Spin chirality induced skew scattering and anomalous Hall effect in chiral magnets

A new mechanism of skew scattering and anomalous Hall effect due to the spin chirality fluctuation is proposed theoretically.

Abstract

Noncoplanar magnetic orders in magnetic metals give rise to an anomalous Hall effect of unconventional origin, which, by the spin Berry phase effect, is known as the topological Hall effect. This effect is pronounced in the low-temperature limit, where the fluctuation of spins is suppressed. In contrast, we here discuss that the fluctuating but locally correlated spins close to the phase boundary give rise to another anomalous Hall effect, that with the opposite sign to the topological Hall effect. Using the Born approximation, we show that the anomalous Hall effect is attributed to the skew scattering induced by the local correlation of spins. The relation of the scalar spin chirality to the skew scattering amplitude is given, and the explicit formula for the Hall conductivity is derived using a semiclassical Boltzmann transport theory. Our theory potentially accounts for the sign change of the anomalous Hall effect observed in chiral magnets in the vicinity of the phase boundary.

INTRODUCTION

Magnetic metals with noncoplanar magnetic orders host rich physics related to magnetic scattering, Berry phase, and topology. One of the key concepts in the noncoplanar magnetism is the scalar spin chirality defined by S₁ ⋅ S₂ × S₃, where ${\mathit{S}}_{\mathit{i}}=({\mathit{S}}_{\mathit{i}}^{\mathit{x}},{\mathit{S}}_{\mathit{i}}^{\mathit{y}},{\mathit{S}}_{\mathit{i}}^{\mathit{z}})$ (i = 1, 2, 3) is the spins. In magnetism, the scalar spin chirality is a quantity that characterizes the noncoplanar structures of spins, such as in antiferromagnets (1–4) and spin glasses (5, 6), and when the magnetic moments form a long-period magnetic structure, it is related to a topological number that characterizes the spin texture (7–9).

When itinerant electrons are coupled to these noncoplanar magnetic orders, it leads to nontrivial consequences in the electron properties. For instance, when the electrons hop between the magnetic atoms with a noncoplanar magnetic texture, it acquires a finite Berry phase that acts as an effective magnetic field. Such a feature of quantum physics is reflected in the transport properties of the system, in particular, in anomalous Hall effect (AHE) (2, 10). In this mechanism, because of the noncoplanar spin structures, the AHE appears even in antiferromagnets (2, 11–13). The sign and the magnitude of the Hall conductivity are often related to the scalar spin chirality, not to the magnetization. This mechanism has been initially discussed for the AHE observed in pyrochlore oxides (3) and is considered as a smoking gun experiment to detect the noncoplanar states (13, 14). A similar physics is also known for long-length magnetic structures, such as skyrmions (15–22), in which the slowly varying moments give rise to the Berry phase in real space (23–27). In these systems, the Berry phase acts as an emergent electromagnetic field, modifying the dynamics of the electrons. This is also experimentally investigated for skyrmions in chiral magnets (28–31). Note that an AHE related to the spin chirality is also known to appear in the weak coupling limit (32, 33), although it is the opposite limit of the Berry phase argument above.

Although most of these pioneering works focus on the ground state, where the spins are considered as a static vector field, there are several studies suggesting rich physics related to spin chirality at a finite temperature where spins are thermally fluctuating. For instance, in frustrated systems, the locally correlated spins due to geometrical frustration can lead to nontrivial electronic properties, such as a Chern insulator (34, 35) and the spin Hall effect (36). Thermal creation of skyrmions in metallic ferromagnets and enhancement of AHE around the magnetic transition temperature in ferromagnetic metals are also studied (24). On the other hand, recent experiments on a chiral magnet found a sign change of AHE close to the critical field (29). The results imply rich physics related to the interplay of thermal fluctuation and magnetic scattering beyond the Berry-phase description.

Motivated by the recent experiments, we theoretically study the AHE in chiral magnets in this paper, focusing on the finite temperature region around and above the magnetic transition temperature. We theoretically show that, in this temperature region, the magnetic scattering gives rise to a skew scattering (37, 38), which is proportional to the thermal average of the scalar spin chirality (or skyrmion number); the skew scattering is a consequence of the quantum phase interference in the three-spin scattering process. From the viewpoint of scattering channels, in this mechanism, a scattering channel with large momentum transfer becomes the dominant source of scattering, in contrast to the small-angle scattering induced by the skyrmion-related Berry phase. These differences show that the two mechanisms are of completely different origin. When we consider the simplest quadratic Hamiltonian for itinerant electrons, we find that the Hall effect by the skew scattering has the opposite sign to that by the topological Hall effect. Our result potentially accounts for the sign change of the Hall conductivity found in chiral magnets (29).

RESULTS

To theoretically study the AHE induced by the spin scattering, in the first half of this section, we study the transport properties of a classical-spin Kondo lattice model. The details of the model we used are described in the subsequent section. In the “Skew scattering” section, we show how scattering by noncoplanar magnetic texture leads to skew scattering. An explicit formula for Hall conductivity is given in the “Boltzmann theory” section using the result we obtained in the “Skew scattering” section. In the latter half of this section, we study the transport properties at a finite temperature by combining the above results with Monte Carlo (MC) simulation. In this section, we reveal the magnetic phase diagram of a classical-spin model relevant for chiral magnets. The field and temperature dependence of AHE are discussed in the “Anomalous Hall effect” section with particular emphasis on comparison with the experiment on MnGe.

Model

Here, we focus on a Kondo lattice model with classical localized spins. The Hamiltonian reads

$$\mathit{H}={\mathit{H}}_0+{\mathit{H}}_{\mathit{K}}$$ (1)

Here,

$${\mathit{H}}_0={\displaystyle \sum _{\mathit{k},\mathrm{\sigma }}}{\mathrm{\epsilon }}_{\mathit{k}\mathrm{\sigma }}{\mathit{c}}_{\mathrm{\sigma }}{(\mathit{k})}^{†}{\mathit{c}}_{\mathrm{\sigma }}(\mathit{k})$$ (2)

is the Hamiltonian for free fermions; ε_k,σ = k²/(2m) is the eigenenergy of an electron with wave number k and spin σ = ±, and c_σ(k) [c_σ(k)^†] is the annihilation (creation) operator for the electron with wave number k and spin σ. In Eq. 1, the second term

$${\mathit{H}}_{\mathit{K}}=\mathit{J}{\displaystyle \sum _{\mathit{i}}}{\mathit{S}}_{\mathit{i}}\cdot {\mathit{c}}_{\mathrm{\sigma }}{({\mathit{R}}_{\mathit{i}})}^{†}{\mathbf{\sigma }}_{\mathrm{\sigma }{\mathrm{\sigma }}^{\prime }}{\mathit{c}}_{{\mathrm{\sigma }}^{\prime }}({\mathit{R}}_{\mathit{i}})$$ (3)

is the Kondo coupling between the spins and itinerant electrons. Here, ${\mathit{S}}_{\mathit{i}}=({\mathit{S}}_{\mathit{i}}^{\mathit{x}},{\mathit{S}}_{\mathit{i}}^{\mathit{y}},{\mathit{S}}_{\mathit{i}}^{\mathit{z}})$ is the spin at the ith site, R_i is the position of the ith site, and J is the exchange coupling between the itinerant electrons and the localized moment.

Skew scattering

To study the AHE induced by the magnetic scattering, we first analyze how multiple-spin scattering contributes to the AHE. In particular, we here focus on how the spin texture gives rise to a skew scattering. For this purpose, we calculate the scattering rate of electrons by the localized moments using the Born approximation. A summary of the approximation is elaborated in Materials and Methods.

In the study of AHE in ferromagnets, it is known that the leading order of the skew scattering by impurities appears as the interference between the first- and second-order terms in the second Born approximation (39, 40). Similarly, we find that the skew scattering due to the spin chirality also appears in the interference terms as the antisymmetric scattering term. Because our focus is on the skew scattering terms, we first define the symmetric $\left({\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{+}\right)$ and antisymmetric $\left({\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}\right)$ terms of the scattering rate by

$${\mathit{w}}_{\mathit{k}\mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{\pm }=\frac{1}{2}({\mathit{W}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}\pm {\mathit{W}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }})$$ (4)

Here, ${\mathit{W}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}$ is the scattering rate from the electron state with momentum k and spin α (|kα〉) to that with momentum k′ and spin β. Because the skew scattering appears as an antisymmetric scattering term, in the rest of this section, we focus on ${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}$. The leading order of ${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}$ in J is given by the asymmetric part of

$$\mathrm{\pi }({\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}(\mathit{k}\prime ,\mathit{k}){[{\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}(\mathit{k}\prime ,\mathit{k})]}^{*}-{\mathit{F}}_{\mathrm{\alpha }\mathrm{\beta }}^{(1)}(\mathit{k},\mathit{k}\prime ){[{\mathit{F}}_{\mathrm{\alpha }\mathrm{\beta }}^{(2)}(\mathit{k},\mathit{k}\prime )]}^{*}+\mathrm{h}.\mathrm{c}.)\mathrm{\delta }({\mathrm{\epsilon }}_{\mathit{k}\mathrm{\alpha }}-{\mathrm{\epsilon }}_{\mathit{k}\prime \mathrm{\beta }})$$ (5)

where

$${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}(\mathit{k}\prime ,\mathit{k})=-\frac{\mathit{J}}{{(2\mathrm{\pi })}^3}{\displaystyle \sum _{\mathit{i}}}{\mathit{S}}_{\mathit{i}}\cdot {\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}{\mathit{e}}^{\mathit{i}(\mathit{k}-\mathit{k}\prime )\cdot {\mathit{R}}_{\mathit{i}}}$$ (6A)

$${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}(\mathit{k}\prime ,\mathit{k})=-\mathit{i}\frac{{\mathit{J}}^2\mathit{m}}{{(2\mathrm{\pi })}^4}{\displaystyle \sum _{\mathit{i}\ne \mathit{j}}}{\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\mathit{S}}_{\mathit{i}}\times {\mathit{S}}_{\mathit{j}}\frac{{\mathit{e}}^{\mathit{i}\mathit{k}{\mathrm{\delta }}_{\mathit{i}\mathit{j}}}}{{\mathrm{\delta }}_{\mathit{i}\mathit{j}}}{\mathit{e}}^{\mathit{i}\mathit{k}\cdot {\mathit{R}}_{\mathit{j}}-\mathit{i}\mathit{k}\prime \cdot {\mathit{R}}_{\mathit{i}}}$$ (6B)

Here, δ_ij = R_i − R_j, δ_ij = |δ_ij|, and ${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}$ and ${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}$ are the scattering amplitudes for the first- and second-order terms in the Born approximation, respectively. Intuitively, these terms correspond to the interference between the one- and two-spin scattering processes as shown in Fig. 1A; the precise definition is in Eq. 29 in Materials and Methods. Substituting Eq. 6 into Eq. 5, we obtain the asymmetric part

$$\begin{array}{c}{\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}=-\frac{{\mathit{J}}^3\mathit{m}}{{(2\mathrm{\pi }\mathit{L})}^3}{\displaystyle \sum _{\mathit{l},\mathit{i}\ne \mathit{j}}}({\mathit{S}}_{\mathit{l}}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\mathit{S}}_{\mathit{i}}\times {\mathit{S}}_{\mathit{j}})\frac{\mathrm{i}{\mathit{e}}^{-\mathrm{i}\mathit{k}{\mathrm{\delta }}_{\mathit{i}\mathit{j}}}}{2{\mathrm{\delta }}_{\mathit{i}\mathit{j}}}[\text{cos}(\mathit{k}\prime \cdot {\mathbf{\delta }}_{\mathit{i}\mathit{l}}-\\ \mathit{k}\cdot {\mathbf{\delta }}_{\mathit{j}\mathit{l}})-\text{cos}(\mathit{k}\cdot {\mathbf{\delta }}_{\mathit{i}\mathit{l}}-\mathit{k}\prime \cdot {\mathbf{\delta }}_{\mathit{j}\mathit{l}})]+\mathrm{h}.\mathrm{c}.\end{array}$$ (7)

Here, we note that, in Eq. 7, the scattering rate is proportional to a three-spin correlation (S_l ⋅ σ_αβ)(σ_βα ⋅ S_i × S_j), which resembles scalar spin chirality S_l ⋅ S_i × S_j.

Fig. 1. Configuration of spins and skew scattering.

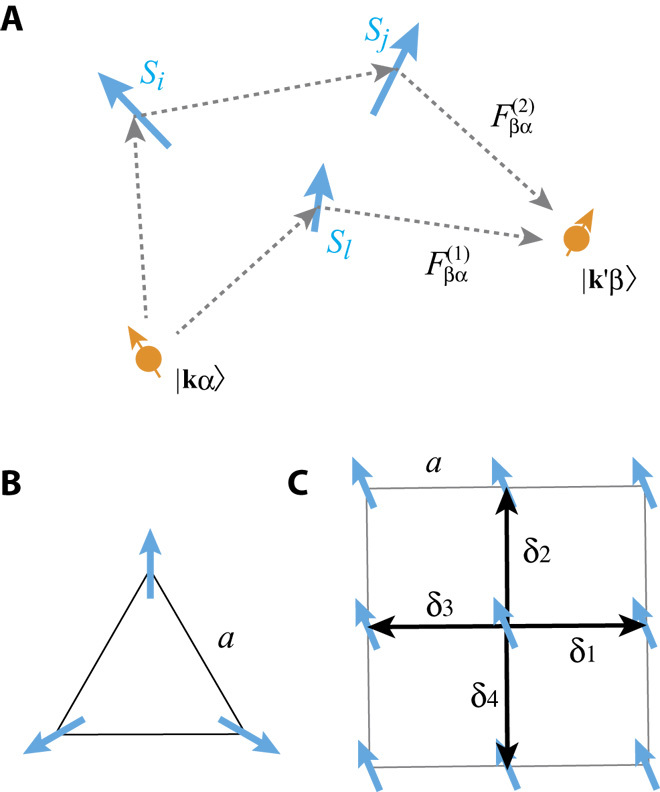
(A) Schematic picture of the scattering process in the second Born approximation in Eq. 5, which contributes to the skew scattering. The blue arrows are the localized spins, and the dotted lines $[{\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}$ and ${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}]$, indicate scattering processes from the first- and second-order terms in the Born approximation, respectively. The skew scattering arises from the interference between the two processes. (B) A schematic figure of the triangular configuration of spins considered in the main text. (C) The square lattice model considered in MC simulation. The arrows show δ_i vectors in Eq. 20, where a is the lattice constant (distance between the localized moments).

To illustrate how the antisymmetric scattering in Eq. 7 contributes to the AHE, we first consider a simple model: itinerant electrons coupled to three magnetic moments. We assume the spins are at R₁ = (0, 0, 0), R₂ = (a, 0, 0), and ${\mathit{R}}_3=(\frac{\mathit{a}}{2},\frac{\sqrt{3}\mathit{a}}{2},0)$. The situation is illustrated in Fig. 1B. Assuming the typical momentum of electrons to be small (that is, ka ≪ 1), we can expand the exponential and trigonometric functions; the result reads

$${\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}={\tilde{\mathit{V}}}_{\mathrm{\beta }\mathrm{\alpha }}\cdot \frac{\mathit{k}\times \mathit{k}\prime }{{\mathit{k}}^2}\mathrm{\delta }({\mathrm{\epsilon }}_{\mathit{k}\mathrm{\alpha }}-{\mathrm{\epsilon }}_{\mathit{k}\prime \mathrm{\beta }})$$ (8)

where

$${\tilde{\mathit{V}}}_{\mathrm{\alpha }\mathrm{\beta }}(\mathit{k})=\frac{3\sqrt{3}}{4}\frac{{\mathit{J}}^3\mathit{m}{\mathit{a}}^2}{{(\mathrm{\pi }\mathit{L})}^3}{\mathit{v}}_{\mathrm{\alpha }\mathrm{\beta }}{\mathit{k}}^3\widehat{\mathit{z}}$$ (9)

Here, v_αβ = ℜ〈(S_l ⋅ σ_αβ)(σ_βα ⋅ S_i × S_j)〉 = ℜ〈(S_j ⋅ σ_αβ)(σ_βα ⋅ S_l × S_i)〉 = ℜ〈(S_i ⋅ σ_αβ)(σ_βα ⋅ S_j × S_l)〉, $\widehat{\mathit{z}}$ is the unit vector along the z axis, and 〈 ⋯ 〉 is the thermal average of ⋯; for simplicity, we assumed here that v_αβ does not depend on the order of sites i, j, and l. We also note that, in Eq. 9, there is another term that is proportional to $\mathfrak{I}\{({\mathit{S}}_{\mathit{l}}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\mathit{S}}_{\mathit{i}}\times {\mathit{S}}_{\mathit{j}})\}$. However, we ignored the term in Eq. 9, because this term does not contribute to the Hall current. For further details, see the “Details of Boltzmann theory” section in Materials and Methods. From Eq. 8, we see that the spin texture gives rise to an antisymmetric scattering, which resembles the skew scattering by nonmagnetic impurities (40). This result suggests that the skew scattering appears in the weak J limit when we have three spins with the finite scalar spin chirality. This phenomenon is fundamentally different from the skew scattering mechanisms studied so far, which is essentially a scattering problem by single impurity (37, 38, 41). In contrast, in this mechanism, the scattering processes that involve multiple spins are essential. In addition, it is distinct from the conventional mechanism in ferromagnets that requires the spin-orbit interaction in the bulk or at the impurity; in our theory, no spin-orbit interaction appears in the scattering process or in the electronic state. Note that, although the purpose of considering the three-spin model is to demonstrate how the skew scattering is related to multiple-spin scattering, the result may directly apply to kagome and pyrochlore magnets (42), because these lattices consist of a tiling of the triangle units.

We next turn to a cubic lattice ferromagnet and consider a case in which the neighboring spins are almost ferromagnetically aligned; that is, only a small difference exists between the direction of two spins. This situation is expected to be realized in chiral magnets under the external field (15–21) and, possibly, in colossal magnetoresistive manganese oxides close to the magnetic transition temperature (24). In this case, S_i can be approximated as S_i ~ S_l + (δ_il ⋅ ∇)S_l because it is close to S_l. To make an evaluation of the scattering rate, we assume that the contribution from the multispin scattering due to nearest-neighbor sites is dominant; that is, we limit i and j in Eq. 7 to the nearest-neighbor sites of l. By replacing S_i and S_j by the differentials, we obtain

$$\begin{array}{c}{\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}=\frac{{\mathit{J}}^3\mathit{m}}{{(2\mathrm{\pi }\mathit{L})}^3}{\displaystyle \sum _{\mathit{l}}}\mathrm{\Re }\langle ({\mathit{S}}_{\mathit{l}}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\partial }_{\mathrm{\mu }}{\mathit{S}}_{\mathit{l}}\times {\partial }_{\mathrm{\nu }}{\mathit{S}}_{\mathit{l}})\rangle \times \\ {\displaystyle \sum _{\mathit{i}\ne \mathit{j}}}\frac{{\mathrm{ϵ}}_{\mathrm{\mu }\mathrm{\nu }\mathrm{\lambda }}}{4}{({\mathbf{\delta }}_{\mathit{i}\mathit{l}}\times {\mathbf{\delta }}_{\mathit{j}\mathit{l}})}_{\mathrm{\lambda }}\mathit{k}[{(\mathit{k}\prime \cdot {\mathbf{\delta }}_{\mathit{i}\mathit{l}}-\mathit{k}\cdot {\mathbf{\delta }}_{\mathit{j}\mathit{l}})}^2-{(\mathit{k}\cdot {\mathbf{\delta }}_{\mathit{i}\mathit{l}}-\mathit{k}\prime \cdot {\mathbf{\delta }}_{\mathit{j}\mathit{l}})}^2]\end{array}$$ (10)

Here, (⋯)_λ is the λ component of the vector in the bracket, and the sum ∑_{i ≠ j} is for all sets of i and j that are nearest-neighbor sites of l. In the same manner as the argument above, we expanded the exponential and trigonometric function by kδ_il and kδ_jl, assuming kδ_il, kδ_jl ≪ 1. For the cubic lattice, if we focus on the scattering in the xy plane, the scattering amplitude reads

$${\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}=\frac{{\mathit{J}}^3\mathit{m}{\mathit{a}}^4}{{(2\mathrm{\pi }\mathit{L})}^3}4\mathit{k}{\mathrm{ϵ}}_{\mathrm{\mu }\mathrm{\nu }\mathit{z}}{(\mathit{k}\times \mathit{k}\prime )}_{\mathit{z}}{\displaystyle \sum _{\mathit{l}}}\mathrm{\Re }\langle [{\mathit{S}}_{\mathit{l}}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }}\rangle [{\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\partial }_{\mathrm{\mu }}{\mathit{S}}_{\mathit{l}}\times {\partial }_{\mathrm{\nu }}{\mathit{S}}_{\mathit{l}}]\}$$ (11)

$$~\frac{{\mathit{J}}^3\mathit{m}\mathit{k}\mathit{a}}{{(\mathrm{\pi }\mathit{L})}^3}{(\mathit{k}\times \mathit{k}\prime )}_{\mathit{z}}\mathrm{\Re }{\displaystyle \int }{\mathit{d}}^3\mathit{x} \langle (\mathit{S}(\mathit{x})\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\partial }_{\mathit{x}}\mathit{S}(\mathit{x})\times {\partial }_{\mathit{y}}\mathit{S}(\mathit{x}))\rangle$$ (12)

where a is the lattice constant; in the second line, we replaced the sum by an integral. Note that, in Eq. 12, the integrand resembles the skyrmion number defined by $\frac{1}{4\mathrm{\pi }}{\displaystyle \int }\mathit{d}{\mathit{x}}^2 \mathit{S}(\mathit{x})\cdot {\partial }_{\mathit{x}}\mathit{S}(\mathit{x})\times {\partial }_{\mathit{y}}\mathit{S}(\mathit{x})$. As we will see in the subsequent section, the anomalous Hall conductivity due to the skew scattering is proportional to the skyrmion number. A difference to the intrinsic mechanism by the Berry phase is that the scattering probability is proportional to $|\mathit{k}\times \mathit{k}\prime |\propto \text{sin}{\mathrm{\theta }}_{\mathit{k}\mathit{k}\prime }$, where ${\mathrm{\theta }}_{\mathit{k}\mathit{k}\prime }$ is the angle between the two wave numbers. Therefore, the skew scattering mechanism induces large-angle scattering of the electrons, in contrast to the small-angle scattering induced by the emergent magnetic field. This indicates that the skew scattering contributes to a distinct scattering channel from that by the emergent magnetic field.

Boltzmann theory

We next investigate how the skew scattering affects the transport property of the system. For this purpose, we calculate the transverse conductivity induced by the spin chirality using a semiclassical Boltzmann theory (39, 43, 44). In the Boltzmann theory, the effect of ${\mathit{W}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}$ (the scattering term that scatters the electron in |kα〉 to |k′β〉) and ${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{+}$ (the symmetric scattering term of the opposite scattering process) is taken into account using the relaxation time approximation. Here, we assume that the relaxation time for |kα〉 is τ_kα = τ, that is, the relaxation time to be independent of k. The resultant Boltzmann equation reads

$$\mathit{q}{\mathit{v}}_{\mathit{k}}\cdot \mathit{E}{\mathit{f}}_0^{\prime }({\mathrm{\epsilon }}_{\mathit{k}})=-\frac{{\mathit{g}}_{\mathit{k}\mathrm{\alpha }}}{\mathrm{\tau }}+{\displaystyle \sum _{\mathrm{\beta }}}{\displaystyle \int }\mathit{d}\mathrm{\phi }\prime \mathit{d}\mathrm{\theta }\prime \text{sin} \mathrm{\theta }\prime \frac{\mathrm{\rho }(\mathit{k})}{4\mathrm{\pi }}{\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}{\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}$$ (13)

where q is the charge of the carriers, v_k = ∇_kε_k,σ is the velocity of electrons with momentum k, E is the uniform electric field, ρ(k) = mk/(2π²) is the density of states for itinerant electrons, and f₀ (ε) and ${\mathit{f}}_0^{\prime }(\mathrm{\epsilon })$ are the Fermi-Dirac distribution function and its energy derivative, respectively. Here, we assumed that the electron occupation f_kα = f₀(ε_k,α) + g_kα is close to that of the Fermi-Dirac distribution and expanded the equation up to leading order in E, assuming ${\mathit{g}}_{\mathit{k}\mathrm{\alpha }}=\mathcal{O}(\mathit{E})$. Because we are interested in the scattering terms discussed in the previous section, we further assume

$${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}={\tilde{\mathit{V}}}_{\mathrm{\alpha }\mathrm{\beta }}(\mathit{k})\cdot \frac{\mathit{k}\mathbf{\times }\mathit{k}\prime }{{\mathit{k}}^2}$$ (14)

where ${\tilde{\mathit{V}}}^{\mathrm{\alpha }\mathrm{\beta }}(\mathit{k})=[{\tilde{\mathit{V}}}_0(\mathit{k}){\mathrm{\sigma }}_0^{\mathrm{\alpha }\mathrm{\beta }}+{\tilde{\mathit{V}}}_1(\mathit{k}){\mathrm{\sigma }}_{\mathit{x}}^{\mathrm{\alpha }\mathrm{\beta }}+\mathrm{i}{\tilde{\mathit{V}}}_2(\mathit{k}){\mathrm{\sigma }}_{\mathit{y}}^{\mathrm{\alpha }\mathrm{\beta }}]\mathit{n}$. Here, n is a unit vector that defines the direction of $\tilde{\mathit{V}}$, σ₀ is the 2 × 2 unit matrix, and σ_a (a = x, y) are the Pauli matrices. Equation 14 is a generalization of the skew scattering term in Eq. 7.

In general, solving the Boltzmann transport equation is a difficult task. However, the Boltzmann equation in Eq. 13 can be solved analytically (45); the details on the solution are elaborated in Materials and Methods. The result for Hall conductivity reads

$${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}=\frac{2{\mathit{n}}_{\mathrm{e}}{\mathit{q}}^2{\mathrm{\tau }}^2}{\mathit{m}}\mathrm{\rho }({\mathit{k}}_{\mathit{F}})\{{\tilde{\mathit{V}}}_0({\mathit{k}}_{\mathit{F}})+{\tilde{\mathit{V}}}_1({\mathit{k}}_{\mathit{F}})\}$$ (15)

where k_F is the Fermi velocity and n_e is the electron density per spin. Therefore, the antisymmetric scattering gives rise to an AHE once we have $\tilde{\mathit{V}}$₀(k) or $\tilde{\mathit{V}}$₁(k). However, $\tilde{\mathit{V}}$₂(k) does not affect the Hall conductivity to the leading order in J; this is the reason we ignored $\mathfrak{I}\{({\mathit{S}}_{\mathit{l}}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot {\mathit{S}}_{\mathit{i}}\times {\mathit{S}}_{\mathit{j}})\}$ in the “Skew scattering” section.

For the case of three spins forming a triangle, $\tilde{\mathit{V}}$₀(k) and $\tilde{\mathit{V}}$₁(k) are calculated from Eq. 9. Using Eq. 33 in Materials and Methods, it reads

$${\tilde{\mathit{V}}}_0({\mathit{k}}_{\mathit{F}})+{\tilde{\mathit{V}}}_1({\mathit{k}}_{\mathit{F}})=\frac{3\sqrt{3}}{2}\frac{{\mathit{J}}^3\mathit{m}{\mathit{a}}^2}{{(\mathrm{\pi }\mathit{L})}^3}{\mathit{k}}_{\mathit{F}}^3\langle {\mathit{S}}_1\cdot {\mathit{S}}_2\times {\mathit{S}}_3\rangle$$ (16)

This result explicitly shows that the Hall conductivity is proportional to the scalar spin chirality.

We next consider the case of chiral magnets, where the generation of skyrmions gives rise to chirality. To be concrete, we consider the cubic lattice model we discussed in Eq. 12. With a similar calculation in Eq. 16, we find

$${\tilde{\mathit{V}}}_0({\mathit{k}}_{\mathit{F}})+{\tilde{\mathit{V}}}_1({\mathit{k}}_{\mathit{F}})={\left(\frac{\mathit{J}{\mathit{k}}_{\mathit{F}}}{\mathrm{\pi }\mathit{L}}\right)}^3\mathit{m}\mathit{a}{\displaystyle \int }{\mathit{d}}^3\mathit{x}[\mathit{S}(\mathit{x})\cdot {\partial }_{\mathit{x}}\mathit{S}(\mathit{x})\times {\partial }_{\mathit{y}}\mathit{S}(\mathit{x})]$$ (17)

This result indicates that the skew scattering induced by the spin texture is proportional to the skyrmion density.

At a glance, this resembles the topological Hall effect in the strong coupling limit where the intrinsic Hall effect occurs because of the Berry phase induced by the noncoplanar spin textures (3, 10, 24, 29). In the semiclassical Boltzmann theory, however, the Berry phase appears as an effective magnetic field (46); that is, it is an effective Lorentz force acting on the electrons. In contrast, the skew scattering in our theory appears as a scattering term in the Boltzmann theory. Therefore, these two are distinct mechanisms. This difference in the mechanism appears in the sign of the Hall effect; for the free electrons we considered above, the sign of the Hall conductivity in our theory is opposite to that of the topological Hall effect. For ferromagnetic Kondo interaction J < 0, the sign of the intrinsic Hall effect is $\text{sgn}[{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}]= \text{sgn}(\mathit{S}\cdot {\partial }_{\mathit{x}}\mathit{S}\times {\partial }_{\mathit{y}}\mathit{S})$, whereas that of the skew scattering is $\text{sgn}[{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}]=-\text{sgn}(\mathit{S}\cdot {\partial }_{\mathit{x}}\mathit{S}\times {\partial }_{\mathit{y}}\mathit{S})$ as in Eq. 17.

MC simulation

In this section, we study the competition between the topological Hall effect and the AHE by skew scattering. In particular, we study how the anomalous Hall conductivity behaves as a function of temperature and magnetic field in chiral magnets, with particular emphasis on the experiment in MnGe. To estimate the magnitude of the Hall effect that appears from the skew scattering, we evaluate the magnitude of the scalar chirality in the chiral magnets above the magnetic transition temperature. For this, we consider a two-dimensional (2D) classical spin model with Heisenberg and Dzyaloshinskii-Moriya (DM) interaction (47)

$$\begin{array}{c}{\mathit{H}}_{\mathit{S}}=-{\mathit{J}}_{\mathit{H}}{\displaystyle \sum _{\mathit{r}}}\mathit{S}(\mathit{r})\cdot \mathit{S}(\mathit{r}+\widehat{\mathit{x}})+\mathit{S}(\mathit{r})\cdot \mathit{S}(\mathit{r}+\widehat{\mathit{y}})\\ -\mathit{K}{\displaystyle \sum _{\mathit{r}}}[\widehat{\mathit{x}}\cdot \mathit{S}(\mathit{r})\times \mathit{S}(\mathit{r}+\widehat{\mathit{x}})+\widehat{\mathit{y}}\cdot \mathit{S}(\mathit{r})\times \mathit{S}(\mathit{r}+\widehat{\mathit{y}})]\\ -\mathrm{\mu }\mathit{h}{\displaystyle \sum _{\mathit{r}}}{\mathit{S}}^{\mathit{z}}(\mathit{r})\end{array}$$ (18)

Here, S(r) is the localized moment at r, and $\widehat{\mathit{x}}$ and $\widehat{\mathit{y}}$ are the unit vectors along x and y axes, respectively. The first term is the Heisenberg interaction between the nearest-neighbor spins and the second term is the DM interaction. The third term is the Zeeman coupling between the spins and the magnetic field h perpendicular to the plane; μ is the size of the magnetic moment. This model is a discretized variant of a continuum model used to study the low-temperature behavior of chiral magnets (21).

Figure 2A shows the phase diagram obtained by MC simulation calculated using system size N = 30². The details of the calculation are elaborated in Materials and Methods. This model shows three phases at zero temperature: helical, skyrmion crystal, and paramagnetic phases. The helical phase appears in the low field, 0 ≤ h/J_H ≲ 1.5, whereas the skyrmion crystal phase becomes the ground state for 1.5 ≲ h/J_H ≲ 2.8, which is taken over by the field-induced ferromagnetic phase at h/J_H ≳ 2.8. The results are consistent with what has been reported in previous studies (21, 47).

Fig. 2. Classical Monte Carlo simulation of two-dimensional chiral magnet.

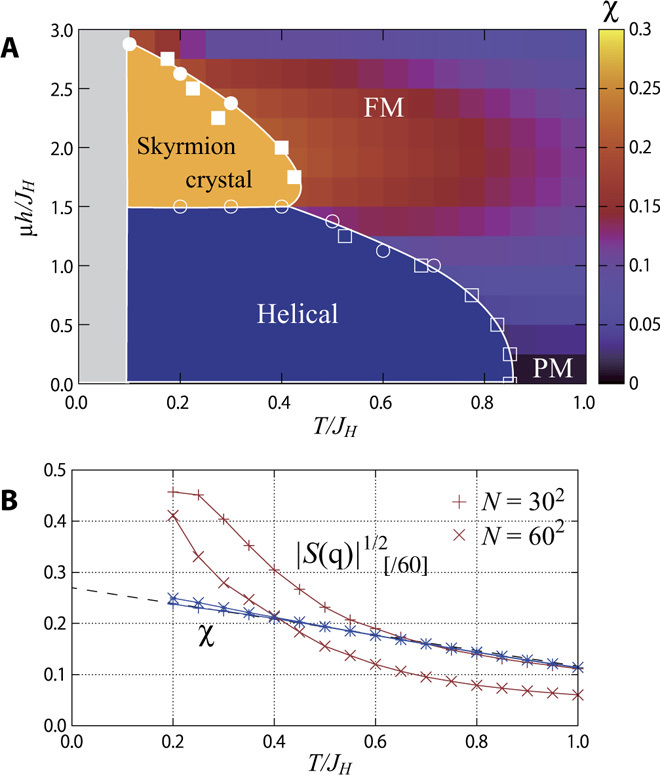
(A) The phase diagram of the 2D chiral magnet in Eq. 18; the transverse axis is the temperature T and the longitudinal axis is the magnetic field h perpendicular to the plane. The squares (circles) are the phase boundary estimated from spin structure factor S(q) using the gradient of S(q) along the T/J_H (μh/J_H) axis. Open (solid) symbols indicate the phase boundary for the helical (skyrmion crystal) order. The lines are merely a guide for the eyes. The contour plot in the paramagnetic (PM)/ferromagnetic (FM) phase shows the thermal average of the scalar spin chirality χ. The low-temperature region shaded in gray is the region where the MC simulation freezes because of low temperature. See the text for details. (B) Temperature dependence of spin structure factor S(q) and chirality χ for h/J_H = 2.0; the two curves are for N = 30² and 60².

At a finite temperature, the helical and skyrmion crystal phases are characterized by the growth of spin structure factor

$$\mathit{S}(\mathit{q})=\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{i}}}{\mathit{S}}_{\mathit{i}}\text{exp}\{\mathrm{i}\mathit{q}\cdot {\mathit{R}}_{\mathit{i}}\}$$ (19)

with nonzero |q| (20). In Fig. 2B, we show the results of ${|\mathit{S}(\mathit{q})|}^{\frac{1}{2}}$ for h/J_H = 0.2, calculated with N = 30² and 60². For N = 30², the result shows growth of the structure factor below T/J_H ~ 0.4, indicating the formation of a skyrmion crystal. The phase boundary between the ferromagnetic and skyrmion crystal phases is determined from the peak of the derivative of |S(q)| with respect to temperature and magnetic field. In Fig. 2A, the squares (circles) indicate the temperature (magnetic field) at which the derivative shows the largest negative value. We note that the result of S(q) for a larger size (N = 60²) shows the same qualitative behavior but with a slightly shifted phase boundary toward the lower temperature. Therefore, the phase boundary in Fig. 2A should be understood as the upper limit for the phase boundary.

The contour plot shown in the background of Fig. 2A is the thermal average of chirality for the nearest-neighbor spins

$$\mathrm{\chi }=\frac{1}{4}{\displaystyle \sum _{\mathit{r},\mathit{i}}}\langle \mathit{S}(\mathit{r})\cdot \mathit{S}(\mathit{r}+{\mathbf{\delta }}_{\mathit{i}})\times \mathit{S}(\mathit{r}+{\mathbf{\delta }}_{\mathit{i}+1})\rangle$$ (20)

where δ_i (i = 1, ⋯ , 4) are the vector connecting nearest-neighbor sites

$${\mathbf{\delta }}_1=(1,0), {\mathbf{\delta }}_2=(0,1)$$ (21)

$${\mathbf{\delta }}_3=(-1,0), {\mathbf{\delta }}_4=(0,-1)$$ (22)

and δ₅ = δ₁ (Fig. 1C). In the phase diagram, χ remains small in the weak field region where the ground state is the helical order. With increasing field, finite χ is induced by the magnetic field h with a maximum around h/J_H ~ 2.0, where the ground state is the skyrmion crystal state. In Fig. 2B, we show the result of χ for N = 30² and 60². The two results almost overlap each other, showing a very small finite size effect. Our results indicate a gradual increase of χ with decreasing temperature with no structure at the transition. The dotted line is the linear fitting of χ for N = 30² in between T/J_H ∈ [0.2, 0.6]; it is used to evaluate the χ at the ground state.

An important feature of the results is that χ is already about 78% of the ground state value above the critical temperature T_c ≳ 0.4; χ does not show a rapid increase at the magnetic transition temperature. This is due to the fact that the finite scalar spin chirality is a consequence of the lattice symmetry and not the spontaneous symmetry breaking, that is, the magnetic phase transition to the skyrmion crystal phase. Therefore, at h ≳ 2.0 and above the magnetic ordering temperature, the spins are in a locally correlated state with finite spin chirality. Because the spins are not ordered in this region, it is expected that the effect of spins on the transport phenomena can be well approximated by the scattering theory discussed in the above sections. Therefore, we expect that the AHE at and around the critical temperature is dominated by the skew scattering.

Anomalous Hall effect

In the previous section, we discussed the competition of the topological Hall effect and skew scattering in chiral magnets. In the Boltzmann transport theory, the Berry phase that gives rise to the topological Hall effect is taken into account as an effective magnetic field in Eq. 13 by replacing qE → qE + v_k × b, where b = (1/2)S ⋅ ∂_xS × ∂_yS (46). Assuming that b (= |b|) and $\mathrm{\rho }(\mathit{k}){\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}$ in the Boltzmann equation are small, we approximate ${\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}={\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{b})}+{\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{w})}+\mathrm{\delta }{\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}~{\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{b})}+{\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{w})}$. Here, ${\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{b})}$ is the deviation of electron occupation in the linear order of b and ${\mathit{g}}_{\mathit{k}\prime \mathrm{\beta }}^{(\mathrm{w})}$ is that in the linear order of $\mathrm{\rho }(\mathit{k}){\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}$ given by Eq. 39 in Materials and Methods. Using this approximation, the current reads

$$\mathit{j}~{\displaystyle \sum _{\mathrm{\alpha }}}{\displaystyle \int }\frac{\mathit{d}{\mathit{k}}^3}{{(2\mathrm{\pi })}^3}{\mathit{v}}_{\mathit{k}}({\mathit{g}}_{\mathit{k}\mathrm{\alpha }}^{(\mathrm{b})}+{\mathit{g}}_{\mathit{k}\mathrm{\alpha }}^{(\mathrm{w})})$$ (23)

Therefore, the anomalous Hall conductivity reads ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}~{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}+{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}$; that is, it is given by the sum of the two contributions.

In the Boltzmann theory, the Hall conductivity due to the topological Hall effect is estimated as ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}~{\mathit{n}}_{\mathrm{e}}{\mathit{q}}^2{\mathrm{\tau }}^2{\mathit{b}}_{\mathit{z}}^{\prime }/{\mathit{m}}^2$, where ${\mathit{b}}_{\mathit{z}}^{\prime }$ is the renormalized emergent magnetic field and 2n_e is the electron density; from dimensional analysis, we here assume ${\mathit{b}}_{\mathit{z}}^{\prime }~{(\mathit{J}\mathit{m}/\mathit{a})}^3{\mathit{b}}_{\mathit{z}}$. On the other hand, the anomalous Hall conductivity due to the skew scattering mechanism is given by Eq. 15 [that is, ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}~{\mathit{n}}_{\mathrm{e}}{\mathit{q}}^2{\mathrm{\tau }}^2\mathrm{\rho }({\mathit{k}}_{\mathit{F}})({\tilde{\mathit{V}}}_0+{\tilde{\mathit{V}}}_1)$]; using Eq. 17, we obtain ${\tilde{\mathit{V}}}_0+{\tilde{\mathit{V}}}_1~{(\mathit{J}{\mathit{k}}_{\mathit{F}})}^3\mathit{m}\mathrm{\chi }~{\mathit{b}}_{\mathit{z}}^{\prime }{({\mathit{k}}_{\mathit{F}}\mathit{a})}^3/{\mathit{m}}^2$. Here, on the basis of the above observation on MC simulation, we assume that χ close to T_c is in the same order as b_z in the ground state. From these relations, the ratio of the two Hall conductivities reads

$$\frac{{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}}{{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}}~\mathrm{\rho }({\mathit{k}}_{\mathit{F}})\mathit{m}\frac{{\tilde{\mathit{V}}}_0+{\tilde{\mathit{V}}}_1}{{\mathit{b}}_{\mathit{z}}^{\prime }}~{({\mathit{k}}_{\mathit{F}}\mathit{a})}^4$$ (24)

Because the chiral magnets are metal, we expect k_Fa ~ 1. Hence, the fluctuating spins at the vicinity of the phase boundary should bring about the skew scattering AHE of similar magnitude to that by the Berry-phase mechanism close to zero temperature.

From the above arguments, we expect ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}$ to be proportional to the spin fluctuation part of scalar spin chirality χ − b_z, where b_z is that for the order parameter; we estimate b_z by

$${\mathit{b}}_{\mathit{z}}=\frac{1}{4}{\displaystyle \sum _{\mathit{r},\mathit{i}}}\langle \mathit{S}(\mathit{r})\rangle \cdot \langle \mathit{S}(\mathit{r}+{\mathbf{\delta }}_{\mathit{i}})\rangle \times \langle \mathit{S}(\mathit{r}+{\mathbf{\delta }}_{\mathit{i}+1})\rangle$$ (25)

On the other hand, the intrinsic Hall conductivity is ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}\propto {\mathit{b}}_{\mathit{z}}$. Therefore, we expect the anomalous Hall conductivity to be

$${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}={\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}+{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}\propto \mathrm{\chi }-(1+\mathrm{\gamma }){\mathit{b}}_{\mathit{z}}$$ (26)

where γ is a parameter that defines the ratio of topological Hall conductivity and skew scattering. Because ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{sk})}/{\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^{(\text{THE})}~1$, we expect γ to be in the order of 1.

At zero temperature, because our model is a classical spin model, the skew scattering does not contribute to the AHE because no thermal fluctuation exists. Therefore, we expect to see only the topological Hall effect. On the other hand, at a finite temperature, we expect to see the contribution from the skew scattering, at least in the vicinity of the phase boundary. In Fig. 3, we plot the field dependence of χ, b_z, and ${\tilde{\mathrm{\sigma }}}_{\mathit{x}\mathit{y}}=\mathrm{\chi }-(1+\mathrm{\gamma }){\mathit{b}}_{\mathit{z}}$ (∝ σ_xy), with γ = 2; Fig. 3A is for T/J_H = 0.1 and Fig. 3B is for T/J_H = 0.5. The blue and yellow shading in Fig. 3A indicates the helical and skyrmion crystal phases, respectively. In the skyrmion crystal phase, b_z become nonzero due to the formation of the long-range order. On the other hand, finite χ exists for a much broader region outside the ordered phase. Reflecting this feature, we find the sign change of ${\tilde{\mathrm{\sigma }}}_{\mathit{x}\mathit{y}}$ in the ordered phase. On the other hand, the result for T/J_H = 0.5 shows a large positive Hall conductivity comparable to the ordered phase, although it is above the magnetic transition temperature to the skyrmion crystal phase. The positive sign shows that the Hall effect comes from the skew scattering mechanism. This implies that, due to the DM interaction, the skew scattering mechanism we discussed in this paper can give rise to a large AHE even above the magnetic transition temperature.

Fig. 3. Field dependence of χ, b_z, and ${\tilde{\mathbf{\sigma }}}_{\mathit{x}\mathit{y}}$ (a quantity that is proportional to the anomalous Hall conductivity) calculated by MC simulation.

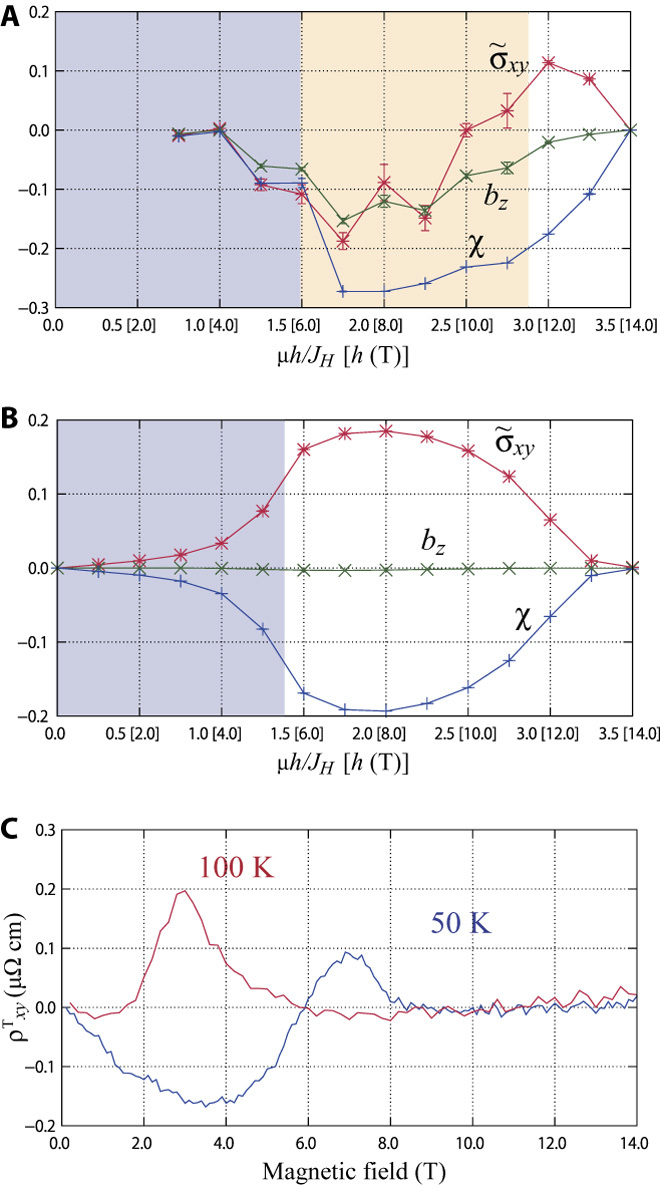
The numbers in square brackets are the magnetic field in Tesla, assuming the upper critical field to be 12 T, which is the case for MnGe. The temperatures are at (A) T/J_H = 0.1 (~20 K) and (B) T/J_H = 0.5 (~100 K) with γ = 2. The definition and description of ${\tilde{\mathrm{\sigma }}}_{\mathit{x}\mathit{y}}$ are given in Eq. 26 and the paragraphs above it. In the figure, the blue and yellow shading indicates helical and skyrmion crystal phases, respectively. See the main text for details. (C) Experimental measurement of Hall conductivity in MnGe at 50 and 100 K. Reproduced from data from the work of Kanazawa et al. (29).

This may explain the sign change of Hall conductivity in MnGe (29). In MnGe, the ground-state magnetic configuration at zero field is proposed to be a 3D magnetic monopole crystal, different from the spiral phase in our model. With an applied magnetic field, however, the strings of skyrmions are expected to develop along the magnetic field (48). Therefore, a similar transition from a skyrmion crystal–like phase to field-induced ferromagnetism is expected in the high field. At low temperatures (≲30 K), MnGe shows a topological Hall effect with a negative sign. On the other hand, at higher temperatures, the result shows unusual behaviors compared to the other chiral magnets.

In Fig. 3C, we show the field dependence of the topological Hall resistivity ρ^T measured in MnGe; the figure is reproduced using the data published by Kanazawa et al. (29). The 50 K result shows a nonmonotonic behavior with a sign change in the Hall resistivity and a peak around the transition to the ferromagnetic phase. The sign change of the Hall conductivity is found in the intermediate temperature 50 K ≲ T ≲ 100 K. In contrast, at 100 K, the result only shows positive Hall resistivity in the intermediate field region, which vanishes in the high field. This behavior persists up to 200 K. The 50 and 100 K results in Fig. 3C should be compared with that of Fig. 3 (A and B, respectively). Assuming that the zero-field critical temperature of our model coincides with that of the MnGe (T_c ~ 170 K), the temperature of Fig. 3A corresponds to 20 K, whereas that of Fig. 3A is 100 K. These numbers match the experiment semiquantitatively.

DISCUSSION

Here, we theoretically studied the AHE induced by fluctuating spins. Using the second Born approximation, we showed that the scalar spin chirality induces skew scattering similar to that by the nonmagnetic impurities with spin-orbit interactions (37, 38). However, this mechanism is distinct from the Berry-phase mechanism; the skew scattering leads to an asymmetric scattering term in the Boltzmann equation, whereas the Berry phase acts as an effective Lorentz force. Combining this result with a semiclassical Boltzmann transport theory, we obtained the explicit formula for the Hall conductivity. The sign of the AHE by the skew scattering mechanism is opposite to that by the Berry-phase one.

In the latter half of the paper, we study a 2D chiral magnet that is relevant for chiral-magnet thin films using MC simulation. We found that, in this model, the thermal average of scalar spin chirality remains in the same order even in the ferromagnetic phase above the skyrmion crystal phase. The MC results, together with the scattering theory, suggest that the AHE induced by the skew scattering mechanism appears around and above the phase boundary between the skyrmion crystal and the ferromagnetic phases.

On the other hand, at a temperature much lower than that during magnetic transition, the electronic structure is expected to change abruptly due to the nonperturbative effect of the formation of magnetic superlattice (49). Because of this effect, the scattering theory discussed in this paper is expected to fail in the low-temperature region. Meanwhile, in the low-temperature region, it is discussed that the emergent magnetic field induced by the skyrmions is responsible for the AHE (25, 26, 50). Therefore, with decreasing temperature, we expect to see a crossover of the AHE, from that by the skew scattering mechanism to the one by the emergent magnetic field. Because the sign of the Hall conductivity differs between the two mechanisms, a sign change of the Hall conductivity is expected; this is demonstrated in Fig. 3 and resembles the experimentally observed anomalous Hall resistivity in MnGe (29). In contrast, in Mn_1−xFe_xSi, no sign change of AHE is observed to date (28, 30, 31). Presumably, this difference is due to the difference in the strength of the electron correlation and spin-orbit interaction. In Mn_1−xFe_xSi, we expect a relatively weak electron correlation compared to MnGe. Therefore, the chiral spin fluctuation is suppressed above the magnetic transition temperature.

In the previous section, we discussed the relation of our work to an earlier work on AHE due to scalar spin chirality. In the study of Tatara and Kawamura (32), using a Green function formalism, it is shown that an AHE proportional to the scalar spin chirality appears in the weak coupling regime. In our work, using the Boltzmann transport theory, we show that the spin chirality contributes to AHE in two ways, that is, as the effective magnetic field that appears in the drift term and as the scatterer in the collision term; we show that the contributions from these two terms have opposite signs.

Regarding the scaling property, in the study of Tatara and Kawamura (32), the anomalous Hall conductivity is quadratically proportional to the quasi-particle lifetime τ′, implying that ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}\propto {\mathrm{\sigma }}_{\mathit{x}\mathit{y}}^2$ [here, we use τ′ in place of τ from the work of Tatara and Kawamura (32), because the definition is somewhat different from τ used in this paper]. We essentially obtain the same result as shown in Eq. 15. However, there is one remark on the mechanism of scattering that contributes to τ. When the scattering by impurities and phonons is dominant, 1/τ is essentially independent of the density of localized moments and the strength of Kondo coupling. In this limit, we expect ${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}\propto {\mathrm{\tau }}^2\propto {\mathrm{\sigma }}_{\mathit{x}\mathit{x}}^2$. In contrast, when the scattering by the localized moments is dominant, we expect 1/τ to be linearly proportional to the density of localized moments. In this case, because ${\tilde{\mathit{V}}}_{\mathit{i}}({\mathit{k}}_{\mathrm{F}})$ is proportional to the density of localized moments, we expect a relation, ${\tilde{\mathit{V}}}_{\mathit{i}}({\mathit{k}}_{\mathrm{F}})\propto 1/\mathrm{\tau }$. Therefore, the resulting scaling relation becomes σ_xy ∝ τ ∝ σ_xx, restoring the scaling relation expected in the skew scattering mechanism (40).

MATERIALS AND METHODS

Born approximation

The scattering rate of electrons was evaluated by the scattering theory using a Born approximation. For the elastic scattering, the rate of scattering an electron with momentum k and spin α to that of k′ and β is

$${\mathit{W}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}=2\mathrm{\pi }{|{\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}(\mathit{k}\prime ,\mathit{k})|}^2\mathrm{\delta }({\mathrm{\epsilon }}_{\mathit{k}\mathrm{\alpha }}-{\mathrm{\epsilon }}_{\mathit{k}\prime \mathrm{\beta }})$$ (27)

where F_βα(k′, k) is the scattering amplitude from kα to k′β. In the Born approximation, the scattering amplitude was estimated by perturbatively expanding the wave functions. In our work, we treated the Kondo coupling term H_K as the perturbation and expanded the wave function up to the second order in J (second Born approximation). The resultant scattering amplitude reads

$${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}(\mathit{k}\prime ,\mathit{k})={\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}(\mathit{k}\prime ,\mathit{k})+{\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}(\mathit{k}\prime ,\mathit{k})$$ (28)

where

$${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(1)}(\mathit{k}\prime ,\mathit{k})=\langle \mathit{k}\prime \mathrm{\beta }|{\mathit{H}}_{\mathit{K}}|\mathit{k}\mathrm{\alpha }\rangle$$ (29A)

$${\mathit{F}}_{\mathrm{\beta }\mathrm{\alpha }}^{(2)}(\mathit{k}\prime ,\mathit{k})=\langle \mathit{k}\prime \mathrm{\beta }|{\mathit{H}}_{\mathit{K}}\mathit{G}({\mathrm{\epsilon }}_{\mathit{k}}){\mathit{H}}_{\mathit{K}}|\mathit{k}\mathrm{\alpha }\rangle$$ (29B)

Here, $|\mathit{k}\mathrm{\alpha }\rangle = \text{exp}(\mathit{i}\mathit{k}\cdot \mathit{r})/{(2\mathrm{\pi })}^{\frac{3}{2}}$ is the eigenstate of H₀ with momentum k and spin α, and G(ω) = (ω − H₀)⁻¹ is the Green function of H₀.

Details of Boltzmann theory

Earlier, we calculated the Hall conductivity using the semiclassical Boltzmann theory. This method is useful for studying AHE, providing not only a microscopic evaluation of the conductivities but also an intuitive understanding of the physical mechanism (39, 43, 44). In the Boltzmann theory, the electron distribution was evaluated by the Boltzmann equation; the transport coefficients were evaluated from the electron distribution by calculating the current. In the presence of the uniform static electric field, the Boltzmann equation reads

$$\begin{array}{c}\mathit{q}{\mathit{v}}_{\mathit{k}}\cdot \mathit{E}{\mathit{f}}_0^{\prime }({\mathrm{\epsilon }}_{\mathit{k}})=-\frac{{\mathit{g}}_{\mathit{k}\mathrm{\alpha }}}{\mathrm{\tau }}+{\displaystyle \sum _{\mathrm{\beta }}}{\displaystyle \int }\mathit{d}\mathrm{\phi }\prime \mathit{d}\mathrm{\theta }\prime \text{sin} \mathrm{\theta }\prime \frac{\mathrm{\rho }(\mathit{k})}{4\mathrm{\pi }}{\mathit{w}}_{\mathit{k}\mathbf{\prime }\mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}{\mathit{g}}_{{\mathit{k}}^{\mathit{\prime }}\mathrm{\beta }}\end{array}$$ (30)

where q is the charge of carriers, v_k = ∇_kε_k is the velocity of electrons with momentum k, ε_k = k²/2m is the eigenenergy for the electron, E is the uniform electric field, and f₀(ε) and ${\mathit{f}}_0^{\prime }(\mathrm{\epsilon })$ are the Fermi-Dirac distribution function and its energy derivative, respectively. Here, we assumed that the electron occupation f_kα = f₀(ε_k) + g_kα is close to that of the Fermi-Dirac distribution and expanded to the equation up to leading order in E, assuming ${\mathit{g}}_{\mathit{k}\mathrm{\alpha }}=\mathcal{O}(\mathit{E})$. For the scattering terms in the right-hand side of Eq. 30, we separated the scattering rate ${\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}$ into symmetric $[{\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{+}=({\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}+{\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }})/2]$ and antisymmetric $[{\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}=({\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}-{\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }})/2]$ terms; ${\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\mathbf{\prime }\mathrm{\beta }}^{+}$ was taken into account by the relaxation time approximation using relaxation time τ, that is, the first term in the right-hand side of Eq. 30. The integral in Eq. 30 is for ${\mathit{w}}_{\mathit{k}\mathrm{\alpha }\to \mathit{k}\prime \mathrm{\beta }}^{-}$. We here used the polar coordinate k′ = (k′ sin θ′ cos φ′, k′ sin θ′ sin φ′, k′ cos θ′); the length of k′ was fixed to k′ = k due to the delta function in ${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}$, because we only consider elastic scattering by the classical moments.

In general, solving Eq. 30 is difficult; it is often solved approximately by using a variational method (39). Here, however, we took an alternative approach (45); we assumed the antisymmetric scattering to be

$${\mathit{w}}_{\mathit{k}\prime \mathrm{\beta }\to \mathit{k}\mathrm{\alpha }}^{-}={\tilde{\mathit{V}}}_{\mathrm{\alpha }\mathrm{\beta }}(\mathit{k})\cdot \frac{\mathit{k}\mathbf{\times }\mathit{k}\mathbf{\prime }}{{\mathit{k}}^2}$$ (31)

where

$${\tilde{\mathit{V}}}^{\mathrm{\alpha }\mathrm{\beta }}(\mathit{k})=({\tilde{\mathit{V}}}_0(\mathit{k}){\mathrm{\sigma }}_0^{\mathrm{\alpha }\mathrm{\beta }}+{\tilde{\mathit{V}}}_1(\mathit{k}){\mathrm{\sigma }}_{\mathit{x}}^{\mathrm{\alpha }\mathrm{\beta }}+\mathrm{i}{\tilde{\mathit{V}}}_2(\mathit{k}){\mathrm{\sigma }}_{\mathit{y}}^{\mathrm{\alpha }\mathrm{\beta }})\mathit{n}$$ (32)

Here, n is a unit vector, σ₀ is the 2 × 2 unit matrix, and σ_x and σ_y are the Pauli matrices; we assumed that V_i(k) (i = 0, 1, 2) are functions of the length of wave number vector k; that is, V_i(k) has no angular dependence. Using relations

$$(\mathit{v}\cdot {\mathbf{\sigma }}_{\mathrm{\alpha }\mathrm{\beta }})({\mathbf{\sigma }}_{\mathrm{\beta }\mathrm{\alpha }}\cdot \mathit{v}\prime )=\{\begin{array}{cc}{\mathit{v}}_{\mathit{z}}{\mathit{v}}_{\mathit{z}}^{\prime }& (\text{if} \mathrm{\alpha }=\mathrm{\beta })\\ ({\mathit{v}}_{\mathit{x}}{\mathit{v}}_{\mathit{x}}^{\prime }+{\mathit{v}}_{\mathit{y}}{\mathit{v}}_{\mathit{y}}^{\prime })+ \text{sgn}(\mathrm{\alpha })\mathrm{i}({\mathit{v}}_{\mathit{x}}{\mathit{v}}_{\mathit{y}}^{\prime }-{\mathit{v}}_{\mathit{y}}{\mathit{v}}_{\mathit{x}}^{\prime })& (\text{if} \mathrm{\alpha }\ne \mathrm{\beta })\end{array}$$ (33)

we see that the scattering probability in Eqs. 8 and 12 is a special form of Eq. 31.

Equation 30 is solvable if we have the above form for antiscattering terms. To solve the Boltzmann equation, we used a self-consistent approach (45); we introduced a parameter P_α(k) defined by

$${\mathit{P}}_{\mathrm{\alpha }}(\mathit{k})={\displaystyle \int }\mathit{d}{\mathrm{\phi }}^{\prime }\mathit{d}\mathrm{\theta }\prime \text{sin} \mathrm{\theta }\prime \mathit{k}\mathit{\prime }{\mathit{g}}_{\mathit{k}\prime }^{\mathrm{\alpha }}$$ (34)

In the integral on the right-hand side, the length of k′ is fixed to k′ = k. Using P_α(k), the Boltzmann equation becomes

$${\mathit{g}}_{\mathit{k}}^{\mathrm{\alpha }}=-\mathrm{\tau }\mathit{q}{\mathit{v}}_{\mathit{k}}\cdot \mathit{E}{\mathit{f}}_0^{\prime }({\mathrm{\epsilon }}_{\mathit{k}})+\frac{\mathrm{\rho }(\mathit{k})\mathrm{\tau }}{4\mathrm{\pi }{\mathit{k}}^2}{\displaystyle \sum _{\mathrm{\beta }}}{\tilde{\mathit{V}}}^{\mathrm{\alpha }\mathrm{\beta }}\cdot \mathit{k}\times {\mathit{P}}_{\mathrm{\beta }}(\mathit{k})$$ (35)

Equation 35 can be diagonalized with respect to the spin indices α and β by the following transformation for ${\mathit{g}}_{\mathit{k}}^{\mathrm{\alpha }}$ and P_α(k)

$${\mathit{g}}_{\mathit{k}}^{\pm }=\frac{\sqrt{1+{\mathit{e}}^{2\mathrm{\eta }}}}{2}({\mathit{g}}_{\mathit{k}}^{\uparrow }\pm {\mathit{e}}^{-\mathrm{\eta }}{\mathit{g}}_{\mathit{k}}^{\downarrow })$$ (36A)

$${\mathit{P}}^{\pm }(\mathit{k})=\frac{\sqrt{1+{\mathit{e}}^{2\mathrm{\eta }}}}{2}\{{\mathit{P}}^{\uparrow }(\mathit{k})\pm {\mathit{e}}^{-\mathrm{\eta }}{\mathit{P}}^{\downarrow }(\mathit{k})\}$$ (36B)

where

$${\mathit{e}}^{-\mathrm{\eta }}=\frac{{\tilde{\mathit{V}}}_1+{\tilde{\mathit{V}}}_2}{\sqrt{{\tilde{\mathit{V}}}_1^2-{\tilde{\mathit{V}}}_2^2}}$$

Using these parameters, we rewrite Eq. 35 as

$$\begin{array}{c}{\mathit{g}}_{\mathit{k}}^{\pm }=-\mathrm{\tau }\mathit{q}{\mathit{v}}_{\mathit{k}}\cdot \mathit{E}{\mathit{f}}_0^{\pm }\prime ({\mathrm{\epsilon }}_{\mathit{k}})\\ +\frac{\mathrm{\rho }(\mathit{k})\mathrm{\tau }}{4\mathrm{\pi }{\mathit{k}}^2}{\tilde{\mathit{V}}}^{\pm }\mathit{n}\cdot \mathit{k}\times {\mathit{P}}^{\pm }(\mathit{k})\end{array}$$ (37)

where ${\tilde{\mathit{V}}}^{\pm }={\tilde{\mathit{V}}}_0\pm \sqrt{{\tilde{\mathit{V}}}_1^2-{\tilde{\mathit{V}}}_2^2}$ and ${\mathit{f}}_0^{\pm }=\frac{\sqrt{1+{\mathit{e}}^{2\mathrm{\eta }}}}{2}(1\pm {\mathit{e}}^{-\mathrm{\eta }}){\mathit{f}}_0$. When n is perpendicular to E, the explicit form of P^±(k) is obtained by substituting Eq. 37 into Eq. 34 using Eq. 36A; it reads

$${\mathit{P}}^{\pm }(\mathit{k})=-\mathrm{\tau }\mathit{q}\frac{2\mathrm{\pi }{\mathit{k}}^2}{\mathit{m}}{\mathit{f}}_0^{\prime }({\mathrm{\epsilon }}_{\mathbf{k}})\frac{\mathit{E}+\frac{\mathrm{\tau }}{2}\mathrm{\rho }(\mathit{k}){\tilde{\mathit{V}}}^{\pm }(\mathit{k})\mathit{E}\times \mathit{n}}{1+{\{\frac{\mathrm{\tau }}{2}\mathrm{\rho }(\mathit{k}){\tilde{\mathit{V}}}^{\pm }(\mathit{k})\}}^2}$$ (38)

Hence, by substituting Eq. 38 into Eq. 37, to the leading order in E, ${\mathit{g}}_{\mathit{k}}^{\pm }$ reads

$${\mathit{g}}_{\mathit{k}}^{\pm }=-\mathrm{\tau }\mathit{q}{\mathit{f}}_0^{\prime }({\mathrm{\epsilon }}_{\mathit{k}}){\mathit{v}}_{\mathit{k}}\cdot (\mathit{E}-\frac{\mathrm{\tau }}{2}\mathrm{\rho }(\mathit{k}){\tilde{\mathit{V}}}^{\pm }(\mathit{k})\mathit{n}\times \mathit{E})$$ (39)

Using the above results, the electric conductivity can be calculated by using the current formula

$$\mathit{j}=\mathit{q}{\displaystyle \sum _{\mathrm{\sigma }}}{\displaystyle \int }\frac{{\mathit{d}}^3\mathit{k}}{{(2\mathrm{\pi })}^3}{\mathit{v}}_{\mathit{k}}{\mathit{f}}_{\mathit{k}\mathrm{\sigma }}$$ (40)

After some calculations, we find that the Hall conductivity is given by

$${\mathrm{\sigma }}_{\mathit{x}\mathit{y}}=\frac{2{\mathit{n}}_{\mathrm{e}}{\mathit{q}}^2\mathrm{\tau }}{\mathit{m}}\frac{\mathrm{\rho }({\mathit{k}}_{\mathrm{F}})\mathrm{\tau }}{2}({\tilde{\mathit{V}}}^0({\mathit{k}}_{\mathrm{F}})+{\tilde{\mathit{V}}}^1({\mathit{k}}_{\mathrm{F}}))$$ (41)

where k_F is the Fermi wave number and ${\mathit{n}}_{\mathrm{e}}={\mathit{k}}_{\mathrm{F}}^3/(6{\mathrm{\pi }}^2)$ is the average density of charges per a spin. Here, we assumed that n is the unit vector along the z axis and that the electric field and the current are in the xy plane. We note that, although we have ${\tilde{\mathit{V}}}_2$ in the scattering rate defined in Eq. 32, it does not affect the transverse conductance, as seen in Eq. 41.

Details of MC simulation

To calculate the phase diagram in Fig. 2, we used a classical MC method with a local update using heat bath algorithm. The calculations were carried out on a model with N = 30² and 60² spins with the periodic boundary condition. To calculate the thermodynamic quantities and its statistical errors, we took an average over five bins for each temperature and magnetic field; in each bin, 2.4 × 10⁶ MC steps were used for calculation after 6 × 10⁵ MC steps for thermalization. Here, one MC step consisted of N local updates using the heat bath method. We also kept track of the acceptance rate and confirmed that the averaged acceptance rate was above 1% for all field when the temperature was above T = 0.2J.