Bayesian-Based Decision Support System for Assessing the Needs for Orthodontic Treatment

Abstract

Objectives

In this study, a clinical decision support system was developed to help general practitioners assess the need for orthodontic treatment in patients with permanent dentition.

Methods

We chose a Bayesian network (BN) as the underlying model for assessing the need for orthodontic treatment. One thousand permanent dentition patient data sets chosen from a hospital record system were prepared in which one data element represented one participant with information for all variables and their stated need for orthodontic treatment. To evaluate the system, we compared the assessment results based on the judgements of two orthodontists to those recommended by the decision support system.

Results

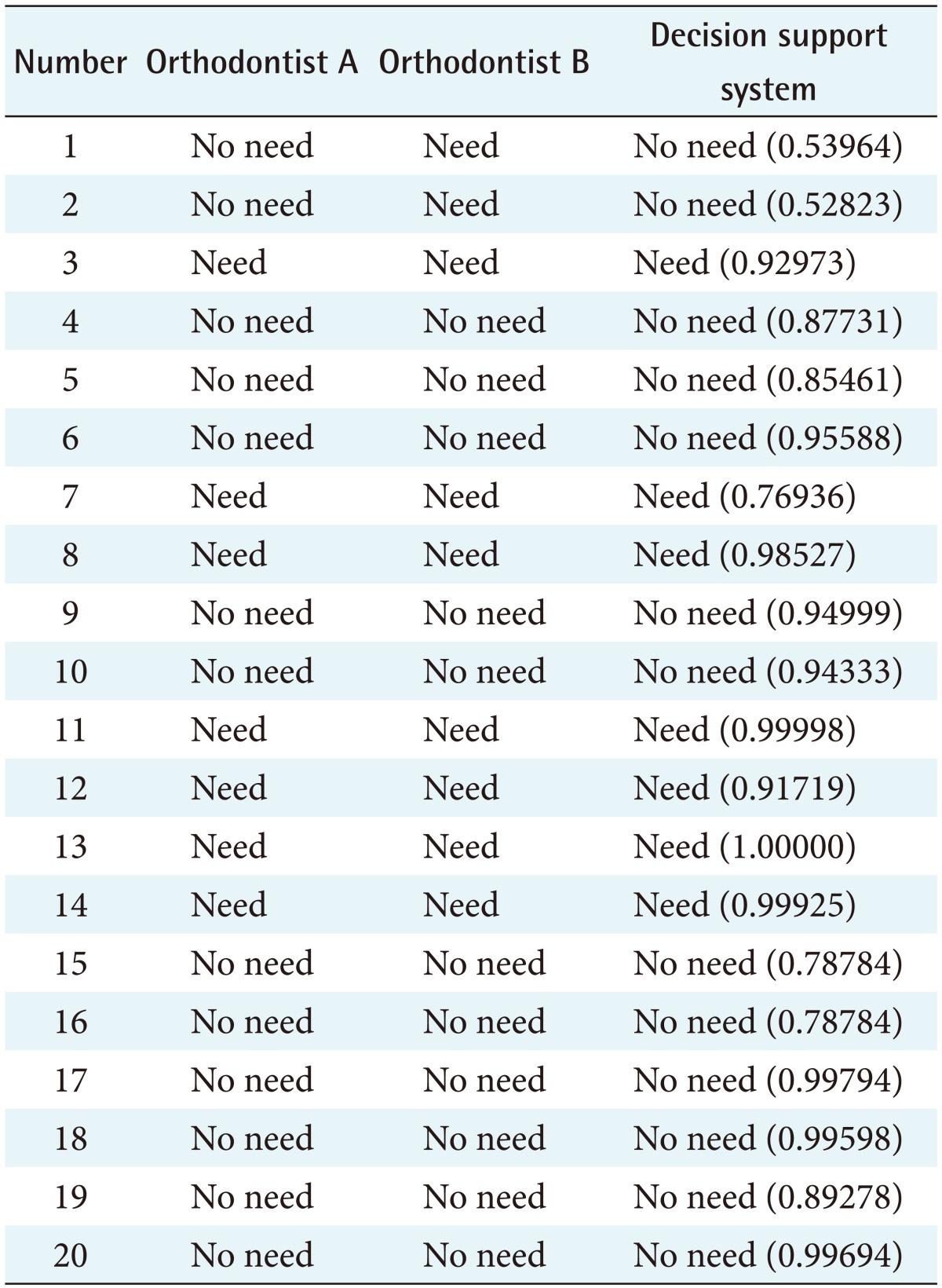
In a BN decision support model, each variable is modelled as a node, and the causal relationship between two variables may be represented as a directed arc. For each node, a conditional probability table is supplied that represents the probabilities of each value of this node, given the conditions of its parents. There was a high degree of agreement between the two orthodontists (kappa value = 0.894) in their diagnoses and their judgements regarding the need for orthodontic treatment. Also, there was a high degree of agreement between the decision support system and orthodontists A (kappa value = 1.00) and B (kappa value = 0.894).

Conclusions

The study was the first testing phase in which the results generated by the proposed system were compared with those suggested by expert orthodontists. The system delivered promising results; it showed a high degree of accuracy in classifying patients into groups needing and not needing orthodontic treatment.

I. Introduction

Malocclusion is a common major dental problem. Several indexes have been developed to classify patients into categories regarding orthodontic treatment need. The occlusal indexes used in various countries include the Handicapping Malocclusion Assessment Record (HMAR) [1], Index of Orthodontic Treatment Need (IOTN) [2], Peer Assessment Rating Index [3], Treatment Priority Index (TPI) [4], Occlusal Index (OI) [5], Dental Aesthetic Index (DAI) [6], Index of Complexity, Outcome and Need (ICON) [7], and Need for Orthodontic Treatment Index (NOTI) [8]. Some indexes are complicated, especially for non-orthodontic dentists. Moreover, the association between these indexes is imprecise, and judgements regarding the need for orthodontic treatment are known to vary substantially between studies [9,10].

Over the past 30 years, computerized applications have been developed to aid the clinician in the decision-making process. Clinical decision support has been defined as “any computer program designed to help health professionals make clinical decisions, deal with medical data about patients or with the knowledge of medicine necessary to interpret such data” [11,12]. Clinical decision support systems have been developed in orthodontic applications for several tasks; Xie et al. [13] used artificial neural network modelling for deciding if extractions are necessary prior to orthodontic treatment. Akcam and Takada [14] developed fuzzy modelling for selecting headgear types. In the present study, a clinical decision support system was developed to help general practitioners analyze the need for orthodontic treatment in patients with permanent dentition.

We chose a Bayesian network (BN) [15] as the underlying model for assessing the need for orthodontic treatment considering essential variables from existing indexes. A BN represents the domain knowledge qualitatively with the use of graphical diagrams containing nodes and arrows that represent variables and the relationships among the orthodontic treatment need variables. Quantitatively, the degree of dependence is expressed by probabilistic terms. The ability of BNs to model uncertainty and causal relationships among variables and to deal with missing clinical data makes them an attractive tool in a number of dental applications [16,17]. The overall purpose of the BN decision support model is to assist dentists in understanding the causal relationships of multiple factors affecting the need for orthodontic treatment thus forming the basis of a decision support system. In this study, we used the information from patients' orthodontic oral examination data sets and applied BN learning algorithms to these data sets to develop a model for assessing the need for orthodontic treatment of these patients. The BN model was an intelligent part of the decision support system. Finally, we evaluated results produced by decision support system for assessing the need for orthodontic treatment in permanent dentition patients.

II. Methods

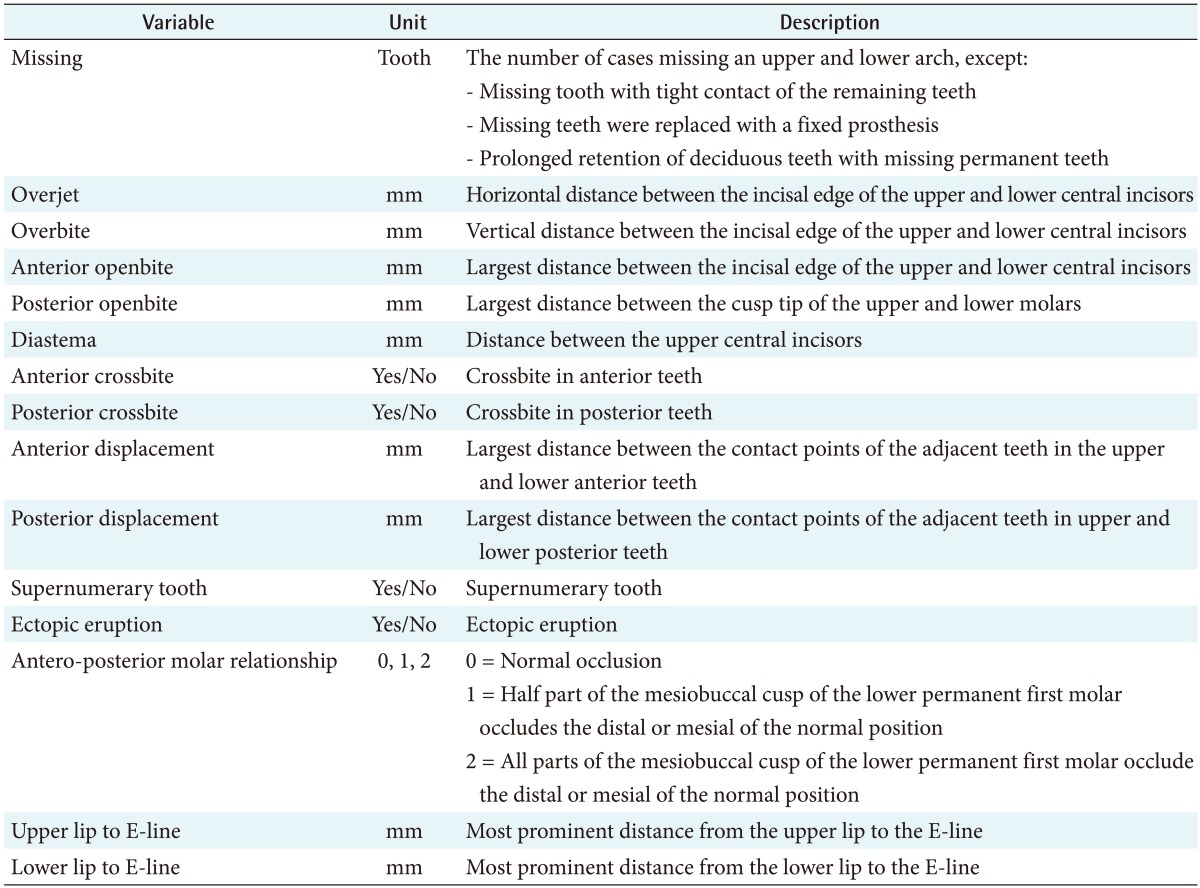
The process began with the identification of variables to be used in the assessment modelling. We referred to articles retrieved using ‘orthodontic treatment need’ as keywords in addition to textbooks on orthodontics supplemented by our experience gained from orthodontic treatment and training; thus, we composed a list of related variables. Fifteen orthodontic treatment need variables were extracted from existing commonly used indexes (IOTN, DAI, and ICON), which included missing tooth, overjet, overbite, anterior openbite, posterior openbite, diastema, anterior crossbite, posterior crossbite, anterior displacement, posterior displacement, supernumerary tooth, ectopic eruption, anterior-posterior molar relationship, upper lip to E-line, and lower lip to E-line.

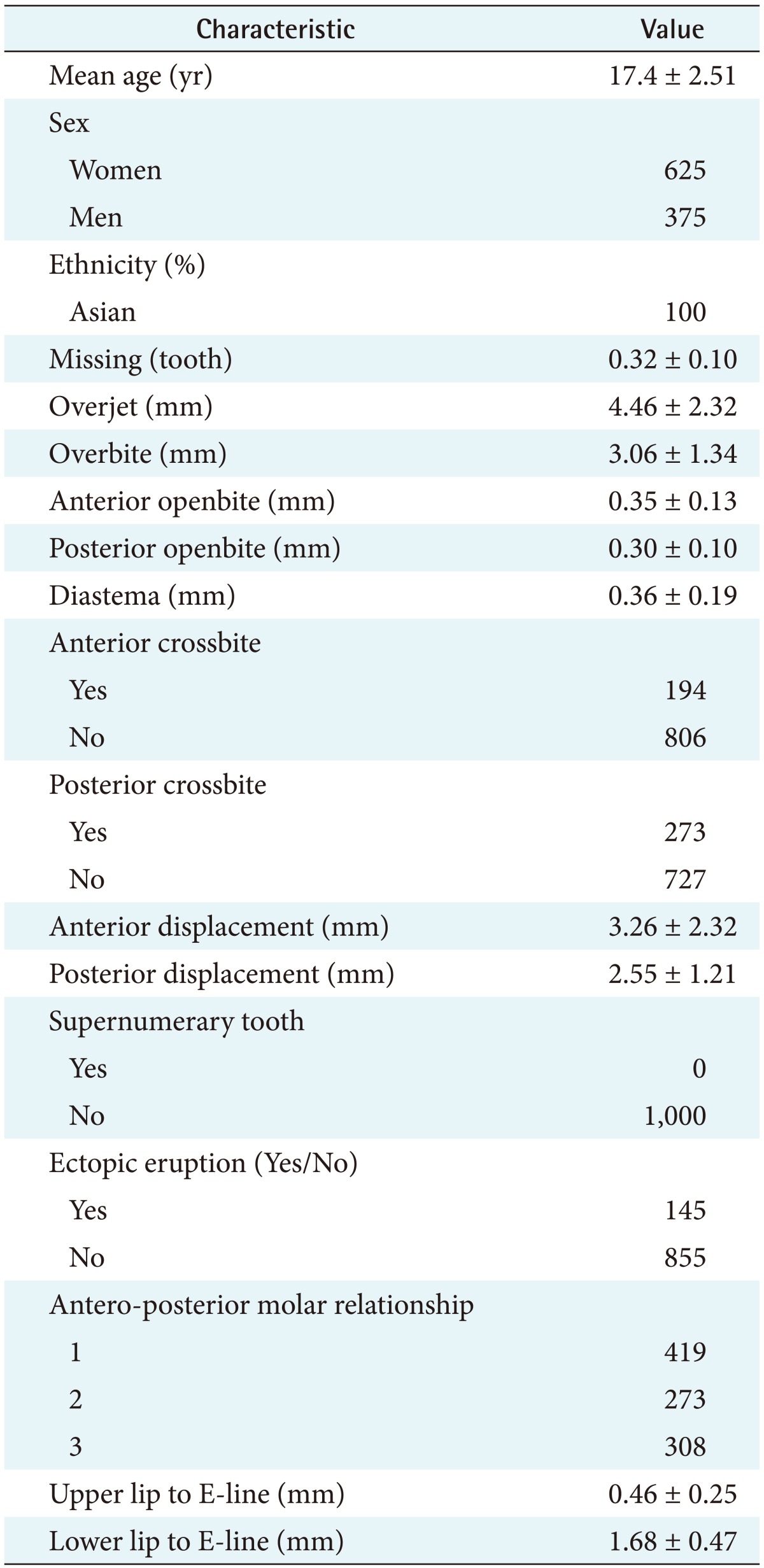
We designed an experiment in which we prepared data sets from patients who needed orthodontic treatment. Ethical permission for this study was obtained from the institutional ethical review board. A random sample of patients' records was selected from the university orthodontic clinic during the period from 2003 to 2013. One thousand participants were selected based on criteria using the purposive sampling method. All participants gave their written informed consent, which was approved by the institutional ethical review board. Dental patients who were 14 to 19 years old, generally in good health, and agreed to participate in this study were eligible for inclusion. Patients who had a history of alginate allergy, were unwilling to participate in this study, or had a history of temporomandibular disorders were excluded. All participants were examined, and upper and lower arch impressions as well as photographs were collected. On the right profile views, the head was in a natural position with the Frankfort horizontal line parallel to the floor (the Frankfort horizontal line extends from the upper tragus to the infraorbital rim). For each participant, each variable was carefully checked, and the data were recorded in an Excel format. Table 1 summarizes the variables and their states for the orthodontic treatment need.

Table 1. Variables and their states regarding the need for orthodontic treatment.

One data element represented one case (participant) with information for all labelled variables. Table 2 summarizes the demographic data and variables of all participants. The data were stored as separate data sets; the data sets were used to train the prediction model (training data) and to evaluate the model's performance (testing data). We applied BN learning algorithms to the training data sets to develop a model for assessing the need for orthodontic treatment. Finally, we tested the accuracy of the model with the validating data sets and implemented the model to predict the need for orthodontic treatment. The data were classified into five groups using random sampling. For each group, 80% were used in turn for training. The remaining 20% were used to test the structure and parameters of the decision support system. To evaluate the accuracy of a probabilistic model, the area under the receiver operating characteristic curve (ROC) is used. The area under the curve (AUC) represents the overall performance of the decision support model, with 1.0 representing a perfect test and 0.5 representing a model with a no discriminating capacity. The procedure was repeated five times, resulting in five candidate BN decision support models. We selected the BN model that achieved the highest performance for integration into the decision support system.

Table 2. Demographic data and each variable of all participants (n = 1,000).

Values are presented as mean ± standard deviation.

To evaluate the system, we randomly recruited 20 new patients from the university orthodontic clinic. All participants gave their written informed consent, which was approved by the institutional ethical review board. Patients who were 14 to 19 years old, in generally good health, and agreed to participate in this study were eligible for inclusion. Patients who had a history of alginate allergy, were unwilling to participate in this study, and had a history of temporomandibular disorders were excluded. We recruited two orthodontists who had at least 5 years of experience in practicing orthodontics after training. The two orthodontists were each asked to examine and assess the orthodontic treatment needs of each participant. We examined each patient and entered the data for each variable into the decision support system, and the automatic assessment results were recorded. This gave us a total of 20 data points to compare between the orthodontists' results and those generated by the decision support system. To test the statistical significance of the agreement between the orthodontists' results and those of the decision support system, we used the kappa statistic. The Kendall W coefficient of concordance was used to summarize the agreement among orthodontists.

III. Results

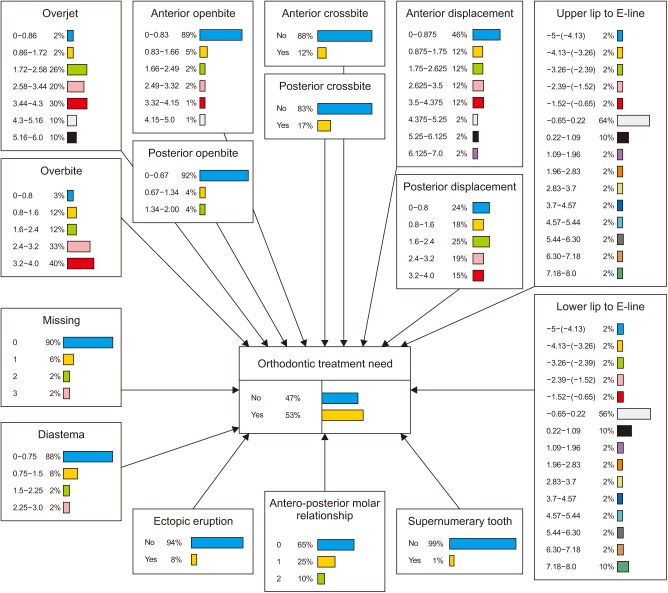
In a BN decision support model, each variable is modelled as a node, and the causal relationship between two variables may be represented as a directed arc. For each node, a conditional probability table is supplied that represents the probabilities of each values of this node, given the conditions of its parents (i.e., all nodes that have arcs pointed to this node) (Figure 1). The structure along with the conditional probability distribution of the BN was built up using training data sets obtained from study models and lateral face image measurement. Figure 1 shows a directed acyclic graph representing the cause-effect relationships among the 15 variables and the conditional probability distribution built up using one training data set. Each node contains a conditional probability table that explains the probabilistic relationships among all variables. The node bars display the normalized conditional probabilities that are compatible with the given state and condition on the evidence, which are normalized to have a maximum value of 100.

Figure 1. Bayesian network representing the possible relationships among factors that influence orthodontic treatment needs. Each arc indicates a causal relationship. Each node contains conditional probability distributions that were learned from the data.

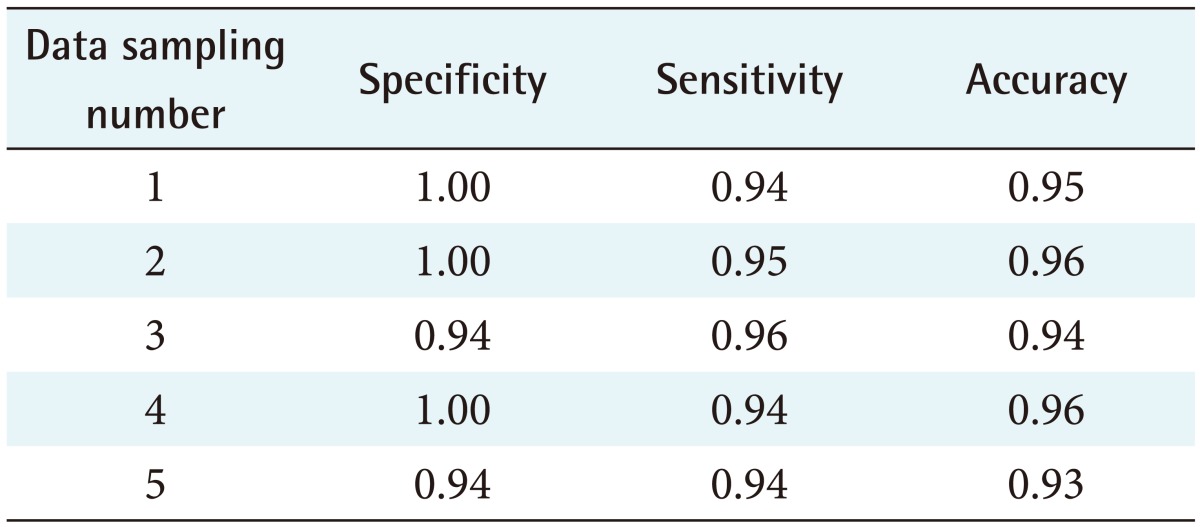
The performance of all candidate decision support systems was classified into five groups by using random sampling, resulting in five candidate decision support systems. The performance of those candidate decision support systems is shown in Table 3. The data sampling, which achieved the highest performance (the specificity, sensitivity, accuracy were 100%, 95%, and 96% respectively), was selected and developed with the software.

Table 3. Specificity, sensitivity, and accuracy of all candidate decision support systems.

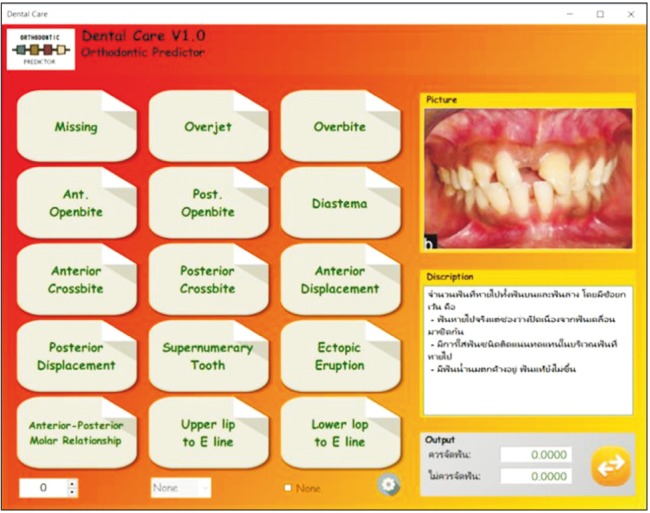
The BN model that showed the highest AUC (= 0.91) was selected for integration into the decision support system. Figure 2 shows the graphic user interface of the software when one participant's data was entered. The user could enter data into 15 variable boxes. These 15 variables consist of both descriptive texts and images (Figure 2). The point of intersection of this study was 0.5. When any possible diagnosis had a value higher than 0.5, it was considered to be the diagnosis for that patient. For example, the oral and facial examinations were: missing = 0, overjet = 2, overbite = 0, anterior openbite = 5, posterior openbite = 0, diastema = 0, anterior crossbite = No, posterior crossbite = Yes, anterior displacement = 2.5, posterior displacement = 3.5, supernumerary = No, ectopic eruption = No, ant-post molar relation = 2, upper lip to E-line = None, and lower lip to E-line = None. After the data were filled completely, the dentists pressed the output button. The result showed that the rate of the need for orthodontic treatment was 0.91491, and the lack of a need to undergo orthodontic treatment was 0.08509. In summary, it was determined that this patient needed orthodontic treatment.

Figure 2. Screen shot of the system user interface showing the prediction of need for orthodontic treatment.

To evaluate the system performance, the data from 20 cases selected by random sampling, including 5 males and 15 females, were used. Table 4 summarizes their need for orthodontic treatment according to two orthodontists and the BN results. There was a high degree of agreement between the two orthodontists (kappa value = 0.894) in their judgements regarding the need for orthodontic treatment. There was a high degree of agreement between the decision support system and orthodontists A (kappa value = 1.00) and B (kappa value = 0.894).

Table 4. Need for orthodontic treatment according to two orthodontists and the Bayesian network results.

IV. Discussion

Clinical decision-making requires that the clinician apply accumulated knowledge to a specific amount of patient information to produce a result that may be the diagnosis, prognosis, course of therapy, or selection of further tests. Too often, decisions are based on limited knowledge, must be made during a limited period of time, and the information upon which they are based is incomplete or imperfect. Bayesian-based decision support systems have been widely used in many organisations. For medical issues, BNs have been used to help diagnose breast cancer [18], to determine the relationship between the environment and genes in the occurrence of disease [19], or to predict pregnancy, as in the study by Corani et al. [20] BNs are very attractive for medical diagnosis systems because they can be applied to make inferences in many cases when the input data are incomplete. This can occur in several clinical settings when a BN is used with limited diagnostic data, and the system can be revised later when more data become available [21].

In this study, we developed a decision support system for assessing the orthodontic treatment needs of permanent dentition patients. The Bayesian decision support module consisted of relevant variables taken from treatment need indexes (IOTN, ICON, and DAI). These three indexes referred to the same variables focusing on anterior teeth, including overbite, anterior openbite, diastema, anterior crossbite, anterior displacement, and anterior-posterior molar relationship. These variables were directly related to the patient's satisfaction, which was influenced by facial aesthetics [22]. We also added the upper lip to E-line and lower lip to E-line variables to the BN model because several studies have suggested that bimaxillary protrusion is the most common aesthetic problem that requires orthodontic correction [23,24,25]. The data considered in the present study showed that most of the protruding profile patients had normal occlusion. The proposed decision support system was evaluated by a comparison of the orthodontic treatment needs assessed by orthodontists with those assessed by the system. Although we used a limited number of training data sets, there was a high degree of agreement between the judgements of the orthodontists and the results produced by the proposed system. In future research, the system should be further developed for orthodontic treatment need assessment in mixed dentition and tested to determine its validity in large community hospitals where there is a lack of orthodontic specialists. In conclusion, this study was the first step in developing a clinical decision support system to help general practitioners analyze the orthodontic treatment needs of their patients. The Bayesian probabilistic model generated decision support results based on patient intra- and extra-oral orthodontic-related data. The first testing phase of comparing the results generated by the system with those suggested by expert orthodontists delivered promising results. It achieved a high degree of accuracy in classifying patients into groups needing and not needing orthodontic treatment.