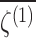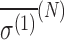Selection of Amino Acid Chirality via Neutrino Interactions with ¹⁴N in Crossed Electric and Magnetic Fields

Abstract

Previous work has suggested that the chirality of the amino acids could be established in the magnetic field of a nascent neutron star from a core-collapse supernova or massive collapsar. The magnetic field would orient the ¹⁴N nuclei, and the alignment of its nuclear spin with respect to those of the electron antineutrinos emitted from the collapsing star would determine the probability of destruction of the ¹⁴N nuclei by interactions with the antineutrinos. Subsequent work estimated the bulk polarization of the ¹⁴N nuclei in large rotating meteoroids in such an environment.

The present work adds a crucial piece of this model by describing the details by which the selective ¹⁴N nuclear destruction would produce molecular chiral selectivity. The effects of the neutrino-induced interactions on the ¹⁴N nuclei bound in amino acids polarized in strong magnetic fields are studied. It is shown that electric fields in the reference frame of the nuclei modify the magnetic field at the nucleus, creating nuclear magnetizations that are asymmetric in chirality. The antineutrino cross sections depend on this magnetization, creating a selective destructive effect. The environmental conditions and sites in which such a selection mechanism could occur are discussed. Selective destruction of D-enantiomers results in enantiomeric excesses which may be sufficient to drive subsequent autocatalysis necessary to produce the few-percent enantiomeric excesses found in meteorites and subsequent homochirality.

Molecular quantum chemical calculations were performed for alanine, and the chirality-dependent effects studied were included. A preference for left-handed molecules was found, and enantiomeric excesses as high as 0.02% were estimated for molecules in the electromagnetic conditions expected from a core-collapse supernova. Key Words: Amino acids—Supernovae—Antineutrinos—Enantiomeric excess—Chirality. Astrobiology 18, 190–206.

1. Introduction

Analyses of inclusions in meteoritic carbonaceous chondrites (Kvenvolden et al., 1970; Bada et al., 1983; Cronin and Pizzarello, 1997; Cronin et al., 1998; Glavin and Dworkin, 2009; Glavin et al., 2010; Herd et al., 2011) have shown that the molecules of life, especially the amino acids, are made in outer space. Furthermore, some of the amino acids so synthesized have the left-handed chirality that is observed almost entirely in earthly amino acids. It is generally accepted that, if some mechanism can introduce an imbalance in the populations of the left- and right-handed forms of any amino acid (Glavin and Dworkin, 2009), successive synthesis or evolution of the molecules via autocatalysis can amplify this enantiomeric excess ultimately to produce a single form. What is not well understood is the mechanism by which the initial imbalance is produced and the means by which it always produces the left-handed chirality observed in the amino acids. This enigma has been discussed in numerous reviews in past years (Frank, 1953; Mason, 1984; Kondepudi and Nelson, 1985; Goldanskii, 1989; Bonner, 1991; Barron, 2008; Blackmond, 2010; Boyd, 2012).

The amount by which one chirality exceeds the other is represented by the enantiomeric excess, ee, defined as

where N_L and N_D represent the number of left- and right-handed amino acids, respectively, of a specific type in an ensemble. Thus, Earth's amino acids (with the exception of the nonchiral glycine) have enantiomeric excesses of 1.0 or 100%.

2. Models of Amino Acid Chirality

The energy states of the left- and right-handed forms have been shown, by detailed computations, to differ at most by infinitesimal amounts due to parity violation (Tranter and MacDermott, 1986; Quack, 2002), so it would be difficult for thermal equilibrium to produce the imbalance. However, some evidence exists that electroweak parity-violating energy shifts could produce an enantiomeric excess if the molecules are in a gas phase (MacDermott et al., 2009).

2.1. Creating amino acid chirality from circularly polarized light

One mechanism that might produce amino acid enantiomeric excesses lies with processing of a population of amino acids in interstellar space by circularly polarized light (CPL) (Bailey et al., 1998; Takano et al., 2007; Takahashi et al., 2009; Meierhenrich et al., 2010; Meinert et al., 2010; de Marcellus et al., 2011); this could select one chirality over the other. This solution does have the benefit of being experimentally verifiable, at least in some of its aspects, a result of the large cross section for interaction of photons with matter. It therefore has been demonstrated to produce an enantiomeric excess in amino acids in laboratory experiments with light in the UV and vacuum UV spectral range (Flores et al., 1977; Norden, 1977; Meierhenrich et al., 2005; Takano et al., 2007; Meinert et al., 2014). Currently, amino acid irradiation by CPL over a limited UV range has yielded the highest ee values in laboratory experiments (Meinert et al., 2012).

A number of different regions of space have been identified as possibilities with light having large-enough circular polarization, at least over some bandwidth, to perform the necessary amino acid processing. Interstellar CPL is thought to have a short wavelength cutoff as well, limiting the bandwidth to the regions necessary for amino acid processing (Bailey et al., 1998). Recent studies have found very large areas of CPL in star-forming regions (Kwon et al., 2016).

This model, however, is not without its difficulties. It does not easily explain why the physical conditions that would select one chirality in one place would not select the other in a different location. Nonetheless, a region as small as a planetary system could be processed by the output from a single star (de Marcellus et al., 2011) so that all the light in that region could be of a single circular polarization. This could explain the observed meteoritic and Earth's results. Another problem, though, is that the CPL must destroy most of the material it is processing in order to produce a significant enantiomeric excess (Bailey et al., 1998; de Marcellus et al., 2011). Finally, UV light could only process to a small depth of the surface of a larger object. Given that much of the material in the interstellar medium is in the form of dust grains, this would not present a problem for processing a large fraction of such material near to the UV source. However, dust grains would not likely reach the surface of a planet if they had to pass through any sort of atmosphere. This could be overcome if the grains could agglomerate into larger entities after they had been exposed to the CPL. If the agglomeration occurred before the amino acids had been processed, however, only the molecules on the surface of the larger objects would be processed, and these would very likely be ablated away as the resulting meteoroid passed through the planetary atmosphere.

2.2. Dark matter and other possibilities

It has been suggested that the differences between ortho- and para-hydrogen pairs (Shinitzky and Elitzur, 2006) in the amino acids could produce a chiral selection. The possibility that dark matter or cosmological neutrinos could select enantiomers has also been studied (Bargueño et al., 2008).

2.3. Creating amino acid chirality via weak interactions

One possibility for producing the chirality of the amino acids (Mann and Primakoff, 1981) invoked selective processing by some manifestation of the weak interaction, which does violate parity conservation, so might perform a chiral selection. This idea was based on earlier work (Vester et al., 1959; Ulbricht and Vester, 1962). Mann and Primakoff focused on the β-decay of ¹⁴C to produce the selective processing. However, it was not possible in that study to show how simple β-decay could produce chiral-selective molecular destruction. A modern update on this possibility (Gusev et al., 2008) does appear to produce some enantiomeric enhancement. Another suggestion (Cline, 2005) assumed that antineutrinos emitted by a core-collapse supernova would selectively process the carbon or the hydrogen in the amino acids to produce an excess of one chirality. However, this also did not explain how a predisposition toward one or the other molecular chirality could evolve from those antineutrino interactions. A similar suggestion (Bargueño and Pérez de Tudela, 2007) involves the effects of antineutrinos from supernovae on molecular electrons.

2.4. The SNAAP model

Recent work (Boyd et al., 2010, 2011; Famiano et al., 2014; Famiano and Boyd, 2016) has suggested that the chirality of the amino acids could be established in the magnetic field of a nascent neutron star from a core-collapse supernova via processing by the antineutrinos—themselves chiral particles—that would be emitted. The antineutrinos occur in an intense few-second burst and are the means by which the collapsing neutron star cools. While the initial burst is intense, the antineutrino emission continues at a reduced rate in the supernova for the next 10 s or so and then at a lower rate for the next ∼10⁵ years as the neutron star continues to cool. This model, the Supernova Neutrino Amino Acid Processing (SNAAP) model, appears to produce a small chiral imbalance. We review this model in more detail below and present details in subsequent sections of calculations that extend it to include details of the connection between the nuclear reactions caused by the antineutrinos and the molecular chirality of the amino acids. Section 3 reviews the SNAAP model. Section 3.1 presents the model used to determine the molecular chiral state selection and determines the resulting population imbalance. Section 4 estimates the magnitude of the enantiomeric excess that might be expected from this model. Section 5 provides an overview of our computational model, and Section 6 shows example results from our model. Section 7 presents some conclusions and discusses questions that must be addressed in determining the veracity of any model.

3. Basic Features of the SNAAP Model

This model assumes that the antineutrinos emitted from a nascent neutron star would interact with the amino acid nitrogen nuclei that had been oriented by the neutron star's magnetic field. These molecules would have to be contained in large enough meteoroids that happened to be passing by the star as it collapsed, that a fraction of them could survive the high-temperature and high-radiation environment existing near the star. The crucial interaction that produces selectivity is

where 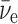is an electron antineutrino and e⁺ is a positron. It was also assumed that some imbalance in the orientation of the molecules would be achieved, perhaps by the Buckingham effect (Buckingham, 2004; Buckingham and Fischer, 2006), which would produce a redistribution in the molecular magnetic substate population that would depend on the coupling of the nuclear spin and the molecular chirality. Then, the conversion from ¹⁴N to ¹⁴C would, because of a spin orientation dependence of the strength of the interaction, preferentially destroy one orientation compared to the other. The geometry surrounding this neutron star is indicated in Fig. 1. Its strong magnetic field will produce a favored chirality as the molecular electronic orbital configuration couples to the nuclear configuration. The strength of the antineutrino interaction that destroys the ¹⁴N depends not only on the orientation of the antineutrino's spin with respect to that of the ¹⁴N but also on conservation of angular momentum. The nucleus ¹⁴N has a spin of 1, in units of 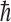(where 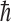is Planck's constant divided by 2π), whereas the and the e⁺ each have spins of 1/2. However, ¹⁴C has a spin of zero.

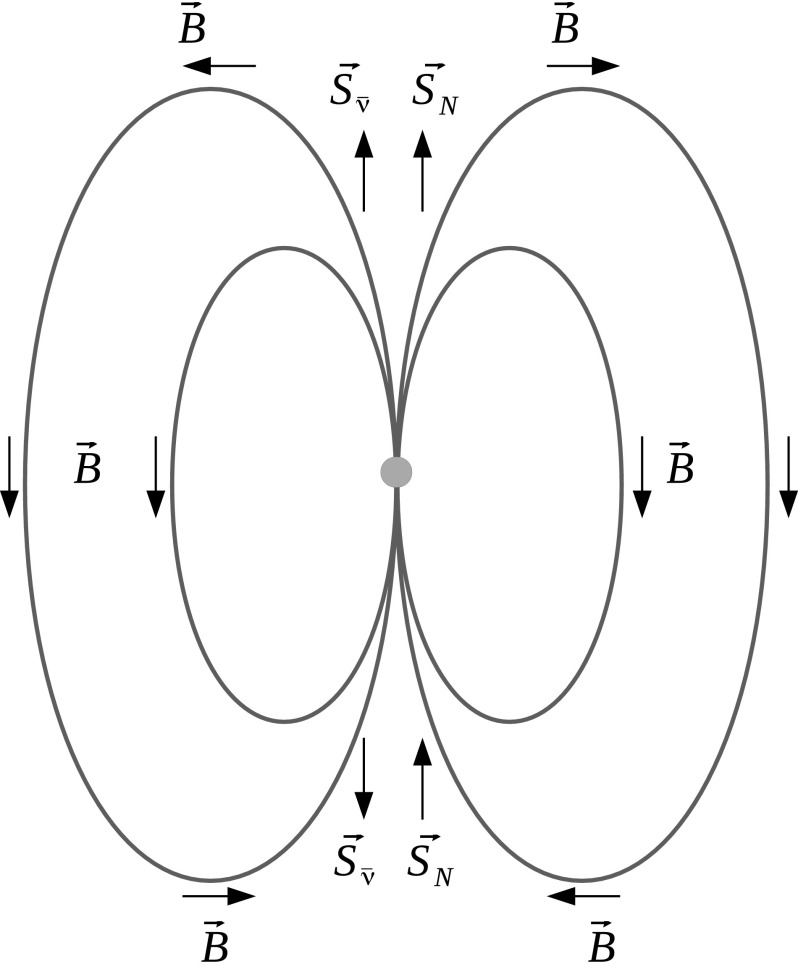
FIG. 1.

Magnetic field around a neutron star, indicated by B; directions of the antineutrino spins, indicated by 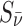; and the alignment direction of the ¹⁴N, indicated by S_N (Boyd et al., 2010, 2011; Famiano et al., 2014).

If the angular momentum is considered in the antineutrino interactions with the ¹⁴N nucleus, then two possible configurations for this reaction exist. One is the case where the antineutrino spin is oriented antiparallel to the ¹⁴N spin. The other is the case in which both spins are aligned:

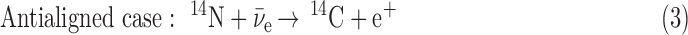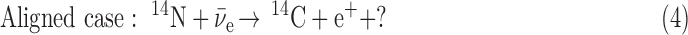In Eq. 3, the antialigned case, the two spin vectors on the left-hand side of the equation can add up to 1/2, so can equal the sum of the spin vectors on the right-hand side. In Eq. 4, though, the aligned case, the two spin vectors on the left-hand side of the equation add up to 3/2, so cannot equal the spin vector sum on the right-hand side without an additional unit of angular momentum, indicated by the question mark. This must come from the wave function of the 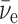or the e⁺, and is known (Boyd, 2008) to inhibit the destruction of ¹⁴N in the aligned case with respect to the antialigned case by about an order of magnitude. This well-known phenomenon can be expressed for antineutrino capture as a relationship of the angle Θ between the antineutrino velocity vector, hence its spin vector, and the ¹⁴N spin vector (Morita, 1973; de Shalit and Feshbach, 1974; Wong, 1998):

The alignment of the nuclear spin in the neutron star's magnetic field and the subsequent destruction of one such orientation will result in a slight preference for one nuclear orientation. The hyperfine interaction will couple the nuclear and electronic spins and has been well studied in stellar environments (Berdyugina and Solanki, 2002; Berdyugina et al., 2005). While the relationship may be more complicated for complex molecules, the molecular chirality can be shown to be related to the electron angular momentum (Prez-Garca et al., 1992). Thus, this selective nuclear destruction would favor one chirality on each side of the neutron star. Although the effects on the two sides of the star would come close to canceling out if the antineutrino fluxes were the same on both sides, that has been shown not to be the case in the strong magnetic field of the star (Horowitz and Li, 1998; Lai and Qian, 1998; Arras and Lai, 1999; Maruyama et al., 2011); thus one of the molecular chiral states would be selected. Although the cross section for the antineutrino-¹⁴N interaction is tiny, roughly 10⁻³⁸ cm⁻², the enormous antineutrino flux that would be emitted in cooling the nascent neutron star would be expected to produce an enantiomeric excess of about a part in 10⁻⁶ in this model (Boyd et al., 2011). This value is certainly lower than values experimentally demonstrated in laboratory CPL experiments (Meinert et al., 2012), for example, though it does represent a value possible in a naturally occurring site. Also, the broad range of conditions possible in this model may result in a large range of possible ees. This broad range is due to the possible sites where this effect can occur.

With any model of chirality selection, amplification, presumably by autocatalysis (Frank, 1953; Mason, 1984; Kondepudi and Nelson, 1985; Goldanskii, 1989), is required to produce the order-of-a-few-percent magnitudes of the enantiomeric excess observed in the meteorites. Autocatalysis has been demonstrated to occur in several situations in laboratory experiments (Soai et al., 1995, 2014; Soai and Sato, 2002; Arseniyadis et al., 2004; Breslow and Levine, 2006), so it does appear to provide a plausible explanation for enantiomeric excess enhancement. Though these experiments do not necessarily apply to prebiotic conditions, they may suggest a partial explanation for autocatalysis in an early Earth environment. Additionally, enantiomeric amplification in racemate crystals has also been shown to occur via selective precipitation of amino acids in solution (Klussmann et al., 2006).

Additional details of the SNAAP model are discussed in Boyd et al. (2011).

3.1. Dynamical model of chiral state selection

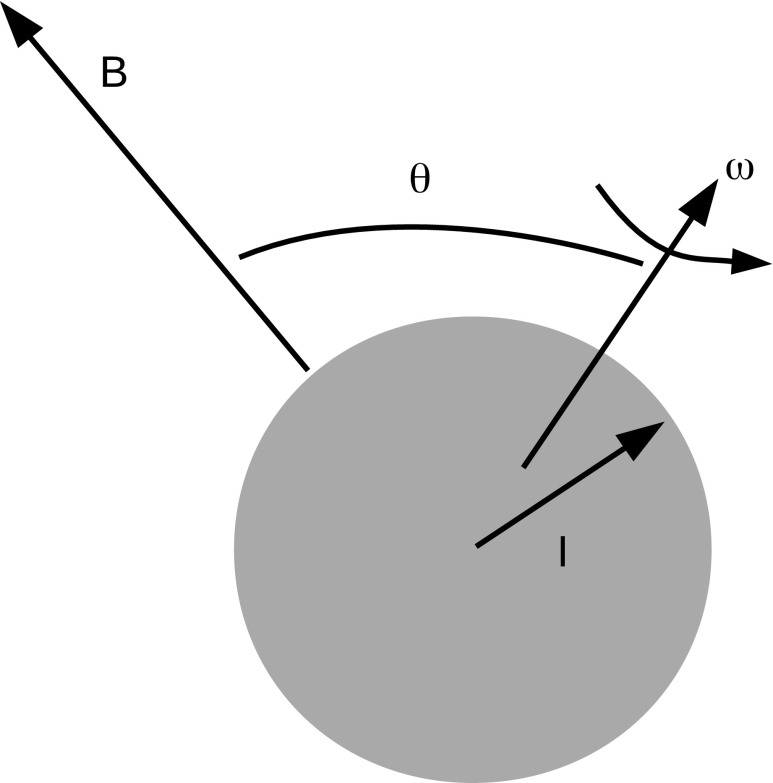
The vectors that are relevant to this model are shown in Fig. 2. These include the magnetic field vector, B; the molecular total angular momentum vector, I; and the vector, ω, that characterizes the rotation of the meteoroid in which the molecules are contained. Clearly the orientation of the rotation vector of the meteoroid is random with respect to the direction of the magnetic field, and the orientation of the molecules within the meteoroid is random with respect to the direction of ω. Thus, any dynamical description of the effects associated with molecular substate reorientation needs to average over the directions of two of the vectors with respect to that of the magnetic field. A Monte Carlo code was written and the averages performed over the directions of the rotation vector of the meteoroid, the orientation of the molecules within the meteoroid, and the magnitude of the magnetic field B.

FIG. 2.

Vectors relevant to the dynamical model of chiral state selection in the SNAAP model. B is the magnetic field vector, I is the total spin of the molecule, and ω is the vector that characterizes the rotation of the meteoroid in which the molecules are contained (Famiano et al., 2014; Famiano and Boyd, 2016).

The quantity calculated by the Monte Carlo code is the bulk polarization of the meteoroid, M, which results from the interaction between the magnetic field of the nascent neutron star and the rotation of the meteoroid. The shift between states is due to an adiabatic transition between the chiral states that results from the interaction between the magnetic field of the neutron star and the rotating total angular momentum of each molecule. The bulk polarization of the molecules trapped in a meteoroid will depend on the strength of the star's field at the meteoroid's location, the gyromagnetic ratio of the molecule, the meteoroid's angular speed, and the orientation of the angular velocity vector with respect to the magnetic field. In the reference frame of the meteoroid, the magnetic field has a component parallel to the angular velocity vector, B₀, and a component perpendicular to this vector, B₁, with the perpendicular component rotating at the angular frequency, ω, of the meteoroid. The polarization is well established in this condition (Bloch, 1946). For a population of polarized states with a rotating component of a magnetic field, the magnetization vector is given by the Bloch equation (Bloch, 1946):

where the bulk magnetization M is initiated in the external magnetic field for a material with number density n and magnetic moment μ_B. The relaxation time, T_R, corresponds to the damping time constant during which a magnetized medium returns to a state of random orientation. The last term in Eq. 6 corresponds to the torque on the magnetic moment from the meteoroid's motion in the external magnetic field. For a material of nonzero magnetic moment in an external magnetic field B₀, the angular momentum vector will precess about the magnetic field axis with the precession frequency ω₀ = γB₀. The rotation of the meteoroid in the magnetic field induces a NMR-like situation in the reference frame of the meteoroid. Equation 6 can then be solved by assuming a rotating reference frame in which B₁ is stationary. The details of this analysis will not be repeated here but can be found in Famiano et al. (2014).

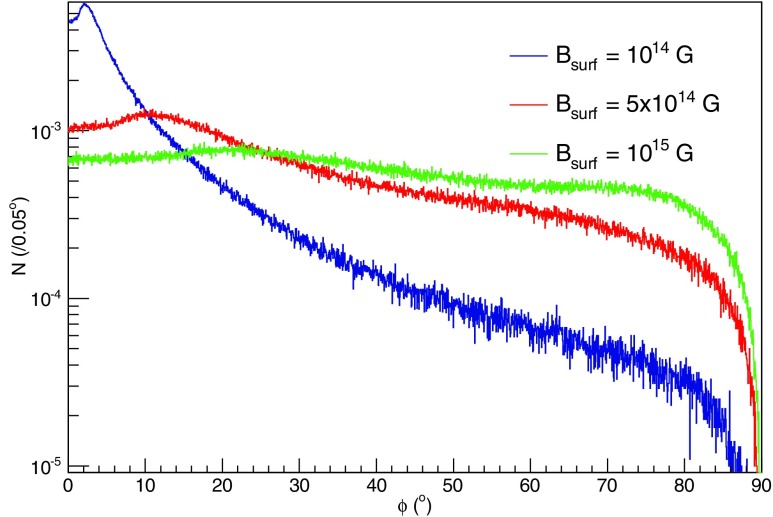
Several Monte Carlo simulations of meteoroids in the vicinity of a neutron star's (dipole) magnetic field were performed to simulate a spatial distribution of meteoroids with varying angular speeds and orientations relative to the external dipole field. In this way, the average bulk polarization angle was determined. For each simulation, meteoroids were assumed to be distributed evenly in a volume of space about the neutron star with random angular orientations and velocities. For each sample in the Monte Carlo calculation, the components of the magnetization were calculated along with the polarization angle. These calculations have ignored the effects of thermalization (which will be considered in this paper at the nuclear magnetization level). If such effects were important, they would produce a competition between the thermalization lifetime and the time associated with producing the substate imbalance, which is the order of the inverse of the meteoroid rotation time. The photostability of amino acids against destruction or racemization via UV radiation has been found to be hundreds of years or even much longer (Ehrenfreund et al., 2001) at the relatively high temperatures assumed in that study. Thus, thermalization times were assumed to be infinite. An example of the bulk polarizations from the SNAAP model is shown in Fig. 3 for three models studied. The angular orientations of the meteoroids' rotation axes were evenly distributed between 0° and 90°. In this figure, the surface field of the star is varied, while a distribution of angular speeds and radii is simulated. While a higher field will exert a stronger initial torque on the molecules, the steady state condition of the system for strong fields becomes more significantly affected by the randomly distributed perpendicular components of the field in the reference frame of the meteoroid. Then, the resonant precession frequency of the external field differs significantly from the angular speed of the meteoroid. The polarization distribution is then more strongly affected by the perpendicular components of the field. Models for the SNAAP model calculation have examined the influence of the neutron star's magnetic field, the meteoroid rotation rate, and the distance from the neutron star's surface; details of these results are given in Famiano et al. (2014).

FIG. 3.

Polarization distribution for three example models. This figure compares the polarization distribution for various neutron star surface magnetic fields (Famiano et al., 2014; Famiano and Boyd, 2016).

While one might conclude that larger radii are more important for this scenario, the antineutrino flux is proportional to the inverse square of the radius, resulting in a reduced selective production effect. Likewise, as the field weakens, the overall polarization may be more susceptible to stochastic effects since the net torque of the external field is much weaker. As discussed previously, a stronger magnetic field may result in a loss of net polarization, so that a model with a distribution of larger magnetic fields has a polarization distribution that is not as pronounced about zero degrees as that with a smaller field (keeping in mind that T_R is assumed to be infinite in this initial evaluation). These particular models are interesting as they enable a quantitative estimate of the enantiomeric excess that could be produced in the SNAAP model than was done previously. In Boyd et al. (2011), the cross section for antineutrino conversion from ¹⁴N to ¹⁴C was estimated from the results of Fuller et al. (1999), and it was assumed that the minimum distance from the nascent neutron star to the meteoroid that would permit survival of the meteoroid would be 0.01 AU. At that distance, the estimated enantiomeric excess was 10⁻⁴%. However, implicit in that assumption was the estimate that the molecular polarization was 100%. The fraction of the molecules that occur within 10° of the direction of the magnetic field of the neutron star, as determined from these calculations, is not 100%, though it can be above 90% under some conditions. The very smallest values occur at the smallest radii, at which the magnetic field becomes so strong that the model probably breaks down anyway. At a radius of 2 AU, the estimate of the bulk polarization is about 50%, and the antineutrino flux will have fallen off from the value used in the estimate of Boyd et al. (2011) by a factor of 4. The result is that the estimated enantiomeric excess becomes 10⁻⁵%, one part in 10⁷. Details of this calculation, along with additional calculations, are described in Famiano et al. (2014).

Does so low a value permit the SNAAP model to drive the ultimate homochirality of Earth or even the few percent enantiomeric excesses found in the meteoritic samples? That required to boost this enantiomeric excess has been demonstrated to occur in laboratory experiments, although, as mentioned above, not at such a small initial enantiomeric excess. Existing experiments have not yet determined the lower limit for autocatalysis to prevail, although that value has been estimated (Meierhenrich, 2008) to be several orders of magnitude less than that expected from the SNAAP model. Since in the SNAAP model the optimal effects are achieved when the neutrino flux is maximum and its velocity vector is aligned with the ¹⁴N spin, a qualitative evaluation of the optimal radius about the neutron star for the SNAAP model to be most effective can be made by maximizing the product of the neutrino flux and the average normalized polarization defined as the average bulk polarization angle normalized to unity after subtracting from π/4:

where the value of π/4 is the average polarization for a flat distribution (similar to the green line in Fig. 3). Thus, a completely unpolarized medium will have an average value of 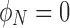, whereas a medium that is completely polarized axially (magnetization pointing toward the pole) will have 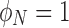, and one that is polarized at 90° with respect to the pole will have 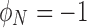. While this definition is somewhat arbitrary, it provides a single number to quantify the amount of bulk polarization in a medium.

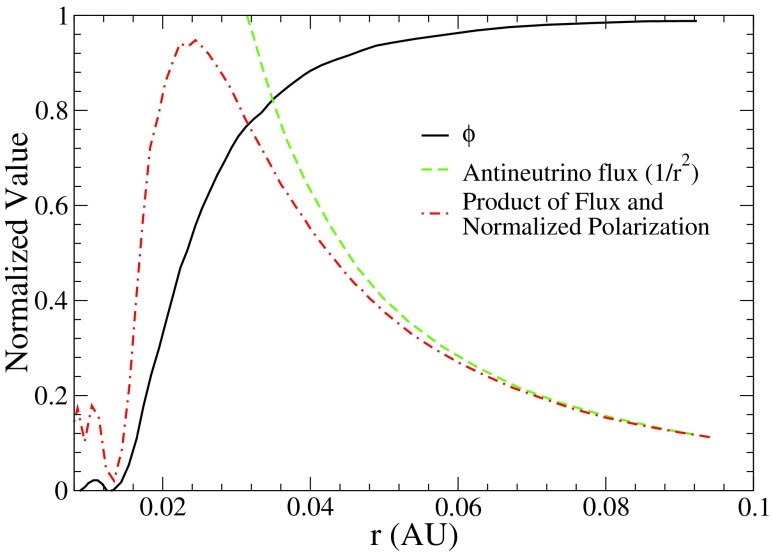
The calculated polarization with respect to the magnetic field vector increases with radius, while the antineutrino flux falls off as 1/r². Thus, the product of the normalized polarization and flux will provide a rough idea of an optimal radius for which chiral selection occurs. This product is shown as a function of radius in Fig. 4 for a surface field of 10¹⁴ G and γ = 2 × 10⁷ rad s⁻¹ T⁻¹.

FIG. 4.

Product of the normalized polarization and 1/r² for a surface field strength of 10¹⁴ G and γ = 2 × 10⁷. Large fluctuations near 0 AU are because fewer events are averaged over in the Monte Carlo calculation in the region closest to the star (Famiano et al., 2014; Famiano and Boyd, 2016).

4. Selection of Amino Acid Chirality

In the previous section, the preliminary work to evaluate the SNAAP model was presented. We now present an extension of that model by evaluating a crucial element which has not yet been examined. This is the coupling of the nuclear spin to the molecular chirality. The effects of the molecular electronic orbitals and molecular orientation are linked to the molecular spin via the nuclear magnetic shielding tensor σ. Here, we evaluate shifts in the shielding tensor via interactions of amino acids in external magnetic and electric fields. Differences in the shielding tensor from different molecular chiral states can affect the magnetic fields at the nucleus and thus the overall spin orientations of the ¹⁴N nuclei with respect to the external field. In this model, external fields can implement this shift.

The isotropic shielding tensor defines the shift in the magnetic field at the nucleus due to the surrounding electron orbitals (Buckingham, 2004; Buckingham and Fischer, 2006):

where the external magnetic field is given by B⁰. This reduction is caused by the motion of the electrons. The superscript (N) indicates values evaluated at the nucleus. (In Eq. 8 and in subsequent equations, the sum over matching indices is implied.) The shielding tensor has been defined perturbatively in the presence of external magnetic and electric fields as a sum of diamagnetic components and paramagnetic components owing to the shift in orbitals from the external electric field. For chiral molecules, the shielding tensor in the presence of an external magnetic field depends on the molecular chirality; off-diagonal elements are asymmetric with external electric field. This is known as the nuclear magnetic shielding polarizability and represents a shift in the shielding tensor in the presence of an external electric field, E⁰:

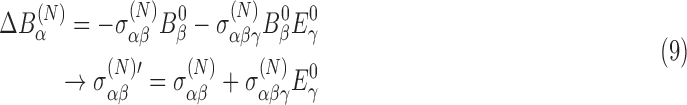where the primed tensor indicates the adjusted tensor in the presence of an external electric field.

The details of the development and calculations of this polarizability and its isotropic components are given in Appendix A. Ultimately, the chirality-dependent shielding tensor changes the nuclear magnetizability and the overall magnetic moment described by the third-rank tensor which couples the change in magnetic field at the nucleus to the external electric field. This rank-3 tensor is also described in the Appendix. The result is that the magnetic field at the nucleus in the presence of an external electric field depends on the molecular chirality.

4.1. The translational Stark effect

A molecule moving in a magnetic field will experience an electric field in its own rest frame equivalent to E_TS ≡ v × B. This electric field is created via the translational (or motional) Stark effect (Rosenbluh et al., 1977; Panock et al., 1980; Zarnstorff et al., 1997). Here, the molecular Hamiltonian contains an additional term from the partial motion in the external field:

where μ_E is the molecular electric dipole moment.

The energy due to the molecular magnetic moment and electric dipole moment in the external field is

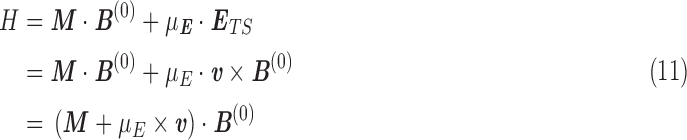For chiral molecules moving in an external magnetic field, the induced electric field in the molecular rest frame thus has two effects. In Eq. A.5, it is seen that the force on the electrons and nuclei in molecules of different shapes results in a reconfiguration of the electron orbital wave functions with respect to the nuclei. This changes the shielding tensor such that the magnetic properties of the molecule change. Equations A.8 and 11 describe the following situation. The electronic wave function of a molecule produces a shift in the total magnetic field at the nuclei of the molecule. An external electric field will cause the electrons to reconfigure. This will cause an additional shift in the magnetic field.

From Eqs. A.9 and A.10, the shift in magnetic field at the nucleus, ΔB^(N), and its contribution to the total magnetic moment, Δm^(N), are, for a constant velocity in a uniform magnetic field:

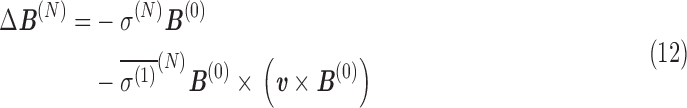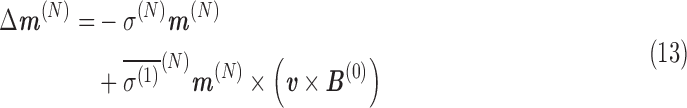Here, the term 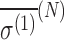is referred to as the isotropic “nuclear magnetic shielding polarizability,” which is described in Appendix A. It is a measure of the average shift in the total magnetic field and magnetization due to an external electric field.

To summarize for chiral molecules in an isotropic medium, any difference in the energy states of the molecules due to the shift in the nuclear magnetization can be expressed as a difference in components of the total magnetic field or magnetization that are parallel and perpendicular to E_TS.

5. Computational Model

Following the example of Buckingham and Fischer (2006), the nuclear magnetic polarizabilities for L-alanine and D-alanine were calculated. The Dalton molecular quantum chemistry code (Aidas et al., 2014) was used to compute the shielding tensor in the presence of external electric fields in the molecular rest frame. Here, the fields are treated perturbatively, and the polarizabilities are calculated. Six field scenarios are calculated for E_x = E_y = E_z = ±0.001 a.u. = ±5.14 × 10⁸ V/m. (The notation “a.u.” indicates atomic units.) Electron orbital wave functions were performed by using a DFT calculation employing a three-parameter hybrid functional (Becke, 1993) with the pcS-2 orbital basis set (Jensen, 2008, 2015).

A test of this basis set with the density functional used was conducted with R-HOOH using a geometry optimized with the aug-cc-pVDZ basis set. The resulting geometry is specified in Table 1. The shielding constants and isotropic magnetic shielding polarizabilities are shown in this table compared to two other calculations (Buckingham and Fischer, 2006). One can see that the results for each geometry compare favorably for each model. For models G1 and G2 in this table, the average over all results from the basis sets used are displayed, and the uncertainty is the standard deviation of all values. One can see a broader range of values for the polarizabilities, though they are similar, and the value computed here is in the range of differences. As this work seeks to approximate the values in amino acids, the R-HOOH-tested values indicate that the choice of basis set and optimization are satisfactory for these purposes.

Table 1.

Comparison of Isotropic Magnetic Shielding Polarizabilities and Nuclear Magnetic Shielding Constants for R-HOOH

	G1	G2	This work
(ppm a.u.)	−3.5 ± 0.43	−5.8 ± 0.19	−4.8
σ(H) (ppm)	26.3 ± 0.99	24.8 ± 0.60	26.68
RO–O (Å)	1.3866	1.452	1.3865
RH–O (Å)	0.9426	0.965	0.9426
∠OOH	103.059°	100.0	103.06°
∠HOOH	111.59°	112.0	111.46°

Model G1 corresponds to Geometry 1 in Buckingham and Fischer (2006), and G2 corresponds to the MP2 result for Geometry 2 in the same reference. Values and uncertainties are described in the text. Units are in ppm for σ^(H) and ppm a.u. for .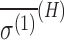

6. Results

The isotropic magnetic polarizability was computed for L- and D-alanine for two different geometries. These geometries were taken from the PubChem database (Kim et al., 2016; PubChem, 2016) and the Protein Data Bank (PDB, Berman et al., 2000) (PDB IDs ALA and DAL; PubChem CID 5950). Geometric coordinates from these databases were taken for the L-enantiomer, and those of the D-enantiomer were determined by a transformation in the z coordinate, (x,y,z) → (x,y,-z). The coordinates of L-alanine are similar in each databank. A schematic of the L-enantiomer is shown in Fig. 5 for both geometries, showing minor differences in each.

FIG. 5.

The structure of L-alanine based on geometry data taken from the Protein Data Bank (left) (Berman et al., 2000), and the PubChem database (right) (Kim et al., 2016; PubChem, 2016).

Here, the geometry used was that of free alanine. Of course, it is possible that the alanine is aqueous or bound to a complex molecule. In this case, the geometry may be modified somewhat. However, we have used the free alanine geometry, as the true geometry is unknown. This will provide a suggestive result, while future work can concentrate on more elaborate or more specific geometries as well as addressing the other uncertainties in this model.

Table 2 shows the isotropic nuclear magnetic shielding polarizabilities for the alanine molecule for four configurations. These are for the D- and L-states for molecular coordinates taken from each database (Berman et al., 2000; Kim et al., 2016).

Table 2.

Isotropic Nuclear Magnetic Shielding Polarizabilities and the Trace of the Nuclear Magnetic Shielding Tensor for Right-Handed (D) and Left-Handed (L) Configurations of Alanine

Configuration		σ(N)		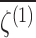χ	μ
Dpub	20.6	196.2	−0.176	−11.42	1.143
Lpub	−20.6		0.176
Dpdb	10.6	195.8	−0.199	−11.43	0.996
Lpdb	−10.6		0.199

The subscripts indicate atomic coordinates taken from the PubChem compilation (pub) (Kim et al., 2016; PubChem, 2016) or from the Protein Data Bank (pdb) (Berman et al., 2000). Units are in ppm for σ^(N), a.u. for and χ, and ppm a.u. for .

These results indicate that Zeeman splitting is modified by an external electric field differently for the D- and L-states independently, as seen by Eqs. 8 and A.5. The relative differences in the magnetic field at the nucleus for the L- and D-enantiomers in the presence of an external electric field E₀ is

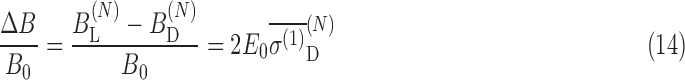The polarizabilities are of opposite sign but equal magnitude for each chirality as shown in Table 2, so the positive value of one enantiomer (the D enantiomer) is used.

For an electric field of 0.001 a.u. (5.14 × 10⁸ V/m) transverse to the external magnetic field of 10 T, the relative difference in magnetic fields between chiralities at the N nucleus is then ∼4 × 10⁻⁹.

6.1. Shielding tensor shifts

The energy shifts are estimated in D- and L-alanine in an isotropic medium with a strong external magnetic field. In the model explored here, the isotropic shielding polarizability tensor 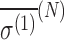is evaluated.

Using the results of Table 2, we calculated the energies of the N nuclei in D- and L-alanine in an external magnetic field taking into account the reduction in field at the nuclei due to electronic shielding. An external field B = B₀ is assumed in an isotropic medium. In molecular results of this model, these are the relevant quantities:

• • D-alanine with the nitrogen magnetic moment μ_B parallel to B.

• • D-alanine with the nitrogen magnetic moment μ_B antiparallel to B.

• • L-alanine with the nitrogen magnetic moment μ_B parallel to B.

• • L-alanine with the nitrogen magnetic moment μ_B antiparallel to B.

In each case, the energy difference between the ground state (the state with μ_B parallel to B) and the state with μ_B antiparallel to B is determined, and the population of N that is spin-aligned and spin-antialigned with the external field is determined in a thermal environment. In the first, simplest evaluation, the maximum energy shift is determined assuming that ΔB is parallel to B. The maximum energy shift from the lowest energy state of the nitrogen nucleus is

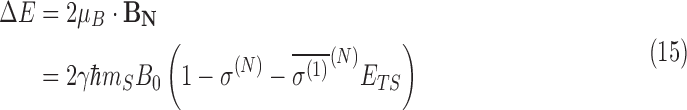where γ is the gyromagnetic ratio and m_S is the z-component of the nitrogen spin; in this case m_S = 1. Here, E_TS is the magnitude of the external electric field. In the case of the translational Stark effect, E_TS = |v × B₀|. Since the shielding polarizability has opposite sign for each chirality, it then follows that

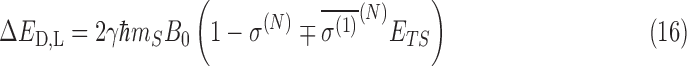where the sign of the last term in the shielding relation is negative (positive) for D(L)-alanine. For the translational Stark effect, the maximum effective difference in chirality occurs for v⊥B. Equation 16 can then be written as

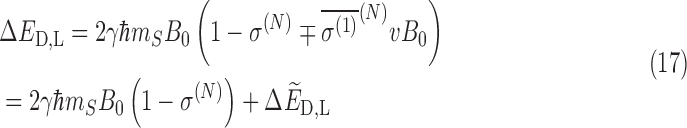Where the first term above is independent of chirality and the chirality-dependent term is given by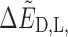

It can be seen that the first term in Eq. 17 is linear in B₀ while the second is quadratic.

As an example, we consider the case of an external field B₀ = 10 T with a velocity of 0.01c. By using the values for the PubChem geometry in Table 2, the values of ΔE and 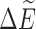are 2.54 × 10⁻⁷ eV and 2.97 × 10⁻¹⁵ eV, respectively, indicating that chiral effects from the translational Stark effect are small. From this, we can compute the ratio R of spin-aligned to spin-antialigned nitrogen nuclei in each chiral state. This ratio is determined by assuming thermodynamic equilibrium of the spin states:

We have simplified this model somewhat by assuming that ¹⁴N has two spin states. In fact, because ¹⁴N has a spin of 1 (in units of 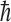), the spin-0 state also contributes to the net population of nuclear states in a magnetic field. This state would not undergo any chirality-dependent preferential destruction but would contribute to the overall state population. However, this would not alter the overall ee to a large extent.

In an isotropic medium, the shielding effects change the evaluated spin states of the nitrogen nucleus by only a small fraction with each chirality. At low temperatures of about 10 K, high magnetic fields of about 10 T, and high velocities of about 0.01c, the ratio above is close to unity, and the variation between L- and D-enantiomers is only a few parts in 10¹⁰.

Using Eqs. A.10 and 13, the shift in the nuclear magnetization can be estimated in an external magnetic field. The precession of the nuclear magnetic moment about the external magnetic field, a result of Eq. 6, can result in a shift in magnetization from the target nucleus ΔM. For an external electric field perpendicular to the magnetic field (a direct result of the Stark effect), the chirality-dependent change in the magnetization vector M is

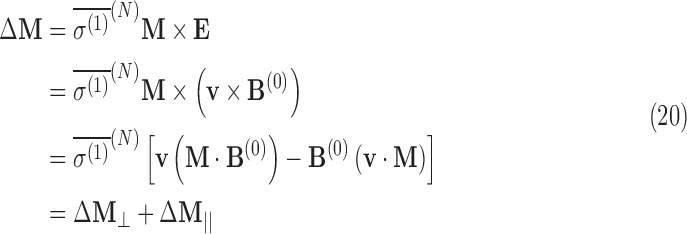where the first term in brackets corresponds to the change in magnetization perpendicular to the external field, and the second term corresponds to the change in magnetization parallel to the magnetic field. Assuming that v⊥B in the SNAAP model,

The above is applicable to the magnetic moments of individual nuclei. For the spin-1 N nucleus, the perpendicular component of the magnetic moment, which precesses about the external magnetic field, induces an oscillation in the parallel component of the magnetic moment. For a spin-1 particle aligned with the external field, M_⊥ = M_||, and the amplitude of the fractional change in magnetization can be approximated:

For a meteoroid with a velocity of 0.01c in a 10 T external field, ΔM_||/M_||∼±10⁻⁹ where the ± corresponds to L and D chiral states.

Given the above evaluation, it can be determined that the effects from the shielding tensor in an isotropic medium may be negligibly small. However, for a medium polarized by the electric dipole moment, the effects could be larger. This is explored in the next section.

6.2. Temperature-dependent electric dipole moment interactions

The effects of the external electric field from the translational motion of the molecule on the shielding tensor were found to be exceedingly small in an isotropic medium. However, the interaction of the electric field with the molecular electric dipole moment may also create a selection in chirality. This influence of the electrical field polarization is explored below.

In addition to the effects from the chiral dependence of the shielding tensor, the electric dipole moments, with reversed sign under a chiral transformation, have been shown to exhibit a temperature dependence in the presence of magnetic fields (Buckingham, 2014; Buckingham et al., 2015). This contribution comes from the temperature-dependent orientation of the mean electric polarization in the external electric field. The molecular electric-dipole moment orients itself in the external electric field much like the nuclear magnetic dipole moment orients itself in an external magnetic field. However, unlike the nuclear magnetic dipole moment, the electric dipole moment depends on the molecular shape. It is thus chirality-dependent. The effect studied here is that the molecule's electronic orbitals are oriented with respect to the external electric field while the nuclei are oriented with respect to the external magnetic field. In crossed electric and magnetic fields naturally resulting from the translational Stark effect, nuclear orientation is thus established relative to the molecular orientation. The shielding tensor then has a “preferred” direction, and an anisotropic shielding tensor contribution can be computed with respect to the molecular (and nuclear) axis. Both the molecular orientation and the nuclear spin state populations are temperature-dependent. For an electric dipole moment μ_E and a nuclear magnetization M in an external electric field E, the shift in the magnetization ΔM_T at the nucleus has been shown to be (Buckingham, 2014; Buckingham et al., 2015)

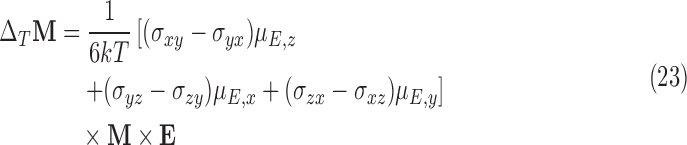In a static electric field, the above is a result of the mean electrical polarization of the molecule oriented in a static external electric field. In this case, the anisotropic components of the shielding tensor times the electric dipole moment vector result in a nonzero contribution to the change in magnetization. This non-isotropic effect can exceed the isotropic effects of the previous section by several orders of magnitude (Buckingham and Fischer, 2006).

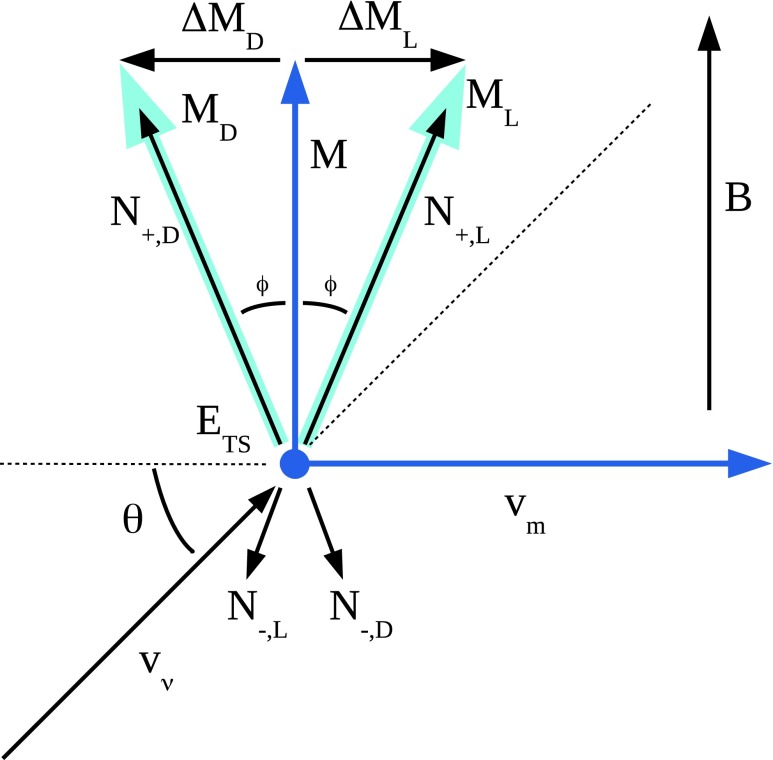
The effects of the shift in the average nuclear magnetization from the electric polarization in the presence of static electric and magnetic fields are diagrammed in Fig. 6. In this diagram v_m is the meteoroid velocity through the static magnetic field B, inducing the electric field E_TS (which is coming out of the page). The antineutrino velocity vector is 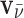which makes an angle θ with respect to v_m. For a meteoroid at rest, the bulk magnetization is M. However, for a nonzero velocity, the induced electric field creates additional transverse magnetization components (from Eq. 23) ΔM_L and ΔM_D for L- and D-chiral states, respectively. This induced magnetization, which is chirality-dependent, produces net positive and negative spins aligned along the magnetization vectors N_+/-,L/D as shown in the figure. This principle can also be conveyed by examining the induced magnetic field from each chiral state ΔB_L,D. The net magnetization vectors M_L and M_D are separated by an angle 2 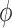as shown, where  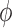= tan⁻¹(ΔM/M). The shift in magnetization between chiral states results in a different angle between the antineutrino spin and the nitrogen spin. Thus, the reaction rates between antineutrinos and chiral states of the same spin vary according to Eq. 5.

FIG. 6.

The vectors relevant to the processing of amino acids in this model. The vectors and labels are explained in the text.

With this model and Eq. 23, the effects of the temperature-dependent polarization on the antineutrino interaction rates are evaluated. The magnitude of the electric dipole moment of alanine is shown in Table 2 (in a.u.). By using the computed components of this value, the change in the chirality-dependent magnetization perpendicular to the external magnetic field can be determined. For a meteoroid velocity of 0.01c, temperature of 10 K, and an external field of 10 T, the fractional change in magnetization for D/L-alanine is ∼±6 × 10⁻⁷—at least 2 orders of magnitude higher than the effect from the isotropic magnetizability. In fact, the electric dipole moment of alanine in aqueous solution may be larger than that computed in the table by over a factor of 10 (Wyman and McMeekin, 1933). However, since we are assuming free alanine, we have conservatively used the value in the table.

It is worthwhile to evaluate whether or not this model is truly chiral. That is, is the model even under a time reversal transformation and odd under a parity transformation for an enantiomer (Barron, 1986; Barron and Buckingham, 2001)? For this, we use Fig. 6 and Eq. 23 to evaluate the time and parity characteristics of the SNAAP model. In the case of time-reversal, the velocities in Fig. 6 change sign, as does the neutrino spin and magnetic field, effectively resulting in a rotation of the figure by 180° about an axis parallel to the electric field. Thus, the model is even under time-reversal. However, under a parity transformation, the electric field and velocities change sign, while the magnetic field and spin do not. Likewise, the result of the change in magnetization (Eq. 23) also changes sign under a parity transformation (because of the change in direction of the electric field, since both the shielding tensor and the electric dipole moment change sign under a parity transformation, the contribution from the value in brackets does not change sign). The net result is that the neutrino helicity in Fig. 6 effectively changes sign. Thus, the time/parity characteristics of our model depend on the neutrino chirality.

A mathematical treatment of this model is described in Appendix B using the temperature-dependent magnetization of Eq. 23. From this, the maximum enantiomeric excess can be estimated. The total parallel component of magnetization is defined as

where N_± is the number of nuclei with spin aligned parallel/antiparallel to the magnetization vector shown in Fig. 6, and μ_B is the nuclear magnetic moment. With this value for ¹⁴N, the thermal-equilibrium magnetization and populations N _± for D- and L-alanine are

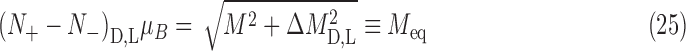where the equilibrium magnetization M_eq has equal magnitudes for each chirality.

The total abundance of a spin state is obtained by summing the components of the spin-state vector from Eq. B.8:

Given the above, the enantiomeric excess of a particular state can now be computed in the SNAAP model.

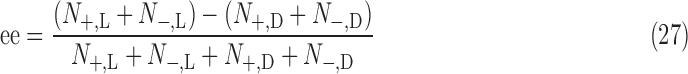In this initial evaluation, a simple calculation is performed for a meteoroid traveling at 0.015c in a 30 T external magnetic field. An ensemble of evenly mixed D- and L-alanine is presumed to populate the interior of the meteoroid. A thermal (spin-lattice) relaxation time of 10 ms is assumed for the nitrogen nucleus. This value is estimated from prior measurements (Troganis et al., 2003), though additional consideration should also be taken for temperature and the possible crystalline nature of the material (Nelson, 2003). The angle θ between the meteoroid and the antineutrino velocity vectors depends on the orbital mechanics of the meteoroid with respect to the nascent neutron star. For meteoroids moving radially away from this star, θ = 0, and for meteoroids moving transversely past the star, θ = 90° at the point of closest approach. Thus, 0 ≤ θ ≤ 90°. For this first evaluation, the angle between the antineutrino and the velocity vector θ is assumed to be zero, providing an estimate of the effects of the antineutrinos on the amino acids.

Equation B.8 shows that one spin-chiral combination is preferentially destroyed, which defines the SNAAP model. Figure 6 shows that the antineutrino spin alignment with the parallel (N₊) nitrogen spin alignment in L-alanine is less than 90° while it is greater than 90° for D-alanine. This means that D-alanine is preferentially destroyed in this orientation for meteoroids that are moving in a net positive radial direction. This is because ΔM_L points in the direction of the velocity vector in this model. For meteoroids moving in a net negative direction, the destruction favors the L-enantiomer. However, since the meteoroid must escape the neutron star in order to populate the interstellar medium, we make the assumption here that meteoroids of interest move in a net positive direction. This effect may be enhanced by meteoroids in non-equatorial hyperbolic orbits; these will experience different magnetic fields on approach and departure from the star. Additional slowing effects may be from meteoroids moving through debris surrounding the neutron star and slowing down as they pass.

The antineutrino interaction rate on ¹⁴N is a parameter of this model. Here, the rate of antineutrino interactions for antineutrino spin aligned parallel to the nitrogen spin is taken to be a factor relative to the inverse of the relaxation time R_p = fλ = f/(2T₁). In terms of reaction rates, this is the only free parameter of the model; it can vary with the stellar dynamics, the collapse of the star, the time at which the meteoroid comes in proximity to the star, the meteoroid distance from the star, and the exact collapse scenario producing the antineutrino flux. For a meteoroid roughly 1 AU from a type II SN, f ∼ 10⁻⁹ (Myra and Burrows, 1990). However, for a meteoroid in close proximity to a neutron star merger, we expect f to be as large as 10⁻⁴ for even nominal values and possibly larger for grazing meteoroids (Perego et al., 2014). Other possible scenarios include meteoroids in close proximity to cooling neutron stars after the initial antineutrino burst, for which we expect f ∼ 10⁻¹⁰ to 10⁻⁸ (Yakovlev and Levenfish, 1995). The reaction rate for neutron star mergers is expected to produce its equilibrium ee rapidly. In the case of cooling neutron stars, the reaction rate is much smaller. However, the antineutrino cooling can last for as long as 10⁵ years, so even this scenario is a possibility as long as the magnetic field persists, and the meteoroid can be in the vicinity of the neutron star for an extended period. Ideally, any situation in which high-speed meteoroids exist in the vicinity of relatively large antineutrino fluxes and high magnetic fields will succeed. The relative values of the reaction rates between spin-aligned and antialigned nuclei R_p and R_a can be estimated from Eq. 5. Figure 6 shows that the nuclear spins are, on average, nearly perpendicular to the antineutrino velocity vectors. The ratio of rates for spins parallel and antiparallel to the ¹⁴N spin is

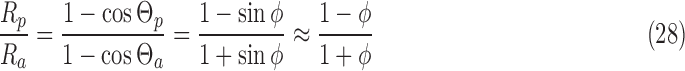For the parameters chosen here, 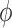 = 10⁻⁶ radians. Thus, (R_a − R_p)/R_p = 2 × 10⁻⁶. We expect resultant ees to be similar to this ratio.

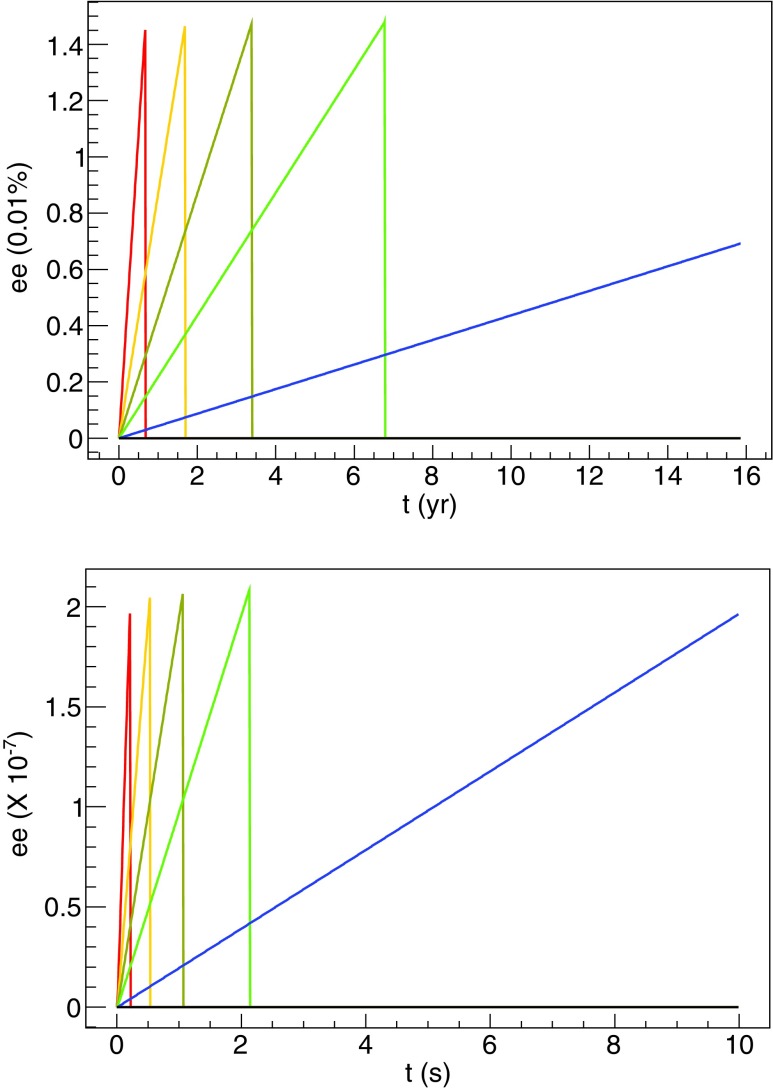
The results of this evaluation are shown in Fig. 7 for two scenarios. In one scenario, representing conditions of a meteoroid in the vicinity of a neutron star, the magnetic field is 800 T, and the meteoroid speed is 0.015c. The antineutrino reaction rates are given by the ratios f = 0, 0, 0.1 × 10⁻⁸, 0.5 × 10⁻⁸, 10⁻⁸, 2 × 10⁻⁸, and 5 × 10⁻⁸. In the second scenario, corresponding more to a meteoroid quite far from a neutron star merger, f = 0, 0.1, 0.5, 1, 2, and 5, indicating antineutrino interaction rates that span from zero to many times the rate of nuclear relaxation. The magnetic field here was assumed to be 30 T with a meteoroid velocity of 0.015c. The net ee for each set of parameters is shown as a function of time after the start of the antineutrino burst. In either scenario, a nonzero ee is produced from a starting ee of zero. Increasing the antineutrino flux pushes the ee to an equilibrium value in a shorter amount of time. However, as expected, for f = 0, corresponding to no external antineutrino interactions, the ee does not deviate from its starting value of 0. While the net magnetization may approach an equilibrium value, and while spins may change, the number of molecules within a chiral state is conserved.

FIG. 7.

The ee as a function of time for a meteoroid penetrating the external magnetic field for two scenarios described in the text. Top: Neutron star cooling scenario. B = 800 T, v = 0.015c, and f = 5 × 10⁻⁸ (red), 2 × 10⁻⁸ (orange), 10⁻⁸ (yellow), 5 × 10⁻⁹ (green), 10⁻⁹ (blue), and 0 (black). Bottom: Neutron star merger scenario. B = 30 T, v = 0.015c, and f = 5 (red), 2 (orange), 1 (yellow), 0.5 (green), 0.1 (blue), and 0 (black).

This figure shows that the ee increases in time in every case. The rate of increase is heavily dependent on f, and it was found that the peak of the function in the figure is dependent on the magnitude of the electric and magnetic fields. In the case of neutron star cooling, which can have an external magnetic field approaching 1000 T at a distance of 500 km from the stellar surface, the maximum ee can be as high as 0.02% for a meteoroid passing near the star at 0.015c.

After a time, the ee drops to zero as the destruction mechanism removes all the alanine from the sample. This means that for a meteoroid exposed to the neutrino flux any time between t = 0 and the time at which the function reaches its peak, any ee between zero and the maximum value is possible. In all cases, this is reasonable, as the neutrino flux in a type II supernova is on the order of seconds, meaning that an ee somewhere between zero and the peak can be formed because the neutrino flux ends prior to the ee reaching its peak. In the second case, that of neutron star cooling, with a much higher field, but lower neutrino flux, the time to peak can be months to several years, which is about the same timescale for a meteoroid to pass the star. In this case, the meteoroid would leave the vicinity of the star prior to the ee reaching its peak.

7. Discussion

A model in which amino acid chiral selection via the interaction between antineutrinos and the ¹⁴N in amino acids in strong external magnetic fields has been developed. The original model predicted an interaction that is selective in chirality because the antineutrino interactions with nuclei of nonzero spin are asymmetric in nature (Boyd et al., 2010). Subsequent developments have examined the effects of bulk spin polarization of the nuclei in rotating reference frames with the possible field strengths available in extreme stellar environments (Famiano et al., 2014; Famiano and Boyd, 2016).

In this work, the model has been expanded to include details of the effects of the nuclear shielding polarizability and its interactions with the molecular electric dipole moment. While the isotropic shielding tensor itself is likely too small to yield changes in the spin states of the nitrogen nuclei, the effects of the electric dipole polarization allow for a coupling between the nitrogen nuclear magnetic moment and the molecular chirality that is sufficient to produce ees in moderate electric and magnetic fields. The temperature-dependent interaction of the electric dipole moment provides a mechanism whereby the molecular chirality is coupled to the nuclear spin and its subsequent magnetization (Buckingham, 2014; Buckingham et al., 2015). By using this coupling, any mechanism in which nuclei in a specific spin state are selectively destroyed will also selectively destroy a specific chirality. In the case of alanine studied in this work, the nitrogen nucleus was the nucleus of choice owing to its relatively large nuclear spin and shielding polarizability compared to hydrogen. Most carbon nuclei have zero spin so are not affected in this model. The assumption of an isotropic medium provided an average assessment of the effects of external magnetic and electric fields on chiral molecules.

The isotropic nuclear polarizability tensor was then computed in Section 6. The effects of a polarized medium were taken into account without assumption of enhancement via NMR-type resonant effects. Thus, any resonance effect could possibly enhance the results of the model presented here.

For this model to work, four things are necessary. An external electric and magnetic field provide the coupling of the molecular chirality to the nuclear spin. Even modest magnetic fields of ∼10 T have been found to be sufficient in this model to produce ees on the order of 10⁻⁷. The external electric field is produced in the reference frame of the molecule via the motion of the molecular substrate (in this case, a meteoroid in which the molecule is embedded) through the magnetic field, though any external electric field will have the same effect. While the magnetic field is assumed to be uniform in this evaluation, movement of the meteoroid through a non-uniform magnetic field will also produce an electric field in the reference frame of the enclosed molecules because of the temporal change in magnetic field as the meteoroid moves through its field gradient. This effect can also be significant, as neutron stars could have large field gradients. Extraordinarily large field gradients are thought to exist around neutron stars and are thought to be responsible for the production of jetlike structures from the interaction of accretion disks with the stellar field (Nakamura et al., 2015). If one assumes a neutron star to have a magnetic dipole with a moderate surface field of 10¹³ G (Bakirova and Folomeev, 2016), then the polar field gradient in the radial direction can be as large as 10⁴ T/km at a distance of 100 km from the star's surface, meaning that even very slow meteoroid velocities may have enormous electric fields in the meteoroid interior—though meteoroids that move too slowly would fall into the star. Such a scenario may be responsible for the creation of strong electric and magnetic fields in the meteoroid reference frame.

The third necessary component of this model is the antineutrino interactions. Here, weak interactions with the slightly polarized nitrogen nucleus are able to selectively destroy nuclei of particular spin states, which are coupled to the molecular chirality.

Finally, the selective destruction of the amino acid is accomplished via the destruction of the nitrogen nucleus, which is possible only because of its nonzero spin. This is the necessary fourth component to drive this model.

While it might be thought that interactions with electrons streaming from the collapsing star may be possible in the magnetic fields here, there are several restraints on this possibility. One is that the electrons must be able to penetrate the interior of the meteoroid. Since extraterrestrial meteoroids must be able to penetrate Earth's atmosphere in order to deliver their chirally selected amino acids, they must exist in their interior since their surfaces would be ablated away. A second constraint is that electrons, though likely spin oriented in the external magnetic field, do not have the definite helicity associated with antineutrinos. This would further constrain the environment in which amino acid chirality can be selected.

As noted from Fig. 7, the antineutrinos are necessary to drive the molecular chirality to an equilibrium value. Without the antineutrinos, molecular chirality cannot exist in the SNAAP model. Of course, we are faced with the drawback of the very low antineutrino cross section with nitrogen (∼10⁻³⁸ cm⁻²). However, the antineutrino flux in the events proposed here can be sufficiently large to produce an appreciable ee. We also see that even slight antineutrino reaction rates can drive the ee to fairly large magnitudes in short timescales. While it is certainly not necessary to produce a nonzero ee in these timescales, such a result is realistic given the rapid antineutrino bursts that accompany collapsing stars. However, even with the longer-timescale fluxes from collapsing stars (∼10 s), or the very long timescale fluxes (∼10⁵ years) from cooling neutron stars, a slower ee production may also be realistic. The possibility for low antineutrino interaction rates greatly relaxes many of the constraints on the environments imposed by this model. It is worth emphasizing, however, that without the antineutrino interactions, the ee of processed nuclei would likely only result from amino acids that form in external electric and magnetic fields, and would only reach values of ∼10⁻¹⁰ at best.

A possible drawback of this model is the possibility that meteoroids may not survive the destruction of massive stars in supernovae explosions. However, one should note that not all massive stars explode upon collapse. In fact, stars with 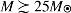are thought to collapse directly to neutron stars or black holes with antineutrino luminosities very similar to—and in some cases exceeding—those of exploding stars (Nakazato et al., 2006, 2013). As discussed, other exotic sites may include non-explosive events such as neutron star and black hole–neutron star mergers or the accretion outflows of black hole and neutron star accretion disks, which are also thought to be associated with relatively high antineutrino luminosities and magnetic fields (Liu et al., 2016; Roberts et al., 2017). Further, neutron star cooling may be sufficient to process amino acids in the interiors of meteoroids without any explosion mechanism.

Also, note that the antineutrinos from supernovae are emitted in roughly 10 s and would therefore process a large volume of space before the matter from the supernova would get to the meteoroids that were passing by. The photons would probably not process the same large volume, as they would be trapped by the matter from the star. While small meteoroids might be destroyed, larger ones could undergo some spallation and still retain their inner amino acids, which would be processed by the antineutrinos.

We also note our assumption that ¹⁴N only has two states. In this simple, preliminary model we expect this assumption to be good enough without altering our results significantly as the third spin state, the spin-0 state, is not affected by the external magnetic field and would not be preferentially destroyed in either chirality. Future work can concentrate on secondary corrections to this model by including the spin-0 state.

7.1. Experimental tests

As proposed in prior works (Buckingham and Fischer, 2006), the possibility of testing some of the features of this model may be within technical reach. NMR-type experiments, with electric fields generated with static plates held at constant voltage, may provide the necessary electric fields to observe the chemical shifts of about 1 part in 10⁹ predicted in these calculations. As proposed previously, low-temperature, high-sensitivity NMR measurements would likely be necessary to obtain such precise values.

Abbreviations Used

CPL

circularly polarized light

SNAAP

Supernova Neutrino Amino Acid Processing

Appendix

Appendix A. Calculation of the Shielding Tensor and the Nuclear Shielding Polarizability

A description of the effects of the shielding tensor of chiral molecules in external electric and magnetic fields, the “Buckingham effect,” is given here. In a molecule, the shielding tensor defines the reduction in the external magnetic field at a specific nucleus N in the molecule (Buckingham, 2004; Buckingham and Fischer, 2006):

where the external magnetic field is given by B⁰. This reduction is caused by the orbital motion of the shielding electrons. The shielding tensor has been defined perturbatively in the presence of an external magnetic field as a sum of diamagnetic components and paramagnetic components. In an isotropic medium, the symmetric diamagnetic term vanishes, and the paramagnetic term is defined perturbatively as (Buckingham and Fischer, 2006)

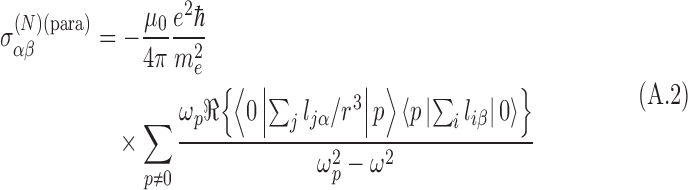where l_i is the orbital angular momentum of electron i at nucleus N. The summation is over all p molecular states with excitation energy ω_p. The resonant frequency of the nucleus is ω = |γ^(N)|B_z^(N)/2π.

This operator is even under a parity transformation and is thus insufficient to distinguish molecular chiral states. However, the perturbation of the shielding tensor by an external electric field may be sensitive to the molecular chirality. This is because this operator is dependent on the electron configuration—a quantity depending on the geometry of the molecule.

Microscopically, the magnetic shielding tensor also describes the change in the nuclear magnetic moment of a molecule due to the change in electronic orbital motion.

The perturbation of the shielding tensor for a molecular nucleus in the presence of an external electric field E⁰ is given by

where the prime indicates the tensor corrected for the perturbation from the external electric field. Here, elements of the third-rank tensor σ_αβγ, also known as the “nuclear magnetic shielding polarizability” (Rizzo et al., 1995) are defined by

This can be deduced by computing the second-rank shielding tensor in the presence of an external magnetic field. For small external fields about zero, the differences in 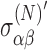can result in an estimate of σ_αβγ. With this, a computation of the shielding tensor from molecular orbitals optimized in an external electric field will allow one to extract σ_αβγ.

For an isotropic medium in external magnetic and electric fields, the isotropic part of the shielding tensor, σ^(N), is given by

and the isotropic component of the nuclear magnetic shielding polarizability, 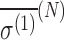, is given by

Using the shielding tensor and the nuclear magnetic shielding polarizability, one can find the shift in the electric dipole moment Δμ₊, magnetic field ΔB^(N), and magnetic moment Δm^(N) at a nucleus in the presence of external electric and magnetic fields (E⁽⁰⁾ and B⁽⁰⁾, respectively) (Buckingham and Fischer, 2006):

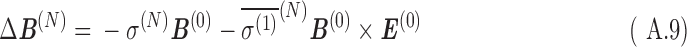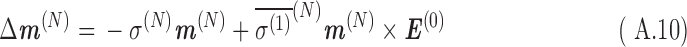Appendix B. Mathematical Treatment of the SNAAP Model

In the SNAAP model, specific spin states are selectively destroyed by an external agent, in this case, antineutrinos. We can then estimate the time evolution of the component of magnetization parallel to the external field. The magnetization is changed by the selective destruction of spin-aligned or spin-antialigned nuclei in the magnetic field. It is also changed by the thermalization of the spins (the relaxation). For one particular chirality,

The first term above is a result of the destruction of specific spin states of the nitrogen nucleus. The second term is the result of redistribution of the spin states due to thermal relaxation. Note that the first term destroys N in a particular spin state while the second term reorganizes spin states. That is, N₊ + N₋ is conserved in the last term so that dN₊/dt = −dN₋/dt. Thus, the spin states can be written in terms of the thermal relaxation:

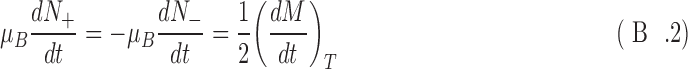where the D and L subscripts have been dropped for readability and are understood.

For the L-enantiomer, for example, the spin states population can be written as

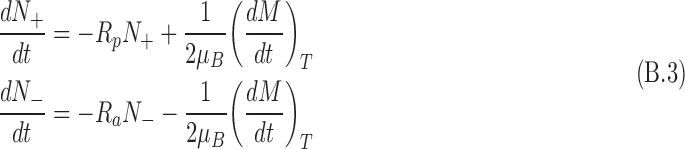where R_p(a) is the antineutrino capture rate for antineutrino spin that is (anti)parallel to the nuclear spin. (Note the change in sign in the second term as the thermalization results in destruction of one spin state while creating another.) From Fig. 6, it is seen that Eq. B.3 applies to the L-enantiomer. For rates of the D-enantiomer, R_p and R_a are exchanged. From Eq. 5, it can be shown that R_a > R_p.

Utilizing the thermal relaxation relationship for a nuclear spin in a magnetic field, Equation B.3 becomes

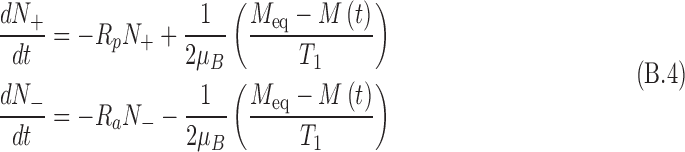where T₁ is the longitudinal relaxation time for the molecular configuration in the medium. Substituting the magnetization into the above equation results in a set of coupled differential equations:

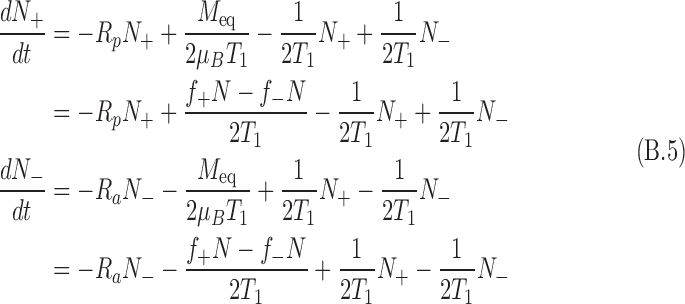where f₊₍₋₎ is the fraction of nuclei in the spin up (down) state in thermal equilibrium with the external magnetic field and Δf = f₊ − f₋. The total nuclear population is N = N₊ + N₋. This can be written as a set of coupled homogeneous first-order differential equations:

where the following are defined:

The above set of equations has solutions:

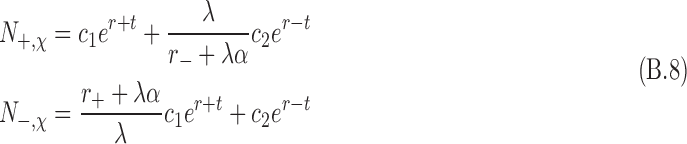In the above, the chirality-dependent terms are r_+/− and α. In this model, Eqs. B.8 are constrained for only positive values of N_±,χ. The values of c₁ and c₂ are determined by the boundary conditions, and the following are defined:

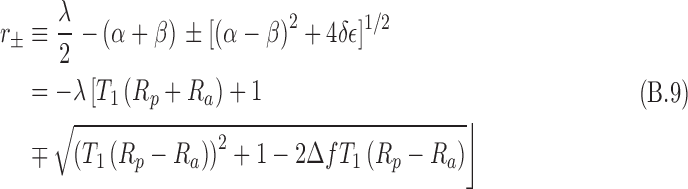In the above, r_± < 0, which means that individual spin state numbers are decaying in time owing to the destruction via antineutrino interactions. The above relationship is for L-enantiomers. For D-enantiomers, the subscripts are reversed.

We evaluate the ee by assuming the boundary conditions N₊(t = 0) = N_-(t = 0) = N/2, where N is the total population of molecular states. Using the same boundary conditions for both chiral states gives N_D(t = 0) = N_L(t = 0) = N/2. One can then set individual combinations of spin and chirality N_+,D = N_−,D = N_+,L = N_−,L = N/4. These initial conditions result in M(t = 0) = ee(t = 0) = 0. With these conditions, the constants c₁ and c₂ are evaluated for each set of chiral equations:

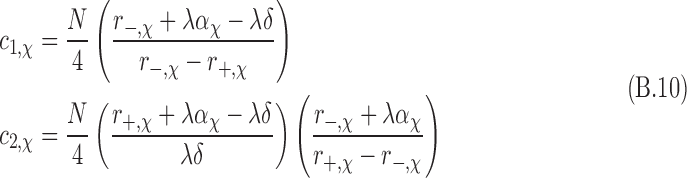where the subscripts have been explicitly inserted to indicate values that are chirality-dependent.

Acknowledgments

M.A.F.'s work was supported by the National Astronomical Observatory of Japan and by NSF grant #PHY-1204486 and by a Western Michigan University Faculty Research and Creative Activities Award (FRACAA).

The authors would like to thank Quinn Martin for his insightful input into this work and Andrew Famiano, who provided assistance with proofreading the final document.

The authors would also like to thank the anonymous referees for their extremely helpful comments on this manuscript.