The Habitability of Proxima Centauri b: Environmental States and Observational Discriminants

Abstract

Proxima Centauri b provides an unprecedented opportunity to understand the evolution and nature of terrestrial planets orbiting M dwarfs. Although Proxima Cen b orbits within its star's habitable zone, multiple plausible evolutionary paths could have generated different environments that may or may not be habitable. Here, we use 1-D coupled climate-photochemical models to generate self-consistent atmospheres for several evolutionary scenarios, including high-O₂, high-CO₂, and more Earth-like atmospheres, with both oxic and anoxic compositions. We show that these modeled environments can be habitable or uninhabitable at Proxima Cen b's position in the habitable zone. We use radiative transfer models to generate synthetic spectra and thermal phase curves for these simulated environments, and use instrument models to explore our ability to discriminate between possible planetary states. These results are applicable not only to Proxima Cen b but to other terrestrial planets orbiting M dwarfs. Thermal phase curves may provide the first constraint on the existence of an atmosphere. We find that James Webb Space Telescope (JWST) observations longward of 10 μm could characterize atmospheric heat transport and molecular composition. Detection of ocean glint is unlikely with JWST but may be within the reach of larger-aperture telescopes. Direct imaging spectra may detect O₄ absorption, which is diagnostic of massive water loss and O₂ retention, rather than a photosynthetic biosphere. Similarly, strong CO₂ and CO bands at wavelengths shortward of 2.5 μm would indicate a CO₂-dominated atmosphere. If the planet is habitable and volatile-rich, direct imaging will be the best means of detecting habitability. Earth-like planets with microbial biospheres may be identified by the presence of CH₄—which has a longer atmospheric lifetime under Proxima Centauri's incident UV—and either photosynthetically produced O₂ or a hydrocarbon haze layer. Key Words: Planetary habitability and biosignatures—Planetary atmospheres—Exoplanets—Spectroscopic biosignatures—Planetary science—Proxima Centauri b. Astrobiology 18, 133–189.

1. Introduction

The discovery of a possibly terrestrial-mass planet sitting squarely in the habitable zone of the Solar System's nearest neighbor (Anglada-Escudé et al., 2016) is a remarkable opportunity to further our understanding of the evolution of terrestrial planets and the distribution of life in the Universe. If confirmed, Proxima Cen b is the closest potentially habitable planet and one of the most accessible examples orbiting a late-type M dwarf host. M dwarfs comprise 70% of all stars, and habitable planets orbiting M dwarfs may be the most common environment for life in the Universe. However, although Proxima Cen b has several promising attributes, including its possibly small size (minimum mass of 1.3 M_⊕) and its position in the conservative habitable zone (Kopparapu et al., 2013) with an effective instellation (i.e., stellar irradiation) 65% that of Earth's (Anglada-Escudé et al., 2016), its habitability is not guaranteed. A determination of the degree to which this planet is habitable, or any other insights into the fate of terrestrial planets orbiting M dwarfs, awaits follow-up information on its orbit, the planet's phase- and time-dependent photometry, and on spectra of the atmosphere and surface. Conversely, Proxima Cen b will ultimately provide an excellent observational laboratory for our current understanding of terrestrial planet evolution, which will in turn inform our knowledge of the prevalence of habitability and life in our galaxy.

In advance of these data, we can synthesize what has been learned over the past several decades on star-planet and planetary environmental interactions for terrestrial planets to make a broad, preliminary assessment of plausible evolutionary processes and current environmental states for Proxima Cen b. This assessment will also be highly relevant to other terrestrial planets found in M dwarf habitable zones, such as the recently discovered TRAPPIST-1 planets (Gillon et al., 2016, 2017) and LHS1140 b (Dittmann et al., 2017). In our companion paper (Barnes et al., 2018), we explored likely evolutionary paths for Proxima Cen b, as it coevolved with the Galaxy, companion stars and planets, and its host star. In this paper, we model several of these possible planetary environmental outcomes with coupled climate-photochemical models that are self-consistently forced by the spectrum of Proxima Cen. We then use radiative transfer and instrument simulation models to generate synthetic phase-dependent light curves, and transmission and direct imaging spectra, which are relevant to missions such as the James Webb Space Telescope (JWST¹; e.g., Cowan et al., 2015), ground-based extremely large telescopes (ELTs; e.g., Kasper et al., 2008), the Wide-Field Infrared Survey Telescope (WFIRST²; Spergel et al., 2015), the Habitable Exoplanet Imaging Mission (HabEx³; e.g., Mennesson et al., 2016), and the Large UltraViolet Optical Infrared Surveyor telescope (LUVOIR⁴; e.g., Kouveliotou et al., 2014; Dalcanton et al., 2015). These spectra can be used to predict possible attributes and necessary measurements to identify discriminants for habitable and uninhabitable environments, and to explore the potential detectability of environmental signs of habitability and life.

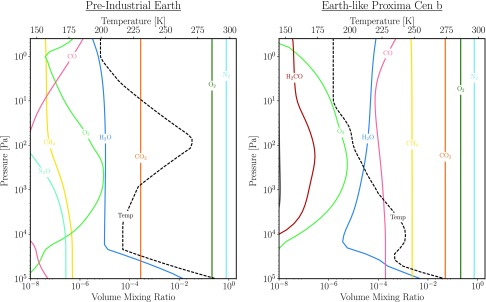
We consider scenarios for atmospheric composition driven by stellar, orbital, and planetary evolution, and use our models to explore the photochemical and climatic outcomes, and observable attributes. Our first scenario is an oxygen-dominated atmosphere, generated by the loss of oceans of water during Proxima Cen's pre-main sequence phase (Luger and Barnes, 2015). In this scenario, the planet can be either desiccated or have retained some of its initial water inventory. In the second class of scenario, the atmosphere is CO₂-dominated and progressively desiccated, and is formed when the majority of O₂ from ocean loss is either lost to space or sequestered in the planetary crust or interior (Schaefer et al., 2016), while CO₂ is outgassed from the mantle. In this case, O₂/CO₂-dominated atmospheres could form and potentially evolve to more CO₂-rich Venus-like states as the O₂ is lost or sequestered. Ultimately, with extreme desiccation, CO₂-dominated atmospheres could photolyze to stable CO₂/CO/O₂ atmospheres (Gao et al., 2015). In the final set of scenarios explored here, the planet is potentially habitable, having evolved as a “Habitable Evaporated Core” (Luger et al., 2015), where an early hydrogen envelope protected a terrestrial or volatile-rich core from water loss. Alternatively, a terrestrial planet initially orbiting farther from the star could have moved to the current orbit of Proxima Cen b via orbital instabilities, possibly triggered by a close passage of Proxima Cen to α Cen A and B (Barnes et al., 2018). Two cases are presented for this habitable scenario: an oxidizing, modern Earth-like atmosphere, and a more reducing Archean (3.8–2.5 billion years ago) early Earth-like atmosphere.

In Section 2, we review the possible evolutionary scenarios for Proxima Centauri b and briefly discuss observable parameters for identification of habitability and biosignatures for terrestrial planets. In Section 3, we describe the radiative transfer, instrument, climate, and photochemical models, along with their model inputs. In Section 4, we present our results. In Section 5, we discuss the implications of our modeling, including an assessment of the scenarios that might lead to habitability for Proxima Cen b. We also identify future observations that will help discriminate between the proposed evolutionary paths, and potentially identify signs of habitability and life. These results are summarized in our conclusions in Section 6.

2. Review of Habitability and Detectability

In this section, we briefly review the factors that can affect terrestrial planet habitability and the plausible evolutionary paths for Proxima Cen b as explored in our companion paper by Barnes et al. (2018). We describe how characteristics of the planet and planetary system could affect Proxima Cen b's current climate. To motivate the detectability simulation results and discussion that follow, we will also briefly review relevant knowledge on observations to identify signs of habitability and life for terrestrial planets.

2.1. Evolutionary processes and the possible habitability of Proxima Cen b

Although Proxima Cen b is possibly small enough to be terrestrial and sits in the habitable zone of its parent star, many factors other than planetary mass and star-planet distance affect a planet's volatile inventory, atmosphere, and surface environment. These factors, in conjunction with the evolution of the star and planet, can maintain or destroy habitability. Classically, exoplanet habitability is defined as the ability to maintain liquid water on the surface of a rocky, terrestrial planet, and the habitable zone is that range of distances from the star over which an Earth-like planet can maintain surface liquid water (Kasting et al., 1993). However, if Proxima Cen b formed in situ, then planet formation models suggest that it may be water-poor (Lissauer et al., 2007; Raymond et al., 2007); but if it migrated in from further out in the system, then it may have been more volatile-rich at formation (Luger et al., 2015). Proxima Cen b's close-in orbit (a = 0.0485 AU; Anglada-Escudé et al., 2016) also leaves it particularly vulnerable to the effects of stellar evolution and longer-term radiative and gravitational interaction between star and planet. These interactions could drive volatile and atmospheric loss processes and orbital changes that could preclude habitability for this planet. These processes are examined in more detail in our companion paper, and an overview of the scope of plausible scenarios is given here to motivate the climate and spectral modeling work that follows.

Perhaps the greatest threat to Proxima Cen b's habitability is the luminosity evolution of its M dwarf host (Luger and Barnes, 2015; Barnes et al., 2018; Ribas et al., 2016). Lower-mass M dwarfs can experience extended pre-main sequence phases of up to a billion years, in which they are more luminous than they will ultimately be when they settle on to the main sequence (Baraffe et al., 1998, 2015). During this superluminous pre-main sequence phase, any terrestrial planet that forms in what will become the main sequence habitable zone is subjected to extremely high levels of radiation, which can vaporize and photolyze oceans and strip lighter elements from the atmosphere (Luger and Barnes, 2015). Simulations performed in our companion paper indicate that, had Proxima Cen b formed at its current location, then its host star would have taken as long as 169 ± 13 million years after formation to dim sufficiently to allow the planet to enter the habitable zone for the first time (Barnes et al., 2018). Consequently, if Proxima Cen b is a terrestrial planet, it may have been in a runaway greenhouse state for the first 169 million years. The vaporized ocean would have been photolyzed by UV from the host star, with subsequent loss of H to space; and between ∼3 and 10 terrestrial ocean equivalents of water could have been lost, depending on the efficiency of oxygen sinks, photochemical shielding, and the planet's initial water endowment (Barnes et al., 2018).

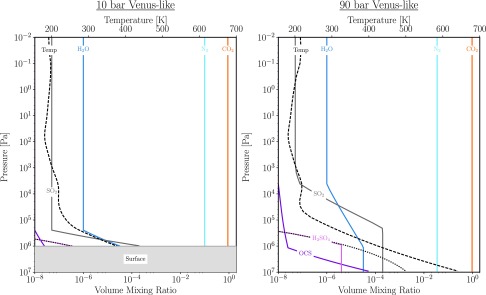
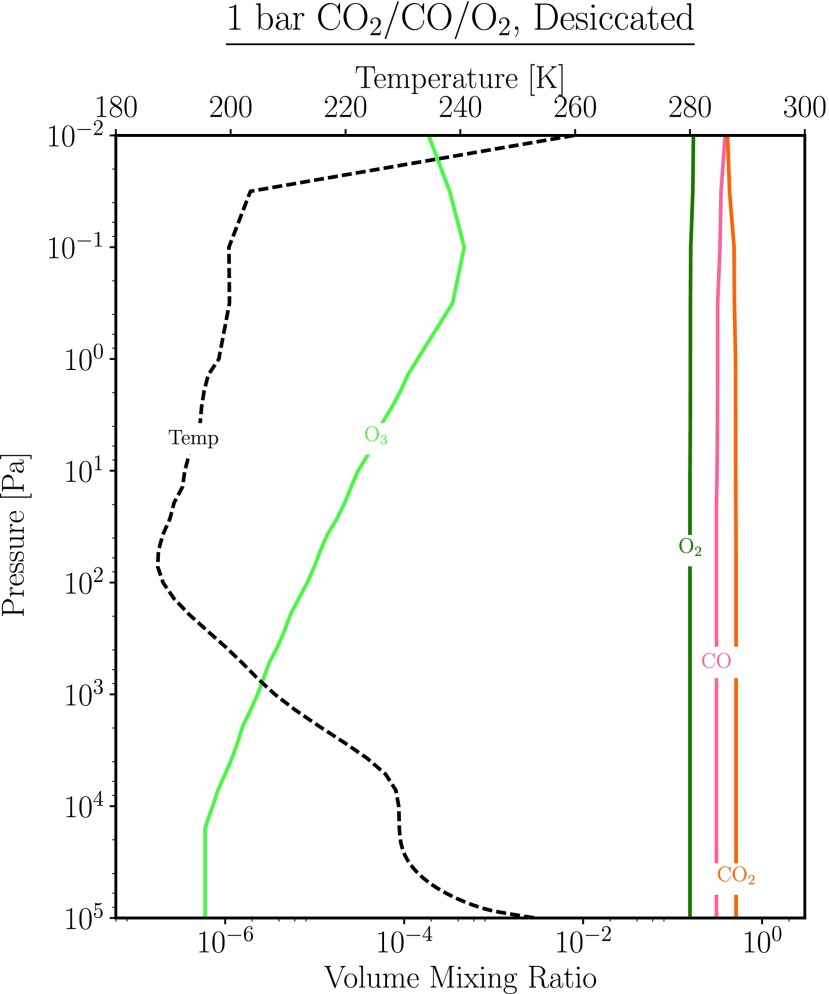
Since loss of one Earth ocean equivalent of water can potentially produce up to 240 bar of atmospheric oxygen (Kasting, 1997), the remaining atmosphere may be strongly oxygen-dominated (Luger and Barnes, 2015) but may transition to being more CO₂-dominated with time as the free oxygen reacts with the surface. The final amount of oxygen will depend on the initial water inventory, the stellar XUV flux, atmospheric losses through hydrodynamic escape and other top-of-atmosphere processes (Collinson et al., 2016; Airapetian et al., 2017; Dong et al., 2017), and the efficiency of planetary sequestration processes (e.g., Schaefer et al., 2016). However, if the atmosphere is retained and oxygen loss and sequestration is efficient—and CO₂ outgassing proceeds via terrestrial geological activity—then the atmosphere may transition from O₂-dominated, through O₂/CO₂-dominated, to a more Venus-like, CO₂-dominated atmosphere, if large quantities of outgassed CO₂ are present (Chassefière, 1996a, 1996b). Note that Barnes et al. (2018) found that the mantle temperature of Proxima Cen b could be maintained at high values due to either tidal heating or increased radiogenic heating, so a high outgassing rate may be likely. If the planet also outgasses SO₂, photochemical processes can result in the formation of a planetwide sulfate cloud and haze deck. If the atmosphere is desiccated, with H₂O abundances of the order of tens of parts per million, HDO may be enhanced as an indicator of early water loss, as is also the case for Venus (de Bergh et al., 1991). Should such a CO₂-dominated planet become significantly more desiccated than Venus—with atmospheric hydrogen inventories <1 ppm—then photochemical processes can split CO₂ while the lack of hydrogen-bearing species inhibits its recombination, resulting in a stable equilibrium mixture of CO₂, CO, O₂, and O₃ (Gao et al., 2015).

However, Proxima Cen b may be more likely to be habitable if it formed at its current position with a dense hydrogen envelope, or formed in a region of the protoplanetary disk rich in ices—and then migrated inward. For these scenarios, rather than stripping water from the planet, the superluminous pre-main sequence phase of the star may have removed enough of the primordial hydrogen (Owen and Mohanty, 2016) to reveal a habitable evaporated core—a potentially volatile-rich planet without the dense hydrogen envelope that may otherwise preclude habitability (Luger et al., 2015). Our calculations suggest that, if Proxima Cen b started with 0.1–1% of its planetary mass in hydrogen, it could have survived the pre-main sequence phase and remained habitable (Barnes et al., 2018). The extreme UV radiation from Proxima Cen would have caused H₂ loss—protecting the water vapor beneath—for the ∼170 million years required for the star to dim and the planet to enter the habitable zone. At this point, the planet would have been safe from further H₂O loss if atmospheric water vapor were cold trapped in the troposphere by a sufficient inventory of noncondensable gases, such as N₂ (Wordsworth and Pierrehumbert, 2014). Even if sufficient N₂ were not initially available, the buildup of O₂ (also a noncondensable gas) from the loss of H₂O could potentially reestablish the cold trap and inhibit subsequent water loss (Wordsworth and Pierrehumbert, 2014). Another potential path to habitability of Proxima Cen b is a later, large-scale dynamical instability of its planetary system possibly caused by Proxima Centauri passing close to α Cen A and B (Barnes et al., 2018). If the planet formed beyond the habitable zone, orbital disruption could have allowed it to arrive in its current orbit after the pre-main sequence phase. In this scenario, the planet would not need an initial thick hydrogen envelope to protect it from desiccation and could start off as a terrestrial body.

Over the 3.5- to 6-billion-year age of the system (Bazot et al., 2007), Proxima Cen's activity levels may have also affected the planet's habitability. Despite its relatively long rotation period (83.5 days, Benedict et al., 1998), which often correlates with lower activity levels, Proxima Cen is a moderately active star with many strong flares per year (Davenport, 2016), and the stellar magnetic field which drives stellar activity is ∼600 times stronger than that of our sun (Reiners and Basri, 2008). Earlier modeling suggested that Earth-mass planets in the habitable zones of M dwarf stars would suffer continuous exposure to strong stellar winds originating from coronal mass ejection events with a subsequent rapid loss of planetary atmosphere (Lammer et al., 2008). This loss could be exacerbated by the shutdown of magnetic dynamo production due to tidal heating of the planet (Driscoll and Barnes, 2015) or higher initial radiogenic abundances than Earth (Barnes et al., 2018). Ribas et al. (2016) also argue that ion pickup processes could remove up to 100 bar of N₂, which would enhance stratospheric water vapor concentrations and potentially lead to the loss of up to 21 Earth ocean equivalents of hydrogen over the age of the system. Airapetian et al. (2017) pointed out that ion loss processes from the early active star could remove oxygen and nitrogen from planets orbiting active M dwarf stars, although this rate is subject to the strength of the planet's magnetic field, and replenishment rates from outgassing and volatile delivery. Garraffo et al. (2016) used magentohydrodynamic models of the stellar wind pressure and conclude that Proxima Cen b's magnetospheric standoff distance undergoes significant stellar wind–induced changes on daily timescales, that are important to consider when calculating atmospheric loss processes. Dong et al. (2017) also modeled atmospheric loss from a CO₂-dominated 1 bar atmosphere for Proxima Cen b and concluded that such a planet may undergo significant atmospheric erosion over billion-year timescales in both the magnetized and unmagnetized cases but that the ionospheric profiles of heavier ions such as O₂⁺ and CO₂⁺ are mostly unaffected by the stellar wind conditions above 200 km. Garcia-Sage et al. (2017) explored enhancement of polar wind losses for a magnetized planet and showed that a 1 bar Earth-like atmosphere could be lost within 365 million years at Proxima Cen b's position, although the current calculated loss rate of H₂⁺ and O₂⁺ did not exceed Earth's current replenishment rate via outgassing and volatile delivery (Holland, 2002), so that maintenance of the atmosphere might be possible. Garcia-Sage et al. (2017) concluded that the habitability of Proxima Cen b requires a different atmospheric history to that of Earth, and indeed none of the above studies considered lifetimes for atmospheres significantly more massive than the current Earth's.

Other processes that may inhibit atmospheric loss also need to be considered, such as cooling to space from upper-atmosphere CO₂ (Tian, 2009) or shielding via formation of ozone from high-O₂ atmospheres. In all cases for atmospheric loss, the resultant atmosphere is dependent on a number of factors including the initial atmospheric inventory, and atmospheric replenishment processes, such as cometary volatile delivery and volcanic outgassing, over the planet's lifetime. In the case of Earth, 80–95% of our volatiles outgassed within the first 50–500 million years (Turner, 1989), but an ocean of water may have remained in the mantle (Albarède, 2009; Sleep et al., 2012), which is being more slowly outgassed. If a similar process works for terrestrial planets orbiting M dwarfs, then these planets would be susceptible to significant loss of water and atmosphere early on, but may, over billions of years, accumulate a surface ocean and atmosphere from volcanic outgassing, after the M dwarf has settled into its more benign main sequence phase.

However, if enough atmosphere is lost via interaction with the star, then the entire atmosphere could potentially be removed by condensation on the cold nightside. This is more likely if the planet is synchronously rotating, and atmospheric transport processes are weak or inefficient (Joshi et al., 1997; Wordsworth, 2015). However, Turbet et al. (2016) used 3-D climate models to show that, if Proxima Cen b retained an ocean, this form of atmospheric collapse into nightside or polar ice is highly unlikely, even if the planet is synchronously rotating. In the worst possible case on a dry, synchronously rotating planet, 4 bar of CO₂ would be required to avoid atmospheric collapse and only 0.1 bar of CO₂ for the asynchronously rotating case. Significantly less CO₂ (as low as a few hundred parts per million) is required if a plausible background gas such as N₂ were present (Turbet et al., 2016).

If, however, the atmosphere survived and is currently Earth-like, protons released via repeated flaring events would destroy any incipient ozone layer, resulting in high surface UV fluxes during flare activity (Segura et al., 2010; M. Tilley, private communication). For even the strongest flares exhibited by Proxima Cen b, which are comparable to the great AD Leo flare (Hawley and Pettersen, 1991; Hawley et al., 2003), previous calculations suggest that UV damage to life can be avoided on an ocean-bearing world at water depths of 9 m or more, while still allowing photosynthesis (Kiang et al., 2007). The resultant flux of photosynthetically active radiation would still be several orders of magnitude above the lower limit for useful light levels set by red algae, but the productivity of such a biosphere would be significantly lower than on Earth, with an estimated 4% of Earth's productivity for a star with AD Leo–type flares (Kiang et al., 2007).

Proxima Cen b's close-in orbit also makes the planet more vulnerable to gravitational tidal interaction with the star (Jackson et al., 2008), which falls off rapidly with semimajor axis, as a^−7.5. Over time, the star could have circularized Proxima Cen b's orbit, trapped it into synchronous rotation, reduced the semimajor axis, and set the obliquity to zero (Barnes et al., 2008, 2009; Heller et al., 2011). However, if Proxima Cen b's orbit has even a small eccentricity, possibly due to a companion planet or a recent perturbation due to a stellar encounter, then the gravitational interaction with the star can induce “tidal heating” due to friction as the body of the planet is flexed due to differential gravitational fields at different points in its orbit (Barnes et al., 2009). Sufficiently high levels of tidal heating could result in surface heat fluxes on the planet that could evaporate oceans of water on the planetary surface (Barnes et al., 2013). Our initial simulations suggest that by 3 billion years ago, for a starting eccentricity close to 0.1, the orbit should have evolved to be currently close to circular (unless it is being perturbed by another planet), in which case the planet is experiencing very little internal heating from tidal forces (Barnes et al., 2018). However, these forces would have been much more significant in the past, exceeding that of the volcanically active Io for the first billion years of the planet's existence (Barnes et al., 2018). However, these heat fluxes fall far short of those required to trigger a runaway greenhouse (Barnes et al., 2013). Instead, the heat deposited into the mantle of the planet may have reduced circulation in the planet's interior and shut down the generation of a protective magnetic field (Driscoll and Barnes, 2015), which could have left the atmosphere more vulnerable to erosion.

Additional considerations for factors that could affect the habitability of Proxima Cen b include the fact that the orbit of Proxima Cen, in relation to α Cen A and B, is very poorly constrained (cf. Wertheimer and Laughlin, 2006; Matvienko and Orlov, 2014). If this orbit takes Proxima Cen closer to its two companions, then the orbit of Proxima Cen b could have been significantly perturbed, resulting in large changes in eccentricity. The existing RV data allows for eccentricity values up to 0.35 for Proxima Cen b's orbit (Anglada-Escudé et al., 2016), which could be the result of the above mechanism or an unseen companion planet (Barnes et al., 2018). Tidally locked exoplanets with eccentric orbits have a much higher probability of being captured into orbital resonance than synchronous rotation (e.g., Rodríguez et al., 2012; Ribas et al., 2016), with eccentricities as low as 0.07 making resonances extremely likely (Ribas et al., 2016; their Fig. 4). In our solar system, Mercury, which is tidally locked with e = 0.21, is in a 3:2 spin-orbit resonance. An eccentric orbit would have made Proxima Centauri b vulnerable to climatic swings (Williams and Kasting, 1997; Williams and Pollard, 2002; Dressing et al., 2010), catastrophic tidal heating (Barnes et al., 2013), and the shutdown of the magnetic field (Driscoll and Barnes, 2015), which could have made atmospheric escape more likely. This disruption of Proxima Cen b's orbit could have occurred at any time in the past and is difficult to predict from the current position of the three stars. On the other hand, as discussed above, orbital instabilities caused by close passage to α Cen A and B may protect extreme water loss during its star's pre-main sequence phase if these instabilities transferred the planet into its current orbit from a more distant one after the pre-main sequence phase ended. Perturbations from stellar encounters could also enhance habitability via impacts, which may generate atmospheric blowoff of a dense H₂ envelope, or deliver volatiles to the planet after formation or after the pre-main sequence phase.

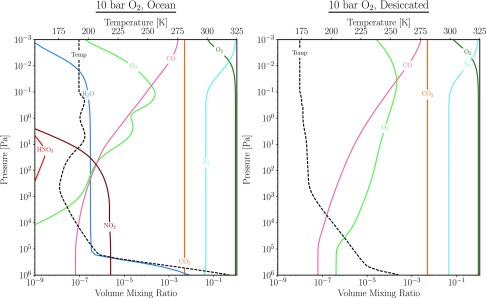
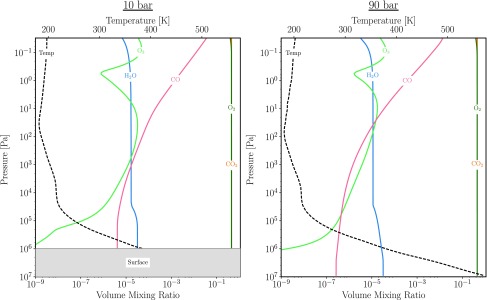
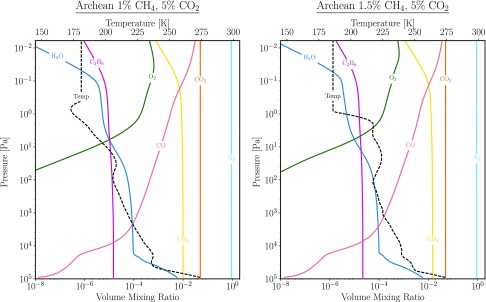
FIG. 4.

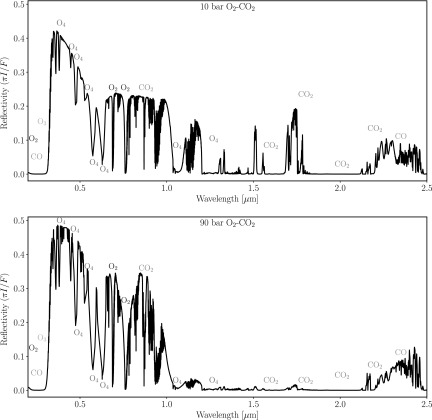
Temperature (top x axes; black dashed) and gas mixing ratio profiles (bottom x axes) for the self-consistent high-O₂ (95%), post-runaway atmospheres with a surface ocean remaining (left) and completely desiccated (right). Differences in temperature and O₃ profiles are primarily driven by the presence or absence of water vapor.

In summary, based on our current knowledge of M dwarf–planet interactions, there are several plausible scenarios for the environmental state of Proxima Cen b: an abiotic O₂-rich atmosphere, a CO₂-rich atmosphere, and a habitable terrestrial environment. Note that early total loss of an atmosphere—without generation or retention of a secondary atmosphere from outgassing—may also be a possible outcome, but we do not consider it for our atmospheric modeling activities. In the abiotic O₂-rich scenarios, Proxima Cen b formed at or close to its current position and suffered catastrophic water loss during the star's superluminous pre-main sequence phase. The resulting steam atmosphere was photolyzed, and H was lost to space. O₂, and possibly remnant water, was left behind, so there could be two cases from this scenario: O₂-rich without water and O₂-rich with water (Luger and Barnes, 2015). Similarly, if massive water loss occurs, and O₂ is lost either via hydrodynamic escape or sequestration in the planet's crust or mantle, or via a magma ocean, then CO₂ may be the dominant gas that persists in the atmosphere. In this case, the atmosphere may consist of remnant O₂ and outgassed CO₂, CO₂-rich and largely desiccated (Venus-like), or a CO₂-dominated, highly desiccated planet (H < 1ppm) which produces a stable CO/CO₂/O₂ atmosphere (Gao et al., 2015). Finally, in the habitable terrestrial environment scenario, Proxima Cen b was a terrestrial body that migrated to its current orbit after the pre-main sequence phase through instability processes, or formed with a protective H₂ layer of no more than 1% of the solid mass of the object, either because a terrestrial planet formed in situ with that envelope or because a more volatile and H₂-rich planet migrated inward from beyond the snowline. That H₂ envelope could have been sufficiently thick to protect the volatile-rich planet underneath during the superluminous pre-main sequence phase but not thick enough to remain and compromise the planet's habitability (Owen and Mohanty, 2016). For these cases, the resultant planet could have had a strongly oxidizing atmosphere, or one that was more reducing, depending on where in the planetary system it formed and how it evolved. Much of the analysis of these scenarios presented here is applicable not just to Proxima Cen b but to potentially habitable worlds orbiting other M dwarfs like those recently found in the TRAPPIST-1 (Gillon et al., 2017) and LHS 1140 (Dittmann et al., 2017) systems.

2.2. Impact of planetary characteristics and star-planet interactions on climate

A planet in the habitable zone can be impacted by the host star's incident spectrum, activity levels, and orbital and tidal interactions. Each of these agents, when interacting with the planet's environment, can strongly impact the current environmental state of the planet, including its atmospheric composition, climate, and potential habitability. For example, the planet's current climate and potentially enhanced ability to maintain surface liquid water are strongly impacted by the interaction of the spectral energy distribution (SED) of the M dwarf star with the planet's atmospheric and surface composition (Shields et al., 2013), any clouds or hazes (Arney et al., 2016, 2017), and the planet's orbital parameters and obliquity (Barnes et al., 2013; Armstrong et al., 2014). In particular, the UV spectrum of the star is critically important for understanding the planet's photochemistry—and therefore the atmospheric composition and climate (Segura et al., 2005; Rugheimer et al., 2015). It is also the key to interpretation of any spectra obtained from the planet. The stellar UV also affects whether or not a UV-absorbing haze will form in a reducing atmosphere (Arney et al., 2017) or an ozone layer in an oxidizing atmosphere (Segura et al., 2005; Domagal-Goldman et al., 2014). The presence and strength of these UV shields will affect the resultant surface UV flux, which could in turn strongly impact habitability. Sufficiently high UV flux could potentially sterilize the land surfaces, although life may still be adequately shielded in an ocean as previously mentioned (Kiang et al., 2007). Stellar flaring activity can also greatly increase stellar UV flux and eject protons, which collide with the planet's atmosphere and drive NO_x chemistry in the stratosphere, potentially damaging or destroying an ozone layer (Segura et al., 2010; M. Tilley, private communication), though the extent to which O₃ is destroyed would be dependent on the activity level (Grenfell et al., 2012). Additionally, HO_x chemistry driven by stellar cosmic rays may efficiently destroy methane and, in combination with NO_x chemistry, generate potentially detectable quantities of HNO₃ (Tabataba-Vakili et al., 2016). Consequently, to assess the current environmental state of the planet, and to interpret any spectra obtained of this object, one of the first steps in planet characterization will be to observe and monitor the UV characteristics and activity of the host star.

Due to the gravitational tidal interactions described above, a terrestrial planet in the habitable zone around an M dwarf star should be tidally locked, and if it has a circular orbit, may be synchronously rotating, with one side of the planet constantly facing the star. This was originally hypothesized to preclude planetary habitability, as the planet's atmosphere would eventually freeze out on the eternal nightside of the planet (Kasting et al., 1993); however, subsequent modeling showed that the presence of a planetary atmosphere of sufficient density would protect against atmospheric collapse onto the dark side (Joshi et al., 1997; Goldblatt, 2016). Leconte et al. (2015) discussed how thermal tides in the planetary atmosphere may cause asynchronous rotation of tidally locked planets. However, Proxima Cen b is currently observationally constrained to have an eccentricity <0.35 (Anglada-Escudé et al., 2016), which does not yet discriminate between a circular orbit with a likely synchronous rotational state and an eccentric orbit with a likely asynchronous rotational state. While models of Proxima Cen b's interaction with its star suggest that the planet is still more likely to be synchronously rotating under most assumptions for orbital position and atmospheric mass, existence in an asynchronous 3:2 spin-orbit resonance (similar to Mercury's) is also possible (Ribas et al., 2016; Turbet et al., 2016), and this possibility is increased if Proxima Cen b has companions in its planetary system (Barnes et al., 2018).

2.3. Identifying planetary habitability

Given the diversity of plausible evolutionary scenarios discussed above, and the star-planet interactions that may sculpt the current environment of the planet, one of the biggest questions posed for Proxima Cen b is, “How do we determine whether or not this planet is habitable?” Habitability can be assessed most straightforwardly by detecting liquid water on the planetary surface. This could be done by using photometric measurements of the distant planet at visible or near-infrared (NIR) wavelengths to search for signs of enhanced reflectivity near crescent phase due to the presence of ocean “glint” (Williams and Gaidos, 2008; Robinson et al., 2010, 2014). Glint is specular reflectance at glancing angles from a smooth surface (Cox and Munk, 1954), which on a terrestrial planet is most likely to come from a liquid—since rock, snow, and snow-covered ice tend to have nonspecular scattering properties.

Robinson et al. (2010) used a sophisticated 3-D spectral model of Earth (Robinson et al., 2011), validated against the EPOXI mission (Livengood et al., 2011) and Earthshine (Pallé et al., 2003) observations of the disk-averaged Earth, to show that Earth deviates strongly from Lambertian (i.e., isotropic) scattering behavior at phases crescent-ward of quadrature. While a similar deviation from Lambertian behavior can occur due to forward scattering from clouds, Robinson et al. (2010) were able to show that an Earth-like planet with realistic (∼50% coverage) forward-scattering water clouds and a specularly reflecting ocean is up to a factor of two brighter than an Earth-like planet with forward-scattering clouds and a Lambertian ocean near crescent phase. This increase in relative brightness due to ocean glint is most apparent between phase angles of 90 and 130 degrees, and is most readily observable at wavelengths between 0.8 and 0.9 μm where Earth's atmosphere is relatively transparent (Robinson et al., 2010, 2014). Consequently, glint from Earth's ocean is potentially detectable as a deviation in the observed reflectivity of the planet near crescent phase, even in the presence of forward-scattering clouds. A potential false positive for ocean glint may occur if the observer is preferentially sounding ice- and/or cloud-covered portions of the planet near crescent phases (Cowan et al., 2015), although this effect may be distinguishable with spectroscopic measurements. Glint may also polarize incident starlight, which could potentially induce a signal in the planet's polarimetric light curve. Williams and Gaidos (2008) used idealized models to show that cloud-free ocean planets with nonpolarizing atmospheres may exhibit a strong (30–70%) polarization signal over an orbit. However, Rayleigh scattering and clouds are also a source of polarization, possibly overwhelming the signal due to a surface ocean (Zugger et al., 2010, 2011) and making it difficult to use polarization to identify water under an atmosphere.

Note that glint is far less ambiguous for surface water detection than the presence of water vapor in the planetary atmosphere, as a planet may maintain a steam atmosphere without being habitable. “Anti-ocean” signatures may also be present in the form of highly soluble gases, for example, SO₂, that would dissolve in an ocean and would not accumulate in the atmosphere unless there was no ocean (or the ocean was already saturated with that gas). Conversely, false negatives for the detection of water can occur, especially in transmission observations, if the water is cold-trapped in the troposphere of a habitable planet, resulting in an appropriately drier stratosphere. Water that is kept near the surface is most valuable for habitability and less susceptible to loss processes. In this case, clouds and refraction in transmission (Bétrémieux and Kaltenegger, 2013, 2014; Misra and Meadows, 2014; Misra et al., 2014b) limit our ability to probe into the relatively water-rich troposphere, where water is more likely to be detected. Drier stratospheres are less likely to affect direct imaging observations, however, except in the presence of high-altitude, planetwide clouds. Even in the presence of broken cloud cover, or some planetwide hazes, direct imaging observations can still sample the lower atmosphere and surface to detect water vapor (Arney et al., 2016).

Another means to assess habitability is to constrain the surface temperature and pressure to determine whether surface liquid water is feasible. This is best assessed with spectra of the planet in the visible and NIR and/or photometry or spectra in the mid-infrared (MIR). While a Rayleigh scattering slope from atmospheric molecules has been proposed as a means of determining atmospheric pressure for a terrestrial planet (Arnold et al., 2002; Woolf et al., 2002; Benneke and Seager, 2012) this method—like all methods for atmospheric pressure assessment—is not robust in the presence of cloud or haze cover, either complete or partial. At best it will return the pressure at the top of the clouds in the former and an average of the cloud top altitudes and surface in the latter. This is graphically demonstrated in our solar system by Venus, which has a 93 bar surface pressure but exhibits extremely weak Rayleigh scattering, because the line of sight into the atmosphere is truncated by sulfuric acid haze at an altitude of 70 km and a pressure near 30 mbar. In direct imaging, which looks at planetary reflectivity, attempts to measure Rayleigh scattering are additionally vulnerable to the spectral properties of the underlying aerosols and surfaces. On Mars, strong absorption by surface iron oxide absorbs Rayleigh scattering in the blue. Similarly, for a CO₂- and CH₄-rich early-Earth-like atmosphere, the formation of a hydrocarbon haze results in strong absorption in the UV and blue, strongly altering the Rayleigh signature (Arney et al., 2016, 2017).

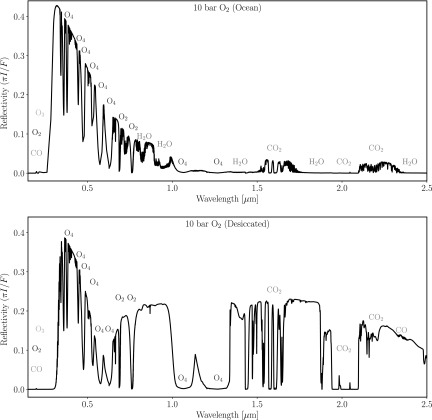
A potentially more promising means for determining atmospheric pressure comes from measurements of collisional absorption from molecules such as N₂ (Schwieterman et al., 2015b) and O₂ (Tinetti et al., 2006; Pallé et al., 2009; Misra et al., 2014a), which are both seen in Earth's disk-averaged spectrum. Unlike Rayleigh scattering, which is degenerate in terms of characterizing the mix of gases that are producing the scattering, observations of collisional absorption can provide a direct measurement of the atmosphere's bulk constituents. However, this method is also subject to path length truncation due to clouds and so will return a composite pressure depending on the available path lengths to clouds and the surface. In the case of O₂, observations of the O₂ molecule can be compared to the strength of the absorption band produced by the O₂-O₂ collisional pair (also referred to as O₄)—which is sensitive to density squared—to quantify the partial pressure of oxygen in the atmosphere (Misra et al., 2014a). The presence of strong O₄ bands in the visible (0.35–0.65 μm) is diagnostic of massive O₂ atmospheres (Schwieterman et al., 2016).

In addition to searching for oceans and determining surface temperature and pressure, habitability could be assessed by undertaking a spectroscopic survey of greenhouse gases and other planetary characteristics that affect climate. In particular, retrieving abundances for greenhouse gases such as CO₂, CH₄, H₂O, SO₂, O₃, and N₂O; obtaining pressure estimates using observations of O₄ and N₄ (the N₂-N₂ collisional pair); and searching for and characterizing hazes and clouds will provide important constraints on planetary climate. These observations could then be used as input to coupled climate and photochemistry models (e.g., Segura et al., 2005) to understand the composition of the atmosphere, and the surface temperature and pressure.

It is important to note that, for terrestrial planets with CO₂ (distinct from Titan, whose atmosphere is extremely reducing), methane and organic hazes could also be a sign of either habitability or life (Arney et al., 2016). Methane in a planet's atmosphere can produce organic haze if the CH₄/CO₂ ratio exceeds 0.1, and these hazes dramatically impact their planet's spectrum. Higher carbon dioxide levels make haze formation more difficult, so larger fluxes of methane are needed to produce haze in the atmospheres of planets with larger CO₂ inventories compared to very reducing atmospheres like Titan. Hazes in Earth-like atmospheres containing CO₂ can therefore be a sign of a high methane production rate. Methane can be sourced from either biological or abiotic processes, but even abiotic methane is a potential habitability marker, as its dominant source on an Earth-like planet is serpentinization—which are liquid water/rock reactions (Kelley et al., 2005). Serpentinization requires freshly exposed seafloor minerals to react, and while a limited area could be obtained from cracking, new seafloor crust would likely be needed for the maintenance of robust serpentinization on long timescales. Consequently, atmospheric methane concentrations requiring large surface fluxes on a terrestrial planet may indicate both liquid water and plate tectonics, two hallmarks of habitability. More intriguingly, existing measurements and models suggest that the presence of an organic haze on an Earthlike exoplanet with >1% CO₂ in the atmosphere may require more vigorous methane production rates than occur on Earth from abiotic processes alone (Kharecha et al., 2005; Etiope and Sherwood Lollar, 2013; Guzmán-Marmolejo et al., 2013), so organic haze in an Earth-like atmosphere could also be suggestive of life if the CO₂ abundance can also be constrained (Arney et al., 2016).

2.4. Biosignature considerations for planets orbiting M dwarfs

Exoplanet biosignatures are biological modifications of a planet's global environment that are potentially observable over interstellar distances. On Earth, biosignatures can be classified into three major groups: atmospheric gases that are produced by life, such as Earth's abundant photosynthetically generated O₂ (Hitchcock and Lovelock, 1967); surface reflectivity signatures like the enhanced “red edge” reflectivity at wavelengths longward of 0.7 μm from vegetation (Gates et al.,1965) or nonphotosynthetic pigments from other organisms (Schwieterman et al., 2015a); and time-dependent phenomena, such as seasonal changes in surface coverage or atmospheric gases (Meadows, 2008).

For planets orbiting M dwarfs, the UV spectrum and stellar activity of the star can work via photochemistry to either enhance or destroy the detectability of potential atmospheric biosignatures. Segura et al. (2005) showed that, for Earth-like surface fluxes of the biogenic gases CH₄ and N₂O, extremely large abundances of these gases can build up in a terrestrial planet atmosphere. In particular, the lifetime and abundance of atmospheric methane is increased from 10–12 years and 1.6 ppm for an Earth-like atmosphere orbiting a Sun-like star to over 200 years and over 300 ppm for a planet orbiting the M3.5V star AD Leo. This is due in large part to the slope of the M dwarf's UV spectrum, which has smaller relative amounts of NUV radiation, and its subsequent relative inefficiency at photolyzing ozone to produce reactive O(¹D) that generates the OH from water vapor that ultimately destroys CH₄ (Segura et al., 2005). On a related note, Segura et al. showed that for the same atmospheric O₂ abundance, ozone column density could be larger or smaller than Earth's by roughly a factor of 2, again depending on the UV spectrum of the star. However, these calculations were performed for quiescent versions of M dwarf spectra. Segura et al. (2010) explored the effect on a planetary atmosphere of large flares, looking at both UV and proton flux on the thickness of an Earth-like planet's ozone layer. For the single flare that they studied, they found that the UV flux had negligible effect on the thickness of the ozone layer, dropping it by of order 1%. However, if the planet intercepted the proton beam from the coronal mass ejection, and did not have a protective magnetic field, the effect on the ozone was devastating, as proton-driven NO_x chemistry from this single flare resulted in a 94% depletion of the ozone layer over a 2-year period (Segura et al., 2010). Consequently, both the stellar spectrum and activity levels need to be well-characterized as an adjunct to interpreting potential biosignatures from planets orbiting M dwarfs.

Other important considerations when interpreting biosignatures of M dwarf planets are the likely detectability of the biosignature gas in question, as well as the likelihood that the planetary environment could produce the biosignature gas without life being present, and thereby exhibit a false positive for the biosignature. Oxygen is a particularly good gas for this discussion, as it has been well studied as a potential biosignature (see Meadows, 2017, for a comprehensive review). Oxygen is produced by photosynthetic organisms on Earth and is particularly attractive as a biosignature gas because it is present in high abundance, is evenly mixed throughout the atmosphere—and so can potentially be detected in the stratosphere by transmission observations—and has strong absorption bands at UV and NIR wavelengths where the first generation of exoplanet telescopes will observe. More exotic potential biosignatures, including organic sulfur compounds (e.g., Domagal-Goldman et al., 2011) are likely to be at lower abundances and be more sensitive to photolysis, so that they are confined closer to the planetary surface. These molecules also tend to absorb predominantly in the MIR, which may be challenging to access for terrestrial planets with upcoming telescopes. However, to offset its advantages as a biosignature, oxygen is now known to have false-positive production mechanisms—abiotic processes that can also produce O₂ in a planetary environment—and the majority of those mechanisms currently known are thought to be more likely to occur for planets orbiting M dwarfs (Domagal-Goldman and Meadows, 2010; Domagal-Goldman et al., 2014; Tian et al., 2014; Gao et al., 2015, Harman et al., 2015; Luger and Barnes, 2015). For these mechanisms, carbon dioxide and water vapor serve as key sources of abiotic oxygen, and the spectrum of the host star and the resultant photochemistry play a significant role, leaving telltale signs in the planetary atmosphere that can be sought to discriminate between biological and abiotic sources for oxygen (Meadows, 2017). In particular, two of the possible atmospheres for Proxima Cen b discussed above—including the massive O₂ atmospheres generated from water loss (Luger and Barnes, 2015) and the CO₂-rich, desiccated atmospheres that may contain large, stable O₂ fractions (Gao et al., 2015)—are both potential false positives for biologically produced oxygen. However, both may be discriminated by searching for either O₄ absorption or both CO and CO₂ absorption in the planetary spectrum (Schwieterman et al., 2016). These studies show the importance of obtaining contextual information about the planetary environment and provide a guide to increasing our confidence in biosignature detection by searching for additional gases and planetary characteristics.

3. Models

We use a suite of planetary climate and photochemistry models to simulate the current environmental state for the evolutionary scenarios described in Sections 1 and 2. We then use a radiative transfer model to predict the potentially observable photometric and spectral parameters that would help discriminate between these environmental states. These models and the stellar and surface albedo inputs are described in the sections below. Table 1 shows a summary of all models used in this study.

Table 1.

Models Used to Simulate Proxima Centauri b

Model name	Type	Model subcomponents/dependencies	Use	References
LBLABC	Absorption coefficients for SMART	n/a	Generate SMART inputs from linelists	Meadows and Crisp, 1996
SMART	1-D radiative transfer	LBLABC	Reflected light spectra	Meadows and Crisp, 1996; Crisp, 1997
VPL Climate	Climate model	LBLABC, SMART radiative transfer core	Climate simulations	This paper; Ty Robinson and David Crisp, private communication
Atmos	1-D photochemical-climate model	Photochemical model, climate model components	Climate and/or photochemical simulations	Arney et al.,2016
SMART-T	1-D radiative transfer–transits	LBLABC, SMART radiative transfer core paired with ScaTrans module	Transit spectra	Robinson, 2017
SMART Phase Curves	Phase curve model	LBLABC, SMART radiative transfer core	Phase curves	This paper
Coronagraph noise model	Instrument simulator	n/a	Add realistic noise for simulated observations to spectra	Robinson et al.,2016

3.1. SMART—direct imaging synthetic spectra

The SMART (Spectral Mapping Atmospheric Radiative Transfer) code is a 1-D line-by-line, multistream, fully multiple scattering radiative transfer model (described in detail in Meadows and Crisp, 1996, and Crisp, 1997) that computes accurate synthetic planetary spectra. SMART combines a multilevel, multistream discrete ordinate algorithm (Stamnes et al., 1988) with a new class of high-resolution spectral mapping techniques to increase computational speed. SMART is used in this study to generate synthetic planetary spectra for both direct imaging and, through the SMART-T modification, for transmission spectroscopy. It also serves as the radiative transfer engine for phase curve generation and for the VPL Climate model. We have validated SMART against observations of Solar System planets, including Mars, Earth, and Venus (Tinetti et al., 2005; Robinson et al., 2011; Arney et al., 2014). SMART requires a number of user inputs, which are described in detail in Section 3.7, such as a pressure/altitude-temperature grid, gas mixing ratios, molecular absorption coefficients, collision-induced absorption data, UV-visible absorption cross sections, a stellar spectrum, and wavelength-dependent surface albedo data. The absorption coefficients for SMART are generated with a separate program called LBLABC (see Section 3.7.4, below) from input line lists (i.e., HITRAN 2012, Rothman et al., 2013; HITEMP 2010, Rothman et al., 2010; and Ames, Huang et al., 2014). SMART can also incorporate the radiative impact of aerosols such as hazes and clouds, by specifying the altitude-dependent optical depths as well as the particle asymmetry parameter and the extinction, scattering, and absorption efficiencies (Q_ext, Q_scat, and Q_abs). SMART can generate spectra at any arbitrary spectral resolution, and its results are valid from the UV to the far-infrared.

3.2. SMART-T—transit transmission spectra

Although Proxima Cen b may not transit (Kipping et al., 2017), the simulations provided here for its plausible environments are potentially relevant to habitable zone planets orbiting late-type M dwarfs that do transit, including the recently discovered TRAPPIST-1 system (Gillon et al., 2016, 2017), where TRAPPIST-1e occupies a similar position in its habitable zone to Proxima Centauri b. Consequently, we simulate transmission as well as direct imaging observations for Proxima Centauri b. To generate the transit transmission spectra, we use the SMART-T model, which updates our original refraction transmission model (Misra and Meadows, 2014; Misra et al., 2014b) by pairing SMART with the full-physics transmission code ScaTrans (Robinson, 2017), which includes the effects of both refraction and transmission. Our new version of SMART-T uses the normal-incidence optical depths of SMART to calculate transmission for a grid of limb-traversing atmospheric paths, which are then integrated over the planetary disk to produce a transit spectrum. The model takes into account the effects of refraction by using the path integration method of van der Werf (2008). Starlight refracted out of the beam of an observer sets a limit on the tangent altitudes at which the atmosphere can be probed (Sidis and Sari, 2010; García Muñoz et al., 2012; Misra and Meadows, 2014; Misra et al., 2014b). SMART-T requires the same inputs as the standard SMART code but additionally requires the radius of the host star, the offset of the planet center from the middle of the star (i.e., the impact parameter), and the altitude-dependent refractivity of the atmosphere. For all transmission spectra presented here, an impact parameter of 0 is assumed, implying the planet is centered on the host stellar disk. We did not use the multiple-scattering capabilities of SMART-T for the spectra presented here, as an initial investigation into the geometry of the problem and the scattering properties of our included aerosols showed that a multiple-scattering calculation was unwarranted.

3.3. SMART phase curves

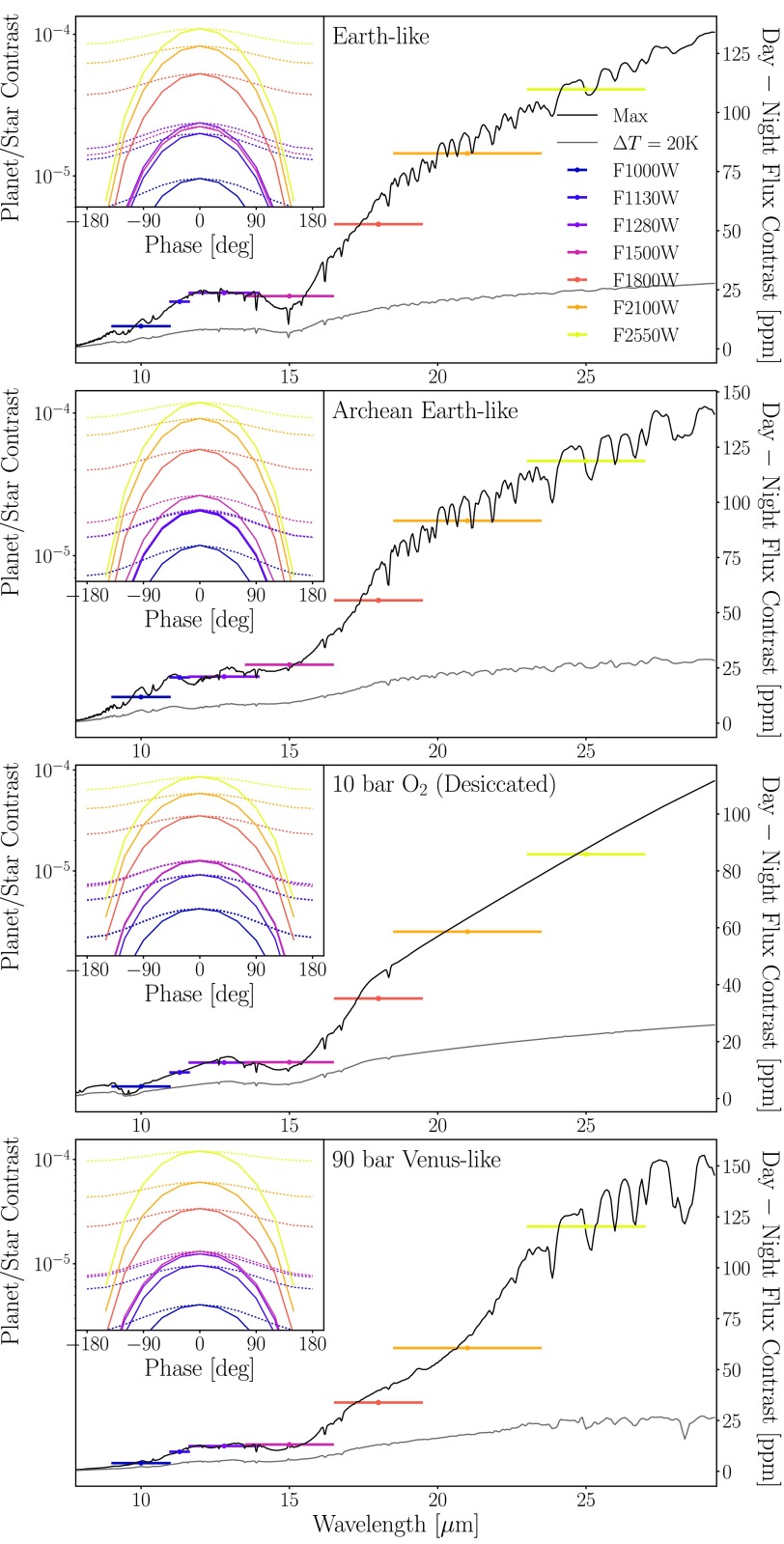
We use the SMART Phase Curve model (developed by T. Robinson and D. Crisp) to calculate the multiband, orbital phase-variability of a planet in reflected and emitted light. This model uses n-point Gaussian quadrature to generate a phase-dependent, disk-integrated spectrum of the planet. Wavelength-dependent radiances at a grid of solar and observer zenith and azimuth angles at Gaussian quadrature are computed by SMART, where the zenith angles form the abscissa for a Gaussian integral computed over the surface of a sphere. The corresponding weights for the integration are determined based on the longitudes of the planetary disk that are visible and illuminated as seen by the observer. We apply this disk integration over a grid of observed planetary phase angles to simulate high-resolution, phase-dependent spectra, which are convolved with JWST/MIRI broadband photometric filters to determine the detectability of the planet's phase variability against the bright stellar background in the MIR.

Our focus is on the phase dependence of the planet due to the vertically resolved atmospheric structure atop a reflecting and emitting surface, and not on the spatially resolved features accessible with a General Circulation Model (GCM). Therefore, the distinguishing observables from one plausible planetary state to another are limited to bulk surface and atmospheric characteristics, such as deviations from Lambertian scattering due to the presence of forward-scattering aerosols or the presence of ocean glint (Robinson et al., 2010, 2014), modulations in the peak amplitude of phase curves as a function of wavelength due to molecular features (Selsis et al., 2011; Stevenson et al., 2014), and thermal phase curve amplitudes due to a day-night temperature contrast. We are not using a GCM in this study, and we have not made self-consistent predictions for the day-night temperature contrast. To simulate phase curves with a thermal emission contribution from the nightside of the planet, we use our self-consistent globally averaged surface temperature, assuming no day-night temperature contrast and extremely efficient heat redistribution (e.g., Venus). We also simulate cases where we assume no thermal contribution from the nightside of the planet to simulate the maximum day-night temperature contrast, and severely inefficient heat redistribution more appropriate for an airless body (Maurin et al., 2012). In this way, we assess the extreme end-member cases for the phase curve amplitude. We also simulate an intermediate case where the nightside surface temperature and temperature-pressure profile is 20 K lower than the dayside to emphasize a plausible phase curve amplitude.

3.4. Instrument simulators and noise model

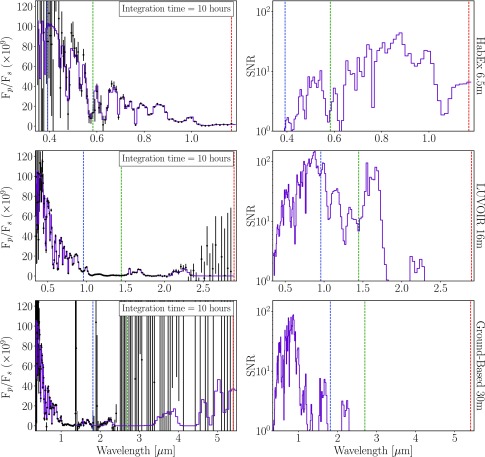
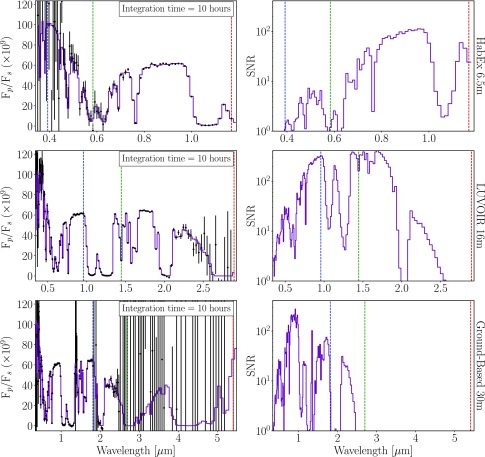
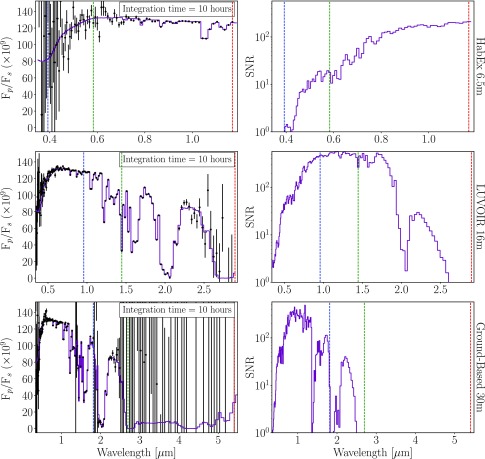
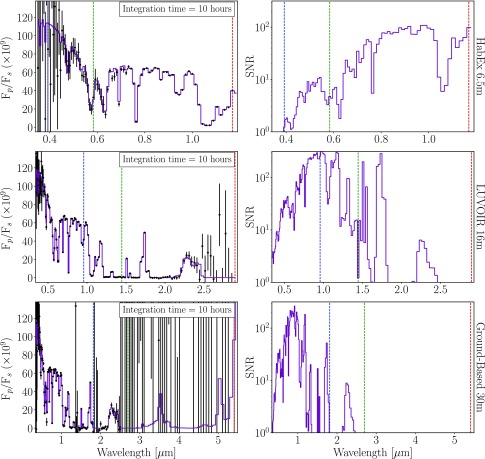
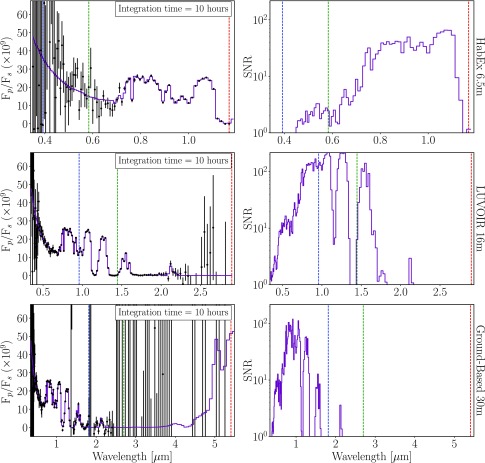
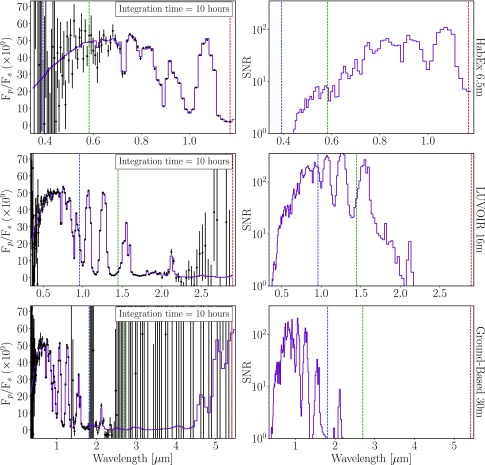
We use a general coronagraph instrument noise model to simulate directly imaged reflectivity spectra for the atmospheric states considered in this work. We refer the reader to Robinson et al. (2016) for a thorough description of the model. In brief, the coronagraph instrument noise model computes wavelength-dependent photon count rates on the detector due to the planet, zodiacal and exozodiacal light, dark current, read noise, speckles, and thermal emission from the mirror. The model also considers the CCD quantum efficiency of assumed detectors, the dependence of dark current on the NIR detector due to detector temperature, and a factor of √2 increase in the shot noise due to the spacecraft roll maneuver required for background subtraction (see Brown, 2005). With the coronagraph noise model, we simulate observations using three future telescope concepts: a space-based 16 m LUVOIR, a space-based 6.5 m HabEx, and a ground-based 30 m telescope assumed to be located in the Atacama Desert, Chile.

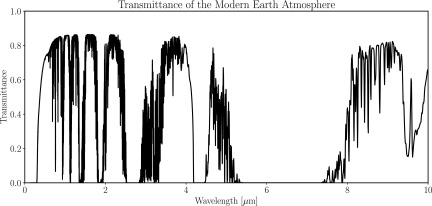
To model ground-based observations, we modified the coronagraph noise model to account for transmission through and downwelling emission from Earth's atmosphere. The wavelength-dependent transmissivity of the Earth atmosphere is calculated with the SMART model (see Fig. 1) and is used to model the effect of telluric absorption such that incident exoplanetary photons are attenuated at high-opacity wavelengths. The sky brightness noise term makes use of the ESO SkyCalc Sky Model Calculator⁵, which is based on the Cerro Paranal Advanced Sky Model (Noll et al., 2012). Sky brightness includes contributions from molecular emission from the lower atmosphere, emission lines from the upper atmosphere, airglow, and scattered starlight, but neglects scattered moonlight, which is dependent on time of observation, and zodiacal light, which is already included in the nominal coronagraph model (Robinson et al., 2016). The downwelling thermal emission from the sky begins to dominate at wavelengths beyond 2.5 microns. For a 30 m telescope, the continuum sky brightness is only ∼2% of the planetary brightness in the PSF core (Hanuschik, 2003). We approximate a sub-optimal Strehl ratio by lowering the planetary flux inside the PSF core by an additional 50% to account for the effects of atmospheric turbulence. We assume a cold planetary surface temperature (269 K) and an observing zenith angle of 30°, which corresponds to the altitude of Proxima Centauri crossing the meridian at La Silla Observatory, Chile. The telescope, instrument, and astrophysical parameters used to simulate coronagraph observations are identical to those given in Robinson et al. (2016; astrophysical in their Table 2, telescope and instrument in their Table 3), except for telescope diameter, detector temperature, raw contrast, and telescope plus instrument throughput, which are presented here in Table 2.

FIG. 1.

Earth's atmospheric transmittance calculated by SMART and used for simulations of ground-based observations.

Table 2.

Parameters Used for the Coronagraph Noise Model

Parameter description	HabEx	LUVOIR	30 m
Telescope diameter	6.5 m	16 m	30 m
Mirror/System temperature	270 K	270 K	270 K
Contrast	10−10	10−10	10−10
Telescope + Instrument Throughput	20%	20%	20%

See Robinson et al. (2016) for a complete list of baseline telescope and astrophysical parameters.

Table 3.

Data Sources for Proxima Centauri Spectrum

Wavelength Range [Å]	Platform/Instrument	Observation ID/References
1200–1215,1216–1691	HST/STISa	o5eo01010[20,30], o5eo02010[20,40]
1215–1216	HST/STIS Ly α reconstruction	MUSCLESb
1691–4569	HST/STIS	MUSCLESb
4569–8499	HST/FOD/RDa	Y2WY0705T, Y2WY0305T
λ > 8499	PHOENIX 2.0 Model	Husser et al. (2013)

^aData obtained from MAST (https://archive.stsci.edu/).

^bData obtained from MUSCLES Treasury Survey (http://cos.colorado.edu/∼kevinf/muscles.html).

3.5. VPL Climate model

Our new 1-D radiative-convective equilibrium (RCE) climate model (Ty Robinson and David Crisp, private communication) incorporates our physically comprehensive, validated radiative transfer model, SMART, which is coupled with a variety of convection and time-stepping methods to determine the equilibrium pressure-temperature structure of an atmosphere. Since our radiative fluxes are computed by using SMART's multistream solver, we avoid inaccuracies that can impact models that use δ 2-stream approximations (Kitzmann et al., 2013). Note that VPL Climate, at present, does not include integration with atmospheric chemistry tools. Therefore, we present results from this model only for cases for which our other 1-D climate model, Atmos (see Section 3.6), lacks key capabilities, such as for high-pressure atmospheres.

Net radiative fluxes in VPL Climate are computed by using a first-order linearized flux-adding approach (Robinson and Crisp, private communication). Full line-by-line, multistream, multiscattering solar and thermal radiative fluxes are computed by SMART, as well as a set of Jacobians that describe the response of the radiative fluxes to changes in key elements in the atmospheric state vector (e.g., layer and surface temperatures). These Jacobians consist of derivatives of the layer-by-layer, wavelength-dependent stellar and thermal source terms, as well as derivatives of layer reflectivity, transmissivity, and absorptivity. This information is used in a linear flux-adding approach to determine the upwelling and downwelling solar and thermal flux profiles at each timestep. If during timestepping the evolved atmospheric state (e.g., the temperature in any given layer) is outside the linear range of the Jacobians, additional iterations of computing Jacobians can be required. The tolerance for the perturbation for computing Jacobians is set by the user, which can be large when starting from an isothermal atmosphere (e.g., 50%) or small when near convergence (e.g., <1%). Since VPL Climate uses SMART to compute fluxes at extremely high spectral resolution, spectral quantities in our flux-adding approach are degraded to a lower resolution (typically 10 cm⁻¹) by convolution with a slit function, which still provides thousands of wavelength intervals.

Our VPL Climate model can implement convection in a number of ways; here, we use mixing length theory (e.g., Gierasch and Goody, 1968), which uses fundamental physical properties for each layer of the atmosphere and requires few assumptions. The required assumptions include surface wind speed U₀ and mixing length z_mix(z), which we calculate for each layer using the asymptotic mixing length calculation from Blackadar (1962):

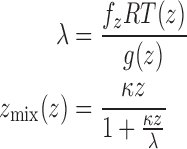where R is the specific gas constant (ideal gas constant/molecular weight of gas), z is altitude, T(z) is temperature, g(z) is the acceleration due to gravity, κ is von Kármán's constant, and f_z is the mixing length proportionality constant, which must be specified. Convective heat transport is computed at every layer from eddy diffusion rates in convectively unstable layers. Convective stability is determined by using the Schwarzchild criterion:

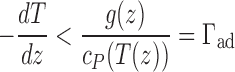where g(z) is the acceleration of gravity, c_P(T(z)) is the specific heat of the atmospheric layer, and Γ_ad is the dry adiabatic lapse rate. For moist cases (comparing to the results of Turbet et al., 2016), we use the moist adiabatic lapse rate for the troposphere, to simulate the effect of condensation and rainfall:

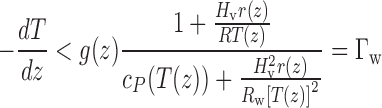where H_v is the latent heat of vaporization of water (2.5 × 10⁶ J K⁻¹), r(z) is the layer-dependent mixing ratio of water, and R_w is the specific gas constant of water vapor (461.5 J kg⁻¹ K⁻¹). The specific heat for common molecules is used from laboratory data⁶ (water vapor, CO₂, N₂O, CO, CH₄, O₂, N₂, NO, SO₂, NO₂, NH₃, HCl, N₂, C₂H₂, C₂H₆, H₂S, C₂H₄, CH₃OH, and H₂). Specific heat for molecules for which data is not available is computed by using an ideal gas law approximation and assuming c_P is temperature-independent:

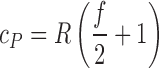where f is the number of degrees of freedom (i.e., 3 for atoms, 5 for diatomic molecules, and 6 for polyatomic molecules). The eddy diffusivity from Gierasch and Goody is

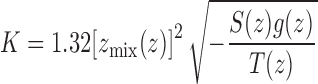where S(z) is the difference from Schwarzchild's criterion. Convective heat flux for each layer is calculated as

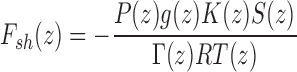Condensation and evaporation are taken into account by adjusting layer mixing ratios of condensable constituents and calculating the heating rate. We assume sufficient condensation nuclei for rapid and efficient condensation in supersaturated layers. Layers are assumed to be supersaturated when the partial pressure of a condensable is above its saturation vapor pressure. The required inputs for this optional feature are the saturation vapor temperature, pressure, and corresponding enthalpy of formation.

The timescales at which we resolve our mixing length model are small, consistent with the time it takes for an air parcel to rise one layer. Since radiative flux calculations are more computationally expensive, we employ a timestep splitting approach where many convective timesteps are resolved within each radiative timestep. Here, we use adaptive methods to calculate the maximum radiative and convective timesteps to more rapidly iterate the temperature-pressure profile to equilibrium. The limit for the radiative timestep is simply an allowed change in temperature for any given layer per timestep (e.g., 0.1 K), while mixing length theory provides for a maximum stable convective timestep in a single layer:

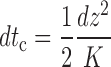We take the smallest of these from all layers as the maximum convective timestep in the convective region.

The model atmosphere constructed for VPL Climate simulations generally consists of 64 plane-parallel layers in hydrostatic equilibrium, spanning from the surface pressure to 10⁻⁷ bar. Half the layers starting at the surface are spaced linearly and comprise 90% of the atmospheric pressure. Coarser, log-spaced layers span the upper atmosphere. Fluxes are computed for the entire stellar spectral energy distribution, divided into ∼8600 intervals, and thermal flux from the planet is computed for the wavelength range ∼1–200 μm, divided into ∼1000 intervals, all spaced at 10 cm⁻¹. Gas absorption is computed in all intervals for which cross sections, collision-induced absorption, or line data are available from HITRAN.

Validations of VPL Climate for Earth, Mars, and Venus have been conducted by Robinson and Crisp (private communication). In particular, our capability to produce Venus-like high-CO₂ atmospheres is validated by the excellent match to the Venus International Reference Atmosphere by Robinson and Crisp (private communication), with a surface temperature of 732 K, compared to Venus' observed global average surface temperature of 733 K. These validations provide confidence that this model can be applied to a variety of planetary climates, including those we discuss for Proxima b. As a further validation, in Section 4.1 we also provide a cross comparison between the VPL Climate model and the LMDz model used by Turbet et al. (2016) for a subset of similar Proxima Cen b calculations.

3.6. Atmos: a coupled climate-photochemical model

We use a 1-D photochemical-climate model, Atmos, to simulate photochemistry and climate of terrestrial planet environments. Atmos generates atmospheres that are both chemically and climatically self-consistent with the atmospheric composition, temperature profile, and incident stellar spectrum. To use Atmos, the photochemical model (which can include particle microphysics) is run first to generate an initial atmospheric state based on user-specified boundary conditions (i.e., gas mixing ratios or fluxes and deposition velocities, the stellar spectrum, the total atmospheric pressure, the initial temperature-pressure profile). The model is described in detail in Arney et al. (2016), and it is publicly available at https://github.com/VirtualPlanetaryLaboratory/atmos. Templates for atmospheres modeled in this paper (including their complete reaction rate lists and species lists) can be found in this repository. The modern Earth photochemical template (which we also use as the basis for our high-O₂ simulations and template, although with different atmospheric boundary conditions) has 233 chemical reactions and includes 50 chemical species, 9 of which are short-lived (meaning atmospheric transport between layers is not considered). Our Archean Earth template includes 392 chemical reactions and 76 chemical species, 11 of which are short-lived. In both base templates, N₂ and CO₂ are assumed to have isoprofiles. Both templates include chemistry for sulfur aerosol formation, and the Archean template includes hydrocarbon haze formation chemistry.

Once the photochemical model reaches a converged state, the photochemical model feeds its outputs into the Atmos climate model. These outputs include the altitude-dependent abundances of H₂O photochemically produced in, or transported to, the stratosphere (tropospheric H₂O is calculated by the climate model), CO₂, O₃, CH₄, O₂, N₂, and C₂H₆. The climate model uses the photochemical model's final state as its initial condition, and the models iterate in this manner until global convergence is reached. These coupling and convergence criteria are described in more detail in the work of Arney et al. (2016).

The photochemical portion of Atmos is based on the 1-D photochemical code originally developed by Kasting et al. (1979). The version we use here has been significantly modernized as described in the work of Zahnle et al. (2006) and can simulate a wide range of planetary redox states ranging from extremely anoxic (pO₂ = 10⁻¹⁶) to 100 bar of O₂ (Schwieterman et al., 2016). An organic haze formation scheme is in place for reducing, methane-rich atmospheres as described in the works of Pavlov et al. (2001), Zerkle et al. (2012), and Arney et al. (2016). For the simulations presented here, the model atmosphere is divided into 200 plane-parallel layers up to 100 km in altitude with a layer spacing of 0.5 km. Hydrostatic equilibrium is assumed. A vertical transport scheme includes molecular and eddy diffusion. Boundary conditions can be set for each species at the top and bottom of the atmosphere, including gaseous mixing ratios and/or fluxes in or out of the atmosphere. Radiative transfer in the photochemical model is done via a δ 2-stream method (Toon et al., 1989). The primary equations solved by the model are the continuity and flux equations, which are, in order,

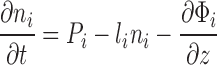and

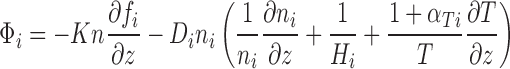where z is altitude (cm), t is model time (s), n_i is the number density (cm⁻³) of species i, P_i is chemical production rate (in molecules cm⁻³ s⁻¹), l_i is the chemical loss frequency (s⁻¹), Φ_i is the flux of species i (cm² s⁻¹), f_i is the mixing ratio of the species i (n_i/n), K is the eddy diffusion coefficient (cm² s⁻¹), n is the total density, D_i is the diffusion coefficient between the background atmospheres and species i, and α_Ti is the thermal diffusion coefficient between species i and the background atmosphere. H_i is the scale height of species i (note H = kT/m_ig). These equations are integrated by a variable timestep reverse Euler method appropriate for stiff systems. This method relaxes to the steady state solution when timesteps are large.

The climate portion of Atmos is based on the 1-D climate model originally developed by Kasting and Pollack (1983), Kasting et al. (1984a, 1984b), and Kasting and Ackerman (1986), but the version we use here has been significantly modernized and was recently used to simulate habitable zones around different stellar spectral types (Kopparapu et al., 2013). The model uses correlated-k coefficients to compute absorption by the spectrally active gases in the model, which include O₂, O₃, CO₂, H₂O, CH₄, and C₂H₆. The effects of pressure broadening (e.g., by N₂) are included in the model. The KSPECTRUM⁷ program was originally used to calculate the correlated-k coefficients using the HITRAN 2008 line lists (Rothman et al., 2009) and updated in the work of Kopparapu et al. (2013) with the HITEMP 2010 line lists (Rothman et al., 2010). As in the photochemical model, this climate model uses a δ 2-stream multiple scattering algorithm (Toon et al., 1989). The shortwave (absorbed stellar radiation) wavelength grid spans from λ = 0.2 to 4.5 μm in 38 spectral intervals; to compute outgoing longwave IR radiation, there is a separate set of correlated-k coefficients in 55 spectral intervals for each gas included in our scheme for wavenumbers 0–15,000 cm⁻¹ (λ > 0.67 μm). The density structure of the atmosphere is calculated assuming hydrostatic equilibrium. The tropospheric temperature profile is calculated by following a wet adiabatic lapse rate to the altitude at which the stratospheric temperature is reached (Kasting, 1988), except in desiccated cases, for which a dry adiabat is assumed. The water vapor distribution with altitude is determined by a Manabe and Wetherald (1967) profile with a surface relative humidity of 80% (Kasting and Ackerman, 1986). Gases in the upper atmosphere can have a heating or cooling effect on the temperature profile depending on the relative abundance of gases in the upper atmosphere and the extent of shortwave heating.

Note that we have been unable to run this climate model to a converged state using the same top-of-atmosphere pressure that the photochemical model has. The photochemical model grid extends to 100 km in altitude, but for 1 bar atmospheres, we are typically unable to run this climate model with pressures above 80 km in altitude at the top of the pressure grid due to model instabilities. Therefore, when this climate model passes its temperature and water profiles to the photochemical model, they are fixed at their values at the top of the climate grid, and they become isoprofiles above the top of this grid. Previous tests (Arney et al., 2016) suggest that this treatment does not strongly impact the resultant photochemistry.

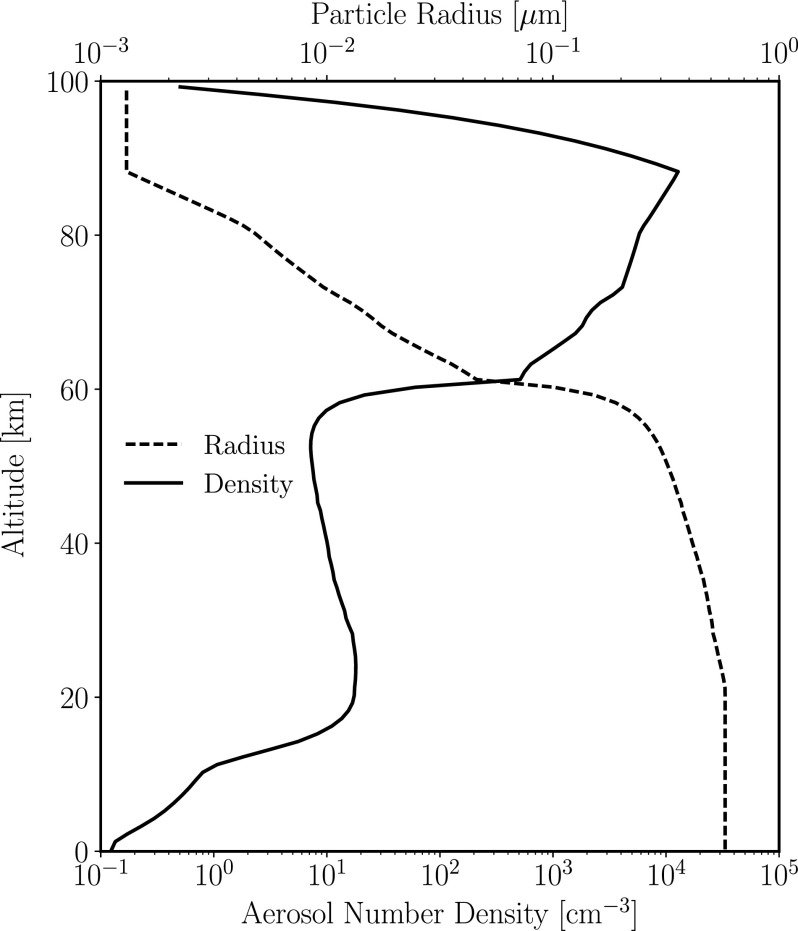
Organic haze particles, which are relevant to some of our simulations, form initially in the model with radii of 0.001 μm. In each layer, the particles are treated as monomodal distributions with the particle size determined by comparing the coagulation lifetime to the particle removal lifetime from the layer by sedimentation and diffusion processes. Particle growth in a layer occurs when the particle growth timescale is shorter than the timescale for particle removal.

Our model's organic haze particles are treated as fractal (rather than spherical) in shape in both the photochemical and climate portions of the Atmos model (Arney et al., 2016). Fractal particles are agglomerates of spherical particles, and studies of organic hazes in the laboratory (e.g., Trainer et al., 2006) and from observations of Titan (e.g., Rannou et al., 1997) suggest that fractal particles are more realistic for organic hazes compared to spherical particles. In particular, we treat our fractal particles as agglomerates of 0.05 μm spherical “monomers.” This size of monomer was chosen because it is similar to the size of the monomers of Titan's haze particles (Rannou et al., 1997; Tomasko et al., 2008), and it was the size used in the first study to simulate fractal hazes in an Earth-like atmosphere (Wolf and Toon, 2010), which our haze input files are based on. Haze scattering and absorption properties are calculated with Mie scattering for our sub-monomer particles (r < 0.05 μm), and the fractal mean-field approximation (Botet et al., 1997) for fractal particles (r > 0.05 μm). Our fractal haze scheme is based on that of Wolf and Toon (2010), and the fractal dimension of our particles varies from 1.5 to 2.4, with larger fractal particles having a larger fractal dimension to account for folding as the particles coagulate. Note that a fractal dimension of 1 describes a linear chain of monomers, and a fractal dimension of 3 describes a perfectly spherical particle. Titan's haze particles have a fractal dimension of about 2 (Rannou et al., 1997). The model includes a grid of optical property files for 51 particle sizes, and particle properties with radii in between grid sizes are defined by interpolating between the nearest grid size properties. A detailed description of our model's haze formation scheme can be found in the work of Arney et al. (2016).

3.7. Model inputs

To simulate planetary environments and observable properties, our models require information on the planetary and stellar characteristics, including stellar parameters and spectrum, planetary physical and orbital parameters, as well as environmental information such as the surface albedo, aerosol and atmospheric molecular absorption properties.

3.7.1. Planetary and stellar parameters

We use the best-fit minimum mass of 1.3 M_⊕ from the work of Anglada-Escudé et al. (2016) and adopt the silicate planet scaling law from the work of Sotin et al. (2007) to obtain a planetary radius of 1.074 R_⊕ (6850 km). Note that this assumes an edge-on, or nearly edge-on, inclination for the system, which is currently unknown. We adopt the best-fit semimajor axis for Proxima Centauri b of 0.0485 AU. We also assume the stellar radius is 0.141 R_⊙ (Boyajian et al., 2012). While the same stellar fluxes are used across our suite of models, the solar zenith angles (SZAs) used in each model were selected to best represent globally averaged behavior resulting from each. The standard SZAs used for Atmos modeling are SZA = 50° in the photochemical model (e.g., Kharecha et al., 2005; Zahnle et al., 2006, Segura et al., 2007) and SZA = 60° in the climate model (e.g., Kopparapu et al., 2013; Arney et al., 2017), and we use these values in our coupled approach here.

3.7.2. The stellar energy distribution of Proxima Centauri

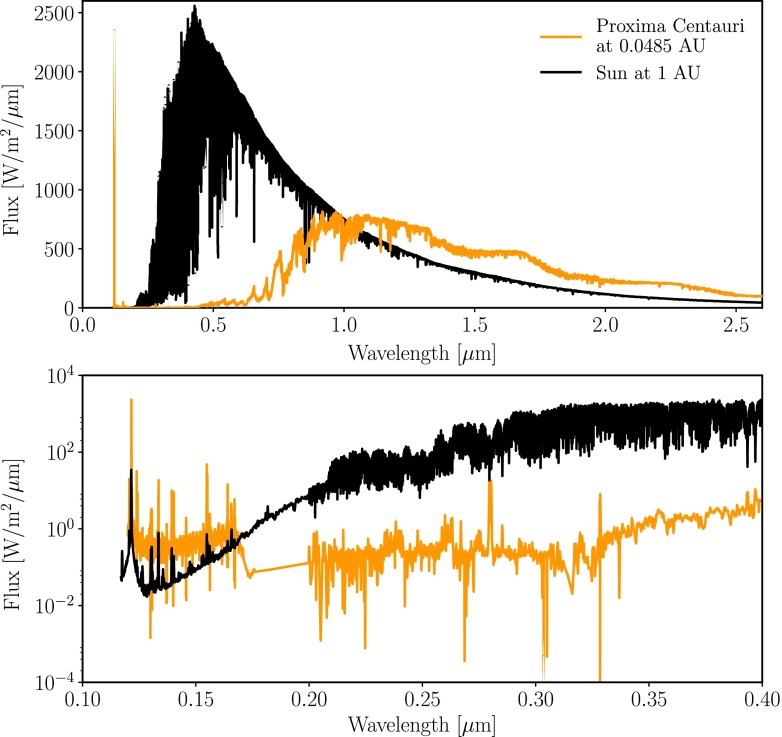
To self-consistently model the photochemistry, climate, and the expected reflectance and transmission spectra from Proxima Centauri b, an EUV to MIR input spectrum is required. Since Proxima Centauri is the nearest star to our Sun, many spectra have been recorded over the years, though no single source provided a calibrated, normalized spectrum for all necessary wavelengths at the time of this work. To facilitate our simulations, we compiled a self-consistent, panchromatic stellar spectrum representative of Proxima Centauri (Fig. 2) combining publicly available data downloaded from the Mikulski Archive for Space Telescopes (MAST)⁸ and MUSCLES⁹, with PHOENIX spectral library v2.0 models¹⁰ at wavelengths where calibrated observations are not yet publicly available (Husser et al., 2013).

FIG. 2.

The spectrum of Proxima Centauri (at the distance of planet b) compared to the solar spectrum. Proxima Centauri b receives about 0.66 times the insolation Earth receives at 1 AU from the Sun.

For UV wavelengths, we combined calibrated HST Space Telescope Imaging Spectrograph (STIS) observations and additional observations processed and compiled by the MUSCLES Treasury Survey. The STIS contribution (λ = 1200–1691 Å) was calculated as the median point at each wavelength of six available calibrated observations (HST Proposal ID: 8040). We used a reconstructed Lyman-α line and calibrated observations for λ = 1691–4569 Å, which were processed and compiled by the MUSCLES Treasury Survey and available on MAST, including details on their calibration methods (v2.1, see also France et al., 2016, and Youngblood et al., 2016). For the visible spectrum (λ = 4569–8499 Å), we used observations from the HST Faint Object Spectrograph (FOD/RD) (HST Proposal ID: 6059). The IR spectrum (λ > 8499 Å) was computed by a linear interpolation of PHOENIX spectral library v2.0 models (Husser et al., 2013) with T_eff = {3000 K, 3100 K} and [Fe/H] = {0.0, 0.5}. The PHOENIX spectrum terminates at 5.5 μm; to extend the spectrum deeper into the MIR for climate modeling and thermal phase curve analysis, we fit a blackbody from the tail of the PHOENIX spectrum to 30 μm. There is little stellar atmospheric absorption in this range and it is well-fit with a blackbody (Roellig et al., 2004; Mainzer et al., 2007). The combined spectrum was normalized to match Proxima Centauri's bolometric luminosity of L/L_⊙ = 0.00155 (Boyajian et al., 2012). Table 3 provides a summary of the sources for our combined spectrum. An important limitation to note for this spectrum is that it is a static representation of the star in its quiescent state and does not account for flare activity (i.e., Davenport, 2016). We have made our compiled spectrum publicly available in the Virtual Planetary Laboratory Spectral Database¹¹.

3.7.3. Input line lists

Our models use a variety of sources to compute gas absorption from line lists, collision-induced absorption coefficients, and UV-visible cross sections. The line lists are primarily from HITRAN 2012 (Rothman et al., 2013) for all species except for high-temperature applications for CO₂ and H₂O, for which we use Ames (Huang et al., 2014) and HITEMP 2010 (Rothman et al., 2010), respectively. Collision-induced absorption is used for CO₂-CO₂, O₂-O₂, and N₂-N₂. The CO₂-CO₂ absorption data, which are included in high-CO₂ models and cover a range of temperatures up to 700 K, are sourced from Moore (1971), Kasting et al. (1984a), Gruszka and Borysow (1997), Baranov et al. (2004), Wordsworth et al. (2010), and Lee et al. (2016). N₂-N₂ collision-induced absorption coefficients are calculated based on the empirical model from Lafferty et al. (1996) as described in Schwieterman et al. (2015b). The O₂-O₂ absorption coefficients are taken from C. Hermans¹² (Hermans et al., 1999) for the 0.333–0.666 μm range and from Greenblatt et al. (1990) and Maté et al. (1999) for the O₂-O₂ absorption at 1.06 μm and 1.27 μm, respectively. UV-visible cross section data is sourced from primary references available from the MPI-Mainz UV/VIS Spectral Atlas of Gaseous Molecules of Atmospheric Interest¹³.

3.7.4. LBLABC

A companion to SMART, the Line-By-Line Absorption Coefficients (LBLABC) code generates pressure- and temperature-dependent, line-by-line absorption coefficients using input line lists as described above (e.g., HITRAN) for given gas mixing ratio profiles (Meadows and Crisp, 1996). LBLABC fully resolves the narrow line cores and wings as far as 1000 cm⁻¹ from the line center and is designed and validated for a wide range of pressures (10⁻⁵ to 100 bar) and temperatures (130–750 K). Unless otherwise specified, a maximum line profile width of 1000 cm⁻¹ is used.

3.7.5. Surface spectral albedo inputs

For Lambertian scattering planetary surfaces, we chose surface spectral albedos to be consistent with the likely surface conditions for the type of atmosphere modeled: basalt, desert, ice, seawater, martian global average, or a composite surface albedo spectrum. The pairing of surface and atmosphere for our experimental scenarios is given in Table 7 in Section 4.2. For modern Earth-like cases, a weighted composite spectrum was used that consists of 65.6% seawater, 13.6% grassland/brush, 4% conifer forest, 5.5% soil/desert (kaolinite), and 11.3% snow/ice, based on a diurnally averaged equatorial Earth view during spring equinox (composite 1; Robinson et al., 2011). For early Earth-like cases, we used a similar composite spectrum with land vegetation removed: 65.6% seawater, 23.1% soil/desert, and 11.3% snow/ice (composite 2). The globally averaged Mars spectrum was compiled by Crisp (1990), who used available observations and laboratory measurements of Mars analog surface materials. The forest spectrum was taken from the ASTER spectral library (Baldridge et al., 2009), while all other surface spectra were taken from the USGS spectral library (Clark et al., 2007). In the subset of cases that included glint, we used the Cox and Munk (1954) glint model as described by Robinson et al. (2010, 2011). Figure 3 shows each of the spectral albedo inputs used over the wavelength range 0.2–2.5 μm.

Table 7.

A Summary of Our Modeled Planetary States, Their Environmental Parameters, and Derived Surface Temperatures

Planet	Surface albedo	Type(s) of haze/clouds	Atmospheric gases	Surface pressure (bar)	Surface temperature (K)
“wet” high O2	Composite 2	None	95% O2, 0.5% CO2 + H2O, N2, trace CO, trace O3	10	318
“dry” high O2	Desert	None	95% O2, 0.5% CO2, N2, trace CO, trace O3	10	256
Evolved O2/CO2	Desert	None	45% CO2, 45% O2, N2, trace CO, trace O3	10	383
Evolved O2/CO2	Desert	None	45% CO2, 45% O2, N2, trace CO, trace O3	90	569
Venus-like 10 bar	Basalt	H2SO4	CO2, 20 ppm H2O	10	379
Venus-like 90 bar	Basalt	H2SO4	CO2, 20 ppm H2O	90	640
Desiccated CO2-dominated	Mars average	None	CO2, O2, CO, trace O3	1	254
Preindustrial Phanerozoic Earth	Composite 1	25% water, 25% ice clouds	78% N2, 21% O2, 280 ppm CO2, 53 ppb H2, 500 ppb CH4, 50 ppb CO, 260 ppb N2O, H2O, O3	1	288
Earth-like Proxima Centauri b	Composite 1	25% water, 25% ice clouds	73% N2, 21% O2, 5% CO2, 53 ppb H2, 2330 ppm CH4, 194 ppm CO, 2.3 ppm N2O, H2O, O3	1	273
Haze-free Archean analogue	Composite 2	water, ice clouds	5% CO2, 1% CH4	1	278
Hazy Archean analogue	Composite 2	water and ice clouds, organic haze	5% CO2, 1.5% CH4	1	277

A more detailed description of the surface albedo types is given in Section 3.7.5. Details of the aerosols used are given in Tables 3 and 4. The surface temperature results are presented in Section 4.2. Note the “Preindustrial Phanerozoic Earth” case represents a fiducial comparison case of actual Earth and was not simulated for a world orbiting Proxima Centauri.

FIG. 3.

Input spectral surface albedos for modeled planetary scenarios. Composite 1 is a weighted average of 65.6% seawater, 13.6% grassland/brush, 4% conifer forest, 5.5% soil/desert (kaolinite), and 11.3% snow/ice. Composite 2 is 65.6% seawater, 23.1% soil/desert, and 11.3% snow/ice. All surface spectral albedos are sourced from the USGS spectral library (Clark et al., 2007), except for the conifer forest, which is from the ASTER spectral library (Baldridge et al., 2009).

3.7.6. Aerosol inputs

Aerosols such as hazes and clouds are incorporated into SMART by providing input containing the altitude-dependent opacities as well as the phase function or particle asymmetry parameter (g) and the extinction, scattering, and absorption efficiencies (Q_ext, Q_scat, and Q_abs). For spherical particles, a full Mie phase function is used; otherwise we use a Henyey-Greenstein phase function (Henyey and Greenstein, 1941). We simulate aerosols in several of our planetary atmospheres: these include organic hazes, sulfuric acid clouds and haze, and water vapor clouds. Table 4 summarizes the aerosol types used in simulated atmospheres.

Table 4.

Summary of Aerosols Used in Our Models

Aerosol type	Optical constants	Particle shape	Particle size (μm)	References
H2SO4	Palmer and Williams, 1975	Spherical	0.49–3.85	Crisp, 1986
Organic haze	Khare et al.,1984	Fractal	0.001–0.5	Botet et al.,1997
Stratocumulus cloud	Hale and Querry, 1973	Spherical	4.07	Wiscombe, 1980; Crisp, 1986
Cirrus cloud	Heymsfield et al.,2002	Columns, plates, rosettes	100a	Baum et al.,2005

^aCross-section weighted mean diameter.

Where we simulate organic hazes, particles of radii >0.05 μm are treated as fractal aggregates of 0.05 μm monomers using the fractal mean-field approximation (Botet et al., 1997), and we use the hydrocarbon refractive indices measured by Khare et al. (1984). The particle sizes, number densities, and vertical distributions for organic hazes used as inputs to the SMART model are derived from our Atmos simulations. Atmos calculates a monomodal size distribution of particles in each layer. The particle size is determined by comparing the particle coagulation lifetime to the timescale for removal from the layer by sedimentation and diffusion processes. Growth occurs when the timescale for coagulation is shorter than the timescale for particle removal. To decrease model run-time for SMART, we bin the many dozens of particle sizes generated by Atmos into 19 particle size bins. Spherical mode particles have radii of 0.001, 0.005, 0.01, and 0.05 μm. Fractal modes particles have radii of 0.06–2 μm: this includes four modes between 0.06 and 0.1 μm, 10 equally spaced modes between 0.1 and 1 μm, and 2 μm.

We also simulate sulfuric acid clouds and hazes in our Venus-like spectral models. Our nominal venusian cloud profiles and particle size populations are based on an empirical Venus cloud model from Crisp (1986). Sulfuric acid refractive indices are derived from Palmer and Williams (1975). The sulfuric acid cloud particle populations are modeled with log-normal size distributions, and the optical efficiencies are calculated by using the code “Miescat” adapted from the code by Wiscombe (1980). Table 5 shows the properties of the Venus cloud particle populations used here. Four particle size populations (called “Modes” in Table 5) are assumed.

Table 5.

Venus Cloud Particle Properties (from Crisp, 1986)

Mode	Effective radius (μm)	Variance
1	0.49	0.22
1.4	1.05	0.16
2	1.4	0.207
3	2.85	0.262

Water vapor (stratocumulus) clouds are modeled by using refractive indices from Hale and Querry (1973). Stratocumulus clouds are modeled with a two-parameter gamma distribution with a = 5.3, b = 1.1, and a mean particle radius of 4.07 μm. Cirrus cloud properties are modeled by using data from B. Baum's Cirrus Optical Property Library (Baum et al., 2005)¹⁴. The optical properties of the cirrus clouds originate from a 45-bin size distribution of three types of ice particle shapes including a weighting of 50% solid columns, 35% plates, and 15% 3-D bullet rosettes. The distribution of cloud particle sizes ranges from 2 to 9500 μm, but the cross-section weighted effective diameter of the distribution used is 100 μm. Patchy clouds on a disk-integrated spectrum are included in the 1-D SMART model by using a weighted average of 50% clear-sky, 25% cirrus cloud, and 25% stratocumulus cloud.

4. Results

To explore possible current environmental states for Proxima Cen b, we present self-consistent atmospheres with constituent vertical mixing ratios and temperature-pressure profiles for the planetary states discussed in Section 2. Most of the simulations presented here are photochemically and climatically self-consistent unless otherwise noted. Following generation of these atmospheres, we simulate phase curves and direct imaging and transmission spectra for these cases. We then outline observational considerations and discuss detectability of spectral features that may be able to discriminate evolutionary histories, current habitability, and biosignatures.

4.1. Comparison with existing 3-D GCM simulations

Our 1-D climate models are computationally efficient and radiatively rigorous but can only approximate the 3-D feedbacks and heat transport processes that can be modeled in detail with 3-D GCMs. Additionally, although we have validated our models on planets in our solar system, the likely evolution of Proxima Centauri b may result in current conditions that differ from those of Earth and Venus. To provide further validation for our model, we compare our results with existing 3-D studies for both Earth-like and non-Earth-like atmospheres. A summary of these comparisons is given in Table 6.

Table 6.

A Comparison of Global Average Surface Temperatures of Our 1-D Climate to 1-D and 3-D Model Results in the Literature

			Comparison result (K)
Atmosphere	Our model	Our result (K)	Asynchronous (3:2)	Synchronous (1:1)
1 bar CO2 (snow)	VPL Climate	264	266a	247a
4 bar CO2	VPL Climate	306	305a	289a
6 bar CO2	VPL Climate	320	324a	309a
1 bar N2, 376 ppm CO2	VPL Climate	238	238a	220a
1 bar N2, 376 ppm CO2, water	VPL Climate	249 (moist adiabat) 257 (fixed H2O)	253a	252a
2% CO2, 0.02% CH4, water	Atmos	282	287b
6% CO2, water	Atmos	285.3	287.9c

^aTurbet et al. (2016), provided by M. Turbet (private communication).

^bCharnay et al. (2013).

^cWolf and Toon (2013).

We compare our new VPL Climate model with the recent work by Turbet et al. (2016), who used a 3-D GCM in a similar study examining the climate of Proxima Centauri b. Although our study's companion paper and the companion paper of Turbet et al. (2016) argue for synchronous rotation as a likely scenario for Proxima Centauri b (Barnes et al., 2018; Ribas et al., 2016), they also note that if Proxima Centauri b has an eccentricity >0.06 or has a companion planet perturbing its orbit, the planet would likely be in a 3:2 spin-orbit resonance. Turbet et al. (2016) demonstrated this resonance results in a longitudinally uniform atmosphere. Since 1-D models implicitly assume a rapidly rotating planet, to calculate a globally averaged surface temperature, the most appropriate comparison for our 1-D models is with the 3:2 spin-orbit results of the 3-D models, although we have also provided their 3-D modeling results for synchronous rotation for comparison, when these were available. First, we assume a rapidly rotating Proxima Cen b and compare our results with the asynchronous 3:2 spin-orbit resonance results from Turbet et al. (2016). The atmospheres selected for comparison include pure CO₂ atmospheres and N₂-dominated atmospheres with trace CO₂. The pure CO₂ cases are for 1, 4, and 6 bar atmospheres. The N₂ cases consist of 1 bar N₂ with 376 ppm CO₂, either without or with water. For the latter case, we begin with the water mixing profile provided by M. Turbet (personal communication) to enable a close comparison. We use a surface albedo of 0.20 from 0–5μm (CO₂ cases) or the idealized wavelength-dependent snow/ice albedo taken from Turbet et al. (2016, their Fig. 2, lower panel) (N₂ cases), and a solar zenith angle of 60 degrees, which approximates the diurnal average in our 1-D model.

Our VPL Climate model appears to be in reasonable agreement with the LMDz model used by Turbet et al. (2016) for the test cases chosen, with at most a discrepancy of 5 K between the surface temperatures derived by the models for similar inputs. However, thin atmospheres depend very strongly on the surface albedo and water vapor profile assumptions. For the pure CO₂ cases, our results agree well with the 3:2 spin-orbit resonance cases of Turbet et al. (2016). We find global average surface temperatures of 264, 306, and 320 K, compared with 266, 305, and 325 K from Turbet et al. (2016) for 1, 4, and 6 bar of CO₂, respectively. For CO₂ cases, these temperatures agree between the models to within 5 K. For the dry 1 bar N₂, 376 ppm CO₂ atmosphere, we agree with Turbet et al. (2016) that this CO₂ amount is insufficient to maintain a globally averaged surface temperature above freezing (we found this initially with an albedo of 0.20 as well, representative of a warm surface). Before comparing the Earth-like (N₂) cases, it is important to point out that surface albedo has a drastic impact on surface temperatures. For example, Godolt et al. (2016) used an updated version of the 1-D Atmos climate model under Earth-like assumptions, and depending on the surface albedo and humidity profile, they produced a range of climates including glaciation and moist greenhouse, spanning 196.4–354.2 K. With VPL Climate, we have also found a strong dependence on surface albedo and water profile. When we use the same albedo assumptions as Turbet et al. for the dry N₂ case with 376 ppm CO₂ we obtain a surface temperature of 238 K, the same as Turbet et al. (see their Fig. 3; private communication, M. Turbet). For the 1 bar N₂ case with 376 ppm CO₂ and H₂O, we calculate a globally averaged surface temperature of 249 K using a fully saturated moist adiabat and 257 K using the globally averaged water mixing ratios from Turbet et al., which compares to 253 K from Turbet et al. (private communication, M. Turbet). Consequently, our surface temperatures are all within ∼5 K of Turbet et al.'s results for the 3:2 spin-orbit cases, and we can reasonably reproduce the global average temperatures of the LMDz GCM for the nonsynchronously rotating planets.

We also show for comparison the globally averaged surface temperatures for the synchronously rotating results of Turbet et al. (2016; M. Turbet, private communication). Our 1-D globally averaged results for dry planets are systematically warmer than the 3-D synchronously rotating cases by 11–18 K. However, our comparison with the wet, Earth-like planet shows only a 3 K difference between the 1-D model and the synchronously rotating case, although, again, for these 1 bar atmospheres, the surface temperature is strongly dependent on water vapor profiles and surface albedos. These results show that the 1-D models are a reasonable match for the 3-D asynchronous result and typically sit between the synchronous and asynchronous 3-D results, which are systematically cooler. Comparable results for exoplanets with 1-D and 3-D models for relatively rapid rotators have been previously shown (Yang et al., 2014) and also for synchronously rotating planets (Godolt et al., 2016), although the latter results are strongly dependent on the assumed surface albedo and water vapor profile. It is also important to note that many 3-D GCM results do not use ocean heat transport, which can be very efficient at reducing day-night temperature differences and potentially deglaciating the nightside of tidally locked planets (Hu and Yang, 2014). Three-dimensional models with ocean heat transport may produce results closer to 1-D results.

We have also previously compared our 1-D Atmos climate model to the temperatures produced by the LMDz GCM and the CAM GCM for Archean Earth-like planets in the work of Arney et al. (2016). For a planet with 2% CO₂, 0.02% CH₄, and a surface albedo of 0.33, the LMDz model produces a global average temperature of 287 K (Charnay et al., 2013), which is 5 K warmer than our model's 282 K for this type of planet. For a planet with 6% CO₂, no CH₄, and an average albedo of 0.317, the CAM model produces a global average temperature of 287.9 K (Wolf and Toon 2013), and our model produces an average temperature of 285.3 K, a difference of 2.6 K. These comparable cases suggest that our 1-D Atmos climate model can produce similar temperatures to GCM models, at least for nonsynchronously rotating planets.

4.2. Temperatures and atmospheres

In this section, we show the simulated atmospheres and resulting temperature profiles for the end states of the evolutionary scenarios described in the work of Barnes et al. (2018), including stages throughout the possible evolutionary sequence from O₂-rich to CO₂-rich atmospheres, and possible habitable planetary environments. A summary of the planetary states considered, including atmospheric composition, surface pressure, and surface albedo, is given in Table 7.

4.2.1. O₂-rich atmospheres

If Proxima Centauri b formed in situ, the extended pre-main sequence phase of its star may have driven substantial water loss and the buildup of potentially hundreds of bar of O₂ (Luger and Barnes, 2015; Barnes et al., 2018). The total O₂ generated depends on several parameters, including the initial volatile inventory of the planet and the rate of destruction or sequestration by geological processes, but plausible scenarios exist where substantial quantities of abiotic oxygen remain in the planet's atmosphere either alongside a remnant liquid water ocean or after complete desiccation of the planet (Barnes et al., 2018).

We used Atmos to self-consistently model the climate and trace gas abundance for two post-runaway, high-O₂ scenarios. In both cases the total pressure of the atmosphere is 10 bar, with 95% O₂ and 0.5% CO₂ by volume (N₂ is a filler gas, constituting the remaining atmospheric volume at each altitude level once all other major and trace gas species are accounted for). In the first high-O₂ case, we assume an ocean remains on the surface with a water vapor profile as described in Section 3.6 (i.e., it is “wet”). In the second case, we assume complete desiccation of the atmosphere and no surface ocean. The choice of 10 bar is motivated by a conservative compromise between the prediction of up to several hundreds of bar of O₂ (Barnes et al., 2018), uncertainties regarding the capacity of effects such as ozone shielding to arrest O₂ buildup, and the extent to which a magma ocean may assimilate that O₂ (Schaefer et al., 2016). A 0.5% CO₂ mixing ratio is assumed for consistency in total CO₂ abundance (mixing ratio times surface pressure) with the modern and Early Earth scenarios described below, which have 5% CO₂ in a 1 bar atmosphere.

Figure 4 shows the temperature and gas mixing ratio profiles for these two cases. The primary differences between the “wet” and desiccated cases, other than the presence and absence of water vapor, are the surface temperatures and O₃ profiles. The surface temperature for the “wet” case is 318 K versus 256 K for the desiccated scenario due to the significant greenhouse impact of water vapor, which is enhanced by pressure broadening effects in the 10 bar atmosphere (e.g., Goldblatt et al., 2009). The presence of water vapor also significantly impacts the O₃ profile, because OH radicals that are primarily formed via interactions between O¹D and water vapor (O¹D + H₂O → 2OH) are efficient at O₃ destruction. Thus, O₃ can build up to significantly higher levels in the desiccated atmosphere, especially near the surface where the H₂O mixing ratio would otherwise be high.

4.2.2. CO₂-rich atmospheres

Although a remnant O₂ atmosphere from massive H escape is possible, if the planet is volcanically active, and lacks a large surface reservoir of water, then the atmosphere may evolve so that significant amounts of both CO₂ and O₂ exist simultaneously in the atmosphere (Section 4.2.2.1). The O₂ would originate from water loss during the pre-main sequence (Luger and Barnes, 2015) and the CO₂ from outgassing from the planetary interior. In the absence of liquid water, the outgassed CO₂ would be unlikely to be dissolved into bodies of water, bound into carbonates, and returned to the mantle, as sequestration by the carbonate-silicate cycle (Walker et al., 1981) requires an active hydrological cycle. In our own solar system, it has been suggested that Venus could have had an O₂- and CO₂-dominated atmosphere today if it had formed with a larger water inventory (Chassefière et al., 1996a). However, if that water inventory is not initially present, or if sufficient time has elapsed that the planet has been able to sequester or lose its O₂, then the planet may be more Venus-like (Section 4.2.2.2) with a CO₂-dominated and largely desiccated atmosphere (< 40 ppm of H). Ultimately, the atmosphere may become heavily H depleted, and in that case, a photochemical equilibrium will develop between O₂, CO, and CO₂ (Gao et al., 2015; Section 4.2.2.3). We model these three cases below for Proxima Centauri b using the VPL Climate model, which is able to simulate massive high-CO₂, high-temperature atmospheres, coupled with the Atmos photochemistry model.

4.2.2.1. Evolved O₂/CO₂ atmospheres

We calculate the photochemistry and climate for 10 and 90 bar mixed CO₂ and O₂ cases. These atmospheres consist of 45% CO₂, 45% O₂, with the remainder comprised of N₂ and photochemically generated trace gases (primarily CO and O₃). We assume a desiccated atmosphere and an initial vertical profile for water vapor consistent with Venus' (∼30 ppmv at the surface). We coupled the photochemical component of Atmos to the VPL Climate model to calculate the self-consistent gas mixing ratios and temperature profiles given in Fig. 5. The photochemically modeled species shown in Fig. 5 (O₂, O₃, CO₂, H₂O, and CO) and the resultant temperature profile from the climate model were passed between the models until global convergence was achieved. Here, the hypothetical 10 bar O₂-CO₂ atmosphere for Proxima Centauri b would produce a surface temperature of 383 K, while the 90 bar case has a surface temperature of 569 K. Neither of these atmospheres would be habitable due to the high surface temperature and the lack of surface water.

FIG. 5.

Temperature (top axes; black dashed) and gas mixing ratio profiles (bottom axes) for a 10 bar (left) and 90 bar (right) O₂-rich and CO₂-rich atmosphere with 45% CO₂, 45% O₂, and ∼10% N₂.

4.2.2.2. Venus-like atmospheres

Venus is our nearest planetary neighbor and represents a class of worlds that may be common throughout the Galaxy (Kane et al., 2014). Studies have suggested that Venus was more Earth-like in its past, possibly with liquid water as inferred from its high D/H ratio (McElroy et al., 1982; Donahue and Hodges, 1992). However, the interpretation of Venus with early liquid water has been called into question by other studies (Grinspoon, 1993; Hamano et al., 2013). Still, desiccation of exoplanets with liquid water by the runaway greenhouse mechanism (Ingersoll, 1969; Kasting and Pollack, 1983; Kasting et al., 1984b; Kasting, 1988; Goldblatt and Watson, 2012; Goldblatt et al., 2013) is likely a common process. This may have occurred on Proxima Centauri b during its star's pre-main sequence phase (Luger and Barnes, 2015) as discussed above. If Proxima Centauri b underwent a runaway greenhouse and lost both its hydrogen and oxygen (e.g., Schaefer et al., 2016; Airapetian et al., 2017), or if it formed without liquid water in the first place (Hamano et al., 2013), then outgassed CO₂ over the last several billion years would have remained in and dominated the atmosphere, and it may be Venus-like.

VPL Climate was used to generate temperature pressure profiles for 10 and 90 bar CO₂ atmospheres with the Venus water vapor vertical mixing ratio profile (e.g., Pollack et al., 1993; Chamberlain et al., 2013; Arney et al., 2014). As in the work of Lee et al. (2016), we also include trace gases SO₂ and OCS (200 ppmv and 35 ppmv at the surface, respectively), which are active greenhouse gases in spectral regions between CO₂ lines. Figure 6 shows the compositions of our Venus-like atmospheres. We specified these gases initially consistent with Venus. Note that the climate simulations in this case are not photochemically self-consistent, nor do they include self-consistent cloud formation or the unknown UV absorber, but they are useful as a first-order approximation of a Venus-like atmosphere for Proxima Centauri b. Our simulations indicate that if Proxima Centauri b had a 10 bar Venus-like atmosphere, its surface temperature would be 385 K; for a 90 bar Venus-like atmosphere, the surface temperature climbs to 654 K. Both are unlikely to be habitable.

FIG. 6.

Temperature (top x axes; black dashed) and gas mixing ratio profiles (bottom x axes) for a 10 bar (left) and a 90 bar (right) Venus-like, CO₂ atmosphere. The H₂SO₄ saturation mixing ratio profile is shown as the black dotted curve, which traces the true H₂SO₄ mixing ratio for much of the atmosphere, indicating that H₂SO₄ is fully saturated and clouds could condense. The differences in gas mixing ratio profiles between these two atmospheres are due to adjustments made to coincide with the regions of cloud formation. Like Venus, H₂SO₄ aerosols are present down to approximately 10 bar in both cases. The temperature profiles are similar above 0.1 bar, where atmospheres are generally optically thin, but the 90 bar atmosphere reaches much hotter temperatures at the surface due to the longer dry adiabat.

If Proxima Centauri b outgasses volcanic SO₂, it may be able to produce sulfuric acid (H₂SO₄) haze and cloud. In Venus' atmosphere, H₂SO₄ aerosols are generated photochemically through reactions such as (Yung and DeMore, 1982)

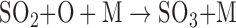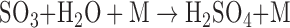Note that the formation of H₂SO₄ requires the presence of H₂O to react with SO₃. Sulfuric acid aerosols therefore cannot form if the atmosphere is completely water-free. Sulfuric acid is an efficient desiccant, so water in the Venus cloud deck gets trapped in the H₂SO₄ droplets, producing a concentrated solution of H₂SO₄ and H₂O. To estimate where a cloud deck could form in our Venus-like atmospheres, we calculated a H₂SO₄ saturation vapor pressure curve following the method described in the work of Gao et al. (2014). We assume an H₂SO₄ vapor mixing ratio of 4 ppm in the lower atmosphere, similar to measurements in Venus' atmosphere (Parkinson et al., 2015), and a cloud droplet acid concentration of 85%, also similar to Venus' (e.g., Barstow et al., 2012).

The intersection of the saturation vapor pressure curves and the temperature-pressure profiles in Fig. 6 shows where H₂SO₄ condensation would occur; a similar technique has been used before to predict cloud condensation in the context of other exoplanets, such as GJ 1214b (Miller-Ricci Kempton et al., 2012). In the 10 bar CO₂ atmosphere, we find that H₂SO₄ condensation can potentially occur throughout the atmosphere, including at the surface. In a 90 bar CO₂ atmosphere, cloud condensation would occur at a pressure of about 5.5 bar, or 25 km in altitude. Since we are not computing photochemistry for these Venus-like atmospheres, we adjust the H₂O, SO₂, and OCS mixing ratios to be consistent with where the cloud deck forms (i.e., all three of these trace gases have lower abundances above the cloud deck than below).

To implement these sulfuric acid cloud decks in our model, we applied a scaling to the Venus cloud model of Crisp (1986) to move the base of the cloud deck to our predicted pressure, shifting the pressures of the entire cloud deck accordingly. However, this procedure does not include feedbacks on the atmospheric temperature structure from the formation of this H₂SO₄ deck. The clouds and haze of Venus reflect over 70% of the total incident solar radiation back to space, and the residual insolation passing through the cloud deck is strongly absorbed. The SMART model shows that only about 3% of the incident radiation at the top of the cloud deck ever reaches the surface of this atmosphere. The clouds themselves are effective absorbers of reradiated longwave radiation for wavelengths longer than 2.7 μm, contributing to the Venus greenhouse (Crisp, 1986). These effects would combine to change the temperature structure of the atmosphere with a cloud deck in place, compared to the temperature profiles shown in Fig. 6.

Future studies of the possibility of H₂SO₄ clouds on Proxima Centauri b should include self-consistent coupled climate-photochemical modeling of the processes that produce H₂SO₄ to determine the efficiency of H₂SO₄ production under Proxima Centauri's UV SED. Our photochemical model cannot currently simulate Venus-like atmospheres, so we were unable to do this here. However, we ran a test of photochemical H₂SO₄ production in an Earth-like atmosphere with the photochemical model for the net reaction SO₃ + H₂O → H₂SO₄. We find that Proxima Centauri's spectrum is less efficient at forming H₂SO₄ by about a factor of 10 compared to an equivalent planet orbiting the sun, and it is also roughly an order of magnitude more efficient at photolytically destroying the precursor molecule SO₃. On Earth, SO₂ oxidation to SO₃ is typically the bottleneck that controls the rate of formation (Lizzio and DeBarr, 1997), rather than the destruction of SO₃ seen for the M dwarf planet. While this may not necessarily preclude the formation of an H₂SO₄ cloud deck on a Venus-like Proxima Centauri b, it suggests that our climate simulations without H₂SO₄ clouds may be reasonable. We include the clouds in our spectral simulations to show the challenges of detecting gaseous spectral features on a cloud-enshrouded Venus-like world.

4.2.2.3. Desiccated CO₂ atmosphere in photochemical equilibrium

In the terrestrial planets of the Solar System, including Venus and Mars, O₂ from CO₂ photolysis does not form a significant fraction of the atmosphere. This is because photolyzed CO₂ is efficiently reformed via recombination reactions catalyzed by Cl and HO_x species (e.g., Yung and DeMore, 1982), with the latter sourced from atmospheric water vapor. If a CO₂-rich atmosphere on a planet orbiting an M dwarf becomes severely desiccated (<1 ppm of total H, significantly lower than on Venus today), then the catalytic recombination of CO₂ after photolysis is inhibited, and within ∼1 million years the planet could form an atmosphere that contains high fractions of CO₂, CO, and O₂ (Gao et al., 2015). Since Proxima Centauri b likely suffered from extreme water loss if it formed in situ (Barnes et al., 2018; Ribas et al., 2016), including possible tidal desiccation of its mantle (Barnes et al., 2018), this scenario is also a plausible end state for its atmosphere.

However, the Atmos photochemical model cannot reproduce these types of atmospheres, as it treats CO₂ as an “inert” species, and the mixing ratio is fixed as an isoprofile. Therefore, to incorporate this scenario into the range of cases we explore, we use intermediate case 4 (0.0320 ppm hydrogen) mixing ratios from Gao et al. (2015), shown in Fig. 7. To determine the equilibrium state of this scenario, Gao et al. (2015) assumed a surface temperature of 240 K, an initial inventory of 1 bar of CO₂ and a given hydrogen abundance (i.e., for case 4, 0.0320 ppm mole fraction of H contained in all H-bearing species), an instellation of 1 S_⊙, and used the UV spectrum of GJ 436 (spectral type M2.5 V; Butler et al., 2004) from France et al. (2013). Photolysis destroyed ∼50% of CO₂, predominantly into CO and O₂ (see Fig. 7). We use the Mars average surface albedo (Crisp, 1990). We find the equilibrium surface temperature for this scenario is 257 K, which, when combined with the severe lack of water, means that this scenario is not habitable. For this particular case, the photochemistry is derived from Gao et al. (2015) and so is not self-consistent with the SED of Proxima Centauri, although the VPL Climate model was used to self-consistently calculate the expected temperature profile for Proxima Cen b, for the specified atmospheric composition.

FIG. 7.

Temperature (top x axis; black dashed) and gas mixing ratios (bottom x axis) for a desiccated CO₂/O₂/CO atmosphere. CO₂, O₂, and CO are the most abundant gases and result from photochemistry of outgassed CO₂. Only major and spectrally observable gases are shown. The temperature profile is the result of VPL Climate using the gas mixing ratio values of Gao et al. (2015; case 4).

4.2.3. Habitable terrestrial atmospheres

If Proxima Centauri b is a “habitable evaporated core” (Luger et al., 2015) that migrated from farther away from the star to its current position, or if it formed in situ with a 1% H₂ envelope, it could have escaped desiccation during its star's pre-main sequence superluminous phase, and it may be a planet hospitable to life. However, depending on where it formed in the protoplanetary disk, and its subsequent evolution, it could be either oxygen-rich or more reducing—as our own Earth's atmosphere has been over time. Here, we model two terrestrial planet examples for a modern, oxidizing Earth-like atmosphere and a more reducing Archean early Earth-like atmosphere.

4.2.3.1. M dwarf modern Earth-like atmosphere

If it survived the pre-main sequence phase and was endowed with and retained sufficient volatiles, Proxima Centauri b's atmosphere could be Earth-like (Barnes et al., 2018; Ribas et al., 2016), with a high-molecular-weight, secondary (outgassed) atmosphere consisting of N₂, CO₂, and H₂O, and, if oxygenic photosynthesis evolved, O₂. However, even if Proxima Centauri b were Earth-like in all other respects, the different SED of its host star would significantly impact its photochemistry and therefore the mixing ratios of trace gas species such as O₃, CH₄, CO, and N₂O, given the same fluxes into the atmosphere and abundances of major species (e.g., Segura et al., 2003, 2005, 2007, 2010; Rugheimer et al., 2015). Additionally, Proxima Centauri b's lower total instellation (0.65 S_⊙) would require higher greenhouse gas abundances to achieve the same globally averaged surface temperature as Earth, though this is partially ameliorated by the shift of the stellar SED to red wavelengths and the corresponding decrease in overall planetary albedo (Kopparapu et al., 2013).

We construct a hypothetical, “modern Earth” atmosphere for Proxima Centauri b that is consistent with the spectrum from the M5.5V host star, following the methodology of Segura et al. (2005). We determined the fluxes of trace gas species, like CH₄, required for the photochemical model to produce the “modern” preindustrial (assuming no anthropogenic sources) mixing ratios for an Earth-Sun case and then applied those gas surface fluxes to determine the mixing ratios for the Proxima Centauri b atmosphere, given the substantially different UV spectrum of the star. CO₂ and H₂ mixing ratios were fixed at 280 ppm and 53 ppb, and the preindustrial mixing ratios from which we derived the surface fluxes were 500 ppb (CH₄), 50 ppb (CO), and 260 ppb (N₂O), all based on ice core data (Haan and Raynaud, 1998; Flückiger et al., 2002; Solomon et al., 2007). (The modern-day mixing ratios—which include anthropogenic sources—are considerably higher, being 1834, ∼100, and 328 ppb, respectively [Blasing, 2016]). The fluxes required to reproduce the lower, preindustrial mixing ratios in our model for modern Earth orbiting the Sun are 5.6 × 10¹⁰ molecules/cm²/s (CH₄), 1.91 × 10¹¹ molecules/cm²/s (CO), and 8.8 × 10⁸ molecule/cm²/s (N₂O), respectively. These molecular fluxes correspond to yearly mass fluxes of 272 Tg/yr for CH₄ (about half the modern value of ∼600 Tg/yr), 1620 Tg/yr for CO, and 11.8 Tg/yr for N₂O. These values are consistent with independent estimates of the fluxes of these gases before the industrial era (Etheridge et al., 1998; Kroeze et al., 1999), though we note that the sources and sinks for these gases also varied naturally through time. In both the modern, preindustrial Earth and Proxima Centauri b cases, we assume a volcanic flux of H₂S of 1.0 × 10⁸ molecules/cm²/s and a flux of SO₂ of 1.0 × 10⁹ molecules/cm²/s.

We applied these fluxes self-consistently to Proxima Centauri b with the coupled Atmos model described in Section 3.6, assuming that the biological and abiotic flux of these gases scales with surface area. We also prescribed a surface pressure of 1 bar, an O₂ mixing ratio of 21%, a CO₂ mixing ratio of 5% (to warm the planet and partially compensate for lower instellation), and an N₂ mixing ratio of 73%. This prescription produced surface mixing ratios of 2330 ppm (CH₄), 194 ppm (CO), and 2.3 ppm (N₂O). We used Atmos to calculate self-consistent profiles for H₂O, O₃, and temperature, and obtained a surface temperature of 273 K, which is at the freezing point of water. However, 3-D GCM studies have shown that Archean Earth can maintain an open ocean fraction of >50%, and thereby remain habitable, for globally averaged surface temperatures as low as 260 K (Wolf and Toon, 2013; Arney et al., 2016), and an equatorial belt of open ocean may also be possible for globally averaged surface temperatures as low as ∼250 K (Charnay et al., 2013). The spectral output of late-type M dwarfs is concentrated in the NIR, where water ice is strongly absorbing, and this interaction can also work to maintain open ocean at cooler temperatures (Shields et al., 2013). Figure 8 compares the gas and temperature mixing ratio profiles for preindustrial concentrations of biogenic trace gas species on modern Earth (Fig. 8, left panel) with those expected for Proxima Centauri b given similar bulk atmospheric constituents (N₂, O₂) and fluxes of trace gas species into the atmosphere, but with 5% CO₂ (Fig. 8, right panel).

FIG. 8.

Temperature (top x axes; black dashed) and gas mixing ratio profiles (bottom x axes) for the preindustrial modern Earth orbiting the Sun (left) and a photochemically self-consistent Earth-like atmosphere for Proxima Centauri b (right). The mixing ratios of trace gas species CH₄, N₂O, and CO for Proxima Centauri b are determined from the flux required to produce their preindustrial concentration in Earth's atmosphere (see Section 4.2.3.1). Given the same fluxes as Earth, CH₄, CO, and N₂O would exist in Proxima Centauri b's atmosphere in much greater abundance. Note that a CO₂ abundance of 5% was used for the Earth-like Proxima Centauri b planet, as that abundance is required to raise the globally averaged surface temperature to 273 K.

A notable difference compared to Earth is the elevated methane abundance on Proxima Centauri b, which is increased by a factor of ∼4760 (2330 ppm vs. 0.5 ppm), for the same surface flux. This effect was described in the work of Segura et al. (2005) and in Section 2, and it is due to Proxima Centauri's low 200–300 nm flux levels that are less efficient at driving the photochemical reactions that destroy methane. This reaction sequence is (Segura et al., 2005)

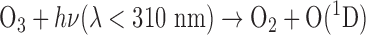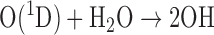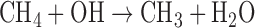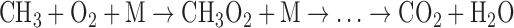Because this reaction primarily takes place in the lower stratosphere and troposphere, overlying O₂ absorbs photons with wavelengths less than 200 nm. The CH₄ content is further enhanced by the lower temperature of this relatively low-instellation planet (compared to Earth), which also lowers H₂O mixing ratios and OH radicals (sourced from H₂O) that would destroy methane. N₂O is enhanced, but only by a factor of ∼10 (2.3 ppm vs. 0.26 ppm). This is also due to the relative lack of >200 nm photons, where N₂O has a significant photodissociative cross section. The climatic effect of enhanced N₂O was not included in the Atmos climate calculations. However, this is unlikely to produce a significant impact, as previous results indicate that increasing the N₂O mixing ratio from 0.3 to 2.3 ppmv in a 1 bar atmosphere would produce a warming effect of ∼1 K (Roberson et al., 2011, their Fig. 3). The water vapor abundance in the stratosphere of Proxima Centauri b would be elevated, 20 ppm at 30 km vs. ∼10 ppm for the Earth-Sun (see Fig. 8 for profiles). This is due to the enhanced methane abundance in its upper atmosphere. The oxidation of methane by molecular oxygen produces additional water vapor through the reaction CH₄ + 2O₂ → CO₂ + 2H₂O (Segura et al., 2005). The difference in surface water mixing ratio is due wholly to the 15 K difference in surface temperature between the Earth-Sun analogue and Proxima Centauri b. Additionally, the temperature profile in the upper atmosphere of Proxima Centauri b is lower primarily due to the lower near-UV fluxes and consequential lack of heating, despite a comparable ozone column. Overall, these results are consistent with those of Segura et al. (2005); and minor differences are due to the different UV spectrum of Proxima Centauri b, our choice of CO₂ mixing ratio, and the use of preindustrial fluxes for biogenic trace gases. It should be noted that our O₃ abundances here are calculated without considering ozone depletion from flares (e.g., Segura et al., 2010), which will be a key consideration for future work.

4.2.3.2. M dwarf Archean Earth-like atmospheres

Early Earth represents another type of habitable planet whose spectral appearance and atmospheric composition are different from modern Earth. In particular, the Archean (roughly 4–2.5 billion years ago) atmosphere is generally believed to have been anoxic (e.g., Farquhar et al., 2000) and may have contained more CO₂ than the modern atmosphere (e.g., Driese et al., 2011), likely on the order of at least about 1% of the total atmosphere—and possibly more (Kanzaki and Murakami, 2015), although there is disagreement in the literature on this point (e.g., Rosing et al., 2010). Early Earth's atmosphere may also have contained a substantial amount of methane before the rise of atmospheric O₂, as there is evidence that methane-producing metabolisms evolved as early as 3.5 billion years ago (Ueno et al., 2006). Because methane can be produced by a number of nonbiological processes as well (Etiope and Sherwood Lollar, 2013), methane-rich, anoxic Earth-like worlds may occur frequently elsewhere in the Galaxy, especially given the propensity for methane to accumulate in Earth-like atmospheres around M dwarfs (Section 4.2.3.1). Earth-like methane-rich atmospheres may also form photochemically induced organic hazes if the CH₄/CO₂ ratio exceeds 0.1 (e.g., Trainer et al., 2006; Domagal-Goldman et al., 2008; Haqq-Misra et al., 2008; Zerkle et al., 2012), cooling the planetary surface environment through the antigreenhouse effect and dramatically altering the spectral appearance of the planet.

We generated 1 bar Archean-like atmospheres with 5% CO₂ in the Atmos climate-photochemical model. This CO₂ amount is reasonable for an Earth-like planet based on constraints on the CO₂ abundance of the Archean atmosphere (Driese et al., 2011; Kanzaki and Murakami, 2015), and it is the same CO₂ amount used to model our modern Earth analog planet. One of these atmospheres contained 1% CH₄ (CH₄/CO₂ = 0.2), and the other contained 1.5% CH₄ (CH₄/CO₂ = 0.3) at the surface. Figure 9 shows the gas and temperature profiles of these two atmospheres. Note the large abundance of CO in these atmospheres from CO₂ photolysis that increases with increasing altitude. Figure 2 shows the UV spectrum of Proxima Centauri compared to the Sun, and it produces excess radiation compared to the Sun for λ < 170 nm, which overlaps with the peak of the CO₂ UV cross section. For an atmosphere with 5% CO₂ and 1% CH₄, the global average surface temperature of the planet is 278 K. For an atmosphere with 5% CO₂ and 1.5% CH₄, a Titan-like organic haze forms, and the surface temperature decreases only slightly to 277 K. Titan-like hazes can cool planetary surface temperatures by 20–25 K on Archean-like planets orbiting solar-type stars (Arney et al., 2016), but these hazes produce less cooling on planets orbiting M dwarfs because M dwarf luminosity is mostly produced at wavelengths where these hazes are more transparent (Arney et al., 2017). The hazy planet's temperature compared to the haze-free world is a function of both the haze and the increased quantity of CH₄ in its atmosphere.

FIG. 9.

Temperature (top x axes; black dashed) and gas mixing ratio profiles (bottom x axes) for Archean analog planets orbiting Proxima Cen b. The moderate temperature inversion seen in the right (1.5% CH₄) plot is due to UV absorption by the haze. UV shielding by the haze in the 1.5% CH₄ plot (right) prevents photolysis of gases such as methane and ethane at higher altitudes than in the 1% CH₄ plot (left). Note the temperature profile becomes an isoprofile above the top of the climate model grid when passed into the photochemical model.

Haze formation depends on the atmospheric CH₄/CO₂ abundance ratio, and more reducing conditions enhance haze production. On an Archean-like planet orbiting a solar-type star, the CH₄/CO₂ ratio needed to initiate haze formation is ∼0.2 (e.g., Trainer et al., 2006), and smaller CH₄/CO₂ ratios are needed for planets around quieter M dwarfs (e.g., CH₄/CO₂ = 0.12 to form haze for an Archean analogue orbiting GJ 876 as discussed in Arney et al. [2017]), but around Proxima Centauri, a CH₄/CO₂ ratio of ∼0.3 is needed to initiate organic haze formation in an Archean-like atmosphere. This higher CH₄ level is easier to achieve compared to a planet around a solar-type star given that the host star spectrum results in a longer atmospheric lifetime for CH₄. Our previous work (Arney et al., 2017) shows that haze formation itself is more difficult on planets that generate larger quantities of photochemical oxygen radicals because these oxygen species consume haze-forming hydrocarbon gases. Therefore, planets with larger amounts of oxygen species in their atmospheres require higher CH₄/CO₂ ratios to form organic hazes. We find that the hazy Archean-like planet around Proxima Centauri produces 1.8, 2.9, and 3.2 times as much O, O₂, and OH, respectively, compared to a similar Archean-like planet around the Sun. This is due to photolysis of CO₂ and water vapor. Thus, the higher CH₄/CO₂ ratio needed to generate haze around Proxima Centauri is consistent with our previous results.

Figure 10 shows the haze particle number density and particle radii for the Archean analog haze particles. Arney et al. (2016) showed that similar number density and particle sizes are obtained for Archean Earth. Haze formation initiates high in the atmosphere, with the peak of the haze particle number density occurring at around 90 km in altitude. The photolysis of methane that initiates haze formation is apparent in the methane profiles in Fig. 9 that decrease at higher altitudes. Haze shields methane (and other gases) from photolysis once it is produced, so the hazy 1.5% CH₄ plot shows photolysis of gases occurring at higher altitudes than the haze-free 1% CH₄ plot. At these high altitudes, however, the particles are very small (∼0.001 μm). Fractal particles begin to form at about 60 km in altitude when the particle radius reaches 0.05 μm. The coagulation of these small, simple spherical particles into fractals causes the decline in particle number density and the increase in particle radius at this altitude. The particles grow to a maximum radius of 0.55 μm through coagulation processes before they fall from the atmosphere.

FIG. 10.

Archean analog haze particle number density (bottom x axis; solid line) and particle radius (top x axis; dashed line) for a hazy planet orbiting Proxima Centauri b. Note the sharp decrease in particle number density (and corresponding increase in particle size) at about 60 km in altitude where fractal particle formation begins to occur.

4.3. Simulated planetary phase curves

If Proxima Centauri b is not transiting, then observations of the planet's reflected and thermal phase variations may be our only option for detecting and characterizing its atmosphere before a next-generation ground or space-based direct imaging coronagraph is built. Thermal phase curves have been used to study the atmospheric dynamics, thermal structure, and molecular composition of hot, thermally bright exoplanets (Cowan et al., 2007, 2012; Knutson et al., 2007, 2012; Crossfield et al., 2010; Zellem et al., 2014). Below, we estimate idealized thermal phase curve variations and planet-star contrast ratios through the MIR.

Simulated phase curves comparing the thermal emission from the planet to the stellar background flux are shown in Fig. 11. In each panel the main plot shows the difference in star plus planet flux between when the planet's dayside is fully visible (superior-conjunction; full phase) and when the planet's nightside is fully visible (inferior-conjunction; new phase), divided by the average star plus planet flux. Following the work of Selsis et al. (2011), we refer to this type of spectrum as a variation spectrum. The upper-left inset shows the planetary phase evolution for two different assumed day-night temperature contrasts in the Mid-Infrared Instrument (MIRI) photometric filter bands longward of 8 μm to avoid detector saturation. Note that neither nightside temperature case is uniquely modeled, but rather, nightside temperatures are assumed to provide conceptual understanding and order-of-magnitude estimates. The case with no thermal flux from the nightside of the planet resembles the expected signal from an airless body, yet here it contains the spectral features from our modeled atmospheres to emphasize the maximum expected signal for the variation spectrum considering the self-consistent globally averaged dayside atmospheric structures that we do rigorously model. Similarly, the case with a 20 K day-night temperature contrast is provided to emphasize a more realistic temperature contrast for a planet with an atmosphere and to depict how the detectability of the variation spectrum scales with the unknown day-night temperature contrast.

FIG. 11.

Synthetic thermal phase curve variation spectrum of the photochemically self-consistent Earth-like atmospheric case with 50% cloud coverage (top panel), the hazy Archean-like atmospheric case with 50% cloud coverage (second panel), the desiccated O₂-rich atmospheric case (third panel), and the 90 bar cloudy Venus-like atmospheric case (bottom panel). The solid and gray lines show the emitted flux from the dayside of the planet (observed at 0°) minus the emitted flux from the nightside of the planet (observed at 180°), divided by the average flux received from the star plus planet. The solid line depicts the maximum possible signal strength for a phase curve spectrum of the planet in the case that there is no flux emitted from the nightside, while the gray line shows the signal strength for a case with a nightside 20 K cooler than the dayside. The colored horizontal lines show the high-resolution model spectrum convolved with the 7 JWST/MIRI filter bands longward of where Proxima Centauri exceeds the instrument brightness limit. Each upper-left inset shows the phase-dependent planet-to-star flux contrast ratios in the MIRI filter bands for the cases with no flux from the nightside (solid lines) and with a 20 K cooler nightside (dotted lines).

The top panel of Fig. 11 shows the modeled phase curves and variation spectrum for the self-consistent Earth-like planet, with the presence of a deep CO₂ feature at 15 μm, numerous H₂O features between 18 and 30 μm, and strong but low-contrast O₃ absorption at 9.6 μm. The second panel of Fig. 11 shows phase curves and the variation spectrum for the hazy, partially cloudy Archean Earth-like planet, with very similar observables to the modern Earth-like case. The third panel of Fig. 11 shows phase curves and the variation spectrum for the desiccated O₂-rich planet, with deep but low-contrast O₃ absorption, relatively weak CO₂ absorption, and no water features. The bottom panel of Fig. 11 shows phase curves and the variation spectrum for the 90 bar cloudy Venus-like planet, with exceptionally strong and broad CO₂ absorption spanning ∼11–22.5 μm. The plots shown in Fig. 11 share the common trend of a general rise in contrast with longer wavelengths, exceeding 10⁻⁴ longward of 20 μm. Our planet-star contrast ratios are in agreement with those computed in the works of Turbet et al. (2016) and Kreidberg and Loeb (2016). Deviations from this steady rise in contrast are due to molecular absorption and emission in the planetary atmosphere and afford the potential for detectability (Selsis et al., 2011). However, the actual detectability of these features ultimately depends on the amplitude of the phase curve (the planet flux is not independently discriminated from the star) and the magnitude of the stellar variability at these wavelengths. In the MIR, the amplitude of the phase curves depends on the day-night temperature contrast.

4.3.1. Thermal phase curve detection with JWST

We compute the detectability of thermal phase curves with the JWST MIRI that operates between 5 and 28 μm. In Section 4.3, we model thermal phase curves for four archetypal planet scenarios assuming two possible day-night temperature contrasts. Following the generalized JWST noise calculations from Greene et al. (2016) and the photon count rate formalism of Robinson et al. (2016), we estimate the integration times required to detect the quoted contrast ratios in each broad spectral band at a signal-to-noise ratio (SNR) of 10 at each phase, assuming photon-limited observations. Such a measurement is likely to be sufficient to resolve the shape of the phase curve, but ultimately the ability to resolve the shape will depend on the amplitude of the phase variations. In an idealized case, resolving the planet at both full and new phase can constrain the amplitude and a day-night brightness temperature contrast.

Using a wavelength-independent combined instrument plus JWST throughput of 0.27 (e.g., Greene et al., 2016), we find that an integration time of 21 h at full phase can detect the planetary emission above the stellar flux with a signal-to-noise of 10 at 8.6 μm after binning to R = 3. These estimates are in agreement with the integration times adopted by Kreidberg and Loeb (2016). For our case with a nightside 20 K cooler than the dayside, we find that an integration time of 62 h is required to resolve the planetary signal at new phase.

Due to the rise of the planet-star contrast ratio toward longer wavelengths in the MIR and the presence of the strong 15 μm CO₂ band in many of our simulated planetary states, it would be advantageous to use the Medium-Resolution Spectrograph (MRS) on JWST/MIRI, which is the only option for spectroscopy beyond 12 μm. However, slit losses and/or imaging slicing with the integral field spectrometer may impede precision exoplanet atmospheric characterization with MRS (e.g., Beichman et al., 2014; Kreidberg and Loeb, 2016). Nonetheless, given that thermal phase curve signals (as well as secondary eclipse signals) for temperate terrestrials increase toward longer wavelengths, significantly improving the planet-to-star contrast, it may be worth revisiting the performance of MRS when on-orbit stability and pointing for JWST are known.

The presence of CO₂ in all the planetary states explored in this paper, and the existence of the strong molecular absorption band at 15 μm, makes it a weak discriminant between the different atmospheric cases, but a strong discriminant between a terrestrial planet with an atmosphere and one without. The variation spectrum of an airless body will appear smooth and consistent with blackbody radiation for the day- and nightsides, while a terrestrial atmosphere will deviate from a blackbody at 15 μm where CO₂ absorbs. Furthermore, 15 μm is well suited for MIRI imaging. The F1500W filter centers on the CO₂ band with a full-width comparable to the full-width of the spectral band. For our Earth-like case with the largest possible day/night temperature contrast, an integration time of 10 h at both full and new phase would be sufficient for a 5σ detection of CO₂. If instead the nightside is only 20 K cooler, 100 h at both full and new would provide a 3.5σ detection. Additional exposures in neighboring MIRI filter bands (e.g., F1130W and F1800W) will be necessary to measure the slope of the variation spectrum and determine if the 15 μm point is lower than the expected continuum value. The integration times necessary to detect CO₂, or any features in a variation spectrum, will strongly depend on the actual day/night temperature contrast. Simply measuring the day/night temperature contrast could provide strong constraints of the presence or lack of an atmosphere that would act to recirculate heat from the dayside to the nightside.

However, there are several caveats for these proposed observations, including possible saturation, systematics, and stellar variability due to flaring. Due to the brightness of Proxima Centauri in the MIR, thermal phase curves with JWST/MIRI will likely run into the brightness limits of the instruments. All MIRI filters will saturate for full frame images, but 64 × 64 subarray photometry should be accessible for short exposures (less than 1 s) using filters longer than 10 microns (F1280W, F1130W, F1500W, F1800W, F2100W, and F2550W). The Low-Resolution Spectrograph (LRS) in “FAST” readout mode will saturate at all wavelengths based on the published saturation curves (Glasse et al., 2015), but shorter exposures or alternate readout modes may salvage LRS data for the longest wavelengths it can access (Kreidberg and Loeb, 2016). The MIRI MRS escapes saturation across its entire wavelength range (4.9–28.8 μm), but its low throughput (2–20%) may require prohibitively long exposures and co-adds. JWST's ability to measure thermal phase curves for terrestrial exoplanets may also be limited by to-be-determined systematics, which could raise the noise floor. Therefore, our performance estimates are likely idealized.

Stellar variability and the effect of flaring in the MIR may also complicate thermal phase curve observations with JWST. Tofflemire et al. (2012) observed NIR (J, H, Ks) counterparts to optical flares on the order of ∼1% in flux for mid M-dwarfs. Knutson et al. (2007) observed variability of about 5 × 10⁻⁴ in the 8 μm phase curve of HD189733b with Spitzer. Although it is unclear how much of the scatter is stellar versus systematic in origin, rotational variability will be seen at these wavelengths and longer, at the known rotation period of the star. For example, considering a starspot with an effective temperature 500 K cooler than the photosphere and with filling factors large enough to get 3–8% optical flux modulations as seen for Proxima Centauri (Davenport, 2016), the MIR variability will be ∼1%. For stars later than mid-M type, cloudlike modulation may become appreciable too (J. Davenport, 2016, personal communication). Proxima Centauri MIR variability is likely to have a greater amplitude than the thermal phase curves. Observations and rigorous modeling of the MIR variability of Proxima Centauri are needed to understand and mitigate its impact on observations of thermal phase curves. Disentangling stellar from planetary modulations will be highly important. Pioneering work in obtaining terrestrial exoplanet phase curves in the MIR and M dwarf variability in the MIR may both be enabled by observing Proxima Cen with JWST.

Further work is needed that combines photochemically and climatically self-consistent potential atmospheres for Proxima Centauri b with a full GCM treatment. Such modeling is necessary for making accurate phase curve predictions that are self-consistent between the altitude-dependent vertical structure and the longitude- and latitude-dependent spatial structure.

Additionally, this study is limited to nearly edge-on inclinations. As the inclination shifts from edge-on to face-on, the phase curve amplitude decays. More work is needed to explore the detectability of thermal phase curves over a complete range of possible inclinations.

4.3.2. Detecting ocean glint in phase curves

Detection of ocean glint in a reflected-light phase curve from Proxima Cen b would provide strong evidence for the presence of surface liquid water. Here, we outline the requirements for glint detection and determine whether it might be feasible to detect using JWST, ground-based telescopes, or future direct imaging missions. As shown in the work of Robinson et al. (2010), strong glint signatures only occur for a subset of all possible orbital inclinations, as orbits near face-on do not allow for crescent-phase viewing geometries. Thus, only inclinations within ±30 degrees of edge-on have the potential to show strong signatures of glint. For this range of inclinations, the glint signature would be strongest at reflected-light wavelengths outside of Rayleigh scattering and gas absorption features. While the atmospheric composition of Proxima Cen b is currently unknown, key wavelength ranges of interest for glint detection would be between the 0.94, 1.1, 1.4, and 1.9 μm water vapor bands. At the phase angles of peak glint contributions for Earth (i.e., 120–165 degrees; Robinson et al., 2010), the planetary phase function will likely decrease the planet-to-star flux ratio by an order of magnitude from its full-phase value (Robinson et al., 2010) to near 10⁻⁸ (Turbet et al., 2016). Since glint could cause up to a 100% increase (i.e., doubling) in planet brightness at these phase angles and wavelengths, the precision of any phase curve measurements aimed at detecting a glint signature at reasonable SNRs would need to be several times smaller than 10⁻⁸. This estimate puts glint detection firmly outside the range of feasibility for JWST, whose systematic noise floor is usually predicted to be in the range of 10⁻⁵ (Greene et al., 2016).

Direct imaging offers better prospects, as noise floors for these types of missions or instruments are typically an order of magnitude below the design contrast for the coronagraph or starshade, which would imply floors near 10⁻¹⁰ to 10⁻¹¹ for next-generation instruments. Here, the challenge for glint detection on Proxima Centauri b becomes angular separation—the planet-star separation at a phase angle near 150 degrees will be roughly 20 milliarcseconds (mas). Imaging the planet at this separation between the 0.94 and 1.1 μm water vapor bands would require an inner working angle (IWA) of better than 1.5λ/D for a 16 m class telescope or 3λ/D for a 30 m class telescope.

4.4. Simulated planetary spectra

To predict the spectral observables of the planets simulated in our study, in this section, we present simulated direct imaging (Section 4.4.1) and transit transmission spectra (Section 4.4.2). Direct imaging observations will be possible with future starlight suppression technologies such as coronagraphs and starshades. Proxima Centauri b is not known to transit (Kipping et al., 2017), but the transit spectra of our simulated worlds show several key diagnostic features that would help discriminate between habitable and uninhabitable scenarios and are applicable not only to Proxima Cen b but also to other terrestrial planets orbiting M dwarfs.

4.4.1. Direct imaging spectra

To anticipate the spectral observables of Proxima Centauri b in reflected light observations that may become possible with future telescopes, we show simulated reflected light spectra generated with SMART in this section. In Section 4.6, we present these same spectra run through coronagraph noise models for several telescope configurations to predict which features will be observable with future technology.

4.4.1.1. Direct imaging spectra for high-O₂ atmospheres

Figure 12 shows clear-sky reflectance spectra for 10 bar, O₂-dominated “wet” and desiccated cases. For the case with a surface ocean remaining, we assumed the second composite albedo described in Section 3.7.5 (ocean and continents with no vegetation), while we assumed a desert surface for the desiccated case. The spectra are dominated by O₄ bands in the UV-visible part of the spectrum at 0.345, 0.36, 0.38, 0.445, 0.475, 0.53, 0.57, and 0.63 μm, and O₄ absorption in the NIR at 1.06 and 1.27 μm (the latter overlaps with the ¹Δ_g 1.27 μm O₂ band). The case with an ocean includes H₂O bands that have been significantly pressure-broadened by the 10 bar atmosphere. Both scenarios contain significant UV absorption by O₃, O₂, and CO. Increased O₃ in the desiccated case produces stronger ozone absorption at 0.3 μm. At short wavelengths there is significant Rayleigh scattering from the large atmospheric mass seen in clear sky, which enhances the albedo even at relatively long wavelengths (∼1 μm). This increases the contrast of the visible O₄ bands with their surrounding continua. The desiccated case is brighter overall at NIR wavelengths due to combination of a higher surface albedo at these wavelengths and a lack of H₂O absorption. Unlike the wet case, the desiccated case shows CO absorption at 2.35 μm that is not obscured by deep H₂O absorption.

FIG. 12.

Reflected light spectra of the 10 bar, high-O₂ (95%) atmospheres (cloud free) with a surface ocean remaining (top) and completely desiccated (bottom). We define the reflectivity (πI/F) of the planet as the outgoing top of atmosphere flux (πI), where I is the radiance, divided by the stellar flux incident at the top of the atmosphere (F). Note the strong O₄ bands present in the UV/VIS/NIR. Both atmospheres were simulated with 0.5% CO₂.

4.4.1.2. Direct imaging spectra for high-CO₂ atmospheres

Figure 13 shows direct imaging reflectance spectra of desiccated, clear O₂-CO₂ atmospheres (45% CO₂, 45% O₂, 10% N₂) with surface pressures of 10 and 90 bar at quadrature (half illuminated). In this environment, we assume Venus levels of water vapor (∼30 ppm), and a desert surface albedo but no H₂SO₄ aerosols. The resulting spectrum is rich in O₄ absorption features like Fig. 12 but with additional strong CO₂ absorption throughout the NIR. Rayleigh scattering contributes to a high planetary albedo at wavelengths shorter than 1 μm, but this high albedo is only seen in the narrow-continuum regions. The absence of high-altitude aerosols and consequent clear-sky paths creates much stronger CO₂ absorption than in the simulated Venus spectrum, particularly in the NIR.

FIG. 13.

Similar to the reflected light spectra of Fig. 12, but for the clear O₂-CO₂ (45% O₂, 45% CO₂, 10% N₂, 20 ppm H₂O) atmospheres with surface pressures of 10 bar (top) and 90 bar (bottom) for comparison with O₂-only and Venus cases.

Figure 14 shows reflected light spectra of Venus-like planets for our 10 bar and 90 bar simulations with an H₂SO₄ cloud deck. There are prominent CO₂ bands—particularly at 1.5 and 2 μm, with weaker CO₂ bands visible near 0.78, 0.87, 1.05, and 1.2 μm. Water vapor, present at 32 ppm at the surface, is observable at 1.35 and 1.85 μm. This uninhabitable planet shows that water in a spectrum is not an unambiguous sign of habitability. An absorption feature from the unknown UV absorber (Moroz et al., 1985), which is responsible for the absorption of most of the incident sunlight in the upper cloud deck in the Solar System's Venus (Pollack et al., 1980), is included in our cloud model and is visible near 0.4 μm. Conspicuously absent are Earth-like absorption features from oxygen, ozone, and methane.

FIG. 14.

Similar to the reflected light spectra of Fig. 12, but for the Venus-like worlds with 10 bar (top) and 90 bar (bottom) CO₂ atmospheres. Strong CO₂ absorption features are present at several wavelengths. The two spectra are similar because the cloud decks in both atmospheres occur at roughly the same pressure, so about the same amount of total atmosphere is sensed in each spectrum.

Figure 15 (top panel) shows the reflectance spectrum of the case of a desiccated CO₂/O₂/CO atmosphere in photochemical equilibrium (Section 4.2.2.3; Gao et al., 2015). In calculating the reflectance spectrum, we used the globally averaged Mars albedo (Crisp, 1990) to simulate a Mars-like oxidized surface. No clouds are included because the desiccation of this atmosphere is almost complete (0.03 ppm H₂O). The spectrum contains strong absorption features from CO₂, O₂, O₃, and CO. The strength of the CO₂ and CO features is notably stronger than for an Earth-like case due to the higher abundance of these gases and is also stronger than the Venus case due to clear paths through the atmosphere that are not truncated by sulfuric acid clouds. As noted by Gao et al. (2015), the lack of H₂O absorption bands would be an indicator that the O₂ is unlikely to be from a biological source.

FIG. 15.

Similar to the reflected light spectra of Fig. 12, but for the 1 bar desiccated CO₂/O₂/CO atmosphere with a wavelength-dependent Mars average surface albedo (top panel), preindustrial Earth (middle panel), and Archean Earth (bottom panel). The top panel shows a desiccated planet with an outgassed CO₂ atmosphere, which can support a stable CO₂/O₂/CO/O₃ atmosphere without life (Gao et al., 2015). The lack of H₂O is an indicator of the abiotic nature of the atmospheric O₂. The middle panel shows Proxima Centauri b simulated as an Earth-like planet with 21% O₂ and 5% CO₂, and 50% cloud cover. The UV to NIR spectrum contains features from Rayleigh scattering, O₃, O₂, H₂O, CO₂, and CH₄. The bottom panel shows Archean Earth-like planets with a photochemically self-consistent organic haze (orange) and without a haze (purple). Note the overlap of some H₂O and CH₄ absorption bands and the strong haze absorption feature at short wavelengths. The surface albedo assumes the composite albedo described in Section 3.7.5 with no vegetation.

4.4.1.3. Direct imaging spectra for Earth-like atmospheres

Figure 15 (middle panel) shows the reflectance spectrum of our photochemically self-consistent modern Earth case using the Earth composite surface spectrum in Section 3.7.5 as our surface spectral albedo. This reflectance spectrum is for a planet with a 50% cloud cover fraction. The composite spectrum is calculated by a weighted average of 50% clear-sky, 25% cirrus (ice) clouds placed at 8.5 km altitude (0.331 bar) with an optical depth of τ = 10, and 25% stratocumulus (liquid) clouds placed at 1.5 km altitude (0.847 bar) also with τ = 10. (The cloud optical properties are fixed and provided in Section 3.7.6). This weighted configuration has been shown to produce a good approximation of Earth's disk-averaged spectrum (Robinson et al., 2011). The synthetic spectrum is rich with molecular features including H₂O, O₂, O₃, CH₄, and CO₂. These include the O₃ Hartley bands at UV wavelengths <0.38 μm and O₃ Chappuis bands from ∼0.5 to 0.7 μm; Rayleigh scattering at blue wavelengths; O₂ absorption at 0.63, 0.69, 0.76, and 1.27 μm; H₂O absorption at 0.65, 0.7, 0.73, 0.8, 0.95, 1.1, 1.4, and 1.8–2.0 μm; CH₄ absorption at 0.9, 1.08, 1.35–1.41, 1.6–1.8, and 2.2–2.4 μm, and CO₂ at 1.6 and 2.0 μm. The spectral slope near 0.7 μm is partly due to the vegetation red edge present in the composite albedo spectrum used as input to the model. Note that N₂O lacks strong absorption bands at these short wavelengths and CO is not abundant enough to make a spectral impact.

The primary differences between the reflectance spectra of an Earth analog planet orbiting Proxima Centauri b and the Earth-Sun case are substantially stronger CH₄ bands for the M dwarf planet. For comparison with this case, Fig. 16 (top panel) shows a simulated Earth-Sun case with that of Proxima Centauri b. Both spectra have the same surface fluxes and 50% cloud cover, but the host star's spectrum changes the photochemical lifetime of gases in the atmosphere, altering its composition and spectral features. Other differences include weaker H₂O bands due to a lower surface temperature and stronger CO₂ bands at 1.6 and 2.0 μm due to higher CO₂ concentrations in the Proxima case.

FIG. 16.

The effect of the host star's SED on the planet's composition and spectrum. For comparison, the Earth orbiting the Sun (orange) and the photochemically self-consistent Earth orbiting Proxima Centauri (purple) are shown in reflected light (top) and in transmission (bottom). For the transmission spectra, the Earth-Sun case is adjusted so that its maximum tangent pressure matches that expected for an Earth-like planet in orbit around Proxima Centauri at Proxima Centauri b's orbital position. The surface fluxes were kept constant in both cases. These plots illustrate the strong impact of the star's spectrum on atmospheric photochemistry and composition, and that Earth itself cannot be used to represent a planet with Earth-like surface fluxes orbiting an M dwarf. The primary differences in the spectra are in the NIR and are due to differences in total methane concentration, which is much higher for Proxima Centauri b. Absorption from O₃ is also sensitive to the host star spectrum, and this is most prominent in the transmission spectrum. Note that differences in the stellar SEDs have been divided out. A cloud cover fraction of 50% is simulated for both cases.

Figure 15 (bottom panel) shows reflected light spectra of Archean Earth-like planets with and without organic haze. The haze is a strong blue and UV wavelength absorber, causing the broad and deep decrease in reflectivity for wavelengths shorter than about 0.55 μm. However, despite its prominence, this feature would be more difficult to detect for a planet like Proxima Centauri b compared to a planet orbiting the Sun (Section 4.5.2) because the star itself produces little flux at these wavelengths. The haze also produces back-scattering at longer wavelengths, which is the cause of the increase in brightness of the hazy spectrum relative to the haze-free spectrum at wavelengths longer than 0.55 μm.

Water, carbon dioxide, and methane all produce absorption bands for wavelengths less than 2.5 μm. Several of the prominent CH₄ and H₂O bands overlap, including the ones near 1.15 and 1.4 μm. H₂O absorption is present at several wavelengths including 0.65, 0.7, 0.73, 0.8, 0.95, 1.1, 1.4, and 1.8–2.0 μm; CH₄ absorption is present at 0.62, 0.73, 0.8, 0.9, 1.08, 1.35–1.41, 1.6–1.8, and 2.2–2.4 μm; CO₂ is present at 1.6 and 2.0 μm and weakly near 1.25 μm.

4.4.2. Transmission spectra

Although no conclusive evidence that Proxima Centauri b transits have been found (Kipping et al., 2017), strong planetary evolution driven by the star's pre-main sequence phase is likely to be common for other planets orbiting M dwarfs. We therefore present transit transmission spectra of our simulated atmospheres, which may be relevant to transiting habitable zone planets orbiting other M dwarfs, including the recently discovered TRAPPIST-1 system (Gillon et al., 2016, 2017) and especially TRAPPIST-1e, which occupies a similar position in its habitable zone to Proxima Centauri b.

Our simulations are intended to demonstrate the size of the signal expected for each atmosphere type, which can be used to determine the required noise floor needed to detect features of interest for terrestrial planets orbiting a star like Proxima Centauri b. For JWST, if the systematic noise floor at the >10 ppm level proposed by Greene et al. (2016) is verified after launch, then it will be difficult to characterize many of the types of planets we simulate for Proxima Centauri b (and small planets in general) with JWST, as some of the features we simulate would not be detectable. However, for similar-sized planets orbiting even smaller stars, such as for the TRAPPIST-1 system (Gillon et al., 2016, 2107) the signals may be even larger than presented here.

4.4.2.1. Transmission spectra for high-O₂ atmospheres

Figure 17 shows the transmission spectra of the modeled 10 bar, O₂-dominated post-runaway atmospheres for the cases of water remaining and complete desiccation. The spectra are in general very similar with strong O₃ and CO₂ features and broad O₄ features at 1.06 and 1.27 μm. The NIR O₄ bands at 1.06 and 1.27 μm may be observable with the JWST NIRISS¹⁵ instrument, which may confirm the existence of an O₂-dominated atmosphere (Schwieterman et al., 2016). For the “wet” 10 bar O₂ case, the 6.3 μm water band is present, although water is not seen at shorter wavelengths, and there is significantly less O₃ absorption at 0.5–0.7 and 9.7 μm. This is due to the presence of H₂O water vapor in the upper atmosphere. Hydroxyl (OH) radicals sourced from H₂O can efficiently remove O₃ from the atmosphere (Segura et al., 2005). O₃ can build up to higher concentrations at most altitudes in the desiccated case. The strong 0.2–0.3 μm O₃ band is sensitive to ozone higher in the atmosphere and is seen in both the desiccated and wet cases. The presence of both strong absorption in the Chappuis band (0.5–0.7 μm) in conjunction with O₄ features in the NIR is indicative of a high-O₂, desiccated atmosphere, with O₃ also present lower in the atmosphere. Detection of O₄ without the Chappuis band suggests lower abundances or absence of O₃ deeper in the atmosphere, which would be the case if water, and associated O₃-destroying OH radicals, are present. Weak O₄ features are apparent at 0.57 and 0.63 μm for the “wet” case, which are otherwise overwhelmed by the Chappuis band.

FIG. 17.

Transmission spectra of the 10 bar, 95% O₂ atmospheres with a surface water ocean (purple) and with complete desiccation (orange). The effective radius of the atmosphere (in km) is shown on the left y axis to emphasize the vertical extent of the absorption features, while the transit depth is shown on the right y axis to emphasize the strength and detectability of spectral features if Proxima Cen b were observed to transit. The contrasts in O₃ absorption stem from the extent to which O₃ remains abundant deep in the atmosphere, which is ultimately due to the presence or absence of water vapor.

4.4.2.2. Transmission spectra for high-CO₂ atmospheres

Figure 18 shows the synthetic transit transmission spectrum for 10 and 90 bar mixed O₂-CO₂ atmospheres. These spectra are similar to Fig. 17, though additional weaker CO₂ bands appear that partially overlap with the 1.06 and 1.27 μm O₄ bands, which are also weaker because their density has been halved at the refraction limit. There are only slight differences in the spectra between the 10 and 90 bar cases because the portion of the atmosphere probed by transmission is almost entirely above 10 bar pressures, though the atmosphere is optically thick at higher altitudes for the 90 bar case.

FIG. 18.

Similar to the transmission spectra of Fig. 17, but for the O₂-CO₂ atmospheres with surface pressures of 10 bar (purple) and 90 bar (orange). The two spectra are almost identical except that the pressure at which the atmosphere becomes optically thick, while the same for both planets, occurs at a higher altitude in the 90 bar case.

Transit transmission spectra of our 10 bar and 90 bar CO₂-rich atmospheres with sulfuric acid cloud decks are shown in Fig. 19. The transit transmission spectra of these Venus-like worlds exhibit flat, featureless spectra at visible wavelengths reminiscent of similar spectra observed on exoplanets that likely have cloud or haze layers of various compositions (e.g., Knutson et al., 2014; Kreidberg et al., 2014).

FIG. 19.

Similar to the transmission spectra of Fig. 17, but for the Venus-like worlds with 90 bar (orange) and 10 bar (purple) CO₂ atmospheres. H₂SO₄ absorption features can be seen at IR wavelengths, and the spectrum is flat at wavelengths shorter than 1 μm.

As discussed in the work of Ehrenreich et al. (2012), a Venus-like transmission spectrum is dominated by H₂SO₄ Mie scattering at λ < 2.7 μm and by H₂SO₄ absorption at λ > 2.7 μm. Because of this, a broad “V” shape can be seen in the Venus spectrum centered near 2.7 μm, especially in the 90 bar atmosphere with a thicker cloud deck. An almost stepwise increase in the H₂SO₄ imaginary refractive index by about 2 orders of magnitude occurs near 2.7 μm, allowing its absorption to dominate at longer wavelengths. This behavior allows H₂SO₄ absorption features to be apparent in Venus' transit transmission spectrum at wavelengths longer than 2.7 μm, providing a means to directly identify sulfuric acid aerosols in the spectrum of a transiting exoplanet. Spectral features from the sulfuric acid clouds are present near 3, 5.8, 8.6, 9.7, and 11.2 μm that correspond to peaks in the H₂SO₄ extinction coefficients. Despite the opacity of Venus-like H₂SO₄ clouds, there are also CO₂ absorption features visible near 2, 2.7, 4.5, and 15 μm. The strongest of these features may be observable at about a 20–30 ppm level.

Figure 20 (top panel) shows the transit transmission spectrum of a 1 bar CO₂/CO/O₂ atmosphere assuming very low hydrogen abundances (∼0.03 ppm total H from all H-bearing species). In contrast to other high-CO₂ cases, this spectrum contains significant CO bands at 2.35 and 4.6 μm, which, together with strong CO₂ bands, suggests active CO₂ photolysis (Harman et al., 2015; Schwieterman et al., 2016). For this high-CO case, when computing the CO absorption coefficients with LBLABC, we specify a wing cutoff of 50 cm⁻¹, because LBLABC treats CO wings as Lorentzian, but the extreme wings have been measured to be sub-Lorentzian (Burch and Gryvnak, 1967). Transmission spectra are especially sensitive to line-shape assumptions of strong absorption bands.

FIG. 20.

Similar to the transmission spectra of Fig. 17, but the top panel is for the heavily H-depleted CO₂/O₂/CO atmosphere in photochemical equilibrium from Section 4.2.2.3 (also see Gao et al., 2015). Note the strong CO bands at 2.35 and 4.6 μm compared to other cases. The middle panel shows the photochemically self-consistent modern Earth (black) with preindustrial biological fluxes of CH₄, CO, and N₂O orbiting Proxima Centauri b. It also shows Earth's spectrum with CH₄ (orange) and H₂O (blue) removed, to show the relative contributions of each to the spectrum. The weak H₂O features result from transmission probing higher, drier altitudes down to about 10 km, but water being mostly concentrated in the lower portion of the troposphere, below ∼12 km. In addition to their intrinsic weakness, the H₂O features are also swamped by CH₄ absorption, which also raises the effective tangent height to drier altitudes. The bottom panel shows the Archean Earth-like planets with (orange) and without (purple) organic haze orbiting Proxima Centauri. A haze absorption feature is present near 6 μm, and haze produces the spectral slope continuing into the NIR for the hazy spectrum.

4.4.2.3. Earth-like transmission spectra

Figure 20 (middle panel) shows a simulated transmission spectrum of the photochemically self-consistent modern Earth orbiting Proxima Centauri, as described in Section 4.2.3.1. The simulated spectrum does not contain clouds and aerosols, although refraction limits altitudes probed to those above ∼12 km, and the majority of clouds are below this altitude and so would not affect the spectrum even if they were present. Strong, broad features from ozone (0.2–0.3, 0.5–0.7, 4.8, and 9.7 μm), CH₄ (0.9, 1.1, 1.4, 2.4, 3.5, 7.5 μm), and CO₂ (1.6, 2.0, 2.7, 4.3, and 15 μm) are present. The water bands are weak because stratospheric water vapor abundance is low (even though it is significantly higher than for the Earth-Sun; see Fig. 8). Additionally, H₂O bands overlap significantly with CH₄, but CH₄ abundances are higher at stratospheric altitudes. This figure panel also illustrates the impact of CH₄ and H₂O on the transmission spectrum by individually removing their contributions, and provides additional evidence that the 1.1 and 1.4 μm features are due to CH₄ and not H₂O in these transmission spectra. For comparison, the lower panel of Fig. 16 shows the differences in the transmission spectra of terrestrial planets with Earth-like surface fluxes, but with the Sun and Proxima Centauri driving their photochemistry. The spectra are markedly different, due primarily to the much stronger absorption from CH₄, which has a longer atmospheric lifetime under Proxima Centauri's spectrum (cf., Segura et al., 2005).

Figure 20 (bottom panel) shows the transit transmission spectra for Archean-like planets with and without organic haze. Gaseous spectral features become weaker in the presence of a haze, and the depth probed into the atmosphere is reduced. The absorption features near 1 μm are present at about 15–42 ppm in the haze-free spectrum, and at 5–23 ppm in the hazy spectrum. The haze becomes more transparent at longer wavelengths, so the difference between the hazy and haze-free spectra diminishes as wavelength increases. A spectral slope caused by Rayleigh scattering is apparent at wavelengths shorter than 0.5 μm in the clear-sky spectrum. The hazy spectrum exhibits a spectral slope that continues into the NIR, which is caused by wavelength-dependent haze extinction. Features from CH₄ (0.62, 0.73, 0.8, 0.9, 1.2, 1.4, 2.4, 3.5, 7.5 μm) and CO₂ (2.0, 2.7, 4.3, and 9.5, 10.5, and 15 μm) may be detectable with a mission like JWST (Arney et al., 2017). A haze absorption feature that occurs near 6 μm, which overlaps with C₂H₆ (6.5, 12 μm), may also be detectable with the JWST MIRI instrument (Arney et al., 2017), if the JWST noise floor were sufficiently low to allow these types of measurements.

4.5. Observational considerations for direct imaging

In this section, we describe the types of observations that may be possible to make with direct imaging telescopes in the coming decades. We discuss the challenges of making these observations and show simulated spectra of Proxima Centauri b using our direct imaging coronagraph noise model in Section 4.5.2.

4.5.1. Inner working angle constraints

Observations of Proxima Centauri b will be constrained by the IWAs of the observatories that may come online in the next decades. The IWA defines the angular distance from the center of the field-of-view within which starlight suppression worsens enough to make planet observations unfeasible. The IWA is typically expressed as nλ/D, where n is a small-valued constant (here, we assume n = 1–3) and D is the telescope diameter. The diffraction limit, which is the smallest angular separation a telescope mirror can resolve, is represented by n ∼ 1. The angular separation between Proxima Centauri and planet b is 37 mas, which is the minimum IWA required to see this planet at quadrature. Note that to observe the planet at any other phase a smaller IWA will be required.

Note also that the IWA is wavelength-dependent, so for the same mirror size, the IWA is larger for a longer wavelength. For a given star-planet separation with a given telescope diameter, this means that there is a maximum wavelength beyond which the wavelength-dependent IWA is larger than the planet-star separation, meaning that the target is effectively unobservable. Table 8 presents long-wavelength cutoffs for IWAs for seven different telescope sizes ranging from a 2.4 m telescope such as WFIRST (Spergel et al., 2015) to a 40 m ground-based observatory such as the European ELT (39 m). These IWAs make no assumptions about starlight suppression technologies; they instead only show the wavelength cutoffs for three potential IWAs.

Table 8.

Inner Working Angles for Future Telescopes and Mission Concepts

Case	λ (IWA = 3λ/D)	λ (IWA = 2λ/D)	λ (IWA = 1λ/D)
Ground (40 m)	2.41 μm	3.61 μm	7.22 μm
Ground (30 m)	1.80 μm	2.71 μm	5.42 μm
LUVOIR (16 m)	0.96 μm	1.44 μm	2.89 μm
LUVOIR (10 m)	0.60 μm	0.90 μm	1.81 μm
LUVOIR (8 m)	0.48 μm	0.72 μm	1.44 μm
HabEx (6.5 m)	0.39 μm	0.59 μm	1.17 μm
HabEx (4 m)	0.24 μm	0.36 μm	0.72 μm
WFIRST (2.4 m)	0.14 μm	0.21 μm	0.43 μm

The ability to characterize Proxima Centauri b varies widely with telescope diameter, and Proxima Centauri b is unlikely to be directly imaged with the current generation of 8–10 m telescopes. Among the mirror diameters simulated here, the best-case scenario is the 40 m ground-based observatory if an IWA ∼ λ/D is achievable: this configuration can reach a wavelength of 7.22 μm. However, observing out to this wavelength is difficult in practice due to the thermal background of the sky and telescope (see Section 4.5.2), and constructing a coronagraph with IWA ∼ λ/D may in practice be hindered by technical challenges. However, we think it is valuable to consider what could be observable with this most optimistic IWA, and also to consider what would be lost if the smallest achievable IWA is larger than this. Large ground-based telescopes have the potential to characterize Proxima Centauri b at shorter wavelengths where the atmospheric background and transmission are more favorable. Even without optimistic assumptions about the IWA, a 30 m ground-based telescope can still reach 1.8 μm for IWA = 3λ/D, and a 40 m ground-based telescope can reach 2.4 μm for the same IWA. However, these Earth-bound observatories must contend with atmospheric turbulence and the limitations of adaptive optics to counteract this. These adaptive optics systems generally perform better at longer wavelengths (e.g., Bouchez et al., 2014), where the IWA is not favorable for Proxima Cen b. Nonetheless, the European Extremely Large Telescope (E-ELT)'s first-generation adaptive optics (AO) instrumentation is planned to function for wavelengths 0.8–2.4 μm¹⁶, and the GMT's planned adaptive optics wavelength range is 1–25 μm (Lloyd-Hart et al., 2006). However, the extreme adaptive optics (ExAO) required to image exoplanets is currently under development at several sites, with the SCExAO instrument serving as a test bed on the Subaru telescope (Guyon et al., 2012), the EPICS (ELT-PCS) instrument being developed as part of the planned suite for the E-ELT (Vérinaud et al., 2010), and current work on the Magellan Telescope MagAO-2K and MagAO-X systems (Males et al., 2016), with the goal to deliver Strehl ratios of over 80% near 0.67 μm and push ExAO into the visible, where the oxygen A band near 0.76 μm, for example, could be accessible.

The most optimistic scenario simulated here for space-based telescopes is a 16 m class LUVOIR (Dalcanton et al., 2015) telescope with IWA = λ/D, which would provide access out to 2.89 μm. This could allow measurement of the 2 μm CO₂ feature, which is the strongest CO₂ feature at wavelengths shorter than 4 μm and may provide the best chance of constraining CO₂ abundance in Earth-like atmospheres that lack strong CO₂ bands elsewhere.

For smaller telescopes, a starshade may be advantageous, potentially allowing measurement of redder wavelengths than the IWA spectral cutoffs shown in Table 8. For WFIRST, the baseline coronagraph design will likely have dramatic throughput losses inside about 2.5 λ/D, corresponding to 120 mas at V band (Traub et al., 2016), which is significantly larger than Proxima Cen b's 37 mas maximum separation from its star. Thus a starshade, with an IWA less than 37 mas, would be required to observe Proxima Cen b with this mission. Note that an effective IWA better than the primary mirror's diffraction limit could be achieved for a starshade-telescope system because most of the starlight never reaches the primary mirror, so the star's central point spread function is strongly suppressed. For a starshade, the IWA can be expressed as IWA = F × λ/R or IWA = (F × λ/z)^1/2, where R is the starshade radius, z is the telescope-starshade separation, and F is the Fresnel number. A large starshade-telescope separation distance would probably be required to observe Proxima Centauri b in the NIR where there are the strongest absorption bands in the atmospheres we simulate. For instance, for a given wavelength and IWA, the telescope-starshade separation distance, z, is given by z = F × λ/IWA². To observe out to 1 μm, Fresnel numbers greater than a factor of a few require starshade-telescope separations that are a large fraction of the distance between Earth and the Moon. The radius of the starshade scales as R = F × λ/IWA, so Fresnel numbers of a factor of a few imply a starshade that is tens or hundreds of meters across in order to reach 1 μm. At a fixed IWA, F/IWA = R/λ = constant, so the required size of the starshade to reach a given wavelength scales linearly with λ. An additional challenge is that observations with a starshade and a small telescope would have a large telescopic PSF (on the order of the size of the star's habitable zone) due to the small size of the mirror. This is especially problematic given that Proxima Centauri is near the plane of the Milky Way galaxy, so the problem of background contamination will likely be significant. A large PSF in a crowded field may make disentangling the photons from Proxima Centauri b and background sources difficult.

Due to the small angular separation between Proxima Centauri b and its parent star, it will be important to push technology toward as small an IWA as possible for the best chance of characterizing this interesting system. Note that if there are Earth-like worlds orbiting nearby, earlier spectral type M dwarfs, the planet-star angular separations may be more favorable for observing the planet outside the IWA.

4.5.2. Coronagraph model simulations

In this section, we show simulated spectra from the previous sections convolved with our coronagraph noise model for different telescope mirror sizes to illustrate the challenges and opportunities for observing Proxima Centauri b with possible future observatories. We show simulated observations for the 10 bar O₂ planet with an ocean (Fig. 21), the desiccated O₂ planet (Fig. 22), the Venus-like planet (Fig. 23), the desiccated CO₂/O₂/CO planet (Fig. 24), the self-consistent modern Earth-like planet (Fig. 25), and the hazy Archean Earth-like planet (Fig. 26). All the spectra in this section are simulated with spectral resolution (λ/Δλ) of R = 70. In the figures below, we choose an IWA of λ/D for our nominal simulations to show what may be theoretically possible. However, in our coronagraph noise model figures, we also indicate where the 2λ/D and 3λ/D cutoffs occur. Note that coronagraph performance tends to decrease with proximity to the IWA, so larger error bars than shown here would be expected at wavelengths near the IWA cutoff. Note also, as mentioned in Section 4.5.1, that a starshade could theoretically observe a smaller IWA than the diffraction limit of the primary mirror and could allow observations to longer wavelengths than shown here.

FIG. 21.

Simulated coronagraph spectrum (left column) and the SNR in each spectral element (right column) for the 10 bar O₂-rich planet with an ocean surface using three different future telescope concepts: a 6.5 m HabEx (top row), a 16 m LUVOIR (middle row), and a 30 m ground-based telescope (bottom row). The simulated observations, showing 1σ errors, and the SNR calculations assume an integration time of 10 h per nulling bandwidth. Dashed vertical lines are placed at IWA = 1λ/D (red), 2λ/D (green), and 3λ/D (blue) to show the long-wavelength limit for the given telescope diameter and planet-star angular separation. All spectra are shown for a spectral resolution of R = 70.

FIG. 22.

Similar to the coronagraph simulations of Fig. 21, but for the desiccated 10 bar O₂-rich planet.

FIG. 23.

Similar to the coronagraph simulations of Fig. 21, but for the 90 bar cloud-covered Venus-like planet.

FIG. 24.

Similar to the coronagraph simulations of Fig. 21, but for the desiccated CO₂/O₂/CO planet.

FIG. 25.

Similar to the coronagraph simulations of Fig. 21, but for the photochemically self-consistent modern Earth-like planet.

FIG. 26.

Similar to the coronagraph simulations of Fig. 21, but for the hazy Archean Earth-like planet.

Figures 21–26 show simulated observations for telescope sizes corresponding to HabEx (6.5 m; top panels), LUVOIR (16 m; middle panels) and a large ground-based observatory (30 m; bottom panels). Signal-to-noise calculations assume a 20% throughput for a coronagraph and telescope instruments. This is an improvement on WFIRST (Robinson et al., 2016) that could occur with off-axis telescope architectures or if the coronagraph has fewer reflections.

Direct imaging of terrestrial exoplanets may become possible from the ground (e.g., Males et al., 2014; Quanz et al., 2015). For the 30 m ground-based telescope simulations, although we include the atmospheric transmittance (Fig. 1), thermal emission from the telescope mirror, and sky brightness, our simulations are optimistic because they do not include wavelength-dependent performance of adaptive optics, and they assume that absorption features from the planet can be perfectly separated from absorption features in Earth's atmosphere. This latter issue will make it difficult to definitively detect gases in any exoplanet's atmosphere if they overlap with strong telluric features. This issue could be resolved by going to very high resolution (e.g., R = 100,000) to disentangle individual planetary spectral lines from Earth's atmosphere's absorption by using the Doppler shift of the planet's motion relative to Earth and a template-matching technique (Snellen et al., 2015).

The right panels of each figure show the SNR in each resolution element for an integration time of 10 h. The left panels of each figure show the simulated spectrum and errors assuming that the planet was observed for 10 h. To retrieve the abundance of an absorbing gas will require SNR ∼ 20 at the bottom of the band (Robinson et al., 2016), although we could also assess concentration from the width of the feature or from combinations of features that appear at different concentrations. As a result, planets with strong oxygen absorption (e.g., Figs. 21 and 22), and consequently lower planet-star flux contrasts in the oxygen A band, will require longer integration times to achieve a SNR of 20 in that spectral element than a planet with little to no oxygen absorption (e.g., Fig. 23). In practice, the full visible to NIR spectrum will be constructed from independent exposures for each coronagraphic nulling bandwidth, and different integration times will be selected for each null based on the expected contrast at that wavelength. In all simulations, there is poorer signal-to-noise at visible wavelengths compared to NIR wavelengths, because the star is dim at visible wavelengths compared to the NIR. The vertical bars illustrate the IWA cutoffs corresponding to λ/D (red), 2λ/D (green), and 3λ/D (blue).

For the 30 m ground-based simulations, the thermal background from Earth's surface and atmosphere makes observations longward of about 2.5 μm difficult at this low spectral resolution, so IWA = λ/D may not actually meaningfully increase our ability to characterize Proxima Centauri b compared to a more modest IWA of 2λ/D for this type of observatory. In the optimistic scenario where the atmosphere can be cleanly corrected for, the base of the oxygen A band for the modern Earth analog planet could be detected with SNR ∼30 in 10 h. Even if the true observing time is longer in reality, this short integration time for a very high-confidence detection suggests that such an observation may be possible for more conservative scenarios.

For a 16 m LUVOIR-class space-based telescope, good signal-to-noise is achievable for the entire wavelength range captured by wavelengths shorter than the λ/D cutoff except for the shorter visible wavelengths where the host star is dim. The base of the oxygen A band on the modern Earth analog could be observed at SNR = 20 in ∼1 h with such an observatory, which is comparable to the 30 m ground-based observatory in the moderately turbulent atmospheric conditions we simulate. If the IWA was as small as λ/D, this could theoretically allow observations out to 2.89 μm. Our simulations assume a mirror temperature of 270 K. Excitingly, because the planet is bright relative to its star, the telescope thermal emission does not swamp the planet signal except for wavelengths longer than about 2.5 μm; by comparison, the signal for an Earth twin orbiting a solar-twin star at 10 pc is swamped by telescope thermal emission for wavelengths longer than about 1.8 μm except when observing with very long integration times on the order of hundreds or thousands of hours. Because the current working design of the LUVOIR NIR detector cuts off at 2.5 μm (M. Bolcar, personal communication), the entire available detector range could obtain useful data from Proxima Centauri b for large telescopes if this optimistic IWA of λ/D could be achieved. This would, for example, allow access to the strong CO₂ band near 2 μm to help constrain the efficiency of Proxima Centauri b's greenhouse and its atmospheric redox state. On the other hand, if an IWA of only 2λ/D is possible, this would still allow access to wavelengths <1.44 μm. If an IWA of only 3λ/D is possible, a 16 m LUVOIR telescope could observe out to 0.96 μm. This would still allow access to the oxygen A band, but a large fraction of this wavelength range would occur at wavelengths where the star is dim and the spectrum lacks strong absorption features.

Observing Proxima Centauri b is naturally more difficult, but still possible, with a smaller telescope like the HabEx concept. A 6.5 m HabEx telescope could observe the deepest part of the oxygen A band in the habitable Earth-like planetary cases at SNR = 20 in over 10 h. However, the oxygen A band is not accessible with a 6.5 m telescope if the IWA achievable is not better than 2λ/D, which cuts off the spectrum longward of 0.59 μm. On the other hand, if HabEx were to fly with a starshade, this could make it possible to observe a smaller IWA and achieve a wider coverage of wavelength space. However, the ability to discriminate the light of the planet from background sources will still be hampered by the PSF of the smaller mirror, and integration times will be longer compared to a larger mirror.

The exposure time necessary to achieve a given signal-to-noise for the flux in the bottom of a band is distinct from the exposure time needed to detect that band itself. As noted in Robinson et al. (2016), for shallow bands, it is relatively simple to measure the flux at the bottom of the band, but it is more difficult to measure the drop in flux due to the band relative to the continuum. Conversely, for strong absorption features, a precise measurement of the bottom-of-band flux may be quite difficult compared to a determination that there is an absorption band at that wavelength.

For atmospheres with high O₂ abundances, the 0.76 μm oxygen A band will be extremely strong and amenable to detection. Following Robinson et al. (2016; Eq. 7), we calculate the exposure time necessary to detect the oxygen A band with a SNR of 5. We find that the oxygen A band can be detected in all the high O₂ atmospheres (Figs. 21, 22, 24) with approximately 1 min exposures for the 16 m LUVOIR and 30 m concepts, while the 6.5 m HabEx concept would require up to 30 min (if the stringent IWA constraint is met). Detecting the oxygen A band for the habitable Earth-like case would require approximately 1 h with the 6.5 m HabEx concept and approximately 3 min with both the 16 m LUVOIR concept and the 30 m ground-based concept. The Archean Earth-like and the Venus-like cases do not contain sufficient oxygen to exhibit detectable oxygen absorption features. Despite having a mirror nearly twice the diameter, the 30 m ground-based telescope and the 16 m LUVOIR concept have comparable performance in the visible due to the sky brightness faced by the ground-based measurements. The advantage of the space-based telescope is further increased beyond 1 μm.

The specific values for the telescope and instrument parameters used here represent notional LUVOIR and HabEx parameters and should be considered preliminary, as these telescope designs are still under early study. Therefore, the integration times and SNR calculations presented here should likewise be understood as notional estimates pending changes to the telescope designs studied by their respective Science and Technology Definition Teams.

4.6. What might Proxima b look like to the human eye?

In addition to all our spectral simulations, we used the Python package ColorPy¹⁷ to visualize the apparent visual color of the range of possible atmospheric states for Proxima Centauri b examined here. ColorPy uses the 1931 Commission Internationale de l'Eclairage (CIE) color matching functions (Smith and Guild, 1931) to calculate the apparent, human-perceived color from an intensity spectrum. We modified ColorPy to take our top-of-atmosphere planetary spectra (Section 4.4) as inputs for these color calculations. Figure 27 shows the visual spectra (380–720 nm) and calculated colors for the star, Proxima Centauri, and our modern Earth-like case with 50% cloud cover, Archean (early) Earth, O₂-dominated, and Venus-like scenarios. For the O₂-dominated cases with substantial (10 bar) atmospheres, the blue color reflectivity enhancement overwhelms the redness of the star in the human visual range, resulting in green planets. The modern Earth case appears yellow because Rayleigh scattering and ocean reflection enhance the blue, but reflection by continents and clouds enhances reflection of red light. The haze-covered Archean Earth and the Venus-like cases are redder than modern Earth: both of these planets have blue wavelength absorbers in their atmospheres and appear orange. Therefore, for plausible sets of both habitable and uninhabitable atmosphere states, Proxima Centauri b might appear as a pale green, pale yellow, or pale orange dot.

FIG. 27.

Optical spectra and the corresponding colors that the human eye would perceive for Proxima Centauri and five of our simulated planetary states. From upper left to lower right: the M5.5V red dwarf star Proxima Centauri, Earth-like with no clouds, hazy Archean with no clouds, O₂-dominated with an ocean, desiccated O₂-dominated, and cloudy Venus-like. The background of each plot is colored as it would appear to the human eye. The shaded area under the curve represents the individual color of each wavelength at the simulated spectral resolution. Each planetary spectrum represents a convolution of the stellar spectrum with the planetary albedo, which is dictated by the planet's surface and atmospheric composition. Furthermore, each perceived color represents a convolution of the planetary spectrum with the human eye.

5. Discussion

The discovery of Proxima Cen b provides a truly remarkable opportunity to learn about the evolution of terrestrial planets orbiting M dwarfs, as well informing our understanding of the range of habitable environments in the Universe. However, although it sits in the habitable zone, which confers a higher probability of being able to support liquid water on its surface, the evolution of the star and planet can work to maintain or destroy habitability for Proxima Cen b (Barnes et al., 2018; Ribas et al., 2016). Consequently, even though Proxima Cen b has the advantages of size and current position in the habitable zone, its habitability is by no means certain and will depend strongly on the evolutionary path taken by the planet and its current interaction with its parent star. Our study has simulated several possible planetary states for Proxima Centauri b that show both habitable and uninhabitable environments.

5.1. The habitability of Proxima Centauri b

We find that Proxima Cen b inspires three fundamental scientific questions: What are the evolutionary paths for Proxima Cen b and for terrestrial planets around other late-type M dwarfs? Is Proxima Cen b currently habitable? How can we best discriminate between possible environmental states for Proxima Cen b and for other M dwarf planets?

The first question was explored in detail in our companion paper by Barnes et al. (2018), which shows that despite the planet's location in its star's habitable zone, this world may not be water-rich, or habitable. The star's luminous pre-main sequence phase represents the biggest barrier to the planet's habitability, and if the planet formed in situ, it may have been desiccated early in its history. However, if the planet retained some of its initial water inventory or migrated to its current orbit from the outer planetary system after the pre-main sequence phase, it may yet be hospitable to life. As formulated here, we identified planetary environmental states that spanned the post-runaway, oxygen-dominated worlds of Luger and Barnes (2015) through terrestrial planet evolution that would lose or sequester the O₂, increase atmospheric CO₂ from geological processes, and progressively desiccate the planet. Habitable scenarios are also possible, especially if H₂ envelopes protect terrestrial planets that formed in situ, or volatile-rich bodies migrate in from beyond the snowline (Luger et al., 2015). We note however that although these scenarios are representative, they are still likely to be a small sample of the possible configurations for M dwarf planet environments.

But is Proxima Centauri b currently habitable? To start to address that question, our climate-photochemical modeling of the possible end-state atmospheres for the evolutionary paths shows environmental states (Table 7) ranging from uninhabitable due to water loss and/or surface temperatures that are too high or low, to worlds that could support liquid water. The uninhabitable planet environments for Proxima Cen b include the desiccated, 10 bar high-O₂ planet with 0.5% CO₂, which has a globally averaged surface temperature of only 256 K and so would be cold and dry. Other uninhabitable planets fell into the hot and dry category, with the evolved, desiccated O₂/CO₂ atmospheres exhibiting surface temperatures of 383–569 K. The Venus-like planets, with a larger atmospheric CO₂ fraction and pressures up to 90 bar, also showed extremely high surface temperatures of 385–654 K at Proxima Centauri b's position within its habitable zone. These results highlight the considerable impact of planetary evolution and atmospheric composition on habitability, even for planets in the habitable zone. For the desiccated (<1 ppm H) atmospheres that initially have 1 bar of CO₂, but then photochemically produce O₂ and CO, which remain stable in their desiccated atmosphere, a temperature of 254 K was obtained. This extremely desiccated planet would not be habitable due to its lack of water and cold conditions. In this case it is interesting to note that the photochemical destruction of CO₂ had a significant impact on the planetary climate. Because of the importance of greenhouse gas abundance for the final climate state, future work should concentrate on understanding the likely outgassing history and plausible atmospheric compositions for terrestrial exoplanets.

The habitable planetary states were also quite varied. If the runaway process halts before all the planetary water inventory is lost, then even a 10 bar O₂ planet with 0.5% CO₂ and an ocean exhibits a globally averaged surface temperature of 320 K, primarily due to the greenhouse effect of the atmospheric water vapor. This is significantly warmer than Earth's current 288 K globally averaged surface temperature, but still potentially habitable. However, it is debatable whether life could start on this planet, as the strongly oxidizing atmosphere would be challenging for the stability of the organic molecules required for the origin of life. We also considered more Earth-like cases, including a modern but photochemically self-consistent Earth-like planet whose atmospheric composition is consistent with the UV radiation from the parent star. The star's UV spectrum resulted in longer lifetimes for, and a buildup of, greenhouse gases such as CH₄ and N₂O, as was previously seen by Segura et al. (2005). This emphasizes the need for both photochemical models and knowledge of the UV spectrum of the host star when trying to model and interpret information on the environments of planets orbiting M dwarfs. For this simulated environment we can obtain cold but habitable surface conditions (273 K) for CO₂ abundances near 5%, with likely open ocean fractions in this case (Charnay et al., 2013; Shields et al., 2013). For the Archean Earth analogue, 5% CO₂ was also specified, but the higher methane fraction resulted in a warmer surface temperature of 278 K in the haze-free case with 1% CH₄, and when CH₄ was increased to 1.5% a haze formed but only modestly cooled the planet to 277 K because hydrocarbon hazes are relatively transparent at the longer wavelengths emitted by late-type M dwarfs (Arney et al., 2017).

Our climate models are 1-D and produce globally averaged results that are most relevant to Proxima Centauri b if the planet is found to be in an asynchronous 3:2 spin-orbit resonance. Since Proxima Cen b's eccentricity is only observationally constrained to be <0.35 (Anglada-Escudé et al., 2016), we cannot discriminate between a circular orbit with a likely synchronous rotational state and an eccentric orbit with a likely asynchronous rotational state. However, it is interesting to discuss under what conditions the asynchronous state is likely for Proxima Centauri b and the consequences to our atmospheric results if the rotation state is not asynchronous. If Proxima Cen b is the only planet in its system, then synchronous rotation may be likely, although the eccentricity data do not rule out asynchronous rotation. While tidal damping of the planetary spin is likely rapid, and for this nominally ∼5-billion-year-old system would result in tidal circularization (Barnes et al., 2018; Ribas et al., 2016), Ribas et al. (2016) also found a significant probability that the planet is in a 3:2 spin-orbit resonance, especially if the planet's eccentricity is >0.1, agreeing with similar results by Rodríguez et al. (2012). There are several mechanisms that would produce a nonzero eccentricity for Proxima Cen b today, including a recent close encounter between Proxima Centauri and α Centauri A and B. However Kepler statistics suggest that at least half of M dwarf systems contain five or more closely packed, coplanar planets (Ballard and Johnson, 2016), and compact planetary systems may be marginally stable, with instabilities that may produce eccentric orbits occurring billions of years after formation (Volk and Gladman, 2015; Ballard and Johnson, 2016). This may result in apparent (to transit) single-planet systems that are the result of a close-packing instability, at least some of the time (Ballard and Johnson, 2016). In both scenarios, other, as yet undetected, planets in the Proxima Cen system could potentially induce significant eccentricities in Proxima Cen b's orbit, which could make capture into the 3:2 resonance much more likely. Barnes et al. (2018) also show that if a currently undetectable companion planet exists in the Proxima Centauri system, such as the putative planet with an orbital period near 200 days (Anglada-Escudé et al., 2016), it could drive an eccentricity in Proxima Cen b's orbit that could be maintained at e > 0.1, even after 7 billion years, and force the planet into supersynchronous rotation (Barnes et al., 2018). Clearly, observations and improved constraints on the current orbit of Proxima Cen b, and the presence and orbital parameters of any companions, are extremely important for our understanding of Proxima Cen b's current orbital state and climate.

However, even if Proxima Centauri b were synchronously rotating, 3-D GCMs of terrestrial exoplanets now routinely show that atmospheric rotation can transfer heat from the dayside to nightside of the planet, and habitable conditions are possible for planets with as little CO₂ as 1 ppm near the inner edge (Kopparapu et al., 2016). Additionally, while 3-D GCMs suggest that reflective clouds could form across the substellar hemisphere of slowly rotating planets and cool them, this effect is likely ameliorated for Proxima Cen b. If Proxima Cen b is synchronously rotating, its relatively short 11-day period could result in some of the substellar cloud deck being advected to the antistellar side of the planet. This process would thin and reduce cloud coverage on the dayside and thereby warm the planet by dropping the dayside albedo from that expected from complete cloud coverage (Yang et al., 2014; Kopparapu et al., 2016). This effect would be even more pronounced if the planet was in a 3:2 spin-orbit resonance with a rotational period close to 7 days, when the reduction in dayside cloud cover due to zonal banding could be larger (Kopparapu et al., 2016).

Atmospheric collapse is another aspect of synchronous rotation that could strongly impact planetary surface temperature and habitability. If the planet is synchronously rotating, the probability that there are significant day-night contrasts—and atmospheric collapse—is strongly dependent on the atmospheric mass, composition, and the presence of an ocean. Turbet et al. (2016) using the LMDz 3-D GCM, for synchronous rotators, showed that one Earth ocean of water is enough to avoid atmospheric collapse for all CO₂ partial pressures above 0.1 bar without a background gas, and 0.01 bar of CO₂ with a background gas such as N₂ or O₂ (their Fig. 1). This is also assuming no ocean heat transport, which would work to equalize day-night temperatures. Three-dimensional modeling work by Hu and Yang (2014) demonstrated that when dynamic ocean heat transport is considered, this process can raise the minimum temperature of the planet when compared to a nondynamic ocean, further protecting the atmosphere from collapse and leading to deglaciation on the nightside. For the case of desiccated worlds, Turbet et al.'s 3-D GCM modeling shows that for ocean-free synchronously rotating worlds, 1 bar of CO₂ is unstable and collapses; but despite large day-night temperature contrasts (<∼75 K), 4 bar of CO₂ does not collapse. So the true atmospheric CO₂ mass required to prevent collapse is probably between 1 and 4 bar. Six bar of CO₂ is sufficient to provide for a world entirely above freezing.

Based on these 3-D GCM results of Turbet et al. (2016), our simulated atmospheres are all likely robust against atmospheric collapse if Proxima Cen b is asynchronously rotating, and most will also avoid collapse even in synchronously rotating situations. Specifically, our 10 and 90 bar CO₂-dominated Venus-like planets and evolved CO₂/O₂ atmospheres (containing 4.5 and 40 bar of CO₂) are stable against collapse for synchronous rotation. Our modern and Archean Earth-like worlds have oceans and 1 bar N₂-dominated atmospheres with 5% CO₂ (so 0.05 bar CO₂, which is greater than the 0.01 bar CO₂ limit with background gas) and so based on the results of Turbet et al. (2016) are also stable against collapse even if synchronously rotating. In other words, a synchronously rotating planet with an Earth-like, N₂-dominated atmosphere would need 25 times Earth's current CO₂ abundance to avoid collapse. Less CO₂ may be required to avoid collapse if there is strong ocean heat transport between the day-night hemispheres (Hu and Yang, 2014). Similarly, our O₂-dominated planets with remnant ocean were given the same amount of CO₂ for comparison with the Earth-like cases and have 0.5% CO₂ in a 10 bar atmosphere, and so 0.05 bar of CO₂ overall, with an ocean, and so are safe from collapse.

However, our desiccated 1 bar CO₂/O₂ atmosphere and the 10 bar O₂-dominated (0.05 bar CO₂) desiccated cases are more susceptible to collapse, but this it is not conclusive and would require further modeling to explore. In the 1 bar case, we have 0.5 bar of CO₂, and Turbet et al. (2016) showed regions of CO₂ condensation for a 1 bar synchronously rotating CO₂ planet. However, an atmosphere with 0.5 bar of CO₂ is more robust to condensation and according to the Clausius-Clapeyron relation will not condense unless the minimum temperature falls below 187 K at the surface, and our atmosphere has an average temperature of 254 K. However, carbon dioxide may begin to condense if parts of the surface drop below 187 K. Again, this would only apply to the synchronously rotating case. In the case of the 10 bar O₂ planet, with 0.05 bar of CO₂, and a background gas, condensation would occur at 164 K, and we find an average surface T of 256 K. We cannot state categorically that these atmospheres would collapse, but it may be possible, although the reduction in condensation temperature with the reduction in partial pressure of CO₂ would need to be modeled to give a more conclusive answer. Turbet et al. (2016) show that all the comparable asynchronous cases are safe from collapse. So if Proxima Cen b was synchronously rotating, these thinner, desiccated atmospheres may be in danger. However, if the planet is asynchronously rotating, these atmospheres would be likely to survive.

So, how should we best use observations to discriminate between these possible environmental states, not only for Proxima Cen b but for other M dwarf planets as well? The post-runaway O₂-dominated worlds are best discriminated by the presence of strong O₄ bands in the visible and NIR for direct imaging, and in the NIR for transmission. Since the atmosphere is strongly oxidizing, and if desiccation has occurred, the presence of aerosols other than dust may be unlikely, making the planet quite bright in the Rayleigh scattering tail. The desiccated case also shows strong ozone absorption because the HO_x products that would destroy it are not present. Water may also be detected in direct imaging, in the case where some of the remnant ocean is retained, but the strong O₄ would sound a warning that the O₂ was most likely formed post-runaway and not from a photosynthetic biosphere (Schwieterman et al., 2016). As the planet evolves to also include abundant CO₂ in addition to the O₂, strong CO₂ bands are seen in both the direct imaging and transmission spectra. Venus-like worlds are dominated by CO₂ features, especially near 1.5 and 2.0 microns, although weaker bands can also be seen even into the visible at 0.78, 0.87, 1.05, and 1.2 microns. In our simulations, weak water vapor was also seen in the spectrum, because there is still water above the cloud deck. In the real venusian atmosphere, there is 6 ppm above the cloud tops on the nightside (Schofield et al., 1982). These planets were also able to form sulfuric acid hazes that increase the planetary albedo and can be spectrally identified by NIR absorption features that may visible in transit transmission spectra (Figs. 14 and 19). The presence of an H₂SO₄ haze may also imply active volcanism on an exoplanet and may hint at internal or tidal energy driving volcanic activity. The amount of SO₂ in the venusian atmosphere required to maintain the sulfuric acid cloud deck has been estimated to be in excess of equilibrated conditions by a factor of 100, implying a source within the past 20 million years (Bullock and Grinspoon, 2001) or possibly within 2 million years (Fegley and Prinn, 1989). Detection of H₂SO₄ would therefore likely be a sign of some level of geological activity. For the highly desiccated, photochemically stable CO₂/CO/O₂ atmospheres, no H₂O would be detectable, but CO₂ and CO would be prominent at 2.35 μm, and O₄ would be absent. The strong CO₂ and CO would also be a useful indication that the O₂ in the atmosphere was likely not biologically produced (Schwieterman et al., 2016).

For the habitable planets, water dominates the simulated direct imaging spectra, with strong bands starting at 0.95 μm and continuing through the NIR. O₂ is also seen, but O₄ is not significant. The other strong discriminant in these cases is the presence of CH₄, which is not seen in the strongly oxidizing, post-runaway terrestrial atmospheres. CH₄ has its strongest bands in the NIR, and interestingly, water absorption features frequently overlap with stronger methane bands. Figures 16 and 20 show how the strong NIR water features at 1.15 and 1.4 μm overlap with methane features. This is particularly problematic given that the UV spectrum of the parent M5.5V star drives the significant photochemical accumulation of CH₄ in the atmosphere of even the modern Earth. In transmission, water is not readily seen for these habitable planets. This is largely due to the fact that habitable planets have cold traps that keep water in the troposphere and desiccate the stratosphere. Due to the effects of refraction and opacity (e.g., Misra et al., 2014b), transmission observations predominantly probe the stratosphere of habitable terrestrial planets where water is scarce. Strong water vapor bands in a transit transmission spectrum would indicate a planet with a wet stratosphere, which may indicate a planet undergoing a moist or runaway greenhouse. Additionally, the photochemically favored buildup of CH₄ works to “cover” the weak stratospheric water signal spectrally and also provides additional opacity to make it more difficult to see into the troposphere. In direct imaging, water vapor can still be seen due to the more direct line of sight, potentially to the planetary surface. Quantifying water and methane abundances in these types of atmospheres without degeneracy will require access to “clean” methane and water bands that do not overlap. The water band near 0.95 μm is relatively clean, as is the methane band near 1.7 μm.

5.2. Potential for future observations

Because Proxima Cen b is so close to Earth, it offers us the unprecedented opportunity to characterize a potentially terrestrial exoplanet that orbits within its star's habitable zone. The proximity of this target offers obvious major advantages, including shorter integration times and a larger IWA relative to more distant planets orbiting M dwarfs—but there are still difficulties.

Because Proxima Cen b orbits so close to its dim host star, the angular separation between it and its star is only 37 mas at maximum elongation. This narrow separation means that to be able to directly image this target out to longer wavelengths, larger telescope apertures are favored to overcome IWA limitations, and they can shorten the required integration times to obtain a good signal relative to smaller telescopes. However, although the angular separation is challenging, for direct imaging Proxima Centauri b provides a relatively high contrast (planet-to-star flux ratio) of tens of parts per billion for a planet with Earth-like brightness orbiting a star significantly fainter than the Sun. This makes Proxima b nearly 100 times more favorable to observe directly than an Earth-Sun analog system, even before considering the advantage of its proximity to our solar system. Large ground-based telescopes may be able to measure the planet's spectrum with the aid of coronagraphy and adaptive optics, but the thermal signature from the telescope and atmosphere will make ground-based direct imaging observations more challenging at wavelengths longer than about 2.5 μm. However, the wavelengths between 1 and 2.5 μm are still extremely useful for atmospheric characterization due to absorption signatures from potentially diagnostic gases, including CO₂ and CH₄.

Since it is unlikely that Proxima Cen b transits (Kipping et al., 2017), one of the most promising observations achievable in the near-term will be thermal phase curves of Proxima Centauri b taken with JWST. The size of any day-night temperature contrasts observed may reveal the presence of an atmosphere. Larger day-night temperature differences indicate poor heat transport, with smaller temperature differences expected for denser atmospheres (Stevenson et al., 2014; Cowan et al., 2015). Because Proxima Centauri b is probably nontransiting, detecting an atmosphere will likely require phase-resolved photometry (e.g., Knutson et al., 2007) or high-dispersion spectroscopy (e.g., Brogi et al., 2013, 2014). Thermal phase curves with JWST may provide our first opportunity to probe the atmospheric composition of Proxima Centauri b. Luger et al. (2017) proposed to leverage the stellar activity and flaring to our advantage and look for sharp oxygen auroral emission from the planetary atmosphere. However, these observations would require the use of high-spectral-resolution, high-contrast coronagraphy, which is still many years away. The most promising effort in that regard may be the coupling of high-resolution imaging and spectroscopy on ground-based telescopes over the 0.6–0.78 μm visible range, which may be achievable over the next 5 years on the Very Large Telescope (Lovis et al., 2017). Kreidberg and Loeb (2016) investigated the detectability of ozone at 9.8 μm with the LRS mounted on JWST/MIRI. Although an ozone detection would be a significant step forward in exoplanet atmospheric characterization, ozone is not an unambiguous biosignature, as it is predicted to accompany abiotically produced O₂ via photochemistry during the super luminous pre-main sequence phase. Detecting ocean glint would also be extremely diagnostic for surface water, but is beyond the capabilities of JWST for Proxima Cen b. Ocean detection will need to wait for a larger-aperture space-based coronagraph or starshade mission, or possibly a large-aperture ground-based telescope with coronagraphic capabilities.

To understand Proxima Cen b's atmosphere, it will also be important to thoroughly characterize its host star. Through photochemical reactions, the star's UV SED can change the atmospheric state of Proxima Cen b sufficiently to distinguish it from an analog planet orbiting the Sun (Section 4.2.3.1). As discussed above, methane builds up to considerably higher amounts detectable in the spectrum of a modern Earth analog planet around Proxima Centauri, but this does not occur around a solar-type star. To study anticipated effects such as this, it is critical to examine potential atmospheres of this planet by using photochemical models with the correct stellar parameters for Proxima Centauri. Additionally, Proxima Centauri is an active star, and our study here has not examined the impact of stellar flares on planet b's atmosphere and photochemistry. Future work will examine the impact of flares on the photochemistry, habitability, surface environment, and detectability of spectroscopic signatures.

6. Conclusions

Proxima Cen b provides an exciting opportunity to learn about the evolution of terrestrial planets orbiting M dwarfs and the nature and extent of habitable environments in the Universe. However, we find that its evolutionary history and current volatile inventory will strongly impact its habitability, even though it resides in the habitable zone. We used coupled climate-photochemistry models to simulate several plausible states for the current environment of Proxima Cen b, for possible scenarios driven by dynamical and stellar evolution. We find several post-runaway states that are uninhabitable either due to extreme water loss or inclement surface temperatures. In particular, a dense Venus-like CO₂ atmosphere will result in extremely high surface temperatures at Proxima Cen's current semimajor axis. However, several evolutionary scenarios may lead to possibly habitable planetary environments, including O₂-rich atmospheres that retain a remnant ocean after extreme water loss, and other, more Earth-like scenarios. These later scenarios include a possible terrestrial planet or volatile-rich core having been protected against the bright early star by a hydrogen envelope, or the late migration via orbital instabilities of a terrestrial world from exterior to the habitable zone. In these more Earth-like cases, only modest amounts of carbon dioxide (0.05 bar) or methane (0.01–0.03 bar) are required to warm the planetary surface. These different scenarios can be discriminated between using observations of thermal phase curves, ocean glint, and spectroscopic diagnostics including O₂, O₃, O₄, CO, CO₂, H₂O, and CH₄, all of which absorb in the 0.3–2.5 μm region. Further information on its planetary characteristics will provide a crucial opportunity for comparative planetology—by broadening our understanding of how terrestrial planetary evolution and processes that operate in our own solar system may be impacted by a very different host star. Upcoming observations with large ground- and space-based telescopes may help illuminate the intriguing environment of our nearest exoplanetary neighbor.

Abbreviations Used

E-ELT

European Extremely Large Telescope

ELTs

extremely large telescopes

ExAO

Extreme Adaptive Optics

GCM

General Circulation Model

HabEx

Habitable Exoplanet Imaging Mission

IWA

inner working angle

JWST

James Webb Space Telescope

LBLABC

Line-By-Line Absorption Coefficients

LRS

Low-Resolution Spectrograph

LUVOIR

Large UltraViolet Optical Infrared Surveyor Telescope

mas

milliarcseconds

MIR

mid-infrared

MIRI

Mid-Infrared Instrument

MRS

Medium-Resolution Spectrograph

NIR

near-infrared

SED

spectral energy distribution

SMART

Spectral Mapping Atmospheric Radiative Transfer

SNR

signal-to-noise ratio

STIS

Space Telescope Imaging Spectrograph

SZAs

solar zenith angles

WFIRST

Wide-Field Infrared Survey Telescope

Acknowledgments

We thank Guillem Anglada-Escudé and his team for sharing their discovery results with us. We are grateful to two anonymous referees whose thoughtful, thorough reviews helped us significantly improve the paper. This work was supported by the NASA Astrobiology Institute's Virtual Planetary Laboratory Lead Team, funded through the NASA Astrobiology Institute under solicitation NNH12ZDA002C and Cooperative Agreement Number NNA13AA93A. This work was facilitated through the use of advanced computational, storage, and networking infrastructure provided by the Hyak supercomputer system at the University of Washington. E.W. Schwieterman is grateful for support from the NASA Postdoctoral Program, administered by the Universities Space Research Association. T. Robinson gratefully acknowledges support from NASA through the Sagan Fellowship Program executed by the NASA Exoplanet Science Institute. D.P. Fleming is supported by an NSF IGERT DGE-1258485 fellowship.

Author Disclosure Statement

No competing financial interests exist.