Neural circuit inference from function to structure

Summary

Advances in technology are opening new windows on the structural connectivity and functional dynamics of brain circuits. Quantitative frameworks are needed that integrate these data from anatomy and physiology. Here we present a modeling approach that creates such a link. The goal is to infer the structure of a neural circuit from sparse neural recordings, using partial knowledge of its anatomy as a regularizing constraint. We recorded visual responses from the output neurons of the retina, the ganglion cells. We then generated a systematic sequence of circuit models that represent retinal neurons and connections, and fitted them to the experimental data. The optimal models faithfully recapitulated the ganglion cell outputs. More importantly, they made predictions about dynamics and connectivity among unobserved neurons internal to the circuit, and these were subsequently confirmed by experiment. This circuit inference framework promises to facilitate the integration and understanding of big data in neuroscience.

Graphical abstract

Neuroscience research faces a need to link big data on brain anatomy and physiology as high-throughput measurements become increasingly feasible. Real et al. present a modeling approach to provide such a link, and test it by inferring the structure of neural circuitry in the retina from sparse physiological recordings.

Introduction

Much of neuroscience seeks to explain brain function in terms of the dynamics in circuits of nerve cells. New parallelized technologies are greatly accelerating the pace of measurements in this field. The structure of brain circuits, namely the shapes of neurons and their connections, can be determined from high-throughput 3-dimensional light and electron microscopy (EM) [1]. The dynamics of signals in those neurons are revealed by a host of parallel recording methods that use optical or electrical readout simultaneously from many hundreds of neurons [2,3]. What is urgently needed is a modeling framework that can integrate these data, provide an explanatory link between structural connectivity and neural dynamics, and finally reveal the overall function of the system.

Neural circuit diagrams (Figures 1 and S1) are a powerful abstraction tool, because they serve as an explanatory link between brain anatomy and physiology [4–7]. In the conventional mode, one proceeds from structure to function: Anatomical studies reveal how neurons are connected. From this one constructs a circuit diagram that predicts the signal flow through the circuit. Those predictions are then tested by physiological experiments. It is worth considering whether this traditional process can be generalized in a way that meets more realistic needs of neuroscience. Typically one has only sparse and incomplete knowledge of the circuit’s structure. For example, even the best EM images cannot reveal the strength of every synapse. Similarly, the functional data are limited, for example to neural recordings from those cells that are most accessible. A circuit model that satisfies both these data sets can serve as the glue needed for their integration. If successful, such a model can make new predictions both for neural connectivity and for neural function that serve to motivate the next round of experiments.

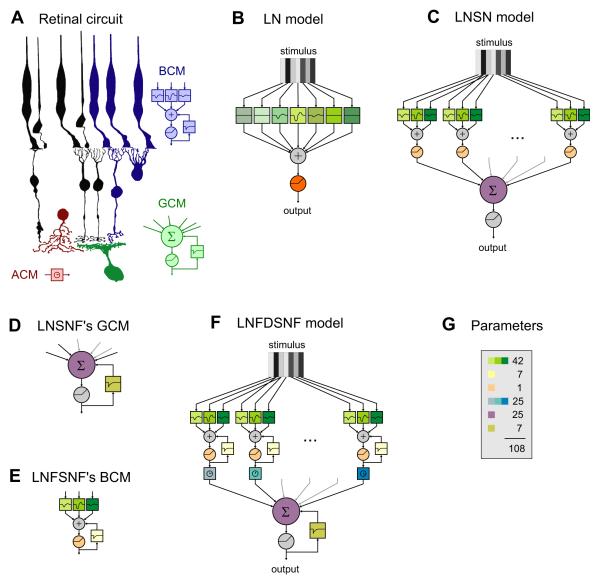
Figure 1. A progression of circuit models constrained by retinal anatomy.

(A) Schematic of the circuit upstream of a ganglion cell in the vertebrate retina. Photoreceptors (P) transduce the visual stimulus into electrical signals that propagate through bipolar cells (B) to the ganglion cell (G). At both synaptic stages one finds both convergence and divergence, as well as lateral signal flow carried by horizontal (H) and amacrine (A) cells. The bipolar cell and its upstream circuitry is modeled by a spatio-temporal filter, a nonlinearity and feedback (bipolar cell module, BCM; blue). The amacrine cell introduces a delay in lateral propagation (amacrine cell module, ACM; red). The ganglion cell was modeled by a weighted summation, another nonlinearity, and a second feedback function (ganglion cell module, GCM; green). Drawings after Polyak, 1941.

(b) LN model. A different temporal filter is applied to the history of each bar in the stimulus. The outputs of all these filters are summed over space. The resulting signal is passed through an instantaneous nonlinearity.

(c) LNSN model. The stimulus is first processed by partially overlapping, identical BCMs, each of which consists of its own spatio-temporal filter and nonlinearity. Their outputs are weighted and summed by the GCM, which then applies another instantaneous nonlinearity to give the model’s output. For display purpose the BCMs are shown here to span only 3 stimulus bars, but they spanned 7 bars in the computations.

(d) LNSNF model. This is identical to the previous one, except that the GCM (depicted here) has an additional feedback loop around its nonlinearity.

(e) LNFSNF model. This is identical to the previous one, except that the BCMs (one of which is depicted here) have an additional feedback loop around their nonlinearities. This new feedback function is the same for all BCMs.

(f) LNFDSNF model. This is identical to the previous one, except that there is a delay inserted between each BCM and the GCM. These delays are allowed to vary independently for each BCM.

(g) A count of the free parameters in the LNFDSNF model, color coded as in the model diagram. Except for the total (108), the numbers here also apply to the LNSN, LNSNF, and LNFSNF models. The LN model has 186 free parameters in the linear filter (31 spatial positions, each with 6-parameter temporal filter as in Error! Reference source not found.–Error! Reference source not found.) and 1 in the nonlinearity. See also Figures S1 and S3.

Here we present an approach for inference of neural circuits from sparse physiological recordings. To test the feasibility of this scheme we worked with a neural system about which a good deal of ground truth is known already: the vertebrate retina [6,8]. In physiological experiments we stimulated the input layer of photoreceptor cells with complex visual stimuli and recorded the output signals from retinal ganglion cells with a multi-electrode array. We then devised a systematic series of models for the intervening circuitry, yielding a best-fit circuit diagram for each ganglion cell type. This method inferred correctly several well-established features of retinal circuitry. It also revealed some unexpected aspects, such as the existence of two different feedback systems. Finally, a critical test of the approach is whether it can predict new circuit structures that were not directly observed. Indeed, the modeling made specific predictions for the response properties and connectivity of bipolar cells, and we subsequently confirmed these quantitatively by direct physiological recordings.

Results

We recorded the spike trains of ~200 ganglion cells in the isolated salamander retina while stimulating the photoreceptor layer with a spatially and temporally rich display: an array of vertical bars that flicker randomly and independently at 60 Hz (Figure S2A). This stimulus drives a wide range of spatio-temporal computations in the retina; at the same time, its restriction to one spatial dimension limits the complexity of analysis and modeling. Repeated presentations of the same flicker sequence reliably evoked very similar spike trains (Figures 2A,B and S2B), as expected from previous studies [9–11]. This suggests that essential features of the retina’s light response can be captured by a deterministic model of the ganglion cell and its input circuitry [4]. In addition we presented a long non-repeating flicker sequence to explore as many spatio-temporal patterns as possible. Thirty ganglion cells were selected for quantitative modeling based on the stability of their responses throughout the extended recording period.

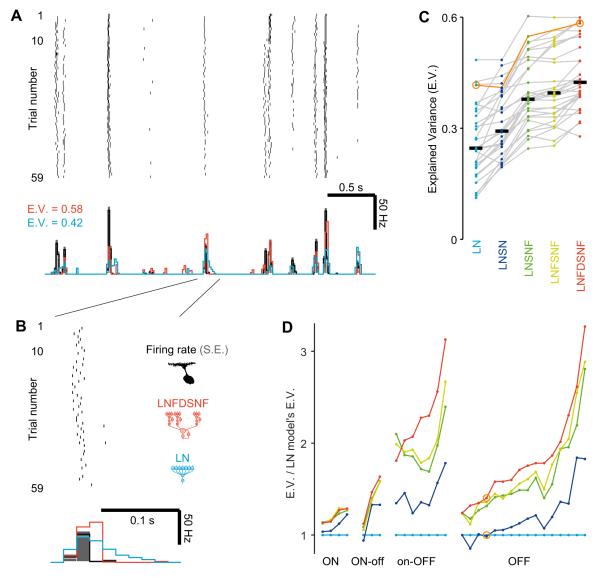
Figure 2. The high precision of retinal responses allows a sensitive discrimination of circuit models.

(A,B) Response of a sample ganglion cell to repetitions of the stimulus (A; zoom-in to one of the firing epoch in B). Top: Each row in the raster denotes spikes from a single stimulus repeat. Bottom: The time course of the firing rate (black; standard error in gray), and that of the output of the models fitted to the same cell (blue, LN model; red, LNFDSNF model). See also Figure S2.

(C,D) A performance summary of all models reveals the most effective circuit features. The example cell in A and B is highlighted in orange. C: Explained variance (E.V.) of individual cells (gray line for each cell) across models (distinct colors). LN, 0.25±0.15; LNSN, 0.29±0.15; LNSNF, 0.38±0.15; LNFSNF, 0.40±0.18; LNFDSNF, 0.42±0.16; median (black horizontal bar) ± interquartile range. D: Variance explained by each model plotted as a ratio to the variance explained by the LN model. Each point along the horizontal axis corresponds to a different ganglion cell, and they are sorted based on their visual response type, and ordered by increasing variance ratio under the most complex model. Note the substantial jump in performance from introducing a nonlinearity at the bipolar cell output (blue to indigo) and from introducing feedback (indigo to green). See also Figure S7.

Modeling approach

We focused on predicting the firing rate of ganglion cells (GCs), namely the expected number of spikes fired in any given 1/60 s interval. Mathematical models were constructed that take the time course of the flicker stimulus as input and produce a time course of the firing rate at the output. The parameters of the model were optimized to fit the long stretch of non-repeating flicker (~80% of the data, the “training set”). Specifically we maximized the fraction of variance in the firing rate that the model explains (Error! Reference source not found.) [11], Then the model performance was evaluated on the remaining data examined with the repeated flicker (~20%, the “test set”). This performance metric was tracked across successive changes in the model structure.

As a formalism we chose so-called cascade models [4,5]. These are networks of simple elements that involve either linear filtering (convolution in space and time) or a static nonlinear transform. They map naturally onto neural circuitry (Figure 1), and can be adjusted from a coarse grained version (every neuron is an element) to arbitrarily fine grained ones (multi-compartment models of every neuron and synapse).

As a reference point we chose the so-called LN model, consisting of a single linear-nonlinear cascade (Figure 1B). This has been very popular in sensory neuroscience [12–14] and serves as a common starting point for fitting neural responses. This model was able to approximate the GC output (Figures 2A,B and S2B), though with a wide range of performance for different neurons (Figure 2C,D). Even with optimized parameters, however, the LN model predicts firing at times when it should not, thus making the peaks of firing events wider and flatter than observed (Figures 2A,B and S2B).

Guided by knowledge of retinal anatomy, we then created a sequence of four cascade models by systematically adding components to the circuits (Figure 1C–F). Each model derives its name from the cascade of components. The last one is the linear-nonlinear-feedback-delayed-sum-nonlinear-feedback (LNFDSNF) model (Figure 1F). For each model class, the components of the circuit were parameterized and the fitting algorithm found the optimal parameter values for each GC (Figure S3). Each model circuit is more general than the previous one and significantly outperformed it in predicting the visual responses of certain GCs (p < 0.001 for every step, sign test; Figure 2C,D). The improvement, however, is not simply due to over-fitting after addition of more free parameters (Figure 1G). In fact, the LN model has the most free parameters among the models we tested. We also used separate training and testing data and achieved equivalent values in the explained variance. This implies that each model truly captures additional aspects of the computations carried out by the retina, and their biological realism will be examined for each case.

LN to LNSN: Multiple bipolar cell modules

Each GC generally pools information from many bipolar cells (BCs) [8]. Previous studies using intracellular recordings have shown that a single BC and its upstream circuitry of photoreceptors and horizontal cells can be well described as a single spatio-temporal linear filter, at least for a moderate dynamic range of stimulus intensity [15]. In addition, transmission at the synapse from BC to GC introduces a nonlinearity, at least for certain BC types [15].

All this suggests a linear-nonlinear-sum-nonlinear (LNSN) model (Figure 1C): This consists of several “bipolar cell-like” modules, each of which is a miniature LN model in itself. Their output is weighted and summed (S), followed by another nonlinear (N) function to produce the GC firing rate [16]. To avoid an excess of free parameters, the bipolar cell modules (BCMs) were all taken to be identical, but placed at different spatial locations in the retina, at increments of one stimulus bar width (66 μm). The BCM outputs are then weighted, pooled together, and rectified by the ganglion cell module (GCM). The second rectification is necessary because some of the pooling weights may be negative, whereas the firing rate of the GC must be positive. In addition, the GCM nonlinearity can express thresholds and rectification in the relationship between synaptic inputs and firing rates.

The fitting algorithm optimized the spatio-temporal filter and nonlinearity of the BCM, as well as the pooling weights of the GCM and its nonlinearity. Owing to the internal nonlinearity in the circuit model, the LNSN model achieved a better performance in predicting the GC visual responses than the LN model (24±5 % increase in the explained variance; mean ± standard error; Figure 2D). Note that this improvement in performance came despite a substantial reduction in the number of free parameters (from 187 to 68). Imposing a structure guided by known anatomy of the retina – the repeating identical subunits from bipolar cells – provides a constraint that regularizes the optimization process and circumvents the “curse of dimensionality” in model fitting. At the same time, this circuit structure seems to be closer to ground truth, as it provides a better match to the system’s function.

Beside this improvement in the model’s performance, several results were robust across all GCs (Figures 3 and 4). First, the spatio-temporal filter of the BCM (Figure 3A) matched existing direct measurements of salamander BC receptive fields in the overall characteristics. In the spatial domain, these BCM filters attained a “Mexican hat” shape – with large values in the center and small opposite polarity values in the surround – and had a much narrower range (106±32 μm, median zero-crossing radius ± interquartile range) than the measured GC receptive fields (180±64 μm; p < 0.001, sign test; Figure 3C). In the time domain, the kinetics of the OFF-type BCMs that depolarize at light-offset were faster than the ON-type ones that depolarize at light-onset (Figure 3A). These characteristics are all consistent with the experimental data [15,17,18].

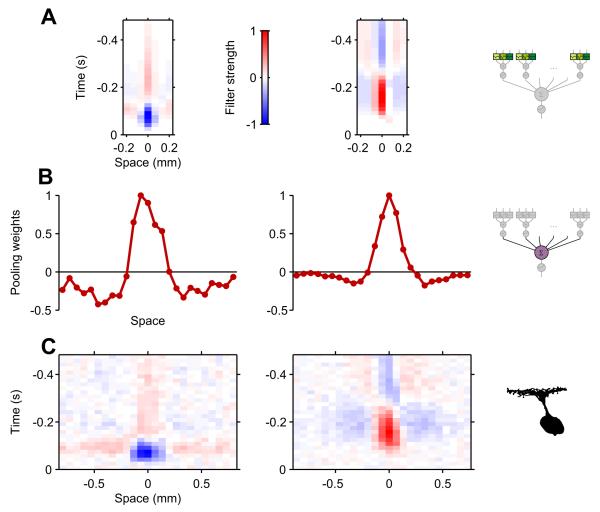
Figure 3. The LNSN model predicts small subunits of the receptive field.

Spatio-temporal filters for the BCM subunits (A) and the GCM pooling functions (B) derived from fits using the LNSN model. Results for two representative GCs (left, OFF type; right, ON type), whose spatio-temporal receptive fields are shown in C. All panels have the same spatial scale. See also Figure S5A,B.

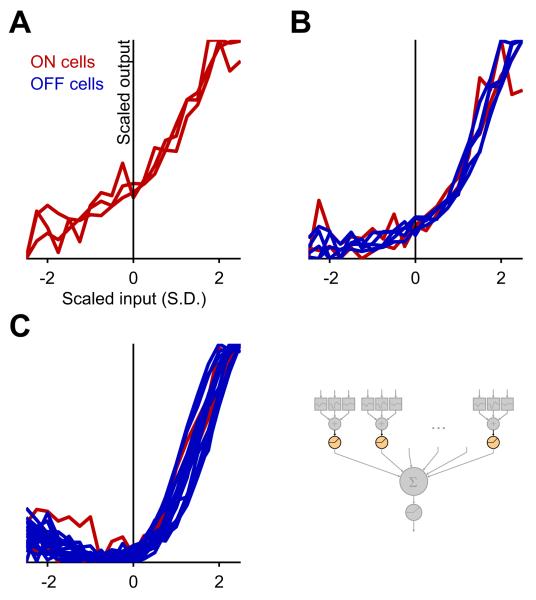
Figure 4. The LNSN model predicts a diversity of transfer functions at the bipolar cell synapse.

The internal nonlinearity of the BCM module inferred by the LNSN circuit model for different ganglion cells. The horizontal axis measures the input to that nonlinearity in units of its standard deviations (S.D.); the vertical axis shows the output of the functions. The nonlinearities are classified into three types: linear (A), monotonic nonlinear (B), and U-shaped (C). The BCM outputs are much more rectified for OFF GCs (blue) than for ON GCs (red; p = 0.005, χ²-test). See also Figure S5C.

Second, the pooling weights of the GCM also attained a center-surround structure but at a considerably larger scale (Figure 3B). The spatial extent of the GCM center (194±39 μm, median zero-crossing radius ± interquartile range) was significantly larger than that of the BCM center (p < 0.001, sign test), and comparable to that of the GC dendritic field in the salamander retina [15,19,20]. The model thus inferred correctly a distinct difference in the spatial pooling properties between circuits in the outer retina (BCM component) and the inner retina (GCM).

Finally, the BCM output nonlinearities fell into three categories (Figure 4): linear, monotonic-nonlinear, and U-shaped. While the linear type was found only in the ON GCs (Figure 4A), the nonlinear types were found more frequently in the OFF GCs (Figure 4B,C). The GCs with the U-shaped BCM nonlinearity likely received excitation from both ON and OFF BCs, and indeed responded to a transition of the stimulus intensity in either direction (data not shown but see, e.g., [21,22]). Nevertheless, the BCM outputs were always highly dominated by one polarity (OFF inputs in most cases) over the other, with about a ten-fold difference in the magnitude (Figure 4C).

For most ganglion cells the BCM nonlinearity had an “expansive” shape with upward curvature [23]. To reduce the number of free parameters, we checked whether this shape could be replaced by a simple half-wave rectifier in subsequent modeling steps. Indeed, this simplification hardly affected the fit (by only 0.01±0.02 in the explained variance; mean ± standard deviation), suggesting that the precise shape of the nonlinearity is not essential for the responses to this broad stimulus set.

LNSN to LNSNF: Ganglion cell output feedback

The models presented so far have an instantaneous nonlinearity at the GCM output. Spike generation, however, involves dynamic processes, such as a slow inactivation of the sodium current in GCs [24]: an increase in firing inactivates the current, which in turn leads to reduced spiking. The inactivation can last for hundreds of milliseconds and is partly responsible for contrast adaptation in retinal responses [24]. In general, any non-instantaneous process that depends on the output cannot be modeled by the LNSN model. A feedback loop around the GCM nonlinearity, however, can emulate these effects [10,11]. Following the rules of cascade modeling, we implemented the feedback as a linear filter, leading to the linear-nonlinear-sum-nonlinear-feedback (LNSNF) model (Figure 1D).

The optimized feedback filter generally consisted of a short positive lobe followed by a longer negative lobe (Figure 5A). The positive lobe was essentially instantaneous, limited to just one stimulus frame (17 ms). The negative lobe could be fit by an exponential with decay time 93±102 ms (median ± interquartile range). With the inclusion of the feedback function, the LNSNF model produced greatly improved fits to the GC visual responses, especially when there is a strong negative feedback (Figure 5B). For most GCs, this was the most beneficial step in the series of the circuit models considered (29±2 % increase in the explained variance from the LNSN model; mean ± standard error; Figure 2D).

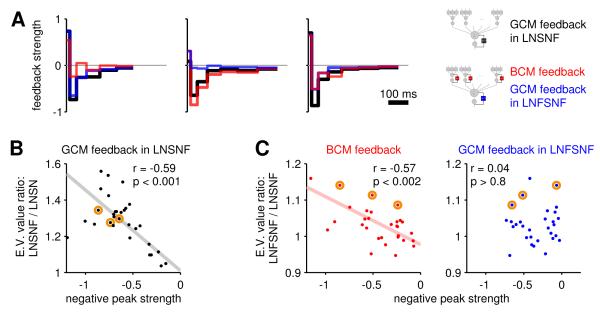
Figure 5. LNFSNF: The importance of feedback at the bipolar and ganglion cell level.

(A) Feedback kernels fitted to three representative cells, using the LNSNF model (black) and the LNFSNF model (GCM, blue; BCM, red).

(B,C) The improvement from models that allow feedback is systematically related to the magnitude of the negative feedback around GCM in the LNSNF model and that around BCM in the LNFSNF model (r, correlation coefficient; p, p-value for testing hypothesis of no correlation; regression line shown in case of significant correlation). Each data point shows the ratio of the explained variance (E.V.) values for each cell either between the LNSNF and LNSN models (B) or between the LNFSNF and LNSNF models (C), as a function of the peak negative feedback strength around BCM or GCM (colors as in A). The representative cells in A are highlighted in orange. See also Figures S4 and S5D.

How does the feedback kernel exert such large effects? The short positive lobe drives the firing rate high as soon as the threshold for firing is crossed, which makes for a sharp onset of firing bursts. Then the later negative lobe eventually suppresses the response following a period of firing – much as in an after-hyperpolarization [25] – with two important effects (Figure S4): First, the early part of the negative lobe (~100 ms) serves to terminate the bursts of firing at the proper duration (Figure S4C,D). Second, the later tail prevents the model from firing for some time after a burst and thus suppresses false responses that would otherwise appear (Figure S4E,F). As a result, the feedback allows the response peaks in the GC output to be taller and sharper, because parameters that control the overall gain are free to grow without incurring a penalty from the appearance of superfluous firing events.

LNSNF to LNFSNF: Bipolar cell synapse feedback

Another site of adaptation in the retina is the BC synapse. The depletion of glutamate vesicles and an activity-dependent reduction in the efficiency of their exocytosis depress the synapse on the timescale of tens to hundreds of milliseconds [26]. A second feedback loop, this time around the BCM nonlinearity, can be used to model this effect. This introduces a BCM feedback and results in the linear-nonlinear-feedback-sum-nonlinear-feedback (LNFSNF) model (Figure 1E). This extension led to small but robust improvements in the fit, primarily for the OFF GCs (3±1 % increase in the explained variance; mean ± standard error; Figure 2D).

The two feedback functions for the BCM and GCM often took on different shapes (Figure 5A). For some GCs, the positive lobe was concentrated in one feedback stage and the negative lobe in the other. These differences were significant: Swapping the two functions degraded the fit, and a subsequent parameter optimization led to a recovery of the original shapes (Figure S5D). For different GCs, the feedback function was dominated either by the component around the GCM or around the BCM (Figure 5A), and cells in the latter category benefited most from introducing a separate BCM feedback to the circuit model. This distinction is prominent especially for the negative portion of the feedback filter (Figure 5C). In summary, feedback plays an important role overall in modeling the responses correctly, yet different GCs vary in the relative importance of the bipolar and ganglion cell feedback stages.

LNFSNF to LNFDSNF: Amacrine cell delay

Previous studies suggest that the negative surround of the GCM pooling function (Figure 3B) arises via inhibition from amacrine cells that carry the information from more distant BCs [8]. Because processing in the intermediary amacrine cells requires extra time, the input to the GCM from BCMs in the distant surround should be delayed with respect to the input from central BCMs. In fact one can observe these delays directly in the spatio-temporal receptive fields (Figure 3C) and the filters of the LN model (Figure S3, top row). This motivated another development of the circuit model: an independent delay parameter for each BCM prior to their pooling. This time delay can be represented by a simple linear filter, and thus the model still conforms to the basic cascade structure. The resulting circuit was called the linear-nonlinear-feedback-delay-sum-nonlinear-feedback (LNFDSNF) model (Figure 1F).

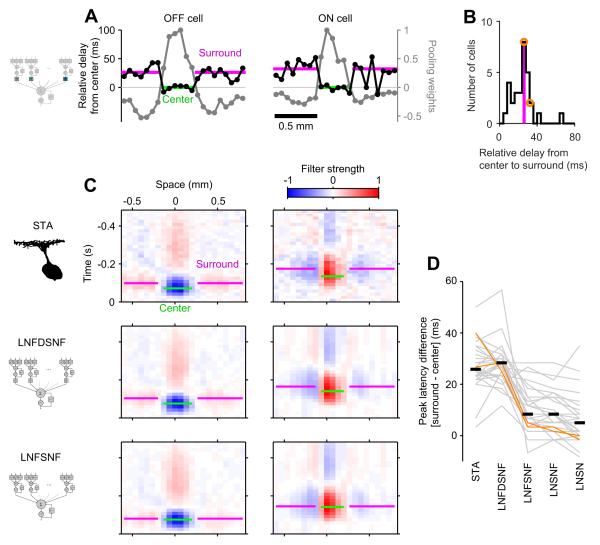
Fitting the LNFDSNF model yielded, in particular, the delays as a function of spatial position (Figure 6A,B). Overlaying this on the simultaneously fitted pooling weights clearly shows that the surround is delayed relative to the center (Figure 6A). This delay ranged from 6 to 66 ms (26±12 ms, median ± interquartile range; Figure 6B), where the GCs with virtually no delay had a very weak surround. The delay did not depend on distance from the center, suggesting it derives from integration in the additional interneuron, not from conduction times along amacrine and ganglion cell processes.

Figure 6. LNFDSNF: Time delays from amacrine cell processing explain the spatio-temporal receptive fields of ganglion cells.

(A) Delay functions (black; relative to the center) and the pooling functions (gray) for two representative cells (left, OFF type; right, ON type). The delays are longer in the surround (magenta; weighted average by the pooling weights) than in the center (green), and the transition occurs at the same spatial location where the pooling function crosses zero.

(B) Population data histogram of the relative delays from the center to the surround (median value in magenta; p < 0.001, sign test). The cells in A are highlighted in orange.

(C) Receptive fields (same cells as in A) calculated from the data (STA, top) show the surround (magenta, peak latency) lagging behind the center (green). Receptive fields calculated from the LNFDSNF model reproduce this feature (middle) but those from the LNFSNF do not (bottom).

(D) The difference in the peak latency between the center and the surround across different models. Each gray line indicates a cell, and the cells in c are highlighted in orange. The black horizontal bars show the median values, with significant differences between the STA and those models without delays (LNSN, LNSNF, and LNFSNF models; all with p < 0.001, rank sum test). The difference in the relative delay between the STA and the LNFDSNF model is not significant (p > 0.9).

The delays affect the model’s predicted receptive fields of GCs, making them more similar to the experimental data (Figure 6C,D). The spike-triggered average analysis, which provides a linear estimate of a neuron’s receptive field [12], shows that the surround of the GC receptive field generally lags behind the center (Figure 6C). This is accurately reproduced by the LNFDSNF model but not by the LNFSNF model (Figure 6D). Even though the LNFSNF model has a delayed surround in its BCMs (Figure S3), this surround is not spatially large enough to account for what is observed in the GC receptive fields. In contrast, the LNFDSNF model has a new way of delaying the receptive field surround independently of the other circuit elements. It can thus accommodate without trade-offs the delayed receptive field surround and achieved a better performance (8±2 % increase in the explained variance; mean ± standard error; Figure 2D).

Experimental tests of the models

An argument for designing response models with a cascade architecture is that they map naturally onto real biophysical circuits of neurons. The ultimate test of this aproach is whether the elements inferred in the fitting process have actual biological counterparts. To explore the biological realism of the models, we next focused on two predictions about bipolar cell (BC) physiology and subjected them to direct experimental tests. Specifically, we measured the receptive and projective fields of real BCs [27,28] and compared them to their predicted counterparts: the BCM filters and the GCM pooling functions, respectively.

These experiments were carried out by combining sharp electrode recordings from BCs and multi-electrode array recordings from GCs. To identify the projection patterns from BCs to GCs, we intracellularly injected current into individual BCs while recording the spiking responses of multiple GCs. This permitted the selection of GCs whose spiking activity was strongly affected by the BC current injection (Figure S6A). To measure the receptive fields of those BC-GC pairs simultaneously, we also recorded their visual responses to the flickering bar movie presented to the photoreceptors. In total, we mapped both the receptive and projective fields in 6 BCs, and 14 BC-GC pairs were selected for the model fitting because they showed strong projections between the cells. This data selection was done before fitting the models to avoid biasing the results.

BCM filters versus BC receptive fields

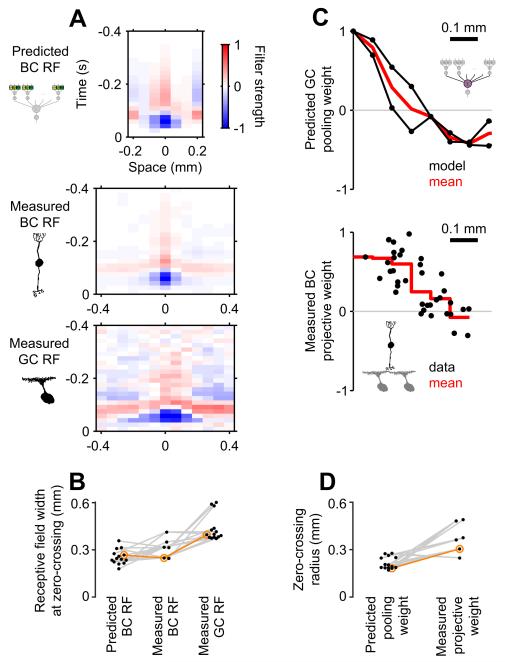
Reverse-correlation methods were applied to bipolar cell recordings to obtain a linear estimate of the bipolar cell receptive field (Figure 7A). This was compared to the BCM filter in a model that fits ganglion cell recordings. We found that the prediction and measurement matched well with each other despite the model’s assumption that a GC receives signals from all identical BCs. Specifically, the spatial characteristics of the BCM filters were consistent with those of the measured BC receptive fields, rather than those of the GC receptive fields (Figures 7A,B and S6B). Moreover, the BCM filters obtained from GCs that receive projections from the same BCs resembled each other more than those from GCs with projections from different BCs (p = 0.02, ANOVA; Figure 7B). All this indicates that the BCMs of the circuit model correspond well to the real biological BCs that provide inputs to the target GC.

Figure 7. Experimental tests confirm the circuit structure predicted by modeling.

(A) Predicted (top) and measured (middle) bipolar cell receptive fields (BC RFs), with the corresponding GC RF (bottom) obtained by a simultaneous BC-GC recording. Note that current injection into this BC significantly affected the spiking activity of this GC (Figure S6A). See also Figure S6B.

(B) Spatial characteristics of the receptive fields across all BC-GC pairs with significant projections (14 GCs, each receiving projections from one of 6 BCs; the example in A is highlighted in orange). The full width of the receptive field center at zero-crossing is significantly smaller in the predicted BC RFs (left, 243±50 μm; median ± interquartile range) than in the measured GC RFs (right, 398±57 μm; p < 0.001, sign test). The difference between the predicted and measured BC RFs (315±68 μm) is not significant (p > 0.1).

(C) The spatial profile of the pooling function of the representative GC (top, with distance from the peak in the horizontal axis) and that of the projective weight of the simultaneously recorded BC (bottom, with each dot representing the projection to a GC). See also Figure S6C.

(D) Comparison between the pooling (197±65 μm) and projective weights (368±178 μm, median ± interquartile range of the zero-crossing radii at the excitation-inhibition transition; p = 0.01, sign test). Each gray line indicates the simultaneously recorded data (the example in C is highlighted in orange).

GCM pooling functions versus BC projective fields

Injecting current into a BC affects the firing of its downstream GCs (Figure S6A). We quantified this effect by the projective weight, defined as a normalized ratio (difference-over-sum as in Error! Reference source not found.) between the GC firing rates in response to BC depolarization and hyperpolarization, and measured its relationship to the distance between the BC and GCs. The resulting projective field represents spatial characteristics of an information flow that is “outward” from a BC onto multiple GCs. In contrast, the GCM pooling function defined in our models refers to information being pooled “inward” from multiple BCMs into a single GCM.

Strictly speaking, the measured projective field and the predicted pooling function are thus different objects, yet we found that these two spatial profiles are comparable. They both had a center-surround structure, with positive (excitatory) weights in the center and weaker negative (inhibitory) ones in the surround (Figures 7C,D and S6C). Together, the similarities between the predicted and measured circuit properties suggest that the cascade model presented here is a powerful tool for inferring the inner details of a neural circuit from simulation and fitting of its overall performance.

Discussion

We set out to derive circuit models of the retina directly from measurements of its input-output function (Figures 2A,B and S2). We considered network models in which the neurons and their connections are explicitly represented. The cells and synapses of the circuit diagram were converted to parametric mathematical expressions (Figures 1 and S1). Then a high-dimensional parameter search yielded the optimal neural circuit to match the functional measurements (Figure 2C,D). The main results of this circuit inference are as follows: (a) The models can reliably distinguish the circuit functions of the inner and the outer retina. Lateral convergence in the inner retina acts over larger distances than in the outer retina (Figures 3 and 7) and distinct feedback functions are employed at the two processing stages (Figure 5). (b) The models inferred correctly that different types of retinal ganglion cells (GCs) have distinct circuit architectures. Major differences involve the spatio-temporal characteristics of bipolar cell (BC) receptive fields (Figure 3) and the degree of rectification at the BC synapses (Figure 4). (c) The circuit models are not merely mathematical abstractions but represent biological reality (Figure 6). For example, circuit inference made accurate predictions for the visual response properties of BCs and their connectivity to GCs, as verified subsequently by direct experimental measurements (Figure 7).

Modeling strategy

Various strategies exist for modeling the input-output function of a neural system [5]. On one end of the spectrum are abstract mathematical techniques that map the stimulus (intensity as a function of space, wavelength, and time) into the firing rate (a function of time), for example using a Volterra series [29,30]. This has the attraction of mathematical completeness along with theorems that govern the inference process for the model parameters and its convergence properties. In practice, however, the structure of such abstract models does not fit naturally to biological data. An accurate fit to neural response data often requires many high-order kernels (Figure S7), whose values cannot be estimated efficiently in reasonable experimental time. Furthermore, the central objects of the model, the kernels, do not relate in any natural way to the biological objects, the neurons and synapses. It is thus difficult to draw further inspiration for biological experiments from the response model.

On the other end of the spectrum one finds models with excessive realism: Here each neuron is represented with a many-compartment biophysical simulation, governed by the morphology of the cell, with many different membrane conductances, and coupled by synapses simulated at molecular detail [31]. A selling point for such models is that they are exhaustive, in that every conceivable molecular parameter can be given a place in the model. But they are also exhausting, in that they require inordinate computing effort to simulate anything. Most of the parameters are unknown, and very few are directly observable or under experimental control. Thus the fitting process to infer this vast number of parameters from data is often computationally intractable.

The modeling style chosen here falls in a golden middle (Figure 1). The neural circuit diagram incorporates biological detail at a level that can actually be observed and manipulated experimentally: neurons, axons, synapses, and dendrites. The signals coursing through the model represent actual electrical signals in neurons. Individual neurons are represented by simple elements with linear summation and a nonlinear output function. Cascade models of this type have been in use for some time [32–34]. In general, one assumes a certain cascade structure and then optimizes the set of parameters that characterize the components. To this our study adds an additional search across different network structures. This allows one to determine which plausible neural circuit best explains the functional data.

Implications for retinal circuits

A good model in biological sciences should give not only a faithful description of a phenomenon but also some insights into the underlying mechanisms along with experimentally testable predictions. We found that the internal circuit structure of the best-fit models agrees with well-established features of retinal circuitry (Figures 3–6) and also with our new experimental observations (Figure 7). Below are two additional predictions to be tested in future experiments, using direct measurements of cellular physiology or synaptic connectivity.

First, our model predicts greater linearity of BC output in ON GCs (Figure 4). At the ganglion cell level, such asymmetry between ON and OFF GCs has been reported in the mammalian retina [35], and was largely attributed to network effects [36,37]. For example, even though the outputs of both ON and OFF BCs are mostly rectified [38], the visual response of ON GCs can be linearized by a feedforward inhibition from OFF amacrine cells (“crossover inhibition”) [39]. The asymmetry between the ON and OFF pathways, however, has not been directly examined in the salamander retina. It also remains to be studied how the output properties of distinct BC types contribute to this asymmetry.

Second, the model predicts distinct feedback processing at the level of BC and GC outputs (Figure 5). The two feedback functions can differ in polarity and dynamics, and such properties also varied across cells. The feedback in the inner retina could arise from a cellular effect such as synaptic depression at the BC synapses [26] and after-hyperpolarization at the GC level [25,38], or from a network effect involving amacrine cells driven by BCs [40,41] or by GCs via gap junctions [42]. Given that addition of the feedback provided the greatest improvement in model performance (Figure 2C,D), it is worth examining how these or other mechanisms contribute to the feedback effects, and how those vary across different ganglion cell circuits.

Future developments of circuit inference

The broad distribution of the model performance (Figure 2C,D) suggests that there is room for improvement. One way to improve the present model is to add more components. Instead of using identical BC modules (BCMs), for example, one could introduce distinct BCM types such as those corresponding to ON BCs and OFF BCs. This will be essential for modeling ON-OFF GCs, such as W3 cells in the mouse retina [43], and may also serve to reveal interesting interactions between the ON and OFF pathways [39,44,45].

Another way of refining the model is to represent amacrine cells explicitly, not just through negative pooling weights and time delays (Figure 6). Amacrine cells are a very diverse class of retinal neurons [8], and participate in distinct circuit functions [6]. For example, narrow-field amacrine cells are needed in modeling direction-selective GCs [46], whereas wide-field amacrine cells can explain the suppression that many GCs receive from distant stimuli [15,22,33,47]. Using a broader range of visual stimuli will likely help in inferring these diverse network features.

Finally, such circuit inference methods should be extended to other brain areas, in particular where one has information about the structural connectome [1] along with large-scale electrical and optical recordings [2,3]. In most instances these recordings will be sparse, covering only a fraction of neurons and synapses. The modeling approach advocated here can fill in the gaps, using known structural information as a guide in parameterizing the circuits, and the available functional observations as a target when optimizing the model parameters. Future developments in this area might consider a broader range of circuit architectures, including recurrent connections between and within areas [48], and exploit other objective functions for data fitting [49,50]. Successful application of such extended models and inference algorithms will help derive insights from the impending flood of structural and functional brain data.

Experimental Procedures

See Supplemental Experimental Procedures for details. No statistical method was used to predetermine sample size. Unless otherwise noted, statistical comparisons across models and corresponding experimental data were performed as sign tests with a significance level of 0.05.

Electrophysiology

Multi-electrode recordings from ganglion cells (GCs) and intracellular recordings from bipolar cells (BCs) in an isolated retina (larval tiger salamander) were performed as described previously [15, 27], following protocols approved by the Institutional Animal Care and Use Committee at Harvard University. The data from simultaneous BC-GC recordings were analyzed similarly as in [28] for estimating the BC projective field (Figure 7). The spatio-temporal receptive fields of the recorded cells (e.g., Figure 3C) were estimated by reverse-correlation methods using randomly flickering bar stimuli (bar width, 66 μm; refresh rate, 60 Hz; Figure S2A) [12].

Modeling

We employed the cascade model framework [4,5] and progressively extended its complexity (Figures 1 and S1), from the linear-nonlinear (LN) model to the linear-nonlinear-feedback-delayed-sum-nonlinear-feedback (LNFDSNF) model. Each stage was modeled as follows:

• “L”: BCM temporal processing was modeled as a sum of two infinite impulse response filters at each spatial location (Eq.S3–Eq.S5); Figure S1A–C).

• “N”: Half-wave rectifiers (Eq.S6; Figure S1D) were used to approximate the nonlinearity in all cases except for the LNSN model that employed a point-wise static nonlinearity on the BCM output (Figure 4).

• “F”: Feedback process was modeled as a linear convolution of a temporal kernel (Eq.S7; Figure S1E).

• “D”: The time delay was introduced by a linear filter that shifts each BCM output in time (Eq.S8; Figure S1F).

• “S”: Spatial pooling of the GCM is formulated as a weighted sum of the BCM outputs (Eq.S9; Figure S1G).

We wrote custom codes in C++ to fit the models to the ganglion cell firing rates (bin size, 1/60 s) in response to the randomly flickering bar stimuli (Figure S3), and analyzed the model performance by the explained variance (Eq.S10) [11].

Highlights.

• We present a computational method to link structure and function in neural circuits

• A series of circuit models with increasing complexity was devised for the retina

• Models progressively performed better in predicting ganglion cell visual responses

• Models correctly inferred inner structure of the retina from ganglion cell function