Abstract
Biomolecular screening research frequently searches for the chemical compounds that are most likely to make a biochemical or cell-based assay system produce a strong continuous response. Several doses are tested with each compound and it is assumed that, if there is a dose-response relationship, the relationship follows a monotonic curve, usually a version of the median-effect equation. However, the null hypothesis of no relationship cannot be statistically tested using this equation. We used a linearized version of this equation to define a measure of pharmacological effect size, and use this measure to rank the investigated compounds in order of their overall capability to produce strong responses. The null hypothesis that none of the examined doses of a particular compound produced a strong response can be tested with this approach. The proposed approach is based on a new statistical model of the important concept of response detection limit, a concept that is usually neglected in the analysis of dose-response data with continuous responses. The methodology is illustrated with data from a study searching for compounds that neutralize the infection by a human immunodeficiency virus of brain glioblastoma cells.
Keywords: Biomolecular screening, constrained least squares, dose-response effects, effect size, Hill equation, logit transformation, median-effect equation, Michaelis-Menten equation, non-linear regression, scaled beta distribution
1. Introduction
The goal of many biomolecular screenings in pharmaceutical research is to select from a set of chemical compounds a subset of compounds that modulate a biochemical or cell-based system. Compounds of interest will make the system produce a continuous response that desirably will have a value higher than a prespecified minimum Rmin (or, in some cases, lower than a prespecified maximum Rmax), if the response were ideally measured without error. An example of response that desirably should be higher than a prespecified Rmin is the percent increase in the number of cancer cells that are killed after a certain time of exposure to a compound, relative to the number of cells that die after spending the same time in the absence of the compound; or the percent reduction in the amount of infection of a target cell by a virus which is observed after certain time of exposure to a compound, relative to the amount of infection after the same time in the absence of the compound. The value of Rmin is chosen so that responses higher than that value are considered pharmacologically or biologically important. An example of a response in which a maximum response Rmax is desirable is the percent increase in the number of non-cancerous cells that are killed after exposure to a potentially anti-cancer agent, relative to no exposure.
In the experiments modeled in this article, the effect of each of m compounds on a continuous bioassay response is investigated, and the same n compound doses D1 < D2 < … < Dn are tested with each of the m compounds. Here, Rij represents the observed response to dose Di of compound j, i = 1, …, n, j = 1, …, m, and the letter R will generically represent the response to a dose D if this response were ideally measured without error. That is, R is the "true" or "adjusted-for-error" response, as opposed to the observed response Rij which is obtained through an experimental procedure that usually involves error. In other words, Rij is a particular measure of a theoretical dimension R.
Here, we are interested in responses R that theoretically are numbers between 0 and 100 inclusive. In practice, however, a particular measure Rij of R may be outside the interval [0, 100]. For instance, suppose that R is the percent reduction of a virus infection of a cell system, produced by a chemical compound, and that the magnitude of a luminescent signal measures the extent of the virus infection. In this case, R can be measured by computing the percent reduction in luminescent signal with respect to the signal of a control bioassay. Because of unavoidable experimental errors, this percent reduction may be < 0 for some compounds, even under the theoretical assumption that none of the investigated compounds may increase the extent of the infection or the assumption that the assay may not detect an infection increase.
Ideally, a particular compound should be selected for future investigations if, after adjusting for experimental error, at least one of its investigated doses yields R > Rmin (or R < Rmax), where Rmin > 0 (or Rmax < 100). However, since many of the examined compounds may satisfy this condition, and only a few compounds can be used in future investigations to minimize project costs, researchers must rank the compounds in order of their overall capability to cause the cell system to produce R > Rmin (or R < Rmax) within the dose range tested. Once the compounds are ranked, the compounds with the highest capabilities would be selected for future investigations.
As described below, the non-linear regression methodology traditionally used in dose response analyses, which fits a parametric curve to the pairs (D1, R1j), …, (Dn, Rnj), is frequently not suitable for conducting this ranking, and never can be used for testing the null hypothesis that none of the n examined doses of a particular compound produced a true response higher (or lower) than the reference response Rmin (or Rmax) (versus the alternative hypothesis that at least one of the examined doses produced a true response higher than the reference response). The objective of this article is to suggest methodology for conducting this ranking and testing.
The most popular approach to comparing the effects of two or more compounds on a continuous response R relies on estimating for each compound the dose D that makes R = 50%, symbolized here as D(50). (Depending on the type of response, this dose is called IC50, ED50, LD50, etc.) This approach assumes that, for each compound and the dose range tested [D1, Dn], the relationship between a dose D and the true response R follows a monotonic dose-response curve. The most frequently used model for this curve is the median-effect equation
| (1) |
which includes as particular cases the well-known Michaelis-Menten and Hill (Goutelle 2008) equations, as well as the Henderson-Hasselbalch and Scatchard equations (Chou 2006). This equation has parameters w ∈ ℝ and D(50) > 0 that are frequently estimated for each compound from observed responses by using non-linear regression with additive errors and least squares estimation.
Admitting that the D(50) measure is widely used in both pharmacological and biological research, this measure has a number of limitations that hinder its applications to compound ranking and statistical testing in biomolecular screening (Diaz et al. 2013). The limitations essentially stem from the fact that the D(50) has to be computed under the assumption of the existence of a dose-response effect and, therefore, the D(50) cannot be used to statistically test the null hypothesis of no dose-response effect for the compound, or the more general null hypothesis that no investigated compound dose has an important effect on the response. Moreover, the D(50) measure cannot be reliably computed in many cases (Diaz et al. 2013). An elaboration of this and other limitations is provided in Section 2.
A central premise of this article is that the research question of interest in a biomolecular screening is not whether there is a monotonic relationship between response and dose for a particular chemical compound, or whether a parametric curve can be fitted to the compound’s dose-response pairs of points, but whether one of the investigated doses really produces a response of importance, where a response is considered important if it is > Rmin (or < Rmax) after adjusting for experimental error. The question of whether some dose outside the examined dose range [D1, Dn] can produce an important response cannot be answered with the types of experiment that are studied in this article, and answering this question is not an objective of this article.
In this article, we show how some further elaborations of equation (1) provide an approach that can be used for compound ranking and compound-effect testing, which does not have the mentioned limitations of a direct application of this equation. This approach is based on a logit transformation of this equation which has been used by other authors for theoretical purposes or for estimating w and D(50) with a limited number of doses (for instance, with only two doses) (Chou 2006), and on a new statistical model of the important concept of response detection limit, a concept that, unfortunately, is usually neglected in dose-response analyses with continuous responses.
The potential of the logit transformation of equation (1) for improving decision making in pharmacological and biological research does not seem to have been fully appreciated. As elaborated in Section 3, this potential stems from the fact that the logit transformation induces a family of dose-response curves that is much larger than the family of curves represented by equation (1). The logit transformation, however, has a limitation of its own: it cannot be applied to observed responses outside the interval (0, 100). To address this issue, this article posits that observed responses that are negative or close to 0 should be considered as mostly generated by a mechanism that is different from (and independent of) the mechanism producing the relationship represented by equation (1). This different mechanism occurs because negative, null or close-to-zero observations are likely measures of true responses that are below the response detection limit, and the experimental conditions cannot correctly quantify such responses. These observations, however, are not excluded from analyses because doing so would bias the decision against the null hypothesis of no compound effects. Instead, they are used to estimate the detection limit through the model proposed in Section 5. The estimated detection limit and the number of negative, null or close-tozero responses are then used to constraint the estimation of the parameters of the linear regression based on the logit-transformed data, as described in Section 9.
Section 2 describes limitations of nonlinear regression and the D(50) in the context of ranking and statistical testing of chemical compound effects. Section 3 gives a mathematical motivation for using a logit-linearized form of the median effect equation in statistical testing of compound effects. Sections 4, 5 and 6 introduce the proposed model. Sections 7 and 8 introduce a measure of pharmacological importance of a compound and the null hypothesis of no importance. Section 9 explains a method to estimate the measure of pharmacological importance of a compound, and Section 10 a method to examine the statistical significance of the estimate. Sections 11 and 12 describe a method of estimating the detection limit for the pharmacological response. Section 13 and 14 present an application to the search for compounds that neutralize HIV infection. A discussion is in Section 15.
2. Limitations of nonlinear regression approaches and the D(50)
In equation (1), the theoretical response R is a strictly increasing function of D when w > 0, and strictly decreasing when w < 0. When w = 0, R = 50 regardless of the dose D and the value of D(50) (Figure 1); thus, D(50) is unambiguously defined only if w ≠ 0, that is, only when R is a strictly monotonic function of D. This fact imposes three major limitations. First, equation (1) by itself does not allow modeling data showing a nearly constant relationship between R and D that may be of pharmacological interest, even if such data is produced by a compound satisfying equation (1) for a dose range wider than the dose range tested. Such relationships may occur, for instance, when all tested doses produce substantially strong responses but the examined dose range is not wide enough to detect an appreciable increase (or a decrease) in response with dose.
Figure 1.
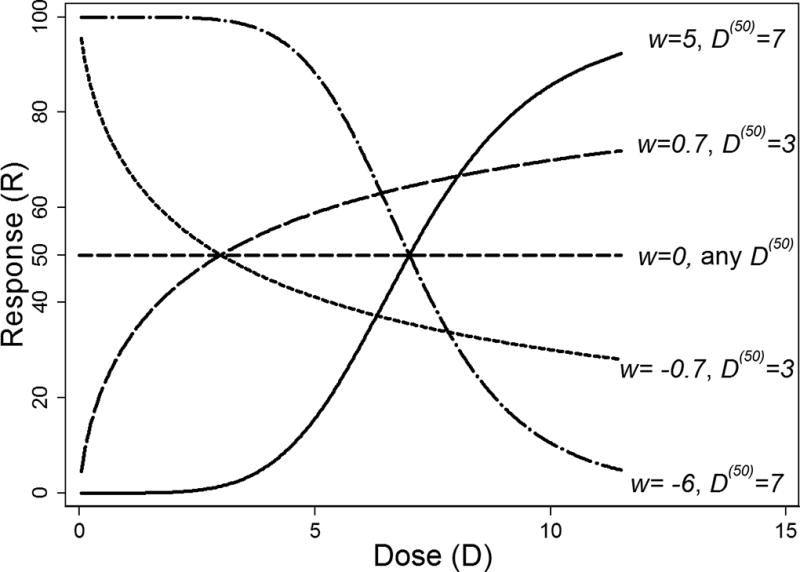
Plot of the median effect equation (1) for different values of w and D(50).
Figure 2 illustrates some problems arising in such situation. The solid line is a plot of equation (1) with D(50) = 3 and w = 0.7. The five points are dose-response pairs that were simulated with these parameter values and a normal random noise with mean 0 and variance 4. The five points may give the impression of a nearly constant dose-response relationship.
Figure 2.
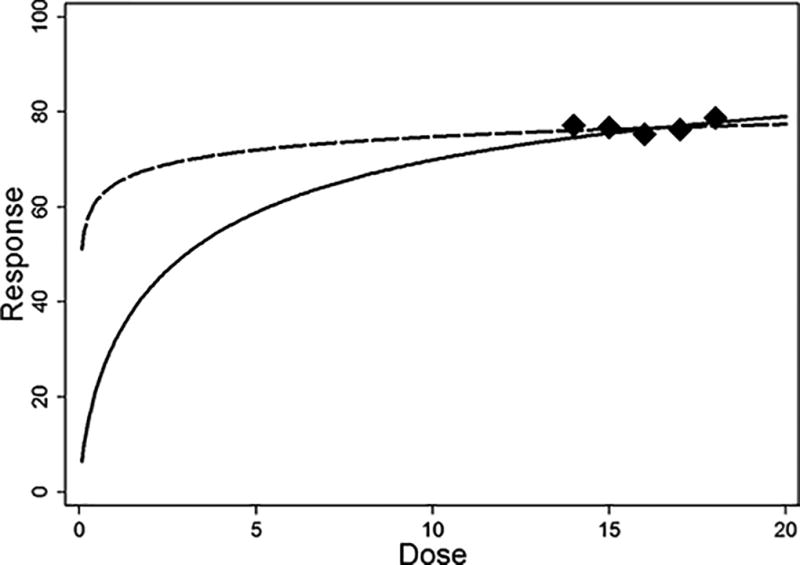
Illustration of a problem that may occur when the range of investigated doses includes doses that produce strong responses but is not wide enough to represent the overall dose-response relationship.
When equation (1) was fitted to the five points in Figure 2 through nonlinear least squares, misleading parameter estimates were obtained, 0.05309 and 0.2077 for D(50) and w, respectively. The dashed line represents the fitted equation. Moreover, data points like the ones illustrated usually produce convergence problems in least squares algorithms when attempting to fit equation (1), because this equation does not include parameters accounting for constant responses other than R = 50 and the parameters of equation (1) are not identifiable for a constant response of R = 50. Thus, some important compounds may not be identified in a biomolecular screening if these algorithms are applied without additional visual inspection, and the D(50) measure cannot even be obtained for some compounds. Moreover, visual inspections may be impractical if the number of examined compounds is relatively large.
Analogous problems occur when small doses are tested. In this case, it is not unusual that the observed dose-response curve of a compound j does not reach a clear plateau, even if the compound has a dose-response effect; as a result, no reliable estimator for the D(50) of compound j can be obtained by fitting equation (1) to the pairs (D1, R1j), …, (Dn, Rnj), and there are even cases in which no D(50) measure can be obtained (Diaz et al. 2013).
Second, the D(50) measure, and indeed equation (1) alone, cannot be used to statistically test the null hypothesis that the investigated doses of the compound do not have a differential effect on the bioassay response, nor the null hypothesis that none of the investigated doses of the compound have an effect on the response (Diaz et al. 2013). The reason is that the parameter space of equation (1), namely {(w, D(50)) ∈ ℝ2; D(50) > 0}, does not include the case in which R = constant (or R ≈ constant) for all D. In other words, since equation (1) can be fitted to observed responses only under the assumption that there is a strictly monotonic relationship between dose and true response, the null hypothesis of no relationship cannot be tested.
Third, also because of the limitations of the parameter space of equation (1), this equation (and therefore the D(50)) cannot be used by itself to model the important case in which R takes on a nearly constant but high (or low) value within the dose range [D1, D2], which may occur if this range is not wide enough (Figure 2). In plain words, constant responses cannot be modeled with equation (1). This is a limitation because excluding from future analyses a compound that showed a constant response solely because its data does not conform with equation (1) may introduce a decision error. In fact, the constant response value to the compound may be substantially larger than Rmin (or lower than Rmax) and, therefore, the compound may be a good candidate for future analyses. Because of these limitations, automated decision rules that distinguish whether (and to what extent) a compound affects the investigated response cannot be designed by using D(50) measurements (Diaz et al. 2013) and, in fact, cannot be designed by using nonlinear regression theory solely based on equation (1).
3. Rationale of the proposed approach to hypothesis testing
To motivate our proposed approach, note that equation (1) can be transformed into
| (2) |
provided that 0 < R < 100, where T is the logit transformation defined as T(x) = log(x/(100 − x)), 0 < x < 100 (Chou 2006). Assuming that equation (1) represents well the dose-response relationship for a compound j, equation (2) could be used to estimate the D(50) of compound j by fitting a simple linear regression model to the points (log (Di), T(Rij)), i = 1, …, n (Chou 2006). However, this would work well only if the range [D1, Dn] of tested doses is sufficiently wide.
Nonetheless, even when D(50) cannot be reliably estimated, the slope and intercept of the estimated linear relationship between T(R) and log(D) have information about the magnitude of the responses to the doses in the dose range tested. Thus, if we focus only on the slope and intercept, we see that equation (2) can be rewritten as
| (3) |
with a, b ∈ ℝ.
Note that, although equation (1) can be algebraically transformed into equation (3), these two equations are not algebraically equivalent, unless both w, a ≠ 0, because there are no restrictions on the values of a and b in equation (3). Specifically, by letting a = w and b = −w log (D(50)), we see that any non-constant dose-response relationship satisfied by equation (1) is also satisfied by equation (3). However, whereas equation (3) is satisfied by all possible constant relationships of the form R ≡ r for all D and some r ∈ (0, 100) [use a = 0 and b = T(r)], the only constant relationship satisfied by equation (1) is the relationship R ≡ 50 which occurs when w = 0 (although, in this case, D(50) is not identifiable).
In summary, the family of relationships between D and R that is represented by equation (3) is larger than the family represented by equation (1). In addition to strictly monotonic relationships, equation (3) includes essentially all constant relationships, which makes equation (3) useful to model relationships that may be pharmacologically or biologically important but are empirically nearly-constant or constant within the investigated dose range (like that suggested by the five points represented in Figure 2). Even more, in contrast to equation (1), the parameter space of equation (3) contains a null subspace representing the null hypothesis of no important pharmacological effects (see Section 8).
4. The concept of detection limit and other preliminary concepts
Our model of the dose-response pairs (Di, Rij), i = 1, …, n, j = 1, …, m, essentially assumes that equation (3) is satisfied by all m examined compounds and doses within the dose-range tested, and that each compound has its own values of a and b. But, the model also postulates the existence of a constant number θ, 0 < θ < 100, such that, if R < θ, then R is unreliably measured. The parameter θ is called the detection limit for R. If the dose Di of compound j produced a true response R < θ, then the measure Rij of R is not considered informative about the parameters of equation (3). These ideas are formally stated in Section 5.
Note that the detection limit θ is postulated to be a constant of the entire set of experiments, that is, θ does not depend on i or j. The detection limit θ is interpreted as a response value below which the biologist accepts that the available experimental setup and instrumentation does not allow measuring the response R with confidence. Thus, the particular value of θ is a consequence of the technology and knowledge used to measure R, and it is not an intrinsic property of any of the examined chemical compounds or of the biological system to which they are applied.
The proposed model is applicable only if it can be reliably assumed either that a ≥ 0 for all compounds tested, or a ≤ 0 for all compounds tested. We stress that the situation a = 0 is included in these two cases, that is, constant responses are accepted as possible in our formulation. For convenience, the methodology will be described only for the case a ≥ 0. In this case, we do not expect that any of the tested compounds will exhibit a strictly decreasing monotonic relationship between response and dose within the investigated dose range, nor an umbrella-shape or other non-monotonic relationship, and we search for compounds producing R > Rmin. The assumption that a ≥ 0 for all compounds is reasonably fulfilled by the data used to illustrate the proposed methodology (Section 13).
The case a ≤ 0 can be handled analogously to the case a ≥ 0 by transforming the response R into 100 − R. Since the usual goal of a biomolecular screening under the case a ≤ 0 is to find compounds producing R < Rmax, the transformation Rmin = T (100 − Rmax) is also needed and, using these two transformations, all that will be described for the case a ≥ 0 applies verbatim to the case a ≤ 0.
In what follows, we say that a random variable X has a scaled beta distribution with parameters α > 0, β > 0 and θ > 0, if the probability density function (pdf) of X is
| (4) |
That is, fX is the pdf of a beta random variable with parameters α and β that has been multiplied by θ. If X has pdf (4), then we say that the distribution of X is Sbeta(α, β, θ).
5. Model assumptions
Let θ be the detection limit for R. The model postulates that, for the entire set of experiments, there exist constant numbers α > 0, β > 0 and γ > 0 in addition to θ, and that for each compound j, with j = 1, …, m, there exist numbers aj ≥ 0 and bj ∈ ℝ, such that
Model Assumption 1: For all i = 1, …, n and j = 1, …, m, if aj log (Di)+bj ≥ Tθ, then P (Rij ≤ 0) = 0 and E[T(Rij)] = aj log (Di) + bj, where Tθ denotes T(θ).
Model Assumption 2: If I is the set of all pairs (i, j) in the Cartesian product {1, …, n} × {1, …, m} satisfying aj log (Di) + bj < Tθ, and if (i, j) ∈ I, there exists an unobserved random variable producing values in the interval (0, θ) such that the conditional distribution of given the event {0 < Rij < 100} is Sbeta(α, β, θ).
Model Assumption 3: If (i, j) ∈ I, the conditional distribution of T(Rij) given both and the event {0 < Rij < 100} is normal with mean T(r) and variance γ2.
Model Assumption 4: If (i, j) ∈ I, then all observed responses Rij with (i, j) ∈ I are mutually independent and identically distributed.
Model Assumption 5: P (Rij ≥ 100) = 0 for all i = 1, …, n and j = 1, …, m.
Model Assumption 6: For a particular compound j, all observations T(Rij) with (i, j) ∉ I are normally distributed with variance , and are mutually independent.
6. Explanation of model assumptions
As mentioned in Section 4, the detection limit θ is not a characteristic of a particular compound but a parameter of the entire set of experiments which depends on the experimental and analytical methods used to measure R. In contrast, aj and bj are parameters whose values reflect the effect of compound j on the response R. The assumption aj ≥ 0 for all j is applicable when strictly monotonically decreasing relationships are not considered possible for the compounds examined.
Model Assumptions 2–4 are informally interpreted as follows: attempting to measure R when R is below the detection limit produces an unwanted artifact R* generated by an Sbeta (α, β, θ) distribution (Model Assumption 2). In that situation, Rij is measuring the artifact R*, not R (Model Assumption 3). As a consequence, when R < θ, Rij does not have any information about aj or bj (Model Assumption 4).
Define , i = 1, …, n, and . By Model Assumption 1, if , then
| (5) |
As described in Section 8, contains all the information we need to statistically test the effect of compound j on the response R in the dose range examined; thus, the statistical test proposed in this article focuses on this parameter. However, both aj and are needed to measure the size of this effect, as described in Section 7.
According to Model Assumption 4, if for some i and j, then the observed response Rij to dose Di of compound j has little or unreliable information on aj and because, in that case, even if aj ≠ 0 or , the distribution of Rij does not depend on aj or . In other words, true responses lower than the detection limit are unreliably measured.
For a particular compound j, we say that the true response produced by a dose Di is below the detection limit θ, or that Di produced a true response below the detection limit, if and only if . In this case, Assumption 4 implies that Rij is uninformative, and therefore, that Rij should not be used to estimate aj or . In practice, Model Assumption 5 means that no observed response is ≥ 100, which is the case in many applications searching for compounds that increase the value of a response, and usually occurs when relatively small compound doses are tested in a biomolecular screening.
7. A measure of the effect size of a chemical compound on a bioassay response
In the following, we assume that Rmin > θ and denote Tmin = T (Rmin). Suppose that we are investigating whether at least one of the n tested doses of compound j can produce, after adjusting for response measurement errors, an important response (i.e. a "true" response higher than Rmin). More precisely, we want to know if for some i, and therefore, if the true response to Di is pharmacologically important (that is, by Model Assumption 1, if E [T(Rij)] > Tmin).
To measure the pharmacological importance of the effect of compound j on the response R, we propose computing the effect size
| (6) |
where [z]+ = max{z, 0}. Note that . Therefore, the integration region in formula (6), the closed interval is the same as the interval . As a consequence, this integration region covers the entire range of tested doses, and only this range. Thus, since Ej is dependent on the particular dose range tested, that is, on the interval [D1, Dn], a comparison of the Ej values of two different compounds is appropriate only if the same dose range was used for examining the two compounds. The higher Ej is, the stronger are the responses to compound j. A convenient computational formula for Ej is presented in Appendix 1.
When Ej > 0, Ej can be geometrically represented in an xy-coordinate system as that portion of the area between the lines and y = Tmin that is relevant to the dose range tested. This interpretation of Ej is illustrated in Figure 3 (A–E), in which the subscript j is dropped for clarity. Also, Ej = 0 essentially means that no true response R to compound j is higher than Rmin within the dose range tested (Figure 3, F–H).
Figure 3.
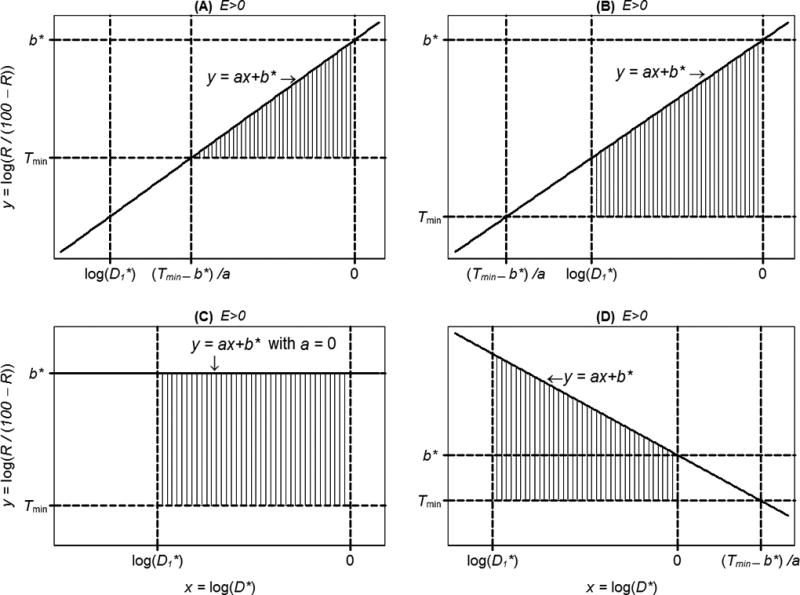
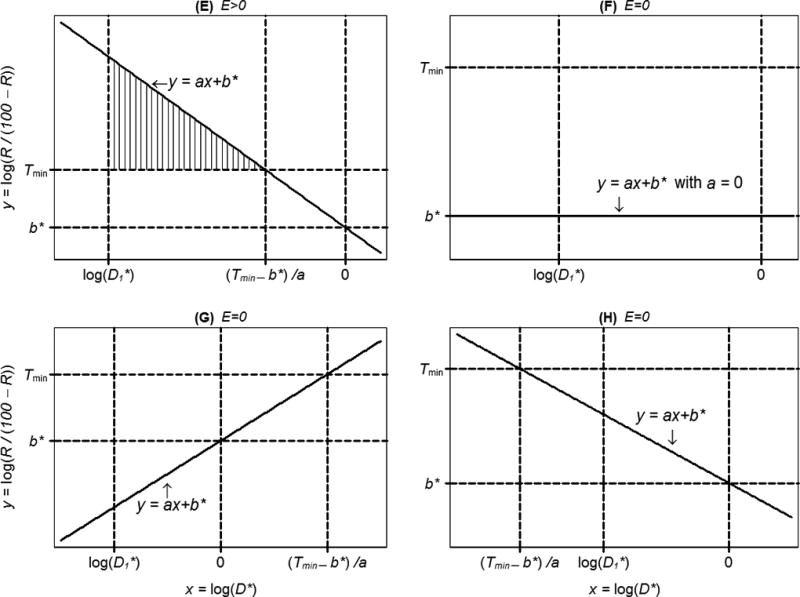
Illustration of five situations producing a compound effect size E > 0 (A–E), and three producing E = 0 (F–H) (continued). In A through E, the area of the region highlighted with vertical lines is equal to E. Referring to formulas (11)–(13), plot (A) corresponds to the case a > 0, b* > Tmin and ; in plot (B), a > 0, b* > Tmin, but ; (C) a = 0, yielding E > 0 because b* > Tmin; (D) a < 0, and min {(Tmin − b*)/a, 0} = 0; (E) a < 0, and min {(Tmin − b*)/ a, 0} = (Tmin − b*)/ a ; (F) a = 0, yielding E = 0 because b* < Tmin ; (G) a > 0, b* < Tmin; (H) a < 0 and .
8. The null hypothesis of no important effect of a compound
Since, in general, Ej ≥ 0, the null hypothesis of no important effects of compound j on the response R within the dose range tested can be stated as H0: Ej = 0, and we should test this hypothesis against the alternative H1: Ej > 0. But, since we are assuming that aj ≥ 0 for all j, the null hypothesis H0: Ej = 0 is equivalent to , and the alternative H1: Ej > 0 is equivalent to . (See Appendix 2 for a proof.)
Provided that at least one true response to compound j is above the detection limit, the maximum possible E [T(Rij)] in the investigated dose range is . Therefore, H0 may be paraphrased as "After adjusting for measurement errors, no response to compound j is above Rmin", and H1 as "At least one dose of compound j produces a response above Rmin".
9. Estimation of the effect size Ej
To estimate Ej for a particular compound j, aj and need to be estimated first. This section describes an approach to estimating aj, and Ej. When there are reasons to believe that some of the true responses R produced by compound j are below the detection limit θ, the value of θ needs to be known or estimated before using this approach. Section 12 describes an approach to estimating θ.
Denote yij = T(Rij) and . Let 1 ≤ k < n and assume that the lowest k doses of compound j produced true responses below the detection limit θ but the remaining doses do not. That is, assume for i ≤ k, and for i > k.
As estimators of aj and , we propose using the values of aj and that minimize the sum of squares function
| (7) |
subject to the k constraints , i = 1, …, k. Since xh < xi for all h < i, and we are assuming aj ≥ 0, these k constraints are equivalent to the unique constraint
| (8) |
Thus, only one constraint is needed to perform the minimization of the sum of squares in (7). The obtained estimators of aj and are denoted âj and .
If no i is assumed to satisfy for compound j, we define k = 0 and estimate aj and by minimizing (7) without any constraint. In this case, the obtained estimators are just ordinary least squares estimators that can be produced with any linear regression software, and are still denoted by âj and . When k ≥ 1, nonlinear regression software can be used to compute âj and as explained in Appendix 3.
In any case, Ej is estimated with . Although we are assuming that aj ≥ 0, we do not impose the additional constraint aj ≥ 0 when minimizing (7). This is not a problem, and it is even advantageous, for three reasons. First, a goal of computing âj and is to compute Êj, which is well defined for any âj, even a negative one. Second, minimizing with respect to under constraint (8) is equivalent to minimizing with respect to , where A = {(a, b*) ∈ ℝ2; axk + b* < Tθ}. Since A is open and convex, standard theory of least squares estimation guarantees that, when aj ≥ 0 and under very general conditions on the distribution of yij for i ≥ k + 1, âj and are consistent estimators of aj and as n − k → ∞ (Shao 2003). As a consequence, Êj is a consistent estimator of Ej under aj ≥ 0.
Third, an advantage of not enforcing the additional constraint aj ≥ 0 in the minimization of (7) is that the adequacy of the assumption aj ≥ 0 can be examined by testing the null hypothesis that aj ≥ 0 versus the alternative aj < 0 by using a standard Wald test based on âj and its standard error. This would not be possible if the additional constraint aj ≥ 0 were imposed because in such case âj would never be negative.
10. Testing the null hypothesis of no important effect for a particular compound
To test H0: Ej = 0 versus H1: Ej > 0 we use Model Assumptions 1 and 6. Under these assumptions, the theory of least squares estimation allows showing that an approximate estimate of the standard error of denoted by , can be computed as the square root of the first diagonal element of the estimated variance-covariance matrix
| (9) |
and (Shao 2003). Now define k = n if all n doses of compound j produced true responses below the detection limit θ. To test H0 at a significance level α, we follow the following decision rule: if n − k − 2 ≥ 1, use the t statistic and reject H0 in favor of H1 if τj > tp,α, where tp,α is a right-tail critical value of a central t distribution with p = n − k − 2 degrees of freedom; and if n − k − 2 < 1, do not reject H0. If desired, a p-value can be computed and corrected for multiple comparisons when n − k − 2 ≥ 1.
11. Practical considerations in the estimation of aj and
In some practical situations, the biologist who conducted the experiments can provide a working value for the detection limit θ, which may be suggested by his/her experience and knowledge. With this provided value, aj and can be estimated for a particular compound j by using the methodology described in Section 9.
If a value for θ is not available from previous experience, θ can be estimated by using the model and approach proposed in Section 12. In any case, a question that needs to be answered before estimating aj and is how to decide whether or not a particular observed response Rij was produced under the inequality , that is, whether the measured response is unreliable.
Biologists usually assume that an observed response less than or equal to 0 reflects the fact that the true response lies below the detection limit, because experimental setup and instrumentation frequently do not allow measuring very small responses with acceptable precision. Guided by practical considerations, we incorporate this biologist’s assumption into our approach by assuming the following:
Working Assumption: Rij ≤ 0 implies for all h ≤ i, even if Rhj > 0 for some h < i.
In other words, since aj ≥ 0 for all j, we also assume that, if Rij ≤ 0, then dose Dh of compound j has produced a true response below the detection limit for all h ≤ i. Thus, if Rij ≤ 0, Rhj is not used directly to estimate the parameters in equation (5) when h ≤ i, although the information that is incorporated into the estimation approach described in Section 9 and Appendix 3.
Our approach, however, does not exclude other possible rules that the biologist or researchers may agree on to incorporate in an automated algorithm that decides whether or not a particular compound dose has produced a true response below the detection limit. Note that the Working Assumption can be viewed as a consequence of Model Assumption 1, because, by the latter, P (Rij ≤ 0) > 0 implies .
12. Estimation of the detection limit
If previous experience or knowledge does not provide a reasonable value for the detection limit θ, Model Assumptions 2–4 can be used to estimate θ, as described in this Section.
Model Assumptions 2 and 3 imply that if dose Di of compound j produced a true response below the detection limit and 0 < Rij < 100, then the unconditional distribution of the observed transformed response T(Rij) is a mixture of normal distributions with a scaled beta as the mixing distribution, where the scaled beta is defined in Section 4. Specifically, it can be shown that the unconditional pdf of T(Rij), is
| (10) |
where −∞ < z < ∞, with parameters α > 0, β > 0, γ2 > 0 and 0 < θ < 100. Note that, consistent with Model Assumption 4, the pdf fT does not depend on particular aj or parameters and depends only on global parameters α, β, θ and γ2.
Although the parameter of interest is θ, we estimate α, β, θ and γ2 simultaneously through maximum likelihood methodology by using the transformed observations T(Rij) satisfying both (i, j) ∈ I and 0 < Rij <100, which, by Model Assumptions 2, 3 and 4, constitute a random sample from fT.
For practical purposes, the parameters in the pdf in (10) will be estimated by using the transformed observations T(Rhj) that satisfy both Rhj > 0 and Rij ≤ 0 for some i > h. By the Working Assumption in Section 11 and Model Assumptions 1–4, the collection of logit-transformed observations satisfying these two conditions can be treated as a random sample from the pdf fT in (10). Once parameter estimates for α, β, θ and γ2 are obtained, the goodness of the fit of pdf (10) is examined by using a quantile-quantile (Q-Q) plot (Coles 2001).
The above approach to estimating the parameters in (10) additionally assumes that the detection limit θ is not substantially greater than 0, because we are not including transformed observations T(Rhj) such that Rij > 0 for all i ≥ h in the random sample from fT. This approach, however, will not bias the maximum likelihood estimator of θ towards 0 if this additional assumption about θ is not correct. The reason is that, by Model Assumption 4, even if θ is substantially large and other observed responses Rij with (i, j) ∈ I are not included in the sample, the observations T(Rhj) satisfying both Rhj > 0 and Rij ≤ 0 for some i > h still can be considered as independent observations from the pdf in (10); therefore, the maximum likelihood estimator of θ will still enjoy its good usual properties.
If θ is relatively large, however, the proposed approach has two limitations: 1) the number of observations T(Rhj) satisfying both Rhj > 0 and Rij ≤ 0 for some i > h may not be large enough to produce a reliable maximum likelihood estimator of θ; and 2) some observations T(Rhj) such that Rij > 0 for all i ≥ h may be rightfully considered as observations from the pdf in (10), but we do not know how to identify them and, more importantly, these unidentified observations may adversely affect the estimation of aj and because they will be wrongfully treated as informative about aj and when implementing the least squares estimation approach described in Section 9.
We stress that the support of fT is the set (−∞, ∞), not the set (0, θ). Thus, in principle, if R < θ, it is possible that Rij > θ and, therefore, that the estimated value of θ be smaller than some of the observations used to estimate θ.
As an additional justification of the proposed approach to estimating θ, observe that a consequence of the Working Assumption in Section 11 is that if Rhj>0 but Rij ≤ 0 for some i > h, then Rhj must contain information about the detection limit θ. For instance, if Rhj were too high, say 70%, since Dh < Di and aj ≥ 0, we would suspect that the experimental setup does not allow measuring strong responses with confidence, and therefore, that the detection limit is far from zero. Our approach extracts this information in order to produce an estimate of θ.
In summary, transformed observations T(Rhj) that satisfy both Rhj> 0 and Rij ≤ 0 for some i > h are viewed as constituting a random sample from a probability distribution that has θ as one of its parameters. A maximum likelihood estimate of θ is thus obtained with these observations.
13. Application: Neutralization of virus infection
Here, the proposed methodology is applied to data from experiments whose goal was to quantify the extent to which each of 62 compounds neutralizes the infection of the sensitive human brain glioblastoma cell line U87+T4+CCR5 by the JR-FL strain of human immunodeficiency virus, described in Krachmarov et al. (2001). Each compound was tested at 7 doses, namely 0.2382, 0.4763, 0.9527, 1.9053, 3.6916, 7.5023 and 15.0045 µM. The 62 compounds were selected from a library of 5,152 small-molecule compounds that were previously screened for their effect on virus infection at a single compound dose of 10 µM each.
The extent of the infection neutralization was indicated by a decrease in luminescent signal from a luciferase cell-based assay system, the magnitude of the luminescent signal reflecting the strength of the infection. The response R to a particular dose is a percent neutralization of virus infection that was defined as the percentage of luminescence that was decreased after the system was exposed to the compound for 72 hours relative to a control. The higher the percent neutralization, the greater the inhibition of virus infection of the U87+T4+CCR5 cells by the compound. Doses of added compounds that neutralized 50–100% of baseline luminescence were searched for. Compounds exhibiting such doses would be considered of pharmacological interest for future studies. Thus, we will use Rmin = 50%.
Here, the effect size Ej will be used as a measure of the overall ability of compound j to neutralize the viral infection, j = 1, …, 62; this measure combines the information produced by the 7 tested doses and treats any error-adjusted neutralization lower than 50% as unimportant. Biochemical methods are described in Appendix 4.
Some negative or zero percent neutralizations occurred when the final luminescent signal in the presence of the compound was equal to or greater than that produced by virus infection in the absence of compound. None of the 62 compounds produced a neutralization of Rij ≥ 100% at the tested doses.
To estimate the detection limit θ through maximum likelihood estimation of the parameters of pdf (10), the commands NIntegrate and NMaximize of the software Mathematica were used (Wolfram Research, Inc.). Table 1 shows the observations Rkj used to estimate these parameters, which satisfied both Rkj>0 and Rij ≤ 0 for some i > k. Parameter estimates for the pdf (10) were α̂ = 35.5616, β̂ = 4.34595, γ̂ = 0.899033 and γ̂ = 4.42281. Figure 4 shows a Q-Q plot built with these estimates, which suggests the adequacy of the proposed detection limit model for the neutralization data in Table 1. Thus, a detection limit of about 4.42% seems to be appropriate for the neutralization response.
Table 1.
Observed percent neutralization responses used to estimate the detection limit θ. The compound concentration (dose) variable was not used in the estimation of the detection limit and is shown here only for reference. The estimated detection limit for the neutralization response was θ = 4.42%.
| Compound | Dose (µM) | Percent neutralization (%) |
|---|---|---|
| KU0103598 | 0.2382 | 0.70 |
| KU0103183 | 0.2382 | 1.22 |
| KU0102611 | 0.2382 | 1.34 |
| KU0103182 | 3.6916 | 1.49 |
| KU0103495 | 3.6916 | 1.59 |
| KU0103598 | 0.9527 | 1.88 |
| KU0102882 | 0.9527 | 2.37 |
| KU0103495 | 1.9053 | 2.37 |
| KU0101694 | 0.4763 | 3.81 |
| KU0103495 | 0.4763 | 4.26 |
| KU0103488 | 0.4763 | 4.33 |
| KU0103560 | 0.2382 | 4.45 |
| KU0102569 | 0.2382 | 5.32 |
| KU0102532 | 0.2382 | 5.91 |
| KU0102620 | 0.9527 | 6.33 |
| KU0102460 | 0.2382 | 7.13 |
| KU0101289 | 3.6916 | 7.55 |
| KU0102882 | 0.2382 | 7.84 |
| KU0103575 | 0.4763 | 9.58 |
| KU0103598 | 0.4763 | 17.34 |
| KU0103575 | 0.2382 | 17.66 |
Figure 4.
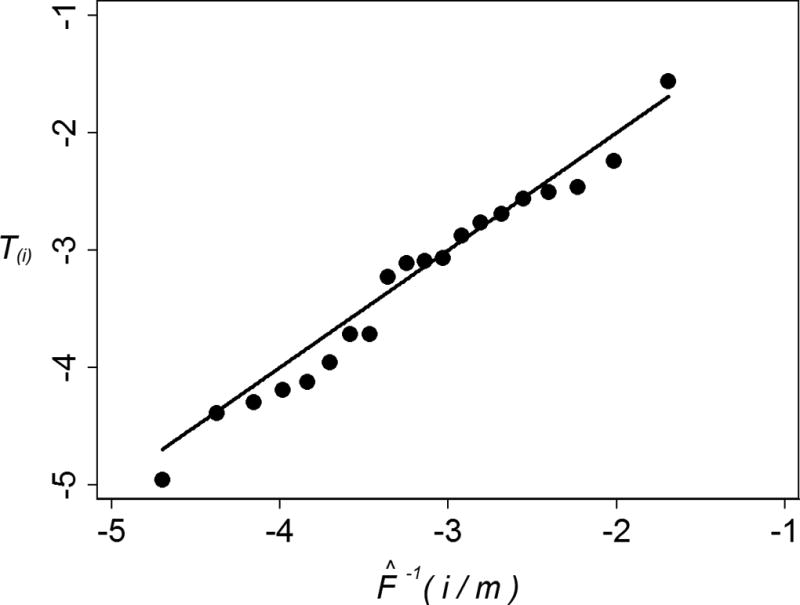
Quantile-quantile (Q-Q) plot for model of detection limit estimated with virus-infection neutralization data. The points tend to align along a straight line with slope 1 and intercept 0, suggesting that pdf (10) is a reasonable model of the detection limit for percent neutralization responses, and therefore, that an estimated detection limit of 4.42% is reasonable for these responses. The Q-Q plot was made with 1 the points (F̂−1(i/m), T(i)), i = 1, …, 21 − 1, where T(1) ≤ … ≤ T(21) are the order statistics of the 21 transformed responses in Table 1 which were used to estimate the parameters α, β, θ and γ2 of pdf (10), and F̂ is an estimate of the cumulative distribution function corresponding to this pdf, which was computed with the maximum-likelihood estimates of these parameters.
The approach described in Sections 9–10 was applied to the neutralization data, using θ = 4.42%. Compound effect sizes (the Ej’s) and their significances were computed by using Rmin = 50%. A Stata program was written to implement the model (Baum 2009). (The program is available from the corresponding author on request.) Stata’s nonlinear regression command (nl) was used for those compounds with k ≥ 1 (Appendix 3). Table 2 shows compound effect sizes Ej and the estimates of aj and for each compound for which these parameters could be estimated (that is, compounds with n − k ≥ 3). In Table 2, compounds were ranked according to estimated effect size. The six compounds with the largest pharmacological effect sizes were KU0104459 (Ej = 11.858), KU0101338 (11.592), KU0102728 (11.155), KU0104328 (10.562), KU0104458 (10.250) and KU0102846 (8.235); these effect sizes were significantly larger than 0. Out of those compounds for which n − k ≥ 3, three had an Ej = 0 (KU0102611, KU0044662 and KU0101694), and 8 had a nonsignificant Ej > 0.
Table 2.
Compound effect sizes (Ej) and statistical tests of the null hypothesis H0: Ej = 0 versus the alternative H1: Ej > 0 for compounds examined in infection neutralization experiments. Effect sizes and statistical tests were computed by assuming that a response of at least 50% neutralization is pharmacologically important.
| Compounda | Numberb,c of responses below detection limit(k) |
Detection limit (%) |
Slope (âj) |
Intercept |
Compound effect size (Ej) |
P-valued | Reject Ho?e |
|---|---|---|---|---|---|---|---|
| KU0104459 | 0 | Not Used | 1.304 | 5.563 | 11.858 | 1.0490E-07 | Reject |
| KU0101338 | 0 | Not Used | 1.265 | 5.419 | 11.592 | 4.6160E-07 | Reject |
| KU0102728 | 0 | Not Used | 0.687 | 4.116 | 11.155 | 4.5050E-06 | Reject |
| KU0104328 | 0 | Not Used | 1.780 | 6.133 | 10.562 | 0.0000080 | Reject |
| KU0104458 | 0 | Not Used | 1.611 | 5.747 | 10.250 | 0.0000009 | Reject |
| KU0102846 | 0 | Not Used | 0.728 | 3.496 | 8.235 | 0.0000001 | Reject |
| KU0104331 | 0 | Not Used | 1.964 | 5.255 | 7.028 | 0.0003487 | Reject |
| KU0104170 | 0 | Not Used | 1.359 | 4.272 | 6.715 | 0.0000042 | Reject |
| KU0104330 | 0 | Not Used | 1.808 | 4.883 | 6.596 | 0.0002132 | Reject |
| KU0101566 | 0 | Not Used | 1.839 | 4.429 | 5.335 | 0.0000242 | Reject |
| KU0104480 | 0 | Not Used | 0.551 | 2.359 | 5.044 | 0.0037141 | Reject |
| KU0102687 | 0 | Not Used | 0.659 | 2.482 | 4.677 | 0.0001547 | Reject |
| KU0103689 | 0 | Not Used | 1.490 | 3.631 | 4.425 | 0.0013418 | Reject |
| KU0104329 | 3 | 4.42281 | 2.975 | 5.128 | 4.420 | 0.0337829 | Reject |
| KU0101570 | 1 | 4.42281 | 1.950 | 4.077 | 4.261 | 0.0001934 | Reject |
| KU0102523 | 0 | Not Used | 0.638 | 2.323 | 4.229 | 0.0000009 | Reject |
| KU0103466 | 0 | Not Used | 0.870 | 2.701 | 4.196 | 0.0000135 | Reject |
| KU0101407 | 2 | 4.42281 | 2.089 | 4.135 | 4.092 | 0.0013082 | Reject |
| KU0104461 | 0 | Not Used | 1.394 | 3.135 | 3.525 | 0.0001186 | Reject |
| KU0101449 | 0 | Not Used | 1.069 | 2.712 | 3.442 | 0.0015486 | Reject |
| KU0103488 | 3 | 4.42281 | 2.641 | 4.208 | 3.352 | 0.0019370 | Reject |
| KU0101601 | 2 | 4.42281 | 1.916 | 3.536 | 3.263 | 0.0002313 | Reject |
| KU0101667 | 3 | 4.42281 | 2.600 | 4.095 | 3.225 | 0.0010664 | Reject |
| KU0101152 | 2 | 4.42281 | 1.906 | 3.501 | 3.216 | 0.0026582 | Reject |
| KU0103568 | 0 | Not Used | 0.865 | 2.142 | 2.654 | 0.0007045 | Reject |
| KU0104351 | 1 | 4.42281 | 1.392 | 2.696 | 2.610 | 0.0294725 | Reject |
| KU0104464 | 1 | 4.42281 | 1.441 | 2.413 | 2.020 | 0.0000274 | Reject |
| KU0101587 | 0 | Not Used | 1.999 | 2.796 | 1.955 | 0.0517520 | Not reject |
| KU0101598 | 1 | 4.42281 | 2.029 | 2.806 | 1.941 | 0.0024013 | Reject |
| KU0104354 | 0 | Not Used | 1.483 | 2.379 | 1.909 | 0.0902165 | Not reject |
| KU0104252 | 3 | 4.42281 | 2.093 | 2.696 | 1.736 | 0.0269597 | Reject |
| KU0101548 | 1 | 4.42281 | 1.278 | 1.960 | 1.503 | 0.0003203 | Reject |
| KU0101288 | 4 | 4.42281 | 2.953 | 2.680 | 1.216 | 0.0369284 | Reject |
| KU0103963 | 1 | 4.42281 | 1.077 | 1.389 | 0.895 | 0.0049965 | Reject |
| KU0103575 | 4 | 4.42281 | 2.496 | 1.584 | 0.502 | 0.2064629 | Not reject |
| KU0103598 | 4 | 4.42281 | 2.139 | 1.342 | 0.421 | 0.0877485 | Not reject |
| KU0102612 | 2 | 4.42281 | 1.287 | 1.030 | 0.412 | 0.0661612 | Not reject |
| KU0106019 | 4 | 4.42281 | 2.099 | 1.259 | 0.378 | 0.1494977 | Not reject |
| KU0102882 | 4 | 4.42281 | 2.520 | 0.606 | 0.073 | 0.2139543 | Not reject |
| KU0102597 | 0 | Not Used | 0.648 | 0.166 | 0.021 | 0.3706192 | Not reject |
| KU0102611 | 4 | 4.42281 | 0.236 | −3.321 | 0 | 0.9579079 | Not reject |
| KU0044662 | 4 | 4.42281 | 0.474 | −2.306 | 0 | 0.9005957 | Not reject |
| KU0101694 | 4 | 4.42281 | 0.617 | −3.069 | 0 | 0.8108476 | Not reject |
Seven doses were tested with each compound, namely 0.2382, 0.4763, 0.9527, 1.9053, 3.6916, 7.5023 and 15.0045 µM.
Of the 62 compounds tested, 19 produced at least 5 responses below the detection limit, namely KU0103495, KU0102692, KU0101209, KU0102460, KU0102569, KU0103517, KU0103668, KU0102553, KU0103597, KU0102850, KU0103576, KU0103262, KU0103560, KU0103182, KU0101695, KU0102620, KU0101289, KU0103183, KU0102532. These compounds are not shown in the Table. Since the model has 3 parameters (slope, intercept and error variance), at least 3 doses producing true responses above the detection limit are required for estimating an effect size. Therefore, the model could not be fitted to data from these compounds.
When k > 0, the slope and intercept were estimated through constrained least squares by using a detection limit of 4.42%.
Uncorrected p-value from t-test testing the null hypothesis that the compound effect size is 0.
Decision using a significance level of 0.05 and Simes correction for multiple comparisons (Benjamini and Hochberg, 1995).
A total of 32 compounds had a significant effect size (Table 2). This apparently large number should not come as a surprise, since the 62 compounds examined in these analyses had been previously selected as the most promising compounds from an initial high throughput screening that explored 5,152 compounds. That is, 32 compounds constitute just 0.62% of the initially explored library of compounds. Also, observing 32 “significant” compounds out of 62 should not be interpreted as an indication of an inflated Type I error for an individual statistical test. In fact, for k = 0, standard theory of least squares guarantees that the probability of Type I error of the test proposed in Section 10 is always ≤ α when the observations T(Rij) are normally distributed.
For the case k > 0, we performed a simulation study using a nominal α = 0.05, which showed that the probability of Type I error for an individual test was not larger than α for fixed k = 1, 2, 3, 4. Observe that, strictly speaking, for a particular compound, k is a random variable. Thus, the conditional probability of Type I error given k was ≤ α for all k = 0, 1, 2, 3, 4. But, a compound was not concluded to be an effective compound when k = 5, 6, 7, where k = 7 if R7,j = 0; that is, for each of these other k’s, the conditional probability of Type I error given k was 0. All this implies that the unconditional probability of Type I error was ≤ α, as desired. The methods and results of this simulation study are available from the corresponding author on request.
All âj’s in Table 2 are non-negative, which suggests that our key assumption that aj ≥ 0 for all j may be valid for these particular infection neutralization experiments. Should one compound exhibit an âj < 0, a Wald test of the null hypothesis H0: aj ≥ 0 versus the alternative H1: aj < 0 could be conducted in order to examine the adequacy of this assumption for the compound.
Observe from Table 2 that there is a trend for high values of k to be associated with small effect sizes Ej. This was expected because Rmin > θ, and therefore, if a large number of tested doses of a particular compound produced true responses below the detection limit then we can infer that the compound did not have important pharmacological effects in the dose range tested (i.e., did not produce R > Rmin for those doses). The effect size Ej just captures this lack of important effects.
14. Further comments about the estimation of the detection limit for infection neutralization response
Table 3 illustrates responses from some compounds. The compounds in Rows 1 and 2 of Table 3 did not produce any non-positive response, so simple linear regression was used to estimate their parameters aj and after logit-transforming their responses. Rows 3–14 of Table 3 show the data from some compounds that produced some true responses below the detection limit according to the Working Assumption in Section 11.
Table 3.
Percent neutralization responses (%) for some compounds.
| Dose (µM)a | ||||||||
|---|---|---|---|---|---|---|---|---|
| Row | Compound | D1 | D2 | D3 | D4 | D5 | D6 | D7 |
| 1 | KU0104459 | 49.88 | 72.34 | 89.96 | 94.80 | 98.14 | 99.11 | 99.50 |
| 2 | KU0104170 | 23.68 | 44.76 | 53.78 | 80.65 | 90.63 | 95.17 | 99.13 |
| 3 | KU0101570 | ≤ 0 | 4.10 | 24.94 | 63.32 | 85.16 | 89.46 | 98.32 |
| 4 | KU0102612 | ≤ 0 | ≤ 0 | 9.48 | 8.25 | 40.14 | 66.10 | 65.60 |
| 5 | KU0101667 | ≤ 0 | ≤ 0 | ≤ 0 | 24.96 | 60.84 | 92.34 | 98.03 |
| 6 | KU0106019 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | 26.42 | 46.01 | 73.57 |
| 7 | KU0102460 | 7.13 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 |
| 8 | KU0102620 | ≤ 0 | ≤ 0 | 6.33 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 |
| 9 | KU0103560 | 4.45 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | 6.98 |
| 10 | KU0101694 | ≤ 0 | 3.81 | ≤ 0 | ≤ 0 | 2.95 | 1.23 | 6.79 |
| 11 | KU0103575 | 17.66 | 9.58 | ≤ 0 | ≤ 0 | 20.03 | 22.75 | 89.36 |
| 12 | KU0103598 | 0.70 | 17.34 | 1.88 | ≤ 0 | 16.37 | 55.02 | 75.14 |
| 13 | KU0102882 | 7.84 | ≤ 0 | 2.37 | ≤ 0 | 4.14 | 32.98 | 59.56 |
| 14 | KU0102692 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 | ≤ 0 |
Doses D1 through D7 were 0.2382, 0.4763, 0.9527, 1.9053, 3.6916, 7.5023 and 15.0045 µM, respectively.
The compound in Row 3 of Table 3 produced a non-positive response at dose D1. One may be tempted to estimate aj and for this compound by using simple linear regression without constraints with only the information from doses Di, i ≥ 2. However, such approach disregards the knowledge that D1 is producing a response below the detection limit, information that may be useful to improve our estimates of aj and . Besides, ignoring this information may bias our conclusions about this compound against the null hypothesis H0: Ej = 0, as explained in the Discussion. Rows 4–6 of Table 3 also show compounds for which some of the smallest doses produced responses below the detection limit. However, no compound in rows 3–6 provided positive responses usable for estimating the detection limit θ.
Row 7 in Table 3 shows an extreme case that helps to motivate the Working Assumption in Section 11. For the compound in this row, R1,j > 0%. However, Rij ≤ 0 for all i ≥ 2. Since we are assuming that aj ≥ 0, there is not doubt that R1,j = 7.13% contains no information about aj and and that the true response produced by D1 should be below the detection limit θ. However, R1,j is valuable in that, if Model Assumptions 2–4 in Section 5 are correct, R1,j carries information about the true value of θ, and therefore, can be used to estimate θ. Similar comments about the observed response R3,j = 6.33% to dose D3 of the compound in Row 8 can be made. In this case, the idea that R3,j carries information about the detection limit is suggested by the fact that all doses higher than D3 produced non-positive observed responses.
To further illustrate, by the Working Assumption, the following observations were used to estimate θ : R1,j = 4.45% for the compound in Row 9 of Table 3; R2,j = 3.81% (Row 10); R1,j = 17.66 and R2,j = 9.58% (Row 11); R1,j = 0.70, R2,j = 17.34 and R3,j = 1.88% (Row 12); and R1,j = 7.84 and R3,j = 2.37% (Row 13).
The compound in Row 14 produced non-positive observed responses at all tested doses. This strongly suggests that, for this compound, the investigated doses did not have any influence on the investigated neutralization response and always produced true responses below the detection limit. Moreover, no observations provided by this compound can be used to estimate θ nor to estimate aj and .
15. Discussion
From a practical point of view, the most important product of this research is that we are able to produce tables like Table 2 that include measures of effect sizes that allow comparing the pharmacological importance of chemical compounds, and p-values that allow testing the significance of these effect sizes.
A major disadvantage of a direct application of the median effect equation in (1) is that this equation does not allow statistically testing the null hypothesis of no effect of the chemical compound on the pharmacological response. Nonlinear regression approaches based on equation (1) alone cannot be used to examine this hypothesis, because equation (1) implicitly assumes that there is a dose-response efffect. In other words, the problem is that the parameter space of equation (1) does not include the possibility of no dose-response effect. In fact, any statistical test procedure based on a parametric model requires that the parameter space contains a null space representing the null hypothesis (Shao 2003). In contrast, in addition to essentially containing all dose-response relationships represented by equation (1), equation (3) allows testing a null hypothesis of no effect.
An added advantage of equation (3) is that dose response relationships that are nearly constant within the investigated dose range can be easily handled with this equation, and a measure of pharmacological effect size (Ej) based on equation (3) can be defined for (and used to compare) many types of relationships. In particular, Ej allows comparing the effect of a compound producing a nearly constant relationship with the effect of a compound producing a relationship represented by the median effect equation. In contrast, a direct use of equation (1) creates problems when analyzing nearly constant relationships, as illustrated in Figure 2, because equation (1) does not include parameters representing constant relationships. As mentioned in the introduction, in a biomolecular screening, non-negligible almost-constant relationships can be found which are produced by compounds with pharmacologically important dose-response effects. This may occur, for instance, if the investigated dose range was not wide enough for those compounds.
Our approach also introduces a formal and precise way of incorporating the important concept of response detection limit in the analysis of dose-response data with continuous responses, a concept that is usually neglected in these types of analysis. A criterion is also suggested for the identification of responses that have taken on values below the detection limit. As described in Section 12, although this criterion will generally produce a reliable estimator of θ, the criterion may not be entirely adequate for estimating Ej when θ is considerably larger than 0. The proposed approach is in general adequate only if θ can be reasonably assumed to be relatively small.
The assumption that the detection limit θ is not large may be reasonable in many biomolecular screenings, and this assumption seems to be reasonably satisfied by the data analyzed in Section 13. However, further research is needed in order to refine the approach proposed in Section 12, and/or propose more approaches amenable to automation. The experience and knowledge of the biologists and pharmacologists involved in measuring continuous responses in cell-based assays are undoubtedly crucial to developing, in future research, further criteria for the identification of data that can be used to estimate the detection limit, especially in situations in which the detection limit is suspected to be large.
Observed null or negative responses cannot be ignored when estimating the parameters of the linearized form (3), which involves a logit transformation T that is undefined for non-positive responses. In fact, when k ≥ 1, minimizing the sum of squares (7) subject to constraint (8) produces a larger estimate of the error variance σ2 than without the constraint. This can be seen by noting that if âu,j and are the unconstrained least squares estimators of aj and , then
But, . Thus, excluding from the analysis responses below the detection limit such as those corresponding to observed null or negative responses, and fitting a simple linear regression model to the remaining (Di, T(Rij)) pairs, underestimates the standard error of the least squares estimate of and, therefore, biases conclusions against the null hypothesis H0: Ej = 0 and increases type II error (because the standard error of is in the denominator of the statistic τj defined in Section 10).
In particular, simply put, since observed non-positive responses are evidence in favor of the null hypothesis of no effects, these responses should not be excluded from the data when fitting the linearized form (3) of the median effect equation. An approach that appropriately handles these responses, such as the one proposed in this paper, should be followed instead.
Moreover, by Model Assumption 4, observed responses obtained when the true response is below the detection limit are independent across (and within) compounds. As a consequence, the presence of many ineffective compounds in the compound sample that is used to estimate θ will not bias θ̂. In fact, the presence of such compounds may even be beneficial to the estimation of θ because the more ineffective compounds are there, the higher the chance of obtaining true responses with low values, including true responses below the detection limit.
It should be noted that, although the transformation T(R) = log(R/(100 − R)) assumes that 0 and 100 are low and upper bounds of R, respectively, the use of equation (3) and the methodology proposed in this article do not require that the scatterplot of the actual dose-response data of a particular compound exhibits a plateau of height 100 at its right side or a plain of height 0 at its left side. Even if the observed maximum response of a particular compound is farther down from 100 or its observed minimum is farther up from 0, the transformation T(R) and the proposed effect size measure and statistical test are still applicable, provided that at least three different doses producing true responses above the detection limit are tested and at least three different observed responses are obtained, and provided equation (3) is valid.
Alternatively, if there are reasons to believe that the dose response curve follows a sigmoidal shape with a minimum response λ1 > 0 and a maximum λ2 < 100, say, where λ1 and λ2 are known values, the transformation R’ = {(R − λ1) / (λ2 − λ1)}×100 should be applied before using the proposed methodology. That is, R’ and T(R’) should be used instead of R and T(R), respectively. However, the effect sizes from a set of compounds can be compared only if the values of both λ1 and λ2 are the same across all compounds.
Acknowledgments
The mathematical and statistical models and procedures described in this article were all conceived and developed solely by Dr. Diaz. These include the model of detection limit, the measure of effect size, and the hypothesis testing procedure. The models were developed during Dr. Diaz part-time work (20% of his time) at the High Throughput Screening Laboratory of the University of Kansas, Lawrence, KS. His salary for this work was provided by the University of Kansas Endowment Association. The neutralization data reported in this article were produced by Drs. Pinter, Chaguturu and McDonald in the context of NIH grant # R21NS067633, which was awarded to Dr. Pinter; Dr. Diaz was not involved in the planning or conduction of the biochemical experiments producing these data, and did not receive any payment from this NIH grant or from Drs. Pinter, Chaguturu or McDonald. The contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH. The authors wish to thank two anonymous reviewers and an Associate Editor who provided comments that substantially contributed to the improvement of the manuscript.
Appendix 1
A computational formula for Ej
The effect size Ej can be computed with the formula
| (11) |
| (12) |
| (13) |
Figure 3 shows graphical representations of Ej made with formulas (11)–(13).
Appendix 2
Appendix 2. Proof of the equivalence of H0: Ej = 0 and when aj ≥ 0
Suppose Ej = 0. Then, for all x in the closed interval , because is a continuous function of x. Thus, for all x in . In particular, using x = 0, we obtain .
Now suppose . For all x in , we have that x ≤ 0 and, therefore, because aj ≥ 0. Thus, for all x in ; this implies Ej = 0.
Appendix 3
Computation of âj and b̂j
The minimization of (7) subject to constraint (8) can be carried out with any nonlinear regression software. In this computational approach, we use the fact that if εij is a random error, then the linear regression model , i = k + 1, …, n, accompanied with constraint (8), is algebraically equivalent to the nonlinear regression model
| (14) |
where aj and γj are unknown parameters that need to be estimated and satisfy . The reason the two models are equivalent is that the constraint is equivalent to eγj > 0, which is always true. When n − k ≥ 3, estimates âj and γ̂j for aj and γj can be obtained by fitting model (14) to the pairs (xi, yij), i = k + 1, …, n, using least squares. Then, the constrained least squares estimate of is computed as . We recommend using this approach for computing the point constrained estimates âj and , as well as , but should be computed separately and should be obtained from matrix (9).
Alternative methods for constrained minimizations are also available in statistical and non-statistical software. For instance, the command NMinimize of the package Mathematica allows implementing constrained minimizations through global optimization algorithms (Wolfram Research, Inc.), although more programming effort is needed to implement this command for the dose-response analyses proposed here than if using standard nonlinear regression software.
Appendix 4
Biochemical methods
The percent neutralization response R was measured through a single-cycle infectivity assay using virions generated from the Env-defective luciferase-expressing HIVNL4-3 genome, pseudotyped with molecularly cloned HIV Env, as previously described (Pinter et al. 2004). Pseudotyped virions in culture supernatants from transfected 293T cells were incubated with serial dilutions of MAbs or polyclonal sera from HIV-infected subjects for 1 h at 37°C, and were then added in the presence of Polybrene (10 g/ml) to U87-T4-CCR5 target cells plated out in 384-well plates. Luciferase activity was determined 72 hours postinfection using assay reagents from Promega (SteadyGlo) and a microtiter plate luminometer (Tecan Safire2).
References
- Baum CF. An introduction to Stata programming. Stata Press; College Station, TX: 2009. [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society B. 1995;57:289–300. [Google Scholar]
- Chou T-C. Theoretical Basis, Experimental Design, and Computerized Simulation of Synergism and Antagonism in Drug Combination Studies. Pharmacological Reviews. 2006;58:621–681. doi: 10.1124/pr.58.3.10. [DOI] [PubMed] [Google Scholar]
- Coles S. An introduction to statistical modeling of extreme values. Springer-Verlag; London: 2001. [Google Scholar]
- Diaz FJ, McDonald PR, Roy A, Taylor B, Price A, Hall J, Blagg BSJ, Chaguturu R. Compound ranking based on a new mathematical measure of effectiveness using time course data from cell-based assays. Combinatorial Chemistry & High Throughput Screening. 2013;16:168–179. doi: 10.2174/1386207311316030002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutelle S, Maurin M, Rougier F, Barbaut X, Bourguignon L, Ducher M, Maire P. The Hill equation: a review of its capabilities in pharmacological modelling. Fundamental & Clinical Pharmacology. 2008;22:633–648. doi: 10.1111/j.1472-8206.2008.00633.x. [DOI] [PubMed] [Google Scholar]
- Krachmarov CP, Kayman SC, Honnen WJ, Trochev O, Pinter A. V3-specific polyclonal antibodies affinity purified from sera of infected humans effectively neutralize primary isolates of human immunodeficiency virus type 1. AIDS Research and Human Retroviruses. 2001;17:1737–1748. doi: 10.1089/08892220152741432. [DOI] [PubMed] [Google Scholar]
- Pinter A, Honnen WJ, He Y, Gorny MK, Zolla-Pazner S, Kayman SC. The V1/V2 domain of gp120 is a global regulator of the sensitivity of primary human immunodeficiency virus type 1 isolates to neutralization by antibodies commonly induced upon infection. Journal of Virology. 2004;78:5205–15. doi: 10.1128/JVI.78.10.5205-5215.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J. Mathematical Statistics. 2. Springer; New York: 2003. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 7.0. Champaign, IL: 2008. [Google Scholar]


