Vinculin forms a directionally asymmetric catch bond with F-actin

Abstract

Vinculin is an actin-binding protein thought to reinforce cell-cell and cell-matrix adhesions. However, how mechanical load affects the vinculin/F-actin bond is unclear. Using a single-molecule optical trap assay, we found that vinculin forms a force-dependent catch bond with F-actin via its tail domain, but with lifetimes that depend strongly on the direction of the applied force. Force toward the pointed end of the actin filament resulted in a bond that was maximally stable at 8 pN, with a mean lifetime (12 s) 10-fold longer than the mean lifetime when force was applied toward the barbed end. A computational model of lamellipodial actin dynamics suggested that the directionality of the vinculin/F-actin bond could establish long-range order in the actin cytoskeleton. The directional and force-stabilized binding of vinculin to F-actin may provide a mechanism by which adhesion complexes maintain front-rear asymmetry in migrating cells.

Cadherin- and integrin-based protein assemblies link cells to each other and to the extracellular matrix (ECM), respectively, and together provide the physical basis for the organization of multicellular tissues (1). Both classes of adhesion complexes are exquisitely sensitive to mechanical load, and change rapidly in size and composition in order to maintain the physical integrity of living tissues (2). These adhesions are also essential in defining the physical asymmetries that underlie both individual and collective cell migration in the context of embryonic development (3), wound healing (4), and cancer metastasis (5). However, the molecular basis of how cadherin- and integrin-based adhesions respond to mechanical stimuli to regulate tissue cohesion and directional cell migration remains poorly understood.

The protein vinculin is a component of both cadherin- and integrin-based adhesion complexes, and is rapidly recruited to both types of adhesions in response to mechanical load through its interactions with α-catenin and talin, respectively (6–8). Vinculin plays a key role in maintaining tissue integrity (9, 10); for example, loss of vinculin in mice results in the death of the developing embryo owing to defects in neural tube closure and heart development (11). Importantly, vinculin is required for persistent directional cell migration, suggestive of a role in generating a polarized connection between adhesions and the actin cytoskeleton (12, 13). Although vinculin is also recruited to cadherin-based adhesions in a force-dependent manner (6, 14), comparatively little is known about how it might regulate actin organization and dynamics at those sites.

Vinculin binds directly to filamentous (F-) actin through its actin-binding tail domain (Vt) (15, 16), but how and whether this bond may be regulated by mechanical load is not known. Defining this mechanism is critical to understanding the role of vinculin as a reinforcing link between adhesion complexes and the actin cytoskeleton. We modified a previously developed optical trap (OT)-based assay (17) to define the load dependence of the binding interaction between vinculin and F-actin (Fig. 1A). Actin binding to full-length, wild-type vinculin is blocked by autoinhibitory intramolecular interactions between the N-terminal head domain and Vt (15). We thus used a well-characterized vinculin construct, termed T12 vinculin, bearing mutations that disrupt the autoinhibitory head-Vt interaction (18). In the OT assay, the displacement of the microsphere (1 μm in diameter) from the trap center typically decreased in several distinct steps (Fig. 1, A and B), indicative of the sequential release of multiple vinculin molecules from the actin filament (17). The last stair step in this series likely reflects a state in which actin is bound by a single vinculin molecule (22), allowing us to determine the effect of mechanical load on the kinetics of vinculin unbinding.

Fig. 1. The optical trap (OT) assay measures vinculin/F-actin bond lifetimes under load.

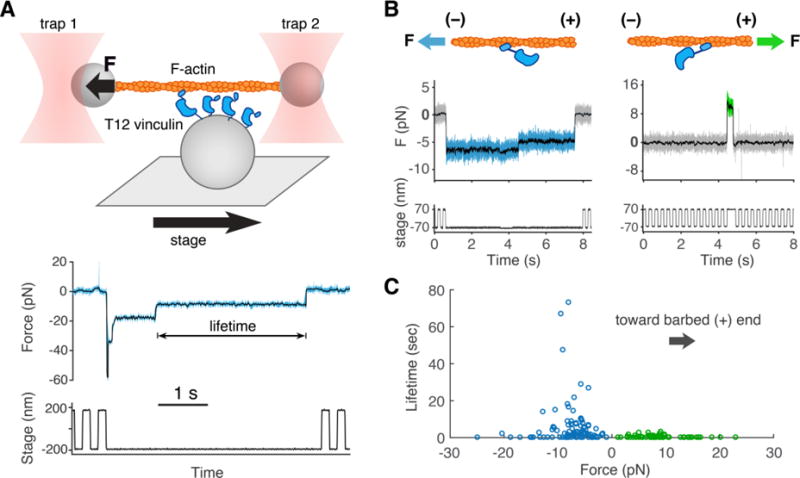
(A) (top) An actin filament attached to two microspheres is held taut by two OTs near a platform bead with vinculin on its surface. A motorized stage moves the platform back and forth. Vinculin binding results in the displacement of one of the optically trapped microspheres. (bottom) Both OTs exert force on the actin filament. Here, we plot the summed force, i.e. the total force transmitted from both traps to the vinculin molecule(s) (22) vs. time, decimated from 40 kHz to 4 kHz (light blue) and median filtered with a 100 point moving window (overlaid in black). If force surpasses a defined threshold, stage motion halts until detachment of the bound vinculin molecule(s). (B) Representative traces where force on T12 vinculin is directed toward the pointed (-) end (blue), or the barbed (+) end (green) of the actin filament. (C) Binding events in which the force on T12 vinculin was directed towards the filament’s pointed (−) end (blue circles, n = 102, mean lifetime of 5.6 s) or barbed (+) end (green circles, n = 65, mean lifetime of 0.54 s).

The duration of vinculin–actin binding events depended on the level of mechanical load: events were short (<1 s) at low 0-3 pN loads; markedly longer (~10 s) at intermediate (7–10 pN) loads, and again short (<1 s) at forces >15 pN (Fig. 1C). This counterintuitive behavior, in which increasing load results in an increase in bond lifetime over a given force range, is termed a catch bond and differs from the more usual behavior of molecular complexes in which increasing load leads to an exponential increase in the dissociation rate (termed a slip bond) (19, 20). Owing to the nature of the loaded OT assay, few binding events were observed at forces less than 2 pN, where catch bond and slip bond models differ greatly in their predicted lifetimes. To measure lifetimes at low forces, we developed an alternative assay in which an actin filament was positioned near a platform oscillating at 200 Hz over 5 nm. Binding of vinculin to the actin filament was detected by a decrease in the amplitude of microsphere fluctuations (Fig. S1). This alternative assay could not resolve sequential unbinding steps, which means that the mean binding lifetimes measured in this way may be overestimated. Nonetheless, the binding events observed near zero force were markedly shorter than those measured at forces higher than 2 pN (p < 0.01 in a one-tailed two sample KS test), consistent with the idea that mechanical load increases the lifetime of the vinculin–actin bond.

A vinculin binding event can displace a trapped actin filament in one of two directions, depending on which direction the platform was moving when binding occurs (Fig. 1B). In all cases, mechanical load applied in one direction resulted in longer mean bond lifetimes than when load was applied in the opposite direction. This result is unlikely to been caused by a systematic error in the OT assay, because the direction yielding longer lifetimes switched when we physically rotated the filament by 180°.

F-actin is polar, with a barbed (+) and pointed (−) end, so we tested whether the observed directionality could arise from the asymmetric binding interface between vinculin and the actin filament. To determine the polarity of a trapped actin filament, we used platforms that were coated with myosin VI (Fig. S2). Myosin VI moves in a processive manner toward the pointed end of the actin filament (21), so the displacement of one of the microspheres from its OT allowed us to assign the polarity of the trapped actin filament (Fig. S3). The same filament, now with known polarity, was moved to a vinculin-coated platform and tested as before. Remarkably, over the range of forces tested (1–30 pN) the vinculin–actin filament bond exhibited a ~10-fold longer mean lifetime when the force experienced by vinculin was directed toward the pointed (−) vs. barbed (+) end of the actin filament (Figs. 1 and S3).

To explain the observed distribution of bond lifetimes, we tested several kinetic models that have been used to describe how bond lifetimes depend on mechanical load (22). Catch bond models that feature a single bound state (23, 24) predict a single exponential distribution of lifetimes at any given force and thus do not accurately describe the mixture of short- and long-lived events that we observed (Fig. S4). We therefore chose a two bound-state model (25) in which the bond can transition between unbound (0), weakly bound (1) and strongly bound (2) states with load-dependent rates given by a modified Bell model,

$$k_{ij}(F)=k_{ij}^0\exp \left(F{x}_{ij}/k_{B}T\right)$$

where the transition rate $k_{ij}(F)$ between two states depends on x_ij, which represents the physical distance between the initial state i and the peak of the energy barrier (i.e. the transition state) between states i and j, as well as the extent to which the applied force is aligned with this direction (Fig. S5A). Using maximum likelihood estimation, we found that this two bound-state model best fit the data for displacements in both the (−) and (+)-end directions (Fig. 2). To obtain accurate parameter estimates, we augmented the force-lifetime dataset in which actin filament polarity was explicitly determined (Figs. 1, S3B) with a dataset in which the actin polarity was inferred from a statistical test (Fig. S3, C and D, and supplemental text). Vinculin bound in the weak-binding state 90% of the time, and equilibrated with the strong-binding state. Importantly, mechanical load lowered the rate at which the strong-binding state transitioned back to the weak-binding state, thereby stabilizing the vinculin–actin filament bond (Fig. S6). The direction of applied force determined the extent to which it stabilized the strongly bound state, which is encoded in the magnitude of the distance parameters x_ij. Thus, the two bound-state catch bond model provides a kinetic basis for the directionality of vinculin–actin filament binding.

Fig. 2. A two bound-state directional catch bond model of T12 vinculin and vinculin tail (Vt) binding lifetimes.

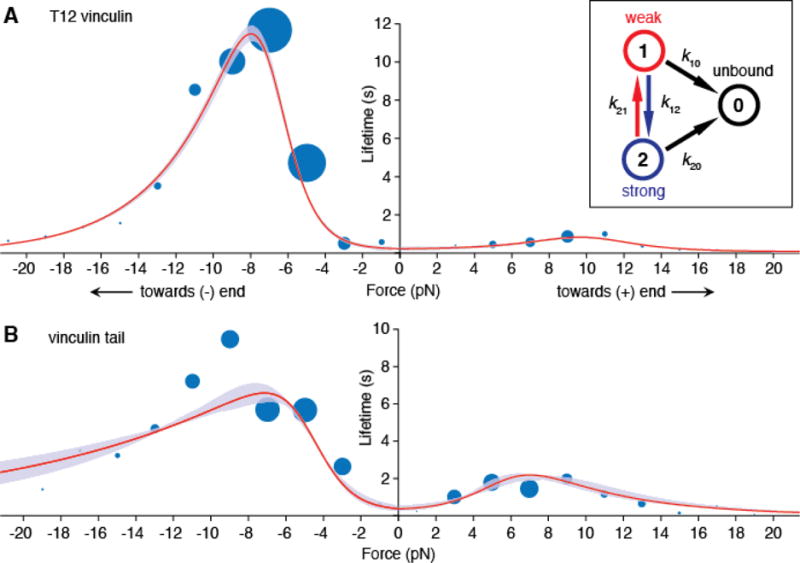
(A) Mean actin binding lifetimes and model of best fit for T12 vinculin (n = 728) and (B) Vt (n = 702). A subset of these events are collected from filaments of known polarity, and the rest are assigned a polarity using a 2D KS test (22). In each 2 pN bin, the area of each blue circle is proportional to the number of events. Red curves show mean lifetimes predicted by the two bound-state catch bond model (inset), and purple envelopes indicate 95% confidence intervals (CIs) for the fit, obtained by parametric bootstrapping. The model was constrained to possess a mean lifetime at zero force that was less than or equal to the lifetime measured using the low-force binding assay (Fig. S1). Survival plots of the data and models are shown in Fig. S8 for T12 vinculin and Fig. S9 for Vt.

We next examined which domain(s) of vinculin were required for the formation of a directional catch bond to F-actin. We tested a protein construct containing only the vinculin tail (Vt) (residues 879-1066), which binds to F-actin. Similar to T12 vinculin, the Vt bond to F-actin was stabilized by mechanical load in either direction, and load directed towards the pointed (-) end resulted in higher stability (Fig. S3, B and D). Thus, Vt alone is sufficient to form a directional catch-bond with the actin filament (Fig. 3B). The less pronounced directionality in Vt binding was reflected in differences in the distance parameter x₂₁ for the strong-to-weak transition (Table I). This parameter is sensitive to the angle of applied load, and the presence of the vinculin head might change the direction of force experienced by the vinculin tail (Fig. S5). Alternatively, the vinculin head may contain cryptic actin-binding site(s) that are revealed upon application of load. In any case, formation of a directionally asymmetric catch bond appears to be intrinsic to the interaction of the vinculin tail with the actin filament.

Fig. 3. Computational model of actin dynamics in a cell protrusion.

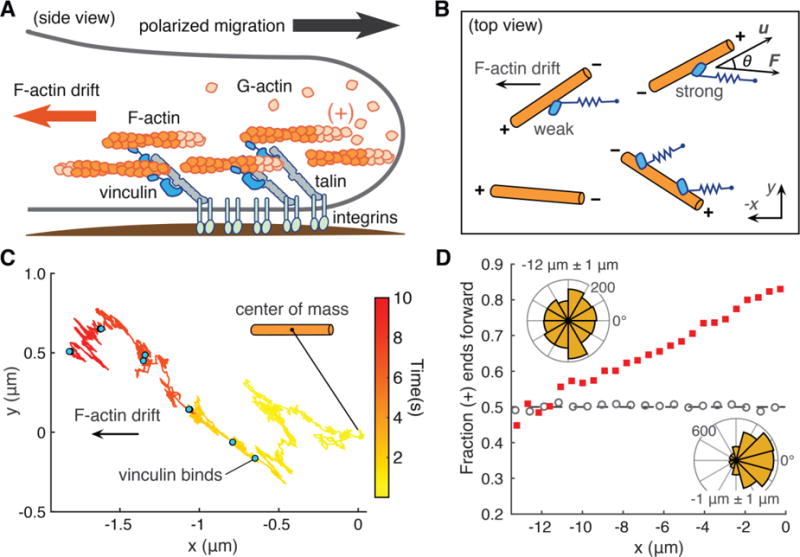
(A) Long-range order of the actin cytoskeleton (orange) induced by adhesion proteins, including vinculin, may reinforce polarized cell migration. (B) Computational model: actin filaments (orange) undergo 2D Brownian diffusion with a drift velocity. The effect of vinculin on filament motion is modeled as a simple spring that dampens diffusion and resists the drift velocity (22). Directionality in the model depends on the angle θ between the filament’s long axis (u) and the force vector (F). (C) Sample trace of the 2D position of a filament’s center of mass over time. Blue dots indicate times at which an additional vinculin binds. (D) Filaments start at x = 0 μm with random initial angle. Red squares show the fraction of filaments with barbed (+) end facing forward after 60 s. Grey circles show a control simulation in which vinculin’s actin-binding kinetics do not depend on actin polarity. Filaments oriented with barbed (+) end to the right are defined as forward facing (angles −90° to 90°). Inset, top left: angles of filaments within x = −12 μm +/− 1 μm. Inset, bottom right: angles of filaments within x = −1 μm +/− 1 μm. For each condition, n = 224000 filaments.

Table I.

Kinetic parameters for the two bound-state catch bond for T12 vinculin (top) and Vt (bottom). State 0 is the unbound state. States 1 and 2 are the weak and strong binding states, respectively. Each parameter is assigned a 95% confidence interval (in brackets) obtained through a parametric bootstrapping method in which 1000 simulated datasets were generated from the fitted model and parameters of best fit for each dataset were obtained through maximum likelihood estimation (17). Transition rate from state i to state j in the absence of load is indicated by k_ij. The application of load alters the equilibrium between state i and state j according to a distance parameter x_ij, which can be positive or negative, indicating that the transition rate is increased or decreased by force, respectively. These distance parameters vary depending on whether force is oriented toward the barbed (+) end or pointed (−) end of the actin filament.

Transition	kij0 (1/s)	CI (1/s)	xij (nm) pointed (−) end direction	CI (nm)	xij (nm) barbed (+) end direction	CI (nm)
1→ 0	5.3	[3.7, 7.6]	0	[0, 0.001]	0	[0, 0.1]
2→ 0	5.5 × 10−3	[0.0054, 0.0059]	1.2	[1.1, 1.2]	1.8	[1.7, 1.8]
1→ 2	6.1	[4.5, 9.4]	0.4	[0.4, 0.5]	0	[0, 0.003]
2→ 1	43	[39, 52]	−3.4	[−3.6, −3.4]	−1.6	[−1.7, −1.6]

Transition	kij0 (1/s)	CI (1/s)	xij (nm) pointed (−) end direction	CI (nm)	xij (nm) barbed (+) end direction	CI (nm)
1→ 0	3.9	[3.3, 4.8]	0	[0.0, 0.1]	0.5	[0.3, 0.5]
2→ 0	0.045	[0.027, 0.058]	0.3	[0.2, 0.5]	0.7	[0.7, 0.9]
1→ 2	2.7	[1.5, 3.5]	0	[0, 0.1]	0	[0, 0.02]
2→ 1	8.3	[3.3, 14.9]	−3.8	[−4.5, −2.9]	−2.8	[−3.6, −1.9]

In migrating cells, actin filaments near the leading edge are almost all oriented with their barbed ends facing the membrane, while filament orientation becomes increasingly isotropic toward the cell center (26–29). We used computational modeling to investigate whether the directional interaction between vinculin and actin could potentially generate long-range order in the actin cytoskeleton (Fig. 3A). In our model, actin filaments underwent 2D Brownian diffusion with a drift velocity that represented retrograde actin flow in a migrating cell (Fig. 3B). Vinculin binding was modeled as the attachment of a simple spring that resisted retrograde actin filament motion. The unbinding kinetics of the vinculin—actin bond were those obtained from the two bound-state model of the OT data, and thus captured both directionality and load-induced stabilization. An ensemble of randomly oriented actin filaments was subjected to a drift velocity, thermal fluctuations and stochastic vinculin binding (Fig. 3C). As the simulation progressed these conditions resulted in the development of orientational asymmetry, with the majority of filaments closer to the starting position (x = 0 μm) oriented with their barbed (+) ends facing the leading edge (Fig. 3D). Thus, the directional asymmetry of the vinculin—actin bond is sufficient to establish a spatial asymmetry in F-actin polarity (Fig. S7), an effect that may underlie the prior observation that vinculin is essential for generating persistent, directional cell migration (12, 13, 30). The directionally asymmetric linkage of vinculin to actin may complement other mechanisms by which cells generate persistent migration, such as the signaling cascade that activates the barbed (+) end nucleators Arp2/3 (31) and formins (32), which reinforce cell polarity by promoting actin polymerization at the cell’s leading edge.

In summary, we have shown that vinculin forms a directionally asymmetric and force-stabilized linkage to F-actin. Directional asymmetry of this sort is not unprecedented; the binding of kinesin with microtubules is destabilized by load, characteristic of a slip bond, but to a different extent depending on loading direction (33), and the binding of the myosin V head with actin, and dynein with microtubules, is asymmetrically stabilized by load, which may promote motor processivity (34, 35). The directional interaction between vinculin and actin may play a critical role in tissue patterning. Consistent with this idea, vinculin null mouse embryos exhibit phenotypes suggestive of failures not only in cell adhesion, but also in tissue patterning driven by cell migration, notably axon outgrowth (11). Vinculin-deficient cells likewise exhibit defects in the formation of stable lamellipodia and filopodia (36), and are more motile (37) but less directionally persistent (13, 30). Thus, vinculin does not appear to be required for adhesion or motility per se, but instead, for stable protrusion and polarized migration. The observation that vinculin forms a catch bond with actin in both directions of applied load (Fig. 3) likely reflects its biological function as a reinforcing linker at adhesions, including those in which actin may not be polarized. A comparison between actin binding by vinculin (Fig. 3A) and the E-cadherin/β-catenin/αE-catenin complex (17)—which vinculin is believed to mechanically reinforce—suggests that under barbed (+) end directed load, vinculin binds with comparable stability as the cadherin-catenin complex, but that under pointed (-) end directed load, vinculin stability is ~10-fold greater. It is interesting to note that, within the limits of our assay, the binding of the cadherin-catenin complex to actin did not exhibit a directional response to force. We suggest that the asymmetric catch bond behavior of vinculin, in addition to enhancing overall resistance to mechanical load, could contribute to organizing the polarity of the actin cytoskeleton in response to internally and externally applied loads at cell-cell contacts.

One Sentence Summary.

The cell adhesion protein vinculin forms a load- and direction-dependent bond with actin filaments that may reinforce directional cytoskeleton assembly.