Scan-rescan of AxCaliber, macromolecular tissue volume and g-ratio in the spinal cord

Abstract

Purpose

Recent MRI techniques have been introduced that can extract microstructural information in the white matter, such as the density or macromolecular content. Translating quantitative MRI to the clinic raises many challenges in terms of acquisition strategy, modeling of the MRI signal, artifact corrections and metric extraction (template registration and partial volume effects). In this work, we investigated the scan-rescan repeatability of several quantitative MRI techniques in the human spinal cord.

Methods

AxCaliber metrics, macromolecular tissue volume (MTV) and the fiber g-ratio were estimated in the spinal cord of eight healthy subjects, scanned and rescanned the same day in two different sessions.

Results

Scan-rescan repeatability deviation was 3% for all metrics, in average in the white matter of all subjects. Intraclass correlation coefficient was up to 0.9. A three-way ANOVA showed significant effects of white matter pathway, laterality and subject.

Conclusion

The present study suggests that quantitative MRI gives stable measurements of white matter microstructure in the spinal cord of healthy subjects. Our findings remain to be evaluated in diseased populations.

Introduction

Quantitative magnetic resonance imaging (qMRI) aims at providing quantitative biomarkers that are insensitive to the protocol parameters, coil excitation and reception profiles. Combined with models of the white matter tissue, quantitative information characterizing microstructure (e.g. the size or density of neuronal fibers) can be inferred from the MRI signal. Using these metrics, investigators would ultimately be able to monitor tissue properties over time in the same individuals, compare subjects, detect lesions based on the biomarker value (as opposed to a detection based on the contrast with the surrounding tissue), and interpret the underlying damage of a tissue, e.g. axonal loss vs. inflammation vs. proliferation of astrocytes.

Quantitative metrics can be obtained from nearly any MRI contrast; diffusion MRI methods such as AxCaliber (1) provide metrics sensitive to the axon diameter and density (metric fr) while T1-weighted images and Macromolecular Tissue Volume (MTV) provide information on myelin content (2). By combining fr and MTV, a quantitative metric sensitive to the fiber g-ratio (defined as the ratio between the inner to the outer diameter of the myelin sheath) can be obtained (3,4).

These techniques, however, are hampered by many challenges in term of acquisition strategy, modeling of the MRI signal, artifact corrections, segmentation, and metric extraction, especially when applied to the spinal cord (5,6). In order to apprehend the repeatability of these pipelines, a common method is to acquire qMRI data on a couple of subjects at different time points and compute the variation of the metrics across time, assuming that the intra-subject variability is zero. Table 1 lists some scan-rescan studies, with an emphasis on spinal cord and qMRI methods. Note that a distinction needs to be made between repeatability and reproducibility: while both are types of measurement precision, repeatability studies use unchanged acquisition conditions whereas reproducibility studies report the impact of varying conditions on the precision (7). The additional sources of variance between scan and rescan in reproducibility studies can be the time delay between the scans, the repositioning of the subject, different MR tech, different centers with potentially different scanners, coils, etc. A particular attention on the post-processing is also necessary in order to compare scan/rescan experiments. For example, a scan/rescan experiment will likely exhibit more variability if metrics are averaged within a small region (e.g., dorsal column between C2 and C4 levels) versus the entire cervical white matter, because of the presence of noise and potential mis-registration. From Table 1 we can conclude that qMRI metrics in the spinal cord have a scan-rescan deviation of 5–10%.

Table 1.

Review of the scan-rescan studies in the spinal cord and brain white matter.

	Region	voxel-wise correlation (R)	ICC (IntraClass Correlation Coefficient)	COV (Within-subject coefficient of variance)	REFERENCE
NODDI fraction of restricted water (fr or vr)	Spinal cord white matter		0.84	7%	(8)
	Brain white matter	0.82			(9)
FA (fractional anisotropy)	Spinal cord white matter			<5%	(10)
	Brain white matter	0.90	0.79	COV across 13 scanners: <5% (Global) 2–8% (per fasciculus)	(11) (9) (12)
λℜ (radial diffusion coefficient)	Spinal cord white matter			<9%	(10)
	Brain white matter		.89	COV across 13 scanners: <3% (Global) 3–10% (per fasciculus)	(11)
λ// (axial diffusion coefficient)	Spinal cord white matter			<4%	(10)
	Brain white matter		0.82	<4% (COV across 13 scanners)	(11,12)
MTR (Magnetization Transfer Ratio)	Spinal cord white matter			<10%	(10)
MWF (Myelin Water Fraction)	Spinal cord			3–10%	(13)
	Brain white matter			2–20%	(14)
qMT (quantitative Magnetization Transfer)	brain white matter			5%	(15)
normalized PD (MTV)	Brain white matter	0.92 (different coils)		<2% (different coils)	(2)

In this work, we investigated the repeatability of quantitative MRI metrics of spinal cord microstructure (AxCaliber and MTV metrics). By definition, scanning conditions were unchanged (same MRI system, same coil, same sequences), but subjects were repositioned between the two scan and rescan.

Methods

Experiments were performed in 8 healthy subjects (28+/−10, 3 males), scanned and rescanned the same day (with subject repositioning between session 1 and 2). The protocol and processing of the data are detailed in (4).

A. Acquisition

Data were obtained using a high-gradient (Gmax=300mT/m per axis) 3T MRI scanner (Skyra CONNECTOM, Siemens) (16) equipped with a 64-channel head/spine coil (17). AxCaliber and MTV protocols were acquired in about 30min (depending on the cardiac rate) with the following parameters.

Diffusion

A cardiac-gated 2D single-shot spin-echo EPI with reduced field of view using two saturation bands placed anterior and posterior to the spinal cord was used with the following parameters: matrix 70x70, voxel size 0.8x0.8x5mm; 4 slices centered at intervertebral disks C1 to C4; 575 diffusion-weighted images (40 b=0, δ=3/3/6/8/10ms, Δ=20/40/20/36/30ms, TE=57/73/67/76/75ms, Gmax=√2*300=424mT/m, and diffusion encoding gradients applied in four directions perpendicular to the spinal cord (XY, -XY, -X-Y, X-Y).

MTV

Proton Density mapping was obtained using three 3D FLASH acquisitions (FA=4,10,20°, TE=2.74ms, TR=30ms, matrix 192x192x22, spacing 0.8x0.8x5mm, GRAPPA R=2). B1+ mapping was acquired using the double-angle method (18) (spin-echo EPI, FA=60/120°, TE=13ms, TR=7s, matrix 64x64x20).

B. Processing

Preprocessing, metric extraction and registration was done as in (4). Briefly, raw diffusion and FLASH volumes were motion-corrected using the Spinal Cord Toolbox¹ (SCT) version 2.2.3 (19); MTV was computed as in (2) and registered to the mean DWI; AxCaliber was computed using qMRLab² and g-ratio was computed as in (20). Lastly, mean DWI volumes were registered slice-by-slice to the MNI-Poly-AMU template using SCT. This processing resulted in four slices located at each intervertebral body C1/C2/C3/C4. An atlas of white matter tracts (21) was used to extract metrics in each spinal cord pathway while accounting for partial volume effect using the maximum a posteriori (MAP) estimation. Ventral tracts were too small to be processed independently and were thus merged into a single region. Values in the CSF were fixed for the MAP estimation: fr_CSF=0, diameter_CSF=10μm, MTV_CSF=0 and gratio_CSF=1. Images for scan and rescan were processed independently (i.e., images of scan and rescan were not co-registered) in order to report the repeatability of the entire processing pipeline (i.e., including registration to the template).

C. Statistics

Repeatability of metric estimation was first assessed in the template space by computing the scan-rescan correlation of white matter voxels. Gray-matter voxels were excluded to prevent artificially high correlations that result when two distinct clusters are fitted by a line and a Pearson’s correlation is reported. Note that scan-rescan correlations were computed globally, without averaging the maps across subjects. Repeatability was then quantified using the absolute scan-rescan deviation in white matter computed per subject, then averaged across subjects:

$$\mathit{Error}=1/M\sum _{{\mathit{subject}}_i=1}^M\mid 1/N\sum _{{\mathit{voxel}}_j=1}^N(m_{{\mathit{vox}}_j,{\mathit{sub}}_i,\mathit{scan}}-m_{{\mathit{vox}}_j,{\mathit{sub}}_i,\mathit{rescan}})\mid$$ (1)

with m_{voxj,subi,scan} the metric value in the voxel j of the white matter, for subject i and session #1 (scan). This repeatability metric was also computed in each tract using values obtained from the atlas-based metric extraction:

$${\mathit{Error}}_{{\mathit{tract}}_j}=1/M\sum _{{\mathit{subject}}_i=1}^M\mid m_{{\mathit{tract}}_j,{\mathit{sub}}_i,\mathit{scan}}-m_{{\mathit{tract}}_j,{\mathit{sub}}_i,\mathit{rescan}}\mid$$ (2)

In order to assess the capability of these metrics to detect reliable differences between subjects, the intraclass correlation coefficient (ICC) was computed in each spinal cord tract. The formula for ICC was:

$$\mathit{ICC}=\frac{{{\sigma }_{\mathit{inter}}}^2}{{{\sigma }_{\mathit{intra}}}^2+{{\sigma }_{\mathit{inter}}}^2}$$ (3)

with σ_intra² = mean_i(1/2 · ((m_i,scan − m_i)² + (m_i,rescan − m_i)²)) and σ_inter² = var_i(m_i). m_i,scan is the metric value measured in a specific tract for subject i, and m_i is the average value between scan and rescan. From this formula, it appears that an ICC close to 1 reveals a much greater inter-subject variation than the scan-rescan error. Because the inter-subject variability includes both the repeatability and the genuine microstructural difference between subjects, then E[σ_intra²] < E[σ_inter²] (E[X] being the expected value of X), and ICC should always be larger than 0.5.

Finally, a three-way ANOVA was done to assess the capability of these metrics to detect significant differences between tracts, subjects and laterality (left/right).

Results

The quality of the scan-rescan and registration to the template can be qualitatively assessed on a GIF animation³ showing in turn the quantitative maps from session #1 (scan), from session #2 (rescan) and the template. This animation shows a consistency across slices and subjects of all metrics in term of contrast (between white matter tracts) and accuracy. Similarly, raw maps at C3 in subject space were visually assessed⁴. Subject #3 was discarded from the rest of the study due to particularly strong movements during the scan.

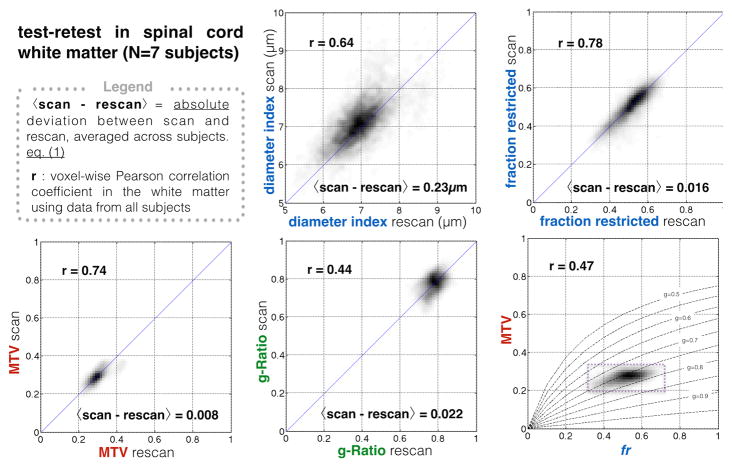
Figure 1 shows the voxel-wise comparison of scan-rescan from all subjects and for each metric. fr and MTV showed a good correlation (r>0.74) and low deviation between scan and rescan (<2%). Deviation between scan and rescan was 3% for all metrics, averaged across white matter voxels and across subjects.

Figure 1.

Scan-rescan repeatability of the different quantitative metrics, assessed voxel-wise, in the template space, in the white matter. Bottom right. the correlation between MTV and fr seems to follow the line of iso-g-ratio g=0.75, thus reducing the dynamic of the g-ratio metric (achievable values are emphasized by the dashed box).

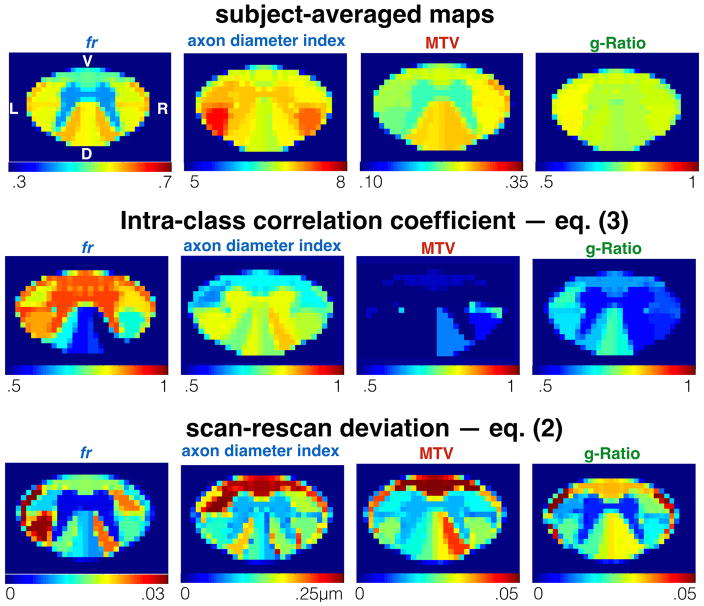
Figure 2 shows the ICC obtained per tract for all subjects (excluding subject #3), and the average scan-rescan deviation per tract. Metric fr was particularly sensitive to differences between subjects (ICC>0.8) in the gray matter, ventral and lateral tracts. The axon diameter index detected differences between subjects in the motor tract, and the left cuneatus (ICC>0.8). Scan-rescan deviation was found to vary between spinal cord regions with values always lower than 5% (reached by metric fr in the spinocerebellar).

Figure 2.

Atlas-based analysis of the repeatability. Top. Average microstructural maps. Values from each tract were averaged across subjects, scan-rescan and vertebral levels. Middle. Intra-class correlation coefficient (ICC, see eq. (3)) assessed per tract. An ICC close to 1 shows the capability of the metric to detect differences between subjects. Bottom. scan-rescan deviation assessed per tract and averaged across subjects (see eq. (2)).

Results of the tract-by-tract analysis (supplementary material S1) are consistent with (4,22), in terms of contrast between tracts (higher axonal density, higher macromolecular content, and smaller fibers in the dorsal column than in the lateral tracts) and statistical results (ANOVA). fr, axon diameter and MTV could detect reproducible differences between tracts and subjects. Axon diameter, MTV and g-ratio could detect significant differences between right and left tracts, with inverse trends between axon diameter and MTV.

Discussion

In previous studies from our group (4,22), we reported the consistency across slices and across subjects, as well as the sensitivity of these metrics to microstructural differences between tracts and between the left and right sides.

In this study, eight new subjects were scanned twice in order to study the performance of the microstructural biomarkers in term of sensitivity to subject variation (ICC), precision (voxel-wise correlation) and repeatability (deviation between scan and rescan).

Voxel-wise correlation

fr and MTV showed good precision and sensitivity to the microstructure based on the voxel-wise correlation and the ANOVA analysis. A worse correlation coefficient was found for g-ratio (r=0.44), that we attribute to (i) unstable g-ratio due to the indeterminate form (0/0) of the equation ( $g=\sqrt{\frac{(1-\mathit{MTV})fr}{\mathit{MTV}+(1-\mathit{MTV})fr}}$) when both fr and MTV are close to 0 (at the periphery of the spinal cord) and (ii) to the small dynamic range of this metric in healthy tissue due to the correlation between MTV and fr (r=0.47) that follows the line of iso-gratio (g=0.75) (Fig 1).

Intra-Class Correlation Coefficient

The large ICC found in ventral and peripheral tracts for the fr metric can be explained by the significant (p<0.05) correlation of fr with the cross-sectional area (CSA) of the spinal cord (r=−0.6 in average in these tracts). This negative correlation shows that smaller spinal cords have higher fr values, which can be explained by higher spatial constraints in smaller spinal cords if we assume approximately the same number of fibers between individuals. Histological studies are necessary to validate this hypothesis. Note that partial volume effect, with CSF or gray matter, would result in a positive correlation between fr and the CSA because fr in the CSF and in the gray matter is very low.

A relatively small ICC was found for MTV (about 0.5), which can be explained by (i) the small dynamic range of this metric in healthy tissue (STD<0.1 in white matter) as shown by histology (23,24), and simulations (25), and (ii) the difficulty to normalize proton density robustly using the CSF in the spinal cord due to CSF pulsation and the presence of spinal roots. The use of an external calibration phantom, or other tissues with known water content could be considered for the normalization of the proton density. Although MTV might not be capable of detecting the subtle variations between healthy subjects, this metric is highly sensitive to demyelination in neurodegenerative diseases (30% contrast in multiple sclerosis lesions) (26,27), and higher ICC is expected if patients are included.

Scan-Rescan deviation

Small tracts, or tracts with partial voluming with gray matter or cerebrospinal fluid (CSF), were found to be less precise (e.g. spinocerebellar or ventral pathways). Metrics fr and axon diameter index showed inverse pattern of repeatability (see figure 2): low fr values are more stable (r=0.5, p=0.04), but axon diameter index is also less stable with lower restriction.

Laterality difference

A significant laterality (left/right) difference was found for MTV (P<10⁻⁴), axon diameter index (P<10⁻²) and g-ratio (p<10⁻²). The fact that this surprising finding is present from two very different sequences (long T1-weighted steady-state sequence for MTV vs short EPI T2-weighted diffusion encoded sequence for axon diameter) makes it seem genuine. Moreover, axon diameter and MTV exhibit inverse trends (large fibers have proportionally less myelin, also see Fig 2), which is expected from simulations (25). However, potential confounds for the significant left/right difference should also be considered. For instance, different thickness between the two gray matter posterior horns would bias the estimated metrics differently between the left and right columns due to different partial voluming. This effect is suspected on the ICC maps with larger values (i.e. large inter-subject variation) close to one of the two horns. Another potential confound is the asymmetrical excitation due to the non-reciprocity of the Maxwell’s equation (28), although this effect should be negligible at 3T. Another potential effect would be a systematic shift in the mis-registration of the template, although we could not qualitatively observe that issue.

Model assumptions

The assumptions (notably the relationship between myelin and MTV) of the biomarkers used in this study were already discussed in these previously published studies (4,22). In this study, the diffusion model assumes a fixed intra-axonal diffusion coefficient; no time-dependence of the extra-axonal perpendicular diffusivity (29); and no free water compartment. However, in pathology, one could expect a different intra-axonal diffusion coefficient, an increased effect of time-dependence due to axonal loss, and presence of a free water compartment due to inflammation and/or oedema. We investigated the impact of these effects on the repeatability and accuracy using simulations in supporting information S2. In summary, a false assumption for the intra-axonal diffusion coefficient biases the axonal diameter metric (slope of −0.8μm/(μm²/ms)); the presence of a free water compartment is mostly compensated by the hindered diffusion coefficient (Dh), but leads to an overestimation for fr and axonal diameter up to 10%; finally, the presence of time dependence leads to overestimation of more than 5% for all parameters (the higher time-dependence the higher the bias is).

Data quality

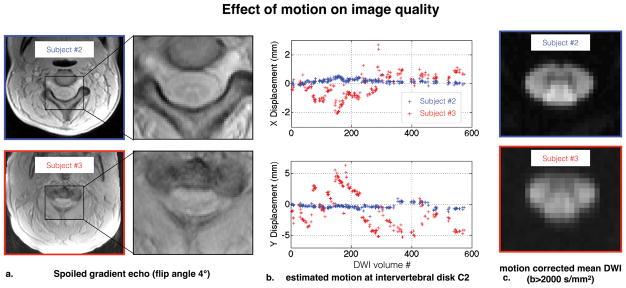
While we acknowledge that the repeatability study is expected to include all possible sources of variation (including subject motion), the motion of subject #3 was particularly large (see figure 3). We decided to remove this subject because it would have strongly affected the repeatability measures without being relevant for the study. The present study assumes that a certain level of data quality is achieved before being considered for the analysis. We would like to stress that quality control is a necessary step in all research and clinical studies, and discarding subject on the basis of large motion is a common routine. Strong motion results in blurry and distorted spoiled gradient echo images (see figure 3.a). This acquisition is particularly sensitive to motion due to the long duration of the 3D scan. Sensitivity to motion could be reduced by using simultaneous multi-slice, reduced field of view or higher bandwidth (at the expense of lower SNR). Navigator-based or camera-based methods to track motion and correct the phase can also be considered but the non-rigid motion of the spinal cord in relation to the rest of the body will limit their performance. Diffusion-weighted EPI images, combined with the motion correction algorithm, are less affected by such strong motion, although we note blurrier borders on the mean DWI of subject #3 (see figure 3.c). Note that in this study, we tried to minimize subject motion by informing subject of the issues of motion (before MRI session and between runs), and by using pads to ensure subject comfort and to minimize head rotation. More restrictive designs could be considered.

Figure 3.

Effect of the large motion of subject #3 on data quality (compared with subject #2 for illustration). a. Raw spoiled gradient echo images. Strong motion blurs the contrast between spinal cord gray and white matter. b. Lateral “X” (top) and antero-posterior “Y” (bottom) translations at C2, as estimated by the motion correction algorithm. Subject #3 showed abrupt motion with much larger amplitude than Subject #2 (~1cm in the Y direction). c. Motion corrected mean DWI (b>2000 s/mm²). Even with motion correction, Subject #3 presents more blurry boundaries suggesting worse data quality.

Applicability of the results

In all repeatability studies the infrastructure and acquisition parameters are a major source of variability, so our results might not be readily applicable to other configurations. Here we used a 300mT/m system with a 64ch head/neck coil. While the strong gradients definitely helped for the diffusion-weighted scans, they had negligible influence for the MTV/T1 protocol we used for quantifying myelin. Therefore, the presented results for the myelin protocol are applicable to clinical systems equipped with similar coils and pulse sequences.

Regarding the diffusion-weighted scans, the present study is still relevant to the community at large, as it sets a lower limit to the variability that can be expected with systems equipped with lower gradients. In a previous ex vivo study, we showed that the restricted water fraction can be measured robustly even at lower b-values (b=4,000mm2/ms), but the lower gradient strength prevents the measurement of the axon diameter index (4). Stimulated echo sequences could also be considered to increase the b-value on clinical systems (30), but the experimenter should be aware of (i) the stronger time-dependence effect (29), (ii) the much higher sensitivity to non-rigid motion of the spinal cord, and (iii) the different T1- and T2- weighting when compared to the PGSE sequence.

It is also important to note that the presented results are bound to a specific acquisition and analysis protocol. For example, lowering spatial resolution or using models with fewer degrees of freedom (compared to AxCaliber) would likely produce better reproducibility results.

Conclusion

It is possible to robustly extract AxCaliber, MTV and g-ratio metrics in the different spinal cord tracts and to detect significant differences of microstructure between spinal cord tracts of healthy subjects. The proposed acquisition and processing framework could be useful for assessing spinal cord demyelination in diseases such as multiple sclerosis.

Supplementary Material

Supp info

Supporting Figure S1: Result of the three-way ANOVA (tracts, subjects, and laterality) for each metric along with the bar plot of metric values in each tract, and scan-rescan error.

Supporting Figure S2. Simulation of the impact of model assumptions (X-axis) on the fitted parameters (Y-axis). In order to improve the precision of fitting parameters, the number of parameters is reduced by fixing some of them to a particular value (vertical dotted lines). Violation of these assumptions can introduce biases, illustrated by the deviation of the average fitted values (blue circles) to the ground truth (horizontal black lines), or reduce precision of the fitted values (blue error bars).