A novel approach to probing in vivo metabolite relaxation: Linear quantification of spatially modulated magnetization

Abstract

Purpose

Conventional sequences for metabolite transverse relaxation quantification all generally measure signal changes at different echo times (TEs). However, quantification results obtained via these conventional methods can be very different and are highly dependent on the type of sequence being applied. TE-dependent effects such as diffusion, macromolecule baseline, and J-coupling modulation contribute significantly to these differences. Here, we propose a novel technique—MAR_ZSS (Multiple flip Angle pulse driven Ratio of longitudinal Steady States)—for preparing magnetization with T₂/T₁ weighting. Using premeasured T₁ values, T₂ values for metabolites can thereby be determined. The measurement procedure does not require varying TE and is TE independent; T₂, diffusion, and J-coupling effects induced by the readout sequence are cancelled.

Method

Longitudinal steady states (M_zss) at different flip angles were prepared with trains of radio frequency (RF) pulses interspersed with field gradients. The resulting spatially modulated longitudinal magnetization was acquired with a PRESS readout module. A new linear equation for quantification of MAR_ZSS was derived from Bloch equations.

Results

By implementing this readout independent method, T₂ measurement of brain metabolites at 7T was demonstrated through Bloch simulations, phantom and in-vivo experiments.

Conclusions

The proposed MAR_ZSS technique can be used to largely avoid multi-TE associated interference, including diffusion, macromolecule s, and J modulation. This MAR_ZSS technology, which is uniquely insensitive to readout sequence type and TE, is a promising technique for more accurately probing in vivo metabolite relaxation.

Introduction

Nuclear magnetic resonance spectroscopy (MRS) allows noninvasive detection of endogenous metabolites in the human brain and can provide valuable metabolic and physiological information. MRS is also a promising tool for diagnosing metabolic disorders and other diverse pathological conditions in human brain, including epilepsy, multiple sclerosis, stroke, cancer, and psychiatric disease [1–4]. The concentrations and relaxation time of metabolites can be used to detect abnormalities in brain regions that appear normal in magnetic resonance imaging (MRI), as well as to characterize pathology underlying MRI-visible abnormalities [5]. For example, many neurological and psychiatric diseases alter the cellular environment, which may be reflected in changes of metabolite T₂ relaxation times [6–7].

In general, two types of techniques are conventionally adopted for T₂ quantification of metabolites in brain. Sequences with simple spin or stimulated echoes [8–10] can be used to measure signals at step-incremented echo times (multi-TEs) for T₂ quantification. Carr-Purcell-Meiboom-Gill (CPMG) sequences [11, 12] are used in a similar manner by repeating more (Carr-Purcell) CP blocks. However, the quantification results obtained via these two types of conventional methods are very different and depend significantly on the sequence type being used. In some circumstances, quantification results may differ even when the same sequence is used, due to selection of parameters such as the TE steps during the spin echo technique or the inter-pulse delay used during the CPMG sequence.

Thus, given that MR exponential decay signal from the multi-TE approaches can be complicated under many scenarios (e.g., confounding spin evolution due to scalar couplings, significant diffusion weighting during readout, or very fast T₂ relaxation of many ³¹P MRS signals), a technique capable of generating variable T₂ weighting without changing TE would be highly valuable.

Tissue signals at steady states driven by rapid pulse trains are frequently used in MRI techniques to quantify different components of tissue water [13]. Balanced steady-state free precession (b-SSFP) serves as a high signal to noise ratio (SNR) imaging tool to generate images with T₂/T₁ weighted contrasts. Quantitative maps can be extracted from those T₂/T₁ weighted images acquired with two or multiple flip angles. However, b-SSFP cannot be directly used to quantify MRS spectra because b-SSFP may have undesirable frequency selective effects; these were previously attributed to the periodic nature of DANTE pulses [14]. Specifically, DANTE pulses interspersed with gradients were previously used as a preparation module for spatial tagging of MR images [15] as well as black blood contrast imaging [16]. When DANTE preparation is used for black blood imaging applications, spatial modulation of longitudinal magnetization (M_z) could give rise to periodic intensity variations in images (dark bandings). To avoid visualizing the dark bandings in the black blood images, the gradient moment in DANTE pulses could be adjusted so that banding size was smaller than voxel size. Under those circumstances, voxel signal amplitude could be quantified [17]. This DANTE-prepared imaging application suggests that the spatial modulation of metabolites at steady state M_zss may also be similarly quantifiable.

This study proposes a novel method— MAR_ZSS (Multiple flip Angle pulse driven Ratio of longitudinal Steady States)—for quantifying spatially modulated magnetization of metabolites. The prepared longitudinal magnetization of longitudinal steady states (M_zss) weighted by T₂/T₁ can be acquired by any readout sequence. When T₁s of metabolites are pre-determined from other techniques, such as inversion recovery or saturation recovery, T₂s and spin densities of metabolites can be correspondingly calculated. Because it is a quantifiable contrast preparation technique, MAR_ZSS does not require varying TE for metabolite relaxation quantification and is independent of the readout module. We hypothesized that using the proposed MAR_ZSS technique instead of conventional multi-TE or CPMG methods would allow us to avoid the readout-sequence-dependent variations associated with diffusion weighting, macromolecule baseline, and J-coupling modulation.

Theory

In order to quantify the longitudinal M_zss of metabolites at steady state by different flip angles, we derived a new linear equation from Bloch equations. Considering a train of radio frequency (RF) pulses interspersed with field gradient (iPFG; shown in Fig. 1), the resulting steady state magnetization (M_zss) is given by [14, 17],

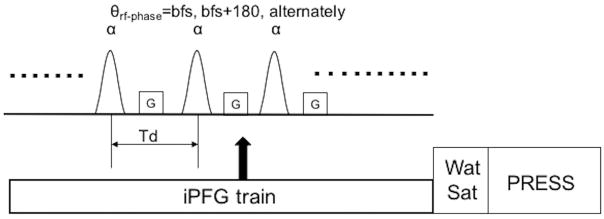
Figure 1.

Diagram of the proposed Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS) module. θ is the phase of the radio frequency (RF) pulse where bfs is the base frequency shift decided by frequency offset of the pulse. α is the flip angle of the pulse train. G is gradient along the z direction. T_d is the interpulse delay of the pulse train. iPFG is the interleaved pulse field gradient. WatSat is the water saturation module. PRESS is the readout module.

$$M_{\mathit{zss}}={\int }_{-(\mathrm{n}+1)\pi }^{(\mathrm{n}+1)\pi }\frac{M_0(1-E_1)[E_2(E_2-\mathit{cos}\theta )+(1-E_2\mathit{cos}\theta )\mathit{cos}\alpha ]}{(1-E_1\mathit{cos}\alpha )(1-E_2\mathit{cos}\theta )-E_1\mathit{cos}\alpha (E_2-\mathit{cos}\theta )E_2}d\theta .$$ Eq. 1

where E₁=exp(−T_d/T₁), E₂ = exp(−T_d/T₂), n is an integer, α is the flip angle of a single RF pulse, and M₀ is the thermal equilibrium signal intensity. T_d is the inter-pulse delay time, which is much shorter than the metabolite T₁ and T₂; within these limitations, E₁=1−T_d/T₁ and E₂=1−T_d/T₂, and θ is the position-dependent linear phase angle induced inside the voxel by the applied field gradient and local field inhomogeneity.

For Eq. 1 to be valid, the minimal gradient moment Gd_G in Fig. 1 must be much greater than π/(γΔr), where γ is the gyromagnetic ratio, d_G is the duration of the applied gradient, and Δr is the voxel size. The above integral yields a closed-form expression for M_zss:

$$M_{\mathit{zss}}=M_0(1-\frac{K\mathrm{C}}{\sqrt{1+K^2{\mathrm{C}}^2}})$$ Eq. 2

where $\mathrm{K}=\sqrt{\frac{{\mathrm{T}}_1}{{\mathrm{T}}_2}}$ and $\mathrm{C}=\sqrt{\frac{1-\text{cos}\mathrm{\alpha }}{1+\text{cos}\mathrm{\alpha }}}=tan\frac{\alpha }{2}(0°\le \alpha \le 90°)$.

Eq. 2 can be rearranged into a linear equation:

$$R_{\mathit{zss}}=\sqrt{\frac{{\mathrm{T}}_1}{{\mathrm{T}}_2}}tan\frac{\alpha }{2}$$ Eq. 3

where $R_{\mathit{zss}}=\frac{M_0-M_{\mathit{zss}}}{\sqrt{M_0^2-{(M_0-M_{\mathit{zss}})}^2}}$, which is the ratio of signal amplitudes from readout sequence. Eq. 3 suggests that T₁/T₂ of metabolites can be calculated by linear fitting. More importantly, Eq. 3 is independent of readout sequence and local inhomogeneity. Because TE in readout is a fixed parameter, the real or complex exponential terms (or effects) induced by readout sequence (for instance, exp(−TE/T₂), exp(−bD), or J evolution f(J,σ)) are common factors that are cancelled in ratio of longitudinal steady states (R_ZSS).

Due to delay of the water suppression module in Fig. 1, M_zss experiences a slight magnetization recovery that can be corrected using Eq. 4 describing T₁ recovery,

$$M_{\mathit{meas}\_z}={\mathrm{M}}_{\mathit{zss}}{e}^{-\frac{t_{ws}}{T_1}}+(1-e^{-\frac{t_{ws}}{T_1}})M_0$$ Eq. 4

where M_{meas_z} is the amplitude from measurement, and t_ws is the delay time of the water suppression module. It is assumed that T₁ of metabolites is pre-determined from other approaches, such as inversion recovery or saturation recovery. Therefore, M_zss can be calculated.

Method

To demonstrate the spatial modulation of metabolite magnetization and its attenuation in longitudinal direction by iPFG, Bloch equation numerical simulations were performed. Code was written using MATLAB (Natick, MA). The M_zss of N-acetylaspartate (NAA) was simulated based on the protocol time series in a single repetition time (TR). For NAA, T₁ and T₂ literature values at 7T of 1730 ms and 170 ms, respectively, were used [18].

All scans were acquired using a 32-channel head coil on a 7T Siemens scanner. A doped water-based sphere phantom was used for phantom measurement of metabolites. Written informed consent was obtained from five healthy volunteers (four females and one male between the ages of 24–40 years).

The iPFG train applied in the measurements shown in Fig. 1 consisted of 500 sinc-Gauss pulses with gradient G_z (along the z direction) interspersed between the RF pulses. The duration of each RF pulse was 4 ms with frequency offset at 2.2 ppm for optimal determination of NAA and a constant inter-pulse delay T_d of 10ms. The phases of the iPFG RF pulses alternated as base frequency shift (bfs) and bfs+180°. Base frequency shift was decided by the frequency offset used in the measurement; in our case, this was 2.2 ppm. The flip angle of the iPFG train was incremented by 10° from 0° to 60° for a total of seven measurements. Gradient amplitude and duration were G_z=2mT/m and 5ms, respectively. Spoil gradients immediately after the preparation module were set along all three directions, G_x=G_y=G_z, with amplitude = 8 mT/m and duration = 1.2 ms.

The sinc-Gaussian pulse used in Fig. 1 has a somewhat nonuniform frequency profile across the metabolites of interest. As a result, different chemical shift experiences slightly different flip angles. Although small, the flip angle at each chemical shift was corrected for data fitting based on Bloch simulation of the sinc-Gaussian pulse.

A water suppression module with an overall duration of 120 ms was applied. Nine sinc-Gauss RF pulses implemented in the water suppression module were all set to an RF duration of 9 ms with a 12 ms interpulse delay time. RF flip angle, RF phase, and spoil gradient amplitudes used after each of the pulses were (flip angle/phase/G): 80.4°/234°/G_x=32 mT/m, 80.4°/585°/G_z=32 mT/m, 152.8°/1053°/G_x=32 mT/m, 80.4/1638°/G_z=16 mT/m, 152.8°/2340°/G_y=16 mT/m, 80.4°/3159°/G_x=16 mT/m, 152.8°/4095°/G_z=40 mT/m, 152.8°/5148°/G_y=40 mT/m and 152.8°/6318°/G_x=G_y=G_z=40 mT/m. Spoil gradient durations were all set to 1.2 ms.

The PRESS sequence was implemented with an isotropic voxel (2 cm × 2 cm × 2 cm) for both in vivo and phantom experiments. The chosen location of in-vivo measurements was in the occipital (OC) lobe as illustrated in Fig. 5. TR of 8.5 s, TE1 (the first PRESS TE) = 69 ms, and TE2 (TE-TE1) = 37 ms were used in both in vivo and phantom experiments. TE1 and TE2 were chosen to minimize contamination of the glutamate (Glu) H4 resonance by glutamine (Gln) and NAA [19]. Two thousand forty-eight data points were acquired for each spectrum. Phantom and in vivo data were acquired with 12 averages and four averages, respectively. Based on previous experience, we believed that four averages would provide adequate SNR for fitting NAA, creatine (Cr), and choline (Cho). When Glu with an inherently lower signal intensity is the target metabolite, increasing the number of averages from four to 12 or more should significantly improve the fitting results. The total scan time for measuring T₁/T₂ using seven flip angles was approximately 18 mins for phantom and 6 mins for in vivo experiments.

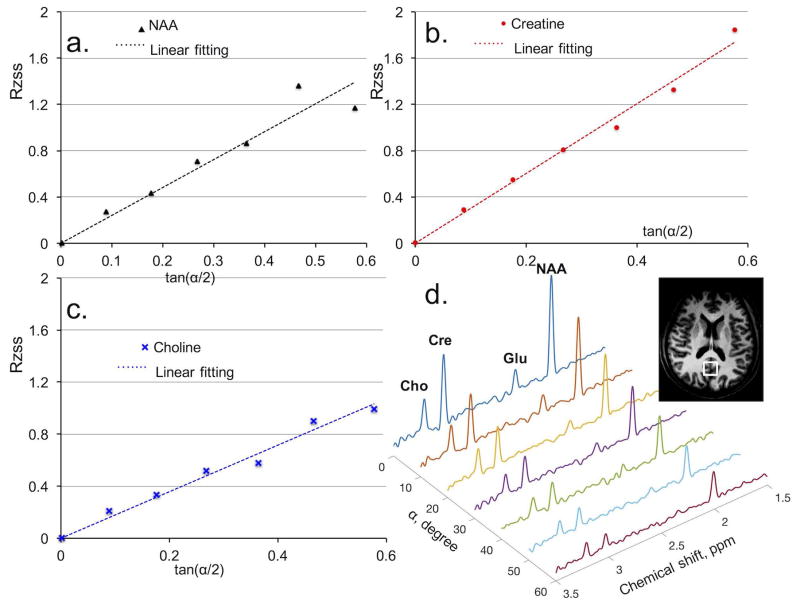
Figure 5.

In vivo metabolite T₂ determination with proposed Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS). (a) Linear fitting as black dotted line for N-acetylaspartate (NAA) data points, extracted with LCModel from spectra in Fig. 5d. (b) Linear fitting as red dotted line for creatine (Cr) data points, extracted from spectra in Fig. 5d. (c) Linear fitting as blue dotted line for choline (Cho) data points, extracted from spectra in Fig. 5d. (d) Signal variation with flip angle in phantom measurements of NAA, Cr, and Cho acquired with flip angle varied from 0° to 60° with 10° increments.

Conventional standard inversion recovery was implemented for independent T₁ determination at the same location. With no change of water saturation or PRESS modules in the MAR_ZSS sequence, the iPFG train was replaced with an inversion recovery pulse. Inversion recovery (TI) times of 425, 625, 825, 1125, 1225, 1425, 1625, 2725, 4725 and 6725 ms were implemented for T₁ measurements. Four scans were conducted for each TI measurement, and TR was 8.5 s. For comparison purposes, a multi-TE PRESS technique for T₂ quantification was also implemented at the same location.

All the metabolite signal amplitudes for MAR_ZSS, IR, and multi-TE measurements were determined using LCModel fitting [20]. The basis set of metabolites for fitting included NAA (NAA acetyl moiety, NAA aspartyl moiety), N-acetylaspartylglutamate (NAAG acetyl moiety, NAAG aspartyl and glutamate moieties), total Cr, total Cho, Aspartate (Asp), Glu, Gln, Lactate (Lac), glutathione (GSH), and γ-aminobutyric acid (GABA).

Two-tailed, unpaired Student’s t-tests were used to compare T₂s obtained via the proposed MAR_ZSS technique and the multi-TE PRESS pulse sequence.

Results

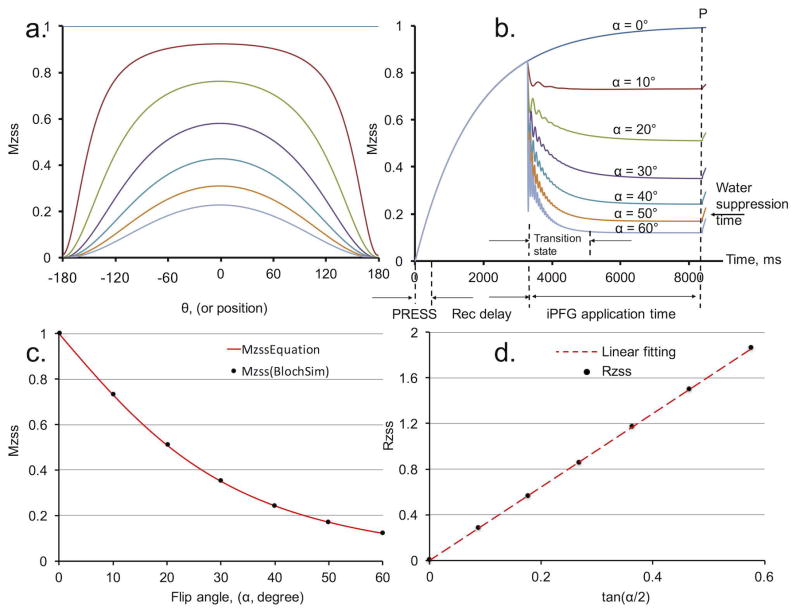
Bloch simulations were implemented to demonstrate changes in longitudinal magnetization (M_z)—both spatially at steady state and temporally at transition state—as a function of different RF flip angles (Fig. 2a and Fig. 2b, respectively). Fig. 2a illustrates the resulting spatial variations of M_z when iPFG trains with different flip angles were applied to saturate NAA to steady states. Although only one of the full spatial modulation periods was simulated in Fig. 2a, for multiple half periods signal attenuation would be identical in the voxel due to symmetry.

Figure 2.

Bloch simulation and equation validation using N-acetylaspartate (NAA) (T₁, 1730 ms, T₂, 170 ms). (a) Spatial variation of longitudinal magnetization at steady states in one period. From top to bottom, lines represent spatial variation induced by Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS) with flip angle from 0° to 60° with 10° increments. (b) Longitudinal steady states (M_zss) temporal variation in one repetition time (TR). PRESS, PRESS sequence readout time (the small effects of two 180° PRESS pulses were omitted.); “Rec delay” is magnetization recovery delay time. (c) M_zss as a function of flip angles. Black dots were extracted from the signal curves evaluated at the dotted line P in Fig. 2b. Alternately, the black dots could be extracted from the areas under the curves in Fig. 2a. The red line is the predicted curve based on equation Eq. 2. (d) Ratio of longitudinal steady states (R_ZSS), in Eq. 3, as a function of tan(α/2). The red dot line is the linear fit.

In the simulation illustrated in Fig. 2a, there is only one period of modulation in the voxel, which corresponds to the gradient moment of 0.23mT/m × 5ms in the iPFG train, given the 2 cm voxel size. In practical applications, significantly larger gradient moments of 2mT/m × 5ms would be employed to avoid the potential quantification error introduced by a non-integer value of n (or a non-half-integer value due to the symmetrical shape of the even function cosθ) in Eq. 1. Approximately 17 half-periods of modulation were present in the 2 cm voxel, which minimized the quantification error introduced at the edges of voxel. The evolution of the M_z over time during an entire TR was numerically simulated using Bloch equations (Fig. 2b), where each signal point as a function of time was averaged over θ values. Fig. 2b illustrates the M_z of NAA evolving from transition states to steady states at different flip angles. Because of the 120 ms duration for the water suppression module, a slight magnetization recovery occurred between the time immediately after the iPFG train and the time before the 90° readout pulse.

Fig. 2c and 2d demonstrate the validation of Eq. 2 and Eq. 3, respectively, using Bloch numerical simulations. The black dots in Fig. 2c were extracted from steady state amplitude at the dotted line P in Fig. 2b. Alternately, the black dots could be identically extracted from integrating (summing) the areas under the symmetrical M_zss spatial variation curve in Fig. 2a. The red line in Fig. 2c illustrates the signal change as a function of flip angle calculated from Eq. 2, showing excellent agreement between the full Bloch simulation and Eq. 2. Linear fitting of the black dots based on Eq. 3 is shown in Fig. 2d. The T₂ value determined from the slope was 167 ms, which is in good agreement with its true value of 170 ms. The small deviation was introduced primarily due to the approximations E₁=1−T_d/T₁ and E₂=1−T_d/T₂.

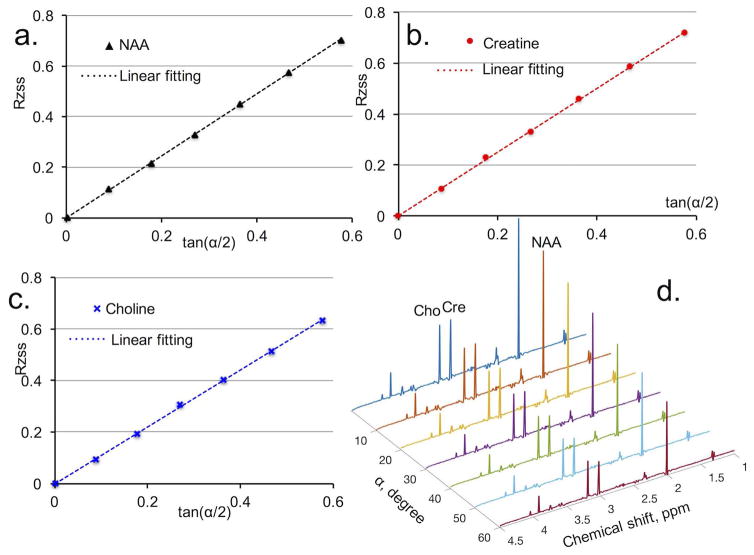
In phantom measurements, signal amplitude ratios R_ZSS (defined in Eq. 3) of NAA, Cr, and Cho as a function of tan(α/2) are shown in Fig. 3a, 3b, and 3c, respectively. The linear relationships between R_ZSS and tan(α/2) predicted by Eq. 3 were clearly confirmed by all three metabolites (Fig. 3). The T₂ of NAA, Cr, and Cho were determined by least square linear fitting (the dotted lines in Fig. 3a, 3b, and 3c). The T₂ results obtained from the proposed MAR_ZSS technique are listed in Table 1 to allow comparison with T₂ results obtained with the multi-TE PRESS method. Fig. 3d shows the phantom spectra acquired by the MAR_ZSS method at different flip angles.

Figure 3.

Phantom metabolite T₂ determination with proposed Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS). (a) Linear fitting as black dotted line for N-acetylaspartase (NAA) data points, extracted with LCModel from spectra in Fig. 3d. (b) Linear fitting as red dotted line for creatine (Cr) data points, extracted from spectra in Fig. 3d. (c) Linear fitting as blue dotted line for choline (Cho) data points, extracted from spectra in Fig. 3d. (d) Signal variation with flip angle in phantom measurements of NAA, Cr, and Cho. Metabolite spectra were acquired with flip angle from 0° to 60° with 10° increment.

Table 1.

Comparisons between phantom metabolite T₂ measurements obtained using the proposed MAR_ZSS and conventional multi-TE PRESS methods.

Method/Metabolite	T2, ms, NAA	T2, ms, creatine	T2, ms, choline
multi-TE PRESS	530±37	310±24	200±23
MARZSS* + PRESS**	494±58	275±31	194±30
Percent diff, %	6.8%	11%	3%

MAR_ZSS*: preparation module; PRESS**: readout module. Metabolite T₁s of the doped phantom were predetermined to be 759 ms, 449 ms, and 297 ms for NAA, creatine, and choline, respectively. Phantom was tested for 3 times and the averaged numbers were shown. NAA, N-acetylaspartate;

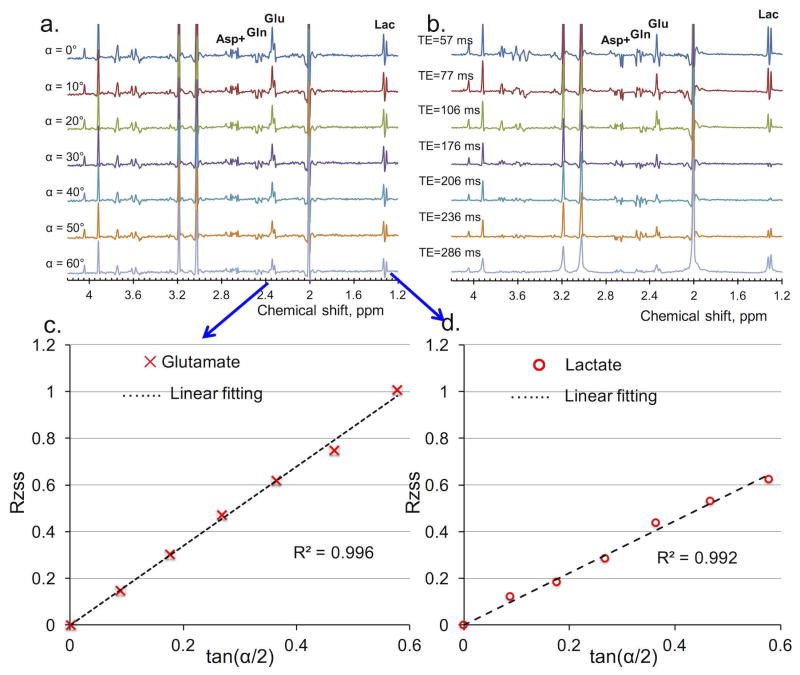
Comparisons of the spectra of metabolites with J-couplings (Asp+, partially contributed from NAA), Gln, Glu, and lactate (Lac) obtained via MAR_ZSS versus multi-TE are demonstrated in Fig. 4a and Fig. 4b. Fig. 4a clearly shows that the proposed MAR_ZSS technique can be implemented with no discernable modulation from J-coupling evolutions because the readout module uses a fixed TE. In contrast, strong signal modulations of metabolites of Asp+, Gln, Glu, and Lac were observed as expected because of J-coupling effects with TE variations (Fig. 4b). Changes in R_ZSS for Glu and Lac in Fig.4a as a function of flip angle were extracted from LCModel and plotted in Fig. 4c and Fig. 4d, respectively. T₂ values for Glu and Lac in the water-based sphere phantom were determined to be 217 ms and 533 ms respectively, based on measured T₁ values of 626 and 658 ms.

Figure 4.

Comparison of phantom results of J-coupled metabolites, such as aspartate (Asp⁺ (with contribution from N-acetylaspartate (NAA) aspartyl moiety), glutamine (Gln), glutamate (Glu), and lactate (Lac), between Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS) and multi-echo time (TE) PRESS techniques. (a) Signal variation with flip angle in phantom measurements acquired by the proposed MAR_ZSS. No discernable sensitivity to J-coupling of MAR_ZSS technique was observed. Flip angles were varied from 0° to 60° with 10° increments (top to bottom). (b) Signal variation with TE in phantom measurements acquired by conventional multi-TE PRESS. High sensitivity to J-coupling of conventional multi-TE PRESS was observed. Echo times were 57, 77, 106, 176, 206, 236, 286 ms (top to bottom). (c) Linear fitting as black dotted line for Glu data points from the proposed MAR_ZSS technique. Glu data were extracted with the LCModel from spectra shown in Fig. 4a. (d) Linear fitting as black dotted line for Lac data points from the proposed MAR_ZSS technique. Lac data were extracted from spectra shown in Fig. 4a.

In vivo signal amplitude ratios (R_ZSS, defined in Eq. 3) of NAA, Cr, and Cho as a function of tan(α/2) acquired from one subject are shown in Fig. 5a, 5b, and 5c, respectively. The linear relationships between R_ZSS and tan(α/2) predicted by Eq. 3 are clearly confirmed by all three metabolites. The T₂s of NAA, Cr, and Cho were determined from the slopes of the dotted straight lines in Fig. 5a, 5b, and 5c, respectively. Table 2 compares T₂ results obtained from the proposed MAR_ZSS technique with T₂ results obtained via the multi-TE PRESS method. In vivo MAR_ZSS spectra using flip angles from 0° to 60° with 10° increments are shown in Fig. 5d.

Table 2.

Comparisons between in vivo metabolite T₂ measurements obtained using the proposed MAR_ZSS and conventional multi-TE PRESS method at 7T.

Method/Metabolites/7T	T2, ms, NAA	T2, ms, creatine	T2, ms, choline	T2, ms, glutamate
Multi-TE PRESS (OC)	171±17	113±9	154±42	N/A
MARZSS+PRESS (OC)	270±36	185±24	263±53	155±45
Percent diff, %	58.2%	63.7%	70.8%	----
t-test (p)	<0.01	<0.004	<0.05	----
7T, CP-LASER (OC) [11]	341	221	N/A	N/A
7T, CPMG(PA) [12]	234	146	194	N/A

NAA, N-acetylaspartate; OC, occipital lobe; PA, parietal lobe; p, t-test of differences between MAR_ZSS and multi-TE PRESS; N/A, not available. Our measurement results from multi-TE PRESS approximate values obtained in the literature at 7T [21]. The T₁s of individual subjects were predetermined for calculation of T₂s. The averaged in vivo T₁s in the OC were 1409 ms, 1396 ms, 1160 ms and 1198 ms for NAA, creatine, choline, and glutamate, respectively.

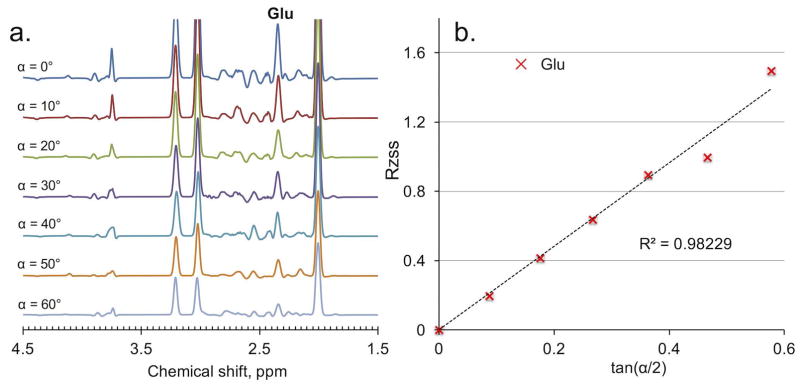
Fig. 6a illustrates the fitted in vivo spectra of Glu obtained using the MAR_ZSS technique; here, the preparation pulses of MAR_ZSS affected monotonically the signal attenuation of Glu. R_ZSS of Glu as a function of tan(α/2) was also extracted, and the result is shown in Fig. 6b. The linear relationship between R_ZSS and tan(α/2) predicted by Eq. 3 is clearly observable, with a fitting coefficient of determination R² = 0.982.

Figure 6.

In vivo results of glutamate (Glu) from the Multiple flip Angle pulse driven Ratio of longitudinal Steady States (MAR_ZSS) technique. (a) Signal variation with flip angle in in vivo measurements of Glu acquired from the proposed MAR_ZSS. This is from fitting data shown in Fig. 5d. No discernable sensitivity to J-coupling of MAR_ZSS technique was observed from Fig. 6a. Flip angles were varied from 0° to 60° with 10° increments (top to bottom). (b) Linear fitting as black dotted line for Glu data points, extracted with the LCModel from spectra in Fig. 6a using the proposed MAR_ZSS technique.

Discussion

This study proposed a new technique— MAR_ZSS—for probing metabolite T₂ relaxation by generating RF-driven longitudinal steady-state magnetization without the need to vary TE. Multiple flip angle iPFG trains were used as preparation modules to generate T₂/T₁ weighting of steady state longitudinal magnetization. In contrast, PRESS sequence served only as a readout module. A new linear equation for quantifying longitudinal magnetization and metabolite relaxation (T₂/T₁) at steady state was derived from Bloch equations. The newly derived equations were validated through Bloch simulations, phantom, and in vivo experiments.

Using conventional techniques such as multi-TE PRESS, spins evolve on the transverse plane with differing evolution time between measurements (i.e., TE), which may result in confounding signal decay from diffusion, physiological motion, and/or signal modulation from J-coupling. When used as a preparation module, the proposed new technique, MAR_ZSS, is independent from the undesirable effects noted above, which are traditionally generated by the readout sequence. Therefore, the readout sequence parameters, especially TE, can be kept consistent between measurements.

It is well known that metabolite T₂s measured by multi-TE PRESS differ substantially from those obtained via CPMG-type methods (Table 2). In contrast, the proposed MAR_ZSS technique is more similar to inversion recovery measurement, whose results are independent of the readout sequence. The three techniques for T₂ measurement have significantly different characteristics.

First, it should be noted that metabolite quantification is complicated by the baseline contributions of broad resonances from macromolecules when spectra are measured at short or even medium TEs [22]. Without a priori knowledge of the concentrations or relaxation times of those macromolecules, accurate extraction of true signal amplitude of the metabolites of interest can be difficult at short TEs [23, 24]. However, using short TE data is unavoidable when measuring T₂ using multi-TE PRESS or CPMG. Because the fitting results of signal amplitude acquired with short TE steps are typically less accurate than those acquired with longer TE steps due to stronger macromolecule baseline at short TE, systematic errors in metabolite T₂ measurement are difficult to eliminate when using either of these two conventional techniques. In contrast, the MAR_ZSS method proposed here completely separated relaxation weighting from readout. As a result, an optimized readout sequence with fixed TE can be used. For example, in this study, the readout sequence was previously optimized to minimize macromolecule baseline and to separate Glu H4 resonance from overlapping signals of Gln and the aspartyl moiety of NAA [21].

Second, for spin echo type sequences, metabolite transverse relaxation measurements can be affected by extra signal attenuation resulting from the diffusion effect. Variations in TE effectively alter diffusion time. In addition, the spoiling gradients used in the sequences and the intrinsic microscopic internal gradient associated with susceptibility inhomogeneity can introduce diffusion attenuation [25, 11]. Furthermore, in cases of in vivo measurements obtained in the presence of internal gradients at different TEs, the potential signal decay induced by physiological motion such as cardiac and respiration cycles can be even stronger than diffusion per se, introducing more errors. Implementing CPMG-type sequences for quantification can reduce various diffusion effects. However, in order to shorten diffusion time, the inter-pulse delay of CPMG has to be decreased while increasing the number of 180° refocusing pulses; this change may result in safety concerns about specific absorption rate in clinical applications. In addition, metabolite T₂ relaxation measured using CPMG-type sequences can be contaminated by relaxation during the refocusing pulses [11, 26].

Third, for spin echo and stimulated echo sequences, the signal amplitude of coupled resonances is complicated due to scalar coupling effect. Introducing T₂ relaxation by varying TE, which is necessary for both multi-TE PRESS and CPMG, introduces additional signal modulation due to scalar coupling but is again unavoidable in conventional methods. The experimenter is often forced to use multiple suboptimal TEs in order to generate different amounts of T₂ weighting for T₂ quantification. These suboptimal TEs can cause significant signal overlap for metabolites of interest. For example, the spectra acquired using the MAR_ZSS technique are demonstrated in Fig. 4a, where the smooth and monotonic signal amplitude attenuation by the progressively larger saturation effects of iPFG trains can be seen. In comparison, the spectra obtained via multi-TE PRESS are shown in Fig. 4b, where the J-coupling effect interferes strongly with the exponential attenuation of transverse relaxation.

While multi-TE PRESS experiments place magnetization entirely on the transverse plane to introduce necessary T₂ weighting, our pulse-driven steady state technique uses a combination of rapid refocusing with 10 ms intervals between adjacent iPFG pulses and longitudinal storage of magnetization. Given that in the MAR_ZSS method, relaxation weighting is prepared longitudinally, we would expect this method to be substantially less susceptible to diffusion and motion effects.

Phantom measurements (listed in Table 1) found that the T₂ of NAA, Cr, and Cho determined by the MAR_ZSS technique agreed reasonably well with the conventional multi-TE PRESS technique. This is likely due to the fact that internal local susceptibility gradients (internal gradients) are not present in the phantom liquid. The free diffusion decay of metabolites is very small with multi-TE PRESS because the time difference of two spoil gradients surrounding the two 180 degree pulses is short, and because diffusion evolution times are not altered in response to different TE values in the multi-TE measurements. Therefore, with phantoms, it is reasonable that MAR_ZSS and multi-TE T₂ values would agree. However, the situation would be completely different in vivo, where internal local susceptibility gradients (internal gradients) are present [11]. TE changes in multi-TE measurements may literally cause variations in the evolution time of diffusion, thereby creating different diffusion decay rates that depend on TE. As a result, substantial, statistically significant differences were found between the two methods in in vivo experiments. Indeed, we found that the T₂s of NAA, Cr, and Cho measured by the proposed MAR_ZSS technique were significantly longer than those measured by multi-TE PRESS (see Table 2). Interestingly, the in vivo T₂ values measured by the MAR_ZSS technique—which has a mechanism of rapid partial refocusing with an inter-pulse interval of only 10 ms—were closer to values obtained using CPMG, which is known to be far less sensitive to diffusion-related effects [11, 12].

The experimental results presented here validate the concepts outlined in the Theory section, above. However, it should be noted that further optimization of this technique is possible. For example, the first measurement with flip angle of 0° is not necessary because the same data are acquired (or extracted from fitting) in the separate T₁ measurements with the same readout sequence. In addition, the simulation results shown in Fig. 2b show that both recovery delay time and iPFG pulse train duration can be significantly shortened to speed up the overall experiment. Our Bloch simulation suggests that TR may be shortened to 4–5 s for flip angles larger than 15°.

This novel MAR_ZSS technique is also associated with certain limitations. First, the accuracy of T₂s depends on the measurement of T₁, which introduces additional errors to the final results. However, measurement of T₁ is relatively more robust, and its result is less controversial than measurement of T₂ because multi-TEs are not involved in the measurements; indeed, we estimated that even when T₁s were averaged across five subjects instead of using individual T₁s, in most cases the deviation from T₁ would be less than 10%. Second, the accuracy of B₁ calibration is another concern, although multi-TE PRESS and CPMG with non-adiabatic pulses can also suffer from B₁ miscalibration or B₁ inhomogeneity. The effect of flip angle error can be evaluated by taking the derivative of Eq. 3: dT₂/T₂ = dα/sin(α). Therefore, a 10% error in flip angle causes an approximately 10% error in T₂ for the range of flip angles (sin(α) ≈ α) used in this study.

Taken together, our findings suggest that the complete separation between relaxation preparation and readout opens many interesting possibilities for practical application in metabolite relaxation experiments. For example, many spectral editing experiments require a fixed TE to maximize editing yield, making it very difficult to effectively measure transverse relaxation of the edited signals using conventional multi-TE PRESS or CPMG methods. The proposed technique, however, allows the straightforward inclusion of various editing schemes (e.g, two-step J editing or multiple quantum filtering) into the readout sequence because TE can be arbitrarily selected and fixed while relaxation weighting is completely generated and quantified by the MAR_ZSS technique. In addition, with the freedom to select an arbitrary TE for readout, TE can be set to zero or close to zero when measuring T₂ relaxation. This can be very convenient for investigating MRS signals with very short T₂s; examples include the ATP signals in ³¹P MRS and labile proton signals that are in fast exchange with water.

Conclusion

We developed a novel technique— MAR_ZSS—for probing metabolite T₂ relaxation by generating RF-driven longitudinal steady-state magnetization without the need to vary TE. An iPFG train was used to create spatial modulation for probing metabolite relaxation in vivo and a new linear equation was derived from Bloch equations. The application of this new concept was demonstrated by Bloch simulations, phantom experiments, and in vivo experiments on human brain. This new technique may have promising applications in a variety of experiments involving relaxation characterization of tissue properties.