Abstract
The α-Fe2O3(11̅02) surface (also known as the hematite r-cut or (012) surface) was studied using low-energy electron diffraction (LEED), X-ray photoelectron spectroscopy (XPS), ultraviolet photoelectron spectroscopy (UPS), scanning tunneling microscopy (STM), noncontact atomic force microscopy (nc-AFM), and ab initio density functional theory (DFT)+U calculations. Two surface structures are stable under ultrahigh vacuum (UHV) conditions; a stoichiometric (1 × 1) surface can be prepared by annealing at 450 °C in ≈10–6 mbar O2, and a reduced (2 × 1) reconstruction is formed by UHV annealing at 540 °C. The (1 × 1) surface is close to an ideal bulk termination, and the undercoordinated surface Fe atoms reduce the surface bandgap by ≈0.2 eV with respect to the bulk. The work function is measured to be 5.7 ± 0.2 eV, and the VBM is located 1.5 ± 0.1 eV below EF. The images obtained from the (2 × 1) reconstruction cannot be reconciled with previously proposed models, and a new “alternating trench” structure is proposed based on an ordered removal of lattice oxygen atoms. DFT+U calculations show that this surface is favored in reducing conditions and that 4-fold-coordinated Fe2+ cations at the surface introduce gap states approximately 1 eV below EF. The work function on the (2 × 1) termination is 5.4 ± 0.2 eV.
1. Introduction
The study of iron oxides is motivated by their abundance in the Earth’s crust, their importance in geochemistry and corrosion processes, and their wide range of applications including catalysis, biomedicine, and spintronics.1 The most stable iron oxide under atmospheric conditions is hematite (α-Fe2O3). This material is a promising candidate for photoelectrochemical (PEC) water splitting because it is stable in water, is nontoxic, and has a bandgap of 1.9–2.2 eV.2,3 In principle, α-Fe2O3 can achieve a maximum solar-to-hydrogen efficiency of 15%,4 which is sufficient for application, but the practical efficiency is hindered by a low absorption coefficient,5 short minority carrier lifetime,6 low conductivity,7,8 and sluggish reaction kinetics.9,10 Several strategies have been developed to improve the performance of α-Fe2O3 photoanodes, including oxygen vacancy engineering,11 doping,12,13 and the addition of cocatalysts,14 and a large foundation of prior work on hematite surfaces exists. However, many aspects of α-Fe2O3 surface structures remain poorly understood at the atomic scale, which limits the understanding of their impact on surface (photo)-chemistry.
One approach to understanding α-Fe2O3 surface chemistry is to study well-defined model systems in a highly controlled environment, thereby reducing complex phenomena to a tractable level. In the so-called surface science method, adsorption and surface chemistry are studied molecule by molecule on low-index single-crystal surfaces, allowing an understanding of the basic interactions to be built up. An accurate and precise knowledge of the atomic-scale surface structure is a prerequisite, and there remain many important metal oxides where this basic knowledge does not exist. To date, most surface-science studies of α-Fe2O3 have utilized thin-film samples grown epitaxially on a metal substrate. This approach usually results in growth of the (0001) facet because an FeO(111) ultrathin film forms at the interface when Fe is deposited in an oxygen background, and this templates further growth with the basal plane parallel to the surface.1,15,16 Unfortunately, it has proven extremely difficult to prepare and measure a stoichiometric α-Fe2O3(0001) surface under UHV conditions,16 and the termination is still debated,1 as are those of several reduced phases that have also been reported.16−23
The nonpolar α-Fe2O3(11̅02) surface (see Figure 1) has attracted considerably less attention, despite the fact that it is prevalent on nanohematite,1,24 and it is reported that a (1 × 1) surface can be easily prepared by annealing a single-crystal sample in ≈10–6 mbar O2.17,25−29 A reduced (2 × 1) termination is formed upon annealing in UHV, and it is possible to cycle reproducibly backward and forward between the two terminations. To date, adsorption studies have primarily focused on water, and both terminations of α-Fe2O3(11̅02) have been shown to be active for dissociative adsorption.26
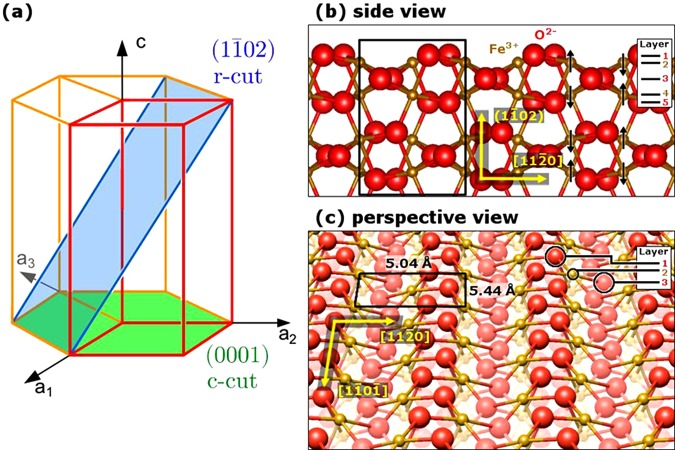
Figure 1.
α-Fe2O3(11̅02) surface. (a) Schematic showing the orientation of the (11̅02) plane within the hexagonal unit cell (red) of α-Fe2O3, which has the corundum structure. The α-Fe2O3 unit cell has dimensions a = 5.04 Å and c = 13.77 Å. The oxygen basal plane lies within the (0001), or c-cut, plane. (b) Side view of the α-Fe2O3 structure looking along the [11̅01̅] direction. Note there is no net dipole moment in the repeat unit perpendicular to the surface (black rectangle), and thus α-Fe2O3(11̅02) is a nonpolar surface. The antiferromagnetic ordering is indicated by black arrows (component perpendicular to the surface, only). The direction perpendicular to the surface is labeled (11̅02) in round brackets because there is no integer–index vector corresponding to that direction for the (11̅02) plane. (c) Perspective view of a bulk truncation at the (11̅02) plane, with oxygen atoms exposed. The surface is characterized by zigzag rows of oxygen and iron atoms and has a unit mesh (black rectangle) measuring 5.04 × 5.44 Å2.
The clean α-Fe2O3(11̅02) (1 × 1) surface is thought to be stoichiometric and bulk-terminated (as depicted in Figure 1(c)), and a few computational papers have studied its properties.30−32 Concerning the (2 × 1) termination, Gautier-Soyer et al.25 proposed that the reconstruction extends about 25–30 Å into the bulk based on LEED and Auger electron spectroscopy (AES) measurements, but this model was challenged by Henderson and co-workers,26−29 who suggested the reconstruction is restricted to the surface layer. Two possible structures were proposed in which every second oxygen row is either completely29 or partially26 missing. The latter model was supported by a molecular mechanics study.33 To date, there are no scanning probe measurements or DFT studies that might support or refute the proposed models.
The present work examines the geometric and electronic structure of the α-Fe2O3(11̅02) (1 × 1) and (2 × 1) terminations using a combination of LEED, XPS, UPS, STM, nc-AFM, and ab initio DFT+U calculations. The results support the stoichiometric, bulk-terminated model for the α-Fe2O3(11̅02)-(1 × 1) surface and show that the bandgap is slightly reduced at the surface. The images of the (2 × 1) termination are in poor agreement with previously proposed models, and a new model based on ordered oxygen vacancies is proposed. The existence of relatively simple, stable surface unit cells together with the possibility to reproducibly cycle back and forth makes α-Fe2O3(11̅02) an ideal model system to study the reactivity of hematite surfaces.
2. Experimental and Computational Details
2.1. Experimental Details
Three independent UHV systems were used to study single-crystal α-Fe2O3(11̅02) samples. The STM data were collected in a setup consisting of a preparation chamber (base pressure <10–10 mbar) and an analysis chamber (base pressure <7 × 10–11 mbar) using an Omicron μ-STM operated in constant current mode. The LEED, XPS, and UPS data were acquired in a vacuum system (base pressure <5 × 10–11 mbar) using a SPECS Phoibos 150 energy analyzer, a SPECS FOCUS 500 monochromatized X-ray source (Al Kα anode), a SPECS UVS10/35 source with both He I and He II discharge, and a commercial LEED setup. Full details of this vacuum system are described in ref (34). Finally, nc-AFM data were taken in a two-vessel UHV setup (preparation chamber <10–10 mbar, analysis chamber <10–11 mbar) based on a commercial Omicron LT-STM equipped with a commercial Omicron q-Plus LT head and tuning-fork-based AFM sensors (k = 1900 N/m, f0 = 30500 Hz, Q ≈ 20 000). Electrochemically etched W tips were glued to the tuning fork and cleaned in situ by self-sputtering in 10–4 Pa Ar,35 followed by treatment on a Cu(100) crystal. While imaging the hematite surface, the tip termination was most likely modified by touching the oxide surface. All the nc-AFM data presented here were taken in the constant-height mode, where the tuning-fork resonance frequency shift is recorded as the primary signal. All nc-AFM and STM images presented in this work were corrected for distortion and creep of the piezo scanner, as described in ref (36).
Experiments were conducted on four natural single-crystal α-Fe2O3(11̅02) samples with consistent results. Two samples were obtained from SurfaceNet GmbH and two from Surface Preparation Laboratories, all with a nominal miscut precision of ±0.1°. After initial cleaning cycles, consisting of 10 min of sputtering with 1 keV Ar+ ions and 20 min of annealing in UHV (T = 540 °C), all contaminants detectable by XPS were successfully removed from the samples. Potassium contamination was observed after high-temperature O2 annealing of one sample, resulting in a (2 × 3) superstructure. Presumably, oxidation caused segregation of K from the bulk of the natural sample. Data from the contaminated crystal are not shown here, although results for the (2 × 1) surface were identical to those of the noncontaminated crystals. At room temperature, all samples initially exhibited charging in LEED below electron energies of about 90 eV. STM measurements were not attempted until the conductivity had increased to a level where no charging was observed in LEED above 20 eV electron energy. This was achieved by 60–100 cycles of sputtering for 10 min with 1 keV Ar+ ions and annealing in UHV (20 min, T = 540 °C). During this preparation process, the samples were also annealed in oxygen (20 min, pO2 = 1 × 10–6 mbar, T = 450 °C) every 5–10 cycles to prevent the surface from being overly reduced, which is a common issue when working with the (0001) surface of hematite.37 The increase in conductivity is most likely linked to the reduction of the sample. Fe interstitials are thought to be the most likely bulk defect in such conditions,38 and these donate electrons into the lattice, resulting in small-polaron-type conductivity.39
The (1 × 1) surface was prepared by directly oxidizing the (2 × 1) surface, or from a freshly sputtered crystal, by annealing in oxygen (pO2 = 1 × 10–6 mbar, 20 min at 450 °C). The (2 × 1) surface could be prepared by annealing (20 min at 540 °C) either a freshly sputtered or a (1 × 1) surface in UHV. A mixed surface was prepared by annealing the (1 × 1) surface in UHV for shorter times or at lower temperatures.
2.2. Density Functional Theory Calculations
Spin-polarized density functional theory (DFT) calculations were performed by using the full-potential augmented plane wave + local orbital method as implemented in the WIEN2k code.40 The PBEsol exchange-correlation functional41 was employed together with a Hubbard U (Ueff = 4 eV)42 to treat the highly correlated Fe 3d electrons.43 This functional was used because it yields bulk lattice constants a = 5.03 Å and c = 13.74 Å, which agree well with experiment,44 and these parameters were subsequently used for the slab setup. All calculations were spin polarized due to the antiferromagnetism of hematite. In bulk hematite, spin-up and spin-down iron atoms are antiferromagnetically ordered along [0001] and ferromagnetically coupled in each (0001) layer. In the (11̅02) planes, this results in alternating spins along the [112̅0] direction, as indicated by black arrows in Figure 1(b). Note that the spin directions are only qualitatively correct as shown. At low temperatures, the spins are oriented antiferromagnetically, but a magnetic transition occurs at the Morin temperature, TM = 260 K, after which spin canting results in weak ferromagnetism.45−48
Both (11̅02) hematite surfaces, (1 × 1) and (2 × 1), were modeled by fully relaxed slabs without inversion symmetry and a vacuum of 19 Å. These slabs contain five Fe2O3 units as depicted in Figure 1(b), with five atomic layers (three oxygen and two iron layers) within every unit (labeled 1–5 in Figure 1). The slabs consist of an upper and a lower surface, which are symmetry-equivalent. The (2 × 1) reconstructions were built from a (2 × 1) supercell of the bulk-terminated surface, removing oxygen or adding iron depending on the model. The models consist of 50 atoms for the bulk-terminated surface and 94–102 atoms for the (2 × 1) reconstructions, respectively.
A plane-wave cutoff of Rkmax = 7.0, where R is the smallest atomic sphere radius, was used, and the Brillouin zones of the surface models were sampled by a 8 × 7 × 1 k-mesh for the bulk terminated model. Atomic-sphere radii of 1.86 and 1.50 bohr were chosen for Fe and O, respectively. All surface models were relaxed until all residual forces were below 1 mRy/bohr. STM simulations were done in constant-height mode by using the Tersoff–Hamann approximation, using a slab with additional vacuum.49 The electron density in the interval between EF and the limit imposed by the sample bias is determined, and the simulated STM images are then obtained by plotting this partial electron density in a plane above the surface at a defined height (3–5 Å).
Ab initio thermodynamics was used to determine the relative stability of the (1 × 1) and (2 × 1) reconstructions. The surface phase diagram was computed with the SCAN (nonempirical strongly constrained and appropriately normed) meta GGA50 due to its more accurate results for energies. Scheffler and Reuter51 define the surface free energy γ of a semi-infinite slab with two equivalent surfaces, which are in contact with a gas-phase reservoir, at temperature T and pressure p as
Here Gslab is the Gibbs free energy; Ni and μi are the number and chemical potentials of the respective atom species; and A represents the surface area. The chemical potentials of Fe and O are linked by the Gibbs free energy of bulk hematite. Hence, the surface free energy can be obtained as a function of the oxygen chemical potential only, which may vary within a reasonable range. This range is constrained by an upper limit, where oxygen would condense on the sample, and a lower limit, where the bulk material would start to turn into magnetite (Fe3O4). Because the total energies for small molecules such as O2 or H2O are not accurately described by semilocal DFT, we use the experimental value for the Gibbs free energy of formation (as was described by Scheffler and Reuter51)
with ΔGfexp(T,p) as the experimental value of the Gibbs free energy of formation and gx(T,p) as the Gibbs free energy per formula unit. This approach allows us to express the Gibbs free energy of formation of O2 with results from calculations of bulk materials only, which are more accurate than total-energy calculations for the O2 molecule.
The Gibbs free energies may be replaced by the total energies computed by DFT+U calculations, disregarding temperature-induced entropic contributions. This approximation allows us to construct a surface phase diagram by using the total energies of the slab, the bulk material, and the molecular species. Based on basic thermodynamics and tabulated experimental data, the range of the chemical potential may be converted into a temperature or pressure scale.
3. Results
3.1. Low-Energy Electron Diffraction
LEED patterns obtained from the clean (1 × 1) and (2 × 1) surfaces are shown in Figure 2. The data were acquired using a 50 eV electron beam energy and are consistent with previous publications.17,25,26 Note that a stoichiometric (1 × 1) surface, as shown in Figure 1(c), contains a glide plane along the [11̅01̅] direction. This should result in every other diffraction spot missing along the main [11̅01̅] axis. We observe these spots to be missing at most energies but weakly present at some energies for both the (1 × 1) and the (2 × 1) surface. This discrepancy could arise because the electron beam is slightly off normal incidence in our experimental setup.
Figure 2.
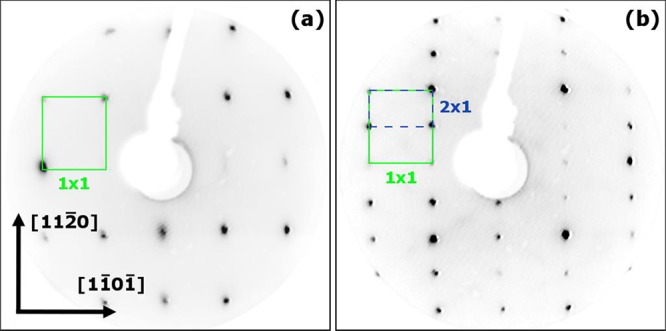
LEED patterns obtained from the clean (1 × 1) (a) and (2 × 1) (b) surfaces of α-Fe2O3(11̅02) with an electron beam energy of 50 eV.
3.2. Photoemission Spectroscopy
Figure 3 shows XPS spectra in the Fe 2p and the O 1s regions acquired from the (1 × 1) and (2 × 1) terminations of α-Fe2O3(11̅02). Measurements were taken at 150 °C to prevent adsorption of water from the residual gas.26 Panels (a) and (b) were acquired at normal emission, whereas panels (c) and (d) were acquired at 75° grazing emission and are thus more surface sensitive. In the absence of a C 1s peak, all energies were referenced to the Fermi edge of the tantalum sample plate. Since the samples were conductive enough for STM, peak shifts due to charging can be ruled out. The position of the O 1s peak of the (2 × 1) terminated surface is consistent across all the data and in agreement with previous measurements of α-Fe2O31,52 and iron oxides in general.53 The same is true for the characteristic shape of the Fe 2p3/2 peak, consisting of several features between 709 and 715 eV due to multiplet splitting.52 The peaks of the (1 × 1) terminated surface are shifted to lower binding energies by a varying degree in the range of VBB = 0.3–0.5 eV, depending on sample history and preparation. We attribute this to upward band bending, which occurs because the Fermi level is closer to the conduction band minimum in the reduced, heavily n-type bulk than it is in the more stoichiometric (1 × 1) surface region. Save for this shift of the entire spectrum, the position of the Fe 2p1/2 and the Fe 2p3/2 peaks for the (1 × 1) surface is consistent with Fe3+-containing compounds and prior measurements of α-Fe2O3,1,52 as is the pronounced shakeup satellite peak located around 719 eV. The Fe 2p3/2 peak from the (2 × 1) surface exhibits a shoulder at ≈708.5 eV, which is more pronounced at 75° grazing emission,1,53 as illustrated in the insets to Figure 3(a,c). This suggests that Fe2+ cations are located at or near the surface in the (2 × 1) termination. In keeping with this, the Fe3+ satellite peak at 719 eV is less pronounced for the (2 × 1) surface, most likely because it overlaps with a Fe2+ shakeup satellite peak at ≈715 eV.1,52 In general, the XPS data from the (2 × 1) surface resemble those obtained from magnetite (Fe3O4), which contains both Fe2+ and Fe3+. Comparing the Fe 2p and O 1s peak areas in grazing emission, we find an increase of ≈11.5% in the Fe:O ratio when going from the (1 × 1) to the (2 × 1) surface. This agrees well with the results of a SESSA54,55 simulation, which predicts an increase of 9.6% for a surface with two oxygen vacancies per (2 × 1) unit cell in the outermost layer. The reduced nature of the (2 × 1) surface is in agreement with previously published electron energy loss spectroscopy (EELS) data of Henderson.27
Figure 3.
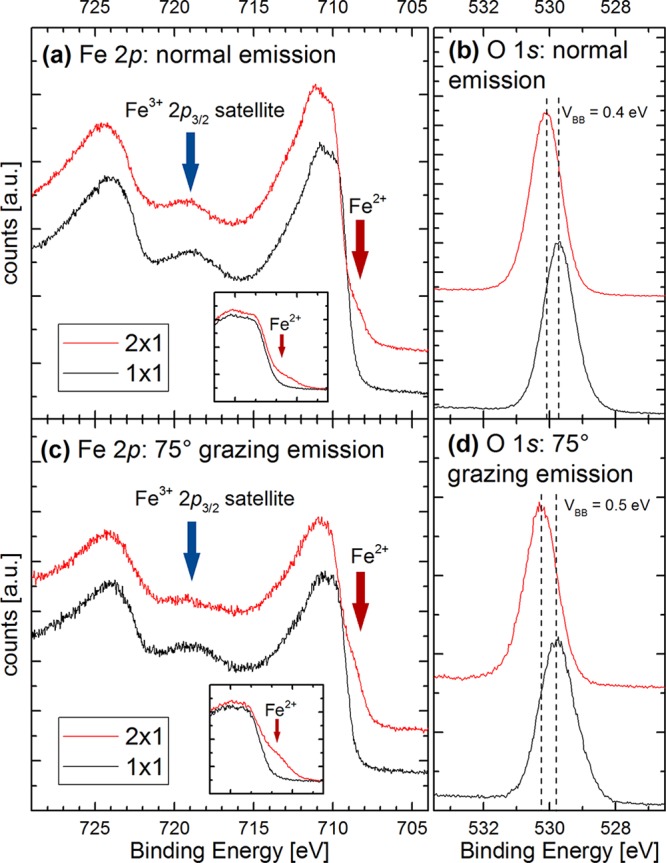
XPS spectra (monochromatized Al Kα) measured at 150 °C of the Fe 2p (a,c) and the O 1s (b,d) peaks for the (1 × 1) and (2 × 1) terminated α-Fe2O3(11̅02) surface acquired at normal (a,b) and 75° grazing emission (c,d). The insets show direct comparisons of the low-binding-energy shoulder on the Fe 2p3/2 peak, aligned to remove the shift determined in (b) and (d) for clarity. The reduction in intensity of the Fe3+ shakeup satellite peak (blue arrows) coupled to the emergence of a low-binding-energy shoulder on the Fe 2p3/2 peak (red arrows) shows that Fe2+ cations are present on the (2 × 1) surface but not on the (1 × 1) surface.52,53
UPS spectra of the (1 × 1) and the (2 × 1) surfaces of α-Fe2O3(11̅02) are shown in Figure 4. The (1 × 1) surface clearly exhibits a band gap, with no photoemission below 1.5 ± 0.1 eV binding energy. The data are consistent with prior UPS measurements of an α-Fe2O3 single crystal56 and thin-film samples.53 Interestingly, ref (56) contains both regular photoemission and inverse photoemission spectroscopy data, from which the authors estimate a total bandgap of ≈2.6 eV. On the (2 × 1) surface, the bulk states appear to be shifted to higher binding energies, with the major valence band contributions appearing at 1.7 ± 0.1 eV binding energy. A small peak is observed closer to the Fermi level, contributing photoemission down to binding energies as low as 0.6 ± 0.1 eV. The data strongly resemble that obtained from Fe3O4 samples,53,57 where the small peak just below EF is attributed to Fe2+-like cations.
Figure 4.
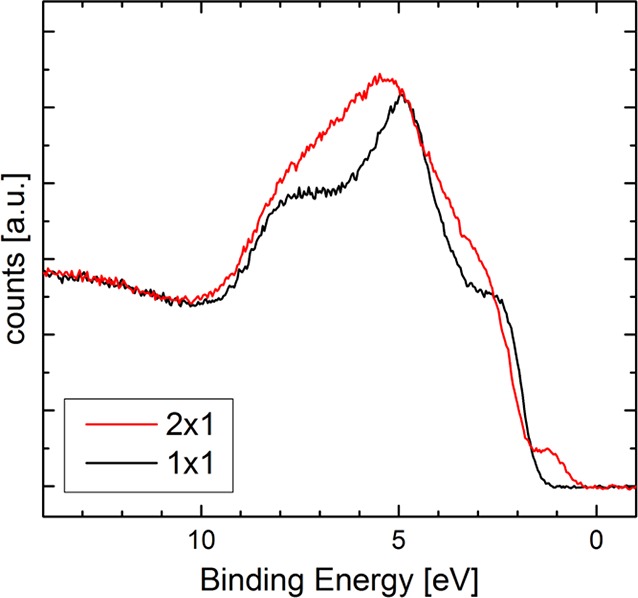
UPS spectra (Helium II line) of (1 × 1) and (2 × 1) terminated surfaces of α-Fe2O3(11̅02), measured at 150 °C. The (2 × 1) surface exhibits states at low binding energies not present on the (1 × 1) surface.
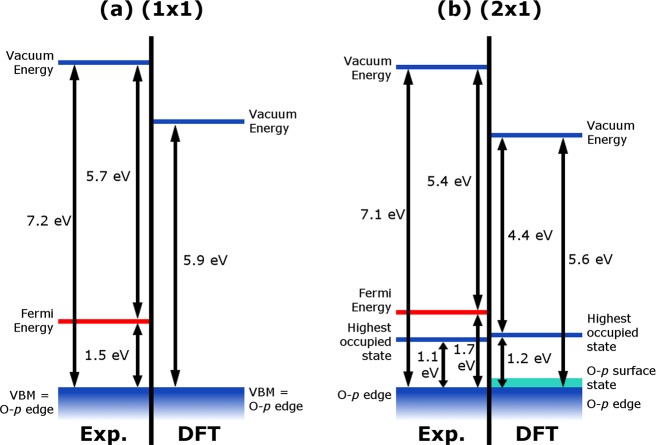
The work function was measured with XPS as 5.7 ± 0.2 eV for the (1 × 1) terminated surface and as 5.4 ± 0.2 eV for the (2 × 1) reconstruction. The work function is determined as the difference between beam energy and high binding energy cutoff (with respect to the Fermi edge of the Ta sample mount). The difference is consistent with the energy shift of the (1 × 1) electronic states observed in both XPS and UPS. Figure 5 shows the interrelation of the energies discussed in this section.
Figure 5.
Schematic of the experimentally and computationally determined energy levels for the (1 × 1)- and the (2 × 1)-terminated α-Fe2O3(11̅02) surface. The computational values are discussed in section 3.5. It should be noted that this figure does not take into account effects such as band bending and that the experimentally measured O-p edge is that of near-surface oxygen, which might be different in energy from the bulk.
3.3. Scanning Tunneling Microscopy
STM images of the α-Fe2O3(11̅02)-(1 × 1) surface are shown in Figure 6. The images were acquired on the same sample area with (a) negative and (b) positive sample bias and thus represent filled and empty states, respectively. Both images are characterized by zigzag lines of bright protrusions running in the [11̅01̅] direction, which are displaced by ≈5.0 Å in the [112̅0] direction. This appearance is consistent with the bulk-truncated structure shown in Figure 1(c), with one sublattice selectively imaged bright. Using point defects as markers (green and orange circles), we infer that the species imaged as bright zigzag lines differs between the filled and empty state images. STM simulations (inset), based on our theoretical calculations (see section 3.5), suggest that the oxygen sublattice is imaged in filled states, whereas the empty state images reveal the surface iron sublattice. The nature of the defects is presently unknown, but some are most likely adsorbates from the residual gas. One possibility is water, which is known to stick on the (1 × 1) surface at room temperature.26
Figure 6.

STM images of the α-Fe2O3(11̅02)-(1 × 1) surface imaging: (a) filled states (10 × 10 nm2, Usample = −3 V, Itunnel = 0.1 nA) and (b) empty states (10 × 10 nm2, Usample = +3 V, Itunnel = 0.1 nA). Both images were acquired on the same sample area and exhibit zigzag rows of bright protrusions running in the [11̅01̅] direction. The relative positions of the defects marked in the green and orange circles suggest that a different sublattice is imaged for each bias polarity. STM simulations (inset), based on the DFT+U calculations described in sections 2.2 and 3.5, are in line with this conclusion. Larger-area STM images of both the (1 × 1) and the (2 × 1) surface are shown in Figure S1.
Figure 7 shows STM images of the α-Fe2O3(11̅02)-(2 × 1) surface acquired with positive and negative sample bias on the same sample area. Both imaging conditions show paired zigzag rows of bright protrusions running in the [11̅01̅] direction. The paired rows have a repeat distance in the [112̅0] direction of 10.1 Å separated by a dark depression, consistent with the (2 × 1) periodicity observed in LEED. High-resolution images (Figure 7(c,e)) of the surface show that the (2 × 1) unit cell contains a protrusion close to the center. A comparison of the point defects in the filled and empty state images (green circles in Figure 7) suggests that the same surface species are imaged in each case. Over the course of many experiments, it was observed that the appearance of the (2 × 1) surface varies somewhat with the tip condition. Although a similar lattice of protrusions is always observed, the apparent depth of the dark depression between the rows varies, and in some conditions it is not resolved.
Figure 7.

STM images of the α-Fe2O3(11̅02)-(2 × 1) surface in (a) filled states (20 × 20 nm2, Usample = −2.5 V, Itunnel = 0.1 nA) and (b) empty states (20 × 20 nm2, Usample = +2.5 V, Itunnel = 0.1 nA), recorded over the same sample area. The bright protrusions form zigzag lines, with a pronounced gap between each zigzag. The common position of the defects (marked in green) in the images suggests that the same sublattice is imaged in both filled and empty states. High-resolution images of the (2 × 1) surface are shown in (c) Usample = −1 V, Itunnel = 0.1 nA and (e) Usample = +2 V, Itunnel = 0.1 nA. The (2 × 1) unit mesh is marked by a yellow rectangle. Note that the unit cell contains a protrusion slightly off center of the rectangle. STM simulations based on the “alternating trench” model are shown in (d) for filled states and (f) for empty states.
Additional information about the (1 × 1) to (2 × 1) transition can be obtained by studying STM images of a mixed-phase surface. The surface in Figure 8 was formed by UHV annealing of the (1 × 1) surface at 500 °C for 15 min. A large domain of the (2 × 1) structure shown in Figure 7(a) is embedded within the (1 × 1) structure, with a dark depression at the boundary. As demonstrated by the green lines in Figure 8, we see that each zigzag row of the (1 × 1) surface (filled states) continues in the (2 × 1) phase with a row of comparatively large, round protrusions. This suggests that the protrusions of the (2 × 1) structure are close to the positions of the O sublattice in the unreconstructed surface.
Figure 8.

STM image (12.5 × 12.5 nm2, Usample = −2 V, Itunnel = 0.1 nA) of a phase boundary between the (1 × 1) and (2 × 1) surface terminations. The green lines demonstrate that the zigzag rows of surface oxygen atoms imaged in the (1 × 1) phase are continued by a row of larger protrusions in the (2 × 1) termination. The (2 × 1) reconstruction domain has formed on a (1 × 1) terrace, as can be seen in the inset (50 × 50 nm2, Usample = −2.5 V, Itunnel = 0.1 nA). The red box in the inset marks the position of the main image.
Given that a (2 × 1) surface can have two possible registries to the underlying bulk, one would also expect to observe antiphase domain boundaries (APDBs) in the (2 × 1) structure. Such APDBs were rarely observed over the course of the STM measurements. The rarity of such features, together with the size of uniform (2 × 1) domains such as the one shown in the inset to Figure 8, is consistent with the prediction by Henderson et al. that growth of existing (2 × 1) domains happens on a short time scale compared to the emergence of new nucleation points.27
3.4. Noncontact Atomic Force Microscopy
The nc-AFM technique provides complementary information to the STM data. Whereas STM reveals electronic structure, nc-AFM is more sensitive to the atom positions and their chemical nature.58
In the (1 × 1) case, the images recorded at large tip–sample distance (Figure 9(a)) resemble the contrast obtained in STM images, with zigzag rows of bright and dark features along the [11̅01̅] direction. In this regime, the AFM contrast is dominated by electrostatic forces,59 and thus the images are sensitive to the distribution of charge at the surface. The reduced surface (Figure 9(b)) exhibits a clear (2 × 1) periodicity with bright, elongated protrusions that rotate by 90° between neighboring rows. The protrusions are too large to correspond to individual surface ions.
Figure 9.
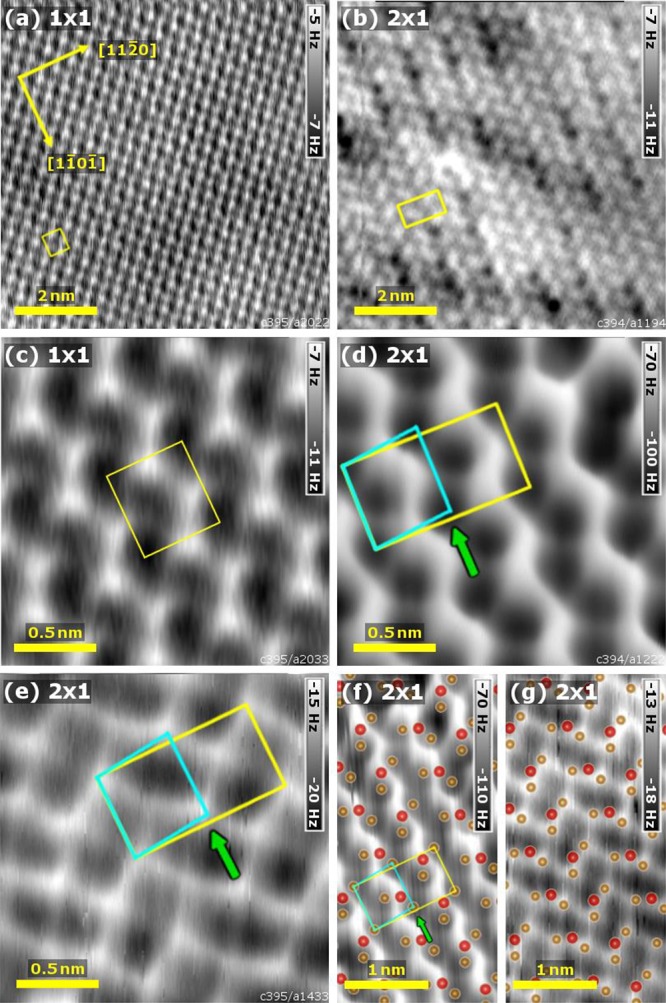
Constant-height noncontact AFM data acquired on (a) the α-Fe2O3(11̅02)-(1 × 1) surface (8 × 8 nm2, T = 78 K, A = 150 pm) and (b) the α-Fe2O3(11̅02)-(2 × 1) surface (8 × 8 nm2, T = 5 K, A = 500 pm). Panels (c) and (d) show detailed images of the same surfaces acquired at smaller tip–sample distances ((c) 2 × 2 nm2, T = 78 K, A = 100 pm, (d) 2 × 2 nm2, T = 5 K, A = 55 pm). Panel (e) shows the (2 × 1) surface measured with a different tip providing inverted contrast (2 × 2 nm2, T = 78 K, A = 250 pm). The (1 × 1) and (2 × 1) unit cells are indicated by yellow boxes. A periodic lateral displacement of neighboring rows along the [11̅01̅] direction is observed in (d), (e), as indicated by the green arrow and the cyan box. Panels (f), (g) show both contrasts obtained on the (2 × 1) surface overlaid with the proposed “alternating trench” model. The positions of the measured dark (f) and bright (e) features correspond to the cation positions in the model.
With a smaller tip–sample separation (Figure 9(c,d,e)), the image contrast becomes dominated by short-range interactions. This short-range tip–surface interaction on oxide surfaces is a mixture of ionic and covalent interactions58,60−62 and may be further influenced by effects such as Pauli repulsion63 or tip bending.64 Therefore, depending on the tip termination and its reactivity with the surface, the information on surface ion positions can be present both in a strong attractive signal and in a highly localized repulsion. On the (2 × 1) reconstruction, we typically observed strong, localized attractive forces as in Figure 9(d). We attribute this to chemical bonding toward the iron sublattice. On the (1 × 1) termination, we observed only weak attractive bonding and repulsion (Figure 9(c)).
In the short-range interaction regime, zigzag rows of bright and dark features are clearly visible on the (1 × 1) surface (Figure 9(c)). Interestingly, the reduced surface (Figure 9(d)) looks very similar, and the (2 × 1) periodicity is not obvious at first glance. On closer inspection, it is present in a slight difference in the interaction measured above every second row of dark features and, more evidently, in a periodic lateral displacement of the dark features along the [11̅01̅] direction (green arrow and cyan box in Figure 9(d)).
Figure 9(e) shows an image of the (2 × 1) surface obtained with a different tip, which exhibits the same underlying structure but with inverted contrast. Similar contrast reversal has been observed in pioneering works on TiO260−62,65 and later on other oxides66 and attributed to tips with opposite polarity. Tips terminated with an anion feel attractive bonding with surface cations, while the interaction with the oxygen sublattice is repulsive and much weaker. Positively terminated tips provide the opposite situation.
Assuming that the contrast shown in Figure 9(d) corresponds to a negatively charged tip, the dark rows in Figures 9(b) and (d) can be interpreted as zigzag chains of Fe cations running in the [11̅01̅] direction. The same pattern is observed as a weak repulsion signal in Figure 9(e), and thus the tip was likely positively terminated here. Figure 9(f) and (g) shows both contrasts overlaid by the top two atomic layers of the proposed “alternating trench” model for the (2 × 1) reconstruction. The positions of the dark features in Figure 9(f) and the bright features in Figure 9(g) correspond to the cation positions of the “alternating trench” model, particularly the characteristic lateral displacement of cations along the [11̅01̅] direction.
3.5. Density Functional Theory Calculations
In Figure 10 we show the results of atomistic thermodynamics calculations for a variety of different possible α-Fe2O3(11̅02) surface structures. Previous models for the (2 × 1) reconstruction26,29 (see Introduction) were relaxed and then tested, as were several new trial structures based on either oxygen vacancies or subsurface Fe interstitials. The plot shows the surface free energy for each structure as a function of the oxygen chemical potential. Clearly, a stoichiometric surface with an essentially bulk-truncated structure (shown in Figure 11(a,b)) is most stable under ambient conditions (horizontal black line). This structure remains the most energetically favorable surface down to an O2 chemical potential of −2.3 eV, which corresponds to an O2 pressure of ≈5 × 10–10 mbar at 1000 K, i.e., well into the UHV regime. Structurally, the stoichiometric (1 × 1) termination differs slightly from a bulk-truncated surface; the outermost five layers relax slightly by +0.06, −0.21, +0.05, +0.10, and −0.07 Å, respectively, in the direction perpendicular to the (11̅02) surface, as shown in Figure 11(a,b). Most of the relaxation is due to layer-2 and layer-4 Fe atoms. All iron cations appear to remain Fe3+, based on their magnetic moment (≈4 μB) and their core-level energies being identical to the bulk atoms. They have bulk-like 6-fold octahedral coordination, apart from layer 2 (top Fe layer, see Figure 11(b)), where all iron atoms are 5-fold coordinated (truncated octahedra, missing the topmost oxygen). The top oxygen atoms are 3-fold coordinated, while all other oxygen atoms show the bulk-like 4-fold coordination with oxygen located at the center of distorted iron tetrahedra.
Figure 10.
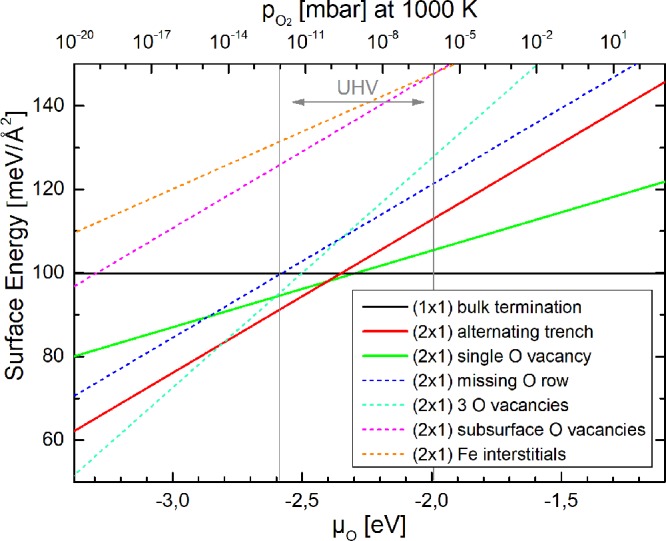
Surface energies calculated by DFT+U for several surface terminations as a function of oxygen chemical potential μO (bottom x axis) and as a function of oxygen pressure at a temperature of 1000 K (top x axis).51 The surfaces calculated to be most stable in experimentally accessible UHV conditions are drawn as bold lines. These correspond to the surface structures shown in Figure 11. The surfaces found to be unfavorable, drawn with dashed lines, are shown in Figure S2.
Figure 11.
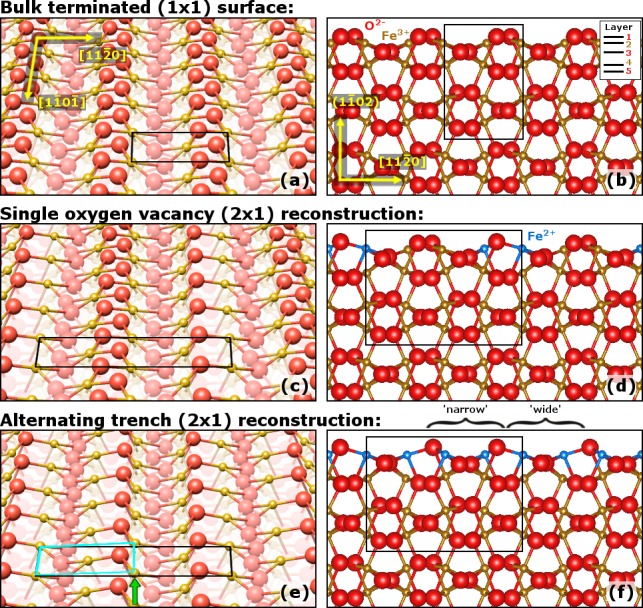
Minimum-energy configurations for the three stable surface terminations shown in perspective (a,c,e) and side views (b,d,f), as determined by density functional theory calculations. (a,b) The (1 × 1) surface exhibits only minor relaxations from a bulk-terminated surface. Two possible models for the (2 × 1) surface are shown: (c,d) a single-oxygen vacancy (2 × 1) reconstruction model previously suggested by Henderson et al.26 and (e,f) a new (2 × 1) reconstruction model based on two oxygen vacancies per unit cell. The latter is termed the alternating trench model, based on the alternating distance of the remaining top-layer oxygen rows. The respective unit cells are drawn in black, oxygen atoms as red, and iron atoms as golden. The layer labeling convention shown in (b) is used for all models throughout this paper. Iron cations predicted to have a nominal charge state of Fe2+ are colored in blue in (d) and (f). A periodic lateral displacement along [11̅01̅] in the iron sublattice of the “alternating trench” model is indicated by the green arrow and the cyan box in (e).
In a narrow window of chemical potentials at more reducing conditions, a (2 × 1) reconstruction previously suggested by Henderson et al.26 becomes competitive. This structure (Figure 11(c,d)) contains one oxygen vacancy per (2 × 1) unit cell, with oxygen atoms removed along a row in the [11̅01̅] direction. Some Fe atoms in layer 2 have a 4-fold coordination and are reduced to an Fe2+-like charge state, and the oxygen zigzag rows in layer 3 tilt out of the (11̅02) plane due to the asymmetric relaxation. This structure does not show the lateral Fe displacement observed in AFM and is only favorable over a very small range of chemical potentials around μO = −2.35 eV. At more reducing conditions, a new structure based on two oxygen vacancies per (2 × 1) unit cell is favorable. This “alternating trench” structure (Figure 11(e,f)) is based on the aforementioned vacancy model, but now two rows of oxygen atoms (the first and the fourth atom of the (2 × 1) bulk unit cell) are removed in the [11̅01̅] direction. This creates alternating wide and narrow trenches, based on the distance of the remaining top-layer oxygen rows. This is the most favorable surface over a broad range of oxygen chemical potentials (i.e., between −2.4 and −2.8 eV). These μO values are low but still experimentally accessible. A fourth model with three oxygen vacancies per (2 × 1) unit cell becomes energetically favorable at oxygen chemical potentials below −2.8 eV; however, this one was not considered further because magnetite (Fe3O4) becomes the stable bulk phase at this μO, and a more extensive reduction is to be expected.24
In the “alternating trench” (2 × 1) model, all surface Fe atoms (layer 2) are 4-fold coordinated and located at the edges of strongly distorted oxygen tetrahedra. The calculated magnetic moments (3.5 μB for Fe2+ and 4 μB for Fe3+ atoms) as well as the partial DOS (Figure 12) suggest that all these atoms have a charge state of Fe2+. This is further supported by a calculated 1 eV Fe 2p core level shift toward lower binding energy of these surface Fe atoms with respect to surface Fe atoms at the (1 × 1) surface, which corresponds well with the experimental XPS data (Figure 3). The coordination and charges of the subsurface atoms (from layer 3 down) in the “narrow” trenches are essentially the same as the (1 × 1) surface. By contrast, in the “wide” trenches, the removal of layer-1 oxygen atoms results in 5-fold-coordinated iron in layer 4. Nevertheless, all layer 4 atoms remain Fe3+, based on their magnetic moments.
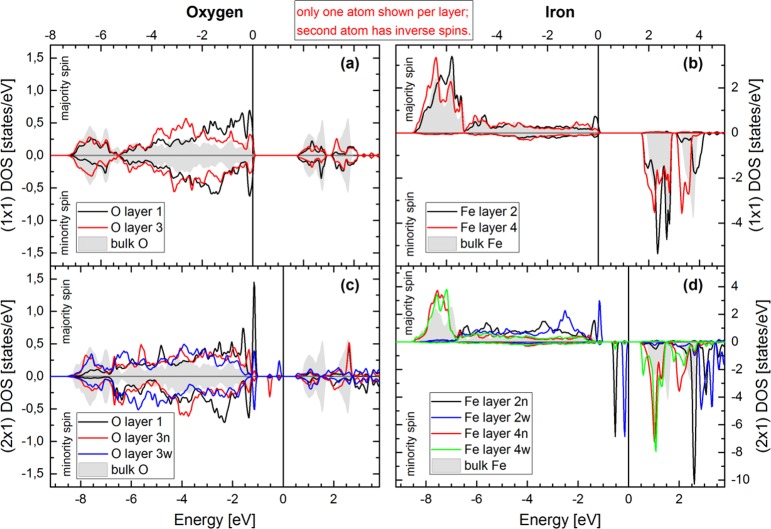
Figure 12.
Calculated density of states (DOS) for the bulk-terminated surface (a,b) and the alternating-trench (2 × 1) reconstruction (c,d). The highest occupied state is marked by a vertical black line, and its energy is set to zero. Layers are numbered by the convention introduced in Figure 11(b), with suffixes in (c) and (d) to distinguish atoms in wide (“w”) and narrow (“n”) trench positions, as defined in Figure 11(f). The partial DOS of the uppermost layers is represented by solid curves, while the DOS of the layers below (labeled “bulk”) is shaded gray. As mentioned above, hematite orders antiferromagnetically along the [0001] direction, which means that in each separate (11̅02) layer the iron spins alternate along the [11̅01̅] direction, with zero net magnetization in each layer. Therefore, two atoms exist in each (11̅02) plane with equivalent but inverse majority/minority spin ordering. Only one of these is shown.
As shown in Figure 11(e,f), the outermost five layers relax perpendicular to the (11̅02) surface by +0.14, −0.25, +0.23, −0.07, and +0.02 Å in the wide trenches and +0.11, −0.14, +0.00, +0.13, and −0.09 Å in the narrow trenches. Due to Fe2+ ions in layer 2, the attraction of layer-1 oxygen atoms is less strong. Hence, we find stronger relaxations of layer-1 oxygen atoms in comparison to the bulk-terminated surface (with Fe3+ surface atoms). Crucially, the layer-2 iron cations in the wide trenches also relax slightly in the [11̅01̅] direction (compare the Fe in the corner of the (2 × 1) unit cell to that in the center in Figure 11(e)), in qualitative agreement with the lateral shift observed in nc-AFM (green arrows in Figure 9(d,e) and Figure 11(e)). It is also notable that the layer-3 oxygen zigzag rows are narrowed in the wide trench, and these atoms relax toward layer 2 by 0.02 Å. The Supporting Information contains structure files for the (1 × 1) and alternating trench (2 × 1) models in CIF file format.
The remaining models considered in Figure 10, shown in Figure S2, proved to be energetically unfavorable. While most of the models considered here are based on ordered oxygen vacancies, it is also possible to construct a reduced surface reconstruction based on a (2 × 1) arrangement of subsurface iron interstitials, which is how the (√2 × √2)R45° reconstruction on Fe3O4(001) is formed,67 and would therefore also seem plausible for hematite. However, no model created in this way yields satisfactory surface energies in the calculations presented here.
The densities of states for the (1 × 1) bulk-terminated surface and for the energetically favorable alternating-trench (2 × 1) reconstruction are shown in Figure 12. The bulk-like partial DOS of O and Fe shows the expected behavior: With the GGA+U method, the occupied Fe-d (spin-up) states are shifted down in energy below the O-p states, but nevertheless, there is a significant overlap between Fe and O states. On the other hand, the unoccupied (spin-down) DOS of Fe is shifted up in energy, forming a gap of about 2 eV between the valence band (which is dominated by O-p character) and the conduction band. For the (1 × 1) surface, the surface oxygen states of layer 1 are shifted upward in energy with respect to bulk or layer-3 oxygens, reducing the overlap with the Fe-d band and dominating in an energy range of about 2 eV below the valence band maximum. This shift can also be seen in the calculated O 1s core level shifts of about 0.6 eV to lower binding energies with respect to the bulk states. Note that we find identical surface O 1s core level shifts for both surfaces, in keeping with the idea that the experimentally observed shift originates from band bending. On the other hand, the surface iron states are shifted to lower energies compared to the bulk in both the valence and the conduction band. This results in a slightly reduced band gap compared to bulk α-Fe2O3.30
On the (2 × 1) reconstructed surface, two new, sharp spin-down Fe d-bands are observed within the original band gap. They originate solely from the outermost layer of iron and are consistent with the reduction of the Fe charge states from 3+ to 2+ at the surface. The calculations show the new in-gap states to be filled, in agreement with the additional peak seen in UPS at low binding energy (Figure 4). The states at lower energy correspond to “narrow” trench Fe and have mainly dz2 character with smaller dxy and dyz contributions, while the states at about 0.4 eV higher energy correspond to “wide” trench Fe and have mainly dyz character with minor dz2 contributions, in both cases with minor contributions of subsurface (layer 3) oxygen states. The layer-4 iron cations exhibit a density of states similar to iron in the (1 × 1) surface, again slightly lowering the conduction band edge. “Narrow” trench layer-4 Fe states are comparable to layer-4 states of the bulk-terminated model. As mentioned above, these Fe cations are octahedrally coordinated in both the bulk-terminated model and the “narrow” trench of the proposed (2 × 1) reconstruction. Their relaxation perpendicular to the (11̅02) surface is also comparable. In contrast, the “wide”-trench layer-4 Fe states are found to be comparable to layer-2 Fe states in the bulk-terminated model. Again, these Fe cations are 5-fold coordinated in both cases.
At the top of the O-p band, a couple of fairly sharp peaks are observed for the reconstructed surface, originating from layer-1 and layer-3 oxygen atoms hybridized with Fe layer-2 states. They exhibit interesting spin splitting and characteristics corresponding to wide and narrow trenches.
The calculated differences between the vacuum potential and the energy of the highest occupied state are 5.9 and 4.4 eV for the (1 × 1) and (2 × 1) surfaces, respectively, which cannot be directly related to the measured work functions. However, this corresponds to a difference between the O-p edge and the vacuum level of 5.9 eV for the (1 × 1) termination and of 5.6 eV for the (2 × 1) reconstruction, respectively, as illustrated in Figure 5. For both terminations, this would imply a lower work function than is observed in experiment. It should however be noted that effects such as band bending are not accounted for here but are observed experimentally (Figure 3) and computationally. In any case, these findings are consistent with previously reported errors of DFT-PBE in predicting ionization potentials of semiconductors,68 as well as the inability of DFT calculations to include image-charge potential effects. Nevertheless, the general trend of a slightly lowered work function on the (2 × 1) reconstruction compared to the (1 × 1) termination is the same in theory and experiment.
To further compare the experimental and theoretical findings, STM simulations were calculated for both surface terminations. The simulations are shown as insets in Figure 6 and in Figure 7(d,f), respectively. On the stoichiometric surface, a zigzag pattern, consisting of bright and dark rows, is found in both positive and negative bias. For negative bias (occupied states), narrow protrusions alternate with dark and thick zigzag lines. Since the partial DOS below the Fermi level is dominated by oxygen surface states, the bright features are mainly caused by layer-1 oxygen atoms. In contrast, wide protrusions separated by thin, dark lines are found in the case of positive bias (filled states). The bright features are offset in the [112̅0] direction with respect to the protrusions in negative bias, and the partial DOS is dominated by Fe surface states in the corresponding region; however, the position of the features does not correspond directly to layer-2 Fe surface atoms. Instead, they are shifted slightly into the trench, due to a hybridized Fe-d orbital, which is tilted with respect to the c-axis.
For the (2 × 1) reconstruction, the STM simulations are more complex. In case of negative bias (filled states), we find two oval features per unit cell located above the Fe–O–Fe trimers, linked by the glide-plane symmetry of the surface. It is not possible to differentiate between Fe and O surface states based on the partial DOS since there are both oxygen and iron states below the Fermi level. The maximum intensity of the oval spots is located near the layer-2 Fe atoms in the wide trench but slightly offset in the [11̅01̅] direction. With positive bias (empty states), droplet-shaped features are observed, with the same glide-plane symmetry as in negative bias. The iron partial DOS suggests that the bright centers are mainly due to layer-2 Fe atoms in the narrow trench (sharp layer-2 states at 2.6 eV, drawn black in Figure 12(d)), with smaller contributions from other atoms, which is supported by comparison with the top view of the unit cell.
4. Discussion
Our results confirm that the α-Fe2O3(11̅02)-(1 × 1) surface is a stoichiometric bulk termination. Such a termination is stable, based on its Tasker type 2 or “non-polar” classification.69 Structurally, the (1 × 1) surface differs little from that of an ideal bulk truncation, with only minor relaxations in the layer spacing near the surface. Interestingly, the 3-fold-coordinated surface oxygen atoms exhibit a significantly higher density of states at the top of the valence band compared to bulk oxygen, which is why these atoms are imaged bright in filled-state STM images (Figure 6(a)). The bottom of the conduction band is dominated by states from the 5-fold-coordinated surface Fe atoms, and these atoms therefore dominate the empty-states images (Figure 6(b)). A slight shift to lower energy of the Fe-related states narrows the surface bandgap by ≈0.2 eV compared to the bulk. Both the XPS and UPS data suggest that all Fe in the surface is Fe3+, which agrees well with the calculated magnetic moments.
The shift to lower binding energies consistently observed in XPS and UPS for the (1 × 1) surface can be explained by the sample preparation. First, the sample is rendered conductive by repeatedly sputtering with Ar+ ions and annealing in UHV. This reducing treatment makes the sample bulk an n-type semiconductor. To form the (1 × 1) termination, the surface is reoxidized, effectively removing the near-surface donors (likely Fe interstitials), resulting in upward band bending. This effect could be useful for photoelectrochemical water splitting since the local field will separate photoinduced electrons and holes and drive holes toward the surface.
The XPS data obtained from the (2 × 1) surface clearly show that the reconstruction involves the reduction of surface iron cations to Fe2+, in line with previous studies.27 In contrast to the (1 × 1) surface, the atomic-scale structure is not immediately apparent from the STM images (Figure 7), but the position of the relatively large protrusions corresponds well to the outermost oxygen atoms of the “alternating trench” model. STM simulations based on this model resemble the experimental data, but the shape of the protrusions differs slightly because the simulations include a contribution from the underlying Fe atoms. Based on the STM simulations, the features on the (2 × 1) surface are expected to line up with rows of oxygen in the (1 × 1) termination, which is in good agreement with the arrangement we find in Figure 8.
Further evidence in favor of the alternating trench model comes from the nc-AFM images. The images acquired at small tip–sample distances are qualitatively similar for the (1 × 1) and (2 × 1) surfaces (Figure 9), suggesting that the surface Fe sublattice remains intact in the reconstruction. Moreover, the small lateral displacement in the registry of neighboring zigzag rows along [11̅01̅] is a feature of the “alternating trench” model, arising because the Fe atoms in the wide and narrow trenches relax differently due to their differing coordination environment. The tip interacts much more strongly with the (2 × 1) surface, consistent with the idea that this surface contains reactive Fe2+ cations. On the other hand, it is difficult to know if the bright contrast observed in Figure 9(d) indicates the positions of surface oxygen atoms or simply the gap between the Fe cations with the least attraction. The strong attraction and poorly localized areas of least attraction suggest the latter scenario.
In general, it seems somewhat counterintuitive that the reduced (2 × 1) reconstruction should be based on oxygen vacancies, given that previous theoretical works have shown that the formation energy of an Fe interstitial is lower than that of an oxygen vacancy in bulk hematite.38 Indeed, iron oxides generally tend to deal with stoichiometric variation by varying the cation lattice, with the close-packed oxygen sublattice remaining intact,38,70 and we have recently shown that the (√2 × √2)R45° reconstruction on Fe3O4(001) is based on a subsurface array of Fe vacancies and interstitials.67 Nevertheless, several (2 × 1) models based on subsurface Fe atoms in octahedral interstitial sites were tested and found to be extremely unstable compared to models based on surface oxygen vacancies.
One of the most convincing factors in favor of the alternating-trench model presented here is that the atomistic thermodynamics calculations predict it to be the most stable surface at an O2 partial pressure below ≈5 × 10–10 mbar at 1000K. Moreover, the predicted transition to the alternating trench model occurs at an oxygen chemical potential of −2.4 eV, which corresponds well with the preparation conditions used to create the (2 × 1) surface in the experiments. Interestingly, the surface phase diagram shown in Figure 10 predicts stability of a third phase with only one oxygen vacancy per (2 × 1) unit cell in a narrow range around −2.35 eV oxygen chemical potential. Since the calculated stability region is so small, and substantial error bars exist in DFT calculations, it is difficult to conclude if this additional phase is, in fact, realized. A relaxed model of this termination is nevertheless shown in Figure 11(c,d). It is not possible to discount the presence of this phase at the (1 × 1)-to-(2 × 1) phase boundaries (Figure 8) since no structure is imaged there. However, since nucleation of the alternating-trench phase appears to be difficult, probably reducing conditions are needed for its formation. It is therefore possible that the one-vacancy phase, even if it should be stable in theory, is never observed due to slow transformation kinetics in its stability range.
Determination of a reliable structural model is the necessary first step toward atomic-scale studies of adsorption, surface chemistry, and (photo)electrochemistry on α-Fe2O3 surfaces. The bulk-truncated nature of the α-Fe2O3(11̅02)-(1 × 1) surface is ideal because it is simple and can easily be prepared in UHV. It will be interesting to see if the UHV-prepared surface is stable in an aqueous environment and how it compares to previous studies of α-Fe2O3 in water. With different types of preparation, such as chemical etching, hydroxylated surface models with missing cations are also reported to be stable in these conditions.32,71−73
The structure proposed for the (2 × 1) model is consistent with all data presented here but certainly requires confirmation by a quantitative structural technique such as surface X-ray diffraction. The possibility to cycle reproducibly between the oxidized and reduced surfaces is ideal to study the impact of Fe2+ cations on surface reactivity. In closing, we note that a (2 × 1) reconstruction has also been observed on the r-cut surface of α-Al2O3, which also has the corundum structure.74,75 It is possible that a similar alternating trench structure might be present there.
Conclusions
The α-Fe2O3(11̅02) surface was successfully imaged with both STM and nc-AFM and studied with LEED, XPS, UPS, and DFT+U calculations. The results support a stoichiometric bulk-termination model for the (1 × 1) surface, but no previously suggested reconstruction explains the STM images acquired on the (2 × 1) terminated surface. A new model for the (2 × 1) reconstruction is proposed in which two oxygen atoms are removed per (2 × 1) unit cell. The proposed model is in good agreement with all existing experimental data and is predicted by DFT+U to be energetically favorable at low oxygen chemical potential.
Acknowledgments
The authors gratefully acknowledge funding through projects from the Austrian Science Fund FWF (START-Prize Y 847-N20 (FK, JH, GSP)), the Special Research Project “Functional Oxide Surfaces and Interfaces” FOXSI (F45 (M Schmid & UD)), the Special Research Project “Vienna Computational Materials Labaratory” ViCoM (F41 (PB)), the European Research Council (UD: ERC-2011-ADG_20110209 Advanced Grant “OxideSurfaces”), the Doctoral College Solids4Fun (MB), and the Doctoral College TU-D (ZJ). The computational results presented have been achieved using the Vienna Scientific Cluster (VSC).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.7b10515.
Contains Figure S1, showing larger-area STM images, and Figure S2, presenting energetically unfavorable (2 × 1) reconstruction models (PDF)
Structure file of the α-Fe2O3(11̅02)-(1 × 1) surface in its minimum energy configuration (CIF)
Structure file of the α-Fe2O3(11̅02)-(2 × 1) alternating trench reconstruction model (CIF)
The authors declare no competing financial interest.
Supplementary Material
References
- Parkinson G. S. Iron Oxide Surfaces. Surf. Sci. Rep. 2016, 71, 272–365. 10.1016/j.surfrep.2016.02.001. [DOI] [Google Scholar]
- Sivula K.; Le Formal F.; Grätzel M. Solar Water Splitting: Progress Using Hematite (α-Fe2O3) Photoelectrodes. ChemSusChem 2011, 4, 432–449. 10.1002/cssc.201000416. [DOI] [PubMed] [Google Scholar]
- Iandolo B.; Wickman B.; Zorić I.; Hellman A. The Rise of Hematite: Origin and Strategies to Reduce the High Onset Potential for the Oxygen Evolution Reaction. J. Mater. Chem. A 2015, 3, 16896–16912. 10.1039/C5TA03362D. [DOI] [Google Scholar]
- Tamirat A. G.; Rick J.; Dubale A. A.; Su W.-N.; Hwang B.-J. Using Hematite for Photoelectrochemical Water Splitting: A Review of Current Progress and Challenges. Nanoscale Horiz. 2016, 1, 243–267. 10.1039/C5NH00098J. [DOI] [PubMed] [Google Scholar]
- Marusak L. A.; Messier R.; White W. B. Optical Absorption Spectrum of Hematite, α-Fe2O3 near IR to UV. J. Phys. Chem. Solids 1980, 41, 981–984. 10.1016/0022-3697(80)90105-5. [DOI] [Google Scholar]
- Cherepy N. J.; Liston D. B.; Lovejoy J. A.; Deng H.; Zhang J. Z. Ultrafast Studies of Photoexcited Electron Dynamics in γ- and α-Fe2O3 Semiconductor Nanoparticles. J. Phys. Chem. B 1998, 102, 770–776. 10.1021/jp973149e. [DOI] [Google Scholar]
- Launay J.; Horowitz G. Crystal Growth and Photoelectrochemical Study of Zr-Doped α-Fe2O3 Single Crystal. J. Cryst. Growth 1982, 57, 118–124. 10.1016/0022-0248(82)90257-3. [DOI] [Google Scholar]
- Warnes B.; Aplan F.; Simkovich G. Electrical Conductivity and Seebeck Voltage of Fe2O3, Pure and Doped, as a Function of Temperature and Oxygen Pressure. Solid State Ionics 1984, 12, 271–276. 10.1016/0167-2738(84)90156-5. [DOI] [Google Scholar]
- Klahr B.; Gimenez S.; Fabregat-Santiago F.; Bisquert J.; Hamann T. W. Electrochemical and Photoelectrochemical Investigation of Water Oxidation with Hematite Electrodes. Energy Environ. Sci. 2012, 5, 7626–7636. 10.1039/c2ee21414h. [DOI] [Google Scholar]
- Klahr B.; Gimenez S.; Fabregat-Santiago F.; Hamann T.; Bisquert J. Water Oxidation at Hematite Photoelectrodes: The Role of Surface States. J. Am. Chem. Soc. 2012, 134, 4294–4302. 10.1021/ja210755h. [DOI] [PubMed] [Google Scholar]
- Rioult M.; Stanescu D.; Fonda E.; Barbier A.; Magnan H. Oxygen Vacancies Engineering of Iron Oxides Films for Solar Water Splitting. J. Phys. Chem. C 2016, 120, 7482–7490. 10.1021/acs.jpcc.6b00552. [DOI] [Google Scholar]
- Magnan H.; Stanescu D.; Rioult M.; Fonda E.; Barbier A. Enhanced Photoanode Properties of Epitaxial Ti Doped α-Fe2O3(0001) Thin Films. Appl. Phys. Lett. 2012, 101, 133908. 10.1063/1.4755763. [DOI] [Google Scholar]
- Rioult M.; Belkhou R.; Magnan H.; Stanescu D.; Stanescu S.; Maccherozzi F.; Rountree C.; Barbier A. Local Electronic Structure and Photoelectrochemical Activity of Partial Chemically Etched Ti-Doped Hematite. Surf. Sci. 2015, 641, 310–313. 10.1016/j.susc.2015.01.002. [DOI] [Google Scholar]
- Zhong D. K.; Sun J.; Inumaru H.; Gamelin D. R. Solar Water Oxidation by Composite Catalyst/α-Fe2O3 Photoanodes. J. Am. Chem. Soc. 2009, 131, 6086–6087. 10.1021/ja9016478. [DOI] [PubMed] [Google Scholar]
- Woodruff D. P. Quantitative Structural Studies of Corundum and Rocksalt Oxide Surfaces. Chem. Rev. 2013, 113, 3863–3886. 10.1021/cr3002998. [DOI] [PubMed] [Google Scholar]
- Kuhlenbeck H.; Shaikhutdinov S.; Freund H.-J. Well-Ordered Transition Metal Oxide Layers in Model Catalysis – a Series of Case Studies. Chem. Rev. 2013, 113, 3986–4034. 10.1021/cr300312n. [DOI] [PubMed] [Google Scholar]
- Lad R. J.; Henrich V. E. Structure of α-Fe2O3 Single Crystal Surfaces Following Ar+ Ion Bombardment and Annealing in O2. Surf. Sci. 1988, 193, 81–93. 10.1016/0039-6028(88)90324-X. [DOI] [Google Scholar]
- Kurtz R. L.; Henrich V. E. Geometric Structure of the α-Fe2O3(001) Surface: A LEED and XPS Study. Surf. Sci. 1983, 129, 345–354. 10.1016/0039-6028(83)90185-1. [DOI] [Google Scholar]
- Condon N.; Murray P.; Leibsle F.; Thornton G.; Lennie A.; Vaughan D. Fe3O4(111) Termination of α-Fe2O3(0001). Surf. Sci. 1994, 310, L609–L613. 10.1016/0039-6028(94)91360-9. [DOI] [Google Scholar]
- Condon N. G.; Leibsle F. M.; Lennie A. R.; Murray P. W.; Vaughan D. J.; Thornton G. Biphase Ordering of Iron Oxide Surfaces. Phys. Rev. Lett. 1995, 75, 1961–1964. 10.1103/PhysRevLett.75.1961. [DOI] [PubMed] [Google Scholar]
- Condon N.; Leibsle F.; Lennie A.; Murray P.; Parker T.; Vaughan D.; Thornton G. Scanning Tunnelling Microscopy Studies of α-Fe2O3(0001). Surf. Sci. 1998, 397, 278–287. 10.1016/S0039-6028(97)00744-9. [DOI] [Google Scholar]
- Lanier C. H.; Chiaramonti A. N.; Marks L. D.; Poeppelmeier K. R. The Fe3O4 Origin of the “Biphase” Reconstruction on α-Fe2O3(0001). Surf. Sci. 2009, 603, 2574–2579. 10.1016/j.susc.2009.06.006. [DOI] [Google Scholar]
- Tang Y.; Qin H.; Wu K.; Guo Q.; Guo J. The Reduction and Oxidation of Fe2O3(0001) Surface Investigated by Scanning Tunneling Microscopy. Surf. Sci. 2013, 609, 67–72. 10.1016/j.susc.2012.11.005. [DOI] [Google Scholar]
- Cornell R. M.; Schwertmann U.. The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses; John Wiley & Sons, 2003. [Google Scholar]
- Gautier-Soyer M.; Pollak M.; Henriot M.; Guittet M. The (1 × 2) Reconstruction of the α-Fe2O3(1̅012) Surface. Surf. Sci. 1996, 352, 112–116. 10.1016/0039-6028(95)01109-9. [DOI] [Google Scholar]
- Henderson M. A.; Joyce S. A.; Rustad J. R. Interaction of Water with the (1 × 1) and (2 × 1) Surfaces of α-Fe2O3(012). Surf. Sci. 1998, 417, 66–81. 10.1016/S0039-6028(98)00662-1. [DOI] [Google Scholar]
- Henderson M. A. Insights into the (1 × 1)-to-(2 × 1) Phase Transition of the α-Fe2O3(012) Surface Using EELS, LEED and Water TPD. Surf. Sci. 2002, 515, 253–262. 10.1016/S0039-6028(02)01917-9. [DOI] [Google Scholar]
- Henderson M. A. Surface Stabilization of Organics on Hematite by Conversion from Terminal to Bridging Adsorption Structures. Geochim. Cosmochim. Acta 2003, 67, 1055–1063. 10.1016/S0016-7037(02)00884-0. [DOI] [Google Scholar]
- Henderson M. A. Low Temperature Oxidation of Fe2+ Surface Sites on the (2 × 1) Reconstructed Surface of α-Fe2O3 (011̅2). Surf. Sci. 2010, 604, 1197–1201. 10.1016/j.susc.2010.04.002. [DOI] [Google Scholar]
- Dzade N. Y.; Roldan A.; de Leeuw N. H. A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces. Minerals (Basel, Switz.) 2014, 4, 89–115. 10.3390/min4010089. [DOI] [Google Scholar]
- Aboud S.; Wilcox J.; Brown G. E. Jr Density Functional Theory Investigation of the Interaction of Water with α–Al2O3 and α–Fe2O3(11̅02) Surfaces: Implications for Surface Reactivity. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 125407. 10.1103/PhysRevB.83.125407. [DOI] [Google Scholar]
- Lo C. S.; Tanwar K. S.; Chaka A. M.; Trainor T. P. Density Functional Theory Study of the Clean and Hydrated Hematite (11̅02). Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 075425. 10.1103/PhysRevB.75.075425. [DOI] [Google Scholar]
- Wang J.; Rustad J. R. A Simple Model for the Effect of Hydration on the Distribution of Ferrous Iron at Reduced Hematite (012) Surfaces. Geochim. Cosmochim. Acta 2006, 70, 5285–5292. 10.1016/j.gca.2006.08.022. [DOI] [Google Scholar]
- Pavelec J.; Hulva J.; Halwidl D.; Bliem R.; Gamba O.; Jakub Z.; Brunbauer F.; Schmid M.; Diebold U.; Parkinson G. S. A Multi-Technique Study of CO2 Adsorption on Fe3O4 Magnetite. J. Chem. Phys. 2017, 146, 014701. 10.1063/1.4973241. [DOI] [PubMed] [Google Scholar]
- Setvin M.; Javorsky J.; Turcinkova D.; Matolinova I.; Sobotik P.; Kocan P.; Ostadal I. Ultrasharp Tungsten Tips — Characterization and Nondestructive Cleaning. Ultramicroscopy 2012, 113, 152–157. 10.1016/j.ultramic.2011.10.005. [DOI] [Google Scholar]
- Choi J.; Mayr-Schmölzer W.; Mittendorfer F.; Redinger J.; Diebold U.; Schmid M. The Growth of Ultra-Thin Zirconia Films on Pd3Zr(0001). J. Phys.: Condens. Matter 2014, 26, 225003. 10.1088/0953-8984/26/22/225003. [DOI] [PubMed] [Google Scholar]
- Lewandowski M.; Groot I. M.; Qin Z.-H.; Ossowski T.; Pabisiak T.; Kiejna A.; Pavlovska A.; Shaikhutdinov S.; Freund H.-J.; Bauer E. Nanoscale Patterns on Polar Oxide Surfaces. Chem. Mater. 2016, 28, 7433–7443. 10.1021/acs.chemmater.6b03040. [DOI] [Google Scholar]
- Lee J.; Han S. Thermodynamics of Native Point Defects in α-Fe2O3: An Ab Initio Study. Phys. Chem. Chem. Phys. 2013, 15, 18906–18914. 10.1039/c3cp53311e. [DOI] [PubMed] [Google Scholar]
- Rosso K. M.; Smith D. M.; Dupuis M. An Ab Initio Model of Electron Transport in Hematite (α-Fe2O3) Basal Planes. J. Chem. Phys. 2003, 118, 6455–6466. 10.1063/1.1558534. [DOI] [Google Scholar]
- Blaha P.; Schwarz K.; Madsen G.; Kvasnicka D.; Luitz J.. WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties; Vienna University of Technology, 2001. [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
- Ovcharenko R.; Voloshina E.; Sauer J. Water Adsorption and O-Defect Formation on Fe2O3(0001) Surfaces. Phys. Chem. Chem. Phys. 2016, 18, 25560–25568. 10.1039/C6CP05313K. [DOI] [PubMed] [Google Scholar]
- Anisimov V. I.; Zaanen J.; Andersen O. K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 44, 943. 10.1103/PhysRevB.44.943. [DOI] [PubMed] [Google Scholar]
- Finger L. W.; Hazen R. M. Crystal Structure and Isothermal Compression of Fe2O3, Cr2O3, and V2O3 to 50 kbars. J. Appl. Phys. 1980, 51, 5362–5367. 10.1063/1.327451. [DOI] [Google Scholar]
- Sandratskii L.; Kübler J. First-Principles LSDF Study of Weak Ferromagnetism in Fe2O3. EPL 1996, 33, 447. 10.1209/epl/i1996-00360-9. [DOI] [Google Scholar]
- Zboril R.; Mashlan M.; Petridis D. Iron (III) Oxides from Thermal Processes Synthesis, Structural and Magnetic Properties, Mössbauer Spectroscopy Characterization, and Applications. Chem. Mater. 2002, 14, 969–982. 10.1021/cm0111074. [DOI] [Google Scholar]
- Searle C.; Dean G. Temperature and Field Dependence of the Weak Ferromagnetic Moment of Hematite. Phys. Rev. B 1970, 1, 4337. 10.1103/PhysRevB.1.4337. [DOI] [Google Scholar]
- Levinson L. M. Temperature Dependence of the Weak Ferromagnetic Moment of Hematite. Phys. Rev. B 1971, 3, 3965. 10.1103/PhysRevB.3.3965. [DOI] [Google Scholar]
- Tersoff J.; Hamann D.. Theory of the Scanning Tunneling Microscope. In Scanning Tunneling Microscopy; Springer: 1985; pp 59–67. [Google Scholar]
- Sun J.; Ruzsinszky A.; Perdew J. P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
- Reuter K.; Scheffler M. Composition, Structure, and Stability of RuO2(110) as a Function of Oxygen Pressure. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 65, 035406. 10.1103/PhysRevB.65.035406. [DOI] [Google Scholar]
- Grosvenor A.; Kobe B.; Biesinger M.; McIntyre N. Investigation of Multiplet Splitting of Fe 2p XPS Spectra and Bonding in Iron Compounds. Surf. Interface Anal. 2004, 36, 1564–1574. 10.1002/sia.1984. [DOI] [Google Scholar]
- Weiss W.; Ranke W. Surface Chemistry and Catalysis on Well-Defined Epitaxial Iron-Oxide Layers. Prog. Surf. Sci. 2002, 70, 1–151. 10.1016/S0079-6816(01)00056-9. [DOI] [Google Scholar]
- Smekal W.; Werner W. S.; Powell C. J. Simulation of Electron Spectra for Surface Analysis (SESSA): A Novel Software Tool for Quantitative Auger-Electron Spectroscopy and X-Ray Photoelectron Spectroscopy. Surf. Interface Anal. 2005, 37, 1059–1067. 10.1002/sia.2097. [DOI] [Google Scholar]
- Werner W. S.; Smekal W.; Powell C. J.. NIST Database for the Simulation of Electron Spectra for Surface Analysis (SESSA). Version: 2.1, 2016. [Google Scholar]
- Zimmermann R.; Steiner P.; Claessen R.; Reinert F.; Hüfner S.; Blaha P.; Dufek P. Electronic Structure of 3d-Transition-Metal Oxides: On-Site Coulomb Repulsion Versus Covalency. J. Phys.: Condens. Matter 1999, 11, 1657. 10.1088/0953-8984/11/7/002. [DOI] [Google Scholar]
- Parkinson G. S.; Mulakaluri N.; Losovyj Y.; Jacobson P.; Pentcheva R.; Diebold U. Semiconductor-Half Metal Transition at the Fe3O4(001) Surface Upon Hydrogen Adsorption. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 125413. 10.1103/PhysRevB.82.125413. [DOI] [Google Scholar]
- Sugimoto Y.; Pou P.; Abe M.; Jelinek P.; Perez R.; Morita S.; Custance O. Chemical Identification of Individual Surface Atoms by Atomic Force Microscopy. Nature 2007, 446, 64–67. 10.1038/nature05530. [DOI] [PubMed] [Google Scholar]
- Gross L.; Schuler B.; Mohn F.; Moll N.; Pavliček N.; Steurer W.; Scivetti I.; Kotsis K.; Persson M.; Meyer G. Investigating Atomic Contrast in Atomic Force Microscopy and Kelvin Probe Force Microscopy on Ionic Systems Using Functionalized Tips. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 155455. 10.1103/PhysRevB.90.155455. [DOI] [Google Scholar]
- Enevoldsen G. H.; Pinto H. P.; Foster A. S.; Jensen M. C. R.; Kühnle A.; Reichling M.; Hofer W. A.; Lauritsen J. V.; Besenbacher F. Detailed Scanning Probe Microscopy Tip Models Determined from Simultaneous Atom-Resolved AFM and STM Studies of the TiO2(110) Surface. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 045416. 10.1103/PhysRevB.78.045416. [DOI] [Google Scholar]
- Enevoldsen G. H.; Foster A. S.; Christensen M. C.; Lauritsen J. V.; Besenbacher F. Noncontact Atomic Force Microscopy Studies of Vacancies and Hydroxyls of TiO2(110): Experiments and Atomistic Simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 205415. 10.1103/PhysRevB.76.205415. [DOI] [Google Scholar]
- Yurtsever A.; Fernandez-Torre D.; Gonzalez C.; Jelinek P.; Pou P.; Sugimoto Y.; Abe M.; Perez R.; Morita S. Understanding Image Contrast Formation in TiO2 with Force Spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 125416. 10.1103/PhysRevB.85.125416. [DOI] [Google Scholar]
- Gross L.; Mohn F.; Moll N.; Liljeroth P.; Meyer G. The Chemical Structure of a Molecule Resolved by Atomic Force Microscopy. Science 2009, 325, 1110–1114. 10.1126/science.1176210. [DOI] [PubMed] [Google Scholar]
- Hapala P.; Kichin G.; Wagner C.; Tautz F. S.; Temirov R.; Jelínek P. Mechanism of High-Resolution STM/AFM Imaging with Functionalized Tips. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 085421. 10.1103/PhysRevB.90.085421. [DOI] [Google Scholar]
- Lauritsen J. V.; Reichling M. Atomic Resolution Non-Contact Atomic Force Microscopy of Clean Metal Oxide Surfaces. J. Phys.: Condens. Matter 2010, 22, 263001. 10.1088/0953-8984/22/26/263001. [DOI] [PubMed] [Google Scholar]
- Rasmussen M. K.; Foster A. S.; Canova F. F.; Hinnemann B.; Helveg S.; Meinander K.; Besenbacher F.; Lauritsen J. V. Noncontact Atomic Force Microscopy Imaging of Atomic Structure and Cation Defects of the Polar MgAl2O4(100) Surface: Experiments and First-Principles Simulations. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 10.1103/PhysRevB.84.235419. [DOI] [Google Scholar]
- Bliem R.; McDermott E.; Ferstl P.; Setvin M.; Gamba O.; Pavelec J.; Schneider M.; Schmid M.; Diebold U.; Blaha P.; et al. Subsurface Cation Vacancy Stabilization of the Magnetite (001). Science 2014, 346, 1215–1218. 10.1126/science.1260556. [DOI] [PubMed] [Google Scholar]
- Jiang H.; Blaha P. GW with Linearized Augmented Plane Waves Extended by High-Energy Local Orbitals. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 115203. 10.1103/PhysRevB.93.115203. [DOI] [Google Scholar]
- Tasker P. The Stability of Ionic Crystal Surfaces. J. Phys. C: Solid State Phys. 1979, 12, 4977. 10.1088/0022-3719/12/22/036. [DOI] [Google Scholar]
- Setvin M.; Wagner M.; Schmid M.; Parkinson G. S.; Diebold U. Surface Point Defects on Bulk Oxides: Atomically-Resolved Scanning Probe Microscopy. Chem. Soc. Rev. 2017, 46, 1772–1784. 10.1039/C7CS00076F. [DOI] [PubMed] [Google Scholar]
- Tanwar K. S.; Lo C. S.; Eng P. J.; Catalano J. G.; Walko D. A.; Brown G. E.; Waychunas G. A.; Chaka A. M.; Trainor T. P. Surface Diffraction Study of the Hydrated Hematite Surface. Surf. Sci. 2007, 601, 460–474. 10.1016/j.susc.2006.10.021. [DOI] [Google Scholar]
- Tanwar K. S.; Catalano J. G.; Petitto S. C.; Ghose S. K.; Eng P. J.; Trainor T. P. Hydrated α-Fe2O3(11̅02) Surface Structure: Role of Surface Preparation. Surf. Sci. 2007, 601, L59–L64. 10.1016/j.susc.2007.04.115. [DOI] [Google Scholar]
- McBriarty M. E.; von Rudorff G. F.; Stubbs J. E.; Eng P. J.; Blumberger J.; Rosso K. M. Dynamic Stabilization of Metal Oxide–Water Interfaces. J. Am. Chem. Soc. 2017, 139, 2581–2584. 10.1021/jacs.6b13096. [DOI] [PubMed] [Google Scholar]
- Gillet E.; Ealet B. Characterization of Sapphire Surfaces by Electron Energy-Loss Spectroscopy. Surf. Sci. 1992, 273, 427–436. 10.1016/0039-6028(92)90079-L. [DOI] [Google Scholar]
- Schildbach M.; Hamza A. Clean and Water-Covered Sapphire (11̅02) Surfaces: Structure and Laser-Induced Desorption. Surf. Sci. 1993, 282, 306–322. 10.1016/0039-6028(93)90936-E. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.