Feasibility and Validation of 4-D Pulse Wave Imaging in phantoms and in vivo

Abstract

Pulse wave Imaging (PWI) is a noninvasive technique for tracking the propagation of the pulse wave along the arterial wall. 3-D ultrasound imaging would aid in objectively estimating the Pulse Wave Velocity (PWV) vector. This study aims to introduce a novel PWV estimation method along the propagation direction, validate it in phantoms and test its feasibility in vivo. A silicone vessel phantom consisting of a stiff and a soft segment along the longitudinal axis and and a silicone vessel with a plaque were constructed. A 2-D array with a center frequency of 2.5 MHz was used. Propagation was successfully visualized in 3-D in each phantom and in vivo in six healthy subjects. In three of the healthy subjects results were compared against conventional PWI using a linear array. PWVs were estimated in the stiff (3.42 ± 0.23 m · s⁻¹) and soft (2.41 ± 0.07 m · s⁻¹) phantom segments. Good agreement was found with the corresponding static testing values (stiff: 3.41 m · s⁻¹, soft: 2.48 m · s⁻¹). PWI-derived vessel compliance values were validated with dynamic testing. Comprehensive views of pulse propagation in the plaque phantom were generated and compared with conventional PWI acquisitions. Good agreement was found in vivo between the results of 4-D PWI (4.80 ± 1.32 m · s⁻¹) and conventional PWI (4.28±1.20 m · s⁻¹) (n = 3). PWVs derived for all of the healthy subjects (n = 6) were within the physiological range. Thus, 4-D PWI was successfully validated in phantoms and used to image the pulse wave propagation in normal human subjects in vivo.

I. Introduction

Arterial stiffness has been reported to be a good predictor of all-cause cardiovascular mortality [1], [2]. Furthermore, risk factors for vascular disease such as age, blood pressure, blood cholesterol and diabetes have been shown to correlate with arterial stiffness. Pulse Wave Velocity (PWV) is widely accepted as a clinical surrogate for arterial stiffness [3]. PWV measurements can be made noninvasively and are highly reproducible [4]. They have been demonstrated to have strong prognostic value for cardiovascular mortality, atherosclerotic vascular burden and target organ damage in the arterial circulation, especially among hypertensive patients [5]. Mechanically, the Young’s modulus of the arteries is related to the PWV through the modified Moens-Korteweg equation [3] as follows:

$$\mathit{PWV}=\sqrt{\frac{\mathit{Eh}}{2R\rho (1-{\upsilon }^2)}}$$ (1)

where E is the Young’s modulus of the arterial wall, h is the wall thickness, ρ is the blood density, R is the inner radius of the vessel and ν is the Poisson’s ratio (the latter partly compensates for the finite thickness of the wall, whereas the original Moens-Korteweg equation makes a thin wall assumption). However, by not having to make assumptions about the thickness of the wall or the vessel circumferential homogeneity, PWV can also be linked to arterial compliance (C) via the Bramwell-Hill equation:

$$\mathit{PWV}=\sqrt{\frac{A}{C\rho }}$$ (2)

where $C=\frac{\mathit{dA}}{\mathit{dP}}$, is the cross-sectional compliance, defined as the change in arterial cross-sectional luminal area dA due to a given change in arterial blood pressure dP and ρ is the blood density.

Currently, in most large-scale longitudinal clinical studies, PWV measurements are obtained noninvasively using applanation tonometry [5], [2], [6]. PWV is usually determined over the carotid-femoral region by dividing the total length of the propagation pathway over the measured propagation time of the pulse wave from the carotid to the femoral arteries. However, carotid-femoral PWV measurements present limitations due to errors in both distance and time-delay measurements. Furthermore, the measured PWV values provide a global estimate accross the entire aorta, thus ignoring spatial variations in arterial stiffness. To address this issue, several medical imaging-based methods have been previously developed for noninvasive measurements of regional PWV, mainly using MRI [7], [8], [9] and ultrasound methods [10], [11], [12], [13], [14], [15], [16].

Drawing inspiration from the seminal work of Meinders et al. [15] our group systematically developed Pulse Wave Imaging (PWI) as a noninvasive, ultrasound-based technique for tracking the propagation of pulse waves along the wall of major arteries at high spatial and temporal resolutions [17], [18], [19]. PWI has previously been optimized by our group with the introduction of piecewise PWI (pPWI), which allows imaging and tracking of the pulse wave propagation along a few mm of the arterial wall [20]. More recently, PWI was expanded using high-frame rate plane wave imaging [13], [16], [21]. Especially in [21], the technique was validated in a phantom setup and further improved by optimizing coherent compounding parameters in vivo. Furthermore, an inverse approach to estimate the spatially varying arterial PWVs and arterial compliance has been proposed [22]. This method maximized the information used from pulse wave propagation maps and showed promise in providing robust PWV estimates with minimal interference from wave reflections.

The PWI technique images the pulse wave propagation in two-dimensional, long-axis views of the arteries. However, using 2-D images to characterize a 3-D phenomenon has some limitations. More specifically, it is assumed that the propagation of the pulse wave is parallel to the imaging plane, an assumption that may lead to erroneous tracking of the pulse wave and ultimately PWV estimation, especially given the high level of tortuosity and branching of the arteries. Furthermore, given two-dimensional, longitudinal views of the arteries, isotropy of both the arterial wall displacements and the pulse wave propagation around the axis of the vessel is assumed. While this assumption could be acceptable in the case of homogeneous disease-free arterial walls, in atherosclerotic or aneurysmal walls, this may not be the case. Moreover, with a 2-D image of the artery, a significant and/or critical segment of the pathological tissue might remain outside of the imaging plane, thus impairing diagnosis.

Developing a three-dimensional imaging platform for PWI would alleviate the aforementioned limitations, with comprehensive views of the arterial walls and objective estimation of the full PWV vector, unaffected by inter- or intra-observer variability. Given the previously mentioned value of PWV in clinical research as an independent predictor of all-cause cardiovascular mortality [23], [2], [4] and atherosclerotic burden [24], [25] its accurate and objective estimation may provide a useful metric in the clinic. Challenges that conventional three-dimensional ultrasound imaging presents, such as increased computational cost and decreased frame-rates [26] have been recently addressed. More specifically, parallel implementation of processing algorithms using graphical processing units (GPUs) as well as the use of efficient 3-D viewing software have rendered the manipulation of large 3-D datasets easier. Furthermore, 3-D high frame rate imaging using plane and diverging waves has led to the acquisition of full 3-D volumes at kHz frame rates [27]. 3-D plane and diverging wave imaging has previously been utilized in imaging of the heart [27], in shear-wave imaging [28], in 3-D and 4-D Doppler imaging of blood vessels [29], [30] and more recently in 3-D quasi-static elastography [31] and in 3-D myocardial elastography in vivo [32].

Previous attempts to obtain elastographic information of arteries in 3-D include three-dimensional phase contrast MRI with flow sensitivity, enabling volumetric coverage and PWV estimation in the aorta even in the case of complex aortic shapes [8], [33]. Furthermore, 3-D strain images of atherosclerotic carotid artery models were produced by estimating the strains from multiple 2-D ultrasonic coherent compounded images and then employing post-acquisition alignment to produce a single 3-D volume [34], [35]. A similar approach was utilized in a simulation study where sparse array imaging was used to produce 3-D strain volumes of a healthy carotid artery [36]. In another study, the complete 3-D strain tensor was acquired by continuous pullback of an intravascular ultrasound catheter inside excised porcine carotid arteries while acquiring images at 30 frames per second [37]. While the aforementioned ultrasonic methods have showed promising results, post-acquisition registration of arterial image slices was employed.

Thus, the objective of this paper is to introduce a novel method of estimating the PWV along the path of the pulse wave propagation, validate it and demonstrate its advantages in silicone phantoms utilizing both static and dynamic testing and test its initial feasibility in healthy human carotid arteries in vivo. It should also be noted that this paper is an expansion upon a study first presented at the 2016 International Ultrasonics Symposium (Tours, France) [38].

II. Materials and Methods

A. 3-D Volume Acquisition

All 3-D imaging in this study was performed using a 16×16 2-D array (Sonic Concepts, Bothell, WA, USA) with a center frequency of 2.5 MHz and a bandwidth of 50%. The spacing of the transducer elements was 0.85 mm. A fully programmable ultrasound system with a sufficient number of channels to accommodate all of the array’s elements in both emission and receive was used to control the probe (Vantage 256, Verasonics, Kirkland, USA). Plane waves were emitted with the 256 elements firing simultaneously. More specifically, a single plane wave acquisition sequence was designed and implemented with plane waves emitted at a transmission angle of 0° (transmission direction being perpendicular to the face of the transducer) at a pulse repetition frequency of 2000 Hz. The imaging field of view corresponded to the 2-D aperture dimensions, i.e. 13.6 × 13.6 mm². A detailed investigation of the lateral resolution of the 2-D array used in the present study obtained with a single plane wave imaging acquisition sequence has been previously performed in a study by Papadacci et al. [39] with the 6 dB width of the point spread function (PSF) in both the x and y dimensions increasing from 1.5 to 3.5 mm as the depth increased from 10 to 60 mm. Subsequently, the received echoes were sampled at 10 MHz and stored in memory. Each acquisition lasted approximately 1 s at a volume rate of 2000 vol/s.

B. Silicone Phantom Design

Silicone gel was used to construct a phantom with a soft and a stiff segment along the longitudinal axis according to [22]. A two-part custom mold was 3-D-printed in polylactic acid (PLA) (MakerBot, New York, NY, USA). The mold is a 240 mm-long cylinder with an internal diameter of 14 mm. An 8 mm-diameter acrylic rod was used to create the lumen. The concentration of the material for the softer part of the phantom was 100% A341 silicone soft gel (Factor II, Lakeside, AZ, USA) and for the stiffer part was 70% A341 and 30% LSR-05 silicone elastomer (Factor II, Lakeside, AZ, USA). Two different concentrations of scatterers were used to distinguish the two parts on the ultrasonic images: 25 g · L⁻¹ of corn starch was added to the ‘soft’ material, 125 g · L⁻¹ was added to the ‘stiff’ material. After mixing, the solutions were vacuum-degassed to prevent the formation of air bubbles. The mold and the central rod were coated with petroleum jelly to ease the extraction of the phantom. The mold was held vertically and layers of soft material were introduced using a syringe to avoid coating the portion of the mold used for subsequent layers with thin layers of silicone. Subsequently, a stiff layer was poured after about an hour of curing time, and it naturally adhered strongly to the existing soft layer. The phantom was carefully extracted from the mold, and then mounted on fittings in a plastic container. A very soft silicone background was constructed from 40% A341 gel and 60% Xiameter PMX-200 100CS silicone fluid (Dow Corning, Midland, MI, USA). Fig. 1a is an image of the resulting phantom.

Fig. 1.

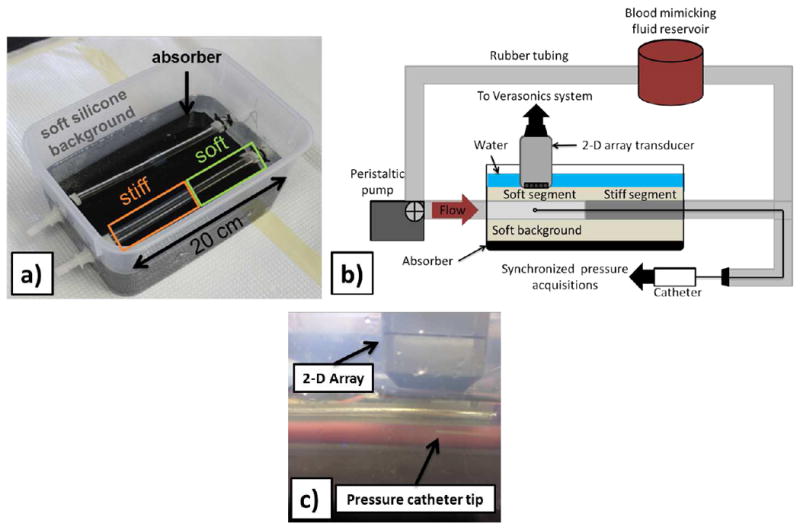
Experimental setup. a) Image of the phantom used in this study. b) Schematic of the experimental setup used in the phantom study with the pressure catheter inserted into the phantom’s lumen and the catheter tip placed beneath the 2-D array at the scanned location. Schematic depicts imaging of the soft phantom part. Imaging of the stiff part was performed by flipping the phantom so that the stiff part would be away from the fixed end of the phantom along the flow direction. c) Close-up of the 2-D array over the silicone phantom with the pressure catheter tip being within the volume of interest.

Static testing was performed similarly to the mechanical testing performed in [22]. As a result, specific points of the pressure-area relationship of the phantom vessel were recovered and used to provide a compliance estimate. The Bramwell-Hill equation (2) was then employed to produce an expected PWV value.

Subsequently, the phantom was connected via rubber tubes to a peristaltic pump, which generated pulse waves at a rate of approximately 2 Hz. Blood-mimicking fluid was used as the circulating fluid. The PWV was estimated under the dynamic conditions of variable pressure while the pump is functioning. It should be noted that care was taken when connecting the phantom to the peristaltic pump so that the imaged segment (soft, stiff) would be as far as possible from the fixed end of the phantom along the flow direction so as to ensure sufficient travel time for the forward wave before mixing with the reflection wave generated at the fixed end of the phantom.

The phantom was also dynamically tested under the aforementioned conditions and the validation was based on deriving the cross-sectional compliance. More specifically, a pressure catheter was introduced into the lumen. A digitizer (CompuScope 14200, Gage Applied Technologies, Lachine, QC, Canada) was used to synchronize the intraluminal pressure measurements with the 3-D ultrasound acquisitions. Care was taken to get the catheter tip within the imaged volume. Consequently, given the synchronized intraluminal pressure and vessel luminal area measurements obtained at the same location, the pressure-area (P – A) relationship of the vessel was recovered at high-frequency sampling and thus dynamic compliance estimates were obtained (C_Dyn = dA/dP ). These were compared to PWI compliance estimates produced via the Bramwell-Hill equation (C_PWI). A schematic of the experimental setup with the 2-D probe and the catheter inserted into the phantom is shown in Fig. 1b. A magnified image of the catheter tip beneath the 2-D array at the imaging location is shown in Fig. 1c.

In order to demonstrate the 3-D capability of the technique, as well as its advantage compared to conventional PWI, a second phantom was constructed with a plaque embedded on the antero-lateral wall. A homogeneous cylindrical phantom was created according to the previously described protocol used for the construction of the soft phantom segment. The plaque was subsequently added by injecting an extra quantity of the “stiff” material mix onto the vessel wall with a syringe. After about an hour of curing time, the generated plaque adhered to the surrounding vessel wall. Next, the phantom was mounted so that the plaque would appear at an antero-lateral location of the phantom wall as shown in Fig. 7a. The phantom segment containing the plaque was scanned with the 2-D array as well as with a standard linear array (L7-4, ATL Ultrasound, Bothell, WA, USA) with 128 elements, a central frequency of 5 MHz, 60% bandwidth and 294 μM of element spacing connected to the Verasonics research system. A conventional PWI acquisition was implemented with the linear array using plane wave imaging. More specifically, coherent compounding was used to achieve high frame rate with improved image signal-to-noise ratio (SNR) [40]. The acquisition sequence consisted of emitting 3 plane waves with the transmission angles being −5°, 5° and 0° at a pulse repetition frequency of 8333 Hz resulting to a frame rate of 2778 Hz. The received channel data were beamformed with a GPU-accelerated delay-and-sum technique and the pulse wave tracking was carried out with the conventional PWI methodology described in [20]. Two conventional PWI acquisitions were made with the plaque being inside and outside of the field of view.

Fig. 7.

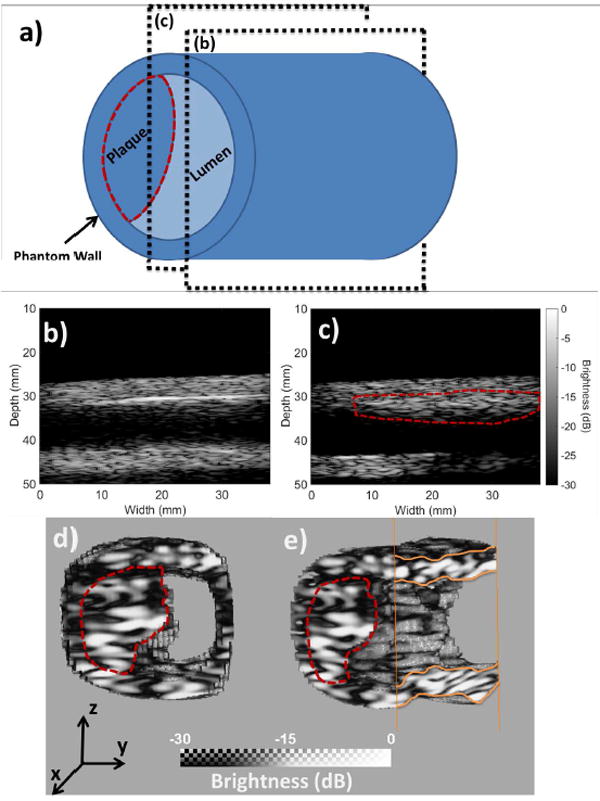
a) Schematic of the constructed plaque phantom. Planes (b) and (c) indicate the imaging planes of the conventional PWI acquisitions. b) B-mode image acquired by imaging along the (b) imaging plane. The plaque is outside of the field of view. c) B-mode image acquired by imaging along the (c) imaging plane. The plaque is within the field of view. d) Segmented vessel acquired with the 2-D array. Cross-sectional front view. e) Segmented vessel acquired with the 2-D array. It has been rotated around the z-axis and clipped in order to visualize the lumen of the phantom. In all of the cases, the plaque has been delineated with a perforated red line

C. In vivo feasibility study design

The right common carotid of six healthy subjects (n = 6) was imaged with the 2-D array previously described. The subjects were 24 to 35 years old, with an average age of 29.2 y.o. The experiments were conducted with the subject in a sitting position, freely breathing. First, the location of the carotid bifurcation was determined with 2-D ultrasound real-time B-mode imaging. The L7-4 linear probe connected to the Verasonics research system was used for the imaging. Subsequently, the 3-D acquisition was performed about 2 cm below the bifurcation. The sample size of six subjects was deemed sufficient to capture a wide range of physiological PWV values.

In order to validate the results, the previously described conventional PWI acquisition sequence was also used to scan the common carotids of three of the healthy subjects at approximately the same location. Subsequently, the resulting PWVs were compared to the ones obtained by 4-D PWI.

D. 4-D PWI Methodology

A parallel delay-and-sum-based algorithm was implemented and used to beamform the acquired channel data. The beamforming algorithm was implemented on the CUDA computing platform (CUDA 6.5, NVIDIA Corporation, Santa Clara, CA, USA). Subsequently, the sub-sample PWI axial wall velocities (v_PWI) were estimated by a GPU-accelerated 1-D normalized cross-correlation algorithm, which parallelizes the sum-table-based method introduced in [41]. Calculations were performed on a Tesla C2075 GPU (Nvidia, Santa Clara, CA, USA).

In order to produce PWI image sequences depicting the pulse wave propagation, the walls of the vessels were isolated in multiple cross-section slices and subsequently interpolated to produce a mask. The v_PWI corresponding to the mask’s borders were used to move the mask accordingly with the vessel’s motion over time. The isolated v_PWI were then color-coded and overlaid onto the corresponding segmented B-modes. 3-D rendering was performed with the Amira software (Visualization Sciences Group, Burlington, MA, USA). A schematic outlining the steps of the post-processing methodology is provided in Fig. 2.

Fig. 2.

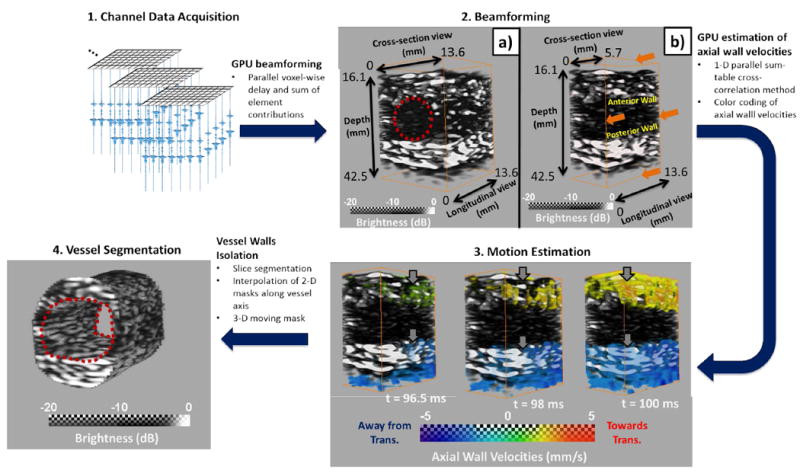
Illustration of the 4-D PWI post-processing methodology in the case of a silicone phantom. 1. Collection of channel data. 2. Beamforming of the channel data to generate sequences of 3-D RF volumes. 2a) Depicts a sample beamformed 3-D volume and 2b)shows a sub-volume by slicing close to the center of the imaged vessel. Red circle indicates the approximate position of the vessel 3. Sequence of 4-D PWI axial wall velocity (V_PWI) volumes indicating the pulse wave propagation. Red indicates motion towards the transducer (top) and blue indicates motion away from it (bottom). Grey arrows indicate the progression of the pulse wave propagation. 4. Segmented vessel.

Points on the anterior wall were manually selected at multiple cross-section slices of the vessel and subsequently interpolated in order to generate a 32 × 32 point grid. The v_PWI at each point of the grid were extracted and plotted as a function of time, thus generating a 3-D spatio-temporal map depicting the directional propagation of the pulse wave. To ensure that the selected grid points correspond to wall locations and more specifically to regions showing adequate signal to noise ratio (SNR), where the quality of the axial wall velocities is expected to be satisfactory, they were selected in regions of the top and bottom walls that exhibited sufficient echogenicity. More specifically, the points of the each walls grid were selected in regions of the B-mode volumes that exhibited a brightness of at least -6 dB (approximately 0.5 of the highest brightness amplitude). Thus, noisy velocities and motion artifacts were mostly avoided. Finally, it should be noted that the lateral walls were also avoided when selecting the points for the anterior and posterior wall grids due to the decreased values and SNR of the v_PWI. Thus, these grids corresponded to broad sections of the anterior and posterior walls where the axial wall velocities were expected to be of higher quality. In cases where there was significant rigid motion, the spatio-temporal maps created for each of the anterior and the posterior walls were subtracted in order to eliminate any potential rigid motion interference and keep only the distension wave.

Subsequently, to maintain consistency with the 2-D case, the 50% upstroke points were used as the pulse wave tracking feature. The 50% upstroke was defined as the time-point, at which the v_PWI was closest in value to the average between the foot and the peak of the v_PWI at each point of the wall grid. The choice of this tracking feature is justified because the early wavefront is less affected by the generated reflected waves [3] and also because previous studies have shown that it is the most robust compared to alternative tracking features (foot, 25% upstroke, 75% upstroke) [42]. The inverse of the gradient of the regression plane fitted between the 50% upstroke arrival time and the point location yielded the PWV along the direction of the pulse wave propagation. A schematic of the methodology of 4-D PWI is shown in Fig. 3.

Fig. 3.

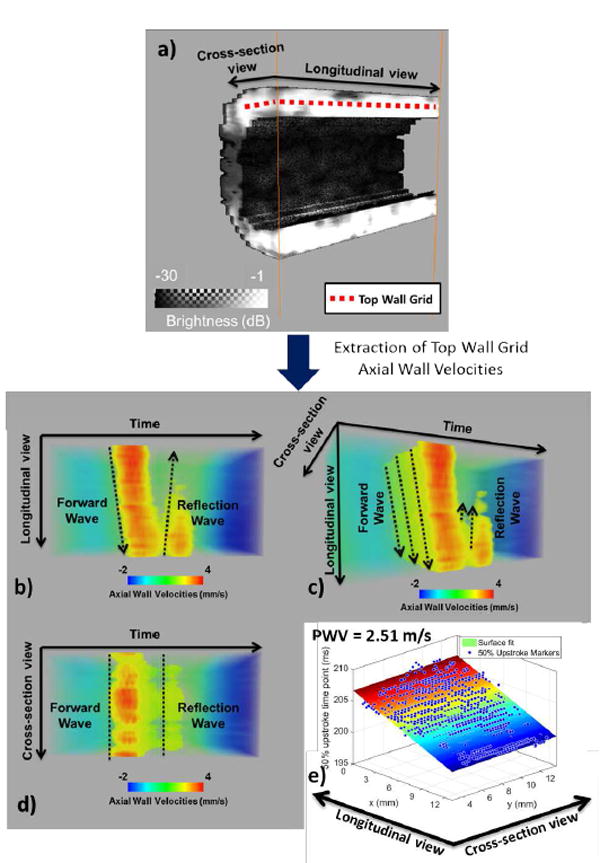
Estimation of PWV in 3-D. a) illustration of the top wall grid overlaid onto the anterior wall cross-sectional and longitudinal section views b), c), d) different views of the 3-D spatio-temporal map e) Estimated 50% upstroke markers and corresponding plane fit. The estimated PWV value is shown in the upper left corner.

III. Results

A. Silicone Phantom Study

Figs. 4a and 4e show segmented 3-D B-mode images of the walls of the soft and the stiff segments of the phantom. Subsequently, the PWI images (Figs.4 b, c and d) show the propagation of a pulse wave in a longitudinal section the soft segment. The propagation is denoted by solid red arrows. Red and blue indicate wall motion towards and away from the 2-D array, respectively. Figs. 4f, g and h show the propagation for the case of the stiff segment.

Fig. 4.

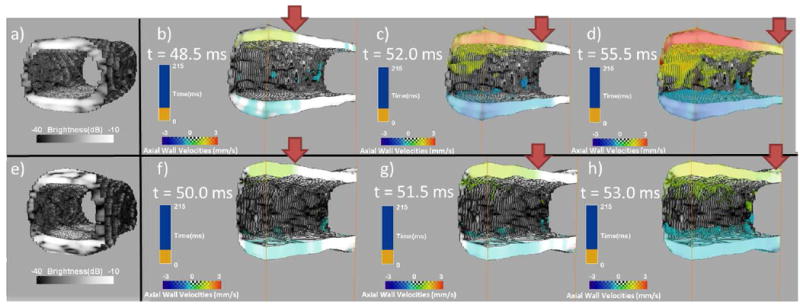
a) Segmented B-mode of the soft part of the phantom, b), c), d) PWI pulse wave propagation image sequence for the soft part, e) Segmented B-mode of the stiff part of the phantom, f), g), h) PWI pulse wave propagation image sequence for the stiff part. The solid red arrows denote the pulse wavefront.

Figs. 5a and 4b depict the 3-D spatio-temporal maps in the cases of a soft and a stiff segment respectively. Figs. 5 b and d show the 50% upstroke markers at their corresponding locations overlaid onto the plane regression that leads to the PWV measurement. The magnitude of each PWV is shown next to the respective surface fitting plot.

Fig. 5.

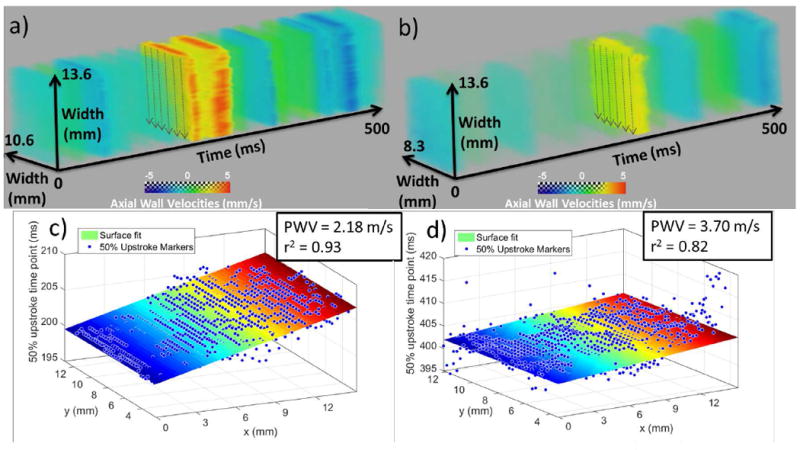
3-D PWI spatio-temporal plots and the corresponding 50% upstroke markers with the plane regression and PWV estimation in the case of a), b) soft segment and c), d) stiff segment of the phantom. The soft segment measurement was obtained from the dynamic testing experiment and the stiff segment measurement was obtained from the static testing experiment.

PWV measurements made for three different cycles (n = 3) in each phantom segment are shown in Table I. The estimated static PWVs are also shown for comparison.

TABLE I.

PWV results (n=3 cycles)

	Soft Segment	Stiff Segment
PWVPWI(m · s−1)	2.41 ± 0.07	3.42 ± 0.23
r2	0.76 ± 0.04	0.72 ± 0.08
PWVstatic(m · s−1)	2.49	3.41

A B-mode slice of the phantom with the catheter in view inside the lumen is depicted in Fig. 6a. The simultaneously acquired vessel diameter and pressure waveforms are depicted in Fig. 6b. Fig. 6c shows the resulting pressure-area relationship along with the corresponding linear regression yielding C_dyn. As seen in Fig. 6c the resulting pressure-area relationship was found to be linear, showing no hysteresis between pressure and area measurements. The mean PWI-derived PWV, r² and compliance in the case of the soft phantom segment was averaged over three different cycles (n = 3) and was found to be PWV = 2.23 ± 0.07 m · s⁻¹, r² = 0.96 ± 0.02 and C_PWI = 71.33±1.63 · 10⁻⁷m² · kPa⁻¹, while the corresponding mean compliance estimated by dynamic testing over three cycles (n = 3) was C_dyn = 73.10 ± 2.39 · 10⁻⁷m² · kPa⁻¹.

Fig. 6.

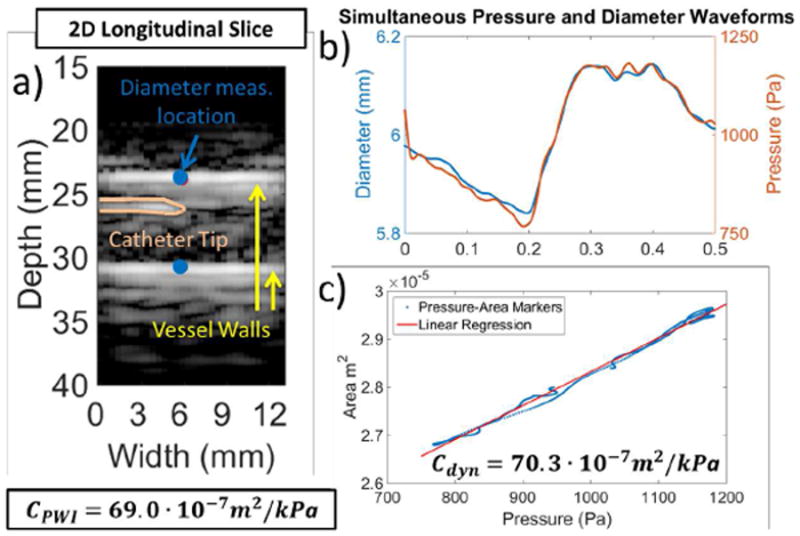
a) Longitudinal section of the phantom at the center of the volume. The catheter tip can be seen within the phantom lumen. Diameter was measured between the points indicated with blue color. b) Pressure and diameter waveforms measured simultaneously at the same location. c) Resulting pressure -area relationship and the corresponding linear fit yielding the dynamic testing compliance C_Dyn. PWI compliance (C_PWI) is also provided.

Fig. 7a shows a schematic of the plaque phantom along with the two imaging planes used by the conventional PWI acquisitions. Imaging plane (b) doesn’t intersect the plaque while imaging plane (c) passes through a plaque section. The 2-D B-mode images corresponding to the imaging planes (b) and (c) are shown in Fig. 7b and c, respectively. Fig 7d and e show the segmented vessel acquired with the 2-D array. Fig 7d corresponds to a front view of the vessel, while in the case of Fig 7e the vessel was rotated around the z-axis and the right lateral wall has been clipped in order to better visualize the lumen of the vessel. In all of the cases the plaque has been delineated with a perforated red line. Fig. 8 shows the corresponding PWI pulse propagation image sequences in the cases of the conventional PWI acquisitions with the plaque outside (Fig. 8a) and within the field of view (Fig. 8b). Figs. 8c and d show the 4-D PWI pulse wave propagation image sequences with the wall clipped outside of the plaque region to visualize propagation within the phantom wall (Fig. 8c) and also clipped at the plaque region to visualize intra-plaque pulse wave propagation.

Fig. 8.

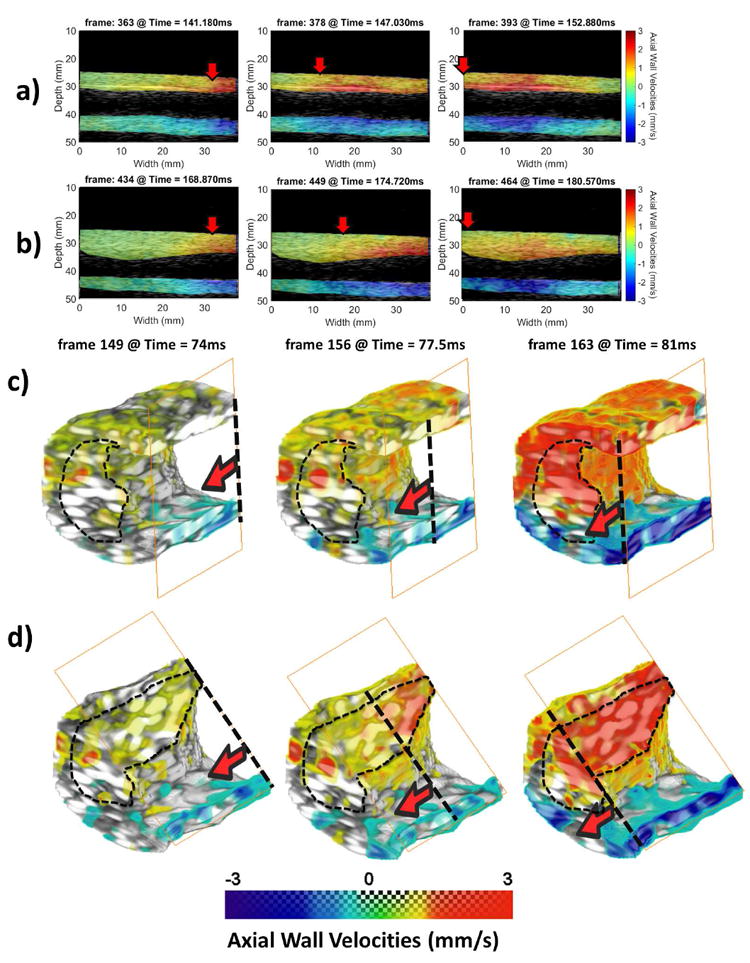
a) Conventional PWI pulse propagation image sequence with the plaque outside of the field of view. b) Conventional PWI pulse propagation image sequence with the plaque within the field of view. c) 4-D PWI pulse propagation image sequence. The phantom wall has been clipped outside of the plaque region to better illustrate pulse wave propagation. d) 4-D PWI pulse propagation image sequence. The phantom wall has been clipped at the plaque region to visualize intra-plaque pulse propagation. The solid red arrows and the transverse perforated lines denote the pulse wavefront and propagation is from right to left side. The extent of the plaque has been delineated with thin black perforated lines

B. In vivo feasibility study

The proposed 4-D PWI processing method was applied to six sets of data from healthy subjects. Snapshots of the propagation of the pulse wave can be seen in Fig. 9. At the anterior and the posterior walls (red/yellow and blue color respectively) the v_PWI wave is propagating over the 13.6 mm length of the artery. The spatio-temporal maps of the propagation of the distension pulse wave were obtained from the 2-D and 3-D acquisitions for three of the subjects (A,B and C) and compared for each one of them, as shown in Fig. 10. Good qualitative agreement between conventional and 3-D spatio-temporal maps was obtained. Additionally, the forward wave, emanating from the heart, and the reflected wave due to the carotid bifurcation were more noticeable in the case of subjects A and B and less so in subject C. Quantitatively, the PWVs estimated with the 4-D PWI technique were close to the PWVs estimated with conventional PWI as shown in Table II. On average, the difference was 0.52 m · s⁻¹. Furthermore, II shows the PWV measured in the remaining healthy subjects (D, E and F) using 4-D PWI. The average PWV recorded for all six scanned healthy subjects was 4.82 ±1.17 m · s⁻¹, (n = 6).

Fig. 9.

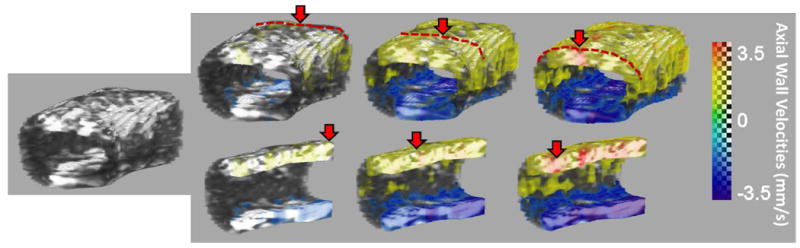
Segmented vessel and PWI pulse wave propagation image sequences showing the 3-D propagation of the pulse wave in a portion of the common carotid of a healthy subject. The same vessel is shown in the bottom row with the arterial wall clipped to show intra-wall pulse propagation. Red dotted lines and red solid arrows indicate the progression of the pulse wave.

Fig. 10.

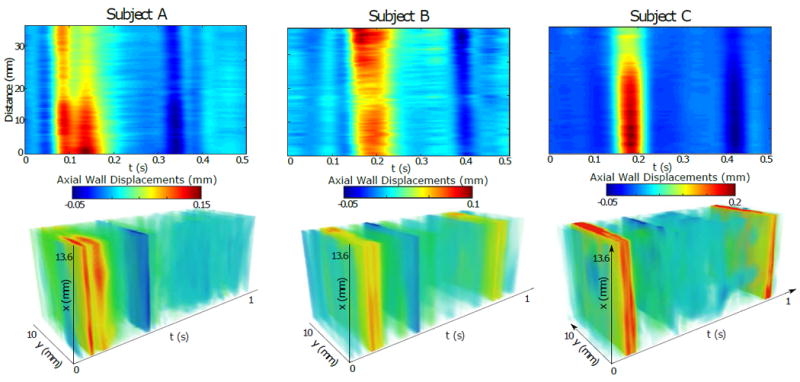
Comparison of the spatio-temporal maps obtained from conventional 2-D measurements (top row) and with the proposed 3-D approach (bottom row) for three different subjects.

TABLE II.

PWV estimated using conventional PWI and 4-D PWI

	conventional PWV (m · s−1)	4-D PWV (m · s−1)
Subject A	3.92	3.98
Subject B	3.03	3.76
Subject C	5.90	6.67
Subject D	-	6.09
Subject E	-	4.73
Subject F	-	3.69

IV. Discussion

In this study, the PWI method was implemented using plane wave imaging in 3-D for the first time using a 2-D matrix array transducer at high volume rates. A novel method to estimate the PWV along the direction of the pulse wave propagation was introduced. PWVs were successfully estimated in 3-D and were validated in a phantom via static and dynamic testing. Utility of 4-D PWI was also shown in a plaque phantom. Furthermore, PWVs were estimated in vivo, in healthy human carotids and were tested against PWVs estimated from 2-D PWI acquisitions.

The walls of both the phantom and the carotid arteries arteries were visualized in 3-D B-mode images. It should be noted that the anterior and posterior walls were more echogenic compared to the lateral walls. This was expected, given the angle of incidence of the transmitted plane wave and can be addressed in the future by implementing 3-D coherent compounding of tilted plane wave acquisitions. This is also expected to increase contrast, image resolution and v_PWI SNR while keeping the frame rate at acceptable levels [27], [21].

The propagation of the pulse waves was visualized in 3-D in both the phantom and the healthy carotid cases. More specifically, as shown in Fig. 4, it was observed that the magnitude of the v_PWI is higher and the duration of the pulse wave propagation is longer in the case of the soft segment compared to the stiff segment. Similar observations have been made in [20] in vivo, between normal and stiffer atherosclerotic aortas in mice. More specifically, atherosclerotic aortas, known to be stiffer compared to healthy ones were shown to have both higher PWVs and lower v_PWI, thus being in agreement with the findings of the current study.

Similarly, in the case of the healthy subjects, common characteristics of the pulse wave propagation at the carotid were observed. More specifically, two waves propagating in opposite directions (forward and reflection waves) were observed followed by a negative peak corresponding to the dicrotic notch and finally repetition of this pattern in the next cardiac cycle. The reflected wave is barely noticeable for subject C. This is because the forward and the reflected waves have mixed due to the high PWV. Additionally, the propagation appears to be relatively homogeneous, an expected result since the subjects were healthy and the arterial wall was homogeneous within the field of view.

3-D spatio-temporal plots depicting the propagation of the pulse waves in three dimensions were generated and subsequently compared to the traditional 2-D spatio-temporal maps where the pulse wave is assumed to travel parallel to the imaging plane. The magnitude of the estimated PWVs was found to be higher in the stiffer segment, as expected. Further validation was achieved as the PWV values were found to be in good agreement with the static estimated ones. A small decrease of the r² values compared to 2-D cases is to be expected given the single unfocused plane wave imaging, which leads to lower image quality as well as noisier motion estimation [27], [40]. Another factor that may have contributed to this decrease is the lower number of 50% upstroke markers in each dimension. Thus, r² is more easily affected by a 50% upstroke marker of a noisier v_PWI waveform.

In the dynamic testing experiment, the PWI-derived compliance C_PWI was found to be similar to the catheter-derived one C_Dyn, thus validating the results of our method with the phantom connected to the peristaltic pump. Another interesting finding of this experiment was the fact that the diameter pulse wave was found to arrive simultaneously with the intraluminal pressure wave, leading to a linear pressure-area relationship and indicating reduced influence of the phantom’s wall viscosity.

Finally, the plaque phantom experiment showcased some advantages of 4-D PWI compared to the conventional technique. More specifically, it showed that while pulse wave propagation was detected using the conventional PWI method with the plaque region both within and outside of the field of view, plaque detection was harder and could have potentially been missed from the PWI analysis. On the contrary, 4-D PWI was able to delineate the full extent of both the phantom’s wall and the plaque attached to it, thus providing comprehensive, angle-independent views of the vessel. This advantage is intrinsically linked to the use of 3-D ultrasound in the diagnosis of atherosclerosis. More specifically, using conventional 2-D imaging, even with a high quality B-mode, plaque severity may be overestimated, underestimated or even completely undetected depending on the orientation of the 2-D imaging plane [43]. Thus, the imaged section of the plaque may not be representative of the plaque morphology [44]. This may induce errors in both the correct diagnosis and the accurate estimation of the plaque and vessel morphological characteristics (i.e. plaque thickness, cross-sectional luminal area). The former has been corroborated by a large scale study where 3-D ultrasound was able to detect more plaques than conventional imaging in an older population [45]. This result shows the objective examination and increased sensitivity provided by 3-D ultrasound and may prove to be crucial for PWI, since it aims at investigating the progression and the mechanical properties of plaques from the earliest stages to the higher risk morphologies.

Additionally, accurate estimation of the plaque and vessel morphological characteristics is very important in the case where compliance is estimated via either the Bramwell-Hill equation or the Pulse Wave Inverse Problem (PWIP), since both of these methods, in addition to the regional PWV, require the correct estimation of the cross-sectional luminal area (A). 4-D PWI, is advantageous in this case, since it is able to provide comprehensive views of the investigated vessels, whereas conventional PWI assumes circumferential homogeneity and symmetry of the vessel, an assumption that often does not hold in the case of atherosclerotic vessels.

Moreover, 4-D PWI is expected to enable precise tracking of the vessel walls regardless of the vessel curvature and tortuosity as long as they lie within the imaged volume, whereas in the case of conventional PWI the probability of having some vessel segments outside of the field of view is higher.

Another advantage of 4-D PWI is that it provides the v_PWI throughout the entire imaged vessels circumference and length simultaneously. On the contrary, conventional PWI only provides the v_PWI at a single slice, dramatically decreasing the amount of available information for further analysis. More specifically, in the plaque phantom as evidenced by 8, by clipping the 3-D segmented vessel, intra-wall and intra-plaque propagation patterns can be studied in more detail and in conjunction with each other. This particular advantage should become clearer in the future with the ongoing development of a robust wall velocity estimator in both the axial and lateral directions.

In the case of healthy subjects, the estimated PWVs were within the range of previously published values of techniques estimating regional carotid artery PWV (3 −9 m · s⁻¹ as seen in [46], [47], [13] [48], [49]) as well as of previous conventional PWI studies ([50] and [21]). Furthermore, good agreement was found between the conventional estimation from 2-D images and the proposed 4-D PWI technique based on 3-D volumes. This is further supported by the fact that in all three cases, the differences between the measured PWVs were less than 1 m · s⁻¹, a finding that applies to PWV values measured during different cardiac cycles of the same subject. More specifically, similar observations on the reproducibility of PWV measurements during different cardiac cycles have been made by previous studies utilizing commercial systems such as Sphygmocor (AtCor Medical, Sydney, Australia) and Complior (Artech Medical, Pantin, France) that estimate global PWVs ([51], [52]) as well as by previous PWI studies testing repeatability of PWI in vivo ([21], [50]). It should be noted that in a previous study estimating regional PWV in the carotid, intra-subject variability of PWVs derived by tracking the systolic foot was found to be up to 1.1 m · s⁻¹ [48]. However, because of the interference between the forward pulse wave and the reflected wave, some discordance between the 4-D and conventional PWI results may exist. To address this issue, the PWI inverse approach developed recently for the 2-D images [22] can be extended to process the 3-D data sets and provide more robust PWV estimates.

Limitations and future directions

The present study suffers from a number of limitations. Firstly, it should be stressed that a comprehensive comparison of 4-D PWI against conventional PWI is beyond the scope of the present study and will be investigated in greater depth in upcoming studies. However, as far as the limited comparison results presented here are concerned, while they are by no means comprehensive, they do provide some indications towards potential applications where 4-D PWI appears to be advantageous compared to conventional PWI (i.e. pulse wave propagation in complex geometry stenosed arteries).

The main drawbacks of the 4-D PWI method compared to conventional PWI are pertinent to the 2-D array used. More specifically, lower image quality and overall SNR can be observed in both the B-mode volumes and the estimated v_PWI, as also discussed in [39], mainly due to the lower number of elements along each direction (16 × 16 elements), lower frequency (2.5 MHz) and lower frequency bandwidth (50%) compared to the linear array used in conventional PWI (128 elements, 5 MHz, 60% bandwidth). These limitations are expected to be alleviated with the acquisition of a new probe with a higher central frequency and more piezo-electric elements. Moreover, larger aperture would aid in performing PWI in more tortuous vessels. It should be noted, however, despite its limitations, the 2-D array was found to be sufficient in demonstrating the feasibility of the proposed technique, showing that lower spatial sampling can still provide adequate depiction of the pulse wave characteristics in 3-D.

Additionally, while the PWVs recorded in both phantom segments (soft and stiff) were low when compared with physiological PWV values, 4-D PWI is expected to be capable of accurately measuring higher PWVs too. The theoretical upper limit of PWV estimation is mainly imposed by the frame rate [42]. It has been previously reported that regional PWV estimation in vivo requires kilohertz rates [53] and has been corroborated in the case of PWI using plane wave imaging in 2-D [21]. Consequently, given that 4-D PWI achieved volume rates of 2 kHz and also yielded sufficient spatial resolution to track vessel walls in 3-D, it is expected to be capable of accurately measuring PWVs in vivo. This was further confirmed by measuring PWVs within the physiological range in six healthy subjects.

Furthermore, there is ongoing research seeking to establish the utility of PWI in characterizing atherosclerotic plaques [54]. Given that both intra-wall and intra-plaque imaging of the pulse wave propagation was feasible in the current study in a phantom setup, the inclusion of 4-D PWI in these studies may aid by providing comprehensive views of the stenotic regions of the arteries and further elucidating the pulse propagation patterns over diseased arterial regions, ultimately helping in the detection of vulnerable plaque.

Finally, a limitation of the current technique is that lateral v_PWI were not estimated and thus pulse wave propagation was based solely on the axial v_PWI. As expected, lateral walls exhibited reduced axial motion and were mostly avoided for the tracking of the pulse wave propagation as discussed in the “Materials and Methods” section. However, it should be noted that the same limitation would apply to conventional PWI, in the case where a 1-D array transducer would image the vessels lateral walls from the same angle as the 2-D array, since also in conventional PWI only the axial v_PWI are tracked. While lateral v_PWI would increase the amount of information provided by 4-D PWI, axial v_PWI were found to be sufficient to enable 4-D PWI’s main functionality and main advantage compared to conventional PWI, the correct tracking of the pulse wave in 3-D along the propagation direction. This is achieved by tracking the axial v_PWI in broader sections of the top and bottom walls along the length of the imaged vessel (grid of points on and around the anterior and posterior walls). Thus, the improved accuracy of PWV estimation is ensured, compared to conventional PWI, which assumes the propagation of the pulse wave parallel to the imaging slice.

Nevertheless, ongoing work aims at the estimation of lateral v_PWI which will ultimately lead to the acquisition of the full vector of the v_PWI and not just their axial component, thus alleviating any perceived angle dependence of the method and also providing increased insight to arterial wall motion. This will be of great importance especially in the case of focal vascular disease exhibiting 3-D motion and complex mechanical behavior.

V. Conclusion

4-D PWI was successfully implemented with plane waves at high volume rates. PWVs were estimated along the direction of the pulse wave propagation and were validated in the case of a silicone phantom against PWV values derived from static testing. Compliance values derived using dynamic testing were also found to be similar to the PWI-derived compliance. Pulse wave propagation was comprehensively visualized in a plaque phantom using 4-D PWI and its advantage was demonstrated against conventional PWI. Finally, the in vivo feasibility was demonstrated by imaging the pulse wave propagation along the carotid artery wall of six healthy subjects.