Abstract
Next-generation sequencing studies on cancer somatic mutations have discovered that driver mutations tend to appear in most tumor samples, but they barely overlap in any single tumor sample, presumably because a single driver mutation can perturb the whole pathway. Based on the corresponding new concepts of coverage and mutual exclusivity, new methods can be designed for de novo discovery of mutated driver pathways in cancer. Since the computational problem is a combinatorial optimization with an objective function involving a discontinuous indicator function in high dimension, many existing optimization algorithms, such as a brute force enumeration, gradient descent and Newton’s methods, are practically infeasible or directly inapplicable. We develop a new algorithm based on a novel formulation of the problem as non-convex programming and non-convex regularization. The method is computationally more efficient, effective and scalable than existing Monte Carlo searching and several other algorithms, which have been applied to The Cancer Genome Atlas (TCGA) project. We also extend the new method for integrative analysis of both mutation and gene expression data. We demonstrate the promising performance of the new methods with applications to three cancer datasets to discover de novo mutated driver pathways.
Keywords and phrases: DNA sequencing, Driver mutations, Optimization, Subset selection, Truncated L1 penalty
1. Introduction
It is known that cancer is characterized by numerous somatic mutations, of which only a subset, named “driver” mutations, contribute to tumor growth and progression. With next-generation whole-genome or whole-exome sequencing, somatic mutations are measured in large numbers of cancer samples (Mardis & Wilson, 2008; Meyerson et al., 2010). To improve understanding and treatment of cancers, it is critical to distinguish driver mutations from neutral “passenger” mutations. A standard approach to predicting driver mutations is to identify recurrent mutations in cancer patients (Beroukhim et al., 2007; Getz et al., 2007), which has its drawback in its inability to capture mutational heterogeneity of cancer genomes (Ding et al., 2008; Jones et al., 2008). An emerging discovery is that in a given sample driver mutations typically target one, but not all, of several genes in cellular signaling and regulatory pathways (Vogelstein & Kinzler, 2004). Hence the research has shifted from the gene level to pathway level (Boca, 2010; Efroni, 2011). Recent studies indicated that mutations arising in driver pathways often cover a majority of samples, but, importantly, for a single sample only a single or few mutations appear because a single mutation is capable to perturb the whole pathway; the latter concept is the so-called mutual exclusivity. By using mutual exclusivity, new pathway-based methods are developed to identify de novo driver mutations and pathways (Ciriello et al., 2012; Masica et al., 2011; Miller et al., 2011). For example, Miller et al. (2011) proposed a method to find functional sets of mutations by using patterns of recurrent and mutually exclusive aberrations; Ciriello et al. (2012) not only used the mutual exclusivity pattern, but also incorporated a gene functional network constructed based on prior knowledge. Recently Vandin et al. (2012) introduced a novel scoring function combining the two concepts, coverage and mutual exclusivity, to identify mutated driver pathways through optimizing this scoring function, which has been used in some large-scale cancer sequencing studies. It is solved by stochastic search methods: a greedy algorithm and a Markov chain Monte Carlo method. Other proposals based on binary linear programming, genetic search algorithm, and integer linear programming have appeared (Zhao et al., 2012; Leiserson et al., 2013), all of which are still relatively slow, especially for large-scale problems. To address these issues, we reformulate the problem of identifying mutated driver pathways as a statistical problem of subset identification to minimize a new cost function, what we call minimum cost subset selection (MCSS). A key component is a novel approximation to a combinatorial problem through regularization, where a discontinuous indicator function is approximated by a continuous and non-convex truncated L1 (TL) function (Shen et al., 2012). Furthermore, we add a truncated L1 penalty (TLP) to the cost function to seek a sparse solution, as well as adding a small ridge penalty to alleviate the problem of multiple solutions. As a result, a combinatorial optimization problem becomes a continuous but non-convex one in the Euclidean space, which can be efficiently solved through a non-convex optimization technique, leading to high computational improvement.
Another advantage of the proposed method is that it is able to find multiple mutated driver pathways. An existing method to identify multiple mutated driver pathways is Multi-Dendrix (Leiserson et al., 2013), in which the number of pathways and the number of the genes in each pathway have to be specified in advance. On the contrary, our proposed method does not need to fix such numbers beforehand. Based on a series of randomly selected initial estimates, a series of low-cost estimates of mutated driver pathways can be obtained. Moreover, the proposed method is general so that other types of information can be incorporated in a simple way. For example, if a gene interaction network is available, it can be incorporated by adding a network-based penalty to the current cost function as in Li & Li (2008); since it is more informative to combine mutation data with other types of data such as gene expression data (Zhang and Zhou, 2014), an integrative version can be developed by adding other cost functions for other types of data into the current one. As a concrete example, we propose a new method to integrate mutation data with gene expression data.
2. Methods
2.1. Problem
Consider mutation data with n patients and p genes, represented as an n × p mutation matrix A with entry Aij = 1 if gene j is mutated in patient i, and Aij = 0 otherwise. For gene j ∈ V = {1, …, p}, let Γ(j) = {i : Aij = 1} be a subgroup of patients whose gene j is mutated. Moreover, given a subset of genes B ⊆ {1, …, p}, let Γ(B) be a subgroup of patients with at least one of the genes in B mutated, i.e. Γ(B) = ∏j∈B Γ(j). Cancer sequencing studies have motivated to identify a set of mutated genes across a large number of patients, whereas only a small number of patients have mutations in more than one gene in the set, that is, these mutations are approximately exclusive. This amounts to finding a set B ⊆ V of genes such that (i) the coverage is high, that is, most patients have at least one mutation in B; (ii) the genes in B are approximately exclusive, that is, most patients have no more than one mutation in B. A measure ω(B) = Σj∈B |Γ(j)| − |Γ(B)| was proposed by Vandin et al. (2012), called the coverage overlap, to balance the trade-off between coverage and exclusivity. To maximize the coverage |Γ(B)| and minimize the coverage overlap ω(B) simultaneously, Vandin et al. (2012) suggests to minimize
| (2.1) |
with respect to B, thus obtaining an estimate B̂. Minimizing f(B) is equivalent to maximizing the weight function −f(B), which is called the maximum weight sub-matrix problem (MWSP). Note that minimizing f(B) is a non-trivial combinatorial problem, to which most existing optimization algorithms based on the gradient descent or Newton’s algorithm cannot be directly applied. A popular method called Dendrix is based on a Monte Carlo search algorithm to seek an approximate solution to minimize f(B) (Vandin et al., 2012).
2.2. New formulation
As indicated in (2.1), MWSP is a combinatorial problem, for which a brute force search is time-consuming and not scalable for large (n, p), while many existing algorithms like gradient descent or Newton’s method cannot be directly applied. Here we formulate it as nonconvex minimization and examine a regularized version by imposing penalties to ensure proper solutions. Specifically, for any β ∈ ℝp, let B = B(β) = {j ∈ V : |βj| ≠ 0}, and we rewrite and |Γ(j)| = A·,j for each j ∈ {1, ⋯, p}. Then (2.1) becomes
| (2.2) |
Minimizing (2.2) in β yields an estimate β̌ = (β̌1, ⋯, β̌p)′, and thus an estimated set B̌ = {j : | β̌j| ≠ 0}. However, due to the discontinuity with the indicator function I(.), it is difficult to minimize (2.2) directly; instead, since min(|βj |/τ1, 1) → I(|βj | ≠ 0) as τ1 → 0+, we propose a surrogate to minimize
| (2.3) |
with respect to β = (β1, …, βp)′ ∈ [0,+∞)p; that is, β is a vector of parameters to be estimated; λ, α, τ1 and τ2 are non-negative tuning parameters to be determined via a grid search in cross-validation (as used in the later experiments); Aij ’s are observed and known. Note that in (2.3), the last two terms, as a TLP and a ridge penalty respectively, ensure sparse and proper solutions.
2.3. Computation
To solve nonconvex minimization (2.3), we employ difference convex (DC) programming by decomposing the objective function into a difference of two convex functions, on which convex relaxation is performed through iterative approximations of the trailing convex function through majorization. Specifically, can be written as a difference of two convex functions: min(z/τ, 1) = z/τ − max (z/τ −1, 0) for any z > 0 and τ > 0. Then, we obtain a sequence of upper approximations S(m)(β) of S(β) at iteration m (up to a constant) as follows:
| (2.4) |
where β ∈ [0,+∞)p, A· = (A·,1, …, A·,p)′, and diag(A·) is a diagonal matrix with elements of A· as diagonals. Now S(m)(β) is strictly convex (since the first term is linear in β, the second is convex while the last is quadratic in β with α ≠ 0), we use some existing convex program package (CVX in Matlab), or more efficiently, the subgradient descent method (as shown in the appendix) (Shor, 1985), to obtain a unique minimizer β̂(m); we repeat the process until convergence to obtain β̃ = β̂(+∞).
Interestingly, one may replace the TLP in S(β) in (2.3) with the L1-penalty, yielding β̂L. This, together with, other randomly generated numbers, can be use as an initial value β̂(0) for our method. For selection of tuning parameters, we may consider cross-validation, as discussed later.
The following algorithm summarizes our computational method.
Algorithm 1.
Given the parameters τ1, τ2, λ, α.
|
The following convergence property of Algorithm 1 has been established.
Theorem 1
β̂(m) in Algorithm 1 converges in finite steps to a local minimizer β̃ of S(β) in (2.3). S(β̂(m)) strictly decreases in m until β̂(m) = β̂(m−1) = β̂(m★−1) for all m ≥ m★.
2.4. Initial estimate
In general, a large number of good or randomly selected initial estimates may be used to obtain multiple solutions, from which a subset of more promising ones with smaller objective or cost function values can be selected. Below, we describe a simple way to obtain a good initial estimate, which was used in later simulations; we modify S(β) such that the modified version SL(β) becomes much easier to optimize. A local condition of (2.3) can be established based on regular subdifferentials
where if βj = 0, if 0 < |βj| < τ1, if |βj| > τ1 and if |βj | = τ1 for j = 1, ⋯, p; if βj = 0, if 0 < |βj| < τ2, if |βj| > τ2 and if |βj | = τ2 for j = 1, ⋯, p. Note that is more complicated as it depends on the values of Aij′ and βj′, j′ ∈ {1, ⋯, p}, and or or for βj > 0. Based on these regular subdifferentials, we develop the following lemma.
Lemma 1
If there exists a non-zero local minimizer β* of S(β) in (2.3) on ℝp, then for each j ∈ {1, ⋯, p}.
Lemma 1 says that the set of all local minimizers of S(β) in (2.3) over [0,+∞]p is the same as that obtained from the following cost function over [0, τ1]p:
| (2.5) |
If we use the L1-penalty as opposed to the truncated L1-penalty in (2.5), then the cost function becomes
which is strictly convex in β ∈ [0, τ1]p, yielding a unique minimizer β̂L.
2.5. Model selection
Tuning parameters (λ, r) need to be estimated from data, where τ2 = rτ1 (0 < r < 1), while α is fixed at a sufficiently small positive number, say α = 10−3, and τ1 is fixed at any positive value, say τ1 = 1. Tuning of (λ, r) can be achieved through sample splitting. As a matter of fact, the term is introduced to yield a unique minimizer of (2.4) so that the bias caused by the ridge penalty is ignorable for sufficiently small α. On the other hand, given the ratio r, an exact value of (τ1, τ2) is unimportant. This is because minβ∈[0,+∞)p S(β;Kτ1, r, λ, α′) = minβ′∈[0,+∞)p S(β′; τ1, r, λ, α′) = minβ∈[0,+∞)p S(β; τ1, r, λ, α′) if S(β;Kτ1, r, λ, α′) = S(β′; τ1, r, λ, α′) with β′ = β/K and for any K > 0. Consequently, given the ratio r, optimization in terms of different choices of τ1 are equivalent. Given a n × p mutation matrix A, a candidate set Λ ⊆ (0,+∞) of the tuning parameter λ and a candidate set R ⊆ (0,+∞) of the tuning parameter r = τ2/τ1, we use a sample splitting procedure to select the tuning parameters λ̂ ∈ Λ and r̂ ∈ R:
Initialization Supply a randomly selected initial estimate β̂(0).
Partition Randomly partition the rows of the mutation matrix A into two parts: training data Atr and tuning data Atu.
Training For each λ ∈ Λ and each r ∈ R, apply Algorithm 1 to the training data Atr with the initial estimate β̂(0) and parameters λ and r to get the corresponding estimate β̂tr (λ, r).
-
Tuning Based on the tuning data Atu, we formulate a tuning error for each β̂tr (λ, r) aswhere ntu denotes the number of rows of Atu, that is, the patient number in the tuning data, and . We select λ and r as
Given λ = λ̂ and r = r̂, we apply Algorithm 1 to the original mutation matrix A to find β̂ ∈ [0,+∞)p that minimizes S(β) in (2.3).
2.6. Integrative analysis
An advantage of the proposed algorithm is its possible extensions to include other types of genomic data, in addition to mutation data. To this end, we modify the proposed cost function and algorithm to incorporate other types of data such as gene expression. Let fME(B) denote the integrative cost function, which is the sum of the original cost function f(B) and a new one fE(B) for gene expression data:
where cjk is the Pearson correlation coefficient of the expression profiles of genes j and k. Note that the integrative cost function is based on the observation that the genes in the same pathway usually collaborate with each other to execute a common function. Therefore, the expression profiles of the genes in the same pathway usually have higher correlations than those from different pathways (Qiu et al., 2010; Zhao et al., 2012).
To minimize fME(B), we develop a similar algorithm as before, called MCSS ME, where S(β) and S(m)(β) are replaced by SME(β) and respectively as follows.
and
where D = C+diag(C.), C = [cjk] (cjj = 0) and C. is the row sum vector of C. Here we use the subgradient descent method (as shown in the appendix) to obtain a minimizer of .
To choose a suitable γ in situations with no prior information, we propose a method to balance the contributions to the new cost function from mutation data and from gene expression data. Specifically, we randomly select a large number of subsets, say B1, B2,…, BR, of the genes from {1, 2, ⋯, p} with the size of each subset |Bj | randomly generated from {2, 3, ⋯, np}, then we choose γ = minj f(Bj)/ minj fE(Bj ), which aims to give an equal weight on the contribution of the mutation data and that of the expression data to the overall cost function fME(). In our following experiments, we always used R = 10000 and np = 8, though other values may be used.
After determining γ, we choose the other tuning parameters similarly as before but according to an integrative version of the tuning error
2.6.1. Evaluation metrics
Several metrics are used for evaluation, including the correct (C) or incorrect (IC) numbers of non-zero estimates for the mutations/genes in the true pathway B0, and average differences of the cost function values (ADC) between the true set B0 and the estimated set B̂ of the driver mutations/genes; that is, C=|B0 ∩ B̂|, , ADC= (f(B0) − f(B̂))/n. We also included the running time (RT) (in minutes) of each algorithm. Note that ADC is important, because the basic task for minimum cost subset selection is to identify a set of mutations with the minimum cost.
In addition to using the correct (C) or incorrect (IC) numbers of non-zero estimates and ADC to measure how close the estimated pathways are close to the true pathway, we also investigate several other metrics in decomposing the cost function into the coverage (cc) and exclusivity (ce), and displaying the proportion of the patients carrying a mutation of a gene in a pathway (c1), as well as the proportion of those carrying multiple mutations in more than one gene in the pathway (c2). Specifically, we define
Due to the coverage and exclusivity of a pathway, c1 is often similar to −cc while c2 is similar to ce.
3. Results
3.1. Real data examples
In this section we first illustrate the application of the proposed method to two cancer datasets that were previously examined by Vandin et al. (2012), then to a more recent and larger dataset including both mutation and expression data. As argued by Vandin et al. (2012), a set of mutated genes with a low cost function value is likely to be a mutated driver pathway, based on which our primary objective is to identify such mutated driver pathways through minimum cost subset selection of mutated genes. For each of the first two datasets, the proposed method was applied with the tuning parameter λ chosen from a tuning set of size 10, while 100 randomly generated initial estimates were used. For each initial estimate, we applied the proposed method, by which we identified multiple low-cost sets of mutations.
3.1.1. Lung adenocarcinoma
The original data set contains 1013 somatic mutations in 623 sequenced genes from 188 lung adenocarcinoma patients in the Tumor Sequencing Project (Ding et al., 2008). For our purpose, we examined 356 genes that were mutated for at least one patient from a group of 162 patients, as in Vandin et al. (2012).
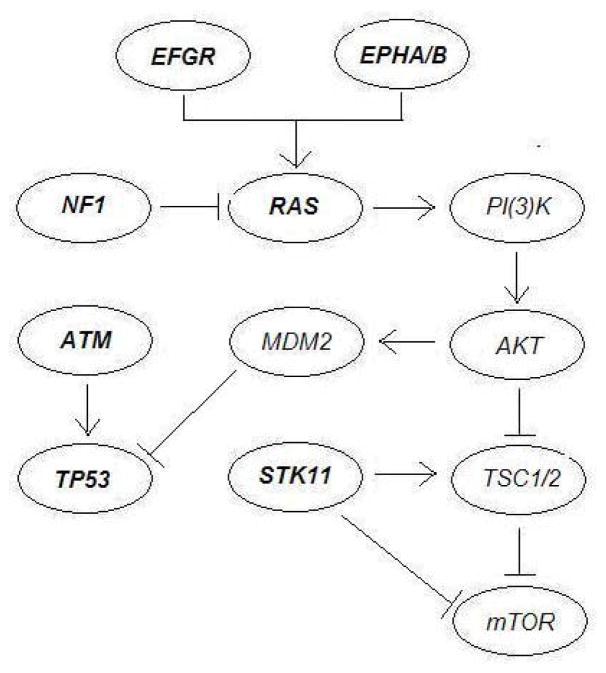
The proposed method was applied to identify multiple sets of mutated genes with low cost function values. Using 100 randomly selected initial values for MCSS, it cost 0.85 minutes and identified some gene sets with low cost. To demonstrate the resulting low-cost sets of mutations as possible candidates for mutated driver pathways, in Table 1 we group these discovered sets in terms of known pathways. In Table 1, all the discovered sets related to two known pathways associated with lung adenocarcinoma: the mTOR signaling pathway and the cell cycle pathway. Gene interactions in these pathways were reported in Ding et al. (2008) as depicted in Figure 1.
Table 1.
Applied to the mutation data of lung adenocarcinoma (Ding et al., 2008), the new method MCSS identified multiple sets of low-cost mutated genes, grouped in terms of associated pathways.
| Pathway | Highly mutated genes | B̂ | f(B̂) | ĉe | ĉc | ĉ1 | ĉ2 |
|---|---|---|---|---|---|---|---|
| mTOR signaling | EGFR, EPHA3, KRAS, NF1, STK11 | (EGFR, KRAS, NF1, STK11) | −0.611 | 0.117 | −0.728 | 0.617 | 0.104 |
| (EGFR, KRAS, STK11) | −0.593 | 0.086 | −0.679 | 0.593 | 0.086 | ||
| (EGFR, KRAS, NF1) | −0.574 | 0.031 | −0.605 | 0.574 | 0.031 | ||
| (EGFR, EPHA3, KRAS, NF1) | −0.574 | 0.061 | −0.636 | 0.586 | 0.037 | ||
| (EGFR, EPHA3, KRAS) | −0.568 | 0.025 | −0.593 | 0.568 | 0.025 | ||
| (EGFR, KRAS) | −0.556 | 0 | −0.556 | 0.556 | 0 | ||
|
| |||||||
| cell cycle | ATM, TP53 | (ATM, TP53) | −0.463 | 0.006 | −0.469 | 0.463 | 0.006 |
|
| |||||||
| mTOR signaling & cell cycle | EGFR, EPHA3, KRAS, NF1, STK11 & ATM, TP53 | (ATM, EGFR, STK11, TP53) | −0.525 | 0.173 | −0.698 | 0.537 | 0.148 |
| (KRAS, TP53) | −0.469 | 0.148 | −0.617 | 0.469 | 0.148 | ||
| (EGFR, TP53) | −0.444 | 0.068 | −0.512 | 0.444 | 0.068 | ||
Fig. 1.
The mTOR signaling pathway and the cell cycle pathway associated with lung adenocarcinoma as reported in Ding et al. (2008). The KRAS gene is one of the three oncogenes in the Ras family.
First, as indicated in Figure 1 (see Figure 6 of Ding et al. (2008)), the mTOR signaling pathway consists of some highly mutated genes, such as EGFR, EPHA3, KRAS, NF1 and STK11. EGFR is a well-known oncogene, whose mutations are strongly associated with lung cancer (da Cunha Santos et al., 2011). In contrast, EPHA3 is one of the most frequently mutated genes in lung cancer, which however has not yet been extensively investigated. As suggested by Zhuang et al. (2012), tumor-suppressive effects of wild-type EPHA3 could be overridden in trans by dominant negative EPHA3 somatic mutations discovered in patients with lung cancer. KRAS is an oncogene associated with non-squamous non-small cell lung cancer. As indicated by many studies as well as our analysis, the mutations of KRAS and EGFR are strongly mutually exclusive. KRAS serves as a mediator between extracellular ligand binding and intracellular transduction of signals from the EGFR to the nucleus. The presence of activating KRAS mutations has been identified as a potent predictor of resistance to EGFR-directed antibodies (Heinemann et al., 2009). STK11 encodes a tumor suppressor enzyme, and its mutations can allow cells to grow and divide uncontrollably, leading to the formation of cancerous cells (Gill et al., 2007). In particular, STK11 mutations are found in non-squamous non-small cell lung cancer, however uncommon in most other types of cancer.
Interestingly, all the identified sets of mutated genes with the cost function values f(B̂) lower than −0.556 = 90/162 are related to these five genes. Recall that in Ding et al. (2008), (EGFR, KRAS) (f(B̂) = −0.556) and (KRAS, STK11) (f(B̂) = −0.420) are the most significant pairs in the mutual exclusiveness test, and in Vandin et al. (2012), the triplet (EGFR, KRAS, STK11) (f(B̂) = −0.593) was found with a lower cost, which was reported as a novel discovery. As indicated in Table 1, we could find not only this triplet (the second set in Table 1), but also another set (EGFR, KRAS, NF1, STK11) (f(B̂) = −0.611) (the first set in Table 1) that contains this triplet and has a lower cost function value. It is a better characterized gene set, containing the already discovered (EGFR, KRAS, STK11). In addition, we also identified four low-cost sets: (EGFR, KRAS, NF1) (f(B̂) = −0.574), (EGFR, EPHA3, KRAS, NF1) (f(B̂) = −0.574), (EGFR, EPHA3, KRAS) (f(B̂) = −0.568) and (EGFR, KRAS) (f(B̂) = −0.556). These discoveries suggest possible roles of these genes related to the mTOR signaling pathway.
Second, the cell cycle pathway includes two highly mutated genes, ATM and TP53. ATM plays a central role in cell division and DNA repair, and the protein encoded by this gene is an important cell cycle checkpoint kinase, which functions as a regulator of a wide variety of downstream proteins. Some studies suggested that ATM mutations may increase the risk for lung cancer (Lo et al., 2010). On the other hand, TP53 encodes a tumor suppressor protein p53 that regulates cell division by keeping cells from growing and dividing too fast or in an uncontrolled way. TP53 mutations are the most common genetic changes found in human cancer, in particular as one of the most significant events in lung cancer while playing an important role in the tumorigenesis of lung epithelial cells (Ding et al., 2008).
The pair (ATM, TP53) was identified by the proposed method with the cost function value of −0.463, which was also discovered in Vandin et al. (2012) by removing the triplet (EGFR, KRAS, STK11) from the original dataset. Note that among the identified low-cost sets in Table 1, the cost function value of (ATM, TP53) was relatively high due to its low value of the coverage: |Γ(B̂)| = 76, much smaller than the maximum value of n = 162. As hypothesized in Vandin et al. (2012), the low coverage is possibly because somatic mutations were measured in only a small subset of genes, or because only single-nucleotide mutations and small indels in these genes were measured, and other types of genomic or epigenetic alterations might occur in the ”unmutated” patients.
In addition, we identified some low-cost sets consisting of the genes related to both the mTOR signaling and the cell cycle pathways, namely, (ATM, EGFR, STK11, TP53) (f(B̂) = −0.525), (KRAS, TP53) (f(B̂) = −0.469) and (EGFR, TP53) (f(B̂) = −0.444). Presumably these discoveries are related to that EGFR and KRAS are upstream regulators of TP53, as suggested by Ding et al. (2008).
3.1.2. Glioblastoma multiforme (A)
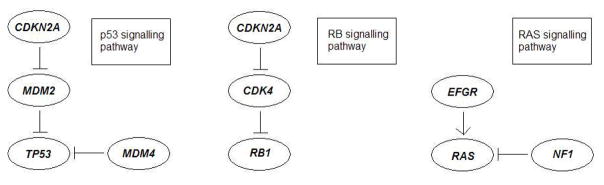
Next, we analyzed the mutation data of 84 glioblastoma multiforme (GBM) patients from The Cancer Genome Atlas (The Cancer Genome Atlas Research Network, 2008), where 601 somatic mutations in these patients occurred. The mutation data consist of 84 patients and 178 genes, with each mutation occurring in at least one patient. The proposed method was applied to identify multiple sets of mutations with low cost values. Using 100 randomly selected initial values for MCSS, it cost 0.66 minutes and identified some gene sets with low cost. In Table 2 we also group the identified low-cost sets in terms of the possibly associated pathways. Most of the sets are associated with three important pathways of glioblastoma multiforme: the p53 signalling pathway, the RB signalling pathway and the RAS/RTK/PI(3)K signalling pathway. Interactions in these pathways were reported in The Cancer Genome Atlas Research Network (2008) as described in Figure 2. Below we discuss each pathway and the discovered sets of mutations.
Table 2.
Applied to the mutation data of glioblastoma multiforme (data GBM A) (The Cancer Genome Atlas Research Network, 2008), the new method MCSS identified multiple sets of low-cost mutated genes, grouped in terms of associated pathways.
| Pathway | Highly mutated genes | B̂ | f(B̂) | ĉe | ĉc | ĉ1 | ĉ2 |
|---|---|---|---|---|---|---|---|
| p53 signalling | CDKN2A, MDM2, MDM4, TP53 | (CDKN2A, MDM2, MDM4, TP53) | −0.655 | 0.167 | −0.821 | 0.667 | 0.143 |
| (CDKN2A, DTX3, TP53) | −0.679 | 0.107 | −0.786 | 0.691 | 0.083 | ||
| (CDKN2A, TP53) | −0.631 | 0.071 | −0.702 | 0.631 | 0.071 | ||
| (CDKN2B, TP53) | −0.631 | 0.107 | −0.738 | 0.631 | 0.107 | ||
|
| |||||||
| RB signalling | CDKN2A/B, CDK4, RB1 | (CDKN2B, CYP27B1, RB1) | −0.738 | 0.048 | −0.786 | 0.738 | 0.048 |
| (CDKN2B, ERBB2, RB1, TSPAN31) | −0.762 | 0.071 | −0.833 | 0.762 | 0.071 | ||
| (CDKN2A, CYP27B1, RB1) | −0.667 | 0.048 | −0.714 | 0.667 | 0.048 | ||
| (CDKN2B, CYP27B1, NF1) | −0.667 | 0.107 | −0.774 | 0.667 | 0.107 | ||
| (CDKN2A, CYP27B1, NF1) | −0.643 | 0.083 | −0.723 | 0.643 | 0.083 | ||
| (CDKN2B, CYP27B1) | −0.643 | 0.036 | −0.679 | 0.643 | 0.036 | ||
|
| |||||||
| RAS signalling | EGFR, NF1 | (EGFR, KDR, NF1) | −0.631 | 0.024 | −0.655 | 0.631 | 0.024 |
|
| |||||||
| Unknown | (MTAP, TP53, TSFM) | −0.667 | 0.131 | −0.798 | 0.679 | 0.107 | |
| (CYP27B1, MTAP, PTEN) | −0.655 | 0.155 | −0.810 | 0.655 | 0.155 | ||
| (CDK4, MTAP, PTEN) | −0.655 | 0.155 | −0.798 | 0.643 | 0.155 | ||
| (EGFR, TP53) | −0.619 | 0.083 | −0.702 | 0.612 | 0.083 | ||
Fig. 2.
Three pathways associated with glioblastoma multiforme as reported in The Cancer Genome Atlas Research Network (2008).
First, the p53 signalling pathway consists of some highly mutated genes, CDKN2A, MDM2, MDM4 and TP53. Importantly, mutations in the tumour suppressor gene TP53 are typical events in primary glioblastoma multiforme, which is characterised by a short clinical history and the absence of a pre-existing, less malignant astrocytoma. In contrast, the cellular oncogene MDM2 is viewed as an important negative regulator of the p53 tumor suppressor, whose overexpression is a characteristic feature of secondary glioblastoma multiforme, progressing from less malignant astrocytoma (Stark et al., 2003).
Interestingly, the set of these four genes (CDKN2A, MDM2, MDM4, TP53) (f(B̂) = −0.655 = −55/84) was identified by the proposed method as a novel discovery unreported before, e.g., in comparison with the pair (CDKN2A, TP53) (f(B̂) = −0.631) identified by Vandin et al. (2012). As indicated in Table 2, the pair (CDKN2A, TP53) was also uncovered by the proposed method, in addition to another two sets, (CDKN2A, DTX3, TP53) (f(B̂) = −0.679) and (CDKN2B, TP53) (f(B̂) = −0.631). Since CDKN2A and CDKN2B are tumor suppressor genes located on a common homozygous deletion region on the human genome, they mutate almost simultaneously, which leads to a low cost function value of (CDKN2B, TP53). However, for (CDKN2A, DTX3, TP53), currently without further biological evidence, we conjecture that it has a low cost function value mainly because it consists of a low-cost set (CDKN2A, TP53) and gene DTX3 with infrequent mutations.
Second, the RB signalling pathway consists of some highly mutated genes, CDKN2A/B, CDK4, RB1, where CDKN2A and CDKN2B are tumor suppressor genes, whose gene products, p16INK4A and p15INK4B, are both able to inhibit the binding of CDK4 and CDK6 to cyclin D, preventing the cell cycle progression at G1 phase. As a result, by negatively controlling cell cycle progression, these genes function as a critical defense against tumorigenesis of a great variety of human cancers, including glioblastoma multiforme (Feng et al., 2012). The main set of mutations identified by the proposed method and associated with this pathway is likely to be (CDKN2B, CYP27B1, RB1) (f(B̂) = −0.738) since it has very low cost and often overlaps with other sets with low cost, which is coincided with that identified by Vandin et al. (2012). Since the mutational profile of CYP27B1 is nearly identical to a metagene including CDK4, Vandin et al. (2012) believed that the triplet (CDKN2B, CDK4, RB1) may be of interest. For (CDKN2B, CYP27B1, RB1), the low cost function value is mainly due to the inclusion of CDKN2B and CYP27B1. As shown in Table 2, we identified several other sets containing CDKN2A/CDKN2B and CYP27B1, namely, (CDKN2A, CYP27B1, RB1) (f(B̂) = −0.667), (CDKN2B, CYP27B1, NF1) (f(B̂) = −0.667), (CDKN2A, CYP27B1, NF1) (f(B̂) = −0.643) and (CDKN2B, CYP27B1) (f(B̂) = −0.643). In addition, we also uncovered a set (CDKN2B, ERBB2, RB1, TSPAN31) (f(B̂) = −0.762), which is another new discovery by the proposed method. Interestingly, TSPAN31 belongs to the same metagene including CDK4.
Third, the RAS/RTK/PI(3)K signalling pathway consists of some highly mutated genes, EGFR, NF1, PI(3)K and PTEN. Associated with this pathway, we identified a set of (EGFR, KDR, NF1) (f(B̂) = −0.619). Its low cost function value is likely due to the inclusion of EGFR and NF1.
Finally, among the other identified low-cost sets in Table 2, (MTAP, TP53, TSFM) (f(B̂) = −0.667), (CYP27B1, MTAP, PTEN) (f(B̂) = −0.655) and (CDK4, MTAP, PTEN) (f(B̂) = −0.655) are not known to be related to the pathways associated with glioblastoma multiforme. Hopefully, these low-cost sets will be useful for suggesting new links to glioblastoma multiforme. For (EGFR, TP53) (f(B̂) = −0.619), its low cost function value is possibly due to the approximate exclusiveness of EGFR and TP53. In particular, tumors in the ‘classical’ subtype of glioblastoma multiforme often carry extra copies of EGFR and are rarely mutated in TP53.
In summary, as shown in the above two real data examples, nearly all of the identified low-cost sets by the proposed method are associated with some known mutated driver pathways. This suggests potential usefulness of the proposed method. More importantly, in comparison with an existing method, some new discoveries were obtained, such as (EGFR, KRAS, NF1, STK11) (f(B̂) = −0.611 = −99/162) associated with the mTOR signalling pathway of lung cancer, and (CDKN2A, MDM2, MDM4, TP53) (f(B̂) = −0.656 = −55/84) associated with the p53 signalling pathway of glioblastoma multiforme.
3.1.3. Glioblastoma multiforme (B)
Finally we analyzed a larger dataset of glioblastoma multiforme (GBM) patients from The Cancer Genome Atlas (Brennan et al., 2013). The mutation data consist of 291 patients and 9539 genes, while the gene expression data include 558 patients and 12042 genes. Focusing on the intersection of the two gene sets, we obtained 5959 genes. Hence, we studied the filtered mutation data with 291 patients and 5959 genes, and the filtered expression data with 558 patients and 5959 genes.
First, the proposed MCSS was applied to identify multiple sets of mutations with low cost values using only the filtered mutation data. Using 10000 randomly selected initial values for all genes and 10000 randomly selected initial values for the subset of the genes with mutation rate larger than 0.05, MCSS identified some top gene sets with the six lowest cost function values (Table 3); note some gene sets with tied cost function values. They are mainly the variations and combinations of two core sets, (EGFR, KEL, NF1, TP53) and (IDH1, PIK3CA, PTEN), as contained in the top two sets identified. The list includes many well-known GBM genes, such as EGFR, PTEN, IDH1, TP53 and NF1 (Frattini et al., 2013). Nevertheless, it is surprising that some top genes identified in Table 2 do not show up in the current list. Accordingly, we examined the top gene sets identified in the previous section but calculated their cost function values using the current data. From Table 4, we see that the top sets obtained earlier all have higher (i.e. worse) cost function values than those obtained in Table 3, indicating some inherent differences between the two datasets. For example, some high-mutation genes in the previous dataset, such as CDKN2A, MDM2, MDM4, CDKN2B, CYP27B1, ERBB2 and TSPAN31, had a low-mutation rate <5% in the current dataset. We use the less frequent mutation (LFM) (i.e. with a mutation rate < 5% among the subjects) ratio (i.e. the proportion of the LFM genes in a gene set) to indicate the presence of LFM genes in Table 4. The inherent differences between the two datasets confirm the genomic heterogeneity of GBM, one of the biggest challenges in current data analysis.
Table 3.
Application to the mutation data of glioblastoma multiforme (data GBM B) (Brennan et al., 2013): the top gene sets with the six lowest cost function values identified by the new method MCSS.
| B̂ | f(B̂) | ĉe | ĉc | ĉ1 | ĉ2 |
|---|---|---|---|---|---|
| (EGFR, KEL, NF1, CNTNAP2, TP53) | −0.515 | 0.127 | −0.642 | 0.526 | 0.106 |
| (EGFR, MUC4, KEL, CNTNAP2, TP53) | −0.509 | 0.103 | −0.612 | 0.512 | 0.096 |
| (FCGBP, IDH1, MUC16, PIK3CA, PTEN) | −0.509 | 0.110 | −0.619 | 0.512 | 0.103 |
| (EGFR, NF1, CNTNAP2, TP53) | −0.505 | 0.103 | −0.608 | 0.509 | 0.096 |
| (EGFR, MUC4, CNTNAP2, TP53, RYR3) | −0.505 | 0.110 | −0.615 | 0.509 | 0.103 |
| (FCGBP, IDH1, MUC16, PTEN) | −0.498 | 0.065 | −0.563 | 0.502 | 0.058 |
| (IDH1, MUC16, PIK3CA, PTEN) | −0.498 | 0.089 | −0.587 | 0.498 | 0.089 |
| (DSP, MUC4, FCGBP, IDH1, NF1, MUC16, PTEN) | −0.498 | 0.175 | −0.673 | 0.512 | 0.148 |
| (IDH1, NF1, MUC16, PTEN) | −0.495 | 0.096 | −0.591 | 0.495 | 0.096 |
| (EGFR, KEL, TP53, FLG) | −0.491 | 0.131 | −0.622 | 0.502 | 0.110 |
| (EGFR, MUC4, CNTNAP2, TP53) | −0.491 | 0.083 | −0.574 | 0.491 | 0.082 |
| (EGFR, USH2A, CNTNAP2, TP53) | −0.491 | 0.096 | −0.587 | 0.498 | 0.082 |
| (DSP, IDH1, MUC16, DNAH3, PTEN) | −0.491 | 0.100 | −0.591 | 0.495 | 0.093 |
| (ATRX, FCGBP, MUC16, PIK3CA, PTEN) | −0.491 | 0.124 | −0.615 | 0.502 | 0.103 |
| (EGFR, CNTNAP2, TP53, RYR3) | −0.491 | 0.089 | −0.581 | 0.491 | 0.089 |
| (EGFR, IDH1, NF1, MUC16, RELN) | −0.491 | 0.110 | −0.601 | 0.495 | 0.103 |
Table 4.
The cost function values of the gene sets in the larger GBM (B) dataset with the gene sets identified from the smaller GBM (A) dataset.
| B̂ | f(B̂) | ĉe | ĉc | ĉ1 | ĉ2 | LFM ratio |
|---|---|---|---|---|---|---|
| (CDKN2A, MDM2, MDM4, TP53) | −0.285 | 0.007 | −0.292 | 0.285 | 0.007 | 3/4 |
| (CDKN2A, TP53) | −0.289 | 0 | −0.289 | 0.289 | 0 | 1/2 |
| (CDKN2B, TP53) | −0.285 | 0 | −0.285 | 0285 | 0 | 1/2 |
| (CDKN2B, CYP27B1, RB1) | −0.103 | 0 | −0.103 | 0.103 | 0 | 2/3 |
| (CDKN2B, ERBB2, RB1, TSPAN31) | −0.103 | 0 | −0.103 | 0.103 | 0 | 3/4 |
| (CDKN2A, CYP27B1, RB1) | −0.107 | 0 | −0.107 | 0.107 | 0 | 2/3 |
| (CDKN2B, CYP27B1, NF1) | −0.124 | 0 | −0.124 | 0.124 | 0 | 2/3 |
| (CDKN2A, CYP27B1, NF1) | −0.124 | 0 | −0.124 | 0.124 | 0 | 2/3 |
| (CDKN2B, CYP27B1) | −0.127 | 0 | −0.127 | 0.127 | 0 | 2/2 |
| (EGFR, KDR, NF1) | −0.354 | 0.024 | −0.378 | 0.354 | 0.024 | 1/3 |
| (EGFR, TP53) | −0.447 | 0.048 | −0.495 | 0.447 | 0.048 | 0/2 |
Finally, MCSS_ME was applied in an integrative analysis of both the filtered mutation and gene expression data. We did not apply the GA method because its current implementation requires the same set of the subjects with both mutation and gene expression data, which did not hold here. Using 10000 randomly selected initial values, MCSS_ME identified its top 10 gene sets shown in Table 5. We note that several genes were also identified from the other dataset in the previous section. Many selected genes are annotated in the Cancer Gene Census in the Catalogue Of Somatic Mutations In Cancer (COSMIC) (Forbes et al., 2015), including well-known GBM genes (EGFR, PTEN, IDH1, TP53 and NF1, among others) (Frattini et al., 2013). Here we only highlight a few examples. Gene ATRX was an important member of the H3.3-ATRX-DAXX chromatin remodelling pathway, among the most frequently mutated genes in paediatric and adult GBM Schwartzentruber et al. (2012). Gene PIK3CA, encoding a protein that antagonizes the function of PTEN protein in the PI3K/Akt pathway; an exclusive mutation pattern was observed in PIK3CA and PTEN (Hartmann et al., 2005). Mutations in a single gene, IDH1, resulted in reorganization of the methylome and transcriptome in glioblastomas and other cancers (Turcan et al., 2012). As reviewed in Sturm et al. (2014), unsupervised clustering of the gene expression data from 200 adult GBM samples from TCGA identified four different molecular subtypes: proneural, neural, classical and mesenchymal. The proneural subtype was largely characterized by abnormalities in platelet derived growth factor receptor α (PDGFRA) or isocitrate dehydrogenase 1 (IDH1), whereas mutation of the epidermal growth factor receptor (EGFR) was found in the classical subgroup and mutations in neurofibromin (NF1) were common in mesenchymal tumours. In particular, Sturm et al. (2014) mentioned the detection of lower-frequency events in both cancer-related as well as previously un-associated genes such as ATRX and KEL.
Table 5.
Application to the mutation data and gene expression data of glioblastoma multiforme (Brennan et al., 2013): the top 10 gene sets identified by the new method MCSS_ME with the automatically selected γ = 0.1. The known cancer genes annotated on COSMIC are underlined.
| B̂ | fME(B̂) | ĉe | ĉc | ĉ1 | ĉ2 | f(B̂) | γfE(B̂) | LFM ratio |
|---|---|---|---|---|---|---|---|---|
| (FCGBP, RYR2, PCLO, CNTP2, TP53) | −0.781 | 0.113 | −0.515 | 0.419 | 0.079 | −0.402 | −0.379 | 1/5 |
| (ATRX, PIK3CA, DOCK5, MUC5B, DH3, PTEN) | −0.779 | 0.113 | −0.519 | 0.419 | 0.086 | −0.405 | −0.374 | 1/6 |
| (EGFR, KEL, NF1, TP53, DH3) | −0.761 | 0.144 | −0.625 | 0.498 | 0.113 | −0.481 | −0.280 | 0/5 |
| (PIK3CA, TP53, PTEN) | −0.754 | 0.137 | −0.549 | 0.419 | 0.124 | −0.412 | −0.342 | 0/3 |
| (PIK3R1, DSP, MUC4, FCGBP, MUC16, PTEN) | −0.753 | 0.162 | −0.612 | 0.474 | 0.113 | −0.450 | −0.303 | 0/6 |
| (ATRX, KEL, PIK3CA, PTEN) | −0.752 | 0.052 | −0.474 | 0.423 | 0.052 | −0.423 | −0.329 | 0/4 |
| (DSP, FCGBP, IDH1, MUC16, DOCK5, PTEN) | −0.751 | 0.124 | −0.612 | 0.502 | 0.096 | −0.488 | −0.263 | 0/6 |
| (KEL, PIK3CA, FRAS1, MUC5B, DH3, PTEN) | −0.745 | 0.117 | −0.529 | 0.426 | 0.089 | −0.413 | −0.332 | 1/6 |
| (FCGBP, IDH1, MUC16, PIK3CA, PTEN) | −0.740 | 0.110 | −0.619 | 0.512 | 0.103 | −0.509 | −0.231 | 0/5 |
| (EGFR, IDH1, KEL, NF1, PIK3CA, DNAH3, PTEN) | −0.739 | 0.244 | −0.701 | 0.495 | 0.168 | −0.457 | −0.282 | 0/7 |
Note that all the gene sets identified with only the mutation data include only high-mutation genes (i.e. with a mutation rate > 5% among the subjects), while it is of interest but difficult to identify driver genes with less frequent mutations (i.e. with a mutation rate ≤ 5%) (LFM). Hence, we show the LFM ratio in Table 5. It is interesting to note the presence of two LFM genes, CNTP2 and DH3. In summary, our preliminary results seem to support the use of integrative analysis as advocated by others (Frattini et al., 2013).
3.2. Simulations
Due to the difficulties in evaluating de novo discoveries with real data, we performed extensive simulations to study the operating characteristics of the proposed method and compared its performance against its competitors. All simulations were performed on a single processor of an Intel(R) Xeon(R) 2.83GHz PC.
3.2.1. Simulation I: a single driver pathway
We first considered the case with only a single driver pathway, in which the focus was on comparing our new method with its strong competitor, the MCMC algorithm of Dendrix as implemented in Python (Vandin et al., 2012), though several other methods were also included.
For the proposed method, we fixed τ1 = 1, τ2 = 0.1 and α = 10−3, and tuned λ over a tuning set Λ. Specifically, λ was selected by minimizing a tuning error over a set of 10 equally-spaced points. We used 100 random initial estimates for MCSS (based on the subgradient descent algorithm), containing the Lasso estimate β̂L, as well as the other 99 random initial estimates. For the algorithm of Dendrix Vandin et al. (2012), 1000000 iterations were run for MCMC with sampling sets of size 4 for every 1000 iterations. Moreover, the algorithm was run with the number of driver mutations varying from 1 to 10 to select the best fitted subset with the lowest cost of f(·) in (2.1) as the final result.
For each simulated dataset, an n × p mutation matrix A was generated with a 1 indicating a mutation and 0 otherwise. For each patient, a gene in a driver pathway B0 = {1, 2, 3, 4} was randomly selected and it mutated with probability p1, and another gene in B0 was randomly selected to have a mutation with probability p2. Consequently, p1 and p2 controlled the coverage and exclusiveness of B0 respectively. Other genes outside B0 mutated with probability p3. Six set-ups were examined with (p1, p2, p3) = (0.95, 0.01, 0.05): (1) n = 50 and p = 1000, (2) n = 100 and p = 1000, (3) n = 1000 and p = 50, (4) n = 1000 and p = 100, (5) n = 50 and p = 10000, (6) n = 100 and p = 10000. With (p1, p2, p3) = (0.8, 0.02, 0.05), we had similar set-ups. The simulation results are summarized in Tables 6 and 7.
Table 6.
Results in Simulation I based on 100 simulation replications with (p1, p2, p3) = (0.95, 0.01, 0.05). The sample means (SD in parentheses) of correct (C) or incorrect (IC) numbers of non-zero estimates, average differences of the cost (ADC) between the true gene subset B0 = {1, 2, 3, 4} and the estimated subset B̂, that is, , and the running time (RT) (in minutes) of the algorithms.
| n | p | Method | C | IC | ADC | ĉ1 [c1] | ĉ2 [c2] | RT |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| 50 | 1000 | MCSS | 4 (0) | 0 (0) | 0 (0) | .95 [.95] | .01 [.00] | .22 (.02) |
| Dendrix-MCMC | 3.80 (.41) | .50 (.94) | −.02 (.04) | .94 [.95] | .01 [.00] | 16.89 (2.01) | ||
| Multi-dendrix-MCMC | 3.90 (.30) | .15 (.36) | −.01 (.03) | .95 [.95] | .01 [.00] | .81 (.01) | ||
| BLP | 3.39 (.86) | 3.82 (2.59) | .05 (.03) | .99 [.95] | .00 [.00] | .01 (.01) | ||
| GA | 3.90 (.38) | 2.13 (1.69) | .04 (.03) | .98 [.95] | .01 [.00] | 2.97 (.25) | ||
|
| ||||||||
| 100 | 1000 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .37 (.04) |
| Dendrix-MCMC | 4 (0) | 1.00 (.53) | .02 (.01) | .95 [.94] | .01 [.01] | 27.01 (3.71) | ||
| Multi-dendrix-MCMC | 4 (0) | 1.1 (.55) | .03 (.02) | .98 [.94] | .01 [.01] | .81 (.01) | ||
| BLP | 4 (0) | 1.76 (1.27) | .01 (.01) | .97 [.94] | .02 [.01] | .05 (.01) | ||
| GA | 4 (0) | 1.68 (1.21) | .01 (.01) | .97 [.94] | .02 [.01] | 1.96 (.16) | ||
|
| ||||||||
| 1000 | 50 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .27 (.01) |
| Dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | 134.34 (27.79) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .78 (.19) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .07 (.01) | ||
| GA | 0 (0) | 0 (0) | −.94 (.00) | 0 [.94] | 0 [.01] | .00 (.00) | ||
|
| ||||||||
| 1000 | 100 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .41 (.03) |
| Dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | 144.46 (28.75) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .68 (.24) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .21 (.01) | ||
| GA | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .11 (.00) | ||
|
| ||||||||
| 50 | 10000 | MCSS | 4 (0) | 0 (0) | 0 (0) | .95 [.95] | .01 [.01] | 1.67 (.29) |
| Dendrix-MCMC | 1.25 (1.02) | 5.96 (3.62) | −.24 (.04) | .83 [.95] | .02 [.01] | 67.06 (5.22) | ||
| Multi-dendrix-MCMC | 1.45 (1.23) | 5.25 (4.02) | −.24 (.03) | .83 [.95] | .03 [.00] | 1.88 (.03) | ||
| BLP | 3.42 (.91) | 2.72 (2.06) | .05 (.03) | .99 [.95] | .01 [.00] | .27 (.48) | ||
| GA | 3.93 (.25) | 1.50 (.92) | .04 (.02) | .98 [.95] | .01 [.00] | 284.92 (32.79) | ||
|
| ||||||||
| 100 | 10000 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | 3.94 (.43) |
| Dendrix-MCMC | 4 (0) | .96 (.41) | .02 (.01) | .95 [.94] | .01 [.01] | 75.46 (8.37) | ||
| Multi-dendrix-MCMC | 4 (0) | .90 (.44) | .02 (.01) | .96 [.94] | .01 [.01] | 3.75 (.02) | ||
| BLP | 3.95 (.22) | 3.90 (1.58) | .04 (.02) | .99 [.94] | .01 [.01] | 2.89 (2.96) | ||
| GA | 3.97 (.14) | 3.45 (1.51) | .04 (.02) | .99 [.94] | .01 [.01] | 275.39 (69.92) | ||
Table 7.
Results in Simulation I based on 100 simulation replications with (p1, p2, p3) = (0.8, 0.02, 0.05).
| n | p | Method | C | IC | ADC | ĉ1 [c1] | ĉ2 [c2] | RT |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| 50 | 1000 | MCSS | 3.70 (.47) | .25 (.44) | −.01 (.02) | .79 [.79] | .02 [.01] | .17 (.02) |
| Dendrix-MCMC | 2.95 (.83) | 3.15 (2.21) | −.03 (.04) | .77 [.79] | .01 [.01] | 16.39 (2.22) | ||
| Multi-dendrix-MCMC | 3.00 (.72) | 3.40 (1.93) | −.01 (.02) | .79 [.79] | .01 [.01] | .59 (.01) | ||
| BLP | 2.85 (1.01) | 6.62 (1.53) | .20 (.05) | 1.00 [.79] | .00 [.01] | .04 (.02) | ||
| GA | 3.63 (.61) | 5.21 (1.04) | .18 (.04) | .97 [.79] | .02 [.01] | 2.58 (.21) | ||
|
| ||||||||
| 100 | 1000 | MCSS | 4 (0) | .05 (.07) | .00 (.00) | .79 [.79] | .01 [.01] | .30 (.05) |
| Dendrix-MCMC | 4 (0) | 2.40 (.60) | .05 (.05) | .84 [.79] | .01 [.01] | 29.60 (1.72) | ||
| Multi-dendrix-MCMC | 4 (0) | 2.25 (.78) | .05 (.01) | .85 [.79] | .05 [.01] | .82 (.02) | ||
| BLP | 3.89 (.31) | 5.90 (.70) | .11 (.02) | .91 [.79] | .04 [.01] | .09 (.01) | ||
| GA | 4 (0) | 5.65 (.67) | .11 (.03) | .90 [.79] | .04 [.01] | 2.00 (.11) | ||
|
| ||||||||
| 1000 | 50 | MCSS | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | .27 (.02) |
| Dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | 163.85 (30.12) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | 1.81 (.34) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | .09 (.01) | ||
| GA | 0 (0) | 0 (0) | −.78 (.01) | 0 [.78] | 0 [.02] | .00 (.00) | ||
|
| ||||||||
| 1000 | 100 | MCSS | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | .36 (.03) |
| Dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | 186.10 (37.15) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | 1.51 (.50) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | .27 (.03) | ||
| GA | 4 (0) | 0 (0) | 0 (0) | .78 [.78] | .02 [.02] | .11 (.00) | ||
|
| ||||||||
| 50 | 10000 | MCSS | 3.15 (.67) | .40 (.68) | −.06 (.05) | .73 [.79] | .02 [.01] | .98 (.27) |
| Dendrix-MCMC | .30 (.42) | 8.70 (1.16) | −.10 (.05) | .71 [.79] | .03 [.01] | 56.09 (4.85) | ||
| Multi-dendrix-MCMC | .15 (.48) | 9.10 (1.07) | −.05 (.02) | .77 [.79] | .03 [.01] | 1.86 (.03) | ||
| BLP | 2.45 (1.40) | 5.44 (2.13) | .20 (.05) | .99 [.79] | .00 [.01] | .83 (1.06) | ||
| GA | 3.24 (1.20) | 3.82 (2.16) | .16 (.04) | .95 [.79] | .01 [.01] | 276.33 (37.50) | ||
|
| ||||||||
| 100 | 10000 | MCSS | 4 (0) | .05 (.07) | .00 (.00) | .79 [.79] | .01 [.01] | 2.70 (.46) |
| Dendrix-MCMC | 3.98 (.00) | 1.87 (.54) | .01 (.01) | .79 [.79] | .01 [.01] | 64.89 (6.75) | ||
| Multi-dendrix-MCMC | 3.64 (.99) | 1.17 (2.35) | .12 (.28) | .94 [.79] | .01 [.01] | 3.82 (.04) | ||
| BLP | 3.85 (.36) | 6.05 (.51) | .17 (.02) | .98 [.79] | .00 [.01] | 12.43 (8.76) | ||
| GA | 4 (0) | 5.33 (.62) | .15 (.02) | .96 [.79] | .01 [.01] | 252.74 (73.58) | ||
As suggested in Tables 6 and 7, the proposed method outperformed the MCMC algorithm of Dendrix, especially in the high-dimensional situations, with respect to the accuracy of selection as well as computational efficiency measured by the values of C, IC, ADC and RT respectively. The amount of improvement of the proposed method over the competitor ranged from low to high. For the running time, the proposed algorithm was overwhelmingly faster than the MCMC algorithm of Dendrix. In particular, it was often more than 50 times faster than the MCMC algorithm of Dendrix. As expected, both methods tended to perform worse as the amount of coverage and exclusiveness of a mutated driver pathway decreased.
We also compared our new method with several other alternative methods that were proposed more recently, including Multi-dendrix-MCMC of Leiserson et al. (2013), BLP (binary linear programming) and GA (genetic algorithm) of Zhao et al. (2012). The numerical results of the three methods are also summarized in Tables 6 and 7. These results suggest that the performance of Multi-dendrix-MCMC was quite similar to that of Dendrix-MCMC but much faster; BLP and GA performed better than their competitors if the algorithms could finish running; however, they were not robust with frequent running errors (up to 15% failing to converge or giving output properly). In particular, BLP ran quite unsteadily in high-dimensional situations, say n = 50 and p = 1000 or 10000, while GA was too slow in high-dimensional situations since it tried to seek an exact solution. As expected, we see that these three methods also tended to perform worse as the amount of coverage and exclusiveness of a mutated driver pathway decreased. Since a rarely mutated gene may by chance satisfy the (approximate) exclusivity property with a highly mutated gene, the union of the highly mutated gene and some rarely mutated genes could drive down the cost function value, leading to false positives. To investigate this issue, we conducted a simulation study. As before, the driver pathway contained four genes. We set the 1st gene to have mutation in a fraction of all n patients, while setting the other three driver genes {2, 3, 4} to have mutations only in the remaining patients, for whom a gene from {2, 3, 4} was randomly selected with probability to have a mutation, and another gene in {2, 3, 4} was randomly selected to have a mutation with probability . Finally, other genes outside B0 = {1, 2, 3, 4} mutated with a background probability . The corresponding simulation results are summarized in Table 8, suggesting that the proposed method still performed well.
Table 8.
Results in Simulation I based on 100 simulation replicates with for .
| n | p | Method | C | IC | ADC | ĉ1[c1] | ĉ2[c2] | RT |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| 50 | 1000 | MCSS | 2.95 (.60) | .20 (.52) | −.05 (.05) | .88 [.94] | .02 [.00] | .48 (.05) |
| Dendrix-MCMC | 2.60 (.50) | 1.55 (1.27) | −.04 (.03) | .90 [.94] | .01 [.00] | 12.58 (.78) | ||
| Multi-dendrix-MCMC | 2.45 (.75) | 2.20 (1.91) | −.04 (.03) | .90 [.94] | .02 [.00] | .46 (.05) | ||
| BLP | 3.32 (.81) | 2.95 (1.50) | .06 (.03) | 1.00 [.94] | .00 [.00] | .02 (.01) | ||
| GA | 3.15 (.93) | 3.25 (1.58) | .06 (.03) | 1.00 [.94] | .00 [.00] | 2.50 (.18) | ||
|
| ||||||||
| 100 | 1000 | MCSS | 3.85 (.41) | .30 (.73) | −.02 (.05) | .91 [.94] | .03 [.00] | .64 (.08) |
| Dendrix-MCMC | 3.95 (.34) | .31 (.61) | −.00 (.01) | .94 [.94] | .01 [.00] | 21.55 (0.84) | ||
| Multi-dendrix-MCMC | 3.95 (.22) | .35 (.93) | −.00 (.01) | .94 [.94] | .01 [.00] | .70 (.07) | ||
| BLP | 3.95 (.22) | 3.00 (1.72) | .03 (.02) | .97 [.94] | .01 [.00] | .05 (.02) | ||
| GA | 4 (0) | 2.60 (1.39) | .03 (.01) | .97 [.94] | .01 [.00] | 1.84 (.11) | ||
|
| ||||||||
| 1000 | 50 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .49 (.04) |
| Dendrix-MCMC | 4 (0) | 0.10 (.31) | −.00 (.01) | .93 [.94] | .01 [.01] | 127.60 (5.49) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .43 (.21) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .04 (.00) | ||
| GA | 0 (0) | 0 (0) | −.94 (.01) | 0 [.94] | 0 [.01] | .00 (.00) | ||
|
| ||||||||
| 1000 | 100 | MCSS | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .65 (.06) |
| Dendrix-MCMC | 4 (0) | .05 (.22) | −.00 (.01) | .94 [.94] | .01 [.01] | 153.12 (7.03) | ||
| Multi-dendrix-MCMC | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | 1.16 (.42) | ||
| BLP | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .08 (.00) | ||
| GA | 4 (0) | 0 (0) | 0 (0) | .94 [.94] | .01 [.01] | .10 (.01) | ||
|
| ||||||||
| 50 | 10000 | MCSS | 2.65 (.68) | .95 (1.10) | −.10 (.05) | .86 [.94] | .04 [.00] | 5.91 (1.52) |
| Dendrix-MCMC | 1.25 (.44) | 3.20 (1.32) | −.07 (.03) | .87 [.94] | .01 [.00] | 40.77 (2.01) | ||
| Multi-dendrix-MCMC | 1.50 (.57) | 3.75 (2.51) | −.08 (.04) | .87 [.94] | .02 [.01] | 1.37 (.09) | ||
| BLP | 2.89 (1.17) | 2.40 (1.27) | .06 (.03) | 1.00 [.94] | .00 [.00] | .15 (.31) | ||
| GA | 2.00 (1.08) | 3.70 (1.62) | .06 (.03) | 1.00 [.94] | .00 [.00] | 224.29 (30.99) | ||
|
| ||||||||
| 100 | 10000 | MCSS | 3.15 (.64) | 0 (0) | −.04 (.03) | .89 [.94] | .00 [.00] | 10.92 (2.57) |
| Dendrix-MCMC | 2.70 (.57) | 1.41 (2.06) | −.06 (.02) | .88 [.94] | .02 [.00] | 49.40 (1.76) | ||
| Multi-dendrix-MCMC | 3.34 (.57) | 2.04 (2.65) | −.04 (.02) | .90 [.94] | .02 [.00] | 2.41 (.15) | ||
| BLP | 3.30 (.92) | 5.45 (1.90) | .06 (.02) | 1.00 [.94] | .00 [.00] | .42 (.24) | ||
| GA | 3.65 (.67) | 4.50 (1.50) | .06 (.02) | .99 [.94] | .00 [.00] | 308.46 (44.10) | ||
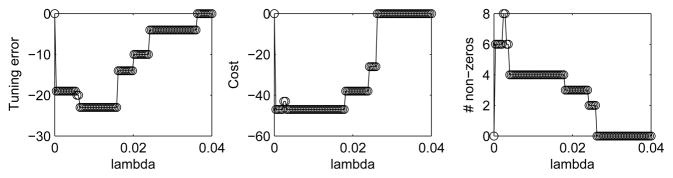
To evaluate the performance involving cross-validation, consider the first set-up: n = 50 and p = 1000 with (p1, p2, p3) = (0.95, 0.01, 0.05). The cross-validation procedure was applied with an enlarged size of Λ, say 100, and Algorithm 1 was applied to A for each λ ∈ Λ separately. The results are displayed in Figure 3, demonstrating that the λ’s minimizing the tuning error corresponded to the minimum cost of (2.1) and the true size of B0, say 4.
Fig. 3.
Tuning error, cost and number of non-zero (i.e. true positive) estimates of MCSS versus the tuning parameter value λ ∈ Λ with |Λ| = 100 for the first simulation set-up: n = 50, p = 1000 and (p1, p2, p3) = (0.95, 0.01, 0.05).
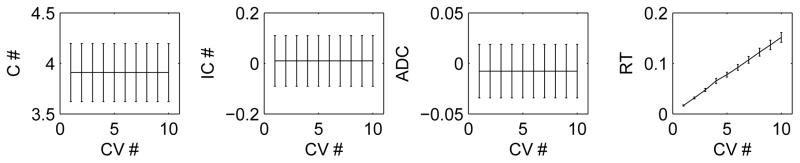
Moreover, the current tuning error is obtained by applying the cross-validation procedure for once in consideration of computational efficiency. For instance, in the first set-up with (n = 50, p = 1000) and (p1, p2, p3) = (0.95, 0.01, 0.05), as indicated in Figure 4, as the cross-validation fold number increased, the performance of the proposed method measured by C, IC and ADC did not improve, while RT increased linearly.
Fig 4.
The correct (C #) and incorrect (IC #) numbers of non-zero (i.e. true positive) estimates, the average difference of the costs (ADC) and running time (RT) of MCSS versus the fold number of cross-validation used in Algorithm 2 (CV #) for the first simulation set-up: n = 50, p = 1000 and (p1, p2, p3) = (0.95, 0.01, 0.05).
3.2.2. Simulation II: multiple driver pathways
We further compared the performance of MCSS against Multi-dendrix in identifying multiple true driver pathways as follows.
The simulation set-up was similar as before except that there were two true driver pathways B1 and B2. We used 100 random initial estimates for MCSS. We compared their performance using the top two estimated sets (with the minimum cost function values) by each method for each dataset. As shown in Table 9, MCSS performed much better for the most challenging high-dimensional case with p = 10000 and n = 50: it correctly identified a much larger number of the genes in the two true driver pathways (i.e. with a larger number of estimated true positives) while yielding fewer false positives. On the other hand, as the sample size n increased to 100, the performance of Multi-dendrix caught up.
Table 9.
Results in Simulation II based on 100 simulation replications with (p1, p2, p3) = (0.8, 0.02, 0.05).
| n | p | Method | C | IC | ADC | RT |
|---|---|---|---|---|---|---|
|
| ||||||
| 50 | 1000 | Multi-dendrix-MCMC | 2.70 (1.65) | 13.40 (6.09) | −.27 (.07) | .59 (.02) |
| MCSS | 7.35 (.67) | .55 (.89) | −.03 (.06) | .35 (.06) | ||
|
| ||||||
| 100 | 1000 | Multi-dendrix-MCMC | 8 (0) | 2.80 (1.19) | .05 (.01) | .85 (.01) |
| MCSS | 8 (0) | 0 (0) | 0 (0) | .57 (.06) | ||
|
| ||||||
| 50 | 10000 | Multi-dendrix-MCMC | .25 (.55) | 18.55 (1.73) | −.37 (.08) | 1.88 (.05) |
| MCSS | 5.52 (1.54) | 1.91 (1.89) | −.14 (.10) | 3.69 (.38) | ||
|
| ||||||
| 100 | 10000 | Multi-dendrix-MCMC | 5.75 (1.06) | 2.75 (3.91) | −.25 (.07) | 3.87 (.04) |
| MCSS | 7.42 (.82) | .65 (.67) | −.14 (.13) | 7.15 (1.11) | ||
3.2.3. Simulation III: with both mutation and gene expression data
We generated the mutation data as in Table 7 and the gene expression data from a multivariate normal distribution N(0, V). Specifically, we divided the genes {1, ···, p} into mutually disjoint subsets B0 = {1, 2, 3, 4}, B1, B2, … BK, where for each k ∈ {1, ···, K}, the gene set size |Bk| was random from {2, ···, 20}. V is a correlation matrix with all diagonal elements Vjj = 1; for any j1 < j2 both in the same Bk, Vj1j2 = Vj2j1 = 0.9; otherwise, Vj1j2 = Vj2j1 = 0.1. The rationale is that, for the genes in the same set, due to their shared function, their expression levels are also highly correlated. We used our proposed method to select all the tuning parameters, including γ. The simulation results for the integrative analysis of both mutation data and gene expression data are summarized in Table 10, where the new method MCSS_ME is compared with GA_ME, the integrative version of GA (Zhao et al., 2012). Note that, to our knowledge, the integrative version of BLP in Zhao et al. (2012) is not yet publicly available. From Table 10, we see that GA_ME failed in situations with the dimension p much smaller than the sample size n; in contrast, the new method MCSS_ME performed well. Furthermore, GA_ME was much time-consuming for large p.
Table 10.
Results in Simulation III for integrative analysis of mutation data and gene expression data. (p1, p2, p3) = (0.8, 0.02, 0.05)
| n | p | Method | C | IC | ADC | RT |
|---|---|---|---|---|---|---|
|
| ||||||
| 50 | 1000 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | 5.11 (.38) |
| GA_ME | 3.61 (.54) | 5.62 (1.67) | −.36 (.04) | 38.22 (1.95) | ||
|
| ||||||
| 100 | 1000 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | 7.96 (.70) |
| GA_ME | 4 (0) | 5.6 (.54) | −.38 (.05) | 30.81 (1.28) | ||
|
| ||||||
| 1000 | 50 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | .58 (.02) |
| GA_ME | 0 (0) | 0 (0) | −1.41 (.01) | .00 (.00) | ||
|
| ||||||
| 1000 | 100 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | .77 (.03) |
| GA_ME | 4 (0) | 0 (0) | 0 (0) | 2.10 (.12) | ||
|
| ||||||
| 50 | 10000 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | 432.55 (35.63) |
| GA_ME | – (–) | – (–) | – (–) | > 1500.00 (–) | ||
|
| ||||||
| 100 | 10000 | MCSS_ME | 4 (0) | 0 (0) | 0 (0) | 100.77 (24.25) |
| GA_ME | – (–) | – (–) | – (–) | > 1500.00 (–) | ||
4. Conclusions
This paper has introduced a new computational method for a combinatorial optimization problem motivated from cancer genomics. It approximates a combinatorial cost function with a continuous and non-convex relaxation. In particular, the indicator function is approximated by a non-convex truncated L1-function. The proposed method is computationally more efficient than an existing approach based on stochastic search, and compares favorably over several existing methods in simulations. Through both real data and simulated data analyses, the proposed method was shown to be promising for discovering mutated driver pathways with tumor sequencing data. In light of that Dendrix and other methods have been successfully applied to the TCGA (Kandoth et al., 2013), it would be interesting to apply our proposed method to on-going large cancer genomics projects. Furthermore, the current problem differs from existing pathway analysis of genome-wide association studies (GWAS) (Wang et al., 2007; Torkamani et al., 2007; Schaid et al., 2012) in two aspects: (i) the current problem is more challenging in the sense that no pathway is given a priori; (ii) however, GWAS data is different with genetic variants (or mutations) present for healthy control subjects, and it is also higher-dimensional with a larger number of genetic variants. It would be interesting to see whether the key concept of mutation exclusivity and associated methodology in the current context can be extended and applied to GWAS for de novo pathway or gene subnetwork (Liu et al., 2014) discovery to handle genetic heterogeneity. Finally, the main idea of our algorithm is quite general and may be modified and extended for other challenging combinatorial search problems.
Matlab code implementing the new method and a manual are available at https://github.com/ChongWu-Biostat/MCSS.
Acknowledgments
We are grateful to the editors and a reviewer for many constructive and helpful comments. This work was supported by NIH grants R01GM113250, R01HL105397 and R01HL116720, by NSF grants DMS-0906616 and DMS-1207771 and by NSFC grant 11571068. The authors thank Dr. Vandin for sharing the data.
APPENDIX
Proof of Theorem1
For convergence of Algorithm 1, by construction, we have, for m ∈ ℕ, S(β̂(m)) = S(m+1)(β̂(m)) ≤ S(m)(β̂(m)) ≤ S(m)(β̂(m−1)) = S(β̂(m−1)). Since S(β) is obviously bounded below, the convergence is proved. Converging finitely follows from the strict decreasing character of S(m)(β̂(m)) in m, uniqueness of minimizer of S(m)(β) and finite possible values of ∇S2(β̂(m−1)) in (2.4). After termination occurs at m★, β̂(m) remains unchanged for m ≥ m★, so does the cost function S(β̂(m)) in (2.3) for m ≥ m★. By construction of S(β), we have that β̃ = β̂(m) = β̂(m★−1), for all m ≥ m★. β̃ is uniquely defined, because for each m ∈ ℕ, the minimizer β̂(m) of S(m)(β) is uniquely defined. Since ∇S(m★)(β̂(m★)) = ∇S1(β̂(m★))−∇S2(β̂(m★−1)) = 0, we get that ∇S1(β̂(m★)) = ∇S2(β̂(m★−1)) = ∇S2(β̂(m★)). Thus, ∇S(β̂(m★)) = ∇S1(β̂(m★)) − ∇S2(β̂(m★)) = 0, which completes the proof.
Proof of Lemma 1
We prove by contradiction. By construction of S(β), we see that is also a local minimum of S(β), β ∈ Rp. Without loss of generality, we assume that . Let
Since and whenever , we see that is not a local minimizer of s*(β1), which is contrary to the assumption.
Proof of Lemma 2
We prove by contradiction. We assume that β* ≠ 0 is a local minimizer of S(β) in (A.1) on ℝp. By construction of S(β), we see that is also a local minimum of S(β), β ∈ Rp. Without loss of generality, we assume that . Let
We first consider the situation of . Denote by the right derivative of at to be b. By construction of , its left derivative at must be . Let c1 and c2 denote the left derivative and right derivative of at respectively. Since s*(β1) achieves a minimum at , we have that and c2 + b ≥ 0, which implies that . On the other hand, since , we have that c1, , and thus because we have assumed that τ12 > 2τ11, which is contrary to the fact that .
Second, we consider the situation of . In this situation, the left derivative of at , b, is , and the left derivative of at , c1, belongs to [ ], which implies b + c1 > 0 and is contrary to the the assumption of local minimum of .
Third, we consider the situation of . We see that the left derivative of at , b, is , and the left derivative of at , c1, belongs to [ ], which implies b + c1 > 0 and is contrary to the the assumption of local minimum of .
Finally, we consider the situation of . Since and whenever , we see that is not a local minimizer of s*(β1), which is contrary to the assumption.
Other choices of the tuning parameters
This section focuses on situations involving different thresholding parameters for different approximations of indicator functions in (2.3). Consider, for β ∈ [0, +∞)p,
| (A.1) |
where τ11 and τ12 may not be equal.
First, we examine the cases of τ12 > 2τ11 (τ2 < τ11, τ12).
Lemma 2
Let τ12 ≥ 2τ11 and τ2 < τ11, τ12. If there exists a local minimizer β* ≠ 0 of S(β) in (A.1), then or for each j ∈ {1, ···, p}.
Letting τ12 ≥ 2τ11, we have that in each iteration of Algorithm 1,
| (A.2) |
It follows from (A.2) that once we have that β̂(m−1) = 0 for some m, S(m)(β) ≥ 0 for all β ∈ [0, +∞)p, which terminates the DC iteration process, because β̂(m) = β̂(m−1) = 0. This indicates that if τ12 ≥ 2τ11, the DC algorithm becomes sensitive to an initial value β̂(0).
Next, we examine the case of 0 < τ12 < 2τ11 (τ2 < τ11, τ12), where the DC algorithm is not sensitive as the first one. However, based on the results of a few numerical examples (not shown), we found that in this situation, even using one more parameter, the performance of finding the minimum cost subset did not improve over the proposed method.
Finally, we consider the case of τ1 = τ11 = τ12 and τ2 ≥ τ1. In this case, similar to Lemma 1, any local minimizer of S(β) belongs to [0, τ2]p, where the truncated L1 penalty becomes a L1 penalty that does not restrict the number of nonzero coordinates of a minimizer as an L0 penalty does. In particular, in the situation with τ1 = τ2, S(β) becomes a strictly convex function on [0, τ2]p, which indicates that for any β1 and β2 with S(β1) = S(β2), . As a result, if there exists two minimum cost subsets B1 and B2 in the finite-sample situation, then by using τ1 = τ2, the corresponding method is more likely to select B1 ∏ B2 as the minimum cost subset.
The subgradient descent algorithm
For MCSS, we denote , use the following subgradient of S(m)(β) at β̂(m,t−1):
and then update β̂(m,t) until convergence to obtain β̂(m):
| (A.3) |
For MCSS_ME, we denote , use the following subgradient of S(m)(β) at β̂(m,t−1):
and then update β̂(m,t) by equation (A.3) until convergence to obtain β̂(m).
References
- An LTH, Tao PD. The DC (difference of convex functions) Programming and DCA revisited with DC models of real world nonconvex optimization problems. Annals of Operations Research. 2005;133:23–46. [Google Scholar]
- Beroukhim R, Getz G, Nghiemphu L, Barretina J, Hsueh T, Linhart D, Vivanco I, Lee JC, Huang JH, Alexander S, et al. Assessing the significance of chromosomal aberrations in cancer: methodology and application to glioma. Proc Natl Acad Sci. 2007;104:20007–20012. doi: 10.1073/pnas.0710052104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boca SM. Patient-oriented gene set analysis for cancer mutation data. Genome Biol. 2010;11:R112. doi: 10.1186/gb-2010-11-11-r112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brennan CW, Verhaak RG, McKenna A, et al. The somatic genomic landscape of glioblastoma. Cell. 2013;155:462–477. doi: 10.1016/j.cell.2013.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciriello G, Cerami E, Sander C, Schultz N. Mutual exclusivity analysis identifies oncogenic network modules. Genome Res. 2012;22:398–406. doi: 10.1101/gr.125567.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Cunha Santos G, Shepherd FA, Tsao MS. EGFR mutations and lung cancer. Annu Rev Pathol. 2011;6:49–69. doi: 10.1146/annurev-pathol-011110-130206. [DOI] [PubMed] [Google Scholar]
- Masica DL, Karchin R. Correlation of somatic mutation and expression identifies genes important in human glioblastoma progression and survival. Cancer Res. 2011;71:4550–4561. doi: 10.1158/0008-5472.CAN-11-0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L, Getz G, Wheeler DA, Mardis ER, McLellan MD, Cibulskis K, Sougnez C, Greulich H, Muzny DM, Morgan MB, et al. Somatic mutations affect key pathways in lung adenocarcinoma. Nature. 2008;455:1069– 1075. doi: 10.1038/nature07423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efroni S. Detecting cancer gene networks characterized by recurrent genomic alterations in a population. PLoS One. 2011;6:e14437. doi: 10.1371/journal.pone.0014437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng J, Kim ST, Liu W, Kim JW, Zhang Z, Zhu Y, Berens M, Sun J, Xu J. An integrated analysis of germline and somatic, genetic and epigenetic alterations at 9p21.3 in glioblastoma. Cancer. 2012;118:232–240. doi: 10.1002/cncr.26250. [DOI] [PubMed] [Google Scholar]
- Forbes SA, Beare D, Gunasekaran P, Leung K, Bindal N, Boutselakis H, Ding M, Bamford S, Cole C, et al. COSMIC: exploring the world’s knowledge of somatic mutations in human cancer. Nucl Acids Res. 2015;43(D1):D805–D811. doi: 10.1093/nar/gku1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frattini V, Trifonov V, Chan JM, Castano A, Lia M, Abate F, Keir ST, Ji AX, Zoppoli P, et al. The integrated landscape of driver genomic alterations in glioblastoma. Nature Genetics. 2013;45:1141–1149. doi: 10.1038/ng.2734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getz G, Hofling H, Mesirov JP, Golub TR, Meyerson M, Tibshirani R, Lander ES. Comment on “The consensus coding sequences of human breast and colorectal cancers”. Science. 2007;317:1500. doi: 10.1126/science.1138764. [DOI] [PubMed] [Google Scholar]
- Gill RK, Yang SH, Meerzaman D, Mechanic LE, Bowman ED, Jeon HS, Roy Chowdhur S, Shakoori A, Dracheva T, Hong KM, et al. Frequent homozygous deletion of the LKB1/STK11 gene in non-small cell lung cancer. Oncogene. 2011;30:3784–3791. doi: 10.1038/onc.2011.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn WC, Weinberg RA. Modelling the molecular circuitry of cancer. Nat Rev Cancer. 2002;2:331–341. doi: 10.1038/nrc795. [DOI] [PubMed] [Google Scholar]
- Hartmann C, Bartels G, Gehlhaar C, Holtkamp N, von Deimling A. PIK3CA mutations in glioblastoma multiforme. Acta Neuropathol. 2005;109:639–642. doi: 10.1007/s00401-005-1000-1. [DOI] [PubMed] [Google Scholar]
- Heinemann V, Stintzing S, Kirchner T, Boeck S, Jung A. Clinical relevance of EGFR- and KRAS-status in colorectal cancer patients treated with monoclonal antibodies directed against the EGFR. Cancer Treatment Reviews. 2009;35:262–271. doi: 10.1016/j.ctrv.2008.11.005. [DOI] [PubMed] [Google Scholar]
- Jones S, Zhang X, Parsons DW, Lin JC, Leary RJ, Angenendt P, Mankoo P, Carter H, Kamiyama H, Jimeno A, et al. Core signaling pathways in human pancreatic cancers revealed by global genomic analyses. Science. 2008;321:1801–1806. doi: 10.1126/science.1164368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandoth C, McLellan MD, Vandin F, Ye K, Niu B, Lu C, Xie M, Zhang Q, McMichael JF, Wyczalkowski MA, et al. Mutational landscape and significance across 12 major cancer types. Nature. 2013;502:333–339. doi: 10.1038/nature12634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leiserson MDM, Blokh D, Sharan R, Raphael BJ. Simultaneous identification of multiple driver pathways in cancer. PLoS Comput Biol. 2013;9:e1003054. doi: 10.1371/journal.pcbi.1003054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li C, Li H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics. 2008;24:1175–1182. doi: 10.1093/bioinformatics/btn081. [DOI] [PubMed] [Google Scholar]
- Liu L, Lei J, Willsey A, et al. DAWN: a framework to identify autism genes and subnetworks using gene expression and genetics. Molecular Autism. 2014;5:22. doi: 10.1186/2040-2392-5-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo YL, Hsiao CF, Jou YS, Chang GC, Tsai YH, Su WC, Chen YM, Huang MS, Chen HL, Yang PC, et al. ATM polymorphisms and risk of lung cancer among never smokers. Lung Cancer. 2008;69:148–154. doi: 10.1016/j.lungcan.2009.11.007. [DOI] [PubMed] [Google Scholar]
- Mardis ER, Wilson RK. Cancer genome sequencing: a review. Hum Mol Genet. 2009;18:R163–R168. doi: 10.1093/hmg/ddp396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masica DL, Karchin R. Correlation of somatic mutation and expression identifies genes important in human glioblastoma progression and survival. Cancer Res. 2011;71:4550–4561. doi: 10.1158/0008-5472.CAN-11-0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyerson M, Gabriel S, Getz G. Advances in understanding cancer genomes through second-generation sequencing. Nat Rev Genet. 2010;11:685–696. doi: 10.1038/nrg2841. [DOI] [PubMed] [Google Scholar]
- Miller CA, Settle SH, Sulman EP, Aldape KD, Milosavljevic A. Discovering functional modules by identifying recurrent and mutually exclusive mutational patterns in tumors. BMC Med Genomics. 2011;4:34. doi: 10.1186/1755-8794-4-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu YQ, Zhang S, Zhang XS, Chen L. Detecting disease associated modules and prioritizing active genes based on high throughput data. Bioinformatics. 2010;11:26. doi: 10.1186/1471-2105-11-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid DJ, Sinnwell JP, Jenkins GD, McDonnell SK, Ingle JN, Kubo M, Goss PE, Costantino JP, Wickerham DL, Weinshilboum RM. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genet Epidemiol. 2012;36:3–16. doi: 10.1002/gepi.20632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartzentruber J, Korshunov A, Liu XY, Jones DT, Pfaff E, Jacob K, Sturm D, Fontebasso AM, Quang DA, Tonjes M, et al. Driver mutations in histone H3.3 and chromatin remodelling genes in paediatric glioblastoma. Nature. 2012;482:226–231. doi: 10.1038/nature10833. [DOI] [PubMed] [Google Scholar]
- Shen X, Pan W, Zhu Y. Likelihood-based selection and sharp parameter estimation. J Am Statist Assoc. 2012;107:223–232. doi: 10.1080/01621459.2011.645783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shor NZ. Minimization methods for non-diffrentiable functions. Springer; 1985. [Google Scholar]
- Stark AM, Witzel P, Strege RJ, Hugo HH, Mehdorn HM. p53, mdm2, EGFR, and msh2 expression in paired initial and recurrent glioblastoma multiforme. J Neurol Neurosurg Psychiatry. 2003;74:779–783. doi: 10.1136/jnnp.74.6.779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturm D, Bender S, Jones DT, Lichter P, Grill J, Becher O, Hawkins C, Majewski J, Jones C, Costello JF, Iavarone A, et al. Paediatric and adult glioblastoma: multiform (epi)genomic culprits emerge. Nat Rev Cancer. 2014;14:92–107. doi: 10.1038/nrc3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature. 2008;455:1061–1068. doi: 10.1038/nature07385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas RK, Baker AC, Debiasi RM, Winckler W, Laframboise T, Lin WM, Wang M, Feng W, Zander T, MacConaill L, et al. High-throughput oncogene mutation profiling in human cancer. Nat Genet. 2007;39:347–351. doi: 10.1038/ng1975. [DOI] [PubMed] [Google Scholar]
- Torkamani A, Topo EJ, Schork NJ. Pathway analysis of seven common diseases assessed by genome-wide association. Genomics. 2008;92:265–272. doi: 10.1016/j.ygeno.2008.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turcan S, Rohle D, Goenka A, Walsh LA, Fang F, Yilmaz E, Campos C, Fabius AWM, et al. IDH1 mutation is sufficient to establish the glioma hypermethylator phenotype. Nature. 2012;483:479–483. doi: 10.1038/nature10866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandin F, Upfal E, Raphael BJ. De novo discovery of mutated driver pathways in cancer. Genome Research. 2012;22:375–385. doi: 10.1101/gr.120477.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogelstein B, Kinzler KW. Cancer genes and the pathways they control. Nat Med. 2004;10:789–799. doi: 10.1038/nm1087. [DOI] [PubMed] [Google Scholar]
- Wang K, Li M, Bucan M. Pathway-based approaches for analysis of genome-wide association studies. Am J Hum Genet. 2007;81:1278–1283. doi: 10.1086/522374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeang CH, McCormick F, Levine A. Combinatorial patterns of somatic gene mutations in cancer. FASEB J. 2008;22:2605–2622. doi: 10.1096/fj.08-108985. [DOI] [PubMed] [Google Scholar]
- Zhao J, Zhang S, Wu L, Zhang X. Efficient methods for identifying mutated driver pathways in cancer. Bioinformatics. 2012;28:2940–2947. doi: 10.1093/bioinformatics/bts564. [DOI] [PubMed] [Google Scholar]
- Zhang S, Zhou XJ. Matrix factorization methods for integrative cancer genomics. Methods Mol Biol. 2014;1176:229–242. doi: 10.1007/978-1-4939-0992-6_19. [DOI] [PubMed] [Google Scholar]
- Zhuang G, Song W, Amato K, Hwang Y, Lee K, Boothby M, Ye F, Guo Y, Shyr Y, Lin L, et al. Effects of cancer-associated EPHA3 mutations on lung cancer. J Natl Cancer Inst. 2012;104:1182–1197. doi: 10.1093/jnci/djs297. [DOI] [PMC free article] [PubMed] [Google Scholar]