Rapid calibration of an intracortical brain computer interface for people with tetraplegia

Abstract

Objective

Brain Computer Interfaces (BCIs) can enable individuals with tetraplegia to communicate and control external devices. Though much progress has been made in improving the speed and robustness of neural control provided by intracortical BCIs, little research has been devoted to minimizing the amount of time spent on decoder calibration.

Approach

We investigated the amount of time users needed to calibrate decoders and achieve performance saturation using two markedly different decoding algorithms: the steady-state Kalman filter, and a novel technique using Gaussian process regression (GP-DKF).

Main Results

Three people with tetraplegia gained rapid closed-loop neural cursor control and peak, plateaued decoder performance within three minutes of initializing calibration. We also show that a BCI-naïve user (T5) was able to rapidly attain closed-loop neural cursor control with the GP-DKF using self-selected movement imagery on his first-ever day of closed-loop BCI use, acquiring a target 37 seconds after initiating calibration.

Significance

These results demonstrate the potential for an intracortical BCI to be used immediately after deployment by people with paralysis, without the need for user learning or extensive system calibration.

1. Introduction

Brain Computer Interfaces (BCIs) use neural information recorded from the brain for the voluntary control of external devices [1–10]. Motor imagery or intention can be decoded using intracortical BCI (iBCI) systems, allowing people with paralysis to control computer cursors [11–18], robotic limbs [13,19–22] and functional electrical stimulation systems [23,24]. Though much progress has recently been made in further improving the speed and robustness of iBCIs in people with tetraplegia resulting from spinal cord injury (SCI), amyotropic sclerosis (ALS), and stroke [16–18], little research has been devoted to minimizing the amount of time it takes a user to gain adequate neural control.

Two approaches have been described to calibrate decoders for motor imagery-based BCIs [25]. The first approach has been to have the users adapt their behavior to a fixed BCI decoder, based on feedback (often visual). While this approach leads to BCI-based control [26–35], the process of developing reliable control requires days to weeks. The second approach has been to adapt the decoder to the user, wherein decoder parameters are computed during an explicit calibration process [3,11–17,19,21,22,36–42]. As part of this calibration process, a baseline statistical model provides the user with initial closed-loop control; we refer to this as decoder seeding. Several methods of seeding have been described that are relevant to users with mobility impairments. First, decoder parameters can be seeded with random or arbitrary values [37,43,44]. Second, in EEG-BCI systems, decoders can be seeded based on large databases of exemplar signals collected from multiple individuals [45–48]. Third, and most commonly applied with human research participants, decoders can be seeded from open-loop imagery [11–13,15–21,43,44,49–52], where users imagine or attempt movements for several minutes, after which their intentions are inferred without real-time external feedback.

In order to provide users with closed-loop control, iBCI decoders are calibrated by modeling a relationship between neural features (e.g. neuronal firing rates) and motor intentions that are inferred from training data (e.g. vectors from the instantaneous cursor position to the target position) [41]. Often, decoder calibration relies on seeding decoders during an open-loop imagery task in which users are asked to attempt, or imagine, controlling a preprogrammed cursor that automatically moves to presented targets [11–18,20,21,24]. The resulting mapping from neural data to movement intention is then used to provide users with closed-loop neural control. Since the tuning of neurons during open-loop imagery doesn’t generalize perfectly to closed-loop contexts [15,37,53–55], parameters are typically re-computed using closed-loop data [15,17,43,44,49,50,56]. Once users are provided with initial closed-loop control, iBCI systems can continue to adapt based on closed-loop data. Adaptation during ongoing use optimizes the quality of control during extended use [9,15,16,25,43,44,49,50,57,58] given signal nonstationarities [16,59]. Strategies for updating decoders during ongoing use include re-computing model parameters continuously [44,56–58] or in short batches on the timescale of minutes [43,49,50].

There are several reasons why the current approach to decoder calibration should be shortened and streamlined. First, some iBCI users will have diseases such as ALS or brainstem stroke, which may impair their ability to remain alert and engaged long enough to participate in prolonged calibration sequences. Second, by rapidly providing users with feedback that the device is working (i.e. by obviating the requirement for an explicit open-loop imagery task), one could anticipate greatly increased user engagement and decreased time required for developing adequate neural control [43,44,60,61]. Third, in the current stage of research, where iBCI devices in humans require percutaneous connections, there is limited time available for data collection during research sessions. A reduction of calibration times on the order of minutes would dramatically streamline data collection, with further time savings gained across days. Finally, the immediate and intuitive calibration of a BCI decoder would make it possible in the future for a patient who has become acutely locked-in due to brainstem stroke to be provided with an immediately useful BCI.

Here, we demonstrate rapid calibration of iBCIs that allows users to achieve closed-loop neural control without an explicit open-loop imagery step [11–18,20,21,24] (Fig 1). Three iBCI users with paralysis developed accurate neural closed-loop cursor control with performance plateauing in under 3 minutes. We found that this approach could be used for two different decoding algorithms. Finally, a BCI-naïve individual with tetraplegia (participant T5) was able to gain continuous, unassisted, two-dimensional closed-loop cursor control when using an iBCI system for the first time.

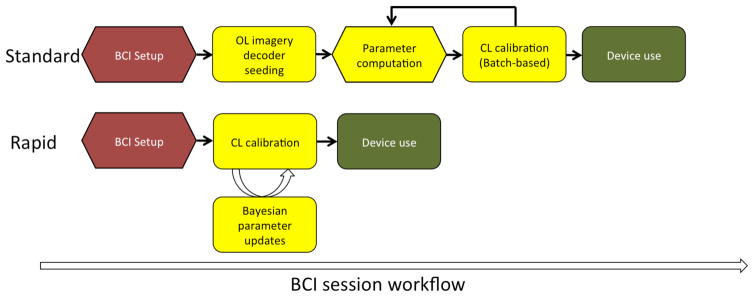
Fig. 1.

Schematic representation of a typical iBCI calibration protocol in humans vs. the rapid calibration sequence. Each black arrow represents a step where a technician currently intervenes. Hexagonal and rounded steps refer to offline and online steps, respectively. The BCI user does not actively participate in offline steps. Red, yellow and green steps refer to the setup, calibration, and use of the BCI system, respectively. Top. Typical use of an intracortical BCI system has several steps. First, the user is connected to the computer and the software is initialized. The user then performs open-loop imagery; decoders are seeded using this initial data; and then closed-loop calibration proceeds, and may be repeated several times depending on the protocol being used. Bottom. No explicit open-loop imagery step is required, and the decoder calibration steps occur without the need for technician oversight or intervention.

2. Methods

2.1 Permissions

The Institutional Review Boards of Brown University, Case Western Reserve University, Partners HealthCare/Massachusetts General Hospital, Providence VA Medical Center, and Stanford Medical Center, as well as the US Food and Drug Administration granted permission for this study (Investigational Device Exemption). The participants in this study were enrolled in a pilot clinical trial of the BrainGate Neural Interface System (ClinicalTrials.gov Identifier: NCT00912041). (Caution: Investigational device. Limited by federal law to investigational use.)

2.2. Participants

The three participants in the study were: T5, a 63 year-old right-handed male with C4 AIS-C spinal cord injury; T8, a 55 year-old right-handed male with C4 AIS-A spinal cord injury; and, T10, a 34 year-old right-handed male with C4 AIS-A spinal cord injury. All three participants underwent surgical placement of two 96-channel intracortical silicon microelectrode arrays [62] (1.5-mm electrode length, Blackrock Microsystems, Salt Lake City, UT) as previously described [11,12]. In T5 and T8, both arrays were placed in the dominant precentral gyrus. In T10, one array was placed in the dominant precentral gyrus and a second was placed in the dominant caudal middle frontal gyrus. Data were used from trial (post-implant) days: 30 and 33 (T5); 660, 662, 665, 927, and 928 (T8); and 84, 112, 187, 188, 194, 195, 203, 215, 216, 236, 355, and 361 (T10).

2.3 Signal acquisition

Raw neural signals for each channel (electrode) were sampled at 30kHz using the NeuroPort System (Blackrock Microsystems, Salt Lake City, UT). Further signal processing and neural decoding were performed using the xPC target real-time operating system (Mathworks, Natick, MA). Raw signals were downsampled to 15kHz for decoding, and de-noised by subtracting an instantaneous common average reference [16,17] using 40 of the 96 channels on each array with the lowest root-mean-square value (selected based on their baseline activity during a one minute reference block run at the start of each session). The de-noised signal was band-pass filtered between 250 Hz and 5000 Hz using an 8^th order non-causal Butterworth filter [63]. Spike events were triggered by crossing a threshold set at 3.5x the root-mean-square amplitude of each channel, as determined by data from the reference block. The neural features used were: (1) the rate of threshold crossings (not spike sorted) on each channel, and (2) the total power in the band-pass filtered signal [14–16]. Neural features were binned in 20ms non-overlapping increments for decoding with T5 and T10. For T8, the 20ms bins were causally smoothed over 60ms.

For closed loop decoding, the neural features, z, were split between threshold crossings and the band power filtered signal [14–16]. We used the top 40 features ranked by signal-to-noise-ratio of neural modulation [64]. For all three participants, 35% (+/− 3%) of the features selected were threshold crossings, and 65% (+/− 3%) were band power. The number of features that were tuned for closed-loop neural cursor control was computed for each participant. A feature was considered tuned if there was a statistically significant relationship between the feature and the direction of movement grouped by octants (ANOVA, p < 0.001). The average fraction of features that were tuned for directional movement was 0.64 (T5, range: 0.53 – 0.70); 0.36 (T8, range: 0.17 – 0.51); and, 0.58 (T10, range: 0.23 – 0.84).

2.4 Calibration task

Task cueing was performed using custom built software running Matlab (Natick, MA). The participants used standard LCD monitors placed 55–60 cm distance from the participant, at a comfortable angle and orientation. Participants engaged in the Radial-8 Task as previously described [12,16]. Briefly, targets (size = 2.4 cm, visual angle = 2.5°) were presented sequentially in a pseudo-random order, alternating between one of eight radially distributed targets and a center target (radial target distance from center = 12.1 cm, visual angle = 12.6°). Successful target acquisition required the user to place the cursor (size = 1.5cm, visual angle = 1.6°) within the target’s diameter for 300ms, before a pre-determined timeout. Target timeouts resulted in the cursor moving directly to the intended target, with immediate presentation of the next target. During the first 60 seconds of calibration with T8, we attenuated 80% of the component of the decoded vector perpendicular to the vector between the cursor and the target [15,39]. No error attenuation was used for T5 or T10.

2.5 Calibration procedure

Previous approaches to iBCI decoder calibration

Prior to the procedure described in this report, decoder calibration was a multi-step process requiring active intervention from a trained technician. We have previously reported two approaches. The first [17,18] used: (i) initial BCI setup, (ii) 5 minutes of open-loop motor imagery, (iii) a technician supervised decoder calibration stage, (iv) 5 minutes of closed-loop control, and finally, (v) a second supervised decoder calibration (Figure 1). Our team has also implemented protocols for initial decoder calibration wherein users performed 2 minutes of open-loop imagined movements, followed by a series of batch-based calibration sequences over 6 minutes [12] or 9 minutes [15,16] of gradually decreasing computer assistance [15,16,39]. Thus, our standard approach to calibration has been to seed decoders with open-loop imagery, and then to perform batch-based decoder updates, taking approximately 8–11 minutes of actual calibration time (excluding the additional time required for manual intervention by the technician between calibration epochs - approximately 0.5–1 minutes between blocks).

We sought to accelerate calibration with three modifications to our standard approach. First, we removed the explicit open loop calibration step. Second, rather than performing batch-based calibration every 2–5 minutes, we updated decoder parameters every 2–5 seconds throughout the calibration phase. Third, we automated the remaining calibration steps normally performed by a technician.

We note that our new approach to calibration performs three processes simultaneously, which we briefly list here and then describe in detail in later sections. First, the decoding algorithm performs real-time predictions of the intended velocity based on the neural features, providing users with closed-loop neural control (Section 2.6). Second, during calibration, data consisting of (y_t, z_t) pairs are collected, where y_t is the 2×1 unit vector pointing from the cursor’s current position to the known target [14–16], and z_t is the corresponding 40×1 vector of neural features. Third, the (y_t, z_t) pairs are used to update the parameters used by the decoding algorithm every 2–5 seconds (Section 2.7).

At the start of the session, the decoder parameters are initialized to values that leave the cursor stationary regardless of the neural features. Nevertheless, training data can be collected since the user has been instructed to attempt to move the cursor to the target on the screen. After the first parameter update (2–5 seconds after the start of the session), the decoder began using neural features to provide users with closed loop neural control, although the user had poor control, as expected. As the calibration task continued, the decoder parameters were re-computed (based on growing amounts of training data, every 2–5 seconds) and the quality of control improved. At the end of the calibration the parameters were locked before assessment with the Grid Task (see below).

2.6 Decoders: Basic models and algorithms

We tested our calibration procedure with two different decoding algorithms: the steady-state Kalman filter, and a novel technique combining Gaussian process regression with the discriminative Kalman filter (GP-DKF), described below. Both decoders are Bayesian sequential filters. Let x_t denote the hidden state at time step t, namely, the unobserved 2×1 vector of intended velocity of the cursor, and let z_t denote the observation at time step t, namely, the 40×1 vector of neural features (Sections 2.3, 2.5). In Section 2.7 we discuss the distinction between x_t and y_t. The initial probability distribution function (PDF) of intended velocity at time 0 is denoted p(x₀), the conditional PDF of intended velocity at time t given the intended velocity at time t-1 is denoted p(x_t | x_t-1), and the conditional PDF of neural features at time t given the intended velocity at time t is denoted p(z_t | x_t). The conditional PDFs p(x_t | x_t-1) and p(z_t | x_t) model, respectively, the temporal dynamics of intended velocity and the instantaneous mapping from intended velocity to neural features. Bayesian sequential filters use these PDFs and the history of observed neural features (z₁,…, z_t) in order to compute the conditional PDF of the intended velocity given the complete history of observed data:

$$\mathrm{p}({\mathrm{x}}_{\mathrm{t}}\mid {\mathrm{z}}_1,\dots ,{\mathrm{z}}_{\mathrm{t}}).$$

Both decoding algorithms used the mean of this conditional PDF as the prediction of the unknown intended velocity at time step t. This prediction was used to update the cursor position.

The two decoding algorithms are derived under differing assumptions for the observation model, p(z_t | x_t), but they share the same model for intended velocity:

$$\begin{gathered} \mathrm{p}({\mathrm{x}}_0)=\mathrm{\eta }({\mathrm{x}}_0\mid 0,{\mathrm{W}}_0) \\ \mathrm{p}({\mathrm{x}}_{\mathrm{t}}\mid {\mathrm{x}}_{\text{t-}1})=\mathrm{\eta }({\mathrm{x}}_{\mathrm{t}}\mid {\text{Ax}}_{\text{t-}1},\mathrm{W}) \end{gathered}$$

where η(x | μ, Σ) denotes the multivariate Gaussian PDF with mean vector μ and covariance matrix Σ evaluated at x. This is the model for the hidden states underlying the well-known Kalman filter [11,65,66]. W and W₀ are 2×2 covariance matrices and A is a 2×2 matrix. The parameters A, W, W₀ were fixed at values that have historically worked well for closed-loop neural control [14–16]. Both A and W noticeably affect the dynamics of cursor control. Loosely speaking, A controls the smoothness of cursor dynamics, whereas W controls the extent to which decoded neural features are used to drive cursor control.

Kalman filter

The first decoder uses the linear, Gaussian observation model

$$\mathrm{p}({\mathrm{z}}_{\mathrm{t}}\mid {\mathrm{x}}_{\mathrm{t}})=\mathrm{\eta }({\mathrm{z}}_{\mathrm{t}}\mid {\text{Hx}}_{\mathrm{t}},\mathrm{Q}),$$

where Q is a 40×40 covariance matrix and H is a 40×2 matrix relating intended velocity to brain activity. The parameters H and Q were learned from the training data collected during the calibration procedure (Sections 2.5 and 2.7). The classical Kalman-update equations use the observed neural features as well as A, W, W₀, H, and Q, in order to compute the mean of p(x_t | z₁,…, z_t), used for closed-loop neural control [11,65,66]. The version of the algorithm that we used is based on the steady-state update Kalman equation [14–16] and uses real-time bias correction [16,19]. During closed-loop calibration, the parameters H and Q were updated every 2–5 seconds. We do not go back to time step 0 and repeat the entire Kalman filtering algorithm with the updated parameters.

Discriminative Kalman filter

In contrast to the standard Kalman filter, the DKF places no constraints on the observation model: it may be nonlinear and non-Gaussian. Although relaxing this Gaussian assumption may better model the non-Gaussian features of neural data, it introduces two fundamental difficulties. First, the standard filtering algorithms become computationally intensive (unlike the fast Kalman-update equations). Second, learning a generic observation model from training data is much more complicated than learning the parameters H and Q in the Kalman model [67,68].

We have recently shown how these two difficulties can be surmounted for our purposes using an approach that we call the discriminative Kalman filter (DKF) [67]. In brief, the DKF solves the problem of computationally intensive Bayesian filtering updates with judicious and theoretically motivated Gaussian approximations. Using these approximations does not require full knowledge of the observation model, but only requires knowing the conditional mean and covariance of the intended velocity given the current neural features. We denote the conditional mean and variance as the functions m(z_t) and S(z_t), respectively. The only requirement in using the DKF is to learn m(z_t) and S(z_t) during calibration (see Sections 2.5, 2.7). Even though m(z) and S(z) are arbitrary functions, we refer to them as parameters of the decoder.

Despite the highly non-linear nature of m(z) and S(z), the calculations needed to compute the predicted intended-velocity (given A, W, W₀) may be performed in real time systems [67]. When the parameters m(z) and S(z) are updated (every 2–5 seconds during the calibration phase), we simply modify their values in the DKF update equations for future updates. We do not go back to time step 0 and repeat the entire DKF filtering algorithm with the updated parameters. We emphasize that the DKF is distinct from the extended Kalman filter, the unscented Kalman filter, and related algorithms, which are based on combining Gaussian approximations with the conditional mean and covariance of the neural features given the intended velocity; instead, the DKF approximates the intended velocity given the neural features. Loosely speaking, the DKF can be viewed as a principled way to do model-based temporal smoothing of direct (nonlinear) regression predictions of intended velocity.

2.7 Decoders: Parameter learning and updating

Each decoder has parameters that relate the intended velocity of the cursor to the neural features, namely, H and Q for the Kalman filter and m(z) and S(z) for the DKF. In principle, parameters could be learned from observed (x_t, z_t) pairs, however, the true intended velocity (x_t) is always unobservable. Instead, we learn the parameters using the (y_t, z_t) pairs that are collected throughout the calibration phase (Section 2.5). Recall that y_t is the unit vector pointing from the cursor’s current position to the known target. Our calibration algorithms simply use y_t as a direct surrogate for x_t, the rationale being based on the assumption that the user intended to move directly to the target at time t. At time step r, say, we horizontally concatenate y₁,…, y_r into a 2×r matrix Y and, similarly, we concatenate z₁,…, z_r into a 40×r matrix Z. The matrices Y and Z comprise the training data at time step r. For certain values of r (every 2–5 seconds), these matrices are used to update the parameters of the decoding algorithm.

Given Y and Z, the calibration for the Kalman filter computes H and Q, and calibration for the DKF computes m(z) and S(z). In both cases, we use standard regression tools: linear regression for H and Q and nonlinear regression for m(z) and S(z). Since closed-loop parameter updates begin updating seconds after the start of calibration, regression methods were chosen that provided non-singular solutions given small amounts of data. In both cases, we used Bayesian regression methods. In a Bayesian approach, uncertainty about a parameter is represented by a probability distribution. The Bayesian prior refers to the probability distribution before data has been collected. As new information becomes available, the parameter’s distribution is updated accordingly (referred to as the posterior distribution). Hence, Bayesian methods provide the experimenter a method for updating their belief of a parameter given evolving information. Note that the term Bayesian is used in two different contexts in this paper. Our decoding algorithms are based on Bayesian filtering, whereas our calibration algorithms incorporate new training data using Bayesian parameter updating. In principle, decoding and parameter learning could be combined into a unified Bayesian procedure, but this would necessitate more complicated decoding algorithms and would be too computationally demanding to perform real-time decoding.

Kalman filter with Bayesian linear regression

Given matrices Y and Z, the parameter H (relating motor intention to neural features) was updated via

$$\mathrm{H}={\text{ZY}}^{\mathrm{T}}{({\text{YY}}^{\mathrm{T}}+\mathrm{\alpha }\mathrm{I})}^{-1},$$

where I is the 2×2 identity matrix and α was a regularization parameter (α = 10⁻³). This particular method of updating H can be viewed equivalently as ridge regression or as Bayesian linear regression [68]. We will describe the Bayesian derivation. Let vec(H) denote the vectorization of H, i.e., the 80×1 vector created by stacking the 40×2 columns of H on top of one another. We set the prior for vec(H) (given Y and Q) to be a multivariate Gaussian with mean zero and covariance α⁻¹I⊗Q, where ⊗ denotes the Kronecker product, and we use the Kalman filter observation model (replacing x_t with y_t) which specifies that p(z_t | Y, H, Q) = η(z_t | Hy_t, Q). Under this model (regardless of the prior on Q), the posterior mean of H is ZY^T(YY^T + αI)⁻¹, and we use this as our estimate of H based on Y and Z. As more data were collected, the impact of the αI term decreased and our estimate for H approached the maximum likelihood estimate that is traditionally used for selecting parameters for the Kalman filter [66]. After H was updated, Q was updated using the covariance of the residuals Z – HY.

Gaussian process regression

Given matrices Y and Z, the nonlinear function m(z) (relating neural features to motor intention) was computed via

$$\mathrm{m}(\mathrm{z})=\mathrm{Y}{(\mathrm{K}(\mathrm{Z},\mathrm{Z})+\mathrm{\alpha }\mathrm{I})}^{-1}\mathrm{K}{(\mathrm{z},\mathrm{Z})}^{\mathrm{T}},$$

where α was a regularization parameter (set to α=0.6), I is the r×r identity matrix, K(z, z′) is the standard radial basis function kernel, K(Z, Z) is an r×r matrix with K_ij(Z, Z)=K(z_i, z_j), and K(z, Z) is a 1×r vector with K_j(z, Z)=K(z, z_j). Intuitively, the function m(z) returns a 2×1 prediction of intended velocity by taking a weighted average of all of the intended velocities in Y (Supplementary Figure 1). The weights were determined by comparing the current vector z of neural features to the neural training data in Z using the radial basis kernel (i.e., a Gaussian kernel in 40 dimensions) as a measure of similarity (Supplementary Fig. 1.). In this case the prior on the function m(z) was a zero mean GP with covariance kernel K and we update using the posterior mean. The function S(z) = S was taken to be constant and was estimated from the covariance of the residuals m(Z) – Y. To emphasize that m(z) is learned with GP regression, we call our second decoder the GP-DKF.

We found evaluating m(z) was slow when the number of training points in Y and Z was too large. We used up to 60 seconds (3000 datapoints) of data for decoding with T5 and T10. For T8, we increased this to 120 seconds (6000 datapoints). The number of datapoints was chosen based on early validation of the GP-DKF method. Early validation of the GP-DKF also suggested higher quality cursor control using only band power for z_t, rather than both band power and threshold crossing counts. For the purposes of comparing performance to the Kalman decoder, we selected 40 features. Neural features were sorted into octants according to the direction of movement. Each octant contained a maximum number of datapoints (i.e. 3000/8 = 375), with corresponding buffer allocations. If the number of datapoints exceeded the buffer size per octant, the oldest data in that octant were replaced.

2.8 Performance measurement

After calibration, we quantified performance using a Grid Task after locking decoder parameters [13,18,52]. This task consisted of a grid of N square targets arranged in a square grid (N = 25, 36, 49, 64, 81 or 100, length of one side of square grid = 24.2cm, visual angle=24.8°). One of N targets was presented at a time in a pseudo-random order. Targets were acquired when the cursor was within the area of the square for 1 second. Incorrect selections occurred if the cursor dwelled on a non-target square for an entire hold period [69]. When comparing the GP-DKF decoder to the previously described standard Kalman calibration scheme [14–16], each comparison block was 3 minutes in length. When performing rapid decoder calibration comparisons with T10, each comparison block was 2 minutes in length. Block lengths were selected based on the participant’s preference.

The Grid Task is designed as a generalized version of a single-channel communication task, designed to measure target selection speed. The achieved bit rate (BR) measures the effective throughput of the system [52]:

$$\text{BR}={log}_2(\mathrm{N}-1)max(\text{Sc}-\text{Si},0)/\mathrm{t}$$

where N is the number of possible selections, Sc and Si are the number of correctly and incorrectly selected targets, respectively, and t is the elapsed time. The max function ensures that the bit rate remains non-negative.

Testing performance as a function of decoder and calibration times

We performed a series of comparisons between the GP-DKF and Kalman decoders with variable amounts of calibration time. Decoders were calibrated using the Radial 8 task, parameters were locked, and the performance was measured using the Grid Task. For instance, when comparing performance of the Kalman decoder at 3 minutes vs. 5 minutes, the Kalman decoder was first calibrated for 3 minutes and then immediately tested (representing condition A). Next, a new Kalman decoder was calibrated for 5 minutes before being tested with the Grid Task (B). Decoder/timing pairs were alternated, in an A-B-A-B format. Only data collected the same day were used for statistical comparisons.

Testing the new rapid calibration protocol vs. the previous standard

To test the performance of the new calibration protocol vs. the standard calibration protocol, we began by calibrating using the technician supervised, computer-assisted, batch-based 11-minute calibration scheme (as previously used in[14–16]). Calibration began with 2 minutes of open loop imagery, which was used to seed a decoder. Next, three blocks (3 minutes each) of closed-loop neural cursor control were performed, while computer assistance was gradually removed. Performance was assessed using the Grid Task. Next, we performed three minutes of closed-loop decoder calibration using the GP-DKF decoder, locked decoder parameters, and then assessed performance with the Grid Task. We used block-based feature mean updates for the standard Kalman decoder[16]. Only data collected the same day were used for statistical comparisons.

Isolating the calibration protocol vs. the previous batch-based protocol

To test the performance effect from the rapid calibration protocol, we compared it to the standard batch-based method while controlling for calibration length. We began by having the participant attempt open loop motor imagery for one minute. The neural features and cursor kinematics were used to seed both the standard Kalman decoder (i.e. decoder parameters did not update for 2 minutes, condition A) and the rapidly updating Kalman decoder (i.e. decoder parameters updated every 3–5 seconds for 2 minutes, condition B). After locking parameters, we then tested performance using the Grid Task, balancing the comparisons by alternating whether A or B was tested first.

Mean angular error measurements

To investigate performance saturation, we performed offline simulations of decoder performance by training decoders with variable amounts of training data. We computed the angular error between the predicted decoder value without filtering (i.e. the Kz term of the Kalman filter) and the label modeled as the vector from cursor to target [14–16]. Data from a single experimental session were concatenated together. A decoder was trained using a random subsample without replacement and then used to predict the mean angular error for another subsample of the same size. Decoder predictions were bootstrapped 100 times.

Additional metrics

In addition to bit-rate and angular error, we also report two additional metrics. The first is time to target, which is the time between target presentation and acquisition by the user. The second is orthogonal direction changes, which is a measure of how consistently the cursor went towards the target[12].

2.9 Additional methods for participant T5’s first day of closed-loop neural control

Though participants often remain in the BrainGate and other BCI research for years [12,18,19,41], there can only be one “first day” of attempted neural control. There is also special interest in understanding how rapidly a BCI-naïve user with tetraplegia might gain useful neural control of a BCI. We had the opportunity to deploy GP-DKF on participant T5’s first day of neural control.

Prior to T5’s first attempt at closed-loop neural control, the following text was read verbatim:

“As you know, we are recording from a part of the brain responsible for controlling movement. In this part of the brain, the nerve cells respond to you attempting to move part of your body. You’ll be presented with a cursor and a target. We’d like you to think about moving your hand/arm/finger towards the target. As you try and do so, the system will be recording from the nerve cells. It will learn that [sic] the pattern of brain activity associated with wanting to go to a direction.

“As you try to move the cursor to more targets, the system will learn a list of different responses. The cursor may not behave as you expect. For example, you may be trying to move the cursor to the right but the cursor moves to the left. This is OK. It’s not your fault. But no matter what the cursor is doing, keep trying to move it towards the target. The system will rapidly learn your brain signals and may start to correct within a few seconds. It’s important to stay consistent with what you’re attempting to do. For example, rather than repeatedly trying to move your hand to the left, you have to attempt to perform a continuous left-moving motion.

“We’re going to try a few different imageries today. Can you think of some motions that would be intuitive to control a computer cursor on a screen?”

We explored a total of six motor imageries with T5. “Joystick” refers to the control of an airplane using a joystick, where the dominant hand is resting comfortably on a surface and moving a joystick in a particular direction driving cursor movement. Left movement occurs through pronation, right through supination, upwards with ulnar deviation, and downwards with radial deviation. “Whole arm” refers to attempting to control the cursor by pointing using the index finger, where the shoulder and elbow are free to move with fixed wrist and finger positions. “Index finger” refers to imagery in which the wrist is resting comfortably on a surface, and the index finger is used to control a pointing stick mouse. “Stirring a pot” refers to the imagery of holding a wooden spoon over a saucepan. The shoulder is fixed, and movement occurs with a combination of arm protraction and retraction, as well as elbow internal and external rotation. The wrist and fingers are fixed. “Pointing at a target” refers to imagery wherein T5 is pointing at the screen where he wants the cursor to go with his arm fully extended, the elbow and wrist locked. Moving left, right, up and down refer to arm adduction, abduction, flexion and extension, respectively. “Mouse ball” refers to the control of a trackball mouse, requiring a combination of elbow and wrist movement, with a fixed wrist/finger orientation. T5 described the mouse ball imagery as being continuous as opposed to repetitive; that is, moving the cursor in a direction did not require repeatedly resetting his hand position. Importantly, due to T5’s injury, he was unable to actually perform these tasks. During all of the imageries, his hand and arm were comfortably at rest at his side. T5 decided to use the “joystick” imagery for the very first attempt at closed-loop control.

The research session began with a one-minute reference block for computing spike threshold values and choosing channels for common average referencing. Thereafter, T5 attempted neural cursor control with the GP-DKF decoder. On the first attempt, the block was stopped after approximately one minute when T5 indicated that he did not understand he was supposed to have been attempting motor imagery (asking “when should I start?”). After being reminded that he should be using the “joystick” imagery, the calibration sequence was repeated and T5 gained closed-loop neural control of the cursor (see Results).

After the “joystick” imagery, T5 then achieved closed-loop control with each of the imageries in the order listed above. T5 was then asked to select the top three imageries that felt most intuitive. He selected “joystick”, “index finger”, and “mouse ball”. We repeated calibration with each of these imageries. We presented him with the results of target acquisition as a function of calibration time (similar in format to Fig. 4), and provided him with the opportunity to select a single motor imagery that felt intuitive to use for the rest of the sessions. He selected “mouse ball”. Thereafter, he was asked to only use “mouse ball” imagery for Radial-8 and Grid Task control.

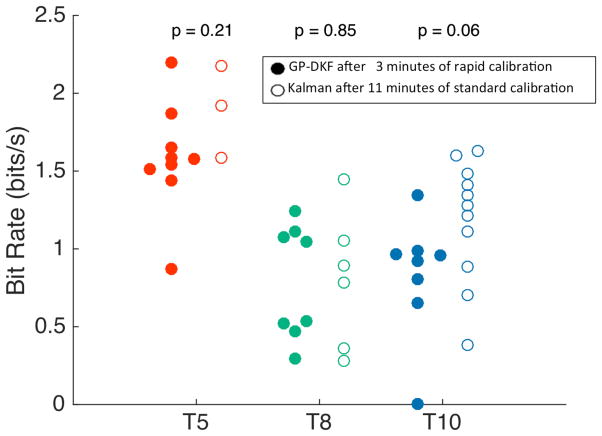
Fig. 4.

Bit rate comparisons between decoder methods. After calibrating the GP-DKF decoder for 3 (T5 - red, T10 - blue) or 4 (T8 - green) minutes, the decoder parameters were locked, and the participants selected targets using the Grid Task. Bit-rates were computed for the GP-DKF decoder and compared to the performance using a Kalman filter using ~10 minutes of calibration data with an explicit open-loop imagery step[16]. Bit rates were not statistically different when comparing decoders within participants (Wilcoxon-rank test). Data were used from trial days: 30 and 33 (T5); 660, 662, 665 (T8); and 84, 112 (T10).

3. Results

3.1 Rapid calibration with both GP-DKF and Kalman decoders

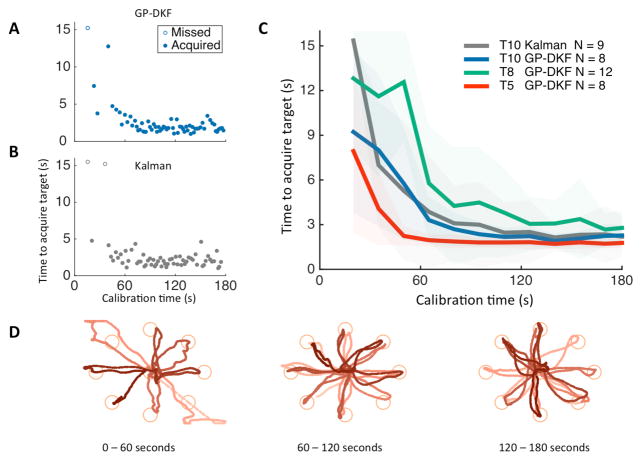
All three iBCI users with tetraplegia rapidly gained closed-loop cursor control during the initial calibration sequence using the GP-DKF decoder (Fig. 2A–D, Supplementary Fig. 2, 3). At the start of calibration, neural control was poor as expected; as more data were collected, each user gained better control in all directions. To assess performance saturation, we fit the calibration performance with an exponential curve, computed the exponential time-constant, and then estimated the amount of calibration data required to achieve 95% maximal performance. We found the time to target performance saturated with the GP-DKF within 3 minutes for all three participants (participant T5: 43s +/− 4s, T8: 136s +/− 54s, T10: 100s +/− 25s). Towards the end of calibration, the time to target acquisition was comparable to state-of-the-art Radial-8 task target acquisition times with fully calibrated decoders and locked parameters [17]. Note that GP-DKF calibration with T5 and T8 did not use computer assistance, whereas T8 used computer assistance for the first 60 seconds (see Methods, [15]).

Fig. 2.

Rapid calibration during the Radial-8 task. Participant T10 performed a three-minute calibration sequence with either the GP-DKF (A) or the Kalman (B) decoders. Targets were acquired when the cursor overlapped the target for 300ms, with a 15-second timeout. (C). Multiple calibration sequences from participants T5 (red), T8 (green) and T10 (blue) were done using the GP-DKF decoder, and with the Kalman decoder in T10 (grey). The thin dark lines are the average amount of time to acquire a target across all blocks (shaded area is +/− 1 standard deviation). Averages are computed by binning data in 15-second increments, with a 5 second offset from calibration start. (D). Example cursor trajectories during calibration using the GP-DKF decoder (participant T5). The brightness goes from light to dark as time elapses during the 60 second interval of closed-loop neural cursor control. Data were used from trial days: 30 and 33 (T5); 662, 665, (T8); and 112, 203, 215, 236 (T10).

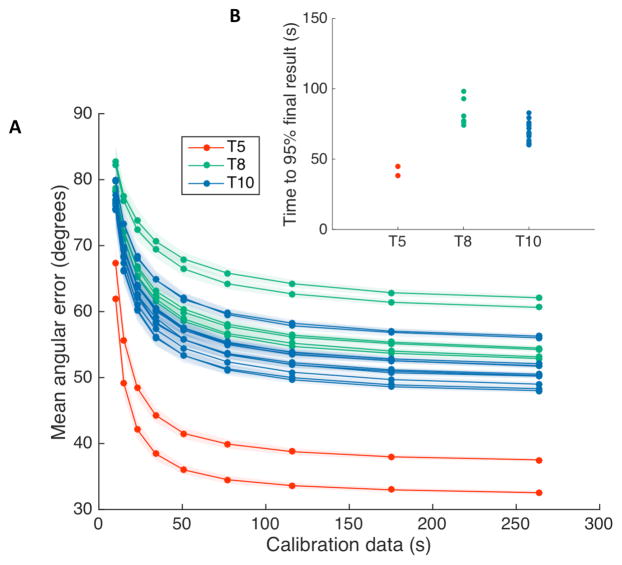
We further evaluated performance saturation for all three participants with offline simulations using a different performance metric. By bootstrapping neural features and cursor kinematics within a single experimental session, we computed the predicted the angular error between the simulated decoded direction and the known vector from cursor to target (see methods). We found that offline predictions of decoder performance had an exponential behavior for all of the experimental sessions we tested (Fig. 3). We fit the angular error curves using a decaying exponential, computed the decay half-lives, and then estimated the amount of neural data required to achieve 95% saturation of the minimum angular error. We found that offline simulations of angular error saturated in under 3 minutes of calibration time (mean +/− standard deviation; participant T5: 41.6s +/− 4.6s; T8: 83.3s +/− 9.9s; T10: 69.3s +/− 7.5s).

Fig. 3.

Bootstrapped angular error as a function of each participant’s neural features used to simulate decoding. (A) For each experimental session, a decoder was trained using a random subsample, without replacement, and then used to mean angular error for another subsample of the same size. Decoder predictions were bootstrapped 100 times. Intuitively, the decoding performance would approach 90 degrees as the amount of data approaches zero, since a poor-quality decoder (e.g. one with limited training data) would decode a random angular error between 0 (perfect) and 180 (opposite) degrees to the target. The average of a large number of random angles drawn between 0 and 180 degrees would average to be 90 degrees. (B) The angular error curves were fit using a decaying exponential, and the amount of data required to achieve 95% saturation of the peak angular error performance was computed. The bootstrapped mean angular error saturated in less than 3 minutes for all three users. (mean +/− standard deviation; participant T5: 41.6s +/− 4.6s; T8: 83.3s +/− 9.9s; T10: 69.3s +/− 7.5s).

Next, we assessed neural closed loop decoder performance at various durations of decoder calibration. We calibrated decoders for 1, 3, and 5 minutes, locked decoder parameters, and then quantified performance using the Grid Task (Table 1, Supplementary Figs. 4, 5). Using the Kalman decoder, we found a statistically significant difference between bit rate at 1 minute and 3 minutes, but did not find a statistically significant difference in bit rate between 3 minutes and 5 minutes (although there was a statistically significant difference in the number of orthogonal direction changes). Thus, we found that closed-loop neural control, as measured by communication bit-rate, saturated within 3 minutes of initializing calibration. For the GP-DKF decoder, we found a statistically significant difference between bit rate performance, time to target, and orthogonal direction changes at 1 minute and 3 minutes. When comparing performance between the Kalman and GP-DKF decoders, we did not find a statistically significant difference between bit rate at 1 minute and 3 minutes (although there was a statistically significant difference in the time to target and orthogonal direction changes).

3.2 Performance after rapid calibration

While closed-loop parameter updates provided users with closed-loop neural decoding that improved during calibration, we investigated whether there was any performance benefit that resulted from this rapid calibration protocol compared to the standard batch-based method (Supplementary Fig. 5). Since the standard calibration method requires parameter initialization in order to provide users with closed-loop control, we initialized both decoding methods using 1 minute of open loop imagery. We then calibrated both methods for 2 minutes without computer assistance, locked decoder parameters, and then tested each resulting decoder using the Grid Task. While neural cursor control improved during calibration (Supplementary movies 1–3), we found no statistically significant difference in bit rate, time to target, or orthogonal direction changes between calibration methods.

Finally, we investigated whether the shortened calibration provided similar performance to our standard calibration method previously described. We calibrated a GP-DKF decoder for 3 minutes and compared the performance against a batch base protocol using 2 minutes of open loop imagery and 9 minutes of closed loop data with gradually decreasing computer assistance [12,14–16]. For each of the three participants, the bit rate (Fig. 4), time to target acquisition, and number of orthogonal direction changes of the shortened calibration method was statistically comparable to the standard calibration method. When participant data was combined, there was no statistically significant difference between calibration methods (median = 1.1 bit/s for GP-DKF vs. 1.3 bit/s for standard Kalman, Wilcoxon Rank-test, p = 0.58).

3.3 Rapid calibration in a BCI-naïve user’s first neural control session

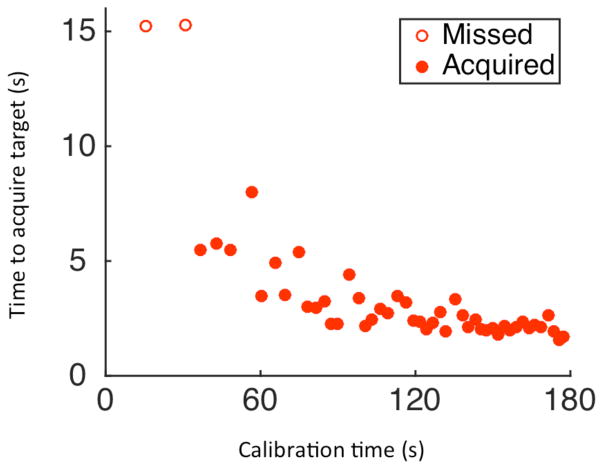
We were interested in investigating the speed and accuracy with which a BCI-naïve user could acquire closed-loop cursor control. Prior to his first-ever BCI research session, we provided participant T5 with a high-level description of the BCI system (as had been discussed over months prior to enrollment) and detailed some principles of motor imagery (see Methods). T5 decided that he would use the imagery of his dominant hand controlling a joystick. On his first-ever BCI control session (Trial Day 30), after reporting that he understood the instructions and indicating that he was ready, T5 gained continuous, unassisted, two-dimensional closed-loop cursor control using the GP-DKF. He acquired his first target approximately 37 seconds after initializing calibration (Fig. 5, Supplementary Video 1). After using the system for 120 seconds, cursor performance was comparable to the most recent state-of-the-art Radial-8 performance described in people [17].

Fig. 5.

Time to target acquisition as a function of time on T5’s first attempt at closed-loop neural control (Trial day 30, block 3).

Although T5 originally selected the “joystick” imagery as being intuitive, we were also interested in exploring whether other motor imageries would be more intuitive, or result in higher quality closed-loop cursor control. Thus, following this initial calibration, we investigated six distinct motor imageries of both the proximal and distal dominant arm, allowing T5 to attempt to gain control using each of them one by one, restarting the calibration task over each time. Consistent with the heterogeneous representation of upper extremity movements at the level of individual neurons in the motor cortex [70–74], T5 was able to achieve closed-loop control using all six imageries within ~60 seconds (Supplementary Figure 7). T5 then selected the imagery he found most intuitive: control of a mouse-ball with the dominant hand. After 3 minutes of calibration with the GP-DKF decoder using mouse ball imagery, the decoder parameters were locked, and performance was assessed in the Grid Task. T5 achieved a bit rate of 1.87 bits/sec on his very first attempt at the Grid Task.

4. Discussion

Three people with tetraplegia rapidly gained high-performance, two-dimensional closed-loop neural control of a computer cursor using two markedly different approaches to neural decoding. Performance for all three participants saturated within three minutes of initiating calibration. Performance with each decoder was comparable to that obtained in previous studies using standard open-loop/closed-loop calibration routines that last ~10 minutes (see methods) [14–16]. In addition, a BCI-naïve man with high cervical spinal cord injury, gained closed-loop two-dimensional neural control on his very first attempt within 2 minutes. This study thus provides additional progress and opportunities toward the goal of providing rapid and intuitive BCIs for people with paralysis.

The rapid calibration protocol reported here improves upon the traditional calibration sequence. Rather than explicitly using an open-loop imagery step, we provided the user with closed-loop control immediately after the first target was presented. This reduced the open-loop imagery phase from 2–5 minutes to ~3 seconds in length.

So as to focus entirely on the decoder calibration methods, the implementation of the Grid Task here relied on users dwelling over targets for a predetermined length of time to make correct (or incorrect) acquisitions. We have previously reported higher bit-rate performance by participants acquiring targets using an additional mouse-click imagery [18]; further research will combine the rapid two-dimensional decoder calibration described here with additional state (e.g., click) detection approaches.

4.1. Future directions for iBCI systems

The ideal iBCI should provide immediate, intuitive restoration of communication and/or mobility. Doing so would make it possible to immediately restore communication for someone who has become acutely locked-in due to brainstem stroke, where the current standard of care in intensive care units has been to rely upon patients’ (often unreliable) eye blinks or vertical eye deviation for communication. Short of achieving this ideal, additional clinical and experimental imperatives include the following: minimizing the amount of user effort required to engage the system; enhancing user engagement during early use [43,44,60,61]; eliminating calibration procedures that provide no feedback (i.e. an explicit open-loop imagery step) for users with impaired levels of alertness; early confirmation to users and caregivers that the BCI is working; and, a dramatic increase in research efficiency. Each of these imperatives is supported by a rapid calibration protocol.

All three participants in this study used intracortical electrode arrays [62] requiring percutaneous connections. As fully implantable iBCI systems [75] are developed that work 24 hours per day, the system should require less active intervention by trained technicians, relying instead on automated procedures to guide everyday use. For example, once the explicit target-based calibration procedure is complete, the user should be able to move on to general computer use, including communication tasks, where the cursor target is not explicitly known by the system.

To continue to calibrate the decoder during self-directed on-screen computer use, we have previously described retrospective target inference as a method of labeling neural data with the BCI users’ intended movement directions based on their own selections, during self-directed on-screen keyboard use [16]. We did not investigate parameter updating during ongoing use; in future work, we hypothesize that combining retrospective target inference with the frequent decoder updates would continue to be an even more effective strategy for maintaining calibration over long periods of practical BCI use. For example, decoders could be updated more frequently - after every click or other action that denotes an intended target - rather than recalibrating only during self-timed pauses in BCI use [16]. We note that we did not explicitly examine long-term effects of learning on decoding performance. Future research would be able to disentangle performance improvements related to a user’s ability to learn a neuromotor (BCI) skill vs. the performance improvements that may result from adaptive decoder recalibration.

4.2 Future directions with Gaussian process regression

The described new strategy for Gaussian process regression neural decoding departs from standard linear methods described in the human iBCI literature [11–17,19–21]. Instead of relying on an explicit function to estimate intended movement from neural data [76], decoding is based on comparing incoming data to activity patterns associated with different intended movement directions. This GP-DKF decoder is computationally tractable using standard BCI hardware, and would be reducible to a fully embedded system [35,75].

As this is an early demonstration of GP-DKF, multiple modeling assumptions remain to be explored. For instance, we focused on the popular radial basis kernel [77]. Additional gains may be sought by learning highly expressive kernel functions or incorporating a fully Bayesian feature selection using automatic relevant determination [77–79]. The highly non-linear nature (combined with multiple options for kernels) of the GP-DKF could provide a useful alternative to linear decoding algorithms for the control of end-effectors such as robotic arms [19–21] or functional electrical stimulation systems [23,24].

5. Conclusions

Brain-computer interfaces have tremendous potential for improving the quality of life for individuals living with motor impairments. As the field looks towards developing BCI systems that can potentially work 24 hours per day, it will be critical to make the calibration process rapid and intuitive. The current study suggests that intracortical BCIs can provide two-dimensional cursor control with performance plateauing within 3 minutes of starting calibration. Such results demonstrate an important step toward a neural prosthetic device that could be used by people with paralysis immediately upon deployment.