Motor cortex embeds muscle-like commands in an untangled population response

Summary

Primate motor cortex projects to spinal interneurons and motor neurons, suggesting that motor cortex activity may be dominated by muscle-like commands. Extensive observations during reaching lend support to this view, but evidence remains ambiguous and much-debated. To provide a different perspective, we employed a novel behavioral paradigm that affords extensive comparison between time-evolving neural and muscle activity. We found that single motor cortex neurons displayed many muscle-like properties, but the structure of population activity was not muscle-like. Unlike muscle activity, neural activity was structured to avoid ‘tangling’: moments where similar activity patterns led to dissimilar future patterns. Avoidance of tangling was present across tasks and species. Network models revealed a potential reason for this consistent feature: low tangling confers noise robustness. Finally, we were able to predict motor cortex activity from muscle activity alone, by leveraging the hypothesis that muscle-like commands are embedded in additional structure that yields low tangling.

Introduction

For fifty years^1–3, a central question in motor physiology has been whether motor cortex activity resembles muscle activity, and if not, why not? Primate motor cortex is as close as one synapse from the motoneurons⁴ and single action potentials in corticospinal neurons can measurably impact muscle activity^5–9, suggesting that motor cortex may encode muscle-like commands^10–16. Yet responses of motor cortical neurons can differ from what would be expected if they encode muscle force, motivating the hypothesis that motor cortex primarily encodes movement velocity or direction^3,17–19. Alternatively, it has been proposed that non-muscle-like response features may be explained by network or feedback dynamics^20–30. Many studies, largely focused on reaching, have produced little consensus^31–42. Progress may thus require new experimental and analytical approaches.

The ubiquity of reaching tasks (and related isometric tasks) has naturally promoted analysis of directional tuning^{2,16,28,43–46} the interpretation of which remains debated^{31,33,39,41,42}. More generally, reaching tasks tend to prompt hypotheses where neurons encode parameters relevant to reaching (hand velocity and position, target direction, etc.)^{3,17,44,47,48} or where the population reflects reach-appropriate dynamics^25,26. A few studies^49–53 have examined primate motor cortex during more extended drawing or tracing movements, but have also largely focused on directional properties (although see^54,55). Given that the defining feature of movement is change with time, we sought a task that afforded detailed comparison of time-evolving patterns of neural and muscle activity.

We developed a novel ‘cycling task’: monkeys manipulated a pedal-like device, endowed with virtual mass and viscosity, to progress through a virtual environment. Cycling involved simple kinematics, but necessitated complex patterns of muscle activity. We found that single neurons and muscles shared many temporal response properties. Yet the neural population as a whole was dominated by signals that were not muscle-like, and could not be explained in terms of velocity / direction coding. These results underscore that we presently lack an explanation for the dominant signals in motor cortex.

We asked whether the dominant signals in motor cortex might relate to a general principle of networks that rely on recurrent and feedback dynamics to generate outputs. Because the current state of activity in such systems strongly influences the future state, two similar patterns of activity (perhaps visited during different movements or at different times during the same movement) should not lead to highly dissimilar patterns in the near future. Violations of this principle, which we refer to as ‘trajectory tangling’, imply that network dynamics are non-smooth and thus potentially non-robust (or more trivially, may imply that the activity under study reflects signals generated elsewhere).

We asked whether motor cortex avoids trajectory tangling, and whether this might explain its dominant signals. We found that tangling was often high for muscle population trajectories, but was dramatically lower for motor cortex population trajectories. This effect was general: it was observed not only during cycling but during a standard reaching task, and in rodent during reach-to-grasp and locomotion. However, this effect was also specific: it was not observed for primary visual or somatosensory cortex.

We employed a novel optimization framework, and predicted motor cortex population activity as the solution to the problem of optimally encoding muscle-like commands while minimizing tangling. The predicted population response was quantitatively similar to the empirical population response, and the two shared the same dominant features. Thus, the structure of motor cortex activity can be accounted for by the hypothesis that neural activity encodes muscle-like commands while displaying additional structure that confers low tangling.

An intriguing finding was that motor cortex activity not only avoided high tangling, but was dominated by structure that resulted in very low tangling. We wondered whether minimal tangling might be computationally advantageous. We examined recurrent neural networks trained to produce the same output, but using varying degrees of internal trajectory tangling. Networks with low tangling were much more robust: they could reliably generate their output in the presence of noise.

Our data reveal a novel and potentially general property of motor cortex: muscle-like signals are present, but are relatively modest ‘ripples’ riding on top of larger signals that confer minimal tangling.

This structure initially seems counter-intuitive – one might expect the outgoing commands to be the dominant signals in the network. However, the empirical structure is expected of networks that must be noise robust. Thus, the dominant signals in motor cortex may serve not a representational function – encoding specific variables – but rather a computational function – ensuring that outgoing commands can be generated reliably.

Results

Task and behavior

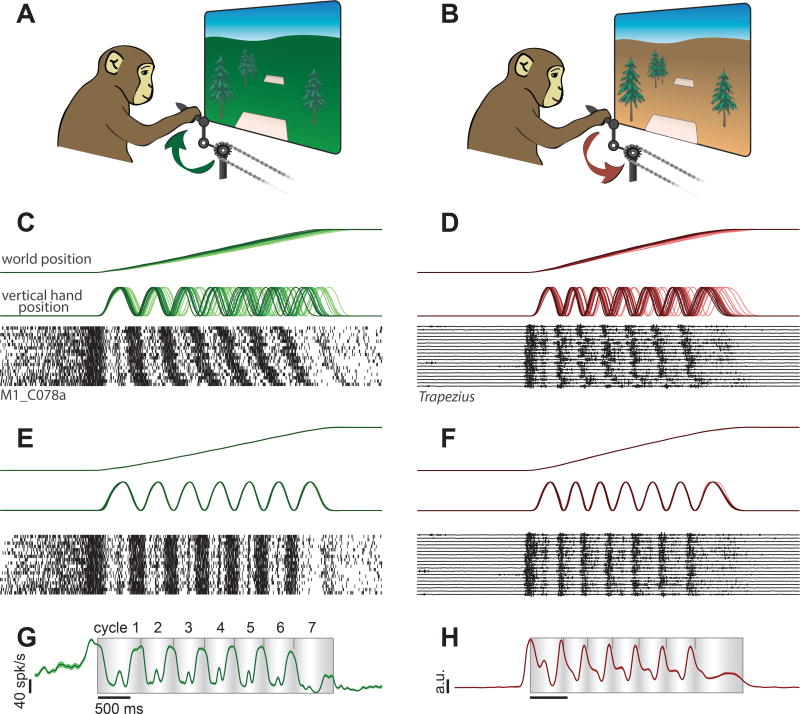
We trained two rhesus macaque monkeys to grasp a pedal with their hand and cycle an instructed number of revolutions for juice reward (Fig. 1). Cycling produced movement through a virtual landscape. Landscape color indicated whether forward virtual movement required ‘forward’ cycling (Fig. 1A) or ‘backward’ cycling (Fig. 1B). During each trial, the monkey moved between a pair of targets. The distance between targets determined the required number of revolutions: 0.5, 1, 2, 4, or 7 cycles. Acquiring a target required stopping with the target positioned ‘under’ the first person perspective (Fig. 1A,B). This location always corresponded to a pedal location that was either straight up (‘top-start’) or straight down (‘bottom-start’). Monkeys performed twenty conditions: all combinations of two cycling directions, two starting pedal orientations, and five distances. Cycling required overcoming simulated inertia and viscosity while countering the weight of an arm extended in front of a vertically oriented body. These requirements differ from those during locomotion, and had to be learned.

Figure 1.

Behavior, neural activity, and muscle activity during the cycling task. A. Schematic illustration of the task during forward cycling. A lush green landscape indicated that progress from one target to the next required cycling in the ‘forward’ direction, as indicated. B. Same for backward cycling. An arid orange landscape indicated that progress required cycling in the opposite, ‘backward’ direction. C. Behavioral data and spikes for individual trials during an example neural recording session. Data are shown for a single condition: forward / seven-cycle / bottom-start (monkey C). Trials are aligned to movement onset, and ordered from fastest to slowest. D. Behavioral data and raw EMG recorded from the trapezius for a single condition: backward / seven-cycle / bottom-start (monkey D). E. Behavioral and neural data from C after temporal scaling to align trials. F. Behavioral and EMG data from D after temporal scaling. G. Trial-averaged and filtered (25 ms Gaussian kernel) neural activity for the example neuron in C,E. Flanking envelopes show standard error of the mean (SEM; often these were no larger than the trace width). The shaded rectangle indicates the interval during which the monkey was actively cycling between targets. Background shading indicates vertical hand position: lightest at top and darkest at bottom. Small tick-marks indicate the completion of each cycle. H. Rectified, filtered (25 ms Gaussian kernel) and trial-averaged muscle activity for the example in D,F.

Behavior was highly stereotyped; note similarity of virtual-world-position traces across trials in (Fig 1C,D. Nevertheless, small trial-to-trial differences in cycling speed caused accumulating misalignment of kinematics (e.g., vertical hand position) with time. We therefore temporally scaled trials so that virtual-world-position traces were closely matched (Fig. 1E,F, top). Doing so revealed considerable temporal structure in neural (Fig. 1E, bottom) and muscle (Fig. 1F, bottom) responses. To summarize such structure, we computed average firing rate (neurons; Fig. 1G) or muscle activation (muscles; Fig. 1H). We used a narrow filter (25 ms Gaussian kernel) relative to the timescale of behavior (~500 ms cycling period) to preserve fine temporal features. Single neurons and muscles displayed temporally structured and statistically reliable response patterns (flanking traces show SEMs).

Hand velocity and muscle activity

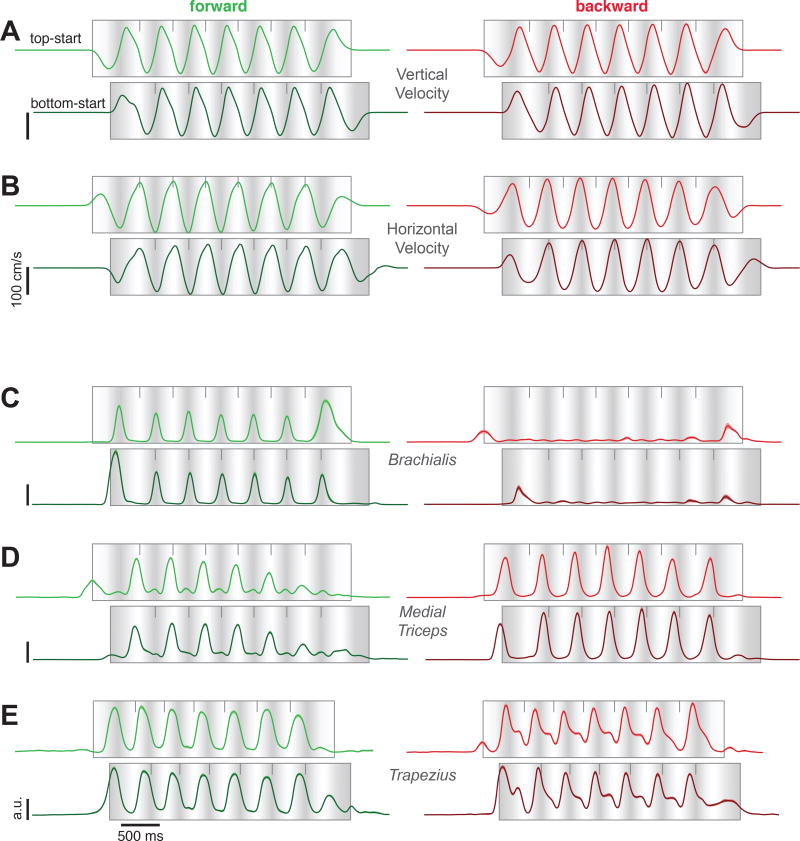
Consistent with the circular pedal motion, vertical and horizontal hand velocity exhibited approximately sinusoidal profiles during forward and backward cycling (Fig. 2A,B). Top- and bottom-start movements differed in phase but were otherwise similar during middle cycles (plots are phase-shifted to aid visual comparison). The temporal profile of hand velocity was repeated consistently across middle cycles. Hand velocity was slightly slower during initial / terminal cycles as angular velocity ramped up and down.

Figure 2.

A. Vertical hand velocity, averaged across trials from a typical session (monkey C). Same format as in Fig 1G. Data are shown for seven-cycle movements for forward cycling (green, left column) and backward cycling (red, right column), and for both top-start and bottom-start movements. The latter have been shifted a half-cycle to visually align hand position between top- and bottom-start movements (light shading indicates the top of each cycle). Flanking traces show the SEM but are generally narrower than the trace width. B. Horizontal hand velocity from the same session, plotted using the same format. C. Activity of brachialis (monkey C) plotted using the same format. Flanking traces (barely visible) show the SEM. D. Activity of the medial triceps (monkey C). E. Activity of the trapezius (monkey D).

Extensive intramuscular electromyographic (EMG) recordings (29 and 35 sites in monkey C and D) concentrated on muscles that moved the upper arm and elbow and to a lesser degree the wrist (which had limited mobility given the pedal design). Muscle activity (Fig. 2C–E) generally followed intuitions from biomechanics. For example, the triceps extends the elbow, moving the hand away from the body. Accordingly, triceps activity (Fig. 2D) peaked near each cycle’s apex (white shading) when pedaling forward, and near its bottom (dark shading) when cycling backward. Some muscle responses were roughly sinusoidal and resembled kinematics, yet deviations from sinusoidal were common (e.g., Fig. 2E). Furthermore, the amplitude and profile of the response often differed between forward and backward cycling. Depending on the muscle, responses during initial / terminal cycles could be either larger or smaller than those during middle cycles.

Single-neuron response

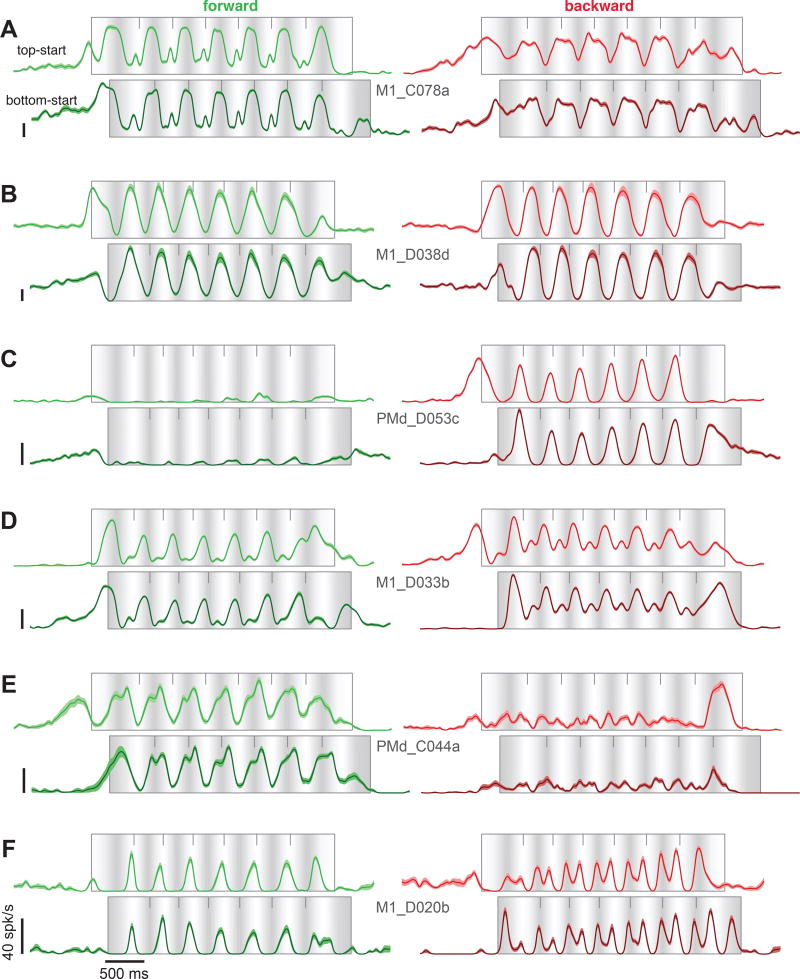
Well-isolated neurons (103 and 109 for monkeys D and C) were recorded from motor cortex, including sulcal and surface primary motor cortex and the immediately adjacent aspect of dorsal premotor cortex (potential differences within this population are explored later). Recordings were localized to the region where microstimulation activated the muscles from which we recorded. Cycling evoked particularly strong responses. Nearly all neurons that could be isolated were modulated during the task. Peak firing rates ranged from 16–184 spikes/s (monkey D, average of 69 spikes/s) and 16–185 spikes/s (monkey C, average of 76 spikes/s). Neurons displayed a variety of intricate response patterns (Fig 3). These patterns were statistically reliable: SEMs (flanking traces) were small and the same pattern could be seen repeatedly across middle cycles (cycles 2–6) for both top-start and bottom-start conditions.

Figure 3.

Firing rates of six example neurons recorded from motor cortex. Same format as for Figure 2. Flanking envelopes show the SEM. Cell names indicate area (M1 versus PMd) and monkey (C and D). All vertical calibrations are 40 spikes/s.

Inspection revealed four features shared between muscles and neurons. First, responses often deviated from the sinusoidal profile of kinematics (e.g., Fig 2E-backward; Fig 3A-forward). Second, responses during initial / terminal cycles often displayed differences in amplitude or temporal profile compared to middle cycles (e.g., Fig 2D-forward; Fig 3D-forward; Fig 3E-backward). This effect presumably relates to the unique force patterns required to start and stop. Third, responses could differ between forward and backward cycling in both amplitude (e.g., Fig 2C, Fig 3C) and structure (e.g., Fig 2E, Fig 3A,F).

Consistent with these shared features, muscle responses could be successfully decoded from the neural population using a linear model (Leave-one-out-cross-validated R² = .80 and .78) consistent with^6,7,10. This is potentially impressive, given that a linear model is almost certainly too simplistic. This finding might suggest that motor cortex activity primarily reflects muscle-like commands. However, decoding neural activity from muscle activity was less successful (Leave-one-out-cross-validated R² = .54 and .50). This discrepancy in fit quality was not due to individual neuron recordings being ‘noisier’ (having higher sampling error) than individual-muscle recordings; the same discrepancy was observed if neural responses were de-noised using dimensionality reduction techniques (methods). Thus, while muscle-like signals can be found in the neural data, there appear to exist additional non-muscle-like neural response patterns, consistent with related observations during reaching^19,35

Non-muscle-like signals dominate the neural population response

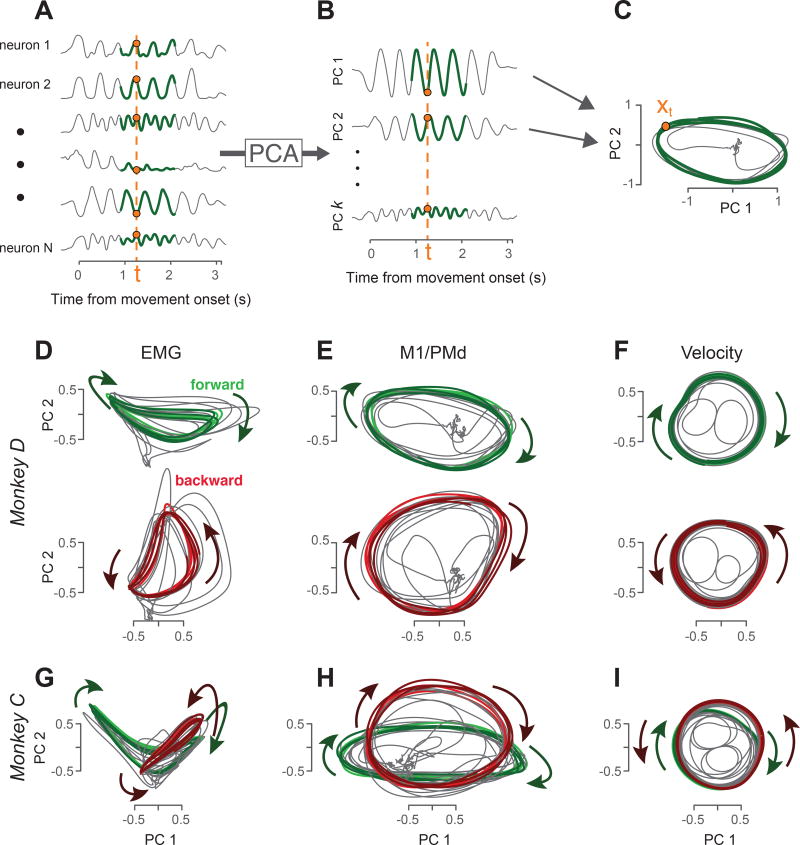
To characterize population responses, we applied principal component analysis (PCA), a standard unsupervised algorithm that identifies the dominant signals in multi-dimensional data (Fig. 4). Each signal identified via PCA is a weighted combination of individual-neuron responses. Those weights (the PCs) allow individual-neuron responses to be faithfully reconstructed from the signals found by PCA. A small number of PCA-derived signals can thus provide a useful summary of the response of a full population.

Figure 4.

Visualization of population structure via PCA. A. PCA operates on a population of responses (six of 103 neurons are shown, monkey D). Green traces highlight the middle three ‘steady state’ cycles, which were used to find the PCs for the present analyses (subsequent analyses consider all times for all conditions). Data are shown for only one condition – forward cycling starting at the bottom – but PCs were computed based on both forward and backward cycling and both top- and bottom-start conditions. B. Projections onto the PCs capture the dominant signals in the data. Orange dashed lines highlight the ‘neural state’ at a single time. That state can be summarized either using the full vector of firing rates (A) or a reduced-dimensional vector containing the values of the projections onto the top PCs (B). C. Neural trajectories revealed by plotting the projection onto the second PC versus the projection onto the first PC (~35% of the total variance is captured in these two dimensions). This is equivalent to projecting the 103-dimensional neural trajectory onto the two dimensions defined by the PCs. Orange dot corresponds to the neural state at the same time as in A and B. D. Muscle trajectories captured by projecting the muscle population response onto its first two PCs (monkey D). Trajectories are shown for forward cycling (green) and backward cycling (red). Each panel overlays trajectories for top-start and bottom-start conditions (lighter and darker colored traces respectively). The same PCs were used to project data for both forward and backward cycling. E. Corresponding neural trajectories for the same monkey and conditions as in D. F. Corresponding hand-velocity trajectories. Trajectories were produced by applying PCA to horizontal and hand velocity traces across multiple sessions. This is exceedingly similar (but for a change of axes) to simply plotting average vertical velocity versus average horizontal velocity. G,H,I. PCA-based muscle, neural, and velocity trajectories for monkey C. Same format as D,E,F, but forward and backward cycling are overlaid.

For visualization, we first examine the signals captured by the top two principal components (PCs). It is often informative to plot one PCA-derived signal versus another, yielding a ‘state-space’ trajectory (Fig. 4C). Each point on the trajectory (e.g., the orange dot in Fig 4C) corresponds to the neural state at that moment (dashed line in Fig 4A). A two-dimensional trajectory provides only a partial summary of the neural state, but the resulting visualization can still be informative, and can suggest hypotheses to be tested using the full population response.

Neural trajectories during both forward and backward cycling (Fig 4E,H) followed a repeating orbit throughout the middle cycles (colored portion of trajectory trace shows cycles 3–5). Muscle trajectories also followed repeating orbits (Fig 4D,G; similarly computed using PCA). Rotating orbits are expected during cycling, in contrast to reaching²⁶, and simply reflect what can be observed in single neurons: middle-cycle responses tend to repeat. Despite this basic similarity, muscle trajectories (Fig 4D,G) differed from neural trajectories in their basic structure. Muscle trajectories counter-rotated: they orbited in opposing directions for forward and backward cycling. Counter-rotation is expected given the reversal of the required force patterns. For example, forward cycling requires lifting before pushing and backward cycling requires pushing before lifting. In contrast, neural trajectories co-rotated: they orbited in the same direction for forward and backward cycling (Fig 4E,H). Other aspects of muscle and neural trajectories also differed. Muscle trajectories tended to depart from circular: the orbit often possessed a kidney- or saddle-like shape. This was moderately true for monkey D (Fig 4D) and pronounced for monkey C (Fig 4G). Neural trajectories were more circular or elliptical. Thus, the dominant signals in the neural population behave rather differently from those in the muscles.

Potential explanations and caveats

A potential explanation for non-muscle-like properties in motor cortex is that they encode directional signals such as hand velocity (e.g.,¹⁷). This explanation initially seems appealing given the present data. For example, the neural trajectory during backward cycling for monkey D (Fig 4E, red) visually resembles the corresponding velocity trajectory (Fig 4F, red). However, velocity trajectories necessarily counter-rotate between forward and backward cycling (the same would be true of hand direction, position, or other kinematic variables). The dominant signals in the neural data do just the opposite. Given this observation, and the fact that single-neuron response profiles typically do not resemble sinusoidal kinematic parameters, it seems unlikely that a representation of kinematic parameters can explain the dominant signals in the neural data.

An alternative explanation is that the dominant signals in the neural data reflect descending commands, but look very non-muscle-like because they will be heavily modified by spinal circuitry. For example, cortical commands are likely integrated / low-pass filtered by the spinal cord⁵⁶, and may encode muscle synergies rather than individual muscle activations⁵⁷. Yet on their own these hypotheses cannot explain the dominant signals in the neural population. Any commands related to force – whether for individual muscles or synergies – are almost certain to reverse between forward and backward cycling due to the reversal of required force patterns. Furthermore, if descending commands are low-pass filtered by the spinal cord, then those commands will necessarily resemble high-pass filtered versions of the final output (muscle activity) with transients and other features becoming more prominent⁵⁷. High-pass filtering the signals in Figure 4D,G would not cause them to co-rotate, and would make them look less circular rather than more.

The above findings do not argue against the idea that muscle-like commands (or kinematic commands) are encoded by neural activity in dimensions beyond the top two PCs. Indeed, we will suggest below that muscle-like commands likely are encoded. The present results do, however, indicate that the dominant signals in the neural data cannot be explained in terms of either muscle encoding or velocity / direction encoding. One thus wonders whether thinking about the dominant signals as ‘encoding’ commands or representations might be misleading. Might there exist an alternative class of explanation?

Smooth dynamics predict low trajectory tangling

Recent physiological and theoretical investigations suggest that the neural state in motor cortex obeys smooth dynamics^{20,24,26,27,29,58,59}. Smooth dynamics imply that neural trajectories should not be ‘tangled’: similar neural states, either during different movements or at different times for the same movement, should not be associated with different derivatives. We quantified trajectory tangling using

$$Q(t)=\underset{t\prime }{\text{max}}\frac{{\Vert {\dot{\mathit{x}}}_t-{\dot{\mathit{x}}}_{t\prime }\Vert }^2}{{\Vert {\mathit{x}}_t-{\mathit{x}}_{t\prime }\Vert }^2+\epsilon }$$ Equation 1

where x_t is the neural state at time t: i.e., a vector containing the neural responses at that time, ẋ_t is the temporal derivative of the neural state, ∥·∥ is the Euclidean norm, and ε is a small constant that prevents division by zero (methods). Q(t) becomes high if there exists a state at a different time, t′, that is similar but associated with a dissimilar derivative. For example, tangling is high if two trajectories pass through similar points but in different directions. We take the maximum to ask whether the state at time t ever becomes tangled with any other state (it is trivially true that two random states will rarely be tangled, as they will rarely be close). This maximum is taken with t indexing across time during all conditions. Q(t) can also be measured for the muscle state, in which case x_t contains muscle responses.

Moments of high tangling are expected in most generic data; a priori there is no reason why two similar states, which may be visited at very different times or during different conditions, should avoid having dissimilar derivatives. Indeed, for many tasks muscle trajectories may need to be tangled. For example, co-contraction of the biceps and triceps at one moment might need to be quickly followed by activation of the biceps and relaxation of the triceps. At a later moment, or during a different movement, co-contraction might instead need to be followed by relaxation of the biceps and activation of the triceps. This would constitute an instance of tangling, because the same state (co-contraction) is followed by different subsequent states. Do these moments of high tangling indeed occur for the muscles? If so, are they mirrored or avoided in the neural responses?

Visualizing trajectory tangling

The state for a given time and condition is a location on the population trajectory. The derivative is the direction in which the trajectory is headed. Two states are thus tangled if they are nearby, but associated with different trajectory directions. For visualization, we consider a subset of the data: the middle five cycles of 7-cycle movements. Two-dimensional projections of muscle (Fig 5A) and neural (Fig 5B) trajectories are shown for forward (green) and backward (red) bottom-start movements. It should be kept in mind that trajectories that cross in these two dimensions may or may not be separated in other dimensions. Thus, the tangling measure (which considers more than two dimensions) does not always agree with what can be seen in a two-dimensional projection. Still, the two-dimensional projections are useful for gaining intuition.

Figure 5.

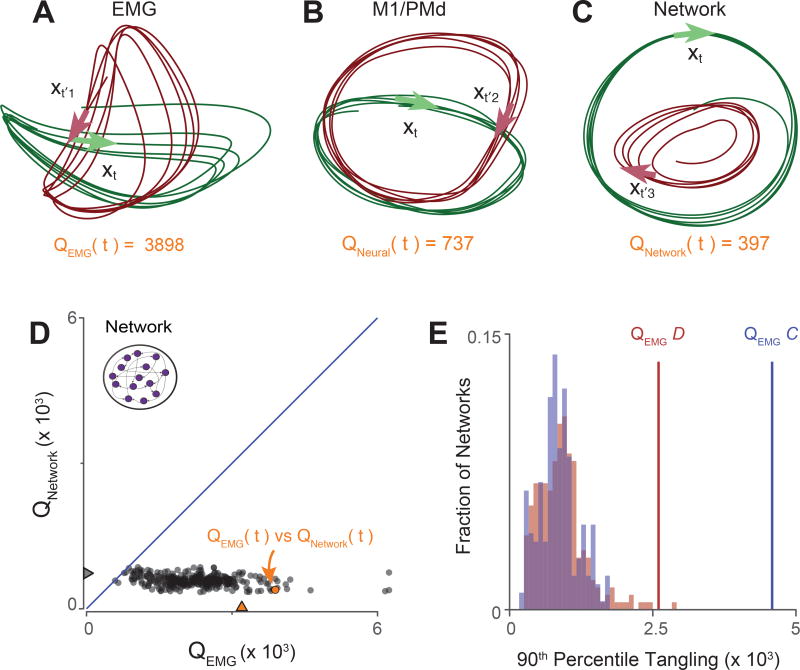
Illustration and validation of the tangling metric. A. Muscle trajectories during the middle five cycles for two conditions: seven-cycle / bottom-start / forward (green) and seven-cycle / bottom-start / backward (red). Arrows illustrate a pair of highly tangled states. Arrows point in the direction of the derivative (the path of the trajectory). The state at time t is maximally tangled with the state at time t₁′, yielding Q_EMG (t)=3898. Tangling was computed in eight dimensions. B. Same as A but for neural trajectories. The state at time t becomes maximally tangled with the state at time t₂′, but this maximum is lower than for the muscles. C. Same but for network trajectories from an artificial recurrent network. The network was trained to produce the activity of all muscles for the times / conditions illustrated in A. D. Scatterplot, with one point per time/condition, of network tangling versus muscle tangling. Orange arrow denotes tangling for time t, corresponding to the time for which tangling was assessed in panels A and C. E. The consistency of the effect in panel D is demonstrated across 247/216 networks, each trained to produce the pattern of muscle activity from monkey D (red) or monkey C (blue). Tangling is summarized by the 90^th percentile value (which highlights how high tangling can become). Lines denote 90^th percentile tangling for the empirical muscle populations.

Muscle trajectories (Fig 5A) show three features suggestive of high tangling. Most obviously, muscle trajectories counter-rotate for forward versus backward cycling. Counter-rotation produces opposing derivatives for similar states: e.g., red traces are moving to the right at the bottom while green traces are moving to the left. Second, muscle trajectories often crossed themselves at right angles, resulting in similar states with very different derivatives. Third, non-circular trajectories sometimes cause nearby muscle states to move in opposite directions (consider the sharp turn on the left-hand-side of the green trace). These features lead to occasional moments of high tangling. For example, the green arrow shows the muscle state and its derivative at a chosen time t. There exists another state, at time $t_1^{\prime }$, that is similar but possesses a very different derivative (red arrow), yielding an instance of high tangling.

Neural trajectories (Fig. 5B) appear potentially less tangled. Co-rotation prevents middle-cycle trajectories from continuously opposing one another between forward and backward cycling. Even within a condition, trajectories are closer to circular with fewer sharp bends. There are moments where trajectories cross in these two dimensions, but this did not result in high tangling because those trajectories were separated in other dimensions. Notably, although the muscle state at time t was strongly tangled, the neural state at that same time was not.

For comparison, we examined trajectories from a simulated recurrent neural network trained to produce muscle activity for the subset of data plotted in Figure 5A. Thus, the dominant signals in the output of the network are approximately the signals in Figure 5A. We wished to observe whether the network – a dynamical system with dynamics determined by connectivity – would indeed show lower tangling than its output. Network trajectories, when projected onto their top PCs (Fig 5C), did not resemble muscle trajectories, and appeared less tangled. For example, although the muscles exhibited a moment of high tangling at time t, the network did not. This illustrates that a network that produces a given output may be dominated by signals that differ from that output. By inspection, such signals appear to be less tangled.

Quantifying trajectory tangling

Are neural (and simulated network) trajectories indeed consistently less tangled than muscle trajectories, as suggested by the visualization in Figure 5A–C? Answering this question requires moving beyond inspection of two-dimensional trajectories, and considering tangling for more than one state. To illustrate our approach, we first consider the simulated network. We measured Q_Network (t) and Q_EMG(t) for every time during both simulated conditions. Note that Q_EMG quantifies tangling for the output of the network, which was trained to produce the activity of all muscles. Plotting Q_Network versus Q_EMG revealed that network-trajectory tangling was consistent lower than muscle-trajectory tangling (Fig 5D).

We repeated this analysis for multiple simulated networks, using different weight initializations and meta-parameters. There was considerable variability in the magnitude of network-trajectory tangling (distributions in Fig 5E) but tangling was nearly always reduced relative to muscle-trajectory tangling. This effect is most clearly observed when plotting network versus muscle tangling for each pair of corresponding states (Fig 5D), but can also be summarized by measuring the 90^th percentile level of tangling (Fig 5E). These simulations reveal that network trajectories can, and indeed strongly tend to be, less tangled that the eventual output. Is this also true of motor cortex, and if so might it explain why the dominant signals in the data are not muscle-like?

Neural-versus muscle-trajectory tangling

For motor cortex, we compared Q_neural and Q_EMG for all times and across all twenty conditions (not just the subset of data used for illustrative purposes in Fig 5). At least four results are possible. First, if motor cortex activity is a straightforward code for muscle activity, Q_neural and Q_EMG should have a linear relationship with a slope near unity. Second, if motor cortex reflects unknown variables, and/or if the tangling metric captures nothing fundamental, Q_neural and Q_EMG may show no clear relationship. Third, if neural activity is more complex, intricate, or ‘noisier’ than muscle activity, Q_neural could be greater than Q_EMG. Finally, neural-trajectory tangling could be reduced relative to muscle-trajectory tanging, as in the case of the simulated networks. If so the slope relating Q_neural to Q_EMG could be less than one, or could even be close to flat.

The data (Fig 6A,B) obeyed the final prediction. The neural state was less tangled than the corresponding muscle state in 99.9% (monkey D) and 96.6% (monkey C) of cases. Distributions of neuraland muscle-trajectory tangling (marginal distributions in Fig 6A,B) were significantly different (paired t-test, p<10⁻¹⁰ for each monkey). The rare instances where neural-trajectory tangling exceeded muscle-trajectory tangling occurred when tangling was low for both. Strikingly, muscle-trajectory tangling could be quite high with no accompanying increase in neural-trajectory tangling.

Figure 6.

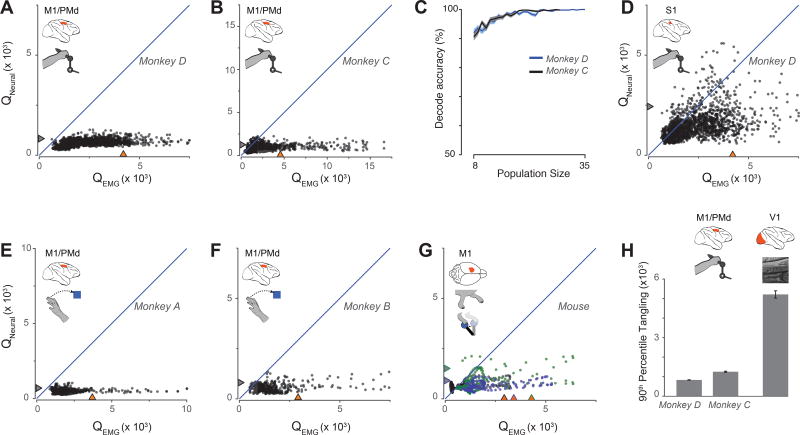
Trajectory tangling for multiple datasets. A. Scatterplot of motor-cortex-trajectory tangling versus muscle-trajectory tangling (monkey D). Each point shows tangling for one moment (one time during one condition). Points are show for all times during movement (sampled every 25 ms) for all twenty conditions. Blue line indicates unity slope. Gray / orange triangles indicate 90% percentile tangling. B. Same as A but for monkey C. C. Neural versus muscle populations could be distinguished based on tangling. For a given number of recordings, we drew that many neurons and muscles and computed tangling for each subpopulation. 500 such draws were made for each subpopulation size. The vertical axis gives the percentage of instances where the neural sub-population was correctly identified based on lower tangling. Flanking standard errors are based on binomial statistics. D. Tangling for S1 neural population trajectories versus muscle trajectories (monkey D). E. Scatterplot of motor-cortex-trajectory tangling versus muscle-trajectory tangling during reaching (monkey A). Each point corresponds to one time during one of eight conditions. F. Same as E but for monkey B. G. Scatterplot of motor-cortex-trajectory tangling versus muscle-trajectory tangling in three mice (black, blue, and green symbols) during both locomotion and lever pulling. Illustration in inset by E. Daubert. H. Comparison of tangling in motor cortex and visual cortex. Motor cortex data are from the cycling task as in panels A and B. V1 data were recorded using natural scenes. Because V1 data contains no corresponding muscle activity, tangling is quantified by the 90^th percentile values. Error bars show the standard error computed via bootstrap: the distribution of tangling values was resampled 200 times, and we computing the sampling distribution of the 90^th percentile values.

The large and consistent difference between Q_neural and Q_EMG contrasts with the observation that visual inspection does not readily reveal whether a set of individual recordings are neural or muscular (compare Fig 3 with Fig 2). Yet the tangling metric readily distinguished between even small populations of neurons versus muscles (Fig. 6C). Thus, tangling captures a robust difference between neural and muscle responses that is only visible at the population level.

When performing the above analyses, we had to choose whether x_t was full-dimensional (containing the response of every neuron / muscle) or reduced in dimensionality (containing the projection onto the top PCs). The latter is computationally efficient and interpretationally conservative; we can compare neural and muscle data using the same number of dimensions, and PCA reduces the impact of measurement noise. All analyses thus employed eight PCs, which captured 70% and 68% (monkey D and C) of the neural data variance, and 94% and 88% of the muscle data variance. In practice, results were remarkably robust regardless of this choice. Effects were virtually identical if x_t was full-dimensional, with no use of PCA (Supp Fig 1). When using PCA, Q_neural was consistently lower than Q_EMG regardless of the analyzed dimensionality (Supp Fig 2). We also considered that we should compare Q_neural and Q_EMG using different dimensionalities. This relates to the hypothesis, developed further below, that neural trajectories contain both muscle-like signals and additional signals that confer low overall tangling. If so, it would be most natural to employ a higher dimensionality for the neural data, such that a similar percentage of variance is captured in both cases. Doing so revealed the same, or perhaps a slightly stronger, effect (Supp Fig 2). Finally, the difference between Q_neural and Q_EMG was not related to the number of measured neurons versus muscles: the difference persisted when population sizes were matched (Supp Fig 2).

Tangling across tasks, species, and areas

Observations made during the cycling task were critical to developing the above approach. But is low neural-versus muscle-trajectory tangling specific to cycling, or a more general property of motor cortex? We leveraged recently collected data⁶⁰ from two monkeys performing a center-out reaching task. Reaching provided fewer data-points than cycling, but the same result was observed: Q_neural was almost always less than Q_EMG (Fig 6E,F). We also compared Q_neural and Q_EMGin mice during an experiment with two behaviors: reaching to pull a joystick and walking on a treadmill [Miri et al., in press]. We observed a slightly weaker, yet similar effect (Fig. 6G) to that seen in primate. Thus, low trajectory tangling in motor cortex appears to be a general property.

We were motivated by the likelihood that tangling is low in a network that obeys strong (internal or feedback) dynamics, such that the present state has a strong influence on the future state. In contrast, tangling could become high in an area where responses are dominated by sensory inputs, especially if those inputs are not a predictable result of the observable network state. Is this range of tangling values indeed observed, or is low tangling a generic property of neural populations? We first examined the population response recorded from the proprioceptive region (area 3a) of primary somatosensory cortex (S1) during cycling. This region is immediately adjacent to motor cortex, and individual-neuron responses (Supp Fig 3) are surprisingly similar to those in motor cortex. Indeed, conclusively discriminating between the two areas typically requires assessing microstimulation thresholds. We also note that both motor cortex and S1 exhibit strong proprioceptive responses, both project to spinal interneuron and motor-neuron populations⁴, and both are believed to contribute to feedback control⁶¹. It is thus a priori unclear whether to expect S1 trajectories to show high or low tangling.

We found that S1 trajectories tended to be less tangled than the muscle trajectories (Fig 6D; 80.7% of neural states were less tangled than their corresponding muscles states). However, this effect was much weaker in S1 than in motor cortex. For moments where the muscle state became highly tangled, the S1 state often also became quite tangled. In contrast, the motor cortex state always remained weakly tangled. All three tangling distributions were significantly different: p < 10⁻¹⁰ when comparing muscle and S1 populations; p < 10⁻¹⁰ when comparing S1 and motor cortex populations (paired t-test).

We also analyzed trajectory tangling for a primary visual cortex (V1) population responding to naturalscene movies²⁹. V1 trajectories were much more tangled than motor cortex trajectories (p<10⁻¹⁰ for both comparisons; two-sample t-test), and occasionally had very high tangling values that were not seen for motor cortex (Fig. 6H). Thus, tangling is a property that can differ dramatically between cortical areas, and cannot be readily inferred from inspection of single-neuron responses.

Noise-robust networks display low tangling

We were surprised to find such a dramatic reduction in tangling between the muscle population and the upstream motor cortex population. Even a purely autonomous dynamical system needn’t show very low tangling (it merely needs to avoid near-maximal tangling). For example, some of the recurrent networks we trained did show modestly high tangling (right tail of the distribution in Fig 5E). Might minimal tangling confer a computational advantage?

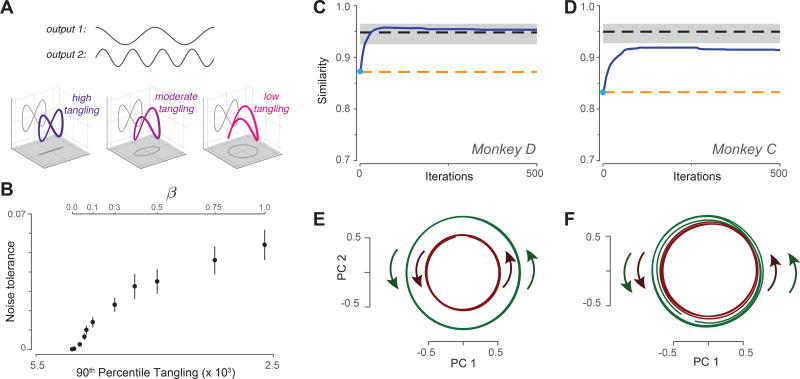
To address this question, we considered a neural network trained to generate a simple idealized output: cos t for one muscle and sin 2t for a second muscle (Fig 7A, top). The resulting output trajectory was thus a figure-eight (left sub-panel). It is not possible for the network’s internal trajectory to follow a pure figure-eight; the center-most state is traversed in different directions and is thus strongly tangled. Tangling can be reduced by employing a third dimension such that the trajectory is [cos t ; sin 2t ; βsin t]. Even a small value of β will reduce tangling modestly (middle sub-panel) such that the trajectory can be produced by the network. The figure-eight trajectory can still be ‘read out’ via projection onto two of the axes. Is there an advantage to further decreases in tangling (right sub-panel)? We examined noise-tolerance across networks whose internal trajectories followed the trajectory cos t; sin 2t ; βsin t, with different values of β. This necessitated the unusual step of training the network not only to produce the desired output (the figure-eight) but to follow the specified internal trajectory (methods).

Figure 7.

Leveraging the observation of low tangling to predict the neural population response. A. Illustration of how the same output can be embedded in a larger trajectory with varying degrees of tangling. Top gray traces: A desired two-dimensional output [cos t; sin 2t] Plotted in state space, the output trajectory is a figure eight, and contains a central point that is maximally tangled. Adding a third dimension (βsin t) reduces tangling at that central point. The figure-eight can still be decoded via projection onto two dimensions, in which case the third dimension falls in the null-space of the decode. B. Noise robustness of recurrent networks trained to follow the internal trajectory [cos t; sin 2t; βsin t]. By varying β, we trained multiple networks that could all produce the same figure-eight output, but had varying degrees of trajectory tangling. For each network, noise tolerance was the largest magnitude of state noise for which the network still produced the figure-eight output. For each value of β we trained 20 networks, each with a different random weight initialization. Error bars show the SEM across such networks. C. Similarity of the predicted and empirical motor-cortex population responses (monkey D). Blue trace: prediction yielded by optimizing the cost function in Equation 2. Light blue dot indicates similarity at initialization. Dashed lines show benchmarks as described in the text. Gray shading indicates 95% confidence interval on the upper benchmark, computed across multiple random divisions of the population. D. Same but for monkey C. E. Projection of the predicted population response (after optimization was complete) onto the top two principal components. Data are for monkey D. Green / red traces show trajectories for three cycles of forward / backward cycling respectively. F. Same but for monkey C.

Low trajectory tangling yielded robustness to external noise (Fig 7B). When tangling is high, small perturbations of the present state can have large ramifications for the future state. For example, the state can be perturbed off the trajectory and relax to an inappropriate point much further along on the trajectory. Reduced tangling makes such events unlikely. Note that β = 1 yields a weakly-tangled trajectory that is a circle in one two-dimensional projection and a figure-eight in another (Fig 7A right sub-panel). The circular aspect of the trajectory does not match the output, but does relate to the robustness with which the output can be generated. We repeated this analysis with more realistic outputs (the empirical patterns of muscle activity) with the same result: low tangling confers noise robustness (Supp Fig 4).

Hypothesis-based prediction of neural responses

The results above suggest a hypothesis: motor cortex may embed outgoing commands (which, if muscle-like, would be quite tangled) in a larger trajectory such that the full orbit is minimally tangled. Inspired by optimizations that successfully predicted aspects of V1 responses⁶², we employed an optimization approach to predict motor cortex activity based on this hypothesis. Optimization found a predicted neural population response, X̂, that could be linearly decoded to produce the empirical muscle activity Z, yet was minimally tangled. Specifically:

$$\widehat{X}=\underset{X}{\text{argmin }}({\Vert Z-Z{X}^{†}X\Vert }_F^2+\lambda {\sum }_t{Q}_X(t))$$ Equation 2

where Z is a matrix describing the muscle population response. The first term of the minimized cost function ensures that neural activity ‘encodes’ muscle activity; ZX^†X is the optimal linear reconstruction of Z from X († indicates the pseudo-inverse and ∥·∥_F indicates the Frobenius norm). This formulation should not be taken to imply that the true neural-to-muscle mapping is linear, merely that the predicted neural activity should yield a reasonable linear readout of muscle activity, consistent with empirical findings^6,7,10. The second term of the cost function encourages low trajectory tangling. The predicted neural population response thus balances optimal encoding of muscle activity with minimal tangling. The constant λ was adjusted to ensure that the second term had an impact, but that muscle activity could still be decoded with >95% accuracy.

We applied optimization to muscle data that included three middle cycles of forward cycling and three middle cycles of backward cycling. Thus, we are attempting to simultaneously predict two ‘steady state’ neural trajectories. We initialized optimization with X̂_init = Z, corresponding to the baseline hypothesis that neural activity is a ‘pure’ code for muscle activity. We used canonical correlation to assess the similarity between predicted and actual neural responses (unity similarity indicates perfect agreement). The similarity for X̂_init (Fig 7C,D, cyan dot) is already high, given that muscle activity shares many basic features with neural activity (e.g., the same fundamental frequency). The key question is whether similarity increases or decreases during optimization, as X̂ is altered to reduce tangling.

Similarity between predicted and empirical populations increased with optimization (Fig. 7C,D blue). That is, similarity increased as optimization moves the prediction away from the hypothesis that neural activity is a pure code for muscle activity, and towards the hypothesis that neural activity encodes muscle commands but also contains non-muscle-like structure that minimizes tangling. The final results of optimization yield a similarity roughly halfway between the initial ‘pure muscle encoding’ hypothesis and perfect similarity. To provide a rough benchmark of good similarity, we computed the average similarity between two random halves of the empirical neural population (black dashed trace with 95% confidence intervals). Similarity between predicted and empirical populations slightly exceeded this benchmark for monkey D and approached it for monkey C.

Similarity increased not because optimization reduced tangling per se, but because the features that emerged during optimization matched prominent features in the neural data. As one example, the reduction in tangling of X̂ was accompanied by the emergence of co-rotational, circular structure in the top two principal components (Fig. 7E,F). Thus, the hypothesis embodied in Equation 2 explains a basic feature not explained by the pure-muscle-encoding (or kinematic-encoding) hypothesis.

Interpreting optimization-based predictions

For both predicted and empirical data, projections onto the top PCs only partially reveal the structure of the population trajectories. In both cases, aspects of structure beyond the first two PCs contributed to low tangling. In particular, trajectories were not coplanar (although also not orthogonal) during forward and backward cycling. The resulting separation further reduced tangling by eliminating crossing points. Structure in the higher PCs also contributed to the ability to decode muscle activity. This was true for both the empirical and predicted populations, and is explored further below.

The optimization approach was motivated by the hypothesis that motor cortex activity reflects both muscle-like commands and additional, dominant structure that reduces tangling. This is possible if aspects of neural activity occupy a ‘null-space’: dimensions that do not directly contribute to the outgoing command^60,63,64. The example in Fig 7A contains a simple one-dimensional null space. This hypothesis implies that neural dimensionality is greater than muscle dimensionality (empirically, a given number of neural PCs did indeed captured less variance than the same number of muscle PCs). Nevertheless, to be conservative, we insisted that the predicted neural population response, X̂, have the same dimensionality as the muscle population response, Z (both were ten-dimensional). This choice aids interpretation: any increase in similarity is noteworthy because some muscle-like features must be lost in order to gain features that reduce tangling. Similarity will thus increase only if the features that are gained are more realistic / prominent than the features that are lost. Had we allowed a higher-dimensional X̂, any increase could have been a trivial result of simply having more structure in X̂ that could correlate with the structure in Z.

We explored a variety of other cost functions, corresponding to other hypotheses (Supp Fig 4). Similarity between predicted and empirical responses increased if we allowed a non-linear decode from neural to muscle activity, but only if optimization also sought to reduce tangling. Optimizations that sought to increase local smoothness (one component of low tangling) increased similarity, but not as much as optimizing for low tangling itself. Optimizations that sought to reduce the norm of activity or to increase sparseness (standard forms of regularization) led to decreases in similarity. Thus, across all the cost functions we explored, only those that reduced tangling led to improved predictions.

Muscle-like signals are embedded in trajectories with low tangling

The above results support the hypothesis that muscle-like signals are embedded in larger, minimally tangled trajectories. A circle is the least tangled rhythmic trajectory. Muscle-like signals may thus be encoded by relatively small ‘ripples’ in dimensions that point off the plane of dominant circular structure. A rough analogy would be a phonograph, where the direction that encodes a temporally complex output is orthogonal to the dominant motion of the record. The above results strongly suggest such structure, but can it be viewed directly?

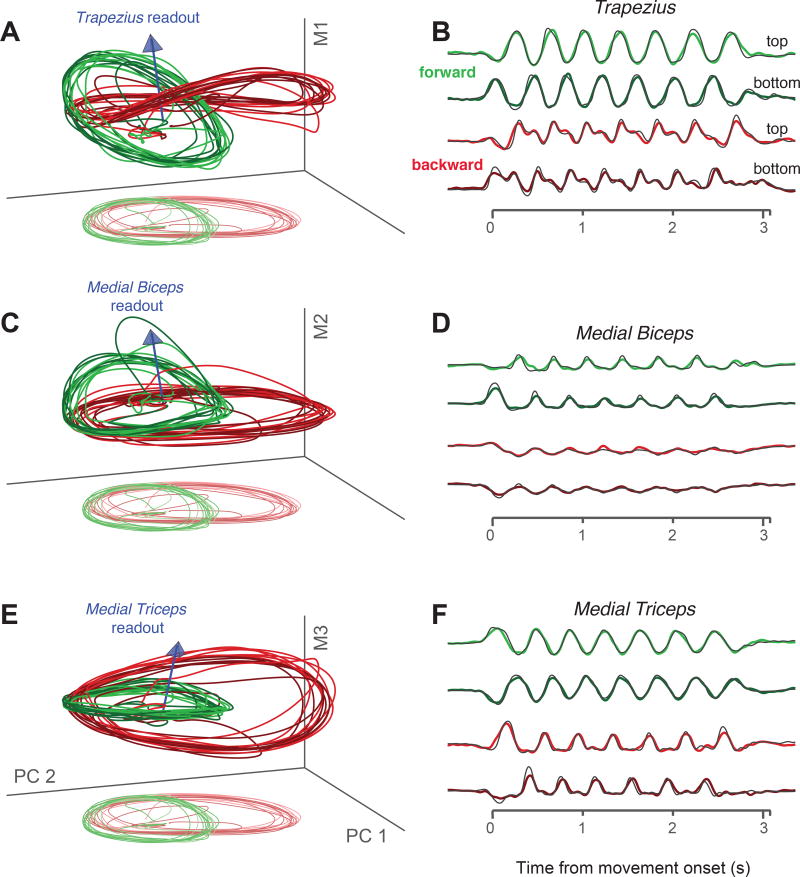
We projected the neural population response onto triplets of dimensions (Fig 8). The first and second dimensions were always the first two PCs, while the third was based on the readout direction of a particular muscle. The readout direction was defined by the set of weights found via linear regression (the arrow in Fig 8A plots the readout direction for the trapezius). The third dimension was then the vector that was orthogonal to the first two PCs, and allowed the three dimensions to span the readout direction.

Figure 8.

Muscle-like signals coexist with signals that contribute to low tangling. Data are for monkey D. A. Three-dimensional subspace capturing trajectories that encode trapezius activity; i.e., can be linearly read out to approximate trapezius activity. Blue arrow indicates the readout direction, defined by the weights identified via linear regression. Axes correspond to the first two PCs and a third dimension that ensures the space spans the readout direction. Trajectories are shown for four conditions: forward (green) and backward (red) seven-cycle movements, starting at the top and bottom (lighter and darker traces). Lighter ‘shadow’ traces at bottom show the projection onto just the first two PCs (perspective has been added). B. Projections, for the four conditions plotted in A, onto the readout direction. Thin black trace plots the true activity of the trapezius. Axis spans the time of movement. C,D. Same as A,B but for the medial biceps. Only the third (vertical) axis is different. E,F. Same but for the medial triceps.

Consider first a triplet of dimensions based on the readout direction of the trapezius (Fig 8A). Trajectories trace out circular paths in the top PCs. Ripples in a third dimension yield the fine temporal structure that matches trapezius activity Fig 8B). The overall trajectory thus has the joint properties of encoding trapezius activity while exhibiting low tangling. Similar structure was observed for other muscles (Fig 8C,E, Supp Fig 5 shows data for monkey C).

The dimensions that encode muscle activity captured only modest variance. In the examples in Figure 8, each muscle-readout dimension captured ~10% as much variance as each of the top two PCs. The vertical dimensions in 8A,C,E are thus shown on an expanded scale for visualization. Similar structure was present for both the network model in Figure 5C and for the predicted population responses in Figure 7E,F: the activity of each ‘encoded’ muscle constituted a set of ripples upon dominant circular structure that yielded low tangling. These ripples cannot be seen in Figures 5C and 7E,F precisely because they point ‘out’ of the page.

Tangling is higher in sulcal motor cortex

The ability to read out muscle activity (Fig 7) suggests that the outputs of motor cortex may be ‘musclelike’, Nevertheless, it remains unclear how heavily those outputs are transformed by the spinal cord (regression can compensate to some degree for any transformation that is not too nonlinear). Ideally, we would have compared neural tangling not with muscle tangling per se, but with the spinally directed output of motor cortex. Fortunately, the potential computational benefits of low tangling are largely agnostic to the details of the particular output. For example, low tangling correlated with noise robustness for both realistic (Supp Fig 4) and idealized (Fig 7A,B) network outputs.

We also considered that descending commands are potentially enriched in sulcal motor cortex, where some neurons make mono-synaptic connections onto motor neurons⁴. We thus compared tangling between a sub-population of surface recordings and a sub-population of sulcal recordings. Tangling was modestly but consistently higher for the sulcal sub-population. This was true for during both cycling and reaching (Supp. Fig. 6). This is consistent with the hypothesis that the broader motor cortex population has tangling lower than its output. The effect was smaller than when comparing neural versus muscle tangling. This is expected: the sulcal sub-population is unlikely to contain only ‘pure’ output signals.

Discussion

Are the dominant signals in motor cortex representational or computational?

We found that the dominant signals in motor cortex were not muscle-like. This result echoes findings during reaching, where aspects of neural responses sometimes (but not always) depart from expectations under a muscle-encoding framework^{1,2,11,17,35,46,65,66}. However, the dominance of non-muscle-like signals is more patent during cycling; non-muscle-like signals are apparent simply via inspection of projections onto the top principal components.

A traditional explanation for non-muscle-like signals is that they represent higher-level movement parameters. The present results are inconsistent with the most common proposal: a representation of direction or velocity. Under that proposal, trajectories should have counter-rotated between forward and backward cycling, and would have been highly tangled as a result. That said, there do exist other ‘representational hypotheses’ that would result in low tangling. For example, a joint representation of hand acceleration, velocity, and position would result in a weakly tangled six-dimensional trajectory. This particular hypothesis does not account for the present results; single-neuron responses did not resemble combinations of acceleration, velocity, and position. Yet this example illustrates that it is conceivable that there exists some set of movement parameters which, if represented in motor cortex, could explain the present findings.

An alternative explanation is that the dominant signals in cortex play a computational, rather than a representational function. Specifically, the dominant signals may fall partly or largely in the null-space of the commands being sent to downstream structures, yet may still be important for ensuring that those commands are generated in a reliable and noise-robust fashion. Put differently, motor cortex is part of a larger dynamical system (spanning many areas, including the spinal cord, and incorporating sensory feedback) that culminates in the generation of muscle commands. Such a system as a whole likely has no ‘choice’ but to contain non-muscle-like signals. It does not of course logically follow that motor cortex itself must show non-muscle-like signals or low tangling; motor cortex could be downstream of the relevant dynamics, or reflect only a small part of the overall network state. Yet empirically, motor cortex displayed very low tangling.

We favor the hypothesis that the dominant signals in motor cortex play a computational role, for three reasons. First, a universal strategy seen in simulated recurrent networks is the production of internal trajectories that possess structure beyond the output. One should thus have a strong prior that aspects of physiological data relate to internal computations rather than to outputs. Second, the hypothesis that motor cortex encodes muscle-like commands, while also displaying low tangling, yielded a concrete prediction of the empirical population response. That prediction was not only successful quantitatively, but reproduced the major qualitative feature of the dominant signals: near-circular co-rotating trajectories. Finally, network simulations demonstrated that low tangling confers noise robustness, suggesting an important computational role.

Notably, the computational explanation for low tangling does not depend on particular assumptions regarding the exact nature of the outgoing commands. A few of our analyses assumed a roughly linear relationship (over the dynamic range being examined) between neural and muscle activity. But the hypothesized computational principle – embed output commands in structure that minimizes tangling – would apply even if outgoing commands were only somewhat muscle-like (e.g., if they were transformed considerably by the spinal cord).

Differences and commonalities across tasks

During both cycling and reaching²⁶, neural trajectories follow circular paths that rotate in a concordant direction, a feature not seen in the muscle population during either task. This shared feature may reflect the combination of two facts. First, muscle activity during both tasks involves rhythmic aspects. This is trivially true during cycling. It is more subtly true during reaching, where the multiphasic patterns of muscle activity are readily constructed from a quasi-oscillatory basis^25,26. Second, a circle is the least-tangled rhythmic trajectory. Rotational trajectories are thus a natural way of encoding muscle activity while maintaining low tangling. This interpretation agrees with recent results from a modeling study. We found that a network model, trained to produce the empirical patterns of muscle activity during reaching, reproduced the circular neural trajectories²⁴. This occurred only if the network was regularized to encourage smooth dynamics. Those findings are consistent with the present results: such regularization would implicitly encourage low tangling.

However, we stress that rotational structure per se is unlikely to be the fundamental principle shared across tasks. There are many ways of adding structure that can reduce tangling. Even if certain motifs are common, the optimal way to reduce tangling will be task-dependent. Thus, we propose that the deeper connection across tasks will not be a specific form of dynamics, but dynamics that produce trajectories with low tangling.

Expectations regarding tangling across areas

Trajectory tangling was very low for motor cortex, considerably higher for S1, and higher still for the muscles. Tangling was also high for V1. Whether tangling is low versus high in a given area may depend on how fully activity in that area reflects global dynamics. Motor cortex may show particularly low tangling because it processes many relevant sources of information. It is not only a major output of the primate motor system, but responds robustly and rapidly to sensory inputs⁶⁷, and lies at the nexus of cerebellar and basal-ganglia feedback loops^68,69. Other areas, even those that participate in the same task, may or may not exhibit low tangling depending on how fully they reflect the overall network state. In particular, S1 responses are likely dominated by sensory feedback, and may very incompletely reflect overall network dynamics. Even within motor cortex, tangling was modestly higher within the sulcus, where activity may be more dominated by output commands. Although V1 presumably does exhibit dynamics, activity is likely dominated by visual inputs which can produce high tangling. These comparisons echo our recent finding that population structure can be fundamentally different depending on whether an area is hypothesized to primarily reflect population dynamics versus external variables²⁹.

It is also possible that tangling might differ within a population, even for the same task. Might the motor system, over the course of learning or development, adopt network trajectories that are increasingly less tangled and thus increasingly noise robust? When a new skill is learned, is performance better if subjects achieve lower tangling? Are pathological conditions associated with increased tangling? Such questions illustrate that many aspects of motor cortex activity may be best understood not in terms of representations of external parameters, but in terms of the computational strategies that allow outputs to be accurately and reliably generated.

Methods

Experimental apparatus

Subjects were two adult male rhesus macaques (monkeys C and D). Animal protocols were approved by the Columbia University Institutional Animal Care and Use Committee. Experiments were controlled and data collected under computer control (Speedgoat Real-time Target Machine). During experiments, monkeys sat in a customized chair with the head restrained via a surgical implant. Stimuli were displayed on a monitor in front of the monkey. A clear acrylic shield was mounted between the monkey and the apparatus and a tube fixed to this shield dispensed juice rewards. The left arm was loosely restrained using a tube and a cloth sling. With their right arm, monkeys manipulated a pedal-like device. The device consisted of a cylindrical rotating grip (the pedal), attached to a crank-arm, which rotated upon a main axel. That axel was connected to a motor and a rotary encoder that reported angular position with 1/8000 cycle precision. In real time, information about angular position and its derivatives was used to provide virtual mass and viscosity, with the desired forces delivered by the motor. The delay between encoder measurement and force production was 1 ms.

Horizontal and vertical hand position were computed based on angular position and the length of the crank-arm (64 mm). To minimize extraneous movement of the wrist, the monkeys’ right wrist rested in a brace attached to the hand pedal. The motion of the pedal was thus almost entirely driven by the shoulder and elbow, with the wrist moving only slightly to maintain a comfortable posture. Wrist movements were monitored via two reflective spheres attached to the wrist brace, which were tracked optically (Polaris system; Northern Digital, Waterloo, Ontario, Canada) and used to calculate wrist angle. The small wrist movements were highly stereotyped across movements of a given type, as were the movements of the other joints (monitored visually using infrared cameras). Eye position and pupil dilation were monitored but are not analyzed here.

Task

The monitor displayed a virtual landscape, generated by the Unity engine (Unity Technologies, San Francisco). Surface texture and landmarks to each side provided visual cues regarding movement through the landscape. Movement was along a linear ‘track’. One rotation of the pedal provided one arbitrary unit of movement. Targets on the landscape surface indicated where the monkey should stop for juice reward.

Each trial of the task began with the appearance of an initial target. To begin the trial, the monkey had to cycle to and to acquire the initial target (e.g., stop on it and remain stationary) within 5 seconds. Acquisition of the initial target yielded a small reward. After a 1000 ms hold period, the final target appeared at a prescribed distance. Following a randomized (500–1000 ms) delay period, a go-cue (a brightening of the final target) was given. The monkey then had to cycle to acquire the final target. After remaining stationary in the final target for 1500 ms, the monkey received a large reward.

Successfully completing a trial necessitated satisfying a variety of constraints. Cycling had to begin between within 650 ms after the go cue. Once cycling began, the final target had to be reached within a distance-dependent time limit. The trial was aborted if this time elapsed, or if cycling speed dropped below a threshold before entering the final target. The trial was also aborted if the monkey moved past the final target, or if the monkey acquired the final target and then moved while waiting for the reward. These constraints, combined with the monkeys’ natural desire to receive reward quickly, produced movements that were both brisk and quite consistent across trials. The primary difference in behavior across trials was modest variation in overall movement duration (e.g., Fig 1). In rare cases, behavior on a successful trial differed notably from typical behavior for that condition. Such trials were removed prior to analysis.

The task included 20 conditions distinguishable by final target distance (half-, one-, two-, four-, and seven-cycles), initial starting position (top or bottom of the cycle), and pedaling direction. A salient visual cue (landscape color) indicated whether pedaling must be ‘forward’ (the had moved away from the body at the top of the cycle) or ‘backward’ (the had moved toward from the body at the top of the cycle) to produce forward progress in the virtual world. Trials were blocked into forward and backward pedaling. Other trials types were interleaved using a block-randomized design.

Neural recordings during cycling

After initial training, we performed a sterile surgery during which monkeys were implanted with a head restraint. Cylinders (Crist Instruments, Hagerstown, MD) were centered over caudal PMd, located according to a previous magnetic resonance imaging scan. Cylinders were placed surface normal to the cortex. The skull within the cylinder was left intact and covered with a thin layer of dental acrylic. Neural recordings were made using conventional single electrodes (Frederick Haer Company, Bowdoinham, ME) driven by a hydraulic microdrive (David Kopf Instruments, Tujunga, CA). Electrodes were introduced through small (3mm diameter) burr holes drilled by hand through the acrylic and skull, under ketamine / xylazine anesthesia.

Sequential recording with conventional electrodes (as opposed to simultaneous recording with an array) allowed us to acquire recordings from a broader range of sites, including sulcal sites inaccessible to most array techniques. Recording locations were guided via microstimulation, light touch, and muscle palpation protocols to confirm the trademark properties of each region. For motor cortex, recordings were made from primary motor cortex (both surface and sulcal) and the adjacent (caudal) aspect of dorsal premotor cortex. For most analyses, these recordings are analyzed together as a single motor cortex population (though see Supp Fig 6). Motor cortex recordings were restricted to regions where microstimulation elicited responses in shoulder, upper arm, chest and forearm. For one monkey, we recorded from area 3a (proprioceptive primary motor cortex). These recordings (44 neurons) were made from the deeper aspects of the posterior bank of the central sulcus, where microstimulation did not produce movement.

Neural signals were amplified, filtered, and manually sorted using Blackrock Microsystems (Digital Hub and 128-channel Neural Signal Processor). A total of 277 isolations were made in monkeys C and D. Nearly all neurons that could be isolated in motor cortex were responsive during cycling. A modest number (21) of isolations were discarded due to low signal-to-noise ratios or insufficient trial counts. No further selection criteria were applied. On each trial, the spikes of the recorded neuron were filtered with a Gaussian (25 ms SD) to produce an estimate of firing rate versus time. These were then averaged across trials as described below.

EMG recordings

Intra-muscular EMG was recorded from the major muscles of the arm, shoulder, and chest using percutaneous pairs of hook-wire electrodes (30mm × 27 gauge, Natus Neurology) inserted ~1 cm into the belly of the muscle for the duration of single recording sessions. Electrode voltages were amplified, bandpass filtered (10–500 Hz) and digitized at 1000 Hz. To ensure that recordings were of high quality, signals were visualized on an oscilloscope throughout the duration of the recording session. Recordings were aborted if they contained significant movement artifact or weak signal. That muscle was then recorded later. Offline, EMG records were high-pass filtered at 40 Hz and rectified. Finally, EMG records were smoothed with a Gaussian (25ms standard deviation, same as neural data) and trial averaged (see below). Recordings were made from the following: the three heads of the deltoid, the two heads of the biceps brachii, the three heads of the triceps brachii, trapezius, latissimus dorsi, pectoralis, brachioradialis, extensor carpi ulnaris, extensor carpi radialis, flexor carpi ulnaris, flexor carpi radialis, and pronator. We often made multiple recordings for a given muscle, especially those that we have previously noted can display responses that vary with recording location (e.g., the deltoid).

Trial alignment and averaging

To preserve response features, it was important to compute the average firing rate across trials with nearly identical behavior. This was achieved by 1) training to a high level of stereotyped behavior, 2) discarding rare aberrant trials, and 3) ‘adaptive alignment’ of behavior on individual trials prior to averaging. Because of the temporally extended nature of cycling movements, standard alignment procedures (e.g., locking to movement onset) often misalign responses later in the movement. For example, a seven-cycle movement lasted ~3500 ms. By the last cycle, a trial 5% faster than normal and a trial 5% slower than normal would thus be misaligned by 350 ms, or over half a cycle.

To ensure response features were not lost to misalignment, we developed a technique to adaptively align trials within a condition. First, trials were aligned so that movement onset occurred at the same moment for every trial. Individual trials were then scaled so that all trials had the same duration (set to be the median duration across trials). Because monkeys usually cycled at a consistent speed (within a given condition) this brought trials largely into alignment: e.g., the top of each cycle occurred at nearly the same time for each trial. The adaptive alignment procedure was used to correct any remaining slight misalignments. The time-base for each trial was scaled so that the position trace on that trial closely matched the average position of all trials. This involved a slight non-uniform stretching, and resulted in the timing of all key moments – such as when the hand passed the top of the cycle – being nearly identical across trials. This ensured that high-frequency temporal response features (e.g., the small peak in Figure 1G) were not lost to averaging.

All variables of interest (firing rate, hand position, hand velocity, EMG, etc.) were computed on each trial before adaptive alignment. Thus, the above procedure never alters the values of these variables, but simply aligns when those values occur across trials. The adaptive procedure was used once to align trials within a condition on a given recording session, and again to align data across recording sessions. This allowed, for example, comparison of neural and muscle responses on a matched time-base.

Other experimental datasets

Data from primate motor cortex during reaching has been analyzed previously⁶⁰. Briefly, two male rhesus monkeys (A and B) performed center-out delayed reaches in eight target directions on a fronto-parallel screen. This task employed three ‘contexts’ in which reach initiation was prompted by different cues. That manipulation was incidental to the present analysis: we analyzed only movement-related responses, which were empirically very similar across the three contexts. We therefore simply computed, for each reach direction, the average time-varying firing rate (smoothed with a 20 ms Gaussian) across all reaches in that direction. Trials were aligned to movement onset and average firing rate was computed from 100 ms before movement onset until 100 ms after the average time of movement offset. Neural populations included 101 and 129 neurons (monkey A and B) recorded from the arm region of motor cortex (including sulcal and surface primary motor cortex and the adjacent aspect of dorsal premotor cortex). During this same task, activity was recorded from the muscles of the upper arm using the same procedures described above (13 and 10 recordings for monkey A and B).

Data from primate V1 were recorded using natural-movie stimuli from an anaesthetized adult monkey (Macaca fascicularis) implanted with a 96-electrode silicon ‘Utah’ array (Blackrock Microsystems, Salt Lake City, UT) in left-hemisphere V1 as previously described²⁹. These data were recorded in the laboratory of Adam Kohn. Procedures were approved by the Animal Care and Use Committees at Albert Einstein College of Medicine (protocol #20150303). The left eye was covered. Receptive field centers (2–4 degrees eccentric) were determined via brief presentations of small drifting gratings. Stimuli, which spanned the receptive fields, were 48 natural movie clips (selected from YouTube) with 50 repeats each. The frame rate was ~95 Hz. Each stimulus lasted 2.63 s (100 movie frames followed by 150 blank frames). Spikes from the array were sorted offline using MKsort (available at https://github.com/ripple-neuro/mksort/). A total of 108 single units and stable multi-unit isolations were included.

Data from mouse motor cortex were recorded from three head-fixed mice during a task that invoked both a reach-to-grasp sub-task and natural treadmill walking (10 cm/s), performed in separate blocks. Procedures were as described previously (Miri et al., Neuron, in press). Multiple neurons / muscles were recorded simultaneously, but were also accumulated across days to allow analysis of larger populations. Populations from each mouse were analyzed separately. Neural recordings were made with independently movable tetrode micro-drives (plated with Platinum Black solution to achieve final impedances of 80–200 kΩ at 1 kHz) implanted into a 3.5 mm diameter craniotomy above the left caudal forelimb area of M1. Tetrodes were lowered over the course of two weeks to target recordings within layer 5. Spike waveforms were acquired at 40 kHz and sorted. A total of 890 well-isolated units from three animals were recorded across 11 behavioral sessions. Muscle activity from the forelimb was recorded from electrodes chronically implanted in the trapezius, pectoralis, biceps, triceps, extensor digitorum communis, and palmaris longus. For two mice, recordings were made from all six of these muscles. For one mice recordings could only be made from four. Each muscle was recorded across eleven sessions. PCA thus extracted the top signals across 66 total records for two mice and 44 for the other. Spike-trains and muscle activity were smoothed with a Gaussian filter (20 ms standard deviation) and averaged across trials.

Preprocessing, PCA, and regression

Because PCA seeks to capture variance, it can be disproportionately influenced by differences in firing rate range (e.g., a neuron with a range of 100 spikes/s has 25 times the variance of a similar neuron with a range of 20 spikes/s). This concern is greater still for EMG, where the scale is arbitrary and can differ greatly between recordings. The response of each neuron / muscle was thus normalized prior to application of PCA. EMG data were fully normalized: response ← response/range(response), where the range is taken across all recorded times and conditions. Neural data were ‘soft’ normalized: response ← response/(range(response) + 5). We standardly^26,29 use soft normalization to balance the desire for PCA to explain the responses of all neurons with the desire that weak responses not contribute on an equal footing with robust responses. In practice, soft normalization was essentially irrelevant for data during cycling, as nearly all neurons had high firing rate ranges.

Following preprocessing, neural data were formatted as a ‘full-dimensional’ matrix, X^full, of size n × t, where n is the number of neurons and t indexes across all analyzed times and conditions. We similarly formatted muscle data as a matrix, Z^full, of size m × t, where m is the number of muscles. Unless otherwise specified, analyzed times were from 100 ms before movement onset to 100 ms after movement offset, for all conditions. Because PCA operates on mean-centered data, we mean-centered X^full and Z^full so that every row had a mean value of zero.

PCA was used to find X, a reduced-dimensional version of X^full with the property that X^full ≈ VX, where V are the principal components (‘neural dimensions’ upon which the data are projected). PCA was similarly used to find Z, the reduced-dimensional version of Z^full. For most analyses, we employed eight principal components, such that X and Z were of size 8×t.

Decoding of muscle activity from neural activity was accomplished via a linear model: Z^full = BX^full. B was found using ridge regression. Performance was assessed using generalization R², using Leave-One-Out Cross Validation. Regularization strength was chosen to maximize Leave-One-Out Cross Validation performance, though in practice a broad range of regularization strengths provided similar performance. For one analysis we also attempted to decode neural activity from muscle activity using the model X^full = BZ^full. Decoding neural activity from muscle activity was less successful than decoding muscle activity from neural activity. Although our neural recordings generally had very good signal-to-noise, it is possible that poor decoding of neural activity from muscle activity (relative to decoding muscle activity from neural activity) could result because neural responses are on average modestly noisier (have higher sampling error) than muscle responses. We therefore re-ran the regression above after de-noising the neural data by replacing each neuron’s response with its reconstruction from the top thirty principal components. The same discrepancy was observed.

Tangling

Tangling was computed as described in the results (Equation 1). The neural state, x_t was the t^th column of X. Muscle tangling was computed analogously, based on Z. Essentially identical results were found if we used X^full (Supp Fig 1) but this was less computationally efficient and did not allow matched dimensionality between neurons and muscles. We computed the derivative of the state as ẋ_t = (x_t − x_t−Δt)/Δt, where Δt was 1 ms When computing tangling, we employed the squared distance between derivatives, ∥ẋ_t − ẋ_t,∥², because its magnitude more intuitively tracks the difference in trajectory direction. For example, if the angle between derivatives doubles from 90° to 180°, the norm grows by only 41%, but the squared norm is doubled. The constant ε (set to 0.1 for all analyses) determines how small the denominator can become, which effectively prevents the measurement of squared distance between states from ever shrinking below 0.1 times the average squared distance. Results were essentially identical across an order of magnitude of values of ε.

The definition of trajectory tangling used here differs somewhat from the recently introduced definition of representational tangling⁷⁰. Representations are tangled if the sets of states corresponding to two stimulus classes cannot be separated by a smooth (e.g., linear) separatrix. Trajectories are tangled if their evolution cannot be accounted for by a smooth dynamical flow-field.

Standard Recurrent Neural Networks

We used two very different approaches to train recurrent neural networks (RNNs). In the first approach, we trained RNNs to produce a target output (Fig 5) as is conventionally done. We used a network with dynamics:

$$\mathit{x}(t+1,c)=f(A\mathit{x}(t,c)+B\mathit{u}(c)+\mathit{w}(t,c))$$

where x is the network state (the ‘firing rate’ of every unit) for time t and condition c. The function f ≔ tanh is an element-wise transfer function linking a unit’s input to its firing rate, Ax captures the influence of network activity on itself via the connection weights in A, Bu captures external inputs (used to instruct the network which output is desired) and the random vector w~N(0, σ_w) adds modest noise. Network output is then a linear readout of its firing rates:

$$\mathit{y}(t,c)=C\mathit{x}(t,c)$$

The parameters A, B, C, and x(0, c) were optimized to minimize the difference between the network output, y and a target, y_targ. That target was the pattern of activity, across all muscles, during the middle five cycles of a seven-cycle movement. We used two conditions with different targets: y_targ (:,1) and y_targ(:,2) contained muscle activity during forward and backward cycling respectively. The input provided the network with the condition identity: u(1) = [1; 0] and u(2) = [0; 1].

The loss function optimized during training contained regularization terms:

$$L=\sum _{t,c}\left[\frac{1}{2}{\Vert {\mathit{y}}_{\text{targ}}(t,c)-\mathit{y}(t,c)\Vert }_2^2\right]+\frac{{\lambda }_A}{2}{\Vert A\Vert }_F^2+\frac{{\lambda }_C}{2}{\Vert C\Vert }_F^2+\sum _{t,c}\left[\frac{{\lambda }_x}{2}{\Vert \mathit{x}(t,c)\Vert }_2^2\right]$$

where the first term is the error between the network output and the target, the second and third terms penalize large recurrent and output weights respectively, and the last term penalizes large firing rates. By varying the hyper-parameters λ_A, λ_C, λ_xσ_w, and the initial weight values, we simulated a family of networks that found different solutions for producing the same output. This allowed us to ask whether low network-trajectory tangling was a common feature of those solutions.

We trained 1000 such networks. Hyper-parameters drawn randomly from log uniform distributions, λ_A ∈ [10⁻⁴, 10⁻¹], λ_C ∈ [10⁻⁶, 10¹], λ_x ∈ [10⁻⁴, 10¹], and σ_w ∈ [10⁻⁴, 10¹]. Each RNN included n = 100 units. Each matrix of the RNN was initialized to a random orthonormal matrix. RNNs were trained using TensorFlow’s Adam optimizer. We discarded RNNs that were not successful (R² < 0.5 between target and actual outputs). Because of the broad range of hyper-parameters, only a subset of networks (463) were successful.

As a technical point, we were concerned that, despite regularization, networks might find overly specific solutions. Each cycle of the empirical muscle activity had different small idiosyncrasies, and optimization might promote overfitting of these small differences. We therefore added ‘new’ conditions to y_targ(t, c). Each new condition looked almost identical to one of the original two conditions, but was modified such that the small idiosyncrasies occurred on different cycles. This ensured that networks produced a consistent output very close to the empirical muscle activity, but did not attempt to perfectly match small idiosyncratic differences. The inclusion of noise via w also encouraged optimization to find robust, rather than overfit, solutions. Noise magnitude, σ_w, was a hyper-parameter that was varied across networks, to encourage varied solutions. However, σ_w was always set to zero when measuring network tangling.

Trajectory-constrained Neural Networks

To examine the relative noise-robustness of different internal trajectories (Fig 7B and Supp Fig 4) we trained RNNs to follow a target internal trajectory. This involved the unconventional approach of employing both a target output, y_targ, and a target internal network trajectory, s_targ. Networks consisted of 100 units. Network dynamics were governed by

$$\mathit{v}(t+1)=\mathit{v}(t)+\mathrm{\Delta }t/\mathrm{\tau }(-\mathit{v}(t)+Af(\mathit{v}(t))+\mathit{w}(t))$$

$$\mathit{y}(t)=Cf(\mathit{v}(t))$$

where f ≔ tanh and w~N(0, σ_w) adds noise. v can be thought of as the membrane voltage and f(v(t)) as the firing rate. Af(v(t)) is then the network input to each unit: the firing rates weighted by the connection strengths. Cf(v(t)) is a linear readout of firing rates.

During training, A was adjusted using recursive least squares⁷¹ so that Af(v(t)) ≈ s_targ. Training thus insured that the synaptic inputs to each unit closely followed the pre-determined trajectory defined by s_targ. Firing rates therefore also followed a pre-determined trajectory. C was adjusted so that y ≈ y_targ. Training was deemed successful if the R² between y and y_targ was > 0.9. Noise robustness was assessed as the largest value of σw for which the network could be trained to accurately produce the target output (R² > 0.9 between y and y_targ) despite being forced to follow the target trajectory.

We set y_targ = [cos t; sin 2t]. To construct s_targ, we began with an idealized low-dimensional target, $\mathit{s}{(t)}_{\text{targ}}^{\prime }=[\text{cos }t;\text{ sin }2t;\mathrm{\beta }\text{sin }t]$. To give each unit a target, we set ${\mathit{s}}_{\text{targ}}=G{\mathit{s}}_{\text{targ}}^{\prime }$ where G is a random matrix of size 100 × 3 with entries drawn independently from a uniform distribution from −1 to 1. (Supplementary simulations use versions of y_targ and $\mathit{s}{(t)}_{\text{targ}}^{\prime }$ derived from muscle activity and predicted neural activity respectively.)

Noise tolerance was tested for a range of values of β, producing target trajectories that varied greatly in their tangling. For each target trajectory, and each tested value of σ_w, we ran multiple simulations with different random initializations of A, C, and G. The noise tolerance reported in Figure 7 is the average (and SEM) across these simulations.

Predicting neural population activity

The optimization described by Equation 2 was performed using Tensorflow. Optimization was initialized with X̂_init = Z. Both X̂ and Z were 10×T; they contained the projection onto the top ten PCs (T is the total number of timepoints across the conditions being considered). Because dimensionality is equal for X̂ and Z, the ability to decode Z from X̂ will suffer as optimization modifies X̂. This will increase the first term of the cost function. However, for ~90% of the variance in muscle population activity was captured in the first 8 PCs. This makes it possible for optimization to add structure to X̂ while compromising the decode only slightly (most trivially, optimization could change the last two rows of X̂ and result in at most 10% error). Thus, the choice of ten dimensions allows ‘room’ for optimization to add structure while keeping decode error low. In practice, decode error was always < 5% (λ was chosen to ensure this). Optimizations employed gradient descent using an inexact line search for the Wolfe conditions c₁ = 0.05 and c₂ = 0.1. Because optimization predicts a single ‘canonical’ middle cycle out of many repeating cycles, we computed the derivative used to compute Q (t_end) based on the assumption that the cycle would repeat. When assessing similarity, we used a modified version of canonical correlation that does not whiten the data (Cunningham & Ghahramani 2015). Similarity was the average of the ten canonical correlations.

Highlights.

• Motor cortex displays a signature of a smooth dynamical system: low ‘tangling’.

• Low tangling explains the previously puzzling dominant signals in motor cortex.

• Low tangling conveys noise robustness and predicts population activity patterns.

• Motor cortex embeds output commands in structure that reduces tangling.