Interpretability of Cancer Clinical Trial Results Using Restricted Mean Survival Time as an Alternative to the Hazard Ratio

Abstract

Importance

In a comparative clinical study with progression-free survival (PFS) or overall survival (OS) as the end point, the hazard ratio (HR) is routinely used to design the study and to estimate the treatment effect at the end of the study. The clinical interpretation of the HR may not be straightforward, especially when the underlying model assumption is not valid. A robust procedure for study design and analysis that enables clinically meaningful interpretation of trial results is warranted.

Objective

To discuss issues of conventional trial design and analysis and to present alternatives to the HR using a recent immunotherapy study as an illustrative example.

Design, Setting, and Participants

By comparing 2 groups in a survival analysis, we discuss issues of using the HR and present the restricted mean survival time (RMST) as a summary measure of patients’ survival profile over time. We show how to use the difference or ratio in RMST between 2 groups as an alternative for designing and analyzing a clinical study with an immunotherapy study as an illustrative example.

Main Outcomes and Measures

Overall survival or PFS. Group contrast measures included HR, RMST difference or ratio, and the event rate difference.

Results

For the illustrative example, the HR procedure indicates that nivolumab significantly prolonged patient OS and was numerically better than docetaxel for PFS. However, the median PFS time of docetaxel was significantly better than that of nivolumab. Therefore, it may be difficult to use median OS and/or PFS to interpret of the HR value clinically. On the other hand, using RMST difference, nivolumab was significantly better than docetaxel for both OS and PFS. We also provide details regarding design of a future study with RMST-based measures.

Conclusions and Relevance

The design and analysis of a conventional cancer clinical trial can be improved by adopting a robust statistical procedure that enables clinically meaningful interpretations of the treatment effect. The RMST-based quantitative method may be used as a primary tool for future cancer trials or to help us to better understand the clinical interpretation of the HR even when its model assumption is plausible.

This comparative clinical study discusses problems with conventional trial design and analysis and presents alternatives to the hazard ratio using a recent immunotherapy study as an illustrative example.

Key Points

Question

For conducting a comparative cancer clinical trial, can we improve the current practice by using a robust procedure-enhancing clinical interpretability of trial results via study design and analysis?

Findings

Trial results using the conventional hazard ratio may be difficult to interpret, especially when the underlying model assumption is not valid; on the other hand, the estimation procedure based on the restricted mean survival time is robust and provides a heuristic, clinically meaningful interpretation for treatment effect.

Meaning

The design and analysis of a conventional cancer clinical trial can be improved by adopting a robust statistical procedure that enables clinically meaningful interpretation of the treatment effect.

Introduction

In a clinical trial to compare a new treatment with a control, the primary end point is generally either the overall survival (OS) or progression-free survival (PFS) time. At the design stage, the hazard ratio (HR) is routinely used to quantify a desirable treatment effect for estimation of the study sample size. The total number of events needed to achieve a specific statistical power can be obtained via a back-of-the-envelope calculation. However, it may not be straightforward to interpret the HR clinically. Thus, a hypothesized HR value (eg, 0.75) is often justified as a relative improvement in median survival time (eg, from 9 to 12 months) due to the treatment. While the median survival time is a clinically meaningful summary measure, it does not capture the long-term survival profile well. Therefore, the difference or ratio between 2 median survival times may not be useful to interpret the HR value at the design stage.

At the end of the study, the OS and/or PFS data are routinely analyzed using the HR estimation and log-rank test. This practice becomes more problematic at the analysis stage. The limitations concerning this summary measure have been discussed extensively in the literature. The validity of using the HR depends on the proportional hazards assumption, that is, the HR for 2 groups is constant over the entire study period. This assumption is rarely valid in practice and without this assumption, the resulting HR estimate is difficult to interpret. In an interview, Professor David Roxbee Cox, FRS, FBA, the creator of the above model, stated, “Of course, another issue is the physical or substantive basis for the proportional hazards model. I think that’s one of its weaknesses…”^(p450)

To ease the difficulty of interpreting the HR, the median survival time estimate is often reported for each group descriptively without formal comparisons. However, in studies with limited follow-up, it may not be possible to estimate the median survival. Moreover, because the median survival estimate is insensitive to long-term survivors and is less stable with respect to precision than the HR, the estimate of the difference in 2 median survival times can result in an inconsistent conclusion about the treatment effect compared with that based on the HR estimate.

The Kaplan-Meier curve provides survival probability information throughout the study follow-up for a group of patients. Visually, the higher the curve is, the better the treatment is. Therefore, the area under the curve within a specific time window is a reasonable summary to quantify the survival curve. This alternative measure is the restricted mean survival time (RMST) or t-year mean survival time. This summary offers an intuitive, clinically meaningful interpretation. The procedure for estimating the difference in 2 RMSTs is always valid without any model assumptions and is more stable in comparison with the estimation of the median survival time. If one is interested only in comparing the long-term survival profiles, the t-year event rate may be an alternative summary. Other group contrast measures such as the “net chance of a longer survival” can also be considered.

There is no single summary measure which can capture the entire survival profile of a group of patients. However, for the design and analysis of a study, a primary summary measure for the between-group difference is needed. The analysis procedure for this summary measure should be robust, not model dependent, and should result in clinically interpretable conclusions about the treatment effect. In this article, we illustrate these points using a recent clinical trial to evaluate an immunotherapy for lung cancer.

Methods

Illustration of Issues for the Conventional Study Design

To illustrate a typical conventional study design, we considered a recent randomized clinical trial (CheckMate 057), which was conducted to evaluate whether nivolumab would be superior to docetaxel for previously treated patients with advanced nonsquamous non–small-cell lung cancer. The primary end point was OS. The study was intended to have enough power to detect a difference of 3.1 months in median OS in favor of nivolumab (the median OS was assumed to be 11.1 months for nivolumab, 8.0 for docetaxel). A natural summary measure of the treatment effect would be the difference or ratio in 2 median OS times. The sample size estimate for the study could then be based on the desired precision of such a difference or based on the desired statistical power for the corresponding test to detect a significant difference between groups.

Instead of taking this straightforward approach to design a trial, the clinical trialists routinely convert the desired median OS difference to HR by assuming that the OS time follows an exponential distribution for each group. One then estimates the sample size based on the log-rank test. For the above example, the resulting HR is 8/11.1 = 0.72. Under this setting, the power of the study would be dependent on the observed number of deaths at the end of study, not on the patient follow-up times. For CheckMate 057, we would need a total of 403 events to have a power of 90%. This resulted in a total of 574 patients required for the study under certain patient accrual and follow-up patterns. Moreover, like other trials, the HR was proposed to quantify the treatment effect.

Why do the trialists convert a heuristically interpretable measure such as the difference or ratio in median OS to HR in designing the study? One major issue of using median survival as a summary is that often at the end of the study, the median survival may not be estimable due to limited study follow-up time. Even when we can estimate the median survival time, the median may not capture the long-term survival profile due to its insensitivity to long-term survivors. Moreover, it is known that the estimate of the median survival time is not stable—its standard error can be quite large—and a substantially larger study would be needed compared with using HR as a measure of the treatment effect.

Illustration of Issues for Conventional Data Analysis

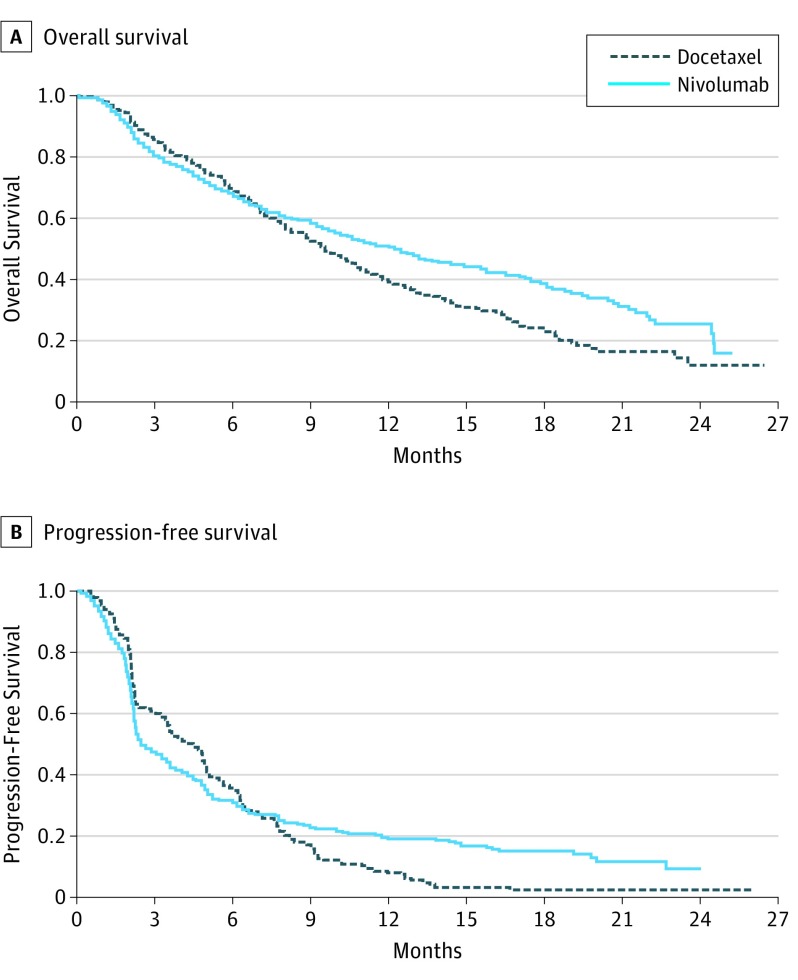
For CheckMate 057, 292 patients were treated with nivolumab and 290 were treated with docetaxel. The total number of observed deaths was 413. We present the Kaplan-Meier curves with reconstructed OS and PFS data (Figure 1) by scanning the survival curves in Figure 1 of Borghaei et al. The HR comparing nivolumab vs docetaxel was 0.73. The 2 survival curves were similar until approximately 7 months after randomization. This suggests that the proportional hazard assumption was not valid, and it is unclear how to interpret HR of 0.73 clinically. To this end, the investigators provided the observed median survival times. The median OS time was 12.2 months (95% CI, 9.7-15.0) for nivolumab and 9.4 months (95% CI, 8.1-10.7) for docetaxel. Since these 2 95% CIs overlapped, it was not clear whether there was a statistically significant difference in the median OS times. It is puzzling that for almost all cancer studies, there are no formal comparisons between 2 median survival times. Using two separate CIs of individual median survival times is not an efficient way to assess the difference of 2 medians. If we apply a simple resampling procedure to estimate the difference in 2 median OS times (nivolumab minus docetaxel), the resulting estimate would be 2.7 months (95% CI, −0.1 to 5.9) with P = .07. In this example, using the difference in 2 median survival times does not help us understand the clinical meaning of the statistically significant HR of 0.73.

Figure 1. Overall Survival and Progression-Free Survival for Patients Taking Docetaxel vs Nivolumab.

Patient-level data was reconstructed from the Kaplan-Meier curves in the study Borghaei et al.

For the PFS end point, the HR is 0.92 with P = .39. Because the Kaplan-Meier curves crossed around month 7 for PFS, this HR is not interpretable. The reported median PFS was 2.3 months for nivolumab and 4.2 months for docetaxel, a difference of 1.9 months. If we apply the above simple inference procedure, the CI for the difference of 2 median PFS (docetaxel minus nivolumab) is 0.4 to 2.6 months with P = .005, indicating that docetaxel was highly significantly superior to nivolumab with respect to median PFS. This result is in contradiction to those from HR analyses for PFS and OS.

Alternatives to the Conventional Study Design and Analysis

Because the study design depends on the statistical methods to be used, we first discuss alternative statistical procedures for analyzing PFS and/or OS data from a comparative trial using CheckMate 057 for illustration. We then discuss in detail how to design a superiority study with the analytical procedure based on the RMST.

Results

An alternative to the median survival is the RMST. Using the reconstructed data in Figure 1A (OS), the estimated RMST at 24 months of follow-up for nivolumab is 13 months. That is, future patients receiving nivolumab followed for 24 months would survive for an average of 13 of 24 months. For docetaxel, RMST estimate is 11.3 months. The difference in RMST is 1.7 months (95% CI, 0.4-3.1; P = .01) in favor of nivolumab. This conclusion is statistically consistent with that from the HR or log-rank test. Graphically this difference is represented by the area between 2 Kaplan-Meier curves in Figure 1A (OS). Note that the standard error estimate for the RMST estimate is obtained without any model assumption in contrast to others proposed in the literature.

For PFS (Figure 1B), the difference of RMSTs is 1.3 months (95% CI, 0.3-2.3; P = .02), which is also significantly in favor of nivolumab. This result is consistent with the observed HR less than 1. For PFS, the HR interacted with time qualitatively over 24 months. For this case, the RMST based procedure can be much more powerful than the log-rank test. Note that at the analysis stage, one can choose any t-year time window until we reach the last death or censored time observation to compute RMST.

One may be interested in estimating the survival curve beyond 2 years with a parametric model to estimate the mean survival time (ie, not restricted within 2-year window). For instance, if we use a Weibull distribution to fit the reconstructed OS data for each group from Figure 1A (OS), the estimated mean survival times are 12.3 and 17.4 months for docetaxel and nivolumab, respectively. The gain from the immunotherapy for OS would be 5.1 months (95% CI, 4.2-6.2). This extrapolation is informative but needs to be interpreted cautiously.

Another alternative measure one may use is the t-year survival rate. On the other hand, this summary does not include the temporal treatment effect before or after t years. For the present example, the OS rates at 2 years are 25.5% and 12.0% for nivolumab and docetaxel, respectively. The 95% CI of the difference is 3.9% to 23.1%.

The statistical analysis for median difference and RMST difference discussed above can be implemented via contributed R packages—surv2sampleComp and survRM2 packages. Both R packages are available from the CRAN website (https://cran.r-project.org/).

To illustrate how to design a study with RMST for the primary analysis, we mimic the CheckMate 057 study setting and estimate the sample size for a study powered to detect a postulated difference of 2 RMSTs. Furthermore, we show how to set the study termination time when conducting the trial. Here is the step-by-step process. Note that this process can be applied to a general, practical setting with an event-time as the end point under any assumed patterns of patient accrual and loss-to-follow-up profiles.

1. Let OS time be the primary end point. Suppose that we are interested in the RMST within a 24-month time window. The duration of this time window may be informed by considerations of both clinical significance and study feasibility. Note that the time window for RMST should be prespecified in the study protocol.

2. Obtain the median or mean survival time for the control arm from historical data, and use a parametric model (for example, exponential) to calculate the RMST with a specific time window. In our example, we fit the reconstructed OS data from docetaxel group with an exponential distribution. This results in an estimated mean survival time of 13.3 months and in a 24-month RMST of 11.1 months.

3. Assume we are interested in detecting an increase of a 24-month RMST of 3 months from docetaxel group in this time window (ie, 14.1 months in nivolumab group) with 90% power. Assuming the exponential distribution, then nivolumab group has an unrestricted mean survival time of 16.3 months.

4. Set the study patient accrual period and follow-up time distribution, which may depend on practical limitations. Here, for illustration, we assume similar accrual and follow-up time patterns as those from CheckMate 057. Figure 2 shows the censoring distribution by pooling the data from both treatment groups from CheckMate 057. Because the primary end point is OS time, we may assume that each patient’s mortality status was known at the end of the study. From Figure 2, it appears that the accrual time was approximately 11 months, with patients entering the study uniformly over this time period, and the last patient enrolled was followed for 15 months. Under these assumptions, future patients who enter the potential trial in the first 2 months are expected to have at least 24 months of follow-up. Therefore, the RMST for each treatment group can be estimated well. Other enrollment and follow-up patterns can be considered as well for designing a study. The key is to ensure that the potential follow-up time for a nontrivial proportion of patients is adequate for estimating the RMST in the specified time window.

5. To estimate the sample size under the above setting, for any given sample size n with 1:1 treatment allocation, we generate a sample of OS times for each group using the above exponential distributions. We then generate corresponding censoring times via the distribution determined by the 11 months of accrual period and additional 16 months of follow-up after the completion of accrual. With these 2 samples of censored OS time data, the estimate of the difference in RMST, its variance estimate using pooled data from two treatment groups, and the corresponding test statistic (ie, z score) are recorded. We repeat this simulation procedure, say, 3000 times, to estimate the power of this potential study. If the power is less (or greater) than 90%, we then increase (or decrease) the sample size n and repeat the above process until the empirical power reaches the target level. This results in a total of 336 patients (168 per arm) to obtain 90% power to detect a 3-month difference in RMST. Note that conventionally, the reciprocal of the average of the above 3000 variance estimates is referred to as the “total information time” of the study. For the present case, the average standard error for the RMST difference estimate is about 0.94 months. With this standard error, the expected 95% CI would be about 1 to 5 months.

6. Like other clinical trials, when we apply a proposed design setting to conduct a real study, patient accrual profile and follow-up time distribution are likely different from the assumed ones. For the present case, one may set the maximum calendar time for study termination being the time of the last patient entering the study plus 24 months. The study may be terminated early when the observed standard “information time” (the reciprocal of variance estimate of the RMST difference) at a specific time point reaches the above total information time specified in Step 5. In fact, the trial may be terminated when, for instance, a handful of patients in each arm has reached 24 months of follow-up.

Figure 2. Distribution of the Censoring Times.

This graph is based on reconstructed data of overall survival.

Note that when using the conventional log-rank test as the primary analysis tool, we set a specific total number of events as the total information time. To estimate the study sample size, we also need to assume the patient accrual and/or follow-up temporal profile. When the event rate is unexpectedly low in the real study, using such a total time information measure may unnecessarily prolong the study duration. On the other hand, with the t-year mean survival time difference or rate as the group contrast measure, the study would have a well-defined maximum duration time.

The procedure for designing a comparative trial with survival data discussed here can be implemented via the contributed R package SSRMST from the CRAN website (https://cran.r-project.org/web/packages/SSRMST/index.html).

Discussion

Generally the primary goal of a comparative clinical study is to estimate an overall treatment effect. However, a “positive” trial based on such an average effect over the entire patient population does not mean every patient would benefit from it. On the other hand, a “neutral or negative” trial does not mean that no patient would benefit from the new therapy. For designing future cancer studies, it is important to have a prespecified procedure based on the patient baseline characteristics collectively to identify a so-called high-value subgroup of patients who would clinically benefit from the new therapy. In a published guidance on the enrichment strategies for clinical trials, the US Food and Drug Administration encourages the clinical trialists to consider such a predictive enrichment strategy. This prespecified procedure would be an ideal tool to identify, for example, a specific subgroup of patients who would benefit from nivolumab or pembrolizumab for treating a specific subpopulation of patients with non–small-cell lung cancer via trials such as CheckMate 057, CheckMate 026, and KeyNote 024 with patient baseline information regarding, for instance, programmed cell death 1 ligand 1, gene signatures, and epitope load collectively.

Conclusions

The design and analysis of a conventional cancer clinical trial with OS and/or PFS outcome can be improved by adopting a robust statistical procedure that enables clinically meaningful interpretation of the treatment effect. The RMST-based statistical method may be used as a primary tool for design and analysis of a comparative study. It may also help us to better understand the clinical interpretation of the HR when the proportional hazards model assumption is plausible.

For the RMST or t-year mean survival time, the choice of t-year is a study characteristic, which should be prespecified in the study protocol with a certain clinical justification. This time point should not be changed for the final primary analysis. Exploratory analysis may be conducted with various time windows.