Adaptive Landscape Flattening Accelerates Sampling of Alchemical Space in Multisite λ Dynamics

Abstract

Multisite λ dynamics (MSλD) is a powerful emerging method in free energy calculation that allows prediction of relative free energies for a large set of compounds from very few simulations. Calculating free energy differences between substituents that constitute large volume or flexibility jumps in chemical space is difficult for free energy methods in general, and for MSλD in particular, due to large free energy barriers in alchemical space. This study demonstrates that a simple biasing potential can flatten these barriers and introduces an algorithm that determines system specific biasing potential coefficients. Two sources of error, deep traps at the endpoints and solvent disruption by hard-core potentials, are identified. Both scale with the size of the perturbed substituent and are removed by sharp biasing potentials and a new soft-core implementation, respectively. MSλD with landscape flattening is demonstrated on two sets of molecules: derivatives of the heat shock protein 90 inhibitor geldanamycin and derivatives of benzoquinone. In the benzoquinone system, landscape flattening leads to two orders of magnitude improvement in transition rates between substituents and robust solvation free energies. Landscape flattening opens up new applications for MSλD by enabling larger chemical perturbations to be sampled with improved precision and accuracy.

Graphical abstract

Introduction

Free energy methods, including free energy perturbation (FEP),^1,2 thermodynamic integration (TI),³ enveloping distribution sampling,^4,5 lambda dynamics,^6–8 and others,^9–11 have become an important class of techniques for obtaining thermodynamic predictions from molecular dynamics simulations. While frequently utilized in computer aided drug design,^12–14 such techniques can also be applied to a wide variety of problems including pK_a predictions,^15,16 peptide binding,^17,18 and solvation free energies¹⁹ (Figure 1). Within most free energy methods, λ is a reaction coordinate that tunes the potential between two systems of interest. FEP and TI rely on several simulations run at closely spaced fixed λ values, while λ dynamics treats λ as a dynamic variable within a single simulation. In addition, λ dynamics can be performed between more than two systems of interest by introducing additional λ coordinates.⁶ For these two reasons, λ dynamics requires far fewer simulations than conventional methods like FEP and TI.

Figure 1.

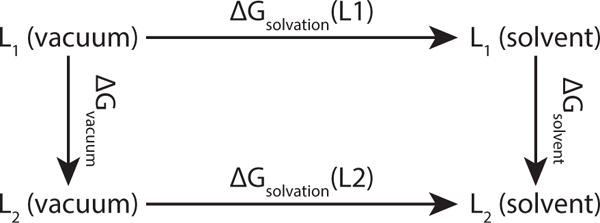
The relative solvation free energy ΔΔG_solvation (L1 → L2) between two ligands L1 and L2 is the difference between the horizontal (physical) processes, ΔG_solvation (L2) − ΔG_solvation (L1). These two free energies are typically difficult to calculate, but their difference is equal to the difference between the two vertical (alchemical) processes, ΔG_solvation − ΔG_vacuum, which can each be readily calculated with free energy methods.

Several recent improvements to λ dynamics have broadened its scope and increased its efficiency. First, λ dynamics was generalized to allow chemical perturbations at multiple sites.²⁰ In that work, multisite λ dynamics (MSλD) was shown to yield precision similar to FEP with about 1/50th of the computational expense. Second, an implicit constraint technique was developed, which simplified constraining λ between the physically relevant endpoints of 0 and 1 and also biased sampling towards those endpoints.²¹ Finally, in a follow-up study, solvation free energy simulations were attempted for 2,5-benzoquinone derivatives with large perturbations at the 2,5 positions. Sampling the large perturbations was facilitated by the enhancement of biasing potential replica exchange (BP-REX) and the concession of lowering the bias of the implicit constraints toward the endpoints.²² Even with these changes, methyl to phenyl perturbations were difficult, and larger volume changes were not sampled adequately. Solvation simulations also demonstrated that grouping substituents by volume improved sampling, so three sets of geldanamycin derivatives with small, medium, and large substituents were simulated bound to heat shock protein 90. Appropriate grouping in chemical space can affect convergence, and has been addressed in FEP and TI through the use of methods like the lead optimization mapper (LOMAP).²³

In this work we revisit the geldanamycin and benzoquinone systems to show that the lack of sampling is due primarily to large alchemical barriers that can be flattened with biasing potentials to enhance transitions between the physically meaningful endpoints. Previously, the bias of the implicit constraints towards the endpoints was weakened to avoid becoming trapped in endpoint wells, but this could give rise to substantial error, since the relative free energy is the difference between endpoints. Landscape flattening improves sampling to such an extent that previous concessions in the implicit constraints are no longer necessary, removing this source of error. Additionally, while in theory hard-core potentials lead to slow convergence, results show that in practice the use of hard-core potentials leads to incorrect relative solvation free energies due to common MSλD approximations. These errors are corrected through the use of soft-core potentials.^24,25 The use of landscape flattening and soft-core interactions allow MSλD to be applied to larger and more complex perturbations with improved precision and accuracy.

Methods

Multisite λ Dynamics

In λ dynamics, λ is a dynamic variable that switches the potential energy function between the potential for one ligand at λ = 0 and another ligand at λ =1. To generalize to MSλD, λ is replaced by the set of dynamic variables {λ_si} that represent the position of the ligand in alchemical space, where s is the index of an attachment site on a core ligand, and i is the index of one of several substituents that may be attached at that site. In MSλD, the potential energy of the system is

$$V=V(x_0,x_0)+{\displaystyle \sum _{s=1}^M{\displaystyle \sum _{i=1}^{N_s}{\lambda }_{si}(V(x_0,x_{si})+V(x_{si},x_{si}))}}+{\displaystyle \sum _{s=1}^M{\displaystyle \sum _{i=1}^{N_s}{\displaystyle \sum _{t=s+1}^M{\displaystyle \sum _{j=1}^{N_t}{\lambda }_{si}{\lambda }_{tj}V(x_{si},x_{tj})+V_{\text{Bias}}\left(\right\{\lambda \left\}\right)}}}},$$ (1)

where x₀ is the set of positions of the particles present in all systems, including the solvent environment, x_si is the set of positions of the particles at site s in substituent i, M is the total number of sites, N_s is the total number of substituents at site s, and V_Bias is a biasing potential on the set of λ coordinates that is used to enhance sampling. V(x, y) is the interaction potential between two groups of atoms x and y, thus V (x₀, x₀) is the interaction of the environment atoms among themselves, V (x₀, x_si) + V (x_si, x_si) is the interaction of substituent i at site s with the environment and with itself, and V (x_si, x_tj) is the interaction potential between substituents i and j at different sites. As is typical in MSλD calculations, bonds, angles, dihedrals, and impropers are not scaled by λ. This ensures the geometry and basic connectivity of a substituent are maintained even when it is in the non-interacting λ = 0 state, which allows efficient reverse transitions. These terms may be kept unscaled without causing artifacts because they cancel with analogous terms in the other thermodynamic half-cycle.

Physically meaningful endpoints are states in which λ_si = 1 for one substituent i at each site s, and all remaining λ_sj = 0 for j ≠ i. Under these conditions, the potential energy in eq 1 reduces to the potential energy for a single ligand and its environment. The constraints

$$0\le {\lambda }_{si}\le 1$$ (2)

$${\displaystyle \sum _{i=1}^{N_s}{\lambda }_{si}=1}$$ (3)

ensure that only one ligand, or one substituent at each site, interacts with the rest of the system at each of the physically relevant endpoints. This set of constraint conditions can be maintained by the implicit constraints

$${\lambda }_{si}=\frac{\exp (c\sin {\theta }_{si})}{{\displaystyle {\sum }_{j=1}^{N_s}\exp (c\sin {\theta }_{sj})}}$$ (4)

previously introduced for use with MSλD.²¹ With these implicit constraints, the dynamic variables θ_si, rather than λ_si, evolve with fictitious masses under the forces due to the potential. The value c = 5.5 was found to be optimal, as lower c values sample the endpoints less and higher c values lead to numerical instability.²¹

The free energy difference between two ligands may then be calculated as

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\left\{{\lambda }_{si}\right\}\to \left\{{\lambda }_{sj}\right\}}\approx -k_{B}T\ln \frac{P(\{{\lambda }_{sj}\}>{\lambda }_c)}{P(\{{\lambda }_{si}\}>{\lambda }_c)}-(V_{\text{Bias}}(\{{\lambda }_{sj}\}=1)-V_{\text{Bias}}(\{{\lambda }_{si}\}=1))$$ (5)

where P ({λ_si} > λ_c) is the probability within the simulation of finding λ_si > λ_c for all M substituents associated with a particular ligand. As λ_c approaches 1, this equation becomes exact. In practice a cutoff of λ_c = 0.8 is typically used to bin states, though this work demonstrates a more stringent cutoff of λ_c = 0.99 reduces error.

Form of the Biasing Potentials in MSλD

In order to accurately determine the relative free energy between two end states, it is necessary, though not always sufficient, to obtain many transitions between the endpoints. Fluctuations in alchemical λ space cannot become statistically independent until barrier crossing occurs, though slower dynamics in the environment may further limit independence. Thus the number of transitions provides a lower bound on the precision of free energy estimates. Transitions can either be limited by high barriers or by low diffusion in the transition region.²⁶ In MSλD, transitions are limited primarily by high barriers, and lowering barriers with biasing potentials substantially improves sampling.

The implicit constraints in eq 4 bias sampling towards the physically meaningful endpoints because large volumes of θ space map to near the endpoints and relatively small volumes of θ space map to alchemical intermediates. This effect grows stronger with increasing c and weaker with increasing number of substituents, N_s. Consequently, the implicit constraints give the endpoints higher entropy and lower free energy in λ space without producing barriers in θ space. The bias of the implicit constraints towards the endpoints is desirable and focuses sampling on the states of interest, but free energy barriers in excess of this bias will inhibit sampling.

The intrinsic entropy of the implicit constraints may be estimated by Monte Carlo sampling the implicit constraints according to the following procedure. Several million random θ values are generated from a uniform distribution, λ values are calculated using eq 4 and sorted into 100 bins according to the same procedure described for estimating free energies in the SI. The intrinsic entropy is then k_B ln p, where p is the probability of occupying a particular λ bin. To prevent the flattening algorithm from flattening the bias of the implicit constraints along with the rest of the barrier, the free energy due to the intrinsic entropy of the implicit constraints is subtracted from the total free energy, and biasing potentials are then used to flatten the remaining free energy.

Previously, two biasing potentials were used: a fixed bias V_Fixed and a variable bias V_Variable.

$$V_{\text{Bias}}=V_{\text{Fixed}}+V_{\text{Variable}}$$ (6)

$$V_{\text{Fixed}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}-F_{si}{\lambda }_{si}}}$$ (7)

$$V_{\text{Variable}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}\{\begin{array}{ll}k{({\lambda }_{si}-0.8)}^2\hfill & {\lambda }_{si}<0.8\hfill \\ 0\hfill & \lambda \ge 0.8\hfill \end{array}}}$$ (8)

The fixed bias ensures that with proper choice of the F_si parameters the endpoints have similar free energies and can be sampled within the same simulation.⁷ This biasing potential alters the free energy of the physically relevant endpoints, so it must be subtracted out when calculating free energies with eq 5. The variable bias has been used as a rough way to tune barriers.²⁰ The cutoff at 0.8 was intended to ensure that the populations near the endpoint were not perturbed, but fails in this regard because the λ’s are linked by eq 3. Furthermore, if different k are used for each substituent si, then this alters the biasing energy of the state λ_si = 1 by −0.64k_si beyond the fixed bias.

This work presents a new set of biasing potentials that are more easily tuned. The fixed bias

$$V_{\text{Fixed}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}{\varphi }_{si}{\lambda }_{si}}},$$ (9)

which is a linear biasing potential, is still absolutely essential and is retained unchanged. The parameters ϕ_si, or equivalently −F_si, are adjusted to ensure the endpoints have similar free energies and can be sampled concurrently. The remaining biasing potentials are chosen to be zero on the endpoints so they only effect nonphysical intermediates.

Early λ dynamics simulations showed a roughly parabolic or quadratic barrier.⁷ Quadratic barriers can be flattened with a potential of the form

$$V_{\text{Quad}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}{\displaystyle \sum _{j>i}^{N_s}{\psi }_{si,sj}{\lambda }_{si}{\lambda }_{sj}}}},$$ (10)

where ψ_si,sj/4 is the amount the biasing potential changes the height of the quadratic barrier between si and sj. This potential has N_s(N_s − 1)/2 independent parameters, allowing each barrier to be tuned independently, to maximize all-to-all transitions. A special case of this potential with fewer parameters is given by

$$V_{\text{Diag Quad}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}{\psi }_{si}({\lambda }_{si}{ }^2-{\lambda }_{si})}},$$ (11)

where eq 3 can be used to show ψ_si,sj = − (ψ_si + ψ_sj) converts the coefficients of eq 11 to the coefficients in eq 10. Eq 11 is closely related to the previously introduced variable bias (eq 8), but with the endpoint differences removed and no cutoff. While eq 10 is used, we find the barriers are within about 1 kcal/mol of the barriers given by the simpler biasing potential of eq 11.

The barriers are more or less quadratic between λ values of 0.1 and 0.9, however, deep free energy wells or traps exist at the endpoints. The free energy increases sharply as λ increases from zero because energy is required to disrupt the solvent and make a solvent cavity for the substituent to occupy. Consequently, larger substituents have deeper wells at λ = 0. Similar traps exist at λ =1 because other competing ligands will be at λ = 0. It can be shown for a simple test system of a methyl converting to a methoxy that the free energy is steep but approximately linear, and quickly saturates with increasing λ (SI Figure S3). A biasing potential which fits this form is given by

$$V_{\text{End}}={\displaystyle \sum _s^M{\displaystyle \sum _i^{N_s}{\displaystyle \sum _{j\ne i}^{N_s}{\omega }_{si,sj}{\lambda }_{si}{\lambda }_{sj}}}/(\alpha +{\lambda }_{si})},$$ (12)

where ω_si,sj is the amount of energy required to make a small amount of substituent si when substituent sj is dominant, and α is the value of λ at which the trap is half of its depth at the endpoint. α = 0.017 was found to give good fits to the free energy for a broad range of substituents in both vacuum and solvent simulations, so these traps are narrow in λ space. The traps can also be several kcal/mol deep for large substituents; for example, the geldanamycin substituents (Figure 2), have depths around 5 kcal/mol, and the largest benzoquinone substituent (Figure 3) has a depth of 12 kcal/mol. While the depths ω_si,sj· vary widely, the widths α are fairly consistent when using hard-core interactions, so the value α = 0.017 was used without further optimization. With the use of soft-core interactions, the shape of the endpoint traps changes, so future work will be needed to fully flatten the endpoint traps and optimize transition rates with soft cores.

Figure 2.

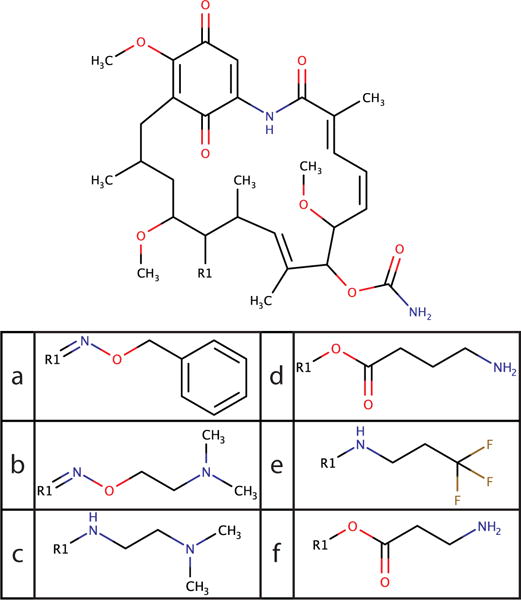
Geldanamycin and the set of large substituents that were previously tested.²²

Figure 3.

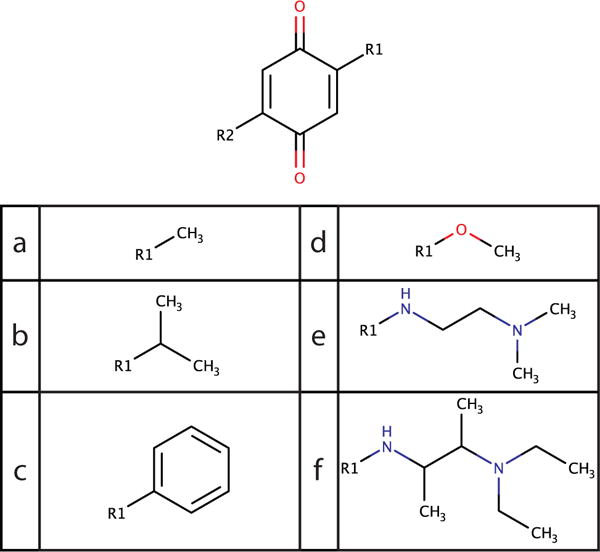
Symmetric benzoquinone derivatives. Several substituents representing a wide variety of sizes were chosen from a previously studied list of ten.²²

Since the endpoint traps are so narrow, when an implicit constraint parameter of c =2.5 is used the trap is not fully accessible. The minimum λ value for c =2.5 is 0.007, and has very low entropy. Thus the previous concession c =2.5 improved sampling by preventing λ from becoming trapped in the endpoint states. However, if endpoint trap depths differ between the vacuum, solvent, or protein binding branches in the thermodynamic cycle, use of the concession c =2.5 introduces errors in computed free energies. By flattening endpoint traps as introduced here, endpoints can be more fully sampled with the optimal c = 5.5 without risk of trapping λ or introducing systematic errors.

Adding Soft-Core Potentials to MSλD

We demonstrate that the use of hard-core potentials for non-bonded interactions in our simulations disrupts the solvent and gives erroneous free energies. Hard-core potentials contain a singularity at an interaction distance of r = 0. As λ approaches 0 at the endpoints, atoms may approach each other more closely, and the potential changes sharply on very short length scales, which may lead to numerical instability. In MSλD, the implicit constraints are bounded from above and below not by 0 and 1, but by (1 + (N_s − 1) exp(±2c))⁻¹, which approach 0 and 1 as c increases. Consequently, MSλD simulations avoid numerical instability due to hard-core interactions because the implicit constraints have a very small but non-zero minimum,²⁰ and the solvent excluded radius is still rather large due to the one twelfth power dependence on λ. However, since this excluded volume radius is non-negligible (still about half the full value for c = 5.5), atoms never completely disappear as λ approaches 0, and this can lead to large solvent inaccessible cavities.

If these solvent cavities are small or inside other atoms, as has mostly been the case for the small substituents sampled in the past,^6,7,20 the errors introduced are small, but if the cavities are larger, as they are for many of the substituents sampled in this work, substantial errors may arise due to approximations made in MSλD. The assumption underlying the calculation of free energies with eq 5 is that the free energy of the λ =1 state is approximately equal to the free energy of the λ_c < λ < (1 + (N_s − 1) exp(−2c))⁻¹ state, up to an additive constant due to bin width that cancels in relative free energies. This assumption is clearly violated if the solvent configurations with which a substituent would interact have been disrupted by solvent cavities. In theory, a more sophisticated analysis involving an FEP calculation between the two λ states could bridge this gap. However, such a calculation would still fail in practice because many of the important states remain inaccessible since their free energies are too high to be adequately sampled at the maximum λ value, and if they were sampled they could lead to further numerical instabilities in the solutions to the equations of motion.

Soft-core interactions are a natural solution to the problem. They remove the singularity from the interaction function so that interactions may be effectively scaled to zero by λ near λ = 0. Consequently, solvent cavities disappear near the endpoints and the assumptions underlying eq 5 are restored. A variety of soft-core potentials exist: some remap interaction distances near r = 0 to some finite value,^24,25 while others extend the potential in a non-singular way inside some radius.²⁷ Soft-core parameters typically vary with λ in such a way that at λ = 1, the hard-core potential is recovered.

The current implementation of soft-core potentials in the CHARMM molecular dynamics package^28,29 has been used effectively in TI calculations and is given in ref 24. In this formulation of soft cores by Zacharias et al., the distance r between two particles is mapped to a distance r′, where

$$r\prime ={\left(r^2+r_0{ }^2(1-\lambda )\right)}^{1/2},$$ (13)

and r′ is substituted into the λ-scaled Van der Waals and Coulomb potentials instead of r. Unfortunately, this soft-core implementation is not available with MSλD in CHARMM and has two undesirable features. First, since r′ ≠ r at the potential energy minimum, the position of the minimum is moved even for λ near one and only approaches the correct position linearly with 1 − λ (SI Figure S4). Second, since distances all the way up to the force cutoff are mapped to r′ ≠ r, the forces become very complex when using shifting and switching functions to mitigate cutoff effects. Consequently, a new soft-core scheme was implemented inside the CHARMM molecular dynamics package for the purpose of this study that mimicked the old soft-core potential without these undesirable features.

In the new soft-core implementation, only inter-particle distances r inside a λ dependent cutoff of r_λ are remapped:

$$r_{\lambda }=2r_0(1-\lambda ),$$ (14)

where λ is the scaling factor for the pairwise interaction (see eq 1) and r₀ = 2 Å. λ = λ_si if atoms in substituent si are interacting among themselves or with the environment, λ = 0 if atoms are in different substituents i and j at the same site s, and λ = λ_siλ_tj if atoms are at different sites s and t. Then the real distance r is mapped to

$$r^{\prime }=\left\{\begin{array}{cc}{r}_{\lambda }\left(\frac{1}{2}+{\left(\frac{r}{r_{\lambda }}\right)}^3-\frac{1}{2}{\left(\frac{r}{r_{\lambda }}\right)}^4\right)& r<r_{\lambda }\\ r& r\ge r_{\lambda }\end{array}\right.$$ (15)

and this r′ is substituted into the potential (eq 1) instead of the real distance between particles r. Thus the potential is undisturbed for r> r_λ which solves both difficulties in the previous implementation. Appropriate derivatives may be taken to obtain the spatial and alchemical forces. For a comparison between eq 13 & 15, see SI Figure S4.

Simulation Details and Learning the Landscape

Simulations were run in the CHARMM molecular dynamics package, developmental version 41a2.^28,29 Simulations used the DOMDEC package³⁰ within CHARMM on CPU for vacuum simulations and GPU for solvent simulations. Timesteps of 1.25 fs were used to ensure simulation stability. (Previously, timesteps of 1.5 fs were used with c = 5.5,²⁰ and timesteps of 2 fs were used with c =2.5.²²) Hydrogen bond lengths were constrained using the SHAKE algorithm.³¹ Van der Waals interactions were switched off between 10 Å and 12 Å, and electrostatic interactions were truncated with force switching over the same interval. The implicit constraint θ coordinates were given a pseudomass of 5 amu·nm² and a Langevin drag coefficient of 5 ps⁻¹. Ligands were prepared using MarvinSketch 16.6.6.0, 2016, from ChemAxon (http://www.chemaxon.com), and forcefield parameters were obtained using MATCH.³² Systems were solvated in boxes with at least 10 Å on each side (20 Å periodic image distance) using TIP3P water.³³ Simulations were performed using an NVT ensemble unless otherwise noted in a Langevin bath with temperature T = 298 K.

A three phase procedure is used to learn the parameters in eqs 9, 10, and 12 that flatten the free energy landscape. First, a 100 ps simulation is performed with a very strong biasing potential (all ψ_si set to 500 kcal/mol or 1000 kcal/mol in eq 11). The slope of the free energy with respect to λ_si can then be computed from the average 〈λ_si〉 as 2ψ_si(1/N_s − 〈λ_si〉). This slope gives an initial estimate for the fixed bias, which is generally accurate to within 10 kcal/mol.

In the second phase this strong biasing potential is removed, and all ψ_si,sj and ω_si,sj are set to 0. We note that more reasonable initial guesses would likely allow biasing parameters to converge in fewer iterations. Up to 50 iterative 100 ps simulations are performed, gradually refining estimates of ϕ_si, ψ_si,sj, and ω_si,sj parameters after each simulation. Results from the previous 10 simulations are combined together using WHAM³⁴ to obtain an estimate of the free energy landscape that is more robust than a single simulation, which can suffer from trapping or a lack of sampling. Older simulations are ignored because they tend to be out of equilibrium and corrupt the free energy estimation. The free energy landscape is used to update estimates for ϕ_si, ψ_si,sj, and ω_si,sj. The exact algorithm for estimating parameters is outlined in the SI. Parameters are not allowed to change very rapidly because very little alchemical space is sampled at first and overshooting degrades sampling. Changes are limited to 1 kcal/mol in ϕ_si and ω_si,sj·and to 4 kcal/mol in ψ_si,sj. In the third phase the same fitting procedure is used, but longer simulations of 1 ns are run. Results from the last 6 simulations are combined with WHAM to estimate the free energy and update ϕ_si, ψ_si,sj, and ω_si,sj. Up to 12 simulations of this length are run. In all, 8 to 17 ns of sampling were used to determine biasing coefficients to flatten the energy landscape. Future simulations should need less time because a method to obtain reasonable initial guesses for the flattening parameters is given in eqs 17 and 18.

Finally, four production runs of 10 ns are run with the optimized biasing potential. Free energies are obtained from populations of λ greater than λ_c = 0.99 using eq 5. This high cutoff was used to minimize the effect of residual variation in the free energy near the endpoints. Relative free energies are obtained by Boltzmann averaging over the n = 4 simulations

$$\mathrm{\Delta }G=-k_{\mathrm{B}}T\ln \left(\frac{1}{n}{\displaystyle \sum _{i=1}^n\exp (-\mathrm{\Delta }{G}_i/k_{\mathrm{B}}T)}\right)$$ (16)

which equates to averaging populations before applying eq 5. Uncertainties were estimated using bootstrap analysis: the standard deviation in fifty free energy estimates was taken to be the uncertainty. Bootstrap analysis requires sampling from a set of independent measurements, so free energies were calculated using the first and second half of each simulation to give n = 8 independent measurements. (Using whole simulations with n = 4 is more susceptible to noise, and using shorter segments approaches the correlation time for some systems, which violates statistical independence.) Each of the fifty free energy estimates was made by choosing eight ΔG_i values randomly with replacement from the eight independent half-simulations and Boltzmann averaging the n = 8 values together.

Results and Discussion

To test the effects of landscape flattening on transition rates and MSλD convergence, relative solvation free energy simulations (Figure 1) were run on two previously characterized systems: geldanamycin and benzoquinone.²² While the primary goal was to improve sampling in order to accelerate convergence and broaden the range of tractable problems, consistency checks that varied the implicit constraint c value and the number of substituents revealed two previous sources of error that this study corrects. The fidelity of results to the correct free energy for the forcefield or to experimental results are not considered and will form the basis of a future study.

Geldanamycin

A previous MSλD study observed that grouping substituents of similar size together optimized transition rates and expedited convergence.²² Consequently, that study explored three sets of geldanamycin substituents: small, medium, and large, with the large substituents proving most challenging. In the present work, the large substituent geldanamycin derivatives (Figure 2) were sampled to test the efficacy of landscape flattening. Only the solvent side of the thermodynamic cycle (ΔG_solvent and not ΔG_vacuum in Figure 1) was run in order to focus on convergence. Four simulations of 10 ns each were run with implicit constraints using c = 5.5 (eq 4). The total transition rate was 188.5/ns (Table 1), which compares well with the 401.5/ns observed previously without landscape flattening, using c =2.5 and BP-REX. While the transition rate is somewhat lower in the present study, this transition rate was obtained without the benefit of replica exchange, and with the use of c = 5.5 rather than c =2.5, which enabled the system to more fully explore the circa 5 kcal/mol wells at the endpoints.

Table 1.

Geldanamycin transition rates

substituent	transitions/ns
a	62.0
b	22.1
c	21.3
d	23.9
e	28.9
f	30.3

The flattened landscape was also sampled using constant pressure NPT simulations and BP-REX with five replicas. Free energies and uncertainties were computed (Table 2). It is noteworthy that the precision with replica exchange (rms uncertainty of 0.13 kcal/mol) was substantially better than without it (rms uncertainty of 0.21 kcal/mol), however this can be explained in terms of sampling. Since the BP-REX results contained five times more sampling, an improvement of a factor of $\sqrt{5}\approx 2.2$ in the precision is expected, which is not too far from the factor of 1.6 that is observed.

Table 2.

Geldanamycin solvent simulation free energies (kcal/mol)

substituent	10 ns NVT	10 ns NPT	10 ns BP-REX
a	0.000 ± 0.13	0.00 ± 0.18	0.00 ± 0.08
b	−4.45 ± 0.30	−4.32 ± 0.31	−4.25 ± 0.06
c	−3.25 ± 0.19	−4.12 ± 0.13	−3.60 ± 0.09
d	−33.48 ± 0.18	−33.95 ± 0.17	−33.84 ± 0.10
e	−24.07 ± 0.22	−24.12 ± 0.19	−23.93 ± 0.11
f	−59.14 ± 0.18	−58.91 ± 0.11	−58.99 ± 0.24

Benzoquinone Derivatives

As a next step, a set of substituents with widely varying sizes were used to test the limits of landscape flattening. The 2,5-benzoquinone derivatives provided an ideal test set (Figure 3). Previously these derivatives were only be sampled in pairs,²² and some of the largest perturbations had very low transition rates, but in this study, landscape flattening enabled all of them to be sampled within the same simulation. In addition, since this system is symmetric, simulation convergence can be assessed not only with the variance of repeated simulations, but also by checking that ΔΔG is the same when substituents at two sites are switched. For benzoquinone derivatives, both the vacuum and solvent simulations were run to obtain relative solvation free energies (Figure 1).

Initially, simulations were performed with only methyl (a) and phenyl (c) at the two sites. Four simulations of 10 ns each were used to assess precision. A transition rate of 160 transitions/ns was obtained with landscape flattening and c = 5.5, a slight improvement over the 134.4 transitions/ns previously observed with c = 2.5 and BP-REX.²² (The vacuum transition rate was 270 transitions/ns.)

Simulations using lower c values are expected to be in error because the narrow endpoint wells cannot be fully explored. In particular, the well depth for phenyl differs by 4 kcal/mol between vacuum and solvent simulations (ω_c,a is 6 kcal/mol in solvent and 2 kcal/mol in vacuum), and since these wells are not fully explored, calculations utilizing c =2.5 will not capture this difference. To assess the error induced by using c =2.5 rather than c = 5.5, the same simulations were performed with the endpoint biases (eq 12) set to zero and c =2.5. As expected, ΔΔG_aa→cc deviated from the c = 5.5 value by 1.2 kcal/mol with the stringent population cutoff of λ_c = 0.99, and by 3.0 kcal/mol when the previously accepted cutoff of λ_c = 0.80 was used (Table 3).

Table 3.

Relative solvation free energies (kcal/mol) of benzoquinone derivatives (a is methyl, c is phenyl) obtained with varying implicit constraints c and population cutoffs λ_c

		λc = 0.80		λc = 0.99
		R2-a	R2-c	R2-a	R2-c
c = 2.5	R1-a	0.00 ± 0.03	−0.76 ± 0.02	0.00 ± 0.06	−1.64 ± 0.04
	R1-c	−0.76 ± 0.03	−1.44 ± 0.01	−1.65 ± 0.05	−3.14 ± 0.02
c = 5.5	R1-a			0.00 ± 0.02	−2.20 ± 0.03
	R1-c			−2.20 ± 0.02	−4.37 ± 0.02

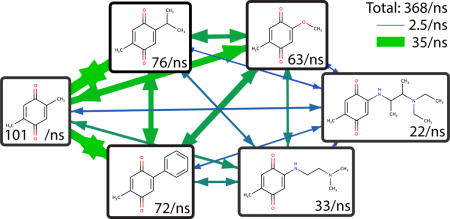
Next, simulations were performed with all six substituents at both sites. Such a simulation with a large variety of substituent volumes would have been intractable without landscape flattening. With c = 2.5, BP-REX, and just two substituents, previous simulations ranged from 242.7 total transitions/ns for a-b to 4.3 total transitions/ns for a-f.²² The total transition rate in the present study of 367.8/ns (Figure 4 and SI Table S1) is a marked improvement of up to two orders of magnitude, and samples a wider variety of substituents simultaneously. The solvation free energies are given in Table 4. The uncertainties are somewhat higher than with two substituents because there are 36 physical ligands to sample instead of 4. The largest deviation between identical symmetric molecules is 0.70 kcal/mol between ce and ec. For substituents a-d, the symmetric errors are all below 0.3 kcal/mol.

Figure 4.

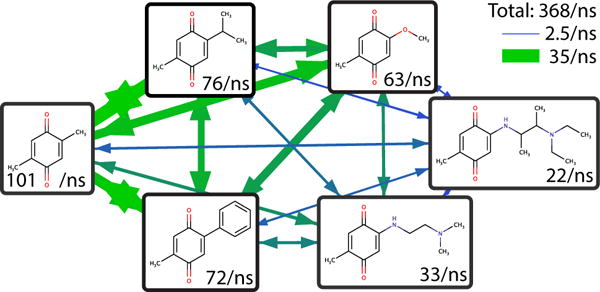
Average transition rates (per ns) of benzoquinone derivatives in solution with flattened free energy landscape.

Table 4.

Hard-Core Benzoquinone Free Energies (kcal/mol)

	R2-a	R2-b	R2-c	R2-d	R2-e	R2-f
R1-a	0.00 ± 0.09	−1.04 ± 0.09a	−4.25 ± 0.10	−6.02 ± 0.12	−6.80 ± 0.13	−4.72 ± 0.13
R1-b	−0.90 ± 0.09a	−1.78 ± 0.11	−5.13 ± 0.12	−7.04 ± 0.16	−7.97 ± 0.15	−5.82 ± 0.16
R1-c	−4.03 ± 0.12	−5.12 ± 0.09	−8.57 ± 0.10b	−10.46 ± 0.14	−11.09 ± 0.20	−9.14 ± 0.17
R1-d	−5.94 ± 0.17	−7.11 ± 0.21	−10.73 ± 0.12	−15.40 ± 0.14	−15.25 ± 0.21	−12.90 ± 0.17
R1-e	−6.46 ± 0.25	−7.84 ± 0.25	−10.45 ± 0.20	−14.67 ± 0.17	−14.70 ± 0.21	−13.02 ± 0.19
R1-f	−5.13 ± 0.25	−5.48 ± 0.29	−9.04 ± 0.44	−13.60 ± 0.51	−13.10 ± 0.83	−11.19 ± 0.31

^aThe difference between symmetric derivatives, ΔG_xy→yx, should be zero to within statistical precision. For example, ΔG_solvation (ab → ba) = (−0.90 ± 0.09) − (−1.04 ± 0.09) = 0.14 ± 0.13. The root mean square difference between symmetric derivatives is 0.35 and the root mean square precision is 0.36.

^bThe ΔG_solvation (aa → cc) value −8.57±0.13 is inconsistent with the two substituent value of −4.37±0.03 from Table 3. This error is corrected in Table 6 through the use of soft-core interactions. (The uncertainties of the (aa) state, 0.09, and the (cc) state, 0.10, are assumed to be uncorrelated, and are thus combined using the root sum of squares to give an uncertainty of 0.13 for ΔG_aa→cc.)

It is worth noting that ΔΔG_aa→ccc is −8.57 kcal/mol in the simulation with 6 substituents while it was −4.37 kcal/mol in the simulation with just a and c. This 4.2 kcal/mol discrepancy signals another source of error. The most likely cause for this discrepancy is in the use of hard-core interactions. While both simulations utilize hard-core interactions, there are more substituents and larger substituents in the six substituent simulation, so the solvent is disrupted to a greater extent in the six substituent simulation.

Hard Cores Cause Solvent Disruption

In order to test the degree of solvent disruption by hard-core interactions, a simple thermodynamic cycle was devised (Figure 5). Benzoquinone site 2 on carbon 5 was given a methyl, while site 1 on carbon 2 was changed from methyl (a) to isopropyl (b) to phenyl (c), and back to methyl (a). In each of the three transitions, only the two substituents involved were included. Consequently, the solvent is disrupted differently at the endpoints when λ ≈ 0 in each simulation. For example, the solvent environment of (ba) (2-isopropyl 5-methyl benzoquinone) is relatively undisturbed in the presence of low levels of (aa), but is more disrupted by the bulky phenyl group in the presence of low levels of (ca).

Figure 5.

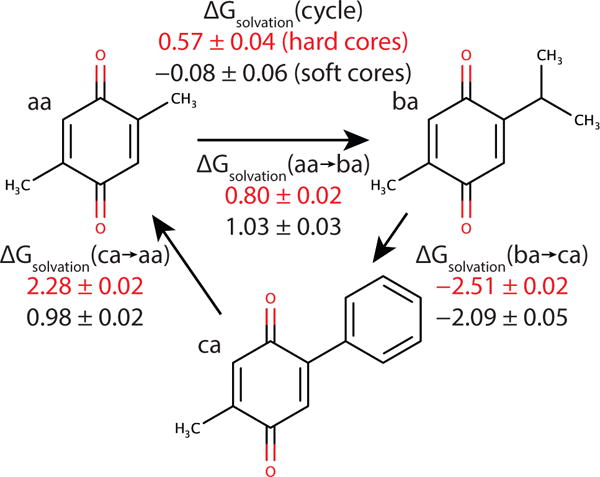
A closed thermodynamic cycle based on the benzoquinone substituents in Figure 3 designed to test solvent disruption by hard-core interactions. The free energy for the cycle sums to zero within statistical uncertainty for the soft-core cycle, but not for the hard-core cycle.

The free energy of this thermodynamic cycle should be zero since it begins and ends with the same state, (aa), but when computed with hard cores, it is not. It deviates from the expected value by 0.57 kcal/mol (Figure 5). (This is smaller than the 4.2 kcal/mol aa → cc discrepancy in the two and six substituent benzoquinone systems because in those systems, two sites are involved rather than one, and in the six substituent case, more and larger substituents are present than in this simple system.)

To make sure this deviation was in fact due to solvent disruption by hard-core interactions, a soft-core interaction potential (eq 15) was implemented in the DOMDEC package³⁰ of CHARMM.^28,29 After re-flattening the landscapes, the change in free energy of the thermodynamic cycle is zero to within statistical precision (Figure 5), demonstrating that the error in the thermodynamic cycle can indeed be attributed to solvent disruption.

Calculations employing soft-core potentials are more consistent with each other as shown by thermodynamic cycle closure, and this, together with the theoretical arguments noted above indicate soft-core calculations almost certainly provide more accurate results. Even in this small, simple, relatively clean system, hard cores at the endpoints give errors of up to 1.3 kcal/mol for ΔΔG_solvation(ca→ aa).

Since soft cores gave improved results on the simple benzoquinone cycle, the two site systems with two and six substituents were re-flattened and rerun with soft cores. Soft-core free energy estimates are shown in Tables 5 and 6. (The infinite uncertainties for five compounds arise because those compounds were not sampled in one or more simulations, but the estimates of ΔG_solvation for those molecules are still in reasonable agreement with their symmetric partners.) With soft-core interactions, the two and six substituent results are consistent (Tables 5 and 6), while with hard cores they were not (Tables 3 and 4). For example, two and six substituent differences in ΔΔG_solvation(αα → cc) were 4.20 ± 0.13 kcal/mol for hard cores and 0.15 ± 0.56 kcal/mol for soft cores.

Table 5.

Soft-Core Benzoquinone Free Energies with Two Substituents (kcal/mol)

	R2-a	R2-c
R1-a	0.00 ± 0.03	−1.07 ± 0.04
R1-c	−1.02 ± 0.04	−1.99 ± 0.04

Table 6.

Soft-Core Benzoquinone Free Energies (kcal/mol)

	R2-a	R2-b	R2-c	R2-d	R2-e	R2-f
R1-a	0.00 ± 0.51	1.25 ± 0.35a	−1.41 ± 0.28	−6.65 ± 0.38	−3.99 ± 0.20	0.65 ± 0.25
R1-b	0.68 ± 0.37a	1.70 ± 0.28	−0.07 ± 0.22	−6.07 ± ∞c	−3.22 ± 0.33	1.39 ± 0.22
R1-c	−1.26 ± 0.29	0.56 ± 0.33	−2.14 ± 0.23b	−8.20 ± 0.31	−4.94 ± 0.22	−0.30 ± 0.19
R1-d	−4.49 ± ∞c	−6.11 ± 0.24	−7.72 ± 0.63	−15.94 ± 0.22	−12.30 ± 0.25	−8.28 ± 0.29
R1-e	−2.58 ± ∞c	−2.09 ± 0.55	−4.73 ± 0.38	−11.39 ± 0.40	−8.04 ± 0.37	−3.98 ± 0.22
R1-f	1.57 ± ∞c	1.88 ± 1.24	0.09 ± ∞c	−8.93 ± 0.54	−5.13 ± 0.61	0.40 ± 0.37

^aThe difference between symmetric derivatives, ΔG_xy→yx, should be zero. ΔG_solvation(ab → ba) = (0.68 ± 0.37) − (1.25 ± 0.35) = −0.57 ± 0.51. Excluding da, ea, fa, and fc, the root mean square difference between symmetric derivatives is 0.71 and the root mean square precision is 0.65.

^bThe ΔG_solvation (aa → cc) value −2.14 ± 0.56 is consistent with the two substituent value of −1.99 ± 0.05 from Table 5, which was not the case with hard-core interactions.

^cNo estimate of precision could be obtained from bootstrap analysis for molecules that were not visited in all production simulations. These molecules are denoted with ±∞. The free energy estimates for these molecules are still within 0.04 to 2.16 kcal/mol of their symmetric derivatives.

Given that soft-core calculations are more accurate, comparison between Tables 4 and 6 reveals that hard cores introduce substantial errors in the full benzoquinone system relative to soft cores: dimethyl (aa) to diphenyl (cc) differs by 6 kcal/mol, and aa → ff differs by 12 kcal/mol. The soft-core results show that hard-core simulations underestimate the solvent affinity of smaller molecules, and the larger the difference in size, the larger the effect. This is because the solvent environment around smaller substituents is severely disrupted by the presence of several very bulky substituents.

It is noteworthy that while soft-core interactions likely give better accuracy, their precision is poorer. For example, uncertainty is about twice as large with soft cores as with hard cores in the two substituent system. Furthermore, in the six substituent system, deviations between symmetric derivatives (which should be zero) are larger with soft cores than with hard cores: e.g. ΔΔG_solvation(ab → ba) is 0.14 ± 0.13 kcal/mol with hard cores and −0.57 ± 0.51 kcal/mol with soft cores. This occurs because the soft-core potentials modify the free energy landscape and especially the endpoints. Eq 12 does not model the endpoint traps as well, so the landscape cannot be as fully flattened, there are fewer transitions, and the uncertainty goes up. The shape of the endpoint well depends rather strongly on the exact form of the soft-core potential so modification of eq 12 or the soft-core potential parameters may be required to optimize sampling and is the subject of ongoing investigation.

Landscape Parameters Depend on Substituent Volume

In this work, a method that found parameters to flatten the energy landscape in λ from many short simulations has been presented. However, reasonable initial estimates for c_si,sj and s_si,sj can further decrease the number of these initial simulations required to learn the landscape. The landscape parameters are strongly correlated with the volume of the substituents. The parameters in vacuum tend to be slightly below half of what they are in solvent, but vacuum simulations are much less expensive, so there is less need to make good initial guesses for the landscape flattening parameters. Therefore, the following analysis focuses on solvent simulation parameters.

The ψ_si,sj parameters in eq 10 can be fairly well approximated by using the simpler ψ_si parameters in eq 11. Using this smaller set of parameters led to a root mean square deviation of 2.6 kcal/mol from the full ψ_si,sj parameters learned by landscape flattening. (A 2.6 kcal/mol error in ψ_si,sj corresponds to a 0.65 kcal/mol error in the barrier). The ψ_si parameters in turn are strongly correlated with volume of the substituent si (Figure 6a). Volumes were obtained using the coordinate volume functionality in CHARMM.^28,29

Figure 6.

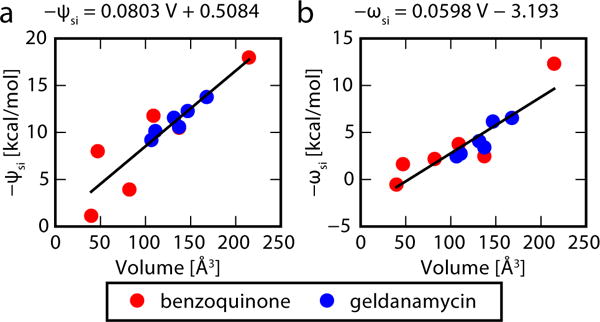
There is a strong correlation between the optimized parameters obtained in this study for solvent simulations and the volume of the substituents. (a) The ψ_si,sj parameters can be decomposed into the sum ψ_si,sj = −(ψ_si + ψ_sj), where ψ_si is strongly correlated with volume. (b) The ω_si,sj parameters are largely independent of sj, and are strongly correlated with the volume of si.

Likewise, the ω_si,sj parameters in eq 12 are largely independent of sj, and can be approximated as ω_si with a 0.6 kcal/mol root mean square deviation. The ω_si parameters are also strongly correlated with the volume of the substituent si (Figure 6b).

The full parameters can then be predicted to be

$$-{\psi }_{si,sj}=m_{\psi }(V_{si}+V_{sj})+2b_{\psi }$$ (17)

with m_ψ = 0.0803 kcal/mol/ų and b_ψ = 0.5084 kcal/mol and

$$-{\omega }_{si,sj}=m_{\omega }{V}_{si}+b_{\omega }$$ (18)

with m_ω = 0.0598 kcal/mol/ų and b_ω= −3.193 kcal/mol.

Discussion

In this work, landscape flattening has proven very effective in lowering barriers and increasing transition rates. This opens up many new possibilities in MSλD simulations. The improved convergence of MSλD calculations can be traded to look at more substituents simultaneously or to examine larger chemical perturbations.

Landscape flattening is most useful in the context of large, flexible substituents, because transition barriers are approximately proportional to substituent volume (Figure 6). Previously, MSλD calculations were limited to perturbations akin to methyl to phenyl in difficulty. The collection of benzoquinone substituents shown in Figure 3 contained substituents with transition rates which previously varied by two to three orders of magnitude.²² In the present work, substituent transition rates vary by about a factor of five, suggesting that even larger perturbations than those considered could potentially be explored, though additional techniques such as solute tempering^2,35 or orthogonal space random walk¹⁰ may be necessary to sample the internal degrees of freedom of large flexible substituents. MSλD has historically focused on modifying small functional groups.^6,7,20 While such calculations have many applications, the ability to look at larger perturbations with landscape flattening opens up new possibilities in fragment-based drug design^13,36 and in exploring the effects of protein mutation on drug binding.^37–39

With larger substituents come new pitfalls, two of which were noted and corrected. Both pitfalls were related to the endpoints. First, the larger the volume of the substituent, the deeper its endpoint trap. This occurs largely because there is an energetic and entropic cost to move water out of the way to make room for the repulsive portion of the Lennard-Jones potential before favorable dispersion and electrostatic interactions begin to have an effect. Without landscape flattening, these traps cannot be fully explored or the simulation will become trapped, yet fully sampling the endpoints is required for accurate results. Landscape flattening allows the simulation to fully sample the endpoints without becoming trapped.

The ability to sample the endpoints fully without becoming trapped is quite useful, as it allows one to return from using c = 2.5 to using c = 5.5 in the implicit constraints (eq 4). The value c = 5.5 was chosen as a compromise between lower c values, which improve simulation stability, and higher c values, which bias sampling towards the endpoints and give better statistics. In subsequent work with larger substituents, biasing λ towards the endpoints promoted trapping, which made biasing λ towards the endpoints a liability, so c =2.5 was a better choice. With landscape flattening, trapping is no longer a consideration and biasing λ towards the endpoints improves sampling, so c = 5.5 is a better choice. As MSλD systems become more complex due to increasing numbers of substituents or sites, the bias of the implicit constraints towards the endpoints becomes less effective, so increasing c beyond 5.5 may improve convergence. Each additional site lowers the fraction of time spent in the physical endpoint states, so increasing c can have a stronger effect on the endpoint sampling for systems with more sites. When increasing c, it may be necessary to lower the timestep or increase the pseudomass of the alchemical particles to maintain stability.

Second, the use of hard-core interactions leaves small solvent inaccessible cavities near the endpoints. For perturbations of one or maybe two heavy atoms, these cavities are few and typically inside other heavy atoms. Consequently, previous MSλD studies suffered very little from the use of hard cores because they focussed on small perturbations. For bigger substituents however, these cavities are quite numerous and seriously disrupt the solvent, leading to errors of up to 12 kcal/mol in the present study. For MSλD simulations with medium or large substituents, soft-core interactions are absolutely essential for accuracy.

In this study the use of landscape flattening improved sampling and precision and the use of soft-core interactions improved accuracy, correcting errors from hard-core calculations of up to 12 kcal/mol introduced by the approximations of eq 5. It is worth asking how well these methods work together, since both precision and accuracy are necessary in many contexts. As previously noted, soft-core interaction change the shape of the endpoint traps. As a result, the landscape is not fully flattened, and there are fewer transitions, which lowers precision. In the benzoquinone system, increases of roughly a factor of two or three were observed in the statistical uncertainty of the results with soft cores. Even with the lower precision, uncertainties were typically less than a kcal/mol, and were small enough to clearly show the improved consistency in the benzoquinone system with changing numbers of substituents. In the future we expect landscape flattening together with soft cores to give accurate results with better than 1 kcal/mol precision even on difficult systems like the large substituents in the benzoquinone system. Further improvements in the endpoint potential and the flattening algorithm may improve soft-core precision to be competitive with the hard-core results.

Conclusions

Free energy calculations are important to a broad range of chemical and biochemical problems, including drug design, peptide binding, pK_a calculations, and solvation free energy. Multi-site λ dynamics is a free energy technique with features that are well suited to address many problems of ligand and receptor optimization because it allows large perturbations, requires fewer simulations, and is highly scalable. In the past MSλD has been limited by high free energy barriers. In this work we presented a new technique to flatten the energy landscape in λ space, thus substantially increasing transitions and improving convergence. We discovered deep traps at the endpoints, and that recent implementations of MSλD were not fully exploring these physically relevant traps due to concessions in the implicit constraints. Flattening of the landscape removed the need for such concessions. With the improved sampling, we also found that the use of hard-core interactions was disrupting the solvent and causing serious errors in even very simple systems. The hard-core errors were removed through the use of a new style of soft-core interaction. These improvements open the way for more aggressive use of MSλD with substantially improved precision and accuracy.