Abstract
Studies of nervous system connectivity, in a wide variety of species and at different scales of resolution, have identified several highly conserved motifs of network organization. One such motif is a heterogeneous distribution of connectivity across neural elements, such that some elements act as highly connected and functionally important network hubs. These brain network hubs are also densely interconnected, forming a so-called rich club. Recent work in mouse has identified a distinctive transcriptional signature of neural hubs, characterized by tightly coupled expression of oxidative metabolism genes, with similar genes characterizing macroscale inter-modular hub regions of the human cortex. Here, we sought to determine whether hubs of the neuronal C. elegans connectome also show tightly coupled gene expression. Using open data on the chemical and electrical connectivity of 279 C. elegans neurons, and binary gene expression data for each neuron across 948 genes, we computed a correlated gene expression score for each pair of neurons, providing a measure of their gene expression similarity. We demonstrate that connections between hub neurons are the most similar in their gene expression while connections between nonhubs are the least similar. Genes with the greatest contribution to this effect are involved in glutamatergic and cholinergic signaling, and other communication processes. We further show that coupled expression between hub neurons cannot be explained by their neuronal subtype (i.e., sensory, motor, or interneuron), separation distance, chemically secreted neurotransmitter, birth time, pairwise lineage distance, or their topological module affiliation. Instead, this coupling is intrinsically linked to the identity of most hubs as command interneurons, a specific class of interneurons that regulates locomotion. Our results suggest that neural hubs may possess a distinctive transcriptional signature, preserved across scales and species, that is related to the involvement of hubs in regulating the higher-order behaviors of a given organism.
Author summary
Some elements of neural systems possess many more connections than others, marking them as network hubs. These hubs are often densely interconnected with each other, forming a so-called rich-club that is thought to support integrated function. Recent work in the mouse suggests that connected pairs of hubs show higher levels of transcriptional coupling than other pairs of brain regions. Here, we show that hub neurons of the nematode C. elegans also show tightly coupled gene expression and that this effect cannot be explained by the spatial proximity or anatomical location of hub neurons, their chemical composition, birth time, neuronal lineage or topological module affiliation. Instead, we find that elevated coexpression is driven by the identity of most hubs of the C. elegans connectome as command interneurons, a specific functional class of neurons that regulate locomotion. These findings suggest that coupled gene expression is a highly conserved genomic signature of neural hubs that may be related to the specific functional role that hubs play in broader network function.
Introduction
Neuronal connectivity provides the substrate for integrated brain function. Recent years have seen several systematic and large-scale attempts to generate comprehensive wiring diagrams, or connectomes, of nervous systems [1] in species as diverse as the Caenorhabditis elegans [2, 3], Drosophila melanogaster [4, 5], zebrafish [6, 7], mouse [8, 9], rat [10], cat [11], macaque [12, 13], and human [14, 15]. One of the most striking findings to emerge from analyses of these diverse data, acquired using different measurement techniques and at resolution scales ranging from nm to mm, is of a strong conservation of certain topological properties of network organization (reviewed in [1, 16–19], see also [20]). These properties include a modular organization, such that subsets of functionally related (and usually spatially adjacent) elements are densely interconnected with each other; a hierarchy of modules, such that modules contain nested sub-modules and so on over multiple scales [21, 22]; economical connectivity, such that wiring costs (typically measured in terms of wiring length) are near-minimal given the topological complexity of the system [22, 23]; a heterogeneous distribution of connections across network nodes, such that most nodes possess relatively few connections and a small proportion of nodes have a very high degree of connectivity [3, 24]; and stronger interconnectivity between hub nodes than expected by chance, leading to a so-called rich-club organization (i.e., the hubs are rich because they are highly connected and form a club because they are densely interconnected) [5, 25–28].
The rich-club organization of hub connectivity is thought to play a central role in integrating functionally diverse and anatomically disparate neuronal systems [26, 29–32]. Consistent with this view, experimental data and computational modeling indicates that hub nodes, and the connections between them, are topologically positioned to mediate a high volume of signal traffic [33–36]. This integrative role comes at a cost, with connections between hubs extending over longer distances, on average, than other types of connections, a finding reported in the human [33], macaque [34], rat [37], mouse [38], and nematode [28]. Human positron emission tomography also suggests that hub nodes consume greater metabolic resources and have higher levels of blood flow than other areas [39–41]. This high metabolic cost may underlie the involvement of hub regions in a broad array of human diseases [17, 29, 31].
Recent studies in mice and humans suggest that the high cost of hub connectivity is associated with a distinct molecular signature, as inferred from brain-wide transcriptomic data. This work has focused on how patterns of expression across many thousands of genes covary between pairs of brain regions. Such patterns of covariation are variously referred to as transcriptional coupling [38], gene coexpression [42] or correlated gene expression [43–45]. The goal of this work is to understand how pair-wise coupling of gene expression corresponds to the pairwise connection topology of the brain, thus drawing a link between molecular function and large-scale network organization. For example, Fulcher and Fornito [38] combined viral tract tracing data on connectivity between 213 regions of the right hemisphere of the mouse brain [8] with in situ hybridization measures of the expression of 17 642 genes in each of those regions. They found that transcriptional coupling, across all genes, is stronger for connected compared to unconnected brain regions and that, in general, this coupling decays with increasing separation distance between brain regions. Countering this general trend, however, connected pairs of hubs (i.e., the “rich club” of the brain) show the highest levels of transcriptional coupling (compared to hub-nonhub and nonhub-nonhub pairs), despite being separated by larger distances, on average, and being distributed across diverse anatomical brain divisions. Moreover, this coupling is driven predominantly by genes regulating the oxidative synthesis and metabolism of adenosine triphosphate (ATP), the primary energetic currency of neuronal signaling [46, 47]. Vértes et al. [48] later combined gene expression data of 20 737 genes through 285 cortical areas of the human brain and found evidence that inter-modular hubs in resting state fMRI connectivity networks also have local transcriptional profiles enriched in oxidative metabolism and mitochondria.
Together, the analyses of Fulcher and Fornito [38] and Vértes et al. [48], which were performed using measures of mesoscale (μm to mm) and macroscale (mm to cm) connectivity, respectively, suggest that the molecular signature of hub connectivity, characterized by elevated coupling of genes regulating oxidative metabolism, may be conserved across species and resolution scales. Here, we sought to test this hypothesis by examining the link between gene expression and microscale connectivity in the nematode C. elegans. C. elegans is the only species to have its connectome mapped almost completely at the level of individual neurons and synapses using electron microscopy [2, 3]. It comprises 302 neurons and around 5600 chemical and electrical synapses [2]. We combined these data on neuronal connectivity with curated information on the binary expression patterns of 948 genes across neurons to examine the relationship between gene expression and the large-scale topological organization of the nematode nervous system. We also used detailed information on neuron spatial positions, birth times, neuronal lineage as well as the functional and chemical composition of each neuron to understand the mechanisms through which gene expression might influence network topology. Paralleling findings in humans and mouse, we find that hub neurons of C. elegans are genomically distinct, with connected hub neurons showing the most similar patterns of gene expression. Genes that contribute most to this effect are involved in regulating glutamate and acetylcholine function, and neuronal communication. We demonstrate that this effect cannot be explained by factors such as neuronal birth time, lineage, neurotransmitter system or spatial position, but may instead be related to the functional specialization of hub neurons in mediating higher order behaviours of the organism.
Materials and methods
We first describe the neural connectivity data used to construct a connectome for C. elegans and the methods used to quantify network connectivity and other properties of individual neurons, including their neurochemical composition, birth times, and lineage relationships. We then describe the gene expression data, how we measure expression similarity between pairs of neurons, and our method for scoring the contribution of individual genes to patterns of correlated gene expression. Note that all data used for analysis in this work were obtained from publicly available sources, and can be downloaded from an accompanying figshare repository (figshare.com/s/797199619fbabdab8c86). Code to process this data and reproduce all figures and analyses presented here is on github (github.com/BMHLab/CElegansConnectomeGeneExpression).
Neuronal connectivity data
The nervous system of C. elegans comprises 302 neurons, divided into the pharyngeal nervous system (20 neurons) and the somatic nervous system (282 neurons). While research detailing the genetic underpinnings that guide the formation of C. elegans nervous system is still ongoing, the spatial positions of neurons, and their interconnections, are known to be stereotypical across organisms [49]. Neuronal connectivity data for the adult hermaphrodite C. elegans was first mapped by White et al. [2] through detailed electron microscopy, and then revised by Chen et al. [50] and Varshney et al. [3]. Here we analyze the larger somatic nervous system using data from Varshney et al. [3], who mapped connectivity between 279 neurons (282 somatic neurons, i.e., excluding CANL/R, and VC6, which do not form synapses with other neurons), which we obtained from WormAtlas [51] (www.wormatlas.org/neuronalwiring.html#NeuronalconnectivityII).
Connectivity data are available for both electrical gap junctions and chemical synapses. The chemical synapse network is both directed (i.e., the pre-synaptic and post-synaptic neurons are identified) and weighted (as the number of synapses from one neuron to another), while gap junctions are conventionally represented as weighted (as the number of electrical synapses connecting two neurons), undirected connections. Previous investigations of C. elegans neuronal connectivity have used differently processed versions of these data, including: (i) only chemical synapses [52]; (ii) a combination of chemical and electrical synapses as a directed network (electrical synapses represented as reciprocal connections) [53, 54]; (iii) a combination of chemical and electrical synapses as an undirected network (representing unidirectional and reciprocal chemical connections equivalently) [28, 55–57]; or (iv) comparing multiple connectome representations [58]. Our analysis here focuses on the combined directed, binary network, treating gap junctions as bidirectional connections. We chose to focus on a binarized network to follow previous studies on C. elegans connectome data [28, 56, 59–61] and to enable a more direct comparison to our previous analysis of the relationship between (binary) connectivity and gene expression in mouse [38]. The resulting connectome contains 279 neurons, with 2 990 unique connections linking 2 287 pairs of neurons.
Note that the qualitative results presented here are not highly sensitive to the types of connections included in the connectome. For example, neuron degree is highly correlated between networks generated using: (i) combined chemical and electrical synapses and (ii) chemical synapses only (Spearman’s ρ = 0.9, p = 3 × 10−107). We also obtained qualitatively similar results for rich-club organization and trends in CGE when excluding gap junctions from our analysis (see S1 Fig).
In addition, we assembled a range of data characterizing other properties of C. elegans neurons. To examine the effect of physical distance between pairs of neurons, we obtained two dimensional spatial coordinates for each neuron as celegans277.mat from www.biological-networks.org/?page_id=25 [62]. Coordinates for three neurons (AIBL, AIYL, SMDVL) were missing in this dataset, and were reconstructed by assigning identical coordinates to the corresponding contralateral neurons (AIBR, AIYR, SMDVR) [59]. To examine the influence of anatomical location, each neuron was labeled by its anatomical location, as: (i) ‘head’, (ii) ‘tail’, or (iii) ‘body’, using data from release WS256 of WormBase [63], (ftp://ftp.wormbase.org/pub/wormbase/releases/WS256/ONTOLOGY/anatomy_association.WS256.wb). These annotations were assigned to individual neurons using the anatomical hierarchy defined in WormBase, which we retrieved using the WormBase API (WormMine: intermine.wormbase.org) [63], propagating each term down the hierarchy to individual neurons. We manually corrected the assignment of twelve head neurons (ALA, AVFL, AVFR, AVG, RIFL, RIFR, RIGL, RIGR, SABD, SABVL, SABVR, SMDVL), which were assigned as ‘head’ in WormAtlas [51] but not on WormBase. To examine the influence of neuronal subtype, all neurons were labeled to one (or multiple) of the following three categories: (i) ‘sensory’ (have clear sensory specializations), (ii) ‘motor’ (make synaptic contacts onto muscle cells), or (iii) ‘interneuron’ (receive synapses from and send synapses onto other neurons) [2]. A total of 79 neurons are annotated as sensory, 121 annotated as motor, and 97 annotated as interneurons (including eighteen neurons assigned to two categories: five are both ‘interneuron’ and ‘sensory’, seven are ‘interneuron’ and ‘motor’, and six are both ‘sensory’ and ‘motor’ neurons). To examine the neurotransmitter systems used by each neuron, neurons were labeled by matching to Table 2 of Pereira et al. [64]. In order to determine the influence of neuron birth time, we obtained neuronal birth time information in minutes from the Dynamic Connectome Lab website (https://www.dynamic-connectome.org/?page_id=25), [59]. To assess the influence of lineage similarity, we obtained a measure of lineage distance for all pairs of neurons from previously published embryonic and post-embryonic lineage trees [65, 66], using data downloaded from WormAtlas (http://www.wormatlas.org/neuronalwiring.html#Lineageanalysis) [51]. In this dataset, the closest common ancestor neuron was identified for each pair of neurons, and then the lineage distance was calculated as the number of cell divisions from the closest common progenitor neuron.
Network analysis
In this section we describe the network analysis methods used to characterize the C. elegans connectome.
Degree
Neuronal connectivity is most simply quantified by counting the number of neurons that a given neuron projects to, known as its out-degree, kout, or by counting the number of neurons that a given neuron receives projections from, known as its in-degree, kin. These quantities can be summed to give the total number of connections involving a given neuron, ktot = kin + kout, which we refer to as simply the degree, k, throughout this work. At a given degree threshold, k, each neuron was classified as either a ‘hub’ (degree > k) or a ‘nonhub’ (degree ≤ k). All connections were subsequently classified in terms of their source and target neurons as either ‘rich’ (hub → hub, or hub ↔ hub), ‘feed-in’ (nonhub → hub), ‘feed-out’ (hub → nonhub), or ‘peripheral’ (nonhub → nonhub, or nonhub ↔ nonhub).
Rich-club organization
We used the rich-club coefficient, ϕ(k), to quantify the interconnectivity of hub neurons:
| (1) |
where N>k is the number of nodes with degree > k, and E>k is the number of edges between them [67]. Thus, ϕ(k) measures the link density in the subgraph containing nodes with degree > k. Because ϕ(k) invariably increases with k (as nodes with higher degree make more connections, yielding a higher expected link density in the subgraph containing nodes with degree > k), we compared ϕ(k) measured from the C. elegans connectome to the mean value of an ensemble of randomized null networks, ϕrand(k) [67]. An ensemble of 1000 null networks was generated by shuffling the links in the empirical network while retaining the same degree sequence [68] (rewiring each edge an average of 50 times per null network) using the randmio_dir function from the Brain Connectivity Toolbox [69]. The normalized rich-club coefficient, Φnorm(k), was computed as the ratio of the rich-club coefficient of the empirical network to the mean rich-club coefficient of the ensemble of randomized networks:
| (2) |
Values of Φnorm > 1 indicate rich-club organization of the network, with statistically significant deviations assessed by computing a p-value directly from the empirical null distribution, ϕrand(k), as a permutation test [25].
Modularity
Another important topological property of neural systems is modularity, whereby network nodes coalesce into tightly connected subsystems that are thought to serve a common function [70]. To investigate whether our results were influenced by the well-known modular organization of the C. elegans connectome [22, 55, 56, 58, 71], we decomposed the network into modules using two methods. The first method involved applying the Louvain community detection algorithm [72] using the community_louvain function in the Brain Connectivity Toolbox [69]. To identify the optimal modular assignment, neurons were assigned to modules using consensus clustering across 1000 repeats of the Louvain algorithm [73], weighting each partition by its modularity, Q, using the agreement_weighted and consensus_und functions of the BCT [69]. The second modular decomposition was taken from a previously-reported nine-module partition derived from an Erdös-Rényi Mixture Model (ERMM) [56].
Gene expression
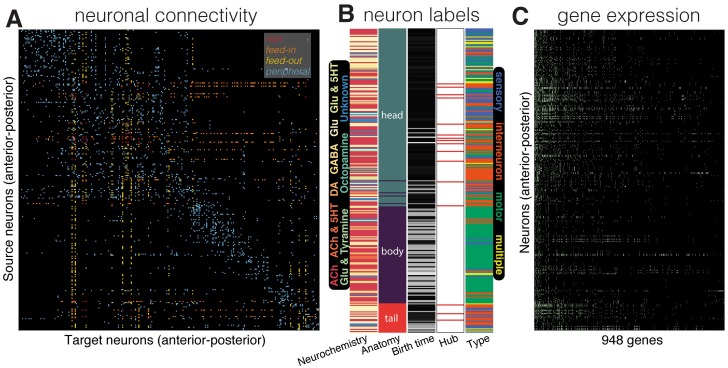
Gene expression is represented as a binary indicator of which genes are expressed in a given neuron using data from many individual experiments compiled into a unified data resource on WormBase [63]. We use release WS256 of this dataset (ftp://ftp.wormbase.org/pub/wormbase/releases/WS256/ONTOLOGY/anatomy_association.WS256.wb) and analyze annotations made ‘directly’ to individual neurons, excluding ‘uncertain’ annotations (see S1 Text). We denote the expression of a gene in a neuron as a ‘1’, and other cases as a ‘0’. Note that a value of ‘0’ indicates either: (i) ‘gene is not expressed’ or (ii) ‘there is no information on whether the gene is expressed’. Expression data are sparse, in part due to incomplete annotations—an average of 30 genes are expressed in each neuron (range: 3 to 138 genes), and each gene is expressed in an average of 9 neurons (range: 1 to 148 neurons). A total of 948 genes are expressed in at least one neuron, allowing us to represent the full expression dataset as a binary 279 (neurons) × 948 (genes) matrix, shown in Fig 1C.
Fig 1. Schematic representation of the data used in this study.
All plots show neurons (rows) ordered by anterior-posterior along the longitudinal axis, from the top of the head (upper, left) to the bottom of the tail (lower, right). (A) Connectivity matrix summarized 2990 directed chemical and electrical connections between 279 neurons from neuron i (row) to neuron j (column). Connections are colored according to how they connect hubs (k > 44) and nonhubs (k ≤ 44), as ‘rich’ (hub → hub), ‘feed-in’ (nonhub → hub), ‘feed-out’ (hub → nonhub), and ‘peripheral’ (nonhub → nonhub). (B) Neurochemistry (types as labeled), anatomical location (as labeled), birth time (from early born neurons, black, to late-born neurons, white), hub assignment (hubs labeled red), and functional type (as labeled). (C) Binary gene expression indicated as a green dot when a gene (column) is expressed in a neuron (row).
Correlated gene expression
Our primary aim in this work is to understand how pairwise patterns of neuronal connectivity (shown in Fig 1A) relate to coupled expression across 948 genes between pairs of neurons (i.e., pairs of rows of Fig 1C). To estimate the coupling between neuronal gene expression profiles, we required a similarity measure for pairs of neurons that captures their similarity of gene expression profiles, or correlated gene expression (CGE). We used a binary analogue of the linear Pearson correlation coefficient, the mean square contingency coefficient [74]:
| (3) |
for two vectors, x and y, of length L(= 948), where nxy counts the number of observations of each of the four outcomes (e.g., n10 = ∑i δxi,1δyi,0 counts the number of times x = 1 and y = 0), and the symbol • sums across a given variable (e.g., n•0 = ∑i δyi,0 counts the number of times y = 0). The coefficient assumes a maximum value rϕ = 1 when x and y are identical (such that n11 + n00 = L), and a minimum value rϕ = −1 when x and y are always mismatched (such that n10 + n01 = L). Note that we use the notation rϕ to denote the phi coefficient, Eq (3); this notation should not be confused with the rich-club coefficient, ϕ(k).
One concern about applying this measure to sparsely annotated data is that it may be biased by differences in the number of expressed genes in a neuron, which ranged from 3 (0.3% of 948 genes analyzed here) to 138 (14.6%). To explore this further, we compared rϕ with several other commonly used metrics of association between binary vectors including Yule’s Q and the Jaccard index. While these other binary similarity metrics exhibited strong bias with the proportion of gene expression annotations made to a given neuron, rϕ was not biased (see S2 Fig and S2 Text).
The 92 bilateral pairs of neurons (e.g., AVAL/AVAR, CEPVL/CEPVR, etc.) exhibit highly correlated gene expression patterns: all bilateral pairs of neurons have rϕ > 0.8, and 96% of bilateral pairs have rϕ > 0.95. Although including bilateral pairs of neurons do not change the main results of this paper, we excluded CGE values of bilateral pairs of neurons from all analyses to ensure that our results are not driven by high CGE between these pairs.
Gene scoring and enrichment
Our CGE measure, rϕ, quantifies the similarity between the expression profiles of two neurons across all 948 genes. To further investigate the role of individual genes in producing different CGE patterns, we developed a method for scoring the contribution of each individual gene to the overall correlation coefficient, following prior work using continuous gene expression data [38]. Performing similar analyses with C. elegans data poses additional challenges due to: (i) binary expression data, making robust quantification difficult; (ii) sparse and incomplete data, posing statistical problems for quantifying a signal in genes with limited expression; and (iii) low genome coverage (less than 5% of the protein coding genes in C. elegans), constraining our ability to perform a comprehensive enrichment analysis, e.g., using the Gene Ontology (GO) [75].
Given that rϕ treats mutual gene expression (i.e., cases in which a gene is expressed in pairs of neurons, n11) the same as mutual absence of gene expression (n00), we started by developing a new analytic measure of the probability of mutual gene expression, given its clearer biological interpretation (see S3 Text). This measure was not biased by differences in the relative number of expressed genes (S2D Fig) and yields qualitatively similar outputs to rϕ on our data. Thus, while we use rϕ throughout this work for its ease of interpretation (as an analogue of the conventional correlation coefficient), our new probability-based CGE measure allowed us to motivate a method for quantifying the contribution of individual genes (and functional groups of genes) to patterns of CGE that addresses some of the above-mentioned challenges. Note that our main findings, obtained using rϕ, are replicated using our new CGE measure (cf. S3 Fig).
As a starting point, we quantified the contribution of individual genes to differences in CGE for different categories of neuron pairs, specifically for (i) increased CGE in connected compared to unconnected pairs of neurons, and (ii) increased CGE in rich and feeder compared to peripheral connections. Note that our method scores genes on their contribution to differences in CGE between categories of pairwise connections. We first scored each gene for whether it is more likely to be expressed in a given class of neuron pair over another as the probability of obtaining at least as many matches (defined as expression in both neurons of a pair) as observed under a random CGE null model using the binomial distribution:
| (4) |
where m is the number of matches (a match indicates that a given gene was expressed in both neurons) on the class of neuron pairs of interest, n is the total number of matches across all neuron pairs considered in the analysis, pclass = nclass/M is the probability of the given class of inter-region pairs, as the total number of neuron pairs of that class, nclass, divided by the maximum number of possible neuron pairs, M, for a given gene, indexed with a. This score, p(a), can be interpreted as a p-value under the null hypothesis that the number of expression matches of gene a is consistent with a purely random pattern of matches/mismatches across edges, giving lower values to genes with more matches in the edge class of interest (compared to an alternative set of edges) than expected by chance. For reasons described earlier, bilateral pairs of neurons were excluded from all scoring procedures and, to ensure that each gene contributes a meaningful score, we imposed a data quality threshold on the number of possible matches, n ≥ 10.
Our first analysis compares two mutually exclusive types of neuron pairs: (i) all pairs of neurons that are connected by at least one chemical or electrical synapse, and (ii) all pairs of neurons that are unconnected. For this analysis, pclass = 0.059 is the proportion of neuron pairs that are connected, n is the total number of neuron pairs that both exhibit expression of gene a, and m is the number of neuron pairs that are structurally connected for which both neurons express gene a. A total of 414 (/948) genes had n ≥ 10 for this analysis. Our second analysis compares pairs of connected neurons for which at least one is a hub (i.e., rich, feed-in, or feed-out connections), to pairs in which both neurons are nonhubs (i.e., peripheral connections). In this case, pclass = 0.35 is the proportion of connected pairs of neurons that involve hubs, n is the number of connected neuron pairs for which gene a is expressed in both, and m counts the number of connected neuron pairs involving hubs for which gene a is expressed. A total of 168 (/948) genes had n ≥ 10 for this analysis.
As well as interpreting the list of individual genes that were significant after correcting for multiple hypothesis comparison, we performed an over-representation analysis (ORA) using the genes that contribute most to a given connectivity pattern to assess whether any gene sets (GO categories) were statistically over-represented in this list. To obtain the gene list, we used the false discovery rate correction of Benjamini and Hochberg [76] on p-values computed using Eq (4), which were thresholded at a stringent level of p = 10−4 (corresponding to approximately the top 20% of genes in each analysis). Over-representation for each biological process GO category with 5 to 100 genes available was quantified as an FDR-corrected p-value (across around 700 GO categories) using version 3.0.2 of ErmineJ software [77]. Biological process GO annotations [75] were obtained from GEMMA [78] (using Generic_worm_noParents.an.txt.gz downloaded on March 31, 2017). Gene Ontology terms and definitions were obtained in RDF XML file format downloaded from archive.geneontology.org/latest-termdb/go_daily-termdb.rdf-xml.gz on March 31 2017.
Results
A schematic overview of our data is in Fig 1, including the directed binary connectome (Fig 1A), additional anatomical data gathered for each neuron (Fig 1B), and binary gene expression across 948 genes (Fig 1C). Our analysis is presented in five parts: (i) given past evidence for a major effect of physical distance on connection probability and CGE [38], we first characterize the spatial dependency of connection probability and CGE; (ii) we confirm the rich-club organization of the C. elegans connectome; (iii) we show that CGE is increased in connected pairs of neurons relative to unconnected pairs, in electrical synapses relative to chemical synapses, and in connected hub neurons relative to other types of connected neuron pairs (mirroring previous results in the mesoscale mouse connectome [38]); (iv) we demonstrate that high CGE between connected hub neurons is not driven by factors like stereotypical interneuron expression, birth time, lineage similarity, neuromodulator types or expression similarity within modules, but may be driven by the high CGE of command interneurons; (v) we characterize the contribution of specific genes, and broader gene ontology categories, to the observed patterns.
Spatial dependency
Previous work has demonstrated the importance of spatial effects in driving patterns of gene expression, with more proximal brain areas [38, 53, 79–84] having both a increased connection probability and more similar gene expression profiles [38, 42, 85, 86] than more distance brain areas. Unlike network analyses of mammalian brains, where all neurons are confined to a spatially contiguous organ, neurons of the C. elegans nervous system are distributed throughout the entire organism, forming a dense cluster of 147 neurons in the head (all within 130 μm), 105 sparser neurons in the body (spanning 1.02 mm), which are predominantly motor neurons (75%), and another dense cluster of 27 neurons in the tail (all within 90 μm of each other), as plotted in Fig 2. In order to examine the relationship between connectivity and CGE, we need to understand the spatial dependence of both connectivity and CGE to characterize the extent to which previously reported spatial dependencies of these measurements apply to the microscale nervous system of C. elegans.
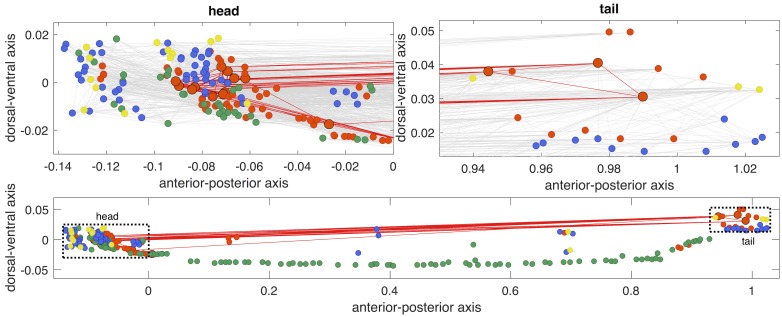
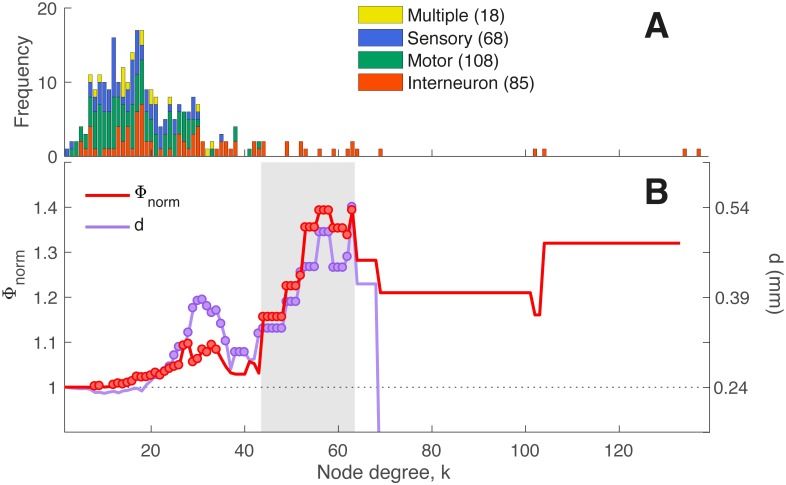
Fig 2. Hub neurons are contained within the head and tail of C. elegans.
Neurons are positioned along the anterior–posterior (horizontal), and dorsal–ventral (vertical) axes, and are colored by type: (i) interneuron (85 neurons, orange), (ii) sensory (68 neurons, blue), (iii) motor (108 neurons, green), or (iv) multiple assignments (18 neurons, yellow). Hub neurons (i.e., neurons with k > 44, see Fig 5) are shown as larger circles and outlined in black. ‘Rich-club’ connections between hub neurons are shown (red), and all other connections are also shown in the upper plots (gray). Axes of each subplot are to scale with each other, and the upper zoomed-in plots of the head and tail are shown as dotted rectangles in the lower plot.
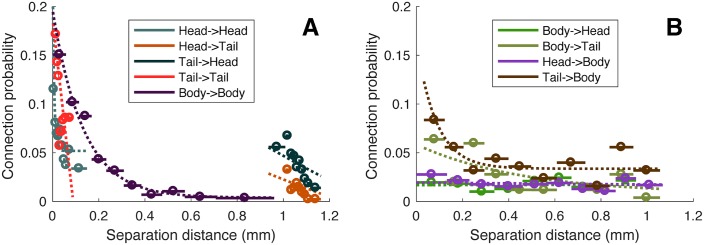
We first characterize the probability that two neurons will be connected given their source and target types, labeling each neuron as being in either the ‘head’, ‘body’, or ‘tail’ of C. elegans. Connection probability is plotted as a function of Euclidean separation distance in Fig 3 for each combination of source and target neuron labels, across 10 equiprobable distance bins (with exponential fits added for visualization). Distinguishing connections by source and target neuron types uncovers clear spatial relationships (that are obscured when all connections are grouped, as in [53]), that differ across connection classes. From the very short distance scale of ⪅ 100 μm of head→head and tail→tail connections to the very longest-range head→tail and tail→head connections (⪆ 1 mm), connection probability decreases with separation distance (Fig 3A). For connections between pairs of neurons located in the body, ranging up to ≈ 1 mm, a near-exponential trend is exhibited, mirroring results in other species and across longer length scales [80], including mouse [38, 87], and in rodents and primates [79]. Other connections do not exhibit strong spatial connectivity relationships, i.e., connections between the body and head or between the body and tail, shown in Fig 3B.
Fig 3. Connection probability decreases with separation distance within and between the head and tail, and within the body.
The connection probability for a pair of neurons as a function of their Euclidean distance is estimated in 10 equiprobable distance bins, shown as a circle (bin centers) and a horizontal line (bin extent). There is a decreasing relationship for connections: within the head (aqua), from head→tail (brown) and from tail→head (stone blue), within the tail (red), and within the body (dark purple). Exponential fits of the form f(x) = A exp(−λx) + B, some of which appear approximately linear across the range of the data, are shown as dotted lines. (B) Plots as in (A), but for connection classes between the body and head/tail: from body→head (forest green), from body→tail (dirt green), connections from head → body (purple), and from tail→body (dark brown). Apart from a small effect at short range for tail→body connections, these connection classes show minimal distance dependence.
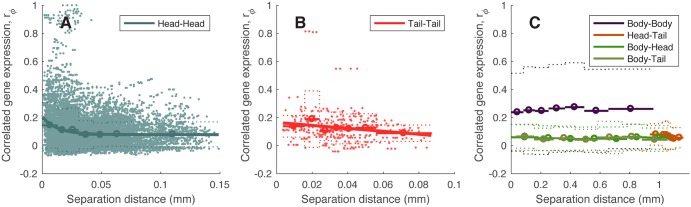
We next investigate the dependence of CGE, rϕ, on the separation distance between neuron pairs, shown in Fig 4. CGE decreases slightly with separation distance for the spatially close neurons within the head (Fig 4A) and within the tail (Fig 4B), but not for pairs of neurons involving the body (Fig 4C). The decreasing trend in CGE with distance within the head and tail is primarily driven by a subset of nearby neurons with high rϕ. It may therefore represent a relationship specific to particular functionally related neurons, rather than a general, bulk spatial relationship seen in macroscopic mammalian brains [38]. Accordingly, attempting to correct for a bulk, non-specific trend by taking residuals from an exponential fitted to the relationship produced artifactual reductions in the CGE of many neuron pairs (shown in S4 Fig). Thus, we found no evidence for bulk spatial relationships of rϕ in the neuronal connectome of C. elegans.
Fig 4. Dependence of correlated gene expression, rϕ, on spatial separation between pairs of neurons.
Correlated gene expression, rϕ (excluding bilateral homologous pairs of neurons), is shown as a function of the pairwise separation distance between pairs of neurons (shown as the mean (solid) ± standard deviation (dotted) in seven equiprobable distance bins, with extent shown as horizontal bars), for (A) all pairs of neurons in the head, (B) all pairs of neurons in the tail, and (C) all other pairs (labeled). Scatters for all neuron pairs are added in (A) and (B). An exponential relationship, f(x) = A exp(−λx) + B, is fitted in (A) and (B). The weak decreasing trend in rϕ with distance, is primarily driven by a small subset of nearby neurons with high rϕ, and may therefore represent a more specific relationship between particular neurons, rather than a general, bulk spatial relationship observed in macroscopic mammalian brains [38, 42].
Hub connectivity
Next we analyze the topological properties of the C. elegans connectome, represented as a directed, binary connectivity matrix between 279 neurons, combining directed chemical synapses and undirected electrical gap junctions (Fig 1). The degree distribution is shown in Fig 5A, where neurons are labeled as sensory neurons, interneurons, motor neurons, or neurons with multiple functional assignments. Consistent with the results of Towlson et al. [28], who used an undirected version of the connectome (by ignoring the directionality of chemical synapses), we found a positively-skewed degree distribution containing an extended tail of high-degree hub interneurons. Hub interneurons of C. elegans are mostly command interneurons and mediate behaviors like coordinated locomotion and foraging [88].
Fig 5. Rich-club organization of the C. elegans connectome.
(A) Degree distribution of neurons, labeled to four categories: (i) interneuron (85 neurons, orange), (ii) motor (108 neurons, green), (iii) sensory (68 neurons, blue), or (iv) multiple assignments (18 neurons, yellow). The distribution features an extended tail of high-degree interneurons. (B) Normalized rich club coefficient, Φnorm (red), as a function of the degree, k, at which hubs are defined (as neurons with degree > k). Also shown is the mean Euclidean separation distance, d (purple) between connected hub regions (across degree thresholds, k). Φnorm > 1 indicates that hubs are more densely interconnected among each other than expected by chance, with red circles indicating values of Φnorm that are significantly higher than an ensemble of 1 000 degree-matched null networks (p < 0.05). Purple circles indicate where the Euclidean distance between connected pairs of hubs is significantly greater than the Euclidean distance for all other pairs of connected regions (right-tailed Welch’s t-test, p < 0.05).
Using the normalized rich-club coefficient, Φnorm, to quantify the extent to which hubs are densely interconnected, we confirmed the results of Towlson et al. [28], finding rich-club organization in the connectome, as shown in Fig 5B. The figure plots the variation of Φnorm across degree thresholds, k, at which hubs are defined (as neurons with degree > k), with red circles indicating a significant increase in link density among hubs relative to 1000 degree-preserving nulls (permutation test, p < 0.05). The plot reveals rich-club organization (Φnorm > 1) at the upper tail of the degree distribution, particularly across the range 44 < k < 63, shaded gray in Fig 5B. Similar results were obtained using weighted representations of the connectome (i.e., using information about the number of synapses in the connectivity network) for two different definitions of the weighted rich-club coefficient [89], shown in S5 Fig. Throughout this work, we define a set of hubs as the sixteen neurons with k > 44, which corresponds to the lowest degree threshold at which the network displays a contiguous region of significant rich-club organization at high k. Our list of hubs includes all of the 11 hub neurons of Towlson et al. [28] at 3σ (see S1 Table), with five additional hubs identified in our analysis of the directed connectome.
The rich-club connectivity of the C. elegans connectome is accompanied by an increase in mean hub-hub connection distance [28], with a significant increase through the topological rich-club regime (right-tailed Welch’s t-test, p < 0.05), shown in Fig 5B. This can be attributed to a relative increase in long-distance hub-hub connections between the head and tail, shown in Fig 2 (cf. S6 Fig). The high connection density and long mean anatomical distance between pairs of hub neurons counters the general trend in the C. elegans connectome, where the probability of connectivity between two neurons decays with their separation distance (Fig 3). These results are consistent with previous findings across diverse neural systems and suggest that the rich club may provide a central yet costly backbone for neuronal communication in C. elegans [28, 33].
Correlated gene expression and connectivity
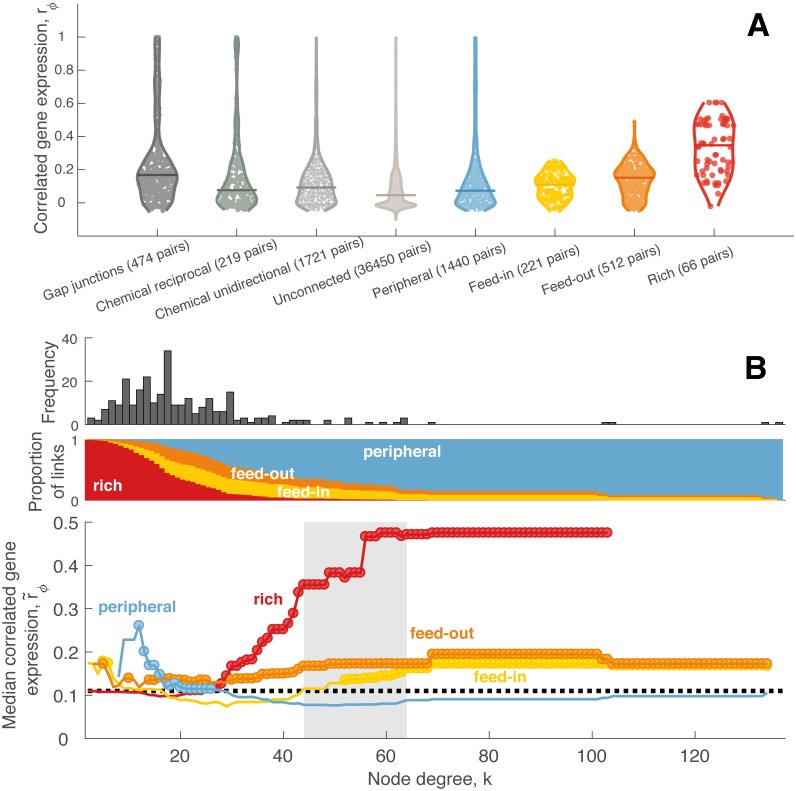
We next investigate how the network connectivity properties of C. elegans relate to patterns of CGE, using the mean square contingency coefficient, rϕ. To test whether CGE varies as a function of connectivity, we compared the distribution of rϕ between (i) all connected pairs of neurons, and (ii) all unconnected pairs of neurons. Connected pairs of neurons have more similar expression profiles than unconnected pairs (Wilcoxon rank-sum test, p = 1.8 × 10−78). Fig 6A (left) shows distributions of rϕ for: (i) all pairs of neurons that are connected via electrical gap junctions (474 pairs, after excluding bilateral pairs), (ii) all pairs of neurons that are connected via reciprocal (291 pairs) and, (iii) unidirectional chemical synapses (1721 pairs) as well as (iv) all pairs of neurons that have neither connection (36 450 pairs). Note that 175 pairs of neurons are connected by both chemical synapses and gap junctions, and are thus included in both chemical and electrical categories. Amongst connected pairs of neurons, those connected via gap junctions exhibit more similar gene expression profiles than those connected via chemical synapses (Wilcoxon rank-sum test, p = 5.4 × 10−22). We found no difference in CGE between pairs of neurons connected reciprocally by chemical synapses (N1 ↔ N2 for two neurons N1 and N2) versus those connected unidirectionally (N1 → N2) (Wilcoxon rank-sum test, p = 0.99).
Fig 6. Correlated gene expression varies as a function of connectedness and connection type.
(A) Left: distribution of CGE for (i) pairs of neurons connected by gap junctions, (ii) pairs of neurons connected by reciprocal chemical synapses, (iii) pairs of neurons connected by unidirectional chemical synapses, (iv) pairs of neurons that are unconnected, shown as a violin plot, with the median of each distribution represented by a horizontal line. CGE is increased in connected (electrical or chemical; reciprocally or unidirectionally) pairs of neurons relative to unconnected pairs (p = 1.8 × 10−78, Wilcoxon rank sum test). Among connected pairs of neurons neurons connected via gap junctions have more similar CGE than connected via chemical synapses (Wilcoxon rank-sum test, p = 5.4 × 10−22). Right: GCE for pairs of neurons labeled as peripheral, feed-in, feed-out, and rich, where hubs are neurons with degree k > 44. The median of each distribution shown as a horizontal line. CGE is significantly higher between hubs (rich links) compared to feeder (p = 5 × 10−22, Wilcoxon rank sum test) and peripheral (p = 3.9 × 10−19, Wilcoxon rank sum test) links. Feed-out links show significantly higher CGE than both feed-in (p = 1.9 × 10−6, Wilcoxon rank sum test) and peripheral links (p = 4.5 × 10−12, Wilcoxon rank sum test). (B) Top: Degree distribution, k, of the C. elegans connectome. Middle: proportion of connections that are: ‘rich’ (hub→hub, red), ‘feed-in’ (nonhub→hub, yellow), ‘feed-out’ (hub→nonhub, orange), or ‘peripheral’ (nonhub→nonhub, blue) as a function of the degree threshold, k, used to define hubs. Note that at high k most neurons are labeled as nonhubs and hence the vast majority of connections are labeled ‘peripheral’. Bottom: Median CGE, , for each connection type as a function of k. The median CGE across all network links is shown as a dotted black line; the topological rich-club regime (determined from the network topology, cf. Fig 5) is shaded gray. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Wilcoxon rank-sum test, p < 0.05).
We next investigated whether CGE varies across different types of connections defined in terms of their hub connectivity. For a given hub threshold, k, we first labeled each neuron as either a ‘hub’ (nodes with degree > k) or a ‘nonhub’ (degree ≤ k), and then labeled each connection as either ‘rich’ (hub → hub), ‘feed-in’ (nonhub → hub), ‘feed-out’ (hub → nonhub), or ‘peripheral’ (nonhub → nonhub). The median CGE, , of each of these four connection types is plotted in Fig 6B, with circles indicating statistically significant increases of a given connection type relative to all other connections (one-sided Wilcoxon rank-sum test, p < 0.05). Correlated gene expression in rich connections increases with degree, k, particularly in the topological rich-club regime where hubs are densely interconnected (shaded gray in Fig 6B). In this topological rich-club regime, both feed-in and feed-out connections exhibit increased CGE relative to peripheral connections, which show the lowest levels of CGE. Full distributions of rϕ for each edge type at a hub threshold of k > 44 are in Fig 6A (right). This plot shows that, compared to all different types of pairs of neurons, connected pairs of hubs showed the highest CGE.
In summary, our results reveal: (i) increased CGE in connected pairs of neurons; (ii) the highest CGE in rich connections; and (iii) lowest CGE in peripheral connections. These results, obtained using incomplete binary annotations of gene expression across 948 genes in a microscale neuronal connectome, are consistent with a prior analysis of the expression of over 17 000 genes across 213 regions of the mesoscale mouse connectome [38].
Potential drivers of elevated correlated gene expression between hubs
The sixteen hub neurons in C. elegans (k > 44): are all interneurons, are all located in either the head or tail, are mostly contained within a single topological module of the network, are mostly cholinergic (13/16), and are all born prior to hatching. We therefore investigated whether the similarity of gene expression profiles between hubs is specific to their high levels of connectivity, or whether it could instead be driven by these other characteristics.
Interneurons
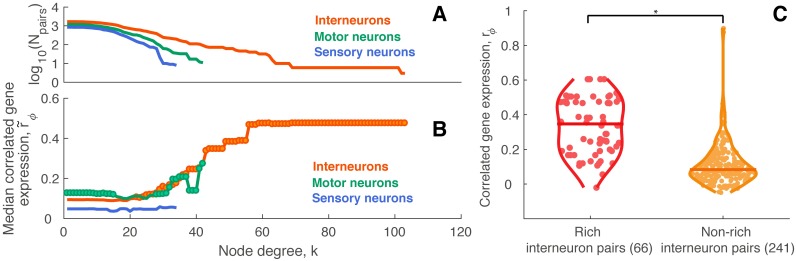
The sixteen hubs in C. elegans are all interneurons. To determine whether the increase in CGE in rich connections was specific to interneurons, we plotted the median CGE for hub-hub connections, , as a function of the degree threshold, k, separately for connections involving interneurons, sensory neurons, and motor neurons, as shown in Fig 7B. For the curve labeled ‘sensory’, for example, each point is the median across connections involving sensory neurons (i.e., at least one neuron of a connected pair is a sensory neuron), for which both neurons have degree > k. The increase in median hub-hub CGE is strongest for connections involving interneurons. Motor neurons show a smaller increase with k, although the absence of motor and sensory neurons with high k makes it difficult to draw firm conclusions. However, we do find that CGE is higher for hub-hub pairs of interneurons compared to connections between all pairs of nonhub interneurons (Wilcoxon rank sum test, p = 5 × 10−21), indicating that the high CGE of rich pairs cannot simply be related to the fact that all hub neurons are interneurons (Fig 7C). We next investigated whether greater CGE of hub-hub pairs of neurons could be driven by specific anatomical properties of hub interneurons. Specifically, we selected a subset of nonhub interneurons that most closely resemble the anatomical properties of hub interneurons in terms of their position and projection pattern; that is, the cells are in similar locations in the head and their axons project to similar targets in the tail. These neurons were AVFL, AVFR, AVHL, AVHR, AVKR, AVJL, and AVJR. Pairs of hub interneurons show higher median CGE than pairs of anatomically-matched nonhub interneurons, with the difference being at the threshold of statistical significance (Wilcoxon rank sum test, p = 0.051), suggesting that the increase in CGE amongst hub interneurons is not a consequence of their classification as interneurons.
Fig 7. Correlated gene expression is highest for hub interneurons.
(A) The number of connected neuron pairs involving interneurons (orange), sensory neurons (blue), and motor neurons (green) across degree threshold, k, represented as log10(number of links). (B) Median CGE as a function of degree for connections involving different types of neurons. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Wilcoxon rank-sum test, p < 0.05). (C) CGE distributions for connected pairs of hub interneurons (red) and connected pairs of non-hub interneurons (dark yellow) (Wilcoxon rank sum test, p = 5 × 10−21). * represents statistically significant difference.
Modular organization
Prior work in humans has shown that functional networks in the brain have elevated transcriptional coupling [45]. The C. elegans connectome has a modular organization, with prior work decomposing it into: (i) modules of neurons with dense intra-module connectivity (and relatively sparse connectivity between modules) [22, 55, 58], or (ii) groups of neurons with more similar connectivity patterns within groups than between groups [56, 71]. We therefore examined the association between topological modularity of the C. elegans connectome and CGE. We used the Louvain community detection algorithm [72] to extract modules from the C. elegans connectome using consensus clustering (see Methods). Four modules were extracted, with eleven hubs in module one (which contains 111 neurons), four hubs in module two (96 neurons), one hub in module three (40 neurons), and no hubs in module four (32 neurons). We also compared the results of this modular partition of neurons to a previously reported nine-module partition derived from an Erdös-Rényi Mixture Model (ERMM) [56]. For the Louvain consensus modules, CGE, rϕ, was significantly increased for connected neurons in the same module (1552 pairs) relative to connected pairs in different modules (687 pairs) (Wilcoxon rank sum test, p = 6.6 × 10−4), but there was no significant difference between intra-modular connected neurons and inter-modular connected neurons for the nine-module ERMM partition (Wilcoxon rank sum test, p = 0.46). The resolution and type of modular decomposition thus affects the relationship between CGE, connectivity, and modular network structure in C. elegans.
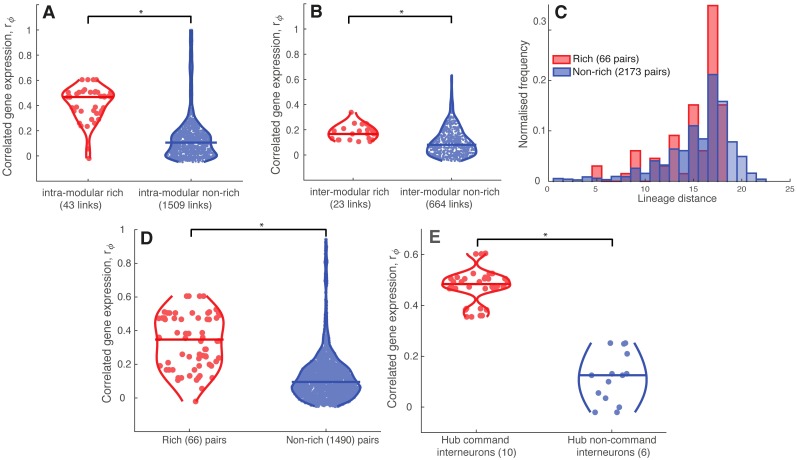
We then tested whether connected hubs exhibit more similar CGE within and between modules (for both the consensus Louvain and ERMM modular decompositions). For pairs of connected neurons within the same module, rϕ is higher for pairs of hubs than pairs of nonhubs (Wilcoxon rank sum test, p = 6.9 × 10−17 for consensus Louvain modules, shown in Fig 8A; 9.3 × 10−7 for ERMM partition). We found a similar result for connected neurons in different modules: pairs of connected hubs exhibit increased CGE than other types of connected pairs of neurons (Wilcoxon rank sum test, p = 1.6 × 10−5 for consensus Louvain modules, shown in Fig 8B; p = 1.6 × 10−16 for ERMM). Thus, for both types of modular decompositions considered, intra-modular and inter-modular connections involving hub neurons exhibit more correlated gene expression patterns than other intra-modular and inter-modular connections.
Fig 8. Increased CGE of hub neurons is not driven by modularity, neuronal birth time, or cell lineage distance.
(A) Distributions of CGE, rϕ, for intra-modular rich (red) non-rich (blue) connections, shown as violin plots with the median shown as a horizontal bar (Wilcoxon rank sum test, p = 6.9 × 10−17). (B) Distributions of CGE, rϕ, for inter-modular rich (red) and non-rich (blue) connections, shown as violin plots with the median shown as a horizontal bar (Wilcoxon rank sum test, p = 1.6 × 10−5). (C) Distributions of lineage distance between rich links (red) and non-rich links (blue), plotted as histograms due to a discrete nature of this measure (Wilcoxon rank sum test, p = 0.079). (D) Distributions of CGE, rϕ, between early born hubs (rich links, red) and nonhubs (non-rich links, blue) shown as violin plots with the median shown as a horizontal bar (Wilcoxon rank sum test, p = 3.9 × 10−22). (E) Distributions of CGE between hub command interneurons (red) and hub non-command interneurons (blue) shown as violin plots with the median shown as a horizontal bar (Wilcoxon rank sum test, p = 3.3 × 10−8). * represents statistically significant differences.
Lineage distance
The lineage distance between a pair of neurons is defined as the sum of total divisions that have taken place since the most recent common ancestor cell [56, 65, 66]. In the mammalian brain, neuronal lineage has been associated with both functional properties [90, 91] as well as connectivity [92]. Moreover, tissue distance (resembling lineage distance on a cellular scale) correlates with gene expression divergence, meaning that tissues from the same branch on the fate map share more similar gene expression patterns in both human and mouse mesoderm as well as ectoderm tissues [93]. Given that the ectoderm eventually differentiates to form the nervous system, this finding suggests a possible relationship between lineage distance and CGE in a microscale neuronal system such as that of C. elegans. However, we find no significant correlation between lineage distance and CGE in C. elegans (Spearman’s ρ = −0.027, p = 0.2). As shown in Fig 8C, there was only a weak tendency for the meadian lineage distance to be increased in non-rich pairs (Wilcoxon rank sum test, p = 0.079). Thus, we can not attribute the transcriptional similarity of connected hub neurons to their neuronal lineage.
Birth time
The genesis of neurons in C. elegans is separated into two distinct time periods: before hatching (birth time < 550 min—‘early-born’) and after hatching (birth time > 1200 min—‘late-born’), with no neurons formed during intermediate times [59]. As a broad group, connected pairs of early-born neurons do not exhibit significantly different CGE compared to connected pairs of late-born neurons (Wilcoxon rank sum test, p = 0.64), but connected pairs of early-born neurons do exhibit significantly higher CGE relative to pairs of connected neurons for which one neuron is born prior to hatching and the other is born after hatching (Wilcoxon rank sum test, p = 4.2 × 10−3). Since all C. elegans hub neurons are born prior to hatching [28] and neurons born at similar times may share similar connectivity properties [28, 59], we investigated whether the increase in CGE between hub neurons of C. elegans may be driven by their similar birth times. Focusing on the 201 neurons born prior to hatching (16 hub and 185 nonhub neurons), connected pairs of hub neurons exhibit significantly increased CGE, rϕ, relative to other pairs of connected early-born neurons (Wilcoxon rank sum test, p < 10−22), as shown in Fig 8D.
Neurochemistry
Hub neurons (k > 44) consist of thirteen cholinergic neurons, two glutamatergic neurons, and one neuron of unknown neurotransmitter type [64]. We find that neuron pairs show different CGE relationships as a function of their neurotransmitter type, e.g., pairs of GABAergic neurons have high median CGE, , while pairs of glutamatergic neurons exhibit a relatively low median CGE, . To determine whether the similarity in CGE between pairs of hub neurons is associated with their neurotransmitter types, we constructed 108 random sets of sixteen neurons of the same neurotransmitter types as hubs (e.g., thirteen random cholinergic neurons, two random glutamatergic neurons, and one random neuron of an unknown neurotransmitter type) and compared the distribution of median CGE of each group to the median CGE of hub neurons as a permutation test. Neurochemical identity is not associated with the elevated CGE of hub neurons, with hubs displaying a significant increase in median CGE relative to random sets of neurons with the same neurotransmitter types as hubs (permutation test, p = 3 × 10−4).
Anatomical location
Of the sixteen hub neurons, thirteen are in the head and three are in the tail; none are located in the body. CGE varies as a function of anatomical location (i.e., ‘head’, ‘body’, and ‘tail’), with pairs of neurons in the same anatomical class exhibiting the highest median CGE (e.g., pairs of neurons within the body have a median , pairs of neurons within the tail have , and pairs of neurons within the head have ), than pairs of neurons in mixed classes (e.g., head-body pairs of neurons have ). Given this variation, we tested whether the increased CGE between hub neurons could be explained by their anatomical distribution using the permutation testing procedure described above for neurochemistry. That is, we compared the distribution of CGE between hubs to a null distribution formed from 108 random permutations of thirteen head neurons and three tail neurons. The median CGE, , between hub neurons is significantly increased relative to random sets of thirteen head neurons and three tail neurons (permutation test, p = 8 × 10−8). Furthermore, CGE is significantly increased amongst hub neurons relative to other pairs of head neurons (Wilcoxon rank sum test, p = 4.1 × 10−11 for 46 hub-hub pairs and 1 186 others), and also amongst head/tail pairs of neurons (Wilcoxon rank sum test, p = 1.6 × 10−14 for 23 hub-hub pairs, 174 others), but not for the three hub neurons in the tail (Wilcoxon rank sum test, p = 0.15 for three hub-hub pairs, 53 others). Thus, anatomical location does not explain the high CGE of hub neurons.
Functional class
C. elegans neurons can be divided into distinct groups that each perform a specialized behavioral function [94]. One of the best-characterised functional classes that is particularly relevant for our analysis is the set of ‘command interneurons’—a functional group of ten neurons that govern forward (AVBL, AVBR, PVCL, PVCR) and backward (AVAL, AVAR, AVDL, AVDR, AVEL, AVER) locomotion [95]. All of these neurons are hubs. Given the overlap between hub neurons and command interneurons, we investigated whether command interneurons exhibit more similar expression than other hub interneurons, and may therefore drive the increase in CGE amongst hubs as a whole. We compared CGE, rϕ, between all pairs of hub command interneurons (ten neurons), and between all pairs of hubs that are not command interneurons (six neurons), shown in Fig 8E. Correlated gene expression between command interneurons is significantly greater than between other hub neurons (Wilcoxon rank sum test, p = 3.3 × 10−8), indicating that command interneurons play a major role in driving the increased CGE amongst hub neurons. Moreover, there is no difference in CGE between pairs of hubs that are not command interneurons (DVA, RIBL, RIBR, AIBR, RIGL, AVKL) and a set of seven anatomically matched nonhub head interneurons (AVFL, AVFR, AVHL, AVHR, AVJL, AVJR, AVKR) (Wilcoxon rank sum test, p = 0.13), indicating that the status of many hub neurons as command interneurons makes a significant contribution to the elevated CGE between hubs.
Genes driving correlated gene expression patterns
Having characterized a robust relationship between CGE and (i) connectivity, and (ii) hub connectivity, we next investigated which specific genes contribute most to this relationship. Despite challenges with the incomplete binary expression measurements in a small proportion of the genome, we developed a method to score genes according to their contribution to a given CGE pattern (see Methods). We characterized individual high-scoring genes, with pcorr < 10−4 (approximately 20% of genes with the highest scores in each analysis), and attempted to summarize functional groups of genes as biological process categories of the gene ontology (GO) that were enriched in high scoring genes using overrepresentation analysis (ORA) [75, 77].
We first investigated which genes drive increased CGE in connected pairs of neurons relative to unconnected pairs. Previous studies in mouse have indicated that genes driving an increase in CGE between connected pairs of brain regions are enriched in GO categories related to neuronal connectivity and communication [38, 96–98]. First, we manually investigated individual high-scoring genes (i.e., those with pcorr < 10−4, see Supplementary Data File (S1 File)). Given that glutamate is a prevalent neurotransmitter in C. elegans (26% of neurons with known neurotransmitter type are glutamatergic [64]), it is appropriate that many high scoring genes are related to glutamate receptors (including glr-1, glr-2, glr-4, glr-5, nmr-1, and nmr-2). Consistent with the importance of innexins in forming electrical synapses [99], our list contained the following innexin genes: unc-9, unc-7, inx-7, inx-19, inx-13. Genes encoding cell adhesion molecules related to axon outgrowth and guidance, cell migration and locomotion (sax-3, cam-1, unc-6, rig-1, unc-5), learning (casy-1) [63, 100–103], as well as genes involved in determining cell polarity (vang-1, prkl-1) [104, 105] were also amongst the top scoring genes for connectivity. These genes have been implicated in neuronal connectivity in both flies and humans [106–108], with our results predicting that they may play a similar role in C. elegans. In addition, transcription factors regulating neuronal development, fate specification (lin-11, unc-3, unc-42, ceh-14, ast-1, cfi-1) [109–114], and locomotion (unc-3) [110]) were also implicated in driving increased CGE amongst connected pairs of neurons. Both adhesion molecules and transcription factors are candidates for facilitating signal transduction and communication.
In order to summarize the above mentioned results and determine if any particular functional groups of genes drive this effect, we performed an enrichment analysis. Top scoring biological process GO categories from ORA analysis (of 85 genes relative to the 414 genes with sufficient data for this analysis) are listed in S2 Table. Although no GO categories are significant at a false discovery rate of 0.05, the top categories are consistent with a connectivity profile, including ‘glutamate receptor signaling’, ‘cell surface receptor signaling’, and ‘ion transport’, with other categories involved in regulation of growth rate and several related to catabolic processes. Thus, despite incomplete gene expression data that do not provide sufficient coverage to detect statistically significant effects, these results indicate that our data-driven gene scoring method is able to yield sensible, biologically relevant insights into the genetic basis of neuronal connectivity in C. elegans connectome.
Having characterized genes that contribute to the increase in CGE between connected pairs of neurons, we next investigated whether particular functional groups of genes drive differences in CGE between connections involving hub neurons (i.e., in rich, feed-in, and feed-out connections) relative to connections between pairs of nonhub neurons (i.e., peripheral connections). In order to investigate which specific genes contribute most to the increase in CGE for connections involving hubs, we first investigated the highest-scoring genes, with pcorr < 10−4 (corresponding to approximately the top 20% of genes in the analysis). In addition to glutamate receptor genes (glr-5, nmr-1, nmr-2, glr-1, glr-2, grld-1) and acetylcholine related genes (ace-2, cho-1, unc-17, deg-3), we again find a high number of genes regulating cell adhesion (cam-1, rig-1, rig-6, unc-6, grld-1, dbl-1, ncam-1) and relevant transcription factors (unc-3, unc-42, ast-1). The implication of glutamate and acetylcholine may be attributable to the importance of glutamate in the regulation of locomotion in command interneurons [115, 116], with acetylcholine being the dominant neurotransmitter in hubs (13 out of 16 hubs are cholinergic). We also find a high overlap between adhesion molecule and transcription factor encoding genes found in the previous analysis and the implication of human orthologs (rig-1, ncam-1, grld-1, corresponding to human genes ROBO4, NCAM2, and RBM15 respectively [63]) for genes regulating cell migration, differentiation and neuron cell adhesion.
While previous work implicated genes regulating oxidative metabolism for connections involving hubs in mouse [38], and for hub regions in human [48], the gene expression dataset used here was not sufficiently comprehensive to investigate these processes. For example, only one of the 948 genes annotated to the GO categories related to hub connectivity in mouse is present in our gene expression dataset (unc-32 is annotated to the GO category: ‘ATP hydrolysis coupled proton transport’). Thus, although a direct test of the metabolic hypothesis for neural hubs is not possible from current data, we investigated whether other biological process GO categories were overrepresented in pairs of connected hubs using ORA (of 30 genes relative to the 168 genes with sufficient data for this analysis), with results listed in S3 Table. Even though no categories are statistically significant at a false discovery rate of 0.05, the list of top categories includes both ‘glutamate receptor signaling pathway’ as well as more general ‘cell surface receptor signaling pathway’ in addition to several ion transport related gene groups (’ion transport’, ‘ion transmembrane transport’, ‘transmembrane transport’). Other top-ranked GO categories include regulation of locomotion, and various metabolism and biosynthesis related processes. Our gene scoring method again yields interpretable insights into the types of genes that contribute to differences in CGE between different classes of neuronal connections in C. elegans. While current data are limited, more comprehensive expression annotations in the future would allow more systematic and statistically powered inferences across GO categories.
Discussion
Highly connected hubs of neural systems play an important role in brain function, with their dense rich-club interconnectivity integrating disparate neural networks [24, 27, 29, 30]. Here, our analysis linking hub connectivity of the microscale connectome of C. elegans to patterns of neuron-specific gene expression has identified a transcriptional signature that appears to be highly conserved, given recent findings reported in a mesoscale investigation of the mouse [38] and a macroscale study of humans [48]. Specifically, we show that: (i) CGE is higher for connected pairs of neurons compared to unconnnected pairs; (ii) the neuron connection probability decays as a function of spatial separation, and; (iii) connected pairs of hub neurons, which are generally separated by longer anatomical distances, show the highest levels of CGE. This association between CGE and hub connectivity followed a gradient, such that CGE was lowest for connected nonhubs, intermediate for hub-nonhub pairs, and highest for connected hubs, consistent with results reported in the mouse brain [38]. Amongst the genes considered here, many of those with the greatest contribution to connectivity are biologically plausible genes related to receptors, neurotransmitters, and cell adhesion, and those with the greatest contribution to hub connectivity are related to glutamate receptors, acetylcholine signaling, and other neuronal communication related genes. The methods we develop here for quantifying CGE, and for scoring the contribution of individuals genes to overall CGE, yield biologically interpretable results from incomplete binary gene expression data. With improvements in gene annotation quality and specificity, and increases in genome coverage, similar methods could be used in future work to characterize the biological basis of a range of neuronal connectivity patterns.
The availability of spatial maps of gene expression with genome-wide coverage has allowed the relationship between gene expression and connectivity to be investigated in species ranging from C. elegans through to mouse and human. For example, Krienen et al. [42] showed that the topography of transcriptional expression of a small number of human supragranular enriched genes mirrors the large-scale brain network organization of rs-fMRI in the healthy human brain, and Romme et al. [117] showed that schizophrenia-related structural disconnectivity is significantly correlated to the expression profiles of schizophrenia risk genes. Recent work has demonstrated a relationship between spatial gene expression maps and cortical hierarchy using structural MRI imaging in macaque and human [118]. Spatial maps of gene transcription will continue to play a key role in uncovering species-conserved mechanisms underlying brain connectivity.
Computational methods to extract relationships between network organization and gene expression can help understand the molecular processes underlying neuronal connectivity. Previous research has related gene expression data in C. elegans to axonal connectivity patterns, focusing on pairwise relationships of genes that might underpin axonal connectivity. Both Kaufman et al. [60] and Baruch et al. [119] developed statistical models to predict the postsynaptic partners of individual neurons in C. elegans (using k-nearest neighbors and boosted decision tree models, respectively). This research found that the targets of some neurons are easier to predict than others [60], and that the prediction can be done with good accuracy using only a small subset of genes [119]. Our results demonstrate differences in CGE across different topological classes of connections, and highlight genes that make the biggest contribution to these differences. More detailed investigations of these relationships (e.g., across C. elegans development) may shed light on the molecular logic underlying the establishment and maintenance of neuronal connectivity.
It is reasonable to expect that the principles of neural organization may differ from the scale of individual neurons to the scale of macroscopic brain regions (in which each brain region contains millions of neurons). However, many of our results in C. elegans suggest a striking conservation of many fundamental spatial trends in neural connectivity and CGE across scales and species. For example, connection probability decreases with spatial separation between brain areas in rodents and primates [79, 80] (including in macaque [81], human [82], mouse [38], and rat [83]), for individual neurons in mouse primary auditory cortex [84], and between neurons in C. elegans (cf. Fig. S1 of [53]). Unlike mammalian brains, where all neurons are confined to a spatially contiguous organ, neurons are distributed across nearly the entire length of C. elegans, including a dense cluster of neurons in the head and in the tail. Despite these distinct morphologies, we report a qualitatively similar spatial dependence of connection probability with separation distance for many classes of connections in C. elegans, including those within the head, body, and tail, indicating that this distance-dependence may be a generic property of evolved neuronal systems that must balance the energetic cost of long-range connections with their functional benefit [17, 23, 33, 55]. Less frequently characterized is the spatial dependence of CGE, with available evidence indicating that more proximal brain areas exhibit more similar gene expression patterns than more distant brain areas in the mouse brain [38] and human cortex [42, 85, 86]. Some of the spatial trends in CGE found in the 948 genes analyzed here mirror these trends of bulk regions of macroscopic mammalian brains. It is therefore possible that these spatial dependences of connectivity and CGE may not be simply due to bulk spatial trends in macroscopic brains containing millions of neurons, but may reflect conserved organizational principles that hold across species and spatial scales. Our results highlight the importance of treating nervous systems as spatially embedded objects, as many seemingly non-trivial properties of brain organization may be well approximated by simple, isotropic spatial rules [22, 50, 79, 82, 120] (see also [17, 23]).
Our analysis indicates that CGE patterns in C. elegans show many surprising similarities to previous work in the mesoscale mouse connectome [38], despite: (i) involving different gene expression annotation data (comprehensive in situ hybridization expression data across ∼20000 genes in mouse versus literature-curated annotations across ∼1000 genes in C. elegans), (ii) being a different type of neural system (from the spatially continuous macroscopic brain of mouse, to the spatially separated nervous system of C. elegans); (iii) orders of magnitude differences in spatial scale. The findings were also robust to a range of data processing choices, including different representations of the connectome (e.g., directed/undirected, or excluding electrical synapses), and across alternative metrics for quantifying transcriptional similarity.
What could drive this highly conserved association between CGE and hub connectivity? Here, we took advantage of the rich and diverse information available for each neuron of the C. elegans connectome to begin to address this question. We show that CGE between hub neurons is not determined by their neuronal type (i.e., the fact that all hubs are interneurons rather than sensory or motor neurons), since CGE between hub neurons is higher than between other pairs of interneurons. The effect cannot be attributed to the modular organization of the network either, since CGE between hubs in the same module is higher than between other pairs of neurons in the same topological module, with a similar increase in CGE for pairs of hubs in different modules. We also show that the effect is not driven by similarities in the birth time nor lineage distance of hub neurons, which exhibit higher CGE than other early-born neurons (prior to hatching) and are not closer in their lineage. Moreover, the abundance of cholinergic signaling of hub neurons cannot explain the effect. Rather, the CGE between pairs of hub neurons in C. elegans may be related to the specific functional role of these cells. Namely, 60% of them are command interneurons, which play a vital role in coordinating forward and backward locomotion in C. elegans [54]. The overlap between command interneurons and hub neurons has interesting parallels with the human cortex, where polymodal association areas tend to be the most highly connected network elements [1]. Association areas sit at atop the cortical hierarchy and support complex behaviors by integrating information from diverse neural systems [121]. Locomotion is arguably one of the most complex behaviors expressed by C. elegans. Thus, the association between hub status and command interneurons may reflect the specialization of these neurons for supporting higher-order functions in the behavioral repertoire of C. elegans.
It is as yet unclear whether CGE between network hubs, regardless of species and scale, is simply a byproduct of tightly coupled hub activity, or some shared morphological or development characteristic between hubs that we have not captured in the present analysis. More comprehensive transcriptomic data (e.g., obtained through systematic single-neuron RNA sequencing), measured through development and coupled with measures of neuronal activity, would allow us to address these questions. Additionally, we cannot rule out the possibility that gene annotations have been influenced by the nature of the curated data that we have used here. Given their functional similarity, command interneurons might have been tested as a group in a set of experiments for the expression of particular genes and consequently assigned similar expression signatures. More precise and systematic measurement of neuron-specific gene expression patterns would be required to address this question. Studies of gene expression often assume that expression levels correspond to protein abundance, but this assumption does not always hold [122–124]. Thus, analyses of transcriptomic data can be viewed as a relatively efficient approach for investigating potential links between molecular function and nervous system organization, that can be more strongly verified using subsequent proteomic analysis.
In this work we developed methods to relate correlations in binary gene expression data to pairwise connectivity and subsequently score and evaluate the contribution of individual genes to these patterns. Compared to continuous in situ hybridization measurements of the expression of > 17000 genes in the mouse brain [125], or microarray measurements of > 20000 genes in the human brain [126, 127], which permit more detailed analysis [38, 48, 96–98, 128], working with C. elegans gene expression data is challenging due to its low coverage (< 5% coverage of the worm genome), binary indications of expression, and incompleteness (an inability to distinguish missing data from lack of expression). Moreover, the data have different qualifiers related to the certainty of gene expression annotations (see S1 Text), requiring choices to be made to appropriately balance sensitivity and specificity. Although gene enrichment analyses did not have enough power to detect significant effects here, top GO categories point us towards biologically relevant categories related to neuronal connectivity, neurotransmitters, and metabolism. We note, however, that the incomplete coverage of the genome in our annotated dataset may mask many true GO associations. Our single gene analysis identified specific genes contributing to increases in CGE for connected pairs of neurons and for connections involving hub neurons. In line with our expectations, genes regulating both chemical and electrical signaling, namely glutamate receptor and innexin genes, were implicated in general connectivity. In addition, we also find multiple cell adhesion molecule genes and transcription factors that regulate neuronal development and fate specification—both groups are important for forming neuronal connections. High overlap between genes encoding adhesion molecules and transcription factors implicated in regulating both general and hub connectivity highlights that related mechanisms might be used in both cases. While we were not able to test GO categories related to neurotransmitter signaling comprehensively, due to insufficient coverage of gene expression annotations, single gene analysis revealed the importance of acetylcholine genes, which may be related to the fact that acetylcholine is the dominant neurotransmitter in hub neurons.
Supporting information
(PDF)
(PDF)
(PDF)
Hubs are defined as neurons with degree k > 44. For each hub, we list (i) the neuron name, (ii) its degree, k, (iii) location (‘head’, ‘body’, or ‘tail’), and function based on information presented in the wormatlas website http://www.wormatlas.org/. Neurons are sorted (descending) by degree.
(PDF)
Top 15 biological process GO categories enriched in genes with the highest mean increase in CGE for connected neurons compared to unconnected neurons. Categories are sorted by p-value (ascending).
(PDF)
Top 15 biological process GO categories enriched in genes with the highest increase in CGE for connections involving hub neurons (i.e., rich, feed-in and feed-out connections) compared to connections between nonhub neurons (i.e., in peripheral connections). Categories are sorted by p-value (ascending).
(PDF)
(A) Rich-club organization of the synaptic C. elegans connectome. Top: Degree distribution of neurons, labelled to four categories: (i) interneuron (85 neurons, orange), (ii) motor (108 neurons, green), (iii) sensory (68 neurons, blue), or (iv) multiple assignments (18 neurons, yellow). The distribution features an extended tail of high-degree neurons. Bottom: Normalized rich club coefficient, Φnorm (red), as a function of the degree, k, at which hubs are defined (as neurons with degree > k). Also shown is the mean Euclidean separation distance, d (purple) between connected hub regions (across degree thresholds, k). Φnorm > 1 indicates that hubs are more densely interconnected among each other than expected by chance, with red circles indicating values of Φnorm that are significantly higher than an ensemble of 1 000 degree-matched null networks (p < 0.05). Purple circles indicate where the Euclidean distance between connected pairs of hubs is significantly greater than the Euclidean distance for all other pairs of connected regions (right-tailed Welch’s t-test, p < 0.05). (B) Top: Degree distribution, k, of the synaptic C. elegans connectome. Middle: proportion of connections that are: ‘rich’ (hub → hub, red), ‘feed-in’ (nonhub → hub, yellow), ‘feed-out’ (hub → nonhub, orange), or ‘peripheral’ (nonhub → nonhub, blue) as a function of the degree threshold, k, used to define hubs. Note that at high k most neurons are labeled as nonhubs and hence the vast majority of connections are labeled ‘peripheral’. Bottom: Median CGE, , for each connection type as a function of k. The median CGE across all network links is shown as a dotted black line; the topological rich-club regime (determined from the network topology, cf. A) is shaded gray. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Wilcoxon rank-sum test, p < 0.05).
(TIF)
We plot the mean value of each metric across 1000 different pairs of random, binary vectors of length 948, which vary only in their proportion of ‘1’s (between 0–0.15; corresponding to a number of ‘1’s ranging from 1 to 150). This is repeated for: (A) mean square contingency coefficient, rϕ, (B) Jaccard index, (C) Yule’s Q, and (D) our developed positive match measure, pmatch, (see S3 Text). Any systematic trend in correlation values indicates a bias driven by the proportion of positive annotations for a pair of vectors, as is seen for the Jaccard index and Yule’s Q. By contrast, rϕ, which is used through this work, and our probability-based measure, pmatch, used to motivate individual gene scoring for enrichment analysis, show no evidence of systematic bias (note the color axis scales).
(TIF)
The matching probability index, pmatch, as introduced in S3 Text. Top: Degree distribution. Middle: Proportion of connections that are ‘rich’ (hub→hub, red), ‘feed-in’ (nonhub→hub, yellow), ‘feed-out’ (hub→nonhub, orange), and ‘peripheral’ (nonhub→nonhub, blue) as a function of the degree threshold, k, used to define hubs. Note that at high k, most neurons are labeled as nonhubs, and hence the vast majority of connections are ‘peripheral’. Bottom: Mean CGE calculated using similarity index from only positive matches, pmatch, for each connection type as a function of k. The mean CGE across all network links shown as a dotted black line; the topological rich-club regime (determined from the network topology, cf. Fig 5) is shaded gray. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Welch’s t test; p < 0.05).
(TIF)
Here we consider correlated gene expression in the head, where the strongest spatial relationship exists (cf. Fig 4. (A) CGE values, rϕ, plotted as a function of Euclidean separation distance for all pairs of neurons within the head (gray dots), with a fitted exponential trend shown in black, f(x) = A exp(−λx) + B. (B) Taking residuals from this trend does not adequately correct the spatial trend. Note the artifactual negative correlations indicated with an arrow. This indicates that the trend is not a bulk, isotropic effect, but may instead be driven primarily by a small number of neuron pairs with high rϕ at short distances (⪅ 50μm), indicated with a circle in (A). For example, neuron pairs with rϕ > 0.8, are all between the following classes of head neurons: CEP, IL1, OLQ, RMD, RME, RMF, SAAD, SAAV, SAB, SIA, SIB, SMB, SMD, URA, URY.
(TIF)
(A) Degree distribution of the C. elegans connectome. Neurons are labeled to four types as in the legend. (B) Normalized weighted rich-club coefficient, (i.e., topology fixed and weights randomized in the null model, shown orange), and normalized mixed rich-club coefficient, (i.e., both topology and weights mixed in the null model, shown green) are plotted as a function of the degree, k, at which hubs are defined (as neurons with degree > k) [129]. Circles indicate values of Φnorm that are significantly higher than an ensemble of 1 000 degree-matched null networks (Welch’s t-test, p < 0.05). Compared to topological rich-club analysis presented in the main text, here the weights of the connections are also accounted for when calculating the rich club coefficient. In the case of the weighted rich-club coefficient, the topology for the null models was kept stable and only the weights of the connections randomized. Results presented here show that connections between higher degree nodes are stronger than expected by chance. On the other hand, in the mixed rich club coefficient both the topology and weights are randomized, therefore we see the combined effect of both types. Distinction between the different null models is discussed in detail in [129]. These results show that connections between high degree nodes are both denser and stronger than expected by chance.
(TIF)
Hub-hub connections (‘rich’) are shown red, and all other connections (‘non-rich’, i.e., feeder and peripheral) are shown gray, where hubs are defined as neurons with degree, k > 44. Anatomical locations are labeled as ‘head’, ‘body’, and ‘tail’, and each connection is labeled according to its source and target neurons, listed on the vertical axis in the form ‘Source-Target’. The plot shows that the increased separation distance between connected hubs relative to other types of connected neurons is driven by a relative increase in long-range connections between the head and tail.
(TIF)
A list of genes that contributed towards the (i) increased CGE in connected compared to unconnected pairs of neurons, and (ii) increased CGE in rich and feeder compared to peripheral connections.
(XLSX)
Acknowledgments
We thank WormBase and particularly Daniela Raciti for providing valuable information regarding the curation of C. elegans gene expression data and Taci Ali for preliminary data processing.
Data Availability
Data used for analysis in this work were obtained from publicly available sources, and can be downloaded from an accompanying figshare repository (figshare.com/s/797199619fbabdab8c86). Code to process this data and reproduce all figures and analyses presented here is on github (github.com/BMHLab/CElegansConnectomeGeneExpression).
Funding Statement
AF was supported by the Australian Research Council http://www.arc.gov.au/ (ID: FT130100589) and the National Health and Medical Research Council https://www.nhmrc.gov.au/ (ID: 3251213). BDF was supported by a National Health and Medical Research Council (https://www.nhmrc.gov.au/) Early Career Fellowship (1089718). RP was supported by Monash University Biomedicine Discovery Fellowship, National Health and Medical Research Council https://www.nhmrc.gov.au/ Project Grant (GNT1105374) and veski innovation fellowship (https://www.veski.org.au/home): VIF 23 to RP. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. van den Heuvel MP, Bullmore ET, Sporns O. Comparative Connectomics. Trends Cogn Sci. 2016;20(5):345–361. doi: 10.1016/j.tics.2016.03.001 [DOI] [PubMed] [Google Scholar]
- 2. White JG, Southgate E, Thomson JN. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci. 1986;314(1165):1–340. doi: 10.1098/rstb.1986.0056 [DOI] [PubMed] [Google Scholar]
- 3. Varshney LR, Chen BL, Paniagua E, Hall DH, Chklovskii DB. Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comp Biol. 2011;7(2):e1001066 doi: 10.1371/journal.pcbi.1001066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Chiang AS, Lin CY, Chuang CC, Chang HM, Hsieh CH, Yeh CW, et al. Three-dimensional reconstruction of brain-wide wiring networks in Drosophila at single-cell resolution. Curr Biol. 2011;21(1):1–11. doi: 10.1016/j.cub.2010.11.056 [DOI] [PubMed] [Google Scholar]
- 5. Shih CT, Sporns O, Yuan SL, Su TS, Lin YJ, Chuang CC, et al. Connectomics-Based Analysis of Information Flow in the Drosophila Brain. Curr Biol. 2015;25(10):1249–1258. doi: 10.1016/j.cub.2015.03.021 [DOI] [PubMed] [Google Scholar]
- 6. Wanner AA, Genoud C, Masudi T, Siksou L, Friedrich RW. Dense EM-based reconstruction of the interglomerular projectome in the zebrafish olfactory bulb. Nat Neurosci. 2016;19(6):816–825. doi: 10.1038/nn.4290 [DOI] [PubMed] [Google Scholar]
- 7. Hildebrand DGC, Cicconet M, Torres RM, Choi W, Quan TM, Moon J, et al. Whole-brain serial-section electron microscopy in larval zebrafish. Nature. 2017;545(7654):345–349. doi: 10.1038/nature22356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, et al. A mesoscale connectome of the mouse brain. Nature. 2014;508(7495):207–214. doi: 10.1038/nature13186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Zingg B, Hintiryan H, Gou L, Song MY, Bay M, Bienkowski MS, et al. Neural Networks of the Mouse Neocortex. Cell. 2014;156(5):1096–1111. doi: 10.1016/j.cell.2014.02.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Bota M, Sporns O, Swanson LW. Architecture of the cerebral cortical association connectome underlying cognition. Proc Natl Acad Sci USA. 2015;112(16):E2093–E2101. doi: 10.1073/pnas.1504394112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Scannell JW, Blakemore C, Young MP. Analysis of connectivity in the cat cerebral cortex. J Neurosci. 1995;15(2):1463–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Markov NT, Ercsey-Ravasz MM, Gomes ARR, Lamy C, Magrou L, Vezoli J, et al. A Weighted and Directed Interareal Connectivity Matrix for Macaque Cerebral Cortex. Cereb Cortex. 2012;24(1):17–36. doi: 10.1093/cercor/bhs270 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Stephan KE, Kamper L, Bozkurt A, Burns GA, Young MP, Kötter R. Advanced database methodology for the Collation of Connectivity data on the Macaque brain (CoCoMac). Philos Trans Roy Soc B: Biol Sci. 2001;356(1412):1159–1186. doi: 10.1098/rstb.2001.0908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, et al. Mapping the Structural Core of Human Cerebral Cortex. PLoS Biol. 2008;6(7):e159 doi: 10.1371/journal.pbio.0060159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: An overview. NeuroImage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Bullmore ET, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10(3):186–198. doi: 10.1038/nrn2575 [DOI] [PubMed] [Google Scholar]
- 17. Bullmore ET, Sporns O. The economy of brain network organization. Nat Rev Neurosci. 2012;13(5):337–349. doi: 10.1038/nrn3214 [DOI] [PubMed] [Google Scholar]
- 18. Sporns O. The non-random brain: efficiency, economy, and complex dynamics. Front Comput Neurosci. 2011;5:5 doi: 10.3389/fncom.2011.00005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Schröter M, Paulsen O, Bullmore E. Micro-connectomics: probing the organization of neuronal networks at the cellular scale. Nat Rev Neurosci. 2017;18(3):131–146. doi: 10.1038/nrn.2016.182 [DOI] [PubMed] [Google Scholar]
- 20. Fornito A, Zalesky A, Bullmore E. Fundamentals of brain network analysis. Academic Press; 2016. [Google Scholar]
- 21. Meunier D, Lambiotte R, Bullmore ET. Modular and Hierarchically Modular Organization of Brain Networks. Front Psychiat. 2010;4:200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bassett DS, Greenfield DL, Meyer-Lindenberg A, Weinberger DR, Moore SW, Bullmore ET. Efficient Physical Embedding of Topologically Complex Information Processing Networks in Brains and Computer Circuits. PLoS Comp Biol. 2010;6(4):e1000748 doi: 10.1371/journal.pcbi.1000748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Betzel RF, Avena-Koenigsberger A, Goñi J, He Y, de Reus MA, Griffa A, et al. Generative models of the human connectome. NeuroImage. 2016;124(Pt A):1054–1064. doi: 10.1016/j.neuroimage.2015.09.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. van den Heuvel MP, Sporns O. Network hubs in the human brain. Trends Cogn Sci. 2013;17(12):683–696. doi: 10.1016/j.tics.2013.09.012 [DOI] [PubMed] [Google Scholar]
- 25. van den Heuvel MP, Sporns O. Rich-Club Organization of the Human Connectome. J Neurosci. 2011;31(44):15775–15786. doi: 10.1523/JNEUROSCI.3539-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Zamora-López G, Zhou C, Kurths J. Cortical Hubs Form a Module for Multisensory Integration on Top of the Hierarchy of Cortical Networks. Front Neuroinf. 2010;4:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. de Reus MA, van den Heuvel MP. Rich Club Organization and Intermodule Communication in the Cat Connectome. J Neurosci. 2013;33(32):12929–12939. doi: 10.1523/JNEUROSCI.1448-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Towlson EK, Vértes PE, Ahnert SE, Schafer WR, Bullmore ET. The rich club of the C. elegans neuronal connectome. J Neurosci. 2013;33(15):6380–6387. doi: 10.1523/JNEUROSCI.3784-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci. 2015;16(3):159–172. doi: 10.1038/nrn3901 [DOI] [PubMed] [Google Scholar]
- 30. van den Heuvel MP, Sporns O. An Anatomical Substrate for Integration among Functional Networks in Human Cortex. J Neurosci. 2013;33(36):14489–14500. doi: 10.1523/JNEUROSCI.2128-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Crossley NA, Mechelli A, Scott J, Carletti F, Fox PT, McGuire P, et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain. 2014;137(Pt 8):2382–2395. doi: 10.1093/brain/awu132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Crossley NA, Mechelli A, Vértes PE, Winton-Brown TT, Patel AX, Ginestet CE, et al. Cognitive relevance of the community structure of the human brain functional coactivation network. Proc Natl Acad Sci USA. 2013;110(28):11583–11588. doi: 10.1073/pnas.1220826110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. van den Heuvel MP, Kahn RS, Goñi J, Sporns O. High-cost, high-capacity backbone for global brain communication. Proc Natl Acad Sci USA. 2012;109(28):11372–11377. doi: 10.1073/pnas.1203593109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Harriger L, van den Heuvel MP, Sporns O. Rich Club Organization of Macaque Cerebral Cortex and Its Role in Network Communication. PLoS ONE. 2012;7(9):e46497 doi: 10.1371/journal.pone.0046497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Mišić B, Sporns O, McIntosh AR. Communication Efficiency and Congestion of Signal Traffic in Large-Scale Brain Networks. PLoS Comp Biol. 2014;10(1):e1003427 doi: 10.1371/journal.pcbi.1003427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Mišić B, Betzel RF, Nematzadeh A, Goñi J, Griffa A, Hagmann P, et al. Cooperative and Competitive Spreading Dynamics on the Human Connectome. Neuron. 2015;86(6):1518–1529. doi: 10.1016/j.neuron.2015.05.035 [DOI] [PubMed] [Google Scholar]
- 37. van den Heuvel MP, Scholtens LH, de Reus MA. Topological organization of connectivity strength in the rat connectome. Brain Struct Funct. 2016;221(3):1719–1736. doi: 10.1007/s00429-015-0999-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Fulcher BD, Fornito A. A transcriptional signature of hub connectivity in the mouse connectome. Proc Natl Acad Sci USA. 2016;113(5):1435–1440. doi: 10.1073/pnas.1513302113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Tomasi D, Wang GJ, Volkow ND. Energetic cost of brain functional connectivity. Proc Natl Acad Sci USA. 2013;110(33):13642–13647. doi: 10.1073/pnas.1303346110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Collin G, Sporns O, Mandl RCW, van den Heuvel MP. Structural and Functional Aspects Relating to Cost and Benefit of Rich Club Organization in the Human Cerebral Cortex. Cereb Cortex. 2014;24(9):2258–2267. doi: 10.1093/cercor/bht064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Liang X, Zou Q, He Y, Yang Y. Coupling of functional connectivity and regional cerebral blood flow reveals a physiological basis for network hubs of the human brain. Proc Natl Acad Sci USA. 2013;110(5):1929–1934. doi: 10.1073/pnas.1214900110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Krienen FM, Yeo BTT, Ge T, Buckner RL, Sherwood CC. Transcriptional profiles of supragranular-enriched genes associate with corticocortical network architecture in the human brain. Proc Natl Acad Sci USA. 2016;113(4):E469–78. doi: 10.1073/pnas.1510903113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Goel P, Kuceyeski A, LoCastro E, Raj A. Spatial patterns of genome-wide expression profiles reflect anatomic and fiber connectivity architecture of healthy human brain. Hum Brain Mapp. 2014;35(8): 4204–4218. doi: 10.1002/hbm.22471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mills BD, Grayson D, Shunmugavel A, Miranda-Dominguez O, Feczko E, Earl E, Neve K, Fair D. Correlated gene expression and anatomical communication support synchronized brain activity in the mouse functional connectome. bioRxiv. [DOI] [PMC free article] [PubMed]
- 45. Richiardi J, Altmann A, Milazzo AC, Chang C, Chakravarty MM, Banaschewski T, et al. Correlated gene expression supports synchronous activity in brain networks. Science. 2015;348(6240):1241–1244. doi: 10.1126/science.1255905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Lennie P. The Cost of Cortical Computation. Curr Biol. 2003;13(6):493–497. doi: 10.1016/S0960-9822(03)00135-0 [DOI] [PubMed] [Google Scholar]
- 47. Laughlin SB, Sejnowski TJ. Communication in neuronal networks. Science. 2003;301(5641):1870–1874. doi: 10.1126/science.1089662 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Vértes PE, Rittman T, Whitaker KJ, Romero-Garcia R, Váša F, Kitzbichler MG, et al. Gene transcription profiles associated with inter-modular hubs and connection distance in human functional magnetic resonance imaging networks. Phil Trans Roy Soc B. 2016;371(1705):735–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Riddle DL, Blumenthal T, Meyer BJ, et al. , editors. C. elegans II. 2nd edition Cold Spring Harbor (NY): Cold Spring Harbor Laboratory Press; 1997. Available from: http://www.ncbi.nlm.nih.gov/books/NBK19997/. [PubMed] [Google Scholar]
- 50. Chen BL, Hall DH, Chklovskii DB. Wiring optimization can relate neuronal structure and function. Proc Natl Acad Sci USA. 2006;103(12):4723–4728. doi: 10.1073/pnas.0506806103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Altun ZF, Herndon LA, Wolkow CA, Crocker C, Lints R, Hall DH. WormAtlas; 2002–2017. Available from: http://www.wormatlas.org.
- 52. Kashtan N, Itzkovitz S, Milo R, Alon U. Topological generalizations of network motifs. Phys Rev E. 2004;70(3 Pt 1):031909 doi: 10.1103/PhysRevE.70.031909 [DOI] [PubMed] [Google Scholar]
- 53. Azulay A, Itskovits E, Zaslaver A. The C. elegans Connectome Consists of Homogenous Circuits with Defined Functional Roles. PLoS Comp Biol. 2016;12(9):e1005021 doi: 10.1371/journal.pcbi.1005021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Kim S, Kim H, Kralik JD, Jeong J. Vulnerability-Based Critical Neurons, Synapses, and Pathways in the Caenorhabditis elegans Connectome. PLoS Comp Biol. 2016;12(8):e1005084 doi: 10.1371/journal.pcbi.1005084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Kim JS, Kaiser M. From Caenorhabditis elegans to the human connectome: a specific modular organization increases metabolic, functional and developmental efficiency. Phil Trans Roy Soc B. 2014;369(1653):20130529 doi: 10.1098/rstb.2013.0529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Pavlovic DM, Vértes PE, Bullmore ET, Schafer WR, Nichols TE. Stochastic Blockmodeling of the Modules and Core of the Caenorhabditis elegans Connectome. PLoS ONE. 2014;9(7):e97584 doi: 10.1371/journal.pone.0097584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Van De Ville D, Demesmaeker R, Preti MG. Guiding Network Analysis using Graph Slepians: An Illustration for the C. Elegans Connectome. arXiv. 2017; p. 1708.04657.
- 58. Pan RK, Chatterjee N, Sinha S. Mesoscopic Organization Reveals the Constraints Governing Caenorhabditis elegans Nervous System. PLoS ONE. 2010;5(2):e9240 doi: 10.1371/journal.pone.0009240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Varier S, Kaiser M, Koh W, Meuli R, Honey C. Neural Development Features: Spatio-Temporal Development of the Caenorhabditis elegans Neuronal Network. PLoS Comp Biol. 2011;7(1):e1001044 doi: 10.1371/journal.pcbi.1001044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Kaufman A, Dror G, Meilijson I, Ruppin E. Gene expression of Caenorhabditis elegans neurons carries information on their synaptic connectivity. PLoS Comp Biol. 2006;2(12):e167 doi: 10.1371/journal.pcbi.0020167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Varadan V, Miller DM, Anastassiou D. Computational inference of the molecular logic for synaptic connectivity in C. elegans. Bioinformatics. 2006;22(14):497–506. doi: 10.1093/bioinformatics/btl224 [DOI] [PubMed] [Google Scholar]
- 62. Choe Y, McCormick B, Koh W. Network connectivity analysis on the temporally augmented C. elegans web: A pilot study In: Soc. Neurosci. Abstr. vol. 30; 2004. p. 921.9. [Google Scholar]
- 63. Harris TW, Antoshechkin I, Bieri T, Blasiar D, Chan J, Chen WJ, et al. WormBase: a comprehensive resource for nematode research. Nucleic Acids Res. 2009;(Database issue):D463–D467. doi: 10.1093/nar/gkp952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Pereira L, Kratsios P, Serrano-Saiz E, Sheftel H, Mayo AE, Hall DH, et al. A cellular and regulatory map of the cholinergic nervous system of C. elegans. eLife. 2015;4:e12432 doi: 10.7554/eLife.12432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Sulston JE, Horvitz HR. Post-embryonic cell lineages of the nematode, Caenorhabditis elegans. Dev Biol. 1977;56(1):110–156. doi: 10.1016/0012-1606(77)90158-0 [DOI] [PubMed] [Google Scholar]
- 66. Sulston JE, Schierenberg E, White JG, Thomson JN. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev Biol. 1983;100(1):64–119. doi: 10.1016/0012-1606(83)90201-4 [DOI] [PubMed] [Google Scholar]
- 67. Colizza V, Flammini A, Serrano M, Vespignani A. Detecting rich-club ordering in complex networks. Nat Phys. 2006;2(2):110–115. doi: 10.1038/nphys209 [Google Scholar]
- 68. Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103 [DOI] [PubMed] [Google Scholar]
- 69. Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage. 2010;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003 [DOI] [PubMed] [Google Scholar]
- 70. Sporns O, Betzel RF. Modular Brain Networks. Annu Rev Psychol. 2016;67(1):613–640. doi: 10.1146/annurev-psych-122414-033634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Achacoso T, Yamamoto W. AY’s Neuroanatomy of C. elegans for Computation. CRC Press, Boca Raton, FL; 1992. [Google Scholar]
- 72. Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. J Stat Mech. 2008;2008(10):P10008 doi: 10.1088/1742-5468/2008/10/P10008 [Google Scholar]
- 73. Lancichinetti A, Fortunato S, Thomson JN, Brenner S, Moon S. Consensus clustering in complex networks. Sci. Rep. 2012;2:336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Warrens MJ. On Association Coefficients for 2x2 Tables and Properties That Do Not Depend on the Marginal Distributions. Psychometrika. 2008;73(4):777–789. doi: 10.1007/s11336-008-9070-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, et al. Gene Ontology: Tool for The Unification of Biology. Nat. Gen. 2000;25(1):25–29. doi: 10.1038/75556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Benjamini Y, Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J Roy Stat Soc B. 1995;57(1):289–300. [Google Scholar]
- 77. Gillis J, Mistry M, Pavlidis P. Gene function analysis in complex data sets using ErmineJ. Nat. Protoc. 2010;5(6):1148–1159. doi: 10.1038/nprot.2010.78 [DOI] [PubMed] [Google Scholar]
- 78. Zoubarev A, Hamer KM, Keshav KD, Luke Mccarthy E, Santos JRC, Van rossum T, et al. Gemma: A resource for the reuse, sharing and meta-analysis of expression profiling data. Bioinformatics. 2012;28(17):2272–2273. doi: 10.1093/bioinformatics/bts430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Horvát S, Gămănut R, Ercsey-Ravasz M, Magrou L, Gămănut B, Van Essen DC, et al. Spatial Embedding and Wiring Cost Constrain the Functional Layout of the Cortical Network of Rodents and Primates. PLoS Biol. 2016;14(7):e1002512 doi: 10.1371/journal.pbio.1002512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Wang XJ, Kennedy H. Brain structure and dynamics across scales: in search of rules. Curr Opin Neurobiol. 2016;37:92–98. doi: 10.1016/j.conb.2015.12.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Markov NT, Ercsey-Ravasz M, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. Cortical High-Density Counterstream Architectures. Science. 2013;342(6158):1238406–1238406. doi: 10.1126/science.1238406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Henderson JA, Robinson PA. Relations Between the Geometry of Cortical Gyrification and White-Matter Network Architecture. Brain Conn. 2014;4(2):112–130. doi: 10.1089/brain.2013.0183 [DOI] [PubMed] [Google Scholar]
- 83. Noori HR, Schöttler J, Ercsey-Ravasz M, Cosa-Linan A, Varga M, Toroczkai Z, et al. A multiscale cerebral neurochemical connectome of the rat brain. PLoS Biol. 2017;15(7):e2002612 doi: 10.1371/journal.pbio.2002612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Levy RB, Reyes AD. Spatial Profile of Excitatory and Inhibitory Synaptic Connectivity in Mouse Primary Auditory Cortex. J Neurosci. 2012;32(16):5609–5619. doi: 10.1523/JNEUROSCI.5158-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Pantazatos SP, Li X. Commentary: BRAIN NETWORKS. Correlated gene expression supports synchronous activity in brain networks. Science 348, 1241-4. Front Neurosci. 2017;11:412 doi: 10.3389/fnins.2017.00412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Richiardi J, Altmann A, Greicius M. Distance Is Not Everything In Imaging Genomics Of Functional Networks: Reply To A Commentary On Correlated Gene Expression Supports Synchronous Activity In Brain Networks. bioRxiv. 2017; p. 132746.
- 87. Goulas A, Uylings HBM, Hilgetag CC. Principles of ipsilateral and contralateral cortico-cortical connectivity in the mouse. Brain Struct Funct. 2017;222(3):1281–1295. doi: 10.1007/s00429-016-1277-y [DOI] [PubMed] [Google Scholar]
- 88. Tsalik EL, Hobert O. Functional mapping of neurons that control locomotory behavior in Caenorhabditis elegans. J Neurobiol. 2003;56(2):178–197. doi: 10.1002/neu.10245 [DOI] [PubMed] [Google Scholar]
- 89. Opsahl T, Colizza V, Panzarasa P, Ramasco JJ. Prominence and control: the weighted rich-club effect. Phys Rev Lett. 2008;101(16):168702 doi: 10.1103/PhysRevLett.101.168702 [DOI] [PubMed] [Google Scholar]
- 90. Ciceri G, Dehorter N, Sols I, Huang ZJ, Maravall M, Marín O. Lineage-specific laminar organization of cortical GABAergic interneurons. Nat Neurosci. 2013;16(9):1199–1210. doi: 10.1038/nn.3485 [DOI] [PubMed] [Google Scholar]
- 91. Li Y, Lu H, Cheng Pl, Ge S, Xu H, Shi SH, et al. Clonally related visual cortical neurons show similar stimulus feature selectivity. Nature. 2012;486(7401):118–121. doi: 10.1038/nature11110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Yu YC, He S, Chen S, Fu Y, Brown KN, Yao XH, et al. Preferential electrical coupling regulates neocortical lineage-dependent microcircuit assembly. Nature. 2012;486(7401):113–117. doi: 10.1038/nature10958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Cui Q, Yu Z, Purisima EO, Wang E, Li X, Schwarz P, et al. MicroRNA regulation and interspecific variation of gene expression. Trends Genet. 2007;23(8):372–375. doi: 10.1016/j.tig.2007.04.003 [DOI] [PubMed] [Google Scholar]
- 94. Hobert O. Behavioral Plasticity in C. elegans: Paradigms, Circuits, Genes. J Neurobiol. 2003;54(1):203–223. doi: 10.1002/neu.10168 [DOI] [PubMed] [Google Scholar]
- 95. Rakowski F, Srinivasan J, Sternberg PW, Karbowski J. Synaptic polarity of the interneuron circuit controlling C. elegans locomotion. Front Comput Neurosci. 2013;7:128 doi: 10.3389/fncom.2013.00128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Ji S, Fakhry A, Deng H. Integrative analysis of the connectivity and gene expression atlases in the mouse brain. NeuroImage. 2014;84:245–253. doi: 10.1016/j.neuroimage.2013.08.049 [DOI] [PubMed] [Google Scholar]
- 97. Fakhry A, Ji S. High-resolution prediction of mouse brain connectivity using gene expression patterns. Methods. 2015;73:71–78. doi: 10.1016/j.ymeth.2014.07.011 [DOI] [PubMed] [Google Scholar]
- 98. French L, Pavlidis P. Relationships between gene expression and brain wiring in the adult rodent brain. PLoS Comp Biol. 2011;7(1):e1001049 doi: 10.1371/journal.pcbi.1001049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Starich T, Sheehan M, Jadrich J, Shaw J. Innexins in C. elegans. Cell Commun. Adhes. 2001;8(4-6):311–314. doi: 10.3109/15419060109080744 [DOI] [PubMed] [Google Scholar]
- 100. Zallen JA, Kirch SA, Bargmann CI. Genes required for axon pathfinding and extension in the C. elegans nerve ring. Development. 1999;126(16):3679–3692. [DOI] [PubMed] [Google Scholar]
- 101. Garriga G, Forrester WC, Dell M, Perens E. A C. elegans Ror receptor tyrosine kinase regulates cell motility and asymmetric cell division. Nature. 1999;400(6747):881–885. doi: 10.1038/23722 [DOI] [PubMed] [Google Scholar]
- 102. Leung-Hagesteijn C, Spence AM, Stern BD, Zhou Y, Su MW, Hedgecock EM, et al. UNC-5, a transmembrane protein with immunoglobulin and thrombospondin type 1 domains, guides cell and pioneer axon migrations in C. elegans. Cell. 1992;71(2):289–299. doi: 10.1016/0092-8674(92)90357-I [DOI] [PubMed] [Google Scholar]
- 103. Ikeda DD, Duan Y, Matsuki M, Kunitomo H, Hutter H, Hedgecock EM, et al. CASY-1, an ortholog of calsyntenins/alcadeins, is essential for learning in Caenorhabditis elegans. Proc Natl Acad Sci USA. 2008;105(13):5260–5265. doi: 10.1073/pnas.0711894105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Wu M, Herman MA. A novel noncanonical Wnt pathway is involved in the regulation of the asymmetric B cell division in C. elegans. Dev Biol. 2006;293(2):316–329. doi: 10.1016/j.ydbio.2005.12.024 [DOI] [PubMed] [Google Scholar]
- 105. Hoffmann M, Segbert C, Helbig G, Bossinger O. Intestinal tube formation in Caenorhabditis elegans requires vang-1 and egl-15 signaling. Dev Biol. 2010;339(2):268–279. doi: 10.1016/j.ydbio.2009.12.002 [DOI] [PubMed] [Google Scholar]
- 106. Paemka L, Mahajan VB, Skeie JM, Sowers LP, Ehaideb SN, Gonzalez-Alegre P, et al. PRICKLE1 Interaction with SYNAPSIN I Reveals a Role in Autism Spectrum Disorders. PLoS ONE. 2013;8(12):e80737 doi: 10.1371/journal.pone.0080737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Ehaideb SN, Wignall EA, Kasuya J, Evans WH, Iyengar A, Koerselman HL, et al. Mutation of orthologous prickle genes causes a similar epilepsy syndrome in flies and humans. Ann Clin Transl Neurol. 2016;3(9):695–707. doi: 10.1002/acn3.334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Sowers LP, Loo L, Wu Y, Campbell E, Ulrich JD, Wu S, et al. Disruption of the non-canonical Wnt gene PRICKLE2 leads to autism-like behaviors with evidence for hippocampal synaptic dysfunction. Mol. Psychiatry. 2013;18(10):1077–1089. doi: 10.1038/mp.2013.71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Sarafi-Reinach TR, Melkman T, Hobert O, Sengupta P. The lin-11 LIM homeobox gene specifies olfactory and chemosensory neuron fates in C. elegans. Development. 2001;128(17):3269–3281. [DOI] [PubMed] [Google Scholar]
- 110. Prasad B, Karakuzu O, Reed RR, Cameron S. unc-3-dependent repression of specific motor neuron fates in Caenorhabditis elegans. Dev Biol. 2008;323(2):207–215. doi: 10.1016/j.ydbio.2008.08.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Baran R, Aronoff R, Garriga G. The C. elegans homeodomain gene unc-42 regulates chemosensory and glutamate receptor expression. Development. 1999;126(10):2241–2251. [DOI] [PubMed] [Google Scholar]
- 112. Cassata G, Kagoshima H, Andachi Y, Kohara Y, Dürrenberger MB, Hall DH, et al. The LIM homeobox gene ceh-14 confers thermosensory function to the AFD neurons in Caenorhabditis elegans. Neuron. 2000;25(3):587–597. doi: 10.1016/S0896-6273(00)81062-4 [DOI] [PubMed] [Google Scholar]
- 113. Schmid C, Schwarz V, Hutter H. AST-1, a novel ETS-box transcription factor, controls axon guidance and pharynx development in C. elegans. Dev Biol. 2006;293(2):403–413. doi: 10.1016/j.ydbio.2006.02.042 [DOI] [PubMed] [Google Scholar]
- 114. Shaham S, Bargmann CI. Control of neuronal subtype identity by the C. elegans ARID protein CFI-1. Genes Dev. 2002;16(8):972–983. doi: 10.1101/gad.976002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Choi S, Taylor KP, Chatzigeorgiou M, Hu Z, Schafer WR, Kaplan JM. Sensory Neurons Arouse C. elegans Locomotion via Both Glutamate and Neuropeptide Release. PLoS Genet. 2015;11(7):e1005359 doi: 10.1371/journal.pgen.1005359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Zheng Y, Brockie PJ, Mellem JE, Madsen DM, Maricq AV. Neuronal Control of Locomotion in C. elegans Is Modified by a Dominant Mutation in the GLR-1 Ionotropic Glutamate Receptor. Neuron. 1999;24(2):347–361. doi: 10.1016/S0896-6273(00)80849-1 [DOI] [PubMed] [Google Scholar]
- 117. Romme IAC., de Reus MA, Ophoff RA, Kahn RS, van den Heuvel MP. Connectome Disconnectivity and Cortical Gene Expression in Patients With Schizophrenia. Biol. Psychiatry 2016;15;81(6):495–502. doi: 10.1016/j.biopsych.2016.07.012 [DOI] [PubMed] [Google Scholar]
- 118.Burt JB, Demirtas M, Eckner WJ, Navejar NM, Ji JL, Martin WJ, Bernacchia A, Anticevic A, Murray JD. Hierarchy of transcriptomic specialization across human cortex captured by myelin map topography. bioRxiv 2017; [DOI] [PMC free article] [PubMed]
- 119. Baruch L, Itzkovitz S, Golan-Mashiach M, Shapiro E, Segal E. Using Expression Profiles of Caenorhabditis elegans Neurons To Identify Genes That Mediate Synaptic Connectivity. PLoS Comp Biol. 2008;4(7):e1000120 doi: 10.1371/journal.pcbi.1000120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Roberts JA, Perry A, Lord AR, Roberts G, Mitchell PB, Smith RE, et al. The contribution of geometry to the human connectome. NeuroImage. 2016;124(Pt A):379–993. doi: 10.1016/j.neuroimage.2015.09.009 [DOI] [PubMed] [Google Scholar]
- 121. Mesulam MM. From sensation to cognition. Brain. 1998;121(Pt 6):1013–1052. doi: 10.1093/brain/121.6.1013 [DOI] [PubMed] [Google Scholar]
- 122. Futcher B, Latter GI, Monardo P, McLaughlin CS, Garrels JI. A sampling of the yeast proteome. Mol. Cell. Biol. 1999;19(11):7357–7368. doi: 10.1128/MCB.19.11.7357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Greenbaum D, Colangelo Ch, Williams K, Gerstein M. Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol. 2003;4(9):117 doi: 10.1186/gb-2003-4-9-117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124. Gygi SP, Rochon Y, Franza BR, Aebersold R. Correlation between protein and mRNA abundance in yeast. Mol. Cell. Biol. 1999;19(3):1720–1730. doi: 10.1128/MCB.19.3.1720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Lein E, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature. 2007;445(7124):168–176. doi: 10.1038/nature05453 [DOI] [PubMed] [Google Scholar]
- 126. Hawrylycz MJ, Lein E, Guillozet-Bongaarts AL, Shen EH, Ng L, Miller JA, et al. An anatomically comprehensive atlas of the adult human brain transcriptome. Nature. 2012;489(7416):391–399. doi: 10.1038/nature11405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. Shen EH, Overly CC, Jones AR. The Allen Human Brain Atlas: comprehensive gene expression mapping of the human brain. Trends Neurosci. 2012;32(12):711–714. doi: 10.1016/j.tins.2012.09.005 [DOI] [PubMed] [Google Scholar]
- 128. Parkes L, Fulcher BD, Yücel M, Fornito A. Transcriptional signatures of connectomic subregions of the human striatum. Genes, Brain Behav. 2017;16(7):647–663. doi: 10.1111/gbb.12386 [DOI] [PubMed] [Google Scholar]
- 129. Alstott J, Panzarasa P, Rubinov M, Bullmore ET, Vértes PE. A unifying framework for measuring weighted rich clubs. Sci. Rep. 2014;4:7258 doi: 10.1038/srep07258 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
Hubs are defined as neurons with degree k > 44. For each hub, we list (i) the neuron name, (ii) its degree, k, (iii) location (‘head’, ‘body’, or ‘tail’), and function based on information presented in the wormatlas website http://www.wormatlas.org/. Neurons are sorted (descending) by degree.
(PDF)
Top 15 biological process GO categories enriched in genes with the highest mean increase in CGE for connected neurons compared to unconnected neurons. Categories are sorted by p-value (ascending).
(PDF)
Top 15 biological process GO categories enriched in genes with the highest increase in CGE for connections involving hub neurons (i.e., rich, feed-in and feed-out connections) compared to connections between nonhub neurons (i.e., in peripheral connections). Categories are sorted by p-value (ascending).
(PDF)
(A) Rich-club organization of the synaptic C. elegans connectome. Top: Degree distribution of neurons, labelled to four categories: (i) interneuron (85 neurons, orange), (ii) motor (108 neurons, green), (iii) sensory (68 neurons, blue), or (iv) multiple assignments (18 neurons, yellow). The distribution features an extended tail of high-degree neurons. Bottom: Normalized rich club coefficient, Φnorm (red), as a function of the degree, k, at which hubs are defined (as neurons with degree > k). Also shown is the mean Euclidean separation distance, d (purple) between connected hub regions (across degree thresholds, k). Φnorm > 1 indicates that hubs are more densely interconnected among each other than expected by chance, with red circles indicating values of Φnorm that are significantly higher than an ensemble of 1 000 degree-matched null networks (p < 0.05). Purple circles indicate where the Euclidean distance between connected pairs of hubs is significantly greater than the Euclidean distance for all other pairs of connected regions (right-tailed Welch’s t-test, p < 0.05). (B) Top: Degree distribution, k, of the synaptic C. elegans connectome. Middle: proportion of connections that are: ‘rich’ (hub → hub, red), ‘feed-in’ (nonhub → hub, yellow), ‘feed-out’ (hub → nonhub, orange), or ‘peripheral’ (nonhub → nonhub, blue) as a function of the degree threshold, k, used to define hubs. Note that at high k most neurons are labeled as nonhubs and hence the vast majority of connections are labeled ‘peripheral’. Bottom: Median CGE, , for each connection type as a function of k. The median CGE across all network links is shown as a dotted black line; the topological rich-club regime (determined from the network topology, cf. A) is shaded gray. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Wilcoxon rank-sum test, p < 0.05).
(TIF)
We plot the mean value of each metric across 1000 different pairs of random, binary vectors of length 948, which vary only in their proportion of ‘1’s (between 0–0.15; corresponding to a number of ‘1’s ranging from 1 to 150). This is repeated for: (A) mean square contingency coefficient, rϕ, (B) Jaccard index, (C) Yule’s Q, and (D) our developed positive match measure, pmatch, (see S3 Text). Any systematic trend in correlation values indicates a bias driven by the proportion of positive annotations for a pair of vectors, as is seen for the Jaccard index and Yule’s Q. By contrast, rϕ, which is used through this work, and our probability-based measure, pmatch, used to motivate individual gene scoring for enrichment analysis, show no evidence of systematic bias (note the color axis scales).
(TIF)
The matching probability index, pmatch, as introduced in S3 Text. Top: Degree distribution. Middle: Proportion of connections that are ‘rich’ (hub→hub, red), ‘feed-in’ (nonhub→hub, yellow), ‘feed-out’ (hub→nonhub, orange), and ‘peripheral’ (nonhub→nonhub, blue) as a function of the degree threshold, k, used to define hubs. Note that at high k, most neurons are labeled as nonhubs, and hence the vast majority of connections are ‘peripheral’. Bottom: Mean CGE calculated using similarity index from only positive matches, pmatch, for each connection type as a function of k. The mean CGE across all network links shown as a dotted black line; the topological rich-club regime (determined from the network topology, cf. Fig 5) is shaded gray. Circles indicate a statistically significant increase in CGE in a given link type relative to the rest of the network (one-sided Welch’s t test; p < 0.05).
(TIF)
Here we consider correlated gene expression in the head, where the strongest spatial relationship exists (cf. Fig 4. (A) CGE values, rϕ, plotted as a function of Euclidean separation distance for all pairs of neurons within the head (gray dots), with a fitted exponential trend shown in black, f(x) = A exp(−λx) + B. (B) Taking residuals from this trend does not adequately correct the spatial trend. Note the artifactual negative correlations indicated with an arrow. This indicates that the trend is not a bulk, isotropic effect, but may instead be driven primarily by a small number of neuron pairs with high rϕ at short distances (⪅ 50μm), indicated with a circle in (A). For example, neuron pairs with rϕ > 0.8, are all between the following classes of head neurons: CEP, IL1, OLQ, RMD, RME, RMF, SAAD, SAAV, SAB, SIA, SIB, SMB, SMD, URA, URY.
(TIF)
(A) Degree distribution of the C. elegans connectome. Neurons are labeled to four types as in the legend. (B) Normalized weighted rich-club coefficient, (i.e., topology fixed and weights randomized in the null model, shown orange), and normalized mixed rich-club coefficient, (i.e., both topology and weights mixed in the null model, shown green) are plotted as a function of the degree, k, at which hubs are defined (as neurons with degree > k) [129]. Circles indicate values of Φnorm that are significantly higher than an ensemble of 1 000 degree-matched null networks (Welch’s t-test, p < 0.05). Compared to topological rich-club analysis presented in the main text, here the weights of the connections are also accounted for when calculating the rich club coefficient. In the case of the weighted rich-club coefficient, the topology for the null models was kept stable and only the weights of the connections randomized. Results presented here show that connections between higher degree nodes are stronger than expected by chance. On the other hand, in the mixed rich club coefficient both the topology and weights are randomized, therefore we see the combined effect of both types. Distinction between the different null models is discussed in detail in [129]. These results show that connections between high degree nodes are both denser and stronger than expected by chance.
(TIF)
Hub-hub connections (‘rich’) are shown red, and all other connections (‘non-rich’, i.e., feeder and peripheral) are shown gray, where hubs are defined as neurons with degree, k > 44. Anatomical locations are labeled as ‘head’, ‘body’, and ‘tail’, and each connection is labeled according to its source and target neurons, listed on the vertical axis in the form ‘Source-Target’. The plot shows that the increased separation distance between connected hubs relative to other types of connected neurons is driven by a relative increase in long-range connections between the head and tail.
(TIF)
A list of genes that contributed towards the (i) increased CGE in connected compared to unconnected pairs of neurons, and (ii) increased CGE in rich and feeder compared to peripheral connections.
(XLSX)
Data Availability Statement
Data used for analysis in this work were obtained from publicly available sources, and can be downloaded from an accompanying figshare repository (figshare.com/s/797199619fbabdab8c86). Code to process this data and reproduce all figures and analyses presented here is on github (github.com/BMHLab/CElegansConnectomeGeneExpression).