Impact of seasonal influenza vaccination in the presence of vaccine interference

Abstract

Background

Annual influenza vaccination is a key to preventing widespread influenza infections. Recent reports of influenza vaccine effectiveness (VE) indicate that vaccination in prior years may reduce VE in the current season, suggesting vaccine interference. The purpose of this study is to evaluate the potential effect of repeat influenza vaccinations in the presence of vaccine interference.

Methods

Using literature-based parameters, an age-structured influenza equation-based transmission model was used to determine the optimal vaccination strategy, while considering the effect of varying levels of interference.

Results

The model shows that, even in the presence of vaccine interference, revaccination reduces the influenza attack rate and provides individual benefits. Specifically, annual vaccination is a favored strategy over vaccination in alternate years, as long as the level of residual protection is less than 58% or vaccine interference effect is minimal. Furthermore, the negative impact of vaccine interference may be offset by increased vaccine coverage levels.

Conclusions

Even in the presence of potential vaccine interference, our work provides a population-level perspective on the potential merits of repeated influenza vaccination. This is because repeat vaccination groups had lower attack rates than groups that omitted the second vaccination unless vaccine interference was at very high, perhaps implausible, levels.

1. Introduction

Annual influenza vaccination is a critical public health measure for preventing widespread influenza infections and their attendant morbidity and mortality. The United States (U.S.) Advisory Committee on Immunization Practices (ACIP) recommends annual influenza vaccination for all individuals six months of age and older [1]. However, in Canada, the United States, and Europe, lower vaccine effectiveness (VE) estimates against influenza A (H3N2 and H1N1) virus illness have been observed ([2–11]) among those vaccinated during the previous season(s), compared to those not vaccinated. Similar results were reported in another multi-season analysis where the highest protection against influenza A (H3N2) illness was observed among vaccinees who had been not been vaccinated in the previous 5 years (VE=65%, 95% CI=36–80) and the lowest VE was among those repeatedly vaccinated in 4 or 5 recent seasons (VE=25%, 95% CI=3–41%) [8]. Such findings are also consistent with results from a household cohort study, which indicated lower VE against A (H3N2) illness among those vaccinated in both the current and prior year than those only vaccinated in the current season [12]. Additionally, in a prospective cohort study of healthcare personnel (HCP) ages 18–65 years, the magnitude of immune response indicated by geometric mean titer or geometric mean ratio declined with the number of inactivated trivalent influenza vaccine(s) (IIV3) received during the prior 4 years, among all age groups [7]. In contrast, a recent meta-analysis found interference only for influenza A (H3N2) and actually found enhanced responses for influenza A (H1N1) and B with repeat vaccination [13]. However, it was also suggested that caution is required in the interpretation of pooled results across multiple seasons, because pooling can mask important variation in repeat vaccination effects among seasons [14].

Taken together, there exists some evidence on negative interference, namely a negative effect of prior vaccination on the current season’s VE that reduces protection against influenza infection (i.e., a lower but still positive vaccine effectiveness point estimate). Furthermore, previous prospective studies have suggested that negative interference from prior influenza vaccination may be especially pronounced when the composition of vaccine antigens has been unchanged and the match with circulating strains is not strong [8, 9, 12].

These findings raise questions about standard flu vaccination recommendations, i.e., should individuals be revaccinated annually to be protected against ever-mutating viruses? In this study, we sought to assess the impact of annual influenza vaccination in the presence of vaccine interference to address this question.

2. Methods

To assess the epidemiological impact of revaccination at various levels of vaccine interference (VI), we present an age-structured model of influenza dynamic transmission and vaccination in which an individual’s VE was assumed to be dependent on age and vaccination status in a prior season (Table S1) [3, 9]. Specifically, the model assumed that the VE in individuals who received influenza vaccine in two consecutive years was generally lower than that of vaccine recipients who were unvaccinated in the prior season [8, 9]. Dynamic models implicitly capture the herd protection conferred by vaccination and thus the incorporate vaccine-induced indirect protection. Model parameters were based on the current age distributions in the U.S. and vaccination rates in age groups [15], and estimated the influenza incidence levels [16].

2.1 Susceptibility and Infectivity

The influenza-related epidemiologic status of individuals was tracked in eight age-dependent classes. All individuals in the population are (partially) susceptible to infection prior to the influenza season. Specifically, individuals in age group k at time t are divided into four epidemiological classes depending on their vaccination status: individuals vaccinated prior season only (T_k(t)), individuals vaccinated in current and prior seasons (W_k(t)), individuals not vaccinated in either season (S_k(t)), and individuals vaccinated in current season only (V_k(t)). We assumed that vaccination provides partial protection, thus resulting in vaccinated individuals being less susceptible than unvaccinated ones.

In addition to these four (partially) susceptible classes, the model has four additional epidemiological classes: exposed individuals who are not infectious yet (E_k(t)), individuals who are infectious and asymptomatic (A_k (t)), individuals who are infectious and symptomatic (I_k(t)), and recovered individuals (R_k(t)). Each epidemiologic class was subdivided into five age groups, which are denoted by the subscript k (k = 1,…, 5) and correspond to 0–8 years, 9–17 years, 18–49 years, 50–64 years, and ≥ 65 years. Those who received an influenza vaccine in a prior season were assigned to the epidemiological class T_k, whereas the others were assigned to the class S_k. Thus, consistent with recent observations [17], the following values were assigned: T₁(0) = 0.62n₁, T₂(0) = 0.53n₂, T₃(0) = 0.33n₃, T₄(0) = 0.44n₄, T₅(0) = 0.63n₅; S_k(0) = n_k − T_k(0) − I_k0; W_k(0) = 0; V_k(0) = 0; E_k(0) = 0; A_k(0) = 0; I_k(0) = I_k0; and R_k(0) = 0 where n_k denotes the size of age group k [8, 17].

2.2 Vaccine Effectiveness (VE) and Vaccine Interference (VI)

We assumed that VE is dependent on both an individual’s age and on his or her history of vaccination (Table 1). For instance, the model assumes that individuals in age group k who were vaccinated in both current and prior seasons would become infected at a fraction (1 − ε_W,k) of the rate at which unvaccinated susceptible individuals (S_k) become infected. Here ε_W,k denotes the VE against infection for individuals who were vaccinated in both prior and current seasons. Similarly, we define ε_V,k as the VE among individuals who are vaccinated in the current season only, while ε_T,k denotes the VE among individuals who are vaccinated in the prior season only. In other words, the level of residual protection by vaccination in the prior year is represented by ε _T,k. For our simulations, we fixed the values of ε_V,k and ε_T,k at baseline values shown in Table 1, and let ε_W,k be determined by various levels of VI. Specifically, to measure the degree of VI, we defined the level of VI as one minus the relative VE of repeat vaccinees compared to that of vaccine recipients who skipped the influenza vaccine in a prior season: $VI=1-\frac{{\epsilon }_{W,k}}{{\epsilon }_{V,k}}$. Thus, at high level of VI, the protection conferred among repeat vaccinees, W_k(t), is assumed to be minimal compared to individuals who are vaccinated in the current season only, V_k(t).

Table 1.

Baseline age-specific efficacy of current and prior vaccination against influenza [30, 32, 33].

Age	Vaccination history	Vaccine efficacy (%)
		Notation	Baseline value
<9 years	Vaccinated both current and prior season	(1-VI) εV,1	Varied between 0
	Vaccinated current season only	εV,1	0.69
	Vaccinated prior season only	εT,1	0.50
9–17 years	Vaccinated both current and prior season	(1-VI) εV,2	Varied between 0 and 0.74
	Vaccinated current season only	εV,2	0.74
	Vaccinated prior season only	εT,2	0.61
18–49 years	Vaccinated both current and prior season	(1-VI) εV,3	Varied between 0 and 0.63
	Vaccinated current season only	εV,3	0.63
	Vaccinated prior season only	εT,3	0.33
50–64 years	Vaccinated both current and prior season	(1-VI) εV,4	Varied between 0 and 0.80
	Vaccinated current season only	εV,4	0.80
	Vaccinated prior season only	εT,4	0.50
≥65 years	Vaccinated both current and prior season	(1-VI) εV,5	Varied between 0 and 0.46
	Vaccinated current season only	εV,5	0.46
	Vaccinated prior season only	εT,5	0.73

2.3 Epidemiology and Infectivity of Influenza

When individuals are infected, they enter a latency period. The latent period (1/τ) was assumed to be 1.2 days, on average [18–20]. Latently infected individuals become infectious with the probability of symptomatic illness, p (p = 0.67) [21, 22]. Infection rate in age group k (λ_k) is proportional to the number of infected individuals, i.e. λ_k = β_k Σ_j θ_kj{bA_j (t) + I_j (t)}/N(t) where we denote the total population size by N(t). Persons with asymptomatic disease were assumed to be half as infectious as those with symptomatic illness, i.e., b = 0.5 [20, 23–25]. We defined θ_kj as the contact rate for infectious individuals of age group j (A_j or I_j) with susceptible individuals of age group k (S_k), where β_k represents the transmission probability per contact in age group k. In the transmission model, contact rates (θ_kj) were parameterized based on the European age-dependent contact matrix that describes age group mixing [26]. The transmission probability per contact in age group k, β_k, was calibrated to capture the patterns of symptomatic influenza incidence and age-specific susceptibility in the U.S, based on influenza illness rates and vaccine coverage levels in the respective age groups (Table S1) [15, 16]. The average infectious period, 1/γ, was assumed to be four days [27–29]. Recovered individuals were assumed to be protected against further influenza infection for the remainder of the outbreak.

Based on our assumptions and definitions, the model can be described as:

$$\begin{gathered} {T_k}^{\text{'}}=-\{{\lambda }_k(1-{\epsilon }_{T,k})+{\phi }_k\}{T}_k, \\ {S_k}^{\text{'}}=-\{{\lambda }_k+{\rho }_k\}{S}_k, \\ {W_k}^{\text{'}}={\phi }_k{T}_k-{\lambda }_k(1-{\epsilon }_{W,k})W_k, \\ {V_k}^{\text{'}}={\rho }_k{S}_k-{\lambda }_k(1-{\epsilon }_{V,k})V_k, \\ {E_k}^{\text{'}}={\lambda }_k\{(1-{\epsilon }_{T,k})T_k+S_k+(1-{\epsilon }_{W,k})W_k+(1-{\epsilon }_{V,k})V_k\}-\tau E_k, \\ {A_k}^{\text{'}}=(1-p)\tau E_k-\gamma A_k, \\ {I_k}^{\text{'}}=p\tau E_k-\gamma I_k, \\ {R_k}^{\text{'}}=\gamma (A_k+I_k) \end{gathered}$$

where λ_k = β_k Σ_jθ_kj{bA_j (t) + I_j (t)}/N(t).

2.4 Vaccination Rates

The model tracked an individual’s vaccine history for two influenza seasons. We defined ϕ_k and ρ_k as the vaccination rate in the current season among epidemiological classes T_k and S_k, respectively. Vaccination acceptance rate was shown to differ between vaccinees and non-vaccinees in a prior season. Thus, based on recent observations, we assumed that the relative ratio of the individuals vaccinated in both seasons to the individuals who were vaccinated in a current season only was 2.29 [30]. The overall vaccine coverage levels in age groups were parameterized based on monthly vaccine coverage levels in the U.S. To calibrate the model, we used the influenza vaccination coverage during the 2012–2013 season, which ranged between 36% in adults (aged 20–64 years) and 70% in younger children (aged 6 months to 4 years) [16, 31]. Across age groups, the vaccine coverage level was 45%. Therefore, the vaccination parameters φ_k and ρ_k were estimated so that ${\displaystyle \underset{t=0}{\overset{T_f}{\int }}}\left({\displaystyle \sum _k}{\varphi }_k{T}_k+{\rho }_k{S}_k\right)dt=0.45$, a final vaccination coverage across age groups, and $\frac{{\displaystyle \underset{t=0}{\overset{T_f}{\int }}}\left({\displaystyle \sum _k}{\varphi }_k{T}_k\right)dt}{{\displaystyle \underset{t=0}{\overset{T_f}{\int }}}\left({\displaystyle \sum _k}{\rho }_k{S}_k\right)dt}=2.29$ where ρ_k = qϕ_k, consistent with empirical observations, resulting in q = 0.27 [30].

The model was run over a 10-month time horizon (i.e., a single influenza season) spanning August through May. Given this short time horizon, aging was ignored in this model. Our numerical simulations and sensitivity analyses were done with the ODE 45 solver of MATLAB 2015b which uses Runge Kutta method of fourth order. Specifically, we defined the system of differential equations and parameters in the body of the function file. In addition, the initial and final times as well as a vector for initial values were defined. We then called MATLAB ODE solver “ode45” to solve the system of differential equations, and retrieved the output of the ODE solver “ode45”.

3. Results

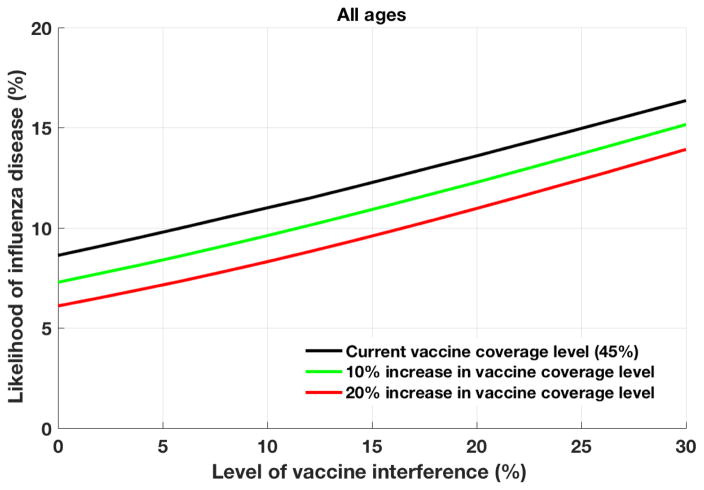
In the base case analysis where the VI was 11% across age groups, the model was fitted to result in a likelihood of influenza disease of 11.3%, consistent with recent observations (Fig. 1) [16]. Using baseline vaccination rates and increasing influenza VI due to the prior year’s vaccination, to 30% in all age groups, the likelihood of influenza disease increased to 16.7%. With an increasing VI, the likelihood of influenza disease generally increased, indicating that VI might significantly reduce the impact of influenza vaccination.

Figure 1.

The likelihood of clinical influenza disease with various vaccine coverage levels.

The probability of clinical influenza disease is calculated, averaged over all ages, at increasing levels of vaccine coverage.

However, the negative effects of VI on VE may be offset by increasing vaccination uptake (Fig. 1). For instance, if vaccine coverage increased by 10%, then the likelihood of influenza disease was slightly lower (9.8%) than the baseline case (11.3%). This held true even in the presence of VI, as long as the degree of VI was <16%. Similarly, increasing vaccine coverage by 20% reduced the likelihood of influenza disease by 2–4% over a range of VI values.

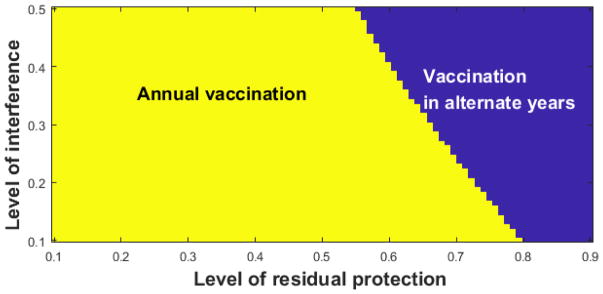
Given the VI observed for annual vaccination without increasing influenza vaccine uptake, two-way sensitivity analysis was used to compare annual vaccination and vaccination in alternate years. The analysis simultaneously varied the level of VI and ε_T,k, i.e., the level of residual protection among individuals vaccinated in the prior season only, which was held constant across all age groups (Fig. 2). The likelihoods of influenza among those vaccinated in the prior season only and those vaccinated in both prior and current seasons were calculated and compared over a range of parameter values of VI and ε_T,k. Annual vaccination was shown to be favored over almost all plausible ranges of VI and ε_T,k. Specifically, annual vaccination would be favored unless the residual protection (ε_T,k) is greater than 55%. In addition, even when the residual protection is over 55%, annual vaccination continues to be favored as long as VI effect is minimal. For instance, even when the level of residual protection (ε_T,k) is 70%, annual vaccination is favored if the level of VI is less than 22%.

Figure 2.

Two-way sensitivity analysis–annual vaccination vs. vaccination in alternate years.

For two-way sensitivity analysis, we simultaneously varied the level of vaccine interference (VI) and ε_T,k, i.e., the level of residual protection among individuals vaccinated in the prior season only. The likelihoods of influenza among those vaccinated in the prior season only and those vaccinated in both prior and current seasons were calculated and compared over a range of parameter values of VI and ε_T,k. The area where the likelihood of influenza among annual vaccinators (W_k) is lower than that among individuals who are vaccinated in alternate years (T_k) is depicted in yellow. The area where vaccination in alternate years results in lower likelihood of influenza than among annual vaccinators is depicted in blue.

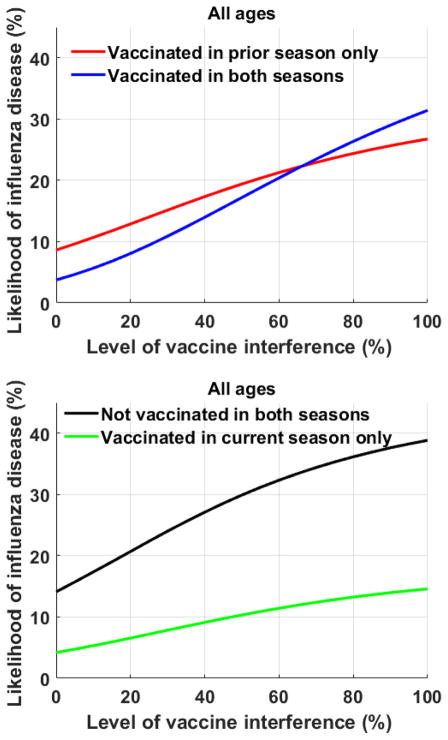
To examine the benefits of vaccination at an individual level, the likelihood of influenza disease was compared between current season vaccinees and non-vaccinees. The level of residual protection (ε_T,k) was fixed at its age-specific baseline levels (Table 1) [30, 32, 33]. Among individuals vaccinated the prior season, the likelihood of influenza disease was lower for those vaccinated in the current season compared to those not vaccinated in the current season, if VI was less than 66% (Fig. 3a). Similarly, among individuals not vaccinated in the prior season influenza disease was lower among those vaccinated in the current season than among those who were unvaccinated, at all levels of VI (Fig. 3b). With increasing levels of VI, the pool of susceptibles grows, resulting in higher infection rates. Individual benefits of annual vaccination even in the presence of VI, were consistent across all age groups, and most pronounced among younger adults (ages 20–64).

Figure 3.

The likelihood of influenza disease.

To examine the benefits of vaccination at an individual level, the likelihood of influenza disease was compared between vaccinees and non-vaccinees a) among individuals receiving influenza vaccine in the prior year; and b) among individuals who skipped influenza vaccine in the prior year.

4. Discussion

Questions about the efficacy of repeated influenza vaccines have been raised for decades. In 1999, it was suggested that in years when a component of the vaccine had changed little or not at all from the previous year’s vaccine and when antigenic drift occurred between the first year’s vaccine and the circulating strain, the second year’s vaccine effectiveness would be reduced–a level of protection referred to as “negative interference” [34]. The negative interference effect by repeat vaccination is hypothesized to be due to antigenic distance [35]; that is, the antibodies produced in one year may neutralize some of the vaccine’s antigens in the subsequent year before it can trigger a full immune response [34]. In recent years, vaccine interference was observed in Canada, the United States, and Europe, showing that revaccination reduces vaccine effectiveness [3, 5, 8, 10, 11]. The level of vaccine interference was shown to be dependent on ages of individuals as well as the influenza strains. Specifically, the level of vaccine interference estimated recently ranged from 5% (when estimated against influenza A (H3N2) among individuals aged >9 years) to 17% (when estimated against influenza B/Yamagata among individuals aged 18–49 years) [30].

As a result, it might be hypothesized that variation in repeat vaccine efficacy is due to differences in antigenic distances among vaccine strains and between the vaccine strains and the epidemic strain in each outbreak. As Belongia et.al. noted, repeated vaccination of low-risk individuals might produce immunologic effects that inhibit response to a new virus [14]. Nevertheless, offering influenza vaccine in alternate years might seem to allow antibody titers to fall and thus reduce negative interference in the following year. However, we show through mathematical modeling, that annual vaccination is likely to be a favored strategy over vaccination in alternate years. This held true based on our simulations, as long as the residual protection was < 55%, over the entire a range of VI considered (0–50%). In fact, annual vaccination reduces the influenza attack rate and provides individual benefits even in the presence of vaccine interference, and individuals vaccinated in a prior season are less likely to be infected if they choose to be revaccinated in a current season, as long as the level of VI is less than 66%. Furthermore, the negative impact of vaccine interference can be offset by increasing the levels of vaccine coverage. The effect of increased vaccination uptake was most apparent among younger adults ages 20–64 years, presumably because this age group has the lowest vaccination rate thus, they have lower indirect protection from herd immunity than other age groups.

4.1 Strengths and Limitations

This study used equation-based dynamic transmission modeling to examine the effects of VI and potential support for alternate year influenza vaccination. Other studies have reported VI from prior years’ vaccine, but this is the first to use modeling to predict the effects of this vaccination policy. Limitations of this model include the fact that VE can be affected by numerous factors that may not have been accounted for. Research is needed to differentiate host, virus, and vaccine technology factors that may contribute to the imperfect immunogenicity and clinical protection afforded by influenza vaccination that may improve the model. The model captured just two years of vaccination history due to lack of data. A meta-analysis or systematic review of interference and the situations in which it arises, as well as the effects of infection history on VE, were published recently [13, 14]; we varied the interference widely to account for these uncertainties (e.g., Fig. 2). Incorporating more years of vaccination history and their effects on vaccine interference into the model would enhance the robustness of the results. The data on interference were generally available over a two-year time frame; thus we did not take a longer perspective which limits the analysis. In addition, a new study conducted by Canada’s Sentinel Practitioner Surveillance Network (SPSN) indicated that the individuals who were vaccinated 3 years in a row beginning in 2012 appeared to have a higher risk of being infected with the dominant flu strain in the latter season [36]. Such negative VE estimate would suggest that vaccine interference might be associated with increased risk of disease, which has not been considered in our modeling study. Memory responses from prior infection with a related subtype are a complex part of the immune response, particularly if imprinting is involved [14, 37]. We address this indirectly by using age-specific susceptibility in the model; a future goal would be to separately incorporate the direct effects of infection and of vaccination, but this requires a highly detailed agent-based model.

4.2 Conclusions

Using an age-structured model of influenza transmission and vaccination, we found that even in the presence of vaccine interference and residual protection from vaccination in a prior year, a policy of annual influenza vaccination still provides benefits to vaccine recipients, and thus continue to be a safe and effective way to reduce influenza-related illnesses and deaths.

Highlights.

• Previous influenza vaccination appears to lower vaccine effectiveness.

• We developed an influenza transmission model with vaccination.

• We compared the effect of annual vaccinations and vaccination in alternate years.

• Annual vaccination was a still effective strategy, even with vaccine interference.