Modeling the Emergence of Antibiotic Resistance in the Environment: an Analytical Solution for the Minimum Selection Concentration

ABSTRACT

Environmental antibiotic risk management requires an understanding of how subinhibitory antibiotic concentrations contribute to the spread of resistance. We develop a simple model of competition between sensitive and resistant bacterial strains to predict the minimum selection concentration (MSC), the lowest level of antibiotic at which resistant bacteria are selected. We present an analytical solution for the MSC based on the routinely measured MIC, the selection coefficient (sc) that expresses fitness differences between strains, the intrinsic net growth rate, and the shape of the bacterial growth dose-response curve with antibiotic or metal exposure (the Hill coefficient [κ]). We calibrated the model by optimizing the Hill coefficient to fit previously reported experimental growth rate difference data. The model fit varied among nine compound-taxon combinations examined but predicted the experimentally observed MSC/MIC ratio well (R² ≥ 0.95). The shape of the antibiotic response curve varied among compounds (0.7 ≤ κ ≤ 10.5), with the steepest curve being found for the aminoglycosides streptomycin and kanamycin. The model was sensitive to this antibiotic response curve shape and to the sc, indicating the importance of fitness differences between strains for determining the MSC. The MSC can be >1 order of magnitude lower than the MIC, typically by the factor sc^κ. This study provides an initial quantitative depiction and a framework for a research agenda to examine the growing evidence of selection for resistant bacterial communities at low environmental antibiotic concentrations.

INTRODUCTION

Effective management of antibiotic risks in the environment requires an understanding of the factors responsible for the emergence, transmission, and maintenance of antibiotic resistance (1). It is particularly important to address the question of when resistant bacteria predominate as a result of environmental antibiotic pollution (1–5). For example, insights are needed into the extent to which antibiotics in aquatic environments contribute to the spread of resistance and to the long-term prevalence of resistant infections in humans (2, 5).

The mutant selection window (MSW) paradigm states that resistant mutants may develop between the lowest boundary concentration of selection for resistance and the upper boundary concentration of growth inhibition of the most resistant potential mutant (the mutant prevention concentration [MPC]) (6, 7). The paradigm further indicates that the lower boundary concentration of the MSW is the MIC (nanograms per milliliter), and the MIC has been useful to evaluate the hazard of selection for resistance in natural aquatic environments (4, 8). Considerable research in vitro and in vivo has demonstrated that resistant mutants develop between the MIC and the MPC (7, 9, 10), but many laboratory and theoretical studies indicate that resistant mutants can also be preferentially selected above the minimum selective concentration (MSC) (nanograms per milliliter), defined as the lowest concentration at which a resistant strain outcompetes and displaces sensitive isolates (1, 11–18). Because the MSC can be lower than the MIC, and to minimize the hazard of resistance occurring in the natural environment (e.g., aquatic systems), further characterization and understanding of the MIC-versus-MSC relationship would be beneficial (8).

Laboratory experiments (11–13, 16, 18) have elegantly demonstrated MSCs ranging from 1/4 to below 1/200 of the MIC for antibiotics of several classes (e.g., macrolides, aminoglycosides, fluoroquinolones, and antifolates) and for two metals in Escherichia coli or Salmonella enterica serovar Typhimurium LT2. This finding may help explain the high levels of resistance found in the environment, particularly at subinhibitory antibiotic concentrations (2, 5, 11). These studies further indicate that the fitness cost of the resistance-conferring mutations is more important than differences in MICs between strains for discerning how much below the MIC the resistant bacteria will predominate (12). However, a mathematical description of the competition between strains would aid in understanding strain- and antibiotic-specific results and generalizing these results to a wider range of situations.

Mechanistic mathematical models, including experimentally validated pharmacodynamic/pharmacokinetic models, describe antibiotic effects better than simple MIC measurements (19–23). For example, the shape of the antibiotic dose-response curve is very important for the microbiological efficacy of antibiotic treatment regimens at high (treatment) levels (19). The implications of this understanding of the dose-response curve shape for low (subinhibitory) antibiotic levels and for calculation of the MSC, while relevant for the selection of resistance, have not been considered in as much depth. To complement recent empirical research (1, 11–13, 16, 18), there remains a need for a quantitative model describing the MSC, i.e., the minimum environmental antibiotic concentration that allows resistant bacterial strains to dominate. Such a model can generate testable predictions, identify the factors that determine water or soil antibiotic concentrations that select for resistance, and be incorporated into hazard assessments for antibiotic resistance development (1). For example, comparisons of the range of observed or modeled antibiotic concentrations to MSC thresholds would aid in comparing the relative likelihoods of selection for resistance under different observed or modeled environmental and management conditions.

An analytical solution for the MSC has two potential uses. First, model sensitivity analysis and examination of the parameter structure may provide insight into the relationship between commonly considered bacterial growth and antibiotic dose-response parameters and the MSC itself. Second, current methodology to accurately measure the MSC requires the direct measurement of competition between bacterial strains and specialized methods such as fluorescent-cell tagging and flow cytometry (12, 16). An analytical solution provides a potential alternative to these methods, instead estimating the MSC based on the bacterial growth rate and antibiotic dose-response parameters that are routinely obtained within microbiology laboratories. To that end, this paper addresses three questions. (i) How do we quantitatively define the MSC via a parsimonious mathematical model in combination with readily available measurements? (ii) How well does such a mathematical model of the MSC fit to reported empirical data? (iii) Which model parameters, representing biological characteristics, are most important to describe the MSC?

The model that we propose in this paper describes the MSC based on the competition between a wild-type strain and a resistant strain of bacteria and the key factors that favor the growth of resistant strains at subinhibitory antibiotic concentrations. The model focuses on conspecific bacteria and is calibrated to the experimental results reported previously by Gullberg et al. (12, 16) for E. coli and S. Typhimurium. The model illustrates the shape of the antibiotic dose-response curve as a measurable and influential driver of the ratio of the MSC and MIC and presents a hypothesized dose-response relationship for use in the risk assessment of resistance development in environmental settings. Finally, we discuss the implications of the MSC results for the increased risk of antibiotic resistance selection at antibiotic concentrations observed in antibiotic-contaminated waste streams and natural waters.

RESULTS

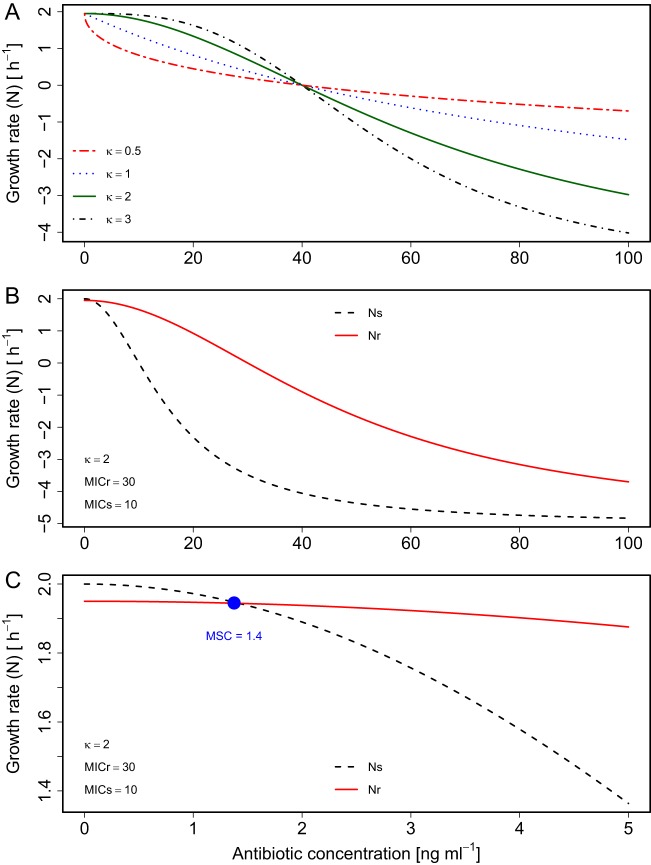
Figure 1 depicts the change in the growth rate (N) versus the antibiotic concentration (see equation 7 in Materials and Methods), the crossover point between the growth rates of sensitive (N_s) and resistant (N_r) strains (i.e., the MSC) (see equation 8), and an analytical solution for the MSC/MIC ratio (see equations 10 and 11). The MSC can be observed as the antibiotic concentration at which N_s (see equation 1) and N_r (see equation 2) cross, indicating identical growth of sensitive and resistant strains (Fig. 1B and C, and see equation 8). The MSC/MIC ratio (12) is of interest because this ratio enables the ready calculation of the MSC given the MIC. The MSC is of particular interest as the environmental antibiotic concentration at which resistance selection could occur among competing bacteria populations (1, 15). The MSC can be calculated by employing this ratio in combination with routinely available MIC data (4, 8, 24) (see the EUCAST database at https://mic.eucast.org/Eucast2/). The obtained MSC can then be directly compared to measured antibiotic concentrations.

FIG 1.

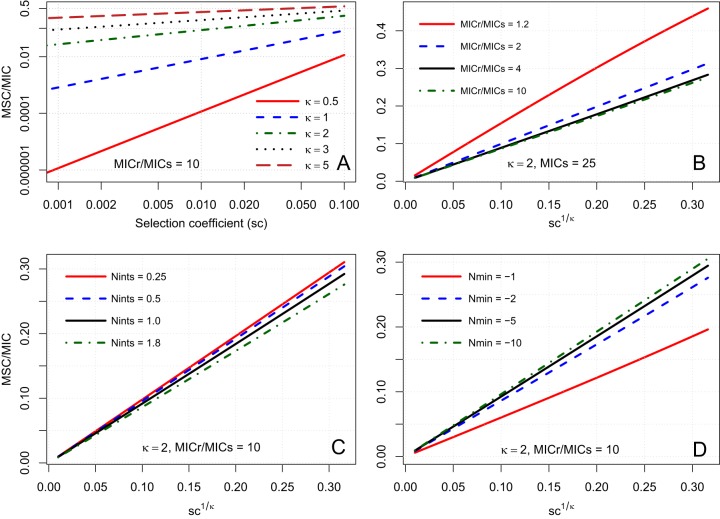
Theoretical comparison of growth rate versus antibiotic concentration (employing equations 1, 2, 5, and 6). (A) Single strain (MIC_r = 40 ng ml⁻¹) with different κ values. (B and C) Sensitive and resistant strains (MIC_s = 10 ng ml⁻¹, MIC_r = 30 ng ml⁻¹, and κ = 2). Panel C shows an enlarged view around the MSC (blue dot), the concentration where growth curves cross (ΔN = 0). Other parameter values were a selection coefficient value of 0.05, an N_int,s of 2 h⁻¹, and an N_min of −5 h⁻¹.

We first evaluate the model by examining the effect of varying κ, the Hill coefficient of the equation representing the loss in net growth due to antibiotic concentration, as well as of N_min, the minimum possible growth rate. We then compare the predicted growth rates and MSC/MIC ratios to previously reported data. We then examine model behavior and implications for MSC/MIC ratio predictions. Finally, we perform a sensitivity analysis to identify the most important parameters for predicting this ratio, looking at κ, N_min, the selection coefficient (sc), and the intrinsic growth rate (N_int).

Model evaluation. (i) Effect of varying κ and N_min for sensitive versus resistant strains.

The analytical solution for equation 10 requires identical κ and N_min values for sensitive and resistant strains. We evaluated the impact of this assumption on model predictions by determining which strain-specific parameter values (i.e., κ_s, κ_r, N_min,s, or N_min,r) were most important for predicting the MSC. To achieve this, we performed a Monte Carlo simulation sensitivity analysis, as detailed in the supplemental material text and in supplemental Table S1. In two simulations, the predicted value of MSC was obtained by using equation 10, assuming separate κ_s, κ_r, N_min,s, and N_min,r values in equations 5 and 6. To be robust to MIC ratio variations, the first simulation had an MIC_r that was 1.5× MIC_s, whereas the second simulation had an MIC_r value equal to 10× MIC_s. In both simulations, the MSC was highly sensitive to κ_s (Spearman rank correlation coefficient [ρ] value of >0.8) but was insensitive to N_min,s or N_min,r (∣Spearman ρ∣ absolute value of ≤0.11). This much stronger influence of κ than of N_min is expected based on the fact that κ is an exponential term (see equations 10 and 11). The MSC was also more sensitive to κ_s than to κ_r, and the ∣Spearman ρ∣ absolute value between κ_s and the MSC (ρ = 0.83) was more than twice the ∣ρ∣ absolute value between κ_r and the MSC (ρ = −0.39). When the MIC_r was 10× MIC_s, almost all variation in the MSC was explained by κ_s (ρ = 0.97), with ρ being equal to −0.09 for κ_r. These results indicate that the MSC will strongly depend on κ_s, the shape of the antibiotic dose response for the sensitive strain. As a result, for the indirect estimation of the MSC using equation 10, κ_s should be well characterized experimentally.

(ii) Model performance for predicting differences in net growth rates.

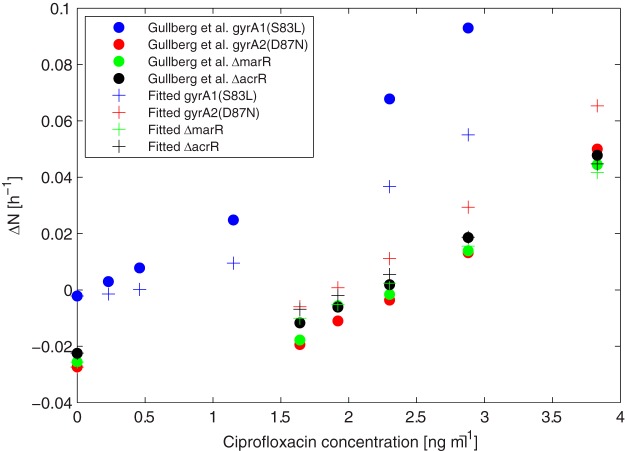
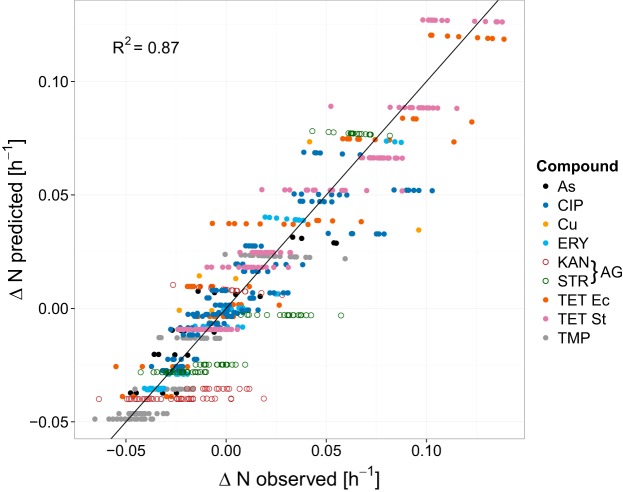
Figures 2 and 3 display the differences in net growth rates for sensitive versus resistant strains (ΔN) for previously reported experimental data in comparison to the model (see equation 7). Figure 2 illustrates how ΔN increases with increasing antibiotic concentrations for the ciprofloxacin (CIP) experiments reported previously by Gullberg et al. (12), with variability being due to the examination of four bacterial strains. Figure 3 directly compares the experimentally observed and model-predicted ΔN values for all antibiotics and metals examined. The model-predicted results overlapped the range of experimental observations under most conditions. Much of the variability was attributable to experimental variation rather than model error, as evident in the horizontal spread of points for each compound. However, the model underpredicted experimental results for the aminoglycosides kanamycin (KAN) and streptomycin (STR) (Fig. 3, open circles) when ΔN was <0.05. Consequently, linear regression indicated that ΔN_modeled = 0.93(ΔN_observed) − 0.002, a slight underprediction. By examining results for individual compounds, the model performances (R², Q², and PRESS/SSY [predictive residual sum of squares/total sum of squares]) were generally similar when either one parameter (κ) or two parameters (κ and N_min) were fitted and for either the raw or averaged experimental data (see Table S2 in the supplemental material). For CIP, erythromycin (ERY), KAN, and STR, the model fit was insensitive to N_min, exhibiting a wide range of possible values and a limited impact on model fit. Therefore, N_min was fixed at a representative literature value of −2 (19, 25, 26), and κ was fitted to experimental observations. The fitted model was generally consistent with raw observations (R² > 0.8), and the model exhibited high predictive value in cross-validation (CV) (Q² > 0.8) for tetracycline (TET), trimethoprim (TMP), ERY, and arsenite in E. coli and for TET in Salmonella Typhimurium (Table 1; see also Fig. S2 to S5 and S9 in the supplemental material). The model fit was moderate for CIP (R² = 0.78) (Fig. 2), Cu (R² = 0.73) (Fig. S7), and STR (R² = 0.67) (Fig. S8). For KAN, the model fit was poor, worse than a simple average of the data, i.e., a slope equal to zero (R² < 0), indicating that it was not possible to fit the model to the KAN data (Fig. S6). The model fit to KAN was also poor for several alternative statistical models, including Weibull, logit, logistic, and probit formulations.

FIG 2.

Comparison between experimentally observed (12) and model-predicted differences in the net growth rates between sensitive and resistant bacterial strains (ΔN, from equation 7) as a function of the ciprofloxacin concentration in E. coli. The model was fit to reported average (12) growth rate differences at each antibiotic concentration for each of four resistant strains, and κ and N_min were fitted (parameter values can be found in Tables S2 and S3 in the supplemental material).

FIG 3.

Model-predicted versus observed ΔN values for all experiments (12, 16). The model was fit to reported raw experimental growth rate differences for each compound, concentration, bacterial species, and resistant strain. κ was separately fitted for each compound-species combination. Abbreviations: As, arsenite; Cu, copper(II) sulfate; AG, aminoglycoside antibiotic; Ec, E. coli; St, Salmonella Typhimurium.

TABLE 1.

Results of model^a optimization to previously reported^b empirical growth rate differences (ΔN) between sensitive and resistant strains, based on the strain-specific selection coefficient, MIC_s, and MIC_r^c

Compoundd	Organism	No. of strains	N	κ	R2	Q2e	PRESS/SSY	MSC/MICs ratio
TET	E. coli	3	60	1.6	0.89	0.89	0.09	0.014
								0.063
TMP	E. coli	2	118	2.5	0.88	0.87	0.07	0.18
ERY	E. coli	3	64	3.5	0.94	0.93	0.07	0.074
								0.27
KAN	E. coli	2	72	10.5	−0.47	−0.48	0.43	0.66
As	E. coli	2	20	0.7	0.84	0.81	0.30	0.0064
Cu	E. coli	2	8	1.9	0.73	0.43	0.80	0.035
CIP	E. coli	5	144	2.0	0.78	0.77	0.31	0.024
								0.088
STR	Salmonellaf	2	87	5.0	0.67	0.66	0.25	0.38
TET	Salmonellaf	2	154	1.2	0.93	0.93	0.04	0.0077

^aSee equation 7.

^bSee references 12 and 16.

^cκ was fitted, and raw experimental ΔN data were employed. Other model parameters were an N_int,s value of 1.8 and an N_min value of −2 (19, 25, 26). The MSC/MIC_s ratio was calculated by using equation 10 with selection coefficients reported previously for resistant strains (12, 16).

^dAs, arsenite.

^eQ² = cross-validated R² = 1 − (PRESS/TSS).

^fSalmonella enterica serovar Typhimurium LT2.

As shown in Table 1, the fitted κ values ranged widely across the nine compounds examined (from 0.7 to 10.5). CV results generally produced a very narrow range, with κ values varying by <0.1 within individual compounds, except for KAN and copper sulfate (Cu) (Table S2). Similarly, CV PRESS/SSY results were <0.4 for all compounds except KAN and Cu. Values of <0.4 are considered to indicate reasonably low model prediction error (27).

Because it was the only experiment that included four resistance genotypes, ciprofloxacin was examined more closely. Overall, the fit and predictive ability were generally reasonable (R² = 0.81, Q² = 0.78, and PRESS/SSY = 0.29) (Table S2), except for the downward bias for the two highest ΔN results (Fig. 2). These were both for the gyrA1(S83L) strain versus the sensitive wild-type strain above 2 ng/ml ciprofloxacin (19). The gyrA1(S83L) comparison had a substantially different curve shape, and the removal of this strain from the data greatly improved the model fit (R² = 0.97, Q² = 0.97, and PRESS/SSY = 0.04). However, the change in predicted κ values was trivial (from 2.0 to 2.1, with N_min fixed at −2).

(iii) Minimum selection concentration.

The MSC/MIC_s ratio was estimated (see equation 10) based on model-fitted κ and empirical values for the selection coefficient (sc), MIC_r, and MIC_s. For these estimates, N_int,s was set at 1.8 h⁻¹, and N_min was either fitted or set at −2 h⁻¹. The chosen N_int,s value is based on the experiments that the model was fitted to, indicates a generation time (doubling time) of about 25 min, and approximately corresponds to the growth rate for a wild-type Salmonella Typhimurium or E. coli strain in Mueller-Hinton medium at 37°C (16; Dan Andersson, Uppsala University, personal communication). Model predictions corresponded well to the observed MSC/MIC_s ratio (12, 16) for all experiments, with either fixed or fitted N_min (Fig. 4), suggesting that the model is appropriate to estimate the MSC/MIC_s ratio. The MSC/MIC_s ratio ranged across 2 orders of magnitude, from 0.006 to 0.66 (Table 1; see also Table S3 in the supplemental material).

FIG 4.

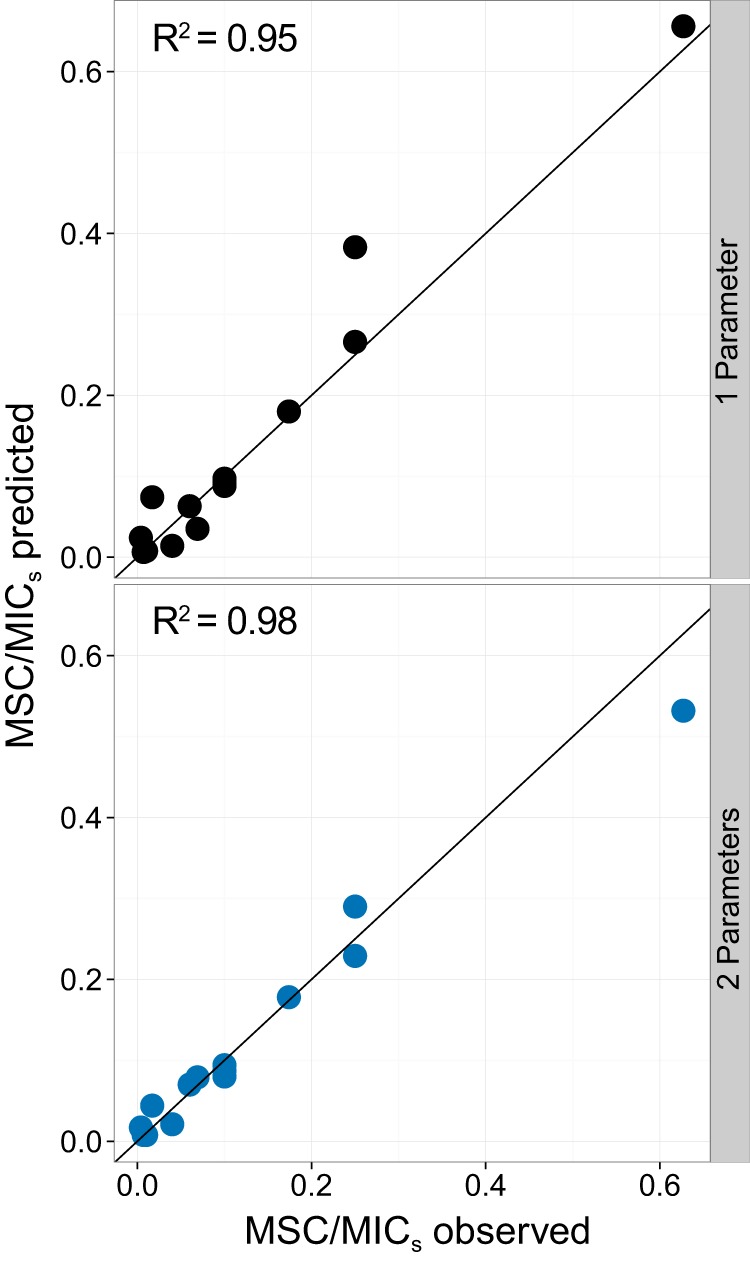
Comparison of observed (12, 16) versus model-predicted (see equation 10) MSC/MIC_s ratios. Symbols represent experimentally evaluated resistant strains (n = 14). The solid line indicates a 1:1 ratio. For one parameter (top), κ was fitted and N_min was fixed at −2 h⁻¹. For two parameters (bottom), both κ and N_min were fitted.

Sensitivity analysis.

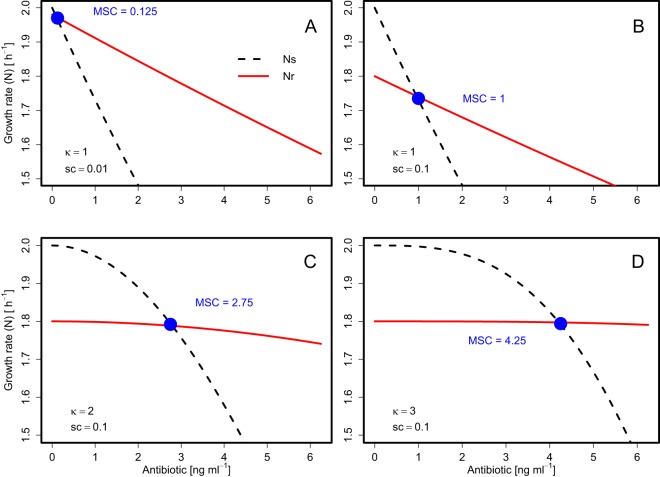
For sensitivity analysis, the behavior of equation 10 was examined across reasonable parameter ranges to examine the sensitivity of the MSC/MIC_s ratio to fitness differences (sc), antibiotic resistance differences (MIC_r/MIC_s ratio), maximum growth rate inhibition (N_min), and the intrinsic growth rate (N_int,s). Equations 10 and 11 indicate that the MSC/MIC_s ratio is primarily a function of sc and κ but is also modified by corrective terms that include N_min, N_int,s, N_int,r, MIC_s, and MIC_r. Figure 5 demonstrates the influences of sc and κ on the MSC/MIC_s ratio. Specifically, increasing the sc value decreases the growth rate of the resistant strain (Fig. 5A and B), whereas increasing κ values increase the curvature of the growth rate of the sensitive strain (Fig. 5B to D), both of which result in increased MSC/MIC_s ratios. As a result, modeled κ is strongly associated with model-predicted MSC/MIC_s ratios. Thus, the Pearson correlation coefficient was very high (r = 0.94) for the κ-versus-MSC/MIC_s results from Table 1.

FIG 5.

Growth rate versus antibiotic concentration for sensitive (N_s) and resistant (N_r) bacteria for different theoretical values of sc (0.01 and 0.1) and κ (1, 2, and 3). For other parameters (all scenarios), the MIC_s was 10, the MIC_r was 40, N_int,s was 2, and N_min was −5. Note the truncated scale on the y axis.

Figure 6 provides plots of the MSC/MIC_s ratio as a solution for equation 10 across different parameter values. Figure 6A confirms the dominant and interdependent influences of sc and κ on the MSC/MIC_s ratio, with the largest influences being found at or below κ values of 1. At a κ value of 1, the MSC/MIC_s ratio is approximately equal to sc (Fig. 6A, blue dashed line). The influences of sc and κ can be combined according to equations 10 and 11, which indicate that the MSC/MIC_s ratio is proportional to sc^1/κ. Figures 6B to D illustrate that the MSC/MIC_s ratio is proportional to sc^1/κ and that the slope of this relationship is modified by MIC_r, N_int,s, and N_min. An increase in the MIC_r will decrease the MSC/MIC_s ratio, but this relationship is sensitive only when the MIC_r approaches the MIC_s (MIC_r/MIC_s ratio close to 1) (Fig. 6B). The generally low sensitivity of the MSC/MIC_s ratio to the MIC values themselves corroborates the empirical findings of Gullberg et al. (12). Increasing the N_int,s value also decreases the MSC/MIC_s ratio, but this exhibits only a minor influence (Fig. 6C). Finally, increasing the N_min value also decreases the MSC/MIC_s ratio, but this is sensitive only when N_min approaches zero (Fig. 6D). N_min indirectly affects the MSC/MIC_s ratio by influencing the MIC-versus-EC₅₀ (50% effective concentration) relationship (see equations S7 and S8 in Text S1.2 in the supplemental material).

FIG 6.

Sensitivity analysis of the MSC/MIC_s ratio (see equation 10) for theoretical values of model parameters as a function of the selection coefficients (sc) for different κ values (log scale) (A) and as a function of sc^1/κ for different values for the MIC_r/MIC_s ratio (B), N_int,s (C), and N_min (D). Other parameters, except as noted, are as follows: MIC_s of 25, MIC_r of 250, N_int,s of 2, and N_min of −5. Note that panel A is on a log scale and that panels B to D are on a linear scale.

Figure 6A also illustrates the expected range of MSC/MIC_s ratios across combinations of sc and κ (the most influential parameters). Over commonly observed sc ranges from 0.001 to 0.1 and κ ranges from 0.5 to 5 (12, 28–30), the MSC/MIC_s ratio ranged widely from 10⁻⁶ to 0.5. With sc equaling 0.01, as κ decreased from 2 to 0.5, the MSC/MIC_s ratio decreased from typically a factor of 0.1 down to less than a factor of 10⁻⁴. This indicates that as the κ value decreases, MSC values become increasingly sensitive to incremental changes in κ. Especially for low sc values, slight decreases in κ may correspond to steep declines in the MSC value (Fig. 6A).

DISCUSSION

This study model is a simple mathematical approach to describe the factors that will drive the MSC, which is a relevant environmental threshold concentration for the selection of resistant bacteria. This model helps us understand the significant issue of the spread of environmental resistance (1, 5, 31) by mathematically formulating the dependence of the MSC (11, 15) on the intrinsic growth rate and the antibiotic-versus-growth dose response. The model would enable an indirect estimation of the MSC using measurements of bacterial growth parameters that are readily obtained in the laboratory and the literature (κ, N_min, and N_int), as an alternative and possible complement to direct measurements (12, 13, 16). More importantly, the model identifies the shape of the antibiotic dose-response curve of the sensitive strain (i.e., κ) and the selection coefficient (sc) as the main parameters determining the MSC/MIC ratio. These traits, combined with MIC ranges reported in the literature (4, 8, 24), can be used to estimate environmental antibiotic concentrations at which resistance could spread.

The model consistently estimated the MSC/MIC ratio across the nine compound-taxon combinations examined, with an overall R² value above 0.95 (Fig. 4). This finding suggests that one could estimate the MSC given (i) the MIC, (ii) the intrinsic bacterial growth rate (i.e., N_int), (iii) fitness loss (either σ or sc measurements), and (iv) the shape of a dose-response curve for the antibiotic concentration versus bacterial growth for the sensitive strain (i.e., κ). The first three values are readily available for a range of strains, resistance mechanisms, and conditions (4, 12, 19, 24, 25, 28, 29, 32, 33). N_int will vary widely for a given species depending on the conditions and media, but the model MSC/MIC ratio is highly insensitive to N_int (Fig. 6C). κ is obtained by means of an antibiotic-concentration-versus-growth-rate dose-response curve. The antibiotic-versus-growth-rate relationship will vary across treatment conditions but is straightforward to obtain, allowing the experimental calculation of κ (references 19, 21, 25, and 34 provide examples). The dose response, based on growth rate data, was traditionally achieved by flask-based culture methods. Currently, automated microtiter plate readers allow growth curves to be obtained within a day (35), and emerging techniques, including PCR-based methods or microfluidics, could streamline growth curve determination even further (36).

To illustrate the use of the model, Fig. 7 displays the MSC/MIC ratio from equation 10 across a range of selection coefficients, based on laboratory growth parameters reported by Regoes et al. (19) and Ankomah et al. (25). Results vary dramatically across experiments, even for the same species-antibiotic combination (Fig. 7), largely due to variations in κ. This suggests a strong impact of specific strains and growth conditions for selection, resulting in differences among systems of multiple orders of magnitude and a need to understand how the antibiotic resistance dose response varies across antibiotic-contaminated environments (1), including water treatment systems, agricultural waste pens, and natural waters and sediments (4, 37–40).

FIG 7.

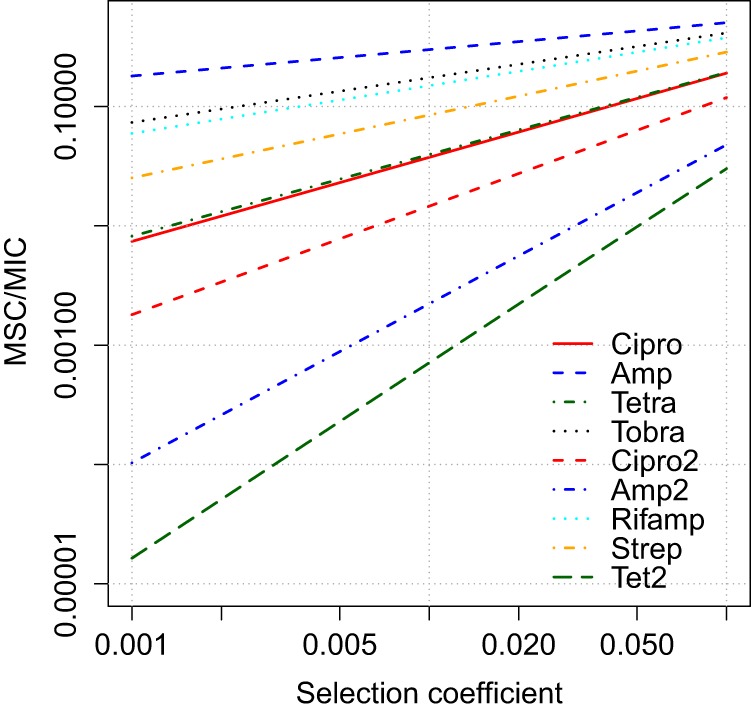
MSC/MIC ratio as a function of the selection coefficient (sc), calculated for parameters obtained in empirical laboratory studies (19, 25). Parameter data can be found in Table S4 in the supplemental material. Cipro, ciprofloxacin; Amp, ampicillin; Tetra, tetracycline; Tobra, tobramycin; Rifamp, rifampin; Strep, streptomycin.

Although the model predicted the MSC/MIC ratio well across the compounds examined, the model inconsistently predicted ΔN values among compounds. ΔN was predicted least well for KAN and STR, both of which are aminoglycosides. In these cases, the inability to fit ΔN well was due to the similarity of the study-observed MSC versus the MIC of the sensitive strain (i.e., high MSC/MIC_s ratio). This amounted to a sudden and dramatic shift from the low experimentally determined ΔN values (∣ΔN∣ < 0.04) around the MSC versus a ΔN value of >1 at the MIC. This steep dose response from high to zero growth of the sensitive strain is evident in high κ values for both STR (κ = 5) and KAN (κ = 10.5). The Hill equation and other common statistical curves could not account for the similar MSC and MIC values. The high κ fitted is also inconsistent with the concentration-dependent (i.e., low κ) bactericidal activity of aminoglycoside antibiotics described previously (34, 41). Instead, the similar net growth rates of susceptible and resistant strains close to the MIC_s may result from adaptive resistance of the susceptible strain. Adaptive resistance to aminoglycosides has been widely observed in Pseudomonas aeruginosa (42, 43), including at sub-MIC exposures (44), as well as in E. coli (22, 26, 45). This occurs due to the elevated production of efflux pumps counteracting growth inhibition and killing at sublethal concentrations (44). In cases of adaptive resistance, the MSC may not be much lower than the MIC. In such cases, the MIC may be a reasonable proxy for the MSC, as is often observed clinically (7).

Experimental data are currently limited to a few species, strains, and antibiotics, possibly limiting the generalizability of the model performance evaluation. Thus, future experimental work is warranted to evaluate the ability to estimate the MSC via equations 10 and 11 across a range of subclinical conditions, species, strains, and antibiotics. This would include a comparison of MSC values directly measured in competition experiments versus MSC values derived from equation 10 based on measurement of the antibiotic dose response of individual strains in isolation (see equations 4 and 5).

Shape of the antibiotic dose response at subinhibitory concentrations.

By emphasizing subinhibitory antibiotic concentrations, this study extends previous findings regarding how the behavior of the Hill equation, and κ in particular, influences the dynamics of bacterial net growth (19, 34). The model predicts that an antibiotic with a lower κ for a given set of conditions (e.g., bacterial strain and medium) exerts a greater selective pressure in the subinhibitory region of concentrations found in the environment, resulting in lower MSC/MIC ratios. With κ approximately equal to 1, there is an approximately linear decrease in growth from the intrinsic rate with no antibiotic to zero growth when the antibiotic concentration is equal to the MIC. As a result, the intersection between the curves for the wild-type and resistant strains can occur at a low antibiotic concentration, and the MSC is approximately equal to the MIC of the wild type multiplied by the selection coefficient. This leads to a low MSC for low selection coefficients.

Under higher-κ conditions, the MSC is closer to the MIC. Thus, a high κ value, in addition to increasing efficacy above the MIC (19), also reduces the hazard of selection for resistance at concentrations below the MIC. Simulated and empirical dose-response measurements in the subinhibitory region are especially needed to evaluate the extent to which the “preselection” of resistant strains may occur at MSCs below the MIC of the sensitive strain, in both clinical and environmental settings.

Implications for resistance development hazard.

Environmental-hazard and -risk assessments would benefit from determining how ambient environmental concentrations in different media compare to the MSC (1). Based on a species sensitivity distribution compared to EUCAST-reported MIC results, Tello et al. found that selective pressure for resistant bacterial communities would be high in swine feces lagoon sediment but low in surface water, ground water, raw sewage, and sewage treatment plant effluent (4). As an example of the implications of the MSC threshold (versus the MIC), we reinterpret the model of Tello et al. (4) to estimate the hazard of selection for resistant bacteria. We employ a model correction factor, assuming a 100-fold-lower species sensitivity distribution, to convert the previously reported MIC₅₀ (see Fig. 4 in reference 4) to an MSC₅₀ by adjusting the reported log-logistic model location (α) parameter by −2. The 100-fold reduction follows our model results and the empirical data reported by Gullberg et al. (12, 16), both of which indicate that MSC/MIC ratios may exhibit values below 0.01. Comparing the adjusted model to the field data reported for ciprofloxacin (see Table 2 in reference 4), the MSC₅₀ model predicted a >25% potentially affected fraction of bacterial taxa in at least one sample for all media reported (surface water, river sediment, raw sewage, and treatment plant effluent). For erythromycin and tetracycline, the MSC₅₀ model predicted 65% and 88% potentially affected fractions in river sediment (versus 2% and 1.6% for the MIC₅₀), respectively (4). Tello et al. used data from systems impacted by human and agricultural development (37, 38), and our 100-fold MSC-MIC correction is more conservative than the 10-fold reduction employed in PNECs (Predicted No Effects Concentrations) developed by Bengtsson-Palme and Larsson (8), thus indicating worst-case conditions. Nevertheless, Bengtsson-Palme and Larsson also reported treatment plant effluent concentrations above PNECs (8) in 28% of cases. These results in combination indicate the likely selection of resistant strains given antibiotic exposure in a wide variety of human-impacted aquatic settings.

Model scope, limitations, and future directions.

The parsimonious analytical solution that we developed addresses vertical gene transfer of antibiotic resistance in a well-mixed environment as a function of fitness loss, competition, and antibiotic concentration. There are many aspects of resistance dissemination that fall outside the scope of this simple exercise, including horizontal gene transfer, interactions among multiple strains, the spatial arrangement of individual colonies, and heterogeneity in antibiotic exposure due to biofilms and other mechanisms (2, 8, 11, 20, 46). Additionally, the model operates on and describes the long-term competition dynamics between bacterial strains rather than stochastic and dynamic changes in net growth and competition over time. Thus, the derivation assumes that the parameters governing growth (e.g., R_int, D_int, and D_ab) will reach relatively stable values when one strain outcompetes another strain. This simplified model does not include parameters for the inoculum effect, biphasic killing, delay functions, drug concentration changes, drug-insusceptible persister cells, or adaptive resistance, all of which may occur in experimental settings. More sophisticated pharmacokinetic/pharmacodynamic models that incorporate these processes are needed to characterize the bacterial time-kill curve and optimal dosing regimens (21–23). However, such models do not lend themselves to an analytical solution similar to what we have provided. Investigation of various initial ratios of resistant to susceptible bacteria indicate no effect on the selection coefficient, suggesting a limited importance of initial conditions, such as inoculum effect (12, 16). Nevertheless, theoretical and experimental investigation of how short-term growth and killing and other dynamic processes would impact the MSC/MIC ratio is warranted in future studies, as is comparison of alternative models.

The primary benefit of the present model is in illustrating the MSC paradigm and the key drivers of selection in simplified systems. As such, this paper adds to the growing scientific understanding of how to interpret laboratory data on the MIC and other parameters for predicting the emergence of resistance at subinhibitory environmental concentrations. It highlights the value of characterizing the antibiotic dose response (i.e., the Hill coefficient [κ]), particularly at antibiotic concentrations below the MIC. Ultimately, this quantification of resistance selection must be integrated into a risk assessment framework that also considers environmental antibiotic contamination, human exposure to and colonization by resistant bacteria, and the association between colonization and infection (1). Such a framework can help quantify the global hazard posed by antimicrobial agents.

MATERIALS AND METHODS

We develop a simple analytical expression of the ratio between the MSC and the MIC for a sensitive strain (i.e., MSC/MIC ratio), which mathematically describes the factors that determine risks of subclinical antibiotic concentrations (11, 12). The model is based on competition between two bacterial strains: a wild-type sensitive strain and a mutant strain that is more resistant.

Model derivation for net growth rate.

We model bacterial growth as a first-order growth rate constant, N (per hour). At a given antibiotic concentration, a (nanograms per milliliter), the net growth rate [N(a) (per hour)] for each strain is given by

$$N_{\text{s}}(a)=N_{\mathrm{int},\text{s}}-D_{\text{ab},\text{s}}(a)=R_{\mathrm{int}}-D_{\mathrm{int}}-D_{\text{ab},\text{s}}(a)$$ (1)

$$N_{\text{r}}(a)=N_{\mathrm{int},\text{r}}-D_{\text{ab},\text{r}}(a)=R_{\mathrm{int}}+\sigma -D_{\mathrm{int}}-D_{\text{ab},\text{r}}(a)$$ (2)

where a subscript s indicates sensitive bacteria; a subscript r indicates resistant bacteria; N_int,s = (R_int − D_int) is the intrinsic net growth rate in the absence of the antibiotic (per hour), calculated as the difference between the intrinsic growth rate (R_int [per hour]) and the intrinsic loss due to mortality (or, in continuous cultures, dilution) (D_int [per hour]); D_ab(a) is the loss in net growth (per hour) due to a given antibiotic concentration, a; and σ is the absolute selection coefficient (per hour).

The absolute selection coefficient (σ [per hour]) represents the loss in fitness of resistance-conferring genes as the absolute difference in the net growth rate between bacterial strains (e.g., sensitive versus resistant) in the absence of antibiotics (i.e., N_int,r = N_int,s + σ). The absolute selection coefficient (σ) is directly related to the fitness cost (see Text S1.1 in the supplemental material for the exact definition of fitness cost and its relation to the absolute selection coefficient). Accurate measurement of the absolute selection coefficient (σ) can be difficult, employing competition experiments with labeled strains and flow cytometry (12, 16, 47). Resistance-conferring mutations exhibit highly variable selection coefficients in comparison to sensitive strains (28, 29, 47, 48), with compensatory mutations often reducing or reversing the fitness cost of resistance mechanisms (29, 30, 49). In principle, σ could be any value greater than −N_int,s. However, in cases where σ is ≥0, there is no fitness loss from resistance, such that MSC equals 0 and the resistant strain would predominate at any antibiotic concentration. For the purposes of this model, we run simulations based on the assumption that resistance-conferring mutations engender a loss in fitness, resulting in lower growth rates than those of less resistant strains, i.e., −N_int,s < σ < 0. This assumption is supported in that the majority of single mutational events entail a loss in fitness (47).

The loss in net growth due to antibiotics can be described by a generalized Hill equation (19, 21, 34, 50, 51):

$$D_{\text{ab}}(a)=k_{\max }\frac{a^{\kappa }}{a^{\kappa }+{(\text{E}{\text{C}}_{50})}^{\kappa }}$$ (3)

in which k_max (per hour) is the maximum death rate due to the antibiotic; EC₅₀ (nanograms per milliliter) is the antibiotic concentration that achieves half of this maximum rate, and will thus increase with increased resistance; and κ is the Hill coefficient (51). For a κ value of 1 in the range of antibiotic concentrations below the MIC, the death rate increases roughly linearly. For a given strain, antibiotics with a high κ value (>1) will have lower efficacy at subtherapeutic levels but higher efficacy at therapeutic levels above the MIC. The opposite relation is true for antibiotics with low κ values (19), as illustrated in Fig. 1A.

To determine k_max from growth and death rates, we note that k_max should correspond to the difference between the maximum possible net growth rate (not limited by resource availability or antibiotics; i.e., N_int) and the minimum possible growth rate, after accounting for the growth-limiting activity of the antibiotic (N_min):

$$k_{\max }=N_{\mathrm{int}}-N_{\min }=R_{\mathrm{int}}-D_{\mathrm{int}}-N_{\min }$$ (4)

For bactericidal drugs, N_min is <0, indicating population decline at the maximum antibiotic exposure level. The EC₅₀ can be directly related to the MIC value (nanograms per milliliter); as a result, the following formulation of D_ab applies for our formalism (the full derivation can be found in Text S1.2 in the supplemental material):

$$D_{\text{ab},\text{s}}(a)=(N_{\mathrm{int},\text{s}}-N_{\min })\frac{a^{\kappa }}{a^{\kappa }+\frac{(-N_{\min })}{N_{\mathrm{int},\text{s}}}{(\text{MI}{C}_s)}^{\kappa }}$$ (5)

$$D_{\text{ab},\text{r}}\left(a\right)=(N_{\text{int},\text{r}}-N_{\min })\frac{a^{\kappa }}{a^{\kappa }+\frac{(-N_{\min })}{N_{\text{int},\text{r}}}({\text{MIC}}_{\text{r}}{)}^{\kappa }}$$ (6)

Equations 5 and 6 are similar to equation 3 from Regoes et al. (19). These equations assume identical κ and N_min values for sensitive and resistant strains, which may not be accurate. In Results, we evaluate the impact of this assumption for the estimation of the MSC.

Difference in net growth rates and derivation of the MSC as a function of the MIC.

Competition between different bacterial strains is expressed by the difference in net growth rates. According to the conceptual model described by Andersson and Hughes (11) and Gullberg et al. (12), N_s is higher than N_r at low antibiotic concentrations due to the fitness cost of resistance, but the greater sensitivity causes more antibiotic-dependent growth inhibition for the sensitive strain. As a result, at high antibiotic concentrations, N_r is higher than N_s, and the MSC is the point of intersection of the two growth curves (N_s = N_r) for which the difference in the net growth rate is zero (Fig. 1B and C).

Analytically, this difference in net growth rates between the resistant and sensitive strains [ΔN(a) (per hour)] is determined by subtracting the value derived by equation 1 from that derived by equation 2, giving

$$\Delta N(a)=N_r(a)-N_s(a)=N_{\mathrm{int},\text{r}}-N_{\mathrm{int},\text{s}}+\left[D_{\text{ab},\text{s}}(a)-D_{\text{ab},\text{r}}(a)\right]=\sigma +D_{\text{ab},\text{s}}(a)-D_{\text{ab},\text{r}}(a)$$ (7)

Thus, the MSC is the antibiotic concentration (i.e., a = MSC) at which the two net growth rates are equal and the difference (equation 7) is zero:

$$\Delta N(\text{MSC})=N_{\text{int},\text{r}}-D_{\text{ab},\text{r}}(\text{MSC})-N_{\mathrm{int},s}+D_{\text{ab},\text{s}}(\text{MSC})=\sigma +D_{\text{ab},\text{s}}(\text{MSC})-D_{\text{ab},\text{r}}(\text{MSC})=0$$ (8)

This is the concentration at which the additional loss in net growth due to the antibiotic in the sensitive strain compared to the resistant strain [D_ab,s(MSC) − D_ab,r(MSC)] compensates for the effect of fitness loss (σ).

To derive the ratio of MSC/MIC, we employ a dimensionless relative selection coefficient (sc) (unitless), obtained by reversing the sign of the reported absolute selection coefficient (σ) (12, 16) and then dividing this value by the net growth rate of the sensitive strain (the full derivation can be found in Text S1.1 in the supplemental material):

$$sc=-\frac{\sigma }{N_{\mathrm{int},\text{s}}}=\frac{N_{\mathrm{int},\text{s}}-N_{\mathrm{int},\text{r}}}{N_{\mathrm{int},\text{s}}}=1-\frac{N_{\mathrm{int},\text{r}}}{N_{\mathrm{int},\text{s}}}$$ (9)

Based on the above-described equations, and further assuming that κ and N_min are the same for sensitive and resistant strains, the following analytical solution for the MSC/MIC_s ratio is obtained (the full derivation can be found in Text S1.4 in the supplemental material):

$$\text{MSC}/\text{MI}{\text{C}}_{\text{s}}={\left[\frac{sc}{1+\frac{N_{\mathrm{int},\text{r}}}{-N_{\min }}-\frac{(1-sc)\left(1+\frac{N_{\mathrm{int},\text{s}}}{-N_{\min }}\right)}{{\left(\frac{\text{MI}{\text{C}}_{\text{r}}}{\text{MI}{\text{C}}_{\text{s}}}\right)}^{\kappa }}}\right]}^{\frac{1}{\kappa }}$$ (10)

In the case of a large difference in resistant versus sensitive MICs, the right-hand term in the denominator approaches zero, and the equation simplifies to

$$\text{MSC}/\text{MI}{\text{C}}_{\text{s}}={\left(\frac{sc}{1-\frac{N_{\mathrm{int},\text{r}}}{N_{\min }}}\right)}^{\frac{1}{\kappa }}$$ (11)

This simplification does not apply to small increases in the MIC, such as with ΔmarR and ΔacrR mutants, which double the MIC for ciprofloxacin (12). Equation 11 becomes appropriate once the MIC_r is >5× MIC_s, at which point the results from equations 10 and 11 become approximately equal (see Fig. S1 in the supplemental material).

Equation 10 is, in essence, a mathematical hypothesis regarding the relationship between the antibiotic dose response and the resulting MSC. The form of equation 10 aids in determining which aspects of the growth rate are likely to be most important for competition at low antibiotic doses. Equations 10 and 11 also represent a potential alternative to direct measurement of the MSC, because all parameters in equation 10 (sc, MIC_s, MIC_r, κ, N_int,s, N_int,r, and N_min) can be directly measured in the laboratory. Additionally, sc, MIC_s, and MIC_r values are readily available in the literature. To obtain κ, N_int,s, and N_min in the laboratory, for example (19, 25), equation 4 would be fit to experimental measures of the sensitive strain's antibiotic-versus-growth dose response, with N_min then being calculated as the strain's intrinsic growth rate (N_int) minus k_max (see equation 5).

As mentioned above, equation 10 rests on the assumption of identical κ and N_min values for sensitive and resistant strains. An analytical solution analogous to equation 10 could not be obtained by assuming separate κ and N_min values (i.e., κ_s, κ_r, N_min,s, and N_min,r). In Results and in the supplemental material, we employ a Monte Carlo simulation sensitivity analysis to critically evaluate this assumption of identical κ and N_min values.

Model evaluation against experimental results.

The analytical solution was evaluated by comparison to the experimental results of Gullberg et al. (12, 16). This evaluation was performed to determine whether the model fit to actual competition data was reasonable and to identify representative parameter sets for N_min and κ parameters, given a set of reported values of MIC_s, MIC_r, σ, and N_int,s (12, 16). The latter four parameters have been characterized for a wide range of strains, conditions, and resistance mechanisms (4, 24, 28–30, 32, 33).

Model fitting was achieved by fitting ΔN values calculated from equation 7 (based on equations 1, 2, and 4 to 6) to the ΔN values observed by Gullberg et al. (12, 16). The NonLinearModel.fit function in MATLAB (Statistics Toolbox, R2013a; MathWorks, Natick, MA, USA) was used to estimate N_min and κ. Fitting was performed separately for seven individual antibiotic-bacterium combinations across the reported range of experimental concentrations as well as for arsenite- and copper-exposed E. coli (12, 16). These metals were included based on coresistance and cross-resistance with antibiotics as well as similar mechanisms of genetic transmission among bacteria (2, 5, 52, 53). For each compound, resistance was compared between a sensitive (wild-type) strain and one to four resistant strains of S. Typhimurium or E. coli. From the reported experiments (12, 16), only the chromosomal mechanism of trimethoprim resistance was excluded because it exhibited an average selection coefficient, σ, of >0, indicating no selective disadvantage of resistance (12).

To evaluate equation 7 and the underlying model assumptions, model-predicted and observed ΔN values were compared. To evaluate robustness to individual observations, CV was also employed. For CV, optimization was performed with each single data point removed in series, and the average and range of N_min and κ results were examined, as were the calculated versus observed ΔN values for the out-of-sample observations. The PRESS statistic was calculated, and PRESS/SSY and Q² (i.e., 1 − PRESS/total sum of squares) were examined to indicate model prediction error and prediction power, respectively (27) (see Text S2.1 in the supplemental material for the definition, implementation, and assumptions regarding these statistics). All analyses were performed on the experimental average results for each strain and antibiotic concentration examined, as reported by Gullberg et al. (12, 16). Analyses were also performed on the raw data for each experimental observation (12, 16) (see the supplemental material), in order to consider the impact of experimental variation on results. All figures were made in MATLAB or in R version 3.4.0 (54).