Compressive Sensing Based Q-Space Resampling for Handling Fast Bulk Motion in Hardi Acquisitions

Abstract

Diffusion-weighted (DW) MRI has become a widely adopted imaging modality to reveal the underlying brain connectivity. Long acquisition times and/or non-cooperative patients increase the chances of motion-related artifacts. Whereas slow bulk motion results in inter-gradient misalignment which can be handled via retrospective motion correction algorithms, fast bulk motion usually affects data during the application of a single diffusion gradient causing signal dropout artifacts. Common practices opt to discard gradients bearing signal attenuation due to the difficulty of their retrospective correction, with the disadvantage to lose full gradients for further processing. Nonetheless, such attenuation might only affect limited number of slices within a gradient volume. Q-space resampling has recently been proposed to recover corrupted slices while saving gradients for subsequent reconstruction. However, few corrupted gradients are implicitly assumed which might not hold in case of scanning unsedated infants or patients in pain. In this paper, we propose to adopt recent advances in compressive sensing based reconstruction of the diffusion orientation distribution functions (ODF) with under sampled measurements to resample corrupted slices. We make use of Simple Harmonic Oscillator based Reconstruction and Estimation (SHORE) basis functions which can analytically model ODF from arbitrary sampled signals. We demonstrate the impact of the proposed resampling strategy compared to state-of-art resampling and gradient exclusion on simulated intra-gradient motion as well as samples from real DWI data.

1. Introduction

Diffusion-weighted (DW) MRI helps reveal the organization of white matter micro-structure - in vivo - through being sensitive to the microscopic random motion of tissue's water molecules. Assuming voxel-wise homogeneous axon population, diffusion tensor imaging (DTI) has shown limitations in modeling brain regions with orientational heterogeneity, such as crossing fibers. With high angular resolution diffusion imaging (HARDI) [1], such brain regions can be modeled using strong gradients and long diffusion times.

Long acquisition times and non-cooperative subjects (e.g. unsedated infants, elderly people and patients in pain) increase the sensitivity of DW-MRI to subject motion [2]. Recently, it has been shown that motion artifacts are inevitable in HARDI acquisitions even under a controlled acquisition environment [3]. The use of high b-values exacerbate motion artifacts even further.

Voluntary or involuntary patient bulk movement during the application of diffusion gradients causes severe signal perturbation [4]. Inter-gradient (a.k.a. slow bulk) motion can cause misalignment among subsequent diffusion images which can be addressed via retrospective motion correction strategies, e.g. [5]. On the contrary, intra-gradient (a.k.a. fast bulk) motion causes inhomogeneous signal dropout/attenuation artifacts [6] which arises due to signal dephasing within the voxels [4, 2] (see Fig. 1 for an example). Such artifacts, even only affecting a few slices, typically lead to unusable diffusion gradient images which have to be discarded. Retrospective correction of such artifacts was considered challenging [4, 6] but finds a promising solution via q-space resampling as discussed here.

Fig. 1.

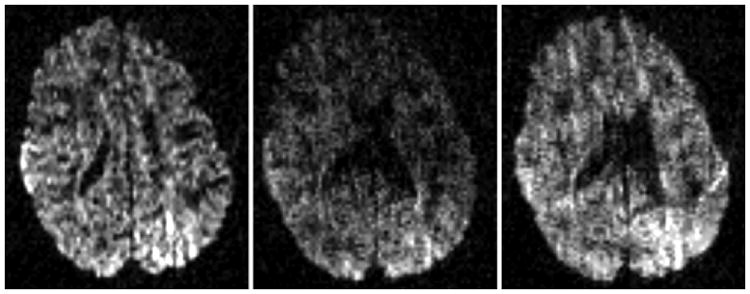
Three consecutive slices in a diffusion gradient suffering from fast bulk motion. Notice signal drop-out in the middle slice which typically causes the exclusion of the full gradient volume from subsequent processing steps.

Common practices to mitigate fast motion artifacts include the identification and exclusion of corrupted images from further processing [4, 7] and/or scheduling for reacquisition during the same scan [2, 4, 8]. However, the reacquisition of motion-corrupted gradients enforces a hardware overhead, e.g. optical tracking systems [8], free-induction decay navigators [9] or volumetric navigators [10], which is not always available on current scanners. It further lengthens the scan acquisition time due to reacquisition and time-consuming calibration steps. The exclusion of entire diffusion images (a.k.a. motion scrubbing), on the other hand, has shown to limit the reconstruction of crossing fibers and anatomical tracts [3]. Further, it introduces inter-subject bias differences that would affect subsequent statistical analysis [11].

The effect of fast bulk motion typically appears as intensity artifacts which span a limited number of axial slices in a diffusion-weighted image (see Fig. 1). Recently, Dubois et al. [12] advocated a resampling strategy as an alternative to discarding gradients, in order to save as many gradients as possible for subsequent reconstruction and tractography. Correction is performed via estimating the intensities of the corrupted (outlier) slices in the q-space through fitting a Q-ball imaging (QBI) diffusion model on the non-corrupted gradients using spherical-harmonics (SH) decomposition of the diffusion signal [13]. Nonetheless, fitting SH basis would require a relatively large number of uncorrupted gradients to yield an accurate diffusion model since the SH basis does not constitute a complete basis in 3D. Further, QBI has been shown to lack representability [14]. The Simple Harmonic Oscillator based Reconstruction and Estimation (SHORE) basis, on the other hand, has been shown to yield better diffusion representation compared to QBI [14]. With recent compressive sensing-based estimation approaches, e.g. [15], resampling can be improved to yield robust reconstructions w.r.t. the number of available uncorrupted gradients.

In this paper, we propose a q-space resampling scheme which makes use of the SHORE-basis to minimize the elimination of full gradient volumes due to fast bulk motion artifacts. Based on synthetic experiments, we present a systematic evaluation framework to study the impact of the exclusion of corrupted gradients versus QBI and SHORE-based resampling strategies on the reconstruction of orientation distribution functions (ODFs) as well as local fiber orientations. Our results show promising performance in favor of SHORE-resampling. We further show preliminary results of the potential impact of our proposed resampling strategy on an infant dataset presenting severe intra-gradient motion corruption.

2. Materials and Methods

2.1. Data Acquisition

In this paper, we are interested in studying the impact of performing q-space resampling, SHORE-based in particular, on subsequent ODF reconstruction and local fiber orientations. To provide a groundtruth to compare to, we decided to rely on acquiring diffusion images from three healthy human subjects (males 30-40 years old) under well controlled environment (Autism Centers for Excellence, Infant Brain Imaging study [16])¹. All subjects were scanned using the same scanner (a 3.0T Siemens Magnetom TrioTim scanner) at the same clinical site to avoid inter-subject variability under multi-scanner/site acquisition. Three DWI datasets (one per subject) were acquired with FOV = 20 × 20 cm, slice thickness = 2.0 mm, matrix size = 106 × 106 with 76 axial slices. The diffusion data consisted of one baseline image with zero b-value and 64 DW-images with b-value = 2000 s/mm².

2.2. Outlier Detection

Fast bulk motion artifacts are typically manifested as slice-wise intensity attenuation, presenting outliers in an acquired dataset. In order to identify corrupted slices, we detect abrupt slice-wise intensity changes. We use normalized cross-correlation (NCC) between successive slices using diffusion images from all the gradients. This metric has been shown to be sensitive to intra-gradient motion while being insensitive to small inter-gradient motion [7]. It is further normally distributed which enables defining outlier slices automatically using the sufficient statistics of its distribution. In particular, at a slice level, a large NCC metric deviation from the mean NCC of all the gradients is indicative to a significant change of intensity where such a slice is marked as corrupted. Moreover, we use the signal dropout score proposed in [4] which is computed for each slice in each volume. Slices with a score greater than 1 can be considered as a suspect for signal dropout.

2.3. Q-space Resampling for Saving Gradients

Q-space resampling amounts to estimating the lost signal during intra-gradient motion using a diffusion model. This is beneficial to save as many usable gradients as possible to be streamed into subsequent processing steps. In our recent analysis [3], we have shown the significant impact of excluding corrupted gradients on ODF reconstruction, tractography and full brain connectivity.

The main idea of resampling strategy can be outlined as follows. When the d–th slice S_d(q) within the gradient acquired along q wave vector in q-space is identified to be corrupted, a diffusion model is fitted using the respective slice in the other non-corrupted gradients. The diffusion signal is then interpolated using this fitted model to fill in the intensities of the corrupted slice (Fig. 2). Note that several gradients may be corrupted for a specific slice, as well several slices may be corrupted within one gradient. This motivates the use of a diffusion model estimation that is robust w.r.t. the number of available uncorrupted measurements. To mitigate under-sampling due to motion-related artifacts, we estimate ODFs using the compressive sensing based formulation proposed in [15] which can handle a limited number of samples.

Fig. 2.

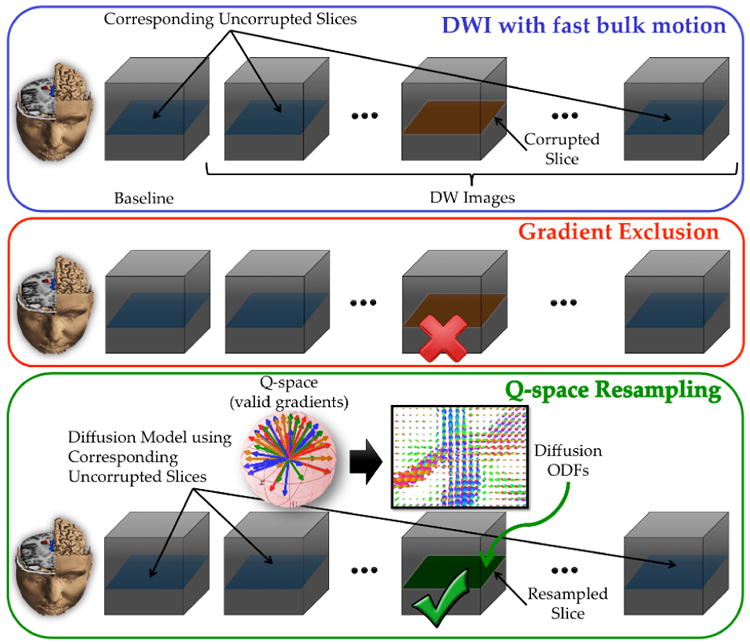
Illustration of q-space resampling strategy compared to gradient exclusion.

The essence of fitting a diffusion model is representing the normalized DWI signal E(q) = S(q)/S(0) in terms of a weighted sum of orthonormal basis, where S(0) is the non-diffusion weighted signal (i.e. baseline). These basis functions separate the radial and spherical parts of q where the SHORE-basis use 3D complete orthonormal basis and is distinguished by their representability [14]. Merlet and Deriche [15] derived the analytical ODF solution in case of SHORE-basis where the diffusion ODF of voxel x_d in the d–th slice and a diffusion gradient orientation u can be written as,

$$\mathrm{\psi }(\mathbf{u},{\mathbf{x}}_d)=\sum _{l=0}^L\sum _{m=-l}^l{\varrho }_{lm}({\mathbf{x}}_d)Y_l^m(\mathbf{u}),$$ (1)

Where $Y_l^m$ is the SH function of order l and degree m and ϱ_lm (x_d) are voxel-wise SHORE coefficients defined in [15]. Once the coefficients ϱ_lm(x_d) for all voxels in the d–th slice are estimated using non-corrupted gradients, the corrupted slice S_d can then be resampled as,

$${\mathbf{S}}_d({\mathbf{x}}_d,\mathbf{q})=S(0)\sum _{l=0}^L\sum _{m=-l}^l{\rho }_{lm}({\mathbf{x}}_d)Y_l^m(\mathbf{u}).$$ (2)

2.4. Reconstruction and Evaluation Metrics

We employ the constrained spherical deconvolution (CSD) technique [17] to reconstruct fiber orientation distributions functions (fODFs) from DWIs. The fiber response function was estimated from voxels with FA higher than 0.7.

To quantify similarities between groundtruth fODFs and those obtained using resampling outlier slices, we use the Jensen-Shannon divergence (JSD) which has been used to quantify differences between ODFs in various studies. Given two probability distributions P and Q, the JSD metric is defined as follows:

$$\text{JSD}(\mathrm{P}\Vert \mathrm{Q})=\frac{1}{2}[D_{\text{KL}}(P\Vert M)+D_{\text{KL}}(Q\Vert M)],$$ (3)

where M = (P + Q)/2 and D_KL is the Kullback-Leibler divergence. In case of discrete distributions; the KL divergence is defined as: $D_{\text{KL}}(P\Vert Q)={\sum }_i{P}_{i}log\frac{P_i}{Q_i}$ where i is the discrete sample index. Note that in order to use the JSD, we normalize the fODFs to sum up to 1.

Assessing deviations in local fiber orientations is also important since their distortion may lead to unreliable tractography and brain connectivity results. We use the mean angular deviation measure θ defined as follows:

$$\begin{array}{cc}{\theta }_{i,j}^k=\frac{180}{\pi }|{cos}^{-1}({\upsilon }_i^k\cdot {\upsilon }_j^k)|,& \theta =\frac{1}{N}\sum _{k=1}^N{\theta }_{i,j}^k,\end{array}$$ (4)

where N is the number of fibers compared, and ${\upsilon }_i^k$ and ${\upsilon }_j^k$ correspond to the orientations of fiber k [3]. Before averaging the deviations, we match the fibers, such that fiber j has the closest direction to fiber i. If the number of fibers is different, we compare the fibers that are present in both voxels. The fiber orientation were computed using DiPy² peak extraction tool where we allowed up to five fiber orientations per voxel.

3. Results

In order to assess the impact of our resampling strategy compared to gradient exclusion (e.g. [11]) and QBI resampling [12], we simulated slice-wise artifacts as follows. We used three DWI datasets from healthy subjects without motion as verified by quality control [3]. Random intra-gradient motion was simulated by introducing different number of outlier gradients in a given slice by zeroing-out their intensities.

For a given slice, we randomly draw 100 subsets of 10%, 30%, 50% and 70% gradients without replacement³ to be declared as corrupted. Three reconstruction scenarios were considered: (1) Gradient exclusion; where ODFs were reconstructed by simply eliminating the corrupted gradients, (2) QBI resampling; where a voxel-wise QBI model was fitted using the uncorrupted gradients, and corrupted gradients were then resampled using the fitted model as in [12]. fODFs were subsequently reconstructed using all the gradients. (3) SHORE resampling; where a voxel-wise SHORE model is fitted and used to resample the corrupted gradients.

Fig. 3 shows the quantitative comparison of the three reconstruction scenarios on fODFs and dominant fiber orientation, respectively, as a function of percentage of corrupted gradients for different brain lobes. One can observe the effect of excluding gradients on the reconstructed fODFs and local fiber orientation which becomes significant with increasing number of corrupted gradients. This complies with our findings in [3]. Further, QBI resampling which is based on SH-basis is showing larger deviations from the groundtruth compared to SHORE resampling, especially with fewer uncorrupted measurements. The deviations shown in Fig. 3 were found to be statistically significant between the three reconstruction scenarios at significance level α = 0.01 for all percentages of corrupted gradients, with SHORE resampling presenting the lowest differences to groundtruth.

Fig. 3.

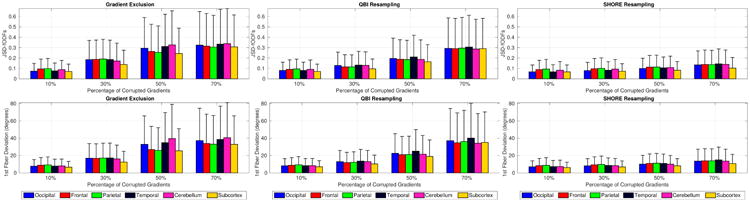
Mean and standard deviations of (top) JSD values and (bottom) dominant fiber orientation deviation in degrees per brain lobe as a function of percentage of corrupted gradients, shown for the three correction schemes (left to right).

Fig. 4 shows the corticospinal tract of a sample low-risk infant (24-month-old) who is a participant of the IBIS study; an ongoing longitudinal study of infants at low and high familial risk for autism. Severe intra-gradient motion was detected, resulting in the exclusion of 26 gradients out of 64 due to on average of 3 outlier slices per gradient (minimum of 1 slice and maximum of 9 slices). Q-space resampling saved 22 gradients where the rest were contaminated with other intensity artifacts. One can notice the effect of gradient exclusion on the resulting tract where the posterior view demonstrates how the tract is not reaching the cortex compared to the resampling strategies.

Fig. 4.

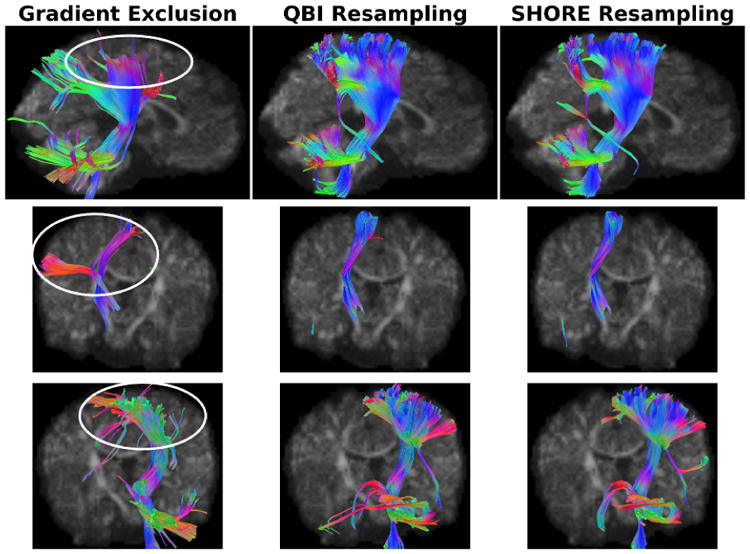
Corticospinal tract of a sample low-risk infant using different reconstruction scenarios. Top row: sagittal view. Middle row: anterior view. Bottom row: posterior view.

Further, we performed full brain tractography and atlas-guided parcellation (detailed in [3]) to visualize brain connectivity of the low-risk infant dataset. In Fig. 5, we use the Circos software [18] where the parcellated structures (refer to [3] for their full names) are displayed on a connectogram representing left and right hemispheres symmetrically positioned along the vertical axis. A normalized connectivity matrix is computed based on [3] where each entry corresponds to an inter-region link with thickness proportional to the entry weight. One can observe the tendency of gradient exclusion to loose connections within a single hemisphere as well as across left and right hemispheres. Further, QBI resampling does not show as many connections as SHORE resampling between left and right hemispheres.

Fig. 5.

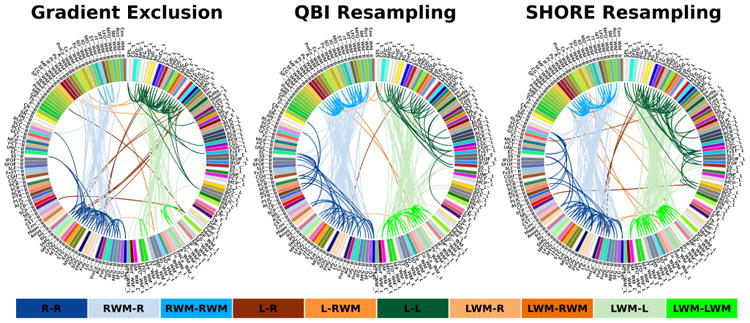
Sample connectomic profile of infant DWI using different reconstruction scenarios. Color legend: L (left), R (right), WM (white matter).

These two examples are limited to showcases of single real dataset and thus do not imply a conclusive validation, with a large-scale evaluation planned for our future research. However, they may serve as demonstrations how different strategies to correct for intra-gradient artifacts will result in differences on subsequent analysis and thus can potentially have a significant impact on clinical studies.

Nonetheless, as a word of caution, a resampling strategy in general implicitly assumes minimal inter-gradient motion where a diffusion model can be estimated using all uncorrupted gradients for a given slice. In case of moderate-to-severe inter-gradient motion, resampling might introduce artifacts due to fitting the diffusion model to motion-corrupted gradients, resulting in discarding gradients even after resampling. Hence, reliability of the resampling step is affected by the severity of motion present in a given dataset. Possible solutions include initial inter-gradient motion correction to bring all the gradients into the same coordinate frame, followed by the intra-gradient resampling scheme for corrupted slices as presented in this paper.