Abstract
Although more patients with congenital heart disease (CHD) are now living longer due to better surgical interventions, they require regular imaging to monitor cardiac performance. There is a need for robust clinical tools which can accurately assess cardiac function of both the left and right ventricles in these patients. We have developed methods to rapidly quantify 4D (3D + time) biventricular function from standard cardiac MRI examinations. A finite element model was interactively customized to patient images using guide-point modelling. Computational efficiency and ability to model large deformations was improved by predicting cardiac motion for the left ventricle and epicardium with a polar model. In addition, large deformations through the cycle were more accurately modeled using a Cartesian deformation penalty term. The model was fitted to user-defined guide points and image feature tracking displacements throughout the cardiac cycle. We tested the methods in 60 cases comprising a variety of congenital heart diseases and showed good correlation with the gold standard manual analysis, with acceptable inter-observer error. The algorithm was considerably faster than standard analysis and shows promise as a clinical tool for patients with CHD.
Keywords: Congenital Heart Disease, Biventricular Modelling, Cardiac function assessment
1 Introduction
Congenital heart disease (CHD) is the most common birth defect, with a prevalence of approximately 10 in every 1000 births [20]. Survival rates have been increasing, with 90% of infants born with CHD now surviving to adulthood due to improvements in surgical interventions. For the first time the population of adults with CHD is larger than the pediatric population [7]. However, heart failure is a significant problem for adults with CHD. As a result, CHD patients undergo regular monitoring in order to correctly time surgical interventions [20]. MRI is the preferred method of evaluation, due to the absence of ionizing radiation, coverage of the whole heart, and high spatial and temporal resolution [20]. However, analysis of the images requires segmentation of the chambers and muscle, which remains a significant bottleneck despite substantial work on improving analysis methods (see [16] for a review).
Although historically the left ventricle (LV) has been viewed as the most important chamber in maintaining cardiac health, later research has shown the importance of the right ventricle (RV) in maintaining overall cardiac function [1, 8, 18]. Interdependence between the ventricles is of particular importance in CHD [3, 8, 19]. Their closely linked anatomy, haemodynamics and shared muscle fibres make it necessary to assess the both ventricles in CHD. While evaluation of biventricular (left and right ventricular) function from cardiac MRI has been widely researched, few studies have considered the additional challenges associated with CHD [22, 17, 16]. Figure 1 shows a four chamber cine view of patients with three different types of CHD. The images are representative of the quality of images typically collected in cardiac MRI examinations in CHD patients. Additional artifacts are caused by septal wires and artificial valves (Figure 1 left image). For clinical evaluation, the standard method is to manually contour the endocardial and epicardial boundaries of both ventricles on all short axis slices at both end-diastole (ED) and end-systole (ES), up to the inflow and outflow valves, and calculate volumes by slice summation. This method has been shown to be prone to inter-observer and intra-observer error as well as being very time-consuming [10]. Although rapid, reproducible analysis is critical for clinical throughput, fully automated methods are currently not robust enough for biventricular analysis in CHD. Semi-automated methods with minimal user interaction are therefore required with fast (real time) interaction.
Fig. 1.
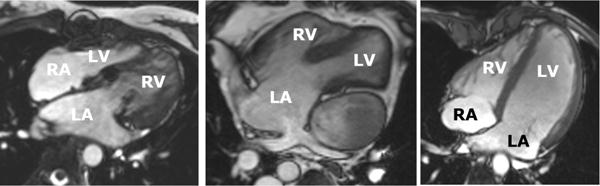
Three ED frames of four-chamber slices in three different types of CHD. Left: Congenitally-corrected transposition of the great arteries, which connects the left atrium to the right ventricle and the right atrium to the left ventricle. Middle: Double outlet right ventricle after a Fontan surgery, showing single ventricle circulation. Right: Dextro-transposition of the great arteries, as well as a ventricular septal defect. The patient has under-gone a Senning procedure, with subsequent arterial switch and mitral regurgitation.
Previous methods for segmenting biventricular geometry have included subdivision surfaces [21] and 4D spatio-temporal models [15], however neither are capable of real-time interaction. Lamata et al. [11] devised a customizable biventricular model, however this study did not model the full cardiac cycle and did not capture the full basal extent of the ventricles (up to the atrioventricular valves). Wang et al. [24] developed a segmentation-free method of assessing biventricular function from MR images, however they did not test the performance of their algorithm on CHD cases. Both [26] and [27] used 3D MRI datasets at the ED frame to create whole heart segmentations. Zhuang et al [26] used spatially encoded mutual information and free form deformation and Zuluaga et al [27] used a multi-atlas segmentation. While both methods reported good correlation with manual delineation, they did not report correlation with clinical measures of heart function, and did not show results in patients.
In this paper we extended and validated a biventricular modelling tool described in a technical conference report [5]. In particular we examined the performance of the method in simulated customizations, and compared results in 60 patients representing a variety of CHD types against manual contours for two independent observers.
2 Methods
2.1 Interactive Biventricular Modelling
Guide-point modelling [25, 6] was used to interactively customize a 3D time-varying finite element model to a patient’s cardiac MRI scan. The biventricular finite element model is shown in Figure 2 and consisted of 82 3D elements with Bézier interpolation and C1 continuity, meaning surfaces were continuous in slope across the element boundaries.
Fig. 2.
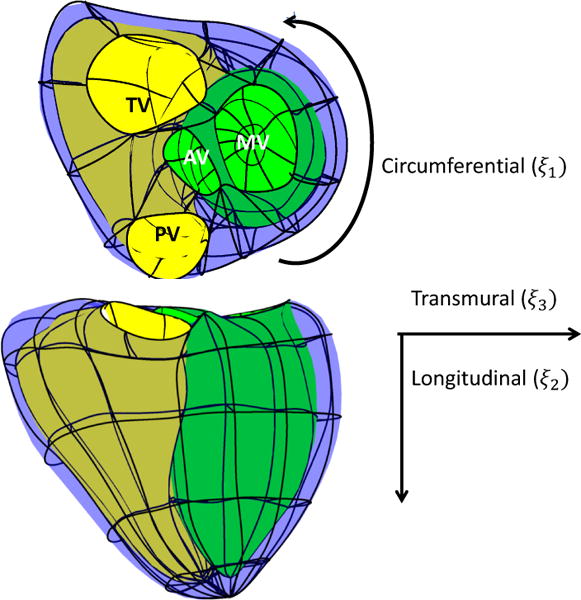
Finite element model showing the four valves and element boundaries. Model coordinates (ξ1, ξ2, ξ3) were defined as shown. MV is the mitral valve, AV is the aortic valve, PV is the pulmonary valve and TV is the tricuspid valve.
The initial model template was scaled and registered to the patient’s images using landmarks defined on the valves (as shown in Figure 3) as well as LV and RV centroids defined on the apical and basal slices, and the apical point of the heart defined on a long axis slice. The apex and valves were tracked throughout the cardiac cycle using image feature tracking by non-rigid registration [13].
Fig. 3.
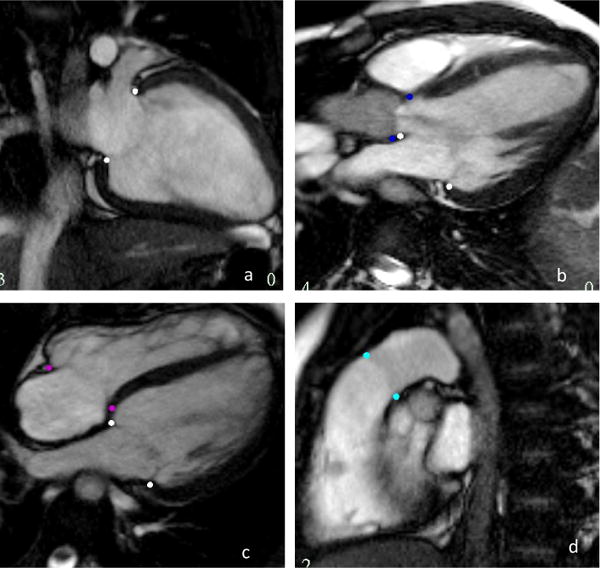
Valve inserts on long axis images. The pink dots are the mitral valve, the dark blue the aortic valve, purple the tricuspid and cyan the pulmonary valve
In order to customise a model to a patient’s anatomy, three types of data points were used: i) guide points, points placed by the user to guide the contour location; ii) predicted points, points generated by the algorithm to predict the model deformation; and iii) tracked contour points, generated from image feature tracking [13]. The model was customised by minimizing the following objective function:
| (1) |
which measures the distance between each user, predicted and tracked contour point, (d) and each corresponding point the model surface. The data points are represented by xd and the corresponding model point is represented by x(ξd). The distance between these two points was weighted by wd to allow for the differing importance of different point types to the model during fitting. For example, if there is a predicted point and a guide point close together, it is better for the model to fit the guide point more accurately as it is user generated thus the guide point would have a higher weighting than the predicted point. S(u) is the smoothing term, which is described in Section 2.1.2. Equation 1 was minimized using a preconditioned conjugate gradient algorithm (see Appendix for details).
2.1.1 Calculating Predicted Points
Predicted points were calculated algorithmically to improve computational efficiency in the optimization process [6] by using a simple model defined in prolate spheroid coordinates to represent the LV endocardial surface and the biventricular epicardial surface [5]. Figure 4 (a) shows the LV prolate model. Briefly, a 16 element model with Bézier interpolation was fitted to the data points and then sampled to provide a set of predicted points. The LV prolate model has been shown to produce efficient and accurate 4D models of the LV geometry [12, 25], but in this application the LV prolate model was used to provide cardiac motion for the LV endocardium and biventricular epicardium only. This was motivated by the observation that, even though the RV is typically non-convex, the biventricular epicardium is approximately convex, as is the LV endocardium. Note that this prediction does not force the final solution to be convex.
Fig. 4.
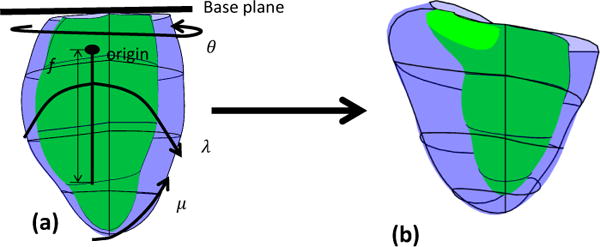
(a) The prolate spheroid coordinate system with the initial prolate model. The origin is one-third the distance from the base towards the LV apex. The coordinate system has four parameters, the radial coordinate (λ), the rotation coordinate (θ), the azimuthal coordinate (μ) and the focal length (f). (b) the customized prolate model.
The prolate spheroid coordinate system was defined as:
| (2) |
where λ > 0 defines the transmural direction from the center of the LV, 0 ≤ μ < π is the azimuthal direction from apex (μ = 0) to base, 0 ≤ θ ≤ 2π is the circumferential direction, and f > 0 is the focal length. We fixed f in this application such that λ at apex is equal to 1.
The prolate model was initialized from the biventricular template, after customization to the anatomical landmarks on the MR images. The basal extent of the prolate model was defined from the mitral valve plane. The prolate coordinate system was permitted to translate and rotate so that the prolate central axis (x axis in Equation 2) passed through the LV apex in all frames. The apex was marked by the user on the end-diastolic frame and was warped through the cardiac cycle using a non-rigid registration method [13]. The prolate surfaces were updated by a linear least squares optimization of the radial (λ) field, as a function of the angular coordinates. The resulting prolate prediction model is shown in Figure 4(b). The predicted points were defined at the locations of the nodes of the biventricular model and were mapped onto the modified prolate model epicardial and LV endocardial surfaces. This mapping was fixed so that after each prolate model update, the position of the predicted points could be found by simple matrix-vector multiplication.
2.1.2 D-Affine smoothing
The smoothing term in Equation 1 is required to regularize the solution in the presence of sparse data. Previously, a Sobolev smoothing term [12, 23] has been used for this purpose [6]; however, this has the disadvantage of being sensitive to large rotations and motions, as are often seen around the RV, leaving artifacts in the model surfaces. In this work we used a D-Affine smoothing term [5], which penalized change in deformation across the model. The D-Affine smoothing term S(u) in Equation 1 was defined to be
| (3) |
where k indicates the model directions in x, y and z, is the Frobenius norm and Ω represents the model domain. J is the Jacobian of motion, which is the deformation gradient tensor and αk is the smoothing weight in the kth direction. The method for incorporating the smoothing term in the conjugate gradient optimization process can be found in the Appendix.
Unlike previous methods such as poly-affine models [14] and locally affine transformations [2], D-Affine smoothing does not require prior knowledge of the number and location of affine transformations. The main advantages of D-Affine smoothing are:
-
–
The method is invariant to affine transformations, including rotations.
-
–
D-Affine smoothing does not require prior knowledge of the displacement fields
-
–
D-Affine smoothing minimises strain across the model
-
–
The method results in a smoothly varying deformation field.
These advantages make D-Affine smoothing useful for modelling CHD, where large deformations, particularly in the RV, are typically observed.
2.1.3 The fitting process
The full customization process, each time a guidepoint is added, included the following steps:
Solve the prolate spheroidal model.
Create a set of predicted points from the polar model
Solve the biventricular model for registration (high smoothing)
Solve the biventricular model with user data (low smoothing)
Solve the time varying model
After each user edit to a landmark or guide-point, the modified prolate model was updated, which was very fast since it involved a low complexity model with a single coordinate field (λ). The predicted point locations at the nodes of the biventricular model were then updated and the biventricular model was then fitted to the predicted point locations with a high smoothing weighting (see Appendix). Then the biventricular model was optimized to the user-placed guide-points, as well as tracked contours from the non-rigid registration, using a normal smoothing weighting. This two step solution process was found to improve the resulting solution by improving the mapping between user defined points and their corresponding model positions. Finally, the time-varying model was updated by fitting all frames using a Fourier harmonic temporal basis function. This acted to provide additional temporal coherence to the final model motion.
2.2 Implementation
The method was implemented in C++ on a Dell OptiPlex 990 running Windows 7 using an Intel® Core i5 3.30GHz with 4GB of RAM, containing 4 cores. The preconditioned conjugate gradient solution was implemented using the Math Kernel Library (Version 10.1.3.028) utilizing the inbuilt routine with multithreading. A solution was possible in 0.15s per frame (including x, y and z), enabling real time updates of the model while dragging a guide-point.
2.3 Experiments
Simulation experiments were performed to test the performance of the smoothing, and the method was validated in 60 patients with CHD.
2.3.1 Simulated Customizations
In order to assess the performance of the D-Affine smoothing, test model behavior and find appropriate smoothing and data weights, a series of simulated customizations were performed. The simulations were designed to test the D-Affine smoothing behavior as well as the performance of the smoothing when combined with other factors, such as guide-points and predicted points. The simulations comprised:
A 10 mm displacement in the x direction using 8 guide-points.
A 45° rotation using eight guide-points.
A displacement of 10 mm in the x and z direction on the LV freewall, using 8 guide-points and a set of predicted points.
A deformation caused by a displacement of one guide-point 10 mm in the x direction, relative to 3 others kept stationary, and a set of predicted points.
A longitudinal scaling simulated by a displacement of 30% towards the apex.
2.3.2 CHD Patients
Ethical approval was obtained from the local ethics committee and 60 participants with CHD gave written informed consent for their images to be used. Table 1 shows the pathologies and surgical interventions represented in the group. There were 25 females and 35 males with an average age of 23 ± 13 (range 7–75) years. The images were acquired using a 1.5 T MRI scanner (Siemens Avanto, Siemens Healthcare, Erlangen, Germany) and all cines were prospectively or retrospectively gated breath-hold steady-state free precession acquisitions. The short axis slices were acquired parallel to the tricuspid annulus plane and spanned both ventricles. Long axis slices were obtained through all valves and spanning both ventricles. Typical imaging parameters were as follows: slice thickness =6mm, flip angle =60°, TE = 1.6ms and TR = 30ms, field of view =360 × 360mm and image matrix =256×208. The images were acquired as part of routine clinical care and the study targeted patients who required assessment of RV function as well as LV function.
Table 1.
Congenital heart disease pathologies and surgeries represented in the dataset.
| Number of patients | CHD type (Other CHD lesions) | Surgery |
|---|---|---|
|
| ||
| 2 | Aortic stenosis | 1 Ross procedure 1 supra aortic stenosis repair |
| 1 | Atrial septal defect, partial anomalous pulmonary venous drainage, pulmonary hypertension | Nil |
| 2 | Bicuspid aortic valve | 1 Ross procedure, 1 balloon dilation |
| 7 | Coarctation of the aorta (3 ventricular septal defect) | 3 aortic arch repair, 1 stent insertion, 3 aortic arch repair, ventricular septal defect repair |
| 1 | Congenitally corrected transposition of the great arteries | Nil |
| 6 | Dextro - transposition of the great arteries | 4 Arterial switch operation, 2 mustard procedure,2 sennings procedure |
| 1 | Double chambered RV | Nil |
| 1 | Ebstiens anomaly | Nil |
| 1 | Marfans syndrome | MV repair, Bentalls procedure |
| 1 | Pulmonary artesia | Pulmonary homograft |
| 2 | Pulmonary artesia with intact ventricular septum | 1 Right ventricle outflow tract repair, tricuspid valve repair, 1 pulmonary valvotomy |
| 27 | Tetralogy of Fallot | 2 pulmonary valve ring preserved, 8 pulmonary homograft, 10 transannular patch, 7 unknown procedures |
| 2 | Tetralogy of Fallot and pulmonary atresia | pulmonary homograft |
| 2 | Truncus arterious | Pulmonary homograft |
| 1 | Ventricular septal defect | Unknown |
| 1 | Ventricular septal defect, transposition of the great arteries and a double outlet right ventricle | Rastelli procedure |
All short axis slices between the apex and the valves were manually contoured either using Argus (Syngo MR2004V, Siemens Healthcare, Erlangen, Germany) or Segment V1.9 (http://segment.heiberg.se) [9] by two independent expert analysts. Myocardial mass and ventricular volumes were calculated using Simpsons rule. Two analysts also assessed the same 60 cases using the biventricular modelling tool.
3 Results
3.1 Simulated Customisations
The D-Affine smoothing was evaluated using the tests described in Section 2.3.1. Tests 1, 2 and 5 did not include predicted points, while tests 3 and 4 did include predicted points. Figure 5 shows the original and fitted models for the five tests.
Fig. 5.
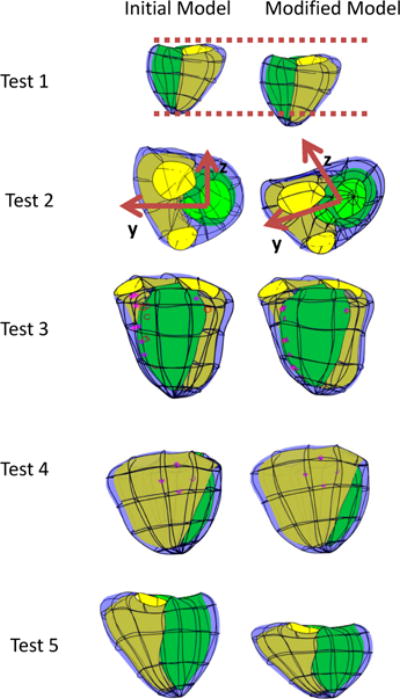
Initial (left) and fitted (right) models for each test. The LV endocardium has a green surface, the RV endocardium has a yellow surface and the epicardium is blue. Guide-points are purple stars and their corresponding model point is a purple circle.
The translation (Test 1) and rotation (Test 2) simulations showed exact solutions to these affine transformations. Tests 3 and 4 show typical customizations, shifting a subset of guide points while others remain constant, similar to what would occur in a typical customization. Test 5 shows the model shortening in the longitudinal direction, while maintaining its size in the y and z direction, similar to the descent of the basal valves towards the apex seen in typical cardiac motion. Similar results were obtained with a range of weights, with good results obtained in all tests with the smoothing matrix given a weight of 1, the predicted points given a weight of 0.01, and the guide-points a weight of 0.1. More detailed tests on the behaviour on the conditioning and numerical accuracy of the smoothing scheme can be found in the Appendix.
3.2 CHD patients
For the patient studies, the smoothing weights represented by αk in Equation 3 were increased 100 times for the high smoothing step, where the biventricular model is registered to the predicted points. Analysis with the biventricular modelling tool took an average of 21 ± 7 minutes per case for all frames compared to over an hour with the manual contouring tools for only end-diastole and end-systole. Each case required approximately 178±36 guide-points to customise the template to the patients images. The prediction of cardiac motion step provided good deformation of the model throughout the cardiac cycle for all hearts, including those with complex congenital defects that cause a large variation in geometry. The end-diastolic volume, the end-systolic volume, mass, stroke volume and ejection fraction were evaluated for the comparison between the manual contours and the biventricular modelling tool.
Table 2 shows the average values for each measure produced by both methods as well as the difference between the methods and the correlation as measured by Pearson product moment correlation coefficient (PPMCC). The PPMCC shows strong correlation in all measures between manual contours and the biventricular modelling tool. Figure 6(a) shows the regression plots of the two methods for all measures of function with R2 values used to measure correlation. Figure 6(b) shows the Bland-Altman plots for all measures. Both plots demonstrate good agreement between the biventricular modelling tool and manual contours. The largest CHD group in our dataset was Tetralogy of Fallot and the results from these 29 cases are shown in Table 4. Figure 7 shows the patient specific model created using the biventricular modelling tool for a 13 year old female with repaired coarctation of the aorta.
Table 2.
Average values for each method as well as the difference and correlation between methods for the full dataset. LV and RV are the left and right ventricles respectively. EDV is the End-diastolic volume, ESV is the End-Systolic volume, SV is stroke volume and EF is the ejection fraction.
| Manual analysis average | Biventricular tool average | Difference between methods | PPMCC | |
|---|---|---|---|---|
| LV EDV (ml) | 157.7 ± 59.5 | 152.5 ± 58.7 | 5.2 ± 11.2(3.4%) | 0.98 |
| LV ESV (ml) | 66.4 ± 31.6 | 71.2 ± 32.3 | −4.9 ± 10.3(−7.1%) | 0.95 |
| LV mass (g) | 112.0 ± 39.3 | 132.2 ± 40.0 | −20.3 ± 11.1(−16.6%) | 0.96 |
| LV SV (ml) | 91.4 ± 35.0 | 81.3 ± 30.3 | 10.1 ± 10.9(11.7%) | 0.96 |
| LV EF (%) | 58.6 ± 8.8 | 54.0 ± 6.1 | 4.7 ± 6.1(8.3%) | 0.73 |
| RV EDV (ml) | 221.6 ± 86.7 | 216.6 ± 80.6 | 5.1 ± 20.2(2.3%) | 0.97 |
| RV ESV (ml) | 119.9 ± 60.6 | 133.8 ± 59.4 | −14.0 ± 16.6(−11.0%) | 0.96 |
| RV mass (g) | 60.1 ± 26.9 | 87.7 ± 31.9 | −27.6 ± 11.9(−37.4%) | 0.93 |
| RV SV (ml) | 101.8 ± 36.1 | 82.8 ± 28.2 | 19.0 ± 17.0(20.6%) | 0.89 |
| RV EF (%) | 47.6 ± 9.3 | 39.4 ± 7.0 | 8.2 ± 6.1(18.9%) | 0.76 |
Fig. 6.
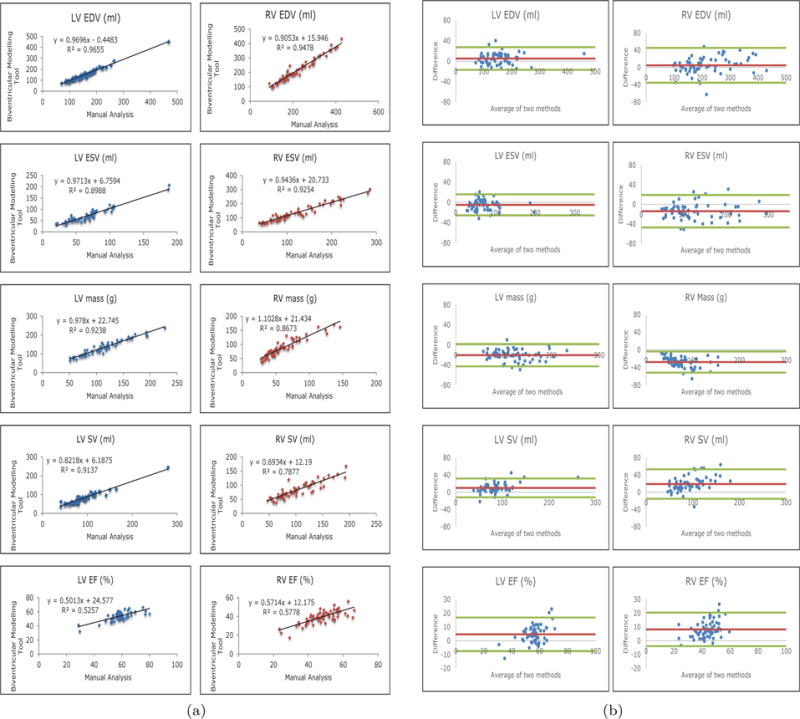
(a) Regression plots showing the correlation between the two measurement methods. (b) Bland-Altman plots comparing the correlation of the manual results and the biventricular modelling tool. The average difference is shown in red and 2 standard deviations are shown in green.
Table 4.
Average values for each method as well as the difference and correlation between methods for the Tetralogy of Fallot Patients. LV and RV are the left and right ventricles respectively. EDV is the End-diastolic volume, ESV is the End-Systolic volume, SV is stroke volume and EF is the ejection fraction.
| Manual analysis average | Biventricular tool average | Difference between methods | PPMCC | |
|---|---|---|---|---|
| LV EDV (ml) | 148.2 ± 43.6 | 145.3 ± 41.9 | 2.9 ± 8.8(2.0%) | 0.979 |
| LV ESV (ml) | 64.4 ± 22.9 | 70.2 ± 22.5 | −5.8 ± 9.6(−8.6%) | 0.911 |
| LV mass (g) | 105.9 ± 34.6 | 127.4 ± 35.3 | −21.5 ± 9.1(−18.4%) | 0.966 |
| LV SV (ml) | 83.8 ± 27.3 | 75.1 ± 22.3 | 8.7 ± 10.6(−11.0%) | 0.929 |
| LV EF (%) | 56.7 ± 7.7 | 1.9 ± 5.0 | 4.8 ± 5.9(8.9%) | 0.644 |
| RV EDV (ml) | 255.0 ± 83.9 | 242.6 ± 77.6 | 12.4 ± 18.4(5.0%) | 0.977 |
| RV ESV (ml) | 142.3 ± 54.9 | 151.7 ± 54.5 | −9.4 ± 18.8(−6.4%) | 0.941 |
| RV mass (g) | 61.2 ± 19.6 | 93.3 ± 26.9 | −32.2 ± 11.0(−41.6%) | 0.936 |
| RV SV (ml) | 112.7 ± 39.8 | 90.9 ± 30.0 | 21.8 ± 17.1(21.4%) | 0.918 |
| RV EF (%) | 44.9 ± 8.8 | 38.0 ± 6.1 | 6.9 ± 6.4(16.7%) | 0.685 |
Fig. 7.
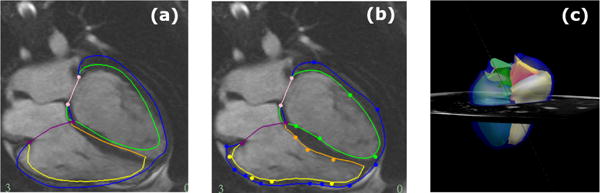
A model fitted to a 13 year old female with coarctation of the aorta, who has undergone an aortic arch repair. The LV endocardium is contoured in green, the RV endocardium in yellow/gold, the biventricular epicardium in dark blue, the mitral valve in pink and the triscupid valve in purple.(a) shows the initial contours presented to the user after fitting to anatomical markers. (b) shows the customised contours for the same four chamber ED frame as (a). (c) shows the resulting ED frame of the model after full customisation to all slices.
Table 3 shows the inter-observer error for both the manual contours and the biventricular modelling tool, on common measures of function. The PPMCC was calculated to assess correlation between the two observers for each method. The inter-observer correlation was high in all measures.
Table 3.
Inter-observer error and correlation for manual analysis and the biventricular modelling tool. LV and RV are the left and right ventricles respectively. EDV is the End-diastolic volume, ESV is the End-Systolic volume, SV is stroke volume and EF is the ejection fraction.
| Manual analysis | Biventricular Modelling Tool | |||
|---|---|---|---|---|
| Inter-observer error | PPMCC | Inter-observer error | PPMCC | |
| LV EDV (ml) | 0.2 ± 8.3(0.2%) | 0.99 | −9.0 ± 14.4(4.1%) | 0.97 |
| LV ESV (ml) | 2.6 ± 5.9(3.9%) | 0.98 | −7.0 ± 10.9(−9.8%) | 0.95 |
| LV mass (g) | 6.5 ± 10.9(5.8%) | 0.98 | −9.8 ± 18.0(−7.4%) | 0.90 |
| LV SV (ml) | −2.4 ± 8.4(−2.6%) | 0.97 | −2.0 ± 10.1(−1.7%) | 0.95 |
| LV EF (%) | −1.6 ± 3.9(−2.8%) | 0.99 | 1.5 ± 4.8(3.1%) | 0.73 |
| RV EDV (ml) | 2.6 ± 13.1(1.2%) | 0.97 | −24.7 ± 32.4(−11.6%) | 0.93 |
| RV ESV (ml) | 7.8 ± 13.8(6.5%) | 0.91 | −17.4 ± 26.7(−13.0%) | 0.92 |
| RV mass (g) | 5.3 ± 7.5(8.7%) | 0.99 | 3.8 ± 18.1(4.3%) | 0.85 |
| RV SV (ml) | −5.3 ± 11.9(−5.2%) | 0.95 | −7.6 ± 15.9(−9.2%) | 0.86 |
| RV EF (%) | −3.0 ± 5.6(−6.3%) | 0.84 | 0.7 ± 5.7(1.8%) | 0.73 |
4 Discussion
This study validated an interactive tool for 4D (3D + time) biventricular mass and volume quantification for CHD patients using a rapid interactive method. A major advantage of the method is that the full basal extent of the biventricular geometry up to all four atrioventricular valves is included, avoiding a major source of error in identifying the basal extent of the ventricles. Long axis slices were used to provide anatomical information which is not well defined on short axis slices due to partial voluming [4]. The biventricular modelling tool showed good correlation with manual contours in 60 cases. The method used fast prediction of surface motion in prolate coordinates, and D-Affine smoothing to constrain motion between data points. The addition of the predicted points benefited the solution time, requiring fewer iterations in Test 3 than Test 1 (Appendix). A previous implementation using Sobolev smoothing and calculation of predicted points using a trilinear host mesh [6], required an average of 19 ± 4 minutes with 318 ± 46 guide-points per case. Although the analysis times were similar with the current method, the average number of guide-points used was almost halved. This suggests that less interaction is required to customize models with the incorporation of D-Affine smoothing and polar prediction. The error between manual analysis and the biventricular modelling tool decreased in the LV ESV (32% to 7%), LV EF (17% to 8%), LV Mass (27% to 17%), RV EDV (5% to 2%), RV ESV (19% to 11%) but increased in RV EF (16% to 19%) and RV mass (33% to 37%) with the inclusion of polar prediction and D-Affine smoothing. However, the cases used in [6] represent a subset of the cases analysed in this paper. The differences in the errors could also be due to a larger variety of CHD cases being analysed. Also, differences in basal extent may account for systematic differences in RV EF.
Compared to the other pathologies, the tetralogy of Fallot cases saw similar differences between the methods in most measures. Differences in RV EDV and ESV may be due to the difficulty defining the pulmonary valves in some ToF cases. Many of these patients have pulmonary homografts, making the valve hard to distinguish.
Our dataset also had five cases where the right ventricle was the systemic ventricle. In these cases, the average differences between the manual analysis and our biventricular modelling tool were as follows: LV EDV - 8.1%, LV ESV - −11.7%, LV Mass - −27.0%, LV SV - 19.5%, LV EF - 10.0%, RV EDV - 1–.5%, RV ESV -−12.1%, RV Mass - −23.2%, RV SV - 24.7%, RV EF -24.4%. While most of the systemic ventricle average differences were somewhat higher than the whole dataset, this would need to be confirmed with more patients. Our dataset did not contain any single ventricle cases and the model developed in this method is currently not flexible enough to fit a single ventricle case to our satisfaction. In these cases a single ventricle model may be appropriate.
While no information was provided on ECG wave forms as part of this study, the method should be applicable in cases of bundle branch blocks and asynchrony. The method described uses non-rigid registration to track features of each image from frame to frames and allows the user to add guidepoints to as many or as few frames as required. The analysts noted the time of minimum volume could be different for RV and LV in some patients, however the causes of this require further study.
The correlation of results from the biventricular modelling tool to the manual analysis results was strong but there was lower inter-observer correlation than in the manual analysis. This was due to the fact that the manual analysis used a consensus approach to determine the the valve locations, where both analysts agreed on basal extent. The basal extent is often very difficult to determine from the short axis images alone, leading to large inter-observer errors in mass and volume if this approach is not taken [10]. In contrast the biventricular analysis was performed completely separately, with analysts with less experience. This difference in protocol was the most likely cause of the lower inter-observer correlation in the biventricular analysis, and improvements are expected with increased training. The long axis slices are particularly useful in defining the valve locations accurately, and use of the long axis slices enables better estimation of the mass and volume of each ventricle when compared to using only the short axis slices [6].
Figure 7 shows the initial (a) and customised (b) contours on the same example frame as well as the 3D model after customisation of all slices. The case fitted in this figure has a relatively good fit; however, there are some CHD lesions which the model does not account for. In the future, the tool should be extended to model ventricular septal defects and valvular regurgitation.
5 Conclusion
In conclusion, we have presented a biventricular modelling tool which can rapidly and accurately create 3D time-varying patient specific models for CHD. A major advantage of our model is that it includes all 4 atrioventricular valves, and includes long axis information to reduce the errors in locating the correct valve position. The model showed good results in comparison with the current clinical standard and can be applied in patients to follow the progression of biventricular remodelling due to disease.
Acknowledgments
This research was supported by the National Institutes of Health (NHLBI R01HL121754). Kathleen Gilbert was funded by Green Lane Research and Education Fund. The authors would also like to gratefully acknowledge the National Heart Foundation of New Zealand.
Appendix
The position of any point on the model in Figure 2 is given by:
| (4) |
where Ψ are the basis functions, i.e. bicubic Bézier in ξ1 and ξ2 and linear in ξ3.
Equation 1 was minimized by linear least squares, by solving the resulting normal equations Ax = b using an iterative preconditioned conjugate gradient method. A matrix was decomposed into:
| (5) |
An effective preconditioner is provided by the following[6]:
| (6) |
This preconitioner was chosen as it is similar to the A matrix and can be precalculated.
In order to find the D-Affine smoothing term (Equation 3, Jacobian of motion can be calculated as follows:
| (7) |
The Kronecker delta is represented by δij. In the case of homogeneous affine motions, the Jacobian is constant, with respect to the model coordinates, and thus the resulting norm is zero. Therefore the D-Affine smoothing scheme penalizes deviations from affine deformations. In fact, S(u) is zero for any global affine transformation, and is therefore invariant to superimposed rigid body motions. It is also quadratic in the displacement parameters, leading to a linear least squares minimisation (each coordinate field being solved separately using the same system of equations). The derivative of the Jacobian is calculated by:
| (8) |
Derivatives of the displacement field are given by:
| (9) |
| (10) |
| (11) |
where Ψn are the basis functions, (Ψn,k are derivatives with respect to the model coordinates, etc) and ξ are the model coordinates. In order to calculate the smoothing terms in each element, we need the derivatives of Equation 3 with respect to the mth parameter in the qth displacement field. Let:
| (12) |
and
| (13) |
Components of the Asmoothing matrix can then be calculated using Gaussian quadrature from the derivatives of Equation 3 with respect to the model field parameters:
| (14) |
where wg are the Gauss point weights and the basis functions are evaluated at the Gauss point positions.
Since the optimum solution is found using a preconditioned conjugate gradient, the conditioning of the A matrix (Equation 5) is important. Table 5 shows the condition number of Ξ−1A and number of PCG iterations required for tests 1 and 3. The condition numbers can be reproduced using different weights, where they have be scaled in the relationship of 10 for the predicted points and guide-points and 102 for the smoothing term. The preconditioned conjugate gradient performed with a tolerance of 1 × 10−6 and a maximum of 100 iterations.
Table 5.
Condition values of tests 1 and 3 with different weights. PP is predicted points and GP guide-points.
| Smoothing Weights | PP weight | GP weight | Condition Number of Ξ−1 | Test 1 | Test 3 | ||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Condition Number of Ξ−1A | PCG iterations | Condition Number of Ξ−1A | PCG iterations | ||||
| 1 | 0.01 | 0.025 | 5.26 × 109 | 310.91 | 24 | 22.42 | 8 |
| 1 | 1 | 2.5 | 1.72 × 109 | 9.80 × 106 | 90 | 3.44 × 104 | 10 |
| 1000 | 1 | 2.5 | 2.15× 109 | 2178.05 | 58 | 35.07 | 10 |
| 10000 | 1 | 2.5 | 5.26 × 109 | 310.93 | 24 | 22.42 | 8 |
| 0.0001 | 0.0001 | .00025 | 5.26 × 109 | 311.08 | 24 | 22.4208 | 8 |
| 1 | 0.01 | 0.1 | 5.26 × 109 | 4196.53 | 45 | 675.34 | 10 |
| 100 | 0.1 | 1 | 5.26 × 109 | 7374.86 | 45 | 675.34 | 12 |
| 10000 | 1 | 10 | 5.26 × 109 | 7374.20 | 45 | 675.34 | 12 |
It was also noted that the numerical accuracy improved with increasing weights. The minimum absolute value (the smallest absolute number) in the A matrix was 2.7 × 10−12 for a smoothing weight of 0.0001, predicted point weight of 0.001 and guide-point weight of 0.0025. For a smoothing weight of 10,000, predicted point weight of 1 and the guide-point weight of 2.5 the smallest absolute value was 2.7 × 10−4. Since a type double (used in all experiments) will store up to 16 decimal places, increasing the minimum absolute value in the A matrix will reduce the effect of truncation errors.
The smoothing weighting must therefore be carefully chosen, considering 1) goodness of fit, 2) conditioning of Ξ(−1)A, and 3) the size of the minimum absolute value. The minimum size of the matrix elements is important as the closer it is to machine precision, the greater the impact of truncation errors.
Contributor Information
K Gilbert, Department of Anatomy and Medical Imaging, Faulty of Medical and health sciences, The University of Auckland, New Zealand.
B Pontre, Department of Anatomy and Medical Imaging, Faulty of Medical and health sciences, The University of Auckland, New Zealand.
C J Occleshaw, Auckland City Hospital, Grafton, Auckland, New Zealand.
B R Cowan, Department of Anatomy and Medical Imaging, Faulty of Medical and health sciences, The University of Auckland, New Zealand.
A Suinesiaputra, Department of Anatomy and Medical Imaging, Faulty of Medical and health sciences, The University of Auckland, New Zealand.
A A Young, Department of Anatomy and Medical Imaging, Faulty of Medical and health sciences, The University of Auckland, New Zealand.
References
- 1.Chahal H, McClelland RL, Tandri H, Jain A, Turkbey EB, Hundley WG, Barr RG, Kizer J, Lima JA, Bluemke DA, et al. Obesity and right ventricular structure and function: the mesa-right ventricle study. CHEST Journal. 2012;141(2):388–395. doi: 10.1378/chest.11-0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Commowick O, Arsigny V, Isambert A, Costa J, Dhermain F, Bidault F, Bondiau PY, Ayache N, Malandain G. An efficient locally affine framework for the smooth registration of anatomical structures. Medical Image Analysis. 2008;12(4):427–441. doi: 10.1016/j.media.2008.01.002. [DOI] [PubMed] [Google Scholar]
- 3.Fogel MA, Weinberg PM, Fellows KE, Hoffman EA. A study in ventricular–ventricular interaction single right ventricles compared with systemic right ventricles in a dual-chamber circulation. Circulation. 1995;92(2):219–230. doi: 10.1161/01.cir.92.2.219. [DOI] [PubMed] [Google Scholar]
- 4.Gentles T, Cowan B, Occleshaw C, Colan S, Young A. Midwall shortening after coarctation repair: the effect of through-plane motion on single-plane indices of left ventricular function. Journal of the American Society of Echocardiography. 2005;18(11):1131–1136. doi: 10.1016/j.echo.2005.05.004. [DOI] [PubMed] [Google Scholar]
- 5.Gilbert K, Cowan BR, Suinesiaputra A, Occleshaw C, Young AA. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2014. Rapid d-affine biventricular cardiac function with polar prediction; pp. 546–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gilbert K, Lam HI, Pontré B, Cowan B, Occleshaw C, Liu J, Young A. An interactive tool for rapid biventricular analysis of congenital heart disease. Clinical physiology and functional imaging. 2015 doi: 10.1111/cpf.12319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guihaire J, Haddad F, Mercier O, Murphy DJ, Wu JC, Fadel E. The right heart in congenital heart disease, mechanisms and recent advances. Journal of clinical & experimental cardiology. 2012;8(10):1. doi: 10.4172/2155-9880.S8-010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Haddad F, Doyle R, Murphy DJ, Hunt SA. Right ventricular function in cardiovascular disease, part II pathophysiology, clinical importance, and management of right ventricular failure. Circulation. 2008;117(13):1717–1731. doi: 10.1161/CIRCULATIONAHA.107.653584. [DOI] [PubMed] [Google Scholar]
- 9.Heiberg E, Sjögren J, Ugander M, Carlsson M, Engblom H, Arheden H. Design and validation of Segment–freely available software for cardiovascular image analysis. BMC medical imaging. 2010;10(1):1. doi: 10.1186/1471-2342-10-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hudsmith LE, Petersen SE, Francis JM, Robson MD, Neubauer S. Normal human left and right ventricular and left atrial dimensions using steady state free precession magnetic resonance imaging. Journal of cardiovascular magnetic resonance. 2005;7(5):775–782. doi: 10.1080/10976640500295516. [DOI] [PubMed] [Google Scholar]
- 11.Lamata P, Niederer S, Nordsletten D, Barber DC, Roy I, Hose DR, Smith N. An accurate, fast and robust method to generate patient– specific cubic Hermite meshes. Medical image analysis. 2011;15(6):801–813. doi: 10.1016/j.media.2011.06.010. [DOI] [PubMed] [Google Scholar]
- 12.Li B, Cowan BR, Young AA. Computer Vision–ACCV 2010. Springer; 2010. Real time myocardial strain analysis of tagged mr cines using element space non-rigid registration; pp. 385–396. [Google Scholar]
- 13.Li B, Liu Y, Occleshaw CJ, Cowan BR, Young AA. In-line automated tracking for ventricular function with magnetic resonance imaging. JACC: Cardiovascular Imaging. 2010;3(8):860–866. doi: 10.1016/j.jcmg.2010.04.013. [DOI] [PubMed] [Google Scholar]
- 14.Mcleod K, Seiler C, Toussaint N, Sermesant M, Pennec X. Functional Imaging and Modeling of the Heart. Springer; 2013. Regional analysis of left ventricle function using a cardiac-specific polyaffine motion model; pp. 483–490. [Google Scholar]
- 15.Perperidis D, Mohiaddin RH, Rueckert D. Spatio–temporal free–form registration of cardiac MR image sequences. Medical image analysis. 2005;9(5):441–456. doi: 10.1016/j.media.2005.05.004. [DOI] [PubMed] [Google Scholar]
- 16.Petitjean C, Dacher JN. A review of segmentation methods in short axis cardiac MR images. Medical image analysis. 2011;15(2):169–184. doi: 10.1016/j.media.2010.12.004. [DOI] [PubMed] [Google Scholar]
- 17.Petitjean C, Zuluaga MA, Bai W, Dacher JN, Grosgeorge D, Caudron J, Ruan S, Ayed IB, Cardoso MJ, Chen HC, Jimenez-Carretero D, Ledesma-Carbayo MJ, Davatzikos C, Doshi J, Erus G, Maier OMO, Nambakhsh CMS, Ou Y, Ourselin S, Peng CW, Peters NS, Peters TM, Rajchl M, Rueckert D, Santos A, Shi W, Wang CW, Wang H, Yuan J. Right ventricle segmentation from cardiac MRI: A collation study. Medical image analysis. 2015;19(1):187–202. doi: 10.1016/j.media.2014.10.004. [DOI] [PubMed] [Google Scholar]
- 18.Pfisterer M, Emmenegger H, Soler M, Burkart F. Prognostic significance of right ventricular ejection fraction for persistent complex ventricular arrhythmias and/or sudden cardiac death after first myocardial infarction: relation to infarct location, size and left ventricular function. European heart journal. 1986;7(4):289–298. doi: 10.1093/oxfordjournals.eurheartj.a062066. [DOI] [PubMed] [Google Scholar]
- 19.Redington AN. Right ventricular function. Cardiology clinics. 2002;20(3):341–349. doi: 10.1016/s0733-8651(02)00005-x. [DOI] [PubMed] [Google Scholar]
- 20.Roest AA, de Roos A. Imaging of patients with congenital heart disease. Nature Reviews Cardiology. 2012;9(2):101–115. doi: 10.1038/nrcardio.2011.162. [DOI] [PubMed] [Google Scholar]
- 21.Sheehan FH, Ge S, Vick GW, Urnes K, Kerwin WS, Bolson EL, Chung T, Kovalchin JP, Sahn DJ, Jerosch-Herold M, et al. Three–dimensional shape analysis of right ventricular remodeling in repaired tetralogy of Fallot. The American journal of cardiology. 2008;101(1):107–113. doi: 10.1016/j.amjcard.2007.07.080. [DOI] [PubMed] [Google Scholar]
- 22.Suinesiaputra A, Cowan BR, Al-Agamy AO, Elattar MA, Ayache N, Fahmy AS, Khalifa AM, Medrano-Gracia P, Jolly MP, Kadish AH, et al. A collaborative resource to build consensus for automated left ventricular segmentation of cardiac mr images. Medical image analysis. 2014;18(1):50–62. doi: 10.1016/j.media.2013.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Victor P. Sobolev regularization of a nonlinear ill-posed parabolic problem as a model for aggregating populations. Communications in partial differential equations. 1998;23(3–4):457–486. [Google Scholar]
- 24.Wang Z, Ben Salah M, Gu B, Islam A, Goela A, Li S. Direct estimation of cardiac biventricular volumes with an adapted bayesian formulation. Biomedical Engineering, IEEE Transactions on. 2014;61(4):1251–1260. doi: 10.1109/TBME.2014.2299433. [DOI] [PubMed] [Google Scholar]
- 25.Young AA, Cowan BR, Thrupp SF, Hedley WJ, Dell’Italia LJ. Left Ventricular Mass and Volume: Fast Calculation with Guide-Point Modeling on MR Images. Radiology. 2000;216(2):597–602. doi: 10.1148/radiology.216.2.r00au14597. [DOI] [PubMed] [Google Scholar]
- 26.Zhuang X, Arridge S, Hawkes DJ, Ourselin S. A nonrigid registration framework using spatially encoded mutual information and free-form deformations. IEEE transactions on medical imaging. 2011;30(10):1819–1828. doi: 10.1109/TMI.2011.2150240. [DOI] [PubMed] [Google Scholar]
- 27.Zuluaga MA, Cardoso MJ, Modat M, Ourselin S. International Conference on Functional Imaging and Modeling of the Heart. Springer; 2013. Multi-atlas propagation whole heart segmentation from mri and cta using a local normalised correlation coefficient criterion; pp. 174–181. [Google Scholar]


