Assembly of multi-flavored two-dimensional colloidal crystals

Abstract

We systematically investigate the assembly of binary multi-flavored colloidal mixtures in two dimensions. In these mixtures all pairwise interactions between species may be tuned independently. This introduces an additional degree of freedom over more traditional binary mixtures with fixed mixing rules, which is anticipated to open new avenues for directed self-assembly. At present, colloidal self-assembly into non-trivial lattices tends to require either high pressures for isotropically interacting particles, or the introduction of directionally anisotropic interactions. Here we demonstrate tunable assembly into a plethora of structures which requires neither of these conditions. We develop a minimal model that defines a three-dimensional phase space containing one dimension for each pairwise interaction, then employ various computational techniques to map out regions of this phase space in which the system self-assembles into these different morphologies. We then present a mean-field model that is capable of reproducing these results for size-symmetric mixtures, which reveals how to target different structures by tuning pairwise interactions, solution stoichiometry, or both. Concerning particle size asymmetry, we find that domains in this model’s phase space, corresponding to different morphologies, tend to undergo a continuous “rotation” whose magnitude is proportional to the size asymmetry. Such continuity enables one to estimate the relative stability of different lattices for arbitrary size asymmetries. Owing to its simplicity and accuracy, we expect this model to serve as a valuable design tool for engineering binary colloidal crystals from multi-flavored components.

1 Introduction

Achieving high-fidelity control over the self-assembly of multi-component colloidal mixtures remains an outstanding objective in material design, and an active area of ongoing research.^1–5 By tuning their pairwise interactions, nano- and microscale colloids can be assembled into a myriad of morphologies with even greater complexity than those found in atomic systems.^6,7 The vast phase space of parameters governing the mathematical form of these potential interactions can be daunting, and determining specific pair potentials that stabilize a desired structure is rarely obvious. Thus, computational tools are often employed to predict pairwise interactions that optimally produce a desired target. Among feasible parameters, directional anisotropy is a common tool for engineering interactions in a highly specific manner to stabilize stereospecific subunits of crystals.^4,8–17 In principle, desired spatial symmetries of a crystal can often be obtained through intuitive design of the shape, size, and orientation of different “patches” on its constituent colloids, making this a highly attractive route for experimental realization.^4,13,14,17 However, for practical reasons not all theoretical or computational designs involving anisotropy can be easily achieved in an experimental setting^4,14 and additional factors, such as structure directing agents, may be required to obtain the desired structure.^18–20 A seemingly simpler alternative is to construct isotropic interactions that can achieve the same end goals.

Indeed, recent work has shown that inverse statistical mechanical methods can be powerful tools for designing purely repulsive pairwise interactions that stabilize specific crystal morphologies in pure-component systems at high density or pressure.^21–24 The assembly of similar purely repulsive binary mixtures have been studied extensively.^25–36 Consequently, it also known that subtle changes to such a pair potential’s form or shape can shift the relative stability of different crystal polymorphs.^37,38 Since it is not always clear how to precisely realize a computationally-engineered potential in an experimental setting, it can be difficult to control the ubiquitous problem of polymorphism with such an approach. Furthermore, the high densities and pressures required to achieve assembly with purely repulsive interactions are not always representative of experimentally realizable systems.

It may be preferable to have a system of isotropically interacting particles that assembles at low density or pressure, whose pairwise interactions have general characteristics that are robustly linked to the resulting morphology into which they self-assemble. An appealing candidate system which meets some of these requirements is DNA-grafted colloids. In traditional DNA-grafted nanoparticle assembly, colloids are coated with a certain single stranded DNA (ssDNA) sequence while strands with a complementary sequence are attached to other particles; base pairing results in highly tunable assembly of this binary mixture. Unfortunately, this approach does not permit the self- and cross-interactions between different colloids to be tuned independently.

However, recently a new approach known as the “multi-flavoring motif” has experimentally demonstrated the capability of decoupling them.^39,40 In this case, more than one sequence (and its complement) is grafted on different particles, which enables one to tune the pairwise cross-interactions between like species and unlike species independent of their self-interactions, making them non-additive. This non-additivity is achieved by controlling the relative concentrations of different strands (and their complements) on different particles. This additional degree of freedom greatly increases the design space for experimentally realizable pair potentials, and may open new avenues to tunable self-assembly with isotropic interactions at low density. Indeed, non-additive pair potentials have been shown to manifest in a breadth of nanoparticle systems⁷ and computational investigations into various colloidal models have revealed a range of intriguing self-assembled structures and phase behavior.^16,41,42

Inspired by this approach, here we use a variety of computational and theoretical methods to interrogate the relative stability of two-dimensional binary crystals assembled from multi-flavored colloids at low densities (pressures) representative of experiments.⁴³ We systematically explore these binary mixtures using a simplified pair potential containing a single order parameter, λ, which smoothly varies the interaction from long-range repulsive to long-range attractive (cf. Section 2).⁴⁴ Thus, for a binary system of “A” and “B” particles, there are three values that need to be specified: 〈λ_A,A, λ_A,B, λ_B,B〉. Physically, these parameters describe the cohesive interaction between like particles, λ_i,i, and the adhesive interaction between unlike particles, λ_i,j. This reduces the pairwise interaction phase space to three scalar coordinates for a binary colloidal mixture. Within this phase space, we determine the regions in which different self-assembled structures are the most stable.

This paper is organized as follows. In Section 2, we describe our model and the computational methodologies we employed. Following, in Section 3, we present our results demonstrating tunable assembly of multi-flavored binary superlattices which requires neither anisotropic interactions nor high pressures. These results can be rationalized on the basis of a simple mean-field model enabling heuristic design of binary systems that need not follow the exact form of the pair potentials we employ here. In addition, this model allows us to systematically explore the impact of solution stoichiometry on the resulting structure.⁴⁵ We found excellent agreement between theoretical predictions and the observed structure in direct simulations, suggesting this model may serve as a valuable tool for guiding experiments. Finally, we conclude by systematically investigating the effect of size asymmetry between the constituent colloids. These conclusions are further summarized in Section 4.

2 Methods

2.1 Multi-flavored pair potential

To capture the essential physics of the multi-flavoring motif, we employed a modified Lennard-Jones potential between all species, as described in ref. 44 (cf. Fig. 1). Here the attractive and repulsive contributions are separated and recombined according to the order parameter, λ, such that:

$$U_{\mathrm{i},\mathrm{j}}(r)=U_{\mathrm{i},\mathrm{j}}^{\mathrm{r}}(r)+{\lambda }_{\mathrm{i},\mathrm{j}}{U}_{\mathrm{i},\mathrm{j}}^{\mathrm{a}}(r),$$ (1)

where

Fig. 1.

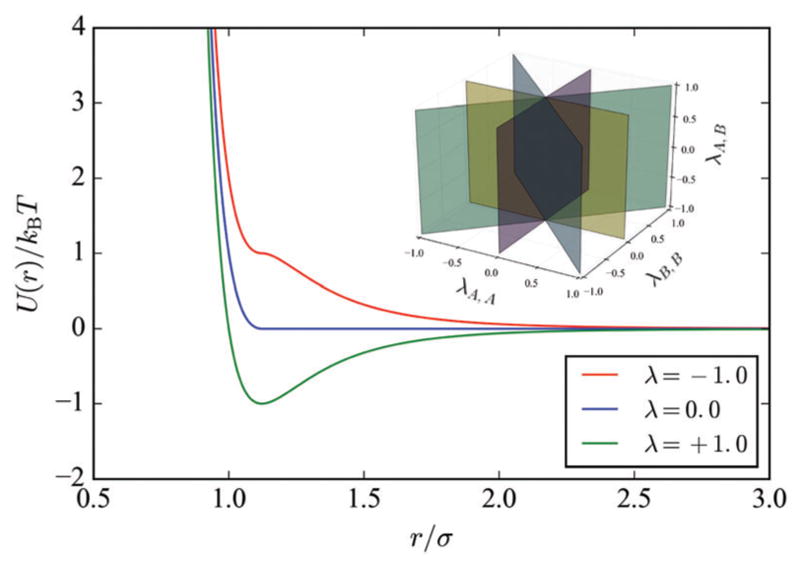
The pair potential we employed describing the interactions between different colloidal species ranging from long-range repulsive (red) to long-range attractive (green), as a function of the order parameter λ. The inset shows how we divide the phase space describing these interactions, 〈λ_A,A, λ_A,B, λ_B,B〉, for all pairs of species into discrete planes which were sampled with Monte Carlo simulations.

$$U_{\mathrm{i},\mathrm{j}}^{\mathrm{r}}(r)=\{\begin{array}{ll}4\left({\left(\frac{{\sigma }_{\mathrm{i},\mathrm{j}}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{\mathrm{i},\mathrm{j}}}{r}\right)}^6\right){\epsilon }_{\mathrm{i},\mathrm{j}}+{\epsilon }_{\mathrm{i},\mathrm{j}}\hfill & r\le 2^{1/6}{\sigma }_{\mathrm{i},\mathrm{j}}\hfill \\ 0\hfill & r>2^{1/6}{\sigma }_{\mathrm{i},\mathrm{j}},\hfill \end{array}$$ (2)

and

$$U_{\mathrm{i},\mathrm{j}}^{\mathrm{a}}(r)=4\left({\left(\frac{{\sigma }_{\mathrm{i},\mathrm{j}}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{\mathrm{i},\mathrm{j}}}{r}\right)}^6\right){\epsilon }_{\mathrm{i},\mathrm{j}}-U_{\mathrm{i},\mathrm{j}}^{\mathrm{r}}(r).$$ (3)

In all our simulations σ_A,A = 1, ε_A,A = ε_A,B = ε_B,B = 1.0, while the diameter of the second species is reduced to explore size asymmetry such that σ_B,B = 1.00, 0.40, 0.14. In all cases, σ_A,B = (σ_A,A + σ_B,B)/2. Temperature is defined in reduced units such that T* = k_BT/ε_A,A, where k_B is Boltzmann’s constant. Furthermore, all lengths reported herein have been implicitly non-dimensionalized by dividing by σ_A,A. In principle, one can use a pair potential derived from statistical mechanics⁴⁶ or simulations,⁴⁷ but here we restrict ourselves to the simple LJ-type potential form for simplicity and generality of the results for other types of binary superlattices.

2.2 Monte Carlo simulations

We performed Wang–Landau Monte Carlo simulations to explore the three dimensional phase space defined by 〈λ_A,A, λ_A,B, λ_B,B〉.^48,49 To cover this pairwise interaction phase space efficiently, we divided it into planes according to fixed ratios of λ_A,A/λ_B,B as depicted in the inset of Fig. 1. Each plane was broken into discrete simulations at different magnitudes of λ_i,i. In each simulation we employed an expanded ensemble in which the adhesion was divided into 11 windows with values of λ_A,B ∈ [0.0, 0.1, 0.2,…,1.0]. The cohesion order parameters, λ_A,A, λ_B,B were fixed, also at values in this range, while the expanded ensemble allows the system to dynamically change its value of λ_A,B over time. These were carried out in a periodic 35σ_A,A × 35σ_A,A simulation cell at T* = 0.05, 0.10, 0.15, 0.175. For equimolar mixtures the cell contained 100 “A”-type colloids and 100 “B”-type colloids. For mixtures at a 2 : 1 ratio we simulated 200 “A” and 100 “B” colloids, whereas for 3 : 1 the cell contained 200 “A” and 66 “B” colloids. Here we report only the representative results from T* = 0.10.

Wang–Landau simulation is a flat-histogram method which constructs the relative probability distribution of a system’s macrostates defined by a given order parameter, in this case, λ_A,B.⁴⁸ This is done by measuring the frequency with which each macrostate is visited during a simulation. The inverse of this estimated distribution is then used to bias the Monte Carlo simulation so that all macrostates may be visited with approximately equal probability. Specific details of our implementation can be found in ref. 50 and 51. In each simulation, we used single particle displacement moves, identity swaps, geometric cluster moves,^52,53 and incremental changes to λ_A,B which occurred in a ratio of 5000 : 5000 : 10 : 1, respectively. This expanded ensemble allows the system to break and reform different morphologies with relative ease facilitating fast equilibration across the range of λ_A,B values used. The subsequent production phase lasted for 2 × 10¹⁰ moves, during which we recorded the instantaneous configuration of the system every 2.5 × 10⁵ steps. This generally resulted in at least 1000 snapshots for each λ_A,B at fixed λ_A,A, λ_B,B. The morphologies in each snapshot were identified visually in each frame and the mean structure we found has been reported here, where the results for each λ_A,B were included with those of their neighboring values. Hence we report the mean structure for λ_A,B ∈ [0.1 ± 0.1, 0.3 ± 0.1, 0.5 ± 0.1, 0.7 ± 0.1, 0.9 ± 0.1]. In these Monte Carlo simulations, all pair potentials were cutoff at r_cut = 3σ_A,A, then shifted to zero at the cutoff.

2.3 Stochastic global structure optimization

We used stochastic global optimization to understand the lowest energy structure of small clusters of size-symmetric colloids (σ_A,A = σ_B,B), used in the Monte Carlo simulations, to identify the most thermodynamically stable structure in the limit of T* → 0. Specifically, we used basin-hopping^54,55 as implemented in the SciPy library⁵⁶ for Python,⁵⁷ for a system of six “A” colloids and six “B” colloids. We considered various cases where λ_i,j ∈ [1, 0.5, 0.1, 0, −0.1, −0.5, −1]. Basin-hopping proceeds via a series of cycles, during which: first, a random perturbation to the coordinates of the colloids is made, second, a local minimization is used to generate a new configuration, and finally, the system is transformed from its old configuration to this new one according to the standard Metropolis criterion⁵⁸ based on the difference in energies between the two configurations:

$$p_{\text{acc}}(\text{old}\to \text{new})=min\left[1,exp\left(-\frac{U_{\text{new}}-U_{\text{old}}}{\widehat{T}}\right)\right].$$ (4)

Here, T̂ is some fictitious temperature which effectively controls the rate at which the system hops between different local basins. Here we chose T̂ = 0.50; note that T̂ is not related to T*. Initially, the colloids were randomly placed in a large, non-periodic cell. Then, a perturbation was generated by choosing random displacements (with magnitudes less than σ_A,A) for each individual colloid 95% of the time, while 5% of the time a randomly chosen number of colloid pairs were selected and their identities were exchanged. Subsequently, the L-BFGS-B algorithm⁵⁹ was employed to locally optimize the structure and produce a new candidate, which was accepted as the new state of the system stochastically. This was repeated 5 × 10⁷ times, over the course of which the energies and configurations of the local minima were recorded. After which, the lowest energy structure was taken as the ground state. To facilitate convergence, interaction energies were truncated at |U(r_cut)| < 0.005. The morphology of the ground state was classified on the basis of its mean coordination number (2, 4, or 6), regardless of its compositional order, unless the resulting structure phase separated. Representative configurations are available in the ESI.^†

2.4 Mean-field model

To estimate the relative stability of different morphologies in the ground state (limit of T* → 0) when the colloids are size-symmetric, we used a simple mean-field approach to energetically rank structures. For a series of candidate structures, we predicted their energies based on the number of i–j contacts in a given structure (regardless of their relative orientation), neglecting edge effects and assuming the result is defect-free. Starting from a chosen stoichiometry of components available, we assumed the colloids aggregate to form a structure whose size is determined by the limiting “reactant” species in the bulk since different structures can have different native stoichiometries than that initially available in the bulk. For simplicity, the remainder is assumed to form a non-interacting homogeneously dispersed phase which contributes no energy. For a structure with a native stoichiometry of x : y, the number of A_xB_y “molecules” that may form is given by:

$$N_{\mathrm{m}}=min\left(\frac{N_{\mathrm{A}}}{x},\frac{N_{\mathrm{B}}}{y}\right),$$ (5)

where N_A and N_B correspond to the number of each colloid type initially available. In each structure, the coordination of each colloid is represented by the vector, C⃗= 〈C_A,A, C_A,B, C_B,B, C_B,A〉. Here, C_i,j refers to the number of colloids of type j in the nearest neighbor shell of a colloid of type i. Values of C are provided in Table 1 for all potential lattices we considered. The total energy of each structure is then given by:

$$U=-\frac{N_{\mathrm{m}}}{2}[x(C_{\mathrm{A},\mathrm{A}}{\lambda }_{\mathrm{A},\mathrm{A}}+C_{\mathrm{A},\mathrm{B}}{\lambda }_{\mathrm{A},\mathrm{B}})+y(C_{\mathrm{B},\mathrm{A}}{\lambda }_{\mathrm{A},\mathrm{B}}+C_{\mathrm{B},\mathrm{B}}{\lambda }_{\mathrm{B},\mathrm{B}})].$$ (6)

Table 1.

Coordination numbers and stoichiometry for candidate morphologies considered in our mean-field model

	Stoichiometry
Morphology	(x : y)	CA,A	CA,B	CB,B	CB,A
Disordered “gas”	1 : 1	0	0	0	0
Alternating string-like aggregate	1 : 1	0	2	0	2
Alternating square lattice	1 : 1	0	4	0	4
Alternating hexagonal layers	1 : 1	2	4	2	4
Mixed hexagonal lattice	1 : 1	3	3	3	3
Phase-separated hexagonal lattices	1 : 1	6	0	6	0
Phase-separated hexagonal lattice + “gas”	1 : 1	6	0	0	0
Honeycomb	2 : 1	3	3	0	6
Kagome	3 : 1	4	2	0	6
Square kagome	3 : 1	4	2	0	6

We also considered the cases where A and B may exchange identities (C_i,j → C_j,i) within the same morphology. From this, we report the lowest energy structure as the most stable. Note that we considered the case where one species forms a pure hexagonal crystal, while the other forms either a “gas” or another pure crystal, as being the same morphology, which we refer to as “phase-separated hexagonal.” This is because the two species demix in both cases, which we consider an uninteresting result, as our objective is to form mixed morphologies corresponding to binary superlattices.

2.5 Molecular dynamics simulation

In addition to Monte Carlo, we also used canonical molecular dynamics simulations, implemented in LAMMPS,⁶⁰ to determine the phases forming ab initio from a disordered fluid phase. For equimolar size-symmetric mixtures we considered λ_A,A, λ_B,B ∈ [1.0, 0.5, 0.0, −0.5, −1.0] and λ_A,B ∈ [1.0, 0.75, 0.5, 0.25, 0.0], where each simulation contained 1000 total colloids. All pairwise interactions were truncated at r_cut = 2.5σ_i,j. These results are presented in the ESI.^† In addition, we replicated the results of Monte Carlo simulations for non-equimolar mixtures at the conditions reported in Fig. 4. The simulations contained 1050 total colloids for a 2 : 1 stoichiometric ratio, and 1000 total colloids for a 3 : 1 ratio. Simulations were performed in a square, periodic box with an edge length of 90σ_A,A. The Verlet algorithm was used to integrate the equations of motion using a time step of $\mathrm{\Delta }t=0.01{\sigma }_{\mathrm{A},\mathrm{A}}\sqrt{m/{\epsilon }_{\mathrm{A},\mathrm{A}}}$, where the mass, m, of all colloids was set to unity. A Langevin thermostat was used with a damping constant of $2{\sigma }_{\mathrm{A},\mathrm{A}}\sqrt{m/{\epsilon }_{\mathrm{A},\mathrm{A}}}$. The system was initially equilibrated for 10⁶ integration steps at T* = 2. Subsequently, the system was run for 2 × 10⁸ integration steps at a constant temperature of T* = 0.1 during which instantaneous configurations were recorded. Visual inspection of the forming structures was conducted using Visual Molecular Dynamics (VMD).⁶¹

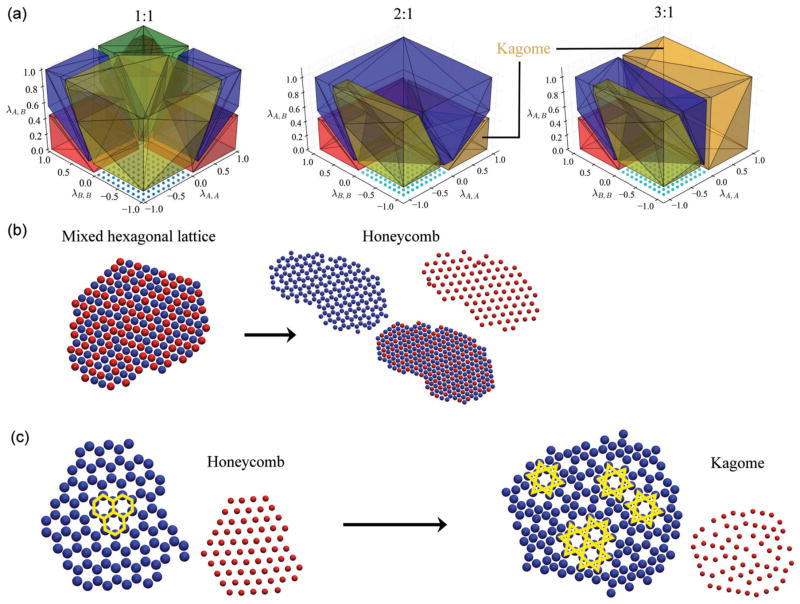
Fig. 4.

Impact of stoichiometry. (a) From left to right, the A : B stoichiometric ratio increases from 1 : 1 to 2 : 1 to 3 : 1 in our mean-field model. The yellow domain corresponds to an alternating square lattice, blue to honeycomb, green to mixed hexagonal, red to phase-separated hexagonal, and orange to kagome. (b) Monte Carlo simulations at 〈λ_A,A, λ_A,B, λ_B,B〉 = 〈0.5, 1.0, 0.5〉 with a 1 : 1 stoichiometric ratio form a mixed hexagonal lattice, while at a 2 : 1 ratio the honeycomb lattice appears instead. (c) Equimolar Monte Carlo simulations at 〈λ_A,A, λ_A,B, λ_B,B〉 = 〈1.0, 1.0, −1.0〉 produce a honeycomb lattice, which instead becomes polymorphic kagome at a 3 : 1 ratio. For clarity, the red colloids have been reduced in size and are depicted next to the blue colloids in whose interstices they exist.

3 Results and discussion

Depending on the grafting density and composition of the ssDNA strands on the colloids, pairwise interactions in a multi-flavored system may range from being attractive to softly repulsive. The potential shown in Fig. 1 mimics this by dividing a Lennard-Jones potential into its attractive and repulsive contributions, then recombining them according to a factor, λ.⁴⁴ Thus, when λ_i,j = 1, particles i and j interact via the conventional Lennard-Jones potential. When λ_i,j = 0, the two have a pseudo-hard-sphere interaction known as the Weeks–Chandler–Andersen potential,⁶² and when λ_i,j = −1 the two colloids have a purely (soft) repulsive interaction. The first case exemplifies when base-pairing results in an attraction between species; the last is representative of when the grafts are non-complementary and exhibit an entropic repulsion between the polymer coronas. Tuning the details of the ssDNA chemistry and composition in the multi-flavoring motif allows one to achieve intermediate states as well.⁴⁰ To identify the most stable crystal or morphology for a given set of pairwise interactions (e.g., 〈λ_A,A, λ_A,B, λ_B,B〉), we first performed flat-histogram Monte Carlo simulations in a λ_A,B-expanded ensemble.

3.1 Monte Carlo simulations

We begin with the size-symmetric case where the two types of colloids have equal diameters (σ_A,A = σ_B,B). Unless otherwise stated, we consider the system at a fixed stoichiometric ratio of 1 : 1. Throughout this work we report only λ_A,B > 0; otherwise the two species demix entirely which is a trivial result. Fig. 2(a) illustrates the results when λ_A,A/λ_B,B = 1 at low temperatures (T* = 0.10) where the mixture can form well-defined crystals for sufficient interparticle attraction. When represented in a two-dimensional cohesion (λ_i,i) vs. adhesion (λ_i,j) diagram, the morphologies we observed display changes which manifest as one traverses the figure in a counterclockwise fashion.

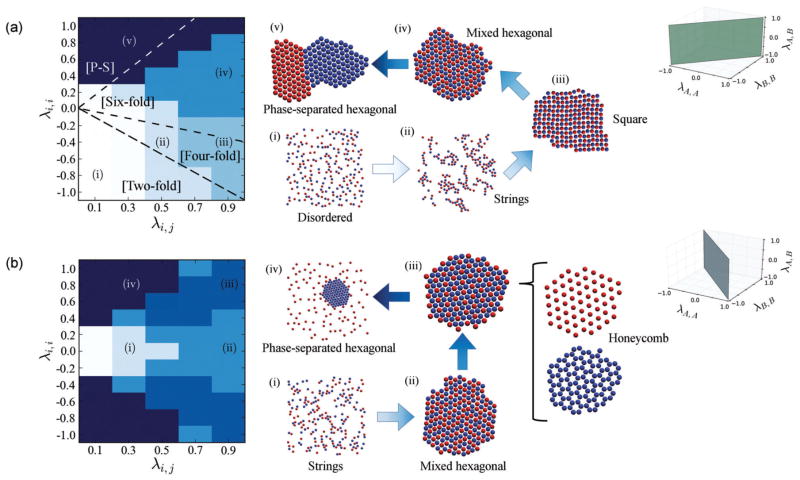
Fig. 2.

Results from Monte Carlo simulations of equimolar, size-symmetric binary mixtures. “A” and “B” colloids are depicted in blue and red, respectively. (a) The case when the cohesive interactions, λ_A,A = λ_B,B = λ_i,i, are identical. Representative snapshots of the morphologies in each colored region, indicated as (i)–(v), are shown on the right. Dashed lines delineate regions of two-, four-, six-fold rotational symmetry, and phase-separated morphologies (counterclockwise, respectively) of small clusters in the limit of absolute zero temperature, when compositional order was ignored. (b) The case when the two colloids have opposite self-interactions, λ_A,A = λ_i,i = −λ_B,B. Representative snapshots are shown on the right. Individual components of the honeycomb lattice from region (iii) are illustrated in more detail.

In region (i) the self-interactions between like colloids display a long-range repulsion, whereas unlike particles are only weakly attractive. Consequently, we find the system in a generally homogeneous, disordered gas-like state. As the adhesive interactions are increased, the system begins to “polymerize” forming compositionally alternating string-like aggregates, as show in region (ii). The emerging compositional order results from an interplay between the long-range cohesive (repulsive) and intermediate-range adhesive (attractive) interactions. Upon further increasing the adhesion, individual string-like aggregates further assemble into an alternating square lattice depicted in region (iii). Next, if one considers the adhesion as fixed, and simply increases the favorability of the cohesive interactions, the alternating square lattice increases its coordination number and transforms into a mixed hexagonal lattice, region (iv), with a loss of compositional order. Finally, if adhesion is reduced at fixed cohesion we reach region (v). The morphology which manifests here is one in which the colloids form hexagonal crystals that have compositionally phase separated into separate grains. Intuitively, this is brought about by reducing the adhesion value below the cohesion values.

With one notable exception, these morphologies represent all of the stable ones found within the range of 〈λ_A,A, λ_A,B, λ_B,B〉 values we explored at a 1 : 1 stoichiometric ratio. This exception may be clearly found along the λ_A,A/λ_B,B = −1 plane, which is depicted in Fig. 2(b). In this case, the cohesive nature of one type of colloid is opposite to the behavior of the other type; e.g., when one is self-repulsive, the other is self-attractive. Again, we find some angular diagrammatic symmetry moving in either a counterclockwise direction from the origin, through the upper half of the order diagram, or clockwise through the lower half. The diagram has reflection symmetry across the λ_i,i = 0 axis, as expected, since crossing this axis simply entails exchanging the identities of the colloids. Once again, starting from an initially homogeneous, disordered state at the origin, increasing the adhesive interactions (λ_A,B) while λ_A,A = −λ_B,B = 0 results in string-like aggregates, depicted in region (i). These transform directly into a randomly mixed hexagonal lattice as the adhesion is further increased, region (ii). However, at this point, because λ_A,A = −λ_B,B, increasing the favorability of one species’ self-interaction implies that the other’s is equally penalized. Consequently, as λ_i,i is increased, species i will energetically favor morphologies with a maximum amount of i-type neighbors, whereas species j will tend to favor avoiding other j-type neighbors. The result is a honeycomb lattice, where species j (in the case shown in Fig. 2(b), the red “B” colloids) situate themselves inside a hexagonal shell of the species i (the blue “A” colloids). Note that upon reducing the adhesion from this state, the system once again phase separates into a hexagonal “A” phase, while the repulsive “B” species forms a disordered gas-like phase around the hexagonal crystal. We refer to both this state and that in Fig. 2(a) when the colloids form two separate grains as a “phase-separated hexagonal” state, which is of little interest here.

3.2 Energetic optimization of small clusters

For all the cases we investigated thus far at a 1 : 1 stoichiometry, we found that the morphologies could be classified as one of the following: a mutually disordered gas-like phase, an alternating string-like aggregate, an alternating square lattice, a (composition-ally) mixed hexagonal lattice, a phase-separated hexagonal lattice, or a honeycomb lattice. To understand the ground-state behavior of this system, we performed stochastic global energy minimization of small clusters of 6 “A” and 6 “B” particles to obtain the most stable morphologies in the zero-temperature limit (cf. ESI^†). To identify any emergent patterns in phase space where different morphologies appear, we performed linear discriminant analysis.^63,64 This analysis revealed that considering the mean cohesive interaction, (λ_A,A + λ_B,B)/2, vs. the adhesive interaction, λ_A,B, often produced a pattern in which morphologies with the same coordination number (or approximately the same n-fold rotational symmetry) fell within regions defined by the angle formed by these two coordinates. The results are summarized as dashed lines on Fig. 2(a) for the case when λ_A,A = λ_B,B. In Fig. 2(a) we have presented the results from Monte Carlo simulations when λ_A,A = λ_B,B, so this mean cohesive interaction is given simply by λ_i,i.

In this ground state, morphologies with the same rotational symmetry may be found between these lines emanating from the origin; however, close to the origin at finite temperature we expect these morphologies to melt into a disordered state (cf. region (i) in Fig. 2(a)) as their pair interactions are overcome by thermal energy, which is indeed what we observed in all Monte Carlo simulations. Thus, we compare the results of the optimized ground state structure with Monte Carlo performed far from the origin. When the self-interactions are predominantly repulsive, any finite amount of cross-interaction results in an alternating string-like morphology in the limit of T* → 0. This aggregate, which may be considered as possessing twofold rotational symmetry, generally resides in regions (i) and (ii) in Fig. 2(a). Here the distinction between the two regions is found only in systems at finite temperature, where there is sufficient thermal energy to break up weakly associating clusters found when close to the origin. Moving counterclockwise, we find a region of well-defined compositionally alternating square lattices (four-fold rotational symmetry) which coincides with Monte Carlo simulations at finite temperature far from the origin (region (iii), Fig. 2(a)). Continuing, we similarly find lattices with six-fold symmetry in the region corresponding to the mixed hexagonal lattices (region (iv)). Finally, when the cohesion is the strongest, but adhesion is relatively weak, we find the ground state phase separates into different compositionally pure grains, as in Monte Carlo (region (v)). We note that as the temperature of the Monte Carlo simulations is reduced, each morphology tends to more completely “fill” the region corresponding to its rotational symmetry, bounded by the dashed lines.

This general increase in the rotational symmetry of the ground state morphology, from strings (two-fold) → square (four-fold) → hexagonal (six-fold), moving counterclockwise in Fig. 2 is most readily observed when λ_A,A = λ_B,B. However, even when λ_A,A ≠ λ_B,B, the general trend still holds, with the caveat that differences in composition order must be neglected. For example, one must include the honeycomb lattice in the six-fold classification together with the mixed hexagonal lattices, without making any distinction between the two (cf. ESI^†). Although this may seem reasonable when considering the morphologies of finite-sized clusters which may be too small to reliably predict the resulting structure of larger systems, this is, in fact, a representation problem that arises in multi-flavored systems. Fundamentally, the presence of three independent pairwise interactions requires, at minimum, a three-dimensional representation of the data, which will be adopted henceforth. Although for specific experimental realizations there may be many variables determining the precise shape and form of these interparticle potentials, apparently, the general nature of having decoupled these pairwise interactions from each other tends to necessitate at least one variable per interaction to preserve information corresponding to morphologies with the same rotational symmetry but different compositional order. Furthermore, the fact that this minimization can reliably predict the morphology observed in Monte Carlo simulations suggests these systems are largely energetically dominated.

3.3 Mean-field model

Encouraged by the close agreement between the simulation and ground-state results, we also developed a mean-field model to predict the structure in the ground state. In this simplified model, we considered an array of different possible arrangements for size-symmetric colloids, including the morphologies discussed above as well as others including kagome lattices (cf. ESI^†). Each lattice was ranked on the basis of its energy, assuming it was defect free and fully periodic. There are two principal components to our model. The first is that each lattice’s energy is based only on the number of nearest neighbor i–j contacts between different species, each of which is assigned an energy of −λ_i,j. The total energy of the lattice is then based on the product of the number of each type of contact and its energy, scaled by the size of the crystal that can be produced from a given stoichiometry.

This stoichiometric effect is the second principal component, which will be addressed further in the next section. We note that a number of similar coarse-grained thermodynamic models for binary mixtures of DNA-coated colloids already exist, such as the complementary contact model.³ However, this model neither accounts for entropic repulsions between particles with non-complementary DNA strands, nor stoichiometric effects.^3,45 Because of the former, it is highly incompatible in its current form with the multi-flavoring motif since λ_i,j < 0 introduces “soft” repulsive interactions. Notably, a recent improvement of this theory was developed which sought to remedy both shortcomings.⁴⁵ In that case, a more advanced approach was adopted to treat the formation of competing morphologies as independent, parallel reactions which requires advanced numerical methods to solve the associated set of non-linear expressions describing equilibrium. In our approach we adopt a significantly simplified tactic (cf. Methods), and find that it is still capable of making accurate predictions about the relative stability of different lattices.

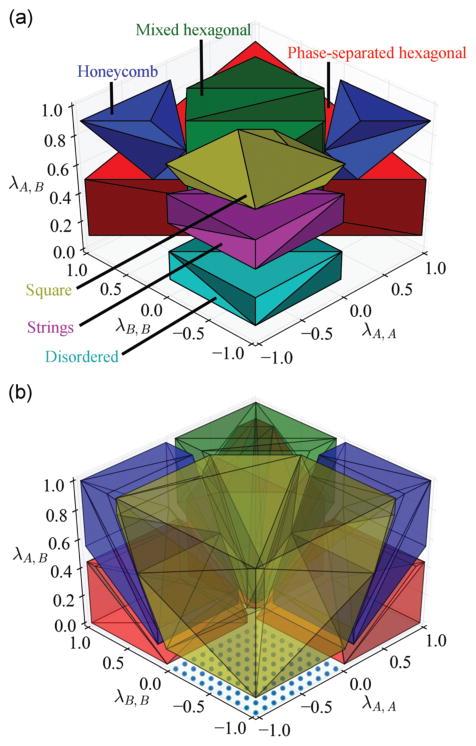
In Fig. 3(a) we took the results of Monte Carlo simulations and plotted them in three-dimensional 〈λ_A,A, λ_A,B, λ_B,B〉 phase space. Remarkably, the regions of phase space corresponding to each morphology can be described by a single contiguous domain, with the exception of the honeycomb lattice which requires two. Comparatively, we found that the simplified mean-field model qualitatively reproduces these domains, suggesting the temperature used in our Monte Carlo simulations (T* = 0.10) is sufficiently low (for most cases) as to be representative of the ground state (cf. Fig. 3(b)). Only some minor differences appear, which are intuitively to be expected. First, the region corresponding to the homogeneously dispersed gas-like phase is reduced from a three-dimensional domain to a two-dimensional plane, indicated by the cyan dots in Fig. 3(b). This is to be expected as any finite, positive λ_A,B implies a favorable energetic interaction between opposite colloidal species. This will result in aggregation in the limit of T* → 0, whereas a finite amount of thermal energy will be able to break these clusters or aggregates when T* > 0. Indeed, this has already been discussed in the context of the energy minimization of small clusters, and is also why the string-like aggregate region (magenta) from Fig. 3(a) does not manifest in part (b). Though, of course, at the interface between the square lattice and the homogeneous gas-like phase one expects intermediate structures, in practice. The mean-field model does not consider the long-ranged nature of the repulsions when λ_i,i are highly negative, which is why ground state optimization, which accounts for these effects, finds a region of string-like aggregates at this interface while the mean-field model does not. Regardless, this region is relatively inconsequential with regards to the assembly of binary superlattices, and its absence does not detract from the applicability of the model.

Fig. 3.

Mean-field model vs. Monte Carlo simulations for a size-symmetric equimolar mixture. (a) Three-dimensional reconstruction of the domains corresponding to each morphology found in Monte Carlo simulation at T* = 0.10. (b) Mean-field predictions in the limit of T* → 0. In both parts, the colors represent different morphologies as indicated in part (a). The dotted cyan region in part (b) indicates that this disordered “gas” morphology is stable only precisely along the plane where λ_A,B = 0, and λ_A,A, λ_B,B ≤ 0.

In Fig. 3(b) we have neglected one morphology from the array of structures we considered, namely an alternating hexagonal layer morphology in which the blue “A” and red “B” colloids are aligned in layers of similar color on a hexagonal lattice. In fact, the mean-field model identifies this structure as slightly lower in energy than the mixed hexagonal lattice, so if it is included, the green region in Fig. 3(b) would now correspond to this morphology rather than the randomly mixed hexagonal morphology also found in Monte Carlo (cf. ESI^†). This, however, has no effect on any of the other domains. The reason for this change is simply due to the fact that the mixed hexagonal lattice has a much higher entropy than its alternating layer counterpart due to its disordered nature. Accordingly, we expect that at finite temperature this morphology should dominate, which is indeed what was observed in both Monte Carlo and molecular dynamics simulations. Regardless, these differences do not detract from the mean-field model’s capacity to predict these regions of stability rather accurately. Given its simplicity, we expect this model to serve as a useful design tool which can provide heuristics for developing pairwise interactions to stabilize desired lattices.

3.4 Stoichiometric control

Next, we consider the impact of mixture stoichiometry on our model. Recent work has shown how the stoichiometric ratio of individual components couples to the assembly of a lattice’s building blocks, thus controlling its equilibrium assembly.⁴⁵ Consequently, stoichiometry can exert a greater degree of control over the self-assembly of colloidal crystal lattices than previously anticipated. To account for this effect, we consider the two size-symmetric colloidal species as reactants whose mixture stoichiometry determines the extent to which an irreversible “reaction” to form a single “unit” of a given lattice or morphology may proceed (cf. Methods). The extent of each reaction determines the maximum size of each morphology, and therefore the extensive energy, associated with each. For example, 100 “A” and 100 “B” colloids could combine to produce 100 units of an alternating square lattice (1 : 1 stoichiometry), but only 50 units of a honeycomb lattice (2 : 1 stoichiometry). This in turn affects the ranking of the different morphologies in the ground state. For simplicity, we assume any excess forms a non-interacting homogeneously dispersed (ideal) “gas” phase which contributes no energy to the final state.

Fig. 4 shows the qualitative changes that result from tuning the solution stoichiometry. Generally speaking, lattices whose stoichiometry is commensurate with that of the initial mixture become favored. In the equimolar case, 1 : 1 lattices are favored in different regions depending on their relative interactions. However, upon increasing the amount of “A” particles to reach a 2 : 1 stoichiometric ratio, the honeycomb lattice primarily dominates the interaction phase space. Indeed, this lattice is the only lattice we considered which has this ratio. This comes at the expense of other 1 : 1 lattices such as the mixed hexagonal lattice and alternating strings, neither of which appear anywhere in phase space. Furthermore, along the λ_A,A axis a new morphology appears which was never stabilized in the equimolar case: the kagome lattice, indicated in orange in Fig. 4(a). Upon further increasing the stoichiometric asymmetry to 3 : 1, the kagome lattice dominates phase space, primarily where λ_A,A > 0. Again, this is consistent with intuition since the kagome lattice has a native 3 : 1 stoichiometric ratio. Note that reversing the stoichiometric ratio, e.g., from 2 : 1 to 1 : 2, simply flips the diagram by exchanging the λ_A,A and λ_B,B axes. Furthermore, increasing the ratio beyond 3 : 1 makes no additional changes since we have not considered lattices beyond this limit, as none were found in either Monte Carlo or molecular dynamics simulations.

To validate these predictions, we performed direct simulations at various points in 〈λ_A,A, λ_A,B, λ_B,B〉 phase space. While we only provide a few examples in Fig. 4(b) and (c), we found general agreement between the predictions of the mean-field model and simulation, both Monte Carlo and molecular dynamics. In Fig. 4(b) we illustrate the results obtained from Monte Carlo simulations at 〈λ_A,A, λ_A,B, λ_B,B〉 = 〈0.5, 1.0, 0.5〉. For an equimolar mixture, a mixed hexagonal morphology manifests with no compositional order. When the ratio is increased to 2 : 1, with an excess of blue “A” colloids, the system instead assembles into a honeycomb lattice. Similarly, equimolar mixtures at 〈λ_A,A, λ_A,B, λ_B,B〉 = 〈1.0, 1.0, −1.0〉 form a well-defined honeycomb structure, which becomes a polymorphic kagome lattice at a 3 : 1 stoichiometric ratio. This lattice generally appears defective, which we attribute to the polymorphic nature of the kagome lattice. As detailed in the ESI,^† there are two polymorphs of this trihexagonal tiling which differ only in their long-range order, while the nearest neighbor shell around each particle type remains unchanged. Consequently, the two polymorphs are indistinguishable for systems dominated by their nearest neighbor interactions. We therefore expect the traditional kagome, and its square polymorph, to manifest simultaneously leading to a structure containing regular polygonal hexagrams (highlighted in yellow in Fig. 4(c)) which lack long range order. Indeed, this is precisely what is observed. These kagome polymorphs were also occasionally found as defects within honeycomb lattices formed from equimolar mixtures (cf. ESI^†), however they were never found to be stable for this stoichiometry.

3.5 Effects of size asymmetry

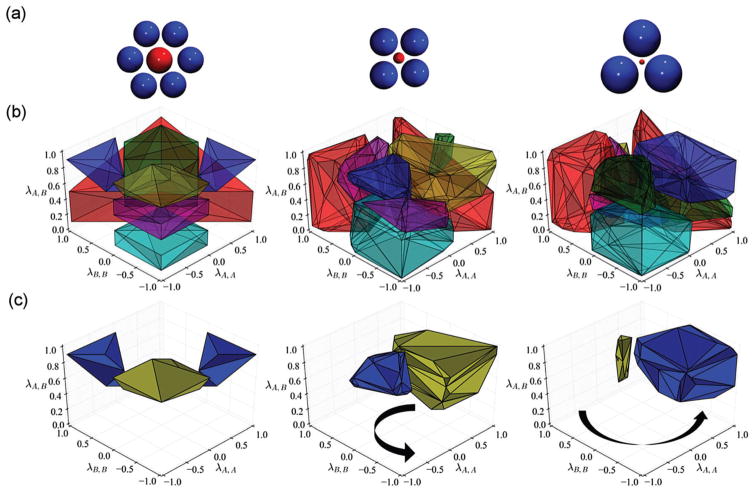
Finally, we consider the impact that size asymmetry has on the resulting morphology of the binary mixture at a 1 : 1 stoichiometric ratio. As the size asymmetry is increased, the smaller component is anticipated to adsorb in the interstices of lattices formed by the larger colloid.^32,65,66 When this occurs, it is common to find multiple smaller colloids within the interstices of the larger one; as a result, the crystal’s stoichiometry deviates from 1 : 1 and the resulting lattices are often reported as being “LS_x” structures, where x denotes the occupancy of the smaller species within the interstices.^32,65 Consequently, we expect the smaller component to behave like a structure directing agent^{16,18,19,67,68} that will bias the formation of the lattice into which the smaller colloid can maximize its energetically favorable nearest neighbor contacts. We fixed σ_A,A = 1.0 and reduced σ_B,B = 0.40, 0.14. At a size ratio of ${\sigma }_{\mathrm{B},\mathrm{B}}/{\sigma }_{\mathrm{A},\mathrm{A}}=\sqrt{2}-1\approx 0.40$, the smaller species “B” can precisely fit into a square formed by four tangent “A” colloids. Similarly, when ${\sigma }_{\mathrm{B},\mathrm{B}}/{\sigma }_{\mathrm{A},\mathrm{A}}=\frac{2}{3}\sqrt{3}-1\approx 0.14$, the smaller colloid can be inscribed inside a tangent triplet of “A” colloids. From simple packing arguments, we anticipate that when σ_B,B/σ_A,A = 0.40 a square lattice of “A” colloids will be favored, whereas when σ_B,B/σ_A,A = 0.14 a lattice with a triangular tiling will be favored (cf. Fig. 5(a)). Fig. 5 illustrates the resulting changes to the location of the domains where different morphologies are found in Monte Carlo simulations.

Fig. 5.

Impact of size asymmetry on an equimolar mixture. (a) The diameter of species “A” (blue) is fixed at σ_A,A = 1.0, while species “B” (red) varies from left to right as σ_B,B = 1.0, 0.40, 0.14. The coloring scheme for the domain corresponding to each morphology is the same as in Fig. 3. (b) Resulting morphology from Monte Carlo simulations for each size ratio. The yellow domain corresponds to an alternating square lattice, blue to honeycomb, green to mixed hexagonal, red to phase-separated hexagonal, and cyan to a disordered “gas.” The magenta regions indicate an amorphous aggregate phase which, in the specific case of a size-symmetric system, manifests as an alternating string-like morphology. (c) Phase space showing only the honeycomb (blue) and alternating square lattice (yellow). Arrows indicate the qualitative “twist” the domains undergo as size asymmetry increases.

We generally find that the classifications used thus far to describe different morphologies in the size-symmetric case remain valid descriptors when the colloids are asymmetric. However, we note that the honeycomb lattice should be taken as synonymous with the hexagonal LS₂ lattices as reported elsewhere.^32,65,66 Furthermore, in both the aggregate and mixed hexagonal domains, we note that the morphologies often resembled the LS₆ and LS₉ phases reported in, e.g., ref. 65. At the temperatures and asymmetries we investigated, we did not find these structures to be well-defined; however, it is likely that these and other LS_x (x > 2) phases may manifest in those domains at lower temperatures, in systems with slightly modified interaction potentials, or at non equimolar stoichiometric ratios. We point out that these domains simply surround the honeycomb, or LS₂ domain, in the our three-dimensional phase space. They may be considered to act as intermediates between the honeycomb lattice and, e.g., phase-separated or square lattice domains. As a result, a detailed characterization of these intermediate structures is beyond the scope of this investigation. We refer the interested reader to the ESI^† for representative snapshots and additional details.

When σ_B,B/σ_A,A = 0.40 we find that regions corresponding to the phase-separated hexagonal lattice and homogeneous disordered gas-like phase are largely the same as when the system is size-symmetric. Instead the domains corresponding to the square (yellow, Fig. 5(a and b)) and honeycomb (blue, Fig. 5(a and b)) lattices undergo the most salient changes. As expected, the volume of the phase space where the square lattice is found has increased substantially, commensurate with expectations based on packing arguments. However, its location has now shifted to the region where the large “A” colloids interact favorably with themselves and even more favorably with the smaller “B” species, while the latter are long-range repulsive with themselves. This is also an intuitive result based on energetic arguments. The volume of the domain corresponding to the honeycomb lattice has not changed significantly, but it has shifted, relative to its location in phase space when the colloids are size-symmetric, in a similar fashion as the square lattice. Magenta and green regions in the center panel of Fig. 5(b) correspond to random aggregates and mixed hexagonal lattices, respectively. In the latter case, the smaller “B” colloids act to adhere the larger colloids into a hexagonal lattice, but do not present with any order themselves (cf. ESI^†). In both cases, these regions manifest as interfaces between lattices of different symmetries, e.g., square and hexagonal; at finite temperature, these intermediate structures are to be expected.

When σ_B,B/σ_A,A = 0.14 the region corresponding to the square lattice for σ_B,B/σ_A,A = 0.40 is now dominated by the honeycomb structure. This is again, expected as this size asymmetry precisely admits one “B” colloid between tangent triplets of “A” colloids which, in this region of strongly favorable cohesion, form a hexagonal lattice with trigonal gaps. Interestingly, a square-like lattice also seems to persist in a narrow region with weaker cohesive interactions, where adhesion remains relative strong. In this case, the smaller species tends to form small clusters which aggregate into the center of interstices formed by the larger “A” colloids when the latter forms a square lattice (cf. ESI^† for representative images). Once again, there is little to no change in the location of the phase-separated hexagonal lattice and homogeneous disordered gas-like domains.

Thus, upon increasing the size asymmetry of the colloids, the domains of 〈λ_A,A, λ_A,B, λ_B,B〉 phase space corresponding to the square and honeycomb lattices tend to undergo what may be envisioned as a counterclockwise rotation in the right-handed coordinate system presented in Fig. 5(c). The relatively uninteresting phase-separated hexagonal lattice and homogeneous disordered gas-like regions remain essentially fixed in place, while the remaining morphologies simply act as interfaces between these structures and the square and honeycomb lattices as they “twist” in phase space. The general absence of any new emerging morphologies, and the seemingly “continuous” nature of the rotation of the domains in phase space, suggest that one may expect to reasonably interpolate the regions of phase space corresponding to each morphology at intermediate size asymmetries not studied here.

4 Conclusions

We systematically studied the low-temperature self-assembly of multi-flavored binary colloidal mixtures in two-dimensions. To represent the experimentally achievable variability in interparticle potentials which occurs in multi-flavored systems, we employed a simple pair potential that spans from long-range repulsive to long-range attractive continuously with a single variable. Thus, our model uses a single variable to describe the nature of each pairwise interaction, resulting in an overall three-dimensional phase space. We used both Monte Carlo and molecular dynamics simulations to investigate the morphology into which binary systems assemble at low temperature throughout this phase space, and observed a range of different structures with n-fold rotational symmetries varying from n = 2 to n = 6. The most thermodynamically stable morphology depends on: (1) the location in three-dimensional phase space describing the pairwise interactions, (2) the mixture’s stoichiometric ratio, and (3) the particle size asymmetry. Using energy minimization, we investigated the ground state structure of small clusters to validate results obtained from larger scale molecular simulations which suggested a nearest neighbor, mean-field description could capture the thermodynamics of this self-assembly. We then demonstrated how this mean-field model can indeed predict the most stable morphology at a given point in phase space for size-symmetric systems with an arbitrary stoichiometry. These predictions were validated with Monte Carlo and molecular dynamics simulations, suggesting this simple model may serve as a valuable design tool for engineering the self-assembly of binary multi-flavored systems. We further considered the consequences of size asymmetry and found that domains in phase space for different morphologies tend to undergo a continuous “rotation” as size asymmetry increases. This continuity suggests how size asymmetry perturbs the predictions made by our model for each point in phase space, enabling qualitative predictions to be made for size-asymmetric systems as well.

We expect the resulting heuristics to enable the experimental and computational realization of targeted two-dimensional colloidal crystals from multi-flavored components. We note that the realization of open structures by this strategy will involve additional postprocessing steps, such as the selective removal of one type of particle,⁶⁹ relative to the design of single-component potentials that can yield such open lattices directly. However, this additional complexity may be acceptable especially when compared to difficulties involved in the latter case.⁷⁰