Abstract
We present a survey of multi-robot assembly applications and methods and describe trends and general insights into the multi-robot assembly problem for industrial applications. We focus on fixtureless assembly strategies featuring two or more robotic systems. Such robotic systems include industrial robot arms, dexterous robotic hands, and autonomous mobile platforms, such as automated guided vehicles. In this survey, we identify the types of assemblies that are enabled by utilizing multiple robots, the algorithms that synchronize the motions of the robots to complete the assembly operations, and the metrics used to assess the quality and performance of the assemblies.
CCS Concepts: Computer systems organization → Robotics, Applied computing → Computer-aided manufacturing, Computing methodologies → Motion path planning, Cooperation and coordination
Additional Key Words and Phrases: Robot assembly, multi-robot coordination, manufacturing robotics, assembly performance metrics
1 INTRODUCTION
The assembly process consists of physically coupling multiple parts together to form a new subcomponent or finished product. While this definition includes processes like welding and riveting, many consider the act of mating the parts together the “assembly task.” The assembly task is generally considered to be more complex when compared to others, such as machining or material handling, in that it typically involves multiple tools and processes to complete (Wick and Veilleux 1987). Given this variability and variety, the assembly process has historically been a manual undertaking. Occasionally, specialized machines are developed to assist and streamline the assembly process, but these all-in-one automated solutions tend to be cost prohibitive and inflexible when accommodating changes in product designs or procedures. For decades, proof-of-concept robotic solutions have successfully demonstrated the feasibility of applying agile robots to the assembly problem in laboratory settings (e.g., Whitney (1982)), and these technologies are just beginning to make their way onto production lines.
Historically, mechanical assembly has been accomplished by means of assembly lines, where station-based workers perform singular, simple, repetitive tasks that are merely a small subset of the total assembly process. Parts and workpieces are fed linearly from one station to the next, while the workers remain in place. The assembly-line methodology minimizes the training required for individual workers, and lends to more modularity in the assembly process. However, assembly lines require more resources (i.e., real estate and workers) to support, and over-specialization limits the ability to compensate for issues originating from the preceding stations.
The assembly-line paradigm for manufacturing, naturally evolved to the robotic assembly line, where robots now perform the singular tasks previously performed by human labor. As technology improved, however, it was demonstrated that the assembly cell—where a single station or cell is responsible for producing a subassembly or finished product—could improve production performance and improve agility to accommodate product variability and customization (Johnson 1999). The assembly cell approach allows for greater parallelization of manufacturing and is more amenable to reconfiguring with minimal impact. Yet the assembly cell approach significantly increases the complexity of the work performed by any given worker or robot, and are more difficult to scale up or down depending on the products being produced.
Traditional assembly work cells consist of a single robot performing a repetitive insertion task with positional uncertainties reduced by means of rigid fixturing. Complex assemblies have also been demonstrated by means of chains of parameterized search motion primitives (e.g., Zhang et al. (2008)). These single-manipulator robotic solutions for assembly are limited in the types and number of assemblies that can be completed, however. Their reliance on expensive fixtures or externally integrated axes makes such systems inherently inflexible, since a given work cell and any associated fixturing must be redesigned with any significant change in the assembly process.
Using multiple robots enables more agile assembly solutions that can readily accommodate changes in manufacturing processes. Using additional robots in the assembly process as dynamic fixtures allows parts to be repositioned and dexterously manipulated to complete more complex assembly procedures. Such solutions are intrinsically more difficult to program and integrate initially and require advanced sensing and control capabilities to enable the assembly algorithms.
This report provides insight into reducing this complexity by presenting algorithms and test methods to complete and assess multi-robot assemblies. We give a landscape overview of solutions for multi-robot manufacturing assembly tasks describing the methods by which multiple robots can be applied to the assembly problem and present metrics by which performance and quality have been evaluated. By giving details of both single- and multi-robot assembly strategies, we provide a basis for (1) developing industrial robotic assembly work cells from the ground up, (2) extending existing assembly work cells to accommodate multiple robots, and (3) evaluating the performances and impacts of using multiple robots in industrial assembly applications. The survey begins with a broad overview of the assembly problem in Section 2, and then highlights single-robot assembly strategies in Section 3. Section 4 describes performance assessment metrics for robotic assembly operations. In subsequent sections, we delve into the strategies for synchronizing and scheduling robots (Section 5), multi-arm robotic assemblies (Section 6), single-chain assemblies using the coordinated motions of a robotic arm and a robotic hand (Section 7), the coordinated efforts of a mobile platform (such as an automated guided vehicle, AVG) and a robotic arm (Section 8), multi-mobile platform assemblies (Section 9), and mixed modality, multi-robot assembly (Section 10).
2 ROBOTIC ASSEMBLY
The existing literature for robotic assembly focuses on the physical mating of parts. Such actions typically take the form of mating operations, specifically inserting and meshing (e.g., interleaving gear teeth) components into an assembled part. The canonical assembly task is the peg-in-hole insertion, which has also served as the benchmark for demonstrating assembly capabilities of robot control algorithms (e.g., Liao and Leu (1998) and Newman et al. (2001)).
The mating task is only a small part of the complete assembly process. In manufacturing, assembly also consists of adding permanence to the components being held together. This permanence is achieved by either mechanically fastening (e.g., by means of threaded fasteners, rivets, retaining rings, or staples) or physically bonding components together (e.g., by adhesives, welds, or joint solders) (Wick and Veilleux 1987). In some cases, the permanence is achieved through the mating task through mechanical mechanisms, such as snap fits. It has also been proposed to further disambiguate assemblies by separating them into two different classifications: rigid and moveable (Niemann 2013). Rigid assemblies produce a new construct that has no moving parts. Movable assemblies, in contrast, produce new constructs that contain both movable and immovable parts. However, the distinction between rigid and movable has less impact on the difficulty of an assembly than the means by which the assembly must come together. Many consider the generalized mating aspects to comprise the harder problems, and so the robotic assembly literature is largely composed of examples of parts being joined together. The survey we present in later sections reflects this trend.
The research presented in the literature does not necessarily map directly to actual manufacturing assembly processes. It is often prohibitively expensive and difficult to automate an assembly task, and the limitations of technology may preclude certain assembly processes from ever being automated. As such, it must be known a priori whether certain assemblies are to be completed manually or by automation so that parts and processes can be engineered accordingly (Wick and Veilleux 1987).
One mechanism for modeling and assessing the feasibility of an assembly is by characterizing the “Assembly Features” of the construction process. Assembly Features were first introduced by Deneux (Deneux 1999) to address the issue of designing and sequencing assemblies. The method applied relationship primitives (e.g., “has,” “links,” and “uses”) between multiple parts and their respective features. This model was then expanded in works by other researchers (e.g., Gayretli and Abdalla (1999), van Holland and Bronsvoort (2000), and Ullah et al. (2006)) to accommodate process optimization, alternative representation as numerical chains, and component-level abstractions.
More commonly, assemblies built by robots are represented in terms of motion primitives that describe assembly actions that are completed at specific stages of the mating operation. These primitives can be chained together to form assembly strategies for complex mechanical assemblies. We now discuss the assembly process for single robot systems and address the inclusion of multiple robots into the process. For the single-robot process, we also provide algorithms for commanding the motions of the robot.
3 ASSEMBLY TYPES AND SEARCH STRATEGIES
The component mating process is achieved by means of search strategies consisting of multiple parameterized motion primitives. In a previous report by Marvel and Falco (2012), we provided a high-level overview of a number of these primitives, including peg-in-hole assemblies (e.g., Chhatpar and Branicky (2001)), gear meshing strategies, and snap fits. In this section, we provide sample algorithms for performing assembly search strategies in terms of moving the robots or their tooling in Cartesian space. For a given assembly search to be considered successful, some desired, assembly-specific termination condition must be satisfied, while failures may be marked by the satisfaction of other termination conditions such as those based on time, distance, or force measures. Termination conditions as metrics are discussed later in this section.
We begin with the single-robot assembly process. The robot must mate a workpiece with an assembly fixture. Here, the workpiece is denoted as being the part that is held and manipulated by the robot, and the fixture is a separate component, or series of components, rigidly held in place, to which the workpiece is added. We assume that the assembly is performed with the workpiece pushed along the tool center point (TCP) +Z axis. Unless noted otherwise, we assume the Cartesian coordinates are in the world coordinate frame, R, which is typically co-aligned with the robot’s base frame.
Each search begins at a nominal starting position, p0 = (x0,y0,z0,rx0,ry0,rz0) of the robot’s TCP, and the individual algorithms calculate position offsets pΔ = (xΔ,yΔ,zΔ,rxΔ,ryΔ,rzΔ) relative to p0 for a given time step, indicated by the iteration count c. Positions are represented by their Cartesian coordinates along the X, Y, and Z axes as x, y, and z, respectively. Orientations are denoted by their respective axis-angle values, rx, ry, and rz. Offsets are calculated based on the iteration count, c, and various input parameters denoted in Table 1. Evaluating offsets on a per-iteration basis enables search interrupts on predefined termination conditions such as timers, force profiles, and travel distances.
Table 1.
Table of Common Variables, Inputs, and Outputs for the Generalized Assembly Search Strategies
| VARIABLE | DEFINITION |
|---|---|
| p0 = (x0,y0,z0,rx0,ry0,rz0) | TCP position at the beginning of the search |
| pΔ = (xΔ,yΔ,zΔ,rxΔ,ryΔ,rzΔ) | Computed TCP position offset |
| c | Iteration counter/time step |
| f | Update frequency |
| t | Total length of search (angular or linear) |
| s | Search speed |
| clocal | Internal counter for search state indication |
| θΔ | Angular change per time step |
| M | Applied moment (torque) |
| F | Applied torque |
| g | Points of contact with an assembly artifact |
| f | Forces measured at points of contact |
The offsets captured in each pΔ are used to move virtual attractors for the robot’s TCP, toward which the controller attempts to move the workpiece. The actual and target poses are not guaranteed to be the same, and the positional errors drive the application of forces to complete the mating process. In the event that the attractor is below the work surface, the robot will maintain a constant contact between the tool and work surface, applying a force proportional to the distance between the actual position of the workpiece and the attractor position. These forces may be applied through either passive (e.g., springs) or active (e.g., force or impedance control) mechanisms. Force-guided assembly operations may be paired with additional sensing modalities to provide initial pose refinement (e.g., Thomas et al. (2007)) and adaptive motion tracking on moving assembly lines.
3.1 Peg-in-Hole Assembly
Peg-in-hole assembly is the quintessential problem domain for assembly research. It consists of inserting a rigid object (i.e., a peg) into an appropriately shaped receptacle (i.e., a hole). Generally speaking, it is assumed that the peg is in constant contact with the surface of the assembly fixture until the hole is found such that the insertion point is located and the peg slips in. However, if constant contact with the assembly cannot be maintained, such searches may also be conducted by gently probing the surface until the insertion point is located. Given sufficiently large hole tolerances and minimal pose uncertainty of both the peg and the hole, peg-in-hole assemblies can be completed using position control with the robot simply moving directly toward a known goal state. However, the large tolerances and a priori knowledge required for success are typically not available in real-world applications.
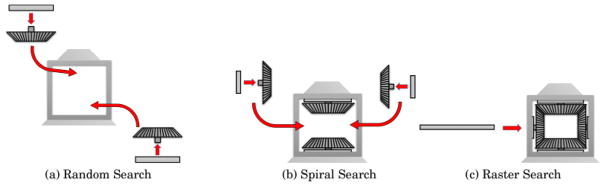
This assembly process is challenging because of the physical contact required between the workpiece rigidly held by a robot’s end effector and some other object. Errors in sensing or control may result in excessive application of force or in the binding of partially engaged parts, thus damaging parts, tooling, and/or robots. Mechanisms to compensate for such errors include the remote center of compliance (RCC), which is passive mechanical tooling that accommodates slight orientation errors of the peg relative to the orientation of the hole. Machine vision can also be applied to identify, localize, and—in the case of moving assembly lines—track insertion locations. With increases in computational and sensing capabilities paired with decreasing costs, force-based control is becoming more commonplace in assembly operations. A number of force-guided peg-in-hole insertion strategies have been implemented in the literature, and robot vendors now provide off-the-shelf software options for their hardware platforms. Most of these solutions reduce the problem to a two-dimensional (2D) problem space, though some researchers have extended the problem into the full three-dimensional (3D) search space (e.g., Fei and Zhao (2003)). In the following subsections, we present these search strategies as they could be implemented on a stock industrial robot controller. Some of these strategies, namely stochastic search, spiral search, and raster search, are illustrated in Figure 1. Algorithms are presented as piecewise adjustments to the current position of the TCP as a function of iteration.
Fig. 1.
Generic, parameterized search strategies for peg-in-hole insertion include the walking stochastic search (A), the spiral search (B), and the raster search (C).
3.1.1 Stochastic Search
The most primitive approach to solving the peg-in-hole insertion problem is to randomly move the workpiece throughout the search space. In a stochastic search, the workpiece is moved in random directions along the XY plane (Figure 1(a)) until the insertion point is found. Algorithmically, this is described as
| (1) |
where rand() is a function that returns a random value with a known distribution in the range of [−1, 1], and kx and ky are search step gains for the X and Y axes, respectively. As computed in Equation (1), the search performs an unbounded random walk, which may be desired if the position of the hole is completely unknown. If an initial estimate of the hole is provided with some level of certainty, then the stochastic search is bounded by removing the offsets from the previous time-step:
| (2) |
Similarly, if the initial position for the search is known to be close to the actual location of the hole, a Gaussian distribution for the rand() function may be preferable to maximize the search in a target region. Otherwise, a uniform distribution will ensure equal coverage of the search region as time progresses.
Searching stochastically is non-deterministic and provides no guarantee of converging to a solution. Rather than exploring all regions of the search space, the robot may reexamine regions already visited. To ensure that the stochastic search fully explores the task space, constraints may be added such that the workpiece moves only to those positions that have not previously been explored. Alternatively, pseudo-random distributions (e.g., Niederreiter (1978)) may be used to guarantee efficient coverage of the search volume. Optimizing these constraints is tantamount to solving the classical traveling salesman problem (e.g., Chhatpar and Branicky (2001)). This approach adds significant computational complexity to the solution, but results in generally good performance.
3.1.2 Spiral Search
When p0 is expected to be near the actual insertion point, a spiral search explores the surrounding region in a gradually increasing search pattern. When commanded, the spiral search performs an Archimedean spiral motion, starting at p0, and moving outward parallel to the XY plane (Figure 1(b)). The input parameters are denoted by t for the number of turns, r for the search radius, and s for the search speed. Given p0, the search call iteration counter, c, and update frequency, f, the total angular search length, θmx, is defined as
| (3) |
and the maximum per-turn change in radius, rΔ, is
| (4) |
Per iteration, the change in degrees, θΔ, is calculated as
| (5) |
To ensure predictable behavior, a local search call iterator is maintained to determine where in the spiral the workpiece should be located. This local iterator, clocal, is defined as
| (6) |
where % is the modulo operator. The clocal value is then used to determine the position inside the spiral based on the number of degrees changed from the initial 0 deg. The degrees changed, θ′, is calculated as
| (7) |
From this, the current radius of the desired point on the spiral, rcur, is computed as
| (8) |
Combined, θ′ and rcur are used to determine the X and Y axes offsets for the workpiece:
| (9) |
Given an appropriately tight spiral, spiral searches are deterministic in that they are guaranteed to find the insertion point provided that that hole lies within the search radius. If the spirals are too far apart, or if there is insufficient chamfering on the hole, then the search may fail to complete the insertion.
3.1.3 Raster Search
When the distance of the insertion point to p0 is unknown, the raster search may explore a large region systematically to find the insertion point. When commanded, the raster search performs a rectangle-shaped motion, starting at p0, and moving back and forth in a square-wave pattern along the X-Y plane (Figure 1(c)). The input parameters are denoted by n for the number of raster scans, l for the raster length, w for the raster width, and s for the search speed. Given the initial starting point p0, the search call iteration counter, c, and update frequency f, the length of each raster step, lstep, is defined as
| (10) |
and the total length of the search motion, ltotal, from beginning to end, is calculated as
| (11) |
The workpiece travel distance per iteration, lΔ, is defined as
| (12) |
The percentage of each width-step combination that consists of the width component, qraster, is calculated as
| (13) |
To ensure predictable behavior, a local search call iterator is maintained to determine where on the raster pattern the workpiece should be located. This local iterator, clocal, is defined as
| (14) |
The clocal value is then used to determine the position on the raster pattern based on the expected travel distance from p0.
To determine if the workpiece is on the X-axis (length) edges of the rectangle or is moving along the Y-axis (width), the ratio of the travel distance to the travel distance of a width and length step of a raster is calculated:
| (15) |
Using this value, the direction of travel is found by evaluating
| (16) |
and
| (17) |
This value then determines the X- and Y-axis offsets of the workpiece according to
| (18) |
Like the spiral search, raster searches are deterministic and guaranteed to succeed provided that the insertion point lies in the path of the raster. The search will fail if the robot is moving away from the hole. The search may also fail if the raster lines are not sufficiently close together to accommodate the hole’s chamfer.
3.1.4 Tilt Strategy
Generalized search strategies, though effective, may impose excessive torque on the robot, tooling, or workpiece of the robot system if not sensitive to exerted forces. For example, if the search speed is too high, or the response to force stimuli is too slow, a partially engaged peg in its insertion point may cause excessive torque on the workpiece or tooling.
If dimensional details of the workpiece are known, however, then the tilt search strategy (Whitney 1982; Chhatpar and Branicky 2001; Caine et al. 1989; Xia et al. 2005) may be employed to discover the position and orientation of the insertion hole explicitly. Here, we describe the principles of the tilt search method as presented in Caine et al. (1989). Though this method was originally generalized for use with a RCC, it is presented in terms of force-guided control of the workpiece position and orientation.
Solving for the tilt strategy requires initial estimates of goal positions to determine velocity of travel and tilt angle based on error models of the actual orientation and position of the peg relative to those of the estimated goal states. The surface of the hole is assumed to be aligned along the coordinate frame R′ (with axes X′, Y′, and Z′). The workpiece is held at a known angle to the Z-axis (i.e., “tilted”) and moved across the X′-Y′ search plane in the direction of +X′ (see Figure 2).
Fig. 2.
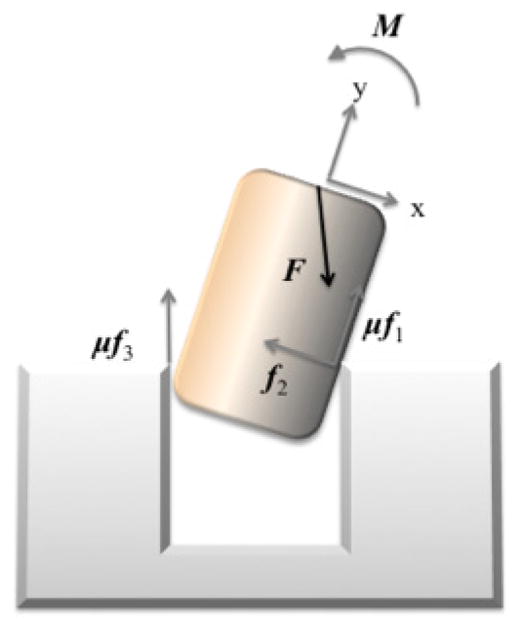
Commanded forces (F) and moments (M) adjust based on measured forces (fi ) to compensate for partial engagements in the tilt strategy.
As the peg is moved across the hole, it becomes partially engaged with one point on the “back” edge of the hole and the bottom edge of the peg at the “front” of the hole. Once the peg has made contact with the hole, the robot rotates the peg around R′ while maintaining at least two points of contact. Maintaining this two-edge sliding contact is achieved by applying appropriate forces and moments to minimize incurred/contact force moments. The quasi-static application of force, F, is minimized by adjusting the controlled force, Fctrl, according to the force law:
| (19) |
Here, ni and vi are the unit normal and unit velocity vectors, respectively, applied to all forces, f. These forces are measured at all k points of contact, i, when a small perturbation, pΔ, is applied. The model assumes the same static coefficient of friction, μ, at all points of contact.
Similarly, the application of moments, M, is minimized by adjusting the controlled torques, Mctrl, around R′:
| (20) |
where g is a contact vector for each of the k points of contact. Strategies for imposing motions of the workpiece include applying either random or cyclic orientation offsets to “wiggle” the parts into place.
When the corner opposite to the initial point of contact clears the top edge of the hole, the orientation of the peg will be, θgoal, and peg will slide into the hole without jamming:
| (21) |
where dpeg is the diameter of the peg, and dhole is the diameter of the hole
3.2 Gear Meshing
The generic “gear meshing” assembly seeks to align complex physical features of freely moving components, typically cogs or chains. With such assembly processes, the risks of damaging the parts, tooling, or robot stem from the potential for binding. When the components cease moving freely, the effort to mate the parts results in high torsional values, which can warp, crack, or shear component features. As such, gear meshing operations are often complex processes that rely on tight control loops with force sensing (e.g., Gravel and Newman (2001)) or dedicated tooling (e.g., Schimmels (2002)). For robotic assembly applications, a common approach is to pair a back-and-forth rotational action with a planar positional offset (here, a circular motion) to alternatingly increase and decrease contact forces through partial cog engagements.
3.2.1 Rotational Search
When commanded, the rotation search rotates the tool back and forth about the Z-axis at the current location of the workpiece. The rotation search is typically used to find an appropriate alignment for gear meshing assemblies. In such gear-meshing assemblies, the robot is pushing toward the assembly while simultaneously moving the tool back and forth to engage the gear teeth.
The magnitude and speed inputs are denoted as m and s, respectively. Given the initial starting point p0, the search call iteration counter, c, and update frequency, f, the Z-axis rotation offset, rzΔ, is calculated as
| (22) |
3.2.2 Circular Search
When commanded, the circular search moves the tool in a circular motion along the X-Y plane. The circular search is intended primarily to provide minor positional offsets to “wiggle” a component into place in tight fits. The stochastic search described earlier may also be used, but the circular search is useful in that it bounds the radius of motion around p0.
From the inputs above, let r be the radius of the circular motion, and s be the speed of the tool motion. Given the initial starting point, p0, search call iteration counter, c, and update frequency, f, the angular change per time step, θΔ, is defined as
| (23) |
To ensure predictable behavior, a local search call iterator is maintained to determine where in the circular pattern the workpiece should be located. This local iterator, clocal, is defined as
| (24) |
The clocal value is then used to determine the position on the circle perimeter based on the angular change:
| (25) |
This value then feeds into the position offset in the form of
| (26) |
3.3 Snap and Press Fits: Linear Search
In some cases, an assembly action consists simply of pushing two components together with sufficient force to engage snap-in tabs or tight, press-in connections. Such assemblies are common in consumer electronics and have been successfully implemented for decades using selective compliance articulated (or assembly) robot arm (SCARA) systems.
In the generalized case, snap and press fits are completed using simple linear searches under force control. The linear search introduces a back-and-forth linear motion along a defined vector from the robot’s initial position. Termination conditions include defined insertion depths, specific force profiles, or audible “snaps” (Genc et al. 1998).
For a linear search, let x be the user-specified X-axis offset, y be the Y-axis offset, z be the Z-axis offset, and s be the desired speed of the tool motion. Depending on the force control loop, s may be defined or limited by the desired applied force. Given the initial starting point p0, search call iteration counter, c, and update frequency f, the linear distance change per time step, lstep, is defined as
| (27) |
and the total length of the search motion, ltotal, is calculated as
| (28) |
The magnitude of the change in position as a function of search speed is calculated as
| (29) |
and the individual axis offsets are computed by
| (30) |
To ensure predictable behavior, a local search call iterator is maintained to determine where along the linear path the workpiece should be located. This local iterator, clocal, is defined as
| (31) |
This value is then used to determine the step-iteration X-, Y-, and Z-axis offsets as
| (32) |
3.4 General Assembly
There exist a number of motion strategies that are not specifically targeted toward completing particular assembly types. However, these general strategies are typically combined with other searches to either avoid or compensate for pose and localization errors and excessive forces and torques.
3.4.1 Dithering and Hopping
Both dithering and “hopping” introduce low magnitude offsets to the robot’s current TCP position and/or orientation. Dithering adds high-frequency random offsets to the TCP pose along the X-, Y-, and/or Z-axis, while hopping adds low frequency Z-axis sinusoidal offsets. Applicable to assembly processes, both dithering and hopping are used to help prevent components from binding during the assembly.
In Cartesian space, dithering can be defined similarly to the random search in Equation (2) given the initial starting point p0:
| (33) |
where the gains ki are necessarily small (e.g., < 0.1mm in the horizontal and vertical planes) to avoid damaging the parts.
For hopping, given the update frequency, f, the angular change per time step, θΔ, is defined as
| (34) |
The Z-axis offset is then calculated as
| (35) |
where m is the magnitude of the hopping motion.
3.4.2 Constant Offset
Although technically not a search function, the constant offset moves the virtual attractor of the workpiece to a constant offset position from the initial search location. Such offsets can be integral in the adjustment of p0 to accommodate biases in the presentation poses of parts to the robot for assembly.
The location and orientation offsets pd = (dx,dy,dz,drx,dry,drz) are applied directly to the robot’s target location:
| (36) |
Note that for large values of dx, dy, dz, drx, dry, and drz, the resulting speed of the robot’s motions may cause unexpected hazards. It is therefore recommended the robot be moved close to the expected target location prior to searching to limit these hazards.
3.4.3 Surface and Contour Matching
Although sometimes considered primitives for force-based control (Marvel and Falco 2012), surface and contour matching are also integral for assembly (Shi and Menassa 2010). Surface and contour matching refer to the processes of aligning and pressing components along flat or curved surfaces, respectively. Like the tilt method presented earlier, both surface and contour matching reflect the application of control laws. For surface/face matching, the control law is such that permutations are added to the TCP’s rotational vector such that the torques along the Cartesian axes are minimized. Often, these permutations are applied to rxΔ and ryΔ while a positive force is applied to the TCP’s Z axis, though there may be multiple surfaces constrained by contact (e.g., tucking an assembly workpiece into a corner). The control law is identical to the moment minimization law (Equation (19)) seen previously in the tilt method:
| (37) |
In this case, the control law attempts to keep an assembly object in a nominal position while minimizing only the rotational torques. As such, typically only the orientation component of pd is non-zero. The torques about the rotational axes are minimized when the face(s) of the assembly objects are aligned.
For contour matching, the control law is such that the TCP follows the orientation of a curved surface by minimizing forces and torques along multiple axes as it is moved along a nominal trajectory path. Such operations are necessary for pressing components together for snap-fit and adhesive applications and may likewise be used in material removal or quality assurance applications. Like the surface matching, the control laws for contour is identical to the force and moment laws from the tilt method:
| (38) |
| (39) |
A notable difference, however, is that the positional offset pt now consists of the robot position along the nominal commanded trajectory at time t together with any offsets imposed by the control law:
| (40) |
As the robot moves along its nominal commanded trajectory, additional offsets are added to maintain a constant contact within some force profile tolerance.
3.4.4 Visual Servoing
Visual servoing introduces positional offsets to the TCP by means of an external, vision-based observer system tracking fiducials on a target assembly fitting or part. Such fiducials may be features on the assembly parts (e.g., screw holes or injection flashing), or explicit markers added to aid with the assembly process. Position and orientation offsets are introduced to the TCP’s current location to compensate for positional errors of the tooling incurred by controller uncertainty, resolver/encoder errors, or movements of the fitting.
The control law is similar to the application of constant offsets as described in Equation 36). However, the application of offsets varies in time as the observer system tracks the fiducials and is dependent on the observer’s coordinate frame. If the observer system is registered with the TCP (e.g., if the camera is mounted on the robot), then offsets are given relative to the TCP’s current pose:
| (41) |
However, if the observer tracks fiducials in a coordinate frame separate from the robot (e.g., the camera is mounted to a rigid fixture), offsets will be given relative to the absolute pose, p0:
| (42) |
3.4.5 Push-Hold/Dynamic Fixturing
Numerous industrial robotic tasks require some form of fixtures to hold a part in place while the robot operates on it. Relying on such fixtures, however, imposes additional cost and complexity on the system. To eliminate the necessity for rigid fixturing, additional robots may be added to the work cell to act as “dynamic fixtures.” Here, one or more robots will acquire the workpiece and rigidly present it to another robot in a known location and orientation such that the other robot may perform assembly operations (e.g., Marvel (2010)).
Such dynamic fixturing may be presented in two different methods. The first, called “push-hold” requires one robot to passively hold the fitting while the other carries out the assembly operation. In such applications, the position of the first robot is held constant while the second robot performs one or more of the aforementioned assembly processes. This is typical of industrial robot programming solutions.
In the second approach, called “push-push,” both robots actively cooperate to engage parts together with each robot holding separate parts. Instead of one robot being held constant, both robots perform assembly motions until some mutual termination condition is met. This is more typical of the way that people carry out similar assembly tasks.
In the multi-robot assembly process, the division between workpiece and assembly fixture is blurred, as the workpiece of one robot may be mated with the workpiece of another robot. Such approaches, however, are sub-optimally efficient, as the dynamic fixture robots are not actively contributing to the assembly process. The use of dynamic fixtures, however, provides a useful baseline for the integration and performance assessment of multi-robot assembly solutions.
3.5 Complex Assembly Strategies
With the exception of the tilt strategy, the general search methods described previously may be logically combined and chained to generate complex assembly actions. Because each search results in positional offsets from the initial pose, p0, simply adding together all j pΔ vectors for a given c results in offsets that reflect multiple transformations:
| (43) |
For instance, assume that an assembly consists of inserting a central sun gear into a planetary gear configuration. The search strategy may consist of a rotational search combined with a circular search and a hopping motion. Summing the offsets from these three search strategies will result in the rigidly held gear simultaneously oscillating back and forth along the Z axis, moving in circular motions along the X-Y plane, and moving up and down on along the Z axis.
Similarly, multi-stage assemblies are accommodated by daisy chaining assembly search strategies predicated on the successful achievement of positive termination conditions (e.g., Marvel et al. (2008)). For instance, the insertion of a sun gear fitted with a shaft into a hole will typically require a two-stage assembly. Stage 1 consists of a spiral search paired with a downward linear search to insert the axle into the bearing, and stage 2 will consist of a rotational search paired with a hopping motion. The circular search is omitted from stage 2, because the axle is engaged with the bearing and adding lateral offsets will impose undue stress on both the axle and the bearing.
4 ASSESSMENT METRICS
The performance of the robots must be evaluated during and after the assembly process to ensure the operations were completed successfully and within operational tolerances. By constantly measuring and evaluating robot and sensor feedback, a watchdog process can assess the state of the assembly process. Such state evaluations can be used to identify when thresholded termination conditions have been met and allow the robot system to know when to transition to the next step of the assembly process. Alternatively, if the assembly is not proceeding as planned, the assembly may be prematurely aborted to minimize the impact on assembly-line bandwidth or the possibility of robot, tool, or component damage. In these cases search parameters could be reinitialized based on in situ assessment and tried again.
4.1 Time Profiles
A given assembly subtask is typically allocated a certain time limit in which the robot must complete its task to maintain production throughput. Tasks that are completed within that timeframe are considered in tolerance and any time spent beyond that limit will impact system performance. When a timer event occurs, a signal is sent to the robot to perform some conditional next step. Such next steps may be to discard the components for a human operator to finish offline or to reassess and restart the assembly operation from a previously known state. Although typically associated with signals to abort an assembly in the event of failures, timers may also be used to indicate task success. For instance, if parts must be held together for a given duration of time to allow adhesives to set, a timer event marks the successful completion of that particular task.
4.2 Force Profiles
In-line forces and torques are often measured and used to transition from the approach stage to subsequent stages of an assembly task. Appropriate deviations from some nominal force, torque, or motor current profile indicate successful interactions with the workpieces. Typically, a search profile will continue until a certain force/torque threshold has been met or exceeded. For instance, force spikes may indicate an object has been found in a “move until touch” motion primitive or completion of a snap-fit task in the presence of steadily increasing force values. Alternatively, force profiles may be used to ensure that components are not damaged during an assembly. For instance, if a nominal force limit has been met, an assembly search may be aborted to prevent excessive wear on the robot, tooling, or workpiece.
4.3 Motion Profiles
Like the force profiles, motion and position profiles may also be used to transition between stages or mark the need to abort a given assembly. If predefined depth thresholds are exceeded, for instance, then a robot may conclude that the part that it is holding has been successfully inserted into its respective receptacle. Similarly, if the lateral distance from p0 exceeds some nominal maximum expected value prior to observing some other signal, the system may conclude that the search has failed and needs to be restarted.
4.4 External Signals
In some instances, a robot system may not know the state of an assembly without the assistance of an external observer system. In such cases, a search may need to be terminated based on external signals prior to the robot system’s own termination conditions being met. Support for such early terminators allow for observer systems to preemptively abort a robot system’s assembly searches with defined “success” or “failure” without requiring complex logic on the robot controller.
5 SCHEDULING AND SYNCHRONIZING ROBOTS
In assembly applications featuring multiple robots, the traditional assembly-line paradigm is maintained to facilitate continuous workflow. Production lines are serialized such that one robot performs its programmed task with a workpiece, checks its work, and then passes the workpiece on to the next station for additional processing. In such cases, each robot is assigned a specific, simple role, and a single-purpose tool. Parts are presented in fixtures, and each robot works independently of any other robots around it.
Regardless of implementation, however, scheduling is considered one of the principal factors when developing multi-robot assembly work cells (Abd et al. 2011). Scheduling includes resource allocations (Nof and Drezner 1993; Hsieh 2003; Fu and Hsu 1993), process distribution (Hsieh 2003; Fu and Hsu 1993; Glibert et al. 1990; Lee and Lee 2010), logistical controls (i.e., part presentations (Nof and Drezner 1993; Bonert et al. 2010)), and collision avoidance (Bonert et al. 2010). In many of these test cases, the physical interaction between robots is restricted or nonexistent, and the robots operate simultaneously in the shared work cell but in a non-supportive manner. When robots physically interact with one another, their trajectories must be defined and timed such that the robots do not collide or impose excessive forces or torques on workpieces, tools, or other robots.
5.1 Multi-Robot Coordination
An entire field of research has been dedicated to the coordination of multiple robot systems for applications ranging from manufacturing to military surveillance. Such applications employ technologies and algorithms ranging from rudimentary collision avoidance to goal-based optimized swarming of robotic agents. This field is necessarily vast, and extends well beyond the scope of this article. For more detailed coverage of multi-robot coordination, it is recommended the reader begin with the surveys by Yan et al. (2013) and Doriya et al. (2015) and the book by Balch and Parker (Balch and Parker 2002). The literature on multi-robot coordination is largely centralized on mobile robotic platforms. Nevertheless, many important lessons can be drawn and extended to other robotic design paradigms used in manufacturing. As such, it is worth providing some basic—albeit brief—coverage of the topic here.
While there are many forms of multi-robot coordination, we want to draw particular attention to synchronization of independently operating robotic systems. Some robot manufacturers provide software solutions that enable several of their robots to be temporally and spatially synchronized using a single controller. Such solutions often provide some handling of process or environment uncertainty, but are otherwise limited in their ability to adapt to large errors given the reliance on strict constraints on the arrangement and control of the system. Independently operating robot systems, however, tend to be more flexible in handling uncertainties, but must be coordinated through communications to achieve any form of synchrony. While there are many approaches to facilitating this coordination, they are ultimately employing some variation of either centralized or distributed control. Similarly, communications may either be explicit in that messages of intent are directly conveyed between robots with or without goals defined a priori (e.g., Rubenstein et al. (2014)), or implicit in that the robots must infer intent by means of sensor-based observations given a shared goal (e.g., Tambe (1997)).
While centralized coordination of multiple robot systems may be used effectively for most assembly tasks, accommodating large uncertainties often requires the distributed coordination of independently intelligent robotic agents. Such coordination requires extensive communication, both implicit and explicit, to accommodate changes in the environment, task, and behaviors of other robotic agents (e.g., Kaminka et al. (2010)). However, such extreme uncertainties are unlikely for the majority of manufacturing tasks, and efforts to facilitate the communication and control complexity necessary for enabling this level of independent coordination in manufacturing robots are likely to experience diminishing returns for both assembly performance and system reliability.
5.2 Coordination Performance and Uncertainty
For any sufficiently advanced mechanical system, some means for evaluating the system and process performance are required to ensure continued operation, optimize production, assess root cause analyses of errors, and predict pending failures. Modern trends in smart manufacturing promote frequent turnover and customization of manufacturing processes to accommodate ever-shifting market demands, which makes developing long-term performance models for prognostics and health monitoring (PHM) particularly challenging (Choo et al. 2016).
Currently, there are no standardized test methods or metrics for the evaluation of multi-robot coordination and control. The basic robot performance standard from the International Organization of Standardization (ISO) (ISO 9283 1998), measures only for the spatial path and end-point accuracy and repeatability of a single robotic manipulator. It does not capture the ability of a given robot platform to coordinate its motions with those of another robot, human, or mechanical system. Moreover, this action-side test methodology does not account for the accuracy of the trajectories or motion plans, themselves, nor is it intended for real-time evaluations. Both of these further confounds PHM efforts, particularly with regards to process monitoring. The test methods in ISO 9283 may be extended and adapted, however, to account for multiple robots’ motions relative to one another as opposed to absolute measures. However, because one cannot expect robots to provide accurate real-time updates of its pose and joint configurations (Marvel and Norcross 2017), means of real-time monitoring by accurate, external observer systems will be required to enable such measures to be used in PHM.
The real-time position and configuration of multiple robots accounts only for a snap-shot of the effects of coordination and individual control of the independent platforms. These physical configuration errors are frequently a resulting symptom of some preceding series of root errors that, if identified earlier, could have been addressed to avoid potential damage to parts, robots, equipment, or human operators. Specifically, physical conflicts such as a lack of temporal or spatial synchronization, collisions, or the excessive build-up of internal stresses or forces of shared workpieces are likely the result of errors or uncertainty in the robots’ software coordination. At the team level, performance metrics have been proposed to evaluate system-wide errors in multi-robot planning (e.g., Sellner et al. (2006), Korsah et al. (2013), and Micalizio and Torasso (2014)), communications (Kalech 2012), and conflict negotiations (Kalech and Kaminka 2007). Alternatively, at the individual robot level, performance errors may result from shortcomings in software agility, possibly inferred based on the robot’s measured efficiency and effectiveness (Downs et al. 2016).
6 MULTI-ARM ASSEMBLY STRATEGIES
Multiple robot arms have been used in manufacturing for several years. Early applications required very careful individual programming of the robots and strict timing to enable them to work together. Another approach was to slave one robot to the other in cases where the actions of one were either same as those of the other or a mirror image. This could be used, for example, to jointly carry a part or to carry out the same operation, such as welding, at adjacent locations on a part. Even today, practical use of multi-robot coordination in industry requires careful programming, specialized controller configurations, and customization for each application. For instance, Sun and Mills (2002) described a generalizable and scalable synchronization control strategy for minimizing coordination errors of multiple robots for assembly tasks. Their approach provided a means for coordinating the motions of multiple robots that were kinematically linked through a shared workpiece and required custom control and feedback interfaces to provide position tracking of the robots along a priori defined trajectories of decentralized robots.
6.1 A Basis for Multiple Arms
A case study showing the benefits of using multiple collaborating robots to reduce the number of fixtures needed for welding in a Body-in-White application is presented in Papakostas et al. (2011). The authors compared two scenarios. In the first, two robots were used for welding components that were held in fixtures. This scenario required a total of six fixtures. In the second situation, three robots were used and the number of fixtures could be reduced to three. They showed a 49% reduction in cycle time for the case in which robots were used to hold the components instead of fixtures. In the first scenario, significant time (nearly 30s) was taken by having to frequently open and close the fixtures and grippers, which was substantially reduced in the second scenario. The use of robots also made the work cell more flexible in comparison to the fixture-based scenario.
Another study of multi-robot assembly was conducted by Rojas and II (2012). The authors used two heterogeneous robots, one of which was an industrial manipulator and the other an anthropomorphic, dual-armed robot. The task was to insert a pipe into a fitting. The “push-hold” and “push-push” strategies were both implemented. The authors found that the “push-push” strategy was quicker at completing the insertion than the “push-hold” scheme and reduced the likelihood of stiction, jamming, and wedging. Another conclusion was made for the case of “push-hold” schemes, where industrial robots are smoother and faster pushers, while compliant robots are better holders.
Shi and Menassa (2010) presented some challenges to assembly in automotive applications. They described a system for loading wheels and tires onto vehicles that used two robots and an automated guided vehicle. Computer vision was used to locate the parts, insert the wheels onto the lugs, and attach the bolts. The two robots worked independently, each on one wheel, but had to synchronize their actions with the motion of the AGV. All of the programming to achieve this was manually developed.
6.2 Multi-Arm Designs
Several multi-arm robotic systems have been developed that are aimed specifically at human-scale manufacturing tasks. For example, in the mid 1980s, Hörmann, Lueth, Nassal, and Rembold developed the mobile, dual-armed Karlsruhe Autonomous Mobile Robot (KAMRO) platform (Hörmann and Rembold 1991; Lueth et al. 1995). The robot consisted of two Puma 260 arms rigidly mounted on a mobile platform. The mobile base moved the dual arms to predefined, dockable locations within a work cell for on-table assembly. The assembly component consisted of several action primitives, including pick, place, and transfer (specifically, for handing parts between arms) (Hörmann et al. 1989). The KAMRO was used principally for test and evaluation of multi-robot control architectures and was applied in research testbeds toward assembly-related material handling problems.
In the 1990s, Yamada et al. (1995) presented their design for a multi-arm robot configuration for performing preprogrammed differential gearboxes assemblies (Figure 3). The robots and their attached parallel grippers were designed to hold a variety of parts while simultaneously maximizing the robots’ combined working volume. Parts were fed to the robots in a fixed kit of parts, and the assembly consisted of (1) the insertion of two sets of vertical pinion gears and spherical washers, (2) the insertion of two sets of horizontal pinion gears and spherical washers, and (3) the insertion of a pinion shaft through the differential case, gears, and washers. The two robot arms used position control and were largely independent of one another. However, each could potentially impact the other’s performance during the phase 2 insertion due to the engagement and rotation of the gears as they were inserted.
Fig. 3.
Generic, parameterized search strategies for peg-in-hole insertion include the walking stochastic search (A), the spiral search (B), and the raster search (C).
In the early 2000s, the HRP2 robot, a dual-armed, humanoid robot, was developed by Kaneko et al. (2002) for generalized task-driven application development of humanoid robotics. Like its predecessors, the HRP2 was targeted for assembly operations due to its dexterous nature. Dauchez et al. (2005), for instance, used a simulation of the HRP2 to perform peg-in-hole assemblies based on the assumption that both the peg and the receptacle were rigid extensions of the robot end effectors. However, no a priori assumptions were made regarding how the parts were held or where they would first make contact when brought together. During the approach phase, the arms would slowly bring the two assembly components together. Once the parts made contact, however, the goal configuration was assumed known, and the robot controller generated a trajectory using a force feedback law to move directly to the goal state while maintaining constant contact between the parts. This represents a simplified application of the tilt method described in Section 2, where the force control law is used to maintain contact and minimize the potential for parts to bind.
More recently, the ABB YuMi robot was developed for assembly tasks for the electronics industry. It focuses on safe operation and easy reconfiguration for new tasks in a human-occupied environment (Kock et al. 2011). Each arm has 7 degrees of freedom (DOF) to ensure that the entire workspace is reachable without bumping into obstacles. The robot uses an integrated industrial controller and requires manual programming. The robot was developed as part of the European RObot control for Skilled ExecuTion of Tasks (ROSETTA) project (Patel et al. 2012), which focused on robot safety, easy programming, and the use of machine learning. It is assumed ABB’s force-based assembly library (ABB) is leveraged to enable and control assembly operations.
6.3 Programming and Control
The use of human-scale robot systems allows for direct teaching of assembly strategies by demonstration. In the system presented by Park et al. (2009), an operator recorded motion trajectories by directly physically interacting with a custom dual-arm robot to complete a peg-in-hole assembly. These trajectories were then played back verbatim to complete subsequent assemblies without further human intervention. In the approach presented by Takamatsu et al. (2007), teaching the robot was done by means of a vision system that recognized and tracked rigid polyhedral structures held by human operators. The assembly task was broken down into defined motion primitives to define the assembly process, which was then replayed by the custom, dual-armed robot after having acquired the parts in its grippers.
A master-slave control strategy was used by Su et al. (2009) to enable two robots to screw a nut onto a bolt. A three-layer architecture was used with the top layer responsible for motion planning of the master robot, computing the kinematics cooperation relation, and computing the motion of the slave robot. The second, servo layer, handled joint control and execution of the motions of each robot. The third layer was responsible for adjusting the poses of the robots based on a sensor that determined the locations of the bolt and nut using a resolved motion rate control method. The master robot held and translated the bolt while the slave robot held and turned the screw. The speeds of the robots were controlled to ensure that the nut meshed with the threads of the bolt during the insertion.
A master-less control strategy developed by Šurdilovic et al. (2001) used two lightweight industrial robot arms modified to enable impedance control to assemble truss structures. Assemblies consisted of rods with locking mechanism integrated to snap fit into the vertex nodes (Figure 4). The structure was systematically assembled using different “push-hold” strategies that were dependent on the assembly operation. In operations where connection nodes were attached to a rod on the assembly structure, one robot would hold the rod by grasping it tightly while the other robot inserted the node over the rod. In contrast, when rods were attached to nodes on the assembly structure, one robot would hold the node by pushing it to keep it in place while the other robot inserted the rod into the node. In both instances, the hold operations were performed by robots operating in position control mode; while in position control, the robot would monitor force magnitudes but would not respond to them. Due to the lack of a defined master, the two robots coordinated through message exchanges to ensure proper timing for correct assembly completion. All of the assembly experiments were evaluated in conditions in which the node and rod alignment errors were kept at a minimum to eliminate the need for positional search. A similar approach was taken by Marvel (2010), in which two industrial robot arms were coordinated via message passing to complete a force-guided snap-fit of cellular telephone case parts.
Fig. 4.
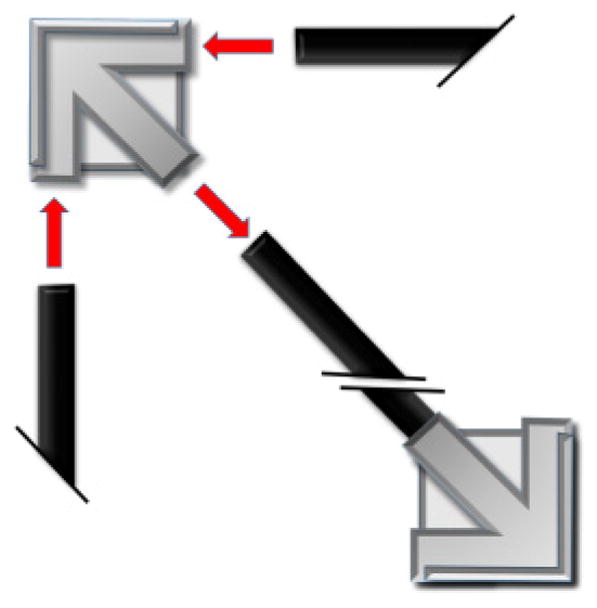
Master-less assembly of truss support rods into central connector nodes from [Šurdilovic et al. 2001]
Much of the academic multi-robot research makes use of agent-based control approaches or behavior-based methods. An approach described as agent based, but that looked like a state-based method, was Zone Logic by van Dyke Parunak (1999). In Zone Logic, each agent was a state-based machine with no knowledge of other agents, although agents could coordinate their actions by propagating constraints or by using an auction mechanism. Zone Logic was developed as a commercial product and has been used to control large transfer lines in factories. Jarvis et al. (2001) developed a system based on Zone Logic but also using a belief-desire-intention (BDI) agent structure. There were two kinds of agents: manufacturing agents controlled devices and machines, while part/product agents planned, scheduled, and executed tasks. A Programmable Logic Controller (PLC) implemented primitive actions for a physical device, such as opening or closing a clamp. The manufacturing agents controlled these actions by setting flags.
In many cases involving multiple arms simultaneously working on an assembly, the arms are used to hold different parts and work either independently or together to complete the assembly task. In contrast, systems like the one presented by Yuan (2006) use two robots to simultaneously hold and control a shared workpiece for assembly. An admittance control law was developed that compliantly moves a shared object across a surface, and then performs a peg-in-hole assembly using the tilt method described in Section 2. In this approach, one robot minimized the incurred forces and torques imposed by part misalignments while the other provided force tracking to maintain part orientation and gravity compensation.
Brogårdh (2009) discussed the evolution of control in industrial robots. He showed how model-based control has greatly improved the speed and accuracy of robots and described the need for expanding the models to include sensor-based control, especially for new and more demanding applications, such as assembly and safety in human-robot collaboration. He stated that the main challenges for multi-robot control are in the architecture of the motion control software. It has to generate servo commands to the robots at exact times and be able to transition smoothly between coordinated and independent robot motions. It also needs to recover from failures without collisions between the robots. Since collaborating robots have serially connected kinematics chains, errors in the servo loops and in the robot models will cause pose deviations between the tool and the work object that are larger than for single robots. This means that collaborative robots must have higher-accuracy servo loops, servo references, feed-forward calculations, dynamic models, and kinematics models.
The ongoing software-driven robotics (SoftRobot) research project by Hoffmann (2014) is principally aimed at reducing the intellectual overhead required for programming complex robotic tasks. As a demonstration of this capability, the researchers have developed a complex assembly task illustrating the performance capabilities of two industrial robot arms and an omnidirectional mobile robot (Hoffmann 2012). The assembly consisted of loose slip-fit metal components held together by machine screws. The parts were delivered on kit trays to the robot arms by the mobile base. The robot arms registered, acquired, and moved these kit trays to locations within the task environment. Parts were then taken from the kit trays in known configurations using specialized tooling, which reduced the complexity of the assembly problem. Once assembled, the completed work pieces were then put back onto the kit trays and transferred back to the mobile base. The assembly process was controlled entirely by the SoftRobot architecture, including (1) the force-based registration of the kit trays, (2) the force-based acquisition of parts, (3) the coordinated motion of the robots for assisted lifting, and (4) the force-based manipulation of parts.
7 ARM-HAND ASSEMBLY STRATEGIES
Dexterity has been identified as an enabling capability for advances in robotic assembly applications (Falco et al. 2013). Robotic hands, in particular, would appear to be at the forefront of the wave of new, dexterous robot platforms. With the ability to grasp and manipulate a broad spectrum of parts presented in arbitrary configurations, such hands promise to revolutionize the robot-application domain. The inclusion of advanced tactile sensing strategies into hand designs offers the ability to handle parts in environments where the parts’ properties (e.g., location and shape) are not well known, or where the behavior of a robot is subject to mechanical noise and positional errors. Indeed, many design reports for dexterous robotic hands specifically convey their applicability and, in some instances, specific design goal toward robot assembly (e.g., Townsend (2000), Krüger et al. (2009), and Diftler et al. (2011)).
The integrated combination of robotic arms and hands is characteristically representative of the macro/micro paradigm. With macro/micro robots, smaller, more accurate robots are connected to larger, less accurate robots to greatly improve the functionality of either system taken individually (Sharon et al. 1993; Quan et al. 2006). In such arm-hand implementations, the arm is used for gross positioning of the hand while the dexterous hand is used for fine repositioning and reorienting the grasped part. The arm-AGV model discussed in Section 8 also reflects this performance goal.
At this report’s publication date there are no documented publications of robot arms and hands being coordinated for the completion of autonomous assembly tasks. Instead, current efforts in robot hand research are focused on addressing the problems of grasp planning and stability; hand design, construction, and control; and in-hand manipulation. One possible exception is related to the arm-hand robotic system developed by the Korea Institute of Industrial Technology (KITECH). Two video demonstrations published by KITECH show peg-in-hole assembly tasks. The first used what appears to be a tilt strategy where a peg is inserted into a hole in a stationary part (Bae 2014a). The second uses two arm/hand systems using a spiral search strategy. One arm/hand pair manipulates the peg, while the second arm/hand pair manipulates the part containing the hole (Bae 2014b). General descriptions of the system shown in the video including the hand design (Bae et al. 2012), arm/hand coordinated control (Kwon et al. 2014), and peg-in-hole assembly (arm only) (Park et al. 2013) are found in the literature with no supporting documentation for the tasks shown in the video.
Other robotic assembly examples of arm-hand combinations have been used principally as illustrative examples to demonstrate unrelated technology advancements. For instance, in the article by Mouri, Kawasaki, and Umebayashi (Mouri et al. 2005), a paired robotic hand and arm were tele-operated by a human operator to perform basic peg-in-hole assembly tasks. The operator wore a sensor-laden glove that provided both control signals and haptic feedback for a human-in-the-loop, master-slave control strategy. Similarly, in the work by Shauri and Nonami (2011), a dual-arm system outfitted with three-fingered hands performed screw assembly operations. Each hand was used as a basic gripper, rigidly holding the parts in each hand while the visually servoed arms performed the actual assembly operations with one arm controlling the bolt and the other controlling the nut. The focus of this research, however, seemed more on image processing and path planning than on arm-hand coordination for assembly tasks. Other instances of arm-hand coordinated solutions focus on pick-and-place operations and rudimentary material handling (e.g., Saut et al. (2010) and Rodríguez et al. (2013)).
8 ARM-AGV ASSEMBLY STRATEGIES
Robot arms onboard mobile robots (“mobile manipulators”) have historically been popular research topics (Shneier and Bostelman 2014) and are now becoming commercial tools for industrial use (e.g., Motoman (2013)). In research, mobile manipulators consider coordination of movements of the robot and the base, since there may be redundant DOFs when a moving base is added. Additionally, researchers have studied mobile manipulator control algorithms, including dynamic motions caused by the onboard manipulator motion, especially in undulating terrain (e.g., outdoors (Hootsman et al. 1992)). Further research includes trajectory planning for a mobile manipulator with stability considerations (Furuno et al. 2003) and task planning, such as opening doors (Petersson et al. 2000). However, industrial AGVs with onboard robot arms that can provide assembly quality accuracy and repeatability have only minimally been researched and demonstrated.
Stroupe et al. (2005) described a behavior-based system in which two mobile-base robots perform assembly tasks. One of the robots acted as a master and one as a slave in the assembly of beams into a structure. Heavy use was made of sensing: stereo vision is used to locate fiducial marks on the components and force-torque sensing is used during transportation and assembly. Tasks were decomposed manually into a sequence of subtasks, such as “drive,” “crab,” “turn in place,” “Ackermann turn,” or “move arm.” These were combined into commands, such as “acquire component” or “clear storage.” Actions like aligning with a component before picking it up made use of vision to locate the fiducial marks and may involve coarse and fine motions. The components were large enough to require that both robots pick them up and transport them collaboratively. In these situations, the slave robot used force-torque velocity control to modify its behavior in response to the motions of the master.
Knepper et al. (2013) described a system that uses multiple robots to cooperatively assemble simple furniture. The system reasoned about connection points to determine feasible assembly sequences and plans the assembly using robots, which took on roles either as part deliverers or part assemblers. The robots could have different roles at different times. Some actions, like screwing components together, required a special tool that had to be acquired before use. The robots were also able to coordinate actions, for example, to jointly turn the completed table onto its legs after assembly. The assembly itself consisted of screwing prethreaded legs onto an inverted table base. A simple peg-in-hole search, visually guided by a motion capture system, aligned the leg-mounted screw with the table base. Both robots then cooperated to turn the entire leg assembly to firmly attach it to the base.
A robot-on-AGV platform was developed by Madsen et al. (2015) for general purpose applications within an industrial environment. To date, however, it has been applied only to simple material handling applications as a proof-of-concept. During these initial trials, the platform was assessed in terms of process efficiency and continuous operation during a single shift trial run.
Hamner et al. (2010) developed an autonomous mobile manipulator that effectively overcomes inherent system uncertainties and exceptions by utilizing control strategies that employ coordinated control, combine visual and force servoing, and incorporate reactive task control. The mobile manipulation system was demonstrated experimentally to achieve peg-in-hole insertion assembly tasks that are commonly encountered in automotive wiring harness assembly.
Researchers at Aalborg University described (Bøgh et al. 2011; Carøe et al. 2012) and demonstrated (Carøe 2012) how their mobile manipulator initially registered itself to a fixture and then performs peg-in-hole assembly of a rotary shaft for a pump. The arm-on-AGV platform consisted of an industrial manipulator mounted on a custom mobile robot base. The mobile base was used to position the robot arm at a workstation while the arm, equipped with a parallel gripper, performed the assembly using a tilt strategy.
9 AGV-AGV ASSEMBLY STRATEGIES
AGVs are anticipated to be an integral component of future agile manufacturing applications (Gravel et al. 2008). The number of AGVs required to fulfill performance requirements for agile manufacturing is an optimization issue, perhaps best solved by mathematical programming (Fazlollahtabar et al. 2010). In the work presented by Fazlollahtabar et al. (2010), a mathematical model was verified for material handling through optimization of a flexible job-shop automated manufacturing system that uses AGVs. Travel and operation times impacting guide-path design, traffic management, vehicle requirements, dispatching, routing, and scheduling were all metrics that also impacted the optimal number of AGVs. Guide-path layout influences the performance of a system as it impacted the travel time to transport a load from its origin to its destination, the number of vehicles required, and the degree of congestion. In Aized (2009), colored Petri nets (CPN) were used to model the AGV system where the data generated by the CPN model was used to develop the response surface models to explore near-optimal conditions of the system.
Tandem material handling using multiple AGVs has also been researched (Sugar and Kumar 2008) and implemented (Systems) for carrying single, heavy, and/or large loads. Sugar and Kumar (2008) described a framework and control algorithms for coordinating multiple autonomous mobile robots with onboard manipulators focusing on tasks that required grasping, manipulation, and transporting large and possibly flexible objects (in this case, large cardboard boxes) without fixtures. Synergy was realized through sensing and communication. The robots cooperatively transported objects in a tightly controlled formation while also having the capability to navigate autonomously.
The system presented by Bolger et al. (2010) demonstrated a swarm of arm-on-mobile-base platforms. Parts were grasped and held by the arms while the mobile platforms were stationary. Additional mobile platforms then coordinated to achieve prioritized delivery of parts for assembly and were not directly involved with the assembly process.
A multi-AGV system was proposed by Hoshino et al. (2008) to process and transport parts in an assembly task. Its purpose was for workload balancing and logistics control for assembly tasks. Other authors have taken similar approaches, in which they attempt to balance the workload and number of AGVs on an assembly line (Rooks 2001; Kilincci and Bayhan 2008; Kilincci 2010; Waurzyniak 2013).
10 OTHER ROBOT CONFIGURATIONS
In the literature, most multi-robot configurations use combinations of robotic arms, hands, and mobile platforms. In some instances, we have found that alternative robotic platforms are used for assembly tasks. Here, we discuss the special considerations of such configurations, since they provide additional insights into the considerations for non-standard robotic system configurations. Bonert et al. (2010) presented a mechanism for scheduling multiple gantry robots for assembling printed circuit boards (PCBs). The article focuses on the collision avoidance problem, which it solves as a modified point-to-point traveling salesman problem for optimal placement of PCB components. Multiple robots are used to optimize the assembly completion time for a complete assembly task, and the robot assembly configuration and control is such that the pick and place operation times are minimized. Each robot is provided parts using separate conveyor feeder systems, and the shared PCB is fixtured on a controllable X-Y table. Because the PCB is fixtured, its position and orientation relative to the two gantry robots is always known with high accuracy. Likewise, the parts are presented in a known position and orientation. As such, the assembly operation consists only of pick and place motion primitives without the requirement for part tracking or sensing.
The system by Sellner et al. (2006) introduced a multi-robot configuration consisting of a mobile manipulator, a mobile observer platform, and a robotic crane (BostelMan et al. 1996) sequentially coordinated and controlled by a remote human operator to assemble a large, node-based, truss system. The crane is used to brace nodes in place, while the mobile manipulator uses visual servoing to guide the connecting beams into place. The system and scenario were selected to simulate possible extra-planetary construction guided by Earth-based human operators. The robots were configured with sliding autonomy (Dorais et al. 1999) to accommodate the operator’s level of attention as he assumed control over each of the three robot systems. Many of the assembly operations were assisted by a simplified vision system for target identification and guidance.
In Simmons et al. (2000) a mobile manipulator was coordinated with an inverted, modular Stew-art platform to complete a construction assembly task. Coordinating their motions, the robots connect a beam to a static post at a predetermined location. An external “foreman” with a mobile observer platform acted as a coordination master and guided the motions of the two robots toward the goal state. The crane was used to support the mass of the beam and position it in the general vicinity of the goal state. The mobile manipulator’s arm provided fine adjustments of the beam’s pose. The performance of the assembly process was monitored visually by means of fiducials mounted on both the beam and the fixed structure. The assembly itself was based on the observed Cartesian poses of the tracked fiducials relative to one another. Throughout the assembly, the wheeled base of the mobile manipulator was parked, reducing the control complexity.
Sequeira and Basson (2009) described a reconfigurable spot-welding assembly work cell for circuit breaker manufacturing. Multiple solutions for robots behaving as dynamic fixtures were considered, including AGVs, gantry robots, rotary tables, linear actuators, and branched track conveyors. Assembly parts were fed into the robotic “fixtures” by feeders at the periphery of the work cell. The system was evaluated in simulation and assessed in terms of their reusability, scalability, agility, and reconfigurability.
11 DISCUSSION
In this report, we discussed general strategies for completing robotic assembly tasks and outlined examples in the literature of such strategies being employed in multi-robot work cells. We focused on multi-arm, arm-hand, arm-AGV, and AGV-AGV robotic assembly strategies and provided insights as to how other, less traditional multi-robot teams may be employed for assembly tasks. These strategies are summarized in Table 2 with a brief summary of the application domain for which the assemblies were programmed. We conclude by reporting on the observed trends in multi-robot assembly strategies and recap briefly the metrics by which such strategies may be assessed.
Table 2.
Summary of Multi-Robot Assembly Strategies Demonstrated in Literature
| Setup | Type | Strategy | Application |
|---|---|---|---|
| Mulit-Arm | Welding | Dynamic fixturing | Spot Welding automotive (Papakostas et al. 2011) |
| Peg-in-Hole | Force-guided part mating | Pipe fitting (Rojas and II 2012) | |
| Demonstration [Hoffmann 2014] | |||
| Vision-guided part mating | Wheel and tire assembly (Shi and Menassa 2010) | ||
| Tilt method | Simulated demonstration (Dauchez et al. 2005) | ||
| Demonstration [Yuan 2006] | |||
| Teach-by-example demonstration [Takamatsu et al. 2007) | |||
| Stochastic search | Transmission assembly (Park et al. 2009) | ||
| Position-based coordination | Bolt fastening (Su et al. 2009) | ||
| Gear Meshing | Rotational search | Differential gear assembly (Yamada et al. 1995) | |
| Parts Alignment | Pick-and-place | Process scheduling (Hörmann et al. 1989) | |
| Snap-Fit | Push-hold strategy | Structural assembly of truss (Šurdilovic et al. 2001) | |
| Cell phone assembly (Marvel 2010) | |||
| Arm-Hand | Peg-in-Hole | Spiral search | Demonstration (Bae 2014a, 2014b) |
| Arm-AGV | Peg-in-Hole | Vision- and force-guided part mating | Structural assembly of truss (Stroupe et al. 2005) |
| Wire harness plug insertion (Hamner et al. 2010) | |||
| Vision-guided part mating | Furniture assembly (Knepper et al. 2013) | ||
| Tilt strategy | Rotary shaft insertion (Bøgh et al. 2011; Carøe et al. 2012; Carøe 2012) | ||
| AGV-AGV | Logistical Support | Parts delivery | Cardboard box material handling (Sugar and Kumar 2008) |
| Workload balancing for part acquisition, transport, and placement (Bolger et al. 2010) | |||
| Scheduling for workload balancing (Fazlollahtabar et al. 2010) | |||
| Other | Parts Alignment | Vision-guided part mating | Structural assembly of truss using a mobile manipulator and a crane (Simmons et al. 2000) |
| Dynamic fixturing | Multiple different robot configurations for circuit breaker welding (Sequeira and Basson 2009) | ||
| Peg-in-Hole | Vision-guided assisted teleoperation | Semi-autonomous assembly of trusses using a mobile manipulator, a robotic crane, and a mobile observer (Sellner et al. 2006) |
11.1 Trade-offs with Multi-Robot Assembly
In Section 1, we briefly discussed the trade-offs associated with the transition from robotic assembly lines to robotic assembly cells. Moving from single- to multi-robot assembly processes introduce additional trade-offs, some of which may be directly measurable (see Section 11.3). When introducing multiple robots, for instance, throughput for a given assembly cell may be increased given the capacity to parallelize processes within a relatively limited footprint. In contrast, a single-robot cell would require serializing the assembly process, frequent tool changes, and, while only housing a single robot, careful planning of the locations and order of operations to accommodate the limited reach of a single robot manipulator. Similarly, by increasing the number of robots in the work cell, one increases agility of the cell. This enables not only a greater variety of assemblies being produced by a single cell, but also allows for multiple assemblies to be created in parallel per cell.
As a trade-off, however, by increasing the number and variety of robots in a given work cell, the challenge of controlling, coordinating, and debugging the robots increases commensurately. Parallelization, in particular, adds to the complexity of the code. A single-robot cell’s serial nature promotes easier tuning of parameters and motions, while a multi-robot system would necessitate optimizing a complex dance of moving manipulators and parts. This takes more time and programming effort to coordinate, which does not necessarily translate to increases in process or product quality. Similarly, with more robots simultaneously active within a confined workspace, the likelihood of collisions increases, thus necessitating increasingly complex observer systems to ensure the safety of human operators, robots, parts, and tools.
11.2 Trends in Multi-Robot Assembly
In general, increasing the number of robots actively servoing to complete an assembly task greatly increases the control complexity while offering some benefit in terms of assembly quality or timing. The principal positive impact of such applications to assembly tasks is measured in terms of process agility and a reduction on infrastructure investment. Specifically, by using a robot as a reconfigurable and dynamic fixture, the required work cell complexity is reduced due to the obsolescence of rigid, non-reconfigurable fixtures, conveyors, and careful planning of real estate. Similarly, a multi-robot work cell may be quickly re-tasked with a different assembly process of similar scale (e.g., with the introduction of a new model year product) with minimal work cell and task redesign.
In small-scale assembly, the active coordination of multiple robots appears to have minimal impact on the actual performance of the assembly in terms of quality or time necessary to complete certain assembly tasks. Many of the successful strategies rely on one robot acting as a modular fixture while the other performs the actual assembly action. Many coordinated applications of robot-robot collaborations for assembly provide proofs of concept but do not demonstrate actual manufacturing capabilities. Regardless, the potential for realizable performance improvements is illustrated, and it is expected that continued research in this domain will net positive results.
In contrast, with large-scale assembly tasks, mobility and component support are key factors in defining the robot system design and effective functionality. Large-scale robots with heavy lift capacities are useful for macro positioning, while dexterous manipulation is a function of smaller, cooperative robotic platforms. Like the small-scale assembly tasks, successfully building large-scale assemblies does not necessitate the coordinated, active servoing of multiple robots. However, the synchronized control of support- and manipulation-role robots will reduce the need for stop-and-go corrections of workpiece positioning and thus improve system cycle time as a whole.
11.3 Multi-Robot Assembly Metrics
As mentioned briefly in Section 2, the most common performance metrics associated with single-robot assembly tasks include profiles of the timing, motions, and forces of the assembly process. Outside of the obvious question of whether the assembly was successful, some of the performance metrics found in and inspired by the literature landscape include:
These metrics hold true also for multi-robot assembly. With additional robots included in the assembly task, however, the motions of a single robot are expected to impact the motions and performances of the others. This results in increased positional errors and incurred forces on the robots’ joints, the tooling, and the assembly workpieces. Assembly strategies that minimize these impacts are expected to improve the quality of the assembly but are also likely to result in increased assembly times and computational complexity of the control laws. For multi-robot configurations, additional metrics include:
-
Efficiency:
How much time is required to configure and tune the multi-robot assembly solution as compared with the time for a single robot to perform the same task?
What is the cost (material) difference between the multi-robot assembly configuration versus the single-robot setup for the same assembly task?
How much additional resources (e.g., space, equipment, or energy) are required to support a multi-robot configuration versus a single-robot solution?
-
Timing:
How does the timing change when adding or changing robots to the assembly application?
-
Forces:
What is the force transfer from one robot to others in the multi-robot configuration?
A brief summary of some common metrics applicable to multi-robot assemblies is given in Table 3. Ultimately, it is worth remembering that robotic assembly tasks in manufacturing are guided by the same tenets that guide any adoption of automation technology: (1) process quality, (2) process efficiency, and (3) return on investment. For any given application of automation technology, there must be a measurable positive impact on the manufacturing process for such solutions to be considered viable. A given solution’s ease of use is anticipated as being one of the key factors when determining broad acceptance of robotic assembly. If the time and effort necessary to accommodate even simple assembly tasks eclipses the expected return on investment, then solutions in robot assembly are unlikely to be accepted. Online and adaptive process optimizations have demonstrated realizable potential for automatically improving the performance of robots performing assembly tasks, but the initial, pre-optimized integration and implementation remain as hurdles to broad adoption.
Table 3.
Example Metrics for Measuring Multi-Robot Assembly Performance
| Metric | Category | Measurement Description | Units |
|---|---|---|---|
| Efficiency | Computational Complexity | Complexity of assembly strategy | O-notation |
| Impact of using alternative assembly strategies | O-notation | ||
| Single- versus multi-robot program complexity | O-notation | ||
| Effort Efficiency | Programming time duration | Seconds | |
| Optimization/tuning duration | Seconds | ||
| Commissioning versus use timing | Seconds | ||
| Single- versus multi-robot program timing | Seconds | ||
| Single- versus multi-robot cost | Monetary units | ||
| Process Quality | Ratio of assembly successes to assembly failures | Seconds | |
| Mean time to failure | Time or cycles | ||
| Timing | Process Timing | Average time to complete a single assembly | Seconds |
| Maximum time to complete a single assembly | Seconds | ||
| Minimum time to complete a single assembly | Seconds | ||
| Standard deviation of assembly times | Seconds | ||
| Impact of using alternative assembly strategies | Seconds | ||
| Sensitivity to parameter changes | Seconds | ||
| Time Spent performing assembly versus other motions | Seconds | ||
| Time required for single- versus multi-robot con- figurations to complete assemblies | Seconds | ||
| Motions | Displacement | Average positional error from the initial assembly search pose to the final assembly pose | Meters |
| Motion Effort | Distance traveled during assembly process | Meters | |
| Joint displacement during assembly process | Radians/degrees | ||
| Energy expended during assembly process | Watts | ||
| Distance traveled performing assembly versus other robot motions | Meters | ||
| Forces | Force Transfer | Maximum incurred force measured by the robot on any given axis | Newtons/Newton-meters |
| Average incurred force Measured by the robot on any given axis | Newtons/Newton-meters | ||
| Maximum and average forces measured independently at the tool, assembly part, and fixture | Newtons/Newton-meters |
11.4 Open Challenges in Multi-Robot Assembly
Despite the technological advances toward robotic assembly, there remain a number of challenges that need addressing. Many of these issues are not limited to the multi-robot assembly problem, however. For instance, ease-of-programming and effective user interfaces are an open challenge. The industry is responding to such calls for improving the user experience, yet progress is slow, and is largely evolving separate from the communities of end users. Similarly, sensor-based, adaptive control of individual manipulators remains difficult, despite increases in computing and sensing capabilities while the cost of entry decreases. Continued research will only improve research, though broad improvements are unlikely to be realized in the near future.
A particular challenge facing multi-robot assembly, however, is centered on the lack of support for heterogeneous robot configurations. Single-manufacturer solutions are already challenging, but the difficulty of integrating, registering, configuring, and coordinating robots increases significantly when one intends to use systems from different manufacturers. System-agnostic solutions will be required to enable the existence of such configurations, let alone effective functionality. While individual research efforts are focused on enabling certain capabilities (e.g., improved calibration and registration (Marvel et al. 2015; Van Wyk and Marvel 2017) and common command languages (Edwards and Lewis 2012)), realizable improvements will require the active cooperation of the robot manufacturers. As is the case with the robot-on-mobile-platform paradigms, garnering such cooperation requires a clear, marketable industry need to exist. Although the needs and technologies exist today, they have yet to grow to the level that warrants concerted effort.
Footnotes
Disclaimer: Commercial equipment and materials are identified in order to adequately specify certain procedures. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials or equipment identified are necessarily the best available for the purpose.
References
- ABB Automation Technologies BA, Robotics. Robotics Application Manual: Force Control for Assembly. Vasteras, Sweden: SE-721 68. [Google Scholar]
- Abd K, Abdhary K, Marian R. A scheduling framework for robotic flexible assembly cells. King Mongkut’s University of Technology North Bangkok: Int J Appl Sci Technol. 2011;4(1):31–38. [Google Scholar]
- Aized Tauseef. Modelling and performance maximization of an integrated automated guided vehicle system using coloured Petri net and response surface methods. Comput Industr Eng. 2009;57:822–831. [Google Scholar]
- Bae Ji-Hun. Peg-in-Hole Assembly by Hand-Arm Coordination. 2014a Retrieved from https://www.youtube.com/watch?v=G-52JZVbBt8.
- Bae Ji-Hun. Robotic Dual Hand-Arm Manipulation: Robotic Peg-in-Hole. 2014b (7 January, 2015 2014). Retrieved from https://www.youtube.com/watch?v=j5qcDDifzpk.
- Bae Ji-Hun, Park Sung-Woo, Park Jae-Han, Baeg Moon-Hong, Kim Doik, Oh Sang-Rok. Development of a low cost anthropomorphic robot hand with high capability. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2012. pp. 4776–4782. [Google Scholar]
- Balch Tucker, Parker Lynne E. Robot Teams: From Diversity to Polymorphism. AK Peters, Ltd; 2002. [Google Scholar]
- Bøgh Simon, Hvilshøj Mads, Kristiansen Morten, Madsen Ole. Autonomous industrial mobile manipulation (AIMM): from research to industry. Proceedings of the 42nd International Symposium on Robotics; 2011. pp. 1–9. [Google Scholar]
- Bolger Adrienne, Faulkner Matt, Stein David, White Lauren, Yun Seung kook, Rus Daniela. Experiments in decentralized robot construction with tool delivery and assembly robots. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2010. pp. 5085–5092. [Google Scholar]
- Bonert M, Shu LH, Benhabib B. Motion planning for multi-robot assembly systems. Int J Comput Integr Manufact. 2010;13(4):301–310. [Google Scholar]
- BostelMan Roger, Albus James, Dagalakis Nicholas, Jacoff Adam. RoboCrane [R] project: An advanced concept for large scale manufacturing. Proceedings of the Association for Unmanned Vehicle Systems International (AUVSI’96); 1996. pp. 509–522. [Google Scholar]
- Brogårdh Torgny. Robot control overview: An industrial perspective. Model Ident Control. 2009;30(3):167–180. [Google Scholar]
- Caine Michael E, Lozano-Pérez Tomas, Seering Warren P. Assembly strategies for chamferless parts. Proceedings of the IEEE International Conference on Robotics and Automation; 1989. pp. 472–477. [Google Scholar]
- Carøe Christian. Rotor Shaft Assembly Using the KUKA LWR. 2012 Retrieved from https://www.youtube.com/watch?v=bR77UhcS0z4.
- Carøe Christian, Hvilshøj Mikkel, Schou Casper. Thesis. Aalborg University; Aalborg, Denmark: 2012. Intuitive Programming of AIMM Robot. [Google Scholar]
- Chhatpar Siddhart R, Branicky Michael S. Search strategies for peg-in-hole assemblies with position uncertainty. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2001. pp. 1465–1470. [Google Scholar]
- Choo Benjamin Y, Adams Stephen C, Weiss Brian A, Marvel Jeremy A, Beling Peter A. Adaptive multi-scale prognostics and health management for smart manufacturing systems. Int J Prognost Health Manage. 2016;7 [PMC free article] [PubMed] [Google Scholar]
- Dauchez Pierre, Fraisse Philippe, Pierrot François. A vision/position/force control approach for performing assembly tasks with a humanoid robot. Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots; 2005. pp. 277–282. [Google Scholar]
- Deneux Dominique. Introduction to assembly features: An illustration synthesis methodology. J Intell Manufact. 1999;10:29–39. [Google Scholar]
- Diftler MA, Mehling JS, Abdallah ME, Radford NA, Bridgwater LB, Sanders AM, Askew RS, Linn DM, Yamokoski JD, Permenter FA, Hargrave BK, Platt R, Savely RT, Ambrose RO. Robotnaut 2 - The first humanoid robot in space. Proceedings of the IEEE International Conference on Robotics and Automation; 2011. pp. 2178–2183. [Google Scholar]
- Dorais Gregory, Peter Bonasso R, Kortenkamp David, Pell Barney, Schreckenghost Debra. Adjustable autonomy for human-centered autonomous systems. Proceedings of the 16th International Joint Conference on Artificial Intelligence Workshop on Adjustable Autonomy Systems; 1999. pp. 16–35. [Google Scholar]
- Doriya Rajesh, Mishra Siddharth, Gupta Swati. A brief survey and analysis of multi-robot communication and coordination. Proceedings of the 2015 International Conference on Computing, Communication, and Automation (ICCCA’15); IEEE; 2015. pp. 1014–1021. [Google Scholar]
- Downs Anthony, Downs Anthony, Harrison William, Harrison William, Schlenoff Craig, Schlenoff Craig. Test methods for robot agility in manufacturing. Industr Robot: Int J. 2016;43(5):563–572. doi: 10.1108/IR-01-2016-0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards S, Lewis C. Applying the robot operating system (ROS) to industrial applications. Proceedings of the IEEE International Conference on Robotics and Automation: ECHORD Workshop.2012. [Google Scholar]
- Falco Joe, Marvel Jeremy, Messina Elena. Report; Proceedings of the NISTIR-7940: Dexterous Manipulation for Manufacturing Applications Workshop; National Institute of Standards and Technology; 2013. [Google Scholar]
- Fazlollahtabar Hamed, Rezaie Borna, Kalantari Hassan. Mathematical programming approach to optimize material flow in an AGV-based flexible jobshop manufacturing system with performance analysis. Int J Adv Manufact Technol. 2010;51:1149–1158. [Google Scholar]
- Fei Yanqiong, Zhao Xifang. An assembly process modeling and analysis for robotic multiple peg-in-hole. J Intell Robot Syst. 2003;36:175–189. [Google Scholar]
- Fu Li-Chen, Hsu Yung-Jen. Fully automated two-robot assembly cell. Proceedings of the IEEE International Conference on Robotics and Automation; 1993. pp. 332–338. [Google Scholar]
- Furuno Seiji, Yamamoto Motoji, Mohri Akira. Trajectory planning of mobile manipulator with stability considerations. Proceedings of the IEEE International Conference on Robotics and Automation; 2003. pp. 3403–3408. [Google Scholar]
- Gayretli A, Abdalla HS. A feature-based prototype system for the evaluation and optimization of manufacturing processes. Proceedings of the 24th International Conference on Computer and Industrial Engineering; 1999. pp. 481–484. [Google Scholar]
- Genc Suat, Messler Robert W, Jr, Gabriele Gary A. A systematic approach to integral snap-fit attachment design. Res Eng Design. 1998;10:84–93. [Google Scholar]
- Glibert PR, Coupez D, Peng YM, Delchambre A. Scheduling of a multi-robot assembly cell. Comput Integr Manufact Syst. 1990;3(4):236–245. [Google Scholar]
- Gravel Dave, Maslar Frank, Zhang George, Nidamarthi Srini, Chen Heping, Fuhlbrigge Tom. Toward robotizing powertrain assembly. Proceedings of the 7th World Congress on Intelligent Control and Automation; 2008. pp. 541–546. [Google Scholar]
- Gravel David P, Newman Wyatt S. Flexible robotic assembly efforts at ford motor company. Proceedings of the 2001 IEEE International Symposium on Intelligent Control; 2001. pp. 173–182. [Google Scholar]
- Hamner Brad, Koterba Seth, Shi Jane, Simmons Reid, Singh Sanjiv. An autonomous mobile manipulator for assembly tasks. Auton Robots. 2010;28:131–149. [Google Scholar]
- Hoffmann Alwin. Factory 2020 - Final Version. 2012 Retrieved from https://www.youtube.com/watch?v=gf3673XkHCw.
- Hoffmann Alwin. SoftRobot. 2014 Retrieved from https://swt.informatik.uni-augsburg.de/softrobot/hauptseite/hauptseite.html.
- Hootsman Norbert AM, Dubowsky Steven, Mo Patrick Z. The experimental performance of a mobile manipulator control algorithm. Proceedings of the IEEE International Conference on Robotics and Automation; 1992. pp. 1948–1954. [Google Scholar]
- Hörmann Andreas, Meier W, Schloen J. A control architecture for an advanced fault-tolerant robot system. Proceedings of the Intelligent Autonomous Systems 2, an International Conference; 1989. pp. 576–585. [Google Scholar]
- Hörmann Andreas, Rembold Ulrich. Development of an advanced robot for autonomous assembly. Proceedings of the IEEE International Conference on Robotics and Autonomous Systems; 1991. pp. 2452–2457. [Google Scholar]
- Hoshino Satoshi, Seki Hiroya, Naka Yuji. Development of a flexible and agile multi-robot manufacturing system. Proceedings of the 17th International Federation of Automatic Control World Congress.2008. [Google Scholar]
- Hsieh Sheng-Fen. Re-configurable dual-robot assembly system design, development and future directions. Industr Robot: Int J. 2003;30(3):250–257. [Google Scholar]
- ISO 9283. Standard. International Organization for Standardization; 1998. ISO 9126 Manipulating Industrial Robots—Performance Criteria and Related Test Methods. [Google Scholar]
- Jarvis Dennis, Jarvis Jacqueline, McFarlane Duncan, Lucas Andrew, Rönnquist Ralph. Implementing a multi-agent systems approach to collaborative autonomous manufacturing operations. Proceedings of the Aerospace Conference; 2001. pp. 2803–2811. [Google Scholar]
- Johnson Danny J. Assembly cells versus assembly lines: Insights on performance improvements from simulation experiments and a case study. Supply Chain and Information Management Conference Papers, Posters and Proceedings; 1999. pp. 999–1001. [Google Scholar]
- Kalech Meir. Diagnosis of coordination failures: A matrix-based approach. Auton Agents Multi-Agent Syst. 2012;24(1):69–103. [Google Scholar]
- Kalech Meir, Kaminka Gal A. On the design of coordination diagnosis algorithms for teams of situated agents. Artific Intell. 2007;171(8):491–513. [Google Scholar]
- Kaminka Gal A, Erusalimchik Dan, Kraus Sarit. Adaptive multi-robot coordination: A game-theoretic perspective. Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA’10); IEEE; 2010. pp. 328–334. [Google Scholar]
- Kaneko Kenji, Kanehiro Fumio, Kajita Shuuji, Yokoyama Kazuhiko, Akachi Kazuhiko, Kawasaki Toshikazu, Ota Shigehiko, Isozumi Takakatsu. Design of prototype humanoid robotics platform for HRP. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2002. pp. 2431–2436. [Google Scholar]
- Kilincci Ozcan. A petri net-based heuristic for simple assembly line balancing problem of type 2. Int J Adv Manufact Technol. 2010;46:329–338. [Google Scholar]
- Kilincci Ozcan, Mirac Bayhan G. A p-invariant-based algorithm for simple assembly line balancing problem of type-1. Int J Adv Manufact Technol. 2008;37:400–409. [Google Scholar]
- Knepper Ross A, Layton Todd, Romanishin John, Rus Daniela. IkeaBot: An autonomous multi-robot coordinated furniture assembly system. Proceedings of the IEEE International Conference on Robotics and Automation.2013. [Google Scholar]
- Kock Soenke, Vittor Timothy, Matthias Bjoern, Jerregard Henrik, Källman Mats, Lundberg Ivan, Mellander Roger, Hedelind Mikael. Robot concept for scalable, flexible assembly automation: A technology study on a harmless dual-armed robot. Proceedings of the IEEE International Symposium on Assembly and Manufacturing; 2011. pp. 1–5. [Google Scholar]
- Ayorkor Korsah G, Stentz Anthony, Bernardine Dias M. A comprehensive taxonomy for multi-robot task allocation. Int J Robot Res. 2013;32(12):1495–1512. [Google Scholar]
- Krüger J, Lien TK, Verl A. Cooperation of human and machines in assembly lines. CIRP Ann Manufact Technol. 2009;58:628–646. [Google Scholar]
- Kwon Jaesung, Yang Woosung, Lee Yosun, Bae Ji-Hun, Oh Younghwan. Biologically inspired control algorithm for an unified motion of whole robotic arm-hand system. Proceedings of the IEEE International Symposium on Robot and Human Interactive Communication; 2014. pp. 398–404. [Google Scholar]
- Lee Jin-Kyu, Lee Tae-Eog. Automata-based supervisory control logic design for a multi-robot assembly cell. Int J Comput Integr Manufact. 2010;15(4):319–334. [Google Scholar]
- Liao Hsin-Te, Leu Ming C. Analysis of impact in robotic peg-in-hole assembly. Robotica. 1998;16(3):347–356. [Google Scholar]
- Lueth Tim C, Nassal Uwe M, Rembold Ulrich. Reliability and integrated capabilities of locomotion and manipulation for autonomous robot assembly. J Robot Auton Syst. 1995;14(1995):185–198. [Google Scholar]
- Madsen Ole, Bøgh Simon, Schou Casper, Andersen Rasmus Skovgaard, Damgaard Jens Skov, Pedersen Mikkel Rath, Krüger Volker. Integration of mobile manipulators in an industrial production. Industr Robot: Int J. 2015;42(1):11–18. [Google Scholar]
- Marvel Jeremy, Messina Elena, Antonishek Brian, Fronczek Lisa, Van Wyk Karl. Report. National Institute of Standards and Technology; 2015. NISTIR 8093: Tools for Collaborative Robots within SME Workcells. Retrieved from http://dx.doi.org/10.6028/NIST.IR.8093. [Google Scholar]
- Marvel Jeremy A. Dissertation. Case Western Reserve University; Cleveland, OH, USA: 2010. Autonomous Learning for Robotic Assembly Applications. [Google Scholar]
- Marvel Jeremy A, Falco Joe. Report. National Institute of Standards and Technology; 2012. NISTIR 7901: Best Practices and Performance Metrics Using Force Control for Robotic Assembly. Retrieved from http://dx.doi.org/10.6028/NIST.IR.7901. [Google Scholar]
- Marvel Jeremy A, Newman Wyatt S, Gravel Dave P, Zhang George, Wang Jianjun, Fuhlbrigge Tom. Automated learning for paramter optimization of robotic assembly tasks utilizing genetic algorithms. Proceedings of the IEEE International Conference on Robotics and Biomimetics; 2008. pp. 179–184. [Google Scholar]
- Marvel Jeremy A, Norcross Rick. Implementing speed and separation monitoring in collaborative robot workcells. Robot Comput-Integr Manufact. 2017;44:144–155. doi: 10.1016/j.rcim.2016.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micalizio Roberto, Torasso Pietro. Cooperative monitoring to diagnose multiagent plans. J Artific Intell Res (JAIR) 2014;51:1–70. [Google Scholar]
- Motoman Yaskawa. Yaskawa Motoman MH80 Robot Unloading Trucks. 2013 Retrieved from https://www.youtube.com/watch?v=8wngL0BnF_4.
- Mouri Tetsuya, Kawasaki Haruhisa, Umebayashi Katsuya. Developments of new anthropomorphic robot hand and its master slave system. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2005. pp. 3225–3230. [Google Scholar]
- Newman Wyatt S, Zhao Yonghong, Pao Yoh-Han. Interpretation of force and moment signals for compliant peg-in-hole assembly. Proceedings of the IEEE International Conference on Robotics and Automation; 2001. pp. 571–576. [Google Scholar]
- Niederreiter Harald. Quasi-monte carlo methods and pseudo-random numbers. Bull Amer Math Soc. 1978;84(6):957–1041. [Google Scholar]
- Niemann Johan. Thesis. Central University of Technology; Free State, Bloemfontein, South Africa: 2013. Development of a Reconfigurable Assembly System with Enhanced Control Capabilities and Virtual Commissioning. [Google Scholar]
- Nof Shimon Y, Drezner Zvi. The multiple-robot assembly plan problem. J Intell Robot Syst. 1993;5(1993):57–71. [Google Scholar]
- Papakostas Nikolaos, Michaelos George, Makris Stiris, Zouzias Dimitris, Chryssolouris George. Industrial applications with cooperaing robots for flexible assembly. Int J Comput Integr Manufact. 2011;24(7):650–660. [Google Scholar]
- Park Chanhun, Park Kyoungtaik, Park Dong IL, Kyung Jin-Ho. Dual arm robot manipulator and its easy teaching system. Proceedings of the IEEE International Symposium on Assembly and Manufacturing; 2009. pp. 242–247. [Google Scholar]
- Park Hyeonjun, Bae Ji-Hun, Park Jae-Han, Baeg Moon-Hong, Park Jaeheung. ntuitive peg-in-hole assembly strategy with a compliant manipulator. Proceedings of the 44th International Symposium on Robotics; 2013. pp. 1–5. [Google Scholar]
- Patel Rajendra, Hedeling Mikael, Lozan-Villegas Pablo. Enabling robots in small-part assembly lines: The “ROSETTA approach”—An industrial perspective. Proceedings of the ROBOTIK 2012: 7th German Conference on Robotics; 2012. pp. 1–5. [Google Scholar]
- Petersson Lars, Austin David, Kragic Danica. High-level control of a mobile manipulator for door opening. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2000. pp. 2333–2338. [Google Scholar]
- Quan Bui Trong, Huang Jian, Harada Minoru, Yabuta Tetsuro. Control of a macro-micro robot system using manipulability of the micro robot. JSME Int J Ser C: Mech Syst Mach Elem Manufact. 2006;49(3):897–904. [Google Scholar]
- Rodríguez Carlos, Monta no Andrés, Suárez Raúl. Manipulation tasks with a dual arm system including obstacles removing. Proceedings of the IEEE 18th Conference on Emerging Technologies and Factory Automation; 2013. pp. 1–7. [Google Scholar]
- Rojas J, Peters Richard A., II Analysis of autonomous cooperative assembly using coordination schemes by heterogeneous robots using a control basis approach. Auton Robots. 2012;32(4):369–383. DOI: http://dx.doi.org/10.1007/s10514-012-9274-3. [Google Scholar]
- Brian Rooks. AGVs find their way to greater flexibility. Assembly Automat. 2001;21(1):38–43. [Google Scholar]
- Rubenstein Michael, Cornejo Alejandro, Nagpal Radhika. Programmable self-assembly in a thousand-robot swarm. Science. 2014;345(6198):795–799. doi: 10.1126/science.1254295. [DOI] [PubMed] [Google Scholar]
- Saut Jean-Philippe, Gharbi Mokhtar, Cortéz Juan, Sidobre Daniel, Siméon Thierry. Planning pick-and-place tasks with two-handed regrasping. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2010. pp. 4528–4533. [Google Scholar]
- Schimmels Joseph M. Method and apparatus for assembling rigid parts. US6408531 B1 US patent. 2002
- Sellner Brennan, Heger Frederik W, Hiatt Laura M, Simmons Reid, Singh Sanjiv. Special Issue Proc IEEE Multi-Robot Syst. IEEE; 2006. Coordinated multi-agent teams and sliding autonomy for large-scale assembly. [Google Scholar]
- Sequeira MA, Basson AH. Case study of a fixture-based reconfigurable assembly system. Proceedings of the IEEE International Symposium on Assembly and Manufacturing; 2009. pp. 387–392. [Google Scholar]
- Sharon Andre, Hogan Neville, Hardt David. The macro/micro manipulator: An improved architecture for robot control. Robot Comput Integr Manufact. 1993;10(3):209–222. [Google Scholar]
- Liza Ruhizan, Shauri Ahmad, Nonami Kenzo. Assembly manipulation of small objects by dual-arm manipulator. Assembly Automat. 2011;31(3):263–274. [Google Scholar]
- Shi Jane, Menassa Roland. Flexible robotic assembly in dynamic environments. Proceedings of the 10th Performance Metrics for Intelligent Systems Workshop; 2010. pp. 271–276. [Google Scholar]
- Shneier Michael, Bostelman Roger. Report. National Institute of Standards and Technology; 2014. NISTIR-8022: Literature Review of Mobile Robots for Manufacturing. [Google Scholar]
- Simmons Reid, Singh Sanjiv, Hershberger David, Ramos Josue, Smith Trey. First results in the coordination of heterogeneous robots for large-scale assembly. Proceedings of the 7th International Symposium on Experimental Robotics (ISER’00); 2000. pp. 323–332. [Google Scholar]
- Stroupe Ashley, Huntsberger Terry, Okon Avi, Aghazarian Hrand, Robinson Matthew. Behavior-based multi-robot collaboration for autonomous construction tasks. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2005. pp. 1495–1500. [Google Scholar]
- Su Liying, Shi Lei, Yu Yucqing, Xia Qixiao. Bolt and screw assemblage throug collaborative kinematics operation of two modular robots based on the position feedback. Proceedings of the IEEE International Conference on Information and Automation; 2009. pp. 1574–1579. [Google Scholar]
- Sugar Thomas, Kumar Vijay. Control and Coordination of Multiple Mobile Robots in Manipulation and Material Handling Tasks. 2008;250:15–24. [Google Scholar]
- Sun Dong, Mills James K. Adaptive synchronized control for coordination of multirobot assembly tasks. IEEE Trans Robot Automat. 2002;18(4):498–510. [Google Scholar]
- Wheelift Systems. Custom Engineered AGV Systems for Heavy Assembly Operations. Retrieved from http://www.wheelift.com/agv_systems.html.
- Takamatsu Jun, Ogawara Koichi, Kimura Hiroshi, Ikeuchi Katsushi. Recognizing assembly tasks through human demonstration. Int J Robot Res. 2007;26:641–659. [Google Scholar]
- Tambe Milind. Agent architectures for flexible. Proceedings of the 14th National Conference on Artificial Intelligence (AI’07); AAAI press; 1997. pp. 22–28. [Google Scholar]
- Thomas U, Molkenstruck S, Iser R, Wahl FM. Multi sensor fusion in robot assembly using particle filters. Proceedings of the IEEE International Conference on Robotics and Automation; 2007. pp. 3837–3843. [Google Scholar]
- Townsend William. The barretthand grasper—Programmbly flexible part handling and assembly. Industr Robot: Int J. 2000;27(3):181–188. [Google Scholar]
- Ullah Hamid, Bohez Erik LJ, Irfan MA. Assembly features: Definition, classification, and instantiation. Proceedings of the IEEE 2006 International Conference on Emerging Technologies; 2006. pp. 617–623. [Google Scholar]
- van Dyke Parunak H. Industrial and Practical Applications of DAI. MIT Press; Cambridge, MA: 1999. pp. 337–421. [Google Scholar]
- van Holland Winfried, Bronsvoort Willem F. Assembly features in modeling and planning. Robot Comput Integr Manufact. 2000;16:277–294. [Google Scholar]
- Van Wyk Karl, Marvel Jeremy A. Strategies for improving and evaluating robot registration performance. IEEE Trans Auto Sci Eng. 2017 doi: 10.1109/TASE.2017.2720478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Šurdilovic Dragoljub, Grassini Francesco, De Bartolemei Maurizio. Synthesis of impedance control for complex co-operating robot assembly task. Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics; 2001. pp. 1181–1186. [Google Scholar]
- Waurzyniak Patrick. Aerospace automation picks up the pace. Manufact Eng. 2013;150(3):55–62. [Google Scholar]
- Whitney Daniel E. Quasi-static assembly of compliantly supported rigid parts. J Dynam Syst Measure Control. 1982;104(1):65–77. [Google Scholar]
- Wick Charles, Veilleux Raymond F., editors. Tools and Manufacturing Engineers Handbook: Volume 4: Quality Control and Assembly. 4. Dearborn, MI, USA: 1987. [Google Scholar]
- Xia Yanchun, Yin Yuehong, Chen Zhaoneng. Dynamic analysis for peg-in-hole assembly with contact deformation. Int J Adv Manufact Technol. 2005;30(1–2):118–128. [Google Scholar]
- Yamada Y, Nagamatsu S, Sato Y. Development of multi-arm robots for automobile assembly. Proceedings of the IEEE International Conference on Robotics and Automation; 1995. pp. 2224–2229. [Google Scholar]
- Yan Zhi, Jouandeau Nicolas, Cherif Arab Ali. A survey and analysis of multi-robot coordination. Int J Adv Robot Syst. 2013;10(399):1–18. [Google Scholar]
- Yuan Peijiang. An adaptive feedback scheduling algorithm for robot assembly and real-time control systems. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2006. pp. 2226–2231. [Google Scholar]
- Zhang George, Bell Arnold, Zhang Hui, He Jianmin, Wang Jianjun, Martinez Carlos. On-pendant robotic assembly parameter optimization. Proceedings of the 7th World Congress on Intelligent Control and Automation; 2008. pp. 547–552. [Google Scholar]