Gibbs Sampler Based λ-Dynamics and Rao-Blackwell Estimator for Alchemical Free Energy Calculation

Abstract

λ-dynamics is a generalized ensemble method for alchemical free energy calculations. In traditional λ-dynamics, the alchemical switch variable λ is treated as a continuous variable ranging from 0 to 1 and an empirical estimator is utilized to approximate the free energy. In the present paper, we describe an alternative formulation of λ-dynamics that utilizes the Gibbs sampler framework which we call Gibbs Sampler λ-dynamics (GSLD). GSLD, like traditional λ-dynamics, can be readily extended to calculate free energy differences between multiple ligands in one simulation. We also introduce a new free energy estimator, the Rao-Blackwell estimator (RBE) for use in conjunction with GSLD. Compared with the current empirical estimator, the advantage of RBE is that RBE is an unbiased estimator and its variance is usually smaller than the current empirical estimator. We also show that the multistate Bennett acceptance ratio (MBAR) equation or the unbinned weighted histogram analysis method (UWHAM) equation can be derived using the RBE. We illustrate the use and performance of this new free energy computational framework by application to a simple harmonic system as well as relevant calculations of small molecule relative free energies of solvation and binding to a protein receptor. Our findings demonstrate consistent and improved performance compared with conventional alchemical free energy methods.

Graphical Abstract

1 Introduction

Free energy calculation is fundamental for understanding many important biophysical processes, such as protein conformational changes, protein-protein interactions, and protein-ligand binding processes.^1,2 Calculating protein-ligand binding free energy has important applications in drug discovery, especially in the lead compound generation and optimization stages.^3–5 These stages only require calculating protein-ligand relative binding free energy, which has been shown to be easier than calculating protein-ligand absolute binding free energy.^3,4

One widely used methodology for calculating protein-ligand relative binding free energy is the alchemical free energy approach.^3–5 This approach utilizes the thermodynamic cycle shown in Figure 1.² This thermodynamic cycle specifies that $\mathrm{\Delta }\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{binding}}=\mathrm{\Delta }{G}_{L_1}^{\text{binding}}-\mathrm{\Delta }{G}_{L_0}^{\text{binding}}=\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{bound}}-\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{unbound}}$. In order to calculate the relative binding free energy between ligand L₀ and L₁ with receptor R, i.e, $\mathrm{\Delta }\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{binding}}$, the alchemical free energy method calculates $\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{unbound}}$ and $\mathrm{\Delta }{G}_{L_0\to L_1}^{\text{bound}}$ by employing alchemical transformations morphing ligand L₀ into ligand L₁ in both unbound and bound environments, respectively.

Figure 1.

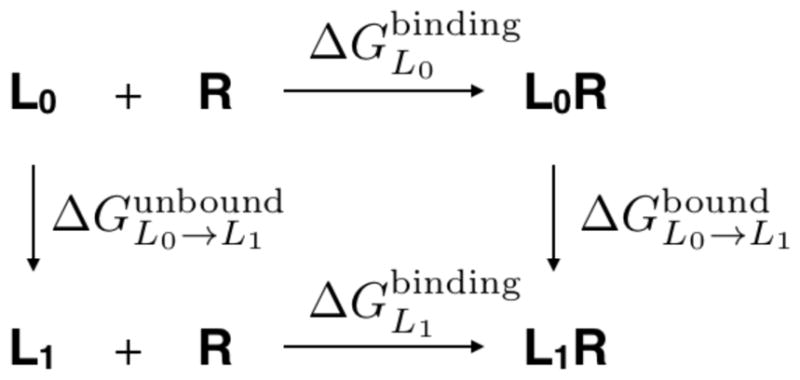
The thermodynamic cycle used for calculating a relative binding free energy between ligand L₀ and L₁ with a receptor R.

Several alchemical free energy calculation methods have been developed over the last several decades, such as free energy perturbation,^6,7 thermodynamic integration,^2,8 enveloping distribution sampling^9,10 and λ-dynamics.^11–17 λ-dynamics is a generalized ensemble method in which the alchemical transformation variable λ is a continuous variable ranging from 0 to 1, with λ = 0, 0 < λ < 1, and λ = 1 corresponding to the ligand being in L₀ state, intermediate hybrid states, and L₁ state, respectively. The potential energy corresponding to λ is

$$V(\lambda ,{\{x_i\}}_{i=0}^1,X)=(1-\lambda )V_0(x_0,X)+\lambda (V_1(x_1,X)+G_1^b)+V_{\text{env}}(X),$$ (1)

where X, x₀ and x₁ are atomic coordinates associated with the environment, the ligand L₀ and the ligand L₁, respectively. V_i(x_i, X) is the potential energy between ligand L_i and the environment and V_env(X) is the potential energy of the environment. $G_1^b$ is a biasing potential to ensure that the two physical states, corresponding to λ = 0 and λ = 1, are both sampled in the simulation. The biasing potential $G_1^b$ is determined iteratively by running multiple short simulations.^14,15,18,19 The dynamics of the system (λ, ${\{x_i\}}_{i=0}^1$, X) is generated from the extended Hamiltonian:

$$H(\lambda ,{\{x_i\}}_{i=0}^1,X)=T_{x,X}+T_{\lambda }+V(\lambda ,{\{x_i\}}_{i=0}^1,X)$$ (2)

where T_{x, X} and T_λ are the kinetic energy associated with coordinates ( ${\{x\}}_{i=0}^1$, X) and λ, respectively. The free energy difference between ligand L₀ and L₁, with the biasing potential $G_1^b$, is

$$\mathrm{\Delta }G=-{\beta }^{-1}ln\frac{P(\lambda =1)}{P(\lambda =0)},$$ (3)

where β is the inverse temperature; P(λ = 0) and P(λ = 1) are probability denisties of λ at points 0 and 1, respectively. In practice, this free energy difference ΔG is estimated using the following empirical estimator based on the trajectory of λ:

$$\mathrm{\Delta }\widehat{G}=-{\beta }^{-1}ln\frac{P(\lambda >{\lambda }_{\text{cutoff}})}{P(\lambda <1-{\lambda }_{\text{cutoff}})},$$ (4)

where λ_cutoff (0 < λ_cutoff < 1) is a cutoff value which is chosen to be close to 1.¹⁴

Although the empirical estimator is straightforward to evaluate based on the λ trajectory, it is not necessarily optimal. One issue is that the empirical estimator is systematically biased as it uses P(λ < 1 – λ_cutoff) and P(λ > λ_cutoff) to approximate P(λ = 0) and P(λ = 1), respectively. Additionally, the bias depends on the cutoff value λ_cutoff, which is chosen empirically and is difficult to quantify as it may vary among different systems.

In the current work, we present a novel form of λ-dynamics called the Gibbs sampler based λ-dynamics (GSLD) with the Rao-Blackwell estimator (RBE). The Gibbs sampler framework for calculating free energy differences between two ligands was first suggested by Chodera and Shirts.²⁰ In their work, λ was treated as a discrete variable and MBAR²¹ was used to estimate the free energy change. In this study, we show that GSLD and RBE can treat λ as either a discrete variable or a continuous variable when calculating free energy differences between two ligands. When λ is treated as a continuous variable, GSLD and RBE can be generalized to simultaneously calculate free energies of multiple ligands in one simulation, as in the generalization of λ-dynamics.¹⁴ We explore these new methods through applications to three model systems in this paper. This paper is organized as follows. In section 2, we describe GSLD and its generalization to multiple ligands. Then we introduce the RBE and show that the MBAR/UWHAM equations^21–23 can be derived from the RBE. In section 3, we give detailed setup information for the setup and simulation of the three systems with which we tested the methods. Our results for these three systems are presented in section 4. We conclude with a discussion of how the GSLD and RBE can be used for other applications.

2 Methods

2.1 Gibbs Sampler Based λ-Dynamics

As a generalized ensemble method, GSLD samples from the joint distribution of λ and the atomic coordinates of the system using the Gibbs sampler. In this section, we first briefly introduce the Gibbs sampler. We then use the Gibbs sampler to formulate pairwise GSLD. We conclude by showing how the GSLD can be generalized to work for multiple ligands.

2.1.1 The Gibbs Sampler

The Gibbs sampler, which is widely used in both statistics and machine learning, is a Markov Chain Monte Carlo (MCMC) method for sampling from multivariate distributions.^24,25 To sample (X, Y ) from the joint distribution: (X, Y ) ~ P(X, Y ), the Gibbs sampler generates a Markov chain of states {(X_t, Y_t), t = 0, 1, 2, …, N} using the following procedure:

• Step 0: initialize the starting state (X₀, Y₀).

• Step t: sample from the conditional distribution

  • Updating X: given the state (X_t−1, Y_t−1) from step t − 1, sample X_t from the conditional distribution of X_t ~ P(X_t|Y_t−1).

  • Updating Y: given X_t from the above update step, sample Y_t from the conditional distribution of Y_t ~ P(Y_t|X_t). The resulting sample (X_t, Y_t) is the state for step t.

Because the above procedure satisfies the detailed balance condition with respect to the joint distribution: (X, Y ) ~ P(X, Y ), the sampled states {(X_t, Y_t), t = 0, 1, 2, …, N} converge to the joint distribution.^24,25 The update steps require sampling from both conditional distributions: X_t ~ P(X_t|Y_t−1) and Y_t ~ P(Y_t|X_t). If direct sampling from the conditional distribution is possible, independent samples can be directly drawn using numerical pseudorandom number generators. Otherwise, samples can be drawn using other Monte Carlo methods or Hamiltonian dynamics, as long as the method satisfies the detailed balance condition with respect to the corresponding conditional distribution.^25,26 This property of the Gibbs sampler makes it quite flexible on choosing appropriate sampling methods based on the conditional distributions.

2.1.2 Pairwise GSLD

Pairwise GSLD calculates the free energy difference between two ligands: ligand L₀ and ligand L₁. In pairwise GSLD, λ can be treated as either a continuous variable or a discrete variable.

Continuous λ

When λ is treated as a continuous variable, pairwise GSLD samples from the joint distribution of (λ, ${\{x_i\}}_{i=0}^1$, X):

$$P(\lambda ,x_0,x_1,X)=\frac{exp(-\beta \left[(1-\lambda )V_0(x_0,X)+\lambda (V_1(x_1,X)+G_1^b)+V_{\text{env}}(X)\right])}{Z},$$ (5)

where Z is the partition function of the generalized ensemble and $G_1^b$ is a biasing potential. $G_1^b$ is determined automatically in the current simulations using a Wang-Landau like algorithm²⁷ which is described in Appendix A. The Gibbs sampler for sampling from the above joint distribution is as follows:

• Step 0: initialize the starting state (λ⁰, ${\{x_i^0\}}_{i=0}^1$, X⁰).

  Step t: sample from the conditional distributions:

  • Updating ( ${\{x_i\}}_{i=0}^1$, X): given the state (λ^t−1, ${\{x_i^{t-1}\}}_{i=0}^1$, X^t−1) from step t − 1, sample ( ${\{x_i^t\}}_{i=0}^1$, X^t) from the conditional distribution: $P({\{x_i^t\}}_{i=0}^1,X^t\mid {\lambda }^{t-1})\propto exp(-\beta \left[(1-{\lambda }^{t-1})V_0(x_0^t,X^t)+{\lambda }^{t-1}\left(V_1(x_1^t,X^t)+G_1^b\right)+V_{\text{env}}(X^t)\right])$, which is the canonical ensemble distribution at the inverse temperature β. A sample can be drawn from this distribution using molecular dynamics simulation.

  • Updating λ: given the atomic coordinates ( ${\{x_i^t\}}_{i=0}^1$, X^t) sampled from the above update step, sample λ^t directly from the conditional distribution $P({\lambda }^t\mid {\{x_i^t\}}_{i=0}^1,X^t)$ using numerical pseudo-random number generator. The conditional distribution $P({\lambda }^t\mid {\{x_i^t\}}_{i=0}^1,X^t)$ is:

    $$\begin{gathered} P({\lambda }^t\mid {\{x_i^t\}}_{i=0}^1,X^t)=\frac{exp(-\beta \left[(1-{\lambda }^t)V_0(x_0^t,X^t)+{\lambda }^t(V_1(x_1^t,X^t)+G_1^b)+V_{\text{env}}(X^t)\right])}{{\int }_0^{1}exp(-\beta \left[(1-{\lambda }^t)V_0(x_0^t,X^t)+{\lambda }^t(V_1(x_1^t,X^t)+G_1^b)+V_{\text{env}}(X^t)\right])d\lambda } \\ =\frac{\beta ·(\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b)exp(-{\lambda }^t·\beta ·[\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b])}{1-exp(-\beta ·[\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b])}(0\le {\lambda }^t\le 1), \end{gathered}$$ (6)
    where $\mathrm{\Delta }{V}_{0\to 1}^t=V_1(x_1^t,X^t)-V_0(x_0^t,X^t)$. This is an exponential distribution of λ^t restricted on the interval of [0, 1]. Therefore, sampling λ^t directly from this distribution can be done using the inverse transformation method:

    $${\lambda }^t=-\frac{1}{\beta ·(\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b)}ln\left[1-[1-e^{\beta ·(\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b)}]·u\right]$$ (7)

    where u is a random sample from the uniform distribution on [0, 1]. The resulting sample (λ^t, ${\{x_i^t\}}_{i=0}^1$, X^t) is the state for step t.

Discrete λ

When λ is a discrete variable specified by the set {l₁, l₂, … l_M}, GSLD samples from the joint distribution

$$P(\lambda =l_j,x_0,x_1,X)\propto exp(-\beta \left[V_0(x_0,X,1-l_j)+V_1(x_1,X,l_j)+G_j^b+V_{\text{env}}(X)\right]),$$ (8)

where $G_j^b$ is the biasing potential added to the state corresponding to λ = l_j. Sampling from this distribution is done in the same way as the case where λ is continuous except that the conditional distribution $P({\lambda }^t\mid {\{x_i^t\}}_{i=0}^1,X^t)$becomes a multinomial distribution:

$$P({\lambda }^t=l_j\mid {\{x_i^t\}}_{i=0}^1,X^t)=\frac{exp(-\beta \left[V_0(x_0^t,X^t,1-l_j)+V_1(x_1^t,X^t,l_j)+G_j^b\right])}{{\sum }_{k=1}^{M}exp(-\beta \left[V_0(x_0^t,X^t,1-l_k)+V_1(x_1^t,X^t,l_k)+G_k^b\right])}$$ (9)

from which samples can also be drawn directly using numerical methods. The biasing potentials $G_j^b$ are determined similarly as the case when λ is continuous. We note that equation 9 is similar to the distribution calculated using the infinite swap limit in replica exchange methods.^28–31

The advantage of using λ as a discrete variable is that the pairwise GSLD still works when the potential energy V_i(x_i, X, λ) is λ dependent, such as when a soft-core Lennard-Jones potential³² is employed to facilitate sampling. When λ is continuous, using λ dependent V_i(x_i, X, λ) will make the normalization constant of the conditional distribution $P(\lambda \mid {\{x_i\}}_{i=0}^1,X)$ not analytically integrable and prevent direct sampling from the conditional distribution $P(\lambda \mid {\{x_i\}}_{i=0}^1,X)$. However, as shown below, the advantage of using λ as a continuous variable is that the GSLD can be generalized for multiple ligands.

2.1.3 Generalizing GSLD for Multiple Ligands

Like λ-dynamics, GSLD can be generalized to calculate the free energies for multiple ligands in one simulation. Assuming there are n ligands, the fraction of the ith ligand in the hybrid state is represented by λ_i, for i = 1, 2, …, n. The hybrid state is specified by the value of (λ₁, λ₂, …, λ_n) which satisfies the conditions ${\sum }_{i=1}^n{\lambda }_i=1$ and 0 ≤ λ_i ≤ 1, i = 1, 2, …, n. The hybrid state’s potential energy is defined as: $V({\{{\lambda }_i\}}_{i=1}^n,{\{x_i\}}_{i=1}^n,X)={\sum }_{i=1}^n{\lambda }_i(V_i(x_i,X)+G_i^b)+V_{\text{env}}(X)$, where x_i and X are atomic coordinates associated with the ith ligand and environment, respectively; $G_i^b$ is the biasing potential added for the ith ligand and can be determined similarly as in the pairwise GSLD. Sampling from the generalized ensemble distribution: $P({\{{\lambda }_i\}}_{i=1}^n,{\{x_i\}}_{i=1}^n,X)\propto exp(-\beta ·V({\{{\lambda }_i\}}_{i=1}^n,{\{x_i\}}_{i=1}^n,X))$ can be done using the following Gibbs sampler procedure:

• Step 0: initialize the starting state ( ${\{{\lambda }_i^0\}}_{i=1}^n,{\{x_i^0\}}_{i=1}^n$, X⁰).

• Step t: sample from the conditional distributions.

  • Updating ( ${\{x_i\}}_{i=1}^n$, X): given the state ( ${\{{\lambda }_i^{t-1}\}}_{i=1}^n,{\{x_i^{t-1}\}}_{i=1}^n$, X^t−1) from step t − 1, sample ( ${\{x_i^t\}}_{i=1}^n$, X^t) from the conditional distribution $P({\{x_i^t\}}_{i=1}^n,X^t\mid {\{{\lambda }_i^{t-1}\}}_{i=1}^n)$ using molecular dynamics simulation.

  • Updating ${\{{\lambda }_i\}}_{i=1}^n$: given the sample ( ${\{x_i^t\}}_{i=1}^n$, X^t) from the above update step, the conditional distribution of ${\{{\lambda }_i^t\}}_{i=1}^n$ in the set $S=\{({\lambda }_1,\dots ,{\lambda }_n)\mid {\sum }_{i=1}^n{\lambda }_i=1\text{and}{\lambda }_i\ge 0,i=1,\dots n\}$ is given by

    $$P({\{{\lambda }_i^t\}}_{i=1}^n\mid {\{x_i^t\}}_{i=1}^n,X^t)=\frac{exp(-\beta \left[{\sum }_{i=1}^n{\lambda }_i^t[V_i(x_i^t,X^t)+G_1^b]+V_{\text{env}}(X^t)\right])}{Z}.$$ (10)
    where

    $$\begin{gathered} Z={\int }_{S}exp(-\beta \left[\sum _{i=1}^n{\lambda }_i^t[V_i(x_i^t,X^t)+G_i^b]+V_{\text{env}}(X^{(t)})\right])d{m}_S(\lambda ) \\ =e^{-\beta V_{\text{env}}(X^t)}\sum _{i=1}^n\frac{e^{-\beta \left[V_i(x_i^t,X^t)+G_i^b\right]}}{{\beta }^{n-1}{\prod }_{j\ne i}(\left[V_j(x_j^t,X^t)+G_j^b\right]-\left[V_i(x_i^t,X^t)+G_i^b\right])}, \end{gathered}$$ (11)
    and dm_S(λ) is the infinitesimal volume element of the simplex S. Because ${\sum }_{i=1}^n{\lambda }_i^t=1$, the conditional distribution $P({\{{\lambda }_i^t\}}_{i=1}^n\mid {\{x_i^t\}}_{i=1}^n,X^t)$ has only n − 1 degrees of freedom. Sampling from this conditional distribution is equivalent to sampling from the n − 1 dimensional distribution:

    $$P({\{{\lambda }_i^t\}}_{i=1}^{n-1}\mid {\{x_i^t\}}_{i=1}^n,X^t)\propto exp(-\beta \left[\sum _{i=1}^{n-1}{\lambda }_i[V_i(x_i^t,X^t)+G_i^b-V_n(x_n^t,X^t)-G_n^b]\right]),$$ (12)

    where $0\le {\sum }_{i=1}^{n-1}{\lambda }_i^t\le 1$, and ${\lambda }_i^t\ge 0$. The environment atom energy term, V_env(X^t), does not appear in equation (12) because it is part of both the numerator and denominator of equation (10) and can be canceled out as a constant when ( ${\{x_i^t\}}_{i=1}^n$, X^t) is fixed. Sampling from this n − 1 dimensional distribution $P({\{{\lambda }_i^t\}}_{i=1}^{n-1}\mid {\{x_i^t\}}_{i=1}^n,X^t)$ is done using the rejection method. In the rejection method, each ${\{{\lambda }_i^t\}}_{i=1}^{n-1}$ is sampled independently from the distribution: $P({\lambda }_i^t)\propto exp(-\beta {\lambda }_i\left[V_i(x_i^t,X^t)+G_i^b-V_n(x_n^t,X^t)-G_n^b\right])$, where $0\le {\lambda }_i^t\le 1$. If the sample ${\{{\lambda }_i^t\}}_{i=1}^{n-1}$ satisfies the condition $0\le {\sum }_{i=1}^{n-1}{\lambda }_i^t\le 1$, it is accepted, otherwise the sample ${\{{\lambda }_i^t\}}_{i=1}^{n-1}$ is rejected. This procedure is repeated until a sample ${\{{\lambda }_i^t\}}_{i=1}^{n-1}$ is accepted. Set ${\lambda }_n^t=1-{\sum }_{j=1}^{n-1}{\lambda }_j^t$ and the resulting sample ( ${\{{\lambda }_i^t\}}_{i=1}^n,{\{x_i^t\}}_{i=1}^n$, X^t) is the state for step t.

2.2 Rao-Blackwell Estimator (RBE)

Although the empirical estimator used in λ-dynamics can also be utilized in GSLD to estimate the free energy, it is not an optimal estimator and may contain a system dependent bias. RBE is introduced here to eliminate these potential issues. RBE is the estimator derived by applying the Rao-Blackwellization transformation to the empirical estimator. Rao-Blackwellization is a statistical method, inspired by the Rao-Blackwell theorem,^33,34 to transform a crude estimator into a better estimator that has smaller mean squared error for estimating the quantity of interest.³⁵

For pairwise GSLD with continuous λ, the quantity of interest is the free energy ΔG = –β⁻¹ ln [P(λ = 1)/P(λ = 0)]. To estimate ΔG, the empirical estimator approximates P(λ = 1) and P(λ = 0) directly by calculating the fraction of λs which are close to 1 and 0, respectively, based on the λ trajectory. In contrast, the RBE ignores the λ trajectory and only uses the atomic coordinate trajectory. It is based on the fact that P(λ = 1) and P(λ = 0) are equal to the expectation of the conditional probability of λ with respect to the atomic coordinates, i.e, $P(\lambda =1)={\mathbb{E}}_{\{{\{x_i\}}_{i=0}^1,X\}}\left[P(\lambda =1)\mid {\{x_i\}}_{i=0}^1,X\right]$ and $P(\lambda =0)={\mathbb{E}}_{\{{\{x_i\}}_{i=0}^1,X\}}[P(\lambda =0)\mid {\{x_i\}}_{i=0}^1,X]$. Therefore, RBE uses the following formula to estimate the free energy ΔG:

$$\begin{gathered} \mathrm{\Delta }{G}_{\text{RBE}}=-{\beta }^{-1}ln\frac{P(\lambda =1)}{P(\lambda =0)} \\ =-{\beta }^{-1}ln\frac{{\mathbb{E}}_{\{{\{x_i\}}_{i=0}^1,X\}}[P(\lambda =1\mid {\{x_i\}}_{i=0}^1,X)]}{{\mathbb{E}}_{\{{\{x_i\}}_{i=0}^1,X\}}[P(\lambda =0\mid {\{x_i\}}_{i=0}^1,X)]} \\ =-{\beta }^{-1}ln\frac{1/N·{\sum }_{t=0}^{N}P(\lambda =1\mid {\{x_i^t\}}_{i=0}^1,X^t)}{1/N·{\sum }_{t=0}^{N}P(\lambda =0\mid {\{x_i^t\}}_{i=0}^1,X^t)} \end{gathered}$$ (13)

where

$$\begin{gathered} P(\lambda =1\mid {\{x_i^t\}}_{i=0}^1,X^t)=\frac{\beta ·(\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b)·exp(-\beta ·[\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b])}{1-exp(-\beta ·[\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b])} \\ P(\lambda =0\mid {\{x_i^t\}}_{i=0}^1,X^t)=\frac{\beta ·(\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b)}{1-exp(-\beta ·[\mathrm{\Delta }{V}_{0\to 1}^t+G_1^b])}, \end{gathered}$$ (14)

and N is the number of samples.

For the generalized GSLD with multiple ligands, the RBE can be derived similarly. To estimate the free energy of the ith ligand given by G(λ_i = 1, λ_j≠i = 0) = –β⁻¹ ln P(λ_i = 1, λ_j≠i = 0), the RBE uses the following formula:

$$\begin{gathered} G_{\text{RBE}}({\lambda }_i=1,{\lambda }_{j\ne i}=0)=-{\beta }^{-1}lnP({\lambda }_i=1,{\lambda }_{j\ne i}=0) \\ =-{\beta }^{-1}ln{\mathbb{E}}_{\{{\{x_k\}}_{k=1}^n,X\}}\left[P({\lambda }_i=1,{\lambda }_{j\ne i}=0\mid \{{\{x_k\}}_{k=1}^n,X\})\right] \\ =-{\beta }^{-1}ln\left[1/N·\sum _{t=0}^{N}P({\lambda }_i=1,{\lambda }_{j\ne i}=0\mid \{{\{x_k\}}_{k=1}^n,X\})\right] \\ =-{\beta }^{-1}ln\left[1/N·\sum _{t=0}^N\frac{exp(-\beta [V_i(x_i^t,X^t)+G_i^b])}{Z}\right], \end{gathered}$$ (15)

where Z is given in equation 11 in section 2.1.3.

As shown in the above formulas, the RBE estimator ΔG_RBE does not depend on the empirical cutoff value of λ_cutoff. Based on the Rao-Blackwell theorem, ΔG_RBE is an unbiased estimator. In addition, if the samples from GSLD are independent, the mean squared error of RBE is guaranteed to be smaller than or equal to that of the empirical estimator. Although the samples from GSLD are usually not truly independent, the advantage of RBE can often be justified empirically.³⁶

2.3 Derivation of the MBAR/UWHAM equations using RBE

Although RBE is originally introduced to estimate free energies based on sampling from GSLD, RBE can also be used when multiple equilibrium states are sampled independently. When RBE is applied to this case, it generates the MBAR/UWHAM equations,^21–23 which are widely used in current alchemical free energy methods.

Let us assume there are M equilibrium states with potential energy function of V_i, i = 1, 2, …, M. Each equilibrium state is sampled independently. The conformations sampled from state i are represented as $x_i^k$, k = 1, 2, …, n_i, where n_i is the number of conformations from state i. The total number of conformations is $N={\sum }_{j=1}^M{n}_j$. The free energy of state i is represented as $G_i^{\ast }$. We use λ ∈ {1, 2, …, M} as an index variable to represent the M equilibrium states, with λ = i corresponding to state i. To calculate the free energies for all the equilibrium states, all the conformations { $x_i^k$, i = 1, 2, …, M, k = 1, 2, …, n_i} are pooled together and viewed as samples from the generalized ensemble $P(\lambda =i,x)\propto e^{-\beta [V_i(x)+G_i^b]}$, where $G_i^b$ is the biasing energy added to state i to adjust the relative weight of state i to be proportional to n_i, i.e, $G_i^b$ needs to satisfy the condition:

$$G_i=G_i^{\ast }+G_i^b=-{\beta }^{-1}ln\frac{n_i}{N},$$ (16)

where G_i is the free energy of state i with the biasing potential of $G_i^b$ and $G_i^{\ast }$ is the unbiased free energy of state i. We note that the biasing potentials $G_i^b$ in equation 16 are unknown variables. They are introduced to make the equation 16 valid, which is the requirement for applying the RBE. These unknown biasing potentials $G_i^b$ can be calculated after the values of $G_i^{\ast }$ are solved. The RBE for this generalized ensemble is:

$$\begin{gathered} G_i=-{\beta }^{-1}\text{ln}P(\lambda =i) \\ =-{\beta }^{-1}\text{ln}\frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{n_i}P(\lambda =i\mid x_j^k) \\ =-{\beta }^{-1}\text{ln}\frac{1}{N}\sum _{j=1}^M\sum _{k=1}^{n_j}\frac{e^{-\beta \left[V_i(x_j^k)+G_i^b\right]}}{{\sum }_{l=1}^M{e}^{-\beta \left[V_l(x_j^k)+G_l^b\right]}} \end{gathered}$$ (17)

Combining equation 16 with equation 17, we have:

$$G_i^{\ast }=-{\beta }^{-1}ln\sum _{j=1}^M\sum _{k=1}^{n_j}\frac{e^{-\beta \left[V_i(x_j^k)\right]}}{{\sum }_{l=1}^M{n}_l·e^{-\beta \left[V_l(x_j^k)-G_l^{\ast }\right]}}$$ (18)

which is the same as the MBAR/UWHAM equations.^21–23 Previously, the MBAR/UWHAM equations were derived as either a result of the maximum likelihood principle or an unbinned extension of the weighted histogram analysis method (WHAM).^21–23 Here we have shown that the MBAR/UWHAM equations can also be derived using RBE.

3 Model Systems and Computational Details

To illustrate how GSLD works and the advantage of RBE over the empirical estimator typically used in λ-dynamics, we applied GSLD and RBE to three test cases: (a) calculation of the free energy difference between two states of a harmonic oscillator system, (b) calculation of the relative hydration free energies of three benzene derivatives, and (c) calculation of the binding free energy difference between benzene and p-xylene bound to the L99A mutant of the protein T4 lysozyme.^37,38 The simulations in these calculations were run using CHARMM³⁹ compiled with OpenMM.⁴⁰ Each calculation was repeated 10 times. Error bars were calculated as the standard variation of the results from these 10 independent repeats.

3.1 Harmonic System

The harmonic system consists of a one dimensional particle that switches between two states: state 0 and state 1. Each state has a harmonic potential energy. The purpose is to calculate the free energy difference of the particle when it changes from state 0 to state 1, i.e, ΔG = G₁ – G₀. Specifically, state 0 has a potential energy given by $\frac{1}{2}{k}_0{(x-x_0^e)}^2$, and state 1 has a potential energy given by $\frac{1}{2}{k}_1{(x-x_1^e)}^2$. In order to prevent the particle from moving too far from the equilibrium position, a restraining potential is added for each state. This restraining potential is not scaled by λ. The resulting hybrid potential energy is:

$$V(\lambda ,x_0,x_1)=(1-\lambda )·\frac{1}{2}{k}_0{(x_0-x_0^e)}^2+\lambda ·\frac{1}{2}{k}_1{(x_1-x_1^e)}^2+\frac{1}{2}{k}_{\text{env}}{(\mid x_0\mid -x_{\text{env}}^e)}^2𝟙\{\mid x_0\mid \ge x_{\text{env}}^e\}+\frac{1}{2}{k}_{\text{env}}{(\mid x_1\mid -x_{\text{env}}^e)}^2𝟙\{\mid x_1\mid \ge x_{\text{env}}^e\},$$

where 𝟙;{condition} is equal to 1 if the condition is true, otherwise it is equal to 0. GSLD is used to sample from the joint distribution of $(\lambda ,{\{x_i\}}_{i=0}^1):P(\lambda ,{\{x_i\}}_{i=0}^1)\propto exp(-\beta ·V(\lambda ,{\{x_i\}}_{i=0}^1))$. Given the value of λ, sampling the coordinates ( ${\{x_i\}}_{i=0}^1$) is accomplished by running Langevin dynamics for 1 ps with a step size of 1 fs, temperature of 300 K, and friction coefficient of 10 ps⁻¹. The total simulation time is 10 ns. The parameters used for $x_0^e,x_1^e,x_{\text{env}}^e$and k_env are −2.0 Å, 2.0 Å, 4.0 Å, and 2.5 kcal/mol · Å⁻², respectively. Two variations of the model system that correspond to setting different values for k₀ and k₁ are used: a symmetrical system with k₀ = k₁ = 0.75 kcal/mol·Å⁻², and an asymmetrical system with k₀ = 0.75 kcal/mol · Å⁻² and k₁ = 0.075 kcal/mol · Å⁻².

3.2 Relative Hydration Free Energies for Three Benzene Derivatives

Relative hydration free energies for three benzene derivatives: benzene, phenol, and benzaldehyde were calculated from the difference between alchemical free energy changes computed in vacuum and in water. The topology and parameter files for the hybrid ligand were generated using MATCH⁴¹ and in-house developed scripts based on the CHARMM General Force Field (CGenFF).⁴² The simulation in water was done in a water box consisting of 800 TIP3P⁴³ water molecules with cubic periodic boundary conditions. The water box had a size of 30.0 Å × 30.0 Å × 30.0 Å. A nonbonded cutoff of 14 Å was used, and the van der Waals switching function and electrostatic force switching function⁴⁴ were used between 12 Å and 14 Å. Sampling from the conditional distribution P(x, X|λ) was accomplished by running Langevin dynamics at 298.15 K for 0.2 ps. The time step size was 2 fs and the friction coefficient was 10 ps⁻¹. The length of all bonds involving hydrogen atoms was fixed during the simulation using the SHAKE algorithm.⁴⁵ The three relative hydration free energies were first calculated by three independent pairwise GSLDs. Then they were calculated simultaneously using the generalized GSLD for multiple ligands. For comparison, the three relative hydration free energies were also calculated using the FEP/MBAR method, in which 11 states corresponding to λ = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1 were used.

3.3 Relative Binding Free Energy between Benzene and p-Xylene with T4 Lysozyme

The L99A mutant of T4 lysozyme has been a model protein system for testing free energy calculation methods.^46–48 It has experimental binding free energy data for a series of benzene derivatives including benzene and p-xylene.^37,38 The relative binding free energy between benzene and p-xylene was calculated using the difference between the alchemical free energy change in water and in the protein environment. The alchemical free energy change in water was calculated using pairwise GSLD with continuous λ. Calculating the alchemical free energy in the protein environment is challenging, even though the binding site of T4 lysozyme is a relatively simple non-polar pocket and the alchemical change from benzene to p-xylene is small. This challenge arises from the fact that T4 lysozyme has a conformational change for the side-chain dihedral angle χ (N-CA-CB-CG1) of residue Val111, which accompanies the alchemical transformation from benzene to p-xylene.⁴⁶ When T4 lysozyme binds with benzene (PDB ID: 181L), the dihedral angle stays in the trans conformation (χ ≈ −180°). When it binds with p-xylene (PDB ID: 187L), the dihedral angle changes into the gauche conformation (χ ≈ −60°). Failing to sample these two relevant conformations in a free energy calculation would cause a quasi-nonergodicity problem, i.e, the calculated free energy will depend on which conformation is used as the starting conformation.^46,48 To address the problem, several methods have been developed. These methods include enhanced sampling methods such as the 2-dimensional replica exchange method (REM)⁴⁷ and the free energy perturbation/replica exchange with solute tempering (FEP/REST) method,⁴⁸ and the potential of mean force (PMF) method, which was first introduced by Tobias and Brooks for addressing a similar problem in 1989⁴⁹ and rediscovered as the “confine-and-release” method by Mobley et al. in 2007.⁴⁶ Here we combined the PMF method with GSLD to calculate the alchemical free energy changes between benzene and p-xylene in the protein environment.

To make our computational protocol clear, we reformulated the PMF method^46,49 using conditional probability as shown in Appendix B. The free energy change ΔG(χ^*) was calculated using pairwise GSLD with a harmonic restraint potential on χ to keep it near χ^* during the pairwise GSLD simulation. The force constant of the harmonic restraint potential was 1195.3 kcal/mol · radius⁻². In our calculations, we chose χ^* to be −180° and −60°, although the final calculated result ΔG did not depend on the choice of χ^*. In the pairwise GSLD, λ was chosen to be a discrete variable specified by the set {l₁, l₂, …, l₁₆}. λ = l₁ corresponds to the physical state that the ligand is benzene and λ = l₁₆ corresponds to the physical state that the ligand is p-xylene. When λ was changed from l₁ to l₁₆, the ligand was alchemically transformed from benzene into p-xylene. During the alchemical transformation, the partial charges on benzene atoms were turned off first. Then the benzene atoms were transformed into p-xylene atoms before the partial charges on p-xylene atoms were turned on. A soft-core Lennard-Jones potential was used during the transformation.⁵⁰ The formula used for both electrostatic potential and the soft-core Lennard-Jones potential is shown in Table S1. The potential energy scaling factors used for each state λ = l_i are also shown in Table S1. The free energy –β⁻¹lnP(χ^*|λ = l₁) and the free energy –β⁻¹lnP(χ^*|λ = l₁₆) were computed by calculating the potential of mean force (PMF) with respect to χ when T4 lysozyme binds with benzene (λ = l₁) and with p-xylene (λ = l₁₆), respectively. The simulations was run inside a TIP3P water box with a size of 79.0Å × 56.4Å × 55.4Å and rectangular periodic boundary conditions were used. The water box had 7112 water molecules in total. The CHARMM36 force field⁵¹ was used for T4 lysozyme and the CHARMM General Force Field (CGenFF)⁴² was used for the ligands. The nonbonded interaction options were the same as that used in the relative hydration free energy calculations.

4 Results

4.1 The Harmonic System

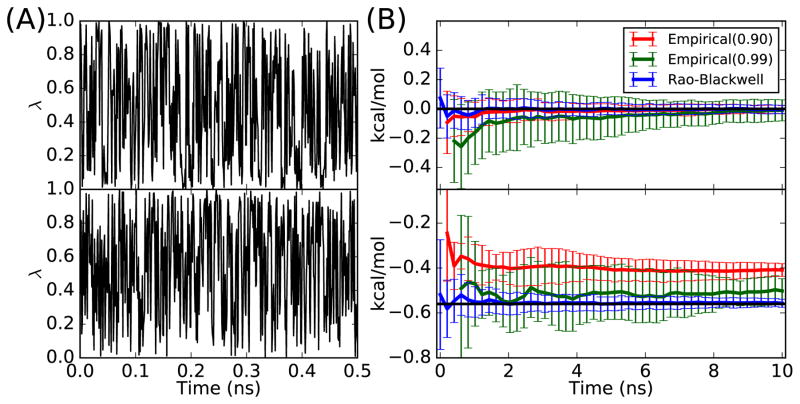
As shown in Figure 2(A), GSLD is able to sample the continuous λ well for both symmetrical and asymmetrical systems. Figure 2(B) shows the estimated free energy changes ΔG using the Rao-Blackwell estimator and two empirical estimators with cutoff values of 0.9 and 0.99. For the symmetrical system, the true value for the free energy changes is equal to 0 kcal/mol because of the symmetry. The RBE and the empirical estimator with cutoff of 0.9 converge to 0 kcal/mol within 2 ns, whereas the empirical estimator with cutoff of 0.99 needs 10 ns of simulation to converge to 0 kcal/mol. Moreover the RBE has the smallest variance among the three estimators. For the asymmetrical system, the empirical estimator with a cutoff of 0.9 converges to −0.41 ± 0.03 kcal/mol and the empirical estimator with a cutoff of 0.99 converges to −0.50 ± 0.06 kcal/mol, whereas the result from numerical integration is −0.56 kcal/mol. This shows that the results of empirical estimators can be biased and the bias depends on the value of the cutoff. Increasing the cutoff value decreases the estimation bias, but it increases the estimation variance because a higher cutoff decreases the number of valid samples used by the empirical estimator. In contrast, the result of RBE converges to −0.56 ± 0.02 kcal/mol, which is closest to the true value and also has the smallest variance. The detailed numerical results can be found in the Table S2. Overall, the results suggest that, for this harmonic system, the GSLD is able to extensively sample the alchemical states and the RBE is better than the empirical estimator in terms of both bias and variance.

Figure 2.

(A) λ trajectories for the symmetrical harmonic system (top) and the asymmetrical harmonic system (bottom); (B) Free energy estimations for the symmetrical system (top) and the asymmetrical system (bottom) using the empirical estimators with a cutoff of 0.9 and 0.99 and the Rao-Blackwell estimator. The horizontal black line is the calculated free energy change using numerical integration.

4.2 Relative Hydration Free Energies for Three Benzene Derivatives

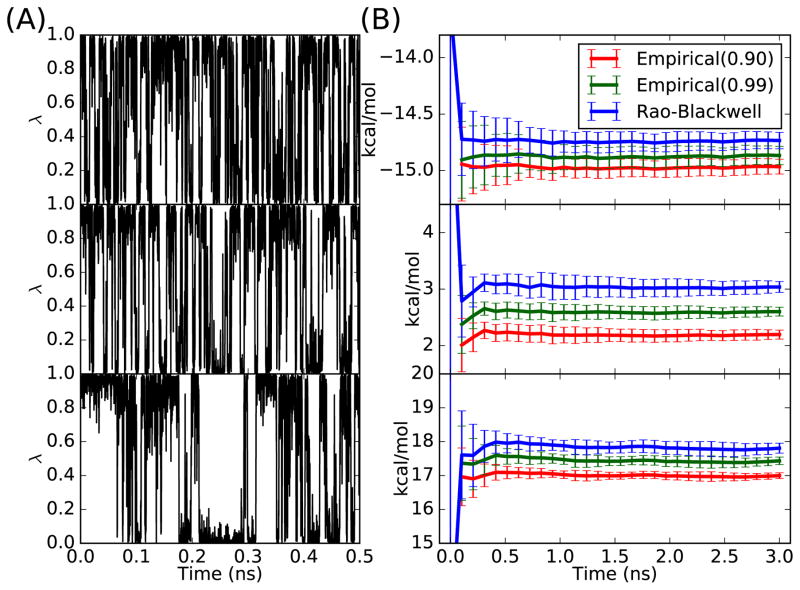
Results of pairwise GSLD simulations in vacuum and in water are shown in Figure S1 and Figure 3, respectively. The pairwise GSLD is able to sample the alchemical states very well for both the simulations in vacuum and the simulations in water. For the simulation in vacuum, the RBE outperforms empirical estimators in terms of both bias and variance, as in the harmonic system. For the simulation in water, the RBE has a similar variance to that of the empirical estimators, because samples from the simulation in water are more correlated than those from the simulations in vacuum. Nevertheless, the RBE is still better than the empirical estimators in terms of the bias. As shown in Figure 3(B), the empirical estimator depends on the cutoff. As the cutoff increases from 0.9 to 0.99, the empirical estimator results move towards to the RBE results. As an example, for the alchemical change from benzene to benzaldehyde, when the cutoff increases from 0.9 to 0.99, the empirical estimator result changes from 2.20 ± 0.08 kcal/mol to 2.60 ± .08 kcal/mol. The RBE result is 3.04 ± 0.09 kcal/mol, which is indistinguishable from the FEP/MBAR result 3.01 ± 0.02 kcal/mol. The detailed numerical values from pairwise GSLD and FEP/MBAR can be found in the Table S3 and S4.

Figure 3.

(A) λ trajectories from simulations in water using GSLD for alchemical changes benzene to phenol (top), benzene to benzaldehyde (middle), and phenol to benzaldehyde (bottom). (B) Estimated alchemical free energy changes in water using empirical estimators with different cutoff values and the Rao-Blackwell estimator for alchemical changes benzene to phenol (top), benzene to benzaldehyde (middle), and phenol to benzaldehyde (bottom).

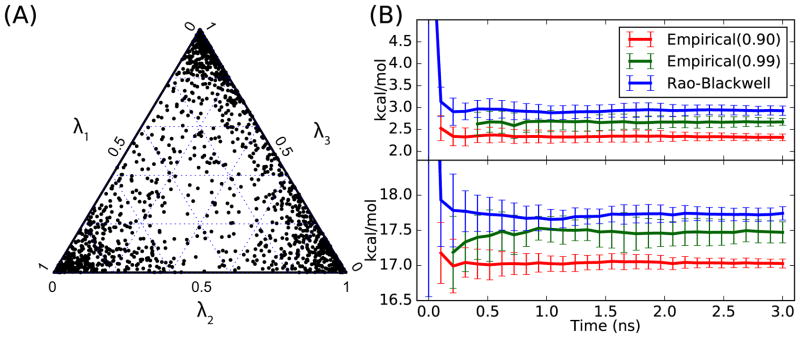
The simulation results in vacuum and in water from generalized GSLD for multiple ligands are shown in Figure S2 and Figure 4, respectively. The ternary plots⁵² of (λ₁, λ₂, λ₃) trajectories show that the generalized GSLD is able to explore the hybrid ligand configuration space of (λ₁, λ₂, λ₃): the unit simplex { $({\lambda }_1,{\lambda }_2,{\lambda }_3)\mid {\sum }_{i=1}^3{\lambda }_i=1$, 0 ≤ λ_i ≤ 1 for i = 1, 2, 3}, in both vacuum and water. In vacuum, the configuration space (λ₁, λ₂, λ₃) is sampled rather uniformly, while in water, the configuration space is sampled mostly close to the physical states, i.e. the corners of the ternary plot in Figure 4. This difference is because the biasing potential energy used in this study is a linear biasing potential ${\lambda }_i{G}_i^b$. With the linear biasing potential, the biased free energy landscape over the configuration space (λ₁, λ₂, λ₃) in vacuum is almost flat. In water, the corresponding biased free energy landscape is not flat due to the polarization energy of the solvent interacting with reactant and product states, and the biased free energies of the physical states is lower than the intermediate non-physical states, which explains why the sampled (λ₁, λ₂, λ₃) are mostly around the physical states. Based on the trajectory from the generalized GSLD simulation, the calculated free energy using RBE and empirical estimators are shown in Figure S2 (B) and Figure 4(B). These results suggests again that, compared with the empirical estimators, the RBE is a better estimator as it has no bias and a smaller variance. The detailed numerical results from the generalized GSLD for multiple ligands is shown in the Table S5.

Figure 4.

(A) Ternary plot of (λ₁, λ₂, λ₃) sampled using GSLD for multiple ligands in water. (B) Estimated free energy changes in water for alchemical changes: benzene to benzaldehyde (top) and phenol to benzaldehyde (bottom) using empirical estimator with different cutoff values and RBE.

The calculated relative hydration free energies for the three benzene derivatives using pairwise GSLD, generalized GSLD for multiple ligands and FEP/MBAR methods are combined in Table 1. The results from all three methods agree well with each other. The total simulation time in water for calculating all three relative hydration free energies is 9 ns for pairwise GSLD, 3 ns for generalized GSLD for multiple ligands and 33 ns for FEP/MBAR methods, which suggests the efficacy of the generalized GSLD for multiple ligands.

Table 1.

Comparison of Relative Hydration Free Energies (ΔΔG in kcal/mol) for The Three Benzene Derivatives. The total simulation time in water for each method is shown in parenthesis.

substituents change	ΔΔGexp	Pairwise GSLD ΔΔG(9ns)	GSLD for Multiple Ligands ΔΔG(3ns)	FEP/MBAR ΔΔG(33ns)
Benzene → Phenol	−5.77	−4.46 ± 0.08	−4.53 ± 0.15	−4.46 ± 0.03
Benzene → Benzaldehyde	−3.18	−3.11 ± 0.11	−3.22 ± 0.11	−3.13 ± 0.03
Phenol → Benzaldehyde	2.59	1.39 ± 0.17	1.31 ± 0.10	1.34 ± 0.14

4.3 Relative Binding Free Energy of Benzene and p-Xylene with T4 Lysozyme

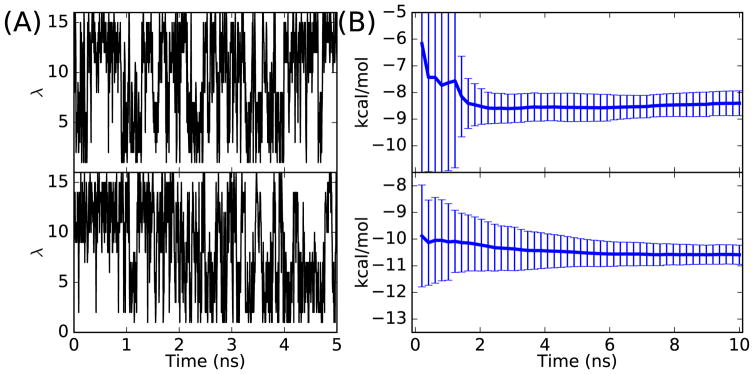
The λ trajectories from the simulation with T4 lysozyme using pairwise GSLD and the free energy estimations using RBE are shown in Figure 5. For both the case where χ is restricted to the trans conformation (χ^* = −180°) and the case where χ is restricted to the gauche (χ^* = −60°) conformation, the pairwise GSLD is able to sample the alchemical switching variable λ well and the RBE estimations converge in 10 ns of simulation. When χ is restricted to the trans conformation, the estimated free energy converges to −8.40 ± 0.46 kcal/mol. When χ is restricted in the gauche conformation, the estimated free energy converges to −10.60 ± 0.36 kcal/mol. These two free energy estimations are different by 2.20 kcal/mol because the dihedral angle χ is restricted to different conformations. Based on the PMF method, in order to get the free energy corresponding to the case where χ is not restricted, the restricting free energies (−β⁻¹ ln P(χ^*|λ = l₁) and –β⁻¹ ln P(χ^*|λ = l₁₆)) need to be considered and used to correct the free energy ΔG(χ^*) using equation 21 in Appendix B. These corrections are shown in Table 2. After the corrections, the estimated free energy ΔG is −9.27 ± 0.50 kcal/mol when χ^* = −180° and −9.01 ± 0.40 kcal/mol when χ^* = −60°. Therefore, after the corrections, the estimated free energy differences (ΔG) agree very well within statistical uncertainty. Based on the these corrected values, the relative binding free energies (ΔΔG) are 0.27 ± 0.56 kcal/mol and 0.43 ± 0.46 kcal/mol when χ^* = −180° and χ^* = −60°, respectively. These results are close to the relative binding free energy from experiment, which is 0.52 ± 0.22 kcal/mol.^37,38

Figure 5.

(A) λ trajectories for simulations with T4 lysozyme using pairwise GSLD for the χ^* = −180° (top) and χ^* = −60° (bottom); (B) Free energy estimation using RBE for χ^* = −180° (top) and χ^* = −60° (bottom).

Table 2.

Alchemical Free Energy Changes (kcal/mol) Between Benzene and p-Xylene Binding with T4 Lysozyme Calculated Using Pairwise GSLD with Corrections from PMFs.

χ*	ΔG(χ*)	–β−1lnP(χ*|λ = 0)	–β−1lnP(χ*|λ = 1)	ΔG	ΔΔG
trans (χ* = −180°)	−8.40 ± 0.46	−0.47 ± 0.01	0.4 ± 0.03	−9.27 ± 0.50	0.27 ± 0.56
gauche (χ* = −60°)	−10.60 ± 0.36	1.14 ± 0.03	−0.45 ± 0.01	−9.01 ± 0.40	0.43 ± 0.46

The alchemical free energy change ΔG in water is −9.44 ± 0.06 kcal/mol and the experimental relative binding free energy ΔΔG is 0.52 ± 0.22 kcal/mol.

5 Discussion and Conclusion

Although the GSLD and RBE are applied only for calculating relative hydration free energy and relative binding free energy in this study, they could also be used for other purposes. One of the applications would be for calculating the pK_a value of protein amino acids by combining with the constant pH molecular dynamics methods (CPHMD),^18,53,54 as several CPHMD methods are based on λ-dynamics. Furthermore, the GSLD framework presented here is not limited to alchemical free energy calculations. The λ variable could be replaced by the pH values, which would correspond to pH generalized ensemble simulations. In these cases, we can also derive the corresponding RBE similarly.

In this study, we have presented the formalism for the Gibbs sampler based λ-dynamics (GSLD) and the Rao-Blackwell estimator (RBE) for alchemical free energy calculations. These methods were successfully demonstrated for three test cases of increasing complexity. The GSLD, a generalized ensemble sampling method, works for the case where λ is a discrete variable and for the case where λ is considered to be continuous. When λ is continuous, the GSLD can be generalized to calculate free energies for multiple ligands simultaneously in one simulation. The RBE not only eliminates the bias problem of the empirical estimator used in the original λ-dynamics, but also has smaller estimation variance than the empirical estimator. Moreover, we have also shown that the RBE can be used to derive the MBAR/UWHAM equations, which provides new understanding for the MBAR/UWHAM method.^21–23

Appendix

A. A Wang-Landau like algorithm to automatically determine the biasing potential $G_1^b$ used in pairwise GSLD when λ is continuous

The purpose of the biasing potential $G_1^b$ used in the pairwise GSLD when λ is continuous is to make the biased free energy landscape over the λ space flat, i.e. to make the simulation spend about equal time at all λ values between 0 and 1. In current study, a linear biasing potential $\lambda G_1^b$ is utilized, because with the linear biasing potential the biased free energy landscape over λ space is quite flat, i.e. the energy barrier between the two physical states λ = 0 and λ = 1 is small enough that the λ is well sampled across the interval [0, 1]. If the linear biasing potential energy cannot make the biased free energy landscape over the λ space flat enough, a quadratic form of biasing potential can be utilized as in Hayes et al.’s flattening method.¹⁹ The biasing potential $G_1^b$ is determined automatically using the following Wang-Landau like algorithm:

• Set the initial biasing potential $G_1^b=0\text{kcal}/\text{mol}$, the decay parameter α such that 0 < α < 1 (α = 0.998 in this study), the biasing potential increment Δ in each step (Δ = 2.0 kcal/mol in this study) and the number of steps R (R = 3000 in this study). Initialize the starting state (λ⁰, ${\{x_i^0\}}_{i=0}^1$, X⁰).

• For t = 1 to R:

  Sample ( ${\{x_i^t\}}_{i=0}^1$, X^t) from the conditional distribution: $P({\{x_i^t\}}_{i=0}^1,X^t\mid {\lambda }^{t-1})$ by running molecular dynamics simulations and then sample λ^t from the conditional distribution $P({\lambda }^t\mid {\{x_i^t\}}_{i=0}^1,X^t)$. Set $G_1^b(t)=G_1^b(t-1)+({\lambda }^t-0.5)\ast \mathrm{\Delta }(t)$ and Δ(t) = α * Δ(t − 1).

• The final value of $G_1^b$ from the above step is fixed and used as the biasing potential in following simulations.

B. Reformulation of the PMF method using conditional probability

The PMF method requires prior knowledge of which slow degree of freedom is affecting the free energy calculation. In the context of T4 lysozyme, the slow degree of freedom is the side-chain dihedral angle N-CA-CB-CG1 (χ) of residue Val111. The joint distribution of (χ, λ) : P(χ, λ) is of most interest, as it encapsulates all the relevant information required to calculate the free energy ΔG = –β⁻¹ln(P(λ = l₁₆)/P(λ = l₁)). Based on the chain rule of conditional probability, we have the following equations:

$$\begin{gathered} P(\chi ={\chi }^{\ast },\lambda =l_{16})=P(\chi ={\chi }^{\ast }\mid \lambda =l_{16})P(\lambda =l_{16})=P(\lambda =l_{16}\mid \chi ={\chi }^{\ast })P(\chi ={\chi }^{\ast }) \\ P(\chi ={\chi }^{\ast },\lambda =l_1)=P(\chi ={\chi }^{\ast }\mid \lambda =l_1)P(\lambda =l_1)=P(\lambda =l_1\mid \chi ={\chi }^{\ast })P(\chi ={\chi }^{\ast }) \end{gathered}$$ (19)

Combining the above two equation gives us:

$$\frac{P(\lambda =l_{16})}{P(\lambda =l_1)}=\frac{P(\lambda =l_{16}\mid \chi ={\chi }^{\ast })}{P(\lambda =l_1\mid \chi ={\chi }^{\ast })}·\frac{P(\chi ={\chi }^{\ast }\mid \lambda =l_1)}{P(\chi ={\chi }^{\ast }\mid \lambda =l_{16})}.$$ (20)

Therefore, we can calculate the free energy ΔG as

$$\begin{gathered} \mathrm{\Delta }G=-{\beta }^{-1}\text{ln}\frac{P(\lambda =l_{16})}{P(\lambda =l_1)} \\ =-{\beta }^{-1}\text{ln}\frac{P(\lambda =l_{16}\mid \chi ={\chi }^{\ast })}{P(\lambda =l_1\mid \chi ={\chi }^{\ast })}-{\beta }^{-1}\text{ln}\frac{P(\chi ={\chi }^{\ast }\mid \lambda =l_1)}{P(\chi ={\chi }^{\ast }\mid \lambda =l_{16})} \\ =\mathrm{\Delta }G(\chi ={\chi }^{\ast })+[-{\beta }^{-1}\text{ln}P(\chi ={\chi }^{\ast }\mid \lambda =l_1)]-[-{\beta }^{-1}\text{ln}P(\chi ={\chi }^{\ast }\mid \lambda =l_{16})], \end{gathered}$$ (21)

where ΔG(χ = χ^*) is alchemical free energy change when χ is fixed at the value χ^*; –β⁻¹lnP(χ = χ^*|λ = l₁) is the free energy required to restrict the dihedral angle χ at the value χ^* when T4 lysozyme binds with benzene, i.e, λ = l₁; –β⁻¹lnP(χ = χ^*|λ = l₁₆) is the corresponding free energy required when T4 lysozyme binds with p-xylene, i.e, λ = l₁₆. The above equation holds regardless of the value of χ^*.