Fast and accurate quantum Monte Carlo for molecular crystals

Significance

Computational approaches based on the fundamental laws of quantum mechanics are now integral to almost all materials design initiatives in academia and industry. If computational materials science is genuinely going to deliver on its promises, then an electronic structure method with consistently high accuracy is urgently needed. We show that, thanks to recent algorithmic advances and the strategy developed in our manuscript, quantum Monte Carlo yields extremely accurate predictions for the lattice energies of materials at a surprisingly modest computational cost. It is thus no longer a technique that requires a world-leading computational facility to obtain meaningful results. While we focus on molecular crystals, the significance of our findings extends to all classes of materials.

Abstract

Computer simulation plays a central role in modern-day materials science. The utility of a given computational approach depends largely on the balance it provides between accuracy and computational cost. Molecular crystals are a class of materials of great technological importance which are challenging for even the most sophisticated ab initio electronic structure theories to accurately describe. This is partly because they are held together by a balance of weak intermolecular forces but also because the primitive cells of molecular crystals are often substantially larger than those of atomic solids. Here, we demonstrate that diffusion quantum Monte Carlo (DMC) delivers subchemical accuracy for a diverse set of molecular crystals at a surprisingly moderate computational cost. As such, we anticipate that DMC can play an important role in understanding and predicting the properties of a large number of molecular crystals, including those built from relatively large molecules which are far beyond reach of other high-accuracy methods.

Computer simulations, in particular those based on the fundamental laws of quantum mechanics, play a key role in modern materials science research. Such electronic structure approaches serve as an indispensable complement to experiment by helping us understand and predict the properties of materials as well as guiding the development of new ones. Density functional theory (DFT) is the leading electronic structure technique in materials science, thanks to its favorable balance between accuracy and computational cost as well as its efficient implementation in modern codes. Indeed, DFT has been described as one of the great success stories of modern science (1), with widespread use in materials science and cognate disciplines (2–4). However, DFT, as generally applied with standard exchange-correlation functionals, suffers from a number of well-known deficiencies (5–8). One notable shortcoming is in the description of weak interactions such as London dispersion forces. Although the last decade has seen impressive developments with the incorporation of dispersion forces in the DFT framework (9–12), and new density functionals with improved accuracy have been developed (13–15), such approaches are not systematically improvable, and their accuracy for condensed phases is open to question. For example, DFT cannot be relied upon to routinely deliver an accuracy below 4 kJ/mol for the lattice energy of molecular crystals. This is the accuracy (so-called chemical accuracy) that is often needed to discriminate between different polymorphs of a given material, and, in some pharmaceutical molecules, even more stringent accuracies (down to 1 kJ/mol) are needed (16, 17).

Traditionally, highly accurate computations of interaction energies have been based on quantum chemistry techniques, in particular, coupled cluster with single, double, and perturbative triple excitations [CCSD(T)]. However, CCSD(T) calculations on solids have been notoriously challenging. Great strides forward have recently been made, and CCSD(T) can now be used to study solids through calculations in periodic boundary conditions (18), or by using approaches based on embedding and fragment decomposition (19, 20). The benzene crystal, for example, was recently considered in a tour de force study using fragment decomposition (21). The recent introduction of local approaches (22) promises to extend the range of applicability of CCSD(T) methods. However, the cost of CCSD(T) calculations for large systems will remain high for the foreseeable future, and their large-scale application is additionally hindered by enormous memory requirements. The random phase approximation (RPA) is emerging as a promising approach for materials, in particular if singles corrections are introduced (23–25). Although it is less accurate than CCSD(T), it is considerably more affordable and currently offers a very good balance between accuracy and computational cost. Quantum Monte Carlo, in particular within the fixed node diffusion Monte Carlo (DMC) scheme (26), is an established method for reference quality calculations of molecular systems and condensed phases. Systematic studies in cases of noncovalent bonding have shown that DMC has an accuracy comparable to CCSD(T) (27). An advantage of DMC over traditional quantum chemical methods like CCSD(T) is that it is essentially unaffected by basis set issues, thanks to the deployment of an efficient ground state projection scheme and the use of B-splines. However, the enormous computational cost of this approach means that DMC studies generally require a world-leading computational facility, and, even then, it remains highly challenging to obtain demonstrably converged results. As a result, DMC studies are often restricted to one-off benchmark calculations of specific systems.

Building upon a recent algorithmic development (28) which significantly reduces the computational cost of DMC, we have developed a scheme (described in Materials and Methods) for obtaining converged DMC energies of molecular crystals in a fully periodic treatment, without the need for fragment decompositions. The approach is effective for both small and large molecules and yields lattice energies of periodic molecular crystals at a computational cost comparable to RPA but with the accuracy of CCSD(T). For example, a chemically accurate lattice energy of a benzene crystal can be computed in as few as ${10}^4$ central processing unit (CPU) hours. In addition, the scheme proposed comes with relatively low manpower costs and can be seen as a step toward the automated DMC treatment of molecular crystals. This opens up horizons for DMC as a tool for accurately and rapidly predicting the properties of molecular crystals, including those built from pharmaceutical molecules. More broadly, the insights obtained from this study should also prove beneficial to DMC studies of other crystalline materials and their surfaces.

Results

The main quantity to consider to assess the stability of a crystal is its lattice energy $E_{\text{latt}}$, which is the energy per molecule gained upon assuming the crystal form with respect to the gas state. It can be computed as

$$E_{\text{latt}}=E_{\text{crys}}-E_{\text{gas}},$$ [1]

with $E_{\text{crys}}$ as the energy per molecule in the crystal state and $E_{\text{gas}}$ as the energy of the isolated molecule. While the accurate computation of $E_{\text{gas}}$ is straightforward, $E_{\text{crys}}$ involves an ideally infinite system. Since any simulated system will be necessarily finite, the evaluation of $E_{\text{crys}}$ will be affected by finite size errors (FSE). The most common approach to tackle crystals is to exploit their periodicity and to simulate a cell within periodic boundary conditions. In DFT, the energy of the infinite system is recovered by simulating the primitive cell and by sampling the first Brillouin zone. In DMC, the wave function is sampled by considering a number of electron configurations, including configurations with local dipoles that, in a small simulation cell (such as the primitive cell), couple with the periodic images, yielding substantial FSE. However, established procedures developed for DMC to reduce or eliminate these errors are available, such as the model periodic Coulomb (MPC) interaction (29), the approach used in this study. MPC treats the explicit two-body interactions within the minimum-image convention in the simulation cell, while, outside the cell, the interaction is with a precalculated charge density normally obtained from a DFT calculation. In principle, MPC can miss some of the correlation energy. Thus, in DMC, it is good practice to simulate supercells of increasing size and to extrapolate the energy of the infinite system. On the other hand, molecular crystals have primitive cells that are already large (and related to the size of the molecule), meaning that calculations in the larger cells needed for the extrapolations can be computationally prohibitive. However, thanks to recent developments (28), it is now possible to simulate large supercells up to cases where FSE are negligible. This, in turn, allows us to establish that accurate results from DMC can, in practice, be obtained in small primitive cells if appropriate corrections for FSE are taken into account.

Typically, the computation of $E_{\text{latt}}$ is performed at zero temperature and considering only the electronic contribution, i.e., quantum nuclear effects are neglected (30). The lattice energy is not directly assessable experimentally, but it can be indirectly obtained from experimental measures of the sublimation enthalpy ${\mathrm{\Delta }}_{\text{sub}}H(T)$ at a given temperature $T$ by including a (theoretically evaluated) energy contribution ${\mathrm{\Delta }}_{\text{T\&QN}}(T)$ accounting for contributions from thermal and quantum nuclear effects,

$${\mathrm{\Delta }}_{\text{sub}}H(T)=-E_{\text{latt}}+{\mathrm{\Delta }}_{\text{T\& QN}}(T).$$ [2]

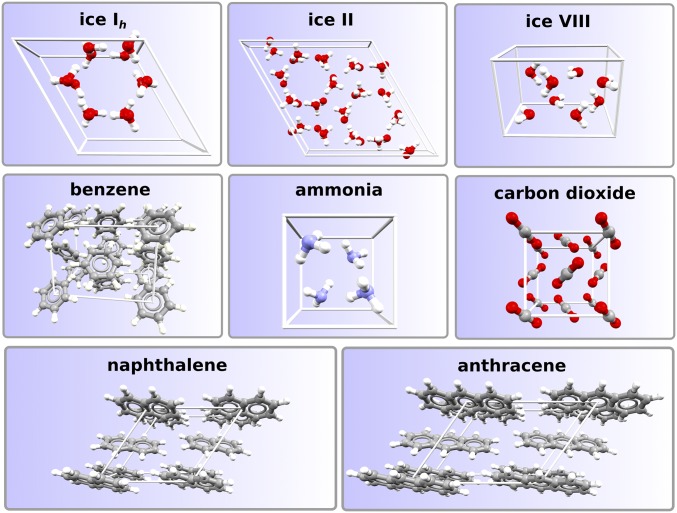
The evaluation of ${\mathrm{\Delta }}_{\text{T\&QN}}(T)$ can be challenging, especially for large molecules where anharmonic contributions are important (31). In SI Appendix, we provide details about the theoretical evaluations of ${\mathrm{\Delta }}_{\text{T\&QN}}(T)$ and the uncertainty associated with experimental evaluations of ${\mathrm{\Delta }}_{\text{sub}}H$. Since both ${\mathrm{\Delta }}_{\text{sub}}H(T)$ and ${\mathrm{\Delta }}_{\text{T\&QN}}(T)$ are affected by errors, accurate theoretical evaluations of $E_{\text{latt}}$ are of help for comparison. To assess the accuracy of a method, one needs to use a diverse test set of systems. In this study, we considered eight molecular crystals (Fig. 1): carbon dioxide (CO₂), ammonia (NH₃), benzene (C₆H₆), naphthalene (C₁₀H₈), and anthracene (C₁₄H₁₀) crystals from the C21 test set of Otero-de-la-Roza and Johnson (32), plus three polymorphs of ice: the hexagonal ice I_h, ice II, and a high-pressure phase ice VIII. This set of molecular crystals comprises a diversity in intermolecular interactions involving strong hydrogen bonds and London dispersion of saturated and unsaturated molecules. A range of interactions such as this is a tough test for any electronic structure method. It is a test that must be passed through if a method is to be truly predictive and applicable to complex molecular crystals, including those of industrial interest (33, 34). DMC values for $E_{\text{latt}}$ of the eight molecular crystals are summarized in Table 1. Two sets of DMC results are reported: DMC(lc) and DMC(sc). The former is obtained using large supercells (containing around a thousand valence electrons); the latter is obtained using smaller cells and relying on the FSE correction via the MPC interaction (see Materials and Methods and SI Appendix). We find that, in all cases, the DMC(sc) results are in excellent agreement with the DMC(lc) results, as a confirmation of the quality of the MPC approach for the correction of FSE. MPC was introduced two decades ago (29), but here, using the algorithm of ref. 28, we have been able to explicitly demonstrate how well MPC performs for complex systems such as molecular crystals. Table 1 also reports lattice energies derived from experiments. The experimental values are obviously not free from error and have an uncertainty coming from both the actual measure of ${\mathrm{\Delta }}_{\text{sub}}H$ and the computed term ${\mathrm{\Delta }}_{\text{T\&QN}}$ on the order of the chemical accuracy, $\sim 4$ kJ/mol. For naphthalene and anthracene, which have the largest values for $E_{\text{latt}}$, the experimental uncertainties are likely to be larger. See SI Appendix for a detailed discussion on the experimental values. Upon comparing DMC to experiment, we find that both DMC(lc) and DMC(sc) always fall within the accuracy of the experimental value. This is remarkable if we consider that this accuracy is achieved over a large range of lattice energies, $E_{\text{latt}}$ from 28 kJ/mol to more than 100 kJ/mol. DMC gets correct lattice energies for hydrogen-bonded, dispersion-bonded and mixed-bonded crystals. DMC also predicts the correct relative energies of the ice polymorphs, yielding slightly improved lattice energies over those reported in ref. 35.

Fig. 1.

Molecular crystals considered in this work with DMC. Only the primitive cell is shown in each case. The systems treated are of considerable size and contain up to 144 molecules (ice VIII) or 1,728 electrons (CO₂).

Table 1.

Lattice energy (kilojoules per mole) for the molecular crystals under consideration in this work, computed with DMC compared with values from experimental measures of sublimation enthalpy

Crystal	DMC(lc)*	DMC(sc)†	Experiment‡
Ice Ih	−59.3 $\pm$ 0.5	−59.2 $\pm$ 0.2	−58.8
Ice II	−59.1 $\pm$ 0.6	−59.0 $\pm$ 0.3	−58.8
Ice VIII	−57.3 $\pm$ 0.6	−57.4 $\pm$ 0.1	−57.4
Carbon dioxide	−28.2 $\pm$ 1.3	−28.5 $\pm$ 0.4	−28.4
Ammonia	−37.1 $\pm$ 0.4	−37.5 $\pm$ 0.1	−37.2
Benzene	−52.1 $\pm$ 0.4	−51.2 $\pm$ 0.2	−50.6
Naphthalene	−78.8 $\pm$ 0.8	−78.0 $\pm$ 0.6	−79.2
Anthracene	−105.5 $\pm$ 1.7	−103.9 $\pm$ 1.0	−105.8

^*DMC using a large supercell.

^†DMC using a small supercell; additional values in SI Appendix.

^‡See SI Appendix, Lattice Energy from Experiments for details.

Discussion

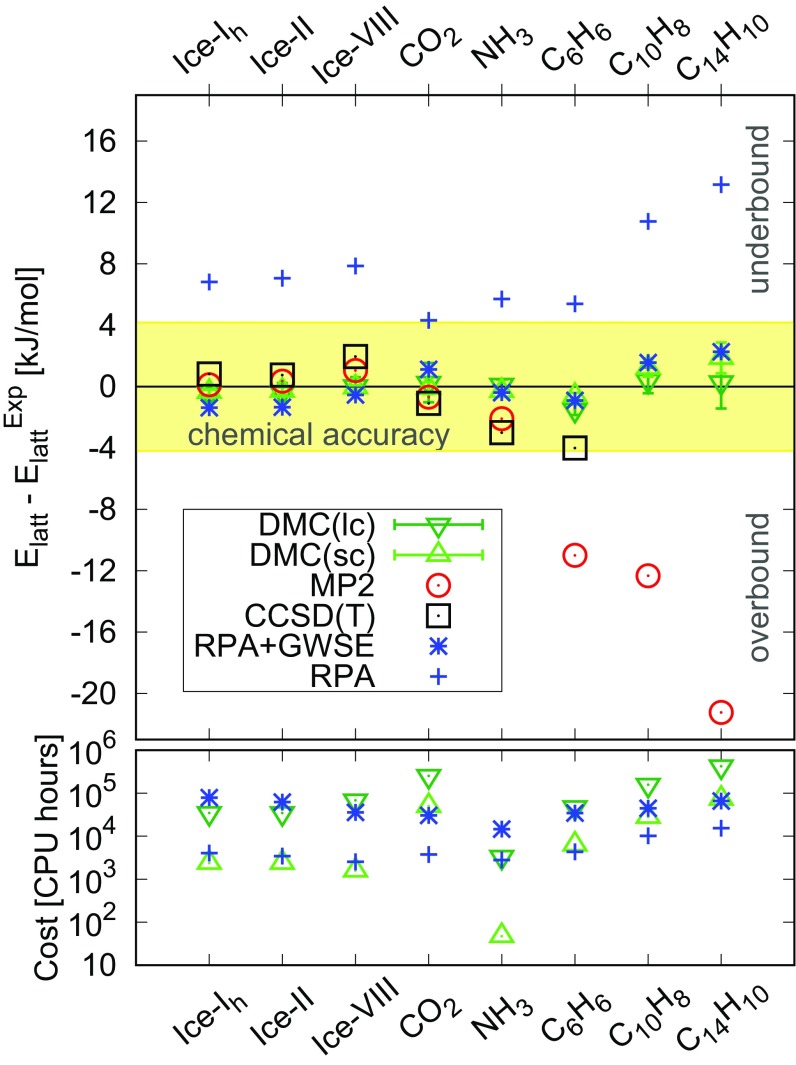
A comparison of the results obtained from DMC to experiment and to other reference quality computational approaches is shown in Fig. 2. This includes second order Møller–Plesset perturbation theory (MP2) results for all systems (36–38), and CCSD(T) for all molecules up to benzene (21, 36, 38). RPA and RPA with GW singles excitations (RPA+GWSE) lattice energies for ice are calculated in this work, and the other values are from ref. 25. From this comparison, we notice that CCSD(T) and RPA+GWSE perform well, whereas RPA systematically underbinds all systems, and MP2 severely overbinds in systems with delocalized electrons such as benzene, naphthalene, and anthracene. Among the computational approaches reported in Fig. 2, only CCSD(T) is acknowledged for an accuracy comparable to DMC, and, indeed, they show excellent agreement. However, all CCSD(T) (and MP2) values reported come from fragment decomposition approaches, which involve the computation of many small contributions to the lattice energy, all of which must be converged to high accuracy, and, typically, the correlation contribution from long-range fragments is computed at a lower level of theory. This can be a painstaking process. Also the range of values obtained from the widely studied benzene crystal (−50 kJ/mol to −56 kJ/mol) (21, 38–41) suggests that the decisions made in carrying out the fragment decomposition can have a noticeable effect on the final result. A big advantage of methods using periodic boundary conditions, such as DMC, is that the $E_{\text{latt}}$ is obtained from a single calculation (provided that FSE are corrected for), which makes such approaches more suitable for rapid screening. As an added bonus, methods such as DMC also yield information on the electronic structure and electron density on the full periodic system, information that can be used for the calculation of experimental observables and to obtain deeper understanding of the system under consideration.

Fig. 2.

Accurate and fast DMC results for a range of molecular crystals. (Top) Difference in the value of $E_{\text{latt}}$ between the experimental value and several computational approaches often used as reference methods. Here DMC(lc) and DMC(sc) indicate that large or small supercells, respectively, have been used. RPA and RPA+GWSE values for ice have been computed in this work; other values are from ref. 25. MP2 and CCSD(T) values for ice are from ref. 36, benzene values are from ref. 21, MP2 values for naphthalene and anthracene are from ref. 37, other values are from ref. 38. (Bottom) Approximate computational cost for DMC(sc), DMC(lc), RPA, and RPA+GWSE (see SI Appendix for details). The DMC cost is intended for a precision of 0.7 kJ/mol. Reported timings are intended only to provide an indication; differences in the codes and computation facilities can yield very different timings.

Computational cost is of utmost importance when making comparisons of computational methods. While DMC(lc) and DMC(sc) produce almost equal values for $E_{\text{latt}}$, each DMC(sc) is much cheaper than DMC(lc). For example, as shown in Fig. 2, Bottom, DMC(sc) is typically one to two orders of magnitude cheaper. Indeed, most of the DMC(sc) results take around ${10}^4$ CPU hours, and can be obtained in around a day on a few hundred processors. This is much more affordable than CCSD(T), which is also only feasible for relatively small molecules with the fragment decomposition approach or small crystals in periodic boundary conditions. RPA+GWSE has, so far, provided a good compromise between accuracy and computational cost. Fig. 2 shows that the cost for DMC(sc), for a precision on $E_{\text{latt}}$ of around 1 kJ/mol, is, in general, comparable to RPA.

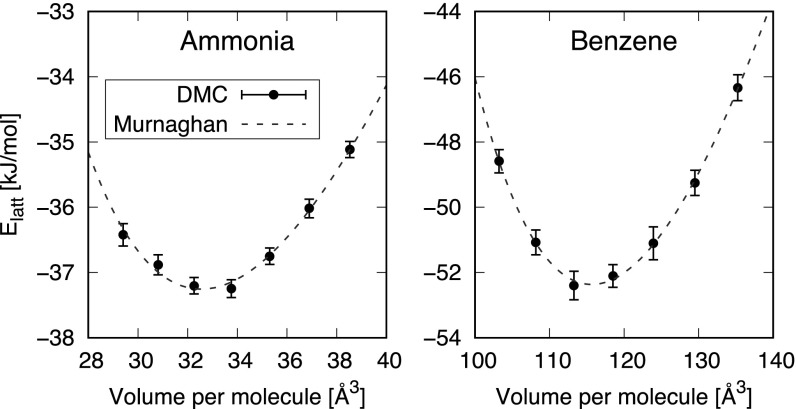
The computational efficiency of the DMC simulations and the fact that we have periodic boundary conditions makes it relatively straightforward to investigate other properties beyond the lattice energy. For instance, we have obtained the equation of state (EOS) for both ammonia and benzene; these are crystals held together predominantly by hydrogen bonds and dispersion interactions, respectively. The results of these simulations, along with fits to the Murnaghan EOS, are reported in Fig. 3. From this, we find that the equilibrium volumes ($V_0$) predicted by DMC agree very well with experiment, coming out $\sim$3% smaller than experiment for both crystals. Slightly smaller DMC volumes are to be expected, since our calculations do not take into account anharmonic thermal expansion and quantum nuclear effects present in experiment. The EOS calculations are also useful because they allow us to test the sensitivity of our computed $E_{\text{latt}}$ to the volume used in our calculations. The DMC $E_{\text{latt}}$ values listed in Table 1 have been obtained at experimentally measured densities. For the two crystals reported in Fig. 3, the bias on $E_{\text{latt}}$ arising from the use of the experimental volume appears very small, less than 0.2 kJ/mol. For the other crystals reported in Table 1, we expect, on the basis of DFT tests (25), a bias on $E_{\text{latt}}$ due to the volume on the order of 1 kJ/mol or less. A second source of bias on the values of $E_{\text{latt}}$ reported in Table 1 is due to the geometries used for the DMC calculations. Indeed, DMC, CCSD(T), MP2, and RPA are typically too expensive for a geometry optimization, which is often performed via DFT with a reliable functional. In SI Appendix, we report the EOS of ammonia and benzene obtained using the geometries from two different DFT functionals. The uncertainty on $E_{\text{latt}}$ appears to be less than 1 kJ/mol for both ammonia and benzene.

Fig. 3.

EOS for the ammonia and benzene crystals (with zero-point motion not accounted for). In both cases, the DMC $E_{\text{latt}}$ values are calculated using the $2\times 2\times 2$ cell, and FSE are corrected for with MPC. The dashed line is the Murnaghan EOS fitting the DMC values, which, for ammonia, yields a minimum $E_0$ of $-37.25\pm 0.05$ kJ/mol at a volume $V_0$ of $32.6\pm 0.1$ ų per molecule and a bulk modulus $B_0$ of $8.5\pm 0.5$ GPa; for benzene, $E_0$ is $-52.37\pm 0.06$ kJ/mol, $V_0$ is $115.7\pm 0.1$ ų per molecule, and $B_0$ is $7.7\pm 0.2$ GPa. The value of $B_0^{\prime }$ in the Murnaghan EOS is set to 4.

To conclude, we have demonstrated that DMC provides a route toward the fast and accurate determination of the properties of molecular crystals. In essence, the scheme makes use of the size-consistent DMC algorithm introduced earlier (28) and an accurate approach for correcting for FSE. We have applied this approach to a range of exemplar systems held together with a range of intermolecular interactions (hydrogen bonds to London dispersion). The calculations have confirmed previous results on water ice polymorphs but with minimal computational cost and with much more control over the numerical accuracy of the results than before. Our results also include EOS calculations for benzene—the “fruitfly” molecular crystal in computational materials science—and anthracene, the largest molecule in the C21 dataset. The consistently high accuracy demonstrated by DMC, along with its moderate computational cost, suggests that DMC can play an increasingly important role in studies of molecular crystals. In particular, DMC could prove to be the method of choice in challenging polymorph prediction studies. Similarly, molecules of direct pharmaceutical interest could now be tackled with DMC, opening up their study with a high-level ab initio approach. To provide full phase diagrams for molecular crystals, our accurate lattice energies have to be combined with estimates of zero-point and thermal effects. This is traditionally computed at the DFT level, where our study will further provide an important benchmark to test and calibrate these approximate methods. Looking farther to the future, we note that several steps of the proposed methodology could be used in a full configuration interaction QMC approach (18), which would yield essentially exact solutions to the Schrödinger equation for molecular crystals. Finally, we note that, beyond molecular crystals, the improved efficiencies and improved understanding of FSE obtained here will also be of direct relevance to DMC simulations on other classes of material, e.g., absorption in metal organic frameworks and binding to surfaces.

Materials and Methods

Geometries for the C21 crystals are taken from ref. 25 [where the geometries for molecules and crystals are optimized via DFT using the optB88-vdW functional (42), and crystals are in the experimental unit cell]. For ice phases, we took the geometries used in ref. 35. DMC simulations were carried out with the casino code (43) to evaluate $E_{\text{crys}}$ and $E_{\text{gas}}$. We used Dirac–Fock pseudopotentials (44, 45) with the locality approximation (46). The trial wave functions were of the Slater–Jastrow type with single Slater determinants and the single-particle orbitals obtained from DFT local-density approximation (LDA) plane-wave calculations performed with pwscf (www.quantum-espresso.org/) and reexpanded in terms of B-splines (47). The Jastrow factor included electron–electron, electron–nucleus, and electron–electron–nucleus terms. Further details on the wave function and the optimization are provided in SI Appendix, as well as some comparative tests with the recently introduced correlated electron pseudopotentials (48).

In the computation of $E_{\text{crys}}$, periodic boundary conditions are used. Simulations with DMC in periodic boundary conditions can be subject to significant FSE, as previously discussed. To assess the converged value of $E_{\text{latt}}$, for any molecular crystal, several simulation cells were considered, as well as twist boundary conditions (49) for the smallest cells. This has revealed that the $E_{\text{latt}}$ obtained from the primitive cell can be overestimated by as much as 300% due to FSE. However, correction schemes to reduce FSE are available in DMC, such as the MPC interaction (29, 50, 51), the correction proposed in ref. 52, and the one in ref. 53. We have tested all of them and observed that MPC provides the best results, as shown in SI Appendix. Here we report results obtained exclusively with MPC. A second and smaller source of FSE in DMC stems from the use of single-particle orbitals obtained from a DFT calculation on a single point in the Brillouin zone (typically the $\mathrm{\Gamma }$-point). This error, called the independent particle finite size error (IPFSE), can be easily estimated and corrected for by performing a few additional DFT calculations. Further computational details are reported in SI Appendix, including the atomic coordinates for each molecular system studied.

The time step, $\tau$, is a key issue affecting the accuracy of DMC calculations. In DMC, a propagation according to the imaginary time Schrödinger equation is performed to project out the exact ground state from a trial wave function (26). A time step $\tau$ must be chosen, keeping in mind that the efficiency of DMC is directly proportional to $\tau$ but the projection is exact only in the continuous limit $\tau \to 0$. Thus, $\tau$ has to be small enough to yield converged results, but as large as possible to make DMC efficient. The time step dependence is system-dependent, so it has to be evaluated on a case-by-case basis. In periodic systems, this can be computationally very expensive, because each supercell is possibly affected by the time step differently. As noted, an improved DMC algorithm (28) was recently presented. The new algorithm, denoted ZSGMA from the authors’ initials, gives better convergence with respect to $\tau$ than the one proposed by Umrigar, Nightingale, and Runge (UNR) (54) which is implemented as standard in DMC codes. In the evaluation of $E_{\text{latt}}$, an important practical point is the influence of the simulation cell size on the time step error. This is shown in Fig. 4 for the example of the ammonia crystal. Specifically, in Fig. 4, the dependence of $E_{\text{latt}}$ on $\tau$ is shown for a range of different unit cells. First, it can be seen that, with ZSGMA, $E_{\text{latt}}$ exhibits almost no dependence on $\tau$ for the range of $\tau$ reported. In contrast, values of $E_{\text{latt}}$ from UNR show a pronounced and nonlinear dependence on $\tau$. This means that, for UNR simulations, small values of $\tau$ (say $\tau \le 0.001$ au) are required to generate a reliable $\tau \to 0$ extrapolation. Second, we find that, with ZSGMA, the time step error on $E_{\text{latt}}$ is independent of the size of the unit cell (compare the 1 × 1 × 1, the 2 × 2 × 2, and the 3 × 3 × 3 cells in Fig. 4). In contrast with UNR, the time step error increases significantly as the size of the simulation cell is increased. This general behavior can be rationalized by the fact that ZSGMA is (approximatively) size-consistent up to relatively large values of $\tau$, while UNR is size-consistent only in the limit $\tau \to 0$.

Fig. 4.

Converged lattice energies from DMC in small and large unit cells. Lattice energies, $E_{\text{latt}}$, for the ammonia crystal, as obtained from DMC (with the MPC interaction to reduce FSE) by using different time steps and cell sizes, from the primitive 1 × 1 × 1 cell (comprising 4 molecules) to a 3 × 3 × 3 supercell (108 molecules). Blue squares represent the results obtained by using the algorithm by ref. 54 (UNR); red circles correspond to the algorithm by ref. 28 (ZSGMA), which consistently yields accurate results. The black dashed line is the value obtained from experimental sublimation enthalpies by ref. 31 (Exp.).

In this work, we have verified the time step convergence with the ZSGMA algorithm for each molecular crystal, as reported in SI Appendix. It is the larger time step that ZSGMA facilitates and the insensitivity of the time step error to the size of the cell that enable the converged DMC calculations on large crystals reported in this study. All results reported in the work are obtained with the ZSGMA algorithm and a time step that yields a bias of $<1$ kJ/mol. With the UNR algorithm, the same accuracy would have required difficult extrapolations and a computational cost around two orders of magnitude larger.

We now describe the scheme used here to compute accurate values of $E_{\text{latt}}$ with DMC. We recommend the use of the ZSGMA algorithm (28) in all DMC calculations, and the use of MPC for all DMC calculations in periodic systems. The following five-step procedure can be used to assess the lattice energy for a given molecular crystal.

• i)Geometries – Obtain geometries for the molecular crystal and the isolated molecule. Since geometry optimizations of large systems are challenging with DMC, we recommend the use of DFT and an exchange-correlation functional that accounts for Van der Waals (vdW) dispersion forces. If reliable experimental structures are available, the optimization should be performed at the experimental volume.
• ii)IPFSE – Using the structure obtained in i, converge the energy per molecule in the crystal, $E_{\text{crys}}^{\text{DFT},\mathrm{\infty }}$, using the functional that is used to obtain the single particle orbitals for the DMC calculations (we generally use LDA). Convergence is reached by considering $l\times m\times n$ Monkhorst–Pack grids of increasing size. The difference $E_{\text{crys}}^{\text{DFT},l\times m\times n}$ - $E_{\text{crys}}^{\text{DFT},\mathrm{\infty }}$ = ${\mathrm{IPFSE}}_{l\times m\times n}^{\text{DFT}}$ provides a good indication of the independent particle contribution to the FSE in DMC calculations for an $l\times m\times n$ supercell; see SI Appendix.
• iii)Jastrow optimization – Take the smallest supercell that is compatible with the Jastrow factor (typically the Jastrow factor has cutoffs related to the size of the simulated cell; we suggest using supercells with the maximum radius of a sphere inscribed within the Wigner–Seitz cell of $>$5 Å) and optimize the Jastrow factor of the quantum Monte Carlo wave function by minimizing the variance (or, alternatively, the variational energy). An optional test of the reliability of the Jastrow can be performed by calculating the DMC binding energy in a molecular dimer extracted from the crystal, and comparing it with a reference value obtained from CCSD(T).
• iv)DMC time step – Check the time step dependence either on the cell used in step iii or on the molecular dimer.
• v)Final DMC calculation of ${\text{𝑬}}_{\text{𝐥𝐚𝐭𝐭}}$ – Take a supercell from step ii with the estimation ${\mathrm{IPFSE}}_{l\times m\times n}^{\text{DFT}}$ smaller than 10 kJ/mol. Perform the DMC simulation for this crystal using MPC, and perform the DMC calculation with open conditions for the molecule. Calculate $E_{\text{latt}}$ and correct for the independent particle FSE using ${\mathrm{IPFSE}}_{l\times m\times n}^{\text{DFT}}$. This yields the final DMC(sc) result. Optionally, consider larger supercells to reduce ${\mathrm{IPFSE}}_{l\times m\times n}^{\text{DFT}}$ and the MPC correction.

The threshold ${\mathrm{IPFSE}}_{l\times m\times n}^{\text{DFT}}$ $<$ 10 kJ/mol (in step v) is motivated by the target accuracy of $\sim$1 kJ/mol and a $\sim$10% reliability of the DFT-based IPFSE correction. A more accurate alternative to evaluate the IPFSE is possible (twist averaging) and is discussed in SI Appendix.

Supporting Information

SI Appendix provides details of the setup for the DMC, RPA, and RPA+GWSE calculations, a discussion of the FSE, and additional DMC results. In addition, the computational cost of DMC is discussed, as well as of RPA and RPA+GWSE. An extended version of Table 1 is given, and the evaluation of lattice energies from experimental sublimation enthalpies is discussed. Geometries of the molecular crystals and reference molecules used for the DMC, RPA, and RPA-GWSE calculations are given.