Pressure-induced structural change in MgSiO₃ glass at pressures near the Earth’s core–mantle boundary

Significance

Knowledge of the structure of MgSiO₃ melt at pressures near the Earth’s core–mantle boundary is important in understanding geochemical and geophysical processes at the region. However, there is no structural determination under such ultrahigh pressures. A double-stage Paris–Edinburgh press combined with multiangle energy dispersive X-ray diffraction enabled in situ structure measurements on MgSiO₃ glass up to 111 GPa. We report direct experimental evidence of a structural change in this glass at pressures greater than 88 GPa, which is shallower than the pressure of the Earth’s core–mantle boundary. Considering similarities in pressure-induced structural changes between silicate melts and glasses, a similar ultrahigh-pressure structural change may occur in MgSiO₃ melts in the deep lower mantle.

Abstract

Knowledge of the structure and properties of silicate magma under extreme pressure plays an important role in understanding the nature and evolution of Earth’s deep interior. Here we report the structure of MgSiO₃ glass, considered an analog of silicate melts, up to 111 GPa. The first (r1) and second (r2) neighbor distances in the pair distribution function change rapidly, with r1 increasing and r2 decreasing with pressure. At 53–62 GPa, the observed r1 and r2 distances are similar to the Si-O and Si-Si distances, respectively, of crystalline MgSiO₃ akimotoite with edge-sharing SiO₆ structural motifs. Above 62 GPa, r1 decreases, and r2 remains constant, with increasing pressure until 88 GPa. Above this pressure, r1 remains more or less constant, and r2 begins decreasing again. These observations suggest an ultrahigh-pressure structural change around 88 GPa. The structure above 88 GPa is interpreted as having the closest edge-shared SiO₆ structural motifs similar to those of the crystalline postperovskite, with densely packed oxygen atoms. The pressure of the structural change is broadly consistent with or slightly lower than that of the bridgmanite-to-postperovskite transition in crystalline MgSiO₃. These results suggest that a structural change may occur in MgSiO₃ melt under pressure conditions corresponding to the deep lower mantle.

Ultralow velocity zones observed in seismological studies suggest the presence of silicate magma immediately above the core–mantle boundary (CMB) (1, 2). Experimental studies have confirmed the possible formation of silicate melts under high pressure and high temperature conditions of the Earth’s deep interior (3, 4), and the melts can be gravitationally stable near the CMB (5, 6). More extensive deep melting may have occurred in the Earth’s early history followed by slow fractional crystallization since, resulting in an unsampled deep geochemical reservoir hosting a variety of incompatible species (especially the missing budget of heat-producing elements) (7). Deep silicate melts may therefore significantly influence geochemical and geophysical processes such as chemical reactions between the mantle and core, thermal transport, and convection patterns. Knowledge of the structure and properties of silicate melts under high pressure condition corresponding to the CMB is a prerequisite in discussing the behavior of silicate melts in the deep earth (ca. 100 GPa). However, such information is scarce owing to well-known experimental challenges.

Pressure-induced structural changes in silicate melts are among the most important issues in understanding the behavior of silicate melts in the Earth’s deep interior and have been predicted by theoretical simulations (8, 9). Efforts have been made to measure the structure of silicate melts at high-pressure conditions in the laboratory (10, 11). However, such experiments have been mostly limited to less than 10 GPa, because of the difficulties in conducting structure measurements at simultaneously high pressure and high temperature conditions. Only a few studies have successfully measured the structure of silicate melt above 10 GPa (12). Given these difficulties, silicate glasses have been studied as an alternate approach to understand structural changes of silicate melts at high pressures, because of similarities in the pressure-induced structural changes in silicate melts and glasses (13).

Pair distribution function measurements showed that SiO₂ glass undergoes gradual structural change with Si coordination increasing from fourfold to sixfold around 15–40 GPa (14–17). Ref. 16 confirmed that the structure with sixfold coordinated Si is stable up to 101.5 GPa. Brillouin scattering measurement (18) found a kink in the pressure dependence of the shear-wave velocity at around 140 GPa, and suggested a possible ultrahigh-pressure structural change with Si-O coordination number greater than 6. A very recent study on SiO₂ glass up to 172 GPa (19) reported an increase of Si-O coordination number to more than 6. This latter study showed continuous increase of Si-O coordination number beyond 6 without sharp structural changes.

Similarly, ref. 20 reported a kink in the pressure dependence of the shear-wave velocity in MgSiO₃ glass above 133 GPa. Based on these observations, ref. 20 argued for the presence of an ultrahigh-pressure structural change in silicate melt at the pressure conditions near the CMB (135 GPa). They further suggested that such a change in structure may result in a gravitationally stable dense silicate magma ocean above the CMB. However, the elasticity data (20) do not provide direct structure information. We have developed a double-stage configuration in a Paris–Edinburgh press for studies of the structure of glasses under ultrahigh pressures using synchrotron radiation (21). In this study, we investigate the pair distribution function of MgSiO₃ glass up to 111 GPa, and report an ultrahigh-pressure structural change in MgSiO₃ glass at pressures higher than 88 GPa.

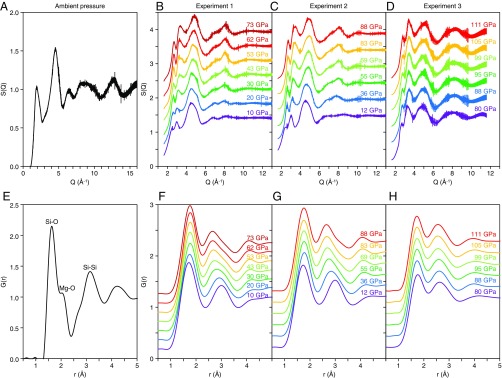
The structure of MgSiO₃ glass was investigated using a multiangle energy dispersive X-ray diffraction technique at a High Pressure Collaborative Access Team (HPCAT) Beamline, 16-BM-B of the Advanced Photon Source (21). Structure factors, S(Q), were determined up to 16 Å⁻¹ at ambient pressure (Fig. 1A), up to 13 Å⁻¹ in experiments 1 and 2 at pressure conditions up to 88 GPa (Fig. 1 B and C), and up to 11.6 Å⁻¹ in experiment 3 at pressures up to 111 GPa (Fig. 1D). Fourier transformation of S(Q) yields the real-space pair distribution function, G(r) (Fig. 1 E–H). Fig. 1 A and E show S(Q) and G(r), respectively, of MgSiO₃ glass measured at ambient pressure. The first (r1) and second (r2) peaks of G(r) are 1.625 ± 0.007 Å and 3.178 ± 0.011 Å, respectively, and are considered to represent Si-O and Si-Si distances, respectively. Our results are consistent with Si-O (1.63 Å) and Si-Si (3.25 Å) distances of MgSiO₃ glass determined by ref. 22. In addition to the main r1 and r2 peaks, there is a shoulder peak at 2.031 ± 0.019 Å (Fig. 1E), which corresponds to the Mg-O distance (2.08 Å) of MgSiO₃ glass (22).

Fig. 1.

Structure factor, S(Q) (A–D), and pair distribution function, G(r) (E–H), of MgSiO₃ glass up to 111 GPa. S(Q) was determined at the Q range up to 16 Å⁻¹ at ambient pressure (A), up to 13 Å⁻¹ for the experiments 1 (B) and 2 (C) and up to 11.6 Å⁻¹ for the experiment 3 (D). S(Q) is displayed by a vertical offset of +0.42 for B and +0.48 for C and D. G(r) is displayed by a vertical offset of +0.18 for F and +0.22 for G and H.

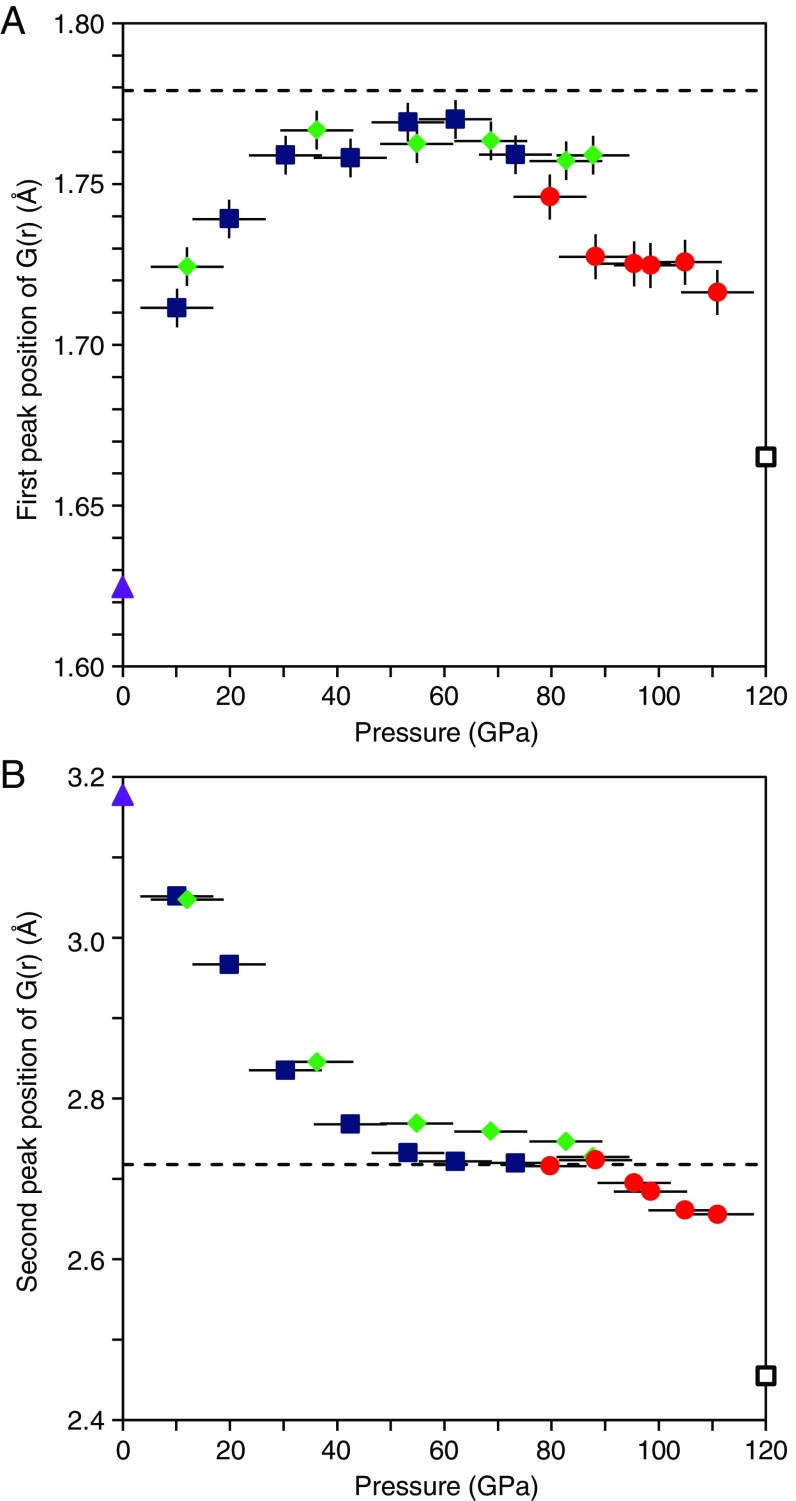
Fig. 1 F–H show G(r) of MgSiO₃ glass at pressures up to 111 GPa. Both r1 and r2 peaks are clearly observed, while the shoulder Mg-O peak cannot be identified, probably because of the increased peak widths at high pressures due to the smaller measured Q range relative to ambient pressure. Both r1 and r2 peak positions shift significantly with pressure (Fig. 2; Table 1). The r1 distance increases rapidly with pressure to 36 GPa, and then remains more or less constant between 36 and 62 GPa (Fig. 2A). Above 62 GPa, the r1 distance turns over, decreasing with increasing pressure. The r2 distance also shows a strong change with increasing pressure (Fig. 2B). It decreases with increasing pressure up to 53 GPa, remains almost constant between 53 and 88 GPa. Both r1 and r2 distances are almost constant at 53–62 GPa.

Fig. 2.

The first (r1) (A) and second (r2) (B) peak position of G(r). Blue, green, and red symbols represent the results of the experiments 1, 2, and 3, respectively. Solid purple triangles represent the r1 and r2 of MgSiO₃ glass measured at ambient pressure. Dashed black line represents average Si-O (1.779 Å) (A) and Si-Si (2.718 Å) (B) distances of crystalline MgSiO₃ akimotoite at 7.8 GPa (23). Open black squares represent average Si-O (1.665 Å) (A) and the shortest Si-Si (2.455 Å) (B) distances of crystalline MgSiO₃ postperovskite at 120 GPa and 0 K (28). Vertical bars represent the error in r1. The error in r2 is smaller than the size of the symbols. Horizontal bars represent the cumulative uncertainty in pressure due to error in the pressure determination, pressure change during the long structure measurement, and pressure gradient in the sample.

Table 1.

Experimental pressure conditions and the results of the first (r1) and second (r2) peak positions of G(r)

Pressure (GPa)	r1 (Å)	r2 (Å)
0.0	1.625 ± 0.007	3.178 ± 0.011
Experiment 1
10.1 ± 1.2	1.712 ± 0.005	3.051 ± 0.010
19.9 ± 1.4	1.739 ± 0.011	2.967 ± 0.010
30.4 ± 1.4	1.759 ± 0.008	2.835 ± 0.018
42.5 ± 0.7	1.758 ± 0.002	2.768 ± 0.018
53.2 ± 1.4	1.769 ± 0.002	2.732 ± 0.010
62.1 ± 1.9	1.770 ± 0.007	2.722 ± 0.006
73.3 ± 2.2	1.759 ± 0.006	2.720 ± 0.004
Experiment 2
12.0 ± 0.4	1.724 ± 0.005	3.047 ± 0.009
36.2 ± 0.7	1.767 ± 0.003	2.845 ± 0.011
54.9 ± 1.2	1.763 ± 0.004	2.769 ± 0.007
68.7 ± 1.1	1.763 ± 0.004	2.759 ± 0.002
82.7 ± 2.5	1.757 ± 0.006	2.747 ± 0.004
87.8 ± 2.0	1.759 ± 0.006	2.727 ± 0.004
Experiment 3
79.7 ± 2.8	1.746 ± 0.006	2.716 ± 0.008
88.2 ± 1.7	1.727 ± 0.007	2.723 ± 0.009
95.4 ± 1.4	1.725 ± 0.007	2.695 ± 0.009
98.5 ± 1.6	1.725 ± 0.006	2.684 ± 0.008
104.9 ± 1.7	1.726 ± 0.006	2.661 ± 0.008
111.0 ± 1.9	1.716 ± 0.005	2.656 ± 0.006

The r1 peak represents the average Si-O distance (22). At 36 GPa, its value (1.767 ± 0.003 Å) is similar to the average Si-O distance of crystalline MgSiO₃ akimotoite with an ilmenite structure (1.779 Å at 7.8 GPa; ref. 23) and that of crystalline MgSiO₃ bridgmanite (1.777 Å at 10.6 GPa; ref. 24) (Fig. 2A). Since both akimotoite- and bridgmanite-type MgSiO₃ are characterized by sixfold coordinated SiO₆ octahedra (23, 24), the increase of the r1 distance of MgSiO₃ glass below 36 GPa may be viewed as an increase in coordination number (CN) for Si from 4 to 6. Above 36 GPa, the r1 distance remains almost constant with increasing pressure, and the r2 distance continues to decrease up to 53 GPa (Fig. 2). The r2 distance of MgSiO₃ glass at 53 GPa (2.732 ± 0.010 Å) (Fig. 2B) is similar to the average Si-Si distance of MgSiO₃ akimotoite (2.718 Å at 7.8 GPa; ref. 23), which consists of edge-shared SiO₆ octahedra. A recent first-principles molecular dynamics simulation of MgSiO₃ glass also reported significant shortening of the Si-Si distance under cold compression (25), which is consistent with our experimental results. On the other hand, MgSiO₃ bridgmanite consists of corner-shared SiO₆ octahedra with an average Si-Si distance of 3.3961 Å at 10.6 GPa (24). This is markedly longer than the r2 distance of MgSiO₃ glass. These observations thus suggest that MgSiO₃ glass undergoes a structural change to sixfold coordinated Si with edge-sharing SiO₆ structural motifs similar to that in the akimotoite structure. The significant shortening of r2 distance in MgSiO₃ glass is structurally related to the decrease of the Si-O-Si bond angle and the folding of the Si-O polyhedra to form edge-shared SiO₆ structural motifs, similar to crystalline MgSiO₃ akimotoite. This interpretation is consistent with predicted structural changes in MgSiO₃ melts (26), based on molecular dynamics (MD) simulations. Hereafter, the akimotoitelike glass structure around 53–62 GPa is referred to as high-pressure structure I (HP-I).

Above 62 GPa, the shift of r1 turns over and begins decreasing with increasing pressure, and r2 remains essentially unchanged up to 88 GPa (Fig. 2), suggesting that although SiO₆ octahedra are continually compressed with increasing pressure, the average Si-Si distance remains more or less constant. We note that in MD simulations (27) Mg CN undergoes significant changes in this pressure interval, with concentrations of MgO₆ and MgO₇ species sharply decreasing while MgO₈ and MgO₉ species sharply increase. This increases the Mg-O distance. Although no reliable high-pressure Mg-O distance data are available for MgSiO₃ glass and melt, information from crystalline structures may be a useful guide. The Mg-O distance of MgO₈ polyhedra [e.g., 2.204 Å at 0 GPa in crystalline MgSiO₃ bridgmanite (24)] is significantly greater than that of MgO₆ polyhedra [e.g., 2.089 Å at 0 GPa in crystalline MgSiO₃ akimotoite (23)]. Furthermore, Mg-O distances of MgO₈ polyhedra in MgSiO₃ bridgmanite and postperovskite are virtually identical at 120 GPa (28), suggesting that this distance of MgO₈ is insensitive of the SiO₆ network topology (corner sharing versus edge sharing). Because Si-O and Mg-O polyhedra share oxygen atoms, the increase in Mg CN and Mg-O distance is expected to open up the Si-O-Si angle in MgSiO₃ glass and melt. The observed continually decreasing r1 (Si-O distance) with a constant r2 (Si-Si distance) in MgSiO₃ glass at 62–88 GPa is therefore interpreted as the result of two competing processes in r2 during compression, namely, the compression of SiO₆ octahedra and the increase of the Si-O-Si angle in the edge-sharing SiO₆ network. Although the former process tends to decrease r2, the latter tends to increase it. Above 88 GPa, however, r1 starts deviating from the compression trend at 62–88 GPa. In addition, r2 begins to decrease again above 88 GPa (Fig. 2B). The marked changes of r1 and r2 above 88 GPa suggest the existence of another structural change in MgSiO₃ glass. Hereafter, this structure is referred to as high-pressure structure II (HP-II).

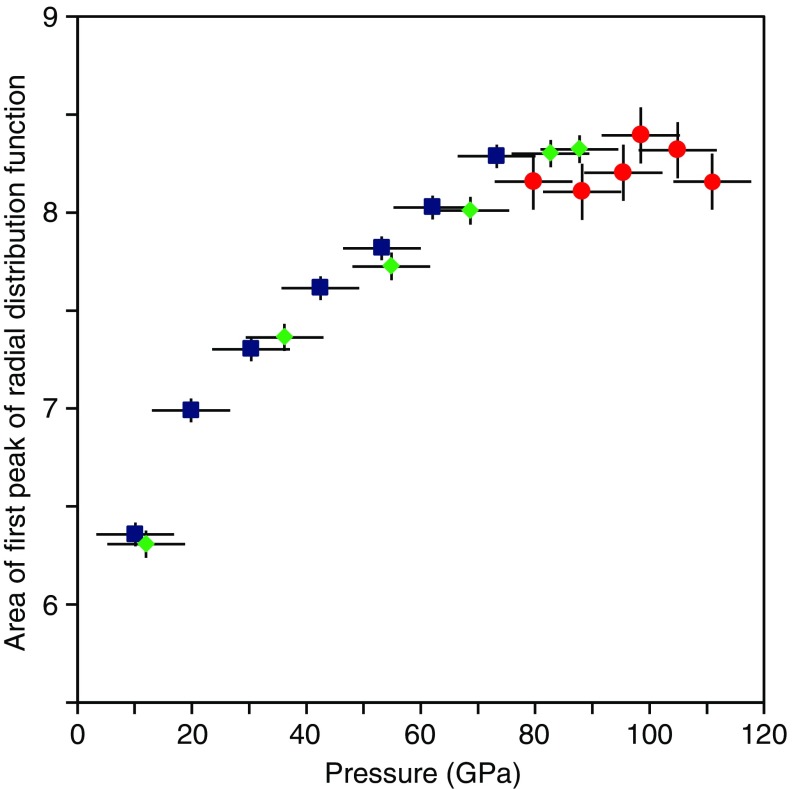
Ref. 20 argued for an ultrahigh-pressure structural change in MgSiO₃ glass with Si-O CN > 6, based on the anomaly in the pressure dependence of the shear wave velocity. To investigate this possibility, we examined the area (A₁) under the first peak of the radial distribution function [=4πr²ρG(r), where ρ is number density, calculated from the equation of state of MgSiO₃ glass (6)] (Fig. 3). Note that A₁ in our observations represents not only the coordination number of Si-O but also some influence of the coordination number of Mg-O, because of the overlap of the Si-O and Mg-O peaks. We therefore only discuss the relative change of A₁ with increasing pressure. A₁ is 6.3 at 10 GPa, and increases strongly with pressure, reaching 8.3 at 73 GPa (Fig. 3). This increase is consistent with a structural change from dominant SiO₄ structural motifs at ambient pressure (22) to akimotoitelike SiO₆ structural motifs. Above 73 GPa, A₁ remains essentially constant up to 111 GPa. This suggests that the CN of Si-O in MgSiO₃ glass remains unchanged across the ultrahigh-pressure structural change above 88 GPa. Our result is consistent with ref. 16 for SiO₂ glass, in that the CN of Si-O remains 6 up to 101.5 GPa. On the other hand, ref. 19 reported a gradual increase of the Si-O CN of SiO₂ glass to more than 6 above ∼100 GPa (19). Ref. 19 showed that the CN of Si-O increases gradually from 6 at ∼60 GPa to 6.8 at 172 GPa although, within the reported error bars, the CN may be viewed as unchanged between 80 and 100 GPa, where we observed no change of A₁ in MgSiO₃ glass. Higher pressure experiments may be important to clarify the possibility of such gradual change of Si-O CN in MgSiO₃ glass. On the other hand, compared with S(Q) measurements with higher Q range in this study (up to 11.6 or 13 Å⁻¹) and ref. 16 (up to 14 Å⁻¹), the limited Q range (up to 10 Å⁻¹) of the S(Q) measurement by ref. 19 along with lack of signal oscillation in the reported S(Q) at >6 Å⁻¹ may be another source of uncertainty in view of the quality of G(r) and the resultant Si-O CN. Higher pressure experiments with high-quality S(Q) measurement to high Q range may be required to clarify the possible change of Si-O CN in MgSiO₃ glass across the structural change above 88 GPa.

Fig. 3.

Area of first peak of radial distribution function (A₁). Blue, green, and red symbols represent the results of the experiments 1, 2, and 3, respectively. Vertical bars represent error of A₁. Horizontal bars represent the cumulative uncertainty in pressure due to error in the pressure determination, pressure change during the long structure measurement, and pressure gradient in the sample.

It is known that MgSiO₃ bridgmanite, which is the next high-pressure polymorph in crystalline MgSiO₃ after akimotoite, has an open network structure of corner-shared SiO₆ octahedra with average Si-Si distance of 3.3961 Å measured at 10.6 GPa (24) and of 3.129 Å calculated at 120 GPa and 0 K (28). The longer Si-Si distance in MgSiO₃ bridgmanite suggests that corner-linked SiO₆ structural motifs are inconsistent with the decrease of r2 distance in MgSiO₃ glass above 88 GPa (Fig. 2B). In fact, MD simulations on both MgSiO₃ (25) and CaSiO₃ (29) glasses show that transitions to SiO₆-dominated structures are accompanied by large fractions of edge- and face-sharing SiO₆ octahedra. The lack of pure corner-sharing SiO₆ octahedra in these glasses (and presumably melts) is likely due to the inefficient packing of corner-sharing structural motifs, as suggested by the much larger bond distances. On the other hand, the crystalline postperovskite structure of MgSiO₃ contains edge-shared SiO₆ octahedra, and the shortest Si-Si distance between the closest edge-shared SiO₆ octahedra is 2.455 Å at 120 GPa and 0 K (28), much shorter than that of akimotoite (Fig. 2B). Therefore, the r1 and r2 distances of MgSiO₃ glass above 88 GPa may be moving toward the average Si-O distance and the shortest Si-Si distance of MgSiO₃ postperovskite (Fig. 2).

The structural change in MgSiO₃ glass at 88 GPa has not been reported in first-principles molecular dynamics simulations for MgSiO₃ melt (9) and glass (25), probably due to the large pressure steps used in these studies (no data point between 55 and 125 GPa in ref. 9 and between ∼65 and ∼110 GPa in ref. 25). On the other hand, another MD simulation study (27) calculated the structure of MgSiO₃ melt with smaller pressure steps, and reported a structural change in MgSiO₃ melt around 100 GPa at 5,000 K, with no marked change in the average coordination numbers of Si-O and Mg-O, whereas the average coordination number of O-O decreases rapidly from ∼15 to ∼12. Ref. 27 interpreted the average O-O CN of ∼12 as corresponding to the number of equal spheres in the maximum dense packing structure (30). This suggests that the oxygen packing structure may be the key to understanding our observed HP-I to HP-II structure change in MgSiO₃ glass at 88 GPa. MgSiO₃ akimotoite consists of irregularly shaped SiO₆ polyhedra with distinct O-O edge distances ranging between 2.300 and 2.649 Å (23), while SiO₆ polyhedra in postperovskite contain more uniform O-O edge distances (2.296–2.456 Å) (28). The shortest Si-Si distance between the closest edge-shared SiO₆ (2.455 Å) in MgSiO₃ postperovskite is also close to the O-O edge distance. These data suggest a more equal distribution of Si and O in the closest edge-shared SiO₆ polyhedra in MgSiO₃ postperovskite. Our observed MgSiO₃ HP-II glass structure may also be due to a denser packing distribution of oxygen atoms with uniform distance, as suggested for MgSiO₃ melt (27).

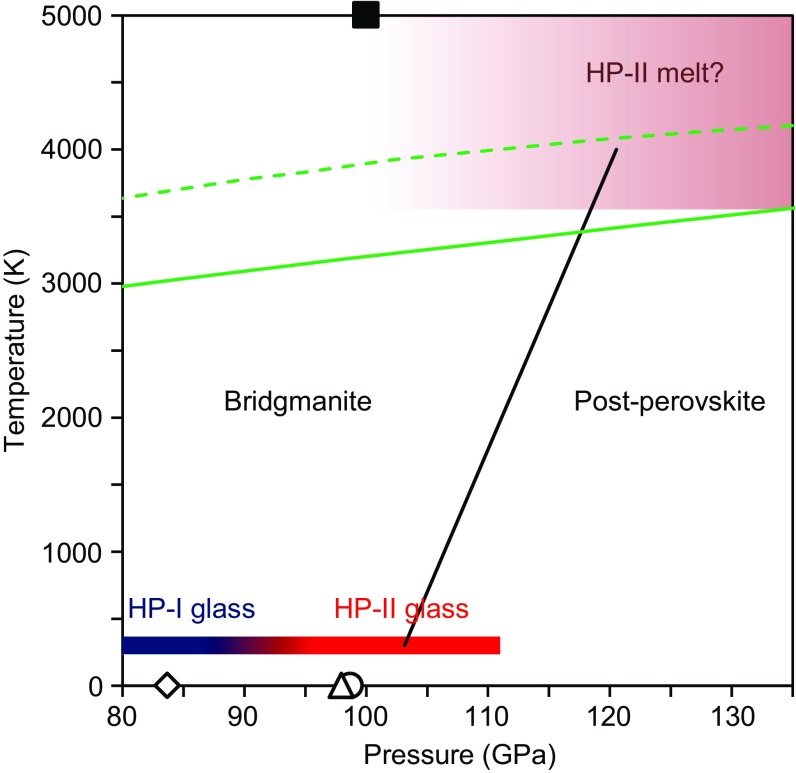
Considering the similarity in the pressure-induced structure changes in silicate glass and melt at very high pressure conditions corresponding to the Earth’s lower mantle (13), we anticipate that a similar ultrahigh-pressure structural change may also occur in MgSiO₃ melt under similar pressure conditions. We note that the pressure condition of the structural change in MgSiO₃ glass at 88 GPa at room temperature is broadly consistent with or slightly lower than that of the bridgmanite-to-postperovskite transition in crystalline MgSiO₃ (28, 31, 32) (Fig. 4). Ref. 32 reported that the postperovskite transition in MgSiO₃ occurs at 113 GPa and 2,400 K with a positive Clapeyron slope of +4.7 MPa/K (Fig. 4). Extrapolating the phase boundary to the melting temperature of peridotite (3) and pyrolite (4), the postperovskite boundary is located around 120 GPa (Fig. 4), shallower than the CMB (135 GPa). In addition, MD simulation (27) predicted a structural change in MgSiO₃ melt around 100 GPa at 5,000 K, which is also lower pressure than the bridgmanite–postperovskite transition pressure and shallower than the CMB (Fig. 4). These results suggest that the ultrahigh-pressure structural change may occur in silicate melts above the CMB, with significant densification and potentially profound influence on the dynamics of melt storage and circulation in the Earth’s deep interior.

Fig. 4.

Pressure condition of the ultrahigh-pressure structural change in MgSiO₃ glass obtained in this study, compared with bridgmanite–postperovskite transition in crystalline MgSiO₃ [open black triangle (28)]; open black circle and diamond: generalized gradient approximation (GGA) and local density approximation (LDA) calculation, respectively, by ref. 31; solid black line (32) and a structural change in MgSiO₃ melt predicted by MD simulation (27) (solid black square). Solid and dashed green line represents melting temperature of pyrolite (4) and peridotite (3), respectively.

Methods

A double-stage large volume cell was developed in the 200-ton Paris–Edinburgh press at HPCAT of the Advanced Photon Source (21). We used a cup-shaped anvil with 12-mm cup diameter with a 3-mm flat bottom as the first stage anvil and (100)-oriented single crystal diamond as the second stage anvil. We used diamond anvils with a 0.8-mm culet in experiment 1 and with a 0.6-mm culet beveled to 0.8-mm diameter in experiments 2 and 3. The two-part gasket was composed of an inner gasket of cubic boron nitride + epoxy (10:1 in weight ratio) with an aluminum alloy (7075) outer gasket for experiments 1 and 2. In experiment 3, an additional steel ring gasket was inserted between the inner and outer gaskets. The initial sample thickness was 0.15 mm for all experiments. The initial sample diameter was 0.3 mm for experiment 1 and 0.23 mm for experiments 2 and 3. The MgSiO₃ glass sample was prepared from a mixture of MgO and SiO₂ powders. The mixed powder, placed in a platinum crucible, was melted in air in a furnace at 1,923 K and quenched by cooling the platinum crucible in water. The MgSiO₃ glass sample was packed in the gasket hole without pressure medium to avoid diffraction peaks from the pressure medium in the X-ray diffraction measurement. A piece of Au (cut from 0.05-mm diameter wire) was placed as a pressure standard at the edge of the sample to avoid contamination of the X-ray spectrum of the MgSiO₃ glass sample by Au diffraction. Pressures were determined by the equation of state of Au (33). We measured pressure before and after each structure measurement of glass, because of the long measurement time (∼3 h for experiments 1 and 2 and ∼5 h for experiment 3). Pressure differences before and after structure measurements were 0.1–3.7 GPa. Table 1 shows the average pressures obtained before and after measurements. In addition, pressure gradient from the center to the edge of the sample is up to 4 GPa at pressures up to 93.4 GPa (21).

The structure of MgSiO₃ glass was investigated using the multiangle energy dispersive X-ray diffraction technique (11). The size of the incident white X-ray in the vertical direction was adjusted to 0.1 mm by a slit. The incident white X-rays were focused to 0.009 mm (full width at half maximum) in the horizontal direction by using a 200-mm-long Pt-coated K-B mirror with an incident angle of 1.25 mrad, which produces an energy cutoff at ∼65 keV. We collected series of energy dispersive X-ray diffraction patterns using a Ge solid-state detector (Canberra) at 2θ angles of 4.6°, 6.6°, 8.1°, 10.6°, 13.6°, 17.1°, 21.1°, and 27.1° for experiments 1 and 2, and 4.6°, 9.1°, 10.6°, 13.6°, 17.1°, and 21.1° for experiment 3. The structure factor was derived from the observed energy dispersive X-ray diffraction patterns using the aEDXD program developed by Changyong Park (11). The Kaplow-type correction using an optimization procedure (34) was applied in determining final structure factor and pair distribution function. The number of iterations in the optimization process was five. The Lorch function was applied to remove the truncation effect on the final pair distribution function determination (35).