Linearization improves the repeatability of quantitative Dynamic Contrast-Enhanced MRI

Abstract

Purpose

The purpose of this study was to compare the repeatabilities of the linear and nonlinear Tofts and reference region models (RRM) for Dynamic Contrast-Enhanced MRI (DCE-MRI).

Materials and Methods

Simulated and experimental DCE-MRI data from 12 rats with a flank tumor of C6 glioma acquired over three consecutive days were analyzed using four quantitative and semi-quantitative DCE-MRI metrics. The quantitative methods used were: 1) Linear Tofts model (LTM), 2) Nonlinear Tofts model (NTM), 3) Linear RRM (LRRM), and 4) Non-linear RRM (NRRM). The following semi-quantitative metrics were used: 1) Maximum enhancement ratio (MER), 2) time to peak (TTP), 3) initial area under the curve (iauc64), and 4) slope. LTM and NTM were used to estimate K, while LRRM and NRRM were used to estimate K relative to muscle (R). Repeatability was assessed by calculating the within-subject coefficient of variation (wSCV) and the percent intra-subject variation (iSV) determined with the Gage R&R analysis.

Results

The iSV for using LRRM was two-fold lower compared to NRRM at all simulated and experimental conditions. A similar trend was observed for the Tofts model, where LTM was at least 50% more repeatable than the NTM under all experimental and simulated conditions. The semi-quantitative metrics iauc64 and MER were as equally repeatable as K and R estimated by LTM and LRRM respectively. The iSV for iauc64 and MER were significantly lower than the iSV for slope and TTP.

Conclusion

In simulations and experimental results, linearization improves the repeatability of quantitative DCE-MRI by at least 30%, making it as repeatable as semi-quantitative metrics.

1. INTRODUCTION

Dynamic contrast-enhanced MRI (DCE-MRI) involves the serial acquisition of T₁-weighted images before, during, and after the injection of a contrast agent (CA) that shortens the T₁ relaxation time of water, resulting in an increase of the MRI signal in tissues or voxels where the agent accumulates [1]. After application of a proper pharmacokinetic (PK) model, parameters related to tissue perfusion [2], blood flow [3], capillary leakage [4], and transit time of the CA can be derived from the dynamic MRI signal in a voxel or a tissue of interest [5].

The two PK parameters most commonly estimated from DCE-MRI data are the rate of CA transfer from blood to tissue (K) and the rate of CA transfer from tissue to blood (k_ep) [1]. Several studies have shown evidence that K can be used to differentiate tumors from normal tissue [6, 7], and to monitor anti-cancer treatment in fibrosarcoma [8], breast [9, 10], and brain neoplasms [11, 12]. Unfortunately, these results are inconsistent with other studies, which showed that K offers little to no utility in monitoring anti-cancer treatment in breast and brain cancers [13, 14]. Because of these limitations, quantitative DCE-MRI descriptors are not part of the standard of care for clinical DCE-MRI.

These contradictory results may be due to the inherent variability of DCE-MRI that is a consequence of a low signal-to-noise ratio (SNR) [15], slow temporal resolution [16, 17], variability in the arterial input function (AIF) needed for PK modeling [18, 19], and/or the model assumed during data analysis [20, 21]. Some of these limitations have been addressed by the introduction of the non-linear reference region model (NRRM) [22, 23] that does not require AIF determination, and the linear reference region model (LRRM) that also does not require the AIF and gives more accurate parameter estimates than the NRRM under low SNR and slow temporal resolution [24, 25]. The standard Tofts model for DCE-MRI has also been linearized, and it was recently demonstrated that such linearization improves its performance under low SNR and low temporal resolution [26]. We recently demonstrated that the relative K (R) estimated by LRRM is a better predictor of response to neoadjuvant chemotherapy in breast cancer than the R estimated using NRRM [24]. An analoguous behavior was observed for K and k_ep estimated using the linear (LTM) and non-linear (NTM) Tofts models [27]. Based on these results, we hypothesized that linearization should improve the repeatability of quantitative DCE-MRI. We performed a retrospective study to compare the repeatability of R and k_ep estimated by NRRM and LRRM. We also compared the repeatability of quantitative NRRM and LRRM descriptors with semi-quantitative descriptors and quantitative NTM and LTM descriptors of DCE-MRI.

2. METHODS

All of the experimental data was downloaded from DataVerse [21], while the code used to simulate and analyze all data are available at https://github.com/JCardenasRdz/Gage-repeatability-DCE-MRI.

2.1 Theory of the quantitative analysis of DCE-MRI and its models

The generalized model for DCE-MRI establishes that the differential equation that describes the PK behavior of a CA within a voxel is:

$$\frac{{\text{dC}}_{\text{TOI}}}{\text{dt}}={\mathrm{K}}^{\text{trans}}·{\mathrm{C}}_{\mathrm{p}}(\mathrm{t})-{\mathrm{k}}_{\text{ep}}·{\mathrm{C}}_{\text{TOI}}$$ (1)

C_TOI is the concentration of the CA in the tissue of interest (TOI) as a function of time. C_p(t) is the concentration of the CA in plasma as a function of time (also known as the AIF), K is the rate transfer constant from the plasma into the TOI and k_ep is the transfer constant from the TOI to plasma. This equation assumes that the fractional plasma volume is equal to zero (v_p=0). The quantitative analysis of DCE-MRI data requires three steps to estimate K and k_ep for any TOI: 1) solve Eq. 1, 2) transform the observed changes in the MRI signal to changes in concentration of the CA, and 3) fit the concentration curves of step 2 to the solution obtained in step 1. The first and most common solution to Eq. [1] was developed by Tofts, et al. [2]:

$${\mathrm{C}}_{\text{TOI}}(\mathrm{t})={\mathrm{K}}^{\text{trans}}·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\mathrm{p}}({\mathrm{t}}^{\prime })·{\mathrm{e}}^{-{\mathrm{k}}_{\text{ep}}·(\mathrm{t}-{\mathrm{t}}^{\prime })}\mathrm{d}{\mathrm{t}}^{\prime }$$ (2)

Equation (2) is non-linear in the parameters, and requires a non-linear fitting routine to estimate K and k_ep. We have named this method the Non-linear Tofts Model (NTM). Non-linear fitting methods are very sensitive to low SNR, while linear fitting methods are more robust and significantly faster. Murase addressed these issues by developing a linear approximation of the NTM, and we have named this method the Linear Tofts Model (LTM; Eq. [3]) [26].

$${\mathrm{C}}_{\text{TOI}}(\mathrm{t})={\mathrm{K}}^{\text{trans}}·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\mathrm{p}}({\mathrm{t}}^{\prime })\mathrm{d}{\mathrm{t}}^{\prime }-{\mathrm{k}}_{\text{ep}}·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\text{TOI}}({\mathrm{t}}^{\prime })\mathrm{d}{\mathrm{t}}^{\prime }$$ (3)

Experimentally measuring C_p(t) is challenging, which is a major limitation for Eq. 2 and Eq. 3. The reference region model (RRM) was introduced to remove the need to measure C_p(t), and instead uses a reference region (RR) as surrogate for C_p(t) (Eq. [4]) [22].

$${\mathrm{C}}_{\text{TOI}}(\mathrm{t})=\frac{{\mathrm{K}}^{\text{trans},\text{TOI}}}{{\mathrm{K}}^{\text{trans},\text{RR}}}·{\mathrm{C}}_{\text{RR}}(\mathrm{t})+\frac{{\mathrm{K}}^{\text{trans},\text{TOI}}}{{\mathrm{K}}^{\text{trans},\text{RR}}}·[{\mathrm{k}}_{\text{ep},\text{RR}}-{\mathrm{k}}_{\text{ep.TOI}}]·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\text{RR}}({\mathrm{t}}^{\prime })·{\mathrm{e}}^{-{\mathrm{k}}_{\text{ep},\text{TOI}}·(\mathrm{t}-{\mathrm{t}}^{\prime })}\mathrm{d}{\mathrm{t}}^{\prime }$$ (4a)

$${\mathrm{C}}_{\text{TOI}}(\mathrm{t})={\mathrm{R}}^{\text{Ktrans}}·{\mathrm{C}}_{\text{RR}}(\mathrm{t})+{\mathrm{R}}^{\text{Ktrans}}·[{\mathrm{k}}_{\text{ep},\text{RR}}-{\mathrm{k}}_{\text{ep.TOI}}]·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\text{RR}}({\mathrm{t}}^{\prime })·{\mathrm{e}}^{-{\mathrm{k}}_{\text{ep},\text{TOI}}·(\mathrm{t}-{\mathrm{t}}^{\prime })}\mathrm{d}{\mathrm{t}}^{\prime }$$ (4b)

C_TOI(t) and C_RR(t) are the concentrations of the CA at time t in the TOI and RR respectively. K and K are the transfer constants between plasma and the extravascular extracellular space (EES) of the TOI and the RR respectively. R = K/K, k_ep,RR and k_ep,TOI are the transfer rates (min) from the TOI and RR back to the plasma. Estimating R, k_ep,RR and k_ep,TOI using Eq. 4 requires a nonlinear fitting method. Thus, we have named Eq. 4 the Non-linear RRM (NRRM). We obtained a linear solution to the RRM, and demonstrated that the Linear RRM (LRRM) is more robust than NRRM to low SNR and low temporal resolution (Eq. 5) [24].

$${\mathrm{C}}_{\text{TOI}}(\mathrm{t})={\mathrm{R}}^{\text{Ktrans}}·{\mathrm{C}}_{\text{RR}}(\mathrm{t})+\frac{{\mathrm{K}}^{\text{trans},\text{TOI}}}{v_{e,RR}}·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\text{RR}}({\mathrm{t}}^{\prime })\mathrm{d}{\mathrm{t}}^{\prime }-k_{ep,\mathit{TOI}}·{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\text{TOI}}({\mathrm{t}}^{\prime })\mathrm{d}{\mathrm{t}}^{\prime }$$ (5)

The same definitions used for Eq. 4 apply to Eq. 5. v_e,RR is the fractional volume of the extravascular extracellular space. The goal of our study was to determine how the model used in DCE-MRI analysis affects the repeatability of DCE-MRI.

2.2 Simulations

Thirty simulated tumor enhancement curves were created using K and v_e values that were randomly selected from a normal distribution (Figure 1). The mean K was set to 0.25 min with a standard deviation of 0.1, and the mean v_e was set to 0.4 with a standard deviation of 0.1. A single muscle reference region enhancement curve was created for all subsequent analyses using a K of 0.1 min and a v_e of 0.1. These values represented reasonable values for tumor and muscle tissues from previous reports [30]. All curves were simulated using Eq. 2, and C_p(t) was simulated using (Eq. 6):

$${\mathrm{C}}_{\mathrm{p}}(\mathrm{t})=\mathrm{A}·\mathrm{t}·e^{-t·C}+\mathrm{D}·(1-e^{-t·E})·e^{-t·F}$$ (6)

where A = 30 mM/min, C = 4.0 min, D = 0.65 mM, E = 5.0 min, and F = 0.04 min. This set of parameters simulated an AIF with an injection speed of 0.005 mL/sec, which is similar to a previously reported AIF [31].

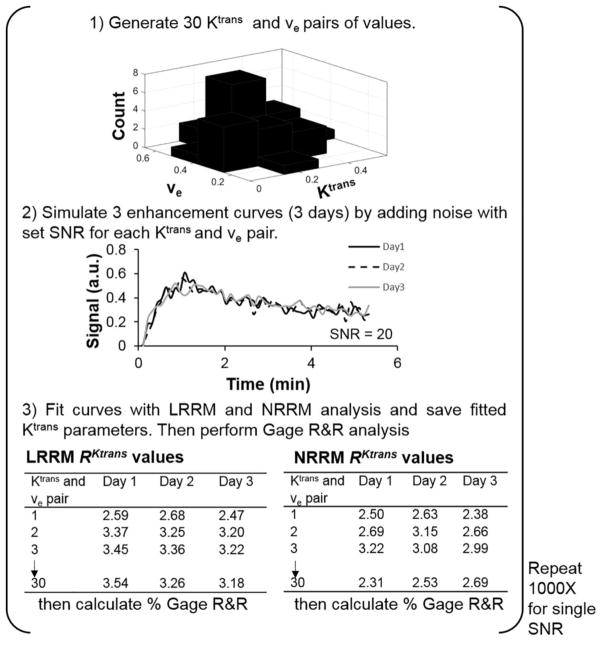
Figure 1.

A diagram of the steps to produce simulated Gage R&R percentage plots. 1) 30 Kand v_e values were generated from a normal distribution. K mean = 0.25 and standard deviation = 0.1. v_e mean = 0.4 and standard deviation = 0.1. The Kand v_e values were paired and the Tofts model was used to simulate 30 enhancement curves. To simulate how DCE MRI data from a single mouse could fluctuate over 3 days, 2) white Gaussian noise (SNR = 20 in this example) was added to an individual enhancement curve 3 times. 3) Each curve with noise was fit by NRRM, LRRM, LTM, and NTM analysis and the fitted Rand K values were stored in their respective tables. This process was repeated for all 30 enhancement curves. After, Gage R&R analysis was conducted and the percent variance (repeatability) value was stored. Steps 1–3 were repeated 1000 times using the same SNR, and the percent variance values were stored each time. After, the median value of the 1000 % variance values generated was taken as the true % variance for the particular SNR.

To simulate potential changes in enhancement curves under the experimental conditions used in this study, white Gaussian noise was added to each of the 30 simulated enhancement curves 3 separate times at the same SNR. White Gaussian noise was also added to a simulated muscle reference region enhancement curve. SNR was defined as the ratio of the signal power over the noise power in decibels.

The R value for each of the 30 curves was estimated using LRRM without a non-negative constraint; LRRM with a non-negative constraint; and NRRM with a non-negative constraint. For NRRM, initial guesses for R were obtained from a gamma distribution with coefficient a = 1.40 and b = 0.56, which corresponds to reasonable values from previous reports. We also estimated values with NRRM using a non-negative constraint and initial guesses for R, k_ep,TOI, and k_ep,RR taken from the estimates from LRRM with a non-negative constraint, which we labeled as NRRM*. Additionally, we determined the rate of transfer from tissue to blood in the tissue of interest (k_ep,TOI), and the rate of transfer from tissue to blood in the reference region (k_ep,RR).

Gage Repeatability and Reproducibility (R&R) analysis (described below) was performed to measure the repeatability of the R values determined using LRRM with and without a non-negative constraint, NRRM and NRRM* by calculating the percent intra-group variances due to the fitting method. These three values were stored and the process starting from the addition of white Gaussian noise was repeated 1000 times. The median Gage R&R percent variance values from the 1000 values generated for each of the three fitting methods were taken as the true Gage R&R percent variance values for that SNR. The process was repeated for SNR values ranging from 5 to 40. Quantitative LTM and NTM analyses and semi-quantitative analyses were also performed in the same manner.

2.3 In vivo study

2.3.1 Animal model and DCE-MRI acquisition

Twelve rats were injected subcutaneously with rat glioma cells and subsequently prepared for imaging [21]. DCE-MRI acquisition was performed on 3 consecutive days. The basics of the DCE-MRI acquisition protocol were as follows: 8 axial images were acquired using a 10 msec repetition time (TR), 1.7 msec echo time (TE), 15 excitation pulse, 16 mm slab thickness (8 slices each 2 mm thick), 469 x 625 μm in-plane resolution, 128 x 80 matrix size, 60 x 50 mm field of view, 50 repetitions, temporal resolution = 6.4 sec, and 1 average. A more detailed description of the MRI protocol is provided in reference 21. Two of the twelve rats had technical scanning failures on 1 of the 3 days of imaging. Data from these 2 rats were excluded from analysis.

2.3.2 Image analysis

A quantitative T₁ map was not obtained in this study. Therefore, we used the signal enhancement ratio (SER, Eq. 7) to replace contrast agent concentration for quantitative DCE-MRI analysis.

$$\text{SER}(\mathrm{t})=\frac{S_t-S_o}{S_o}$$ (7)

SER(t) is the SER at time t, St is the MR signal at time t, and S_o is the signal before injection of the CA (t=0).

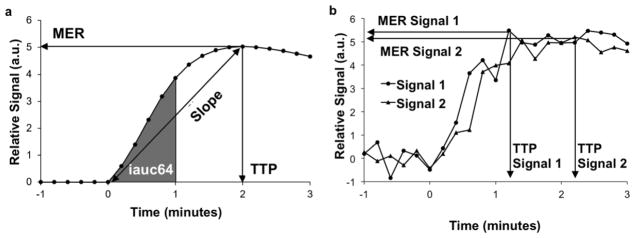
The following semi-quantitative metrics were used in this work: a) maximum enhancement ratio (MER), b) time to peak (TTP), c) initial area under the curve (iauc64), and d) slope (Fig. 2). The MER was defined as the maximum of each SER(t) curve. The TTP was determined by subtracting the time at the final baseline time point (10 image) from the time of the MER. iacu64 was determined from the area under the curve from the first post-baseline time point (11 image) to the time point acquired 64 seconds post-baseline (20 image). The slope was determined by dividing MER by TTP.

Figure 2.

Semi-quantitative analyses. a) Mean Enhancement Ratio (MER) is the maximum of the curve, Time To Peak (TTP) is the time from the last baseline image (0 minutes) to the time at the maximum (2.0 minutes), slope is MER divided by TTP, and iauc64 is the area under the curve from the last baseline image to 64 seconds post-baseline (shaded area). b) TTP is affected by noise more than MER.

As mentioned earlier, the NTM and NRRM require a non-linear fitting algorithm and an initial guess to estimate their respective PK parameters. An initial guess of K = 0.5 and k_ep,TOI = 5.0 were used for the NTM, while the following initial guesses were used for the NRRM: R= 2.0, k_ep,TOI = 5.0, and k_ep,RR = 5.0. The MATLAB function lsqcurvefit was used for all non-linear fittings, while constraining all possible solutions between 0 and 10. The function tolerance was set to 1 x 10 and the maximum number of iterations was set to 100,000. Estimates for the linear methods were obtained with and without a constraint of greater than or equal to zero. This was accomplished using non-negative least squares as implemented in the MATLAB function lsqnonneg. Finally, we studied the effect of using the parameters estimated with the LTM as the initial guesses for the NTM (NTM*), and the parameters estimated by the LRRM as the initial guesses for the NRRM (NRRM*).

Our quantitative analysis of experimental DCE-MRI data using the NTM (Eq. 2) and LTM (Eq. 3) assumed a population-based averaged AIF, which was derived from the AIFs for individual rats in reference 21 (Eq. 8). The fitting for the NRRM and LRRM used muscle as a surrogate for the AIF.

$${\mathrm{C}}_{\mathrm{p}}(\mathrm{t})=0.64·e^{-0.033·t}+0.42·e^{-0.0010·t}$$ (8)

To analyze the average signal of the tumor, a region of interest (ROI) for each tumor and muscle were drawn by a single observer (KMJ) on slices 4, 5, and 6 of the 8 slices imaged for each rat. The three slices chosen showed the largest tumor volume. The same ROIs for any given rat were used for LTM, NTM, LRRM and NRRM analyses. For each rat, the average intensity of the whole tumor ROI and muscle reference region ROI from all time points were used to generate the enhancement curve that was fit with LRRM and NRRM analyses. The average signal intensity of the population AIF was used for the LTM and NTM analyses.

For pixelwise analyses, each pixel within the ROI chosen for the tumor region was used to compute R, k_ep,TOI, and k_ep,RR. A single enhancement curve for the muscle reference region, generated by taking the average signal value of the whole muscle reference region ROI from all time points, was used for all tumor pixelwise analyses. Based on the SNR of these data sets, pixels within the tumor ROI that showed less than 10% enhancement were excluded from analysis. This exclusion criterion was also used in a previous study that used this data [21]. Additionally, pixels that showed poor fits based on the R value were excluded from analysis. A range of R values from 0 – 0.9 were used as the cutoff point to ensure that comparisons between LRRM and NRRM were not affected by the selected R cutoff point. After removing the pixels with poor fits, the median value of the remaining pixels was determined for R, k_ep,TOI, and k_ep,RR.

2.4 Statistical Analysis

A summary of the parameter values generated from quantitative and semi-quantitative DCE-MRI analyses were provided in the form of mean, range, and within-subject coefficient of variation (wSCV). The values were taken on a global scale meaning that values from all rats over each of the three time points were included in the calculation. The wSCV was calculated as follows: 1) the base-10 logarithm was applied to estimated quantitative and semi-quantitative descriptors, 2) the within-subject variance (variance for each row) was calculated, 3) the mean within-subject standard deviation (wSD) was calculated by taking the square root of the within-subject variance, 4) wSCV= antilog(wSD)-1 [32, 33]. The medians of the estimates of the parameters R and k_ep,TOI, as determined by the methods LRRM and NRRM, were compared using a t-test, with the significance set to the 95% confidence level.

The Gage R&R methodology was initially developed to determine the sources of variation in a manufacturing system [34]. Gage R&R analysis uses ANOVA to determine the percent of the observed variation in a system that is due to the parts (process), measurement protocol (repeatability), and the operator (reproducibility). This analysis method is often performed to test variations between multiple operators who are measuring a characteristic of multiple parts with one measurement protocol. In this study, we compared different measurement protocols rather than comparing different operators. One researcher (one operator) analyzed DCE-MRI data from multiple rats (multiple parts) to determine the repeatability of fitting algorithms used for the analysis of DCE-MRI data (multiple measuring protocols). Each fitting algorithm was assigned a unique measurement protocol identification and each rat was assigned a unique part identification for Gage R&R analysis. The measured percent variance (iSV) represented the variance in the fitting method compared to the total variation. This analysis was performed for both the simulations and the experimental data. The Gage R&R methodology was implemented using the gagerr function in Matlab R2015a [28].

3. RESULTS

3.1 Simulations

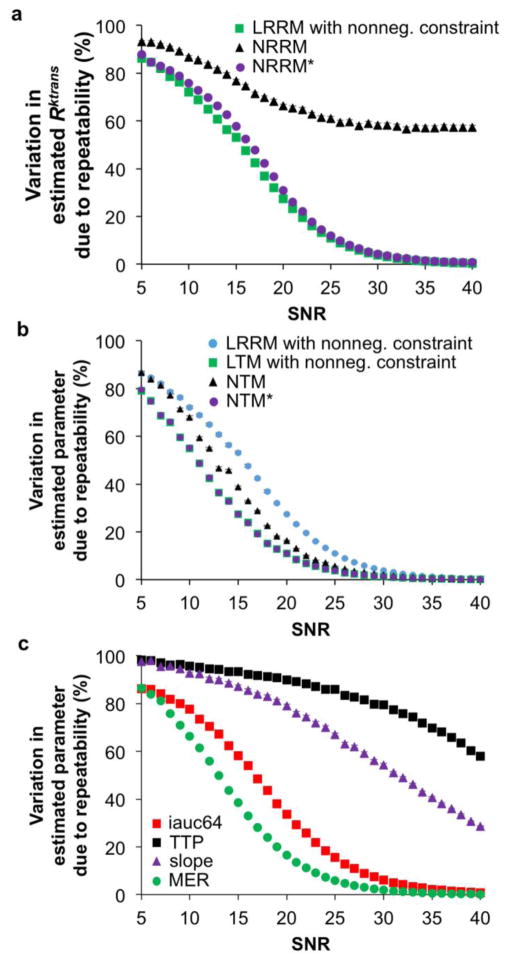
A total of 3.15 million simulated enhancement curves were generated. These curves were subsequently analyzed with quantitative and semi-quantitative methods, and then with Gage R&R analysis. The use of 30 enhancement curves was sufficient for convergence as evidenced by the tight confidence intervals in the Gage R&R plots (Fig. 3). The median percent variance due to repeatability was obtained from the 1000 Gage R&R analyses performed at each SNR. The median percent variance value and its corresponding 95% confidence interval were evaluated over the range of SNRs tested from each DCE-MRI fitting method. Comparisons between LRRM with and without non-negative constraints showed no difference in percent variance over the range of SNRs tested (data not shown). Thus, LRRM with a non-negative constraint was compared with NRRM, which also had a non-negative constraint, to avoid erroneous negative R, k_ep,TOI, and k_ep,RR values from being generated.

Figure 3.

Dependence of Gage R&R on signal-to-noise. The median Gage R&R percent of the 1000 repetitions (described in Figure 1) is displayed for each SNR tested for a) quantitative reference region analyses, b) semi-quantitative analyses, and c) quantitative Tofts analyses with the LRRM added as a reference. The LRRM analysis without and with a non-negative constraint produced almost identical Gage R&R percentages. Also note that the 95% CIs were smaller than the marker size for most plots.

LRRM showed a significantly lower Gage R&R percent variance compared to NRRM at all SNRs tested (Fig. 3a). A significant difference was defined as non-overlapping 95% confidence intervals. Interestingly, when repeating the analysis with NRRM* (NRRM initialized using LRRM-derived coefficients as the initial guess), the Gage R&R percent variance values were similar between LRRM and NRRM*. This result emphasizes that the repeatability of R estimated via the NRRM is highly dependent on a proper initial guess. LTM showed a significantly lower Gage R&R percent variance compared to NTM and LRRM at low SNRs (Fig. 3b). The significant difference between LTM and NTM at low SNRs further emphasizes that linearizing a model improves repeatability. Additionally, when repeating analysis with NTM* (NTM initialized using LTM-derived coefficients as initial guesses), the Gage R&R percent variance values were similar between LTM and NTM, which was observed with LRRM and NRRM as well. The analysis of semi-quantitative descriptors showed the best repeatability measurements with iauc64 and MER (Fig. 3c). The variability of these two descriptors was significantly lower than the variability of the slope and TTP at all SNRs, and similar to the variability of R values estimated via the LRRM and NRRM*. The Gage R&R value of the slope was significantly lower than TTP at all SNRs and similar to the variability of NRRM with a random initial guess at mid-range SNRs.

3.2 In vivo Results

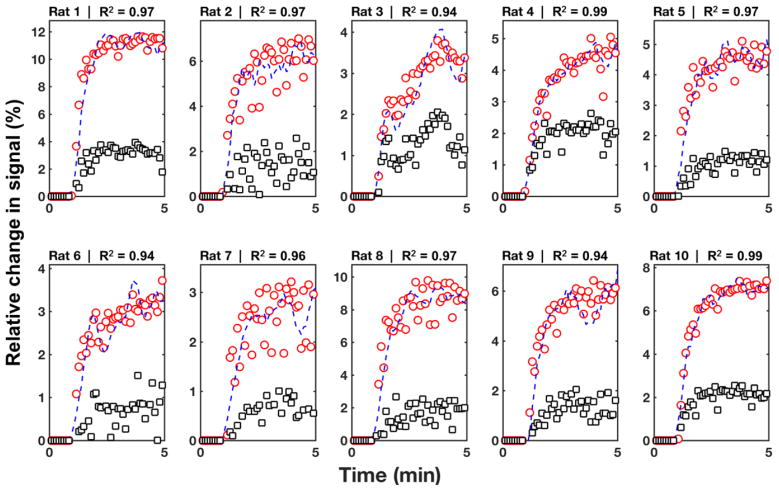
Fitting in vivo results with the LRRM correctly described the PK of the agent in the tumor, as demonstrated by an excellent goodness-of-fit between the fit and the experimental results (R ≥ 0.94; Fig. 4). The semi-quantitative measurements, LTM, and LRRM measurements showed lower wSCVs than the NRRM measurements (Table 1). Notably, the wSCVs of R measurements were lower with LRRM vs. NRRM in pixelwise analysis. The wSCVs of R measurements were also lower with NRRM* vs. NRRM in pixelwise analysis. The R values from all rats at all time points were significantly higher with LRRM compared to NRRM in pixelwise analysis (p<0.01) and ROI analyses (p<0.01). Also, k_ep,TOI values were significantly lower with LRRM compared to NRRM in both pixelwise analysis (p<0.01) and ROI analysis (p < 0.01). Similarly, the R values were significantly higher with NRRM* compared to NRRM in pixelwise analysis (p = 0.04) and the k_ep,TOI values were significantly lower with NRRM* compared to NRRM in pixelwise analysis (p < 0.01).

Figure 4.

Representative example of the performance of the LRRM on experimental data for all rats on Day 2. Circles represent the observed signal for the tumor; squares represent the observed signal for the reference region (RR); dash lines represent the predicted signal for the tumor. The LRRM showed an excellent goodness-of-fit metric as measured by the R value for all rats.

Table 1.

Results of DCE MRI Analyses

Model	Parameter	ROI			Pixel
		Mean	IQR	wSCV	Mean	IQR	wSCV
Quantitative Parameters (Reference Region)
LRRM	RKtrans	2.57	1.86–3.23	0.41	2.40	1.67–3.16	0.40
	kep,TOI	0.11	0.01–0.73	0.74	0.03	0.0–0.04	0.68
NRRM	RKtrans	1.52	1.02–2.61	0.97	1.99	1.13–2.97	0.92
	kep,TOI	1.03	0.62–1.47	0.91	1.33	0.81–1.55	0.73
NRRM*	RKtrans	1.24	0.73–1.68	0.74	1.99	1.13–2.97	0.63
	kep,TOI	0.45	0.12–0.71	0.61	0.30	0.07–0.43	0.53
Quantitative Parameters (Tofts Model)
LTM	Ktrans	0.25	0.03–0.34	0.43	0.22	0.09–0.24	0.66
	kep,TOI	0.85	0.64–1.10	0.37	0.90	0.73–1.05	0.21
NTM	Ktrans	0.16	0.09–0.24	0.57	0.18	0.17–0.21	0.20
	kep,TOI	7.64	6.89–8.04	0.19	8.20	8.67–9.48	0.45
NTM*	Ktrans	0.08	0.05–0.11	0.43	0.05	0.04–0.05	0.27
	kep,TOI	1.87	1.04–2.32	0.26	2.21	1.59–2.83	0.29
Semi-Quantitative Parameters
	MER	5.93	4.56 – 8.22	0.44	7.46	6.22 – 8.81	0.25
	TTP	3.79	3.20 – 4.05	0.15	3.09	2.99 – 3.20	0.07
	iauc64	0.21	0.15 – 0.29	0.48	0.22	0.18 – 0.26	0.29
	slope	1.56	1.31 – 2.60	0.41	2.46	2.13 – 2.82	0.27

LRRM = linear reference region model

NRRM = nonlinear reference region model with set initial guess

NRRM* = nonlinear reference region model with initial guess from LRRM estimates

LTM = linear tofts model

NTM = nonlinear tofts model with set initial guess

NTM* = nonlinear tofts model with initial guess from LTM estimates

MER = mean enhancement ratio, TTP = time to peak, iauc64 = initial area under the curve

IQR: inter-quartile range

wSCV: within subject coefficient of variation. Bounds: 95% lower and upper confidence intervals

Interestingly, the R and the k_ep,TOI values from analyzing ROIs were similar when NRRM* and NRRM were used. This was also seen in the K and the k_ep,TOI values when analyzing ROIs with NTM* and NTM. Therefore data with high SNR produced the same estimates for the quantitative metrics regardless of the initial guess. Conversely, analysis of pixelwise data showed different R and k_ep,TOI values when NRRM* and NRRM were used, while the use of NRRM* and LRRM estimated similar values. This similarity is based on median values produced by LRRM and NRRM*. This result suggests that data with low SNR requires a good initial guess to obtain a good analysis with the NRRM method.

For Gage R&R analysis of the experimental DCE-MRI study, a single percent variance value was generated for the dataset for each of the quantitative and semi-quantitative methods and these values were compared to each other (Table 2). A student’s t-test could not be performed to test for statistical significance because only a single value could be measured with Gage R&R analysis for the quantitative and semi-quantitative methods.

Table 2.

Summary of Gage R&R Percent Variances (%)

	Pixelwise Analysis	ROI Analysis
Reference Region Model
LRRM	45.1	65.7
NRRM	78.3	93.5
NRRM*	53.3	86.7
Tofts Model
LTM	59.5	62.4
NTM	86.9	84.3
NTM*	62.7	71.8
Semi-quantitative
MER	46.1	65.5
Slope	50.9	48.2
TTP	88.7	100
Iauc64	46.5	66.4

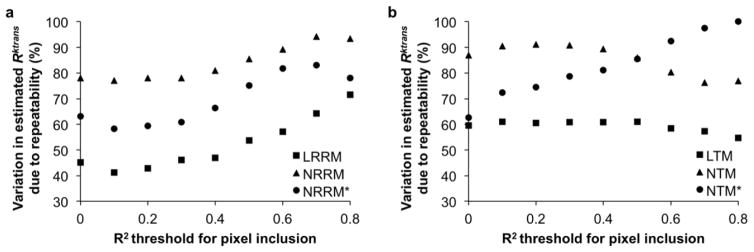
For analyses of in vivo results, the median Gage R&R percent variance value was lower with LRRM compared to NRRM and lower with LTM compared to NTM in both pixelwise and ROI analysis. This difference held true for all thresholds set for pixel inclusion based on the R of the fit (Figs. 5a and 5b). An R value of 0.9 was not chosen as a threshold because of the high number of pixels that were discarded when doing so. The median Gage R&R percent variance value was lower with NRRM* compared to NRRM and NTM* compared to NTM for pixelwise analysis but similar for ROI analysis, which matched with wSCV results. The Gage R&R percent variance value for R with LRRM was similar to percent variance values for LTM, MER, slope, and iauc64 in both pixelwise and ROI analysis (Table 2). The Gage R&R percent variance values for R with NRRM, NTM, and TTP were similar, and were also higher than all other Gage R&R percent variance values in both pixelwise and ROI analysis. We attribute the lower repeatability of TTP to the stronger dependence of TTP on image noise relative to the dependence of MER and iauc64 on image noise (Fig. 2b).

Figure 5.

In vivo pixelwise percent Gage R&R plots. a) LRRM, NRRM, and NRRM* and b) LTM, NTM, and NTM* Gage R&R percent variances by pixelwise analysis as a function of the R correlation coefficient of the fit. Pixels that had R coefficients less than the threshold were excluded from analysis.

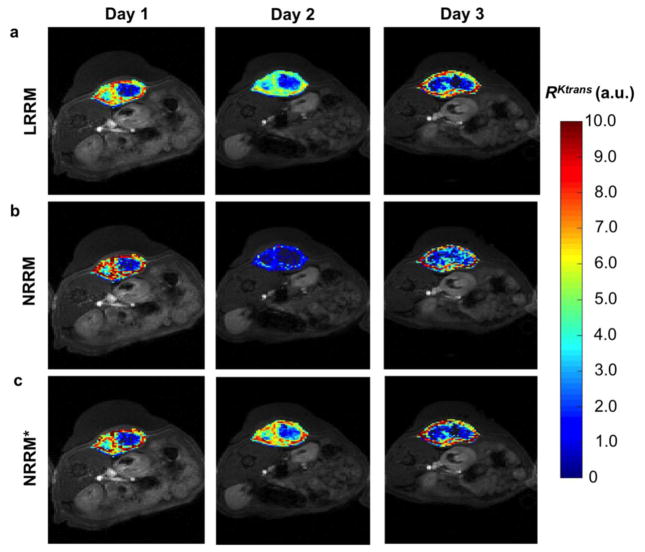
R pixelwise maps from a representative rat over the three days of DCE-MRI showed the distribution of R values with LRRM, NRRM, and NRRM* (Fig. 6). The median R values from the maps for days 1, 2, and 3 were 3.44, 3.08, and 3.16 min respectively for LRRM; 3.52, 1.26, and 3.17 min respectively for NRRM; and 3.51, 2.89, and 2.97 min respectively for NRRM*. These results indicated a larger variability with NRRM as compared to LRRM and NRRM* in measuring R over multiple days. Additionally, the pixelwise distributions for NRRM had larger standard deviations and were more highly skewed than the pixelwise distributions with LRRM. For the rat shown in Fig. 6, the standard deviations of the pixels for days 1, 2, and 3 were 2.0, 2.16, and 2.63 respectively for LRRM; 2.50, 0.84, and 2.97 respectively for NRRM; and 2.22, 1.87, and 2.31 respectively for NRRM*.

Figure 6.

R parametric maps. a) LRRM b) NRRM and c) NRRM* R parametric maps of an individual rat imaged on three consecutive days.

4. DISCUSSION

The results of this study support our hypothesis that linearization can be used to improve the repeatability of the reference region model for DCE-MRI, making quantitative DCE-MRI as repeatable as LTM and semi-quantitative DCE-MRI. Our Gage R&R analyses of simulations showed that a lower percentage of the variability in the measurement system is due to the algorithm when the LRRM is used instead of the NRRM, regardless of the SNR of the DCE-MRI data. This result was consistent with previous reports that concluded that linearization improves the accuracy of the Tofts and reference region models for DCE-MRI [24, 26]. In addition, our experimental results showed lower wSCV and iSV values for R with LRRM compared to NRRM, for pixelwise analyses. This improved repeatability was also evident in the pixelwise parametric maps of R. The improvement in the repeatability of the pixelwise analyses with LRRM indicated that LRRM is especially useful under conditions of lower SNR. We believe our work is a useful contribution to the understanding of the repeatability and reproducibility of quantitative DCE-MRI with variations of the Tofts model and the reference region model [32, 35–38].

The accuracy and precision of the algorithms most commonly used for non-linear curve fitting of DCE data are highly dependent on the initial guess of the true values of K and k_ep (R for the RRM) [24, 26, 36]. This long-standing issue in quantitative DCE-MRI is often ignored, causing the results of quantitative DCE-MRI to be highly variable if the wrong initial guess is used. As evidence, we demonstrated that the repeatability of NRRM and NTM approached the repeatability of LRRM and LTM if the results of LRRM and LTM were used as the initial guess for NRRM (NRRM*) and NTM (NTM*). Also, the median value and interquartile range of R determined using NRRM* was similar to values determined using LRRM for pixelwise analyses. This result indicated that an “ideal” initial guess can overcome the variability of NRRM analysis induced by image noise. However, it is fundamentally impossible to know the “ideal” initial guess for each pixel in practice, and therefore the quality of NRRM analysis is fundamentally limited under practical conditions. To address this fundamental problem of the “ideal” initial guess, each voxel could be fit with a non-linear algorithm multiple times using different initial guesses [36]. However, hundreds-to-thousands of initial guesses may be needed to properly evaluate this issue of the “ideal” initial guess. Therefore this approach is computationally impractical for pixelwise analyses, and the improvement in the analysis does not scale linearly with the number of initial guesses. Our LRRM completely avoids this fundamental problem because our methods use a linear regression that does not require an initial guess [24, 26].

A recently published study concluded that the linear compartmental tissue uptake model (similar to the Tofts model) is less robust to low SNR than its nonlinear equivalent, which would seem to contradict our study [39]. However, this previous study used the initial values used to simulate data as the initial guesses for the non-linear fitting routines. An “ideal” initial guess is only available during simulation studies such as this recently published study, and an “ideal” initial guess is fundamentally impossible to obtain during practical experiments. Thus, the LRRM is a superior approach for analyzing DCE-MRI data as compared to NRRM.

The repeatability of R estimated with the LRRM was comparable to the repeatability of LTM, MER and iauc64 measurements, as shown by Gage R&R analyses of simulated and experimental data. A previous study showed that MER and iauc64 measurements have good reproducibility [35], which suggests that LRRM also has good reproducibility (where repeatability tests measurements under the same conditions, and reproducibility tests measurements under different conditions). TTP measurements, R estimated with the NRRM, and K estimated with the NTM showed the lowest repeatability, which was attributed to the stronger sensitivity to noise for these measurements.

The wSCV for R determined by the LRRM in our study is in good agreement with the wSCV (~0.40) for R reported in previous repeatability studies of the reference region model [35, 38]. The data analyzed in our study were acquired at lower temporal resolution than the previous repeatability studies. The wSCV for R determined by the NRRM showed that the NRRM was only half as repeatable relative to results from these previous reports. Therefore, linearization improves the repeatability of the RRM under conditions of slower temporal resolution, which are often encountered in clinical studies [38, 40]. This result regarding temporal resolution complements previous studies that have shown how LRRM can estimate accurate R values at temporal sampling rates as slow as 60 seconds [24], while NRRM requires temporal sampling rates less than 32.0 seconds to estimate accurate R values [39], and the Tofts model requires a temporal sampling rate of 5.0 seconds or faster [15, 16]. Furthermore, these previous studies showed that NRRM underestimates R and overestimates k_ep,TOI especially with low SNR, which matched the results of our study. In these previous studies, the calculation speed of LRRM was shown to be 1350–8200 times faster than NRRM (depending on the SNR) [24].

Our results also demonstrate the benefits of using Gage R&R analysis as a means to compare repeatability between different MRI analysis methods. Gage R&R analysis calculates the percentage of variation due to the measurement source compared to the total variation, and thus is not subject to the scale of the DCE-MRI parameter being measured. For comparison, wSCV is subject to the scale of the DCE-MRI parameter, and thus wSCV is inherently smaller for DCE-MRI parameters that have a small absolute value like TTP, compared to larger DCE-MRI parameters like MER. In our experimental results, wSCV values for TTP compared to MER were lower, while Gage R&R analyses clearly showed better repeatability measurements for MER compared to TTP, for both pixelwise and ROI analysis, during simulations and experimental analyses.

Despite the promising results presented in this work, three limitations still remain. First, the Gage R&R method assumes that the biologic variability of the tumors were zero over the three time points. However, the tumors inevitably changed in size and possibly in perfusion characteristics over the three time points. Therefore, the fitting method variability and the day-today variability could be confounded in the estimation of iSV. Unfortunately, performing repeat scans 24 hours apart was the shortest timeframe allowed by the IACUC. Second, we used the change in MR signal to represent the change in concentration in the tumor and reference region during our DCE-MRI analyses. However, the MR signal has a non-linear relationship with CA concentration, which could lead to erroneous estimations of the absolute values of PK constants. Our study focused on the repeatability of measuring the estimated PK constants, which pertains to precision rather than accuracy, thus this potential pitfall should not significantly affect the conclusions of our study. Also, the relationship between MR signal and concentration becomes more linear at lower, clinically-relevant magnetic fields. To test this potential pitfall, a future DCE-MRI clinical study can be performed at ≤ 3T magnetic field strength with the acquisition of T₁ parametric maps before injection of the Gd-based CA.

5. CONCLUSION

In conclusion, this report introduces the Gage R&R analysis as a convenient method to determine the repeatability of DCE-MRI, while also demonstrating that linearization increase the repeatability of the Tofts and reference region models for DCE-MRI by approximately 40%.