Characteristic Impedance: Frequency or time domain approach?

Abstract

Characteristic impedance (Zc) is an important component in the theory of hemodynamics. It is a commonly used metric of proximal arterial stiffness and pulse wave velocity. Calculated using simultaneously measured dynamic pressure and flow data, estimates of characteristic impedance can be obtained using methods based on frequency or time domain analysis. Applications of these methods under different physiological and pathological conditions in species with different body sizes and heart rates show that the two approaches do not always agree. Considering the interpretation and role of Zc as an important hemodynamic parameter, we have investigated the discrepancies between frequency and time domain estimates accounting for uncertainties associated with experimental processes and physiological conditions. We have used published data measured in different species including humans, dogs, and mice to investigate: (a) the effects of time delay and signal noise in the pressure-flow data, (b) uncertainties about the blood flow conditions, (c) periodicity of the cardiac cycle versus the breathing cycle, on the frequency and time domain estimates of Zc, and (d) if discrepancies observed under different hemodynamic conditions can be eliminated. We have shown that the frequency and time domain estimates are not equally sensitive to certain characteristics of hemodynamic signals including phase lag between pressure and flow, signal to noise ratio and the end of systole retrograde flow. The discrepancies between two types of estimates are inherent due to their intrinsically different mathematical expressions and therefore it is impossible to define a criterion to resolve such discrepancies. We propose that the frequency and time domain estimates of Zc should be further assessed as two different hemodynamic parameters in a future study.

1. Introduction

Analyses of vascular impedance provides insight into arterial structure and function. It is, intrinsically, a frequency domain quantity that characterizes the opposition to pulsatile flow by quantifying the level of dissipation and storage of hydraulic energy. Impedance can be separated into four components including: input, longitudinal, transverse and characteristic impedance (Milnor 1989).

Input impedance (Z) is defined as the ratio of pressure to flow harmonics. Assuming that the cardiovascular system is operating in a periodic steady state, i.e. the pulse waves start and end at the same point, Z can be obtained by frequency analysis of simultaneous pressure (p(t)) and flow (q(t)) over a single or multiple heartbeats. The resulting complex spectrum can be expressed as moduli and phase over a range of frequencies and provides information about local and downstream vascular properties and wave reflections. Longitudinal impedance is defined as the ratio of the longitudinal pressure gradient to the flow and the transverse impedance is defined as the ratio of the pressure to the longitudinal flow gradient, both computed in the frequency domain under the aforementioned assumptions for the input impedance. These two impedances quantify resistive and elastic properties of the blood vessels, which are determined by physical properties of the blood and vessels including kinematic viscosity of the blood, vascular dimensions, thickness and elasticity of the arterial walls. Finally, the characteristic impedance (Zc) is defined as the ratio of harmonics of the incident pressure to the incident flow. It can be quantified by the input impedance in the absence of wave reflections. Since wave reflections carry information about the distal vasculature, their exclusion makes Zc a local vessel parameter, which remains independent of the heart rate (HR) as well as properties of the downstream vascular beds.

Using linearized theory, one can show that the characteristic impedance can be computed as a function of the product of longitudinal and transverse impedances (Milnor 1989, Nichols et al 2011). The theoretical result show that Zc varies directly with the elastic modulus of the vessel wall and inversely with its diameter, i.e. the stiffer the vessel and smaller its diameter, the higher the value of Zc. This property alone makes Zc an important physiomarker. However, wave reflections are always present in real arterial networks due the their branching nature and spatially varying elastic properties. Therefore, in practice, a straight forward computation of Zc from measured hemodynamic data is not possible. Consequently, Zc has to be inferred, either from the input impedance spectrum at high frequencies where reflections have less impact (Nichols et al 2011, Milnor 1989) or from pressure and flow data measured during early ejection phase before the reflected waves have returned to the point of measurement (Dujardin et al 1980). Under assumptions of dominant inertial and weak viscous forces as well as linear elastic wall properties, the two approaches can only give an approximation of true characteristic impedance.

Characteristic impedance is an important parameter in the theory of hemodynamics. In fact most applications analyzing input impedance involve approximation of the characteristic impedance to assess the behavior of arterial stiffness and pulse wave velocity (Hughes & Parker 2009, Borlotti et al 2014, Zuckerman 1985). The results of these studies have also been used to quantify the effects of different interventions, drugs, and disease on pulsatile hemodynamics and arterial stiffness (Bak et al 2007, Mitchell 2009, Mitchell et al 2011, Li & Andrew 2012, Zuckerman 1985). In view of this, many investigators have introduced methods in the in the time and frequency domain to approximate the characteristic impedance using experimental data from a range of species under different hemodynamic conditions, (e.g. Nichols et al 2011, Milnor et al 1969, Dujardin & Stone 1981, Lucas et al 1988). Below we provide a brief review of frequency and time domain analysis and highlight the advantages and disadvantages of each approach.

1.1. Frequency Domain Analysis

In the frequency domain, Fourier analysis is the most common method for calculating the input impedance spectrum (Nichols et al 1977, Dujardin & Stone 1981, Mitchell et al 1994, Nichols et al 2011, Huez et al 2004, Zuckerman 1985). As shown in Figure 1, given normal pressure and flow waveforms in the aorta and main pulmonary artery (a)–(d), the impedance moduli (e) and (g) fall steeply from zero until a minimum is reached. At this point the impedance moduli increase gradually until reaching a local maximum, after which it continues to oscillate. The critical frequency (f_c) associated with the first minimum is often accompanied by a phase cross-over from negative to positive. After this the phase is expected to stay close to zero. Data, compiled by Milnor (1989, p183), showed that in humans f_c varies between 3.3–4.2 Hz in the aorta and 2.0–4.0 Hz in the pulmonary artery, for dogs f_c varies between 6.0–8.0 Hz in the aorta and 2.0–3.5 Hz in the pulmonary artery, for rabbits the variation ranges from 4.5–9.8 Hz in the aorta to 3.0 Hz in the pulmonary artery, and for rats it was found to be 12.0 Hz in the aorta.

Figure 1.

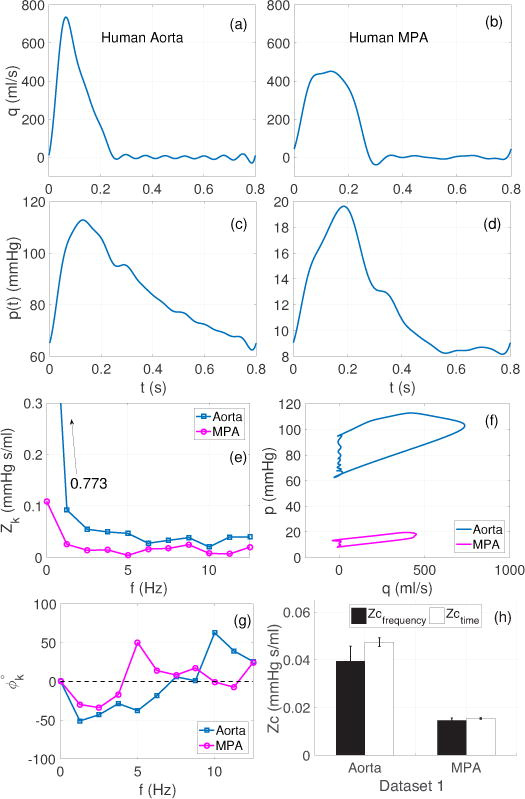
Dataset 1 (Section 2.1): Frequency and time domain analysis using pressure and flow wave forms from the human aorta and main pulmonary artery (MPA). (a)–(d): pressure (left), flow (right). Note the difference in scale between the aortic and MPA pressures. (e) and (g): corresponding impedance moduli and phase spectra, (f): pressure-flow loops, used for estimating Zc with the time domain up-slope methods, (h): comparison of Zc in the aorta and MPA across both domains. The bars show mean ± SD values of Zc, across all the frequency and time domain methods listed in Table 1.

Most frequency domain methods use f_c to determine the frequency band or harmonic range where Zc is estimated by averaging the associated moduli. The argument behind this approach is that after f_c, near zero phase at higher frequencies indicate cancellation of in- and out-of-phase incident and reflected waves and that the associated impedance moduli oscillate around the true value Zc. Therefore averaging the impedance moduli associated with high frequency harmonics yields a reasonable approximation of the true Zc (Milnor 1989). However, a strict application of this approach may yield less accurate estimates due to an asymmetric arrangement of the impedance moduli above and below the true value of Zc. Ideally, the full spectrum, above f_c, should be analyzed, but as Milnor (1989) showed, harmonics above 25 Hz are less reliable due to a low signal to noise ratio (SNR). Therefore, the frequency domain methods rely on determining an appropriated frequency band or the harmonic range that is less susceptible to noise.

As pointed out in (Nichols et al 2011, p307), the determination of frequency band is somewhat arbitrary, but provides reasonably accurate estimates of Zc when applied to data where the first impedance minimum is reached at a low frequency. The estimates are inaccurate and misleading if f_c is well above 2.0 Hz, as observed in small animals like rats. The accuracy of the f_c prediction is relative to the accuracy of the fundamental frequency. Since all frequencies are integer multiples of the fundamental frequency, (heart rate (HR)), a greater HR variability leads to a less accurate fundamental frequency, and hence f_c. This can lead to a shift in the minimum of the impedance moduli and phase cross over. In particular, a higher HR is associated with a less accurate f_c (Milnor 1989). To improve the presumed accuracy of Zc, many investigators do not make the choice on the basis of frequency but on harmonics. This also makes the choice animal-independent (see Table 1 for a partial list of such methods).

Table 1.

Frequency and time domain methods for estimating the characteristic impedance (Zc).

Frequency range	Notation	Reference
2.0 – 12 Hz	Zc(2–12)	Pepine et al (1979)
2.0 – 16 Hz	Zc(2–16)	Lucas et al (1988)
3.5 – 10 Hz	Zc(3.5–10)	Westerhof et al (1973)
5.0 – 15 Hz	Zc(5–15)	Dujardin et al (1980)
9.0 – 18 Hz	Zc(9–18)	Cox & Bagshaw (1975)
15 – 25 Hz	Zc(15–25)	O’Rourke & Taylor (1967)
Harmonics range
1 – 8	Zc1–8	Clarke et al (1978)
1 – 9	Zc1–9	Peluso et al (1978)
2 – 10	Zc2–10	Gary et al (1994)
3 – 10	Zc3–10	Hughes & Parker (2009)
4 – 10	Zc4–10	Tabima et al (2012)
k – 10a	Zck–10	Gary et al (1994)
6 – 8	Zc6–8	Abel (1971)
4 – 8	Zc4–8	This study
Time domain techniques
Early systole up-slopeb	Zcqc	Dujardin & Stone (1981)
max(p′)/max(q′)	Zc′	Lucas et al (1988)

^aHere k is the harmonic corresponding to the first impedance minimum provided that it appears before the 5’th harmonic.

^bq_c varies between 25% and 95%. In this study, q_c = 25%, 50%, 90% and 95%.

1.2. Time Domain Analysis

In 1981, Dujardin & Stone (1981) introduced a time domain method to estimate Zc. This method is also known as the ‘up-slope method’ (Lucas et al 1988). Referring to a parametric graph relating simultaneously measured pressures and flows, they hypothesized that Zc can be estimated from the slope of the pressure-flow loop during the early ejection phase. To test this hypothesis, they carried out experiments under different flow conditions in dog ascending aortas. They found that time domain estimates of Zc are in close agreement with frequency domain estimates under all flow conditions. Subsequently, variations of this approach have been used by several researchers to estimate Zc in the time domain (e.g. Bollache et al 2015, Fourie & Coetzee 1993, Lucas et al 1988).

The up-slope method assume that the initial upstroke during systole is free of reflections, that the pressure and flow are in phase, and that the relation between pressure and flow is linear. The latter can only be established if the flow and pressure waveforms are measured simultaneously at the same location. These assumptions are not easy to verify. In particular, it is difficult to determine if a measured time-lag between a pressure and flow waveform is due to experimental or physiological conditions. Moreover, as discussed by Lucas et al (1985), any portion of the pressure-flow loop may be used in this analysis as long as the reflection free condition is satisfied. However, as discussed earlier, an ideal reflection free condition does not exist in the real system and it is difficult to quantify the contribution of reflections from the linear or nonlinear parts of the pressure-flow relationships.

Both the frequency and time domain approaches have advantages and disadvantages, and both are only valid under specific assumptions. Frequency domain methods may be more difficult to apply, yet there are arguably far more studies carried out analyzing properties of the cardiovascular system in terms of the input impedance spectra (Nichols et al 2011, Milnor et al 1969, Taylor 1966). Not only is the theory of vascular impedance is rooted in the frequency domain, the test of linearity of the pressure-flow relationship is also well-defined in the frequency domain (Milnor 1989, p188). However, without careful consideration of uncertainties associated with f_c and the harmonic range, different values of Zc can be obtained using the same impedance spectrum (O’Rourke & Taylor 1967). On the other hand, time domain methods are fast and believed to be independent of data preprocessing. Therefore they are easy to integrate in clinical settings (Bollache et al 2015) and/or mathematical algorithms of interest, such as the method of wave separations (Hughes et al 2008, Parker 2009). However, to determine which portion of the pressure-flow loop ensures minimal wave reflection is equally challenging. Finally, it should be noted that the true characteristic impedance is a parameter independent of the HR (Milnor 1989), but the data analyzed here are obtained in-vivo (with a heart), given a specific cardiac cycle. Since both methods rely on the accuracy of HR, due to the determination of f_c in the frequency domain and the length of the cardiac cycle during the ejection phase, cardiac conditions has an impact on both methods.

One study by Lucas et al (1985) compared the time domain method with a frequency domain method averaging the impedance moduli between 2–16 Hz. They used aortic and pulmonary arterial pressure and flow measurements, before and after surgery, recorded in 125 patients with congenital heart disease. They observed a strong correlation between the two estimates, which lead them to conclude that the time domain estimates of Zc are adequate if no other features of the input impedance spectrum are of interest. These results were contrasted in a study by Fourie & Coetzee (1993), who showed that time and frequency domain approaches yield different estimates of Zc.

Importantly, past comparisons of the frequency and time domain methods have been based on experimental observations only and lacks a rigorous mathematical analysis to support their equivalence. Despite this, both estimates have been used to infer vascular properties related to Zc (Hughes & Parker 2009, Borlotti et al 2014). Recent editions of McDonalds (Nichols et al 2011, p175), advocate the time domain approach as fairly accurate for systemic arteries when both pressure and flow are measured at the same location. However, Milnor (1989) does not mention the time domain methods, despite the fact that its latest edition was published eight years after Dujardin & Stone’s (1981) study. Since there is no gold standard, one must be wary of choosing a particular method. Comparisons, limitations, interpretations, and therefore conclusions should be explained within the context of the chosen approach.

This study investigates the sensitivities of the two approaches to various physiological and experimental conditions. To do so, we have set up a number of hypothetical scenarios and conducted numerical tests with the aim to investigate agreement or disagreement of the two methods. We have used functional waveforms from Milnor (1989) that mimic typical pressure and flow waves in the aorta and main pulmonary artery in an adult human subject. We have also used a digitized dataset from Dujardin & Stone (1981), which represents pressure and flow in a dog ascending aorta over multiple cardiac cycles as well as from dogs and mice (Dujardin et al 1980, Tabima et al 2012) under different hemodynamic conditions.

2. Methods

This section includes a description of methods, and data acquisition tools, used in this study. We first describe available data followed by two sections describing the frequency and time domain methods. The last section presents four different case studies pertinent to experimental and physiological uncertainties. For the sake of convenience, the term ‘impedance’ when used alone will refer to ‘input impedance’ in the rest of this manuscript.

2.1. Digital Waveforms

Pressure and flow waveforms analyzed here were extracted from previous studies in humans, dogs, and mice under different physiological and pathological conditions. Below we have described the steps involved in reproducing each dataset.

Dataset 1

Aortic and pulmonary arterial pressure (mmHg) and flow (ml/s) waveforms from an adult human subject (from Milnor (1989)). This subject had a HR of 75 beats/min and a cardiac output of 6.6 L/min. The waveforms shown in Figure 1(a)–(d) were generated by constructing Fourier series of the form (1) using 10 harmonics at a sampling frequency (Fs) of 1.0 kHz. (see Milnor (1989, p158) and Appendix A for more detail). Even though the original waveforms include high-frequency oscillations (12.5 Hz being being the highest frequency), it was stated that the reconstructed waveforms contain more than 95% of the total oscillatory hydraulic power contained in the original data (see equation (4)).

Dataset 2

Pressure and flow waveforms from a dog ascending aorta (from Dujardin et al (1980, figure 1) and Dujardin & Stone (1981, figure 1)). Data were obtained by digitizing waveforms^‡ (using GraphClick^§) resampled in Matlab to ensure a uniform sampling rate. Data were measured under four flow conditions: control (C), volume expansion (V), new control (NC), and hemorrhage (H). Dataset 2A (from Dujardin et al (1980)) was measured over two cardiac cycles under all four conditions. Dataset 2B (from Dujardin & Stone (1981)) includes the volume expansion case measured over five cardiac cycles. For all datasets, hemodynamic parameters including mean pressure, vascular resistance, HR, stroke volume and pulse pressure were matched with the corresponding ranges provided by Dujardin et al (1980) and Dujardin & Stone (1981).

Dataset 3

Flow and pressure waveforms from mice pulmonary arteries under normoxic and hypoxic conditions (see Tabima et al (2012) and Gen et al (2007) for details). The data, recorded at 5 kHz, was obtained from male C57BL6/J mice, 12-13 weeks old with an average body weight of 24 g. The mice were obtained from the Jackson Laboratory (Bar Harbor, ME) and they were divided into control (n = 7) and chronic hypoxia groups (n = 5). The mice in the hypoxic group were exposed to 21 days of chronic hypoxia (10% Oxygen) and both groups were exposed to a 12 hour light-dark cycle. All procedures associated with obtaining the flow and pressure waveforms were performed as described in (Tabima et al 2012). Two representative datasets from one cardiac cycle encoding ensemble averages were analyzed in this study.

2.2. Frequency Domain Analysis

Under the assumptions of periodicity and linearity, pulsatile pressure and flow waveforms can be approximated by a Fourier series of the form

$$\stackrel{\sim }{s}\left(t_n\right)=\overline{S}+{\displaystyle \sum _{k=1}^K{S}_k}\cos ({\omega }_k{t}_n+{\phi }_k),=\overline{S}+{\displaystyle \sum _{k=1}^K\mathrm{\Re }}[S_k{e}^{i({\omega }_k{t}_n+{\phi }_k)}];n=0,\dots N,$$ (1)

where $\stackrel{\sim }{s}(t_n)$ is the Fourier series approximation of the original waveform s(t_n), t_n = n/Fs is the time vector, T = N/Fs the period of s(t_n), and N = 60×Fs/HR. ω_k = 2kπ/T (k = 1, …, K) are the angular frequencies, $\overline{S}$ is the mean of s(t_n), and S_k and φ_k (rad) are the moduli and phase spectra associated with each harmonic numbered k, and K is the smallest resolution of harmonics required for the impedance analysis. Both, S_k and φ_k, are defined in terms of a_k and b_k, the coefficients of basic trigonometric Fourier series, i.e.

$$S_k=\sqrt{a_k^2+b_k^2},{\phi }_k={\tan }^{-1}(b_k/a_k),$$

$$\text{where}{a}_k\approx \frac{2}{N}{\displaystyle \sum _{n=0}^{N}s(t_n})\cos {\omega }_k{t}_n,b_k\approx \frac{2}{N}{\displaystyle \sum _{n=0}^{N}s(t_n})\sin {\omega }_k{t}_n.$$ (2)

Setting s(t_n) as p(t_n) and q(t_n) in (1) and (2), the impedance spectrum, Z(ω_k), can be computed as the ratio of the pressure and flow harmonics by

$$Z({\omega }_k)=\frac{\mathrm{\Re }[P_k{e}^{i({\omega }_k{t}_n+{\alpha }_k)}]}{\mathrm{\Re }[Q_k{e}^{i({\omega }_k{t}_n+{\beta }_k)}]}=\frac{P_k}{Q_k}\mathrm{\Re }[e^{i({\alpha }_k-{\beta }_k)}]=Z_k\mathrm{\Re }{e}^{i{\varphi }_k},$$ (3)

where P_k and Q_k are the moduli and α_k and β_k the phase angles of the pressure and flow harmonics, respectively. Z_ks are the impedance moduli and ϕ_k = α_k − β_k the corresponding phases at a given frequency. Note if ϕ_k < 0 then the k’th pressure harmonic lags the k’th flow harmonic, and vice versa. The 0’th harmonic represents the steady or mean component known as the vascular resistance (Z₀), whose phase angle is ‘zero’ by definition.

Generally, for a continuous periodic function s(t), K → ∞ in equation (1). It is possible to specify an upper integer bound on K as long as equation (1) adequately reproduces the actual waveforms. Most studies predict dynamics using sums of 10 or less harmonics (Milnor 1989, Nichols et al 2011), but for any given dataset the finite limit on K can be determined as follows. First, noting the similarity of S_k and ϕ_k with the complex polar form of the discrete Fourier transform, one can exploit properties of FFT algorithms for a given discrete signal s(t_n). This implies that K is bounded by N and provided that the data satisfies the Nyquist frequency limit, only half of the harmonics are useful, i.e. K = N/2+1 (Briggs & Henson 1995). Second, for the purpose of impedance analysis, K should be set to satisfy the oscillatory power criterion defined as the oscillatory power (W (J/s)) generated by the ventricle can be computed by

$$W=\frac{1}{2}{\displaystyle \sum _{k=1}^{\frac{N}{2}+1}{Q}_k}{P}_k\cos {\varphi }_k,$$ (4)

According to the criterion, K can be determined such that the approximated oscillatory power $(\stackrel{\sim }{W})$, associated with K number of pressure and flow harmonics, is at least 95% of total oscillatory power. In other words, for a given K, $\stackrel{\sim }{W}\ge 0.95W$.

The frequency domain estimates of the characteristic impedance (Zc) can be obtained by averaging the higher frequency impedance moduli associated with the i’th–j’th harmonics (Milnor 1989, O’Rourke & Taylor 1967), i.e.

$$\text{Zc}=\frac{1}{j-i+1}{\displaystyle \sum _{r=i}^i{Z}_r}\equiv \frac{1}{j-i+1}{\displaystyle \sum _{r=i}^j\frac{P_r}{Q_r}},$$ (5)

where i ≥ 2 and j ≤ K. For most practical purposes, to avoid introducing frequency components attributable to noise, the computation of impedances is restricted to less than 25 Hz (Milnor 1989). A partial list of frequency domain methods is given in Table 1.

2.3. Time Domain Analysis

The original time domain method proposed by Dujardin & Stone (1981) estimates Zc by fitting a straight-line to manually selected points on the pressure-flow loop during the early ejection phase. The slope of this line defines Zc. To eliminate the effect of early reflections, this technique was later modified by requiring that the pressure-flow slope should be calculated by using no more than 95% of the peak flow rate (q_max) (Lucas et al 1988). In this study, this percentage is assumed constant, representing the critical flow threshold, denoted by q_c, which we set to 95%, 75%, 50% and 25% of q_max of the early ejection phase. Based on the above description, one can provide a mathematical expression of the time domain Zc value given by

$$\text{Zc}=\frac{dp}{dq}\forall p\in [p(t_0)p(t_m)],m<N:q(t_m)\le q_c\cdot q_{\text{max}},$$ (6)

where dp/dq represents the slope of best-fit line to the pressure-flow loop over [t₀ t_m].

Another time domain technique is based on relating the derivatives of the pressure and flow signals. This method calculates Zc by dividing the peak derivative of pressure by the peak derivative of flow that is Zc′ = max(p′)/max(q′), where the prime in the left hand side (LHS) denotes time differentiation. In this study, we implement and compare the up-slope and peak derivative methods. A detailed review of time domain techniques and their comparison can be found in Lucas et al (1988).

2.4. Case Studies

Methods for estimating Zc using any approach are operator dependent, which means that the operator has to decide the level of signal preprocessing, the number of harmonics or points on a certain portion of the pressure-flow loops to be included (Lucas et al 1988). This decision is based on assumed experimental conditions, such as the time delay between pressure and flow waves due to the distance between pressure and flow probes and the quality of the signal in terms of the signal to noise ratio (SNR). In this context we have defined four hypothetical cases, which were evaluated using datasets 1–3 to calculate time and frequency domain estimates from Table 1.

Case 1 time-lag between the pressure and flow waveforms

The propagation of the pulse-wave along the arterial network induces a small time-lag between the pressure and flow waves (Nichols et al 2011). This can easily be exaggerated if the pressure and flow probes are not positioned exactly at the same location (Gary et al 1994). To minimize the effect on the analysis, time-lags should be removed before the data are analyzed. To study the effects of time-lag on the Zc estimates, we introduced an artificial time-lag between the pressure and flow waveforms in dataset 1. This was achieved by shifting the pressure waves by 10 ms forward (p₊) and backward (p₋), while keeping the flow wave unaltered.

Case 2 Effects of noise

Pressure and flow measurements are typically noisy, and thus most studies filter the signals before analyzing them, typically using a low-pass filter (Lucas et al 1988). In order to study the effects of the signal quality, we contaminated the composite pressure and flow signals in dataset 1 with a small level of Gaussian white noise. To do so, we added noise to pressure and flow signals to obtain signals with a 40 dB SNR. The noise was generated using the built in Matlab function awgn, part of the communication toolbox.

Case 3 Periodicity of the cardiac cycle versus breathing cycle

In-vivo measurements of HR and blood pressure include natural beat-to-beat variation, which is higher in young people than in the elderly. Both methods analyzed here assume that signals are periodic, requiring that the natural beat-to-beat variation is removed before analysis (Parker 2009). Commonly used approaches include a) averaging over multiple cardiac cycles with selection and/or exclusion of specific cycles (Lucas et al 1988), b) analysis of individual cardiac cycles with subsequent averaging of the resulting information, and c) analysis over multiple cardiac cycles (typically over a respiratory cycle) (Dujardin et al 1980, Dujardin & Stone 1981). In the latter case, the fundamental frequency of the resultant spectra reflects the breathing rate, not the HR. Depending on the length of the respiratory cycle, the frequency of the HR usually appears after the first few harmonics. This case uses dataset 2B to compare the Zc estimates from single-beat and multi-beats.

Case 4 Qualitative comparison under different hemodynamic conditions

This case analyzes the effects of hemodynamic variation on the Zc estimates. We used datasets 2A, 2B and 3 to study the effects of four different flow conditions, including C, V, NC and H, on a frequency domain (Zc_5–15) and a time domain estimate (Zc₉₅). These two estimates were chosen for comparison since Dujardin & Stone (1981) claimed that their impedance measures were identical, under all four conditions. In addition, we modified dataset 2B to investigate the effects of retrograde flow at the end of systole. This analysis was motivated by the observation, that the up-slope method in the time domain completely ignores the late systole and diastole part of the signals. Dataset 3 was used to investigate the effects of chronic hypoxia as a model of pulmonary vascular disease (see Table 1).

3. Results

This section presents results of the frequency and time domain analyses. We analyzed three datasets under four cases as described in Section 2. Specifically, we calculated and compared multiple estimates of Zc from each dataset by applying the methods listed in Table 1. For most cases, comparisons of the two approaches were made by computing the mean ± SD of Zc estimates (referred as grouped averaged Zc hereafter) across the frequency and time domain methods listed in Table 1. However, in some cases only selected methods from each domain were used to compare the Zc estimates. For the sake of reproducibility, units of primary (pressure and flow) and secondary (components of impedance) quantities were kept the same as those in the source studies.

3.1. Dataset 1

Dataset 1 was used to compare all Zc estimates listed in Table 1 and to analyze cases 1 and 2, focused on studying the effects of time-lags between the pressure and flow and noise on Zc estimates.

Figure 1 gives an overview of the frequency and time domain analysis of dataset 1. Panels (a)–(d) show the flow and pressure waveforms in the aorta and the MPA of a human subject over one cardiac cycle. Panels (e) and (g) show the impedance moduli and phase spectra, plotted for the first 10 harmonics after the mean component Z₀. The fundamental frequency (HR) in this subject is 1.25 Hz and the first impedance minimum for aorta occurs at 6.25 Hz (5’th harmonic), which is accompanied by the phase crossover between 6.25–7.5 Hz (5’th–6’th harmonic). For the MPA, the first impedance minimum is at 5 Hz (4’th harmonic), with a phase crossover between 3.75–5.0 Hz (3rd–4’th harmonic). The total resistance (Z₀) in the aorta and the MPA was observed to be 0.77 and 0.11 mmHg s/ml, respectively. Panel (f) shows the pressure-flow loops in the respective arteries. These loops were used to calculate Zc using the up-slope method at q_c = 95%, 75%, 50% and 25% of q_max during the early ejection phase.

Panel (h) compares the frequency and time domain estimates for the aorta and MPA. The group averaged Zc in the frequency domain were found to be 17% and 5% smaller than the time domain values for the aorta and the MPA, respectively.

Case 1

Figure 2 shows the effects of time-lags between the pressure and flow waveforms on the Zc estimates, calculated using dataset 1. Panel (a) shows the normalized pressure and flow waveforms, plotted with forward (p₊) and backward shifted pressures (p₋). The time shift (t_s) was set to 10 ms in reference to original timing of the pressure wave. The timing of the wave refers to time coordinate associated with the foot of the wave on abscissa. A forward shift in pressure, while keeping the flow unaltered, causes the flow to precede pressure and vice versa. Panel (b) shows the effect of an induced time-lag on the so-called linear portion of the pressure-flow loop during the early ejection phase. A time-shift, in either direction, breaks the linear relationship between the pressure and flow waves, while the shape and magnitude of both waveforms are preserved. A distinctive effect of the time shift is that the area bounded by the pressure-flow loop increases when flow precedes pressure (magenta dashed curve) and decreases when the flow lags the pressure (blue dot-dashed curve). Panels (c) and (d) show plots of the impedance moduli and phase corresponding to the original and shifted pressure waves. As anticipated, the impedance moduli remain insensitive to the time shift. However, the phase spectrum is shifted above or below the original phase by an angle ∆ϕ_k = ω_kt_s (Rad). As a result, the phase crossover shifts from 8.75–10 Hz (7’th-8’th harmonic), when flow precedes pressure, and from 5.0–6.25 Hz (4’th-5’th harmonic) when flow lags pressure.

Figure 2.

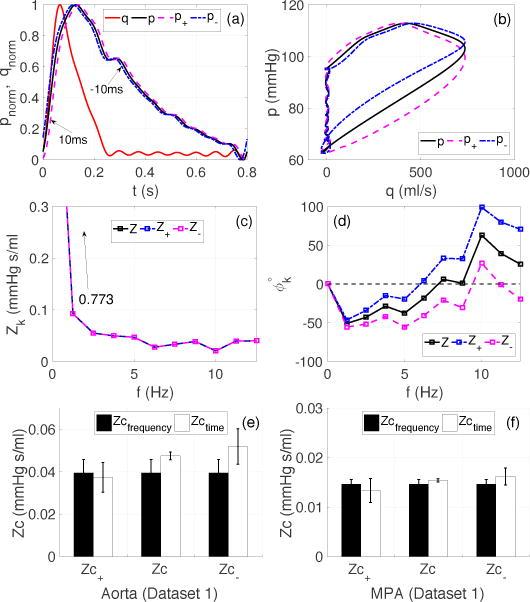
Case 1 (Dataset 1): Effects of a time-lag between pressure and flow on the Zc estimates. (a): Normalized pressure and flow (dimensionless) in the aorta; p₊ and p₋ denote the forward and backward shifted wave by 10 ms. (b): Effect of a 10 ms time shift on the early ejection phase of the pressure-flow loop (in units of mmHg and ml/s), (c)–(d): impedance moduli (mmHg s/ml) and phase spectra (degrees), (e)–(f): effects of time-lag on the resultant Zc values for the aorta and MPA. Zc_± correspond to the Zc estimates obtained using p±.

The last two panels, (e) and (f), quantify the effects of the time-lag on the Zc estimates in the aorta and MPA. All frequency domain estimates were insensitive to the time-lag. Yet the time domain estimates, calculated usin g the up-slope method, were very sensitive to the time-lag. Interestingly, the Zc′ computed using the derivates peak method was insensitive to the time-lag. In the case of the aorta, when flow preceded the pressure by 10 ms, the relative error between the two types of estimates was reduced to 5%, from an original value of 17%. However, the error jumped to 24%, when flow lagged pressure. For the MPA the relative error increased to 9.5% and 9.7%, respectively for the forward and backward shift in time, compared to the 5% relative error observed in the original signals.

Case 2 (Dataset 1)

Figure 3 shows how random noise in the data affects the Zc estimates. Panel (a) shows the noisy pressure and flow waveforms (normalized) whereas panel (b) depicts the corresponding pressure-flow loop (in dimensional form). Panels (c) and (d) show that the noise level affects the impedance moduli and phase above 12.5 Hz (10’th harmonic), the frequency cut-off used when generating dataset 1. The effect on the mean component (Z₀) was negligible (it increased from 0.773 to 0.775 mmHg s/ml). Panels (e) and (f) illustrate the quantitative effects of noise on the frequency and time domain calculations of Zc. Analysis of noisy data over all frequency or time domain methods listed in Table 1 yield a high variance of the Zc predictions (bars in the center). However, the effects of noise can be eliminated by excluding methods requiring analysis of frequencies above 12.5 Hz (bars on the left). Similarly, excluding peak derivative methods also improved time domain estimates.

Figure 3.

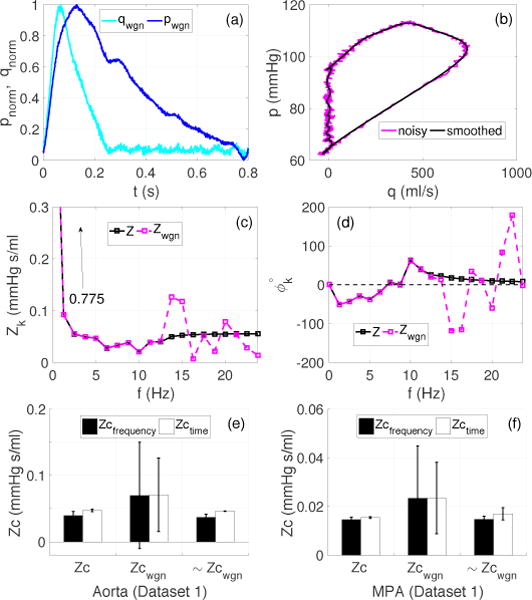
Case 2 (Dataset 1): Effects of noise on the Zc estimates. (a): Normalized pressure and flow waveforms (dimensionless) in the aorta, contaminated with Gaussian white noise generating a 40 dB SNR, (b): pressure-flow loops from normal (see Figure 1 (a)) and noisy pressure (p_wgn) and flow (q_wgn) signals, (c)–(d) impedance moduli and phase for the first 19 harmonics computed using normal (Z) and noisy (Z_wgn) datasets, (e)–(f): effects of noise on the grouped averaged Zc for the aorta and MPA, where Zc and Zc_wgn are the group averaged Zc accounting for all the methods listed in Table 1. ~Zc_wgn excludes all frequency domain methods, which require harmonics above 12.5 Hz, and the peak derivative method (Zc′) in the time domain.

3.2. Dataset 2B

This dataset was used to analyze cases 3 and 4. Case 3 studies the effects of different approaches, including analysis of single or multiple cardiac cycles or the ensemble encoding of number of cardiac cycles. Case 4 investigates the effects of retrograde flow usually observed at the end on systole. For these cases, one frequency, Zc_(5–15), and one time domain, Zc₉₅, method were considered.

Case 3 (Dataset 2B)

Figure 4 compares Zc values obtained by analyzing the data in three alternative ways: (a) beat by beat analysis of one cardiac cycle, (b) analysis of an ensemble encoding multiple cardiac cycles, and (c) analyzing multiple cardiac cycles encoding a complete breathing cycle. For the cardiac cycle, shown in in panels (b), the mean and pulse pressures were 20.2 ± 0.3 kPa and 4.7 ± 0.1 kPa, respectively. Moreover, the cycle length was found to be 0.47±0.01s, i.e an approximate HR of 2.13 Hz (~128 beats/min) whereas the breathing frequency was 0.43±0.001 Hz (~26 breaths/min).

Figure 4.

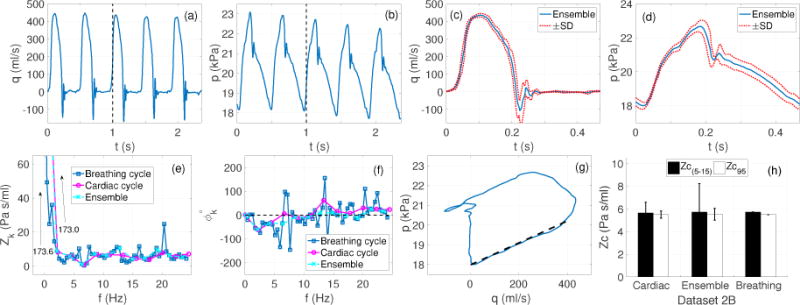
Case 3 (Dataset 2B): Effects of single beat, breathing cycle (multi-beat) and ensemble encoding approach on the Zc estimates (Murgo et al 1980). (a)–(b): Pressure and flow data over five cardiac cycles reproduced with permission from Dujardin & Stone (1981) (c)–(d): ensemble encoding (blue curves)±SD (dotted red curves) of the flow and pressure waveforms, (e)–(f): impedance moduli and phase spectra obtained by subjecting all five cycles (blue curve representing breathing cycle analysis), a representative cardiac cycle (magenta curve representing beat by beat analysis) and ensemble encoding (cyan curve), to the Fourier analysis (g): the pressure-flow loop (blue curve) from the ensemble encoded waveform with the fitted line at q_c = 0.95 (dashed balck), (h): comparison of Zc_(5–15) and Zc₉₅ using the three approaches: (left) the cardiac cycle approach, error bars show mean±SD Zc values over five cardiac cycles analyzed individually, (center) ensemble encoding approach, the error bars show the estimates corresponding to dotted red curves in (c) and (d), (right) breathing cycle approach.

Panel (e) shows a clear minimum at 6.4 Hz in the moduli spectrum for all three approaches. These minima were accompanied by phase crossovers at the same frequency except for the ensemble data, which was shifted between10.7–12.8 Hz (5’th-6’th harmonic). This introduces an uncertainty about the occurrence of f_c, which in this case is determined to be 6.4 Hz using the full dataset. However, this frequency is associated with the 3rd harmonic for the single and ensemble cycles compared to 15’th harmonic for the breathing cycle. It should be noted that two local minima were found in the breathing cycle moduli spectrum, at about 0.8 Hz (2nd harmonic) and 3.4 Hz (8’th harmonic), respectively. The former minimum was accompanied by a phase crossover, yet neither of these frequencies can be determined as f_c nor should they be part of the Zc calculation because they do not represent multiples of the fundamental frequency (HR). Therefore, when using the breathing cycle approach, all harmonics whose frequency do not correspond to the HR should be excluded from the analysis.

It is interesting to note, panel (h), that all estimates are in agreement except the ones computed using the extreme bounds of the ensemble encoding, which yielded significantly different results for the frequency domain Zc_(5–15). However, the time domain Zc₉₅ was observed to be relatively insensitive even to the extreme bounds of the ensemble encoding and the error was found to be comparable to that in the beat-to-beat analysis in the time domain.

Case 4 (Modified Dataset 2B)

Figure 5 analyzes the effects of presence or absence of retrograde flow at the end of systole. The flow waveforms shown in panel (a) were obtained by modifying dataset 2B to eliminate retrograde flow at the end of systole, without significantly affecting the cardiac output. Removing retrograde flow leads to a 2% increase in the cardiac output. The pressure-flow loops, show a similar behavior during the early ejection phase, while they differ in the last part of the cycle. Panel (c) shows a significantly different oscillatory behavior for the modified flow (Q_no–Retro) than for the actual flow (Q_Retro). Selected Zc estimates, Zc_(5–15) and Zc₉₅, were calculated using ensemble encoding of the modified flow and compared with those presented in Figure 4(h). Results, panel (d), show that the Zc_(5–15) corresponding to the modified flow is 33% higher than the Zc_(5–15) computed from the actual flow. On the other hand, Zc₉₅ is found to be insensitive to any modification in the end of systole flow behavior, leading to a relative error of 36% between Zc_(5–15) and Zc₉₅ in the absence of end of systole retrograde flow compared to 3% in the presence of retrograde flow. This predicts a much higher discrepancy between the time and frequency domain method in the absence of end of systole retrograde flow and indicates a strong dependency of the frequency domain methods on the entire cardiac cycle.

Figure 5.

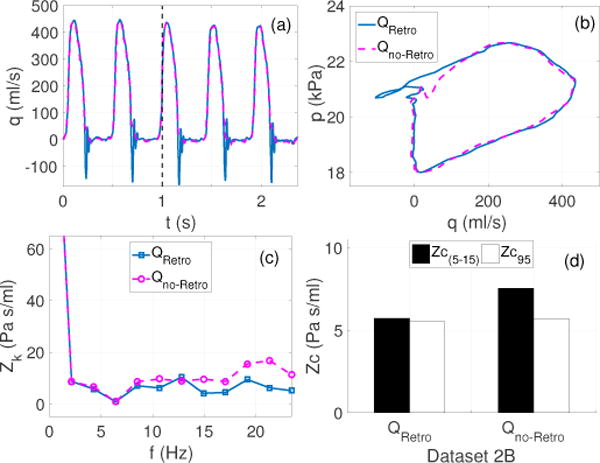
Case 4 (Modified dataset 2B): Effects of retrograde flow at the end of systole examined using a frequency and time domain estimate. (a): The original flow from Figure 4 (solid blue) with retrograde flow (Q_Retro), and modified flow (dashed meganta) without retrograde flow (Q_no–Retro), (b): corresponding pressure-flow loops from ensemble encoding, (c): corresponding impedance moduli spectra including 0–11 harmonics, (d): comparison of Zc_(5–15) and Zc₉₅ in the presence and absence of the retrograde flow.

3.3. Dataset 2A

This dataset was used in case 4 comparing frequency and time domain approaches under different hemodynamic conditions. Results were obtained for Zc_(2–12), Zc_(5–15) and Zc₉₅, and for estimates of Zc₉₅₊ that analyzes the impact of delayed pressures waveforms (by 7 ms).

Case 4

Figure 7 shows that the qualitative features of both, moduli and phase spectra, mimic those presented in the original study (Dujardin et al 1980). In all cases a clear minimum in the moduli spectra can be observed at the 3rd harmonic. Each of these are accompanied by a phase crossover around the same harmonic. However, the critical frequency (f_c) associated with the first impedance minimum varies depending on the HRs associated with each flow condition. Specifically, f_c was observed to be 6.5 and 6.4 Hz for the control (C), and new control (NC), and 6.3 and 7.2 Hz for the volume expansion (VE) and hemorrhage (H) cases, respectively. Moreover, it should be observed that during hemorrhage, the phase remains negative between the 4’th and 9’th harmonics. This is interesting given that pressure and flow look similar (see figure 6(d), 6((h)), suggesting minimal wave reflections. A negative phase suggests that the pressure wave lags the wave at these frequencies. This can be explained by the fact that hemorrhage acts as a sink in the fluid channel causing a suction effect leading to acceleration of the flow and a drop in the pressure. The latter is likely a result of an out of phase reflected pressure wave causing the flow to lead pressure at higher frequencies.

Figure 7.

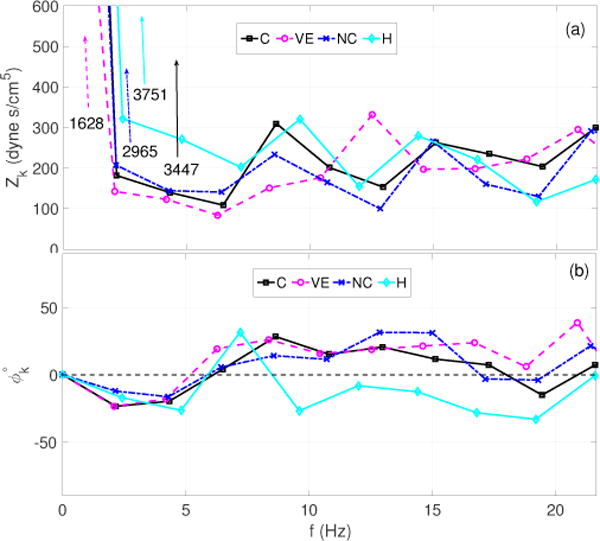
Dataset 2A: Impedance moduli (a) and phase spectra (b) corresponding to each case (C, VE, NC and H) presented in Figure 6. The spectra are generated using the second cardiac cycle in the in the sequence of pressure and flow waveforms and only show 0–10 harmonics after the mean component.

Figure 6.

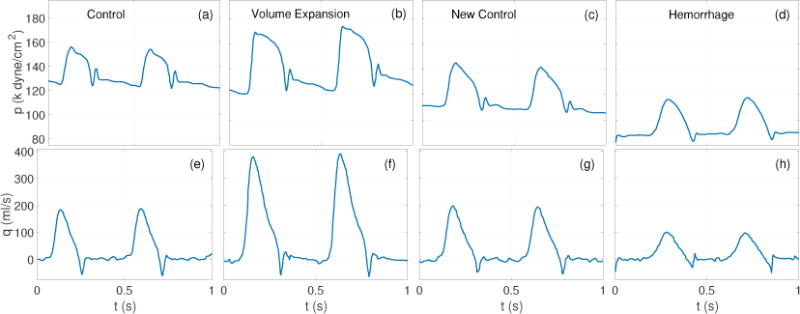
Dataset 2A: Pressure (top row) and flow (bottom row) waveforms reproduced with permission from Dujardin et al (Dujardin et al 1980). The measurements were recorded in a dog ascending aorta under four d flow conditions, labeled in top row panels. Variations in the cycle lengths should be noted for each flow condition.

Figure 8 illustrates the Zc₉₅ computation using actual (panels (a)–(d)) and modified (panels (e)–(h)) pressure-flow loops. In the later cases the pressure waves were delayed by 7 ms. Panels (i)–(l) compare Zc₉₅ and Zc₉₅₊ (delayed) with selected frequency domain estimates, Zc_(2–12) and Zc_(5–15). In the source study (Dujardin et al 1980), only Zc_(5–15) was calculated.

Figure 8.

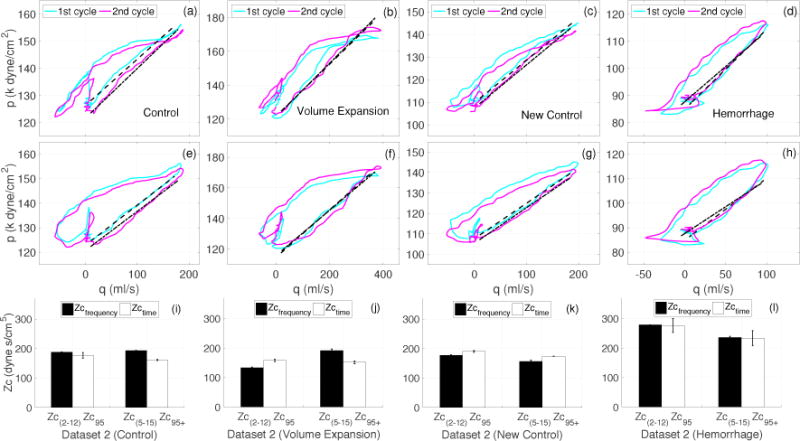
Case 4 (Dataset 2A): Comparison of frequency and time domain estimates of Zc calculated form the dataset 2A (Figs. 7 and 6. (a)–(d): Pressure-flow loops with q_c = 0.95 providing Zc₉₅. (e)–(h): Pressure-flow loops with pressure delayed by 7 ms, and q_c = 0.95 providing modified Zc₉₅₊, (i)–(l): comparison of frequency domain Zc_(2–12), Zc_(5–15) (see Table 1) with time domain Zc₉₅ and Zc₉₅₊. The bar charts show the mean±SD of all estimates computed from each cardiac cycle shown in Figure 6.

Figure (i)–(l) show that for a given case there were discrepancies between the time and frequency domains estimates as well as between the two frequency domain estimates. We observed discrepancies between Zc_(2–12) and Zc_(5–15) for all cases, where relative errors of 3%, 30%, 14% and 18% were observed for C, VE, NC, and H, respectively. As for the comparison with Zc₉₅ and Zc₉₅₊, for case C (panel (i)) Zc₉₅ was smaller than both Zc_(2–12) (by 6%) and Zc_(5–15) (by 9.5%). However, the error was further increased (to 16.5% and 19%, respectively) when Zc_(2–12) and Zc_(5–15) were compared with time shifted estimate, Zc₉₅₊. For the VE case (panel (j)), Zc₉₅ was greater than Zc_(2–12) (by 15%) but smaller than Zc_(5–15) (by 21%). However, in this case, the time shifted estimate, Zc₉₅₊, improved the agreement with Zc_(2–12) (reducing the error to 12%) but further increased the error (to 26%) for Zc_(5–15). As for the NC case (panel k), the trend was opposite to that of the C case. For this case, both of the frequency domain estimates were smaller than Zc₉₅ (by 7% and 18%) respectively. However, the errors were reduced (to 2% and 10%) when these frequency domain estimates were compared with the time shifted Zc₉₅₊. In the final case H (panel (l)), Zc_(2–12) agreed with Zc₉₅, but Zc_(5–15) was found to be smaller than Zc₉₅ (by 15%). Once again, the introduction of a time delay increased the discrepancy (to 19%) between Zc_(2–12) and Zc₉₅₊ but, nevertheless, it also lead to an agreement between Zc_(5–15) and Zc₉₅₊.

Figure 9 shows that there is a relatively strong linear relationship between Zc_(2–12) and Zc₉₅ (see panel (a)), in comparison to the relationship observed between Zc_(5–15) and Zc₉₅ (see panel (b)). For each of these comparisons, the coefficient of determination (R²) was found to be 0.93 and 0.41, respectively.

Figure 9.

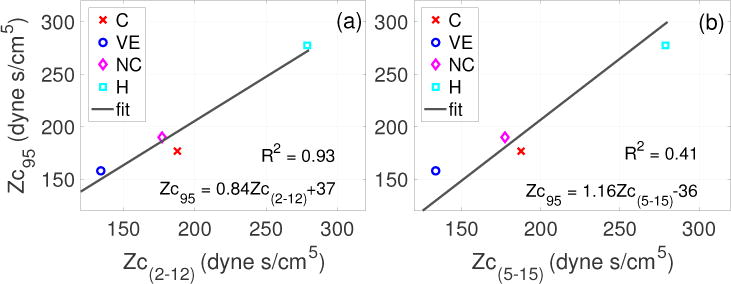
Case 4 (Dataset 2A): Following Murgo et al (1980), regression line depicting the linear relationship between Zc₉₅ and Zc_(2–12) (a), and Zc₉₅ and Zc_(5–15). Coefficient of correlation, R², is 0.93 and 0.41, respectively.

In summary, in all cases, Zc_(2–12) was observed to be in better agreement with Zc₉₅ than Zc_(5–15). However, the qualitative trends of these comparisons were unpredictable. For instance, for the VE case (panel (j)) Zc₉₅ was greater than Zc_(2–12) but smaller than Zc_(5–15), making it impossible to guess the nature of the discrepancy. Moreover, in some cases the introduction of a time shift improves the agreement while in other cases it augment the discrepancies.

3.4. Dataset 3

This dataset was used to analyze the performance of frequency and time domain Zc estimates in mice pulmonary arteries under normal and hypoxic conditions (case 4). Results were obtained by analyzing the representative pressure and flow waveforms. The representative waveforms were obtained from ensemble encoding of pressure and flow across two groups, a healthy control group (7 mice) and a hypoxic group (5 mice).

Case 4

Figure 10 presents frequency and time domain analysis of dataset 3. For the control case, the first impedance minimum in the moduli spectra was observed at 20 Hz (2nd harmonic) and is accompanied by a phase crossover around the same frequency. This was followed by a spike at 30 Hz (3rd harmonic) with a modulus value (59 mmHg s/ml) very close to the mean value (Z₀ = 70.6 mmHg s/ml). This feature is rather uncommon in the context of the data analyzed so far. As for the hypoxic case, the first impedance minimum occurred at 40 Hz (4’th harmonic) whereas the phase crossover takes place at 70 Hz (7’th harmonic). Unlike the control case, there is no spike comparable to the mean value (Z₀ = 153 mmHg s/ml) in the moduli spectrum for the hypoxic mice. Moreover, for both groups, the impedance moduli gradually tailed off at higher frequencies within the plotted range of harmonics.

Figure 10.

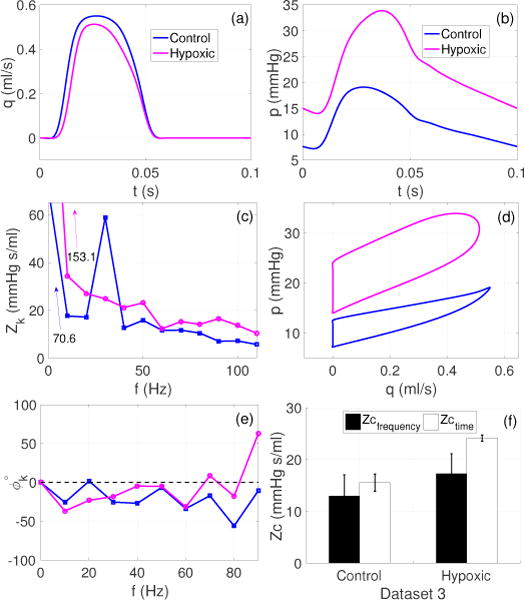
Dataset 3. Estimates of Zc in mice pulmonary arteries during control and hypoxia. (a)–(b): Representative pressure (p) and flow (q) waveforms plotted for one cardiac cycle for the control and hypoxic groups, (c) and (e): corresponding impedance moduli (Z_k) and phases (ϕ_k) spectra for 0–10 harmonics, (d): corresponding pressure-flow loops for the control and hypoxic cases, and (f): comparison of frequency and time domain estimates where the bars show the mean ± SD values of Zc, across all the frequency and time domain methods listed in Table 1.

The comparison of the frequency and time domain methods, illustrated in panel (f), uses all methods listed in Table 1. However, due to a much higher basal HR (10 Hz), the Zc estimates based on the frequency range were considered after multiplying the frequencies by 10. So, for example, Zc_(2–12) in Table 1 uses all frequencies between 2 and 12 Hz. But in the case of mice Zc_(2–12) will use all frequencies between 20 and 120 Hz. Consequently, the grouped averaged values of Zc were compared. In general, for both the control and hypoxic cases, the frequency domain estimates were found to be smaller than the time domain estimates by 16.6% and 28.5%, respectively. It was also observed that Zc increases during hypoxia irrespective of the choice of method. More specifically, during hypoxia the frequency and time domain estimates were increased by 25% and 36%, respectively.

4. Discussion

In this study, we scrutinized frequency and time domain methods to understand the sources of discrepancies and the effects physiological and experimental factors on the values of Zc. As a result, some interesting features of both frequency and time domain approaches were identified. Some of these results can be useful in setting the path straight for more accurately estimating the characteristic impedance.

The usefulness of time and frequency domain analysis for estimating characteristic impedance relies on the assumptions that the pressure-flow relationships are linear and that the portions of the waveforms being analyzed are free of wave reflections. A linear pressure-flow relationship is well-defined in the frequency domain i.e. a purely sinusoidal flow oscillation should produce a purely sinusoidal pressure oscillation of the same frequency, and the impedance in a linear system is independent of the shape and magnitude of the applied pressure pulse as long as the physical properties of the vessels, the blood density and viscosity remain constant (Nichols et al 2011). As for wave reflections, the frequency domain analysis assumes that a higher dissipation rate at higher frequencies limits the effect of reflections. In the time domain, the effects of reflections are usually excluded by ignoring a large portion of the pressure-flow loops from the analysis. It is assumed that the initial disturbance due to cardiac contraction does not have enough time to travel to a distal location, be reflected, and meet the incident wave during the early ejection phase (Parker 2009). It is also assumed that wave reflection from the previous cardiac cycles have dissipated. However, it is not clear how the linearity of pressure-flow relationships should be interpreted in the time domain. Is the observation of a visually linear relationship during the early ejection phase adequate or should one define an analytical time domain criterion that must be transformable to the equivalent frequency domain criterion? This leads us to the question of mathematical equivalence of the two approaches.

To our knowledge, only one previous study, by Lucas et al (1988) has attempted to establish a mathematical connection between the two approaches. This study used transmission line theory (Milnor 1989, Nichols et al 2011) to assert that the two approaches are equivalent. They postulated that under the assumptions of negligible viscous losses, purely elastic blood vessels, and in the absence of wave reflections Zc ≈ dp/dq. However, their particular study (Lucas et al 1988) lacked mathematical details and appropriate references to establish the reliability of their formula. Moreover, most of the aforementioned assumptions are rendered invalid as soon as the arterial waves meet a reflecting junction in the proximal vasculature or the properties of blood and arteries behave in a non-Newtonian and non-linear manner. Even when the assumptions remain intact, the mathematical equivalence of the two methods is non-trivial, as discussed below.

Ignoring the mean component, the instantaneous slope of the pressure flow relation can be calculated from (1),

$$\frac{dp}{dq}\equiv \frac{p\prime (t_n)}{q\prime (t_n)}=\frac{{\displaystyle \sum _{k=1}^K{P}_k{\omega }_k}\cos ({\omega }_k{t}_n+({\alpha }_k-\pi /2))}{{\displaystyle \sum _{k=1}^K{Q}_k{\omega }_k}\cos ({\omega }_k{t}_n+({\beta }_k-\pi /2))},$$ (7)

where the right hand side (RHS) represents the Fourier representation of dp/dq whose values at any instant of time depend on the amplitude and phase of all the harmonics of pressure and flow. For a given time t_m < T during early ejection, one can substitute dp/dq from (7) into (6) in Section 2.3, i.e. the expression for the time domain Zc. It is clear that the resultant expression would not be comparable with (5) in Section 2.2, i.e. the expression for the frequency domain Zc. Thus it is not possible to analytically prove the equivalence of the two approaches. For this reason the ability of each method, in both domains, to produce quantitatively consistent results on a case by case basis remains an open question (Fourie & Coetzee 1993).

In this study, numerical experiments based on case 1, (see Figure 2) through case 4 (see Figure 5) suggest that time domain estimates are more sensitive to experimental uncertainties, whereas the frequency domain approaches are more dependent on the actual flow conditions. Specifically, the time domain analyses are highly dependent on the time-lag between the pressure and flow during early ejection. This is due to the fact that the apparent linear behavior in the pressure-flow loops during the early ejection phase is dependent on this time-lag. Although, there is a natural time-lag between the pressure and flow waves (Nichols et al 2011), it can also be introduced due to experimental setup involving the positioning of pressure and flow probes in the blood stream (Gary et al 1994). Therefore, time-lag correction becomes vital if the time domain analysis is proposed to estimate the characteristic impedance. This however requires a record of all the parameters and variables of the experimental setup, such as the sampling rate and frequency response of the flow meter and pressure transducer systems. On the contrary, the frequency domain estimates remain insensitive to the time-lag, assuming that the phase crossover is not the necessary condition for determining the critical frequency (f_c). This is due to the fact that the spectrum of the impedance moduli, is not affected by the time-lag, given that the shape and magnitudes of the actual waves remain preserved. This aspect alone will always be a major source of uncertainty and discrepancy between the frequency and time domain estimates of Zc from a given dataset.

Another source of discrepancy among the two types of estimates lies in the end of systole flow conditions. As revealed by the analyses of case 4 (Figure 5), retrograde flow at the end of systole significantly impacts the frequency domain estimates of Zc. In contrast, by design, the up-slope methods completely ignore the hemodynamic conditions beyond the time of peak systole. The case is further complicated due to the fact that the presence of retrograde flow is not the source of discrepancy but the absence is. Had this observation been otherwise, one could address the discrepancies by excluding the harmonics which constitute the retrograde flow. But in this case, there is no possible modification that can be proposed to make the two types of estimates equal. This also suggests that any preprocessing of the data that results in modification of flow behavior may yield an erroneous value of Zc in the frequency domain.

Another aspect that may significantly impact the outcomes of frequency and time domain analyses is the presence of noise in the pressure and flow data. Although both types of estimates are prone to errors due to different levels of noise, the analysis presented in Figure 3 suggests that a certain time domain Zc estimate is highly sensitive to noise. In the frequency domain, the high frequency noise components can easily be removed by imposing an upper bound on the frequency or number of harmonics. However, in the time domain, it is inevitable that noise is inherent to the data within the context of linear curve fitting or computing the derivatives of pressure and flow. Therefore the level of preprocessing as well as the choice of a particular approach and its specifics should be based on the overall quality of available data.

Analysis of case 3 (see Figure 4) suggests that there is a consistency among the outcomes obtained using different approaches, pertinent to signal selection. If the signals are reasonably periodic, then one should expect identical outputs from the beat-to-beat or the multi-beat analysis, and the ensemble encoding over number of beats can be used as a good representation of all the cardiac cycles. However, in the event of significantly non-periodic data, the results from each approach will be subject to higher uncertainty.

The outcomes discussed above, related to figures 2 and 5, are not surprising. The identification of source of discrepancies between the two approaches is strongly connected to the problem of mathematical equivalence. The very apparent differences between the definitions and applications of the frequency and time domain approaches for estimating the characteristic impedance assure the existence of such discrepancies. It is evident from equation (5) that frequency domain estimates will always be independent of the phase values, which are affected by the time-lag between the pressure and flow waves. They only depend on the impedance moduli associated with a selected harmonic range, starting from the i’th harmonic. For most applications i ≥ 2. On the other hand, equation (7) shows a clear dependence of the time domain estimate on the moduli as well as the phase of both pressure and flow harmonics. The early ejection behavior of the pressure-flow loops predominantly depend on the first two harmonics of the pressure and flow, which are usually excluded form the calculation of the frequency domain estimates of Zc.

In Table 2, we compiled key values of Zc and other hemodynamics parameters computed using datasets 1–3, representing different physiological and pathological conditions in three species. For comparison across these datasets, we converted the units of pressure and flow to mmHg and ml/s for all datasets. The analyses suggests a qualitatively consistent behavior of the two types of estimates. In particular, for dataset 1 all the frequency and time domain estimates were observed to be much smaller in the MPA than the aorta (see Figure 9(i)). Similarly, in dataset 3, the Zc estimates in mice were observed to be significantly larger during hypoxia than in control (see Figure 10(f)). Finally, in dataset 2A, estimates of Zc_(2–12) and Zc₉₅ suggest that the characteristic impedance decreases with volume expansion (VE) and increases with hemorrhage. However, when the qualitative behavior of Zc_(5–15) was assessed for the same dataset, the decrease in the characteristic impedance during VE and the increase during hemorrhage were considerably smaller compared to the behavior of Zc_(2–12) (see Figure 8(i)-(l)). In addition, Zc_(5–15) further decreased in the new control condition instead of retrieving the control value. This behavior was opposite to that observed for Zc_(2–12) and Zc₉₅. As a result, a very weak correlation between Zc_(5–15) and Zc₉₅ was observed with coefficient of determination R² = 0.41 compared to R² = 0.93 for Zc_(2–12) and Zc₉₅.

Table 2.

Estimates of characteristic impedance and hemodynamic parameters under various conditions. The table lists critical frequency (f_c), HR, cardiac output (CO), mean pressure (P_mean), and pulse pressure (P_pulse). Values correspond to the hemodynamic conditions described by datasets 1–3 in Section 2.1. For comparison, pressure and flow units are converted to mmHg and cm/s for all datasets. Zc estimates listed below were also plotted, with original units, in the figures mentioned in last column.

Z0	Zctime	Zcfrequency	fc	HR	CO	Pmean	Ppulse	Artery	Species	Condition	Dataset	Figure no.
(mmHg ml/s)×102			(Hz)		(ml/s)	(mmHg)
77.3	4.7	3.9	6.25	1.25	110	85	50	Aorta	Human	Healthy	1	1(h)
10.9	1.5	1.5	5.00	1.25	110	12	11	MPA	—	—	—	—
129.8	4.2a,e	4.3d,e	6.39	2.13	117	172	35	Aorta	Dog	VE	2B	4(h)
265.8	13.2a,e	14.1c,e	6.49	2.16	38	101	24	—	—	C	2A	8(i)
—	12.1b,e	14.5d,e	—	—	—	—	—	—	—	—	—	—
122.6	11.9a,e	10.0c,e	6.27	2.09	87	106	38	—	—	VE	—	8(j)
—	11.4b,e	14.4d,e	—	—	—	—	—	—	—	—	—	—
223.7	14.3a,e	13.3c,e	6.43	2.14	40	89	27	—	—	NC	—	8(k)
—	13.0b,e	11.7d,e	—	—	—	—	—	—	—	—	—	—
288.6	20.8a,e	20.9c,e	7.04	2.35	25	72	25	—	—	H	—	8(l)
—	17.6b,e	17.7d,e	—	—	—	—	—	—	—	—	—	—
7065.0	1553.8	1296.3	20.0	10.0	0.18	12.6	11.9	MPA	Mouse	Control	3	10(f)
15307.0	2412.3	1724.7	40.0	10.0	0.15	22.9	19.9	—	—	Hypoxic	—	—

^aZc₉₅.

^bZc₉₅₊ (see caption of Figure 9).

^cZc_(2–12).

^dZc_(5–15).

^evalue represents averaged Zc over number of cycles.

no symbol: value represents average of all the frequency and time domain methods listed in Table 1.

In summary, even if the qualitative behavior is consistent, the rate of change in the characteristic impedance obtained from different frequency and time domain methods can be highly variable under the same hemodynamic conditions. This not only makes the inter-domain quantitive comparison impossible, but the comparison of intra-domain methods can also lead to contradictions in qualitative behavior. This means that, qualitative behavior and dimensions of parameter estimates do not warrant a comparison with other quantities with the same dimensions, just like Z₀ and Zc cannot be compared to infer the same information about the vascular properties. Therefore the frequency and time domain estimates of characteristic impedance should also be considered as two different hemodynamic parameters. If desired, a certain frequency or time domain estimate should be compared with itself only. Although extensive literature is available, both based on experiments and mathematical models, which studies the effects of various vascular properties on the impedance spectra (see Milnor (1989, ch.7) and Nichols et al (2011, ch.12) for a detailed review of the subject), there are hardly any studies that investigate the effects of hemodynamic conditions and vascular properties on the time domain estimates of Zc, or the behavior of pressure-flow loops in general. In particular, a criterion for selecting the portion of pressure-flow loop is missing and no quantitative comparison is available that compares the estimates using nonlinear and diastolic portions of the pressure-flow loop with other available estimates. One way to improve the understanding of physical differences between the two estimates is to use a 1D pulse wave propagation network model with known parameters and boundary conditions. Using this type of model enables us to calculate the true characteristic impedance, which can then be compared with the two estimates from the frequency and time domain methods, and to quantify the effects of the reflection free assumption. Alternatively, one could set up an in-vitro experiment generating pulse waves at different frequencies and propagate these along a network of tubes with known elastic modulus and reflection coefficients, e.g. the network developed by Segers et al (1998).

5. Conclusion

The goal of this study was to estimate and compare the characteristic impedance using frequency and time domain approaches. Based on our analysis, we conclude that there is no mathematical equivalence relation between the two approaches and demanding them to yield an identical solution for any given dataset is not a mathematically feasible problem. Nevertheless, the two approaches do behave in a qualitatively similar manner and it is possible to obtain identical solutions by multi-run trials using a combination of options. Given their intrinsically different mathematical expressions, frequency and time domain impedance estimates should be assessed as two different hemodynamic parameters. To gain more insight into these differences, we suggest conducting a detailed modeling study or setting up an in-vitro experiment that investigates the effects of system parameters and flow conditions on the two types of estimates.

Appendix A

Table A1.

Dataset 1: Typical harmonics of flow and pressure in the ascending aorta and pulmonary artery of in man. The values are taken from Chapter 6 in Hemodynamics by Milnor (1989) and only provided for the sake of reproducibility of Example 1 in the text.

	Aorta				Pulmonary Artery
	Flow		Presure		Flow		Presure
Harmonic Number	Modulus (ml/s)	Phase (Rad)	Modulus (mmHg)	Phase (Rad)	Modulus (ml/s)	Phase (Rad)	Modulus (mmHg)	Phase (Rad)
0	110	−0.00	85.0	−0.00	110	−0.00	12.00	−0.00
1	202	−0.78	18.6	−1.67	195	−1.02	4.95	−1.54
2	157	−1.50	8.6	−2.25	132	−2.04	1.83	−2.63
3	103	−2.11	5.1	−2.61	58	−3.05	0.85	2.94
4	62	−2.46	2.9	−3.12	10	−1.34	0.04	−0.50
5	47	−2.59	1.3	−2.91	28	−2.14	0.46	−1.90
6	42	−2.91	1.4	−2.81	20	2.98	0.35	3.12
7	31	2.92	1.2	2.93	02	−2.72	0.05	−2.47
8	19	2.66	0.4	−2.54	10	−2.80	0.08	−2.80
9	15	2.73	0.6	−2.87	06	2.48	0.04	2.38
10	15	2.42	0.6	2.87	02	−3.05	0.04	−3.10