Current hypotheses to explain genetic chaos under the sea

Abstract

Chaotic genetic patchiness (CGP) refers to surprising patterns of spatial and temporal genetic structure observed in some marine species at a scale where genetic variation should be efficiently homogenized by gene flow via larval dispersal. Here we review and discuss 4 mechanisms that could generate such unexpected patterns: selection, sweepstakes reproductive success, collective dispersal, and temporal shifts in local population dynamics. First, we review examples where genetic differentiation at specific loci was driven by diversifying selection, which was historically the first process invoked to explain CGP. Second, we turn to neutral demographic processes that may drive genome-wide effects, and whose effects on CGP may be enhanced when they act together. We discuss how sweepstakes reproductive success accelerates genetic drift and can thus generate genetic structure, provided that gene flow is not too strong. Collective dispersal is another mechanism whereby genetic structure can be maintained regardless of dispersal intensity, because it may prevent larval cohorts from becoming entirely mixed. Theoretical analyses of both the sweepstakes and the collective dispersal ideas are presented. Finally, we discuss an idea that has received less attention than the other ones just mentioned, namely temporal shifts in local population dynamics.

Introduction

Soon after protein electrophoresis enabled access to molecular variation, geneticists interested in marine coastal species were surprised by observations of micro-scale genetic heterogeneity that could not easily be explained. Finding significant, temporally unstable genetic differentiation at short scale in the face of planktonic larval dispersal, Johnson and Black (1982) described the genetic structure of Siphonaria jeanae limpets as “chaotic genetic patchiness” (CGP). The term has prevailed as similar observations from a variety of molecular markers have accumulated for a wide array of marine species (reviewed, e.g., in Larson and Julian 1999; Hellberg et al. 2002; Broquet et al. 2013).

These patterns often involve meagre genetic differences that may have little biological effect themselves (Selkoe et al. 2006). Yet they are interesting, because, as we will see, the mechanisms that could hypothetically create such patterns are relevant to a species’ life cycle, demography, ecology, or evolution. They pertain also to population genetic theory as we struggle to understand both how evolutionary forces shape these patterns and how one may infer life-history parameters from genetic observations (there are currently very few methods for the genetic inference of parameters in cases of high spatiotemporal variability in genetic structure).

Our objective is to review the current knowledge and hypotheses regarding the formation of CGP. We will: (1) describe what are the patterns characterized as CGP, (2) discuss each process that has been proposed as a potential cause, and (3) outline emerging issues and perspectives. Hedgecock and Pudovkin (2011) point out that the gap between theory and practice in marine population genetics remains large. Here we start to build some bridges between theoretical and empirical analysis by presenting both empirical and theoretical arguments for the drivers of CGP.

Chaotic Genetic Patchiness: Patterns

The initial description of CGP by Johnson and Black (1982; see also Johnson and Black 1984a, 1984b) contains all the specificities that are still food for thought today. CGP refers to unexpected, small-scale patterns of genetic differentiation inconsistent in space and time. These patterns do not follow any simple spatial distribution (in particular, genetic differentiation does not build up with distance) and local allelic frequencies and spatial differentiation fluctuate rapidly across time (in particular, from one generation to the other). This peculiar type of genetic structure can be described as a fluctuating genetic mosaic (David et al. 1997b). See Boxes 1 and 2 for examples of empirical studies that show CGP.

The key point of CGP is that it occurs at a relatively small spatial scale. That is, genetic differentiation is observed at distances way below the presumed range of dispersal distances of a given species (e.g., <50 m for the limpet S.jeanae in spite of its potentially long planktonic dispersal phase; Johnson and Black 1982). We must be clear that patchiness alone is not a matter of surprise. The dynamics of genetic variation in structured populations was formalized long before chaotic patchiness was described (Wright 1931, 1943), and theory shows how spatial genetic structure can be shaped by mutation, recombination, migration, drift, and selection. The surprise and interest in CGP come from the fact that genetic structure is observed at a scale where theory predicts that gene flow should completely homogenize neutral genetic variation across post-dispersal individuals. In some cases, genetic structure may even be higher at small versus large spatial scale.

Although this definition of CGP is globally accepted in the literature, the scale at which gene flow is thought to be overwhelming for a given species is a matter for debate. There is thus considerable variation in what situations are defined as chaotic patchiness in case studies (see examples in Boxes 1 and 2). A good share of this variation across studies seems to derive from 3 main causes. First and foremost, dispersal is particularly difficult to quantify for the concerned species, leading to uncertainty about the spatial scale at which one can expect to observe CGP. These are almost exclusively marine fish and invertebrates with pelagic larval dispersal (but see Becheler et al. 2010 for an example with the marine phanerogam Zostera marina). Despite a great deal of efforts in the fields of larval biology, hydrodynamic modelling, genetic inference, and geochemical analysis, solid quantitative estimates of larval dispersal have been obtained only for a limited number of species, and even an approximate idea of the dispersal scale remains difficult to obtain for many marine species (reviewed, e.g., in Kinlan and Gaines 2003; Pineda et al. 2007; Selkoe and Toonen 2011). So there is room for interpretation as to what patterns of genetic differentiation appear unexpected at a given spatial scale and different authors may disagree on what should be called chaotic.

Second, a theoretical model which adequately predicts CGP has not yet been introduced (but see Eldon and Wakeley 2009; Broquet et al. 2013 for steps in this direction). This means that conclusions based on observed patterns are rarely, if ever, backed up by quantitative estimates of what should have been observed in theory. Obviously, this does not mean that the conclusions are wrong, but it leaves more room for variation in data interpretation across studies.

Third, beyond inevitable differences in sampling strategies (including pre-/post-dispersal sampling and different types of genetic markers), different studies may use different statistical descriptors of genetic diversity and genetic structure. Global or local gene diversity ($H_{\mathrm{T}}$ and $H_{\mathrm{S}}$) and global or pairwise spatial differentiation ($F_{\text{ST}}$) are commonly used to describe CGP, but there is variation in the use of other descriptors such as temporal $F_{\text{ST}}$ at a sampling point, the distribution of pairwise relatedness between individuals, and various estimators of differentiation such as $D_{\text{est}-\text{Chao}}$ (Jost 2008; “Chao” incidentally stands for Chao et al. 2008, not chaotic patchiness). Different statistics may bring useful, complementary information about the distribution of genetic diversity in a given species (but see box 1 in Gagnaire et al. 2015 for a discussion on $F_{\text{ST}}$ estimators in high gene flow situations). For instance, relatedness estimates are increasingly being used to characterize CGP and identify its cause (e.g., Iacchei et al. 2013, box 1). At the same time, we need to derive theoretical expectations for these statistics in order to make stronger conclusions as to what can explain the observed patterns.

Alongside this issue of comparing empirical estimates with theoretical expectations, theory is useful for at least 2 other reasons. One is that it helps to test for the effect of sampling artefacts: variation in $F_{\text{ST}}$ estimates due to small sample size can easily be interpreted as CGP. Along the same lines, non-significant isolation-by-distance (or time) is often used to suggest that a species’ genetic structure is chaotic. However, this claim should be accompanied by a power analysis (Mantel test has low power for sample sizes that are commonly used in genetic structure analyses) and a good understanding of the conditions under which isolation-by-distance is theoretically expected to be happening (Rousset 2004). The other reason is that formalizing the drivers of genetic patchiness into equations forces us to consider the quantitative effect of clearly defined evolutionary forces (that is, the direct effects of migration, drift or selection on genetic structure) rather than using verbal arguments only.

Chaotic Genetic Patchiness: Processes

In this section, we discuss 4 processes that may generate CGP, namely selection, sweepstakes reproductive success, collective dispersal, and asynchronous local population dynamics.

A chaotic effect of diversifying selection

Diversifying selection due to fluctuating environmental conditions at a local spatial scale was the first process proposed to explain CGP (Johnson and Black 1982; Johannesson and Tatarenkov 1997; Schmidt and Rand 1999). However, many examples resulted from environmental gradients leading to predictable clinal genetic structure (Schmidt et al. 2008), such as salinity gradients in estuaries (Hilbish and Koehn 1985), latitudinal gradient of temperature along European or American coasts (Place and Powers 1979), or bathymetry (Siebenaller and Somero 1978; Rogers 2002).

In some other examples, genetic differentiation was due to the mixing of cryptic species and gene introgression after hybridization in specific places (e.g., in the blue mussel, Bierne et al. 2003). Local admixture was therefore likely to accentuate the impression of chaos because some introgressed individuals are performing better than others under specific local conditions (Bierne et al. 2003, 2006), or hybridization is favored in specific areas or at certain depths (Muths et al. 2006). For example, hybridization between the intertidal echinoderm Acrocnida brachiata and the related subtidal species A. spatulispina is largely prevented by their bathymetric position over the shore and a 15-day shift in reproductive period (Muths et al. 2010). But hybridization still occurs in specific sheltered areas, which results in patches of differentially introgressed demes.

There are, however, situations where selection might be truly responsible for small-scale genetic differentiation. In particular, post-larval settlement selection under different environmental conditions has been argued to create CGP. This is particularly true on rocky shore habitats where emersion time and substrate fixation vary strongly with bathymetric position (Wilkins 1977; Johannesson and Tatarenkov 1997; Schmidt and Rand 1999, 2001). In more homogeneous sandy substrata, specific enzyme-coding loci can also be under direct selection driven by more subtle, unpredictable environmental variations (David and Jarne 1997). However, post-settlement selection on a heterogeneous substratum can be very costly, and habitat choice occurring either at the larval stage (Bierne et al. 2003) or through active migration at the adult stage can be another mechanism whereby the environment drives genetic differentiation.

There are a number of examples of environmental segregation via either differential mortality or active habitat choice, for instance, in gastropods such as Patella aspersa (Wilkins 1977; Riddoch 1993), Littorina saxatilis (Johannesson and Tatarenkov 1997), and Nucella lapidus (Day 1990). These studies found post-settlement differential mortality and phenotypic differences between individuals depending on wave exposure and duration of emergence at low tide. Wave exposure may differ even on the exposed parts of the shelf at a very restricted spatial scale (i.e., a few decimeters to a few meters). It can explain local chaotic patchiness at some genes involved in specific tasks such as attachment on the rocky surface (e.g., shell flatness, foot enlargement in gastropods [Johnson and Black 1998], or byssus strength in bivalves [Willis and Skibinski 1992]). For instance, the spatial juxtaposition of sheltered/exposed rocky habitats accounted for small-scale genetic patchiness in the Mytilus complex (Gosling and Wilkins 1981; Skibinski et al. 1983; Gardner and Skibinski 1991; Gardner et al. 1993), especially for the Glu gene involved in byssus strength (Gerard et al. 2015).

Finally, CGP at some adaptive genes may also result from chaotic variations of the environment itself. This is particularly likely in very unstable, patchy, and unpredictable environments such as deep-sea hydrothermal vents. In this peculiar ecosystem, the chaotic nature of thermo-chemical conditions is driven by the hydrothermal fluid discharge and thus the dual effect of tectonic movements and local effusive eruptions, leading to a series of highly fluctuating microhabitats from very hot and anoxic diffuse systems to older and cooler edifices (Jollivet 1996). In such an extreme system, diversifying selection is likely to occur locally, thereby promoting chaotic alternations of allelic frequencies at some loci involved in thermal adaptation or stress responses to hypoxia and various toxic compounds such as $H_{2}S$, CO₂, CH₄, ammonia, and dissolved metals. In alvinellid worms in particular, allozyme frequency variations among demes were locally (i.e., at the meter scale) significant and as high as between very distant populations located several thousand kilometers apart (Jollivet et al. 1995a). In this particular case, small-scale genetic differentiation at some specific loci such as the phosphoglucomutase gene was partly driven by the average temperature at the opening of the worm’s tubes (Piccino et al. 2004), and allozyme frequencies were linked with their catalytic performance and thermo-resistance (Jollivet et al. 1995b; Piccino et al. 2004).

Although costly, diversifying selection can thus generate CGP in the face of high gene flow provided that, at least, 2 main pre-requisites are simultaneously met: (1) large fecundity for enough recruits to be left after selection by the environment, and (2) a fine-grained mosaic of contrasted habitats able to impose a strong differential selective sieve or a target for the habitat choice in larvae. Such conditions are difficult to find in the open ocean or in the abyssal plain. They could be more frequent in coastal areas of temperate regions with a high diversity of habitats such as the surf and estuarine/brackish zones or in extreme habitats such as deep-sea vents or the upper part of the intertidal habitat where conditions can fluctuate quite rapidly and with a great amplitude over time and space.

The literature cited above show that specific loci under direct or indirect selection have been identified. Genomic studies should bring new information regarding the consequence of these selective effects at the scale of the genome, and they will help identify new selection targets (reviewed by Gagnaire and Gaggiotti, this issue). For instance, combining genome-wide SNP genotyping and transcriptomics, Eierman and Hare (2016) were able to find adaptive loci in the oyster Crassostrea virginica. Individuals subjected to different salinity conditions displayed contrasted gene expression patterns, some of them matching $F_{\text{ST}}$ outliers that correspond to genes known to play a role in osmoregulation. This type of approach is providing interesting information regarding the role of selection within the context of small-scale genetic differentiation.

Sweepstakes reproductive success

The 3 other potential causes of CGP that we discuss are not linked with exogenous effects on specific genomic regions. They are neutral processes generated by a species’ life cycle and life-history traits, more particularly reproductive systems and dispersal. We start here with the sweepstakes reproductive success hypothesis, first by presenting a verbal argument and then we provide some theoretical details.

From variance in reproductive success to CGP

Many marine species are characterized by broadcast spawning reproduction and/or a free-swimming larval stage, with large amounts of gametes and/or larvae released per reproductive event (e.g., 5–20 million eggs released per reproductive event in Crassostrea gigas, Suquet et al. 2016 and 1–11 million in Gadus morhua, Oosthuizen and Daan 1974). High fecundity mitigates the effects of high mortality at early-life stages (Type III survivorship curve). Mortality has been mainly attributed to the stochastic environment in which they are released, although recent studies suggests that it is largely due to genetic load (Plough et al. 2016; Plough, this issue). Many cohorts (here defined as pools of larvae produced by a breeding group during a short period of time) will meet unfavorable conditions and suffer high mortality. Few cohorts may, however, experience milder conditions, and survive. This results in high variance in reproductive success among individuals, notably attributed to high variance in mortality among cohorts, a pattern referred to as the “Sweepstakes Reproductive Success” hypothesis (SRS; Hedgecock 1994; Hedgecock and Pudovkin 2011).

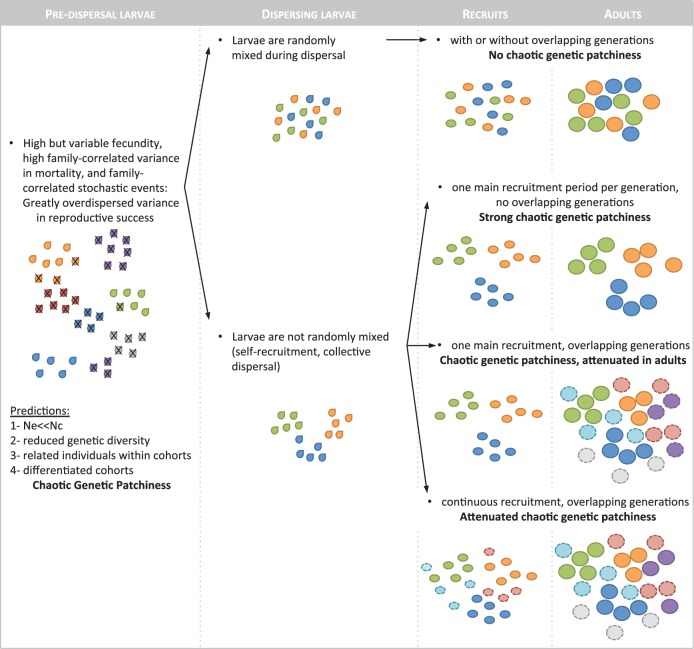
To understand how SRS may drive CGP, 2 key points need to be clarified. First, the spatial scale of the SRS hypothesis must be specified. Sweepstakes reproduction can be considered within a single population but one might also consider sweepstakes events happening within local demes or subpopulations connected via migration (e.g., Eldon and Wakeley 2009; Broquet et al. 2013, see also discussion in Selkoe et al. 2006; Christie et al. 2010). The second point is to decipher expectations for the different life cycle stages of a given species. This is especially critical for early-life stages (pre- vs. post-dispersal larvae). These aspects are important when one discusses the predictions of SRS in terms of spatial genetic structure. Below we consider a substructured population and we first detail SRS expectations for samples taken before dispersal, then after dispersal; and we discuss how SRS may or may not drive CGP in each case (illustrated in Figure 1 with the use of simplified scenarios).

Figure 1.

Simplified scenarios where sweepstakes reproductive success may or may not drive CGP in samples taken at different stages of the bentho-pelagic life cycle. Dashed circles represent recruits or adults that were present before younger recruits or adults appear in the population. In this figure, we consider a spatial scale where dispersal is not limited by distance (see the synthesis section for a discussion of the effects of spatially limited dispersal, self-recruitment, and collective dispersal). Note also that whereas in this figure the sweepstakes reproduction effect is represented only at the pre-dispersal stage, it can be enhanced during dispersal in cases when larvae are not well mixed and mortality can thus affect cohorts differently. This figure gives a qualitative idea of the conditions under which CGP may emerge, but our ability to actually observe genetic patterns (“predictions”) depends also on sampling and data analysis. Quantitative predictions, obtained through analytical theory or simulation, should help interpreting empirical observations.

Inherent to the SRS hypothesis is the idea that variance in reproductive success is extremely high. As few individuals efficiently reproduce and most individuals fail to reproduce, a decrease of the effective population size (Ne) compared with the census population size (Nc) is expected, and a generally low Ne/Nc ratio should be observed (Hedrick 2005; Hauser and Carvalho 2008; Waples, forthcoming). As mentioned above, the SRS hypothesis is explicitly based on the idea that many entire cohorts may die, whereas others will be more successful, thereby introducing family-correlated survival. As shown by Crow and Morton (1955), this can greatly reduce effective population size. See Waples (2002) for a detailed treatment of the effect of family-correlated survival on effective population size and an empirical example in salmons. Waples (forthcoming) further showed that tiny Ne/Nc ratios cannot be explained without involving strong variations in reproductive success among individuals (in particular, the effect of overlapping generations, which is not dealt with explicitly in the theoretical sections below, is necessarily much more modest). SRS is predicted to accelerate genetic drift, with strong consequences for the genetic structure of populations. This process can be formalized using different theoretical approaches. One could use coancestry modeling (recursive equations for identity by descent for pairs of gene copies), as, for instance, in Broquet et al. (2013). With this method, the effect of SRS could be introduced using Waple’s 2002 approach. Another method is to analyze the effect of SRS using coalescent theory, and this approach is presented in detail in the next section.

The genetic effect of SRS will first be visible in offspring from a single reproduction event sampled before they disperse: gene diversity among pre-dispersal offspring should be reduced relative to the adult population (e.g., Li and Hedgecock 1998). An additional key prediction of the SRS hypothesis is the presence of related individuals in pre-dispersal larvae as few individuals largely contribute to the next generation (St-Onge et al. 2015). Genetic differentiation at a small spatial scale in samples taken before dispersal may then be viewed as a prediction of the SRS hypothesis, i.e., SRS should generate instantaneous and ephemeral CGP.

In contrast to genetic drift, larval dispersal will redistribute genetic variation across space, thereby reducing genetic differentiation between locations. Genetic differentiation (CGP) will persist in post-dispersal larvae or recruits if (1) dispersal is limited in space (that is, the study scale is larger than effective dispersal distances), (2) larvae from different cohorts are not completely mixed during dispersal (a situation that we call here collective dispersal, detailed in section 3.3), or (3) a fraction of larvae settle in their natal site (self-recruitment; we consider this situation in the theoretical analysis of SRS below).

By contrast, if dispersal effectively mixes larvae from different cohorts, genetic differentiation is largely attenuated or lost in recruits and adults. Whether or not CGP is completely erased also depends on the dynamics of recruitment (continuous recruitment and/or overlapping generations, Figure 1).

High fecundity, skewed offspring distribution, and multiple-merger coalescents

Population genetics theory is—in large part—based upon 2 main classes of models describing how gene copies are passed on from one generation to the next. The Wright–Fisher model is a discrete-time model of non-overlapping generations. In each generation, each individual (thought of as a gene copy) independently contributes a huge number of potential offspring. The next generation is then formed by sampling the same fixed number (N) from the pool of potential offspring. In the Moran model, at each time step a single individual contributes exactly one offspring (there is no intermediate step of potential offspring), and exactly one individual (other than the offspring) dies, whereas all others survive to the next time step. With this model, generations are overlapping. The classical Wright–Fisher and Moran population models can be viewed as models of “low fecundity,” in the sense that a single individual cannot contribute a large fraction of the next generation (the probability that the number of surviving offspring of a given individual is on the order of the population size vanishes in the limit of a large population). The theory of coalescence can be used to understand the dynamics of genetic variation in these classical population models, and, more importantly here, it can be developed to account for “high fecundity” and sweepstakes reproductive events.

The coalescent approach is the mathematical description of the random genealogy of gene copies sampled from a natural population. It describes inheritance relationships among alleles (gene tree) and allows observations of genetic diversity in a sample to be related to population processes (including drift, mutation, recombination, migration, selection, demographic changes, etc.). It is closely related to the concept of identity by descent (IBD) (Malécot 1948, 1975), which is a concept of pairwise genetic similarity. See, for example, Wakeley (2009) for an introduction to coalescent theory and discussion of the relation between IBD and the coalescent. The random gene-genealogy of a sample of gene copies taken from a Wright–Fisher or Moran population is described (in a large population limit) by the Kingman coalescent (Kingman 1982a, 1982b, 1982c). The Kingman coalescent provides an approximate description of the true genealogy of the sampled individuals, obtained by assuming that the population size is arbitrarily large. The Kingman coalescent approximation holds for a large class of population models provided that the variance in the offspring distribution does not increase with population size. Moreover, it could be unsuitable for highly fecund populations which (potentially) exhibit SRS. It may also be unsuitable for managed wild populations that are effectively replenished by many offspring from a few captive parents (Waples et al., this issue).

Population models which admit high fecundity and SRS have multiple-merger coalescents as their ancestral limit processes (Donnelly and Kurtz 1999; Pitman 1999; Sagitov 1999; Schweinsberg 2000; Möhle and Sagitov 2001; Tellier and Lemaire 2014). In multiple-merger coalescents, an arbitrary number of active ancestral lineages can coalesce at the same time, rather than at most 2 as in the Kingman coalescent. Two different types of multiple-merger coalescents exist (Figure 2). The most general type are so-called Ξ-coalescents (Schweinsberg 2000; Möhle and Sagitov 2001), in which many distinct multiple mergers can occur simultaneously (Figure 2C). A specific case of Ξ-coalescents are Λ-coalescents (Donnelly and Kurtz 1999; Pitman 1999; Sagitov 1999; see Figure 2B), in which at most one multiple merger occurs each time. The general form of the coalescent rate in a Λ-coalescent is given by

$${\lambda }_{b,k}={\int }_0^1{x}^k{(1-x)}^{b-k}{x}^{-2}\Lambda (dx),2\le k\le b$$ (1)

where Λ is a finite measure on $[0,1]$, and (1) gives the rate at which a given group of k lines coalesce out of b lines. The integrand in Equation (1) can be thought of as representing the binomial probability of merging k lines, where x is the probability that a given line participates in the merger, and the term $x^{-2}\Lambda (dx)$ represents the probability density of the law that governs x. The Kingman coalescent is a special case of Λ-coalescents, when $\Lambda (dx)={\delta }_0(x)dx$ (unit mass at 0).

Figure 2.

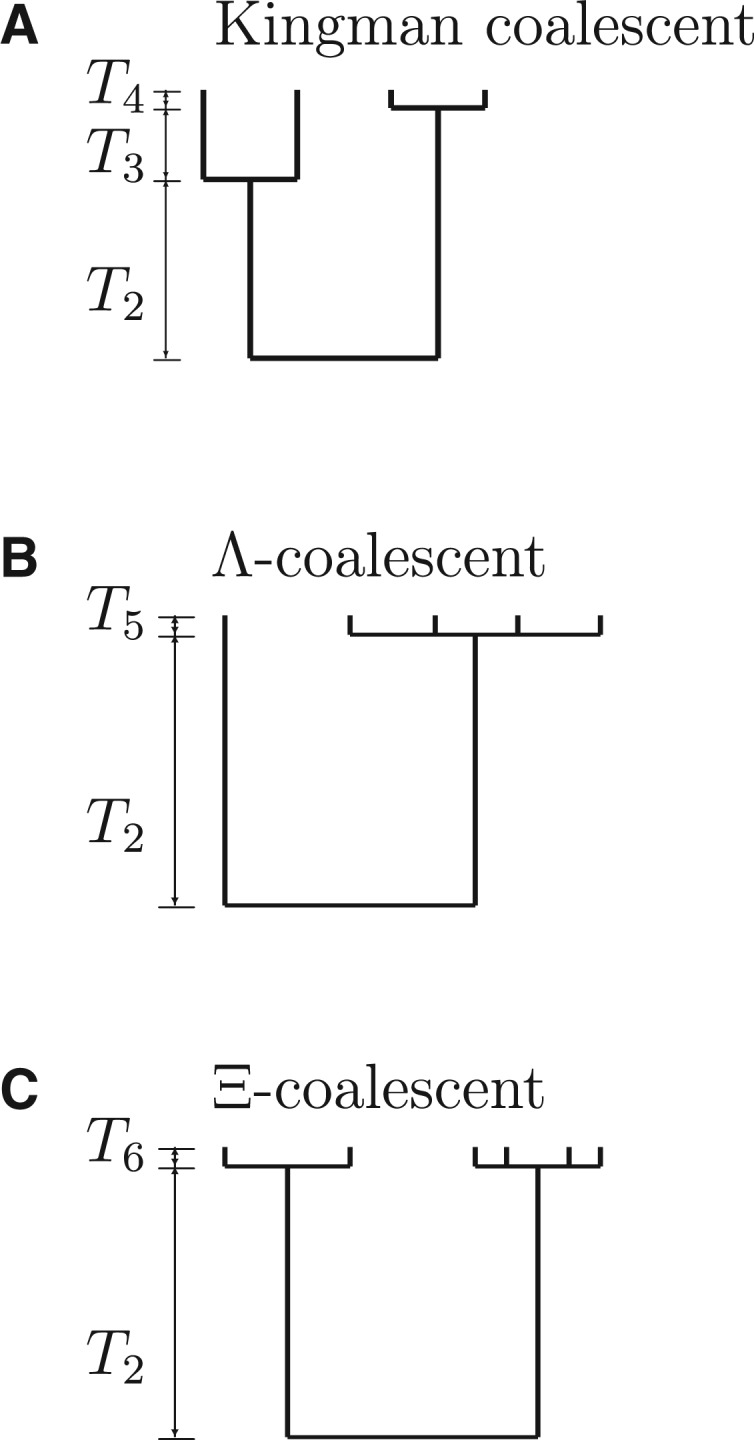
Examples of gene genealogies associated with (A) Kingman coalescent; (B) Λ-coalescent; (C) Ξ-coalescent. The times T_j, where j denotes the number of active lines in each interval, are independent exponentials with rates given by the coalescence rates associated with each coalescent. In (A), at most 2 ancestral lines can coalesce at the same time. In (B), at most one multiple merger occurs each time (a multiple merger of 4 lines in this example). In (C), many distinct multiple mergers can occur simultaneously (here we see a simultaneous merger in which 2 lines and 4 lines merge at the same time in 2 distinct groups).

The work of Birkner et al. (2013a) and Möhle and Sagitov (2003) suggests that Ξ-coalescents are appropriate for analysis of population genetic data of autosomal loci in diploid (or polyploid) highly fecund populations with SRS; whereas Λ-coalescents would be appropriate for analysis of mtDNA, because mtDNA is inherited in a haploid fashion. Indeed, one can model diploidy (where selfing is excluded), by requiring a pair of distinct diploid individuals (the parents), sampled uniformly at random without replacement, to contribute diploid offspring to the next generation. Each diploid offspring samples one chromosome from each of the 2 parents. There are, therefore, 4 parental chromosomes involved in each reproduction event. In an event when the number of diploid offspring is large, many ancestral lines will be involved, and this leads to simultaneous mergers (Möhle and Sagitov 2003; Birkner et al. 2013a). We emphasize that to obtain multiple-merger coalescent processes from some population model, the population model necessarily needs to allow both high fecundity and SRS. These models have in common that the variance in the offspring distribution is huge.

The first (haploid) population model of high fecundity and SRS was introduced by Schweinsberg (2003). In each generation, each individual independently contributes a random number X of potential offspring. The distribution of X is skewed in a way that

$$\mathbb{P}(X\ge k)\approx C{k}^{-\alpha },k\to \infty$$ (2)

where C > 0 is a normalizing constant, and the parameter $\alpha >0$ represents the skewness. If $\alpha \ge 2$ the chance of an individual contributing, a huge number of viable offspring are negligible (the skewness is negligible); whereas if $0<\alpha <2$, the skewness is non-negligible. One can think of the relation (2) between $\mathbb{P}(X\ge k)$ and $C{k}^{-\alpha }$ as approximating the probability distribution of the number of potential offspring (or gametes) produced by a single individual from a highly fecund population (recall the large number of gametes released by Atlantic cod and Pacific oysters). The relation between $\mathbb{P}(X\ge k)$ and $C{k}^{-\alpha }$ only holds for very large k, but it is the tail-end (the probability of a single individual having a large number of offspring) behavior of the model, which determines the resulting coalescent process, i.e., if multiple mergers become visible or not. For instance, an individual has a much higher chance of contributing huge numbers of potential offspring under model (2) than under a Poisson distribution with a fixed mean.

The next generation of individuals is then generated by sampling N individuals from the pool of potential offspring. With this haploid model, the condition $\mathbb{E}[X]>1$ ($\mathbb{E}[X]$ is the expected number of potential offspring by a single individual) ensures that enough potential offspring are produced to maintain a constant population size (N). In case $1\le \alpha <2$ the resulting coalescent process is a special case of a Λ-coalescent, where the rate at which k out of b active ancestral lines coalesce is given by (Schweinsberg 2003):

$${\lambda }_{b,k}=\left(\begin{array}{c}b\\ k\end{array}\right)\frac{\Gamma (k-\alpha )\Gamma (b-k+\alpha )}{\Gamma (b)\Gamma (2-\alpha )\Gamma (\alpha )},2\le k\le b;$$ (3)

where $\Gamma (·)$ is the gamma function. In case $0<\alpha <1$ a discrete-time Ξ-coalescent is obtained (Schweinsberg 2003). However, such a process may not have biological relevance, because the time for mutations to generate variation may be too short.

In general, coalescence theory uses continuous time. It is computationally advantageous, but it makes less biologically intuitive sense than other approaches where time is measured as discrete time units, that is, generations. To understand the predictions from coalescence theory, it is thus important to consider how a continuous-time coalescent process is derived from a discrete-time population model. Assuming Wright–Fisher reproduction in a haploid population of size N (or 2N if diploid), one coalescent time unit (in continuous time) corresponds to N (or 2N) generations; which is the average number of generations it takes 2 genes to find a common ancestor in a haploid (or diploid) population. For instance, if μ is the per generation mutation rate, then the expected number of mutations along a single lineage over one unit of time (that is, N generations) is $N\mu$. Similarly to the scaled mutation rate $N\mu$, one defines a scaled migration rate Nm in structured population models.

With multiple mergers, the time for 2 genes to find a common ancestor can be much reduced. That is, the timescale of the multiple-merger coalescent processes can be very different from the one usually associated with the Kingman coalescent. We define that one coalescent time-unit corresponds to $1/c_N$ generations. The quantity c_N is the probability of the event that 2 individuals, randomly sampled from the population, derive from the same parent. In a haploid Wright–Fisher population model with population size N, $c_N=1/N$. The timescale in the model (2) of Schweinsberg (2003) is given by, when $1<\alpha <2$, and $B(·,·)$ is the beta function,

$$c_N\approx \frac{C\alpha B(2-\alpha ,\alpha )}{{(\mathbb{E}[X])}^{\alpha }{N}^{\alpha -1}},N\to \infty ,$$ (4)

(Schweinsberg 2003, Lemma 13). Because $\mathbb{E}[X]$ is unknown in most cases, one usually approximates $c_N\approx N^{1-\alpha }$ in applications.

A driver of CGP

In classical coalescent theory of structured populations (e.g., Herbots 1997), the migration rate between subpopulations is usually defined for one unit of time that consists of N generations, where N is the population size of each subpopulation. This scaled migration rate Nm follows from the timescale of the underlying Wright–Fisher model (as explained above), but the structured coalescent process of a Moran model would be the same, as long as individuals have negligible chance (in a large population at least) of contributing very many offspring (e.g., Eldon 2009). Given a sweepstakes reproductive success population model with timescale $1/c_N$, the standard “Nm” quantity is replaced by $c_N^{-1}m$. If $1/c_N\ll N$, one needs to model migration as occurring on a much shorter timescale than in the classical models.

In general we do not know $\mathbb{E}[X]$, the mean of the number of viable offspring contributed by a given individual in the model of Schweinsberg (2003). For simplicity, we approximate c_N from (4) with $c_N^{(\mathrm{B})}=N^{1-\alpha }$, and denote the c_N associated with the classical haploid Wright–Fisher model as $c_N^{(\text{WF})}=N^{-1}$. Then $c_N^{(\text{WF})}/c_N^{(\mathrm{B})}=N^{\alpha -2}$, when $1<\alpha <2$. Hence, for large N, the ratio $c_N^{(\text{WF})}/c_N^{(\mathrm{B})}$ can be very small. The “effective size” of a deme is usually defined in reference to the haploid Wright–Fisher model. If we define the deme effective size as $N_e=1/c_N$, then we have $N_e^{(\mathrm{B})}=1/c_N^{(\mathrm{B})}$, and $N_e^{(\mathrm{W}F)}=1/c_N^{(\text{WF})}$. Then

$$\frac{c_N^{(\text{WF})}}{c_N^{(\mathrm{B})}}=\frac{N_e^{(\mathrm{B})}}{N_e^{(\mathrm{W}F)}},$$

and the deme effective size associated with model (2) can be much smaller than the deme effective size associated with the Wright–Fisher model, for same census deme size N.

Eldon and Wakeley (2009) derive expressions for $F_{\text{ST}}$ when the offspring distribution is assumed to be skewed (imitating a situation where sweepstakes reproductive success can take place). The migration rate in the model of Eldon and Wakeley (2009) necessarily follows the coalescent timescale c_N, with scaled migration rate $M=c_N^{-1}m$. The probability m (which, therefore, must be regarded as a function of the population size N) that a single individual resided in a different subpopulation in the previous generation is given by $m=M{c}_N$. Eldon and Wakeley (2009) obtain the following expression, in which $D\ge 2$ denotes the number of subpopulations,

$$F_{\text{ST}}=\frac{1}{1+\frac{M}{\lambda }{\left(\frac{D}{D-1}\right)}^2+\frac{\theta D}{2(D-1)\lambda }},$$ (5)

θ is the (appropriately rescaled) mutation rate, and $\lambda ={\lambda }_{2,2}$ in (1) is the rate at which 2 lines coalesce. Equation (5) was obtained from a population model of a structured population (a simple island model), in which the migration rate is assumed equal between demes. Sweepstakes reproduction is allowed to occur in every subpopulation (see Eldon and Wakeley 2009, for details).

If one rescales time with c_N, λ equals 1, regardless of the population model. However, both θ and M are in units of $c_N^{-1}$, and thus could be small relative to 1. The value of $F_{\text{ST}}$ can therefore be close to 1 (Figure 3), even if the rates of migration or mutation would be very high measured over N generations. In Figure 3, we set θ = 1 to keep focus on varying migration rate. We can rewrite Equation (5) in terms of the coalescent timescale c_N (with λ = 1), and obtain, in which μ and m denote the per-generation mutation and migration rates,

$$F_{\text{ST}}^{(c_N)}=\frac{1}{1+\frac{m}{c_N}{\left(\frac{D}{D-1}\right)}^2+\frac{2\mu }{c_N}\frac{D}{D-1}}.$$ (6)

Using the approximation $c_N\approx N^{1-\alpha }$, Equation (6) becomes

$$F_{\text{ST}}^{(c_N^{(\mathrm{B})})}=\frac{1}{1+m{N}^{\alpha -1}{\left(\frac{D}{D-1}\right)}^2+2\mu N^{\alpha -1}\frac{D}{D-1}}.$$ (7)

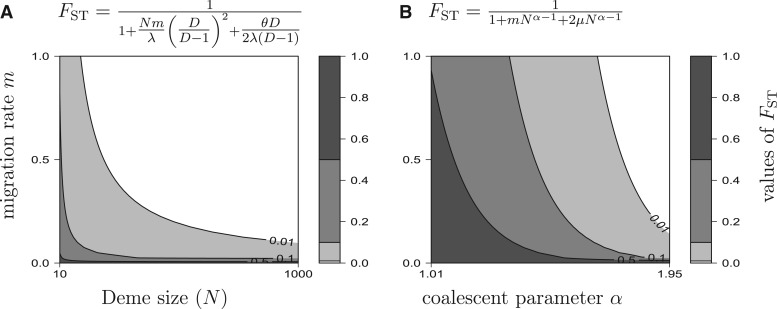
Figure 3.

Values of $F_{\text{ST}}$ from expressions as shown. In (A), $\theta =\lambda =1$; in (B), N = 1,000 and $\mu ={10}^{-5}$. Number of subpopulations set at D = 100 in both graphs. In (B), the effect of skewness (and thus the intensity of SRS) is greater for smaller values of α.

Equation (6) is obtained from a structured coalescent model in which migration is forced to occur on the coalescent timescale $1/c_N$. Migration could be strong when measured over the timescale of N generations, but much weaker when measured over the possibly much shorter timescale of $1/c_N$ generations. This is what $F_{\text{ST}}$ picks up. Consider Equation (6), and assume $m/c_N\ll 1$, but also that $m/(1/N)=Nm\gg 1$, then $1/N\ll c_N$. Thus, $F_{\text{ST}}$ in Equation (6) can be away from zero if the coalescence timescale $1/c_N$ is much shorter than the usual Wright–Fisher timescale. We should also keep in mind that the coalescent might be a version of the Kingman coalescent, only with a timescale dictated by c_N.

If migration is weak relative to the coalescent rate on the timescale $1/c_N$, we effectively observe one of the scenarios illustrated in Figure 1, where SRS is able to generate CGP. Collective dispersal, discussed in the next section, may enhance the effect of SRS by keeping the cohorts which derive from the same parents together.

Collective dispersal

How can collective dispersal generate CGP

Collective dispersal is a general term for any process leading to gene flow by groups of individuals (Yearsley et al. 2013). It can be described as any dispersal process where 2 immigrants in the same population have a higher than random chance of having originated from the same natal population. This type of dispersal may arise from individual dispersal strategies (e.g., spider mites form collective balls of individuals in order to promote dispersal by wind; Clotuche et al. 2013) or it may be a consequence of the environment constraining individuals to disperse in groups (e.g., dispersal by ocean currents Siegel et al. 2008).

The hypothesis that collective dispersal can produce CGP was qualitatively proposed by a number of authors (Campton et al. 1992; Hedgecock 1994; David et al. 1997b) and quantitatively formalized by Broquet et al. (2013) and Yearsley et al. (2013). Collective dispersal can generate CGP because gene flow due to collective dispersal has reduced power to mix the genetic diversity of different populations. This means that the force of gene flow relative to genetic drift is weakened and the equilibrium genetic differentiation between populations is increased. The power of collective dispersal can be intuitively appreciated from the extreme case of a metapopulation with many demes, where all individuals in a deme are immigrants from the same source deme and local extinction does not occur. In this extreme case of high dispersal (m = 1) and high collective dispersal, individuals from different demes never mix despite the high dispersal and strong genetic differentiation can therefore emerge.

Another feature of CGP is a high temporal turnover in genetic diversity. In systems with high potential for dispersal the temporal turnover (e.g., quantified as a temporal version of $F_{\text{ST}}$; Lehmann 2007) is close to spatial turnover in genetic diversity, $F_{\text{ST}}$. Collective dispersal therefore increases temporal turnover to the same extent as its effect on spatial genetic diversity. Extinction of local breeding populations can also be responsible for increasing temporal turnover in genetic diversity without having a significant impact upon $F_{\text{ST}}$ (Broquet et al. 2013).

Because collective dispersal involves pairs of immigrants, immigration rate must be at least 2 immigrants per deme (Nm > 2). In practice, immigration rates must be much higher than 2 for the impact of collective dispersal on genetic diversity to be detectable relative to random dispersal. Collective dispersal is therefore of most interest in systems with high immigration rates ($m\approx 1$). It is therefore relevant in metapopulations of marine fish or invertebrates with a bentho-pelagic life cycle with large-scale larval dispersal.

The effect of collective dispersal can also be explained in terms of coalescence (Wakeley 2009). In a metapopulation with many demes and no collective dispersal (i.e., each individual disperses to a randomly selected deme), 2 immigrants sampled in the same deme are very unlikely to have come from the same source deme (probability $1/D$, where D is the number of demes). The probability of a coalescence event between 2 immigrants is therefore very small (for coalescence, 2 individuals must share a parent, which requires them to have the same source deme). Almost by the definition of collective dispersal, the probability of 2 immigrants having the same source population is increased. Therefore, the probability of coalescence is also increased and the expected time until coalescence is decreased under collective dispersal.

The plausibility of collective dispersal and its empirical support

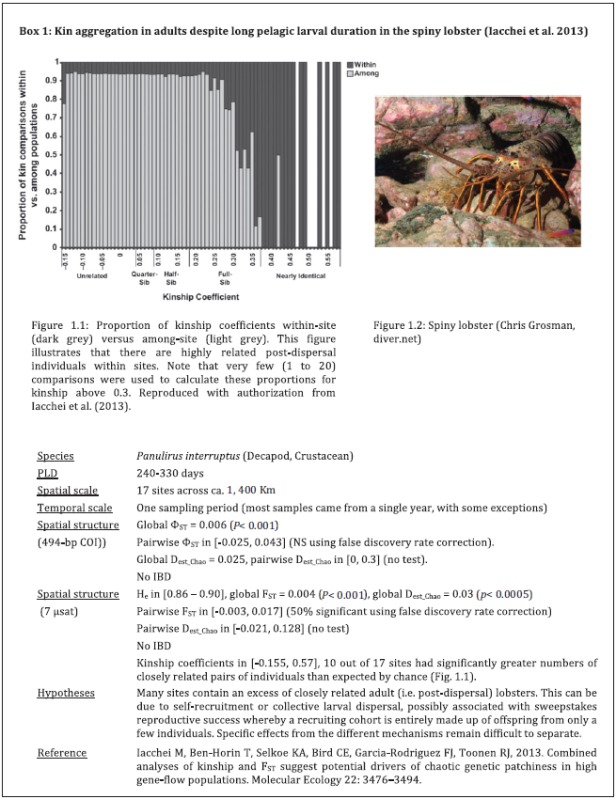
We are not aware of studies that estimate the strength of collective dispersal in real systems, but there is evidence that collective dispersal exists. The strongest evidence for the presence of collective dispersal in marine systems comes from the observation of greater than expected levels of kinship within sampling sites (e.g., Hedgecock et al. 2007; Iacchei et al. 2013; Aglieri et al. 2014).

Evidence of increased kinship within a sample has been found for the humbug damselfish Dascyllus aruanus (Buston et al. 2009) and Naso unicornis (Planes et al. 2002). More evidence is now emerging from specific pairwise relatedness between recruits in the same sample. Genetic evidence of full-sibs (Bernardi et al. 2012; Iacchei et al. 2013; Aglieri et al. 2014) and half-sibs (Selkoe et al. 2006; Hedgecock et al. 2007) in cohorts of larval recruits is particularly suggestive of collective dispersal.

There is also some direct evidence that marine larvae can have correlated dispersal pathways. In a study of 2 species of coral-reef fish (Neopomacentrus miryae and Chromis viridis), Ben-Tzvi et al. (2012) found similarity in otolith microchemistry between pairs of individuals from cohorts of N. miryae. This intra-cohort similarity suggests that N. miryae larval fish move together during their pelagic dispersal. Intra-cohort similarity of C. viridis otolith microchemistry was no different from the expectation, giving no evidence for collective dispersal in this species. This data from otolith microchemistry seems particularly powerful when combined with genetic data.

Finally, observations of heterozygosity-fitness correlations in marine species may be interpreted as an indirect evidence of collective dispersal: Such correlations require mating between closely related mates, and this happens when closely related individuals dispersed together (e.g., David et al. 1995).

Collective dispersal could be an active dispersal strategy in marine invertebrates and fish (e.g., kin recognition, shoaling), but it could also be driven by the physical dispersal environment. Biophysical modelling of larval dispersal supports the possibility of collective larval dispersal being driven by eddies that maintain packets of larvae during their transport by ocean currents (Siegel et al. 2008). Another, more speculative possibility is that dispersal is constrained by species interactions (e.g., Phyllosoma larvae associated with Medusae, Herrnkind et al. 1976)

If we accept that collective dispersal is present in marine invertebrates, then to generate the observed levels of CGP also requires quite strong genetic drift (equivalent to local breeding groups of less than roughly 50 individuals). Genetic drift is required to generate genetic differentiation between demes whereas collective dispersal is required to reduce the power of gene flow at removing the differentiation generated by the drift. Collective dispersal would thus theoretically be a stronger driver of spatial genetic structure when sweepstakes reproductive success occurs in a structured population, as advocated by Broquet et al. (2013). Limited empirical data supports small local breeding groups, but very few studies have empirically estimated the effective size of breeding groups. Hedgecock et al. (2007) found only 10–20 breeders contributing to a cohort of juvenile flat oysters Ostrea edulis. Slipper limpets (Crepidula fornicata) have a maximum of 10–15 parents in a breeding group simply because breeding groups are fixed stacks of individuals (Dupont et al. 2006; Proestou et al. 2008; Broquet et al. 2015), although collective dispersal of slipper limpet larvae may not happen at a scale such that 2 or more related larvae settle in the same breeding group (stack).

Broader consequences of collective dispersal

The hypotheses of collective dispersal and SRS have several parallels. Collective dispersal has the consequence that the natal sources of immigrants into a deme are overly represented by individuals from one, or a few, source demes. Sweepstakes reproductive success has the consequence that immigrants into a deme are overly represented by the offspring of one, or a few, individuals.

If collective dispersal plays a role for marine organisms then it is expected to affect the evolution of life history beyond genetic chaotic patchiness. Collective dispersal has been shown to favor female-biased sex ratio (Gardner et al. 2009) and altruistic behavior (Gardner and West 2006). Consistent with collective dispersal being associated with altruistic behavior, kin recognition has been demonstrated in marine invertebrate larvae that also settle in aggregations stronger than expected under random dispersal (Grosberg and Quinn 1986). If collective dispersal is itself a trait that can evolve then it is expected to be favored by high within-group relatedness, low costs of dispersal and reproductive skew in favor of “followers” (Koykka and Wild 2015). Heritability in the dispersal behavior of a marine invertebrate (a requirement for evolution to occur) has been demonstrated in the tube worm Hydroides dianthus (Toonen and Pawlik 2001).

Parallels with asymmetric dispersal

Asymmetric dispersal patterns are likely to be common in marine systems (see discussion in Riginos et al., this issue). For example, oceanographic currents have prevailing directionality that provide an underlying asymmetry to the dispersal of passive particles. Asymmetric dispersal may also arise from patterns of dispersal that randomly fluctuate from one generation to the next. Fluctuating dispersal patterns may be driven by peaks in local larval production that occur in different generations for different local populations.

There are strong parallels between the genetic consequences of collective dispersal and the genetic consequences of asymmetric dispersal. Both collective dispersal and asymmetric dispersal increase the probability of sampling 2 immigrants that had the same natal population. Both, therefore, increase the rate of coalescence events between pairs of lineages. Many of the qualitative results for collective dispersal also apply to asymmetric dispersal (Yearsley et al. 2013). Asymmetric dispersal is therefore expected to increase population differentiation, relative to the symmetric dispersal scenario. Simulations that compare the effects of asymmetric dispersal and collective dispersal show that asymmetric dispersal can be more effective at creating population differentiation when asymmetric dispersal patterns are constant through time (Yearsley et al. 2013).

Theoretical test of the collective dispersal hypothesis

The ability of collective dispersal to increase genetic differentiation in systems with high immigration rates and small local breeding groups can be theoretically investigated by 2-sample coalescent theory (Yearsley et al. 2013) and computer simulation (Broquet et al. 2013). The theory considers a metapopulation with D demes, each containing N individuals, an extinction probability e, and an immigration rate of m. It is assumed that the population is at equilibrium, the number of demes is not small (D > 20) and that immigration is constant. Collective dispersal can be represented as the probability that 2 immigrants into the same deme also originated from the same deme, $\phi$ (random dispersal corresponds to $\phi =1/(D-1)$). Consider the probability that 2 individuals in the same deme had ancestors who also shared a deme, α. This can arise if the 2 individuals stay in their natal deme (with probability ${(1-m)}^2$) or if the 2 individuals dispersed collectively (with probability $m^2\phi$). Collective dispersal therefore increases the probability that pairs of individuals stay together in a deme

$$\alpha ={(1-m)}^2+m^2\phi ,$$ (8)

but the collective dispersal term ($\phi$) is quadratic in m, and hence, most important for $m\approx 1$.

Genetic differentiation (F_ST) can be simply expressed when immigration rate is close to 1 and in the many deme limit with no selfing,

$$F_{ST}\approx \frac{1}{1+\frac{2N}{\phi }\left[(1-\phi )+2(1-e)(1-m)\right]}$$ (9)

where terms of ${(1-m)}^2$ and higher in the denominator have been neglected. Setting extinction rate to zero (e = 0) gives the simplified equation,

$$F_{ST}\approx \frac{1}{1+\frac{2N}{\phi }\left[(1-\phi )+2(1-m)\right]}.$$ (10)

This shows that at very high immigration rates genetic differentiation is determined by the level of collective dispersal and local genetic drift. Reducing immigration rate in this scenario counter-intuitively reduces genetic differentiation.

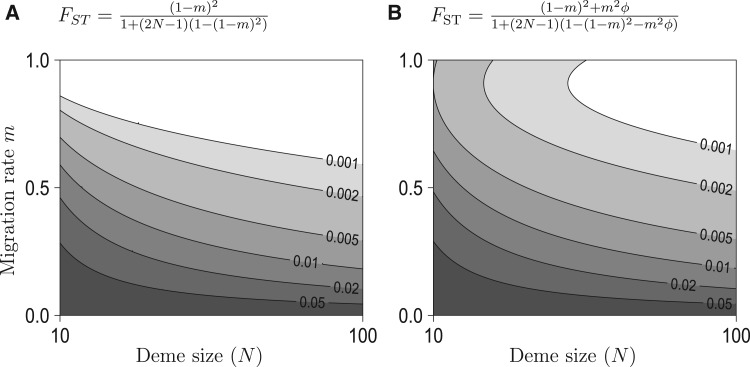
In this scenario, the global population size (ND) is not determining genetic differentiation. Rather it is the local breeding group size (N) that is determining the strength of genetic drift. Figure 4 shows that predicted levels of differentiation from equation 10 can be consistent with observed levels for realistic values of local breeding group sizes (N) and a moderate level of collective dispersal $\phi$.

Figure 4.

Effect of collective dispersal on predicted equilibrium $F_{\text{ST}}$ (gray levels) in an infinite island model for a range of deme size (N). In (A), there is no collective dispersal (island model, $\varphi$= 0). In (B), 10% of the immigrants in a given deme come from the same source deme ($\phi$= 0.1). This figure shows that collective dispersal enhances genetic differentiation at a spatial scale where all larvae are migrants (m = 1) and this effect is visible when drift is strong (small deme size N).

Asynchronous local population dynamics

In addition to selection, sweepstakes reproductive success, and collective dispersal, CGP may also be caused by differences in phenology leading to asynchronous local population dynamics. In particular, spawning asynchrony among patches of ripe individuals and the subsequent history of cohorts before settlement can drive genetic differentiation at a short spatial scale (Watts et al. 1990; David et al. 1997a; Andrade and Solferini 2007). This may be particularly true for semelparous species with non-overlapping generations (Jolly et al. 2003, 2009, 2014).

In most marine species, individuals are often gregarious during reproduction and mainly distributed in discrete patches (Heip 1975). Generally speaking, in case of external reproduction, gamete release can be locally synchronized both by extrinsic factors that may vary locally (e.g., increase of temperature, lunar cycle and/or lack of turbulence at low tide: Minchin 1992; Marshall et al. 2004; Mangubhai and Harrison 2008), and intrinsic factors (e.g., release of pheromones by the first spawners: Hardege et al. 1998; Zeeck et al. 1998; Ram et al. 2008). The timing of larval release can thus vary from one patch to another. Moreover, this remains true even for continuous populations, where egg release and fertilization are often density-dependent and highly restricted to local patches as fertilization severely decreases a few meters from the point of emission (Levitan 1991; Levitan et al. 1992; Babcock et al. 1994; Yund 2000). On the one hand, aggregations of conspecifics increase the likelihood of fertilization success but, on the other hand, also affect their growth and maturation rates because of strong intra-specific competition for food. As a consequence, individuals of neighboring patches are not always able to spawn at the same time simply because both the neighborhood size and local conditions vary. This variation can affect gonadic maturation, as shown in the ophiuroid A.brachiata for which individuals located a few meters apart display a shift of about 15 days in their gamete maturation because of their position on the shore (Muths et al. 2010). This was shown also in the polychaete Pectinaria koreni, which lives on muddy sediments that display differing levels of organic matter (Jolly et al. 2014). Changes in density among and between patches thus generate a high level of heterogeneity in the period at which individuals reproduce, resulting in a series of discrete spawning events over different portions of the population during the breeding season (Muths et al. 2010; Jolly et al. 2014). Such a situation has been well depicted in the tubeworm P.koreni in the Baie de Seine (France), where the population is made of a series of patches that spatially differ both in terms of population density (from a few tens to thousands of individuals per meter square) and individual growth rate (Jolly et al. 2014). This heterogeneous distribution of individuals has a profound impact on the metapopulation dynamics of this semelparous and univoltine species with several discrete spawning events during the breeding season (May–September) leading to a high level of spatiotemporal heterogeneity of the settlement patterns at the scale of the bay and subsequent month-dependent genetic patchiness.

Asynchronous reproduction and development may thus generate genetic patchiness. Yet this differentiation can be observed between patches of adults only if dispersal is not efficiently homogenizing the genetic pool between reproduction events (similarly to the conditions discussed earlier for the SRS hypothesis, section 3.2). In the case of P.koreni that is detailed above, the co-occurrence of genetically differentiated cohorts was maintained by differences in the hydrodynamic regime prevailing at the dates of spawning. A similar situation was also suspected by Johnson and Black (1984a) and David et al. (1997b) to explain the genetic heterogeneity of recently settled recruits in the gastropod S.jeanae and the bivalve Spisula ovalis.

Moreover, the persistence of genetic differentiation requires additional conditions: (1) the number of parents contributing to the offspring must be limited at each spawning event, so that genetic drift is strong enough to create differentiation between offspring cohorts, (2) spawning events should be well separated over time, and (3) parents and offspring should not be able to cross-fertilize subsequently to avoid the genetic re-homogenization from one generation to the next. This situation is usually met in semelparous species, but it is also achievable in species with overlapping generations if parents and offspring are spatially well separated (specific case of sink populations when several sources co-occur) or if maturation rate is heritable. In this latter case, populations can be subdivided into groups of early and late reproducers that weakly interact through time, leading to the possibility of isolation by time as proposed by Hendry and Day (2005). For example, this process was shown to produce a mosaic of genetically differentiated groups of individuals in the catadromic fish Anguilla anguilla (Maes et al. 2006).

In a few cases, another explanation for CGP at both micro- and meso-spatial scales is the co-occurrence of distinct propagule types (i.e., poecilogony) within a given species according to either its environmental surroundings or the reproductive season (Collin 2012). Although quite rare, this situation is found in some annelid polychaetes, which harbor a great plasticity in developmental mode (Kruse et al. 2003; Kesaniemi et al. 2014a, 2014b). For instance, high temporal genetic variation was found between cohorts of the polychaete Pygospio elegans in the Baltic Sea for populations with more than one developmental mode. The alternance of developmental modes produced a high level of genetic relatedness in some cohorts, essentially due to the nearly direct development of the worms at specific localities (mainly the ends of fjörds). The co-occurrence of several developmental strategies within a single species is therefore likely to fuel genetic differentiation among populations.

Synthesis and Perspectives

Reviewing the mechanisms that can generate unexpected genetic differentiation in the face of dispersal in marine species, we found that selection can be responsible for locus-specific signatures whereas genome-wide patterns are more parsimoniously explained by several neutral processes (sweepstakes reproductive success, collective dispersal, and asynchronous population dynamics).

An important conclusion is that these 3 neutral processes all require that (1) drift is strong enough to create genetic differentiation between cohorts of larvae, and (2) dispersal is not efficiently homogenizing the genetic variability in space across the study area.

The first condition is met when the size of local breeding groups is limited (e.g., because of the short lifetime of gametes in species with external fertilization, or the limited mating opportunities in not-too-mobile species with internal fertilization). Drift can be greatly enhanced by SRS (Waples 2002; Hedrick 2005; Eldon 2009), and SRS is, perhaps, even required in cases where CGP is observed. However, sweepstakes reproductive success and drift alone cannot result in CGP if dispersal is efficient and homogeneous across the study scale.

The second condition is met when: (1) dispersal happens at smaller distances than anticipated, (2) a fraction of individuals recruit in the site or population where they were produced (i.e., migration rate m < 1 in population genetics models) and in that case theory shows that SRS can be a strong promoter of local genetic structure in the face of gene flow, and (3) an individual’s dispersal is not completely random and at least a few related individuals end up in the same breeding group after dispersal (a situation that we call here collective dispersal and that can have a particularly strong effect when combined with SRS or asynchronous population dynamics).

In case (1), there is no puzzle, and the genetic structure should perhaps not be called CGP. This is a situation where geographic patterns such as isolation by distance can be expected if genetic drift is not too weak. Case (2) can also be considered a classic situation of population genetic structure, but it is remarkable in species with a bentho-pelagic life cycle because it requires that a proportion of larvae recruit where they were produced. Self-recruitment can be driven by active larval behavior (e.g., swimming fish larvae), particular hydrodynamics favoring retention, or a mixture of both (such as selective tidal stream transport in invertebrate larvae). Case (3) is the most intriguing, and surely the most speculative, because it requires that larvae are not completely mixed during dispersal but instead sufficiently aggregated for genetic structure to be observable in post-dispersal stages (recruits and adults). Yet random (or constant) asymmetric gene flow between populations has the same (or stronger) consequences as collective dispersal (Yearsley et al. 2013), and such asymmetries could result from asymmetric current flow. It remains to be tested whether hydrodynamics, coupled with larval behavior, can produce asymmetries that are strong enough to result in chaotic genetic structure. This question enters the research agenda of seascape genetics (Riginos et al., this issue).

The “variable source hypothesis” is another idea often mentioned in the literature to explain CGP. This hypothesis states that juveniles that recruit in different local populations come from differentiated sources, thereby maintaining spatial genetic heterogeneity at a local scale (e.g., Kordos and Burton 1993; Selkoe et al. 2006). The intriguing point with this idea is that immigrants dispersed as cohorts (or variable mixtures of cohorts, e.g., Hogan et al. 2010) rather than a mixture of individuals from all potential sources (otherwise there would be no genetic structure maintained post-dispersal). This can happen in case of temporal asynchrony or collective dispersal. In this article, we separated these 2 mechanisms, which is why the “variable source hypothesis” is not treated as such.

In the context of the “variable source hypothesis,” it is also important to realize that the sources need not be genetically differentiated to generate differentiated cohorts of offspring. Genetic drift can do that alone, and differentiation between cohorts will be proportional to 1/N (Broquet et al. 2013). This effect of genetic drift on differentiation in pre-dispersal offspring was termed the “Allendorf-Phelps” effect by Waples (1998), by reference to an example of pre-dispersal genetic differentiation reported by Allendorf and Phelps (1981). More information on pre- and post-dispersal dynamics of the genetic variation can be found in Vitalis (2002), Fontanillas et al. (2004) and Rousset (2004).

In this article, we have focused essentially on unexpected fine scale patterns (where “fine” means that we look at a spatial scale where dispersal is thought to be spatially unlimited). Note, however, that another aspect of CGP that is sometimes observed is that the level of differentiation at a very large spatial scale (way beyond a species’ dispersal capability) remains constant. None of the 4 processes that we list satisfactorily explain cases where genetic differentiation at a very large spatial scale is of the same order as small-scale patterns (except perhaps for enzyme polymorphism under selection). To our knowledge, this precise question has never been tackled using theoretical formalism and will need to be addressed in future studies.

In this discussion article, we have struggled to start bridging the gap between theoretical and empirical research. We met a number of difficulties, including comparing overlapping generation coalescent models and non-overlapping generation co-ancestry models, and understanding in what conditions a given model can be used to understand observations from the wild. We have merely started to build some connections between different theoretical approaches and between theory and empirical results, and we encourage others to go in that direction as theory and quantitative predictions help to understand empirical datasets.

New theory can also be developed. Barton et al. (2010, 2013) consider a population evolving in a spatial continuum, in which reproduction at any given time only affects individuals located within a given area, which can change in size and location between reproduction events. Under certain conditions, the associated gene genealogies admit multiple mergers. Further analysis of models of populations evolving in continuous space could yield new insights into CGP; in particular coastal marine species could be modeled as being continuously distributed along a coastline. Common statistics for structured populations, such as $F_{\text{ST}}$, are based on the spatial structure being discrete, i.e., the population is structured into discrete subpopulations. Other statistics such as relatedness coefficients that quantify the “degree of substructure” in models of continuous space can provide interesting information for describing and understanding CGP (Iacchei et al. 2013).

Predictions or even inference can be made based upon the different hypotheses. Some inference methods to infer the value of, for example, the parameter α in Equation (2), or to distinguish between population growth models and SRS models, have been developed (Birkner and Blath 2008; Birkner et al. 2013b; Eldon et al. 2015; Spence et al. 2016, forthcoming). Because $F_{\text{ST}}$, when derived from a structured population model which admits multiple mergers, necessarily is a function (implicitly or explicitly) of associated coalescent parameters, one may need to develop new statistics (modified versions of $F_{\text{ST}}$), which allow for multiple mergers, and make the dependence on coalescent parameters explicit, so that it is clear what one is measuring. Likelihood methods could also be developed; either based on the full DNA sequence data (cf., e.g., Birkner and Blath 2008; Koskela et al. 2015), or approximate likelihoods based on summary statistics such as the (normalized) site-frequency spectrum (cf., e.g., Eldon et al. 2015). Another idea regarding SRS would be to explore the consequences of this demographic process on the distribution of genetic differentiation across the genome. For instance, it would be useful to determine if false positive outliers are generated, and if these can be used to detect SRS.

Finally, after its original description from a marine invertebrate, CGP has since been discussed almost exclusively in the field of marine biology. As we have detailed above, this could be due to the fact that this genetic structure is linked with peculiar life-history traits found in marine species. Yet one might ask whether the particular combination of evolutionary forces that shape these patterns could be observed in other, terrestrial systems. For instance, sweepstakes reproductive success could also be happening in a variety of highly fecund terrestrial species, as suggested by Hedrick (2005). Wind-dispersed seeds could also lead plant species to experience some of the scenarios explored above. However, only marine environments provide favorable conditions for a specialized dispersive life stage (free floating larvae) that can survive and grow for long periods of time (and much more so than the airborne stage of terrestrial organisms, Burgess et al. 2015). As advocated by Burgess et al. (2015), “benthic marine organisms with a biphasic life cycle […] exemplify the greatest contrast with life cycles in most terrestrial organisms.” Being nearly exclusively found in species with such a bentho-pelagic life cycle (invertebrates and coastal fish), CGP might thus well be truly associated with the marine environment.

Funding

B.E. acknowledges the support of the DFG Priority Programme SPP 1819 “Rapid Evolutionary Adaptation” through DFG Grant STE 325/17-1 to Wolfgang Stephan. T.B. has been supported by the Region Bretagne (Grant SAD Volet 1 - DYNAMIC 6626), the French ministers “Affaires étrangères et Européennes” and “Enseignement supérieur et Recherche” (Grant Ulysses 25778NF), and the French Agence Nationale de la Recherche (grant ANR-13-JSV7-0001-01).