Model for screened, charge-regulated electrostatics of an eye lens protein: Bovine gammaB-crystallin

Abstract

We model screened, site-specific charge regulation of the eye lens protein bovine gammaB-crystallin (γ B) and study the probability distributions of its proton occupancy patterns. Using a simplified dielectric model, we solve the linearized Poisson-Boltzmann equation to calculate a 54 × 54 work-of-charging matrix, each entry being the modeled voltage at a given titratable site, due to an elementary charge at another site. The matrix quantifies interactions within patches of sites, including γB charge pairs. We model intrinsic pK values that would occur hypothetically in the absence of other charges, with use of experimental data on the dependence of pK values on aqueous solution conditions, the dielectric model, and literature values. We use Monte Carlo simulations to calculate a model grand-canonical partition function that incorporates both the work-of-charging and the intrinsic pK values for isolated γB molecules and we calculate the probabilities of leading proton occupancy configurations, for 4 < pH < 8 and Debye screening lengths from 6 to 20 Å. We select the interior dielectric value to model γB titration data. At pH 7.1 and Debye length 6.0 Å, on a given γB molecule the predicted top occupancy pattern is present nearly 20% of the time, and 90% of the time one or another of the first 100 patterns will be present. Many of these occupancy patterns differ in net charge sign as well as in surface voltage profile. We illustrate how charge pattern probabilities deviate from the multinomial distribution that would result from use of effective pK values alone and estimate the extents to which γB charge pattern distributions broaden at lower pH and narrow as ionic strength is lowered. These results suggest that for accurate modeling of orientation-dependent γB-γB interactions, consideration of numerous pairs of proton occupancy patterns will be needed.

I. INTRODUCTION

In considering interactions between proteins in solution, one interesting feature is that many different protonation patterns of the titratable, possibly charged amino acid residues coexist in equilibrium [1–3]. Because its acidic and basic residues continually exchange protons with the surrounding solution, an individual protein molecule presents many different spatial patterns of positive and negative charges to its neighbors, and the corresponding voltage patterns around each molecule keep changing. Each possible pair of such charging patterns can in principle give rise to a distinct spatial and orientational dependence of the screened electrostatic interaction between two nearby protein molecules [4–6], and the basins of attraction and repulsive parts of the corresponding potential energy landscape may change in depth or height, angular and spatial extent, and number.

The probabilities of individual charging patterns on molecules that are close enough, approximately within one or two Debye electrostatic screening lengths, also change in response to the altered voltages at neighboring sites on the two surfaces [2,7–11]. Such proximity can already occur more than 20% of the time even at protein volume fractions near 1% [12] and is of critical importance at the high macromolecular volume fractions in living cells, which have been estimated to range from 0.07 to 0.40 [13].

Phase transitions are ubiquitous in the normal and pathological physiology of living cells and tissues [14–19]. Many of these transitions involve multiple chemical equilibria, such as the protonation equilibria studied here. Such protonation and other ligand-binding features, in solutions of proteins and other macromolecules that undergo phase transitions, are analogous to the simultaneous multiple chemical equilibria and phase transitions occurring in micellar solutions, microemulsions, and other self-associating systems [20–24]. How do the relevant chemical equilibria and kinetics affect phase transitions in macromolecular solutions?

For a protein with 20 residues that may change charge at a particular pH, by accepting or donating protons from its surroundings, there are 2²⁰ or about 10⁶ such coexisting protonation patterns. Even if most of these patterns are highly unlikely, it still may be necessary to consider the interactions of many different pairs of charging patterns in order to build quantitative models of their consequences for protein-protein interactions. For example, within a given pair of γB molecules at pH 7.1, the present model predicts that on each molecule, one or more of the most frequent 100 charging patterns will be present about 90% of the time. Thus, in order to account for 80% of the possible pair interaction potentials between these molecules, in principle one then needs to consider the approximately 5050 distinct pairings that can occur between members of these top 100 charging patterns.

Therefore, one important element for understanding protein-protein interactions is to know how often each charge pattern occurs in the isolated molecules, which is the focus of the present work. While the probabilities of each of these charge patterns will change with increasing protein concentration, their probability distributions for the isolated protein molecules nevertheless form part of the groundwork for characterizing pairwise and higher-order orientation-dependent interactions between proteins.

In order to evaluate how often a given pattern occurs, it is important to account for the fact that substantial electrostatic coupling can occur between charge patterns on a single protein, as well as between neighboring proteins, in the phenomenon known as charge regulation. Due to these electrostatic couplings, the probability of a given pattern is not, in principle, given by the product of the probabilities for each titratable residue to be occupied with a proton. Indeed, on a lattice such couplings can give rise to a charge-patterning phase transition [25].

That is, knowledge of the individual pH values at which each titratable residue is occupied with a proton half the time on average, called the pK_1/2 values, in combination with the Henderson-Hasselbalch dependence [26] of occupancy on pH − pK_1/2, is in principle not sufficient to evaluate the pattern probabilities. A better description is that effective pK values for given groups change in response to neighboring charges [27–30]. However, because neighboring titratable site occupancies can be substantially altered [31–34] from the Henderson-Hasselbalch form, a more comprehensive description can be given by a grand-canonical distribution model or equivalent consideration [2,7,10,11,25,29,32,33,35,36] that incorporates screened electrostatic couplings, as we pursue here for γB-crystallin (Protein Data Bank ID 1AMM).

In the present model we calculate a work-of-charging matrix that models screened electrostatic links between titratable sites on the protein, which are assumed to be fixed in position relative to the protein. In so doing it is important to recognize that other factors can contribute that we do not incorporate, including changes in conformation that are important in allosteric effects and in calculations that use more microscopic representations of dielectric properties [31,37–42], hydration and the hydrophobic effect [43], hydrogen-bonding [44,45], static dipole potentials [45–47], and ion binding [48], each of which can also be expected to produce changes in local charge patterns. We note that γ B-crystallin is believed to have a fairly robust internal structure; for example, circular dichroism measurements [49] showed no significant spectroscopic changes between −20 °C and 60 °C, though this does not rule out the possible role of conformational flexibility in affecting the present model. In the larger context of protein-protein interactions, we note that the work-of-charging matrix also involves sites on neighboring proteins and itself depends on the relative positions and orientations of the protein neighbors [10].

We focus the present model on studying the probability distributions of the protonation patterns of an eye lens protein, bovine γB-crystallin (γB). In aqueous solution, the eye lens γ-crystallins show liquid-liquid phase separation with an upper consolute temperature [12,50–53], a phenomenon that can compromise transparency of the eye lens and has been linked to cataract disease [54]. The human counterpart of bovine γ B-crystallin, human γ D-crystallin (HGD), exhibits many single amino acid mutations that lead to congenital cataracts. The effects of a number of these mutations on the phase diagrams of HGD or HGD–α-crystallin mixtures are consistent with cataractogenesis [55–60]. These findings motivate the present work, as an aid to building models of how particular amino acid changes affect protein interactions, the resulting phase diagram, and ultimately lens transparency and the cataract.

We build our model for the probability distributions using the notation of a previous paper [10], though it is important to note that study of protein charge regulation has a very long history [1,2,7,27,29,32,33,35,36,61–63] (for a recent review see Ref. [3]) and there are other equivalent sets of notation. Briefly, we use a linearized Poisson-Boltzmann equation to compute a work-of-charging matrix. This matrix enables modeling of the work required to assemble a given pattern of charges on the protein. The linearized Poisson-Boltzmann equation is a useful starting point for this purpose because its linearity allows for the use of superposition in considering the effects of many charges and the work of charging is a symmetric quadratic form in the vectors of site charges [10]. We model the pK values of the titratable residues, with a simplified consideration of their dielectric environments. The combined work-of-charging matrix and pK values enter into a grand-canonical distribution that models the relative probabilities of occupancy patterns. We fix an assumed constant interior dielectric value through comparison with existing experimental charge vs pH data for γ B. We then use Monte Carlo simulations and direct calculations to study the resulting probability distributions of protonation patterns. We note that while numerical Poisson-Boltzmann solvers are available that provide calculations of the screened electrostatic environment around proteins and other biological macromolecules (see, e.g., Refs. [64–67]) and corresponding acid-base titration characteristics [68], we developed a program with a view towards flexibility in analyzing model systems [10], including the protonation pattern probability distributions studied here, and for ongoing work on protein-protein interactions.

Figure 1 sets the stage for this work, by depicting the screened electrostatic potential that corresponds to the top proton occupancy pattern near neutral pK, modeled to occur about 17% of the time. Interestingly, in view of the attractive interactions that lead to liquid-liquid phase separation of this protein [50], the contours of zero voltage extend fairly far from the protein, in comparison with the Debye length, here 6 Å. For a 1:1 electrolyte in water at 298 K, a Debye length of 6 Å corresponds to an ionic strength of 257 mM, close to that at which the γB phase diagram has been studied [12,50,52,69–72]. One might expect that negative and positive patches on neighboring molecules, separated by one or more Debye lengths, are quite capable of creating attractions by facing one another at relatively specific orientations.

FIG. 1.

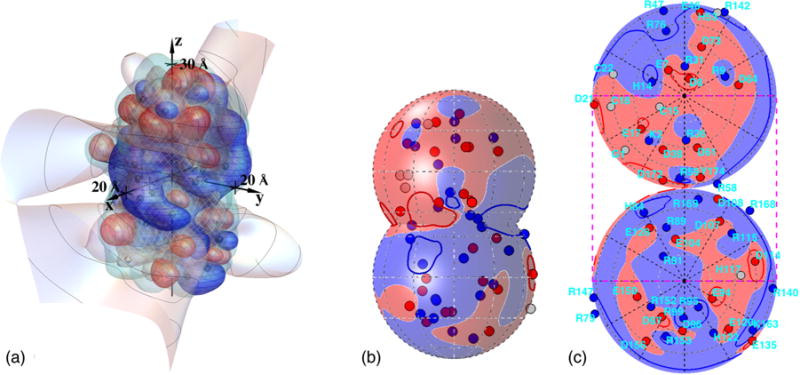
(a) Screened potential contours produced by the charges of γ B-crystallin, for the most common protonation pattern occurring at pH = 7.1 and Debye length 6.0 Å, corresponding to an ionic strength of 257 mM for a 1:1 electrolyte in water at 298 K: +k_BT/e V (blue with horizontal curves), 0 V (light), and −k_BT/e V (red with vertical curves). Black spheres, gray octahedra, and white spheres show positive, neutral, and negative sites, respectively. Curves on the 0 V contour are spaced by two Debye lengths from the center of the protein. The netted surface is the low-dielectric boundary and the plain (light blue) surface just outside it is the electrolyte boundary (see Fig. 2). (b) To aid in visualization, auxiliary spheres of radius 18.5 Å were placed over top and bottom parts of the molecule, and the potential and charges are shown in blue (+) (dark gray and nearly black, respectively) or red (−) (potential light and charges dark gray). Neutral charges are lightest in (b). (c) A simultaneous view of voltages around the entire protein surface can be given with the use of two Lambert azimuthal equal-area projections, one for each of the top and bottom spheres; projected locations of amino-acid residues of possibly charged sites are indicated. The grayscale description of (c) is like that in (b). The dashed rectangle in (c) shows the portion that is visible in (b). The top and bottom perimeter circles in (c) are both images of the crease between the auxiliary spheres in (b). Darker curves in (b) and (c) show +k_BT/e and −k_BT/e V contours.

To help study the resulting voltage variation, Fig. 1(b) shows the sign of the potential on auxiliary spheres that were placed over the top and bottom portions of the molecule for this purpose, about a one-half Debye length from the surface of the protein, with projected positions of possibly charged residues also indicated. Figure 1(c) shows conjoined Lambert azimuthal equal-area projections of the top and bottom auxiliary spheres, which provide a single view of the voltages around the entire protein surface.

Thus, the electrostatic interactions between γB molecules can contribute to the short-range, orientation-dependent interactions long known to be important for understanding the broad widths of γ-crystallin liquid-liquid coexistence curves and the position of the crystal solubility boundary, or liquidus [52]. However, because the voltage patterns depend on which γB residues are protonated, different protonation patterns may significantly affect the relative orientations that lead to attraction and repulsion, much like the problems that can occur in attempting to fit jigsaw pieces together. Our purpose here is to build groundwork for studying the distribution of orientation-dependent interactions that result from probable protonation patterns.

The paper is organized as follows. We briefly recap the relevant theory as it is presented in [10,25]. We then describe the construction of our simplified dielectric model for γ B, and model pK values that would occur in the hypothetical absence of electrostatic interactions between sites, termed the intrinsic, or pK_int, values, as defined by Tanford and Kirkwood [2]. The pK_int values are functions of the geometry of the interior dielectric environment, because of its effect on the energy stored in the electrostatic field. We then calculate the work-of-charging matrix as a function of the electrostatic screening length in the solvent and the internal dielectric environment, as input to the model grand-canonical partition function. The resulting function gives predictions for the charge vs pH, or titration, curve of the protein, which we compare with existing titration [73] and isoelectric point [74,75] data. Because the predictions depend on the assumed internal dielectric coefficient, we make use of the data for tuning this coefficient. We then quantify and study the resulting probability distributions of protonation patterns. Although very few protonation patterns occur compared to the possible ones, we find that their probability distributions are nevertheless broad. We study the extent to which charge pattern probabilities deviate from the multinomial distribution that would result from use of variously defined effective pK values, called pK_eff,α* below, and study how the distributions broaden at lower pH and narrow at lower ionic strength. It turned out, somewhat to our surprise, that seemingly subtle changes in the work-of-charging matrix, for example, ignoring entries smaller than 0.2k_BT, can still produce changes in the modeled rank order of protonation patterns and we analyze why this is so. We briefly discuss possible implications for protein interactions and refinements before concluding.

II. MODEL

A. Screened electrostatic model

As in previous work [10,25], we model the response of the electrostatic potential ϕ(r) to a specified distribution of fixed charge per unit volume ρ(r) through use of the linearized Poisson-Boltzmann equation [76], written here for a medium with spatially varying relative dielectric coefficient ε_r(r) and Debye screening parameter $\stackrel{\sim }{\kappa }(\mathbf{r})$:

$$\mathbf{\nabla }\cdot [{\epsilon }_0{\epsilon }_r(\mathbf{r})\mathbf{\nabla }\varphi (\mathbf{r})]-{\stackrel{\sim }{\kappa }}^2(\mathbf{r})\varphi (\mathbf{r})-\rho (\mathbf{r}).$$ (1)

In Eq. (1), ε₀ is the vacuum permittivity, ε_r(r) is the local, relative static dielectric coefficient, ϕ(r) is the local electrostatic potential, ρ(r) is the local free charge per unit volume, and κ is related to the standard Debye screening length in water 1/κ by $\kappa =\tilde{\kappa }/\sqrt{{\epsilon }_w}$, where ε_w is the static dielectric coefficient of liquid water. More sophisticated models of electrolyte solutions are needed in order to accurately model ionic solutions that are not dilute or contain divalent ions and explicit solvent [76–80], to incorporate important physical effects such as finite ion size and ion-specific interactions, including ion absorption [81–83], to include dipolar and polarizability-related interactions [84,85], and to take account of nonlinear dielectric response [86,87]. In the case of ion absorption, for example, one could construct expanded grand-canonical distribution models that would incorporate equilibria with ions other than protons or with polar ligands (see, e.g., [31,88]). Also, the application of Eq. (1) to molecular length scales, on which the protein and the solvent are heterogeneous, involves inherent problems that call for the use of more microscopic, quantum-mechanical approaches, as have been studied for many years (see, e.g., [37,40,89–93] and references therein). Nevertheless, at low ionic strengths and surface charge densities [94], Eq. (1) is a useful starting point for investigating patterned, charge regulation-mediated electrostatic interactions, because its linearity allows the use of superposition in considering the effects of many charges. Also, the work of charging a given configuration of titratable sites may be expressed as a symmetric quadratic form in the vectors of site charges [10].

B. Grand canonical partiton function

In the present model [10], the grand-canonical partition function $\mathcal{Q}$ can be written formally as a sum over the occupancy patterns, indexed by α, of protons on the protein

$$\mathcal{Q}={\displaystyle \sum _{\alpha }{e}^{-\mathrm{\Delta }{G}_{\alpha }/k_{B}T}}={\displaystyle \sum _{\alpha }{\zeta }^{k_{\alpha }}{e}^{-(\mathbf{\Delta }{\mathit{\mu }}^0\cdot {\mathbf{O}}_{\alpha })/k_{B}T}{e}^{-W_{\text{el},\alpha }/k_{B}T}}$$ (2)

in which ΔG_α is the free energy of formation of pattern α, ζ = 10^−pH, k_α is the total number of protons bound to the protein in configuration α, and $\mathbf{\Delta }{\mathit{\mu }}^0=(\mathrm{\Delta }{\mu }_1^0,\mathrm{\Delta }{\mu }_2^0,\dots ,\mathrm{\Delta }{\mu }_N^0)$ is a vector of standard chemical potential differences for the occupancy of each site. Each $\mathrm{\Delta }{\mu }_i^0$ is related to the corresponding intrinsic pK_int,i value of a titratable site by

$$\exp \left(\frac{\mathrm{\Delta }{\mu }_i^0}{k_{B}T}\right)={10}^{-p{\mathrm{K}}_{\mathrm{int},i}}.$$ (3)

By the pK_int,i value we mean the value of the pK that site i would have hypothetically in the absence of electrostatic interactions with charges on other sites and in the absence of the electrolytes in the solvent, as in Ref. [2]. That is, it is not the pK_1/2 that would be measured as the value of the pH at which that amino acid residue is, on average, 50% occupied, for example, with use of appropriate nuclear magnetic resonance (NMR) experiments. Instead, pK_1/2 values emerge as a consequence of models of the present type [2,10,29,32–34]. In Sec. II D below we describe the model we used for estimating the pK_int,i values.

The vector O_α in Eq. (2) is the occupancy pattern in configuration α, for example, {1,0,0,1,1,0,0, …}. The quantity W_el,α in Eq. (2) denotes the work of charging contribution to the free energy when the protein assumes occupancy pattern α. The W_el,α is a quadratic form constructed from the work-of-charging matrix W, which in this formulation is dimensionless. Each entry W_ij in W is the screened electrostatic potential produced at site i by a unit charge at site j, multiplied by the electronic charge e, and divided by k_BT. That W_ij = W_ji can be shown with use of Eq. (1) [10]. In this notation, W_el,α is given by

$$\frac{W_{\text{el},\alpha }}{k_{B}T}=\frac{1}{2}{(q_1,q_2,\dots ,q_n)}_{\alpha }\cdot W\cdot {(q_1,q_2,\dots ,q_n)}_{\alpha }=\frac{1}{2}({\mathbf{Q}}_b+{\mathbf{O}}_{\alpha })\cdot W\cdot ({\mathbf{Q}}_b+{\mathbf{O}}_{\alpha }).$$ (4)

Here the vector (q₁,q₂, …, q_n)_α denotes the actual signed charge numbers on the protein for a specific pattern α and Q_b denotes the vector of signed, bare charge numbers of the titratable groups, for example,−1 or 0. The bare charge numbers are 0 for arginine, histidine, and lysine residues, as well as the terminal amino group, and −1 for aspartate, glutamate, cysteine, and the terminal carboxylate. The probability of occupancy pattern α, P_α(x), is given by

$${\mathit{P}}_{\alpha }=\frac{{\mathit{e}}^{-\mathrm{\Delta }{G}_{\alpha }}/k_{B}T}{\mathcal{Q}}.$$ (5)

We note that the grand-canonical partition function $\mathcal{Q}$ is also called the binding polynomial [31], because it can be written as a polynomial in powers of the proton activity ζ, as in Eq. (2).

C. Interior dielectric model and salt exclusion zone

We now describe our model for the quantities ε_r(r) and ${\stackrel{\sim }{\kappa }}^2(\mathbf{r})$ that appear in Eq. (1). We use a simplified model in which ε_r(r) is assumed to be a scalar that takes a low and constant value inside the protein and a high value outside. After constructing the grand-canonical distribution, we adjusted the interior dielectric coefficient so as to best match the available experimental protein net charge vs pH titration data [73,75], as described below in Sec. II F. The value that gave the best match to these data was ε_r,in = 3.0. Outside the protein, we take a value experimentally determined for water at 25 °C, ε_r,out = 78.5 [95]. We modeled the boundary of the low dielectric to be a surface that is 1.4 Å outside the Protein Data Bank (PDB) coordinates of the appropriate atoms (PDB entry 1AMM, from Ref. [96]) and a salt-exclusion zone to extend 3.3 Å beyond this boundary, in approximate accord with hydrated radii of monovalent ions in aqueous solvent [97]. The resulting surfaces are illustrated in Fig. 2.

FIG. 2.

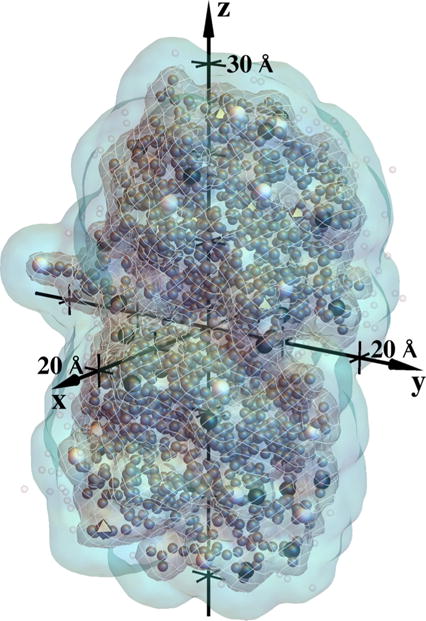
Illustration of the dielectric and salt-exclusion zone model for bovine γ B-crystallin, based on PDB entry 1AMM [96], rotated and translated to the coordinate system used for numerical solution of Eq. (1). The dark gray netted surface is the boundary of the low-dielectric region and the light plain surface is the boundary of the salt-exclusion zone, described in the text. Larger black and white spheres and gray octahedra show titratable sites that are positive, negative, and neutral, respectively, for the most probable configuration at pH 7.0, modeled to occur about 20% of the time [see Fig. 13(a)]. Smaller dark gray spheres are locations of nonhydrogen atoms in the 1AMM structure and smaller lighter spheres are positions of heteroatoms.

D. Model for pK_int values

In view of our primary present purpose of studying the nature of the probability distributions of the protonation patterns on γB-crystallin, we adopted a simple classical approach to modeling the pK_int values. We start from tabulated pK values in water for relevant charged groups [98–100] and then calculate the change in the integral that, in a linear dielectric, gives the free energy stored in the electrostatic field per unit volume [101,102], (1/2)D(r) · E(r). The integral is taken over the volume outside spheres of radii r₀ surrounding the group in question, when water is replaced by a heterogeneous dielectric environment like that near the surface of the protein. This approach omits a number of factors that also affect pK values, many of which call for molecular mechanics and/or quantum mechanical treatment [37,39,93,103–107]. These include hydrogen bonding [44,45,108], bound ions, and nonlinear dielectric effects [86,87] that require a different integration of E(r) δD(r) than that which yields (1/2)D(r) · E(r) [86,101,102].·Hydrogen bonds can stabilize charged carboxylates [44], among other effects, and the presence of metal or other ions, often bound between titratable residues [109], would call for a grand-canonical formulation that involves more exchangeable components [88]. These phenomena are not modeled here. In addition, there are problems involved in characterizing dielectric response at molecular length scales [37,40,89–93], as mentioned above. A related factor not modeled here is the local electrostatic potential from strong static dipoles such as backbone and side-chain amide groups [45–47,110]. There are also solvent effects that can be studied with liquid-state theory approaches [111–113]. However, the present approach is useful as a first approximation; its value may be illustrated, for example, by its remarkable ability to help understand the dependence of salt solubilities on a solvent’s static dielectric coefficient [97]. The resulting modeled contribution to the change in pK, ΔpK, can be written as

$$\mathrm{\Delta }pK\ln (10)=\pm \frac{1}{2k_{B}T}{\displaystyle {\iiint }_{r>r_0}\mathbf{D}(\mathbf{r})\cdot \mathbf{E}(\mathbf{r})dV}-\frac{q^2}{8\pi {\epsilon }_0{\epsilon }_w{r}_0{k}_{B}T}$$

$$(\text{if in uniform solvent})=\pm \frac{q^2}{8\pi {\epsilon }_0{r}_0{k}_{B}T}\left(\frac{1}{{\epsilon }_0}-\frac{1}{{\epsilon }_w}\right).$$ (6)

In Eq. (6), the + sign is appropriate for groups that become charged when they are not occupied by a proton, that is, for glutamate, aspartate, cysteine, and the terminal carboxylate, while the − sign is appropriate for groups that become charged when they are occupied by a proton, that is, for lysine, arginine, histidine, and the terminal amino group. To evaluate the needed integral in Eq. (6), as described in detail in the Appendix, we took advantage of the fact that a rough approximation to the shape of our more complicated dielectric model can be constructed by conjoining two spheres, each of radius 15.5 Å. Then we used Kirkwood’s analytical solution for the potential due to a charge placed in a low-dielectric sphere, near its surface [61]. We placed the charges a depth of 1.4 Å inside this sphere. We used Gauss’s theorem to convert the volume integral of (1/2)D · E in Eq. (6) to a surface integral over the small sphere of radius r₀; symmetry then permits the needed integral to be converted to a one-dimensional integral, also given in the Appendix, that we evaluated numerically.

To estimate appropriate values of an effective r₀ for use in Eq. (6), we used a facility within the quantum-chemistry package GAUSSIAN09 that provides for estimating recommended radii for self-consistent reaction field calculations [114]. For each titratable side-chain group and for the terminal amino and carboxyl groups, we constructed the test molecules listed in Table I, which included the side-chain titratable group in its charged form, and calculated the r₀ values in Table I from repeated runs, for which the test ions were surrounded by a medium having the static dielectric coefficient of water. We first used Hartree-Fock calculations with the 6-31G(d,p) basis set to optimize the test molecules in the presence of implicit solvent. Vibration frequency analyses were performed on the optimized structures to determine whether they represented true minima. No structure exhibited imaginary frequencies. We did not perform a conformational analysis of the test molecules or optimize them in their protein environment, for simplicity and consistent with the fact that the present model does not incorporate cross-talk between conformational changes and charge regulation, as noted in the Introduction. We performed r₀ calculations at least 10 times for each of the test molecules, which yielded standard deviations (Table I) that ranged from 0.1 to 0.2 Å. For modeling the solvent, we used the GAUSSIAN09 program’s default implementation of the integral equation formulation of a polarizable continuum model. The needed $p{\mathrm{K}}_{{\mathrm{H}}_2\mathrm{O}}$ values were estimated with use of the tables given in the work of Dawson et al. [98], Ellenbogen [99], and Serjeant and Dempsey [100]. Because this work is spurred by our interest in building models for γB-γB interactions in the range 4 < pH < 8, we did not include the titration of tyrosine side chains, which typically occurs in the range 10 < pH < 10.3 [110].

TABLE I.

Estimated pK_int values used (see the text). Corresponding model $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values for individual residues are given in [122] for α_* equal to the top pattern at pH 7.1.

Residue	Abbreviation	r0±s.d.a (Å)	$p{\mathrm{K}}_{{\mathrm{H}}_2\mathrm{O}}$	ΔpK	pKint,ε=3	No.
arginine	Arg(R)	3.68 ± 0.2	12.48	−1.18	11.30 ± 0.2	20
aspartate	Asp(D)	3.31 ± 0.15	3.86	+1.55	5.41 ∓ 0.2	13
cysteine	Cys(C)	3.35 ± 0.2	10.50b	+1.50	12.00 ∓ 0.2	3
glutamate	Glu(E)	3.31 ± 0.15	4.25	+1.55	5.80 ∓ 0.2	9
N-glycine	Gly(G)	2.65 ± 0.2	7.60	−2.72	4.88 ± 0.5	1
histidine	His(H)	3.65 ± 0.2	6.00	−1.20	4.80 ± 0.2c	5
histidine	H14				7.05d	1
histidine	H53				6.04d	1
histidine	H84				6.91d	1
histidine	H117				6.37d	1
histidine	H122				6.32d	1
lysine	Lys(K)	2.65 ± 0.2	10.70	−2.72	7.98 ± 0.5	2
C-tyrosine	Tyr(Y)	3.31 ± 0.15	3.40	+1.55	4.95 ∓ 0.2	1

^aIons used in GAUSSIAN09 calculations with H₂O solvent were methylguanidinium(Arg); acetate[Asp, Glu, Y174(carboxyl)]; ammonium[Lys, G1(amino)]; mean of imidazolium, 4-methyl imidazolium(His); and methanethiolate(Cys).

^bSee the text.

^cValue not used; see the text.

^dFrom PROPKA 3.1 [115–118]. Note that these values are not intended as pK_int values; see Sec. II F for discussion.

The resulting pK_int values and uncertainties are listed in Table I. The values calculated for the charged sites just inside the low-dielectric sphere are designated as pK_{int,ε =3}. Here we are anticipating the fact that, as explained below, the grand-canonical distribution model was used to predict titration curves as functions of ε, which were then compared with experiment to settle on an assumed, continuum model internal static dielectric coefficient value ε = 3.

However, when carrying out this process, we found that there was a discrepancy between the modeled titration curve and the data, displayed in Fig. 4(a) below, which suggested that our modeled values for the histidine pK were lower than would be compatible with the titration curve [73] and the measured isoelectric point of bovine γB-crystallin, pH = 7.8 [74,75]. Therefore, as input to the grand-canonical simulations we instead tried using the PROPKA (version 3.1) web server estimates [115–118] to replace the initially estimated histidine pK_int values for γB, again with use of the PDB entry 1AMM, while leaving all the other pK_int D · E integral method described above. The resulting PROPKA histidine pK estimates are listed in Table I. The comparison of the modeled titration curve with the data, for various assumptions about the inner dielectric coefficient and the histidine pK values, is described and shown in Sec. II F below, in connection with Fig. 4. As the authors emphasize [115–118], PROPKA uses a phenomenological approach to achieve speed and scope in estimating pK values for a large variety of proteins. It incorporates factors that the present approach does not, including hydrogen bonding and varying degrees of penetration of residues into the interior. For histidines PROPKA starts from a higher model pK of 6.5 than the 6.0 initially used here and it assigns smaller pK reductions to H14, H84, H117, and H122 than the Table I ΔpK of −1.20, due to their varying degrees of penetration. PROPKA also predicts that hydrogen bonds raise the pK values of H14, H53, and H84, by from 0.6 to almost 0.9 pK units.

FIG. 4.

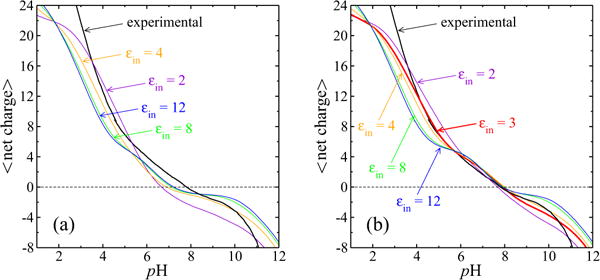
Selection of interior dielectric coefficient and pK values through comparison of modeled titration curves with experiment. The experimental data [73] are shown by the labeled curve. The work-of-charging matrix W was calculated as described in the text, for different choices of ε_in. (a) Calculated titration curves when all $p{K}_{\mathrm{int},{\epsilon }_{\text{in}}}$ values were calculated according to the D(r) · E(r) integral method described in Sec. II D, for the same ε_in values used for solution of Eq. (1) to yield the matrix W. (b) Calculated titration curves when all but the histidine $p{K}_{\mathrm{int},{\epsilon }_{\text{in}}}$ values were estimated with the integral method, as functions of ε_in, while PROPKA 3.1 values were used for histidine (Table I) pK_int values (see the text). In (b) the red (bold) ε_in = 3 curve is that of the model adopted for further study of the probability distributions.

The Table I cysteine $p{\mathrm{K}}_{{\mathrm{H}}_2\mathrm{O}}$, 10.5, chosen to be near the pK values for methanethiol (10.33) and ethanethiol (10.5 and 10.61) [100], leads to pK_int values of 12, well above the 9–9.5 typical of protein cysteines [110]; indeed, many proteins exhibit cysteine pK_1/2 values much less than 9, due primarily to hydrogen bonding [119] and somewhat to nearby amide dipole potentials [47,119]. We did not alter the present approach given our focus on 4 < pH < 8, although better modeling of cysteine pK values is of interest, given the importance of cysteine oxidation for gamma crystallins and other lens proteins [54–56,120,121]. In particular, the present model does not attempt to model hydrogen bonding of C18 with both C78 and S20, predicted by PROPKA to lower the C18 pK to 6.88. We included only C15, C18, and C22 in our model, which appear less buried than C32, C41, C78, and C109. However, due to the high model cysteine pK_int, C15, C18, and C22 were charged only rarely in simulations, at higher pH values, as tabulated in the Supplemental Material [122].

We will find it instructive to study the ability of “effective” pK values, $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$, defined below, to model the probability distributions of the protonation patterns. These effective pK values are closely related to those used in Refs. [27–29], among others; briefly, the difference is that here we study the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ with respect to particular choices α_* of on-or-off charge patterns ${\mathbf{Q}}_b+{\mathbf{O}}_{{\alpha }_{\ast }}$, as contrasted with patterns of average residue charge values at a given pH, ${\mathbf{Q}}_b+\langle {\mathbf{O}}_{{\alpha }_{\ast }}\rangle$ in the present notation, as analyzed, for example, in Ref. [29].

In the present notation, the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ are expressed as follows [27]. For any particular protonation pattern α on the protein, the numerator of Eq. (5) can be written

$$\mathcal{Q}{P}_{\alpha }\equiv {\stackrel{\sim }{Q}}_{\alpha }={10}^{(p\mathbf{K}-p\mathbf{H})\cdot {\mathbf{O}}_{\alpha }}{\mathit{e}}^{-{\mathbf{q}}_{\alpha }^{\top }W{\mathbf{q}}_{\alpha }/2},{\mathbf{q}}_{\alpha }={\mathbf{Q}}_b+{\mathbf{O}}_{\alpha },$$ (7)

in which Q_b is the vector of bare charges of the titratable residues; pK, pH, and q_α also denote vectors; and the symmetric work-of-charging W is defined above Eq. (4). The idea is now to use a chosen configuration ${\mathbf{O}}_{{\alpha }_{\ast }}$, which could be, for example, the most probable configuration at a certain pH, as a reference configuration; the algebraic development given here also applies for the reference configuration choice ⟨O_α⟩, as used in Refs. [27–29]. The probabilities of other configurations can now be expressed in terms of how much their occupancy vectors differ from that of the reference configuration. For configuration α, the occupancy vector is ${\mathbf{O}}_{\alpha }={\mathbf{O}}_{{\alpha }_{\ast }}+({\mathbf{O}}_{\alpha }-{\mathbf{O}}_{{\alpha }_{\ast }})={\mathbf{O}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha }$, where $\delta {\mathbf{O}}_{\alpha }={\mathbf{O}}_{\alpha }-{\mathbf{O}}_{{\alpha }_{\ast }}$. Letting ${\mathbf{q}}_{{\alpha }_{\ast }}={\mathbf{Q}}_b+{\mathbf{O}}_{{\alpha }_{\ast }}$ and ${\mathbf{q}}_{\alpha }={\mathbf{q}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha }$ one finds

$${\stackrel{\sim }{Q}}_{\alpha }={10}^{(p\mathbf{K}-p\mathbf{H})\cdot ({\mathbf{O}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha })}{\mathit{e}}^{-{({\mathbf{q}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha })}^{\top }W({\mathbf{q}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha })/2}={10}^{(p\mathbf{K}-p\mathbf{H})\cdot {\mathbf{O}}_{{\alpha }_{\ast }}}{\mathit{e}}^{-{\mathbf{q}}_{{\alpha }_{\ast }}^{\top }W{\mathbf{q}}_{{\alpha }_{\ast }}/2}{10}^{(p\mathbf{K}-p\mathbf{H})\cdot \delta {\mathbf{O}}_{\alpha }}\times e^{-(2\delta {\mathbf{O}}_{\alpha }^{\top }W{\mathbf{q}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha }^{\top }W\delta {\mathbf{O}}_{\alpha })/2}.$$

The first two multiplicative factors in the above expression are common to all ${\stackrel{\sim }{Q}}_{\alpha }$. In the expression for the probabilities P_α, these factors cancel with the same common factors in the denominator, $\mathcal{Q}$. Therefore, we have $P_{\alpha }={\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )/{\mathcal{Q}}_{{\alpha }_{\ast }}$, in which we define ${\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )$ and ${\mathcal{Q}}_{{\alpha }_{\ast }}$ via

$$Q_{\alpha }\equiv {10}^{(p\mathbf{K}-p\mathbf{H})\cdot {\mathbf{O}}_{{\alpha }_{\ast }}}{\mathit{e}}^{-{\mathbf{q}}_{{\alpha }_{\ast }}^{\top }W{\mathbf{q}}_{{\alpha }_{\ast }}/2}{\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha ),$$

$$\mathcal{Q}\equiv 10^{(p\mathbf{K}-p\mathbf{H})\cdot {\mathbf{O}}_{{\alpha }_{\ast }}}{e}^{-{\mathbf{q}}_{{\alpha }_{\ast }}^{\top }W{\mathbf{q}}_{{\alpha }_{\ast }}/2}{\mathcal{Q}}_{{\alpha }_{\ast }}.$$

With these definitions,

$${\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )={10}^{(p\mathbf{K}-p\mathbf{H})\cdot \delta {\mathbf{O}}_{\alpha }}{\mathit{e}}^{-(2\delta {\mathbf{O}}_{\alpha }^{\top }W{\mathbf{q}}_{{\alpha }_{\ast }}+\delta {\mathbf{O}}_{\alpha }^{\top }W\delta {\mathbf{O}}_{\alpha })/2}={10}^{(p\mathbf{K}-p\mathbf{H})\cdot \delta {\mathbf{O}}_{\alpha }}{\mathit{e}}^{-(W{\mathbf{q}}_{{\alpha }_{\ast }})\cdot \delta {\mathbf{O}}_{\alpha }}{\mathit{e}}^{-\delta {\mathbf{O}}_{\alpha }^{\top }W\delta {\mathbf{O}}_{\alpha }/2}={10}^{(p\mathbf{K}-p\mathbf{H})\cdot \delta {\mathbf{O}}_{\alpha }}{10}^{-(W{\mathbf{q}}_{{\alpha }_{\ast }})\cdot \delta {\mathbf{O}}_{\alpha }/\ln 10}{\mathit{e}}^{-\delta {\mathbf{O}}_{\alpha }^{\top }W\delta {\mathbf{O}}_{\alpha }/2}={10}^{[(p\mathbf{K}-W{\mathbf{q}}_{{\alpha }_{\ast }}/\ln 10)-p\mathbf{H}]\cdot \delta {\mathbf{O}}_{\alpha }}{\mathit{e}}^{-\delta {\mathbf{O}}_{\alpha }^{\top }W\delta {\mathbf{O}}_{\alpha }/2}.$$ (8)

With $\delta q_{\alpha }=q_{\alpha }-q_{{\alpha }_{\ast }}=\delta O_{\alpha }$, Eq. (8) can be written as

$${\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )={10}^{[(pK-W{\mathbf{q}}_{{\alpha }_{\ast }}/\ln 10)-pH]\cdot \delta O_{\alpha }}{e}^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2}.$$ (9)

From a comparison of Eqs. (7) and (9), it is natural to define a vector $p{\mathbf{K}}_{\text{eff},{\alpha }_{\ast }}$ of $p{K}_{\text{eff},{\alpha }_{\ast }}$ values by

$$p{\mathbf{K}}_{\text{eff},{\alpha }_{\ast }}=p\mathbf{K}-W{\mathbf{q}}_{{\alpha }_{\ast }}/\ln 10,$$ (10)

so that

$${\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )={10}^{(p{\mathbf{K}}_{\text{eff},{\alpha }_{\ast }}-p\mathbf{H})\cdot \delta {\mathbf{q}}_{\alpha }}{e}^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2},$$ (11)

$$P_{\alpha }=\frac{{\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha )}{{\mathcal{Q}}_{{\alpha }_{\ast }}}\text{with}{\mathcal{Q}}_{{\alpha }_{\ast }}={\displaystyle \sum _{\alpha }{\stackrel{\sim }{Q}}_{{\alpha }_{\ast }}(\alpha ).}$$ (12)

Equations (10)–(12) correspond to the combination of Eqs. (2)–(4) of Ref. [27], as expressed there in terms of a particular constellation of charges (here symbolized by the vector $q_{{\alpha }_{\ast }}$). As indicated above, except by its use of a particular on-off pattern α_*, Eq. (10) is also related to Eqs. (1a), (1b), and (16) in Ref. [29], where the average pH-dependent approach introduced in Ref. [27] is expressed and its mean-field-approximation nature is elucidated. In this connection we note that the use of $p{K}_{\text{eff},{\alpha }_{\ast }}$ below, to study its capability to approximate probability distributions of protonation patterns, has a different focus than the study of the reduced-site approximation also introduced in Ref. [29]; that approximation becomes better as the criteria to regard less-labile sites as fixed become progressively more strict. Reference [29] demonstrates that the reduced-site approximation is more effective than the mean-field approach for representing the average occupancy states of particular sites, while typically more efficient computationally than using the exact expressions.

Equation (10) expresses the fact that for configurations that are similar to the chosen configuration ${\alpha }_{\ast }$, the effective pK values are typically biased by charges ${\mathbf{q}}_{{\alpha }_{\ast }}$ on neighboring sites. These charges, in turn, produce voltages that bias the occupancy of a given site. Thus, at a given pH, one expects that the site occupancies can be fairly well described by $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values for a well-chosen ${\alpha }_{\ast }$, say, the most common configuration. The extent to which this is not the case is clearly afunction ofthequantities $e^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2}$, according to Eqs. (11) and (12). We will find below that a given set of $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values accurately represent only part of the probability distribution of the protonation patterns at a given pH, precisely because of this latter factor.

E. Calculation of the potential and work-of-charging matrix

The numerical methods we used to calculate the potential are those described previously [10]. We used grid sizes from 0.3 to 0.6 Å, the domain was 100 × 100 × 120 ų, and the protein was placed at its center. We used the Neumann boundary condition that the normal component of the field is zero there. While we expect that a more accurate boundary condition would be that a linear combination of the normal field component and the potential would be zero, for the Debye lengths investigated here, the zero-field condition suffices. To calculate the ith row of the work-of-charging matrix W, a charge is placed at site i; the potential at site j then gives the entry w_ij. Each such work-of-charging matrix was symmetric, providing an important check on the calculation.

We note that there are also self-energies associated with the interaction of each charge with its counterion cloud. In principle, this factor also changes the effective pK of a site, above and beyond the fact that the site is near a dielectric boundary. We calculated the magnitudes of these effects from our numerical solutions of Eq. (1), by evaluating the potential at a given charged site produced by the nearby net charge within its surrounding, screening ionic atmosphere. The magnitudes we calculated for this effect were very uniform and would produce changes in the given pK on the order of only ±0.1 pK units, which we regard as insignificant compared with the uncertainties in the modeled pK_int values themselves. Accordingly, we simply set the diagonal entries of the work-of-charging matrices to 0 for further calculations.

Figure 3 illustrates a work-of-charging matrix calculated in this fashion. To find a permutation of the residue order that would yield the approximately block-diagonal forms shown in Fig. 3, we used simulated annealing, with an objective function that was linearly proportional to the distance of (the symmetric) work-of-charging entries from either the diagonal or the upper right or lower left corners. On repeated runs, this yielded a robust grouping of sites. While we grouped the sites in this fashion in order to identify patches of residues predicted by the model to be more highly correlated, we left all entries intact for computing the partition function. That is, this grouping does not represent a block-diagonal approximation method, an avenue that has been pursued by a number of investigators (see Ref. [123] and references therein).

FIG. 3.

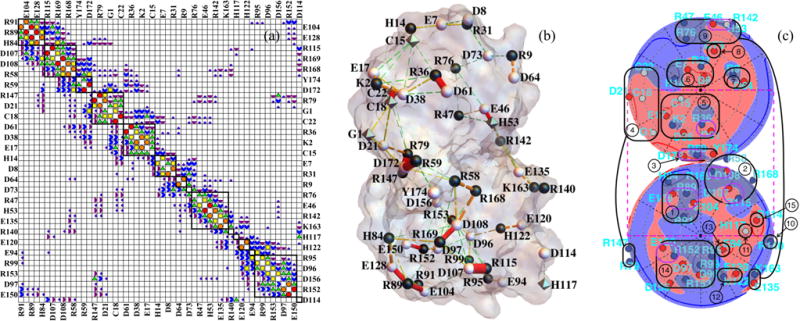
(a) Approximate block-diagonal form of the dimensionless work-of-charging matrix W for interior dielectric coefficient 3 and Debye length 6.0 Å. The W_ij magnitude categories are as follows: white < 0.05 ≤ dark purple quarter circles < 0.1 ≤ purple half circles < 0.2 ≤ blue 3/4 circles < 0.4 ≤ green triangles < 0.8 ≤ yellow squares < 1.6 ≤ orange pentagons < 3.2 ≤ red circles. The matrix includes all 54 titratable residues used in the present model, which as noted in the text omits the tyrosine residues and four of the cysteine residues; the entire protein contains 174 residues. Designations for the 54 residues considered alternate between left and right (and top and bottom) margins. (b) Cylinders with radii proportional to W_ij mapped onto the PDB 1AMM structure of γ B-crystallin. The W_ij magnitude categories are as follows: 0.4 ≤ green cylinders with three gaps < 0.8 ≤ yellow cylinders with two gaps < 1.6 ≤ orange cylinders with one gap < 3.2 ≤ red cylinders. (c) Lambert projections with potential and charges indicated as in Fig. 1(c). Groups of titratable sites participating in approximate blocks of W are circled in black and numbered in (c) and indicated by black squares in (a). Group numbering corresponds to the order of sites in W in Fig. 3(a), from top to bottom, and group numbers are those to which Figs. 7 and 8 refer. In (b) and (c) the protonation configuration is that modeled to be the most common one at pH 7.1.

Figure 3(a) displays an approximate block-diagonal form of the work-of-charging matrix W, for the adopted inner dielectric value ε_in = 3.0. The symbol code for W_ij magnitude categories is given in the caption, ranging from white for entries less than 0.05k_BT/e to red circles for entries greater than or equal to 3.2k_BT/e. The prominent entries adjacent to the main diagonal show a high degree of charge pairing, long noted to occur for γ-crystallins [124]. The 0.05 lower cutoff is close to the value below which we observed very little change in the order of probabilities of the protonation patterns, if smaller entries were ignored [see Fig. 10(a)]. Residue identities are indicated on the borders of Fig. 3(a). A perspective view of the work-of-charging matrix of Fig. 3(a) is given in Fig. 2 of the Supplemental Material [122]. Figure 3(b) displays the work-of-charging entries in the form of line segments that link the titratable groups on the protein, using the same symbol code as in Fig. 3(a). Figure 3(c) shows labeled sets of titratable sites, circled in black, that participate in approximate blocks of W, with use of the same projection as in Fig. 1(c). The corresponding blocks are outlined by the thick black squares in Fig. 3(a). In addition, prominent charge pairs are circled in purple (lighter) in Fig. 3(c). Tables of the work-of-charging matrices we calculated for Debye lengths 6, 12, and 20 Å are given in Figs. 6–11 of the Supplemental Material [122].

FIG. 10.

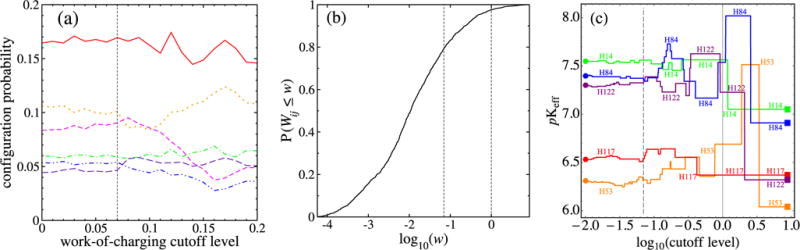
(a) Dependence on dimensionless work-of-charging cutoff level of the six most common proton configurations at pH 7.1 and Debye length 6.0 Å. At each cutoff level on the horizontal axis, all of the entries in W below the given level were set to zero and the probabilities of the configurations were recalculated using Eq. (5). At this pH, the order of the configurations is stable up to a cutoff level of 0.07, which is shown by the vertical dashed line. (b) Cumulative distribution function of the work-of-charging matrix entries (see the text). The left vertical line in (b) corresponds to the cutoff level of 0.07 indicated in (a). The right vertical line is at 1. (c) Changes in $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values of the indicated histidine residues, whose protonation switches produce the top-ranked configurations shown in (a). Above a cutoff of 0.07, the H84 $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ value changes are the primary reasons for the configuration probability changes in (a) (see the text).

F. Calculation of the grand-canonical distribution function and the protonation pattern probabilities

We performed Metropolis Monte Carlo simulations that included all 54 sites of the present model to determine the grand-canonical partition function (GCPF) and the associated statistics of the distributions of protons on the protein. Protonation pattern statistics were studied using Monte Carlo runs of 10⁸ iterations. We determined GCPF vs pH in 0.1 pH increments by finding top protonation configuration probabilities in 10⁶ iteration runs and using Eq. (5) with that configuration’s ΔG_α. While the results given here were calculated from the simulations, it is convenient to note that in the Monte Carlo simulations, many of the residues, primarily the arginines with the highest $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values, never changed their occupation states at some of the p_H values in the range of primary interest here, 4–8, or did so very few times, even in 10⁸ iterations. A table of the number of times each residue switched protonation state, as a function of pH, and a table that includes individual $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values appear as Figs. 4 and 5, respectively, in the Supplemental Material [122]. Therefore, to speed calculations, it can be convenient to omit such residues from calculation of the partition function, as was done in the reduced sites approximation of Ref. [29], and with fewer titratable sites, about 25 or 30, the model partition function $\mathcal{Q}$ can be evaluated exactly. By either method, once $\mathcal{Q}$ is known, the probability of protonation pattern α is then given by Eq. (5). Likewise, the average number of protons ⟨n⟩ on a protein can be found from

$$\langle n\rangle =\frac{\zeta }{\mathcal{Q}}\frac{\partial \mathcal{Q}}{\partial \zeta }=\frac{\partial \ln \mathcal{Q}}{\partial \ln \zeta },$$ (13)

in which ζ = 10^−pH.

FIG. 5.

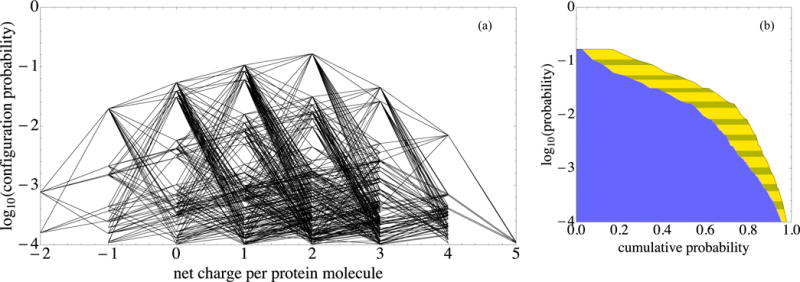
Protonation patterns that have opposite net protein charge readily occur at pH 7.1. In both panels, log₁₀ P is plotted vertically for the most prominent pH 7.1 configurations that together account for over 97% of the configuration probability. (a) The net protein charge of each configuration is plotted horizontally. Line segments join configurations that can be transformed into one another with a single-residue protonation switch. (b) (i) The horizontal coordinate of the yellow-striped–clear boundary is the sum of the probabilities of that configuration and more common ones, that is, their cumulative probability. (ii) The horizontal coordinate of the blue–yellow-striped boundary is the square of the same cumulative probability. The blue–yellow-striped boundary estimates the fraction of pairs of neighboring proteins, both molecules of which have one of the configurations down to a given log₁₀ P level; this estimate neglects biasing of pattern probabilities due to protein proximity.

Titration curves calculated in this manner are shown in Fig. 4. The experimental data [73] are shown by the black curve in each panel. These data were obtained with use of an aqueous 100 mM potassium chloride solvent, corresponding to a Debye length of 9.6Å, the value we therefore used in the 54 solutions of Eq. (1) for each choice of ε_in, to generate the matrices W needed for the comparisons shown in Fig. 4. Figure 4(a) shows the calculated titration curves when the $p{\mathrm{K}}_{\mathrm{int},{\epsilon }_{\text{in}}}$ values were calculated according to the D·E integral method described above. Note that in this case both the work-of-charging matrix W resulting from application of Eq. (1) and the $p{\mathrm{K}}_{\mathrm{int},{\epsilon }_{\text{in}}}$ values resulting from the first two lines of Eq. (6) are functions of the interior dielectric coefficient value ε_in and were calculated as input to the GCPF simulations for the values ε_in = 2, 4, 8, and 12. Therefore, the calculated $p{\mathrm{K}}_{\mathrm{int},{\epsilon }_{\text{in}}}$ values relevant to the curves in Fig. 4(a) are not those listed in Table I for ε_in = 3. In Fig. 4(a) each test model titration curve predicts a lower isoelectric point (pI) than that observed experimentally for γ B-crystallin, pI = 7.8 for the native protein [74,75], though in Ref. [74] a minor component was also observed at a lower pI of 7.3, a component that was sensitive to the presence of reducing agents [74]. Also, note that bovine γ B-crystallin was termed γ-II at the time of publication of Refs. [74,75].

In addition to the purpose of studying the probability distributions of the protonation patterns, we have a goal of modeling small-angle neutron scattering data from γ B-crystallin solutions in the pH range between 4.5 and 7.1, and as a preliminary step want to create a charge-regulation model in a pH range that spans these values and reproduces the observed isoelectric point. Therefore, as described above, we used the PROPKA estimates for the needed histidine pK_int values, while continuing to use the D · E integral procedure for the other residues. Figure 4(b) shows the resulting model titration curves. Although there is clearly a range of ε_in values that could be used and there is room for improvement, the highlighted red curve, with W and nonhistidine pK values generated using ε_in = 3.0, provides a relatively good match to the experimental titration curve in the range 4 < pH < 8 of particular interest and we took it to be sufficient for studying the general nature of the protonation pattern probability distributions. We did so despite the fact that the PROPKA estimates include a model of charge-charge interactions [117] and therefore are not intended to be intrinsic pK_int values as they are used here.

We anticipate that as NMR assignment and titration data become available for γ B-crystallin, it will become possible to test and refine the present model in much more detail. Accordingly, we postponed detailed study of using different histidine $p{\mathrm{K}}_{{\mathrm{H}}_2\mathrm{O}}$ values, which are expected to depend on their tautomeric states [125], in addition to the possible hydrogen bonding, dipolar potential, and other effects mentioned above.

The value ε_in = 3.0 of the model we use here is compatible with calculations of continuum-model static dielectric coefficients of 2–4 for interior regions of many proteins and with measurements of dry protein powders [90,126–129]. The quoted range is approximate, depending on the protein and the method of calculation, and represents an ongoing area of investigation, as noted above [92]. Recent analyses of NMR chemical shifts within proteins, in particular their dependence on modeled local electric fields, found that values of ε_in near 3 gave the best matches to data [130,131].

III. PROBABILITY DISTRIBUTIONS OF PROTONATION PATTERNS

A. Features of the distributions at constant pH

In this section we address the following questions. How broad are the distributions at a given pH? How different are these distributions from the multinomial distribution that would occur if the off-diagonal work-of-charging entries were all zero? What simple approximations provide good quantitative agreement with the exact model probabilities? How different are the patterns of surface voltage that correspond to probable protonation patterns? In order to study these questions, in Figs. 5, 7, and 8 we plot the base-10 logarithm of the modeled probability of each protonation pattern vertically vs its net charge. In each figure, the line segments join two configurations that differ by a single switch in proton occupancy. We call such configurations adjacent. In addition to giving a visual picture of the protonation pattern probabilities and the possible single-step transitions between them, these and related diagrams can help to study how pattern probabilities are distributed with respect to factors that can affect protein-protein interactions, here net charge.

FIG. 7.

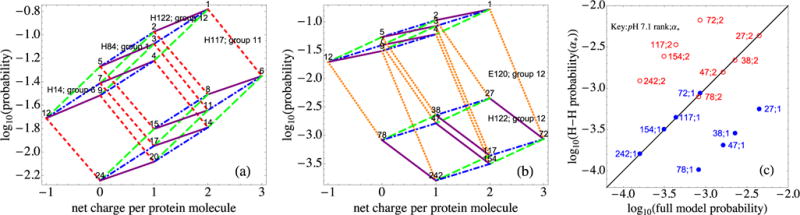
(a) Because H117 is only weakly linked to other residues [see Fig. 3(c), group 11], when H117 switches charge (red short-dashed lines), the eight-vertex polygon representing the possible switches of H122 (purple solid lines), H84 (blue dash-dotted lines), and H14 (green long-dashed lines) undergoes translation with very little distortion (see the text). (b) Because E120 and H122 interact strongly, when E120 changes from charge −1 to 0 the H122 switching segments markedly change slope, distorting the same polygon. (c) Further analysis of the changes in (b), by comparing the full model probabilities with those of a Henderson-Hasselbalch approach. Agreement would correspond to all points being on the solid diagonal line. (c) Illustration that the E120 switch markedly alters some probabilities from Henderson-Hasselbalch values (see the text).

FIG. 8.

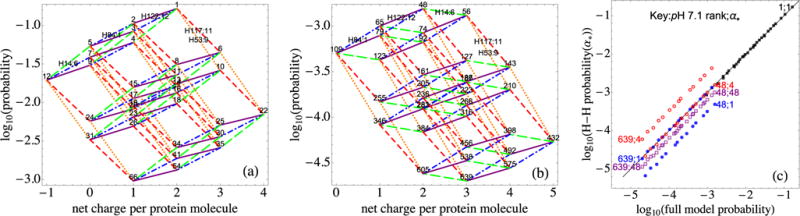
(a) Most common 32-vertex polygon representing possible switches of all five histidine residues at pH 7.1; H53 switches (orange dotted lines) are shown as well as the H122 (purple solid lines), H84 (blue dash-dotted lines), and H14 (green long-dashed lines) depicted in Fig. 7. (b) The 32-vertex polygon of histidine switches that occurs under the condition that E7, a neighbor of H14, has gained a proton to become neutral. The positively charged state of H14, which had been stabilized by a neighboring negative charge, is now less probable than its neutral state and the green long-dashed segments have negative slopes, while the others retain their slopes. Note the change in the vertical scale. (c) Comparison of probabilities from the full model and a Henderson-Hasselbalch approach for the topmost 32-vertex polygon in (a) (black squares), using α_* = 1, and the choices α_* = 1 (blue closed circles), α_* = 4 (red open circles), and α_* = 48 (purple open squares) for the polygon in (b). The diagonal solid line is that of agreement between the two methods.

Figure 5 shows that γ B protonation patterns that have both positive and negative net protein charge readily occur at pH 7.1. Figure 5(a) shows the most prominent pH 7.1 configurations that together account for 97% of the configuration probability.

In Fig. 5(b) the cumulative probability down to a given level is plotted horizontally as the curve on the far right, the boundary of the striped yellow region. This curve, taken together with Fig. 5(a), shows that each of the topmost 70% of the configurations has a non-negative net charge. However, below that level quite a few pH 7.1 configurations have net negative charge. Because oppositely charged proteins are more likely to exhibit attractive interactions, Fig. 5 gives rise to the interesting possibility that at high concentrations, where proteins have many near neighbors, the probability distributions of net charge may even become bimodal. In this work we do not analyze the biasing of the distributions because of protein proximity.

The square of the cumulative probability is filled in blue (dark) in Fig. 5(b). It provides an estimate of the fraction of pairs of neighboring proteins, both molecules of which have a configuration with a probability above a given level. This estimate again neglects biasing of probabilities due to protein proximity. The blue-yellow boundary suggests that close pairs of proteins, both of which have net non-negative charge, will account for only the top half of neighboring protein pairs. Also, to account for about 80% of the configuration pair types, configurations that range down to those that occur only one one-thousandth of the time must be included. Thus the blue-yellow boundary gives a rough guide to how many configurations to include in a model of electrostatic interactions for this protein.

Figure 6 compares the voltage patterns around the 12 most probable proton configurations at pH = 7.1 and Debye length 6 Å. Residues that have gained or lost protons, with respect to the next more common configuration, are shown by blue (darker) and red (lighter) arrows, respectively. At this pH, histidine protonation switches are modeled to account for the first 20 patterns. It is very interesting that as a consequence of the majority of these switches, the connectivity of the positive [blue (darker)] and negative [red (lighter)] potential regions on the projection spheres also changes, much like straits and isthmuses in continental drift. Thus one might expect that in the presence of neighboring proteins that also have charged patches, the ease of reorientation of each protein could depend on voltage channels that open and close, as each of their protonation configurations changes. The similarity of many of the voltage patterns that result from different protonation patterns, illustrated in Fig. 6, suggests that larger classes of such pairs may be sufficient for creating accurate models of the relevant pair potentials. Thus a very interesting question is how best to construct a good coarse-grained level of detail in the protonation pattern distributions in order to model protein interactions accurately. In the present work we do not focus on the protein interaction consequences of the patterns shown in Fig. 6.

FIG. 6.

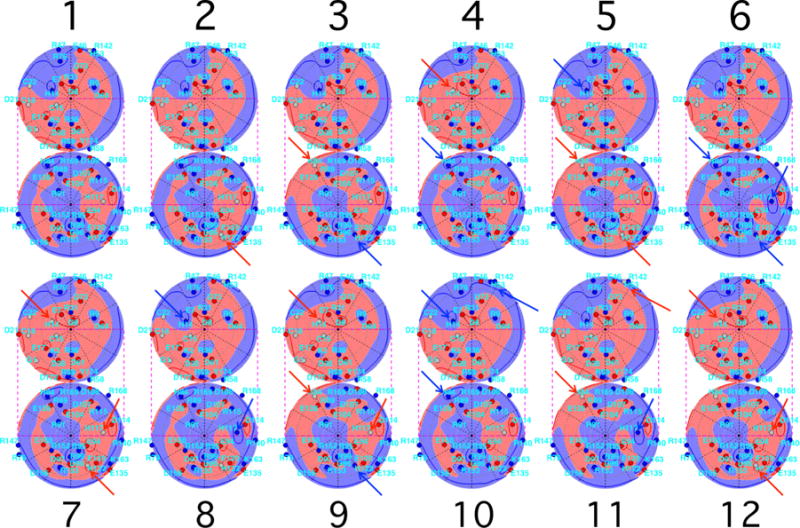
Lambert projections, with potentials and charges indicated as in Fig. 1(c), for the 12 most probable configurations at pH = 7.1 and Debye length 6 Å, in order of probability (see Table II). Residues that have gained or lost a proton, with respect to the more common configuration that is adjacent in order, are shown by blue (darker) and red (lighter) arrows, respectively. For many protonation switches, positive [blue (darker)] and negative [red (lighter)] voltage regions change connectivity.

We now study the origins of the switching pattern shown in Fig. 5(a) in more detail, in a residue-by-residue manner. Each line segment in Fig. 5(a) can be identified with the particular residue that gained or lost a proton. The probabilities of protonation patterns reflect both the affinity of each residue for protons and the correlations between sites that are strongly affected by their mutual electrostatic interaction.

The quantitative consequences are illustrated in Fig. 7. If two residues are uncorrelated, as are H122 and H84, the change in the pattern probability when one of them switches protonation state will not depend on the state of the other. Because their occupation probabilities are essentially independent, when H122 changes its charge, the logarithm of the pattern probability will change by a given amount that does not depend on whether H84 is protonated. Thus, the slope of the line segment that links H122-adjacent patterns (purple solid line) will not depend on the state of H84 and vice versa. In contrast, if two sites are strongly correlated, their protonation probabilities are no longer independent and the corresponding slopes that link adjacent configurations will depend on the protonation of the second residue.

Consider Figs. 7(a) and 7(b). In Fig. 7(a), because residue H117 is uncorrelated with residues H122, H84, and H14, protonating H117 simply translates (red short-dashed lines) the line segments for switches of the three other residues. In Fig. 7(b), because E120 is in residue group 12, as is H122 [see the lower right corner of Fig. 3(c)], H122-adjacent pattern probabilities change in different ways that depend on the state of E120.

If the work-of-charging matrix were diagonal, the distribution of protonation patterns would be multinomial and a translation-without-distortion property would hold exactly for all line segments in a diagram such as the ones in Figs. 5, 7, and below in Fig. 8. Thus the deviations from congruence of residue-switch polygons in the coordinates (net protein charge log₁₀ P) display the degree to which parts of the protonation pattern distribution differ from multinomial. We note that in the present work the choice of net charge on the horizontal axis underlies this polygon translation property, simply because the net charge is here assumed to be solely due to protonation switches. Clearly, if ion absorption played a significant role or if other coordinates were used in place of or in addition to net charge, such as the percentage of the surface that has a positive voltage, a more complex picture would result.

Figure 7(c) focuses on the configurations in the lower, eight-vertex polygon in Fig. 7(b). It illustrates the deviation of the probabilities calculated from the full model from those of the Henderson-Hasselbalch approximation, in a log-log plot. The blue closed circles compare these two probabilities using the topmost configuration as the reference (α_* = 1) for calculating $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values in the Henderson-Hasselbalch approximation. In this case the Henderson-Hasselbalch probability of configuration 72, which is found by a direct single-proton switch from configuration 1, agrees with the probability predicted by the full model, together with the configurations in its attached, translated blue-green polygon, namely, 117, 154, and 242 [see Fig. 7(b)], while the other four configurations (27, 38, 47, and 78) have probabilities that are 10 times those predicted by the Henderson-Hasselbalch model. In contrast, if α_* = 2, the open red circles show that the two methods of estimating probability agree for configurations 27, a direct switch from 2, together with 38, 47, and 78, while the other four no longer agree. Because E120 is in the same group as H122, there is no reference state for which all of the pattern probabilities can be computed with use of the Henderson-Hasselbalch approach. Indeed, the factors $e^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2}$ in Eqs. (10)–(12), in which the vectors δq_α depend on both α and α_*, together with the existence of nonzero off-diagonal elements of W, imply that, in general, some full GCPF pattern probabilities will differ from Henderson-Hasselbalch ones, regardless of the choice of α_*. Some individual residue protonation probabilities must then also differ from Henderson-Hasselbalch values. This can occur whether or not the residue is charged as it is in α_*; this can be shown by expressing individual residue protonation probabilities as sums of the P_α of Eq. (12) over the appropriate patterns α, the key point being that each summand can carry a different factor of $e^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2}$.

Figure 8 is a larger-scope version of the translating polygons picture. In the present γB-crystallin model, at pH 7.1 the switching of protonation states of the five histidines accounts for a large fraction of the topmost protonation configurations of the entire protein. Thus for this pH it is interesting to construct sets of 32-vertex polygons, in which the vertices represent all of the 2⁵ histidine protonation patterns that occur for a given configuration of all the other residues. Figure 8(a) shows the topmost such polygon.

The entire probability distribution of protonation patterns can be represented as the family of all such 32-vertex polygons; each possible pattern belongs to just one such polygon. Figure 8(b) illustrates the distortion of the topmost polygon that results when residue E7, strongly coupled to H14, switches protonation. It is now harder for H14 to become protonated, which is reflected in the fact that the slopes of the green long-dashed segments that represent the H14 protonation switches become smaller; in this case they go from positive to negative. As in Fig. 7, Fig. 8(c) shows that when E7 switches, the Henderson-Hasselbalch approach does not work well for the resulting polygon, even though it does work well for the topmost polygon. The choice α_* = 48, suggested by the fact that it is the topmost configuration in Fig. 8(b), produces a linear arrangement that is parallel to but displaced from the line of agreement.

Figure 9 compares full model configuration probabilities with those calculated using $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values, at pH 4.5 and 7.1. Figures 9(a), 9(b), 9(d), and 9(e) show that a large number of the configurations have quite different probabilities from those calculated using $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values alone, due to linkage between groups of titratable residues. Because the protein becomes more highly charged as pH is decreased (see Fig. 4), it is natural to expect that the broader distribution of probabilities relative to the Henderson-Hasselbalch approximation may be associated with this increased net charge. Also, there might be more charged residues at the lower pH, which might bias the probabilities from Henderson-Hasselbalch values.

FIG. 9.

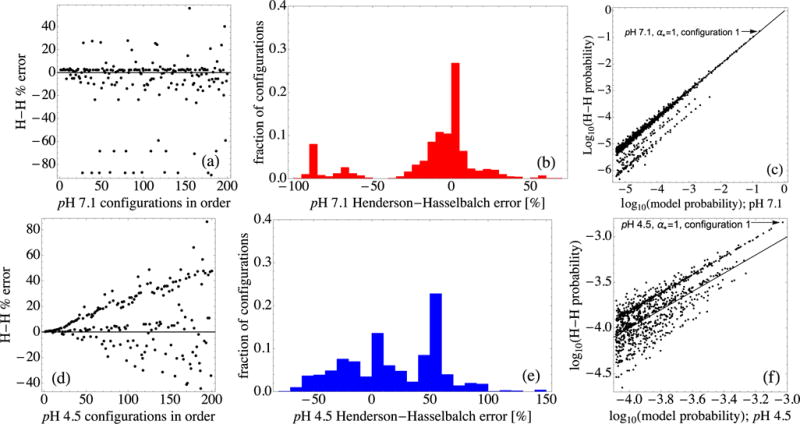
(a) Percentage deviation of the Henderson-Hasselbalch probabilities of the top-ranked 200 configurations from those of the full model at pH 7.1. Panels (a)–(c) all use α_* = 1 for pH 7.1 to determine $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values for use in calculating Henderson-Hasselbalch probabilities. (b) Histogram of the same deviations, for the top-ranked 1000 configurations at pH 7.1. (c) A log-log comparison of the top-ranked 1000 configuration probabilities from the full model with the Henderson-Hasselbalch probabilities. Note the clustering along diagonal lines. (d) Similar percentage deviations of the top-ranked 200 configurations at pH 4.5. Panels (d)–(f) all use α_* = 1 for pH 4.5 to determine $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values for use in calculating Henderson-Hasselbalch probabilities. (e) Histogram of the deviations at pH 4.5. (f) A log-log comparison of the top-ranked 1000 configuration probabilities; note the changed scales.

However, the Henderson-Hasselbalch probabilities in Fig. 9 already incorporate the influence of the most common charge patterns because they use the top configuration α_* appropriate for each pH to construct the needed $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values, via Eq. (10). Thus, the existence of residues that are charged differently at the two pH values is not, by itself, sufficient to account for the broader distribution in Fig. 9(d), as compared with that in Fig. 9(b).

Also, for the very top configurations at each pH, fewer residues, 43, are modeled as charged at pH 4.5 (28 positive, 15 negative, 11 neutral, net charge +13) than at pH 7.1, where 48 are charged (25 positive, 23 negative, 6 neutral, net charge +2). Thus, positively and negatively charged residues, taken together, make for a larger total number of charges at pH 7.1, despite the fact that the net charge is lower at pH 7.1. This situation is physically reasonable because it corresponds mainly to the fact that at pH 4.5, eight glutamate and aspartate residues that carried negative charges at pH 7.1 are neutral, which can readily occur because the pH is much closer to their $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values; H53, H117, G1, and Y174 also change charge. Thus the fact that there are fewer titratable groups that carry charge (positive or negative) at pH 4.5 than there are at pH 7.1 depends on the set of $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values [see Fig. 15(a) herein and Fig. 5 in the Supplemental Material [122]), combined with the bare charge numbers. This is not directly connected with the fact that the deviation from the Henderson-Hasselbalch distribution is greater at pH 4.5.

FIG. 15.

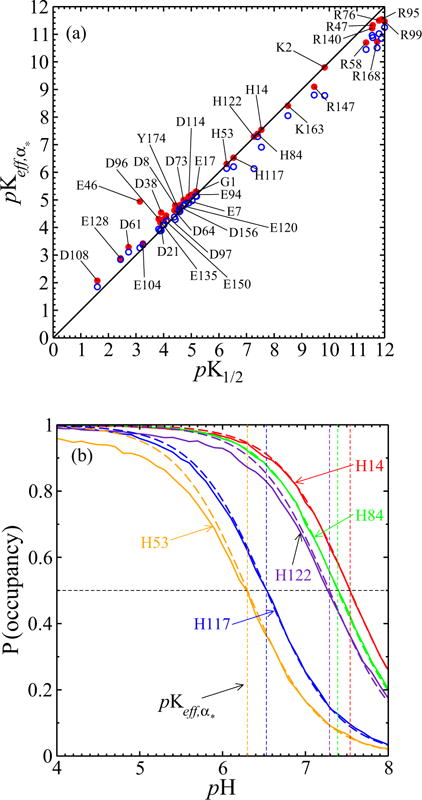
(a) The pK_1/2 values from simulations of the full model with interactions, on the horizontal axis, are close to the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values. Red dots result from taking α_* to be the most prominent protonation configuration within 6.6 < pH < 7.3; pK_1/2 values farther from 6.6 < pK_1/2 < 7.3 differ from those $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$, as expected. Blue open circles result from taking α_* to be the most prominent configuration within 4.4 < pH < 4.6; again pK_1/2 values farther from that of α_* differ more from those of $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$. (b) Except for H53 and H122 below their respective pK_1/2, histidine titration curves from the full model (solid line) also agree well with Henderson-Hasselbalch curves (dashed line) as parametrized by the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values of the α_* used in (a).

Rather, Eqs. (11) and (12) indicate that the broader width of the distribution of protonation pattern probabilities must arise from the switches δq_α of charge patterns from that of α_* that contribute significantly to the factors $e^{-\delta {\mathbf{q}}_{\alpha }^{\top }W\delta {\mathbf{q}}_{\alpha }/2}$. More specifically, the broader width of the protonation pattern probabilities relative to the Henderson-Hasselbalch approximation at pH 4.5, as compared with that at pH 7.1, is due to Glu and/or Asp residue pairs in the same work-of-charging group [see Fig. 3(c)]. Frequent charge switches of these residues at pH 4.5 produce the most probable protonation patterns, while at the same time their work-of-charging linkages bias pattern probabilities away from Henderson-Hasselbalch ones. At pH 7.1, histidine residue switches produce the most probable patterns, but because each histidine is in a different work-of-charging group, pattern probabilities more closely track the Henderson-Hasselbalch approximation. Figures 9(c) and 9(f) show log-log plots similar to those in Figs. 7(c) and 8(c) for the top-ranked 1000 configurations. At pH 7.1, the deviations cluster along lines parallel to the diagonal line of agreement. At pH 4.5 this clustering feature is less clear; the scale was expanded to make it apparent.

The polygons linking protonation patterns shown in Figs. 7 and 8 suggest that the use of effective pK values holds both value and danger. If the effective pK values were to be considered as fixed, they would not account for the lack of independence of the protonation pattern probabilities that is represented graphically by the distortion of the polygons shown. Nevertheless, as suggested by Figs. 9(c) and 9(f), one might accurately model the probability distributions with use of judicious choices of a changing set of base configurations α_* for calculating effective pK values according to Eq. (10).

How large do off-diagonal parts of the work-of-charging matrix need to be before they significantly affect the probability distribution of protonation configurations, at a given pH? Figure 10 examines the sensitivity of the probabilities of the topmost few configurations to the omission of elements of the work-of-charging matrix that are smaller than chosen cutoff levels. Figure 10(a) shows that at pH 7.1, the order of the top-ranked six configurations is stable up to a cutoff level of only 0.07, a level that is shown by the vertical dashed line. Such a dimensionless work-of-charging level corresponds to an electrostatic potential φ, produced at one member of a pair of titratable groups by the other, charged member, of 0.07k_BT/e, or approximately 2 mV. This rather small value to which the ranking of protonation patterns is sensitive occurs for two principal reasons, which are illustrated in Figs. 10(b) and 10(c), respectively.

First, while many of the entries in W are quite small, there are many such entries. To quantify this, Fig. 10(b) shows the cumulative distribution function of the work-of-charging matrix entries. While for 0.07 < W_ij < 1, individual titratable site pairs have relatively little effect on one another, a large number of such pairs occurs; 1133 entries are less than 0.07, 262 entries are between 0.07 and 1, and 36 entries are more than 1.

Second, and more specifically, the cutoff values depend on how close the pH is to one or more $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values. At the pH illustrated, the titration of histidine residues is modeled to account for the relative prominence of the top-ranked configurations, as discussed above and shown by the polygons in Figs. 7 and 8. Further, the agreement between the Henderson-Hasselbalch probabilities and those of the full model for the topmost 32-vertex polygon, shown in Fig. 8(c), suggests that the changes shown in Fig. 10(a) should correspond to changing $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values.

This is borne out by Fig. 10(c), which shows how the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values of the five histidines change as the work-of-charging cutoff value is increased from 0.01 to 10, all at a pH of 7. The 0.07 level is again shown by the vertical dashed line. At cutoffs lower than 0.07, the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values show small fluctuations much like those of a random walk, a feature that corresponds to the large number of small work-of-charging entries below this level, shown in Fig. 10(b). The ranking of configuration probabilities [shown in Fig. 10(a)] consequently remains stable until the net result of these fluctuations overcomes the difference between two neighboring $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values. This occurs just beyond the 0.07 cutoff level, when the H84 $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ crosses below that of H122. As a result, the H84 $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ is now closer to the ambient pH 7.1 and its deprotonation would now be modeled as more probable than that of H122. In terms of the configuration probability polygon in Fig. 7(a), the H84 segments will now be less positively sloped than those of H122. Such a change corresponds precisely to the fact that the configurations initially ranked 2 and 3 switch their order in Fig. 10(a) just above cutoff level 0.07. It is also consistent with the fact that configurations 5 and 6 also switch their rankings at a very similar cutoff level. Further comparison shows that the prominent migration of the H84 $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ value with increasing cutoff level, shown in Fig. 10(c), is largely responsible for the further configuration ranking changes shown in Fig. 10(a). Finally, Fig. 10(c) shows that at higher cutoff levels, many additional switches occur, until the cutoff level is so high that it is larger than any off-diagonal values.

In summary of the implications of Fig. 10, off-diagonal elements of the work-of-charging matrix that are quite small in the dimensionless units eϕ/k_BT can nevertheless change the ranking of protonation configuration probabilities. Also, as larger and larger off-diagonal elements are set to zero, a random-walk-like migration of $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values provides an approximate accounting for the ranking changes of the top configurations, whose probabilities are well represented by the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values at this pH.

B. The pH dependence of protonation pattern distributions

The modeled probability distributions of protonation configurations show a marked dependence on pH, which we now study. By way of introduction, Fig. 11 shows how the screened potential contours change with pH for the most common protonation patterns, those occurring at pH = 7.1 [Fig. 11(a), as in Fig. 1(a)], pH = 6.5 [Fig. 11(b)], pH = 5.0 [Fig. 11(c)], and pH = 4.5 [Fig. 11(d)]. The contour values displayed are for +k_BT/e V (blue with horizontal curves), 0 V [gray with curves as in Fig. 1(a)], and −k_BT/e V (red with vertical curves). In each case the Debye length is 6 Å. Prior experimental results, to be analyzed and reported with the help of the model being developed here, led to the choice of pH values for Fig. 11. Specifically, at pH 7.1, 6.5, and 5.5, at a Debye length of 6 Å, we observe reversible liquid-liquid phase separation in concentrated γB-crystallin solutions, strongly suggesting attractive net protein-protein interactions. However, we see no phase separation at pH 4.5, and at this pH small-angle neutron scattering indicates repulsive interactions.

FIG. 11.

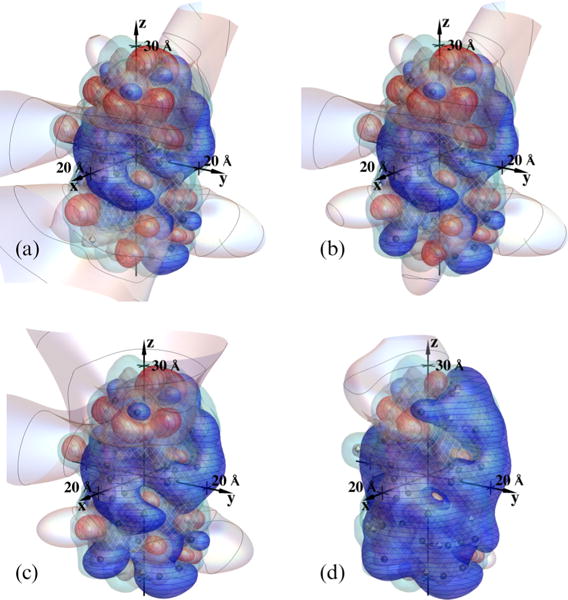
Screened potential contours of γ B-crystallin, for the most common protonation patterns at (a) pH = 7.1 (as in Fig. 1), (b) pH = 6.5, (c) pH = 5.0, and (d) pH = 4.5. The Debye length is 6.0 Å; contour values are +k_BT/e V (blue with horizontal curves), 0 V [gray with curves as in Fig. 1(a)], and −k_BT/e V (red with vertical curves); dielectric and electrolyte boundaries are designated as in Fig. 1(a). Note the changing balance between positive and negative voltage regions with pH and an accompanying shrinkage of zero-voltage contours, most of which, at pH 4.5, extend to less than a Debye length from the protein.

It is interesting that in this context the balance between the positive and negative voltage regions is fairly even at pH 7.1 and pH 6.5, while in contrast the positive regions progressively dominate at pH 5.0 and pH 4.5. Further, the zero potential contours extend far from the protein at the upper three pH values shown, but collapse to inside or near the protein at pH 4.5. In combination with the findings mentioned above, Fig. 11 suggests that with the more even balance of positive and negative surface regions modeled at the higher pH values, neighboring proteins may readily bias their orientations so that oppositely charged surface patches can face one another and interact so as to produce net attractive forces. However, if the balance between positive and negative surface regions becomes skewed beyond that corresponding to Fig. 11(c), net repulsive forces can result. Figure 11(d) illustrates that at pH 4.5 the majority of the protein surface is positive. At this pH, the angular-averaged interprotein interactions may be relatively insensitive to changes in the particular configuration of protons. It is important to note that a quantitative model will also need to include dispersion forces and hard-core interactions, at least.

Figure 12 shows log₁₀ P vs net protein charge for configurations in the modeled distributions at pH 5.5 and pH 4.5, together with their single-protonation switch line segments, accompanied by the pH 7.1 distribution shown in Fig. 5. As pH decreases within this range, there is a substantial spread of net charge and the topmost configuration becomes considerably reduced in probability, reaching below 1 part in a thousand at pH 4.5.

FIG. 12.

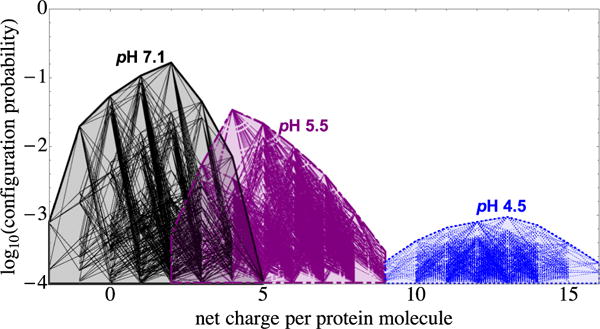
Plot of log₁₀ P vs net charge, with line segments indicating single-residue protonation switches, for protonation patterns that occur at pH 7.1 (black solid line, the same as in Fig. 5), pH 5.5 (purple dash-dotted line), and pH 4.5 (blue dotted line) (see the text).

Figure 13 illustrates summary statistics of the configuration probability distributions vs pH. Figure 13(a) shows that near neutral pH the distributions are relatively narrow for this protein; for example, one of the top 100 patterns is expected to occur about 90% of the time. Because 2⁷ = 128, this corresponds to on the order of seven sites switching their protonation status. As discussed in connection with Fig. 5, even though the distribution is relatively narrow near pH 7.0, Fig. 13(a) implies that a large number of pairs of patterns may be needed in order to model electrostatically mediated interactions between the proteins. The needed number of pairs can be estimated from the figure. For example, assuming for the purpose of illustration that neighboring patterns do not bias each other’s probabilities, it would mean that considering (100 × 101)/2 distinct pairs of patterns would enable one to model a fraction 0.9 × 0.9 of the pairs that contribute to the effective interaction strength. The distributions are much broader at lower pH values; the pH 4.5 curve in Fig. 13(a) shows that at that pH, one of the first 1000 patterns will be present only 20% of the time. Figure 13(b) shows the contours of the cumulative probabilities of the top sets of patterns at each pH, in the [pH, log₁₀(number of configurations)] plane.

FIG. 13.

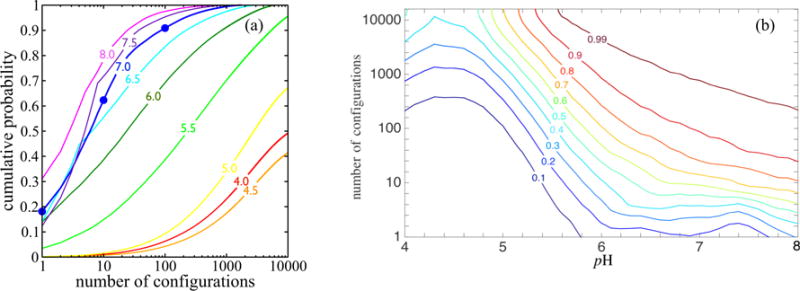
(a) Cumulative probabilities of the most probable protonation patterns at a Debye length of 6.0 Å. For example, the dots on the pH 7.0 curve show that under these conditions, the top γB occupancy pattern occurs nearly 20% of the time, one of the first 10 patterns will be present 60% of the time, and one of the top 100 patterns occurs 90% of the time. The pH 4.5 curve shows that one of the first 1000 patterns will be present 20% of the time. (b) Contours of the cumulative probabilities displayed in the [pH,log₁₀(number of configurations)] plane. For example, the 0.99 contour indicates that at pH ≈ 6.8, 1000 configurations account for 99% of the probability.

Figure 14(a) shows the pH dependence of the probabilities of patterns that are each the top pattern within some interval of pH. To understand these probabilities more thoroughly, consider any pattern α that has a specified number k_α = n of protons bound. Such a pattern has the probability

$$P_n=\frac{{\zeta }^n{e}^{-(\mathbf{\Delta }{\mathit{\mu }}^{\mathbf{0}}\mathbf{·}{\mathbf{O}}_{\mathit{\alpha }})/k_{B}T}{e}^{-W_{\text{el},\alpha }/k_{B}T}}{\mathcal{Q}}\equiv \frac{{\zeta }^{n}B(O_{\alpha })}{\mathcal{Q}},{\log }_{10}{P}_n={\log }_{10}B(O_{\alpha })-np\mathrm{H}-{\log }_{10}\mathcal{Q},$$ (14)

in which ζ = 10^−pH and B(O_α) denotes a Boltzmann factor for occupancy vector O_α; B(O_α) includes the intrinsic pK values as well as the work-of-charging contribution. Note that all of the pH dependence in the last line of Eq. (14) occurs in the last two terms; the partition function $\mathcal{Q}$ in the final term depends on pH through ζ. Therefore, for a given value of n, all of the curves of log₁₀ P_n vs pH are simply vertically displaced with respect to one another, because they differ only due to the quantities log₁₀ B(O_α). This feature is illustrated in Fig. 3(a) in the Supplemental Material [122]. The nearly parabolic shapes in the coordinates (pH, log₁₀ P_n) correspond to nearly Gaussian shapes when P_n is plotted vs pH, as shown in Fig. 14(b) for the top-ranked 12 configurations at pH 7.1; these are the configurations illustrated in Fig. 6. In Fig. 14(c) we show the partition function in the form ${\log }_{10}\mathcal{Q}$ in the range 4 < pH < 8. In this pH range, ${\log }_{10}\mathcal{Q}$ can be represented well by cubic or quartic polynomials, specifically ${\log }_{10}\mathcal{Q}=474.27-86.407\times p\mathrm{H}+7.414\times p{\mathrm{H}}^2-0.30492\times p{\mathrm{H}}^3(1-\text{adjusted}{R}^2=6\times {10}^{-6})$ and ${\log }_{10}\mathcal{Q}=545.64-136.56\times p\mathrm{H}+20.392\times p{\mathrm{H}}^2-1.7713\times p{\mathrm{H}}^3+0.061101\times p{\mathrm{H}}^4(1-\text{adjusted}{R}^2=5\times {10}^{-7})$, respectively. Such fits can be convenient for estimating $\mathcal{Q}$ in Eq. (5) or (14) for protonation pattern probabilities. The fit residuals in Fig. 14(c) illustrate the degree of error to be expected in using such a fit for $\mathcal{Q}$ and show their polynomial appearance; such correlation of residuals can be detected using, for example, the Durbin-Watson statistic. Physically, such an appearance is to be expected given that $\mathcal{Q}$ is a polynomial of essentially higher order than 4, because more than four prominent overall protonation numbers occur in 4 < pH < 8 [see Eq. (2) and Fig. 14(a)]. A perspective view of the joint dependence of pattern probabilities on net charge and pH is given in Fig. 3(b) in the Supplemental Material [122].

FIG. 14.

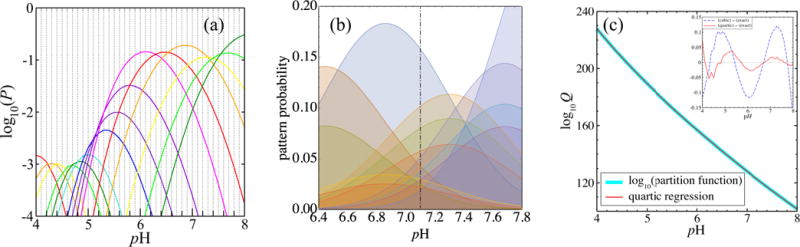
(a) The pH dependence of the probabilities of patterns that are each the top pattern in some interval of pH. (b) The P_α vs pH for the top 12 configurations at pH 7.1 have nearly Gaussian distributions with respect to pH. (c) The ${\log }_{10}\mathcal{Q}$ from the present model, determined using Monte Carlo simulations (10 × 10⁶ samples per pH, in 0.1 pH steps). The inset shows the residuals to two of the fits, which for the quartic fit in this pH interval have a range of about 1 part in 4000 of ${\log }_{10}\mathcal{Q}$.

The finding that the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values are useful for predicting the ranking of configurations suggests that it is interesting to compare them with the pK_1/2 values calculated using the full model. Figure 15 makes such a comparison, with use of $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values that take α_* to be the top-ranked configuration for 6.6 < p_H < 7.3 (red closed circles) and to be the top-ranked configuration for 4.4 < pH < 4.6 (blue open circles). Figure 15(a) shows that for the histidines that are modeled to titrate near neutral pH, the $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values are indeed almost exactly equal to the corresponding pK_1/2 values. This is to be expected from the agreement shown by the black squares in Fig. 8(c). It is instructive to compare the order in which histidine residues first switch to the difference between pH 7.1 and their respective $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values. From Fig. 6 or from Table I, the order of switching is H122, H84, H14, H117, and H53, consistent with the corresponding $|p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}-p\mathrm{H}|$ values of 0.19, 0.29, 0.44, 0.57, and 0.80.

Figure 15(a) also shows that for residues whose $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ values are further from the range for which the chosen α_* configuration is appropriate, the pK_1/2 and $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ differ more strongly. Thus, when using $p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}$ as a tool for estimating experimental pK_1/2 values, it is important to choose α_* configurations that are prominent, and representative, in a pH range that ideally includes the pK_1/2 in question. We note that because 1 < pH < 12 in the simulations used to create Fig. 15(a), residues with model pK_1/2 values outside this range are not shown; in addition to 12 of the arginines and the three cysteines, these included D72 and D107.

Figure 15(b) shows that, except for H53 and H122 below their respective pK_1/2 values, the histidine titration curves from the full model agree well with Henderson-Hasselbalch curves, as expected because they are in different work-of-charging groups [Fig. 3(c)]. Thus, although many protonation configuration probabilities are not well predicted by a Henderson-Hasselbalch approach, this may not show up prominently in the titration curves of selected residues.

C. Dependence of the distributions on ionic strength

The possible effects of ionic strength on solutions of γ B-crystallin and other proteins are very interesting, in that one expects that they will depend on both the balance and shapes of the negative and positive voltage surface regions. On one hand, if attractive interactions are in part created by protein orientations that put negative and positive surface regions of neighboring proteins face-to-face to some degree, lowering ionic strength would be expected to increase attractions, because then the negative and positive regions would affect one another over a larger range of protein separations. On the other hand, if the net electrostatic portion of the interaction is repulsive, lowering ionic strength would be expected to increase the repulsion. In this context it is interesting to see how large the effects of ionic strength are on the distribution of protonation patterns, which could also play some role in mediating such effects.

Figures 16(a) and 16(b) show that the off-diagonal work-of-charging entries, as expected, can increase substantially as ionic strength is lowered. Figure 16(c) shows the corresponding changes in the configuration distribution at pH 7.1. In these coordinates the changes appear modest for the case illustrated. However, the effect is nevertheless evident; it is to make the most prominent configurations slightly more probable, at the expense of some of the less probable configurations. Figure 16(d) shows this in summary fashion. Note the crossover between the changes shown by the top-ranked configurations, whose probabilities generally increase (blue curve above black curve), at the expense of lower-ranked configurations, whose probabilities generally decrease, though not without exception.

FIG. 16.

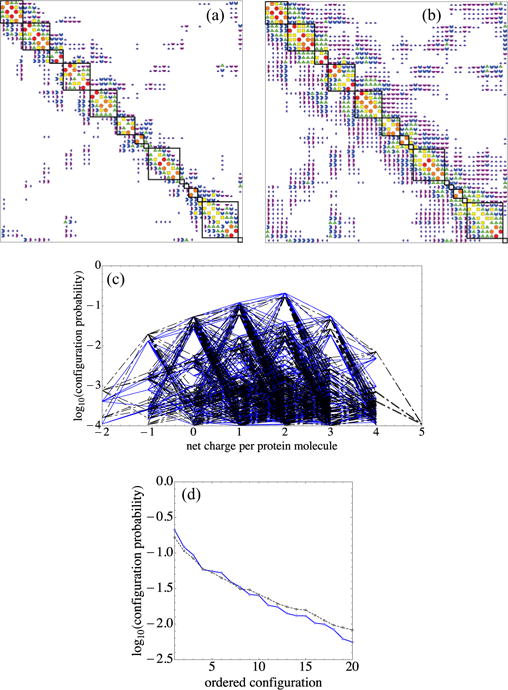
Lowering ionic strength, corresponding to increasing the Debye length λ_D from (a) 6 Å to (b) 20 Å, increases off-diagonal work-of-charging entries and makes the top configurations more prominent while suppressing others, as shown in (c) and (d). In (a) and (b) W_ij magnitude codes are as in Fig. 3(a). A 1:1 electrolyte in water at 298 K corresponds to ionic strengths of (a) 257 mM and (b) 23.1 mM. In going from (a) to (b), in all categories but the top (red circles), entries above 0.05k_BT increase in number with increased λ_D. (c) Plot of log₁₀ P vs net charge, as in Fig. 5. Black dash-dotted lines show λ_D = 6 Å and blue solid lines λ_D = 20 Å. (d) Plot of log₁₀ P for the top 20 configurations; note the changed vertical scale. The black dashed line shows λ_D = 6 Å and the blue solid line λ_D = 20 Å. The contrast between changes in top- and lower-ranked probabilities is shown by the crossing of the dashed and solid curves.

D. Possible implications for protein-protein interactions

As discussed in the Introduction, our primary purpose here is to provide part of a basis for further investigation of the molecular properties that determine the magnitude of interactions between γ B- and related γ-crystallin and other eye lens crystallin proteins, investigation that we hope can eventually achieve sufficient detail to provide for quantitative, predictive modeling of the origin of the cataractogenic effects of single-residue mutations. Because many known cataractogenic mutations of γ-crystallins involve changes of residue charge, it is natural to study the protonation configuration probability distributions in detail. While many models of orientation-dependent protein-protein interactions have been developed at various levels of coarse graining [3–6,11,132–134], some of which incorporate charge regulation, including models for lysozyme interactions [4–6,132,135,136] and for gamma crystallin interactions [52,88,137], achieving the degree of fine graining for the more predictive modeling needed in many contexts remains an outstanding challenge [19].

Although a quantitative investigation of the consequences of the present model for how site-specific chemical changes influence interactions is not the focus of the present work, we nevertheless comment here on three features that illustrate the scope of the problem. These include (i) the small fraction of the pairs of configurations accounted for by each choice of individual protonation configurations in neighboring proteins, even if those choices are each the top-ranked choice, (ii) the six-dimensional space of the relative positions of two neighboring proteins, and (iii) the biasing of protonation configuration probabilities because of protein proximity [10], a biasing that is itself a function in that same six-dimensional space. Of course, additional relative position and orientation dimensions are needed if the concentration is high enough so that clusters of more than two neighboring proteins are needed to represent the situation adequately. We now briefly discuss each of these features.

First, Fig. 17 shows the calculated voltage contours around two neighboring γB-crystallin molecules, at pH 7.1 and Debye length 6 Å. Each of these molecules has been given the most common protonation configuration, that illustrated in Fig. 1. Note that the zero voltage contours appear dramatically altered from those surrounding the isolated protein in Fig. 1(a). Yet the corresponding pair of proton occupancy patterns accounts for only about 0.165 × 0.165 = 0.0272 of the contributions to the protein-protein interactions. An illustration of interaction contributions by common pairs of patterns is given in Fig. 1 of the Supplemental Material [122].

FIG. 17.

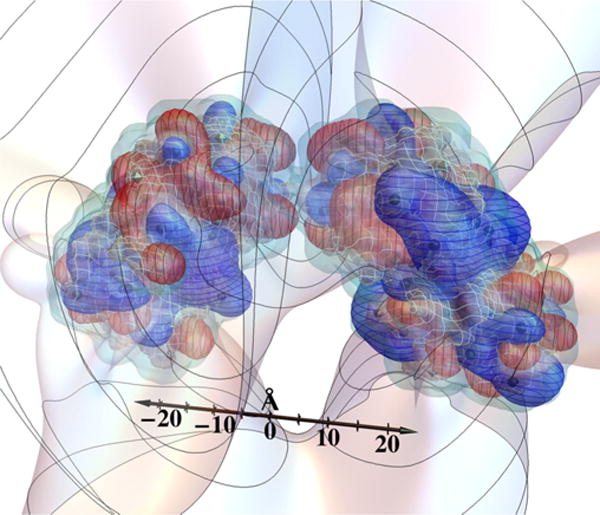
Screened voltage contours around neighboring γ B-crystallin molecules, with pH 7.1 and Debye length 6 Å. The voltage contour surface designations are as in Fig. 1(a), except that the curves on the 0 V contour surface are spaced by 12 Å from the calculation box center. Each molecule has the top-ranked protonation configuration.

Now, for each chosen pair of protonation configurations, the space of relative orientations of the two proteins has five dimensions, two for each protein to choose the surface points that are in closest proximity and one more for the relative twist about the line joining their centers. Radial separation gives a sixth dimension. Among the many choices of how to visualize the space of possible relative orientations, one shown in Fig. 18 is to make a projection so as to be able to plot the voltages around both protein surfaces above and below two planes and to represent the space of possible proximities by the collection of all line segments or arrows that join pairs of points, one from each plane. Twist can then be added as a position along each line segment, if desired. In Fig. 18,a few such line segments are drawn that indicate connections that could correspond to strong electrostatic attractions between neighboring γ -crystallins, for the most common pair of protonation configurations, shown at left. While the few connections shown in Fig. 18 simply join positive to negative peaks, nonpeak locations can also show electrostatic attractions, depending on the twist angle. With use of calculations that consider the possible relative orientations, one can find prominent basins of attraction and saddle points in the five- or six-dimensional space and illustrate these by points on the appropriate connection lines.

FIG. 18.

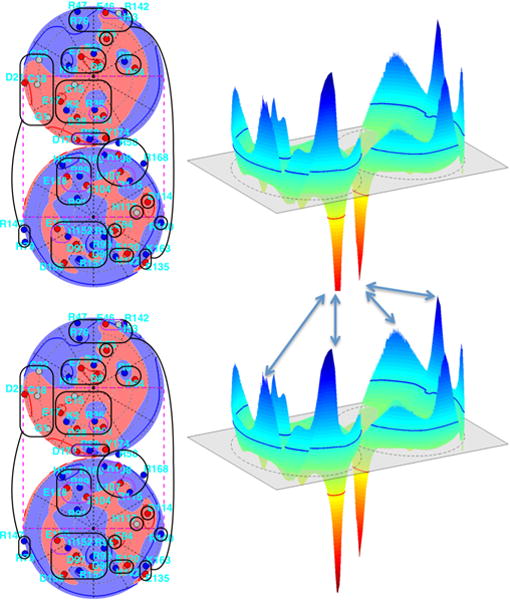
Visualization of the sets of relative orientations that could give electrostatic attractions between neighboring γ-crystallins. Lambert projections, as in Fig. 3(c) and described there, of the electrostatic potential at about one-half Debye length from two copies of the most common pH 7.1 protonation configuration are shown on the left. Voltages on the same surfaces are plotted vertically on the right, above and below the Lambert projections, with positive up. While the arrows here simply join positive to negative peaks, nonpeak locations can also attract, depending on twist angle.

Returning now to Fig. 17, protein proximity dramatically alters the surrounding voltage zero contours, as mentioned above. As a consequence the protonation pattern probability distribution will now reflect between-protein, off-diagonal elements of an enlarged work-of-charging matrix. The existence of these elements means that the joint configuration probabilities can only be approximately represented by the products of probabilities of the individual configurations of hypothetical isolated proteins. As a consequence, the study of the probability distributions of protonation patterns becomes much more intricate for close protein neighbors. Figure 19 gives an example in which changing the relative orientations of two neighboring proteins alters the expanded, two-protein work-of-charging matrix. This example illustrates that the expanded matrices are now functions of the six-dimensional space of the relative positions of the two proteins. Figure 19 also shows that only a small portion of the protein-protein blocks in the expanded matrices differ substantially from zero, which suggests that a perturbation approach might accurately represent the resulting joint probability distributions. To create Fig. 19, we streamlined the needed calculation by using a simpler dielectric boundary than that used above, which consisted of two conjoined, interpenetrating low-dielectric spheres, and by omitting the three cysteine residues that are incorporated in the 54 titratable residues considered above.

FIG. 19.

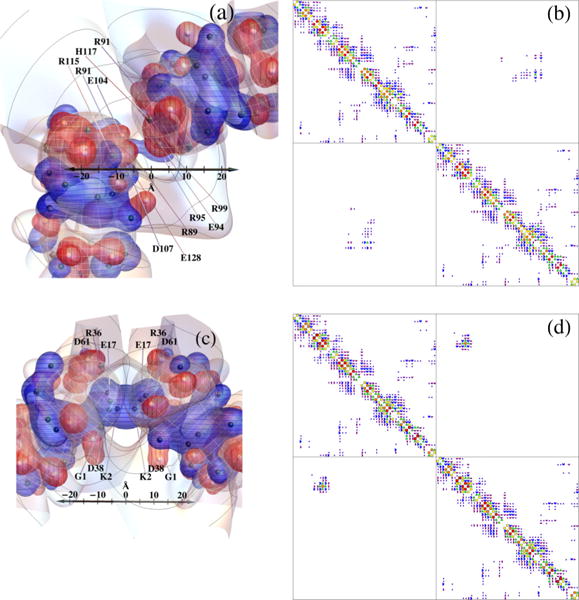
Changing the relative orientations of two neighboring proteins alters the expanded, two protein work-of-charging matrix. The voltage contour surface designations in (a) and (c) are the same as in Fig. 1(a), except that the curves on the 0 V contour surface are spaced by 12 Å from the calculation box center. The dielectric surfaces are outlined by white longitude and latitude curves. (b) and (d) Same color code as in Fig. 3. (b) and (d) Upper left and lower right squares show the within-protein recalculated work-of-charging matrix entries, while the off-diagonal squares show the between-protein entries. (a) and (c) Different sets of residues are adjacent to one another, as indicated, producing differences in the corresponding work-of-charging matrices shown in (b) and (d), respectively. The order of residues is the same for each protein in (b) and (d), but differs from that in Fig. 3.

Note that close protein proximity can be quite common even at rather low concentrations compared with those that occur in the living eye lens, which can range into the hundreds of milligrams per milliliter. For example, in a square-well model of the phase behavior of γB-crystallin [12], Monte Carlo simulations using parameters that gave the closest fit to the observed critical temperature and concentration (a square-well width over diameter of 0.25 and square-well depth of 1.267k_BT) indicate that even at a concentration of 0.5 mM protein, the mean-field estimate of the average number of contacts per particle [Eq. (30) in [12]] is 0.2; that is, a given protein will already have an essentially close neighbor about 20% of the time. This concentration, which for γB-crystallin is close to 10.5 mg/ml, corresponds to a volume fraction of 0.0074, a small fraction of its critical volume fraction of 0.18–0.20, and small compared with estimates of the macromolecular volume fraction in living cells [13], which range from 0.07 to 0.40. Thus one expects altered protonation probability distributions, due to molecular proximity, to contribute substantially to the thermodynamics of protein and other macromolecular solutions within living cells.

IV. CONCLUSION

We have used the linearized Debye-Hückel approximation to model the probability distributions of protonation patterns on bovine γB-crystallin as functions of pH. The breadth of the probability distributions indicates that a very large number of pairs of such patterns will be needed in order to account for how the distribution of protonation patterns affects γB- γB interactions. The key to such an analysis will be to understand not simply the distribution of protonation patterns of a single protein, but rather the probability distribution of protonation patterns, spatial variations of electrostatic potential, and consequent electrostatic interaction free energies present on pairs and larger tuples of neighboring proteins, as functions of their relative positions and orientations.

Accurate, angle-dependent potential of mean force models are needed to provide a sound molecular basis for understanding the statistical thermodynamics and the liquid structure of protein solutions [111–113] and the corresponding dramatic effects of mutations, post-translational modifications, and solution environment on protein phase separation and aggregation in solution. The present model is a step towards building an accurate angle-dependent model of electrostatic contributions to the potential of mean force for γ -crystallin interactions. Clearly, such a model will also need to encompass other aspects of protein-protein interactions not considered here, including dispersion interactions, the hydrophobic effect, and hydration forces.

TABLE II.

Occupancies of the residues that switch protonation states in the top ten configurations at pH 7.1 (see also Fig. 6). Residues switch in the order H122, H84, H14, H117, and H53, consistent with increasing $|p{\mathrm{K}}_{\text{eff},{\alpha }_{\ast }}-7.1|$ (see the text).

	Configuration rank
Residue	1	2	3	4	5	6	7	8	9	10
H14	1	1	1	0	1	1	0	1	0	1
H53	0	0	0	0	0	0	0	0	0	1
H84	1	1	0	1	0	1	1	1	0	1
H117	0	0	0	0	0	1	0	1	0	0
H122	1	0	1	1	0	1	0	0	1	1
probability	0.165	0.106	0.084	0.060	0.054	0.045	0.039	0.031	0.030	0.026

APPENDIX: EVALUATION OF ELECTROSTATIC ENERGY INTEGRALS AND CORRESPONDING pK SHIFTS

Consider a single charge on the z axis located at (0,0,z₀). We wish to compute $\frac{1}{2}{\displaystyle \iiint D·\mathit{EdV}}$ over the unbounded volume V exterior to a small sphere (neighborhood) of radius R, centered at the charge. To do so, we make use of the linearized Poisson-Boltzmann equation

$$\mathbf{\nabla }\cdot \left[\epsilon \left(\mathbf{x}\right)\mathbf{\nabla }u\left(\mathbf{x}\right)\right]={\epsilon }_{\mathit{out}}{\kappa }^2\left(\mathbf{x}\right)u\left(\mathbf{x}\right)-\rho \left(\mathbf{x}\right).$$

Within V, ρ(x) = 0, and in the absence of ionic screening (κ = 0), the equation reduces to

$$\mathbf{\nabla }\cdot [\epsilon (\mathbf{x})\mathbf{\nabla }u(\mathbf{x})]=0.$$ (A1)

To compute the volume integral

$$\frac{1}{2}{\displaystyle {\iiint }_{V}D\cdot \mathit{EdV}=\frac{1}{2}}{\displaystyle {\iiint }_V\epsilon (\mathbf{x})\mathbf{\nabla }u(\mathbf{x})\cdot \mathbf{\nabla }u(\mathbf{x})dV,}$$

we use the relation

$$\mathbf{\nabla }\cdot [\epsilon (\mathbf{x})u(\mathbf{x})\mathbf{\nabla }u(\mathbf{x})]=\epsilon \mathbf{\nabla }u\cdot \mathbf{\nabla }u+u\mathbf{\nabla }\cdot [\epsilon \mathbf{\nabla }u].$$

The second term on the right-hand side of the relation is equal to zero by Eq. (A1), in which case we have

$$\epsilon (\mathbf{x})\mathbf{\nabla }u(\mathbf{x})\cdot \mathbf{\nabla }u(\mathbf{x})=\mathbf{\nabla }\cdot [\epsilon (\mathbf{x})u\mathbf{\nabla }u(\mathbf{x})].$$

Then the integral can be written as

$$\frac{1}{2}{\displaystyle {\iiint }_{V}D\cdot \mathit{EdV}=\frac{1}{2}}{\displaystyle {\iiint }_V\mathbf{\nabla }\cdot [\epsilon (\mathbf{x})u(\mathbf{x})\mathbf{\nabla }u(\mathbf{x})]dV.}$$

The integral can be evaluated using Gauss’s divergence theorem by closing the volume with a second concentric sphere of radius R′ > R and letting R′ approach infinity. Let V′ be the volume bounded by the two spheres and let ∂R and ∂R′ denote the spherical boundary surfaces of radius R and R′, respectively. Then

$$\frac{1}{2}{\displaystyle {\iiint }_{V^{\prime }}\mathbf{\nabla }\cdot [\epsilon u\mathbf{\nabla }u]dV=-\frac{1}{2}}{\displaystyle {\iint }_{\partial R}\epsilon (\mathbf{x})u(\mathbf{x})\mathbf{\nabla }u(\mathbf{x})}\cdot \mathbf{n}dS+\frac{1}{2}{\displaystyle {\iint }_{\partial R^{\prime }}\epsilon (\mathbf{x})u(\mathbf{x})\mathbf{\nabla }u(\mathbf{x})}\cdot {\mathbf{n}}^{\prime }dS$$ (A2)

where the unit vectors n and n′ are normal to the respective boundary surfaces. We choose the unit normal vectors to be directed outward relative to the spheres, rather than to the volume itself. The second integral on the right-hand side of Eq. (A2) approaches zero as R′ approaches infinity. In this limit, we are left with

$$\frac{1}{2}{\displaystyle {\iiint }_{V}D\cdot \mathit{EdV}=-\frac{1}{2}}{\displaystyle {\iint }_{\partial R}\epsilon (\mathbf{x})u(\mathbf{x})\mathbf{\nabla }u(\mathbf{x})}\cdot \mathbf{n}dS.$$

It is convenient to evaluate the integral in spherical coordinates with the origin translated to the charge location at (0,0,z₀). Since the point charge is located on the z axis and ε is assumed to be symmetric about the z axis, the integrand is independent of the azimuthal angle θ. Therefore, the surface integral reduces to a single-variable integral given by

$$\frac{1}{2}{\displaystyle {\iiint }_{V}D\cdot \mathit{EdV}=-\pi R^2}{\displaystyle {\int }_0^{\pi }\epsilon (\varphi )u(\varphi )\frac{\partial u}{\partial r}}(\varphi )\sin \varphi d\varphi .$$

Outside a sphere of radius r₀, surrounding an isolated charge of magnitude q, placed in a dielectric having relative dielectric coefficient ε_r,

$$\frac{1}{2}{\displaystyle {\iiint }_{r>r_0}D\cdot \mathit{EdV}=\frac{q^2}{8\pi {\epsilon }_0{\epsilon }_r{r}_0}}.$$ (A3)

Therefore, if we transfer a charged group surrounded by water, which has dielectric coefficient ε_w, into a medium with coefficient ε_r, the work required is

$$\frac{q^2}{8\pi {\epsilon }_0{\epsilon }_r{r}_0}-\frac{q^2}{8\pi {\epsilon }_0{\epsilon }_w{r}_0}=\frac{q^2}{8\pi {\epsilon }_0{r}_0}\left(\frac{1}{{\epsilon }_r}-\frac{1}{{\epsilon }_w}\right).$$ (A4)

The corresponding change in the pK of such a group, ΔpK, is therefore given by

$$\mathrm{\Delta }p\mathrm{K}\ln (10)=\pm \frac{q^2}{8\pi {\epsilon }_0{r}_0{k}_{B}T}\left(\frac{1}{{\epsilon }_r}-\frac{1}{{\epsilon }_w}\right)=\pm \left[\frac{1}{2k_{B}T}{\displaystyle {\iiint }_{r>r_0}D\cdot \mathit{EdV}-\frac{q^2}{8\pi {\epsilon }_0{\epsilon }_w{r}_0{k}_{B}T}}\right],$$ (A5)

which corresponds to Eq. (6) in the text. Whereas the last substitution may seem superfluous, in view of Eq. (A3), it is the last equality that enables calculation of how pK values can be expected to change in a nonuniform (scalar) dielectric environment, such as the one being used for the present model. This is how we have proceeded (except for the histidines) to model γB-crystallin’s pK values.

To understand which sign is to be used in Eq. (A5), it is valuable to recognize that for a lower dielectric than water, that is, ε_r < ε_w, the right-hand side of Eq. (A4) is positive, corresponding to the fact that one must do work to bury a charge, of either sign, in a low-dielectric environment. Consider first an acidic residue such as glutamic or aspartic acid. In that case, partially surrounding the charge site with a low-dielectric environment will favor the protonated state, which is uncharged, and therefore a lower concentration of protons (higher pH) will suffice for protonation. Thus, the pK will shift upward and the + sign should be used in Eq. (A5). The opposite is true for basic residues such as lysine, arginine, and histidine, for which a higher concentration of protons will be needed in order to protonate the site.