Abstract
This article reviews the physics and technology of producing large quantities of highly spin-polarized 3He nuclei using spin-exchange (SEOP) and metastability-exchange (MEOP) optical pumping. Both technical developments and deeper understanding of the physical processes involved have led to substantial improvements in the capabilities of both methods. For SEOP, the use of spectrally narrowed lasers and K-Rb mixtures has substantially increased the achievable polarization and polarizing rate. For MEOP nearly lossless compression allows for rapid production of polarized 3He and operation in high magnetic fields has likewise significantly increased the pressure at which this method can be performed, and revealed new phenomena. Both methods have benefitted from development of storage methods that allow for spin-relaxation times of hundreds of hours, and specialized precision methods for polarimetry. SEOP and MEOP are now widely applied for spin-polarized targets, neutron spin filters, magnetic resonance imaging, and precision measurements.
I. INTRODUCTION
A. Overview and roadmap
Gases of nuclear spin-polarized 3He, highly or “hyper”- polarized to close to 100% in quantities on the order of a standard liter, have extensive scientific applications. As a target for nuclear and particle physics with charged particle and photon beams (see Sec. VI), polarized 3He provides a reasonable approximation to a polarized free neutron target. Neutron spin filters (Sec. VII) can polarize neutron beams because of the large spin dependence of the cross section for the absorption of neutrons by 3He. For hyperpolarized magnetic resonance imaging (MRI, Sec.VIII), long relaxation times in vivo due to the chemical inertness of He and the absence of an electric quadrupole moment, along with a large magnetic moment, yield the highest resolution imaging of human air spaces. Relaxation times of hundreds of hours (Sec. IV) make polarized 3He extremely stable and sensitive for precision measurements (Sec. IX).
These applications are enabled by specialized optical pumping methods that polarize large volumes of 3He nuclei to polarizations approaching unity. This review focuses on the significant developments in the theory, practice and applications of these methods in the last two to three decades.
Due to the small hyperfine splitting in the 3He 1s2p state and resulting long hyperfine mixing time relative to the short excited-state lifetime, it is not possible to directly optically pump 3He to a useful polarization level using the 1s2 −1s2p transition, even if the required 58 nm radiation were conveniently available. Hence two indirect optical pumping methods, spin-exchange (SEOP) and metastability-exchange (MEOP), are employed to hyperpolarize 3He nuclei.
In the SEOP method (Sec. II), electronic polarization produced in alkali metal atoms by optical pumping at bar-scale pressures is slowly transferred to 3He nuclei during collisions via the Fermi-contact hyperfine interaction between the alkali electron and the 3He nucleus. The MEOP method (Sec. III) rapidly produces nuclear polarization in metastable 3He atoms at mbar-scale pressures by a combination of optical pumping and hyperfine mixing. The metastable nuclear spin polarization is then rapidly transferred to the ground state population via metastability exchange collisions. Typically the gas is then compressed for use in applications.
Brief overviews of the two techniques are presented in Secs. I.B and I.C, with a comparison of their relative merits in Sec. I.D. Although limited by different issues, the polarizations achievable by each method for applications have remained roughly comparable, with the current achievable time-averaged values between 55% and 85%, depending on conditions. The polarizations and polarizing rates and thus the capabilities for applications have dramatically improved with the advent of new lasers and their continual progress in capability and convenience. In both methods, increased capabilities have led to deeper examinations of their respective physical limits.
For SEOP (Sec. II) the discovery of an unexpected 3He relaxation mechanism proportional to the alkali-metal density has modified our view of the maximum attainable polarization, but the limit is still not completely clear. Motivated by the potential of lower alkali-metal spin relaxation rates, studies of optical pumping with K and “hybrid” K-Rb mixtures have been performed with hybrid K-Rb emerging as the favored approach at this time. With the elucidation of the physical processes that increase the laser power demand, the sophistication of SEOP models has increased but they are still not fully mature and verified.
Major thrusts for MEOP (Sec. III) have been the parallel development of different compression approaches and extensions to high-pressure (~0.1bar), high-field (~1 T) operation. Large scale piston compressors are now used with mbar-scale MEOP to rapidly produce highly polarized gas at pressures of up to several bar. For MRI applications, compact inexpensive peristaltic pumps are being employed that exploit the reduced compression ratio requirements allowed by high pressure, high field MEOP. For MEOP itself, there have been advances in the theory of this complex process. Recent studies of the maximum attainable polarization have revealed a light-induced relaxation mechanism that is particularly important at high pressures.
Spin-relaxation remains a key issue for practical application of polarized 3He (Sec. IV). Despite much technical progress, with relaxation times in the hundreds of hours now quite common, new unexplained aspects of wall relaxation have been observed and the subject remains poorly understood from a fundamental perspective. Extensive work has been done on storage of polarized 3He in glass containers of various types, and with a variety of coatings. Magnetostatic cavities allow long 3He relaxation times to be maintained even in the large magnetic field gradients of neutron scattering experiments. At cryogenic temperatures cesium has been employed to inhibit wall relaxation and superfluid film flow.
Accurate absolute polarization metrology (Sec. V) methods are crucial for target and neutron spin filter applications. Techniques now include water-calibrated NMR, neutron transmission, and magnetometry. Method-specific approaches include alkali-metal electron paramagnetic resonance (EPR) polarimetry for SEOP, and calibrated fluorescence and light absorption polarimetry for MEOP optical pumping cells.
All of these improvements have greatly enhanced applications of polarized 3He. As an example, order-of-magnitude increases in the luminosity of polarized 3He targets for nuclear and particle physics with charged particle and photon beams (Sec.VI) have enabled high precision studies of topics such as nucleon electric and magnetic form factors, spin structure functions, and three-body nuclear physics.
The large spin dependence of the cross section for absorption of neutrons by 3He allows polarization of neutron beams (Sec. VII). Such “neutron spin filters” (NSFs) are being developed worldwide and applications to neutron scattering are growing rapidly. Examples of topics and materials under study include magnetic ordering, magnetic multilayers and magnetic nanoparticles. Applications of NSFs to fundamental neutron physics include studies of neutron beta decay, measurements of parity-violating asymmetries, and measurements of the spin dependence of the neutron-3He scattering length.
A variety of polarized 3He apparatus are being employed for medical studies of human lung airways (Sec. VIII). Although the range of imaging studies with 129Xe is larger because it dissolves in water and fat, the larger magnetic moment and generally higher attainable polarizations for 3He generally makes it the preferred choice for the highest resolution lung images.
Precision spectroscopy on 3He (Sec. IX) has resulted in, for example, new magnetometry methods, searches for violations of fundamental symmetries, and searches for interactions mediated by axion-like particles.
3He has been used for other applications that we will not consider further in this paper. Newbury et al. (1991) studied polarized muonic He by capturing muons on polarized 3He. The macroscopic behavior of spin-polarized 3He fluids is modified at low temperature by polarization of the 3He nuclei (Castaing and Nozieres, 1979; Lhuillier and Laloë, 1979, 1982; Owers-Bradley, 1997). Nonlinear spin dynamics (Akimoto et al., 2000; Desvaux, 2013), and NMR time reversal (Baudin et al., 2008) have been studied in 3He-4He mixtures.
We conclude the review by discussing future trends in Sec. X.
B. Overview of SEOP physics and apparatus
In the SEOP method, electronic polarization produced in alkali metal atoms by optical pumping is slowly transferred to 3He nuclei during collisions via the Fermi-contact hyperfine interaction between the alkali electron and the 3He nucleus (Bouchiat et al., 1960; Walker and Happer, 1997). 3He gas at typical pressures between 1 bar and 10 bar1 is contained in sealed glass cells along with on the order of 0.1 g of alkali-metal, usually rubidium or a rubidium-potassium mixture. Pure Rb or K-Rb cells are typically heated to 170 °C or 220 °C, respectively, to establish an alkali-metal density around 3 × 1014 cm−3. Due to the short diffusion length of the alkali-metal atoms, the entire volume of the cell must be immersed in circularly polarized laser light, typically provided by diode laser arrays with output power on the order of 100 W, an air wavelength of 794.7 nm and a typical linewidth of 0.25 nm. A number of factors such as absorption by optically thick alkali-metal vapor, focusing and/or distortion of the laser light by non-uniform blown glass cells, and in some cases poor spatial mode quality make it difficult to realize the goal of uniform optical pumping rate at all points in the cell, which can be partially addressed by pumping from opposing directions (Chann et al., 2003; Chen et al., 2014a). The absorption width of the Rb vapor is determined by pressure broadening of 0.038 nm/bar (Kluttz et al., 2013; Romalis et al., 1997), so the atomic pressure broadened width is comparable to the laser linewidth for high density (10 amg2) targets but substantially smaller than the laser linewidth for typical neutron spin filters (1.5 amg). The degree of the circular polarization (99% or better is usually attained with commercial wave plates) is not highly critical because the relatively high alkali-metal density strongly absorbs the undesired photon spin state (Bhaskar et al., 1979; Chann et al., 2002b). To suppress radiation trapping from radiative decay of the excited alkali-metal atoms, on the order of 0.1 amg of nitrogen gas is added to provide rapid collisional de-excitation (Lancor and Walker, 2010; Walker and Happer, 1997).
The alkali-metal polarization PA is determined by the ratio of the electronic spin relaxation rate to the optical pumping rate. Rubidium spin relaxation rates are typically a few hundred s−1 whereas optical pumping rates are much higher, hence PA near unity is established on a very short time scale. The temperature must be maintained at a low enough value so that absorption of the laser light by the optically thick alkali-metal vapor does not yield too low an optical pumping rate in the interior of the cell. Alkali-metal spin relaxation results primarily from alkali-alkali collisions (dominant at low 3He gas pressures) and alkali-3He collisions (dominant for high 3He gas pressures), with some contribution from alkali-nitrogen collisions (Ben-Amar Baranga et al., 1998). For the same spin-exchange rate, the spin relaxation for potassium is typically about five times lower than that of rubidium, hence the use of K-Rb mixtures or pure K increases the efficiency of SEOP (Babcock et al., 2003). In practice K-Rb mixtures are typically employed because of greater laser availability at 795 nm for Rb pumping as compared to K pumping at 770 nm (Chen et al., 2007b).
The 3He polarization is determined by the ratio of 3He nuclear spin relaxation to the spin-exchange rate. The spin-exchange rate is typically on the order of 0.1 h−1, hence a day is required to approach the maximum polarization. This slow time scale makes long 3He relaxation times critical. Sealed cells made from fully blown aluminosilicate glass are typically employed for charged particle and photon scattering and neutron spin filters, whereas borosilicate glass and/or open systems are more common for polarized gas MRI and other applications. Aluminosilicate glass has low 3He permeability and is alkali-metal resistant, and for neutron applications GE1803 is particularly desirable because it is boron-free. The use of fully blown glass (Chen et al., 2011; Newbury et al., 1993) and the presence of the alkali-metal (Heil et al., 1995) are both important for achieving the longest relaxation times. 3He cells with room temperature relaxation times on the order of 100 h or longer (Chen et al., 2011) obstensibly make wall relaxation a minor contributor to limiting 3He polarization, but a strongly temperature-dependent relaxation mechanism has been found to limit the achievable 3He polarization (Babcock et al., 2006). For poorer cells, short wall relaxation times can in principle be overcome by increasing the alkali density (and using hybrid pumping) and thus increasing the spin-exchange rate, but this is only possible to the extent that sufficient laser power is available.
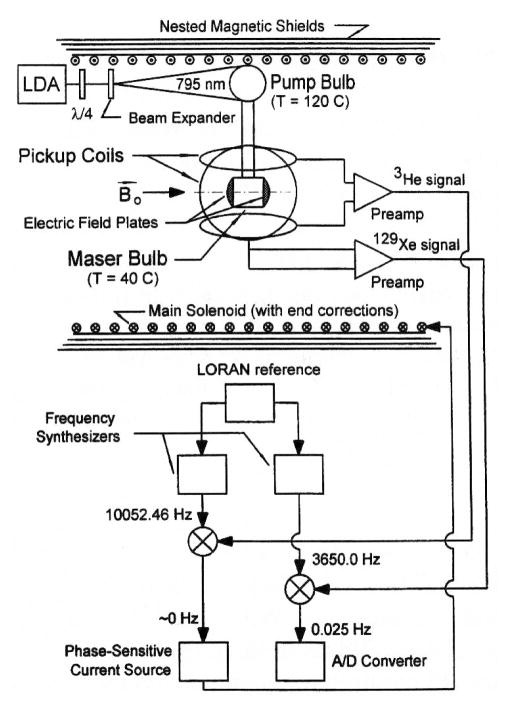
A typical SEOP apparatus (Fig. 1) consists of a non-magnetic oven to heat a 3He cell, a uniform magnetic field provided by Helmholtz coils, and a spectrally-narrowed high-power diode array laser with suitable optics for producing circular polarization and focusing and steering the laser beam. Hot air is typically used for heating but non-magnetic electrical heating has also been employed (Babcock et al., 2016; Tong et al., 2010). Although Helmholtz coils are the most common, four-coil systems, compensated solenoids, and magnetostatic cavities have also been used. Diode laser bars are spectrally narrowed with diffraction gratings (Babcock et al., 2005a) or volume holographic gratings (VHGs) (Chen et al., 2014b; Liu et al., 2015; Nikolaou et al., 2013). 3He polarization is monitored using either adiabatic fast passage (AFP) or free induction decay (FID) NMR. AFP typically requires a pair of drive coils large enough to immerse the cell in a reasonably uniform radiofrequency (RF) field and pickup coil(s) to detect the precessing magnetization. FID can also be performed in this scheme but more often a small surface coil that both transmits a short RF pulse and detects the small precessing transverse magnetization is employed. SEOP apparatus may also employ other diagnostics such as EPR (Romalis and Cates, 1998), Faraday rotation (Vliegen et al., 2001), and transmission spectrum monitoring with a small diffraction grating spectrometer. Other characteristics of SEOP apparatus are discussed under individual applications.
FIG. 1.
An example of an apparatus for spin-exchange optical pumping (SEOP). This apparatus has been employed for photon scattering experiments. Whereas SEOP is typically performed in single cells for neutron spin-filter and magnetic resonance imaging applications, both electron and photon scattering applications employ a double cell configuration in which a target cell (TC) is linked to an optical pumping cell (OPC) through a connecting tube. Electron paramagnetic resonance and nuclear magnetic resonance are employed to measure the 3He polarization in the OPC and TC, respectively. Adapted from Ye et al. (2010)
C. Overview of MEOP physics and apparatus
In the MEOP method, nuclear polarization is produced in metastable 3He atoms by a combination of optical pumping and hyperfine mixing, and then rapidly transferred to the ground state population via metastability exchange collisions (Batz et al., 2011; Colegrove et al., 1963). Traditional low-field MEOP is performed in pure 3He or 3He - 4He mixtures (Stoltz et al., 1996a) at pressures on the order of 1 mbar, whereas high-field MEOP has been performed at pressures up to a few hundred millibar (Nikiel-Osuchowska et al., 2013). An electrical discharge produced by external electrodes is employed to produce metastable densities on the order of 1010 cm−3. Low gas-phase impurity levels are required because metastable atoms have 20 eV of energy, which is sufficient to ionize most common impurities, resulting in destruction of the metastable atoms. In practice, highly pure source gas and baked and discharge-cleaned glass walls are required to achieve an adequate high metastable density. A hand-held spectrometer provides a simple and convenient method to evaluate the purity of the 3He gas, since the light emitted from an MEOP cell should not show broadband background and/or impurity emission lines.
Due to the relatively low metastable density the gas is optically thin, hence long cells can be employed to absorb more laser light and thus yield larger quantities of hyperpolarized gas. However, due to the weak absorption, the degree of circular polarization is more critical than for SEOP. The spatial profile of the light somewhat underfills the pumping cell, approximately matching the metastable density profile that vanishes at the cell walls. Radiation trapping is not a major issue since the diameter of the cells are typically less than ≈7 cm to avoid this consideration. Optical pumping is typically performed with Yb fiber lasers with output power on the order of 10 W, an air wavelength of 1083 nm, and a typical linewidth of 2 GHz to match the Doppler-broadened absorption width. The polarizations of the ground state and metastable populations are strongly coupled (Nacher and Leduc, 1985) and evolve together on typical time scales of seconds to minutes, depending on the cell size and laser power (Gentile and McKeown, 1993). The 3He ground state relaxation time is generally dominated by the discharge and ranges from a fraction of a minute to several minutes. Stronger discharges yield higher metastable densities and thus higher polarizing rates, but also increased relaxation. In many applications the polarized gas is compressed to obtain pressures of between 1 bar and 4 bar at polarizing rates of the order of 1 amg-L/h, with a typical time scale of a few hours or less to fill a cell (Batz et al., 2005; Lelievre-Berna, 2007). Storage cells are typically made of fused quartz or aluminosilicate glass and coated with alkali-metal (usually cesium) to reduce relaxation (Heil et al., 1995).
A typical MEOP apparatus (Fig. 2) consists of a radio-frequency discharge, a uniform magnetic field provided by a set of coils or solenoid, and a Yb fiber laser with suitable optics for producing circular polarization and focusing and steering the laser beam (Andersen et al., 2005). Although Helmholtz coils are common, multiple-coil systems are also used, in particular for large compression apparatus. In the optical pumping cell, 3He polarization is monitored by measuring the degree of circular polarization from the 668 nm 3He emission line or absorption of a probe laser at the pumping wavelength. Compression apparatus range from large-scale piston compressors for a range of applications to small-scale peristaltic pumps typically employed for polarized gas MRI (Nacher et al., 1999; Nikiel et al., 2007). In these small-scale systems high-field pumping in the bore of the MRI magnet can be employed. After compression, either AFP or FID NMR is used. Other characteristics of MEOP apparatus are discussed under individual applications.
FIG. 2.
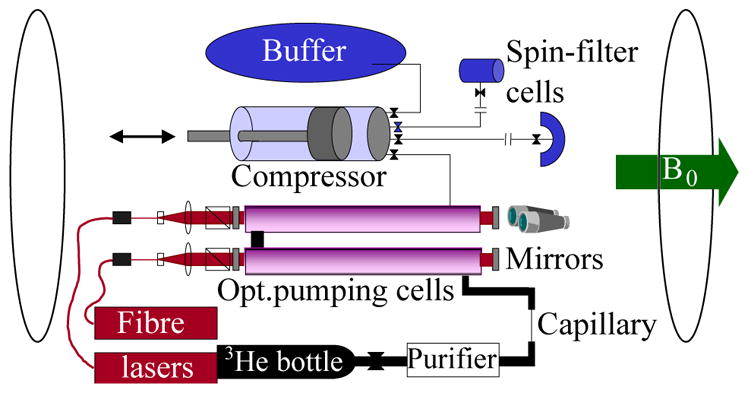
An example of an apparatus for metastability exchange optical pumping, adapted from Andersen et al. (2005). This apparatus has been employed for compressing gas into neutron spin filter cells. Nine 2 m diameter coils provide the uniform magnetic field for the 2.3 m long optical pumping cells (OPC). 3He gas is purified, polarized in the OPCs, compressed in two stages with an intermediate buffer cell, and dispensed into detachable neutron spin filter cells. The capillary serves to control the flow rate and restrict diffusion for the typical 1 mbar pressure in the OPCs.
D. SEOP/MEOP compare and contrast
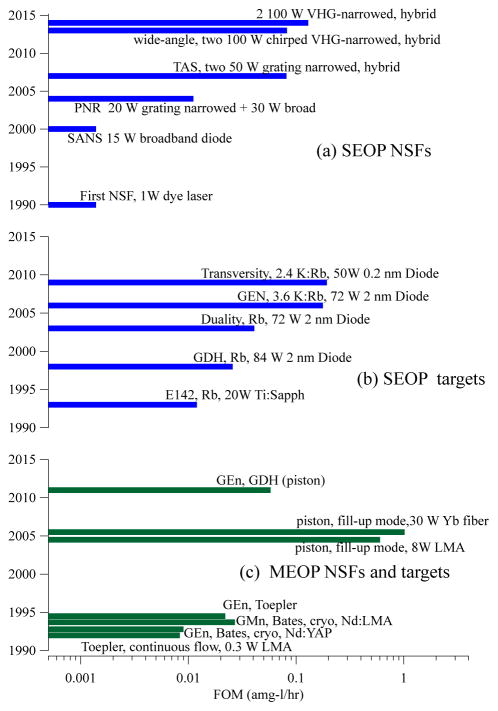
Although SEOP and MEOP address the problem of polarizing 3He nuclei quite differently, the needs of applications are met by both methods, with comparable practical results. Figure 3 shows representative performance of the two methods as the advances discussed in this review occurred.
FIG. 3.
Development of neutron spin filters (NSFs) and spin-polarized 3He targets, illustrated by representative devices and experiments. In each case, key parameters are listed to show how advances for each method improved performance, e.g. spectrally narrowed lasers and K-Rb mixtures for spin-exchange optical pumping (SEOP), and filling of cells with piston compressors and high power laser sources for metastability exchange optical pumping (MEOP). See Secs. VI and VII for definitions of identifiers in this plot. The FOM is defined to be for SEOP NSFs and targets, and MEOP cryogenic targets, where PHe is the 3He polarization, N is the total number of atoms in the cell in units of amg-L, and τ is the time constant for polarizing the cell. (Reminder: to reach 90% of the maximum polarization requires 2.3 time constants.) For compression-based MEOP NSFs and targets, τ is replaced by T, where T is the time to refresh the gas for continuous flow or the time between cell exchange for remotely operated compression. (a) SEOP NSFs: First NSF (Coulter et al., 1990)), SANS (Gentile et al., 2000; Jones et al., 2000), PNR (Chen et al., 2004), TAS (Chen et al., 2007a), wide-angle (Ye et al., 2013), and VHG-narrowed (Chen et al., 2014a). (b) SEOP targets for electron-scattering experiments. Here the FOM is equivalent to the potential effective luminosity of Singh et al. (2015). Data provided by J. Singh. E142 (Anthony et al., 1993), GDH (Amarian et al., 2002), GEN (Riordan et al., 2010), Duality (Solvignon et al., 2008), Transversity (Qian et al., 2011) (c) MEOP NSFs and targets. GEn (Bates, cryogenic, Nd:YAP) (Jones et al., 1993), GMn (Bates, cryogenic, Nd:LMA) (Gao et al., 1994), GEn (Toepler pump) (Meyerhoff et al., 1994), GEn, GDH (piston) (Krimmer et al., 2011, 2009; Schlimme et al., 2013), (Toepler pump) (Eckert et al., 1992), piston fill-up mode (Batz et al., 2005).
The key feature of SEOP is the ability to polarize 3He directly at a wide range of pressures (typically between 0.5 bar and 13 bar), which is required for most applications. In contrast MEOP is typically performed at pressures of order 1 mbar, thus requiring polarization preserving compression. The key feature of MEOP is the ability to produce polarized 3He at rates of a few amg-L/h (Batz et al., 2005), typically an order of magnitude faster than most SEOP apparatus. Most applications have been approached by both methods, but in some cases one may be preferred, e.g. dual species masers, in which both 3He and 129Xe can be simultaneously polarized by SEOP, and internal targets, for which the low operating pressure and high polarizing rate are well-matched to MEOP.
A comparison of the key parameters of each method reveals how their practical performance is comparable. MEOP starts off with a rate constant nearly nine orders of magnitude higher than SEOP, primarily because of the inherent weakness of the spin-exchange cross section between alkali-metal atoms and 3He nuclei as compared to the nearly gas-kinetic cross section for metastability exchange. However, this advantage is dramatically reduced because the typical alkali-metal density is about four orders of magnitude higher than the typical metastable density thus resulting in a difference of nearly five orders of magnitude in the polarizing time constant, e.g. 15 h for pure Rb SEOP and 1 s for low-field MEOP. SEOP is performed at pressures 103 to 104 times higher than low-field MEOP, hence overall the polarizing rate for MEOP is about an order of magnitude faster than SEOP (see Fig. 3). The operational approach of each method reflects exploitation of their respective strengths: SEOP is slow but compact and can operate unattended, hence one operates continuously on charged particle beam lines and/or makes use of overnight operation with multiple polarizing stations to remotely polarize cells for neutron beam lines. MEOP is fast but compression requires greater attention and the speed is maximized with large optical pumping volumes, hence one operates with replaceable cells that are rapidly filled with polarized gas by a remote compressor.
In recent years the limitations of each method are being addressed by new methods. More compact piston compression apparatus have been developed (Beecham et al., 2011; Kraft et al., 2014; Mrozik et al., 2011) and for MRI applications MEOP has been extended to optical pumping pressures up to hundreds of millibar at high magnetic fields (Nikiel-Osuchowska et al., 2013). The use of K-Rb mixtures has increased the polarizing rate for SEOP (Chen et al., 2007b; Singh et al., 2015) and large scale production of polarized 3He via SEOP is under development (Hersman et al., 2013).
II. SPIN-EXCHANGE OPTICAL PUMPING
Spin-exchange optical pumping of 3He was pioneered by Bouchiat et al. (1960) using lamps. With some exceptions (Fitzsimmons et al., 1969; Gamblin and Carver, 1965; Grover, 1978) the topic was largely ignored until the proposal and initial demonstration of Chupp et al. (1987) for producing high density polarized targets using SEOP with tunable lasers. Subsequent experimental developments are described in detail throughout this review. Basic descriptions of SEOP physics (Chupp et al., 1987; Wagshul and Chupp, 1994; Walker and Happer, 1997) have been presented previously, as well as much more detailed discussions (Appelt et al., 1998; Happer et al., 2009). In this section we present the current understanding of SEOP physics, with particular emphasis on new understanding obtained since the RMP Colloquium of 1997 (Walker and Happer, 1997).
A. Spin-exchange collisions
Spin-exchange optical pumping of 3He transfers spin-polarization between alkali-metal electron spins (A) and 3He nuclear spins during binary collisions:
| (1) |
The dominant interactions experienced during A-He collisions are
| (2) |
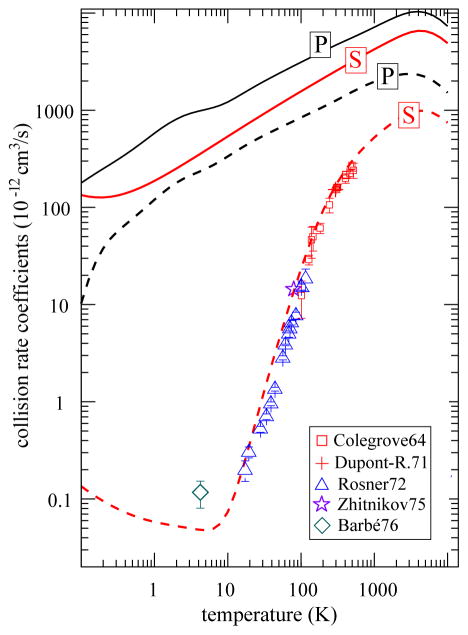
where V0(ξ) is the spin-independent interaction potential between the two atoms separated by ξ and α(ξ) is the strength of the Fermi-contact hyperfine interaction between the alkali electron spin S and the 3He nuclear spin IHe. Recent theoretical calculations (Partridge et al., 2001; Tscherbul et al., 2011) of these for K-3He are shown in Fig. 4. The extremely weak attractive portion of V0, supporting at most one bound state, (Kleinekathöfer et al., 1999) is imperceptible on the scale of typical thermal collision energies so that the dominant spin-transfer occurs at the inner turning points of binary collisions. The spin-rotation interaction γ(ξ)N ·S, which couples the electron spin to the rotational angular momentum N of the alkali-metal-He pair, is a major source of angular momentum loss in the system and governs the maximum possible efficiency with which spin exchange can occur.
FIG. 4.

Calculated spin-independent (V0(ξ)) (Partridge et al., 2001) and Fermi-contact (α(ξ)) (Tscherbul et al., 2011) potentials for K-3He molecules, as a function of interatomic separation ξ in atomic units.
The curves of Fig. 4 can be used with time-dependent perturbation theory to estimate the spin-exchange rate coefficient, kSE ≈ vσ(ατ/ħ)2, to be within a factor of two or so of the measured spin-exchange rate coefficients, around 6 ×10−20 cm3/s. Here vσ is the gas-kinetic rate coefficient and τ the collision time. The probability of spin-exchange during a single collision, (ατ/ħ)2, is on the order of 10−10. With alkali-metal densities [A]in the range of 1014 −1015 cm−3, this implies a spin-exchange time constant (kSE[A])−1 of 5–50 hours. These numbers illustrate why the technical development of storage containers with 3He lifetimes of hundreds of hours (Sec. IV) is vital to attaining polarizations that approach unity.
The 3He polarization dynamics due to spin exchange and other sources of relaxation (rate Γw, usually dominated by wall collisions) can under most conditions be accurately modeled as
| (3) |
where the alkali-metal electron polarization PA, due to its sub-second relaxation times, is essentially constant compared to the hour-scale variations of PHe. Thus the noble gas polarization builds up to a steady-state value
| (4) |
with a time constant τ obeying
| (5) |
This latter relation seems to imply a simple method for measuring kSE, namely measure the time constant as a function of the alkali density [A]. This method does not work, however, since for reasons not yet understood the wall relaxation rate Γw in spin-exchange cells is observed to increase rapidly with temperature. This issue is discussed in detail in Sec. II.E.2.
1. Measurements of spin-exchange collision rates
Several wall-independent methods have been used to determine kSE for different species. The repolarization method (Ben-Amar Baranga et al., 1998; Chann et al., 2002a) measures the alkali polarization produced by spin-exchange in the absence of optical pumping,
| (6) |
where ΓA is the measured alkali spin-relaxation rate. The rate balance method (Chann et al., 2002a) measures PHe∞, τ, PA, and the alkali density to deduce kSE from Eq. (4). A combination of these two methods, measuring the time rate of change of the repolarization signal, was used by Borel et al. (2003). For alkali atoms with small ΓA, the spin-exchange rate can also be deduced by measuring the difference between ΓA for 3He and for 4He, with a correction for the reduced-mass scaling of the spin-relaxation contribution (Walker et al., 2010). Most recently, Singh et al. (2015) used absolute alkali polarimetry and density measurements, combined with the initial slope from Eq. (3), to infer kSE. Table I shows the status of wall-independent spin-exchange rate coefficient measurements for the various alkali-metal atoms. For potassium, the recent result of Singh et al. (2015) is 30 % higher than the weighted average of three prior measurements. They speculated that this difference may be due to their operation at substantially higher temperature, but the origin of the disagreement has not been established.
TABLE I.
Spin-exchange rate coefficient(kSE) measurements, in units of 10−20 cm3/s, using wall-independent methods; EPR frequency shift enhancement factors κ0 and dκ0/dT (units K−1; see Sec. II.F). Throughout this paper, numbers in parentheses represent the uncertainty in the last digit(s).
| Na | K | Rb | |
|---|---|---|---|
|
| |||
| 6.1(4)a | |||
| kSE | 6.1(6)b | 5.5(2)c | 6.7(6)d |
| 6.1(7)e | 6.8(2)f | ||
| 7.5(5)g | |||
|
| |||
| κ0 | 4.72(09)h | 6.01(11)i | 6.15(09)j |
|
| |||
| dκ0/dT | 0.00914(56)k | 0.0086(20)l | 0.00934(14)m |
| 0.00916(26)n | |||
(Babcock et al., 2005b), 200 °C
(Babcock et al., 2005b), 200 °C
(Romalis and Cates, 1998), 175°C
(Babcock et al., 2005b), 210–350°C
(Babcock et al., 2005b), 150–220°C
(Romalis and Cates, 1998), 110–172 °C
(Babcock et al., 2005b), 170–350°C
2. Spin-exchange efficiency
Despite the very slow time constants associated with spin-exchange pumping of 3He, the efficiency of transfer of angular momentum from the photons in the optical pumping light to the nuclei can, under ideal conditions, be surprisingly high. If fully polarized alkali metal atoms are assumed not to scatter optical pumping light (an assumption to be examined in Sec. II.B.3), the loss of angular momentum by [A]V polarized alkali metal atoms in volume V occurs at a rate [A]V ΓAPA. Comparing this to the rate V[He]dPHe/dt at which angular momentum is added to the noble-gas nuclei, gives the collisional efficiency
| (7) |
The collisional efficiency is maximum at low He polarizations, then decreases at higher polarizations as significant amounts of angular momentum are returned to the alkali metal atoms via spin-exchange collisions from the polarized He nuclei. Direct measurements of the efficiency (Ben-Amar Baranga et al., 1998) were made using Eq. (6) rewritten as . Variations from atom to atom in ΓA are the primary determining factor in the efficiency.
There are many contributing processes to the alkali spin-relaxation rate ΓA (Sec. II.B.2), but at a given [He] the minimum relaxation rate is ΓA = (kSR + kSE)[He], where kSR is the rate coefficient for relaxation due to the spin-rotation interaction. Thus when relaxation due to He atoms dominates the alkali-metal spin-relaxation, the spin-exchange limited efficiency is
| (8) |
Measurements of the spin-exchange efficiency for Rb and K (Ben-Amar Baranga et al., 1998), shown in Fig. 5, obtained ηSE ~ 1/50 and 1/6 under typical conditions. For Na the spin-exchange efficiency is consistent with 1 (Borel et al., 2003). The unmeasured Cs spin-exchange efficiency is predicted to be about 7 times lower than Rb using estimates from Happer et al. (2009).
FIG. 5.
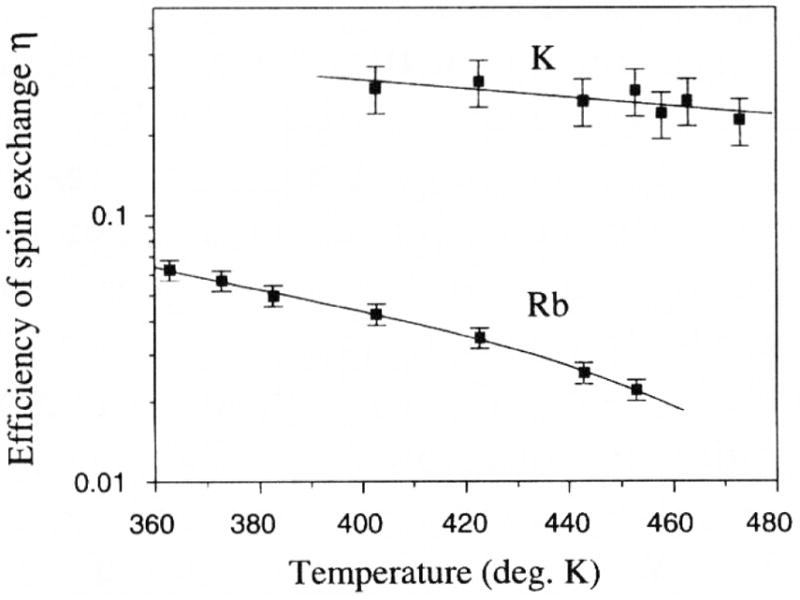
Spin-exchange efficiency (ηSE) measurement for K and Rb, from Ben-Amar Baranga et al. (1998).
B. Optical pumping
In order to produce substantial quantities of highly polarized 3He by SEOP, it is necessary to spin polarize large volumes of high density alkali-metal vapor interacting with 3He gas at densities ranging from 0.5 amg for neutron spin filters to 10 amg for targets. The optical pumping is typically done using 100 W scale lasers whose spectral line widths are comparable to or broader than the atomic lines. These extreme conditions raise a number of issues that are typically not encountered in other optical pumping contexts4. The breakdown of free-atom light selection rules, light propagation and spectral evolution in optically thick conditions, and dissipation of heat are examples of issues that are key to understanding the SEOP process. These and other effects are discussed in this section.
1. High pressure optical pumping
Figure 6 shows the energy levels and photon absorption rates relevant for optical pumping of alkali-metal atoms in the S1/2 ground state using circularly polarized light tuned to the P1/2 “D1” resonance. In the presence of He atoms, there is collisional mixing of the P1/2 and P3/2 levels, so that the P1/2 level acquires some P3/2 character, indicated by the dashed Zeeman sublevels in the figure. The relative absorption probability, parameterized by P∞, for atoms in the mS =−1/2 Zeeman sublevel is 1 + P∞, much greater for atoms than the relative absorption probability 1 −P∞ for those in the mS = 1/2 sublevel. Thus atoms in the −1/2 sublevel are selectively excited by the light. The excited atoms experience rapid spin-relaxation in collisions with the He and N2 buffer gases, randomizing populations among the P1/2 and, to a significant extent, P3/2 sublevels. Quenching collisions with N2 molecules then resonantly transfer the P-state energy to excited N2 vibrational levels, returning the alkali atoms to the ground S1/2 state. Atoms that return to the mS =1/2 state only rarely absorb the polarized light, while those that return to mS = −1/2 will be efficiently re-excited. In this manner atoms will preferentially populate the mS =1/2 state, reaching a steady-state population of P∞ (Lancor et al., 2010a).
FIG. 6.
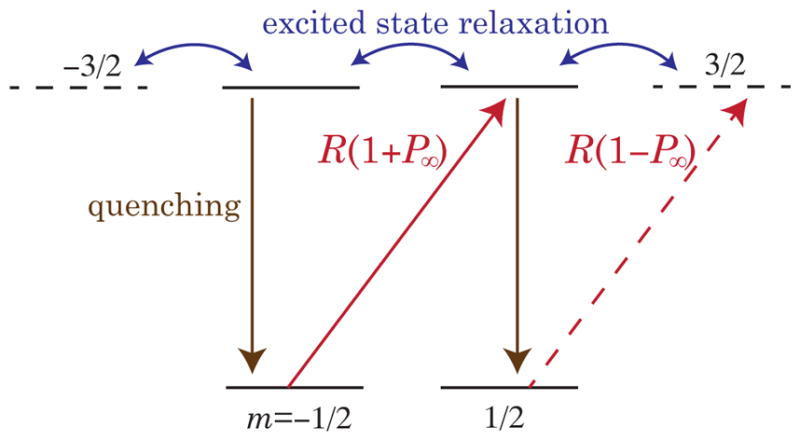
Key elements of the optical pumping cycle for light tuned to the alkali metal S1/2—P1/2 resonance in the presence of high pressure He gas. Collisions with the He atoms mix the P1/2 and P3/2 levels, altering the selection rules for light absorption. Atoms in the ms = ±1/2 Zeeman ground-state sublevels absorb photons with relative probabilities 1ŦP∞. Once excited, rapid collisional spin-relaxation occurs. Quenching collisions with N2 molecules randomly repopulates the ground-state sublevels. The atoms accumulate in the mS = 1/2 sublevel, acquiring a steady-state spin-polarization of P∞ in the absence of ground-state spin-relaxation.
Rapid quenching of the excited atoms by N2 molecules plays an essential role in this process (Lancor and Walker, 2010). Since SEOP typically takes place in extremely optically thick cells, the reabsorption probability for photons emitted by the excited alkali atoms can be considered to be nearly unity. Since such photons constitute an essentially unpolarized background of resonant light, they act as a relaxation mechanism and decrease the efficiency of optical pumping.
In the limit of large pressure broadening and short excited-state quenching times, the alkali-metal nuclear spin IA can be considered to be conserved in the optical pumping cycle, an excellent approximation for SEOP in the 5 to 10 amg He density range. At lower densities, however, as the electrons are rapidly relaxed in the excited state, hyperfine coupling with the nuclei causes some nuclear spin-relaxation, reducing the optical pumping efficiency and requiring more photons per atom to reach full polarization (Lancor and Walker, 2010).
Under the high alkali density conditions of SEOP, spin-exchange collisions between the alkali metal atoms are by far the dominant spin-dependent collision process. Since alkali-metal spin-exchange collisions conserve total angular momentum, they mainly serve, in concert with the hyperfine coupling between the nuclei and electrons, to reach a spin-temperature equilibrium where the fraction of atoms in any total angular momentum state F,mF is ρ(F,mF) ∝ eβmF (Anderson et al., 1959; Appelt et al., 1998; Happer, 1972). The spin-temperature parameter β is related to the alkali-metal electron spin-polarization by PA =tanh(β/2), and either of these numbers (β, PA) is sufficient to completely describe the states of the alkali-metal spins. It is often convenient to account for the alkali-metal nuclei by the “slowing-down factor” q = 〈Fz〉/〈Sz〉 which is approximately 2IA +1 (isotopic average of 5.4 for Rb) under the usual high polarization conditions of SEOP (Appelt et al., 1998). Sometime it is useful to note that, at small magnetic fields where F is a good quantum number, the electron spin-polarization arises solely from the populations of the two states F = IA +1/2, mF = ±(IA +1/2), i.e. PA =ρ(F,F)−ρ(F,−F).
Since the rapid alkali-alkali spin-exchange collisions keep the electronic and nuclear spins in spin-temperature equilibrium, regardless of the collision mechanism we can write the optical pumping process using conservation of angular momentum:
| (9) |
where ΓA is an effective electron spin-relaxation rate and R(r)is the local photon absorption rate (Fig. 6) for unpolarized atoms at position r in the cell. The local steady-state polarization in the bulk of the cell is therefore
| (10) |
The photon scattering rate is
| (11) |
The first term is the scattering rate required to make up for spin-relaxation collisions, while the second term represents the scattering rate from a maximally polarized atom and would be zero for idealized D1 pumping (Happer et al., 2009; Happer and Van Wijngaarden, 1987; Lancor et al., 2010a).
2. Alkali spin relaxation
There are many collision processes that can relax the alkali-metal spin polarization in SEOP cells. We have already mentioned (Secs II.A, II.A.2) the relaxation due to the spin-rotation interaction VγN =γ(ξ)S·N that couples the electron spin to the rotational angular momentum N of a colliding alkali-He pair at distance ξ (Walker et al., 1997). VγN arises from spin-orbit interactions induced by s-p mixing during collisions, and is therefore proportional to the spin-orbit splitting in the alkali excited state. This is a primary motivation for using K, with its smaller fine-structure interaction, over Rb as a preferred spin-exchange partner. This collision process has a strong T4 temperature dependence (Ben-Amar Baranga et al., 1998). Analogous interactions are presumably responsible for relaxation in alkali-N2 collisions.
Also of practical importance is the small non-conservation of spin angular momentum in alkali-metal-alkali-metal interactions. This relaxation arises from the spin-axis interaction VSS = 2λ(ξ)S ·(ξ̂ξ̂ −1/3)·S, with about 1/2 of the relaxation coming from binary collisions (Kadlecek et al., 2001b) and 1/2 from formation of triplet molecules (Erickson et al., 2000; Kadlecek et al., 1998). The molecular contribution can be isolated by magnetic decoupling with 0.1 T-scale magnetic fields, and has a surprising and as yet unexplained persistence at high He pressures. The low-field rate coefficients are 1.0 × 10−18 cm3/s for K-K collisions and 9.3 × 10−18 cm3/s for Rb-Rb. Again, the smaller rate for K relaxation makes it attractive for 3He SEOP. At very low pressures, a few tens of mbar, relaxation from Rb2 singlet molecules becomes important (Kadlecek et al., 2001a); this is a minor contribution for most SEOP situations but has a similar pressure dependence to diffusion and care has to be taken to account for both in relaxation experiments.
Spin-relaxation rates and optical pumping rates are generally much larger than the characteristic diffusion rates of the alkali atoms to the cell walls. Thus throughout most of the cell the alkali polarization varies slowly (cm length scales) as the pumping light is attenuated during propagation through the cell. Near the cell walls, however, there is a thin “diffusion layer” of unpolarized atoms. The alkali polarization is nearly zero at the walls, so to a good approximation the polarization at a distance z from the wall is modified from Eq. (10) to PA(r)(1 −exp(−z/Λ)), where the diffusion layer length scale is approximately at the entrance to the cell (Appelt et al., 1998; Wagshul and Chupp, 1994; Walker and Happer, 1997). At 3 amg, D ≈ 0.15 cm2/s (Nelson and Walker, 2001), and assuming R = 100ΓA = 40000 s−1 gives Λ ~ 60 μm.
3. Light propagation and circular dichroism
As already noted, the slow spin-exchange rates for SEOP require optical pumping of high density alkali-metal vapors. For unpolarized atoms, the optical depth OD0 is typically of order 100, i.e. the transmission of light through the cell is e−100. For uniformly polarized atoms, the optical depth of circularly polarized light is OD =OD0(1 −PAP∞). Thus the light can only significantly penetrate the cell if 1 −PAP∞ ≪1, so the atoms must be polarized to nearly 100% (PA ~1) and they must become transparent when maximally polarized (P∞ ~1). These conditions are only met for pumping light tuned to the P1/2 D1 resonance.
Under the high density conditions of SEOP, absorption of light during alkali-metal-He (or N2) collisions does not obey the selection rules for isolated atoms (Lancor et al., 2010a,b). This is because the fine-structure states are mixed during collisions with He atoms, as illustrated in Fig. 7. The normal D1 atomic selection rules are slightly violated, allowing absorption of circularly polarized light by fully polarized atoms. Thus in the presence of He gas the alkali atoms do not become fully spin-polarized in the limit of high pumping rates; they instead acquire a maximum polarization P∞ <1.
FIG. 7.
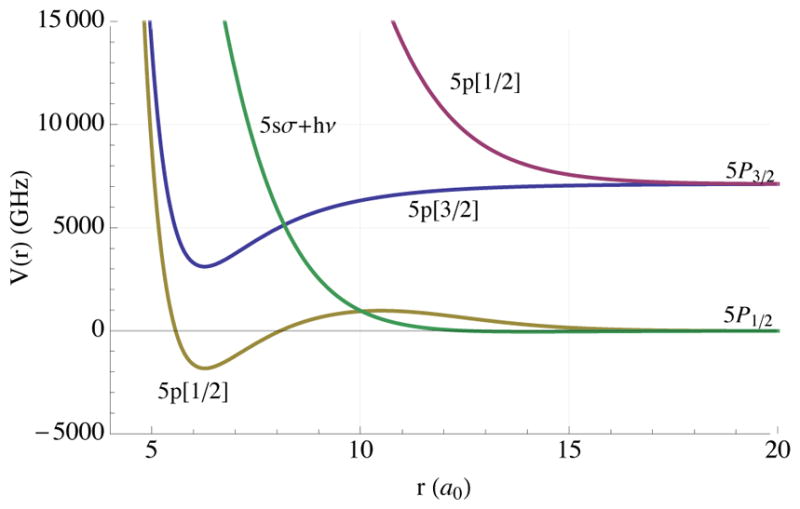
Energy levels of RbHe molecules in the presence of optical pumping light (Lancor et al., 2010a; Pascale, 1983). The green curve, the ground state potential energy plus 1 photon, crosses 2 excited-state potentials at two different interatomic separations. The 5p[M = 3/2] curve is of purely P3/2 nature while the 5p[1/2] is of mixed P1/2-P3/2 character. The projection of the electronic angular momentum along the interatomic axis is M. For both crossings the colliding atom pair can absorb the circularly polarized optical pumping light even when each is fully spin-polarized. From Lancor et al. (2010a).
Figure 8 shows measurements of the circular dichroism P∞ of maximally polarized Rb atoms in the presence of 3He gas (Lancor et al., 2010a,b). While the dichroism peaks at very close to 1 right on resonance, at only 1 nm (475 GHz) detuning from the line center, the dichroism has already dropped to 0.9. The strong reduction of the circular dichroism for off-resonant pumping implies that narrowband lasers will not only yield more efficient optical pumping, but also higher maximum polarization.
FIG. 8.
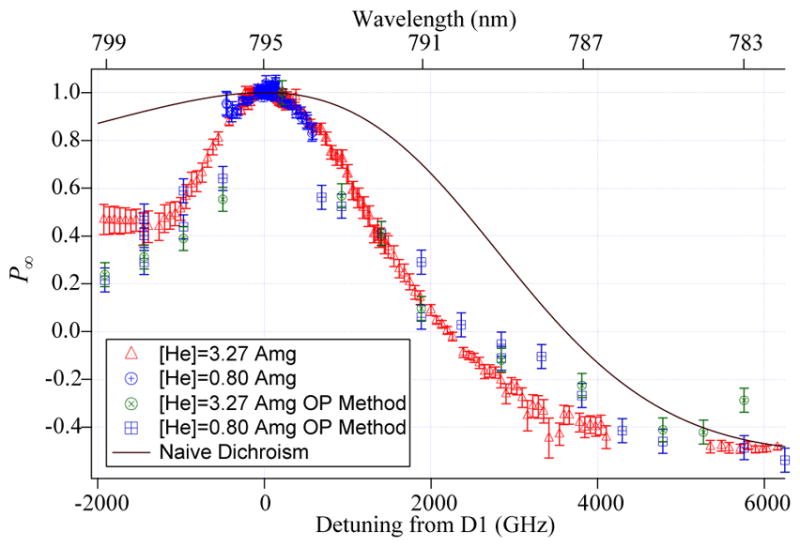
Circular dichroism of Rb atoms in the presence of He gas. Near the D1 line, the dichroism approaches 1, reaching −1/2 for the D2 line. The solid line shows the dichroism neglecting He collisions. The very significant reduction near the D1 line is responsible for excess photon absorption under SEOP conditions. Adapted from Lancor et al. (2010a).
For narrowband pumping in the bulk of the cell, the photon flux density I(r) (cm−2s−1) obeys (suppressing from now on the implied spatial dependence of I, PA, and 𝒜)
| (12) |
where the pumping rate and the photon flux density are related, R = σI, by the optical absorption cross section σ for unpolarized atoms. For pumping by resonant, narrowband light the first term, which leads to a linear decay (Bhaskar et al., 1979; Walker and Happer, 1997), dominates. The light is attenuated purely to compensate for loss of angular momentum in ground state collisions. The transparency of nearly fully polarized atoms allows the light to be only weakly attenuated despite the great optical thickness of SEOP cells.
When there are significant off-resonant light components, however, the second term becomes important. For high optical pumping rates, PA ≈P∞, and Eq. (12) leads to exponential attenuation of the flux density in the usual fashion, . The absorption length of the light is increased by over what it would be for unpolarized atoms, but can still be smaller than the cell length when P∞ deviates from 1.
The excess photon scattering due to the circular dichroism effect is exacerbated by pumping with unnarrowed diode array bars with linewidths on the order of 2 nm (1000 GHz). One can define a photon efficiency analogous to the ideal spin-exchange efficiency of Eq. (7), namely the ratio of the rate of production of polarized 3He to the photon scattering rate:
| (13) |
For ideal circular dichroism, P∞ =1, ηγ =ηSE. At high optical pumping rates, which can be much less than ηSE. Measured photon efficiencies for pumping with a particularly poor laser are shown in Fig. 9.
FIG. 9.
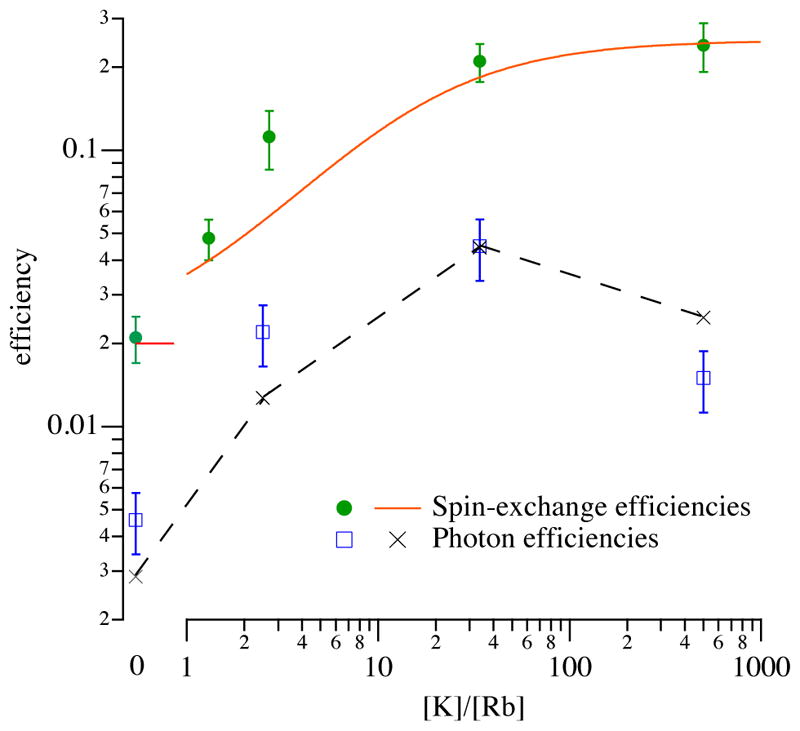
Measured efficiencies at 190°C as a function of density ratio 𝒟 = [K]/[Rb]. The spin-exchange efficiency, ηSE, which is the maximum possible efficiency with which the angular momentum of the pumping light can be transferred to the nuclei, shows the clear increases predicted by Eq. (15), solid line, as the vapor approaches pure K. Measured and modeled photon efficiencies, ηγ, are much smaller, thanks to dichroism effects, see Sec II.B.3. From Babcock et al. (2003).
4. Laser linewidth issues
The early laser-based SEOP experiments (late 1980’s, early 1990s) with 3He used Ar+-pumped tunable dye lasers (Chupp et al., 1987; Coulter et al., 1990) or Ti:Sapphire lasers (Larson et al., 1991b) to optically pump Rb vapor. With the notable exception of the early SLAC5 3He targets that used up to six Ti:Sapphire lasers (Johnson et al., 1995), these large, expensive and often unreliable sources were generally limited to <10 W of pumping light. The first application to SEOP with diode lasers was performed with relatively low power individual diodes (Wagshul and Chupp, 1989).
With the introduction of inexpensive, high power laser diode array bars in the early 1990s, SEOP experiments rapidly converted to these new sources that were readily available at a fraction of the cost (Cummings et al., 1995). The drawback of laser diode array bars is their relatively broad spectral profile (typically 2 nm or 900 GHz) that is not well-matched to the 20 GHz linewidth of Rb atoms at 1 amg of He density. Thus only a small fraction of the laser light is actually available for resonant pumping of the Rb atoms. It thus became common practice to use higher He densities (between 3 and 10 amagat) and rely on high optical thickness of the SEOP cells to absorb a significant fraction of the broad spectral profile of the pumping light (Driehuys et al., 1996). Such pressures were well matched to high luminosity targets for electron scattering. For MRI pressure of a few bar is convenient for gas delivery; for this reason and for optical pumping efficiency high He densities were also employed (MacFall et al., 1996; Middleton et al., 1995).
In practice, though these high power lasers were able to polarize larger volumes of 3He, the attainable 3He polarizations using these lasers were generally found to be limited to 50 % or less for these applications. Examination of Fig. 8 shows that a polarization reduction could be at least qualitatively explained because of optical pumping by off-resonant light. In optically thick SEOP cells this effect is exacerbated because the central core of the spectral profile of the light is depleted in the front portion of the cell, so that in the back of the cell the atoms are generally being pumped by off-resonant light with a substantially reduced value of P∞. The broad line width of diode lasers was a particularly bad match to neutron spin filters. Although pressures of 3 bar were employed in the early development of SEOP-based NSFs (Gentile et al., 2000; Jones et al., 2000), simpler construction and long lifetimes made pressures of closer to one bar preferable (Rich et al., 2002b).
Attainable 3He polarizations increased with the introduction of narrower diode laser sources, first using long external cavities (Babcock et al., 2005a; Chann et al., 2003) similar to those used in pulsed dye lasers and later using compact volume holographic gratings (VHG) (Chen et al., 2014b; Volodin et al., 2004) Both narrowing methods generally reduce the laser linewidth to 0.2 nm (90 GHz), thus both giving a much better match to the atomic absorption spectrum and also increasing the value of P∞. SEOP experiments utilizing such frequency narrowed lasers generally produce 3He polarizations of 70% or greater, and recently have demonstrated 85% (Chen et al., 2014b). Scaling of narrowing techniques to stacks of diode laser bars (Zhu et al., 2005) have reached kilowatt levels (Hersman et al., 2016).
Full simulations of propagation of broad and narrowband laser light due to competing spin-relaxation and circular dichroism effects have been made for SEOP in 1 to 3 bar spin-filter type cells (Lancor et al., 2010b), and for 8–10 bar cells (Singh et al., 2015). Such models generalize Eq. (12) to account for both spectral and spatial evolution of the optical pumping light, and do not yet include dual-sided pumping. They also generally attempt to account for heating effects (Sec. II.B.5) in a simplified manner. Such models generally predict higher polarizations than are observed experimentally, though they do semiquantitatively explain the much higher polarizations achieved with narrow-band pumping over broad-band pumping. An important gap in the literature is a quantitative comparison of such models with three-dimensional alkali-metal polarization mapping techniques using EPR spectroscopy (Young et al., 1997).
5. Heating
With the common use of 100 W scale diode lasers for SEOP, it is natural and important to ask about how this energy is dissipated in the vapor. The first work addressing this topic was Walter et al. (2001). They used Raman spectroscopy to measure the rotational and vibrational spectra of the N2 molecules under SEOP conditions. The picture painted by this study is as follows. The N2 quenching collisions that are so important for preventing radiation trapping leave the N2 molecules with 1.5 eV of excitation contained in 5 or 6 vibrational quanta. The vibrational energy relaxes slowly, while the rotational degrees of freedom rapidly thermalize with the local translational temperature. Therefore the rotational spectroscopy can be used to infer the internal temperature of the vapor. The spatial dependence of the internal temperature was inconsistent with conductive heat transfer, indicating convective heat transport inside the cell. While the convection tends to reduce temperature gradients, striking high temperature increases were observed. For example, a 95°C internal temperature increase with respect to the wall temperature occurred with only 22 W of deposited light power in an 8.4 bar cell.
Parnell et al. (2010) measured the temperature rise in a 2.3 bar 3He SEOP cell under illumination by a 100 W narrowed diode array bar. Using a gradient spin-echo sequence, they were able to measure the spatial profile of the local diffusion coefficient and observed an increase in diffusion at the center of cell consistent with a 30 K temperature rise. Double cells provide a means for measuring the temperature rise during SEOP by the resulting drop in gas density in the SEOP cell, and a consequent increase in the non-SEOP cell. Singh et al. (2015) compared 3He NMR signals with and without pumping light to deduce 20 to 50 K temperature increases for high pressure electron scattering cells. Normand et al. (2016) used neutron transmission to observe the reduction in the 3He gas density in the SEOP cell under optical pumping conditions. Their results indicated a remarkable 135 K temperature increase in a 1 bar SEOP cell with 200 W of laser illumination. Systematic studies using these kind of techniques on cells with varied nitrogen and 3He pressures, hybrid mixtures, and laser illumination would fill in an important gap in our understanding of the the interior conditions of SEOP cells.
C. SEOP with pure K or Na
As compared to traditional SEOP with rubidium, the efficiency of SEOP should be much greater for potassium due to its lower spin destruction rate (Ben-Amar Baranga et al., 1998; Walker et al., 1997). Increased spin-exchange efficiency for K, up to a factor of 10 above that of Rb for the same temperature, was observed (Ben-Amar Baranga et al., 1998). Enthusiasm for exploiting this substantial advantage has been tempered by potential pumping of the D2 line due to the small (3.4 nm) fine-structure splitting of the 4p state. The first reported SEOP application yielded 46 % in a mid-sized double cell target, using a Ti:Sapphire laser (Wang et al., 2003) operating at the potassium 770 nm D1 transition wavelength. 770 nm diode lasers have had limited availability and lower power compared to their 795 nm counterparts for pumping Rb. Thus hybrid SEOP with Rb/K mixtures has remained the preferred approach. The single study of 770 nm pumping (Chen et al., 2007b), which focused on NSF applications, did find increased efficiency as compared to pure Rb SEOP but also observed that the excess laser power demand and decline of alkali-metal polarization with increasing spin-exchange rate was similar to pure Rb cells, with poorer performance relative to Rb/K hybrid pumping. These observations are not well-understood and merit future investigations. Although 770 nm pumping was found to be preferable for the special case of high mixture ratio hybrid cells (see Sec. II.D), it is generally desirable to use the same laser for all cells and so hybrid SEOP has remained favored. In principle, SEOP with Na would yield even higher efficiency (Borel et al., 2003) but practical application is hampered by cell browning at the required temperatures of ≥300 °C and the absence of convenient laser sources at 590 nm.
D. Hybrid spin exchange
The idea of hybrid SEOP is to optically pump Rb in the presence of a higher density vapor of K. Rapid spin-exchange collisions between the Rb and K atoms lead to spin-temperature equilibrium between them; thus the K atoms become collisionally polarized to a level equal to that of the Rb atoms. The K-rich K-Rb vapor loses less angular momentum per atom due to spin-relaxation as compared to a pure Rb vapor, so that the fraction of the angular momentum of the light that gets transferred to 3He increases. The spin-relaxation rate of the Rb atoms in the presence of K is increased due to spin-exchange collisions with the K atoms. The rapid K-Rb spin-exchange thereby causes the effective Rb spin-relaxation rate to increase from its K-free value ΓRb to
| (14) |
where 𝒟 = [K]/[Rb] and the total K relaxation rate is ΓK. The spin-exchange efficiency becomes
| (15) |
which approaches at large 𝒟. Measurements of the spin-exchange efficiency as a function of 𝒟 are shown in Fig. 9.
The earliest experiments indicated that the maximum attainable alkali polarization drops at high 𝒟 (Fig. 10). This comes from off-resonant pumping of the K atoms by the resonant Rb light (Lancor and Walker, 2011) and limits the useful density ratios to 𝒟 < 10. Chen et al. (2007b) observed similar results and found that the polarization decline was not observed if hybrid cells were optically pumped with 770 nm light.
FIG. 10.
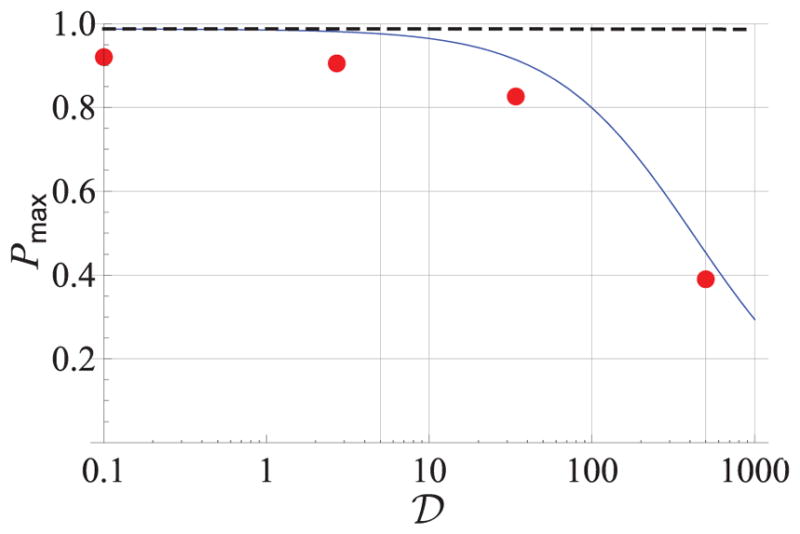
Alkali polarization as a function of K-Rb density ratio. The solid line shows the density limit for a narrowband pumping laser, using the measured K absorption cross section at 795 nm. The dots are experimental measurements using a broad pumping laser whose maximum polarization is limited by the dichroism effect to 0.92. The dashed line shows expected polarization limits predicted from a naive line-broadening model. From Lancor and Walker (2011).
The reduced collisional loss per atom for hybrid pumping means that for a given laser power the volume of 3He can be increased or the alkali density and thus the polarizing rate can be increased. Practical application of hybrid SEOP has been investigated for neutron spin filters (Chen et al., 2011, 2007b) and targets for electron scattering (Singh et al., 2015; Ye et al., 2013). Vapor mixture ratios, 𝒟, between 2 and 7 were found to yield the best results. Because of the difference in vapor pressures for a given temperature, ≈25 times more condensed phase K than Rb is required to yield 𝒟 = 4. In Chen et al. (2011, 2007b), individual Rb and K distillation is described whereas Singh et al. (2015) describe premixing Rb and K in a glove box. Variations in 𝒟 occur in both methods but can be minimized; in the individual approach 𝒟 can be checked before the cell is sealed off and in the pre-mix approach experimental feedback on the pre-mix ratio to account for fractional distillation improves the reproduceability. For NSFs 𝒟 has been determined by white light absorption and the pumping rate for a given temperature (Chen et al., 2011, 2007b) and for targets by laser light absorption and Faraday rotation (Singh et al., 2015). After a newly filled cell has been heated one or more times, the mixture ratio may increase, perhaps due to curing effects (Ma et al., 2009).
Although Fig. 9 indicates six times higher efficiency for hybrid SEOP in the optimum regime, hybrid cells are operated at typically 40°C higher temperature than pure Rb cells in order to obtain the same spin-exchange rate. For NSF cells at pressures near 1 bar, alkali-metal spin destruction from alkali-alkali collisions dominates, which decreases the efficiency and/or rate gain. In this regime, a resulting efficiency or rate gain approaching 3 or , respectively, has been calculated and observed. For high pressure targets, alkali-metal spin destruction from alkali-3He collisions dominates, and thus both the efficiency and rate gain is expected to be closer to that shown in Fig. 9. An additional benefit observed for hybrid cells is an observed slower decline of the alkali-metal polarization with increasing spin-exchange rates. Whereas this result was found to be in agreement with modeling, a steeper decline was observed for both pure Rb and pure K pumping in disagreement with modeling (Chen et al., 2007b).
Hybrid SEOP has substantially increased the quantity and production rate of polarized gas for both NSFs and polarized targets. For NSFs cells 85% 3He polarization in cells approaching one liter in volume with pumping time constants of between 4 h and 8 h (Chen et al., 2014a) has been achieved and for double cell polarized targets up to 70% has been reached with similar time constants (Singh et al., 2015).
E. Limits to 3He polarization
Combining the capability of polarizing high density alkali vapors to near 100% polarization, the developments of glass cells with hundreds of hour room temperature wall relaxation times, and rapid spin-exchange with hybrid pumping, the attainable 3He polarizations should be nearly 100%. The issues limiting the polarization are not yet fully understood. We briefly review here what is known about this issue. More details on most of these topics are discussed in other sections of this review.
1. Anisotropic spin exchange
Walter et al. (1998) pointed out that the long-range portion of the 3He nuclear magnetic field causes an additional term in the alkali-3He Hamiltonian:
| (16) |
This anisotropic spin-exchange interaction tends to polarize the 3He nuclei towards PHe = −PA/2, and so serves to limit the maximum 3He polarization to
| (17) |
where kα and kβ are the respective rate coefficients for the (isotropic) Fermi-contact interaction and the anisotropic interaction in Eq. (16). A theoretical estimate of the effect of anisotropic spin-exchange yielded PHe∞ = 0.95 for SEOP with either Rb or K (Walter et al., 1998), and more recent calculations yielded a similar value of 0.96 (Tscherbul et al., 2011).
There are no definitive experimental measurements of anisotropic spin-exchange. Wall-independent techniques (II.A.1) for measuring spin-exchange rates are sensitive to the combination kα −kβ/2. As discussed below (Sec. II.E.2), spin-exchange transients are generally sensitive to kSE[A]+Γw, where kSE =kα +kβ, but the strong temperature dependence of Γw makes it difficult to isolate kβ from Γw. However, Walker et al. (2010) pointed out that comparison of spin-relaxation rates of K in 3He and 4He, when combined with kSE measurements, allow kβ to be isolated without any assumptions about wall relaxation. A first attempt gave PHe∞ = 0.90 ± 0.11.
An upper limit on anisotropic spin-exchange can be deduced from absolute 3He polarimetry. The highest 3He polarization obtained to date is 0.88 ± 0.03 (Chen, 2016) in a 𝒟=4 K-Rb hybrid cell, giving kβ ≤(0.09 ± 0.02)kα.
2. X-factor
Studies of the time constants for spin-exchange obey the phenomenological relation (Babcock et al., 2006; Chann et al., 2002a, 2003; Chen et al., 2007b, 2014b; Singh et al., 2015; Walker, 2011)
| (18) |
where Γr is the room temperature relaxation rate, taken to be independent of temperature. This relation, experimentally verified for both Rb and K-Rb hybrid cells, indicates that the wall relaxation rate has an exponential increase with temperature that mimics the variation of alkali vapor pressure with temperature. This limits the 3He polarization to
| (19) |
for 100% Rb polarization and negligible Γr. That the “X-factor” originates from a temperature dependence of the wall relaxation rate is suggested by the tremendous variations in measured values of X for many different cells. Figure 11 shows a sample of such data. If it is a wall relaxation effect, X =χS/V should hold, where S/V is the cell surface-to-volume ratio and the relaxivity χ is a poorly controlled parameter. Indeed, there are greater fluctuations in X for small cells (large S/V) than for large cells (Walker, 2011). For large cells (eg. S/V ≤1 cm−1) X was found to be typically ≈0.3, thus limiting the maximum 3He polarization to between 75 % and 80 %. Direct determinations of X by measurements of the relaxation of heated cells were found to be consistent with measurements of the maximum 3He polarization.
FIG. 11.

NIST measurements of the X-factor, deduced from 3He polarization limits at high temperature, for both blown (filled, red) and flat-windowed (open, blue) neutron spin filter cells with a range of surface to volume ratios S/V. Adapted from Babcock et al. (2006).
Further determinations of X in spin filter cells (Parnell et al., 2009) and double cells for 3He targets (Singh et al., 2015; Ye et al., 2010) have been reported. The temperature dependence of relaxation in quartz cells has also been studied with deviation from the characteristic linear dependence on alkali-metal density (Ino and Muto, 2007) and larger X values observed (Ye et al., 2013). For this reason quartz presents issues for achieving the best 3He polarization values for SEOP, even if a long relaxation time at room temperature can be obtained.
Recently, the polarization of NSFs (Chen et al., 2014b) pumped by 100 W VHG-narrowed lasers have found polarization limits over 85%, compared to the 75 to 80% found in earlier studies (Babcock et al., 2006; Chen et al., 2007b). These polarization increases were also observed in cells that were studied over a decade time scale. The polarization increases with time (or perhaps equivalently, narrowband laser power) suggest that at least some of the polarization limits attributed to the X-factor may be insufficiently polarized Rb vapor in those early experiments. However, the Rb polarizations measured in those experiments using EPR spectroscopy were found to be conservatively in excess of 95%, generally 98% or above (Babcock, 2005).
3. Rb polarization limits
When the spin-exchange rates dominate over any other relaxation mechanisms, the 3He polarization can never exceed the spatial average of the alkali polarization.
The first rather obvious implication of this statement is that due to the high pressures used in SEOP, so that there is little alkali polarization diffusion, care must be taken to provide sufficient pumping light to all regions of the cell, including ensuring that the light exiting the cell is not fully depleted of useful pumping light. Because most SEOP experiments use lasers with spectral linewidths greater than the pressure-broadened line width of the atoms, it is essential to measure the spectral profile of the transmitted light, checking that the useful resonant portion of the light is not fully depleted.
Due to the imperfect dichroism of Rb pumped in the presence of high pressure 3He (Sec. II.B.3), spectrally broad lasers have been observed to have 10% reduction in their maximum Rb polarization, even under low Rb density conditions (Babcock et al., 2003). This effect is exacerbated as the light propagates through the optically thick cell and the resonant portion is depleted, further lowering the dichroism. These effects are now understood to be largely responsible for the 20% increases in polarization observed when experimenters first used frequency narrowed diode array bars (Chann et al., 2003; Gentile et al., 2005b).
Due to the locally enhanced spin-relaxation of alkali atoms within a diffusion length of the wall, correspondingly large light absorption occurs at the entrance to the cell, leading to reduced pumping rates and Rb polarizations within the bulk of the cell. For single frequency pumping with dye or Ti:Sapphire lasers, where the spectrum of the light is much narrower than that of the atoms, this effect can be somewhat mitigated by purposely tuning the laser off resonance (Wagshul and Chupp, 1994). For broad or frequency narrowed diode array bars, typically up to 10% of the useful light can be absorbed by this layer, again reducing pumping rates and hence alkali polarizations within the bulk of the cell.
Finally, even for narrow band pumping hybrid K:Rb mixtures exhibit reduced maximum polarizations at high 𝒟 due to off-resonant absorption of the Rb pumping light by the K atoms (Lancor and Walker, 2011), see Fig 10. This effect limits the useful values of 𝒟 <10.
4. EPR spectroscopy
It is often useful to complement 3He polarimetry with diagnostics to measure and even image the Rb polarization. In the very simplest version, one can simply monitor the transmission of the optical pumping light. Assuming the pump light is approximately circularly polarized, the light transmission is minimum when the laser is tuned directly on resonance. Then as the circular polarization of the light is adjusted, the transmission will be a maximum when the pumping light is maximally circularly polarized. The sensitivity of this technique is enhanced by monitoring the transmitted pumping light with a diffraction grating spectrometer. Then the greater polarization sensitivity of the on-resonant spectral components is easy to observe. Such a diagnostic can however only identify the alkali polarization as “high”. For a more sensitive alkali polarization monitor, a linearly polarized Faraday probe, co-propagating with the pumping light but tuned near the D2 optical resonance (so it can be distinguished from the pumping light by a spectrometer or interference filter), can be used. The high optical depth in SEOP make the polarization rotations large (~rad) even for light tuned a number of linewidths off resonance. The Faraday rotation is proportional to PA[A], so absolute calibration of PA is difficult without a precise alkali number density measurement. Indeed, assuming PA ≈ 1, the Faraday rotation can be used to measure [A](Chann et al., 2002a).
For a more quantitative alkali polarization assessment, electron paramagnetic resonance (EPR) spectra can be obtained by monitoring the transmitted intensity of the pumping light, Faraday rotation of a co-propagating probe laser, or residual cell fluorescence as a transverse oscillating magnetic field is swept through the alkali Zeeman resonances, slightly changing the alkali polarization (Chann et al., 2002a; Kramer et al., 2007; Romalis and Cates, 1998). These detection modalities are all proportional to the longitudinal alkali spin-polarization, so the “longitudinal EPR” signal is proportional to the square of the oscillating magnetic field strength. At small magnetic fields, the splitting between adjacent EPR lines arises largely from the second-order Zeeman effect and is q(μBB)2/(h2δν), where μB is the Bohr magneton, δν the hyperfine splitting, h is Planck’s constant, and q =2/9 for 85Rb with nuclear spin IA =5/2 and q =1/2 for the IA = 3/2 species 87Rb and K. This neglects the nuclear Zeeman interaction, which slightly splits the RF resonances for the two hyperfine levels. Under the strong pumping conditions typical for SEOP, the two primary EPR lines are m =Fmax → Fmax − 1 and Fmax − 1 → Fmax − 2, where the maximum angular momentum of the atom is Fmax =IA+1/2. The Fmax line is narrowed due to having little spin-exchange broadening, while the Fmax − 1 line experiences substantial spin-exchange broadening (Appelt et al., 1999). The Rb polarization is simply related to the areas of the RF resonances. In 85Rb, for example, assuming spin-temperature equilibrium one gets
| (20) |
where Am is the area of the EPR peak originating from mF =m. This is valid when the F,m = 3, 2 and 2, 2 lines are not resolved.
A more sensitive technique for EPR alkali polarimetry, and the first to be demonstrated, is to directly detect the transverse alkali polarization induced by the oscillating magnetic field(Ben-Amar Baranga et al., 1998; Young et al., 1997). This is done by demodulating the Faraday rotation of a transversely propagating probe laser. The transverse polarization is linear in the oscillating magnetic field amplitude, so weaker oscillating fields are required to observe these “transverse EPR” signals. Again, ratios of the areas of resonance peaks allow the alkali polarization to be measured. Lancor (2011) compared simultaneous longitudinal and transverse EPR signals using Faraday rotation of a skew off-resonant laser. He observed that the spatially averaged alkali polarizations deduced by the two methods differed, with the longitudinal EPR generally yielding 0–10% higher alkali polarization estimates than transverse EPR. The origin of this discrepancy is not known, though both transverse and longitudinal methods gave distributions consistent with a spin-temperature. Thus earlier studies relying on longitudinal EPR for alkali polarimetry may have overestimated alkali polarizations.
Young et al. (1997) and Ben-Amar Baranga et al. (1998) also demonstrated the use of EPR spectroscopy for alkali polarization imaging. In this case the most convenient approach is to work at low fields where the individual EPR lines are not resolved, and apply a longitudinal magnetic field gradient ∂Bz/∂x so that the Faraday rotation of the probe beam, propagating along the x-direction, arises solely from a small voxel of atoms that satisfy the EPR resonance condition. Sweeping the longitudinal field Bz then produces a spatial map of the Rb polarization along the x-direction. Moving the probe laser allows the polarization to be mapped in 3-dimensions.
F. EPR frequency shift
The spin-polarized alkali-metal atoms that are present in the SEOP cell can serve as a sensitive in-situ magnetometer, detecting the magnetic field produced by the polarized 3He. The magnetic field at position x with respect to a spin-polarized nucleus with magnetic moment m is the sum of the classical dipole field and a contact term: B(x)=[3xx·m−x2m]|x|−5+8πm/3δ(x)(Jackson, 1999). The average field experienced by the alkali atoms due to the polarized 3He is (Barton et al., 1994; Romalis and Cates, 1998; Schaefer et al., 1989)
| (21) |
| (22) |
where μHe is the magnetic moment of 3He, and κ0 is a frequency shift enhancement factor whose value is proportional to the average alkali electron spin-density at the 3He nucleus. For a gas that is uniformly polarized inside a spherical cell, the spatial average of Bcl vanishes so that only the contact term, responsible for the hyperfine interaction (second term of Eq. (2)), contributes, κ =κ0. The field BHe produces an EPR frequency shift δν =γABHe =γSBHe/(2IA +1), where γS ≈28 MHz/mT is the electron gyromagnetic ratio. For the most common 85Rb isotope, the numerical value of the shift is 1.13κ0 kHz for fully polarized 3He at a density of 1 amg.
Using two orientations of a long cylindrical cell, for which Bcl can be accurately calculated, Romalis and Cates (1998) isolated the classical and contact contributions, thus enabling a precision measurement of κ0 for Rb-3He, with an uncertainty of 1.5%. This result agreed with a prior calibrated absolute NMR polarimetry measurement (Newbury et al., 1993) and forms the basis of precision absolute polarimetry of electron scattering targets. EPR frequency shift polarimetry has also been indirectly tested using neutron transmission (Ye et al., 2013).
The resulting alkali EPR frequency shifts δν (Schaefer et al., 1989) are typically tens of kHz for high density 3He SEOP and are easily measured using any of the EPR methods. AFP is often used to briefly reverse the 3He polarization with respect to the magnetic field and hence isolate the EPR frequency shift. The results are improved when the bias external magnetic field is stabilized using an auxiliary magnetometer (fluxgate or atomic). Since the temperature dependence of κ0 yields a typical change in the EPR frequency shift of 0.14%/°C, the gas temperature must be carefully determined in order to retain the full precision in the absolute polarimetry. The effect of internal heating (Sec. II.B.5) has not generally been investigated as a source of error and uncertainty. If unaccounted for, a 10 °C temperature rise of the gas sampled for the EPR measurement would yield a 1.4 % error, which would be comparable to the uncertainty in current values for κ0.
Using the carefully measured Rb3He enhancement factor as a reference, the enhancement factors for K and Na have also been measured, and the temperature range for Rb-3He extended as needed for hybrid pumping (Babcock et al., 2005b). The values of κ0(T) for the various alkali-metal atoms are given in Table. I. The temperature dependence dκ0/dT, also given in Table I, is sufficiently large that 10% variations are seen over common SEOP temperature ranges.
III. METASTABILITY-EXCHANGE OPTICAL PUMPING
Metastability-exchange optical pumping mainly involves two processes: optical pumping on the optically closed 23S-23P transition of He at 1083 nm, described in Sec. III.C, and nuclear orientation transfer to the ground state of 3He through metastability-exchange (ME) collisions, described in Sec. III.B. MEOP is usually performed in pure 3He gas, and it is often sufficient to consider these two processes for 3He atoms only. However, the addition of 4He to 3He gas can lead to higher nuclear polarizations and faster build-up rates, with potential applications whenever the admixture of 4He atoms has no adverse effect (e.g., for neutron spin filters). In isotopic mixtures, optical pumping advantageously operates on 4He atoms (Stoltz et al., 1996a). From another point of view, traces of 4He are often found in 3He cells, resulting for instance from cell preparation or from permeation through glass walls. The impact of even sub-% 4He fractions on MEOP efficiency or optical measurement of polarization can be significant (Batz, 2011; Talbot et al., 2011). Therefore the knowledge of features and processes relevant for MEOP may be needed and they will be examined for both helium isotopes in this section, starting with the relevant He level structures in Sec. III.A.
A. Atomic levels involved in MEOP
Figure 12 schematically displays the optical pumping and ME collisions processes and the most relevant atomic levels for S both He isotopes. The 23S state of 4He (J = =1) has three magnetic sublevels (mS =−1, 0, and 1), linearly split at all values of the applied magnetic field B by the Zeeman energy. They are named Y1 to Y3 (for all sets of Zeeman sublevels indices increase with increasing energies). The 23P state of 4He has three fine-structure levels with J =0, 1 and 2, hence nine Zeeman sublevels (Z1 to Z9). Due to its two nuclear spin states 3He has twice as many Zeeman sublevels: six in the 23S state (A1 to A6) and eighteen in the 23P state (B1 to B18). The magnetic sublevels Ai can be written using the decoupled basis states |mS,mI 〉. A1 = |−1, −〉 and A4 = |1, +〉 are pure states while the states for which mF =±1/2 involve two mixing parameters θ± (Courtade et al., 2002):
| (23) |
FIG. 12.
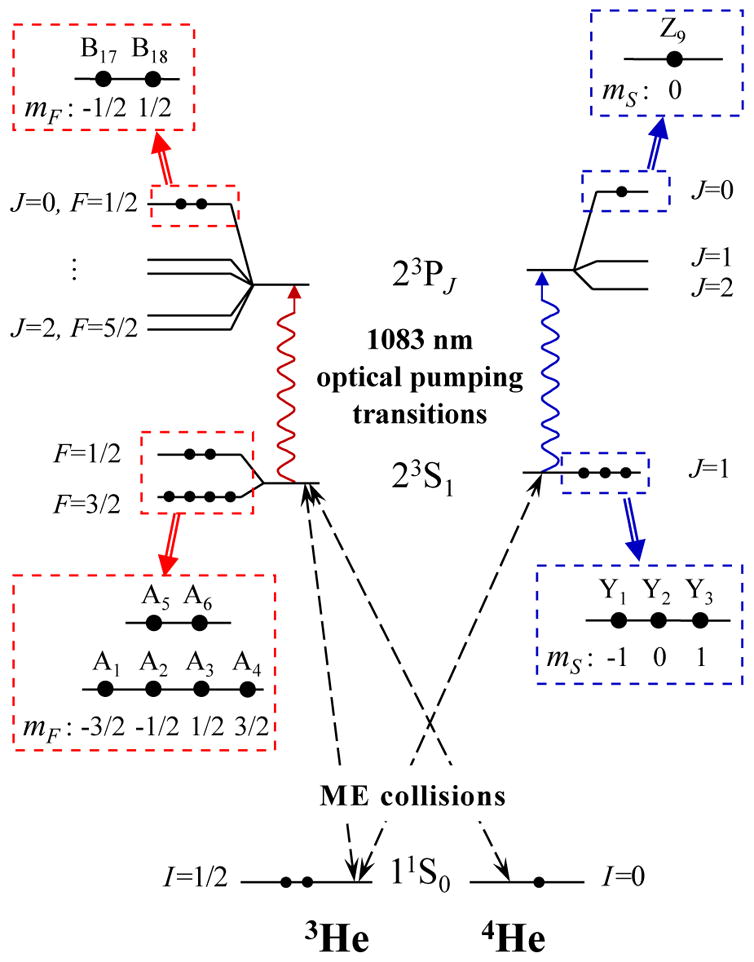
Fine- and hyperfine-structures of the atomic states of He involved in the metastability-exchange optical pumping process, for the 3He (left) and 4He (right) isotopes, in low magnetic field (for negligible magnetic Zeeman energies, i.e. below a few mT). The values of the total angular momenta (J for 4He, F for 3He) are indicated. Details and names of the magnetic sublevels of the 23S and 23P0 states are given in blown-up boxes (with notations of Courtade et al. 2002.) The shifts and splittings are not displayed to scale.
For simplicity, only the highest-lying Zeeman sublevels of the 23P0 states are displayed in Fig. 12.
At low magnetic field, the F = 3/2 and F = 1/2 hyperfine levels of the 23S state of 3He are well resolved and split by 6.74 GHz. Strong mixing of electronic and nuclear angular momenta yields large values of the mixing parameters θ±: sin2 θ− =2/3 and sin2 θ+ =1/3. The 23P states levels extend over 32.91 GHz for 4He and 32.60 GHz for 3He. The isotope shifts of the energy levels result in an increased optical pumping transition energy (by 33.67 GHz) and a higher 23S state energy (by 259.6 GHz, i.e. 12 K in temperature units) for 4He (Drake et al., 2005).
At high magnetic field, the Zeeman energy is no longer a small correction to the fine- and hyperfine-structure energy contributions and the angular momentum structures of the 23S and 23P levels are deeply modified. For instance, the mixing parameters in Eq. (23) have small and almost equal values θ± ≈0.11/B, with the field strength B in T. This has a strong impact on ME and optical pumping mechanisms alike. Therefore, in each of the following sections, the low-field and high-field situations will be separately discussed as limiting cases. Traditional low-field corresponds to field strengths B ≤10 mT, with θ± decreasing by less than 3% and Zeeman shifts significantly lower than Doppler widths at room temperature. Conversely, B ≥ 1 T will be considered a high-field situation with small mixing parameters θ± and a strongly modified level structure (see Sec. III.C.3).
B. Metastability-exchange collisions
1. Treatment of the metastability-exchange collision process
Metastability exchange collisions are binary collisions in which the electronic excitation is transferred from a He* atom in the metastable 23S state to one in the ground state. For a gas confined in a cell, the quantum states of the atoms can be statistically described by density operators depending on atomic positions and velocities. The position-dependent parameters include the local plasma characteristics and the optical pumping light intensity. This intensity has a spatial dependence because of the pumping beam transverse shape and divergence (if any) and of atomic absorption. The velocity dependence mainly results from the velocity-selective character of optical pumping with a narrowband laser and will be addressed in Sec. III.C.2 below. Using a standard approach (Partridge and Series, 1966), the effect of a ME collision between He* and He atoms characterized by density operators ρm and ρg can be described as:
| (24) |
The ground state density operator of 3He is directly related to the populations of the two spin states |+〉 and |−〉, which are functions of the nuclear polarization PHe:
| (25) |
while the He* density operator can be written as:
| (26) |
for 4He* or 3He*, respectively. The relative populations of the 23S state sublevels Yi and Ai are noted yi and ai, respectively, with Σyi =Σai =1. The local number density of 23S state atoms in the Zeeman sublevels are thus and , where and are the local number densities of 23S state atoms of each isotope. Their ratio depends on the gas composition and temperature, due to the lower energy of the 3He* state (Courtade et al., 2002; Nacher, 1985; Zhitnikov et al., 1975). At room temperature (T ≫12 K), where and are the number densities of ground state atoms of the isotopes. Number densities are simply noted nm and Ng in a pure gas.
For an outgoing 3He atom:
| (27) |
is simply obtained using the trace operator Tre over the electronic variables of the incoming 3He* atom. For the outgoing He* atom in 3He-3He* collisions the density operator is written as:
| (28) |
The tensor product is the density operator immediately after the collision. Off-diagonal terms (coherences) between the F = 1/2 and F = 3/2 hyperfine sublevels are created during metastability exchange collisions, but they can be neglected for usual MEOP conditions, at low enough pressure or high enough field (Courtade et al., 2002). Therefore the restricted expression of can be used (Eq. (28), where PF is the projection operator onto the F hyperfine substate).
Note that off-diagonal elements can also be created if coherent light is used for pumping with a V-type or Λ-type scheme, with two optical transitions addressing at least one common sublevel in the lower state or the upper state, respectively. However, such schemes are avoided in MEOP since well-polarized light of given helicity is used.
For isotopic He mixtures, Eq. (24) generically refers to three different ME processes depending on the isotopic nature of the colliding atoms (see Fig. 12, dashed lines). Two additional equations, similar to Eq. (28), are used for collisions between atoms of different isotopes (Courtade et al., 2002). The fourth type of collisions, between 4He* and 4He atoms, plays no role in the evolution of nuclear or electronic spin variables, and therefore no direct link is sketched in Fig. 12.
The initial approach of Partridge and Series was subsequently improved to quantitatively link the time evolution of selected atomic observables with ME collision cross sections in weak pumping and low polarization conditions (Dupont-Roc et al., 1971, 1973; Pinard and Laloë, 1980). It was then used in models suitable for the description of MEOP with lasers, in which the evolution of all Zeeman sublevel populations is evaluated for arbitrary pumping conditions (Batz et al., 2011; Nacher and Leduc, 1985). Rate equations are derived from Eq. (28) for the populations in the 23S state. They explicitly depend linearly on PHe due to the linear dependence of ρg on PHe in Eq. (25). For pure 3He they are written as:
| (29) |
The ME collision rate γe =NgkME is proportional to the number density of atoms in the ground state and depends on temperature through the ME rate coefficient kME (Sec. III.B.2 below). The matrices E(3) and F(3) involve B-dependent parameters (Courtade et al., 2002, Tables 16 and 17). For the ground state, the contribution of ME collisions to the rate equation describing the evolution of PHe is obtained by computing Trn ρgIz using Eqs. (27) and (26):
| (30) |
| (31) |
The nuclear polarization is usually uniform in the ground state since the diffusion rate in a low pressure gas is much larger than typical rates of evolution for PHe. On the contrary, both the nuclear polarization PHe* and the density nm of atoms in the 23S state depend on local pumping light and discharge intensities and may strongly vary with position. Hence Eq. (30) involves a spatial average over the cell volume Vcell. PHe* is directly derived from the set of populations using the field-dependent parameters Lk (Courtade et al., 2002, Table 13).
This formalism has been extended to mixtures of 3He and 4He, and the corresponding rate equations have been established (Courtade et al., 2002). If isotopic mixtures are optically pumped using a 4He atomic transition, the electronic polarization created in the 23S state of 4He atoms is first transferred to the 23S state of 3He atoms by ME collisions with ground state 3He atoms. The nuclear polarization which subsequently develops in 3He* atoms due to hyperfine interactions is then transferred to the ground state of 3He atoms via further ME collisions. The larger light absorption probability of 4He atoms (see Sec. III.C.2) contributes to make this indirect process more efficient (Stoltz et al., 1996a).
2. Temperature dependence of metastability-exchange collision rates
Early studies of the magnetic resonance linewidth in the 23S state of 3He have shown that ME collision cross sections and collision rate coefficients strongly decrease with decreasing temperatures between 4.2 K and 550 K (Colegrove et al., 1964). These experimental data were found to be consistent with computations using empirically determined potential parameters (Fitzsimmons et al., 1968), but the values inferred for the cross sections need to be corrected to take into account the partial character of the loss of orientation in ME collisions (Dupont-Roc et al., 1971). These data and the results of more accurate measurements performed at low temperatures are compiled in Fig. 13 together with the results of ab-initio calculations of different rates for collisions between 23S or 23P and ground state He atoms (Vrinceanu and Sadeghpour, 2010). The first set of data points in Fig. 13 is evaluated from the plot of reduced linewidths Δν/N in the temperature range 100 K to 550 K (Colegrove et al., 1964, Fig. 7) using the correcting relation kME =9/4×πΔν/N.6 Other experimental data for the exchange rate coefficients kME are derived from published values of linewidth Δνex (Rosner and Pipkin, 1972), exchange rate 1/τ (Dupont-Roc et al., 1971), cross section σex (Barbé, 1976; Zhitnikov et al., 1975), and number densities N using:
| (32) |
where is the average relative velocity of colliding He atoms at temperature T (kB is the Boltzmann constant, M the 3He atomic mass). The experimental and calculated values of ME rate coefficients are in fair agreement (the expected effect of isotope mass difference through v̄rel is of the order of symbol size). For convenience, values of kME and of their local temperature variations inferred from the compiled experimental data are listed in Table II.
FIG. 13.
Temperature dependence of calculated and experimentally assessed collision rate coefficients in He. Ab-initio calculated rates are plotted for excitation transfer (dashed lines) and total (solid lines) rates of collisions for the 23S state (red curves, labeled ‘S’) and the 23P state (black curves, ‘P’). Experimental kME data (symbols, see legend) are derived from published values of linewidths or ME cross sections in 3He (see text). Three calculated rate coefficients slowly decrease with decreasing temperature and thermal velocities, but the rate coefficients kME for ME collisions (the dashed red line and symbols) abruptly decrease below room temperature. This is attributed to a weak repulsive barrier at large distance in the He*-He interaction potential. Adapted from Vrinceanu and Sadeghpour (2010, Fig. 3) for the calculated curves.
TABLE II.
Table of metastability-exchange rate coefficients kME and of corresponding typical rates 1/τtyp = NtypkME for a gas number density Ntyp = 2.653×1016 cm−3, i.e. 10−3 amg, which is a typical value in metastability-exchange optical pumping experiments (1 mbar at 293 K)
| T [K] | kME [10−12 cm3/s] | 1/τtyp [106s−1] |
|---|---|---|
| around 300 | 154 × (T/300)1.09 | 4.09 × (T/300)1.09 |
| around 77 | 6.6 × (T/77)2.91 | 0.175 × (T/77)2.91 |
| 4.2 | 0.12 | 0.32 × 10−2 |
An interesting feature of the ab-initio calculated rates in Fig. 13 is the comparatively high value of the exchange rate between ground state and 23P state atoms, approximately ten times larger than the ME rate at room temperature and more than 1000 times larger at a few Kelvin (the dashed curves labeled P and S, respectively). In spite of this, this coupling channel is traditionally not considered in the transfer of angular momentum to the ground state, due to the comparatively low number density usually achieved in the 23P state.
3. Metastability exchange and spin-temperature distribution
An important property of ME collisions in helium is the negligible depolarization that occurs during the very short collisions (10−12 s), due to the fact that all involved angular momenta are spins (Pinard and Laloë, 1980). This accounts for the very efficient transfer of angular momentum in MEOP from the absorbed polarized light to the nuclear orientation. This also enforces a Boltzmann-like distribution in angular momentum for the relative populations of all sublevels coupled by ME collisions: a so-called spin-temperature distribution. Anderson et al. have proposed that such a distribution is enforced, e.g., by fast spin-exchange (Anderson et al., 1959; Happer, 1972). For He, whenever the effects of pumping light and relaxation can be neglected, the spin-temperature distribution can be derived from ME equations on density operators (Courtade et al., 2002). Defining eβ = (1 + PHe)/(1 − PHe) as the ratio of the populations in the ground state with nuclear polarization PHe (1/β plays the role of a spin temperature), one finds that the ME-driven ratios of populations in the 23S state of 3He are field-independent, and given by eβΔmF for any two sublevels with a magnetic quantum number difference ΔmF. Similarly, in an isotopic mixture, the ME-driven ratios of populations for the three magnetic sublevels in the 23S state of 4He are given by eβΔmS. Therefore, one may write for populations and , where the upper index indicates spin-temperature distribution values:
| (33) |
| (34) |
This yields explicit expressions:
| (35) |
| (36) |
The spin-temperature values of populations of Eq. (35) can be checked to yield, using Eq. (31), a nuclear polarization in the 23S state of PHe* = PHe, as expected.
These distributions of populations have a strong impact on the absorption of light on the 23S–23P optical pumping transition. The consequences on the efficiency of MEOP at high nuclear polarization will be discussed in Sec. III.C, and the resulting features of polarimetry using the optical pumping transition in Sec. III.D.
C. Optical pumping of the 23S - 23P transition
Besides the ME collisions described above, two kinds of processes jointly affect the populations in the 23S and 23P states: population transfers between Zeeman sublevels within the 23S and 23P states, usually modeled as relaxation processes, and optical pumping that combines absorption and spontaneous or induced emission of light on the closed 23S - 23P transition. They are successively considered below.
1. Relaxation in the 23S and 23P states
Population transfers between sublevels occur with very different rates for the two states (Batz et al., 2011):
In the 23S state, the L = 0 orbital angular momentum is not affected by collisions: relaxation is slow, with rates typically of order 103 s−1. It is attributed to excitation quenching (e.g., at cell wall or in 3-body dimer-forming collisions) and re-excitation in the gas discharge. Its effect on populations is simply written as:
| (37) |
In the 23P state, J-changing collisions occur at a much faster rate, proportional to gas pressure and of order a few 107 s−1/mbar (Schearer, 1967; Vrinceanu et al., 2004). These collisions may induce significant population transfer during the radiative lifetime, which is phenomenologically described in MEOP models using a single rate in rate equations ruling the evolutions of the populations bj of the sublevels Bj:
| (38) |
For convenience, the bjs are defined so that the number density of atoms in each sublevel Bj of the 23P state is nmbj. Consequently they are not true populations (i.e., diagonal elements of a trace-1 density matrix), and Σbk < 1 depends on the pumping light intensity. When isotopic mixtures are considered, additional phenomenological equations similar to Eqs. (37) and (38) are used, with possibly different rates for different isotopes due to the thermal velocity difference.
A more realistic treatment of the effects of collisions in the 23P state, in particular at high magnetic field, remains to be implemented and tested in MEOP models (Batz et al., 2011).
2. Traditional low-field optical pumping
Optical pumping selectively promotes atoms from a sub-set of Zeeman sublevels of the 23S state to corresponding sublevels of the 23P state according to selection rules depending on the frequency and polarization of the pumping light. Figure 14(a) displays typical absorption spectra for 3He and 4He at 1083 nm.
FIG. 14.
Low-field metastability-exchange optical pumping transitions: (a) computed absorption spectra for the 23S-23P transition for a low-pressure, optically thin gas at room temperature. The linewidths essentially arise from Doppler broadening. (b) Fine- and hyperfine-sublevels involved in the transition (see Fig. 12). The three transitions to the 23P0 levels are schematically represented, and the names and positions of the corresponding line components in the spectra are highlighted. (c) The inset displays the optical transitions involved for C8, σ+ pumping (straight arrows, see text). The curved arrow represents population transfer between Zeeman sublevels of the 23P state. Note that no direct transfer, corresponding to a nuclear spin flip, is expected to occur between these two sublevels.
The action of optical pumping in pure 4He is quite straightforward: each of the two strong low-energy components of the pumping transition (partly resolved in Fig. 14(a)) can be used to efficiently obtain a high electronic polarization in the 23S state by depopulating, for instance, the Y1 and Y2 sublevels, whereas using the D0 component depopulates only one sublevel and therefore yields a maximum polarization of 0.5 (Giberson et al., 1982; Wallace et al., 1995). In a similar way, optical pumping can efficiently depopulate selected sublevels of 3He* atoms whenever ME collisions have a negligible rate, for instance at low temperature (see Fig. 13) or in atomic beams (Stas et al., 2004). Achieving full nuclear polarization would require depopulating all sublevels except A1 or A4 by suitably addressing both hyperfine levels (see Eq. 23 and Fig. 12).
The effect of pumping light in a gas of 3He or in isotopic mixtures is quite different due to the strong coupling enforced by ME collisions between the Zeeman sublevels of the 23S state (Eq. 29). In a weak pumping limit, one may consider that PHe* ≈ PHe and derive a simple phenomenological model at low PHe (Colegrove et al., 1963), or more generally consider the effect of optical pumping cycles on the PHe-dependent spin-temperature populations of Eqs. 35 and 36 for arbitrary PHe. In usual MEOP conditions, ME therefore not only transfers nuclear orientation to the ground-state atoms but also plays a key role in the way the pumping light is absorbed. In that case full polarization could in principle be achieved even if a single Zeeman sublevel is addressed by optical pumping. The actual limit for the polarization results from a balance of angular momentum gain from the pumping light and loss through relaxation. In practice, MEOP is usually performed by tuning the pumping light to one of the high-energy components of the spectra to selectively populate the 23P0 level, using the D0 component for 4He or the C8 or C9 component for 3He (see Fig. 14(b)). These are the most efficient and widely used transitions for pumping with tunable lasers. In the early days of MEOP, pumping light was usually obtained from 4He lamps to polarize 3He gas with fair efficiency, thanks to the isotope shift (Colegrove et al., 1963).
Figure 14(c) displays in more details the full optical pumping cycle process in the simple case of the C8 component. Right-handed circular (σ+) polarization excites atoms from the A5 sublevel (mF = −1/2) to the B17 sublevel (mF = 1/2). Radiative decay brings atoms back to the 23S state by spontaneous and stimulated emissions with well-defined branching ratios from the directly populated B17 sublevel and from any other sublevel that may have been indirectly populated by J-changing collisions, as described in the previous section III.C.1. There are two extreme situations for the impact of these collisions: low-pressure optical pumping (Kastler, 1957) for , where γ=1.022 × 107 s−1 is the radiative decay rate of the 23P state, and depopulation optical pumping (Dehmelt, 1957), a high pressure regime where all 23P populations are equalized, for .
All radiative processes can be modeled by sets of coupled rate equations for the populations. For 3He they are written as (Nacher and Leduc, 1985):
| (39) |
| (40) |
where Tij is the transition matrix element, and γij is the optical pumping rate of the transition Ai →Bj. γij is proportional to the pump light intensity and to Tij. On the right-hand sides of these equations, the first terms account for spontaneous emission and the second terms for the net difference between absorption and stimulated emission.
Adding up contributions of ME, relaxation, and radiative processes (Eqs. (29) and (37) to (40)), one obtains a set of coupled rate equations for the populations of all sublevels of the 23S and 23P states. Given that the rate parameters are in the range 103 to 107 s−1 in these equations, while the rate of change of the nuclear polarization is usually smaller than 1 s−1, steady-state solutions for the populations are adiabatically computed taking PHe as a static input parameter.
Figure 15 displays examples of computed populations, pump absorption coefficients, and 23S state laser-induced over-polarization for parameters corresponding to typical MEOP experiments. Competition between metastability-exchange and optical pumping is illustrated in Fig. 15(a), in which the steady-state populations of the 23S state are represented for different values of PHe and of the pumping rate γij on the C8 transition component. In that case, absorbed light directly depletes level A5 while other populations are differently affected, which enforces systematic deviations from the spin-temperature distribution (the red boxes) that is obeyed in the absence of optical pumping and assumed in simple MEOP models. The effect of relaxation in the 23S state on populations is too weak to be seen on this figure.
FIG. 15.
Results of the MEOP rate equations obtained using the same computer code as in (Batz et al., 2011) for typical operating conditions: 0.5 mbar 3He gas, T = 293 K, B = 1 mT, nm = 1.2 × 1010 cm−3, . Atoms of all velocity classes are pumped with the same rates γij (see text). (a) Distributions of the 23S populations ai for C8, σ+ optical pumping and γij = γ/10, γ, and 10γ (bars from left to right and from light grey to black in each group) Surrounding red boxes are the spin-temperature populations. (b) Computed absorption coefficients are plotted as functions of reduced pumping rates for C8 and C9 optical pumping and different nuclear polarizations (see legend). For C9 the two pumping rates for the two pumped sublevels jointly scale with the pumping light intensity, with a fixed ratio T1,18/T2,17 = 3. Introducing Tij in the horizontal scales makes the reduced pumping rates identically proportional to the pump intensity. (c) Differences between nuclear polarizations in the 23S and ground states are plotted as a functions of PHe for C8 and C9 pumping and different reduced pumping rates (see legend)
Figure 15(b) displays the computed variation of the gas absorption coefficient with the reduced pumping rate γij/(γTij) for both C8 and C9 components. A strong decrease of the absorption results from the modifications of populations in the 23S state as well as from stimulated emission of atoms promoted to the 23P state by optical pumping. Absorption also significantly decreases when nuclear polarization increases. It is therefore increasingly difficult to efficiently deposit angular momentum at increasing polarization and pumping intensity.
Another meaningful quantity derived from the solutions of the rate equations is represented in Fig. 15(c): the nuclear over-polarization PHe* − PHe, which acts as a driving term for the ground state polarization PHe in Eq. (30). The parameters in Eq. (31) are (Lk) = (−1, L−, L+, 1, −L−, −L+), with L± ≈ ±1/3 in low field. Therefore PHe* is fairly sensitive to the modifications of all populations enforced by optical pumping in the 23S state. The decrease of this driving term with PHe and its saturating increase at high pumping rates mainly result from the decrease in pumping light absorption. Introducing the optical pumping photon efficiency η as the net change of atomic angular momentum projection mF upon the absorption and emission of a photon, these correlated decreases can be quantitatively linked (Batz et al., 2011). For C8, η has a fixed value ranging from 0.5 to 0.9 depending on , while for C9 η also depends on PHe and the optical pumping rate, ranging from 0.5 to 1.25.
So far, the pumping rates have not been explicitly related to the pumping light parameters. They depend on the local characteristics of the pumping light (intensity, direction of propagation, spectral characteristics) and on the atomic velocity projection v on the direction of propagation of the pumping light. Velocity-selective optical pumping, i.e. a strong correlation between v and populations or PHe*, may occur if an intense narrowband laser is used, with spectral width L smaller than the Doppler width D (Aminoff and Pinard, 1982; Pinard et al., 1979). Velocity-dependent pumping rates γij(v, r) can be computed for a single-frequency pump laser (Courtade et al., 2002). The maximum rate is experienced by atoms in the velocity class v* that is resonant with the laser frequency, and is given by:
| (41) |
where Ilas(r) is the laser intensity, ω its angular frequency, α the fine structure constant, f the oscillator strength of the transition, and me the electron mass; the numerical value of the first fraction is 0.149 m2/W. The total damping rate of the optical coherence of the transition, Γ′/2 = γ + πw, results from the combined effects of the radiative decay rate γ and of the pressure-dependent collisional broadening w, with a value for w/p of order 20 MHz/mbar (Vrinceanu et al., 2004) or 12 MHz/mbar (Nikiel-Osuchowska et al., 2013) that remains to be confirmed. In the low-pressure limit (w ≪ γ), γij = Tij γ for Ilas = 6.7 W/m2.
Pumping rates can also be evaluated for broadband lasers of known spectral intensity distribution. For instance, for a laser of Gaussian width L tuned to the center of the Doppler absorption profile, the rate is (Batz et al., 2011):
| (42) |
where is the most probable speed and D=(ω/2π)v̄/c is the associated Doppler width. Due to the second factor on the right hand side, the rates are typically 100 to 1000 times smaller than in Eq. (41) for a given pumping intensity. This accounts for the much higher total power absorption for a pump laser with a suitable bandwidth L ≈ D (Tastevin et al., 2004).
One may be tempted to make an exact treatment of velocity-selective optical pumping effects by explicitly keeping a dependence of populations and collision rates on the atomic velocity projection v. However, solving sets of rate equations for various velocity classes would be a difficult task since their populations are coupled by velocity-changing and by ME collisions, with ill-known collision rates. Instead, a coarse description with only two broad velocity classes has been proposed to account for the Maxwell distribution of atomic velocities in the pumped gas: strongly pumped atoms, in the center of the velocity distribution, and weakly pumped atoms, in the wings of the velocity distribution (Batz et al., 2011; Nacher and Leduc, 1985). Each class is pumped with an effective pumping rate depending on the pump spectral profile, and their populations are coupled by ME and velocity-changing collisions. This is a crude model, however it is sufficient to capture key features of velocity-selective optical pumping effects with few free parameters and it usually provides meaningful quantitative results.
Velocity-independent optical pumping models can be reliably used in specific cases: if (i)- broadband (“white”) pumping light is used, with L sufficiently larger than D, or if (ii)-the rate of change of populations from Eqs. (39) and (40), γγij/(γ + γij), is much smaller than ME and velocity-changing collision rates. Condition (ii) is automatically fulfilled if γ ≪ γe. Because γe scales with gas pressure p, high pressure optical pumping is immune to velocity-selective effects and a single set of populations can be used to locally characterize the effect of MEOP on the gas. In pure 3He at room temperature, γe = γ p/p*, where p* = 2.72 mbar is the crossover pressure for which γe = γ (from data in Sec. III.B.2). At lower pressure, a velocity-independent optical pumping regime is obtained only for laser intensities much smaller than a crossover value depending on pressure and laser linewidth, which can be evaluated using for instance a two-class model.
Indeed, during experiments where polarization decay occurs following the interruption of optical pumping, velocity-independent values of the populations are expected to be enforced by ME collisions as well.
3. High-field optical pumping
As mentioned above (Sec. III.A), the angular momentum structures of the 23S and 23P levels and the 1083 nm transition are deeply modified in high magnetic field. Figure 16 displays the absorption spectra and the energies of all Zeeman sublevels of 3He for B = 1.5 T, a field strength commonly met in MRI systems and thus of practical importance for applications. The six sublevels of the 23S state are organized in three pairs of states (Fig. 16(b) and (c), bottom graphs). In each pair the sublevel energy is mostly determined by the common dominant value of mS and the nuclear spin projections are almost opposite. Similarly, hyperfine coupling only weakly mixes levels of different mI values in the 23P state (Fig. 16(b) and (c), upper graphs). As a result, high-field spectra for a given light polarization comprise six main components clustered in two groups: a pair and a quartet, each group being unresolved at room temperature (Fig. 16(a)).
FIG. 16.
High-field metastability-exchange optical pumping transitions: (a) Computed absorption spectra at B = 1.5 T for the 23S-23P transition (low-pressure, optically thin gas at room temperature) for both circular polarizations. The strong unresolved components in the spectra are labeled , where n=2 or 4 refers to the number of involved transitions and ± to the sign of the circular polarization. Doublets of resolved weaker transitions of interest for optical detection purpose are highlighted. (b) and (c) Energies of the 3He sublevels at 1.5 T for the 23S and 23P states. The transitions induced by the σ−-polarized pumps (thick lines) and the suitable probes (thin lines) are displayed ( pump, σ+ probe in (b); pump, σ− probe in (c)).
In high-field, the parameters in Eq. (31) are (Lk) = (−1, L−, L+, −L−, 1, −L+), with L± ≃ 1; the change in the order of levels results from crossings occurring around 0.16 T and 4.7 T. Simplified models as well as full resolution of the rate equations of MEOP show that a large number of ME collisions, proportional to B2, are required to transfer a single unit of angular momentum between ground state and 23S state atoms (Abboud et al., 2004; Courtade et al., 2002). For instance, at null ground state polarization, strong pumping with the pair of lines may depopulate the A5 and A6 sublevels while a1 = … = a4 = 1/4 if spin-temperature is still obeyed for the unpumped sublevels. Hence PHe* = (L+ − 1)/4 = −sin2 θ+/2 with sin2 θ+ = 5.62 × 10−4 at 1.5 T. Similarly, strong pumping depopulates A1 to A4, so that a5 = a6 = 1/2 and PHe* = (1 − L+)/2. pumping is thus expected to yield positive nuclear polarization in spite of its negative circular polarization, with a (twice) faster pump-up rate, in fair agreement with experimental observations (Abboud et al., 2005; Nikiel et al., 2007). Over a wide range of field strengths and gas pressures, σ− pumping has been reported to be more efficient, possibly because the and groups are imperfectly resolved, especially at high pressure, and have opposite polarizing actions. The σ− pumping schemes are thus detailed in Fig. 16(b) and (c), together with the corresponding probing transitions that will be discussed in Sec. III.D.2.
The photon efficiency of these high-field optical pumping schemes can be as high as in low field (η ≈ 1 for pumping at high pressure) but this remains to be systematically studied (Batz et al., 2011; Nikiel-Osuchowska et al., 2013). With modified He level structures and only weak hyperfine couplings remaining in the excited states, high-field MEOP has two distinct features: highly absorbing lines can be used, with absorption coefficients ≃ 10 times larger than for C8 or C9 pumping at low field, and the transfer of angular momentum to the ground state is orders of magnitudes slower than in low field at a given pressure. For this last point, ME collisions fail to enforce a strong coupling between the 23S state populations, which is reminiscent of the low-field, low-temperature situation with its ME cross sections orders of magnitude lower than at room temperature.
It was initially argued that, due to the weak hyperfine coupling, MEOP would be inefficient in high field and early attempts were driven by applications and were limited to moderate field strengths: 0.1 T (Darrasse et al., 1997; Flowers et al., 1990) and 0.6 T (Flowers et al., 1997). It was only later that a key benefit of high-field MEOP was recognized: its efficient operation at high gas pressures (Courtade et al., 2000). More recently, high-field MEOP of 3He at low pressure has been shown to be efficient as well (Abboud et al., 2004; Maxwell et al., 2016; Nikiel et al., 2014). To date, no study of high-field MEOP in isotopic mixtures has been reported. Ultimately, the performance of MEOP for weakened ME coupling crucially depends on the balance between impeded polarization transfer and reduced polarization losses in the ground state, which will be discussed in Sec. III.E.
D. Optical methods of polarimetry
The measurement of the nuclear polarization of 3He gas in optical pumping cells can be made using a direct magnetic measurement (see Sec. V). However, optical methods relying on polarimetry of the visible fluorescence light emitted by He gas or on 1083 nm light absorption measurements are more widely used since they are simple to perform, provide high sensitivity, and operate in the presence of the discharge sustained for MEOP.
1. Fluorescence light polarimetry
Nuclear spin polarization is conserved during collisions which excite atoms from the ground state and hyperfine interaction subsequently couples electronic and nuclear orientations in the excited states. The electronic orientation, and therefore the degree of circular polarization of the fluorescence light emitted by atoms losing their excitation, both reflect the value of the ground state polarization (Pavlović and Laloë, 1970). The circular polarization Pfluo of the fluorescence light emitted along the direction of B is experimentally monitored using a rotating quarter-wave plate and a fixed linear polarizer (Bigelow et al., 1992; Lorenzon et al., 1993; Pinard and van der Linde, 1974), a 2-channel polarimeter consisting of a static quarter-wave plate and a beam-splitting polarizer (Stoltz et al., 1996b), or an electro-modulated polarimeter comprising a liquid crystal wave retarder (Maxwell et al., 2014b). Light of two spectral lines, at 668 nm and 588 nm, are significantly polarized and yield high signal-to-noise-ratio (SNR) measurements, with typical polarization ratios Pfluo/PHe ≈ 0.1 (Stoltz et al., 1996b). The ratios significantly decrease with B above about 10 mT due to the weakening of hyperfine coupling efficiency and decrease with gas pressure p. In spite of these variations and of its sensitivity to the discharge strength for the 588 nm line, fluorescence polarimetry is a convenient and accurate polarization measurement technique for low-p and low-B MEOP experiments. The two existing calibrations of the technique, performed at 668 nm using different methods (Bigelow et al., 1992; Lorenzon et al., 1993), agree within typical uncertainties of 2%.
2. Light absorption polarimetry
Since the early days of MEOP (Colegrove et al., 1963; Daniels and Timsit, 1971; Greenhow, 1964), 1083 nm light absorption measurements have been used to evaluate nuclear polarization in cells. The method is based on the fact that the ME-enforced spin-temperature distribution establishes a strong link between PHe and 23S state populations (Sec. III.B.3, Eqs. (35) and (36)). Probing absorption by two suitable Zeeman sublevels, or combinations of sublevels, is sufficient to infer the spin temperature β, and hence PHe, from the ratio of measured absorption coefficients. Additionally, the 23S state density nm integrated over the probe beam path can usually be inferred as well from such measurements.
At low B, two different probe beam polarizations are used to address different sublevels. For a longitudinal beam, propagating along B, σ+ and σ− polarizations selectively probe a5 and a6 when tuned to C8 or a1 + a2/3 and a4 + a3/3 when tuned to C9. For a transverse beam, the orthogonal linear polarizations (π : ⊥B and σ :|| B) provide independent combinations of populations only when tuned to C9. In isotopic mixtures the D0 transition component can be used in both geometrical arrangements. For longitudinal probe polarimetry the ratios of absorption coefficients for σ+ and σ− light (the subscript i is 8 or 9 for C8 or C9, 0 for D0) are:
| (43) |
This configuration offers the highest sensitivity at low polarizations, with linear coefficients −2, −5, and −4, respectively. For transverse probe polarimetry the ratios of absorption coefficients for π and σ light are:
| (44) |
The transverse configuration has a weak sensitivity at low polarizations since it only depends on . This is actually a useful feature for measurements performed while an intense pumping light is applied: the method is almost insensitive to the potentially large pump-induced deviations of populations from their spin-temperature values, such as displayed in Fig. 15 (Talbot et al., 2011).
As is done for fluorescence polarimetry, a mechanically or electrically modulated polarization or a 2-channel static scheme can be used for light absorption polarimetry. The probe beams must be weak enough so as not to locally affect the measured populations (low intensity) nor globally deposit angular momentum of the wrong sign (low absorbed power) (Talbot et al., 2011). In static schemes, a small geometrical separation of the two probe beams should be used to avoid coherently addressing common levels with the two beams, which has been observed to induce sizable artifacts in the measurements (Talbot et al., 2011).
At high B, all energy degeneracies of the Zeeman sublevels are lifted and two different probe beam frequencies are used to address different sublevels. Due to hyperfine decoupling, ME collisions imperfectly enforce the link between PHe and the 23S state populations, so that systematic measurement errors may appear even for moderate pump intensities. Fortunately, an adequate choice of optical transitions can be made to avoid such difficulties, by probing a pair of sublevels that are not addressed by the pump (Abboud et al., 2004; Nikiel-Osuchowska et al., 2013; Suchanek et al., 2007). This is achieved using the convenient line doublets highlighted in Fig. 16a: a periodic frequency sweep of the probe (at fixed circular polarization) sequentially yields values of two absorption coefficients that are used to infer both nm and PHe.
In spite of the need for a probe laser at 1083 nm, absorption polarimetry is preferred for high field or high pressure situations, and for measurements in isotopic mixtures, since it yields accurate results if adequate care is taken.
E. Relaxation in MEOP cells and steady-state polarizations
1. Discharge-induced polarization decay
MEOP apparatus and cells are designed so as to avoid significant polarization loss due to diffusion in field inhomogeneities or wall relaxation. When the discharge used to populate the 23S state is off, relaxation times of one to several hours are usually achieved. When the discharge is on and the pumping light is interrupted following polarization build-up, decay times 1/ΓD of order 1 min are typical. As the discharge intensity is increased, the metastable density nm and thus the polarizing rate increases but the achievable 3He polarization usually decreases. These dependencies vary with gas pressure and discharge frequency; Gentile and McKeown, 1993, reported on studies with pressures between 0.13 mbar and 6.5 mbar and frequencies between 0.1 MHz and 10 MHz. Several other groups have studied the influence of cell size and shape, configuration of external discharge electrodes, and frequency: over a wide range of pressures (up to hundreds of mbars) and fields (up to 4.7 T), nm and ΓD are found to positively correlate, with nm increasing less rapidly than ΓD with the discharge excitation power (Batz, 2011; Nikiel-Osuchowska et al., 2013).
The effect of an applied field exceeding usual low holding fields depends on pressure. At low pressures (p < 1 mbar), the ratios ΓD/nm increase in the applied field (at 30 mT and above). At higher pressures, on the contrary, ΓD/nm decreases in the applied field, which is potentially beneficial for efficient MEOP. For instance, at p = 2.45 mbar, ΓD is decreased by a factor of 2 to 4 at fixed nm for B = 30 mT (Batz, 2011). At higher p (tens of mbar) and B (1.5 T) the decrease can exceed a factor of 10. However, at such high pressures, the radial distribution of nm has an inverted distribution (with a minimum on cell axis) correlated to a plasma localisation near the cell wall (Dohnalik et al., 2011). This distribution is sensitive to B, which makes it delicate to quantitatively compare ΓD/nm ratios between low and high B.
Part of the polarization decay is due to relaxation in the 23S state, which drives a flow of angular momentum from the ground state reservoir with a rate ΓME. The remainder of the decay, with a rate Γg, is due to various relaxation processes directly affecting polarization in the ground state, for instance collisions with excited ionic or molecular He, or electronic excitation and loss of angular momentum by emission of polarized light in the radiative cascade (see Sec. III.D). Altogether, the decay rate is:
| (45) |
ΓME scales as the volume average over the cell of with a -dependent computed factor equal to 11/3 in pure 3He at low polarization (Batz et al., 2011). Moreover, nm is experimentally found to depend on during polarization decays at fixed discharge excitation levels, changing by up to ±20%. nm depends on the local balance of excitation to the 23S state in the discharge (involving ionization by electron impact, recombination, and radiative cascade), local decay through various processes (e.g., quenching by chemical impurities in the helium gas, 3-body conversion to metastable He2 molecules, Penning ionizing collisions), and atomic diffusion in the helium gas combined with excitation loss at the cell wall. Optogalvanic effects may also play a role in the balance of processes occurring in the plasma. Therefore nm may depend on and on MEOP conditions due, for example, to the influence of electronic orientation on the cross section of Penning collisions (Fedichev et al., 1996; Hill et al., 1972). In spite of the expected -dependency of ΓME, decays are systematically observed to be accurately exponential with PHe-independent rates ΓD over a wide range of gas pressures and field strengths, a so far unexplained observation (Batz et al., 2011; Nikiel-Osuchowska et al., 2013).
2. Optical-pumping-induced polarization loss
When the pumping light is applied, the time evolution of PHe as well as its steady-state value, PHe∞, can be inferred from the balance between the inflow of angular momentum of Eq. (30) and the loss term −ΓgPHe. This approach provides a detailed insight on the key relevant processes at play in MEOP, but it requires providing a trusted MEOP model with values for all physical and phenomenological parameters. A more pragmatic approach can be preferred for its robustness: a global angular momentum budget in which the rate of change of the ground state nuclear polarization is written as the net balance between the angular momentum actually transferred through optical pumping cycles to the 23S atoms and an angular momentum loss directly associated to the ground state atoms (Batz et al., 2011):
| (46) |
where Wabs is the pumping light power absorbed by the gas. The global polarization loss rate ΓR introduced in this approach is not a constant but may vary with PHe and MEOP conditions as does the photon efficiency η. Equation (46) involves known parameters and experimentally measurable quantities (PHe and Wabs), plus two unknown ones: η and ΓR. The photon efficiency η can be evaluated using a MEOP model or directly inferred from transient buildup measurements at PHe = 0 for which the loss term in Eq. (46) vanishes. For C8 or D0 optical pumping in low field, where η does not vary with PHe, ΓR can thus be fully inferred from experimentally determined quantities.
This pragmatic approach has been used to analyze experimental data for which the absorbed pump power was measured. Figure 17 displays selected results obtained at various pressures in low and high fields. Data obtained in steady-state (once PHe∞ has been reached, with a null left-hand side term in Eq. (46)) as well as data collected during polarization build-ups towards PHe∞ (three series of closely clustered symbols) are displayed. Despite the qualitatively different behavior of build-ups: exponential approaches towards PHe∞ at high fields (Nikiel-Osuchowska et al., 2013) contrasting with non-exponential build-ups having decreasing rates at high PHe (Batz et al., 2011; Gentile and McKeown, 1993), all corresponding data nicely collapse with the steady-state data. The decay rates ΓD for the various experiments tend to increase with pressure, and are strongly reduced, at fixed p, in high field (inset in Fig. 17). The polarization loss rates ΓR are found to significantly differ from ΓD for most of the data points. The differences ΓR − ΓD plotted in Fig. 17 for low-field data (open symbols) span over 4 orders of magnitude when experimental parameters are varied. The absorbed power Wabs is varied by changing the incident power or the absorption coefficient, through nm (in steady-state) or PHe (during build up); different cell diameters yield different cell volumes Vcell. The pumping-induced additional relaxation rates reveal a consistent linear-like variation only when plotted versus the ratio Wabs/Vcell. The 1.5-T-data display a similar pumping-enhanced relaxation behavior, but with a significantly reduced rate coefficient (the two lines in Fig. 17 correspond to linear laws with a ratio 30 of their slopes). Data obtained at 30 mT (Batz, 2011, Fig. 6.59) for p up to 2.45 mbar are identical to the corresponding low-B results. This field strength is sufficient to suppress the angular momentum loss which occurs in the radiative cascade and plays a key role in fluorescence polarimetry. The absence of effect of a 30-mT field on the data suggests that angular momentum loss in the radiative cascade plays no role in the pumping-induced polarization loss, but that larger hyperfine structures are involved.
FIG. 17.
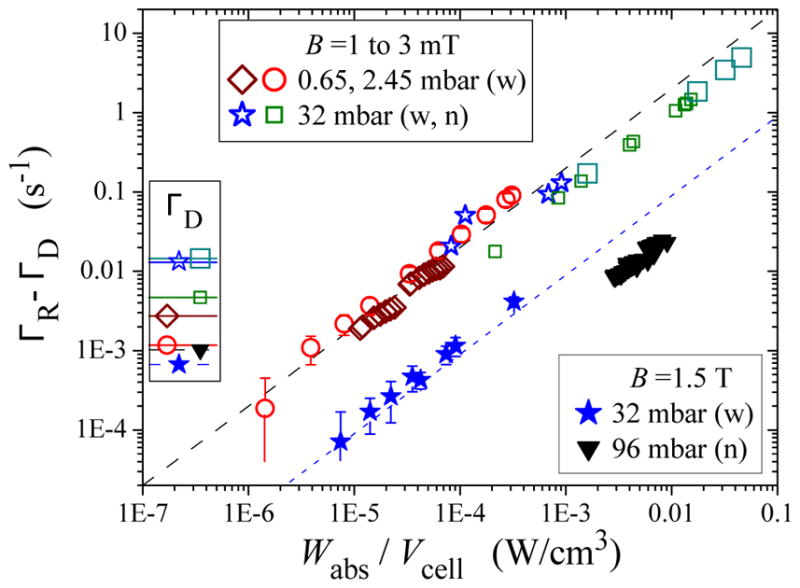
Optical-pumping-induced additional loss rates are plotted vs absorbed pumping power per unit volume for various gas pressures and fields (see legends) and cell diameters: wide (w: ≥ 5 cm) and narrow (n: 1.5 cm). Each of the two logarithmic scales spans 6 decades. The lines are guides for the eye corresponding to linear variations with linear coefficients 200 cm3/J (dashed line, low B) and 9 cm3/J (dotted line, 1.5 T). The ordinates of the horizontal lines in the box next to the left axis are the values of the pumping-free decay rates ΓD for the different sets of data. They range from 0.67 × 10−3 s−1 (filled stars) to 14.5 × 10−3 s−1 (large open squares). The figure is adapted from (Batz, 2011, Fig. 6.62); it compiles data from Mainz (
 ), Cracow (▼), and Paris (all other symbols; the small and large squares stand for weak and strong discharges in the same cell).
), Cracow (▼), and Paris (all other symbols; the small and large squares stand for weak and strong discharges in the same cell).
The physical processes causing such strong pumping-enhanced polarization losses remain to be elucidated. Radiation trapping (i.e., re-absorption of 1083 nm fluorescence light) or plasma modification by light-enhanced creation of a relaxing long-lived species through the 23P state have been considered as possible origins of pumping-induced loss mechanisms, but they could not account for the observations (Batz, 2011).
3. Steady-state polarization limits
Since the development of powerful lasers for MEOP, it has been noted that the achievable steady-state polarizations PHe∞ are in practice obtained at moderate laser intensities and that higher intensities only yield faster build up rates. Moreover, very high PHe∞ > 0.8 can be obtained only in a narrow pressure range. Figure 18 displays a compilation of steady-state polarizations obtained at low fields (open symbols) and high fields (filled symbols, B ≥ 1 T) over a wide range of pressures. A moderate field increase, just sufficient to impede angular momentum loss in the radiative cascade (30 mT, half-filled circles), reduces ΓD and increases PHe∞ for weak discharges, but the rapid decrease of PHe∞ with pressure is still observed. At higher fields, on the contrary, large polarizations can be achieved at 10- to 100-fold higher pressures.
FIG. 18.
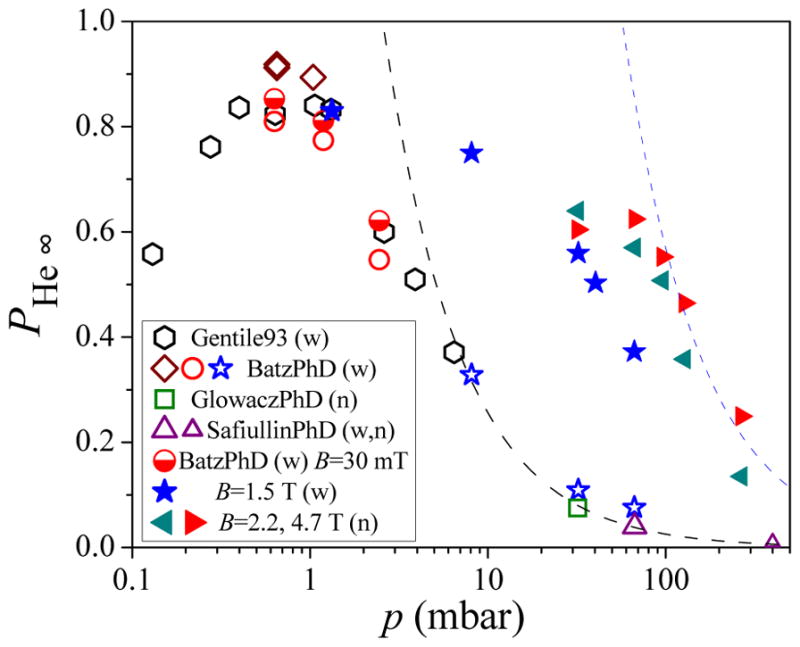
Variation with pressure of highest steady-state polarizations achieved by various groups at low fields (open symbols, 1 to 3 mT) and high fields (filled symbols, see legend). The two lines (PHe = 2.56/p and PHe = 57/p) are upper bounds derived from the lines in Fig. 17 (see text). The figure is adapted from (Batz, 2011, Fig. 6.48), with additional data from (Glowacz, 2011) and (Safiullin, 2011); it compiles data from Caltech (
 ), Mainz (
), Mainz (
 ), Cracow (
), Cracow (
 ,
,
 ), and Paris (all other symbols). Wide and narrow cells (w, n): see Fig. 17.
), and Paris (all other symbols). Wide and narrow cells (w, n): see Fig. 17.
Using the steady-state solution of Eq. (46) to relate PHe∞ to the absorbed power Wabs, one obtains strikingly different behaviors using for ΓR an optical-pumping-independent loss rate, such as ΓD, or the pumping-enhanced loss rate which has been consistently inferred from observations at high laser powers. The steep decease of PHe∞ with p above a few mbar is not reproduced by MEOP models assuming fixed losses. For instance, PHe∞ > 0.8 instead of 0.5 to 0.6 would be achieved for p = 2.45 mbar (Batz, 2011, Fig. 6.47). On the contrary, if the approximate scaling (ΓR − ΓD) ∝ Wabs/Vcell (the lines in Fig. 17) is substituted in Eq. (46) as a lower bound for ΓR, an upper bound for PHe∞ is found to be independent of Wabs, hence of the incident laser power, and to decrease as 1/p with pressure. The lines in Fig. 18 are upper bounds corresponding to the lines in Fig. 17 using η = 1.25 in Eq. (46). The angular momentum budget approach therefore provides a link between the observed pumping-enhanced polarization losses of the previous Section and the limits in the experimentally achieved PHe∞, especially at high pressures. Additionally, the spectacular increase in efficiency of MEOP at high pressure in high field can be attributed to the increasingly strong reduction of the pumping-enhanced loss for B > 1 T.
Achieving very high polarizations in low fields requires operating at a suitably low pressure with pumping light tuned to the most efficient transition component (usually C8 or D0) and carefully tailored to the needs:
a bandwidth of order the Doppler width to avoid velocity-selective pumping and the associated optical saturation,
a spatial transverse profile matched to the pressure-dependent density profile of the 23S state atoms, and
a very high degree of circular polarization because sub-% fractions of an opposite polarization are more efficiently absorbed and have thus a strong adverse effect at high PHe (Leduc et al., 2000).
At higher fields and pressures, stronger transition components are the most efficient ( or with a slight detuning from the composite line center, Abboud, 2005, Chap. 6) and the constraints 1 and 3 listed above can be somewhat relaxed thanks to collisional broadening and to large Zeeman splittings making the opposite polarization non-resonant. Recently, MEOP relying on the 23S -33P transition at 389 nm instead of the usual 1083-nm transition was demonstrated (Maeda et al., 2010). It was found to yield much lower polarizations than standard MEOP for comparable laser powers; this may be due to the smaller line component splittings (Sulai et al., 2008) and larger Doppler width for this transition which prevents selecting an isolated efficient component.
F. Lasers for MEOP
A succession of continually improving lasers has been used for MEOP. For traditional, low field MEOP a match to the 2 GHz Doppler-broadened absorption width is ideal. The first work in laser optical pumping was performed with color center lasers (Nacher and Leduc, 1985), and argon-ion pumped Nd:LMA lasers (Eckert et al., 1992). Velocity selective optical pumping was an issue for narrowband lasers, but increased efficiency was obtained by frequency modulation (Elbel et al., 1990). Frequency stabilization to the helium absorption lines was demonstrated (Heil et al., 1990). These early approaches were superseded in both performance and simplicity by the arc-lamp pumped Nd:LMA laser, which was constructed by replacing the Nd:YAG crystal rod in a commercial arc lamp-pumped laser and adding one or two etalons to produce a 2 GHz linewidth (Aminoff et al., 1991; Schearer and Tin, 1990). Tuning the laser was accomplished by varying the temperature and/or angle of the etalons. These lasers produced an output of several watts, but performance was highly dependent on crystal quality. Although the spectrum was actually a series of narrow peaks with substantial jitter the influence of velocity-changing collisions yielded efficient optical pumping (Elbel et al., 1990; Gentile et al., 2003), resulting in a substantial improvement in polarization and pumping rate (Gentile and McKeown, 1993). More recently Nd:LMA has been superseded by Yb fiber lasers (Chernikov et al., 1997; Gentile et al., 2003; Mueller, 2001; Tastevin et al., 2004). A Yb fiber oscillator and amplifier, properly constructed for MEOP, yields a fairly uniform spectrum with a ≈2 GHz spectral width. An alternative scheme is to use a diode laser oscillator and Yb fiber amplifier, which requires modulation for efficient optical pumping (Mueller, 2001). Comparable performance for a given power is obtained for Nd:LMA and both types of Yb lasers (Gentile et al., 2003), but Yb lasers have higher available power as well as greater convenience and a smaller footprint. For small sealed cells, 1083 nm diode lasers (≈50 mW) have been used to produce up to 40 % 3He polarization in pure 3He and 80 % in 3He - 4He mixtures (Stoltz et al., 1996a).
G. Compression approaches
Application to polarized targets for charged particle and photon scattering, MRI, and neutron spin filters requires compressing 3He gas polarized by MEOP. Following the path of an early attempt to use a Toepler pump (Timsit et al., 1971a), a successful compressor was developed for electron scattering at MAMI7 (Becker et al., 1999; Eckert et al., 1992). This compressor employed a mercury column to compress gas polarized by MEOP at a pressure of ≈ 1 mbar into a 100 cm3 target cell at ≈ 1 bar. For this device 50 % 3He polarization was achieved. At Mainz, this apparatus was replaced by a titanium piston compression apparatus (Becker et al., 1994; Surkau et al., 1997) that achieved pressures of a few bar. With subsequent improvements this compressor could produce between 60 % and 80 % 3He polarization with corresponding polarizing rates of between 4 bar-L/h and 1 bar-L/h (Batz et al., 2005). For this apparatus, the best achievable polarization in the open compression system under static conditions was 84 %, not far from the record high value of 91% achieved in a sealed cell. At Indiana University an aluminum piston compressor developed for neutron spin filters reached 50 % 3He polarization (Hussey et al., 2005). Both the Mainz and Indiana University apparatus employed two stages of compression with a buffer cell between the stages. In these and subsequent piston compressors, the polarization loss in the compressor itself was a few percent or less, but additional polarization losses are incurred due to gas flow and relaxation in the buffer cell, storage cell, and interconnecting tubing. A similar compressor was installed at the ILL8, but eventually replaced by a new apparatus, denoted “Tyrex”, for filling neutron spin filter cells. With further improvements, a typical value of 75 % 3He polarization has been obtained in NSF cells (Lelievre-Berna, 2007). A compression system denoted HELIOS was put into operation at the FRM II reactor in Munich (Hutanu et al., 2007a) and more recently a compression apparatus is also planned for use at ISIS (Beecham et al., 2011).
In parallel with the development of these large scale piston compression apparatus, smaller scale compressors based on peristaltic (Nacher et al., 1999) and diaphragm pumps (Gentile et al., 2001) have been employed for polarized gas MRI. For the peristaltic approach with flow rates of 0.1 bar-L/h and polarization preservation near unity, a polarization of between 30 % and 40 % could be achieved in the storage cell. Typically, 0.04 bar-L was used routinely for MRI applications (Bidinosti et al., 2003). More recently a similar apparatus was reported (Collier et al., 2012). The diaphragm pump (Gentile et al., 2001) method produced between 20 % and 35 % 3He polarization using pure 3He or between 35 % and 50 % polarization using 3He-4He mixtures. The typical outlet pressure was one bar, polarization preservation was 0.75, and the polarizing rate was 0.4 bar-L/h. However, further development of this approach has not been pursued.
IV. 3HE RELAXATION
A. Dipole-dipole
Newbury et al (Newbury et al., 1993) calculated that dipole-dipole interactions in bulk 3He limit the longitudinal relaxation time of polarized 3He to T1 = 807/p h (where p is the 3He pressure in bar, for a cell temperature of 296 K), where the polarization decays as exp(−t/T1) for 3He polarized along the applied magnetic field. This expression was verified for 3He pressure in the range between 4 bar and 12 bar in sealed SEOP cells made from aluminosilicate glass (Corning 1720)9. The observed limiting relaxation time T1 was extended to lower pressures in borosilicate glass (T1 = 300 h observed for p=2.5 bar (Smith et al., 1998)) and sol-gel coated borosilicate glass (Corning Pyrex) (T1 = 344 h observed for p=2.1 bar (Hsu et al., 2000)). The development of neutron spin filters led to practical interest in pressures near 1 bar, in which relaxation times of several hundred hours have been observed (Chen et al., 2011; Parnell et al., 2009; Rich et al., 2002b; Salhi et al., 2014) in SEOP GE180 cells,10 corresponding to relaxation times of order several thousand hours from wall relaxation and other sources. All of these cells contained Rb or Rb/K mixtures for the SEOP process, films of which have been shown to suppress wall relaxation as compared to bare glass cells (Heil et al., 1995).
B. Wall
1. Room temperature
In most practical situations, wall relaxation limits the achievable T1 but is not well understood. Nearly a half century ago it was found that, for bare glass cells at room temperature, aluminosilicate glass yielded relaxation times of tens of hours as compared to a few hours for the borosilicate glass Pyrex (Fitzsimmons et al., 1969). The temperature dependence of the relaxation times for both types of glass indicated that Pyrex relaxation at room temperature is dominated by permeation whereas adsorption dominates for aluminosilicate cells. In Pyrex, T1 becomes shorter at high temperatures due to increased permeation of He into the glass. A detailed model of 3He relaxation on the surface of borosilicate glass which accurately predicted observed relaxation rates and their temperature dependence was reported (Jacob et al., 2003).
For bare aluminosilicate glasses, which have negligible permeation and adsorption energies of order 100K, higher temperatures result in longer T1 due to reduced adsorption. This discovery (Fitzsimmons et al., 1969), plus the much better alkali metal chemical resistance, led to the dominance of aluminosilicate glass for SEOP. Nearly complete suppression of wall relaxation was achieved in the study of dipole-dipole relaxation with SEOP cells made from aluminosilicate glass (Newbury et al., 1993). It was found that cells made from fully blown glass yielded the best results and cleaning with nitric acid was suggested if a fully blown cell was not possible. The term “fully blown” indicates that all interior surfaces of the glass have been thoroughly melted; the resulting changes in these surfaces has generally been found to decrease 3He relaxation. Wall relaxation times of several thousand hours have also been observed in SEOP neutron spin filter cells and the importance of fully blown glass verified (Chen et al., 2011; Parnell et al., 2009; Rich et al., 2002b; Salhi et al., 2014).
In SEOP cells, alkali-metal coatings are always present. In a series of measurements with various glasses and metal coatings, the importance of metal coatings for reducing wall relaxation was demonstrated by Heil et al. (1995). Relaxation times of 68 h and 120 h were reported for cesium-coated Pyrex and cesium-coated aluminosilicate glass (Schott supremax)11, respectively. (It is interesting to note that Fitzsimmons et al. (1969) reported a relaxation time of 250 h for a SEOP cell.) In a later study that also included alkali-metal oxide coatings, it was found that despite the substantial role of the coating, the longest relaxation times were still obtained with aluminosilicate glass (Deninger et al., 2006). Hence the substrate still plays a role and it was speculated that this role could be associated with imperfections in the coating.
Whereas for both methods the longest relaxation times are usually obtained with aluminosilicate glasses, Pyrex SEOP cells have been employed for MRI applications (Jacob et al., 2002) and sol-gel coatings developed for SEOP cells (Hsu et al., 2000). More recently this technique was employed for a 3He target to avoid the substantial barium content in GE180 (Ye et al., 2010). MEOP storage cells typically employ cesium coatings; long relaxation times have also been obtained in fused silica (Deninger et al., 2006) and silicon-windowed Pyrex cells (Lelievre-Berna, 2007).
For compressor and target applications relaxation on various materials has been studied (Gamblin and Carver, 1965; Hussey et al., 2005; Jones et al., 1993; Katabuchi et al., 2005; Korsch et al., 1997; Timsit et al., 1971b).
2. Magnetic field and orientation effects
The advent of polarized gas MRI led to studies of relaxation in strong magnetic fields, which has revealed yet further unexplained aspects of 3He relaxation. In the first study (Jacob et al., 2001), it was found that the 3He relaxation rate could be increased by a factor of between 2 and 20 solely by exposure of SEOP cells to a magnetic field of a few tenth of a Tesla (few-kG). The original T1 could be restored by degaussing the cell, leading to the term “T1 hysteresis” to describe the observed behavior. Soon thereafter a significant dependence of T1 in SEOP cells due only to the physical orientation of the cell in a 3 mT (30 G) applied magnetic field was observed (Jacob et al., 2004). The presence of both alkali metal and heating of the cells associated with the SEOP process were necessary to produce this low-field orientation dependence. Later studies showed that the relaxation time can depend on the direction and strength of the magnetic field (Chen et al., 2011). More recently, the angular dependence of T1 was measured and found to be characteristic of a dipolar effect (Boag et al., 2014). Based on studies of boundary collisions of random walks, Bicout et al. (2013) concluded that the depolarizing effect of rare magnetic impurities may be much larger than expected and speculated that this enhancement could explain T1 hysteresis. In a test on a pure Rb, sealed SEOP cell, the T1 was observed to decrease by an order of magnitude for a field strength of only 40 mT (Chen et al., 2011).
T1 hysteresis was also observed in both Cs-coated and bare-glass, valved, MEOP cells (Hutanu et al., 2007b). The variation of T1 with magnetic field was measured and found to decrease exponentially with a constant of (30 mT)−1 [(300 G)−1]. Superconducting quantum interference device (SQUID) measurements revealed that most of the magnetization was associated with the glass valves, in particular the plastic parts and O-ring (Hutanu et al., 2007c).
C. Field gradients
Relaxation due to static and oscillating magnetic field gradients in a variety of regimes has been addressed in several references (Bohler and McGregor, 1994; Cates et al., 1988a, 1988b; Gamblin and Carver, 1965; Hasson et al., 1990; McGregor, 1990; Schearer and Walters, 1965). At room temperature, a practical expression for the relaxation rate 1/T1 in a uniform field gradient is given by (McIver et al., 2009)
| (47) |
where p is the gas pressure in bar and and are the gradients in the transverse components of the magnetic field (ie. the nuclear polarization is along the z-axis) in units of cm−1 (Cates et al., 1988a). For a cell at a pressure of one bar in a uniform gradient the gradient-induced relaxation time is 830 h. We note that Eq. (47) is valid as long as the product of Larmor precession frequency and the collision time is small compared to unity, valid for SEOP and also for MEOP at 20 G and typical pressures of order 1 mbar. For MEOP at very low pressures and high fields corrections to this are necessary (Schearer and Walters, 1965).
In more recent work, Zheng et al. (2011b) reported an approach based on calculating the autocorrelation function of spins to derive the magnetic field gradient-induced transverse and longitudinal relaxation of spins undergoing restricted diffusion. Guigue et al. (2014) performed a theoretical analysis of spin relaxation, for a polarized gas of spin 1/2 particles undergoing restricted adiabatic diffusive motion within a container of arbitrary shape, due to magnetic field inhomogeneities of arbitrary form. This analysis provided a theoretical justification for the usual assumption that the relaxation rate is determined by the volume average of the relevant gradients. Studies of gradient-induced relaxation in the transfer of gas into high magnetic fields has been also been reported (Maxwell et al., 2015; Zheng et al., 2011a).
D. Magnetostatic cavities
Neutron spin filters have motivated a variety of magnetostatic cavities to provide a uniform magnetic field for 3He gas on neutron beam lines. For these applications, there may be space constraints and significant stray fields, as well as neutron spin transport fields to be matched (see Sec. VII.A). In early applications of NSFs on the IN20 triple-axis spectrometer at the ILL, an end-compensated solenoid surrounded by a μ-metal box and a cubic iron box (40 cm3 by 40 cm3 by 40 cm3) was employed (Heil et al., 1999a). Soon thereafter a superconducting magnetostatic cavity (Cryopol) was developed for the D3 spectrometer that is capable of shielding an NSF from a nearby superconducting sample magnet operating at several Tesla (Dreyer et al., 2000). For moderate stray fields a magnetic parallel plate capacitor was developed, which provided a uniform 1 mT field transverse to the neutron beam (known as a “Magic Box” because when first made, the performance was better than predicted by finite element calculations) (Petukhov et al., 2006). This cavity consisted of a μ-metal box with sides that are magnetized by either coils or permanent magnets. The field lines enter the top plate and traverse the gap to the bottom plate. The original box was 80 cm along the beam line, but in a later, permanent-magnet design this distance was reduced to 40 cm (Hutanu et al., 2008) and the field increased to 1.7 mT. An end-compensated design shortened the length along the beam line to 28.4 cm (McIver et al., 2009), with field strengths up to 3.6 mT (Chen et al., 2014a). Magnetically shielded solenoids are also employed and typically provide greater protection from stray fields in space-constrained applications. Typical achievable gradients from magnetically shielded solenoids and magic boxes are between 2 × 10−4 cm−1 and 6 × 10−4 cm−1, corresponding to gradient-induced relaxation times of between 3700 h and 600 h, respectively (Chen et al., 2014a). Polarized gas MRI also provided a motivation for compact, light-weight and inexpensive magnetized boxes for transporting polarized gas, in some cases via air freight (Hiebel et al., 2010).
E. Ionizing radiation
Relaxation from 3 MeV protons for 3He polarized at mbar pressures by MEOP was reported in (Milner et al., 1987). Soon thereafter relaxation from 18 MeV 4He alpha particles for 3He polarized at 0.8 bar by SEOP was reported in (Coulter et al., 1988). Theoretical studies (Bonin et al., 1988a,b) showed that relaxation is caused by hyperfine coupling in 3He+ and spin-rotation coupling in . This relaxation source is greatly reduced in SEOP cells because nitrogen efficiently destroys these species. For application of MEOP cells to electron scattering, addition of a small ([N2]/[3He] ≈ 10−4) quantity of nitrogen after compression has been employed to quench these species (Meyerhoff et al., 1994). Nevertheless, there is substantial relaxation induced by high current charged particle beams, thus motivating the use of hybrid SEOP and rapid exchange of gas in double cell targets (Dolph et al., 2011; Singh et al., 2015). Due to the much greater sensitivity of pure 3He cells to ionization, large effects on 3He relaxation have been observed in MEOP cells due to neutron beams (Petukhov, 2016). For in-situ SEOP on neutron beam lines, beam-induced alkali-metal relaxation and other effects have been observed (see Sec. VII.E.3).
F. Low Temperatures
Motivated by the need fordense polarized 3He targets, as well as by studies of thermodynamic and transport properties of polarized 3He liquid, attempts to dynamically polarize liquid 3He from optically pumped room temperature gas were made soon after the first MEOP experiments were reported. In this seminal work (McAdams, 1968), polarized 3He gas was transported from a room temperature MEOP region through a connecting tube to a cold sample volume either by atomic diffusion or by transient gas flow during sample cool down. Most of the polarization was lost in the process, presumably due to fast wall relaxation in the cold part of the connecting tube or in the sample, with a maximum polarization of 0.15% achieved in a small liquid 3He volume. This work triggered studies of wall relaxation of 3He gas and liquid at low temperatures by several groups, using either Boltzmann-polarized or MEOP-polarised 3He. It was confirmed that clean, bare Pyrex glass walls induce increasing relaxation rates 1/T1 at decreasing temperatures below ≈ 100 K (Fitzsimmons et al., 1969; Lefevre-Seguin and Brossel, 1988), with T1 < 1 s below 20 K for a low-density gas (Barbé et al., 1975; Chapman and Richards, 1974).
In order to reduce the dwell time and polarization loss of 3He atoms colliding with cold glass walls, weak-binding diamagnetic cryogenic coatings have been added onto cell walls: Ne (Chapman and Bloom, 1976; Chapman, 1975), H2 (Barbé et al., 1975), or liquid 4He (Himbert et al., 1983). The adsorption energies of 3He atoms on these coated walls and the relaxation mechanisms of atoms or adsorbed layers on weakly relaxing substrates have been extensively studied and are well understood (Himbert and Dupont-Roc, 1989; Lefevre-Seguin et al., 1985; Lefevre-Seguin and Brossel, 1988; Lusher et al., 1988a,b). Depending on experimental conditions, different relaxation regimes can be observed. For instance, for low-density adsorbed 3He layers, T1 does not depend on the bulk gas density N and scales as exp(−2ΔW/kBT), where ΔW is the adsorption energy and kBT the thermal energy. On the contrary, for high enough gas density or low enough temperature, a complete 3He monolayer is condensed and T1 ∝ N is essentially temperature-independent. H2 coatings, for which ΔW ≈ 12 K, yield long T1s (up to several days) at 4 K (for comparison, ΔW ≈ 150K on bare glass). H2 coatings are efficient up to ≈ 6 K where they desorb and down to ≈ 2 K where a 3He monolayer is formed. 4He films extend the temperature range over which polarized 3He gas can be prepared or stored down to below 0.5 K (where the gas eventually liquefies if its pressure exceeds a few mbar).
Alternatively, cesium can be used to coat cell walls. With a 3He adsorption energy as low as ΔW ≈ 2.3 K (Tastevin, 1992a) cesiated glass (i.e. glass that has been in contact with cesium) is a weakly relaxing material from room temperature down to hundreds of mK. This property is plausibly linked with the non-wetting of alkali metal surfaces by 4He liquid and films (Nacher and Dupont-Roc, 1991), and was initially demonstrated at low temperature before being assessed at room temperature (Chéron et al., 1995).
Motivated by an experiment to measure the neutron electric dipole moment, new relaxation studies in liquid mixtures of 3He and 4He have been performed for the relevant polymer-coated materials at cryogenic temperatures (Ye et al., 2008, 2009).
With suitably coated walls, the way was open for reliable measurements of the bulk (dipole-dipole) relaxation in 3He gas (Lusher et al., 1988b) and 3He-4He liquid mixtures, for which T1 exceeding 10 hours have been recorded at low 3He concentration (Piegay and Tastevin, 2002). More importantly, McAdams’ strategy to prepare polarized cold 3He samples from optically polarized gas could be successfully applied. For instance, polarization was nearly fully preserved when transferred to a gas sample at 4.2 K, therefore exceeding 50% (Crampton et al., 1984; Leduc et al., 1984). Transient polarizations exceeding 40% were reported for liquid 3He just after liquefaction (Tastevin et al., 1988), subsequently decaying due to a bulk T1 of ≈ 300 s. Thermally-driven convective flow between the low- and high-temperature regions was used to sustain up to 56% nuclear polarization in steady-state in 3He-4He liquid mixtures (Candela et al., 1994). Such high polarizations could not be achieved by MEOP directly performed at low temperature due to the highly reduced rate of ME collisions (see Sec. III.B.2), but room temperature OP with polarized gas transfer enabled a series of low-temperature studies of 3He as a quantum fluid: characterization of spin waves (Nacher et al., 1984; Tastevin et al., 1985) and heat conduction changes (Larat et al., 1990; Leduc et al., 1987) in 3He gas and of phase coexistence for liquid 3He (Candela et al., 1994; Tastevin, 1992b; Villard et al., 2000). A similar technique was used with refillable cells to repeatedly prepare larger samples of polarized liquid in which magnetic interactions play a key role in non-linear NMR dynamics (Baudin et al., 2008; Hayden et al., 2007).
Let us also mention two alternative hyperpolarization techniques, not using MEOP but instead relying on nuclear relaxation and well-controlled phase transitions: rapid melting which yields up to 70% transient polarization in liquid 3He (Bonfait et al., 1984, 1987; Buu et al., 2000) and spin distillation which provides up to a sevenfold enhancement of the Boltzmann equilibrium polarization in the steady-state (Nacher et al., 1991; Rodrigues and Vermeulen, 1997; van Steenbergen et al., 1998).
V. 3HE POLARIZATION METROLOGY AND CONTROL
Absolute polarization measurements methods for dense samples of polarized 3He include water-calibrated NMR (Lorenzon et al., 1993; Romalis et al., 1998), EPR (Babcock et al., 2005b; Romalis and Cates, 1998), neutron transmission (Chupp et al., 2007; Jones et al., 2000), and magnetometry (Noël et al., 1996; Wilms et al., 1997). In all of these methods except neutron transmission, the absolute 3He polarization is determined by measuring both the 3He magnetization and the 3He density. The 3He density is determined at the time a cell is filled with gas. For SEOP cells the density can also be determined after the cell is filled from the width and/or shift of the alkali-metal absorption lines (Kluttz et al., 2013; Romalis et al., 1997). For SEOP electron-scattering targets, the two methods of determining the density have been reported to agree within 2% (Romalis and Cates, 1998) and 1% (Singh et al., 2015). Since SEOP cells contain both 3He and N2 gas, the pressure width and/or shift coefficients for both gases are required, although the shift and width is typically dominated by the 3He gas. These coefficients were measured for the Rb D1 and D2 lines with a typical accuracy of 2% (Romalis et al., 1997), and more recently for both Rb and K with a typical accuracy for the width coefficient of 1% (Kluttz et al., 2013). For neutron transmission, the density is replaced with the opacity, which is determined from the transmission through an unpolarized cell.
A. NMR
1. Adiabatic fast fassage
In the technique of adiabatic fast passage (AFP) NMR (Abragam, 1961), an RF magnetic field is applied transverse to the static magnetic field. If the magnetic field is swept such that the Larmor frequency passes through the RF frequency (or the RF frequency is swept so that it passes through the Larmor frequency), the 3He polarization will invert. From a quantum-mechanical point of view, this process is essentially an avoided crossing due to perturbation from the RF field (Rubbmark et al., 1981). The sweep rate and RF amplitude are adjusted to minimize losses resulting from polarization inversion. If a pickup coil transverse to both the static and RF magnetic fields is employed, a signal proportional to the magnetization is obtained. In order to minimize the large background from inadvertent pickup of the applied RF field, the pickup coil must be carefully adjusted to be orthogonal to the driving RF magnetic field. An absolute 3He polarization measurement can be obtained if the response of the pickup coil and associated electronics is calibrated using a thermally polarized water cell with exactly the same size and geometry as the 3He cell. Despite the extremely small thermal polarization of order 10−8 in typical holding fields of a few millitesla, these calibrations can be performed with uncertainties of a few percent. (In principle the magnitude of the AFP signal could be determined absolutely for a given apparatus, but in a study of this approach discrepancies of between 20%–50% were observed with cell to cell variations (Chen et al., 2011).) Further descriptions of this technique and its application to electron scattering targets (Chupp et al., 1987; Romalis et al., 1998), polarimetry of low pressure MEOP cells (Lorenzon et al., 1993), and polarized gas MRI12 have been reported.
Whereas losses of a few tenths of a percent are typically encountered for AFP, techniques have been developed to reduce these losses substantially. The primary motivation has been for neutron spin filter cells that are not actively optically pumped on the beam line, but in which the 3He polarization may be frequently inverted during use so as to invert the neutron polarization. Besides the usual optimization of RF magnetic field strength and sweep rate, the RF field is modulated by a Gaussian envelope during the sweep (McKetterick et al., 2011; Petoukhov et al., 2006). Using this approach, losses of 10−5 per flip have been obtained. In a compact RF solenoid with shielding to confine the RF field, loss as low as 0.03% was reported (Ye et al., 2013).
2. Free induction decay
Monitoring of 3He polarization can also be performed by free induction decay (FID) (Bloch, 1946), in which an RF pulse tips the 3He spins and a pickup coil detects the freely precessing transverse component of the magnetization following the tip. This approach avoids the need for orthogonal drive and pickup coils. The measurement can be non-destructive by either using small tip angles for a coil of comparable size to the cell and/or a small coil. The decay of the signal is given by the transverse relaxation time , which is typically dominated by dephasing due to magnetic field gradients and thus given in high-pressure cells by , where γ/2π=32.4 kHz/mT (3.24 kHz/G) is the gyromagnetic ratio and ΔB is the variation in the magnetic field B over the gas volume sampled by the coil. Values of in typical applications range from a few milliseconds to a few hundred milliseconds. For the typical low pressures employed for low field MEOP, averaging of the field gradient (motional narrowing (Cates et al., 1988b; Pines and Slichter, 1955)) can increase substantially above this value. The use of FID is discussed in several references (Chen et al., 2011; Krimmer et al., 2009; Lorenzon et al., 1993; Parnell et al., 2008). Whereas FID is typically used for relative measurements, Gentile et al. (2001) employed an FID system with large coils that was calibrated against fluorescence light polarimetry in an MEOP cell and then applied to determine absolute 3He polarization in compressed gas.
3. Radiation damping issues and control
For pickup coils with a high filling factor, or dense samples with a high polarization, the nuclear magnetization can be significantly affected by radiation damping, i.e. the action of the resonant RF field generated by NMR-precession-driven current in the coils. For 3He gas polarized in the low Zeeman energy state, the lifetime of the observed FID signals is decreased whereas for the high energy state it is increased and unstable precession or maser operation can occur (Gentile et al., 2001). During AFP magnetization reversal, radiation damping affects the applied RF field and therefore modifies lineshapes and may increase losses, even if the unstable regime is avoided. Radiation damping is traditionally reduced using weakly coupled coils (at the expense of detected signal amplitudes) or applying a suitable field gradient to the sample (Romalis and Happer, 1999; Zheng, 2002). Active feedback schemes can also be used to control radiation damping without signal-to-noise penalty (Baudin et al., 2011; Hoult, 1979).
B. Neutron transmission
3He polarization measurement by neutron transmission relies on the simple equations governing a neutron spin filter (Coulter et al., 1990; Jones et al., 2000). The neutron polarization Pn is given by
| (48) |
where λ is are the neutron wavelength and T0(λ) and Tn(λ) are the transmissions of unpolarized neutrons through the unpolarized and polarized 3He cell, respectively. Hence Pn, which is typically what is of the greatest interest for spin filter applications, can be accurately determined with only a relative transmission measurement. Using the relationship
| (49) |
where O(λ) is the opacity, the 3He polarization PHe can be determined. The opacity is determined from T0 = Te exp(−O(λ)), where Te is the transmission of the cell without 3He gas. Hence to determine PHe from Pn requires an absolute measurement of T0(λ) and determination of Te. The opacity is given by the product of the neutron absorption cross section (which typically increases linearly with neutron wavelength), the 3He density, and the 3He path length. Because of the dependence on neutron wavelength, neutron transmission measurements are typically performed with monochromatic beam lines at reactors or with the use of time-of-flight (TOF) analysis at pulsed neutron sources. Neutron transmission has been used to calibrate NMR-based polarization measurements for routine 3He polarimetry on reactor beams for a wide variety of neutron spin filter cells with typical accuracy of a few percent (Chen et al., 2011). Te can be determined by neutron transmission measurements before the cell is filled, but for routine applications is often determined from measured values for glass transmission (eg. see (Chupp et al., 2007)) and estimated glass thickness; a typical value and uncertainty is Te = 0.88 and 0.02, respectively. With TOF analysis, T0 vs. wavelength can be fit, allowing extraction of the opacity and Te for a filled cell. Using this approach, determinations of PHe at pulsed sources with uncertainties of 2% have been reported (Chupp et al., 2007; Tong et al., 2012).
C. Detection by magnetometry
Accurate magnetometry has also been applied to measure 3He polarization in a 5 bar MEOP-based target for electron scattering with accuracy of 3% (Krimmer et al., 2009). This approach relies on the known dipolar field for a spherical sample of polarized gas. Since the field due to the gas is only ≈1 mG or 0.02% of the holding field, the change in field strength is determined by a fluxgate magnetometer upon inverting the 3He polarization with low-loss AFP (Wilms et al., 1997). In addition, a spherical phantom with equidistant current loops was employed to calibrate the exact location of the magnetic field sensor.
VI. CHARGED PARTICLE AND PHOTON SCATTERING TARGETS
Polarized 3He provides a reasonable approximation to a polarized neutron target because the proton spins are primarily paired off. Hence about 87% of the 3He spin is carried by the lone neutron (Friar et al., 1990; Laskaris et al., 2015, 2013). It is this property of the 3He nucleus that yields its utility for studies of the spatial distribution of charge, magnetization, (Bernauer, 2012) and spin in the neutron. 3He targets for nuclear and particle physics with charged particle and photon beams fall into four groups: 1) continuously polarized SEOP external targets for electron (Singh et al., 2015), photon (Ye et al., 2010), proton (Häusser et al., 1995; Katabuchi et al., 2005), and pion (Larson et al., 1991a) scattering, 2) MEOP external targets that are polarized remotely and transported to electron (Krimmer et al., 2009) and photon beam lines (Krimmer et al., 2011), 3) MEOP internal targets for electron storage rings (DeSchepper et al., 1998), and 4) continuously polarized MEOP external targets for electron scattering (Eckert et al., 1992; Jones et al., 1993). In addition, an MEOP-based polarized 3He ion source is under development for RHIC13 (Maxwell et al., 2014a). Fig. 19 shows two current target designs.
FIG. 19.
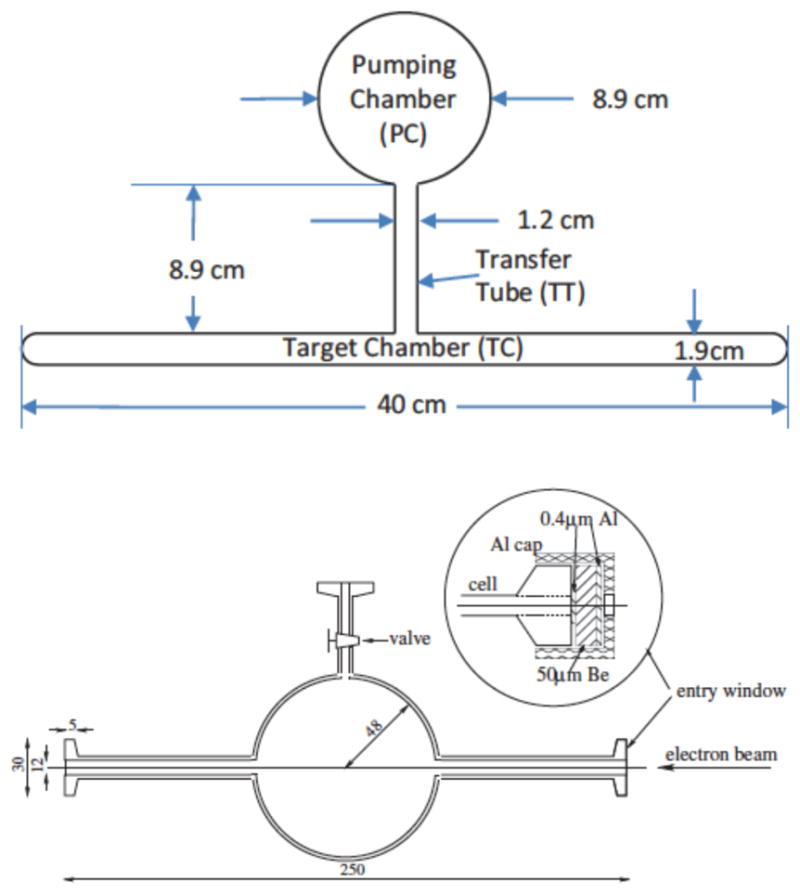
Diagrams of current electron beam target designs. Top: JLAB, from Dolph et al. (2011). Bottom: Mainz, from Krimmer et al. (2009). Dimensions are in mm.
A. SEOP
1. TRIUMF, Bates LINAC, SLAC
Early SEOP targets were constructed from Corning 1720 glass cells between 10 cm3 and 35 cm3 in volume, filled to pressures of several bar, and optically pumped with several watts of laser light from Ti-Sapphire lasers. Typical 3He polarization of 50 % was obtained for pion (Larson et al., 1991a) and proton (Häusser et al., 1995) scattering at TRIUMF14, and production of polarized muonic helium at LAMPF15 (Newbury et al., 1991). Application to electron scattering followed soon thereafter but required the use of double cells (Chupp et al., 1987) due to the strong ionization produced by electron beams with energies of several hundred MeV and several μA beam currents. In the double cell configuration, diffusion links the polarization produced in an optical pumping cell to the target cell via a transfer tube. The first double cell targets (Chupp et al., 1992) were employed for quasielastic scattering of polarized electrons at the Bates Linear Accelerator Center, which provided some of the first double-polarization results for determination of the neutron’s electric form factor (Thompson et al., 1992). Using a few watts of laser light from a Tisapphire laser, an ≈50 cm3 cell was polarized up to 40 % in tests and was maintained between 10 % and 27 % during the experiment. Double cell targets were then applied for deep inelastic scattering experiments (Johnson et al., 1995) with ≈25 GeV energy electrons at SLAC for the first studies of the neutron’s spin structure functions (Anthony et al., 1993, 1996). In this experiment, 3He polarization between 30 % and 40 % was maintained in a 9 bar, 200 cm3 double cell with 20 W of laser light from five Ti-sapphire lasers, each pumped with a 20W argon-ion laser (Johnson et al., 1995). With improved polarimetry, further studies of spin structure functions were performed with this target. (Abe et al., 1997a,b).
2. JLAB and TUNL targets
Double cell targets based on the design employed at SLAC were developed for electron scattering experiments at Jefferson Laboratory with typical energies of ≈6 GeV, and have steadily improved in performance and capability. As shown in Fig. 19, these targets typically have an optical pumping cell between 6 cm and 9 cm in diameter, a ~2 cm diameter target cell between 25 cm and 40 cm long, end windows ~120μm thick, densities of 7–12 amg, and relaxation times of 20 h to 70 h (Alcorn et al., 2004; Singh et al., 2015). They have been constructed from Corning 1720 and, more recently, GE180 glass. Optical pumping is typically performed with ≈90 W of laser light from three fiber-coupled diode laser systems. The typical 3He polarization achieved was 30% to 40% in the first experiments on electromagnetic form factors (Xiong et al., 2001; Xu et al., 2000) and neutron spin structure functions (Amarian et al., 2004, 2002; Zheng et al., 2004a,b). With the use of hybrid SEOP, the 3He polarization was increased to ~45% for a more recent measurement of the neutron’s electric form factor (Riordan et al., 2010). For hybrid SEOP with spectrally narrowed lasers, the polarization has been increased to between 50 % and 55 % for studies of asymmetries in scattering from transversely or vertically polarized targets generally aimed at improved understanding of the origin of the neutron’s spin (Allada et al., 2014; Huang et al., 2012; Katich et al., 2014; Parno et al., 2015; Qian et al., 2011; Zhang et al., 2014; Zhao et al., 2015). In a detailed study of these targets, a maximum off-line value of 70 % and a detailed analysis of achievable polarization was reported (Singh et al., 2015). Future experiments with even higher luminosity are expected to employ a new type of double cell in which exchange of gas between the optical pumping and target cells is increased by convection (Dolph et al., 2011). In this new design, there are two transfer tubes and gas circulation is produced by heating one tube.
Recently, two different SEOP targets have also been employed at TUNL16 A target was developed for measurements of spin-correlation coefficients in p + 3He elastic scattering (Daniels et al., 2010; Katabuchi et al., 2005), in which the 3He was polarized by SEOP at 8 bar and transferred through a plastic tube to spherical Pyrex cells with Kapton film covering the apertures for the beam and scattered particles. For application to gamma-ray beams, a sol-gel coated Pyrex double cell was employed to avoid background signals scattered off the barium present in GE180 glass (Ye et al., 2010). The relaxation time in the 7 bar target was 35 h and a maximum off-line 3He polarization of 62 % was obtained. In experiments to study three-body physics, ≈ 40 % 3He polarization was maintained (Laskaris et al., 2015, 2014).
B. MEOP
1. Early targets, Bates LINAC, internal targets
The high efficiency of MEOP allowed for early targets based on optical pumping with lamps (Baker et al., 1969; Phillips et al., 1962). The first laser-pumped targets were based on a double cell approach with a cryogenic target cell to increase the density (Alley and Knutson, 1993; Milner et al., 1989). Such a target operated at a gas pressure of 2.6 mbar and a target cell temperature of 17 K was employed for quasielastic scattering of polarized electrons at the Bates Linear Accelerator Center, which provided some of the first double-polarization results to determine the neutron’s electric form factor (Jones et al., 1993; Jones-Woodward et al., 1991; Woodward et al., 1990). In this experiment, between 20 % and 30 % 3He polarization was maintained using 0.3 W of laser light. The 10 cm long copper target cell was coated with frozen nitrogen to permit target cell relaxation times between 400 s and 1000 s, depending on beam current. The same target design was employed in subsequent experiments to determine the neutron’s magnetic form factor (Gao et al., 1994) and to further study quasielastic scattering (Hansen et al., 1995). Employing optical pumping with a few watts of laser light from a Nd:LMA laser (Gentile and McKeown, 1993) allowed for over 38 % 3He polarization at 2.5 times higher average electron beam current (Gao et al., 1994).
Concurrently with these external targets, MEOP was applied to internal targets for storage rings. In these targets, gas flows from an optical pumping cell through a capillary to a open target cell. The first polarized 3He internal target (Lee et al., 1993) was employed at the Indiana University Cyclotron Facility for measurements of quasielastic scattering of polarized protons from polarized 3He to study the ground state spin structure of the 3He nucleus (Bloch et al., 1995; Lee et al., 1993; Miller et al., 1995). A Nd:LMA laser was used for optical pumping and the average 3He polarization in the target was 46 % at a 3He flow rate of 1.2 × 1017 atoms/s. Soon thereafter, an internal target with a cryogenic target cell (DeSchepper et al., 1998; Korsch et al., 1997; Kramer et al., 1995a,b) was employed for spin-dependent deep inelastic scattering of 27.5 GeV polarized positrons at DESY17 (Ackerstaff et al., 1997; DeSchepper, 1998). For an ultrapure aluminum target cell cooled to 25 K, the 3He polarization was 46 % during the experiments. This target also used a variation of the fluorescence polarimetry method: rather than a discharge, high energy positrons provided the required atomic excitation and the 3He polarization was determined from the circular polarization of 492 nm light from the 4 1D - 2 1P transition. An internal target at NIKHEF 18 operating at a nominal atomic flow rate of 1 × 1017 s−1 yielded a nuclear polarization of 0.50 for a target thickness of 0.7 × 1015 cm−2 at a target temperature of 17 K (Poolman et al., 2000).
2. MAMI
Early 3He targets for electron scattering at MAMI employed a Toepler pump (Eckert et al., 1992), in which a mercury column compressed gas polarized by MEOP at a pressure of ≈ 1 mbar into a 100 cm3 target cell at ≈ 1 bar. The polarized gas was continuously recirculated from the target cell to the optical pumping cell for repolarization at a flow rate of 1018 atoms/s. Optical pumping with a few watts of laser light from a Nd:LMA laser (Eckert et al., 1992) yielded an average 3He polarization of 38 % in the first MAMI experiment to determine the neutron’s electric form factor (Meyerhoff et al., 1994). In a later experiment on the same topic (Becker et al., 1999), several improvements, including a cesium coated cell with a relaxation time of 6 h, yielded 50 % 3He polarization. The continuous flow Toepler pump apparatus was replaced by remotely polarized cells filled using a piston compression apparatus (Becker et al., 1994; Surkau et al., 1997) to a pressure of 4 bar. This approach was employed for further measurements of the neutron’s electric form factor (Bermuth et al., 2003). More recently, an improved piston compression apparatus yielded 72 % 3He polarization in a 25 cm long, cesium-coated, quartz, 5 bar target cell with beryllium and aluminum foil windows (Krimmer et al., 2009), see Fig. 19. Relaxation induced by the electron beam (see Sec. IV.E) yielded typical beam-on relaxation times between 30 h and 40 h, hence the cells were replaced twice a day. A time-averaged 3He polarization of 56 % was maintained over the course of a three week measurement of the neutron electric to magnetic form factor ratio (Schlimme et al., 2013). Similar targets (Krimmer et al., 2011) have also been applied for the tagged photon beam facility at MAMI (Costanza et al., 2014).
C. Brief summary of physics enabled
The complex and diverse subatomic physics studied with 3He targets is clearly beyond the scope of this review. Nevertheless, we briefly summarize the overall topics of the majority of experiments. The charge and magnetization distributions are typically characterized by the electric and magnetic form factors of the neutron, and , respectively, which nonrelativistically can be considered to be the Fourier transforms of the charge and magnetization distributions. The first experiments with polarized 3He focused on measuring these form factors and on testing the three-body nuclear physics calculations needed to quantitatively validate the approximation of a polarized 3He target as a neutron target. Since the neutron is neutral overall, measuring the electric form factor is particularly difficult. In addition, measurements must be performed over a wide range of momentum transfer to test theoretical predictions. In the last 25 years, these measurements have greatly improved the knowledge of these form factors, yielding more precise tests of nucleon models (Qattan and Arrington, 2012). Whereas the uncertainty for the earliest measurements were larger than the values themselves and were performed at only a single value of relatively low momentum transfer, recent measurements have fractional uncertainties of 15 % or better and cover a wide range of momentum transfer (Gentile and Crawford, 2011). Although is generally the more difficult and desired measurement, is also important because typically is actually determined from a measurement of the ratio combined with separate measurements of .
Analogous to the electric and magnetic form factors are the more complex spin structure functions that are related to the distribution of angular momentum in the neutron (Aidala et al., 2013). These studies have been primarily motivated by understanding the origin of the spin of the neutron. Improvements in the polarized 3He targets have allowed for a substantial improvement in the precision of tests of the fundamental sum rules for spin structure from quantum chromodynamics. Decades ago it was determined that contrary to expectations, the intrinsic quark spins contribute only a small fraction of the nucleon spin. Despite many years of effort, studies of the origin of the spin of the nucleon are still incomplete. Continuing studies with polarized 3He targets have focused on the possible contribution to the nucleon spin from the orbital angular momentum of the quarks.
VII. NEUTRON SPIN-FILTERS
Neutron spin-filters (NSFs, Ioffe et al. (2011)) produce highly spin-polarized beams of low energy neutrons, or analyze the neutron spin state, by passing the neutrons through a glass cell of polarized 3He in a uniform magnetic field. The near 100% contrast in the spin dependence of the 3He neutron absorption cross section (Coulter et al., 1990) results in highly polarized neutron beams or very efficient spin analyzers. Although other devices such as supermirrors (Mezei, 1976) and Heusler alloy (Freund et al., 1983) are employed for polarizing neutron beams (Williams, 1988), NSFs are advantageous for large area and large divergence beams, can be used for cold, thermal, and epithermal neutrons, and decouple polarization selection from wavelength selection. For both MEOP and SEOP, NSF cells are typically polarized offline, transported to the neutron beam line, and stored in various magnetostatic cavities. In addition, there has been increasing use of SEOP-based in-situ NSF systems.
A. Principles
The large cross section for neutron absorption by 3He arises from a broad, unbound, resonance that yields a proton and a triton. The strong spin dependence arises because absorption only occurs if the neutron and 3He spins have their spins antiparallel. Whereas the cross section for capture of 25 meV neutrons with spin antiparallel to the 3He nuclear spin is 10666 barns, the ratio of the absorption for neutrons with parallel and antiparallel spin has been determined experimentally to be less than a few percent and estimated theoretically to be less than 0.5 % (Huber et al., 2014), and the scattering cross section is only a few barns (Mughabghab et al., 1981). Hence for a sufficient opacity (product of gas density, cross section, and cell length) of 100 % polarized 3He, all neutrons with antiparallel spin would be absorbed, while nearly all neutrons with parallel spin would be transmitted, resulting in 100 % neutron polarization and 50 % transmission. Although imperfect 3He polarization reduces the achievable neutron polarization and transmission for a given opacity, increasing the opacity allows any neutron polarization to be achieved at the expense of transmission. The absorption cross section is directly proportional to wavelength, hence higher energy (shorter wavelength) neutrons require greater opacities. Typical room temperature pressure-length products vary between 4 bar-cm and 25 bar-cm for neutrons with energies between 2 meV and 80 meV (wavelengths between 0.6 nm and 0.1 nm). For a 3He polarization of 75 %, 90 % neutron polarization with 28 % neutron transmission can be obtained. These values include the transmission of 0.88 due to neutron scattering from a typical glass NSF cell. The basic equations governing the relationships between opacity, 3He polarization, and neutron polarization and transmission appear in many publications (Coulter et al., 1990; Jones et al., 2000). These relationships allow both the neutron and 3He polarization to be determined by neutron transmission measurements. NSFs are also used to analyze neutron polarization; in this case an analyzing power of 90 % with a transmission for the desired spin state of 54 % can be obtained. Fig. 20 shows the variation of the neutron polarization and transmission with the pressure-length-wavelength product for 3He polarizations of 0.5, 0.75 and 1. The ideal opacity factor depends on the type of experiment and its optimization has been addressed with different approaches (Gentile et al., 2005a; Goossens and Cussen, 2002; Tasset and Ressouche, 1995; Williams, 1999); a typical value is 3 bar-cm-nm.
FIG. 20.
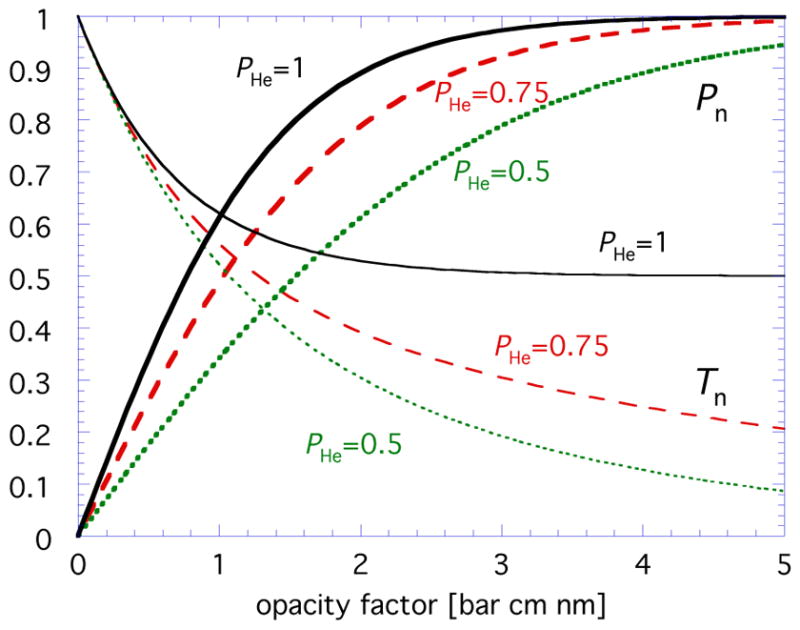
The variation of the neutron polarization Pn and transmission Tn with the opacity factor, where the opacity factor is given by the pressure-length-wavelength product in bar cm nm, for 3He polarizations (PHe) of 0.5, 0.75 and 1. The neutron transmissions shown do not include the transmission of 0.88 due to neutron scattering from a typical glass NSF cell.
The strong neutron absorption cross section for boron restricts the choice of materials for NSFs. For SEOP, GE180 is generally employed due to issues with 3He permeation and temperature-dependent relaxation for quartz (Ino and Muto, 2007; Ino et al., 2005; Ye et al., 2013). Sapphire (Chen et al., 2011; Masuda et al., 2005) and silicon-windowed Pyrex cells (Chen et al., 2011) have also been investigated for SEOP, but use has been limited due to relaxation issues. For MEOP cells, which do not need to be heated, both quartz and silicon-windowed Pyrex cells are routinely used (Hutanu and Rupp, 2005; Lelievre-Berna, 2007). Neutron transmission and scattering from glasses are important practical issues for NSFs and have been studied by various groups (Babcock et al., 2014; Chen et al., 2004; Chupp et al., 2007; Sakaguchi et al., 2011b). A variety of MEOP and SEOP cells are shown in Fig. 21 and discussed below.
FIG. 21.

Neutron spin filter (NSF) cells. Clockwise from top left: MEOP silicon-windowed cells (largest cell is 14 cm diameter by 10 cm long, Lelievre-Berna (2007)), MEOP wide-angle cell (6 cm inner diameter, 20 cm outer diameter, 12 cm tall, Andersen et al. (2009)), cells for neutron interferometry (larger cell is 4 cm diameter by 6 cm long, Huber et al. (2014)), horseshoe SEOP cell (9 cm inner diameter, 23 cm outer diameter, 7.5 cm tall, Chen (2016)), SEOP wide-angle cell (14 cm inner diameter, 30 cm outer diameter, 8 cm tall, Ye et al. (2013)), typical SEOP NSF cell (12 cm diameter by 7 cm long, Chen et al. (2011)).
As discussed in Sec. IV.D, various magnetostatic cavities are employed to provide the highly homogeneous magnetic field required to maintain the 3He polarization. Polarized neutron beam lines typically have magnetic fields to maintain the neutron polarization from the polarizer to the analyzer (“guide fields”) and fields for various types of neutron spin flippers. Often a sample under study may be immersed in a strong magnetic field provided by electromagnets or superconducting magnets, hence protecting the NSF from field gradients is an important practical consideration. In addition, maintaining the polarization of the neutron beam during transitions between the homogeneous magnetic field for the 3He to the sample and/or neutron spin flipper fields can be difficult, in particular on space-constrained apparatus not originally designed for NSFs. In some cases AFP NMR is used to flip the 3He polarization (and thus the neutron polarization or analyzer direction) so as to avoid the need for traditional neutron spin flippers. For some applications, the polarizer NSF, sample, and analyzer NSF are all immersed in the same field, thus bypassing neutron spin transport issues but also precluding the use of strong sample fields (Ye et al., 2013).
B. Neutron scattering implementation: SEOP
The first test of an NSF based on SEOP was performed at LANSCE19 (Coulter et al., 1990) and applied to the search for parity violation in neutron resonances. A 3He polarization of 70 % was obtained in a 3 cm3 cell optically pumped with 1 W of laser light with a line width of 40 GHz that was provided by a standing-wave dye laser pumped by a krypton ion laser. A neutron polarization of 20 % was produced in a beam of epithermal neutrons (energy of 0.734 eV, 0.03 nm wavelength). Soon thereafter an SEOP-based NSF was tested at the ILL (Tasset et al., 1992), but the ILL program shifted to MEOP (see Sec. VII.C).
For neutron scattering, an ongoing program in SEOP-based NSFs was begun at the NCNR20 (Jones et al., 2000), first demonstrated for small angle neutron scattering (SANS) (Gentile et al., 2000), and subsequently applied to polarized neutron reflectometry (PNR) (Chen et al., 2004), triple-axis spectrometry (TAS) (Chen et al., 2007a), and wide-angle neutron polarization analysis (Ye et al., 2013). For these applications, SEOP cells are polarized off-line, transported to the neutron beam line, and stored in magnetostatic cavities. Typical NSF cells for SANS, PNR and TAS are blown from GE180 glass, between 8 cm and 12 cm diameter, and filled to pressures between one and two bar. Cells for wide-angle analysis have been formed by optically sealing three sections of blown glass together so as to cover a 110 degree angular range (Ye et al., 2013). More recently, fully blown cells for wide-angle analysis have been fabricated by first blowing a toroidal GE180 cell and then closing off a 270 degree section from the toroid (Chen et al., 2016). The current state of the NCNR program has been summarized recently (Chen et al., 2014a).
The relatively small size of SEOP apparatus is well-matched to in-situ operation on neutron beam lines (Jones et al., 2006). An in-situ NSF has been operated routinely on the Magnetism Reflectometer at the SNS 21 (Tong et al., 2012) and smaller in-situ systems have been developed for the HB3 triple-axis spectrometer and the hybrid spectrometer (HYSPEC) at the SNS (Jiang et al., 2014). At LENS22, a continuously pumped analyzer has been demonstrated for spin echo small angle neutron scattering (SESANS) (Parnell et al., 2015). Compact NSFs with low loss AFP NMR for on-beam operation have been developed at KEK23 (Ino et al., 2012, 2005). More recently, there has been spin filter development at the Materials and Life Science Facility at J-PARC24 and at the High-flux Advanced Neutron Application Reactor at KAERI25 (Lee et al., 2016). At J-PARC, in-situ SEOP neutron spin filters have been demonstrated for SANS (Sakaguchi et al., 2011a), PNR, and polarized neutron imaging (Hayashida et al., 2016).
The SEOP programs at the Forschungzentrum Jülich (Babcock et al., 2016) and the ISIS spallation source26 (Beecham et al., 2011) have also focused on in-situ systems for continuously polarized 3He. An apparatus was developed in which a 3He polarization of 80 % was maintained in a 100 cm3 cell by SEOP with two 100 W diode lasers, each spectrally narrowed to 0.2 nm bandwidth with an external cavity (Babcock et al., 2011b). It has been applied to PNR and SANS (Babcock et al., 2016). Cells for wide-angle polarization analysis (Salhi et al., 2016) fabricated from sections of fully blown doughnut-shaped GE180 cells (Salhi et al., 2014) are under development. More recently, two compression apparatus have been bult at the ILL for use at the ISIS pulsed neutron and muon source (Beecham et al., 2011) and the Australian Nuclear Science and Technology Organization (Lee and D’Adam, 2016).
C. Neutron scattering implementation: MEOP
Due to the large size of most compression apparatus, NSFs based on MEOP are typically polarized off-line and transported to neutron beam lines. The first demonstration of an MEOP-based NSF was performed at the Univ. of Mainz with polarized 3He from a piston compression system (Surkau et al., 1997). A similar compressor was installed at the ILL, with the capability to produce between 50 % and 55 % 3He polarization for a variety of cell designs (Heil et al., 1999a). The first application was on the IN20 triple-axis spectrometer (Kulda et al., 1998). With the development of the superconducting magnetostatic cavity “Cryopol” (Dreyer et al., 2000), an NSF was applied for spherical neutron polarimetry (SNP) with hot (0.08 nm wavelength) neutrons on the D3 instrument (Lelievre-Berna et al., 2005). Large solid-angle polarization analysis at thermal neutron wavelengths was demonstrated on the two-axis diffractometer D1B using a cesium-coated quartz cell that analyzed a 90 degree range of scattering angles (Heil et al., 2002). The 530 cm3 banana-shaped cell exhibited a relaxation time of 92 h. With improved optical pumping using a 30 W ytterbium fiber laser instead of an 8 W Nd:LMA laser, a spin filter with a 3He polarization of up to 70 % was demonstrated at the Mainz reactor (Batz et al., 2005). Concurrently a new compressor, denoted “Tyrex”, was constructed at the ILL and employed to fill spin filter cells with 65 % – 70 % polarized 3He gas at rates of 1 bar-L/h to 2 bar-L/h (Petoukhov et al., 2006). An NSF employing a 14 cm diameter silicon-windowed, valved, spin filter cell was demonstrated on the D17 reflectometer, along with a “local filling” approach for refreshing the 3He daily (Andersen et al., 2006). With further improvements, a typical value of 75 % 3He polarization has been obtained in NSF cells, enabling a large range of neutron scattering applications (Andersen et al., 2009; Lelievre-Berna, 2007; Lelievre-Berna et al., 2010; Stewart et al., 2006). A similar compression system, denoted HELIOS, was put into operation at the FRM II reactor27 (Hutanu et al., 2007a) and has been applied to SNP at the hot neutrons single crystal diffractometer POLI-HEiDI (Hutanu et al., 2011). More recently a compression apparatus is also planned for use at ISIS (Beecham et al., 2011).
D. Brief summary of neutron scattering physics enabled
The primary application of NSFs in neutron scattering is in the study of magnetic materials. Neutron polarization analysis allows for separation of nuclear from magnetic scattering (Moon et al., 1969; Williams, 1988). SNP and TAS have been employed to study magnetic ordering in antiferromagnetic crystals (Blanco et al., 2006; Hiess et al., 2001; Hiess et al., 2001; Poole et al., 2007; Zaharko et al., 2006), magnetization distributions (Boehm et al., 2003; Brown et al., 2002), magnetoelectric and multiferroic crystals and films (Brown et al., 2005; Cabrera et al., 2009; Lee et al., 2008; Ratcliff et al., 2011; Tian et al., 2008), and the interplay between magnetism and superconductivity (Chen et al., 2008; Schneider et al., 2006; Wang et al., 2011). The ability of NSFs to analyze the polarization of diffusely reflected neutrons has been applied to magnetic multilayers (Nickel et al., 2001), domain walls in magnetic thin films (Radu et al., 2003, 2005), periodic magnetic rings (Ogrin et al., 2007), and superlattices (Wildes et al., 2008). For SANS, NSFs allow for polarization analysis which has been implemented via SEOP at the NCNR (Gentile et al., 2000; Krycka et al., 2009), and via MEOP at the Hahn-Meitner Institute in Berlin, Germany (Keiderling et al., 2008; Wiedenmann, 2005) and the ILL (Honecker et al., 2010). At the NCNR, several recent studies have focused on understanding the structure of magnetic nanoparticles (Hasz et al., 2014; Krycka et al., 2014, 2009, 2010, 2013, 2011). SANS with NSFs has also been employed to study multiferroics (Ramazanoglu et al., 2011; Ueland et al., 2010), magnetostriction (Laver et al., 2010a), exchange-bias (Dufour et al., 2011), and nanowires (Pimpinella et al., 2013). Polarization analysis also allows for separation of coherent from spin-incoherent scattering (Moon et al., 1969; Williams, 1988), which is relevant to biological samples due to the substantial spin-incoherent scattering from hydrogen. Applications of NSFs to this technique are emerging (Babcock et al., 2016; Sakaguchi et al., 2011a).
NSFs have advantages over neutron optical devices for polarized neutron imaging because they can provide a uniform analyzing power without optical distortions of the neutron beam. At the ILL, polarized neutron imaging using NSFs from the Tyrex compressor was demonstrated and applied to visualize small-scale magnetic features and trapped magnetic flux (Dawson et al., 2011). In addition, depolarization imaging has been used to image ferromagnetic phase separation in real space (Laver et al., 2010b).
E. Application to fundamental neutron physics
1. Accurate neutron polarimetry
For a monochromatic neutron beam, the neutron polarization produced by an NSF can be determined from the ratio of the transmission of unpolarized neutrons with the NSF polarized and unpolarized. If the NSF is used as a polarization analyzer, the analyzing power can be determined by this method and then employed to accurately measure the polarization of a neutron beam. This simple approach allows for highly accurate measurements of neutron polarization or analyzing power (Coulter et al., 1990; Jones et al., 2000). However, fundamental neutron physics experiments often require high neutron flux for statistics and thus polychromatic beams. With time of flight analysis, typically available at a pulsed neutron source, accurate polarimetry can be extended to polychromatic beams. At LANSCE neutron beam polarization was measured with an absolute accuracy of 0.3 % in the neutron energy range from 40 meV to 10 eV (Rich et al., 2002a). More recently, Ino et al. (2011) reported a measurement of the near-unity average neutron beam polarization produced by supermirror benders at J-PARC with an absolute accuracy of 0.03% in the neutron wavelength range from 0.1 nm (81 meV) to 0.7 nm (1.7 meV). At continuous sources, one can use “opaque” spin filters, i.e. NSFs with sufficient opacity such that the analyzing power is near unity for the relevant wavelengths (Zimmer et al., 1999). This approach has been applied to neutron beta-decay (see Sec. VII.E.2).
2. Applications
The first application of NSFs to fundamental neutron physics was for measurements of the parity-violating neutron spin rotation in the 0.734 eV resonance in lanthanum. Measurements were performed at KEK in Japan (Sakai, 1997; Sakai et al., 1998), LANSCE (Haseyama et al., 2002), and the ILL (Heil et al., 1999b). At LANSCE, SEOP with diode lasers was employed with 56% (polarizer) and 29% (analyzer) 3He polarization obtained in 6 bar cells. At the ILL, the MEOP compression system was employed to obtain 50 % 3He polarization in a 5 cm diameter, 20 cm long NSF analyzer filled to 3 bar. More recently, a new experiment to search for time reversal violation in neutron transmission has been proposed (Bowman and Gudkov, 2014).
An SEOP-based, large area NSF for long term continuous operation (Chupp et al., 2007) was employed for the study of parity violation in the absorption of cold neutrons by compound nuclei (Gericke et al., 2006) and hydrogen (the “NPDGamma” experiment) (Gericke et al., 2011). With two 30 W fiber-coupled diode lasers (between 1.5 nm and 2 nm bandwidth), 57 % 3He polarization was obtained in 11 cm diameter GE180 cells (Gentile et al., 2005b). The NSF was successfully operated for one year, but the 3He polarization declined to ≈30 % due to long term effects on the cell from the neutron beam (see Sec. VII.E.3.) The neutron polarization was determined with an accuracy of 0.1 % with time of flight analysis.
Measurements of the electron (A), neutrino (B) and proton (C) asymmetries in polarized neutron beta-decay provide accurate tests of the Standard Model (Jackson et al., 1957). These experiments require highly accurate determinations of the neutron polarization. For these experiments, the use of a series of opaque spin filters (see Sec. VII.E.1) has been employed to determine neutron polarization to 0.1 % accuracy, thus substantially reducing this contribution to the overall uncertainty budget (Mund et al., 2013; Schumann et al., 2008, 2007). An NSF was also used to determine the neutron polarization in a measurement of the neutron electric dipole moment via spin rotation in a non-centrosymmetric crystal (Fedorov et al., 2010).
Polarized 3He has also been used to determine the spin dependence of the neutron scattering length for 3He, which is important for nuclear few body models. Two different methods were used. In the first method, the pseudomagnetic precession of an unpolarized neutron beam passing through a sample of polarized 3He was detected using a neutron spin-echo spectrometer (Zimmer et al., 2002). A 6 cm diameter, 10 cm long glass cell with flat, parallel, silicon windows was filled with polarized gas using the ILL MEOP compression system. In the second method, the spin-dependence of the phase shift for polarized neutrons passing through a sample of polarized 3He was determined by neutron interferometry (Huber et al., 2014). A 2.4 cm diameter, 4.2 cm long glass cell with flat, parallel glass windows was polarized off-line by SEOP and installed inside a neutron interferometer. The relaxation times observed during the experiments were between 75 h and 120 h (Zimmer et al., 2002) and between 135 h and 150 h (Huber et al., 2014). For the interferometry experiment, the polarization of the monochromatic neutron beam was determined with NSFs to better than 0.1% absolute accuracy. The two measurements differ by two standard deviations (Huber et al., 2014).
3. Neutron beam effects
Effects of the neutron beam on the operation of in-situ SEOP NSFs were first observed in the NPDGamma experiment (see Sec. VII.E.2) and soon thereafter studied at LANSCE (Sharma et al., 2008). Further studies at the ILL revealed that at a neutron particle flux density of 4.7 ×109 cm−2s−1, the alkali-metal relaxation rate increased from 100 s−1 to 1000 s−1 (Babcock et al., 2009). The relaxation rate was found to vary with the square root of the neutron flux, consistent with the source being the ionization produced by the energetic triton and proton produced in neutron absorption by 3He. The alkalimetal relaxation rate was found to increase rapidly (time scale <1 s), followed by a further slow rise on a time scale of hundreds of seconds. Studies of the cell whitening that had been previously reported after long term exposure to the neutron beam (Chupp et al., 2007) indicated that this problem may be reduced in K-Rb hybrid cells. The origin of this whitening is unknown, but speculated to be due to the production of RbH and/or alkali azides. It was demonstrated that a double cell configuration, an approach already long employed for electron scattering, is a practical method to bypass these neutron beam effects. In a later study (Babcock et al., 2011a), it was observed that the slow component of alkali-metal relaxation increases with increasing nitrogen density in the SEOP cell.
VIII. MAGNETIC RESONANCE IMAGING
A. Introduction and History
The application to MRI (Leawoods et al., 2001; Möller et al., 2002) arguably provides the most visible and salient connection of hyperpolarized noble gases to commercial (in this case, medical) technologies. The two noble gases with nuclear spin 1/2, 3He and 129Xe, yield relatively long relaxation times due to absence of a nuclear quadrupole moment that can interact with electric fields at surfaces. Conventional 1H MRI of lung tissues is very challenging, mainly due to the very short (microseconds) NMR-signal lifetimes (Cutillo et al., 1991) resulting from the large magnetic susceptibility broadening in the lung microstructures (alveolar spaces and connecting bronchioles). Rapidly moving gases average away this broadening, but their low density relative to protons in water introduces a severe sensitivity problem. A hyperpolarized inert gas is potentially the ideal signal source for investigating lung function: it serves as a tracer of gas-flow in an organ whose principal function is to move gas, it is not metabolized and interacts minimally with the body, and the enhanced magnetization overcomes the intrinsic sensitivity problem (Kastlér, 1950).
In the early 1980’s, even as MRI itself was still being developed for clinical use, Bhaskar et al. (1982) noted that about 11 bar·cm3/h of highly polarized 129Xe might be produced with 1 W of laser power, although at the time, attention was focused on the ability this would afford to produce dense polarized targets. Some combination of the biological relevance of xenon (an anesthetic, which dissolves in lipid tissue), relatively fast spin-exchange rates (Zeng et al., 1985), and the ability to freeze and transport xenon with minimal polarization loss (Cates et al., 1990) led to the first rudimentary MR images of excised mouse lungs (Albert et al., 1994). However, the tipping point for the technology was not so much the marriage itself of hyperpolarized noble gases to MRI, as it was two major improvements in related technology. For SEOP, the advent in the early 1990’s of inexpensive high-power high-efficiency solid-state diode lasers increased the available photon flux from a few to many tens, even hundreds of watts (utilizing arrays of such lasers), at a fraction of the size and cost of Ti:Sapphire lasers (Wagshul and Chupp, 1989). For MEOP, where the intrinsic efficiency of the process does not put a premium on high-power lasers, the principal problem solved was compression of 3He gas polarized at very low pressure up to atmospheric pressure without substantial loss of polarization; this was accomplished at large scales through use of titanium piston pumps (Becker et al., 1994) and at smaller scales with peristaltic (Nacher et al., 1999) and diaphragm (Gentile et al., 2001) pumps.
The dramatic scaling up of production rates necessary for human-lung imaging occurred for both SEOP and MEOP at about the same time in the early 1990’s, leading rapidly in both cases to the first human lung MR images using hyperpolarized 3He, reported in 1996 (Ebert et al., 1996; MacFall et al., 1996). For the next decade or so, the field was dominated by imaging with 3He, which was available for ≈ $100/(barL) at near 100% isotopic abundance, has a large magnetic moment (75% of the proton’s moment) and for which the physics (and hence the scale-up) of SEOP and MEOP were generally better understood than for 129Xe SEOP. In comparison, naturally abundant xenon (26% 129Xe) costs ≈ $50/(bar L) (isotopically enriched samples cost about an order of magnitude more), and the 129Xe nuclear moment is roughly one-quarter that of the proton. Commercial development of SEOP began in 199628; currently two small companies 29 offer high volume 3He and 129Xe SEOP systems.
In small-animal work, MR microscopy with 3He (Chen et al., 1998) was developed to resolve airways down to the fifth generation of branching in the guinea pig lung. In humans, stunning 3-D data sets of the lung with resolution of a few millimeters can now be acquired in a ten-second breath-hold (Qing et al., 2015). A variety of diseases have been studied, among them cystic fibrosis (Flors et al., 2016; Mentore et al., 2005; Paulin et al., 2015) (see Fig. 22), asthma (Kruger et al., 2014; Tustison et al., 2010), and emphysema (Kirby et al., 2013; Quirk et al., 2011; Spector et al., 2005).
FIG. 22.
Coronal (view from the front of the body) 3He magnetic resonance images from a healthy subject (left) and three patients with cystic fibrosis (CF). The number of ventilation defects increases with worsening results of a standard global ventilation test, FEV1 (forced expiratory volume in one second). FEV1 is shown as a percentage of the predicted value for a healthy subject. From Mentore et al. (2005).
B. Gas handling and delivery
Using SEOP, 3He can be polarized in reusable valved glass cells at pressures of up to 10 bar prior to being released for use in imaging. Jacob et al. (2002) provided a recipe for making such cells from inexpensive borosilicate (Corning Pyrex) glass, with a length of capillary tube separating the main cell volume from the wetted valve materials. The high pressure limits T1 due to the 3He-3He dipolar mechanism (Newbury et al., 1993) and cells are frequently dispensed and refilled, so that using the low-permeability glasses that produce the longest wall-relaxation times (see Section IV.B.1) is not necessary. When polarized by MEOP for imaging, 3He is typically compressed to a few bar and stored in separate long-T1 storage cells (Heil et al., 1995). Such cells have not only been used to supply 3He for imaging experiments performed locally, but have also been transported by air in compact magnetized boxes (?), for use in MRI at distant sites around the world (Schmiedeskamp et al., 2013; Thien et al., 2008; Wild et al., 2002).
While more sophisticated ventilation systems have been employed, both for small-animal (Nouls et al., 2011) and human (Guldner et al., 2015) imaging, the most straightforward and widely used method to deliver hyperpolarized 3He to human subjects has been the use of plastic-valved flexible bags made of and or coated with one or more fluoropolymer materials; the most used among these is Tedlar30. Both the cell containing polarized 3He and the bag are connected to a gas-handling manifold via a plastic valve built into the bag. Once the bag is filled with the requisite gas mixture, it is detached from the manifold and handed to the subject inside the magnet. We note that imaging protocols often call for 3He to be mixed with nitrogen to conserve it in cases where there is plenty of signal intensity available. The use of 3He for human lung MRI is subject to country-specific regulations, such as FDA regulation in the United States, where it requires an exemption as an investigational new drug (IND).
C. Imaging modalities
Several important characteristics of hyperpolarized 3He are of immediate consequence to MRI and necessitate rethinking of the pulse-sequence and signal-acquisition techniques commonly used for conventional 1H MRI. First, there is no relevant thermal recovery of the magnetization: the thermally polarized signal is negligible and typically characterized by a long recovery time T1. Hence, while no (time-consuming) signal averaging is required, strategies are necessary to ration the magnetization inhaled in one breath to acquire the hundreds to thousands of data sets with different applied magnetic-field gradients needed to obtain an image. The imaging sequences in early work employed successive small-angle excitations (Kauczor et al., 1997; de Lange et al., 1999) or successions of rapidly refocused gradient echoes (Saam et al., 1999). Strategies for variable-strength excitations (variable flip angle) were also explored to make more efficient use of the magnetization (Deppe and Wild, 2012; Markstaller et al., 2000; Santyr et al., 2008). Thus, while total imaging time is ultimately limited by T1 relaxation of the inhaled gas, the fact that there is no waiting period due to thermal recovery means that image acquisition speed is not T1-limited; this was exploited to make frame-by-frame animations of gas motion during breathing (Saam et al., 1999; Salerno et al., 2001), pointing toward the use of 3He to study lung function (van Beek et al., 2004; Fain et al., 2010) as well as structure. More recently, a wide range of more sophisticated pulse sequences and imaging protocols has been introduced (Ajraoui et al., 2010; Horn et al., 2016; Salerno et al., 2003).
Second, the available 3He polarization depends only on the process (SEOP or MEOP) and the subsequent prevention of T1 relaxation in the stored sample prior to the start of image acquisition. Contrary to the case in conventional 1H imaging, it does not depend on the applied magnetic field. Most human and animal MR imaging is ultimately dominated by conductive currents that produce Johnson noise in the sample and not in the probe. One can combine these facts to conclude that the SNR across a wide parameter space is approximately independent of applied field, although Parra-Robles et al. (2005) identifies an optimal low field of ≈ 0.1 T, with a factor of two loss in SNR occurring near the edges of the range 0.01 to 1 T. In the lung, there is the added prospect of improving image fidelity at low field by reducing artifacts due to susceptibility broadening created by multiple air-water interfaces (Salerno et al., 2005). Low-field MRI using 3He has been developed and implemented both by Owers-Bradley et al. (2003) at 0.15 T and by Durand et al. (2002), the latter using a commercial 0.1 T MR imager to obtain images with higher SNR and greater fidelity than achieved at the more standard 1.5 T field. In principle, one should be able to image with 3He at even lower fields (< 50 mT). In practice, the results have been mixed, as one has to contend with increased pick-up and 1/f-noise at lower Larmor frequencies, and concomitant gradients, i.e., the inability at very low fields to assume that gradients orthogonal to the applied-field direction are negligible (Yablonskiy et al., 2005). There is often the need to develop dedicated pulse-sequences, probes, gradient coils, and other components, since commercial MRI has developed for several decades almost exclusively at ever-increasing applied fields. Despite these limitations, ultra-low-field MRI with 3He has been developed and implemented by Venkatesh et al. (2003), Bidinosti et al. (2004), and by Tsai et al. (2008), who studied the orientation-dependence of ventilation in the human lung with a custom-built 5-mT Helmholtz-coil pair in which a human subject could stand.
Third, paramagnetic molecular oxygen strongly relaxes 3He (at a rate of about 0.5 s−1) for pure O2 at 1 bar (Saam et al., 1995), typically limiting imaging time in vivo to about 30 s for a single inhaled bolus of gas. Conventional MRI hardware is more than up to the task of using the magnetization during this time to acquire biologically relevant information, but one must be aware and account for the fact that a change in 3He density cannot easily be discerned from a change in magnetization, potentially confounding image interpretation. Schemes for continuous or quasi-continuous breathing of 3He have been developed for humans and for small animals. This apparent limitation can also be turned around to quantify regional pulmonary oxygen pressure in human lungs (Deninger et al., 1999; Hamedani et al., 2013; Miller et al., 2010).
While state-of-the-art spin-density-weighted 3He lung images are quite spectacular in terms of brightness and resolution (see Fig. 22), there are several other mechanisms that can be used to generate MRI contrast. T1-weighting via interaction with O2 has already been discussed; highly mobile 3He is also particularly suited to diffusion imaging (Schmidt et al., 1997), where the attenuation of signal due to diffusion through applied magnetic-field gradients (Stejskal and Tanner, 1965) can be used to map the mean-squared displacement of spins during some characteristic time interval. This is particularly useful in the study of emphysema and related diseases, which are characterized by disintegration of the walls separating the many tiny (≈ 300 μm) alveolar (gas-exchange) spaces. The characteristic MRI diffusion time is easily chosen for 3He to be significantly greater than the diffusion time across alveolar spaces in a healthy lung, but on the order of or less than the diffusion time across the larger spaces that are created as the disease destroys the alveolar walls. Bright regions are those where 3He diffusion is restricted by many boundaries; diseased areas, where there is strong attenuation, show up darker. The quantitative measure of mean-squared displacement mapped in such images is known as the apparent diffusion coefficient (ADC). Several groups have developed and refined this technique (Conradi et al., 2006; Fain et al., 2005; Wang et al., 2008). A quantitative model based on anisotropic 3He diffusion and ADC measurement was developed by Yablonskiy et al. (2009) and supported through comparison to histologic sections of healthy and diseased tissue (Woods et al., 2006). An alternate competing view of such modeling and its limitations was put forth by Parra-Robles and Wild (2013).
D. Current Limitations and the Future of 3He MR Imaging
While substantial progress has been made during the last two decades in improving image quality and applying various contrasts to study healthy and diseased lungs, these applications to date are generally termed “pre-clinical,” meaning that the technique has yet to find a specific application that warrants regular clinical use. One of the more promising avenues may be MR imaging of neonates (Krjukov et al., 2007; Tkach et al., 2014; Walkup et al., 2015), where it is known that lung development is the limiting factor for survival of premature infants and where MRI is particularly attractive for longitudinal studies due to the absence of ionizing radiation.
Knowledge of the physics and correlated technological issues surrounding production of highly polarized 129Xe has improved somewhat in the last decade (Freeman et al., 2014; Nelson and Walker, 2001; Nikolaou et al., 2013). Coupled with native interest in the more biologically active xenon gas as a signal source and with the scarcer (and much more expensive) availability of 3He (Shea and Morgan, 2010), it would appear that, short of mining the moon for 3He (Woods, 2013), future further development of hyperpolarized-gas MRI as a clinical tool will primarily focus on 129Xe.
IX. PRECISION MEASUREMENTS
Although most applications of hyperpolarized 3He exploit the large achievable magnetizations, 3He has tremendous potential itself for precision spectroscopy due to both large magnetization and long coherence times(T2). In a generic spectroscopy experiment, the uncertainty principle implies a measurement uncertainty for a single measurement on a single particle. For the N = [He]V polarized nuclei, and repeating the measurement times, the quantum-limited precision of frequency measurement becomes . Defining the equivalent frequency noise spectrum δν through implies a quantum projection frequency noise of
| (50) |
for a V = 1 cm3 volume if T2 is limited by dipole-dipole relaxation (Sec. IV.A). The corresponding magnetic (Romalis, 2013) and rotation (Donley and Kitching, 2013; Walker and Larsen, 2016) sensitivities are and . As such samples are now realizable, the primary challenges are detection and, for non-magnetic applications, compensation for environmental magnetic noise. Detection strategies to date include inductive pickup (Chupp et al., 1988), SQUID detection (Gemmel et al., 2010; Greenberg, 1998; Savukov et al., 2008), external atomic magnetometers (Cohen-Tannoudji et al., 1969; Koch et al., 2015a, b; Kraft et al., 2014), fluxgate magnetometers (Guigue et al., 2015; Wilms et al., 1997) and, specific to SEOP implementations, using the embedded alkali atoms to detect the 3He precession (Kornack and Romalis, 2002; Zou et al., 2016).
The magnitude of the magnetic field produced by the precessing 3He nuclei is of order
| (51) |
for 1 amg of hyperpolarized 3He. The factor κ ~ 6 is, for imbedded alkali detection, the frequency shift enhancement factor exploited for EPR polarimetry (Sec. II.F), while for the other methods that detect the classical magnetic field produced by the nuclei it is a geometrical factor, typically less than 1, that depends on cell and detector geometry. Inside a multi-layer magnetic shield made of high permeability metal, the magnetic noise can be or better, giving a potential SNR for the 3He detection approaching 150 dB in a 1 Hz bandwidth. No experiment has yet attained this value, but a recent experiment (Allmendinger et al., 2014a; Gemmel et al., 2010) showed for a 2 mbar cell with in a He-Xe co-magnetometer experiment, with the He contribution likely substantially better than this.
Both SEOP and MEOP involve spin-polarized paramagnetic species (alkali atoms, metastable He atoms, free electrons) that produce effective paramagnetic fields BA that in turn cause NMR frequency shifts of the 3He analogous to the EPR frequency shift of Eq. (22):
| (52) |
The field is 2 mG for fully polarized Rb at a density of 1014 cm−3. This shift must be carefully managed in any precision measurement in which the 3He is in the same region as the paramagnetic species. Most precision NMR experiments to date manage the problem by transporting the polarized 3He to a region free of paramagnetic species, with a key exception being the alkali co-magnetometer approach of Sec. IX.C.
A. Co-magnetometry
Any use of 3He beyond magnetometry (symmetry violations, rotation) must account for the inevitable magnetic field fluctuations in any environment. Thus a second species is required to separate out magnetic from non-magnetic interactions, generally by either locking one species to an atomic clock (Bear et al., 1998), comparing the precession phase directly (Allmendinger et al., 2014a; Chupp et al., 1988), or taking frequency ratios (Chupp et al., 1988).
A special case to note is the proposed use of 3He as a comagnetometer for neutron electric dipole moment (EDM) experiments (Borisov et al., 2000; Chu and Peng, 2015; Kim and Clayton, 2013; Savukov et al., 2008; Tsentalovich and nEDM Collaboration, 2014). The cryogenic compatibility of 3He is very attractive to co-locate with the neutrons, and the small 10% difference in the magnetic moments of 3He and neutrons allows dressing techniques to give them effectively the same moment, thus allowing common-mode rejection of magnetic field noise (Golub and Lamoreaux, 1994). Recent experiments have shown the viability of this approach (Chu et al., 2011; Eckel et al., 2012).
Dual 3He-129Xe magnetometry was demonstrated by Gemmel et al. (2010) using SQUID detection of MEOP-produced 3He and SEOP-produced 129Xe. They demonstrated magnetic sensitivity of 1 fT in about 200 s of integration. Further developed versions of this approach, reaching coherence times of more than 100 hours (Heil et al., 2013) were used to set new limits on monopole-dipole interactions (Tullney et al., 2013) and charge-parity-time (CPT)/Lorentz invariance (Allmendinger et al., 2014a). In this latter experiment, an anomalous phase precession was attributed to interactions between the precessing nuclei due to the internal fields produced by the nuclei themselves, the magnitude of the effect being consistent with κ0 = 1 (Eq. (22)), implying a significant contact interaction between the species (Romalis et al., 2014) that would call into question the geometrical calibration of the EPR frequency shift (Romalis and Cates, 1998). This argument was disputed by Allmendinger et al. (2014b). Similar Xe-He techniques are being developed for new Xe EDM experiments (Heil et al., 2013; Kuchler et al., 2016).
He-Xe co-magnetometry using the embedded magnetometer possible in SEOP was studied by Sheng et al. (2014). The alkali field shifts were nulled by strongly driving the Rb EPR resonance during free precession of the spins. Of particular emphasis was systematic shifts caused by magnetic field and temperature gradients.
B. Masers
The first demonstration of the potential of hyperpolarized 3He for precision measurements was in a maser configuration, by Robinson and Myint (1964), who reported a statistical uncertainty of using a lamp-pumped MEOP setup. This experiment also pioneered the use of a dual cell system, with the MEOP process occurring in one bulb, connected by a few mm diameter tube to the spherical maser chamber. The use of a relatively low frequency (100 kHz) means that the resonant cavity used for most electron spin masers is replaced by an open LRC circuit. Nearly 25 years later, Richards et al. (1988) and Flowers et al. (1990) built similar systems for precision magnetometry at fields up to 0.1 T. Later, Gilles et al. (2003) built a laser-pumped MEOP maser for earth field measurements, comparing the performance to a metastable 4He magnetometer and obtaining a field sensitivity of .
In 1994, dual species SEOP-pumped 3He and 129Xe masers were introduced (Chupp et al., 1994). The maser bulb was again isolated from the pumping bulb, in order to suppress frequency shifts from optically pumped Rb. With dual species operation (shown in Fig. 24) (Bear et al., 1998; Stoner et al., 1996), the common mode magnetic field fluctuations were cancelled to a high precision, enabling the dual species maser to be sensitive to non-magnetic interactions such as permanent electric dipole moments. Using 3He as comagnetometer, Rosenberry and Chupp (2001) reported the most precise limits on a possible 129Xe EDM to date. An earlier version demonstrated the development of molybdenum electrodes with long relaxation times (Oteiza, 1992). A dual species maser under development for future EDM tests is described in Funayama et al. (2015).
FIG. 24.
Dual species maser, from Stoner et al. (1996)
The dual species maser was used in a series of symmetry violation tests by Walsworth and co-workers. Bear et al. (2000) set new limits on Lorentz and CPT violations, further improved by Cane et al. (2004). These experiments search for sidereal variation in the relative precession of the two nuclei as the laboratory rotates with respect to the distant stars (Walsworth, 2006; Walsworth et al., 2000). Glenday et al. (2008) used the dual species maser and a nearby SEOP 3He cell inside a separate magnetic shield to search for anomalous interactions between neutrons. Extensive modeling and details of the experimental implementation of the dual species maser, which reaches a precision of about 10 nHz, are given by Glenday (2010).
C. Alkali-He co-magnetometer
The maser and FID approaches to precision spectroscopy and comagnetometry with 3He avoid systematic shifts due to alkali spin-exchange fields by making measurements in the absence of the alkali atoms. Another approach, pioneered by Romalis and co-workers (Kornack et al., 2005; Kornack and Romalis, 2002) is to use the spin-exchange fields in an alkali-3He SEOP setup to null the magnetic sensitivity while maximizing sensitivity to non-magnetic interactions. Taking advantage of both the spin-exchange field BHe from the 3He nuclei (Eq. (22)) and the analogous field from the polarized alkali atoms, they show that when the alkali metal atoms experience no response to transverse magnetic fields. The application of a transverse magnetic field causes precession of the 3He whose spin-exchange field cancels the applied field. However, when a non-magnetic interaction is present, the nuclei and alkali metal atoms do not respond proportionately to their gyromagnetic ratios and the electrons then precess. The alkali atoms acquire a sensitivity to non-magnetic interactions with the 3He nucleus that is amplified by the factor γS/γHe = 617.
The K-3He co-magnetometer was used to demonstrate a sensitive gyroscope (Kornack et al., 2005), set new limits on anomalous nuclear spin-dependent forces (Vasilakis et al., 2009), and set new limits on Lorentz/CPT violation (Brown et al., 2010). These experiments exhibit a frequency sensitivity in the range of 18 pHz.
D. Magnetometry
Optically pumped metastable 4He magnetometers have been extensively developed (Schearer, 1985) and used for military, geomagnetic, and planetary magnetic field measurement applications (Dunlop, M.W. and Dougherty, M.K. and Kellock, S. and Southwood S., 1999)31. Despite their greater potential sensitivity, He-3 NMR-based magnetometers have not been commercialized due to challenges of the NMR readout. Development has been primarily for specialized precision physics measurements, especially neutron EDM experiments. Borisov et al. (2000) pioneered a scheme where they measured the absolute 3He polarization in a MEOP cell, let the gas expand into the measurement volume, applied a π/2–T –π/2 Ramsey sequence, then recompressed the gas into the MEOP cell where the final polarization was measured. The magnetic field measurement precision was 24 fT.
Extensive studies of 3He-Cs magnetometers have been made for integration into the ultra-cold neutron EDM experiment being developed at PSI32. The basic principle is to transport 3He from a MEOP pumping setup inside the magnetic shield where the EDM experiment is located. They detect free-induction-decay of the 3He with lamp-pumped (Kraft et al., 2014) or multiple laser-pumped (Koch et al., 2015a, b) Cs magnetometers.
For measurements of Tesla-scale magnetic fields, 3He is very attractive due to its immunity to systematic errors. Nikiel et al. (2014) demonstrate astounding relative accuracy of 10−12 at 1 T, with further advances promised from the use of essentially perfect spherical containers for the 3He (Maul et al., 2016).
E. Searches for axion-like interactions
Since 3He has similar spin and electromagnetic properties as a free neutron, it can be used to investigate possible exotic spin-dependent interactions with matter. In particular, hypothetical axion-like particles would generate a CP-violating scalar-pseudoscalar coupling of strength gsgp (Moody and Wilczek, 1984) with a Yukawa-like spatial dependence of length-scale Λ, which is inversely proportional to the axion-like mass. The most straightforward approach is to search for a shift in the 3He resonance frequency as the distance between a macroscopic mass and the 3He gas is modulated (Tullney et al., 2013). Another remarkable approach, proposed by Pokotilovski (2010), is to use the fact that spin relaxation of 3He is sensitive to magnetic field gradients, which in this case means gradients of the hypothetical Yukawa scalar-pseudoscalar coupling. Measurements of the transverse spin relaxation rates are particularly sensitive to these non-magnetic gradients and, in particular, the long coherence times of Gemmel et al. (2010) were used to set new limits (Kostelecky, 2010; Petukhov et al., 2010). For Λ smaller than the cell size, the classic transverse relaxation, Eq. (47) must be modified(Petukhov et al., 2011). Measurements of 3He transverse relaxation rate as a function of parameters such as bias magnetic field, density, and mass distribution then potentially reveal the existence of the scalar-pseudoscalar coupling. A series of experiments have been done along these lines (Chu et al., 2013; Fu et al., 2011; Guigue et al., 2015; Yan et al., 2015). At the shortest distances Λ < 20 μm, this method is the most sensitive (Guigue et al., 2015); for Λ > 50 μm the 3He-Xe comagnetometry prevails (Tullney et al., 2013); the small intermediate regime is limited by a dual isotope Xe comagnetometer (Bulatowicz et al., 2013). A new approach for improving axion limits using a resonance method has been proposed as well (Arvanitaki and Geraci, 2014).
X. FUTURE TRENDS
We close with some of the scientific and technical challenges in the theory and practice of SEOP and MEOP. The limiting polarization for SEOP is still not clear. Although the discovery of excess relaxation that scales with alkali-metal density has modified our understanding of this limit, the present analysis is purely phenomenological as the origin of this cell-dependent relaxation is not fundamentally understood. Indeed both its origin and magnetic field effects on 3He cells are new twists in the quest for understanding of wall relaxation, but perhaps they will turn out to be clues rather than simply a new source of confusion. The recent higher polarizations from SEOP observed at the NCNR (Chen et al., 2014a) also suggest that there is more to the limit than excess relaxation. These results must be reproduced by other groups.
Hybrid SEOP has yielded a significant gain in the polarizing rate. A possibility for a further increase in rate is operation in a ≈ 50 mT magnetic field, which has been shown to reduce alkali-alkali relaxation by a factor of ≈2 (Kadlecek, 1999; Kadlecek et al., 1998). This approach would be the most useful for the typical 1.5 bar pressure in NSFs, for which this contribution dominates over alkali-buffer gas relaxation. However, the detrimental effect of even such modest magnetic fields on 3He wall relaxation (Chen et al., 2011; Jacob, 2003) would have to be substantially reduced to employ this approach. Employing the very low relaxation rate for sodium (Borel et al., 2003) is hampered by browning of aluminosilicate glass at the high temperatures required (Babcock, 2005; Chen et al., 2011). Although this issue could be addressed with the use of sapphire (Masuda et al., 2005), practical construction of such cells for routine applications would be required. Again, we see that poorly understood wall-relaxation properties limit the performance of SEOP.
The continuing development of laser technology has greatly benefitted SEOP. Cost-effective laboratory systems can presently make use of chirped VHGs to narrow 100 W single diode bars to 0.25 nm bandwidth. However, fiber-coupled lasers are required or preferred for various in-situ systems. If VHG-narrowed, fiber-coupled systems (Liu et al., 2015) were commercialized and could reach this power level with similar bandwidth and comparable cost, the performance of targets and in-situ NSFs could be improved. Similarly, ultra-narrow lasers could yield benefits, but their utility has not been experimentally investigated. A study of the practical improvement in SEOP for narrowing high power diode lasers from 2 nm to 0.2 nm was reported (Chann et al., 2003), However, no such study has been reported for further narrowing from 0.2 nm to 0.04 nm (Gourevitch et al., 2008), even though this is now commercially available33. Another possible approach to future lasers is alkali-metal lasers (Zhdanov and Knize, 2012). If 770 nm lasers were to become as available as 795 nm lasers for the same cost, pure K pumping should be further investigated. Despite tremendous progress in the last two decades, a mature, common model for SEOP in both Rb/K hybrid and pure alkalimetal cells remains to be developed and tested.
The most significant new trend in MEOP is high field/high pressure operation. To date the achievable polarization at high field has not exceeded that obtained at low field and low pressure. Whereas operation in low field is typically easier, operation at high field is under development for a polarized 3He ion source at RHIC (Maxwell et al., 2016) and for high-accuracy magnetic field measurements (Maul et al., 2016; Nikiel et al., 2014). Recent studies have revealed a light-induced relaxation mechanism that wastes most of the angular momentum deposited of the pumping light and limits the achievable polarization at higher pressures, but is not well understood. Whereas the lower polarizations currently obtained at higher pressure are acceptable for MRI applications, NSF and electron scattering applications typically demand the highest polarizations. However, the current remote mode of operating large compressors inherently introduces lower time-averaged polarization because of the need to replace cells or perform local refilling operations. If future work revealed the origin of this relaxation and a path to its elimination, there is the potential for simplifying and shrinking large-scale compression apparatus for these applications and thus perhaps allowing for continuous operation, as well as for more efficient use of available pumping light and larger production rates for MRI applications.
The high luminosity planned for future experiments at JLAB will put new demands on SEOP targets for electron scattering. The high polarizing rates achievable with hybrid pumping make it possible to tolerate the 3He relaxation produced by higher beam currents, but reducing the transfer time between the two volumes of the double cell is desirable. Since the 3He polarimetry is typically done using EPR in the optical pumping cell, more rapid transfer increases the accuracy of the determination of the polarization in the target cell. Towards that end, targets employing convective transfer between the two volumes (see Fig. 25) are under development for these future experiments.
FIG. 25.
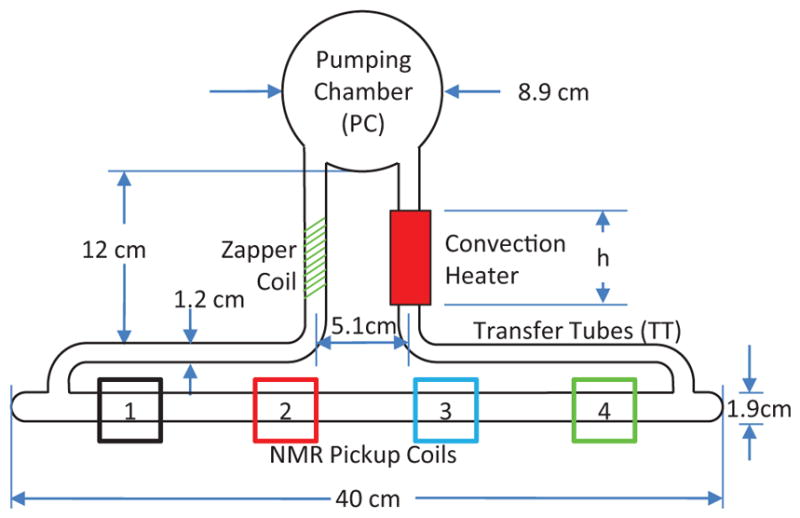
Design of a convection cell for decreased transfer time between the two volumes of a double cell, from Dolph et al. (2011). The flow of gas was monitored using an NMR tagging technique, in which the zapper coil was used to depolarize a slug of gas and NMR signals were then detected at each of four locations along the target chamber (labelled 1,2,3 and 4).
As NSFs are employed on an increasing range of neutron scattering instruments, there will be new challenges for both methods. For neutron scattering, NSFs have been typically polarized remotely and transferred to neutron beam lines, but it is becoming of increasing interest to operate NSFs continuously or pseudo-continuously so as to maximize the figure of merit and decrease polarization correction uncertainties. For SEOP, apparatus that can fit within difficult space constraints and satisfy laser safety requirements are required. For MEOP, local filling is likely to be used more extensively. Increasing the range of applications will require NSFs with large and/or complex cells and/or greater tolerance to stray magnetic fields. Finally, some NSFs may provide the greatest impetus for achieving the highest possible 3He polarizations for two reasons: 1) some NSFs are relatively simple, single, cells at pressures near one bar, for which the limiting polarization in a practical application can be close to that possible under ideal conditions and 2) high neutron polarization and/or analyzing power are typically desirable for neutron scattering experiments in which a small component of magnetic scattering is separated from a much large component of nuclear scattering (Gentile et al., 2005a). In contrast with the typical figure of merit proportional to for the running time of an experiment, such situations yield a stronger dependence that is closer to .
In the area of 3He polarimetry, the high polarizations achievable in NSFs provide both the impetus and a methodology for tests and possible improvements. For example, if an accurate EPR apparatus were operated on an in-situ NSF, a careful comparison of the two methods would enable a potential improvement in the determination of κ0 In the other direction, improved EPR, water-based NMR, and/or magnetometry could provide the means for a determination or better limit on the small cross section for neutron absorption by 3He with parallel spins (Huber et al., 2014). Finally if NSFs are to be used to polarize high flux beams for fundamental neutron physics applications, double cells for neutron beams will have to be developed.
While the long-term future availability of 3He for medical imaging remains uncertain, 129Xe is naturally abundant and relatively inexpensive. The advancements in 129Xe polarization technology and work comparing 3He and 129Xe support 129Xe being a viable alternative to 3He in many, but not all, instances. Thad Furthermore, the unique physical properties of 129Xe allow for dissolved-phase imaging capable of measuring biomarkers related to gas uptake and exchange. In patient populations where the slight dissolution of 129Xe into blood is a potential issue, such as infants, 3He may continue to be the preferred hyperpolarized gas.
Spin-polarized 3He can be expected to be desirable for many applications in precision measurements. The insensitivity of 3He to non-magnetic interactions, plus its extremely small fundamental bandwidth, make it ideal for co-magnetometry applications for symmetry tests like searches for electric dipole moments. The 3He is relatively immune to chemical shifts, so it can be considered a primary magnetic field standard. In a synchronous SEOP configuration (Korver et al., 2015, 2013) there is promise to avoid systematic shifts from the alkali fields for making absolute magnetic field measurements or rotation measurements with the inherently high sensitivity of an imbedded alkali magnetometer.
FIG. 23.
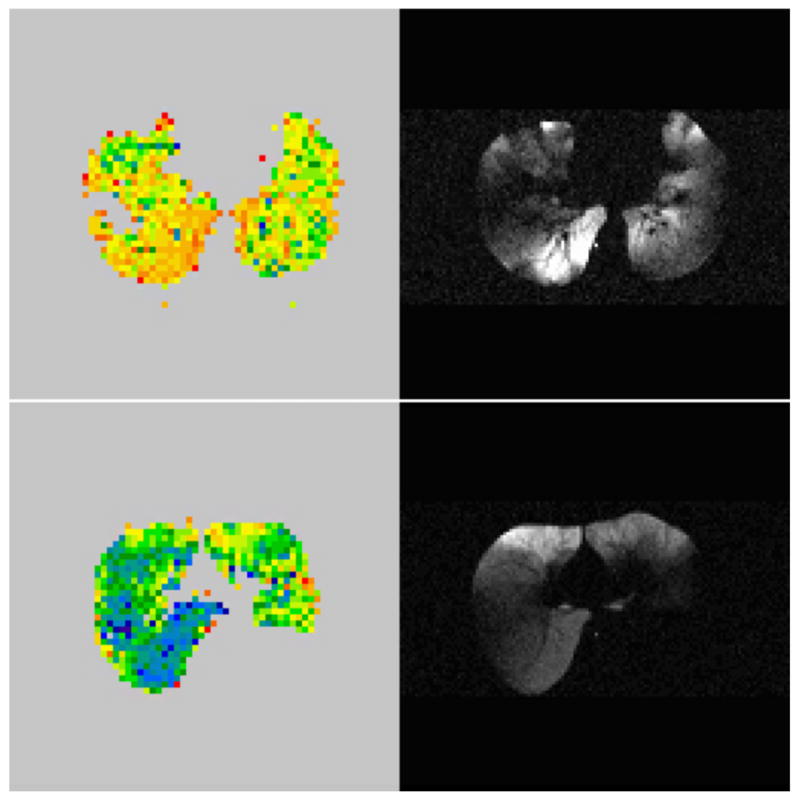
Axial (perpendicular to the spine) 3He magnetic resonance images of a cross section of the ventilated lung in two emphysema patients, top and bottom. Images on the right are spin-density weighted while those on the left are maps of apparent diffusion coefficient (ADC), where red represents the most restricted air spaces regions and blue the least restricted. The blue regions correspond to the most diseased tissue, where the alveolar walls have been destroyed. These regions do not necessarily correlate with the poorly ventilated regions seen in the spin-density weighted images, which demonstrates the potential for greater specificity with ADC mapping. From Conradi et al. (2006).
Acknowledgments
The National Science Foundation (PHY-1607439) and Northrop-Grumman Corp. funding supported T.W.’s work on this paper.
Footnotes
All pressures refer to room temperature unless otherwise noted.
1 amagat (amg)=2.69×1019 cm−3 is the density of an ideal gas at standard temperature and pressure.
GE Lighting Component Sales, Cleveland, OH Certain trade names and company products are mentioned in the text or identified in an illustration in order to adequately specify the experimental procedure and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose.
Recent treatments of optical pumping include Auzinsh et al. (2010) and Happer et al. (2009). The classic review of the subject is Happer (1972), and a good introduction is Happer and Van Wijngaarden (1987).
Stanford Linear Accelerator Center, Menlo Park, CA
The total number density N and the ground state number density Ng are almost equal in He gas discharges under MEOP conditions, with at most a few ppm of the atoms in an excited state. N is used instead of Ng whenever necessary or convenient.
Mainz Microtron, Mainz, Germany
Institut Laue-Langevin, Grenoble, France
Corning Glass, Corning, NY.
GE Lighting Component Sales, Cleveland, OH
SCHOTT North America, Inc., Louisville, KY
Polarean Inc., Durham, NC
Relativistic Heavy Ion Collider, Brookhaven, NY
Canada’s national laboratory for particle and nuclear physics and accelerator-based science, Vancouver BC
Los Alamos Clinton P. Anderson Meson Physics Facility, Los Alamos, NM
Triangle Universities Nuclear Laboratory, Durham, NC
Deutsches Elektronen Synchrotron, Hamburg, Germany
Dutch National Institute for Subatomic Physics, Amsterdam, Netherlands
Los Alamos Neutron Scattering Center, Los Alamos, NM
National Institute for Standards and Technology Center for Neutron Research, Gaithersburg, MD
Spallation Neutron Source, Oak Ridge, TN
Low Energy Neutron Source, Bloomington, IN
National Laboratory for High Energy Physics, Tsukuba, Japan
Japan Proton Accelerator Research Complex, Tokai, Japan
Korean Atomic Energy Research Institute, Daejeon, Korea
Rutherford Appleton Laboratory, Oxfordshire, United Kingdom
Forschungs-Neutronquelle Heinz Maier-Leibnitz, Munich, Germany
Magnetic Imaging Technologies, Inc., later acquired by GE Healthcare
Polarean Inc. (Research Triangle Park, NC); Xemed LLC (Durham, NH)
Jensen Inert Products, Coral Springs, FL
Polatomic Inc., Polatomic, Inc., Richardson, TX
Paul Scherrer Institute, Villigen PSI, Switzerland
Optigrate Corp., Oviedo, Florida
Contributor Information
T. R. Gentile, National Institute of Standards and Technology (NIST), Gaithersburg, Maryland 20899, USA
P. J. Nacher, Laboratoire Kastler Brossel, ENS-PSL Research University, CNRS, UPMC-Sorbonne Universités, Collège de France, Paris, France
B. Saam, Department of Physics and Astronomy, University of Utah, Salt Lake City, Utah 84112, USA
T. G. Walker, Department of Physics, University of Wisconsin-Madison, Madison, Wisconsin 53706, USA.
References
- Abboud M, Sinatra A, Tastevin G, Nacher PJ, Maitre X. Metastability exchange optical pumping of helium-3 at high pressures and 1.5 T: Comparison of two optical pumping transitions. Laser Physics. 2005;15(4):475–479. [Google Scholar]
- Abboud Marie. Pompage optique de l’hélium-3 à forte pression dans un champ magnétique de 1.5 Tesla. PhD Thesis. 2005 http://tel.archives-ouvertes.fr/tel-00011099 (UPMC - Paris 6)
- Abboud Marie, Sinatra Alice, Maître Xavier, Tastevin Genevieve, Nacher P-J. High nuclear polarization of 3He at low and high pressure by metastability exchange optical pumping at 1.5 Tesla. Europhys Lett. 2004;68(4):480. [Google Scholar]
- Abe K, Akagi T, Anderson BD, Anthony PL, Arnold RG, Averett T, Band HR, Berisso CM, Bogorad P, Borel H, et al. Measurement of the neutron spin structure function and asymmetry . Phys Lett B. 1997a;404(3):377–382. [Google Scholar]
- Abe K, Akagi T, Anderson BD, Anthony PL, Arnold RG, Averett T, Band HR, Berisso CM, Bogorad P, Borel H, et al. Precision Determination of the Neutron Spin Structure Function . Phys Rev Lett. 1997b;79(1):26. [Google Scholar]
- Abragam Anatole. The principles of nuclear magnetism. Oxford University Press; 1961. International series of monographs on physics No. 32. [Google Scholar]
- Ackerstaff K, Airapetian A, Akushevich I, Akopov N, Amarian M, Aschenauer EC, Avakian R, Avakian H, Avetissian A, Bains B, et al. Measurement of the neutron spin structure function with a polarized 3He internal target. Phys Lett B. 1997;404(3):383–389. [Google Scholar]
- Aidala CA, Bass SD, Hasch D, Mallot GK. The spin structure of the nucleon. Rev Mod Phys. 2013;85(2):655. [Google Scholar]
- Ajraoui S, Lee KJ, Deppe MH, Parnell SR, Parra-Robles J, Wild JM. Compressed sensing in hyperpolarized 3He Lung MRI. Magn Reson Med. 2010;63:1059–69. doi: 10.1002/mrm.22302. [DOI] [PubMed] [Google Scholar]
- Akimoto H, Adams ED, Candela D, Mullin WJ, Shvarts V, Sullivan NS, Xia JS. Nonlinear spin dynamics of dilute 3He–4He at very high B/T. Physica B. 2000;284:313–314. [Google Scholar]
- Albert MS, Cates GD, Driehuys B, Happer W, Saam B, Springer CS, Wishnia A. Biological magnetic resonance imaging using laser-polarized 129Xe. Nature. 1994;370:199. doi: 10.1038/370199a0. [DOI] [PubMed] [Google Scholar]
- Alcorn J, Anderson BD, Aniol KA, Annand JRM, Auerbach L, Arrington J, Averett T, Baker FT, Baylac M, Beise EJ, et al. Basic instrumentation for Hall A at Jefferson Lab. Nucl Instrum Methods Phys Res, Sect A. 2004;522:294–346. [Google Scholar]
- Allada K, Zhao YX, Aniol K, JR, Annand M, Averett T, Benmokhtar F, Bertozzi W, Bradshaw PC, Bosted P, Camsonne A, et al. Jefferson Lab Hall A Collaboration. Single spin asymmetries of inclusive hadrons produced in electron scattering from a transversely polarized 3He target. Phys Rev C. 2014;89:042201. [Google Scholar]
- Alley MT, Knutson LD. Spin correlation measurements for p-3He elastic scattering between 4.0 and 10.0 MeV. Phys Rev C. 1993;48(4):1890. doi: 10.1103/physrevc.48.1890. [DOI] [PubMed] [Google Scholar]
- Allmendinger F, Heil W, Karpuk S, Kilian W, Scharth A, Schmidt U, Schnabel A, Sobolev Yu, Tullney K. New Limit on Lorentz-Invariance-and C P T-Violating Neutron Spin Interactions Using a Free-Spin-Precession 3He-129Xe Comagnetometer. Phys Rev Lett. 2014a;112(11):110801. doi: 10.1103/PhysRevLett.112.110801. [DOI] [PubMed] [Google Scholar]
- Allmendinger F, Heil W, Karpuk S, Kilian W, Scharth A, Schmidt U, Schnabel A, Sobolev Yu, Tullney K. Reply to “Comment on ’New limit on Lorentz-invariance- and CPT-violating neutron spin interactions using a free-spin-precession 3He -129Xe comagnetometer”. Phys Rev Lett. 2014b;113:188902. doi: 10.1103/PhysRevLett.112.110801. [DOI] [PubMed] [Google Scholar]
- Amarian M, Auerbach L, Averett T, Berthot J, Bertin P, Bertozzi B, Black T, Brash E, Brown D, Burtin E, et al. Q2 Evolution of the Neutron Spin Structure Moments using a 3He Target. Phys Rev Lett. 2004;92(2):022301. doi: 10.1103/PhysRevLett.92.022301. [DOI] [PubMed] [Google Scholar]
- Amarian M, Auerbach L, Averett T, Berthot J, Bertin P, Bertozzi W, Black T, Brash E, Brown D, Burtin E, et al. Q2 Evolution of the Generalized Gerasimov-Drell-Hearn Integral for the Neutron using a 3He e Target. Phys Rev Lett. 2002;89(24):242301. doi: 10.1103/PhysRevLett.89.242301. [DOI] [PubMed] [Google Scholar]
- Aminoff CG, Pinard M. Velocity selective optical pumping. J Phys. 1982;43(2):263–277. [Google Scholar]
- Aminoff CG, Essabaa S, Brissaud I, Arianer J. A high power lamp-pumped LNA laser with thermally tuned etalon. Opt Commun. 1991;86(2):99–105. [Google Scholar]
- Andersen KH, Chung R, Guillard V, Humblot H, Jullien D, Lelievre-Berna E, Petoukhov A, Tasset F. First results from Tyrex, the new polarized-3He filling station at ILL. Physica B. 2005;356(1):103–108. [Google Scholar]
- Andersen KH, Cubitt R, Humblot H, Jullien D, Petoukhov A, Tasset F, Schanzer C, Shah VR, Wildes AR. The 3He polarizing filter on the neutron reflectometer D17. Physica B. 2006;385:1134–1137. [Google Scholar]
- Andersen KH, Jullien D, Petoukhov AK, Mouveau P, Bordenave F, Thomas F, Babcock E. SANS polarization analysis at V4 SANS instrument of HMI Berlin. Physica B. 2009;404:2652–2654. [Google Scholar]
- Anderson LW, Pipkin FM, Baird JC. N14-N15 Hyperfine Anomaly. Phys Rev. 1959;116:87. [Google Scholar]
- Anthony PL, Arnold RG, Band HR, Borel H, Bosted PE, Breton V, Cates GD, Chupp TE, Dietrich FS, Dunne J, et al. Determination of the neutron spin structure function. Phys Rev Lett. 1993;71(7):959. doi: 10.1103/PhysRevLett.71.959. [DOI] [PubMed] [Google Scholar]
- Anthony PL, et al. Deep inelastic scattering of polarized electrons by polarized 3He and the study of the neutron spin structure. Phys Rev D. 1996;54:6620. doi: 10.1103/physrevd.54.6620. [DOI] [PubMed] [Google Scholar]
- Appelt S, Ben-Amar Baranga A, Erickson CJ, Romalis MV, Young AR, Happer W. Theory of spin-exchange optical pumping of 3He and 129Xe. Phys Rev A. 1998;58(2):1412. [Google Scholar]
- Appelt S, Ben-Amar Baranga A, Young AR, Happer W. Light narrowing of rubidium magnetic-resonance lines in high-pressure optical-pumping cells. Phys Rev A. 1999;59(3):2078. [Google Scholar]
- Arvanitaki Asimina, Geraci Andrew A. Resonantly Detecting Axion-Mediated Forces with Nuclear Magnetic Resonance. Phys Rev Lett. 2014;113(16):161801. doi: 10.1103/PhysRevLett.113.161801. [DOI] [PubMed] [Google Scholar]
- Auzinsh Marcis, Budker Dmitry, Rochester Simon M. Optically Polarized Atoms: Understanding Light-Atom Interactions. Oxford University Press; 2010. [Google Scholar]
- Babcock E. PhD thesis. University of Wisconsin-Madison; 2005. Spin-Exchange Optical Pumping with Alkali Metal Vapors. [Google Scholar]
- Babcock E, Boag S, Becker M, Chen WC, Chupp TE, Gentile TR, Jones GL, Petukhov AK, Soldner T, Walker TG. Effects of high-flux neutron beams on 3He cells polarized in situ with spin-exchange optical pumping. Phys Rev A. 2009;80(3):033414. [Google Scholar]
- Babcock E, Boag S, Beecham C, Chupp TE, Gentile TR, Jones GL, Petukhov AK, Walker TG. Effects of high intensity neutron flux on in-situ spin-exchange optical pumping of 3He. J Phys Conf Ser. 2011a;294:012011. [Google Scholar]
- Babcock E, Chann B, Walker TG, Chen WC, Gentile TR. Limits to the Polarization for Spin-Exchange Optical Pumping of 3He. Phys Rev Lett. 2006;96(8):083003. doi: 10.1103/PhysRevLett.96.083003. [DOI] [PubMed] [Google Scholar]
- Babcock E, Mattauch S, Ioffe A. High level of 3He polarization maintained in an on-beam 3He spin filter using SEOP. Nucl Instrum Methods Phys Res, Sect A. 2011b;625(1):43–46. [Google Scholar]
- Babcock E, Salhi Z, Pistel P, Simeoni G, Ioffe A. Magic-PASTIS for XYZ polarization analysis using SEOP polarized 3He gas. J Phys Conf Ser. 2014;528:012018. [Google Scholar]
- Babcock Earl, Chann Bien, Nelson Ian A, Walker Thad G. Frequency-narrowed diode array bar. Appl Optics. 2005a;44(15):3098–3104. doi: 10.1364/ao.44.003098. [DOI] [PubMed] [Google Scholar]
- Babcock Earl, Nelson Ian, Kadlecek Steve, Driehuys Bastiaan, Anderson LW, Hersman FW, Walker Thad G. Hybrid Spin-Exchange Optical Pumping of 3He. Phys Rev Lett. 2003;91(12):123003. doi: 10.1103/PhysRevLett.91.123003. [DOI] [PubMed] [Google Scholar]
- Babcock Earl, Nelson Ian A, Kadlecek Steve, Walker Thad G. 3He polarization-dependent EPR frequency shifts of alkali-metal–3He pairs. Phys Rev A. 2005b;71(1):013414. [Google Scholar]
- Babcock Earl, Salhi Zahir, Theisselmann Tobias, Starostin Denis, Schmeissner Johann, Feoktystov Artem, Mattauch Stefan, Pistel Patrick, Radulescu Aurel, Ioffe Alexander. SEOP polarized 3He Neutron Spin Filters for the JCNS user program. J Phys Conf Ser. 2016;711(1):012008. [Google Scholar]
- Baker SD, McSherry DH, Findley DO. Elastic Scattering of Protons by Polarized 3He. Phys Rev. 1969;178(4):1616. [Google Scholar]
- Barbé R. Measurement of the helium metastability-exchange cross section at 4.2K. J Phys B: At Mol Phys. 1976;9(6):995. [Google Scholar]
- Barbé René, Laloë Franck, Brossel Jean. Very Long 3He Nuclear Relaxation Times at 4 K Using Cryogenic Coatings. Phys Rev Lett. 1975;34(24):1488. [Google Scholar]
- Barton AS, Newbury NR, Cates GD, Driehuys B, Middleton H, Saam B. Self-calibrating measurement of polarization-dependent frequency shifts from Rb-3He collisions. Phys Rev A. 1994;49(4):2766. doi: 10.1103/physreva.49.2766. [DOI] [PubMed] [Google Scholar]
- Batz M, Baessler S, Heil W, Otten EW, Rudersdorf D, Schmiedeskamp J, Sobolev Y, Wolf M. 3He Spin Filter for Neutrons. J Res Natl Inst Stan. 2005;110(3):293–298. doi: 10.6028/jres.110.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batz Marion. Metastability exchange optical pumping in 3He gas up to 30 mT: Efficiency measurements and evidence of laser-induced nuclear relaxation. PhD Thesis. 2011 http://tel.archives-ouvertes.fr/tel-00665393 (UPMC -Paris 6 and Johannes Gutenberg-Universität Mainz)
- Batz Marion, Nacher P-J, Tastevin Genevieve. Fundamentals of metastability exchange optical pumping in helium. J Phys Conf Ser. 2011;294:012002. [Google Scholar]
- Baudin E, Safiullin K, Morgan SW, Nacher PJ. An active feedback scheme for low field NMR experiments. J Phys Conf Ser. 2011;294(1):012009. [Google Scholar]
- Baudin Emmanuel, Hayden Michael E, Tastevin Geneviève, Nacher Pierre-Jean. NMR Time Reversal Experiments in Highly Polarised Liquid 3He-4He Mixtures. J Low Temp Phys. 2008;150(3–4):168–173. [Google Scholar]
- Bear D, Chupp TE, Cooper K, DeDeo S, Rosenberry M, Stoner RE, Walsworth RL. Improved frequency stability of the dual-noble-gas maser. Phys Rev A. 1998;57(6):5006. [Google Scholar]
- Bear D, Stoner RE, Walsworth RL, Alan Kosteleckỳ V, Lane Charles D. Limit on Lorentz and CPT violation of the neutron using a two-species noble-gas maser. Phys Rev Lett. 2000;85(24):5038. doi: 10.1103/PhysRevLett.85.5038. [DOI] [PubMed] [Google Scholar]
- Becker J, Andresen HG, Annand JRM, Aulenbacher K, Beuchel K, Blume-Werry J, Dombo Th, Drescher P, Ebert M, Eyl D, et al. Determination of the neutron electric form factor from the reaction 3He(e,e′n) at medium momentum transfer. Eur Phys J A. 1999;6(3):329–344. [Google Scholar]
- Becker J, Heil W, Krug B, Leduc M, Meyerhoff M, Nacher PJ, Otten EW, Prokscha Th, Schearer LD, Surkau R. Study of mechanical compression of spin-polarized 3He gas. Nucl Instrum Methods Phys Res, Sect A. 1994;346(1):45–51. [Google Scholar]
- Beecham CJ, Boag S, Frost CD, McKetterick TJ, Stewart JR, Andersen KH, Bentley PM, Jullien D. 3He polarization for ISIS TS2 phase I instruments. Physica B. 2011;406(12):2429–2432. [Google Scholar]
- van Beek Edwin J, Wild Jim M, Kauczor Hans-Ulrich, Schreiber Wolfgang, Mugler John P, III, de Lange Eduard E. Functional MRI of the lung using hyperpolarized 3-helium gas. J Magn Reson Imaging. 2004;20(4):540–554. doi: 10.1002/jmri.20154. [DOI] [PubMed] [Google Scholar]
- Ben-Amar Baranga A, Appelt S, Romalis MV, Erickson CJ, Young AR, Cates GD, Happer W. Polarization of 3He by spin exchange with optically pumped Rb and K vapors. Phys Rev Lett. 1998;80(13):2801. [Google Scholar]
- Bermuth J, Merle P, Carasco C, Baumann D, Böhm R, Bosnar D, Ding M, Distler MO, Friedrich J, Friedrich JM, et al. The neutron charge form factor and target analyzing powers from 3He(e,e′n) scattering. Phys Lett B. 2003;564(3):199–204. [Google Scholar]
- Bernauer JC. Precise form factors from elastic electron scattering. J Phys Conf Ser. 2012;381:012006. [Google Scholar]
- Bhaskar N, Happer W, McClelland T. Efficiency of spin exchange between rubidium spins and 129Xe nuclei in a gas. Phys Rev Lett. 1982;49:25. [Google Scholar]
- Bhaskar ND, Hou M, Suleman B, Happer W. Propagating, Optical-Pumping Wave Fronts. Phys Rev Lett. 1979;43:519. [Google Scholar]
- Bicout Dominique J, Kats Efim I, Petukhov Alexander K, Whitney Robert S. Size Independence of Statistics for Boundary Collisions of Random Walks and Its Implications for Spin-Polarized Gases. Phys Rev Lett. 2013;110(1):010602. doi: 10.1103/PhysRevLett.110.010602. [DOI] [PubMed] [Google Scholar]
- Bidinosti CP, Choukeife J, Nacher P-J, Tastevin G. In vivo NMR of hyperpolarized 3He in the human lung at very low magnetic fields. J Magn Reson. 2003;162(1):122–132. doi: 10.1016/s1090-7807(02)00198-2. [DOI] [PubMed] [Google Scholar]
- Bidinosti CP, Choukeife J, Tastevin G, Nacher P-J, Vignaud A. MRI of the lung using hyperpolarized 3He at very low magnetic field (3 mT) Magn Reson Mater Phy. 2004;16(6):255–258. doi: 10.1007/s10334-004-0035-y. [DOI] [PubMed] [Google Scholar]
- Bigelow NP, Nacher P-J, Leduc M. Accurate optical measurement of nuclear polarization in optically pumped 3He gas. J Phys II France. 1992;2(12):2159–2179. [Google Scholar]
- Blanco JA, Brown PJ, Stunault A, Katsumata Koichi, Iga Fumitoshi, Michimura Shinji. Magnetic structure of GdB4 from spherical neutron polarimetry. Phys Rev B. 2006;73(21):212411. [Google Scholar]
- Bloch C, Doskow J, Goodman CD, Jacobs WW, Leuschner M, Meyer HO, Von Przewoski B, Rinckel T, Savopulos G, Smith A, et al. Spin-dependent scattering of polarized protons from a polarized 3He internal gas target. Nucl Instrum Methods Phys Res, Sect A. 1995;354(2):437–457. [Google Scholar]
- Bloch Felix. Nuclear induction. Phys Rev. 1946;70(7–8):460. [Google Scholar]
- Boag S, Jiang CY, Tong X, Parnell SR. Lifetime behaviour and polarization stability in 3He neutron spin filter cells. J Phys Conf Ser. 2014;528(1):012019. [Google Scholar]
- Boehm M, Roessli B, Schefer J, Wills AS, Ouladdiaf B, Lelievre-Berna E, Staub U, Petrakovskii GA. Complex magnetic ground state of CuB2O4. Phys Rev B. 2003;68(2):024405. [Google Scholar]
- Bohler CL, McGregor DD. Transverse relaxation in spin-polarized 3He gas due to dc and ac magnetic-field gradients. Phys Rev A. 1994;49:2755–2758. doi: 10.1103/physreva.49.2755. [DOI] [PubMed] [Google Scholar]
- Bonfait G, Puech L, Greenberg AS, Eska G, Castaing B, Thoulouze D. Strongly Polarized Liquid 3He: Experimental Access to the Melting Curve. Phys Rev Lett. 1984;53:1092–1095. [Google Scholar]
- Bonfait G, Puech L, Halperin WP, Castaing B. Sound Velocity in Highly Polarized 3He. Europhys Lett. 1987;3(4):489. [Google Scholar]
- Bonin KD, Saltzberg DP, Happer W. Relaxation of gaseous spin-polarized 3He targets due to creation of 3He+ Phys Rev A. 1988a;38(9):4481. doi: 10.1103/physreva.38.4481. [DOI] [PubMed] [Google Scholar]
- Bonin KD, Walker TG, Happer W. Relaxation of gaseous spin-polarized 3He targets due to ionizing radiation. Phys Rev A. 1988b;37(9):3270. doi: 10.1103/physreva.37.3270. [DOI] [PubMed] [Google Scholar]
- Borel Peter Ingo, Søgaard LV, Svendsen Winnie Edith, Andersen N. Spin-exchange and spin-destruction rates for the 3He- Na system. Phys Rev A. 2003;67(6):062705. [Google Scholar]
- Borisov Yu, Heil W, Leduc M, Lobashev V, Otten EW, Sobolev Yu. Feasibility study of a 3He-magnetometer for neutron electric dipole moment experiments. Nucl Instrum Methods Phys Res, Sect A. 2000;440(3):483–488. [Google Scholar]
- Bouchiat M, Carver TR, Varnum CM. Nuclear Polarization in 3He Gas Induced by Optical Pumping and Dipolar Exchange. Phys Rev Lett 5 1960 [Google Scholar]
- Bowman J David, Gudkov Vladimir. Search for time reversal invariance violation in neutron transmission. Phys Rev C. 2014;90(6):065503. [Google Scholar]
- Brown JM, Smullin SJ, Kornack TW, Romalis MV. New Limit on Lorentz-and C P T-Violating Neutron Spin Interactions. Phys Rev Lett. 2010;105(15):151604. doi: 10.1103/PhysRevLett.105.151604. [DOI] [PubMed] [Google Scholar]
- Brown P Jane, Bruce Forsyth J, Tasset Francis. Studies of magneto-electric crystals using spherical neutron polarimetry. Solid State Sci. 2005;7(6):682–689. [Google Scholar]
- Brown PJ, Forsyth JB, Tasset F, et al. Determination of the magnetization distribution in Cr2O3 using spherical neutron polarimetry. J Phys: Condens Matter. 2002;14(8):1957. [Google Scholar]
- Bulatowicz M, Griffith R, Larsen M, Mirijanian J, Fu CB, Smith E, Snow WM, Yan H, Walker TG. Laboratory Search for a Long-Range T-Odd, P-Odd Interaction from Axionlike Particles Using Dual-Species Nuclear Magnetic Resonance with Polarized 129Xe and 131Xe Gas. Phys Rev Lett. 2013;111(10):102001. doi: 10.1103/PhysRevLett.111.102001. [DOI] [PubMed] [Google Scholar]
- Buu O, Puech L, Wolf PE. Polarization Decreases the Specific Heat of Liquid 3He. Phys Rev Lett. 2000;85:1278–1281. doi: 10.1103/PhysRevLett.85.1278. [DOI] [PubMed] [Google Scholar]
- Cabrera I, Kenzelmann M, Lawes G, Chen Y, Chen WC, Erwin R, Gentile TR, Leao JB, Lynn JW, Rogado N, et al. Coupled Magnetic and Ferroelectric Domains in Multiferroic Ni3V2O8. Phys Rev Lett. 2009;103(8):087201. doi: 10.1103/PhysRevLett.103.087201. [DOI] [PubMed] [Google Scholar]
- Cagnac B, Brossel J, Kastler A. Résonance magnétique nucléaire du mercure 201hg, aligné par pompage optique. Compt Rend. 1958;246(1):1827–1830. [Google Scholar]
- Candela D, Hayden ME, Nacher PJ. Steady-State Production of High Nuclear Polarization in 3He-4He Mixtures. Phys Rev Lett. 1994;73(19):2587. doi: 10.1103/PhysRevLett.73.2587. [DOI] [PubMed] [Google Scholar]
- Cane F, Bear D, Phillips DF, Rosen MS, Smallwood CL, Stoner RE, Walsworth RL, Kostelecky VA. Bound on Lorentz and CPT violating boost effects for the neutron. Phys Rev Lett. 2004;93(23) doi: 10.1103/Phys-RevLett.93.230801. [DOI] [PubMed] [Google Scholar]
- Castaing B, Nozieres P. Phase-transitions of spin polarized He-3 - Thermodynamical nuclear orientation technique. J Phys. 1979;40:257–268. [Google Scholar]
- Cates GD, Benton DR, Gatzke M, Happer W, Hasson KC, Newbury NR. Laser production of large nuclear-spin polarization in frozen xenon. Phys Rev Lett. 1990;65:2591. doi: 10.1103/PhysRevLett.65.2591. [DOI] [PubMed] [Google Scholar]
- Cates GD, Schaefer SR, Happer W. Relaxation of spins due to field inhomogeneities in gaseous samples at low magnetic fields and low pressures. Phys Rev A. 1988a;37(8):2877. doi: 10.1103/physreva.37.2877. [DOI] [PubMed] [Google Scholar]
- Cates GD, White DJ, Chien TR, Schaefer SR, Happer W. Spin relaxation in gases due to inhomogeneous static and oscillating magnetic fields. Phys Rev A. 1988b;38(8):5092–5106. doi: 10.1103/physreva.38.5092. [DOI] [PubMed] [Google Scholar]
- Chann B, Babcock E, Anderson LW, Walker TG. Measurements of 3He spin-exchange rates. Phys Rev A. 2002a;66(3):032703. [Google Scholar]
- Chann B, Babcock E, Anderson LW, Walker TG. Skew light propagation in optically thick optical pumping cells. Phys Rev A. 2002b;66(3):033406. [Google Scholar]
- Chann B, Babcock E, Anderson LW, Walker TG, Chen WC, Smith TB, Thompson AK, Gentile TR. Production of highly polarized 3He using spectrally narrowed diode laser array bars. J Appl Phys. 2003;94(10):6908–6914. [Google Scholar]
- Chapman R, Bloom M. Nuclear spin-lattice relaxation of 3He on neon surfaces. Can J Phys. 1976;54(8):861–869. [Google Scholar]
- Chapman R, Richards MG. Longitudinal Spin Relaxation in 3He Gas at 4.2 K. Phys Rev Lett. 1974;33(1):18. [Google Scholar]
- Chapman Ross. Temperature dependence of the relaxation time in dilute 3He gas: An investigation of the He-He potential. Phys Rev A. 1975;12(6):2333. [Google Scholar]
- Chen Wangchun. Private communication. 2016.
- Chen WC, Armstrong G, Chen Y, Collett B, Erwin R, Gentile TR, Jones GL, Lynn JW, McKenney S, Steinberg JE. 3He spin filters for a thermal neutron triple axis spectrometer. Physica B. 2007a;397(1):168–171. [Google Scholar]
- Chen WC, Gentile Thomas R, O’Donovan Kevin V, Borchers Julie A, Majkrzak Charles F. Polarized neutron reflectometry of a patterned magnetic film with a 3He analyzer and a position-sensitive detector. Rev Sci Instrum. 2004;75(10):3256–3263. [Google Scholar]
- Chen WC, Gentile TR, Erwin R, Watson S, Ye Q, Krycka KL, Maranville BB. 3He spin filter based polarized neutron capability at the NIST Center for Neutron Research. J Phys Conf Ser. 2014a;528(1):012014. [Google Scholar]
- Chen WC, Gentile TR, Fu CB, Watson S, Jones GL, McIver JW, Rich DR. Polarized 3He cell development and application at NIST. J Phys Conf Ser. 2011;294(1):012003. [Google Scholar]
- Chen WC, Gentile TR, Walker TG, Babcock E. Spin-exchange optical pumping of 3He with Rb-K mixtures and pure K. Phys Rev A. 2007b;75(1):013416. [Google Scholar]
- Chen WC, Gentile TR, Ye Q, Kirchhoff A, Watson SM, Rodriguez-Rivera JA, Qiu Y, Broholm C. Recent advancements of wide-angle polarization analysis with 3He neutron spin filters. J Phys Conf Ser. 2016;746(1):012016. [Google Scholar]
- Chen WC, Gentile TR, Ye Q, Walker TG, Babcock E. On the limits of spin-exchange optical pumping of 3He. J Appl Phys. 2014b;116(1):014903. doi: 10.1103/PhysRevLett.96.083003. [DOI] [PubMed] [Google Scholar]
- Chen X Josette, Chawla Mark S, Hedlund Laurence W, Möller Harald E, Macfall James R, Allan Johnson G, Elaine G. MR microscopy of lung airways with hyperpolarized 3He. Magn Reson Med. 1998;39:79–84. doi: 10.1002/mrm.1910390113. [DOI] [PubMed] [Google Scholar]
- Chen Ying, Lynn JW, Li J, Li G, Chen GF, Luo JL, Wang NL, Dai Pengcheng, Cruz Clarina dela, Mook HA. Magnetic order of the iron spins in Nd-FeAsO. Phys Rev B. 2008;78(6):064515. [Google Scholar]
- Chernikov SV, Taylor JR, Platonov NS, Gapontsev VP, Nacher PJ, Tastevin G, Leduc M, Barlow MJ. 1083 nm ytterbium doped fibre amplifier for optical pumping of helium. Electron Lett. 1997;33(9):787–789. [Google Scholar]
- Chéron B, Gilles H, Hamel J, Leduc M, Moreau O, Noël E. 3He Nuclear Spin Relaxation in Cesium Coated Cells at Room Temperature. J Phys III France. 1995;5(8):1287–1295. [Google Scholar]
- Chu P-H, Dennis A, Fu CB, Gao H, Khatiwada R, Laskaris G, Li K, Smith E, Snow WM, Yan H, Zheng W. Laboratory search for spin-dependent short-range force from axionlike particles using optically polarized 3He gas. Phys Rev D. 2013;87(1):011105. [Google Scholar]
- Chu P-H, Esler AM, Peng JC, Beck DH, Chandler DE, Clayton S, Hu B-Z, Ngan SY, Sham CH, So LH, et al. Dressed spin of polarized 3He in a cell. Phys Rev C. 2011;84(2):022501. [Google Scholar]
- Chu Ping-Han, Peng Jen-Chieh. Simultaneous pi/2 rotation of two spin species of different gyromagnetic ratios. Nucl Instrum Methods Phys Res, Sect A. 2015;795:128–131. [Google Scholar]
- Chupp TE, Oteiza ER, Richardson JM, White TR. Precision frequency measurements with polarized 3He, 21Ne, and 129Xe atoms. Phys Rev A. 1988;38:3998–4003. doi: 10.1103/physreva.38.3998. [DOI] [PubMed] [Google Scholar]
- Chupp TE, Coulter KP, Kandes M, Sharma M, Smith TB, Jones G, Chen WC, Gentile TR, Rich DR, Lauss B, et al. A large area polarized 3He neutron spin filter. Nucl Instrum Methods Phys Res, Sect A. 2007;574(3):500–509. [Google Scholar]
- Chupp TE, Hoare RJ, Walsworth RL, Wu Bo. Spin-exchange-pumped 3He and 129Xe Zeeman masers. Phys Rev Lett. 1994;72(15):2363. doi: 10.1103/PhysRevLett.72.2363. [DOI] [PubMed] [Google Scholar]
- Chupp TE, Loveman RA, Thompson AK, Bernstein AM, Tieger DR. Tests of a high density polarized 3He target for electron scattering. Phys Rev C. 1992;45(3):915. doi: 10.1103/physrevc.45.915. [DOI] [PubMed] [Google Scholar]
- Chupp TE, Wagshul ME, Coulter KP, McDonald AB, Happer W. Polarized, high-density, gaseous 3He targets. Phys Rev C. 1987;36(6):2244. doi: 10.1103/physrevc.36.2244. [DOI] [PubMed] [Google Scholar]
- Cohen-Tannoudji C, Dupont-Roc J, Haroche S, Laloë F. Detection of the Static Magnetic Field Produced by the Oriented Nuclei of Optically Pumped 3He Gas. Phys Rev Lett. 1969;22:758–760. [Google Scholar]
- Colegrove FD, Schearer LD, Walters GK. Polarization of 3He gas by optical pumping. Phys Rev. 1963;132(6):2561. [Google Scholar]
- Colegrove FD, Schearer LD, Walters GK. Temperature Dependence of Helium Metastability Exchange Cross Section. Phys Rev. 1964;135(2A):A353. [Google Scholar]
- Collier Guilhem, Suchanek Mateusz, Wojna Anna, Cieslar Katarzyna, Palasz Tadeusz, Glowacz Bartosz, Olejniczak Zbigniew, Dohnalik Tomasz. Metastability exchange optical pumping low field polarizer for lung magnetic resonance imaging. Opt Appl. 2012;42(1):223–239. [Google Scholar]
- Conradi Mark S, Saam Brian T, Yablonskiy Dmitriy A, Woods Jason C. Hyperpolarized 3He and perfluorocarbon gas diffusion MRI of lungs. Prog Nucl Mag Res Sp. 2006;48(1):63–83. [Google Scholar]
- Costanza S, Mushkarenkov A, Rigamonti F, Romaniuk M, Aguar Bartolomé P, Ahrens J, JR, Annand M, Arends HJ, Beck R, Braghieri A, et al. (A2 Collaboration) Helicity dependence of the γ3He → πX reactions in the Δ(1232) resonance region. Eur Phys J A. 2014;50(11):173. [Google Scholar]
- Couch Marcus J, Blasiak Barbara, Tomanek Boguslaw, Ouriadov Alexei V, Fox Matthew S, Dowhos Krista M, Albert Mitchell S. Hyperpolarized and Inert Gas MRI: The Future. Mol Imaging Biol. 2015;17(2):149–162. doi: 10.1007/s11307-014-0788-2. [DOI] [PubMed] [Google Scholar]
- Coulter KP, Chupp TE, McDonald AB, Bowman CD, Bowman JD, Szymanski JJ, Yuan V, Cates GD, Benton DR, Earle ED. Neutron polarization with a polarized 3He spin filter. Nucl Instrum Methods Phys Res, Sect A. 1990;288(2):463–466. [Google Scholar]
- Coulter KP, McDonald AB, Happer W, Chupp TE, Wagshul ME. Neutron polarization with polarized 3He. Nucl Instrum Methods Phys Res, Sect A. 1988;270(1):90–94. [Google Scholar]
- Courtade E, Marion F, Nacher PJ, Tastevin G, Dohnalik T, Kiersnowski K. Spectroscopy of the helium 23S–23P transition above 0.01 Tesla – Application to optical pumping studies. Hyperfine Interact. 2000;127(1–4):451–454. [Google Scholar]
- Courtade Emmanuel, Marion François, Nacher P-J, Tastevin Geneviève, Kiersnowski K, Dohnalik Tomasz. Magnetic field effects on the 1083 nm atomic line of helium. Eur Phys J D. 2002;21(1):25–55. [Google Scholar]
- Crampton SB, Nacher PJ, Leduc M, Laloë F. Nuclear polarization of 3He gas at and below 4.2 K by room temperature laser optical pumping. AIP Conference Proceedings. 1984;117(1):153–156. [Google Scholar]
- Cummings WJ, Häusser O, Lorenzon W, Swenson DR, Larson B. Optical pumping of Rb vapor using high-power Ga1–xAlxAs diode laser arrays. Phys Rev A. 1995;51(6):4842. doi: 10.1103/physreva.51.4842. [DOI] [PubMed] [Google Scholar]
- Cutillo AG, Ganesan K, Ailion DC, Morris AH, Durney CH, Symko SC, Christman RA. Alveolar air-tissue interface and nuclear magnetic resonance behavior of lung. J Appl Physiol. 1991;70:2145–54. doi: 10.1152/jappl.1991.70.5.2145. [DOI] [PubMed] [Google Scholar]
- Daniels JM, Timsit RS. Determination of polarization of He-3 by optical methods. Can J Phys. 1971;49(5):539. [Google Scholar]
- Daniels Timothy Vaughn, Arnold CW, Cesaratto JM, Clegg TB, Couture AH, Karwowski HJ, Katabuchi T. Spin-correlation coefficients and phase-shift analysis for p+ 3He elastic scattering. Phys Rev C. 2010;82(3):034002. [Google Scholar]
- Darrasse Luc, Guillot Geneviève, Nacher Pierre-Jean, Tastevin Geneviève. Low-field 3He nuclear magnetic resonance in human lungs. CR Acad Sci, Ser IIb: Mec, Phys, Chim, Astron. 1997;324(11):691–700. [Google Scholar]
- Dawson M, Kardjilov N, Manke I, Hilger A, Jullien D, Bordenave F, Strobl M, Jericha E, Badurek G, Banhart J. Polarized neutron imaging using helium-3 cells and a polychromatic beam. Nucl Instrum Methods Phys Res, Sect A. 2011;651(1):140–144. [Google Scholar]
- Dehmelt HG. Slow Spin Relaxation of Optically Polarized Sodium Atoms. Phys Rev. 1957;105(5):1487–1489. [Google Scholar]
- Deninger A, Heil W, Otten EW, Wolf M, Kremer RK, Simon A. Paramagnetic relaxation of spin polarized 3He at coated glass walls. Eur Phys J D. 2006;38(3):439–443. [Google Scholar]
- Deninger AJ, Eberle B, Ebert M, Grossmann T, Heil W, Kauczor H-U, Lauer L, Markstaller K, Otten E, Schmiedeskamp J, et al. Quantification of regional intrapulmonary oxygen partial pressure evolution during apnea by 3He MRI. J Magn Reson. 1999;141(2):207–216. doi: 10.1006/jmre.1999.1902. [DOI] [PubMed] [Google Scholar]
- Deppe MH, Wild JM. Variable flip angle schedules in bSSFP imaging of hyperpolarized noble gases. Magn Reson Med. 2012;67:1656–64. doi: 10.1002/mrm.23155. [DOI] [PubMed] [Google Scholar]
- DeSchepper D, Kramer LH, Pate SF, Ackerstaff K, Carr RW, Court GR, Dvoredsky A, Gao H, Golendoukhin A, Hansen J-O, et al. The HERMES polarized 3He internal gas target. Nucl Instrum Methods Phys Res, Sect A. 1998;419(1):16–44. [Google Scholar]
- DeSchepper Dirk. Spin-dependent deep inelastic positron scattering from 3He with HERMES. Nucl Instrum Methods Phys Res, Sect A. 1998;402(2):256–259. [Google Scholar]
- Desvaux Herve. Non-linear liquid-state NMR. Prog Nucl Magn Reson Spectrosc. 2013;70:50–71. doi: 10.1016/j.pnmrs.2012.11.001. [DOI] [PubMed] [Google Scholar]
- Dohnalik T, Nikiel A, Pałasz T, Suchanek M, Collier G, Greńczuk M, Głowacz B, Olejniczak Z. Optimization of the pumping laser beam spatial profile in the MEOP experiment performed at elevated 3He pressures. Eur Phys J Appl Phys. 2011;54(2):20802. [Google Scholar]
- Dolph PAM, Singh J, Averett T, Kelleher A, Mooney KE, Nelyubin V, Tobias WA, Wojtsekhowski B, Cates GD. Gas dynamics in high-luminosity polarized 3He targets using diffusion and convection. Phys Rev C. 2011;84(6):065201. [Google Scholar]
- Donley EA, Kitching J. Chap Nuclear Magnetic Resonance Gyroscopes. Cambridge University Press; 2013. Optical magnetometry; p. 369. [Google Scholar]
- Drake GWF, Nörtershäuser W, Yan Z-C. Isotope shifts and nuclear radius measurements for helium and lithium. Can J Phys. 2005;83(4):311–325. [Google Scholar]
- Dreyer J, Regnault L-P, Bourgeat-Lami E, Lelievre-Berna E, Pujol S, Thomas F, Thomas M, Tasset F. Cryopol: a superconducting magnetostatic cavity for a 3He neutron spin filter. Nucl Instrum Methods Phys Res, Sect A. 2000;449(3):638–648. [Google Scholar]
- Driehuys B, Cates GD, Miron E, Sauer K, Walter DK, Happer W. High-volume production of laser-polarized 129Xe. Appl Phys Lett. 1996;69(12):1668–1670. [Google Scholar]
- Dufour C, Fitzsimmons MR, Borchers JA, Laver Mark, Krycka KL, Dumesnil K, Watson SM, Chen WC, Won J, Singh S. Nanometer-size magnetic domains and coherent magnetization reversal in a giant exchange-bias system. Phys Rev B. 2011;84(6):064420. [Google Scholar]
- Dunlop MW, Dougherty MK, Kellock S, Southwood S. Operation of the dual magnetometer on Cassini: science performance. Planetary and Space Science. 1999;47:1389–1405. [Google Scholar]
- Dupont-Roc J, Leduc M, Laloë F. New value for the metastability exchange cross section in helium. Phys Rev Lett. 1971;27(8):467–470. [Google Scholar]
- Dupont-Roc J, Leduc M, Laloë F. Contribution à l’étude du pompage optique par échange de métastabilité dans 3He. - Première partie et deuxième partie. J Phys. 1973;34(11–12):961–976. 977–987. [Google Scholar]
- Durand E, Guillot G, Darrasse L, Tastevin G, Nacher PJ, Vignaud A, Vattolo D, Bittoun J. CPMG measurements and ultrafast imaging in human lungs with hyperpolarized helium-3 at low field (0.1 T) Magn Reson Med. 2002;47:75–81. doi: 10.1002/mrm.10047. [DOI] [PubMed] [Google Scholar]
- Ebert M, Grossmann T, Heil W, Otten EW, Surkau R, Thelen M, Leduc M, Bachert P, Knopp MV, Schad LR. Nuclear magnetic resonance imaging with hyperpolarised helium-3. The Lancet. 1996;347(9011):1297–1299. doi: 10.1016/s0140-6736(96)90940-x. [DOI] [PubMed] [Google Scholar]
- Eckel S, Lamoreaux SK, Hayden ME, Ito TM. Time-dependent spin dressing using a 3He atomic beam. Phys Rev A. 2012;85:032124. [Google Scholar]
- Eckert G, Heil W, Meyerhoff M, Otten EW, Surkau R, Werner M, Leduc M, Nacher PJ, Schearer LD. A dense polarized 3He target based on compression of optically pumped gas. Nucl Instrum Methods Phys Res, Sect A. 1992;320(1):53–65. [Google Scholar]
- Elbel M, Larat C, Nacher PJ, Leduc M. Optical pumping of helium-3 with a frequency electromodulated laser. J Phys Paris. 1990;51(1):39–46. [Google Scholar]
- Erickson CJ, Levron D, Happer W, Kadlecek S, Chann B, Anderson LW, Walker TG. Spin relaxation resonances due to the spin-axis interaction in dense rubidium and cesium vapor. Phys Rev Lett. 2000;85(20):4237. doi: 10.1103/PhysRevLett.85.4237. [DOI] [PubMed] [Google Scholar]
- Fain S, Schiebler ML, McCormack DG, Parraga G. Imaging of lung function using hyperpolarized helium-3 magnetic resonance imaging: Review of current and emerging translational methods and applications. J Magn Reson Imaging (USA) 2010;32:1398–408. doi: 10.1002/jmri.22375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fain SB, Altes TA, Panth SR, Evans MD, Waters B, Mugler JP, III, Korosec FR, Grist TM, Silverman M, Salerno M, Owers-Bradley J. Detection of age-dependent changes in healthy adult lungs with diffusion-weighted 3He MRI. Acad Radiol (Netherlands) 2005;12:1385–93. doi: 10.1016/j.acra.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Fedichev PO, Reynolds MW, Rahmanov UM, Shlyapnikov GV. Inelastic decay processes in a gas of spin-polarized triplet helium. Phys Rev A. 1996;53(3):1447–1453. doi: 10.1103/physreva.53.1447. [DOI] [PubMed] [Google Scholar]
- Fedorov VV, et al. Measurement of the neutron electric dipole moment via spin rotation in a non-centrosymmetric crystal. Phys Lett B. 2010;694:22–25. [Google Scholar]
- Fitzsimmons WA, Lane NF, Walters GK. Diffusion of He(23S1) in Helium Gas; 23S1 –11S0 Interaction Potentials at Long Range. Phys Rev. 1968;174(1):193–200. [Google Scholar]
- Fitzsimmons WA, Tankersley LL, Walters GK. Nature of surface-induced nuclear-spin relaxation of gaseous 3He. Phys Rev. 1969;179(1):156. [Google Scholar]
- Flors Lucia, Mugler John P, III, de Lange Eduard E, Miller Grady W, Mata Jaime F, Tustison Nick, Ruset Iulian C, William Hersman F, Altes Talissa A. Hyperpolarized Gas Magnetic Resonance Lung Imaging in Children and Young Adults. J Thorac Imag. 2016;31:285–295. doi: 10.1097/RTI.0000000000000218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flowers JL, Petley BW, Richards MG. An optically pumped 3He maser operating at 0.1 T. J Phys B: At, Mol Opt Phys. 1990;23(8):1359–1362. [Google Scholar]
- Flowers JL, Bickley CJ, JosephsFranks PW, Petley BW. Optically pumped He-3 NMR and atomic hydrogen ESR at 0.6 T. IEEE T Instrum Meas; Conference on Precision Electromagnetic Measurements (CPEM 96); Braunschweig, Germany. Jun 17–20, 1996.1997. pp. 104–107. [Google Scholar]
- Freeman MS, Emami K, Driehuys B. Characterizing and modeling the efficiency limits in large-scale production of hyperpolarized 129Xe. Phys Rev A. 2014;90:023406. doi: 10.1103/physreva.90.023406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund A, Pynn R, Stirling WG, Zeyen CME. Vertically focussing Heusler alloy monochromators for polarised Neutrons. Physica B+C. 1983;120(1):86–90. [Google Scholar]
- Friar JL, Gibson BF, Payne GL, Bernstein AM, Chupp TE. Neutron polarization in polarized 3He targets. Phys Rev C. 1990;42:2310–2314. doi: 10.1103/physrevc.42.2310. [DOI] [PubMed] [Google Scholar]
- Fu CB, Gentile TR, Snow WM. Limits on possible new nucleon monopole-dipole interactions from the spin relaxation rate of polarized 3He gas. Phys Rev D. 2011;83(3):031504. [Google Scholar]
- Funayama C, Furukawa T, Sato T, Ichikawa Y, Ohtomo Y, Sakamoto Y, Kojima S, Suzuki T, Hirao C, Chikamori M, Hikota E, Tsuchiya M, Yoshimi A, Bidinosti CP, Ino T, Ueno H, Matsuo Y, Fukuyama T, Asahi K. Performance assessment of a new laser system for efficient spin exchange optical pumping in a spin maser measurement of 129Xe EDM. Hyperfine Interact. 2015;236(1):59–64. [Google Scholar]
- Gamblin Rodger L, Carver Thomas R. Polarization and Relaxation Processes in 3He Gas. Phys Rev. 1965;138(4A):A946. [Google Scholar]
- Gao Haiyan, Arrington J, Beise EJ, Bray B, Carr RW, Filippone BW, Lung A, McKeown RD, Mueller B, Pitt ML, et al. Measurement of the neutron magnetic form factor from inclusive quasielastic scattering of polarized electrons from polarized 3He. Phys Rev C. 1994;50(2):R546. doi: 10.1103/physrevc.50.r546. [DOI] [PubMed] [Google Scholar]
- Gemmel C, Heil W, Karpuk S, Lenz K, Ludwig Ch, Sobolev Yu, Tullney K, Burghoff M, Kilian W, Knappe-Grüneberg S, Müller W, Schnabel A, Seifert F, Trahms L, Baeßler St. Ultra-sensitive magnetometry based on free precession of nuclear spins. Eur Phys J D. 2010;57(3):303–320. [Google Scholar]
- Gentile Thomas R, Hayden Michael E, Barlow Michael J. Comparison of metastability-exchange optical pumping sources. J Opt Soc Am B. 2003;20(10):2068–2074. [Google Scholar]
- Gentile Thomas R, McKeown Robert D. Spin-polarizing 3He nuclei with an arc-lamp-pumped neodymium-doped lanthanum magnesium hexaluminate laser. Phys Rev A. 1993;47(1):456. doi: 10.1103/physreva.47.456. [DOI] [PubMed] [Google Scholar]
- Gentile TR, Babcock E, Borchers JA, Chen WC, Hussey D, Jones GL, Lee WT, Majkzrak CF, O’Donovan KV, Snow WM, et al. Polarized 3He spin filters in neutron scattering. Physica B. 2005a;356(1):96–102. [Google Scholar]
- Gentile TR, Chen WC, Jones GL, Babcock E, Walker TG. Polarized 3He Spin Filters for Slow Neutron Physics. J Res Natl Inst Stan. 2005b;110(3):299–304. doi: 10.6028/jres.110.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentile TR, Crawford CB. Neutron charge radius and the neutron electric form factor. Phys Rev C. 2011;83:055203. [Google Scholar]
- Gentile TR, Jones GL, Thompson AK, Barker J, Glinka CJ, Hammouda B, Lynn JW. SANS polarization analysis with nuclear spin-polarized 3He. J Appl Crystallogr. 2000;33(3):771–774. [Google Scholar]
- Gentile TR, Rich DR, Thompson AK, Snow WM, Jones GL. Compressing Spin-Polarized 3He With a Modified Diaphragm Pump. J Res Natl Inst Stan. 2001;106(4):709–730. doi: 10.6028/jres.106.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gericke MT, Alarcon R, Balascuta S, Barron-Palos L, Blessinger C, Bowman JD, Carlini RD, Chen W, Chupp TE, Crawford C, et al. Measurement of parity-violating γ-ray asymmetry in the capture of polarized cold neutrons on protons. Phys Rev C. 2011;83(1):015505. [Google Scholar]
- Gericke MT, Bowman JD, Carlini RD, Chupp TE, Coulter KP, Dabaghyan M, Dawkins M, Desai D, Freedman SJ, Gentile TR, et al. Upper bounds on parity violating gamma-ray asymmetries in compound nuclei from polarized cold neutron capture. 2006 arXiv preprint nucl-ex/0608006. [Google Scholar]
- Giberson KW, Cheng Chu, Onellion M, Dunning FB, Walters GK. Optical pumping of He(23S) atoms by a color-center laser. Rev Sci Instrum. 1982;53(11):1789–1790. http://dx.doi.org/10.1063/1.1136864. [Google Scholar]
- Gilles H, Monfort Y, Hamel J. 3He maser for Earth magnetic field measurement. Rev Sci Instrum. 2003;74(10):4515–4520. [Google Scholar]
- Glenday Alexander G. PhD thesis. Harvard University; 2010. Progress in Tests of Fundamental Physics Using a 3He and 129Xe Zeeman Maser. [Google Scholar]
- Glenday Alexander G, Cramer Claire E, Phillips David F, Walsworth Ronald L. Limits on Anomalous Spin-Spin Couplings between Neutrons. Phys Rev Lett. 2008;101(26) doi: 10.1103/PhysRevLett.101.261801. [DOI] [PubMed] [Google Scholar]
- Glowacz Bartosz. Detection of metastable He2* molecules in helium plasma. PhD Thesis. 2011 http://tel.archives-ouvertes.fr/tel-01360241 (UPMC -Paris 6 and Jagiellonian Univ. Cracow, Poland)
- Golub Robert, Lamoreaux Steve K. Neutron electric-dipole moment, ultracold neutrons and polarized 3He. Phys Rep. 1994;237(1):1–62. [Google Scholar]
- Goossens DJ, Cussen LD. Optimising neutron polarizers - measuring a single cross section. Nucl Instrum Methods Phys Res, Sect A. 2002;490:316–333. [Google Scholar]
- Gourevitch A, Venus G, Smirnov V, Hostutler DA, Glebov L. Continuous wave, 30 W laser-diode bar with 10 GHz linewidth for Rb laser pumping. Opt Lett. 2008;33(7):702–704. doi: 10.1364/ol.33.000702. [DOI] [PubMed] [Google Scholar]
- Greenberg Ya S. Application of superconducting quantum interference devices to nuclear magnetic resonance. Rev Mod Phys. 1998;70:175–222. [Google Scholar]
- Greenhow RC. Optical Pumping in 3He. Phys Rev. 1964;136(3A):A660. [Google Scholar]
- Grover BC. Noble-Gas NMR Detection through Noble-Gas-Rubidium Hyperfine Contact Interaction. Phys Rev Lett. 1978;40:391–392. [Google Scholar]
- Guigue M, Jullien D, Petukhov AK, Pignol G. Constraining short-range spin-dependent forces with polarized 3He. Phys Rev D. 2015;92:114001. [Google Scholar]
- Guigue M, Pignol G, Golub R, Petukhov AK. Universality of spin relaxation for spin-1/2 particles diffusing over magnetic-field inhomogeneities in the adiabatic regime. Phys Rev A. 2014;90(1):013407. [Google Scholar]
- Guldner M, Becker S, Wolf U, Duber C, Friesenecker A, Gast KK, Heil W, Hoffmann C, Karpuk S, Otten EW, Rivoire J, Salhi Z, Scholz A, Schreiber LM, Terekhov M. Application unit for the administration of contrast gases for pulmonary magnetic resonance imaging: optimization of ventilation distribution for 3he-mri. Magn Reson Med (USA) 2015;74:884–93. doi: 10.1002/mrm.25433. [DOI] [PubMed] [Google Scholar]
- Hamedani H, Kadlecek SJ, Ishii M, Emami K, Kuzma NN, Xin Yi, Rossman M, Rizi RR. A variability study of regional alveolar oxygen tension measurement in humans using hyperpolarized 3He MRI. Magn Reson Med (USA) 2013;70:1557–66. doi: 10.1002/mrm.24604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen J-O, Titko MA, DeSchepper D, Dodson G, Donnelly TW, Dow R, Ent K, Farkhondeh M, Korsch W, Kramer LH, Lee K, et al. Transverse-Longitudinal Asymmetry in the Quasielastic 3H⃗e(e⃗, e′) Reaction. Phys Rev Lett. 1995;74(5):654. doi: 10.1103/PhysRevLett.74.654. [DOI] [PubMed] [Google Scholar]
- Happer, Jau WY-Y, Walker TG. Optically Pumped Atoms. Wiley; 2009. [Google Scholar]
- Happer W, Van Wijngaarden WA. An optical pumping primer. Hyperfine Interact. 1987;38(1):435–470. [Google Scholar]
- Happer William. Optical pumping. Rev Mod Phys. 1972;44(2):169. [Google Scholar]
- Haseyama T, et al. Measurement of parity-nonconserving rotation of neutron spin in the 0.734-eV p-wave resonance of 139La. Phys Lett B. 2002;534:39–44. [Google Scholar]
- Hasson KC, Cates GD, Lerman K, Bogorad P, Happer W. Spin relaxation due to magnetic-field inhomogeneities: quartic dependence and diffusion-constant measurements. Phys Rev A. 1990;41:3672–3688. doi: 10.1103/physreva.41.3672. [DOI] [PubMed] [Google Scholar]
- Hasz K, et al. Particle moment canting in CoFe2O4. Phys Rev B. 2014;90:180405(R). [Google Scholar]
- Häusser O, Larson B, Alford WP, Chan C, Delheij PPJ, Henderson RS, Jackson KP, Landau RH, Mefford T, Miller CA, et al. Elastic scattering of polarized protons from polarized 3He. Phys Lett B. 1995;343(1):36–40. [Google Scholar]
- Hayashida H, Oku T, Kira H, Sakai K, Hiroi K, Ino T, Shinohara T, Imagawa T, Ohkawara M, Ohoyama K, et al. Development of a 3He nuclear spin flip system on an in-situ SEOP 3He spin filter and demonstration for a neutron reflectometer and magnetic imaging technique. J Phys Conf Ser. 2016;711(1):012007. [Google Scholar]
- Hayden ME, Baudin E, Tastevin G, Nacher PJ. NMR Time Reversal as a Probe of Incipient Turbulent Spin Dynamics. Phys Rev Lett. 2007;99(13):137602. doi: 10.1103/PhysRevLett.99.137602. [DOI] [PubMed] [Google Scholar]
- Heil W, Andersen KH, Cywinski R, Humblot H, Ritter C, Roberts TW, Stewart JR. Large solid-angle polarisation analysis at thermal neutron wavelengths using a 3He spin filter. Nucl Instrum Methods Phys Res, Sect A. 2002;485(3):551–570. [Google Scholar]
- Heil W, Dreyer J, Hofmann D, Humblot H, Lelievre-Berna E, Tasset F. 3He neutron spin-filter. Physica B. 1999a;267:328–335. [Google Scholar]
- Heil W, Humblot H, Hofmann D, Krasnoschekova I, Lelievre-Berna E, Petoukhov A, Petrov G, Serebrov A, Tasset F, Valsky G. Neutron optics P-violation effects near p-wave resonance. Physica B. 1999b;267:289–293. [Google Scholar]
- Heil W, Werner M, Meyerhoff M, Schearer LD. Frequency stabilization of LNA laser to the helium absorption lines. Rev Sci Instrum. 1990;61(10):2549–2551. [Google Scholar]
- Heil Werner, Gemmel Claudia, Karpuk Sergei, Sobolev Yuri, Tullney Kathlynne, Allmendinger Fabian, Schmidt Ul-rich, Burghoff Martin, Kilian Wolfgang, Knappe-Grueneberg Silvia, et al. Spin clocks: Probing fundamental symmetries in nature. Annalen Der Physik. 2013;525(8–9) SI:539–549. [Google Scholar]
- Heil Werner, Humblot Hubert, Otten Ernst, Schafer Matthias, Sarkau Reinhard, Leduc Michèle. Very long nuclear relaxation times of spin polarized helium 3 in metal coated cells. Phys Lett A. 1995;201(4):337–343. [Google Scholar]
- Hersman FW, Distelbrink JH, Ketel J, Wilson J, Watt DW. Power scaling of a wavelength-narrowed diode laser system for pumping alkali vapors 2016 [Google Scholar]
- Hersman William, Watt David W, Ruset Iulian C, Distelbrink Jan H, Ketel Jeff. High-volume 100 Liter-per-day SEOP Polarization of 3He. Physcs Proc. 2013;42:171–182. [Google Scholar]
- Hiebel S, Großmann T, Kiselev D, Schmiedeskamp J, Gusev Y, Heil W, Karpuk S, Krimmer J, Otten EW, Salhi Z. Magnetized boxes for housing polarized spins in homogeneous fields. J Magn Reson. 2010;204(1):37–49. doi: 10.1016/j.jmr.2010.01.017. [DOI] [PubMed] [Google Scholar]
- Hiess A, Brown PJ, Aso N, Roessli B, Bernhoeft N, Sato NK, Lander GH. Neutron scattering study of the static and dynamic magnetic properties of UNi2Al3. J Magn Magn Mater. 2001;226:54–56. [Google Scholar]
- Hiess A, Brown PJ, Lelievre-Berna E, Roessli B, Bernhoeft N, Lander GH, Aso N, Sato NK. Spherical neutron polarimetry of the magnetic structure in UNi2Al3. Phys Rev B. 2001;64(13):134413. [Google Scholar]
- Hill JC, Hatfield LL, Stockwell ND, Walters GK. Direct demonstration of spin-angular-momentum conservation in the reaction He(23S1)+He(23S1) → He(11S0)+He++e−. Phys Rev A. 1972;5(1):189–195. [Google Scholar]
- Himbert M, Dupont-Roc J. Liquid4He as a cryogenic coating for gaseous spin polarized3He. J Low Temp Phys. 1989;76(5–6):435–452. [Google Scholar]
- Himbert Marc, Lefevre-Seguin Valérie, Nacher Pierre-Jean, Dupont-Roc Jacques, Leduc Michèle, Laloë Franck. Nuclear polarization through optical pumping of gaseous 3He below 1 K. J Phys Lett Paris. 1983;44(13):523–529. [Google Scholar]
- Honecker D, et al. Longitudinal polarization analysis in small-angle neutron scattering. Eur Phys J B. 2010;76:209–213. [Google Scholar]
- Horn Felix C, Rao Madhwesha, Stewart Neil J, Wild Jim M. Multiple breath washout of hyperpolarized 129Xe and 3He in human lungs with three-dimensional balanced steady-state free-precession imaging. Magn Reson Med 2016 doi: 10.1002/mrm.26319. ??, n/a–n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoult DI. Fast recovery, high sensitivity nmr probe and pre-amplifier for low-frequencies. Review of Scientific Instruments. 1979;50(2):193–200. doi: 10.1063/1.1135786. [DOI] [PubMed] [Google Scholar]
- Hsu Ming F, Cates GD, Kominis I, Aksay IA, Dabbs DM. Sol-gel coated glass cells for spin-exchange polarized 3He. Appl Phys Lett. 2000;77(13):2069–2071. [Google Scholar]
- Huang J, Allada K, Dutta C, Katich J, Qian X, Wang Y, Zhang Y, Aniol K, Annand M, JR, Averett T, et al. Beam-Target Double-Spin Asymmetry ALT in Charged Pion Production from Deep Inelastic Scattering on a Transversely Polarized 3He Target at 1.4 < Q2 < 2.7 GeV2. Phys Rev Lett. 2012;108:052001. doi: 10.1103/PhysRevLett.108.052001. [DOI] [PubMed] [Google Scholar]
- Huber MG, Arif M, Chen WC, Gentile TR, Hussey DS, Black TC, Pushin DA, Shahi CB, Wietfeldt FE, Yang L. Neutron interferometric measurement of the scattering length difference between the triplet and singlet states of n- 3He. Phys Rev C. 2014;90(6):064004. [Google Scholar]
- Hussey DS, Rich DR, Belov AS, Tong X, Yang H, Bailey C, Keith CD, Hartfield J, Hall GDR, Black TC, et al. Polarized 3He gas compression system using metastability-exchange optical pumping. Rev Sci Instrum. 2005;76(5):053503. [Google Scholar]
- Hutanu V, Masalovich S, Meven M, Lykhvar O, Borchert G, Heger G. Polarized 3He Spin Filters for Hot Neutrons at the FRM II. Neutron News. 2007a;18(4):14–16. [Google Scholar]
- Hutanu V, Meven M, Sazonov A, Heger G. Development of compact magnetostatic cavities for 3He spin filter cells. Meas Sci Technol. 2008;19(3):034010. [Google Scholar]
- Hutanu V, Rupp A. Research on 3He spin filter cells made of quartz glass. Physica B. 2005;356(1):91–95. [Google Scholar]
- Hutanu V, Rupp A, Klenke J, Heil W, Schmiedeskamp Jörg. Magnetization of 3He spin filter cells. J Phys D: Appl Phys. 2007b;40(15):4405. [Google Scholar]
- Hutanu V, Rupp A, Sander-Thömmes T. SQUID measurements of remanent magnetisation in refill-able 3He spin-filter cells (SFC) Physica B. 2007c;397(1):185–187. [Google Scholar]
- Hutanu Vladimir, Meven M, Masalovich S, Heger Gernot, Roth Georg. 3He spin filters for spherical neutron polarimetry at the hot neutrons single crystal diffractometer POLI-HEiDi. J Phys Conf Ser. 2011;294(1):012012. [Google Scholar]
- Ino T, Arimoto Y, Yoshioka T, Mishima K, Taketani K, Muto S, Shimizu HM, Kira H, Sakaguchi Y, Oku T, et al. Measurement of the neutron beam polarization of BL05/NOP beamline at J-PARC. Physica B. 2011;406(12):2424–2428. [Google Scholar]
- Ino Takashi, Arimoto Yasushi, Shimizu Hirohiko M, Sakaguchi Yoshifumi, Sakai Kenji, Kira Hiroshi, Shinohara Takenao, Oku Takayuki, Suzuki Jun-ichi, Kakurai Kazuhisa, et al. A compact SEOP 3He neutron spin filter with AFP NMR. J Phys Conf Ser. 2012;340(1):012006. [Google Scholar]
- Ino Takashi, Muto Suguru. Measurements of the 3He spin relaxation below room temperature. Physica B. 2007;397(1):182–184. [Google Scholar]
- Ino Takashi, Muto Suguru, Masuda Yasuhiro, Kim Guinyun, Skoy Vadim R. Development of 3He polarized neutron spin filters at KEK. Physica B. 2005;356(1):109–113. [Google Scholar]
- Ioffe Alexander, Babcock Earl, Gutberlet Thomas. JCNS Workshop on Modern Trends in Production and Applications of Polarized 3He. J Phys Conf Ser. 2011;294(1):011001. [Google Scholar]
- Jackson JD, Treiman SB, Wyld HW. Possible tests of time reversal invariance in beta decay. Phys Rev. 1957;106:517–521. [Google Scholar]
- Jackson John David. Classical electrodynamics. 3. Wiley; New York, NY: 1999. [Google Scholar]
- Jacob RE, Driehuys B, Saam B. Fundamental mechanisms of 3He relaxation on glass. Chem Phys Lett. 2003;370(1):261–267. [Google Scholar]
- Jacob RE, Morgan SW, Saam B. 3He spin exchange cells for magnetic resonance imaging. J Appl Phys. 2002;92(3):1588–1597. [Google Scholar]
- Jacob RE, Morgan SW, Saam B, Leawoods JC. Wall relaxation of 3He in spin-exchange cells. Phys Rev Lett. 2001;87:143004. doi: 10.1103/PhysRevLett.87.143004. [DOI] [PubMed] [Google Scholar]
- Jacob RE, Teter J, Saam B, Chen WC, Gentile TR. Low-field orientation dependence of 3He relaxation in spin-exchange cells. Phys Rev A. 2004;69(2):021401. [Google Scholar]
- Jacob Richard Emil. PhD thesis. The University of Utah; 2003. Studies of hyperpolarized relaxation 3He at glass surfaces. [Google Scholar]
- Jiang CY, Tong X, Brown Daniel R, Chi S, Christianson AD, Kadron BJ, Robertson JL, Winn Barry L. Development of a compact in situ polarized 3He neutron spin filter at Oak Ridge National Laboratory. Rev Sci Instrum. 2014;85(7):075112. doi: 10.1063/1.4890391. [DOI] [PubMed] [Google Scholar]
- Johnson JR, Thompson Alan K, Chupp TE, Smith TB, Cates GD, Driehuys B, Middleton H, Newbury NR, Hughes EW, Meyer W. The SLAC high-density gaseous polarized 3He target. Nucl Instrum Methods Phys Res, Sect A. 1995;356(1):148–152. [Google Scholar]
- Jones CE, Beise EJ, Belz JE, Carr RW, Filippone BW, Lorenzon W, McKeown RD, Mueller BA, O’Neill TG, Dodson GW, et al. 3H⃗e(e⃗, e′) quasielastic asymmetry. Phys Rev C. 1993;47(1):110. doi: 10.1103/physrevc.47.110. [DOI] [PubMed] [Google Scholar]
- Jones GL, Dias F, Collett B, Chen WC, Gentile TR, Piccoli PMB, Miller ME, Schultz AJ, Yan H, Tong X, et al. Test of a continuously polarized 3He neutron spin filter with NMR-based polarization inversion on a single-crystal diffractometer. Physica B. 2006;385:1131–1133. [Google Scholar]
- Jones GL, Gentile Thomas R, Thompson Alan K, Chowdhuri Z, Dewey MS, Snow WM, Wietfeldt FE. Test of 3He-based neutron polarizers at NIST. Nucl Instrum Methods Phys Res, Sect A. 2000;440(3):772–776. [Google Scholar]
- Jones-Woodward CE, Beise EJ, Belz JE, Carr RW, Filippone BW, Lorenzon W, McKeown RD, Mueller BA, O’Neill TG, Dodson G, et al. Determination of the neutron electric form factor in quasielastic scattering of polarized electrons from polarized 3He. Phys Rev C. 1991;44(2):R571. doi: 10.1103/physrevc.44.r571. [DOI] [PubMed] [Google Scholar]
- Kadlecek S. PhD thesis. University of Wisconsin-Madison; 1999. Spin Relaxation in Alkali Vapors. [Google Scholar]
- Kadlecek S, Anderson LW, Erickson CJ, Walker TG. Spin Relaxation in Alkali-metal Dimers. Phys Rev A. 2001a;64:52717. [Google Scholar]
- Kadlecek S, Anderson LW, Walker TG. Field dependence of spin relaxation in a dense Rb vapor. Phys Rev Lett. 1998;80(25):5512. [Google Scholar]
- Kadlecek S, Walker T, Walter DK, Erickson C, Happer W. Spin-axis relaxation in spin-exchange collisions of alkali-metal atoms. Phys Rev A. 2001b;63(5):052717. [Google Scholar]
- Kastlér A. Quelques Suggestions Concernant la Production Optique et la Détection Optique d’une Inégalité de Population des Niveaux de Quantifigation Spatiale des Atomes. Application a L’Expérience de Stern et Gerlach et a la Résonance Magnétique. J Phys Radium. 1950;11:255–65. [Google Scholar]
- Kastler A. Optical Methods of Atomic Orientation and of Magnetic Resonance. J Opt Soc Am. 1957;47(6):460–465. [Google Scholar]
- Katabuchi T, Buscemi S, Cesaratto JM, Clegg TB, Daniels TV, Fassler M, Neufeld RB, Kadlecek S. Spin-exchange optically pumped polarized 3He target for low-energy charged particle scattering experiments. Rev Sci Instrum. 2005;76(3):033503. [Google Scholar]
- Katich J, Qian X, Zhao YX, Allada K, Aniol K, Annand M, JR, Averett T, Benmokhtar F, Bertozzi W, Bradshaw PC, et al. Measurement of the Target-Normal Single-Spin Asymmetry in Deep-Inelastic Scattering from the Reaction 3He↑(e, e′)X. Phys Rev Lett. 2014;113:022502. doi: 10.1103/PhysRevLett.113.022502. [DOI] [PubMed] [Google Scholar]
- Kauczor Hans-Ulrich, Ebert Michael, Kreitner Karl-Friedrich, Nilgens Helge, Surkau Reinhard, Heil Werner, Hofmann Dirk, Otten Ernst W, Thelen Manfred. Imaging of the lungs using 3He MRI: preliminary clinical experience in 18 patients with and without lung disease. J Magn Reson Imaging. 1997;7(3):538–543. doi: 10.1002/jmri.1880070314. [DOI] [PubMed] [Google Scholar]
- Keiderling U, Wiedenmann A, Rupp A, Klenke J, Heil W. SANS polarization analysis at V4 SANS instrument of HMI Berlin. Meas Sci Technol. 2008;19:034009. [Google Scholar]
- Kim Young Jin, Clayton Steven M. Development of a SQUID-Based He-3 Co-Magnetometer Readout for a Neutron Electric Dipole Moment Experiment. IEEE T Appl Supercon. 2013;23(3):1. doi: 10.1109/TASC.2012.2229773. [DOI] [Google Scholar]
- Kirby M, Kanhere N, Etemad-Rezai R, McCormack DG, Parraga G. Hyperpolarized helium-3 magnetic resonance imaging of chronic obstructive pulmonary disease exacerbation. J Magn Reson Imaging. 2013;37:1223–7. doi: 10.1002/jmri.23896. [DOI] [PubMed] [Google Scholar]
- Kleinekathöfer U, Lewerenz M, Mladenović M. Long Range Binding in Alkali-Helium Pairs. Phys Rev Lett. 1999;83:4717–4720. [Google Scholar]
- Kluttz Kelly A, Averett Todd D, Wolin Brian A. Pressure broadening and frequency shift of the D1 and D2 lines of Rb and K in the presence of 3He and N2. Phys Rev A. 2013;87(3):032516. [Google Scholar]
- Koch Hans-Christian, Bison Georg, Zoran Grujić D, Heil Werner, Kasprzak Malgorzata, Knowles Paul, Kraft Andreas, Pazgalev Anatoly, Schnabel Allard, Voigt Jens, Weis Antoine. Investigation of the intrinsic sensitivity of a 3He/Cs magnetometer. Eur Phys J D. 2015a;69:1–11. [Google Scholar]
- Koch Hans-Christian, Bison Georg, Grujic Zoran D, Heil Werner, Kasprzak Malgorzata, Knowles Paul, Kraft Andreas, Pazgalev Anatoly, Schnabel Allard, Voigt Jens, Weis Antoine. Design and performance of an absolute 3He/Cs magnetometer. Eur Phys J D. 2015b;69:262. [Google Scholar]
- Kornack TW, Ghosh RK, Romalis MV. Nuclear spin gyroscope based on an atomic comagnetometer. Phys Rev Lett. 2005;95(23):230801. doi: 10.1103/PhysRevLett.95.230801. [DOI] [PubMed] [Google Scholar]
- Kornack TW, Romalis MV. Dynamics of two overlapping spin ensembles interacting by spin exchange. Phys Rev Lett. 2002;89(25):253002. doi: 10.1103/PhysRevLett.89.253002. [DOI] [PubMed] [Google Scholar]
- Korsch W, Carr RW, DeSchepper D, Dvoredsky A, Kramer LH, Li Y, McKeown RD, Milner RG, Pate SF, Pitt ML, et al. Temperature dependence of 3He polarization in aluminum storage cells. Nucl Instrum Methods Phys Res, Sect A. 1997;389(3):389–397. [Google Scholar]
- Korver A, Thrasher D, Bulatowicz M, Walker TG. Synchronous Spin-Exchange Optical Pumping. Phys Rev Lett. 2015;115:253001. doi: 10.1103/PhysRevLett.115.253001. [DOI] [PubMed] [Google Scholar]
- Korver A, Wyllie R, Lancor B, Walker TG. Suppression of Spin-Exchange Relaxation Using Pulsed Parametric Resonance. Phys Rev Lett. 2013;111:043002. doi: 10.1103/PhysRevLett.111.043002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kostelecky Alan., editor. Constraints on MonopoleDipole Interactions of WISPS from Polarized Gas Relaxation Time. Vol. Proceedings of the Fifth Meeting on CPT and Lorentz Symmetry; Bloomington, USA. 28 June - 2 July 2010.2010. [Google Scholar]
- Kraft A, Koch H-C, Daum Manfred, Heil Werner, Lauer Thorsten, Neumann Daniel, Pazgalev Anatoly, Sobolev Yuri, Weis Antoine. Development of a 3He magnetometer for a neutron electric dipole moment experiment. EPJ Techn Instrum. 2014;1:8. [Google Scholar]
- Kramer Kevin, Zong Xing, Lu Rongchun, Dutta Dipangkar, Gao Haiyan, Qian Xin, Ye Qiang, Zhu Xiaofeng, Averett Todd, Fuchs Sabine. A high-pressure polarized 3He gas target for the High Intensity Gamma Source (HIγS) facility at Duke Free Electron Laser Laboratory. Nucl Instrum Methods Phys Res, Sect A. 2007;582(2):318–325. [Google Scholar]
- Kramer LH, DeSchepper D, Milner RG, Pate SF, Shin T. An internal polarized 3He target for electron storage rings. Nucl Instrum Methods Phys Res, Sect A. 1995a;362(1):32–35. [Google Scholar]
- Kramer LH, Kelsey JF, Milner RG, Winn P, McGuire J. A cryogenic storage cell for polarized internal gas targets. Nucl Instrum Methods Phys Res, Sect A. 1995b;365(1):49–53. [Google Scholar]
- Krimmer J, Aguar Bartolomé P, Ahrens J, Altieri S, Arends HJ, Heil W, Karpuk S, Otten EW, Pedroni P, Salhi Z, et al. A polarized 3He target for the photon beam at MAMI. Nucl Instrum Methods Phys Res, Sect A. 2011;648(1):35–40. [Google Scholar]
- Krimmer J, Distler M, Heil W, Karpuk S, Kiselev D, Salhi Z, Otten EW. A highly polarized target for the electron beam at MAMI. Nucl Instrum Methods Phys Res, Sect A. 2009;611(1):18–24. [Google Scholar]
- Krjukov E, Fichele S, Wild JM, Paley MNJ. Design and evaluation of a low field system for hyperpolarized 3He gas imaging of neonatal lungs. Concepts Magn Reson Part B. 2007;31:209–17. [Google Scholar]
- Kruger SJ, Niles DJ, Dardzinski B, Harman A, Jarjour NN, Ruddy M, Nagle SK, Francois CJ, Sorkness RL, Burton RM, Munoz del Rio A, Fain SB. Hyperpolarized Helium-3 MRI of exercise-induced bron-choconstriction during challenge and therapy. J Magn Reson Imaging. 2014;39:1230–7. doi: 10.1002/jmri.24272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krycka KL, Borchers JA, Booth RA, Ijiri Y, Hasz K, Rhyne JJ, Majetich SA. Origin of Surface Canting within Fe3O4 Nanoparticles. Phys Rev Lett. 2014;113:147203. doi: 10.1103/PhysRevLett.113.147203. [DOI] [PubMed] [Google Scholar]
- Krycka KL, Booth R, Borchers JA, Chen WC, Conlon C, Gentile TR, Hogg C, Ijiri Yumi, Laver M, Maranville BB, Majetich SA, Rhyne J, Watson SM. Resolving 3D magnetism in nanoparticles using polarization analyzed SANS. Physica B. 2009;404(17):2561–2564. [Google Scholar]
- Krycka KL, Booth Ryan A, Hogg CR, Ijiri Y, Borchers JA, Chen WC, Watson SM, Laver M, Gentile TR, Dedon LR, et al. Core-shell magnetic morphology of structurally uniform magnetite nanoparticles. Phys Rev Lett. 2010;104(20):207203. doi: 10.1103/PhysRevLett.104.207203. [DOI] [PubMed] [Google Scholar]
- Krycka KL, Borchers JA, Laver M, Salazar-Alvarez German, López-Ortega A, Estrader M, Surinach S, Baró MD, Sort J, Nogués J. Correlating material-specific layers and magnetic distributions within onion-like Fe3O4/MnO/γ-Mn2O3 core/shell nanoparticles. J Appl Phys. 2013;113:17B531. [Google Scholar]
- Krycka KL, Jackson AJ, Borchers JA, Shih J, Briber R, Ivkov R, Grüttner C, Dennis CL. Internal magnetic structure of dextran coated magnetite nanoparticles in solution using small angle neutron scattering with polarization analysis. J Appl Phys. 2011;109(7):07B513. [Google Scholar]
- Kuchler F, Babcock E, Burghoff M, Chupp T, Degenkolb S, Fan I, Fierlinger P, Gong F, Kraegeloh E, Kilian W, et al. A new search for the atomic EDM of 129Xe at FRM-II. Hyperfine Interact. 2016;237(1):1–5. [Google Scholar]
- Kulda J, Wildes A, Martin-Martin A, Müller W, Heil W, Humblot H, Tasset F. The 3He filter on a polarized thermal neutron three-axis spectrometer. Physica B. 1998;241:136–138. [Google Scholar]
- Lancor B, Babcock E, Wyllie R, Walker TG. Breakdown of angular momentum selection rules in high pressure optical pumping experiments. Phys Rev Lett. 2010a;105(8):083003. doi: 10.1103/PhysRevLett.105.083003. [DOI] [PubMed] [Google Scholar]
- Lancor B, Walker TG. Effects of nitrogen quenching gas on spin-exchange optical pumping of 3He. Phys Rev A. 2010;82(4):043417. [Google Scholar]
- Lancor Brian. PhD thesis. University of Wisconsin-Madison; 2011. Studies of the Efficiency of Spin-Exchange Optical Pumping. [Google Scholar]
- Lancor Brian, Babcock Earl, Wyllie Robert, Walker TG. Circular dichroism of RbHe and RbN2 molecules. Phys Rev A. 2010b;82(4):043435. [Google Scholar]
- Lancor Brian, Walker Thad G. Polarization limits in K-Rb spin-exchange mixtures. Phys Rev A. 2011;83(6):065401. [Google Scholar]
- de Lange Eduard E, Mugler John P, III, Brookeman James R, Knight-Scott Jack, Truwit Jonathon D, David Teates C, Daniel Thomas M, Bogorad Paul L, Cates Gordon D. Lung air spaces: MR imaging evaluation with hyperpolarized 3He gas. Radiology. 1999;210(3):851–857. doi: 10.1148/radiology.210.3.r99fe08851. [DOI] [PubMed] [Google Scholar]
- Larat C, Leduc M, Nacher P-J, Tastevin G, Vermeulen G. Heat-conduction in Spin-polarized Gaseous He-3 at Low-temperature. J Low Temp Phys. 1990;80(5–6):299–314. [Google Scholar]
- Larson B, Häusser O, Brash EJ, Chan C, Rahav A, Bennhold C, Delheij PPJ, Henderson RS, Jennings BK, Mellinger A, et al. Asymmetries in elastic scattering of 100 MeV π+ from a polarized 3He target. Phys Rev Lett. 1991a;67(24):3356. doi: 10.1103/PhysRevLett.67.3356. [DOI] [PubMed] [Google Scholar]
- Larson B, Häusser O, Delheij PPJ, Whittal DM, Thiessen D. Optical pumping of Rb in the presence of high-pressure 3He buffer gas. Phys Rev A. 1991b;44(5):3108. doi: 10.1103/physreva.44.3108. [DOI] [PubMed] [Google Scholar]
- Laskaris G, Yan X, Mueller JM, Zimmerman WR, Xiong W, Ahmed MW, Averett T, Chu P-H, Deltuva A, Flower C, Fonseca AC, Gao H, Golak J, Heideman JN, Karwowski HJ, Meziane M, Sauer PU, Skibiński R, Strakovsky II, Weller HR, Witała H, Wu YK. Measurement of the doubly-polarized reaction at 16.5 mev and its implications for the {GDH} sum rule. Physics Letters B. 2015;750:547–551. [Google Scholar]
- Laskaris G, Ye Q, Lalremruata B, Ye QJ, Ahmed MW, Averett T, Deltuva A, Dutta D, Fonseca AC, Gao H, et al. Spin-dependent cross sections from the three-body photodisintegration of 3He at incident energies of 12.8 and 14.7 MeV. Phys Rev C. 2014;89:024002. doi: 10.1103/PhysRevLett.110.202501. [DOI] [PubMed] [Google Scholar]
- Laskaris G, Ye Q, Lalremruata B, Ye QJ, Ahmed MW, Averett T, Deltuva A, Dutta D, Fonseca AC, Gao H, et al. First Measurements of Spin-Dependent Double-Differential Cross Sections and the Gerasimov-Drell-Hearn Integrand from 3H⃗e (γ⃗, n)pp at Incident Photon Energies of 12.8 and 14.7 MeV. Phys Rev Lett. 2013;110(20):202501. doi: 10.1103/PhysRevLett.110.202501. [DOI] [PubMed] [Google Scholar]
- Laver M, et al. Magnetostriction and magnetic heterogeneities in iron-gallium. Phys Rev Lett. 2010a;105:027202. doi: 10.1103/PhysRevLett.105.027202. [DOI] [PubMed] [Google Scholar]
- Laver M, et al. Search for electronic phase separation at quantum phase transitions. J Low Temp Phys. 2010b;161:167–181. [Google Scholar]
- Leawoods Jason C, Yablonskiy Dmitriy A, Saam Brian, Gierada David S, Conradi Mark S. Hyperpolarized 3He gas production and MR imaging of the lung. Concept Magnetic Res. 2001;13(5):277–293. [Google Scholar]
- Leduc M, Crampton SB, Nacher PJ, Laloë F. Nuclear polarization in gaseous 3He by optical pumping. Nucl Sci Appl. 1984;2:1–20. https://hal.archives-ouvertes.fr/hal-01383488. [Google Scholar]
- Leduc M, Nacher PJ, Betts DS, Daniels JM, Tastevin G, Laloë F. Nuclear Polarization and Heat Conduction Changes in Gaseous 3He. Europhys Lett. 1987;4(1):59. [Google Scholar]
- Leduc M, Nacher PJ, Tastevin G, Courtade E. Kinetics of helium 3 laser optical pumping. Hyperfine Interact. 2000;127(1–4):443–449. [Google Scholar]
- Lee K, Hansen J-O, Van Den Brand JFJ, Milner RG. A laser optically pumped polarized 3He target for storage rings. Nucl Instrum Methods Phys Res, Sect A. 1993;333(2):294–303. [Google Scholar]
- Lee S, Moon MK, Kim J, Cho SJ, Lee JH, Lee C-H, Lee SW, Ino T. In-situ compact 3He neutron spin polarizer based on a magneto-static cavity with built-in NMR coils. J Phys Conf Ser. 2016;711(1):012014. [Google Scholar]
- Lee Seongsu, Choi Taekjib, Ratcliff W, II, Erwin R, Cheong SW, Kiryukhin V. Single ferroelectric and chiral magnetic domain of single-crystalline BiFeO3 in an electric field. Phys Rev B. 2008;78(10):100101. [Google Scholar]
- Lee WT, D’Adam T. Placeholder. J Phys Conf Ser. 2016 in press. [Google Scholar]
- Lefevre-Seguin V, Nacher PJ, Brossel J, Hardy WN, Laloë F. Nuclear relaxation of 3He at the surface of solid H2. J Phys Paris. 1985:46. [Google Scholar]
- Lefevre-Seguin Valérie, Brossel Jean. Attempts to increase the nuclear relaxation time of a 3He gas at low temperatures. J Low Temp Phys. 1988;72(1):165–188. [Google Scholar]
- Lelievre-Berna E. Mid-term report of the NMI3 neutron spin filter project. Physica B. 2007;397(1):162–167. [Google Scholar]
- Lelievre-Berna E, Bourgeat-Lami E, Gibert Y, Kernavanois N, Locatelli J, Mary T, Pastrello G, Petukhov A, Pujol S, Rouques R, et al. ILL polarised hot-neutron beam facility D3. Physica B. 2005;356(1):141–145. [Google Scholar]
- Lelievre-Berna E, et al. Powder diffraction with spin polarized neutrons. Meas Sci Technol. 2010;21:055106. [Google Scholar]
- Lhuillier C, Laloë F. Spin polarized He-3 - New quantum fluid. J Phys. 1979;40(3):239–256. [Google Scholar]
- Lhuillier C, Laloë F. Transport-properties in a spin polarized gas, 1 and 2. J Phys. 1982;43:197–224. [Google Scholar]
- Liu Bo, Tong Xin, Jiang Chenyang, Brown Daniel R, Robertson Lee. Development of stable, narrow spectral line-width, fiber delivered laser source for spin exchange optical pumping. Appl Optics. 2015;54(17):5420–5424. doi: 10.1364/AO.54.005420. [DOI] [PubMed] [Google Scholar]
- Lorenzon W, Gentile TR, Gao H, McKeown RD. NMR calibration of optical measurement of nuclear polarization in 3He. Phys Rev A. 1993;47(1):468. doi: 10.1103/physreva.47.468. [DOI] [PubMed] [Google Scholar]
- Lusher CP, Secca MF, Richards MG. Nuclear magnetic relaxation of 3He gas. I. Pure3He. J Low Temp Phys. 1988a;72(1–2):25–69. [Google Scholar]
- Lusher CP, Secca MF, Richards MG. Nuclear magnetic relaxation of 3He gas. II. 3He-4He mixtures. J Low Temp Phys. 1988b;72(1–2):71–97. [Google Scholar]
- Ma J, Kishinevski A, Jau Y-Y, Reuter C, Happer W. Modification of glass cell walls by rubidium vapor. Phys Rev A. 2009;79(4):042905. [Google Scholar]
- MacFall James R, Cecil Charles H, Black Robert D, Middleton Hunter, Swartz John C, Saam Brian, Driehuys Bastiaan, Erickson Christopher, Happer William, Cates Gordon D, et al. Human lung air spaces: potential for MR imaging with hyperpolarized He-3. Radiology. 1996;200(2):553–558. doi: 10.1148/radiology.200.2.8685356. [DOI] [PubMed] [Google Scholar]
- Maeda Shingo, Tabata Yutaka, Yamada Hiroki, Kumagai Hiroshi. Comparative study of laser-induced metastability-exchange optical pumping of He3 atoms through 23S1 –33PJ transition at 389nm with 23S1 – 23PJ transition at 1083nm. Opt Eng. 2010;49(9) 091014-091014-5. [Google Scholar]
- Markstaller K, Eberle B, Schreiber WG, Weiler N, Thelen M, Kauczor H-U. Flip angle considerations in 3Helium-MRI. NMR Biomed (UK) 2000;13:190–3. doi: 10.1002/1099-1492(200006)13:4<190::aid-nbm644>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Masuda Y, Ino T, Skoy VR, Jones GL. 3He polarization via optical pumping in a birefringent cell. Appl Phys Lett. 2005;87(5) [Google Scholar]
- Maul Andreas, Bluemler Peter, Heil Werner, Nikiel Anna, Otten Ernst, Petrich Andreas, Schmidt Thomas. Spherical fused silica cells filled with pure helium for nuclear magnetic resonance-magnetometry. Rev Sci Instrum. 2016;87(1) doi: 10.1063/1.4938251. [DOI] [PubMed] [Google Scholar]
- Maxwell J, Epstein C, Milner R, Alessi J, Beebe E, Pikin A, Ritter J, Zelenski A. Development of a Polarized Helium-3 Source for RHIC and eRHIC. Int J Mod Phys: Conf Ser. 2016;40:1660102. [Google Scholar]
- Maxwell J, Milner R, Epstein C. Development of a polarized 3He ion source for RHIC. Phys Part Nuclei. 2014a;45:301–302. [Google Scholar]
- Maxwell James D, Epstein Charles S, Milner Richard G. Liquid crystal polarimetry for metastability exchange optical pumping of 3He. Nucl Instrum Methods Phys Res, Sect A. 2014b;764:215–219. [Google Scholar]
- Maxwell James D, Epstein Charles S, Milner Richard G. Diffusive transfer of polarized 3He gas through depolarizing magnetic gradients. Nucl Instrum Methods Phys Res, Sect A. 2015;777:194–198. [Google Scholar]
- McAdams HH. Dynamic nuclear polarization of liquid helium-three by optical pumping. Phys Rev. 1968;170(1):276–285. [Google Scholar]
- McGregor DD. Transverse relaxation of spin-polarized 3He gas due to a magnetic field gradient. Phys Rev A. 1990;41(5):2631. doi: 10.1103/physreva.41.2631. [DOI] [PubMed] [Google Scholar]
- McIver JW, Erwin R, Chen WC, Gentile TR. End-compensated magnetostatic cavity for polarized 3He neutron spin filters. Rev Sci Instrum. 2009;80(6):063905. doi: 10.1063/1.3154386. [DOI] [PubMed] [Google Scholar]
- McKetterick TJ, Boag S, Stewart JR, Frost CD, Skoda MWA, Parnell SR, Babcock E. Optimised adiabatic fast passage spin flipping for 3He neutron spin filters. Physica B. 2011;406(12):2436–2438. [Google Scholar]
- Mentore K, Froh DK, de Lange EE, Brookeman JR, Paget-Brown AO, Altes TA. Hyperpolarized 3He MRI of the lung in cystic fibrosis: assessment at baseline and after bronchodilator and airway clearance treatment. Acad Radiol. 2005;12:1423–9. doi: 10.1016/j.acra.2005.07.008. [DOI] [PubMed] [Google Scholar]
- Meyerhoff M, Eyl D, Frey A, Andresen HG, Annand JRM, Aulenbacher K, Becker J, Blume-Werry J, Dombo Th, Drescher P, et al. First measurement of the electric form factor of the neutron in the exclusive quasielastic scattering of polarized electrons from polarized 3He. Phys Lett B. 1994;327(3):201–207. [Google Scholar]
- Mezei F. Novel polarized neutron devices: super-mirror and spin component amplifier. Commun Phys. 1976;1:81–85. [Google Scholar]
- Middleton Hunter, Black Robert D, Saam Brian, Cates Gordon D, Cofer Gary P, Guenther Robert, Happer William, Hedlund Lawrence W, Alan Johnson G, Juvan Kim, et al. MR imaging with hyperpolarized 3He gas. Magnet Reson Med. 1995;33(2):271–275. doi: 10.1002/mrm.1910330219. [DOI] [PubMed] [Google Scholar]
- Miller GW, Mugler JP, III, Altes TA, Cai Jing, Mata JF, de Lange EE, Tobias WA, Cates GD, Brookeman JR. A short-breath-hold technique for lung pO2 mapping with 3He MRI. Magn Reson Med. 2010;63:127–36. doi: 10.1002/mrm.22181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MA, Lee K, Smith A, Hansen J-O, Bloch C, van den Brand JFJ, Bulten HJ, DeSchepper D, Ent R, Goodman CD, et al. Measurement of Quasielastic 3He(p⃗, pN) Scattering from Polarized 3He and the Three-Body Ground State Spin Structure. Phys Rev Lett. 1995;74(4):502. doi: 10.1103/PhysRevLett.74.502. [DOI] [PubMed] [Google Scholar]
- Milner RG, McKeown RD, Woodward CE. Study of spin relaxation by a charged particle beam in a polarized 3He gas target. Nucl Instrum Methods Phys Res, Sect A. 1987;257(2):286–290. [Google Scholar]
- Milner RG, McKeown RD, Woodward CE. A polarized 3He target for nuclear physics. Nucl Instrum Methods Phys Res, Sect A. 1989;274(1):56–63. [Google Scholar]
- Möller Harald E, Josette Chen X, Saam Brian, Hagspiel Klaus D, Allan Johnson G, Altes Talissa A, de Lange Eduard E, Kauczor Hans-Ulrich. MRI of the lungs using hyperpolarized noble gases. Magnet Reson Med. 2002;47(6):1029–1051. doi: 10.1002/mrm.10173. [DOI] [PubMed] [Google Scholar]
- Moody JE, Wilczek Frank. New macroscopic forces? Phys Rev D. 1984;30:130–138. [Google Scholar]
- Moon RM, Riste T, Koehler WC. Polarization analysis of thermal-neutron scattering. Phys Rev A. 1969;181:920–931. [Google Scholar]
- Mrozik C, Endner O, Hauke C, Heil W, Karpuk S, Klemmer J, Otten EW. Construction of a compact 3He polarizing facility. J Phys Conf Ser. 2011;294(1):012007. [Google Scholar]
- Mueller Robert M. The Yb fiber laser for metastable 3He optical pumping at Jülich. Physica B. 2001;297(1):277–281. [Google Scholar]
- Mughabghab SF, Divadeenam M, Holden NE. Neutron Resonance Parameters and Thermal Cross Sections, vol 1 of Neutron Cross Sections. Academic Press; New York: 1981. [Google Scholar]
- Mund D, et al. Determination of the weak axial vector coupling λ =gA/gV from a measurement of the β-asymmetry parameter A in neutron beta decay. Phys Rev Lett. 2013;110:172502. doi: 10.1103/PhysRevLett.110.172502. [DOI] [PubMed] [Google Scholar]
- Nacher P-J. Observation d’ondes de spin dans un gaz d’3He polarisé par pompage optique laser. PhD Thesis. 1985 https://tel.archives-ouvertes.fr/tel-00011855 (Univer-sité Pierre et Marie Curie)
- Nacher P-J, Leduc M. Optical pumping in 3He with a laser. J Phys Paris. 1985;46(12):2057–2073. [Google Scholar]
- Nacher Pierre-Jean, Tastevin Geneviève, Leduc Michèle, Crampton SB, Laloë Franck. Spin rotation effects and spin waves in polarised gaseous 3He. J Phys Lett Paris. 1984;45(9):441–448. [Google Scholar]
- Nacher PJ, Dupont-Roc J. Experimental evidence for nonwetting with superfluid helium. Phys Rev Lett. 1991;67(21):2966. doi: 10.1103/PhysRevLett.67.2966. [DOI] [PubMed] [Google Scholar]
- Nacher PJ, Shinkoda I, Schleger P, Hardy WN. Nuclear polarization enhancement by distillation of liquid 3He-4He solutions. Phys Rev Lett. 1991;67(7):839. doi: 10.1103/PhysRevLett.67.839. [DOI] [PubMed] [Google Scholar]
- Nacher PJ, Tastevin G, Maitre X, Dollat X, Lemaire B, Olejnik J. A peristaltic compressor for hyperpolarized helium. Eur Radiol. 1999;9:B18. [Google Scholar]
- Nelson IA, Walker TG. Rb-Xe spin relaxation in dilute Xe mixtures. Phys Rev A. 2001;65(1):012712. [Google Scholar]
- Newbury NR, Barton AS, Bogorad P, Cates GD, Gatzke M, Saam B, Han L, Holmes R, Souder PA, Xu J, et al. Laser polarized muonic helium. Phys Rev Lett. 1991;67(23):3219. doi: 10.1103/PhysRevLett.67.3219. [DOI] [PubMed] [Google Scholar]
- Newbury NR, Barton AS, Cates GD, Happer W, Middleton H. Gaseous 3He–3He magnetic dipolar spin relaxation. Phys Rev A. 1993;48(6):4411. doi: 10.1103/physreva.48.4411. [DOI] [PubMed] [Google Scholar]
- Nickel B, Rühm A, Donner W, Major J, Dosch H, Schreyer A, Zabel H, Humblot H. Spin-resolved off-specular neutron scattering maps from magnetic multilayers using a polarized 3He gas spin filter. Rev Sci Instrum. 2001;72(1):163–172. [Google Scholar]
- Nikiel A, Palasz T, Suchanek M, Abboud M, Sinatra A, Olejniczak Z, Dohnalik T, Tastevin G, Nacher PJ. Metastability exchange optical pumping of 3He at high pressure and high magnetic field for medical applications. Eur Phys J Special Topics. 2007;144(1):255–263. [Google Scholar]
- Nikiel Anna, Blümler Peter, Heil Werner, Hehn Manfred, Karpuk Sergej, Maul Andreas, Otten Ernst, Schreiber Laura M, Terekhov Maxim. Ultrasensitive 3He magnetometer for measurements of high magnetic fields. Eur Phys J D. 2014;68(11):1–12. [Google Scholar]
- Nikiel-Osuchowska A, Collier G, Gowacz G, Palasz T, Olejniczak Z, Weglarz WP, Tastevin G, Nacher P, Dohnalik T. Metastability exchange optical pumping of 3He gas up to hundreds of millibars at 4.7 Tesla. Eur Phys J D. 2013;67:200. [Google Scholar]
- Nikolaou P, Coffey AM, Walkup LL, Gust BM, Whiting N, Newton H, Barcus S, Muradyan I, Dabaghyan M, Moroz GD, Rosen MS, Patz S, Barlow MJ, Chekmenev EY, Goodson BM. Near-unity nuclear polarization with an open-source 129xe hyperpolarizer for nmr and mri. Proc Natl Acad Sci USA. 2013;110:14150–5. doi: 10.1073/pnas.1306586110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noël E, Gilles H, Hamel J, Moreau O, Chéron B. Measurements of the Nuclear Polarisation of Optically Pumped 3He Atoms Using a 4He Magnetometer. J Phys III France. 1996;6(8):1127–1132. [Google Scholar]
- Normand E, Jiang CY, Brown DR, Robertson L, Crow L, Tong X. Measuring gas temperature during spin-exchange optical pumping process. J Phys Conf Ser. 2016;711(1):012012. [Google Scholar]
- Nouls J, Fanarjian M, Hedund L, Driehuys B. A constant-volume ventilator and gas recapture system for hyperpolarized gas mri of mouse and rat lungs. Concepts Magn Reson B, Magn Reson Eng (USA) 2011;39B:78–88. doi: 10.1002/cmr.b.20192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogrin FY, Weekes SM, Cubitt B, Wildes A, Drew A, Ross CA, Jung W, Menon R, Toperverg B. Polarized Neutron Reflectivity Investigation of Periodic Magnetic Rings. IEEE Trans Magn. 2007;43(6):2731–2733. [Google Scholar]
- Oteiza ER. PhD thesis. Harvard; 1992. Search for a Permanent Electric Dipole Moment in 129Xe Using Simultaneous 3He Magnetometry. [Google Scholar]
- Owers-Bradley John R. Spin-polarized-liquids. Rep Prog Phys. 1997;60(11):1173. [Google Scholar]
- Owers-Bradley JR, Fichele MS, Bennattayalah A, Smith McGloin CJ, Bowtell RW, Morgan PS, Moody AR. MR tagging of human lungs using hyperpolarized 3He gas. J Magn Reson Imaging. 2003;17:142–146. doi: 10.1002/jmri.10226. [DOI] [PubMed] [Google Scholar]
- Parnell SR, Babcock E, Nünighoff K, Skoda MWA, Boag S, Masalovich S, Chen WC, Georgii R, Wild JM, Frost CD. Study of spin-exchange optically pumped 3He cells with high polarisation and long lifetimes. Nucl Instrum Methods Phys Res, Sect A. 2009;598(3):774–778. [Google Scholar]
- Parnell SR, Washington AL, Li K, Yan H, Stonaha P, Li F, Wang T, Walsh A, Chen WC, Parnell AJ, et al. Spin echo small angle neutron scattering using a continuously pumped 3He neutron polarisation analyser. Rev Sci Instrum. 2015;86(2):023902. doi: 10.1063/1.4909544. [DOI] [PubMed] [Google Scholar]
- Parnell Steven R, Deppe Martin H, Ajraoui Salma, Parra-Robles Juan, Boag Stephen, Wild Jim M. Measurement of laser heating in spin exchange optical pumping by NMR diffusion sensitization gradients. J Appl Phys. 2010;107(9):094904. [Google Scholar]
- Parnell Steven R, Woolley Elliot B, Boag Stephen, Frost Christopher D. Digital pulsed NMR spectrometer for nuclear spin-polarized 3He and other hyperpolarized gases. Meas Sci Technol. 2008;19(4):045601. [Google Scholar]
- Parno DS, Flay D, Posik M, Allada K, Armstrong W, Averett T, Benmokhtar F, Bertozzi W, Camsonne A, Canan M, et al. Precision measurements of in the deep inelastic regime. Phys Lett B. 2015;744:309–314. [Google Scholar]
- Parra-Robles J, Cross AR, Santyr GE. Theoretical signal-to-noise ratio and spatial resolution dependence on the magnetic field strength for hyperpolarized noble gas magnetic resonance imaging of human lungs. Med Phys. 2005;32:221–9. doi: 10.1118/1.1833593. [DOI] [PubMed] [Google Scholar]
- Parra-Robles J, Wild JM. Response to Commentary on “The influence of lung airways branching structure and diffusion time on measurements and models of short-range 3He gas MR diffusion. J Magn Reson. 2013;239:143–146. doi: 10.1016/j.jmr.2013.10.019. [DOI] [PubMed] [Google Scholar]
- Partridge Harry, Stallcop James R, Levin Eugene. Potential energy curves and transport properties for the interaction of He with other ground-state atoms. J Chem Phys. 2001;115(14):6471–6488. [Google Scholar]
- Partridge RB, Series GW. The transfer of coherence by collisions of 3He atoms. Proc Phys Soc. 1966;88(4):983–993. [Google Scholar]
- Pascale J. Use of l-dependent pseudopotentials in the study of alkali-metal-atom—He systems. The adiabatic molecular potentials. Phys Rev A. 1983;28:632–644. [Google Scholar]
- Paulin GA, Svenningsen S, Jobse BN, Mohan S, Kirby M, Lewis JF, Parraga G. Differences in hyper-polarized 3He ventilation imaging after 4 years in adults with cystic fibrosis. J Magn Reson Imaging. 2015;41:1701–7. doi: 10.1002/jmri.24744. [DOI] [PubMed] [Google Scholar]
- Pavlović Milica, Laloë Franck. Étude d’une nouvelle méthode permettant d’orienter, par pompage optique, des niveaux atomiques excités. Application à la mesure de la structure hyperfine de niveaux 1D de 3He. J Phys Paris. 1970;31(2–3):173–194. [Google Scholar]
- Petoukhov AK, Andersen KH, Jullien D, Babcock E, Chastagnier J, Chung R, Humblot H, Lelièvre-Berna E, Tasset F, Radu F, et al. Recent advances in polarised 3He spin filters at the ILL. Physica B. 2006;385:1146–1148. [Google Scholar]
- Petukhov AK, Pignol G, Golub R. Comment on “Limits on possible new nucleon monopole-dipole interactions from the spin relaxation rate of polarized 3He gas. Phys Rev D. 2011;84:058501. [Google Scholar]
- Petukhov AK. Private communication. 2016.
- Petukhov AK, Guillard V, Andersen KH, Bourgeat-Lami E, Chung R, Humblot H, Jullien D, Lelievre-Berna E, Soldner T, Tasset F, et al. Compact magnetostatic cavity for polarised 3He neutron spin filter cells. Nucl Instrum Methods Phys Res, Sect A. 2006;560(2):480–484. [Google Scholar]
- Petukhov AK, Pignol G, Jullien D, Andersen KH. Polarized 3He as a Probe for Short-Range Spin-Dependent Interactions. Phys Rev Lett. 2010;105(17):170401. doi: 10.1103/PhysRevLett.105.170401. [DOI] [PubMed] [Google Scholar]
- Phillips GC, Perry RR, Windham PM, Walters GK, Sc-hearer LD, Colegrove FD. Demonstration of a polarized 3He target for nuclear reactions. Phys Rev Lett. 1962;9(12):502. [Google Scholar]
- Piegay N, Tastevin G. Study of bulk longitudinal spin relaxation in He-3-He-4 liquid mixtures. J Low Temp Phys. 2002;126(1–2):157–162. [Google Scholar]
- Pimpinella RE, Zhang D, McCartney MR, Smith DJ, Krycka KL, Kirby BJ, O’Dowd BJ, Sonderhouse L, Leiner J, Liu X, et al. Magnetic properties of GaAs/Fe core/shell nanowires. J Appl Phys. 2013;113(17):17B520. [Google Scholar]
- Pinard M, Aminoff CG, Laloë F. Velocity-selective optical pumping and Doppler-free spectroscopy. Phys Rev A. 1979;19(6):2366–2370. [Google Scholar]
- Pinard M, Laloë F. The role of the Pauli principle in metastability exchange collisions. J Phys. 1980;41(8):799–818. [Google Scholar]
- Pinard M, van der Linde J. Disorientation of 3He 1D states in 3He–3He collisions. Can J Phys. 1974;52:1615–1621. [Google Scholar]
- Pines D, Slichter CP. Relaxation times in magnetic resonance. Phys Rev. 1955;100(4):1014. [Google Scholar]
- Pokotilovski Yu N. Limits on short-range spin-dependent forces from spin relaxation of polarized 3He. Phys Lett B. 2010;686(2):114–117. [Google Scholar]
- Poole A, Wills AS, Lelievre-Berna E. Magnetic ordering in the XY pyrochlore antiferromagnet Er2Ti2O7: a spherical neutron polarimetry study. J Phys: Condens Matter. 2007;19(45):452201. [Google Scholar]
- Poolman HR, Van Den Brand JFJ, Bulten HJ, Doets M, Ent R, Ferro-Luzzi M, Geurts DG, Harvey M, Mul FA. A polarized 3He internal target for storage rings. Nucl Instrum Methods Phys Res, Sect A. 2000;439(1):91–110. [Google Scholar]
- Qattan IA, Arrington J. Flavor decomposition of the nucleon electromagnetic form factors. Phys Rev C. 2012;86:065210. [Google Scholar]
- Qian X, Allada K, Dutta C, Huang J, Katich J, Wang Y, Zhang Y, Aniol K, Annand JRM, Averett T, et al. Single Spin Asymmetries in Charged Pion Production from Semi-Inclusive Deep Inelastic Scattering on a Transversely Polarized 3He Target at Q2=1.4–2.7 GeV2. Phys Rev Lett. 2011;107(7):072003. doi: 10.1103/PhysRevLett.107.072003. [DOI] [PubMed] [Google Scholar]
- Qing K, Altes TA, Tustison NJ, Feng X, Chen X, Mata JF, Miller GW, de Lange EE, Tobias WA, Cates GD, Jr, Brookeman JR, Mugler JP., 3rd Rapid acquisition of helium-3 and proton three-dimensional image sets of the human lung in a single breath-hold using compressed sensing. Magn Reson Med (USA) 2015;74:1110–5. doi: 10.1002/mrm.25499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quirk JD, Lutey BA, Gierada DS, Woods JC, Senior RM, Lefrak SS, Sukstanskii AL, Conradi MS, Yablonskiy DA. In vivo detection of acinar microstructural changes in early emphysema with (3)he lung morphometry. Radiology. 2011;260:866–74. doi: 10.1148/radiol.11102226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radu F, Vorobiev A, Major J, Humblot H, Westerholt K, Zabel H. Spin-resolved off-specular neutron scattering from magnetic domain walls using the polarized 3He gas spin filter. Physica B. 2003;335(1):63–67. [Google Scholar]
- Radu Florin, Leiner Vincent, Westerholt Kurt, Zabel Hartmut, McCord Jeffery, Vorobiev Alexei, Major Janos, Jullien David, Humblot Hubert, Tasset Francis. Magnetic induction and domain walls in magnetic thin films at remanence. J Phys: Condens Matter. 2005;17(10):1711. [Google Scholar]
- Ramazanoglu M, Laver Mark, Ratcliff W, II, Watson SM, Chen WC, Jackson A, Kothapalli K, Lee Seongsu, Cheong S-W, Kiryukhin V. Local weak ferromagnetism in single-crystalline ferroelectric BiFeO 3. Phys Rev Lett. 2011;107(20):207206. doi: 10.1103/PhysRevLett.107.207206. [DOI] [PubMed] [Google Scholar]
- Ratcliff William, Kan Daisuke, Chen Wangchun, Watson Shannon, Chi Songxue, Erwin Ross, McIntyre Garry J, Capelli Sylvia C, Takeuchi Ichiro. Neutron diffraction investigations of magnetism in BiFeO3 epitaxial films. Adv Funct Mater. 2011;21(9):1567–1574. [Google Scholar]
- Rich DR, Bowman JD, Crawford BE, Delheij PPJ, Espy MA, Haseyama T, Jones G, Keith CD, Knudson J, Leuschner MB, et al. A measurement of the absolute neutron beam polarization produced by an optically pumped 3He neutron spin filter. Nucl Instrum Methods Phys Res, Sect A. 2002a;481(1):431–453. [Google Scholar]
- Rich DR, Gentile Thomas R, Smith TB, Thompson AK, Jones GL. Spin exchange optical pumping at pressures near 1 bar for neutron spin filters. Appl Phys Lett. 2002b;80(12):2210–2212. [Google Scholar]
- Richards MG, Cowan BP, Secca MF, Machin K. The 3He nuclear Zeeman maser. J Phys B: At, Mol Opt Phys. 1988;21(4):665. [Google Scholar]
- Riordan S, Abrahamyan S, Craver B, Kelleher A, Kolarkar A, Miller J, Cates GD, Liyanage N, Wojtsekhowski B, Acha A, et al. Measurements of the Electric Form Factor of the Neutron up to Q2=3.4 GeV2 using the reaction 3H⃗e(e⃗, e′n)pp. Phys Rev Lett. 2010;105(26):262302. doi: 10.1103/PhysRevLett.105.262302. [DOI] [PubMed] [Google Scholar]
- Robinson HG, Myint Than. 3He Nuclear Zeeman Maser. Appl Phys Lett. 1964;5:116–118. [Google Scholar]
- Rodrigues Alexandre, Vermeulen Gerard. Phase equilibrium in a polarized saturated 3He-4He mixture. J Low Temp Phys. 1997;108(1):103–142. [Google Scholar]
- Romalis MV. Chap Quantum Noise in Atomic Magnetometers. Cambridge University Press; 2013. Optical magnetometry; p. 25. [Google Scholar]
- Romalis MV, Happer W. Inhomogeneously broadened spin masers. Phys Rev A. 1999;60:1385–1402. [Google Scholar]
- Romalis MV, Bogorad PL, Cates GD, Chupp TE, Coulter KP, Hughes EW, Johnson JR, Kumar KS, Smith TB, Thompson AK, et al. Toward precision polarimetry of dense polarized 3He targets. Nucl Instrum Methods Phys Res, Sect A. 1998;402(2):260–267. [Google Scholar]
- Romalis MV, Cates GD. Accurate 3He polarimetry using the Rb Zeeman frequency shift due to the Rb-3He spin-exchange collisions. Phys Rev A. 1998;58(4):3004. [Google Scholar]
- Romalis MV, Miron E, Cates GD. Pressure broadening of Rb D1 and D2 lines by 3He, 4He, N2, and Xe: Line cores and near wings. Phys Rev A. 1997;56(6):4569. [Google Scholar]
- Romalis MV, Sheng D, Saam B, Walker TG. Comment on “New limit on Lorentz-invariance- and CPT-violating neutron spin interactions using a free-spin-precession 3He -129Xe comagnetometer. Phys Rev Lett. 2014;113:188901. doi: 10.1103/PhysRevLett.113.188901. [DOI] [PubMed] [Google Scholar]
- Rosenberry MA, Chupp TE. Atomic electric dipole moment measurement using spin exchange pumped masers of 129Xe and 3He. Phys Rev Lett. 2001;86(1):22. doi: 10.1103/PhysRevLett.86.22. [DOI] [PubMed] [Google Scholar]
- Rosner SD, Pipkin FM. Temperature dependence of helium metastability-exchange cross-section in range 15–115 degrees K. Phys Rev A. 1972;5(4):1909. [Google Scholar]
- Rubbmark Jan R, Kash Michael M, Littman Michael G, Kleppner Daniel. Dynamical effects at avoided level crossings: A study of the Landau-Zener effect using Rydberg atoms. Phys Rev A. 1981;23:3107–3117. [Google Scholar]
- Saam B, Happer W, Middleton H. Nuclear relaxation of 3He in the presence of O2. Phys Rev A. 1995;52(1):862. doi: 10.1103/physreva.52.862. [DOI] [PubMed] [Google Scholar]
- Saam B, Yablonskiy DA, Gierada DS, Conradi MS. Rapid imaging of hyperpolarized gas using EPI. Magn Reson Med. 1999;42:507–14. doi: 10.1002/(sici)1522-2594(199909)42:3<507::aid-mrm13>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- Safiullin Kajum. Magnetic resonance of hyperpolarised helium-3 at low magnetic fields. PhD Thesis. 2011 https://tel.archives-ouvertes.fr/tel-00753219 (UPMC -Paris 6)
- Sakaguchi Y, Kira H, Oku T, Shinohara T, Suzuki J, Sakai K, Nakamura M, Aizawa K, Arai M, Noda Y, et al. Applications of 3He neutron spin filters on the small-angle neutron scattering spectrometer SANS-J-II. J Phys Conf Ser. 2011a;294(1):012017. [Google Scholar]
- Sakaguchi Y, Kira H, Oku T, Shinohara T, Suzuki J, Sakai K, Nakamura M, Suzuya K, Aizawa K, Arai M, et al. Research on glass cells for 3He neutron spin filters. Physica B. 2011b;406(12):2443–2447. [Google Scholar]
- Sakai K. Observation of parity-violating spin rotation in the n-139La p-wave resonance. Phys Lett B. 1997;391:11–14. [Google Scholar]
- Sakai K, Sato H, Yoshimi A, Asahi K, Masuda Y, Muto S. Development of polarized 3He gas system as a spin analyzer for low energy neutrons. Nucl Instrum Methods Phys Res, Sect A. 1998;402(2):244–246. [Google Scholar]
- Salerno M, Altes TA, Brookeman JR, de Lange EE, Mugler JP., III Dynamic spiral MRI of pulmonary gas flow using hyperpolarized 3He: preliminary studies in healthy and diseased lungs. Magn Reson Med (USA) 2001;46:667–77. doi: 10.1002/mrm.1244. [DOI] [PubMed] [Google Scholar]
- Salerno M, Altes TA, Brookeman JR, de Lange EE, Mugler JP., 3rd Rapid hyperpolarized 3He diffusion MRI of healthy and emphysematous human lungs using an optimized interleaved-spiral pulse sequence. J Magn Reson Imaging(USA) 2003;17:581–8. doi: 10.1002/jmri.10303. [DOI] [PubMed] [Google Scholar]
- Salerno M, Brookeman JR, de Lange EE, Mugler JP., III Hyperpolarized 3He lung imaging at 0.5 and 1.5 Tesla: a study of susceptibility-induced effects. Magn Reson Med (USA) 2005;53:212–16. doi: 10.1002/mrm.20329. [DOI] [PubMed] [Google Scholar]
- Salhi Zahir, Babcock E, Pistel P, Ioffe A. 3He Neutron Spin Filter cell development program at JCNS. J Phys Conf Ser. 2014;528(1):012015. [Google Scholar]
- Salhi Zahir, Babcock Earl, Gainov Ramil, Bussmann Klaus, Kaemmerling Hans, Pistel Patrick, Russina Margarita, Ioffe Alexander. First result from the magic-PASTIS using large 3He SEOP-polarized GE180 doughnut cell. J Phys Conf Ser. 2016;711(1):012013. [Google Scholar]
- Santyr GE, Lam WW, Ouriadov A. Rapid and efficient mapping of regional ventilation in the rat lung using hyperpolarized 3He with flip angle variation for offset of RF and relaxation (FAVOR) Magn Reson Med (USA) 2008;59:1304–10. doi: 10.1002/mrm.21582. [DOI] [PubMed] [Google Scholar]
- Savukov I, Matlashov A, Volegov P, Espy M, Cooper M. Detection of He-3 spins with ultra-low field nuclear magnetic resonance employing SQUIDs for application to a neutron electric dipole moment experiment. J Magn Reson. 2008;195(2):129–133. doi: 10.1016/j.jmr.2008.09.008. [DOI] [PubMed] [Google Scholar]
- Schaefer SR, Cates GD, Chien Ting-Ray, Gonatas D, Happer W, Walker TG. Frequency shifts of the magnetic-resonance spectrum of mixtures of nuclear spin-polarized noble gases and vapors of spin-polarized alkalimetal atoms. Phys Rev A. 1989;39(11):5613. doi: 10.1103/physreva.39.5613. [DOI] [PubMed] [Google Scholar]
- Schearer LD. Collision-Induced Mixing in the 23P Levels of Helium. Phys Rev. 1967;160(1):76. [Google Scholar]
- Schearer LD. Optically pumped helium-a spin dependent probe. Ann Phys Paris. 1985;10:845–858. [Google Scholar]
- Schearer LD, Tin Padetha. Tunable lasers at 1080 nm for helium optical pumping. J Appl Phys. 1990;68(3):943–949. [Google Scholar]
- Schearer LD, Walters GK. Nuclear spin-lattice relaxation in the presence of magnetic-field gradients. Phys Rev. 1965;139(5A):A1398. [Google Scholar]
- Schlimme BS, Achenbach P, Ayerbe Gayoso CA, Bernauer JC, Böhm R, Bosnar Damir, Challand Th, Distler MO, Doria L, Fellenberger F, et al. Measurement of the Neutron Electric to Magnetic Form Factor Ratio at Q2=1.58 GeV2 Using the Reaction 3 H⃗e(e⃗, e′n)pp. Phys Rev Lett. 2013;111(13):132504. doi: 10.1103/PhysRevLett.111.132504. [DOI] [PubMed] [Google Scholar]
- Schmidt David M, George John S, Penttila Seppo I, Caprihan Arvind, Fukushima Eiichi. Diffusion imaging with hyperpolarized 3He gas. J Magn Reson. 1997;129(2):184–187. doi: 10.1006/jmre.1997.1258. [DOI] [PubMed] [Google Scholar]
- Schmiedeskamp J, Wild JM, Paley MNJ, Filbir F, Fichele S, Knitz F, Mills GH, Woodhouse N, Swift A, Heil W, Wolf M, Otten E. Hyperpolarized 3He MR imaging of the lungs: testing the concept of a central production facility. Eur Radiol. 2013;13:2583–86. doi: 10.1007/s00330-003-2094-2. [DOI] [PubMed] [Google Scholar]
- Schneider Mi, Zaharko O, Gasser U, Kreyssig A, Brown PJ, Canfield PC. Spherical neutron polarimetry of the magnetic structure in HoNi2B2C: Interplay between magnetic phases and superconductivity. Phys Rev B. 2006;74(10):104426. [Google Scholar]
- Schumann M, et al. Measurement of the proton asymmetry parameter in neutron beta decay. Phys Rev Lett. 2008;100:151801. doi: 10.1103/PhysRevLett.100.151801. [DOI] [PubMed] [Google Scholar]
- Schumann Marc, Soldner T, Deissenroth M, Glück F, Krempel J, Kreuz M, Märkisch B, Mund D, Petoukhov A, Abele H. Measurement of the neutrino asymmetry parameter B in neutron decay. Phys Rev Lett. 2007;99(19):191803. doi: 10.1103/PhysRevLett.99.191803. [DOI] [PubMed] [Google Scholar]
- Sharma M, Babcock E, Andersen KH, Barron-Palos Libertad, Becker M, Boag S, Chen WC, Chupp TE, Danagoulian A, Gentile TR, et al. Neutron Beam Effects on Spin-Exchange-Polarized 3He. Phys Rev Lett. 2008;101(8):083002. doi: 10.1103/PhysRevLett.101.083002. [DOI] [PubMed] [Google Scholar]
- Shea DA, Morgan D. Tech Rep R41419. United States Congress; Washington DC: 2010. The Helium-3 Shortage: Supply, Demand, and Options for Congress. [Google Scholar]
- Sheng D, Kabcenell A, Romalis MV. New Classes of Systematic Effects in Gas Spin Comag-netometers. Phys Rev Lett. 2014;113(16) doi: 10.1103/Phys-RevLett.113.163002. [DOI] [PubMed] [Google Scholar]
- Singh Jaideep T, Dolph Peter AM, Al Tobias William, Averett Todd D, Kelleher Aiden, Mooney KE, Nelyubin Vladimir V, Wang Yunxiao, Zheng Yuan, Cates Gordon D. Development of high-performance alkali-hybrid polarized 3He targets for electron scattering. Phys Rev C. 2015;91(5):055205. [Google Scholar]
- Smith TB, Chupp TE, Coulter KP, Welsh RC. Recent advances in spin-exchange pumped polarized 3He target technology. Nucl Instrum Methods Phys Res, Sect A. 1998;402(2):247–249. [Google Scholar]
- Solvignon P, Liyanage N, Chen J-P, Choi Seonho, Aniol K, Averett T, Boeglin W, Camsonne A, Cates GD, Chang CC, et al. (Jefferson Lab E01-012 Collaboration) Quark-Hadron Duality in Neutron (3He) Spin Structure. Phys Rev Lett. 2008;101:182502. doi: 10.1103/PhysRevLett.101.182502. [DOI] [PubMed] [Google Scholar]
- Spector ZZ, Emami K, Fischer MC, Zhu J, Ishii M, Vahdat V, Yu J, Kadlecek S, Driehuys B, Lipson DA, et al. Quantitative Assessment of Emphysema Using Hyperpolarized 3He Magnetic Resonance Imaging. Magn Reson Med. 2005;53:1341–6. doi: 10.1002/mrm.20514. [DOI] [PubMed] [Google Scholar]
- Stas RJW, McNamara JM, Hogervorst W, Vassen W. Simultaneous Magneto-Optical Trapping of a Boson-Fermion Mixture of Metastable Helium Atoms. Phys Rev Lett. 2004;93:053001. doi: 10.1103/PhysRevLett.93.053001. [DOI] [PubMed] [Google Scholar]
- van Steenbergen AS, Wiegers SAJ, Perenboom JAAJ, Maan JC. Distillation of Nuclear Polarization of 3He-4He Mixtures in Very High Magnetic Fields. J Low Temp Phys. 1998;113(1):101–122. [Google Scholar]
- Stejskal EO, Tanner JE. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42(1):288–292. [Google Scholar]
- Stewart JR, Andersen KH, Babcock E, Frost CD, Hiess A, Jullien D, Stride JA, Barthélémy J-F, Marchal F, Murani AP, et al. PASTIS: An insert for polarization analysis studies on a thermal inelastic spectrometer. Physica B. 2006;385:1142–1145. [Google Scholar]
- Stoltz E, Meyerhoff M, Bigelow N, Leduc M, Nacher P-J, Tastevin G. High nuclear polarization in3He and 3He-4He gas mixtures by optical pumping with a laser diode. Appl Phys B. 1996a;63:629–633. [Google Scholar]
- Stoltz Eric, Villard Bérengère, Meyerholf Michael, Nacher Pierre-Jean. Polarization analysis of the light emitted by an optically pumped 3He gas. Appl Phys B. 1996b;63(6):635–640. [Google Scholar]
- Stoner RE, Rosenberry MA, Wright JT, Chupp TE, Oteiza ER, Walsworth RL. Demonstration of a Two Species Noble Gas Maser. Phys Rev Lett. 1996;77:3971–3974. doi: 10.1103/PhysRevLett.77.3971. [DOI] [PubMed] [Google Scholar]
- Suchanek K, Suchanek M, Nikiel A, Pałasz T, Abboud M, Sinatra A, Nacher P-J, Tastevin G, Olejniczak Z, Dohnalik T. Optical measurement of 3He nuclear polarization for metastable exchange optical pumping studies at high magnetic field. Eur Phys J Special Topics. 2007;144(1):67–74. [Google Scholar]
- Sulai IA, Wu Qixue, Bishof M, Drake GWF, Lu Z-T, Mueller P, Santra R. Hyperfine suppression of 23S1–33PJ transitions in 3He. Phys Rev Lett. 2008;101(17):173001. doi: 10.1103/PhysRevLett.101.173001. [DOI] [PubMed] [Google Scholar]
- Surkau R, Becker J, Ebert M, Grossmann T, Heil W, Hofmann D, Humblot H, Leduc M, Otten EW, Rohe D, et al. Realization of a broad band neutron spin filter with compressed, polarized 3He gas. Nucl Instrum Methods Phys Res, Sect A. 1997;384(2):444–450. [Google Scholar]
- Talbot Cavin, Batz Marion, Nacher P-J, Tastevin Genevieve. An accurate optical technique for measuring the nuclear polarisation of 3He gas. J Phys Conf Ser. 2011;294(1):012008. [Google Scholar]
- Tasset F, Chupp TE, Pique JP, Steinhof A, Thompson A, Wasserman E, Ziade M. First test at ILL of a gaseous 3He neutron polarization filter. Physica B. 1992;180:896–898. [Google Scholar]
- Tasset F, Ressouche E. Optimum transmission for a 3He neutron polarizer. Nucl Instrum Methods Phys Res, Sect A. 1995;359(3):537–541. [Google Scholar]
- Tastevin G. Investigation of adsorption and wetting of 3He on cesium and cesiated glass. J Low Temp Phys. 1992a;89(3–4):669–672. [Google Scholar]
- Tastevin G. NMR characterization of phase separation in highly polarized 3He-4He solutions above 450 mK. J Low Temp Phys. 1992b;89(1):317–324. [Google Scholar]
- Tastevin G, Nacher PJ, Leduc M, Laloë F. Direct detection of spin waves in gaseous polarized 3He. J Physique Lett. 1985;46(6):249–254. [Google Scholar]
- Tastevin Genevieve, Grot Sébastien, Courtade Emmanuel, Bordais Sylvain, Nacher P-J. A broadband ytterbium-doped tunable fiber laser for 3He optical pumping at 1083 nm. Appl Phys B. 2004;78(2):145–156. [Google Scholar]
- Tastevin Geneviève, Nacher Pierre-Jean, Wiesen-feld Laurent, Leduc Michèle, Laloë Franck. Obtaining polarized liquid helium 3 from optically oriented gas. J Phys Paris. 1988;49(1):1–6. [Google Scholar]
- Thien F, Friese M, Cowin G, Mailet D, Wang D, Galloway G, Brereton I, Robinson PJ, Heil W, Thompson B. Feasibility of functional magnetic resonance lung imaging in Australia with long distance transport of hyperpolarized helium from Germany. Respirology. 2008;13:599–602. doi: 10.1111/j.1440-1843.2008.01262.x. [DOI] [PubMed] [Google Scholar]
- Thompson AK, Bernstein AM, Chupp TE, DeAngelis DJ, Dodge GE, Dodson G, Dow KA, Farkhondeh M, Fong W, Kim JY, et al. Quasielastic Scattering of Polarized Electrons from Polarized 3He and Measurement of the Neutron’s Form Factors. Phys Rev Lett. 1992;68(19):2901. doi: 10.1103/PhysRevLett.68.2901. [DOI] [PubMed] [Google Scholar]
- Tian Wei, Li Jiying, Lynn Jeffrey W, Zarestky Jerel L, Vaknin David. Spin dynamics in the magnetoelectric effect compound LiCoPO4. Phys Rev B. 2008;78(18):184429. [Google Scholar]
- Timsit RS, Daniels JM, Dennig EI, Kiang AKC, May AD. An experiment to compress polarized 3He gas. Can J Phys. 1971a;49(5):508–516. [Google Scholar]
- Timsit RS, Daniels JM, May AD. Nuclear relaxation of 3He gas on various solid surfaces. Can J Phys. 1971b;49(5):560–575. [Google Scholar]
- Tkach JA, Merhar SL, Kline-Fath BM, Pratt RG, Loew WM, Daniels BR, Giaquintol RO, Rattan MS, Jones BV, Taylor MD. Mr imaging in the neonatal intensive care unit: Initial experience using a small footprint 1.5 t system. Am J Roentgenol. 2014;202:W95–W105. doi: 10.2214/AJR.13.10613. [DOI] [PubMed] [Google Scholar]
- Tong X, Jiang CY, Lauter V, Ambaye H, Brown D, Crow L, Gentile TR, Goyette R, Lee WT, Parizzi A, et al. In situ polarized 3He system for the Magnetism Reflectometer at the Spallation Neutron Source. Rev Sci Instrum. 2012;83(7):075101. doi: 10.1063/1.4731261. [DOI] [PubMed] [Google Scholar]
- Tong X, Pierce J, Lee WT, Fleenor M, Chen WC, Jones GL, Robertson JL. Electrical heating for SEOP-based polarized 3He system. J Phys Conf Ser. 2010;251(1):012087. [Google Scholar]
- Tsai LL, Mair RW, Rosen MS, Patz S, Walsworth RL. An open-access, very-low-field MRI system for posture-dependent 3He human lung imaging. J Magn Reson. 2008;193(2):274–285. doi: 10.1016/j.jmr.2008.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tscherbul TV, Zhang Peng, Sadeghpour Hossein R, Dalgarno Alexander. Anisotropic Hyperfine Interactions Limit the Efficiency of Spin-Exchange Optical Pumping of 3He Nuclei. Phys Rev Lett. 2011;107(2):023204. doi: 10.1103/PhysRevLett.107.023204. [DOI] [PubMed] [Google Scholar]
- Tsentalovich EP Collaboration nEDM. The nEDM experiment at the SNS. Phys Part Nuclei. 2014;45(1):249–250. [Google Scholar]
- Tullney Kathlynne, Allmendinger Fabian, Burghoff Martin, Heil Werner, Karpuk Sergej, Kilian Wolfgang, Knappe-Grüneberg Silvia, Müller Wolfgang, Schmidt Ulrich, Schnabel Allard, et al. Constraints on spin-dependent short-range interaction between nucleons. Phys Rev Lett. 2013;111(10):100801. doi: 10.1103/PhysRevLett.111.100801. [DOI] [PubMed] [Google Scholar]
- Tustison NJ, Altes TA, Song G, de Lange EE, Mugler JP, 3rd, Gee JC. Feature analysis of hyperpolarized helium-3 pulmonary mri: a study of asthmatics versus nonasthmatics. Magn Reson Med (USA) 2010;64:1448–55. doi: 10.1002/mrm.22390. [DOI] [PubMed] [Google Scholar]
- Ueland BG, Lynn JW, Laver M, Choi YJ, Cheong S-W. Origin of electric-field-induced magnetization in multiferroic HoMnO3. Phys Rev Lett. 2010;104(14):147204. doi: 10.1103/PhysRevLett.104.147204. [DOI] [PubMed] [Google Scholar]
- Vasilakis G, Brown JM, Kornack TW, Romalis MV. Limits on New Long Range Nuclear Spin-Dependent Forces Set with a K-3He Comagnetometer. Phys Rev Lett. 2009;103(26):261801. doi: 10.1103/PhysRevLett.103.261801. [DOI] [PubMed] [Google Scholar]
- Venkatesh AK, Zhang AX, Mansour J, Kubatina L, Oh C-H, Blasche G, Ünlü MS, Balamore D, Jolesz FA, Goldberg BB, Albert MS. MRI of the lung gas-space at very low-field using hyperpolarized noble gases. Magn Reson Imaging. 2003;21(7):773–776. doi: 10.1016/s0730-725x(03)00178-4. [DOI] [PubMed] [Google Scholar]
- Villard Bérengère, Nacher Pierre-Jean, Tastevin Geneviève. Vapour pressure changes in spin-polarised liquid 3He and 3He-4He mixtures. Physica B. 2000:178–179. [Google Scholar]
- Vliegen E, Kadlecek S, Anderson LW, Walker TG, Erickson CJ, Happer William. Faraday rotation density measurements of optically thick alkali metal vapors. Nucl Instrum Methods Phys Res, Sect A. 2001;460(2):444–450. [Google Scholar]
- Volodin BL, Dolgy SV, Melnik ED, Downs E, Shaw J, Ban VS. Wavelength stabilization and spectrum narrowing of high-power multimode laser diodes and arrays by use of volume Bragg gratings. Opt Lett. 2004;29(16):1891–1893. doi: 10.1364/ol.29.001891. [DOI] [PubMed] [Google Scholar]
- Vrinceanu D, Kotochigova S, Sadeghpour HR. Pressure broadening and shift of He(23P0,1,2)-He(23S) lines. Phys Rev A. 2004;69(2):022714+. [Google Scholar]
- Vrinceanu D, Sadeghpour HR. Spin polarization transfer in ground and metastable helium atom collisions. New J Phys. 2010;12(6):065039. [Google Scholar]
- Wagshul ME, Chupp TE. Optical pumping of high-density Rb with a broadband dye laser and GaAlAs diode laser arrays: Application to 3He polarization. Phys Rev A. 1989;40(8):4447. doi: 10.1103/physreva.40.4447. [DOI] [PubMed] [Google Scholar]
- Wagshul ME, Chupp TE. Laser optical pumping of high-density Rb in polarized 3He targets. Phys Rev A. 1994;49(5):3854. doi: 10.1103/physreva.49.3854. [DOI] [PubMed] [Google Scholar]
- Walker TG, Larsen MS. Spin-Exchange-Pumped NMR Gyros. Adv At Mol Opt Phys. 2016;65:373–401. [Google Scholar]
- Walker TG, Nelson IA, Kadlecek Steve. Method for deducing anisotropic spin-exchange rates. Phys Rev A. 2010;81(3):032709. [Google Scholar]
- Walker Thad G. Fundamentals of spin-exchange optical pumping. J Phys Conf Ser. 2011;294(1):012001. [Google Scholar]
- Walker Thad G, Happer William. Spin-exchange optical pumping of noble-gas nuclei. Rev Mod Phys. 1997;69(2):629. [Google Scholar]
- Walker Thad G, Thywissen Joseph H, Happer William. Spin-rotation interaction of alkali-metal–He-atom pairs. Phys Rev A. 1997;56(3):2090. doi: 10.1103/PhysRevLett.54.1921. [DOI] [PubMed] [Google Scholar]
- Walkup LL, Tkach JA, Higano NS, Thomen RP, Fain SB, Merhar SL, Fleck RJ, Amin RS, Woods JC. Quantitative magnetic resonance imaging of bronchopulmonary dysplasia in the nicu environment. Am J Respir Crit Care Med. 2015;192:1215–22. doi: 10.1164/rccm.201503-0552OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace CD, Bixler DL, Monroe TJ, Dunning FB, Walters GK. Optical pumping of a He(23S) metastable atom beam using a diode laser. Rev Sci Instrum. 1995;66(1):265–266. [Google Scholar]
- Walsworth RL. Tests of Lorentz symmetry in the spin-coupling sector. In: Ehlers J, Lammerzahl C, editors. Special Relativity: Will it Survive the Next 101 years?; 271st WE-Heraeus Seminar on Special Relativity; Potsdam, Germany. 2005.2006. pp. 493–505. Lecture Notes in Physics. [Google Scholar]
- Walsworth RL, Bear D, Humphrey M, Mattison EM, Phillips DF, Stoner RE, Vessot RFC. New clock comparison searches for Lorentz and CPT violation. In: Guo XH, Thomas AW, Williams AG, editors. Symmetries in Subatomic Physics; 3rd International Symposium on Symmetries in Subatomic Physics (SYMM 2000); Adelaide Australia. 2000.IUPAP; Ctr Subatom Struct Matter; Natl Inst Theoret Phys; 2000. pp. 119–129. AIP Conference Proceedings. [Google Scholar]
- Walter DK, Griffith WM, Happer W. Energy transport in high-density spin-exchange optical pumping cells. Phys Rev Lett. 2001;86(15):3264. doi: 10.1103/PhysRevLett.86.3264. [DOI] [PubMed] [Google Scholar]
- Walter DK, Happer W, Walker TG. Estimates of the relative magnitudes of the isotropic and anisotropic magnetic-dipole hyperfine interactions in alkalimetal–noble-gas systems. Phys Rev A. 1998;58(5):3642. [Google Scholar]
- Wang Chengbo, Miller GW, Altes TA, de Lange EE, Cates GD, Mata JF, Brookeman JR, Mugler JP. Extending the range of diffusion times for regional measurement of the 3He ADC in human lungs. Magn Reson Med (USA) 2008;59:673–8. doi: 10.1002/mrm.21543. [DOI] [PubMed] [Google Scholar]
- Wang Guodong, Shao Wenjin, Hughes Emlyn W. Highly polarized 3He by spin exchange with potassium. Phys Rev A. 2003;68(6):065402. [Google Scholar]
- Wang Meng, Wang Miaoyin, Li GN, Huang Q, Li CH, Tan GT, Zhang CL, Cao Huibo, Tian Wei, Zhao Yang, et al. Antiferromagnetic order and superlattice structure in nonsuperconducting and superconducting RbyFe1.6+xSe2. Phys Rev B. 2011;84(9):094504. [Google Scholar]
- Wiedenmann Albrecht. Polarized SANS for probing magnetic nanostructures. Physica B. 2005;356(1):246–253. [Google Scholar]
- Wild JM, Schmiedeskamp J, Paley MNJ, Filbir F, Fichele S, Kasuboski L, Knitz F, Woodhouse N, Swift A, Heil W, Mills GH, Wolf M, Griffiths PD, Otten E, van Beek EJR. MR imaging of the lungs with hyperpolarized helium-3 gas transported by air. Phys Med Biol (UK) 2002;47:185–90. doi: 10.1088/0031-9155/47/13/401. [DOI] [PubMed] [Google Scholar]
- Wildes AR, Björck M, Andersson G. Some observations on polarized neutron reflectivity in applied fields. J Phys Condens Matter. 2008;20:295216. [Google Scholar]
- Williams W Gavin. Polarized Neutrons, Oxford Series on Neutron Scattering in Condensed Matter. Clarendon Press; Dordrecht: 1988. [Google Scholar]
- Williams WG. Polarisation modulated cross correlation neutron spectroscopy using 3He polarizing filters on a pulsed source. Nucl Instrum Methods Phys Res, Sect A. 1999;428:446–453. [Google Scholar]
- Wilms E, Ebert M, Heil W, Surkau R. Polarimetry on dense samples of spin-polarized 3He by magnetostatic detection. Nucl Instrum Methods Phys Res, Sect A. 1997;401(2):491–498. [Google Scholar]
- Woods JC. Mine the moon for 3He MRI? Not yet. J Appl Physiol. 2013;114:705–6. doi: 10.1152/japplphysiol.00035.2013. [DOI] [PubMed] [Google Scholar]
- Woods JC, Choong CK, Yablonskiy DA, Bentley J, Wong J, Pierce JA, Cooper JD, Macklem PT, Conradi MS, Hogg JC. Hyperpolarized 3He diffusion MRI and histology in pulmonary emphysema. Magn Reson Med (USA) 2006;56:1293–300. doi: 10.1002/mrm.21076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodward CE, Beise EJ, Belz JE, Carr RW, Filippone BW, Lorenzon WB, McKeown RD, Mueller B, O’Neill TG, Dodson G, et al. Measurement of inclusive quasielastic scattering of polarized electrons from polarized 3He. Phys Rev Lett. 1990;65:698–700. doi: 10.1103/PhysRevLett.65.698. [DOI] [PubMed] [Google Scholar]
- Xiong F, Dutta Dipangkar, Xu W, Anderson Bryon, Auberbach L, Averett Todd, Bertozzi William, Black Timothy, Calarco John, Cardman Larry, et al. Precision Measurement of the Spin-Dependent Asymmetry in the Threshold Region of 3 H⃗e(e⃗, e′) Phys Rev Lett. 2001;87(24):242501. doi: 10.1103/PhysRevLett.87.242501. [DOI] [PubMed] [Google Scholar]
- Xu W, Dutta D, Xiong F, Anderson B, Auberbach L, Averett T, Bertozzi W, Black T, Calarco J, Cardman L, et al. Transverse Asymmetry AT′ from the quasi elastic 3 H⃗e(e⃗, e′) Process and the Neutron Magnetic Form Factor. Phys Rev Lett. 2000;85(14):2900. doi: 10.1103/PhysRevLett.85.2900. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA, Sukstanskii AL, Ackerman JJH. Image artifacts in very low magnetic field MRI: the role of concomitant gradients. J Magn Reson. 2005;174:279–86. doi: 10.1016/j.jmr.2005.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA, Sukstanskii AL, Woods JC, Gierada DS, Quirk JD, Hogg JC, Cooper JD, Conradi MS. Quantification of lung microstructure with hyperpolarized 3He diffusion MRI. J Appl Physiol. 2009;107:1258–1265. doi: 10.1152/japplphysiol.00386.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan H, Sun GA, Peng SM, Zhang Y, Fu C, Guo H, Liu BQ. Searching for New Spin- and Velocity-Dependent Interactions by Spin Relaxation of Polarized 3He Gas. Phys Rev Lett. 2015;115:182001. doi: 10.1103/PhysRevLett.115.182001. [DOI] [PubMed] [Google Scholar]
- Ye Q, Dutta D, Gao H, Kramer K, Qian X, Zong X, Hannelius L, McKeown RD, Heyburn B, Singer S, et al. Relaxation of spin polarized 3He in mixtures of 3He and 4He below the 4He lambda point. Phys Rev A. 2008;77(5):053408. [Google Scholar]
- Ye Q, Gao H, Zheng W, Dutta D, Dubose F, Golub R, Huffman P, Swank C, Korobkina E. Relaxation of spin-polarized 3He in mixtures of 3He and 4He at about 330 mK. Phys Rev A. 2009;80(2):023403. [Google Scholar]
- Ye Q, Gentile TR, Anderson J, Broholm C, Chen WC, De-Land Z, Erwin RW, Fu CB, Fuller J, Kirchhoff A, et al. Wide Angle Polarization Analysis with Neutron Spin Filters. Physcs Proc. 2013;42:206–212. [Google Scholar]
- Ye Q, Laskaris G, Chen W, Gao H, Zheng W, Zong X, Averett T, Cates GD, Tobias WA. A high-pressure polarized 3He gas target for nuclear-physics experiments using a polarized photon beam. Eur Phys J A. 2010;44(1):55–61. [Google Scholar]
- Young AR, Appelt S, Ben-Amar Baranga A, Erickson C, Happer W. Three-dimensional imaging of spin polarization of alkali-metal vapor in optical pumping cells. Appl Phys Lett. 1997;70(23):3081–3083. [Google Scholar]
- Zaharko O, Rønnow H, Mesot J, Crowe SJ, McK Paul D, Brown PJ, Daoud-Aladine A, Meents A, Wagner A, Prester M, et al. Incommensurate magnetic ordering in Cu2Te2O5X2 (X= Cl, Br) studied by single crystal neutron diffraction. Phys Rev B. 2006;73(6):064422. doi: 10.1103/PhysRevLett.93.217206. [DOI] [PubMed] [Google Scholar]
- Zeng X, Wu Z, Call T, Miron E, Schreiber D, Happer W. Experimental determination of the rate constants for spin exchange between optically pumped K, Rb, and Cs atoms and 129Xe nuclei in alkali-metal-noble-gas van der Waals molecules. Phys Rev A. 1985;31:260. doi: 10.1103/physreva.31.260. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Qian X, Allada K, Dutta C, Huang J, Katich J, Wang Y, Aniol K, Annand M, JR, Averett T, et al. (Jefferson Lab Hall A Collaboration) Measurement of “pretzelosity” asymmetry of charged pion production in semi-inclusive deep inelastic scattering on a polarized 3He target. Phys Rev C. 2014;90:055209. doi: 10.1103/PhysRevLett.107.072003. [DOI] [PubMed] [Google Scholar]
- Zhao YX, Allada K, Aniol K, Annand M, JR, Averett T, Benmokhtar F, Bertozzi W, Bradshaw PC, Bosted P, Camsonne A, et al. (Jefferson Lab Hall A Collaboration) Double spin asymmetries of inclusive hadron electroproduction from a transversely polarized 3He target. Phys Rev C. 2015;92:015207. [Google Scholar]
- Zhdanov Boris V, Knize Randy J. Review of alkali laser research and development. Opt Eng. 2012;52(2):021010. [Google Scholar]
- Zheng W, Cleveland ZI, Möller HE, Driehuys B. Gradient-induced longitudinal relaxation of hyperpolarized noble gases in the fringe fields of superconducting magnets used for magnetic resonance. J Magn Reson. 2011a;208:284–290. doi: 10.1016/j.jmr.2010.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W, Gao H, Liu J-G, Zhang Y, Ye Q, Swank C. General solution to gradient-induced transverse and longitudinal relaxation of spins undergoing restricted diffusion. Phys Rev A. 2011b;84(5):053411. [Google Scholar]
- Zheng Xiaochao. PhD Thesis. MIT; 2002. Precision Measurement of Neutron Spin Asymmetry at Large xBj Using CEBAF at 5.7 GeV. [Google Scholar]
- Zheng Xiaochao, Aniol K, Armstrong DS, Averett TD, Bertozzi W, Binet S, Burtin E, Busato Emmanuel, Butuceanu C, Calarco J, et al. Precision measurement of the neutron spin asymmetry and spin-flavor decomposition in the valence quark region. Phys Rev Lett. 2004a;92(1):012004. doi: 10.1103/PhysRevLett.92.012004. [DOI] [PubMed] [Google Scholar]
- Zheng Xiaochao, Aniol Konrad, Armstrong DS, Averett TD, Bertozzi William, Sebastien Binet, Burtin Etienne, Busato Emmanuel, Butuceanu Cornel, Calarco John, et al. Precision measurement of the neutron spin asymmetries and spin-dependent structure functions in the valence quark region. Phys Rev C. 2004b;70(6):065207. doi: 10.1103/PhysRevLett.92.012004. [DOI] [PubMed] [Google Scholar]
- Zhitnikov RA, Kartoshkin VA, Klementev GV, Usacheva LV. Metastability exchange in a mixture of helium isotopes at liquid-nitrogen temperature. JETP Lett. 1975;22(5):136–137. [Google Scholar]
- Zhu H, Ruset IC, Hersman FW. Spectrally narrowed external-cavity high-power stack of laser diode arrays. Opt Lett. 2005;30(11):1342–1344. doi: 10.1364/ol.30.001342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmer O, Ehlers G, Farago B, Humblot H, Ketter W, Scherm R. A precise measurement of the spin-dependent neutron scattering length of 3He. EPJ direct. 2002;4(1):1–28. [Google Scholar]
- Zimmer O, Müller TM, Hautle P, Heil W, Humblot H. High-precision neutron polarization analysis using opaque spin filters. Phys Lett B. 1999;455(1):62–68. [Google Scholar]
- Zou Sheng, Zhang Hong, Chen Xi-yuan, Chen Yao, Lu Jixi, Hu Zhao-hui, Shan Guang-cun, Quan Wei, Fang Jian-cheng. Ultra-sensitive atomic magnetometer for studying magnetization fields produced by hyperpolarized helium-3. J Appl Phys. 2016;119(14):143901. http://dx.doi.org/10.1063/1.4945670. [Google Scholar]