Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 21;9(2):313–318. doi: 10.1021/acs.jpclett.7b02921

Molecular Dynamics Simulations Reveal an Interplay between SHAPE Reagent Binding and RNA Flexibility

Vojtěch Mlýnský 1,*, Giovanni Bussi 1,*
PMCID: PMC5830694  PMID: 29265824

Abstract

graphic file with name jz-2017-02921p_0004.jpg

The function of RNA molecules usually depends on their overall fold and on the presence of specific structural motifs. Chemical probing methods are routinely used in combination with nearest-neighbor models to determine RNA secondary structure. Among the available methods, SHAPE is relevant due to its capability to probe all RNA nucleotides and the possibility to be used in vivo. However, the structural determinants for SHAPE reactivity and its mechanism of reaction are still unclear. Here molecular dynamics simulations and enhanced sampling techniques are used to predict the accessibility of nucleotide analogs and larger RNA structural motifs to SHAPE reagents. We show that local RNA reconformations are crucial in allowing reagents to reach the 2′-OH group of a particular nucleotide and that sugar pucker is a major structural factor influencing SHAPE reactivity.

Ribonucleic acid (RNA) is involved in a large number of functional processes in cells.1 RNA function depends not only on its sequence and secondary structure but also on its specific 3D fold and structural dynamics.2,3 Thus there is a longstanding interest in developing tools that can be used to predict or directly determine RNA structure. Chemical probing techniques are popular methods used to determine RNA secondary structure by distinguishing among base-paired and unpaired nucleotides. Hydroxyl radical footprinting, dimethylsulfate probing, selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE), and in-line probing are used most frequently.4 The number of available data sets obtained by chemical probing techniques has exploded in the last years and has already surpassed by two orders of magnitude the number of RNA 3D structures obtained with traditional X-ray or NMR methods.5 Statistics from the freely available RMDB database6 shows that almost half of the chemical probing data sets were obtained by using SHAPE protocols. SHAPE was designed as a method providing a sequence-independent and time-effective analysis of RNAs with single nucleotide resolution.7,8 Chemically, 2′-hydroxyl (2′-OH) groups are modified by electrophilic molecules (SHAPE reagents) during the acylation reaction, resulting in adducts that are subsequently detected as stops in primer extension by gel electrophoresis or with mutational profiling.9−11 Recent protocols allow one to analyze massive structures,12−14 have success in probing RNA in vivo,15−21 and can also detect motifs participating in RNA–protein interactions.13,14 Additionally, SHAPE data serve in guiding structure models and improving the accuracy of popular secondary structure prediction tools22−30 and have been fruitfully combined with a plethora of computational methods and algorithms.9,19,28,31−33

Flexible nucleotides are presumed to be more reactive toward SHAPE reagents because they were shown to sample multiple conformations, where few of those could enhance the reactivity of 2′-OH group.4,8 Thus certain efforts focused on the relationship between SHAPE reactivity and specific geometry of RNA residues.31,34−36 In particular, Bindewald and coworkers found that SHAPE reactivities are correlated with structural properties of nucleotides, that is, base pairing (cis-Watson–Crick/Watson–Crick) and base stacking.31 McGinnis and coworkers compared reactivities of small nucleotide analogs with ∼1500 different nucleotides from the small ribosomal subunit and identified three important structural parameters: (i) sugar-pucker of the ribose ring, (ii) conformation of the adjacent phosphate moiety, and (iii) presence of a RNA functional group within hydrogen-bond (H-bond) distance from 2′-OH group.34 More specifically, the sugar pucker of the ribose ring was identified as an important structural factor37 and nucleotides with C2′-endo sugar pucker appeared to be more reactive toward SHAPE reagents.34 Interestingly, transient pucker reconformations of RNA nucleotides can also be observed in NMR studies.38 Finally, SHAPE data sets were correlated with structural fluctuations obtained from both molecular dynamics (MD) simulations and elastic network models (ENMs), where the best fits surprisingly considered neither 2′-OH groups nor phosphate moieties but rather fluctuations in the distance between consecutive nucleobases.36 Overall, there is a general consensus that nucleotide flexibility and dynamics are important in yielding SHAPE modifications, but a microscopic interpretation of this statement is totally missing. Indeed, to the best of our knowledge, neither SHAPE reagent interactions with RNA nor atomistic details of the interplay between reagent binding and local nucleotide dynamics have been analyzed in detail.

To reveal the effects of SHAPE reagent on RNA structural dynamics, we report here a computational analysis of reagent interactions with diverse RNA systems, that is, the RNA core of the signal recognition particle (SRP–RNA), GNRA tetraloop, and two RNA nucleotide analogs. Classical as well as enhanced sampling MD simulations revealed that reagent is mostly stabilized in conformations required for the acylation reaction by stacking interaction with ribose sugar rings. Reaction rates are dependent on the dynamics of the whole RNA motif and on the ability of each nucleotide to accommodate the reagent in close proximity of its 2′-OH group.

The SRP–RNA (Figure 1) containing several unpaired as well as Watson–Crick (WC) and noncanonical (NC) base-paired nucleotides was used to investigate the accessibility of nucleotides toward fast acting benzoyl cyanide (BzCN) SHAPE reagent. We mostly used BzCN in our simulations because interactions between complex RNA systems and larger reagents, for example, N-methylisatoic anhydride (NMIA), appeared to be more complicated (see the Supporting Information (SI) part 3 for details). Starting structure was taken from the protein–RNA complex determined by X-ray crystallography.39 Structural dynamics of individual nucleotides was first quantified by running a 500 ns long classical MD simulation and some enhanced sampling simulations.40 Namely, bias-exchange MD simulations41 were applied to enforce C3′-endo/C2′-endo sugar-pucker flips, and a similar approach41,42 was then used to investigate the interplay between reagent binding and RNA reconformation to overcome binding free-energy barriers and bring the reactive carbon of the BzCN reagent toward the 2′-OH group of each SRP–RNA nucleotide. Results were correlated against a recent experiment using BzCN reagent for investigating cotranscriptional folding of SRP–RNA.43 SHAPE data sets from this experiment are freely available and were retrieved from the RMDB database.6 In addition, we performed other tests involving smaller RNA systems: (i) a gccGUAAggc GNRA tetraloop with BzCN SHAPE reagent and (ii) two nucleotide analogs, that is, 3′-5′-cyclic-adenosine monophosphate (cAMP) and 3′-5′-cyclic-cytosine monophosphate (cCMP), for which we used larger (NMIA) SHAPE reagent to directly compare results with available experimental data.7 All simulations were performed using GROMACS44 and PLUMED45 (see the SI part 2 for details). We note that the simulation setup of SRP–RNA motif contained soft restrains that were required to (i) compensate for previously reported force-field deficiencies46−50 and to (ii) avoid unfeasibly long simulations in an attempt to capture the whole structural ensemble upon multiple RNA unfolding/refolding events. Restraints were applied using an RNA-dedicated metric (ϵRMSD)49,51 (see the SI parts 1−7 for details).

Figure 1.

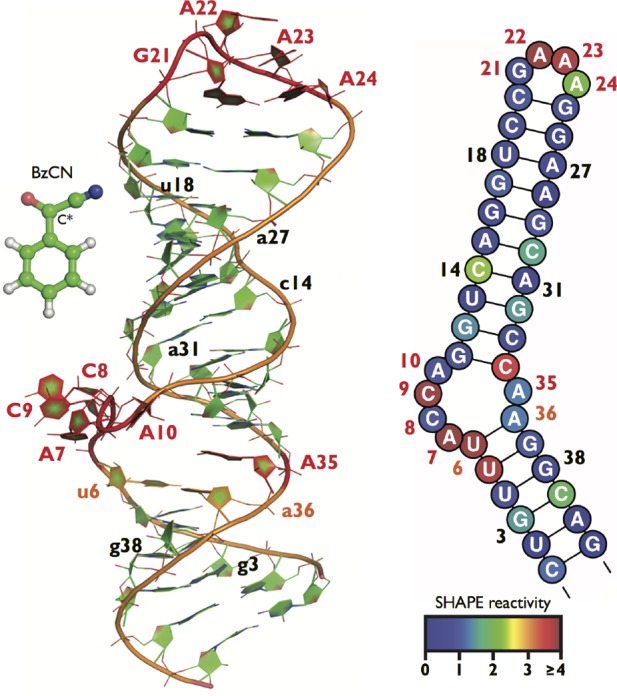
Figure 1

Open in a new tab

Tertiary and secondary structures of SRP–RNA motif. The left panel shows the tertiary structure used as starting point for MD simulations (PDB ID 1DUL).39 Nucleotides from GNRA tetraloop, first and last noncanonical base pairs from the symmetric loop, all nucleotides from the asymmetric internal loop, and U6-A36 closing base pair from the asymmetric loop are labeled (unpaired nucleotides in capital letters). Structural model of small BzCN reagent is displayed (not to scale) on the left side with the reactive carbon (C*) highlighted. The right panel shows the corresponding secondary structure model, where the coloring scheme for each nucleotide is based on experimentally measured SHAPE reactivity.43

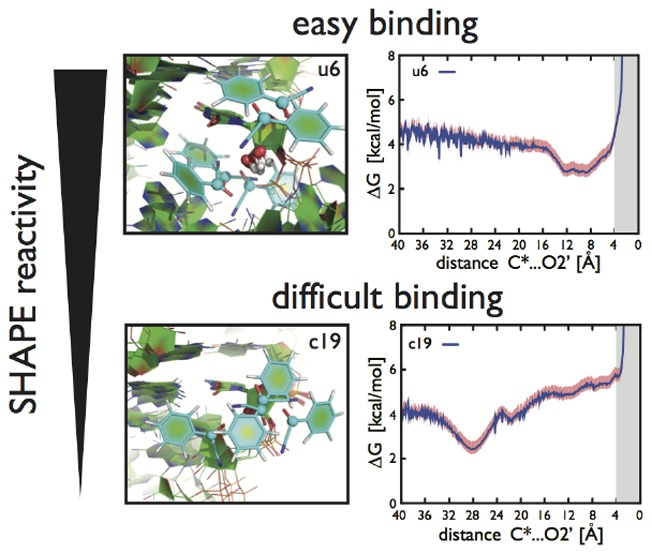
As a preliminary step, we analyzed the X-ray structure and the plain MD trajectory using previously proposed approaches, namely, computing solvent accessibility of 2′-OH and fluctuations of base–base distances. Results are reported in the SI (part 7, Figures S1–S3) and are in agreement with previously reported analyses of different RNA molecules.7,34,36,52 We then analyzed RNA structural dynamics, in particular, monitoring the transient C2′-endo sugar puckers. Nucleotides from SRP–RNA were enforced to undergo C3′-endo/C2′-endo sugar-pucker flips during enhanced sampling simulations. The C2′-endo population analysis revealed that the data are correlated with experimental reactivity (Pearson’s linear R value of ∼0.5, Figure 2) and the sugar pucker could be considered as a possible structural factor for distinguishing among reactivity patterns (see the SI part 7 for details). To explicitly take into account the RNA–reagent dynamical interplay, we performed enhanced sampling simulations and modeled the propensity of the reagent to reach a reactive conformation. We estimated relative binding constants between BzCN reagent and 2′-OH groups of nucleotides from SRP–RNA. The results from these bias-exchange-like simulations revealed rather poor correlation (∼0.3) against experimental SHAPE reactivities (see Figure S5 in the SI). However, the correlation could be enhanced up to ∼0.6 by combining the two above-mentioned procedures, that is, by applying the sugar-pucker population analysis to the results from enhanced sampling simulations (Figure 2). An equivalent analysis made on a simulation where RNA was kept completely frozen lead to zero correlation, unambiguously revealing that RNA flexibility is a fundamental determinant for SHAPE reactivity (Figure 2). In a further attempt to increase the correlation, we analyzed the presence of nearby RNA groups with the ability to function as general bases in deprotonation of 2′-OH,34 but the overall correlation was not improved. Interestingly, the outputs from two different MD-based approaches involving a completely different analysis, that is, (i) monitoring fluctuations of distance between consecutive nucleobases36 in classical MD simulations and (ii) combining bias-exchange-like simulations with sugar-pucker analysis, appear to capture the same phenomena as their results are highly correlated against each other (R ∼ 0.8, see Figure S6 in the SI). In summary, all of the successful approaches discussed here explicitly take into account RNA dynamics, supporting the fact that flexibility is crucial for SHAPE reactivity.

Figure 2.

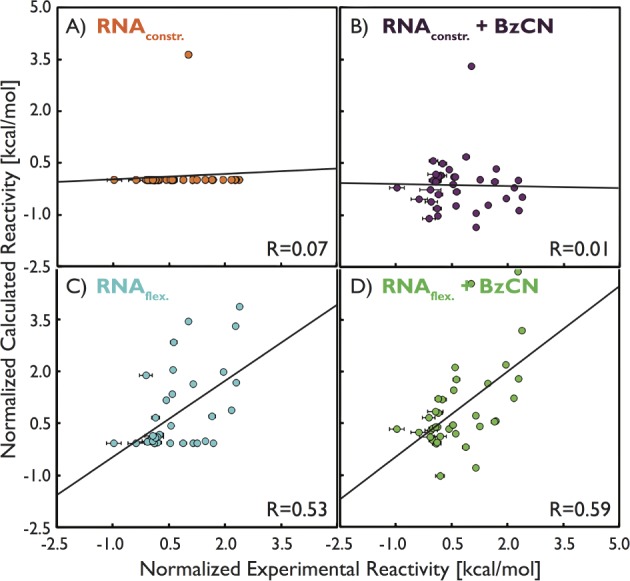
Figure 2

Open in a new tab

Correlations between experimental and calculated SHAPE reactivities of nucleotides from SRP–RNA. Top (A,B) and bottom (C,D) panels show results from simulations with frozen (X-ray like) RNA and flexible RNA, respectively. On the left side (A,C), results based on RNA-only structural analysis are shown, that is, the distribution of C2′-endo puckers in the X-ray structure and their respective populations from enhanced sampling simulations (see Figure S4 in the SI for the comparison between classical MD and enhanced sampling simulations). On the right side (B,D), both structural analysis of sugar puckers and relative binding rate constants from bias-exchange-like simulations with BzCN reagent were used. See Figure S5 in the SI for the results from enhanced sampling simulations not modified by additional sugar-pucker population analysis. Computed and experimental reactivities were derived as a free energy (as logarithm of SHAPE reactivity) and subsequently normalized against one particular WC base-paired nucleotide (see the SI part 4 for details).

We notice that experimental reactivities from four independent experiments are available,43 but attempts to correlate our predictions against different experimental data sets revealed minimal differences. Hence, only R values against the first data set are discussed in the main text (see Table S1 in the SI for all raw data sets and selected cross-correlations). Experimental data sets are significantly correlated against each other (R values from 0.73 to 0.98, see the SI part 5 for details), confirming that the obtained reactivities are reproducible. However, the R values indicate that any prediction on the order of 0.75 or better would be practically undistinguishable from experimental data sets.

Our results from bias-exchange-like simulations with the SRP–RNA system might be influenced by the choice of the X-ray structure used as a starting point for MD simulations, which was taken from a protein–RNA complex.39 Other X-ray structures of SRP–RNA are available, but they are either in complex with proteins as well or display sequences that are different from the one used in SHAPE experiment (especially in less structured parts). The protein is interacting with the symmetrical loop of SRP–RNA stabilizing five NC base pairs (from C14-A31 to U18-A27, see Figure 1).39 NMR data in solution are, however, available for only a small part of SRP–RNA (terminal RNA hairpin) and suggest that NC duplex region may prefer different structural order.53 In particular, considering the X-ray structure, the classical 500 ns long MD simulation (see the SI part 2 and 7 for details), as well as all enhanced sampling simulations, one of the reported nuclear Overhausser effect (NOE) contacts53 involving adenine H2 protons, that is, A15(H2)...G29(H1′), is never formed, and the other (C19(H6)...A27(H2)) is often violated during both classical and enhanced sampling simulations. In addition, NMR data suggest that U13, A23, A24, and C30 should transiently sample C2′-endo pucker,53 but we did not detect any repuckering of these nucleotides either in classical MD or during bias-exchange-like simulations with BzCN reagent. The bias-exchange simulation enforcing pucker flips revealed only minimal populations of C2′-endo pucker for C13, A23, A24, and C30 nucleotides (probing them as nonreactive, Table S1 in the SI). Thus our choice to initialize the simulations from the X-ray structure could explain the disagreements in reactivity between prediction and experiment that were observed in NC duplex and tetraloop regions (Figure S7 in the SI). On the contrary, we propose that discrepancies between our calculations and experimental SHAPE data could be used to identify dynamical regions, where a single X-ray structure might not be representative. This is probably the case for the asymmetric loop (NMR data not available), which contains a closing U6-A36 base pair (Figure 1) and is probably dynamic, as suggested by both experimental43 and computed SHAPE reactivities (see Figures S7 and S8 in the SI).

On the basis of our results, we propose that the modification of a particular RNA nucleotide by SHAPE reagent occurs in a sequence of stages (Figure 3). First, reagent reaches the nucleotide and is stabilized in the close proximity of its 2′-OH group mainly by stacking with sugar rings and nucleobases and by some (rather weak) H-bond contacts. We clustered all possible reactive conformations of SRP–RNA nucleotides and identified that stacking to sugar rings is the most frequent in unpaired as well as WC and NC base-paired nucleotides (Figures S9 and S10 in the SI). WC paired nucleotides mostly accommodated BzCN on their sugar ring, whereas unpaired and NC paired rather favored stacking on other sugars or nucleobases. This is not surprising because stacking in canonical A-RNA duplex is mostly saturated.35 Our limited sample of diverse nucleotides shows that reactive geometries of WC and NC paired nucleotides typically provided a similar number of different clusters, whereas the number of clusters from unpaired nucleotides was slightly (∼1.3 times) higher on average (Figures S9 and S10 in the SI). Notice that identified stacking preference to sugars here could be driven by the specific SHAPE reagent (BzCN) or due to the number of restrains required for the simulations (see the SI part 3 for details). In general, we expect more frequent reagent stacking to nucleobases, larger reconformations of RNA motifs, and other structural changes to be induced, especially by larger SHAPE reagents (like NMIA and its derivative).

Figure 3.

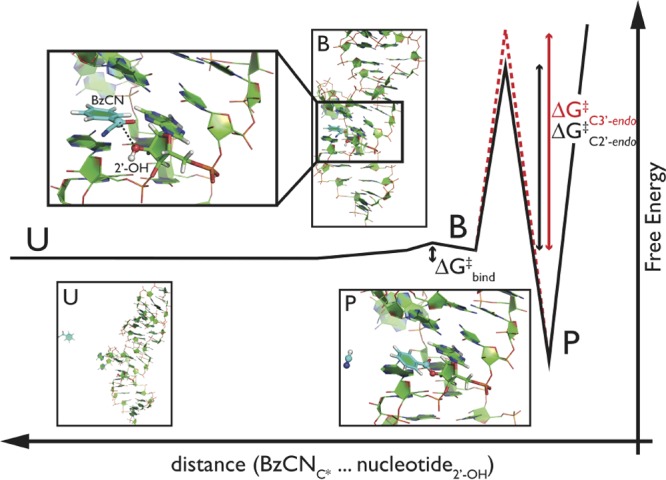
Figure 3

Open in a new tab

Hypothetical mechanism of RNA modification by SHAPE reagent. Schematic profile, where the free energy depends on the distance between reactive carbon (C*) of BzCN reagent and O2′ oxygen from particular nucleotide. Insets represent snapshots of SRP–RNA motif with BzCN in unbound state (U), bound state in close proximity from 2′-OH group (B, highlighted in double-inset), and anticipated reaction adduct after the acylation reaction (P). Bound states are here defined as structures for which the distance between C* and O2′ is <4.0 Å. Water molecules and counterions are not shown for clarity. We find that the barrier for binding (ΔGbind‡) and unbinding is marginal (∼1 kcal/mol, Figure S11) in comparison with the activation barrier of the acylation reaction (estimated ∼20 kcal/mol; see the SI part 4 for details). The activation free energy could be affected by some structural factors, for example, by the sugar pucker of the particular nucleotide in a reaction complex with reagent (in the range of a few kcal/mol favoring C2′-endo sugar pucker in a free energy; Table S2 in the SI).

After the initial binding, a reaction undergoes with a rate proportional to exp(−ΔGreact‡/RT). Considering the acylation reaction producing SHAPE adduct as irreversible, the measured amount of each adduct is directly proportional to the reactivity of the corresponding nucleotide. We here find that a simple model where the reaction barrier (ΔGreact) only depends on the sugar conformation such that the C2′-endo pucker is more reactive is sufficient to obtain a high correlation with experiments. The typical barriers that we observe for unbinding are very small (∼1 kcal/mol, see Figure S11 in the SI for calculated free-energy binding profiles of all analyzed SRP–RNA nucleotides) and certainly much lower than the expected ΔGreact‡ of the following chemical reaction (Figure 3). The reactivity of a particular nucleotide is thus proportional to the binding rate constant of the SHAPE reagent toward the corresponding 2′-OH group with a correction taking into account the sugar pucker. Consequently, we are able to distinguish reactivity patterns without the need to explicitly simulate the acylation reaction. This makes the presented protocol robust even without usage of computationally demanding ab initio methods or problematic semiempirical potentials that were required for a recent investigation of inline probing experiments.54 Assuming the typical reagent concentration in SHAPE experiments (∼100 mM)9,10,43 and our calculated absolute binding constants (from 0.2 to 6.4 M–1) between BzCN and nucleotides in a common structural motif, the roughly estimated ΔGreact should be ∼20 kcal/mol to get one modification per molecule under experimental time scale of minutes, which is a reasonable value for this type of reaction (see the SI part 4 for details). In addition, the estimated absolute binding constants indicate that the reagent binding likely occurs before the activation (deprotonation) of the particular 2′-OH group.

The original study of Weeks and coworkers identified that nucleotide analogs with 3′-phosphodiester moiety constrained away from the 2′-OH group by 3′-5′-linkage have one of the highest reaction rates with NMIA reagent among various nucleotide analogs7 and are thus denoted as “hyper-reactive”.34 We used two of these analogs (cAMP and cCMP) for additional simulations to test if our designed simulation setup was able to detect possible differences in reactivity among different nucleotides, that is purines and pyrimidines. We analyzed NMIA reagent binding toward cAMP and cCMP and estimated absolute binding constants of 6.6 and 2.9 M–1 for cAMP and cCMP, respectively (see the SI part 4 for details). In other words, NMIA reagent established a measurably stronger interaction with cAMP (here used as an analog of purine nucleotides) than cCMP (as corresponding analog of pyrimidine nucleotides). A similar observation was reported from an experimental analysis of large data sets, where cytosines were shown to be the least reactive among nucleotides with relative reactivities almost two times lower than adenines.55 Those differences could partly originate from the different pKa of 2′-OH groups between purine and pyrimidine residues.55,56 On the basis of our results, we speculate that the difference could be rather explained by the better ability of purine nucleotides to stabilize SHAPE reagents in the close proximity of 2′-OH groups, namely, by stronger stacking interaction. However, this systematic difference in reactivity between purine and pyrimidine nucleotides could be hidden or even reversed when analyzing individual structural motifs.8 For instance, considering results for SRP–RNA, the average reactivity of pyrimidine nucleotides is ∼1.5 times higher than that of purines, both in our prediction and in the experimental data set.43 Indeed, other effects such as stacking interactions with other residues and ribose repuckering might be more important than nucleobase identity.

In summary, we here provide a computational attempt to characterize the interactions between RNA nucleotides and SHAPE reagents. We developed and applied a novel protocol to predict reactivity patterns of small RNA structural elements as well as larger RNA motifs, estimated the reagent’s binding constants, and compared results with experimental SHAPE data sets. Our analysis shows that RNA flexibility is crucial to allow the reagent to reach the 2′-OH group, which requires some local RNA reconformations. Indeed, among all of the tested methods, only those where RNA dynamics was explicitly or implicitly (as in the ENM approach) included were capable of reaching a significant correlation with experiments. The explicit simulation of RNA–reagent binding allowed us to reach important structural insight on the SHAPE modification of nucleotides. Sugar rings and nucleobases are directing the reagent to the close proximity of 2′-OH group by the stacking interaction, and moieties from neighboring and other residues located further away along the RNA chain are frequently involved in stabilizing the reagent in the reactive conformation. The sugar pucker of the ribose ring is also an important structural factor that can determine the reactivity of particular nucleotides. Ultimately, our data show that the probability to observe the reagent in the binding position at the usually employed concentrations is much higher than the probability to observe a deprotonated 2′-OH group, which is required for the following acylation reaction to happen. We speculate that the protocol developed here could be employed to compute the reactivity patterns of predicted structures associated with sequences for which SHAPE data are available and, subsequently, to rank those putative structures by their agreement with experimental data. If the capability to discriminate decoy structures will be confirmed, then this procedure may allow the direct utilization of SHAPE data in 3D structure prediction. In addition, because many RNA chemical probing methods are based on the idea of using small molecules to probe equivalent sites located on different nucleotides, we anticipate that the introduced protocol may be suitably adapted to predict reactivities obtained using other experimental techniques.

Acknowledgments

We thank Rhiju Das, Alisha Jones, Anthony M. Mustoe, Kevin Weeks, and anonymous reviewers for critical reading of the manuscript and providing a number of useful suggestions. Richard A. Cunha, Alejandro Gil-Ley, and Andrea Cesari are also acknowledged for helpful discussions. This work has been supported by European Research Council under the European Union’s Seventh Framework Program (FP/2007-2013)/ERC grant agreement no. 306662, S-RNA-S.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b02921.

  • Details of structure preparation, simulation protocols, applied restrains, fitting procedure, analysis of calculated and experimental reactivities, solvent accessibility of 2′-OH groups and other structural analysis, and supporting tables and figures. (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz7b02921_si_001.pdf (19.2MB, pdf)

References

  1. Morris K. V.; Mattick J. S. The rise of regulatory RNA. Nat. Rev. Genet. 2014, 15, 423–437. 10.1038/nrg3722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Walter N. G. The blessing and curse of RNA dynamics: Past, present, and future. Methods 2009, 49, 85–86. 10.1016/j.ymeth.2009.09.002. [DOI] [PubMed] [Google Scholar]
  3. Lilley D. M. How RNA acts as a nuclease: Some mechanistic comparisons in the nucleolytic ribozymes. Biochem. Soc. Trans. 2017, 45, 683–691. 10.1042/BST20160158. [DOI] [PubMed] [Google Scholar]
  4. Weeks K. M. Advances in RNA structure analysis by chemical probing. Curr. Opin. Struct. Biol. 2010, 20, 295–304. 10.1016/j.sbi.2010.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cordero P.; Lucks J. B.; Das R. An RNA Mapping DataBase for curating RNA structure mapping experiments. Bioinformatics 2012, 28, 3006–3008. 10.1093/bioinformatics/bts554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Merino E. J.; Wilkinson K. A.; Coughlan J. L.; Weeks K. M. RNA structure analysis at single nucleotide resolution by selective 2’-hydroxyl acylation and primer extension (SHAPE). J. Am. Chem. Soc. 2005, 127, 4223–4231. 10.1021/ja043822v. [DOI] [PubMed] [Google Scholar]
  8. Weeks K. M.; Mauger D. M. Exploring RNA structural codes with SHAPE chemistry. Acc. Chem. Res. 2011, 44, 1280–1291. 10.1021/ar200051h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Smola M. J.; Rice G. M.; Busan S.; Siegfried N. A.; Weeks K. M. Selective 2’-hydroxyl acylation analyzed by primer extension and mutational profiling (SHAPE-MaP) for direct, versatile, and accurate RNA structure analysis. Nat. Protoc. 2015, 10, 1643–1669. 10.1038/nprot.2015.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Wilkinson K. A.; Merino E. J.; Weeks K. M. Selective 2’-hydroxyl acylation analyzed by primer extension (SHAPE): Quantitative RNA structure analysis at single nucleotide resolution. Nat. Protoc. 2006, 1, 1610–1616. 10.1038/nprot.2006.249. [DOI] [PubMed] [Google Scholar]
  11. Tian S.; Cordero P.; Kladwang W.; Das R. High-throughput mutate-map-rescue evaluates SHAPE-directed RNA structure and uncovers excited states. RNA 2014, 20, 1815–1826. 10.1261/rna.044321.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Watts J. M.; Dang K. K.; Gorelick R. J.; Leonard C. W.; Bess J. W. Jr.; Swanstrom R.; Burch C. L.; Weeks K. M. Architecture and secondary structure of an entire HIV-1 RNA genome. Nature 2009, 460, 711–716. 10.1038/nature08237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Smola M. J.; Calabrese J. M.; Weeks K. M. Detection of RNA–protein interactions in living cells with SHAPE. Biochemistry 2015, 54, 6867–6875. 10.1021/acs.biochem.5b00977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Smola M. J.; Christy T. W.; Inoue K.; Nicholson C. O.; Friedersdorf M.; Keene J. D.; Lee D. M.; Calabrese J. M.; Weeks K. M. SHAPE reveals transcript-wide interactions, complex structural domains, and protein interactions across the Xist lncRNA in living cells. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 10322–10327. 10.1073/pnas.1600008113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Spitale R. C.; Crisalli P.; Flynn R. A.; Torre E. A.; Kool E. T.; Chang H. Y. RNA SHAPE analysis in living cells. Nat. Chem. Biol. 2012, 9, 18–20. 10.1038/nchembio.1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. McGinnis J. L.; Weeks K. M. Ribosome RNA assembly intermediates visualized in living cells. Biochemistry 2014, 53, 3237–3247. 10.1021/bi500198b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Spitale R. C.; Flynn R. A.; Zhang Q. C.; Crisalli P.; Lee B.; Jung J.-W.; Kuchelmeister H. Y.; Batista P. J.; Torre E. A.; Kool E. T.; et al. Structural imprints in vivo decode RNA regulatory mechanisms. Nature 2015, 519, 486–490. 10.1038/nature14263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. McGinnis J. L.; Liu Q.; Lavender C. A.; Devaraj A.; McClory S. P.; Fredrick K.; Weeks K. M. In-cell SHAPE reveals that free 30S ribosome subunits are in the inactive state. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 2425–2430. 10.1073/pnas.1411514112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Watters K. E.; Yu A. M.; Strobel E. J.; Settle A. H.; Lucks J. B. Characterizing RNA structures in vitro and in vivo with selective 2’-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Methods 2016, 103, 34–48. 10.1016/j.ymeth.2016.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Takahashi M. K.; Watters K. E.; Gasper P. M.; Abbott T. R.; Carlson P. D.; Chen A. A.; Lucks J. B. Using in-cell SHAPE-Seq and simulations to probe structure–function design principles of RNA transcriptional regulators. RNA 2016, 22, 920–933. 10.1261/rna.054916.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Chan D.; Feng C.; Zhen Y.; Flynn R. A.; Spitale R. C. Comparative analysis reveals furoyl in vivo selective hydroxyl acylation analyzed by primer extension reagents form stable ribosyl ester adducts. Biochemistry 2017, 56, 1811–1814. 10.1021/acs.biochem.7b00128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Reuter J. S.; Mathews D. H. RNAstructure: Software for RNA secondary structure prediction and analysis. BMC Bioinf. 2010, 11, 129. 10.1186/1471-2105-11-129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Sükösd Z.; Swenson M. S.; Kjems J.; Heitsch C. E. Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res. 2013, 41, 2807–2816. 10.1093/nar/gks1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hajdin C. E.; Bellaousov S.; Huggins W.; Leonard C. W.; Mathews D. H.; Weeks K. M. Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 5498–5503. 10.1073/pnas.1219988110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hsiao C.; Lenz T. K.; Peters J. K.; Fang P.-Y.; Schneider D. M.; Anderson E. J.; Preeprem T.; Bowman J. C.; O’Neill E. B.; et al. Molecular paleontology: A biochemical model of the ancestral ribosome. Nucleic Acids Res. 2013, 41, 3373–3385. 10.1093/nar/gkt023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lorenz R.; Luntzer D.; Hofacker I. L.; Stadler P. F.; Wolfinger M. T. SHAPE directed RNA folding. Bioinformatics 2015, 32, btv523. 10.1093/bioinformatics/btv523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Wu Y.; Shi B.; Ding X.; Liu T.; Hu X.; Yip K. Y.; Yang Z. R.; Mathews D. H.; Lu Z. J. Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data. Nucleic Acids Res. 2015, 43, 7247–7259. 10.1093/nar/gkv706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kutchko K. M.; Laederach A. Transcending the prediction paradigm: Novel applications of SHAPE to RNA function and evolution. Wiley Interdiscip. Rev. RNA 2017, 8, e1374. 10.1002/wrna.1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Tan Z.; Sharma G.; Mathews D. H. Modeling RNA secondary structure with sequence comparison and experimental mapping data. Biophys. J. 2017, 113, 330–338. 10.1016/j.bpj.2017.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Spasic A.; Assmann S. M.; Bevilacqua P. C.; Mathews D. H. Modeling RNA secondary structure folding ensembles using SHAPE mapping data. Nucleic Acids Res. 2017, gkx1057. 10.1093/nar/gkx1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Bindewald E.; Wendeler M.; Legiewicz M.; Bona M. K.; Wang Y.; Pritt M. J.; Le Grice S. F.; Shapiro B. A. Correlating SHAPE signatures with three-dimensional RNA structures. RNA 2011, 17, 1688–1696. 10.1261/rna.2640111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kirmizialtin S.; Hennelly S. P.; Schug A.; Onuchic J. N.; Sanbonmatsu K. Y. Integrating molecular dynamics simulations with chemical probing experiments using SHAPE-FIT. Methods Enzymol. 2015, 553, 215–234. 10.1016/bs.mie.2014.10.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Krokhotin A.; Mustoe A. M.; Weeks K. M.; Dokholyan N. V. Direct identification of base-paired RNA nucleotides by correlated chemical probing. RNA 2017, 23, 6–13. 10.1261/rna.058586.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. McGinnis J. L.; Dunkle J. A.; Cate J. H.; Weeks K. M. The mechanisms of RNA SHAPE chemistry. J. Am. Chem. Soc. 2012, 134, 6617–6624. 10.1021/ja2104075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Steen K.-A.; Rice G. M.; Weeks K. M. Fingerprinting non-canonical and tertiary RNA structures by differential SHAPE reactivity. J. Am. Chem. Soc. 2012, 134, 13160–13163. 10.1021/ja304027m. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pinamonti G.; Bottaro S.; Micheletti C.; Bussi G. Elastic network models for RNA: a comparative assessment with molecular dynamics and SHAPE experiments. Nucleic Acids Res. 2015, 43, 7260–7269. 10.1093/nar/gkv708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Gherghe C. M.; Mortimer S. A.; Krahn J. M.; Thompson N. L.; Weeks K. M. Slow conformational dynamics at C2’-endo nucleotides in RNA. J. Am. Chem. Soc. 2008, 130, 8884–8885. 10.1021/ja802691e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Clay M. C.; Ganser L. R.; Merriman D. K.; Al-Hashimi H. M. Resolving sugar puckers in RNA excited states exposes slow modes of repuckering dynamics. Nucleic Acids Res. 2017, 45, e134. 10.1093/nar/gkx525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Batey R. T.; Rambo R. P.; Lucast L.; Rha B.; Doudna J. A. Crystal structure of the ribonucleoprotein core of the signal recognition particle. Science 2000, 287, 1232–1239. 10.1126/science.287.5456.1232. [DOI] [PubMed] [Google Scholar]
  40. Mlýnský V.; Bussi G.. Exploring RNA structure and dynamics through enhanced sampling simulations. 2017, arXiv:1709.02342 [q-bio.BM]. arXiv.org e-Print archive. https://arxiv.org/abs/1709.02342v1. [DOI] [PubMed] [Google Scholar]
  41. Piana S.; Laio A. A bias-exchange approach to protein folding. J. Phys. Chem. B 2007, 111, 4553–4559. 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
  42. Cunha R. A.; Bussi G. Unraveling Mg2+–RNA binding with atomistic molecular dynamics. RNA 2017, 23, 628–638. 10.1261/rna.060079.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Watters K. E.; Strobel E. J.; Yu A. M.; Lis J. T.; Lucks J. B. Cotranscriptional folding of a riboswitch at nucleotide resolution. Nat. Struct. Mol. Biol. 2016, 23, 1124–1131. 10.1038/nsmb.3316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tribello G. A.; Bonomi M.; Branduardi D.; Camilloni C.; Bussi G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
  46. Bergonzo C.; Henriksen N. M.; Roe D. R.; Cheatham T. E. III Highly sampled tetranucleotide and tetraloop motifs enable evaluation of common RNA force fields. RNA 2015, 21, 1578–1590. 10.1261/rna.051102.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Condon D. E.; Kennedy S. D.; Mort B. C.; Kierzek R.; Yildirim I.; Turner D. H. Stacking in RNA: NMR of four tetramers benchmark molecular dynamics. J. Chem. Theory Comput. 2015, 11, 2729–2742. 10.1021/ct501025q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Kuhrová P.; Best R. B.; Bottaro S.; Bussi G.; Šponer J.; Otyepka M.; Banáš P. Computer folding of RNA tetraloops: Identification of key force field deficiencies. J. Chem. Theory Comput. 2016, 12, 4534–4548. 10.1021/acs.jctc.6b00300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Bottaro S.; Banáš P.; Šponer J.; Bussi G. Free energy landscape of GAGA and UUCG RNA tetraloops. J. Phys. Chem. Lett. 2016, 7, 4032–4038. 10.1021/acs.jpclett.6b01905. [DOI] [PubMed] [Google Scholar]
  50. Zgarbová M.; Jurečka P.; Banáš P.; Havrila M.; Šponer J.; Otyepka M. Noncanonical α/γ backbone conformations in RNA and the accuracy of their description by the AMBER force field. J. Phys. Chem. B 2017, 121, 2420–2433. 10.1021/acs.jpcb.7b00262. [DOI] [PubMed] [Google Scholar]
  51. Bottaro S.; Di Palma F.; Bussi G. The role of nucleobase interactions in RNA structure and dynamics. Nucleic Acids Res. 2014, 42, 13306–13314. 10.1093/nar/gku972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Gherghe C. M.; Shajani Z.; Wilkinson K. A.; Varani G.; Weeks K. M. Strong correlation between SHAPE chemistry and the generalized NMR order parameter (S2) in RNA. J. Am. Chem. Soc. 2008, 130, 12244–12245. 10.1021/ja804541s. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Schmitz U.; Freymann D.; James T.; Keenan R.; Vinayak R.; Walter P. NMR studies of the most conserved RNA domain of the mammalian signal recognition particle (SRP). RNA 1996, 2, 1213–1227. [PMC free article] [PubMed] [Google Scholar]
  54. Mlýnský V.; Bussi G. Understanding in-line probing experiments by modeling cleavage of nonreactive RNA nucleotides. RNA 2017, 23, 712–720. 10.1261/rna.060442.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Wilkinson K. A.; Vasa S. M.; Deigan K. E.; Mortimer S. A.; Giddings M. C.; Weeks K. M. Influence of nucleotide identity on ribose 2’-hydroxyl reactivity in RNA. RNA 2009, 15, 1314–1321. 10.1261/rna.1536209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Velikyan I.; Acharya S.; Trifonova A.; Földesi A.; Chattopadhyaya J. The pKa’s of 2’-hydroxyl group in nucleosides and nucleotides. J. Am. Chem. Soc. 2001, 123, 2893–2894. 10.1021/ja0036312. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b02921_si_001.pdf (19.2MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES