Effects of rogue ryanodine receptors on Ca²⁺ sparks in cardiac myocytes

Abstract

Ca²⁺ sparks and Ca²⁺ quarks, arising from clustered and rogue ryanodine receptors (RyRs), are significant Ca²⁺ release events from the junctional sarcoplasmic reticulum (JSR). Based on the anomalous subdiffusion of Ca²⁺ in the cytoplasm, a mathematical model was developed to investigate the effects of rogue RyRs on Ca²⁺ sparks in cardiac myocytes. Ca²⁺ quarks and sparks from the stochastic opening of rogue and clustered RyRs are numerically reproduced and agree with experimental measurements. It is found that the stochastic opening Ca²⁺ release units (CRUs) of clustered RyRs are regulated by free Ca²⁺ concentration in the JSR lumen (i.e. [Ca²⁺]_lumen). The frequency of spontaneous Ca²⁺ sparks is remarkably increased by the rogue RyRs opening at high [Ca²⁺]_lumen, but not at low [Ca²⁺]_lumen. Hence, the opening of rogue RyRs contributes to the formation of Ca²⁺ sparks at high [Ca²⁺]_lumen. The interplay of Ca²⁺ sparks and Ca²⁺ quarks has been discussed in detail. This work is of significance to provide insight into understanding Ca²⁺ release mechanisms in cardiac myocytes.

1. Introduction

Ca²⁺ sparks regulate the excitation–contraction coupling in heart muscle [1–3], and are activated by the opening of clustered ryanodine receptors (RyRs) on the junctional sarcoplasmic reticulum (JSR) membrane [4–6]. Recently, the discovery of quarky Ca²⁺ releases (QCRs or Ca²⁺ quarks) due to the opening of rogue RyRs has been shown as a significant Ca²⁺ release mechanism relevant to ‘invisible Ca²⁺ leak’ [7–9]. Here, rogue RyRs refer to RyR channels located near clustered RyRs within a JSR, defined as ‘junctional rogue RyRs’. Although Ca²⁺ sparks and quarks occur spontaneously and concurrently in the cytoplasm under physiological conditions, Ca²⁺ quarks feature different properties from Ca²⁺ sparks, e.g. a smaller amplitude with a high firing frequency and a longer duration [10].

Zima et al. [11] demonstrated experimentally that single RyR opening could mediate Ca²⁺ leak but fails to trigger Ca²⁺ sparks when free Ca²⁺ concentration in the JSR lumen ([Ca²⁺]_lumen) is below a threshold level. On the other hand, mathematical models have been developed to investigate the dynamics of Ca²⁺ sparks and quarks. Sobie et al. [12] proposed a model to solve the paradox of [Ca²⁺]_lumen to support the existence of rogue RyRs. Models of Ca²⁺ leak from JSRs have been used to characterize differences between Ca²⁺ sparks and quarks [13]. Walker et al. [14] included the computational nonspark-based Ca²⁺ leak from JSRs to explain the exponential rise of Ca²⁺ spark frequency. They further presented that Ca²⁺ sparks could be triggered by spontaneous opening of a single RyR in a cluster [15]. A stochastic contact network model of the Ca²⁺ initiation process was applied to realistic RyR cluster structures, which revealed that the Ca²⁺ sparks probability depends on the position of the initial RyR in the cluster. Their works provided insight into the Ca²⁺ release process in the heart and a framework for evaluating functional heterogeneity in populations of receptor clusters under normal and pathological conditions. Lu et al. [16,17] investigated ‘non-junctional rogue RyRs’ located away from the release sites and showed their effects on Ca²⁺ waves with heart failure. It suggested that Ca²⁺ dynamics was unstable and Ca²⁺ waves were likely to be triggered when ‘non-junctional rogue RyRs’ were taken into consideration. The variation of membrane potential depolarization was indicated to be dependent on the distribution density of rogue RyR channels, which is important for understanding the arrhythmogenic mechanism for heart failure from the subcellular to cellular level. Sato and Bers [18] used a mathematical model of JSR Ca²⁺ releases to show that single RyR opening at low [Ca²⁺]_lumen could not recruit Ca²⁺ sparks from Ca²⁺ release units (CRUs). However, the effects of rogue RyRs on Ca²⁺ sparks at high [Ca²⁺]_lumen remain unknown. The anomalous subdiffusion of cytoplasmic Ca²⁺ and the random distribution of JSR RyRs, unnoticed in these models, could unveil the temporal and spatial properties of Ca²⁺ sparks and quarks.

The objective of the study is to develop a mathematical model of JSR Ca²⁺ release to quantify the interplay of rogue and clustered RyRs for a detailed explanation of spontaneous Ca²⁺ sparks and quarks in cardiac myocytes under physiological conditions. A mathematical model was proposed to simulate the temporal and two-dimensional (2D) spatial distributions of Ca²⁺ sparks and quarks in a cardiac myocyte with consideration of the distribution of clustered and rogue RyRs on the JSR membrane and the anomalous subdiffusion of Ca²⁺ in the cytoplasm [19]. The model could explain various Ca²⁺ release events from a JSR and predict the firing probability of clustered RyRs activated by Ca²⁺ release through rogue RyRs. The stochastic opening of rogue and clustered RyRs was regulated by free Ca²⁺ concentrations in both cytoplasm and JSR lumen of a cardiac myocyte. The line-scan experimental measurements were carried out in cardiac myocytes of rats to validate the present model. The significance was discussed to improve the understanding of Ca²⁺-induced-Ca²⁺-release events in cardiac myocytes.

2. Material and methods

2.1. Experimental methods

Similar to previous studies [20–22], eight Sprague-Dawley rats (about 2.5 months old, 225–300 g) were anaesthetized with pentobarbital sodium (40 mg kg⁻¹) by peritoneal injection. Hearts were rapidly excised from animals. An isolated heart was immediately put into ice cold buffer, mounted in a Langendorff system, and perfused with a Ca²⁺-free buffer containing (in mM): 137 NaCl, 5.4 KCl, 1.2 MgCl₂, 1.2 Na₂HPO₄, 20 HEPES, 10 taurine, and 10 glucose (at a pH value of 7.35, aerated with 95% O₂ and 5% CO₂) for 5 min. The heart was then digested in a buffer containing 0.5 mg ml⁻¹ collagenase, 1 mg ml⁻¹ bovine serum albumin, 0.06 mg ml⁻¹ protease (type X-IV) and 50 µM CaCl₂ until becoming pale. The left ventricle was sectioned into small pieces and incubated in the digesting solution. Myocytes were harvested and stored in Tyrode's solution containing (in mM): 135 NaCl, 1 CaCl₂, 4 KCl, 1.2 MgCl₂, 1.2 Na₂HPO₄, 10 glucose, and 10 HEPES with a pH value of 7.35. Before imaging, myocytes were loaded with the dye Fluo-4-AM for 5 min and washed twice using the Tyrode's solution. A confocal microscope (Nikon A1+, Japan) equipped with a 40 × 1.3 NA oil immersion objective was used for line-scan images at a sample rate of 512 frames s⁻¹. The samples were excited at 488 nm. All line-scan measurements were performed at room temperature (23–25°C). Images were processed by the SparkMaster software [23].

2.2. Geometrical model

In a 2D model similar to Izu et al. [24], the regular intervals between Ca²⁺ release sites are l_x (= 2 µm) in the longitudinal direction (x-axis) and l_y (= 0.8 µm) in the transverse direction (y-axis). Figure 1a shows the geometrical model of a cardiac myocyte. Each Ca²⁺ release site represents a JSR. The schematic representative of a JSR is shown in figure 1b, which includes randomly distributed clustered RyRs and rogue RyRs. A CRU of clustered RyRs has 22 RyR channels and a rogue RyR has 3 RyR channels [5]. Figure 1c shows the distribution of clustered and rogue RyRs on a JSR for simulation. CRUs of clustered RyRs (blue dots, approx. 2 in a JSR) are surrounded by randomly distributed rogue RyRs (red dots, approx. 8 in a JSR). The number and location of clustered and rogue RyRs in each JSR are random in simulations.

Figure 1.

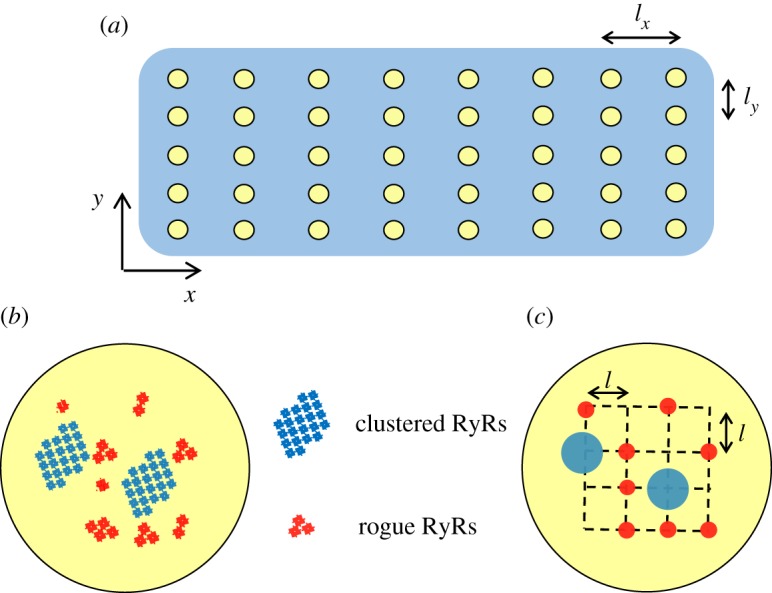
Geometrical model. (a) Schematic representation of the 2D geometrical model of a cardiac myocyte. The yellow dots denote JSRs with regularly spaced intervals: l_x= 2 µm and l_y = 0.8 µm. (b) Schematic representation of a JSR, which includes randomly distributed clustered and rogue RyRs. (c) The distribution of clustered and rogue RyRs in a JSR for simulation (l = 0.1 µm). Two CRUs of clustered RyRs (blue dots) are surrounded by eight rogue RyRs (red dots) on the JSR as shown in (b). The number and location of clustered and rogue RyRs are random in simulations.

2.3. Computational model

The balanced equation for free Ca²⁺ concentration in the cytoplasm, ${[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}$, with consideration of the anomalous subdiffusion of Ca²⁺ in the cytoplasm and the distribution of clustered and rogue RyRs, can be written as:

$$\begin{array}{rl}\frac{\mathrm{\partial }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}}{\mathrm{\partial }t}& =D_x\frac{{\mathrm{\partial }}^{\beta }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}}{\mathrm{\partial }{x}^{\beta }}+D_y\frac{{\mathrm{\partial }}^{\beta }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}}{\mathrm{\partial }{y}^{\beta }}\\ & +J_{\mathrm{dye}\text{-}\mathrm{cyto}}+J_{\mathrm{buffer}\text{-}\mathrm{cyto}}+J_{\mathrm{pump}}+J_{\mathrm{clustered}}+J_{\mathrm{rogue}},\end{array}$$ 2.1

where t is time, x and y denote the spatial coordinates, D_x (= 300 µm² s^-1) and D_y (= 150 µm² s⁻¹) refer to the Ca²⁺ diffusion coefficients. The anomalous subdiffusion order β is 2.25. Anomalous space subdiffusion corresponds to the short jump of the random walker and is defined though the relations [25]

$$\frac{{\mathrm{\partial }}^{2.25}{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,y,t)}{\mathrm{\partial }{x}^{2.25}}=\frac{1}{\mathit{\Gamma }(0.75)}\frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{x}^3}{\int }_0^x\frac{{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(\tau ,y,t)}{{(x-\tau )}^{0.25}}\text{d}\tau$$ 2.2

and

$$\frac{{\mathrm{\partial }}^{2.25}{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,y,t)}{\mathrm{\partial }{y}^{2.25}}=\frac{1}{\mathit{\Gamma }(0.75)}\frac{{\mathrm{\partial }}^3}{\mathrm{\partial }{y}^3}{\int }_0^y\frac{{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,\tau ,t)}{{(y-\tau )}^{0.25}}\text{d}\tau ,$$ 2.3

where Γ denotes the Gamma function. $J_{\mathrm{dye}\text{-}\mathrm{cyto}}$ and $J_{\mathrm{buffer}\text{-}\mathrm{cyto}}$ are the fluxes due to the Ca²⁺ fluorescent indicator dye (i.e. Rhod-2 or Fluo-4-AM, in the cytoplasm) and the endogenous stationary buffers respectively. J_pump is the pumping rate of SR Ca²⁺-ATPase. SR pumps are started when ${[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}$ exceeds the resting Ca²⁺ concentration level (0.1 µM) in the cytoplasm. These variables can all be defined as:

$$\begin{array}{r}{J}_{\mathrm{dye}\text{-}\mathrm{cyto}}=-k_{\mathrm{F}}^{+}{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}({[\text{F}]}_{\mathrm{T}}-[\text{CaF}])+k_{\mathrm{F}}^{-}[\text{CaF}],\end{array}$$ 2.4

$$\begin{array}{r}{J}_{\mathrm{buffer}\text{-}\mathrm{cyto}}=\sum _{\mathrm{n}}-\frac{\mathrm{\partial }[\text{Ca}{\text{B}}_{\mathrm{n}}]}{\mathrm{\partial }t},\end{array}$$ 2.5

$$\begin{array}{r}\frac{\mathrm{\partial }[\text{Ca}{\text{B}}_{\mathrm{n}}]}{\mathrm{\partial }t}=k_{\mathrm{n}}^{+}{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}({[\text{B}]}_{\mathrm{T}}-[\text{Ca}{\text{B}}_{\mathrm{n}}])-k_{\mathrm{n}}^{-}[\text{Ca}{\text{B}}_{\mathrm{n}}]\end{array}$$ 2.6

$$\begin{array}{r}\text{and}{J}_{\mathrm{pump}}=-\frac{V_{\mathrm{pump}}^{max}{({[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}})}^{\mathrm{h}}}{{(K_{\mathrm{pump}})}^{\mathrm{h}}+{({[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}})}^{\mathrm{h}}},\end{array}$$ 2.7

where the subscript ‘n’ refers to each buffer in the cytoplasm, the superscript ‘h’ refers to the Hill constant; [F]_T and [B_n]_T represent the total concentrations of indicator and buffers, respectively. [CaF] and [CaB_n] are the concentrations of Ca²⁺-bound complexes; $k_{\mathrm{F}}^{+}$, $k_{\mathrm{F}}^{-}$, $k_{\mathrm{n}}^{+}$ and $k_{\mathrm{n}}^{-}$ are the reaction kinetic parameters. K_pump is the affinity constant, and $V_{\mathrm{pump}}^{max}$ is the maximum rate for SR pumps. Values of the parameters are based on a previous study [26]. Moreover, J_rogue and J_clustered are the Ca²⁺ fluxes released by rogue and clustered RyRs respectively, which can be written as:

$$J_{\mathrm{rogue}}={\sigma }_{\mathrm{rogue}}\sum _{i,j}\delta (x-x_i^{\mathrm{rogue}},y-y_j^{\mathrm{rogue}})S(x_i^{\mathrm{rogue}},y_j^{\mathrm{rogue}},t;\hspace{0.17em}{T}_{\mathrm{rogue}})$$ 2.8

and

$$J_{\mathrm{clustered}}={\sigma }_{\mathrm{clustered}}\sum _{i,j}\delta (x-x_i^{\mathrm{clustered}},y-y_j^{\mathrm{clustered}})S(x_i^{\mathrm{clustered}},y_j^{\mathrm{clustered}},t;\hspace{0.17em}{T}_{\mathrm{clustered}}),$$ 2.9

where δ is the Dirac delta function and S is a stochastic function for the opening of clustered and rogue RyRs; $(x_i^{\mathrm{rogue}},\hspace{0.17em}{y}_j^{\mathrm{rogue}})$ and $(x_i^{\mathrm{clustered}},\hspace{0.17em}{y}_j^{\mathrm{clustered}})$are the positions of rogue RyRs and clustered RyRs in the 2D plane respectively. The release times for rogue and clustered RyRs are defined as T_rogue= 20 ms [10] and T_clustered= 10 ms [27]. The equivalent source strength of rogue RyRs and clustered RyRs [28] are expressed by

$${\sigma }_{\mathrm{rogue}}=\frac{0.64I_{\mathrm{rogue}}({[\text{C}{\text{a}}^{2+}]}_{\mathrm{lumen}}-{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}})}{2F}$$ 2.10

and

$${\sigma }_{\mathrm{clustered}}=\frac{0.64I_{\mathrm{clustered}}({[\text{C}{\text{a}}^{2+}]}_{\mathrm{lumen}}-{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}})}{2F},$$ 2.11

where the Faraday constant F is 96 500 C mol⁻¹, and I_rogue and I_clustered are the average currents through rogue and clustered RyRs, set to be 0.07 pA mM⁻¹ and 0.7 pA mM⁻¹. Note that Ca²⁺ is released from the JSR lumen into a 3D volume in the cytoplasm of a cardiac myocyte. The conversion factor 0.64 in equations (2.10) and (2.11) is used to give the identical Ca²⁺ distribution in 2D [24]. Equation (2.1) can describe the Ca²⁺ release mechanism of Ca²⁺ sparks only when J_rogue = 0, or QCRs only when J_clustered = 0.

Conversely, the balance equation for free Ca²⁺ concentration in each JSR lumen, ${[\text{C}{\text{a}}^{2+}]}_{\mathrm{lumen}}$, can be written as

$$\frac{\mathrm{\partial }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{lumen}}}{\mathrm{\partial }t}=J_{\mathrm{release}\text{-}\mathrm{lumen}}+J_{\mathrm{dye}\text{-}\mathrm{lumen}}+J_{\mathrm{buffer}\text{-}\mathrm{lumen}}+J_{\mathrm{refill}},$$ 2.12

where $J_{\mathrm{release}\text{-}\mathrm{lumen}}$ denotes the decreased Ca²⁺ release flux caused by opening of clustered RyRs (J_clustered) and rogue RyRs (J_rogue) in a JSR. J_refill is the refilled Ca²⁺ flux and expressed by

$$J_{\mathrm{refill}}=\frac{{[\text{C}{\text{a}}^{2+}]}_{\mathrm{NSR}}-{[\text{C}{\text{a}}^{2+}]}_{\mathrm{lumen}}}{{\tau }_{\mathrm{refill}}},$$ 2.13

where free Ca²⁺ concentration in network sarcoplasmic reticulum (NSR) [Ca²⁺]_NSR is 1.0 mM, time constant for Ca²⁺ transfer between JSR and NSR ${\tau }_{\mathrm{refill}}$ is 10 ms, and the volume of a JSR lumen is 1 × 10⁻¹¹ µl [29]. [Ca²⁺]_lumen is less than the beginning level 1.0 mM as a result of Ca²⁺ release at a certain time. $J_{\text{dye-lumen}}$ and $J_{\text{buffer-lumen}}$ are the Ca²⁺ fluxes due to indicator dye (i.e. Fluo-5N) and buffer (i.e. calsequestrin) in a JSR lumen, respectively. Their expressions are similar to that in the cytoplasm. Various parameters of dyes (Rhod-2 [30], Fluo-4-AM [26] and Fluo-5N [31]) and buffers [26,32] in the cytoplasm and JSR lumen are listed in table 1.

Table 1.

Standard parameter values for dyes and buffers.

dyes or buffers	[F]T or [Bn]T (μM)	kF+ or kn+ (μM−1 s−1)	kF− or kn− (s−1)
parameters in cytoplasm
Rhod-2	5	130	69
Fluo-4-AM	50	80	90
calmodulin	24	100	38
troponin	70	39	20
SR	47	115	100
SL	1124	115	1000
parameters in JSR lumen
Fluo-5N	20	48.8	19 520
calsequestrin	14 000	100	60 000

2.4. Firing probability of rogue and clustered RyRs

The firing probability per unit time of RyRs is determined by Ca²⁺ concentrations in both cytoplasm and JSR lumen [33–35], which can be expressed as

$$P_{\mathrm{firing}}=P_{\mathrm{cyto}}\cdot {\mathit{\Phi }}_{\mathrm{lumen}},$$ 2.14

where P_cyto refers to the firing probability per unit time of calcium release events controlled by ${[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}$. ${\mathit{\Phi }}_{\mathrm{lumen}}$ represents a [Ca²⁺]_lumen-dependent regulation term of Ca²⁺ release events. According to the coupled RyR gating model [5], P_cyto can be expressed as

$$P_{\mathrm{cyto}}=1-{(1-P{}_{\mathrm{RyR}})}^{n{}_{\mathrm{RyR}}},$$ 2.15

where $P_{\mathrm{RyR}}$ is the firing probability per unit time of a single RyR channel [36]. Here, ${\mathit{\Phi }}_{\mathrm{lumen}}$ is written as

$${\mathit{\Phi }}_{\mathrm{lumen}}={\varphi }^m,$$ 2.16

where ϕ is an empirical power function given in Walker et al.'s model [14], m is the regulation coefficient for rogue (m = 1) or clustered (m = 10) RyRs.

2.5. Numerical solutions

Equations (2.1–2.16) were solved using a FORTRAN-developed program. A 2D computational domain (5 µm × 5 µm) was meshed with a size of 0.025 µm to simulate Ca²⁺ release events from a single Ca²⁺ release site. Moreover, a computational domain of 20 µm × 20 µm was meshed with a size of 0.1 µm to simulate Ca²⁺ release events from multiple Ca²⁺ release positions. For the fractional differential term in equation (2.1), the shifted Grünwald formula of centre difference [37] was used to discretize the computational domain as

$$\frac{{\mathrm{\partial }}^{\alpha }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,y,t)}{\mathrm{\partial }{x}^{\alpha }}=\frac{1}{h^{\alpha }}\underset{M\to \mathrm{\infty }}{lim}\sum _{k=0}^M{g}_k{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x-(k-1)h,y,t)$$ 2.17

and

$$\frac{{\mathrm{\partial }}^{\alpha }{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,y,t)}{\mathrm{\partial }{y}^{\alpha }}=\frac{1}{h^{\alpha }}\underset{M\to \mathrm{\infty }}{lim}\sum _{k=0}^M{g}_k{[\text{C}{\text{a}}^{2+}]}_{\mathrm{cyto}}(x,y-(k-1)h,t),$$ 2.18

where $g_k=\mathit{\Gamma }(k-\alpha )/\mathit{\Gamma }(k+1)$, α = β − 1 = 1.25, k is an integer with α < k < α + 1, and h is the mesh size. Free Ca²⁺ concentrations in the cytoplasm and JSR were calculated simultaneously. The variable time-step algorithm was used. The zero-flux boundary condition was taken in the Monte Carlo simulations.

3. Results and discussion

3.1. Ca²⁺ quarks and Ca²⁺ sparks

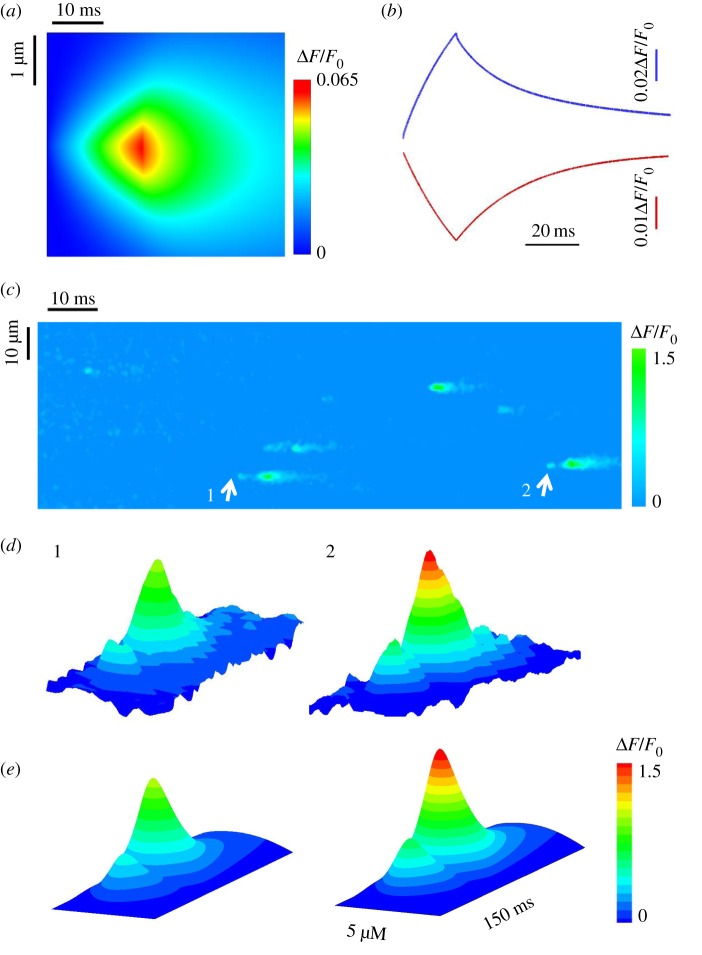
Figure 2a shows a computational Ca²⁺ quark through a rogue RyR to mimic the line-scan measurements when the release time is set to 20 ms. The computational domain is a square of 5 × 5 µm² with the distribution of clustered and rogue RyRs on the JSR membrane in figure 1c. The dyes, Rhod-2 and Fluo-5N, were used to indicate Ca²⁺ in the cytoplasm and JSR lumen, respectively. The shape of the Ca²⁺ quark is consistent with that in a previous study [10]. Figure 2b plots the time courses of a QCR–QCD pair (i.e. a quarky Ca²⁺ release–quarky Ca²⁺ depletion pair) corresponding to figure 2a. The values of t₆₇ and ΔF/F₀ were computed to be 22.0 and 22.5 ms and 0.065 and 0.025 for QCR and QCD, respectively. They are within 1 s.d. of experimental measurements, i.e. t₆₇ = 20.1 ± 1.1 ms for a QCR and 20.8 ± 1.9 ms for a QCD and ΔF/F₀ = 0.069 ± 0.006 for a QCR and 0.025 ± 0.002 for a QCD [10].

Figure 2.

Properties of Ca²⁺ quarks and Ca²⁺ sparks. (a) A computational line-scan Ca²⁺ quark through a rogue RyR (5 µm × 50 ms). (b) The corresponding time courses of a QCR–QCD pair. (c) A representative line-scan image (50 µm × 1 s) of Ca²⁺ release events measured in a cardiac myocyte. Arrows point to Ca²⁺ sparks activated by QCRs. (d) Experimental results for line-scan images of sparks activated by QCRs. (e) Computational results in agreement with (d).

Figure 2c shows the line-scan measurements of Ca²⁺ release events in an isolated myocyte. The arrows refer to Ca²⁺ sparks due to the firing of clustered RyRs after QCR events owing to the opening of rogue RyRs, which were further analysed using the SparkMaster software [23] in figure 2d. The peak ΔF/F₀ of the two Ca²⁺ spark is 1.02 and 1.44 in figure 2d (1) and (2), respectively. To avoid the background noise, we did not measure QCR events with ΔF/F₀ < 0.2. The number of recorded Ca²⁺ sparks is 1125 in all measurements. The proportion of sparks that are triggered by QCRs is approximately 11.6%. Accordingly, figure 2e shows the computational results of Ca²⁺ sparks in a JSR with random distribution of clustered and rogue RyRs in figure 1c. The regular Ca²⁺ spark (left) due to an opening CRU of clustered RyRs is initiated by three opening rogue RyRs. The large spark (right) results from two CRUs of clustered RyRs activated by four opening rogue RyRs. An agreement between experimental and computational results (figure 2d versus figure 2e) validates the 2D mathematical model.

3.2. Interplay of rogue and clustered RyRs in a junctional sarcoplasmic reticulum

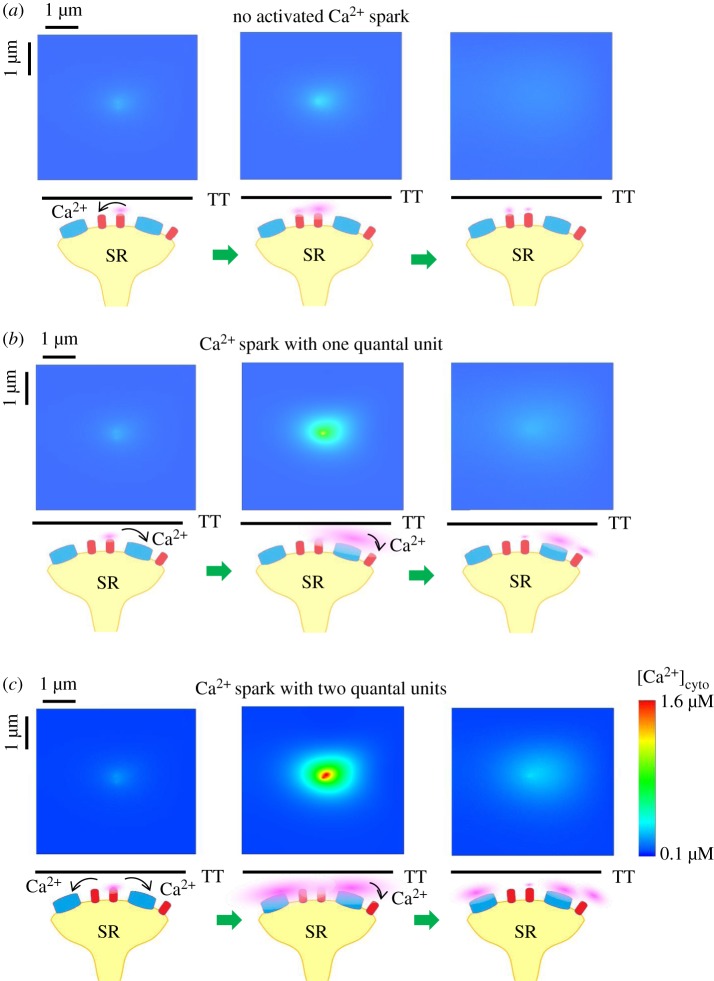
We simulated three modes of elemental Ca²⁺ release events that could coexist at a Ca²⁺ release site, as shown in figure 3a–c. Snapshots of elemental Ca²⁺ release events in a computational domain of 5 × 5 µm² are taken at 10, 20 and 40 ms when three rogue RyRs are fired at the same time. Given the polymorphism of Ca²⁺ sparks at a release site, there are three distinct modes: no activated Ca²⁺ spark, a Ca²⁺ spark with one quantal unit (i.e. a fired Ca²⁺ spark from a CRU of clustered RyRs), and a Ca²⁺ spark with two quantal units (i.e. a fired Ca²⁺ spark from two CRUs of clustered RyRs). It demonstrates that QCRs from the opening rogue RyRs could activate the neighbour CRUs of clustered RyRs in a JSR to form a Ca²⁺ spark with different quantal units. Moreover, rogue RyRs could be activated by the Ca²⁺ release of clustered RyRs in the same JSR, which was recorded in the snapshots and shown in figure 3b,c. On the other hand, the amplitude of a Ca²⁺ spark is mainly determined by the firing number of clustered RyRs regardless of rogue RyRs because QCR events have a low Ca²⁺ flux.

Figure 3.

Interplay of rogue and clustered RyRs in a JSR. Snapshots of Ca²⁺ release events in a region of 5 µm × 5 µm are taken at 10, 20 and 40 ms from left to right when three rogue RyRs are fired at the same time. There are three distinct modes. Schematic interplay of Ca²⁺ release events is plotted below the snapshots. Clustered and rogue RyRs are distinguished by blue and red colours similar to figure 1c. Cytoplasmic Ca²⁺ is displayed by pink colour. Arrows denote that Ca²⁺ diffuses and activates neighbour clustered and rogue RyRs in the cytoplasm. SR, sarcoplasmic reticulum; TT, T-tubule. (a) No activated Ca²⁺ spark. Neighbour rogue RyRs are activated by Ca²⁺ quarks. (b) A Ca²⁺ spark with one quantal unit. One CRU of clustered RyRs is initiated by Ca²⁺ quarks. Then Ca²⁺ spark from the CRU of clustered RyRs contributes to activation of neighbour rogue RyRs. (c) A Ca²⁺ spark with two quantal units. Two CRUs of clustered RyRs are triggered and then activate neighbour rogue RyRs.

This model explains the coexistence of the three modes of elemental Ca²⁺ release in a Ca²⁺ release site as well as predicting the properties of a Ca²⁺ spark. QCRs do not always activate clustered RyRs because luminal Ca²⁺ depletion reduces the probability of activating clustered RyRs. The probability of Ca²⁺ sparks of the three modes activated by different initial opening numbers of rogue RyRs is shown in figure 4. The results reveal that clustered RyRs have the highest frequency of being triggered by four opening rogue RyRs simultaneously.

Figure 4.

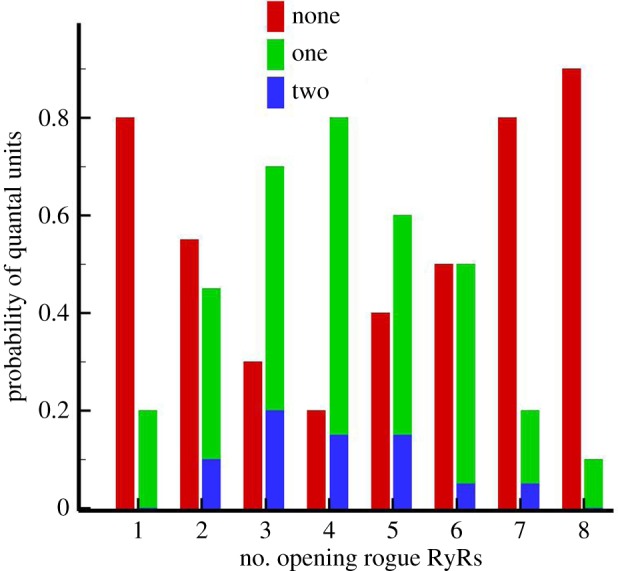
The probability of activated quantal units in a JSR calculated by Monte Carlo simulations (n = 20).

3.3. The effects of [Ca²⁺]_lumen on Ca²⁺ release events

The effects of [Ca²⁺]_lumen on the firing frequency of Ca²⁺ sparks and quarks are quantified in a computational domain of 20 × 20 µm², as shown in figure 5. The beginning levels of [Ca²⁺]_lumen is set from 0.2 to 1.0 mM. The computational results show a higher firing frequency of spontaneous QCR events than that of spontaneous Ca²⁺ sparks consistent with previous experimental observations [10]. A computational study also showed a steep increase in the firing frequency of spontaneous Ca²⁺ sparks despite a slight change in the firing frequency of spontaneous QCR events with the increase of [Ca²⁺]_lumen [18]. Moreover, we show a threshold value of [Ca²⁺]_lumen (i.e. less than 0.3 mM) where spontaneous Ca²⁺ quarks become a major pathway of SR Ca²⁺ leak. The present study shows the incidence of 12.2 ± 1.1 Ca²⁺ sparks [100 µm]⁻¹ s⁻¹ under physiological conditions ([Ca²⁺]_lumen = 1.0 mM), which agrees with experimental measurements [38]. The statistical proportion of sparks that are triggered by QCRs is 34.7% because one or two openings of rogue RyRs were neglected in experimental measurements in figure 2c.

Figure 5.

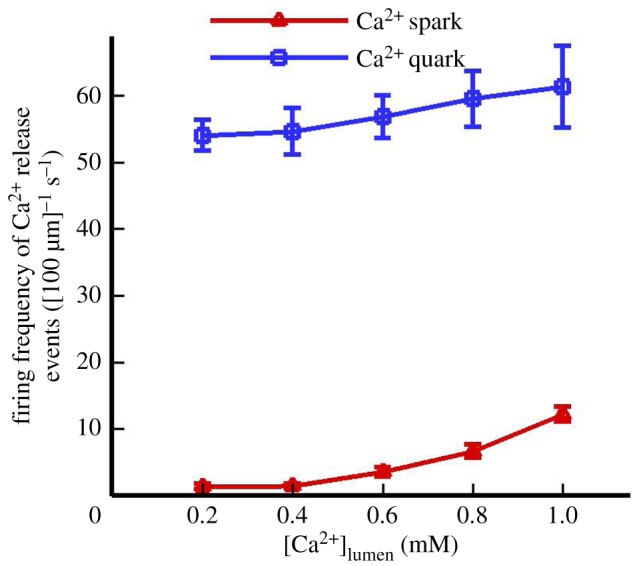
The firing frequency of Ca²⁺ sparks (red line) and quarks (blue line) determined by Monte Carlo simulations (n = 10) when [Ca²⁺]_lumen varies from 0.2 mM to 1.0 mM.

3.4. Effects of rogue RyRs on Ca²⁺ sparks with consideration of [Ca²⁺]_lumen

We examined how rogue RyRs affect Ca²⁺ sparks at different levels of [Ca²⁺]_lumen. A comparison of computational line-scan Ca²⁺ release events with consideration of rogue RyRs or not is displayed in a square of 20 × 20 µm² (the intervals between JSRs are l_x= 2 µm and l_y= 0.8 µm) for 2 s (figure 6a versus figure 6b) at different [Ca²⁺]_lumen. The Ca²⁺ spark frequency has values of 1.3 ± 0.4 and 1.2 ± 0.3 [100 µm]⁻¹ s⁻¹ with consideration of rogue RyRs or not when [Ca²⁺]_lumen = 0.2 mM. Therefore, the stochastic opening of rogue RyRs at low [Ca²⁺]_lumen fails to trigger spontaneous Ca²⁺ sparks owing to the decreased driving force ([Ca²⁺]_lumen− [Ca²⁺]_cyto) and sensitivity of clustered RyRs as well as the shortened firing possibility of neighbouring RyRs. Conversely, the frequency of spontaneous Ca²⁺ sparks increases with consideration of rogue RyRs at 1.0 mM [Ca²⁺]_lumen. QCR events are hence responsible for the formation of Ca²⁺ sparks at high [Ca²⁺]_lumen. Moreover, sensitivity analysis on the firing frequency of Ca²⁺ sparks was performed with respect to the number of rogue RyRs varying in the range of 2–14 in figure 6c. The opening of clustered RyRs monotonically increases with the increase of the number of rogue RyRs at high [Ca²⁺]_lumen. But it does not change obviously at low [Ca²⁺]_lumen. The firing frequency of Ca²⁺ sparks has a bigger slope at higher [Ca²⁺]_lumen.

Figure 6.

Effects of rogue RyRs on Ca²⁺ sparks as [Ca²⁺]_lumen varies. (a) Computational line-scan Ca²⁺ release events (20 µm × 2 s) with effects of rogue RyRs when [Ca²⁺]_lumen = 1.0 mM, 0.6 mM and 0.2 mM. Ca²⁺ sparks are marked by white ovals. (b) Computational line-scan Ca²⁺ release events without effects of rogue RyRs under the same conditions as (a). (c) Sensitivity analysis on the firing frequency of Ca²⁺ sparks as a function of the number of rogue RyRs in a JSR at various [Ca²⁺]_lumen determined by Monte Carlo simulations (n = 10).

3.5. A comparison with previous models

Sato et al. [18] showed that a RyR channel in a cluster of RyRs could trigger adjacent RyR channels in the same cluster to form a Ca²⁺ spark when [Ca²⁺]_lumen is above a threshold. Walker et al. [14,15] further investigated the structural effects of clustered RyRs on Ca²⁺ sparks. Moreover, Lu et al. [16,17] indicated that non-junctional RyRs increased the probability of occurrence of spontaneous Ca²⁺ waves. The present study showed the temporal and spatial properties of Ca²⁺ quarks and sparks relevant to both rogue and clustered RyRs, where rogue RyRs randomly surround clustered RyRs within a single junctional space. We showed that Ca²⁺ quarks and sparks coexist at a Ca²⁺ release site, which agrees with experimental measurements from line-scan imaging. The opening of rogue RyRs leads to the formation of Ca²⁺ sparks at high [Ca²⁺]_lumen, but not at low [Ca²⁺]_lumen. This supports the conclusion of Sato et al. [18].

On the other hand, the present model simulated Ca²⁺ quarks and sparks based on the anomalous subdiffusion in comparison with previous models from Fickian diffusion [14–18]. Hence, we solved the paradox of full width at half-maximum (FWHM) due to Fickian diffusion. This study addresses the importance of rogue RyRs for understanding Ca²⁺ release mechanisms from JSRs.

3.6. Potential implications

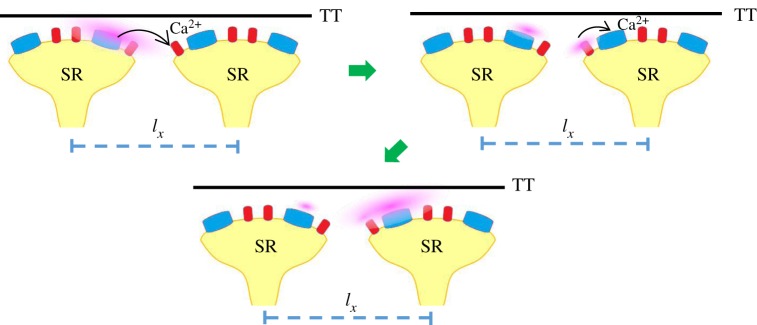
Ca²⁺ sparks could trigger clustered RyRs in neighbour JSRs with the help of rogue RyRs. This mode is marked by the arrow in figure 6a and shown in figure 7 schematically. Ca²⁺ quarks may trigger the opening of clustered RyRs in self-propagating succession along the length of a cell. The sum of Ca²⁺ sparks and quarks gives rise to the global Ca²⁺ transient for the formation of a Ca²⁺ wave. Furthermore, the changes in the number of rogue RyRs in a JSR may induce potential heart diseases. For example, a reduction of the number of rogue RyRs could lead to an inhibition of Ca²⁺ waves and dyssynchronous Ca²⁺ transients in myocytes of congestive heart failure [39]. Atrial fibrillation associated with overactive Ca²⁺ release could be related to the increased number of rogue RyRs [40].

Figure 7.

Schematic interplay of clustered and rogue RyRs in neighbour JSRs. Clustered RyRs are triggered by Ca²⁺ sparks in a neighbour JSR with the help of rogue RyRs.

3.7. Critique of the study

In the study, the duration and current of Ca²⁺ release events from JSRs were fixed similar to previous studies [10,27]. However, Ca²⁺ release flux should be regulated by the SR structure, functional properties and the size of RyR cluster [41]. The impact of time-dependent Ca²⁺ release flux from RyRs can give us new inspiration for the relation between Ca²⁺ release events and the interplay of rogue and clustered RyRs. The spatial arrangement of RyRs within clusters influences the frequency of Ca²⁺ sparks [14]. The detailed structure of clustered RyRs should be taken into consideration when a high-performance supercomputer is used to satisfy the requirement of large computation. Furthermore, the present study comes from the assumption that 3D geometry is simplified to a 2D model in healthy myocytes. Modelling 3D distribution of the JSRs in cardiac cells is more realistic and the 3D simulations of Izu et al. [42] indicated that it could reveal more complex RyR interactions between neighbour JSRs. Hence, a 3D model should be developed to investigate spontaneous Ca²⁺ release events under both physiological and pathological conditions in future studies.

4. Conclusion

A mathematical model is developed to investigate Ca²⁺ sparks and quarks in the cytoplasm and show the significance of rogue RyRs. The Ca²⁺ release events from JSRs agree with experimental measurements in cardiac myocytes. The computational results show a steep increase in the firing frequency of spontaneous Ca²⁺ sparks despite a slight change in the firing frequency of spontaneous Ca²⁺ sparks with the increase of [Ca²⁺]_lumen. The frequency of spontaneous Ca²⁺ sparks is remarkably affected by the rogue RyRs opening at high [Ca²⁺]_lumen, but not at low [Ca²⁺]_lumen. This study is of importance to understand basic mechanisms of Ca²⁺ release events in cardiac myocytes.

Ethics

All animal experiments were performed in accordance with Chinese National and Peking University ethical guidelines regarding the use of animals in research, consistent with the NIH guidelines (Guide for the care and use of laboratory animals) on the protection of animals used for scientific purposes. The experimental protocols were approved by the Animal Care and Use Committee of Peking University, China.

Data accessibility

Statistical data of Ca²⁺ release events used in this paper can be accessed at: http://dx.doi.org/10.6084/m9.figshare.5450719.

Authors' contributions

X.C., Y.H. and W.T. designed and performed the numerical calculation. Y.F. analysed data. X.C., Y.H. and W.T. wrote the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Natural Science Foundation of China (11732001 and 11328201) and the Leading Talents of Guangdong Province Program.