Electromagnetically induced transparency in vacuum and buffer gas potassium cells probed via electro-optic frequency combs

Abstract

Electromagnetically induced transparency (EIT) in ³⁹K and ⁴¹K was probed using electro-optic frequency combs generated by applying chirped waveforms to a phase modulator. The carrier tone of the frequency comb served as the pump beam and induced the necessary optical cycling. Comb tooth spacings as narrow as 20 kHz were used to probe potassium in both buffer gas and evacuated cells at elevated temperatures. Atomic absorption features as narrow as 33(5) kHz were observed allowing for the ³⁹K lower state hyperfine splitting to be optically measured with a fit uncertainty of 2 kHz. Due to the ultranarrow width of the EIT features, long-lived optical free induction decays were also observed which allowed for background-free detection.

Due to their flexibility, agility, and low phase noise electro-optic frequency combs [1–3] have seen widespread adoption for numerous applications including measurements of atomic (e.g., [4–6]) and molecular transitions (e.g., [7–9]), astronomical calibrations [10], and for frequency metrology [11]. As their comb tooth spacing is controlled via the driving radiofrequency waveform, rather than a physical length dimension as for mode-locked lasers, combs with ultranarrow tooth spacings (≪1 MHz) can readily be produced. These combs are ideal for multiplexed spectroscopy of narrow atomic resonances such as electromagnetically induced transparency (EIT) [12, 13] which can be orders of magnitude more narrow than even the natural linewidth of the given atomic system. Here we use electro-optic frequency combs with tooth spacings as small as 20 kHz to probe EIT features in the D₁ line of ³⁹K and ⁴¹K using evacuated and buffer gas cells. EIT features as narrow as 33 kHz are observed, well below the potassium natural linewidth of 6.0 MHz [14].

A schematic of the instrument can be found in Fig. 1. An electro-optic frequency comb was generated by applying a frequency-chirped, repeating waveform to an electro-optic phase modulator [5]. The resulting frequency comb had a tooth spacing given by the inverse of the waveform repetition rate and a span given by twice the chirp range. The probe laser was an external-cavity diode laser with a tuning range of 745 nm to 785 nm which was tuned near the D₁ ³⁹K hyperfine transitions at 770.1 nm. The laser linewidth was given by the manufacturer as 15 kHz in 10 ms. We employed a self-heterodyne configuration [4, 5, 15] in which the heterodyne signal between this electro-optic frequency comb and the external-cavity diode laser from which it originated was monitored on a fast photodiode. An acousto-optic modulator (AOM) was driven at 384.22 MHz in order to shift the heterodyne frequencies away from DC and to ensure that positive and negative phase modulator sidebands occurred at unique radiofrequencies. The AOM drive frequency was phase-locked to an external frequency reference in order to enable coherent time-domain averaging [8]. The laser wavelength was stabilized using a low bandwidth (varied from 1 Hz to 100 Hz) proportional-integral-derivative servo in conjunction with a commercial wavelength meter having 0.5 MHz optimal resolution.

Fig. 1.

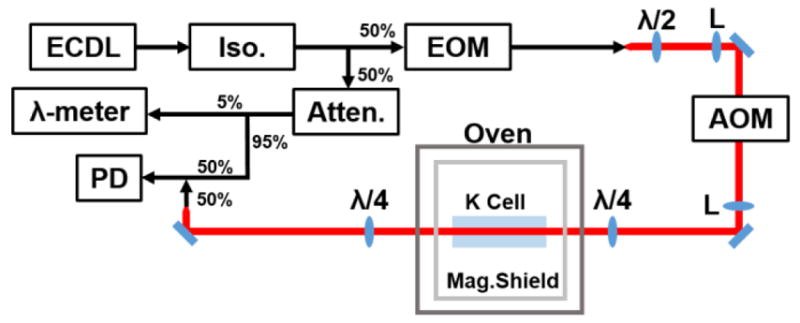
Instrument optical schematic. The abbreviated components are an external-cavity diode laser (ECDL), a fiber coupled isolator (Iso.), an electro-optic phase modulator (EOM), half-wave and quarter-wave plates (λ/2 and λ/4, respectively), 100 mm lenses (L), an acousto-optic modulator (AOM), a potassium cell (K Cell), a triply shielded magnetic chamber (Mag. Shield), a variable fiber attenuator (Atten.), a high precision wavelength meter (λ-meter), and a 1 GHz photodiode (PD). Fiber couplers are shown with their relevant split ratios. Only the 1^st-order output of the AOM is shown (the 0^th order is sent into a beam block). Fiber optics are shown in black while red lines denote free-space beam paths.

Two separate cylindrical potassium cells with uncoated walls were used for these measurements. The first cell was 7.5 cm in length with a diameter of 25.4 cm and contained potassium metal as well as 2.67 kPa of argon buffer gas. The second cell was 46 cm in length with a 1.27 cm diameter containing potassium metal with no buffer gas (i.e., evacuated). For a given measurement the cell of interest was placed inside a triply shielded nickel-iron alloy chamber to reduce stray magnetic fields (measured to be approximately 80 μT) by roughly three orders of magnitude. Due to its length, the evacuated cell extended approximately 2 cm from this chamber. As a result, an additional single layer of nickel-iron alloy was wrapped around this protruding portion. This chamber was then placed inside an oven consisting of insulated walls with a thermoelectric heat exchanger. A proportional-integral-derivative servo was used to maintain constant temperature based upon the reading of a calibrated platinum resistance thermistor. Measurements were made between 34 °C and 35 °C in order to increase the potassium vapor number density.

As the amplitude of the carrier frequency of the comb (i.e., the unmodulated light) is several orders of magnitude greater than that of any given comb tooth [5], it served as the pump beam for these measurements (commonly referred to as the cycling laser in the nomenclature of EIT). After the circularly polarized comb beam passed through the potassium cell (approximately 300 μW of total incident power) it was injected back into fiber and combined with the local oscillator beam to produce the self-heterodyne signal at the output of the 1 GHz bandwidth, AC-coupled photodiode.

This self-heterodyne signal was amplified and split for data acquisition and the AOM phase lock. The data acquisition channel was low-pass filtered at 264 MHz to remove the strong carrier tone (at 384.22 MHz, i.e., the AOM frequency) thus allowing for optimal use of the digitizer’s 12 bit depth. This filtration reduces our number of observed comb teeth by a factor of two (i.e., to just negative sidebands) but following amplification leads to a substantial increase in the observed signal-to-noise ratio.

After coherent time domain averaging, the signal was converted into the frequency domain using a fast Fourier transform. The signal magnitude and phase at each comb tooth frequency were extracted and then normalized against reference signals recorded by an identical procedure when the laser frequency was detuned by several GHz away from the D₁ transition [5].

Amplitude and phase absorption spectra for the evacuated cell can be found in Fig. 2. Combs spanning 200 MHz to 650 MHz were employed with a comb tooth spacing of 200 kHz. In addition to the prominent ³⁹K EIT feature at −462 MHz, we can also clearly observe the broader hyperfine pumping features [16, 17] which are separated by the upper state hyperfine splitting (i.e., 55 MHz). Finally, consistent with the high signal-to-noise ratio of these spectra we can further observe the ⁴¹K EIT feature near −254 MHz despite its low isotopic abundance of 6.7% [18]. The ³⁹K feature has a considerably larger amplitude than we previously observed using a counter-propagating beam approach [5] because of the improved magnetic shielding and elevated temperature.

Fig. 2.

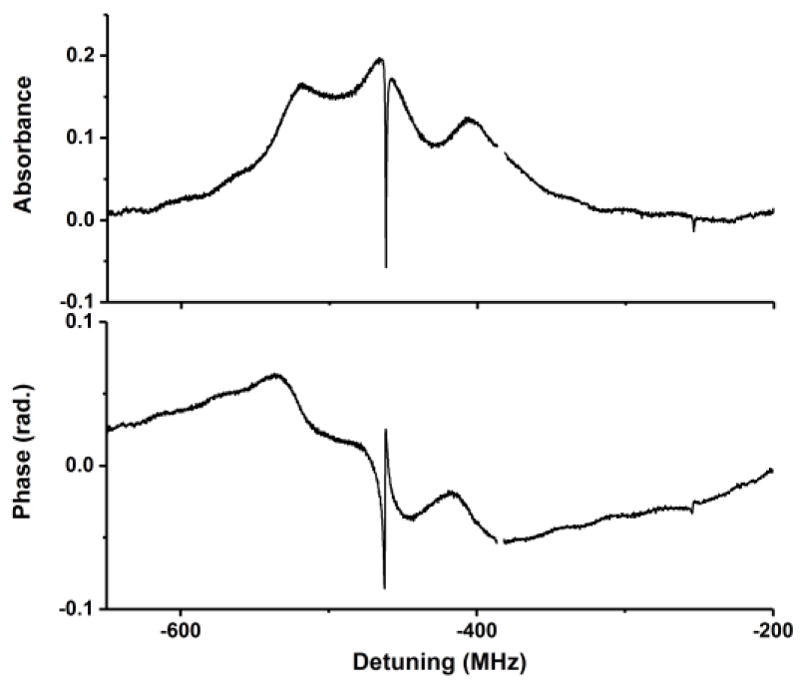
Normalized amplitude (top panel) and phase (bottom panel) spectra of the EIT and hyperfine pumping peaks for the evacuated cell at 34 °C. Linear background absorption was modeled by a 4^th order polynomial for the amplitude spectrum and a 2^nd order polynomial for the phase spectrum. Two thousand interferograms were averaged in the time domain before being fast Fourier transformed. Each component interferogram contained 300 kS recorded at 750 MS/s. Typical duty cycles were 25 % to 40 %, corresponding to a total acquisition time near 3 s for the probe spectrum. The full-width at half-maximum of the ³⁹K EIT feature is approximately 800 kHz which is consistent with the expected transit time broadening.

Based upon a fit of these spectral features (see Ref. [5] for further details on the fitting procedure), we determine 461.828(9) MHz and 254.12(7) MHz for the ³⁹K and ⁴¹K lower state hyperfine splittings where the shown uncertainties are statistical spectroscopic fit uncertainties which do not include any sources of systematic uncertainty. Difficulties in modeling the underlying strong optical pumping features and the Doppler pedestal, each of which exhibits strong asymmetries represents the dominant source of systematic uncertainty and likely accounts for the deviation from the well known microwave values [19].

The predominant source of broadening of these EIT features is transit time broadening which occurs due to the large mean free path of potassium atoms in the evacuated cell and dephasing interactions with the cell walls. This broadening can be reduced through the use of a buffer gas which confines the potassium atoms within the beam [20, 21]. Importantly, the use of a buffer gas cell should also remove the velocity selective optical pumping features which were likely the dominant source of uncertainty in the measurements of the EIT feature when using the evacuated cell.

Through the use of the argon buffer gas cell and combs spanning 400 MHz to 650 MHz with a comb tooth spacing of 20 kHz we were able to reduce the observed ³⁹K EIT full-width at half-maximum linewidth to 33(5) kHz (see Figure 3). The observation of this ultranarrow feature is possible because of the mutually coherent nature of the pump and probe [7]. As expected the hyperfine pumping features, which are velocity selective, are not observed in the presence of the buffer gas. Based upon a complex Lorentzian fit to this spectrum we retrieve a lower state hyperfine splitting of 461.724(2) MHz (where the uncertainty is the standard fit uncertainty) which agrees with the microwave value of 461.7197201(6) [19] at the 2σ level. We note that pressure shifting of the ground state hyperfine splitting by argon is negligible at this pressure (i.e., approximately 9 Hz [22]). The most prominent systematic uncertainty in our measurement of the lower state splitting is likely the dynamic Stark effect, due to the strong optical pumping, which we estimate to be near 85 kHz (based upon the assumption that roughly one half of the total optical power is in the carrier tone). As a result of the triply shielded magnetic chamber, Zeeman splitting is expected to be only roughly 1 kHz.

Fig. 3.

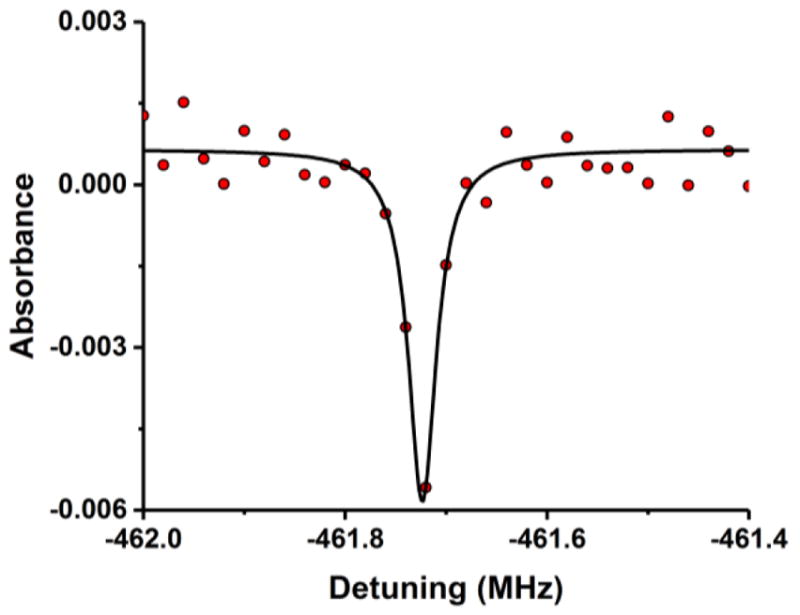
A portion of an absorption spectrum and corresponding Lorentzian fit of the EIT feature for a buffer gas cell containing Ar buffer gas at 35 °C. Two thousand interferograms were averaged in the time domain before being fast Fourier transformed. Each component interferogram contained 300 kS recorded at 750 MS/s. As an additional level of averaging, 40 normalized spectra were then averaged to produce the shown spectrum.

We note that the amplitude of the EIT feature in the buffer gas cell is far smaller than observed with the evacuated cell (even after accounting for the difference in cell length) while this observation is in agreement with the observed behavior for Cs [23], it differs from a previous examination of EIT in K using a Hanle configuration [24] which found the buffer gas amplitude to be larger. This enhancement was attributed to optical pumping compensation due to the overlapping Doppler profiles [24].

Due to the narrow intensity linewidth of the ³⁹K EIT feature, and its correspondingly long lifetime, we were able to observe the optical free induction decay by pulsing the arbitrary waveform generator signal which drove the electro-optic phase modulator (see Fig. 4). The pulses, which were separated by 5 μs and had a pulse duration of 1 μs, had a single frequency of 461.7 MHz, which matches that of the hyperfine splitting of the ³⁹K ground state. The observed free induction decay corresponds to a lifetime of 0.25 μs for the EIT feature in the evacuated cell at room temperature. This corresponds to an intensity linewidth of 640 kHz.

Fig. 4.

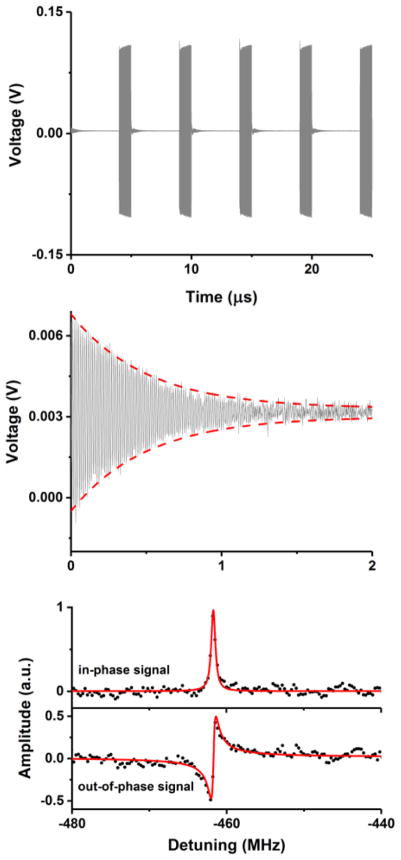
(Upper panel) Time domain self-heterodyne signal for pulsed modulation using the evacuated cell at room temperature. The shown trace is the average of 20 000 acquisitions. The sampling rate was 750 MS/s. An unresolved technical issue leads to a very slight baseline distortion for some of the free induction decays (e.g., the second one). This may be because there are not an integer number of cycles of 461.7 MHz in 5 μs. (Middle panel) Same data as the upper panel but with the x- and y-axes reduced. The gray trace shows the acquired data while the red traces correspond to models of the free induction decay of the form V(t) = Ae^−t/(2τ) + V₀, where the factor of two in the exponent accounts for the heterodyne nature of the measurement. (Lower panel) In-phase and out-of-phase components of the fast Fourier transform (FFT) of the self-heterodyne signal after a chirped pulse (black points) and corresponding model (solid red line). The x-axis was shifted to account for the AOM offset of 384.22 MHz. Twenty thousand time-domain signals were averaged, with each individual acquisition containing 10 000 samples recorded at 3 GS/s.

In light of these observed free induction decays we were able to go a step further and use chirped pulses to probe the EIT feature using the evacuated potassium cell at 34 °C. A chirp of 400 MHz to 650 MHz was employed with a 500 ns duration and 5000 ns between successive pulses. Taking the fast Fourier transform of the self-heterodyne signal after the chirped pulse yields a background-free EIT feature (see Fig. 4). The shown models for the in-phase (real) and out-of-phase (imaginary) components of the spectrum were $s_r(\omega )=\frac{e_0{e}_{lo}}{\mathrm{\Delta }{\omega }^2+1/(4{\tau }^2)}\frac{1}{2\tau }$ and $s_i(\omega )=-\frac{e_0{e}_{lo}}{\mathrm{\Delta }{\omega }^2+1/(4{\tau }^2)}\mathrm{\Delta }\omega$, respectively, where e₀ and e_lo are the probe and local oscillator field amplitudes and Δω is the angular frequency detuning. The amplitude, center, and baselines were floated while τ was held fixed to the known value.

This approach is analogous to the commonly used chirped pulse Fourier-transform microwave and THz techniques [25, 26] but is possible in the optical domain because of the ultranarrow EIT features which are probed. We note that free induction decays are routinely observed with femtosecond mode-locked lasers (e.g., [27]).

Through the use of electro-optic frequency combs with comb tooth spacings as narrow as 20 kHz we have observed electromagnetically induced transparency in a self-heterodyne configuration. The common-mode and coherent nature of both the excitation and acquisition enabled us to determine the ³⁹K lower state hyperfine splitting with a standard uncertainty less than 2 kHz. The flexibility of electro-optic frequency combs makes this approach amenable to present problems in atomic and molecular spectroscopy. Efforts to extend these measurements to other wavelengths and systems as well as the implementation of an open-path instrument for remote sensing are presently under way.