Abstract
Charged and polar groups, through forming ion pairs, hydrogen bonds, and other less specific electrostatic interactions, impart important properties to proteins. Modulation of the charges on the amino acids, e.g., by pH and by phosphorylation and dephosphorylation, have significant effects such as protein denaturation and switch-like response of signal transduction networks. This review aims to present a unifying theme among the various effects of protein charges and polar groups. Simple models will be used to illustrate basic ideas about electrostatic interactions in proteins, and these ideas in turn will be used to elucidate the roles of electrostatic interactions in protein structure, folding, binding, condensation, and related biological functions. In particular, we will examine how charged side chains are spatially distributed in various types of proteins and how electrostatic interactions affect thermodynamic and kinetic properties of proteins. Our hope is to capture both important historical developments and recent experimental and theoretical advances in quantifying electrostatic contributions of proteins.
Graphical Abstract
1. INTRODUCTION
Amino acids with ionizable side chains, e.g., Asp, Glu, His, Lys, and Arg, impart important properties to proteins. Modulation of the charges on these amino acids, e.g., by pH,1 may result in significant changes such as protein denaturation.2 Charge alteration by phosphorylation and dephosphorylation of Ser, Thr, and Tyr is key to inducible protein–protein interactions, which underlie the switch-like response of signal transduction networks.3 Other types of posttranslational charge-altering modifications, such as acetylation of Lys, can moderate the strength of protein–DNA association, most notably in the nucleosome. Charged residues can play critical roles in regulating protein condensation, as illustrated by the β subunit Glu6 → Val mutation in the polymerization of sickle hemoglobin.4,5 Nucleic acids and cell membranes have surface charges; thus binding of proteins to these targets is expected to be strongly influenced by electrostatic interactions. Charges also have profound effects in processes such as conduction of ions through transmembrane channels and binding of metals (e.g., Ca2+) or charged ligands (e.g., ATP) to specific sites in proteins. In addition to residues carrying net charges, polar residues have significant partial charges and form hydrogen bonds and other less specific electrostatic interactions among themselves and with charged residues. This review aims to present a unifying theme among the various effects of protein charges and polar groups. Simple models will be used to illustrate basic ideas about electrostatic interactions in proteins, and these ideas in turn will be used to elucidate the roles of electrostatic interactions in protein structure, folding, binding, condensation, and related biological functions.
Charged residues differ from nonpolar residues (e.g., Leu and Ile) in crucial ways. The hydrophobic interactions of nonpolar residues are a driving force for the folding stability of proteins.6–10 On the other hand, because charges can be either positive or negative and opposite charges attract whereas like charges repel, interactions between charged residues can confer specificity. Interactions of charged residues with polar groups, in particular in the form of hydrogen bonds, reinforce specificity. In addition, charge–charge interactions can be strong even at a distance (e.g., of 5–10 Å). Such “long-range” interactions can be a crucial factor in determining the rate constants of proteins binding with small and macromolecular partners.11,12
There are strong energetic penalties for burying charged residues in nonpolar environments, probably much stronger than those encountered in exposing nonpolar residues to aqueous environments. It is this strong penalty that prevents normal hemoglobin from forming the sort of polymers formed by sickle hemoglobin. In general, charged residues help keep proteins from aggregation and contribute significantly to the solubility of water-soluble proteins.
In addition to the foregoing generic roles, charged residues are often found in functional sites and directly participate in functions. For example, as part of the catalytic triad in serine proteases, an Asp residue is involved in shepherding the catalytic process. Acidic residues are recognized as key sites for facilitating the transport of protons through proteins.13–15 Charged residues often line binding sites for metal ions such as Ca2+ and charged ligands such as ATP.16–18 DNA-binding proteins such as transcription factors may use Arg residues to sense whether a specific site is found.19,20 Basic residues are an essential part of the sequences that serve as signals for nuclear import of many proteins.21,22
Side-chain charges can be changed through protonation–deprotonation and posttranslational modifications such as phosphorylation–dephosphorylation. The former can be controlled internally by changes of protein conformations and externally by changes of pH. The latter are typically controlled by enzymes (i.e., kinases and phosphatases). The strengths of charge–charge interactions can be further modulated by variations in salt concentrations in and dielectric constants of the cellular milieus. In particular, the dielectric constants in the middle of a membrane bilayer and in the surrounding aqueous environment are drastically different,23,24 and the resulting “dielectric barrier” explains the low permeability of small ions through the membrane.25 Dielectric constants can also be very different in different protein phases26,27 and have a significant dependence on temperature.28 The influences of salts and temperature can be particularly relevant for proteins in halophilic and thermophilic organisms. This multitude of controls affords ample opportunities for electrostatic interactions to be fine-tuned in order to achieve optimal effects on protein functions in their cellular contexts.
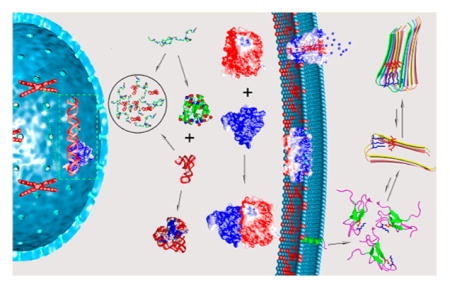
Different aspects of protein electrostatics have been reviewed.29–48 Our goal here is to present a comprehensive coverage on the uses of electrostatic interactions by proteins in tuning their basic biophysical properties and in performing their biological functions, with emphasis on conceptual understanding and connections among the various effects. We will consider various types of proteins (Figure 1), including both those that form globular structures and those that are intrinsically disordered; both water-soluble proteins and integral as well as peripheral membrane proteins; and proteins that form complexes with other proteins or nucleic acids. We will examine how charged side chains are distributed in these proteins and how electrostatic interactions affect thermodynamic and kinetic properties of processes including protein folding and binding. Our hope is to capture both important historical developments and recent experimental and theoretical advances in quantifying electrostatic contributions of proteins.
Figure 1.
The ever presence of electrostatic interactions in various proteins that participate in a wide range of biochemical processes at different subcellular localizations (cytoplasm, nucleus, and cell membrane). Folding, binding to different targets (other proteins, nucleic acids, and cell membrane), and two different forms of condensation (fibrillation and droplet formation) are illustrated.
2. THEORETICAL BACKGROUND
When it comes to the interactions between charges, the surrounding medium exerts a strong influence. For example, in vacuum the energy of interaction between two charges q1 and q2 at a distance r is, according to Coulomb’s law
| (1a) |
However, in a solvent with a dielectric constant εs, the interaction is weakened by a factor of εs:
| (1b) |
In these expressions, charges are in units of proton charge, distances are in angstroms (Å), and energies are in kilocalories per mole (kcal/mol); the numerical factor 332 (more precisely, 332.064) is determined by the vacuum permittivity and proton charge in units of coulomb as well as the conversion factor for energy from joules to kcal/mol. Events such as folding and binding change both the distances between and the medium around protein charges, and therefore the electrostatic energies will change significantly.
Accounting for electrostatic interactions in proteins is complicated because the medium around protein charges is not homogeneous. The solvent, water for aqueous solutions, is very polar (as reflected by a large dielectric constant of ~80 at room temperature), but the protein interior is very nonpolar (with a dielectric constant generally taken as 2–4, although values as high as 40 have been used49–52).53 Each charge inside the protein will interact with the solvent. When other charges are present, the charges also interact with each other, but the interactions are screened by the solvent. The charge–solvent interactions and solvent screening of charge–charge interactions significantly affect the electrostatic energies of proteins.
2.1. Models of Born, Debye and Hückel, and Linderström-Lang
An important fact about charges is that they interact very favorably with polar solvents over nonpolar ones. This was recognized by Born,54 who developed the now well-known Born model, originally to explain how the cloud chamber worked as a particle detector. When charged particles passed through the saturated water vapor in the chamber, water droplets formed along the paths. This early (charged) particle detector won its inventor C. T. R. Wilson the 1927 Nobel Prize in Physics. Born modeled a charged particle or ion as a sphere with radius a and charge q (here assumed to be distributed uniformly over the surface). The energy of the ion due to its interaction with the surrounding medium with a dielectric constant ε, by solving the Poisson equation for the electrostatic potential, is
| (2a) |
If the ion is transferred from a nonpolar environment (e.g., water vapor or protein interior) with a dielectric constant εp to a polar solvent with dielectric constant εs, the solvation energy is
| (2b) |
This last result is valid for any spherically symmetric charge distribution within the ion. With a = 2.5 Å, q = ±1, εp = 4, and εs = 80, the solvation energy is −15.8 kcal/mol. This very favorable solvation energy then explains the traces of water droplets left by passing ions in the Wilson cloud chamber. Because an ion is so much more favorable in liquid water than in water vapor, the vapor condenses into liquid in order to solvate the ion. The same explanation applies to the melting of snow by salt spray and the releasing of water from cooking leafy vegetables upon adding table salt. These daily experiences make it easy to understand the strong tendency for charged residues to be near the surfaces of water-soluble proteins.
Debye and Hückel55 realized that mobile ions in water affect charge–solvent interactions. By a mean-field treatment of the ion distribution in the solvent, the Poisson equation for the electrostatic potential ϕ becomes56
| (3) |
where κ = (8πNAe2I/εskBT)1/2 with NA denoting Avogadro’s number, e proton charge, I the ionic strength, kB Boltzmann’s constant, and T the absolute temperature. For water at room temperature, κ ≈ I1/2/3.04 Å−1 when I is in molar. Equation 3 is known as the linearized Poisson–Boltzmann equation. For the charged solute considered in the Born model, one now has
| (4a) |
where a′ is the radial distance to which mobile ions are excluded. If now the ionic solute is transferred from the nonpolar to the polar solvent, the solvation energy becomes
| (4b) |
The second term, due to the redistribution of mobile ions, makes the solvation even more favorable. Though the magnitude of this term is relatively small for a single ion, we will see that the effects of this term on proteins can be important, e.g., when studying the dependence on salt concentrations (in particular, section 2.3).
Mobile ions also affect interactions between charges. For two spherical solutes with charges q1 and q2 and closest-approach distances a1′ and a2′ for mobile ions, the energy of interaction at a large distance r is57
| (5) |
which amounts to treating each solute as a test charge inside the electrostatic potential of the other solute. When κ = 0, eq 5 reduces to eq 1b. The strength of charge–charge interaction decreases with increasing ionic strength.
Linderström-Lang1 adapted the Born model for proteins with the Debye–Hückel effect included. A folded protein was approximated as an impenetrable sphere (with radius R). Replacing a by R and a′ by R′ (closest-approach distance for mobile ions) in eq 4a, the energy of interaction of the protein with solvent is
| (6) |
q now represents the net charge on the protein.
2.2. Tanford–Kirkwood Model
In eq 6, the net charge q was modeled as smeared uniformly over the protein surface. Tanford and Kirkwood58,59 introduced a more realistic treatment by using discrete charges. For a point charge qi located at radial distance ri inside the spherical protein with dielectric constant εp, the solvation energy is
| (7) |
where Ll = 1 + l + (εp/εs)l, Xl = κR′Kl−1/2(κR′)/Kl+1/2(κR′), and Ml = Ll + (Ll + Yl)Xl/(2l+1), with Yl = (1 − εp/εs)l(R/R′)2l+1 and Kl+1/2(x) denoting modified Bessel functions of the second kind. The first summation is the extension of the Born equation (eq 2b) and accounts for charge–water interaction, while the second summation accounts for the effect of mobile ion redistribution in response to the protein charge. If the charge is distributed with spherical symmetry, only the l = 0 term survives in each summation. Equation 7 then reduces to eq 4b (with R and R′ of the protein replaced by a and a′ for the ionic solute).60 As the charge is moved from the center of the protein toward the surface, its interaction with the solvent becomes more and more favorable (Figure 2a, purple curve). This result explains why charged residues are usually found near surfaces in water-soluble proteins. The favorable charge–solvent interaction is the basic reason why charged residues contribute significantly to the solubility of water-soluble proteins (see section 2.3 and section 5.3.1). Conversely, the energetic cost of desolvating small ions in the middle of cell membranes explains why their transport requires channels or carriers.25
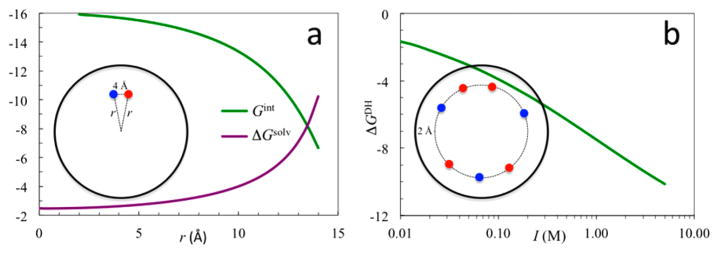
Figure 2.
(a) Solvation energy (purple curve) of a unit charge and interaction energy (green curve) between two unit charges inside a spherical protein. The two charges have opposite signs and are at the same radial distance (r) with a distance of 4 Å between them. (b) Effect of salt ions on the electrostatic energy of a charge distribution in a spherical protein. There are 46 charges of ±1, randomly distributed at 2 Å below the protein surface. The common parameters are εp = 4, εs = 80, and R = 16 Å. For (a), κ = 0; for (b), R′ = 18 Å and κ = I1/2/3.04 Å−1. Energies are in units of kcal/mol.
When two point charges qi and qj are located inside the protein, their interaction energy is
| (8) |
where ri and rj are the radial distances of the charges, rij is the distance between them, θij is the angle between their radial vectors, and Pl(x) are Legendre polynomials. The first term is just the Coulomb interaction between the charges in the protein dielectric, the second term is due to screening of the interaction by water, and the last term accounts for the screening by mobile ions. The strength of interaction decreases when the charge pair is moved from the center of the protein toward its surface due to increased solvent screening (Figure 2a, green curve).
When multiple charges are present, the solvation energy (eq 7) should be summed over all charges and the interaction energy (eq 8) summed over all charge pairs. The addition of the two contributions
| (9a) |
is the electrostatic energy of the total charge distribution. There are different ways of partitioning eq 9a. Gel would be given by the first term (Coulomb interaction energy) of eq 8 if the protein dielectric were extended to infinity. Hence the remaining terms constitute the solvation energy for the set of protein charges, when the protein is embedded in the solvent. We then write
| (9b) |
In particular, a dipole p0 can be mimicked by a pair of opposite charges ±q at a separation rij → 0 but with qrij = p0. If the midpoint of the charge pair is at the center of the protein (hence ri = rj = rij/2 and θij = 180°), then the solvation energy of the dipole at κ = 0 is
| (9c) |
This result was first obtained by Bell61 and Onsager.62
The first term of eq 7 and the first and second terms of eq 8 together give the electrostatic energy in the absence of salt ions (i.e., κ = 0), hereafter denoted as Gel0. The contribution of added salt ions, accounted for by the last terms of eqs 7 and 8, will be referred to as the Debye–Hückel term, ΔGDH. We then have
| (9d) |
As an example, let us consider a spherical protein with 46 point charges, 26 with a charge of +e and the rest with charge −e (the net charge is thus +6e). All the point charges have the same radial distance of 14 Å, but the directions of their radial vectors are random with the provision that no two charges are closer than 4 Å. For this charge distribution, Gel0 has a value of −403 kcal/mol. The dependence of ΔGDH on ionic strength is shown in Figure 2b.
The Tanford–Kirkwood model can be used to illustrate various effects of protein electrostatic interactions.63 In particular, it has sometimes been mistakenly assumed that mobile ions at high concentrations can completely screen out electrostatic interactions inside the protein. Figure 2b shows that, as the ionic strength → ∞, the magnitude of the electrostatic energy increases continually.64 However, at high ionic strengths, mobile ions will compete for hydration water and a new effect comes into play.
2.3. Salting In and Salting Out
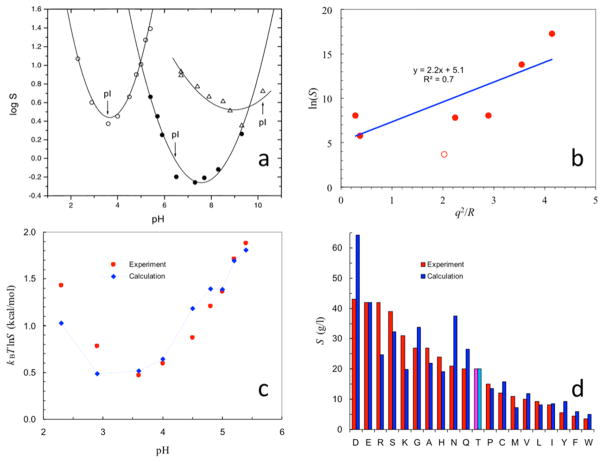
High salt concentrations tend to precipitate proteins, a phenomenon documented by Hofmeister in 188865 and now known as the Hofmeister effect. As we have noted, ions favor a polar environment over a nonpolar one. It is thus energetically unfavorable for the ions to move from the bulk solvent to the surface of a protein molecule, even though such redistribution of ions lowers the electrostatic energy of the protein charges. (In essence the ions are repelled by their dielectric images.66) Salts thus exert two opposing effects: the electrostatic energy of the protein charges favors distribution of counterions around the protein surface, but the solvation energy of the mobile ions favors hydration in the bulk solvent. If the protein molecule can exist in two states (such as folded and unfolded) or two phases (such as solution and solid) that differ in surface exposure to the solvent, then, depending on their concentrations, salts may shift the equilibrium in either direction.
Kirkwood67 made calculations of the two opposing energetic contributions in an effort to explain the dependence of protein solubility on salt concentration. He showed that, at low salt concentrations, the Debye–Hückel term dominates and salts thus shift the equilibrium toward the solution phase, i.e., an increase in solubility, or salting in. On the other hand, at high salt concentrations, the contribution from hydration of the ions (to be called the Kirkwood term) dominates and salts then shift the equilibrium toward the solid (either amorphous or crystalline) phase, i.e., a decrease in solubility, or salting out.
In 2005 these ideas were put into a more rigorous framework.68 The Kirkwood term was shown to be the work of charging up ions around the protein low-dielectric cavity (assumed to be spherical). Distribution of the ions was modeled by the Poisson–Boltzmann equation. Results for both the nonlinear and linearized equations were obtained, but here only those from the linearized version are presented for illustration. The work of charging up a single ion of species α, with charge eα, at radial distance r from the protein, in the presence of all other ions, is
| (10a) |
where
| (10b) |
with Il+1/2(x) denoting modified Bessel functions of the first kind. A special case of eq 10a with R′ = R has been derived previously.69 The work to charge up an equilibrium distribution of all the ions is
| (10c) |
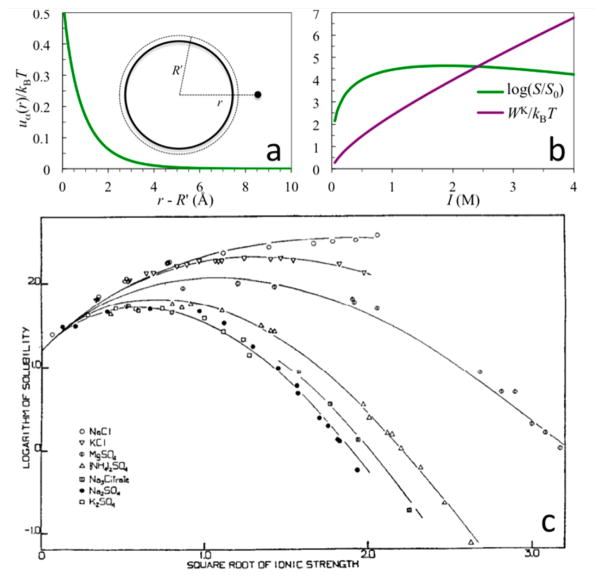
where ρα is the bulk concentration of ion species α. WK measures the dehydration cost of all the ions surrounding the protein. Figure 3a shows the energetic cost, uα(r), for bringing an ion of species α from bulk solution to a spherical protein in the presence of 1 M 1:1 salt; Figure 3b shows the Kirkwood term as a function of ionic strength.
Figure 3.
(a) Dehydration cost for bringing a single ion to the surface of a spherical protein in the presence of 1 M 1:1 salt (parameters are as given in Figure 2b; kBT = 0.59 kcal/mol). r is the final radial distance of the ion. (b) Ionic strength dependences of the dehydration cost WK for an equilibrium distribution of ions around the protein and the protein solubility. The latter is calculated from the WK term shown and the ΔGDH term shown in Figure 2b. (c) Dependence of hemoglobin solubility on concentrations of various salts; curves are fits to an empirical formula that has the same form as eq 12 but with simplified expressions for ΔGDH and WK. Panel c reprinted with permission from ref 70. Copyright 1932 American Society for Biochemistry and Molecular Biology.
The solubility, S, is the protein concentration of the solution phase in equilibrium with the solid phase. This equilibrium requires the equality of the chemical potentials, denoted as μs and μc, respectively, of a protein molecule in the two phases. To illustrate, we model the solution phase as dilute and the solid phase as a crystalline lattice of solvated protein molecules. The equality of the respective chemical potentials is
| (11) |
where μex is the excess chemical potential of a protein molecule in the solution, arising from interactions with the solvent environment; Ec is the free energy of a protein molecule in the crystalline lattice, arising from interactions with the solvent environment and neighboring protein molecules; vc is an effective free volume that is accessible to the protein molecule in the crystalline lattice; and C° is an arbitrary reference concentration. Assuming that salts affect μs (specifically μex) but not μc (see next paragraph), the ratio of the protein solubility levels, S/S0, in the presence and absence of salts is given by68,71,72
| (12) |
As illustrated by using the ΔGDH term shown in Figure 2b, eq 12 predicts a biphasic dependence of the solubility on salt concentration (Figure 3b). As I increases from zero, S initially increases but then turns over. The initial increase in S is due to the favorable ΔGDH term. At higher I, WK has a much stronger dependence than ΔGDH, leading to the turnover in S. Eventually, WK becomes dominant and S can ultimately decrease to less than S0. Most salts at lower concentrations (I < ~1 M) have a salt-in effect on proteins (Figure 3c), as predicted by a favorable Debye–Hückel term in eq 12 (Figure 2b).68,70,72 Some salts have a salt-out effect, qualitatively consistent with the Kirkwood term in eq 12.
Salts can freely diffuse between the solution and crystalline phases73 (for a protein with a net charge, counterions should be in slight excess over co-ions in the crystalline phase in order to maintain overall charge neutrality). In theory, salts in the solvent region of the crystalline phase can affect Ec in the same way as they affect μex. However, each protein molecule in the crystalline phase has less surface exposure to the solvent than in the solution phase, so correspondingly the magnitudes of both the Debye–Hückel and Kirkwood terms should be less than those in the solution phase. Additionally, salts in the solvent region may screen the repulsion between like-charged protein molecules (see eq 5) in the crystalline lattice, thereby countering the effect of the Kirkwood term of the crystalline phase. This screening effect has sometimes been claimed as the main role of salts on protein solubility. If this claim were correct, one would only predict salting out, which contradicts with the experimental observation of salting in for most salts at I < ~1 M. An increase in salt concentration required for lysozyme crystal formation at pHs with higher protein net charges was observed, and was explained in terms of salt screening of the repulsion between net charges (presumably with a greater effect in the crystalline phase than in the solution phase).74 We note that this observation can have a different explanation: a higher net charge means that the protein–solvent interactions in the solution phase become more favorable (see section 5.3.1), and therefore an increase in salt concentration is required for the Kirkwood term to drive the protein into the crystalline phase.
Although eq 12 predicts that all salts at high concentrations favor the state or phase of a protein with less surface exposure (e.g., folded over unfolded state and solid over solution phase), different ions actually have very different effects on protein stability and solubility (among other properties). The variation of the effects of different ions generally follows similar orders for different properties, and is known as the Hofmeister series. Ions at one end of the series are called kosmotropes (e.g., SO42−, HPO42−, Mg2+, Ca2+, Li+, and Na+), which at high concentrations stabilize and salt out proteins, in agreement with expectation from ion dehydration cost. In contrast, ions at the other end of the Hofmeister series (SCN−, I−, and (NH2)3C+), called chaotropes, tend to destabilize and salt in proteins. Relative to kosmotropic ions, chaotropic ions were noted to have smaller charge densities (low valency and/or large radius).75 In comparison to Cl− (a moderate kosmotrope), SCN− and I− were found to have preferential binding with protein backbone amides.76–79
Finally, we mention that protein–ion interactions at low salt concentrations also exhibit ion-specific variations, beyond what can be captured by the Debye–Hückel term. In particular, the levels of preferential accumulation of anions around a positively charged protein followed the order SO42− > SCN− > I− > Cl−, which, with the exception of SO42−, is almost the Hofmeister series in reverse and has been termed the electroselectivity series.80 Conversely, polyvalent cations (e.g., Y3+) can bind tightly to acidic residues and even lead to inversion of the protein net charge.81 In addition to interacting with proteins in various ways and mediating protein–protein interactions, salts also exert an indirect effect on protein stability and solubility through increasing the protein–water interfacial tension,66,68 thereby strengthening hydrophobic interactions in proteins.82
2.4. pKa Shift
The side chains of some amino acids, notably Asp, Glu, His, Lys, and Arg, can uptake or release a proton, depending on the proton concentration (i.e., pH) of the solution. The protonated fractional population of a side chain varies with pH through the relation
| (13a) |
where pKa is the pH at which f = 1/2. Equation 13a is equivalent to a Boltzmann distribution with an “energy” function
| (13b) |
where x = 0 for the unprotonated state and 1 for the protonated state. The probability of the protonated state predicted by the Boltzmann distribution is exactly f, and the probability of the unprotonated state is 1 − f. The average protonation, x̄, of the side chain is then 1·f + 0·(1 − f), which, as desired, equals f.
When isolated in solution (as found for model compounds), the pKa values of the side chains are approximately the following: Asp, 4.0; Glu, 4.4; His, 6.3; Lys, 10.4; and Arg, 12.0. The N- and C-termini of proteins are also ionizable, with model-compound pKa values of 7.5 and 3.8, respectively. Protonation changes the net charge of Asp, Glu, and the Cterminus from −1 to 0 and the net charge of His, Lys, Arg, and the N-terminal from 0 to +1. We introduce a parameter γ to distinguish the two classes of ionizable groups, with values of −1 for the former and +1 for the latter. For either class, the net charge is either 0 or γ and its value in protonation state x can be written as ξ = x + ξ0, with ξ0 = (γ − 1)/2.
In the folded protein environment, electrostatic interactions with the solvent and the rest of the protein will shift the balance between the two protonation states of an ionizable group.83 If the electrostatic energy of the protein changes by ΔGel when ξ changes from 0 to γ and the corresponding change in the model compound is ΔGel;model, then the energy function can be written as
| (13c) |
where is the pKa for the model compound and ΔΔGel = ΔGel − ΔGel;model. Comparison of eqs 13b and 13c gives
| (13d) |
The protonation site in the protein differs from its counterpart in the model compound both by its exposure to the solvent and by the presence of other protein charges. Thus, ΔΔGel consists of two terms:
| (13e) |
The desolvation cost ΔΔGsolv is always positive for a protein charge and thus favors the uncharged state (i.e., ξ = 0), thereby upshifting the pKa of Asp or Glu and downshifting that of His, Lys, or Arg. On the other hand, favorable interactions with nearby charged and/or polar groups lead to a negative interaction energy Gint, thereby downshifting the pKa of Asp or Glu and upshifting that of His, Lys, or Arg.
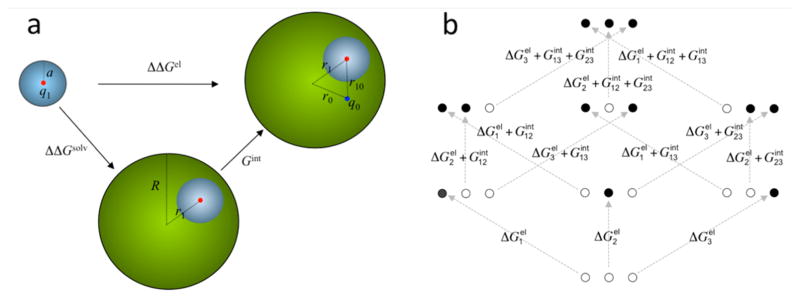
To illustrate the two opposite effects, consider a protein modeled as a sphere with a radius R and a model compound as a sphere with a radius a (Figure 4a). Let us assume that all the charge of the ionizable group in the charged state (i.e., ξ = γ) is located at a point, at a radial distance r1 in the protein and at the center in the model compound. The desolvation cost, ΔΔGsolv, of the net charge q1 = γe, calculated as the difference in solvation energy between the protein (eq 7) and the model compound (eq 2b), is 5.5 kcal/mol for R = 16 Å, r1 = 14 Å, and a = 2.5 Å.84 This corresponds to a pKa shift of 4 pH units. If there is a charge of q0 = −γe preexisting in the protein, at a radial distance r0 = 14 Å and a distance r10 = 4 Å from the protonation site, then the interaction with the ionizable group makes an energetic contribution of Gint = −6.7 kcal/mol (eq 8). Adding ΔΔGsolv and Gint together, the pKa shift is a moderate 0.8.
Figure 4.
(a) Difference (ΔΔGel) in the electrostatic energies for creating a charge q1 in a model compound (small sphere) and in a protein (large sphere). The model compound becomes buried in the protein, resulting in the desolvation cost ΔΔGsolv. Interaction with a preexisting protein charge q0 contributes an additional energy Gint. This model can also be adopted for reduction potential and for protein folding. In those cases, the model compound becomes the redox center or a charged group of the protein. (b) Differences in electrostatic energies among the eight protonation states of a protein with three protonation sites. Solid and open circles represent charged and neutral sites, respectively. In the former case the net charge at each site can be either positive or negative. The situation for protonation inside the protein is shown. For the counterpart in the model compounds, there are no interactions among the three sites.
Proteins typically have dozens of ionizable groups. The protonation probabilities at different sites influence each other. To illustrate, consider a protein with three ionizable sites (Figure 4b). Each site can be either protonated or unprotonated, hence there is a total of 23 = 8 protonation states. Let the γ parameter of site i be γi and the protonation state be xi. The protonation states of the three sites are specified by (x1, x2, x3), collectively referred to as x, which have binary values 000, 100, 010, …, 111. The all-neutral state is specified by x = (−ξ01, −ξ02, −ξ03), where ξ0i = (γi − 1)/2. The statistical weight of state x is proportional to a Boltzmann-like factor exp[− ℋ(x)/kBT]. Relative to the all-neutral state, the energy function of the state x = (x1, −ξ02, −ξ03), where two sites stay neutral, is given by (see eq 13d)
| (14a) |
where ξi = xi + ξ0i. Similarly expressions can be written for x = (−ξ01, x2, −ξ03) and (−ξ01, −ξ02, x3). When only one site stays uncharged, the remaining sites, say 1 and 2, can interact, giving rise to an energy . The overall energy has the form
| (14b) |
Similarly, when no site is fixed at the neutral state, the total energy has the form
| (14c) |
Of the total of eight protonation states, four have site 1 protonated. These are 100, 110, 101, and 111. The average protonation on site 1 is thus
| (15) |
where Q is the sum of all eight statistical weights.
In general, for a protein with N ionizable sites, the energy of a protonation state has the form
| (16) |
with a corresponding statistical weight exp[−Δℋ(x)/kBT]. Again, represents the difference between the energies for charging up site i in the protein and in a model compound; in calculating the former, all sites j ≠ i are assumed to be neutral. The average protonation of site i is
| (17) |
where the sums are over the 2N possible protonation states. The sums can be carried out by exhaustive enumeration for N up to ~20 (corresponding to 1 048 576 states). For larger N, Monte Carlo simulations can be used to sample the protonation states.85,86 The average protonation as a function of pH can be fit to eq 13a to obtain the apparent pKa value appropriate for site i in the protein environment.
2.5. Reduction Potential
Oxidation–reduction reactions are processes involving the transfer of electrons. They yield most of the free energy required by living organisms.87 Many proteins such as cytochrome c specialize in electron transfer. The reduction of a species A to A− in an aqueous (aq) solution by accepting an electron
is characterized by the reduction potential
| (18) |
where μS is the chemical potential of the species specified by a subscript and ℱ = 23.06 kcal/mol/V is the Faraday constant.88 Hypothetically one can first bring A to the gas phase, letting the reduction occur there, and then bring A− back to the aqueous solution (Figure 5a). We have
Figure 5.
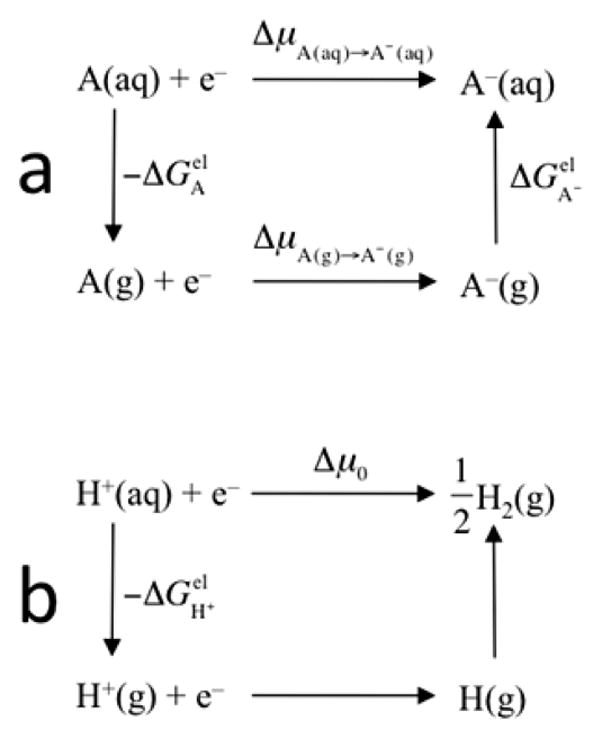
(a) Reduction of A in aqueous solution and its connection with the corresponding reaction in gas phase. (b) Reduction in the hydrogen electrode and hypothetical intermediate steps of proton dehydration and hydrogen atom formation.
| (19) |
where is the change in electrostatic energy when the solvent is changed from vacuum to water, i.e., the hydration energy. The concentration of species S is assumed to be identical in the solution and in the gas phase and will be denoted as [S]. The change in chemical potential in the gas phase is89
| (20) |
where ΔEelectronic(A) is the difference in electronic energy between A and A−, commonly referred to as the ionization energy (IE).
Reduction potentials are typically measured against the hydrogen electrode, which involves the reaction
The reduction potential of this electrode is
| (21) |
By envisioning the reduction to occur in the gas phase, first forming atomic hydrogen and then hydrogen molecule (Figure 5b), we find
| (22) |
The chemical potentials of H and H2 in the gas phase are90
| (23a) |
| (23b) |
where mH is the mass of the hydrogen atom, σe = 2 accounts for the degeneracy of the electron spin in H, h is Planck’s constant, Θr = 85.4 K is the characteristic temperature for the rotation of the hydrogen molecule, D0(H2) is the dissociation energy for the hydrogen molecule, and σs = 2 accounts for the indistinguishability of the two nuclei in H2. Substituting these results in eq 22, we have
| (24a) |
The standard hydrogen electrode (SHE) is specified by [H+] = 1 M, T = 298 K, and a 1-atm pressure in the gas phase. The last two conditions correspond to [H2(g)] = 0.041 M according to the ideal gas law. At the standard conditions
| (24b) |
The ionization energy of H and the dissociation energy of H2 are 13.60 and 4.48 eV, respectively.91 The hydration energy of proton is −264 kcal/mol = −11.45 eV (with an uncertainty of approximately 5 kcal/mol).92 With these values, eqs 21 and 24b predict an SHE reduction potential of ψ0° = 4.52 V. A number of measurements and previous estimates put the value of ψ0° in the range 4.43–4.73 V.93 Measured against the SHE, the reduction potential Δψ° ≡ ψ° − ψ0° at standard state (with [A] = [A−] = 1 M) of A is then given by
| (25a) |
| (25b) |
Sometimes electron transfer is coupled to protonation, such as in iron-containing superoxide dismutase.94 In such a case one can in principle measure reduction potentials (Δψ°p and Δψ°u) for the protonated and unprotonated states separately. Similarly, one can also measure pKa’s (pKao and pKar) for the oxidized and reduced states separately. The four quantities are related by
| (26a) |
At a given pH, the protonation site will be partially protonated and partially unprotonated. The apparent reduction potential is given by
| (26b) |
In a protein, the accepted electron can be assumed to be distributed within a redox center. Then ΔEelectronic(A) refers to the gas-phase ionization energy of the redox center, while (S = A or A−) refers to the change in electrostatic energy of the oxidized or reduced redox center when it is moved from the gas phase to within the solvated protein matrix. This can be separated into two terms:
| (27) |
The first term arises from the change in solvent environment, whereas the second term arises from the interaction of the redox center with the charges in the protein matrix.
To illustrate, consider an electron-transfer protein modeled as a sphere with radius R that embeds a redox center, represented as a small sphere with radius a and a point charge q1 at the center (see Figure 4a). The charge q1 in the center changes from noxe to (nox − 1)e upon reduction. Let the redox center be located at a distance r1 from the center of the protein. If the redox center were directly located in the aqueous solution, its solvation energy would be given by the Born equation (eq 2b). When embedded in the protein, the solvation energy is given by eq 7. With a = 5 Å, R = 16 Å, and r1 = 10 Å, the desolvation cost of the redox center (upon moving from the aqueous solution to the protein matrix) is 3.9nox2 or 3.9(nox − 1)2 kcal/mol in the oxidized and reduced states, respectively. The difference, 3.9(2nox − 1) kcal/mol, can be either positive (when nox > 0.5) or negative (when nox < 0.5). For nox = 0, 1, and 2, the resulting change in reduction potential is −169, 169, and 506 mV, respectively.
Protein charges around the redox center also affect the reduction potential. For example, if a change q0 preexists at a radial distance r0 and a distance r10 from the redox center (see Figure 4a), the interaction energy between q0 and the redox center is given by eq 8. For r0 = 14 Å and r10 = 5 Å, the change in interaction energy from the reduced to the oxidized state is 6.7(q0/e) kcal/mol. This interaction will increase the reduction potential by 291 mV if q0 = +e and decrease the reduction potential by the same amount if q0 = −e.
In short, the reduction potential of a protein can be modulated by the nature of the redox center (affecting ΔEelectronic), the depth of burying the redox center (affecting the solvation energy), and the surrounding protein charges (affecting the interaction energy). These and related effects have been calculated in many studies.95–108
2.6. Folding Free Energy and Thermostability
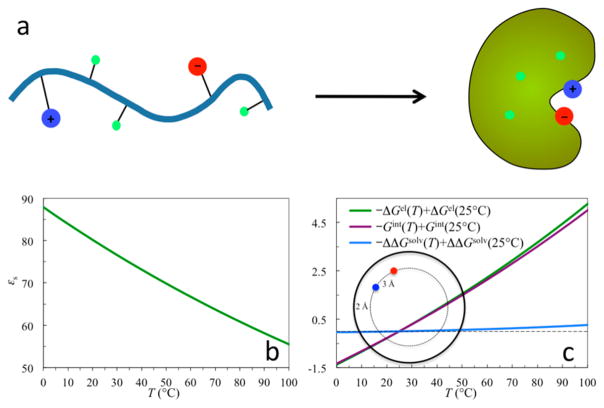
While hydrophobic interactions of nonpolar residues are a driving force for protein folding,6–10 electrostatic interactions of polar and charged residues can significantly modulate the folding stability. In the folded state, a protein molecule is compact; in the unfolded state, it samples vastly different conformations and has its groups (including charged ones) highly exposed to the solvent (Figure 6a). The charge–solvent and charge–charge interactions are thus very different in the two states. This difference contributes to the folding stability. If the individual residues are modeled as separately solvated in the unfolded state, then the electrostatic contribution to the folding free energy is
Figure 6.
(a) Model for protein folding. (b) Dielectric constant of water in the temperature range 0–100 °C. (c) Temperature dependences of the electrostatic energy (ΔGel) for forming 10 ion pairs upon folding a protein, the solvation cost (ΔΔGsolv), and the interaction energy (Gint). Each ion pair is modeled as two point charges +e and −e at a distance of 3 Å. The ion pairs are assumed not to interact with each other. Energies are given in kcal/mol and are relative to those at 25 °C.
| (28a) |
| (28b) |
where i and j refer to protein residues. The first term consists of the desolvation cost of individual residues, and the second term consists of their interactions in the folded state. Their interactions in the unfolded state are neglected for now, but will be addressed in section 4.1. The electrostatic contribution, , to binding stability of proteins can be similarly formulated.
The electrostatic contribution can be illustrated by modeling the folded protein as a sphere with radius R and each charged residue as an ion with radius a (see Figure 4a). The desolvation cost of the residue upon folding is the difference of eqs 7 and 2b. Figure 2a illustrates that the solvation energy (and hence the desolvation cost) rapidly decreases as the charged residue approaches the protein surface. The desolvation cost is 5.5 kcal/mol for a residue with charge q1 = ±e that is modeled as a sphere with a radius a = 2.5 and becomes buried at 2 Å from the surface of a protein with radius R = 16 Å.
Favorable interactions between charges compensate for the desolvation cost (see sections 2.7 and 4.2 for further discussion). For a pair of opposite charged residues with a distance of 3 Å and both at a radial distance of 14 Å, the interaction energy is −11.6 kcal/mol. This amount more than compensates for the desolvation cost of 2 × 5.5 = 11 kcal/mol. Thus, the net effect of pairing the two opposite charges upon folding is stabilization by 0.6 kcal/mol.
The message from these simple calculations is 2-fold. (i) The desolvation cost of a charged residue upon folding is sensitive to its exposure to the solvent in the folded state. (ii) Favorable interactions of charge pairs can overcome the desolvation cost and increase the folding stability.
Contribution of ion pairs (formed by oppositely charged residues at close range) to stabilization of thermophilic proteins over their mesophilic counterparts was first proposed by Perutz.29,109 Thermophilic proteins have much higher melting temperatures (e.g., close to or even above 100 °C). As the dielectric constant of water (εs) decreases significantly with temperature (Figure 6b),28 it may be anticipated that electrostatic interactions may be anticipated to have more favorable contributions to folding stability at higher temperatures. The enhanced contributions may come either by decreasing the desolvation cost110,111 or by strengthening the charge–charge interactions.112,113
Again let us illustrate using the Tanford–Kirkwood model (Figure 4a) the effect of high temperature on the effect of electrostatic contribution to folding stability, assuming that temperature only affects the dielectric constant of water. Figure 6c shows the temperature dependences of the desolvation cost, the interaction energy, and the net contribution to the folding free energy of 10 isolated ion pairs. It can be seen that the desolvation cost is nearly constant over the temperature range 0–100 °C. The interaction energy thus accounts for almost all the temperature dependence of the electrostatic contribution to the folding free energy.114 Note also that the net electrostatic contribution has a slight upward curvature as temperature increases. This feature will be further analyzed in section 4.3.
2.7. Numerical Poisson–Boltzmann and Generalized Born Models
In the previous sections the Tanford–Kirkwood model is used for qualitative illustration of electrostatic effects. For realistic calculations one can use the Poisson–Boltzmann (PB) model, in which the detailed protein surface is specified by the radii of the individual atoms and each atom is assigned a partial charge.115 Within the linearized PB equation, the electrostatic energy of the protein is
| (29) |
where qi are the atomic partial charges and are the electrostatic potentials at the atomic positions, with the prime indicating that the infinite self-potentials of the charges at their own positions are excluded. The PB model can only be solved numerically. A number of solvers based on a finite-difference representation of the PB equation, such as Delphi,30 UHBD,32 PBEQ,116 and APBS,117 are now widely used; an alternative, boundary-element approach, based on transforming the PB equation to an integral equation on the protein–solvent boundary, has undergone continued development.118–125
Even given all the atomic radii, there is still freedom in precisely specifying the dielectric boundary between the protein and the solvent (Figure 7a). The first obvious choice is the van der Waals (vdW) surface (consisting of the exposed surfaces of individual van der Waals spheres). Another choice, widely used and commonly referred to as the molecular surface, is the surface to which a spherical solvent probe, typically with a 1.4 Å radius, is excluded from the protein interior. It consists of contact and reentrant parts, as defined by Richards.126 For specificity this choice will be referred to as the solvent-exclusion (SE) surface. The vdW surface leaves interstitial voids as a part of the solvent high dielectric, which has been used as an argument against its use, since a spherical solvent probe will not be able to reach such voids if the protein structure is rigid. Of course proteins are not rigid, and water indeed can penetrate deeply into interior sites, as shown by NMR spectroscopy and molecular dynamics simulations.127,128
Figure 7.
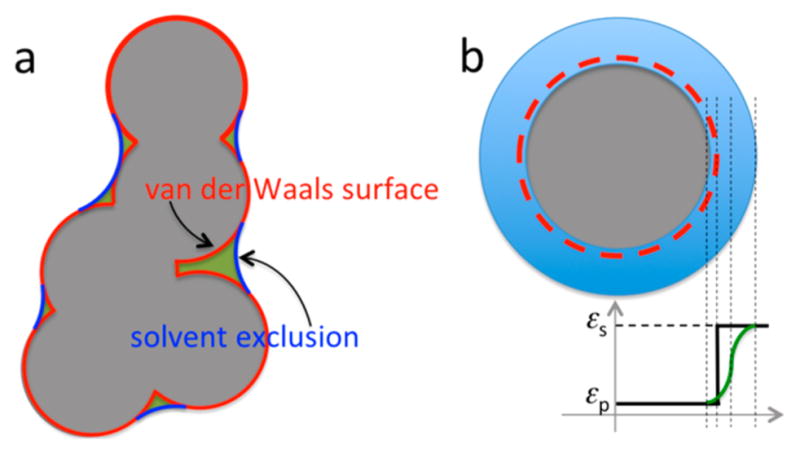
(a) Two different dielectric boundaries. The vdW protocol defines the gray shaded region as the solute dielectric; the SE protocol adds the crevices, shaded in green, not accessible to a spherical solvent probe to the solute dielectric. (b) Smoothed vdW dielectric boundary. From left to right, the first, third, and fourth vertical dashed lines indicate the start, midpoint, and end of the dielectric transition region; the second vertical dashed line indicates the location of the original atomic surface.
The issue of which surface to choose is important because calculation results are sensitive to the choice.129 Relative to the vdW protocol, the SE protocol apportions more regions as the protein low dielectric (Figure 7a); as a result protein charges are less solvent-exposed. Qualitatively we then expect the desolvation cost to be higher and the interaction energy to be stronger. However, the magnitude of the difference between the vdW and SE results was somewhat a surprise. For example, for a salt bridge formed by residues Arg69 and Asp93 in barnase, the desolvation cost and the interaction energy calculated according to the vdW surface were 2.86 and −4.52 kcal/mol, respectively, resulting in a favorable contribution of 1.66 kcal/mol to the folding stability. On the other hand, according to the SE surface, the desolvation cost and interaction energy were 8.23 and −8.45 kcal/mol, respectively, leading to a marginal effect on the folding stability. Because the substantial desolvation cost of SE-based PB calculations for burying charges in folded proteins and in protein–protein complexes is seldom completely compensated by favorable charge–charge interactions, a widely held view has been that electrostatic interactions affect either marginally or adversely protein folding and binding stability,130–132 although counter-examples have been presented.133
In light of the sensitivity of PB results on the choice of the dielectric boundary, this view, formed from a particular choice of the dielectric boundary (i.e., the SE surface), has been reassessed.129,134–139 For many protein complexes, , the electrostatic component of the binding free energy, has a positive sign in SE-based PB calculations, signifying net destabilization, but the sign becomes negative in vdW-based calculations.135,137,138 Unfortunately, the overall electrostatic component of the folding or binding free energy cannot be isolated from experimental measurements. However, effects of charge mutations, presumably dominated by the electrostatic component, can be measured and used to discriminate protocols of PB calculations. In a series of studies, effects of charge mutations on protein folding and binding free energies were predicted from vdW- and SE-based PB calculations. Consistently, better agreement with experimental data was achieved for the vdW-based calculations. In particular, the experimental coupling energy, −3.2 kcal/mol, for the Arg69–Asp93 salt bridge in barnase, obtained from a double mutant cycle analysis140 and, serving as a proxy for the interaction energy of the two charged residues, was accurately reproduced by the vdW-based calculations but overestimated by more than 2-fold by the SE-based calculations.129
The apparently overestimated charge–charge interaction energies by SE-based PB calculations led to overly perturbed predicted pKa’s, which in turn led to a “fix” using an inflated value of 20 for the protein dielectric constant εp.141 The inflated εp has a similar effect as the interstitial solvent high dielectric voids found in the vdW-based protocol. In particular, from SE-based PB calculations switched sign (from positive to negative) for many protein complexes when εp was increased from 4 to 20.135,137 For 8 out of 12 mesophilic and thermophilic proteins, from SE-based PB calculations underwent a similar sign switch.142
A computationally cheaper version of the PB model is the generalized Born (GB) model.143 The model was originally developed for the absence of salt ions (i.e., κ = 0), and the solvation and interaction energies have the form (cf. eqs 7 and 8)
| (30a) |
| (30b) |
with
| (30c) |
The parameter bi in eq 30a mimics the radius of a Born ion and is referred to as the Born radius. In theory it should be found by minimizing the discrepancy between eq 30a and the solvation energy given by the PB model. The function fij was designed to approach the correct limits at rij = 0 (which corresponds to two overlapping charges, hence fij = bi = bj) and at rij = ∞ (which corresponds to two infinitely separated charges, hence fij = rij; see eq 5 with κ = 0). For a spherical protein, it has been shown that the Tanford–Kirkwood model leads to fij ≈ (rij2 + bibj)1/2.144 A number of methods have been developed for practical calculations of the Born radii and the overall electrostatic energy of proteins.145–154 In calculating the Born radii, many GB methods defined the dielectric boundary as the vdW surface;155 some were then reparametrized to match PB results calculated using the SE surface.148,152 The low computational cost of the GB model has been used to accelerate molecular dynamics simulations of biomolecules, 156–161 in particular to study protonation/deprotonation of ionizable groups at constant pH.162–165
As alluded to above, vdW- and SE-based PB results can be brought into agreement when different εp values are used for the two protocols. Agreement can also be achieved by using different atomic radii in defining the respective dielectric boundaries. When the SE protocol was used as the benchmark, the required inflation in atomic radii for the vdW protocol was investigated for 55 proteins (with the number of atoms ranging from 145 to 3564) and for the 20 types of amino acids (with the number of atoms ranging from 6 to 24).166 The amounts of inflation (from Bondi radii167 used for SE-based PB calculations) were mostly within 10–20% for the proteins but 2–5% for the amino acids. The greater inflation for the proteins reflects the increasing tendency of the larger molecules to contain interstitial voids that are eliminated by the SE surface. The dependence of the extent of atomic radius inflation on solute size (and other factors such as compactness of the solute structure) raises caution about transferring parameters obtained from small molecules to proteins. For example, as mentioned in the preceding paragraph, some GB methods defined the dielectric boundary as the vdW surface in calculating the Born radii but were then reparametrized to match SE-based PB results.148,152 It is possible that reparametrizations that work for small molecules may not work for proteins and vice versa. A similar problem may arise when the GB and PB models are parametrized against solvation energies, generally available only for small molecules, either from experimental measurements145,168 or from free energy calculations in explicit-solvent molecular dynamics simulations (see section 2.8). The differences in atomic radii parametrized on such data are likely to be relative small (e.g., <5%) between the vdW and SE protocols. However, using these respective radii, the vdW and SE protocols may lead to very divergent predictions for the solvation energies of proteins.
The dielectric boundary defined above (Figure 7a) represents a discontinuity in the dielectric constant, which jumps from εp in the solute region to εs in the solvent region. This discontinuity can give rise to large changes in the electrostatic energy from small changes in the solute structure, and result in ill-defined derivatives (as when calculating forces on solute atoms in molecular dynamics simulations). These and other considerations have led to the development of dielectric boundaries that feature a smooth transition in the dielectric constant from εp to εs.116,169–171 In essence, the width of the dielectric boundary is stretched from zero to a finite (but still relatively small) value. In particular, transition functions based on overlapping atom-centered polynomials or Gaussians have been proposed by Im et al.116 and Grant et al.,169 respectively; when the width of Im et al.’s transition function is reduced to zero, one recovers the vdW surface (Figure 7b). Even with a finite width, these atom-centered transition functions can still leave interstitial voids as part of the high dielectric region; in this sense these smoothed dielectric boundaries are qualitatively similar to the vdW surface and are referred to hereafter as smoothed vdW or smvdW. To reproduce the original vdW-based PB results, the starting point, not the midpoint, of Im et al.’s transition function needs to be located near the atomic surfaces172 (Figure 7b). The nominal atomic radii, defined by the midpoint of the transition region, are thus increased from the original atomic radii by an amount nearly equal to the half-width of the transition region.
The work of Dzubiella et al.170 and Chen et al.171 deserves special mentioning, because these authors self-consistently determine the solute–solvent boundary, by minimizing free energy functionals. Moreover, these functionals represent the total free energy, including both electrostatic and nonelectrostatic terms, and therefore potential coupling between electrostatic and nonelectrostatic effects can be accounted for.
The PB equation is based on a crude mean-field approximation for the mobile ions in the solvent. It has been extended by numerous authors, to account for, e.g., correlations, sizes, and dielectric images of the mobile ions.173–185 Some of these extensions predict the interesting result that mediation by polyvalent counterions can lead to attraction between like-charged macromolecules. This result may help explain DNA condensation, with possible implications for genome packaging. However, explicit-solvent molecular dynamics simulations reveal that ions exhibit a wide range of behaviors around charged molecular surfaces, from tightly bound to loosely bound to diffuse.186–189 It is not clear whether even these extended implicit-solvent models can adequately capture all these details, though progress is continuously made.
2.8. Explicit-Solvent Molecular Dynamics Simulations
The electrostatic energy given by eq 29 is the work required for charging the solute in the dielectric environment (and hence a free energy). When charges are created in a dielectric medium, the resulting electric field polarizes the medium. The work can be obtained through a charging process in which the solute atomic charges are changed gradually from 0 to the final values qi. At a particular point along the charging process, the atomic charges have values λqi, with λ changing from 0 to 1. If the corresponding electrostatic potential (excluding the self-potential) has values at the atomic positions, then the total work of charging is
| (31) |
Equation 29 is obtained if linear response (i.e., ) is assumed, although nonlinearity has been shown by some explicit-solvent molecular dynamics simulations.190 In general, there are two mechanisms to dielectric polarization: electronic polarization via distortion of electronic distribution (see section 2.9) and dipole (actually multipole) reorientation involving atomic and molecular motions. When the PB model is used for a protein with fixed (i.e., permanent) atomic charges and a rigid structure, neither mechanism of solute polarization is treated explicitly. Rather, their effects are supposed to be accounted for by the protein dielectric constant εp. The effects of solvent polarization are of course implicitly accounted for by the solvent dielectric constant εs.
A similar charging process can be used to calculate the free energy Gel from explicit-solvent molecular dynamics simulations. If the potential energy of the system (solute plus solvent) is U(λ) when the solute atomic charges have values λqi, then
| (32) |
where 〈···〉λ denotes averaging for the system with solute atomic charges λqi. This calculation of Gel provides a way to directly test and parametrize the PB model, as done in a number of studies.191–198 To facilitate the test, the solute molecules were usually made rigid in the explicit-solvent simulations, so the same solute structures could be used in the corresponding calculations for the PB model. The molecular mechanics force fields in these studies were nonpolarizable; i.e., electronic polarization was lacking. The use of rigid solute structures and lack of electronic polarization mean that neither of the mechanisms of dielectric polarization was operative for the solutes in the explicit-solvent simulations. Accordingly the appropriate solute dielectric constant should be 1 in the corresponding PB calculations.
Jean-Charles et al.191 were the first to make this type of direct comparison between implicit and explicit solvent models. They found a good match in Gel (or rather, the solvation component ΔGsolv; see eq 9b) for 20 small molecules (including a dipeptide in three different conformations) between explicit-solvent and SE-based PB calculations with atomic radii inflated by 12% from the Lennard-Jones radii (i.e., σ/2) in the explicit-solvent force field.
In the study of Nina et al.,192 covering 20 dipeptides, the atomic radii for vdW-based PB calculations were initially chosen as the largest radial distances at which solvent charge densities were still negligible in explicit-solvent simulations. These solvent charge density based atomic radii (e.g., 2.04 Å for carbonyl carbon of the peptide backbone) were overall larger than typical van der Waals radii (e.g., Bondi radius of 1.7 Å for any carbon). Optimal agreement of vdW-based PB ΔGsolv results with their explicit-solvent counterparts was achieved after only slight adjustments from these initial values for the atomic radii. The explicit-solvent results could also be reproduced by SE-based PB calculations if the atomic radii were reduced by 2%. As commented in section 2.7, the offsets in atomic radii between vdW- and SE-based calculations depend on solute size, and the 2% reduction is a reflection of the small solutes studied by these authors. Lastly, the explicit-solvent results could be reproduced by smvdW-based PB calculations, provided, as noted in section 2.7, that the nominal atomic radii were increased by an amount close to the half-width of the transition region.172
That the appropriate atomic radii for generating the dielectric boundary (of the vdW type) were larger than typical van der Waals radii was previously suggested by Luque et al.,199 also based on solvent distribution functions around solute molecules in explicit-solvent simulations. Specifically, from the locations of the first peak in the water oxygen distribution functions, Luque et al. reasoned that the suitable atomic radii for generating the dielectric boundary should be 1.2 times those of van der Waals radii. The interest of these authors is in the quantum mechanical treatment of (small) solutes in a PB (continuum) model for the solvent, to account for solute electronic polarization (see section 2.9). In these so-called quantum mechanical continuum solvation models, it is common practice to use the vdW-type dielectric boundary and apply an inflation factor of 1.2 for the atomic radii.200,201
Swanson et al.195 extended the study of Nina et al.,192 choosing to match explicit-solvent simulation results with smvdW-based PB calculations on ΔGsolv for short peptides. The transferability of these optimized radii seemed poor, as much greater mismatch between explicit- and implicit-solvent results were found for peptides not used for the atomic radius optimization.
The smvdW dielectric boundary allows for the calculation of forces on solute atoms.116 Wagoner et al.202 showed that these solvent-averaged mean forces, in contrast to the solvation energy, can be easily calculated for large protein molecules in explicit-solvent simulations. Solvation forces thus open the door for explicit-solvent simulations of large proteins to be used for parametrizing the PB model. With the inclusion of solvation forces in atomic radius optimization, Swanson et al.197 found improved parameter transferability for short peptides but still “limitations for highly solvated protein systems”.
Onufriev and Aguilar198 expanded the comparison of explicitand implicit-solvent ΔGsolv results from small molecules and short peptides to small proteins (around 30 residues). Starting from Bondi radii,167 they found vdW-based PB results with uniform 0.2 Å inflation of atomic radii performed as well as or better than SE-based PB results with the common 1.4-Å probe radius in reproducing explicit-solvent results. However, even when Gel values matched, partitioning into the self-terms and interactions terms (see eq 9a) differed significantly between the vdW and SE protocols for a small protein (though not for a small molecule). As discussed in section 2.7, protein atoms are less solvent-exposed in the SE protocol, hence smaller magnitudes for the self-terms are predicted along with larger magnitudes for the interaction terms. The latter could lead to overestimation of coupling energies of salt bridges and overly perturbed pKa’s in proteins.
Several studies195,196 also targeted the pair potential of mean force, i.e., the electrostatic energy of a pair of polar or charged small molecules over a range of intermolecular distances. The SE protocol produces a low dielectric intermolecular region when the intermolecular separation is about half the solvent probe diameter (i.e., too narrow to fully accommodate the solvent probe). The resulting low magnitudes of the self-terms of the electrostatic energy can lead to a barrier in the potential of mean force. The superficial resemblance of this barrier to those in potentials of mean force from explicit-solvent simulations has been used as a support for the SE protocol.194 However, it should be pointed out that, while the barrier in the SE protocol has a purely electrostatic origin, the actual potentials of mean force of all molecules, polar or nonpolar, are oscillatory, with not just one but a series of barriers separated at distances roughly equal to the solvent diameter. The origin of these barriers is entropic, due to the packing of solvent molecules around the pair of solute molecules, as well illustrated by the hard-sphere liquid. Of course, for polar or charged solutes solvated by water, electrostatic interactions can accentuate the barriers and minima in the potentials of mean force.
The explicit-solvent simulations discussed above lacked electronic polarization and used rigid solute structures, partly to facilitate direct comparison with PB calculations. Real proteins respond to the creation of charges by both electronic polarization and atomic displacements, giving rising to an εp that is greater than 1. The benchmarking of the PB model against explicit-solvent simulations with electronic polarization and flexible solute molecules (see section 2.9) is largely untouched. A study193 in which charging energies were calculated for peptides bound to a protein presents a glimpse into the added complexity. When the protein, which was really part of the solvent as far as the peptide solutes were concerned, was allowed to relax in the explicit-solvent simulations, water exposure of the peptides was increased. Therefore, change in water exposure would likely conflate the dielectric response of solute molecules.
A final note of caution on explicit-solvent simulations is that there is no consensus on an explicit water model, and ΔGsolv values calculated using different water models differ significantly.203 Therefore, despite the much higher computational cost, explicit-solvent simulations suffer from high sensitivity to model parametrization, just like PB and other implicit-solvent calculations.
2.9. Electronic Polarization
Of the two mechanisms of dielectric polarization, molecular dynamics simulations with nonpolarizable force fields account for dipole reorientation but neglect electronic polarization. For proteins, dipole reorientation is limited (in comparison to a small polar molecule like water) and hence the contribution of electronic polarization becomes important.
2.9.1. Onsager Model
Let us illustrate the effect of solute electronic polarization using the Onsager model,62 consisting of a polarizable dipole at the center of a spherical solute cavity with (radius R) in a dielectric continuum solvent. If the solute molecule has permanent dipole moment p0 and polarizability α, then in the solvent its total dipole moment is the sum of the permanent dipole moment and the induced dipole moment:
| (33a) |
| (33b) |
where ER is the reaction field, due to solvent polarization by the dipole p. The reaction field is
| (33c) |
Combining these two equations, we find
| (33d) |
Electronic polarization thus effectively increases the magnitude of the dipole moment. The energy of the dipole due to the solute–solvent mutual polarization is
| (33e) |
Compared to the corresponding result for a nonpolarizable dipole given in eq 9c, the magnitude of the energy is increased, by the same factor, p/p0, that the dipole moment is increased.
In nonpolarizable force fields, atomic partial charges are typically inflated to compensate for the lack of electronic polarization. For example, partial charges for neutral polar groups are scaled up by a factor of 1.16 in the CHARMM force field.204 However, as recognized by Berendsen et al.,205 treating the inflated charges as permanent charges results in an erroneous expression for the electrostatic energy. For example, if the total dipole moment p in the Onsager model were treated as permanent charges, then the energy would be given by eq 9c but with p0 replaced by p. The resulting energy would be an increase from that for the original permanent dipole p0 by a factor of (p/p0)2. The discrepancy from the correct result in eq 33e is
| (33f) |
This correction is typically not included in nonpolarizable force field.
The correction in eq 33f is but an indication of the many subtleties of dielectric polarization. Onsager is known to have said, “The theory of dielectrics has more booby traps than a Gamma function has poles.”206
2.9.2. Quantum Mechanical Treatment of Electronic Polarization for Continuum Solvent
In the Onsager model the polarizability appears as a parameter that requires specification. This requirement is eliminated when the solute electronic polarization is treated quantum mechanically. The quantum mechanical problem for the solute electrons and the resulting solvent polarization need to be solved self-consistently. 200,201,207–209 The solution can be obtained through an iterative process.
The iteration starts with the gas-phase Hamiltonian of the solute ℋ0(x; X), where x and X refer to the electron and nucleus coordinates, respectively; the latter are fixed according to the Born–Oppenheimer approximation. Solution of the Schrödinger equation yields the ground-state energy E0(X) and the corresponding wave function Ψ0(x;X). From the latter, the charge density in the solute can be found:
| (34) |
where Zi are nuclear charges (in units of the proton charge). The “reaction” potential, , due to solvent polarization by the solute charge density can then be obtained from solving the PB equation, in particular by the boundary-element approach.200,201 Approximations based on treating the solute dielectric cavity as spherical along with a multipole expansion of the reaction potential (cf. eq 8)207,208 and based on the GB model (cf. eq 30b)209 have also been made. The potential energy arising from the reaction potential acting on the solute charge density
| (35) |
is then added to the initial Hamiltonian ℋ0(x; X), and a new wave function is obtained. This process is repeated until convergence. Let the final converged quantities be denoted by a subscript “f”. Assuming solvent response, the electrostatic solvation energy of the electronically polarized solute is
| (36a) |
| (36b) |
The results from the foregoing approach can be used to parametrize electronic polarizability. The model as presented has fixed nuclei, and thus does not treat the other mechanism of dipolar polarization, i.e., dipole reorientation. The computational cost of the quantum calculations also precludes applications to large molecules such as proteins. Both of these limitations are lifted in the models presented next.
2.9.3. Classical Treatment for Explicit Solvent
A number of ideas have been presented to model electronic polarization classically, thus enabling molecular dynamics simulations of proteins in explicit solvent.210–214 The model developed by Ren and Ponder,211 based on using atomic induced dipoles, is particularly appealing and is outlined here.
Suppose that an external electric field E(r) is applied to a molecular system, in which atom i possesses polarizability αi. Each induced dipole generates an additional electric field, which acts to induce dipoles at all the other atoms. The induced dipole pi is proportional to the total electric field at atom i, which includes both the external field E(ri) and the fields generated by all other induced dipoles. The electric field at atom i due to an induced dipole pj at atom j can be written as 𝒮̃ij·pj. In a vacuum, one has
| (37) |
where ℐ̃ is a 3 × 3 identity matrix. Adding up all the contributions to the total electric field, one finds
| (38) |
This equation is a self-consistent relation for determining the induced dipoles.
Now suppose that the electric field E arises from the permanent charges (and higher permanent multiples) on the atoms. In particular, for point charges in vacuum215
| (39) |
The change in electrostatic energy due to electronic polarization is
| (40) |
The foregoing model has been implemented in the AMOEBA polarizable force field.216
3. SPATIAL DISTRIBUTIONS OF CHARGED RESIDUES
The amino acid sequences of proteins result from evolution for function, subject to the constraints of physical laws. The energetics of charged residues interacting among themselves and with other polar groups and the solvent environment influence how the charged residues are spatially distributed in proteins and their complexes. Charged residues are present in proteins for many functional reasons, including solubility, prevention of aggregation, and interactions with different partners. These functional roles also affect the spatial distributions of charged residues.
Below we detail a variety of characteristics observed for the spatial distributions of charged residues in different types of proteins (structured versus intrinsically disordered; water-soluble versus transmembrane), and in interfaces formed by proteins with different types of partners (membranes, other proteins, and nucleic acids). We also briefly discuss residues that become charged by phosphorylation.
3.1. Water-Soluble Proteins
It is now widely accepted that hydrophobic interactions serve as a driving force for protein folding stability.6–10 For water-soluble proteins, the burial of nonpolar side chains in protein cores is well appreciated as a result of hydrophobic interactions. It should also be appreciated that charged side chains are usually found in protein surfaces to avoid considerable desolvation cost. For example, modeling a charged side chain and a folded protein as dielectric cavities with radii of 3 and 16 Å, respectively, we can estimate a desolvation cost of 10.7 kcal/mol upon burying the charged side chain at the center of the protein. In comparison, the energy cost for exposing a nonpolar side chain can be estimated to be 2.5 kcal/mol using a surface area of 100 Å2 and a solvation parameter of 25 cal/mol/Å2.217,218 It stands to reason that avoidance of burial by charged side chains may rival avoidance of exposure by nonpolar side chains in contributing to the stability of the folded structures of water-soluble proteins.
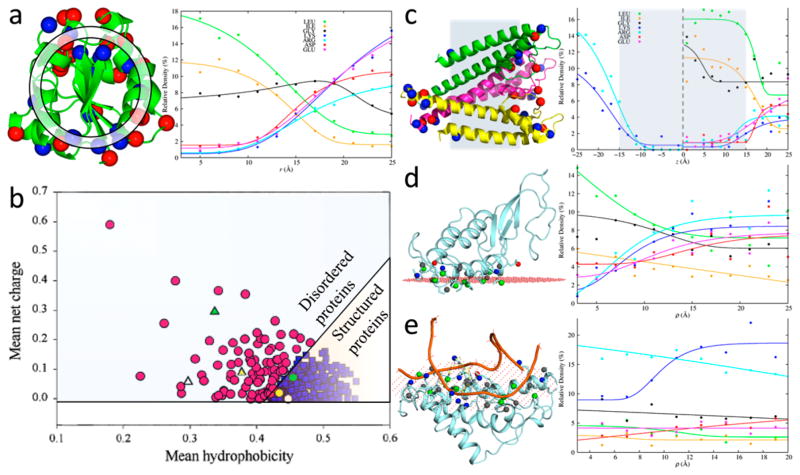
The foregoing opposite trends of the spatial distributions of nonpolar and charged side chains in the structures of globular water-soluble proteins were quantified by Vijayakumar and Zhou.219 These authors calculated the radial distributions of the 20 types of side chains in a set of globular proteins (Figure 8a, left panel). In these calculations, each protein was divided into spherical shells centered at the center of geometry; the radial distances of all the side chains, each represented by a single “tip” atom (e.g., Nζ atom for Lys but Cα for Gly), were then used to identify the spherical shells where they were located. The relative density of each type of side chain in a given shell was finally obtained as the ratio of the total number of that type of side chains (accumulated over all the proteins in the set) to the total number of all side chains in the same shell.
Figure 8.
Spatial distributions and compositions of residues in different types of proteins and interfaces. (a) Relative densities of residues along the radial distance in water-soluble proteins. (left) Basic and acidic residues are displayed as blue and red spheres, respectively; a spherical shell used for defining relative density is shown. (right) r dependences of relative densities of nonpolar, Gly, and charged residues. (b) Separation of intrinsically disordered proteins from structured proteins according to hydrophobicity and net charge, by the line q̄ = 2.785h̄ − 1.151. Adapted with permission from ref 221. Copyright 2000 John Wiley & Sons Ltd. (c) Relative densities of residues along the membrane normal in α-helical transmembrane proteins. (left) Basic and acidic residues are displayed as blue and red spheres, respectively; shaded region indicates the membrane hydrophobic core. (right) z dependences of relative densities of nonpolar, Gly, and charged residues. (d) Relative densities of residues along the two-dimensional radial distance ρ in protein–membrane interfaces. (left) Interfacial side chains are displayed as sticks, with tip atoms of basic, acidic, nonpolar, and other residues displayed as blue, red, green, and gray spheres, respectively; the membrane hydrocarbon boundary plane (as calculated in the OPM database222) is represented by red dots. (right) ρ dependences of relative densities of nonpolar, Gly, and charged residues. (e) Similar results for protein–nucleic acid interfaces.
The radial distributions are protein-size dependent. In Figure 8a, right panel, we display the results for six types of side chains, calculated here on 507 proteins with radii of gyration between 13 and 17 Å (taken from a larger nonredundant set of globular proteins with high-resolution structures220). These results largely recapitulate those calculated previously on a smaller set of 85 proteins.219 Specifically, for nonpolar side chains (as represented by Leu and Ile; not shown for Val, Phe, Met, Cys, and Ala) and for Trp, the radial distributions decay sharply as a function of the radial distance r. In contrast, for charged side chains (Lys, Arg, Glu, and Asp), the radial distributions are a sharply growing function of r. The latter trend is also true for polar side chains Asn, Gln, and Ser and for Pro. The radial distributions of other side chains (as represented by Gly; not shown for Thr, His, and Tyr) are more uniform.
Vijayakumar and Zhou also extended the analysis to residue–residue pairs, following earlier developments.223–225 Compared to an appropriately scrambled reference, both nonpolar pairs (e.g., Leu–Ile) and oppositely charged pairs (e.g., Lys–Asp) are clearly enriched at short tip–tip distances (around 4 and 2.75 Å, respectively). Both may serve to stabilize the folded structures. Similar ideas have been used to develop residue–residue statistical pair potentials for protein structure prediction.226–229
3.2. Intrinsically Disordered Proteins
Since the 1990s, proteins (or regions thereof) that do not autonomously fold into well-defined three-dimensional structures have gained ever-increasing attention.230–237 It is estimated that some 30% of eukaryotic proteins either are wholly intrinsically disordered or contain intrinsically disordered regions.233 These intrinsically disordered proteins/regions (IDPs/IDRs) are heavily involved in transcription regulation and signal transduction, through binding to macromolecular targets, whereupon they often (but not always) undergo disorder-to-order transitions. Not surprisingly, IDPs are also associated with numerous diseases.233,238,239 Early on it was recognized that IDPs/IDRs have sequence characteristics that are distinct from structured proteins, and these distinctions have formed the basis of many machine-learning programs that predict disordered regions.240
An insightful observation by Uversky et al.221 is that IDPs are characterized by low hydrophobicity and high net charge (Figure 8b). In the plane defined by mean hydrophobicity h̄ and mean net charge q̄, the line q̄ = 2.785h̄ − 1.151 can separate IDPs from structured proteins. Apparently, both reduced hydrophobic interactions (due to low h̄) and increased desolvation cost and charge–charge repulsion (due to high q̄) are important for maintaining structural disorder. The charge-mediated effects are also likely crucial in mitigating aggregation, for which IDPs would otherwise have a heightened propensity.
Several recent studies have shown that the sizes (as measured by, e.g., the radius of gyration) of IDPs expand as the net charge per residue increases, when results for IDPs of different sequences or for the same IDP at different pHs or with and without phosphorylation are compared.241–246 Moreover, salt effects suggest that charge–charge repulsion can result in significant size expansion at high q̄, but charge–charge attraction can lead to size contraction at low q̄.242,245 The contraction is especially notable for sequences with oppositely charged blocks, which lead to strong charge–charge attraction and hairpin-like conformations.243
When IDPs undergo disorder-to-order transitions upon binding macromolecular targets, the resulting conformations are often extended, suggesting that they rely more on intermolecular interactions and less on intra-molecular interactions for structural stability.231,232,247,248 These features influence the mechanism of the coupled binding and folding process of IDPs (see section 6.2.3 for further discussion).
Like the interfaces formed by structured protein pairs (see section 3.4.2), the interfaces formed by IDPs and their partner proteins have higher levels of nonpolar residues around the center than at the rim and the opposite is true for charged and polar residues.249 Intuitively, it seems obvious that the resulting electrostatic interactions should stabilize the protein complexes. However, a recent study249 has again used SE-based PB calculations to propagate the view that favorable charge–charge interactions are hardly sufficient to compensate for the desolvation cost of burying charges at protein–protein interfaces. Electrostatic contributions to binding stability and kinetics will be addressed in later sections.
3.3. Transmembrane Proteins
Transmembrane proteins play a central role in many cellular activities, including signal transduction and transport of ions and small molecules across membranes, energy conversion (as, e.g., in photosynthesis), and intercellular communication. About 20–30% of all genes in most genomes are estimated to encode α-helical transmembrane proteins,250 yet approximately 60% of drug targets are membrane-associated.251,252 Prominent among them are G-protein coupled receptors (GPCRs), ligand-gated ion channels, and voltage-gated ion channels.
Anfinsen is often misquoted as stating that the amino acid sequence alone dictates the structure of a protein. Rather, Anfinsen’s thermodynamic hypothesis stated that “the three-dimensional structure of a native protein in its normal physiological milieu (solvent, pH, ionic strength, presence of other components such as metal ions or prosthetic groups, temperature, etc.) is the one in which the Gibbs free energy of the whole system is lowest; that is that the native conformation is determined by the totality of interatomic interactions and hence by the amino acid sequence, in a given environment.”253 The solvent environment is as important for the structures of transmembrane proteins as for the structures of water-soluble proteins. Indeed, lipid bilayers that constitute the heterogeneous solvent environment of transmembrane proteins possess unique biophysical properties; membrane mimetics such as detergents used for sample preparations in structure determination may not model well these biophysical properties and consequently lead to protein structure distortions.254 Most notable among the unique biophysical properties of lipid bilayers are a sharp variation in dielectric constant, from a value of approximately 2 in the hydrocarbon core of bilayers, to approximately 5 in the carbonyl/glycerol regions, to approximately 150 in the headgroup regions, and finally to 80 in the aqueous phase,23,24 and corresponding sharp variations in hydrophobicity and in water density.255
The heterogeneous environment in lipid bilayers impacts the sequence and structure as well as positioning and orientation of a membrane protein. Nonpolar side chains should be favored in the hydrocarbon core of lipid bilayers, whereas charged and polar side chains should be favored in the carbonyl/glycerol and headgroup regions. Therefore, amino acid sequences are expected to be characterized by motifs consisting of stretches of (about 10–30) nonpolar residues flanked by polar and charged residues. Most transmembrane proteins form α-helix bundles, but some form β-barrels and are located in outer membranes of bacteria, mitochondria, and chloroplasts. Many machine-learning programs have exploited the sequence characteristics of transmembrane proteins to predict secondary structures.256
The two leaflets of cell membranes are asymmetric, and nearly all transmembrane proteins have a defined orientation (often referred to as topology) with respect to the membranes. It was observed by von Heijne257 quite early that positively charged residues are more frequently found on the cytoplasmic side, compared to the noncytoplasmic side. This so-called positive-inside rule is the basis of topology prediction.256 Why it holds is not fully understood; part of the reason may be interactions between basic side chains and anionic phospholipid headgroups.258 As supporting evidence, the introduction of basic residues was able to invert the orientation of a protein in the Escherichia coli inner membrane, but the propensity of inversion decreased with decreasing level of anionic phospholipids. 259 Interestingly, in both the plasma membrane and the membranes of some intracellular organelles of eukaryotic cells, anionic phospholipids are enriched in the cytoplasmic leaflet.260
Ulmschneider et al.261 carried out detailed analysis on the spatial distributions of the 20 types of amino acids in 46 α-helical transmembrane protein structures. Consistent with expectations, the hydrocarbon core of membranes is over-populated by nonpolar side chains, underpopulated by long polar side chains, and severely so by charged side chains. Outside the hydrocarbon core, acidic residues Asp and Glu occur on both sides of membranes to similar extents, but basic residues Lys and Arg, the latter especially, show preference for the cytoplasmic side, in line with the positive-inside rule. These conclusions are confirmed by Schramm et al.262 and also here (Figure 8c) by a similar analysis on 26 α-helical transmembrane protein structures that were previously assessed to be native-like (i.e., free of overt distortions by membrane mimetics in structure determination).263 The transmembrane domains were oriented to maximize the sum of the distances of charged residues from the membrane central plane;263 others chose to minimize either the sum of the tilt angles of transmembrane helices261 or an implicit solvation energy function called PPM (positioning of proteins in membranes), in which burials of nonpolar and charged residues in the membrane hydrophobic core are rewarded and penalized, respectively.264 Comparing parts a and c of Figure 8, the distributions along the radial direction in water-soluble globular proteins and along the membrane normal in α-helical transmembrane proteins show clear resemblance for both charged and nonpolar side chains. However, relative to the core (radial distance <15 Å) of water-soluble proteins, in the membrane hydrophobic core (|z| < 15 Å) charged side chains appear to be further depleted and nonpolar side chains (Leu in particular) elevated, consistent with the exceedingly low water density there.24,255 Gly residues are also enriched in the |z| < 15 Å region, often involved in tight helix–helix packing (and hence not exposed to the lipid hydrocarbon tails).263
Recently, Slusky and Dunbrack,265 following an earlier study,266 found that β-barrel proteins in bacterial outer membranes also exhibit charge asymmetry. Charged residues, both basic and acidic, on the lipid-facing surface occur on the extracellular side three times as frequently as on the periplasmic side. Moreover, this charge asymmetry correlates with the higher hydrophilicty of the outer leaflet of the outer membranes.
In addition to dictating the orientation of membrane proteins, charged residues, by their strong preference for the carbonyl/glycerol and headgroup regions, are also a determinant for the positioning of membrane proteins along the membrane normal, working in concert with Trp and Tyr, which favor the carbonyl/glycerol regions. Monne et al.267 investigated the effects of introducing charged residues to a model nonpolar transmembrane helix on membrane positioning. Asp and Glu mutations in the C-terminal two turns of the helix expectedly led to movements of the helix toward the membrane–water interface, but more centrally placed Asp and Glu had little effect, possibly due to charge neutralization via protonation. In contrast, Lys and Arg mutations in the C-terminal two turn had little effect, and more centrally placed basic residues led to moderate movements of the helix toward the membrane–water interface; these observations could be explained by the long basic side chains snorkeling into the carbonyl/glycerol and headgroup regions.268 An isolated transmembrane helix may also be able to change its tilt angle to help move its charges out of the hydrocarbon core.
Charged residues may also be positioned in transmembrane proteins to serve functional purposes. Specifically, residues around permeation pathway entrances and with charges opposite to the permeant ions have been suggested to facilitate transport in many ion channel and transporter proteins. Examples are the KcsA K+ channel (Figure 8c, left panel),269 the NhaA Na+/H+ antiporter,14 and a CLC transporter.15
3.4. Binding Interfaces
3.4.1. Protein–Membrane Complexes
Peripheral membrane proteins reversibly bind to membrane surfaces (e.g., for targeting membrane-bound ligands) or to outer regions of transmembrane proteins (e.g., for regulating transmembrane receptors such as GPCRs and ion channels, and for participating in the transient assembly of other membrane-associated protein complexes). As an example, the highly water-soluble protein cytochrome c can, through interaction with the mitochondrial phospholipid cardiolipin, associate with the outer leaflet of the mitochondrial inner membrane, where it shuttles electrons from the cytochrome bc1 complex to cytochrome c oxidase, leading to a proton gradient across the inner membrane that powers the synthesis of ATP. Elevation in the concentration of mitochondrial reactive oxygen species enhances the peroxidase activity of cardiolipin-bound cytochrome c. The resulting oxidation of cardiolipin and release of cytochrome c from the intermembrane space into the cytoplasm start the apoptotic process. The cytochrome c–cardiolipin interaction has a strong electrostatic component, as implicated by the opposite charges on the two molecules and the diminished strength at increasing salt concentration.270 Electrostatic interactions, in particular between basic residues (or bound Ca2+ ions) and anionic phospholipid headgroups, contribute to the subcellular targeting of many other peripheral membrane proteins.40,271
Lomize et al.272 used their PPM solvation energy function to calculate the orientations and depths of peripheral membrane proteins, relative to a plane coinciding with the boundary of the membrane hydrocarbon core (which is approximately 5 Å beneath the phosphate atoms). According to these calculations, nonpolar side chains can penetrate into the membrane hydrophobic core whereas charged side chains stay atop to interact with the lipid headgroups (Figure 8d, left panel).
To gain a general sense on the spatial distribution of amino acids in the protein–membrane interfaces, here we collected 329 representative peripheral membrane protein structures from the OPM database (one from each family in the “monotopic/peripheral” type).222 Tip atoms within 5 Å of the hydrocarbon boundary plane and on the protein surface (i.e., with greater than 15% solvent exposure, based on the NACCESS program273) were identified as interfacial. The interfacial tip atoms of some proteins formed two or three separate patches (based on manual inspection). For each of the 355 interfacial patches, distances (denoted as ρ) to the membrane normal passing through the center of geometry were calculated for the tip atoms. Figure 8d, right panel, displays the relative densities of four charged residues, two nonpolar residues, and Gly along ρ. The opposite trends between charged and nonpolar residues seen in Figure 8a,c are again seen along ρ, though the increases and decreases here are more gradual. The moderated dependence on ρ can be attributed to the fact that peripheral membrane proteins are not permanently bound to the membrane surface, but exchange between the membrane surface and an aqueous environment. In the latter environment, the charged side chains are solvent-exposed whether it is at the center or the rim of a membrane-binding patch.
As already alluded to, interfacial charged side chains are overwhelmingly located on the side of the boundary plane distal to the membrane hydrocarbon core. Compared to elsewhere of the protein surface, a membrane-binding patch typically has higher levels of nonpolar residues and lower levels of charged residues. Whereas oppositely charged residues are roughly equal in numbers in water-soluble proteins (Figure 8a), basic residues outnumber acidic ones in the membrane-binding patches of peripheral membrane proteins (Figure 8d), possibly because many of them target anionic phospholipids. Basic residues may contribute to membrane binding stability and may be especially important for the binding kinetics (see section 6.3).
3.4.2. Protein–Protein Complexes
Most biological functions involve the binding between proteins to form stereospecific complexes. The interactions that govern the structures of the protein–protein complexes and their binding stability and kinetics (see sections 5.2 and 6.2) are largely dictated by the composition and spatial distribution of amino acids forming the interfaces. Analysis of surface residues on subunits of protein–protein complexes led to the discovery that interface residues have composition and spatial distribution that are distinct from those of noninterface residues, and these differences were exploited by machine-learning programs to predict protein interaction sites.274,275 Such predictions may assist the structural modeling of protein–protein complexes276,277 and may potentially even be targets for drug design.278,279
It is well recognized that protein–protein interfaces have higher levels of nonpolar residues around the center than at the rim and the opposite is true for charged residues.249,280,281 So once again the same trends in relative densities on going from the center of a protein (or an interface) to the surface (or rim) are observed. Indeed, ρ dependences of relative densities similar to those shown in Figure 8d for protein–membrane interfaces are found for protein–protein interfaces. However, overall the latter interfaces have fewer nonpolar residues as well as fewer Arg residues and more Asp and Glu residues, such that opposite charges are nearly balanced. The distribution characteristics of amino acids along ρ may be useful for improving interface prediction.
3.4.3. Protein–Nucleic Acid Complexes
Nucleic acids, either DNA or RNA, are polymers of nucleotides, each of which carries a negatively charged phosphate. Double-stranded DNA molecules have the well-known double-helix structure, whereas single-stranded RNA molecules form tertiary structures somewhat reminiscent of proteins. DNA and RNA mainly function in encoding, transmitting, and expressing genetic information. Interactions between proteins and these highly acidic molecules are expected to have a significant electrostatic component. In particular, the interactions drive the formation of the nucleosome, which comprises approximately 146 base pairs of genomic DNA wrapped around a histone octamer and is the basic unit of the chromatin. Not surprisingly, nucleic acid binding sites on proteins are highly enriched in basic residues (Figure 8e, left panel). This property features prominently in machine-learning programs that predict nucleic acid binding sites.282–291
To achieve a more fine-grained picture, here we calculated the ρ dependences of the relative densities of amino acids in the nucleic acid binding sites of previously curated sets of 264 protein–DNA complexes and 106 protein–RNA complexes.284 As displayed in Figure 8e, right panel, with increasing ρ, nonpolar residues still show decaying relative densities whereas charged residues show growing relative densities, except for Arg. The relative density of Arg is nearly uniform in RNA-binding proteins and shows even a modest increase toward the center of binding sites in DNA-binding proteins. The latter trend reflects the preponderance of Arg residues forming multiple interactions with the backbone phosphate and the nucleotide base of DNA (Figure 8e, left panel).
3.5. Phosphorylation Sites
Phosphorylation is one of the most important posttranslational modifications, affecting the majority of human proteins292,293 and responsible for regulating protein function, localization, degradation, interaction, and conformation. In human, over 500 kinases specialize in adding a phosphate group to Ser, Thr, and Tyr residues,294 thereby imparting them with two units of negative charge at pH 7. The reverse process, dephosphorylation, occurs with the help of phosphatases. Phosphorylation sites should be solvent-exposed, because of their necessary accessibility to the active sites of kinases and phosphatases and because of the double negative charge on the phosphorylated residues. Hence these residues are found on the surfaces of structured proteins, and very often in IDRs.295,296 Phosphorylation can directly affect the conformational ensemble (such as the average size) of an IDR or even induce a disorder-to-order or order-to-disorder transition.246,297,298 Notably, an IDP was induced to fold by multisite phosphorylation.299
In addition to the phosphorylated residue, 10 or so sequentially neighboring residues are in contact with the kinase active site. The neighboring positions show distinct patterns, such as preference of upstream positions for Asp and Glu in the case of phospho-Tyr and for Arg and Lys in the cases of phospho-Ser/Thr.300 Machine-learning programs based on such sequence patterns have been developed to predict phosphorylation sites.300–305
Bacterially expressed proteins lack posttranslational modifications and hence typically are not phosphorylated. In the laboratory, an Asp or Glu mutation is often used as a substitute for phosphorylation. This practice is an indication that the negative charge at the phosphorylated site is important for fulfilling the functional role of phosphorylation.3 There is some evidence that phosphorylation sites evolved from Asp and Glu residues.306
It would be remiss not to note the fact that other posttranslational modifications, including acetylation of Lys and deimination of Arg, also change the charges on side chains. In particular, acetylation of Lys residues in histones, by neutralizing the positive charge on the side chains, weakens electrostatic interactions with DNA and reduces nucleosome stability, as demonstrated experimentally307 and by theoretical modeling.308 This presumably leads to a less compact chromatin structure, which in turn facilitates DNA access for transcription and other purposes.309 Histone acetylation also either enables or prevents the binding of chromatin-remodeling complexes and other chromatin-associated factors.
4. PROTEIN FOLDING STABILITY
When a protein folds, both the distances between charges and the solvent environment change significantly (Figure 6a). It is difficult to compute or measure the total electrostatic contribution to the folding stability. However, the effects of pH, charge mutations, temperature, and salts on the electrostatic contribution have been extensively studied and significantly broadened our understanding of protein folding stability.
4.1. pH-Dependent Effects
Although aqueous environments in and around cells are generally thought to have a pH around 7, through their lifetimes many proteins actually encounter pHs far from 7. For example, some intracellular compartments (e.g., endosomes and lysosomes) are known to have acidic pHs.310 Proteins are generally denatured at pH extremes, where uniform protonation or deprotonation of ionizable groups results in enormous repulsion between like charges. The mammalian stomach relies on this acid denaturation for protein digestion. On the other hand, bacteria that live in or pass through the stomach have evolved to survive this acidic environment.
The pH dependence of folding free energies has been measured for numerous proteins. This dependence is governed by the rigorous relation2
| (41) |
where qf and qu are the net charges on the protein in the folded and unfolded states, respectively, assuming that a pH change affects the protein charge only through proton binding or release. In practice, pH changes may also affect protein charges in indirect ways, e.g., pH-induced ion binding or release. Neglecting such complications, the folding free energy as a function of pH can be determined, up to a constant (i.e., ΔGfold at a reference pH), using qf and qu calculated from the pKa’s or pH-dependent extents in protonation of ionizable groups in the folded and unfolded states. A number of attempts to compute the pH dependence of folding free energy were made, e.g., using PB-based pKa predictions for the folded state.141,311–313 All these attempts assumed that, in the unfolded state, ionizable groups could be treated as model compounds and hence devoid of charge–charge interactions.
The pKa’s of ionizable groups in the folded state can be routinely determined by NMR spectroscopy. With the resulting qf and experimental data for the pH-dependent folding free energy, eq 41 allows for a test of the model-compound treatment for the unfolded state. This test on many proteins has shown large errors of the model-compound treatment, hence implicating significant charge–charge interactions in the unfolded state.314–321
Experimental determination of pKa’s in the unfolded state is impractical for most proteins because of the negligible population of this state under native conditions. However, for a marginally stable protein, Tollinger et al.322 measured the pKa’s in the unfolded state. These pKa’s are significantly perturbed from model-compound values, but, when used in eq 41, yield a pH dependence of the folding free energy consistent with direct measurement. pKa’s have now been determined for the unfolded state of at least one other marginally stable protein323 and for several intrinsically disordered proteins (or fragments).324–326 Using a new NMR methodology, it is even possible to determine pKa’s for a sparsely populated folding intermediate and deduce its pH-dependent stability relative to the folded state.327 Again, in all these cases, perturbed pKa’s implicate charge–charge interactions.
The first serious effort at modeling charge–charge interactions in the unfolded state was made by Elcock,328 who represented the unfolded state by a single “native-like” conformation obtained by unfolding molecular dynamics simulations. This representation improved the prediction of the pH dependence of folding free energy over the model-compound treatment, but the corrections tended to overshoot.
Zhou329 took a very different approach, modeling the unfolded protein as a Gaussian chain, in which the distribution of each inter-residue distance has a Gaussian form, with a variance depending linearly on the sequence separation. At a given distance rij, the interaction energy between two charged residues was assumed to take the Debye–Hückel form
| (42) |
Then an average was taken over the distribution of rij. Tests against experimental data on the pH dependence of folding free energy have shown that the Gaussian-chain model captures well charge–charge interactions in the unfolded state for many proteins.329–334 In the two cases where individual pKa’s were measured in the unfolded state,322,323 the experimental values were predicted well by the Gaussian-chain model.330,332 According to this model, pKa perturbations in the unfolded state are dominated by sequentially neighboring charged residues, which statistically have higher chances of being at short distances than residues farther apart along the sequence. The Gaussian-chain model would fail if the unfolded state contained persistent structures for parts of the protein. The latter scenario was explored in a variety of ways, e.g., by generating a range of conformations335 and using coarse-grained336,337 or constant-pH338 molecular dynamics simulations. Influences of charges on the conformational ensembles (and sizes in particular) of IDPs are further stimulating interest in modeling electrostatic effects in states without fixed structures.241–246
For the folded state, PB-based pKa predictions have highlighted the desolvation cost and interactions with neighboring charged and polar groups as key determinants (see section 2.4), and do reasonably well when shifts from model-compound values are modest.85,86,141,339–344 However, cases where pKa shifts are large, as for ionizable groups engineered into deeply buried sites by Garcia-Moreno and coworkers, 345,346 often involve unanticipated structural reorganization and possibly water penetration upon ionization, posing great challenges. These are being tackled by more sophisticated computational methods such as free energy perturbation with overcharging,347 quantum mechanics/molecular mechanics treatment,348 or enhanced sampling,349 and constant-pH molecular dynamics simulations in explicit solvent.350–353
While proteins can respond to subtle changes in intracellular pH in a variety of modes,354 acid destabilization may be a general mechanism for biological processes that are mediated by pH-dependent conformational transitions of proteins. For example, when enveloped viruses enter host cells through endocytosis, viral and endosomal membrane fusion, involving conformational transitions of “fusion proteins” triggered by endosomal acidic pH, allows the release of genetic materials into the cytoplasm. In the influenza A virus, the fusion protein is hemagglutinin, which is a trimer with each subunit composed of two disulfide-linked fragments (HA1 and HA2) produced by proteolytic cleavage of a precursor. The structural differences between pre- and postfusion hemagglutinin include a dramatic extension, by 38 residues, of the central helix of HA2, thereby relocating the N-terminus by over 100 Å and positioning it for insertion into the endosomal membrane (Figure 9).355 Several observations suggested that acid destabilization of the prefusion structure is key to the fusion activity of hemagglutinin.356 First, at pH 5.6 (endosomal pH), hemagglutinin fused membranes at 37 °C; at pH 7.3 (neutral pH), fusion still occurred, but only at an elevated temperature of 62 °C, meaning that destabilization could be achieved by heat in lieu of acid. Second, the latter temperature of fusion coincided with the denaturation temperature of hemagglutinin at neutral pH (presumably in the prefusion form). Third, when incubated at pH 5, hemagglutinin became heat stable even up to 80 °C, presumably because the protein transitioned into the postfusion form, which evidently was more stable. Lastly, mutations (including HA2 D112G) that destabilized the prefusion form also raised the pH of fusion commensurately.
Figure 9.
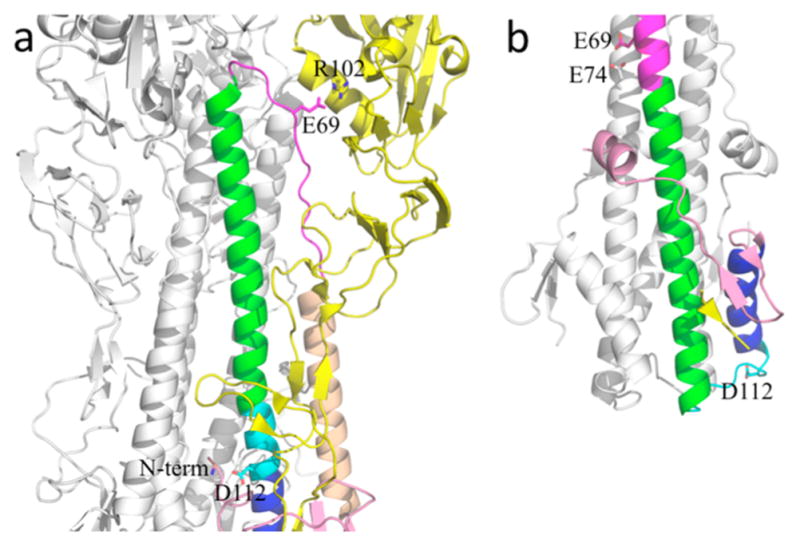
pH-dependent conformational transition of hemagglutinin. (a) In the prefusion form (Protein Data Bank entry 1JSD), HA2 Asp112 forms an ion pair with the N-terminal amino group, and HA2 Glu69 forms a salt bridge with HA1 Arg102. (b) In the postfusion form (PDB entry 1HTM), the N-terminus of the HA2 central helix extends from residue 74 to residue 37, while residues 106–113 (in cyan) become a loop, allowing the C-terminal helical segment (in blue) to fold back. HA2 Asp112 is now exposed on the surface, and Glu69 forms a pair with Glu74 of a neighboring chain.
Possible pH sensors of hemagglutinin are N- and C-termini and Asp, Glu, and His residues, due to their ability to change protonation states on going from neutral to endosomal pH. In the prefusion structure, HA2 Asp112 forms an ion pair with the N-terminal amino group (Figure 9a). The resulting stabilization would be lost if Asp112 were protonated upon decreasing pH, making this residue a candidate for a pH sensor. The D112G mutation has the same charge neutralization effect as protonation, and therefore less destabilization of the prefusion form and less decrease in pH are required for fusion. Recently Harrison et al.357 proposed that residue pairs involving His, Glu, and Asp are vehicles for acid destabilization. Specifically, pairs of Asp/Glu residues can potentially be stabilizing when at least one partner is protonated (e.g., featuring a short hydrogen bond between the carboxylic groups) but destabilizing, due to charge–charge repulsion, when both partners are deprotonated. The situation is reversed when His is paired with a basic residue (i.e., Arg or Lys); here destabilization occurs upon His protonation. As supporting evidence, Harrison et al. found that the numbers of Asp/Glu pairs are higher whereas the number of His–basic pairs are lower in the postfusion forms of hemagglutinin and fusion proteins in two other viruses than in the prefusion forms. Figure 9b displays a Glu–Glu pair in the postfusion form of hemagglutinin.
In the influenza A virus, another envelope protein, M2, forms a tetrameric acid-activated proton channel. The conductance of protons by M2, prior to fusion with the endosomal membrane, results in acidification of the viral core and subsequent dissociation of viral nucleoprotein particles from the matrix protein, M1, thereby preparing the viral nucleoprotein particles for release and nuclear import.358 The pore-lining His37 residues of M2 have been established as the pH sensor and proton selectivity filter (Figure 10a).359 The channel is nonconducting until the third of the four His37 residues is protonated.360,361 The doubly protonated His37 tetrad forms two short hydrogen bonds, each between an imidazole and an imidazolium. The third proton breaks up this stable arrangement, and the ensuing rearrangement brings the proton across the His37 tetrad (Figure 10b).361,362 The responses at the tertiary and quaternary structural levels are subtle and have yet to be well characterized.
Figure 10.
Acid activation and proton conductance of the influenza A M2 protein. (a) Structure in the closed state (PDB entry 2L0J). (left) Structure embedded in the membrane; concentration of basic residues in the inner leaflet is in line with the positive-inside rule. (right) His37 and other key pore-lining residues. Reprinted with permission from ref 362. Copyright 2010 American Association for the Advancement of Science. (b) External proton attack of a His37 imidazole–imidazolium hydrogen-bonded dimer may end with a proton returned to the same aqueous compartment (futile cycle) or transferred to the internally exposed compartment (conductance cycle). Reprinted with permission from ref 361. Copyright 2015 Elsevier.
As another example, the acid-activated chaperone activity of a small periplasmic protein HdeA is essential for enteric bacterial pathogens such as E. coli to survive passage through the acidic environment of the mammalian stomach (pH ~2).363 At neutral pH, HdeA is a chaperone-inactive, structured dimer,364 but upon going to low pH, HdeA dissociates into disordered monomers that are chaperone-active.363,365,366 The dimer interface is stabilized by not only hydrophobic interactions but also electrostatic attraction of oppositely charged residues.363,364 Evidently, at low pH, protonation of Asp and Glu residues leads to lost electrostatic attraction with basic residues both within and between monomers, leading to not only the breakup of the dimer but also an order-to-disorder transition of the resulting monomers. By neutralizing two Asp residues (at positions 20 and 51) using Ala mutations, Foit et al.367 produced a mutant that was mainly monomeric, partially unfolded, and chaperone-active at neutral pH.
4.2. Charge Mutations
As discussed in section 2.7, PB-based predictions of electrostatic contributions to folding stability are highly dependent on the choice of the boundary between the protein low dielectric and the solvent high dielectric. Choosing the SE surface as the dielectric boundary led to the conclusion that electrostatic interactions make marginal net contributions to folding stability or are destabilizing.130,131 This view still persists due to the popularity of the SE protocol. In contrast, we have advocated the vdW protocol, in part because it consistently leads to better predictions for the effects of charge mutations.129,134,139 For example, experimentally, neutralizing a semiburied salt bridge in T4 lysozyme by the double mutation H31N/D70N resulted in approximately 2.5 kcal/mol decrease in stability.368 The SE protocol predicted a 1.3 kcal/mol increase in stability, but the vdW protocol predicted a decrease of 1.6 kcal/mol in stability, in much better agreement with the experimental result.134,369 Experimental data of Perl et al.370,371 showed that the stability gap of a mesophilic–thermophilic pair of cold shock proteins was closed two-thirds of the way by a single charge reversal, R3E, in their sequences and also significantly diminished by adding salts, strongly hinting at an electrostatic origin. Indeed, vdW-based PB calculations on R3E and other charge and polar mutations at different ionic strengths and temperatures matched well with experimental measurements.372
Enlarging εp in the SE protocol (for pKa predictions141) achieves similar effects of tempering the desolvation cost of buried charges as the vdW protocol. Schwehm et al.373 found that this εp enlargement was necessary to achieve correlation between SE-based PB calculations and experimental data for the effects of neutralizing or reversing surface charges on Staphylococcal nuclease. Moreover, in agreement with other studies,129,134,135,137 the calculated results using the SE protocol with an enlarged εp were comparable to those using the vdW protocol with a normal, low εp.
Based on reviewing a large body of experimental data for the effects of mutations on folding stability, Pace10 presented compelling arguments that both hydrophobic interactions and hydrogen bonds make large contributions. He estimated that a hydrogen bond on average increases stability by approximately 1 kcal/mol. Hydrogen bonds are predominantly electrostatic in nature. Electrostatic interactions, in contrast to hydrophobic interactions, can be both specific and longer ranged, and are highly dependent on the dielectric environment. The contributions of hydrogen bonds in particular and electrostatic interactions in general are therefore context dependent. Gao et al.374 found that hydrogen bonds can provide up to 1.2 kcal/mol more stabilization when sequestered in nonpolar environments than when solvent exposed. Similarly, a computational study came to the conclusion that, while surface charges may not reliably contribute to protein stability, semiburied salt bridges can provide significant stabilization.134
A number of laboratories have now reported successes in modifying surface charges for stability enhancement.16,375–384 A simple strategy is to reduce charge repulsion, as for proteins that have a large net charge at neutral pH (corresponding to very low or high isoelectric point, pI)377 or have patches with concentrated like charges.16,376 However, these charges may be present for function, and therefore the enhanced stability may compromise function16,376 (see sections 5.1 and 6.2). Makhatadze and co-workers378,380,383 have developed a computational method, based on optimizing surface charge–charge interactions (as calculated by a modified Tanford–Kirkwood model), that has proven very effective.
4.3. Thermophilic and Halophilic Proteins
Thermophilic organisms have to survive temperatures near or above 100 °C. Sequence and structure comparisons of thermophilic proteins and their mesophilic homologues have suggested a variety of physical factors for thermostability, among which enrichment of ion pairs and hydrogen bonds has consistently been noted.29,109,370,385–390 As noted in section 4.2, the contributions of ion pairs in a cold shock protein have been quantitatively measured370,371 and calculated.372 Recently, Porebski et al.391 used consensus sequence to design a protein that has a melting temperature exceeding 100 °C. Again, an extended ion pair network, along with an optimized hydrophobic core, was identified as a key feature of the design. Extrinsic factors, including macromolecular crowding,392 may also contribute to thermostability.
According to thermodynamics, the temperature dependence of the folding free energy is given by393,394
| (43) |
where Ts is a reference temperature and ΔCp is the change in heat capacity upon unfolding, assumed to be temperature independent. Unfolding of water-soluble proteins is characterized by a positive ΔCp. Corresponding to the positive ΔCp, the −ΔGfold vs T curve (known as the stability curve) has a downward, near-parabolic shape (Figure 11). Here we choose Ts to be the temperature at which −ΔGfold reaches the maximum. Thermophilic proteins must have a high melting temperature (Tm; the upper of the two temperatures at which ΔGfold = 0). This can be achieved by changing the three parameters in eq 43 independently and in combination.395,396 That is, an increase in −ΔGfold(Ts), a decrease in ΔCp, and an increase in Ts, resulting in upward shift, flattening, and rightward shift of the stability curve, respectively, all lead to a higher Tm (Figure 11). In a stability comparison between thermophilic proteins and their mesophilic counterparts, Razvi and Scholtz396 found that a majority (18 out of 26) used decreases in ΔCp (either alone or in combination with increases in the other two parameters) for increased Tm.
Figure 11.
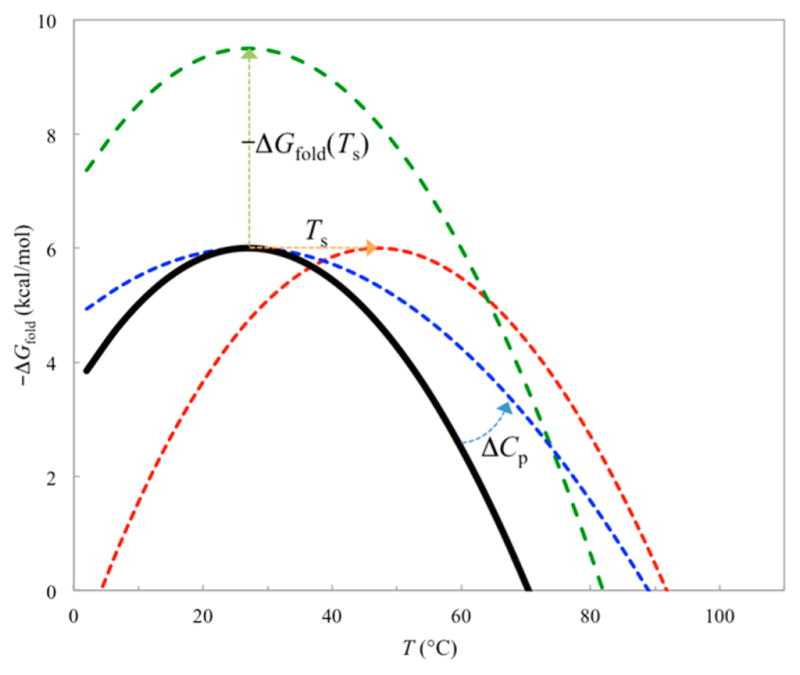
Temperature dependence of the unfolding free energy −ΔGfold. The melting temperature increases with increasing −ΔGfold(Ts), decreasing ΔCp, and increasing Ts, as illustrated by the green, blue, and red curves, respectively.
It has long been known that the hydration heat capacities are positive for nonpolar groups and negative for charged and polar groups,8,397,398 a fact that serves as crucial evidence for hydrophobic effects as a driving force for folding stability. Evidently the positive sign of ΔCp is determined by the solvent exposure of nonpolar groups upon unfolding, although the solvent exposure of charged and polar groups modulates the magnitude of ΔCp.8 A number of workers have recognized that the decrease of the dielectric constant of water with increasing temperature (Figure 6b) can result in a more favorable electrostatic contribution ( ) to folding stability.110–113,372 Zhou also noted that the resulting temperature dependence of , as illustrated in Figure 6c with an upward curvature, corresponds to a negative contribution to ΔCp. This negative contribution qualitatively explains the observed negative hydration heat capacities of charged and polar groups. He further suggested that the enrichment of ion pairs and hydrogen bonds in thermophilic proteins can result in decreases in ΔCp. Therefore, additional ion pairs and hydrogen bonds found in thermophilic proteins may both increase −ΔGfold(Ts) and decrease ΔCp. Charge mutation studies of a thermophilic protein by Wong and co-workers have provided support for this idea.399,400
Salt ions at low concentrations can increase the desolvation cost and screen charge–charge interactions of proteins in the folded state (sections 2.1 and 2.2). When the charge–charge interactions are mostly favorable, the net effect of salt ions is expected to be reduced folding stability.68,333,371,372,401–406 On the other hand, at higher salt concentrations, the salting-out effect (section 2.3) can dominate and lead to increased folding stability.68,333,371,403–405,407–409 The latter consequence may be at play for cytoplasmic proteins in some halophilic organisms, where cytoplasmic KCl can reach 4 M.410,411 However, the salting-out effect can also lead to protein precipitation. This problem was solved by enrichment of acidic residues (and possible concomitant loss of Lys)412–418 (see section 5.3.1). The potential destabilizing effect of the like charges (akin to acid denaturation) is mitigated by the screening of the concentrated salt ions,419 and may be one of the main reasons why these halophilic organisms cannot survive in low salt environments.
4.4. Transmembrane Proteins
Experimental data for the folding stability of a number of transmembrane proteins in lipid bilayers (not detergents) have been reported, after overcoming significant technical challenges. 420–422 As has been emphasized, interactions with the membrane environment are essential for the structural integrity and the stability of the natively folded state.254,423
The imprint of the membrane environment on the energetics of membrane proteins is recognizable in many ways. In particular, the scarcity of charged residues in the membrane hydrocarbon core is noted in section 3.3 (Figure 8c). Consequently, backbone hydrogen bonds between amides and carbonyls and occasional backbone-side chain hydrogen bonds involving Ser and Thr residues are the predominant polar interactions in the membrane hydrocarbon core. Due to the low dielectric environment, these hydrogen bonds can be particularly strong. Indeed, relative to α-helices of water-soluble proteins, transmembrane α-helices are more regular, the peptide planes are closer to being parallel to the helical helix so the amides and carbonyls are more protected,424,425 and the backbone hydrogen bonds are shorter.424,426,427 The tertiary (and quaternary) structural stability of helical transmembrane proteins relies on close packing of transmembrane helices.254 The small size of Gly allows very close approach of helix backbones and thereby promotes the formation of interhelical CαH···OC hydrogen bonds and other interhelical polar and van der Waals interactions.263,428–431 Future folding studies of membrane proteins, e.g., through using mutations, will lead to better quantitative understanding of these stabilization factors.422
5. THERMODYNAMICS OF PROTEIN BINDING AND CONDENSATION
As discussed above, in the folded structures of proteins, charged residues are largely present on or near the surface. It is easy to imagine that these charges can be pre-positioned or even preorganized to either stabilize or disrupt the interactions of proteins with their partner molecules. These opposite effects are exemplified by electrostatic stabilization of the transition state in enzyme-catalyzed reactions and prevention of polymerization by the β subunit Glu6 residues of normal hemoglobin.
5.1. Transition-State Stabilization in Enzyme Catalysis
Enzyme-catalyzed reactions take place in pockets, or active sites, that are accessible to but often significantly shielded from solvent. In such a site, a relatively small number of residues interact with the substrate (and cofactors if present), and an even smaller number directly participate in the catalytic reaction. Holliday et al.432 curated the functional roles, as annotated in the literature, of the latter catalytic residues among many subclasses of enzymes. With a few exceptions, only the (nominally) charged side chains of Asp, Glu, Lys, and Arg and the polar side chains of Ser, Thr, His, Tyr, Trp, and Cys are chemically active to allow them to serve as catalytic residues. Two functional roles of these catalytic residues were predominantly annotated: stabilization of the transition state or other intermediates, generally through electrostatic interactions, and proton shuttling, through protonation and deprotonation. Of the 891 catalytic residues collected by Holliday et al., 40% were described by others as providing stabilization and 36% as for proton shuttling, with the remaining 24% spread among five other roles. These results show that, from a chemistry perspective, electrostatic effects dominate in the functional roles of catalytic residues. A related observation is that catalytic residues often have substantially perturbed pKa’s and remain partially protonated over an extended pH range (due to proximity of multiple ionizable groups).433,434
Warshel39 has been a strong proponent of the idea that catalytic activity mostly derives from electrostatic stabilization of the transition state. His group used electrostatic calculations to demonstrate that “enzyme active sites provide a preorganized polar environment that stabilizes the transition state much more than the corresponding environment in water.” The essence of a preorganized electrostatic microenvironment can be easily illustrated by a nonenzymatic protein designed for Ca2+ binding, where a cluster of five Asp and Glu residues was engineered (Figure 12a).16 Prior to coordinating a Ca2+ ion (akin to the ground state), the acidic side chains repel each other, such that the designed protein is significantly destabilized relative to the original protein (ΔTm = −20 °C). Upon Ca2+ coordination (akin to the transition state), the short-distance charge–charge attraction confers strong stabilization of the complex (as shown by Ca2+-dependent increase in Tm). Charge neutralization increases the thermostability of the protein but also compromises its Ca2+-binding affinity.
Figure 12.
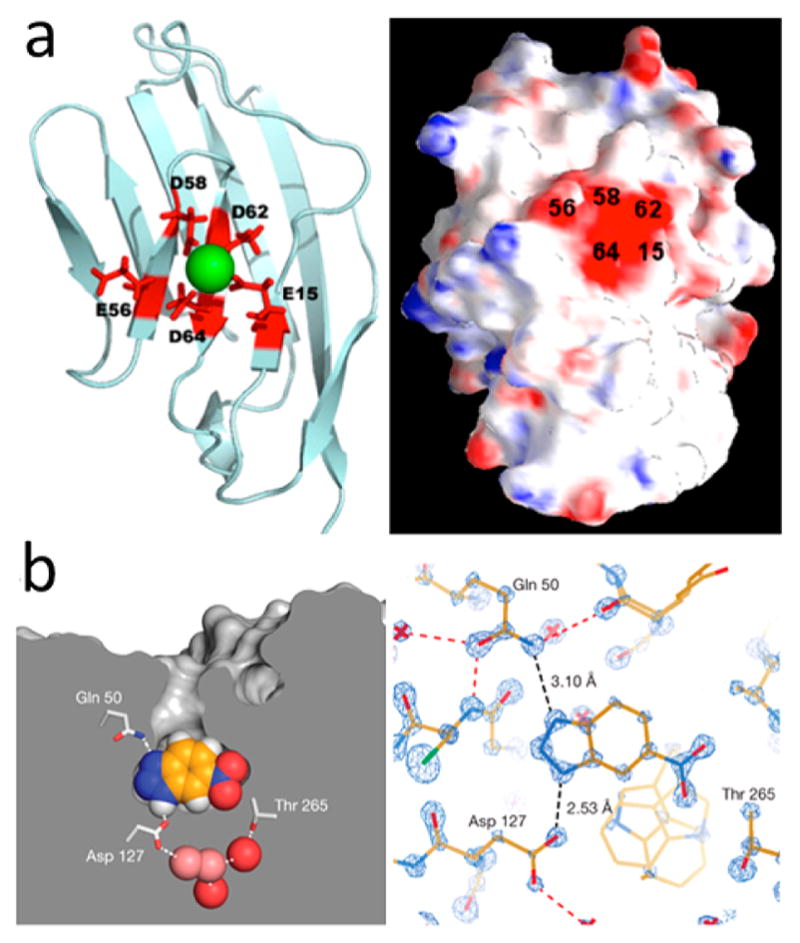
Designed and evolved binding sites. (a) Nonenzyme protein with a site designed to bind Ca2+. Reprinted with permission from ref 16. Copyright 2009 BioMed Central Ltd. http://creativecommons.org/licenses/by/2.0. (b) Artificial enzyme, HG3.17, obtained through directed evolution, shown bound with a transition state analogue. In the substrate, the NH moiety forming a short hydrogen bond with Asp127 is replaced by a scissile CH, and the nitrogen atom hydrogen bonded to Gln50 is replaced by oxygen. Reprinted with permission from ref 435. Copyright 2013 Macmillan Publishers Ltd.
Of course the protein matrix of an enzyme is not static during the catalytic reaction. The movements of the participating moieties in the catalytic reactions are coupled, at least to some degree, to the motions of the protein matrix. Therefore, the free energy landscape of the protein matrix in conformational space can influence the energy barrier of the catalytic reaction. An efficient enzyme is one where the necessary motions of the protein matrix do not encounter a significant energy barrier and serve to optimize the electrostatic microenvironment, e.g., by properly positioning and orienting charged and polar groups of catalytic and nearby residues and by changing the solvent exposure of the active site, for shepherding the catalytic reaction. One of the enzymes for which the interplay of protein motions and electrostatics is well characterized is dihydrofolate reductase, where the influence of the protein matrix’s motions was demonstrated by effects of distal mutations on the catalytic rate.436 This influence may also be the basis of allosteric regulation of catalytic activity.437
When a catalytic reaction involves charge displacement or transfer, electrostatic stabilization of the transition state can be conferred by a strong local electric field. The electric fields can be measured based on the vibrational Stark effect, whereby the vibrational frequencies of certain bonds are shifted linearly by the electric fields experienced.438,439 This was done for a carbonyl bond of an inhibitor bound to the enzyme ketosteroid isomerase;438 the corresponding carbonyl bond in the substrate is transformed to an enolate (while a nearby proton is abstracted) during the first half of the catalytic reaction. The electric field experienced by the carbonyl bond is extremely strong, at 150 MV/cm, and shows little variability (as indicated by the narrow width of the vibrational band), suggesting that it is preorganized and largely fixed. As the dipole moment of the carbonyl bond in the substrate is increased in the transition state by the charge displacement during the catalytic reaction, the electric field likely accounts for a substantial portion of the decrease in reaction energy by the enzyme. Indeed, mutations of two proximal catalytic residues reduced the catalytic rate and the electric field in proportion to each other. Combined experimental and computational studies of vibrational Stark effects in dihydrofolate reductase also revealed a strong electric field along its hydride transfer route.436 We note in passing that the electric field calculated within a nonpolar cavity in the core of a protein was suggested to stabilize the presence of water, through interaction with the latter’s dipole.127
A recent highly successful artificial enzyme, HG3.17, optimized through directed evolution of a computational design, HG3,440 and reaching a kcat/KM of 2.3 × 105 M−1 s−1, highlights the critical importance of precise electrostatic stabilization.435 Structural comparison of HG3.17 and HG3 in complex with a transition state analogue reveals the decisive factors for the high catalytic activity (Figure 12b). In a binding pocket that possesses extraordinary shape complementarity to the ligand and is almost totally secluded from bulk solvent, Asp127 forms a short hydrogen bond with the ligand and is precisely aligned for proton abstraction, and Gln50 is well positioned to stabilize the developing negative charge in the transition state. These are exactly the features noted for natural enzymes (see the first paragraph of the present section). Further optimization to raise kcat/KM to a level typical of “perfected” enzymes (~109 M−1 s−1; ref 441) may have to rely on long-range electrostatic attraction conferred by surface charges to speed up the bimolecular rate constant for binding to the active site442–445 (see also section 6.2).
5.2. Stability of Protein–Protein Complexes
As noted in section 3.4.2, protein–protein interfaces typically have nonpolar residues concentrated at the center and charged residues localized at the rim, suggesting that hydrophobic interactions are a driving force for binding (as for folding) but electrostatic interactions may contribute to the structural specificity and the thermodynamic stability of the complexes. Shape complementarity and electrostatic complementarity between subunits have long been recognized as twin hallmarks of protein interfaces.446,447 In a number of cases, it has been observed that coarse-grained energy functions select structural models that have an incorrect, flipped (i.e., 180° rotated) orientation between the subunits.448–450 An accurate treatment of the intersubunit electrostatic interactions may allow discrimination of the correct orientation from the flipped one.
On the net contribution to the thermodynamic stability of protein binding, the early view, arising from SE-based PB calculations, that electrostatics generally opposes binding still persists.249,451 As has been argued, the SE-based protocol likely overestimates the desolvation cost of charges upon binding; an alternative, i.e., the vdW-based protocol, predicts that, in most cases, the desolvation cost is more than compensated by favorable charge–charge interactions, resulting in net electrostatic stabilization (section 2.7).135,137,138 The histogram of , the electrostatic component of the binding free energy, calculated for 132 protein–protein complexes is displayed in Figure 13a.452 The histogram peaks at −2.4 kcal/mol, with being negative for 74% of the complexes. Also, protein binding can significantly shift pKa’s, which in turn result in pH dependence of binding stability.46,135,453,454 The latter is governed by a relation analogous to eq 41.
Figure 13.
Electrostatic contributions to protein–protein binding stability and rate constants. (a) Electrostatic components, , of the interaction energies in 132 protein–protein native complexes. (b) Electrostatic interaction energies, ΔGel*, in the transient complexes of the 132 protein pairs. Reprinted with permission from ref 452. Copyright 2013 John Wiley & Sons Ltd.
Phosphorylation, like pH, can regulate protein–protein binding by modifying charges of residues. Indeed, phosphorylation is commonly stated to elicit inducible (i.e., turn on or off) protein–protein interactions.3 For example, phosphorylation can either generate a motif that interacts with a phospho-specific-binding domain such as SH2, or disrupt the interaction between two proteins via a phospho-dependent conformational transition or placing the doubly negatively charged phosphate group in the interface (akin to the Glu6 residue in the β subunits of normal hemoglobin). Often, disruption of the interaction with one (e.g., intramolecular) partner frees the phosphorylated protein to interact with another (e.g., intermolecular) partner; thereby phosphorylation serves as a precise trigger for the familiar regulatory mechanism of partner swap.455,456
Instead of turning on or off a protein–protein interaction, phosphorylation at a single site is more likely to merely modulate the stability of the interaction.458 The on/off behavior of complex formation can be achieved by the accumulative effects of multisite phosphorylation on the binding stability, via phosphate-mediated specific or nonspecific interactions.459–462 However, even if multisite phosphorylation can turn on or off a critical protein–protein interaction, the response of the signal transduction network is still graded instead of switch-like, unless the level of phosphorylation also responds in a switch-like fashion to a graded kinase signal. In the cellular context, ultrasensitive switch-like responses may involve a variety of mechanisms, including processive or cooperative multisite phosphorylation, coordination among kinase, phosphatase, and other regulatory proteins, and positive or negative feedback.463–465 The physical basis of these mechanisms remains poorly understood. Moreover, the timing of the responses also has to be precise, but how that precision arises from the integration of individual protein–protein binding events is even less clear.
5.3. Solubility, Assembly, and Liquid–Liquid Phase Separation
The protein complexes discussed above are binary, stabilized by highly specific contacts between subunits. When each subunit can simultaneously engage in contacts with multiple partners, oligomeric complexes such as the ribosome can form. From a thermodynamic standpoint, these oligomeric complexes can be constituted by a finite number of binary steps. In this section we are interested in states that grow in size indefinitely when more monomers are supplied. The multimeric contacts that stabilize these condensed states can be solid-like in some cases (e.g., the crystalline phase in protein solubility) and liquid-like in other cases (e.g., the droplet phase in liquid–liquid phase separation, characterized by large, dynamic protein clusters466). Notably, the solvation environment of protein molecules in a crystalline lattice can be very different from that in a dilute solution. In particular, the effective dielectric constant and hydrophobicity may deviate significantly from the properties of bulk solvent.
5.3.1. Protein Solubility
As alluded to in section 2.3, our view is that favorable protein–solvent interactions are the driving force for protein solubility. Below we first use this view to qualitatively rationalize a number of experimental observations, including the increase in solubility with increasing net charge, and then put this view to a quantitative test, by examining effects of pH and point mutations on solubility.
Protein solubility has a strong dependence on pH, which affects the protein net charge. The solubility usually reaches a minimum at a pH around the isoelectric point (where the net charge is zero; Figure 14a).467,468 Hence the higher the net charge, the higher the solubility. Solubility can also be increased by replacing exposed nonpolar residues with charged ones.469 In fact, an important reason for the presence of charged residues in proteins is to ensure solubility and prevent aggregation. Proteins free of charged residues have been engineered (by mutation or in combination with pH titration and chemical modification), but with low solubility or a significant decrease in solubility from the parent protein.470–472 The increase in solubility with increasing net charge is usually attributed to repulsion between like-charged protein molecules in the solid phase. However, we suggest that the primary cause for the increase in solubility is the favorable interactions between the protein charges and the solvent in the solution phase.
Figure 14.
Effects of pH, net charges, and mutations on protein solubility. (a) Dependence of solubility on pH for wild-type ribonuclease Sa and two charge mutants with very different isoelectric points (pI values; indicated by arrows). Reprinted with permission from ref 468. Copyright 2001 John Wiley & Sons Ltd. (b) Solubility data for seven proteins,473 linearly correlated with q2/R, according to eq 44a. Net charge q from ref 473; radius R estimated as 0.89MW1/3 Å, where MW denotes molecular weight in daltons. (c) Calculated pH dependence of wild-type ribonuclease Sa solubility. (d) Calculated results for ribonuclease Sa solubility when Thr76 is mutated into the other 19 types of amino acids. Panels c and d reprinted with permission from ref 27. Copyright 2008 Elsevier.
To illustrate, let us model the protein molecule as a sphere with a radius R and a net charge q uniformly distributed on the surface. Equation 6 then gives the excess chemical potential in the solution (assuming absence of any mobile salts for now). A similar expression, with an effective dielectric constant εc for the crystalline phase replacing εs, applies to the free energy Ec. Equation 11 then leads to
| (44a) |
where S0 denotes the solubility at zero net charge. We expect εc < εs (see below) and hence predict an increase in solubility with increasing net charge. Thus highly charged proteins have high solubility for the same reason as simple salts, by favorably interacting with the solvent.
Kramer et al.473 determined the solubility of seven proteins and observed a correlation with the fraction of negatively charged surface area. In Figure 14b we plot their solubility data (extrapolated to zero salt) as a function of q2/R (where R is estimated from the molecular weight), as suggested by eq 44a. The data hint at a linear relation between ln S and q2/R, although the scatter is too much to be conclusive. Interestingly, the slope of 2.2 from a linear fit is very close to what is predicted by eq 44a with εs = 80 and εc = 50 (see below).
Organic solvents such as ethanol have much lower dielectric constants than water, and their water mixtures have intermediate dielectric constants commensurate with mixing ratios. Addition of organic solvents to water has long been known to reduce protein solubility.467 The usual explanation is that the lower dielectric constant leads to stronger attraction in the solid phase—somehow like-charged protein molecules no longer repel each other! Again, we suggest that the primary reason lies in the solution phase, not in the solid phase. Compared to εs, εc is closer in value to the dielectric constants of organic solvents, and hence the latter are less likely to produce a significant reduction of dielectric constant in the solid phase. Moreover, in protein crystals formed in water mixtures of organic solvents, water molecules occupy most of the protein surface while organic molecules bind to a few positions.474 To a crude approximation we can thus assume εc is unaffected by organic solvents. If we further assume that the dielectric environment in the solution is modeled by the dielectric constant εm of the solvent mixture, then the organic solvent changes the solubility from S to Sm according to
| (44b) |
In essence, the solubility decreases due to less favorable interactions of protein charges with the less polar solvent mixture.
Trevino et al.475 systematically studied how different types of amino acids modulate the solubility of ribonuclease Sa at 1.1 M (NH4)2SO4 by mutating the exposed residue Thr76 into all of the other 19 amino acids. They found that, when the net charge is small, both acidic and basic residues modestly increase solubility. However, with higher net charges, acidic but not basic residues significantly increase solubility. The authors attributed the superior effects of Asp and Glu to their “water-binding” ability, which is distinct from hydrophilicity. However, it is unclear how this water-binding ability affects the free energy difference between the solution and solid phases. In this context, it is worth noting that, relative to Asp and Glu, Lys has a large nonpolar group in addition to the charged moiety. A loss of Lys residues in some halophilic proteins relative to their nonhalophilic homologues has been found to largely account for a reduction in the fraction of nonpolar surface area.418
The effects of pH and point mutations on solubility have been quantitatively computed,27 by combining constant-pH molecular dynamics simulations162 with modeling of the free energy change upon transferring a protein molecule from the crystalline phase to the solution phase. The latter was decomposed into two terms:
| (45) |
where the electrostatic component was based on the PB model and the nonelectrostatic component was based on solvent accessible surface area. Assuming that a pH change (from pH0 to pH) does not affect the nonelectrostatic component, then the corresponding change in solubility (from S0 to S) is given by
| (46) |
As the pH deviates from the pI in either direction, the net charge increases in magnitude and becomes more and more negative due to favorable charge–solvent interactions in the solution phase (see eq 44a). Equation 46 thus provides a qualitative explanation for the observation that the solubility is usually minimal around the isoelectric point (Figure 14a).
The foregoing discussion assumes that the solution phase is a much more polar dielectric environment than the crystalline phase; i.e., εs is much higher than εc. This observation is consistent with the experimental observation that the dielectric constant of dry protein powder is around 4 and increases with increasing hydration level.26 To determine the value of εc, Tjong and Zhou27 calculated the electrostatic solvation energy (see eq 9b) of a protein molecule in a crystalline lattice (with charges present only on the central protein molecule) using the PB model, with all the protein molecules on the crystalline lattice assigned a dielectric constant of 4 and the solvent regions assigned a dielectric constant of 78.5. The solvation environment of the central protein molecule was then replaced by a uniform dielectric, with the dielectric constant εc varied to reproduce the solvation energy in the crystalline lattice. The resulting value for εc was 53.5. With this εc, the pH dependence of ribonuclease Sa solubility predicted by PB calculations for on protein conformations sampled from constant-pH simulations is in good agreement with experiment468 (Figure 14c).
To rationalize the variations in the ribonuclease Sa solubility when the exposed Thr76 was mutated into different amino acids,475 Tjong and Zhou27 modeled the nonelectrostatic component of the transfer free energy based on solvent accessible surface area.217,218 The surface area was divided into nonpolar and polar portions, and the change in the nonelectrostatic component upon a T → X mutation was
| (47) |
where ΔA denotes the change in (nonpolar or polar) surface area upon mutation, and bc→s denotes the corresponding change in the nonelectrostatic contribution per unit area. For transferring from a hydrocarbon solvent to water, the bnp value is around 25 cal/mol/Å2.217,218 The crystalline environment should be less hydrophobic than a hydrocarbon solvent, so is expected to be less than 25 cal/mol/Å2. Choosing values of 8.6 and 1.1 cal/mol/Å2 for and , respectively, and modeling the electrostatic component as described above, the measured solubility results at pH 4.25 for the Thr76 mutations are well reproduced (Figure 14d). At pH 7, the mutations of Thr76 to Asp, Lys, and Arg were calculated to change the solubility from 41 g/L to 196, 23, and 28 g/L, respectively; the latter are to be compared with experimental values of 160, 60, and 50 g/L. The much higher solubility of the Asp mutant relative to the Lys and Arg mutants comes from two sources: the acidic residue increases but the basic residues decrease the magnitude of the net charge by 1; the basic residues, but not the acidic Asp, have a significant portion of nonpolar surface area. These may be the same reasons that halophilic proteins choose acidic residues for mitigating low solubility due to salting out.
Finally, we mention that machine-learning programs have been developed to classify proteins as soluble and insoluble, highlighting the importance of acidic residues to protein solubility.476,477
5.3.2. Polymerization and Fibrillation
While protein crystals grow in all three directions, for some proteins, monomers are added along one direction to form linear polymers or filaments. For example, the eukaryotic cytoskeleton is made up of three types of filaments: actin filament, intermediate filament, and microtubule. Assembly of these filaments is influenced by electrostatic interactions, as illustrated by strong pH and salt effects on actin filament nucleation and elongation.478,479 However, hemoglobin remains the best example for the roles of electrostatics in polymer formation. Whereas sickle hemoglobin forms polymers that lead to deformation of red blood cells into a sickle shape and ultimately anemia, polymer formation is prevented for normal hemoglobin by a charged residue, Glu6, in the two β subunits of the tetrameric protein. This charge would be buried in the interface between two neighboring tetramers in the polymer and thus incur a tremendous desolvation cost. This cost is eliminated when the charged residue is replaced by a nonpolar one, Val, as in sickle hemoglobin.
Amyloid fibrils are another form of polymers that have gained greater attention due to their connection with diseases, including Alzheimer’s and type 2 diabetes. These fibrils consist of a stack of two or more parallel β-sheets that grow indefinitely (Figure 15). For example, in fibrils formed by Alzheimer’s amyloid-β peptide Aβ40, the stacking is between two β-strands within each subunit, which are bent into a “U” shape, with the bend stabilized by a salt bridge between Asp23 and Lys28 (Figure 15a).480 By cross-linking the two residues, the typical lag phase in the kinetics of the fibrillogenesis was eliminated, indicating that the nucleus for fibril formation can be stabilized by stabilizing the bend.481 In Aβ42 fibrils, each subunit forms three β-strands in an “S” shape; a salt bridge, between Lys28 and the C-terminus, also makes an important contribution to fibril stability (Figure 15b).482–484 The 37-residue islet amyloid polypeptide (IAPP, or amylin) associated with type 2 diabetes has three basic residues, Lys1, Arg11, and His18, all in the N-terminal half, and no acidic residues. Adding salts led to speedup of fiber formation, presumably by screening intra- and intersubunit electrostatic repulsion, but the extents of the speedup were different among different anions of the salts, indicating additional effects.485 The orders of the anions in the speedup were different at high and low salt concentrations. At a high salt concentration (600 mM), the order followed the Hofmeister series, as expected for the Hofmeister effect (section 2.3). On the other hand, at a low salt concentration (20 mM), the order followed the electroselectivity series, suggesting anion-specific binding to clusters of basic residues on the nucleus and fibril (section 2.3). Anion-specific binding has also been implicated in speeding up the formation of other fibrils.486,487
Figure 15.
Influence of charged residues on fibril structures of self-assembling peptides. (a) Aβ40 fibril, where a salt bridge between Asp23 and Lys28 (indicated by arrows) stabilizes a bend between two β-strands within each subunit. Reprinted with permission from ref 480. Copyright 2002 National Academy of Sciences. (b) Aβ42 fibril, stabilized by an intrasubunit salt bridge between Lys28 and the C-terminus. Reprinted with permission from ref 482. Copyright 2015 Macmillan Publishers Ltd. (c) Model of an IAPP fibril, where charged residues project outward. A dot between two subunits indicates that the direction of the fibril axis is perpendicular to the page. Reprinted from ref 485. Copyright 2012 American Chemical Society. (d) Model of an RADA16 nanofiber. (top) β-Strand formed by a single subunit, with charged Arg and Asp projecting to one face and nonpolar Ala to the other face. (middle) Three classes of model for stacking two β-sheets where the charged residues are all projected outward. (bottom) Two views of the nanofiber molecular model. Reprinted from ref 488. Copyright 2013 American Chemical Society.
As enlightened by the prevention of polymerization of normal hemoglobin, it is important to avoid burying charged residues at interfaces. This idea was apparently at play in building a structural model for an IAPP fibril (Figure 15c).485 It certainly was extremely helpful in reducing the number of possible structural models for the nanofiber formed by a 16-residue peptide termed RADA16 (Figure 15d).488 This peptide has a patterned sequence, RADA repeated four times, designed for β-strand propensity.489 In the resulting β-sheet, the nonpolar Ala residues project to one face while the charged Arg and Asp residues project to the opposite face. In theory there are eight classes of models,490 involving aligning strands in a β-sheet parallel or antiparallel to each other, orienting two β-sheets in a stack parallel or antiparallel to each other, and placing the nonpolar or charged face of each β-sheet in the interface. By requiring that the charged face of neither β-sheet was placed in the interface, five of the eight classes of models were eliminated. Distance restraints from solid-state NMR spectroscopy allowed the development of a structural model for the RADA16 nanofiber, in which strands in each β-sheet aligned in parallel but had a registry shift, the two β-sheets stacked in a parallel fashion, and the charged faces of both β-sheets projected outward.
5.3.3. Liquid–Liquid Phase Separation
Protein solubility is determined by the equilibrium between the solution and solid phases. For simple molecules like water, the separation between two phases occurs when the molecules can achieve the same low free energy by adopting two distinct types of configurations, with different densities and different extents of intermolecular contacts. Typically the low free energy results from low enthalpy in one phase (e.g., solid) and high entropy in the other phase (e.g., liquid). A homogeneous mix of the two phases, with a density falling in the gap between the two phases, would have a higher free energy and hence only be metastable. The same principle applies to proteins (dissolved in solvent). Indeed, proteins can exist in three phases that are reminiscent of solid, liquid, and gas for simple molecules. The solution and solid phases discussed above correspond to solid and liquid, respectively. Under certain conditions (in particular, at temperatures below a “critical” value, Tc), the solution phase can further separate into a dilute phase and a concentrated phase, akin to the gas and liquid phases, respectively, of simple molecules. This process is known as liquid–liquid phase separation (LLPS), since the protein molecules are liquid-like in both of the phases. In the concentrated phase, protein molecules cluster into droplets, typically micrometers in size, that are detectable by various types of microscopes. The droplets scatter light, and consequently the protein sample appears cloudy to the naked eye (in the same way as we observe clouds in the sky).
For structured proteins, LLPS usually occurs within the gap between the solution and solid phases, and hence is metastable.491 Nevertheless LLPS has been observed for a number of proteins (e.g., when crystallization occurs very slowly),492 including γ-crystallins, which are a main protein component of the eye lens.493,494 At temperatures below Tc, protein droplets emerge in the lens and scatter light, leading to lens opacification, a phenomenon known as “cold cataract.”495 Interestingly, highly homologous γ-crystallins, e.g., γD and γF with 83% sequence identity, can have critical temperatures that differ by over 30 °C.494 Indeed, a cataract-associated mutation, R14C, of γD-crystallin496 increased Tc by over 20 °C, apparently via disulfide-linked oligomerization.497 Also interestingly, a negatively charged globular protein, bovine serum albumin (BSA), was found to undergo LLPS upon adding the trivalent cation Y3+, but only between two critical concentrations of the salt. This “reentrant” condensation behavior was attributed to tight binding of Y3+ to acidic residues, resulting in charge neutralization across the first critical salt concentration and, with excess Y3+ binding, charge inversion at the second critical salt concentration.81 It has now become possible to compute subtle effects of point mutations and ion-specific binding on LLPS, by representing interprotein interactions at the atomic level.466 By computing the chemical potential of a protein over a range of concentrations, the coexistence curve of LLPS (the concentrations of the two phases versus temperature) can be constructed.
Recent years have seen renewed interest in LLPS,498–505 because it is thought to underlie the genesis of membraneless organelles inside cells.506–509 Recombinantly expressed components of these organelles have been shown to undergo LLPS.510–523 These proteins typically contain disordered regions and/or bind RNA. Presumably IDPs do not crystallize, and hence for them LLPS is thermodynamically stable (no competition from solution–solid phase separation) and easily observable. Indeed, the fragments of the disordered regions alone often are sufficient for LLPS.510,511,513–516,518–520,522 RNA can reduce the protein concentration required for the onset of LLPS,513,514,520,521 but excessive RNA has the opposite effect,519,524 an observation reminiscent of Y3+-dependent reentrant condensation. The enrichment of charged residues in IDPs (see section 3.2) and the involvement of RNA make LLPS extremely susceptible to changes in salt concentration. Cells likely use this and other changes in solvent conditions such as pH and temperature, as well as posttranslational modifications and protein or RNA concentrations, to regulate LLPS.503 Droplet formation can facilitate the assembly of multicomponent complexes for biochemical processes, 500,504,512,523 but the resulting condensation of disordered proteins is also inductive to fibrillation and degenerative diseases.500,503,513–515,517,519 Therefore, exquisite regulation of LLPS is crucial.
6. KINETICS OF PROTEIN FOLDING AND BINDING
Electrostatic interactions can (de)stabilize intermediates along kinetic pathways and accelerate (or impede) intramolecular and intermolecular relative diffusion, and are thus expected to modulate the magnitudes of folding and binding rate constants. Numerous studies have confirmed this basic expectation and have also revealed the myriad ways by which electrostatic interactions affect folding and binding mechanisms.
6.1. Protein Folding
Folding refers to the process where the protein chain rearranges to acquire the native structure. The simplest scenario of this process is a transition between two states, i.e., from the unfolded to the folded state. The rate constant of this transition, as a unimolecular reaction in solution, generally follows Kramers’ theory525
| (48) |
where ΔG‡ is the free energy barrier separating the unfolded and folded states, and the pre-exponential factor kf0 depends on the shape of free energy surface and the effective diffusion constant along the reaction coordinate.
The pair of cold shock proteins where an electrostatic origin for the stability gap was implicated (see section 4.2) also serves to illustrate that folding kinetics can be significantly affected by electrostatic interactions. The folding and unfolding rates of the thermophilic protein were 10-fold higher and 20-fold lower, respectively, compared with the mesophilic counterpart.526 The R3E mutation of the thermophilic protein slowed the folding rate by 20-fold and accelerated the unfolding rate by 3-fold, implicating strong electrostatic contributions to the differences in folding kinetics between the thermophilic and mesophilic homologues. These proteins form a five-stranded β-barrel, with the N-terminal three strands in one sheet and the C-terminal two strands in another. In the thermophilic protein, Arg3 on strand 1 is sandwiched between Glu21 on strand 2 and Glu46 on strand 4.527 An extensive mutational analysis (including Φ-value analysis528) by Perl et al.526 revealed that, in the transition state, the N-terminal two strands are formed, and the Arg3–Glu46 interaction is present to provide tertiary stabilization. These features were largely confirmed in transition-state conformations identified by high-temperature unfolding simulations. 529 The same conclusion was drawn from simulations based on a native-centric coarse-grained model that included electrostatic interactions.530
Tzul et al.383 examined how stabilizing mutations from redesigned surface charge–charge interactions (see section 4.2) affected folding kinetics. These mutations accelerated the folding rates while they left the unfolding rates largely unaffected, leading the authors to conclude that the transition state of folding was stabilized by the redesigned surface electrostatics. Halskau et al.531 compared the folding barriers of two homologous proteins, lysozyme and α-lactalbumin (38% sequence identity). The barriers were high (8.4 kcal/mol) for lysozyme but only marginal (1.3 kcal/mol) for α-lactalbumin. The latter result was attributed to electrostatic stabilization of the transition state.
When the surface of a protein is clustered with like charges (for binding partner proteins; see sections 5.1 and 6.2), adding salts can screen the expected charge–charge repulsion in the transition state and thereby accelerate the folding rate. This was precisely the result observed on the human peripheral subunit-binding domain (PSBD) of the pyruvate dehydrogenase multienzyme complex, which uses basic residues for binding catalytic subunits in shuttling prosthetic groups.532 For a bacterial PSBD, BBL, with less concentration of basic residues, adding salts still increased folding stability, as expected from screening of charge–charge repulsion in the folded state, but, paradoxically, decreased the folding rate (4-fold at 4 M LiCl).533 The latter result was explained by proposing that the folding of BBL was barrierless, a scenario first proposed on theoretical grounds, when the folding barrier disappeared due to extreme energetic bias toward the native state.534 Relaxation on the resulting single-well free energy surface can still have an approximately exponential time dependence, with the relaxation rate, analogous to the pre-exponential factor kf0 in eq 48, determined by the curvature of the surface and the effective diffusion constant. The 4-fold decrease in folding rate at 4 M salt was accounted for by a combination of (i) broadening of the free energy surface, which was corroborated by a broadened (i.e., less cooperative) equilibrium denaturation transition with high temperature, and (ii) an increase in solvent viscosity, which would slow down intramolecular relative diffusion. Whether the folding of BBL is barrierless and whether the particular experimental system is appropriate for invoking the native-bias scenario of the theoretical model are hotly contested.535 Removal of charges on two poorly solvated Lys residues in the fast-folding small protein villin headpiece introduced native bias, presumably by decreasing the desolvation cost and charge–charge repulsion, and was suggested to push the folding toward the barrierless scenario.536
Lastly, we note that nonnative electrostatic interactions, such as between sequentially neighboring charged residues as postulated in the Gaussian-chain model329–332 (see section 4.1), can form in the unfolded state and persist in the transition state for folding. Cho et al.537 mutated the exposed Lys12 in the N-terminal domain of the ribosomal protein L9 to Met, and found a 1.9 kcal/mol increase in folding stability. The authors presented several lines of evidence to suggest that the stabilization resulted not from native state effects but from elimination of repulsion of Lys12 by other basic residues in the unfolded state. Incidentally, the charge–charge interactions in the unfolded state of this protein are modeled well by the Gaussian-chain model, as judged by a close match between predicted individual pKa’s and subsequently measured values in the unfolded state.323,330 Kinetic experiments of Cho et al.537 further showed that the K12M mutation resulted in a 2.3-fold increase in folding rate and an 11-folding decrease in unfolding rate. The greater effect on the unfolding rate was interpreted as indicating the persistence of Lys12-mediated charge–charge repulsion in the transition state.
6.2. Protein–Protein Association
The measured rate constants of protein–protein association span approximately 10 orders of magnitude, from 1 to 1010 M−1 s−1 (Figure 16). Association involves the approach of two partner proteins (A and B), via translational and rotational diffusion, toward each other with appropriate relative orientations and further conformational change. Hence there are two potential rate-limiting mechanisms, which can be captured by Scheme 1,538 where A*B denotes the initial (or encounter) complex formed by diffusion, k1 and k−1, respectively, are the rate constants for the formation and disassembly of this intermediate, and k2 is the rate constant for conformational change leading to the native complex C. Below we will assign specific meanings to the intermediate A*B and the elementary rate constants in different contexts, but for now we keep things generic. It should be pointed out that Scheme 1 is only the simplest reaction scheme that possesses all the essential ingredients for protein association; more complex schemes may, e.g., contain more than one intermediate. Making the steady-state approximation for A*B, the overall association rate constant is given by
Figure 16.
Wide spectrum of values for the rate constants (ka) of protein–protein association. Four pairs of proteins are illustrated by their electrostatic surfaces; in each pair, the partner proteins are separated and rotated just enough to expose the binding interface. Red vertical lines indicate experimental ka values (at low ionic strengths when data available) for DNase E9 and Im9,539 barnase and barstar,540 interleukin 4 (IL4) and IL4 binding protein (IL4BP),541 and FtsY and Ffh (in the absence of RNA).542 Significant charge complementarity is present in the first three protein pairs. For FtsY and Ffh, charge complementarity is present to some degree between the N subdomains (toward the left), which were implicated in forming the interface of a kinetic intermediate,543,544 but absent between the G subdomains (to the right), which form the interface in the native complex.545,546
Scheme 1.
Major Rate-Limiting Mechanisms in Protein Association
| (49) |
Note that k1 always serves as an upper bound for ka. If the conformational change is fast (i.e., k2 ≫ k−1), then the association is diffusion-limited and ka ≈ k1. Conversely, if the conformational change is slow (i.e., k2 ≫ k−1), then it becomes the rate-limiting mechanism, and the association rate constant is approximately (k2/k−1)k1 and much lower than k1.
It becomes apparent that the upper range of the ka spectrum is diffusion-limited whereas the lower range is conformational-change-limited.11,538 The dividing line between these two regimes falls in the interval between 104 and 106 M−1 s−1, where proteins form stereospecific complexes at the limit of unbiased diffusion.457,538 Rate constants that are higher than 106 M−1 s−1 are likely achieved through accelerated diffusion due to interprotein electrostatic attraction, which can be easily confirmed by complementary charge distributions across the binding interfaces of protein complexes, as exemplified by those between interleukin 4 and interleukin 4 binding protein,541 between barnase and barstar,540 and between DNase E9 and immunity protein Im9.539 Incidentally, the accumulation of like charges on each partner protein, needed for across-interface charge complementarity, reduces folding stability.376 On the other hand, rate constants that are lower than 104 M−1 s−1 implicate slow conformational change, as illustrated by the association between Ffh and FtsY GTPase domains.542,545,546 Work up to 2009, mostly in the diffusion-limited regime, was previously reviewed;11 another brief overview, focusing on the computational side, appeared in 2013.547 Below we highlight recent advances in the association kinetics of structured proteins, in both the diffusion-limited and conformational-change-limited regimes, and of IDPs, which may have features of both regimes.
6.2.1. Automated Prediction of ka in the Diffusion-Limited Regime
The important physical factors in the diffusion-limited regime are well understood. Association becomes diffusion-limited when there are little differences between unbound and bound structures or when the change in conformation is rapid on the time scale of intermolecular relative diffusion. For this regime, the free energy surface in the six-dimensional space of relative translation and rotation is essentially barrierless, with a single deep well defining the bound state. Described in terms of Scheme 1, the A*B species represents the rim of the bound state and kc → ∞. The association rate constant is then determined by intermolecular diffusion, with the bound-state rim treated as absorbing. Electrostatic interactions between the partner proteins can have a significant effect on the speed to reach the bound-state rim and hence ka, especially when this rim is highly localized, as would be the case for stereospecific complex formation. A quantitative model for ka prediction requires the specification of the bound-state rim and efficient treatment of electrostatic interactions. These issues were solved in the transient-complex theory for protein–protein association,538 and the resulting computational method called TransComp has been implemented as a web server (http://pipe.sc.fsu.edu/transcomp/).457
Alsallaq and Zhou538 used the term “transient complex” to designate the bound-state rim, to signify it as a late, on-pathway intermediate where the two partner proteins have near-native separation and relative orientation but have yet to form most of the stereospecific native contacts. The bound state features numerous contacts but is restricted in relative rotation. As the two partners start to separate, a sharp decrease in the number of (native and nonnative) contacts is accompanied by a sudden increase in the freedom of relative rotation. In TransComp, the midpoint of this transition was identified as the transient complex, where an absorbing boundary condition for calculating the diffusion-limited ka would be imposed.457 In other studies, the location of the absorbing boundary was adjusted, often to reach agreement with experimental values for ka, thereby compromising the predictive power of computation. 548–550 Note that the transient complex does not correspond to a barrier in the free energy surface. In fact, it may be electrostatically stabilized to such an extent that the resulting (low) population becomes detectable by paramagnetic relaxation enhancement NMR spectroscopy.551,552
Once the location of the transient complex is specified, ka can be calculated from simulations of the translational and rotational diffusion of a pair of proteins. The costly treatment of electrostatic interactions in such Brownian dynamics simulations has necessitated approximations. Analytical theories have led to a remarkably simple formulation for the electrostatic contribution to the association rate constant:553,554
| (50) |
where ka0 is the “basal” rate constant, calculated when electrostatic interactions are turned off, and ΔGel* is the electrostatic interaction energy in the transient complex. The validity of eq 50 relies on both the stereospecificity of the native complex and the long-range nature of electrostatic interactions. TransComp uses eq 50, with ΔGel* calculated from solving the PB model using the vdW-based protocol.555
The performance of TransComp is illustrated by results on a sample of 49 complexes, with experimental ka values spanning 5 orders of magnitude (from 2.1 × 104 to 1.3 × 109 M−1 s−1) (Figure 17a). The predicted and experimental log ka values have a root-mean-square deviation of 0.73, corresponding to a 5-fold error in ka. These complexes encompass different biological functions and have different sizes and shapes (Figure 17b). Successes in ka modeling have also been achieved in other web servers,556,557 and with empirical correlations between ka and various structural and physical features.558–560
Figure 17.
Sample results from the TransComp web server. (a) Comparison between predicted and experimental ka values for 49 protein complexes. Ionic strengths were chosen to be close to a physiological value (i.e., 0.15 M) when possible. Reprinted with permission from ref 457. Copyright 2011 Elsevier. (b) Collage of structures for a subset of the 49 protein complexes. Protein structures were modified in two cases before TransComp calculations: for 40 (hirudin and thrombin), only the docking segment (shown in green ribbon) of hirudin was used; for 46 (ribonuclease A and inhibitor protein), the cleft of the inhibitor protein (red surface) was widened by a normal-mode analysis based on an elastic network model.
Equation 50 not only simplifies the calculation of ka but also provides better physical insight into how different physical factors differently dictate the magnitude of ka. Specifically, short-range interactions specify the location of the transient complex and hence the basal rate constant, whereas the effect of long-range electrostatic interactions is contained in ΔGel*. The latter appears in the exponent, and hence differences of a few kilocalories per mole in ΔGel* correspond to several orders of magnitude changes in ka. For example, four 4-helix bundle cytokines associate with their receptors with rate constants spanning a 5000-fold range.541,561–563 Calculations using eq 50 revealed that, with ka0 differing by no more than 3-fold, the vast span in ka arises mostly from the differences in ΔGel*, by as much as 4.1 kcal/mol, due to the varying extents of charge complementarity across the binding interfaces.564 Values of ΔGel* calculated on 132 complexes ranged from less than −5 kcal/mol to greater than 2 kcal/mol (Figure 13b).
Very recently Cohen-Khait and Schreiber565 used yeast surface display to select mutations of TEM1 β-lactamase that increased the association rate with the protein inhibitor BLIP. The selected clones were enriched in charge mutations proximal to the binding interface, and nearly all were predicted by TransComp to have increased ka. Moreover, seven of the clones were purified, and the measured ka values showed excellent agreement with TransComp predictions.
Lastly, we note that TransComp has been adapted to predict association rate constants under cell-like crowded conditions, by accounting for the effects of crowding on protein diffusion and interprotein interaction energy.566,567 Interestingly, the two effects of crowding oppose each other and nearly cancel, leaving ka nearly unaffected. The association rate constant of TEM1 and BLIP measured in the cytoplasm of HeLa cells was indeed close to the value in buffer.568
6.2.2. Characterization of Intermediates in the Conformational-Change-Limited Regime
In the conformational-change-limited regime, the partner proteins have at least one slow step of conformational change. The intermediate preceding the slow step may accumulate to become detectable experimentally, as illustrated by two protein complexes. When modeled with Scheme 1, the A*B species now represents the detectable intermediate.
The association between the signal recognition particle and its receptor is a crucial step in delivering newly synthesized proteins from the cytoplasm to the appropriate membrane location. In E. coli, the signal recognition particle consists of a single protein, Ffh, and a small RNA referred as 4.5S, and the receptor is a protein called FtsY. The native complex is formed between the structurally homologous GTPase domains of Ffh and FtsY, stabilized by interactions mostly between the G subdomains of the two subunits, and involves significant conformational rearrangements, including bending between the G and N subdomains of each subunit.545,546 In the absence of the 4.5S RNA, the associate rate constant was very low, at 180 M−1 s−1; the 4.5S RNA accelerated the rate substantially, to 5.7 × 104 M−1 s−1.542 A subsequent kinetic experiment revealed an intermediate, which could be trapped by removing nucleotides from the GTPase domains (but only in the presence of the 4.5S RNA).569 In the presence of the 4.5S RNA, this intermediate formed at a rate constant (k1) of 5.6 × 106 M−1 s−1 and disassembled at a rate (k−1) of 60 s−1, and proceeded to form the native complex at a rate (k2) of approximately 1 s−1. The acceleration of the 4.5S RNA was achieved by stabilizing the intermediate; the intermediate was too weak to be detectable, as indicated by the absence of any complexation between the nucleotide-free GTPase domains, without the 4.5S RNA. Using electron paramagnetic resonance and fluorescence resonance energy transfer, the binding interface of the intermediate was mapped to the N subdomains of the two subunits, with electrostatic attraction providing stabilization (Figure 16).543 This intermediate has been captured in a cryoelectron microscopy structure.544
The second example concerns the dimerization of the E-cadherin extracellular domains, a process central to cell adhesion. The native complex has a domain-swapped interface, 570 but an alternative, X-shaped dimer was formed by mutants incapable of domain swapping and was implicated as an on-pathway intermediate by an enormous decrease in dimerization rate when a salt bridge in the X-dimer interface was disrupted by a charge reversal mutation (K14E).571,572 The values of ka were 1.0 × 104 M−1 s−1 for the wild-type protein but only 2.2 M−1 s−1 for the K14E mutant. NMR relaxation dispersion experiments detected the X-dimer as a minor population, formed with a rate constant of 2.3 × 105 M−1 s−1 and disassembled at a rate of 1.8 × 103 s−1. Together with the overall ka value, a rate of 86 s−1 for the transition from the Xdimer to the domain-swapped dimer could be deduced. With the K14E mutation, the intermediate was no longer detectable by NMR relaxation dispersion. Incidentally, this experimental technique has also been used to study the overall association between the H2A.Z-H2B histone dimer and the histone chaperone Chz1573 and between an SH3 domain and peptides with varying charges,574 implicating the potential for significant electrostatic ka enhancement in both cases.
6.2.3. Binding of IDPs to Structured Targets
When binding to structured targets such as partner proteins, many IDPs undergo a disorder-to-order transition. The conformations adopted on the target surfaces often are extended, with stabilization provided less by intramolecular and more by intermolecular interactions (see Figure 17b (#40 complex) and Figure 18). Simultaneous formation of all these latter interactions upon approaching a target surface would severely restrict the association rate constant; a more likely scenario is sequential formation of the extended conformation.457 Specifically, it was proposed that the binding of an IDP follows a dock-and-coalesce mechanism, whereby one segment of the IDP first docks to its subsite on the target surface and the remaining segments subsequently coalesce around their respective subsites (Figure 18). The docking segment approaches its subsite by translational and rotational diffusion, and at the same time undergoes rapid conformational exchange to reach a kinetic intermediate, referred to as a docked complex (the A*B species in Scheme 1), where the docking segment is natively bound but the remaining segment(s) of the IDP are still loose.575 The docking step likely is rate-limited by the diffusional approach, and the rate constant k1 can be calculated by the TransComp method. In the subsequent coalescing step, the remaining segments evolve toward their native conformations, with energy barriers determined by secondary structure propensities of the coalescing segments576,577 and their short-range intermolecular interactions with the target surface.578
Figure 18.
Dock-and-coalesce mechanism, illustrated on the binding of a WASP disordered region to Cdc42. WASP is shown as a ribbon, with different colors for three segments, and Cdc42 is shown by its electrostatic surface. Reprinted with permission from ref 589. Copyright 2017 John Wiley & Sons Ltd.
According to eq 49, the docking rate constant k1 provides an upper bound for the overall association rate constant ka, but slow coalescing may result in a much lower ka in a given dock- and-coalesce pathway. Binding of the IDP can proceed along multiple pathways, each starting with the docking of some initial segment of the IDP and ending with the structural coalescence of some final segment on the target surface.457,579 However, it is quite possible that a single pathway has a ka much higher than all other alternatives, and hence becomes dominant. The most likely dominant pathway is the one where the docking step is rate-enhanced by electrostatic attraction and is close to being rate-limiting for the overall ka of that pathway. By applying the TransComp method to different segments of an IDP, one can identify the docking segment of the dominant pathway and predict the rate constant of the docking step, thereby providing an upper bound for the rate constant of the overall binding process. This adaptive use of TransComp was first tested on the binding of the partially disordered hirudin to thrombin (#40 complex in Figure 17b), where the docking segment was identified as the highly acidic C-terminal tail.457 The predicted docking rate constant, 1.3 × 108 M−1 s−1, closely approximated the experimental value, 7.5 × 107 M−1 s−1 for ka.580 These and experimental and computational data on other proteins suggest that dock-and-coalesce is a general mechanism for the binding of IDPs.579
With the adaptive use of TransComp, the rate constants of three IDPs, along with four structured proteins, that all bind to G-actin and regulate actin polymerization were calculated.581 These results showed that, for both IDPs and structured proteins, electrostatic attraction is the main determinant for the magnitudes of ka. For a phosphopeptide binding to two different SH2 domains, while the rate constants are electrostatically enhanced in both cases, as shown by decreased rates with increasing extents of dephosphorylation,582,583 the binding mechanisms were different, one forming the native complex all at once while the other involving dock-and-coalesce.584 Interestingly, for the binding of the disordered Wiskott–Aldrich syndrome protein (WASP) to the Cdc42 GTPase (Figure 18), when the docking step with one segment was slowed down substantially by charge mutations, docking with another segment came into play, so that multiple dock-and- coalesce pathways started to contribute to the overall binding process.575 Significant electrostatic rate enhancement has also been observed in the binding of other IDPs, again implicating a diffusion-limited docking step playing a major rate-determining role.585–587
The coalescing step is likely to play a greater rate-determining role in the binding of many other IDPs. It is then of greater interest to trap and probe the docked complex as an intermediate (e.g., ref 588), analogous to the studies illustrated in section 6.2.2 for structured proteins. Given that the docking and coalescing steps are dictated by distinct physical factors, solvent conditions such as temperature can be used to differentially change the influences of these physical factors, therefore providing a way to dissect the docking and coalescing steps.585,589 Lastly, we note that, by tuning down electrostatic attraction in one segment and tuning up electrostatic attraction in another segment, it might be possible to alter the dominant dock-and-coalesce pathway.
6.3. Protein Binding to Specific Sites on DNA and to Cell Membranes
How transcription factors and other site-specific DNA-binding proteins achieve conflicting goals of specificity and speed when binding to a specific site on genomic DNA with up to billons of base pairs has attracted the attention of theoreticians and experimentalists for many decades. A seminal idea, proposed by Adam and Delbrück,590 is that nonspecific binding to the DNA surface, mediated, e.g., by electrostatic interactions between basic residues of a protein and acidic phosphates of DNA (see section 3.4.3), reduces the dimensionality of the search space, from three and one, and thereby enhances the binding rate constant for a specific site. Berg et al.591 proposed three phenomenological modes of translocation between nonspecific sites: continuous sliding along the DNA, hopping between near sites, and intersegmental transfer between far sites. Zhou and Szabo592 treated nonspecific binding in a physically transparent way, by introducing an attractive interaction potential between the protein and the entire DNA surface. A more recent idea is that proteins use conformational switch to help resolve the conflict between specific and speed: one conformation allows for fast scanning of many sites and another conformation allows for recognition of a specific site.593,594 Nonspecifically bound protein structures have been characterized experimentally and contrasted with specifically bound structures, revealing in particular that Arg side chains interact with DNA phosphates in the former but insert more deeply to interact with DNA bases in the latter.19,20 Zandarashvili et al.595 engineered protein–DNA and interdomain salt bridges to shift the balance between specificity and speed in a predictive manner.
Not only proteins but also DNA may undergo conformational switches upon specific binding. In particular, many proteins induce substantial DNA bending, and the driving force has been speculated and interrogated. Based on the observation that histones bind to nucleosomal DNA mostly from one face of the DNA double helix and thereby asymmetrically neutralize the phosphate charges, Mirzabekov and Rich596 proposed that electrostatic repulsion between phosphates on the opposite face of the DNA is part of the driving force for DNA bending. Asymmetric phosphate neutralization by methylation has indeed been found to induce DNA bending.597 EcoRV endonuclease bends its specific target sequence, GATATC, by 50° toward the major groove at the central TA step.598 Although an initial complex with unbent (or mildly bent) DNA is a likely intermediate toward forming the native complex, simultaneous monitoring of binding and bending indicated fast bending such that the overall process was rate-limited by the initial binding step, with a rate constant exceeding 108 M−1 s−1 (measured on a 14 base pair oligonucleotide).599 Hancock et al.600 presented data using charge neutralization on both EcoRV and a GATATC-containing 24 base pair oligonucleotide to demonstrate that asymmetric phosphate neutralization makes a significant contribution to DNA bending. In particular, neutralization of two DNA-contacting basic residues, Lys119 and Arg226, reduced the association rate constant by 11-fold and 23-fold, respectively, which are in line with the magnitudes of effects found for charge neutralization on protein–protein association rates.575,579,584 In comparison, the effects of these mutations on the stability (and hence the dissociation rate constant) of the native complex with bent DNA were much more dramatic, with 6500-fold and 13000-fold decreases in the binding constant. These basic residues must experience a much more intense negative electrostatic potential from the phosphates brought closer by DNA bending.
On the other hand, Hancock et al.600 found that increasing salt concentration significantly decreased the association rate constant but only weakly affected the dissociation rate constant. These disparate salt effects conform to a pattern for electrostatically enhanced diffusion-limited protein–protein association, which was explained by suggesting that most of the electrostatic interactions subject to salt screening are already formed in a tight transient complex along the way to the native complex (cf. section 6.2.1).601 Vivas et al.602 used salt dependences of the binding constant and the relaxation rate after temperature jump to dissect the initial binding step and subsequent DNA bending step of the integration host factor, a protein involved in DNA compaction. To reduce the number of fitting parameters, these authors assumed a linear dependence, on a log–log scale, of each elementary rate constant on salt concentration. They found that the rate constant most affected by salts was for the disassembly of the initial complex, in contrast to the results for EcoRV,602 and explained their finding by invoking a very loose transient complex for the initial binding.
Protein binding to membrane-bound receptors presents another case where a reduction in dimensionality of the search space, now from three to two, can enhance the rate constant. As an example, the activation of protein kinase C starts with the targeting of its C2 domain to the membrane-bound ligand, phosphatidylinositol-4,5-bisphosphate. We are not aware of any study on the binding kinetics of the C2 domain to the membrane-bound ligand, but a study on the binding to the whole surface of an anionic lipid vesicle is quite interesting.603 Mutations of both (positively) charged and hydrophobic residues in the protein–membrane interface had greater effects on the dissociation rate constant than on the association rate constant. This trend, opposite to that of salt effects on stereospecific association between proteins,601 has been predicted by rate calculations using the theoretical model of Zhou and Szabo.592,604 For binding to a specific site on a membrane, the effect of a surface potential on the binding constant nearly all resides with accelerating the association rate constant. In contrast, for binding to the whole membrane surface, the effects of the surface potential become modest on the association rate constant but significant on the dissociation rate constant.
7. CHARGE MODIFICATIONS LINKED TO DISEASES
Here we showcase the importance of electrostatic interactions in protein structure and function by highlighting a number of charge modifications, either through gene mutation or attained posttranslationally, that can be linked to the pathogenesis of human diseases. Once again, the β subunit Glu6 → Val mutation of sickle hemoglobin serves as a prime example. Like sickle cell anemia and Alzheimer’s disease, cataract is a protein condensation disease, where light scattering by protein aggregates leads to lens opacification.605 The cataractogenic R14C mutation of γD-crystallin significantly expands the temperature range where LLPS occurs and promotes aggregation, likely via disulfide-linked oligomeriztion.497 Two other cataractogenic mutations of γD-crystallin also involve charge neutralization of Arg residues, R36S606 and R58H.607 These mutations led to significant solubility decreases and rapid crystallization.608 In fact, crystallization of the R36S mutant was observed in situ and believed to be the mechanism for cataractogenesis.606 One more cataract-associated mutation, E107A,609 involves neutralization of an acidic residue. The mutation did not affect the LLPS coexistence curve of pure γD-crystallin, but dramatically changed the protein compositions of the two phases for mixtures of γD-crystallin and α-crystallin (another main protein component of the eye lens).610 For mixtures of α-crystallin and wild-type γD-crystallin, the concentrated phase was mostly γD-crystallin whereas the dilute phase was mostly α-crystallin. With the mutation, the compositions for both phases were more evenly split between the two protein types. The change in phase behavior upon mutation, attributed to more favorable interactions between the two protein types, resulted in stronger light scattering, which was suggested to contribute to cataractogenesis.
There are numerous other reports of charge mutations altering intra- or intermolecular interactions and thereby contributing to pathogenesis. For example, a number of charge mutations in GPCRs have been found to increase constitutive activity by disrupting interactions that stabilize an inactive form.611,612 In rhodopsin, the GPCR for vision, the inverse agonist 11-cis-retinal is covalently linked to the ε-amino group of Lys296 and thereby inhibits the basal activity. Absorption of light switches the inverse agonist to an all-trans conformation and activates the receptor. Mutations of Lys296 prevent the covalent linkage of 11-cis-retinal and cause autosomal dominant retinitis pigmentosa, by keeping the protein in an apo, constitutively active form and ultimately leading to retinal degeneration. In addition to covalently linking 11-cis-retinal, Lys296 also forms a salt bridge with Glu113 that helps keep the basal activity in check. This salt bridge is interfered by G90D and A292E mutations, by providing alternative partners to Lys296; the resulting constitutive activation leads to congenital night blindness. Similarly, in many rhodopsin-like GPCRs, an “ionic lock” between Arg(3.50) and Asp(6.30) suppresses basal activity, and a number of disease-associated mutations of Asp(6.30) have been identified. Protein–protein interfaces are also hot spots for disease-causing mutations, often by disrupting electrostatic interactions between proteins.613,614
Posttranslational modifications can also change the charges on side chains, and dysregulation of these modifications has been linked to many diseases. In particular, many cancer-associated mutations either inactivate or activate kinases, leading to hypo- or hyperphosphorylation of substrate proteins.615 As an example, the R776H mutation of the epidermal growth factor kinase results in constitutive activity, by disrupting an autoinhibitory interaction involving Arg766.616 Mutations may also destroy phosphorylation sites or generate new ones (see section 3.5).615 We note that intracellular pHs are elevated by approximately 0.4 unit in cancer cells relative to normal cells, which can alter the charges of ionizable groups and potentially affect structure and function of many proteins.617 Arg to His mutations, as exemplified by the aforementioned R776H, are enriched in cancer mutations.618 The new His residues could increase sensitivity to changes in intracellular pH.
Aberrant profiles of histone modifications, in particular Lys acetylation, are closely linked to cancer.309 Erroneous histone acetylation may result in anomalous recruitment of chromatin-associated factors (see section 3.5) and hence deregulated expression of oncogenes and tumor repressors. Changes in histone modifications may also impair genomic stability and thereby increase the risk of developing cancer.
Deimination of Arg residues in myelin basic protein (MBP) has been implicated in the pathogenesis of multiple sclerosis.619–621 MBP is a major component of the myelin membrane protecting nerve axons. Interactions between basic residues of MBP and anionic phospholipids (see section 3.4.1) help maintain a compact myelin sheath. These interactions are weakened when the positive charges on Arg residues in MBP are lost upon deimination, leading to a more open myelin sheath. The degree of deimination correlated well with the severity of the disease.
8. CONCLUDING REMARKS
In this review, we have emphasized a basic, unified framework for understanding protein electrostatic effects, and used only the simplest theoretical models, in particular the PB model, to illustrate basic ideas. In reality, protein electrostatics is complex and there is much ongoing work addressing these complexities, including the many effects of salt ions. Certainly there is ample room for developments of both models and methodologies in the future. Moreover, compared to our cumulative knowledge on protein folding and binding, our understanding of electrostatic effects in more complex processes involving protein clusters (as in various protein condensation phenomena) and networks (as in signal transduction and many human diseases) is lagging. These problems will present challenges to theoreticians and experimentalists alike.
Continuum electrostatic models such as the PB model have greatly advanced our physical understanding of proteins. For example, one can easily rationalize why charged residues are generally found on the surface of structured proteins and why disordered proteins tend to have a higher content of charged residues. Similarly, the pKa shifts of many ionizable groups can be explained in terms of desolvation cost and interactions with neighboring charged and polar groups. At the same time, these models have severe limitations. For example, the PB model would totally miss the mitigation of desolvation cost by transient opening of a deeply buried site. In addition, salt ions have many facets that are beyond the mean-field treatment of the PB model. These include finite ion size, ion–ion correlation, ion hydration, and ion dielectric image. Models that account for them have yet to be widely disseminated to the protein community. As a result, preferential binding of chaotropic ions to protein backbone amides, preferential accumulation of anions around basic residues, and tight binding of polyvalent ions to proteins and nucleic acids are still not as well understood as ion screening of protein charge–charge interactions. Testing the accuracy of advanced electrostatic models and developing computationally efficient implementations for realistic applications to proteins will be a fruitful direction for future studies.
Most implicit-solvent models have treated electrostatic effects in isolation from nonelectrostatic effects, assuming additivity of their combined effects. This assumption is intuitively appealing and has sometimes met with remarkable successes, as in modeling diffusion-limited protein–protein association. Here the physical factors for the association rate constant can be teased out, with short-range interactions specifying the location of the transient complex and hence the basal rate constant while long-range electrostatic forces controlling the speed to reach the transient complex and hence the magnitude of the overall rate constant.538 However, there are many examples where electrostatic and nonelectrostatic effects are coupled. In particular, salt ions can strengthen hydrophobic interactions in proteins.66,68 The use of total free energy functionals that include both electrostatic and nonelectrostatic terms offers one way to account for their coupling.170,171 Unique benefits of explicitly treating electrostatic and nonelectrostatic coupling have yet to be fully explored for proteins.
There likely will always be limits to what implicit-solvent models can achieve, regardless of their levels of sophistication. In many cases, discrete microscopic effects of solvent molecules can be important for both correct physical understanding and for numerical accuracy of computed energetics. A promising approach that incorporates details of solvation response from the physics of an explicit solvent and yet is computationally fast is semiexplicit assembly, where solvation properties of water precomputed in explicit-solvent simulations of simple spheres are assembled to predict solvation free energies of arbitrary solutes.622 So far this approach has only been applied to small solute molecules, and it will be interesting to investigate possible adaptation for use on protein molecules. Although in theory very powerful, explicit-solvent simulations of proteins require careful attention to convergence of computed thermodynamic and kinetic properties (and hence the associated computational cost). This is especially true for problems with slow events such as transient opening of a deeply buried site. Unfortunately, the computational challenge is confounded by persistent concerns for inaccuracy of force-field parameters. In any event, it is always important that those who carry out simulations are diligent in uncovering mechanistic insight from their simulations, so that physical understanding improves along with numerical accuracy.
While electrostatic modeling for protein folding and binding, which involve a single or a few protein molecules, has been detailed and extensive, similar efforts for condensed states such as the solid phase in solubility and the droplet phase in liquid–liquid phase separation are lagging. Advanced methods for fast calculations of interaction energies in large systems (e.g., ref 623) will be valuable. In contrast to the situation for protein binding that leads to stereospecific binary complexes, for liquid–liquid phase separation and other situations with highly concentrated macromolecules, such as found in cellular environments, nonspecific interprotein interactions become central players, leading to large, dynamic clusters.466,624 The interaction sites therein are neither stereospecific nor random, but preferential, resulting from favorable superposition of many weak interatomic interactions.504 Capturing and characterizing these protein clusters experimentally will require novel approaches.
Modulation of side chain charges by pH has been intensively studied, both experimentally and computationally. Experimental studies that specifically target charge modifications by posttranslational modifications such as phosphorylation at the molecular level are relatively sparse, and computational studies are even fewer (e.g., on phosphorylation-induced conformational changes625 and on the kinetics of phosphopeptide-SH2 binding584). More such studies and, even more importantly, studies into how these “local” effects are integrated to achieve ultrasensitive, precisely timed responses in signal transduction networks will be crucial to advance the physical understanding of biology in both health and disease.
Sickle cell anemia, the first disease characterized at the molecular level, has its root cause at a single charge mutation.4,5 The double-helix model of DNA was correctly built only after placing the negatively charged phosphate groups on the surface.626 These examples remind us to never underestimate the power of electrostatics.
Acknowledgments
While working on this review in the past 10 years, H.-X.Z. has benefited from discussions with many scientists, including Robert Baldwin, Nick Pace, and Brian Matthews. We thank them as well as past and current members of the Zhou group for helping shape the ideas presented in this review. This work was supported in part by Grants GM58187, GM88187, and GM118091 from the National Institutes of Health.
Biographies
Huan-Xiang Zhou received his Ph.D. from Drexel University in 1988. He did postdoctoral work at the National Institutes of Health with Attila Szabo. After faculty appointments at Hong Kong University of Science and Technology, Drexel University, and Florida State University, he moved in 2017 to the University of Illinois at Chicago, where he is professor of chemistry and physics and holds an LAS Science endowed chair. He has served on a number of grant review panels and journal editorial boards. His group currently does theoretical, computational, and experimental research on protein association, on crowding and emergent properties in cellular environments, on structures and functional mechanisms of ion channels and other membrane proteins, and on self-assembly of peptides.
Xiaodong Pang received his Ph.D. in biophysics from Fudan University (China) under the supervision of Prof. Xinyi Zhang in 2010. Since then he has been a postdoctoral fellow with Prof. Huan-Xiang Zhou at Florida State University, conducting research on protein association and structure determination and prediction.
Footnotes
Notes
The authors declare no competing financial interest.
References
- 1.Linderström-Lang K. On the Ionisation of Proteins. C R Trav Lab Carlsberg, Ser Chim. 1924;15:1–29. [Google Scholar]
- 2.Tanford C. Protein Denaturation. C. Theoretical Models for the Mechanism of Denaturation. Adv Protein Chem. 1970;24:1–95. [PubMed] [Google Scholar]
- 3.Hunter T. Why Nature Chose Phosphate to Modify Proteins. Philos Trans R Soc, B. 2012;367:2513–2516. doi: 10.1098/rstb.2012.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pauling L, Itano HA, Singer SJ, Wells IC. Sickle-Cell Anemia, a Molecular Disease. Science. 1949;110:543–548. doi: 10.1126/science.110.2865.543. [DOI] [PubMed] [Google Scholar]
- 5.Ingram VM. A Specific Chemical Difference between the Globins of Normal Human and Sickle-Cell Anaemia Haemoglobin. Nature. 1956;178:792–794. doi: 10.1038/178792a0. [DOI] [PubMed] [Google Scholar]
- 6.Kauzmann W. Some Factors in the Interpretation of Protein Denaturation. Adv Protein Chem. 1959;14:1–63. doi: 10.1016/s0065-3233(08)60608-7. [DOI] [PubMed] [Google Scholar]
- 7.Dill KA. Dominant Forces in Protein Folding. Biochemistry. 1990;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 8.Makhatadze GI, Privalov PL. Energetics of Protein Structure. Adv Protein Chem. 1995;47:307–425. doi: 10.1016/s0065-3233(08)60548-3. [DOI] [PubMed] [Google Scholar]
- 9.Baldwin RL. Energetics of Protein Folding. J Mol Biol. 2007;371:283–301. doi: 10.1016/j.jmb.2007.05.078. [DOI] [PubMed] [Google Scholar]
- 10.Pace CN, Scholtz JM, Grimsley GR. Forces Stabilizing Proteins. FEBS Lett. 2014;588:2177–2184. doi: 10.1016/j.febslet.2014.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schreiber G, Haran G, Zhou HX. Fundamental Aspects of Protein-Protein Association Kinetics. Chem Rev. 2009;109:839–860. doi: 10.1021/cr800373w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pang X, Zhou HX. Rate Constants and Mechanisms of Protein-Ligand Binding. Annu Rev Biophys. 2017;46:105–130. doi: 10.1146/annurev-biophys-070816-033639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Iwata S, Ostermeier C, Ludwig B, Michel H. Structure at 2.8 Å Resolution of Cytochrome C Oxidase from Paracoccus Denitrif icans. Nature. 1995;376:660–669. doi: 10.1038/376660a0. [DOI] [PubMed] [Google Scholar]
- 14.Hunte C, Screpanti E, Venturi M, Rimon A, Padan E, Michel H. Structure of a Na+/H+ Antiporter and Insights into Mechanism of Action and Regulation by pH. Nature. 2005;435:1197–1202. doi: 10.1038/nature03692. [DOI] [PubMed] [Google Scholar]
- 15.Feng L, Campbell EB, Hsiung Y, MacKinnon R. Structure of a Eukaryotic CLC Transporter Defines an Intermediate State in the Transport Cycle. Science. 2010;330:635–641. doi: 10.1126/science.1195230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maniccia AW, Yang W, Johnson JA, Li S, Tjong H, Zhou HX, Shaket LA, Yang JJ. Inverse Tuning of Metal Binding Affinity and Protein Stability by Altering Charged Coordination Residues in Designed Calcium Binding Proteins. PMC Biophys. 2009;2:11. doi: 10.1186/1757-5036-2-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ennion S, Hagan S, Evans RJ. The Role of Positively Charged Amino Acids in ATP Recognition by Human P2X(1) Receptors. J Biol Chem. 2000;275:29361–29367. doi: 10.1074/jbc.M003637200. [DOI] [PubMed] [Google Scholar]
- 18.Jiang LH, Rassendren F, Surprenant A, North RA. Identification of Amino Acid Residues Contributing to the Atp-Binding Site of a Purinergic P2X Receptor. J Biol Chem. 2000;275:34190–34196. doi: 10.1074/jbc.M005481200. [DOI] [PubMed] [Google Scholar]
- 19.Kalodimos CG, Biris N, Bonvin A, Levandoski MM, Guennuegues M, Boelens R, Kaptein R. Structure and Flexibility Adaptation in Nonspecific and Specific Protein-DNA Complexes. Science. 2004;305:386–389. doi: 10.1126/science.1097064. [DOI] [PubMed] [Google Scholar]
- 20.Iwahara J, Zweckstetter M, Clore GM. NMR Structural and Kinetic Characterization of a Homeodomain Diffusing and Hopping on Nonspecific DNA. Proc Natl Acad Sci U S A. 2006;103:15062–15067. doi: 10.1073/pnas.0605868103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Conti E, Uy M, Leighton L, Blobel G, Kuriyan J. Crystallographic Analysis of the Recognition of a Nuclear Localization Signal by the Nuclear Import Factor Karyopherin Alpha. Cell. 1998;94:193–204. doi: 10.1016/s0092-8674(00)81419-1. [DOI] [PubMed] [Google Scholar]
- 22.Pang X, Zhou HX. Design Rules for Selective Binding of Nuclear Localization Signals to Minor Site of Importin Alpha. PLoS One. 2014;9:e91025. doi: 10.1371/journal.pone.0091025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Stern HA, Feller SE. Calculation of the Dielectric Permittivity Profile for a Nonuniform System: Application to a Lipid Bilayer Simulation. J Chem Phys. 2003;118:3401–3412. [Google Scholar]
- 24.Nymeyer H, Zhou HX. A Method to Determine Dielectric Constants in Nonhomogeneous Systems: Application to Biological Membranes. Biophys J. 2008;94:1185–1193. doi: 10.1529/biophysj.107.117770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Parsegian A. Energy of an Ion Crossing a Low Dielectric Membrane: Solutions to Four Relevant Electrostatic Problems. Nature. 1969;221:844–846. doi: 10.1038/221844a0. [DOI] [PubMed] [Google Scholar]
- 26.Bone S, Pethig R. Dielectric Studies of the Binding of Water to Lysozyme. J Mol Biol. 1982;157:571–575. doi: 10.1016/0022-2836(82)90477-6. [DOI] [PubMed] [Google Scholar]
- 27.Tjong H, Zhou HX. Prediction of Protein Solubility from Calculation of Transfer Free Energy. Biophys J. 2008;95:2601–2609. doi: 10.1529/biophysj.107.127746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Archer DA, Wang P. The Dielectric Constant of Water and Debye-Huckel Limiting Law Slopes. J Phys Chem Ref Data. 1990;19:371–411. [Google Scholar]
- 29.Perutz MF. Electrostatic Effects in Proteins. Science. 1978;201:1187–1191. doi: 10.1126/science.694508. [DOI] [PubMed] [Google Scholar]
- 30.Sharp KA, Honig B. Electrostatic Interactions in Macromolecules: Theory and Applications. Annu Rev Biophys Biophys Chem. 1990;19:301–332. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 31.Warshel A, Aqvist J. Electrostatic Energy and Macromolecular Function. Annu Rev Biophys Biophys Chem. 1991;20:267–298. doi: 10.1146/annurev.bb.20.060191.001411. [DOI] [PubMed] [Google Scholar]
- 32.Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, et al. Electrostatics and Diffusion of Molecules in Solution: Simulations with the University of Houston Brownian Dynamics Program. Comput Phys Commun. 1995;91:57–95. [Google Scholar]
- 33.Gilson MK. Theory of Electrostatic Interactions in Macromolecules. Curr Opin Struct Biol. 1995;5:216–223. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 34.Honig B, Nicholls A. Classical Electrostatics in Biology and Chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 35.Ullmann GM, Knapp EW. Electrostatic Models for Computing Protonation and Redox Equilibria in Proteins. Eur Biophys J. 1999;28:533–551. doi: 10.1007/s002490050236. [DOI] [PubMed] [Google Scholar]
- 36.Simonson T. Macromolecular Electrostatics: Continuum Models and Their Growing Pains. Curr Opin Struct Biol. 2001;11:243–252. doi: 10.1016/s0959-440x(00)00197-4. [DOI] [PubMed] [Google Scholar]
- 37.Baker NA. Improving Implicit Solvent Simulations: A Poisson-Centric View. Curr Opin Struct Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 38.Koehl P. Electrostatics Calculations: Latest Methodological Advances. Curr Opin Struct Biol. 2006;16:142–151. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 39.Warshel A, Sharma PK, Kato M, Xiang Y, Liu H, Olsson MH. Electrostatic Basis for Enzyme Catalysis. Chem Rev. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 40.Mulgrew-Nesbitt A, Diraviyam K, Wang J, Singh S, Murray P, Li Z, Rogers L, Mirkovic N, Murray D. The Role of Electrostatics in Protein-Membrane Interactions. Biochim Biophys Acta, Mol Cell Biol Lipids. 2006;1761:812–826. doi: 10.1016/j.bbalip.2006.07.002. [DOI] [PubMed] [Google Scholar]
- 41.Grochowski P, Trylska J. Continuum Molecular Electrostatics, Salt Effects, and Counterion Binding–a Review of the Poisson-Boltzmann Theory and Its Modifications. Biopolymers. 2008;89:93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 42.Grimsley GR, Scholtz JM, Pace CN. A Summary of the Measured pK Values of the Ionizable Groups in Folded Proteins. Protein Sci. 2009;18:247–251. doi: 10.1002/pro.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Pace CN, Grimsley GR, Scholtz JM. Protein Ionizable Groups: pK Values and Their Contribution to Protein Stability and Solubility. J Biol Chem. 2009;284:13285–13289. doi: 10.1074/jbc.R800080200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ren P, Chun J, Thomas DG, Schnieders MJ, Marucho M, Zhang J, Baker NA. Biomolecular Electrostatics and Solvation: A Computational Perspective. Q Rev Biophys. 2012;45:427–491. doi: 10.1017/S003358351200011X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lund M, Jonsson B. Charge Regulation in Biomolecular Solution. Q Rev Biophys. 2013;46:265–281. doi: 10.1017/S003358351300005X. [DOI] [PubMed] [Google Scholar]
- 46.Onufriev AV, Alexov E. Protonation and pK Changes in Protein-Ligand Binding. Q Rev Biophys. 2013;46:181–209. doi: 10.1017/S0033583513000024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cisneros GA, Karttunen M, Ren P, Sagui C. Classical Electrostatics for Biomolecular Simulations. Chem Rev. 2014;114:779–814. doi: 10.1021/cr300461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lin YL, Aleksandrov A, Simonson T, Roux B. An Overview of Electrostatic Free Energy Computations for Solutions and Proteins. J Chem Theory Comput. 2014;10:2690–2709. doi: 10.1021/ct500195p. [DOI] [PubMed] [Google Scholar]
- 49.Gilson MK, Honig BH. The Dielectric Constant of a Folded Protein. Biopolymers. 1986;25:2097–2119. doi: 10.1002/bip.360251106. [DOI] [PubMed] [Google Scholar]
- 50.Simonson T, Brooks CL. Charge Screening and the Dielectric Constant of Proteins: Insights from Molecular Dynamics. J Am Chem Soc. 1996;118:8452–8458. [Google Scholar]
- 51.Schutz CN, Warshel A. What Are the Dielectric “Constants” of Proteins and How to Validate Electrostatic Models? Proteins: Struct, Funct Genet. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 52.Rossini E, Knapp EW. Protonation Equilibria of Transition Metal Complexes: From Model Systems toward the Mn-Complex in Photosystem II. Coord Chem Rev. 2017;345:16–30. [Google Scholar]
- 53.It should be noted that the protein dielectric constant is not uniquely defined. In a given continuum electrostatic model, the protein dielectric constant may take different values for best predictions of two different properties (e.g., pKa shifts versus protein solubility). Similarly, in two different continuum electrostatic models, the protein dielectric constant may take different values for best predictions of the same property.
- 54.Born M. Volumen Und Hydratationswärme Der Ionen. Eur Phys J A. 1920;1:45–48. [Google Scholar]
- 55.Debye P, Hückel E. Zur Theorie Der Elektrolyte. I. Gefrierpunktserniedrigung Und Verwandte Erscheinungen (On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena) Phys Z. 1923;24:185–206. [Google Scholar]
- 56.For typical proteins electrostatic energies calculated from the nonlinear equation are not significantly different from those calculated from the linearized version. See: Zhou H-X. Macromolecular Electrostatic Energy Within the Nonlinear Poisson-Boltzmann Equation. J Chem Phys. 1994;100:3152–3162.
- 57.Debye P. Reaction Rates in Ionic Solutions. Trans Electrochem Soc. 1942;82:265–272. [Google Scholar]
- 58.Kirkwood JG. Theory of Solutions of Molecules Containing Widely Separated Charges with Special Application to Zwitterions. J Chem Phys. 1934;2:351–361. [Google Scholar]
- 59.Tanford C, Kirkwood JG. Theory of Protein Titration Curves. I. General Equations for Impenetrable Spheres. J Am Chem Soc. 1957;79:5333–5339. [Google Scholar]
- 60.Equation 4b gives the solvation energy of an ionic solute as long as its charge distribution has spherical symmetry.
- 61.Bell RP. The Electrostatic Energy of Dipole Molecules in Different Media. Trans Faraday Soc. 1931;27:797–802. [Google Scholar]
- 62.Onsager L. Electric Moments of Molecules in Liquids. J Am Chem Soc. 1936;58:1486–1493. [Google Scholar]
- 63.For a perspective of the Tanford–Kirkwood model among other electrostatic models see: Davis ME, McCammon JA. Electrostatics in Biomolecular Structure and Dynamics. Chem Rev. 1990;90:509–521.
- 64.At infinite ionic strength the electrostatic potential must be zero in the solvent (see eq 3) but cannot be zero inside the protein because of the protein charges. This statement also holds for the nonlinear Poisson–Boltzmann equation. Note that taking the solvent dielectric constant to infinity has the same effect (i.e. forcing the electrostatic potential to be zero in the solvent); this extreme case of the solvent is referred to as conductor-like. See: Klamt A, Schuurmann G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy Its Gradient. J Chem Soc Perkin Trans 2. 1993;2:799–805.
- 65.Hofmeister F. Zur Lehre Von Der Wirkung Der Salze (About the Science of the Effect of Salts) Naunyn-Schmiedeberg’s Arch Pharmacol. 1888;24:247–260. [Google Scholar]
- 66.Onsager L, Samaras NNT. The Surface Tension of Debye-Huckel Electrolytes. J Chem Phys. 1934;2:528–536. [Google Scholar]
- 67.Kirkwood JG. In: Proteins, Amino Acids and Peptides as Ions and Dipolar Ions. Cohn EJ, Edsall JT, editors. Reinhold Publishing Corp; New York: 1943. [Google Scholar]
- 68.Zhou HX. Interactions of Macromolecules with Salt Ions: An Electrostatic Theory for the Hofmeister Effect. Proteins: Struct, Funct Genet. 2005;61:69–78. doi: 10.1002/prot.20500. [DOI] [PubMed] [Google Scholar]
- 69.Zhou HX. Brownian Dynamics Study of the Influences of Electrostatic Interaction and Diffusion on Protein-Protein Association Kinetics. Biophys J. 1993;64:1711–1726. doi: 10.1016/S0006-3495(93)81543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Green AA. Studies in the Physical Chemistry of the Proteins. X. The Solubility of Hemoglobin in Chlorides and Sulfates of Varying Concentration. J Biol Chem. 1932;95:47–66. [Google Scholar]
- 71.Tanford C. Physical Chemistry of Macromolecules. John Wiley & Sons, Inc; New York: 1961. [Google Scholar]
- 72.Arakawa T, Timasheff SN. Theory of Protein Solubility. Methods Enzymol. 1985;114:49–77. doi: 10.1016/0076-6879(85)14005-x. [DOI] [PubMed] [Google Scholar]
- 73.Matthews BW. Determination of Molecular Weight from Protein Crystals. J Mol Biol. 1974;82:513–526. doi: 10.1016/0022-2836(74)90245-9. [DOI] [PubMed] [Google Scholar]
- 74.Poon WCK, Egelhaaf SU, Beales PA, Salonen A, Sawyer L. Protein Crystallization: Scaling of Charge and Salt Concentration in Lysozyme Solutions. J Phys : Condens Matter. 2000;12:L569–L574. [Google Scholar]
- 75.Collins KD. Sticky Ions in Biological Systems. Proc Natl Acad Sci U S A. 1995;92:5553–5557. doi: 10.1073/pnas.92.12.5553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Scatchard G, Coleman JS, Shen AL. Physical Chemistry of Protein Solutions. VII. The Binding of Some Small Anions to Serum Albumin. J Am Chem Soc. 1957;79:12–20. [Google Scholar]
- 77.Schrier EE, Schrier EB. The Salting-out Behavior of Amides and Its Relation to the Denaturation of Proteins by Salts. J Phys Chem. 1967;71:1851–1860. doi: 10.1021/j100865a049. [DOI] [PubMed] [Google Scholar]
- 78.Nandi PK, Robinson DR. Effects of Salts on the Free Energy of the Peptide Group. J Am Chem Soc. 1972;94:1299–1308. doi: 10.1021/ja00759a042. [DOI] [PubMed] [Google Scholar]
- 79.Rembert KB, Paterova J, Heyda J, Hilty C, Jungwirth P, Cremer PS. Molecular Mechanisms of Ion-Specific Effects on Proteins. J Am Chem Soc. 2012;134:10039–10046. doi: 10.1021/ja301297g. [DOI] [PubMed] [Google Scholar]
- 80.Gokarn YR, Fesinmeyer RM, Saluja A, Razinkov V, Chase SF, Laue TM, Brems DN. Effective Charge Measurements Reveal Selective and Preferential Accumulation of Anions, but Not Cations, at the Protein Surface in Dilute Salt Solutions. Protein Sci. 2011;20:580–587. doi: 10.1002/pro.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Zhang F, Skoda MW, Jacobs RM, Zorn S, Martin RA, Martin CM, Clark GF, Weggler S, Hildebrandt A, Kohlbacher O, et al. Reentrant Condensation of Proteins in Solution Induced by Multivalent Counterions. Phys Rev Lett. 2008;101:148101. doi: 10.1103/PhysRevLett.101.148101. [DOI] [PubMed] [Google Scholar]
- 82.Baldwin RL. How Hofmeister Ion Interactions Affect Protein Stability. Biophys J. 1996;71:2056–2063. doi: 10.1016/S0006-3495(96)79404-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.As a historical note, the model of Tanford and Kirkwood (ref 59) was motivated by the prediction of pKa shifts in folded protein.
- 84.All results for the remainder of this section are calculated with εp = 4, εs = 80, and I = 0.
- 85.Beroza P, Fredkin DR, Okamura MY, Feher G. Protonation of Interacting Residues in a Protein by a Monte Carlo Method: Application to Lysozyme and the Photosynthetic Reaction Center of Rhodobacter Sphaeroides. Proc Natl Acad Sci U S A. 1991;88:5804–5808. doi: 10.1073/pnas.88.13.5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Gilson MK. Multiple-Site Titration and Molecular Modeling: Two Rapid Methods for Computing Energies and Forces for Ionizable Groups in Proteins. Proteins: Struct, Funct Genet. 1993;15:266–282. doi: 10.1002/prot.340150305. [DOI] [PubMed] [Google Scholar]
- 87.Nelson DL, Cox MM. Lehninger Principles of Biochemistry. Freeman; New York: 2004. [Google Scholar]
- 88.When only a single species of particles is involved in a process (such as the solvation of an ion), the chemical potential is just the free energy per particle.
- 89.In the convention adopted here, the electron is assumed to be at rest by itself in the gas phase, and thus has a chemical potential of zero.
- 90.Hill TL. An Introduction to Statistical Thermodynamics. Dover Publications, Inc; New York: 1986. [Google Scholar]
- 91.Balakrishnan A, Smith V, Stoicheff BP. Dissociation Energy of the Hydrogen Molecule. Phys Rev Lett. 1992;68:2149–2152. doi: 10.1103/PhysRevLett.68.2149. [DOI] [PubMed] [Google Scholar]
- 92.Donald WA, Williams ER. Gas-Phase Electrochemistry: Measuring Absolute Potentials and Investigating Ion and Electron Hydration. Pure Appl Chem. 2011;83:2115–2212. [Google Scholar]
- 93.Reiss H, Heller A. The Absolute Potential of the Standard Hydrogen Electrode: A New Estimate. J Phys Chem. 1985;89:4207–4213. [Google Scholar]
- 94.Yikilmaz E, Rodgers DW, Miller AF. The Crucial Importance of Chemistry in the Structure-Function Link: Manipulating Hydrogen Bonding in Iron-Containing Superoxide Dismutase. Biochemistry. 2006;45:1151–1161. doi: 10.1021/bi051495d. [DOI] [PubMed] [Google Scholar]
- 95.Churg AK, Warshel A. Control of the Redox Potential of Cytochrome C and Microscopic Dielectric Effects in Proteins. Biochemistry. 1986;25:1675–1681. doi: 10.1021/bi00355a035. [DOI] [PubMed] [Google Scholar]
- 96.Zheng C, Davis ME, McCammon JA. Electric-Field Distribution inside the Bacterial Photosynthetic Reaction Center of Rhodopseudomonas Viridis. Chem Phys Lett. 1990;173:246–252. [Google Scholar]
- 97.Langen R, Brayer GD, Berghuis AM, McLendon G, Sherman F, Warshel A. Effect of the Asn52–> Ile Mutation on the Redox Potential of Yeast Cytochrome C: Theory and Experiment. J Mol Biol. 1992;224:589–600. doi: 10.1016/0022-2836(92)90546-v. [DOI] [PubMed] [Google Scholar]
- 98.Zhou HX. Effects of Mutations and Complex Formation on the Redox Potentials of Cytochrome C and Cytochrome C Peroxidase. J Am Chem Soc. 1994;116:10362–10375. [Google Scholar]
- 99.Zhang LY, Friesner RA. Ab Initio Electronic Structure Calculation of the Redox Potentials of Bacteriochlorophyll and Bacteriopheophytin in Solution. J Phys Chem. 1995;99:16479–16482. [Google Scholar]
- 100.Zhou HX. Control of Reduction Potential by Protein Matrix: Lesson from a Spherical Protein Model. JBIC, J Biol Inorg Chem. 1997;2:109–113. [Google Scholar]
- 101.Ullmann GM, Noodleman L, Case DA. Density Functional Calculation of pKa Values and Redox Potentials in the Bovine Rieske Iron-Sulfer Protein. JBIC, J Biol Inorg Chem. 2002;7:632–639. doi: 10.1007/s00775-002-0342-6. [DOI] [PubMed] [Google Scholar]
- 102.Li GH, Zhang XD, Cui Q. Free Energy Perturbation Calculations with Combined QM/MM Potentials Complications, Simplifications, and Applications to Redox Potential Calculations. J Phys Chem B. 2003;107:8643–8653. [Google Scholar]
- 103.Mao J, Hauser K, Gunner MR. How Cytochromes with Different Folds Control Heme Redox Potentials. Biochemistry. 2003;42:9829–9840. doi: 10.1021/bi027288k. [DOI] [PubMed] [Google Scholar]
- 104.Olsson MH, Hong G, Warshel A. Frozen Density Functional Free Energy Simulations of Redox Proteins: Computational Studies of the Reduction Potential of Plastocyanin and Rusticyanin. J Am Chem Soc. 2003;125:5025–5039. doi: 10.1021/ja0212157. [DOI] [PubMed] [Google Scholar]
- 105.Ishikita H, Knapp EW. Control of Quinone Redox Potentials in Photosystem II: Electron Transfer and Photoprotection. J Am Chem Soc. 2005;127:14714–14720. doi: 10.1021/ja052567r. [DOI] [PubMed] [Google Scholar]
- 106.Machuqueiro M, Baptista AM. Molecular Dynamics at Constant pH and Reduction Potential: Application to Cytochrome C(3) J Am Chem Soc. 2009;131:12586–12594. doi: 10.1021/ja808463e. [DOI] [PubMed] [Google Scholar]
- 107.Gámiz-Hernández AP, Kieseritzky G, Galstyan AS, Demir-Kavuk O, Knapp EW. Understanding Properties of Cofactors in Proteins: Redox Potentials of Synthetic Cytochromes B. ChemPhysChem. 2010;11:1196–1206. doi: 10.1002/cphc.200900889. [DOI] [PubMed] [Google Scholar]
- 108.Hughes TF, Friesner RA. Development of Accurate DFT Methods for Computing Redox Potentials of Transition Metal Complexes: Results for Model Complexes and Application to Cytochrome P450. J Chem Theory Comput. 2012;8:442–459. doi: 10.1021/ct2006693. [DOI] [PubMed] [Google Scholar]
- 109.Perutz MF, Raidt H. Stereochemical Basis of Heat Stability in Bacterial Ferredoxins and in Haemoglobin A2. Nature. 1975;255:256–259. doi: 10.1038/255256a0. [DOI] [PubMed] [Google Scholar]
- 110.Elcock AH. The Stability of Salt Bridges at High Temperatures: Implications for Hyperthermophilic Proteins. J Mol Biol. 1998;284:489–502. doi: 10.1006/jmbi.1998.2159. [DOI] [PubMed] [Google Scholar]
- 111.Karshikoff A, Ladenstein R. Ion Pairs and the Thermotolarance of Proteins from Hyperthermophiles: A ‘Traffic Rule’ for Hot Roads. Trends Biochem Sci. 2001;26:550–556. doi: 10.1016/s0968-0004(01)01918-1. [DOI] [PubMed] [Google Scholar]
- 112.Kumar S, Ma B, Tsai CJ, Nussinov R. Electrostatic Strengths of Salt Bridges in Thermophilic and Mesophilic Glutamate Dehydrogenase Monomers. Proteins: Struct, Funct Genet. 2000;38:368–383. doi: 10.1002/(sici)1097-0134(20000301)38:4<368::aid-prot3>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 113.Zhou HX. Toward the Physical Basis of Thermophilic Proteins: Linking of Enriched Polar Interactions and Reduced Heat Capacity of Unfolding. Biophys J. 2002;83:3126–3133. doi: 10.1016/S0006-3495(02)75316-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.The fact that the interaction energy has a much stronger temperature dependence than the desolvation cost can be understood as follows. The desolvation cost can be seen as arising from the interaction of a charge with its dielectric image and hence varies little with εs as long as εs/εp is large. On the other hand, the solvent has a greater chance to mediate the interaction between two charges. In the limit that the two charges are fully positioned in the solvent, the interaction energy is inversely proportional to εs according to Coulomb’s law.
- 115.Warwicker J, Watson HC. Calculation of the Electric Potential in the Active Site Cleft Due to Alpha-Helix Dipoles. J Mol Biol. 1982;157:671–679. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
- 116.Im W, Beglov D, Roux B. Continuum Solvation Model: Computation of Electrostatic Forces from Numerical Solutions to the Poisson-Boltzmann Equation. Comput Phys Commun. 1998;111:59–75. [Google Scholar]
- 117.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of Nanosystems: Application to Microtubules and the Ribosome. Proc Natl Acad Sci U S A. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Zauhar RJ, Morgan RS. A New Method for Computing the Macromolecular Electric Potential. J Mol Biol. 1985;186:815–820. doi: 10.1016/0022-2836(85)90399-7. [DOI] [PubMed] [Google Scholar]
- 119.Yoon BJ, Lenhoff AM. A Boundary Element Method for Molecular Electrostatics with Electrolyte Effects. J Comput Chem. 1990;11:1080–1086. [Google Scholar]
- 120.Juffer AH, Botta EFF, Vankeulen BAM, Vanderploeg A, Berendsen HJC. The Electric Potential of a Macromolecule in a Solvent: A Fundamental Approach. J Comput Phys. 1991;97:144–171. [Google Scholar]
- 121.Zhou HX. Boundary Element Solution of Macromolecular Electrostatics: Interaction Energy between Two Proteins. Biophys J. 1993;65:955–963. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. The Fast Multipole Boundary Element Method for Molecular Electrostatics: An Optimal Approach for Large Systems. J Comput Chem. 1995;16:898–913. [Google Scholar]
- 123.Boschitsch AH, Fenley MO, Zhou HX. Fast Boundary Element Method for the Linear Poisson-Boltzmann Equation. J Phys Chem B. 2002;106:2741–2754. [Google Scholar]
- 124.Lu B, Cheng X, Huang J, McCammon JA. Order N Algorithm for Computation of Electrostatic Interactions in Biomolecular Systems. Proc Natl Acad Sci U S A. 2006;103:19314–19319. doi: 10.1073/pnas.0605166103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Geng WH, Krasny R. A Treecode-Accelerated Boundary Integral Poisson-Boltzmann Solver for Electrostatics of Solvated Biomolecules. J Comput Phys. 2013;247:62–78. [Google Scholar]
- 126.Richards FM. Areas, Volumes, Packing and Protein Structure. Annu Rev Biophys Bioeng. 1977;6:151–176. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 127.Ernst JA, Clubb RT, Zhou HX, Gronenborn AM, Clore GM. Demonstration of Positionally Disordered Water within a Protein Hydrophobic Cavity by NMR. Science. 1995;267:1813–1817. doi: 10.1126/science.7892604. [DOI] [PubMed] [Google Scholar]
- 128.Damjanovic A, García-Moreno B, Lattman EE, García AE. Molecular Dynamics Study of Water Penetration in Staphylococcal Nuclease. Proteins: Struct, Funct Genet. 2005;60:433–449. doi: 10.1002/prot.20486. [DOI] [PubMed] [Google Scholar]
- 129.Vijayakumar M, Zhou HX. Salt Bridges Stabilize the Folded Structure of Barnase. J Phys Chem B. 2001;105:7334–7340. [Google Scholar]
- 130.Hendsch ZS, Tidor B. Do Salt Bridges Stabilize Proteins? A Continuum Electrostatic Analysis. Protein Sci. 1994;3:211–226. doi: 10.1002/pro.5560030206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Honig B, Yang AS. Free Energy Balance in Protein Folding. Adv Protein Chem. 1995;46:27–58. doi: 10.1016/s0065-3233(08)60331-9. [DOI] [PubMed] [Google Scholar]
- 132.Sheinerman FB, Norel R, Honig B. Electrostatic Aspects of Protein-Protein Interactions. Curr Opin Struct Biol. 2000;10:153–159. doi: 10.1016/s0959-440x(00)00065-8. [DOI] [PubMed] [Google Scholar]
- 133.Kumar S, Nussinov R. Salt Bridge Stability in Monomeric Proteins. J Mol Biol. 1999;293:1241–1255. doi: 10.1006/jmbi.1999.3218. [DOI] [PubMed] [Google Scholar]
- 134.Dong F, Zhou HX. Electrostatic Contributions to T4 Lysozyme Stability: Solvent-Exposed Charges Versus Semi-Buried Salt Bridges. Biophys J. 2002;83:1341–1347. doi: 10.1016/S0006-3495(02)73904-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Dong F, Vijayakumar M, Zhou HX. Comparison of Calculation and Experiment Implicates Significant Electrostatic Contributions to the Binding Stability of Barnase and Barstar. Biophys J. 2003;85:49–60. doi: 10.1016/S0006-3495(03)74453-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Wang T, Tomic S, Gabdoulline RR, Wade RC. How Optimal Are the Binding Energetics of Barnase and Barstar? Biophys J. 2004;87:1618–1630. doi: 10.1529/biophysj.104.040964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Dong F, Zhou HX. Electrostatic Contributions to the Binding Stability of Protein-Protein Complexes. Proteins: Struct, Funct Genet. 2006;65:87–102. doi: 10.1002/prot.21070. [DOI] [PubMed] [Google Scholar]
- 138.Qin S, Zhou HX. Do Electrostatic Interactions Destabilize Protein-Nucleic Acid Binding? Biopolymers. 2007;86:112–118. doi: 10.1002/bip.20708. [DOI] [PubMed] [Google Scholar]
- 139.Pang X, Zhou HX. Poisson-Boltzmann Calculations: Van Der Waals or Molecular Surface? Commun Comput Phys. 2013;13:1–12. doi: 10.4208/cicp.270711.140911s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Tissot AC, Vuilleumier S, Fersht AR. Importance of Two Buried Salt Bridges in the Stability and Folding Pathway of Barnase. Biochemistry. 1996;35:6786–6794. doi: 10.1021/bi952930e. [DOI] [PubMed] [Google Scholar]
- 141.Antosiewicz J, McCammon JA, Gilson MK. Prediction of pH-Dependent Properties of Proteins. J Mol Biol. 1994;238:415–436. doi: 10.1006/jmbi.1994.1301. [DOI] [PubMed] [Google Scholar]
- 142.Xiao L, Honig B. Electrostatic Contributions to the Stability of Hyperthermophilic Proteins. J Mol Biol. 1999;289:1435–1444. doi: 10.1006/jmbi.1999.2810. [DOI] [PubMed] [Google Scholar]
- 143.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J Am Chem Soc. 1990;112:6127–6129. [Google Scholar]
- 144.Grycuk T. Deficiency of the Coulomb-Field Approximation in the Generalized Born Model: An Improved Formula for Born Radii Evaluation. J Chem Phys. 2003;119:4817–4826. [Google Scholar]
- 145.Hawkins GD, Cramer CJ, Truhlar DG. Parametrized Models of Aqueous Free Energies of Solvation Based on Pairwise Descreening of Solute Atomic Charges from a Dielectric Medium. J Phys Chem. 1996;100:19824–19839. [Google Scholar]
- 146.Schaefer M, Karplus M. A Comprehensive Analytical Treatment of Continuum Electrostatics. J Phys Chem. 1996;100:1578–1599. [Google Scholar]
- 147.Bashford D, Case DA. Generalized Born Models of Macromolecular Solvation Effects. Annu Rev Phys Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 148.Onufriev A, Bashford D, Case DA. Modification of the Generalized Born Model Suitable for Macromolecules. J Phys Chem B. 2000;104:3712–3720. [Google Scholar]
- 149.Lee MS, Feig M, Salsbury FR, Jr, Brooks CL., III New Analytic Approximation to the Standard Molecular Volume Definition and Its Application to Generalized Born Calculations. J Comput Chem. 2003;24:1348–1356. doi: 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
- 150.Gallicchio E, Levy RM. Agbnp: An Analytic Implicit Solvent Model Suitable for Molecular Dynamics Simulations and High-Resolution Modeling. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 151.Tjong H, Zhou HX. Gbr(6): A Parameterization-Free, Accurate, Analytical Generalized Born Method. J Phys Chem B. 2007;111:3055–3061. doi: 10.1021/jp066284c. [DOI] [PubMed] [Google Scholar]
- 152.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. Generalized Born Model with a Simple, Robust Molecular Volume Correction. J Chem Theory Comput. 2007;3:156–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Haberthur U, Caflisch A. Facts: Fast Analytical Continuum Treatment of Solvation. J Comput Chem. 2008;29:701–715. doi: 10.1002/jcc.20832. [DOI] [PubMed] [Google Scholar]
- 154.Mukhopadhyay A, Aguilar BH, Tolokh IS, Onufriev AV. Introducing Charge Hydration Asymmetry into the Generalized Born Model. J Chem Theory Comput. 2014;10:1788–1794. doi: 10.1021/ct4010917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Feig M, Brooks CL., 3rd Recent Advances in the Development and Application of Implicit Solvent Models in Biomolecule Simulations. Curr Opin Struct Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 156.Schaefer M, Bartels C, Karplus M. Solution Conformations and Thermodynamics of Structured Peptides: Molecular Dynamics Simulation with an Implicit Solvation Model. J Mol Biol. 1998;284:835–848. doi: 10.1006/jmbi.1998.2172. [DOI] [PubMed] [Google Scholar]
- 157.Dominy BN, Brooks CL. Development of a Generalized Born Model Parametrization for Proteins and Nucleic Acids. J Phys Chem B. 1999;103:3765–3773. [Google Scholar]
- 158.Tsui V, Case DA. Molecular Dynamics Simulations of Nucleic Acids with a Generalized Born Solvation Model. J Am Chem Soc. 2000;122:2489–2498. [Google Scholar]
- 159.Zhu JA, Shi YY, Liu HY. Parametrization of a Generalized Born/Solvent-Accessible Surface Area Model and Applications to the Simulation of Protein Dynamics. J Phys Chem B. 2002;106:4844–4853. [Google Scholar]
- 160.Gotz AW, Williamson MJ, Xu D, Poole D, Le Grand S, Walker RC. Routine Microsecond Molecular Dynamics Simulations with Amber on GPUs. 1. Generalized Born. J Chem Theory Comput. 2012;8:1542–1555. doi: 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Nguyen H, Roe DR, Simmerling C. Improved Generalized Born Solvent Model Parameters for Protein Simulations. J Chem Theory Comput. 2013;9:2020–2034. doi: 10.1021/ct3010485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Mongan J, Case DA, McCammon JA. Constant pH Molecular Dynamics in Generalized Born Implicit Solvent. J Comput Chem. 2004;25:2038–2048. doi: 10.1002/jcc.20139. [DOI] [PubMed] [Google Scholar]
- 163.Lee MS, Salsbury FR, Jr, Brooks CL., 3rd Constant-pH Molecular Dynamics Using Continuous Titration Coordinates. Proteins: Struct Funct Genet. 2004;56:738–752. doi: 10.1002/prot.20128. [DOI] [PubMed] [Google Scholar]
- 164.Chen J, Brooks CL, 3rd, Khandogin J. Recent Advances in Implicit Solvent-Based Methods for Biomolecular Simulations. Curr Opin Struct Biol. 2008;18:140–148. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Itoh SG, Damjanovic A, Brooks BR. pH Replica-Exchange Method Based on Discrete Protonation States. Proteins: Struct, Funct Genet. 2011;79:3420–3436. doi: 10.1002/prot.23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Tjong H, Zhou HX. On the Dielectric Boundary in Poisson-Boltzmann Calculations. J Chem Theory Comput. 2008;4:507–514. doi: 10.1021/ct700319x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Bondi A. Van Der Waals Volumes and Radii. J Phys Chem. 1964;68:441–451. [Google Scholar]
- 168.Sitkoff D, Sharp KA, Honig B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J Phys Chem. 1994;98:1978–1988. [Google Scholar]
- 169.Grant JA, Pickup BT, Nicholls A. A Smooth Permittivity Function for Poisson-Boltzmann Solvation Methods. J Comput Chem. 2001;22:608–640. [Google Scholar]
- 170.Dzubiella J, Swanson JM, McCammon JA. Coupling Hydrophobicity, Dispersion, and Electrostatics in Continuum Solvent Models. Phys Rev Lett. 2006;96:087802. doi: 10.1103/PhysRevLett.96.087802. [DOI] [PubMed] [Google Scholar]
- 171.Chen Z, Baker NA, Wei GW. Differential Geometry Based Solvation Model I: Eulerian Formulation. J Comput Phys. 2010;229:8231–8258. doi: 10.1016/j.jcp.2010.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Nina M, Im W, Roux B. Optimized Atomic Radii for Protein Continuum Electrostatics Solvation Forces. Biophys Chem. 1999;78:89–96. doi: 10.1016/s0301-4622(98)00236-1. [DOI] [PubMed] [Google Scholar]
- 173.Oosawa F. Polyelectrolytes. Marcel Dekker; New York: 1971. [Google Scholar]
- 174.Outhwaite CW, Bhuiyan LB. An Improved Modified Poisson-Boltzmann Equation in Electric-Double-Layer Theory. J Chem Soc Faraday Trans 2. 1983;79:707–718. [Google Scholar]
- 175.Chandler D, Mccoy JD, Singer SJ. Density Functional Theory of Nonuniform Polyatomic Systems. 1. General Formulation. J Chem Phys. 1986;85:5971–5976. [Google Scholar]
- 176.Attard P. Electrolytes and the Electric Double Layer. Adv Chem Phys. 1996;92:1–159. [Google Scholar]
- 177.Borukhov I, Andelman D, Orland H. Steric Effects in Electrolytes: A Modified Poisson-Boltzmann Equation. Phys Rev Lett. 1997;79:435–438. [Google Scholar]
- 178.Ha BY, Liu AJ. Counterion-Mediated Attraction between Two Like-Charged Rods. Phys Rev Lett. 1997;79:1289–1292. [Google Scholar]
- 179.Kovalenko A, Hirata F. Self-Consistent Description of a Metal-Water Interface by the Kohn-Sham Density Functional Theory and the Three-Dimensional Reference Interaction Site Model. J Chem Phys. 1999;110:10095–10112. [Google Scholar]
- 180.Yu YX, Wu JZ, Gao GH. Density-Functional Theory of Spherical Electric Double Layers and Zeta Potentials of Colloidal Particles in Restricted-Primitive-Model Electrolyte Solutions. J Chem Phys. 2004;120:7223–7233. doi: 10.1063/1.1676121. [DOI] [PubMed] [Google Scholar]
- 181.Chu VB, Bai Y, Lipfert J, Herschlag D, Doniach S. Evaluation of Ion Binding to DNA Duplexes Using a Size-Modified Poisson-Boltzmann Theory. Biophys J. 2007;93:3202–3209. doi: 10.1529/biophysj.106.099168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Luchko T, Gusarov S, Roe DR, Simmerling C, Case DA, Tuszynski J, Kovalenko A. Three-Dimensional Molecular Theory of Solvation Coupled with Molecular Dynamics in Amber. J Chem Theory Comput. 2010;6:607–624. doi: 10.1021/ct900460m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Wong GCL, Pollack L. Electrostatics of Strongly Charged Biological Polymers: Ion-Mediated Interactions and Self-Organization in Nucleic Acids and Proteins. Annu Rev Phys Chem. 2010;61:171–189. doi: 10.1146/annurev.physchem.58.032806.104436. [DOI] [PubMed] [Google Scholar]
- 184.Tan ZJ, Chen SJ. Ion-Mediated RNA Structural Collapse: Effect of Spatial Confinement. Biophys J. 2012;103:827–836. doi: 10.1016/j.bpj.2012.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Lipfert J, Doniach S, Das R, Herschlag D. Understanding Nucleic Acid-Ion Interactions. Annu Rev Biochem. 2014;83:813–841. doi: 10.1146/annurev-biochem-060409-092720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Yi M, Nymeyer H, Zhou HX. Test of the Gouy-Chapman Theory for a Charged Lipid Membrane against Explicit-Solvent Molecular Dynamics Simulations. Phys Rev Lett. 2008;101:038103. doi: 10.1103/PhysRevLett.101.038103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Tolokh IS, Pabit SA, Katz AM, Chen Y, Drozdetski A, Baker N, Pollack L, Onufriev AV. Why Double-Stranded RNA Resists Condensation. Nucleic Acids Res. 2014;42:10823–10831. doi: 10.1093/nar/gku756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Giambasu GM, Luchko T, Herschlag D, York DM, Case DA. Ion Counting from Explicit-Solvent Simulations and 3d-RISM. Biophys J. 2014;106:883–894. doi: 10.1016/j.bpj.2014.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Yoo J, Kim H, Aksimentiev A, Ha T. Direct Evidence for Sequence-Dependent Attraction between Double-Stranded DNA Controlled by Methylation. Nat Commun. 2016;7:11045. doi: 10.1038/ncomms11045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Muddana HS, Sapra NV, Fenley AT, Gilson MK. The Electrostatic Response of Water to Neutral Polar Solutes: Implications for Continuum Solvent Modeling. J Chem Phys. 2013;138:224504. doi: 10.1063/1.4808376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Jean-Charles A, Nicholls A, Sharp K, Honig B, Tempczyk A, Hendrickson TF, Still WC. Electrostatic Contributions to Solvation Energies: Comparison of Free-Energy Perturbation and Continuum Calculations. J Am Chem Soc. 1991;113:1454–1455. [Google Scholar]
- 192.Nina M, Beglov D, Roux B. Atomic Radii for Continuum Electrostatics Calculations Based on Molecular Dynamics Free Energy Simulations. J Phys Chem B. 1997;101:5239–5248. [Google Scholar]
- 193.Zhang LY, Gallicchio E, Friesner RA, Levy RM. Solvent Models for Protein-Ligand Binding: Comparison of Implicit Solvent Poisson and Surface Generalized Born Models with Explicit Solvent Simulations. J Comput Chem. 2001;22:591–607. [Google Scholar]
- 194.Swanson JM, Mongan J, McCammon JA. Limitations of Atom-Centered Dielectric Functions in Implicit Solvent Models. J Phys Chem B. 2005;109:14769–14772. doi: 10.1021/jp052883s. [DOI] [PubMed] [Google Scholar]
- 195.Swanson JMJ, Adcock SA, McCammon JA. Optimized Radii for Poisson-Boltzmann Calculations with the Amber Force Field. J Chem Theory Comput. 2005;1:484–493. doi: 10.1021/ct049834o. [DOI] [PubMed] [Google Scholar]
- 196.Tan C, Yang L, Luo R. How Well Does Poisson-Boltzmann Implicit Solvent Agree with Explicit Solvent? A Quantitative Analysis. J Phys Chem B. 2006;110:18680–18687. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 197.Swanson JMJ, Wagoner JA, Baker NA, McCammon JA. Optimizing the Poisson Dielectric Boundary with Explicit Solvent Forces and Energies: Lessons Learned with Atom-Centered Dielectric Functions. J Chem Theory Comput. 2007;3:170–183. doi: 10.1021/ct600216k. [DOI] [PubMed] [Google Scholar]
- 198.Onufriev AV, Aguilar B. Accuracy of Continuum Electrostatic Calculations Based on Three Common Dielectric Boundary Definitions. J Theor Comput Chem. 2014;13:1440006. doi: 10.1142/S0219633614400069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Luque FJ, Negre MJ, Orozco M. An AM1-SCRF Approach to the Study of Changes in Molecular-Properties Induced by Solvent. J Phys Chem. 1993;97:4386–4391. [Google Scholar]
- 200.Tomasi J, Persico M. Molecular-Interactions in Solution - an Overview of Methods Based on Continuous Distributions of the Solvent. Chem Rev. 1994;94:2027–2094. [Google Scholar]
- 201.Tomasi J, Mennucci B, Cammi R. Quantum Mechanical Continuum Solvation Models. Chem Rev. 2005;105:2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 202.Wagoner J, Baker NA. Solvation Forces on Biomolecular Structures: A Comparison of Explicit Solvent and Poisson-Boltzmann Models. J Comput Chem. 2004;25:1623–1629. doi: 10.1002/jcc.20089. [DOI] [PubMed] [Google Scholar]
- 203.Izadi S, Aguilar B, Onufriev AV. Protein-Ligand Electrostatic Binding Free Energies from Explicit and Implicit Solvation. J Chem Theory Comput. 2015;11:4450–4459. doi: 10.1021/acs.jctc.5b00483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204.MacKerell AD., Jr . In: Computational Biochemistry and Biophysics. Becker OM, MacKerell AD Jr, Roux B, Watanabe M, editors. Marcel Dekker; New York: 2001. [Google Scholar]
- 205.Berendsen HJC, Grigera JR, Straatsma TP. The Missing Term in Effective Pair Potentials. J Phys Chem. 1987;91:6269–6271. [Google Scholar]
- 206.Longuet-Higgins HC, Fisher ME. Lars Onsager. National Academy of Sciences; Washington, DC: 1991. [Google Scholar]
- 207.Rinaldi D, Rivail JL. Molecular Polarizability and Dielectric Effect of Medium in Liquid-Phase: Theoretical Study of Water Molecule and Its Dimers. Theor Chim Acta. 1973;32:57–70. [Google Scholar]
- 208.Rivail JL, Rinaldi D. Quantum Chemical Approach to Dielectric Solvent Effects in Molecular Liquids. Chem Phys. 1976;18:233–242. [Google Scholar]
- 209.Cramer CJ, Truhlar DG. A Universal Approach to Solvation Modeling. Acc Chem Res. 2008;41:760–768. doi: 10.1021/ar800019z. [DOI] [PubMed] [Google Scholar]
- 210.Kaminski GA, Stern HA, Berne BJ, Friesner RA, Cao YX, Murphy RB, Zhou R, Halgren TA. Development of a Polarizable Force Field for Proteins Via Ab Initio Quantum Chemistry: First Generation Model and Gas Phase Tests. J Comput Chem. 2002;23:1515–1531. doi: 10.1002/jcc.10125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Ren PY, Ponder JW. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J Phys Chem B. 2003;107:5933–5947. [Google Scholar]
- 212.Lamoureux G, MacKerell AD, Roux B. A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J Chem Phys. 2003;119:5185–5197. [Google Scholar]
- 213.Patel S, Mackerell AD, Jr, Brooks CL., 3rd Charmm Fluctuating Charge Force Field for Proteins: II Protein/Solvent Properties from Molecular Dynamics Simulations Using a Nonadditive Electrostatic Model. J Comput Chem. 2004;25:1504–1514. doi: 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
- 214.Wang J, Cieplak P, Cai Q, Hsieh MJ, Wang JM, Duan Y, Luo R. Development of Polarizable Models for Molecular Mechanical Calculations. 3. Polarizable Water Models Conforming to Thole Polarization Screening Schemes. J Phys Chem B. 2012;116:7999–8008. doi: 10.1021/jp212117d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 215.The formulation in the rest of the present subsection applies also to a solute molecule embedded in a continuum solvent dielectric, when the reaction field arising from solvent polarization by the solute permanent charges is added to the “vacuum” electric field.
- 216.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, Ren P. The Polarizable Atomic Multipole-Based Amoeba Force Field for Proteins. J Chem Theory Comput. 2013;9:4046–4063. doi: 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Reynolds JA, Gilbert DB, Tanford C. Empirical Correlation between Hydrophobic Free Energy and Aqueous Cavity Surface Area. Proc Natl Acad Sci U S A. 1974;71:2925–2927. doi: 10.1073/pnas.71.8.2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 218.Wimley WC, Creamer TP, White SH. Solvation Energies of Amino Acid Side Chains and Backbone in a Family of Host-Guest Pentapeptides. Biochemistry. 1996;35:5109–5124. doi: 10.1021/bi9600153. [DOI] [PubMed] [Google Scholar]
- 219.Vijayakumar M, Zhou HX. Prediction of Residue-Residue Pair Frequencies in Proteins. J Phys Chem B. 2000;104:9755–9764. [Google Scholar]
- 220.Kochanczyk M. Prediction of Functionally Important Residues in Globular Proteins from Unusual Central Distances of Amino Acids. BMC Struct Biol. 2011;11:34. doi: 10.1186/1472-6807-11-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 221.Uversky VN, Gillespie JR, Fink AL. Why Are “Natively Unfolded” Proteins Unstructured under Physiologic Conditions? Proteins: Struct, Funct Genet. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 222.Lomize MA, Pogozheva ID, Joo H, Mosberg HI, Lomize AL. OPM Database and PPM Web Server: Resources for Positioning of Proteins in Membranes. Nucleic Acids Res. 2012;40:D370–376. doi: 10.1093/nar/gkr703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Tanaka S, Scheraga HA. Medium- and Long-Range Interaction Parameters between Amino Acids for Predicting Three-Dimensional Structures of Proteins. Macromolecules. 1976;9:945–950. doi: 10.1021/ma60054a013. [DOI] [PubMed] [Google Scholar]
- 224.Miyazawa S, Jernigan RL. Estimation of Effective Interresidue Contact Energies from Protein Crystal-Structures: Quasi-Chemical Approximation. Macromolecules. 1985;18:534–552. [Google Scholar]
- 225.Sippl MJ. Calculation of Conformational Ensembles from Potentials of Mean Force. An Approach to the Knowledge-Based Prediction of Local Structures in Globular Proteins. J Mol Biol. 1990;213:859–883. doi: 10.1016/s0022-2836(05)80269-4. [DOI] [PubMed] [Google Scholar]
- 226.Samudrala R, Moult J. An All-Atom Distance-Dependent Conditional Probability Discriminatory Function for Protein Structure Prediction. J Mol Biol. 1998;275:895–916. doi: 10.1006/jmbi.1997.1479. [DOI] [PubMed] [Google Scholar]
- 227.Lu H, Skolnick J. A Distance-Dependent Atomic Knowledge-Based Potential for Improved Protein Structure Selection. Proteins: Struct, Funct Genet. 2001;44:223–232. doi: 10.1002/prot.1087. [DOI] [PubMed] [Google Scholar]
- 228.Zhou H, Zhou Y. Distance-Scaled, Finite Ideal-Gas Reference State Improves Structure-Derived Potentials of Mean Force for Structure Selection and Stability Prediction. Protein Sci. 2002;11:2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229.Shen MY, Sali A. Statistical Potential for Assessment and Prediction of Protein Structures. Protein Sci. 2006;15:2507–2524. doi: 10.1110/ps.062416606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 230.Wright PE, Dyson HJ. Intrinsically Unstructured Proteins: Re-Assessing the Protein Structure-Function Paradigm. J Mol Biol. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- 231.Dunker AK, Brown CJ, Lawson JD, Iakoucheva LM, Obradovic Z. Intrinsic Disorder and Protein Function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
- 232.Uversky VN. Natively Unfolded Proteins: A Point Where Biology Waits for Physics. Protein Sci. 2002;11:739–756. doi: 10.1110/ps.4210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233.Uversky VN, Oldfield CJ, Dunker AK. Intrinsically Disordered Proteins in Human Diseases: Introducing the D2 Concept. Annu Rev Biophys. 2008;37:215–246. doi: 10.1146/annurev.biophys.37.032807.125924. [DOI] [PubMed] [Google Scholar]
- 234.Wright PE, Dyson HJ. Linking Folding and Binding. Curr Opin Struct Biol. 2009;19:31–38. doi: 10.1016/j.sbi.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 235.Zhou HX. Intrinsic Disorder: Signaling Via Highly Specific but Short-Lived Association. Trends Biochem Sci. 2012;37:43–48. doi: 10.1016/j.tibs.2011.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 236.Oldfield CJ, Dunker AK. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu Rev Biochem. 2014;83:553–584. doi: 10.1146/annurev-biochem-072711-164947. [DOI] [PubMed] [Google Scholar]
- 237.Wright PE, Dyson HJ. Intrinsically Disordered Proteins in Cellular Signalling and Regulation. Nat Rev Mol Cell Biol. 2015;16:18–29. doi: 10.1038/nrm3920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 238.Babu MM, van der Lee R, de Groot NS, Gsponer J. Intrinsically Disordered Proteins: Regulation and Disease. Curr Opin Struct Biol. 2011;21:432–440. doi: 10.1016/j.sbi.2011.03.011. [DOI] [PubMed] [Google Scholar]
- 239.Uversky VN, Dave V, Iakoucheva LM, Malaney P, Metallo SJ, Pathak RR, Joerger AC. Pathological Unfoldomics of Uncontrolled Chaos: Intrinsically Disordered Proteins and Human Diseases. Chem Rev. 2014;114:6844–6879. doi: 10.1021/cr400713r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240.He B, Wang K, Liu Y, Xue B, Uversky VN, Dunker AK. Predicting Intrinsic Disorder in Proteins: An Overview. Cell Res. 2009;19:929–949. doi: 10.1038/cr.2009.87. [DOI] [PubMed] [Google Scholar]
- 241.Mao AH, Crick SL, Vitalis A, Chicoine CL, Pappu RV. Net Charge Per Residue Modulates Conformational Ensembles of Intrinsically Disordered Proteins. Proc Natl Acad Sci U S A. 2010;107:8183–8188. doi: 10.1073/pnas.0911107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Muller-Spath S, Soranno A, Hirschfeld V, Hofmann H, Ruegger S, Reymond L, Nettels D, Schuler B. Charge Interactions Can Dominate the Dimensions of Intrinsically Disordered Proteins. Proc Natl Acad Sci U S A. 2010;107:14609–14614. doi: 10.1073/pnas.1001743107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 243.Das RK, Pappu RV. Conformations of Intrinsically Disordered Proteins Are Influenced by Linear Sequence Distributions of Oppositely Charged Residues. Proc Natl Acad Sci U S A. 2013;110:13392–13397. doi: 10.1073/pnas.1304749110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 244.Sawle L, Ghosh K. A Theoretical Method to Compute Sequence Dependent Configurational Properties in Charged Polymers and Proteins. J Chem Phys. 2015;143:085101. doi: 10.1063/1.4929391. [DOI] [PubMed] [Google Scholar]
- 245.Sizemore SM, Cope SM, Roy A, Ghirlanda G, Vaiana SM. Slow Internal Dynamics and Charge Expansion in the Disordered Protein CGRP: A Comparison with Amylin. Biophys J. 2015;109:1038–1048. doi: 10.1016/j.bpj.2015.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 246.Chin AF, Toptygin D, Elam WA, Schrank TP, Hilser VJ. Phosphorylation Increases Persistence Length and End-to-End Distance of a Segment of Tau Protein. Biophys J. 2016;110:362–371. doi: 10.1016/j.bpj.2015.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 247.Gunasekaran K, Tsai CJ, Kumar S, Zanuy D, Nussinov R. Extended Disordered Proteins: Targeting Function with Less Scaffold. Trends Biochem Sci. 2003;28:81–85. doi: 10.1016/S0968-0004(03)00003-3. [DOI] [PubMed] [Google Scholar]
- 248.Meszaros B, Tompa P, Simon I, Dosztanyi Z. Molecular Principles of the Interactions of Disordered Proteins. J Mol Biol. 2007;372:549–561. doi: 10.1016/j.jmb.2007.07.004. [DOI] [PubMed] [Google Scholar]
- 249.Wong ETC, Na D, Gsponer J. On the Importance of Polar Interactions for Complexes Containing Intrinsically Disordered Proteins. PLoS Comput Biol. 2013;9:e1003192. doi: 10.1371/journal.pcbi.1003192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 250.Krogh A, Larsson B, von Heijne G, Sonnhammer EL. Predicting Transmembrane Protein Topology with a Hidden Markov Model: Application to Complete Genomes. J Mol Biol. 2001;305:567–580. doi: 10.1006/jmbi.2000.4315. [DOI] [PubMed] [Google Scholar]
- 251.Overington JP, Al-Lazikani B, Hopkins AL. Opinion - How Many Drug Targets Are There? Nat Rev Drug Discovery. 2006;5:993–996. doi: 10.1038/nrd2199. [DOI] [PubMed] [Google Scholar]
- 252.Rask-Andersen M, Masuram S, Schioth HB. The Druggable Genome: Evaluation of Drug Targets in Clinical Trials Suggests Major Shifts in Molecular Class and Indication. Annu Rev Pharmacol Toxicol. 2014;54:9–26. doi: 10.1146/annurev-pharmtox-011613-135943. [DOI] [PubMed] [Google Scholar]
- 253.Anfinsen CB. Principles That Govern the Folding of Protein Chains. Science. 1973;181:223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 254.Zhou HX, Cross TA. Influences of Membrane Mimetic Environments on Membrane Protein Structures. Annu Rev Biophys. 2013;42:361–392. doi: 10.1146/annurev-biophys-083012-130326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 255.Wiener MC, White SH. Structure of a Fluid Dioleoylphosphatidylcholine Bilayer Determined by Joint Refinement of X-Ray and Neutron Diffraction Data. III. Complete Structure. Biophys J. 1992;61:434–447. doi: 10.1016/S0006-3495(92)81849-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256.Elofsson A, von Heijne G. Membrane Protein Structure: Prediction Versus Reality. Annu Rev Biochem. 2007;76:125–140. doi: 10.1146/annurev.biochem.76.052705.163539. [DOI] [PubMed] [Google Scholar]
- 257.von Heijne G. The Distribution of Positively Charged Residues in Bacterial Inner Membrane Proteins Correlates with the Trans-Membrane Topology. EMBO J. 1986;5:3021–3027. doi: 10.1002/j.1460-2075.1986.tb04601.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.von Heijne G. Membrane-Protein Topology. Nat Rev Mol Cell Biol. 2006;7:909–918. doi: 10.1038/nrm2063. [DOI] [PubMed] [Google Scholar]
- 259.van Klompenburg W, Nilsson I, von Heijne G, de Kruijff B. Anionic Phospholipids Are Determinants of Membrane Protein Topology. EMBO J. 1997;16:4261–4266. doi: 10.1093/emboj/16.14.4261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 260.van Meer G, Voelker DR, Feigenson GW. Membrane Lipids: Where They Are and How They Behave. Nat Rev Mol Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261.Ulmschneider MB, Sansom MS, Di Nola A. Properties of Integral Membrane Protein Structures: Derivation of an Implicit Membrane Potential. Proteins: Struct, Funct Genet. 2005;59:252–265. doi: 10.1002/prot.20334. [DOI] [PubMed] [Google Scholar]
- 262.Schramm CA, Hannigan BT, Donald JE, Keasar C, Saven JG, Degrado WF, Samish I. Knowledge-Based Potential for Positioning Membrane-Associated Structures and Assessing Residue-Specific Energetic Contributions. Structure. 2012;20:924–935. doi: 10.1016/j.str.2012.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 263.Dong H, Sharma M, Zhou HX, Cross TA. Glycines: Role in Alpha-Helical Membrane Protein Structures and a Potential Indicator of Native Conformation. Biochemistry. 2012;51:4779–4789. doi: 10.1021/bi300090x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 264.Lomize AL, Pogozheva ID, Lomize MA, Mosberg HI. Positioning of Proteins in Membranes: A Computational Approach. Protein Sci. 2006;15:1318–1333. doi: 10.1110/ps.062126106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 265.Slusky JS, Dunbrack RL., Jr Charge Asymmetry in the Proteins of the Outer Membrane. Bioinformatics. 2013;29:2122–2128. doi: 10.1093/bioinformatics/btt355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 266.Jackups R, Jr, Liang J. Interstrand Pairing Patterns in Beta-Barrel Membrane Proteins: The Positive-Outside Rule, Aromatic Rescue and Strand Registration Prediction. J Mol Biol. 2005;354:979–993. doi: 10.1016/j.jmb.2005.09.094. [DOI] [PubMed] [Google Scholar]
- 267.Monne M, Nilsson I, Johansson M, Elmhed N, von Heijne G. Positively and Negatively Charged Residues Have Different Effects on the Position in the Membrane of a Model Transmembrane Helix. J Mol Biol. 1998;284:1177–1183. doi: 10.1006/jmbi.1998.2218. [DOI] [PubMed] [Google Scholar]
- 268.Segrest JP, De Loof H, Dohlman JG, Brouillette CG, Anantharamaiah GM. Amphipathic Helix Motif: Classes and Properties. Proteins: Struct, Funct Genet. 1990;8:103–117. doi: 10.1002/prot.340080202. [DOI] [PubMed] [Google Scholar]
- 269.Doyle DA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT, MacKinnon R. The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 270.Hanske J, Toffey JR, Morenz AM, Bonilla AJ, Schiavoni KH, Pletneva EV. Conformational Properties of Cardiolipin-Bound Cytochrome C. Proc Natl Acad Sci U S A. 2012;109:125–130. doi: 10.1073/pnas.1112312108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 271.Yeung T, Gilbert GE, Shi J, Silvius J, Kapus A, Grinstein S. Membrane Phosphatidylserine Regulates Surface Charge and Protein Localization. Science. 2008;319:210–213. doi: 10.1126/science.1152066. [DOI] [PubMed] [Google Scholar]
- 272.Lomize AL, Pogozheva ID, Lomize MA, Mosberg HI. The Role of Hydrophobic Interactions in Positioning of Peripheral Proteins in Membranes. BMC Struct Biol. 2007;7:44. doi: 10.1186/1472-6807-7-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 273.Hubbard S, Thornton J. NACCESS. Department of Biochemistry and Molecular Biology, University College London; 1993. [Google Scholar]
- 274.Zhou HX, Shan Y. Prediction of Protein Interaction Sites from Sequence Profile and Residue Neighbor List. Proteins: Struct, Funct Genet. 2001;44:336–343. doi: 10.1002/prot.1099. [DOI] [PubMed] [Google Scholar]
- 275.Zhou HX, Qin S. Interaction-Site Prediction for Protein Complexes: A Critical Assessment. Bioinformatics. 2007;23:2203–2209. doi: 10.1093/bioinformatics/btm323. [DOI] [PubMed] [Google Scholar]
- 276.Qin S, Zhou HX. A Holistic Approach to Protein Docking. Proteins: Struct, Funct Genet. 2007;69:743–749. doi: 10.1002/prot.21752. [DOI] [PubMed] [Google Scholar]
- 277.Mukherjee S, Zhang Y. Protein-Protein Complex Structure Predictions by Multimeric Threading and Template Recombination. Structure. 2011;19:955–966. doi: 10.1016/j.str.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 278.Wells JA, McClendon CL. Reaching for High-Hanging Fruit in Drug Discovery at Protein-Protein Interfaces. Nature. 2007;450:1001–1009. doi: 10.1038/nature06526. [DOI] [PubMed] [Google Scholar]
- 279.Jin L, Wang W, Fang G. Targeting Protein-Protein Interaction by Small Molecules. Annu Rev Pharmacol Toxicol. 2014;54:435–456. doi: 10.1146/annurev-pharmtox-011613-140028. [DOI] [PubMed] [Google Scholar]
- 280.Janin J, Bahadur RP, Chakrabarti P. Protein-Protein Interaction and Quaternary Structure. Q Rev Biophys. 2008;41:133–180. doi: 10.1017/S0033583508004708. [DOI] [PubMed] [Google Scholar]
- 281.Levy EDA. Simple Definition of Structural Regions in Proteins and Its Use in Analyzing Interface Evolution. J Mol Biol. 2010;403:660–670. doi: 10.1016/j.jmb.2010.09.028. [DOI] [PubMed] [Google Scholar]
- 282.Ahmad S, Gromiha MM, Sarai A. Analysis and Prediction of DNA-Binding Proteins and Their Binding Residues Based on Composition, Sequence and Structural Information. Bioinformatics. 2004;20:477–486. doi: 10.1093/bioinformatics/btg432. [DOI] [PubMed] [Google Scholar]
- 283.Kuznetsov IB, Gou Z, Li R, Hwang S. Using Evolutionary and Structural Information to Predict DNA-Binding Sites on DNA-Binding Proteins. Proteins: Struct, Funct Genet. 2006;64:19–27. doi: 10.1002/prot.20977. [DOI] [PubMed] [Google Scholar]
- 284.Tjong H, Zhou HX. Displar: An Accurate Method for Predicting DNA-Binding Sites on Protein Surfaces. Nucleic Acids Res. 2007;35:1465–1477. doi: 10.1093/nar/gkm008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 285.Gao M, Skolnick J. DBD-Hunter: A Knowledge-Based Method for the Prediction of DNA-Protein Interactions. Nucleic Acids Res. 2008;36:3978–3992. doi: 10.1093/nar/gkn332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 286.Wu J, Liu H, Duan X, Ding Y, Wu H, Bai Y, Sun X. Prediction of DNA-Binding Residues in Proteins from Amino Acid Sequences Using a Random Forest Model with a Hybrid Feature. Bioinformatics. 2009;25:30–35. doi: 10.1093/bioinformatics/btn583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Ozbek P, Soner S, Erman B, Haliloglu T. Dnabindprot: Fluctuation-Based Predictor of DNA-Binding Residues within a Network of Interacting Residues. Nucleic Acids Res. 2010;38:W417–W423. doi: 10.1093/nar/gkq396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 288.Xiong Y, Liu J, Wei DQ. An Accurate Feature-Based Method for Identifying DNA-Binding Residues on Protein Surfaces. Proteins: Struct, Funct Genet. 2011;79:509–517. doi: 10.1002/prot.22898. [DOI] [PubMed] [Google Scholar]
- 289.Chen YC, Wright JD, Lim C. Dr_Bind: A Web Server for Predicting DNA-Binding Residues from the Protein Structure Based on Electrostatics, Evolution and Geometry. Nucleic Acids Res. 2012;40:W249–W256. doi: 10.1093/nar/gks481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 290.Zhu X, Ericksen SS, Mitchell JC. DBSI: DNA-Binding Site Identifier. Nucleic Acids Res. 2013;41:e160. doi: 10.1093/nar/gkt617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 291.Miao Z, Westhof E. Prediction of Nucleic Acid Binding Probability in Proteins: A Neighboring Residue Network Based Score. Nucleic Acids Res. 2015;43:5340–5351. doi: 10.1093/nar/gkv446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 292.Hornbeck PV, Zhang B, Murray B, Kornhauser JM, Latham V, Skrzypek E. Phosphositeplus, 2014: Mutations, PTMs and Recalibrations. Nucleic Acids Res. 2015;43:D512–520. doi: 10.1093/nar/gku1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 293.As of January 2016; the PhosphoSitePlus database (http://www.phosphosite.org) of these authors contains 211 136 phosphorylation sites on 17 547 human proteins.
- 294.Manning G, Whyte DB, Martinez R, Hunter T, Sudarsanam S. The Protein Kinase Complement of the Human Genome. Science. 2002;298:1912–1934. doi: 10.1126/science.1075762. [DOI] [PubMed] [Google Scholar]
- 295.Iakoucheva LM, Radivojac P, Brown CJ, O’Connor TR, Sikes JG, Obradovic Z, Dunker AK. The Importance of Intrinsic Disorder for Protein Phosphorylation. Nucleic Acids Res. 2004;32:1037–1049. doi: 10.1093/nar/gkh253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 296.Holt LJ, Tuch BB, Villen J, Johnson AD, Gygi SP, Morgan DO. Global Analysis of Cdk1 Substrate Phosphorylation Sites Provides Insights into Evolution. Science. 2009;325:1682–1686. doi: 10.1126/science.1172867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 297.Xiang S, Gapsys V, Kim HY, Bessonov S, Hsiao HH, Moehlmann S, Klaukien V, Ficner R, Becker S, Urlaub H, et al. Phosphorylation Drives a Dynamic Switch in Serine/Arginine-Rich Proteins. Structure. 2013;21:2162–2174. doi: 10.1016/j.str.2013.09.014. [DOI] [PubMed] [Google Scholar]
- 298.De Simone A, Gustavsson M, Montalvao RW, Shi L, Veglia G, Vendruscolo M. Structures of the Excited States of Phospholamban and Shifts in Their Populations Upon Phosphorylation. Biochemistry. 2013;52:6684–6694. doi: 10.1021/bi400517b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 299.Bah A, Vernon RM, Siddiqui Z, Krzeminski M, Muhandiram R, Zhao C, Sonenberg N, Kay LE, Forman-Kay JD. Folding of an Intrinsically Disordered Protein by Phosphorylation as a Regulatory Switch. Nature. 2015;519:106–109. doi: 10.1038/nature13999. [DOI] [PubMed] [Google Scholar]
- 300.Blom N, Gammeltoft S, Brunak S. Sequence and Structure-Based Prediction of Eukaryotic Protein Phosphorylation Sites. J Mol Biol. 1999;294:1351–1362. doi: 10.1006/jmbi.1999.3310. [DOI] [PubMed] [Google Scholar]
- 301.Obenauer JC, Cantley LC, Yaffe MB. Scansite 2.0: Proteome-Wide Prediction of Cell Signaling Interactions Using Short Sequence Motifs. Nucleic Acids Res. 2003;31:3635–3641. doi: 10.1093/nar/gkg584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 302.Kim JH, Lee J, Oh B, Kimm K, Koh I. Prediction of Phosphorylation Sites Using SVMs. Bioinformatics. 2004;20:3179–3184. doi: 10.1093/bioinformatics/bth382. [DOI] [PubMed] [Google Scholar]
- 303.Gnad F, Ren S, Cox J, Olsen JV, Macek B, Oroshi M, Mann M. PHOSIDA (Phosphorylation Site Database) Management, Structural and Evolutionary Investigation, and Prediction of Phosphosites. Genome Biol. 2007;8:R250. doi: 10.1186/gb-2007-8-11-r250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 304.Trost B, Kusalik A. Computational Prediction of Eukaryotic Phosphorylation Sites. Bioinformatics. 2011;27:2927–2935. doi: 10.1093/bioinformatics/btr525. [DOI] [PubMed] [Google Scholar]
- 305.Chen X, Shi SP, Suo SB, Xu HD, Qiu JD. Proteomic Analysis and Prediction of Human Phosphorylation Sites in Subcellular Level Reveal Subcellular Specificity. Bioinformatics. 2015;31:194–200. doi: 10.1093/bioinformatics/btu598. [DOI] [PubMed] [Google Scholar]
- 306.Pearlman SM, Serber Z, Ferrell JE., Jr A Mechanism for the Evolution of Phosphorylation Sites. Cell. 2011;147:934–946. doi: 10.1016/j.cell.2011.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 307.Andrews AJ, Chen X, Zevin A, Stargell LA, Luger K. The Histone Chaperone Nap1 Promotes Nucleosome Assembly by Eliminating Nonnucleosomal Histone DNA Interactions. Mol Cell. 2010;37:834–842. doi: 10.1016/j.molcel.2010.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 308.Fenley AT, Adams DA, Onufriev AV. Charge State of the Globular Histone Core Controls Stability of the Nucleosome. Biophys J. 2010;99:1577–1585. doi: 10.1016/j.bpj.2010.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 309.Bannister AJ, Kouzarides T. Regulation of Chromatin by Histone Modifications. Cell Res. 2011;21:381–395. doi: 10.1038/cr.2011.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 310.Anderson RG, Orci L. A View of Acidic Intracellular Compartments. J Cell Biol. 1988;106:539–543. doi: 10.1083/jcb.106.3.539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 311.Yang AS, Honig B. On the pH Dependence of Protein Stability. J Mol Biol. 1993;231:459–474. doi: 10.1006/jmbi.1993.1294. [DOI] [PubMed] [Google Scholar]
- 312.Roca M, Messer B, Warshel A. Electrostatic Contributions to Protein Stability and Folding Energy. FEBS Lett. 2007;581:2065–2071. doi: 10.1016/j.febslet.2007.04.025. [DOI] [PubMed] [Google Scholar]
- 313.Dudek MJA. Detailed Representation of Electrostatic Energy in Prediction of Sequence and pH Dependence of Protein Stability. Proteins: Struct, Funct Genet. 2014;82:2497–2511. doi: 10.1002/prot.24613. [DOI] [PubMed] [Google Scholar]
- 314.Oliveberg M, Arcus VL, Fersht AR. Pka Values of Carboxyl Groups in the Native and Denatured States of Barnase: The pKa Values of the Denatured State Are on Average 0. 4 Units Lower Than Those of Model Compounds. Biochemistry. 1995;34:9424–9433. doi: 10.1021/bi00029a018. [DOI] [PubMed] [Google Scholar]
- 315.Swint-Kruse L, Robertson AD. Hydrogen Bonds and the pH Dependence of Ovomucoid Third Domain Stability. Biochemistry. 1995;34:4724–4732. doi: 10.1021/bi00014a029. [DOI] [PubMed] [Google Scholar]
- 316.Tan YJ, Oliveberg M, Davis B, Fersht AR. Perturbed Pk (a)-Values in the Denatured States of Proteins. J Mol Biol. 1995;254:980–992. doi: 10.1006/jmbi.1995.0670. [DOI] [PubMed] [Google Scholar]
- 317.Kuhlman B, Luisi DL, Young P, Raleigh DP. pKa Values and the pH Dependent Stability of the N-Terminal Domain of L9 as Probes of Electrostatic Interactions in the Denatured State. Differentiation between Local and Nonlocal Interactions. Biochemistry. 1999;38:4896–4903. doi: 10.1021/bi982931h. [DOI] [PubMed] [Google Scholar]
- 318.Whitten ST, Garcia-Moreno EB. pH Dependence of Stability of Staphylococcal Nuclease: Evidence of Substantial Electrostatic Interactions in the Denatured State. Biochemistry. 2000;39:14292–14304. doi: 10.1021/bi001015c. [DOI] [PubMed] [Google Scholar]
- 319.Lindman S, Linse S, Mulder FAA, Andre I. pKa Values for Side-Chain Carboxyl Groups of a PGB1 Variant Explain Salt and pH-Dependent Stability. Biophys J. 2007;92:257–266. doi: 10.1529/biophysj.106.088682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 320.Arbely E, Rutherford TJ, Neuweiler H, Sharpe TD, Ferguson N, Fersht AR. Carboxyl pKa Values and Acid Denaturation of BBL. J Mol Biol. 2010;403:313–327. doi: 10.1016/j.jmb.2010.08.052. [DOI] [PubMed] [Google Scholar]
- 321.Bradley J, O’Meara F, Farrell D, Nielsen JE. Highly Perturbed pKa Values in the Unfolded State of Hen Egg White Lysozyme. Biophys J. 2012;102:1636–1645. doi: 10.1016/j.bpj.2012.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 322.Tollinger M, Crowhurst KA, Kay LE, Forman-Kay JD. Site-Specific Contributions to the pH Dependence of Protein Stability. Proc Natl Acad Sci U S A. 2003;100:4545–4550. doi: 10.1073/pnas.0736600100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 323.Meng W, Raleigh DP. Analysis of Electrostatic Interactions in the Denatured State Ensemble of the N-Terminal Domain of L9 under Native Conditions. Proteins: Struct, Funct Genet. 2011;79:3500–3510. doi: 10.1002/prot.23145. [DOI] [PubMed] [Google Scholar]
- 324.Pujato M, Navarro A, Versace R, Mancusso R, Ghose R, Tasayco ML. The pH-Dependence of Amide Chemical Shift of Asp/Glu Reflects Its pKa in Intrinsically Disordered Proteins with Only Local Interactions. Biochim Biophys Acta, Proteins Proteomics. 2006;1764:1227–1233. doi: 10.1016/j.bbapap.2006.04.014. [DOI] [PubMed] [Google Scholar]
- 325.Croke RL, Patil SM, Quevreaux J, Kendall DA, Alexandrescu AT. NMR Determination of pKa Values in Alpha-Synuclein. Protein Sci. 2011;20:256–269. doi: 10.1002/pro.556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 326.Mosley PL, Daniels KG, Oas TG. Electrostatic Energetics of Bacillus subtilis Ribonuclease P Protein Determined by Nuclear Magnetic Resonance-Based Histidine pKa Measurements. Biochemistry. 2015;54:5379–5388. doi: 10.1021/acs.biochem.5b00138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 327.Hansen AL, Kay LE. Measurement of Histidine pKa Values and Tautomer Populations in Invisible Protein States. Proc Natl Acad Sci U S A. 2014;111:E1705–1712. doi: 10.1073/pnas.1400577111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 328.Elcock AH. Realistic Modeling of the Denatured States of Proteins Allows Accurate Calculations of the pH Dependence of Protein Stability. J Mol Biol. 1999;294:1051–1062. doi: 10.1006/jmbi.1999.3305. [DOI] [PubMed] [Google Scholar]
- 329.Zhou HXA. Gaussian-Chain Model for Treating Residual Charge-Charge Interactions in the Unfolded State of Proteins. Proc Natl Acad Sci U S A. 2002;99:3569–3574. doi: 10.1073/pnas.052030599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 330.Zhou HX. Residual Electrostatic Effects in the Unfolded State of the N-Terminal Domain of L9 Can Be Attributed to Nonspecific Nonlocal Charge-Charge Interactions. Biochemistry. 2002;41:6533–6538. doi: 10.1021/bi025580m. [DOI] [PubMed] [Google Scholar]
- 331.Zhou HX. Residual Charge Interactions in Unfolded Staphylococcal Nuclease Can Be Explained by the Gaussian-Chain Model. Biophys J. 2002;83:2981–2986. doi: 10.1016/S0006-3495(02)75304-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 332.Zhou HX. Direct Test of the Gaussian-Chain Model for Treating Residual Charge-Charge Interactions in the Unfolded State of Proteins. J Am Chem Soc. 2003;125:2060–2061. doi: 10.1021/ja0298491. [DOI] [PubMed] [Google Scholar]
- 333.Spencer DS, Xu K, Logan TM, Zhou HX. Effects of pH, Salt, and Macromolecular Crowding on the Stability of FK506-Binding Protein: An Integrated Experimental and Theoretical Study. J Mol Biol. 2005;351:219–232. doi: 10.1016/j.jmb.2005.05.029. [DOI] [PubMed] [Google Scholar]
- 334.Lindman S, Bauer MC, Lund M, Diehl C, Mulder FAA, Akke M, Linse S. pKa Values for the Unfolded State under Native Conditions Explain the pH-Dependent Stability of PGB1. Biophys J. 2010;99:3365–3373. doi: 10.1016/j.bpj.2010.08.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 335.Fitzkee NC, Garcia-Moreno EB. Electrostatic Effects in Unfolded Staphylococcal Nuclease. Protein Sci. 2008;17:216–227. doi: 10.1110/ps.073081708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 336.Weinkam P, Pletneva EV, Gray HB, Winkler JR, Wolynes PG. Electrostatic Effects on Funneled Landscapes and Structural Diversity in Denatured Protein Ensembles. Proc Natl Acad Sci U S A. 2009;106:1796–1801. doi: 10.1073/pnas.0813120106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 337.Azia A, Levy Y. Nonnative Electrostatic Interactions Can Modulate Protein Folding: Molecular Dynamics with a Grain of Salt. J Mol Biol. 2009;393:527–542. doi: 10.1016/j.jmb.2009.08.010. [DOI] [PubMed] [Google Scholar]
- 338.Shen JK. Uncovering Specific Electrostatic Interactions in the Denatured States of Proteins. Biophys J. 2010;99:924–932. doi: 10.1016/j.bpj.2010.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 339.Bashford D, Karplus M. pKa’s of Ionizable Groups in Proteins: Atomic Detail from a Continuum Electrostatic Model. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 340.Zhou HX, Vijayakumar M. Modeling of Protein Conformational Fluctuations in pKa Predictions. J Mol Biol. 1997;267:1002–1011. doi: 10.1006/jmbi.1997.0895. [DOI] [PubMed] [Google Scholar]
- 341.Georgescu RE, Alexov EG, Gunner MR. Combining Conformational Flexibility and Continuum Electrostatics for Calculating pKas in Proteins. Biophys J. 2002;83:1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 342.Alexov E, Mehler EL, Baker N, Baptista AM, Huang Y, Milletti F, Nielsen JE, Farrell D, Carstensen T, Olsson MH, et al. Progress in the Prediction of pKa Values in Proteins. Proteins: Struct, Funct Genet. 2011;79:3260–3275. doi: 10.1002/prot.23189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 343.Nielsen JE, Gunner MR, Garcia-Moreno EB. The pKa Cooperative: A Collaborative Effort to Advance Structure-Based Calculations of pKa Values and Electrostatic Effects in Proteins. Proteins: Struct, Funct Genet. 2011;79:3249–3259. doi: 10.1002/prot.23194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 344.Meyer T, Knapp EW. pKa Values in Proteins Determined by Electrostatics Applied to Molecular Dynamics Trajectories. J Chem Theory Comput. 2015;11:2827–2840. doi: 10.1021/acs.jctc.5b00123. [DOI] [PubMed] [Google Scholar]
- 345.Fitch CA, Karp DA, Lee KK, Stites WE, Lattman EE, Garcia-Moreno EB. Experimental pKa Values of Buried Residues: Analysis with Continuum Methods and Role of Water Penetration. Biophys J. 2002;82:3289–3304. doi: 10.1016/s0006-3495(02)75670-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 346.Isom DG, Castaneda CA, Cannon BR, Velu PD, Garcia-Moreno EB. Charges in the Hydrophobic Interior of Proteins. Proc Natl Acad Sci U S A. 2010;107:16096–16100. doi: 10.1073/pnas.1004213107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 347.Kato M, Warshel A. Using a Charging Coordinate in Studies of Ionization Induced Partial Unfolding. J Phys Chem B. 2006;110:11566–11570. doi: 10.1021/jp061190o. [DOI] [PubMed] [Google Scholar]
- 348.Ghosh N, Cui Q. pKa of Residue 66 in Staphylococal Nuclease. I. Insights from QM/MM Simulations with Conventional Sampling. J Phys Chem B. 2008;112:8387–8397. doi: 10.1021/jp800168z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 349.Zheng L, Chen M, Yang W. Random Walk in Orthogonal Space to Achieve Efficient Free-Energy Simulation of Complex Systems. Proc Natl Acad Sci U S A. 2008;105:20227–20232. doi: 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 350.Donnini S, Tegeler F, Groenhof G, Grubmüller H. Constant pH Molecular Dynamics in Explicit Solvent with λ-Dynamics. J Chem Theory Comput. 2011;7:1962–1978. doi: 10.1021/ct200061r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 351.Goh GB, Laricheva EN, Brooks CL. 3rd Uncovering pH-Dependent Transient States of Proteins with Buried Ionizable Residues. J Am Chem Soc. 2014;136:8496–8499. doi: 10.1021/ja5012564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 352.Swails JM, York DM, Roitberg AE. Constant pH Replica Exchange Molecular Dynamics in Explicit Solvent Using Discrete Protonation States: Implementation, Testing, and Validation. J Chem Theory Comput. 2014;10:1341–1352. doi: 10.1021/ct401042b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 353.Huang Y, Chen W, Wallace JA, Shen J. All-Atom Continuous Constant pH Molecular Dynamics with Particle Mesh Ewald and Titratable Water. J Chem Theory Comput. 2016;12:5411–5421. doi: 10.1021/acs.jctc.6b00552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 354.Schonichen A, Webb BA, Jacobson MP, Barber DL. Considering Protonation as a Posttranslational Modification Regulating Protein Structure and Function. Annu Rev Biophys. 2013;42:289–314. doi: 10.1146/annurev-biophys-050511-102349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 355.Skehel JJ, Wiley DC. Receptor Binding and Membrane Fusion in Virus Entry: The Influenza Hemagglutinin. Annu Rev Biochem. 2000;69:531–569. doi: 10.1146/annurev.biochem.69.1.531. [DOI] [PubMed] [Google Scholar]
- 356.Ruigrok RW, Martin SR, Wharton SA, Skehel JJ, Bayley PM, Wiley DC. Conformational Changes in the Hemagglutinin of Influenza Virus Which Accompany Heat-Induced Fusion of Virus with Liposomes. Virology. 1986;155:484–497. doi: 10.1016/0042-6822(86)90210-2. [DOI] [PubMed] [Google Scholar]
- 357.Harrison JS, Higgins CD, O’Meara MJ, Koellhoffer JF, Kuhlman BA, Lai JR. Role of Electrostatic Repulsion in Controlling pH-Dependent Conformational Changes of Viral Fusion Proteins. Structure. 2013;21:1085–1096. doi: 10.1016/j.str.2013.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 358.Bui M, Whittaker G, Helenius A. Effect of M1 Protein and Low pH on Nuclear Transport of Influenza Virus Ribonucleoproteins. J Virol. 1996;70:8391–8401. doi: 10.1128/jvi.70.12.8391-8401.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 359.Pinto LH, Lamb RA. The M2 Proton Channels of Influenza A and B Viruses. J Biol Chem. 2006;281:8997–9000. doi: 10.1074/jbc.R500020200. [DOI] [PubMed] [Google Scholar]
- 360.Hu J, Fu R, Nishimura K, Zhang L, Zhou HX, Busath DD, Vijayvergiya V, Cross TA. Histidines, Heart of the Hydrogen Ion Channel from Influenza a Virus: Toward an Understanding of Conductance and Proton Selectivity. Proc Natl Acad Sci U S A. 2006;103:6865–6870. doi: 10.1073/pnas.0601944103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 361.Miao Y, Fu R, Zhou HX, Cross TA. Dynamic Short Hydrogen Bonds in Histidine Tetrad of Full-Length M2 Proton Channel Reveal Tetrameric Structural Heterogeneity and Functional Mechanism. Structure. 2015;23:2300–2308. doi: 10.1016/j.str.2015.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 362.Sharma M, Yi M, Dong H, Qin H, Peterson E, Busath DD, Zhou HX, Cross TA. Insight into the Mechanism of the Influenza a Proton Channel from a Structure in a Lipid Bilayer. Science. 2010;330:509–512. doi: 10.1126/science.1191750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 363.Gajiwala KS, Burley SK. HDEA, a Periplasmic Protein That Supports Acid Resistance in Pathogenic Enteric Bacteria. J Mol Biol. 2000;295:605–612. doi: 10.1006/jmbi.1999.3347. [DOI] [PubMed] [Google Scholar]
- 364.Yang F, Gustafson KR, Boyd MR, Wlodawer A. Crystal Structure of Escherichia coli HDEA. Nat Struct Biol. 1998;5:763–764. doi: 10.1038/1796. [DOI] [PubMed] [Google Scholar]
- 365.Hong W, Jiao W, Hu J, Zhang J, Liu C, Fu X, Shen D, Xia B, Chang Z. Periplasmic Protein HDEA Exhibits Chaperone-Like Activity Exclusively within Stomach pH Range by Transforming into Disordered Conformation. J Biol Chem. 2005;280:27029–27034. doi: 10.1074/jbc.M503934200. [DOI] [PubMed] [Google Scholar]
- 366.Tapley TL, Korner JL, Barge MT, Hupfeld J, Schauerte JA, Gafni A, Jakob U, Bardwell JC. Structural Plasticity of an Acid-Activated Chaperone Allows Promiscuous Substrate Binding. Proc Natl Acad Sci U S A. 2009;106:5557–5562. doi: 10.1073/pnas.0811811106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 367.Foit L, George JS, Zhang BW, Brooks CL, 3rd, Bardwell JC. Chaperone Activation by Unfolding. Proc Natl Acad Sci U S A. 2013;110:E1254–1262. doi: 10.1073/pnas.1222458110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 368.Anderson DE, Becktel WJ, Dahlquist FW. pH-Induced Denaturation of Proteins: A Single Salt Bridge Contributes 3–5 kcal/mol to the Free Energy of Folding of T4 Lysozyme. Biochemistry. 1990;29:2403–2408. doi: 10.1021/bi00461a025. [DOI] [PubMed] [Google Scholar]
- 369.In these calculations, accounting for charge–charge interactions in the unfolded state by the Gaussian-chain model led to a modest improvement in the accuracy of predicted effects of charge mutations.
- 370.Perl D, Mueller U, Heinemann U, Schmid FX. Two Exposed Amino Acid Residues Confer Thermostability on a Cold Shock Protein. Nat Struct Biol. 2000;7:380–383. doi: 10.1038/75151. [DOI] [PubMed] [Google Scholar]
- 371.Perl D, Schmid FX. Electrostatic Stabilization of a Thermophilic Cold Shock Protein. J Mol Biol. 2001;313:343–357. doi: 10.1006/jmbi.2001.5050. [DOI] [PubMed] [Google Scholar]
- 372.Zhou HX, Dong F. Electrostatic Contributions to the Stability of a Thermophilic Cold Shock Protein. Biophys J. 2003;84:2216–2222. doi: 10.1016/S0006-3495(03)75027-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 373.Schwehm JM, Fitch CA, Dang BN, Garcia-Moreno EB, Stites WE. Changes in Stability Upon Charge Reversal and Neutralization Substitution in Staphylococcal Nuclease Are Dominated by Favorable Electrostatic Effect. Biochemistry. 2003;42:1118–1128. doi: 10.1021/bi0266434. [DOI] [PubMed] [Google Scholar]
- 374.Gao J, Bosco DA, Powers ET, Kelly JW. Localized Thermodynamic Coupling between Hydrogen Bonding and Microenvironment Polarity Substantially Stabilizes Proteins. Nat Struct Mol Biol. 2009;16:684–690. doi: 10.1038/nsmb.1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 375.Serrano L, Horovitz A, Avron B, Bycroft M, Fersht AR. Estimating the Contribution of Engineered Surface Electrostatic Interactions to Protein Stability by Using Double-Mutant Cycles. Biochemistry. 1990;29:9343–9352. doi: 10.1021/bi00492a006. [DOI] [PubMed] [Google Scholar]
- 376.Schreiber G, Buckle AM, Fersht AR. Stability and Function: Two Constraints in the Evolution of Barstar and Other Proteins. Structure. 1994;2:945–951. doi: 10.1016/s0969-2126(94)00096-4. [DOI] [PubMed] [Google Scholar]
- 377.Grimsley GR, Shaw KL, Fee LR, Alston RW, Huyghues-Despointes BM, Thurlkill RL, Scholtz JM, Pace CN. Increasing Protein Stability by Altering Long-Range Coulombic Interactions. Protein Sci. 1999;8:1843–1849. doi: 10.1110/ps.8.9.1843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 378.Loladze VV, Ibarra-Molero B, Sanchez-Ruiz JM, Makhatadze GI. Engineering a Thermostable Protein Via Optimization of Charge-Charge Interactions on the Protein Surface. Biochemistry. 1999;38:16419–16423. doi: 10.1021/bi992271w. [DOI] [PubMed] [Google Scholar]
- 379.Wunderlich M, Martin A, Schmid FX. Stabilization of the Cold Shock Protein Cspb from Bacillus subtilis by Evolutionary Optimization of Coulombic Interactions. J Mol Biol. 2005;347:1063–1076. doi: 10.1016/j.jmb.2005.02.014. [DOI] [PubMed] [Google Scholar]
- 380.Strickler SS, Gribenko AV, Gribenko AV, Keiffer TR, Tomlinson J, Reihle T, Loladze VV, Makhatadze GI. Protein Stability and Surface Electrostatics: A Charged Relationship. Biochemistry. 2006;45:2761–2766. doi: 10.1021/bi0600143. [DOI] [PubMed] [Google Scholar]
- 381.Pedelacq JD, Cabantous S, Tran T, Terwilliger TC, Waldo GS. Engineering and Characterization of a Superfolder Green Fluorescent Protein. Nat Biotechnol. 2006;24:79–88. doi: 10.1038/nbt1172. [DOI] [PubMed] [Google Scholar]
- 382.Bi Y, Cho JH, Kim EY, Shan B, Schindelin H, Raleigh DP. Rational Design, Structural and Thermodynamic Characterization of a Hyperstable Variant of the Villin Headpiece Helical Subdomain. Biochemistry. 2007;46:7497–7505. doi: 10.1021/bi6026314. [DOI] [PubMed] [Google Scholar]
- 383.Tzul FO, Schweiker KL, Makhatadze GI. Modulation of Folding Energy Landscape by Charge-Charge Interactions: Linking Experiments with Computational Modeling. Proc Natl Acad Sci U S A. 2015;112:E259–E266. doi: 10.1073/pnas.1410424112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 384.Batra J, Tjong H, Zhou HX. Electrostatic Effects on the Folding Stability of FKBP12. Protein Eng, Des Sel. 2016;29:301–308. doi: 10.1093/protein/gzw014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 385.Argos P, Rossmann MG, Grau UM, Zuber H, Frank G, Tratschin JD. Thermal Stability and Protein Structure. Biochemistry. 1979;18:5698–5703. doi: 10.1021/bi00592a028. [DOI] [PubMed] [Google Scholar]
- 386.Jaenicke R, Bohm G. The Stability of Proteins in Extreme Environments. Curr Opin Struct Biol. 1998;8:738–748. doi: 10.1016/s0959-440x(98)80094-8. [DOI] [PubMed] [Google Scholar]
- 387.Kumar S, Tsai CJ, Nussinov R. Factors Enhancing Protein Thermostability. Protein Eng, Des Sel. 2000;13:179–191. doi: 10.1093/protein/13.3.179. [DOI] [PubMed] [Google Scholar]
- 388.Szilagyi A, Zavodszky P. Structural Differences between Mesophilic, Moderately Thermophilic and Extremely Thermophilic Protein Subunits: Results of a Comprehensive Survey. Structure. 2000;8:493–504. doi: 10.1016/s0969-2126(00)00133-7. [DOI] [PubMed] [Google Scholar]
- 389.Vieille C, Zeikus GJ. Hyperthermophilic Enzymes: Sources, Uses, and Molecular Mechanisms for Thermostability. Microbiol Mol Biol Rev. 2001;65:1–43. doi: 10.1128/MMBR.65.1.1-43.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 390.Petsko GA. Structural Basis of Thermostability in Hyperthermophilic Proteins, or “There’s More Than One Way to Skin a Cat”. Methods Enzymol. 2001;334:469–478. doi: 10.1016/s0076-6879(01)34486-5. [DOI] [PubMed] [Google Scholar]
- 391.Porebski BT, Nickson AA, Hoke DE, Hunter MR, Zhu L, McGowan S, Webb GI, Buckle AM. Structural and Dynamic Properties That Govern the Stability of an Engineered Fibronectin Type III Domain. Protein Eng, Des Sel. 2015;28:67–78. doi: 10.1093/protein/gzv002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 392.Zhou HX. Polymer Crowders and Protein Crowders Act Similarly on Protein Folding Stability. FEBS Lett. 2013;587:394–397. doi: 10.1016/j.febslet.2013.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 393.Privalov PL, Khechinashvili NN. A Thermodynamic Approach to the Problem of Stabilization of Globular Protein Structure: A Calorimetric Study. J Mol Biol. 1974;86:665–684. doi: 10.1016/0022-2836(74)90188-0. [DOI] [PubMed] [Google Scholar]
- 394.Becktel WJ, Schellman JA. Protein Stability Curves. Biopolymers. 1987;26:1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
- 395.Nojima H, Ikai A, Oshima T, Noda H. Reversible Thermal Unfolding of Thermostable Phosphoglycerate Kinase. Thermostability Associated with Mean Zero Enthalpy Change. J Mol Biol. 1977;116:429–442. doi: 10.1016/0022-2836(77)90078-x. [DOI] [PubMed] [Google Scholar]
- 396.Razvi A, Scholtz JM. Lessons in Stability from Thermophilic Proteins. Protein Sci. 2006;15:1569–1578. doi: 10.1110/ps.062130306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 397.Edsall JT. Apparent Molal Heat Capacities of Ammo Acids and Other Organic Compounds. J Am Chem Soc. 1935;57:1506–1507. [Google Scholar]
- 398.Spolar RS, Livingstone JR, Record MT., Jr Use of Liquid Hydrocarbon and Amide Transfer Data to Estimate Contributions to Thermodynamic Functions of Protein Folding from the Removal of Nonpolar and Polar Surface from Water. Biochemistry. 1992;31:3947–3955. doi: 10.1021/bi00131a009. [DOI] [PubMed] [Google Scholar]
- 399.Lee CF, Allen MD, Bycroft M, Wong KB. Electrostatic Interactions Contribute to Reduced Heat Capacity Change of Unfolding in a Thermophilic Ribosomal Protein L30e. J Mol Biol. 2005;348:419–431. doi: 10.1016/j.jmb.2005.02.052. [DOI] [PubMed] [Google Scholar]
- 400.Chan CH, Yu TH, Wong KB. Stabilizing Salt-Bridge Enhances Protein Thermostability by Reducing the Heat Capacity Change of Unfolding. PLoS One. 2011;6:e21624. doi: 10.1371/journal.pone.0021624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 401.Ogasahara K, Lapshina EA, Sakai M, Izu Y, Tsunasawa S, Kato I, Yutani K. Electrostatic Stabilization in Methionine Aminopeptidase from Hyperthermophile Pyrococcus Furiosus. Biochemistry. 1998;37:5939–5946. doi: 10.1021/bi973172q. [DOI] [PubMed] [Google Scholar]
- 402.Ramos CH, Kay MS, Baldwin RL. Putative Interhelix Ion Pairs Involved in the Stability of Myoglobin. Biochemistry. 1999;38:9783–9790. doi: 10.1021/bi9828627. [DOI] [PubMed] [Google Scholar]
- 403.Dominy BN, Perl D, Schmid FX, Brooks CL. 3rd The Effects of Ionic Strength on Protein Stability: The Cold Shock Protein Family. J Mol Biol. 2002;319:541–554. doi: 10.1016/S0022-2836(02)00259-0. [DOI] [PubMed] [Google Scholar]
- 404.Apetri AC, Surewicz WK. Atypical Effect of Salts on the Thermodynamic Stability of Human Prion Protein. J Biol Chem. 2003;278:22187–22192. doi: 10.1074/jbc.M302130200. [DOI] [PubMed] [Google Scholar]
- 405.Bye JW, Falconer RJ. Thermal Stability of Lysozyme as a Function of Ion Concentration: A Reappraisal of the Relationship between the Hofmeister Series and Protein Stability. Protein Sci. 2013;22:1563–1570. doi: 10.1002/pro.2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 406.Shi Y, Zheng D, Xie J, Zhang Q, Zhang H. Thermal Stability of Thermoanaerobacter Tengcongensis Ribosome Recycling Factor. Protein Pept Lett. 2014;21:285–291. doi: 10.2174/09298665113206660118. [DOI] [PubMed] [Google Scholar]
- 407.Sedlak E, Stagg L, Wittung-Stafshede P. Effect of Hofmeister Ions on Protein Thermal Stability: Roles of Ion Hydration and Peptide Groups? Arch Biochem Biophys. 2008;479:69–73. doi: 10.1016/j.abb.2008.08.013. [DOI] [PubMed] [Google Scholar]
- 408.Tadeo X, Lopez-Mendez B, Castano D, Trigueros T, Millet O. Protein Stabilization and the Hofmeister Effect: The Role of Hydrophobic Solvation. Biophys J. 2009;97:2595–2603. doi: 10.1016/j.bpj.2009.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 409.Pegram LM, Wendorff T, Erdmann R, Shkel I, Bellissimo D, Felitsky DJ, Record MT., Jr Why Hofmeister Effects of Many Salts Favor Protein Folding but Not DNA Helix Formation. Proc Natl Acad Sci U S A. 2010;107:7716–7721. doi: 10.1073/pnas.0913376107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 410.Ginzburg M, Sachs L, Ginzburg BZ. Ion Metabolism in a Halobacterium. I. Influence of Age of Culture on Intracellular Concentrations. J Gen Physiol. 1970;55:187–207. doi: 10.1085/jgp.55.2.187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 411.Oren A, Heldal M, Norland S, Galinski EA. Intracellular Ion and Organic Solute Concentrations of the Extremely Halophilic Bacterium. Extremophiles. 2002;6:491–498. doi: 10.1007/s00792-002-0286-3. [DOI] [PubMed] [Google Scholar]
- 412.Dym O, Mevarech M, Sussman JL. Structural Features That Stabilize Halophilic Malate-Dehydrogenase from an Archaebacterium. Science. 1995;267:1344–1346. doi: 10.1126/science.267.5202.1344. [DOI] [PubMed] [Google Scholar]
- 413.Frolow F, Harel M, Sussman JL, Mevarech M, Shoham M. Insights into Protein Adaptation to a Saturated Salt Environment from the Crystal Structure of a Halophilic 2Fe-2S Ferredoxin. Nat Struct Biol. 1996;3:452–458. doi: 10.1038/nsb0596-452. [DOI] [PubMed] [Google Scholar]
- 414.Kennedy SP, Ng WV, Salzberg SL, Hood L, DasSarma S. Understanding the Adaptation of Halobacterium Species NRC-1 to Its Extreme Environment through Computational Analysis of Its Genome Sequence. Genome Res. 2001;11:1641–1650. doi: 10.1101/gr.190201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 415.Oren A, Mana L. Amino Acid Composition of Bulk Protein and Salt Relationships of Selected Enzymes of Salinibacter Ruber, an Extremely Halophilic Bacterium. Extremophiles. 2002;6:217–223. doi: 10.1007/s007920100241. [DOI] [PubMed] [Google Scholar]
- 416.Fukuchi S, Yoshimune K, Wakayama M, Moriguchi M, Nishikawa K. Unique Amino Acid Composition of Proteins in Halophilic Bacteria. J Mol Biol. 2003;327:347–357. doi: 10.1016/s0022-2836(03)00150-5. [DOI] [PubMed] [Google Scholar]
- 417.Mongodin EF, Nelson KE, Daugherty S, Deboy RT, Wister J, Khouri H, Weidman J, Walsh DA, Papke RT, Sanchez Perez G, et al. The Genome of Salinibacter Ruber: Convergence and Gene Exchange among Hyperhalophilic Bacteria and Archaea. Proc Natl Acad Sci U S A. 2005;102:18147–18152. doi: 10.1073/pnas.0509073102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 418.Britton KL, Baker PJ, Fisher M, Ruzheinikov S, Gilmour DJ, Bonete MJ, Ferrer J, Pire C, Esclapez J, Rice DW. Analysis of Protein Solvent Interactions in Glucose Dehydrogenase from the Extreme Halophile. Proc Natl Acad Sci U S A. 2006;103:4846–4851. doi: 10.1073/pnas.0508854103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 419.Elcock AH, McCammon JA. Electrostatic Contributions to the Stability of Halophilic Proteins. J Mol Biol. 1998;280:731–748. doi: 10.1006/jmbi.1998.1904. [DOI] [PubMed] [Google Scholar]
- 420.Moon CP, Kwon S, Fleming KG. Overcoming Hysteresis to Attain Reversible Equilibrium Folding for Outer Membrane Phospholipase A in Phospholipid Bilayers. J Mol Biol. 2011;413:484–494. doi: 10.1016/j.jmb.2011.08.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 421.Chang YC, Bowie JU. Measuring Membrane Protein Stability under Native Conditions. Proc Natl Acad Sci U S A. 2014;111:219–224. doi: 10.1073/pnas.1318576111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 422.Hong H. Toward Understanding Driving Forces in Membrane Protein Folding. Arch Biochem Biophys. 2014;564:297–313. doi: 10.1016/j.abb.2014.07.031. [DOI] [PubMed] [Google Scholar]
- 423.White SH, Wimley WC. Membrane Protein Folding and Stability: Physical Principles. Annu Rev Biophys Biomol Struct. 1999;28:319–365. doi: 10.1146/annurev.biophys.28.1.319. [DOI] [PubMed] [Google Scholar]
- 424.Kim S, Cross TA. Uniformity, Ideality, and Hydrogen Bonds in Transmembrane Alpha-Helices. Biophys J. 2002;83:2084–2095. doi: 10.1016/S0006-3495(02)73969-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 425.Page RC, Kim S, Cross TA. Transmembrane Helix Uniformity Examined by Spectral Mapping of Torsion Angles. Structure. 2008;16:787–797. doi: 10.1016/j.str.2008.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 426.Hildebrand PW, Preissner R, Frommel C. Structural Features of Transmembrane Helices. FEBS Lett. 2004;559:145–151. doi: 10.1016/S0014-5793(04)00061-4. [DOI] [PubMed] [Google Scholar]
- 427.Joh NH, Min A, Faham S, Whitelegge JP, Yang D, Woods VL, Bowie JU. Modest Stabilization by Most Hydrogen-Bonded Side-Chain Interactions in Membrane Proteins. Nature. 2008;453:1266–1270. doi: 10.1038/nature06977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 428.MacKenzie KR, Prestegard JH, Engelman DM. A Transmembrane Helix Dimer: Structure and Implications. Science. 1997;276:131–133. doi: 10.1126/science.276.5309.131. [DOI] [PubMed] [Google Scholar]
- 429.Javadpour MM, Eilers M, Groesbeek M, Smith SO. Helix Packing in Polytopic Membrane Proteins: Role of Glycine in Transmembrane Helix Association. Biophys J. 1999;77:1609–1618. doi: 10.1016/S0006-3495(99)77009-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 430.Senes A, Ubarretxena-Belandia I, Engelman DM. The Calpha—H···O Hydrogen Bond: A Determinant of Stability and Specificity in Transmembrane Helix Interactions. Proc Natl Acad Sci U S A. 2001;98:9056–9061. doi: 10.1073/pnas.161280798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 431.Mueller BK, Subramaniam S, Senes A. A Frequent, GxxxGMediated, Transmembrane Association Motif Is Optimized for the Formation of Interhelical Calpha-H Hydrogen Bonds. Proc Natl Acad Sci U S A. 2014;111:E888–895. doi: 10.1073/pnas.1319944111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 432.Holliday GL, Mitchell JB, Thornton JM. Understanding the Functional Roles of Amino Acid Residues in Enzyme Catalysis. J Mol Biol. 2009;390:560–577. doi: 10.1016/j.jmb.2009.05.015. [DOI] [PubMed] [Google Scholar]
- 433.Ondrechen MJ, Clifton JG, Ringe D. Thematics: A Simple Computational Predictor of Enzyme Function from Structure. Proc Natl Acad Sci U S A. 2001;98:12473–12478. doi: 10.1073/pnas.211436698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 434.Harris TK, Turner GJ. Structural Basis of Perturbed pKa Values of Catalytic Groups in Enzyme Active Sites. IUBMB Life. 2002;53:85–98. doi: 10.1080/15216540211468. [DOI] [PubMed] [Google Scholar]
- 435.Blomberg R, Kries H, Pinkas DM, Mittl PRE, Grutter MG, Privett HK, Mayo SL, Hilvert D. Precision Is Essential for Efficient Catalysis in an Evolved Kemp Eliminase. Nature. 2013;503:418–421. doi: 10.1038/nature12623. [DOI] [PubMed] [Google Scholar]
- 436.Hanoian P, Liu CT, Hammes-Schiffer S, Benkovic S. Perspectives on Electrostatics and Conformational Motions in Enzyme Catalysis. Acc Chem Res. 2015;48:482–489. doi: 10.1021/ar500390e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 437.Guo J, Zhou HX. Protein Allostery and Conformational Dynamics. Chem Rev. 2016;116:6503–6515. doi: 10.1021/acs.chemrev.5b00590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 438.Fried SD, Bagchi S, Boxer SG. Extreme Electric Fields Power Catalysis in the Active Site of Ketosteroid Isomerase. Science. 2014;346:1510–1514. doi: 10.1126/science.1259802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 439.Fried SD, Boxer SG. Measuring Electric Fields and Noncovalent Interactions Using the Vibrational Stark Effect. Acc Chem Res. 2015;48:998–1006. doi: 10.1021/ar500464j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 440.Privett HK, Kiss G, Lee TM, Blomberg R, Chica RA, Thomas LM, Hilvert D, Houk KN, Mayo SL. Iterative Approach to Computational Enzyme Design. Proc Natl Acad Sci U S A. 2012;109:3790–3795. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 441.Knowles JR, Albery WJ. Perfection in Enzyme Catalysis: The Energetics of Triosephosphate Isomerase. Acc Chem Res. 1977;10:105–111. [Google Scholar]
- 442.Sharp K, Fine R, Honig B. Computer Simulations of the Diffusion of a Substrate to an Active Site of an Enzyme. Science. 1987;236:1460–1463. doi: 10.1126/science.3589666. [DOI] [PubMed] [Google Scholar]
- 443.Sines JJ, Allison SA, McCammon JA. Point Charge Distributions and Electrostatic Steering in Enzyme/Substrate Encounter: Brownian Dynamics of Modified Copper/Zinc Superoxide Dismutases. Biochemistry. 1990;29:9403–9412. doi: 10.1021/bi00492a014. [DOI] [PubMed] [Google Scholar]
- 444.Getzoff ED, Cabelli DE, Fisher CL, Parge HE, Viezzoli MS, Banci L, Hallewell RA. Faster Superoxide Dismutase Mutants Designed by Enhancing Electrostatic Guidance. Nature. 1992;358:347–351. doi: 10.1038/358347a0. [DOI] [PubMed] [Google Scholar]
- 445.Zhou HX, Wong KY, Vijayakumar M. Design of Fast Enzymes by Optimizing Interaction Potential in Active Site. Proc Natl Acad Sci U S A. 1997;94:12372–12377. doi: 10.1073/pnas.94.23.12372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 446.McCoy AJ, Chandana Epa V, Colman PM. Electrostatic Complementarity at Protein/Protein Interfaces. J Mol Biol. 1997;268:570–584. doi: 10.1006/jmbi.1997.0987. [DOI] [PubMed] [Google Scholar]
- 447.Gabb HA, Jackson RM, Sternberg MJE. Modelling Protein Docking Using Shape Complementarity, Electrostatics and Biochemical Information. J Mol Biol. 1997;272:106–120. doi: 10.1006/jmbi.1997.1203. [DOI] [PubMed] [Google Scholar]
- 448.van Dijk M, van Dijk AD, Hsu V, Boelens R, Bonvin AM. Information-Driven Protein-DNA Docking Using Haddock: It Is a Matter of Flexibility. Nucleic Acids Res. 2006;34:3317–3325. doi: 10.1093/nar/gkl412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 449.Fleishman SJ, Corn JE, Strauch EM, Whitehead TA, Andre I, Thompson J, Havranek JJ, Das R, Bradley P, Baker D. Rosetta in CAPRI Rounds 13–19. Proteins: Struct, Funct Genet. 2010;78:3212–3218. doi: 10.1002/prot.22784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 450.Qin S, Zhou HX. Structural Models of Protein-DNA Complexes Based on Interface Prediction and Docking. Curr Protein Pept Sci. 2011;12:531–539. doi: 10.2174/138920311796957694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 451.Chakavorty A, Li L, Alexov E. Electrostatic Component of Binding Energy: Interpreting Predictions from Poisson-Boltzmann Equation and Modeling Protocols. J Comput Chem. 2016;37:2495–2507. doi: 10.1002/jcc.24475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 452.Qin S, Zhou HX. Using the Concept of Transient Complex for Affinity Predictions in CAPRI Rounds 20–27 and Beyond. Proteins: Struct, Funct Genet. 2013;81:2229–2236. doi: 10.1002/prot.24366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 453.Kundrotas PJ, Alexov E. Electrostatic Properties of Protein-Protein Complexes. Biophys J. 2006;91:1724–1736. doi: 10.1529/biophysj.106.086025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 454.Mason AC, Jensen JH. Protein-Protein Binding Is Often Associated with Changes in Protonation State. Proteins: Struct, Funct Genet. 2008;71:81–91. doi: 10.1002/prot.21657. [DOI] [PubMed] [Google Scholar]
- 455.Nelson ML, Kang HS, Lee GM, Blaszczak AG, Lau DKW, McIntosh LP, Graves BJ. Ras Signaling Requires Dynamic Properties of Ets1 for Phosphorylation-Enhanced Binding to Coactivator Cbp. Proc Natl Acad Sci U S A. 2010;107:10026–10031. doi: 10.1073/pnas.0915137107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 456.Wu SY, Lee AY, Lai HT, Zhang H, Chiang CM. Phospho Switch Triggers Brd4 Chromatin Binding and Activator Recruitment for Gene-Specific Targeting. Mol Cell. 2013;49:843–857. doi: 10.1016/j.molcel.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 457.Qin S, Pang X, Zhou HX. Automated Prediction of Protein Association Rate Constants. Structure. 2011;19:1744–1751. doi: 10.1016/j.str.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 458.Nishi H, Hashimoto K, Panchenko AR. Phosphorylation in Protein-Protein Binding: Effect on Stability and Function. Structure. 2011;19:1807–1815. doi: 10.1016/j.str.2011.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 459.Nash P, Tang X, Orlicky S, Chen Q, Gertler FB, Mendenhall MD, Sicheri F, Pawson T, Tyers M. Multisite Phosphorylation of a Cdk Inhibitor Sets a Threshold for the Onset of DNA Replication. Nature. 2001;414:514–521. doi: 10.1038/35107009. [DOI] [PubMed] [Google Scholar]
- 460.Borg M, Mittag T, Pawson T, Tyers M, Forman-Kay JD, Chan HS. Polyelectrostatic Interactions of Disordered Ligands Suggest a Physical Basis for Ultrasensitivity. Proc Natl Acad Sci U S A. 2007;104:9650–9655. doi: 10.1073/pnas.0702580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 461.Lee CW, Ferreon JC, Ferreon ACM, Arai M, Wright PE. Graded Enhancement of P53 Binding to Creb-Binding Protein (CBP) by Multisite Phosphorylation. Proc Natl Acad Sci U S A. 2010;107:19290–19295. doi: 10.1073/pnas.1013078107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 462.Kumar P, Chimenti MS, Pemble H, Schonichen A, Thompson O, Jacobson MP, Wittmann T. Multisite Phosphorylation Disrupts Arginine-Glutamate Salt Bridge Networks Required for Binding of Cytoplasmic Linker-Associated Protein 2 (Clasp2) to End-Binding Protein 1 (Eb1) J Biol Chem. 2012;287:17050–17064. doi: 10.1074/jbc.M111.316661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 463.Koivomaegi M, Valk E, Venta R, Iofik A, Lepiku M, Balog ERM, Rubin SM, Morgan DO, Loog M. Cascades of Multisite Phosphorylation Control Sic1 Destruction at the Onset of S Phase. Nature. 2011;480:128–131. doi: 10.1038/nature10560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 464.Lu LX, Domingo-Sananes MR, Huzarska M, Novak B, Gould KL. Multisite Phosphoregulation of Cdc25 Activity Refines the Mitotic Entrance and Exit Switches. Proc Natl Acad Sci U S A. 2012;109:9899–9904. doi: 10.1073/pnas.1201366109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 465.Koivomaegi M, Oerd M, Iofik A, Valk E, Venta R, Faustova I, Kivi R, Balog ERM, Rubin SM, Loog M. Multisite Phosphorylation Networks as Signal Processors for Cdk1. Nat Struct Mol Biol. 2013;20:1415–1424. doi: 10.1038/nsmb.2706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 466.Qin S, Zhou HX. Fast Method for Computing Chemical Potentials and Liquid-Liquid Phase Equilibria of Macromolecular Solutions. J Phys Chem B. 2016;120:8164–8174. doi: 10.1021/acs.jpcb.6b01607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 467.Green AA, Hughes WL. Protein Fractionation on the Basis of Solubility in Aqueous Solutions of Salts and Organic Solvents. Methods Enzymol. 1955;1:67–90. [Google Scholar]
- 468.Shaw KL, Grimsley GR, Yakovlev GI, Makarov AA, Pace CN. The Effect of Net Charge on the Solubility, Activity, and Stability of Ribonuclease Sa. Protein Sci. 2001;10:1206–1215. doi: 10.1110/ps.440101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 469.Trevino SR, Scholtz JM, Pace CN. Measuring and Increasing Protein Solubility. J Pharm Sci. 2008;97:4155–4166. doi: 10.1002/jps.21327. [DOI] [PubMed] [Google Scholar]
- 470.Loladze VV, Makhatadze GI. Removal of Surface Charge-Charge Interactions from Ubiquitin Leaves the Protein Folded and Very Stable. Protein Sci. 2002;11:174–177. doi: 10.1110/ps.29902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 471.Kurnik M, Hedberg L, Danielsson J, Oliveberg M. Folding without Charges. Proc Natl Acad Sci U S A. 2012;109:5705–5710. doi: 10.1073/pnas.1118640109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 472.Hojgaard C, Kofoed C, Espersen R, Johansson KE, Villa M, Willemoes M, Lindorff-Larsen K, Teilum K, Winther JR. A Soluble, Folded Protein without Charged Amino Acid Residues. Biochemistry. 2016;55:3949–3956. doi: 10.1021/acs.biochem.6b00269. [DOI] [PubMed] [Google Scholar]
- 473.Kramer RM, Shende VR, Motl N, Pace CN, Scholtz JM. Toward a Molecular Understanding of Protein Solubility: Increased Negative Surface Charge Correlates with Increased Solubility. Biophys J. 2012;102:1907–1915. doi: 10.1016/j.bpj.2012.01.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 474.Mattos C, Ringe D. Proteins in Organic Solvents. Curr Opin Struct Biol. 2001;11:761–764. doi: 10.1016/s0959-440x(01)00278-0. [DOI] [PubMed] [Google Scholar]
- 475.Trevino SR, Scholtz JM, Pace CN. Amino Acid Contribution to Protein Solubility: Asp, Glu, and Ser Contribute More Favorably Than the Other Hydrophilic Amino Acids in Rnase Sa. J Mol Biol. 2007;366:449–460. doi: 10.1016/j.jmb.2006.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 476.Smialowski P, Martin-Galiano AJ, Mikolajka A, Girschick T, Holak TA, Frishman D. Protein Solubility: Sequence Based Prediction and Experimental Verification. Bioinformatics. 2007;23:2536–2542. doi: 10.1093/bioinformatics/btl623. [DOI] [PubMed] [Google Scholar]
- 477.Diaz AA, Tomba E, Lennarson R, Richard R, Bagajewicz MJ, Harrison RG. Prediction of Protein Solubility in Escherichia coli Using Logistic Regression. Biotechnol Bioeng. 2010;105:374–383. doi: 10.1002/bit.22537. [DOI] [PubMed] [Google Scholar]
- 478.Drenckhahn D, Pollard TD. Elongation of Actin Filaments Is a Diffusion-Limited Reaction at the Barbed End and Is Accelerated by Inert Macromolecules. J Biol Chem. 1986;261:12754–12758. [PubMed] [Google Scholar]
- 479.Crevenna AH, Naredi-Rainer N, Schonichen A, Dzubiella J, Barber DL, Lamb DC, Wedlich-Soldner R. Electrostatics Control Actin Filament Nucleation and Elongation Kinetics. J Biol Chem. 2013;288:12102–12113. doi: 10.1074/jbc.M113.456327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 480.Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. A Structural Model for Alzheimer’s Beta -Amyloid Fibrils Based on Experimental Constraints from Solid State NMR. Proc Natl Acad Sci U S A. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 481.Sciarretta KL, Gordon DJ, Petkova AT, Tycko R, Meredith SC. Aβ40-Lactam (D23/K28) Models a Conformation Highly Favorable for Nucleation of Amyloid. Biochemistry. 2005;44:6003–6014. doi: 10.1021/bi0474867. [DOI] [PubMed] [Google Scholar]
- 482.Xiao Y, Ma B, McElheny D, Parthasarathy S, Long F, Hoshi M, Nussinov R, Ishii Y. Aβ (1–42) Fibril Structure Illuminates Self-Recognition and Replication of Amyloid in Alzheimer’s Disease. Nat Struct Mol Biol. 2015;22:499–505. doi: 10.1038/nsmb.2991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 483.Colvin MT, Silvers R, Ni QZ, Can TV, Sergeyev I, Rosay M, Donovan KJ, Michael B, Wall J, Linse S, et al. Atomic Resolution Structure of Monomorphic Aβ42 Amyloid Fibrils. J Am Chem Soc. 2016;138:9663–9674. doi: 10.1021/jacs.6b05129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 484.Wälti MA, Ravotti F, Arai H, Glabe CG, Wall JS, Böckmann A, Güntert P, Meier BH, Riek R. Atomic-Resolution Structure of a Disease-Relevant Aβ (1–42) Amyloid Fibril. Proc Natl Acad Sci U S A. 2016;113:E4976–4984. doi: 10.1073/pnas.1600749113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 485.Marek PJ, Patsalo V, Green DF, Raleigh DP. Ionic Strength Effects on Amyloid Formation by Amylin Are a Complicated Interplay among Debye Screening, Ion Selectivity, and Hofmeister Effects. Biochemistry. 2012;51:8478–8490. doi: 10.1021/bi300574r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 486.Munishkina LA, Henriques J, Uversky VN, Fink AL. Role of Protein-Water Interactions and Electrostatics in Alpha-Synuclein Fibril Formation. Biochemistry. 2004;43:3289–3300. doi: 10.1021/bi034938r. [DOI] [PubMed] [Google Scholar]
- 487.Jain S, Udgaonkar JB. Salt-Induced Modulation of the Pathway of Amyloid Fibril Formation by the Mouse Prion Protein. Biochemistry. 2010;49:7615–7624. doi: 10.1021/bi100745j. [DOI] [PubMed] [Google Scholar]
- 488.Cormier AR, Pang X, Zimmerman MI, Zhou HX, Paravastu AK. Molecular Structure of Rada16-I Designer Self-Assembling Peptide Nanofibers. ACS Nano. 2013;7:7562–7572. doi: 10.1021/nn401562f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 489.Holmes TC, de Lacalle S, Su X, Liu G, Rich A, Zhang S. Extensive Neurite Outgrowth and Active Synapse Formation on Self-Assembling Peptide Scaffolds. Proc Natl Acad Sci U S A. 2000;97:6728–6733. doi: 10.1073/pnas.97.12.6728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 490.Sawaya MR, Sambashivan S, Nelson R, Ivanova MI, Sievers SA, Apostol MI, Thompson MJ, Balbirnie M, Wiltzius JJ, McFarlane HT, et al. Atomic Structures of Amyloid Cross-Beta Spines Reveal Varied Steric Zippers. Nature. 2007;447:453–457. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 491.Asherie N, Lomakin A, Benedek GB. Phase Diagram of Colloidal Solutions. Phys Rev Lett. 1996;77:4832–4835. doi: 10.1103/PhysRevLett.77.4832. [DOI] [PubMed] [Google Scholar]
- 492.Zhang FJ, Roosen-Runge F, Sauter A, Wolf M, Jacobs RMJ, Schreiber F. Reentrant Condensation, Liquid-Liquid Phase Separation and Crystallization in Protein Solutions Induced by Multivalent Metal Ions. Pure Appl Chem. 2014;86:191–202. [Google Scholar]
- 493.Tanaka T, Ishimoto C, Chylack LT., Jr Phase Separation of a Protein-Water Mixture in Cold Cataract in the Young Rat Lens. Science. 1977;197:1010–1012. doi: 10.1126/science.887936. [DOI] [PubMed] [Google Scholar]
- 494.Broide ML, Berland CR, Pande J, Ogun OO, Benedek GB. Binary-Liquid Phase Separation of Lens Protein Solutions. Proc Natl Acad Sci U S A. 1991;88:5660–5664. doi: 10.1073/pnas.88.13.5660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 495.Lo WK. Visualization of Crystallin Droplets Associated with Cold Cataract Formation in Young Intact Rat Lens. Proc Natl Acad Sci U S A. 1989;86:9926–9930. doi: 10.1073/pnas.86.24.9926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 496.Stephan DA, Gillanders E, Vanderveen D, Freas-Lutz D, Wistow G, Baxevanis AD, Robbins CM, VanAuken A, Quesenberry MI, Bailey-Wilson J, et al. Progressive Juvenile-Onset Punctate Cataracts Caused by Mutation of the Gammad-Crystallin Gene. Proc Natl Acad Sci U S A. 1999;96:1008–1012. doi: 10.1073/pnas.96.3.1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 497.Pande A, Pande J, Asherie N, Lomakin A, Ogun O, King JA, Lubsen NH, Walton D, Benedek GB. Molecular Basis of a Progressive Juvenile-Onset Hereditary Cataract. Proc Natl Acad Sci U S A. 2000;97:1993–1998. doi: 10.1073/pnas.040554397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 498.Garber K. Cell Biology. Protein ’Drops’ May Seed Brain Disease. Science. 2015;350:366–367. doi: 10.1126/science.350.6259.366. [DOI] [PubMed] [Google Scholar]
- 499.Strzyz P. Molecular Networks: Protein Droplets in the Spotlight. Nat Rev Mol Cell Biol. 2015;16:639. doi: 10.1038/nrm4070. [DOI] [PubMed] [Google Scholar]
- 500.Aguzzi A, Altmeyer M. Phase Separation: Linking Cellular Compartmentalization to Disease. Trends Cell Biol. 2016;26:547–558. doi: 10.1016/j.tcb.2016.03.004. [DOI] [PubMed] [Google Scholar]
- 501.Babu MM. The Contribution of Intrinsically Disordered Regions to Protein Function, Cellular Complexity, and Human Disease. Biochem Soc Trans. 2016;44:1185–1200. doi: 10.1042/BST20160172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 502.Courchaine EM, Lu A, Neugebauer KM. Droplet Organelles? EMBO J. 2016;35:1603–1612. doi: 10.15252/embj.201593517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 503.Mitrea DM, Kriwacki RW. Phase Separation in Biology; Functional Organization of a Higher Order. Cell Commun Signaling. 2016;14:1. doi: 10.1186/s12964-015-0125-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 504.Qin S, Zhou HX. Protein Folding, Binding, and Droplet Formation in Cell-Like Conditions. Curr Opin Struct Biol. 2017;43:28–37. doi: 10.1016/j.sbi.2016.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 505.Weber SC. Sequence-Encoded Material Properties Dictate the Structure and Function of Nuclear Bodies. Curr Opin Cell Biol. 2017;46:62–71. doi: 10.1016/j.ceb.2017.03.003. [DOI] [PubMed] [Google Scholar]
- 506.Brangwynne CP, Eckmann CR, Courson DS, Rybarska A, Hoege C, Gharakhani J, Julicher F, Hyman AA. Germline P Granules Are Liquid Droplets That Localize by Controlled Dissolution/Condensation. Science. 2009;324:1729–1732. doi: 10.1126/science.1172046. [DOI] [PubMed] [Google Scholar]
- 507.Li P, Banjade S, Cheng HC, Kim S, Chen B, Guo L, Llaguno M, Hollingsworth JV, King DS, Banani SF, et al. Phase Transitions in the Assembly of Multivalent Signalling Proteins. Nature. 2012;483:336–340. doi: 10.1038/nature10879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 508.Hyman AA, Weber CA, Julicher F. Liquid-Liquid Phase Separation in Biology. Annu Rev Cell Dev Biol. 2014;30:39–58. doi: 10.1146/annurev-cellbio-100913-013325. [DOI] [PubMed] [Google Scholar]
- 509.Brangwynne CP, Tompa P, Pappu RV. Polymer Physics of Intracellular Phase Transitions. Nat Phys. 2015;11:899–904. [Google Scholar]
- 510.Burke KA, Janke AM, Rhine CL, Fawzi NL. Residue-by-Residue View of in Vitro FUS Granules That Bind the C-Terminal Domain of RNA Polymerase II. Mol Cell. 2015;60:231–241. doi: 10.1016/j.molcel.2015.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 511.Elbaum-Garfinkle S, Kim Y, Szczepaniak K, Chen CCH, Eckmann CR, Myong S, Brangwynne CP. The Disordered P Granule Protein LAF-1 Drives Phase Separation into Droplets with Tunable Viscosity and Dynamics. Proc Natl Acad Sci U S A. 2015;112:7189–7194. doi: 10.1073/pnas.1504822112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 512.Jiang H, Wang S, Huang Y, He X, Cui H, Zhu X, Zheng Y. Phase Transition of Spindle-Associated Protein Regulate Spindle Apparatus Assembly. Cell. 2015;163:108–122. doi: 10.1016/j.cell.2015.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 513.Lin Y, Protter DSW, Rosen MK, Parker R. Formation and Maturation of Phase-Separated Liquid Droplets by RNA-Binding Proteins. Mol Cell. 2015;60:208–219. doi: 10.1016/j.molcel.2015.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 514.Molliex A, Temirov J, Lee J, Coughlin M, Kanagaraj AP, Kim HJ, Mittag T, Taylor JP. Phase Separation by Low Complexity Domains Promotes Stress Granule Assembly and Drives Pathological Fibrillization. Cell. 2015;163:123–133. doi: 10.1016/j.cell.2015.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 515.Murakami T, Qamar S, Lin JQ, Schierle GSK, Rees E, Miyashita A, Costa AR, Dodd RB, Chan FTS, Michel CH, et al. ALS/FTD Mutation-Induced Phase Transition of FUS Liquid Proplets and Reversible Hydrogels into Irreversible Hydrogels Impairs RNP Granule Function. Neuron. 2015;88:678–690. doi: 10.1016/j.neuron.2015.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 516.Nott TJ, Petsalaki E, Farber P, Jervis D, Fussner E, Plochowietz A, Craggs TD, Bazett-Jones DP, Pawson T, Forman-Kay JD, et al. Phase Transition of a Disordered Nuage Protein Generates Environmentally Responsive Membraneless Organelles. Mol Cell. 2015;57:936–947. doi: 10.1016/j.molcel.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 517.Patel A, Lee HO, Jawerth L, Maharana S, Jahnel M, Hein MY, Stoynov S, Mahamid J, Saha S, Franzmann TM, et al. A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated by Disease Mutation. Cell. 2015;162:1066–1077. doi: 10.1016/j.cell.2015.07.047. [DOI] [PubMed] [Google Scholar]
- 518.Xiang S, Kato M, Wu LC, Lin Y, Ding M, Zhang Y, Yu Y, McKnight SL. The LC Domain of hnRNPA2 Adopts Similar Conformations in Hydrogel Polymers, Liquid-Like Droplets, and Nuclei. Cell. 2015;163:829–839. doi: 10.1016/j.cell.2015.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 519.Zhang H, Elbaum-Garfinkle S, Langdon EM, Taylor N, Occhipinti P, Bridges AA, Brangwynne CP, Gladfelter AS. RNA Controls PolyQ Protein Phase Transitions. Mol Cell. 2015;60:220–230. doi: 10.1016/j.molcel.2015.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 520.Feric M, Vaidya N, Harmon TS, Mitrea DM, Zhu L, Richardson TM, Kriwacki RW, Pappu RV, Brangwynne CP. Coexisting Liquid Phases Underlie Nucleolar Subcompartments. Cell. 2016;165:1686–1697. doi: 10.1016/j.cell.2016.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 521.Mitrea DM, Cika JA, Guy CS, Ban D, Banerjee PR, Stanley CB, Nourse A, Deniz AA, Kriwacki RW. Nucleophosmin Integrates within the Nucleolus Via Multi-Modal Interactions with Proteins Displaying R-Rich Linear Motifs and rRNA. eLife. 2016;5:e13571. doi: 10.7554/eLife.13571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 522.Pak CW, Kosno M, Holehouse AS, Padrick SB, Mittal A, Ali R, Yunus AA, Liu DR, Pappu RV, Rosen MK. Sequence Determinants of Intracellular Phase Separation by Complex Coacervation of a Disordered Protein. Mol Cell. 2016;63:72–85. doi: 10.1016/j.molcel.2016.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 523.Su X, Ditlev JA, Hui E, Xing W, Banjade S, Okrut J, King DS, Taunton J, Rosen MK, Vale RD. Phase Separation of Signaling Molecules Promotes T Cell Receptor Signal Transduction. Science. 2016;352:595–599. doi: 10.1126/science.aad9964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 524.Banerjee PR, Milin AN, Moosa MM, Onuchic PL, Deniz AA. Reentrant Phase Transition Drives Dynamic Substructure Formation in Ribonucleoprotein Droplets. Angew Chem, Int Ed. 2017;56:11354–11359. doi: 10.1002/anie.201703191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 525.Kramers HA. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica. 1940;7:284–304. [Google Scholar]
- 526.Perl D, Holtermann G, Schmid FX. Role of the Chain Termini for the Folding Transition State of the Cold Shock Protein. Biochemistry. 2001;40:15501–15511. doi: 10.1021/bi011378s. [DOI] [PubMed] [Google Scholar]
- 527.Mueller U, Perl D, Schmid FX, Heinemann U. Thermal Stability and Atomic-Resolution Crystal Structure of the Bacillus caldolyticus Cold Shock Protein. J Mol Biol. 2000;297:975–988. doi: 10.1006/jmbi.2000.3602. [DOI] [PubMed] [Google Scholar]
- 528.Matouschek A, Kellis JT, Jr, Serrano L, Fersht AR. Mapping the Transition State and Pathway of Protein Folding by Protein Engineering. Nature. 1989;340:122–126. doi: 10.1038/340122a0. [DOI] [PubMed] [Google Scholar]
- 529.Huang X, Zhou HX. Similarity and Difference in the Unfolding of Thermophilic and Mesophilic Cold Shock Proteins Studied by Molecular Dynamics Simulations. Biophys J. 2006;91:2451–2463. doi: 10.1529/biophysj.106.082891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 530.Su JG, Chen WZ, Wang CX. Role of Electrostatic Interactions for the Stability and Folding Behavior of Cold Shock Protein. Proteins: Struct, Funct Genet. 2010;78:2157–2169. doi: 10.1002/prot.22730. [DOI] [PubMed] [Google Scholar]
- 531.Halskau O, Perez-Jimenez R, Ibarra-Molero B, Underhaug J, Munoz V, Martinez A, Sanchez-Ruiz JM. Large-Scale Modulation of Thermodynamic Protein Folding Barriers Linked to Electrostatics. Proc Natl Acad Sci U S A. 2008;105:8625–8630. doi: 10.1073/pnas.0709881105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 532.Arbely E, Neuweiler H, Sharpe TD, Johnson CM, Fersht AR. The Human Peripheral Subunit-Binding Domain Folds Rapidly While Overcoming Repulsive Coulomb Forces. Protein Sci. 2010;19:1704–1713. doi: 10.1002/pro.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 533.Desai TM, Cerminara M, Sadqi M, Munoz V. The Effect of Electrostatics on the Marginal Cooperativity of an Ultrafast Folding Protein. J Biol Chem. 2010;285:34549–34556. doi: 10.1074/jbc.M110.154021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 534.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, Pathways, and the Energy Landscape of Protein Folding: A Synthesis. Proteins: Struct, Funct Genet. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 535.Neuweiler H, Sharpe TD, Johnson CM, Teufel DP, Ferguson N, Fersht AR. Downhill Versus Barrier-Limited Folding of BBL 2: Mechanistic Insights from Kinetics of Folding Monitored by Independent Tryptophan Probes. J Mol Biol. 2009;387:975–985. doi: 10.1016/j.jmb.2008.12.056. [DOI] [PubMed] [Google Scholar]
- 536.Kubelka J, Chiu TK, Davies DR, Eaton WA, Hofrichter J. Sub-Microsecond Protein Folding. J Mol Biol. 2006;359:546–553. doi: 10.1016/j.jmb.2006.03.034. [DOI] [PubMed] [Google Scholar]
- 537.Cho JH, Sato S, Raleigh DP. Thermodynamics and Kinetics of Non-Native Interactions in Protein Folding: A Single Point Mutant Significantly Stabilizes the N-Terminal Domain of L9 by Modulating Non-Native Interactions in the Denatured State. J Mol Biol. 2004;338:827–837. doi: 10.1016/j.jmb.2004.02.073. [DOI] [PubMed] [Google Scholar]
- 538.Alsallaq R, Zhou HX. Electrostatic Rate Enhancement and Transient Complex of Protein-Protein Association. Proteins: Struct, Funct Genet. 2008;71:320–335. doi: 10.1002/prot.21679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 539.Wallis R, Moore GR, James R, Kleanthous C. Protein-Protein Interactions in Colicin E9 Dnase-Immunity Protein Complexes. 1. Diffusion-Controlled Association and Femtomolar Binding for the Cognate Complex. Biochemistry. 1995;34:13743–13750. doi: 10.1021/bi00042a004. [DOI] [PubMed] [Google Scholar]
- 540.Schreiber G, Fersht AR. Rapid, Electrostatically Assisted Association of Proteins. Nat Struct Biol. 1996;3:427–431. doi: 10.1038/nsb0596-427. [DOI] [PubMed] [Google Scholar]
- 541.Shen BJ, Hage T, Sebald W. Global and Local Determinants for the Kinetics of Interleukin-4/Interleukin-4 Receptor Alpha Chain Interaction. A Biosensor Study Employing Recombinant Interleukin-4-Binding Protein. Eur J Biochem. 1996;240:252–261. doi: 10.1111/j.1432-1033.1996.0252h.x. [DOI] [PubMed] [Google Scholar]
- 542.Bradshaw N, Walter P. The Signal Recognition Particle (SRP) RNA Links Conformational Changes in the SRP to Protein Targeting. Mol Biol Cell. 2007;18:2728–2734. doi: 10.1091/mbc.E07-02-0117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 543.Zhang X, Lam VQ, Mou Y, Kimura T, Chung J, Chandrasekar S, Winkler JR, Mayo SL, Shan SO. Direct Visualization Reveals Dynamics of a Transient Intermediate During Protein Assembly. Proc Natl Acad Sci U S A. 2011;108:6450–6455. doi: 10.1073/pnas.1019051108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 544.Estrozi LF, Boehringer D, Shan SO, Ban N, Schaffitzel C. Cryo-EM Structure of the E. coli Translating Ribosome in Complex with SRP and Its Receptor. Nat Struct Mol Biol. 2011;18:88–90. doi: 10.1038/nsmb.1952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 545.Focia PJ, Shepotinovskaya IV, Seidler JA, Freymann DM. Heterodimeric GTPase Core of the SRP Targeting Complex. Science. 2004;303:373–377. doi: 10.1126/science.1090827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 546.Wild K, Bange G, Motiejunas D, Kribelbauer J, Hendricks A, Segnitz B, Wade RC, Sinning I. Structural Basis for Conserved Regulation and Adaptation of the Signal Recognition Particle Targeting Complex. J Mol Biol. 2016;428:2880–2897. doi: 10.1016/j.jmb.2016.05.015. [DOI] [PubMed] [Google Scholar]
- 547.Zhou HX, Bates PA. Modeling Protein Association Mechanisms and Kinetics. Curr Opin Struct Biol. 2013;23:887–893. doi: 10.1016/j.sbi.2013.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 548.Frembgen-Kesner T, Elcock AH. Absolute Protein-Protein Association Rate Constants from Flexible, Coarse-Grained Brownian Dynamics Simulations: The Role of Intermolecular Hydrodynamic Interactions in Barnase-Barstar Association. Biophys J. 2010;99:L75–77. doi: 10.1016/j.bpj.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 549.Fields JB, Hollingsworth SA, Chreifi G, Heyden M, Arce AP, Magana-Garcia HI, Poulos TL, Tobias DJ. “Bind and Crawl” Association Mechanism of Leishmania Major Peroxidase and Cytochrome C Revealed by Brownian and Molecular Dynamics Simulations. Biochemistry. 2015;54:7272–7282. doi: 10.1021/acs.biochem.5b00569. [DOI] [PubMed] [Google Scholar]
- 550.Saglam AS, Chong LT. Highly Efficient Computation of the Basal kon Using Direct Simulation of Protein-Protein Association with Flexible Molecular Models. J Phys Chem B. 2016;120:117–122. doi: 10.1021/acs.jpcb.5b10747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 551.Suh JY, Tang C, Clore GM. Role of Electrostatic Interactions in Transient Encounter Complexes in Protein-Protein Association Investigated by Paramagnetic Relaxation Enhancement. J Am Chem Soc. 2007;129:12954–12955. doi: 10.1021/ja0760978. [DOI] [PubMed] [Google Scholar]
- 552.Bashir Q, Volkov AN, Ullmann GM, Ubbink M. Visualization of the Encounter Ensemble of the Transient Electron Transfer Complex of Cytochrome C and Cytochrome C Peroxidase. J Am Chem Soc. 2010;132:241–247. doi: 10.1021/ja9064574. [DOI] [PubMed] [Google Scholar]
- 553.Zhou HX. Effect of Interaction Potentials in Diffusion-Influenced Reactions with Small Reactive Regions. J Chem Phys. 1996;105:7235–7237. [Google Scholar]
- 554.Zhou HX. Enhancement of Protein-Protein Association Rate by Interaction Potential: Accuracy of Prediction Based on Local Boltzmann Factor. Biophys J. 1997;73:2441–2445. doi: 10.1016/S0006-3495(97)78272-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 555.Using the SE-based protocol would lead to positive values for ΔGel*, contradicting the higher-than-basal-value rate constants for many protein complexes (see ref 538).
- 556.Shaul Y, Schreiber G. Exploring the Charge Space of Protein-Protein Association: A Proteomic Study. Proteins: Struct, Funct Genet. 2005;60:341–352. doi: 10.1002/prot.20489. [DOI] [PubMed] [Google Scholar]
- 557.Yu X, Martinez M, Gable AL, Fuller JC, Bruce NJ, Richter S, Wade RC. Websda: A Web Server to Simulate Macromolecular Diffusional Association. Nucleic Acids Res. 2015;43:W220–224. doi: 10.1093/nar/gkv335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 558.Bai H, Yang K, Yu D, Zhang C, Chen F, Lai L. Predicting Kinetic Constants of Protein-Protein Interactions Based on Structural Properties. Proteins: Struct, Funct Genet. 2011;79:720–734. doi: 10.1002/prot.22904. [DOI] [PubMed] [Google Scholar]
- 559.Moal IH, Bates PA. Kinetic Rate Constant Prediction Supports the Conformational Selection Mechanism of Protein Binding. PLoS Comput Biol. 2012;8:e1002351. doi: 10.1371/journal.pcbi.1002351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 560.Das M, Basu G. Protein-Protein Association Rates Captured in a Single Geometric Parameter. Proteins: Struct, Funct Genet. 2015;83:1557–1562. doi: 10.1002/prot.24860. [DOI] [PubMed] [Google Scholar]
- 561.Darling RJ, Kuchibhotla U, Glaesner W, Micanovic R, Witcher DR, Beals JM. Glycosylation of Erythropoietin Affects Receptor Binding Kinetics: Role of Electrostatic Interactions. Biochemistry. 2002;41:14524–14531. doi: 10.1021/bi0265022. [DOI] [PubMed] [Google Scholar]
- 562.Bernat B, Sun M, Dwyer M, Feldkamp M, Kossiakoff AA. Dissecting the Binding Energy Epitope of a High-Affinity Variant of Human Growth Hormone: Cooperative and Additive Effects from Combining Mutations from Independently Selected Phage Display Mutagenesis Libraries. Biochemistry. 2004;43:6076–6084. doi: 10.1021/bi036069b. [DOI] [PubMed] [Google Scholar]
- 563.Jomain JB, Tallet E, Broutin I, Hoos S, van Agthoven J, Ducruix A, Kelly PA, Kragelund BB, England P, Goffin V. Structural and Thermodynamic Bases for the Design of Pure Prolactin Receptor Antagonists: X-Ray Structure of Del1–9-G129R-hPRL. J Biol Chem. 2007;282:33118–33131. doi: 10.1074/jbc.M704364200. [DOI] [PubMed] [Google Scholar]
- 564.Pang X, Qin S, Zhou HX. Rationalizing 5000-Fold Differences in Receptor-Binding Rate Constants of Four Cytokines. Biophys J. 2011;101:1175–1183. doi: 10.1016/j.bpj.2011.06.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 565.Cohen-Khait R, Schreiber G. Low-Stringency Selection of TEM1 for BLIP Shows Interface Plasticity and Selection for Faster Binders. Proc Natl Acad Sci U S A. 2016;113:14982–14987. doi: 10.1073/pnas.1613122113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 566.Qin S, Cai L, Zhou HX. A Method for Computing Association Rate Constants of Atomistically Represented Proteins under Macromolecular Crowding. Phys Biol. 2012;9:066008. doi: 10.1088/1478-3975/9/6/066008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 567.Phillip Y, Harel M, Khait R, Qin S, Zhou HX, Schreiber G. Contrasting Factors on the Kinetic Path to Protein Complex Formation Diminish the Effects of Crowding Agents. Biophys J. 2012;103:1011–1019. doi: 10.1016/j.bpj.2012.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 568.Phillip Y, Kiss V, Schreiber G. Protein-Binding Dynamics Imaged in a Living Cell. Proc Natl Acad Sci U S A. 2012;109:1461–1466. doi: 10.1073/pnas.1112171109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 569.Zhang X, Kung S, Shan SO. Demonstration of a Multistep Mechanism for Assembly of the SRP•SRP Receptor Complex: Implications for the Catalytic Role of SRP RNA. J Mol Biol. 2008;381:581–593. doi: 10.1016/j.jmb.2008.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 570.Posy S, Shapiro L, Honig B. Sequence and Structural Determinants of Strand Swapping in Cadherin Domains: Do All Cadherins Bind through the Same Adhesive Interface? J Mol Biol. 2008;378:954–968. doi: 10.1016/j.jmb.2008.02.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 571.Harrison OJ, Bahna F, Katsamba PS, Jin X, Brasch J, Vendome J, Ahlsen G, Carroll KJ, Price SR, Honig B, et al. Two-Step Adhesive Binding by Classical Cadherins. Nat Struct Mol Biol. 2010;17:348–357. doi: 10.1038/nsmb.1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 572.Li Y, Altorelli NL, Bahna F, Honig B, Shapiro L, Palmer AG. 3rd Mechanism of E-Cadherin Dimerization Probed by NMR Relaxation Dispersion. Proc Natl Acad Sci U S A. 2013;110:16462–16467. doi: 10.1073/pnas.1314303110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 573.Hansen DF, Zhou Z, Feng HQ, Jenkins LMM, Bai YW, Kay LE. Binding Kinetics of Histone Chaperone Chz1 and Variant Histone H2a.Z-H2b by Relaxation Dispersion NMR Spectroscopy. J Mol Biol. 2009;387:1–9. doi: 10.1016/j.jmb.2009.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 574.Meneses E, Mittermaier A. Electrostatic Interactions in the Binding Pathway of a Transient Protein Complex Studied by NMR and Isothermal Titration Calorimetry. J Biol Chem. 2014;289:27911–27923. doi: 10.1074/jbc.M114.553354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 575.Pang X, Zhou HX. Mechanism and Rate Constants of the Cdc42 Gtpase Binding with Intrinsically Disordered Effectors. Proteins: Struct, Funct Genet. 2016;84:674–685. doi: 10.1002/prot.25018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 576.Giri R, Morrone A, Toto A, Brunori M, Gianni S. Structure of the Transition State for the Binding of C-Myb and Kix Highlights an Unexpected Order for a Disordered System. Proc Natl Acad Sci U S A. 2013;110:14942–14947. doi: 10.1073/pnas.1307337110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 577.Arai M, Sugase K, Dyson HJ, Wright PE. Conformational Propensities of Intrinsically Disordered Proteins Influence the Mechanism of Binding and Folding. Proc Natl Acad Sci U S A. 2015;112:9614–9619. doi: 10.1073/pnas.1512799112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 578.Rogers JM, Oleinikovas V, Shammas SL, Wong CT, De Sancho D, Baker CM, Clarke J. Interplay between Partner and Ligand Facilitates the Folding and Binding of an Intrinsically Disordered Protein. Proc Natl Acad Sci U S A. 2014;111:15420–15425. doi: 10.1073/pnas.1409122111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 579.Zhou HX, Pang X, Lu C. Rate Constants and Mechanisms of Intrinsically Disordered Proteins Binding to Structured Targets. Phys Chem Chem Phys. 2012;14:10466–10476. doi: 10.1039/c2cp41196b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 580.Stone SR, Dennis S, Hofsteenge J. Quantitative Evaluation of the Contribution of Ionic Interactions to the Formation of the Thrombin-Hirudin Complex. Biochemistry. 1989;28:6857–6863. doi: 10.1021/bi00443a012. [DOI] [PubMed] [Google Scholar]
- 581.Pang X, Zhou KH, Qin S, Zhou HX. Prediction and Dissection of Widely-Varying Association Rate Constants of Actin-Binding Proteins. PLoS Comput Biol. 2012;8:e1002696. doi: 10.1371/journal.pcbi.1002696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 582.Groesch TD, Zhou F, Mattila S, Geahlen RL, Post CB. Structural Basis for the Requirement of Two Phosphotyrosine Residues in Signaling Mediated by Syk Tyrosine Kinase. J Mol Biol. 2006;356:1222–1236. doi: 10.1016/j.jmb.2005.11.095. [DOI] [PubMed] [Google Scholar]
- 583.Chen CH, Martin VA, Gorenstein NM, Geahlen RL, Post CB. Two Closely Spaced Tyrosines Regulate Nfat Signaling in B Cells Via Syk Association with Vav. Mol Cell Biol. 2011;31:2984–2996. doi: 10.1128/MCB.05043-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 584.Pang X, Zhou HX. Distinct Mechanisms of a Phosphotyrosyl Peptide Binding to Two SH2 Domains. J Theor Comput Chem. 2014;13:1440003. doi: 10.1142/s0219633614400033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 585.Rogers JM, Steward A, Clarke J. Folding and Binding of an Intrinsically Disordered Protein: Fast, but Not ’Diffusion-Limited’. J Am Chem Soc. 2013;135:1415–1422. doi: 10.1021/ja309527h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 586.Ganguly D, Zhang W, Chen J. Electrostatically Accelerated Encounter and Folding for Facile Recognition of Intrinsically Disordered Proteins. PLoS Comput Biol. 2013;9:e1003363. doi: 10.1371/journal.pcbi.1003363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 587.Xue Y, Yuwen T, Zhu F, Skrynnikov NR. Role of Electrostatic Interactions in Binding of Peptides and Intrinsically Disordered Proteins to Their Folded Targets. 1. NMR and MD Characterization of the Complex between the c-Crk N-SH3 Domain and the Peptide Sos. Biochemistry. 2014;53:6473–6495. doi: 10.1021/bi500904f. [DOI] [PubMed] [Google Scholar]
- 588.Sugase K, Dyson HJ, Wright PE. Mechanism of Coupled Folding and Binding of an Intrinsically Disordered Protein. Nature. 2007;447:1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
- 589.Ou L, Matthews M, Pang X, Zhou HX. The Dock-and- Coalesce Mechanism for the Association of a Wasp Disordered Region with the Cdc42 Gtpase. FEBS J. 2017;284:3381–3391. doi: 10.1111/febs.14197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 590.Adam G, Delbrück M. In: Structural Chemistry and Molecular Biology. Rich A, Davidson N, editors. W. H. Freeman; San Francisco: 1968. [Google Scholar]
- 591.Berg OG, Winter RB, von Hippel PH. Diffusion-Driven Mechanisms of Protein Translocation on Nucleic Acids. 1. Models and Theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 592.Zhou HX, Szabo A. Enhancement of Association Rates by Nonspecific Binding to DNA and Cell Membranes. Phys Rev Lett. 2004;93:178101. doi: 10.1103/PhysRevLett.93.178101. [DOI] [PubMed] [Google Scholar]
- 593.Mirny L, Slutsky M, Wunderlich Z, Tafvizi A, Leith J, Kosmrlj A. How a Protein Searches for Its Site on DNA: The Mechanism of Facilitated Diffusion. J Phys A: Math Theor. 2009;42:434013. [Google Scholar]
- 594.Zhou HX. Rapid Search for Specific Sites on DNA through Conformational Switch of Nonspecifically Bound Proteins. Proc Natl Acad Sci U S A. 2011;108:8651–8656. doi: 10.1073/pnas.1101555108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 595.Zandarashvili L, Esadze A, Vuzman D, Kemme CA, Levy Y, Iwahara J. Balancing between Affinity and Speed in Target DNA Search by Zinc-Finger Proteins Via Modulation of Dynamic Conformational Ensemble. Proc Natl Acad Sci U S A. 2015;112:E5142–5149. doi: 10.1073/pnas.1507726112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 596.Mirzabekov AD, Rich A. Asymmetric Lateral Distribution of Unshielded Phosphate Groups in Nucleosomal DNA and Its Role in DNA Bending. Proc Natl Acad Sci U S A. 1979;76:1118–1121. doi: 10.1073/pnas.76.3.1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 597.Strauss JK, Maher LJ. 3rd DNA Bending by Asymmetric Phosphate Neutralization. Science. 1994;266:1829–1834. doi: 10.1126/science.7997878. [DOI] [PubMed] [Google Scholar]
- 598.Winkler FK, Banner DW, Oefner C, Tsernoglou D, Brown RS, Heathman SP, Bryan RK, Martin PD, Petratos K, Wilson KS. The Crystal Structure of EcoRV Endonuclease and of Its Complexes with Cognate and Non-Cognate DNA Fragments. EMBO J. 1993;12:1781–1795. doi: 10.2210/pdb4rve/pdb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 599.Hiller DA, Fogg JM, Martin AM, Beechem JM, Reich NO, Perona JJ. Simultaneous DNA Binding and Bending by EcoRV Endonuclease Observed by Real-Time Fluorescence. Biochemistry. 2003;42:14375–14385. doi: 10.1021/bi035520w. [DOI] [PubMed] [Google Scholar]
- 600.Hancock SP, Hiller DA, Perona JJ, Jen-Jacobson L. The Energetic Contribution of Induced Electrostatic Asymmetry to DNA Bending by a Site-Specific Protein. J Mol Biol. 2011;406:285–312. doi: 10.1016/j.jmb.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 601.Zhou HX. Disparate Ionic-Strength Dependencies of on and Off Rates in Protein-Protein Association. Biopolymers. 2001;59:427–433. doi: 10.1002/1097-0282(200111)59:6<427::AID-BIP1047>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- 602.Vivas P, Velmurugu Y, Kuznetsov SV, Rice PA, Ansari A. Global Analysis of Ion Dependence Unveils Hidden Steps in DNA Binding and Bending by Integration Host Factor. J Chem Phys. 2013;139:121927. doi: 10.1063/1.4818596. [DOI] [PubMed] [Google Scholar]
- 603.Scott AM, Antal CE, Newton AC. Electrostatic and Hydrophobic Interactions Differentially Tune Membrane Binding Kinetics of the C2 Domain of Protein Kinase Calpha. J Biol Chem. 2013;288:16905–16915. doi: 10.1074/jbc.M113.467456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 604.Qin S, Zhou HX. Prediction of Salt and Mutational Effects on the Association Rate of U1A Protein and U1 Small Nuclear Rna Stem/Loop II. J Phys Chem B. 2008;112:5955–5960. doi: 10.1021/jp075919k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 605.Benedek GB. Cataract as a Protein Condensation Disease: The Proctor Lecture. Invest Ophthalmol Visual Sci. 1997;38:1911–1921. [PubMed] [Google Scholar]
- 606.Kmoch S, Brynda J, Asfaw B, Bezouska K, Novak P, Rezacova P, Ondrova L, Filipec M, Sedlacek J, Elleder M. Link between a Novel Human Gamma D-Crystallin Allele and a Unique Cataract Phenotype Explained by Protein Crystallography. Hum Mol Genet. 2000;9:1779–1786. doi: 10.1093/hmg/9.12.1779. [DOI] [PubMed] [Google Scholar]
- 607.Heon E, Priston M, Schorderet DF, Billingsley GD, Girard PO, Lubsen N, Munier FL. The Gamma-Crystallins and Human Cataracts: A Puzzle Made Clearer. Am J Hum Genet. 1999;65:1261–1267. doi: 10.1086/302619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 608.Pande A, Pande J, Asherie N, Lomakin A, Ogun O, King J, Benedek GB. Crystal Cataracts: Human Genetic Cataract Caused by Protein Crystallization. Proc Natl Acad Sci U S A. 2001;98:6116–6120. doi: 10.1073/pnas.101124798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 609.Messina-Baas OM, Gonzalez-Huerta LM, Cuevas-Covarrubias SA. Two Affected Siblings with Nuclear Cataract Associated with a Novel Missense Mutation in the Crygd Gene. Mol Vision. 2006;12:995–1000. [PubMed] [Google Scholar]
- 610.Banerjee PR, Pande A, Patrosz J, Thurston GM, Pande J. Cataract-Associated Mutant E107A of Human Gamma D-Crystallin Shows Increased Attraction to Alpha-Crystallin and Enhanced Light Scattering. Proc Natl Acad Sci U S A. 2011;108:574–579. doi: 10.1073/pnas.1014653107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 611.Tao YX. Constitutive Activation of G Protein-Coupled Receptors and Diseases: Insights into Mechanisms of Activation and Therapeutics. Pharmacol Ther. 2008;120:129–148. doi: 10.1016/j.pharmthera.2008.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 612.Stoy H, Gurevich VV. How Genetic Errors in GPCRs Affect Their Function: Possible Therapeutic Strategies. Genes Dis. 2015;2:108–132. doi: 10.1016/j.gendis.2015.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 613.Teng S, Madej T, Panchenko A, Alexov E. Modeling Effects of Human Single Nucleotide Polymorphisms on Protein-Protein Interactions. Biophys J. 2009;96:2178–2188. doi: 10.1016/j.bpj.2008.12.3904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 614.David A, Razali R, Wass MN, Sternberg MJE. Protein-Protein Interaction Sites Are Hot Spots for Disease-Associated Nonsynonymous Snps. Hum Mutat. 2012;33:359–363. doi: 10.1002/humu.21656. [DOI] [PubMed] [Google Scholar]
- 615.Creixell P, Schoof EM, Simpson CD, Longden J, Miller CJ, Lou HJ, Perryman L, Cox TR, Zivanovic N, Palmeri A, et al. Kinome-Wide Decoding of Network-Attacking Mutations Rewiring Cancer Signaling. Cell. 2015;163:202–217. doi: 10.1016/j.cell.2015.08.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 616.Ruan Z, Kannan N. Mechanistic Insights into R776H Mediated Activation of Epidermal Growth Factor Receptor Kinase. Biochemistry. 2015;54:4216–4225. doi: 10.1021/acs.biochem.5b00444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 617.Webb BA, Chimenti M, Jacobson MP, Barber DL. Dysregulated pH: A Perfect Storm for Cancer Progression. Nat Rev Cancer. 2011;11:671–677. doi: 10.1038/nrc3110. [DOI] [PubMed] [Google Scholar]
- 618.Kan Z, Jaiswal BS, Stinson J, Janakiraman V, Bhatt D, Stern HM, Yue P, Haverty PM, Bourgon R, Zheng J, et al. Diverse Somatic Mutation Patterns and Pathway Alterations in Human Cancers. Nature. 2010;466:869–873. doi: 10.1038/nature09208. [DOI] [PubMed] [Google Scholar]
- 619.Gyorgy B, Toth E, Tarcsa E, Falus A, Buzas EI. Citrullination: A Posttranslational Modification in Health and Disease. Int J Biochem Cell Biol. 2006;38:1662–1677. doi: 10.1016/j.biocel.2006.03.008. [DOI] [PubMed] [Google Scholar]
- 620.Harauz G, Musse AA. A Tale of Two Citrullines–Structural and Functional Aspects of Myelin Basic Protein Deimination in Health and Disease. Neurochem Res. 2007;32:137–158. doi: 10.1007/s11064-006-9108-9. [DOI] [PubMed] [Google Scholar]
- 621.Ishigami A, Maruyama N. Importance of Research on Peptidylarginine Deiminase and Citrullinated Proteins in Age-Related Disease. Geriatr Gerontol Int. 2010;10:S53–S58. doi: 10.1111/j.1447-0594.2010.00593.x. [DOI] [PubMed] [Google Scholar]
- 622.Fennell CJ, Kehoe CW, Dill KA. Modeling Aqueous Solvation with Semi-Explicit Assembly. Proc Natl Acad Sci U S A. 2011;108:3234–3239. doi: 10.1073/pnas.1017130108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 623.Qin S, Zhou HX. Further Development of the FFT-Based Method for Atomistic Modeling of Protein Folding and Binding under Crowding: Optimization of Accuracy and Speed. J Chem Theory Comput. 2014;10:2824–2835. doi: 10.1021/ct5001878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 624.Yu I, Mori T, Ando T, Harada R, Jung J, Sugita Y, Feig M. Biomolecular Interactions Modulate Macromolecular Structure and Dynamics in Atomistic Model of a Bacterial Cytoplasm. eLife. 2016;5:e19274. doi: 10.7554/eLife.19274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 625.Narayanan A, Jacobson MP. Computational Studies of Protein Regulation by Post-Translational Phosphorylation. Curr Opin Struct Biol. 2009;19:156–163. doi: 10.1016/j.sbi.2009.02.007. [DOI] [PubMed] [Google Scholar]
- 626.Watson JD, Crick FH. Molecular Structure of Nucleic Acids; a Structure for Deoxyribose Nucleic Acid. Nature. 1953;171:737–738. doi: 10.1038/171737a0. [DOI] [PubMed] [Google Scholar]