Enhancing NMR Sensitivity of Natural-Abundance Low-γ Nuclei by Ultrafast Magic-Angle-Spinning Solid-State NMR Spectroscopy

Abstract

Although magic-angle-spinning (MAS) solid-state NMR spectroscopy has been able to provide piercing atomic-level insights into the structure and dynamics of various solids, the poor sensitivity has limited its widespread application, especially when the sample amount is limited. Herein, we demonstrate the feasibility of acquiring high S/N ratio natural-abundance ¹³C NMR spectrum of a small amount of sample (≈2.0 mg) by using multiple-contact cross polarization (MCP) under ultrafast MAS. As shown by our data from pharmaceutical compounds, the signal enhancement achieved depends on the number of CP contacts employed within a single scan, which depends on the T_1ρ of protons. The use of MCP for fast 2D ¹H/¹³C heteronuclear correlation experiments is also demonstrated. The significant signal enhancement can be greatly beneficial for the atomic-resolution characterization of many types of crystalline solids including polymorphic drugs and nanomaterials.

Solid-state NMR spectroscopy has been playing very important roles by rendering substantial insights into the atomic-resolution molecular structures and dynamics of various types of solids including polymers,^[1,2] protein assemblies,^[3–8] bone,^[9–11] amyloid aggregates,^[12–15] and pharmaceutical compounds,^[16,17] However, its poor sensitivity has severely limited the application of this mighty technique. In fact, many exciting applications cannot utilize the benefits of sophisticated multidimensional solid-state NMR techniques. Use of a large sample quantity, longer data collection, modification of the sample to include specific isotopes or dopants, and/or data collection at cryogenic temperatures is mandatory for most solid-state NMR studies. Although a low temperature dynamic nuclear polarization (DNP) experiment^[18–21] can be used to enhance the sensitivity, there are issues with low spectral resolution, structural perturbation due to the inclusion of a polarizing agent, denaturing the sample due to freezing, and expense in carrying out the experiments. There is also considerable interest in developing proton-detection based techniques that can fully utilize the high gyromagnetic ratio and abundance of protons.^[22–30] However, in addition to the need for an additional frequency dimension, the resolution of low-γ nuclei spectrum obtained by proton detection can be compromised due to insufficient chemical shift evolution time in the indirect dimension. Therefore, there is still a need for methods to enhance the sensitivity of NMR experiments that utilize natural-abundance low-γ nuclei.

Heteronuclear cross-polarization (CP)^[31,32] has been widely employed in solid-state NMR experiments. Even though CP enhances the signal intensity of low-γ nuclei by a factor of γ_H/γ_X, the acquisition of natural-abundance ¹³C signal is still a challenge when the sample quantity is limited. In the pioneering work by Pines et al.,^[31] multiple-contact CP (MCP) along with multiple acquisition was suggested to fully utilize the proton magnetization. However, to the best of our knowledge, such a pulse sequence has not been demonstrated to its full potential and is not practical under slow or moderate spinning speeds. On one hand, under moderate spinning speeds, high radio-frequency (RF) power continuous-wave (CW) irradiation has to be applied in order to spin-lock the proton magnetization as well as to achieve proton decoupling. On the other hand, the use of high-power CW will unavoidably reduce the number of CP contacts and signal acquisitions due to the probe duty cycle and potential sample heating. These problems could be well overcome by using low-power CW decoupling of protons under ultrafast MAS. In this study, we experimentally demonstrate the feasibility of using MCP to significantly enhance the signal intensity of natural-abundance ¹³C nuclei under very fast MAS conditions. In addition to comparing the efficiencies of 1D MCP and the well-established ramp-CP^[33] experiments, we also demonstrate the use of MCP in 2D ¹H-¹³C heteronuclear correlation (HETCOR) experiments on small amounts (≈2.0 mg) of pharmaceutical compounds.

The 1D and 2D RF pulse sequences used in this study are shown in Figure 1. For experiments using MCP, as shown in Figure 1a, a double spin-lock with a ramp on the ¹³C spin-lock followed by a CW proton decoupling during ¹³C signal acquisition is repeated N times. At the end of final ¹³C signal acquisition, a ¹H 90° pulse is applied to flip the remaining proton transverse magnetization to the +z axis to accelerate the proton spin-lattice relaxation (T₁) process.^[34–36] Significant signal enhancement obtained using MCP at 60 kHz MAS is well demonstrated on a danazol/vanillin cocrystalline sample as shown in Figure 2. The effect of the last flip-back 90° pulse on the ¹H RF channel is demonstrated in Figure S1, where an additional ≈22% signal enhancement is achieved. It should be noted that if the ¹H magnetization is decayed to zero after multiple CP contacts, then the final flip-back 90° pulse will have negligible effect on accelerating the T₁ relaxation of protons, as there is no residual transverse magnetization to flip back to the +z axis. Details on the sample preparation, NMR experiments, theoretical explanation, and additional 2D ¹H/¹³C HETCOR spectra are given in the Supporting Information.

Figure 1.

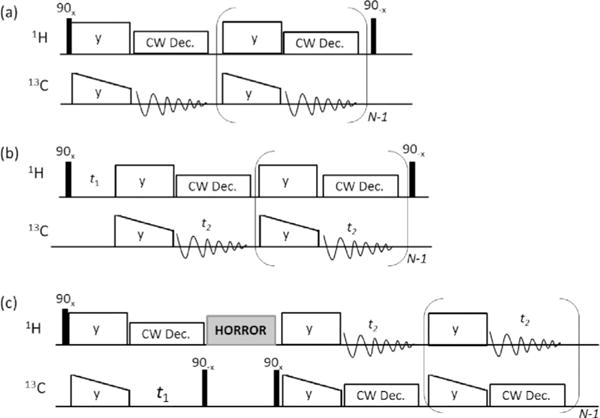
Multiple-contact CP (MCP) based NMR pulse sequences. a) 1D MCP experiment for recording natural-abundance 1D ¹³C spectrum. b) ¹³C-detected MCP 2D ¹H/¹³C HETCOR experiment. c) ¹H-detected MCP 2D ¹H/¹³C HETCOR experiment. The final 90° pulse (in a and b) was used to flip the remaining ¹H transverse magnetization back to the +z axis to enhance the T₁ relaxation of protons.

Figure 2.

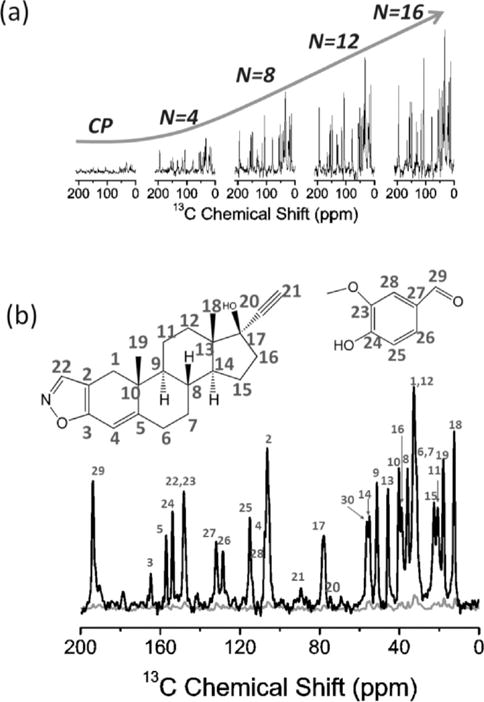
Natural-abundance ¹³C NMR spectra of danazol/vanillin co-crystalline sample. a) Comparison of spectra obtained by conventional ramp-CP and MCP with the indicated number (N) of CP contacts. b) Comparison of spectra obtained with conventional ramp-CP (grey) and MCP with N=16 (black). The molecular structure and resonance assignment are shown on top of the spectrum in (b) according to the work of Atta-Ur-Rahman et al.^[37] A linear ramp of 28% was applied on all the ¹³C spin-lock RF pulses as shown in Figure 1. Other experimental parameters used to obtain the spectra are: 60 kHz MAS, CP contact time of 1 ms, 6 ms data acquisition time, 2100 scans, 14 kHz decoupling and 10 s recycle delay. The total experimental time was ≈5.9 hours for each spectrum. A 600 MHz Agilent solid-state NMR spectrometer and a 1.2 mm triple-resonance MAS probe were used. The ¹H and ¹³C resonance frequencies were 599.8 and 150.8 MHz, respectively.

Significant suppression of ¹H-¹H dipolar couplings under 60 kHz MAS enhanced the efficiency of RF spin-locks of protons during MCP and resulted in a slow ¹H T_1ρ relaxation rate even when a weak RF field strength of ≈14 kHz was used for spin-locking protons. Because of the ability to retain proton transverse magnetization for a very long time, it is possible to utilize many CP contact blocks in the MCP experiment to acquire ¹³C spectra with better sensitivity. As shown in Figure 2a, increasing the number of CP contacts (N) within each experimental scan, remarkably increased the ¹³C signal-to-noise (S/N) ratio, needless to mention that the signal enhancement rendered by MCP is dramatic when compared to that obtained via the conventional ramp-CP as shown in Figure 2b. Indeed, only the aliphatic signals in the 10–60 ppm region could be observed in the conventional ramp-CP spectrum, and they are all very weak in intensity (Figure 2a). On the contrary, all the ¹³C signals, including that of the quaternary carbons resonating in the 150–200 ppm region, could be clearly observed in the MCP_N=16 spectrum (Figure 2b). Due to the extremely long ¹H T_1ρ, the 16 FIDs obtained in the single scan have very similar intensity, as shown in Figure S2, which should result in a overall theoretical S/N ratio enhancement of 4.0 (Equation S7). A theoretical analysis of the S/N ratio enhancement is included in the Supporting Information. However, it is remarkable that the overall S/N ratio enhancement achieved by MCP_N=16 is ≈4.6 times as that obtained using ramp-CP, higher than the theoretical value of 4.0 This is because of the use of a ¹H flip-back 90° pulse after the final ¹³C signal acquisition to accelerate ¹H T₁ relaxation. The efficiency of MCP is also further demonstrated on a different polymorphic compound, ibuprofen (Figure 3a,b), where all ¹³C peak intensities are dramatically enhanced by MCP. In particular, as compared to conventional ramp-CP, the S/N ratio enhancement rendered by MCP for the peaks associated with quaternary carbons (C1, C4, and C7) are remarkably high. It is worth noting that the noise observed in the MCP spectrum is stronger than that of the conventional ramp-CP spectrum. Although we employed five CP contacts in the 1D MCP experiment, the signal decreased very fast due to ¹H T_1ρ relaxation, and there was not much signal observed in the fourth and fifth FIDs (as shown in Figure S3). As a result, the S/N ratio is compromised by the superposition of fourth and fifth FIDs.

Figure 3.

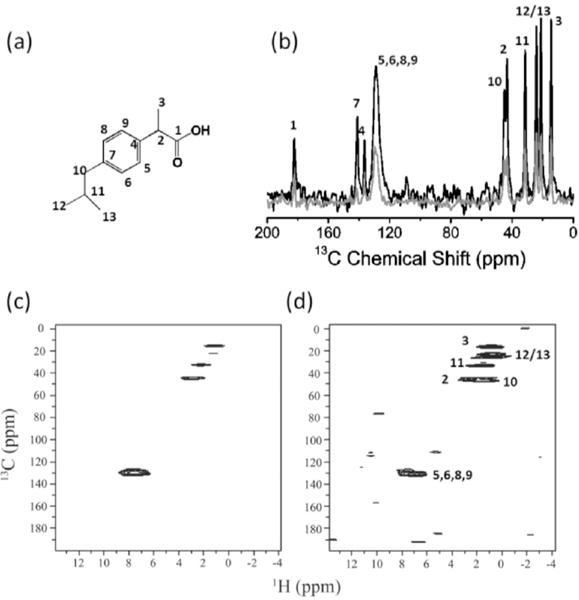
Natural-abundance 1D and 2D NMR spectra of ibuprofen powder. a) Chemical structure of ibuprofen. b) Comparison of spectra obtained using conventional ramp-CP (grey) and MCP with N=5 (black). Other experimental parameters used to obtain the spectra are: 60 kHz MAS, 1 ms CP contact time, 7 ms acquisition time, 1200 scans, 14 kHz proton decoupling and 4 s recycle delay. The total experimental time was ≈1.8 hours for each spectrum. c,d) ¹H-detected HETCOR spectra of ibuprofen obtained using the pulse sequence shown in Figure 1c with N= 1 and N=3, respectively. The initial ¹H→¹³C CP contact time was 2.0 ms, and each ¹³C→¹H CP contact time was 0.4 ms. Other experimental parameters include 7 ms of each signal acquisition, 3 s recycle delay, and 20 scans for each t₁ increment.

To further realize the advantage of MCP, it was incorporated into 2D ¹³C- and ¹H-detected ¹H/¹³C HETCOR experiments for sensitivity enhancement as shown in the RF pulse sequences given in Figure 1b and 1c. In the case of the ¹³C-detected HETCOR experiment, ¹H chemical shifts are expressed during the incrementable t₁ period before repeating the CP-¹³C-acquisition block N times (Figure 1b). On the other hand, in the ¹H-detected HETCOR experiment, ¹³C chemical shift is expressed during t₁ after the first CP and then following the z-filter the CP-¹H-acquisition block is repeated N times as shown in Figure 1c. Therefore, these two types of HETCOR pulse sequences differ in the use of MCP: ¹H to ¹³C CP (Figure 1b) versus ¹³C to ¹H CP (Figure 1c).

The 2D ¹³C-detected ¹H/¹³C HETCOR spectra of danazol/vanillin co-crystals and ibuprofen are shown in Figures S4 and S5, respectively. Although significant signal enhancement could be achieved compared to the regular ¹³C-detected HETCOR experiment, the proton spin diffusion during multiple CW decoupling periods may extend ¹³C-¹H correlations; an example is the case of danazol/vanillin co-crystals as shown in Figure S4b. The use of N=20 in the ¹³C-detected HETCOR experiment resulted in a total CW decoupling duration of ≈120 ms. Though ¹H-¹H dipolar couplings were largely suppressed by the ultrafast MAS as well as the spin-locking (reduces by half),^[1] the use of a very long total CW decoupling duration can still allow the exchange of ¹H proton magnetization either through direct un-averaged ¹H-¹H dipolar couplings (high-order homonuclear dipolar coupling terms) or via relayed polarization transfer. Then, the “exchanged” proton magnetization can further be transferred to nearby carbons in the successive CP periods. Because of this effect, most of the carbon resonances are correlated with proton resonances in the resultant 2D ¹³C-detected MCP HETCOR spectra (Figure S4b). In contrast, when a small N value was used, such as the ¹³C-detected MCP HETCOR spectrum of ibuprofen shown in Figure S5b, the total CW decoupling time was reduced to ≈28 ms and therefore the effect of spin diffusion was much reduced. As a result, only the non-bonded ¹³C-¹H correlations between aromatic carbon and aliphatic protons were observed in Figure S5b, while the ¹³C-¹H correlation between aromatic proton and aliphatic carbon is absent, which is due to the larger number of aliphatic protons than that of aromatic protons. Although proton spin diffusion is a major limitation for the ¹³C-detected MCP HETCOR experiment, it might not be a problem for heavily deuterated samples, where the proton dipolar couplings can be completely averaged out by the ultrafast MAS. In such samples, the 13C-detected MCP HETCOR spectrum can directly provide heteronuclear proximity information.

As mentioned above, the effect of proton spin diffusion in the ¹³C-detected HETCOR experiment should be taken into account when employing a large number of CP-acquisition blocks. On the other hand, in the ¹H-detected MCP HETCOR experiment (Figure 1c), the ¹³C spin diffusion can be safely ignored due to the very low natural-abundance of ¹³C (≈1%) as well as weak ¹³C-¹³C couplings; and there is no role for≈ proton spin diffusion. As a result, the ¹H-detected MCP HETCOR experiment can greatly enhance the S/N ratio and also render the same information as that of a regular ¹H-detected HETCOR experiment but with enhanced sensitivity as demonstrated on ibuprofen (Figure 3) and danazol/vanillin cocrystal (Figure 4) samples.

Figure 4.

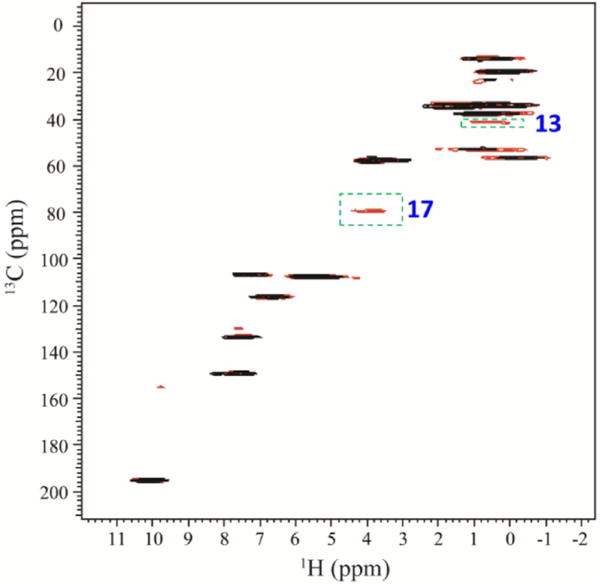
¹H-detected 2D ¹H/¹³C HETCOR spectrum of danazol/vanillin co-crystals obtained using the pulse sequence shown in Figure 1c with N=1(black) and N=3(red). The initial ¹H→¹³C CP contact time was 2.0 ms, and each ¹³C→¹H CP contact time was 0.4 ms. Other experimental parameters include 6 ms of each signal acquisition, 7 s recycle delay, and 36 scans for each t₁ increment.

As shown in Figures 3 and 4, the use of MCP significantly increases the S/N ratio of ¹H-detected HETCOR spectra. For ibuprofen sample, all the correlation signals are dramatically enhanced. However, due to the limited amount of ¹³C magnetization from the initial single CP for the t₁ evolution (Figure 1c), the signals observed in the second and third FIDs were weaker than that observed in the first FID in the ¹H-detected MCP HETCOR experiment with N=3, because most of the ¹³C magnetization has been transfer to ¹H in the first CP contact. However, the noise is constant in all the three FIDs. Therefore, the noise is a little high in the ¹H-detected MCP HETCOR spectrum in comparison to the regular HETCOR spectrum. However, for the ¹H-detected MCP HETCOR spectrum, an overall S/N ratio enhancement of ≈30% is still achieved.

Similarly, signal enhancement was also achieved on the danazol/vanillin co-crystal sample (Figure 4). It is worth noting that resonances of most of the quaternary carbons (except C17 and C13) are absent in the regular HETCOR spectrum, because a contact time of 0.4 ms is too short to enable significant remote ¹H→¹³C polarization transfer directly through the weak non bonded ¹³C-¹H dipolar couplings. However, in the ¹H-detected MCP HETCOR experiment, the ¹³C magnetization remaining after the first ¹³C to ¹H CP is transferred to proton in the subsequent CP contacts, and thus enhancing remote ¹³C-¹H correlations in the resultant 2D spectrum.

The experimental results presented above clearly demonstrate the significant signal enhancement by MCP that has considerable advantages for ¹³C and other low-γ nuclei based solid-state NMR experiments under ultrafast MAS conditions. As shown by the experimental and theoretical (see the Supporting Information) analyses, the sensitivity enhancement rendered by MCP directly relies on the number of CP contacts (i.e. N) used in the experiment. As long as there is ¹H or ¹³C magnetization remaining after the CW decoupling period, CP could further be applied for ¹H→¹³C or ¹³C→¹H polarization transfer, respectively. For natural-abundance samples, N is mainly determined by the proton relaxation time during the CP spin-lock and CW decoupling periods. Therefore, a system with a long ¹H T_1ρ would allow the use of a very large number of CP contacts in the MCP experiment within the capability of the probe, and hence the feasibility of a dramatic enhancement of sensitivity; this is the case under ultrafast MAS as discussed below. It should also be mentioned that to avoid the loss of proton magnetization during decoupling periods, only CW decoupling can be used. The use of other decoupling schemes, such as the efficient composite-pulse based sequences, would destroy the ¹H magnetization. As a result, the CW decoupling power required to obtain high spectral resolution, which depends on the spinning speed of the sample, should be carefully optimized. Fortunately, ultrafast spinning speed does not require a high RF power for efficient decoupling^[38,39] and thus avoids potential sample heating. Indeed, MCP would be less rewarding under slow or moderate spinning speeds mainly because of the inefficiency of CW decoupling. These factors suggest that there are unique advantages of performing MCP based experiments under ultrafast spinning speeds (>100 kHz) in addition to the higher spectral resolution. For example, efficient suppression of dipolar couplings among protons by ultrafast MAS would: a) increase the T_1ρ of protons and therefore enable the use of more CP-acquisition blocks in the pulse sequence to render higher sensitivity enhancement; b) enhance the CW decoupling efficiency and/or reduce the RF power required for decoupling.

We also note that there is another way to implement multiple-contact CP as used in the literature.^[40–43] In these published approaches, instead of signal acquisition immediately following the CP, the rare spin magnetization is generally stored along the +z-axis for a delay of ≈T_1H to enable the recovery of ¹H magnetization which then allows for the subsequent cross polarization from protons to rare nuclei. Although this approach enhances the signal intensity, the experimental time for each scan is longer than the MCP-based method presented in this study. In particular, for a heterogeneous sample with a broad range of ¹³C T₁ values, a short T_1z filter delay between two neighboring CP periods will not be able to recover the lost ¹H magnetization during the previous CP, while a long T_1z filter delay will result in a significant signal loss (due to ¹³C T₁ relaxation). Though other recent approaches that employed multiple acquisitions to utilize the residual magnetization of low-γ nuclei are valuable to obtain multiple 2D spectra of labeled biological solids, the number of acquisitions is quite limited by the initial signal-contact proton-enhanced CP.^[44,45] On the other hand, using the MCP approach proposed in this study could significantly broaden the benefits of such approaches under ultrafast MAS.

In conclusion, the dramatic enhancement of S/N ratio obtained in 1D ¹³C CPMAS and ¹H or ¹³C-detected 2D ¹H/¹³C HETCOR experiments clearly demonstrated the feasibility of high-resolution natural-abundance ¹³C based ultrafast MAS experiments on a small amount of sample (≈2.0 mg). We foresee that the reported MCP approach will be valuable for a broad range of applications and the development of new techniques under ultrafast spinning speeds (>100 kHz). High-throughput characterization of pharmaceutical compounds by solid-state NMR and NMR crystallography studies would also be possible with the use of MCP under ultrafast MAS.