Failure and Redemption of Statistical and Nonstatistical Rate Theories in the Hydroboration of Alkenes

Abstract

Our previous work found that canonical forms of transition state theory incorrectly predict the regioselectivity of the hydroboration of propene with BH₃ in solution. In response, it has been suggested that alternative statistical and nonstatistical rate theories can adequately account for the selectivity. This paper uses a combination of experimental and theoretical studies to critically evaluate the ability of these rate theories, as well as dynamic trajectories and newly developed localized statistical models, to predict quantitative selectivities and qualitative trends in hydroborations on a broader scale. The hydroboration of a series of terminally substituted alkenes with BH₃ was examined experimentally, and a classically unexpected trend is that the selectivity increases as the alkyl chain is lengthened far from the reactive centers. Conventional and variational transition state theories can neither predict the selectivities nor the trends. The canonical competitive nonstatistical model makes somewhat better predictions for some alkenes but fails to predict trends, and it performs poorly with an alkene chosen to test a specific prediction of the model. Added nonstatistical corrections to this model make the predictions worse. Parameterized RRKM-master equation calculations correctly predict the direction of the trend in the selectivity versus alkene size but overpredict its magnitude, and the selectivity with large alkenes remains unpredictable with any parameterization. Trajectory studies in explicit solvent can predict selectivities without parameterization but are impractical for predicting small changes in selectivity. From a lifetime and energy analysis of the trajectories, “localized RRKM-ME” and “competitive localized noncanonical” rate models are suggested as steps toward a general model. These provide the best predictions of the experimental observations and insight into the selectivities.

Graphical abstract

INTRODUCTION

Rate theories are scientific models¹ of chemical reactivity. As models, they are simplifications of reality that may qualitatively or quantitatively account for particular observations, or on the whole perhaps a great preponderance of observations. Models are of supreme value in chemistry; it might be said that a central goal of theoretical chemistry is the development of models that provide insight and detailed predictions. The simplifications and assumptions in models make chemistry tractable, but they also inherently pose a problem. That is, real systems need not conform to a model’s ideals, and subtle observations may expose their inadequacy. We describe here how this idea applies to the attempts to understand alkene hydroboration in solution using known and newly developed statistical and nonstatistical rate theories. On close inspection, current theories fail. We find that one may fall back on the primordial consideration of trajectories to account for the selectivity in these reactions, but this is impractical for understanding or predicting subtle trends. We suggest here two new semi-statistical models for solution reactions as steps toward an accurate and physically realistic accounting for experimental observations.

The hydroboration of alkenes with BH₃ provides a classic example of regioselectivity for undergraduate textbooks of organic chemistry. To highlight the contrast with the “Markovnikov” addition of acids to alkenes, Brown described hydroboration as occurring in an “anti-Markovnikov” fashion.² That is, the preferred product with simple alkenes results from addition of a BH₂ group to the less-substituted olefinic carbon (eq 1). This selectivity is not normally observed directly, but rather is observed as a combination of selectivities in three separate reactions – hydroboration by BH₃, hydroboration by RBH₂, and hydroboration by R₂BH – followed normally by oxidation to the ultimate alcohol products.

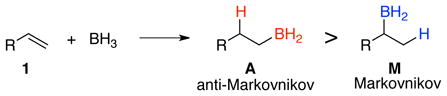(1)

Implicitly assuming the applicability of conventional transition state theory (TST), early theoretical studies had correctly predicted the direction of this selectivity.³ However, the quantitative accuracy of TST in this reaction or any comparable solution reaction had never been definitively checked. Doing so required overcoming several problems, including the composite nature of the experimentally observed product ratios and the limited level of the prior theoretical calculations. Our previous work addressed each of these problems.⁴ Experimentally, we found that the hydroboration of propene with BH₃ alone afforded a 90:10 ratio of anti-Markovnikov (A, R = Me) to Markovnikov (M, R = Me) products. In contrast, the best calculations, assuming TST, predicted a 99:1 – 98: 2 ratio. Consideration of ordinary sources of inaccurate predictions, such as the role of solvent and the harmonic approximation, did not account for the discrepancy between experiment and theory.

We argued that this failure of a TST prediction had its origin in the excess energy that is available from the formation of the intermediate π-complex (INT, Figure 1). At the time, two mechanisms were considered by which this excess energy could affect the selectivity. In one mechanism, the excess energy is specifically channeled, i. e. in a nonstatistical process, into motions that overcome the barriers to formation of products A and M, allowing direct passage over the transition states TSA and TSM. This would be considered a form of “dynamic matching” as discussed by Carpenter.⁵ A second mechanism is that statistically distributed excess energy would affect the selectivity, just so long as the reaction occurs faster than thermal equilibration with solvent. A key observation was that the fastest-finishing gas-phase dynamic trajectories were particularly unselective, while slower-finishing trajectories approached RRKM expectations for selectivity. In this way, the trajectories appeared to support a combination of the two mechanisms, one statistical, the other not. Our results here will support the importance of a third mechanism by which the excess energy affects the selectivity.

Figure 1.

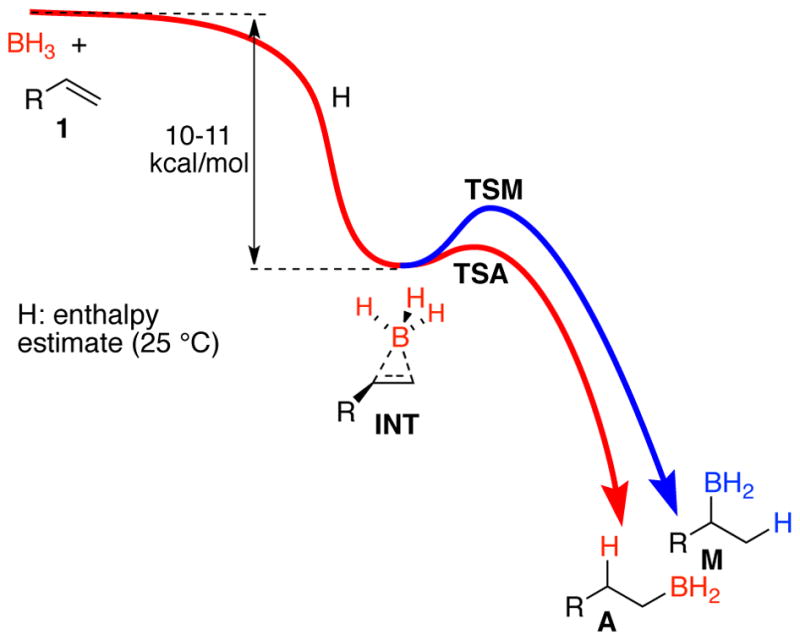
Energy diagram for the hydroboration of a terminal alkene.

These results attracted significant interest from theoreticians with the goal of applying or developing rate theories that could account for the selectivity in hydroboration or other reactions subject to the same complication. In an effort to account for the hydroboration selectivity within the confines of known statistical models, Glowacki et al applied a weak collision RRKM-Master Equation (RRKM-ME) model to the reaction.^6,7 Such models allow for collisional energy loss from intermediates as they react. There has been some contention over the best way to model the energy loss, but on the whole such models have been highly successful for gas-phase calculations, and have started to see use in condensed phases.^6,7,8,9 Importantly, the selectivity expected for propene in the absence of collisional cooling would be lower than experiment while the selectivity expected if INT (R = Me) cooled fully is higher than experiment. As a result, any model for the energy loss would necessarily be able to reproduce experiment with a fitted cooling parameter. The interesting question then is not whether an RRKM-ME model can reproduce observed selectivity, but rather whether it can make accurate predictions for diverse alkenes with a single realistic cooling model and parameters. We will address that question here. A more subtle issue in applying RRKM-ME calculations to solution arises from consideration of timescales. In the gas phase, the time between collisions is generally long compared to the time required for intramolecular vibrational energy redistribution (IVR) in molecules. Gas-phase RRKM-ME calculations can then defensibly make the critical assumption of a statistical distribution of energy in intermediates. The central tenet of ME calculations, that of history independence, depends on this assumption. In solution, however, the interaction with solvent is continuous and the time between collisions in any collisional model is sub-picosecond, while IVR can take many picoseconds.^10,11,12 It will be important to consider how the overlap of timescales affects the accuracy of the models.

A distinct and innovative approach to understanding hydroboration selectivity was taken by Zheng, Papajak, and Truhlar.¹³ Their canonical competitive nonstatistical model (CCNM) divides the selectivity for reaction coordinates of the type in Figure 1 into two limiting parts arising from an “indirect mechanism” and a “direct mechanism.” For the indirect part, intermediates (INT in the hydroboration case) are treated as thermally equilibrated, and the selectivity would be dictated by transition state energies and the temperature in an ordinary way. For the direct part, the products are weighted either statistically or non-statistically based on the product energy levels, in the manner of phase-space theory. In the simplest, statistical form of CCNM (which is still nonstatistical in its division of mechanisms), the direct part reflects the equilibrium mixture of the products. In its nonstatistical form, a correction factor is included to allow for incomplete coupling of the complex with the product states. The direct part of the CCNM model has the significant virtue that it attempts to account for the selectivity of trajectories that rapidly afford product. In this way, the CCNM model more closely fits with observations in trajectories. The direct part also provides a straightforward prediction of selectivity when there is no intermediate, and the CCNM model provides a smooth continuum of predictions as the barrier for reaction of the intermediate disappears. The RRKM-ME approach can do neither. Our concern however was that the simplifications involved in the CCNM model, particularly its reliance on phase-space theory for the direct part of the reaction and its assumption of thermal equilibration for the indirect part, would not lead to successful predictions in alternative reactions. This concern is investigated here, as we search for a rate theory that can account for a broader range of observations.

RESULTS AND DISCUSSION

Experimental Selectivities

Regardless of whether the problem of selectivity in hydroboration is approached using trajectories or RRKM-ME calculations or the CCNM model, the physical models were considered successful if they could account for a single data point, the product ratio for the hydroboration of propene.¹⁴ To provide more stringent tests of the models, we sought to expand the range of experimental observations to consider.

We have previously described the utility of studying product ratios in homologous reactions as a probe for nonstatistical dynamics.¹² The idea is that a series of extended alkyl group substituents, e.g. butyl versus hexyl versus decyl, will likely differ little in electronic and steric effects on transition state energies, but they will differ substantially in their ability to absorb excess energy in intermediates. The changes in product ratios can then be analyzed versus statistical predictions. This was the purpose behind the hydroboration of 1-hexene (3), 1-octene (4), and 1-dodecene (5). The study of tert-butylethylene (6) was for a different purpose. That is, since the CCNM model effectively weighs equilibrium product ratios into its predictions, it makes the clear prediction that a high equilibrium product ratio will lead to high reaction selectivity. The reaction of the sterically perturbed 6 tests this prediction.

These four alkenes were each reacted with a large excess of freshly prepared BH₃ in THF at 25 °C, and the borane products were immediately oxidized with H₂O₂ / NaOH. The crude alcohols were recovered by an extraction process, and their ratio analyzed directly by ¹H NMR. In control workups, the recovery process did not change the product ratio. The percentage Markovnikov product calculated from these ratios for six independent reactions for each alkene are summarized in Table 1. Table 1 includes the previously reported result for propene-d₆, obtained by a somewhat different procedure and product ratio analysis.⁴

Table 1.

Experimental and predicted selectivities for hydroborations of alkenes (25 °C unless noted).

Alkene	Experimental Markovnikov (M)	TSTa,b	CVT/SCTc,b	statistical CCNMd	nonstatistical CCNMd	best-fit RRKM-ME	localized RRKM-ME	competitive local- ized noncanonical
propene	10.0 ± 0.3%e	1.4%	2.2%	4.2%	3.3%	13.0%	8.7%	10.0%
propene at 70 °C	11.2 ± 0.3%e	2.4%	3.5%	6.4%	5.2%	13.7%	10.3%	11.1%
1-butene (2)	–	1.9%	2.8%	5.6%	4.4%	11.7%	10.9%	12.3%
1-hexene (3)	10.7 ± 0.5%f	2.0%	2.8%	6.2%	4.1%	9.5%	10.9%	11.6%
1-octene (4)	9.8 ± 0.4%f	2.1%g	2.9%g	6.1%g	4.5%g	6.8%	10.6%g	10.8%
1-dodecene (5)	9.2 ± 0.2%f	2.2%g	2.9%g	6.2%g	4.5%g	5.7%	10.1%g	10.3%
(6)	11.2 ± 0.4%f	1.8%	2.6%	1.9%	1.7%	8.6%	11.4%	11.3%

^aBased on CCSD(T)//B3LYP/6-31G* energies.

^bThe basis set for CCSD(T) calculations was aug-cc-pvtz unless otherwise noted.

^cBased on VTST-ISPE calculations,¹⁷ using CCSD(T) energies at 0.1 a.u. increments along the minimum-energy path.

^dThe CCNM calculations employed the procedures of reference 13, using the CVT/SCT rate constants, CCSD(T) energies, and B3LYP/6-31G* frequencies and paths.

^eTaken from ref 4, for propene-d₆, at 21 °C.

^fThe uncertainty shown is the 95% confidence limit based on six measurements.

^gThe results for 1-octene and 1-dodecene are extrapolated from the 1-hexene results employing an aug-cc-pvtz basis set and the differences in the results for the three alkenes using an aug-cc-pvdz basis set. See the SI for the complete details and results.

The most striking observation is that the unbranched terminal alkenes 3–5 exhibit higher selectivity as the alkenes become larger. Considering the distance of the extra carbons from the reactive centers, it would seem immoderate to explain this trend as either a steric effect or an electronic effect of the substituent, though the latter possibility will be more closely examined below. The effect of the alkyl groups is not attributable to a medium effect; addition of pentane to the reaction mixture had no effect on the selectivity. It is also notable that the hindered alkene 6 exhibited lower selectivity than the unbranched alkenes.

Computational Methods

CCSD(T) calculations were used as the primary standard for relative potential energies. For the two largest systems these calculations were limited to an aug-cc-pvdz basis set. For 1-hexene, and tert-butylethylene, the basis set was extended to aug-cc-pvtz. For propene and selected butene structures, basis sets were explored up to aug-cc-pvqz, and the effect on relative energies versus aug-cc-pvtz was negligible (see the SI). For consistency, most of the energies presented are based on CCSD(T)/aug-cc-pvtz calculations. The underlying geometries, reaction paths, frequencies, and trajectories were usually obtained from B3LYP/6-31G* calculations. We had previously found that B3LYP/6-31G* performed the best out of 61 method / basis set combinations in modeling a grid of points in the critical part of the energy surface (near INT) in comparison with CCSD(T)/aug-cc-pvtz energies.⁴

Using the GAUSSRATE / POLYRATE set of programs,^15,16 variational transition structures were located in canonical variational transition state theory (CVT) with interpolated single-point energies (VTST-ISPE),¹⁷ using CCSD(T) energies at 0.1 a.u. increments along the B3LYP/6-31G* minimum-energy path. Tunneling was included using the small-curvature tunneling (SCT) approximation.¹⁸

It should be noted that no calculation, at any level, can be expected to reliably predict product ratios for a solution reaction at the experimental third-digit level of precision, even when the reaction is fully governed by statistical rate theories. The goal instead will be to evaluate the ability of rate theories to qualitatively predict product ratios and especially predict trends in the observations. Reasonable systematic errors in the relative energies of INT, TSA, and TSM for the various alkenes should not preclude this goal. At times the “predictions” here will involve the choice of one or more parameters, for example in the rate of cooling of INT. Any choices made (see the SI) were limited to effects on the overall level of selectivity, not affecting the trends in the predictions.

TST and CVT Predictions

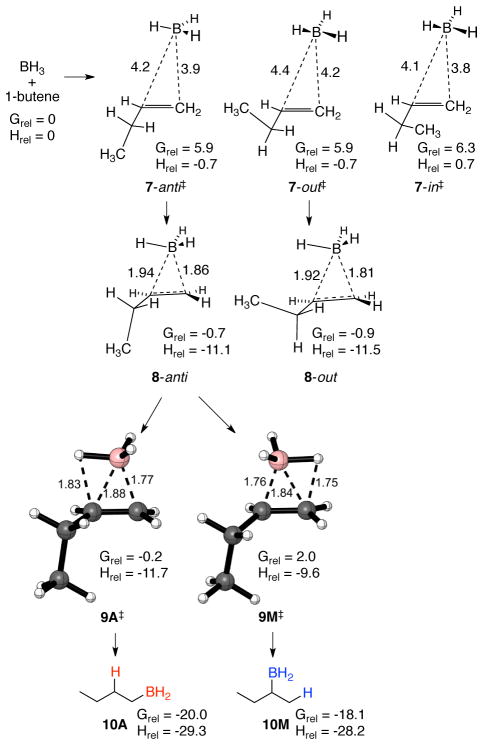
As discussed in our previous paper, the weight of experimental evidence favors a hydroboration mechanism involving interaction of the alkene with free BH₃, as opposed to interaction with a solvent-complexed BH₃.⁴ We will assume for now that this is correct; later we will consider the alternative mechanism. The approach of BH₃ to terminal alkenes is enthalpically barrierless but approximate CVT transition structures (TSs) were located as the maximum in free energy (CCSD(T)/aug-cc-pvdz//B3LYP/6-31G*) as the BH₃ descends a mass-weighted steepest descent path, using the no-saddle procedure of Truhlar.¹⁹ Such structures are intrinsically highly approximate owing to the crudeness of the free energy calculation for loosely associated molecules, but their relevance will be supported later in trajectory studies. Three CVT TSs were located with 1-butene. Approach of the BH₃ to either face of the 1-butene’s most stable conformation gives rise to 7-anti^‡ and 7-out^‡, while approach to its less stable conformation gives rise to 7-in^‡ (Scheme 1).

Scheme 1.

As will be seen, the addition step occurs in less than 1 ps after the CVT TSs, and this is too little time for significant interconversion of alkyl-group conformers (barrier 2.4 kcal/mol). The addition is then in a non-Curtin-Hammett realm²⁰ where it would be formally correct to follow separate mechanistic tracks for each pathway following the CVT TSs. In calculating product ratios for alkenes 2–5, it was assumed that TSs analogous to 7-anti^‡ and 7-out^‡ contributed equally to product formation. Inclusion of the 7-in^‡-derived products had a negligible effect on the product ratio with 1-butene, and this pathway was not calculated for 3–5. The remaining alkyl chain was in all cases assumed to be in an extended anti conformation.

The CVT TSs lead by steepest-descent paths in mass-weighted coordinates (intrinsic reaction coordinates, IRCs²¹) to π-complexes 8-anti and 8-out. The π-complexes, which resemble nonclassical carbocations, are just specific examples of INT from Figure 1 (see the SI for structures derived from 7-in^‡). Although the π-complexes are similar in free energy to the separate reactants, there is no opportunity for them to reverse because the barriers for going forward are very low. This makes the formation of the π-complexes 8 via the loose CVT TSs 7 rate-limiting. Klein proposed this in 1967 based on a lack of correspondence between intermolecular and intramolecular selectivity.²² Klein’s proposal explained many observations in hydroborations but was surprisingly ignored.

Each π-complex can lead to TSA and TSM addition transition states. The CCSD(T)/aug-cc-pvtz//B3LYP CVT TSs following 8-anti for the anti-Markovnikov and Markovnikov additions of BH₃ to 1-butene are shown as structures 9A^‡ and 9M^‡; see the SI for the structures derived from 8-out and for the complete set of structures obtained for alkenes 3–5. The CVT TSs are slightly later than the potential-energy saddle points due to a decrease in entropy and increase in zero-point energy (zpe) as the addition proceeds.

As we had previously reported for the hydroboration of propene, the selectivity in the hydroboration of larger alkenes is not accurately predicted by TST. In conventional TST, the CCSD(T)//B3LYP free-energy difference between TSA and TSM structures is 2.2–2.5 kcal/mol for 2–6. This corresponds to ~2% M in each case (Table 1). The inclusion of tunneling favors M; tunneling accelerates the Markovnikov addition by about 50% but adds little to the rate of the anti-Markovnikov addition. This is because the latter barrier is so low that the over-the-barrier process dominates. With the effect of tunneling in CVT/SCT calculations, the predicted M with 2–6 goes up to 2.6–2.9%.

We considered whether the ordinary errors associated with calculations could account for the discrepancy between prediction and experiment. One issue is that these are gas-phase calculations, and the effect of solvent on the selectivity must be considered. However, the TSA structures are more polar than the TSM structures. For example, the CCSD(T)/cc-pvtz dipole moment for 9A^‡ is 3.53 D, while that for 9M^‡ is 2.93 D. As a result, the inclusion of a PCM solvent model for THF in the calculations favors the anti-Markovnikov TS by 0.2 kcal/mol, taking predictions further from experiment.²³ The B3LYP-calculated solvent effect changed <0.04 kcal/mol for dodecene versus butene. Another issue is that the accuracy of the free-energy barrier is limited by the harmonic approximation. However, anharmonic frequency calculations on 9A^‡ and 9M^‡ changed their relative energies by only 0.02 kcal/mol.

Could the discrepancy result from a systematic error in the relative potential energies of the TSAs versus TSMs? In this regard, it is notable that the TST and CVT/SCT calculations do not account for the trend in selectivity observed with 3–5, predicting instead a very modest effect in the opposite direction (Table 1). The TST and CVT/SCT calculations also do not account for the lower selectivity seen with 6. Finally, the calculations substantially overpredict the proportional effect of temperature on the selectivity in the propene reaction. No simple systematic error could alleviate the inaccuracy of these predictions.

Why TST is not Appropriate

Figure 2 shows detailed energetics along the anti track for the reaction with 1-butene. The CVT TS 7-anti^‡ is an irreversible dynamical bottleneck for the reaction and within the tenets of CVT this structure would be thermally equilibrated. The enthalpy difference of 10.4 kcal/mol between 7-anti^‡ and π-complex 8-anti then reflects the average excess energy that could in principle be present in 8-anti to promote the subsequent hydroboration. We will be concerned below with how much of this energy is still present during the hydroboration transition states, but for now it is sufficient to note that the excess energy far surpasses the enthalpic barriers for passage through 9A^‡ and 9M^‡. (There is no enthalpic barrier for 9A^‡, though the ΔH^‡ of −0.6 kcal/mol simply reflects the non-counting of a low-energy normal mode’s contribution to the enthalpy as it morphs into the transition vector.) By itself, the excess energy relative to the barrier would not guarantee that the hydroboration step would occur before thermal equilibration, but it signals the possibility.

Figure 2.

Energy diagram (CCSD(T)/aug-cc-pvtz//B3LYP/6-31G*) for the hydroboration of 1-butene along the anti conformational track. Free energies are shown in blue and enthalpies in red, in kcal/mol.

Although a growing number of exceptions are being recognized,^12,24,25 in most solution reactions intermediates cool and thermally equilibrate before proceeding through the next transition state, even when their initial excess energy far exceeds the next barrier. Accordingly, TST is usually the appropriate theory to apply for predicting the behavior of intermediates. In hydroboration, the failure of TST to adequately predict the product ratios is the key evidence that the π-complex intermediate has not thermally equilibrated. In the absence of thermal equilibration, an assumption of TST has been violated and TST should not be applied. This circular reasoning, that the failure of the TST prediction signals its inapplicability, emphasizes that that failure lies not in TST itself but in the initial choice to apply it to this reaction. In the general case, however, the applicability of any rate theory assuming a canonical ensemble will depend on the relative rates of reaction of hot intermediates versus their rate of thermal equilibration. The latter in particular is sufficiently nebulous that chemistry has no clear criteria for recognizing when TST will not work.

Statistical CCNM Predictions

As described above, the CCNM model of Zheng, Papajak, and Truhlar divides the reaction into indirect and direct parts, with the indirect part reflecting the ordinary rate constants (CVT/SCT here) for reaction of the intermediate complexes, and with the direct part in simplest form reflecting the equilibrium mixture of products. For hydroboration, the latter is subject to a significant complication because the products are conformationally complex. Because the cyclic TSs perforce initially afford an unstable eclipsed conformation, trajectories initiated from TSA (such as 9A^‡) can afford both C₁-C₂-gauche and C₁-C₂-anti conformations of product A. Additionally, there are differing rotamers associated with the C₁-BH₂ bond. The choice of product conformations is important because the CCNM-predicted product ratio depends sensitively on the relative energies of the products. For the CCNM calculations here, we used the product conformations formed most often within 200 fs after the hydroboration TSs. This was usually the same conformation as obtained by an IRC, but in the cases of 9A^‡ and the anti-Markovnikov addition to 6, the IRC falls into shallow minima that are mostly bypassed by trajectories.

For the CCNM model, the proportion of the reaction assigned to the direct mechanism depends largely on the relative energies of TSA and TSM versus INT. When the barriers are very low, the direct mechanism dominates. When the barriers are large, the indirect mechanism dominates. For the anti conformational track with 1-butene, the reaction would be 41% direct and 59% indirect.

Since the indirect portion of the selectivity is defined by the CVT/SCT rate constants, the CCNM model can only improve on the overly-selective CVT/SCT predictions when the direct portion of the mechanism would be less selective. In the statistical CCNM model, the selectivity assigned to the direct mechanism is just the equilibrium constant for the products. For unbranched alkenes, this equilibrium favors the A by a factor of 8–15. The weighted inclusion of this lower selectivity increases the predicted amount of M, bringing the predictions closer to experiment (Table 1). The predicted selectivity is however still too high, though the potential for systematic error in the energetics should be recalled in considering this. More decisively, the predictions do not account for the observed trends in selectivity with the series of alkenes.

In the case of 6, the steric effect of the bulky tert-butyl group increases the equilibrium preference for A to a factor of 86. Because the CCNM model includes this in the direct portion of its selectivity prediction, it makes the specific qualitative and quantitative prediction that the selectivity should be very high. The CCNM prediction fails entirely. The likelihood of this failure was considered in the choice to study 6. In complex reactions, the phase-space relationship of the branching ratio to the stability of the products is physically dubious, and the tert-butylethylene example demonstrates this. The partial success of the statistical CCNM model with unbranched alkenes arises from a favorable product equilibrium constant that is arguably simply fortuitous.

Nonstatistical CCNM Predictions

The nonstatistical CCNM model, following ideas from nonstatistical phase-space theory,²⁶ allows for a finite intramolecular energy relaxation time versus the time required for the structure to traverse from the transition states to the products. The latter depends on the distance (in mass-weighted coordinates) between the transition state and product. A shorter distance to a product provides less time for energy relaxation, decreasing the effective partition function of a product and decreasing its predicted formation.

In the Zheng, Papajak, and Truhlar work, the nonstatistical CCNM correction led to improved agreement with experiment. However, those calculations had made the unfortunate approximation that the distance between the transition state and the product was the same for both the Markovnikov and anti-Markovnikov pathways. In fact, the distance to A is always substantially larger (by a factor of 1.7 with propene and 2.2–2.7 with 1-hexene). This difference is because the path to M requires a simple methyl-group rotation from the transition state, while formation of A requires the rotation of a bigger CH₂BH₂ group, followed by an additional BH₂ rotation. The result of the difference in distances is that the correct nonstatistical corrections consistently favor A. In contrast to the prior work, this takes the predictions further from experiment (Table 1). It had been suggested by Zheng, Papajak, and Truhlar that the inclusion of additional nonstatistical factors could lead to improved predictions, but considering the distance effect, it is not clear to us how additional corrections within the same physical framework can take the predictions in the right direction.

As with TST and CVT/SCT, the statistical and nonstatistical CCNM calculations overpredict the proportional effect of temperature on the selectivity in the propene reaction. In each of these rate models, the selectivity is ultimately linked to enthalpic differences that would lead to a large temperature effect in any calculation based on a canonical distribution of energy.

Overall, the statistical and nonstatistical CCNM methods cannot be described as successful in their prediction of the selectivity of the hydroboration reaction, as they miss in specific predictions and fail to reproduce trends in the observations. The critical problem in these methods is what is lacking in their physics, in that they do not fully allow for the excess energy that is present in the intermediate and selectivity-determining transition states. This was clearly recognized as a potential problem by Zheng, Papajak, and Truhlar, and the results here suggest that the problem leads to qualitative errors. We will suggest below an improvement of the CCNM physics after considering the more conventional RRKM-ME approach of Glowacki et al.

RRKM-ME Predictions

In applying an RRKM-ME model to a solution reaction, the key question is how best to model and parameterize the collisional energy loss from intermediates. This is a complex issue even in the gas phase, and in solution it is complicated by uncertainty in what constitutes a collision. We will return to this issue, but our initial goal was to evaluate the straightforward exponential-down model used by Glowacki et al.⁶ These calculations were carried out using the MESMER program²⁷ and included a small correction for the effect of tunneling (see the SI).

The RRKM-ME calculations involve a number of reaction-dependent parameters that may be set based on literature data in a consistent way, such as the Lennard-Jones parameters for the solvent and each reactant, affecting the collision frequency. (See the SI for a full description.) The RRKM-ME predictions then depend on a single critical adjustable parameter, E_down, that represents the average energy lost in a collision. This parameter was adjusted to fit experimental data, with the provision that the same E_down was used for all reactions. It should be understood that changing other parameters, such as those affecting the effective size of the solvent molecules, has no impact other than to change the fitted value of E_down. As a first-order approximation, other systematic errors (such as a systematic error in the relative energies of TSA versus TSM across the series) would also change the fitted E_down without changing the final predictions.

The RMS error in the RRKM-ME predictions versus the experimental observations was minimized with an E_down of 860 cm⁻¹. However, the predictions do not fit experiment well (Table 1). The amount of M is overpredicted for propene and underpredicted for larger alkenes, with the error increasing as the size of the alkene increases. The temperature effect on the selectivity is underpredicted. The greatest virtue of the RRKM-ME predictions is that they get the direction of selectivity change versus alkene size for the 1-hexene / 1-octene / 1-dodecene series, which was a qualitative failing of the TST, CVT/SCT, and CCNM calculations. The trend in these predictions is understandable, since each INT homolog has the same amount of excess energy distributed statistically (as assumed in RRKM and RRKM-ME calculations) over molecules that increase in size substantially along the series. However, the RRKM-ME calculation overpredicts the change in selectivity for 3–5, predicting a change of 3.8% versus 1.5% observed experimentally. Including propene in the series makes the comparison worse. Increasing the size of the alkyl group makes an experimentally significant difference in the selectivity, but by much less than would be expected from the statistical treatment.

It is important to note that there is no choice of parameters that can lead to an adequate RRKM-ME prediction of the selectivity for 1-dodecene. Setting E_down at 0 provides a tunneling-corrected RRKM calculation that calculates an upper bound on M of 6.1%. For an arbitrarily large linear terminal alkene, the RRKM-ME result will asymptotically approach the CVT/SCT prediction of 2.9% M, but considering the sequence of results with 1-hexene, 1-octene, and 1-dodecene, it seems unlikely that any size alkene would afford less than 8% M. Outside of the full relaxation limit, RRKM-ME calculations unambiguously must fail for any sufficiently large intermediate because the time required for the assumed statistical IVR grows continually with the size of the system while the times for reaction and intermolecular energy equilibration do not. What is seen here with 1-dodecene is just the initial manifestation of this inevitable forced error.

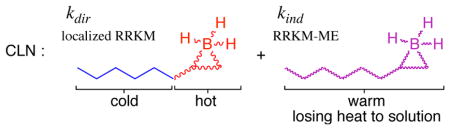
Localized RRKM-ME

The inadequacy of the simple RRKM-ME model suggests that the excess energy in INT is not statistically distributed as the subsequent formations of A and M occur. A plausible hypothesis is that the larger alkyl chains can only slowly take up a statistical share of the excess energy, so that the reaction occurs before IVR is complete. If so, the larger molecules would act like smaller molecules. This nonstatistical effect was largely anticipated by Rice in 1930.²⁸ Building on the work of Rabinovitch,²⁹ we have previously suggested a “localized RRKM” model for such reactions in which structurally large intermediates are modeled as if they were smaller molecules.¹² This is done by simply replacing the large-molecule vibrational frequencies used in an RRKM calculation by frequencies for a smaller model. This approach has aided the understanding of the reactions of hot intermediates in ozonolysis¹² and alkoxy radical cleavage reactions.²⁴

We consider here a new “localized RRKM-ME” model that, as above with the localized RRKM model, treats a large molecule as a smaller piece of the molecule that is chosen to mimic the “molecular reaction area,” but then allows for cooling of that piece in an RRKM-ME fashion. This model was applied by replacing the various frequencies used for the RRKM-ME calculations for the reactions of 2–6 by those for the propene reaction. It should be noted that the choice of propene, as opposed to for example 1-butene, is an unavoidable qualitative choice inherent to the model. The E_down was then modified to obtain a best fit with experiment. The results in Table 1 provide the lowest error versus experiment among the models explored so far, and are far superior to regular RRKM-ME.

The regular RRKM-ME and the localized RRKM-ME calculations may be viewed as the extremes of a continuum of possibilities, the former corresponding to complete IVR in INT before reaction and the latter corresponding to no IVR beyond the core atoms. In this regard, it is striking that the two models bracket every experimental result. In each case the localized RRKM-ME model provides a closer prediction, but with some displacement toward the regular RRKM-ME values. Due to the E_down–fitted nature of each set of numbers, this observation should be taken with a grain of salt, but the combination of results is consistent with the idea that the excess energy in INT is largely localized with some degree of energy loss to the rest of the molecule.

The fitted nature of the RRKM-ME approach masks weaknesses. One weakness is that the appropriateness of the exponential down model and any particular E_down is difficult to judge a priori, though significant progress has been made in recent years.^30,7,9 A more fundamental weakness is the dubiousness of any simplistic assumption of a statistical energy distribution, whether full-molecule or localized. To make progress along these fronts, we shall have to consider the behavior of trajectories in explicit solvent.

An alternative reaction mechanism in which the π-complex is formed by a direct transfer of BH₃ from a THF molecule was considered briefly. By applying the classical single-trajectory method of Hase to this mechanism in the case of dodecene,³¹ it was found that the direct transfer process affords a less energetic π-complex having only ~3.0 kcal/mol of excess vibrational energy. This mechanism would then give only 3.6% of M with E_down set at 0 and using the localized RRKM-ME model. This mechanism appears inconsistent with the observed selectivities, in keeping with other lines of argument previously described.⁴

Trajectory Studies

Two differing QM/QM ONIOM model surfaces were employed for the study of the hydroboration of propene, 1-hexene, and 1-dodecene in explicit THF. The first used B3LYP/6-31G* for the alkene / BH₃ along with PM3 for 53 THF molecules in a sphere with a diameter of ~24.6 Å and density ~0.88. The second used B3LYP/6-31G* for the alkene / BH₃ and PM6-D3H4 for 80 THFs in a sphere with a diameter of ~29 Å and density ~0.91. The second surface also included a small additional empirical dispersion correction adapted from Grimme’s D2 model³² (see the SI for details). PM3 greatly underestimates intermolecular attractions but was initially employed in the first model for practical reasons. The larger and more realistic second model became practical with the development of a new program, ProgdynONIOM, described in the SI. Despite substantially differing intermolecular forces, the results with the two systems were comparable.

The trajectories in explicit solvent are necessarily fully classical and they are calculated on a B3LYP/6-31G* surface. We considered whether these limitations would skew the results versus the quantum mechanical reality including zpe and tunneling. In this regard, the CVT/SCT CCSD(T)/aug-cc-pvtz relative rates for formation of A versus M (44:1) from propene may be compared with the ratio derived from fully classical TST on the B3LYP surface (59:1). Also, the predicted absolute rate for reaction of INT (R = Me) from B3LYP / fully classical TST is very close to the CCSD(T) / CVT/SCT prediction (1.6 × 10¹² s⁻¹ versus 2.0 × 10¹² s⁻¹). Finally, the predicted B3LYP / classical RRKM amount of M is 15.4%, while the tunneling-corrected CCSD(T)/aug-cc-pvtz / quantum RRKM predicted amount of M is 14.2%. These differences should have little effect on the results, though the last point suggests that the trajectories will overestimate the amount of M versus experiment. A more subtle issue, considered later, is how the classical simulation affects solute-solvent energy transfer.

The starting points for trajectories on these surfaces were obtained from a series of independent simulations that were equilibrated at 25 °C with the BH₃ boron atom loosely constrained by a harmonic biasing potential to ~3.4 Å and ~3.8 Å from the terminal and internal olefinic carbons, respectively. These distances were chosen to approximate the calculated gas-phase variational transition state for approach of BH₃ to propene, and they are somewhat shorter than the distances calculated for larger alkenes (see 7 in Scheme 1). If this choice of variational transition state geometry is accurate, it would be expected that 50% of the trajectories released at random would afford addition products and 50% would form reactants. The actual percentage of product-forming trajectories across all simulations was 57% with a range of 40% to 77%, depending on the alkene and choice of ONIOM model. This suggests that the trajectory staring points were reasonably close to the variational TS.

With propene, 1-hexene, and 1-dodecene in each ONIOM model, structures and velocities were extracted at 250 fs intervals from the equilibrating systems and integrated forward and backward in time using a Verlet algorithm with no constraint until either A or M had formed or the alkene and BH₃ had dissociated into separate reactants (separated by > 4.5 Å). The results from trajectories connecting separate reactants to the products are summarized in Table 2. Recrossing trajectories, passing either from reactants to reactants or products to products, were disregarded.

Table 2.

Results from trajectories in explicit solvent and energy values obtained in their analysis.^a

Alkene	ONIOM model	A: M (% M)	median timeb (fs)	ΔEaverage (kcal/mol)	ΔElocal-ave (kcal/mol)	ΔE”experimental” (kcal/mol)	ΔEchain-ave (kcal/mol)
propene	53 THF	115:11 (8.7%)	643	−4.0 ± 0.7	−4.0 ± 0.7c	−3.4	-
	80 THF	153:26 (14.5%)	803	−2.8 ± 0.4	−2.8 ± 0.4c		-
1-hexene (3)	53 THF	108:15 (12.2%)	650	−3.5± 0.6	−4.5 ± 0.9	−4.7	+0.7 ± 0.6
	80 THF	184:36 (16.4%)	784	−4.1 ± 0.5	−5.1 ± 0.6		+0.8 ± 0.5
1-dodecene (5)	53 THF	71:10 (12.3%)	672	−5.1 ± 1.1	−4.7 ± 1.2	−5.6	−0.5 ± 1.0
	80 THF	108:15 (12.2%)	831	−5.4 ± 1.4	−5.4 ± 0.9		+1.0 ± 0.8

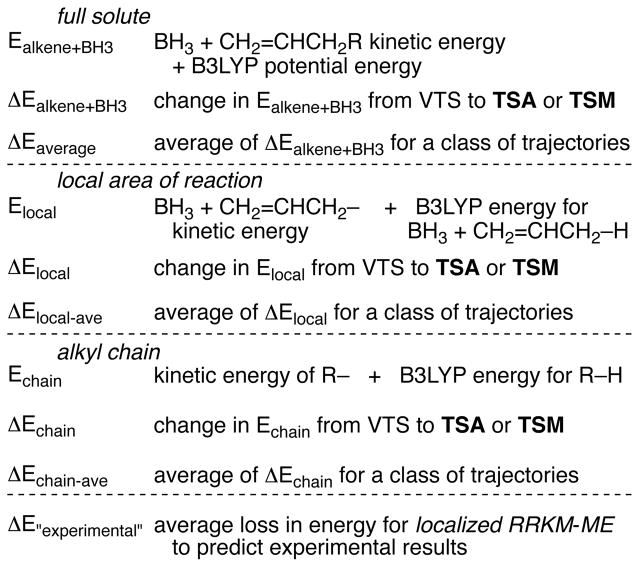
^aSee Chart 1 for a description of the energy values.

^bThis is the time from the release point at the approximate VTS to the formation of A or M.

^cFor simplicity, the ΔE_local-ave for propene calculated as including the full molecule, making it equivalent to ΔE_average. This differs from the definition of ΔE_local-ave for 3 and 5 by the change in energy for one methyl-group C-H bond, which averaged <0.2 kcal/mol in exploratory calculations.

Owning to its reliance on ratios of chance events, product-ratio predictions based on trajectories have an associated uncertainty, and precise predictions require large numbers of trajectories. Due to practical limitations in the number of trajectories calculated, the predicted percentages of M in Table 2 are uncertain (95% confidence) by 4–6%. This substantial disadvantage of trajectories precludes their use to predict trends in the selectivity such as that seen with 3–5. In this regard, the trajectory approach fails in practice, if not in principle. As noted above, the B3LYP /classical trajectories should modestly overestimate the amount of M versus an accurate quantum model. Given these limitations, the predictions of the amount of M formed in Table 2 are highly successful. Most importantly, this success comes without any ad hoc theory or adjustable parameter.

The total trajectory time to proceed from the VTSs to the products is complicated by a broad variation in the time required for the collision forming the π-complex (a median of ~450 fs). A more interesting and readily analyzed parameter is the π-complex lifetime, i.e., the time from first formation of the π-complex (defined by C-B distances < 2.0 Å) to passage through TSA or TSM. Approximately 30% of the trajectories have π-complex lifetimes less than 50 fs, and these trajectories are best described as reacting in the first BH₃ / alkene collision with no intermediate. The decay of the π-complex is then fascinatingly bimodal, as shown in Figure 3. (Figure 3 is a composite of all data. The individual sets of trajectories show more noise but are similar.) After the initial burst of reactions, few π-complexes react between 50 and 120 fs. This lull in the reaction represents the time required for the rebound and reapproach of the BH₃ versus the alkene after an initial unproductive collision. After 120 fs, the complexes continue their decay but at a much slower rate.

Figure 3.

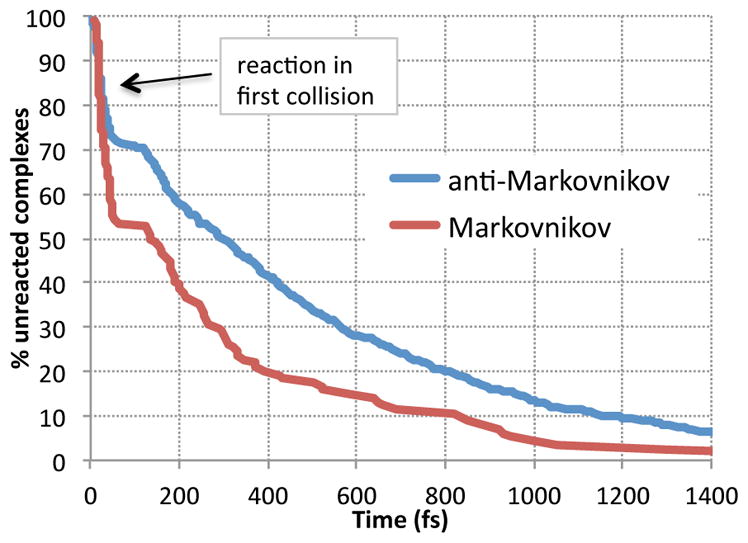
Decay of BH₃ / alkene π-complexes after formation, combining all data.

The low selectivity of the reactions occurring in the first collision is of particular importance. Almost half of the overall M product is formed at this stage of the reaction, and the selectivity in the first 50 fs is 20.2% M. This %M is somewhat higher than predicted by any of the statistical models, even within the localized RRKM-ME model with no energy lost to solution (which would give 16% M classically with B3LYP energetics). This is consistent with the selectivity in the initial collision being nonstatistical, but the evidence is weak due to the intrinsic differences between the trajectory / explicit solvent model and the gas-phase harmonic-approximation statistical model. The initial burst is a relatively large proportion of the reaction but its impact on the overall product ratio versus the ratio if the burst were statistical (16% M instead of 20.2% M) is small, adding 1.2% to the M. Such an error is readily obscured by the RRKM-ME parameterization.

The burst is responsible for over one-third of the increase in M over TST. Still, most of the deviation from TST is the result of more slowly reacting complexes. The selectivity increases for longer-lived π-complexes but never reaches the TST selectivity; the % M after 1000 fs is still 4.7%. For comparison, trajectories started from a thermally equilibrated BH₃ / dodecene π-complex afforded a 6: 198 ratio of M: A (2.9 ± 1.6% M). This is within statistical error of classical TST expectations.

A similar burst is seen in gas-phase classical trajectories started from the VTS (see the SI). The main difference in the gas phase is that trajectories that fail to form a product on the initial collision tend to have the BH₃ rebound further from the alkene. As a result, fewer BH₃ molecules quickly reapproach the reactive area and 37% of the trajectories remain unreactive after 1000 fs. In solution, the solvent cage has the dynamic role of limiting the motion of the BH₃,³³ in addition to its role of slowly removing heat from the complex. Without that cooling effect, the gas-phase trajectories remain relatively unselective after 1000 fs, as previously described.⁴

Energy Analysis

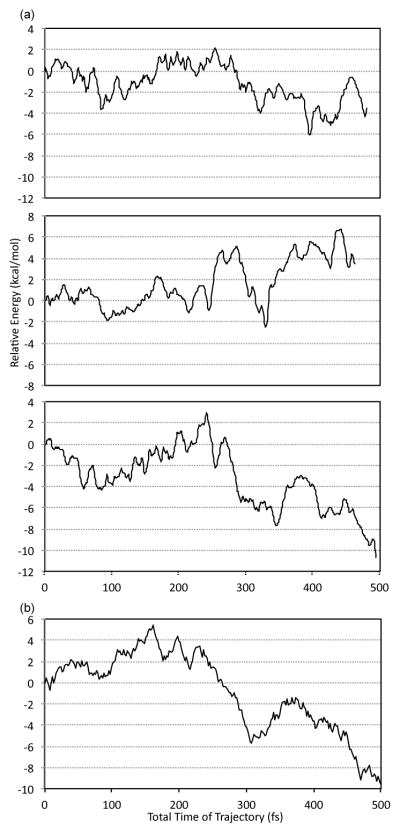
With these series of trajectories in hand, we examined the energy change versus time in the alkene / BH₃ systems. The total energy in the complete sphere is constant, of course, but the energy within the alkene / BH₃ solute combination changes due to interaction with the solvent. The energy in the alkene / BH₃ solute is a combination of the atomic kinetic energies, their potential energies versus the gas phase, and an energy of interaction with the solvent sphere. The last of these terms is the most difficult to calculate but in limited studies it varied little on average as the reactions proceeded. It was then satisfactory for the current purposes to approximate the alkene / BH₃ solute energy as the sum of the gas phase B3LYP potential energy and the atomic kinetic energies in a center-of-mass frame (see the SI). This energy, E_alkene+BH3, and its relative change between the VTS and passage through the TSA or TSM, ΔE_alkene+BH3, was followed for each trajectory. We also followed a local energy (E_local) in the area of the alkene as the combination of the kinetic energy for the BH₃ and the terminal allyl atoms (CH₂=CHCH₂–) plus the potential energy for the BH₃ / allyl combination (obtained by replacing the extended chain with a hydrogen atom at a C-H distance of 1.09 Å). A chain energy (E_chain) was defined in a similar way as the kinetic energy of the atoms of R of R–CH₂CH=CH₂ plus the potential energy of R-H. The changes in E_local and E_chain between the VTS and TSA or TSM are ΔE_local and ΔE_chain. Notably, the sum of ΔE_local and ΔE_chain. is approximately ΔE_alkene+BH3, but not exactly so due to interactions between the two pieces of the system. Table 2 summarizes the average values of ΔE_alkene+BH3 (ΔE_average), ΔE_local (ΔE_local-ave), and ΔE_chain (ΔE_chain-ave) for the various sets of trajectories, while Figure 4a graphs E_alkene+BH3 versus time for three example trajectories with 1-hexene / BH₃. Chart 1 provides a summary of the energies under discussion.

Figure 4.

(a) Graphs of E_alkene+BH3 versus time for three trajectories with 1-hexene / BH₃ that form product in ~500 fs. (b) A biased random walk in the energy, with E(t+2fs)=E(t)+0.54*rand−0.016, where rand is a random number between −1 and 1. The parameters were chosen to mimic ΔE_average and the variation in ΔE_alkene+BH3 over 180 fs (see the SI for details and additional graphs).

Chart 1.

Energies of interest in the analysis of trajectories.

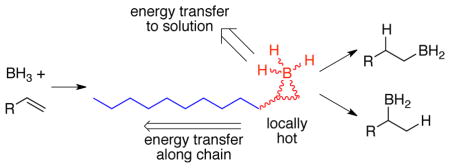
The results are striking in a long series of ways: (1) the full solute energy E_alkene+BH3 varies continually. The solute is always subject to a force field exerted by the solvent, and its energy is constantly changing in response to this force field.¹⁰ (2) The variation in E_alkene+BH3 versus time appears nearly indistinguishable from simulations employing a random walk in the energy, as in Figure 4b. That is, the hills and valleys in Figure 4a that might give the appearance of discrete events, suggesting solute-solvent “collisions,” can be simulated approximately by completely random fluctuations in the energy. The autocorrelation time for changes in E_alkene+BH3 was only ~2 fs. The E_alkene+BH3 curves then provide no evidence for descriptively meaningful collisions in solution. (3) The excess energy generated in the solute on formation of INT, 11.8 kcal/mol on the B3LYP surface, is on average only partially lost to the solvent by the time the trajectory passes through TSA or TSM. The average energy lost in the solute, ΔE_average in Table 2, varies in the simulations from 2.8 to 5.4 kcal/mol, with an apparent trend of increasing ΔE_average with increasing alkene size. (4) Within a trajectory, the solute energy E_alkene+BH3 might go up or down, with a wide distribution. The ΔE_alkene+BH3 values for individual trajectories have a standard deviation of 3.8 kcal/mol for propene, 4.9 kcal/mol for 1-hexene, and 6.7 kcal/mol for 1-dodecene. Figure 4a shows examples with 1-hexene where the solute loses 4 kcal/mol (near the average), 11 kcal/mol (matched or exceeded in 10% of the trajectories), and gains 4 kcal/mol (matched or exceeded 8% of the time). (5) the full solute ΔE_average and the local ΔE_local-ave are similar, most surprisingly for the dodecyl chain, so that the ΔE_chain-ave values are all small (from +1.0 to −0.5 kcal/mol with relatively large uncertainties). This means that most of the energy lost from the localized reaction area ends up in solution, not in the alkyl chain! (6) If we assume the applicability of the semi-statistical localized RRKM-ME model, then the experimental product selectivity can be used to calculate the average energy lost from the local area of the reaction, ΔE_{”experimental”}. The most striking observation of all is that the ΔE_{”experimental”} values match closely the ΔE_average and ΔE_local-ave values from the simulation.

We consider below each of these last three observations in more detail.

The Variation in ΔE_alkene+BH3

The broad variation in the change in solute energy ΔE_alkene+BH3 across the trajectories provides information about energy transfer in and out of the molecular normal modes, allowing consideration of how the quantum real system would differ from the classical simulation. For the propene, 1-hexene, and 1-dodecene systems involving 33, 60, and 114 classical normal modes, the average total internal energies are 33RT, 60RT, and 114RT, and the standard deviations on the energies in individual molecules at 25 °C would be 3.4, 4.6, and 6.6 kcal/mol, respectively (see the SI for this calculation). The close correspondence of these numbers to the observed variation in ΔE_alkene+BH3 values indicates that the energies in the classical normal modes have varied essentially randomly over the course of the ~1 ps between the VTS and product formation. In other words, the molecular energies at TSA or TSM are ~uncorrelated with their starting energy. This loss of correlation takes time. To study the rate of decorrelation, the distribution of energies in 1-hexene / BH₃ at the VTS was compared with 180 fs prior to the VTS (a time period in which no reaction occurs). The standard deviation on ΔE_alkene+BH3 was 2.9 kcal/mol, 63% of its asymptotic value. Crudely, the decorrelation of the energy with its initial value is happening with a half-life of ~140 fs.

The quantum real system would be subject to a tighter distribution of ΔE_alkene+BH3 because the high energy normal modes are rarely excited. For the propene, 1-hexene, and 1-dodecene systems, the standard deviations on the Boltzmann-random energies in individual molecules at 25 °C would be 1.6, 2.3, and 3.2 kcal/mol, respectively (see the SI). These are approximately half of the variations in the classical systems. From Fermi’s Golden Rule, the quantum system should be subject to lower rates of energy interchange with solvent than the classical system. This would be particularly true of high-energy modes, as supported by experimental observations.^10,34 However, most of the excess energy will be in low-energy modes that should behave closer to the classical limit seen in the simulations.

The Low ΔE_chain-ave

The surprisingly low average change in energy in the alkyl chain ΔE_chain-ave requires a more detailed consideration of IVR. The potential energy lost as the BH₃ approaches the alkene is initially manifest as kinetic energy in the approaching motion of the BH₃ and alkene atoms. This approaching motion may be viewed as the coherent superposition of a series of delocalized normal modes. Some of the energy is then transferred down the alkyl chain by the simple dephasing of the modes, without any change in their vibrational quantum numbers. This is ballistic energy transfer, and it is fast; linear alkyl chains ballistically transfer energy at speeds greater than 10 Å/ps.^35,36,37 Other energy is transferred diffusively by the excitation of new modes due to their anharmonic coupling with overlapping excited modes. (From the perspective of molecular eigenstates, diffusive energy transfer is itself a dephasing process.) Solvent interactions can have a strong effect on the rate of this form of IVR.^38,39 Diffusive energy transfer is much slower.⁴⁰

To examine each mode of energy transfer to the alkyl chain without the confounding effect of solvent, we applied the single-trajectory method of Hase to gas-phase reactions of BH₃ with each alkene conformation.³¹ Trajectories were initiated with the BH₃ 5.0 Å from the olefinic carbons, providing no energy to the normal modes. The BH₃ was then allowed to fall into the alkene with the motion propagated in the manner of an ordinary trajectory. Because the approaching motion is not complicated by orthogonal motions, the trajectories fall directly into the deepest area of the π-complex potential energy well. Figure 5 shows how the local potential energy and E_local evolve with time for the anti and out conformations of 1-dodecene. In the anti case (Figure 5a), the π-complex is formed and persists to ~2000 fs before reacting. In the out case (Figure 5b), the momentum built up in the approaching atoms carries them directly over TSM to afford M. This last observation interestingly suggests, albeit weakly, that dynamic matching⁵ relatively favors formation of the Markovnikov product. This idea fits with the enhanced %M in trajectories that form products in the initial alkene / BH₃ collision.

Figure 5.

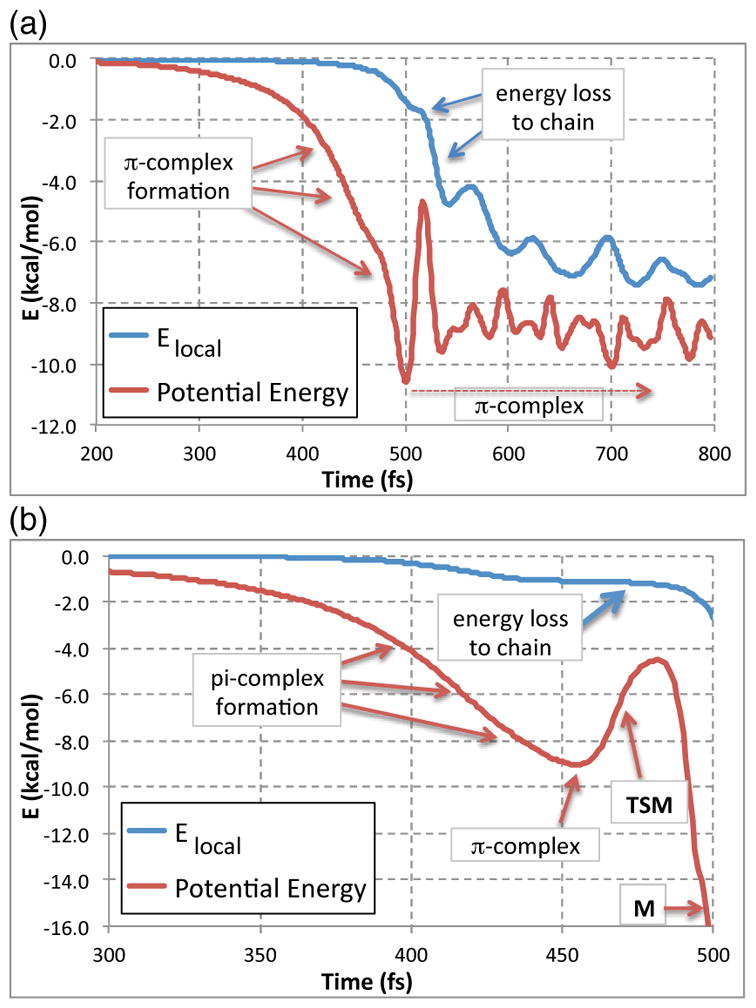
Single-trajectory studies of the reaction of BH₃ with 1-dodecene in the gas phase. (a) With the anti mode of approach, the trajectory forms a persistent π-complex. (b) With the out mode of approach, the trajectory immediately passes through TSM to afford M.

The π-complex formation of Figure 5a allows consideration of how fast energy can be transferred to the alkyl chain. As the BH₃ approaches the alkene, the potential energy drops and kinetic energy concomitantly builds in the atoms involved in the π-complex. The passage of this energy to the alkyl chain, as seen in the drop in E_local, lags the potential energy drop by roughly 100 fs. Much of the energy loss is rapid, assumedly ballistic, and the loss reaches 6 kcal/mol within 100 fs after formation of the π-complex. After this, the energy loss is slower, and it reaches its equilibrium value of 8.3 kcal/mol in about 1500 fs (see the SI). With 1-hexene (not shown), less energy is lost to the chain ballistically but it still exceeds 4 kcal/mol within 100 fs (see the SI).

These results suggest that ballistic energy transfer is fast and large, once the potential energy from π-complex formation become available to the molecule. However, both the solution trajectories and the experimental results suggest that the actual energy transfer to the alkyl chain of 1-dodecene is on average less than half of the >6 kcal/mol that could be transferred ballistically within 100 fs. Experimentally, it is clear that the alkyl chain of 1-dodecene takes up some extra energy relative to smaller alkenes, based on the higher selectivity observed, but to account for the selectivity statistically the extra energy absorbed with 1-dodecene over 1-hexene and propene would be 0.9 and 2.2 kcal/mol, respectively (based on the ΔE_{”experimental”} values). The solution trajectories agree with a relatively low amount of energy transferred to the alkyl chain of 1-dodecene in two ways. The first is that the ΔE_local-ave for 1-dodecene is only moderately lower than the ΔE_local for propene, roughly 1.9 kcal/mol (with a large uncertainty). The second way is the set of low values for ΔE_chain-ave. The low ΔE_chain-ave values do not show directly how much energy is transferred to the chain, but little is left there at the time of the reaction.

Why is the amount of energy actually transferred down the alkyl chain so much lower than could be rapidly transferred ballistically? For the ~30% of trajectories reacting on the first collision, the answer is straightforward. In the M-forming single trajectory of Figure 5b, only 1.2 kcal/mol of energy has been transferred to the chain when the trajectory passes through TSM. The corresponding trajectory with 1-hexene, which also forms M, has lost only 0.8 kcal/mol to the chain at TSM. For the 70% of trajectories that do not react on the first collision, many of the initial collisions will be glancing blows that do not initially pass through the bottom of the π-complex well and so do not have the full alkene / BH3 complexation energy available to distribute. Such trajectories may then react on their second collision with still little energy passed to the chain. About 30% of the trajectories persist for 500 fs after the first collision, and such trajectories would be expected to pass 6–8 kcal/mol of energy to the chain of 1-dodecene, but the average from all trajectories ends up low. The alkyl chain makes a difference in the rate of energy loss, but the observation that ΔE_average for propene is greater than half of ΔE_local-ave for 1-dodecene suggests that most of the cooling after π-complex formation arises from a direct passage of energy from the area of the π-complex to the solution. In small molecules it has often been observed that IVR precedes energy loss to solution,⁴¹ but in the large system here the two are competitive.

The Similarity of ΔE_{”experimental”} and ΔE_local-ave

The calculation of the local energy change from the experimental selectivity, ΔE_{”experimental”}, assumes that the product formation is statistical, at least within the confines of our localized RRKM-ME model. This assumption may be incorrect, due to the high %M in the 30% of trajectories that react on initial collision, but the low impact of this burst on the final product ratio limits its impact on the statistical ΔE_{”experimental”} calculation, even if the burst is nonstatistical.

We then consider the similarity of ΔE_{”experimental”} and ΔE_local-ave as a notably successful correlative prediction of the localized RRKM-ME model and the trajectory studies. That is, the RRKM-ME model allows the calculation of how much energy is lost from the local area of a reaction in order to account for experiment, and this amount matches well with the local energy loss seen in the trajectories. This supports the underlying physical relevancy of the localized RRKM-ME model. (It should be noted that there is no assumption of either collisions in solution or an exponential-down model in the ΔE_{”experimental”} calculation – see the SI.)

Taking the localized RRKM-ME model seriously, the effect of the various alkyl chains on the cooling of the reaction area may be analyzed. One way to view the effect of the alkyl chains is to ask how their cooling effect compares to that of the solvent. This may be done by retaining the exponential-down formalism using a set value for E_down (106 cm⁻¹) that reproduces experiment for propene in neat THF, then calculating the effective concentration of THF, relative to neat solution, that would bring localized RRKM-ME predictions in line with experiment for the other alkenes. For 1-hexene, 1-octene, 1-dodecene, and tert-butylethylene, solvent concentrations of 1.55, 1.81, 1.91, and 1.53 times that of neat THF, respectively, would account for experiment. So, the alkyl chain in 1-hexene has a cooling effect that is 55% of that of the solvent, and the alkyl chain in 1-dodecene is almost as cooling as the solvent. The sequence from 1-hexene to 1-octene to 1-dodecene shows that the cooling effect of a small chain is large but additional chain length has a diminishing effect as the chain grows. It also appears that the branched chain in tert-butylethylene and the linear chain in 1-hexene have a roughly equivalent cooling effect. Each of these trends makes qualitative sense, and they fall out solely from the experimental observations and the assumptions of the localized RRKM-ME model.

A Competitive Localized Noncanonical Model

The scientific strategy in the CCNM model of Zheng, Papajak, and Truhlar is that it seeks to understand a complex observation as the combination of two well-understood extreme cases, one being a reaction involving a fully equilibrated intermediate and the other being a reaction with no intermediate at all. We hypothesized that this general strategy might work better if the extremes are brought closer to the reality suggested by the trajectories. Toward that end, we have explored a “competitive localized noncanonical” (CLN) model.

In the CLN model, the reaction is divided into limiting “direct” and “indirect” parts, just as in the CCNM model. For simplicity, the CLN model uses the same division algorithm as was used in the CCNM model,¹³ based in effect on the relative energies of the intermediate versus its flanking transition states. This algorithm provides a rate constant for the direct mechanism, k_dir, and obtains the rate constant for the indirect mechanism, k_ind, by subtracting k_dir from a unified statistical total rate constant.⁴² A virtue of the CCNM division algorithm is that it is correct at its extremes, with a high indirect component for intermediates facing high barriers and a high direct component for intermediates facing low barriers. Improved division algorithms might be readily envisioned for future work.

Our CLN model then assigns the branching ratio for the direct mechanism, $R_{A/B}^{\mathit{loc}\mathit{RRKM}}$, based on a localized RRKM model, equivalent to the localized RRKM-ME model above except with no collisional cooling. In other words, it treats the direct portion of the reaction as if a propene / BH₃ complex were reacting statistically in the gas phase low-pressure limit. This portion of the reaction is meant to correspond to the trajectories that react most rapidly after collision. The CLN model then assigns the branching ratio for the indirect mechanism, $R_{A/B}^{\mathit{RRKM}-ME}$, based on an RRKM-ME calculation for the full alkene / BH₃ system. The cooling from molecular collisions in the RRKM-ME calculation is based on an exponential-down model, using the same E_down for all reactions.

$$k_{\mathrm{A}}^{\mathit{CLN}}=\frac{R_{A/B}^{\mathit{loc}\mathit{RRKM}}}{1+R_{A/B}^{\mathit{loc}\mathit{RRKM}}}{k}_{\mathit{dir}}+\frac{R_{A/B}^{\mathit{RRKM}-ME}}{1+R_{A/B}^{\mathit{RRKM}-ME}}{k}_{\mathit{ind}}$$ (1)

$$k_{\mathrm{B}}^{\mathit{CLN}}=\frac{1}{1+R_{A/B}^{\mathit{loc}\mathit{RRKM}}}{k}_{\mathit{dir}}+\frac{1}{1+R_{A/B}^{\mathit{RRKM}-ME}}{k}_{\mathit{ind}}$$ (2)

The results are shown in the last column of Table 1. With E_down adjusted to make the CLN selectivity for propene at 25 °C match the experimental selectivity, the CLN model predicts the propene selectivity at 70 °C and the selectivity for tert-butylethylene with high accuracy. The CLN model then overpredicts the M with 1-hexene by 0.9%, but predicts with high accuracy the change in selectivity from 1-hexene to 1-octene and 1-dodecene. Any fitted prediction is to some degree an exercise in numerology, but the striking agreement of the CLN predictions with experiment, using only a single adjustable parameter, supports its physical relevancy.

The CLN model then provides intuitive explanations for some of the trends in the experimental selectivity. The change in selectivity for propene at 25 °C versus 70 °C is a combination of a low change in the selectivity in the direct (RRKM) mechanism, 0.5%, and a larger change in the indirect (RRKM-ME) mechanism, 1.3%. The tert-butylethylene reaction is predicted to be less selective than the propene reaction in the CLN model because the low-selectivity direct mechanism is increased in importance (47% versus 33% for propene) due to somewhat lower barriers for reaction of the π-complex intermediate. The selectivity increases from 1-hexene to 1-octene to 1-dodecene because the alkyl chains distribute the energy in the indirect mechanism, but the change is less than expected from simple RRKM-ME calculations because of a constant contribution of low-selectivity reaction from the localized direct mechanism. The real reactions are of course more complex than the extremes of the CLN model, but the CLN model provides both quantitative predictions and an attractive qualitative intuitive basis for understanding observations.

Conclusions

Canonical versions of transition state theory fail to account for the regioselectivity of hydroboration of a series of terminal alkenes. This failure is both quantitative, with respect to inaccurate predictions of specific selectivities, and qualitative, with respect to their inability to predict notable trends in the observations. Canonical transition state theory by definition was not designed to handle reactions of intermediates containing excess energy, so it can be argued that transition state theory should not have been applied in the first place. However, the inapplicability of transition state theory to mechanistic intermediates is not known a priori, only from the failure of its predictions. Surely most of the time transition state theory is applicable to intermediates in solution, but great care must be taken when the intermediate initially has enough energy to overcome a subsequent barrier rapidly. We would note with emphasis that the failure / inapplicability of transition state theory in hydroboration was only recognizable by a coincidence of factors that aid this observation. This includes that the reaction produces a mixture of products, that the selectivity is in a range that is readily observable, and that the excess energy in the intermediate substantially changes the selectivity. For reactions involving a similar reaction coordinate but lacking any one of these factors, transition state theory may be inapplicable without it being so readily experimentally discernable.

The CCNM model approaches the prediction of the selectivity in hydroboration by combining two extreme cases, one in which the intermediate reacts only after thermal equilibration and the other in which there is no intermediate so that the selectivity is governed by phase-space theory. This simplicity aids intuition, minimizing the need to consider the complex physics of what happens in the intermediate cases. In one respect, the trajectory studies here provide intriguing support for the direct-mechanism portion of the CCNM model. That is, ~20% of the trajectories react in their initial collision while the CCNM model predicts ~33% of the direct mechanism with propene. However, the extreme cases composing the CCNM model include no allowance for either IVR or intermolecular energy transfer. They are also susceptible to a general limitation of phase-space approaches, in that the selectivity may be determined in a structural area that little resembles the products of the reaction. This makes the CCNM model subject to designed failures, as in the case of tert-butylethylene. Overall, it should not be surprising that the statistical and nonstatistical CCNM models as originally formulated cannot account for a complex series of experimental observations in hydroboration.

RRKM-master equation calculations are by design aimed at gas-phase reactions where the time for IVR is short compared to both the time between collisions and the lifetime of the intermediate. In solution, the time scale is per force contracted; the high-pressure limit of RRKM-ME calculations (the TST result) can only be avoided in solution if the lifetime is very short. With such a short lifetime, the time required for IVR can no longer be ignored. As a result, the RRKM-ME calculations for hydroboration err systematically, overpredicting the effect of molecular size. From the consideration of time scales, this will be a persistent shortcoming in the application of RRKM-ME calculations to solution reactions.

Trajectory studies in explicit solvent appear adequate for predicting the approximate selectivity in hydroborations, with minimal physical assumptions and no parameterization, but their impracticality for precise predictions precludes their use in the prediction of the subtle experimental changes in selectivity versus alkene size. Their greatest value lies in the insight they provide into the nature of a reaction of this type in solution. A substantial portion of the trajectories react in the initial collision of the BH₃ with the alkene. After this burst of reaction, the decay of the trajectories is slowed and the selectivity increases at longer times. The energy in the alkene / BH₃ complex is varying continually, with no discernable discrete collisions, but on average less than half of the excess energy gained in the formation of the complex is lost before product formation. More is lost for larger alkenes, so the alkyl chain has a definite cooling effect on the reaction area, but energy loss to solution remains the major process and little excess energy remains in the alkyl chain on reaction. Overall, the energy lost from the molecular reaction area fits with the experimental observations when interpreted through the lens of a localized RRKM-ME rate model. The covalently attached alkyl chain can then be thought of as an additional cooling mechanism for the reaction area, instead of the statistical energy reservoir assumed in ordinary RRKM-ME calculations. The efficacy of this cooling mechanism versus solvent cooling can then be analyzed from the experimental data, and the results provide an intuitively attractive measure of the effect.

The localized RRKM-ME model is one of two semi-statistical rate models suggested here. The second, the CLN model, is an adaptation of the CCNM model of Zheng, Papajak, and Truhlar using extreme cases that appear more realistic based on the trajectory observations. In this model, the overall reaction is considered to be a combination of very fast reactions where the energy is retained in the local molecular area, with no cooling, and slower reactions with distributed energy following RRKM-ME results. With a single parameter, as inherent to all RRKM-ME calculations, the CLN model is able to reproduce the trends in the experimental observations with impressive accuracy.

Correct understanding allows accurate control. The CCNM model suggested that increased selectivity in hydroboration could be approached by sterically favoring one of the products thermodynamically, but this was not the case with tert-butylethylene. The ordinary RRKM-ME model suggested that hydroboration selectivity could be increased greatly by attaching large groups to the alkene, but the actual effect was much smaller. The CLN model suggests an approach to the accurate prediction of the effect of changes in structure in the control of selectivity.

The hydroboration of alkenes with BH₃ is certainly an example of nonstatistical dynamics, at the least from the perspective that neither canonical transition state theories nor ordinary RRKM-ME theory can account for the experimental observations. Put another way, the reaction is nonstatistical by a mechanism in which the intermediate contains excess energy and that excess energy is not distributed statistically throughout the molecule. The importance of this mechanism of nonstatistical dynamics seems firmly established here. The mechanism of nonstatistical dynamics that we originally proposed, a form of dynamic matching, is supported by the low selectivity in reactions forming product in the initial collision, but this mechanism is not the major contributor to the overall selectivity. Philosophically, it is difficult to defend the application of statistical theories to reactions that occur within 50 fs of an initial collision, but the selectivity observed in these trajectories is not so different from statistical predictions.

Despite the nonstatistical nature of hydroboration, the results here suggest that adaptations of statistical theories to localized areas of large molecules, as suggested by Rice long ago,²⁸ may be tremendously useful in understanding the reactions of large short-lived intermediates in solution. This would be expected to include short-lived intermediates in biological reactions. The localized approach still needs improvement, for example to avoid the current qualitative choice of the local system, but the models here appear to be useful steps toward an accurate rate theory. Our plan is to continue to explore the applicability of these localized statistical models to unusual experimental observations in ordinary reactions in solution.