Abstract
We develop a multivariate analysis of brain anatomy to identify the relevant shape deformation patterns and quantify the shape changes that explain corresponding variations in clinical neuropsychological measures. We use kernel Partial Least Squares (PLS) and formulate a regression model in the tangent space of the manifold of diffeomorphisms characterized by deformation momenta. The scalar deformation momenta completely encode the diffeomorphic changes in anatomical shape. In this model, the clinical measures are the response variables, while the anatomical variability is treated as the independent variable. To better understand the “shape—clinical response” relationship, we also control for demographic confounders, such as age, gender, and years of education in our regression model. We evaluate the proposed methodology on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database using baseline structural MR imaging data and neuropsychological evaluation test scores. We demonstrate the ability of our model to quantify the anatomical deformations in units of clinical response. Our results also demonstrate that the proposed method is generic and generates reliable shape deformations both in terms of the extracted patterns and the amount of shape changes. We found that while the hippocampus and amygdala emerge as mainly responsible for changes in test scores for global measures of dementia and memory function, they are not a determinant factor for executive function. Another critical finding was the appearance of thalamus and putamen as most important regions that relate to executive function. These resulting anatomical regions were consistent with very high confidence irrespective of the size of the population used in the study. This data-driven global analysis of brain anatomy was able to reach similar conclusions as other studies in Alzheimer’s Disease based on predefined ROIs, together with the identification of other new patterns of deformation. The proposed methodology thus holds promise for discovering new patterns of shape changes in the human brain that could add to our understanding of disease progression in neurological disorders.
Keywords: Computational Anatomy, Deformation Momenta, Kernel Partial Least Squares (PLS), Alzheimer’s Disease, Prediction
1. Introduction
Recently, there has been widespread interest within the neuroimaging community about machine learning and shape analysis techniques. This has provided effective tools for learning patterns in morphological shape changes occurring in the human brain during healthy aging and disease progression. Some of these studies exhibit potential for prognosis and prediction of neurological diseases. Traditional brain imaging studies have used the brain anatomy as the outcome variable and have correlated changes in the brain anatomy to age, gender, and cognitive status. However, only recently, there have been very few attempts that try and predict cognitive function from brain MRI, specifically to determine the extent to which changes in the brain anatomical structure account for the variance of cognitive function in normal aging and Alzheimer’s disease.
Alzheimer’s disease is a neurological disorder that is characterized by severe cognitive decline and distinctive neuroanatomical shape changes. Cognitive decline is measured by clinical tests for neuropsychological function. The complex and subtle shape changes that occur during disease progression can be extracted from structural information available in MR brain images. In previous work, Large Deformation Diffeomorphic Metric Mapping (LDDMM) has been used for the characterization of anatomical changes associated with various diseases [Ashburner et al. (2003); Twining and Marsland (2003); Miller et al. (2005)], including the analysis of changes in anatomy with normative aging [Davis et al. (2007)]. Most of the earlier studies on characterization of neuroanatomical changes have focused on the statistical analysis of deformation maps, either using the associated Jacobian of the transformations, as in the now ubiquitous deformation-based morphometry [Ashburner et al. (1998); Mechelli et al. (2005)], or have done the analysis directly on the displacement maps. Most of the recent studies using large deformation diffeomorphic transformations have focused on the characterization of group differences in the shape of specific substructures, such as the hippocampus [Wang et al. (2007)]. In another substructure focussed study, Miller et al. (2012) performed statistical analysis on surface-based deformation markers to characterize differential atrophy in amygdala between the mild cognitive impairment (MCI) and the AD group. More recently, Li et al. (2012) studied variety of sparse regression methods on summary measures derived only from left and right hippocampus, such as volumes and surface deformations of hippocampi.
In this article, we present a multivariate analysis of diffeomorphic transformations of the whole brain for relating complex anatomical changes with neuropsychological responses, such as clinical measures of cognitive abilities, audio-verbal learning, logical memory, and measures of executive functions. Rather than using the associated Jacobian of transformations or the vector-valued velocity or deformation fields, we formulate the regression problem in terms of scalar initial momenta maps that completely encode the geodesics on the manifold of diffeomorphisms. Deformation momenta are a scalar-valued signature that summarize the complete shape variability information for an individual [Vialard et al. (2011)]. The scalar momenta are comprised of both the local divergence and curl components of associated deformation fields and not only the local scaling represented by the Jacobians. We use kernel Partial Least Squares (kernel PLS) to study covariance of the anatomical structures in the entire brain volume without any segmentation or a priori regions of interest identification. The methodology helps us extract and identify shape deformation patterns in brain anatomy that relate to observed clinical scores depicting cognitive abilities. Furthermore, this regression scheme under the LDDMM framework enables us to visualize and quantify the amount of localized shape atrophy observed and relate it to attenuation in neuropsychological response. Another interesting question about the interpretation of relationship between variables in regression concerns the confounding effect of extraneous variables, which may lead to false interpretation in the statistical analysis. Frank (2000) gives a comprehensive account of such issues. Since we attempt to understand the “neuroanatomical shape—neurological response” relationship, this particularly is of considerable importance for our shape analysis and regression modeling. Both the anatomical shape and clinical response are well known to be affected by several demographic variables. We formulate a modeling approach that takes into account a control for these variables in order to avoid spurious interpretations of our results. We also report the prediction accuracy to understand the stability of the model and find the results comparable to some of those reported in previous attempts. Our results also show that anatomical measures, such as cortical thickness, hippocampal volume and atrophy in amygdala, putamen and thalamus emerge naturally as in previous studies of Alzheimer’s and related dementia.
The details about some of the closest works to this study are covered in the next section. We detail the specifics of our proposed methodology in Section 3. Section 4 details about our extensive experiments with the ADNI data and comparisons with other regression methodologies such as Relevance Vector Regression (RVR). Analysis of stability of the regression estimates and applications to multi-modal image analysis using our proposed method are also presented in this section. Finally, we summarize and conclude with the discussion about the scope and the impact of this study to neuroimaging community in Section 5.
2. Related Work
Several studies have used machine learning methodologies to predict cognitive and disease states from neuroimaging data. Some of these works in Alzheimer’s disease are by Vemuri et al. (2008), Davatzikos et al. (2008), Fan et al. (2008), Cuingnet et al. (2011), Zhang et al. (2011) and Li et al. (2012) (see Weiner et al. (2012) for detailed review on this ongoing research). Vemuri et al. (2008) used linear support vector machines (SVM) to build classifiers to discriminate Alzheimer’s disease from cognitively normal patients using tissue densities extracted from structural MR brain images. In another study, Davatzikos et al. (2008) used high-dimensional pattern classification to develop efficient classifiers on a smaller cohort comprising of individuals with AD and frontotemporal dementia (FTD). Disease categorization between AD and FTD was performed based on features summarizing the amount of gray matter and white matter in brain tissues. Extensive analysis is presented in Cuingnet et al. (2011), summarizing disease categorization performances of classifiers targeting primarily the classification between AD, MCI (convertors and non-convertors) and control groups. This study evaluates multiple feature extraction methodologies such as voxel based summaries, cortical thickness and the hippocampus volume. Zhang et al. (2011) proposed a multi-kernel method to combine both structural and functional imaging modalities and evaluated their method on the classification of MCI group. Batmanghelich et al. (2013) have recently developed approximate inference algorithm to solve probabilistic models based on classification of disease phenotypes: AD, MCI and healthy controls, utilizing features derived from both the structural MRI as well as from genetic sequences in the form of single nucleotide polymorphisms (SNPs). However, this framework in its current form, is also not generalizable to regression with continuous clinical variables.
While many of above studies involve categorical classifications of disease, regression-based predictive analysis of continuous clinical measures have been given little attention. Modeling symptomatic measures of neuropsychological response as a function of anatomy has recently found increasing interest within the neuroimaging community. The progression of disease associated with aging such as the AD is characterized by gradual and continuous changes. Thus, regression analysis using continuous clinical response variables is a natural choice and more informative of disease progression than just the classification-based approach for the study of such neurological disorders. Cohen et al. (2011) give a comprehensive review of such techniques and covers a gamut of studies that relate continuous clinical variables with neuroimaging data in various neurological disorders. Another review article by Filipovych et al. (2011) also suggests the use of clustering-based approaches for categorical analysis and high-dimensional pattern regression approaches for understanding continuous clinical progression.
Some of the works to predict neuropsychological characteristics from imaging data in Alzheimer’s disease are from Duchesne et al. (2009) and more recently by Stonnington et al. (2010) and Wang et al. (2010). Duchesne et al. (2009) have used linear regression models on features derived from MRI data to predict clinical decline for the Mild Cognitive Impairment (MCI) disease group. The latter two works, however, are more closely related and comparable to our study. They have considered a continuum of disease states in Alzheimer’s and have used similar predictive modeling on the ADNI neuroimaging and neuropsychological data. For comparison, we report the correlation of predicted vs. actual value for test data (rtest) in leave-one-out cross-validation as reported in these studies. Stonnington et al. (2010) employed Relevance Vector Regression (RVR) techniques on the ADNI baseline MR scans and baseline clinical evaluation scores for a continuum of disease states, with the similar datasets as has been used in this study. They reported the best numbers for prediction to be around rtest = 0.48 for mmse (Mini Mental State Examination score). The estimated prediction accuracy using leave-one-out cross validation obtained in our work is: rtest = 0.52 for mmse (rtest = 0.53 after control for confounders). Wang et al. (2010) have employed regional-based clustering approach on tissue density maps (TDM) for feature selection, followed by RVR based bagging model. Although they report higher correlation, Wang et al. (2010) used only a subset of the baseline MRI scans from ADNI, and their response variable was the average clinical score over timepoints. We perform a detailed comparison of our results with these related works in Section 5.
Deformation momenta have been previously used for statistical analysis. Singh et al. (2010, 2012) used scalar deformation momenta to build models to explain covariance of shape and clinical data in the form of latent directions extracted in the two spaces but did not develop models summarizing functional relationship between anatomy and clinical variables. These models hence were not directly applicable for the prediction of continuous clinical response. Besides neuroimaging, momenta under the currents framework have been used as summary measure of shape changes in a cardiac study. Mansi et al. (2011) evaluate the regional impact of valve regurgitation and heart growth upon the end-diastolic right ventricle (RV) using shape changes summarized by deformation momenta. With the motivation of addressing problem of multicollinearity in high dimensional regression problem this work also employs partial least squares regression and reports improved predictions when compared to using principal component analysis (PCA) regression. This work applies the PLS method on moments using L2 scalar product between moments which is ill-defined. The regression coefficient thus obtained does not have a strict interpretation within the metric space of momenta and hence such an L2 based analysis is not intrinsic to the manifold.
Some of the other works that have recently provided more insights in the understanding of Alzheimer’s disease dynamics include those by Lorenzi et al. (2011), Lorenzi et al. (2012) and Niethammer et al. (2011); Hong et al. (2012). Lorenzi et al. (2011) have developed a hierarchical approach that combines subject specific tissue atrophy to obtain population level longitudinal changes. This framework is used to investigate the effects of positivity of CSF Aβ1–42 levels on brain atrophy in healthy aging. In the work that followed, Lorenzi et al. (2012) suggest a methodology to decompose individual’s brain atrophy into complementary components comprising of AD specific and healthy aging based on the projections defined under stationary velocity fields (SVF) framework. Niethammer et al. (2011) proposed a novel idea of generalizing the notion of least squares regression to manifold of diffeomorphisms that is effective in summarizing changes in atrophy along with age for a single individual. Hong et al. (2012) further extend geodesic regression to derive an approximate algorithm under metamorphosis framework. This method of geodesic regression, in its current form, is generally applicable to explaining atrophy with aging. The anatomical shape is treated as a response variable to independent aging progression. These methods are not applicable where neuropsychological characteristics are sought to be modeled as a functions of anatomy.
The focus of pattern recognition and machine learning methods for both classification and regression analysis in recent neuroimaging studies has primarily been to predict. Even though these approaches were able to extract and visualize the pattern-maps of brain atrophy that are most informative for prediction, none of the above studies answered questions about interpretation of the model in a way that would enable them to quantify the amount of anatomical shape changes. Our goal here is centered around quantifying the shape deterioration observed in brain tissue that would explain continuous clinical progression. An important statistical consideration towards this end is the need to control for the confounding variables, such as age, gender, handedness, and patient education. Previous predictive-modeling approaches have not included any explicit control for such confounding variables and does bring into question the biological interpretability of the patterns recognized by the regression coefficients obtained in these approaches. We address this by formulating a regression model between the residual in deformation momenta and residuals in clinical response, obtained after regressing out confounders such as age, gender, and education.
3. Methods
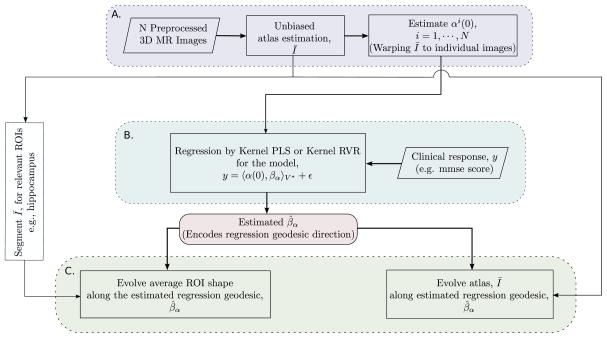
The focus of this work is to build regression models to study nonlinear geometry changes in the complex anatomy of human brain. In our proposed methodology, we use deformation momenta as signature representations of infinite dimensional diffeomorphic shape changes. Geometric regression models on brain anatomy using deformation momenta are formulated as kernel variants of high-dimensional regression methods such as the partial least squares (PLS) or the relevance vector regression (RVR). We further discuss the geometrical interpretation of regression estimates on the manifold of diffeomorphisms (Figure 1). Figure 2 summarizes the key steps of this regression modeling.
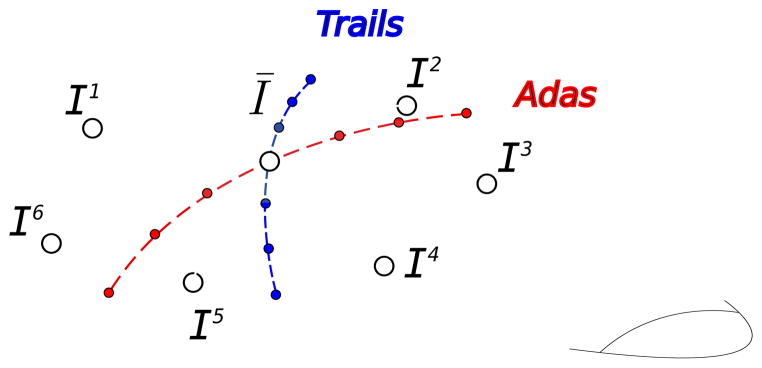
Figure 1.
Tangent space at the atlas (Ī) and emanating geodesics towards contributing images. The geodesics in red and blue represent regression coefficient for clinical variables and need to be estimated.
Figure 2.
Shape—clinical response regression modeling framework. Block A. represents initial shape feature extraction process, Block B. represents the regression on manifold and Block C. represents the interpretation of the estimated regression coefficient on the manifold and quantifying corresponding anatomical shape deformations.
3.1. Atlas building and deformation momenta
We use the general framework of computational anatomy by Dupuis et al. (1998) in which the anatomical variation within a population is characterized by a template or an atlas and the space of transformations that maps the atlas to each individual subject of the population. We follow the now well-established framework of large deformation diffeomorphic transformations. We briefly review the mathematical framework as it is central to the subsequent statistical analysis. Let Ω be the coordinate space of the atlas. Diffeomorphic transformations are continuously differentiable with a differentiable inverse. This definition implies that the set of all diffeomorphisms of Ω has a group structure. A convenient and natural machinery for generating diffeomorphic transformations is by the integration of ordinary differential equations (ODE) on Ω defined via the smooth time-indexed velocity vector fields v(t, y) : (t ∈ [0, 1], y ∈ Ω) → ℝ3. The function ϕv(t, x) given by the solution of the ODE with the initial condition y(0) = x defines a diffeomorphism of Ω. In other words, y(t) denotes the path of each voxel along the flow while x denotes the starting location in the coordinate grid, Ω. Thus, ϕv(t, x) = y(t), represents the diffeomorphism of the entire grid as a function of time, t. One defines a Riemannian metric on the space of diffeomorphisms by inducing an energy via a Sobolev norm with the partial differential operator L on these velocity fields. The distance between the identity transformation and a diffeomorphism ψ is defined as the minimization
| (1) |
The distance between any two diffeomorphisms is defined as d(ϕ, ψ) = d(id, ψ ∘ ϕ−1).
This Riemannian metric defined on the space of diffeomorphisms can now be used to compute a deformation that matches two images. If the problem is to register an image I over the target image J, then image at time t is defined as , i.e., I0 = I. The goal is to generate the diffeomorphism ϕ parameterized by the ‘optimal’ time-varying velocity field v that best aligns It with J.
It has been shown in Miller et al. (2002); Miller and Younes (2001) that the distance metric in Equation (1) on diffeomorphisms also establishes the notion of distance between two anatomical images, I and J. The length of the shortest path on diffeomorphisms connecting images I to J defines a metric on the image orbit under the group action of diffeomorphisms. For exact matching where I ∘ ϕ−1 = J, the distance between images is written as,
| (2) |
Motivated from the above, for inexact matching, a penalization to force closeness of the match is usually added [Miller et al. (2002); Miller and Younes (2001)] resulting in the minimization problem:
| (3) |
where σ is a free parameter controlling the tradeoff between exactness of the match and smoothness of the velocity fields. The existence of a minimizer in Equation (3) is shown in Dupuis et al. (1998).
3.1.1. Shooting-based Image Matching and Deformation Momenta
The minimizer in Equation (3) solves the LDDMM image matching problem. An important consequence is that the Euler-Lagrange equations associated with the LDDMM problem coincide with the Euler-Lagrange equations of geodesics on the group of diffeomorphisms. As shown in Younes et al. (2009), the geodesic equations are completely determined via the initial momenta Lv0, and furthermore it is in the direction of the gradient of deforming image. The vector image, α0 ∇ I (or the scalar image, α0) is referred to as the initial momenta. The scalar quantity, α0 completely encodes the geodesic flow from the initial image to the final image for the metric defined by the choice of operator L as per Equation (1) and the gradient of the initial image, ∇ I.
A very effective and standard algorithm for the solution of above LDDMM problem was proposed by Beg et al. (2005). While the energy minimization of
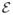 (v) over v is efficient in matching complex shapes, at convergence, this algorithm does not yield accurate estimates of the initial momenta. Vialard et al. (2011) has suggested another algorithm to accurately estimate the initial momenta. This shooting algorithm optimizes directly on scalar initial momenta by solving the adjoint system of Hamiltonian equations.
(v) over v is efficient in matching complex shapes, at convergence, this algorithm does not yield accurate estimates of the initial momenta. Vialard et al. (2011) has suggested another algorithm to accurately estimate the initial momenta. This shooting algorithm optimizes directly on scalar initial momenta by solving the adjoint system of Hamiltonian equations.
The minimization of the functional in Equation (3) can be done efficiently by ensuring the accuracy of estimated initial velocity, and thus the initial momenta, when the optimization is carried over the set of geodesic flows as in Vialard et al. (2011). The time integral over velocity can be replaced by the Hamiltonian of the system at t = 0 expressed in terms of initial momenta, α(0). This leads to minimization of the functional,
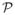 (a(0)) over initial momenta:
(a(0)) over initial momenta:
| (4) |
subject to the geodesic evolution constraints given by:
| (5) |
| (6) |
| (7) |
Equation (7) is the infinitesimal action of the velocity field v on the image, while (6) is the conservation of momenta.
The gradient for energy functional in (4) is expressed in terms of time-dependent Lagrangian multiplier over the path of geodesics. The gradient of
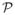 is given by:
is given by:
| (8) |
α̂(0) is computed by solving the following system of adjoint equation by backward time-integration:
| (9) |
| (10) |
| (11) |
subject to initial conditions
and α(t) and It are the solution of the system of shooting equations (5)–(7). Thus, to estimate α(0) for matching image I to target image J, a gradient descent based iterative algorithm is implemented. Since the gradient of energy functional as per Equation (8) is dependent upon the values of the adjoint variable, α̂(0) at t = 0, the Equations (9) to (11) are integrated backward in time in every iteration. Thus, the gradient descent step on initial momenta is taken based on computed gradient of energy as per Equation (8) using these adjoints until convergence.
3.1.2. Atlas Construction
The empirical estimate of Fréchet mean of images, Ī can now be presented using the distance metric on images defined in Equation (2). The goal is to compute the unbiased atlas image, Ī that minimizes the sum of squared distances to the given population of images (Joshi et al. (2004)). Given a collection of anatomical images {Ii, i = 1, ···, n}, the atlas can be defined as a solution to the minimum mean square energy criteria,
The minimum mean squared energy atlas construction problem is that of jointly estimating an image Ī and n individual deformations.
The algorithm described in Section 3.1.1 is effective for image matching but is numerically unstable when a template estimation is involved. The numerical instabilities of geodesic shooting-based template construction algorithms are studied in Singh et al. (2013). The problem of instabilities is not well understood and remains a key concern to investigate in future. Therefore, we present an alternative method to estimate the atlas and the geodesics emanating from it towards each of the contributing images. In our study, the atlas construction step is decoupled from the geodesic shooting-based image matching optimization because the template construction using scalar deformation momenta is known to suffer from numerical instabilities and is difficult to converge to a stable mean image. Therefore, for template construction, we have used the standard algorithm mentioned in Joshi et al. (2004) that does not involve geodesic shooting based optimization. The accurate shooting-based deformation momenta are estimated by solving N image matching problems as a secondary step. Following is the two-step approach used in this study to estimate deformation momenta that accurately encode geodesics:
Estimating the unbiased atlas, Ī using the truncated mean or the least-trimmed square minimization as per the framework of Joshi et al. (2004) and
Estimating the initial momenta from this atlas by registering, Ī to all images individually using the iterative backward-integration based gradient descent algorithm as described in Section 3.1.1.
For the atlas construction step, we note that both the estimate of the mean anatomy and the stable convergence of the estimation algorithm can be affected by outliers, often resulting from errors during automated image preprocessing such as poor skull-stripping. As the number of images used in atlas construction increases, thorough hand-validation of each input image becomes prohibitive. To mitigate the effects of such outliers, we compute a truncated mean in place of the full mean, where at each iteration of the atlas estimation algorithm all deformations are updated, but the estimate of the mean is updated based on the current most-central 90% of the deformations using the distance metric, d(Ī, Ik) as per Equation (2).
For the second step, atlas image Ī is registered to each image to solve the n LDDMM image matching problems thereby resulting in the estimate of n geodesics emanating from the atlas towards each image. The geodesic equations are completely determined via the initial momenta, Lv0 corresponding to each individual image deformation direction. This implies that for each of the n image matching problems, the initial velocity is given by the equation . The quantity completely encodes the geodesic flow from the atlas image to each of the individual images, i.e., ’s have all that we need to know to traverse the geodesic joining the atlas to the contributing images.
The two-step approach above not only improves the accuracy of the initial momenta computation but also decouples the individual subjects by recomputing deformation fields from the atlas to individual subjects. This allows separation between training and testing data, which is important for prediction-based regression modeling. Another benefit is that one can choose any atlas and model the shape variations from any coordinate system of choice.
3.2. GPU implementation
Two main challenges exist in implementing the LDDMM atlas building framework: the intensive computational cost and large memory requirements. Even with a very low-resolution time discretization, and efficient multithreaded implementation, atlas generation takes lot of time and memory on a high-end, multi-core, shared-memory machine. This makes parameter tuning and cross-validation schemes impractical, and limits the size of the population for which an atlas can reasonably be generated.
We implemented the GPU version of the algorithm as in Joshi et al. (2004). For a fixed atlas image Ī, the n individual deformations are updated by performing a gradient step of (3). This is implemented as a parallel alternating algorithm by interleaving the updates of the optimal deformations and the estimate of the atlas image Ī. These deformations are completely independent of each other, naturally yielding to a distributed memory implementation. Further, the parallel nature of many of the image processing algorithms used in the deformation update process lend themselves to an efficient and massively parallel GPU-based implementation. An implementation of LDDMM atlas building for use on a GPU computing cluster was therefore developed, based on MPI and the GPU image processing framework by Ha et al. (2009). Individual deformation calculations are distributed across computing nodes, and nodes further distribute deformation calculations among GPUs. In this manner, the only inter-GPU and inter-node communication required is in the atlas update step. Inter-GPU atlas computation is done in host (node) shared memory, and inter-node atlas computation is efficiently done by a parallel-reduce summation MPI call.
The GPU cluster used consists of 64 8-core computing nodes and 32 NVIDIA Tesla s1070 computing servers, each containing four GPUs. Each node controls two of the four GPUs contained in a s1070. Using 55 nodes of the GPU cluster, the resulting implementation generated the atlas of the population of 566 brain images with much higher time discretization in under 40 minutes.
3.3. Partial Least Squares (PLS) on manifold
The statistical analysis pertaining to data configuration with high dimensions but a small number of observations has been referred to as a ‘high dimensional low sample size’ (HDLSS) [Hall et al. (2005)] problem. This has also been popular in the probability and statistics literature as the ‘small n large p’ problem (Portnoy (1984), Bai and Yin (1993)). This characteristic property is typical to the neuroimaging data where the dimensionality of the acquired images far outpaces the number of subjects in the study. The statistical technique of Partial Least Squares (PLS) has been shown to be effective in the HDLSS regression setting where the problem is particularly susceptible to multicollinearities. There are several variants of PLS both for univariate and multiple response setting (Phatak and Jong (1997), Boulesteix and Strimmer (2007)). We review the PLS regression problem under the Euclidean setup and adopt this technique to model the regression in the tangent space of the manifold of the group of diffeomorphisms acting on images.
The PLS regression is a supervised dimensionality reduction technique based on a latent decomposition model. This is done by extracting a small number of latent components or projection scores that are linear combinations of the original variables to avoid multicollinearity. Unlike Principal Component Regression (PCR) [Jolliffe (1982)], where the dimensionality reduction of the data is carried out independent of the response variable by maximizing the variance within the regressors alone, PLS models the regression by maximizing the covariance between the regressors and response. The latent components are extracted in the independent and dependent data spaces such that the covariance between the two is maximum.
We discuss here the formulation of regression modeling to predict q-dimensional response variable, y1, y2 ···, yq represented by a vector y, using p predictor variables, x1, x2, ···, xp represented by a vector x. If we denote the n observations as (xi, yi)i=1, ···, n, the data matrices X and Y can be formulated as:
The matrix X is n × p where n ≪ p and the matrix Y is n × q.
PLS decomposes the matrices, X and Y into latent components of the form:
| (12) |
where T and U are the matrices of extracted scores while the matrices P and Q represent the loadings. The matrices E and F are the error matrices respectively. In its classical form, PLS method is based on the nonlinear iterative partial least squares (NIPALS) algorithm due to Wold (1975) which solves the following optimization problem to estimate weight vectors w and c:
subject to wT w = 1, cT c = 1. The cov(t, u) denotes the sample covariance between score vectors, t and u. The above optimization problem can be solved by the Singular Value Decomposition (SVD) of the matrix XT Y by using the square root transformation resulting in the equivalent formulation:
| (13) |
subject to wT w = cT c = 1. NIPALS algorithm, based on similar principles as the power method, is a robust procedure for solving singular valued decomposition problems. The NIPALS algorithm initializes a random estimate of u and iteratively updates u until converge according to the sequence:
t = Xw
u = Yc
After convergence, the loading vectors, p and q are extracted by regressing out t and u from X and Y respectively as per regression equations in (12) using least-squares estimates such that:
The above process for estimation of score and loading vectors is repeated on the rank-one deflation of matrices X and Y to compute the successive latent variables. There are several variants of PLS algorithm which primarily differ in the deflation step. For this study, we focus on the most widely used variant based on the assumption that PLS score vectors, are good predictors of response, Y. This added asymmetry of predictor and response is encoded in the deflation scheme such that the component of the regression of Y on t is removed from Y at each iteration of PLS:
| (14) |
The regression problem for PLS can also be written in the form that relates the input data matrices X and Y as:
where B is the regression coefficient and F is the error matrix. The matrix B is of the form:
As derived in Rosipal and Trejo (2002) using the relations between W, T, U and P from Manne (1987), Höskuldsson (1988) and Rännar et al. (1994), the expression for B takes the form:
| (15) |
Notice that in this resulting expression, B, a) depends upon the data inner product matrix XXT and b) is invariant of scalings of score vectors in matrices T and U.
3.3.1. Kernel Partial Least Squares Regression
The kernel version of PLS algorithm as in Rosipal and Trejo (2002) attempts to find the relationship between datablocks when the dependent variable, xi is an element of the Reproducing Kernel Hilbert space,
 equipped with the inner product. The goal is to formulate the PLS model in the Hilbert space,
equipped with the inner product. The goal is to formulate the PLS model in the Hilbert space,
 . We denote the matrix of inner products (Gram matrix) of the data points in
. We denote the matrix of inner products (Gram matrix) of the data points in
 as G. The NIPALS algorithm described above can be extended to use this inner product matrix, G of the data points. This can be seen by merging steps 1 to 3 to give the following algorithm:
as G. The NIPALS algorithm described above can be extended to use this inner product matrix, G of the data points. This can be seen by merging steps 1 to 3 to give the following algorithm:
t = Gu
c = YTt
u = Yc
Similar to the deflation Equation 14 for the Euclidean case, the deflation of Gram matrix, G can be written as:
Moreover, we can write the regression coefficient for the regression with kernel Gram matrix, B̃ as:
| (16) |
For prediction on the test data we need to get the Gram matrix for test data that comprises of the inner products of test data points with the training data points. Also, the estimate of B as in Equation (15) can be obtained by linear combination of input data points i.e., the B = XT B̃.
3.3.2. On the manifold of diffeomorphisms
We utilize this machinery provided by the kernel PLS methodology and extend this idea to regression on a manifold (Figure 1). We do this by incorporating the innerproduct structure of the manifold of diffeomorphisms into the PLS framework. Given the Fréchet mean atlas of the image ensemble, the initial velocities ( , i = 1, ···, n) and corresponding initial momenta ( , i = 1, ···, n) for all contributing images defined in the tangent space at the atlas obtained as a consequence of solving the LDDMM energy minimization problem, we can construct a kernel formulation of the PLS algorithm.
The Sobolev operator mentioned in Section 3 which also relates to deformation momenta (Section 3.1.1) as Lv = −α ∇ I, defines the kernel function for the mapping. Here, L is the self-adjoint differential operator of the form:
| (17) |
where the first two terms controls the smoothness of the registration while the last term ensures the invertibility of the operator. These operators are borrowed from the theory of fluid mechanics and were introduced in image registration by Christensen et al. (1996). Holden (2008) review the class of such operators for fluid image registration in detail. The compact self-adjoint smoothing operator, K is thus related to operator L as:
For a pair of geodesics emanating from the atlas towards each image, we can compute the inner product between initial velocities and in the tangent space at the atlas and relate it to the inner product between initial momenta as:
| (18) |
Now, if we were given only the initial deformation momenta, and and the common gradient image ∇ I, we represent this inner product between a pair of initial deformation momenta as:
| (19) |
where V* represents the space of deformation momenta.
As detailed in Section 3.3.1, for the kernel extension of the PLS formulation, the space,
 is the Hilbert space of momenta maps, V* equipped with the inner product defined by Equation (18). The initial momenta,
capture the shape variations from the atlas in the form of the geodesic direction it encodes.
is the Hilbert space of momenta maps, V* equipped with the inner product defined by Equation (18). The initial momenta,
capture the shape variations from the atlas in the form of the geodesic direction it encodes.
Now, we define the anatomical shape vs. clinical response regression on the manifold of diffeomorphism (in the space of momenta maps, V*). Specifically, the problem is to find a direction governing the geodesic flow that predicts the clinical response y. For single clinical measure represented by a univariate response variable, y, this can be modeled as per the regression set up:
| (20) |
for a given geodesic characterised by the initial momenta α0. Note that α0 ∈ V* is an initial momenta map image for the geodesic corresponding to the regressor shape data and y the univariate dependent response. βα ∈ V* is the regression coefficient that needs to be estimated under the PLS formulation. We use the subscript α with the regression coefficient to emphasize that it represents a deformation momenta map. To solve this, projection operations in the PLS formulation must all be carried out in the tangent space using the Sobolev inner product in the space of momenta as per Equation (19). We further define βα as a linear combination of input data points, , i = 1, ···, n and represent:
| (21) |
The regression problem in (20) becomes:
This implies that the regression is formulated using only inner product evaluations of the input data points. Further, the kernel PLS algorithm can be written entirely in terms of the kernel Gram matrix G of inner products between all data points in vector space V*. For solving this kernel PLS problem, we use the kernel algorithm presented in Section 3.3.1. Given the initial momenta maps for each individual, we can compute the Gram matrix, G of Sobolev innerproducts on the tangent space pairwise for all geodesics. The kernel PLS performed up to l latent vectors yields the estimate of β̃ which can then be transformed to βα, into the space of initial momenta using (21), and interpreted as a scalar momenta map image representing a geodesic direction for this regression.
We also note that this framework extends naturally for multivariate response using the kernel PLS when q > 1. This implies that we learn multiple clinical tasks simultaneously for prediction as per the kernel PLS formulation in Section 3.3.1. However, for multivariate response there in no direct interpretation of the regression coefficient, B on the manifold of diffeomorphisms without ignoring the correlations within the dependent outcome variable. The following section covers the details about interpretation of the PLS and the regression coefficient in the tangent space for univariate response.
3.4. Interpreting β: quantifying shape changes
To quantify the local anatomical deformations corresponding to the evolution of the atlas for changing clinical response, we interpret the regression coefficient as the direction governing the geodesic flow that best predicts the clinical response y.
In matrix notation, the inner product can be interpreted as:
where
and αi are vectorized into momenta ai for computations in matrix notation.
Note that
 is never computed since the kernel algorithms utilize the pre-computed Gram matrix, G of innerproducts.
is never computed since the kernel algorithms utilize the pre-computed Gram matrix, G of innerproducts.
The regression problem in (20) can be written for training and test data in matrix notation as:
where βa is the vectorized form of the regression coefficient βα (in image domain). Since, PLS gives the solution estimate β̃PLS to: ytest = Gtest β̃PLS +ε, or equivalently for the problem: , we have,
Here, the matrix Atrain is the matrix of all initial momenta for the training data (ai’s) augmented row-wise. The βa vector can further be converted back to the momenta map image, βα.
The regression coefficient, βα thus obtained lies in the space of momenta. βα can be interpreted as the initial momenta for the atlas image corresponding to a particular geodesic. Moreover, the direction represented by the initial velocity, vβ corresponding to initial momenta βα (obtained from the evolution EPDiff equation: Lv0 = −α ∇ I) is the direction for the geodesic flow, the magnitude of which can be interpreted as quantifying the units of the response variable with respect to units of deformation. Moving along the geodesic direction represented by βα, the response variable y can be directly related to the amount of deformation. We can shoot with βα to quantify change in response y per unit of deformation corresponding to the initial momenta for regression. Traveling along this geodesic, the atlas deforms along the direction of clinical progression and the distance traveled is related to the change in clinical response. Since the inner product (Equation (19)) is linear, this interpretation is analogous to the way we talk about regression coefficients as slope in classical linear regression.
4. Results
We performed a comprehensive analysis of the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database for the baselines. The results section details our extensive study on the structural Magnetic Resonance Image (MRI) and clinical data from ADNI. The next section (4.1) begins with a description of the ADNI data. Section 4.2 explains the pipeline of our methodology. Section 4.3 reports the detailed analysis of the results of our method including the stability of regression estimates using bootstrap. We further report results of our proposed method on prospective applications such as prediction of rate of cognitive decline and multi-modal image analysis for detection of individuals at high risk of developing AD in Sections 4.4 and 4.5.
4.1. DATA: MRI and Clinical Variables
All the baseline and screening T1 weighted, bias-field-corrected and N3 scaled structural Magnetic Resonance Images were downloaded from the ADNI. The brainmasks for skull stripping and Talairach transforms that had passed ADNI QA were also retrieved and matched against the images. The corresponding neuropsychological data was also downloaded from ADNI. We included only the subjects for which the clinical scores were recorded within 3 months of their MRI scans. The above filtering procedure from the ADNI database resulted in a total of 566 subjects. The population of subjects downloaded primarily consisted of three diagnostic groups: Healthy Individuals or Normals (NL, N=153), Mild Cognitive Impairment (MCI, N=265) and Alzheimer’s Disease (AD, N=132) and 16 subjects without any diagnosis information. In this paper we consider the AD, MCI and NL subjects as a continuous class rather than discrete classes.
We used thirteen global cognitive and functional assessment test scores for the analysis (Table 1). The first two were variants of the modified Alzheimer’s Disease Assessment Scale modified cognitive battery (adas-cog) a) One that includes delayed word recall and number cancellation (adastotalmod); and b) The other that does not include delayed word recall and number cancellation (adastotal11). The next two were the Mini Mental State Examination (mmse) and the Clinical Dementia Rating scale, Sum of Boxes (cdrsb). Episodic memory was assessed using the Rey Auditory Verbal Learning Test (AVLT) and the Logical Memory test of the Wechsler Memory Scale-Revised. Both memory tests had immediate recall (avlt.imm, logic.imm) and 30 minute delayed recall (avlt.del, logic.del). Boston Naming Test score (bnt) is also included. Note the AVLT used the immediate recall after the 5th learning trial. The tests for executive functions: Trail Making Test (trailsA & trailsB), constructional ability: Clock Drawing Test (clock), and working memory: Digits Span Forward Test (digit) were also considered. Preprocessing the MRI involved skull stripping and registration to Talairach coordinates using Freesurfer [Dale et al. (1999)] as a part of ADNI preprocessing pipeline. We performed the tissue-wise intensity normalization for white matter, gray matter, and cerebrospinal fluid using the expectation maximization (EM) based segmentation followed by the histogram matching for each region.
Table 1.
Response Variables: Total of 566 MRI imaging data
| n | μ | σ | range | |
|---|---|---|---|---|
| adastotal11 | 548 | 11.9276 | 6.6093 | 1.00 – 42.67 |
| adastotalmod | 544 | 18.7096 | 9.4361 | 1.67 – 54.67 |
| mmse | 565 | 26.6690 | 2.7564 | 18 – 30 |
| cdrsb | 566 | 1.8498 | 1.8754 | 0 – 9 |
| trailsA | 548 | 47.9854 | 26.9674 | 17 – 150 |
| trailsB | 539 | 135.1095 | 80.2142 | 0 – 300 |
| clock | 550 | 4.0745 | 1.1452 | 0 – 5 |
| logicimm | 566 | 8.1343 | 4.9335 | 0 – 22 |
| logicdel | 566 | 5.6961 | 5.4836 | 0 – 22 |
| avltimm | 549 | 32.1421 | 11.8276 | 0 – 69 |
| avltdel | 549 | 3.5883 | 3.9993 | 0 – 15 |
| digit | 546 | 37.1282 | 13.3481 | 0 – 80 |
| bnt | 544 | 25.2188 | 4.9519 | 1 – 30 |
4.2. Procedure
Figure 2 summarizes the key steps of our regression modeling framework. It starts from preprocessed MR brain images and follows three steps of processing. (A) The first step computes a stable and unbiased atlas and estimates the geodesics emanating from this estimated atlas towards each subject. This is analogous to shape feature-extraction such that the estimated initial deformation momenta are compact representations of anatomical shape variations corresponding to each subject.
(B) We compute the Gram matrix of pairwise inner products and solve the regression model for shape–clinical response regression using kernel PLS or kernel RVR to give the estimate of the regression coefficient that encodes a geodesic direction. (C) Finally, we deform the atlas image and segmented ROIs from the atlas along this estimated geodesic via geodesic shooting to quantify the amount of shape deformations.
PLS and RVR both work on the kernel Gram matrices of size N × N, where N is the number of subjects in the study. Thus, the running time of the entire procedure is dominated by the deformation momenta estimation step, Block A, that works on all p voxels of the image. Each gradient descent iteration for momenta computations involves forward integration of shooting equations (5)–(7) followed by backward integration of adjoint equations in (9)–(11). These set of equations involve gradient and divergence computation operations that are linear in p. The integration is domination by convolution with the kernel, K, which is done in Fourier domain. Thus, the order of complexity for one gradient descent step for an individual deformation is O(kp log p), where k is the number of intervals of discretized time for the integration.
Registration parameters
The registration parameters were fixed a priori in the beginning of the analysis. The smoothness and invertibility of deformation fields are controlled by the parameters of the fluid operator L as mentioned in Equation (17). In our experiments, these parameters are fixed to the standard values of α = 0.01, β = 0.01, and γ = 0.001. These fluid parameters have been used in previous studies in Davis et al. (2007); Singh et al. (2010, 2012) and are known to ensure sufficient smoothness of deformations fields for registration of MRI brain images. The parameter σ that controls the trade-off between the exactness of the match and smoothness regularity term in Equation (3) was also set a priori to the least possible value that ensured successful registration and also resulted in smooth and invertible deformation fields. The σ = 1 was selected for the image intensity range between [0, 1]. Ten timesteps were used during integration of EPDIFF for forward and backward adjoints.
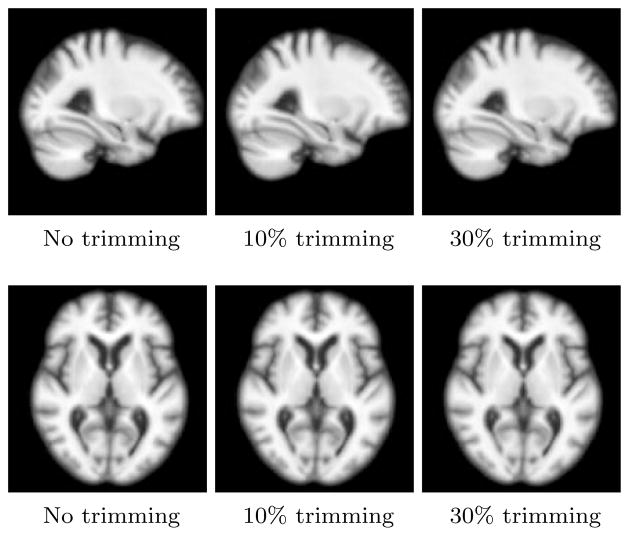
Using the framework discussed in Section 3.1.2, we generated the atlas with the 566 subjects on the GPU cluster. To assess the stability of atlas construction, we generated atlases using truncated mean with different percentage of outliers removed each time. Figure 3 shows the atlas obtained for first two trimming levels. The generated atlases were stable and did not change up to 30% of truncation. Thus, as a conservative estimate and with the assumption that there are no more than 10% outliers in the preprocessed imaging data, we selected the atlas with 10% trimming level. The difference in average image residuals with 10% trimming and without trimming was less than 3%. We did the accurate estimation of geodesics by computing initial momenta via registering the atlas to each individual subjects MRI by the iterative gradient descent using shooting optimization and backward integration scheme as detailed in Section 3.1.1. We evaluated the underlying smooth deformations, ϕi corresponding to estimated momenta for stability and invertibility. We deformed the atlas forward using the estimated deformation field (ϕ) and the subject’s MRI backward using inverse of this deformation field (ϕ−1). The underlying Jacobian images for the deformation and the difference images for matching of the deformed images with the the corresponding target endpoints were confirmed visually for all the subjects.
Figure 3.
Stability of atlas using trimmed mean.
Using the inner product (Equation (19)), we performed the kernel-PLS on initial deformation momenta with the smoothing kernel against the clinical response variables (Section 3.3.2). We assessed the stability of the model by evaluating the accuracy of prediction on the regression model using the leave-one- out cross-validation (LOOCV) scheme. The atlas, deformation momenta and regression model were recomputed each time using only the training data and the resulting regression model was tested on the left-out individual. Further, the stability of resulting regression coefficients were evaluated using bootstrap experiments. Finally, we quantified the deformations by shooting the atlas using an appropriately scaled regression coefficient (Section 3.4). The amount of deformation was visualized by overlaying the log of Jacobians of deformations over the atlas achieved at the end point of the geodesic. To further evaluate the stability of modeling we also did the regression of initial momenta with clinical variables using RVR. For details about RVR, see Appendix B.
We controlled for confounding demographic variables using the regression procedure described in Appendix A. Table 2 details the demographic information such as age, gender, handedness, and years of education for the population under consideration. The effect of age for instance can be seen by visualizing the regression coefficient obtained from the regression of shape with age. In this case, we performed the linear regression of initial momenta and visualized the regression coefficient by shooting the atlas along the geodesic encoded by the coefficient (Figure 15 in Suppl.). Figure 16 (in Suppl.) shows the regression of individual clinical variables with demographic variables. In general, the ADAS, MMSE score and TrailsA score reported some correlation with years of education with p-values 0.001, 0.000 and 0.004 (The significance test for correlation (null hypothesis, r = 0) while no such trend was observed with age. Table 3 details the residuals in the clinical response obtained after regressing out age, gender and education.
Table 2.
Demographic Info
| diagnosis | 153 Normals, 265 MCI, 132 AD, 16 no diagnosis |
| education | μ = 15.43 and σ = 3.14 |
| age | μ = 75.45 and σ = 7.01 |
| gender | 268 Females and 302 Males |
| handedness | 530 Right and 36 Left |
Table 3.
Residuals in clinical response after regressing out demographic variables
| n | σ | range | |
|---|---|---|---|
| adastotal11 | 548 | 6.5218 | −10.3468 to 30.0943 |
| adastotalmod | 544 | 9.3098 | −17.5333 to 35.1846 |
| mmse | 565 | 2.6859 | −8.5865 to 5.0305 |
| cdrsb | 566 | 1.8554 | −2.6515 to 7.4980 |
| trailsA | 548 | 26.7489 | −32.5173 to 106.2147 |
| trailsB | 539 | 77.8597 | −149.5055 to 194.6877 |
| clock | 550 | 1.1225 | −4.0949 to 1.6570 |
| logicimm | 566 | 4.7171 | −9.5218 to 13.2546 |
| logicdel | 566 | 5.2864 | −8.8638 to 15.2274 |
| avltimm | 549 | 11.3933 | −31.2308 to 37.6304 |
| avltdel | 549 | 3.9245 | −5.0557 to 11.8789 |
| digit | 546 | 12.8555 | −41.2448 to 42.7871 |
| bnt | 544 | 4.7129 | −24.2047 to 9.1309 |
To control for confounders, we repeated the PLS and cross-validation analysis with the residuals in momenta and residuals in clinical scores; the residuals were from their respective regressions with confounding variables. We ensured the training and test data separation right at the first step, i.e., the residuals were computed under complete isolation in the cross-validation (refer Appendix A).
4.3. Analysis
The goal of our regression analysis is to relate anatomical shape changes and neurological response and to quantify the shape changes that are most predictive of clinical decline. Table 4 reports the correlation of predicted vs. actual value, rtest, for test data in leave-one-out cross-validation for two independent regression schemes (PLS and RVR). The table also reports comparisons of the analysis done with and without the control for demographics. In terms of execution time PLS outperformed RVR for the same input—up to three orders of magnitude for all the clinical variables. For detailed analysis, we have focussed on the results obtained for regression with adas, mmse and trailsA. This is because the predicted adas reported best correlation with actual adas for regression with anatomical shape. The mmse score was selected since it reported the best improvement in prediction when compared to that reported in previous studies. Similarly, the trailsA test was selected since it reported the best numbers within all the regression results of shape with clinical scores for test of executive function.
Table 4.
Leave one out cross-validation – correlation of predicted vs actual for test data
| Without control | Control for demographics | |||
|---|---|---|---|---|
| Kernel PLS (rtest) | Kernel RVR (rtest) | Kernel PLS (rtest) | Kernel RVR (rtest) | |
| adastotal11 | 0.53 | 0.52 | 0.56 | 0.55 |
| adastotalmod | 0.57 | 0.56 | 0.60 | 0.59 |
| mmse | 0.52 | 0.49 | 0.53 | 0.49 |
| cdrsb | 0.54 | 0.50 | 0.59 | 0.53 |
| trailsA | 0.35 | 0.34 | 0.40 | 0.37 |
| trailsB | 0.34 | 0.32 | 0.39 | 0.36 |
| clock | 0.30 | 0.29 | 0.32 | 0.29 |
| logicimm | 0.46 | 0.44 | 0.53 | 0.50 |
| logicdel | 0.45 | 0.43 | 0.50 | 0.48 |
| avltimm | 0.47 | 0.44 | 0.45 | 0.43 |
| avltdel | 0.37 | 0.34 | 0.38 | 0.34 |
| digit | 0.36 | 0.33 | 0.38 | 0.34 |
| bnt | 0.42 | 0.39 | 0.41 | 0.35 |
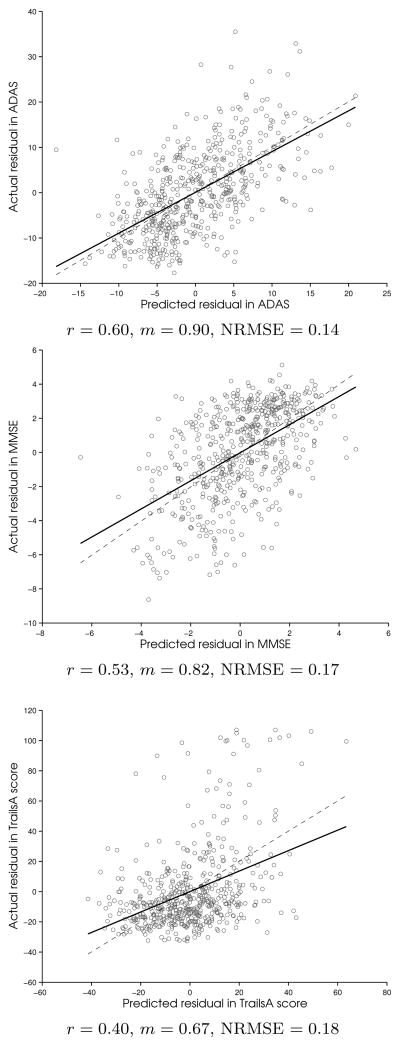
The LOOCV predicted scores vs actual scores correlation plots for adas, mmse, and trailsA regression are shown in Figure 4 for PLS with residuals. Together with rtest, we also report the slope of correlation fit between actual clinical score and predicted score, m, and the normalized root mean squared error of cross-validation (NRMSE). Here,
Figure 4.
PLS with residuals: Regression of LOOCV predicted residuals vs actual residuals (solid line) for the left-out test data. The correlation, r and slope, m are reported. The dashed line corresponding to slope 1 is shown for comparison. Normalized Mean Squared Error (NRMSE) for PLS cross-validation is also reported. The significance test for correlation (null hypothesis, r = 0) resulted in p-values < 10−15 for all.
4.3.1. Cross-validation accuracies and regression geodesics
We noticed in general that predictive power in terms of cross-validation correlation values between actual and predicted response variables (rtest) improved after adding the control of confounding demographic variables in the regression. Moreover, the cross-validation performance results for PLS and RVR were comparable. The most stable regression results were obtained for regression with adas (adastotalmod: rtest = 0.60 for PLS, rtest = 0.59 for RVR after control for confounders).
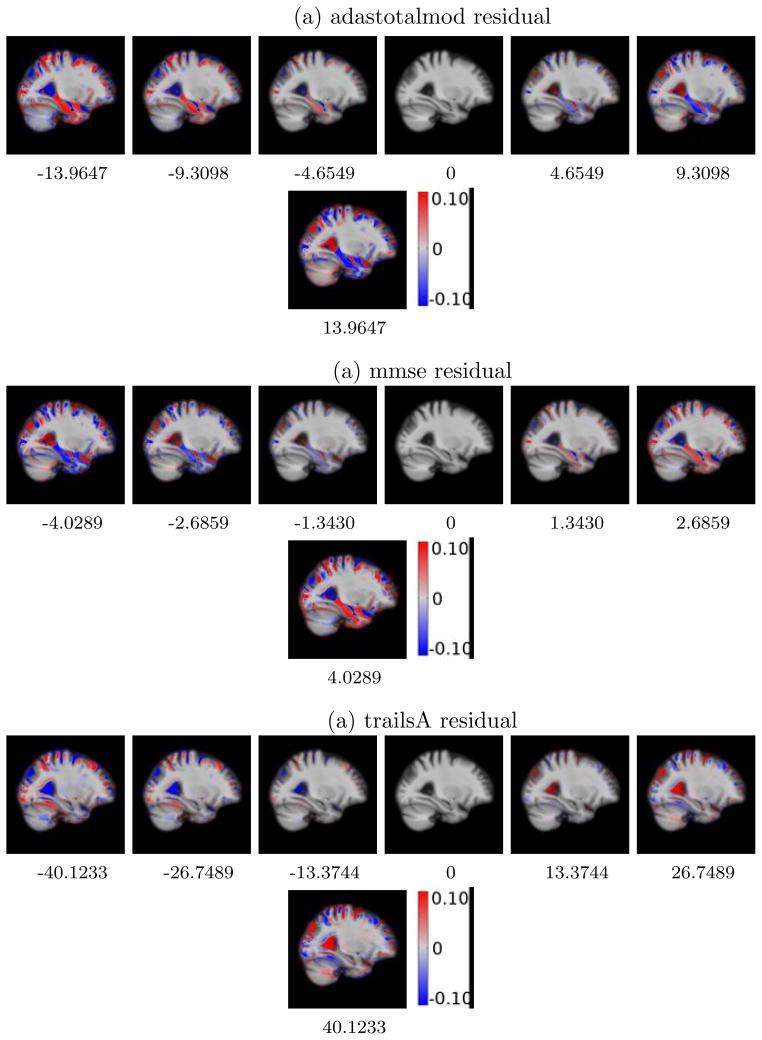
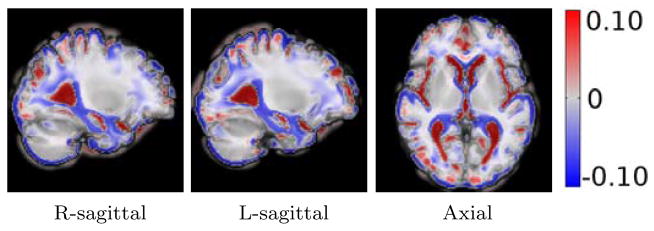
For visualizing the direction and the amount of local anatomical deformations, we present the Jacobians of the deformation of the atlas image at different points along the regression geodesic for regression with residuals in Figure 5. Visualizations for these deformations without controlling for demographics are detailed in Figure 17 in Suppl. Selected slices from this 3D overlay capture relevant regions of the neuro-anatomical structures, such as hippocampus, amygdala and ventricles, pertinent to cognitive impairment in Alzheimer’s and related dementia. Figure 5 shows the local shape deformation patterns that overlay the atlas image for the kernel PLS regression geodesic shooting results for adas, mmse and trailsA. We notice the expansion of the lateral ventricles and CSF with increasing adas residual scores. The most critical observation is the clearly evident shrinkage of the hippocampus and amygdala along this geodesic direction. Such patterns of atrophy are known to characterize the disease progression in AD and related dementia.
Figure 5.
PLS WITH RESIDUALS: Deformation of atlas with changing clinical residual score. The middle column represents the atlas with zero average clinical residual. Red denotes the regions of local expansion and blue denotes the regions of local contraction.
The RVR analysis also resulted in very similar shape deformation patterns as were obtained with PLS. For comparison, Figure 6 shows the deformation patterns for the regression geodesic obtained for RVR analysis with adas. This suggests that our proposed methodology of regression on the shape manifold of diffeomorphisms is generic and generate reliable shape deformation patterns under different choices of regression schemes.
Figure 6.
RVR WITH RESIDUALS: Deformation of atlas with changing adastotalmod residual score.
The other global measures of dementia such as mmse and cdrsb also reported good numbers. The mmse score regression particularly showed improvement in prediction accuracy over results reported by some of the previous work (refer Section 5). For mmse score, we found the rtest = 0.52 for PLS and rtest = 0.49 for RVR. The analysis with the mmse residuals reported rtest = 0.53 for PLS and rtest = 0.49 for RVR. We again noticed the corresponding shape changes obtained in traversing along mmse regression geodesic (Figure 17) for mmse showed patterns dominating in hippocampus, amygdala and CSF shape changes - the expansion CSF regions and the shrinking hippocampus and amygdala with decreasing mmse from the mean mmse of 26.58. The pattern maps looked very similar when this analysis was done with residuals in mmse (Figure 5 for mmse). Overall, in terms of predictive accuracy and shape deformation patterns extracted, our method fared well for regression with global measures of cognition and memory scores.
For regression with tests for executive function, the cross-validation correlation results were not very promising. Other than the tests for global measures of dementia and memory functions, our best results were for regression with the trailsA executive function score: correlation values for cross-validation, rtest = 0.35 for PLS, rtest = 0.34 for RVR, rtest = 0.40 for PLS with residuals and rtest = 0.37 for RVR with residuals. However, we found interesting shape-changes trends for regression with trailsA. We noticed that no shape variations in hippocampus or amygdala were reported when the atlas was deformed along the geodesic direction for the trailsA score (Figure 5). While the hippocampus and amygdala emerge as mainly responsible for regression with global measures of dementia and changes in memory function, they does not seem be a determinant factor for the executive function.
4.3.2. Region-of-interest based validations
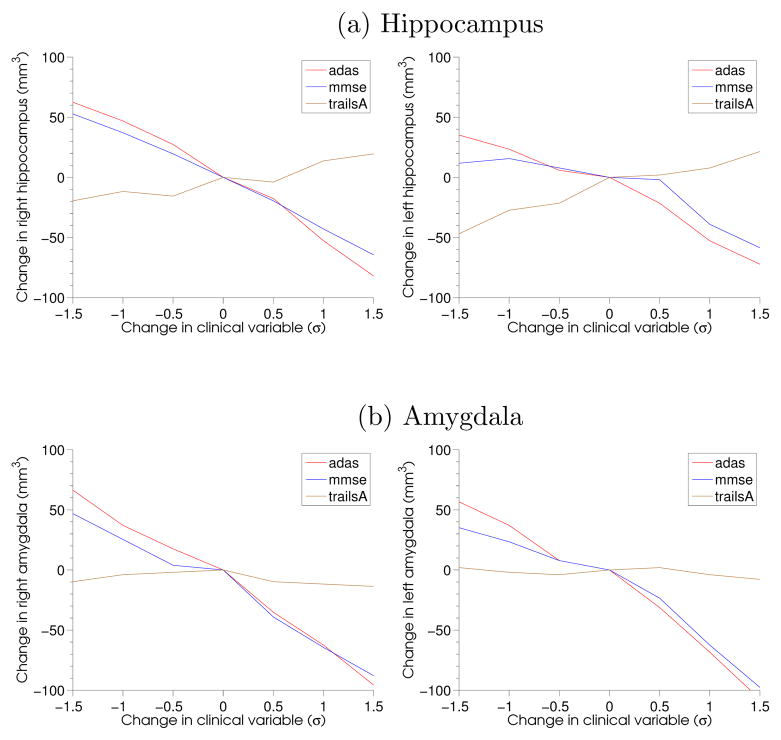
To verify this observation further, we evolved the left and the right hippocampus and amygdala along the estimated regression geodesic encoded by deformation momenta. For this purpose, the atlas image, Ī was segmented for the hippocampus and the amygdala. The smooth segmented regions were then deformed along the geodesics represented by the regression coefficients for each clinical variable. Since v = K ★ (α∇I), such an evolution of segmentations effectively is governed by only the momenta at the boundaries of hippocampus and amygdala in the atlas, Ī. Table 7 details the difference in the volume of these tissues obtained after traversing along the geodesic in the direction, one standard deviation away along the corresponding clinical variable and one standard deviation opposite to it. With clinical scores for global measures of Alzheimer’s dementia i.e., adas and mmse, we noticed clear trends in tissue atrophy while not much was seen for executive function score trailsA. Figure 7 also shows this comparison in hippocampus and amygdala atrophy for adas, mmse and trailsA score. The volume change is reported at multiple timepoints away from the atlas on the estimated geodesic, both in the direction of dementia and opposite to it. This also suggests the clear atrophy in right and left hippocampi and amygdalae with increasing adas and decreasing mmse as compared to that with trailsA. The changing shape of these substructures for along changing adas score is also visualized in Figure 18 in Suppl.
Table 7.
Volume changes (mm3) in hippocampus and amygdala along extracted regression coefficient from −σ to +σ of change in clinical response.
| Left Amygdala | Right Amygdala | Left Hippocampus | Right Hippocampus | |
|---|---|---|---|---|
| adastotalmod | −105.47 | −99.609 | −76.172 | −99.609 |
| mmse | 85.938 | 89.844 | 54.688 | 80.078 |
| trailsA | −1.9531 | −7.8125 | 35.156 | 25.391 |
Figure 7.
Change in volume compared to change in clinical residual in terms of standard deviations (σ). To capture the tissue atrophy towards neurodegeneration, the X-axis for mmse score is reversed for comparison.
4.3.3. Stability of regression coefficient
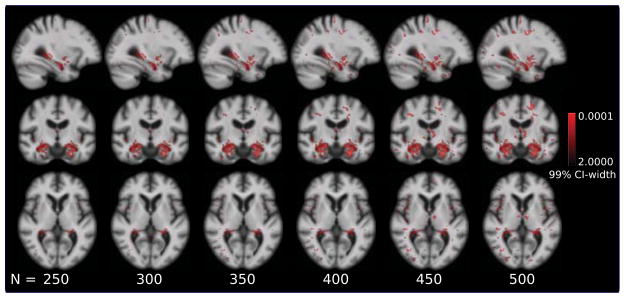
An important consideration for regression analysis under the HDLSS regime is the effect of size of the population on the estimates of regression coefficient. To assess the robustness of the proposed method when population size is varied, bootstrap experiments were performed by sampling with replacement, the momenta and clinical response pair. The regression coefficient was estimated for each the bootstrap replicate. The 99% confidence bounds were computed based on the percentile of the empirical distribution of 1000 bootstrap replicates[Efron and Tibshirani (1993)]. Brain regions were extracted where regression coefficient is different from zero with 99% confidence i.e., the regions where zero does not lie within the 99% confidence interval. These maps represent anatomical regions that have high weights in regression coefficient with low standard error. It was observed that high regression weights were concentrated on boundaries of relevant regions even when the sample size was varied with N = 250, 300, 350, 400, 450, 500. For instance, Figure 9 details the width of the confidence interval in these regions of high weight and high confidence of the regression coefficients for regression with ADAS score (adastotalmod). It clearly exhibits the consistent patterns around the boundaries of hippocampus and amygdala for different population size. More regions emerge when sample size is increased along with consistent appearance of hippocampus and amygdala. Bootstrap confidence results for stability of regression with mmse and trailsA are detailed in Figures 19 and 20 in Suppl.
Figure 9.
Bootstrap stability of regression coefficient as a function of sample size for PLS regression with ADAS. Red denotes regions where regression coefficient is different from zero with 99% confidence. Regions with high confidence increase with sample size. Regression coefficient is consistent around hippocampus and amygdala regions with changing sample size.
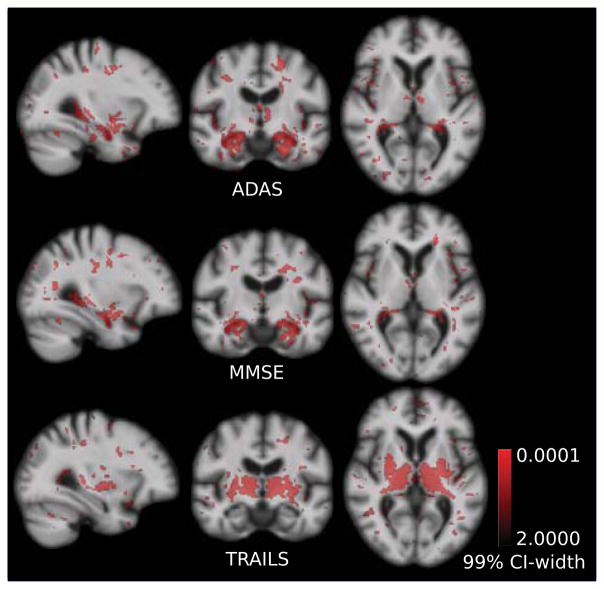
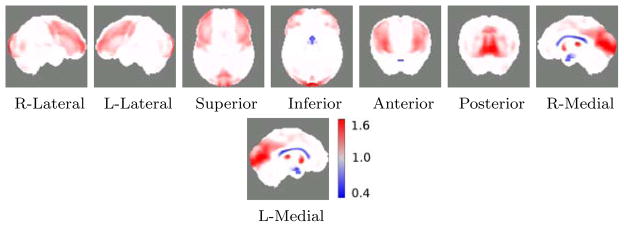
Figure 8 compares extracted regions with high regression weights and high confidence for PLS regression with adas, mmse and trailsA score. Hippocampus and amygdala are the most important regions among all the voxels in the brain for regression with adas and memory scores. However, neither the hippocampus, nor the amygdala regions are high weights regressors for the executive function score, trailsA. A critical finding was the appearance of thalamus and putamen as most important regions that relate to executive function. Atrophy in putamen and thalamus is known to be related to cognitive performance in neurodegenerative disorders such as the Alzheimer’s disease and the Huntington’s disease [de Jong et al. (2008); Braak and Braak (1991); Kassubek et al. (2005)]. These resulting anatomical regions were consistent with very high confidence irrespective of the size of the population used in the study (Figure 8 and Figure 20 in Suppl.).
Figure 8.
Bootstrap width of the 99% confidence interval (CI-width) for PLS. With 99% confidence, regions in red have regression coefficient different from zero. Coefficients are concentrated around hippocampus and amygdala that relate to test scores for memory: MMSE and ADAS. However, putamen and thalamus are more important for regression with executive function score, Trails.
Further, we extend the regression methodology with control for demographic confounders to learn all thirteen clinical variables simultaneously using multivariate kernel PLS as explained in Section 3.3.1. Table 5 details the cross-validation results. The results are similar to separate learning of clinical variables. We do not get any improvement in predictive power while predicting multiple variables together.
Table 5.
Leave one out cross-validation for multivariate kernel PLS with control for confounders
| Kernel PLS (rtest) | |
|---|---|
| adastotal11 | 0.56 |
| adastotalmod | 0.60 |
| mmse | 0.53 |
| cdrsb | 0.58 |
| trailsA | 0.32 |
| trailsB | 0.41 |
| clock | 0.32 |
| logicimm | 0.53 |
| logicdel | 0.52 |
| avltimm | 0.48 |
| avltdel | 0.40 |
| digit | 0.38 |
| bnt | 0.41 |
4.4. Extension to predicting rate of cognitive decline
The early detection of Alzheimer’s disease is of high clinical relevance. Timely detection of memory loss or cognitive impairment is important to assess the risk of AD and other dementia in elderly population. It is therefore important to not only relate the anatomical shape with current neuropsychological function at baseline but also to answer questions about the future trends of cognitive function decline. The anatomical shape regression framework presented in this work can be extended to relate the rate of change of clinical response using only the information available from baseline scans. For this purpose we extract the information that describes the linear trend in terms of the slope of the regression with cognitive decline for clinical measures obtained from measurements done on a subject for subsequent visits. The slope of the linear regression for clinical scores regression along time for each subject can be related to shape anatomical variation across the population of subjects. The “anatomical shape vs. rate of clinical decline” model thus learned on training data is used to predict the rate of the cognitive decline of the new subject using only the baseline MRI scan. The ADNI data consists of follow-up clinical measurements at an interval of 6 months from baseline for up to 48 months. For this part of the study, we selected all the subjects that had at least three or more clinical follow-ups recorded so as to get an estimate of the trend in linear least squares sense. The slope thus obtained was regressed against the corresponding deformation momenta using the kernel PLS (Section 3.3.1) with the control of demographic confounders (Section Appendix A). Table 6 reports the correlation of predicted vs actual rates of clinical change residuals for leave-one-out cross-validation. In general, the baseline anatomical shape did not offer much predictive power for prediction of the rate of clinical decline. Relatively, we obtained the best correlation of predicted and actual rates of decline, rtest = 0.41 for regression with global measures of dementia i.e., adas, mmse and cdrsb.
Table 6.
Leave one out cross-validation for predicting rate of cognitive decline
| Kernel PLS (rtest) | |
|---|---|
| adastotal11 | 0.39 |
| adastotalmod | 0.40 |
| mmse | 0.41 |
| cdrsb | 0.41 |
| trailsA | 0.18 |
| trailsB | 0.16 |
| clock | 0.20 |
| logicimm | 0.23 |
| logicdel | 0.18 |
| avltimm | 0.26 |
| avltdel | 0.03 |
| digit | 0.18 |
| bnt | 0.21 |
4.5. Extension to combining multiple imaging modalities and genetic risk factors for prediction of MCI conversion to AD
We further extend this analysis to combine high-dimensional imaging modalities with several other low-dimensional disease risk factors. The motivation is to discover new imaging biomarkers and use them in conjunction with other known biomarkers for prognosis of individuals at high risk of developing AD. This framework also has the ability to assess the relative importance of imaging modalities for predicting AD conversion. Mild cognitive impairment (MCI) is an intermediate stage between healthy aging and dementia. Patients diagnosed with MCI are at high risk of developing Alzheimer’s disease (AD), but not everyone with MCI will convert. Accurate prognosis for MCI patients is an important prerequisite for providing the optimal treatment and management of the disease. Decreased synaptic response and brain function can be measured using functional imaging modalities, such as [18F]-fluorodeoxyglucose Positron Emission Tomography (FDG-PET). Additional potential risk biomarkers include blood and cerebrospinal fluid (CSF) markers, including genetic susceptibility assessed by apolipoprotein E (APOE) genotype and plaque deposition assessed by concentration of Aβ-42 and ptau181. The challenge for predicting conversion is to combine these heterogeneous data sources, some of which are high-dimensional (MRI and PET) and some low-dimensional (clinical, CSF, APOE carrier), by selecting features that optimally weight the relative contribution from each modality.
This data-driven formulation finds the optimal combination of these high-dimensional modalities that best characterize the disease progression. The goal to assess the combined predictive capability of this model for early detection of conversion of MCI to AD by using only the information available at baseline.
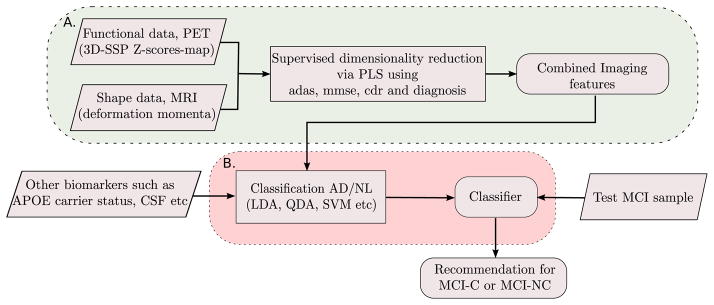
Since the anatomical shape and neuronal metabolic activity are two separate measures obtained from independent imaging modalities, we combine the two to form a product space of the joint imaging modalities. To make pattern analysis robust, we propose a supervised dimensionality reduction to represent this high-dimensional data in terms of a few features, specifically selected to best explain factors relevant to dementia. Further, the extracted imaging features are used in conjunction with APOE genotype and/or CSF biomarkers for assessing the risk of conversion of an MCI individual to AD. Figure 10 summarizes our feature selection and classification framework.
Figure 10.
MCI-C/MCI-NC prediction framework. Block A: Feature extraction process from high-dimensional imaging data. Block B: Classification.
4.5.1. Combining structure & function
The shape space represented by the space of deformation momenta,
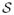 , and the space of neuronal metabolic activity represented by 3D-SSP,
, and the space of neuronal metabolic activity represented by 3D-SSP,
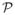 , are both high-dimensional spaces. We define the combined space of imaging modalities,
, are both high-dimensional spaces. We define the combined space of imaging modalities,
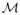 such that: M =
such that: M =
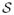 ×
×
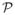 . Inner product between a pair mi = (αi, pi) ∈
. Inner product between a pair mi = (αi, pi) ∈
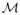 and mj = (αj, pj) ∈
and mj = (αj, pj) ∈
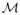 is defined via a their convex combination as:
is defined via a their convex combination as:
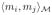 = η
= η
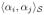 + (1 − η)
+ (1 − η)
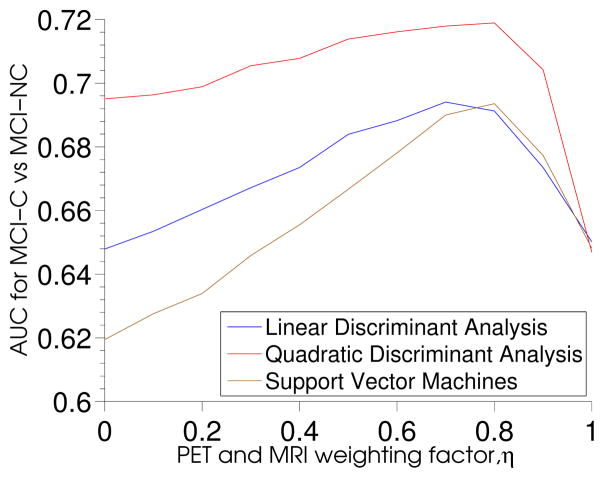
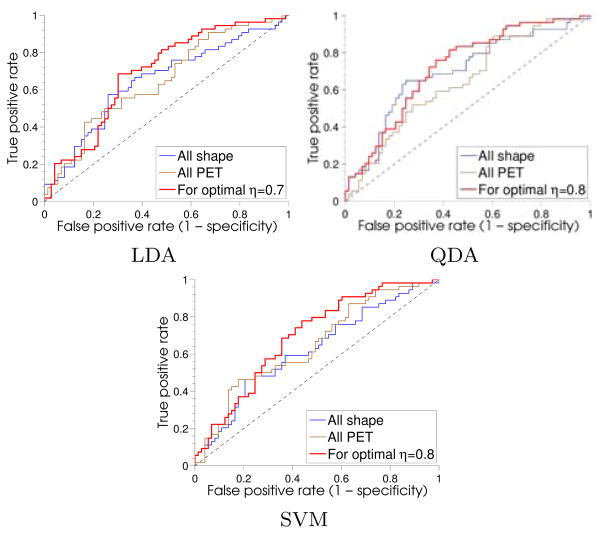
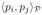 . The factor, η is interpretable as a relative weight when both the modalaties are normalized to have unit variance.
. The factor, η is interpretable as a relative weight when both the modalaties are normalized to have unit variance.
4.5.2. Supervised Dimensionality Reduction via Partial Least Squares
The structural and functional information extracted from two imaging modalities results in a feature space with much higher dimension than the population size. We adapt the PLS methodology for the purpose of extracting relevant features from the combination of shape and 3D-SSP data supervised by the clinical scores such as MMSE, ADAS, CDR and clinical cognitive status that are treated as global measures of dementia. The idea is to ensure that during dimensionality reduction we retain those dimensions in imaging data that not only explain variability within imaging data but also retain the variability that is relevant to dementia. We find directions m̂ in the combined product space of imaging modalities,
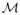 , and directions ŷ in the clinical response space,
, and directions ŷ in the clinical response space,
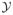 , that explain their association in the sense of their common variance. The projections of shape and pet data along the directions, m̂i are treated as the features for the classifier. For the symmetric PLS, the maximum number of possible latent vectors are limited by the inherent dimensionality of the two spaces, i.e., by min(dim(
, that explain their association in the sense of their common variance. The projections of shape and pet data along the directions, m̂i are treated as the features for the classifier. For the symmetric PLS, the maximum number of possible latent vectors are limited by the inherent dimensionality of the two spaces, i.e., by min(dim(
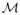 ), dim(
), dim(
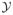 )).
)).
The projection scores, thus obtained by PLS, have combined information of anatomical shape and glucose metabolic activity that is used as features together with low-dimensional modalities such as genetic biomarkers of APOE carrier status and/or CSF biomarker available from spinal tap tests.
4.5.3. APOE carrier status—genetic biomarker
A confirmed risk factor for Alzheimer’s disease is the status of apolipoprotein E (APOE) gene in an individual. APOE exhibit polymorphisms with three major isomorphisms or alleles: APOE ε2, APOE ε3 and APOE ε4. Majority of the population with late-onset of AD is found to be dominant in APOE ε4 allele. APOE carrier status is computed based on the allele copy inherited from parents in an individual. We consider the binary status for APOE genetic risk based on whether the individual has at least one copy of allele ε4 and treat those subjects as APOE-carrier.
4.5.4. Prediction of conversion to AD
Distinguishing the probable convertors from the population of MCI is a binary classification problem. While there are several ways to look at this problem, we present here a formulation of the classifier supervised by the AD group and healthy control group (NL). In other words, the classifier is trained on the AD and NL but is used as a “recommender” for the test MCI subject. Based on the classification score obtained on the MCI subject, the prediction of the classifier is interpreted. We denote the test MCI subject as “AD-like” when the classifier recommends AD and treated as predicted MCI-C otherwise termed as “Stable-MCI” or predicted MCI-NC. The classifier accuracy is assessed by comparing the predicted MCI-C or MCI-NC status with the conversion status from the follow-up study for that test MCI subject. The proposed methodology is evaluated using the LDA, its quadratic variant–Quadratic Discriminant Analysis (QDA), and SVM as binary classifiers.
Figure 11 shows area under the receiver operating characteristic curve (AUC) as a function of the weighting factor, η, for the three separate classifiers discriminating MCI-C vs MCI-NC. The accuracy of prediction of MCI to AD conversion and the associated η is given in Table 9. The reported numbers correspond to optimal η, based on AUC. QDA performed the best with accuracy of 66% and AUC of 0.72 at η = 0.8. Also, the optimal combination of PET and shape performed much better as compared to only using PET or anatomical shape information irrespective of the choice of classifier used (Figure 12). The analysis was repeated using only the left and right hippocampus volumes for predicting MCI conversion. The AUCs and accuracies for prediction using hippocampus volumes obtained for three classifiers were: accuracy=60.7%, AUC=63.8% for LDA, accuracy=61.6%, AUC=63.8% for QDA and accuracy=58.9%, AUC=63.4% for SVM. Overall, our proposed method resulted in improved prediction when compared to using only the hippocampus volumes for predicting MCI conversion.
Figure 11.
Shape and PET weighting factor, η for different classifiers based on AUC.
Table 9.
MCI-C vs. MCI-NC classification results for ηOPT.
| AUC | Acc (%) | Sen(%) | Spec(%) | η | |
|---|---|---|---|---|---|
| QDA | 0.72 | 66.14 | 64.81 | 67.12 | 0.8 |
| LDA | 0.69 | 63.78 | 74.07 | 56.16 | 0.7 |
| SVM | 0.69 | 64.57 | 72.20 | 58.90 | 0.8 |
Figure 12.
Receiver operating characteristic curves (ROC) for MCI-C/MCI-NC classification with only shape information, only PET information and optimal combination of shape and PET as per ηOPT.
Besides APOE carrier status, the above analysis was also done after adding log transformed CSF-biomarkers: Aβ-42 and ptau181 concentration, which reduced the study sample-size to only: 29 NL, 36 AD and 59 MCI. With CSF-biomarkers, a slight increase in accuracy was observed for QDA: accuracy=68% and AUC= 0.72 (η = 0.8).
The log Jacobians of the deformation, overlaid on atlas image Ī, resulting from evolving Ī along the geodesic represented by the classifier weights are shown in Figure 13. The selected slices from this 3D overlay shown here capture relevant regions of the neuro-anatomical structures, such as hippocampus, pertinent to cognitive impairment in Alzheimer’s and related dementia. Similarly, the PET classifier weights are translated back in the Z-score space of 3D-SSP (Figure 14).
Figure 13.
Shape: Discriminating regions obtained from classifier weights for prediction of MCI conversion to AD. Log of Jacobians overlaid on atlas. Red denotes regions of local expansion and blue denotes regions of local contraction.
Figure 14.
FDG-PET: Discriminating regions obtained from classifier weights for prediction of MCI conversion to AD in 3D-SSP Z-score space.
The spatial patterns of anatomical shape changes were primarily the expansion of lateral ventricles and CSF, together with the shrinkage of the cortical surface. Another critical observation was the clearly evident shrinkage of the hippocampus and cortical and sub-cortical gray matter along the discriminating directions. Such patterns of atrophy are well known to characterize the disease progression in AD and related dementia. We observed that the shape component dominated the model with up to 80% contribution compared to only 20% contribution from the PET component, irrespective of the classifier used.
5. Discussion and conclusion
This paper presents a novel approach to study the nonlinear changes in geometry of local anatomical regions in the brain and accounts for the shape variations that relate to clinical response for neuropsychological functions. More generally, the proposed methodology enables us to investigate high-dimensional, nonlinear trends in shape variations in an ensemble of complicated shapes that can be treated as regressors for the prediction of Euclidean response variables.
We utilize computational differential geometry to model shape variations on the manifold of diffeomorphisms and statistical machine learning techniques to model prediction-based shape regression on this manifold-valued shape data. We harness the properties of the Hilbert space of momenta, V* equipped with the inner product to compare geodesic trends. Kernel Partial Least Squares (kernel PLS) enables us to study the high dimensional covariance of the anatomical structures in the entire brain volume, without any segmentation or a priori regions of interest identification, directly on the tangent space at the atlas. Furthermore, this regression scheme under the LDDMM framework enables us to visualize and quantify the amount of localized shape atrophy observed and relate it to attenuation in neuropsychological response.
Comparison to previous work
We compare the predictive accuracy results with some of the previous closest works (refer Section 2) that have formulated predictive models for clinical response using shape information extracted from the structural MRI. Using Relevance Vector Regression (RVR), Stonnington et al. (2010) has reported the best numbers for LOOCV predictive accuracy to be around rtest = 0.57 for ADAS-cog and rtest = 0.48 for mmse, using the ADNI baseline MRI scans and baseline clinical evaluation scores. The LOOCV accuracy of prediction attained by our kernel PLS modeling on manifold gives rtest = 0.60 for ADAS-cog. For mmse, we found further improved accuracy with rtest = 0.53. In another related work, Wang et al. (2010) has employed a regional based clustering approach on tissue density maps (TDM) for feature selections, followed by RVR-based machine learning bagging predictive models on subsampled ADNI data to give a much more successful model using the baseline MRI scans (rtest = 0.75), with average mmse over timepoints taken at an interval of 6-months. It is important to note that the study in Wang et al. (2010) is done on the very different and sampled subset of the ADNI data. Moreover, the response variable that this RVR regression model predicts is different from our work and that of Stonnington et al. (2010). Their approach also differs fundamentally from ours at the bagging framework setup, where they build ensemble regressors derived from multiple bootstrap training samples. Thus, we stress that the numbers presented in Wang et al. (2010) are not directly comparable to that reported in our work. In contrast, the regression modeling and the independent and dependent data as presented in the work of Stonnington et al. (2010), are much closer in principle to our work and hence we can draw a direct comparison to their approach. Furthermore, both Stonnington et al. (2010) and Wang et al. (2010) use segmentation of individual tissue types—gray matter (GM), white matter (WM), cerebro spinal fluid (CSF) or Tissue Density Maps (TDM) and do subsequent feature extraction. However, in our study we consider raw MRI as a whole without any segmentation. This enables us to talk about anatomical shape changes more naturally since the results and its interpretability can be directly translated back to original structural MRI space.
Stability of modeling and generalizability properties: RVR vs. PLS
To answer the question about stability of our modeling in general and choice of regression schemes in particular, we have also reported results with the RVR style of formulation as used in both of the above related works under discussion. We also stress that the method of analysis proposed in this paper is generic. We can use any choice of regression analysis as long as it can be kernelized, i.e., valid regression schemes that can be formulated as inner products of the mapped data. We notice that in the comparative study for the choice of two such schemes, kernel PLS and kernel RVR, reported stable results. The pattern maps obtained using two independent regression methodologies yield very similar geodesics of regression coefficients for all the clinical response variables. The leave-one-out predictive accuracy obtained in both are also comparable. In terms of execution times we found PLS to be much faster than RVR; up to three orders of magnitude for all the clinical variables.
Deformation based morphometry and LDDMM momenta
The scope of LD-DMM based methods is much beyond just their predictive capabilities and the potential to extract relevant deformation patterns. The LDDMM framework although computationally more intensive, has several advantages over conventional Jacobian based statistical analysis akin to deformation based morphometry (DBM)[Mechelli et al. (2005)]. Deformation momenta obtained in LDDMM are scalar-valued signatures that summarize the voxel-wise large deformation information about anatomical variability. The scalar momenta are comprised of both the local divergence and curl components of associated deformation fields and not just the local scaling represented by the Jacobians. Another important difference between these two approaches is the interpretation of the resulting coefficients in regression analysis. In DBM, even though the regression coefficients can be visualized to understand the patterns or weight maps of clusters important for prediction, the scaling of the regression coefficient does not tie with the inherent non-linearity of the underlying space. The scaled coefficients cannot be naturally interpreted under the nonlinear regression framework. In LDDMM, since the statistics are done on Riemannian manifold of diffeomorphism, the regression coefficient has a meaning as a mathematical quantity—it is an element of V*. The amount of scaling of the regression coefficient translates naturally to how far along the geodesic we intend to travel away from the Fréchet mean image in deformations—which correspond to scaled units of changes in clinical response.
The proposed modeling enables us to identify local shape deformation patterns by performing a global analysis of the structure of the human brain. We notice that the evolving atlas shows distinct trends in hippocampus and amygdala shape changes whenever the regressed response variable is a measure of memory and cognitive function, the determinants of Alzheimer’s Disease progression. Putamen and thalamus were found to be important to the regression with executive function. The results were consistent with both the PLS as well as the RVR. These resulting anatomical regions were consistent with very high confidence irrespective of the size of the population used in the study.
We stress the fact that no additional clinical prior on the hippocampus was added and no priori information about the disease state was used in modeling. This is unlike most of the contemporary shape analysis studies in AD and related dementia, where the statistics are performed on the specific region of interests already clinically known to be affected. The style of global analysis presented in this paper holds promise for discovering new patterns of shape changes in the human brain that could add to our understanding of disease progression in AD.
Supplementary Material
Table 8.
ADNI data details
| Diagnosis | 54 Stable NL controls, 127 MCI, 61 AD |
| Education | μ = 15.27 and σ = 3.23 |
| Age | μ = 75.56 and σ = 6.65 |
| Gender | 98 Females and 144 Males |
| Handedness | 229 Right and 13 Left |
| APOE positive | 13 NL’s, 70 MCI’s, 41 AD’s |
| Follow-up | From baseline up to 48 months |
| MCI-C/NC status | 54 out of 127 MCI converted to AD |
Highlights.
Propose PLS in tangent space of diffeomorphisms: methodology for global analysis of brain anatomy without apriori region of interest.
Extract shape deformation patterns that predict clinical progression.
Continuous geodesic evolution quantifies the shape changes in the units of clinical response.
The model incorporates controls for counfounding variables in regression such as age, education.
Acknowledgments
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in the analysis or writing of this report. The research in this paper was also supported by NIH grant 5R01EB007688, the University of California, San Francisco (NIH grant P41 RR023953), NSF grant CNS-0751152, and NSF CAREER Grant 1054057.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ashburner J, Csernansk J, Davatzikos C, Fox N, Frisoni G, Thompson P. Computer-assisted imaging to assess brain structure in healthy and diseased brains. The Lancet Neurology. 2003;2 (2):79–88. doi: 10.1016/s1474-4422(03)00304-1. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Hutton C, Frackowiak R, Johnsrude I, Price C, Friston K. Identifying global anatomical differences: deformation-based morphometry. Human Brain Mapping. 1998;6 (5–6):348–357. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<348::AID-HBM4>3.0.CO;2-P. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai ZD, Yin YQ. Limit of the smallest eigenvalue of a large dimensional sample covariance matrix. The Annals of Probability. 1993 Jul;21 (3):1275–1294. [Google Scholar]
- Batmanghelich N, Dalca A, Sabuncu M, Golland P. Joint modeling of imaging and genetics. In: Gee J, Joshi S, Pohl K, Wells W, Zllei L, editors. Information Processing in Medical Imaging. Vol. 7917 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2013. pp. 766–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beg M, Miller M, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision. 2005;61 (2):139–157. [Google Scholar]
- Boulesteix A, Strimmer K. Partial least squares: a versatile tool for the analysis of high-dimensional genomic data. Briefings in Bioinformatics. 2007;8 (1):32. doi: 10.1093/bib/bbl016. [DOI] [PubMed] [Google Scholar]
- Braak H, Braak E. Alzheimer’s disease affects limbic nuclei of the thalamus. Acta Neuropathol (Berl) 1991;81 (3):261–268. doi: 10.1007/BF00305867. [DOI] [PubMed] [Google Scholar]
- Christensen G, Joshi S, Miller M. Visualization in Biomedical Computing. Springer; 1996. Individualizing anatomical atlases of the head; pp. 343–348. [Google Scholar]
- Cohen J, Asarnow R, Sabb F, Bilder R, Bookheimer S, Knowlton B, Poldrack R. Decoding continuous variables from neuroimaging data: basic and clinical applications. Frontiers in Neuroscience. 2011:5. doi: 10.3389/fnins.2011.00075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuingnet R, Gerardin E, Tessieras J, Auzias G, Lehricy S, Habert MO, Chupin M, Benali H, Colliot O. Automatic classification of patients with alzheimer’s disease from structural mri: a comparison of ten methods using the ADNI database. Neuro Image. 2011;56 (2):766–781. doi: 10.1016/j.neuroimage.2010.06.013. [DOI] [PubMed] [Google Scholar]
- Dale A, Fischl B, Sereno M. Cortical surface-based analysis I. Segmentation and surface reconstruction. Neuro Image. 1999;9 (2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Davatzikos C, Resnick S, Wu X, Parmpi P, Clark C. Individual patient diagnosis of {AD} and {FTD} via high-dimensional pattern classification of {MRI} Neuro Image. 2008;41 (4):1220–1227. doi: 10.1016/j.neuroimage.2008.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis B, Fletcher P, Bullitt E, Joshi S. Population shape regression from random design data. Proceeding of ICCV.2007. [Google Scholar]
- de Jong LW, van der Hiele K, Veer IM, Houwing JJ, Westendorp RG, Bollen EL, de Bruin PW, Middelkoop HA, van Buchem MA, van der Grond J. Strongly reduced volumes of putamen and thalamus in Alzheimer’s disease: an MRI study. Brain: A Journal of Neurology. 2008 Dec;131 (Pt 12):3277–3285. doi: 10.1093/brain/awn278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchesne S, Caroli A, Geroldi C, Collins D, Frisoni G. Relating one-year cognitive change in mild cognitive impairment to baseline mri features. Neuro Image. 2009;47 (4):1363–1370. doi: 10.1016/j.neuroimage.2009.04.023. [DOI] [PubMed] [Google Scholar]
- Dupuis P, Grenander U, Miller MI. Variational problems on flows of diffeomorphisms for image matching. Quarterly of Applied Mathematics. 1998;56 (3):587. [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman & Hall; New York: 1993. [Google Scholar]
- Fan Y, Batmanghelich N, Clark CM, Davatzikos C. Spatial patterns of brain atrophy in mci patients, identified via high-dimensional pattern classification, predict subsequent cognitive decline. Neuro Image. 2008;39 (4):1731–1743. doi: 10.1016/j.neuroimage.2007.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filipovych R, Wang Y, Davatzikos C. Pattern analysis in neuroimaging: beyond two-class categorization. International Journal of Imaging Systems and Technology. 2011;21 (2):173–178. doi: 10.1002/ima.20280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank K. Impact of a confounding variable on a regression coefficient. Sociological Methods & Research. 2000;29 (2):147. [Google Scholar]
- Ha L, Kruger J, Fletcher PT, Joshi S, Silva CT. Fast parallel unbiased diffeomorphic atlas construction on multi-graphics processing units. Proceedings of Eurographic Symposium on Parallel Graphic and Visualization (EGPGV); 2009. pp. 41–48. [Google Scholar]
- Hall P, Marron JS, Neeman A. Geometric representation of high dimension, low sample size data. Journal of the Royal Statistical Society Series B. 2005;67 (3):427–444. [Google Scholar]
- Holden M. A review of geometric transformations for nonrigid body registration. Medical Imaging, IEEE Transactions on. 2008;27 (1):111–128. doi: 10.1109/TMI.2007.904691. [DOI] [PubMed] [Google Scholar]
- Hong Y, Joshi S, Sanchez M, Styner M, Niethammer M. Metamorphic geodesic regression. In: Ayache N, Delingette H, Golland P, Mori K, editors. Medical Image Computing and Computer-Assisted Intervention MIC-CAI 2012. Vol. 7512 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2012. pp. 197–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höskuldsson A. Pls regression methods. Journal of Chemometrics. 1988;2 (3):211–228. [Google Scholar]
- Jolliffe IT. A note on the use of principal components in regression. Journal of the Royal Statistical Society Series C (Applied Statistics) 1982;31 (3):300–303. [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. Neuro Image. 2004;23:151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- Kassubek J, Juengling FD, Ecker D, Landwehrmeyer GB. Thalamic atrophy in Huntington’s disease co-varies with cognitive performance: a morphometric MRI analysis. Cereb Cortex. 2005 Jun;15 (6):846–853. doi: 10.1093/cercor/bhh185. [DOI] [PubMed] [Google Scholar]
- Li T, Wana J, Zhang Z, Yan J, Kim S, Risacher SL, Fang S, Beg MF, Wang L, Saykin AJ, Shen L. Hippocampus as a predictor of cognitive performance: comparative evaluation of analytical methods and morphometric measures. MICCAI Workshop on Novel Imaging Biomarkers for Alzheimer’s Disease and Related Disorders (NIBAD’12); 2012. pp. 133–144. [Google Scholar]
- Lorenzi M, Ayache N, Frisoni G, Pennec X. Mapping the effects of Aβ1–42 levels on the longitudinal changes in healthy aging: hierarchical modeling based on stationary velocity fields. In: Fichtinger G, Martel A, Peters T, editors. Medical Image Computing and Computer-Assisted Intervention MICCAI 2011. Vol. 6892 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2011. pp. 663–670. [DOI] [PubMed] [Google Scholar]
- Lorenzi M, Pennec X, Ayache N, Frisoni G. Disentangling the normal aging from the pathological Alzheimer’s disease progression on cross-sectional structural MR images. MICCAI workshop on Novel Imaging Biomarkers for Alzheimer’s Disease and Related Disorders (NIBAD’12); Nice, France. 2012. pp. 145–154. [Google Scholar]
- Manne R. Analysis of two partial-least-squares algorithms for multivariate calibration. Chemometrics and Intelligent Laboratory Systems. 1987;2 (1–3):187–197. [Google Scholar]
- Mansi T, Voigt I, Leonardi B, Pennec X, Durrleman S, Sermesant M, Delingette H, Taylor AM, Boudjemline Y, Pongiglione G, Ayache N. A statistical model for quantification and prediction of cardiac remodelling: application to tetralogy of fallot. Medical Imaging, IEEE Transactions on. 2011;30 (9):1605–1616. doi: 10.1109/TMI.2011.2135375. [DOI] [PubMed] [Google Scholar]
- Mechelli A, Price CJ, Friston KJ, Ashburner J. Voxel-based morphometry of the human brain: methods and applications. Current Medical Imaging Reviews. 2005;1:105–113. [Google Scholar]
- Miller M, Younes L. Group actions, homeomorphisms, and matching: a general framework. International Journal of Computer Vision. 2001;41 (1–2):61–84. [Google Scholar]
- Miller MI, Beg MF, Ceritoglu C, Stark C. Increasing the power of functional maps of the medial temporal lobe by using large deformation diffeomorphic metric mapping. Proceedings of the National Academy of Sciences of the United States of America. 2005;102 (27):9685–9690. doi: 10.1073/pnas.0503892102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MI, Trouv A, Younes L. On the metrics and euler-lagrange equations of computational anatomy. Annual Review of Biomedical Engineering. 2002;4 (1):375–405. doi: 10.1146/annurev.bioeng.4.092101.125733. [DOI] [PubMed] [Google Scholar]
- Miller MI, Younes L, Ratnanather JT, Brown T, Reigel T, Trinh H, Tang X, Barker P, Mori S, Albert M. Amygdala atrophy in MCI/Alzheimers disease in the BIOCARD cohort based on diffeomorphic morphometry. MICCAI workshop on Novel Imaging Biomarkers for Alzheimer’s Disease and Related Disorders (NIBAD’12); 2012. pp. 155–166. [PMC free article] [PubMed] [Google Scholar]
- Niethammer M, Huang Y, Vialard F-X. MICCAI 2011. Vol. 6892. Springer; Berlin Heidelberg: 2011. Geodesic regression for image time-series; pp. 655–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phatak A, Jong SD. The geometry of partial least squares. Journal of Chemometrics. 1997;11 (4):311–338. [Google Scholar]
- Portnoy S. Asymptotic behavior of M-Estimators of p regression parameters when p2/n is large. i. consistency. The Annals of Statistics. 1984 Dec;12 (4):1298–1309. [Google Scholar]
- Rännar S, Lindgren F, Geladi P, Wold S. A pls kernel algorithm for data sets with many variables and fewer objects. Part 1: theory and algorithm. Journal of Chemometrics. 1994;8 (2):111–125. [Google Scholar]
- Rosipal R, Trejo L. Kernel partial least squares regression in reproducing kernel hilbert space. The Journal of Machine Learning Research. 2002;2:97–123. [Google Scholar]
- Singh N, Fletcher PT, Preston JS, Ha L, King R, Marron JS, Wiener M, Joshi S. Medical Image Computing and Computer-assisted Intervention: Part III. MICCAI’10. Springer-Verlag; Berlin, Heidelberg: 2010. Multivariate statistical analysis of deformation momenta relating anatomical shape to neuropsychological measures; pp. 529–537. [DOI] [PubMed] [Google Scholar]
- Singh N, Hinkle J, Joshi S, Fletcher P. A vector momenta formulation of diffeomorphisms for improved geodesic regression and atlas construction. Biomedical Imaging (ISBI), 2013 IEEE 10th International Symposium; 2013. pp. 1219–1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh N, Wang A, Sankaranarayanan P, Fletcher P, Joshi S. Genetic, structural and functional imaging biomarkers for early detection of conversion from mci to ad. In: Ayache N, Delingette H, Golland P, Mori K, editors. Medical Image Computing and Computer-Assisted Intervention MICCAI 2012. Vol. 7510 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2012. pp. 132–140. [DOI] [PubMed] [Google Scholar]
- Stonnington C, Chu C, Klöppel S, Jack C, Jr, Ashburner J, Frackowiak R. Predicting clinical scores from magnetic resonance scans in alzheimer’s disease. Neuro Image. 2010;51 (4):1405–1413. doi: 10.1016/j.neuroimage.2010.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tipping ME. Sparse bayesian learning and the relevance vector machine. J Mach Learn Res. 2001 Sep;1:211–244. [Google Scholar]
- Twining C, Marsland S. Constructing diffeomorphic representations of non-rigid registrations of medical images. In: Taylor C, Noble J, editors. Information Processing in Medical Imaging. Vol. 2732 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2003. pp. 413–425. [DOI] [PubMed] [Google Scholar]
- Vemuri P, Gunter JL, Senjem ML, Whitwell JL, Kantarci K, Knopman DS, Boeve BF, Petersen RC, Jr, CRJ Alzheimer’s disease diagnosis in individual subjects using structural {MR} images: validation studies. Neuro Image. 2008;39 (3):1186–1197. doi: 10.1016/j.neuroimage.2007.09.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vialard F-X, Risser L, Rueckert D, Cotter C. Diffeomorphic 3d image registration via geodesic shooting using an efficient adjoint calculation. International Journal of Computer Vision. 2011:1–13. doi: 10.1007/s11263-011-0481-8. [DOI] [Google Scholar]
- Wang L, Beg M, Ratnanather J, Ceritoglu C, Younes L, Morris J, Csernansky J, Miller M. Large deformation diffeomorphism and momentum based hippocampal shape discrimination in dementia of the Alzheimer type. IEEE Transactions on Medical Imaging. 2007;26 (4):462. doi: 10.1109/TMI.2005.853923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Fan Y, Bhatt P, Davatzikos C. High-dimensional pattern regression using machine learning: from medical images to continuous clinical variables. Neuro Image. 2010;50 (4):1519–1535. doi: 10.1016/j.neuroimage.2009.12.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Liu E, Morris JC, Petersen RC, Saykin AJ, Schmidt ME, Shaw L, Siuciak JA, Soares H, Toga AW, Trojanowski JQ. The alzheimers disease neuroimaging initiative: a review of papers published since its inception. Alzheimer’s and Dementia. 2012;8 (1, Supplement):S1–S68. doi: 10.1016/j.jalz.2011.09.172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wold H. Quantitative Sociology: International Perspectives on Mathematical and Statistical Model Building. 1975. Path models with latent variables: the NIPALS approach. [Google Scholar]
- Younes L, Arrate F, Miller M. Evolutions equations in computational anatomy. Neuro Image. 2009;45 (1S1):40–50. doi: 10.1016/j.neuroimage.2008.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Wang Y, Zhou L, Yuan H, Shen D. Multimodal classification of alzheimers disease and mild cognitive impairment. Neuro Image. 2011;55 (3):856–867. doi: 10.1016/j.neuroimage.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.