Cooperative metal ion binding and general base activation in hammerhead ribozyme catalysis

Abstract

The hammerhead ribozyme is a well-studied nucleolytic ribozyme that catalyzes the self-cleavage of the RNA phosphodiester backbone. Despite experimental and theoretical efforts, there remain key questions about details of the mechanism with regard to the activation of the nucleophile by the putative general base guanine (G12). Straight-forward interpretation of the measured activity-pH data implies the pK_a value of the G12 nucleobase is significantly shifted by the ribozyme environment. Recent crystallographic and biochemical work has identified pH-dependent divalent metal ion binding at the N7/O6 position of G12, leading to the hypothesis that this binding mode could induce a pK_a shift of G12 towards neutrality. We present computational results that unify the interpretation of available structural and biochemical data, and paint a detailed mechanistic picture of the general base step of the reaction. Electronic structure calculations quantify the magnitude of predicted pK_a shifts induced by Mg²⁺ binding in several Mg²⁺-guanine complexes. Molecular dynamics and free energy simulations using newly developed 12-6-4 parameters for divalent metal ion binding to nucleic acids are used to characterize the ribozyme active site environment and evaluate the pK_a of G12 in HHR with and without the Mg²⁺ ion bound. The results suggest that Mg²⁺ is able to down-shift the pK_a of G12 by −1.2 units in accord with the apparent pK_a value determined from activity-pH measurements. In addition, ab initio quantum mechanical/molecular mechanical simulations are performed to explore the free energy profile for the general base step in the presence and absence of Mg²⁺. Taken together, these results are in quantitative agreement with available experimental data, and support a cooperative mechanism whereby Mg²⁺ binding at the N7/O6 position serves to stabilize G12 in the functional, deprotonated form that can abstract a proton from the nucleophile in the general base step of the reaction. In this scenario, site-specific Mg²⁺ ion binding acts as a switch to activate the general base in HHR. Finally, experimentally-testable predictions are made on the mutational and rescue effects on G12, which will give further insights into the catalytic mechanism. These results contribute to our growing knowledge of the potential roles of divalent metal ions in RNA catalysis.

The hammerhead ribozyme (HHR) is a prototype catalytic RNA system that has been extensively studied(1–9) for almost three decades since it was first discovered by Uhlenbeck in 1987(10). The HHR catalyzes the cleavage transesterification of the RNA sugar-phosphate backbone(8). In the generally accepted acid-base mechanism, the nucleophile (the 2′-hydroxyl of residue C17) is deprotonated by a general base to form an activated precursor that then goes on an inline attack to the adjacent scissile phosphate. Departure of the O5′ leaving group is then facilitated by a general acid, leading to a 2′,3′-cyclic phosphate.

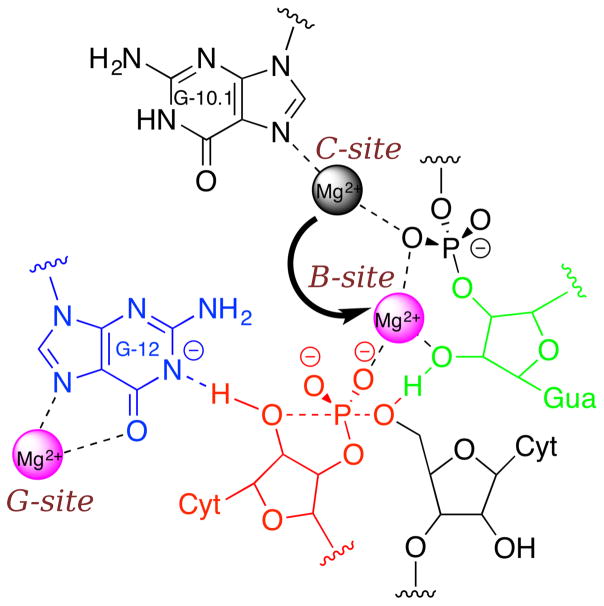
Despite the wealth of structural(11–16), biochemical(6, 17–40) and computational(3, 8, 41–49) data available, certain details of the catalytic mechanism remain unclear. In particular, the specific mechanism whereby the nucleophile becomes activated by a general base is not yet resolved. Biochemical studies(30, 31, 36) have suggested that the guanine nucleobase in residue G12 may act as the general base in HHR, which is also supported by crystal structures(13, 15) in which the N1 site of G12 is well-positioned to interact with the 2′-hydroxyl group of C17 (Fig. 1). Interestingly, guanine is observed to interact with the 2′-hydroxyl nucleophile in many other ribozyme systems(9), including the hairpin(50, 51), glmS(52, 53), Varkud satellite(54), twister(55, 56) and pistol(?) ribozymes, and thus appears to be a common theme in RNA catalysis.

Figure 1.

Illustration of the active site interactions in HHR and its self-cleavage mechanism. The N1 position of guanine in the putative general base G12 (blue) needs to be deprotonated before acting as a proton acceptor to deprotonate the 2′-OH in C17 (red), which will then act as the nucleophile to attack the phosphorous. Recent studies(15, 16) indicate that there could be a Mg²⁺ directly bound at the Hoogsteen face of G12 (“G-site”) to facilitate its deprotonation. Another Mg²⁺ is believed to play the role of activating the 2′-OH of the general acid G8 (green) by migrating from the binding site at N7 of G10.1 (“C-site”) observed crystallographically into a bridging position (“B-site”) with the scissile phosphate, in accord with thio/rescue effect experiments(29, 39, 57). In this bridging position, the Mg²⁺ can coordinate the 2′-OH of G8, increasing its acidity, and facilitating proton transfer to the O5′ leaving group in the general acid step of the reaction(8).

A conceptual objection to the hypothesis that G12 may act as the general base is that the apparent pK_a values derived from activity-pH profiles (around 8(15, 30, 31, 36)), are somewhat lower than the pK_a value of guanine in aqueous solution (9.2). In order to reconcile these observations, the most straight-forward interpretation is that the pK_a of G12 would need to be considerably down-shifted by the ribozyme active site. This prospect seems unlikely given the high degree of localized negative charge in the active site(46), the proximity of G12 to the scissile phosphate and the lack of nearby divalent metal ions in the active site of an earlier crystallographic data with resolved solvent structure(43).

Recently, a new set of crystal structures(15, 16) of a full length hammerhead ribozyme (RzB) has been obtained that indicate a Mg²⁺ ion bound directly to the Hoogsteen face of G12 at pH 8. This binding mode is similar to the position of an electron density peak found in the previous crystal structures and interpreted as a likely water molecule(43) or Na⁺ ion(14). Divalent metal ions have been predicted to be capable of considerably shifting the pK_a of certain residues in ribozyme environment to facilitate catalysis(58–60). It is thus of considerable interest to understand whether this binding mode could represent an effective catalytic strategy for general base activation in nucleolytic ribozymes.

In this paper, we explore the feasibility of a Mg²⁺ ion, bound to G12, to shift the pK_a at the N1 position as required by its implicated role as general base in the reaction, and make quantitative predictions that are experimentally testable. Electronic structure calculations are performed to quantify the magnitude of pK_a shifts induced by Mg²⁺ binding in several Mg²⁺-guanine complexes. Molecular dynamics (MD) simulations are carried out with newly developed force field parameters for divalent metal ion binding to nucleic acids(61) to characterize the ribozyme active site environment and thermodynamic integration (TI) is used to evaluate the pK_a shift of G12 in HHR with and without the Mg²⁺ bound. Ab initio quantum mechanical/molecular mechanical (QM/MM) simulations with rigorous long-range electrostatic interactions (62) are performed to explore the free energy profile for the general base step in the presence and absence of Mg²⁺ bound at the newly identified position. Taken together, these results are in quantitative agreement with available experimental data, and support a mechanism whereby Mg²⁺ serves to stabilize G12 in an active (deprotonated) form that will ultimately facilitate deprotonation of the nucleophile in the general base step of the reaction. In addition, quantum mechanical calculations on the binding free energies between different divalent metal ions and guanine/6-thioguanine predict that a 6-thio substitution at G12 in HHR will decrease the catalytic reaction rate by knocking out the Mg²⁺ binding while replacing Mg²⁺ by Mn²⁺ or Cd²⁺ could have rescue effects, which could be tested by future experimental works.

Methods

Electronic structure calculations

All electronic structure calculations were carried out in the Gaussian09 package(63) using M06-2X(64) density functional with 6–311++G(3df,3pd) basis set. The PCM solvation model(65–68) was used to treat the solvation effects, whose solvation cavity is constructed from the UFF radii set scaled by a factor of 1.1(69). Harmonic vibrational analysis was performed on the optimized geometries using rigid rotor and harmonic oscillator approximations to verify the nature of the stationary points and obtain the thermal corrections to free energies. The relative pK_as (i.e., the pK_a shifts) are calculated from:

$$\mathrm{\Delta }\mathrm{p}{K}_a=(\mathrm{\Delta }{G}^{\prime }-\mathrm{\Delta }G)/\mathit{RT}ln(10)$$ (1)

where ΔG′ and ΔG are the deprotonation reaction free energies of Mg²⁺-guanine and guanine, respectively. Free energy difference between two deprotonation reactions in kcal/mol were converted to pK_a shift in pK_a units by dividing by RT ln(10). The pK_a shift is further corrected by taking the Mg²⁺ ion concentration and Mg²⁺-guanine binding affinity into account. By considering a kinetic model that consists of deprotonation of guanine, Mg²⁺-guanine binding equilibrium and deprotonation of Mg²⁺-guanine complex, we obtained estimates for the corrected pK_a of Mg²⁺-guanine complex as (see supporting information for details):

$$\mathrm{p}{K}_a(\text{Mg-Gua},\text{corr.})=-{log}_{10}\left(\frac{{10}^{-\mathrm{p}{K}_a(\text{Gua})}+c_{\text{Mg}}\times e^{-\beta \mathrm{\Delta }{G}_{\text{bind}}}\times {10}^{-\mathrm{p}{K}_a(\text{Mg:Gua},\text{uncorr.})}}{1+c_{\text{Mg}}\times e^{-\beta \mathrm{\Delta }{G}_{\text{bind}}}}\right)$$ (2)

where c_Mg is the concentration of Mg²⁺ ion (0.01 M is used in this work) divided by the standard molar concentration 1.0 M (thus dimensionless), and ΔG_bind is the Mg²⁺-guanine binding affinity which has been experimentally measured to be −0.34 kcal/mol(61, 70) (see Supporting Information for details). Electron population analysis was performed on the guanine and Mg²⁺-guanine complex molecules (both neutral and deprotonated) at their optimized geometries using the natural bond orbital (NBO) analysis(71) method, as implemented in Gaussian09.

For the binding free energy calculations between different metal ions and guanine/6-thioguanine, the chemical equations that define the binding free energy are:

$$\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_6^{2+}+\mathrm{G}\to {[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_5:\mathrm{G}]}^{2+}+{\mathrm{H}}_2\mathrm{O}$$ (3)

$$\text{or}\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_6^{2+}+{\mathrm{G}}^{-}\to {[\mathrm{M}{({\mathrm{H}}_2\mathrm{O})}_5:\mathrm{G}]}^{+}+{\mathrm{H}}_2\mathrm{O}$$ (4)

in which M could be Mg²⁺, Mn²⁺ or Cd²⁺ and G could be guanine or 6-thioguanine. For Mn and Cd atoms, the SDD effective core potential(72) is used. The cavity radii of S atom was adjusted from 2.0175 (default as implemented in Gaussian09) to 2.6 which correctly reproduces the experimentally measured(73) pK_a between guanine and 6-thioguanine.

Molecular dynamics simulations

All molecular dynamics simulations were carried out in the Amber14 package(74). Starting from the recent crystal structure of the RzB hammerhead ribozyme with divalent metal ion bound at G12(15, 16) (PDB code 5DI2), the RNA was solvated in a box of TIP4P-Ew(75) water molecules with a 12 A buffer. 67 Na⁺ and 15 Cl⁻ ions were added to neutralize the system and solvate it with 0.14 M NaCl (roughly physiological salt conditions). The RNA was treated by the AMBER-ff14SB force field(76, 77) which includes the corrections for alpha/gamma conformers(78) and glycosidic torsions(79) in nucleic acids. The monovalent ions were described using the TIP4P-Ew-compatible parameters developed by Joung & Cheatham(80). To better characterize the interaction between Mg²⁺ and nucleic acids, we apply the recently developed m12-6-4 parameter set developed by Panteva, Giambaşu and York(61) to accurately describe balanced interactions between Mg²⁺ and nucleic acids. This model was based on pioneering work by Li and Merz(81) to include effects of ion-induced polarization, using a simple pairwise approximation that does not require further alteration of conventional moleecular simulation force fields. This model provides outstanding agreement with structural, thermodynamic, kinetic and mass transport properties of Mg²⁺ in aqueous solution(82), and has recently been extended so as to give balanced interactions with nucleic acids through adjustment of specific pairwise parameters(61). This model was used to describe all 6 Mg²⁺ ions that were present in the crystal structure and in the simulations. The system was then slowly heated up to 300 K and equilibrated for a total of >30 ns simulation (refered as HHR · Mg²⁺:G12). To justify the effect of the G12-bound Mg²⁺, another system was built by removing the G12-bound Mg²⁺ and went through the same equilibration process (refered as HHR:G12). Also, a reference system was set up by solvating a single guanosine monophosphate residue (CH₃-capped at the O3′ position and CH₃O-capped at P position) in a box of TIP4P-Ew water with a 20 A buffer along with 13 Na⁺ and 12 Cl⁻ ions. This system was heated up to 300 K and equilibrated for a total of 5 ns simulation. All simulations employ an 8 A nonbond cutoff and make use of Particle Mesh Ewald to account for the electrostatics beyond the cutoff. (83)

Thermodynamic integration calculations

Starting from the equilibrated structures, all 3 systems (solvated guanosine, HHR:G12 and HHR · Mg²⁺:G12) were prepared for thermodynamic integration (TI) calculations to compute the free energy of deprotonating guanine or G12. The net free energy change is: ΔG_DEPR = G_G⁻ − G_GH, where G_GH is the free energy of the neutral guanine state (both in the reference system and at the G12 position in the HHR) and G_G⁻ is the free energy of the guanine deprotonated at the N1 position, which carries a net 1-charge. In order to stabily compute the net free energy change from a reasonable amount of statistical sampling, it is advantageous to decompose the net free energy change as a sum of 3 stages(84) that pass through intermediate states:

$$\mathrm{\Delta }{G}_{\text{DEPR}}=\mathrm{\Delta }{G}_{\text{decharge}}+\mathrm{\Delta }{G}_{\text{bond-removal}}+\mathrm{\Delta }{G}_{\text{recharge}}$$ (5)

where ΔG_decharge, ΔG_bond-removal, and ΔG_recharge are refered to as the “decharging”, “bondremoval”, and “recharging” stages, respectively. The advantage of this decomposition is that less sampling is required to compute each stage than what would otherwise be necessary through a direct transformation between the two end states. In the decharging stage, the partial charge on H1 is removed. In the bond-removal stage, the bond, angle, torsion and Lennard-Jones interaction terms in the force field involving the H1 are removed. In the recharging stage, the partial charges on the entire residue are transformed to the charge set for the deprotonated guanine derived from RESP charge fitting(85). The free energy of each stage is computed from TI:

$$\mathrm{\Delta }{G}_{\text{stage}}={\int }_0^1{\langle \frac{\partial {\mathcal{H}}_{\text{stage}}(\lambda )}{\partial \lambda }\rangle }_{\lambda }d\lambda$$ (6)

where ℌ_stage(λ) is a linear combination of Hamiltonians that define the end-states of the stage:

$${\mathcal{H}}_{\text{stage}}(\lambda )=(1-\lambda ){\mathcal{H}}_{\text{stage}}^{(0)}+\lambda {\mathcal{H}}_{\text{stage}}^{(1)}$$ (7)

${\mathcal{H}}_{\text{stage}}^{(0)}$ and ${\mathcal{H}}_{\text{stage}}^{(1)}$ are the Hamiltonians for the stage’s initial and final states, respectively. As an exception to Eq. 7, the removal of the Lennard-Jones interaction within the “bondremoval” stage is performed through a non-linear “soft-core” potential(61, 86):

$$V_{\text{sc}}(\lambda )=4\epsilon (1-\lambda )\left[\frac{1}{{[\alpha \lambda +{(r/\sigma )}^6]}^2}-\frac{1}{\alpha \lambda +{(r/\sigma )}^6}\right]$$ (8)

where ε and σ are standard LJ parameters, r is atomic distance and α is an adjustable constant that was set to 0.5 by default(86). The free energy change of each stage is evaluated by performing 11 simulations (TI “windows”) corresponding to 11 evenly-spaced values of λ, and numerically integrating Eq. 6 from the trapezoid rule. Each TI window is equilibrated for 100 ps at λ = 0.5, and statistics are sampled from 1 ns of production simulation.

The TI calculations described above involves 33 TI window simulations per system (3 stages/system and 11 windows/stage) to compute a net free energy change. To ascertain the reliability of the result, we perform the procedure 3 times for each system (99 windows/system) to compute 3 estimates of the system’s net free energy change. For each system, we report (see Table 3) the average ΔG_DEPR value and its standard error from the 3 estimates.

Table 3.

Deprotonation free energies (kcal/mol), pK_as and pK_a shifts (in pK_a units) of G12 in HHR from different sets of TI simulations and experiments.

Model	ΔGDEPR	pKa	pKa shift
Guanine (ref.)	−114.1 ± 0.5	9.2	–
HHR:G12	−108.9 ± 0.3	12.9 ± 0.2	3.7 ± 0.2
HHR · Mg2+:G12	−115.8 ± 0.5	8.0 ± 0.4	−1.2 ± 0.4
Experiments(15)	–	8.0	−1.2

Quantum mechanical/molecular mechanical simulations

After G12 is deprotonated, it is suited to act as a general base that activates the nucleophile by facilitating a proton transfer from the nucleophile C17:O2’ to G12:N1. Ab initio QM/MM umbrella sampling simulations were performed to obtain the free energy profile of the proton transfer reaction for both HHR:G12 and HHR · Mg²⁺:G12. The PBE0 hybrid density functional(87, 88) with the 6–31+G(d) basis set was used to model the 47 atom (HHR:G12) or 48 atom (HHR · Mg²⁺:G12) QM region. The QM region includes the guanine base in the G12 residue, the Mg²⁺ bound at G12 (but not the coordinating water molecules), and the entire C17 residue (cytosine base, sugar, and phosphate). The simulations were performed with an 8 A nonbond cutoff, and the Ambient-Potential Composite Ewald method(62) was used to describe the long-range electrostatics in the system.

The reaction coordinate (ξ = R₁ − R₂) is the difference between two distances. R₁ is the distance from the proton donor C17:O2′ to the proton C17:HO2′, and R₂ is the distance from the proton acceptor G12:N1 to the proton C17:HO2′. The umbrella biasing potential

$$U_{\text{bias}}(\xi )=k{(\xi -{\xi }_0)}^2$$ (9)

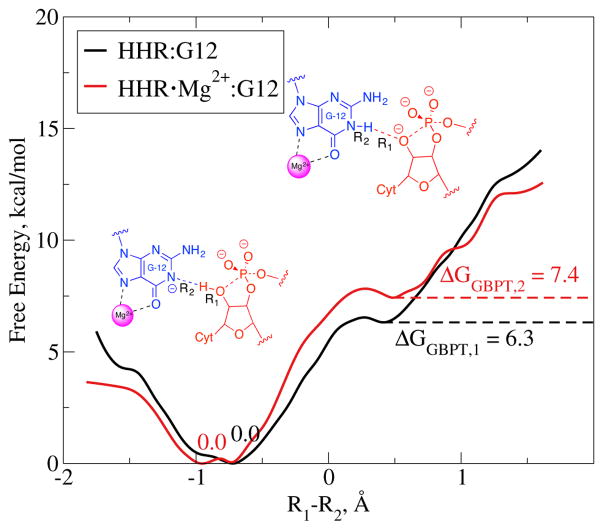
where ξ₀ is the reference coordinate for the window, and k = 50 kcal mol⁻¹ A⁻² is a force constant. Each profile is generated from 16 simulation windows whose reference coordinate evenly samples the range −1.6 A ≤ ξ₀ ≤ 1.4 A. Each window is equilibrated for 2.5 ps, and statistics were drawn from 10 ps of production simulation. The statistics gathered from the biased simulations are analyzed using the variational free energy profile (vFEP) method(89) to generate the unbiased free energy profiles shown Fig. 9.

Figure 9.

Potential of mean force (PMF) for the general base proton transfer (GBPT) reaction in HHR · Mg²⁺:G12 (red) and HHR:G12 (black) generated by ab initio QM/MM umbrella sampling. The two chemical structures depict the reactant (left) and product (right) states. Reaction coordinate is the difference (R₁–R₂) between the distance from C17:O2′ to C17:HO2′ (R₁) and the distance from G12:N1 to C17:HO2′ (R₂). Free energies of the reactant and product states are marked.

Results and Discussion

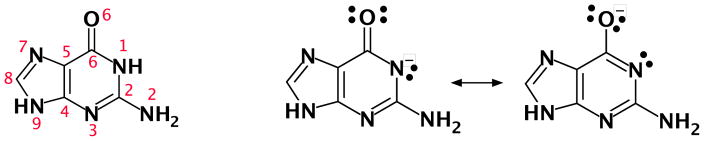
Guanine nucleobases are often encountered in ribozyme active sites, and have been implicated as acting as the general base in catalysis. In order to act as a general base, the guanine nucleobase should be deprotonated at the N1 position (Fig. 2). In the deprotonated state, resonance stabilization allows the negative charge to be distributed between the N1 and O6 positions. Divalent metal ion bining at the O6 position, therefore, would be expected to have a large infleunce on the microscopic pK_a at the N1 position by stabilizing the deprotonated form. In the following sections, we build up models for Mg²⁺ binding to guanine and related chemically modified analogs used in mechanistic experiments, and make predictions about the induced pK_a shift at the N1 position, and on the free energy of the general base step in the chemical reaction.

Figure 2.

(Left) Canonical numbering of guanine nucleobase. (Right) Resonance structures of guanine deprotonated at N1 position with formal charge alternately on the N1 and the O6.

pK_a shifts of Mg²⁺-guanine complexes

In order to get a more detailed picture of the Mg²⁺-guanine interaction and its effect on the pK_a, we designed model compounds that mimic the Mg²⁺-guanine complex in HHR crystal structure and performed density functional electronic structure calculations. To validate the computational protocol and quantum chemical model chemistry, we calculated the pK_a shifts of three chemically modified guanines: substitution of N3/N7 to CH which makes 3/7-deaza-guanine and replacement of exocyclic NH₂ with H which yields inosine (Fig. 3). From Table 1, the calculated pK_a shift of all three chemically modified guanines agree very well with experimental values (maximum error of 0.4 pK_a units).

Figure 3.

Chemical structures of guanine and several chemically modified guanine molecules studied in this work. Experimental pK_a values at the N1 position (taken from Refs. 90, 91) are shown.

Table 1.

Calculated and experimental pK_a shifts of guanine, chemically modified guanine and Mg²⁺-guanine complexes. The calculated pK_a shifts have been corrected for Mg²⁺-guanine binding affinity and Mg²⁺ concentration (0.01 M) using Eq. 2. Error estimates are not available because the method used to obtain those values are deterministic and do not involve sampling.

Model	pKa shift (calc.)	pKa shift (expt.)
guanine (ref.)	–	–
inosine	−0.3	−0.5 (90)
3-deaza-guanine	3.2	3.1 (91)
7-deaza-guanine	1.5	1.1 (91)
Mg2+-(H2O)5-guanine	−7.0	–
Mg2+-(H2O)5-inosine	−7.0	–
Mg2+-(H2O)5-3-deaza-guanine	−4.4	–
HHR G12	–	−1.2 (15)

Next, we examined several Mg²⁺-guanine model complexes that mimicked the metal ion binding mode observed in the crystal structure of reactant state HHR in which the hexacoordinated Mg²⁺ has inner sphere contact with N7 and outer sphere coordination with O6. We also picked two of the three chemically modified species (3-deaza-guanine and inosine) and built complexes with Mg²⁺ in the same way. These two species were chosen because, unlike the 7-deaza modification, neither directly alters the chemical environment of the Hoogsteen face, therefore preserving the observed binding mode of the native guanine. For 7-deaza-guanine, it’s expected that the Mg²⁺ binding would be considerably disrupted. As seen in Table 1, the magnitude of pK_a shifts induced by Mg²⁺ (≈−7 pK_a units) is quite large, making the N1 position considerably more acidic. This large shift agrees with previous arguments(58, 60, 92) that metal-ion binding could induce large pK_a shifts of nucleobase residues. The experimentally observed pK_a shift of G12 in the ribozyme environment is a much smaller shift toward neutrality (≈−1.2 pK_a units). As will be discussed in more detail in the next section, the accumulated negative charge of the ribozyme active site in the hammerhead ribozyme leads to a considerable positive pK_a shift that requires divalent metal ion binding at the G site in order to offset. The main point of the current section is to establish a baseline for the expected pK_a shifts that a Mg²⁺ would be expected to induce if it were bound to an isolated guanine (or modified guanine) nucleobase in solution, before making predictions about the pK_a shifts in the more complex active site of the HHR.

To examine the effect of Mg²⁺ binding on the electronic structure of guanine, we performed NBO analysis to calculate the partial atomic charges in the neutral and deprotonated species (Table 2). Of the key atoms listed, the largest negative charge is seen to reside at the O6 position in both protonation states and in the presence and absence of Mg²⁺. The O6 position also exhibits the greatest increase in negative charge upon deprotonation, both in the presence and absence of Mg²⁺. The O6 position is also seen to considerably increase in negative charge, for both neutral and deprotonated guanine, upon Mg²⁺ binding, but not as dramatically as at the N7 position where the ion has direct inner-sphere coordination. Overall, the charge transfer from guanine to the hydrated Mg²⁺ ion is relatively modest for both neutral and deprotonated (anionic) guanine (0.17 and 0.23 e, respectively). These results indicate that the interaction between Mg²⁺ and guanine is mostly electrostatic in nature, providing justification for the use of fixed-charge molecular mechanical (MM) force fields to model the Mg²⁺-guanine interaction that will be introduced in the next subsection.

Table 2.

Partial atomic charges of selected atoms in guanine and Mg²⁺-guanine complexes derived from NBO analysis.

Model	N1	H1	N3	O6	N7	Guanine
Guanine	−0.663	0.472	−0.603	−0.687	−0.510	0.000
Mg2+-(H2O)5-guanine	−0.635	0.484	−0.582	−0.743	−0.582	0.168
(Difference)	(0.028)	(0.012)	(0.021)	(−0.056)	(−0.071)	(0.168)
Guanine(−)	−0.716	–	−0.659	−0.792	−0.533	−1.000
Mg2+-(H2O)5-guanine(−)	−0.651	–	−0.617	−0.830	−0.602	−0.767
(Difference)	(0.065)	–	(0.042)	(−0.038)	(−0.069)	(0.233)

To better characterize the effects of the complicated enzyme environment, molecular dynamics (MD) simulation on the full HHR was conducted and the pK_a shift of guanine N1 position in G12 was then evaluated using thermodynamic integration (TI) technique. The reference system was the deprotonation of a single guanine nucleotide in solution which has known experimental pK_a of 9.2. For the HHR system, both HHR:G12 and HHR · Mg²⁺:G12 were simulated. The two pK_a shift values were then determined using Eq. 1. This approach has been adopted to predict pK_a shifts in ribozymes induced by the enzyme environments(56, 93) and a closely-related protein enzyme system where the leading factor of pK_a shift was also a Mg²⁺(94) in previous works and was shown to be giving reasonable results.

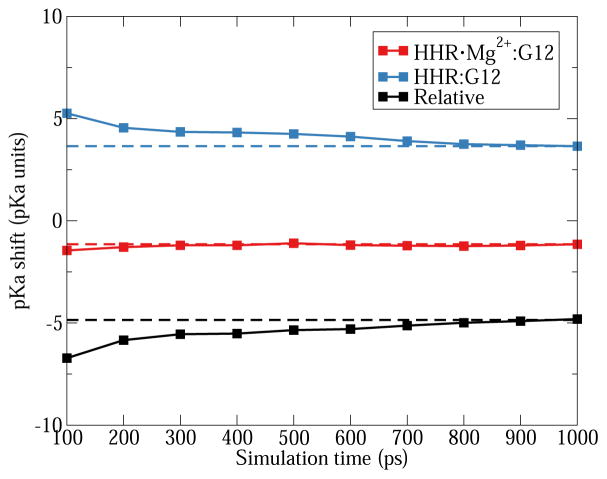
As seen in Table 3, the simulations predicted that in HHR · Mg²⁺:G12, the pK_a of N1 in G12 is shifted down by −1.2, while in HHR:G12, the pK_a is shifted up by 3.7 units. The convergence of the TI simulations in terms of the target observable pK_a shifts was measured (Fig. 6) and showed that the simulations reached reasonable convergence after 1 ns, which was similar to the timescales investigated in related work(56, 93, 94). Experimental activity-pH profiles indicate that the apparent pK_a of the general base in HHR is around 8 in the presence of Mg²⁺(15). If guanine is assumed to be the general base, and the most straight forward interpretation of the apparent pK_a values are made, this would imply an expected shift of the pK_a of G12 by *ap; −1.2 units.

Figure 6.

Convergence of pK_a shift values from TI simulations. Filled squares connected by solid lines are the pK_a shift values evaluated using all available data at certain simulation time, with an increment of 100 ps per point. Dashed lines are drawn to help show the convergence.

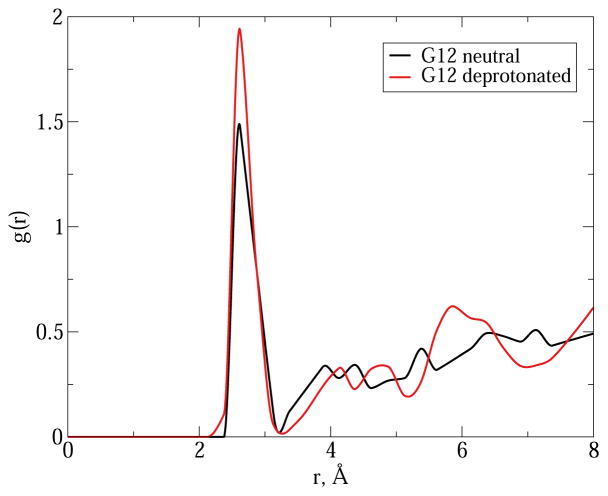
As mentioned above, an electron density peak was found in the vicinity of G12 in the previous crystal structure of HHR obtained at pH 6.5(43) (PDB code 2OEU) and was interpreted as a solvent water molecule. In the recent work(15), the G12-bound Mg²⁺ was found in the crystal obtained at pH 8.0 but not in the one obtained at pH 5.0. Here, we analyzed the solvent distribution around the O6 position of G12 from the HHR:G12 simulations by calculating the radial distribution functions (RDFs). As seen in Fig. 8, there is a clear peak at around 2.6 A in both RDFs, which is consistent with the previous structure in which the oxygen in the G12-bound water is 2.54 A away from the O6 of G12. Also, in the RDF where G12 is deprotonated, the height of the peak is greater than in the other one, which suggests that the deprotonated G12, which is carrying a −1 charge, needs stronger electrostatic interactions to stabilize the negative charges that are buiding up on O6 and N7, than the neutral form. These results indicate that the Mg²⁺-G12 binding in HHR might have pH-dependence, which could be the reason why the G12-bound Mg²⁺ is only found in high-pH crystal structures but not in the low-pH ones.

Figure 8.

Radial distribution function (RDF) of water oxygens around the O6 position of neutral and deprotonated G12 in HHR. Both sets of data are extracted from 1 ns of MD simulation of HHR:G12 with G12 in neutral and deprotonated forms, respectively. RDF data points are calculated using window size of 0.2 A and are interpolated using the Akima spline.

Taken together, the results reported here are consistent with a model whereby a Mg²⁺ ion binds at the G site and results in an overall pK_a shift of G12 toward neutrality by 1.2 pK_a units. In the absence of the metal ion binding at the G site, the pK_a of G12 is predicted to be considerably shifted to higher pK_a values (12.9), making it highly unlikely to be activated as the general base in the biologically relevant pH range. This scenario would contradict the interpretation of activity-pH data in terms of apparent pK_a values. As our calculated result is in striking agreement with experiment suggests that the apparent pK_a values observed experimentally may have this straight forward interpretation.

These results are consistent with previous calculations that indicate that HHR folds to form an electrostatically strained active site, which acts as an electronegative recruiting pocket for a threshold cationic charge required for efficient activity(46). If the local environment around G12 in HHR is overall negatively charged, then it’s expected that the pK_a of G12 will be shifted up in HHR compared to in aqueous solution. By recruiting divalent metal ions, this shift is offset and even reversed. By comparing the pK_a shifts with/without Mg²⁺ in Table 3, we can estimate the net effect of Mg²⁺ on the pK_a of G12 to be (−1.2) − 3.7 = −4.9 pK_a units, which is in qualitative agreement with our DFT result −7.0. In the hepatitis delta virus (HDV) ribozyme, which has a similar divalent metal ion requirement under physiological conditions, a pK_a shift of similar magnitude (~−4 units) on the 2′-hydroxyl nucleophile induced by Mg²⁺ was predicted by 3D-RISM calculations(95). Further, Amaro and co-workers have reported the Mg²⁺-induced pK_a shift of lysine K82 in guanylyltransferase mRNA capping enzyme to be −4.2(94) which is very close to the result reported here using a similar TI approach. Rosta and co-workers have also observed that Mg²⁺ plays the role of altering pK_a in dUTPase which catalyzes phosphate hydrolysis(96, 97).

It is noteworthy that, at high concentrations (≥ 1.0 M) of monovalent salts, HHR can undergo self-cleavage in the absence of divalent metal ions with only a modest rate reduction(98–100). It is conceivable that at high monovalent salt concentrations, cationic charge stabilization at the G12:O6 position may produce a similar catalytic effect as divalent metal ion binding. Alternatively, it may be the case that under high salt conditions, a different mechanism is available, although it is likely that at least a small part of the full HHR rate enhancement does require at least one divalent metal ion(100). It is likely that more probing study of the dependence of HHR kinetics on ionic conditions may shed light into these and other important mechanistic details.

Free energy profile for the general base step

From TI-MD simulations, we found that the G12-bound Mg²⁺ in HHR could activate the general base G12 by down-shifting its pK_a to facilitate its deprotonation. Nonetheless, since the next step after general base activation is the proton transfer from nucleophile to general base, one might expect that having a Mg²⁺ bound at G12 could make this step thermodynamically less favorable because Mg²⁺ binding to deprotonated G12 makes it a a worse proton acceptor. One possibility is that the Mg²⁺ could “leave the scene” after the deprotonation of G12 to avoid the energy penalty in the following step. However, in the crystal structure of the vanadate transition state mimic(16) (PDB code 5EAQ) which mimics the state after general base proton transfer step is completed, the Mg²⁺ was still found to be bound at G12. This suggested that the Mg²⁺ might be bound at G12 all the time despite the energy penalty of the general base proton transfer step, which could potentially be compensated by providing electrostatic stabilization to the overall negatively-charged active site.

To evaluate the energy penalty induced by Mg²⁺, we carried out ab initio QM/MM umbrella sampling simulations of the general base proton transfer step for both HHR:G12 and HHR · Mg²⁺:G12. As seen in Fig. 9, the reaction in HHR · Mg²⁺:G12 did have a higher free energy cost. However, the decrease in the free energy cost of the G12 deprotonation induced by Mg²⁺ was more than enough to compensate for this (Table 4). Overall, the free energy required to get the system into the state that is ready for phosphoryl transfer is 5.6 kcal/mol less when a G12-bound Mg²⁺ is present, which again supports the existence and the catalytic effect of that Mg²⁺ in HHR.

Table 4.

Summary of predicted free energy costs in different steps for HHR:G12 and HHR · Mg²⁺:G12. (Relative) ΔG_DEPR values are taken from Table 3 while ΔG_GBPT values are from QM/MM free energy profiles as labeled in Fig. 9. All numbers are in kcal/mol. Error estimates for ΔG_DEPR values are from Table 3 while for ΔG_GBPT are from bootstrapping (see supporting information for details). Standard errors of ΔG_TOTAL are obtained using the propagation rule.

Model	ΔGDEPR	ΔGGBPT	ΔGTOTAL
HHR:G12	6.7 ± 0.6	6.3 ± 0.2	13.0 ± 0.6
HHR · Mg2+:G12	0.0 ± 0.0	7.4 ± 0.2	7.4 ± 0.2

Effect of 6-thio substitution on G12 and rescue effects

All the results and discussions above support the hypothesis that the G-site Mg²⁺ could facilitate the catalysis by down-shifting the pK_a of G12. To further test the hypothesis and make predictions that could be directly tested by experiments, we examine the effects of changing a guanine to a 6-thioguanine. The 6-thioguanine molecule (sometimes referred to as tioguanine) has been used in medications for the treatment of leukemia and other diseases, but has not, to our knowledge, been used extensively at a mechanistic probe in ribozymes. The pK_a of 6-thioguanine has been experimentally measured to be 8.3(73), almost a full unit lower than the pK_a of guanine (9.2). In a mechanistic scenario whereby there is no divalent metal ion bound at the G-site, one would expect the lower pk_a of 6-thioguanine would lead to slightly increased activity at neutral pH due to the higher probability of being in deprotonated form and able to accept a proton from the nucleophile in the general base step, and the activity-pH profile would be accordingly shifted. If, however, a divalent metal ion did bind at the G-site, thio substitution at the 6 position could create a thio/rescue effect scenario.

In order to test this, we employed electronic structure calculations to obtain the binding free energies of Mg²⁺, Mn²⁺ and Cd²⁺ ions to guanine and 6-thioguanine, both in neutral and deprotonated (at the N1 position) form. Results are shown in Table 5, including normalization adjustments such that binding free energies are relative to guanine in its normal protonation state at neutral pH, and the column corresponding guanine is taken from the experimental binding affinities(61, 70). As one can see, the Mg²⁺-6-thioguanine binding is unfavorable relative to Mg²⁺-guanine binding, and suggests that the G-site Mg²⁺ could be knocked out upon 6-thio substitution at G12. Mn²⁺ and Cd²⁺, which are softer, more thiophilic ions, show more favorable binding to 6-thioguanine than Mg²⁺, which implies a partial rescue effect to the 6-thio substitution at G12 upon replacing Mg²⁺ with Mn²⁺ and particularly Cd²⁺. This is an experimentally testable prediction that could help to further reconcile the role of divalent metal ions in general base activation.

Table 5.

Comparison of estimated binding free energies (kcal/mol) between different divalent metal ions and guanine/6-thioguanine in both neutral and deprotonated forms. Numbers in the first column are converted from experimental binding affinities(61, 70). In each row, the numbers are normalized according to the corresponding experimental values in the first column.

Metal	Guanine	Guanine−	6-thioguanine	6-thioguanine−
Mg2+	−0.3	−11.7	6.4	5.0
Mn2+	−0.6	−12.4	0.7	−0.7
Cd2+	−2.0	−10.8	−3.2	−4.5

Conclusions

This work presents a series of quantum chemical calculations and molecular simulations to probe the activation mode of general base in hammerhead ribozyme (HHR). The hypothesis, motivated by recent crystallographic data, is that the presumed general base G12 is activated by a Mg²⁺ ion causing a pK_a shift toward neutrality that would allow it to have increased probability of being in an ionized state where the N1 position is able to extract a proton from the 2′OH nucleophile. The electronic structure calculations on small model systems suggest that a Hoogsteen face-bound Mg²⁺ ion could greatly down-shift the pK_a of the N1 position in guanine, primarily due to electrostatic interactions. Free energy simulations in the full ribozyme environment support a model whereby the pK_a of G12 in HHR is shifted by a Mg²⁺ ion bound at the experimentally observed G site by −1.2 units, in agreement with the apparent pK_a value derived from measured activty-pH profiles. QM/MM simulations of the general base proton transfer reaction further support the catalytic significance of this metal ion binding mode, and role of the G-site Mg²⁺. Based on binding free energy calculations, 6-thio substitution on G12 is predicted to reduce the catalytic activity but could be partially rescued by replacing Mg²⁺ with more thiophilic metal ions, which could be tested by experiments that measure the metal-ion dependence on activity-pH profiles for chemically modified HHRs. The suggested role of metal ions in the activation of a guanine general base may represent a general catalytic strategy used by other RNA enzymes.

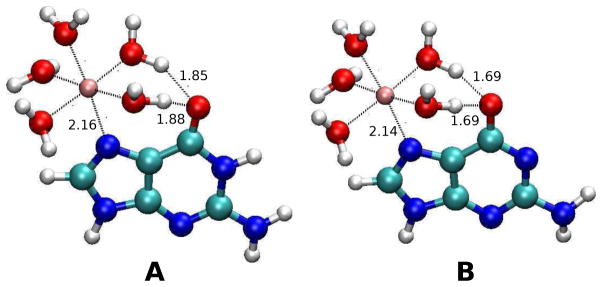
Figure 4.

Optimized geometries of Mg²⁺-guanine (A) and Mg²⁺-deprotonated guanine (B) complexes. Selected bond lengths shown are in A.

Figure 5.

Thermodynamic cycle used in TI calculations.

Figure 7.

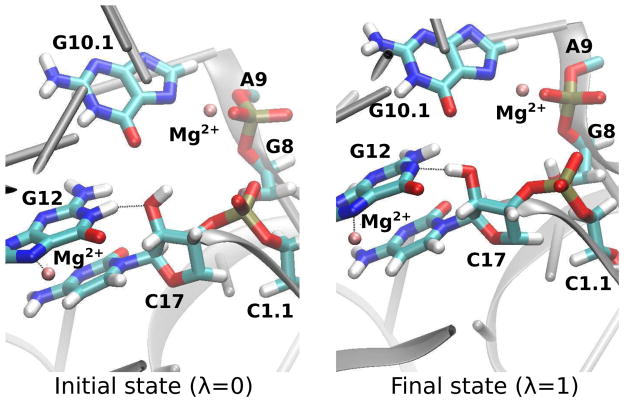
Representative active site conformation of the initial (left) and final (right) states from the free energy (TI) simulation of HHR · Mg²⁺:G12. The conformations from the simulation of HHR:G12 are very similar, and therefore not shown here. For clarity, water molecules and some other atoms/residues are not displayed. White, cyan, blue, red, pink and gold spheres stand for H, C, N, O, Mg and P atoms, respectively.