Abstract
We present a Bayesian adaptive design for dose finding in cancer phase I clinical trials. The goal is to estimate the maximum tolerated dose (MTD) after possible modification of the dose range during the trial. Parametric models are used to describe the relationship between the dose and the probability of dose limiting toxicity (DLT). We investigate model reparameterization in terms of the probabilities of DLT at the minimum and maximum available doses at the start of the trial. Trial design proceeds using escalation with overdose control (EWOC), where at each stage of the trial, we seek the dose of the agent such that the posterior probability of exceeding the MTD of this agent is bounded by a feasibility bound. At any time during the trial, we test whether the MTD is below or above the minimum and maximum doses, respectively. If during the trial, there is evidence that the MTD is outside the range of doses, we extend the range of doses and complete the trial with the planned sample size. At the end of the trial, a Bayes estimate of the MTD is proposed. We evaluate design operating characteristics in terms of safety of the trial design and efficiency of the MTD estimate under various scenarios and model misspecification. The methodology is further compared to the original EWOC design. We showed by comprehensive simulation studies that the proposed method is safe and can estimate the MTD more efficiently than the original EWOC design.
Keywords: Cancer phase I trials, Maximum tolerated dose, Escalation with overdose control, Dose limiting toxicity, Flexible dose range
1. Introduction
Cancer phase I clinical trials are small sequential studies designed to investigate the safety and tolerability of investigational new agents or combination of existing cytotoxic and/or biologic agents. These trials enroll late stage patients who have exhausted all standard therapy (Roberts et al., 2004). The primary objective of these trials is to estimate a dose level that is associated with a predetermined level of dose limiting toxicity (DLT). Such a dose is referred to as the maximum tolerated dose (MTD) or phase II dose. A review of single agent dose-finding methods can be found in (Chevret, 2006; Le Tourneau, Lee and Siu, 2009; Ting, 2006). The most commonly used design for cancer phase I trials is the 3+3 algorithm (Rogatko et al., 2007) although many authors showed that it is inefficient in estimating the MTD and can lead to many patients in the trial receiving sub-therapeutic doses, see e.g (Babb, Rogatko and Zacks, 1998; Hansen et al., 2014; Rogatko et al., 2015). A recent comparative review of the 3+3 design relative to some model based designs further confirmed the inefficiency of the these algorithm based designs and emphasized their dependence on the target probability of DLT rate (Ananthakrishnan et al., 2017).
Existing statistical designs such as the continual reassessment method (CRM) (Cheung and Chappell, 2000; Faries, 1994; Goodman, Zahurak and Piantadosi, 1995; Møller, 1995; O’Quigley, Pepe and Fisher, 1990; O’Quigley and Shen, 1996; Piantadosi, Fisher and Grossman, 1998) and escalation with overdose control (EWOC) (Babb et al., 1998; Babb and Rogatko, 2001; Chen, Tighiouart and Kowalski, 2012; Tighiouart, Cook-Wiens and Rogatko, 2012a, b; Tighiouart, Liu and Rogatko, 2014; Tighiouart and Rogatko, 2010; Tighiouart and Rogatko, 2012; Tighiouart, Rogatko and Babb, 2005; Zacks, Rogatko and Babb, 1998) and algorithmic designs such as the standard ‘3+3′ and its modifications (Derman, 1957; Durham, Flournoy and Rosenberger, 1997; Storer, 1989) or accelerated titration design (Simon et al., 1997) consist of searching for the MTD among a pre-determined set of discrete doses or within a bounded interval of doses specified by the clinicians. If the true MTD happens to be below the minimum dose available in the trial Xmin, then such designs lead to stopping the trial using some type of statistical or deterministic stopping rules. As a result, enrollment to the trial is either suspended and the clinical protocol is amended to expand the dose range or the trial is closed to enrollment. On the other hand, if the true MTD is above the maximum dose available in the trial Xmax, these designs will usually proceed and enroll the planned number of patients in the trial and recommend the last dose as the phase II dose or the clinicians amend the protocol to include one or more doses above Xmax. This situation is not uncommon based on our experience reviewing amendments of protocols describing early phase cancer trials. For instance, we recently reviewed an amendment of a protocol for a phase I trial of a synthetic copolymer-drug conjugate (SDX-7320) in patients with advanced refractory or late-stage solid tumors. The trial design used the 3+3 algorithm exploring seven dose levels of the drug. The amendment consisted of adding 3 dose levels above the maximum dose level originally proposed because there were no DLTs among all 21 patients enrolled to the trial.
In this manuscript, we extend the EWOC design by expanding the dose range [Xmin, Xmax] during the trial if there is evidence that the true MTD is outside this range. Clinicians specify a discrete set of doses {d1, …, dk} or a range of available doses in the interval [Xmin, Xmax] based on their prior belief or preliminary data about the safety of the dose Xmin and the location of the true MTD in [Xmin, Xmax]. We next ask clinicians to specify a range of doses they are willing to expand below Xmin if there is statistical evidence that Xmin is too toxic. We further ask them to pre-specify a range of doses to be expanded beyond Xmax if there is statistical evidence that the probability of DLT at Xmax is way below the target probability of DLT. This approach will allow us to search for the MTD beyond [Xmin, Xmax] and without suspending accrual, stopping the trial, or recommending a suboptimal dose as the phase II dose. Moreover, design operating characteristics are carried out at the design stage of the trial and will take into account any dose range expansion below Xmin or above Xmax.
The manuscript is organized as follows. In section 2, we give a detailed description of the methodology and describe the trial design with a possible dose range expansion. In section 3, we present the operating characteristics of the design using continuous and discrete dose levels and under model misspecification. Section 4 contains some final remarks and discussion of practical implementations.
2. Model
2.1 Dose-Toxicity Model
Consider the problem of identifying a tolerable dose x > 0 of a cytotoxic agent. We consider the dose-toxicity model of the form
| (2.1) |
where Y is the indicator of dose limiting toxicity (DLT), Y = 1 if a patient given dose x exhibits DLT within one cycle of therapy, and Y = 0 otherwise, and F is a known cumulative distribution function. Let Xmin and Xmax be the minimum and maximum doses available in the trial.
We will assume that β1 > 0 so that the probability of DLT increases with dose. The MTD is defined as the dose γ > 0 such that
| (2.2) |
The value of the target probability θ is pre-specified by the clinicians and depends on the nature and clinical manageability of the DLT; it is set relatively high when the DLT is a transient, reversible or non-fatal condition, and low when it is life threatening. It follows from (2.1) and (2.2) that
| (2.3) |
Using the transformation h(u) = (u − Xmin)/(Xmax − Xmin), we standardize the dose levels to be in the interval [0, 1] so that Xmin corresponds to dose level 0 and Xmax to dose level 1. The original EWOC design (Babb et al., 1998) assumes that γ ε [Xmin, Xmax] with prior (and hence posterior) probability 1. This assumption may be very restrictive in some applications and the performance of the design is suboptimal if the true MTD γtrue is near the boundaries of the dose range. When γtrue is close to Xmax, the dose escalation rate slows down resulting in a large bias of the estimate of the MTD. Tighiouart et al. (Tighiouart et al., 2005) introduced a class of flexible priors by expanding the support of γ to [Xmin, ∞). If γtrue is close to Xmin, the method results in an excessive number of DLTs and ad hoc stopping rules are introduced. One way to further expand the support of γ to [0, ∞) is to reparameterize model (2.1) in terms of ρ0, the probability of DLT at dose level 0, and ρ1, the probability of DLT at dose level 1. This reparameterization is convenient to clinicians since prior information on ρ0 and ρ1 may be available from other trials. It can be shown that
| (2.4) |
The standardized MTD in (2.3) becomes
| (2.5) |
Let Dn = {(xi,yi), i = 1, …, n} be the data after enrolling n patients in the trial. The likelihood function for the model parameters is
| (2.6) |
where
| (2.7) |
2.2 Prior and Posterior Distributions
We assume that ρ1 ~ beta(a1, b1) and conditional on ρ1, ρ0 / ρ1 ~ beta(a2, b2). Under lack of prior information about these parameters, we take ai = bi, i = 1,2. Let Dn = {(xi, yi), i = 1,…, n} be the data after enrolling n patients in the trial. Using Bayes rule, the posterior distribution of the model parameters is
| (2.8) |
where
| (2.9) |
Features of this posterior distribution are estimated using WinBUGS (Lunn et al., 2000) and JAGS. In the design described below, the posterior distribution of the standardized MTD π(γ |D1) obtained using (2.5) is truncated to the interval [−Xmin/(Xmax − Xmin), ∞) since the dose is always positive.
2.3 Trial Design
The adaptive design uses the EWOC scheme where at each stage of the trial, the posterior probability of overdosing a future patient is bounded by a feasibility bound α. Furthermore, at each stage of the trial, we check whether or not the minimum dose Xmin is likely to be too toxic and the maximum dose Xmax is likely to be very safe. If either condition holds, the dose range is expanded accordingly. Let L be the largest amount of the drug the clinician is willing to expand from below in case Xmin is too toxic and U be the largest amount to be added to Xmax in case Xmax is very safe. Denote by П−1(·| Di) the inverse cumulative distribution function of the posterior distribution of the MTD γ given the data Di.
The first patient (or cohort of m patients) receives dose x1 = Xmin.
- The second patient receives dose x2 corresponding to the α-th percentile of π(γ |D1), the posterior distribution of the MTD given the data. In general, the i-th patient receives dose
- For i=1,…,n−1, if
expand the range of doses to [Xmin − L, Xmax] and patient i+1 receives the dose(2.10)
If
expand the range to [Xmin, Xmax + U] and patient i+1 receives the dose(2.11) Repeat steps 2 and 3 until n patients are enrolled to the trial.
At the end of the trial, we estimate the MTD as the median of the posterior distribution π(γ |Dn). Step 2 of the algorithm states that the dose allocated to the i-th patient in the trial is П−1(α | Di−1) provided that this dose is within the range of doses available in the trial. Otherwise, the dose allocated to the i-th patent is either Xmin or Xmax depending on whether П−1(α | Di−1) is below the minimum dose or above the maximum dose available in the trial. Step 3 states that anytime during the trial, if there is evidence that either the minimum dose is likely to be to toxic or the maximum doses is likely to have a probability of DLT below the target θ, then the dose range is expanded either below Xmin or above Xmax and dose allocation proceeds as in step 2 with this expanded range of doses.
The design parameters δ, δ1, and δ2, are selected to produce good operating characteristics. L and U control the size of the dose range expansion and are pre-specified by the clinicians. The parameter α is the feasibility bound and controls the probability of overdosing patients. It is set at 0.1 at the onset of the trial, and then increases by increments of 0.05 to a maximum value of 0.5 after each patient is enrolled to the trial. Although the use of a varying feasibility bound may violate the coherence (Cheung, 2005) property of EWOC (Bartroff and Leung Lai, 2011; Wheeler, 2016), we found that this occurred in less than 7% of the simulated trials when the true MTD is below the minimum dose. When the true MTD is in the middle of the dose interval or above the maximum dose, violation of the coherence property never occurred. In the simulation results we studied, the parameters associated with the stopping rules are δ1 = δ2 = 0 and δ = 0.8.
The possibility of modifying the range of doses during the trial is very useful to clinicians and can help salvage a trial that shows a high rate of DLTs around the minimum dose or a low rate of DLTs around the maximum dose. In such cases, the proposed design expands the range of doses without suspending enrollment to the trial and future amendments to the clinical protocol may be avoided if the dose expansion is big enough to include the true MTD.
3. Simulation Studies
3.1 Simulation Set-up and Scenarios
We studied the performance of this design by simulating m = 1000 trials under three scenarios of the true MTD using the logistic function F(u) = (1 + e−u)−1 as the true and working model with both continuous doses and a discrete set of doses. Model misspecification was examined using a normal distribution function as the response for the true model and the logistic function in the working model for the continuous doses. In all cases, the target probability of DLT is θ = 0.33, planned trial sample size is n = 30 patients, and aj = bj = 1, j = 1, 2 which corresponds to vague priors for ρ0 and ρ1. For a hypothetical trial, we took Xmin = 100 mg/m2 and Xmax = 500 mg/m2, L = 100 mg/m2, U = 200 mg/m2 and the following scenarios for the true MTD, γ = 37 mg/m2, 308 mg/m2, and 586 mg/m2. The doses are standardized to the interval [0, 1] and the true standardized MTDs are −0.16, 0.52, and 1.22. The corresponding true parameters for the reparameterized logistic dose-toxicity model are (ρ0, ρ1) = (0.45, 0.95), (0.05, 0.8), and (0.01, 0.2).
In the case of continuous dose levels, we compared the safety of a trial and efficiency of the estimated MTD between the following three designs, (1) Dose expansion (DE) design: this is the proposed design where a stopping rule is put in place and the range of doses expanded if needed. (2) No dose expansion (NDE) design: this design uses the stopping rule but does not expand the range of doses, and (3) No stopping rule (NS): this design does not use a statistical stopping rule as in the original EWOC (Babb et al., 1998; Tighiouart and Rogatko, 2010), i.e., step 3 of the algorithm in Section 2.3 is skipped and all n patients are enrolled to the trial. We further compared the performance of the proposed design (DE) with the NS design but starting with the expanded dose range [Xmin − L, Xmax + U] to assess the safety of the trial and efficiency of the estimate of the MTD had we started the trial with a much wider dose range instead of expanding it during the trial. This latter design is called expanded range design (ERD).
Let Yi,j be the binary indicator of DLT of the j-th patient in the i-th trial. Safety of each design is assessed by computing the average percent of DLTs
| (3.1) |
and the percent of trials that have a DLT rate exceeding θ + δ, for δ = 0.05, 0.1,
| (3.2) |
The threshold θ + 0.1 is usually considered to be an indication of an excessive DLT rate. Efficiency of the trial is evaluated by calculating the average bias
| (3.3) |
where is the estimate of the MTD for the i-th trial and γtrue is the true MTD under a particular scenario, the root mean square error
| (3.4) |
the percent of trials with estimated MTD within (100×p)% of the dose range of the true MTD, 0 < p < 1,
| (3.5) |
and the percent of trials with estimated MTD within (100×p)% of the value of the true MTD, 0 < p < 1,
| (3.6) |
The statistics in (3.5) and (3.6) can be interpreted as the percent of MTD recommendation within a neighborhood of the true MTD. They differ with respect to the structure of this neighborhood. In (3.5), the width of the tolerance interval is a fraction of the dose range and is constant regardless of the value of γtrue, see (Tighiouart et al., 2012a). In (3.6), the width of the tolerance interval is a fraction of γtrue so that wider intervals are tolerated for high values of γtrue and tighter neighborhoods are imposed for values of γtrue near the minimum dose Xmin. Such a statistic was used for single agent dose finding trials in (Van Meter, Garrett-Mayer and Bandyopadhyay, 2011) and dose combination trials in (Tighiouart, Piantadosi and Rogatko, 2014).
The discrete dose simulations used a set of six dose levels evenly distributed on the original dose range at increments of 80 mg/m2, which corresponds to the set {0, 0.2, 0.4, 0.6, 0.8, 1} on the standardized dose scale. We considered a case where the lower bound might be extended by one dose level to 50 mg/m2 (−0.125 standardized dose) if the stopping rule indicates a high posterior probability of toxicity. Similarly, the upper bound might be extended to 600 mg/m2 (1.25 standardized dose). The true MTDs were chosen to be the same as in the continuous dose simulation scenarios. The calculation of the next dose proceeded as in the continuous case, but the next dose assigned was the highest discrete dose that was less than the dose recommended by the algorithm. Under each scenario of the true MTD m = 1000 trials were simulated with the same stopping rules in place to expand the set of doses either below or above the original range. In addition to these dose expansion simulations, m = 1000 trials were run with no stopping rule and no dose expansion as a comparison to original EWOC with the six discrete doses. Each set of m = 1000 trials was summarized by calculating the true probability of DLT at each dose level, the percent of patients in all trials allocated to each dose level, and the percent of MTD recommendation.
Model robustness was studied using a normal link function (true model) so that the probability of toxicity at the true MTD was θ, and the probability of toxicity at the minimum dose, ρ0, was higher or lower than the corresponding logistic function (working model). There were two normal models for each scenario of the true MTD. For the logistic parameters (ρ0, ρ1) = (0.45, 0.95) the two scenarios for misspecification chosen were (A) ρ0 = 0.55 and (B) ρ0 = 0.42. For the (ρ0, ρ1) = (0.05, 0.8) logistic model the two normal models chosen were (C) ρ0 = 0.15 and (D) ρ0 = 0.01, and for the (ρ0, ρ1) = (0.01, 0.2) logistic model the two normal models chosen were (E) ρ0 = 0.1 and (F) ρ0 = 0.0001. The probabilities of toxicity as a function of standardized dose for these models are shown in the response profiles of Figure 1. The model misspecification simulations were run with the stopping rules to expand the dose range in the same way as in the main simulation results.
Figure 1.
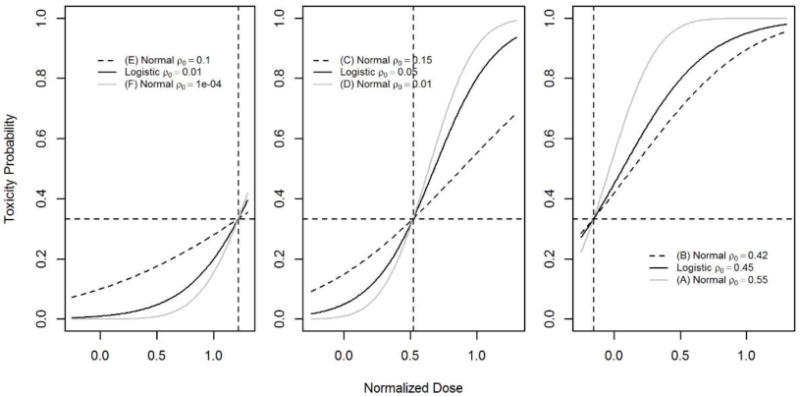
Response profiles for probability of toxicity as a function of standardized dose in logistic and normal models for each scenario of the true MTD. Dotted lines show dose and probability of the true MTD under the three scenarios.
3.2 Results
Table 1 gives the probability of expanding the dose range under the three scenarios along with the median trial sample size where the dose range was expanded and 90% confidence interval. When γtrue is below the minimum dose Xmin, the probability of expanding the dose range from below is 0.81 with a median sample size of 11. The probability of expanding the dose range from above is 0.96 when γtrue is above the maximum dose Xmax and the corresponding median sample size is 6. Similar results are obtained when using discrete dose levels. When the model is misspecified, the probability of expanding the dose range depends on the location of γtrue and the toxicity probability of the true model relative to the working model around γtrue. For instance, when the true MTD is below Xmin, the probability of expanding the dose range from below when the true model is the normal link function (B) is 0.66 and this probability increases to 0.99 under the normal link function (A). This is expected since the probability of DLT under (B) is much lower relative to the logistic link function and is higher under (A) relative to the logistic link function as shown in the right panel of Figure 1. Similar patterns are observed when the true MTD is above Xmax when the true models are the normal links (E) and (F), see the right panel of Figure 1. We conclude that the probability of expanding the dose range when the true MTD is outside the dose range is reasonably high under slight departure from the true model around the true MTD.
Table 1.
Probability of expanding dose range and CI for sample size n where stopping rule was applied.
| Logistic response | True MTD | |||
|---|---|---|---|---|
| −0.16 | 0.52 | 1.22 | ||
| Continuous doses | P(expand) | 0.810 | 0.048 | 0.960 |
| Median n | 11 | 6 | 6 | |
| 90% CI for n | [4, 27] | [6, 6] | [6, 19.1] | |
| Discrete doses | P(expand) | 0.804 | 0.025 | 0.931 |
| Median n | 11.5 | 7.0 | 7.0 | |
| 90% CI for n | [4, 27] | [6.2. 11] | [7, 22] | |
| Normal response | (B) | (D) | (F) | |
| P(expand) | 0.664 | 0.010 | 0.985 | |
| Median n | 12.5 | 6.0 | 6.0 | |
| 90% CI for n | [4, 27] | [6, 6] | [6, 18] | |
| Normal response | (A) | (C) | (E) | |
| P(expand) | 0.987 | 0.139 | 0.643 | |
| Median n | 8.0 | 6.0 | 6.0 | |
| 90% CI for n | [4, 19] | [6, 18.1] | [6, 25] | |
3.2.1 Trial Safety
Table 2 shows that when the true MTD is below the minimum dose available in the trial, the average percent of DLTs computed using (3.1) is lower using the proposed design (DE) relative to a design where no stopping rule is used (NS) or the design that stops the trial but does not expand the range of doses (NDE). When the true MTD is in the middle of the dose range, the average percent of DLTs is close to the target probability of DLT θ = 0.33 for all three designs. In the case where the true MTD is above Xmax, aveDLT using design DE is much closer to the target θ = 0.33 than the other two designs. The high DLT rate of 45.9% using DE is probably due to the fact that a much higher rate of DLT is observed prior to the dose range expansion from below. The same conclusion holds for the percent of trials with an excessive DLT rate. When the true MTD is either in the middle of the dose range or above Xmax, the percent of trials with DLT rate exceeding θ computed using (3.2) are 4.7% and 0.1%, respectively. When the true MTD is below Xmin, this percent is lower using design DE relative to the other two designs, but is still high in the order of 79%. Again, this is due to the fact that the median sample size before expanding the dose range is 11.
Table 2.
Operating Characteristics comparing the three designs using continuous dose logistic responses
| True MTD | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −0.16 | 0.52 | 1.22 | ||||||||
| Design | DE | NDE | NS | DE | NDE | NS | DE | NDE | NS | |
| Safety | Average % DLTs | 45.900 | 56.100 | 48.600 | 34.100 | 32.300 | 34.000 | 28.200 | 4.700 | 16.600 |
| % trials w. DLT rate > θ + 0.1 | 79.0 | 92.7 | 84.8 | 4.7 | 3.6 | 4.7 | 0.1 | 0.0 | 0.0 | |
| Efficiency | Average MTD | −0.058 | 0.018 | 0.013 | 0.519 | 0.542 | 0.521 | 1.212 | 0.999 | 0.996 |
| Average bias | 0.099 | 0.174 | 0.169 | −0.001 | 0.022 | 0.001 | −0.004 | −0.217 | −0.220 | |
| RMSE | 0.128 | 0.178 | 0.172 | 0.105 | 0.148 | 0.097 | 0.150 | 0.218 | 0.221 | |
| % trials with MTD estimate in | (γ − 0.10, γ + 0.10) | 56.7 | 0.0 | 0.0 | 66.3 | 62.4 | 71.3 | 49.4 | 0.0 | 0.0 |
| (γ − 0.15, γ + 0.15) | 72.9 | 0.0 | 0.0 | 84.8 | 79.9 | 88.6 | 67.2 | 0.0 | 0.0 | |
| (γ − 0.15γ, γ + 0.15γ) | 16.3 | 0.0 | 0.0 | 55.0 | 53.4 | 58.9 | 74.5 | 0.0 | 0.0 | |
| (γ − 0.20γ, γ + 0.20γ) | 21.0 | 0.0 | 0.0 | 68.5 | 64.3 | 73.1 | 87.8 | 99.0 | 96.0 | |
Comparing the different response functions under model misspecification showed similar average rates of DLTs within each scenario of the true MTD, but larger differences in the proportion of trials that exceeded a DLT rate of 0.43 when he true MTD is below Xmin. The percent of trials that were unsafe was 79% for the logistic response model, but was 89.2% for model (A) and 72.1% for model (B). When the true MTD was in the middle of the dose range all three models had average DLT rates within one percent of each other near the target DLT rate of 33%. The percent of unsafe trials for the logistic model in this scenario was 4.7%, whereas model (C) had 6.9% and model (D) had 4%. When the true MTD was above the dose range all models were under the target average DLT rate of 33%. The logistic response model and model (F) had the same average DLT rate of 28.2%, and model (E) had a slightly lower average of 26.6%. The percent of unsafe trials was less than one percent in all three response models in this case. We conclude that the logistic model is reasonably robust with respect to the safety of the trial.
Simulation results in the case of discrete doses using the dose expansion rule also had a lower proportion of DLTs and lower proportion of trials with excessive DLT rates when the true MTD was below the minimum dose compared to the designs NDE and NS, see Table 3. All of the discrete dose simulations had DLT rates that were below the target rate of 0.33 when the true MTD was in the middle of the dose range or above the maximum dose. The trials with dose expansion rules achieved an average DLT rate closer to the target rate than the designs NDE and NS.
Table 3.
Operating Characteristics comparing the three designs using discrete dose logistic responses
| Standardized Dose Level | True Prob. of DLT | Percent Patients at Dose Level | Percent Trials with Dose Level as MTD | |||||
|---|---|---|---|---|---|---|---|---|
| DE | NDE | NS | DE | NDE | NS | |||
|
True MTD −0.16 |
−0.125 | 0.356 | 36.5 | – | – | 71.7 | – | – |
| 0 | 0.45 | 51 | 77.71 | 86.4 | 27.6 | 99.3 | 99.2 | |
| 0.2 | 0.605 | 10.2 | 18.08 | 10.6 | 0.7 | 0.7 | 0.8 | |
| 0.4 | 0.742 | 1.97 | 3.546 | 2.35 | 0.0 | 0.0 | 0.0 | |
| 0.6 | 0.844 | 0.33 | 0.599 | 0.51 | 0.0 | 0.0 | 0.0 | |
| 0.8 | 0.91 | 0.03 | 0.06 | 0.06 | 0.0 | 0.0 | 0.0 | |
| 1 | 0.95 | 0.003 | 0.006 | 0.01 | 0.0 | 0.0 | 0.0 | |
| 1.25 | 0.977 | 0 | – | – | 0.0 | – | – | |
| Average % DLTs: DE 42.4, NDE 52.3, NS 46.1; % trials w. DLT rate > θ + 0.1: DE 52.3, NDE 83.2, NS 71.5 | ||||||||
|
True MTD 0.52 |
−0.125 | 0.03 | 0 | – | – | 0.0 | – | – |
| 0 | 0.05 | 8.27 | 8.43 | 8.3 | 0.0 | 0.0 | 0.0 | |
| 0.2 | 0.111 | 13.84 | 14.06 | 14.7 | 9.4 | 9.2 | 9.2 | |
| 0.4 | 0.229 | 40.98 | 41.27 | 42.9 | 61.4 | 60.1 | 63.6 | |
| 0.6 | 0.414 | 28.86 | 28.54 | 26.6 | 27.9 | 26.9 | 26.3 | |
| 0.8 | 0.627 | 6.27 | 6.12 | 5.8 | 1.3 | 1.3 | 0.9 | |
| 1 | 0.8 | 1.647 | 1.58 | 1.7 | 0.0 | 2.5 | 0.0 | |
| 1.25 | 0.922 | 0.12 | – | – | 0.0 | – | – | |
| Average % DLTs: DE 28.5, NDE 27.6, NS 28.2; % trials w. DLT rate > θ + 0.1: DE 0.1, NDE 0.0, NS 0.0 | ||||||||
|
True MTD 1.22 |
−0.125 | 0.007 | 0 | – | – | 0.0 | – | – |
| 0 | 0.01 | 6.83 | 17.98 | 6.85 | 0.0 | 0.0 | 0.0 | |
| 0.2 | 0.019 | 3.68 | 9.68 | 3.7 | 0.0 | 0.0 | 0.0 | |
| 0.4 | 0.035 | 4.23 | 11.14 | 3.98 | 0.0 | 0.0 | 0.0 | |
| 0.6 | 0.065 | 5.75 | 14.59 | 5.69 | 0.7 | 0.6 | 0.3 | |
| 0.8 | 0.116 | 11.47 | 21.1 | 10.36 | 7.3 | 2.8 | 5.0 | |
| 1 | 0.2 | 28.14 | 25.51 | 69.41 | 40.9 | 96.6 | 94.7 | |
| 1.25 | 0.358 | 39.91 | – | – | 51.1 | – | – | |
| Average % DLTs: DE 21.9, NDE 5.3, NS 15.6; % trials w. DLT rate > θ + 0.1: DE 0.0, NDE 0.0, NS 0.0 | ||||||||
3.2.2 Trial Efficiency
Table 2 shows that the average bias of the estimate of the MTD computed using (3.3) is always lower when using the proposed design DE relative to the other two designs when the true MTD is outside the range of doses available in the trial. This is expected since designs NDE and NS cannot allocate doses or recommend MTD estimates outside the dose range [Xmin, Xmax]. When the true MTD is in the middle of the dose range, the average bias is very small, similar to the NS design. Similar conclusions hold for the RMSE computed using (3.4). Similarly, the percent of trials with estimated MTD in a neighborhood of the true MTD as measured by (3.5, 3.6) is almost always higher when using design DE relative to the other two designs when the true MTD is outside the range of doses. When the true MTD is in the middle of the dose range, design NS does better than design DE with an excess of 4 to 5% in the percent of trials with MTD estimate within a given neighborhood of the true MTD. In the case of discrete dose levels, Table 3 shows that when the true MTD is below the minimum dose available in the trial, designs NDE and NS recommend the minimum dose as the MTD 99% of the time whereas design DE recommends this dose 28% of the time. However, design DE does recommend the expanded dose from below 72% of the time. Similar conclusions can be drawn when the true MTD is above the maximum dose available in the trial. When the true MTD is in the middle of the dose range, there is essentially no difference in the three design in recommending either dose level 3 or 4 as the MTD. Based on these results, we conclude that the method is useful in estimating the MTD efficiently and is an improvement over the original EWOC design in the case where the true MTD turns out to be outside the range of doses available in the trial.
3.2.3 Model misspecification
Model robustness was assessed by comparing the operating characteristics of the DE model using the logistic link function as the true model to the DE models using normal link functions as the true models. Table 4 shows that the average rate of DLTs are similar across all scenarios for the three models and the percent of trials with an excessive rate of DLT are fairly close except when γtrue is below Xmin and when using model (A), the model with the greatest departure from the true logistic model, see the third panel of Figure 1. Based on these results, we conclude that safety of the trial is in general not compromised. The largest difference in the average bias between the true and misspecified model is 0.09 and is achieved when using model (E), again a model with the highest departure from the logistic model. In any case, this highest difference corresponds to 9% of the dose range and is practically not very significant. Similar conclusions can be drawn using the RMSE for the various models. When using the measures of efficiency REC1 and REC2 in equations (3.5–3.6), there is a big difference in the percent of trials recommending the MTD in a neighborhood of the true MTD, with the largest differences obtained when using models with big departures from the logistic model (A, C, E). This is probably due to the small sample size, width of the interval around the true MTD defining the neighborhood, and extent of the departure from the true model. These differences are less pronounced when using discrete dose levels (results not shown). In the case of discrete doses, Table 3 shows that the percent selection of the MTD using the proposed design is 72% when γtrue is below the minimum dose and is 51% when γtrue is above the maximum dose. The corresponding percentages for the proposed design and the design with no dose range expansion are very close. Similar conclusions are achieved when comparing the number of patients treated at or near the true MTD between the two designs.
Table 4.
Operating Characteristics comparing the three response models using continuous doses
| True MTD | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −0.16 | 0.52 | 1.22 | ||||||||
| Response ρ0 | (B) | Logistic | (A) | (D) | Logistic | (C) | (F) | Logistic | (E) | |
| Safety | Average % DLTs | 45.000 | 45.900 | 47.800 | 33.600 | 34.100 | 33.500 | 28.200 | 28.200 | 26.600 |
| % trials w. DLT rate > θ + 0.1 | 72.1 | 79.0 | 89.2 | 4.0 | 4.7 | 6.9 | 0.3 | 0.1 | 0.1 | |
| Efficiency | Average MTD | −0.018 | −0.058 | −0.116 | 0.519 | 0.519 | 0.556 | 1.211 | 1.212 | 1.1246 |
| Average bias | 0.139 | 0.099 | 0.041 | −0.001 | −0.001 | 0.036 | −0.005 | −0.004 | −0.091 | |
| RMSE | 0.225 | 0.128 | 0.064 | 0.082 | 0.105 | 0.199 | 0.122 | 0.150 | 0.307 | |
| % trials: MTD estimate is in | (γ − 0.10, γ + 0.10) | 42.1 | 56.7 | 87.3 | 78.9 | 66.3 | 37.6 | 62.0 | 49.4 | 16.9 |
| (γ − 0.15, γ + 0.15) | 56.6 | 72.9 | 96.7 | 93.1 | 84.8 | 55.4 | 77.6 | 67.2 | 24.7 | |
| (γ − 0.15γ, γ + 0.15γ) | 7.9 | 16.3 | 35.3 | 66.8 | 55.0 | 29.0 | 85.7 | 74.5 | 28.6 | |
| (γ − 0.20γ, γ + 0.20γ) | 10.7 | 21.0 | 45.4 | 81.2 | 68.5 | 39.4 | 94.3 | 87.8 | 46.9 | |
Finally, operating characteristics comparing the performance of the proposed design (DE) and the design starting with the expanded dose range (ERD) for the continuous and discrete dose levels cases are listed in Tables 5 and 6, respectively. As expected, the percent of DLTs for the ERD design is lower relative to the DE design when the true MTD is below Xmin and the ERD design is more efficient in estimating the MTD since the dose range (Xmin − L, Xmax + U) includes the true MTD. However, when the true MTD is within the range (Xmin, Xmax) or above Xmax, safety of the trial is not compromised but there is a significant loss of efficiency of the estimate of the MTD when using the ERD design relative to the DE design since the dose range has been extended from (100, 500) to (0, 700), an increase of 75% in the width of the dose range. For instance, when γtrue = 1.22, the average bias using the ERD design is −0.213 compared to −0.004 for the DE design and the percent of trials with MTD estimate within a neighborhood of γtrue is much higher using the ED design relative to the ERD design, see the last four rows of Table 5 when γtrue = 0.53, 1.22. Similar conclusions can be made for the discrete dose level case, see Table 6.
Table 5.
Operating Characteristics comparing the DE and ERD designs for continuous doses.
| True MTD | |||||||
|---|---|---|---|---|---|---|---|
| −0.16 | 0.52 | 1.22 | |||||
| Design | DE | ERD | DE | ERD | DE | ERD | |
| Safety | Average % DLTs | 45.900 | 34.800 | 34.100 | 20.200 | 28.200 | 14.000 |
| % trials w. DLT rate > θ + 0.1 | 79.0 | 12.9 | 4.7 | 0.0 | 0.1 | 0.0 | |
| Efficiency | Average MTD | −0.058 | −0.169 | 0.519 | 0.409 | 1.212 | 1.003 |
| Average bias | 0.099 | −0.012 | −0.001 | −0.111 | −0.004 | −0.213 | |
| RMSE | 0.128 | 0.059 | 0.105 | 0.156 | 0.150 | 0.275 | |
| % trials with MTD estimate in | (γ − 0.10, γ + 0.10) | 56.7 | 94.2 | 66.3 | 42.5 | 49.4 | 18.3 |
| (γ − 0.15, γ + 0.15) | 72.9 | 97.8 | 84.8 | 65.9 | 67.2 | 30.4 | |
| (γ − 0.15γ, γ + 0.15γ) | 16.3 | 23.3 | 55.0 | 21.8 | 74.5 | 17.8 | |
| (γ − 0.20γ, γ + 0.20γ) | 21.0 | 31.4 | 68.5 | 28.4 | 87.8 | 25.0 | |
Table 6.
Operating Characteristics comparing the DE and ERD designs for discrete doses.
| Standardized Dose Level | True Prob. of DLT | Percent Patients at Dose Level | Percent Trials with Dose Level as MTD | ||||
|---|---|---|---|---|---|---|---|
| DE | ERD | DE | ERD | ||||
|
True MTD −0.16 |
−0.125 | 0.356 | 36.500 | 82.850 | 71.7 | 96.9 | |
| 0.000 | 0.450 | 51.000 | 15.250 | 27.6 | 3.1 | ||
| 0.200 | 0.605 | 10.200 | 1.780 | 0.7 | 0.0 | ||
| 0.400 | 0.742 | 1.970 | 0.130 | 0.0 | 0.0 | ||
| 0.600 | 0.844 | 0.330 | 0.000 | 0.0 | 0.0 | ||
| 0.800 | 0.910 | 0.030 | 0.000 | 0.0 | 0.0 | ||
| 1.000 | 0.950 | 0.003 | 0.000 | 0.0 | 0.0 | ||
| 1.250 | 0.977 | 0.000 | 0.000 | 0.0 | 0.0 | ||
| Average % DLTs: DE 42.4, ERD 36.2; % trials w. DLT rate > θ + 0.1: DE 52.3, ERD 23.5 | |||||||
|
True MTD 0.52 |
−0.125 | 0.030 | 0.000 | 2.080 | 0.0 | 0.0 | |
| 0.000 | 0.050 | 8.273 | 21.380 | 0.0 | 2.3 | ||
| 0.200 | 0.111 | 13.843 | 39.950 | 9.4 | 43.4 | ||
| 0.400 | 0.229 | 40.977 | 30.170 | 61.4 | 48.6 | ||
| 0.600 | 0.414 | 28.863 | 5.890 | 27.9 | 5.4 | ||
| 0.800 | 0.627 | 6.273 | 0.490 | 1.3 | 0.3 | ||
| 1.000 | 0.800 | 1.647 | 0.040 | 0.0 | 0.0 | ||
| 1.250 | 0.922 | 0.123 | 0.000 | 0.0 | 0.0 | ||
| Average % DLTs: DE 28.5, ERD 15.1; % trials w. DLT rate > θ + 0.1: DE 0.1, ERD 0.0 | |||||||
|
True MTD 1.22 |
−0.125 | 0.007 | 0.000 | 0.350 | 0.0 | 0.0 | |
| 0.000 | 0.010 | 6.830 | 11.130 | 0.0 | 0.0 | ||
| 0.200 | 0.019 | 3.680 | 10.760 | 0.0 | 0.1 | ||
| 0.400 | 0.035 | 4.230 | 15.330 | 0.0 | 2.7 | ||
| 0.600 | 0.065 | 5.750 | 21.330 | 0.7 | 16.4 | ||
| 0.800 | 0.116 | 11.470 | 21.400 | 7.3 | 38.2 | ||
| 1.000 | 0.200 | 28.140 | 14.700 | 40.9 | 34.2 | ||
| 1.250 | 0.358 | 39.910 | 5.000 | 51.1 | 8.4 | ||
| Average % DLTs: DE 21.9, ERD 9.5; % trials w. DLT rate > θ + 0.1: DE 0.0, ERD 0.0 | |||||||
4. Discussion
We described a dose finding design for cancer phase I clinical trials which uses a flexible dose range. In this design, clinicians propose a dose range [Xmin, Xmax] for searching for the MTD with the flexibility to expand this range to [Xmin − L, Xmax + U] if there is statistical evidence that the lowest dose is too toxic or the largest dose level is too safe. The approach is an extension of the method described in (Babb et al., 1998) and is more general than the extension described in (Tighiouart et al., 2005). When there is evidence that the lowest dose is too toxic or the highest dose has a low probability of DLT, the method has several advantages over previous approaches. For instance, there is no need to suspend accrual, amend the clinical protocol, or close the trial since the consequences of expanding the dose range are evaluated using the design operating characteristics at the design stage of the trial. However, this approach may not prevent future amendments to the trial if the expanded dose range is not wide enough to include the true MTD.
We assessed the performance of the approach using three scenarios for the true MTD and by comparing the proposed design with a design that does not expand the range of doses and a design that does not use a statistical stopping rule as in the original EWOC. We showed that our method is safer and can estimate the MTD more efficiently. Specifically, about 36% of the patients are treated at the MTD when γtrue is below the minimum dose level available in the trial initially and 40% are treated at the MTD when γtrue is above the maximum dose using our approach compared to 0.0% if the dose range is not expanded. Model robustness was assessed using various link functions and we found that safety of the trial was not compromised in general. Furthermore, the method was fairly robust when comparing the average bias between the true and misspecified models but the percent of MTD recommendations can differ substantially between the true and misspecified model depending on the width of the interval around the true MTD defining the neighborhood. Although these differences are less pronounced for trials that use discrete dose levels (results not shown), these considerations should be carefully evaluated at the design stage of the trial and discussed with the clinician before the trial is moved forward. For instance, alternative statistics such as percent of trials with MTD estimate within 20% or 25% of the dose range around the true MTD may also be considered to assess the performance of the method. Furthermore, when the true MTD is outside the range of doses, the probability of expanding the dose range is consistently high under model misspecification. Based on these results, we conclude that the method is fairly robust under small departures from the true model around the true MTD.
We further compared the performance of the proposed design with the one starting with the expanded dose range instead. We found that if the true MTD is below the minimum dose available in the trial, the later design is safer and more efficient than the DE design but the DE design is worth using when the true MTD is within the dose range or above the maximum dose available in the trial as assessed by the high gain in efficiency of the estimate of the MTD. In any case, the choice of the minimum dose in a real prospective trial is based on the clinician’s best knowledge of the drug from other similar trials or is taken as a small fraction of the lethal dose in 10% of mice or rats (LD10) for new agents. If this dose happens to be too toxic, then the DE design is superior relative to the NDE and NS designs as discussed above. Although the methodology described here uses EWOC, it can be applied to any model based dose finding method such as CRM (O’Quigley et al., 1990) or mTPI (Ji and Wang, 2013) designs. We plan to adapt the methodology to dose combination trials by extending the work described in (Tighiouart, Li and Rogatko, 2017).
Acknowledgments
We thank the reviewers and associate editor for their thorough review and valuable comments which helped improve the quality of the manuscript. This work is supported in part by the National Institute of Health Grant Number 1 R01 CA188480-01A1 (M.T, A.R, and Q.L), the National Center for Research Resources, Grant UL1RR033176, and is now at the National Center for Advancing Translational Sciences, Grant UL1TR000124 (M.T and A.R), and 2 P01 CA098912 (M.T).
References
- Ananthakrishnan R, Green S, Chang M, Doros G, Massaro J, LaValley M. Systematic comparison of the statistical operating characteristics of various Phase I oncology designs. Contemporary Clinical Trials Communications. 2017;5:34–48. doi: 10.1016/j.conctc.2016.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babb J, Rogatko A, Zacks S. Cancer phase I clinical trials: efficient dose escalation with overdose control. Statistics in Medicine. 1998;17:1103–1120. doi: 10.1002/(sici)1097-0258(19980530)17:10<1103::aid-sim793>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- Babb JS, Rogatko A. Patient specific dosing in a cancer phase I clinical trial. Statistics in Medicine. 2001;20:2079–2090. doi: 10.1002/sim.848. [DOI] [PubMed] [Google Scholar]
- Bartroff J, Leung Lai T. Incorporating individual and collective ethics into phase I cancer trial designs. Biometrics. 2011;67:596–603. doi: 10.1111/j.1541-0420.2010.01471.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen ZJ, Tighiouart M, Kowalski J. Dose escalation with overdose control using a quasi-continuous toxicity score in cancer Phase I clinical trials. Contemporary Clinical Trials. 2012;33:949–958. doi: 10.1016/j.cct.2012.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung YK. Coherence principles in dose-finding studies. Biometrika. 2005;92:863–873. [Google Scholar]
- Cheung YK, Chappell R. Sequential designs for phase I clinical trials with late-onset toxicities. Biometrics. 2000;56:1177–1182. doi: 10.1111/j.0006-341x.2000.01177.x. [DOI] [PubMed] [Google Scholar]
- Chevret S. Statistical Methods for Dose-finding Experiments. Chichester: Wiley; 2006. [Google Scholar]
- Derman C. Nonparametric up and down experimentation. Annals of Statistics. 1957;28:795–798. [Google Scholar]
- Durham SD, Flournoy N, Rosenberger WF. A random walk rule for phase I clinical trials. Biometrics. 1997;53:745–760. [PubMed] [Google Scholar]
- Faries D. Practical Modifications of the Continual Reassessment Method for Phase I Cancer Clinical Trials. Journal of Biopharmaceutical Statistics. 1994;4:147–164. doi: 10.1080/10543409408835079. [DOI] [PubMed] [Google Scholar]
- Goodman SN, Zahurak ML, Piantadosi S. Some Practical Improvements in the Continual Reassessment Method for Phase-I Studies. Statistics in Medicine. 1995;14:1149–1161. doi: 10.1002/sim.4780141102. [DOI] [PubMed] [Google Scholar]
- Hansen AR, Graham DM, Pond GR, Siu LL. Phase 1 trial design: is 3 + 3 the best? Cancer Control. 2014;21:200–208. doi: 10.1177/107327481402100304. [DOI] [PubMed] [Google Scholar]
- Ji Y, Wang SJ. Modified Toxicity Probability Interval Design: A Safer and More Reliable Method Than the 3+3 Design for Practical Phase I Trials. Journal of Clinical Oncology. 2013;31:1785–1791. doi: 10.1200/JCO.2012.45.7903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Tourneau C, Lee JJ, Siu LL. Dose Escalation Methods in Phase I Cancer Clinical Trials. Journal of the National Cancer Institute. 2009;101:708–720. doi: 10.1093/jnci/djp079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS - A Bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing. 2000;10:325–337. [Google Scholar]
- Møller S. An Extension of the Continual Reassessment Methods Using a Preliminary up-and-Down Design in a Dose Finding Study in Cancer Patients, in Order to Investigate a Greater Range of Doses. Statistics in Medicine. 1995;14:911–922. doi: 10.1002/sim.4780140909. [DOI] [PubMed] [Google Scholar]
- O’Quigley J, Pepe M, Fisher L. Continual reassessment method: A practical design for phase I clinical trials in cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- O’Quigley J, Shen LZ. Continual reassessment method: a likelihood approach. Biometrics. 1996;52:673–684. [PubMed] [Google Scholar]
- Piantadosi S, Fisher JD, Grossman S. Practical Implementation of a Modified Continual Reassessment Method for Dose-Finding Trials. Cancer Chemotherapy and Pharmacology. 1998;41:429–436. doi: 10.1007/s002800050763. [DOI] [PubMed] [Google Scholar]
- Roberts TG, Goulart BH, Squitieri L, et al. Trends in the risks and benefits to patients with cancer participating in phase 1 clinical trials. Jama-Journal of the American Medical Association. 2004;292:2130–2140. doi: 10.1001/jama.292.17.2130. [DOI] [PubMed] [Google Scholar]
- Rogatko A, Cook-Wiens G, Tighiouart M, Piantadosi S. Escalation with Overdose Control is More Efficient and Safer than Accelerated Titration for Dose Finding. Entropy. 2015;17:5288–5303. doi: 10.3390/e17085288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogatko A, Schoeneck D, Jonas W, Tighiouart M, Khuri FR, Porter A. Translation of innovative designs into phase I trials. Journal of Clinical Oncology. 2007;25:4982–4986. doi: 10.1200/JCO.2007.12.1012. [DOI] [PubMed] [Google Scholar]
- Simon R, Freidlin B, Rubinstein L, Arbuck SG, Collins J, Christian MC. Accelerated titration designs for phase I clinical trials in oncology. Journal of the National Cancer Institute. 1997;89:1138–1147. doi: 10.1093/jnci/89.15.1138. [DOI] [PubMed] [Google Scholar]
- Storer BE. Design and Analysis of Phase-I Clinical-Trials. Biometrics. 1989;45:925–937. [PubMed] [Google Scholar]
- Tighiouart M, Cook-Wiens G, Rogatko A. Escalation with Overdose Control Using Ordinal Toxicity Grades for Cancer Phase I Clinical Trials. Journal of Probability and Statistics. 2012a;2012:18. [Google Scholar]
- Tighiouart M, Cook-Wiens G, Rogatko A. Incorporating a Patient Dichotomous Characteristic in Cancer Phase I Clinical Trials Using Escalation with Overdose Control. Journal of Probability and Statistics. 2012b;2012:10. [Google Scholar]
- Tighiouart M, Li Q, Rogatko A. A Bayesian adaptive design for estimating the maximum tolerated dose curve using drug combinations in cancer phase I clinical trials. Statistics in Medicine. 2017;36:280–290. doi: 10.1002/sim.6961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tighiouart M, Liu Y, Rogatko A. Escalation with Overdose Control using Time to Toxicity for Cancer Phase I Clinical Trials. Plos One. 2014;9 doi: 10.1371/journal.pone.0093070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tighiouart M, Piantadosi S, Rogatko A. Dose finding with drug combinations in cancer phase I clinical trials using conditional escalation with overdose control. Statistics in Medicine. 2014;33:3815–3829. doi: 10.1002/sim.6201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tighiouart M, Rogatko A. Dose Finding with Escalation with Overdose Control (EWOC) in Cancer Clinical Trials. Statistical Science. 2010;25:217–226. [Google Scholar]
- Tighiouart M, Rogatko A. Number of Patients per Cohort and Sample Size Considerations Using Dose Escalation with Overdose Control. Journal of Probability and Statistics. 2012;2012:16. [Google Scholar]
- Tighiouart M, Rogatko A, Babb JS. Flexible Bayesian methods for cancer phase I clinical trials. Dose escalation with overdose control. Statistics in Medicine. 2005;24:2183–2196. doi: 10.1002/sim.2106. [DOI] [PubMed] [Google Scholar]
- Ting N. Dose Finding in Drug Development. First. New York: Springer; 2006. [Google Scholar]
- Van Meter EM, Garrett-Mayer E, Bandyopadhyay D. Proportional odds model for dose-finding clinical trial designs with ordinal toxicity grading. Statistics in Medicine. 2011;30:2070–2080. doi: 10.1002/sim.4069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler GM. Incoherent dose-escalation in phase I trials using the escalation with overdose control approach. Statistical Papers. 2016 doi: 10.1007/s00362-00016-00790-00367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zacks S, Rogatko A, Babb J. Optimal Bayesian-feasibile dose escalation for cancer phase I trials. Statistics & Probability Letters. 1998;38:215–220. [Google Scholar]


