A network model of behavioural performance in a rule learning task

Abstract

Humans demonstrate differences in performance on cognitive rule learning tasks which could involve differences in properties of neural circuits. An example model is presented to show how gating of the spread of neural activity could underlie rule learning and the generalization of rules to previously unseen stimuli. This model uses the activity of gating units to regulate the pattern of connectivity between neurons responding to sensory input and subsequent gating units or output units. This model allows analysis of network parameters that could contribute to differences in cognitive rule learning. These network parameters include differences in the parameters of synaptic modification and presynaptic inhibition of synaptic transmission that could be regulated by neuromodulatory influences on neural circuits. Neuromodulatory receptors play an important role in cognitive function, as demonstrated by the fact that drugs that block cholinergic muscarinic receptors can cause cognitive impairments. In discussions of the links between neuromodulatory systems and biologically based traits, the issue of mechanisms through which these linkages are realized is often missing. This model demonstrates potential roles of neural circuit parameters regulated by acetylcholine in learning context-dependent rules, and demonstrates the potential contribution of variation in neural circuit properties and neuromodulatory function to individual differences in cognitive function.

This article is part of the theme issue ‘Diverse perspectives on diversity: multi-disciplinary approaches to taxonomies of individual differences’.

1. Introduction

Humans demonstrate important cognitive capacities for rule learning and symbolic processing. Rule learning includes the ability to generalize from previous experience, to allow previously unseen sensory input to be interpreted in terms of a previously learned rule to generate the correct response [1]. Humans show a range of capabilities for learning and detecting rules and applying them to new sensory input, as shown for example by the differences in rule learning performance on the Raven's progressive matrices task [2–4] that are a reflection of probabilistic abilities, and on other rule learning tasks such as the context-dependent association task described here [5].

The mechanisms of rule learning involve neural circuits in cortical structures such as the prefrontal cortex [6,7], but the detailed circuitry for rule learning has not been determined. The ability to flexibly apply rules to new input requires circuits for symbolic processing. Here we focus on symbolic processing as the capacity for a specific cognitive role in a rule to be flexibly filled by different sensory inputs. This flexible linking of roles to different fillers contributes to the productivity, systematicity and compositionality of cognitive function [1]. This flexible application of rules to different fillers has been modelled in different ways, including the synchrony of oscillations [8–10], the use of compression operators to link codes [11,12] or the flexible gating between different cortical working memory buffers by the basal ganglia [13,14] consistent with previous theories of flexible routing in prefrontal cortex [6]. The model presented in this paper demonstrates how the concept of flexible gating could be implemented by circuits within neocortex to allow learning and generalization of rules. This builds on previous models using interacting populations of neurons to gate selection of motor actions [15,16] or selection of memory actions loading information into working memory or episodic memory for solving behavioural tasks [15,17,18].

The fundamental feature of this model is the direct influence of gating neurons on the synaptic spread of activity between other neurons, which could arise via different possible mechanisms. This gating could involve synapses on the dendritic tree of pyramidal cells that interact via voltage-dependent N-methyl-d-aspartate (NMDA) conductances, such that a conjunction of nearby synaptic inputs is necessary to generate an output [19,20]. This model is supported by the fact that neurons receive multiple different functional synaptic inputs, but commonly only respond to a subset of these inputs [21,22]. Alternately, it could involve axo-axonic inhibitory interneurons that can directly regulate spiking output [23,24].

The range of human cognitive function could reflect a range of neuromodulatory influences in different individuals [25,26]. This could involve different neuromodulatory systems including dopamine, norepinephrine, serotonin and acetylcholine, which could regulate different aspects of cognitive function [25]. This paper will focus on the potential neuromodulatory role of acetylcholine in cortical circuits. Extensive data indicate an important role of acetylcholine in regulating cortical cognitive function. A broad range of medical anecdotes indicate that blockade of muscarinic acetylcholine receptors by high doses of drugs such as scopolamine or atropine (present in some plant species) causes a breakdown of cognitive function resulting in delirium and hallucinations [27], and this has been proposed to contribute to cognitive dysfunction in diseases such as Lewy body dementia [28]. The essential role for muscarinic receptors in cognition is further supported by studies showing more selective cognitive impairments including impaired encoding of lists of words and impaired working memory with lower levels of muscarinic blockade [29–31].

The cognitive effects of muscarinic receptor blockade appear to result from blockade of specific physiological effects at the cellular and circuit level within cortical structures. These muscarinic effects are present in most cortical regions that have been tested including hippocampus, entorhinal cortex and prefrontal cortex [32]. Nicotinic receptors also contribute to the effects of acetylcholine, but blockade of nicotine receptors has weaker effects on cognitive function. The model presented here contains features of neural function that are inspired by data on physiological effects of muscarinic cholinergic receptors [32,33]. Data show that acetylcholine is released during waking in cortical structures including the neocortex and hippocampus [34,35]. This release of acetylcholine causes a number of strong physiological effects that could be important for cognitive function.

Cholinergic modulation strongly influences the spiking activity of cortical neurons by regulating different conductances. Muscarinic receptors cause a direct depolarization of neurons through the block of a leak potassium current [36]. In addition, by blocking calcium-dependent potassium currents [37–39] and activating a calcium-sensitive non-specific cation current (CAN current), acetylcholine can cause persistent spiking in a subset of neurons when spiking activity causes calcium influx that activates the calcium-sensitive cation current [40–43]. This persistent spiking could provide a means for maintaining working memory of prior activity [44], which could allow gating neurons to bridge the sequential gaps between inputs. In vivo studies show that acetylcholine increases the firing rate and reliability of the spiking response of cortical neurons to sensory input [45–47]. Variation in cognitive function between individuals could result from genetic variation in the structure of muscarinic receptor proteins. For example, it has been shown that a mutation in a potassium channel regulated by muscarinic receptors (KCNQ) can cause an inherited epilepsy syndrome [48].

Cholinergic modulation also regulates the induction and expression of synaptic modification, as shown in studies in which acetylcholine enhances long-term potentiation [49–51] and the NMDA conductances that could contribute to long-term potentiation [52]. At the same time that cholinergic modulation enhances synaptic modification, the cholinergic activation of muscarinic receptors also causes strong presynaptic inhibition of glutamatergic synaptic transmission which is stronger at excitatory feedback synapses compared to afferent input [32,33,53] and depends upon M4 muscarinic receptors [54]. This presynaptic inhibition has been shown to be stronger at excitatory intrinsic synapses within neocortex [55], in contrast to the afferent input which often undergoes nicotinic enhancement [56,57]. Modelling shows how increases of acetylcholine would cause muscarinic presynaptic inhibition of recurrent synapses that would prevent retrieval of previously stored associations from interfering with encoding of new patterns [32,58], whereas lower levels of acetylcholine could allow stronger synaptic feedback to mediate consolidation [33], consistent with the enhancement of consolidation seen with quiet rest after encoding [59,60].

In this paper, we present a model of cognitive rule learning that shows the capacity to learn a rule across a large number of stimulus examples, and to generalize this rule to previously unseen examples. The model also shows how variation in cortical parameters could alter the performance of the network to effectively learn the rule, and could thereby underlie the large individual variation seen in data from human performance on this task [5]. The variations in parameters that could influence performance include: (i) variation in the amount of excitatory noise added to the network, which influences the capacity to explore different representations (equation (2.1)); (ii) variation in the efficacy of synaptic modification based on correct output (equations (2.3) and (2.4)); and (iii) variation in the presynaptic inhibition of previously modified synapses to allow incorrect responses to update the pattern of network connectivity.

2. Methods

(a). Overview of task

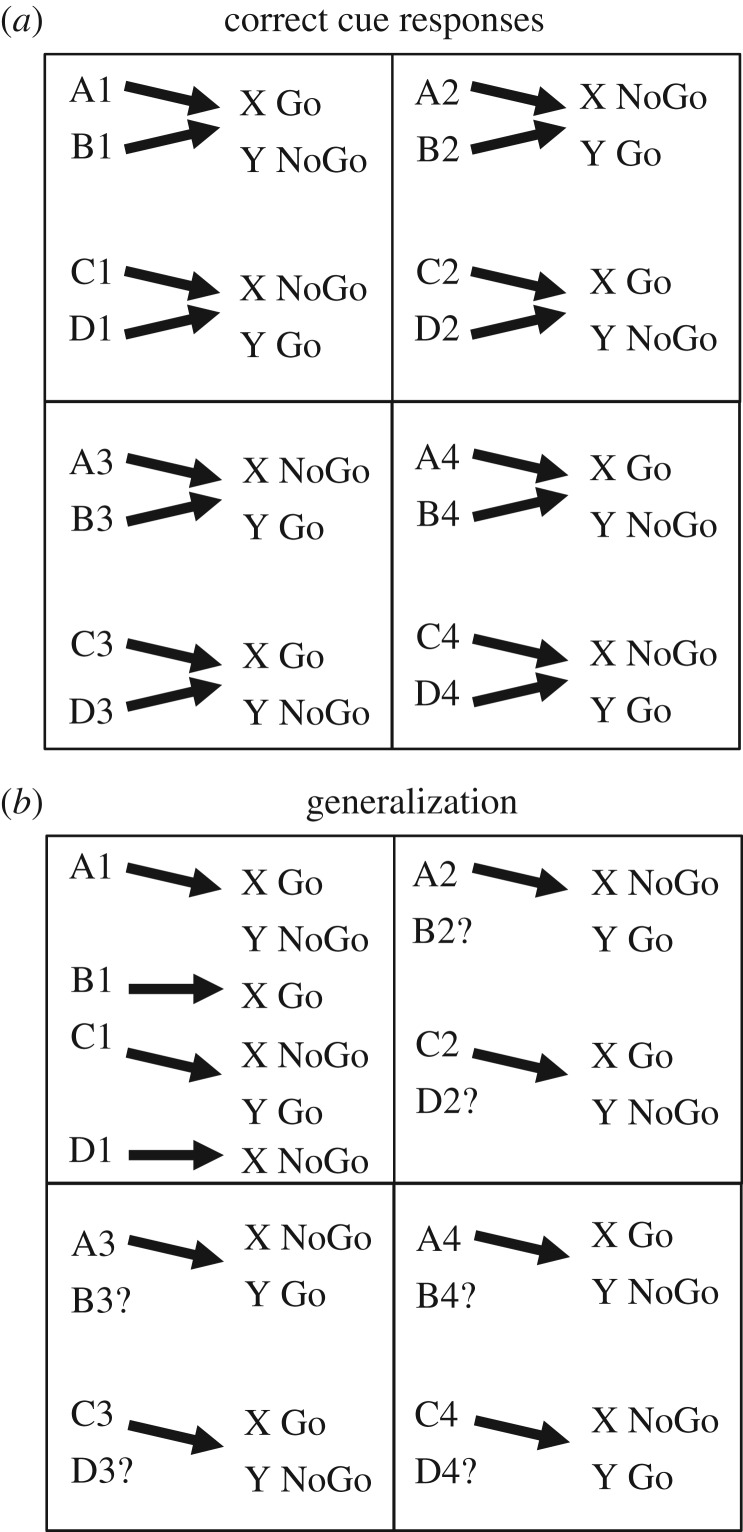
The task being modelled requires behavioural go or no-go responses to easily identifiable pairs of items, as illustrated in figure 1. The correct response on each trial is determined by the rules determined by the current pair of items and the context of spatial location. On each trial, human participants are presented with two different item stimuli in the same spatial context (screen location) separated by a short memory delay. Participants make a keyboard response based on whether the presented items are paired in a ‘Go’ or ‘NoGo’ configuration. The stimulus pairings for correct ‘Go’ responses are summarized in figure 1, where the first stimuli are indicated by A,B,C,D and the second stimulus by X or Y. Feedback indicates whether the response is correct or incorrect for each response. Importantly, participants are naive to the fact that pairings are made based on spatial location. For example, in context 1, item cue A followed by cue X requires a correct Go response, but in context 2 item cue A followed by X would require a NoGo response, whereas in context 2 item cue A followed by Y would require a Go response. These form some of the context-dependent rules that participants must learn. Participants must learn the correct behavioural responses and rules for each pair of items using the feedback provided. In the behavioural data [5], human subjects show a wide variety of capacities for learning this task. Some subjects show rapid learning over a small set of trials that indicates rapid learning and generalization of the basic rule structure of the task. Other subjects do not learn the correct rule structure at all over an extensive period of training, whereas other subjects correctly learn the rule structure at an intermediate stage during learning.

Figure 1.

(a) Diagram of the behavioural task. Participants learn associations between four items A,B,C,D and two other items X,Y. The association rules change with spatial quadrant, but pairs of quadrants have the same associations (e.g. 1 and 4, 2 and 3), allowing participants to extract a common higher order rule. For example, item A followed by item X in quadrant 1 requires a Go response to be correct. There are 16 Go pairings and 16 NoGo pairings. (b) Task with probe stimuli testing generalization. The task is the same as A, except that in each quadrant, about half of the cue combinations are not shown during training (indicated by the question mark ‘?’). All examples of A and C are shown, but only a single example for B and D are shown. After training, simulations are presented with the missing cue and have to infer the correct paired associate (X, Y) from experience in the equivalent quadrant.

(b). Overview of model

To understand how these rules could be learned and generalized, and to understand the range across human subjects in capacity for learning the rules, the performance of the task has been modelled within a neural network structure that uses gating of weights. Gating of weights refers to a subset of active units in the model that determine the nature of synaptic interactions between other units in the model.

The basic function of the model is similar to most neural network models, in which the activity a_i(t) of neuron population 1 at time t influences the activity a_j(t + 1) of neuron population 2 at time t + 1. The activity is influenced via a set of synaptic weights with values represented by the matrix W_ij at time t, as follows:

2.1

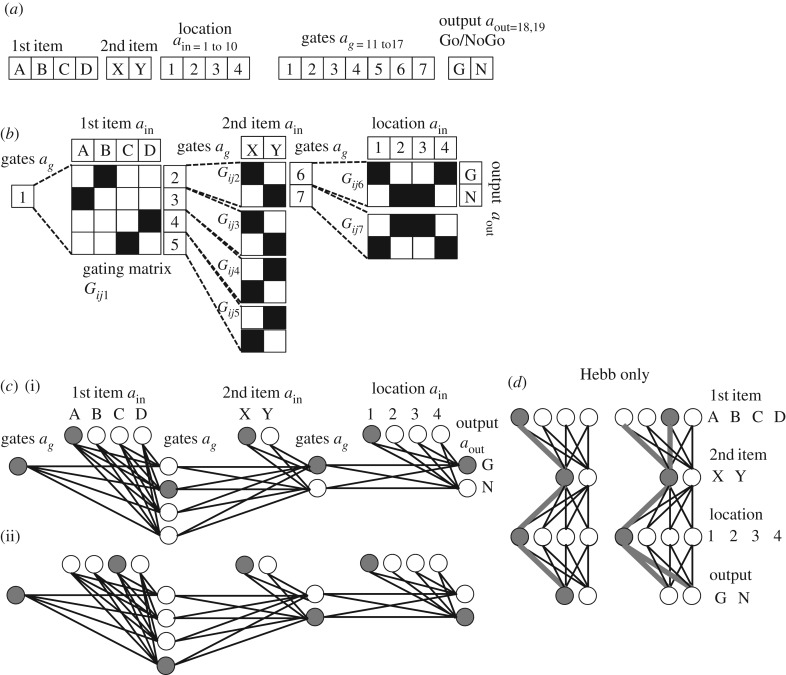
Note that this activation equation also includes an added noise term where μ is 0.1 and σ is the rand function from MATLAB which produces random numbers drawn from a uniform distribution between 0 and 1. This noise gives the network flexibility for exploring different activity patterns. The full activity vector summarized in figure 2a contains input units (indices 1–10) responding to the first item (A,B,C,D), the second item (X,Y) and the location (1,2,3,4). The vector also includes gating units (with indices 11–17 in most simulations) and two output units representing the Go or NoGo response (with indices 18–19).

Figure 2.

Network structure. (a) The activity array used in simulations. Units are assigned to the first items A,B,C,D, second items X,Y, locations 1,2,3,4 and gates 1,2,3,4,5,6,7 and output Go, NoGo. (b) The network connectivity of gating in the model. Gate 1 regulates gated weights G_ij1 between first patterns A,B,C or D and gates 2,3,4,5. Black squares indicate strengthened connections in a specific example of function also shown in figure 3. Gates 2,3,4,5 then regulate gated weights G_ij2, G_ij3, G_ij4, G_ij5 between second patterns X or Y and gates 6 or 7. Gates 6 or 7 then regulate gated weights G_ij6 and G_ij7 between location inputs 1,2,3 or 4 and outputs Go (G) or NoGo (N). (c) The same network connectivity as in b, but shown with circles representing units and lines (instead of matrices) representing weights. Filled circles represent active units for the examples described in the main text. (d) Example of a network without gating units or gated weights. Synapses between neurons representing patterns are strengthening with Hebbian modification only. This results in overlap for the association of pattern A with pattern X in location 1 versus pattern C with pattern X in location 1. The need for two different outputs cannot be accommodated in this structure.

Figure 2b,c summarizes the overall network connectivity. The simulations use three functional sets of weights that link the input arriving at different time points in the task to different sets of gating units. The gating units then regulate gating matrices that determine the currently functional set of connections within the network. Each trial starts with gate 1 active (gate 1 has index 11 within the overall activity vector because the vector includes 10 input neurons with indices 1–10). Gate 1 regulates the first set of gating weights that link input from neurons 1–4 that respond to the first item (A,B,C or D in figure 1) and send output to update activity in another set of gating units (numbered 2–5 in figure 2, and corresponding to indices 12–15 in the overall vector). Gates 2–5 regulate the second set of weights that link inputs from neurons 5–6 that respond to the second item (X or Y in figures 1 and 2) and send output to update activity in a second set of gates (numbered 6–7 in the figure, and corresponding to indices 16–17 in the overall vector). The third set of weights links input from neurons 7–10 that represent the spatial location 1,2,3,4 of the input (upper left, upper right, lower left, lower right) and send output to neurons representing the selection of a Go or NoGo output. For ease of programming, these three sets of functional weights were all implemented with single gating matrices in which the functional weights are just subsets of all possible connections between elements of the activity vector. Thus, in figure 3, the grey scale plots of weight matrices show all possible connections between units 1–19 and the same set of units 1–19, but only a subset of weights are modified during the performance of the task.

Figure 3.

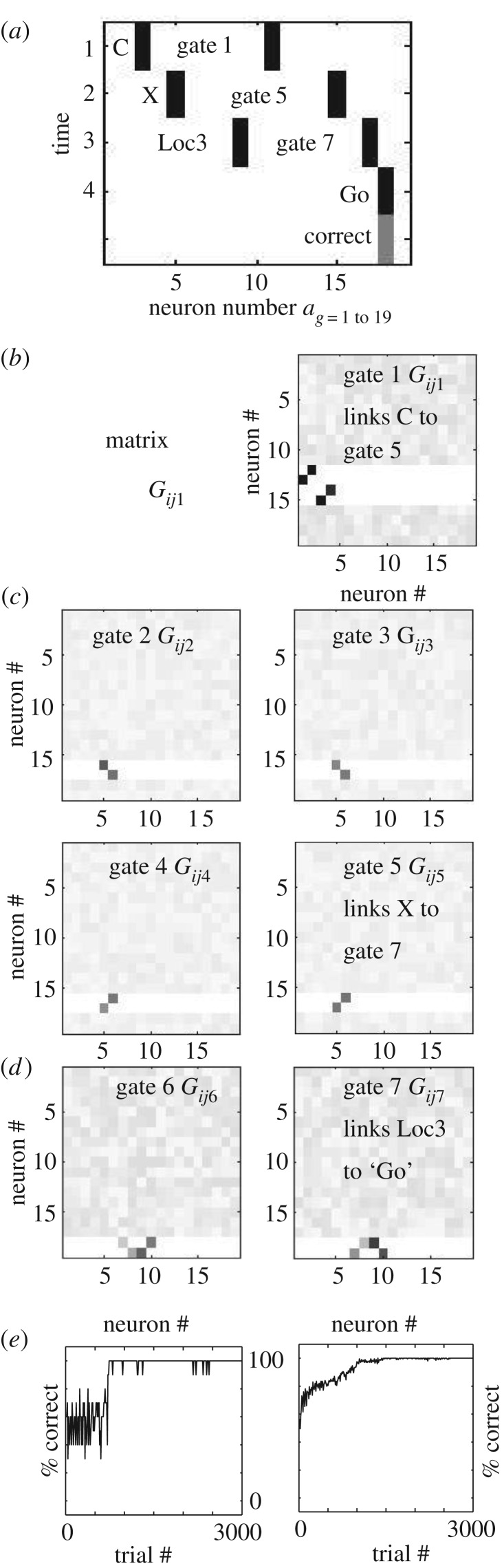
Simulation of task after training. (a) On each trial, the full network was presented with a sequence of binary patterns with active units (black rectangles) representing one item from A,B,C,D (top row, ‘C’) followed by one item from X,Y (second row, ‘X’) followed by one of 4 location cues (third row, ‘Loc3’). Each trial started with activity in gate 1 (index 11), and after learning cue C activates gate 5 (index 15), cue X activates gate 7 (index 17), and Loc3 activates the Go response via weights shown in part b. These network weights were previously strengthened when the network was rewarded for a correct Go response or NoGo based on the combinations shown in figure 1. The network learned to correctly respond to all combinations. (b) After learning, gate 1 has a weight matrix G_ij1 with four strong weights (black squares) linking the four first cues to specific gates, so input ‘C’ in column 3 activates output row corresponding to gate 5 (index 15). The grey scale values represent the random initial weights that were not modified due to the absence of pre- or post-synaptic activity. Darker grey represents stronger weights. (c) The next four gates link the second cue to a different set of gates. In this example, active gate 5 (index 15) allows input X to activate gate 7. (d) The next two gates link the location context to a correct response. In this example, active gate 7 (index 17) allows Loc3 to activate Go. (e) Left: Performance of a single network over 3000 training trials, showing relatively rapid increase in performance from random (50%) to 100% correct around trial 800. Right: Performance change averaged over 20 networks, showing that all networks converge over time to 100% correct responses on all 32 trial types.

(c). Gating of weights

The regulation of the weights W in this model is somewhat different from most neural network models. Most neural network models update a single matrix W based on Hebbian learning rules or backpropagation of error. By contrast, the essential novel feature of this model is the gating of the spread of activity in the network. This corresponds to an extensive connectivity pattern W that is selectively gated by individual gating units that activate gating matrices G that regulate the influence of component synapses in W, potentially through multiplicative interactions of the gating neuron input with adjacent synapses in W. Neurophysiologically, this could involve nonlinear interactions between synapses on a dendritic tree such that one synapse only has a significant effect on spiking when accompanied by input at a nearby synapse on the same dendritic tree. This was modelled in previous studies in the Hasselmo laboratory [61], based on earlier models of nonlinear dendritic interactions involving NMDA receptors [19,20].

This property is here represented by allowing the pattern of synaptic weights to be directly regulated by the effect of activity in a set of gating units that are part of the vector of activity. Thus, as shown in figure 2, the activity vector a_i is divided up into different sets of units a_in (input units), a_out (output units) and a_g (gating units). Note that for simulations, all of these separate components are combined in a single vector, so the indices in, out and g all fall within the larger vector index i in equation (2.1).

The gating of weights is represented by a gating matrix of weights G_ijg that map activity of the gating units a_g to weights W_ij as follows:

2.2

At each time step, the active gating units a_g determine how each gating matrix G_ijg contributes to the pattern of weights W_ij within the network. In this notation, the subscripted index ijg indicates the indices of the interaction from an individual active gating unit a_g with index g to the gated weights ij associated with that index. As noted above, the units a_g used to influence gating are a separate set of gating units within the overall population of units. The notation with square brackets and the plus sign indicates a threshold linear function with output of zero if the function within the square brackets is negative (i.e. when a_g(t) falls below threshold θ) and linear when a_g(t) is above threshold θ. The maintenance of the activity of gating units is proposed to involve muscarinic activation of the mechanisms of intrinsic persistent spiking within individual neurons [42,62].

The effect of gating units on the matrix W_ij is rapid in equation (2.2), but the matrix gating weights G_ijg change slowly over time depending on learning as described below. The learning occurs initially due to noise causing random activity of units within the network that randomly generates correct responses, which result in the modification of the gating weights. Learning of the rule progresses to asymptotic performance, during which the gating depends upon the updating or control of W at each time step by a subset of active units within a(t) that act on W via weights G_ijg. The essential learning within the network concerns the modification of weights G_ijg so that the appropriate sets of units get activated to implement the appropriate gating of interactions between specific roles within the rule and the associated fillers such as the stimuli. For example, a specific active gating unit would activate the gating weights that link a specific stimulus location (e.g. 2′) to a specific output (Go).

(d). Updating of internal weights

The update of the gating weights G depends upon the generation of correct responses in the network, which initially occurs due to noise causing random selection of activity of gating units. If a correct response is generated randomly, the gating weights are updated. The updating based on correct responses is proposed to involve the release of a neuromodulator such as dopamine or acetylcholine, which has been shown to enhance mechanisms of long-term potentiation [63].

The gating weight matrices G_ijg all start out with random initial weights. Sections 1 and 2 below describe the spread of activity as described in equations (2.1) and (2.2) above, and then sections 3–5 describe how the activity results in the modification of weights G in equations (2.3)–(2.5) below.

(1) As shown in equation (2.1) above, presynaptic activity spreads across the current synaptic weight matrix W_ij to influence postsynaptic activity with added noise. Because of the restrictions on connectivity described above, the postsynaptic activity on each time step is distributed across the gating units. The network then selects the gating unit with the highest activity (winner-take-all).

(2) As shown in equation (2.2) above, on a given trial, the current weight matrix W_ij depends upon the sum of the gating matrices G_ijg that are associated with currently active gating units g. These are summarized in figure 2. To provide an initial gate, the gating unit 1 (index 11) is set to be active at the start of each trial. In the simulations shown here, the weight matrix for gate 1 is restricted to only allow connections from units 1–4 representing cues A,B,C,D to the four gates 2,3,4,5 (indices 12–15). Gates 2–5 are restricted to regulate weights between input units with indices 5, 6 representing cues X,Y to the two gates 6,7 (indices 16–17). The gates 6 and 7 are restricted to regulate weights between units with indices 7–10 representing the four quadrant locations (Location 1: upper left, 2: upper right, 3: lower left, 4: lower right), with postsynaptic targets being the output units (indices 18,19) representing the Go or NoGo responses.

(3) The network then computes Hebbian learning based on the association of the currently active presynaptic input unit a_j(t) and the currently active postsynaptic gating unit selected by winner-take-all a_g(t) (or output unit representing Go or NoGo). Note that the change of G_ijg(t)(t) is associated with the index of the active gating unit g(t) determined by the current time step t as seen in the index. This Hebbian learning is not immediately implemented, but is stored as a possible change in the manner described as synaptic tagging [64,65].

2.3

(4) The strengthening of tagged synapses is determined by the match of network output to desired output. The network output activity (Go or NoGo) in the final layer of the network is determined either by the gated weights or by random input. This output activity a_o(t) is then compared with the desired output activity o(t) at that final stage. The desired output o(t) is determined by the reward structure of the task, so in the desired output vector o(t), the Go or NoGo unit is set to one as defined by the behavioural rule shown in figure 1. If the network is correct, then the release of a neuromodulator (possibly dopamine) updates the gates G based on the Hebbian learning stored previously. Note that this process updates the weight matrices for each of the gating units for the three steps of update. Thus, the gating unit active on the first time step (gate 1, index 11) updates based on the synaptic tag from that time step (t = 1) and so on.

2.4

(5) In addition to the synaptic modification, there is also postsynaptic normalization of the weights so that the sum of the row of weights entering a particular postsynaptic gate or output does not change. This uses the following equation:

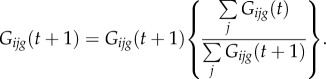2.5

This normalization ensures that weights do not grow explosively and also causes heterosynaptic depression of other weights that are not associated with the current postsynaptic activity.

(6) Because the postsynaptic activity is being chosen randomly, the network has the potential to get stuck in incorrect response structures, even though the neuromodulatory updating of weights depends upon correct output. Because of this, the network has an additional feature that incorrect responses are associated with a small probability of resetting the gating matrices associated with active gates on that trial. On incorrect trials if a uniformly distributed random number is r < 0.2, then the matrices G_ijg of all active gating units a_g(t) are set to random initial connectivity. This is motivated by the idea that an incorrect response causes release of acetylcholine. The acetylcholine would then cause a diffuse presynaptic inhibition that could reduce synaptic transmission at all previously strengthened synapses (specifically influencing the gating matrices associated with currently active gating units) and thereby allow a change in postsynaptic activity and an alternation in the pattern of connectivity.

3. Results

The network model described in the Methods section (figure 2) can be successfully trained on the behavioural task described in the same section (figure 1). As shown in figure 3, after training the network can generate the correct Go or NoGo response to each of the 32 pattern combinations. In addition, as shown in figure 4, the network can also generalize to previously unseen pattern combinations that fit the same rule learned by the network. The subsequent sections of the results below will describe the detailed activity and gating weights associated with correct function of the network.

Figure 4.

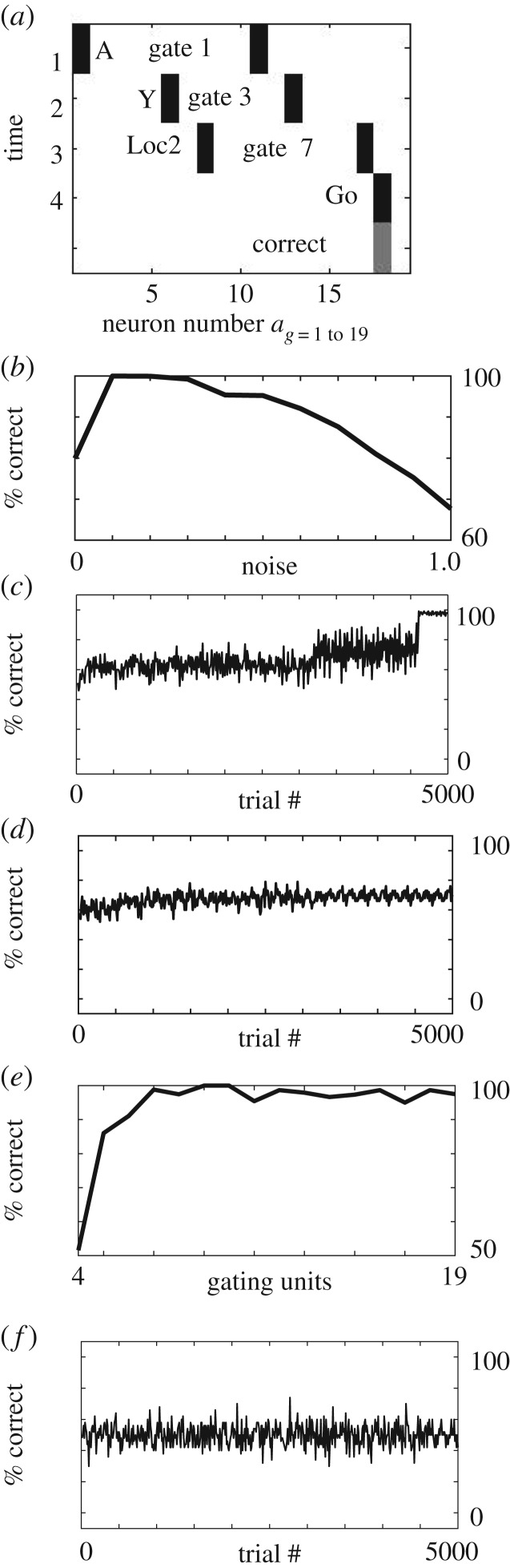
More examples of neural networks trained on task. (a) A different example, after different training. In this case, gate 1 (index 11) links input cue ‘A’ to gate 3 (index 13). Gate 3 links cue ‘Y’ to gate 7 (index 17). Gate 7 links ‘Loc2’ to Go response which is correct. (b) Performance of the network for different levels of noise (0.0 to 1.0) when trained on all 32 combinations. The network does not perform well with zero noise, because it does not explore enough gating patterns, but does perform well for noise of 0.1 and 0.2. Higher levels of noise cause a decrease in correct steady state responding. (c) Example of generalization from average across 20 networks, showing that when presented with only 18 of the 32 combinations, the networks attain about 75% performance. Then on the last 400 trials, most of the networks (19 out of 20) can correctly generalize to 100% correct responses when presented with all 32 pattern combinations (without further learning). (d) With noise set to zero, the average performance of 20 networks does not learn the rules and remains at 50% performance and does not generalize, indicating sensitivity to specific network parameters. (e) Performance of the network for different numbers of gating units, showing that insufficient numbers prevent good performance. Best performance is attained first with seven units, which allows four gating units to be activated by the four input items A,B,C,D. (f) With purely Hebbian connectivity without gating units and gated weights, a network cannot learn to attain better than 50% performance, due to incompatible responses that must be routed through the same neuron.

Figure 2 illustrates how the gating units provide a mechanism for learning and applying the rule across all 32 pattern combinations. Figure 2b illustrates the pattern of weights that were learned in one instance of training. These patterns can be used to trace the generation of correct responses for the example of this specific set of learned gating weights, as summarized in figure 2c. The first gate 1 is always active at the start of the trial, and has weight G_ij1 in figure 2c(i). In this example, this gating matrix allows input item A to activate gate 3. Then gating matrix G_ij3 allows input X to activate gate 6. Then gating matrix G_ij6 allows input location 1 to activate output G (Go). Figure 2c(ii) shows a different set of inputs, illustrating that gate 1 allows input item C to activate gate 5. Gate 5 allows input X to activate gate 7 (instead of 6). This then allows input location 1 to activate gate N (NoGo). So the gating matrices allow different initial items (A versus C) to activate nonoverlapping representations to generate distinct output responses, even though the intervening stimuli are the same (X and location 1).

By contrast, figure 2d illustrates that a purely Hebbian network without gating cannot learn these distinct context-dependent associations. The Hebbian network can learn associations between input pattern A to pattern X, from pattern X to location 1 and from location 1 to output G. However, when input pattern C is presented, the overlapping components (X and location 1) prevent location 1 from being associated with an unambiguous correct response. During learning, location 1 gets associated with both Go and NoGo responses, and the network will not be able to attain better than 50% correct responses. The performance of the simulation for the Hebbian case is shown in figure 4f, and the performance across different numbers of gating units is shown in figure 4e (fewer gates result in poor performance).

Figure 3 shows a specific example trial after training on all 32 pattern combinations, as well as showing the summary of performance over trials. In figure 3a, the activity of the network is shown for each time step, with each row showing the vector of activity for a single time step. At the start of the example trial shown here, the network receives an input representing the pattern ‘C’ on the first time step (each trial starts with one of the four cues A,B,C,D). In addition, at the start of all trials, the network starts with gate 1 active at the start of the trial (seen as ‘gate 1’ in the figure). Gate 1 activates the gating matrix shown in figure 3b which becomes the connectivity W_ij of the network. As can be seen in this gating matrix in figure 3b, the previous learning strengthened connections that link each of the input cues A,B,C,D with one of the gating units. When this matrix is multiplied by the matrix containing the cue ‘C’, it generates the output that activates gate 5. Note that input ‘C’ corresponds to column 3, which has a strengthened weight (black square) at column 3 and row 15 (gate 5), so that the activity spreads from input 3 to gate 5.

Now that gate 5 is active, it can be seen on row 2 of figure 3a, and it activates the gating matrix shown in figure 3c (lower right). In addition, as seen in row 2 of figure 3a, on time step 2 the network receives the input representing cue ‘X’. This input cue then spreads across the element of the weight matrix. As can be seen in the weight matrix in figure 3c (gate 5), the gating matrix contains a strengthened synapse that will gate the input from column 5 (representing the cue ‘X’) to output row 17 (activating postsynaptic gating unit 7).

Now that gate 7 is active, this can be seen on row 3 (time step 3) of figure 3a. This activates the gating matrix shown in figure 3d (right). In addition, as seen in row 3 of figure 3a, on time step 3, the network receives the input representing the spatial location in the lower left (labelled as ‘Loc3’ on row 3). This input activity spreads across the weight matrix shown for gate 7 in figure 3d. The input at column 9 spreads across the strengthened weight in column 9 row 18 (black square) to cause postsynaptic activity in the output unit representing a ‘Go’ response. As can be seen, this corresponds to the correct desired output for this combination of input cues and location. Thus, for this particular example trial, the response is correct. This network is able to also generate the correct ‘Go’ responses for the full set of 16 combinations requiring a ‘Go’ response, as summarized in figure 1. In addition, the network generates the correct NoGo responses for the full set of 16 combinations requiring a NoGo response, as summarized in figure 1.

As shown in figure 3e, during training a single network (left) initially performs at around 50% (due to random selection of Go or NoGo responses), but then at one point relatively rapidly increases to 100% performance. This is consistent with the rapid improvement of performance on the task when some individuals discover the rule [5]. Consistent with the data, many of the example networks achieve 100% more rapidly, but this example was selected to show that performance can increase at a later stage. The network activates random gates that form associations between the relevant inputs and gating outputs at each time step. In the case shown here, the initial randomly selected gates do not give good performance and performance only improves when the correct output causes strengthening of weights in the gating matrices to select specific gates.

The plot on the right side of figure 3e shows the performance averaged over 20 different networks with different initial conditions. Each of the individual networks achieves good performance relatively rapidly at different times, but the average shows a smooth approach to 100% performance. The full set of 32 combinations is presented during training, and every single network increases to 100% performance over the 3000 training trials. The noise component of the activation rule is turned off for the last 400 trials, so that the incorrect responses generated by the noise no longer perturb the performance, causing a smoother line at the end. If noise is kept large throughout the simulations, then the noise will perturb the performance as shown in the plot in figure 4b, which shows performance over the last 100 trials for different levels of noise when all patterns are trained. Note that as noise increases, the steady state of the network decreases. However, the network cannot function well with the absence of noise, because noise assists with the selection of different gating units that allow the random generation of correct responses that allow effective learning of the full set of rules. Thus, when noise is set to 0, the network does not attain good performance as shown on the left side of the plot in figure 4b.

As shown in figure 4, the network can effectively generalize to unseen patterns. Figure 4a shows an example of a sequence of patterns that was not seen during training, but generates a correct response due to generalization. Figure 4c shows the performance of networks tested for generalization, using the set of patterns summarized in figure 1b. In this test, the network has seen all examples for pattern A and pattern C, but is only shown a single example of pattern B and pattern D. Because the network received only about 50% of the input patterns during training on time step 1 to 4600, its initial performance during this period is around 75% because it is only being presented with about 50% of the patterns, and then it guesses correctly on 50% of the remaining trials, but it is being evaluated relative to the full set of 32 patterns. Then once the full set of 32 patterns is presented during the final 400 trials, it demonstrates effective generalization to respond correctly to all of the patterns. Figure 4c shows the average performance across 20 different networks. Nineteen out of 20 networks correctly generalize to all 32 patterns at the end of training, even though they were only trained on 18 pattern combinations (as shown in figure 1b). Thus, the network can generalize to 14 previously unseen stimuli based on the rule that it has extracted. Effective generalization was also seen with many other configurations of learned stimuli and stimuli not seen during learning.

For correct performance, the network depends upon a number of specific parameters. In particular, if the noise term μ is set to zero, the network does not explore enough of the activation space and does not effectively create enough new gating units and therefore cannot effectively learn the rules. In this case, activity stays at about 50% as shown in the average across 20 networks in figure 4d. The importance of the potential modulatory reset of weights was shown in other simulations that are not illustrated. When the code for the network was modified to remove the capacity for reset of weights, then performance stayed at about 80% during training because there were more cases of failure to learn the full rule.

The network needed gating units to perform effectively, as already illustrated schematically in figure 2d. Simulations shown in figure 4f demonstrate that when there was only Hebbian modification of connections between layers responding to sensory input, then the network could not perform better than about 50% correct. The performance of the network with different numbers of gating units is shown in figure 4e for numbers ranging from 4 gating units (one for each set of connections in figure 2b) to 19 gating units. The number of gating units was specifically varied for the gating units activated by the first input items A,B,C,D. Note that the best performance first appears for seven gating units, which is the number of gating units shown in figure 2b,c. This allows four gating units to be activated by each of the four input items A,B,C,D. As the number is increased, the performance remains high, as a subset of four gating units for the first item input are selected by each network. However, increasing the number of second input gating units beyond two causes a decrease in performance.

4. Discussion

The simulations presented here provide a general framework for the role of neural gating in the learning of rules shown in figure 1. As shown in figures 2 and 3, the neural network model can learn complex rules and generate correct responses based on this rule across a large number of combinations of patterns. As shown in figure 4, the network can perform generalization based on learning of about half of the training set to generate correct answers for the other half of the learned combinations. More complex combinations of gating could allow learning of more sophisticated hierarchical rule structures.

The network model also indicates how differences in neural circuit parameters could influence the cognitive capabilities of different individuals, consistent with the wide variety of learning capabilities demonstrated in behavioural tests using the training set illustrated in figure 1. Experimental data shows that when trained on this set of stimuli, human subjects vary from immediate learning and application of the rule, to delayed acquisition of the rule, to complete inability to implement the rule across the full training set [5]. As shown in figures 3 and 4, the network presented here shows a similar diversity of behaviour that can arise from a number of different sources. One source is the level of noise in equation (2.1). The noise is necessary for the network to explore a range of different gating representations through noisy postsynaptic activation that is necessary to set up distinct rules. With noise set at 0.1, the network can achieve 100% performance (figure 3) and generalize the rule to new patterns (figure 4). With noise set at 0, the network does not learn and only achieves 75% performance due to random guessing of responses (figure 4e). Even when parameters are kept at the same value, the influence of noise results in different runs of the same network achieving correct performance at different training times. This illustrates how a relatively simple parameter of neural function could influence behaviour on a broad scale. The noise is necessary for the network to learn, and could be considered as a component of arousal allowing exploration of different internal representations [25].

Another aspect of performance depends on the ability of the network to respond to incorrect responses by weakening the influence of previously modified weights, to allow the activation of new alternative representations. This could correspond to the presynaptic inhibition of synaptic transmission in cortical structures by acetylcholine [32,33] or norepinephrine [55,66] that might be activated during pulses of cholinergic or noradrenergic activity evoked by errors during performance; or it could involve presynaptic inhibition by GABA_B receptors [67,68], or metabotropic glutamate receptors [69]. Another component that is important to the function of the network is the modulatory expression of synaptic modification at tagged synapses dependent upon the reward associated with a correct response. This could correspond to the cholinergic enhancement of long-term potentiation shown in a number of studies. Thus, the model presented in this paper demonstrates that the diversity of cognitive rule learning function across individuals could arise from variation in the impact of different neuromodulators across individuals.

Currently, we do not have an accepted scientific framework for modelling how flexible symbolic processing allows generalization of performance within cognitive tasks. If the neural mechanisms for human rule learning can be modelled computationally in terms of basic elements of cognitive function that are combined into higher order cognitive functions, this could then form the basis of a systematic taxonomy of cognitive function. As a distantly related analogy, one could think of the breakthrough in chemistry and physics when chemical elements were described and shown to systematically combine with different stoichiometries into different chemical compounds. Cognitive science does not have such a systematic framework for adding to knowledge of the elements of cognitive function, but the interaction of individual cognitive gates could involve different internal processing functions that could be characterized as different elements of cognitive function. As a simple first step, the analysis of learning and performance patterns in models such as the one presented here could indicate the behavioural manifestation of differences in parameters of cognitive function (for example, the different properties described here as noise in response selection and as weakening of previously modified weights). The manifestation of these behavioural differences in rule learning and generalization could allow analysis of human cognitive behaviour in terms of the potential parameters of neural circuit elements.

Data accessibility

This article has no additional data.

Competing interests

The authors have no conflicts of interest.

Funding

This work supported by the National Institutes of Health, grant numbers R01 MH60013, R01 MH61492 and by the US Office of Naval Research MURI award number N00014-16-1-2832.