Primordial sex facilitates the emergence of evolution

Abstract

Compartments are ubiquitous throughout biology, and they have very likely played a crucial role at the origin of life. Here we assume that a protocell, which is a compartment enclosing functional components, requires N such components in order to be evolvable. We calculate the timescale in which a minimal evolvable protocell is produced. We show that when protocells fuse and share information, the timescales polynomially in N. By contrast, in the absence of fusion, the worst-case scenario is exponential in N. We discuss the implications of this result for the origin of life and other biological processes.

1. Introduction

A defining characteristic of living organisms is their ability to replicate and evolve [1]. A major objective of research on the origin of life is, therefore, to find plausible chemical systems that are capable of self-replication. The ‘RNA world hypothesis’ is a leading framework encompassing theories about the role of RNA in the origin of life. It postulates that RNA or a similar biopolymer, being both an information-carrying molecule, as well as an enzymatic one, must have played a central role in initiating self-replication [2–4]. But formidable difficulties remain for developing this narrative into a complete and rigorous theory of the origin of life [5–8]. Both theoretical and experimental investigations show that well-mixed populations of RNA or similar biopolymers often suffer from calamitous pitfalls, including the error catastrophe for replicases [9] and parasitism for cooperative enzymes [10–13]. Moreover, the complexity of long RNA sequences that could serve as efficient catalysts creates a challenge for explaining their spontaneous prebiotic synthesis [14]. Indeed, despite decades of efforts in prebiotic chemistry (and some exciting progress, e.g. [15,16]), building efficient, stable and prebiotically plausible replicases (sometimes called the holy grail of the RNA world) has remained a challenge [17,18].

In modern cells, lipid membranes compartmentalize information-carrying and enzymatic molecules akin to those sought after by RNA world researchers. Hence, at some point in the development of life, either before, during or after the emergence of self-replicating genetic elements, such compartmentalization must have occurred. There is evidence in support of the prebiotic availability of lipid membranes. It has been shown that amphiphilic molecules, like simple fatty acids that are building blocks for the lipid membrane, can be produced in a prebiotically plausible manner [19]. Alternatively, lipids could have been imported to earth by chondrite meteorites [20–22]. Hence, such molecules were likely abundantly present on the prebiotic Earth [23–27]. These molecules are able to spontaneously assemble into lipid vesicles in aqueous conditions [27,28], forming compartments, which in this context are known as protocells.

Protocells alleviate some of the pitfalls that can impede the transition from prelife to life. The contents of protocells are held near each other and share the same fate. This results in increased interactions within the protocell and decreased interactions with the outside environment. It also means that the protocell can house a segmented genome, i.e. the information within the protocell need not be stored in one contiguous polymer (e.g. [23,29]). It can also dampen the effects of side reactions for any auto-catalytic cycles that may be required to start and maintain a metabolism [30]. Protocells can also divide into new protocells that inherit parts of their contents [31,32]. These properties of protocells enable them to help in selection for cooperative polymers, in particular replicases [10,11,33–38]. In addition to enclosing information and dividing, protocells are able to merge, thereby sharing their contents [30,39–41]. In biology, sharing information content between two individuals is considered a defining property of sex.

The implications of this information-sharing ability among protocells, which is a form of ‘primordial sex’, have not received much attention. For reasons outlined in the rest of this study, we suggest that the ability for these compartments to merge categorically changes the time required to produce an evolvable protocell. Hence, we propose that early presence of membranes, possibly even before the advent of replication, could have vastly improved the chances of producing complicated cells by luck. In such cases, it would not be unreasonable to assume that the starting set of molecules from which an evolvable cell emerges could be large. This assumption is rarely made in origin of life models, because it is considered a probabilistic miracle.

2. Model

To test this hypothesis, we investigate a simple first-passage process [42,43]. We assume that in order to be evolvable, a protocell needs to contain a certain number, N, of component types (i.e. distinct molecules of various complexity) [29,44–47]. In early life, these could be molecules as simple as ions, activated monomers, molecules that stabilize the membrane or more complicated polymers, like oligo-peptides, and even elementary ribozymes and simple unlinked genes [16,23,29,30,34,35,48–53]. More precisely, the target set should result in an auto-catalytic network that results in a evolvable cell with non-negligible probability. Such a scheme has been proposed since Oparin, and has been defended more recently [53]. We term the smallest set of necessary and sufficient components from which an evolvable protocell can be made a minimal evolvable protocell.

We can accordingly represent the functional (or genetic) content of each protocell as a binary string of length N. For simplicity, we ignore the redundancy (or dose) of each component in the protocell, and are only concerned with each component's presence. If a protocell contains a particular component i, then the string will have a value of 1 at the ith position and 0 otherwise. Whenever a protocell randomly assembles, we assume that it contains each of the N component types independently (components do not compete for positions) with probability p. That is, protocell assembly uniformly samples each type (with sufficient abundance) from the environment with probability p. Whenever two protocells merge, the value of the resulting string at every position i is simply determined by a bitwise OR operation on the ith bits of the two parent protocells (i.e. if either of the original cells contain a component, the resulting cell will also contain it). This is shown schematically in figure 1.

Figure 1.

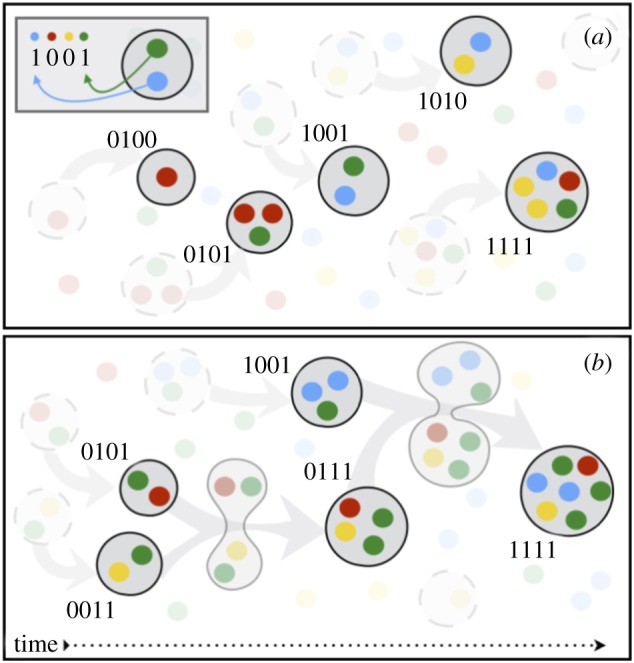
Merging occurs between randomly assembled protocells. (a) Each colour (and a ‘1’ bit at each corresponding position on a protocell's representative binary string) indicates the presence of one of the four components needed for the protocell to be evolvable (here, N = 4). Randomly assembled lipid membranes form around the components. (b) Whenever two protocells merge, they share their contents. Sharing of contents is computed as a bitwise OR operation between each of the two parent strings of length N. (Online version in colour.)

The dynamical process is as follows. On the first step, the accumulator—the object of our attention—consists of a randomly assembled protocell. If less than N components are enclosed, then one of two things can happen: with probability δ, the accumulator loses its contents, and on the second step, the accumulator consists of a new randomly assembled protocell, with the accumulation process starting over. The accumulator can lose its contents if, for example, its membrane's integrity is lost, it is infected by a parasite, or it divides, and the parameter δ accounts for all such possibilities. Or with probability 1 − δ, on the second step, the accumulator merges with a randomly assembled protocell from the environment, possibly gaining additional components. In this case, if the accumulator still has less than N components after merging, then one of two things can happen: with probability δ, the accumulator loses its contents, and on the third step, the accumulator consists of a new randomly assembled protocell, with the accumulation process starting over. Or with probability 1 − δ, on the third step, the accumulator merges with another randomly assembled protocell from the environment, possibly gaining additional components. This process continues until the accumulator gains all N components necessary for evolvability. The total number of steps (or time units), Z, needed to gain all N components is equal to the total number of random assembly and merging events in the accumulation process.

The time, Z, needed to form a minimal evolvable protocell is thus a random variable that depends on the particular accumulator being tracked. If we track many such accumulators, then what is the mean first-passage time, E[Z], for an accumulator to achieve all N components necessary for evolvability?

Begin by considering the simple case δ = 1 (no merging occurs). If the accumulator consists of a randomly assembled protocell that has all N components, then the minimal evolvable protocell has been achieved. But if there are less than N components, then the accumulator is reset without merging. Thus, the expected number of such random assembly events required to accumulate all N components necessary for evolvability, E_δ=1[Z], grows exponentially with N, i.e.

Under this model of independent components, for large values of N, the spontaneous generation of a minimal evolvable protocell would be a probabilistic miracle. This is the worst-case scenario. We now focus our attention on understanding how E[Z] grows with N when 0 < δ < 1.

In what follows, it is convenient to use the parameter q ≡ 1 − p. Denote by S(q, δ, N) the probability that, starting from a randomly assembled protocell, the accumulator achieves all N components before being reset. We determine S(q, δ, N) as follows. First, assume that there is no death of the accumulator. Then 1 − q^z is the probability that, after z steps, the accumulator has achieved a particular component. Therefore, 1 − (1 − q^z)^N is the probability that the accumulator has not achieved all N components after z steps. It follows that (1 − q^z)^N − (1 − q^z−1)^N is the probability that the accumulator achieves all N components in exactly z steps. Then, considering death of the accumulator, since the probability that the accumulator survives for z steps without being reset is simply (1 − δ)^z−1 , we have

This can be simplified as

2.1

Denote by T(z; q, δ, N) the probability mass function for the number of steps, z, needed for the accumulator to gain all N components (i.e. reach its target) when starting from a randomly assembled protocell, given that all N components are accumulated before being reset. We have

2.2

Roughly speaking, T is the distribution of how many steps it takes to succeed in hitting the target set starting from a reset without being reset again. Denote by R(z; q, δ, N) the probability mass function for the number of steps, z, taken before the accumulator is reset when starting from a randomly assembled protocell, given that the accumulator is reset before gaining all N components. We have

2.3

Roughly speaking, R is the distribution of the number of steps the accumulator takes until it resets starting from a reset without hitting the target. In what follows, we omit explicitly writing the functional dependencies on q, δ and N for notational convenience.

For all 0 < δ < 1, the mean first-passage time, E[Z], needed to form a minimal evolvable protocell is calculated directly from

2.4

Substituting equations (2.1)–(2.3) into equation (2.4) and simplifying, we obtain

2.5

To extract the large-N behaviour of E[Z] from equation (2.5), we simplify the summation in equation (2.1) for large N using the following procedure. For a smooth function f(x), we use the notation f⁽ⁱ⁾(x) = dⁱf(x)/dxⁱ. We can express an integration of f⁽ⁱ⁾(x) with respect to x from 0 to ∞ as

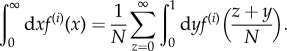Next, we write a Taylor expansion of f⁽ⁱ⁾((z + y)/N) in powers of y/N and perform the integration over y. We have

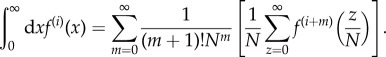2.6

Substituting equation (2.6) into equation (2.1) to express the summation as an integration, substituting the integral form of the Beta function, 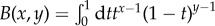, and henceforth using ∼ to denote asymptotic equivalence as , we obtain

2.7

Substituting equation (2.7) into equation (2.5), expressing the beta function using gamma components, B(x, y) = Γ(x)Γ(y)/Γ(x + y), using Stirling's formula for the gamma function, 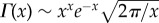, and simplifying for large N, we find that E[Z] grows asymptotically as

2.8

where

and

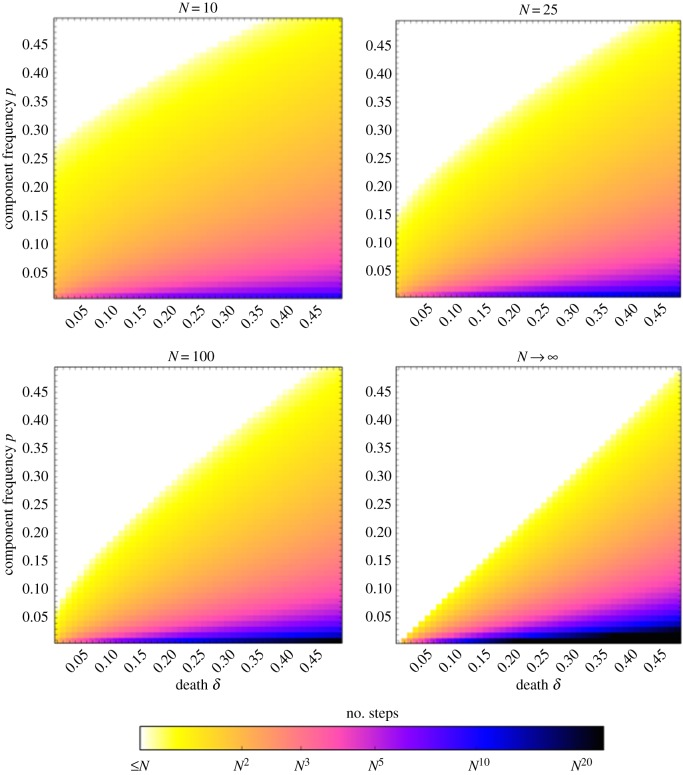
The time complexity of concurrence of components is thus fundamentally altered: for any slight amount of merging, i.e. for any value 0 < δ < 1, E[Z] grows algebraically with N. Intriguingly, for many values of p and δ, E[Z] grows only as a small power of N, and for many other values of p and δ, E[Z] grows only sublinearly with N (figure 2).

Figure 2.

Minimal evolvable protocells are achieved in polynomial time for the vast majority of parameter space. For N = 10, N = 25 and N = 100, we perform Monte Carlo simulations of the accumulation of components, and we plot N^log_N(E[Z]) as a function of p and δ. For , we plot N^k as a function of p and δ. (Online version in colour.)

For the particular case in which δ ≪ 1, p ≪ 1 and δ is not too large relative to p, equation (2.8) admits a simple approximation:

2.9

The exact form of E[Z] for all values of N given by equation (2.5), E[Z] measured using a Monte Carlo simulation of the accumulation of components, the exact asymptotic result for E[Z] given by equation (2.8), and the approximation for E[Z] given by equation (2.9) are plotted in figure 3 for several values of p, δ and N.

Figure 3.

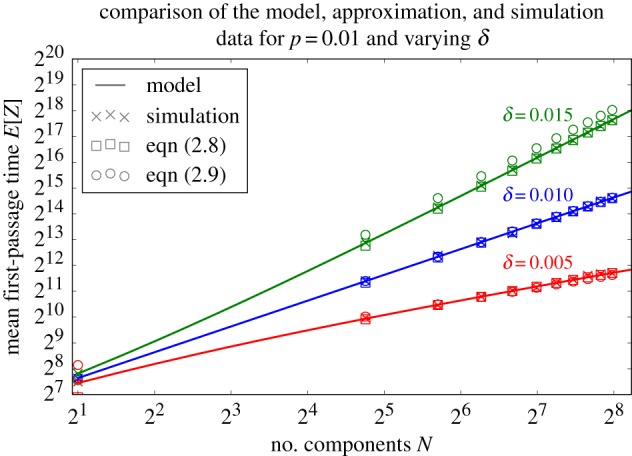
For p = 0.01 and δ = 0.005, δ = 0.01 and δ = 0.015, we plot the exact form of E[Z] for any value of N given by equation (2.5) (solid lines), E[Z] measured using a Monte Carlo simulation of the accumulation of components (cross), the asymptotically exact form of E[Z] given by equation (2.8) (square) and the approximation for E[Z] given by equation (2.9) (circle). (Online version in colour.)

For the particular case δ = 0, the accumulator begins as a randomly assembled protocell, and it is never reset. For this case, the mean first-passage time, E_δ=0[Z], grows logarithmically with N, i.e.,¹

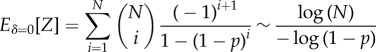Also of interest for the biologically realistic case 0 < δ < 1 is the probability mass function, P(Z = z), for the number of steps needed to achieve a minimal evolvable protocell. P(Z = z) is given by

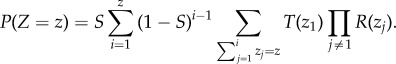2.10

In essence, this equation splits the total number of steps z into the runs in which the accumulator resets without success (i − 1 times), and the final run in which the accumulator hits the target set. For simplicity, the number of steps taken in the successful run is labelled as z₁, and the rest are denoted by z_j.

If N is small, then there is typically a small number of resets before the accumulator gains all components, which corresponds to each z_j being comparable in magnitude to z in the summations in equation (2.10). But if N is large, then there is typically a large number of resets before the accumulator gains all components, which corresponds to having z_j ≪ z for all j in the summations in equation (2.10). In this case, the total number of steps, Z, is the sum of many independent and identically distributed random variables.

To provide a sense of how good of an estimator E[Z] is for the variable Z, we look at its concentration 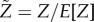. Denote μ as the average number of steps before an accumulator resets given that the accumulator resets before gaining all N components. Denote σ² as the variance in the number of steps before an accumulator resets given that the accumulator resets before gaining all N components. We have 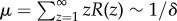and 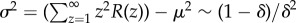. Since both μ and σ² are finite, the central limit theorem enables a simplification of equation (2.10) for large values of N: we obtain the probability density function for :

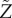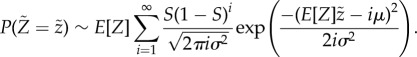2.11

The moments of 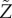are directly computed from equation (2.11)

Since the corresponding moment-generating function is that of the exponential distribution, it follows that Z is exponentially distributed about E[Z]:

For large N, the natural production of minimal evolvable protocells via random assembly and repeated fusion is therefore simply a Poisson process.

3. Discussion

It is noteworthy that E[Z], equation (2.5), provides an upper bound on the time to construct a minimal evolvable protocell for many natural variations of this process. There are many ways in which the first-passage time can be shortened. For instance, the expected time to reach the target set of N components is reduced if cells divide (and retain some components) instead of losing all components through death. Redundancy in components, where a protocell might have one or more backup copies of each component, can have a similar effect. Additionally, random assembly does not necessarily take exponential time if the components are not independently sampled. Yet, regardless of the worst-case time complexity, we show that fusion helps in reducing the hitting time. Our simple model is specified by only three parameters. Our model is, therefore, robust for exploring the time complexity of a myriad of compartmentalization scenarios by simply tuning the values of p, δ and N.

Doing so will help in understanding several biological questions and relates our work to other studies that are interested in the timescale of evolutionary events. For instance, Wilf & Ewens [54] arrive at exactly the same formula for δ = 0 when looking for the time it takes for evolution (on a smooth landscape with a single peak, hence δ = 0) to reach a target set of genes. This analysis is also favourable to viewing sex as the default biological state. Computational and experimental analyses of sex suggest that it may make evolutionary search over a landscape more efficient [55–58]. Our analysis adds that this advantage could be present, and aid, in starting cellular replication itself. While biologists have considered the possibility of early sex before [40,59], it was soon observed that parasitism could be a serious problem [30]. However, our exact asymptotic analysis instead suggests that sex is a good strategy, even in the presence of parasites.

Oceanic currents in early earth could have brought together primitive protocells with disparate components, which subsequently merged and eventually spawned an evolvable protocell. In this scenario, protocell formation and merging act as a necessary bridge between physically and chemically heterogeneous prebiotic environments for biological construction. Indeed, there is exciting, ongoing experimental work on creating ‘self-sustaining’ protocells, which can divide and subsequently restore their viable composition via fusion for a few generations [60]. Similarly, recent experiments have demonstrated predation-like behaviour and phagocytosis in communities of semi-permeable colloidal objects which encapsulate biological molecules [61,62]. As these mechanisms mirror merging, they provide a potential platform where protocells with novel functionality can be searched for through parallelization and random merging.

Our mathematical model is also appropriate for investigating the biological activation of modern viruses. In particular, our model captures a process known as multiplicity reactivation. In this process, multiple non-functional, mutant viruses of the same strain combine, thereby covering each other's loss-of-function mutations and producing a functioning virus. Our analysis readily provides the expected number of such viral particles required that would reactivate a virus (although in many cases N is too small for the speed-up to be of interest). In a similar scenario, in multi-compartment viruses, multiple distinct components need to co-infect the same host in order to produce a new virion. In numerous plant viruses, such as the genus Tymovirus, the infection occurs when two or more functionally distinct virions infect the same host [63,64]. The occurrence of this type of combinatorial reproduction in many RNA viruses, which are thought to be ancient, is consistent with the thesis that primordial sex played an integral role in early life [65,66].

Research into minimal synthetic cells has shown that cells with a few hundred genes are able to self-sustain in complex media [67–69]. This suggests that even for low values of p, in this case the probability of required genes versus random protein-coding genes, novel self-sustaining cells (and possibly viruses) could be produced, either in the laboratory or in early life, by a feasible number of fusions. The feasibility of finding novel viable combinations through a merging process in the laboratory should also be of help in order to understand the density of viable solutions within the fitness landscape, a problem of interest in algorithmic perspectives of evolution and origin of life [55,70,71].

We may never know with certainty what path has resulted in the emergence of life on earth. There are likely many possible paths to evolvability, none of which have been fully delineated to this date. So far, virtually all models of protocells assumed a small initial set size, precisely because co-occurrence of many components together is unlikely. We show that even if the number of required components N is large, there are tenable paths to construct such an assembly. The merging mechanism is not as critical if N is small, but in the presence of merging compartments we are no longer restricted to this scenario. Here, we have devised and analysed a model that captures a general set of possibilities for an evolvable protocell to emerge. It is noteworthy that our model remains agnostic about whether template-directed replication or metabolism emerged first and it can apply in both scenarios as well as different levels of complexity (from chemicals to enzymes and genes) in the underlying components.

To the best of our knowledge, our study is the first to provide a rigorous and quantitative blueprint for comparing the plausibility of a subset of paths to life: those that involve compartmentalization.

Data accessibility

Monte Carlo simulations were used to validate the model. The Python code for these simulations is available upon request.

Authors' contributions

S.S. and M.A.N. conceived the study. S.S., J.O., I.A.N. and M.A.N. performed mathematical analysis and simulations. All authors contributed to the preparation of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was conducted using the resources at the Program for Evolutionary Dynamics (PED). PED is supported by the John Templeton Foundation and, in part, by a grant from B. Wu and Eric Larson.