Graphical abstract
Keywords: Distributed learning, Support vector machine, Decision support systems, Predictive models, Dyspnea
Highlights
-
•
Developed and implemented IT infrastructure in 5 radiation clinics across 3 countries.
-
•
Proof-of-principle for ‘big data’ infrastructure and distributed learning studies.
-
•
General framework to execute learning algorithms on distributed data.
Abstract
Machine learning applications for personalized medicine are highly dependent on access to sufficient data. For personalized radiation oncology, datasets representing the variation in the entire cancer patient population need to be acquired and used to learn prediction models. Ethical and legal boundaries to ensure data privacy hamper collaboration between research institutes. We hypothesize that data sharing is possible without identifiable patient data leaving the radiation clinics and that building machine learning applications on distributed datasets is feasible.
We developed and implemented an IT infrastructure in five radiation clinics across three countries (Belgium, Germany, and The Netherlands). We present here a proof-of-principle for future ‘big data’ infrastructures and distributed learning studies. Lung cancer patient data was collected in all five locations and stored in local databases. Exemplary support vector machine (SVM) models were learned using the Alternating Direction Method of Multipliers (ADMM) from the distributed databases to predict post-radiotherapy dyspnea grade . The discriminative performance was assessed by the area under the curve (AUC) in a five-fold cross-validation (learning on four sites and validating on the fifth). The performance of the distributed learning algorithm was compared to centralized learning where datasets of all institutes are jointly analyzed.
The euroCAT infrastructure has been successfully implemented in five radiation clinics across three countries. SVM models can be learned on data distributed over all five clinics. Furthermore, the infrastructure provides a general framework to execute learning algorithms on distributed data. The ongoing expansion of the euroCAT network will facilitate machine learning in radiation oncology. The resulting access to larger datasets with sufficient variation will pave the way for generalizable prediction models and personalized medicine.
Introduction
Medical research revolves around accumulation and analysis of (patient) data. Collecting sufficient quantities of data to explain a phenomenon is arguably a major impediment to scientific progress in a technology-driven discipline such as radiation oncology. This obstacle becomes even more eminent in light of the recent adoption of machine learning [1] to foster the goal of personalized medicine: machine learning algorithms require access to large databases with sufficient variation in the collected data to answer complex research questions.
Single institutes struggle to collect the necessary data volumes with sufficient diversity to learn from. Furthermore, data collected in radiation oncology is influenced and biased by technological (e.g., vendor-specific properties [2]), human (e.g., local patient characteristics, physician’s opinions [3]), as well as organizational (e.g., treatment guidelines) factors which can change rapidly. Research questions in such contexts may remain unanswerable by isolated data collection efforts: the data may be too biased or simply lack the necessary variation to successfully model relationships between the collected variables. Data homogeneity may not only be an issue for single institutes but nationwide due to national treatment guidelines [4]. Hence, generalizable machine learning models to answer these research questions should be created by incorporating data from multiple institutes in a continuous manner (i.e., rapid learning health care [5]). Systematic data sharing among research institutes will become an indispensable means for personalized medicine to thrive in radiation oncology. At present, data sharing is characterized by one-off exchanges of datasets with limited standardization of data collection and data characterization. Further, data sharing is impeded by each institute’s legal and ethical concern to protect their patients’ privacy rights.
In this study, we present euroCAT, an IT infrastructure for systematic data sharing among research institutes. A video summary is available here: https://youtu.be/ZDJFOxpwqEA
The hypotheses of the study are
-
(1)
Data sharing for machine learning is possible without identifiable patient data leaving an institute’s IT systems. Thus, the institutes remain in control of their data, preserve data privacy, and thereby overcome legal and ethical issues common to other forms of data exchanges.
-
(2)
Running machine learning applications on these data is feasible and, given the appropriate methodology, the resulting models only minimally differ from centrally learned models, which makes efforts to centralize data largely unnecessary. As an example, support vector machines (SVM) predicting severe dyspnea after radiotherapy (henceforth simply called dyspnea) are learned from the data provided in five institutes.
The aim of the study was to deploy the euroCAT system in five partner institutions within three European countries (Belgium, Germany, and The Netherlands) and in four languages (Dutch, English, French, and German) and test the above hypotheses.
euroCAT focusses on multi-centric machine learning in radiation oncology, similar work to implement privacy-preserving data analysis exists, e.g., for Genome-Wide Association Studies (GWAS) [6]. Constable et al. concisely discuss existing literature for distributed learning and the accompanying risks. A web service for distributed logistic regression analysis is presented by Jiang et al. [7] to facilitate collaborative regression analysis.
Material & methods
euroCAT infrastructure
Institutes within the euroCAT network (a site) dedicate a server within their IT infrastructure that hosts the local databases and local learning connector (Varian Medical Systems, Palo Alto, USA). The global learning environment (Varian Learning Portal) spans the sites, and connects a central server (the master) outside the sites’ IT infrastructure to the learning connectors inside the sites. Master and sites communicate via file-based, asynchronous messaging. The user interacts with the learning environment via a web browser-based interface in which s/he can upload learning applications (MATLAB, MathWorks, Natick, MA, USA) and can initiate machine learning runs. Every learning application consists of two parts, one site algorithm which runs inside the sites’ infrastructure and interacts with the learning connector and one master algorithm which runs in the global learning environment and can send and receive messages to and from the site algorithms.
Data
Each participating center (Aachen (Germany), Eindhoven (The Netherlands), Hasselt (Belgium), Liège (Belgium), and Maastricht (The Netherlands)) was asked to retrospectively select at least 50 patients which fulfilled the inclusion criteria (non-small cell lung cancer, high-dose radiotherapy, no surgical treatment). The centers were provided with an overview of variables that were needed for the study. Initially, survival outcome, dysphagia outcome, and dyspnea outcome were scored. For this proof-of-principle paper, we only used the dyspnea outcome. The data was stored in a spreadsheet. An euroCAT researcher visited each center and manually checked 20% of the collected data for inconsistencies/mistakes. Post-treatment dyspnea was recorded for 268 patients. Given availability in the databases, three features were manually selected to construct an exemplary prediction model for post-treatment severe dyspnea: lung function tests (FEV1 (in %), forced expiratory volume in 1 s, in %, adjusted for age and gender), cardiac comorbidity (non-hypertension cardiac disorder at baseline, for which treatment at a cardiology department has been given), and timing of chemotherapy. Severe dyspnea was defined as Grade 2 dyspnea after treatment. The variables are listed in Table 1.
Table 1.
Overview of patient characteristics per hospital.
| Variable | Maastricht |
Eindhoven |
Hasselt |
Liège |
Aachen |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Count | % | Count | % | Count | % | Count | % | Count | % | |
| Post-RT dyspnea | ||||||||||
| 89 | 72% | 50 | 89% | 8 | 57% | 20 | 61% | 36 | 86% | |
| 34 | 28% | 6 | 11% | 6 | 43% | 13 | 39% | 6 | 14% | |
| Missing | 0 | 0% | 0 | 0% | 0 | 0% | 0 | 0% | 0 | 0% |
| Cardiac comorbidity | ||||||||||
| No | 90 | 73% | 44 | 79% | 2 | 14% | 27 | 82% | 24 | 57% |
| Yes | 33 | 27% | 12 | 21% | 3 | 21% | 6 | 18% | 12 | 29% |
| Missing | 0 | 0% | 0 | 0% | 9 | 64% | 0 | 0% | 6 | 14% |
| Chemotherapy timing | ||||||||||
| None | 16 | 13% | 5 | 9% | 3 | 21% | 0 | 0% | 2 | 5% |
| Sequential | 22 | 18% | 24 | 43% | 2 | 14% | 2 | 6% | 4 | 10% |
| Concurrent | 85 | 69% | 27 | 48% | 8 | 57% | 31 | 94% | 33 | 79% |
| Missing | 0 | 0% | 0 | 0% | 1 | 7% | 0 | 0% | 3 | 7% |
| FEV1 (in %) | ||||||||||
| Mean & Standard Dev | 78 | 21 | 80 | 25 | 80 | 25 | 72 | 23 | 66 | 19 |
| Missing Count & Percentage | 0 | 0% | 20 | 36% | 2 | 14% | 0 | 0% | 20 | 48% |
From the spreadsheets, data was extracted using an open source data warehousing tool (Pentaho) and stored in an open-source database (PostgreSQL). From this database, data elements were mapped to the Semantic Web data model (Resource Description Framework, RDF) using an open source tool (D2RQ) and stored in an open-source RDF store (Sesame, Eclipse RDF4J). During mapping to RDF the data elements were coded using Uniform Resource Identifiers (URIs) which are defined in a domain ontology (Radiation Oncology Ontology) and reference ontologies (NCI Thesaurus, Unit Ontology) in the Web Ontology Language (OWL, available on the Bioportal [8]). The learning connector uses the Semantic Web query language SPARQL to query data from the RDF store [9] and can parse that data to the site learning algorithm.
Distributed learning
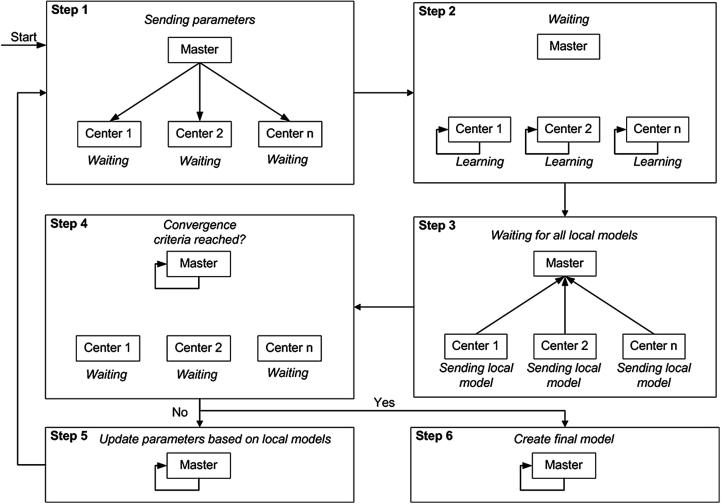
The process of carrying out distributed learning inside euroCAT is presented schematically in Fig. 1. At each iteration, the data stored at different sites is processed simultaneously and separately. Updated model parameters are then sent from each site to the master. At the master, an algorithm compares the model parameters and updates them further. The algorithm also checks whether the learning process has converged sufficiently (according to pre-set convergence criteria). If the convergence criteria are not yet met, the master sends the parameters back to each of the sites. Once the sites receive updated parameters, they are used as a starting point for adjusting the model parameters further (given the local data) once again. This completes one iteration cycle. The learning iterations continue until the convergence criteria are satisfied.
Fig. 1.
Distributed learning flow in euroCAT.
Using this infrastructure allows models to use data for learning without transferring these data across the network. The learned model is a support vector machine (SVM) classifier, solved with the Alternating Direction Method of Multipliers (ADMM) method [10].
Support vector machines (SVM) & the Alternating Direction Method of Multipliers (ADMM)
A support vector machine determines two parallel hyperplanes, forming a ‘border’ which separates the feature space into two large regions and a margin between the planes. Each dimension of this feature space represents one patient feature (e.g., FEV1 (in %) or cardiac comorbidity) and each patient is represented by one point in this space. For simple problems, the intention would be to identify hyperplanes that separate all patients with dyspnea from the group of patients without dyspnea. This is not possible in most cases, therefore the objective becomes to find hyperplanes such that
-
–
most of the dyspneic patients are on one and non-dyspneic patients are on the other side
-
–
if there is a patient on the ‘wrong’ side of the border, the distance to the border is as small as possible
-
–
the border between the groups of dyspneic and non-dyspneic patients is as large as possible.
The optimal hyperplanes ( and , where are the features of a patient) are determined by a vector of coefficients that minimizes a cost function under a set of constraints (see Appendix A for details).
Boyd et al. [10] discuss a distributed formulation of a support vector machine using the Alternating Direction Method of Multipliers (ADMM) and provide MATLAB code [11]. The ADMM algorithm gained popularity in the machine learning community as it allows to split up large datasets into smaller portions and distribute the analysis over multiple machines. In our multi-centric learning context, the same property is exploited to overcome the restriction that data may not be centralized. ADMM requires a multitude of iterations in which estimates for are refined using each site’s data. See Appendix A for a more detailed description of SVMs and ADMM.
Learning & validation
For details on additional data processing steps, parametrization of the ADMM algorithm, and the code used to execute the algorithm, we refer to Appendix B.
To display the capabilities of the distributed learning network, support vector machines are once trained on all sites and once trained and validated in a cross-validation design: the SVM is fitted using data from four sites and validated on the remaining site. This process is repeated four times with validation on another site. The average values for training and validation constitute the cross-validation result.
The models’ performance is measured in terms of discriminative performance expressed as the area under the curve (AUC) of the Receiver Operating Characteristic curve (ROC).
To demonstrate the validity of the distributed learning approach with respect to a centralized learning algorithm, we compare the ADMM results to solutions from a centralized SVM optimizer. To this end, we centralize the data from all sites and solve the SVM optimization problem (Eqs. (1), (2), (4), Appendix A). Missing value imputation is still done per site to ensure comparability of centralized and distributed results. For this demonstration, the distributed algorithm is run in a local simulation environment.
Results & discussion
The results for learning and validation on all sites and the 5-fold cross-validation can be found in Table 2. The discriminative performance in the cross-validation is modest with a validation AUC of 0.66 but stable across training (0.62) and validation (0.66). Training AUCs are stable across folds (0.60–0.64) while inter-fold validation AUCs vary considerably (0.57–0.77). Published models [12], [13] show similar discriminative performance. The sole purpose of the presented SVM models is to display the infrastructure’s functionality and it is advised not to use these models in a clinical setting.
Table 2.
Discrimination performance (AUC) obtained by learning an SVM on all sites and in a 5-fold CV in distributed learning (ADMM, following the formulation shown in Eqs. (4), (5), (6), (7), Appendix A).
| CV | |||||||
|---|---|---|---|---|---|---|---|
| Train on | All | All except Maastricht | All except Eindhoven | All except Hasselt | All except Liège | All except Aachen | |
| Validate on | Maastricht | Eindhoven | Hasselt | Liège | Aachen | ||
| Training AUC | 0.63 | 0.61 | 0.60 | 0.64 | 0.62 | 0.64 | 0.62 |
| Validation AUC | 0.58 | 0.77 | 0.57 | 0.72 | 0.64 | 0.66 |
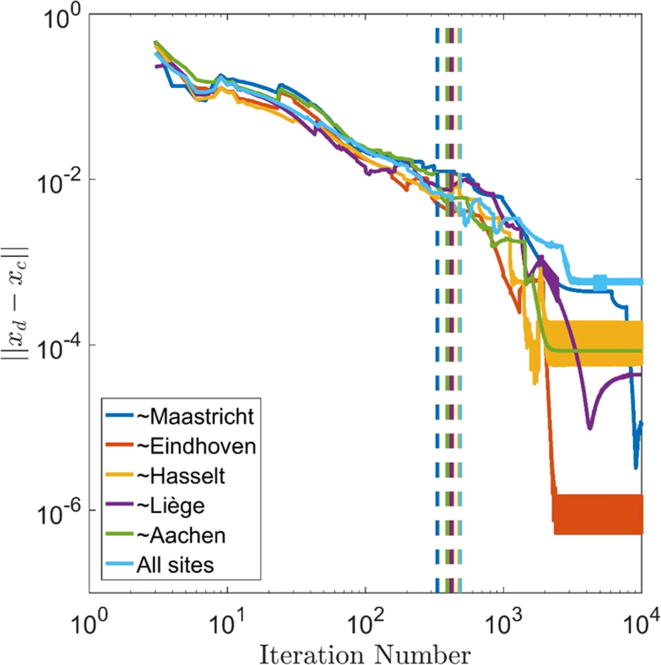
The coefficients of the SVM trained in the euroCAT network and in centralized learning can be found in Table 4. The individual run time of the 6 learning runs in the current euroCAT network was approximately 2 h or less with an iteration count between 300 and 500. Fig. 2 illustrates the convergence of the ADMM results to the centralized optimization results for all six learning runs. The iteration number is listed on the x-axis, the norm of the difference between ADMM and centralized results is shown on the y-axis. The algorithm was run for iterations and the iterations in which the internal convergence criteria are met in the euroCAT network are indicated by vertical lines. In all six cases, the solution approaches the centralized solution non-monotonically until the convergence criteria are met and the ADMM algorithm stops. The ADMM-based SVMs do not completely coincide with centralized models (see Table 4) as the convergence criteria were relaxed to accommodate for the relatively long network communication time in each iteration. A centralized learning algorithm determines SVM coefficients in less time as there is no network communication. Thus, when using ADMM-based distributed learning (or other distributed learning methods with repeating master-site communication), one faces a trade-off between solution precision and computation time. While the network communication time will surely force large-scale simulation studies to be maximally parallelized (to minimize the impact of network communication), the impact on prediction model development and performance is expected to be limited: the impact on AUC-based discriminative performance is small for the exemplary SVM models (compare Table 2, Table 3) and can be further reduced with stricter convergence criteria (see Fig. 2). Viewed differently, ‘early stopping’ is employed in machine learning as a regularization technique to avoid overfitting [14]. Models that suffer from overfitting explain the training data but fail to correctly predict outcomes in other datasets. Therefore, the trade-off between solution precision and computation time should not harm the goal of developing robust machine learning models for personalized medicine.
Table 4.
SVM coefficients learned by distributed and centralized learning.
| Trained on | ||||||
|---|---|---|---|---|---|---|
| All | Distributed | 0.01 | −0.32 | −0.20 | −0.25 | −0.55 |
| Centralized | 0.01 | −0.31 | −0.20 | −0.25 | −0.55 | |
| All except Maastricht | Distributed | −0.03 | −0.31 | −0.20 | −0.29 | −0.51 |
| Centralized | −0.02 | −0.31 | −0.20 | −0.29 | −0.51 | |
| All except Eindhoven | Distributed | 0.01 | −0.28 | −0.06 | −0.33 | −0.48 |
| Centralized | 0.02 | −0.28 | −0.06 | −0.33 | −0.48 | |
| All except Hasselt | Distributed | 0.00 | −0.32 | −0.20 | −0.26 | −0.55 |
| Centralized | 0.00 | −0.31 | −0.20 | −0.26 | −0.55 | |
| All except Liège | Distributed | 0.00 | −0.31 | −0.20 | −0.25 | −0.55 |
| Centralized | −0.01 | −0.31 | −0.20 | −0.26 | −0.55 | |
| All except Aachen | Distributed | 0.00 | −0.34 | −0.19 | −0.24 | −0.53 |
| Centralized | 0.00 | −0.34 | −0.19 | −0.24 | −0.53 | |
Fig. 2.
Convergence graphs of distributed ADMM solutions to centralized solutions for iterations. Vertical lines indicate the iterations in which internal convergence criteria were met in the euroCAT network. The data was created in local simulations. ‘∼’ indicates ‘Trained on all sites except’.
Table 3.
Discrimination performance (AUC) obtained by learning an SVM on all sites and in a 5-fold CV in centralized learning (solving the optimization problem shown in Eqs. (1), (2), (4), Appendix A).
| CV | |||||||
|---|---|---|---|---|---|---|---|
| Train on | All | All except Maastricht | All except Eindhoven | All except Hasselt | All except Liège | All except Aachen | |
| Validate on | Maastricht | Eindhoven | Hasselt | Liège | Aachen | ||
| Training AUC | 0.63 | 0.61 | 0.60 | 0.63 | 0.61 | 0.64 | 0.62 |
| Validation AUC | 0.58 | 0.77 | 0.59 | 0.72 | 0.64 | 0.66 |
A challenge of distributed learning is that the user is not able to inspect the data which is used as input for the machine learning applications. S/he must rely on summary statistics to ascertain that the data is in the desired format. This obstacle can be overcome by collaboration between users from the respective institutes and strictly following the agreed data collection and storage protocols. An euroCAT umbrella protocol [15] was provided to the participating institutes to guide future lung data collection. Protocols for other diseases are also available: for a data sharing project between MAASTRO Clinic and the Sacred Heart University Hospital (Rome) on rectal cancer, a corresponding umbrella protocol was developed [16].
Systematic data sharing not only requires an IT infrastructure, as developed in this study, but it also depends on systematic data collection in routine clinical care. It has been argued that data from routine care is a valuable source of information to improve the standard of care [5], [17]. However, this data is often not treated as such. Consequently, data collection and standardization have the potential to be improved as also observed in this study.
Even though routine clinical care might become a cornucopia of clinical data, this data needs to be handled with care: McGale et al. [18] show that conclusions from routine clinical care data may contradict findings from randomized clinical trials. Routine care data is subject to many biases contrary to data from carefully designed trials. The conclusion should not be to discard routine care data altogether but rather to develop means to profit from this data: i.e., develop appropriate methodology, e.g., extensive correction for confounders [19], and to expand standardized data collection to capture all data necessary to detect confounders, e.g., collect accompanying patient data from referring hospitals/physicians and details on the (quality of the) treatment given. Viewed differently, the purpose of data collection, regardless whether it is data from randomized clinical trials or routine care, is to improve treatment quality for all patients. Peters et al. [20] show that even within clinical trials treatment quality is highly variable among institutes, i.e., institutes treating fewer patients delivering lower quality treatments. Given these difference, it is debatable whether conclusions drawn from trials which were conducted at selected institutes translate into routine clinical care where the standard of care may be generally lower and patient populations differ [21], [22]. Data collected in routine clinical care is directly sampled from the population in question unlike trial data derived from a biased proxy. Therefore, systematic data collection in routine clinical care will not only provide new opportunities for further analyses (with the abovementioned necessary caution) but it will also allow systematic studies of the general patient population and tracking whether treatment benefits observed in clinical trials arrived in routine clinical care.
Continued concerns over patient privacy might render institutes reluctant to participate in systematic data sharing. Illegal access to data is prevented within the euroCAT learning environment: the web browser-based learning interface is only accessible with registered user accounts and learning runs are always linked to such account. Learning algorithms circulating in the network need to be authenticated by a digital file signer that is available only to registered members of the euroCAT network. Furthermore, permission to learn on an institute’s data is granted by the respective institute’s principal investigators per user account or on a run-by-run basis. Additionally, illegal data transfers can be identified and shut down: standard master/site communication is limited to small volumes like model parameters, prediction outcomes, and summary statistics. Limits on the communication volume therefore render high volume data transfers impossible. Collaboration with external parties always comes with a risk of losing control over one’s data. Mutual trust and legal assurance to safeguard other parties’ data are key aspects in scientific collaboration. However, in comparison to the traditional data exchange collaborations, a data sharing network such as euroCAT adds technical control mechanisms to manage and limit access to an institute’s data.
The pilot study was restricted to sharing a dataset of limited size in three countries. However, the range of variables, number of patients, and number of institutes is variable: linking an entire hospital’s EHR and PACS to the learning environment is theoretically possible. Further, the ontologies used for euroCAT to match variables across institutes bear the potential to facilitate data sharing around the globe. For euroCAT, data was shared across clinics located in three different countries, i.e., with three different national data collection guidelines and three different languages (Dutch, French, and German). This pilot study has led to follow-up projects in, among others, the Netherlands (duCAT), Italy (VATE), the USA (meerCAT), Australia (ozCAT), Canada (canCAT), and China (sinoCAT).
The potential of the euroCAT infrastructure exceeds the presented results. The capability to learn SVMs is just one example for applications of the distributed learning infrastructure. The ADMM algorithm used for SVMs is extendable to other existing machine learning methods like linear/logistic regressions and feature selection methods like (logistic) LASSO [10]. Independent of the ADMM algorithm, the infrastructure can facilitate other machine learning techniques such as Bayesian Networks learned from distributed data [23]. More generally, any desirable computation requiring access to an institute’s data with subsequent aggregation on the master is feasible. Systematic data sharing efforts such as euroCAT will likely profit from the ongoing research in the flourishing fields of machine learning and artificial intelligence.
The presented IT infrastructure facilitates modeling of multi-centric data without direct access to said data. This method bears the risk that inter-institutional bias in variables, e.g., due to inconsistent (toxicity) scoring, varying reporting standards, different patient populations, or data collection errors remain unnoticed. Future work will be focused on the systematic detection of such affected data in a distributed learning network.
Conclusion
Multi-centric rapid learning for health care is feasible as shown by the support vector machines developed in the euroCAT network. We have no doubts that the clinical decision support systems of the future would routinely use models based on data available in distributed databases across national borders. One solution for surmounting accompanying technical, legal, and ethical issues with data sharing is already delivered across three countries by the euroCAT system and has shown to scale globally. We believe that distributed learning is the best way to go for building clinically reliable models that are universally applicable, personalized, and robust.
Funding
Authors acknowledge financial support from ERC advanced grant (ERC-ADG-2015, n° 694812 – Hypoximmuno). This research is also supported by the Dutch technology Foundation STW (grant n° 10696 DuCAT & n° P14-19 Radiomics STRaTegy), which is the applied science division of NWO, and the Technology Programme of the Ministry of Economic Affairs. Authors also acknowledge financial support from the EU 7th framework program (ARTFORCE – n° 257144, REQUITE – n° 601826), SME Phase 2 (EU proposal 673780 – RAIL), EUROSTARS (SeDI, CloudAtlas, DART), the European Program H2020-2015-17 (BD2Decide – PHC30-689715 and ImmunoSABR – n° 733008), Kankeronderzoekfonds Limburg from the Health Foundation Limburg, Alpe d’HuZes-KWF (DESIGN), and the Dutch Cancer Society. This publication was supported by the Dutch national program COMMIT (Prana Data project).
Declaration of interests
Timo Deist holds a part-time employment with ptTheragnostic BV, The Netherlands. Philippe Lambin is in the advisory board of ptTheragnostic BV, The Netherlands.
Acknowledgement
We would like to thank Varian Medical Systems for providing the distributed learning manager, and Wolfgang Wiessler and Tim Hendriks for their dedicated support.
Appendix A
A support vector machine determines two parallel hyperplanes, forming a ‘border’ which separates the feature space into two large regions and a margin between the planes. Each dimension of this feature space represents one patient feature (e.g., FEV1 (in %) or cardiac comorbidity) and each patient is represented by one point in this space. For simple problems, the intention would be to identify hyperplanes that separate all patients with dyspnea from the group of patients without dyspnea. This is in not possible in most cases, therefore the objective becomes to find hyperplanes such that
-
–
most of the dyspneic patients are on one and non-dyspneic patients are on the other side
-
–
if there is a patient on the ‘wrong’ side of the border, the distance to the border is as small as possible
-
–
the border between the groups of dyspneic and non-dyspneic patients is as large as possible.
The optimal hyperplanes are determined by
| (1) |
such that
| (2) |
| (3) |
is the normal vector of the separating hyperplanes, is the bias term. characterizes the hyperplanes. is an auxiliary variable for sample representing the classification error. is a parameter to assign more importance to the first or the second term of the objective. needs to be positive. is the label of training sample . is the vector of features for sample . Minimizing the first term in the objective function, , maximizes in the margin, i.e., the space between both hyperplanes. Minimizing minimizes the classification error. The objective is split into two terms, and The latter is separable among data samples such that the value for can be obtained by slicing up the dataset into multiple parts, computing the contribution of each slice independently and merging the results afterwards. This property (and other) can be exploited such that the SVM optimization problem is solvable in a distributed fashion. Boyd et al. [10] discuss a distributed formulation of a support vector machine using the Alternating Direction Method of Multipliers and provide MATLAB code [11]. The ADMM algorithm gained popularity in the machine learning community as it allows to split up large datasets into smaller portions and distribute the analysis over multiple machines. In our multi-centric learning context, the same property is exploited to overcome the restriction that data may not be centralized. The formulation is
| (4) |
| (5) |
| (6) |
| (7) |
where , is the number of sites, and and are model parameters.
In each iteration , is computed at each site and transmitted to the master. At the master, a relaxation function (6) is applied to yielding . The average of all sites is used to compute and , which are transmitted to the sites and are used as input for the computation of in the next iteration. is calculated to reduce the classification error, is calculated to increase the margin, and is the dual variable inherent to the ADMM algorithm.
ADMM requires a multitude of iterations in which estimates for are refined using each site’s data. Once an estimate of is chosen and the algorithm is stopped, Platt scaling [24] is applied: the values per training sample are fitted to the dyspnea outcomes using a logistic regression. is a measure of training sample i’s location in space relative to the two hyperplanes. The logistic regression equation allows to assign a dyspnea probability to patients in the training and validation datasets.
Appendix B
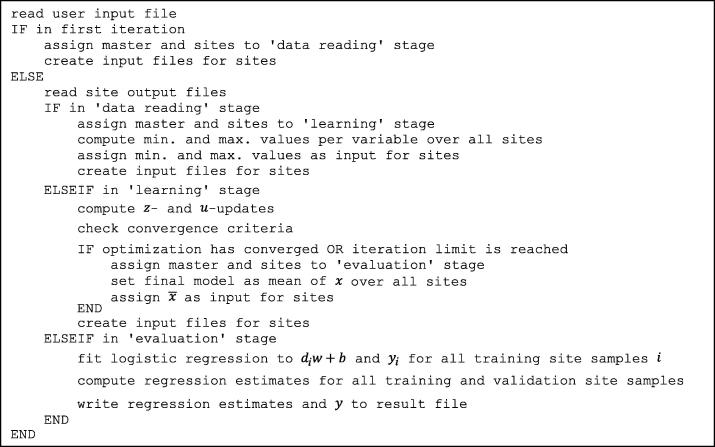
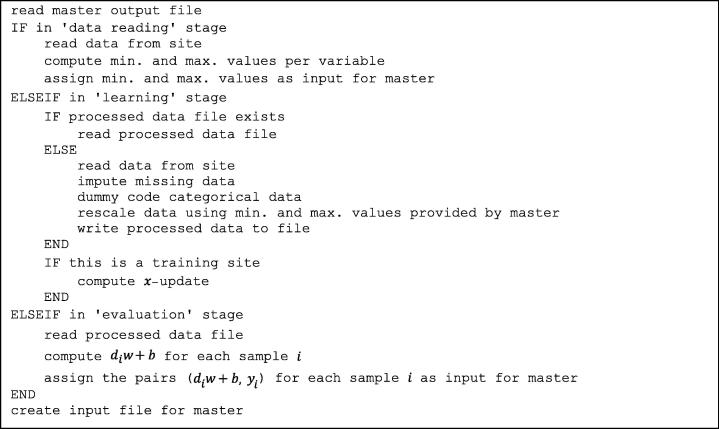
Data processing was done in MATLAB (MathWorks, Natick, MA, USA). Pseudocodes of the MATLAB functions executed on the master and sites are shown in Fig. B1, Fig. B2, respectively.
Fig. B1.
Pseudocode of the MATLAB function executed on the master.
Fig. B2.
Pseudocode of the MATLAB function executed on the sites.
Patient features were rescaled before learning to improve algorithm performance. A variable was rescaled to according to
where and are minimal and maximal feature values, respectively, found within the entire learning network. This step requires centralizing minimal and maximal feature values for each site. This poses no threat to patient privacy since no value can be allocated to a single patient assuming that each site’s database contains more than one patient. Future work should be dedicated to replacing this normalization by a generally privacy-preserving method.
The categorical variables cardiac comorbidity and chemotherapy timing were each coded as dummy variables, being equal to the variable’s cardinality.
Missing values were imputed using the mean for continuous variables and mode for categorical variables. Means and modes were derived per site.
The code designed to guide the machine learning process within the IT infrastructure is available on www.eurocat.info with further information about the infrastructure and how to join the CAT project.
The chosen model parameters are , , and . The convergence criteria are set as described by [11] with absolute tolerance and relative tolerance . , , and are initialized at the zero vector. Parameters have been set manually and based on choices found in [11]. Future work on deriving clinically-relevant prediction models exceeding an exemplary nature should also comprise systematic parameter tuning.
References
- 1.Lambin P. Predicting outcomes in radiation oncology–multifactorial decision support systems. Nat Rev Clin Oncol. 2013;10(1):27–40. doi: 10.1038/nrclinonc.2012.196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mackin D. Measuring computed tomography scanner variability of radiomics features. Invest Radiol. 2015;50(11):757–765. doi: 10.1097/RLI.0000000000000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rosewall T. Inter-professional variability in the assignment and recording of acute toxicity grade using the RTOG system during prostate radiotherapy. Radiother Oncol. 2009;90(3):395–399. doi: 10.1016/j.radonc.2008.12.003. [DOI] [PubMed] [Google Scholar]
- 4.Dekker A. Rapid learning in practice: a lung cancer survival decision support system in routine patient care data. Radiother Oncol. 2014;113(1):47–53. doi: 10.1016/j.radonc.2014.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lambin P. ‘Rapid learning health care in oncology’ – an approach towards decision support systems enabling customised radiotherapy’. Radiother Oncol. 2013;109(1):159–164. doi: 10.1016/j.radonc.2013.07.007. [DOI] [PubMed] [Google Scholar]
- 6.Constable S.D., Tang Y., Wang S., Jiang X., Chapin S. Privacy-preserving GWAS analysis on federated genomic datasets. BMC Med Inform Decis Mak. 2015;15(5):S2. doi: 10.1186/1472-6947-15-S5-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jiang W. WebGLORE: a web service for Grid LOgistic REgression. Bioinformatics. 2013:btt559. doi: 10.1093/bioinformatics/btt559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Welcome to the NCBO BioPortal | NCBO BioPortal. [Online] Available: <http://bioportal.bioontology.org/>; 2016 [accessed 26.10.16].
- 9.Prud’Hommeaux E, Seaborne A. SPARQL query language for RDF. W3C Recomm., vol. 15; 2008.
- 10.Boyd S., Parikh N., Chu E., Peleato B., Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn. 2011;3(1):1–122. [Google Scholar]
- 11.Distributed optimization and statistical learning via the alternating direction method of multipliers. [Online] Available: <http://web.stanford.edu/~boyd/papers/admm_distr_stats.html>; 2016 [accessed: 26.10.16].
- 12.Dehing-Oberije C., Ruysscher D.D., van Baardwijk A., Yu S., Rao B., Lambin P. The importance of patient characteristics for the prediction of radiation-induced lung toxicity. Radiother Oncol. 2009;91(3):421–426. doi: 10.1016/j.radonc.2008.12.002. [DOI] [PubMed] [Google Scholar]
- 13.Nalbantov G. Cardiac comorbidity is an independent risk factor for radiation-induced lung toxicity in lung cancer patients. Radiother Oncol J Eur Soc Ther Radiol Oncol. 2013;109(1):100–106. doi: 10.1016/j.radonc.2013.08.035. [DOI] [PubMed] [Google Scholar]
- 14.Prechelt L. Early stopping — but when? In: Montavon G., Orr G.B., Müller K.-R., editors. Neural networks: tricks of the trade. Springer; Berlin Heidelberg: 2012. pp. 53–67. [Google Scholar]
- 15.Oberije Cary. 2013. EuroCAT umbrella protocol for NSCLC. [Google Scholar]
- 16.Meldolesi E. An umbrella protocol for standardized data collection (SDC) in rectal cancer: a prospective uniform naming and procedure convention to support personalized medicine. Radiother Oncol J Eur Soc Ther Radiol Oncol. 2014;112(1):59–62. doi: 10.1016/j.radonc.2014.04.008. [DOI] [PubMed] [Google Scholar]
- 17.Abernethy A.P. Rapid-learning system for cancer care. J Clin Oncol Off J Am Soc Clin Oncol. 2010;28(27):4268–4274. doi: 10.1200/JCO.2010.28.5478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McGale P., Cutter D., Darby S.C., Henson K.E., Jagsi R., Taylor C.W. Can observational data replace randomized trials? J Clin Oncol. 2016;34(27):3355–3357. doi: 10.1200/JCO.2016.68.8879. [DOI] [PubMed] [Google Scholar]
- 19.Chavez-MacGregor M., Giordano S.H. Randomized clinical trials and observational studies: is there a battle? J Clin Oncol. 2016;34(8):772–773. doi: 10.1200/JCO.2015.64.7487. [DOI] [PubMed] [Google Scholar]
- 20.Peters L.J. Critical impact of radiotherapy protocol compliance and quality in the treatment of advanced head and neck cancer: results from TROG 02.02. J Clin Oncol Off J Am Soc Clin Oncol. 2010;28(18):2996–3001. doi: 10.1200/JCO.2009.27.4498. [DOI] [PubMed] [Google Scholar]
- 21.Murthy V.H., Krumholz H.M., Gross C.P. Participation in cancer clinical trials: race-, sex-, and age-based disparities. JAMA. 2004;291(22):2720–2726. doi: 10.1001/jama.291.22.2720. [DOI] [PubMed] [Google Scholar]
- 22.Movsas B. Who enrolls onto clinical oncology trials? a radiation patterns of care study analysis. Int J Radiat Oncol Biol Phys. 2007;68(4):1145–1150. doi: 10.1016/j.ijrobp.2007.01.051. [DOI] [PubMed] [Google Scholar]
- 23.Jochems A. Distributed learning: developing a predictive model based on data from multiple hospitals without data leaving the hospital – a real life proof of concept. Radiother Oncol. 2016 doi: 10.1016/j.radonc.2016.10.002. [DOI] [PubMed] [Google Scholar]
- 24.Platt J.C. Advances in large margin classifiers. 1999. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods; pp. 61–74. [Google Scholar]