On the role of visual experience in mathematical development: Evidence from blind mathematicians

Abstract

Advanced mathematical reasoning, regardless of domain or difficulty, activates a reproducible set of bilateral brain areas including intraparietal, inferior temporal and dorsal prefrontal cortex. The respective roles of genetics, experience and education in the development of this math-responsive network, however, remain unresolved. Here, we investigate the role of visual experience by studying the exceptional case of three professional mathematicians who were blind from birth (n = 1) or became blind during childhood (n = 2). Subjects were scanned with fMRI while they judged the truth value of spoken mathematical and nonmathematical statements. Blind mathematicians activated the classical network of math-related areas during mathematical reflection, similar to that found in a group of sighted professional mathematicians. Thus, brain networks for advanced mathematical reasoning can develop in the absence of visual experience. Additional activations were found in occipital cortex, even in individuals who became blind during childhood, suggesting that either mental imagery or a more radical repurposing of visual cortex may occur in blind mathematicians.

1. Introduction

Humans exhibit a unique ability for advanced mathematical thought. This ability seems to be rooted in evolutionarily ancient non-verbal systems for numbers and geometry that all humans possess from birth and share with other animal species. Indeed, human adults with or without full access to education, young infants, and a variety of non-human animal species all share a capacity to estimate numerosity from visual or auditory sets and to perform arithmetical operations over these quantities (Feigenson et al., 2004, Gilmore et al., 2007, Gilmore et al., 2010, Izard et al., 2009, Pica, 2004). Similarly, they are endowed with basic geometrical skills (Dehaene et al., 2006, Lee and Spelke, 2008, Spelke and Lee, 2012). Recent work has suggested that formal mathematics builds upon this core set of non-verbal proto-mathematical abilities. Behaviorally, some studies have revealed a correlation between the accuracy of the primitive approximate number system and math achievement at schools (Feigenson et al., 2013, Halberda et al., 2008, Libertus, 2015, Piazza et al., 2013, Starr, 2015). In geometry, it has been suggested that non-symbolic knowledge of geometry predicts the ability to use symbolic geometrical cues in 4-year-old children (Dillon et al., 2013). Furthermore, neuroimaging studies of advanced mathematical reflection (Amalric and Dehaene, 2016, Monti et al., 2012) and deductive inference (Monti et al., 2007) have revealed that the neural substrate for advanced formal mathematics strongly overlaps regions involved in basic numerical and spatial abilities (Daitch et al., 2016, Husain and Nachev, 2007, Nieder and Dehaene, 2009, Shum et al., 2013).

However, the mechanisms by which formal mathematics emerges from proto-mathematical systems for numbers and space remain unknown. A possibility is that mathematical representations are rooted in visuospatial thinking and develop through visual experience. This hypothesis transpires in many mathematicians’ introspective reports on their invention processes. For instance, Albert Einstein wrote to fellow mathematician Jacques Hadamard that "[t]he psychical entities which seem to serve as elements in thought are certain signs and more or less clear images which can be ‘voluntarily' reproduced and combined…. The above mentioned elements are, in my case of visual and muscular type” (Hadamard, 1975). Support for this “visual” hypothesis can be found in several recent findings. In Stoianov and Zorzi (2012), a deep learning network trained with visual arrays containing different numbers of objects spontaneously developed representations of numerosity similar to those identified in monkeys (Nieder, 2005). Some studies also suggest that numerosity is an early visual feature whose extraction is grounded, at least in part, on a form of texture perception (Burr and Ross, 2008, Morgan et al., 2014). At a more abstract level, it has been suggested that the perception of specific features in our environment, such as symmetries or angles, shapes our basic understanding of geometry (Giaquinto, 2005, Howe and Purves, 2005). Visual processing has also proven to be relevant to mathematical problem solving, especially in the domain of algebra where the covert “movements” involved in resolving equations were found to interact with actual motion (Goldstone et al., 2010, Landy et al., 2008).

Neuroimaging studies of mathematical processing are also compatible with the hypothesis of a visual support. In fact, the brain regions involved in mathematical reflection, regardless of domain (arithmetic, analysis, algebra, topology or geometry) or problem difficulty (Amalric and Dehaene, 2016, Dehaene et al., 2003, Monti et al., 2012), include the bilateral intraparietal sulci (IPS) and bilateral infero-temporal regions. The latter are located just lateral to the ventral visual pathway and overlap with the recently discovered “Visual number form areas” (VNFA) (Shum et al., 2013) that systematically activate to the visual presentation of Arabic numerals. Moreover, in (Amalric and Dehaene, 2016), during mathematical reflection, participants’ ratings of imageability of highly-advanced mathematical statements correlated with brain activity in a left occipito-temporal region close to the VNFA. As for the parietal lobe, it is known to be involved in visually guided eye and hand movements, but is also activated conjointly with frontal eye fields during mental arithmetical problems (Knops et al., 2009). It also intervenes in mental rotation (Culham and Kanwisher, 2001, O’Boyle et al., 2005).

One major issue for a visual origin of mathematical abilities, however, lies in the fact that mathematical knowledge also develops in the blind (Landau et al., 1981, Abboud et al., 2015, Kanjlia et al., 2016). The so-called “visual” number form area may, in fact, be activated in congenitally blind subjects when numerals are presented auditorily via visual-to-auditory sensory substitution (Abboud et al., 2015). Blind subjects may even become professional mathematicians, although this is much less documented scientifically (Jackson, 2002). There are actually many examples of famous blind mathematicians in the history of mathematics, such as Leonhard Euler who was blind during the two last decades of his life, or Nicholas Saunderson who went blind in his first year and yet became the Lucasian professor of Mathematics at Cambridge University. In fact, blind mathematicians can be top-of-the-class geometers, like the French mathematician Bernard Morin who first constructed a sphere eversion, topologists such as the famous Russian mathematician Pontryagin, or analysts like the American mathematician Lawrence Baggett.

Two alternative hypotheses may account for the existence of talented blind mathematicians. The first one assumes that blind mathematicians learn mathematics by compensating through other modalities. In this case, the same behavioral outcome – high-level mathematics – would arise from very different cerebral substrates (e.g. areas involved in auditory or tactile processing). The second hypothesis assumes that mathematical activity is in fact based on highly abstract representations which are amodal rather than primarily visual. Several findings indeed suggest that the mental representation of numbers consists of highly abstract entities that can be accessed indifferently from visual, auditory or tactile input (Piazza et al., 2006, Riggs et al., 2006, Tokita et al., 2013). There is also evidence of integration of numerical information presented in two different modalities in newborns (Izard et al., 2009), in 6-month old infants (Feigenson, 2011), in children (Barth et al., 2005), in human adults (Barth et al., 2003) and in monkeys (Jordan et al., 2005, Jordan et al., 2008).

Recently, Kanjlia et al. (2016) used fMRI to investigate the brain mechanisms of mental arithmetic in the blind. Congenitally blind adults were asked to decide whether two equations (e.g. 7 − 2 = x; 6 − 1 = x) had the same result. The results indicated that (1) they performed similarly to blindfolded sighted participants and (2) they activated a classical bilateral fronto-parietal network, very similar to what was observed in sighted subjects, the only difference being an additional activity in occipital cortex. These findings show that numerical thinking can develop in the absence of visual experience and is rooted in typical number-related brain circuits, therefore lending support to our second hypothesis.

Many mathematicians, however, argue that simple numerical knowledge may not be representative of the broader field of mathematics, which encompasses domains such as geometry or topology which might conceivably depend on visual experience. Here, we intended to bring some light to bear on this topic through neuroimaging studies of advanced mathematical concepts (rather than the basic arithmetic studied by Kanjlia et al., 2016) in three exceptional cases of blind professional mathematicians. Those subjects accepted to participate in two fMRI experiments similar to our prior work (Amalric and Dehaene, 2016). During fMRI, they were asked to quickly evaluate the truth value of various auditory mathematical and nonmathematical statements with high-level content.

Note that, although our fMRI images were acquired in adults and therefore reflected the end point of a long developmental process, they should still be informative on the role of visual experience in mathematical development. This is because, amongst our three participants, one was blind from birth and all had become blind before the age of 11, and therefore acquired high-level mathematical concepts in the absence of visual experiment. If visual experience plays a dominant role in shaping cerebral representations of advanced mathematical concepts, then different brain regions should activate in the blind compared to sighted mathematicians. In this case, even the two blind mathematicians who have developed basic mathematical knowledge while they could still see may recruit different brain regions for advanced mathematical concepts. On the contrary, if mathematical representations develop independently of visual experience, then the same brain regions should activate during mathematical reflection irrespective of blindness. Finally, if occipital cortex can be recycled (Dehaene and Cohen, 2007) or re-used in blind subjects, as previously observed for instance by Kanjlia et al. (2016) for arithmetic and by Bedny et al. (2011) for language processing, then we might expect an additional activation of occipital cortex in blind subjects.

2. Results

2.1. Description of the blind participants

Subject A, a 46-years-old male, progressively became blind over a period extending from 3 to 10 years of age, because of optic nerve damage arising from a neurological impairment that also caused facial hemiplegia. He nevertheless followed regular schooling and exhibited precocious mathematical skills. Notably, he explained that mathematical Braille was not well adapted to mathematical lessons in high school, so that he had to do mathematics only mentally. He is now teaching arithmetic and geometry in a top-ranking French university. Surprisingly perhaps, he declared having strong number-color synesthesia to this present day.

Subject B, a 54-years-old male, became blind at the age of 11 as a combined result of glaucoma and Marfan syndrome, a genetic disorder of connective tissue that commonly affects the eyes by inducing lens dislocation. He is a prominent mathematician, essentially known for a major breakthrough in the domain of contact geometry. Like subject A, subject B reported a vivid number-color synesthesia.

Subject C, a 36-years-old male, is congenitally blind due to bilateral anophthalmia. He followed typical university training in mathematics and computer sciences, and defended a PhD thesis on Lambda calculus. He now works as a research engineer in a French computer science laboratory.

2.2. Experiment 1: advanced mathematical statements

In a first experiment, participants were presented with the difficult mathematical and nonmathematical statements used in (Amalric and Dehaene, 2016) and had to judge whether they were true, false or meaningless. Stimuli spanned various domains of math including analysis (e.g. “Any compact topological group admits a unique probability measure invariant under left-translations”; true), algebra (e.g. “There exists an infinite order group that admits a finite number of sub-groups”; false), topology (e.g. “The graph of the completion of a compact group is dense in a partially connected open set”; meaningless) and geometry (e.g. “The Euclidean orthogonal group has exactly two connected components”; true), as well as nonmath problems (e.g. “In Ancient Greece, a citizen who could not pay his debts was made a slave”; true). After fMRI, participants were presented again with all statements and were asked to give ratings about various aspects of these statements, including their “imageability” (see Amalric and Dehaene, 2016, for a full description of the Methods). Within the group of sighted mathematicians, we had previously found that bilateral intraparietal sulci (IPS), bilateral inferior temporal regions (IT), and bilateral sites in dorsolateral, superior and mesial prefrontal cortex (PFC) showed greater activation to meaningful math than to meaningful nonmath judgements during the reflection period, regardless of the mathematical domain or the perceived difficulty (Fig. 2A, for more details, see Amalric and Dehaene (2016)).

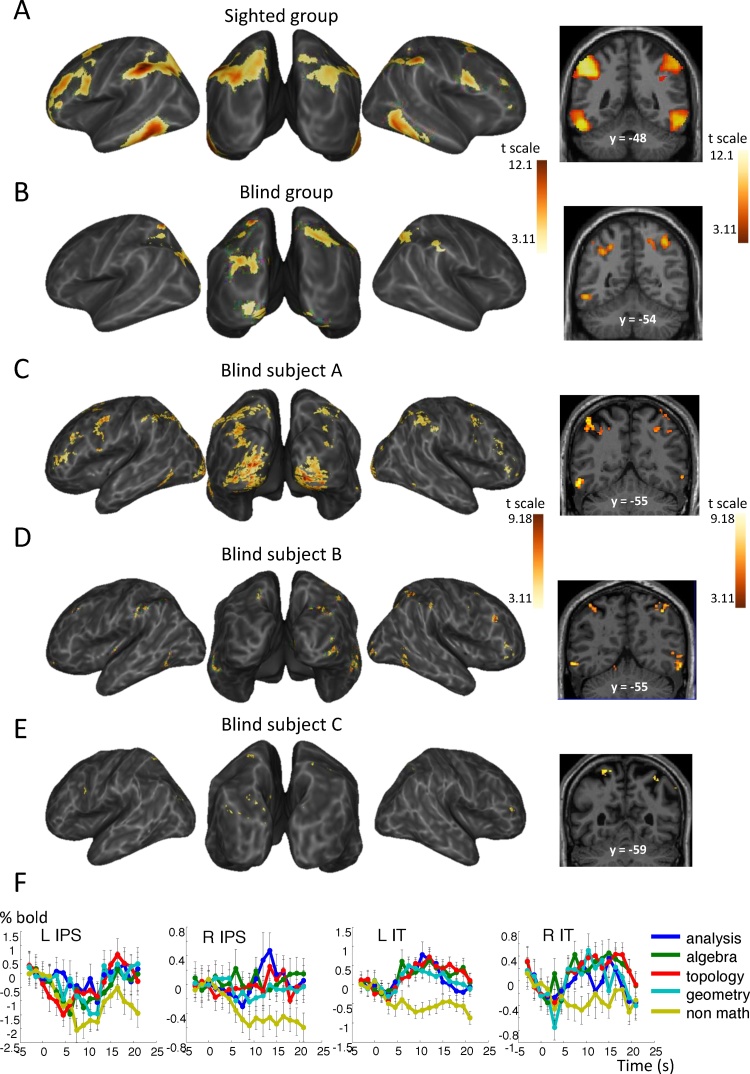
Fig. 2.

Math-responsive network in blind and sighted mathematicians in experiment 1. Whole-brain inflated maps and coronal slice showing the contrast of meaningful math versus meaningful nonmath reflection in 15 sighted mathematicians (A), 3 blind mathematicians (B), and each blind subject individually (C–E). Contrast maps are display at p_unc < 0.001 uncorrected at the voxel level, and p_FDR < 0.05 corrected for multiple comparisons at the cluster level. (F) Average time course of the fMRI signal in subjects A, B and C in representative areas of activation: bilateral intraparietal sulci (IPS) and inferior temporal (IT) regions.

Note: explore these data yourself at http://www.unicog.org/webdemo/Amalric_oct2016/.

Behaviorally, an ANOVA with group and problem type as factors revealed no significant main effect of group (F(1,16) = 0.005, p = 0.95) or math domain (F(3,48) = 0.93, p = 0.43), nor a group by domain interaction (F(3,48) = 2.65, p = 0.059). Subject A answered correctly to 66.7% of the math statements and 62.5% of the nonmath statements, which is very similar to the group of sighted mathematicians (math: 63%, nonmath: 65%). Subject B responded correctly to 78.6% of math statements and 73.3% of nonmath statements, which is slightly but not significantly above the average of our previous group of 15 sighted professional mathematicians. Subject C found experiment 1 challenging: he succeeded only with 44.4% of math statements, compared to 64.3% of nonmath statements.

For subject A, examination of the contrast of meaningful math versus meaningful nonmath during the reflection period revealed activation in bilateral IPS, IT, mesial and inferior PFC (Fig. 2C, Table S1). The time course of activation in representative areas of this math-responsive network showed that the fMRI signal increased for all four domains of math, while nonmath statements induced a slow deactivation (Fig. 2F). Additional activation was observed in bilateral occipital cortex (Figs. 2 C, 4, Table S1). Virtually the same activation was observed when comparing meaningful versus meaningless mathematical statements. Subject A’s average imageability rating equaled 42.7% for math statements and 10.3% for nonmath statements. This imageability rating correlated with activation in bilateral middle frontal gyri (BA6), occipital cortex along the calcarine sulci and more dorsal occipital sites, and at several parietal foci (Table S3).

For subject B, math reflection induced more activation than nonmath reflection in several bilateral parietal, occipito-parietal and occipital sites, in bilateral IT regions, as well as in bilateral prefrontal foci (Fig. 2D, Table S1). Again, similar activation was observed when examining the contrast of meaningful versus meaningless math judgments. Global imageability rating equaled 29.2% for math statements, and 13.5% for nonmath statements. Imageability rating for math statements correlated with activation in bilateral occipital cortices, including at the junction with the precuneus, and bilateral superior frontal sulci (Table S3).

Despite subject C’s difficulties with math problems, there was small but significant activation elicited by mathematical reflection more than nonmathematical reflection in a few bilateral occipito-parietal and occipital foci, in right IPS and right MFG (Fig. 2E, Table S1). Subject C reported no mental imagery in this experiment, therefore preventing us from studying the correlation of imageability with brain activation.

These results suggest that activations observed in each individual blind mathematician and in the group of sighted mathematicians were similar apart from an occasional additional activation in occipital cortex. This conclusion was confirmed by a group analysis comparing 15 sighted versus 3 blind mathematicians. The main effect of math > nonmath in the blind again revealed a parieto-occipital network, plus bilateral activation in inferior temporal regions (Fig. 2B). There was a significant intersection of the math > nonmath networks in sighted and blind mathematicians in bilateral intraparietal sulci and inferior temporal cortices. The interaction with group, searching for greater activation to mathematics in blind than in sighted mathematicians (Blind > Sighted × math >  nonmath), revealed activation exclusively in left occipital cortex (Fig. 4). A symmetrical activation was seen in the right hemisphere when relaxing the cluster-wise threshold (p < 0.05 uncorrected). Examination of fMRI signal for subject A revealed that even if both math and nonmath reflection activated those occipital regions, activation remained transient for nonmath statements (Fig. 4).

Fig. 4.

Additional occipital activation elicited by math in blind mathematicians. (A) Occipital coronal slices showing the interaction of group (Blind > Sighted) and statement type (math > non-math) in experiment 1 (top panel) and experiment 2 (bottom panel). (B) Occipital coronal slices show the activation elicited by math > nonmath in each blind subject and each experiment. (C) Temporal profile of activation in left and right occipital cortices in subject A in each experiment.

2.3. Experiment 2:simpler mathematical facts

We sought to replicate those results in a second experiment focusing on simpler mathematics. Statements were either true or false and consisted in well-known mathematical facts such as classical algebraic identities (e.g. “(a + b)² equals a² + b² + 2ab”) or trigonometric formulae (“cos(a + b) equals cos(a)cos(b)-sin(a)sin(b)”), algebraic equations (“(z − 1)² equals z² −  2z + 1”),trigonometric equations (“sin(x + π) equals − sin(x)”), complex number properties (“the angle between i and 1 + i equals π/4”), and non-metric Euclidean geometry (“Any equilateral triangle can be divided into two right triangles”). These were compared to declarative nonmathematical facts about art (“Pantomime relies on attitude and gesture, without speaking”). Auditory controls consisting of series of beeps were also presented.

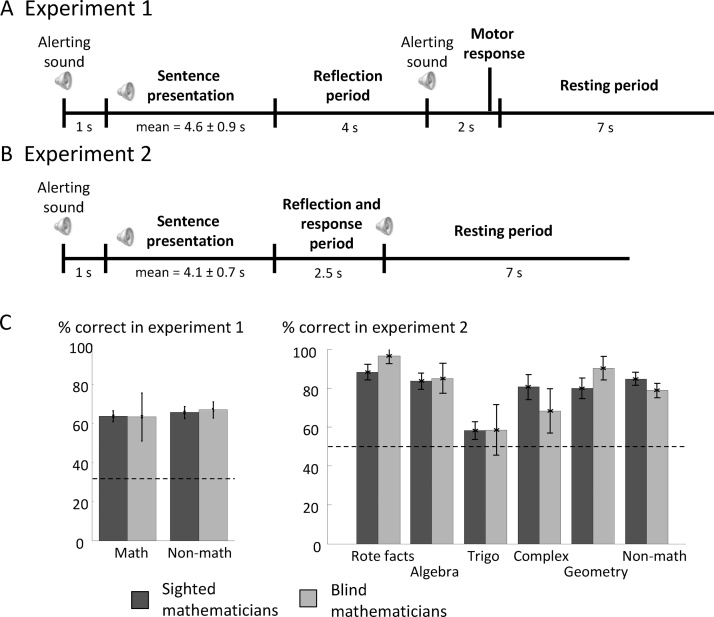
Overall performance for math statements reached 78.6% correct in both groups of sighted and blind mathematicians, thus confirming that the statements were simpler than in experiment 1. For example, ∼90% of classical algebraic identities (called rote facts in Fig. 1) were correctly classified, as were ∼84% of algebraic equations. Trigonometric formulae were the most difficult, with an average performance of 58.1% correct. Complex number properties were quite easy for sighted mathematicians (80.6%), and subjects A and B (75% and 80%), but appeared to be harder for subject C (50%). If anything, geometrical statements were responded slightly better by blind mathematicians (respective correct rates: 100%, 87.5% and 83.3%) than by sighted mathematicians (79.9%). Overall, however, an ANOVA with group and problem type as factors revealed no significant main effect of group (F(1,15) = 0.07, p = 0.80) nor a group by type interaction (F(4,60) = 1.46, p = 0.23).

Fig. 1.

Experimental paradigms and behavioral results. (A) In experiment 1, auditory math and nonmath statements were announced by a beep and followed by a 4 s reflection period. Another beep announced the 2 s response period during which subjects were asked to press one of three buttons placed in right hand to indicate whether they judged the statement as true, false, or meaningless. A resting period of 7 s ended each trial. (B) Experiment 2 was similar to experiment 1 except that math and nonmath statements were simpler so that subjects were asked for a speeded response during a single 2.5 s period ending with a beep. (C) The two bar plots represent the percentage of correct responses in experiments 1 and 2 (bars = one standard error of the mean). On average, sighted and blind mathematicians performed virtually identically. Dashed lines represent the chance level (33.3% in experiment 1, 50% in experiment 2).

In fMRI, within the group of sighted mathematicians, extensive activations were again elicited by math more than by nonmath statements in bilateral IPS, bilateral IT regions, bilateral superior, and middle frontal regions (Brodmann areas 9 and 46) (Fig. 3A, Table S2). These results, which will be detailed in another publication, indicate that the classical mathematical network is highly reproducible even when simple and well-known mathematical facts are used.

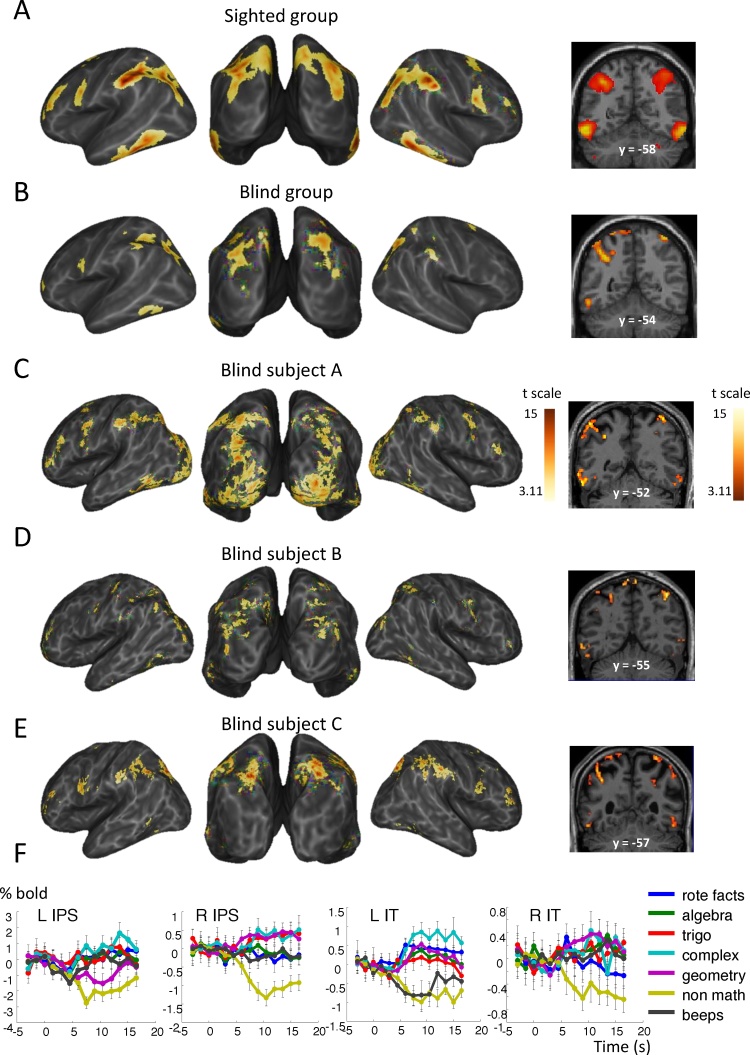
Fig. 3.

Math-responsive network in blind and sighted mathematicians in experiment 2. Same format as Fig. 2.

In blind subject A, the contrast of math versus nonmath statements again revealed activation in bilateral IPS and bilateral IT and bilateral MFG (BA 9), plus activation in a left occipito-parietal region and bilateral lateral occipital foci (Fig. 3C, Table S2). Examination of the time course of activation in bilateral IPS and IT also revealed a sharp and sustained activation for all categories of math, a slow deactivation for declarative nonmath facts, and no activation for auditory control beeps (Fig. 3F).

For subject B, the same contrast revealed activation in various bilateral parietal and occipital sites, bilateral IT regions, and some bilateral middle prefrontal foci (Fig. 3D, Table S2).

For subject C, math statements, relative to nonmath statements, elicited more activation in bilateral IPS, IT, MFG (BA 9 and BA46), plus one occipital focus near the calcarine sulcus (Fig. 3E, Table S2). Examination of the time course of activation in bilateral IPS and IT also revealed a sharp and sustained activation for all categories of math, a slow deactivation for declarative nonmath facts, and no activation for auditory control beeps. We note here that, while complex statements from experiment 1 did not elicit any mental imagery in subject C, he informally reported vivid mental imagery for trigonometry, complex numbers and geometrical statements in this experiment.

At the group level, pooling over our three blind mathematicians, math versus nonmath problems elicited activation in bilateral IPS, occipito-parietal junction, left IT regions and left MFG (Fig. 3B). There was again a significant intersection of the math > nonmath networks in sighted and blind mathematicians in bilateral intraparietal sulci, left inferior temporal cortex and MFG (BA9). The only group difference between blind and sighted mathematicians during the resolution of math problems more than during the resolution of nonmath problems, was located in two bilateral occipital regions located close to but slightly anterior and inferior to the left occipital region identified in experiment 1 (Fig. 4). Examination of the fMRI signal over time in these regions revealed a profile of activation similar to the one observed in the rest of the math-responsive network: a fast activation for all types of math problems and no activation or even a slow deactivation for nonmath problems and the auditory control condition.

3. Discussion

In two high-resolution fMRI experiments contrasting math versus nonmath reflection, we observed in blind mathematicians a consistent and systematic activation of the math-responsive network that we had previously identified in sighted professional mathematicians (Amalric and Dehaene, 2016). Indeed, bilateral intraparietal, inferior temporal and dorsal prefrontal sites were activated in both experiments in the group of sighted mathematicians as well as in each individual blind mathematician. The only exception was in experiment 1 for subject C who exhibited very little activation. This negative finding may be due to the fact that subject C received less math training than the others and found experiment 1 harder. In experiment 2, however, subject C exhibited activations to simpler math statements in a set of areas that were very similar to the network exhibited in the sighted group and in subjects A and B.

Previous studies have shown that the parietal lobe, involved in mathematical skills, also houses a diversity of areas for visuospatial functions such as orienting of visual gaze and attention, visually guided hand movements, mental rotation of objects, or the maintenance of visuospatial information in working memory (Hubbard et al., 2005, Husain and Nachev, 2007, Simon et al., 2002, Zacks, 2008). Similarly, inferior temporal activation during mathematical reflection has previously been linked to the recognition of visual Arabic numerals (Shum et al., 2013) and visually presented mathematical expressions (Amalric and Dehaene, 2016). Nevertheless, the present results, together with similar prior findings on number recognition and calculation in blind subjects (Abboud et al., 2015, Kanjlia et al., 2016) refute the hypothesis of a link between mathematical expertise and visual experience. Instead, they suggest that cortical representations of advanced mathematics, involving the IPS and inferior temporal regions as essential nodes, can develop independently of visual experience.

It may seem surprising that all blind participants exhibited activation in bilateral inferior temporal regions that have been described as the visual number form areas (VNFA), because these areas have been reported to be specifically responsive to written Arabic numerals (Shum et al., 2013). However, a similar activation was observed using sight-to-sound sensory substitution in congenitally blind individuals trained to hear colored-shapes and asked to interpret the shapes I, V, and X as Roman numerals (Abboud et al., 2015). Our result thus supports the idea that the VNFA encodes mathematical symbols and concepts in an abstract way, regardless of any specific sensory modality. Indeed, we found that this area is also responsive to written mathematical formulas in professional mathematicians (Amalric and Dehaene, 2016). A recent intracranial study indicates that this region contains distinct but intermingled sites sensitive to Arabic numerals and to calculation itself (Daitch et al., 2016). Thus, the contribution of this region to mathematics appears to be much broader than its label suggests, and it is probably only because of difficulties in imaging this temporal region with fMRI that this region was not previously considered as a core region for number sense.

The behavioral performance of sighted and blind mathematicians did not provide any evidence that training via nonvisual modalities gives blind individuals any specific advantage or disadvantage in mathematical processing compared to sighted individuals. Indeed, unlike in (Castronovo and Seron, 2007) where blind participants performed better in numerosity estimation than sighted subjects, blind individuals in our tasks did not judge the truth value of mathematical statements significantly better than sighted participants. However, we examined only the endpoint of mathematical training in adults, and our findings do not preclude the possibility that differences in mathematical skills and conceptual understanding would be observed during development.

Turning to brain-imaging results, a comparison of blind and sighted participants in our experiments revealed an additional activation in the occipital cortex of blind mathematicians while they were thinking about math problems. This finding is compatible with many recent observations that blindness does not lead to a lack of activity of “visual” cortex during tactile or auditory tasks (Bedny et al., 2011, Raz et al., 2005). In particular, a similar activation of occipital cortex has recently been observed in congenitally blind adults performing mental calculation (Kanjlia et al., 2016). To the best of our knowledge, however, this is the first time that occipital activation is observed in an activity as abstract and high-level as professional mathematics.

We note in passing that, in our study, even though all three blind mathematicians exhibited occipital activation during mathematical thinking, the amount and location of such activation differed among the three individuals. While an extensive activation was seen in bilateral occipital cortex in subject A, who became blind between the age of 3 and 10, smaller clusters of activation in right occipital cortex and in the calcarine sulcus were observed in subject B (who became blind at the age of 11), and only very small but significant activation was seen in the calcarine sulcus in subject C (who was congenitally blind). It is however hard to explain such inter-individual differences by applying the conclusions extracted from group analysis in the literature. Indeed, our results do not agree for example with studies showing greater occipital activation to auditory verbal tasks in early-blind than in late-blind people (Bedny et al., 2012; Burton, 2003). Note however that all our participants became blind before ages that usually mark the limit between early and late blindness, i.e. 14 (Cohen et al., 1999, Wan et al., 2010) or 16 (Sadato et al., 2002). Some studies have also suggested that the visual cortex is recruited at a level that depends on performance (Amedi et al., 2008, Amedi et al., 2003). However, again, this claim does not seem to apply to the present study, given that subject B performed slightly better than subject A but showed less activation in occipital cortex. In the present study, it would in fact be bold to draw any conclusions regarding the causes of the observed differences in occipital activation in only three subjects whose individual histories differed massively in the onset and the cause of blindness (optic nerve damage, glaucoma, and anophthalmia).

How can we account for the additional occipital activation in blind participants compared to sighted subjects? We might first speculate that they entertained a form of mental imagery. Indeed, subject A, who exhibited the most extensive occipital activation, also reported a great amount of imageability during math in experiment 1. Furthermore, the two participants who were not congenitally blind reported number-color synesthesia. Subject C also reported that statements dealing with trigonometry or geometry elicited vivid mental imagery. Similar reports of mental imagery have already been discussed in blind individuals during mental rotation of objects (Arditi et al., 1988), drawing (Amedi et al., 2008), or Braille reading (Striem-Amit et al., 2012). There is nothing contradictory in the possibility that blind subjects develop sufficient intuitions of what vision is as to end up forming and manipulating mental images. Indeed, Denis Diderot, in his celebrated Letter on the Blind (1749), already noted how

“Saunderson was extremely successful as professor of mathematics at the University of Cambridge. He gave lessons in optics, he lectured on the nature of light and colors, he explained the theory of vision; he wrote on the properties of lenses, the phenomena of the rainbow, and many other subjects connected with sight and its organ.”

Assuming the mental imagery hypothesis, our results however query the necessity of mental imagery to mathematical processing. Indeed, the amount of occipital activation varied across blind participants, even though they all performed similarly in experiment 2. We might thus think that the mathematical concepts that we studied here are likely to be encoded in an abstract manner, allowing blind individuals to manipulate them through nonvisual representations. According to this view, vision could simply be the preferred or the most “advantageous” (Poincaré, 1902) modality by which to convey mathematical information in sighted people. This hypothesis is compatible with studies showing that visual features are relevant to mathematical understanding (Goldstone et al., 2010, Stoianov and Zorzi, 2012).

Furthermore, the mental imagery hypothesis conflicts with the fact that occipital activations were absent in sighted participants, even though they too reported high levels of imageability. An alternative to this hypothesis, therefore, is that the occipital activation reflects “neuronal recycling” (Dehaene and Cohen, 2007), i.e. a repurposing of part of the visual cortex towards a related function which would be useful to mathematical processing. Indeed, activation in occipital cortices of blind individuals overlap with areas that, in sighted individuals, are heavily influenced by top-down visual attention (Martínez et al., 1999) and include retinotopic maps or topographically organized visual areas that may constitute a topographic buffer (Kosslyn, 2005) depicting shapes (Vinberg and Grill-Spector, 2008). Such retinotopic maps might therefore be particularly appropriate to support the mental manipulation of geometrical shapes or spatial diagrams that are central to mathematics, regardless of the modality in which they are initially conveyed.

Finally, a third account of the occipital activation may also be proposed, namely a radical reorientation of visual cortex for a completely novel use, unrelated to the normal role of this region in forming retinotopic maps and processing shapes. Indeed, several studies have shown that occipital cortex may be also activated in congenitally blind individuals during nonmathematical tasks such as sentence processing and verbal working memory, with a profile similar to the one observed in Broca’s area (Amedi et al., 2003, Bedny et al., 2011, Lane et al., 2015, Röder et al., 2002. It is hard to see what kind of visual imagery or neuronal recycling could explain these language-related occipital activations. Rather, it seems plausible that a broad form of plasticity, particularly in the developing brain, could lead to a radical repurposing of occipital cortices towards high-level cognitive functions, including mathematical thinking. This radical plasticity hypothesis, however, would still need to explain the recent observation that, in the blind, distinct and reproducible sectors of occipital cortex are allocated to number-related and language-related functions, whose resting-state activity patterns correlate respectively with the frontoparietal number network and the left-hemispheric language network (Kanjlia et al., 2016). This result, suggesting that pre-existing connectivity to distant areas may account for the specialization of occipital cortex in the blind, is in agreement with the neuronal recycling hypothesis (Hannagan et al., 2015). We acknowledge that, at present, our observations are simply insufficient to convincingly distinguish among those three interpretations of occipital activation during mathematical processing in the blind.

Regarding our original question, however, the results are unambiguous in supporting the hypothesis that visual experience is not necessary for the development of a normal cerebral representation of advanced mathematical concepts. Given that the activation during mathematical judgments overlapped with regions classically involved in the mental representation of space and number, in both sighted and blind subjects, our results are compatible with the hypothesis that advanced mathematics builds upon abstract and amodal systems for number and space, which can develop in the absence of visual experience.

4. Methods

4.1. Participants

Three blind mathematicians and 20 sighted mathematicians participated in this study. The latter were all professional mathematicians, i.e. full-time researchers and/or professors in mathematics. For more details regarding the subjects who participated in the first experiment (n = 15), see Amalric and Dehaene (2016). The second experiment (n = 14) comprised 5 subjects who already participated in experiment 1 and 9 new subjects with equivalent academic background. All experiments were approved by the regional ethical committee for biomedical research, and subjects gave informed consent after they read or heard (in case of the blind) consent information.

4.2. Experiment 1

Participants were presented, in semi-random order, with spoken mathematical statements that belonged to analysis, algebra, topology and geometry, and to non-mathematical statements. Within each category, 6 statements were true, 6 were false, and 6 were meaningless. All meaningful statements bore upon non-trivial facts which required logical reflection. Immediately after fMRI, a paper questionnaire allowed to reexamine all statements in the same order. For each of them, participants were asked to rate, on a scale from 0 to 7, several subjective features such as their confidence in their answer or the “imageability” of the statements. Blind participants were read each question by the experimenter and responded orally.

4.3. Experiment 2

Participants were exposed to a simpler set of spoken mathematical and non-mathematical statements than in experiment 1. Each statement was either true or false. One category of mathematical statements consisting in canonical algebraic identities and trigonometric formulae was likely to be known by heart. Another category consisted in algebraic equations. The three remaining categories (trigonometry, complex numbers, and geometry) required to visualize a simple mathematical fact concerning the trigonometric circle, the complex plane, or geometrical shapes. Finally, non-mathematical statements were declarative facts about music, painting, literature or movies. Series of pure tone beeps with the same average duration as the statements were also presented as a control for the presence of auditory activation. When the last beep had a higher pitch than the others, subjects were asked to respond “true”, and “false” otherwise. This experiment was divided into 7 runs of 12 statements each, including at least one exemplar of each sub-category.

All statements were recorded using Audacity by a female native French speaker who was familiar with mathematical concepts. Within each experiment, statements from the different categories were matched in syntactic construction, number of syllables and duration.

Note that all statements used in experiments 1 and 2 can be found online at http://www.unicog.org/webdemo/Amalric_oct2016/.

4.4. Procedure

In both experiments, the only display on screen was a fixation cross on a black background, which sighted participants had to fixate continuously. Each trial started with a beep and a color change of the fixation cross (which turned to red), announcing the onset of the statement. In experiment 1, participants were given a fixed reflection period of 4 s following auditory presentation. In experiment 2, they were asked to answer as quickly as they could. In the latter case, a maximum of 2.5 s was left for the reflection and the response. In both experiments, the response period started and ended with a beep, and was signaled by the fixation cross turning to green. In experiment 1, subjects gave their evaluation of the sentence (true, false, or meaningless) by pressing one of three corresponding buttons held in the right hand. In experiment 2, they pressed the button held in the right hand for true, and held in the left hand for false. Each trial ended with a 7-s resting period (Fig. 1).

4.5. fMRI data acquisition and analysis

We used two 3-T whole body systems (Siemens Trio and Prisma) with high-resolution multiband imaging sequences developed by the Center for Magnetic Resonance Research (CMRR) (Xu et al., 2013) (multiband factor = 4, Grappa factor = 2, 80 interleaved axial slices, 1.5 mm thickness and 1.5 mm isotropic in-plane resolution, matrix = 128 × 128, TR = 1500 ms, TE = 32 ms). For sighted mathematicians, a 32 channel head-coil was used for experiment 1 and a 64 channel head-coil for experiment 2. All three blind mathematicians were scanned with a 32 channel head-coil.

Using SPM8 software, functional images were first corrected for slice timing, realigned, normalized to the standard MNI brain space, and spatially smoothed with an isotropic Gaussian filter of 2 mm FMWH. A two-level analysis was then implemented in SPM8. For each participant, fMRI images were high-pass filtered at 128s. Then, time series from experiment 1 and experiment 2 were modelled separately. For experiment 1, two regressors were defined for each sentence, one capturing the activation to the sentence itself (kernel = sentence duration) and the other capturing the activation during reflection (kernel = reflection duration). For experiment 2, time series was modelled using a single regressor per statement, with a kernel corresponding to statement presentation plus the mean reaction time for that subject. We then defined subject-specific contrasts by comparing the activation evoked by two subsets of sentences during the reflection period. We also used subjective imageability ratings of math statements to compute a normalized and centered SPM contrast. Regressors of non-interest included the six movement parameters for each run. Within each auditory run, additional regressors of non-interest were added to model activation to the alert signals and to the button presses.

For the second-level group analysis, individual contrast images for each of the experimental conditions relative to rest were smoothed with an isotropic Gaussian filter of 5 mm FWHM, and entered into a second-level whole-brain ANOVA with stimulus category as within-subject factor. All brain activation results are reported with a clusterwise threshold of p < 0.05 corrected for multiple comparisons across the whole brain, using an uncorrected voxelwise threshold of p < 0.001. Individual and averaged time courses of activation were plotted after averaging over spheres of 6 mm centered on the principal peaks of activation observed in the contrast of math versus nonmath statements when pooling across both experiments.

Appendix A. Supplementary data

The following is Supplementary data to this article: