Trends and fluctuations in the severity of interstate wars

Advanced statistical models suggest that the likelihood of a large interstate war has not changed over 200 years.

Abstract

Since 1945, there have been relatively few large interstate wars, especially compared to the preceding 30 years, which included both World Wars. This pattern, sometimes called the long peace, is highly controversial. Does it represent an enduring trend caused by a genuine change in the underlying conflict-generating processes? Or is it consistent with a highly variable but otherwise stable system of conflict? Using the empirical distributions of interstate war sizes and onset times from 1823 to 2003, we parameterize stationary models of conflict generation that can distinguish trends from statistical fluctuations in the statistics of war. These models indicate that both the long peace and the period of great violence that preceded it are not statistically uncommon patterns in realistic but stationary conflict time series. This fact does not detract from the importance of the long peace or the proposed mechanisms that explain it. However, the models indicate that the postwar pattern of peace would need to endure at least another 100 to 140 years to become a statistically significant trend. This fact places an implicit upper bound on the magnitude of any change in the true likelihood of a large war after the end of the Second World War. The historical patterns of war thus seem to imply that the long peace may be substantially more fragile than proponents believe, despite recent efforts to identify mechanisms that reduce the likelihood of interstate wars.

INTRODUCTION

Over the next century, should we expect the occurrence of another international conflict that kills tens of millions of people, as the Second World War did in the last century? How likely is such an event to occur, and has that likelihood decreased in the years since the Second World War? What are the underlying social and political factors that govern this probability over time?

These questions reflect a central mystery in international conflict (1–4) and in the arc of modern civilization: Are there trends in the frequency and severity of wars between nations, or more controversially, is there a trend specifically toward peace? If such a trend exists, what factors are driving it? If no such trend exists, what kind of processes governs the likelihood of these wars, and how can they be stable despite changes in so many other aspects of the modern world? Scientific progress on these questions would help quantify the true odds of a large interstate war over the next 100 years and shed new light on whether the great efforts of the 20th century to prevent another major war have been successful and whether the lack of such a conflict can be interpreted as evidence of a change in the true risk of war.

Early debates on trends in violent conflict tended to focus on the causes of wars, particularly those between nation states (5). Some researchers argued that the risk of these wars is constant and fundamentally inescapable, whereas others argued that warfare is dynamic, and its frequency, severity, and other characteristics depend on malleable social and political processes (1, 2, 6–9). More recent debates have focused on whether there has been a real trend toward peace, particularly in the postwar period that began after the Second World War (3, 10–13).

In this latter debate, the opposing claims are associated with liberalism and realism perspectives in international relations (14). The liberalism argument draws on multiple lines of empirical evidence, some spanning hundreds or even thousands of years [for example, see the works of Pinker (3) and Roser et al. (15)], to identify a broad and general decline in human violence and a specific decline in the likelihood of war, especially between the so-called great powers. Arguments supporting this perspective often focus on mechanisms that reduce the risk of war, such as the spread of democracy (16, 17), peace-time alliances (9, 18–20), economic ties, and international organizations (9, 21).

In contrast, the realism argument draws on empirical evidence, some of which also spans great lengths of time [for example, see the studies of Harrison and Wolf (22) and Cirillo and Taleb (23)], to identify an absence of discernible trends toward peace within observed conflict time series. A key claim from this perspective is that the underlying conflict-generating processes in the modern world are stationary, an idea advanced in the early 20th century by the English polymath L. F. Richardson (24, 25) in his seminal work on the statistics of war sizes and frequencies.

This debate has been difficult to resolve because the evidence is not overwhelming, war is an inherently rare event, and there are the multiple ways to formalize the notion of a trend (4, 5, 17, 26, 27). Should we focus exclusively on international conflicts, or should other types of conflict be included, such as civil wars, peace-keeping missions, or even the simple use of military force? Should we focus on conflicts between major powers or between geographically close nations, or should all nations be included? What conflict variables should we consider? How should we account for the changing number of states, which have increased by nearly an order of magnitude over the past 200 years? What about other nonstationary characteristics of conflicts, such as the increasing frequency of asymmetric or unconventional conflicts, the use of insurgency, terrorism, and radicalization, improvements in the technology of war and communication, or changes in economic development? Different answers to these questions can lead to opposite conclusions about the existence or direction of a trend in conflict (1, 2, 7, 8, 22, 23, 26–28).

Ultimately, the question of identifying trends in war is inherently statistical. Answering it depends on distinguishing a lasting change in the dynamics of some conflict variable from a temporary pattern—a fluctuation—in an otherwise stable conflict-generating process. More formally, a trend exists if there is a measurable shift in the parameters of the underlying process that produces wars, relative to a model with constant parameters. Identifying these trends is a kind of change-point detection task (29), in which one tests whether the distributions observed before and after a change point are statistically different. The ease of making these distinctions depends strongly on the natural variance of the observed data.

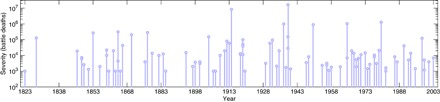
This article presents a data-driven analysis of the general evidence for trends in the sizes of and years between interstate wars worldwide and uses the resulting models to characterize the plausibility of a trend toward peace since the end of the Second World War. This analysis focuses on the 1823–2003 period and on the interstate wars in the Correlates of War interstate conflict data set (Fig. 1) (30, 31), which provides comprehensive coverage in this period, with few artifacts and relatively low measurement bias. The underlying variability in these data is captured using an ensemble approach, which then specifies a stationary process by which to distinguish trends from fluctuations in the timing of war onsets, the severity of wars, and the joint distribution of onsets and severity.

Fig. 1. The Correlates of War interstate war data (30) as a conflict time series, showing both severity (battle deaths) and onset year for the 95 conflicts in the period 1823–2003.

The so-called long peace (10)—the widely recognized pattern of few or no large wars since the end of the Second World War—is an important and widely claimed example of a trend in war. However, the analysis here demonstrates that periods like the long peace are a statistically common occurrence under the stationary model, and even periods of profound violence, like that of and between the two World Wars, are within expectations for statistical fluctuations. Hence, even if there have been genuine changes in the processes that generate wars over the past 200 years, data on the frequency and severity of wars alone are insufficient to detect those shifts. The long peace pattern would need to endure for at least another 100 to 150 years before it could plausibly be called a genuine trend. These findings place an upper bound on the magnitude of any underlying changes in the conflict-generating processes for wars, if they are to be consistent with the observed statistics. These results imply that the current peace may be substantially more fragile than proponents believe.

MATERIALS AND METHODS

War sizes and war onsets

Trends in war are implicitly statements about changing likelihoods of rare events, and their rarity necessarily induces uncertainty in any statistical estimate. To control for this uncertainty in the analysis here, the entire distribution of a conflict variable is modeled, and the ensembles of these models are used to quantify the uncertainty in the distribution’s shape. For concreteness, the analysis focuses on the sizes of wars and their timing in the historical record. Initially, these variables are considered independently, and subsequently, a joint model is formulated to numerically estimate the likelihood of historical patterns, such as the long peace, relative to well-defined stationary models of interstate conflict.

The sizes or severities of wars, commonly measured in battle deaths, have been known since the mid-20th century to follow a right-skewed distribution with a heavy tail, in which the largest wars are many orders of magnitude larger than a “typical” war. In Richardson’s original analysis of interstate wars from 1820 to 1945 (32), he argued that war sizes followed a precise pattern, called a power-law distribution, in which the probability that a war kills x people is Pr(x) ∝ x^−α, where α > 1 is called the “scaling” parameter and x ≥ x_min > 0. He also argued that the timing of wars followed a simple Poisson process, implying a constant annual hazard rate and an exponential distribution for the time between wars (24, 25). Although Richardson’s analysis would not be considered statistically rigorous today, these patterns—a power-law distribution for war sizes and a Poisson process for their onsets—represent a simple stationary model for the statistics of interstate wars worldwide.

Here, this model is improved upon by first testing the statistical plausibility of its two key assumptions, then estimating their structure from empirical data, and finally combining them computationally to investigate the likelihood that the end of the Second World War and its subsequent long peace pattern represent a change point in the observed statistics of interstate wars. Before examining the marginal distributions of war sizes and timing between war onsets, a brief overview is given of relevant mathematical and statistical issues to specify these models and use them to distinguish trends from fluctuations in conflict time series.

Statistical concerns

Power-law distributions have unusual mathematical properties (33, 34), which can require specialized statistical tools [for a primer on power-law distributions in conflict, see the studies of Cederman (6) and Clauset et al. (35)]. For instance, when observations are generated by a power law, time series of summary statistics, such as the mean or variance, can exhibit large fluctuations that can resemble a trend. The largest fluctuations occur for α ∈ (1, 3), when one of or both the mean and variance are mathematically undefined. In the context of interstate wars, this property can produce long transient patterns of low severity or the absence of wars, making it difficult to distinguish a genuine trend toward peace from a transient fluctuation in a stationary process.

Identifying a power law in the distribution of an empirical quantity can indicate the presence of exotic underlying mechanisms, including nonlinearities, feedback loops, and network effects (33, 34), although not always (36), and power laws are believed to occur broadly in complex social, technological, and biological systems (37). For instance, the intensities or sizes of many natural disasters, such as earthquakes, forest fires, and floods (34, 38, 39), as well as many social disasters, such as riots and terrorist attacks (35, 40), are well described by power laws.

However, it can be difficult to accurately characterize the shape of a distribution that follows a power-law pattern (37). Fluctuations in heavy-tailed data are greatest in the distribution’s upper tail, which governs the frequency of the largest and rarest events. As a result, data tend to be sparsest precisely where the greatest precision in model estimates is desired.

Recent interest in heavy-tailed distributions has led to the development of more rigorous methods to identify and estimate power-law distributions in empirical data (37, 41, 42), to compare different models of the upper tail’s shape (37), and to make principled statistical forecasts of future events (43). This branch of statistical methodology is related to but distinct from the task of estimating the distribution of maxima within a sample (44, 45) and is more closely related to the peaks-over-threshold literature in seismology, forestry, hydrology, insurance, and finance (41, 42, 45–48).

Although Poisson processes pose fewer statistical concerns than power-law distributions, a similar statistical approach is used in the analysis here of both war sizes and years between war onsets. In particular, an ensemble approach is used (43) on the basis of a standard nonparametric bootstrap procedure (49) that simulates the generative process of events to produce a series of synthetic data sets {Y} with similar statistical structure as the empirical data X. Fitting a semiparametric model Pr(y|θ) to each Y yields an ensemble of models {θ} that incorporate the empirical data’s inherent variability into a distribution of estimated parameters. This distribution is then used to weight models by their likelihood under the bootstrap distribution and to numerically estimate the likelihood of specific historical or future patterns (43).

Within the 1823–2003 time period, the end of the Second World War in 1945 is widely viewed as the most plausible change point in the underlying dynamics of the conflict-generating process for wars and marks the beginning of the subsequent long peace pattern (10). Determining whether 1945 marks a genuine a shift in the observed statistics of wars and, hence, whether the long peace is plausibly a trend or a fluctuation represents a broad test of the stationary hypothesis of war (23). Evaluating other theoretically plausible change points in these data is left for future work.

Finally, some studies choose to limit or normalize war onset counts or war sizes (battle death counts) by a reference population. For instance, onset counts can be normalized by assuming that war is a dyadic event and that dyads independently generate conflicts (26), implying a normalization that grows quadratically with the number of nations. However, considerable evidence indicates that dyads do not independently generate conflicts (9, 16–21). Similarly, limiting the analysis to conflicts among “major powers” introduces subjectivity in defining such a scope, and there is not a clear consensus about the details, for example, when and whether to include China or the occupied European nations, or certain wars, such as the Korean War (26). War size can be normalized by assuming that individuals contribute independently to total violence, which implies a normalization that depends on either the population of the combatant nations (a variable sometimes called war “intensity”) or of the world (3, 23). However, there is little evidence for this assumption (3, 50), although such a per capita variable may be useful for other reasons. In the analysis performed here, war variables are analyzed in their unnormalized forms, and all recorded interstate wars are considered. The analysis is thus at the level of the entire world, and results are about absolute counts.

RESULTS

The sizes of wars

Considering the sizes of wars alone necessarily ignores other characteristics of conflicts, including their relative timing, which may contain independent signals about trends. A pattern in war sizes alone thus says little about changes in declared reasons for conflicts, the way they are fought, their settlements, aftermaths, or relationships to other conflicts past or future, or the number of nations worldwide, among other factors. One benefit of ignoring these factors, at least at first, is that they may be irrelevant for identifying an overall trend in wars, and their relationship to a trend can be explored subsequently. Hence, focusing narrowly on war sizes simplifies the range of models to consider and may improve the ability to detect a subtle trend.

The Correlates of War data set includes 95 interstate wars, the absolute sizes of which range from 1000 (the minimum size by definition) to 16,634,907 (the recorded battle deaths of the Second World War) (Fig. 2). The estimated power-law model has two parameters: x_min, which represents the smallest value above which the power-law pattern holds, and α, the scaling parameter. Standard techniques are used to estimate model parameters and model plausibility (section S1) (37).

Fig. 2. Interstate wars sizes, 1823–2003.

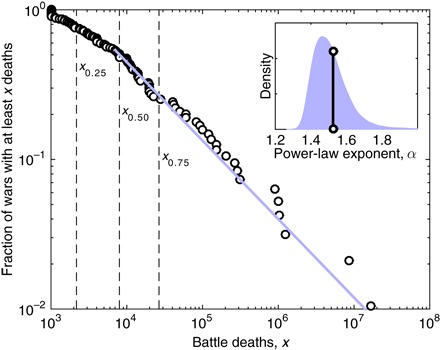
The maximum likelihood power-law model of the largest-severity wars (solid line, $\widehat{\mathrm{\alpha }}$ = 1.53 ± 0.07 for $\mathit{x}={\widehat{\mathit{x}}}_{\text{min}}=7061$) is a plausible data-generating process of the empirical severities (Monte Carlo, p_KS = 0.78 ± 0.03). For reference, distribution quartiles are marked by vertical dashed lines. Inset: Bootstrap distribution of maximum likelihood parameters Pr($\widehat{\mathrm{\alpha }}$), with the empirical value (black line).

The maximum likelihood power-law parameter is $\widehat{\mathrm{\alpha }}=1.53\pm 0.07$ for wars with severity x ≥ x_min = 7061 (Fig. 2, inset), and 95% of the bootstrap distribution of $\widehat{\mathrm{\alpha }}$ falls within the interval [1.37, 1.76]. However, these estimates do not indicate that the observed data are a plausible independent and identically distributed (iid) draw from the fitted model. To quantitatively assess this aspect of the model, we used an appropriately defined statistical hypothesis test (37), which indicates that a power-law distribution cannot be rejected as a data-generating process (p_KS = 0.78 ± 0.03). That is, the observed data are, as a group, statistically indistinguishable from an iid draw from the fitted power-law model. This finding is consistent with past analyses of war intensities (population-normalized war size) over a similar period of time, which found a power law to be statistically plausible and at least as good a model as alternative heavy-tailed distributions, including a power-law distribution with an upper, exponential cutoff (37).

The statistical plausibility of a power-law distribution here provides only circumstantial evidence for the stationary hypothesis because this analysis does not consider the exchangeability of the sequence of wars or whether the Second World War is a plausible change point in the observed statistics of wars. The size of the Second World War is not statistically anomalous, given the historical distribution of war sizes (section S2). Furthermore, the distribution of war sizes in the postwar period, defined as onsets that occurred during 1940–2003, is not statistically distinguishable from the distribution in the preceding period, 1823–1939 (section S3).

The relatively small sample size of the data set necessarily reduces the statistical power of these tests; thus, a trend may still exist within these events and be obscured by the large fluctuations that power laws naturally produce. In addition, the above distributional analysis only models the relative frequencies of the 51 largest conflicts (x ≥ 7061, the upper 54% of the distribution), and nearly half of all interstate wars fall outside this domain. Small wars could thus follow a different pattern or trend than large wars. In the subsequent model of the joint distribution of war sizes and timing, a semiparametric approach is used to capture the full distribution of war sizes (section S1) and to investigate the statistical power of the stationary hypothesis over time.

The time between wars

A trend toward peace could also manifest as a trend in the time between new wars. That is, the sizes of wars may not be changing, but the time between consecutive wars overall or those of at least a certain size may be lengthening.

Delays between consecutive wars in the data set range from 0 years (representing wars that began in the same year) to 18 years (the delay between the Russo-Turkish War in 1828 and the Mexican-American War in 1846). However, long delays are uncommon, and in the postwar period, no delay exceeded the 7 years between the onsets of the Franco-Thai War in 1940 and the Indo-Pakistani War in 1947. Overall, wars have occurred at a relatively steady pace since 1823, with an average time of 1.91 years between consecutive war onsets. In only 14 of the 181 years (8%) were there multiple new war onsets in the same year, and all other years had either 0 or 1. Most wars ended no more than 2 years after their onset (79%), and hence, the temporal analysis here focuses on the distribution of times between war onsets.

If the generation of war onsets follows a Poisson process, the distribution of years between onsets is given by a geometric distribution since onsets are binned by year. For interstate conflicts, the maximum likelihood parameter for a geometric model of time between wars is $\widehat{\mathit{q}}=0.428\pm 0.002$ for delays of at least t ≥ t_min = 1 year (Fig. 3, inset), and 95% of the bootstrap distribution of $\widehat{\mathit{q}}$ falls within the interval [0.354, 0.520].

Fig. 3. Times between interstate war onsets, 1823–2003.

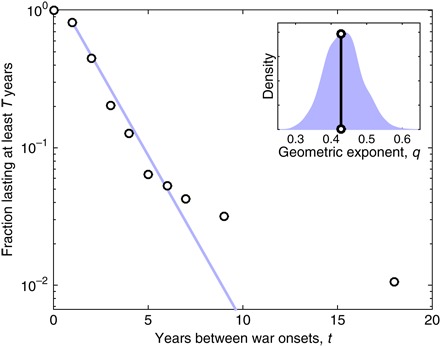
The maximum likelihood geometric model (solid line, $\widehat{\mathit{q}}=0.428\pm 0.002$ for t ≥ 1) is a plausible data-generating process of the empirical delays (Monte Carlo, p_KS = 0.13 ± 0.01), implying that the apparent discontinuity at t = 5 is a statistical artifact. Inset: Bootstrap distribution of maximum likelihood parameters $\text{Pr}(\widehat{\mathit{q}})$, with the empirical estimate (black line).

To assess whether the observed data are plausibly an iid draw from this model, we used an appropriately defined statistical hypothesis test (37), with a geometric distribution as the null rather than a power law. This test indicates that a geometric model cannot be rejected as a data-generating process (p_KS = 0.13 ± 0.01), implying that the observed delays are statistically indistinguishable from an iid draw from the fitted geometric model. Hence, although, visually, there appears to be a discontinuity in the empirical distribution around t = 5 years, this pattern is not statistically significant.

As with war sizes, the statistical plausibility of a simple geometric model for years between war onsets provides circumstantial evidence for a stationary process because it does not test for exchangeability. However, the distribution of time between wars in the postwar period, 1940–2003, is also not statistically distinguishable from that of the preceding period, 1823–1939 (section S4). This finding supports the basic realist argument for a lack of any trend in the timing of wars, and it agrees with Richardson’s original hypothesis that war onsets are well described by a simple Poisson process (24, 25).

Distinguishing trends from fluctuations

The liberalism thesis argues that, after the Second World War, large wars became relatively less common than they were before it. In other words, the joint distribution of war sizes and their timing changed at a particular time. This idea is evaluated quantitatively here by combining the results on war size and timing to develop stationary models that can generate synthetic histories, or futures, of war onset times and corresponding sizes. Under such a model, a genuine trend like the long peace should be statistically unlikely. If it is not, then the dynamics of the stationary process may be extrapolated into the future to estimate how long a long peace pattern must endure before it becomes statistically distinguishable from a long but transient excursion under stationarity. In this way, the statistical power of these tests may be investigated.

The long peace pattern is commonly described as a change in the frequency of large wars, and, here, a “large” war is defined as one with severity in the upper quartile of the historical distribution, that is, x ≥ x_0.75 = 26,625 battle deaths. Over the initial 1823–1939 period, there were 19 large wars, with a new large war occurring on average every 6.2 years. The “great violence” pattern of 1914–1939, which spans the onsets of the First and Second World Wars, was especially violent, with 10 large wars or about one every 2.7 years. In contrast, the long peace of the 1940–2003 postwar period contains only five large wars or about one every 12.8 years, a marked reduction in the most severe conflicts relative to earlier periods. These patterns are represented quantitatively using an accumulation curve, which gives the cumulative count over time of wars whose size exceeds some threshold (Fig. 4).

Fig. 4. Cumulative counts of wars by general severity.

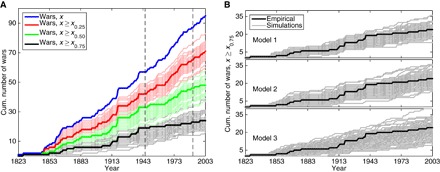
(A) Empirical counts of wars of different sizes (dark lines) over time against ensembles of simulated counts from a stationary model, in which empirical severities are replaced iid with a bootstrap draw from the empirical severity distribution (model 1). For reference, dashed lines mark the end of the Second World War and the end of the Cold War. (B) For the largest-severity wars alone, empirical and simulated counts for three models of stationarity, which incorporate progressively more variability in the underlying data-generating process (see main text).

The likelihood of the postwar pattern can now be evaluated under three stationary models of war size and timing. Each model first chooses a sequence of onset years and then independently assigns a war size to each. Hence, these models differ only in their variability in generating the timings or sizes of wars, and each set of simulated wars is an exchangeable sequence of random variables.

For war onsets, models 1 and 2 use the empirical onset dates, as observed, producing 95 wars in each simulation. Model 3 generates a new war in each year according to a Bernoulli process, with the empirically observed production rate (on average, a new war every 1.91 years) in agreement with the fitted geometric distribution of delays. For war sizes, model 1 draws a size value iid from the empirical distribution (a bootstrap), whereas models 2 and 3 draw a size iid from a uniformly random member of the ensemble of semiparametric power-law models obtained above. Intuitively, models 1 to 3 represent a sequence of increasing variance in the posterior distribution of war sizes and delays, with model 1 producing the smallest variance and model 3 producing the largest.

Within the empirical accumulation curve for large wars, the long peace is a visible pattern, in which the rate of production (slope of the accumulation curve) is substantially more flat than in the preceding great violence period (Fig. 4A and section S5). However, under all three models, the long peace pattern falls comfortably within the distribution of simulated curves (Fig. 4B), implying that the observed pattern is not statistically distinguishable from a long transient of the heavy-tailed distribution of historical war sizes.

Most war sequences (57 to 68%) produced by the three stationary models contain a period of peace at least as long in years and at least as peaceful in terms of large wars as the long peace (Table 1). These results show that long periods of relatively few large wars are downright common even when the hazard rate of a large war is constant and unchanging. Hence, observing a long period of peace is not necessarily evidence of a changing likelihood for large wars.

Table 1. Stationary likelihood of empirical conflict patterns.

Under three models of stationary conflict generation (see main text), estimated likelihoods of observing one of three large-war patterns over the period 1823–2003: a “great violence,” meaning 10 or more large war onsets (x ≥ x_0.75) over a 27-year period (the empirical count of these onsets, 1914–1939); a “long peace,” meaning five or fewer large war onsets over a 64-year period (the empirical count of these onsets, 1940–2003); or a great violence, followed by a long peace. Probabilities are estimated by Monte Carlo. Parenthetical values indicate the SE (standard error) of the least significant digit.

Empirical pattern	Formalization	Model 1	Model 2	Model 3
Great violence	Pr(V ≡ n ≥ 10 large wars over t ≤ 27 years)	0.107(1)	0.159(1)	0.121(1)
Long peace	Pr(P ≡ n ≤ 5 large wars over t ≥ 64 years)	0.622(2)	0.569(2)	0.681(2)
Violence, then peace	Pr(V followed by P)	0.0030(2)	0.0029(2)	0.0055(2)

In contrast, few war sequences (11 to 16%) contain a period of violence at least as large and over no more time than the great violence, implying that this period was relatively unusual, although still not statistically rare, in the degree of clustering in time for large war onsets. Moreover, the joint probability of a period of great violence, immediately followed by a long period of peace, is genuinely rare, occurring in less than 1% of simulated sequences across models. This estimate is consistent with the liberalism hypothesis that some learning or adaptation resulting from the World Wars (14) may have changed the subsequent conflict-generating process for subsequent wars. However, the magnitude of this statistic should be interpreted cautiously because all sufficiently specific sequences of events under a stationary process have small likelihoods.

Peering into the future

If the postwar pattern of relatively fewer large wars were permanent, at what future date could we reasonably conclude that this pattern is a trend, that is, a genuine change in the statistics of large wars, and not a fluctuation? This question can be answered by extrapolating the simulated war sequences into the future. The variable of interest is then the fraction of simulations with a greater accumulation of large wars than either observed in the past or expected in the future, under a linear extrapolation of the long peace pattern, in which a new large war occurs every 12.8 years on average. This fraction’s trajectory describes the evolution of the statistical likelihood of the empirical accumulation pattern of large wars over time.

To generate war sequences that cover both the historical 1823–2003 period and a future period of chosen length, we modified models 1 and 2 to generate a new war in each year beyond 2003 according to the same Bernoulli process of model 3. Otherwise, all features of all models remain the same. The result is a distribution of accumulation curves of any length required, which quantify the natural variability of the accumulation of large wars under a stationary process (Fig. 5A). As before, model 1 produces the smallest variance in the posterior distribution, and model 3 produces the largest.

Fig. 5. How long must the peace last?

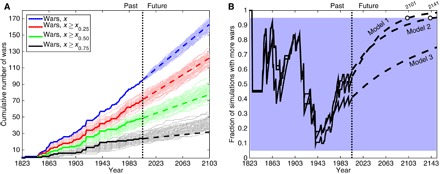
(A) Simulated accumulation curves for wars of different sizes under a simple stationary model (model 1; see main text), overlaid by the empirical curves up to 2003 (dark lines) and linear extrapolations of the empirical postwar trends (the long peace) for the next 100 years (dashed lines). Quartile thresholds are derived from empirical severity data. (B) Fraction of simulated conflict time series that contain more large wars (x ≥ x_0.75) than observed in the past or than expected in the future relative to a linear extrapolation of the postwar tend. Years at which the postwar trend (the long peace) becomes statistically unlikely under a stationary model, relative to 95% of simulated time series, are marked with open circles.

Over the historical period, the observed accumulation of large wars fluctuates throughout the middle 90% of simulated trajectories, confirming the above results that the historical record of large wars is not itself statistically unusual under a stationary process (Fig. 5B). However, the great violence pattern of 1914–1939 resulted in a marked shift in the significance of the observed number of large wars, moving from a point where most stationary sequences had more large wars than were observed empirically to a point where most had fewer. Nonetheless, the extent of this shift was not large enough to make the overall accumulation pattern statistically significant relative to the stationary hypothesis. The subsequent long peace pattern then moved the relative significance back to the middle of the null distribution.

In other words, the sparsity of large wars in the postwar 1940–2003 period thus served to counterbalance the large density of these wars in the preceding 1914–1939 period. Hence, in a purely statistical accounting sense, the long peace has simply balanced the books relative to the great violence. Had the great violence contained fewer large wars or were the long peace substantially longer, the recent empirical pattern of relatively few large wars would appear marginally more significant.

In the extrapolated future, the postwar pattern of relatively few large wars becomes progressively more unlikely under a stationary hypothesis (Fig. 5B). The particular year at which the long peace pattern becomes significant differs by stationary model, with crossing points around 100 to 140 years in the future for models 1 and 2. Model 3 yields a much longer estimate because its stochastic process for war onsets leads to substantially larger variance in the accumulation statistics over time. In general, however, the long peace would need to hold for at least another century to be statistically distinguishable from a large but random fluctuation in an otherwise stationary process for war sizes and onsets. The consistency of the historical record of wars with a stationary model places an implicit upper bound on the magnitude of change in the underlying conflict-generating process since the end of the Second World War. Such a change in the production of wars cannot be ruled out by this statistical analysis, but if it exists, it is evidently not a marked shift. That is, these results can be consistent with evidence of genuine changes in the international system, but they constrain the extent to which these changes could have affected the production of interstate wars.

The long view

If the long peace does not reflect a fundamental shift in the production of large wars (23), then in the years between now and when such a pattern becomes statistically significant, the hazard of a very large war would remain constant. In this case, a stationary model may be used to estimate the likelihood of a very large war occurring over 100 years, one like the Second World War, which produced x_* = 16,634,907 battle deaths. Using the ensemble of semiparametric models for the sizes of wars and assuming a new war onset every 1.91 years on average (43), the probability of observing at least one war with x_* or more deaths is p_* = 0.43 ± 0.01 (Monte Carlo), and the expected number of these events over the next 100 years is 0.62 ± 0.01. Hence, under stationarity, the likelihood of a very large war over the next 100 years is not particularly small.

Under an even stronger assumption of stationarity, the model can estimate the waiting time for a war of truly spectacular size, such as one with x = 1,000,000,000 (one billion) battle deaths. A conflict this large would be globally catastrophic and would likely mark the end of modern civilization. It is also not outside the realm of possibility, if current nuclear weapons were used widely.

Using the ensemble of semiparametric models of war sizes and a longer Monte Carlo simulation, the model estimates that the median forecasted waiting time for such an event is 1339 years. Reflecting the large fluctuations that are natural under the empirical war size distribution, the distribution of waiting times for such a catastrophic event is enormously variable, with the 5 to 95% quantiles ranging from 383 to 11,489 years. A median delay of roughly 1300 years does not seem like a long time to wait for an event this enormous in magnitude, and humans have been waging war on each other, in one way or another, for substantially longer than that.

The plausibility of this prediction is likely unknowable. However, a genuinely stationary process would hold equally well for the past as for the future, and there is no evidence of such an event in the long history of human conflict (50). Its absence suggests that some aspects of conflict generation are probably not stationary in the way they have been modeled here, and hypotheses are easy to enumerate. For example, changes in world population, technology, and political structures have likely all played some role in increasing or decreasing the sizes of wars over very long periods of time, but none of these processes are represented directly in observed war sizes (51). Looking toward the future, however, stationarity may be more plausible (52); hence, the prospect of a civilization-ending conflict in the next 13 centuries is sobering.

DISCUSSION

The absence of a large war between major powers and relatively few large wars of any kind since the end of the Second World War is an undeniable international achievement. However, whether this peaceful pattern should be expected to endure has been a central mystery in conflict research now for several decades. On the one hand, a substantial body of scholarship now presents a compelling argument that the postwar peace reflects a genuine trend based on mechanisms that reduce the likelihood of war (9, 16, 20) and on statistical signatures of a broad and centuries-long decline in general violence (3, 7, 12, 13) or the improvement of other aspects of human welfare (15). The result is not unreasonable support for the optimistic perspective espoused by liberalism, despite reality’s frequent disregard for the direction of the trend.

However, focusing only on mechanisms that explain a trend toward peace commits a kind of scientific fallacy by selecting on the dependent variable. A full accounting of the likelihood that the long peace will endure must consider not only the mechanisms that reduce the likelihood of war but also the mechanisms that increase it [for example, see previous works (53–55)]. War-promoting mechanisms certainly include the reverse of established peace-promoting mechanisms, for example, the unraveling of alliances, the slide of democracies into autocracy, or the fraying of economic ties, but may also include completely novel mechanisms.

In the long run, some of the processes that promote interstate war may be intimately related to the ones that reduce it over the shorter term, through feedback loops, trade-offs, or backlash effects. For example, the persistent appeal of nationalism, the spread of which can increase the risk of interstate wars (56), is not independent of deepening economic ties via globalization (57). The investigation of these interactions will be a vital direction of future work in conflict research. However, without a complete understanding of mechanisms that promote interstate war, especially the large ones, it is unclear whether the postwar pattern of peace will continue or whether the formation and eventual dissolution of periods of peace are part and parcel for a dynamical but ultimately stationary system.

Three key difficulties for evaluating the changing likelihood of war from a mechanistic viewpoint are (i) the incomplete accounting of mechanisms, that is, it seems unlikely that every peace- or war-promoting process has been identified, (ii) the lack of understanding of “meta-mechanisms,” that is, processes that govern over very long periods of time the emergence and relevance of more specific mechanisms, and (iii) the difficulty of integrating these varied mechanisms into a single calculation. In contrast, a statistical analysis of the historical record, like the one performed here, does not require accounting for all possible mechanisms. Hence, it provides both an alternative approach to arrive at some kind of answer to a difficult question and a quantitative means by which to identify unusual patterns in need of explanation.

The analysis here finds that the postwar pattern of peace is remarkably unsurprising (Table 1). Similarly long periods of relative peace are common occurrences in the naturally variable statistics of interstate wars [a point recently made by Cirillo and Taleb (23)]. The more unusual pattern in the past two centuries is not a long period of relative peace but the markedly violent period that preceded it (in which 42% of large wars occurred over 15% of the total time). This period was so violent over such a short period of time that the subsequent long peace simply balanced the statistical books (Fig. 5B), making it entirely plausible that the timing and sizes of interstate wars since 1823 were generated by a stationary process. Hence, the long peace is not evidence by itself of a change in the underlying mechanisms that generate conflict (Fig. 4B). The analysis here estimates that the postwar pattern of relative peace would need to endure in its current form for at least another 100 years before it would become statistically unusual enough to justify a claim that it represents a genuine trend (Fig. 5B).

A related finding is the remarkable stability of war onsets of any size since 1823 (Figs. 3 and 4B), whose statistics are consistent with a simple Poisson process, as originally proposed by Richardson (24, 25). In other words, the annual hazard rate of a new interstate war is evidently also stationary, despite changes in many relevant factors (14), including the number of states, which increased by nearly an order of magnitude over this time period.

These results undermine the optimism of liberalism by implying that the enormous efforts after the Second World War to reduce the likelihood of large interstate wars have not yet changed the observed statistics enough to tell whether they are working. This does not lessen the face value achievement of the long peace because the severity of a large war between major powers using modern military technology could be very large, and there are real benefits beyond lives saved (15) that have come from increased economic ties, peace-time alliances, and the spread of democracy. However, it does highlight the continued relevance of the realist perspective and the appropriateness of a stationary process as the null hypothesis for patterns in interstate war. It also highlights the difficulty of understanding the role that human agency plays in driving trends and fluctuations in the statistics of interstate wars. Specifically, how can so much concerted effort, by so many individuals and organizations over so many decades of time, not be evidence of a genuine trend?

The answer may be simply a shift in perspective. Evidence from the study of complex social and biological systems (58) suggests that we often underestimate the importance of complexity and overestimate our ability to understand complicated causes of complicated effects, especially those that represent the aggregation of many inconsequential individual actions. Human agency certainly plays a critical role in shaping shorter-term dynamics and specific events in the history of interstate wars. However, the distributed and changing nature of the international system evidently moderates the impact that individuals or coalitions can have on longer-term and larger-scale system dynamics.

In this sense, the correct level of description to understand trends in conflict may be the entire system, above the level of individual states, individual conflicts, or even individual peace- or war-promoting mechanisms. A pattern like the long peace could thus be real and understandable, produced by mechanisms that have genuinely reduced the likelihood of war over this period, and yet still be consistent with an overall stationary process running at a larger scale.

To illustrate this point, consider a professional basketball game and the ups, downs, and reversals in the lead size by one team over the other. As a spectator or player, one can readily explain why the lead size increased at one time or decreased at another. Each scoring event can be tied to specific actions and individuals within the game and to individual or team strategies. At this level, scoring trends have interpretable causes that depend on actions at the same scale as the events themselves.

However, when thousands of individual games across teams and seasons are aggregated to consider basketball as a system, the relevance of these explanations blurs. Patterns at this scale cannot be attributed to specific actions or individuals and, instead, emerge from subtle correlations within or constraints on collective behavior. At this scale, the empirical statistics of lead sizes in basketball are nearly indistinguishable from those of a simple unbiased random walk (59, 60), and exciting trends within individual games are just statistical fluctuations at the system level.

Counterintuitively, the stationary pattern of scoring in basketball appears despite the strategic efforts of highly skilled players to make it otherwise. It may be precisely these independent efforts of skilled individuals in competition with each other that produce the observed stationary statistics (60). This analogy suggests a new direction in conflict research, one aimed at identifying and testing mechanisms that could cause stationary statistics in the long term to emerge out of nonstationary dynamics at smaller temporal and spatial scales. A related direction would seek to understand what actions are necessary to genuinely alter these mechanisms and to change the characteristics of the stationary process.

Without a clearer understanding of the underlying mechanisms that drive the production of conflicts over long periods of time or access to sufficiently broad and reliable data by which to identify them, a satisfying answer to the debate over trends in war may remain out of reach. Progress may be further complicated by the fact that interstate wars are only one conflict variable among many (4), which are surely interdependent. The analysis here indicates that none of the variations in the frequency and severity of wars since 1823 are statistically plausible trends. However, this finding may occur in part because there are compensatory trends in other variables that mask a subtle underlying change in the conflict-generating processes. Proponents of the trend toward peace cite patterns across multiple conflict variables or focus on patterns among developed nations, as evidence of a broad shift toward less violence (3, 7, 12, 13). However, not all conflict variables support this conclusion, and some, such as military disputes and the frequency of terrorism, exhibit the opposite pattern (22, 43). Untangling the interactions of various conflict variables, and characterizing both their trends and their differences across different groups of nations, is a valuable line of future work.

For instance, a stationary process for interstate wars is not inconsistent with an overall decline in per capita violence (3) because the human population has grown markedly over the same period (23, 27). The nonstationarity dynamics in human population, in the number of recognized states, in commerce, communication, public health, and technology, and even in the modes of war itself make it all the more puzzling that the hazard of interstate war in general has remained evidently so constant.

If the statistics of interstate wars are genuinely stationary, the risk over the next century of a very large war is uncomfortably high. The results here thus highlight the importance of continued efforts to ensure that the long peace endures and to prevent fragile peace-promoting institutions or systems from falling in the face of stable or contingent processes that drive the production of war. Much of this work must be done on the policy side. In the long run, however, research will play a crucial role by developing and evaluating mechanistic explanations, ideally at the system scale, of the likelihood of war (61, 62), which will help shed new light on what policies at what scales will promote peace.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/2/eaao3580/DC1

section S1. Distribution models

section S2. The likelihood of a large interstate war

section S3. War severities before and after 1940

section S4. War onsets before and after 1940

section S5. Variability in onset rate by war size

fig. S1. Power-law tail models fitted to bootstrap samples of conflict sizes (1823–2003).

fig. S2. Estimated war size distribution parameter over time.

fig. S3. Cumulative number of wars, 1823–2003.

table S1. Observed and expected fractions of war sizes, by order of magnitude, for the postwar period (1940–2003).

table S2. Observed and expected fractions of durations of peace (no new war onsets) for the postwar period.

References (63, 64)