Abstract
Background
In recent years, investigators have asserted that the 3 + 3 design lacks flexibility, making its use in modern early-phase trial settings, such as combinations and/or biological agents, inefficient. More innovative approaches are required to address contemporary research questions, such as those posed in trials involving immunotherapies.
Design
We describe the implementation of an adaptive design for identifying an optimal treatment regimen, defined by low toxicity and high immune response, in an early-phase trial of a melanoma helper peptide vaccine plus novel adjuvant combinations.
Results
Operating characteristics demonstrate the ability of the method to effectively recommend optimal regimens in a high percentage of trials with reasonable sample sizes.
Conclusions
The proposed design is a practical, early-phase, adaptive method for use with combined immunotherapy regimens. This design can be applied more broadly to early-phase combination studies, as it was used in an ongoing study of two small molecule inhibitors in relapsed/refractory mantle cell lymphoma.
Keywords: immunotherapy, clinical trials, early-phase, melanoma, combination
Introduction
The current landscape of oncology drug development poses a challenge to widely accepted methods used in early-phase clinical trials. In recent years, novel statistical methods have been developed in order to address more complex research questions in early-phase studies. However, broad implementation of novel methods has been limited, with traditional or modified 3 + 3 designs remaining in frequent use [1]. A recent paper by Paoletti et al. [1] described the rigidity of the 3 + 3 design in meeting the challenges of studies involving combinations and/or biological agents, and called for wider use of more innovative methods to achieve the goals of contemporary research objectives. This call is present throughout the statistical and medical literature, with reviews, justification, and recommendations on the use of innovative designs [2–4]. More complex problems have created the need to adapt early-phase trial design to the specific agents being investigated, and the corresponding endpoints.
The Food and Drug Administration (FDA) published a report acknowledging the need for alternative dose-escalation strategies in cancer vaccines [5]. This report states that many cancer vaccine trials that employ the 3 + 3 design fail to identify a maximum tolerated dose, mainly due to the lack of dose-limiting toxicities (DLTs), and that model-based designs may be more appropriate. It continues by saying that when few DLTs are expected, designs guided by alternative outcomes, such as immune response, may be more valuable [5]. In this article, we present a model-based, early-phase design for combination immunotherapies that accounts for both safety and immunologic response in order to identify an optimal treatment strategy. The statistical modeling framework is outlined in Wages and Conaway [6]. We describe the implementation of the method in an ongoing trial (Mel63) investigating a helper peptide vaccine plus local and systemic adjuvant combinations for the treatment of melanoma (NCT02425306) designed at the University of Virginia (UVA) Cancer Center. This design extends the one outlined in Wages et al. [7]. Recently published guidelines [8, 9] for implementing novel early-phase methods were followed in executing the described design.
Design
Mel63 is an early-phase evaluation of the safety and immunogenicity of a vaccine comprised of a mixture of 6 synthetic melanoma helper peptides (6MHP) [10] administered with one of the two local adjuvant combinations, Incomplete Freund’s Adjuvant (IFA) or IFA + the toll-like receptor 3 agonist polyICLC, alone or with systematic low-dose cyclophosphamide (mCy), as shown in Table 1. Treatment combinations are grouped into ‘zones’ based on the number of adjuvants in a regimen (1, 2, or 3). The trial was designed to find the range of optimal treatment combinations (OTC), defined as a combination with early and durable immunologic response and an acceptable level of toxicity. An adaptive design is being used to guide accrual decisions with toxicity assessments and the potential for a durable immune response characterizing the main decision measures. The decision endpoints are DLTs and durable immune response (dRsp) as measured by CD4+ T cell responses to 6MHP during the time period of vaccination administration.
Table 1.
Treatment regimen/combination/zone definitions
| Zone | Regimen/Combination | 6MHP+ |
|---|---|---|
| 1 | A | IFA |
| 2 | B | IFA + mCy |
| 2 | C | IFA + PolyICLC |
| 3 | D | IFA + PolyICLC + mCy |
In monitoring safety, adverse events (AEs) are being assessed and acute toxicity graded using the National Cancer Institute (NCI) Common Terminology Criteria (CTCAE) Version 4.03. A participant is classified as experiencing a DLT (yes/no) based on protocol-specified criteria. In this study, a DLT is defined as any unexpected AE that is possibly, probably, or definitely related to treatment and meets the following criteria; (i) grade ≥ 3, (ii) grade 1 ocular AEs, and (iii) grade 2 allergic/autoimmune reactions. An early dRsp is defined as at least a 5-fold increase in immune response to the 6MHP peptide as measured by CD4+ T cells over two consecutive time periods during vaccination (days 0–85). As data accumulate, each participant is classified as experiencing a DLT (yes/no) and experiencing a dRsp (yes/no). Treatment-related grade 3 or higher AE data from our prior studies [11, 12, NCT01585350] are being used to gauge DLT rates. Using these data, the DLT tolerance level was chosen to be 25% (i.e. any optimal combination that we are satisfied has an estimated DLT probability ≤25% to be considered ‘acceptable’ in terms of safety).
Allocation decisions presented in this manuscript depend on the definition (and measure) of an immune response as a yes/no (binary) endpoint. In particular, the endpoint must be defined prospectively and ideally is one that has biologic relevance and/or is associated with clinical response. Many immunologic endpoints depend on continuous variables, and, in this design strategy, it is important to define prospectively a criterion for defining a ‘positive’ or ‘negative’ result along a continuum of data values. In the present study, we have defined criteria based on prior reports [13]. Another important consideration is that the result of the immune response measure must be available in a reasonable timeframe if it is to be useful in guiding trial enrollment. Thus, it is important to select an immunologic endpoint that occurs early enough to be meaningful and to design processes for collecting samples and assaying them rapidly so that the data may guide participant enrollment in accord with the study design.
Estimation
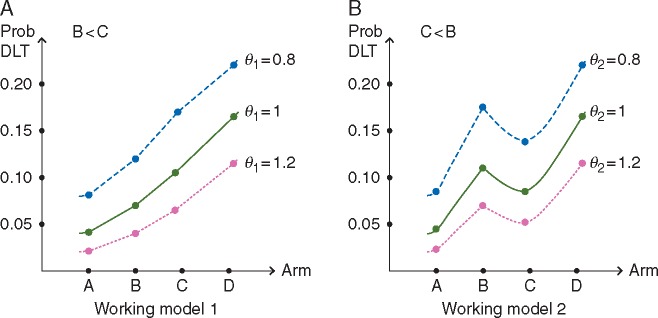
Model-based allocation is being based upon a continual reassessment method (CRM) [14] that accounts for two binary endpoints (DLT, dRsp) in combinations of agents [6]. Safety assessments are based on the assumption that, as the number of adjuvants increases, the probability of DLT is non-decreasing. It is reasonable to assume that regimens in higher zones do not have lower probabilities of DLT than regimens in lower zones. This assumption is based on data from previous melanoma studies in which these adjuvant preparations were combined with other peptide vaccines. It is unknown whether regimens have higher or lower DLT probabilities than other regimens within the same zone. It could be that B < C or C < B in terms of their respective DLT probabilities. We express this uncertainty through specification of multiple one-parameter models in Table 2 that reflect different orderings of the DLT probabilities. We then rely on model selection techniques to choose the model most consistent with the data. A common model choice [15] in the CRM is to raise a set of initial DLT probability estimates, also referred to as the ‘skeleton’ of the model, to a power to be estimated by the data, where indexes the skeleton. Figure 1 illustrates how the model works, and that is a parameter to be estimated. The skeleton values displayed in Table 2 for each model were generated using the algorithm of Lee and Cheung [16]. Using the accumulated toxicity data, the CRM is fit for each DLT probability working model, and the parameter is estimated for each model by maximum likelihood estimation. The working model with the largest likelihood is chosen and, using the selected model, DLT probability estimates are updated for each combination. If there is a tie between the likelihood values of two or more models, then the selected model is randomly chosen from among those with tied likelihood values.
Table 2.
Working models/skeletons of DLT probabilities
| Zone | 1 | 2 |
3 | |
|---|---|---|---|---|
| Working model | A | B | C | D |
| 1 | ||||
| 2 | ||||
Figure 1.
Illustration of the working models for toxicity under various values of the parameter to be estimated.
The working models for dRsp probabilities are formulated under two different assumptions: (1) the probabilities are increasing with increasing zone, or (2) the probabilities increase initially and then plateau after a certain zone, as displayed in Table 3. Like toxicity, these possible shapes for the regimen–immune response curve are expressed through multiple skeletons of CRM models. We again rely on a class of one-parameter power models, indexed by , and the algorithm of Lee and Cheung [16] to formulate working models for the dRsp probabilities. Using the accumulated immune response data, the CRM is fit for each dRsp probability working model, and the parameter is estimated for each model by maximum likelihood estimation. Again, the working model with the largest likelihood is chosen and, using the selected model, dRsp probability estimates are updated for each regimen. We make allocation decisions based on the probability estimates for both DLT and dRsp.
Table 3.
Working models/skeletons of dRsp probabilities
| Regimens |
||||
|---|---|---|---|---|
| Working model | A | B | C | D |
| Under the assumption of increasing dRsp probability across zones | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| Under the assumption of plateau dRsp probability across zones | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
For regimens B–D, a two-sided 80% confidence interval is calculated using the estimated DLT probability for that regimen, based on confidence interval estimation for CRM models [17]. If the lower bound of this confidence interval exceeds the maximum toxicity tolerance of 25%, then this regimen is deemed too toxic and excluded from the acceptable set of combinations. If regimen A is excluded from the acceptable set, then no regimen is considered acceptable and the trial is stopped for safety. Therefore, for regimen A the level of confidence is set at 90% instead of 80%.
Once the set of acceptable combinations is determined, the recommended combination will be based upon how many participants have been entered into the study to that point. For the first third of the trial (i.e. one-third the maximum sample size), the combination recommendation is based on randomization using a weighted allocation scheme. Randomization prevents the design from getting ‘stuck’ at a sub-optimal regimen based on limited data [18]. The recommended combination for the next entered participant is chosen at random from the ‘acceptable’ combinations, with each acceptable combination weighted by its estimated dRsp probability. That is, acceptable combinations with higher estimated dRsp probabilities have a higher chance of being randomly chosen as the next recommended combination. For the latter third of the trial (i.e. final two-third of maximum sample size), the recommended combination for the next entered participant is defined as the ‘acceptable’ combination with the highest estimated dRsp probability.
Stopping the trial
Accrual to the study will be halted and trigger a safety review by the study investigators and the Data and Safety Monitoring Committee to determine whether the study should be modified, or permanently closed to further accrual according to the following: (i) accrual would have been halted for safety if the first two entered participants in Zone 1 experience a DLT, (ii) if at any point in the study, no regimens are considered acceptable in terms of safety, the trial will stop, (iii) otherwise, accrual to the study will end if the recommendation is to assign the next participant to a combination that already has 30 participants treated at that combination.
Sample size and accrual
Target sample size for the optimal combination is based upon acquiring sufficient information to assess the objective of estimating dRsp rates, assuming at least one optimal combination has been found. Based upon results from the Mel 44 clinical trial [11], 30 eligible participants treated at the optimal combination will provide adequate data to assess dRsp. The target of 30 participants was chosen based on having sufficient information to determine whether the optimal regimen shows an increase dRsp rate compared with the baseline rate observed in the 6MHP regimens of Mel 44 of 18% (90% CI [11, 26%]). If at least 13/30 (43%; 90% C.I. (28, 60%)] participants on the optimal regimen experience a dRsp the results will be considered promising since the lower limit of the confidence interval exceeds the upper limit from the Mel 44 estimated rate. Total study sample size is estimated from the simulations (Appendix), and is determined by the stopping rules in the section above. We set the maximum total sample size to 70 eligible participants; however, as indicated in the simulation results the maximum average trial size over all scenarios is 52 participants.
Results
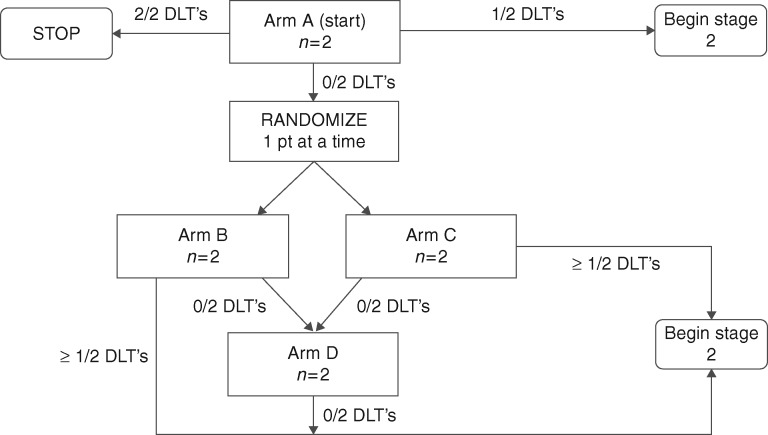
Accrual to regimens occurs in two stages, as illustrated in the schema of Figure 2. The initial stage accrued eligible participants in cohorts of two on each regimen, until a participant experienced a DLT. The second stage is allocating eligible participants in cohorts of one according to the above estimation procedure.
Figure 2.
Schema illustrating the two stages of the design.
Allocation in completed stage 1
The escalation plan for the first stage was based on the zones. With this design participants could be accrued and assigned to other open regimens within a zone but escalation would not occur outside the zone until the minimum follow-up period was observed for the first participant accrued to a regimen. The minimum follow-up period for escalation between Zones was 3 weeks after the initial vaccine. Initial allocation within a zone was based upon random allocation (1:1) between the possible regimens. Escalation to a higher zone occurred only when all regimens in the lower zone had been tried, and no DLT had been observed. Participant allocation to subsequent regimens within the new zone followed the same accrual strategy. This allocation strategy was followed for accrual to increasing zones until a participant experienced a DLT or a stopping rule was triggered. The seventh participant accrued to the study experienced the first DLT on regimen D, at which time the second stage using multidimensional CRM modeling began. The 8th participant had already been accrued to regimen D in stage 1 when the DLT occurred.
Allocation in ongoing stage 2
Stage 2 is allocating eligible participants based upon the multidimensional CRM modeling approach described above. Model-based estimation of DLT probabilities began for the accrual of the ninth participant to the study. After each new accrual in stage 2, the estimated DLT probabilities are being updated and used to define a set of ‘acceptable’ combinations in terms of safety. If the minimum follow-up period is not satisfied at the time a new participant is ready to be put on-study, then the participant may be accrued to any regimen, by random allocation, which has accrued at least one participant and is in the acceptable set.
Model-based estimation of dRsp probabilities began at the beginning of stage 2, since a dRsp was observed in stage 1 (participant 5). After each participant, a new recommended combination is obtained, and the next entered participant is allocated to the recommended combination. The trial will stop once sufficient information about the optimal regimen range has been obtained, according to the stopping rules. Currently, the trial has accrued 30 participants, with model-based allocation (stage 2) having been utilized after the first 8 participants, as illustrated in Table 4. Allocation based on weighted randomization occurred for the first 15 participants in stage 2, which is approximately one-third the maximum sample size, minus the stage 1 participants [i.e. (70/3) – 8].
Table 4.
Summary data (by stage and combined current total) of partially completed Mel 63 trial
| Stage | Total | Regimen | Toxicity | Immune response |
|---|---|---|---|---|
| Accrual (n) | # of DLT/# treated | # of dRsp/# treated | ||
| 1 | 2 | A | 0/2 | 0/2 |
| 1 | 2 | B | 0/2 | 1/2 |
| 1 | 2 | C | 0/2 | 0/2 |
| 1 | 2 | D | 1/2 | 2/2 |
| 2 | 1 | A | 0/1 | 0/1 |
| 2 | 5 | B | 1/5 | 1/5 |
| 2 | 4 | C | 0/4 | 4/4 |
| 2 | 12 | D | 0/12 | 10/12 |
| 1 + 2 | 3 | A | 0 (0%) | 0 (0%) |
| 1 + 2 | 7 | B | 1 (14%) | 2 (29%) |
| 1 + 2 | 6 | C | 0 (0%) | 4 (67%) |
| 1 + 2 | 14 | D | 1 (7%) | 12 (86%) |
Conclusions
The development of novel methods in early-phase dose-finding has been rapid in the last decade, yet, the use of innovative designs remains infrequent. In this article, we have outlined a novel early-phase adaptive design, implemented in an ongoing trial of four treatment combinations for participants with high-risk melanoma. In this study, all doses of each adjuvant are fixed, and it is the regimens that vary by number of adjuvants. The design could be used in trials where dose is varied, however, that was not done in this trial because we wanted to focus on the high-priority challenge in combination immunotherapy where there are a growing number of active agents with defined doses that may be useful in combination. Arguably, for cancer vaccines in particular, the choice of adjuvant is a way to modify the effective ‘dose’ of the vaccine by increasing the immune response. The method presented serves as an alternative to the 3 + 3 design for cancer vaccine trials, which are being called for by the FDA and by others [3, 5]. Simulation studies were carried out to evaluate the performance of the design characteristics and are reported in the Appendix. The simulation results in supplementary Table S1, available at Annals of Oncology online demonstrate the method's ability to effectively recommend the OTC, defined by acceptable toxicity and high immune response rates, in a high percentage of trials with manageable sample sizes. Software in the form of R [19] code for both simulation and implementation of the method is available upon request of the first author. The method we outline in this work can be viewed as an extension of the CRM, utilizing multiple skeletons for DLT and dRsp probabilities, increasing the ability of CRM designs to handle more complex dose-finding problems. The numerical results presented in the Appendix include the type of simulation information that aid review entities in understanding design performance, such as average sample size, frequency of early trial termination, etc., which we hope will augment early-phase trial design in cancer immunotherapy. This design can be applied more broadly in early-phase combination studies [20], as it was used in an ongoing study of two small molecule inhibitors in relapsed/refractory mantle cell lymphoma (NCT02419560).
Funding
This work was supported by the National Cancer Institute (K25CA181638 to NAW, R01CA142859 to GRP, and R01CA178846 to GRP and CLS); and the Biostatistics Shared Resource, University of Virginia Cancer Center, University of Virginia (P30 CA044579).
Disclosure
CLS is an inventor on patents of peptides for use in clinical trials of cancer vaccines; these patents are held by the University of Virginia Licensing and Ventures Group. He also serves, and the University receives funding for his roles, as external advisory board member for Immatics, Inc., and as PI for a clinical trial of a cell-based vaccine sponsored by Polynoma. He also receives support for investigator-sponsored cancer immunotherapy clinical trials from GlaxoSmithKline and Merck. All remaining authors have declared no conflicts of interest.
Supplementary Material
References
- 1. Paoletti X, Ezzalfani M, Le Tourneau C.. Statistical controversies in clinical research: requiem for the 3 + 3 design for phase I trials. Ann Oncol 2015; 26: 1808–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Iasonos A, O’Quigley J.. Adaptive dose-finding studies: a review of model-guided phase I clinical trials. J Clin Oncol 2014; 32: 2505–2511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Rahma OE, Gammoh E, Simon R. et al. Is the “3 + 3” dose-escalation phase I clinical trial design suitable for therapeutic cancer vaccine development? A recommendation for alternative design. Clin Cancer Res 2014; 20: 4758–4767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Nie L, Rubin EH, Mehrotra N. et al. Rendering the 3 + 3 design to rest: more efficient approaches to oncology dose-finding trials in the era of targeted therapy. Clin Cancer Res 2016; 22: 2623–2629. [DOI] [PubMed] [Google Scholar]
- 5. FDA USDoHaHS, Administration FaD, Research CfBEa. Guidance for industry clinical considerations for therapeutic cancer vaccines 2011; [cited 2011 October 2011]. http://www.fda.gov/downloads/Biologics Blood Vaccines/GuidanceComplianceRegulatoryInformation/Guidances/Vaccines/UCM278673.pdf (31 December 2016, date last accessed).
- 6. Wages NA, Conaway MR.. Phase I/II adaptive design for drug combination oncology trials. Stat Med 2014; 33: 1990–2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Wages NA, Slingluff CL Jr, Petroni GR.. A phase I/II adaptive design to determine the optimal treatment arm from a set of combination immunotherapies in high-risk melanoma. Contemp Clin Trials 2015; 41: 172–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Iasonos A, Gönen M, Bosl GJ.. Scientific review of Phase I protocols with novel dose-escalation designs: how much information is needed? J Clin Oncol 2015; 33: 2221–2225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Petroni GR, Wages NA, Paux G, Dubois F.. Implementation of adaptive methods in early-phase clinical trials. Stat Med 2016. doi: 10.1002/sim.6910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Slingluff CL Jr, Petroni GR, Olson W. et al. Helper T-cell responses and clinical activity of a melanoma vaccine with multiple peptides from MAGE and melanocytic differentiation antigens. J Clin Oncol 2008; 26: 4973–4980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Slingluff CL Jr, Petroni GR, Chianese-Bullock KA. et al. A randomized multicenter trial of the effects of melanoma-associated helper peptides and cyclophosphamide on the immunogenicity of a multipeptide melanoma vaccine. J Clin Oncol 2011; 29: 2924–2932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Slingluff CL Jr, Petroni GR, Olson W. et al. A randomized pilot trial testing the safety and immunologic effects of MAGE-A3 protein plus AS15 immunostimulant administered into muscle or into dermal/subcutaneous sites. Cancer Immunol Immunother 2016; 65: 25–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Slingluff CL Jr, Petroni GR, Chianese-Bullock KA. et al. Immunologic and clinical outcomes of a randomized phase II trial of two multipeptide vaccines for melanoma in the adjuvant setting. Clin Cancer Res 2007; 13: 6386–6395. [DOI] [PubMed] [Google Scholar]
- 14. O’Quigley J, Pepe M, Fisher L.. Continual reassessment method: a practical design for phase I clinical trials in cancer. Biometrics 1990; 46: 33–48. [PubMed] [Google Scholar]
- 15. Paoletti X, Kramar A.. A comparison of model choices for the continual reassessment method in phase I clinical trials. Statist Med 2009; 28: 3012–3028. [DOI] [PubMed] [Google Scholar]
- 16. Lee SM, Cheung YK.. Model calibration in the continual reassessment method. Clin Trials 2009; 6: 227–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Natarajan L, O’Quigley J.. Interval estimates of the probability of toxicity at the maximum tolerated dose for small samples. Statist Med 2003; 22: 1829–1836. [DOI] [PubMed] [Google Scholar]
- 18. Thall PF, Nguyen HQ.. Adaptive randomization to improve utility-based dose-finding with bivariate ordinal outcomes. J Biopharm Stat 2012; 22: 785–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2016; https://www.R-project.org/. [Google Scholar]
- 20. Wages NA, Conaway MR, Slingluff CL Jr. et al. Recent developments in the implementation of novel designs for early-phase combination studies. Ann Oncol 2015; 26: 1036–1037. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.