Statistical controversies in clinical research: building the bridge to phase II—efficacy estimation in dose-expansion cohorts

Abstract

Background

Regulatory agencies and others have expressed concern about the uncritical use of dose expansion cohorts (DECs) in phase I oncology trials. Nonetheless, by several metrics—prevalence, size, and number—their popularity is increasing. Although early efficacy estimation in defined populations is a common primary endpoint of DECs, the types of designs best equipped to identify efficacy signals have not been established.

Methods

We conducted a simulation study of six phase I design templates with multiple DECs: three dose-assignment/adjustment mechanisms multiplied by two analytic approaches for estimating efficacy after the trial is complete. We also investigated the effect of sample size and interim futility analysis on trial performance. Identifying populations in which the treatment is efficacious (true positives) and weeding out inefficacious treatment/populations (true negatives) are competing goals in these trials. Thus, we estimated true and false positive rates for each design.

Results

Adaptively updating the MTD during the DEC improved true positive rates by 8–43% compared with fixing the dose during the DEC phase while maintaining false positive rates. Inclusion of an interim futility analysis decreased the number of patients treated under inefficacious DECs without hurting performance.

Conclusion

A substantial gain in efficiency is obtainable using a design template that statistically models toxicity and efficacy against dose level during expansion. Design choices for dose expansion should be motivated by and based upon expected performance. Similar to the common practice in single-arm phase II trials, cohort sample sizes should be justified with respect to their primary aim and include interim analyses to allow for early stopping.

Introduction

In phase I oncology trials, a dose expansion cohort (DEC) enrolls additional patients after the maximum tolerated dose (MTD) is estimated [1–4]. These cohorts may be stratified by genetic aberration or disease site, providing additional information on the effectiveness and safety of a targeted therapy in specific subpopulations and thus answering questions traditionally left to single-arm phase II trials. For this reason, dose expansion has increasingly become the norm [1, 2], outpacing the development of foundational design principles for such trials [4, 5] and prompting concern from the FDA about a lack of rigor in the design of such studies [6, 7]. The present article seeks to bridge this disconnect.

Expansion cohorts are often large, with sample sizes exceeding those of phase II trials [2, 3, 8]. Mullard writes of ‘investigational new drug applications…designed to enroll up to 1000 patients’ [8], including several anti-PD-1 agents [9, 10]. The FDA granted accelerated approval to ceritinib for the treatment of ALK-rearranged non-small-cell lung cancer on the basis of promising efficacy data from a 163-patient cohort [11, 12]. Although large sample sizes in DEC trials are motivated by efficacy as a primary study endpoint, they are seldom formally justified [13]. Dose expansion trials are also complicated [14], sometimes ‘encompass[ing] an entire drug development program in a single trial’ [7]. The clinical trial of the anti-PD-1 agent nivolumab ultimately enrolled cohorts at multiple dose levels, based upon multiple protocol amendments [9, 14].

Subsequent to efficacy, trials with expansion should consider patient safety [6]. Because the selected MTD from dose escalation is based on a small number of patients, it may turn out not to have been a good choice for use in the much larger dose expansion. Paoletti et al. [15] note that a ‘seamless transition [from escalation to expansion] with continuous monitoring of the risk of DLT’ is the more natural application of dose expansion. Iasonos and O’Quigley [3] report several trials in which the recommended phase II dose differed from the MTD. Therefore, it is important to monitor toxicity during expansion and adjust the dose accordingly [4]. In our experience, most protocols describe how an individual patient’s dosing will be held or reduced in the presence of toxicity, but few include plans for monitoring the overall toxicity rate during expansion or adjusting the MTD. Several innovative designs base dose-finding on both toxicity and efficacy [16–21]. While promising, these require an efficacy outcome that can be observed quickly enough to inform dosing for future patients and are not designed for trials with multiple patient cohorts. Seamless phase I/II designs define expansion cohorts based on multiple dose levels rather than patient subpopulations [22].

There is a critical need for efficient designs and metrics upon which to base expansion cohort sample sizes that protect patients and are equipped to identify efficacious anti-cancer therapies [6, 7]. These goals overlap significantly with phase II objectives. The goal of this article is to (i) assess common designs for dose expansion and (ii) recommend sensible design templates and principles for trials with dose expansion.

Methods

The typical conduct of a phase I trial with dose expansion is to enroll a group(s) of patients at the estimated MTD from ‘3 + 3’ dose escalation. In the context of a single DEC looking exclusively at toxicity, we have previously argued for keeping open the dose-escalation mechanism during dose expansion [4]. The point of departure from that work is a specific focus on trials having multiple and/or large cohorts in which efficacy is of primary interest, two examples being the ceritinib and nivolumab studies previously mentioned [9, 11, 12]. The prevalence of such trials is increasing and likely to continue to do so [7, 8]. We address the following critical questions recently posed by regulatory agencies and others [6–8], namely (i) How should unexpectedly high (or low) toxicity in one cohort impact the dose assignment in another?; (ii) What is the appropriate number of patients to enroll in each cohort?; (iii) At what point should a cohort be closed for apparent futility? To do so, we emulate design templates, which we define as a toxicity-based dose-assignment mechanism plus an analytic approach for estimating efficacy, that we see or would like to see in practice, testing them against a variety of dose-toxicity-efficacy scenarios. Our aim was to determine what designs increase the likelihood of making the best decision in each cohort.

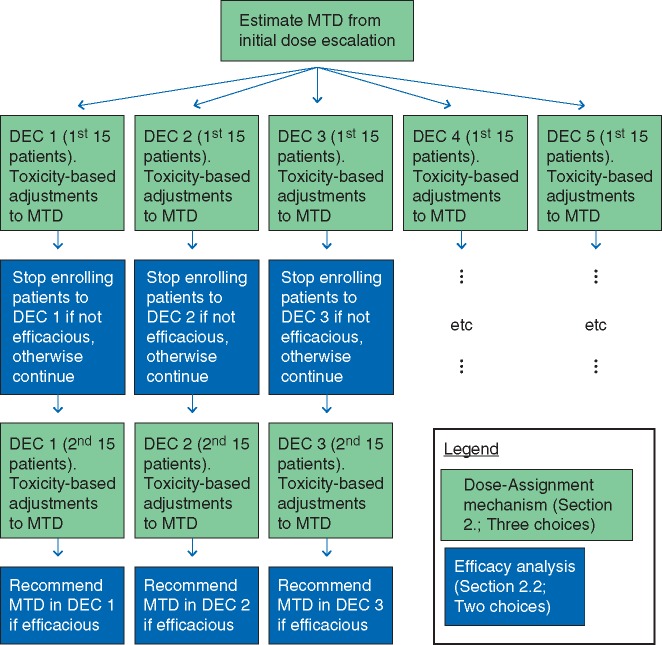
We simulated the kinds of trials we most often see in practice: dose escalation is based upon toxicity, but the recommendation for pursuing further study of the treatment in a particular cohort is based on efficacy. We first describe three mechanisms for toxicity-based dose assignments during dose escalation and during expansion. We then describe two analyses for using the efficacy data in each cohort to inform a futility analysis and make separate recommendations as to whether to pursue study of the treatment in a future trial of that subpopulation. One analysis uses more information within the DEC than the other by modeling the underlying dose-efficacy curve. Each of the six combinations of dose-assignment mechanism and analysis represents a ‘design template’, a description of the trial’s general conduct without any specific contextual details (e.g. number of doses, number of cohorts, sample size). We tested these templates against a total of 10 such dose-toxicity-efficacy scenarios. One simulated trial consisted of dose escalation followed by expansion to K ≥ 1 cohorts, opened simultaneously, each starting at the estimated MTD as determined by dose-escalation. A flowchart of an exemplar trial with K = 5, 30-patient cohorts, with futility analyses, is given in Figure 1. For illustration, we limited each cohort to just two possible sample sizes The estimated MTD may be revised up or down during expansion, as more data are collected, resulting in fewer than 30 patients at the final estimate, but we did not extend enrollment in any cohort beyond 30 patients. In actual trials, specific choices of samples size should be justified using, for example, the metrics for evaluating performance that are discussed in this article. We averaged these metrics across 2500 simulated trials, so as to precisely estimate these metrics. Complete details of our full approach are in supplementary data S1, available at Annals of Oncology online. The study was done in the R statistical environment [23–25], and code is available at http://www.umich.edu/∼philb.

Figure 1.

Flowchart for the 30-patient, five-DEC design with futility analysis used in the simulation study. There are three choices of dose-assignment mechanism (the light box, green online) and two choices of efficacy analysis (the dark box, blue online). Every box represents a decision to continue enrolling patients or stop enrolling patients due to toxicity (the light boxes) or futility (the dark boxes), and so, after initial dose escalation is complete, recommendations can be made separately for each DEC.

Dose-assignment mechanisms

We evaluated three mechanisms for making dose assignments in response to toxicity during escalation and/or expansion. Supplementary data S2, available at Annals of Oncology online, provides comprehensive details.

Local

Dose-escalation is according to the 3 + 3 [26], at which point K cohorts open at the estimated MTD. An extension of the 3 + 3 philosophy monitors for toxicity in each cohort: beginning with the 4th patient receiving the current assigned dose level, if the proportion of patients in that cohort at that dose level with toxicity exceeds 1/3, the dose level is reduced by one. If already at the lowest dose level, patient enrollment is stopped within that cohort only. Multiple dose de-escalations during the cohort are possible but escalation is not.

Global

This also begins with the 3 + 3 and de-escalates during dose-expansion if a toxicity threshold is crossed. In contrast to Local, this monitoring is conducted and acted upon globally over all cohorts. The Global threshold is constructed such that, when the true rate of toxicity is 0.25 (which lies between the 3 + 3 critical thresholds of 1/6 and 2/6), the cumulative probability of one incorrect de-escalation over all 75 or 150 patients is ∼0.05 [27]. Any de-escalation applies to all cohorts. As with Local, Global allows for multiple dose de-escalations but no dose escalation.

Continual reassessment method

This is a modification of the continual reassessment method (CRM) [28], a statistical model wherein each subject is assigned the dose level that is estimated to have a rate of toxicity closest to 0.25. Thus, the dose assignment changes up or down over time as more subjects enroll and toxicity data are collected. As in Global, all patients at a given dose level are assumed to have the same probability of toxicity. From a toxicity perspective, therefore, there is little distinction between escalation and expansion: the same mechanism assigns dose levels for the entire trial and across all DECs. The model runs until a planned sample size is enrolled, in our case the average sample size that a 3 + 3 trial would enroll plus 75 or 150, so as to match the Local and Global sample sizes [29]. To monitor toxicity, if the estimated rate of toxicity at the lowest dose level ever exceeds 0.30, the target rate of 0.25 plus a margin of 0.05, enrollment in all cohorts stops. All other settings are as in Boonstra et al. [4], including over-riding modifications to preserve patient safety [30, 31].

In all cases, the final estimated MTD is the dose level that would be assigned to the next patient following completion of that cohort. If a cohort is stopped early due to excessive toxicity, there is no MTD. For Local, the estimated MTD may differ between cohorts, but for Global and CRM, it is the same across cohorts.

Efficacy analysis

At an interim futility analysis and the end of the trial, the response rate at the estimated MTD is estimated separately for each DEC. These estimates are the basis for deciding whether the treatment merits further study in each subpopulation. We considered two options. Supplementary data S3, available at Annals of Oncology online, provides details.

Empiric

When an estimated response rate is required, it is calculated based upon those patients at the current estimated MTD. Two-stage phase II designs compare the observed, or empiric, number of responses to a required minimum number of responses [32, 33]. This approach may not be applicable in our context: the overall DEC sample size is fixed in advance and toxicity-based dose modifications may occur, meaning that the number of patients treated at the estimated MTD is unknown in advance and may be less than nominal. For all possible sample sizes, we calculate the corresponding smallest number of responders that would yield sufficient evidence, via a confidence interval compared with the null efficacy rate, to warrant further study. These are in supplementary Table S1 (supplementary data S3, available at Annals of Oncology online). At the interim analysis, enrollment is stopped for futility in any DEC in which this minimum number of responses is observed. Similarly, no further study is recommended following completion of DECs with fewer than the specified number of responses.

Model

This approach uses data from all patients in the DEC, rather than only those treated at the current estimated MTD, increasing the precision of estimated response rates. It does so using a Bayesian logistic regression, with dose level coded as an integer (1, …, 5). From this fitted model, we estimated the response rate at the final estimated MTD and constructed confidence intervals for this response rate. As with the Empiric analysis, the recommendation is based on these intervals.

Alternatively, to ensure a minimum number of patients at the final estimated MTD, one could amend the protocol after dose modification in the cohort. A reviewer noted that randomization within a DEC is ideal. We elected not to include a randomized control arm, instead viewing these efficacy analyses as phase IIA trials: not intended to be definitive but rather to triage inefficacious treatments.

Dose-toxicity-efficacy scenarios

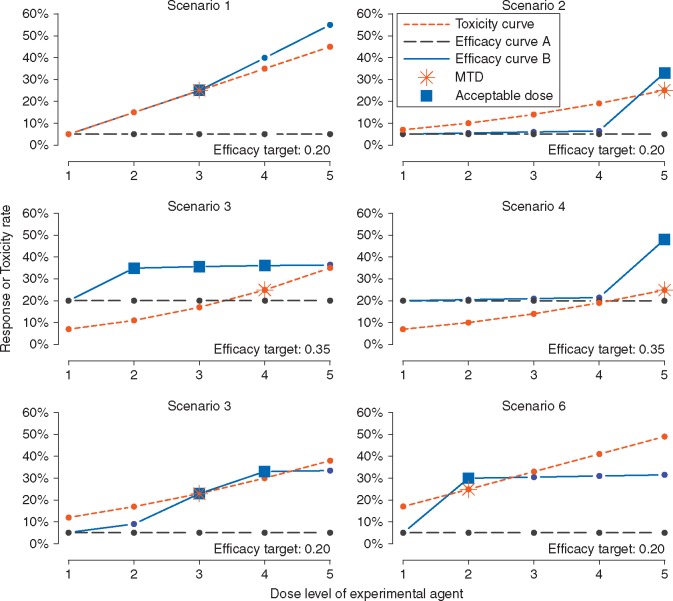
For each of the six combinations of dose-assignment mechanism and efficacy analysis, we examined 10 dose-toxicity-efficacy scenarios, as presented in Figure 2 (scenarios 1–6) and supplementary Figure S5, available at Annals of Oncology online (scenarios 7–10). Each scenario consisted of a toxicity curve common to all patients and two different efficacy curves (labeled A and B). Efficacy within a cohort was characterized by one of these two curves, reflecting that a therapy is not expected to be equally efficacious in all subpopulations. Toxicity and efficacy outcomes were recorded as ‘yes’ or ‘no’. The true MTD is the dose level with a rate of toxicity closest to 0.25 but not exceeding 0.30, indicated by a star in Figure 2. Efficacy curve A is flat at either a constant 0.05 response rate (i.e. for single agent trials or when there is no effective standard therapy) or a constant 0.20 response rate (i.e. when there is a backbone treatment with some activity). The goal was to find a tolerable dose that improves upon this null response rate by at least 0.15: to 0.05 + 0.15 = 0.20 or 0.20 + 0.15 = 0.35, respectively. At least one such dose always exists in efficacy curve B, indicated with a box in Figure 2. In each trial, we opened K = 5 cohorts: three of the five followed the flat efficacy curve A, the ‘inefficacious DECs’, and two followed curve B, the ‘efficacious DECs’. Thus, the ideal outcome for the whole trial was to recommend no further study in the three inefficacious DECs and recommend a good dose level for further study in the two efficacious DECs. In a real trial, the number of cohorts will be motivated by contextual details that are not germane to our study.

Figure 2.

Six toxicity-efficacy scenarios. The desired targeted response, or efficacy, rate is in the lower-right of each panel. After dose-escalation, five DECs are simulated according to a common toxicity curve (short dashed). The MTD is indicated with a star. For three DECs, the targeted response rate is not achievable (long dashed; efficacy curve A); for two, it is achievable (solid; efficacy curve B). Acceptable dose levels in efficacy curve B, i.e. those with efficacy greater than the stated target and DLT rate no greater than 0.30, are boxed.

Two sample sizes per cohorts, 15 or 30, yield 75 or 150 patients across all five cohorts in one trial. In 30-patient cohorts, we implemented an interim futility analysis after patient 15, described below. For comparison, we also simulated 30-patient cohorts without an interim analysis. Interim analyses are not feasible in a 15-patient cohort due to variability in response rates.

Evaluation

In typical clinical practice, a treatment at a particular dose level is recommended if it is found to be safe and efficacious. For each cohort in each simulated trial, we recorded the recommended dose level, or that no dose was recommended and why, and the estimated response rate at the final estimated MTD. We also recorded the average number of patients enrolled in a cohort, which may be less than 15 or 30 due to stopping for toxicity or futility. We calculated the following two performance metrics.

True positive rate

For a given dose-assignment/analysis/sample size, the true positive rate (TPR) is the proportion of 5000 simulated efficacious cohorts (2500 trials × two efficacious cohorts per trial) in which any dose level is recommended for further study. TPR is similar to statistical power, although TPR includes recommending a dose level that is lower or higher than the true MTD, on the assumption that later-phase study will hone this finding.

False positive rate

The false positive rate (FPR) is the proportion of 7500 inefficacious cohorts (2500 trials × three inefficacious cohorts per trial) in which any dose level is recommended for further study. FPR is similar to type I error. The ideal design has TPR = 1 and FPR = 0.

TPR only captures whether any dose level is recommended. However, it is most preferable to recommend one of the ‘boxed’ dose levels in Figure 2. For this reason, we report more granular results for the efficacious DECs. The possible outcomes are the following: (i) no recommendation due to excess toxicity; (ii) no recommendation due to futility; (iii) recommending a sub-therapeutic dose; (iv) recommending a ‘boxed’ or acceptable dose; or (v) recommending a toxic dose. In the scenarios, we considered, there is a partial ordering of preference for these outcomes. Least preferred is (i), because there is always a tolerable dose level(s), followed by (ii). Next are (iii) and (v), since a dose was recommended but not the correct one. Finally, (iv) is ideal, corresponding to identifying an acceptable dose level. The sum of (iii), (iv) and (v) is equal to TPR, being the probability of recommending any dose level, and the sum of (i) and (ii) is equal to 1 − TPR.

Results

Comparison between dose-assignment mechanisms

Table 1 presents TPR and FPR under each scenario. In all cases, CRM has a greater TPR than either Global or Local. In terms of TPR, CRM exceeds Local by 1–27% under 15-patient cohorts and 8–45% under 30-patient cohorts with an interim analysis. FPR is comparable between mechanisms, with most differences <10%. While none of the mechanisms is uniformly preferred in terms of FPR, Local usually has the lowest FPR by a small margin.

Table 1.

True and false positive rates (TPR, FPR) for the six scenarios of toxicity/efficacy curves in Figure 2 under 18 combinations of dose-assignment mechanism, efficacy analysis, and 15-patient DECs, 30-patient DECs with no futility analysis, or 30-patient DECs with a futility analysis

	TPR						FPR
	CRM	Global	Local	CRM	Global	Local	CRM	Global	Local	CRM	Global	Local
# in DEC=15
	Set 1			Set 2			Set 1			Set 2
Model	98	87	81	87	72	69	53	53	50	53	54	53
Empiric	90	86	74	77	72	61	41	52	46	43	53	49
	Set 3			Set 4			Set 3			Set 4
Model	97	95	91	93	88	80	74	80	71	80	81	73
Empiric	94	96	93	90	89	84	76	83	79	77	83	79
	Set 5			Set 6			Set 5			Set 6
Model	93	79	73	86	72	61	51	52	48	48	45	37
Empiric	85	78	65	78	71	51	39	51	44	39	44	34
# in DEC=30 (no futility analysis at 15)
	Set 1			Set 2			Set 1			Set 2
Model	96	76	63	78	46	34	14	17	14	20	19	15
Empiric	94	76	64	77	46	35	18	19	18	18	19	18
	Set 3			Set 4			Set 3			Set 4
Model	81	75	69	75	45	31	21	19	16	25	20	17
Empiric	78	79	75	73	48	36	21	24	23	21	24	23
	Set 5			Set 6			Set 5			Set 6
Model	89	62	47	76	58	35	15	17	13	12	15	9
Empiric	87	62	49	76	58	35	17	18	17	17	17	12
# in DEC=30 (with futility analysis at 15)
	Set 1			Set 2			Set 1			Set 2
Model	93	75	58	72	44	31	13	16	12	16	17	13
Empiric	85	74	53	64	44	26	12	16	13	13	17	13
	Set 3			Set 4			Set 3			Set 4
Model	83	75	64	73	45	30	20	18	15	25	19	16
Empiric	76	79	68	69	49	32	19	23	20	20	23	20
	Set 5			Set 6			Set 5			Set 6
Model	87	62	43	75	59	37	13	16	12	11	14	9
Empiric	79	62	39	70	58	31	12	16	13	12	14	9

TPR (left-hand columns) is the probability that a dose was recommended in an efficacious DEC, i.e. a DEC having at least one dose level with sufficiently large response rate. FPR (right-hand columns) is the probability that a dose was recommended in an inefficacious DEC, i.e. a DEC having no dose levels with sufficiently large response rate.

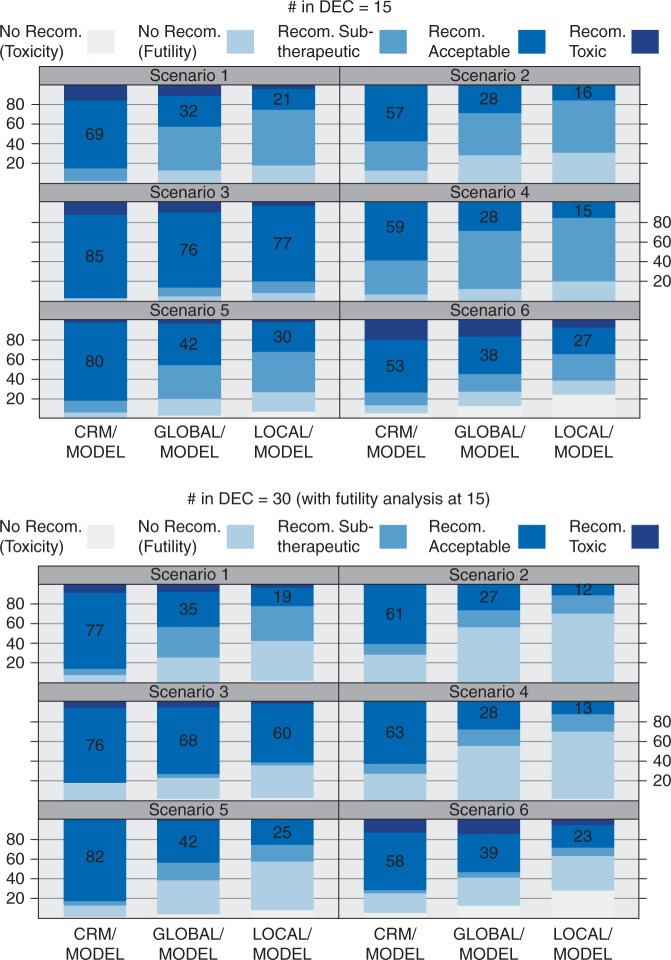
Figure 3 breaks down the frequency of outcomes for the efficacious cohorts of size 15 (top) and 30 (bottom) for the Model-based analyses; the Empiric analyses are in supplementary Figure S1 (supplementary data S4, available at Annals of Oncology online). Because Figure 3 only considers efficacious cohorts, there is always a dose level(s) with an acceptable toxicity/efficacy profile. Recommending an acceptable dose level is ideal, and the proportion of simulations in which this occurs is annotated. This proportion is lowest for Local and highest for CRM. By monitoring for toxicity both within and across cohorts, Global and CRM correctly leverage the common toxicity curve.

Figure 3.

Breakdown of simulation-based frequencies of five possible outcomes in an efficacious DEC for the six scenarios of toxicity/efficacy curves in Figure 2 under each dose-assignment mechanism and for 15-patient DECs (top plot) and 30-patient DECs with a futility analysis (bottom). Only the Model-based efficacy analyses are given; the Empiric efficacy analyses are in supplementary figure S1 (supplementary data S4, available at Annals of Oncology online). The ideal outcome is to recommend an acceptable, i.e. tolerable and efficacious, dose level; the proportion of simulated DECs recommending such a dose level is annotated.

Another factor in CRM’s performance advantage is that, in addition to de-escalating dose levels, it can escalate the dose at any point in the trial, including during dose expansion.

Comparison between efficacy analyses

By definition, each dose-assignment mechanism makes toxicity-based adjustments during expansion, so that multiple dose levels may be assigned. Thus, Model-based estimation of the response rate, which ‘shares’ information across dose levels within a cohort, allows for more precise estimates of response rates. For patient cohorts, the Empiric analysis is more conservative, having smaller TPR/FPRs. With 30 patients, the Model-based analysis tends to have a larger TPR with a proportionally smaller increase in FPR, at least in the case of the CRM. The true efficacy curves are described in Figure 2; none of these follows a logistic curve, which the Model-based analysis assumes. Thus, this performance gain is not based upon an unrealistic modeling assumption.

Interim futility analysis

An interim futility analysis after 15 patients decreases average enrollment by ∼6 patients per inefficacious DEC and 2 patients per efficacious DEC (Table 2). The decrease in average enrollment to efficacious DECs is smallest for CRM. The addition of an interim analysis to the 30-patient cohort reduces the TPR and FPR by ∼2% each.

Table 2.

Average decrease in number of patients enrolled per 30-patient DEC as a result of the interim futility analysis for the six scenarios of toxicity/efficacy curves in Figure 2 under each dose-assignment and efficacy analysis, stratified by the efficacious DECs (left) and inefficacious DECs (right)

	Efficacious DECs						Inefficacious DECs
	CRM	Global	Local	CRM	Global	Local	CRM	Global	Local	CRM	Global	Local
	Set 1			Set 2			Set 1			Set 2
Model	0.4	1.9	2.4	2.0	4.4	4.8	7.0	6.9	7.4	6.9	6.9	7.2
Empiric	1.5	2.0	3.5	3.6	4.5	6.0	8.8	7.0	8.0	8.6	7.0	7.7
	Set 3			Set 4			Set 3			Set 4
Model	0.4	0.5	0.9	1.0	1.8	2.9	3.7	2.9	4.2	2.9	2.7	4.1
Empiric	0.9	0.4	0.8	1.4	1.6	2.4	3.8	2.5	3.1	3.4	2.4	3.1
	Set 5			Set 6			Set 5			Set 6
Model	0.8	2.6	3.2	1.2	2.6	2.4	7.1	6.9	7.0	7.1	6.9	6.2
Empiric	2.1	2.7	4.3	2.3	2.8	3.8	9.0	7.1	7.6	8.4	7.1	6.6

Size of expansion cohort

At this early stage of research, sensible designs must ensure a large TPR, necessarily resulting in a large FPR for 15-patient cohorts. Increasing to a maximum of 30 patients reduces the FPR considerably, while also slightly reducing TPR. For example, in scenario 1, the CRM/Model design has TPR/FPR equal to 98/53 under a 15-patient cohort versus 93/13 under a 30-patient cohort (Table 1).

Additional scenarios

Supplementary Figures S2–S4 and Tables S2–S3 (supplementary data S5, available at Annals of Oncology online) present results for four additional scenarios, including flat toxicity and/or efficacy curves. Scenarios 8 and 10 have low toxicity across all dose levels and are thus less challenging. All designs do well in this case. In scenario 7, the toxicity rate is also flat but larger and closer to the target. In this case, CRM outperforms Global and Local, with TPRs ∼20% larger.

Discussion

We have quantified how expansion cohort design templates—some common, some not—operate in realistic phase I/II settings, where the term ‘design template’ refers to a choice of dose-assignment mechanism coupled with an analytic approach to estimating efficacy. Put succinctly, the use of statistical modeling techniques during dose expansion to analyse the substantial amount of patient data increases the likelihood of making the most appropriate decision within each cohort. We are making a similar argument statisticians and clinical trialists have been making for nearly 30 years (with little success) [34], since the development of the CRM design [28]. However, the order of magnitude increase in numbers of patients enrolled to modern dose-expansion trials increases the ethical stakes by that much. Broken down into greater detail, our findings and recommendations directly correspond to three statistical questions that Prowell et al. [7] recently posed to guide development of protocols employing dose expansion.

Is the sample-size range consistent with the stated objectives and end points? [7]

A recent survey of 105 expansion-based phase I trials reported that only four justified a sample size [13]. One explanation for this is that sample size formulas for single-arm phase II studies [33] do not apply to expansion cohorts allowing for dose modification. In this context, we propose performance metrics, the true and false positive metrics, that quantify how well a specific sample size (in the context of the rest of the design) achieves the stated objectives. Our use of 15 or 30 patients per cohort is not meant to be prescriptive but illustrative. In a given cohort, a reasonable technique for determining an appropriate per-cohort sample size is to identify the sample size that achieves a desired TPR subject to a specified FPR under an expected dose-efficacy relationship, in much the same way that traditional sample size calculations seek to achieve a desired power subject to a specified type I error under an expected effect size. What our study highlights is the potential efficiency gain—effectively a gain in sample size—from using statistical models in the trial design.

Is there a defined end to the trial, in terms of both efficacy and futility? [7]

We outline an approach for implementing futility analyses in the interim of large expansion cohorts and efficacy analyses at each cohort’s end. Importantly, both account for dose modifications during expansion. If both dose-toxicity and dose-efficacy relationships are expected to differ between cohorts, such as those DECs distinguished by unique dosing schedules in Topalian et al. [9], the cohorts could be considered parallel phase I/II trials falling under a single protocol, in which case neither toxicity nor efficacy information would be ‘shared’ between cohorts. One reviewer suggested that this could be an additional design template, which might be called a ‘local CRM’. Alternatively, recent work by Neuenschwander et al. [35] outlines how the extent of sharing may be data-adaptive using hierarchical regression with random effects. In any case, the guidelines exposited in this article, namely stating how toxicity will be monitored, justifying sample sizes, and implementing futility analyses, still apply.

Is there an appropriate statistical analysis plan for all stated end points? [7]

The designs and analyses that performed the best in our study are arguably complicated. They require additional work by clinicians and statisticians in advance of and during the trial. However, our results suggest that this additional effort is more than compensated by a substantially increased likelihood of discriminating among efficacious and inefficacious treatments/patient populations. What might be called a standard dose-assignment mechanism, namely de-escalating during a cohort whenever a simple cumulative (over all patients) toxicity threshold is exceeded, i.e. Local monitoring, often incorrectly de-escalates the dose level and thus results in poor efficacy estimation. In both Local and Global monitoring, dose assignments are not escalated during expansion if the observed rate of toxicity is unexpectedly low. A low toxicity rate is problematic because the 3 + 3 tends to conservatively estimate the MTD [3], and this tendency is exacerbated as the size of the cohort increases. As a result, efficacy is often estimated at too low a dose in Local and Global. A dose-assignment mechanism that can escalate the dose during expansion is preferred. Of the three mechanisms we examined, only the Model-based CRM incorporates dose-escalation, although the Global mechanism could be extended to do so. Thus, the CRM estimates the MTD most accurately, and efficacy is likely to be estimated well at a desired dose level.

As with all simulations of clinical trials, the present study has limitations. The role of a data safety monitoring committee varies between trials, and protocols seldom describe whether the committee monitors cumulative toxicity at a particular dose level. Therefore, it is possible that many dose-expansion trials fail to monitor cumulative toxicity. Although we did not simulate a design that does not monitor toxicity during expansion, the expected impact would be to increase the number of patients treated at a toxic dose (a bad feature), while preventing dose de-escalation due to variability in observed toxicity outcomes in a small group of patients (a good feature). Also, we reiterate that our use of five DECs here is neither optimal nor necessary; the number of cohorts should be determined by the context of the therapy and its targets. Although we only report results for trials having three inefficacious and two efficacious DECs, our qualitative conclusions are not sensitive to these numbers or proportions, because all efficacy analyses are performed separately for each cohorts, i.e. we do not share efficacy information between cohorts within a trial.

The conceptual goal of using DECs to increase sample size makes sense in the framework of the 3 + 3, because few patients are treated at each dose. However, some phase I trials now enroll several hundreds of patients across multiple cohorts, a trend described as ‘getting out of hand’ [8]. Combined with a growing interest in early efficacy estimation, this has led to a radical change in the philosophy and complexity of phase I oncology trials. Putting these in the phase II framework helps create efficient and ethical designs for such trials.

Funding

This work was supported by the National Institutes of Health [grant number P30 CA046592].

Key Message

The prevalence and size of dose-expansion cohorts in phase I oncology trials have been increasing, but the development of design principles for such trials has not kept pace. Using a simulation study, we explore several design templates specifically tailored to dose expansion. The use of statistical models makes efficient use of the substantial amount of patient data coming from such trials and increases the likelihood of making the most appropriate decision for each cohort.

Disclosure

The authors have declared no conflicts of interest.