On-chip dual-comb source for spectroscopy

A compact, integrated dual-comb source is developed on a single chip to demonstrate fast, real-time spectroscopy of materials.

Abstract

Dual-comb spectroscopy is a powerful technique for real-time, broadband optical sampling of molecular spectra, which requires no moving components. Recent developments with microresonator-based platforms have enabled frequency combs at the chip scale. However, the need to precisely match the resonance wavelengths of distinct high quality-factor microcavities has hindered the development of on-chip dual combs. We report the simultaneous generation of two microresonator combs on the same chip from a single laser, drastically reducing experimental complexity. We demonstrate broadband optical spectra spanning 51 THz and low-noise operation of both combs by deterministically tuning into soliton mode-locked states using integrated microheaters, resulting in narrow (<10 kHz) microwave beat notes. We further use one comb as a reference to probe the formation dynamics of the other comb, thus introducing a technique to investigate comb evolution without auxiliary lasers or microwave oscillators. We demonstrate high signal-to-noise ratio absorption spectroscopy spanning 170 nm using the dual-comb source over a 20-μs acquisition time. Our device paves the way for compact and robust spectrometers at nanosecond time scales enabled by large beat-note spacings (>1 GHz).

INTRODUCTION

Optical frequency combs (1) are a revolutionary technology with widespread applications in precision spectroscopy (2), microwave signal synthesis (3, 4), frequency metrology (5), optical clocks (6), communications (7, 8), and astronomical spectrograph calibration (9, 10). A frequency comb consists of a sequence of hundreds or thousands of narrow, discrete spectral lines equidistant in frequency, separated by the repetition rate f_rep. Many of the previous demonstrations of frequency comb sources have used femtosecond mode-locked lasers (11, 12). In recent years, there has been significant development of chip-scale comb sources based on the Kerr nonlinearity using high quality-factor (Q) microresonators. The past decade has seen the development of numerous platforms for generating these microresonator-based frequency combs, including silica (13), silicon nitride (Si₃N₄) (14), crystalline fluorides (15–17), Hydex glass (18), aluminum nitride (19), diamond (20), silicon (21), and AlGaAs (22). These microresonators, when pumped by a monochromatic continuous-wave (cw) laser, generate frequency sidebands through four-wave mixing (FWM) parametric oscillation and undergo nontrivial nonlinear dynamics to produce a comb of frequencies that can span an octave of bandwidth (23, 24).

Dual-comb spectroscopy (DCS) enables broadband optical sampling of molecular absorption spectra with a high signal-to-noise ratio (SNR) and tens-of-microsecond acquisition times, without any moving parts, through the use of the high coherence of the comb lines (25–30). This technique uses two frequency combs with slightly different repetition rates, f_rep1 and f_rep2 = f_rep1 + Δf_rep. The heterodyne beating between these two combs generates a sequence of beat notes in the radio frequency (rf) domain, spaced by the difference in repetition rates Δf_rep, ensuring a one-to-one mapping of the optical comb lines to the rf beat notes. This beating down-converts the spectral information spanning tens to hundreds of terahertz in the optical domain to a few gighertz in the rf domain (Fig. 1). The resolution of DCS is determined by the repetition rate of the combs. DCS has been traditionally implemented using stabilized (28), as well as free-running (30, 31), mode-locked Ti:sapphire or fiber lasers and therefore often requires bulky tabletop setups. Chip-based frequency combs have the potential to implement DCS in a compact and robust integrated platform. These combs typically have larger line spacings (f_rep > 10 GHz) than their counterparts based on mode-locked lasers. Because Δf_rep << f_rep to prevent aliasing, a larger repetition rate permits a larger Δf_rep, which corresponds to a smaller minimum acquisition time to resolve the beat notes. This enables faster measurements than those possible with laser-based dual combs, especially for spectroscopy in the solid or liquid phase, where materials exhibit broad spectral features. The improvement in speed is in addition to the usual benefits of conventional dual-comb spectrometers, namely, the absence of moving mechanical parts and the ability to perform absorptive and dispersive measurements with a single photodetector (25). The large Δf_rep introduces a trade-off in the number of optical comb lines that can be down-converted within a fixed rf bandwidth, but this trade-off can be mitigated by commercially available high-speed photodetectors with very large rf bandwidths approaching 100 GHz or more. The dual-comb heterodyning technique in microresonators has also been used for massively parallel coherent detection for communications (8).

Fig. 1. Cascaded microring resonators for dual comb generation.

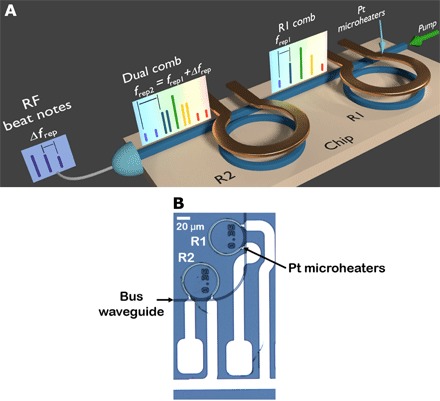
(A) Schematic of the device. A cw laser pumps the silicon nitride waveguide, which is coupled to two silicon nitride rings: R1 and R2. Through parametric oscillation and cascaded FWM, rings R1 and R2 generate frequency combs with repetition rates f_rep1 and f_rep2, respectively. The insets show schematic optical spectra after the first and second rings. The spectrum detected at the output of the chip using a fast photodiode shows a series of beat notes in the rf domain. Note that although the optical spectrum insets span several tens of terahertz, the rf spectrum spans only a few gigahertz, enabling ease of detection in the electronic domain. (B) Optical microscopy image of the fabricated device showing the silicon nitride rings with integrated platinum microheaters.

The challenge in performing DCS using an integrated platform lies in the requirement for mode-locking each of the combs generated in both microcavities and aligning their resonance wavelengths to a single external pump laser wavelength (to ensure high relative coherence between the two spectral combs). Two experiments have demonstrated on-chip integration of dual combs using semiconductor disk lasers (32) and quantum cascade lasers (33) with narrow optical bandwidths of 0.08 and 0.96 THz, respectively. The development of a dual-comb source based on Kerr nonlinear microresonators, used in combination with dispersion-engineered waveguides, has the potential to increase the bandwidth by orders of magnitude without compromising the device footprint or the on-chip integration capability. In this vein, Suh et al. (34) recently demonstrated dual combs based on wedge resonators using two separate chips pumped by two independent lasers, but these combs are limited in their optical bandwidth due to dispersion and in their achievable relative coherence time without using active locking of the two lasers. Similarly, Yu et al. (21) reported mid-infrared (IR) DCS using two separate chips pumped by an optical parametric oscillator. On the other hand, soliton dual combs with low beat-note spacings have been reported by Pavlov et al. (35), but spectroscopy was hindered by the short lifetimes of the combs due to thermal effects.

Here, we present the generation of dual Kerr frequency combs on a single chip using a single pump laser and dispersion-engineered Si₃N₄ microrings to produce wide optical bandwidths and long coherence times. We demonstrate soliton mode-locking of both combs using integrated thermal tuning, leading to narrow microwave beat notes with linewidths of <10 kHz and sech²-shaped optical spectra spanning 51 THz with minimal mode crossings. Thermal tuning based on platinum microheaters also allows us to use a low-noise nontunable laser as the pump, resulting in a long mutual coherence time of 100 μs even without active feedback and stabilization. Furthermore, we use one of the soliton mode-locked combs as a reference and investigate the generation dynamics of the second comb as the latter is tuned into the mode-locked state by measuring the intercomb beat note, thus illustrating the power of the dual-comb heterodyne technique to study the formation dynamics of frequency combs. Finally, we perform time-domain absorption spectroscopy of dichloromethane spanning a 170-nm wavelength range over a fast acquisition time of 20 μs using the demonstrated dual-comb source.

RESULTS

Device design

The dual comb is generated using cascaded Si₃N₄ microring resonators pumped with a single cw laser. The cascaded rings (R1 and R2) have slightly different nominal radii of 50.04 and 49.98 μm, respectively (Fig. 1A), and are coupled to the same bus waveguide. Si₃N₄ has proven to be a versatile platform for on-chip photonics due to its low linear loss (~0.8 dB m⁻¹) (36–39), high refractive index (~2), negligible nonlinear absorption in the near-IR, and compatibility with complementary metal-oxide semiconductor fabrication processes (40). Si₃N₄ waveguides are particularly attractive for integrated nonlinear photonics because of the high nonlinear index (n₂ ~ 2 × 10⁻¹⁹ m² W⁻¹) (14, 41), high confinement (41, 42), and the ability to tailor the group velocity dispersion (GVD) by engineering the waveguide geometry (43, 44). In our device, the waveguides have a height of 730 nm and a width of 1500 nm to ensure low anomalous GVD around the pump wavelength of 1561 nm, which allows for broadband comb generation (23, 24). The coupling gap between the waveguide and the resonator is 350 nm.

We overcome the challenge of aligning the resonances of both high-Q rings (loaded Q > 600,000) to the pump wavelength by fabricating integrated platinum microheaters on top of the Si₃N₄ rings to tune the resonance wavelength of the rings using the thermo-optic effect. This is in contrast to what has been carried out in most previous experiments with Kerr combs, where the laser wavelength is tuned to a cavity mode of the microresonator (45). The microheaters have highly localized heat flow, reduced thermal cross-talk (46), and fast response times and enable us to stably and repeatedly tune the rings into resonance with the pump in tandem (47–50). The heaters can tune the resonance by more than one full free spectral range (FSR) and hence compensate for fabrication variations in the rings’s radius (see the Supplementary Materials). The rise and fall times of the microheaters are 24 and 22 μs, respectively (fig. S2), which allow us to tune into resonance at speeds of ~50 MHz/μs (49); this is significantly faster than using Peltier elements to tune the temperature of the entire chip. Details of the fabrication process can be found in Materials and Methods.

Dual-comb optical spectra

The heaters enable tuning of either one or both rings into resonance to generate frequency comb spectra spanning 51 THz (400 nm) near the pump wavelength of 1561.4 nm, as shown in Fig. 2 (A to C). We excite ring R1 with ~105 mW of power in the bus waveguide and tune its heater without tuning the heater on R2 to generate the spectrum shown in Fig. 2A. Similarly, Fig. 2B shows the spectrum obtained by tuning the heater on R2 without tuning the heater on R1. These individual comb spectra allow us to characterize the mode spacings of the combs to within the 0.01-nm resolution of the optical spectrum analyzer (OSA). Both rings generate a spectrum spanning 400 nm (51 THz). We infer a mode spacing f_rep1 = 451.4 ± 0.4 GHz for the R1 comb and f_rep2 = 452.8 ± 0.4 GHz for the R2 comb. The difference between the mode spacings of the combs is Δf_rep = 1.4 ± 0.8 GHz, which is well within the bandwidth of commercially available fast photodiodes, whereas the repetition-rate frequency of each individual comb is much larger than what can be directly detected with fast photodiodes. In general, this is true for microresonator combs, which have repetition rates from tens to hundreds of gigahertz. Thus, the dual-comb technique frequency down-converts the repetition rate of the microresonator combs, making it amenable to study the repetition-rate beat note using fast photodiodes. Note that the large error bar in Δf_rep is limited by the resolution of the OSA, and rf heterodyne beating measurements shown later determine Δf_rep to a much higher accuracy. Figure 2C shows the spectrum of the dual comb generated when both R1 and R2 are on resonance with the laser. As can be seen from the inset of Fig. 2C, pairs of closely spaced modes are distinguishable, indicating a dual-comb spectrum. Note that Δf_rep is much larger than the linewidth of each cavity mode (230 MHz for R1 and 310 MHz for R2), so that the comb lines generated in R1 are not resonant with the cavity modes of R2, except for the pump. This ensures that the comb lines from R1 do not couple into the R2 resonances and do not interact with the comb lines in R2, despite the cascaded geometry (see the Supplementary Materials).

Fig. 2. Optical spectra.

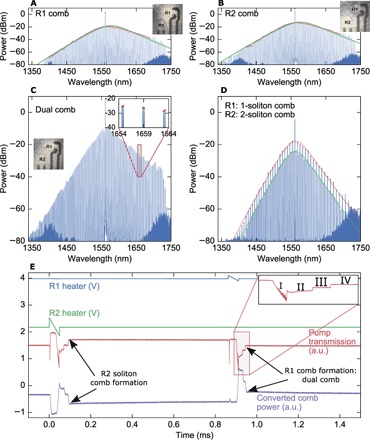
(A to C) Generated spectrum when the heaters on (A) R1, (B) R2, and (C) both rings are tuned into resonance with the pump laser at 1561.4 nm. OSA resolution, 0.01 nm. The insets are top-view IR camera images showing which of the two rings are on resonance. The combs are in the single-soliton mode-locked state. Solid red and green lines are fits to a sech² spectral envelope.(D) Dual-comb state with a single soliton in R1 and two solitons in R2. The zoomed-in inset in (C) and (D) reveals dual combs with pairs of lines closely spaced in wavelength. By changing the magnitude of the final upward voltage ramp shown in (E), one can choose the number of solitons in the final state. As an example, the state shown here has a single soliton in R1 and two solitons half a roundtrip apart in R2 (harmonic mode-locking). All spectra span 400 nm (51 THz). (E) Time domain traces of the voltage ramp used to access the mode-locked states of both the rings. The blue (green) line represents the voltage applied to the heater on R1 (R2). The red and purple lines represent the transmitted pump power and the converted comb power (excluding the pump and vertically offset for clarity), respectively. Discrete steps are seen in the pump power, as well as the comb power, characteristic of multisoliton states in the ring. The inset shows the stages of comb formation in R1, including the high-noise state (I), the multisoliton state (II and III), and the single-soliton state (IV). a.u., arbitrary units.

By engineering the thermal tuning of the heaters with respect to the comb, we independently tune the two rings at sufficiently fast time scales and achieve mode-locking of the two spectral combs using a fixed-frequency pump laser. The combs generated in R1 and R2 exhibit single-soliton mode-locking with sech² spectral envelopes without significant mode crossings. We tune into the low-noise, mode-locked states of both the combs by applying a voltage ramp to the microheaters of rings R1 and R2 over a period of 50 μs using an arbitrary waveform generator (AWG), corresponding to a scan speed of 20 kHz as shown in Fig. 2E and as detailed in the study of Joshi et al (49). The corresponding rate of change of the ring’s resonance frequency is estimated to be ~50 MHz/μs. The downward voltage ramp is applied on a ring when the pump laser is initially on the blue-detuned side of the ring resonance, which blueshifts the ring resonance toward the pump laser. A final increase in voltage redshifts the resonance, providing us deterministic access to the soliton states. When the pump wavelength is on the red-detuned side of the resonance, we observe a series of abrupt steps in the pump transmission concomitant to the formation of multisoliton states with different numbers of solitons propagating per roundtrip around the microring, similar to what has been routinely observed in recent work on soliton mode-locking (45, 49, 51). Optimization of the voltage ramp parameters permits us to reach the same mode-locked state for single frequency combs on each microheater scan. Dual-comb generation, although successful on each scan, occasionally requires multiple scans to reach a desired soliton state due to the influence of R1’s transmitted pump on R2 (see the Supplementary Materials). The single-soliton state corresponds to a shallow pump extinction of 12 to 15%, which enables the rest (>85%) of the transmitted pump after the first ring to be used for pumping the second ring. This makes the cascaded geometry more power-efficient than a parallel geometry, where the pump would have to be split 50:50 before the rings. The soliton powers are pinned by the double balance between nonlinearity and dispersion on the one hand and dissipation and parametric gain on the other hand (45, 52). Thus, the spectral intensities of the two combs are very similar despite the different pump power levels for the two rings. By controlling the magnitude of the final upward voltage ramp, one can control the number of solitons present in the comb. For example, Fig. 2D depicts a spectrum with a single soliton state in R1 and a two-soliton harmonic mode-locked state in R2. Note that previous experiments have demonstrated soliton mode-locking in fiber ring resonators (52), as well as in single microresonators using pump wavelength tuning (45), two-step pump power control (51), and integrated thermal tuning (49). Here, we choose thermal tuning because it allows us to use a fixed-frequency, nontunable, low-noise laser (see Materials and Methods and the Supplementary Materials) as the pump and enables independent tuning of the two rings at sufficiently high speeds. Tunable external-cavity diode lasers, conventionally used for Kerr frequency comb generation, have a broader linewidth (>100 kHz), have higher phase noise and frequency jitter, and are typically not amenable to tuning at required speeds. Note that the soliton states, once generated, stably exist for hours without any active feedback, in spite of the drifts in fiber-to-chip coupling and pump power.

Multiheterodyne beat notes

We observe multiheterodyne beat notes between the combs when both rings are tuned into resonance with the pump laser to generate dual combs. For this measurement, the output of the chip is sent to a wavelength-division multiplexing filter to remove the pump. Because the comb lines are symmetric in frequency relative to the pump, the beat notes of the comb lines on the red side of the pump overlap with the beat notes on the blue-detuned side. To avoid this and hence enable one-to-one mapping of the rf beat notes to the optical wavelength, we use shortpass and longpass filters to characterize the beat notes on the shorter and longer wavelength sides of the dual comb (see the Supplementary Materials). In principle, an acousto-optic modulator could be used to frequency-shift the pump for one of the rings to obviate the need for optical filtering (28, 29, 53). The filtered comb is sent to a 45-GHz photodiode followed by a 40-GHz rf amplifier, and the resulting rf signal is monitored on a 36-GHz real-time oscilloscope. In Fig. 3A, we plot the time-domain interferogram over 20 μs. Figure 3B shows the same interferogram expanded 2000 times, and a periodic signal is visible, repeating every 900 ps (=1/Δf_rep). To further elucidate the details of the time-domain interferogram, we amplify the filtered dual comb using an L-band erbium-doped fiber amplifier (EDFA) and plot the amplified and expanded version of the interferogram in Fig. 3C. It is worth emphasizing that optical amplification of the generated combs was only used for visual clarity of the interferogram shown in Fig. 3C. The rest of the interferograms and the rf domain spectra, as well as the spectroscopy results shown later, were acquired without any optical amplifier after the combs. The use of optical amplifiers after the dual combs would restrict the optical bandwidth of DCS due to the limited range of C- and L-band amplifiers (<50 nm).

Fig. 3. Time-domain interferogram and rf heterodyne beat notes.

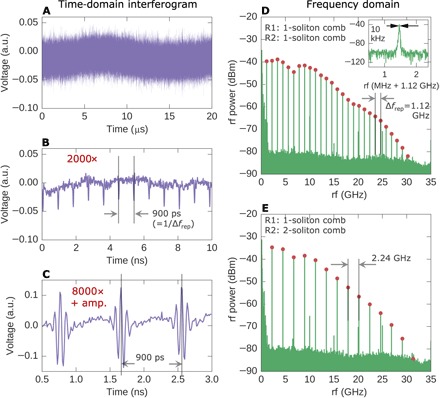
(A) Twenty microsecond time-domain interferogram of the mode-locked dual comb. (B) The same time-domain interferogram expanded 2000 times shows periodic pulses at the inverse of the beat-note frequency (1/Δf_rep). (C) The dual comb is amplified by an L-band EDFA and detected on a fast photodiode to highlight features of the time domain interferogram. This trace is zoomed in by a factor of 8000 compared to (A). Note that the interferogram in (C) represents a filtered version of the real time-domain trace because of the ~40-nm gain bandwidth of the L-band EDFA. Comb lines close to the pump (1561 to 1570 nm) and those beyond 1610 nm are attenuated by the EDFA. (D) rf multiheterodyne beat notes obtained by a fast Fourier transform (FFT) of the interferogram in (A). The data were taken with a longpass filter and represent the dual comb lines on the red side of the pump. The beat notes correspond to the dual comb shown in Fig. 2C, where both combs are in the single-soliton mode-locked state. A beat-note spacing of 1.12 GHz is observed. The inset shows the linewidth of the first beat note, measured using an rf spectrum analyzer with a resolution bandwidth of 2 kHz. We measure a high SNR (60 dB) with a linewidth of 10 kHz, which corresponds to a relative coherence time of 100 μs. (E) rf beat notes of the comb shown in Fig. 2D, where the comb generated in R1 is in the single-soliton mode-locked state and the comb in R2 is in the two-soliton harmonic mode-locked state. The beat notes are spaced by 2.24 GHz because the R2 comb is missing a line in every alternate mode of the ring. In both (D) and (E), the beat notes close to the pump have a high SNR in excess of 40 dB. The spurious peaks at 5, 10, 15, 20, and 25 GHz are artifacts of the FFT analyzer.

An FFT of the time-domain signal yields 27 rf beat notes spaced by 1.12 GHz, which corresponds to the difference in mode spacings of the two combs (Fig. 3D). The number of beat notes detected is limited by the noise floor of the FFT and the decreasing power in the comb lines away from the pump. The beat notes below 10 GHz have very high SNR in excess of 40 dB. The center frequency of the first beat note is 1.12 GHz, which is commensurate with the difference in mode spacings estimated from the OSA scans within the uncertainty of the OSA measurement. It also matches reasonably well with the difference in mode spacings calculated on the basis of the radii of R1 and R2 (see the Supplementary Materials). Although the results shown in Fig. 3 were obtained with a longpass filter and correspond to the optical spectrum on the red side of the pump, similar spectra were also observed with a shortpass filter for the blue half of the comb.

The soliton mode-locked dual comb exhibits low-noise rf beat notes with a narrow 3-dB linewidth of 10 kHz (Fig. 3D), which ensures a long relative coherence time [τ_rel = (10 kHz)⁻¹ = 100 μs]. The first beat note has an SNR exceeding 60 dB over a span of 2 MHz with a sweep time of 500 μs. Our high SNR over fast acquisition times is enabled by (i) a short single-shot acquisition time (limited by τ_acq,min = 2/Δf_rep = 1.79 ns to resolve individual beat notes) and (ii) our ability to perform complete spectral acquisitions well within the relative coherence time τ_rel = 100 μs. We choose an acquisition time τ_rel = 20 μs to satisfy the condition τ_acq,min < τ_acq < τ_rel. Note that the relative coherence between the two mode-locked combs is high, although the combs are in the free-running state (that is, there is no active feedback and stabilization), because both the combs are generated from the same low-noise pump laser. The observed beat-note linewidth of 10 kHz is not fundamental but is limited by the noise in the AWG used to control the heaters on the rings. Shorter linewidths (<1 kHz) at the repetition-rate beat note have been reported for single combs without active feedback (45, 54), and hence, it should be possible to reach even longer coherence times using a lower-noise voltage source to control the heaters.

To underscore the importance of mode-locking for the generation of narrow beat notes, we also study the dual comb in the high-noise state, which exhibits a much broader beat-note 3-dB linewidth. The linewidth of the dual-comb beat note in this state is ~300 MHz, which is rather broad for precision spectroscopy or microwave signal generation (fig. S6). This is because in the high rf-amplitude noise state, the frequencies and the relative phases of the comb lines randomly fluctuate in time.

Evolution of beat notes

We show that the integrated dual-comb source enables one to directly observe the comb formation dynamics, without the need for a secondary laser or microwave oscillator. A microresonator frequency comb starts as primary sidebands, which develop into minicombs that further evolve into a high-noise state and finally undergo a transition to a mode-locked state through higher-order FWM interactions (45, 54, 55). These dynamics have been studied experimentally by characterizing the repetition-rate beat note but that often requires auxiliary lasers or rf local oscillators for heterodyne downmixing (55, 56). Here, we use the dual-comb heterodyne technique for the same purpose, obviating the need for an auxiliary laser.

We monitor the evolution of the rf noise of the comb from R2 as it is tuned into the soliton mode-locked state by beating it with a mode-locked comb from R1. Specifically, here, we study the beat note around the radiofrequency Δf_rep, which is formed by the mixing of the first R2 comb line on the red side of the pump and the corresponding comb line in R1, with the latter acting as the local oscillator. We can choose a different radiofrequency (= nΔf_rep) to study the evolution of a comb line n FSRs away from the pump. The rings used in this measurement have a difference in radius of 1 μm, corresponding to an 8.6-GHz beat-note spacing. The larger beat-note spacing allows us to study the noise characteristics of combs, which typically span up to several gigahertz in the high-noise state. We used a longpass filter to observe the comb on the red side of the pump. A voltage ramp is applied initially to the heater on R1, as described in the previous section, to generate a soliton mode-locked comb, which is then used as a reference to probe the different stages of comb formation in R2. The voltage applied to the heater on R2 is changed, and the rf spectrum around the first heterodyne beat note at 8.6 GHz is simultaneously recorded. Figure 4 shows the evolution of the beat note as R2 goes through several stages of comb formation, finally culminating in the narrow, high-SNR beat-note characteristic of dual mode-locked combs described in the previous section. On the blue-detuned side, we observed a single (stage I) or multiple (stage II) low-SNR beat note/s. With further tuning, the number of beat notes, as well as the width of each beat note, increases, eventually leading to the broad rf beat note characteristic of the high-noise state (stages III and IV). By continuing the scan, we access the red-detuned side of the resonance, resulting in the formation of a high-SNR narrow beat note (stage V; see also movie S1). Scanning further in the same direction leads to the ring falling out of resonance with the laser. The rf spectra in Fig. 4 do not include the dynamics of the primary comb lines, because they are formed several FSRs away from the pump at larger blue detunings than what is shown here. Note that because there is a one-to-one mapping between each pair of closely spaced lines of the dual comb and the corresponding beat note in the downmixed rf spectrum, one can, in principle, study the dynamics of the comb line-by-line by experimentally analyzing the desired rf heterodyne beat note.

Fig. 4. Dual-comb heterodyne technique to study beat-note evolution.

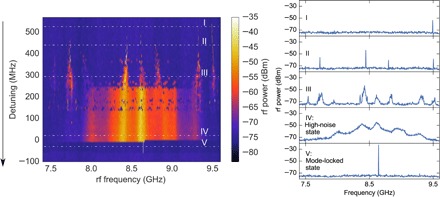
The device used in this measurement had a beat-note spacing of 8.6 GHz. Keeping the comb generated in R1 in the mode-locked state, the resonance of R2 is tuned with respect to the pump laser and the rf spectrum is recorded. The left panel shows the spectrum of the first beat note as the heater power on R2 is varied starting from a far–blue-detuned state to the mode-locked state on the red-detuned side. The spectra on the right show the formation of beat notes (stages I and II), which broaden to form a wide beat note in the high-noise state (stage III and IV). On tuning further to the red-detuned side, we observe an abrupt transition to a narrow and high-SNR beat note as shown in Fig. 3. (see also the Supplementary Materials and movie S1).

DCS of dichloromethane

We perform liquid-phase absorption spectroscopy of dichloromethane near the pump wavelength of 1561 nm using the dual-comb source and show that the recorded spectrum using DCS agrees very well with the corresponding spectrum obtained using an OSA and a broadband supercontinuum (Fianium SC-450-4) as a light source. Dichloromethane is a widely used organic solvent with broad absorption features in the near-IR. For spectroscopy, the output of the chip is collected with an aspheric lens and sent directly through a cuvette containing dichloromethane (Fig. 5A). The absorption spectrum is obtained by recording the rf heterodyne beating of the dual combs with and without the sample of dichloromethane, and it is then corroborated with the corresponding optical spectrum (Fig. 5B). As stated earlier, we acquire a time-domain interferogram over 20 μs at 80 gigasamples/s and perform an FFT to extract the beat-note information in the rf domain. We achieved a high SNR without averaging multiple spectra, thus indicating the real-time nature of the acquisition system. The quartz cuvette showed no significant absorption in this wavelength range. Note that the optical bandwidth of 170 nm accessible by the dual comb is narrower in our experiment than the full extent of the dual-comb spectrum (400 nm) due to the photodiode’s sharp roll-off in responsivity beyond 1640 nm and the decreasing power of the comb lines in accordance with the sech²-shape, which restricts the SNR of wavelengths shorter than 1460 nm.

Fig. 5. DCS of dichloromethane.

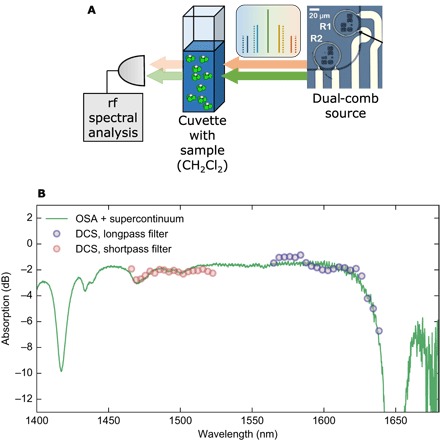
(A) Schematic of the setup. The output of the chip generating a dual comb is sent to a 10-mm cuvette containing dichloromethane, and the transmitted light is sent to a 45-GHz photodiode and analyzed with an rf spectrum analyzer or with a fast oscilloscope. (B) Spectrum of dichloromethane acquired using DCS and corroborated with the same spectrum measured with a broadband supercontinuum source and an OSA. The solid line represents the absorption spectrum measured with a supercontinuum source (Fianium SC-450-4) and an OSA. The red (blue) circles represent the absorption spectrum acquired using the rf beat notes and a shortpass (longpass) filter. All spectra are normalized by the corresponding spectrum without dichloromethane.

DISCUSSION

We have demonstrated the generation of two frequency combs based on Si₃N₄ microresonators, with slightly different repetition rates on the same chip. The generated combs have a broadband spectrum spanning 400 nm (51 THz), with high repetition rates of 450 GHz with a repetition-rate difference of 1.12 GHz. Dispersion engineering by tailoring the waveguide dimensions (23, 24) or external nonlinear broadening in fibers (6) should allow us to further broaden the bandwidth of the combs up to an octave. The combs have a high degree of relative coherence because they are generated from the same fixed-frequency low-noise cw pump laser, as evidenced by narrow rf heterodyne beat notes with a linewidth of 10 kHz. Both the combs are operated in the single-soliton mode-locked state, with the help of integrated heaters to tune the resonance wavelengths of the microresonators.

The approach we have developed can be extended to other wavelength ranges, such as the mid-IR “molecular fingerprint” region, where several molecules have their strongest fundamental rovibrational resonances, as shown in recent experiments by Yu et al. (21). The repetition rate of our dual comb (450 GHz) provides sufficient resolution for spectroscopy of liquids and solids, which typically have broad absorption features of a few terahertz or more, as demonstrated in the real-time DCS measurement of dichloromethane reported here. Higher-resolution spectroscopy, as required typically for gases, is possible by tuning the laser and the resonator synchronously once the comb is generated (57) or by using longer resonators with smaller FSRs (54). High repetition-rate combs, such as the ones shown here, are desirable for fast acquisition time scales, because the speed of acquisition scales with an increase of the comb-tooth spacing f_rep (29). These combs are promising for investigating rapid dynamical processes, such as chemical reactions (58), or single-shot measurements in turbulent environments (29).

Here, the dual-comb source is coupled out of the chip using a single waveguide, which is adequate for absorption spectroscopy because it requires detecting only the amplitude information. Dispersive measurements, which require phase-sensitive detection (25, 28), could be enabled by designing two separate outputs for the two combs: one used as the reference arm and the other sent to the sample to be measured. This would require incorporating either drop ports on both the rings or splitting the pump laser before sending them to two waveguide-coupled rings in noncascaded geometry. The latter configuration also permits combs with smaller difference in repetition rates (Δf_rep < 10 MHz; see the Supplementary Materials), making time-domain measurements more feasible, at the cost of increasing the minimum time needed for acquiring a single-shot spectrum. Combined with these improvements, a chip-scale microresonator-based dual-comb source opens the door to realize a compact portable spectrometer for stand-off molecular sensing in the field.

MATERIALS AND METHODS

Device fabrication

The devices were fabricated using a process similar to those described in our previous work (36, 39). We started with a 4-inch-diameter virgin Si wafer and thermally oxidized it to obtain a 4-μm buried oxide layer to be used as the undercladding. Trenches were defined before nitride deposition on the oxide to mitigate stress-induced crack propagation in the film. A 730-nm-thick layer of stoichiometric silicon nitride was grown using a low-pressure chemical vapor deposition in two steps. The waveguides and resonators were patterned with electron beam lithography on a JEOL 9500FS system using ma-N 2403 resist. An alternative procedure uses an oxide hard mask to better transfer patterns to the nitride layer from the resist. This oxide was deposited using plasma-enhanced chemical vapor deposition (PECVD). The pattern was etched using inductively coupled plasma reactive-ion etching with CHF₃, N₂, and O₂ gases. The devices were annealed in an argon atmosphere at 1200°C after stripping the resist to remove residual N–H bonds, which introduce optical loss in the nitride film. The devices were cladded with 500 nm of high-temperature oxide at 800°C followed by a 2.5-μm-thick overcladding of PECVD oxide. We sputtered 100 nm of platinum on top of the oxide cladding and defined the heaters using photolithography and lift-off. The heaters had a width of 6 μm and were sufficiently far from the waveguide layer so as not to introduce any optical loss due to interaction with the metal (39, 47, 50).

Experimental setup

A cw RIO Orion laser at 1561.4 nm with a narrow linewidth of <3 kHz was used as the pump. It was amplified by an EDFA and filtered by a 27.5-GHz bandwidth dense wavelength division multiplexing (DWDM) add-drop filter centered at 1561.42 nm to mitigate the amplified spontaneous emission noise generated by the EDFA. A fiber polarization controller before the chip and a polarizer after the chip were used to couple to the fundamental transverse electric mode of the bus waveguide using a lensed fiber. The waveguide was coupled to rings R1 and R2, which had platinum microheaters on them to enable thermal tuning of the rings’s resonance wavelength using the thermo-optic effect. Light was coupled out of the chip using a 40× aspheric lens. The microheaters were driven using tungsten probes by an AWG in burst mode, with a staggered delay of 0.85 ms between the burst triggers of the two voltages V1 and V2 applied to the heaters on rings R1 and R2, respectively. On coupling 110 mW of power into the bus waveguide and applying the requisite voltages to the rings (shown in Fig. 2E), soliton mode-locked dual combs are generated. A part of the output of the chip was sent to an OSA to monitor comb formation. The rest was sent to another DWDM add-drop filter to separate the pump and the dual comb. The pump and the generated dual comb were both sent to separate photodiodes, and the dc component was monitored on an oscilloscope. The dual comb was also sent to a 45-GHz fast photodiode (Newport 1014). For DCS, a cuvette with a path length of 10 mm, containing the sample to be measured (dichloromethane in our experiment), was placed in the path of the dual comb. The rf output of the fast photodiode was amplified using a three-stage broadband amplifier (Centellax OA4MVM3) with a bandwidth of 40 GHz and sent to a 36-GHz oscilloscope (LeCroy LabMaster 10 Zi-A, 8-bit resolution, 80 GSa/s). A time domain trace of the dual-comb multiheterodyne beating was acquired, followed by an FFT to obtain the rf beat notes. The fast oscilloscope can also be used as an rf spectrum analyzer for measuring the linewidth of the beat notes. A detailed outline of the experimental setup can be found in fig. S1.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/3/e1701858/DC1

Details of soliton mode-locking using heaters

Details of rf multiheterodyne spectroscopy

Filtering

Beat-note spacing

Evolution of combs in the high-noise state

Details of the experimental setup

fig. S1. Detailed experimental setup.

fig. S2. Heater response.

fig. S3. Frequency comb filtered with a longpass filter.

fig. S4. Quality factor of microrings.

fig. S5. Optical spectra of combs in the high-noise state.

fig. S6. Evolution of dual-comb beat note when the R1 comb is in the high-noise state.

movie S1. Beat-note evolution.

References (59–64)