Abstract
According to implicit ligand theory, the standard binding free energy is an exponential average of the binding potential of mean force (BPMF), an exponential average of the interaction energy between the unbound ligand ensemble and a rigid receptor. Here, we use the Fast Fourier Transform (FFT) to efficiently evaluate BPMFs by calculating interaction energies when rigid ligand configurations from the unbound ensemble are discretely translated across rigid receptor conformations. Results for standard binding free energies between T4 lysozyme and 141 small organic molecules are in good agreement with previous alchemical calculations based on (1) a flexible complex (R ≈ 0.9 for 24 systems) and (2) flexible ligand with multiple rigid receptor configurations (R ≈ 0.8 for 141 systems). While the FFT is routinely used for molecular docking, to our knowledge this is the first time that the algorithm has been used for rigorous binding free energy calculations.
Keywords: Noncovalent Binding Free Energy, Implicit Ligand Theory, Fast Fourier Transform, Protein-Ligand, T4 Lysozyme
Graphical abstract
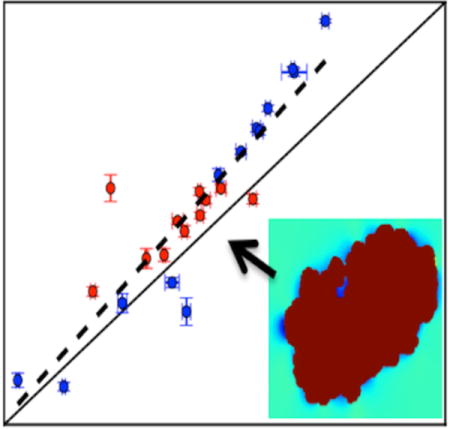
We demonstrate the feasibility of using the fast Fourier transform to calculate binding free energies between proteins and small molecules. A key part of the algorithm involves calculating interaction energies when the small molecule is translated across the binding site on the receptor (lower right inset). Upon averaging over the interaction energies and over multiple protein conformations, the resulting binding free energy is consistent with those from more expensive alchemical methods (scatter plot).
INTRODUCTION
To accelerate absolute binding free energy calculations between proteins and small molecules, we developed a method based on the fast Fourier transform and then tested it, finding reasonable agreement with more expensive calculations.
The binding of small molecules to biological macromolecules plays a critical role in cellular processes including enzymatic reactions, signal transduction, and gene regulation. Moreover, noncovalent associations with specific targets are essential to the mechanism of most drugs. Molecular simulations have been used to calculate binding free energies between small molecules and biomacromolecules and, increasingly, have become important for understanding biological mechanisms1–5 and for computer-aided drug design6–10.
The most rigorous methods for evaluating binding free energies are alchemical pathway methods11, in which conformations of both the ligand and receptor are sampled from a series of possibly nonphysical thermodynamic states along a pathway connecting two end states of interest. These methods are designed to determine either relative or absolute binding free energies. In relative binding free energy calculations, the pathway involves transforming one ligand into another. In absolute binding free energy calculations, the pathway may involve turning off interactions between the ligand and receptor or physically separating them12–14. Simulations may be done in explicit or implicit15,16 solvent, with the latter increasing speed at the expense of accuracy17. In an increasing number of publications, alchemical pathway methods have been successful at accurately calculating protein-ligand binding free energies17–25.
If the binding free energies of many ligands are desired, however, sampling from a series of thermodynamic states for each receptor-ligand pair can be computationally expensive. The ability to perform large-scale free energy calculations efficiently is desirable for the purposes of computer-aided drug discovery. Absolute binding free energy calculations for a large library of diverse compounds are useful for the discovery of drug leads. Relative binding free energy calculations between a congeneric series are useful for lead optimization.
A number of strategies are emerging to facilitate large-scale free energy calculations. In the λ-dynamics simulation method26, the alchemical parameter specifying the identity of a substituent is treated as a dynamical variable instead of a fixed value. Its extension to multiple substituents at multiple locations on a scaffold, multi-site λ-dynamics27,28, enables many relative binding free energy calculations based on a single simulation. Another strategy involves pre-computing ensembles of the protein complexed with a reference molecule29,30, with a reference ligand31, or of the protein by itself (the apo ensemble)32,33. This approach is advantageous because it allows for receptor conformations to be exhaustively sampled once and used for a large set of ligands. For a series of molecules that are similar to the reference molecule29–31, a one-step perturbation is often sufficient to estimate their relative binding free energies.
Implicit ligand theory (ILT)32 is a formalism that enables large-scale absolute binding free energy calculations based a pre-computed ensemble of the receptor. The theoretical basis for ILT is similar to the basis for calculating standard binding free energies based on implicit solvent11,15. While the implicit solvent formalism involves an integral over all solvent degrees of freedom to obtain a potential of mean force for solvation, ILT invokes an integral over all ligand degrees of freedom to obtain a binding potential of mean force (BPMF) – the binding free energy between a flexible ligand and rigid receptor. The solvent potential of mean force is typically obtained by a continuum dielectric electrostatics model. In contrast, the BPMF has hitherto been determined by an alchemical pathway method32,33.
In ILT, receptor conformations can be sampled from any statistical distribution as long as they can be reweighted to reproduce the apo ensemble32. However, in order to obtain accurate binding free energies, it is necessary to sample receptor conformations that are relevant to the holo (bound) ensemble for a particular ligand. This sampling requirement also pertains to, but is not always achieved in, alchemical binding free energy calculations with a flexible receptor34. Recently, Xie et al.33 demonstrated the feasibility of using ILT32 to calculate absolute binding free energies based on multiple receptor conformations drawn from alchemical binding free energy calculations between T4 lysozyme and 6 different ligands. The BPMF was then calculated between 141 ligands and each of the receptor conformations. In accordance with ILT, the standard binding free energy was calculated as an exponential average of the BPMFs, weighted by the apo ensemble. ILT-based calculations closely reproduced (with Pearson’s R = 0.9 and RMSE = 1.59 kcal/mol) results obtained by YANK16, a program based on alchemical pathway calculations with a flexible receptor.
Here, we perform similar calculations using an alternate way to compute BPMFs. Xie et al.33 computed BPMFs using the program Alchemical Grid Dock35 (AlGDock), which implements an alchemical pathway method in which the receptor is held rigid. While these calculations were much faster than simulations with a flexible receptor, they still required sampling from multiple thermodynamic states. To understand this alternate approach, it is helpful to consider the definition of the BPMF between a flexible ligand and a rigid receptor32,
| (1) |
where kB is Boltzmann’s constant and T is the temperature. Internal coordinates of the complex, rRL, include internal coordinates of the receptor and ligand, rR and rL, respectively, and external degrees of freedom of the ligand, ζL. The external degrees of freedom are translation and rotation. I(ζL) is an indicator function, either 0 or 1, that specifies whether or not the receptor and ligand are bound. Ψ(rRL) is the effective interaction energy between the receptor and ligand, the difference in solvated potential energy between the complex and its substituents, the receptor and ligand. The bracket denotes the ensemble average over the external and conformational degrees of freedom of the ligand in the apo ensemble. In this paper, the apo ensemble of a ligand (or receptor) refers to the probability density of the molecule in the unbound state, alone in implicit solvent. Equation 1, therefore, demonstrates that BPMFs can be obtained by sampling ligand internal coordinates rL from the apo ensemble and external degrees of freedom from the uniform distribution in the region where I(ζ) = 1. The ensemble average, in practice, is obtained as the mean of N samples of (rL, ζL),
| (2) |
The indicator function I(ζ) does not appear in Equation 2 because it is always 1 when ligand external degrees of freedom are sampled from the region where the receptor and ligand are considered to be bound.
The fast Fourier transform (FFT) facilitates the use of Equation 2 by providing an efficient way to compute interaction energies when the ligand is translated across the receptor. If interaction energies are calculated at M translational positions per dimension, the number of direct calculations is O(M6). Katchalski-Katzir et al.36 pioneered an alternate procedure based on the FFT in which interaction energies are calculated from the cross-correlation between three-dimensional grids that represent each binding partner. Their “interaction energy” was very simple — with values 0 outside the protein, 1 on its surface, and a large penalty for the interior — but more recent studies have incorporated elements of molecular mechanics nonbonded interaction energies, including electrostatics37, van der Waals interactions38, or both39,40. After mapping binding partners onto the grids, a discrete Fourier transform is performed, the two grids are convoluted, and an inverse Fourier transform is performed, yielding interaction energies for relative translations specified by grid point positions. Using the FFT, this algorithm is of order M3 ln(M3)! Due to this speedup, algorithms based on the FFT are routinely used for protein-protein docking36,37,41–46 and have been applied to docking fragments to proteins47,48 to search for binding poses with low interaction energies. Qin and Zhou39,40 have implemented an FFT-based method for calculating an exponential average of intermolecular interaction energies (similar to Equation 2) as a route to determining the chemical potential of a tracer protein in a crowded macromolecular solution.
In this study, we develop a similar FFT-based method for evaluating interaction energies and calculating BPMFs and standard binding free energies. We test our method, which we refer to as FFTΔG, on T4 lysozyme L99A and the same set of ligands as in Xie et al.33. To our knowledge, this is the first time that the FFT has been used for rigorous binding free energy calculations.
METHODOLOGY
Our calculations were performed on the same systems as in a prior study demonstrating the feasibility of ILT for protein-ligand systems Xie et al.33: T4 lysozyme L99A complexed with 141 ligands for which experimentally measured binding activity information is available.
The ligands are diverse: some are linear aliphatic chains, many have one aromatic ring, and some have two rings. They contain various functional groups, including alcohol and halogen groups. A complete list of ligand names is the legends of Figures S1 and S2 in the supplementary material, and more information is available in Table S1 of Xie et al.33. In a thermal denaturation shift assay, 69 of the ligands were determined to be active and 71 inactive49–55. The remaining ligand, iodobenzene, was determined to be active by isothermal titration calorimetry. The same AMBER56 topology and coordinate files for the ligands and receptor from Xie et al.33, based on the AMBER ff14 force field for protein and generalized AMBER force field for ligands, were used. BPMFs were calculated between these ligands and the same T4 lysozyme conformations, extracted from alchemical pathway simulations for six ligands: 1-methylpyrrole, benzene, p-xylene, phenol, N-hexylbenzene, and (±)-camphor. The first four ligands were chosen because they were used in Wang et al.16 and the latter two because their large size could favor opening of the binding pocket.
Ligand Sampling
To sample ligand conformations from the apo ensemble, we performed parallel tempering57,58 in the gas phase with a script based on OpenMM 6.3.159,60. Langevin dynamics simulations were performed at eight geometrically spaced temperatures between 300 and 600 K for 1 ns at each temperature using a time step of 2 fs. Exchanges between nearest neighboring temperatures were attempted every 1 ps. Ligand snapshots from the simulation at 300 K were saved every 1 ps, resulting in the total of 1000 snapshots per ligand. In the apo state, the energy should be isotropic with respect to translation and rotation. To sample from this state, therefore, each snapshot was randomly rotated about its centroid. Translational sampling was based on the FFT.
FFT-based BPMF Determination
BPMFs between each ligand and receptor snapshot were obtained using the thermodynamic cycle shown in Figure 1. Solvent contributions to the BPMF are (1) the desolvation of the rigid receptor and flexible ligand from state (A) to (B), and (2) the solvation of the complex from state (C) to (D). The gas-phase BPMF is the free energy difference between states (B) and (C), obtained by using the FFT to calculate interaction energies for a set of discrete translations of the ligand relative to the receptor.
Figure 1.
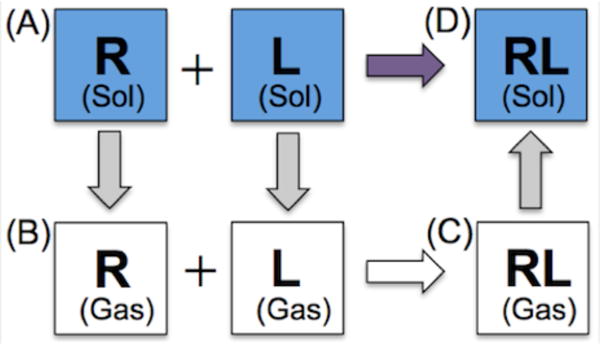
Thermodynamic cycle for calculating BPMFs based on the FFT.
Gas-phase BPMFs
We first describe the determination of the gas-phase BPMF, i.e., the free energy difference between states (B) and (C). This part largely follows Qin and Zhou40, and we give some detail here for sake of completeness. In the FFT-based approach, interaction energies are calculated using grid-based forms of pairwise interaction terms, including electrostatic and van der Waals interactions. The general form for the interaction terms is61,62,
| (3) |
where the inner sum is over all receptor atoms and the outer one over all the ligand atoms. V (rij) is a function of the distance rij between atoms i and j. γi and γj are constants associated with each ligand and receptor atom, respectively, such that the energy due to the pairwise interaction between atoms i and j is γiγjV(rij). As a specific example, consider the electrostatic energy,
| (4) |
where γi = qi and γj = qj are atomic partial charges. As partial charges were specified in electronic charge units and rij in Å, ΨELE was multiplied by 332.05 such that the energy is in units of kcal/mol. The van der Waals interaction energy is based on the Lennard-Jones potential using the geometric (instead of arithmetic) means for combining the well depths of two atoms as and their radii as . It is necessary to separately treat the repulsive term,
| (5) |
and attractive term,
| (6) |
Combining all three terms, the total interaction energy is ΨELE + ΨLJr + ΨLJa.
Each of these terms was calculated by discretizing Equation 3 onto a pair of three-dimensional grids: one for the receptor and one for the ligand. The inner sum of Equation 3,
| (7) |
is assigned to the receptor grid, where n is the position vector of a grid point. The generalized “charges” γi of ligand atoms in the outer sum of Equation 3 are then assigned to the ligand grid. Because ligand atoms generally do not fall precisely on grid points, it is necessary to “distribute” the generalized charges to grid points. Following Qin and Zhou40, we distribute γi for each ligand atom onto the 10 nearest grid points. The value of the ligand grid function GL(n) at position n is the sum of generalized charges distributed from all the surrounding atoms. With these discretizations, the interaction energy between the protein, in its original position, and the ligand, translated by the vector m, is approximated by the cross-correlation function,
| (8) |
where the approximation is due to discretization. According to the cross-correlation theorem63, it is possible to evaluate the cross-correlation function C for every position on the grid by,
| (9) |
where FT and FT−1 denotes the forward and inverse discrete Fourier transforms, respectively, the dot symbol · denotes the element-wise product of matrices, and the asterisk * denotes a complex conjugate. While direct evaluation of grid-based interaction energies for all points has a complexity of O(M6), the complexity of FFT-based calculations scales as M3 ln(M3) or better, where M is number of translations per dimension.
FFT-based interaction energy calculations were performed for two grid sizes. In one set of calculations, we used a smaller cubic grid of 16 Å along each dimension, centered around the binding site (as defined in Xie et al.33). For a subset of 21 ligands for which experimental binding free energies are available, we also performed calculations with a larger cubic grid of 62 Å along each dimension, which encompasses the whole receptor surface.
Interaction energies computed directly and by the FFT-based method were compared for three grid spacings: 0.125 Å, 0.25 Å, and 0.5 Å. Direct calculations based on equations 4, 5, and 6 were performed using a custom python script. Based on the comparison, grid spacings of 0.25 Å and 0.125 Å were used for the small grid and a spacing of 0.25 Å was used for the larger grid.
While the FFT evaluates interaction energies at all grid points, not all of the points are useful for evaluating BPMFs. First, because the FFT is periodic, an interaction energy can be evaluated for an unphysical situation where a ligand is split between opposite sides of a receptor grid. To filter out configurations corresponding to these unphysical translations, a ligand box was defined as a rectangular region containing all ligand coordinates and two additional grid spacings. Interaction energies corresponding to translations where the ligand box is split across the system were discarded. Second, translations n that lead to a steric clash are labeled as such and the contribution of that grid point to the exponential average is set to zero. To keep track of translational positions that give rise to a steric clash, we used occupancy grids, defined the same way for both the receptor and ligand as,
| (10) |
The FFT correlation function of the ligand and receptor occupancy grids gives positive values whenever there is at least one pair of atoms that sterically clash. It gives zero otherwise. Interaction energies for translations that have steric clashes were assumed to be infinite.
Interaction energies (including infinite values) were collected for all sampled translations, random ro-tations, and conformations of the ligand to evaluate the BPMF using Equation 2.
Solvent contributions to BPMFs
Two (de)solvation steps were needed to transform the gas-phase BPMFs into their counterparts in solution. Solvent contributions were calculated according to a single-step perturbation,
| (11) |
where is the free energy difference between the sampled state j and target state k and ΔUj,k(rRL,n) is the difference in the potential energy of the complex between state k and state j. In the target state, the receptor, ligand, or complex, was solvated in
Onufriev-Bashford-Case (OBC2) generalized Born / surface area implicit solvent64, implemented in OpenMM 6.3.159,60; or
Poisson-Boltzmann / surface area (PBSA) implicit solvent, implemented in the sander program from AmberTools56.
For the free energy difference between states (A) and (B) — the desolvation of the rigid receptor and flexible ligand —, the sampled state was (B) and the target state was (A). To calculate the free energy difference between states (C) and (D), we first needed to obtain samples of state (C) or (D). Since the FFT approach does not directly sample from either state, we performed “sampling importance resampling” to obtain samples of state (C) from the conformations in state (B). Specifically, 100 conformations were drawn from state (B) with weight proportional to e−βΨ, where Ψ is the total interaction energy. The weight, e−βΨ, is the probability ratio between the bound state and apo state. Subsequently, the free energy difference was determined according to Equation 11 with state (C) as the sampled state and (D) the target state.
Determination of Standard Binding Free Energies
According to implicit ligand theory32, the standard binding free energy ΔG° is given by an exponential average of BPMFs over the apo ensemble of receptor conformations,
| (12) |
where Ω = ∫ I(ζL)dζL = 8π2Vsite. The 8π2 comes from an integral over the rotational degrees of freedom of the ligand. Because there are no restraints on this rotation, the integral is over the full range of Euler angles. Vsite is the volume of the binding site, defined as the rectangular region where the ligand box does not go outside of the receptor grid (see above for the definition of the “ligand box”). Since each FFT translation yields a slightly different box size, the average volume of all rectangular regions is used to calculate Vsite. C° is the standard state concentration.
The exponential average was determined as a weighted sample mean of the BPMFs of different receptor snapshots, leading to
| (13) |
where W(rR) is the normalized weight associated with each receptor configuration rR in the apo ensemble. Xie et al.33 explained in detail why we used the weighted mean and how to obtain the weights. Briefly, receptor conformations were not sampled from the apo state but from a series of alchemical states in the presence of a ligand using the program YANK16. This approach was used to obtain receptor conformations more relevant to holo ensembles with other ligands. Therefore we had to reweigh these conformations to the apo ensemble. To this end we used the multistate Bennett Acceptance Ratio65 to obtain weights for all the receptor snapshots in the apo ensemble.
The set of receptor conformations selected for BPMF calculations, however, is just a small subset of all the snapshots from the YANK simulations. There are several possible ways to assign weights to the selected subset given the weights of all the snapshots: assign each snapshot its own MBAR weight and neglect the weights of snapshots without BPMF calculations; assign each snapshot the cumulative MBAR weight for the thermodynamic state it represents; assign MBAR weights of all snapshots to the most structurally similar counterparts with BPMF calculations. The first choice theoretically is most rigorous but numerically can be unstable. The latter two are approximate but numerically stable. Additionally, we have different ways to combine weights from simulations with different ligands. We considered two strategies: giving each YANK simulation equal weight or giving the apo state of each YANK simulation equal weight. As in Xie et al.33, these strategies led to a total of six weighting schemes:
Each snapshot is assigned its own MBAR weight; each YANK simulation has equal weight.
Each snapshot is assigned its own MBAR weight; each apo state has equal weight.
Each snapshot is assigned the cumulative MBAR weight of the thermodynamic state it represents; each YANK simulation has equal weight.
Each snapshot is assigned the cumulative MBAR weight of the thermodynamic state it represents; each apo state has equal weight.
Each snapshot is assigned the MBAR weight of its neighbors; each YANK simulation has equal weight.
Each snapshot is assigned the MBAR weight of its neighbors; each apo state has equal weight.
Correlation and Error Statistics
To quantify the agreement between different data sets, we used Pearson’s R, the root mean square error (RMSE), and adjusted RMSE (aRMSE). The RMSE between two series of data points {x1, x2, …, xN} and {y1, y2, …, yN} is,
| (14) |
The aRMSE is33,
| (15) |
where the and are the sample means of x and y, respectively. The aRMSE accounts for systematic deviation between the series and is useful for assessing whether relative binding free energies are accurate.
RESULTS AND DISCUSSION
FFT-Based Interaction Energy Accuracy Depends on Grid Spacing
Distributing ligand generalized charges onto a grid results in a discretization error that is more pronounced for a larger grid spacing (Figure 2). For a grid spacing of 0.125 Å, the FFT interaction energies are very close to the direct computation values based on Equations 4, 5, and 6, and discretization error is essentially nonexistent. Increasing grid spacing to 0.25, 0.5, and 0.8 Å leads to a gradual reduction of Pearson’s R from nearly 1 to 0.89 and increase of the RMSE from nearly zero to 0.63 kcal/mol (Figure S3 in the supplementary material).
Figure 2.
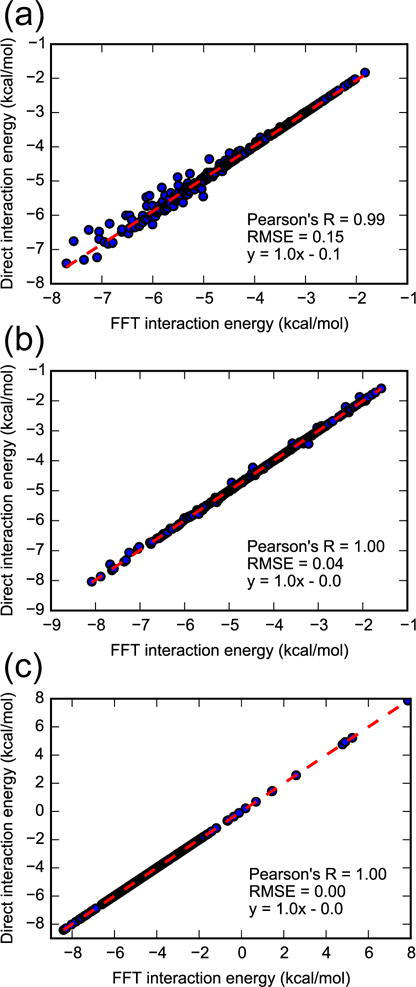
FFT-based vs direct interaction energies based on Equations 4, 5, and 6, between benzene and a snapshot of T4 lysozyme with a grid spacing of (a) 0.5 Å, (b) 0.25 Å, and (c) 0.125 Å.
While the accuracy at larger spacing may still be acceptable, increased spacing also reduces the number of samples. Therefore, for BPMF calculations with the smaller grid with 16 Å edges, we used grid spacings of 0.25 Å and 0.125 Å. For the larger grid with 62 Å edges, we reduced computational expense by only using a grid spacing of 0.25 Å.
Our free energy calculations employ a finer grid spacing than Qin and Zhou39,40 used to evaluate the excess chemical potential of proteins in a crowded solution. In these studies, grid spacings between 0.15 Å and 0.75 Å were all sufficient to calculate the fraction of proteins that do not clash with a crowding molecule39. However, chemical potential estimates were found to suffer from a systematic bias that increases with the grid spacing, and is approximately 0.75 kcal/mol at 0.6 Å40. To improve accuracy while retaining the speed of a larger spacing, Qin and Zhou40 corrected for these discretization errors by adjusting atomic radii and partial charges; this strategy may be pursued in future work on FFT-based protein-ligand interaction energies.
FFT-Based Interaction Energies Favor the Binding Site and Protein Surface
A cross-section of the interaction energy grid between benzene and the whole protein (Figure 3) shows the lowest values in the binding site and near the protein surface and many infinite values within the protein. Low values in the binding site are expected, but low values on the surface may indicate either alternative binding sites or an artifact of the force field. The existence of alternative sites was suggested by Wang et al.16, who predicted that several ligands including benzene bind to multiple sites on T4 lysozyme and that each site contributes to the binding affinity. Interaction energies for surface sites may be comparable to the main binding site because the gas phase interaction energy does not account for solvation. To elaborate, placing the small hydrophobic molecule benzene in the main binding site would be favorable because it would be almost entirely desolvated, but this effect is not captured in our treatment of the interaction energy. The infinite interaction energies result from steric clashes between the ligand and receptor. The existence of many translational positions with steric clashes as the ligand is translated across the binding pocket is common in FFT-based docking, evident from even the first paper in the area36.
Figure 3.
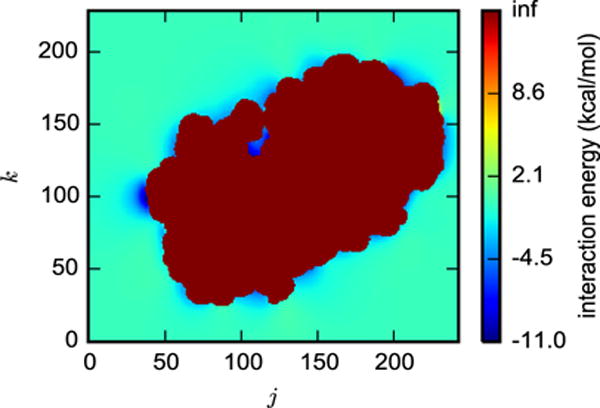
A cross-section of FFT-based interaction energies between fixed configurations of benzene and T4 lysozyme, shown as a cross-section of Ψ(i, j, k) with i = 160. Translations that result in steric clashes are colored dark red.
BPMF Calculations Apparently Converge
Ligand conformational and binding pose sampling appears to be thorough. Parallel tempering and random rotation leads to ligands being uniformly oriented in three-dimensional space (Figure 4a).
Figure 4.

Conformations of p-xylene (a) sampled from the gas phase or (b) in the binding pocket. Panel (a) includes 1000 conformations sampled from the parallel tempering simulation in the gas phase, randomly rotated around the centroid. Panel (b) are poses with finite FFT-based interaction energies obtained when these 1000 configurations are translated across the receptor binding pocket.
Although a large number of translational vectors m result in steric clashes and infinite interaction energies, due to the diversity of sampled ligand conformations and orientations, a substantial number of poses have finite interaction energies (Figure 4b).
Ligand sampling is sufficient for BPMF calculations to apparently converge (Figure 5). As the number of ligand conformations increases, the standard deviation of the BPMF decreases and, for the nine arbitrarily chosen systems in the figure, starts to level off at around 500 configurations. At this point, the standard deviations of the BPMFs range from 0.03 to 0.5 kcal/mol. For all 141 systems, bootstrapping analysis suggests that after 2000 configurations, standard deviation of the BPMFs are within 0.5 kcal/mol.
Figure 5.
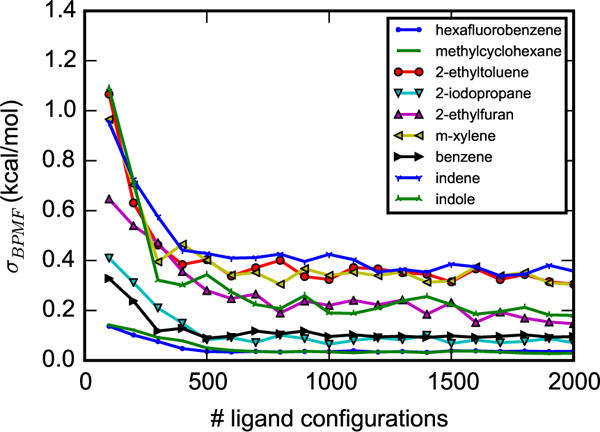
Convergence of BPMF calculations. Standard deviations (σBPMF) of BPMF calculations as a function of the number of ligand configurations, shown for nine arbitrarily chosen ligands. σBPMF are obtained by repeating the BPMF calculations 10 times, using different sets of ligand configurations. Figures S1 and S2 in the supplementary material show the bootstrapping estimate of σBPMF for all 141 ligands.
The main caveat of this analysis is that exponential averages such as Equation 2 are known to suffer from convergence issues due to conformational sampling limitations and finite sample bias66,67. As ligand conformations important to the holo ensemble may differ from those in the apo ensemble, many ligand conformations may be required to sample from the energetic minima in the holo ensemble. Moreover, a large number of samples may need to be sampled from within each minima in order to observe rare events that have the largest contribution to the exponential average. The established approach to address these issues of configuration space overlap and finite sample bias is to compute free energy differences between similar thermodynamic ensembles in an alchemical pathway. Comparison to the alchemical pathway method in AlGDock allows us to evaluate the severity of this approximation in FFT-based single-step perturbation.
FFT-based and AlGDock BPMF calculations are highly correlated but there is an error of 3.31 ± 0.21 kcal/mol (Figure 6). As seen in Figure 6b, much of the deviation from AlGDock stems from using a single-step perturbation instead of an alchemical pathway to obtain the gas-phase BPMF. Some error also results from the complex solvation free energy, but the ligand solvation free energies obtained are very consistent.
Figure 6.
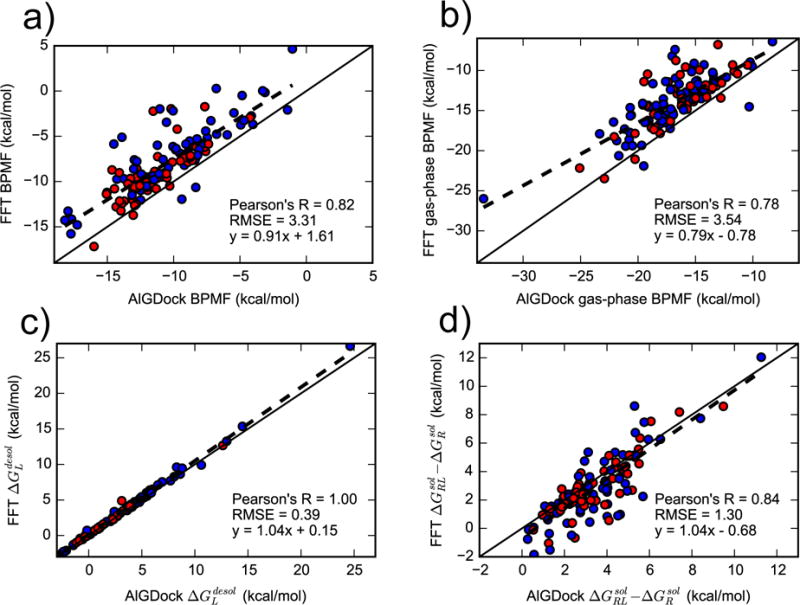
Comparing contributions to the BPMF from AlGDock (x-axis) and FFTΔG (y-axis). Contributions are for the (a) total BPMF in GBSA implicit solvent, (b) gas-phase BPMF, (c) ligand desolvation free energy, and (d) the difference between the complex and receptor solvation free energy. Active and inactive molecules are shown with red and blue markers, respectively.
FFTΔG is Consistent with YANK
The alchemical pathway method in YANK is our gold standard for standard binding free energies based on a specific force field. In Xie et al.33, YANK calculations were performed for 24 ligands binding to T4 lysozyme: 1-methylpyrrole, benzofuran, 4-ethyltoluene, allyl ethyl sulfide, benzene, hexafluorobenzene, indole, m-xylene, N-hexylbenzene, nitrobenzene, p-xylene, DL-camphor, 1-propanol, 1,1-diethylurea, 1,4-diiodobenzene, 1,2-diiodobenzene, 2-bromoethanol, 2-iodoethanol, benzyl alcohol, benzaldehyde oxime, phenol, ethanol, methanol, and dimethyl-sulfoxide.
There are multiple ways to combine interaction energies to estimate binding free energies. The simplest approach, which is akin to molecular docking, is to use the minimum interaction energy from all receptor structures as a free energy estimate. These results are highly correlated with YANK free energies, with a Pearson’s R of 0.90, but the slope is much greater than one and the RMSE is large, at 12.70 kcal/mol (Figure 7). Another approach is to use the minimum interaction energy as an approximation to the BPMF. In the context of ILT, this is known as the dominant state approximation32. The approach yields results that are highly correlated with YANK, but with large error. Using an exponential average of BPMFs estimated by the dominant state approximation instead of the minimum retains the high correlation with a reduction in RMSE. This performance is in line with expectations because it involves fewer approximations.
Figure 7.
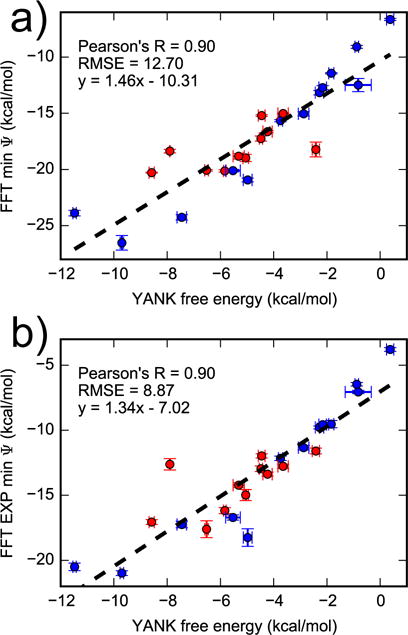
Comparing FFT minimum interaction energy with YANK free energy. The minimum interaction from multiple snapshots were combined by taking the (a) minimum or (b) exponential average. Active and inactive molecules are shown with red and blue markers, respectively.
Finally, the full FFTΔG procedure of using Equation 2 yields binding free energies that are highly correlated with YANK and have much smaller error (Figure 8 and Table 1). The RMSE for the full set of ligands ranges between 2.07 and 2.31 kcal/mol and Pearson’s R between 0.87 and 0.90 (with the exact value depending on the weighting scheme). The slope of the linear regression line is close to 1 (≈ 1.2). When considering only the 11 active ligands, the RMSE is only slightly different from the full data set but the Pearson’s R much lower and has greater uncertainty. This large uncertainty in the Pearson’s R likely results from the relatively small spread of free energies among active ligands. On the other hand, due to a large spread in YANK free energies of inactive ligands, the subset of 13 inactive ligands achieves even higher correlation (Pearson’s R ≈ 0.96) than the full set of 24 ligands.
Figure 8.
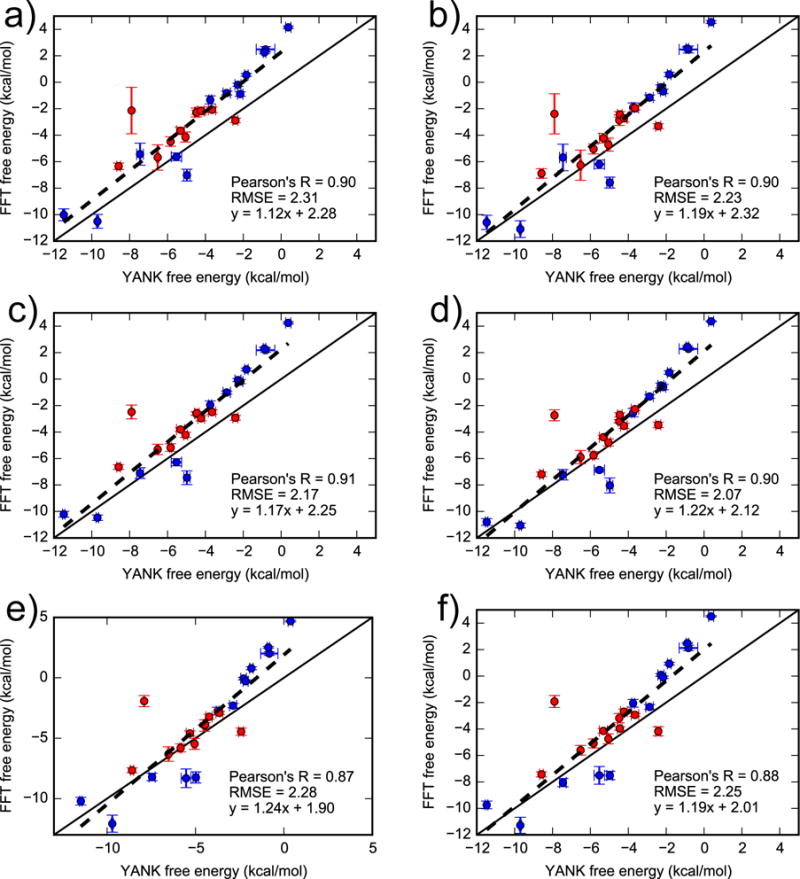
Comparing binding free energies for 24 ligands obtained using YANK (x-axis) and FFTΔG (y-axis). For the FFTΔG calculations, the grid spacing was 0.125 Å and grid size was 16 Å cubed, encompassing only the binding pocket. Active and inactive molecules are shown with red and blue markers, respectively. The labels (a) to (f) correspond to different weighting schemes, as defined in the main text. Error bars denote the standard deviation from three independent YANK calculations (x-axis) or from bootstrapping BPMFs (y-axis), with the range of error bars representing a single standard deviation. The solid line is y = x and the dashed line is a linear regression based on all data points. For a similar plot with a grid spacing of 0.25 Å, see Figure S4 in the supplementary material.
Table 1.
Comparing binding free energies for 24 ligands obtained using YANK and FFTΔG. The FFT-based free energies were calculated using different weighting schemes, as defined in the main text. RMSE is in units of kcal/mol.
| Full (24) | Active (11) | Inactive (13) | |||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Weighting scheme | Linear regression | RMSE | R | RMSE | R | RMSE | R |
|
| |||||||
| a | y = 1.12x + 2.28 | 2.31(0.28) | 0.90(0.06) | 2.35(0.57) | 0.59(0.21) | 2.28(0.24) | 0.96(0.02) |
| b | y = 1.19x + 2.32 | 2.23(0.31) | 0.90(0.06) | 2.09(0.54) | 0.58(0.18) | 2.34(0.26) | 0.96(0.02) |
| c | y = 1.17x + 2.25 | 2.17(0.28) | 0.91(0.05) | 2.09(0.59) | 0.62(0.13) | 2.24(0.26) | 0.96(0.02) |
| d | y = 1.22x + 2.11 | 2.07(0.29) | 0.90(0.06) | 1.86(0.60) | 0.59(0.13) | 2.24(0.28) | 0.96(0.03) |
| e | y = 1.24x + 1.90 | 2.28(0.37) | 0.87(0.07) | 1.99(0.84) | 0.38(0.23) | 2.50(0.30) | 0.94(0.03) |
| f | y = 1.19x + 2.01 | 2.25(0.32) | 0.88(0.07) | 2.08(0.74) | 0.41(0.19) | 2.39(0.27) | 0.94(0.03) |
A notable outlier is N-hexylbenzene, whose free energy is calculated to be around −2.5 and −8 kcal/mol by FFTΔG and YANK, respectively. N-hexylbenzene is the largest active ligand and possesses a long and flexible hydrocarbon chain. As it is difficult to sample the bound conformation of this chain from a simulation of the ligand by itself, its binding free energy is overestimated.
The performance of different weighting schemes are fairly similar to one another. Overall, weighting scheme (d) gives the lowest RMSE for the full set of ligands and sets containing only active or inactive ligands (see Tab. 1). However, the differences among weighting schemes in the present work are not significant due to the sizable error bars of the RMSE and Pearson’s R. To be consistent with Xie et al.33, who found that scheme (c) led to the greatest consistency between AlGDock (which uses an alchemical pathway to calculate BPMFs) and YANK (which uses an alchemical pathway to calculate standard binding free energies) results, we will hitherto use weighting scheme (c).
In recapitulating YANK, FFTΔG (which evaluates the gas-phase BPMF with a single-step perturbation) is less accurate than AlGDock (which evaluates it with an alchemical pathway). AlGDock yields RMSEs in the range 1.49 to 1.76 kcal/mol33. This reduction in accuracy may be linked to ligand being sampled only from the apo ensemble in the FFT approach as opposed to a thorough sampling from a series of alchemical states in AlGDock method35. With both methods, the slope of the linear regression compared to YANK is slightly greater than one, likely because we used the same receptor conformations and these conformations did not include those relevant to the weakest-binding ligands. This makes the weakest-binding ligands appear even weaker, leading to an increased slope.
Consistency with YANK requires a Diverse Set of Receptor Snapshots
The consistency between FFTΔG and the “gold standard” YANK free energy is sensitive to the choice of receptor snapshots. If only snapshots from a single alchemical simulation are used, there is generally a weaker correlation and larger RMSE (and uncertainty in the RMSE) compared to YANK (Table 2). However, there are exceptions. When only snapshots from alchemical simulations of T4 lysozyme in complex with p-xylene or (±)-camphor are used, FFTΔG gives rather strong correlation and relatively low RMSE compared to YANK. These two ligands are the second largest active and the largest inactive ligands, respectively. The quality of these calculations can be attributed to the fact that larger ligands tend to open up the binding pocket more widely and hence improve the FFT translational sampling of ligands. However, N-hexylbenzene, the largest active ligand with a long carbon chain, gives the worst FFT-based free energies. YANK simulations with this ligand may have induced a binding pocket shape that is unfavorable for binding to most of other ligands. These trends are consistent with our previous results33, although N-hexylbenzene snapshots did not perform as poorly when using AlGDock.
Table 2.
Correlation coefficients and RMSE of FFT free energies with respect to YANK. The FFT free energies were obtained using weighting scheme (c) and different sets of receptor snapshots, obtained from separate YANK simulations for T4 Lysozyme in complex with six different ligands (listed in the first column).
| Snapshots used in FFT calculations | Pearson’s R with respect to YANK | RMSE with respect to YANK (kcal/mol) |
|---|---|---|
| all 576 snapshots | 0.90 (0.06) | 2.07 (0.29) |
| 384 active snapshots | 0.79 (0.15) | 2.77 (0.72) |
| 1-methylpyrrole1 | 0.71 (0.11) | 5.38 (0.40) |
| benzene1 | 0.64 (0.12) | 5.44 (0.50) |
| p-xylene1 | 0.87 (0.05) | 2.50 (0.45) |
| phenol2 | 0.13 (0.20) | 6.93 (0.78) |
| N-hexylbenzene1 | 0.34 (0.25) | 7.77 (0.82) |
| (±)-camphor2 | 0.92 (0.04) | 2.77 (0.59) |
active
inactive
In contrast to Xie et al.33, using only snapshots from alchemical simulations of T4 lysozyme complexes with four active ligands (Tab. 2) results in worse consistency with respect to YANK than using all snapshots. This suggests that FFTΔG may require a larger set of receptor snapshots to obtain converged binding free energies, likely due to the large number of steric clashes.
FFTΔG Correlates with AlGDock
For 141 ligands, binding free energies based on FFTΔG and AlGDock, our standard BPMF calculation method, are highly correlated (Figure 9 and Figure S5 in the supplementary material). The RMSE for 140 ligands (excluding one ligand with high free energies) is 2.24 (0.13) kcal/mol and Pearson’s R is 0.82 (0.04). The subsets of 69 active and 71 inactive ligands maintain essentially the same level of consistency with AlGDock results with RMSE/Pearson’s R at 0.70 (0.08) / 2.23 (0.18) kcal/mol for active ligands and 0.86 (0.04) / 2.24 (0.19) kcal/mol for inactive ligands. For the full set of 141 ligands, the performance is similar (Figure S5 in the supplementary material). In the majority of deviations between the two estimates, FFTΔG has a higher value. The likely cause of these deviations is that the FFT-based procedure does not sample poses with sufficiently low interaction energies.
Figure 9.
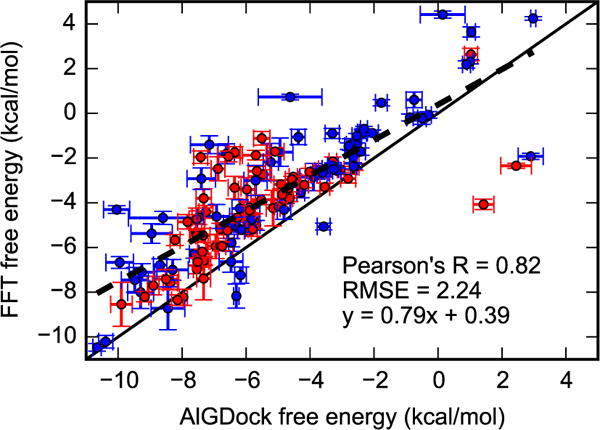
Binding free energies for 140 ligands estimated using AlGDock33 (x-axis) and FFT (y-axis) using weighting scheme (c). For FFT calculations, the grid spacing was 0.125 Å and grid size was 16 Å cubed, encompassing only the binding pocket. Active and inactive molecules are shown with red and blue markers, respectively. Error bars denote the standard deviation from bootstrapping BPMFs, with the range of error bars representing a single standard deviation. The solid line is y = x and the dashed line is the linear regression line. One ligand with high free energies, 1,2-benzenedithiol, is excluded from this plot but is included in Figure S5 in the supplementary material.
Using a larger grid spacing of 0.25 Å does not appear to have a significant effect on the accuracy of FFTΔG with respect to YANK, but reduces accuracy with respect to AlGDock (Figures S4 and S6 in the supplementary material). With respect to YANK, the Pearson’s R is not much lower and RMSE not much higher. However, accuracy is more sensitive to the weighting scheme. On the other hand, for the larger data set of 141 ligands, the Pearson’s R and RMSE with respect to AlGDock is 0.73 and 3.28 kcal/mol, respectively; the RMSE is slightly higher than with 0.125 Å grid spacing. Because interaction energies are fairly accurate at 0.25 Å grid spacing, the likely cause of the deviation is reduced sampling of translational positions.
The overall consistency with respect to YANK and AlGDock suggests that it is feasible to estimate protein-ligand binding free energies using FFTΔG.
FFTΔG Convergence Requires More Receptor Sampling than AlGDock
Compared to AlGDock, FFTΔG requires a greater number of receptor snapshots in order for ΔG° calculations to converge. If receptor snapshots are randomly selected, AlGDock requires about 200 snapshots in order for the free energy to converge33. In contrast, the Pearson’s R and RMSE values do not level off until about 400 snapshots processed by FFTΔG (red curves in Figure 10). When receptor snapshots are selected in the order of increasing the DOCK 6 scores, the convergence of Pearson’s R and RMSE is improved significantly (green curves in Figure 10). They all level off after about 100 snapshots. Nevertheless, the convergence of FFT method is still much slower that AlGDock33, which needs only a few snapshots to recover the best possible correlation and RMSE when snapshots were selected from lowest to highest docking scores. The best convergence can be achieved by selecting receptor snapshots in the order of increasing BPMF as shown by blue curves in Figure 10. These curves serve as an ideal unobtainable reference point because a priori, we do not know which snapshots in the set give lowest BPMFs unless we carry out the calculation for all of them. The convergence analysis done here and in Xie et al.33 suggest that it is better to use docking scores to sort out receptor snapshots before performing BPMF calculations. Convergence is likely worse with FFTΔG than with AlGDock because the ligand has no flexibility and must truly fit as a lock-and-key into the selected receptor conformations to obtain accurate free energies.
Figure 10.
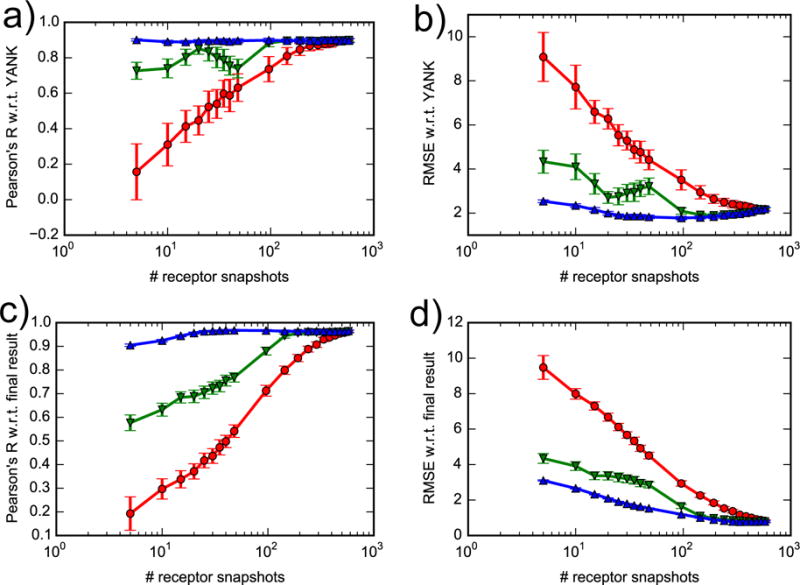
Convergence of free energy calculations. Correlation coefficient and RMSE of FFT free energies with respect to YANK (a, b) and to final result (c, d). Receptor snapshots were selected randomly (red line), with lowest docking scores (green line) or with lowest BPMFs (blue line).
FFTΔG is Consistent with Experiment
Binding free energy calculations based on FFTΔG are moderately consistent with experimental results (Figure 11), with similar but slightly worse performance than AlGDock. Isothermal titration calorimetry has been used to measure binding free energies between T4 lysozyme L99A and 21 active ligands50,54. Calculated binding free energies for iodine-containing ligands, as in Xie et al.33, were found to be highly overestimated. Therefore, iodobenzene was excluded from the present analysis (but is included in the supplementary material). The correlation of calculated and measured binding free energies is dependent on the solvent model. Comparing the results from the OBC2 model and experiment, the RMSE is 1.29 ± 0.14 kcal/mol, aRMSE is 1.08 ± 0.08 kcal/mol, and Pearson’s R is 0.49 ± 0.17. When the PBSA implicit solvent model is used, the RMSE is 3.42 ± 0.42 kcal/mol, aRMSE is 1.99 ± 0.28 kcal/mol, and Pearson’s R is 0.52 ± 0.19, which has slightly worse error but comparable correlation. For a point of comparison, Xie et al.33 used the PBSA implicit solvent model in AlGDock to attain a RMSE of 2.81 ± 0.32, aRMSE of 1.35 ± 0.27, and Pearson’s R of 0.65 ± 0.05. In both the present results and in Xie et al.33, the reason for the poor RMSE is that the PBSA model causes a positive shift in the estimated binding free energies.
Figure 11.
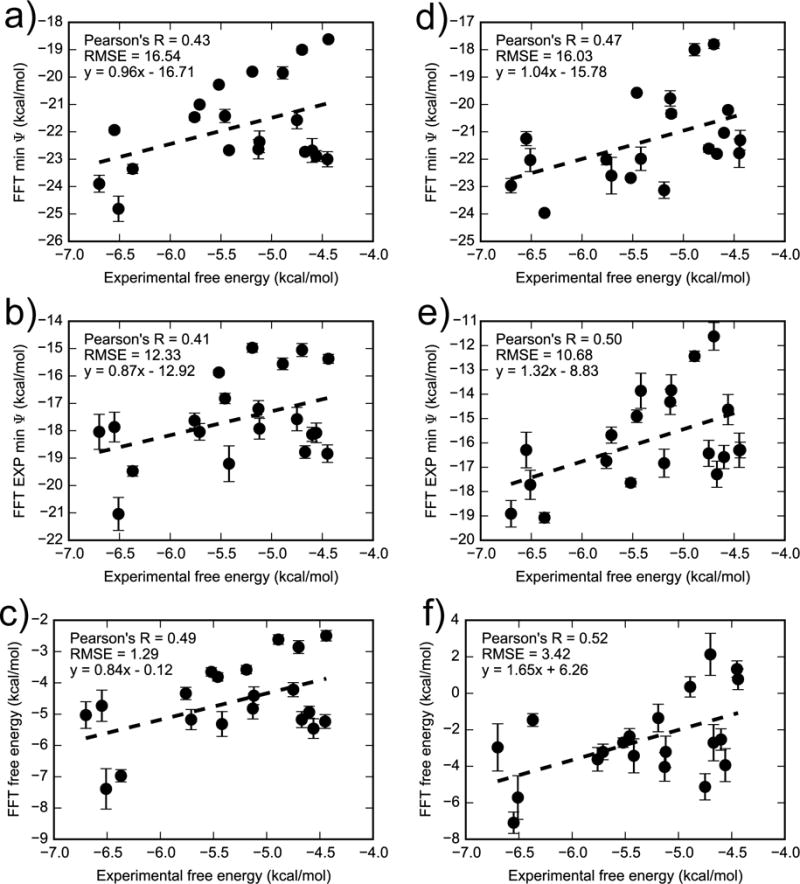
Comparing FFT free energy calculations in (a–c) OBC2 and (d–f) PBSA implicit solvent with experiment for 20 ligands excluding iodobenzene. The top row are minimum interaction energies for all receptor snapshots, middle row are the exponential average of the interaction energies, and bottom row are the full FFTΔG estimate. Note that each set of axes have different limits. Figure S7 in the supplementary material is similar but includes the outlier iodobenzene.
Using alternate estimators for the binding free energy increases the error but does not significantly reduce the correlation with experiment. The error is largest using the dominant state approximation, the minimum interaction energy, as the BPMF. Error is reduced by taking the exponential average of the minimum interaction energy, and is least with FFTΔG. These results are consistent with comparisons to YANK, where we found that these approximations also increase the error with respect to YANK calculations. They are also consistent with Nunes-Alves and Arantes68, who found that using the exponential average is no better than the minimum energy for T4 lysozyme. However, they found that in other, more complex systems, an exponential average was superior to the minimum interaction energy for reproducing experimental free energies.
We hypothesized that agreement with experiment could be improved by using a larger grid (62 Å on each side) to account for binding to alternative sites. This grid size encompasses the whole surface of the receptor. However, in spite of being more computationally demanding, the FFT calculations with large grid size do not lead to improved agreement with experiment (Figure 12). When the OBC2 solvent model is used, the Pearson’s R, RMSE, and aRMSE with respect to experiment are 0.43 ± 0.18), 2.30 ± 0.19 kcal/mol, and 1.04 ± 0.12 kcal/mol, respectively. When PBSA solvent model is used, the Pearson’s R slightly increases to 0.53 ± 0.13 but the RMSE becomes slightly larger, 3.50 ± 0.24 kcal/mol, and the aRMSE is 1.08 ± 0.16 kcal/mol. The lack of improvement in agreement with experiment suggests that weak binding of these ligands outside of the L99A cavity may not make a significant contribution to their binding free energy.
Figure 12.
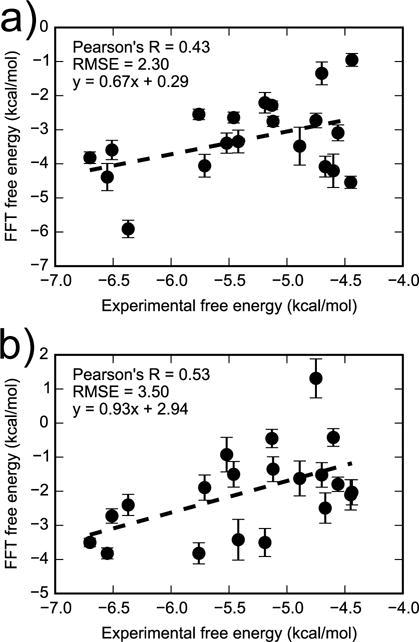
Comparing FFT free energies with experiment for 20 ligands excluding iodobenzene. The FFT free energies were estimated with large grid size (62 Å × 62 Å × 62 Å) in OBC2 (a) and PBSA (b) implicit solvents. Figure S8 in the supplementary material is similar but includes the outlier iodobenzene.
FFTΔG is a Slightly Better Binary Classifier than Molecular Docking
Binding free energy methods can also be used to predict whether a molecule is active or inactive against a target. Here we use receiver operating characteristic (ROC)69 curves, the area under the ROC curve (AUC), and the area under the semi-log ROC curve (AUlC) to assess the ability of FFT free energy calculations to discern active from inactive molecules. A ROC curve illustrates the fraction of true positives versus the fraction of false positives as the threshold separating two categories is changed. An ideal ROC consists of a vertical line from (0,0) to (0,1), and then a horizontal line from (0,1) to (1,1), meaning that all active molecules are more highly ranked than any inactive molecules. The AUC ranges from 0 for completely incorrect to 0.5 for random to 1 for completely correct classification. The intent of the AUlC70 metric is to emphasize top-ranked molecules, which are more likely to be pursued in subsequent experiments and calculations. For a random classifier, the AUlC is 0.14.
These different metrics show that DOCK 6 is essentially random, FFTΔG is slightly better, and AlGDock is the best binary classifier (Figure 13 and Table 3). With the OBC2 model, ROC curves of AlGDock and FFT methods (based on the minimum interaction energy or BPMF) are about the same and slightly better than DOCK 6. With the PBSA implicit solvent model, AlGDock has better, but FFTΔG has worse ROC curves. The relatively poor binary classification performance of FFTΔG with the PBSA implicit solvent model is consistent with its relatively poor correlation with experimental ΔG° measurements.
Figure 13.
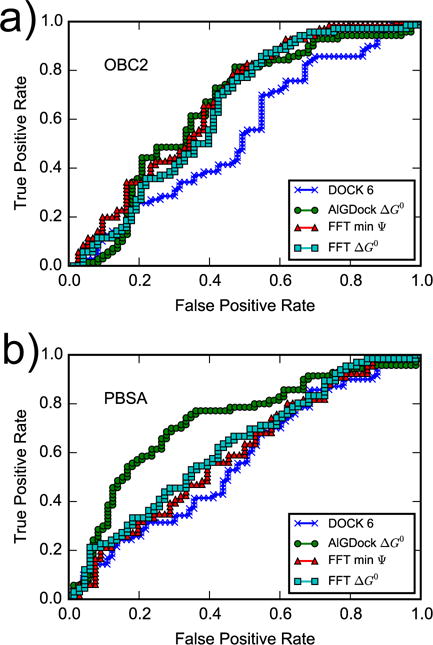
Receiver operating characteristic (ROC) curves for the DOCK 6 score, AlGDock ΔG°, FFT min Ψ, and FFT ΔG° calculated using the OBC2 (a) or PBSA (b) implicit solvent models.
Table 3.
AUC and AUlC of the ROC curves.
| OBC2 | PBSA | |||
|---|---|---|---|---|
|
| ||||
| Scoresa | AUC | AUlC | AUC | AUlC |
|
| ||||
| AlGDock ΔG° | 0.65 (0.05) | 0.18 (0.03) | 0.72 (0.04) | 0.26 (0.04) |
| FFT min Ψ | 0.67 (0.04) | 0.20 (0.03) | 0.60 (0.05) | 0.18 (0.04) |
| FFT ΔG° | 0.64 (0.05) | 0.18 (0.03) | 0.63 (0.05) | 0.21 (0.04) |
AUC and AUlC of Dock 6 are 0.53 (0.05) and 0.15 (0.02), respectively.
As observed in Xie et al.33, computing a binding free energy opposed to the minimum or mean interaction energy has no benefit to binary classification of active and inactive ligands to T4 lysozyme L99A. As the ligands for T4 lysozyme are small and relatively rigid, the entropic contribution to binding may not change much from ligand to ligand.
FFTΔG is Faster than AlGDock for Coarse and Small Grids
While FFTΔG is less accurate than AlGDock, its main potential benefit is speed. To compare the computational cost of FFTΔG and AlGDock, we carried out BPMF calculations for a small and a large ligand. Both methods basically consist of two steps: sampling and post-processing with implicit solvent. The post-processing step happens in the same way for both methods and expected to consume more or less the same amount of CPU time. Therefore we only compare timing for the sampling step. For the purposes of this comparison, we sampled the binding pose using AlGDock35 based on Hamiltonian replica exchange as previously described33 and in FFTΔG using random rotation and the cross-correlation.
Our benchmark calculations (Table 4) show that FFTΔG is faster than AlGDock for coarse (0.25 Å spacing) and small grids (16 Å on each edge) and is less sensitive to the ligand size. For a finer grid with 0.125 Å spacing, the speed of FFTΔG is comparable or slower than AlGDock. It is considerably slower for a large grid, but the comparison is unfair because the AlGDock calculation is restricted to smaller binding site opposed to the entire protein surface. One apparent advantage of the FFT approach is that it is less sensitive to the size of the ligand. That is, the larger ligand, N-hexylbenzene, requires approximately twice the amount of computer time with AlGDock, but takes around the same amount of time with FFTΔG. The reason that the calculations take about the same amount of time is that they depend on the number of ligand grid points, not the number of ligand atoms.
Table 4.
CPU time for gas phase BPMF calculations, in H:M:S format.
A comparison between FFTΔG and YANK is less meaningful because YANK calculations were performed on graphical processing units. As mentioned in Xie et al.33, each YANK calculation took about one week on a single graphical processing unit.
CONCLUSIONS
We have demonstrated that the FFT may be used to estimate standard binding free energies based on implicit ligand theory. To our knowledge, this is the first time that the FFT has been used to calculate noncovalent binding free energies. For the binding of T4 lysozyme to 141 small molecules, FFTΔG is less accurate than AlGDock (which uses an alchemical pathway instead of a single-step perturbation for the gas-phase BPMF) at reproducing YANK, less correlated with experiment, and less capable of classifying active and inactive molecules. With small grids, however, FFT-based sampling is considerably faster than AlGDock and less sensitive to ligand size.
For the T4 lysozyme complexes tested, we find that the free energy estimate has a lower RMSE but is not better correlated with experiment than approximations based on the minimum interaction energy. This suggests that the loss of entropy upon binding is fairly consistent among T4 lysozyme ligands with measured affinities.
Given the benefits and limitations of FFTΔG, the approach is mostly likely to be useful for larger chemical libraries than AlGDock. Virtual screening can be performed by first using FFTΔG on a large library. Subsequently, AlGDock may be used for a refined library with the greatest predicted affinity. Finally, a flexible-receptor technique such as YANK may be used on yet a smaller library prior to experimental validation.
Reflecting a niche of FFT-based docking, another possible use of FFTΔG may be for computing binding free energies between relatively inflexible fragments and a protein. The FFT is an efficient approach for translating the ligand across an entire protein surface. ILT provides a rigorous formalism for combining interaction energies from multiple sites into a single binding free energy.
Due to its relative insensitivity to the number of ligand atoms, FFTΔG is likely to be useful for larger ligands than AlGDock. However, FFTΔG may not be efficient if the large ligands are too flexible. Ultimately, another niche of FFTΔG may be the same as the present niche of FFT-based molecular docking: docking of folded protein domains to each other. In these cases, the ligands are large but relatively ordered; it may be feasible to recapitulate their flexibility with molecular dynamics simulations.
As a closing comment, we would like to point out a possible way to improve the scoring function of FFT-based docking methods. The current paradigm in FFT-based docking, as in other docking strategies, is to search for the configuration with the lowest interaction energy between binding partners. Once this position is obtained, all other interaction energies are ignored and the binding strength is scored solely based on the lowest value. We suggest an alternative approach that requires essentially no additional computational expense: following the approach of our present study, one may calculate an exponential average of the interaction energy and use the BPMF to score the strength of binding.
Supplementary Material
Acknowledgments
We thank Paula Bianca Viana Pinheiro for participating in this project as an undergraduate summer intern through the Brazil Scientific Mobility Program. We thank Robert “Wes” Ludwig and anonymous reviewers for suggestions on improving the clarity of the manuscript. We thank OpenEye scientific software for providing a free academic license to their software. Computer resources were provided by the Open Science Grid71. This research was supported by the National Institutes of Health (R15GM114781 to DDLM and R35GM118091 to HXZ).
Footnotes
Additional Supplementary Material may be found in the online version of this article. It includes a table with all 141 ligands. Also, it has figures comparing FFT-based vs direct interaction energies with a grid spacing of 0.8 Å, binding free energies for 24 ligands estimated using YANK and FFTΔG with a grid spacing of 0.25 Å, binding free energies for 141 ligands estimated using AlGDock and FFTΔG with grid spacings of 0.125 and 0.25 Å, and FFT free energy calculations with experiment for 21 ligands (including iodobenzene) for different grid sizes.
References
- 1.Dadarlat VM, Skeel RD. Biophys J. 2011;100:469. doi: 10.1016/j.bpj.2010.11.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cong X, Campomanes P, Kless A, Schapitz I. PLoS ONE. 2015;10:e0135998. doi: 10.1371/journal.pone.0135998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lee HS, Seok C, Im W. J Chem Theory Comput. 2015;11:1255. doi: 10.1021/ct5008907. [DOI] [PubMed] [Google Scholar]
- 4.Calabro G, Woods CJ, Powlesland F, Mey ASJS, Mulholland AJ, Michel J. J Phys Chem B. 2016;120:5340. doi: 10.1021/acs.jpcb.6b03296. [DOI] [PubMed] [Google Scholar]
- 5.Li Y, Nam K. Chem Sci. 2017;8:3453. doi: 10.1039/c7sc00055c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jorgensen WL. Science. 2004;303:1813. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 7.Michel J, Essex JW. J Comput-Aided Mol Des. 2010;24:639. doi: 10.1007/s10822-010-9363-3. [DOI] [PubMed] [Google Scholar]
- 8.Chodera JD, Mobley DL, Shirts MR, Dixon RW, Branson K, Pande VS. Curr Opin Struct Biol. 2011;21:150. doi: 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mobley DL, Klimovich PV. J Chem Phys. 2012;137:230901. doi: 10.1063/1.4769292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Parenti MD, Rastelli G. Biotechnol Adv. 2012;30:244. doi: 10.1016/j.biotechadv.2011.08.003. [DOI] [PubMed] [Google Scholar]
- 11.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys J. 1997;72:1047. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deng Y, Roux B. J Phys Chem B. 2009;113:2234. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bekker G-J, Kamiya N, Araki M, Fukuda I, Okuno Y, Nakamura H. J Chem Theory Comput. 2017;13:2389. doi: 10.1021/acs.jctc.6b01127. [DOI] [PubMed] [Google Scholar]
- 14.Heinzelmann G, Henriksen NM, Gilson MK. J Chem Theory Comput. 2017;13:3260. doi: 10.1021/acs.jctc.7b00275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gallicchio E, Lapelosa M, Levy RM. J Chem Theory Comput. 2010;6:2961. doi: 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang K, Chodera JD, Yang Y, Shirts MR. J Comput-Aided Mol Des. 2013;27:989. doi: 10.1007/s10822-013-9689-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Michel J, Essex JW. J Med Chem. 2008;51:6654. doi: 10.1021/jm800524s. [DOI] [PubMed] [Google Scholar]
- 18.Boyce SE, Mobley DL, Rocklin GJ, Graves AP, Dill KA, Shoichet BK. J Mol Biol. 2009;394:747. doi: 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ge X, Roux B. J Phys Chem B. 2010;114:9525. doi: 10.1021/jp100579y. [DOI] [PubMed] [Google Scholar]
- 20.Wang L, Berne BJ, Friesner RA. Proc Natl Acad Sci USA. 2012;109:1937. doi: 10.1073/pnas.1114017109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhu S, Travis SM, Elcock AH. J Chem Theory Comput. 2013;9:3151. doi: 10.1021/ct400104x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, Lupyan D, Robinson S, Dahlgren MK, Greenwood J, et al. J Am Chem Soc. 2015;137:2695. doi: 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- 23.Aldeghi M, Heifetz A, Bodkin MJ, Knapp S, Biggin PC. Chem Sci. 2016;7:207. doi: 10.1039/c5sc02678d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aldeghi M, Heifetz A, Bodkin MJ, Knapp S, Biggin PC. J Am Chem Soc. 2017;139:946. doi: 10.1021/jacs.6b11467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wan S, Bhati AP, Zasada SJ, Wall I, Green D, Bamborough P, Coveney PV. J Chem Theory Comput. 2017;13:784. doi: 10.1021/acs.jctc.6b00794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kong X, Brooks CL., III J Chem Phys. 1996;105:2414. [Google Scholar]
- 27.Knight JL, Brooks CL., III J Chem Theory Comput. 2011;7:2728. doi: 10.1021/ct200444f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hayes RL, Armacost KA, Vilseck JZ, Brooks CL., III J Phys Chem B. 2017;121:3626. doi: 10.1021/acs.jpcb.6b09656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mark AE, Xu Y, Liu H, Van Gunsteren WF. Acta Biochim Pol. 1995;42:525. [PubMed] [Google Scholar]
- 30.Oostenbrink C, van Gunsteren WF. Proc Natl Acad Sci USA. 2005;102:6750. doi: 10.1073/pnas.0407404102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Raman EP, Vanommeslaeghe K, Mackerell AD. J Chem Theory Comput. 2012;8:3513. doi: 10.1021/ct300088r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Minh DDL. J Chem Phys. 2012;137:104106. doi: 10.1063/1.4751284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Xie B, Nguyen TH, Minh DDL. J Chem Theory Comput. 2017;13:2930. doi: 10.1021/acs.jctc.6b01183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lim NM, Wang L, Abel R, Mobley DL. J Chem Theory Comput. 2016;12:4620. doi: 10.1021/acs.jctc.6b00532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Minh DDL. arXiv p. 1507.03703v1. 2015 [Google Scholar]
- 36.Katchalski-Katzir E, Shariv I, Eisenstein M, Friesem AA, Aflalo C, Vakser IA. Proc Natl Acad Sci USA. 1992;89:2195. doi: 10.1073/pnas.89.6.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gabb HA, Jackson RM, Sternberg MJE. J Mol Biol. 1997;272:106. doi: 10.1006/jmbi.1997.1203. [DOI] [PubMed] [Google Scholar]
- 38.Bliznyuk AA, Gready JE. J Comput Chem. 1999;20:983. doi: 10.1002/jcc.10122. [DOI] [PubMed] [Google Scholar]
- 39.Qin S, Zhou HX. J Chem Theory Comput. 2013;9:4633. doi: 10.1021/ct4005195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Qin S, Zhou HX. J Chem Theory Comput. 2014;10:2824. doi: 10.1021/ct5001878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ritchie DW, Kemp GJ. Proteins: Struct, Funct, Genet. 2000;39:178. [PubMed] [Google Scholar]
- 42.Mandell JG, Roberts VA, Pique ME, Kotlovyi V, Mitchell JC, Nelson E, Tsigelny I, Ten Eyck LF. Protein Eng. 2001;14:105. doi: 10.1093/protein/14.2.105. [DOI] [PubMed] [Google Scholar]
- 43.Chen R, Li L, Weng Z. Proteins: Struct, Funct, Genet. 2003;52:80. doi: 10.1002/prot.10389. [DOI] [PubMed] [Google Scholar]
- 44.Eisenstein M, Katchalski-Katzir E. C R Biol. 2004;327:409. doi: 10.1016/j.crvi.2004.03.006. [DOI] [PubMed] [Google Scholar]
- 45.Kozakov D, Brenke R, Comeau SR, Vajda S. Proteins: Struct, Funct, Bioinf. 2006;406:392. doi: 10.1002/prot.21117. [DOI] [PubMed] [Google Scholar]
- 46.Moal IH, Bates PA. Int J Mol Sci. 2010;11:3623. doi: 10.3390/ijms11103623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Brenke R, Kozakov D, Chuang GY, Beglov D, Hall D, Landon MR, Mattos C, Vajda S. Bioinformatics. 2009;25:621. doi: 10.1093/bioinformatics/btp036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ngan CH, Bohnuud T, Mottarella SE, Beglov D, Villar EA, Hall DR, Kozakov D, Vajda S. Nucleic Acids Res. 2012;40:W271. doi: 10.1093/nar/gks441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Morton A, Baase WA, Matthews BW. Biochemistry. 1995;34:8564. doi: 10.1021/bi00027a006. [DOI] [PubMed] [Google Scholar]
- 50.Morton A, Matthews BW. Biochemistry. 1995;34:8576. doi: 10.1021/bi00027a007. [DOI] [PubMed] [Google Scholar]
- 51.Su AI, Lorber DM, Weston GS, Baase WA, Matthews BW, Shoichet BK. Proteins: Struct, Funct, Genet. 2001;42:279. doi: 10.1002/1097-0134(20010201)42:2<279::aid-prot150>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 52.Wei BQ, Baase W, Weaver L, Matthews B, Shoichet BK. J Mol Biol. 2002;322:339. doi: 10.1016/s0022-2836(02)00777-5. [DOI] [PubMed] [Google Scholar]
- 53.Graves AP, Brenk R, Shoichet BK. J Med Chem. 2005;48:3714. doi: 10.1021/jm0491187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA. J Mol Biol. 2007;371:1118. doi: 10.1016/j.jmb.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Graves AP, Shivakumar DM, Boyce SE, Jacobson MP, Case DA, Shoichet BK. J Mol Biol. 2008;377:914. doi: 10.1016/j.jmb.2008.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Case D, Cerutti D, Cheatham ITE, Darden T, Duke R, Giese T, Gohlke H, Goetz A, Greene D, Homeyer N, et al. Amber. 2017;2017 [Google Scholar]
- 57.Swendsen RH, Wang JS. Phys Rev Lett. 1986;57:2607. doi: 10.1103/PhysRevLett.57.2607. [DOI] [PubMed] [Google Scholar]
- 58.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141. [Google Scholar]
- 59.Eastman P, Pande VS. Comput Sci Eng. 2010;12:34. doi: 10.1109/MCSE.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Eastman P, Friedrichs M, Chodera J. J Chem Theory Comput. 2013;9:461. doi: 10.1021/ct300857j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Pattabiraman N, Levitt M, Ferrin TE, Langridge R. J Comput Chem. 1985;6:432. [Google Scholar]
- 62.Meng EC, Shoichet BK, Kuntz ID. J Comput Chem. 1992;13:505. [Google Scholar]
- 63.Rabiner LR, Schafer RW. Digital Processing of Speech Signals. Prentice Hall; Upper Saddle River, NJ: 1978. [Google Scholar]
- 64.Onufriev A, Bashford D, Case DA. Proteins: Struct, Funct, Bioinf. 2004;55:383. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 65.Shirts MR, Chodera JD. J Chem Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wood RH, Muhlbauer WCF, Thompson PT. J Phys Chem. 1991;95:6670. [Google Scholar]
- 67.Zuckerman DM, Woolf TB. J Stat Phys. 2004;114:1303. [Google Scholar]
- 68.Nunes-Alves A, Arantes GM. J Chem Inf Model. 2014;54:2309. doi: 10.1021/ci500301s. [DOI] [PubMed] [Google Scholar]
- 69.Swets JA, Dawes RM, Monahan J. Sci Am. 2000;283:82. doi: 10.1038/scientificamerican1000-82. [DOI] [PubMed] [Google Scholar]
- 70.Mysinger MM, Shoichet BK. J Chem Inf Model. 2010;50:1561. doi: 10.1021/ci100214a. [DOI] [PubMed] [Google Scholar]
- 71.Pordes R, Petravick D, Kramer B, Olson D, Livny M, Roy A, Avery P, Blackburn K, Wenaus T, Würthwein F, et al. J Phys: Conf Ser. 2007;78:012057. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


