Choosing non-redundant representative subsets of protein sequence data sets using submodular optimization

Abstract

Selecting a non-redundant representative subset of sequences is a common step in many bioinformatics workflows, such as the creation of non-redundant training sets for sequence and structural models or selection of “operational taxonomic units” from metagenomics data. Previous methods for this task, such as CD-HIT, PISCES and UCLUST, apply a heuristic threshold-based algorithm that has no theoretical guarantees. We propose a new approach based on submodular optimization. Submodular optimization, a discrete analogue to continuous convex optimization, has been used with great success for other representative set selection problems. We demonstrate that the submodular optimization approach results in representative protein sequence subsets with greater structural diversity than sets chosen by existing methods, using as a gold standard the SCOPe library of protein domain structures. In this setting, submodular optimization consistently yields protein sequence subsets that include more SCOPe domain families than sets of the same size selected by competing approaches. We also show how the optimization framework allows us to design a mixture objective function that performs well for both large and small representative sets. The framework we describe is the best possible in polynomial time (under some assumptions), and it is flexible and intuitive because it applies a suite of generic methods to optimize one of a variety of objective functions.

1 Background

Redundancy is ubiquitous in biological sequence data sets, and this redundancy often impedes analysis. For example, because some proteins, such as those involved in disease or industrial applications, are studied by many more researchers than proteins with less important or unknown functions, protein sequence databases contain hundreds or thousands of slight variants of well-studied proteins and only one or a few copies of the sequences of less-studied proteins. Removing this redundancy has two benefits. First, doing so removes computational and statistical problems introduced by this redundancy. Second, members of a non-redundant set of sequences can be interpreted as representatives of the whole set, such as using sequences to represent species or “operational taxonomic units” in a metagenomics study¹.

Redundancy can be handled by selecting a representative subset of the original data set. A representative subset is a subset of sequences from the original data set that (1) minimizes the redundancy in the representative sequences, and (2) maximizes the representativeness of the subset; that is, every sequence in the full data set has at least one representative that is similar to it. The selected representative subset is then used in downstream analysis in place of the full data set. However, the task of choosing a high quality subset can be computationally challenging because finding the best representative subset out of N sequences requires, in principle, considering all 2^N possible subsets.

Many methods have been developed for the problem of finding a representative subset of a sequence data set^{2;3;4;5;6;7;8;9;10}, including the popular CD-HIT¹¹, PISCES¹² and UCLUST⁵ algorithms. These sequence selection methods are very widely used—for example, the CD-HIT papers have been cited a total of >3,000 times (Google Scholar)—and are a standard preprocessing step applied to data sets of protein sequences, cDNA sequences and microbial DNA. Additional methods have been proposed for the related problem of sequence clustering; see Related Methods below for a discussion of these methods and the distinction between clustering and representative set selection.

All of these existing methods (with the exception of some clustering methods) are based on the following Threshold algorithm (Supplementary Algorithm 1): start with an empty representative set; order the sequences by length; then, for each sequence v, add v to the representative set if no sequence currently in the set is more similar to v than some threshold (usually either 40% or 90% sequence identity). This algorithm was introduced in², which proposed it instead of the previous practice of selecting protein sequence data sets manually, and the algorithm was subsequently implemented in all of the sequence representative set selection methods referenced above. The algorithm was first motivated as reducing the redundancy of the reported set by aiming to solve the optimization problem

$${\text{maximize}}_{R\subset S}\mid R\mid \text{such}\text{that}\text{sim}(s_1,s_2)<\tau \text{for}\text{all}{s}_1,s_2\in R$$ (1)

for an input set of sequences S and threshold τ, and where sim(s₁, s₂) is the percent identity between s₁ and s₂. This optimization problem is sometimes known as the independent set problem. The algorithm is also sometimes motivated as maximizing the representativeness of the chosen set (for example in the case of metagenomics analysis¹) because Threshold guarantees that every input sequence will get a representative with identity no less than the threshold.

However, there is no theoretical reason to choose the Threshold algorithm over any other. In particular, this algorithm has two drawbacks. First, it ignores all similarities less than the specified threshold. This behavior can result in many pairs of representative sequences with similarities that are very close to the threshold (for example, pairs of sequences with 89% identity in the case of a 90% threshold). This behavior often occurs in practice (Results). Second, the Threshold algorithm makes no guarantees about the size of the identified representative set. The desired subset size usually depends on the downstream application of the representative set: if the user is interested in maximizing representativeness, they are usually interested in the smallest sufficiently-representative set. In contrast, if they are interested in minimizing redundancy, they are usually interested in the largest set without too much redundancy. In either case, Threshold can fail catastrophically. For example, consider a set of sequences {s₁, …, s_N}, in which the similarities between sequences 1 and i is greater than the threshold for i = 2…N and less for all other pairs. Further suppose that s₁ is slightly shorter than the other sequences. The smallest subset that represents the full data set is just {s₁}, whereas the threshold algorithm picks {s₂, …, s_N}. If the user was instead interested in maximizing the size of the set without including any pairs with similarity greater than the threshold, the opposite problem can occur: Suppose that s₁ is slightly longer than the other sequences. In that case, the best subset is {s₂, …, s_N}, but Threshold chooses just {s₁}. Here we argue that due to these two deficiencies, the widely-used Threshold algorithm is suboptimal.

In order to develop a better algorithm than Threshold, we are motivated by representative set selection methods from other fields based on submodular optimization. The class of submodular functions is analogous to the class of convex functions, in the sense that both classes of functions are amenable to optimization. Submodular functions, however, are defined over subsets of a given set of data items, whereas convex functions are defined over real-valued vectors. Submodular functions are those that satisfy the property of diminishing returns: If we think of a function f(R) as measuring the quality of a given representative subset R of a larger set of sequences S, then the submodular property means that the incremental “value” of a adding a sequence s to a given representative set R decreases as the size of R grows. (See Methods for a formal definition.) In many applications, it is common to search for a subset of maximal quality, as measured by a function f(R). The resulting optimization problem is hopelessly difficult for an arbitrary set function, but when the set function is submodular, the quality can be approximately maximized (i.e. the quality of the identified solution is a least constant factor times optimal) in low-order polynomial time^13;14;15 (Methods). Moreover, the approximation ratio achieved by these optimization algorithms are provably the best achievable in polynomial time, assuming P ≠ NP.

For these reasons, submodular optimization has a long history in economics^16;17, game theory^18;19, combinatorial optimization^20;21;22, electrical networks²³, and operations research²⁴. Furthermore, submodular optimization has recently been used with great success for selecting representative subsets of text documents ^25;26;27, recorded speech^28;29;30, machine translation³¹ and image analysis³², and we recently successfully applied it to the prioritization of genomics assays³³. However, submodular optimization is not yet widely used in sequence analysis.

In this work, we propose a principled framework for representative protein sequence subset selection using submodular optimization. This approach involves defining a submodular objective function that quantifies the desirable properties of a given subset of sequences, and then applying a submodular optimization algorithm to choose a representative subset that maximizes this function.

We have produced a software package, Repset, that implements this approach. Repset is implemented in Python and takes as input a fasta file, runs PSI-BLAST⁷ to compute pairwise similarities between sequences, runs submodular optimization, and outputs the chosen representative set. The number of PSI-BLAST iterations is configurable with an option; in this work we used a single iteration for efficiency, which is equivalent to standard BLAST. The package is configurable to support multiple objective functions and mixtures of functions. Moreover, the software is highly modular such that it can be modified to support a new submodular objective function simply by adding a new objective function object that implements a standard interface. The package is available at https://github.com/mlibbrecht/submodular_sequence_repset.

In the remainder of this paper, we demonstrate empirically that submodular optimization method does a better job of selecting representative protein sequence sets than competing methods, when evaluated relative to a protein structure gold standard. We also demonstrate how optimization-based method development offers practical advantages over an approach in which the algorithm and the property it tries to optimize (its objective function) are inextricably intertwined. In particular, we demonstrate how a hybrid optimization function allows us to design a method that excels at selecting both large and small representative sets. We also demonstrate how a hybrid function can allow the user to encourage the returned set to include long sequences.

Note that the task of representative subset selection is distinct from that of clustering. Clustering focuses on sets of similar sequences, whereas representative subset selection focuses on the individual sequences chosen to represent a larger set. (See Methods for a review of sequence clustering algorithms.) Applying these methods to representative subset selection requires specifying, in addition, a procedure for selecting an exemplar sequence from each cluster. In practice, clustering methods are rarely used for selecting representative sets of sequence data sets. Nonetheless, we empirically demonstrate below that our submodular selection approach outperforms several commonly used clustering algorithms.

2 Methods

2.1 Set notation

We use the following notation to handle sets. We use capital letters to denote sets and lowercase letters to denote items (i.e. sequences).

• {a, b, c} denotes a set with items a, b and c. ∅ is the empty set.

• A ∪ B is the union of A and B

• A \ B is the set of all items in A but not in B.

• a ∈ A is true when a is an item in A and false otherwise.

• A ⊂ B is true when A is a subset of B, and false otherwise. A ⊆ B is the same, but also true when the sets are identical.

2.2 Submodularity

The property of submodularity is important for the optimization of the set functions defined below. A submodular function³⁴ is defined as follows: given a finite set S = {s₁, s₂, …, s_n}, a discrete set function f : 2^S → ℝ is submodular if and only if:

$$f(A\cup (s))-f(A)\ge f(B\cup \{s\})-f(B),\forall A\subseteq B\subseteq S,s\notin B.$$ (2)

In other words, the incremental gain of adding sequence s to the set decreases when the set to which s is added to grows from A to B. Intuitively, most reasonable measures of the quality or “informativeness” of a set of items are submodular because the gain from adding a given item is reduced when the set already contains other items similar to it.

Two other properties of set functions are relevant to their optimization. First, a set function f is defined as monotone non-decreasing if

$$f(R\cup \{s\})-f(R)\ge 0,\forall v\in S\backslash R,R\subseteq S.$$ (3)

Second, we say that f is normalized if f(∅) = 0.

2.3 Similarity functions

The measures of subset quality described below are based on pairwise similarities of sequences. Such similarity measures are real-valued functions sim(r, s) defined on pairs of sequences. We considered two measures to quantify the similarity between a pair sequences: (1) the fraction of residues that match between the two sequences (fraction identical), and (2) the similarity measure used by the Rankprop method, defined as exp(–E-value/100)³⁵. Both measures have been used successfully in previous work on protein sequences, and can be calculated efficiently using an index-based method like BLAST³⁶. In both cases, we define the similarity between all pairs of sequences not reported by BLAST as 0. Note that, due to differing sequence lengths and amino acid content, both measures are not symmetric.

2.4 Subset quality measures

Let S be the full set of sequences and let sim(r, s) be a measure of similarity between a pair of sequences r, s ∈ S. A subset quality function is defined over subsets f(R), where R ⊆ S. In all cases, a higher value of the function is desired.

In this work we focus on two measures of the quality of a set of protein sequences. We chose these two functions because (1) they quantify the two qualitative criteria (minimizing redundancy and maximizing representativeness respectively) that we aimed to optimize, respectively, (2) they are both submodular, and (3) optimizing them resulted in the best performance on our performance metrics (Results). See Supplementary Note 1 for a discussion of other potential objective functions. The two functions are as follows.

First, we define the facility-location function as

$$f_{\text{facility-location}}(R)\triangleq \frac{1}{\mid S\mid }\sum _{s\in S}\underset{r\in R}{max}\text{sim}(s,r).$$ (4)

Intuitively, this function takes a high value when every sequence in S has at least one similar representative in R. This function is also the objective function of the k-medoids clustering method. The facility-location function is submodular, normalized and monotone non-decreasing.

Second, we define the sum-redundancy function as

$$f_{\text{sum-redundancy}}(R)\triangleq {\kappa }_{\text{sum}}-\sum _{r_1,r_2\in R}\text{sim}(r_1,r_2),$$ (5)

where κ_sum = Σ_a,b∈V sim(a, b). Intuitively, for sets R of a given size |R|, this function takes a very small value when R includes many pairs of similar sequences, and it takes a large value when all the sequences in R are very dissimilar from one another. In other words, the sum-redundancy function penalizes the redundancy in R. The sum-redundancy is submodular and normalized, but not monotone non-decreasing (in fact, it is monotone non-increasing).

2.5 Optimization algorithms

We are interested in choosing a subset of sequences R that maximizes a given measure of quality of the subset.

Maximizing an arbitrary set function in general requires considering all 2^|S| possible subsets and is therefore impractical for large sets of sequences. In fact, even when this set function is submodular, maximizing it exactly is NP-hard³⁷. However, fast approximation algorithms for submodular functions exist that find a solution that is guaranteed to be within a constant factor of optimal. In this work we apply the following two optimization algorithms.

The first algorithm is the Greedy algorithm (Supplementary Algorithm 2). At each iteration, this algorithm computes the difference in the objective function obtained by adding each sequence and adds the sequence with the largest difference. It turns out that when the objective function is submodular, monotone nondecreasing and normalized, this simple algorithm is guaranteed to produce a solution within a factor of 1 – 1/e ≈ 0.63 of optimal¹⁴. This is the best approximation ratio achievable in polynomial time unless P=NP³⁷.

The second algorithm is the BidirectionalGreedy algorithm (Supplementary Algorithm 3). This randomized algorithm maintains a “growing set”, which is initialized to the empty set, and a “shrinking set”, which is initialized to the full set. It considers each sequence s in turn, and either adds s to the growing set or removes it from the shrinking set randomly with probability proportional to the gain in the objective resulting from either change, respectively. At the end of the algorithm, it can be observed that the growing set and shrinking set are always identical; this set is returned. When the objective function is submodular and normalized (but not necessarily monotone nondecreasing), the mean of the objective values found over many randomized runs of this algorithm is guaranteed to be at least $\frac{1}{2}$ of optimal³⁸. This is the best approximation ratio achievable in polynomial time (independent of whether or not P=NP)³⁹. In theory, it is possible to optimize the results of BidirectionalGreedy by running it multiple times and choosing the best result. However, on our data sets, we found that the variance in performance due to the algorithms’ random choices was tiny relative to the difference between algorithms (likely indicating that many of the algorithm’s choices have independent effects), so in our experiments we ran the algorithm just once (Supplementary Figure 8).

We term the algorithm used by most previous sequence subset selection methods, including CD-HIT, UCLUST and PISCES, the Threshold algorithm (Supplementary Algorithm 1). This algorithm starts with an empty return set. It considers each sequence in decreasing order of sequence length, adding a given sequence to the return set if there is no sequence currently in the return set with similarity greater than some threshold τ. The value of τ controls the size of subset returned: a small τ results in a small set, while a large τ results in a large set.

In order to facilitate comparison, we implemented our own version of the threshold algorithm instead of using an existing implementation. The primary difference between our implementation and existing Threshold-based implementations (such as CD-HIT, PISCES and UCLUST) is that our implementation uses pre-computed BLAST alignments, while other Threshold-based methods use an on-the-fly index-based alignment method similar to BLAST. The main advantage of this on-the-fly method is that it does not require an expensive database construction preprocessing step. However, when comparing multiple methods on a single data set, it is much more efficient to perform a single alignment step. Using a single set of alignments also removes the possibility that artifactual differences in alignments (due to, for example, issues of numerical precision) could result in a difference in performance. Note that the on-the-fly method could in principle be used in the context of either the threshold method or submodular optimization. As expected, existing Threshold-based methods and our Threshold implementation all produce nearly identical subsets (Supplementary Figure 1).

2.6 Size of output representative set

In practice, the user often wants to control the number of sequences in the output representative set. We give the user control differently depending on the optimization method used. Greedy outputs an ordering s_o1 …s_on such that, for any size k, s_o1 …s_ok is the output subset of size k. Therefore a single run of MonotoneGreedy effectively outputs a representative subsets of all possible sizes.

In the case of BidirectionalGreedy, we add a term to the objective that is proportional to the size of the subset, scaled by a hyperparameter λ_size, and we optimize the unconstrained function

$$\text{maximize}f(R)+{\lambda }_{\text{size}}\mid R\mid .$$ (6)

The second term expresses a preference for a particular size of subset: a large value of λ_size results in a large output representative set; a small (or negative) value results in a small set. Similarly, Threshold takes as input a threshold hyperparameter τ, where a small τ results in a small set and a large τ results in a large set.

In the case of BidirectionalGreedy and Threshold, the user may control size either by directly inputting a hyperparameter value (λ_size or τ, respectively) or by specifying a desired representative set size (or range of sizes) and performing binary search on the hyperparameter space. The former, direct method is most commonly used in practice by existing Threshold-based methods.

This binary search procedure is expensive because it requires running the respective optimization method multiple times. Specifically, if we let input min and input max be the minimum and maximum possible hyperparameter values and output_min and output_max be the minimum and maximum hyperparameter value that yield representative sets in the desired range of sizes, then the number of binary search iterations grows according to $O(log\frac{\text{input}\_\text{range}}{\text{output}\_\text{range}})$. In practice, we do not know the value of output_range. However, in the reasonable case that the representative set size is linear in the hyperparameter and the tolerance in desired size grows linearly as a function of the input database size, then output_range is constant as a function of database size. In fact, in practice, we found that binary search usually converged in 5–10 iterations independent of database size for both BidirectionalGreedy and Threshold (Supplementary Figure 9).

Alternatively, the user may want to use some other statistic of the returned representative set to control its size. For example, the user may want to return a set such that the average similarity between each sequence in the input set and its most-similar representative is no less than a particular value. Any such statistic can be controlled in the same way as above. For Greedy, we run the algorithm once to produce an ordering, then calculate the statistic each subset of increasing size and choose the size that achieves the required value for the statistic. For Bidirectional or Threshold, we perform binary search on the desired statistic instead of the subset size.

2.7 Running time

The asymptotic running times of the algorithms in question are as follows. Let n be the number of sequences in the input database; let k be the number of sequences in the output representative set (k = n in the worst case); let d be average the number of neighbor sequences with nonzero similarity to any given sequence (i.e. the average degree of the similarity graph); and let diff_f be the running time to compute f(R∪{v})–f(R). Greedy has a worst-case running time of O(kn diff_f). Bidirectional has a worst-case running time of O(n diff_f). Threshold has a worst-case running time of O(kd). For the sum-redundancy function, it is easy to see that diff_{fsum-redundancy} = O ( d). For the facility-location function diff_{ffacility-location} for an arbitrary A and v is O(nd). However, we can speed up optimization over the facility-location function by caching the value, for each s, of max_r∈R sim(s, r), for a fixed R that is updated once per iteration. It is easy to see that, given this cache, diff_{ffacility-location} = O ( d). (This cost includes the time to update the cache.)

Greedy has the most expensive worst-case running time; however, it can be sped up significantly in several ways. First, observe that the submodular property guarantees that, if adding a sequence v to A would result in a difference of d in the objective, then adding v to a larger set A ∪ B will result in an objective difference d′ ≤ d. This property allows the algorithm to skip considering many sequences in each iteration, and in practice has been observed to improve running time by many orders of magnitude¹⁵.

Second, two strategies allow us to trade off performance and running time for Greedy. The first strategy, called StochasticGreedy, evaluates the gain in objective on a random subset of sequences T at each iteration, rather than the full set S⁴⁰. It turns out that StochasticGreedy has an expected approximation ratio of 1 – 1/e – ε (compared to 1 – 1/e ≈ 0.63 for Greedy), where |T| = (n/k)log(1/ε). Stochastic-Greedy has a worst-case running time of $O(nlog\frac{1}{\epsilon }\text{diff})$. The second strategy, called ApproxGreedy, adds a sequence v to A if it can guarantee that f(A ∪ {v}) – f(A) ≥ β(f(A ∪ {v}) – f(A)) for some user-specified tolerance β⁴¹. This allows the algorithm to skip considering some sequences at each iteration (more so than using only the strategy described in the previous paragraph). ApproxGreedy has an expected approximation ratio of 1 – exp(–β). ApproxGreedy has the same worst-case running time as Greedy but is much faster in practice (Results).

2.8 Related methods

Threshold-based methods

As mentioned above, the most widely-used methods for selecting representative subsets of sequence data sets are based on the Threshold algorithm. This method was first proposed by², which proposed it instead of the previous practice of selecting protein sequence data sets manually. Currently, the most widely-used representative subset methods are CD-HIT¹¹, PISCES¹² and UCLUST⁵. PISCES is primarily applied to protein sequences, and supports filtering according to structural quality criteria. CD-HIT and UCLUST are applied to both nucleotide and protein sequences; they differ from previous Threshold-based methods in their methods for computing sequence similarities. A large number of other Threshold-based methods have also been proposed^{2;3;4;5;6;7;8;9;42}.

Clustering methods

A large number of methods have been proposed for protein sequence clustering, including those based on Markov clustering⁴³, connected component detection⁸, generative modeling⁴⁴, minimal spanning trees⁴⁵, clique detection⁴⁶, and spectral clustering⁴⁷. As discussed above, clustering methods are rarely used for selecting representative sets of sequence data sets.

Baseline methods

Two intuitive methods for choosing representative sets turn out to be special cases of the submodular optimization approach. First, the popular clustering algorithm k-medoids++⁴⁸ is identical to optimizing a facility-location function with MonotoneGreedy. Second, optimizing a sum-redundancy function with MonotoneGreedy is identical to the following heuristic: Start with an empty representative set; at each iteration, choose the sequence with the least sum of similarity to the sequences in the representative set.

2.9 Protein sequence data

To test these methods, we downloaded the full Structural Classification Of Proteins–extended (SCOPe) database version 2.04 from http://scop.berkeley.edu⁴⁹. SCOPe is a hierarchical structural classification database, consisting of four levels with increasing granularity: class, fold, superfamily, and family. In this work, we focus primarily on the family and superfamily levels because these represent a reasonable level of granularity for subset selection.

We also downloaded the ASTRAL database from http://scop.berkeley.edu⁵⁰. ASTRAL is a database of protein domain sequences, some of which are associated with SCOPe categories. We used only ATOM-derived sequence records, and we chose the subset of ASTRAL sequences that are associated with a SCOPe family, removing eight sequences that were labeled with multiple SCOPe families. This resulted in a set of 78,048 sequences.

We also downloaded the results from all-by-all BLAST on the ASTRAL sequences from http://scop.berkeley.edu. BLAST was run using the command line blastpgp -d DBNAME -i SEQ.fa -j 1 -h 1e-2 -v 5000 -b 5000 -a2 -z 100000000 -J T -O OUTPUT. This results in all pairwise relationships with an E-value less than 0.01, where the similarity of each pair is measured by an E-value and a fraction sequence identity.

In order to avoid overfitting to SCOPe, we performed all development (such as testing our implementation, and choosing hyperparameters) on just the 16,880 ASTRAL sequences with the SCOPe Class “All beta proteins.” Note that we opted to use a single SCOPe class rather than a random subset of all classes, because we expect a random subset to exhibit very different redundancy properties than the full set. In particular, a random subset is likely to have much less redundancy than the full set because, if the full set has a pair of similar sequences, then the random subset is likely to include just one of the pair. We applied our methods to all of ASTRAL only after we had settled on which experiments to perform.

3 Results

3.1 An example illustrates how a subset can be representative of the whole data set

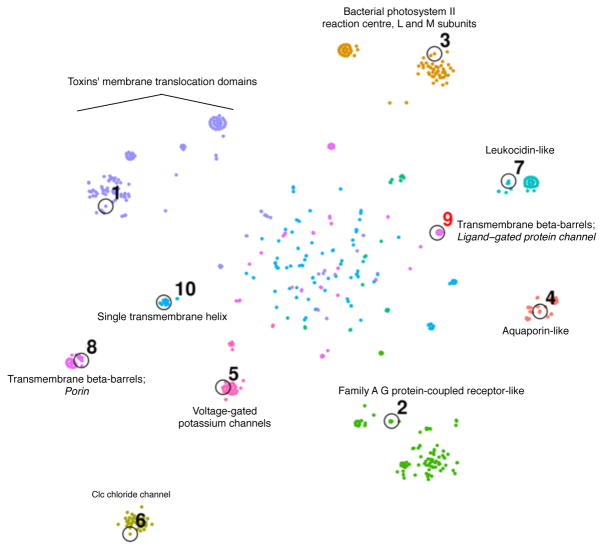
To illustrate this approach, we applied our submodular optimization framework to protein domain sequences drawn from a single class (“Membrane and cell surface proteins and peptides”) within the Structural Classification of Proteins—extended (SCOPe) database⁴⁹. The availability of protein structures provide an orthogonal gold standard for judging the quality of a given representative subset. The results (Figure 1) suggest that the submodular approach does a good job of selecting protein sequences with diverse structural properties. In particular, among the nine folds that comprise our selected class, the submodular method successively chooses one exemplar sequence from each fold before selecting two sequences from the same fold. The only exception is that the method chooses two “transmembrane beta-barrel” protein domains before selecting the first “single transmembrane helix” domain; however, as illustrated in Figure 1, this choice is not particularly surprising, given that the “transmembrane beta-barrel” fold is comprised of two superfamilies with quite different structural properties. These results of this qualitative analysis were similar for most methods we tried, so we turned to quantitative analysis to compare different methods.

Figure 1. Protein sequence representative set selection.

Points represent protein sequences, projected into 2D based on their pairwise similarities according to BLAST using t-SNE⁵³. All sequences are depicted from the SCOPe Class “Membrane and cell surface proteins and peptides.” Color with text labels indicates SCOPe fold, and italicized text indicates SCOPe family within a given fold. Black circles indicate the top ten representative sequences chosen by the greedy algorithm on a mixture of facility-location (Rankprop sim; 0.5 weight) and sum-redundancy (percent ID sim; 0.5 weight). Numbers labeling these circles indicate choice order. Choice #9 is colored red because it is the second chosen sequence within the same fold. To produce the 2D embedding, we first computed a n × n pairwise distance matrix (for a set of n sequences) with the formula: distance(i, j) = 1 – percent id(i, j)/100. We used multidimensional scaling (MDS) to project this distance matrix to a 30 × n feature matrix. This MDS preprocessing step is similar to the standard preprocessing step used by t-SNE that applies principle component analysis (PCA) to project a high-dimensional feature matrix to a 30 × n feature matrix⁵³. We used t-SNE to project this 30 × n matrix into a 2 × n matrix, which is plotted. The diffuse points in the center are a common feature of t-SNE plots, and are a consequence of the algorithm imperfectly recapitulating the n-dimensional similarity matrix in two dimensions.

3.2 Submodular optimization can effectively minimize redundancy and maximize representativeness in sequence data sets

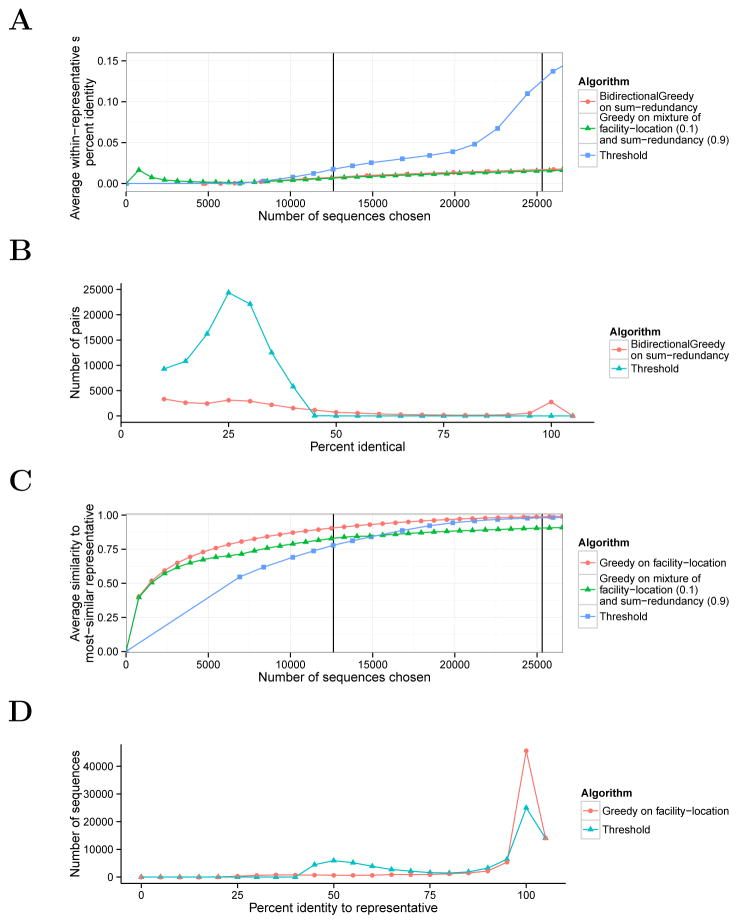
To evaluate how well submodular optimization can remove redundancy in protein sequence data sets, we applied it to sequences from the ASTRAL database (Methods). We used the sum-redundancy function to quantify redundancy; this function measures the total amount of identity within a given representative set (Methods). Applying submodular optimization methods to this function produced representative subsets with less redundancy than those generated by the existing Threshold method (Figure 2A). For small sets (12,614 sequences, the size chosen by Threshold at 40%), the set chosen by Threshold has an average pairwise identity of about 1.5%, while the set chosen by BidirectionalGreedy is somewhat less redundant, at 0.8%. The effect is more dramatic for large sets (25,310 sequences, 90% threshold); in this case, Threshold’s chosen set has 12.6% average redundancy while BidirectionalGreedy’s has just 1.7%. This improvement is expected, because the submodular optimization approach explicitly aims to optimize this quantity. The improvement primarily comes from the fact that the threshold method chooses many pairs of sequences with identity just under the threshold, whereas optimizing sum-redundancy results in choosing very few sequences with any detectable identity at the cost of choosing a small number of closely-related pairs (Figure 2B).

Figure 2. Redundancy and representativeness of chosen representative sets.

(A) Redundancy as a function of set size. The vertical axis is calculated for a representative set R as 1/(|R|(|R| – 1)/2)Σ_r1,r2∈R sim(r₁, r₂), where sim(r₁, r₂) is percent identity. Vertical lines correspond to the sizes of subsets selected by Threshold using 40% and 90% sequence identity thresholds. (B) Histogram of pairwise identity. Vertical axis indicates the number of pairs of sequences with a given percent identity bin within size-12,614 representative chosen by each algorithm. (We chose this size because Threshold chooses this size with a 40% threshold.) The histogram omits the column corresponding to 0 percent identity, as the vast majority of pairs fall into this category. (C) Representativeness as a function of set size. Same as (A), but the vertical axis for a representative set R is: $(1/\mid R\mid )\frac{1}{\mid S\mid }{\sum }_{s\in S}{max}_{r\in R}\text{sim}(s,r)$, where sim(s, r) is percent identity. (D) Histogram of representation. Same as (B), except histogram is defined over the similarity of each sequence to its nearest representative (for a given s, max_r∈R sim(s, r).

As a control, we additionally evaluated random subsets and found that both Threshold and submodular optimization reduced redundancy far more than could be achieved by chance (Supplementary Figure 12).

We similarly found that submodular optimization could effectively maximize representativeness (Figure 2C). We used the facility-location function to quantify representativeness; this function measures the similarity of each sequence in the original database (ground set) to its nearest representative in the chosen set. For small representative sets (12,614), the idenity of the average sequence in the ground set to its nearest representative was just 77.9% in Threshold’s representative set, compared to 90.6% in Greedy’s set. For large sets (25,310), these quantities were 98.0% for Threshold and 98.8% for Greedy, again showing a small advantage to the submodular optimization approach. Again, it is not surprising that the submodular approach performs well, because it is specifically optimizing this quantity. The improvement primarily comes from the fact that Threshold assigns many sequences a representative with identity that is just over the threshold, whereas optimizing facility-location results in choosing a very-similar representative for almost every sequence, at the cost of leaving a few sequences with only a distant representative (Figure 2D).

3.3 Representative subsets chosen by submodular optimization exhibit high structural diversity

In order to evaluate the quality of a subset of sequences independently of a specific objective function, we compared these subsets to the Structural Classification Of Proteins–extended (SCOPe) database. SCOPe contains 78,048 protein domain sequences, each assigned to one of 4,994 protein families. These assignments are based on experimentally determined protein structures, so they are independent from the sequence-based information used by the optimization methods. Intuitively, a good representative subset should include one sequence from each family, whereas a poor subset may include many sequences from the same family while leaving other families with no representatives. Therefore, we defined the quality of a subset as the number of SCOPe protein families with at least one sequence from that family in the subset.

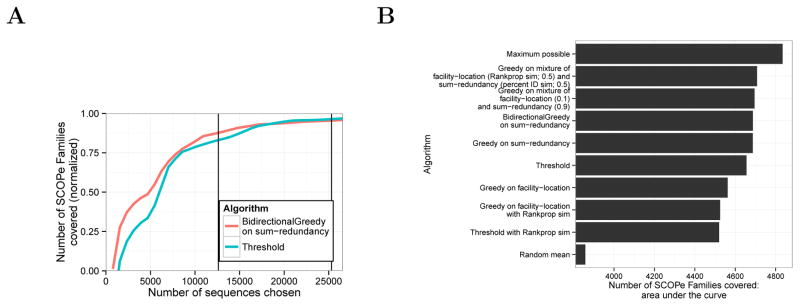
Among the three submodular objective functions that we considered, we found that optimizing the sumredundancy function produced the best results on this evaluation metric. Our evaluation considered 12 possible approaches: two submodular optimization algorithms on three different objective functions, each computed using two different measures of sequence similarity (Supplementary Figure 7). To avoid overfitting to SCOPe, we performed all development and comparison of objective functions on a subset of the data (~21%) and applied only the best method to the full data set (Methods). We found that optimizing sum-redundancy with BidirectionalGreedy results in much better coverage of SCOPe families than Threshold (Figure 3). For small representative sets (12,614 sequences, the size chosen by Threshold at 40%), the set chosen by submodular optimization leaves 27% fewer SCOPe families uncovered (276 compared with 379) than the threshold method does. The two methods perform about the same on large subsets (25,310 sequences, 90% threshold), with Threshold and the submodular approach leaving 48 and 59 uncovered respectively. We reached a similar conclusion when performing the evaluation on SCOPe superfamilies and folds rather than families (Supplementary Figures 2–7).

Figure 3. Coverage of SCOPe families.

(A) The vertical axis indicates is the number of families with at least one representative, normalized to the range [0, 1] using the formula $f^{\prime }(x)=\frac{f(x)-E(x)}{M(x)-E(x)}$, where x is a subset size, f(x) is the value for the method in question on that subset size, E(x) is expected (random mean) and M(x) is maximum possible (defined as M(x) = x if x < F, and M(x) = F otherwise, where F = 4,994 is the total number of SCOPe families). Vertical lines correspond to the sizes of subsets selected by Threshold using 40% and 90% sequence identity thresholds. (B) Area under the curve comparison. Horizontal axis indicates area under the “family” coverage curve, calculated as follows. Let V be the full set of sequences, i ∈ 1 …|V | be a subset size, m be a particular method, $A_i^{(m)}$ be the subset of size i chosen by m, and f(A) be the number of SCOPe Families covered by A. $\text{Area under}\text{the curve}=\frac{1}{\mid V\mid }{\sum }_{i=1}^{\mid V\mid }f(A_i^{(m)})$. Bars indicate selection algorithms, ordered by their area under the curve. For subset sizes for which we did not compute a subset, f() is imputed with linear interpolation.

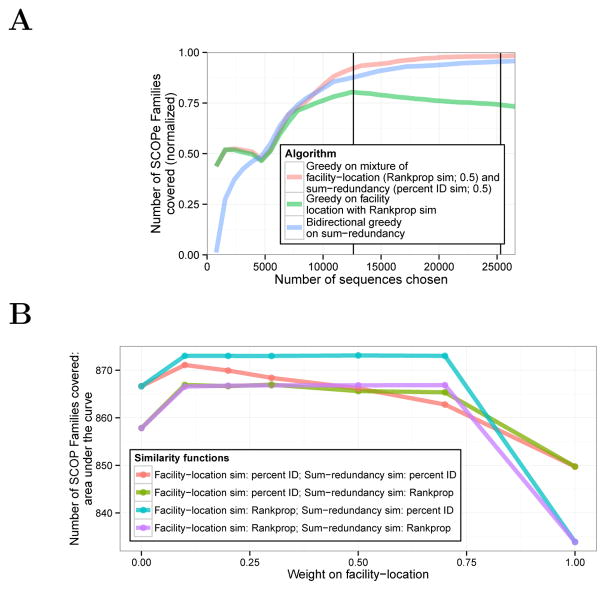
3.4 A mixture of submodular objective functions outperforms any single component objective

Although optimizing sum-redundancy performs best on the SCOPe-based evaluation metric for large subsets, we found that optimizing a different function resulted in better performance for very small subsets (<5,000 sequences; Figure 4A). Specifically, this good performance resulted from optimizing the facility-location function using the similarity function used by the Rankprop method³⁵ that takes into account the statistical confidence of an alignment, instead of percent identity (Methods). This observation suggests that sum-redundancy with the percent identical similarity metric and facility-location with the Rankprop similarity metric may provide different types of information. To test this hypothesis we defined a mixture objective function

Figure 4. Optimizing a mixture of objective functions.

(A) Same as 3A, but including mixture objectives. (B) Comparison of mixture weights. Each mixture objective is a combination of facility-location and sum-redundancy objectives, each with either a percent ID or Rankprop similarity function. Horizontal axis indicates weight on facility-location (weight on sum-redundancy equals one minus the weight on facility-location). Line color indicates mixture objective. Vertical axis indicates area under the curve for SCOPe family coverage (see Supplementary Figure 4). To avoid overfitting, the statistics in (B) were computed on the subset of sequences with the SCOPe Class “All beta proteins”.

$$f_{\text{mix}}(R)={\lambda }_{\text{mix}}{f}_{\text{facility-location}}(R)+(1-{\lambda }_{\text{mix}})f_{\text{sum-redundancy}}(R).$$ (7)

We optimized a mixed objective function using the greedy algorithm and evaluated the resulting representative subsets against the SCOPe evaluation metric. Indeed, we found that this mixture performed much better on SCOPe coverage than either function individually, both for small and large subsets (Figure 4A). Moreover, this performance is quite insensitive to mixture weight (Figure 4B). These results show that a mixture of objective functions can better represent the quantity of interest than a single function. This demonstrates a significant advantage of the submodular optimization framework: optimizing mixtures of objective functions is very natural using this framework, but would be very difficult to achieve in a non-optimization-based framework such as Threshold.

3.5 Representative subset selection methods perform better than repurposed clustering methods

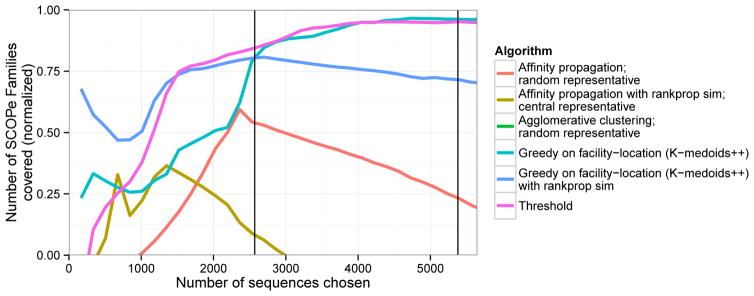
An alternative to applying a representative subset selection method is to apply a clustering method and then choose a representative from each identified cluster. Using the SCOPe evaluation metric, we compared representative subset selection using submodular optimization to eight variants of this clustering-based approach. We compared two similarity functions: percent identity and Rankprop; three clustering methods: k-medoids++⁴⁸, affinity propagation⁵¹ and agglomerative hierarchical clustering; and two methods for choosing a representative from each cluster: “random” and “central”. Central representative selection chooses the cluster member with the highest total similarity to the other cluster members (i.e. it optimizes a facility-location objective for a single item). Random representative selection chooses a random member. Note that k-medoids++ is identical to optimizing facility-location with the submodular greedy algorithm.

We found that none of these clustering methods performed as well as either the submodular optimization-based methods or the threshold heuristic (Figure 5 and Supplementary Figure 7). The exception, as noted above, is that optimizing facility-location with the Rankprop similarity metric performs well for small representative sets. This is likely because clustering methods aim to optimize the quality of the entire cluster, whereas representative set selection methods focus solely on identifying good representatives.

Figure 5. Performance of clustering methods repurposed for representative set selection.

Plot is same as Figure 3, but includes clustering-based methods instead of submodular optimization-based. Results are computed on our development set, composed of the subset of the data (~21%) with the SCOPe Class “All beta proteins”.

3.6 The submodular optimization framework enables simultaneously optimizing for multiple criteria

Because sequence databases often contain both full-length protein sequences as well as fragments of the same protein, it is sometimes desirable to encourage a representative set to include long sequences where possible. Indeed, most methods based on the Threshold algorithm sort sequences by length first in order to give a preference to longer sequences. We found that, even though the submodular optimization method does not have this preference, the returned subsets have comparable average sequence length to those from the threshold algorithm (Figure 6), likely because both algorithms primarily focus on reducing redundancy. However, if a user has a strong preference for longer sequences, the submodular optimization framework provides a naturable and flexible way to achieve this goal. To demonstrate this flexibility, we ran submodular optimization on the following mixture of objective functions:

$$\text{maximize}(1-{\lambda }_{\text{length}})f_{\text{sum-redundancy}}(R)+{\lambda }_{\text{length}}\sum _{r\in R}\text{length}(r),$$ (8)

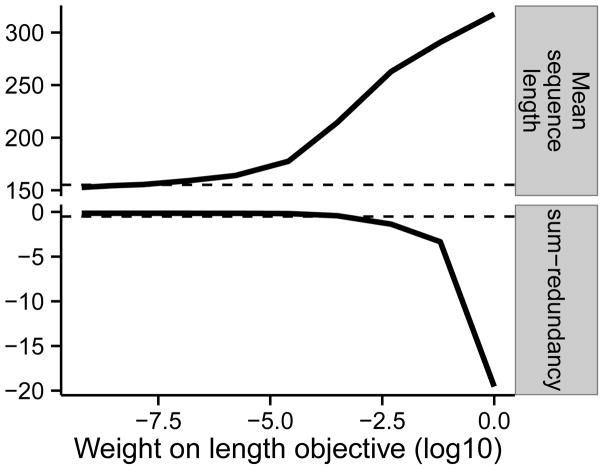
where λ_length is a hyperparameter that determines the relative weight of the two terms. The second term adds a preference for the representative set to contain long sequences. It is easy to show that, because the first term is submodular and the second term adds a constant value for each sequence in A (functions with this property are known as modular functions), this objective function is submodular as well. As expected, performing optimization in the presence of the second term results in representative sequences with longer average length, at the cost of a small increase in redundancy (Figure 6). For example, setting λ = 0.1 results in choosing sequences that are 72% longer (mean length 262.9 aa compared to 152.7 aa) and increases the average pairwise identity from 0.29% to 2.6%. This example demonstrates how the submodular optimization framework allows the user to optimize for a variety of criteria simply by tweaking the objective function; such multi-criterion optimization is not possible when using a fixed algorithm such as Threshold.

Figure 6. Simultaneously minimizing redundancy and maximizing sequence length.

Horizontal axis indicates weight on length term λ from Equation 8. The sum-redundancy values are scaled by a factor of 10⁵ to improve legibility. Dashed lines indicate performance by the threshold algorithm. Results are computed on our development set, composed of the subset of the data (~21%) with the SCOPe class “All beta proteins”. Results are for representative sets of size 3222 (size chosen by Threshold at 40% on the development set).

3.7 A modified submodular approach can ensure that every input sequence is represented

We showed above that optimizing the facility-location results in finding a representative subset such that most input sequences get a very similar representative, but there remains the possibility that the algorithm leaves some sequences with poor representatives in order to maximize the representation of other sequences. Indeed, in the example in Figure 2D, it can be seen that a small number of sequences end up represented at less than 40% identity. If the user wishes to be sure that every sequence is well represented, we can also use submodular optimization to satisfy this need. This case corresponds to the optimization problem

$$\text{minimize}\mid R\mid \text{such}\text{that}\underset{s\in S}{min}\underset{r\in R}{max}\text{sim}(s,r)\ge \tau$$ (9)

for some threshold τ. This is closely related to the Threshold method, which guarantees that the above criterion is met. This optimization problem is not obviously submodular; however, we can address it using submodular optimization as follows. We optimize the normalized, monotone, submodular function f_{threshold-facility-location}(R) = Σ_s∈S 1[max_r∈R sim(s, r) ≥ τ ], where 1[a ≥ b] equals 1 if a ≥ b and 0 if a < b. This function is similar to the facility location function, except that it thresholds representativeness, so that a sequence gets a score of 1 as long as is it represented with a similarity of at least τ. For a given threshold τ, we use Greedy to find a set R such that f_{threshold-facility-location}(R) = |S|; this ensures that the criterion in equation 9 is met. This approach is guaranteed to produce a set that is at most (1 + ln n) times the size of the smallest possible set that satisfies this criterion ⁵²; moreover, this is the best approximation possible in polynomial time unless P=NP³⁷.

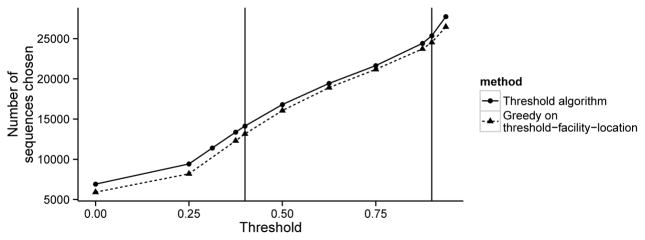
We applied this strategy to our data set for varying thresholds, and found that it identified subsets of sequences that are small but nonetheless represent every input sequence (Figure 7). For example, we found that Greedy required just 13,159 sequences to represent every input sequence with an identity of 40%. In contrast, Threshold required slightly more sequences to achieve the same level of representativeness: 14,137 sequences, or an increase of 7.4%. The results are similar if we require each sequence to get a representative with 90% similarity: Greedy requires just 24,532 sequences, while Threshold requires 25,361, or 3.3% more. This approach performs similarly to Threshold according to the SCOPe evaluation metric (Supplementary Figure 7,10).

Figure 7. Ensuring that every sequence is represented.

Horizontal axis indicates threshold on percent identity. Vertical axis indicates size of representative set chosen by a given method such that every input sequence has at least one representative with identity greater than the threshold. Vertical lines mark 40% and 90% identity.

3.8 Submodular optimization algorithms have practical computational costs

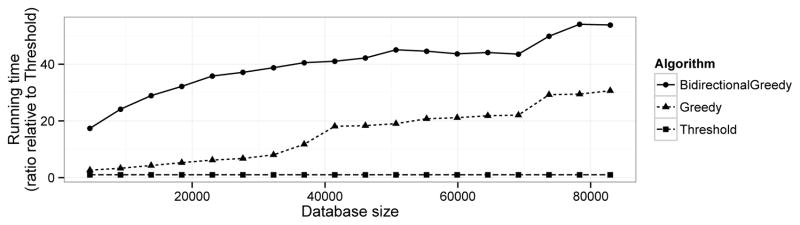
To evaluate whether the proposed algorithms are practical to run in practice, we compared their respective running times (Figure 8A). We found that Threshold has the fastest running time; this is expected, as it is a simple heuristic. The BidirectionalGreedy algorithm is the most expensive algorithm, taking approximately 30–100 times the running time of Threshold. Despite the fact that Greedy has worst-case quadratic running time (Methods), we found that it ran faster than BidirectionalGreedy on most data sets due to the lazy evaluation approach that utilizes the submodularity property to skip some calculations (Methods¹⁵). However, on the full ASTRAL data set, Bidirectional took just four minutes; therefore, computational cost is unlikely to be an important consideration for either algorithm on anything but the largest data sets. It is worth noting that computational cost may have been a more important concern 20 years ago, when Threshold was first introduced.

Figure 8. Running time.

Running time relative to Threshold (running time / Threshold running time) as function of database size. We ran Threshold with a 40% threshold, BidirectionalGreedy with λ = 9, and Greedy to generate a set a subset of 15% of the original size. We generated smaller databases by taking random subsets of ASTRAL.

The Greedy method can be even further sped up using the approximation algorithms ApproxGreedy and StochasticGreedy (Methods). We found that these two algorithms could greatly reduce the running time of Greedy with only a small cost in optimization performance. In certain instances, we found that ApproxGreedy achieved up to 7× speedup relative to Greedy while maintaining better performance than Threshold (Supplementary Figure 11). However, we found that this improvement depends greatly on the target representative set size: the approximations greatly speed up selection of large representative sets, but cannot significantly speed up selection of small sets without a large optimization performance cost.

4 Discussion

In this work, we introduced a method for selecting representative sets of sequence data sets using submodular optimization. This optimization-based approach is preferable to the existing Threshold algorithm for several reasons. First, we can optimize the feature we’re interested in—either minimizing redundancy or maximizing representativeness—much more effectively by optimizing it directly. We showed that doing so also improves the quality of the representative sets according to an independent gold standard, SCOPe, which is based on protein structure data that was not available to the representative set selection method.

Second, an optimization-based approach gives great flexibility in what criteria we optimize. This flexibility let us devise a mixture objective that, when optimized, produced better performance on SCOPe than any individual objective. In addition, this flexibility allows the method to be modified to optimize alternative criteria, such as encouraging long sequences. Combining and modifying objective functions this way is very natural in the submodular optimization framework, but would be very difficult in a non-optimization-based framework.

Third, the submodular optimization algorithms we used here have theoretically constant-factor approximation guarantees, in contrast to Threshold, which has no guarantee. It is worth noting that these guarantees are useful for guiding our intuition about which algorithms are likely to perform best, even when the theoretical worst-case performance would be much worse than we expect them to perform in practice. This is similar to the reason why asymptotic analysis (i.e. O(·)) is useful even though algorithms could have huge constant factors: in practice, the algorithms that have the best asymptotic running time often also have the best empirical running time.

In this work we presented a number of variants of the submodular approach; we make the following recommendations for its use in practice. For general-purpose representative set selection, we recommend using Greedy to optimize a 50% mixture of sum-redundancy on percent identity and facility-location on Rankprop similarity with a small (λ_length = 10⁻³) length objective, because this mixture provides a good balance of simultaneously optimizing many desirable criteria without significantly sacrificing any single one. When the goal is solely to minimize redundancy, Bidirectional with sum-redundancy on percent identity should be used. In addition, the user should consider whether there are other criteria that would be desirable for their application; these can be easily implemented using Repset’s modular design.

The algorithms we present here achieve better results at the cost of increased computation time relative to Threshold. This is unlikely to be an issue on moderately sized data sets (less than 100k-1M sequences), but will be too expensive on huge data sets. For extremely large data sets, we recommend that users take a two-step approach of first applying a Threshold-based method to reduce down to 100,000 sequences, then applying Repset to reduce from 100,000 to the final desired size.

In this work we have explored only a small number of submodular functions; the submodular optimization framework supports many other objective functions that may provide even better results, including those based on cluster coverage, those based on the sequences directly rather than alignments, and others. Because the SCOPe evaluation function is itself submodular, a submodular objective function could also potentially be learned from training data such that the objective function correlates well with it.

For these reasons, we expect this submodular optimization method to replace the existing ubiquitous Threshold method for choosing representative sets from sequence data sets. Moreover, this application may serve as a model for how submodular optimization can be applied to other discrete problems in biology, such as selecting representative sets of protein structures, genomic loci, or mass spectra.